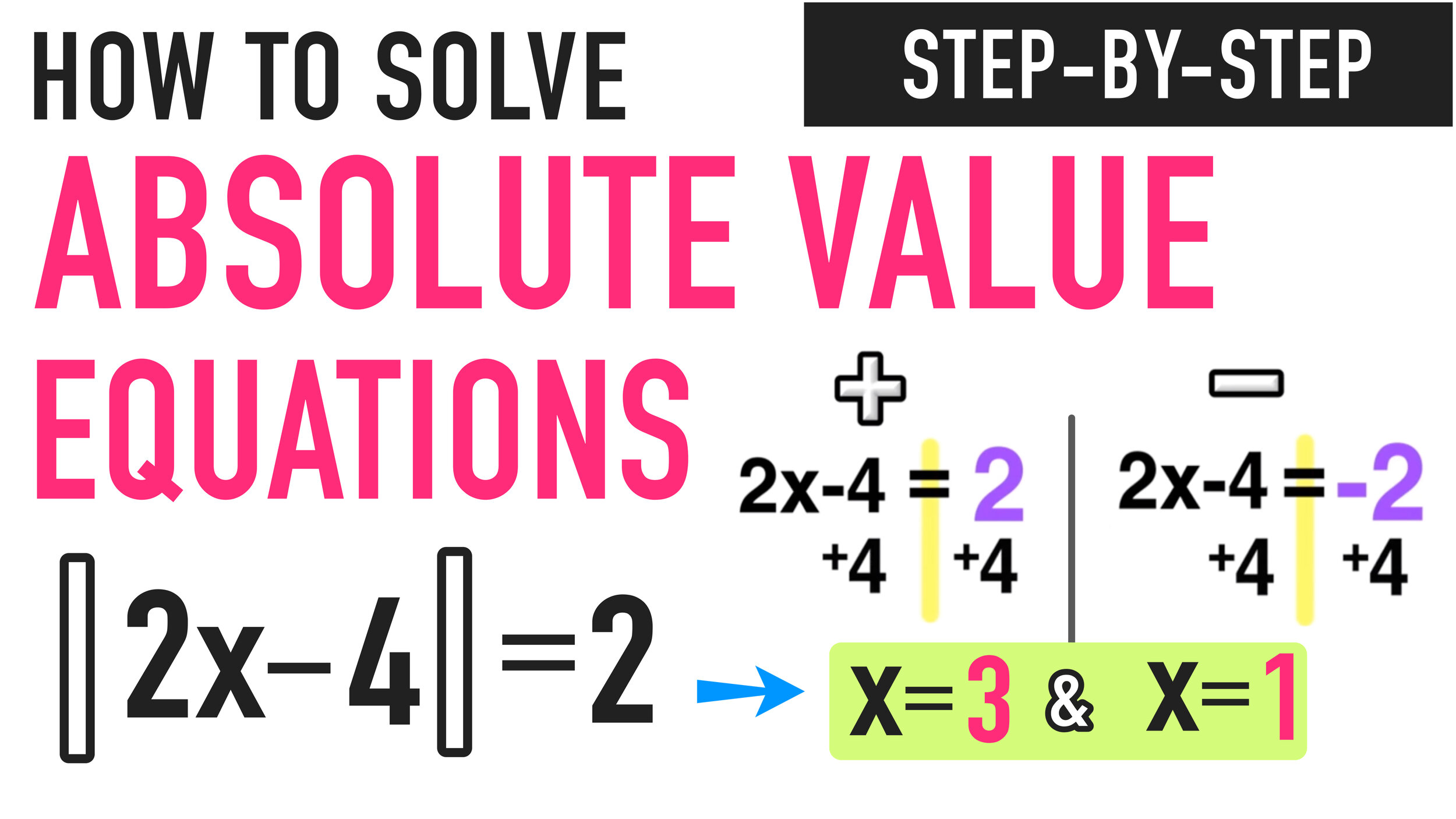

Solving Absolute Value Equations: Complete Guide
April 16, 2020 by Anthony Persico
Learn How to Solve Absolute Value Equations in 3 Easy Steps!
The following step-by-step guide will show you how to solve absolute value equations and absolute value functions with ease (algebra).
Welcome to this free lesson guide that accompanies this Solving Absolute Value Equations Tutorial where you will learn the answers to the following key questions and information:
How to solve an absolute value equation
How to solve an absolute value function
How to find both solutions to an absolute value equation
Why is absolute value always positive?
This Complete Guide to Solving Absolute Value Equations includes several examples, a step-by-step tutorial and an animated video tutorial.

*This lesson guide accompanies our animated Solving Absolute Value Equations Explained! video.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Intro to Solving Absolute Value Equations
Before you work on a few absolute value equations examples, let’s quickly review some important information:.
Fact: Any value inside of absolute value bars represents either a positive number or zero.
Notice that the absolute value graph in Figure 1 has a range of y is greater than or equal to 0 (it is never negative)

Figure 1: The parent function for absolute value.
Furthermore, consider the example below:
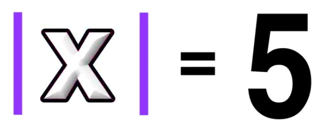
There are two values that would make this equation true!

The absolute value of 5 AND the absolute value of -5 both equal positive 5.
This should make sense when you graph the line y=5 over the absolute value function graph because you can see that there are two intersection points, and thus two solutions.

Absolute value functions can have up to two solutions!
Now you know that ABSOLUTE VALUE EQUATIONS CAN HAVE TWO SOLUTIONS.
Now you are ready to try a few examples.
Solving Absolute Value Equations Example #1

We will be using the following 3-step process that can be used to solve any absolute value equation:
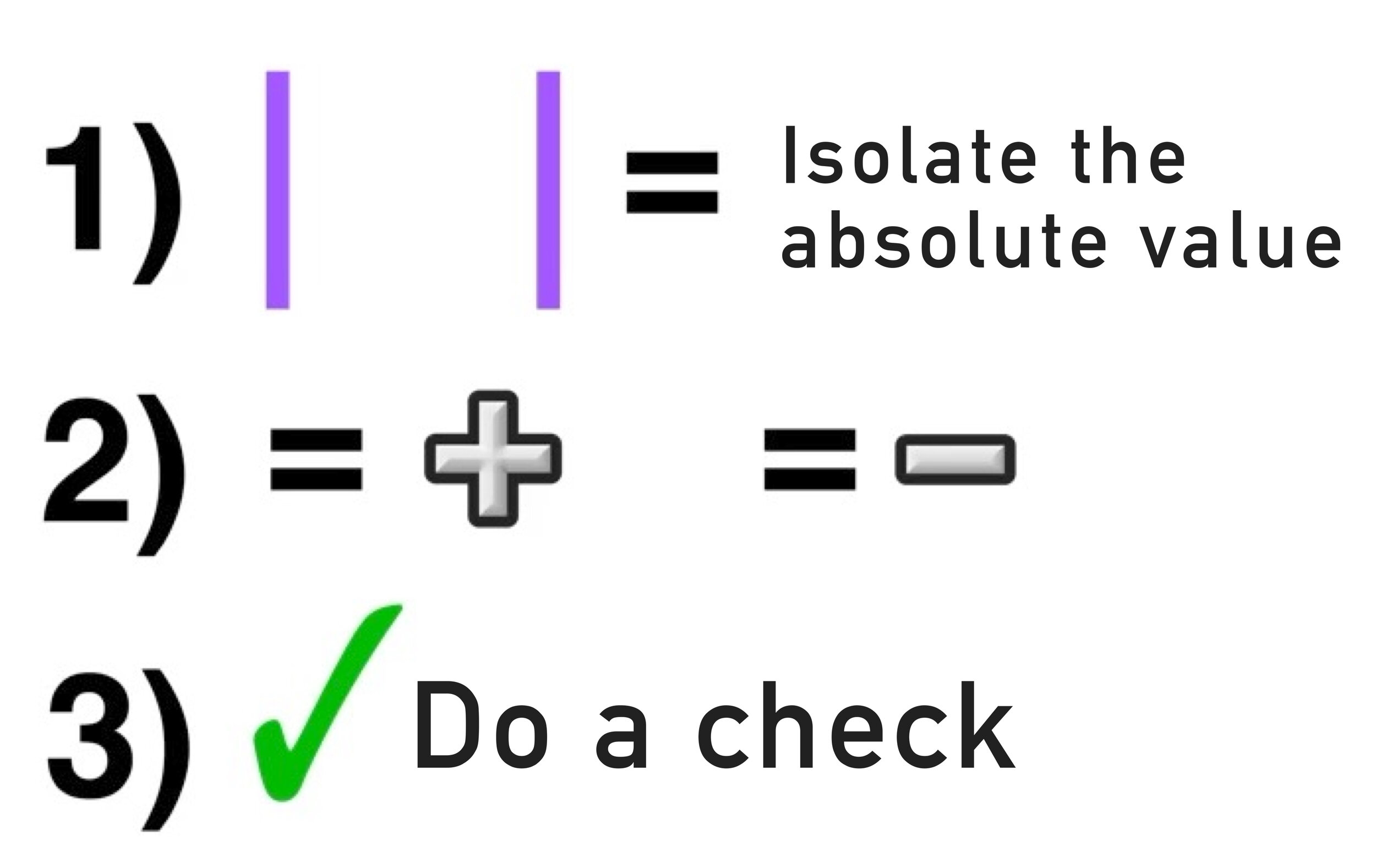
STEP ONE: Isolate the Absolute Value
In this example, the absolute value is already isolated on one side of the equals sign, which means that there are no other terms outside of the absolute value, so you can move onto step two.
STEP TWO: Solve for Positive AND Solve for Negative
For step two, you have to take the original equation |x+3| = 6 and split it up into two equations, one equal to POSITIVE 6 and the other equal to NEGATIVE 6. You also get rid of the absolute value bars.
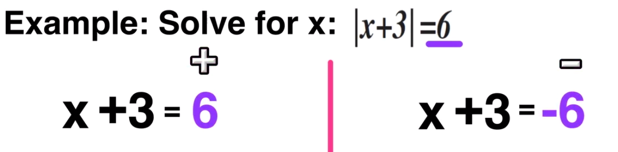
Set up two equations (positive and negative) and ditch the absolute value bars.
Now you just have to solve each equation for x as follows:
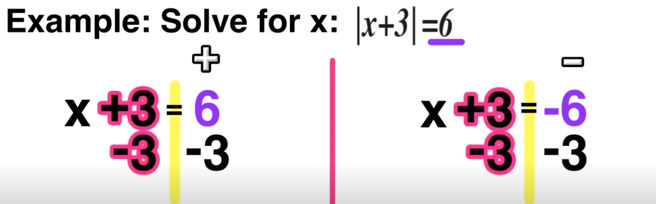
And now you have concluded that there are two solutions to |x+3|=6, x=3 and x=-9.
STEP THREE: Check Your Answer
Finally, do a quick check by plugging both answers into the original equation, |x+3|=6, to make sure that they are correct:

Left: replace x with 3. Right: replace x with -9

Both equations are true.
Since the checks worked out, you can conclude that:
Final Answer: The solutions to |x+3|=6 are x=3 and x=-9
Solving Absolute Value Equations Example #2

Again, you will follow the three-step process to solving this absolute value equation:

Unlike the last example, the absolute value is not already isolated on one side of the equal sign, because there is a +8 outside of it that needs to be moved to the other side as follows:

Step One: Isolate the absolute value!
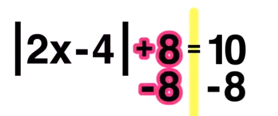
Now the absolute value is isolated.
Now that you have isolated the absolute value on one side of the equal sign, you are ready for the next step.
The next step is to ditch the absolute value bars and solve the following equations:
Positive: 2x-4=2 and Negative: 2x-4=-2
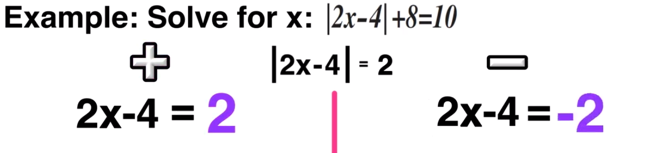
Now you have TWO solutions: x=3 and x=1
The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are finished!
Go ahead and check the solution to Example 2 on your own! Did it work out?
Still Confused?
Check out this animated video tutorial on solving absolute value equations.
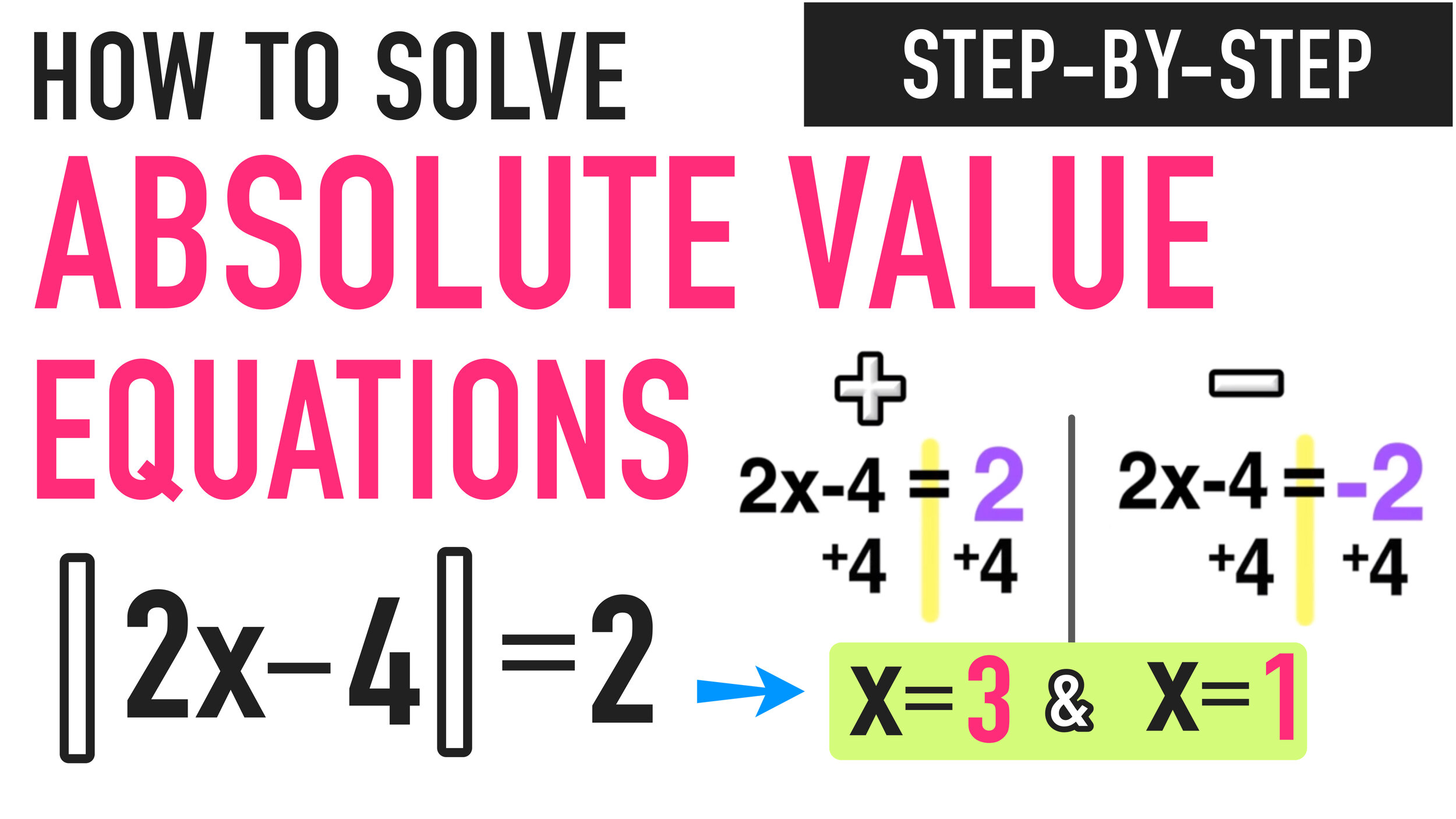
Looking for more practice with absolute value?
Check out the following free cube root resources:.
Free Tutorial
Absolute Value Calculator Basics: How to Graph and Solve Absolute Value Equations
How to find x and y intercepts of a function explained, keep learning with more free lesson guides:.

Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.
Reset password New user? Sign up
Existing user? Log in
Absolute Value Equations
Already have an account? Log in here.
- Pranshu Gaba
- Alan Enrique Ontiveros Salazar
- Kai Hsien Boo
- Agnishom Chattopadhyay
- Aditya Virani
- Prince Loomba
- Keshav Ramesh
Absolute value equations are equations involving expressions with the absolute value functions . This wiki intends to demonstrate and discuss problem solving techniques that let us solve such equations.
A very basic example would be as follows:
Find all values of \(x\) satisfying \(|x-2| + |x-4| = 4.\)
Usually, the basic approach is to analyze the behavior of the function before and after the point where they reach 0. For example, for \(|x-a|\) one could analyze the cases where \(x > a\) or \(x < a\), or even \(x = a\) if required. However, these problems are often simplified with a more sophisticated approach like being able to eliminate some of the cases, or graphing the functions. In this wiki, we intend to discuss this techniques along with strategies on when to use which.
Methodology
Technique - squaring both sides, technique - casework, technique - sketching graph, problem solving - miscellaneous.
Introduction to absolute value equations
Methodology to solve absolute value equations: the techniques used to solve absolute value equations and when to use which one
Take an example to describe the following methodology:
1) Understanding absolute value--positive, negative case (or graph approach) 2) Determining possible solutions 3) Verifying solutions
Explain - How do we use this technique to solve absolute value equations?
Remember to verify the possible solutions - why and how?
2-3 examples in increasing order of difficulty - explaining how we squared both sides to solve more difficult problems
Followed by 1-2 TIY problems - relevant to be solved by case work technique
Suppose we have an equation of the form \(\lvert a \rvert = \lvert b \rvert\). Since both sides are positive, we can square them without adding extraneous solutions: \[a^2=b^2.\] Then solve it as an ordinary equation: \[\begin{align} a^2-b^2&=0 \\ (a+b)(a-b)&=0. \end{align}\] So we see that \(a=-b\) or \(a=b\).
Solve the equation \(\lvert 3x+4 \rvert = \lvert 2x-7 \rvert\) for real \(x\). We square both sides to obtain \[(3x+4)^2=(2x-7)^2.\] Here we don't need to expand both sides; just apply the difference of two squares to find the factors: \[\begin{align} (3x+4+2x-7)(3x+4-2x+7)&=0 \\ (5x-3)(x+11)&=0. \end{align} \] The solutions are \(\left\{\frac{3}{5}, -11\right\}. \ _ \square\)
Because absolute value can be defined as piecewise functions, depending on where the value of \(x \) is with respect to the number line, you have to work with a different "piece" of the piecewise function.
General steps:
Using the definition of absolute value as a piecewise function, "undo" the absolute value sign(s) and write cases. For example, we know that the expression in the absolute value sign can either be positive or negative.
Solve each case for \( x\).
Verify the solutions.
Find all real values of \(x\) such that \( | 3x – 4 | – 2 = 3.\) We first isolate the absolute value onto one side: \[\begin{align} | 3x – 4 | – 2 & = 3\\ | 3x – 4 | &= 5. \end{align}\] Now, we "undo" the absolute value signs and split the equation into its two cases, the positive case and the negative case: \[\begin{array}{rlcccrl} (3x – 4) &= 5 &&\text{ or } && –(3x – 4) &= 5\\ 3x – 4 &= 5 &&\text{ or } && –3x + 4 &= 5\\ 3x &= 9 &&\text{ or } && –3x &= 1\\ x &= 3 &&\text{ or } && x &= –\frac{1}{3}. \ _\square \end{array}\]
Find all real values of \(x \) such that \( |x+1| + |2x+3| = 5 \). There are four possible cases, but one will be eliminated due to impossibility: Case 1. If \(x+1 \) and \( 2x+3 \) are both positive, then \[\begin{align} x+1 + 2x+3 &= 5 \\ 3x + 4 &= 5 \\ 3x &= 1 \\ x &= \dfrac{1}{3}. \end{align} \] Case 2. If \( x+1 \) is negative and \( 2x + 3 \) is positive, then \[\begin{align} - x - 1 + 2x + 3 &= 5 \\ x + 2 &= 5 \\ x &= 3. \end{align} \] However, when \( x = 3 \), \( x+1 \) and \( 2x+3 \) are both positive, so this is not a valid solution to the equation. Case 3. If \( x+1 \) and \( 2x+3 \) are both negative, then \[\begin{align} -x - 1 - 2x - 3 &= 5 \\ -3x - 4 &= 5 \\ -3x &= 9 \\ x &= -3. \end{align} \] Case 4. If \( x +1 \) is positive and \( 2x + 3 \) is negative, it is an impossible case. Graph the two lines if you are not convinced. Therefore, the solution set is \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\)
Find all real values of \(x\) such that \[|x+2|+|2x+6|+|3x-3|=12.\] In this problem we are dealing with 3 terms of absolute values. Their turning points (the values of \(x\) such that they change sign) of the three terms are \(x=-2, x=-3, x=1,\) respectively. Hence, we need to check the cases \(-\infty < x \leq -3\), \(-3<x\leq -2\), \(-2 < x \leq 1\), \(1<x<\infty\). Case 1. \(\, -\infty < x \leq -3\) In this case, the three terms will always be negative. Hence, \[\begin{aligned} -(x+2)-(2x+6)-(3x-3)&=12 \\ x &= -\frac{17}{6}. \end{aligned}\] However, \(x=-\frac{17}{6} >-3\) is not within the domain \(-\infty < x \leq -3\). Thus this solution is not valid. Case 2. \(\, -3<x\leq -2\) In this case, the three terms will be negative, positive, and negative, respectively. Hence, \[\begin{aligned} -(x+2)+(2x+6)-(3x-3)&=12 \\ x &= -\frac{5}{2}. \end{aligned}\] \(x=-\frac{5}{2}\) lies between \(-3\) and \(-2\). Thus \(\boxed{x=-\frac{5}{2}}\) is one of the solutions. Case 3. \(\, -2 < x \leq 1\) In this case, the three terms will be positive, positive, and negative, respectively. However, \[\begin{aligned} (x+2)+(2x+6)-(3x-3)=11 \neq 12. \end{aligned}\] Thus there is no solution within this domain. Case 4. \(\, 1<x<\infty\) In this case, the three terms are always positive. Hence, \[\begin{aligned} (x+2)+(2x+6)+(3x-3)&=12 \\ x &= \frac{7}{6}, \end{aligned}\] which lies between \(1\) and \(\infty\). Thus \(\boxed{x=\frac{7}{6}}\) is another solution. In conclusion, \(x=-\frac{5}{2}\) and \(x=\frac{7}{6}\) are the solutions for the given equation. \(_\square\)
Find all real values of \( x \) such that \( |x||x+1| = 2 \). Case 1. \(\, x, x+1 \) both positive \[\begin{align} x(x+1)-2 &= 0 \\ x^2 +x - 2 &= 0 \\ x &= 1, x = -2. \end{align} \] Reject \( x = -2 \) because it does not make both \(x \) and \( x +1 \) positive. Case 2. \(\, x\) negative, \( x + 1 \) positive \[\begin{align} -x(x+1)-2 &= 0 \\ -x^2 - x - 2 &= 0 \\ x^2 + x + 2 &= 0 \\ x &= \dfrac{-1 \pm \sqrt{1 - 4 \cdot 1 \cdot 2 }}{2}. \end{align} \] We only asked for real solutions, so at this point we ignore this case because we're going to get imaginary results. Case 3. \(\, x\) positive, \( x +1 \) negative This is an impossible case (graph the lines and you'll see why), so we can ignore it. Case 4. \(\, x, x+1 \) both negative Because they're both negative, the negatives end up "canceling" and become positive, which was what we had in Case 1. However, the restriction is different from Case 1 (here, both \( x \) and \( x +1 \) have to be negative, not positive ), so instead of rejecting \( x = -2 \), we reject \( x = 1 \) from this case. Basically, in this specific case 4, \( x = 1 \) is not a possible solution, but it does not mean it's not a possible solution for Case 1 because we're simply going piece by piece in this piecewise function--in the end we will take the union of all possible solutions. Thus, the solutions are \( \left \{ -2, 1 \right \} \). \(_\square\)
Sometimes absolute value equations have a ridiculous number of cases and it would take too long to go through every single case. Therefore, we can instead graph the absolute value equations using the definition of absolute value as a piecewise function. To get each piece, you must figure out the domain of each piece. This method is highly beneficial when the question writer asks for the number of solutions instead of the actual solutions. Let's work through some examples to see how this is done.
Find all real solutions to \( |3x-4| = 5 \). To graph this, there are two possible cases: when \( 3x - 4\) is positive, and when \( 3x-4 \) is negative. When is \( 3x-4 \) positive? \[\begin{align} 3x - 4 &> 0 \\ 3x &> 4 \\ x &> \dfrac{4}{3}. \end{align} \] (Also, when \( x < \frac{4}{3} \), \( 3x- 4 \) will be negative.) We know that there will be a "turning point" at \( x = \frac{4}{3} \) for the graph of \( y = |3x-4| \). Finally, using the definition of absolute value, we know that when \( x > \frac{4}{3} \), \( y = 3x - 4 \), and when \( x \leqslant \frac{4}{3} \), \( y = -3x + 4 \). We now just need to graph \( y = 5 \) and look for the intersections. You can see that the solutions are \(\left \{ -\frac{1}{3} , 3 \right \}.\ _\square\). Another benefit of this graphing technique is that you do not need to verify any of the solutions--since we are only graphing the pieces that are actually mathematically possible, we get all the solutions we are looking for, no less and no more. If you could not discern the solutions from the picture, you can simply solve the equation for each case.
Find all real solutions to \( |x+1| + |2x+3| = 5 \). The possible cases are that \(\hspace{0.5cm}\) 1. \( \, x+1, 2x+3 \) are both positive; \(\hspace{0.5cm}\) 2. \( \, x+1 \) is negative and \( 2x+3 \) is positive; \(\hspace{0.5cm}\) 3. \( \, x+1 , 2x + 3 \) are both negative. We need to figure out the domains for which each of these holds. Case 1 holds when \( x > -1 \). Case 2 holds when \( -\frac{3}{2} < x< -1 \). Case 3 holds when \( x < -\frac{3}{2} \). Now, let's write our piecewise function. When \( x > -1 \), we have \( y = x+1 + 2x + 3 = 3x + 4 \). When \( -\dfrac{3}{2} < x< -1 \), we have\( y = -x -1 + 2x + 3 = x + 2 \). When \( x < - \dfrac{3}{2} \), we have \( y = -x - 1 -2x - 3 = -3x -4 \). As you can see in the graph, the solutions for the given equation are \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\) .
Find all real solutions to \( |x||x+1| = 2 \). To graph this, we again only look at the possible cases and when they would occur: \(\hspace{0.5cm}\) 1. \(\, x, x+1 \) both positive \(\hspace{0.5cm}\) 2. \(\, x \) negative, \( x+1 \) positive \(\hspace{0.5cm}\) 3. \(\, x, x+1 \) both negative. Case 1 is true when \( x>0 \). Case 2 is true when \( -1 < x < 0 \). Case 3 is true when \( x<-1 \). When \( x>0 \) and when \( x< -1 \), we have \( y = x(x+1) = x^2 + x \). When \( -1 < x < 0 \), we have \( y = -x(x+1) = -x^2 - x \). It is evident that the solutions are \(\{-2, 1\}.\ _\square\)
Any other technique (fact, definition) you can use to solve the problems? Otherwise move on to the followings.
3-4 examples solved by using a mix of more than one of above techniques
Add guiding text in between. Guiding text means phrasing the section in a way that it keeps on telling the reader what's going on in this section.
3-4 TIY problems - using multiple techniques to solve
What is the sum of all real numbers \(x\) satisfying \[ x^2-\sqrt{x^2} = \lvert x-1 \rvert +5?\] Observe that \(\sqrt{x^2}=\lvert x \rvert.\) Then the given equation becomes \[ x^2-\lvert x \rvert= \lvert x-1 \rvert +5.\] If \(x<0,\) then we rewrite the equation to obtain \[\begin{align} x^2-(-x)&=-(x-1)+5\\ x^2+2x-6&=0\\ x&=-1\pm \sqrt{7}\\ x&=-1-\sqrt{7}. \qquad (\text{since } x<0) \end{align}\] If \(0\le x<1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=-(x-1)+5\\ x^2&=6\\ x&=\pm \sqrt{6}, \end{align}\] which do not satisfy the assumption \(0\leq x<1.\) Thus there are no solutions in this interval. If \(x\ge 1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=x-1+5\\ x^2-2x-4&=0\\ x&=1\pm \sqrt{5}\\ x&=1+\sqrt{5}. \qquad (\text{since } x\ge 1) \end{align}\] Therefore, the above three cases give two solutions \(x=-1-\sqrt{7}\) and \(x=1+\sqrt{5},\) the sum of which is \(\sqrt{5}-\sqrt{7}.\) \(_\square\)
[IMO 1959/2] Solve the equation \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=A\) for real \(x\) (where the square roots are only defined for non-negative values), when \(A=\sqrt{2}\); \(A=1\); \(A=2\). Here we don't see any absolute value involved with the equation. Before doing anything, note that our first restriction for \(x\) is \(x \geq \frac{1}{2}\) and for \(A\) is \(A>0\). Intuitively, we could square both sides to get rid of some square roots: \[\begin{align} x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{x^2-(2x-1)}&=A^2 \\ 2x+2\sqrt{(x-1)^2}&=A^2. \end{align}\] Great! We find a perfect square inside the square root, so an absolute value will appear: \[2x+2|x-1|=A^2.\] Now we are going to find the possible cases for \(A\): When \(x-1 > 0\), we have \[\begin{align} 2x+2(x-1)&=A^2 \\ x&=\dfrac{A^2+2}{4}. \end{align}\] Then, by our assumption of \(x-1 > 0\), we get that this solution only works when \(A^2 > 2\). When \(x-1 \leq 0\), something interesting happens: \[\begin{align} 2x-2(x-1)&=A^2 \\ 2&=A^2. \end{align}\] So, when \(A^2=2 (\text{or }A=\sqrt{2})\), the equation becomes independent of \(x\), implying that any value of the interval \(x \in \left[\frac{1}{2},1\right]\) will be a solution for the first point. When \(A=1\), there are no solutions by our restriction of \(A^2 \geq 2\). Finally, when \(A=2\) we have \[x=\dfrac{2^2+2}{4}=\frac{3}{2}.\ _\square\] What happens if we allow the square roots to admit negative values?
Sometimes, in minimization problems, it often helps us to see that the value of an expression inside the absolute value is at least 0.
No problem found with slug "absolute-warm-up"
Problem Loading...
Note Loading...
Set Loading...

How to solve absolute value equations
|x + 5| = 3.
Worksheet on Abs Val Equations Abs Val Eqn Solver
The General Steps to solve an absolute value equation are:
- Rewrite the absolute value equation as two separate equations, one positive and the other negative
- Solve each equation separately
- After solving, substitute your answers back into original equation to verify that you solutions are valid
- Write out the final solution or graph it as needed
It's always easiest to understand a math concept by looking at some examples so, check outthe many examples and practice problems below.
You can always check your work with our Absolute value equations solver too
Practice Problems
Example equation.
Solve the equation: | X + 5| = 3
Click here to practice more problems like this one , questions that involve variables on 1 side of the equation.
Some absolute value equations have variables both sides of the equation. However, that will not change the steps we're going to follow to solve the problem as the example below shows:
Solve the equation: |3 X | = X − 21
Solve the following absolute value equation: | 5X +20| = 80
Solve the following absolute value equation: | X | + 3 = 2 X
This first set of problems involves absolute values with x on just 1 side of the equation (like problem 2 ).
Solve the following absolute value equation: |3 X −6 | = 21
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

- EXPLORE Random Article
How to Solve Absolute Value Equations
Last Updated: January 31, 2023 References
This article was co-authored by wikiHow Staff . Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 23,151 times.

Setting up the Problem

- For example, |9| = 9; |-9| = -(-9) = 9.

Calculating the Values

Check Your Work

Expert Q&A
- Remember that absolute value bars are distinct from parentheses and function differently. Thanks Helpful 0 Not Helpful 0
- Once you've solved for any variables, remember to simplify absolute values accordingly. Thanks Helpful 0 Not Helpful 0
You Might Also Like

- ↑ http://tutorial.math.lamar.edu/Classes/Alg/SolveAbsValueEqns.aspx
- ↑ https://www.mathsisfun.com/numbers/absolute-value.html
- ↑ http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations
- ↑ http://www.purplemath.com/modules/solveabs.htm
- ↑ https://www.khanacademy.org/math/algebra/absolute-value-equations-functions/absolute-value-equations/v/absolute-value-equations
About this article

To solve absolute value equations, first isolate the absolute value terms by moving anything outside of the vertical bars to the other side of the equation. Next, solve for the positive value of the equation by isolating the variable. Since the absolute variable can represent 2 numbers, then solve for the negative value by putting a negative sign outside the vertical bars. Then, move the negative by dividing both sides by -1 and solve for the variable. If you want to learn how to check your answers for an absolute value equation, keep reading the article! Did this summary help you? Yes No
Did this article help you?

- About wikiHow
- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
- Solving Absolute Value Equations – Methods & Examples
JUMP TO TOPIC
What is Absolute Value?
Practice questions, solving absolute value equations – methods & examples.
Solving equations containing an absolute value is as simple as working with regular linear equations . Before we can embark on solving absolute value equations, let’s take a review of what the word absolute value means.
In mathematics, the absolute value of a number refers to the distance of a number from zero, regardless of direction. The absolute value of a number x is generally represented as | x | = a, which implies that, x = + a and -a.
We say that the absolute value of a given number is the positive version of that number . For example, the absolute value of negative 5 is positive 5, and this can be written as: | − 5 | = 5.
Other examples of absolute values of numbers include: |− 9| = 9, |0| = 0, − |−12| = −12 etc. From these examples of absolute values, we simply define absolute value equations as equations containing expressions with absolute value functions.
How to Solve Absolute Value Equations?
The following are the general steps for solving equations containing absolute value functions:
- Isolate the expression containing the absolute value function.
- Get rid of the absolute value notation by setting up the two equations so that in the first equation, the quantity inside absolute notation is positive. In the second equation, it is negative. You will remove the absolute notation and write the quantity with its suitable sign.
- Calculate the unknown value for the positive version of the equation.
- Solve for the negative version of the equation, in which you will first multiply the value on the other side of the equal sign by -1, and then solve.
In addition to the above steps, there are other important rules you should keep in mind when solving absolute value equations.
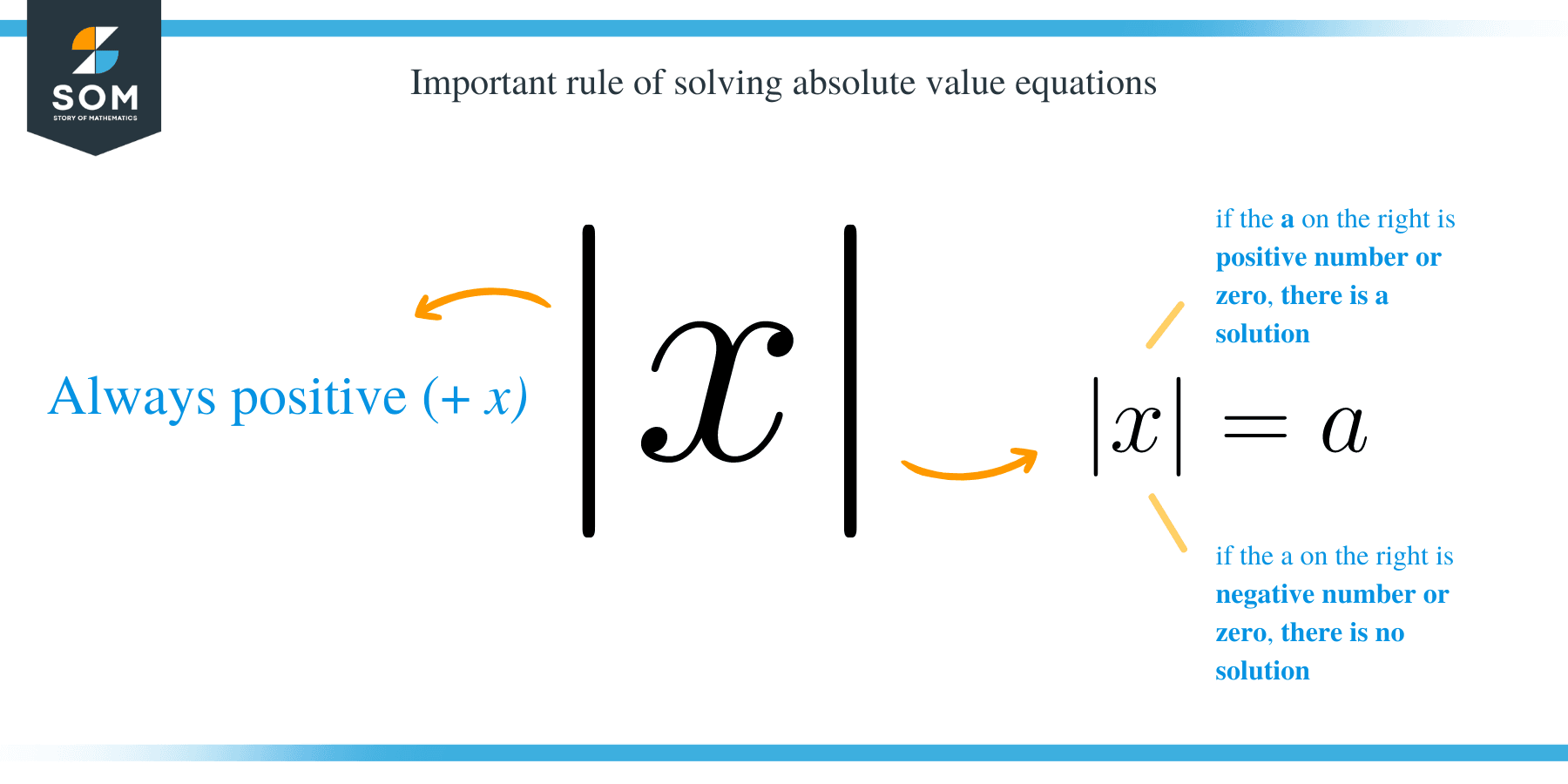
- The ∣x∣is always positive: ∣x∣ → +x.
- In | x| = a, if the a on the right is a positive number or zero, then there is a solution.
Solve the equation for x: |3 + x| − 5 = 4.
- Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain;
| 3 + x | − 5 + 5 = 4 + 5
| 3 + x |= 9
- Calculate for the positive version of the equation. Solve the equation by assuming the absolute value symbols.
| 3 + x | = 9 → 3 + x = 9
Subtract 3 from both sides of the equation.
3 – 3 + x = 9 -3
- Now calculate for the negative version of the equation by multiplying 9 by -1.
3 + x | = 9 → 3 + x = 9 × ( −1)
Also subtract 3 from both side to isolate x.
3 -3 + x = – 9 -3
Therefore 6 and -12 are the solutions.
Solve for all real values of x such that | 3x – 4 | – 2 = 3.
- Isolate the equation with absolute function by add 2 to both sides.
= | 3x – 4 | – 2 + 2 = 3 + 2
= | 3x – 4 |= 5
Assume the absolute signs and solve for the positive version of the equation.
| 3x – 4 |= 5→3x – 4 = 5
Add 4 to both sides of the equation.
3x – 4 + 4 = 5 + 4
Divide: 3x/3 =9/3
Now solve for the negative version by multiplying 5 by -1.
3x – 4 = 5→3x – 4 = -1(5)
3x – 4 = -5
3x – 4 + 4 = – 5 + 4
Divide by 3 on both sides.
Therefore, 3 and 1/3 are the solutions.
Solve for all real values of x: Solve | 2 x – 3 | – 4 = 3
Add 4 to both sides.
| 2 x – 3 | -4 = 3 →| 2 x – 3 | = 7
Assume the absolute symbols and solve for the positive version of x.
2 x – 3 = 7
2x – 3 + 3 = 7 + 3
Now solve for the negative version of x by multiplying 7 by -1
2 x – 3 = 7→2 x – 3 = -1(7)
Add 3 to both sides.
2x – 3 + 3 = – 7 + 3
x = – 2
Therefore, x = –2, 5
Solve for all real numbers of x: | x + 2 | = 7
Already the absolute value expression is isolated, therefore assume the absolute symbols and solve.
| x + 2 | = 7 → x + 2 = 7
Subtract 2 from both sides.
x + 2 – 2 = 7 -2
Multiply 7 by -1 to solve for the negative version of the equation.
x + 2 = -1(7) → x + 2 = -7
Subtract by 2 on both sides.
x + 2 – 2 = – 7 – 2
Therefore, x = -9, 5
Previous Lesson | Main Page | Next Lesson

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Solving Simpler Absolute-Value Equations
Simpler Harder Special Case
When we take the absolute value of a number, we always end up with a positive number (or zero). Whether the input was positive or negative (or zero), the output is always positive (or zero). For instance, | 3 | = 3 , and | −3 | = 3 also.
This property — that both the positive and the negative become positive — makes solving absolute-value equations a little tricky. But once you learn the "trick", they're not so bad. Let's start with something simple:
Content Continues Below
MathHelp.com
Solving Absolute Value Equations
Solve | x | = 3
I've pretty much already solved this, in my discussion above:
| −3 | = 3
So then x must be equal to 3 or equal to −3 .
But how am I supposed to solve this if I don't already know the answer? I will use the positive / negative property of the absolute value to split the equation into two cases, and I will use the fact that the "minus" sign in the negative case indicates "the opposite sign", not "a negative number".
For example, if I have x = −6 , then " − x " indicates "the opposite of x " or, in this case, −(−6) = +6 , a positive number. The "minus" sign in " − x " just indicates that I am changing the sign on x . It does not indicate a negative number. This distinction is crucial!
Whatever the value of x might be, taking the absolute value of x makes it positive. Since x might originally have been positive and might originally have been negative, I must acknowledge this fact when I remove the absolute-value bars. I do this by splitting the equation into two cases. For this exercise, these cases are as follows:
a. If the value of x was non-negative (that is, if it was positive or zero) to start with, then I can bring that value out of the absolute-value bars without changing its sign, giving me the equation x = 3 .
b. If the value of x was negative to start with, then I can bring that value out of the absolute-value bars by changing the sign on x , giving me the equation − x = 3 , which solves as x = −3 .
Then my solution is
x = ±3
We can, by the way, verify the above solution graphically. When we attempt to solve the absolute-value equation | x | = 3 , we are, in effect, setting two line equations equal to each other and finding where they cross. For instance:
In the above, I've plotted the graph of y 1 = | x | (being the blue line that looks like a "V") and y 2 = 3 (being the green horizontal line). These two graphs cross at x = −3 and at x = +3 (being the two red dots).
If you're wanting to check your answers on a test (before you hand it in), it can be helpful to plug each side of the original absolute-value equation into your calculator as their own functions; then ask the calculator for the intersection points.
Of course, any solution can also be verified by plugging it back into the original exercise, and confirming that the left-hand side (LHS) of the equation simplifies to the same value as does the right-hand side (RHS) of the equation. For the equation above, here's my check:
x = −3
LHS: | x | = | −3 |
LHS: | x | = | +3 |
If you're ever in doubt about your solution to an equation, try graphing or else try plugging your solution back into the original question. Checking your work is always okay!
The step in the above, where the absolute-value equation was restated in two forms, one with a "plus" and one with a "minus", gives us a handy way to simplify things: When we have isolated the absolute value and go to take off the bars, we can split the equation into two cases; we will signify these cases by placing a "minus" on the opposite side of the equation (for one case) and a "plus" on the opposite side (for the other). Here's how this works:
Solve | x + 2 | = 7 , and check your solution(s).
Advertisement
The absolute value is isolated on the left-hand side of the equation, so it's already set up for me to split the equation into two cases. To clear the absolute-value bars, I must split the equation into its two possible two cases, one each for if the contents of the absolute-value bars (that is, if the "argument" of the absolute value) is negative and if it's non-negative (that is, if it's positive or zero). To do this, I create two new equations, where the only difference between then is the sign on the right-hand side. First, I'll do the "minus" case:
x + 2 = −7
x = −9
Now I'll do the non-negative case, where I can just drop the bars and solve:
Now I need to check my solutions. I'll do this by plugging them back into the original equation, since the grader can't see me checking plots on my graphing calculator.
x = −9:
LHS: |(−9) + 2|
= |−7| = 7 = RHS
LHS: |(5) + 2|
= |7| = 7 = RHS
Both solutions check, so my answer is:
x = −9, 5
Solve | 2 x − 3 | − 4 = 3
First, I'll isolate the absolute-value part of the equation; that is, I'll get the absolute-value expression by itself on one side of the "equals" sign, with everything else on the other side:
| 2 x − 3 | − 4 = 3
| 2 x − 3 | = 7
Now I'll clear the absolute-value bars by splitting the equation into its two cases, one for each sign on the argument. First I'll do the negative case:
2 x − 3 = −7
2 x = −4
x = −2
And then I'll do the non-negative case:
2 x − 3 = 7
The exercise doesn't tell me to check, so I won't. (But, if I'd wanted to, I could have plugged "abs(2X−3)−4" and "3" into my calculator (as Y1 and Y2, respectively), and seen that the intersection points were at my x -values.) My answer is:
x = −2, 5
URL: https://www.purplemath.com/modules/solveabs.htm
Page 1 Page 2 Page 3
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Advertisement
How Absolute Value Works in Equations and Graphs
- Share Content on Facebook
- Share Content on LinkedIn
- Share Content on Flipboard
- Share Content on Reddit
- Share Content via Email
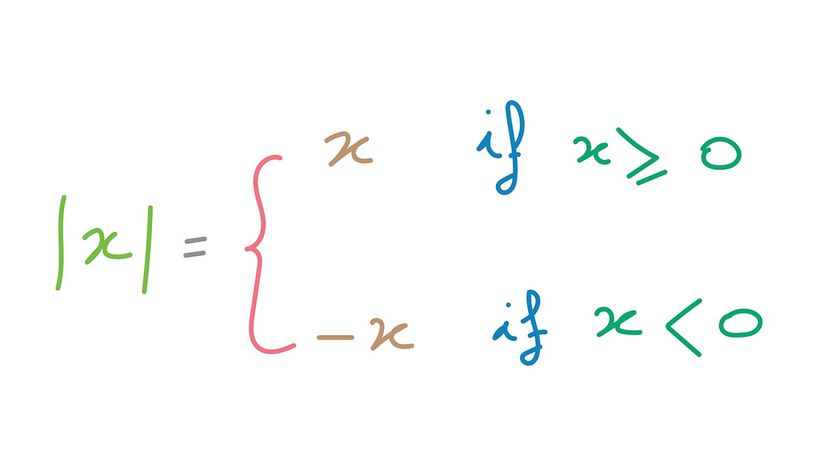
Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.
To illustrate this concept, regard your house as the origin point "zero," with steps toward the west as negative numbers, and steps toward the east as positive numbers. Whether you traveled a mile east or a mile west, you are an equal distance away from your home.
Walking west didn't mean you were taking a negative number of steps, and going east isn't equivalent to a positive number of steps. They have the same positive value from the origin point. Therefore, a mile in either direction has the same absolute value.

What Does an Absolute Value Symbol Look Like?
4 fundamental properties of absolute values, solving absolute value equations, absolute value function graphs.
Absolute value symbols are vertical bars on each side of a number. For instance, instead of writing "the absolute value of five," you can simply write |5|.
Now that you understand the general meaning of absolute value from the distance example above, read on to learn how you can use the following four fundamental properties to quickly identify and define a specific instance of this mathematical concept.
1. Non-negativity
An absolute value will always be a positive or non-negative value.
2. Positive-definiteness
In regards to absolute value, positive definiteness means that a number's absolute value is zero only when the number is explicitly denoted as zero |0|.
3. Multiplicativity
The absolute value of the product of two numbers is the same as the product of the absolute values because of what the negative sign becomes in an absolute value. Let's look at the following example.
The absolute value of the product of -3 and 5 is 15:
The product of |-3| and |5| is also 15:
4. Subadditivity
The concepts of subadditivity are typically illustrated in the following expression:
This means that the absolute value of the sum of two real numbers is less than or equal to the total of the absolute values of the two numbers. Let's plug in some numbers to see how this plays out in a real example:
Whether a is -2 or 2, |a| is 2. Similarly, whether b is -5 or 5, |b| is 5. Therefore:
Now let's look at the other side of that inequality: |a + b| . The expression a + b (before you take the absolute value of the expression) can play out any of the following ways:
The absolute value of the first and last examples is 7:
The same goes for the second and third examples:
Now, let's go back to the initial inequality: |a + b| ≤ |a| + |b| . No matter what values you plug into a and b, you'll find that the absolute value of the sum ( |a + b| ) is less than or equal to the sum of the absolute values ( |a| + |b| ).
First, separate the absolute value expression from the rest of the equation. Identify whether it is a positive or negative value and how it will affect the corresponding numbers. Solve the unknown and double-check your work by graphing it.
In mathematical settings it is always important to proof your work to validate your answer. The graph of the common form of the absolute value function is f(x) = |x| .
This formula can also be expressed as f(x) = x, if x ≥ 0 and -x, if x < 0 (as depicted in the image at the beginning of the article).
Jean-Robert Argand coined the term "module" in 1806 to represent the complicated absolute value. The term evolved to "modulus" 50 years later. Then, in 1841, Karl Weierstrass invented the vertical bar notation to simplify complex equations using this mathematical component.
Please copy/paste the following text to properly cite this HowStuffWorks.com article:
Absolute Value Equation Calculator
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Example (Click to try)
About absolute value equations.
- Get the absolve value expression by itself.
- Set up two equations and solve them separately.
Absolute Value Equation Video Lesson
- Khan Academy Video: Absolute Value Equations
Need more problem types? Try MathPapa Algebra Calculator
Clear Absolute Value Equation Calculator »
Absolute Value Calculator
Table of contents
In this absolute value calculator, we provide all of the necessary information about the absolute value function and its inequalities, and, obviously, we help you calculate the absolute value of any number . To help you understand better what an absolute value is, we have included some absolute value graphs and a few practical examples of solving absolute value equations. So come in and enjoy learning new things about absolute value!
🙋 Once you've mastered the absolute value of a number, you can go beyond and use our absolute value equation calculator .
What is "absolute value"? – definition
Let's start from the beginning, shall we? The term absolute value might have different meanings, depending on the context, but here, in the mathematical world, it is very clearly defined . The absolute value definition is simply the value of the number, regardless of the sign. This absolute value definition is not the most technical one, but it's sure to confuse no one while explaining what absolute value is.
For those who like more technicality when it comes to their mathematical definitions, we haven't forgotten about you:
The absolute value, or modulus |x|, of a real number x is the non-negative value of x without regard to its sign. Namely, |x| = x for a positive x, |x| = −x for a negative x (in which case −x is positive), and |0| = 0.
Now that you know what absolute value is, we can talk about how to write it and operate with it in mathematical terms. The mathematical symbol for absolute value is |x| , where x would denote whatever number we want the absolute value of. For example, the absolute value of 3 is written as |3| while the absolute value of -5.3 would be written as |-5.3| .
To calculate the absolute value of a number , you simply "take the sign off" of the number. One can also think about it as "making the number inside positive." If you want to sound fancier, you can always make up your own way to explain, depending on what you'd like to compute. For example, "you find the distance between the number you're interested in and the value 0 (zero)".
It is important to know that the absolute value operation is not just limited to numbers . It can be applied to expressions and equations like this: |-3x + 3| where x would be an unknown value.
We will explain later how to calculate the absolute value of equations or the absolute value of a graph/function. For now, let's go step by step.
Is absolute value useful?
You bet it is!
Oh! I guess you want some reasons and examples of what is absolute value useful for, right? Well, let's start with the easiest: any situation in which we care about differences and only differences . For example, when we are talking about the distance between two things. The obvious one is the distance between two points, which is, for example, necessary alongside time when calculating speed .
For example, if a car starts at x = 5 and moves to x = 2 , how far has it traveled? You can simply say it's 5 - 2 = 3 , but that is technically incorrect since the distance is actually the absolute value of the difference between the starting finish and the finishing point. In this case, the equation to solve this would be |2 - 5| = |-3| = 3 , which gives us the same result as before but much more technical prowess to show off ;)
We can also use the absolute value as a way of abbreviating our writing . For example, if we want a function that gives only positive numbers, we could write a set of 'if...else' conditions, but that would get too long. This is where absolute value comes to the rescue: we can simply wrap our function inside the absolute value signs to give us permanent positive values. This means that |f(x)| is always positive no matter the value of f(x) .
Absolute value functions and absolute value graphs
And this usefulness leads directly to absolute value graphs and absolute values inside of functions . Both are simple things in theory, but both are tricky in the beginning.
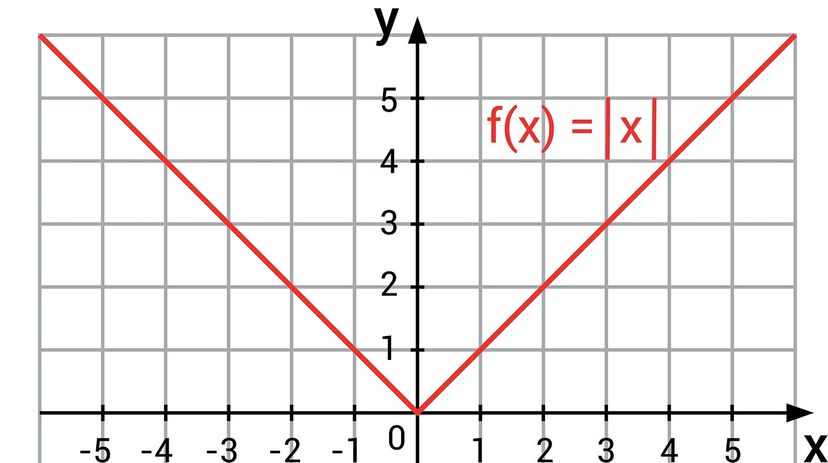
Let's start with the most basic absolute value function: f(x) = |x| . Before we think about its shape, we already know that this absolute value function can only have values above and on the x-axis; that is, f(x) only has positive and zero values.
Digging a bit deeper, we can start with the positive part, x > 0 . In this case, f(x) = x , so we get a straight line at exactly 45º which bisects the first graph quadrant of the Cartesian plane. The part for negative x, x < 0 , can be rewritten as f(x) = -x , which gives a line symmetrical to the positive x part with the y-axis acting as the axis of symmetry. This part bisects the second quadrant and forms an angle of 135º with the x-axis. For the sake of completeness, we should add that f(0) = |0| = 0 , completing the symmetry.
Things get a bit more sophisticated when we get a more complicated expression inside the absolute value. As long as the absolute value surrounds the whole expression, we can use a small trick . If we look back at f(x) = |x| as a modification on f(x) = x , we can see that the difference is that the negative part of f(x) = x has been altered to have positive values. More precisely, what we've done is flipped it around the x-axis so that it is now a mirror image of the original part.
This same trick can be used for any absolute value function. Just draw the function ignoring the absolute value, and then flip over whatever part is below y = 0 , which you can calculate using our slope intercept form calculator . The result is a perfect representation of the absolute value graph without any headaches.
As a side note for those interested, any absolute value graph is as continuous as the non-absolute one , but will also have a sharp, non-differentiable point wherever the values have begun to change from positive to negative. For example, in the function f(x) = |x| , we get a sharp point at f(0) = 0 .
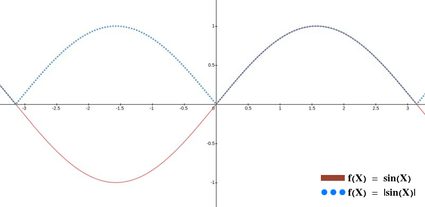
For more complicated expressions where the absolute value function is inside the expression (like in f(x) = 2x + 3 / |x| ), things get more complicated and require more thorough mathematical analysis . It is not impossible to do, and it's more about labor than complexity. However, that goes beyond the scope of this calculator, so we will stop here and swiftly move on to absolute value equations and inequalities.
Absolute value equations and absolute value inequalities
A common place to find absolute values is when solving absolute value equations (or any kind of equation, really). Equations that have absolute values are known as absolute value equations ; if instead of an equals ( = ) sign, we have a greater than ( > ), less than ( < ), greater than, or equal to ( ≥ ), or less than or equal to ( ≤ ) sign, then we have what is called an absolute value inequality .
The way to deal with absolute values in both cases is similar. When solving absolute value equations, you want to operate on and simplify things as much as possible while avoiding touching the absolute value part until you absolutely (pun intended) have to.
Once we hit the point where we need to deal with the absolute value, we isolate it on one side of the sign and decompose it into its possible options: positives and negatives. This process is the same for both absolute value equations and absolute value inequalities.
Let's see how that would look with a very simple example. Imagine you've managed to simplify everything to the point where you have the following equation:
4x + 1 = |2x - 3|
We know that the part |2x - 3| is always going to be positive but 2x - 3 could be positive OR negative. If it's positive , the equation would be:
4x + 1 = 2x - 3
while it is negative , the absolute value would change the sign, giving us the following:
4x + 1 = -(2x - 3) => 4x + 1 = 3 - 2x
Both equations represent potential solutions of the initial equation and would yield:
a) Positive: x = -2 b) Negative: x = 1/3
If we pay close attention we can see that we are not done , since x = -2 means that 2x - 3 = -4 - 3 = -7 . As the result is a negative number, this violates the assumption we made that |2x - 3| > 0 , so we know that x = -2 cannot be a solution . This is confirmed if we check this:
4·(-2) + 1 = |2·(-2) - 3| => -8 + 1 = |-4 - 3| => -7 = +7 ,
which is a mathematical absurdity.
This same process of dividing the absolute value equation or absolute value inequality, then checking what solutions make sense, is very useful and standard. You can use it when solving any absolute value equation (even if it's a quadratic formula ), and your success is pretty much guaranteed.
We used a very simple example here to keep it brief. Still, the same techniques can be used to solve very complex inequalities or find important points in absolute value functions so that you can draw the absolute value graphs we mentioned earlier.
How to use the absolute value calculator
Using the absolute value calculator is as easy as it gets. As a mathematical operation, the absolute value is very easy to find in and of itself, but we're going to try and talk you through a couple of tips that might help you.
First of all, the absolute value calculator works by turning any number you input into a positive number, which is all the absolute value really is. So you should introduce a number in the input box of the calculator, and you will get its absolute value as a result.
You can use this tool to check certain points of your absolute value graph and equation to make that sure your sketch, drawing, or solution is correct.
It is a very simple calculator, and that is why we have provided all the information above : to turn this simple absolute value calculator into a tool to gain more knowledge, bound to be helpful in your life (or at least in your math class).

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

2.2: Absolute Value Functions
- Last updated
- Save as PDF
- Page ID 149144

- Carl Stitz & Jeff Zeager
- Lakeland Community College & Lorain County Community College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Math 370 Learning Objectives
Most of the topics in this section are provided for you to review on your own, if needed; however, the following two should be covered in lecture.
- True Definition of the Absolute Value: Understand and use the piecewise definition of the absolute value.
- Graphing Absolute Value Functions: Graph transformations of absolute value functions.
True Definition of the Absolute Value
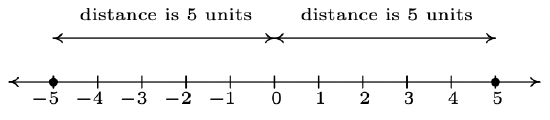
There are a few ways to describe what is meant by the absolute value \(|x|\) of a real number \(x\). You may have been taught that \(|x|\) is the distance from the real number \(x\) to \(0\) on the number line. So, for example, \(|5| = 5\) and \(|-5| = 5\), since each is \(5\) units from \(0\) on the number line.
Another way to define absolute value is by the equation \(|x| = \sqrt{x^2}\). Using this definition, we have \(|5| = \sqrt{(5)^2} = \sqrt{25} = 5\) and \(|-5| = \sqrt{(-5)^2} = \sqrt{25} = 5\). The long and short of both of these procedures is that \(|x|\) takes negative real numbers and assigns them to their positive counterparts while it leaves positive numbers alone. This last description is the one we shall adopt, and is summarized in the following definition.
Definition: Absolute Value
The absolute value of a real number \(x\), denoted \(|x|\), is given by
\[ |x| = \left\{ \begin{array}{rcl} x, & \text{ if } & x \geq 0 \\ -x, & \text{ if } & x \lt 0 \\ \end{array} \right. \label{AbsValDefn} \]
Note that we define \(|x|\) using a piecewise-defined function (see Section 1.4 ). To check that this definition agrees with what we previously understood as absolute value, note that since \(5 \geq 0\), to find \(|5|\) we use the rule \(|x| = x\), so \(|5|=5\). Similarly, since \(-5 < 0\), we use the rule \(|x| = -x\), so that \(|-5| = -(-5) = 5\). This is one of the times when it’s best to interpret the expression "\(-x\)" as "the opposite of \(x\)" as opposed to "negative \(x\)." Before we begin studying absolute value functions , we remind ourselves of the properties of absolute value.
Properties of the Absolute Value
Theorem \(\pageindex{1}\): properties of the absolute value.
Let \(a\), \(b\), and \(x\) be real numbers and let \(n\) be an integer. 1 Then
Product Rule for Absolute Values 2 : \(|ab|= |a||b|\)
Power Rule for Absolute Values: \(\left| a^{n} \right| = |a|^{n}\) whenever \(a^{n}\) is defined
Quotient Rule for Absolute Values: \(\left| \dfrac{a}{b} \right| = \dfrac{|a|}{|b|}\), provided \(b \neq 0\)
Equality Properties for Absolute Values:
\(|x| = 0\) if and only if \(x = 0\).
For \(c > 0\), \(|x| = c\) if and only if \(x = c\) or \(-x = c\).
For \(c < 0\), \(|x| = c\) has no solution.
The proof of the Quotient Rule is very similar to the proof of the Product Rule, with the exception that \(b \neq 0\). The Power Rule can be shown by repeated application of the Product Rule. The Equality Properties can be proved using Equation \( \ref{AbsValDefn} \) and by looking at the cases when \(x \geq 0\), in which case \(|x| = x\), or when \(x < 0\), in which case \(|x| = -x\). For example, if \(c > 0\), and \(|x| = c\), then if \(x \geq 0\), we have \(x = |x| = c\). If, on the other hand, \(x < 0\), then \(-x = |x| = c\), so \(x = -c\). The remaining properties are proved similarly and are left for the Exercises.
Subsection Footnotes
1 See Section 1.1 if you don’t remember what an integer is.
2 Some texts will call this the Product Rule without saying "for Absolute Values"; however, it turns out that we have many different "Product Rules" in Mathematics. I will try my best to name them accordingly to make them distinct.
Solving Absolute Value Equations
Our first example reviews how to solve basic equations involving absolute value using the properties listed in Theorem \( \PageIndex{1} \) .
Example \( \PageIndex{1} \)
- \(|3x-1| = 6\)
- \(3 - |x+5| = 1\)
- \(3|2x+1| - 5 = 0\)
- \(4 - |5x+3| = 5\)
- \(|x| = x^2-6\)
- \(|x-2| + 1 = x\)
- The equation \(|3x-1| = 6\) is of the form \(|x| = c\) for \(c > 0\), so by the Equality Properties, \(|3x - 1| = 6\) is equivalent to \(3x - 1=6\) or \(3x - 1 = -6\). Solving the former, we arrive at \(x = \frac{7}{3}\), and solving the latter, we get \(x = -\frac{5}{3}\). We may check both of these solutions by substituting them into the original equation and showing that the arithmetic works out.
- To use the Equality Properties to solve \(3 - |x+5| = 1\), we first isolate the absolute value.\[ \begin{array}{rcl} 3 - |x+5| & = & 1 \\ -|x+5| & = & -2 \\ |x+5| & = & 2 \\ \end{array} \nonumber \]Hence, \( x + 5 = 2 \) or \( x + 5 = -2 \). In the former case, we get \( x = -3 \), and in the latter case we get \( x = -7 \).
- As in the previous example, we first isolate the absolute value in the equation \(3|2x+1| - 5 = 0\) and get \(|2x+1| = \frac{5}{3}\). Using the Equality Properties, we have \(2x+1 = \frac{5}{3}\) or \(2x+1 = -\frac{5}{3}\). Solving the former gives \(x = \frac{1}{3}\) and solving the latter gives \(x = -\frac{4}{3}\). As usual, we may substitute both answers in the original equation to check.
- Upon isolating the absolute value in the equation \(4 - |5x+3| = 5\), we get \(|5x+3| = -1\). At this point, we know there cannot be any real solution, since, by definition, the absolute value of anything is never negative. We are done.
- The equation \(|x| = x^2-6\) presents us with some difficulty, since \(x\) appears both inside and outside of the absolute value. Moreover, there are values of \(x\) for which \(x^2-6\) is positive, negative and zero, so we cannot use the Equality Properties without the risk of introducing extraneous solutions, or worse, losing solutions. For this reason, we break equations like this into cases by rewriting the term in absolute values, \(|x|\), using Equation \( \ref{AbsValDefn} \). For \(x < 0\), \(|x| = -x\), so for \(x < 0\), the equation \(|x| = x^2-6\) is equivalent to \(-x = x^2-6\). Rearranging this gives us \(x^2+x-6 = 0\), or \((x+3)(x-2) = 0\). We get \(x = -3\) or \(x=2\). Since only \(x=-3\) satisfies \(x<0\), this is the answer we keep. For \(x \geq 0\), \(|x| = x\), so the equation \(|x| = x^2-6\) becomes \(x = x^2-6\). From this, we get \(x^2-x-6 =0\) or \((x-3)(x+2) = 0\). Our solutions are \(x=3\) or \(x = -2\), and since only \(x=3\) satisfies \(x \geq 0\), this is the one we keep. Hence, our two solutions to \(|x| = x^2-6\) are \(x=-3\) and \(x=3\).
- To solve \(|x-2| + 1 = x\), we first isolate the absolute value and get \(|x-2| = x-1\). Since we see \(x\) both inside and outside of the absolute value, we break the equation into cases. The term with absolute values here is \(|x-2|\), so we replace "\(x\)" with the quantity "\((x-2)\)" in Equation \( \ref{AbsValDefn} \) to get \[ |x-2| = \left\{ \begin{array}{rclcl} x-2, & \text{ if } & (x-2) \geq 0 & \implies & x \geq 2 \\ -(x-2), & \text{ if } & (x-2) \lt 0 & \implies & x \lt 2 \\ \end{array} \right. \nonumber \]So, for \(x < 2\), \(|x - 2| = -x + 2\) and our equation \(|x - 2| = x - 1\) becomes \(-x + 2 = x - 1\), which gives \(x = \frac{3}{2}\). Since this solution satisfies \(x < 2\), we keep it. Next, for \(x \geq 2\), \(|x - 2| = x - 2\), so the equation \(|x - 2| = x - 1\) becomes \(x - 2 = x - 1\). Here, the equation reduces to \(-2 = -1\), which signifies we have no solutions here. Hence, our only solution is \(x = \frac{3}{2}\).
Graphing Absolute Value Functions
Next, we turn our attention to graphing absolute value functions. Our strategy in the next example is to make liberal use of Equation \( \ref{AbsValDefn} \) along with what we know about graphing linear functions (from Section 2.1 ) and piecewise-defined functions (from Section 1.4 ).
Example \( \PageIndex{2} \)
Graph each of the following functions. Find the zeros of each function and the \(x\)- and \(y\)-intercepts of each graph, if any exist. From the graph, determine the domain and range of each function, list the intervals on which the function is increasing, decreasing or constant, and find the relative and absolute extrema, if they exist.
- \(f(x) = |x|\)
- \(g(x) = |x-3|\)
- \(h(x) = |x| -3\)
- \(i(x) = 4 - 2|3x+1|\)

- To find the zeros of \(g\), we set \(g(x) = |x-3|=0\). By Theorem \( \PageIndex{1} \) , we get \(x-3=0\) so that \(x=3\). Hence, the \(x\)-intercept is \((3,0)\). To find our \(y\)-intercept, we set \(x=0\) so that \(y = g(0) = |0-3| = 3\), which yields \((0,3)\) as our \(y\)-intercept. To graph \(g(x) = |x-3|\), we use Equation \( \ref{AbsValDefn} \) to rewrite \(g\) as \[ g(x) = |x-3| = \left\{ \begin{array}{rclcl} x-3, & \text{ if } & x-3 \geq 0 & \implies & x \geq 3 \\ -(x-3), & \text{ if } & x -3 \lt 0 & \implies & x \lt 3 \\ \end{array} \right. \nonumber \]For the graph, see Figure \( \PageIndex{4}A \). As before, the open circle we introduce at \((3,0)\) from the graph of \(y = -x+3\) is filled by the point \((3,0)\) from the line \(y = x-3\). We determine the domain as \((-\infty, \infty)\) and the range as \([0,\infty)\). The function \(g\) is increasing on \([3,\infty)\) and decreasing on \((-\infty,3]\). The relative and absolute minimum value of \(g\) is \(0\) which occurs at \((3,0)\). As before, there is no relative or absolute maximum value of \(g\).

Note that all of the functions in the previous example bear the characteristic "\(\vee\)" shape of the graph of \(y=|x|\). We could have graphed the functions \(g\), \(h\) and \(i\) in Example \( \PageIndex{2} \) starting with the graph of \(f(x)=|x|\) and applying transformations as in Section 1.7 as our next example illustrates.
Example \( \PageIndex{3} \)
Graph the following functions starting with the graph of \(f(x) = |x|\) and using transformations.
- \(h(x) = |x| - 3\)
- \(i(x) = 4-2|3x+1|\)
We begin by graphing \(f(x) = |x|\) and labeling three points, \((-1,1)\), \((0,0)\) and \((1,1)\).
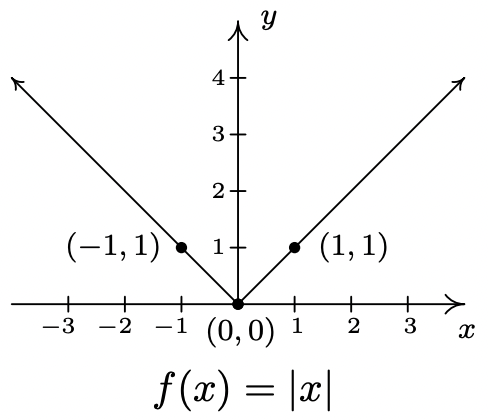
While the methods in Section 1.7 can be used to graph an entire family of absolute value functions, not all functions involving absolute values posses the characteristic "\(\vee\)" shape. As the next example illustrates, often there is no substitute for appealing directly to the definition.
Example \( \PageIndex{4} \)
Graph each of the following functions. Find the zeros of each function and the \(x\)- and \(y\)-intercepts of each graph, if any exist. From the graph, determine the domain and range of each function, list the intervals on which the function is increasing, decreasing or constant, and find the relative and absolute extrema, if they exist.
- \(f(x) = \frac{|x|}{x}\)
- \(g(x) = |x+2| - |x-3|+1\)

Many of the applications that the authors are aware of involving absolute values also involve absolute value inequalities. For that reason, we save our discussion of applications for Section 2.4 .
3 Actually, since functions can have at most one \(y\)-intercept (Do you know why?), as soon as we found \((0, 0)\) as the \(x\)-intercept, we knew this was also the \(y\)-intercept.

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
Graph your math problems
Practice, practice, practice

Number Line
- x^4-5x^2+4=0
- \sqrt{x-1}-x=-7
- \left|3x+1\right|=4
- \log _2(x+1)=\log _3(27)
- 3^x=9^{x+5}
- What is the completing square method?
- Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
- What is the golden rule for solving equations?
- The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
- How do you simplify equations?
- To simplify equations, combine like terms, remove parethesis, use the order of operations.
- How do you solve linear equations?
- To solve a linear equation, get the variable on one side of the equation by using inverse operations.
equation-calculator
- High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...
Please add a message.
Message received. Thanks for the feedback.

Game Central

IMAGES
VIDEO
COMMENTS
Solving Absolute Value Equations. Solving absolute value equations is as easy as working with regular linear equations. The only additional key step that you need to remember is to separate the original absolute value equation into two parts: positive and negative (±) components.Below is the general approach on how to break them down into two equations:
To solve absolute value equations, find x values that make the expression inside the absolute value positive or negative the constant. To graph absolute value functions, plot two lines for the positive and negative cases that meet at the expression's zero. The graph is v-shaped. Created by Sal Khan and CK-12 Foundation.
The next step is to ditch the absolute value bars and solve the following equations: Positive: 2x-4=2 and Negative: 2x-4=-2. Now you have TWO solutions: x=3 and x=1. STEP THREE: Check Your Answer. The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are ...
Solution. Step 1: Isolate the absolute value to obtain the form . Step 2: Set the argument of the absolute value equal to . Here the argument is and . Step 3: Solve each of the resulting linear equations. Step 4: Verify the solutions in the original equation. Check.
This topic covers: - Solving absolute value equations - Graphing absolute value functions - Solving absolute value inequalities If you're seeing this message, it means we're having trouble loading external resources on our website.
2) The absolute values (besides being the distance from zero) act as grouping symbols. Once you get to the point that you can actually drop the absolute values, if there is a number in front, that number must be distributed. Example: 14 |x+7| = 2 becomes 14 (x+7) = 2 and 14 (x+7) = -2.
To solve an absolute value equation, we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations. How to Solve Absolute Value Equations. Example \(\PageIndex{4}\)
This algebra video tutorial provides a basic introduction into absolute value equations. it explains how to solve absolute value equations the easy way. It...
For example, should you want to solve the equation \(|2x − 4| = 6\), you could divide both sides by 2 and apply the quotient property of absolute values. Distance Revisited Recall that for any real number x, the absolute value of x is defined as the distance between the real number x and the origin on the real line.
Absolute value equations are equations involving expressions with the absolute value functions. This wiki intends to demonstrate and discuss problem solving techniques that let us solve such equations. A very basic example would be as follows: Usually, the basic approach is to analyze the behavior of the function before and after the point where they reach 0.
This math video tutorial explains how to solve absolute value equations with variables on both sides. It contains plenty of examples and practice problems.S...
The General Steps to solve an absolute value equation are: Rewrite the absolute value equation as two separate equations, one positive and the other negative. Solve each equation separately. After solving, substitute your answers back into original equation to verify that you solutions are valid. Write out the final solution or graph it as needed.
1. Set up the equation for the positive value. An equation involving absolute value will have two possible solutions. To set up the positive equation, simply remove the absolute value bars, and solve the equation as normal. [6] For example, the positive equation for is .
1. Isolate the absolute value expression to one side of the equal sign. 2. Set the inside of the absolute value equal to + and to - the value on the other side of the equal sign (remove the absolute value bars in this step). 3. If needed, solve for the variable in these 2 new equations. 4.
Learn how to solve absolute value equations in this free math video tutorial by Mario's Math Tutoring. We discuss how to rewrite an absolute value equation ...
Example 1. Solve the equation for x: |3 + x| − 5 = 4. Solution. Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain; | 3 + x | − 5 + 5 = 4 + 5. | 3 + x |= 9. Calculate for the positive version of the equation.
Here's how this works: Solve | x + 2 | = 7, and check your solution (s). The absolute value is isolated on the left-hand side of the equation, so it's already set up for me to split the equation into two cases. To clear the absolute-value bars, I must split the equation into its two possible two cases, one each for if the contents of the ...
Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.. To illustrate this concept, regard your house as the origin point "zero," with steps toward the west as negative ...
About absolute value equations. Solve an absolute value equation using the following steps: Get the absolve value expression by itself. Set up two equations and solve them separately.
Well, normally, you solve equations with an absolute value in them by considering two cases. In the first case, you assume that the stuff inside the parentheses is already a positive number, so you can just get rid of the absolute value signs and solve the problem as though they aren't even there. Then, once you've finished doing the problem ...
Free absolute value equation calculator - solve absolute value equations with all the steps. Type in any equation to get the solution, steps and graph
With its help, you'll easily deal with all kinds of absolute value equalities, in particular equations where the absolute value is equal to 0. If you want to learn more about this topic, scroll down and learn: How to solve absolute value equations by hand; and; How to find an absolute value equation from a graph.
In this absolute value calculator, we provide all of the necessary information about the absolute value function and its inequalities, and, obviously, we help you calculate the absolute value of any number.To help you understand better what an absolute value is, we have included some absolute value graphs and a few practical examples of solving absolute value equations.
Graphing Absolute Value Functions: Graph transformations of absolute value functions. True Definition of the Absolute Value There are a few ways to describe what is meant by the absolute value \(|x|\) of a real number \(x\).
In this video, I show you how to solve absolute value equations.If you would like to check out my Teachers Pay Teachers store, here is the link:https://www.t...
Solve long equations, draw in landscape! Get step-by-step explanations. See how to solve problems and show your work—plus get definitions for mathematical concepts. Graph your math problems. Instantly graph any equation to visualize your function and understand the relationship between variables.
The values of x that satisfy the equation are called solutions of the equation, and roots or zeros of the expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root.
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Type in any equation to get the solution, steps and graph
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.