how to solve mixed fraction questions

• Maths Questions

Mixed Fractions Questions

Mixed fractions questions and answers will help students grasp the topic more quickly. Many “Mixed Fractions” questions appear on almost every board test. Students can use these questions to get a fast overview of the topics and practise answering them to improve their understanding. To double-check your answers, learn the complete explanations for each question. Click here to learn more about mixed fractions .

For learning and practising, here are some mixed fractions questions and answers.

Mixed Fractions Questions with Solutions

1. Convert 75/6 into a mixed fraction.

Step 1: Divide 75/6.

Step 2: If we divide 75/6, we get the quotient 12 and the remainder 3.

Step 3: Now, arrange the sequence in the form: 12 (3/6).

Now, the fractional part 3/6 is further simplified as ½.

Hence, 75/6 in a mixed fraction is 12 ½.

2. Convert the mixed fraction 2 (6/13) into an improper fraction.

Given mixed fraction: 2 (6/13)

To convert the mixed fraction into an improper fraction, multiply 2 by 13 and add the product value with 6 to get the numerator and keep the denominator 13.

Finding numerator:

= (2 × 13) + 6

Hence, the mixed fraction 2 (6/13) into an improper fraction is 32/13.

3. How to write 4 ⅗ as an improper fraction?

Given mixed fraction: 4 (3/5)

For converting the mixed fraction into an improper fraction, multiply 4 by 5 and add the product value with 3 to get the numerator and keep the denominator 5.

= (4 × 5) + 3

Hence, the mixed fraction 4 (3/5) into an improper fraction is 23/5.

4. Add the mixed fractions: 4 (¼) + 2 (¼).

Step 1: Convert the mixed fractions 4 (¼) and 2 (¼) into an improper fraction.

4 (¼) = 17/4

2 (¼) = 9/4

Step 2: Check whether the denominators of both the improper fractions are the same.

The fractions 17/4 and 9/4 have the same denominator.

Step 3: Now, add the numerators of the fractions:

4 (¼) + 2 (¼) = (17/4) + (9/4)

4 (¼) + 2 (¼) = (17 + 9)/4

4 (¼) + 2 (¼) = 26/4

Now, the obtained fractions can be simplified further.

Hence, we get

4 (¼) + 2 (¼) = 13/2.

5. Find the sum: 3(¼) + 3(⅝).

Step 1: Convert 3(¼) and 3(⅝) into an improper fraction.

3(¼) = 13/4

3(⅝) = 29/8

Step 2: Now, check the denominators of the fractions, whether they are equal or not.

Step 3: Since the denominators are not equal, take the LCM of 4 and 8.

Thus, The LCM of 4 and 8 is 8.

3(¼) + 3(⅝) = (13/4) + (29/8)

3(¼) + 3(⅝) = (26 + 29)/8

3(¼) + 3(⅝) = 55/8.

6. Subtract the mixed fractions: 8 ½ – 4 ½.

First, convert the mixed fraction to an improper fraction.

Since the denominators are equal, now subtract the numerators.

8 ½ – 4 ½ = (17/2) – (9/2)

8 ½ – 4 ½ = (17 – 9)/2

8 ½ – 4 ½ = 8/2.

This can be further simplified as follows:

8 ½ – 4 ½ = 4/1.

7. Find the difference: 6 ¾ – 2 ⅙.

6 ¾ – 2 ⅙ = (27/4) – (13/6)

Since the denominators of the improper fractions are not equal, take the LCM of 4 and 6.

Thus, the LCM of 4 and 6 is 12.

(27/4) – (13/6) = (81 – 26) /12

(27/4) – (13/6) = 55/12.

8. Multiply 4 ⅘ × 3 ⅘.

4 ⅘ × 3 ⅘ is written as 24/5 × 19/5.

Now, multiply the numerator with the numerator and the denominator with the denominator.

4 ⅘ × 3 ⅘ = (24 × 19) / (5 × 5)

4 ⅘ × 3 ⅘ = 456/25

Hence, the product of 4 ⅘ × 3 ⅘ is 456/25.

9. Find the product of 7 ⅔ and 11 ½.

First, convert the mixed fraction into an improper fraction.

11 ½ = 23/2

7 ⅔ × 11 ½ = (23/3) × (23/2)

7 ⅔ × 11 ½ = (23×23) / (3×2)

7 ⅔ × 11 ½ = 529/6.

Thus, the product of 7 ⅔ and 11 ½ is 529/6.

10. Divide 4½ by 2 ¼.

Convert the mixed fractions 4½ and 2¼ into an improper fraction.

First fraction: 4½ = 9/2

Second fraction: 2¼ = 9/4

Now, take the reciprocal of the second fraction.

Thus, the reciprocal of 9/4 is 4/9.

To divide 4½ by 2 ¼, multiply the first fraction by the reciprocal of the second fraction.

4½ ÷ 2 ¼ = (9/2) × (4/9)

4½ ÷ 2 ¼ = 2/1.

Explore More Articles

Practice questions.

1. Find the sum of 6 ⅘ and 11 ⅗.

2. Subtract 5 (3/7) from 12 (1/7).

3. Multiply 12 ⅘ and 17 ⅓.

To learn more Maths-related concepts quickly, register with BYJU’S – The Learning App and download the app today!

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Fraction Questions in Math

Last Updated: May 29, 2024 Fact Checked

This article was co-authored by Mario Banuelos, PhD and by wikiHow staff writer, Sophia Latorre . Mario Banuelos is an Associate Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,202,406 times.

Fraction questions can look tricky at first, but they become easier with practice and know-how. Start by learning the terminology and fundamentals, then pratice adding, subtracting, multiplying, and dividing fractions. [1] X Research source Once you understand what fractions are and how to manipulate them, you'll be breezing through fraction problems in no time.

How to Solve Fractions

• If two fractions have the same denominator, add or subtract the numerators from each other.
• If the fractions don’t have the same denominator, change them to a common multiple. For example, 4/5 and 3/2 can become 8/10 and 15/10.
• Multiply fractions by multiplying the numerators, then the denominators. Divide fractions by inverting one and then multiplying the new fractions’ numerators and denominators.

Doing Calculations with Fractions

• For instance, to solve 5/9 + 1/9, just add 5 + 1, which equals 6. The answer, then, is 6/9 which can be reduced to 2/3.

• For instance, to solve 6/8 - 2/8, all you do is take away 2 from 6. The answer is 4/8, which can be reduced to 1/2.

• For example, if you need to add 1/2 and 2/3, start by determining a common multiple. In this case, the common multiple is 6 since both 2 and 3 can be converted to 6. To turn 1/2 into a fraction with a denominator of 6, multiply both the numerator and denominator by 3: 1 x 3 = 3 and 2 x 3 = 6, so the new fraction is 3/6. To turn 2/3 into a fraction with a denominator of 6, multiply both the numerator and denominator by 2: 2 x 2 = 4 and 3 x 2 = 6, so the new fraction is 4/6. Now, you can add the numerators: 3/6 + 4/6 = 7/6. Since this is an improper fraction, you can convert it to the mixed number 1 1/6.
• On the other hand, say you're working on the problem 7/10 - 1/5. The common multiple in this case is 10, since 1/5 can be converted into a fraction with a denominator of 10 by multiplying it by 2: 1 x 2 = 2 and 5 x 2 = 10, so the new fraction is 2/10. You don't need to convert the other fraction at all. Just subtract 2 from 7, which is 5. The answer is 5/10, which can also be reduced to 1/2.

• For instance, to multiply 2/3 and 7/8, find the new numerator by multiplying 2 by 7, which is 14. Then, multiply 3 by 8, which is 24. Therefore, the answer is 14/24, which can be reduced to 7/12 by dividing both the numerator and denominator by 2.

• For example, to solve 1/2 ÷ 1/6, flip 1/6 upside down so it becomes 6/1. Then just multiply 1 x 6 to find the numerator (which is 6) and 2 x 1 to find the denominator (which is 2). So, the answer is 6/2 which is equal to 3.

Joseph Meyer

Think about fractions as portions of a whole. Imagine dividing objects like pizzas or cakes into equal parts. Visualizing fractions this way improves comprehension, compared to relying solely on memorization. This approach can be helpful when adding, subtracting, and comparing fractions.

Practicing the Basics

• For instance, in 3/5, 3 is the numerator so there are 3 parts and 5 is the denominator so there are 5 total parts. In 7/8, 7 is the numerator and 8 is the denominator.

• If you need to turn 7 into a fraction, for instance, write it as 7/1.

• For example, if you have the fraction 15/45, the greatest common factor is 15, since both 15 and 45 can be divided by 15. Divide 15 by 15, which is 1, so that's your new numerator. Divide 45 by 15, which is 3, so that's your new denominator. This means that 15/45 can be reduced to 1/3.

• Say you have the mixed number 1 2/3. Stary by multiplying 3 by 1, which is 3. Add 3 to 2, the existing numerator. The new numerator is 5, so the mixed fraction is 5/3.

Tip: Typically, you'll need to convert mixed numbers to improper fractions if you're multiplying or dividing them.

• Say that you have the improper fraction 17/4. Set up the problem as 17 ÷ 4. The number 4 goes into 17 a total of 4 times, so the whole number is 4. Then, multiply 4 by 4, which is equal to 16. Subtract 16 from 17, which is equal to 1, so that's the remainder. This means that 17/4 is the same as 4 1/4.

Fraction Calculator, Practice Problems, and Answers

Community Q&A

• Check with your teacher to find out if you need to convert improper fractions into mixed numbers and/or reduce fractions to their lowest terms to get full marks. Thanks Helpful 2 Not Helpful 1
• Take the time to carefully read through the problem at least twice so you can be sure you know what it's asking you to do. Thanks Helpful 2 Not Helpful 2
• To take the reciprocal of a whole number, just put a 1 over it. For example, 5 becomes 1/5. Thanks Helpful 1 Not Helpful 1

You Might Also Like

• ↑ https://www.sparknotes.com/math/prealgebra/fractions/terms/
• ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
• ↑ https://www.mathsisfun.com/fractions_multiplication.html
• ↑ https://www.mathsisfun.com/fractions_division.html
• ↑ https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
• ↑ https://www.youtube.com/watch?v=PcEwj5_v75g
• ↑ https://sciencing.com/solve-math-problems-fractions-7964895.html

About This Article

To solve a fraction multiplication question in math, line up the 2 fractions next to each other. Multiply the top of the left fraction by the top of the right fraction and write that answer on top, then multiply the bottom of each fraction and write that answer on the bottom. Simplify the new fraction as much as possible. To divide fractions, flip one of the fractions upside-down and multiply them the same way. If you need to add or subtract fractions, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Sebastian Maxwell

Jun 1, 2017

Did this article help you?

Jul 19, 2017

Sep 16, 2017

Kamaria Albert

Feb 28, 2017

Oct 17, 2016

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

Game Central

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 4th grade   >   Unit 8

• Writing mixed numbers as improper fractions
• Writing improper fractions as mixed numbers
• Write mixed numbers and improper fractions

Mixed numbers and improper fractions review

What is an improper fraction?

What is a mixed number, rewriting a mixed number as an improper fraction.

• Your answer should be
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  

Rewriting an improper fraction as a mixed number

• a mixed number, like 1   3 / 4 ‍  

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Special May offer - 7 days free unlimited access to all premium content Try Premium

• Fifth Grade

Mixed Fractions

Fifth grade mixed fractions.

Filter by Grade:

Filter by subject:, smart practice.

Comparing Fractions

Simplifying Fractions

Adding Fractions

Improper Fractions, Mixed Numbers Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Rational numbers
• Combined operations with fractions

In this article we explain the combined operations between fractions : additions, subtractions, multiplications, divisions, powers and roots. We will see a complete guide with formulas, explanations and exercises solved step by step.

Table of Contents

How to solve combined operations with fractions

It should be noted that grouping symbols such as parentheses, brackets, and braces indicate that within them there is a number that cannot be separated. For example, *(2+3)\cdot 5* is different from *2+3\cdot 5*, in the first expression it indicates that the number 2+3 is multiplied by 5, resulting in 25; in the second expression, it indicates that 2 is added to the multiplication of 3 and 5, resulting in 17. The same idea applies when dealing with fractions.

When performing calculations involving fractions, it is convenient to follow a specific order for solving the operations. This is commonly known as order of operations and helps avoid arriving at incorrect results.

The order of operations suggests following these steps in order to solve combined calculations:

• Solve operations within parentheses, brackets, and braces from innermost to outermost.
• Solve exponents and roots from left to right.
• Perform multiplication and division from left to right.
• Perform addition and subtraction from left to right.

If there are mixed numbers , they need to be converted into fractions before proceeding with the first step. This can be done by adding the whole number to the fractional part. For example: *5~\dfrac{1}{2}=5+\dfrac{1}{2}=\dfrac{11}{2}*

If there are numbers written in decimal form , they should be converted into fractions. If there are whole numbers , it is convenient to write them as fractions with a denominator of 1, for example: *4=\dfrac{4}{1},* this will make operations easier when performing calculations.

Combined calculations with addition and subtraction

These are the simplest cases, to perform them we can follow the following steps:

• Perform the operations within parentheses, brackets, and braces from the inside out.
• Calculate additions and subtractions from left to right.

*\left(\dfrac{1}{2}+\dfrac{2}{7}\right)-\dfrac{5}{4}+\dfrac{3}{2}*

Step 1: First, we solve what's inside the parentheses. In this case, the fractions in red will be added. It's better to write the result in a simplified form.

*{\color{red}\left(\dfrac{1}{2}+\dfrac{2}{7}\right)}-\dfrac{5}{4}+\dfrac{3}{2}*

*=\dfrac{11}{14}-\dfrac{5}{4}+\dfrac{3}{2}*

Step 2: Now we solve the remaining additions and subtractions. Simplify the final result.

*\dfrac{11}{14}-\dfrac{5}{4}+\dfrac{3}{2}*

*=-\dfrac{13}{28}+\dfrac{3}{2}*

*=\dfrac{29}{28}*

*\left(\dfrac{2}{3}+\dfrac{5}{7}\right)+2~\dfrac{1}{3}-\left(\dfrac{5}{17}-\dfrac{14}{8}\right)*

Before starting, we convert the mixed number into a fraction. This is equal to adding the whole part to the fractional part: *2~\dfrac{1}{3}=2+\dfrac{1}{3}=\dfrac{7}{3}*. So, the exercise becomes:

*\left(\dfrac{2}{3}+\dfrac{5}{7}\right)+\dfrac{7}{3}-\left(\dfrac{5}{17}-\dfrac{14}{8}\right)*

Step 1: We solve the two parentheses. The result is as follows:

*\dfrac{29}{21}+\dfrac{7}{3}-\left(-\dfrac{99}{68}\right)*

We apply the sign rule to the last fraction.

*\dfrac{29}{21}+\dfrac{7}{3}+\dfrac{99}{68}*

Step 2: We calculate the remaining additions and subtractions.

*\dfrac{26}{7}+\dfrac{99}{68}*

*=\dfrac{2461}{476}*

*\left[\dfrac{2}{3}+1.5-\left(\dfrac{3}{7}-\dfrac{1}{5}\right)+\dfrac{2}{9}\right]-\dfrac{5}{4}*

Before we begin, we convert the decimal to a fraction:

*\left[\dfrac{2}{3}+\dfrac{3}{2}-\left(\dfrac{3}{7}-\dfrac{1}{5}\right)+\dfrac{2}{9}\right]-\dfrac{5}{4}*

Step 1: We first solve what's inside the grouping symbols, from the inside out. We start with the parentheses and then proceed to the brackets.

*\left[\dfrac{2}{3}+\dfrac{3}{2}-{\color{green}\left(\dfrac{3}{7}-\dfrac{1}{5}\right)}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{2}{3}+\dfrac{3}{2}-\dfrac{8}{35}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{13}{6}-\dfrac{8}{35}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{407}{210}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\dfrac{1361}{630}-\dfrac{5}{4}*

Step 2: Now that we have removed the grouping symbols, we solve the remaining subtraction:

*\dfrac{1361}{630}-\dfrac{5}{4}=\dfrac{1147}{1260}*

Combined operations with multiplications and divisions

Now, let's increase complexity by including multiplications and division of fractions. The steps for performing these calculations are as follows:

• Perform the operations within parentheses, brackets, and braces from inside to outside.
• Carry out multiplications and divisions from left to right.
• Perform additions and subtractions from left to right.

*\left(\dfrac{7}{8}\cdot \dfrac{2}{5}+\dfrac{3}{5}\right):\dfrac{1}{2}+\dfrac{3}{5}*

Step 1: We first solve what's inside the parentheses, from left to right. According to the hierarchy, multiplication is done first, followed by addition. The results will always be simplified.

*\left(\dfrac{7}{20}+\dfrac{3}{5}\right):\dfrac{1}{2}+\dfrac{3}{5}*

*=\dfrac{19}{20}:\dfrac{1}{2}+\dfrac{3}{5}*

Step 2: Now, we solve the multiplications and divisions. In this case, only division is left.

*\dfrac{19}{20}:\dfrac{1/2}+\dfrac{3}{5}*

*=\dfrac{19}{10}+\dfrac{3}{5}*

Step 3: We calculate the addition.

*\dfrac{19}{10}+\dfrac{3}{5}=\dfrac{5}{2}*

*\left[\dfrac{2}{3}+\left(\dfrac{3}{5}:\dfrac{1}{2}\right)-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\left(\dfrac{7}{4}+1\right)*

Step 1: We solve what's inside the parentheses first. Then, we calculate what's inside the brackets.

*\left[\dfrac{2}{3}+\dfrac{6}{5}-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\left[\dfrac{28}{15}-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\dfrac{67}{60}\cdot \dfrac{6}{7}-\dfrac{11}{4}*

Step 2: We calculate the remaining multiplication.

*\dfrac{67}{60}\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\dfrac{67}{70}-\dfrac{11}{4}*

Step 3: We calculate the subtraction.

*\dfrac{67}{70}-\dfrac{11}{4}=-\dfrac{251}{140}*

*1:\left[\left(\dfrac{3}{5}:\dfrac{1}{2}\right)\cdot \dfrac{5}{6}+3.5\right]+\left(\dfrac{2}{8}:\dfrac{5}{3}-1\right)+5~\dfrac{1}{3}*

Before we begin, convert the decimal and mixed number into fractions.

*1:\left[\left(\dfrac{3}{5}:\dfrac{1}{2}\right)\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]+\left(\dfrac{2}{8}:\dfrac{5}{3}-1\right)+\dfrac{16}{3}*

*1:\left[\dfrac{6}{5}\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]+\left(\dfrac{3}{20}-1\right)+\dfrac{16}{3}*

*1:\left[\dfrac{6}{5}\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]-\dfrac{17}{20}+\dfrac{16}{3}*

*1:\left[1+\dfrac{7}{2}\right]-\dfrac{17}{20}+\dfrac{16}{3}*

*1:\dfrac{9}{2}-\dfrac{17}{20}+\dfrac{16}{3}*

Step 2: We calculate the division that's left.

*=\dfrac{2}{9}-\dfrac{17}{20}+\dfrac{16}{3}*

Step 3: Since there are only additions and subtractions left, we calculate them.

*\dfrac{2}{9}-\dfrac{17}{20}+\dfrac{16}{3}*

*=-\dfrac{113}{180}+\dfrac{16}{3}*

*=\dfrac{847}{180}*

*\left[\left(\dfrac{1}{2}-\dfrac{3}{4}\right)+\dfrac{5}{8}:\dfrac{8}{4}\right]\cdot \dfrac{5}{11}*

We apply the same steps as we've been doing.

*\left[-\dfrac{1}{4}+\dfrac{5}{8}:\dfrac{8}{4}\right]\cdot \dfrac{5}{11}*

*=\left[-\dfrac{1}{4}+\dfrac{20}{64}\right]\cdot \dfrac{5}{11}*

*=\dfrac{1}{16}\cdot \dfrac{5}{11}*

*=\dfrac{5}{176}*

Combined operations with powers and roots of fractions

Now we include exponents and fractional roots . The steps for performing these calculations are:

• Perform operations within parentheses, brackets, and braces from the inside out.
• Calculate multiplications and divisions from left to right.

*\left[\sqrt{\dfrac{1}{2}+\dfrac{1}{16}}+\dfrac{5}{4}\right]^2-1*

Step 1: First, we resolve what's inside the brackets. What's inside the square root also counts as a parenthesis, so we resolve it.

*\left[\sqrt{\dfrac{9}{16}}+\dfrac{5}{4}\right]^2-1*

*=\left[\dfrac{3}{4}+\dfrac{5}{4}\right]^2-1*

Step 2: Since we've removed the brackets, we proceed to do the exponentiation and then the addition.

*2^2-1=4-1=3*

*\left[\left(\dfrac{1}{2}-\dfrac{1}{6}\right)^3\cdot \sqrt{\dfrac{25}{16}}\right]\cdot \left(\dfrac{1}{5}+\dfrac{7}{15}\right)^2-10\cdot \dfrac{5}{2}*

Step 1: First, we solve what's inside parentheses, then what's inside brackets.

*\left[\left(\dfrac{1}{3}\right)^3\cdot \sqrt{\dfrac{25}{16}}\right]\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

*\left[\dfrac{1}{27}\cdot \dfrac{5}{4}\right]\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

*\dfrac{5}{108}\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

Step 2: Now we solve the exponent.

*\dfrac{5}{108}\cdot \dfrac{4}{9}+\dfrac{157}{243}*

Step 3: We solve the multiplication now.

*\dfrac{5}{243}+\dfrac{157}{243}*

Step 4: Now we can solve the addition.

*\dfrac{5}{243}+\dfrac{157}{243}=\dfrac{2}{3}*

$$(-0.7)^3\cdot \dfrac{10}{21}\cdot 20+\sqrt{0.\overline{4}}:\dfrac{10}{11}-1.\overline{5}$$

Before starting, let's convert the integers and decimal expressions into fractions. The rewritten problem becomes:

$$\left(-\dfrac{7}{10}\right)^3\cdot \dfrac{10}{21}\cdot \dfrac{20}{1}+\sqrt{\dfrac{4}{9}}:\dfrac{10}{11}-\dfrac{95}{90}$$

Step 1: Since the only operation within parentheses is a power, let's proceed to solve powers and roots.

$$-\dfrac{343}{1000}\cdot \dfrac{10}{21}\cdot \dfrac{20}{1}+\dfrac{2}{3}:\dfrac{10}{11}-\dfrac{95}{90}$$

Step 2: Let's solve the multiplications and divisions from left to right.

$$-\dfrac{49}{15}+\dfrac{22}{30}-\dfrac{19}{18}$$

Step 3: Now, calculate the additions and subtractions from left to right, and we'll have the final answer.

$$-\dfrac{49}{15}+\dfrac{22}{30}-\dfrac{19}{18}=-\dfrac{323}{90}$$

$$\sqrt{\dfrac{25}{16}\cdot \dfrac{36}{4}}-\left(\dfrac{5}{2}+\dfrac{3}{7}-\dfrac{7}{4}\right)$$

This combined exercise can be solved in different ways; we'll explore two of them.

First approach: Applying the order of operations, we solve what is inside the parentheses and within the square root, then the square root, and finally the additions and subtractions.

$$=\sqrt{\dfrac{900}{64}}-\dfrac{33}{28}$$

$$=\dfrac{30}{8}-\dfrac{33}{28}$$

$$=\dfrac{18}{7}$$

Second approach: We apply a property of the square root of a product to distribute the square root and the rule of signs to eliminate the parentheses.

$$=\sqrt{\dfrac{25}{16}}\cdot \sqrt{\dfrac{36}{4}}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

$$=\dfrac{5}{4}\cdot \dfrac{6}{2}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

$$=\dfrac{15}{4}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

Daniel Machado

Advanced student of Mathematics at Facultad de Ciencias Exactas, Químicas y Naturales. Universidad Nacional de Misiones, Argentina.

Other articles that may interest you

Operations with fractions

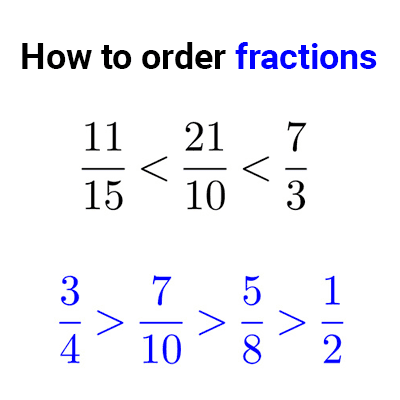
Ordering fractions

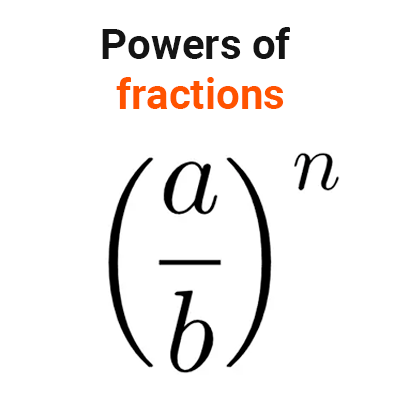
Powers of fractions

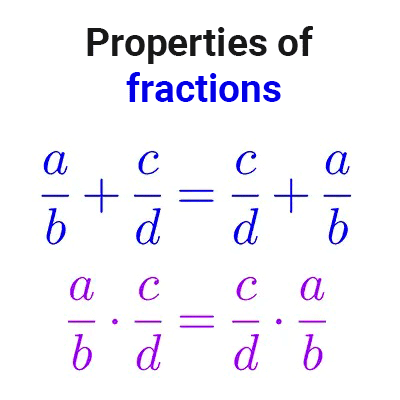
Properties of fractions

We use cookies to improve your browsing experience, show personalized ads or content, and analyze our traffic. More information

Talk to our experts

1800-120-456-456

• Mixed Fraction Addition

Introduction to Mixed Fractions

A fraction, which derives from the Latin word fractus, which means "broken," is a portion of a whole or, more broadly, any number of equal pieces. A fraction, such as one-half, eight-fifths, or three-quarters, indicates how many components of a particular size there are when stated in ordinary English. The mixed fraction is the combination of a whole number or integer and a fraction. To find out the addition of the mixed fraction, you should convert the mixed fraction into simplified regular fractions . Example: \[4\dfrac{7}{2}\] In the given mixed fraction 4 is the whole number or integer and \[\dfrac{7}{2}\]is the fraction.

How To Add Mixed Fractions

The addition of a mixed fraction is like finding the sum or the total of two or more mixed fractions . There are two types of methods by which we can find out the sum of various mixed fractions: one is by separating the whole number, and another is by converting the mixed fraction into a simpler form. Before applying any arithmetic operations such as addition, subtraction , multiplication , etc., we need to change the mixed fractions to improper fractions.

Mixed Fraction Addition Method Explanation

We will now learn different methods of adding mixed fractions

Method 1. Separating the Whole Number

Mixed Fraction Example:

Add \[1\dfrac{1}{2}\] and \[2\dfrac{1}{2}\].

Step 1: Find the whole or integer number from a mixed fraction.

The whole number of \[1\dfrac{1}{2}\] is 1. And for \[2\dfrac{1}{2}\] is 2.

Step 2: Separate the whole number and add it.

Now we separate the whole number from the fraction and add it separately

\[ = (1 + 2) + \dfrac{1}{2} + \dfrac{1}{2}\]

\[ = 3 + \dfrac{1}{2} + \dfrac{1}{2}\]

Step 3: Taking LCM as 2

\[ = \dfrac{{3 \times 2}}{{1 \times 2}} + \dfrac{1}{2} + \dfrac{1}{2}\]

\[ = \dfrac{{6 + 1 + 1}}{2}\]

\[ = \dfrac{8}{2}\]

Hence, the answer is 4.

Method 2. Converting into a Simpler Fraction

\[ = 1\dfrac{1}{2} + 2\dfrac{1}{2}\]

Step 1. Convert mixed fractions into improper fractions.

( In this we have multiplied the denominator with the whole number and added it to the numerator we have converted the mixed fraction into a simpler fraction)

\[ = \dfrac{{2 \times 1 + 1}}{2} + \dfrac{{2 \times 2 + 1}}{2}\]

Step 2. Taking LCM as 2

\[ = \dfrac{3}{2} + \dfrac{5}{2}\]

Mixed Fraction Questions (Solved)

Question 1.

Add the fraction \[7\dfrac{1}{4}\] and \[4\dfrac{2}{4}\]

Solution: \[7\dfrac{1}{4} + 4\dfrac{2}{4}\]

\[ = (7 + 4) + \dfrac{1}{4} + \dfrac{2}{4}\]

\[ = 11 + \dfrac{1}{4} + \dfrac{2}{4}\]

\[ = \dfrac{{11 \times 4}}{{1 \times 4}} + \dfrac{1}{4} + \dfrac{2}{4}\]

\[ = \dfrac{{44}}{4} + \dfrac{1}{4} + \dfrac{2}{4}\]

\[ = \dfrac{{44 + 1 + 2}}{4}\]

\[ = \dfrac{{47}}{4}\]

Hence, The fraction is \[ = \dfrac{{47}}{4}\]

Question 2.

Add \[4\dfrac{1}{2}\] and \[2\dfrac{1}{4}\]

Solution: \[4\dfrac{1}{2} + 2\dfrac{1}{4}\]

\[ = \dfrac{{2 \times 4 + 1}}{2} + \dfrac{{4 \times 2 + 1}}{4}\]

\[ = \dfrac{9}{2} + \dfrac{9}{4}\]

\[ = \dfrac{{9 \times 2}}{{2 \times 2}} + \dfrac{9}{4}\]

\[ = \dfrac{{18}}{4} + \dfrac{9}{4}\]

\[ = \dfrac{{27}}{4}\]

Hence, The fraction is \[ = \dfrac{{27}}{4}\].

As we have solved the above example using both methods of adding mixed fractions. Now, we can see that the addition of mixed fractions can be done by two methods. This topic has covered two methods: separating the whole number and converting the mixed fraction into a simpler form. The answer obtained from both methods will be the same.

FAQs on Mixed Fraction Addition

1. What is the Definition of a Fraction?

A fraction is a mathematical number that illustrates the components of a whole.

2. What is meant by the whole number?

All positive integers from 0 to infinity are included in the group of numbers known as whole numbers.

3. Can a proper number be written as a mixed number?

No, a proper number cannot be written as a mixed number, only improper numbers can be written as mixed numbers.

Subtracting Mixed Fractions

Mixed fractions are another form of representing an improper fraction composed of a whole number and a proper fraction. Subtracting mixed fractions is the subtraction operation performed between any two mixed fractions. We will be studying different methods and rules to understand subtracting mixed fractions in this article.

Subtracting Mixed Fractions with Like Denominators

Two or more fractions having a common denominator are known as like fractions . Hence, mixed fractions with like denominators will have the same denominators such as \(3\dfrac{2}{7}\) and \(2\dfrac{1}{7}\). Look at the following points to be kept in mind while subtracting mixed fractions.

• A mixed fraction \(a\dfrac{b}{c}\) can also be written as a + (b/c).
• To convert a mixed number to an improper fraction, the whole number is multiplied by the denominator and the result is added to the numerator of the proper fraction by retaining the denominator. For example, to convert \(1\dfrac{6}{11}\) to an improper fraction, we multiply 1 and 11 i.e, 1 × 11 = 11 and the result is added to 6 i.e., 11 + 6 = 17. Thus the improper fraction is 17/11.
• To convert an improper fraction to a mixed number we will divide the numerator of the improper fraction by its denominator. The quotient becomes the whole number part, the remainder becomes the numerator of the proper fraction and the denominator remains as it is. For example, to convert 22/3 to a mixed number, we first divide 22 by 3 and get the quotient as 7 and the remainder as 1. Thus, the mixed number is \(7\dfrac{1}{3}\).

Now let us understand the steps of subtracting mixed fractions with like denominators.

Example: Subtract the mixed fraction \(2\dfrac{1}{3}\) from \(4\dfrac{2}{3}\).

We have to perform \(4\dfrac{2}{3}\) - \(2\dfrac{1}{3}\). Let's look into the steps.

• Step 1: We will subtract the whole numbers of both the fractions. i.e., 4 - 2 = 2.
• Step 2: Now we will subtract the fractional parts. i.e., (2/3) - (1/3) = 1/3.
• Step 3: We will combine the result of the last two steps to get the result. i.e., 2 + (1/3) = \(2\dfrac{1}{3}\).

Hence the value of \(4\dfrac{2}{3}\) - \(2\dfrac{1}{3}\) is \(2\dfrac{1}{3}\).

Subtracting Mixed Fractions with Unlike Denominators

Fractions with unequal denominators are known as unlike fractions. Thus, some examples of mixed fractions with unlike denominators are \(5\dfrac{2}{3}\) and \(1\dfrac{2}{5}\). Let us take an example to understand the steps of subtracting mixed fractions with unlike denominators.

Example: Subtract \(3\dfrac{1}{6}\) from \(5\dfrac{2}{3}\).

We have to perform \(5\dfrac{2}{3}\) - \(3\dfrac{1}{6}\). We have two ways to perform the subtraction.

Method I: By subtracting the whole numbers separately and the fractions separately by making their denominators equal.

• Step 1: Subtract the whole numbers of both the fractions. i.e., 5 - 3 = 2.
• Step 2: Now we will subtract the fractional parts. To do so we have to make the denominators of 2/3 and 1/6 equal by finding their LCM.
• Step 3: Since the LCM of 3 and 6 is 6, we will write 2/3 as (2 × 2) / (3 × 2) = 4/6.
• Step 4: We will now subtract the fractions. i.e., (4/6) - (1/6) = 3/6.
• Step 5: The result obtained in the previous step will be simplified. i.e., 3/6 = 1/2.
• Step 6: The result of step 1 and step 5 will be combined to get the final result. i.e., 2 + (1/2) = \(2\dfrac{1}{2}\).

Method II: By converting them into improper fractions , followed by subtracting them by making their denominators equal.

• Step 1: Convert the given mixed fractions to improper fractions. i.e., \(5\dfrac{2}{3}\) = 17/3 and \(3\dfrac{1}{6}\) = 19/6.
• Step 2: For the obtained fractions in the last step, we will make the denominators equal by taking their LCM.
• Step 3: LCM of the denominators 3 and 6 is 6. Thus, 17/3 can be written as (17 × 2) / (3 × 2) = 34/6.
• Step 4: Now, we will subtract the fractions. i.e., (34/6) - (19/6) = 15/6.
• Step 5: The result of the previous step will be simplified. i.e., 15/6 = 5/2.
• Step 6: Finally we convert the result obtained in the last step to a mixed fraction. i.e., 5/2 = \(2\dfrac{1}{2}\).

Hence the value of \(5\dfrac{2}{3}\) - \(3\dfrac{1}{6}\) is equal to \(2\dfrac{1}{2}\).

Subtracting Mixed Fractions with Regrouping

While subtracting mixed fractions, there might arise a situation wherein the fraction to be subtracted is greater than the fraction from which it is being subtracted. In such cases, we will use the concept of regrouping. Let's now understand subtracting mixed fractions with regrouping by taking an example.

Example: Subtract \(7\dfrac{2}{3}\) from \(10\dfrac{4}{9}\).

We have to perform \(10\dfrac{4}{9}\) - \(7\dfrac{2}{3}\).

• Step 1: Consider the fractional parts of both the mixed fraction and compare them by making their denominators equal. i.e., we will be comparing 4/9 and 2/3.
• Step 2: The LCM of the denominators 9 and 3 is 9. Thus, 2/3 can be written as (2 × 3) / (3 × 3) = 6/9. Hence we see that 6/9 > 4/9 or we can say 2/3 > 4/9.
• Step 3: As seen in the previous step 4/9 < 6/9, we cannot subtract 6/9 from 4/9. Hence, now 4/9 will borrow 1 from the whole number part of the mixed fraction \(10\dfrac{4}{9}\).
• Step 4: The whole number 10 gives away 1 as borrow to 4/9. We know that 1 can also be written as 9/9. Hence, when the borrow 9/9 is added to 4/9, we get 4/9 + 9/9 = 13/9.
• Step 5: We will now rewrite the fraction after regrouping. The whole number 10 becomes 9 after giving a borrow to 4/9 and 4/9 becomes 13/9. Hence, \(10\dfrac{4}{9}\) = \(9\dfrac{13}{9}\).
• Step 6: Now we will subtract the mixed fractions easily as they have like denominators. i.e., \(9\dfrac{13}{9}\) - \(7\dfrac{6}{9}\) = \(2\dfrac{7}{9}\).

Related Articles on Subtracting Mixed Fractions

Check these articles related to the concept of subtracting mixed fractions.

• Mixed fractions
• Improper fractions
• Proper fraction

Subtracting Mixed Fractions Examples

Example 1: Subtract the mixed fraction \(15\dfrac{1}{3}\) from \(20\dfrac{2}{3}\) .

Solution: We will use the concept of subtracting mixed fractions to solve this question. Given mixed fractions are \(15\dfrac{1}{3}\) and \(20\dfrac{2}{3}\) that has a like denominator. We have to perform \(20\dfrac{2}{3}\) - \(15\dfrac{1}{3}\). We will be subtracting the whole numbers and the fractional parts separately and combining them as shown below.

= (20 - 15) + [(2/3) - (1/3)]

= 5 + (1/3)

= \(5\dfrac{1}{3}\)

Thus, the value of \(20\dfrac{2}{3}\) - \(15\dfrac{1}{3}\) is equal to \(5\dfrac{1}{3}\).

Example 2: Subtract the mixed fraction \(16\dfrac{1}{4}\) from \(27\dfrac{1}{12}\) using the concept of regrouping.

Solution: We will use the steps of subtracting mixed fractions with regrouping to solve this question. We have to perform \(27\dfrac{1}{12}\) - \(16\dfrac{1}{4}\). Regrouping is needed here because when we compare the fractions 1/12 and 1/4 we see that 1/12 < 1/4. This is because the fractions are unlike and on converting them to like fractions we get 1/4 = 3/12. Thus, 1/12 < 3/12. We cannot subtract a bigger fraction from a smaller one thus, we use the concept of regrouping. In the fraction \(27\dfrac{1}{12}\), 1/12 needs to borrow 1 from 27. Therefore, we will modify this fraction. 27 gives a borrow of 1 whole to 1/12 and itself becomes 26. This borrow of 1 whole is added to 1/12. We know that 1 can also be represented as 12/12. Thus, 1/12 + 12/12 = 13/12. Therefore, the modified fraction is \(27\dfrac{1}{12}\) = \(26\dfrac{13}{12}\).

Now, we will perform \(26\dfrac{13}{12}\) - \(16\dfrac{3}{12}\).

= (26 - 16) + (13/12) - (3/12)

= 10 + (10/12)

= \(10\dfrac{10}{12}\)

On simplifying we get,

= \(10\dfrac{5}{6}\)

Therefore, the value of \(27\dfrac{1}{12}\) - \(16\dfrac{1}{4}\) is \(10\dfrac{5}{6}\).

go to slide go to slide

Book a Free Trial Class

Practice Questions on Subtracting Mixed Fractions

Faqs on subtracting mixed fractions, how to solve subtracting mixed fractions.

Subtracting mixed fractions can be done in two ways. For like denominators, the whole numbers can simply be subtracted and the fractional part of the mixed fractions can also be subtracted and the two results are combined to get the result. The other way to do it is, by converting the mixed fractions to improper fractions and subtracting them. For unlike denominators, they can be first converted to like denominators by finding the LCM and the same steps can be followed as subtracting mixed fractions with like denominators.

How to Borrow when Subtracting Mixed Fractions?

While subtracting mixed fractions, if the proper fractional part of the mixed fraction from which the other mixed fraction is getting subtracted is smaller, then the whole number gives a borrow to the proper fraction to make it larger. For example, to perform \(3\dfrac{1}{3}\) - \(1\dfrac{2}{3}\) we see that 2/3 > 1/3. Thus, 1/3 will borrow 1 whole from 3. 1 whole can be written as 3/3. The whole number 3 after giving a borrow of 1 becomes 3 - 1 = 2 and the fraction 1/3 becomes (1/3) + (3/3) = 4/3. Thus, the new modified mixed fraction after borrowing is \(2\dfrac{4}{3}\). Now, the subtraction will be \(2\dfrac{4}{3}\) - \(1\dfrac{2}{3}\) = \(1\dfrac{2}{3}\).

How to Regroup when Subtracting Mixed Fractions?

Regrouping is done when a greater fraction is subtracted from a smaller fraction. For example, let's perform \(8\dfrac{4}{9}\) - \(5\dfrac{2}{3}\) . We will be making the denominators of 4/9 and 2/3 equal to compare them. The fraction 2/3 can also be written as 6/9. But 6/9 > 4/9. We cannot subtract a larger fraction from a smaller fraction. Thus, 4/9 has to be made larger. To do so, 4/9 borrows a 1 from 8. 1 whole can also be written as 9/9. Now, the whole number 8 becomes 8 - 1 = 7 and the fraction 4/9 becomes (4/9) + (9/9) = 13/9. Thus, the new fraction will be \(7\dfrac{13}{9}\). Thus, now the subtraction is as follows: \(7\dfrac{13}{9}\) - \(5\dfrac{6}{9}\) = \(2\dfrac{7}{9}\).

How to Subtract Mixed Fractions with Same Denominators?

Subtracting mixed fractions with the same denominators is done by subtracting the whole number part and fractional part of the mixed fractions separately followed by combining them to get the result. For example, let's perform \(23\dfrac{3}{4}\) - \(21\dfrac{1}{4}\) = (23 - 21) + (3/4) - (1/4) = 2 + (2/4) = \(2\dfrac{2}{4}\)

On simplifying we get, = \(2\dfrac{1}{2}\)

How to Subtract Mixed Fractions with Different Denominators?

Subtracting mixed fractions with different denominators can be done by converting them into an improper fraction followed by converting them into like denominators by taking their LCM and finally subtracting their numerators. The final result is then converted back to a mixed fraction. For example, let's perform \(6\dfrac{2}{3}\) - \(2\dfrac{1}{4}\) = (20/3) - (9/4) = [(20 × 4) / (3 × 4)] - [(9 × 3) / (4 × 3)] = (80/12) - (27/12) = 53/12 = \(4\dfrac{5}{12}\)

How to Subtract Mixed Fractions from Whole Numbers?

The whole numbers can be modified and be written as a mixed fraction. Once the whole number is written in the form of a mixed fraction, the general steps of subtracting the mixed fractions can be followed. For example, let's perform 5 - \(2\dfrac{2}{3}\) Note that 5 can also be written as 4 + 1 = 4 + (3/3) = \(4\dfrac{3}{3}\) Thus, we will perform \(4\dfrac{3}{3}\) - \(2\dfrac{2}{3}\) = (4 - 2) + (3/3) - (2/3) = 2 + (1/3) = \(2\dfrac{1}{3}\)

How to do Adding and Subtracting Mixed Fractions?

Mixed fractions will be subtracted from mixed fractions by first converting them into improper fractions and subtracting their numerators if they have the same denominator. If they have different denominators, then they are first converted into the same denominators by taking their LCM followed by subtracting their numerators. The final result will be converted back to a mixed fraction. The steps to add mixed fractions also remain the same. The only difference is we add the numerators instead of subtracting. For example, let's perform \(4\dfrac{2}{7}\) - \(3\dfrac{1}{6}\) = (30/7) - (19/6) = [(30 × 6) / (7 × 6)] - [(19 × 7) / (6 × 7)] = (180/42) - (133/42) = 47/42 = \(1\dfrac{5}{42}\)

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Word Problems on Addition of Mixed Fractions | Adding Mixed Numbers Word Problems

Mixed Fractions are the ones having a Whole Number and a Fraction. Learn how to solve problems on adding mixed fractions by availing our quick resource on Word Problems on Addition of Mixed Fractions. Try to solve the Questions on Adding Mixed Numbers available on your own before you cross-check with the respective Solutions and explanations. For better understanding, we have provided the Examples on Mixed Numbers Addition step by step. Understand the Problem Solving Strategy Used and Solve the Related Problems on your own.

Also, Refer:

• Addition of Mixed Fractions

Addition of Mixed Fractions Word Problems with Answers

Example 1. Ram walked 1\(\frac { 3 }{ 5 } \)  km on Monday, 3 \(\frac { 1 }{ 6 } \) km on Tuesday, and 2 \(\frac { 1 }{ 12 } \)  km on Wednesday. Find out the distance he walked in all? Solution: Ram walked on monday= 1 \(\frac { 3 }{ 5 } \) Ram walked on tuesday=3 \(\frac { 1 }{ 6 } \) Ram walked on wednesday=2 \(\frac { 1 }{ 12 } \) The distance he walked in all days= 1 \(\frac { 3 }{ 5 } \) + 3\(\frac { 1 }{ 6 } \) + 2 \(\frac { 1 }{ 12 } \) =\(\frac { 8 }{ 5 } \) +\(\frac { 19 }{ 6 } \) + \(\frac { 25 }{ 12 } \) =\(\frac {8 × 12  }{ 5 ×12 } \) +\(\frac {19 × 10  }{ 6 ×10 } \) +\(\frac {25 ×5   }{ 12 ×5 } \) ( LCM of 5,6,12 is 60) = \(\frac { 96 }{ 60 } \)+\(\frac { 190 }{ 60 } \)1 +\(\frac { 125 }{ 60 } \) =\(\frac { 411 }{ 60 } \) =\(\frac { 137 }{ 20 } \) =6 \(\frac { 17 }{ 20 } \) Hence, Ram walked 6 \(\frac { 17 }{ 20 } \) km.

Example 2. Laxman bought 2 \(\frac { 1 }{ 2 } \) kg wheat, 4\(\frac { 1 }{ 4 } \)  of sugar, 10 \(\frac { 1 }{ 2 } \) kg rice. How many kg of items did he buy? Solution: Laxman bought wheat= 2 \(\frac { 1 }{ 2 } \) kg Laxman bought sugar=4 \(\frac { 1 }{ 4 } \) kg Laxman bought rice=10 \(\frac { 1 }{ 2 } \) kg Total no. of kg of items Laxman bought  = 2 \(\frac { 1 }{ 2 } \)  + 4 \(\frac { 1 }{ 4 } \) + 10 \(\frac { 1 }{ 2 } \) =\(\frac { 5 }{ 2 } \) +\(\frac { 17 }{ 4 } \) +\(\frac { 21 }{ 2 } \) =\(\frac { 5 ×2}{ 2×2 } \) + \(\frac { 17}{ 4 } \)  +\(\frac { 21 ×2 }{ 2×2 } \) = \(\frac { 10 }{ 4 } \) +\(\frac { 17 }{ 4 } \) + \(\frac { 42 }{ 4 } \) =  \(\frac { 69 }{ 4 } \) =17 \(\frac { 1 }{ 4 } \) . Therefore, Laxman bought 17 \(\frac { 1 }{ 4 } \) kg of items.

Example 3. Rajesh donated 19 \(\frac { 1 }{ 2 } \) kg of rice, 25 \(\frac { 1 }{ 4 } \) kg of wheat, and 11 \(\frac { 3 }{ 4 } \) of oil. Find how many kgs of groceries he donated? Solution: Rajesh donated rice=19 \(\frac { 1 }{ 2 } \) Rajesh donated wheat=25 \(\frac { 1 }{ 4 } \) Rajesh donated oil=11\(\frac { 3}{ 4 } \) Total no. of kg of groceries Rajesh donated =19 \(\frac { 1 }{ 2 } \)+ 25 \(\frac { 1 }{ 4 } \) + 11 \(\frac { 3 }{ 4 } \) =\(\frac { 39 }{ 2 } \)+\(\frac { 101 }{ 4 } \)+\(\frac { 47 }{ 4 } \) = \(\frac { 39 × 2 }{ 2 × 2 } \)+\(\frac { 101 }{ 4 } \)+ \(\frac { 47 }{ 4 } \) =\(\frac { 78 }{ 4 } \)+\(\frac { 101 }{ 4 } \)+ \(\frac { 47 }{ 4 } \)47/4 =\(\frac { 226 }{ 4 } \)=\(\frac { 113 }{ 2 } \)=56\(\frac {1 }{ 2 } \) Hence, Rajesh donated 56 \(\frac {1 }{ 2 } \) kgs of groceries.

Example 4. Giri went on walking 3 \(\frac {1 }{ 2 } \)  km, and then cycling by 4 \(\frac {1 }{ 4 } \) km and then he took a lift and traveled 8 \(\frac {3 }{ 8 } \) km. Find out how much distance he traveled? Solution: Giri went on walking =3 \(\frac {1 }{ 2 } \)  km Giri went on cycling=4 \(\frac {1 }{ 4 } \) km Giri took a lift and travelled=8 \(\frac {3}{ 8 } \) km The total distance he travelled= 3 \(\frac {1 }{ 2 } \)+4 \(\frac {1 }{ 4 } \) + 8 \(\frac {3}{ 8 } \) =\(\frac {7}{ 2 } \)+\(\frac {9 }{ 4 } \)+\(\frac {67 }{ 8 } \) =\(\frac {7 × 4 }{ 2 ×4 } \) + \(\frac {9 × 2 }{ 4 × 2} \)  + \(\frac {67}{ 8 } \) (LCM of 2,4,8 is 8) =\(\frac {28}{ 8 } \)+\(\frac {18}{ 8 } \)+ \(\frac {67}{ 8 } \) =\(\frac {113}{ 8 } \)=14 \(\frac {1}{ 8 } \)

Example 5. Sameera went to a market and bought mangoes 3 \(\frac {3}{ 4 } \) and her sister bought 4 \(\frac {5}{ 8 } \) mangoes. Find how many kgs of mangoes bought by Sameera and her sister? Solution: Sameera bought mangoes= 3 \(\frac {3}{ 4 } \) Sameera sister bought mangoes=4 \(\frac {5}{ 8 } \) Total no. of kg of mangoes bought by Sameera and her sister=3 \(\frac {3}{ 4 } \)  + 4 \(\frac {5}{ 8 } \) = \(\frac {15}{ 4 } \) + \(\frac {29}{ 8 } \) = \(\frac {15 × 2}{ 4× 2} \)+\(\frac {29}{ 8 } \) =  \(\frac {30}{ 8 } \)+\(\frac {29}{ 8 } \)=\(\frac {59}{ 8 } \) =7\(\frac {3}{ 8 } \) Therefore, Sameera and her sister bought 7\(\frac {3}{ 8 } \)  kg of mangoes.

Example 6. For a birthday party, Akhil distributed 14 \(\frac {1}{ 2 } \) liters of Pepsi, 10 \(\frac {3}{ 4 } \) liters of sprite, and 12 \(\frac {5}{ 8 } \) liters of thum sup. Find how many liters of cool drinks he distributed at the birthday party? Solution: Akhil distributed pepsi= 14 \(\frac {1}{ 2 } \) Akhil distributed sprite=10 \(\frac {3}{ 4 } \) Akhil distributed thums up=12 \(\frac {5}{ 8 } \) Total no. of liters of cool drinks Akhil distributed in the party=14 \(\frac {1}{ 2 } \) +10 \(\frac {3}{ 4 } \) +12 \(\frac {5}{ 8 } \) =\(\frac {29}{ 2 } \)+\(\frac {43}{ 4 } \)+\(\frac {101}{ 8 } \) =\(\frac {29 ×4}{ 2 ×4 } \)+\(\frac {43 ×2}{ 4 ×2 } \)+\(\frac {101}{ 8 } \) =\(\frac {116}{ 8 } \)+ \(\frac {86}{ 8 } \)+\(\frac {101}{ 8 } \) =\(\frac {303}{ 8 } \)=37 \(\frac {7}{ 8 } \) Akhil distributed 37 \(\frac {7}{ 8 } \) liters of cool drinks at the birthday party.

Example 7. In a competition between two friends, Anjana prepared 20 \(\frac {1}{ 2 } \) lit of orange juice and Sanjana prepared 22 \(\frac {5}{ 8 } \) of orange juice. Find how many liters of juice are prepared by both of them? Solution: Anjana prepared orange juice= 20 \(\frac {1}{ 2 } \) Sanjana prepared orange juice=22 \(\frac {5}{ 8} \) No. of liters of juice prepared by both of them= 20 \(\frac {1}{ 2 } \) + 22 \(\frac {5}{ 8 } \) = \(\frac {41}{ 2 } \)+ \(\frac {181}{ 8 } \) =\(\frac {41 ×4}{ 2 ×4 } \) +\(\frac {181}{ 8 } \) =\(\frac {164}{ 8 } \)+\(\frac {181}{ 8 } \)=\(\frac {345}{ 8 } \) =43\(\frac {1}{ 8 } \) Anjana and sanjana both prepared 43 \(\frac {1}{ 8 } \) liters of juice.

Example 8.  Sriram has wires of length 6 \(\frac {3}{ 4 } \)  m, 10 \(\frac {5}{ 8 } \). Find the length of both the wires? Solution: First wire length= 6 \(\frac {3}{ 4 } \) Second wire length=10 \(\frac {5}{ 8 } \) Length of both the wires= 6 \(\frac {3}{ 4 } \)  +10 \(\frac {5}{ 8 } \) =\(\frac {27}{ 4 } \)  +\(\frac {85}{ 8 } \) = \(\frac {27 × 2}{ 4 × 2 } \) +\(\frac {85}{ 8 } \) =\(\frac {54}{ 8 } \)  +\(\frac {85}{ 8 } \) =\(\frac {139}{ 8 } \) =17 \(\frac {3}{ 8 } \) The length of both wires is 17 \(\frac {3}{ 8 } \) .

Example 9. Bhaskar spent 8 \(\frac {1}{ 2 } \) hours on work, 2 \(\frac {1}{ 2} \)  hours on the playground. He spent 1 \(\frac {3}{ 4 } \)on  walking. Find how much time he spent on the day? Solution: Bhaskar spent on work=8 \(\frac {1}{ 2 } \) Bhaskar spent on playground=2 \(\frac {1}{ 2 } \) Bhaskar spent on walking=1 \(\frac {3}{ 4} \) Bhaskar spent on the day= 8 \(\frac {1}{ 2 } \) + 2 \(\frac {1}{ 2 } \) + 1\(\frac {3}{ 4 } \) = \(\frac {17}{ 2 } \) +\(\frac {5}{ 2 } \) +\(\frac {7}{ 4 } \) = \(\frac {17 × 2}{ 2 ×2 } \) + \(\frac { 5× 2}{ 2 ×2 } \)  +\(\frac {7}{ 4 } \) =\(\frac {34}{ 4 } \) + \(\frac {10}{ 4 } \) +\(\frac {7}{ 4 } \) =\(\frac {51}{ 4 } \) =12 \(\frac {3}{ 4 } \) Therefore, Bhaskar spent 12 \(\frac {3}{ 4 } \)  hours a day.

Example 10. Srikrishna bought 5 \(\frac {1}{ 4 } \) of vegetables, 20 \(\frac {3}{ 4 } \)  kg of groceries, and 1 \(\frac {1}{ 2} \)  kg of chicken. Find how many kgs he bought? Solution: Srikrishna bought vegetables= 5 \(\frac {1}{ 4 } \) kg Srikrishna bought groceries=20 \(\frac {3}{ 4 } \)   kg Srikrishna bought chicken= 1 \(\frac {1}{ 2 } \)  kg Srikrishna bought all=5 \(\frac {1}{ 4 } \) +20 \(\frac {3}{ 4 } \) +1 \(\frac {1}{ 2 } \) = \(\frac {21}{ 4 } \) +\(\frac {83}{ 4 } \) +\(\frac {3}{ 2 } \) =\(\frac {21}{ 4 } \) +\(\frac {83}{ 4 } \)+ \(\frac {3 ×2}{ 2 × 2 } \) =\(\frac {21}{ 4 } \) +\(\frac {83}{ 4 } \) + \(\frac {6}{ 4 } \) =\(\frac {110}{ 4 } \)=\(\frac {55}{ 2 } \)=27 \(\frac {1}{ 2 } \) Srikrishna bought 27 \(\frac {1}{ 2 } \) kg.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

Fraction Worksheets

Conversion :: Addition :: Subtraction :: Multiplication :: Division

Conversions

Fractions - addition, fractions - subtraction, fractions - multiplication, fractions - division.

The 7 Best AI Tools to Help Solve Math Problems

Quick links, the test questions, wolframalpha, microsoft mathsolver.

While OpenAI's ChatGPT is one of the most widely known AI tools, there are numerous other platforms that students can use to improve their math skills.

I tested seven AI tools on two common math problems so you know what to expect from each platform and how to use each of them.

I used two math problems to test each tool and standardize the inputs.

• Solve for b: (2 / (b - 3)) - (6 / (2b + 1)) = 4
• Simplify the expression: (4 / 12) + (9 / 8) x (15 / 3) - (26 / 10)

These two problems give each AI tool a chance to show reasoning, problem-solving, accuracy, and how it can guide a learner through the process.

Thetawise provides more than simple answers; you can also opt to have the AI model tutor you by sharing a detailed step-by-step breakdown of the solution. Using the platform is fairly straightforward, given that all you need to do is navigate to the platform and key in the math problem at hand. Alternatively, you can even upload a photo of the math problem onto the platform, and the AI will analyze the image and provide you with an answer.

The AI platform gave us a step-by-step breakdown of the problem:

It resulted in the answer:

While the answer is correct, the tool also provides further options for students to generate a more detailed breakdown of the steps or ask more specific questions.

WolframAlpha is an AI tool capable of solving advanced arithmetic, calculus, and algebra equations. While WolframAlpha's free version provides you with a direct answer, the paid version of the tool generates step-by-step solutions. If you want to make the best use of WolframAlpha's capabilities, you can sign up for the Pro version, which costs $5 per month for the annual plan if you're a student.

As expected, Wolfram Alpha solved both problems, showcasing its ability to handle different problems and provide precise answers quickly.

Julius works pretty similarly to the other AI tools on this list. That said, the highlight of this platform is that it has a built-in community forum, which users can use to discuss their prompts, results, or even issues they might be facing with the platform. Its active user base helps you quickly exchange ideas and receive feedback or advice. The platform's default version uses a combination of GPT-4 and Calude-3, based on whichever model best suits the prompt you input.

We tested the platform's accuracy by submitting the same problems that we did with the other AI tools. When submitting your prompt, you have the option of typing your question or uploading an image or a Google Sheet.

Julius provided correct solutions and offered options to help users verify the solution.

One of the oldest AI platforms, Microsoft's MathSolver is a great option if you want a tool capable of providing free step-by-step solutions to calculus, algebra, and other math problems. Here's how it fared when we submitted our math problems.

Microsoft's MathSolver provided the correct answers, and you can view the steps to the solution, take a quiz, solve similar problems, and more. This can be a great way to practice and perfect your understanding of different concepts.

Symbolab allows you to practice your math skills via quizzes, track your progress, and provide solutions to mathematical problems of different types, including calculus, fractions, trigonometry, and more. You can also use the Digital Notebook feature to keep track of any math problems you solve and share them with your friends. Another highlight of this platform is that educators can use the tool to create a virtual classroom, generate assessments, and share feedback, among other things.

The platform not only displays the answer but also lets you view a breakdown of the steps involved in solving the problem. You can also share the answers and steps via email or social media or print them for reference.

Anthropic launched its Claude 3 AI models in March 2024. Anthropic stated that Claude Opus, the most advanced Claude 3 model, outperforms comparable AI tools on most benchmarks for AI systems, including basic mathematics, undergraduate-level expert knowledge, and graduate-level expert reasoning. To test the platform's accuracy and ease of use, we submitted our two math problems. Here's how the platform performed:

While Claude initially got the answer wrong, probing it and requesting further clarification led to a correct solution.

Remember that we used the free version of Claude to solve this problem; subscribing to Opus (its more advanced model) is recommended if you want to take advantage of Claude's more advanced problem-solving capabilities.

Given that Claude got the previous problem wrong, our second, more basic fraction-based problem will indicate if the AI's performance was an anomaly or part of a consistent pattern.

As you can see, Claude correctly solved this problem and provided a detailed step-by-step breakdown of how it arrived at the answer.

GPT-4 can solve problems with far greater accuracy than its predecessor, GPT-3.5. If you're using the free version of ChatGPT, you'll likely only have access to GPT 3.5 and GPT-4o . However, for $20 per month, you can subscribe to the Plus model, which gives you access to GPT-4 and allows you to input five times the number of messages per day compared to the free version. That said, let's check how it performs with math problems.

In both cases, GPT-4o provided the correct answer with a detailed breakdown of the steps. While the platform is free, unlike other models, it does not have a quiz feature or a community forum.

These AI tools offer unique features and capabilities that make them a good option for math problems. Ultimately, the best way to pick a tool is by testing different models to determine which platform best fits your preferences and learning needs.

Question.AI-Math Calculator 4+

Scan&solve all subject problem.

• #3 in Education
• 4.6 • 19.6K Ratings
• Offers In-App Purchases

Screenshots

Description.

Experience the future of communication with Question.AI, the ultimate AI Chatbot app that's revolutionizing the way you gather information, communicate, and stay informed across various facets of life. Whether you're a student, a professional at work, an inquisitive mind, or a business enthusiast, our app is designed to make your life easier, smarter, and more efficient in any context. 【Key Features】 - Simplicity at its Best: Seeking answers has never been easier. Just ask your questions, and our intuitive AI will promptly provide you with accurate responses. No need for complex commands or jargon - it's like having a knowledgeable friend by your side 24/7. - Your Personal Assistant: From quick facts to in-depth research, Question.AI is your personal assistant ready to assist you. Need a definition, explanation, or summary? Count on us to deliver information tailored to your needs. - Global Connectivity: Break language barriers effortlessly. With the ability to translate into 140+ languages, Question.AI ensures you can communicate and connect with individuals from all around the world. Expand your horizons and broaden your perspectives with ease. - Intelligent Writing: Enhance your writing with AI-powered suggestions. Whether you're crafting an email, composing a report, or writing creatively, our app's intelligent writing feature offers insightful recommendations to make your content shine. - Adaptable Across Occasions: Question.AI is your versatile companion across various occasions, whether it's for studying, working, managing your business, or simply enhancing your daily life. We're here to assist you in every scenario. 【Why Choose Question.AI?】 With a commitment to excellence and user satisfaction, Question.AI stands out as the ultimate AI Chatbot app: - User-Friendly: Our user-centric design prioritizes simplicity and accessibility, ensuring a seamless experience for users of all ages. - Instant Insights: Get answers in real-time, allowing you to make informed decisions and impress others with your newfound knowledge. - Trusted Accuracy: Our AI's responses are backed by robust algorithms, ensuring that the information you receive is reliable and up-to-date. - Empowering Communication: Break down language barriers, foster connections, and engage with a global community effortlessly. - Unleash Creativity: Elevate your writing and communication skills with AI-powered suggestions that refine and elevate your content. Ready to embark on a journey of knowledge and connection? Download Question.AI now and experience the future of communication in the palm of your hand. Get started today! 【Contact us】 Email: [email protected] Official Website: www.questionai.com Instagram: @question.ai_app YouTube: @QuestionAI-Official Facebook: bit.ly/QuestionAI_FB TikTok: @question.ai_app Discord: bit.ly/QuestionAI_DC Messenger Group: https://m.me/j/AbaNe6U1Rhv5NAiL/ Privary Policy: https://www.questionai.com/privacy-policy Terms and Conditions: https://www.questionai.com/useTerm

Version 2.6.0

We’ve optimized the user experience. Update now!

Ratings and Reviews

19.6K Ratings

Literal LIFE SAVER

Your math teacher don't explain stuff like this and you know it. All you gotta do is just take a picture and it'll explain everything step by step. The app is free, but the pro cost money. Yes, the pro helps, but the app itself without any add-ons is still amazing and literally life-saving. If you are ever in doubt in math just snap a pic. And to make it even better is does others subject if you need any more help. Its just so awesome in general , like whoever came up with this stuff is a genius and so relatable. The videos would be so helpful but I don't pay for pro because my mom won't let me😭 Anywho, the step by step process is really easy to understand as well. Just get this app if you are in need of a math tutor, and tbh I think everyone needs a lil help on math especially, just consider downloading this app. Super easy to use and super easy to understand. THANK YOU DEARLY QUESTION A.I!!!🤗🤗

Developer Response ,

We're thrilled to know that you're satisfied with our app! Your positive experience is our greatest reward. Thank you for choosing us!

Love this app!!

I love this app so much usually you have to pay a monthly fee but with this you don’t, I didn’t buy it at first. I thought that we would have to pay monthly and I didn’t feel like getting the app but I gave it out a try. After I gave it a few tries and math questions I realize it really does help and that I love it so much,being in middle school and having tough math helps me so much with this even though I don’t really read the videos on how to do it sure helps with the answers and that is what it’s great about this app because you can help me with with my homework and if I need help it’ll give me. I love this app so much definitely recommended you don’t have to pay any monthly fee and this is the first app. I’ve actually waited five stars and left a comment because usually these apps aren’t good, but this one is amazing. Love it so much. Thanks.

We have always focused on providing high-quality service and user experience. Thank you for your recognition and support!

I’ve never been so greatful towards an app before, usually there was a deal with other apps that you had only a few tries before you had to pay for the full thing or wait your time…which 90% of the time didn’t even give you an answer or help… I’ve never had something this smooth be so dang helpful 😭❤️ Not only did it help me pass my test (88% omg 😍) but it also gave helpful advice and dumbed it down for me so i didn’t have to read through everything. Quite literally gave me the information i wanted and also the answer which is AMAZING 😨❤️Helped me better understand the questions SO THANK YOU 🙏 will definitely be using this on math 🥶 hoping for the same smoothness on math since it’s what i struggle with but overall just from a first time use i’m deeply thankful for this app!! 😭🙏❤️

Thank you for your positive feedback! I'm delighted to hear that you're enjoying the application. Please feel free to share any suggestions you have directly, and I'll do my best to assist or pass them along to the appropriate team for consideration.

App Privacy

The developer, 3HOUSE , indicated that the app’s privacy practices may include handling of data as described below. For more information, see the developer’s privacy policy .

Data Used to Track You

The following data may be used to track you across apps and websites owned by other companies:

Data Not Linked to You

The following data may be collected but it is not linked to your identity:

• Identifiers

Privacy practices may vary, for example, based on the features you use or your age. Learn More

Information

English, Arabic, Dutch, French, German, Indonesian, Italian, Japanese, Korean, Malay, Portuguese, Russian, Simplified Chinese, Spanish, Traditional Chinese, Vietnamese

• Question.AI DPro - Monthly $9.99
• Question.AI Plus-Monthly $11.99
• Question.AI Pro-Monthly $8.99
• Question.AI DPro - yearly $99.99
• Question.AI Plus-Yearly $99.99
• Question.AI Plus-yearly $34.99
• Question.AI Plus Special Offer $9.99
• Question.AI DPro - Monthly New $9.99
• Question.AI Plus- Monthly Free $9.99
• Questionai Pro - Monthly $9.99
• Developer Website
• App Support
• Privacy Policy

You Might Also Like

Answer.AI - Your AI tutor

Quizard AI - Scan and Solve

Ai Homework Helper: Scan Solve

Pic Answer - AI Solver

TutorEva: Campus AI Study Help