solving percent problems using decimals

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

4.2: Percents Problems and Applications of Percent

Last updated
Save as PDF
Page ID 142718

Morgan Chase
Clackamas Community College via OpenOregon

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

You may use a calculator throughout this module.

$sale-tag.jpg$

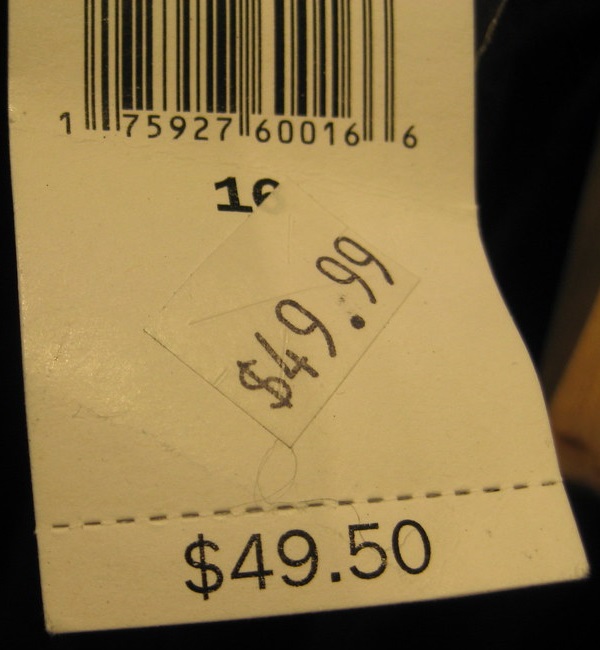
Recall: The amount is the answer we get after finding the percent of the original number. The base is the original number, the number we find the percent of. We can call the percent the rate.

When we looked at percents in a previous module, we focused on finding the amount. In this module, we will learn how to find the percentage rate and the base.

$\text{Amount}=\text{Rate}\cdot\text{Base}$

$A=R\cdot{B}$

We can translate from words into algebra.

“is” means equals
“of” means multiply
“what” means a variable

Solving Percent Problems: Finding the Rate

Suppose you earned $56$ points on a $60$-point quiz. To figure out your grade as a percent, you need to answer the question “$56$ is what percent of $60$?” We can translate this sentence into the equation $56=R\cdot60$.

Exercises $\PageIndex{1}$

1. $56$ is what percent of $60$?

2. What percent of $120$ is $45$?

1. $93\%$ or $93.3\%$

2. $37.5\%$

Be aware that this method gives us the answer in decimal form and we must move the decimal point to convert the answer to a percent.

Also, if the instructions don’t explicitly tell you how to round your answer, use your best judgment: to the nearest whole percent or nearest tenth of a percent, to two or three significant figures, etc.

Solving Percent Problems: Finding the Base

Suppose you earn $2\%$ cash rewards for the amount you charge on your credit card. If you want to earn $ $50$ in cash rewards, how much do you need to charge on your card? To figure this out, you need to answer the question “$50$ is $2\%$ of what number?” We can translate this into the equation $50=0.02\cdot{B}$.

3. $ $50$ is $2\%$ of what number?

4. $5\%$ of what number is $36$?

3. $ $2,500$

5. An $18\%$ tip will be added to a dinner that cost $ $107.50$. What is the amount of the tip?

6. The University of Oregon women’s basketball team made $13$ of the $29$ three-points shots they attempted during a game against UNC. What percent of their three-point shots did the team make?

7. $45\%$ of the people surveyed answered “yes” to a poll question. If $180$ people answered “yes”, how many people were surveyed altogether?

5. $ $19.35$

6. $44.8\%$ or $45\%$

7. $400$ people were surveyed

Solving Percent Problems: Percent Increase

When a quantity changes, it is often useful to know by what percent it changed. If the price of a candy bar is increased by $50$ cents, you might be annoyed because it’s it’s a relatively large percentage of the original price. If the price of a car is increased by $50$ cents, though, you wouldn’t care because it’s such a small percentage of the original price.

To find the percent of increase:

Subtract the two numbers to find the amount of increase.
Using this result as the amount and the original number as the base, find the unknown percent.

Notice that we always use the original number for the base, the number that occurred earlier in time. In the case of a percent increase, this is the smaller of the two numbers.

8. The price of a candy bar increased from $ $0.89$ to $ $1.39$. By what percent did the price increase?

9. The population of Portland in 2010 was $583,793$. The estimated population in 2019 was $654,741$. Find the percent of increase in the population. [1]

8. $56.2\%$ increase

9. $12.2\%$ increase

Solving Percent Problems: Percent Decrease

Finding the percent decrease in a number is very similar.

To find the percent of decrease:

Subtract the two numbers to find the amount of decrease.

Again, we always use the original number for the base, the number that occurred earlier in time. For a percent decrease, this is the larger of the two numbers.

10. During a sale, the price of a candy bar was reduced from $ $1.39$ to $ $0.89$. By what percent did the price decrease?

11. The number of students enrolled at Clackamas Community College decreased from $7,439$ in Summer 2019 to $4,781$ in Summer 2020. Find the percent of decrease in enrollment.

10. $36.0\%$ decrease

11. $35.7\%$ decrease

Relative Error

In an earlier module, we said that a measurement will always include some error, no matter how carefully we measure. It can be helpful to consider the size of the error relative to the size of what is being measured. As we saw in the examples above, a difference of $50$ cents is important when we’re pricing candy bars but insignificant when we’re pricing cars. In the same way, an error of an eighth of an inch could be a deal-breaker when you’re trying to fit a screen into a window frame, but an eighth of an inch is insignificant when you’re measuring the length of your garage.

The expected outcome is what the number would be in a perfect world. If a window screen is supposed to be exactly $25$ inches wide, we call this the expected outcome, and we treat it as though it has infinitely many significant digits. In theory, the expected outcome is $25.000000...$

To find the absolute error , we subtract the measurement and the expected outcome. Because we always treat the expected outcome as though it has unlimited significant figures, the absolute error should have the same precision (place value) as the measurement , not the expected outcome .

To find the relative error , we divide the absolute error by the expected outcome. We usually express the relative error as a percent. In fact, the procedure for finding the relative error is identical to the procedures for finding a percent increase or percent decrease!

To find the relative error:

Subtract the two numbers to find the absolute error.
Using the absolute error as the amount and the expected outcome as the base, find the unknown percent.

Exercisew $\PageIndex{1}$

12. A window screen is measured to be $25\dfrac{3}{16}$ inches wide instead of the advertised $25$ inches. Determine the relative error, rounded to the nearest tenth of a percent.

13. The contents of a box of cereal are supposed to weigh $10.8$ ounces, but they are measured at $10.67$ ounces. Determine the relative error, rounded to the nearest tenth of a percent.

12. $0.1875\div25\approx0.8\%$

13. $0.13\div10.8\approx1.2\%$

$6509400855_aaaf915871.jpg$

The tolerance is the maximum amount that a measurement is allowed to differ from the expected outcome. For example, the U.S. Mint needs its coins to have a consistent size and weight so that they will work in vending machines. A dime (10 cents) weighs $2.268$ grams, with a tolerance of $\pm0.091$ grams. [2] This tells us that the minimum acceptable weight is $2.268-0.091=2.177$ grams, and the maximum acceptable weight is $2.268+0.091=2.359$ grams. A dime with a weight outside of the range $2.177\leq\text{weight}\leq2.359$ would be unacceptable.

$dime-under-microscope-300x225.jpg$

A U.S. nickel (5 cents) weighs $5.000$ grams with a tolerance of $\pm0.194$ grams.

14. Determine the lowest acceptable weight and highest acceptable weight of a nickel.

15. Determine the relative error of a nickel that weighs $5.21$ grams.

A U.S. quarter (25 cents) weighs $5.670$ grams with a tolerance of $\pm0.227$ grams.

16. Determine the lowest acceptable weight and highest acceptable weight of a quarter.

17. Determine the relative error of a quarter that weighs $5.43$ grams.

14. $4.806$ g; $5.194$ g

15. $0.21\div5.000=4.2\%$

16. $5.443$ g; $5.897$ g

17. $0.24\div5.670\approx4.2\%$

www.census.gov/quickfacts/fact/table/portlandcityoregon,OR,US/PST045219 ↵
https://www.usmint.gov/learn/coin-and-medal-programs/coin-specifications and https://www.thesprucecrafts.com/how-much-do-coins-weigh-4171330 ↵

+ ACCUPLACER Mathematics
+ ACT Mathematics
+ AFOQT Mathematics
+ ALEKS Tests
+ ASVAB Mathematics
+ ATI TEAS Math Tests
+ Common Core Math
+ DAT Math Tests
+ FSA Tests
+ FTCE Math
+ GED Mathematics
+ Georgia Milestones Assessment
+ GRE Quantitative Reasoning
+ HiSET Math Exam
+ HSPT Math
+ ISEE Mathematics
+ PARCC Tests
+ Praxis Math
+ PSAT Math Tests
+ PSSA Tests
+ SAT Math Tests
+ SBAC Tests
+ SIFT Math
+ SSAT Math Tests
+ STAAR Tests
+ TABE Tests
+ TASC Math
+ TSI Mathematics
+ ACT Math Worksheets
+ Accuplacer Math Worksheets
+ AFOQT Math Worksheets
+ ALEKS Math Worksheets
+ ASVAB Math Worksheets
+ ATI TEAS 6 Math Worksheets
+ FTCE General Math Worksheets
+ GED Math Worksheets
+ 3rd Grade Mathematics Worksheets
+ 4th Grade Mathematics Worksheets
+ 5th Grade Mathematics Worksheets
+ 6th Grade Math Worksheets
+ 7th Grade Mathematics Worksheets
+ 8th Grade Mathematics Worksheets
+ 9th Grade Math Worksheets
+ HiSET Math Worksheets
+ HSPT Math Worksheets
+ ISEE Middle-Level Math Worksheets
+ PERT Math Worksheets
+ Praxis Math Worksheets
+ PSAT Math Worksheets
+ SAT Math Worksheets
+ SIFT Math Worksheets
+ SSAT Middle Level Math Worksheets
+ 7th Grade STAAR Math Worksheets
+ 8th Grade STAAR Math Worksheets
+ THEA Math Worksheets
+ TABE Math Worksheets
+ TASC Math Worksheets
+ TSI Math Worksheets
+ AFOQT Math Course
+ ALEKS Math Course
+ ASVAB Math Course
+ ATI TEAS 6 Math Course
+ CHSPE Math Course
+ FTCE General Knowledge Course
+ GED Math Course
+ HiSET Math Course
+ HSPT Math Course
+ ISEE Upper Level Math Course
+ SHSAT Math Course
+ SSAT Upper-Level Math Course
+ PERT Math Course
+ Praxis Core Math Course
+ SIFT Math Course
+ 8th Grade STAAR Math Course
+ TABE Math Course
+ TASC Math Course
+ TSI Math Course
+ Number Properties Puzzles
+ Algebra Puzzles
+ Geometry Puzzles
+ Intelligent Math Puzzles
+ Ratio, Proportion & Percentages Puzzles
+ Other Math Puzzles

How to Using Decimals, Grid Models, and Fractions to Represent Percent

A percentage is a rate per 100. You can use 10×10 grids to develop a percentage. To find a percentage of a number, merely multiply. To convert a decimal into a percentage, multiply by 100 (merely move the decimal point two spaces to the right). To obtain the percent equivalent, move the decimal point 2 spaces to the right-hand side.

Step-by-Step Guide to Using Decimals, Grid Models, and Fractions to Represent Percent

Understand the problem: Read the problem carefully and identify the information provided and the information that needs to be found.
Convert the percent to a decimal: Divide the percent by 100 and write it as a decimal. For example, 25% can be written as 0.25.
Use the decimal to complete a grid model: Draw a grid with labeled columns and rows to represent the given and unknown information. Fill in the known values, such as the decimal and the whole, into the grid.
Write the equation: Write the equation using the information provided in the grid. For example, if the problem states that an item is 25% off, the equation is: part = (decimal) * whole
Solve the equation: Substitute the known values into the equation and solve for the unknown value.
Convert the decimal to a fraction: Write the decimal as a fraction with a denominator of 100. For example, 0.25 can be written as 25/100.
Simplify the fraction: Reduce the fraction to its simplest form. For example, 25/100 can be simplified to 1/4.
Write the final answer in a complete sentence: Use the simplified fraction or decimal to express the final answer.

Using Decimals, Grid Models, and Fractions to Represent Percent – Examples 1

Problem: A shirt is on sale for 25% off. The original price of the shirt is $50. What is the sale price of the shirt?

We are given that the shirt is on sale for 25% off and the original price is $50.
Convert the percent to a decimal: 25% can be written as 0.25
Draw a grid model with labeled columns and rows: Original price, discount and sale price columns, and whole, decimal and part rows.
Write the equation: part = (decimal) * whole
Fill in the grid:

Original price $50 Discount 0.25 Sale price x

Solve the equation: part = (decimal) * whole => x = 0.25 * 50 => x = 12.5
Check your work: $50 – $12.5 = $37.5, which is the price of the shirt after a 25% discount.
The sale price of the shirt is $37.5 or 25/100 of the original price.

It’s worth noting that this is just one way to use decimals, grid models, and fractions to represent percent, and you can use different methods depending on the information provided in the problem

Using Decimals, Grid Models, and Fractions to Represent Percent – Examples 2

Show 49% on the grade and write as a fraction and decimal. Solution: Shade 49 of the 100 squares to represent 49% of the grid model. As a fraction, 49% is equivalent to $\frac{49}{100}$. As a decimal, $49÷100=0.49$

Using Decimals, Grid Models, and Fractions to Represent Percent – Examples 3

Show 72% on the grade and write as a fraction and decimal. Solution:

Shade 72 of the 100 squares to represent 72% of the grid model. As a fraction, 72% is equivalent to $\frac{72}{100}$. As a decimal, $72÷100=0.72$ Divide the numerator and denominator by 4 to write the in the simplest form. $\frac{72}{100}=\frac{72÷4}{100÷4}=\frac{18}{25}$

by: Effortless Math Team about 1 year ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

How to Motivate your Child to Learn Math?
Top 10 Algebra 1 Books in 2024 (Expert Recommendations)
Case File: How to Solve Multi-step Problems Involving Percent
How to Distinguishing Numbers: Prime vs. Composite
How to Find the Area of a Quarter Circle?
Half-Angle Identities
Full-Length 8th Grade Common Core Math Practice Test-Answers and Explanations
How to Use Division Properties
Exterior Angle Theorem
Cofunction Identities

What people say about "How to Using Decimals, Grid Models, and Fractions to Represent Percent - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

10 Full Length Keystone Algebra I Practice Tests The Practice You Need to Ace the Keystone Algebra I Test

10 full length ndsa grade 7 math practice tests the practice you need to ace the ndsa grade 7 math test, 10 full length mcas grade 7 math practice tests the practice you need to ace the mcas grade 7 math test, 10 full length mca grade 7 math practice tests the practice you need to ace the mca grade 7 math test, 10 full length maap grade 7 math practice tests the practice you need to ace the maap grade 7 math test, 10 full length m-step grade 7 math practice tests the practice you need to ace the m-step grade 7 math test, 10 full length nhsas grade 7 math practice tests the practice you need to ace the nhsas grade 7 math test, 10 full length ilearn grade 7 math practice tests the practice you need to ace the ilearn grade 7 math test, 10 full length k-prep grade 7 math practice tests the practice you need to ace the k-prep grade 7 math test, 10 full length kap grade 7 math practice tests the practice you need to ace the kap grade 7 math test, 10 full length gmas grade 7 math practice tests the practice you need to ace the gmas grade 7 math test, 10 full length mea grade 7 math practice tests the practice you need to ace the mea grade 7 math test, 10 full length dcas grade 7 math practice tests the practice you need to ace the dcas grade 7 math test, 10 full length common core grade 7 math practice tests the practice you need to ace the common core grade 7 math test, 10 full length azmerit grade 7 math practice tests the practice you need to ace the azmerit grade 7 math test.

ATI TEAS 6 Math
ISEE Upper Level Math
SSAT Upper-Level Math
Praxis Core Math
8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

Math Worksheets
Math Courses
Math Topics
Math Puzzles
Math eBooks
GED Math Books
HiSET Math Books
ACT Math Books
ISEE Math Books
ACCUPLACER Books
Premium Membership
Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

Bulk Orders
Refund Policy

Number Charts
Multiplication
Long division
Basic operations
Telling time
Place value
Roman numerals
Fractions & related
Add, subtract, multiply, and divide fractions
Mixed numbers vs. fractions
Equivalent fractions
Prime factorization & factors
Fraction Calculator
Decimals & Percent
Add, subtract, multiply, and divide decimals
Fractions to decimals
Percents to decimals
Percentage of a number
Percent word problems
Classify triangles
Classify quadrilaterals
Circle worksheets
Area & perimeter of rectangles
Area of triangles & polygons
Coordinate grid, including moves & reflections
Volume & surface area
Pre-algebra
Square Roots
Order of operations
Scientific notation
Proportions
Ratio word problems
Write expressions
Evaluate expressions
Simplify expressions
Linear equations
Linear inequalities
Graphing & slope
Equation calculator
Equation editor
Elementary Math Games
Addition and subtraction
Math facts practice
The four operations
Factoring and number theory
Geometry topics
Middle/High School
Statistics & Graphs
Probability
Trigonometry
Logic and proof
For all levels
Favorite math puzzles
Favorite challenging puzzles
Math in real world
Problem solving & projects
For gifted children
Math history
Math games and fun websites
Interactive math tutorials
Math help & online tutoring
Assessment, review & test prep
Online math curricula

Key to Percents Workbooks

Key to Percents first emphasizes mental computation and estimation skills--since most work with percents is done without pencil and paper. Then students are taught to solve percent problems using equal fractions and decimal multiplication. Finally, percents are used to solve word problems in a variety of applications. Key to Percents assumes only a knowledge of fraction and decimal computation. Book 1 covers Percent Concepts. Book 2 covers Percents and Fractions. Book 3 covers Percents and Decimals.

Percentages Worksheets

Welcome to the percentages math worksheet page where we are 100% committed to providing excellent math worksheets. This page includes Percentages worksheets including calculating percentages of a number, percentage rates, and original amounts and percentage increase and decrease worksheets.

As you probably know, percentages are a special kind of decimal. Most calculations involving percentages involve using the percentage in its decimal form. This is achieved by dividing the percentage amount by 100. There are many worksheets on percentages below. In the first few sections, there are worksheets involving the three main types of percentage problems: calculating the percentage value of a number, calculating the percentage rate of one number compared to another number, and calculating the original amount given the percentage value and the percentage rate.

Most Popular Percentages Worksheets this Week

$Calculating the Percent Value of Whole Number Amounts and All Percents$

Percentage Calculations

$solving percent problems using decimals$

Calculating the percentage value of a number involves a little bit of multiplication. One should be familiar with decimal multiplication and decimal place value before working with percentage values. The percentage value needs to be converted to a decimal by dividing by 100. 18%, for example is 18 ÷ 100 = 0.18. When a question asks for a percentage value of a number, it is asking you to multiply the two numbers together.

Example question: What is 18% of 2800? Answer: Convert 18% to a decimal and multiply by 2800. 2800 × 0.18 = 504. 504 is 18% of 2800.

Calculating the Percentage Value (Whole Number Results) Calculating the Percentage Value (Whole Number Results) (Percents from 1% to 99%) Calculating the Percentage Value (Whole Number Results) (Select percents) Calculating the Percentage Value (Whole Number Results) (Percents that are multiples of 5%) Calculating the Percentage Value (Whole Number Results) (Percents that are multiples of 25%)
Calculating the Percentage Value (Decimal Number Results) Calculating the Percentage Value (Decimal Number Results) (Percents from 1% to 99%) Calculating the Percentage Value (Decimal Number Results) (Select percents) Calculating the Percentage Value (Decimal Number Results) (Percents that are multiples of 5%) Calculating the Percentage Value (Decimal Number Results) (Percents that are multiples of 25%)
Calculating the Percentage Value (Whole Dollar Results) Calculating the Percentage Value (Whole Dollar Results) (Percents from 1% to 99%) Calculating the Percentage Value (Whole Dollar Results) (Select percents) Calculating the Percentage Value (Whole Dollar Results) (Percents that are multiples of 5%) Calculating the Percentage Value (Whole Dollar Results) (Percents that are multiples of 25%)
Calculating the Percentage Value (Decimal Dollar Results) Calculating the Percentage Value (Decimal Dollar Results) (Percents from 1% to 99%) Calculating the Percentage Value (Decimal Dollar Results) (Select percents) Calculating the Percentage Value (Decimal Dollar Results) (Percents that are multiples of 5%) Calculating the Percentage Value (Decimal Dollar Results) (Percents that are multiples of 25%)

Calculating what percentage one number is of another number is the second common type of percentage calculation. In this case, division is required followed by converting the decimal to a percentage. If the first number is 100% of the value, the second number will also be 100% if the two numbers are equal; however, this isn't usually the case. If the second number is less than the first number, the second number is less than 100%. If the second number is greater than the first number, the second number is greater than 100%. A simple example is: What percentage of 10 is 6? Because 6 is less than 10, it must also be less than 100% of 10. To calculate, divide 6 by 10 to get 0.6; then convert 0.6 to a percentage by multiplying by 100. 0.6 × 100 = 60%. Therefore, 6 is 60% of 10.

Example question: What percentage of 3700 is 2479? First, recognize that 2479 is less than 3700, so the percentage value must also be less than 100%. Divide 2479 by 3700 and multiply by 100. 2479 ÷ 3700 × 100 = 67%.

Calculating the Percentage a Whole Number is of Another Whole Number Calculating the Percentage a Whole Number is of Another Whole Number (Percents from 1% to 99%) Calculating the Percentage a Whole Number is of Another Whole Number (Select percents) Calculating the Percentage a Whole Number is of Another Whole Number (Percents that are multiples of 5%) Calculating the Percentage a Whole Number is of Another Whole Number (Percents that are multiples of 25%)
Calculating the Percentage a Decimal Number is of a Whole Number Calculating the Percentage a Decimal Number is of a Whole Number (Percents from 1% to 99%) Calculating the Percentage a Decimal Number is of a Whole Number (Select percents) Calculating the Percentage a Decimal Number is of a Whole Number (Percents that are multiples of 5%) Calculating the Percentage a Decimal Number is of a Whole Number (Percents that are multiples of 25%)
Calculating the Percentage a Whole Dollar Amount is of Another Whole Dollar Amount Calculating the Percentage a Whole Dollar Amount is of Another Whole Dollar Amount (Percents from 1% to 99%) Calculating the Percentage a Whole Dollar Amount is of Another Whole Dollar Amount (Select percents) Calculating the Percentage a Whole Dollar Amount is of Another Whole Dollar Amount (Percents that are multiples of 5%) Calculating the Percentage a Whole Dollar Amount is of Another Whole Dollar Amount (Percents that are multiples of 25%)
Calculating the Percentage a Decimal Dollar Amount is of a Whole Dollar Amount Calculating the Percentage a Decimal Dollar Amount is of a Whole Dollar Amount (Percents from 1% to 99%) Calculating the Percentage a Decimal Dollar Amount is of a Whole Dollar Amount (Select percents) Calculating the Percentage a Decimal Dollar Amount is of a Whole Dollar Amount (Percents that are multiples of 5%) Calculating the Percentage a Decimal Dollar Amount is of a Whole Dollar Amount (Percents that are multiples of 25%)

The third type of percentage calculation involves calculating the original amount from the percentage value and the percentage. The process involved here is the reverse of calculating the percentage value of a number. To get 10% of 100, for example, multiply 100 × 0.10 = 10. To reverse this process, divide 10 by 0.10 to get 100. 10 ÷ 0.10 = 100.

Example question: 4066 is 95% of what original amount? To calculate 4066 in the first place, a number was multiplied by 0.95 to get 4066. To reverse this process, divide to get the original number. In this case, 4066 ÷ 0.95 = 4280.

Calculating the Original Amount from a Whole Number Result and a Percentage Calculating the Original Amount (Percents from 1% to 99%) ( Whole Numbers ) Calculating the Original Amount (Select percents) ( Whole Numbers ) Calculating the Original Amount (Percents that are multiples of 5%) ( Whole Numbers ) Calculating the Original Amount (Percents that are multiples of 25%) ( Whole Numbers )
Calculating the Original Amount from a Decimal Number Result and a Percentage Calculating the Original Amount (Percents from 1% to 99%) ( Decimals ) Calculating the Original Amount (Select percents) ( Decimals ) Calculating the Original Amount (Percents that are multiples of 5%) ( Decimals ) Calculating the Original Amount (Percents that are multiples of 25%) ( Decimals )
Calculating the Original Amount from a Whole Dollar Result and a Percentage Calculating the Original Amount (Percents from 1% to 99%) ( Dollar Amounts and Whole Numbers ) Calculating the Original Amount (Select percents) ( Dollar Amounts and Whole Numbers ) Calculating the Original Amount (Percents that are multiples of 5%) ( Dollar Amounts and Whole Numbers ) Calculating the Original Amount (Percents that are multiples of 25%) ( Dollar Amounts and Whole Numbers )
Calculating the Original Amount from a Decimal Dollar Result and a Percentage Calculating the Original Amount (Percents from 1% to 99%) ( Dollar Amounts and Decimals ) Calculating the Original Amount (Select percents) ( Dollar Amounts and Decimals ) Calculating the Original Amount (Percents that are multiples of 5%) ( Dollar Amounts and Decimals ) Calculating the Original Amount (Percents that are multiples of 25%) ( Dollar Amounts and Decimals )
Mixed Percentage Calculations with Whole Number Percentage Values Mixed Percentage Calculations (Percents from 1% to 99%) ( Whole Numbers ) Mixed Percentage Calculations (Select percents) ( Whole Numbers ) Mixed Percentage Calculations (Percents that are multiples of 5%) ( Whole Numbers ) Mixed Percentage Calculations (Percents that are multiples of 25%) ( Whole Numbers )
Mixed Percentage Calculations with Decimal Percentage Values Mixed Percentage Calculations (Percents from 1% to 99%) ( Decimals ) Mixed Percentage Calculations (Select percents) ( Decimals ) Mixed Percentage Calculations (Percents that are multiples of 5%) ( Decimals ) Mixed Percentage Calculations (Percents that are multiples of 25%) ( Decimals )
Mixed Percentage Calculations with Whole Dollar Percentage Values Mixed Percentage Calculations (Percents from 1% to 99%) ( Dollar Amounts and Whole Numbers ) Mixed Percentage Calculations (Select percents) ( Dollar Amounts and Whole Numbers ) Mixed Percentage Calculations (Percents that are multiples of 5%) ( Dollar Amounts and Whole Numbers ) Mixed Percentage Calculations (Percents that are multiples of 25%) ( Dollar Amounts and Whole Numbers )
Mixed Percentage Calculations with Decimal Dollar Percentage Values Mixed Percentage Calculations (Percents from 1% to 99%) ( Dollar Amounts and Decimals ) Mixed Percentage Calculations (Select percents) ( Dollar Amounts and Decimals ) Mixed Percentage Calculations (Percents that are multiples of 5%) ( Dollar Amounts and Decimals ) Mixed Percentage Calculations (Percents that are multiples of 25%) ( Dollar Amounts and Decimals )

Percentage Increase/Decrease Worksheets

$solving percent problems using decimals$

The worksheets in this section have students determine by what percentage something increases or decreases. Each question includes an original amount and a new amount. Students determine the change from the original to the new amount using a formula: ((new - original)/original) × 100 or another method. It should be straight-forward to determine if there is an increase or a decrease. In the case of a decrease, the percentage change (using the formula) will be negative.

Percentage Increase/Decrease With Whole Number Percentage Values Percentage Increase/Decrease Whole Numbers with 1% Intervals Percentage Increase/Decrease Whole Numbers with 5% Intervals Percentage Increase/Decrease Whole Numbers with 25% Intervals
Percentage Increase/Decrease With Decimal Number Percentage Values Percentage Increase/Decrease Decimals with 1% Intervals Percentage Increase/Decrease Decimals with 5% Intervals Percentage Increase/Decrease Decimals with 25% Intervals
Percentage Increase/Decrease With Whole Dollar Percentage Values Percentage Increase/Decrease Whole Dollar Amounts with 1% Intervals Percentage Increase/Decrease Whole Dollar Amounts with 5% Intervals Percentage Increase/Decrease Whole Dollar Amounts with 25% Intervals
Percentage Increase/Decrease With Decimal Dollar Percentage Values Percentage Increase/Decrease Decimal Dollar Amounts with 1% Intervals Percentage Increase/Decrease Decimal Dollar Amounts with 5% Intervals Percentage Increase/Decrease Decimal Dollar Amounts with 25% Intervals

Solving Percent Problems

Learning Objective(s)

· Identify the amount, the base, and the percent in a percent problem.

· Find the unknown in a percent problem.

Introduction

Percents are a ratio of a number and 100. So they are easier to compare than fractions, as they always have the same denominator, 100. A store may have a 10% off sale. The amount saved is always the same portion or fraction of the price, but a higher price means more money is taken off. Interest rates on a saving account work in the same way. The more money you put in your account, the more money you get in interest. It’s helpful to understand how these percents are calculated.

Parts of a Percent Problem

Jeff has a coupon at the Guitar Store for 15% off any purchase of $100 or more. He wants to buy a used guitar that has a price tag of $220 on it. Jeff wonders how much money the coupon will take off the original $220 price.

Problems involving percents have any three quantities to work with: the percent , the amount , and the base .

The percent has the percent symbol (%) or the word “percent.” In the problem above, 15% is the percent off the purchase price.

The base is the whole amount. In the problem above, the whole price of the guitar is $220, which is the base.

The amount is the number that relates to the percent. It is always part of the whole. In the problem above, the amount is unknown. Since the percent is the percent off , the amount will be the amount off of the price .

You will return to this problem a bit later. The following examples show how to identify the three parts, the percent, the base, and the amount.

The previous problem states that 30 is a portion of another number. That means 30 is the amount. Note that this problem could be rewritten: 20% of what number is 30?

Solving with Equations

Percent problems can be solved by writing equations. An equation uses an equal sign (= ) to show that two mathematical expressions have the same value.

Percents are fractions, and just like fractions, when finding a percent (or fraction, or portion) of another amount, you multiply.

The percent of the base is the amount.

Percent of the Base is the Amount.

Percent · Base = Amount

Once you have an equation, you can solve it and find the unknown value. To do this, think about the relationship between multiplication and division. Look at the pairs of multiplication and division facts below, and look for a pattern in each row.

Multiplication and division are inverse operations. What one does to a number, the other “undoes.”

When you have an equation such as 20% · n = 30, you can divide 30 by 20% to find the unknown: n = 30 ÷ 20%.

You can solve this by writing the percent as a decimal or fraction and then dividing.

n = 30 ÷ 20% = 30 ÷ 0.20 = 150

You can estimate to see if the answer is reasonable. Use 10% and 20%, numbers close to 12.5%, to see if they get you close to the answer.

10% of 72 = 0.1 · 72 = 7.2

20% of 72 = 0.2 · 72 = 14.4

Notice that 9 is between 7.2 and 14.4, so 12.5% is reasonable since it is between 10% and 20%.

This problem is a little easier to estimate. 100% of 24 is 24. And 110% is a little bit more than 24. So, 26.4 is a reasonable answer.

Using Proportions to Solve Percent Problems

Let’s go back to the problem that was posed at the beginning. You can now solve this problem as shown in the following example.

You can estimate to see if the answer is reasonable. Since 15% is half way between 10% and 20%, find these numbers.

10% of 220 = 0.1 · 220 = 22

20% of 220 = 0.2 · 220 = 44

The answer, 33, is between 22 and 44. So $33 seems reasonable.

There are many other situations that involve percents. Below are just a few.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability