direct variation problems with graphs and tables

Direct Variation

Direct variation is a type of proportionality wherein one quantity directly varies with respect to a change in another quantity. This implies that if there is an increase in one quantity then the other quantity will experience a proportionate increase. Similarly, if one quantity decreases then the other quantity also decreases.  Direct variation is a linear relationship hence, the graph will be a straight line.

Further, if two quantities are in direct variation then one will be a constant multiple of the other. In this article, we will elaborate on direct variation, its definition, formula, graph and associated examples.

What is Direct Variation?

Direct variation exists between any two variables when one quantity is directly dependent on the other i.e. if one quantity increases with respect to the other quantity and vice versa. It is the relationship between two variables where one of the variables is a constant multiple of the other. Since the two variables are directly related to each other it is also termed as directly proportional. 

Direct variation and inverse variation are two types of proportionalities. Proportionality refers to a relationship where two quantities are multiplicatively connected by a constant. In a direct variation, the ratio of the two quantities remains the same whereas in an inverse variation the product of the two quantities remains constant. Here we shall check in detail the definition and examples of direct variation.

Direct Variation Definition

Two quantities as said to follow a direct variation if both increase or decrease by the same factor. Thus, an increase in one quantity leads to an increase in the other while a decrease in one quantity leads to a decrease in the other. In other words, if the ratio of the first quantity to the second quantity is a constant term, then the quantities are said to be directly proportional to each other. This constant value is known as the coefficient or constant of proportionality .

Direct Variation Example

The following two quick examples are helpful for an easy understanding of this concept of direct variation.

Example I: The formula for the circumference of a circle is given by C = 2πr or C = πd. Here, r is the radius and d is the diameter . This is an example of a direct variation. Thus, the circumference of a circle and its corresponding diameter are in direct variation with π being the constant of proportionality.

Example II:  The quantity of Iron boxes made is directly proportional to the number of iron blocks. The number of iron blocks needed for 40 boxes is 160. How many iron blocks are needed for a box?

In the given problem, the number of iron blocks needed for 40 boxes is referred to as y = 160, and the number of boxes is referred to as x = 40. The number of iron blocks needed for a box is k. Here we use the direct variation formula of y = kx.

160 = k × 40 k = 160/40 k = 4

Thus 4 iron blocks are needed for a box.

What Is Direct Variation Formula?

Direct variation formula helps relate two quantities, having a mathematical relationship such that one of the variables is a constant multiple of the other. When two quantities are directly proportional to each other or are in direct variation they are represented using the symbol "\(\propto\)". Suppose there are two quantities x and y that are in direct variation then they are expressed as follows:

y \(\propto\) x

When the proportionality sign is removed then the direct variation formula is given as follows.

Direct Variation Formula: y = kx

Here k is the constant of proportionality. If x is not equal to zero then the value of the constant of proportionality can be given as k = y/x. Thus, the ratio of these two variables is always a constant number. Another way of expressing the direct variation equation is x = y / k. This means that x is directly proportional to y with the constant of proportionality equalling 1 / k.

The formula for the direction variation for a set of two quantities that are linearly dependent is as follows. 

Let us understand the formula of direct variation with the help of a simple example. Example: Let us assume that y varies directly with x, and y = 30 when x = 6. What is the value of y when x = 100?

The given quantities are y 1   = 30, x 1  = 6, x 2  = 100, y 2  = ? Using direct variation formula we have the following expression.

y 1  / x 1  = y 2  / x 2 30/6 = y 2  / 1005 = y 2  / 100 y 2  = 500

Therefore the value of y when x = 100 is 500.

Direct Variation Graph

The graph of two quantities in a direct variation will result in a straight line. Thus, direct variation represents a linear equation in two variables . The linear equation is given by y = kx. The ratio of change \(\frac{\Delta y}{\Delta x}\) is also equal to k. This change represents the slope of the line . The direct variation graph is given as follows:

Difference Between Direct Variation and Inverse Variation

The difference between direct variation and inverse variation provides the relationship between two mathematical quantities. The two quantities are said to be in direct variation if one quantity is proportionally increasing with respect to another quantity, and the two quantities are said to be in inverse variation if one quantity is increasing and the other quantity is simultaneously decreasing. The relationship between the two quantities, y, and x is as follows.

Inverse and direct variation are both types of proportionalities. The difference between inverse and direct variation is given in the table below:

Related Articles:

• Direct Proportion
• Ratio and Proportion
• Percent Proportion

Important Notes on Direct Variation

• A direct variation is a proportionality relationship in which two quantities follow a direct relationship. This implies that an increase (or decrease) in one quantity leads to a corresponding increase (or decrease) in another quantity.
• The direct variation equation is a linear equation in two variables and is given by y = kx where k is the constant proportionality.
• The direct variation graph in a coordinate plane is a straight line.
• The ratio of two quantities in a direct variation is a constant.

Examples on Direct Variation

• Example 2: If x = 10 and y = 20 follow a direct variation then find the constant of proportionality Solution: As x and y are in a direct variation thus y = kx or k = y / x. k = 20 / 10 = 2 Answer: k = 2
• Example 3: Let x and y be in direct variation, x = 6 and y = 21. Then find the direct variation equation. Solution: As x and y are in a direct variation thus y = kx or k = y / x. k = 21 / 6 = 7 / 2 y = \(\frac{7}{2}x\) Answer: The direct variation equation is y = \(\frac{7}{2}x\)

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Direct Variation

go to slide go to slide

FAQs on Direct Variation

When one quantity directly varies with respect to another quantity it is known as direct variation . This implies that if one quantity increases or decreases the other quantity also increases or decreases proportionately.

What is the Direct Variation Equation?

The direct variation equation is given as y = kx where y and x are the two varying quantities and k is the constant of proportionality.

What is a Real-Life Direct Variation Example?

One example of direct variation is the speed of a car and the distance covered by it. If the speed increases the distance traveled within a certain time will also increase. Similarly, if the speed of the car decreases the distance covered within that interval of time will also decrease.

How to Solve Direct Variation?

To solve questions on direct variation the formula used is y = kx. If the constant of proportionality needs to be determined then y is divided by x to get the result. Suppose k is given and either x or y need to be determined then these values can be substituted in the aforementioned equation to find the unknown value.

How to Tell if an Equation is a Direct Variation?

If an equation is not in the form of y = kx then it does not follow a direct variation. For example y = 3x + 5 is not of the form y = kx hence, it doesn't represent a direct variation. On the other hand, y = 1.2x is of the form y = kx and denotes a direct variation.

How to Graph a Direct Variation Equation?

To graph a direct variation equation, y = kx, the steps are as follows:

• Substitute x with numerical values.
• Find the corresponding values of y using the direct variation formula.
• Using these test points, plot a graph. The graph will be a straight line passing through the origin.

Is y = 2x a Direct Variation?

Yes. As y = 2x is of the form y = kx thus, it represents a direct variation. The value of y will increase or decrease with an increase or decrease in the value of x.Yes. 

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Direct Variation

Key Questions

Take note of the behavior of one variable and compare with the corresponding behavior of the other.

If you increase the value of one variable, what happens to the value of the other variable? If it increases, you have a direct variation . If it decreases, you have a inverse variation

In this video, we are going to discuss a category of functions called direct variation functions, how to write and solve equations involving direct variation, and how to identify examples of direct variation from data given in tables.

By now you’ve seen plenty of examples of functions. Some form flat lines, while others form slanted or even curvy lines. Some pass through the origin, while others do not. The topic of this video is direct variation functions , which are graphically represented as straight lines that pass through the origin.

Algebraically, direct variation functions can be written in the form \(y=kx\), where \(k\) determines the slope of the line. \(k\) can be any number, whether positive or negative, whole or otherwise.

Let’s look at an example of direct variation.

This function satisfies the conditions of direct variation because we can easily see that it is written in the form \(y=kx\). In this case, \(k=3\).

Since this function is an example of direct variation and follows the form \(y=kx\), where \(x\) is raised only to the first power, we are guaranteed that the function is a straight line. Additionally, whenever \(x=0\), \(y=k\times 0=0\), so the line also passes through the origin. Sure enough, this can be seen in the graph of \(y=3x\).

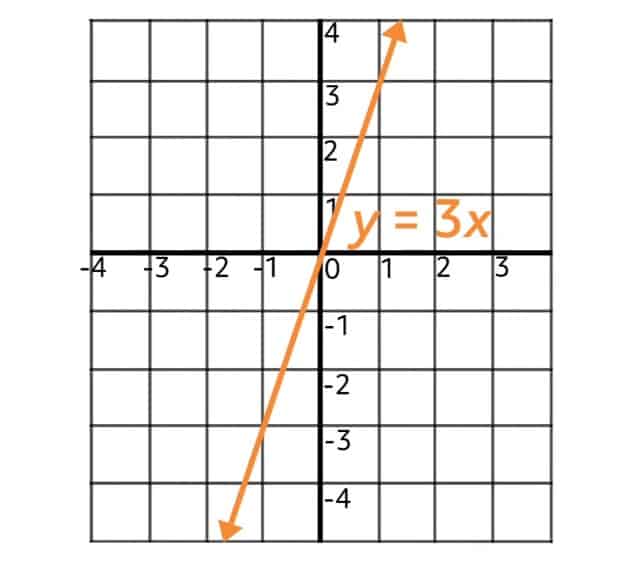
Direct variation functions like these can be helpful in solving real-life problems, as we’ll see in the next example.

Air Force One can fly at the astonishing speed of 600 mph. If the number of air miles traveled by the president is represented by \(y\), and varies directly to the number of hours flown, represented by \(x\), how far would Air Force One travel after 4 hours?

To answer this question, we need to realize that the phrase “varies directly” is used in the problem statement. This means we will use the direct variation formula, \(y=kx\). We are told that \(y\) is the number of miles traveled, and that \(x\) is the number of hours flown. We are also told that the plane travels at about 600 mph. This is our \(k\).

Putting this \(k\) into the direct variation formula, we have \(y=600x\).

miles   hours

The amount of time we are concerned with is four hours, so let’s plug in \(x=4\).

Simplifying, we see that \(y=2,400\) miles. That is, after four hours, Air Force One could have traveled an astounding 2,400 miles! That’s the distance from New York to California!

When it comes to direct variation problems, you may sometimes receive information in other forms. Let’s now discuss another type of direct variation problem, where you are given a table of information. To make it clear what kind of information such tables can hold, let’s jump into an example.

Vivian lives on a small hen farm, and each morning she collects eggs to sell at the market. On Monday she gathered and sold 2 dozen eggs for $4.00. On Tuesday she gathered and sold 3 dozen eggs for $6.00. Finally, on Wednesday she gathered and sold 2 dozen eggs for $4.00. We can arrange this information in a table, where one column shows the dozens of eggs sold, and the other shows the amount received.

Or, if we wanted to present this information in a more clearly mathematical way, we could write the table with the first column called \(x\) and the second called \(y\).

Now that we have arranged the information in this way, it’s time to ask: is this an example of direct variation?

Before we can answer that question though, we need an extra tool. So far, we have been using the form \(y=kx\) to determine whether or not a function is an example of direct variation. But since we don’t have \(y\) written as a function this time, we need to do a slick trick to change \(y=kx\) into something we can use. Notice that from the equation \(y=kx\), we can divide both sides by \(x\) to get \(k\) by itself.

  Now we have that \(\frac{y}{x}\) is equal to \(k\). This is equivalent to the expression \(y=kx\), but we can use it to help us in problems involving tables.

The key to the problem now is solving for \(k\) from each of the three days that Vivian gathered and sold eggs, and then checking whether the values for \(k\) are all the same across all days. If all values of \(k\) are the same, then this is an example of direct variation.

Since Vivian sold 2 dozen eggs for $4.00 on Monday, the \(k\) for Monday is equal to \(\frac{y}{x}=\frac{4}{2}=2\). For Tuesday, she sold 3 dozen eggs for $6.00, so the \(k\) for Tuesday is \(\frac{y}{x}=\frac{6}{3}=2\). Finally, on Wednesday she sold 2 dozen eggs for $4.00, so the \(k\) for Wednesday is \(\frac{y}{x}=\frac{4}{2}=2\).

The \(k\) for each day is equal to 2, and since they are all the same, this is indeed an example of direct variation. In fact, now that we know that \(k=2\), we also know that we can write a function describing egg prices per dozen in the form \(y=kx\) as \(y=2x\).

Direct variation has many different applications. Let’s run through one more example to cover the last type of problem you’ll encounter.

Paul has a drippy kitchen faucet, so he leaves a cup underneath it and waters his plants each time it fills up so that no water is wasted. The cup fills once every two hours. Based on this information, write a direct variation equation, and then use it to determine how many times the cup fills after 7 hours.

We need to apply the formula \(y=kx\) to this scenario. Here’s what we have to work with: number of hours passed, times the cup fills up, and the rate at which the cup fills.

Remember in the Air Force One example, we said the speed of the plane was \(k\). In other words, the rate of the plane’s travel was \(k\). When writing direct variation equations, we will always assign \(k\) to be the rate we are given in the problem.

That means that for this problem, \(k\) will represent the rate at which the cup fills up, once every two hours. We write this as

because the cup is halfway full after one hour. Now, we must determine what \(x\) represents and what \(y\) represents. To do this, let’s consider the units of \(k\). \(k\) can be described with the units “cups per hour” because the cup fills one time after two hours.

Now, remember from the previous example that \(k\) is also equal to \(\frac{y}{x}\) in direct variation problems. This tells us that the numerator of \(k\) will have the same units as \(y\) and that the denominator of \(k\) will have the same units as \(x\).

Our direct variation equation is then \(y=12x\), where \(y\) is the number of cups, and \(x\) is the number of hours passed.

Now, we are interested in finding out how many times the cup will fill up after 7 hours pass, so we set hours (\(x\)) equal to 7.

Solving for \(y\), the number of cups, we have

And we are done!

In this video, we’ve learned the two formulas to remember for direct variation are \(y=kx\) and \(k=\frac{y}{x}\). We have also encountered multiple word problems and learned some important phrases to look for, including “varies directly” and “rate” (or the word “per”). For problems involving writing direct variation equations, set \(k\) to be the rate, then notice which units should correspond with \(x\) and with \(y\). With a little practice, you’ll have direct variation mastered in no time.

Thanks for watching, and happy studying!

by Mometrix Test Preparation | This Page Last Updated: December 19, 2023

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Ratios and proportions

Constant of variation

Direct variation

Here you will learn about direct variation, including the constant of variation, the equation that represents direct variation, and interpreting the graphs of direct variation.

Students first learn about proportional relationships on a graph in the 6th grade with ratio tables in ratios and proportional relationships.

What is direct variation?

Direct variation is a proportional relationship between the x -coordinate (an independent variable) and the y -coordinate (a dependent variable), where the ratio between the x -coordinate and the y -coordinate is constant.

Direct variation is represented algebraically by the equation,

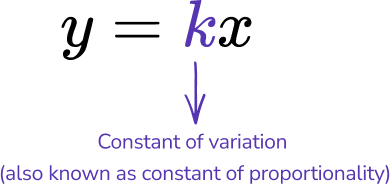
Direct variation is represented graphically by a line that goes through the origin.

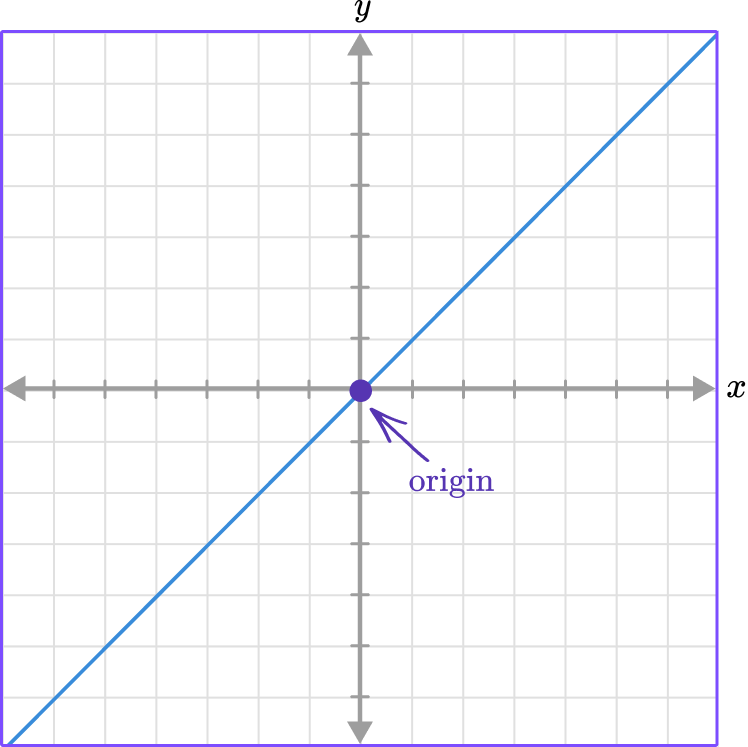
Let’s look at some examples,

The equation y=\cfrac{1}{6} \, x represents direct variation. What is the constant of variation?

The constant of variation is represented by k in the equation y=kx.

So in this case, \, \cfrac{1}{6} \, is the constant of variation.

k=\cfrac{1}{6}

You can use a graph to determine the constant of variation.

For example, use the graph to find the constant of variation.

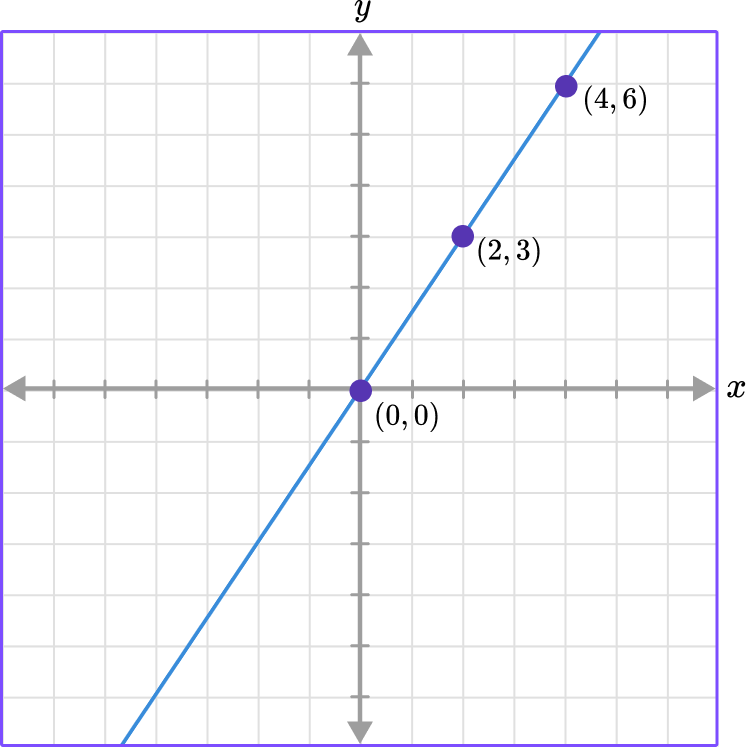
The line goes through the origin and also contains the points of (2, 3) and (4, 6).

To find the constant of variation or the constant of proportionality you can write the ratio of the points in the form of \, \cfrac{y}{x} \, because k=\cfrac{y}{x} .

Choosing the point (2, 3) the ratio is \, \cfrac{3}{2} \, which means that k=\cfrac{3}{2} .

The constant of variation, k, can also be found by counting the units from one point to the next. You can see that from (0, 0) to (2, 3) you moved to the right 2 units and up 3 units, and from points (2, 3) to (4, 6) the same movement occurred.

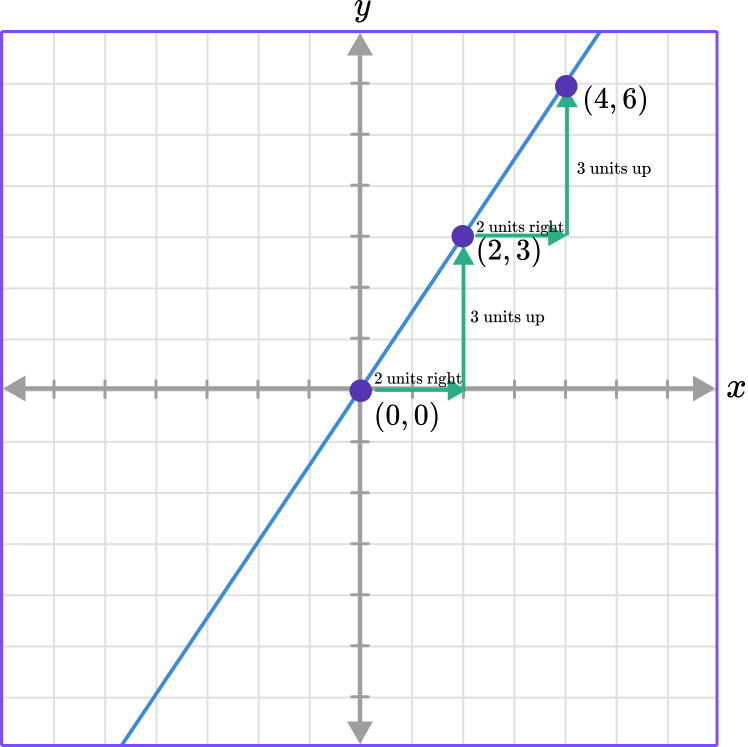
The constant movement from one point to the next is also called the constant rate of change.

Common Core State Standards

How does this relate to grade 7 math and grade 8 math?

• Grade 7 – Ratios and Proportional Relationships (7.RP.A.2.b) Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.
• Grade 7 – Ratios and Proportional Relationships (7.RP.A.2.c) Represent proportional relationships by equations.
• Grade 8 – Expressions and Equations (8.EE.B.5) Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.

How to use direct variation

In order to find the constant of variation from an equation:

Compare the equation to \textbf{y = kx} to determine the value of \textbf{k} .

Write the value of \textbf{k} .

In order to find the constant of variation from a graph:

Select a point.

• Write the point as a ratio in the form of \cfrac{\textbf{y}}{\textbf{x}} \, .

In order to find the equation of direct variation from a point:

Select a point and define the \textbf{x} value and the \textbf{y} value.

Substitute the values into the equation \textbf{y = kx} to find \textbf{k} .

Solve for \textbf{k} .

Write the equation of direct variation.

[FREE] End of Year Math Assessments (Grade 4 & Grade 5)

Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!

Direct variation examples

Example 1: find the constant of variation from an equation.

What is the constant of variation in the equation y=\cfrac{3}{5} \, x ?

Comparing the equation y=\cfrac{3}{5} \, x to y=kx , you can see that \, \cfrac{3}{5} \, represents the constant of variation.

2 Write the value of \textbf{k} .

k=\cfrac{3}{5}

Example 2: find the constant of variation from an equation

What is the constant of variation in the equation y=-6x?

Comparing the equation y=-6x to y=kx, you can see that the -6 represents the constant of variation.

Example 3: find the constant of variation from a graph

Use the graph to find the constant of variation.

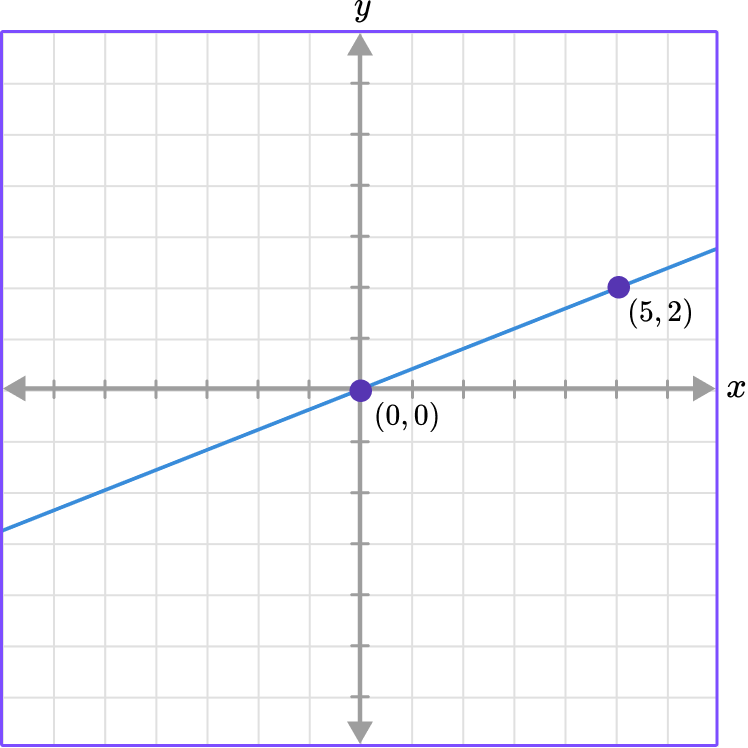
Use the point (5, 2) .

Write the point as a ratio in the form of \, \cfrac{\textbf{y}}{\textbf{x}} \, .

(5,2) \rightarrow \cfrac{2}{5}

k=\cfrac{2}{5}

Example 4: find the constant of variation from a graph

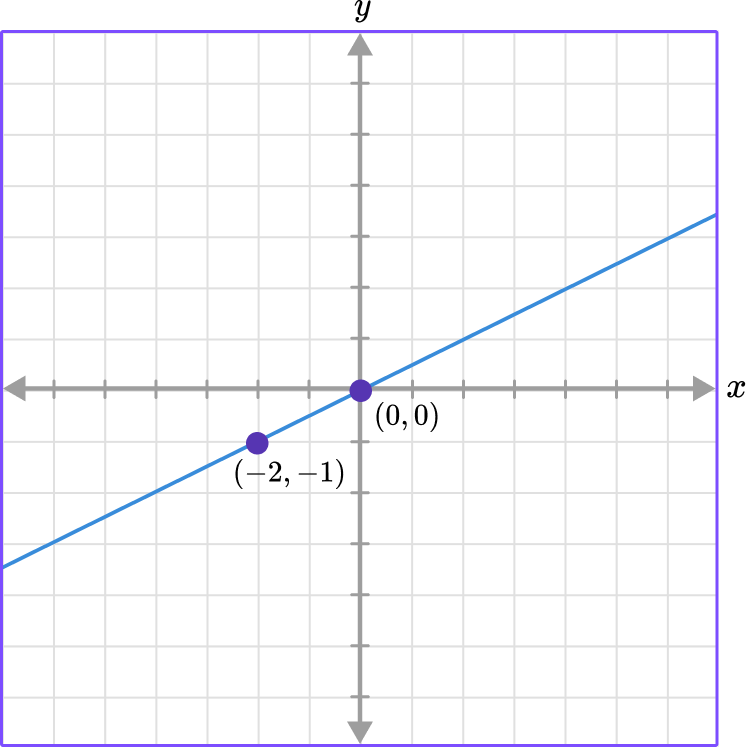
Use the point (-2, -1).

(-2,-1) \rightarrow \cfrac{-1}{-2}=\cfrac{1}{2}

k=\cfrac{1}{2}

Example 5: finding the equation of direct variation

If x varies directly with y, find the equation of direct variation from the point (7, 3).

The point is (7, 3) which means that x=7 and y=3.

\begin{aligned} & y=k x \\\\ & 3=k( 7) \end{aligned}

\begin{aligned} & 3=k (7) \\\\ & \cfrac{3}{7}=\cfrac{k (7)}{7} \\\\ & \cfrac{3}{7}=k \end{aligned}

k=\cfrac{3}{7}

So, y=\cfrac{3}{7} \, x .

Example 6: finding the equation of direct variation

The graph represents a direct variation. Find the equation.

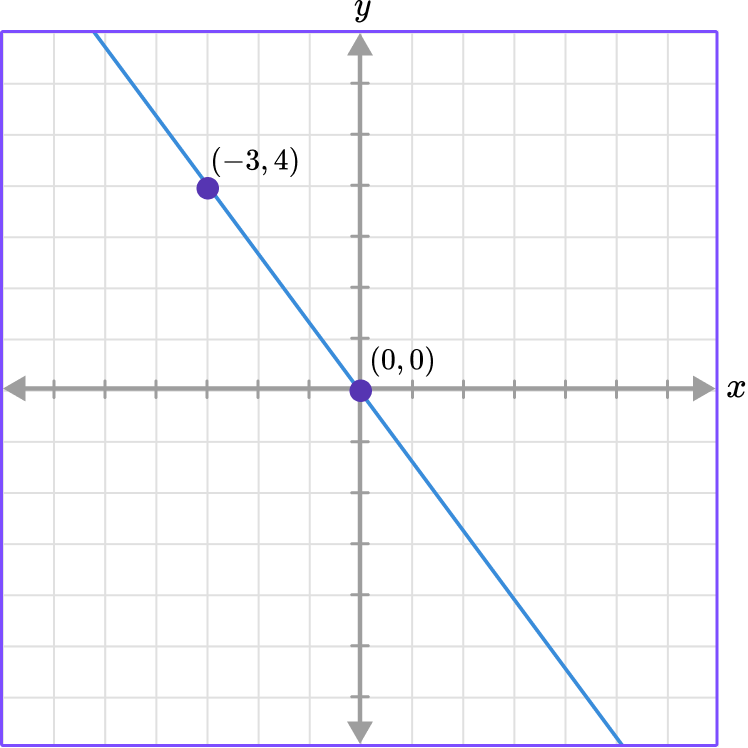
Use the point (-3, 4) where x=-3 and y=4 .

\begin{aligned} & y=k x \\\\ & 4=k(-3) \end{aligned}

\begin{aligned} & 4=k(-3) \\\\ & \cfrac{4}{-3}=\cfrac{k(-3)}{-3} \\\\ & \cfrac{4}{-3}=k \end{aligned}

k=\-cfrac{4}{3}

So, y=-\cfrac{4}{3} \, x .

Teaching tips for direct variation

• Reinforce to students that the common ratio of points is the constant of proportionality which is the constant of variation k.
• Using digital graphing platforms such as Desmos or actual graphing calculators helps students make connections between the visual representation of direct variation and the equation that represents the direct variation.
• Create situations where students can connect the constant of variation with the slope of the line or the constant rate of change of the line.
• Use real life direct variation word problems and graphs for students to analyze and see the relevance of the concept in the world around them.
• Although practice worksheets help students practice skills, focus on making the math relevant to their everyday lives.
• Through discovery based activities and questioning strategies, lead students to think about the direct variation equation, y=kx, where the constant of variation is the constant rate of change, which will eventually be the slope, and the origin is the y -intercept.

Easy mistakes to make

• Thinking that the constant of variation has to be positive The constant of variation, k, can be positive or negative. k is the ratio of the y -coordinate to the x -coordinate.
• Thinking that the line that represents direct variation does not have to go through the origin Direct variation is a linear, proportional relationship, which means it must pass through the origin. If the line does not pass the origin, it is not a representation of direct variation.

Related types of graphs lessons

• Types of graphs
• Linear graphs
• Interpreting graphs
• x and y axis
• Coordinate plane
• Plot points on a graph
• Independent and dependent variables

Practice direct variation questions

1. What is the constant of variation of the equation, y=-7x?

The equation y=-7x compared to y=kx, shows that -7 represents the constant of variation. k=-7

2. What is the constant of variation from the graph?

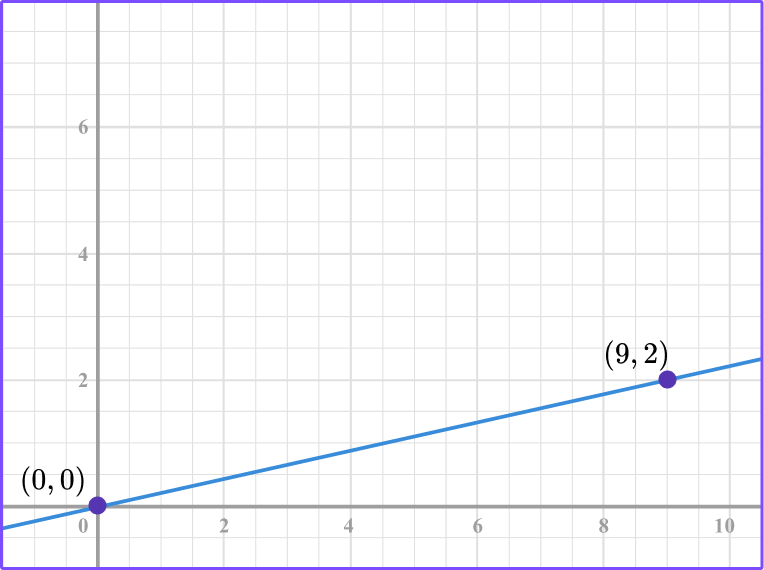
From the graph you can see that the line passes through (0, 0) and (9, 2).

Using the point (9, 2) , the ratio of the point in the form of \, \cfrac{y}{x} \, is \, \cfrac{2}{9} \, .

Another way to interpret the constant of variation is to count from the origin to the point (9, 2).

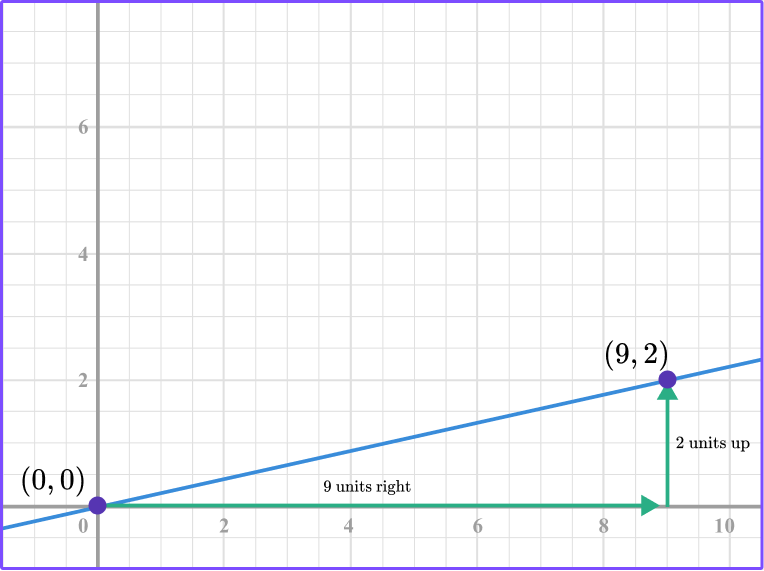
9 units right and 2 units up is the constant rate of \, \cfrac{2}{9} .

3. What is the constant rate of change of the direct variation graph?

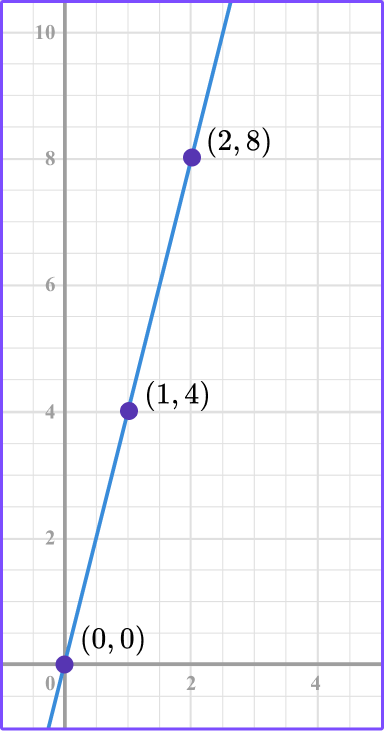
The constant rate of change is the constant of variation or the constant of proportionality.

Looking at the graph, the line passes through the points (0, 0), (1, 4) , and (2, 8).

Selecting the point (1, 4) , the ratio of the point in the form of \, \cfrac{y}{x} \, is \, \cfrac{4}{1} \, .

You can also count the movement from one point to the next to find the constant rate of change.

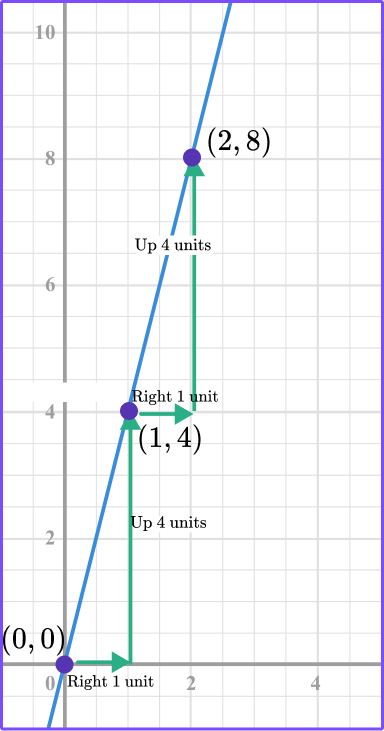
1 unit right and 4 units up \, \cfrac{4}{1} .

4. A rabbit can hop at top speed 6 miles in 10 minutes. This represents a proportional relationship as shown in the graph below. How long will it take the same rabbit to hop 12 miles at the same speed?

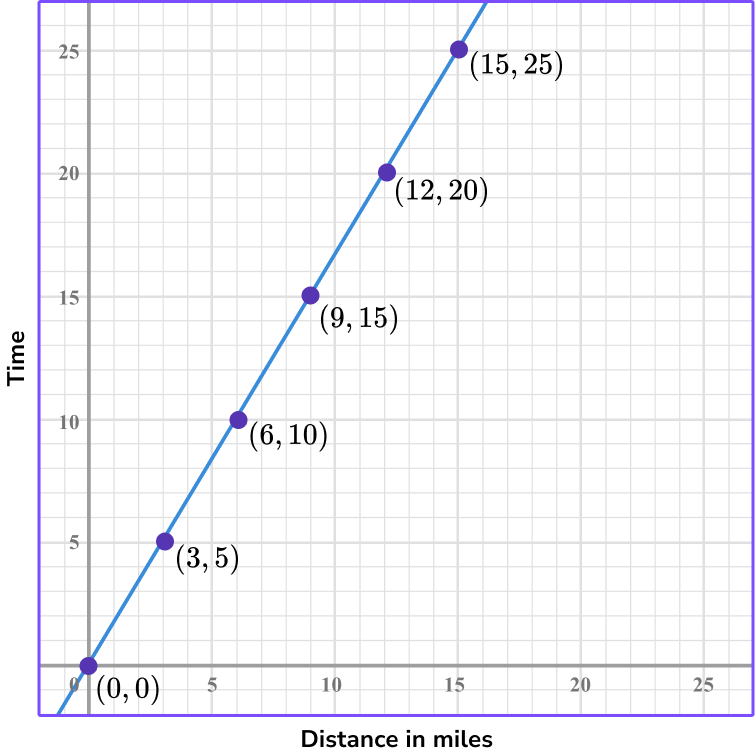
The point (6, 10) represents the rabbit hopping 6 miles in 10 minutes. Where x represents the distance and y represents the time.

Looking at the points, you can see that the coordinate (12, 20) represents 12 miles in 20 minutes.

Another way to do it is to find the constant of variation.

The constant of variation is \, ​​\cfrac{10}{6} \, which can be simplified to be \, \cfrac{5}{3} \, .

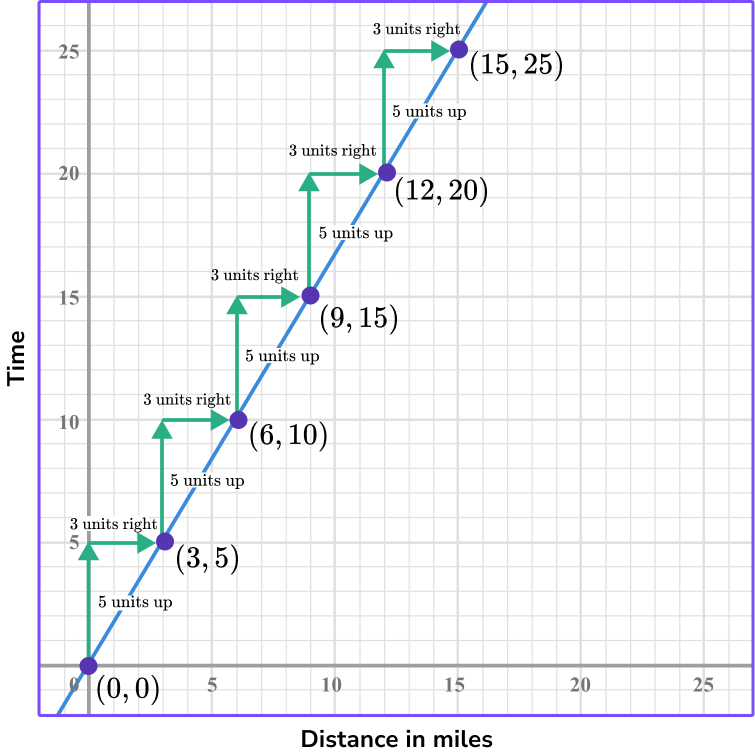
To find how long it will take the rabbit to hop 12 miles you can multiply 12 \times \cfrac{5}{3}=20 or use the graph and count out the constant of variation 5 units up and 3 units right until you get to the point where 12 is the x -coordinate.

5. If x and y vary directly, find the equation of direct variation that contains the point (2, 8).

Using the direct variation equation y=kx and the given point, (2, 8), you can substitute x with 2 and y with 8.

8=k(2) and then solve for k.

\begin{aligned} &8=k(2)\\\\ &\cfrac{8}{2}=\cfrac{k \, (2)}{2} \\\\ &4=k \end{aligned}

Since k=4, the equation will be y=4 x .

6. If x and y vary directly, find the equation of direct variation that contains the point (-6, 12).

Using the direct variation equation y=kx and the given point, (-6, 12), you can substitute x with -6 and y with 12.

12=k \cdot(-6) and then solve for k.

\begin{aligned} & 12=k(-6) \\\\ & \cfrac{12}{-6}=\cfrac{k \, (-6)}{-6} \\\\ & -2=k \end{aligned}

Since k=-2, the equation will be y=-2 k .

Direct variation FAQs

Yes, when you graph direct variation equations, they will go through the origin because direct variation equations are proportional.

Direct variation represents a direct proportion between the x variable and the y variable. When the x increases, the y increases, and vice versa. The graph of a direct variation equation is a straight line that passes through the origin. With inverse variation, when the x increases, the y decreases, and vice versa. The graph of inverse variation is a curve.

Yes, the constant of variation represents the proportional relationship between x and y , where the vertical and horizontal movement from one point to the next is the same. The constant rate of change of a line is the vertical and horizontal movement from one point to the next. In algebra, the constant rate of chance of a linear equation is the slope of a line.

Yes, the constant of variation can be a decimal or a fractional number.

The next lessons are

• Number patterns

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.9: Use Direct and Inverse Variation

• Last updated
• Save as PDF
• Page ID 15181

Learning Objectives

By the end of this section, you will be able to:

• Solve direct variation problems
• Solve inverse variation problems

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

• Find the multiplicative inverse of −8 If you missed this problem, review Exercise 1.10.13 .
• Solve for n: 45=20n If you missed this problem, review Exercise 2.2.1 .
• Evaluate \(5x^2\) when x=10 If you missed this problem, review Exercise 1.3.25 .

When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.

Solve Direct Variation Problems

Lindsay gets paid $15 per hour at her job. If we let s be her salary and h be the number of hours she has worked, we could model this situation with the equation

Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.

Definition: DIRECT VARIATION

For any two variables x and y , y varies directly with x if

y=kx, where \(n \ne 0\)

In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates x and y . Then we can use that equation to find values of y for other values of x .

How to Solve Direct Variation Problems

Example \(\PageIndex{1}\)

If y varies directly with x and y=20 when x=8, find the equation that relates x and y .

Example \(\PageIndex{2}\)

If y varies directly as x and y=3, when x=10, find the equation that relates x and y .

\(y=\frac{3}{10}x\)

Example \(\PageIndex{3}\)

If y varies directly as x and y=12 when x=4, find the equation that relates x and y .

We’ll list the steps below.

Definition: SOLVE DIRECT VARIATION PROBLEMS

• Write the formula for direct variation.
• Substitute the given values for the variables.
• Solve for the constant of variation.
• Write the equation that relates x and y.

Now we’ll solve a few applications of direct variation.

Example \(\PageIndex{4}\)

When Raoul runs on the treadmill at the gym, the number of calories, c , he burns varies directly with the number of minutes, m , he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.

• Write the equation that relates c and m .
• How many calories would he burn if he ran on the treadmill for 25 minutes?

Example \(\PageIndex{5}\)

The number of calories, c , burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising.

• Write the equation that relates c and t .
• How many calories would he burn if he exercises for 90 minutes?
• 432 calories

Example \(\PageIndex{6}\)

The distance a moving body travels, d , varies directly with time, t , it moves. A train travels 100 miles in 2 hours

• Write the equation that relates d and t .
• How many miles would it travel in 5 hours?

In the previous example, the variables c and m were named in the problem. Usually that is not the case. We will have to name the variables in the next example as part of the solution, just like we do in most applied problems.

Example \(\PageIndex{7}\)

The number of gallons of gas Eunice’s car uses varies directly with the number of miles she drives. Last week she drove 469.8 miles and used 14.5 gallons of gas.

• Write the equation that relates the number of gallons of gas used to the number of miles driven.
• How many gallons of gas would Eunice’s car use if she drove 1000 miles?

Notice that in this example, the units on the constant of variation are gallons/mile. In everyday life, we usually talk about miles/gallon.

Example \(\PageIndex{8}\)

The distance that Brad travels varies directly with the time spent traveling. Brad travelled 660 miles in 12 hours,

• Write the equation that relates the number of miles travelled to the time.
• How many miles could Brad travel in 4 hours?

Example \(\PageIndex{9}\)

The weight of a liquid varies directly as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.

• Write the equation that relates the weight to the volume.
• If a liquid has volume 13 gallons, what is its weight?

In some situations, one variable varies directly with the square of the other variable. When that happens, the equation of direct variation is \(y=kx^2\).

Example \(\PageIndex{10}\)

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 4” will support a maximum load of 75 pounds.

• Write the equation that relates the maximum load to the cross-section.
• What is the maximum load that can be supported by a beam with diagonal 8”?

Example \(\PageIndex{11}\)

The distance an object falls is directly proportional to the square of the time it falls. A ball falls 144 feet in 3 seconds.

• Write the equation that relates the distance to the time.
• How far will an object fall in 4 seconds?
• \(d=16t^2\)

Example \(\PageIndex{12}\)

The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.

• Write the equation that relates the area to the radius.
• What is the area of a pizza with a radius of 9 inches?
• \(A=3.14r^2\)
• 254.34 square inches

Solve Inverse Variation Problems

Many applications involve two variable that vary inversely . As one variable increases, the other decreases. The equation that relates them is \(y=\frac{k}{x}\).

Definition: INVERSE VARIATION

For any two variables x and y , y varies inversely with x if

y=\(\frac{k}{x}\),where \(k \ne 0\)

The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is \(\frac{1}{x}\).

We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.

Definition: SOLVE INVERSE VARIATION PROBLEMS

• Write the formula for inverse variation.

Example \(\PageIndex{13}\)

If y varies inversely with x and y=20 when x=8 x and y .

Example \(\PageIndex{14}\)

If p varies inversely with q and p=30 when q=12 find the equation that relates p and q.

\(p=\frac{360}{q}\)

Example \(\PageIndex{15}\)

If y varies inversely with x and y=8 when x=2 find the equation that relates x and y.

\(y=\frac{16}{x}\)

Example \(\PageIndex{16}\)

The fuel consumption (mpg) of a car varies inversely with its weight. A car that weighs 3100 pounds gets 26 mpg on the highway.

• Write the equation of variation.
• What would be the fuel consumption of a car that weighs 4030 pounds?

Example \(\PageIndex{17}\)

A car’s value varies inversely with its age. Elena bought a two-year-old car for $20,000.

• What will be the value of Elena’s car when it is 5 years old?
• \(v=\frac{40,000}{a}\)

Example \(\PageIndex{18}\)

The time required to empty a pool varies inversely as the rate of pumping. It took Lucy 2.5 hours to empty her pool using a pump that was rated at 400 gpm (gallons per minute).

• How long will it take her to empty the pool using a pump rated at 500 gpm?
• \(t=\frac{1000}{r}\)

Example \(\PageIndex{19}\)

The frequency of a guitar string varies inversely with its length. A 26” long string has a frequency of 440 vibrations per second.

• How many vibrations per second will there be if the string’s length is reduced to 20” by putting a finger on a fret?

Example \(\PageIndex{20}\)

The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees.

• How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?
• \(h=\frac{130}{t}\)
• \(1\frac{2}{3}\) hours

Example \(\PageIndex{21}\)

The force needed to break a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-foot long board.

• How many pounds of pressure is needed to break a 5-foot long board?
• \(F=\frac{48}{L}\)

Algebra Examples

• Privacy Policy--New
• Terms ( Premium )
• DO NOT SELL MY INFO
• Mathway © 2024

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Direct Variation: Definition, Formula, Equation, Examples, FAQs

What is direct variation in math, what is a direct variation equation (direct variation formula), difference between direct variation and inverse variation, solved examples of direct variation, practice problems on direct variation, frequently asked questions about direct variation.

Direct variation is a type of proportionality in which one quantity directly varies with respect to a change in another quantity, by the same factor. 

This means that an increase in one quantity results in a proportionate increase in the other quantity. Similarly, a decrease in one quantity results in a proportionate decrease in the other quantity. There will be a proportionate increase or decrease.

Note that the ratio between two quantities that are in direct proportion or direct variation always remains the same. 

In direct variation, the variable that represents the cause of the relationship is called the independent variable, generally denoted by x. The other variable depends on the value of the independent variable; it is called the dependent variable, generally denoted by y. 

( Note: It’s important to note that the roles of independent and dependent variables vary depending on the specific context and the relationship between the defined variables. It is always better to first understand the relationship between two quantities in comparison.)

Direct variation real-life example:

Suppose you are working on an hourly pay basis. In this case, the number of hours you work is directly proportional to your earnings. The more you work, the more you earn. You can earn double by working twice as many hours.  

Here, $x =$ Number of hours you work and $y =$ The amount of money you earn

Direct Variation Definition

Direct variation or direct proportionality is a mathematical relationship between two variables where one variable varies in direct proportion with respect to the other variable.

Direct Variation Symbol

Suppose that a variable y is directly proportional to x. In other words, y varies directly as x.

We can write this mathematically as

$y \propto x$

Symbol “$\propto$” stands for “is proportional to.”

The relationship between two variables x and y, which are in direct variation, can be represented by an equation

$k = \frac{y}{x}$ is the constant of variation representing the constant ratio between the two variables.

Here, k is a non-zero real constant. The value of k can be both positive or negative.

The above equation can be decoded as “y varies directly with x” or “y varies directly as x.” The equation can be used to derive different formulas according to the requirements of a solution. 

Different forms of the direct variation formula are as follows:

• To solve for the constant of variation, k, we can shuffle the formula.

$k = \frac{y}{x}$ and $x \neq 0$

• To solve for one of the variables (x or y), we can shuffle the formula.

$x = \frac{y}{k}$

Direct Variation on a Graph

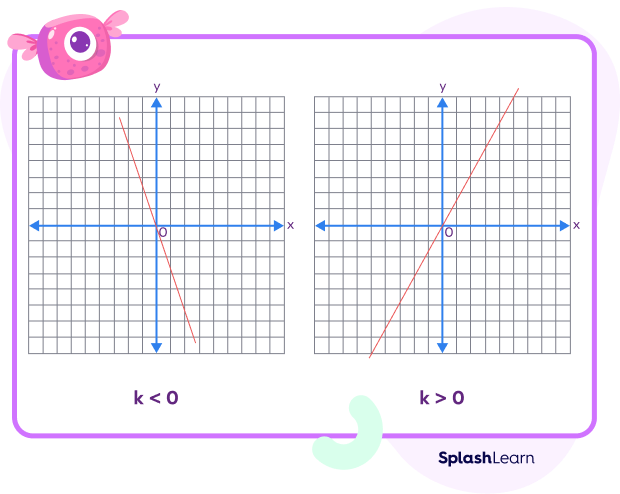
Note that the graph of the direct variation linear equation $y = kx$ is a straight line passing through the origin.

• If k is positive, then the line will rise from left to right, passing through the origin.
• If k is negative, then the line will fall from left to right, passing through the origin.

The slope of the line represents the constant of variation in a direct variation. It indicates how much the dependent variable changes for each unit increase in the independent variable.

So, to understand how to graph direct variation, we will identify the plot points satisfying the equation $y = kx$.

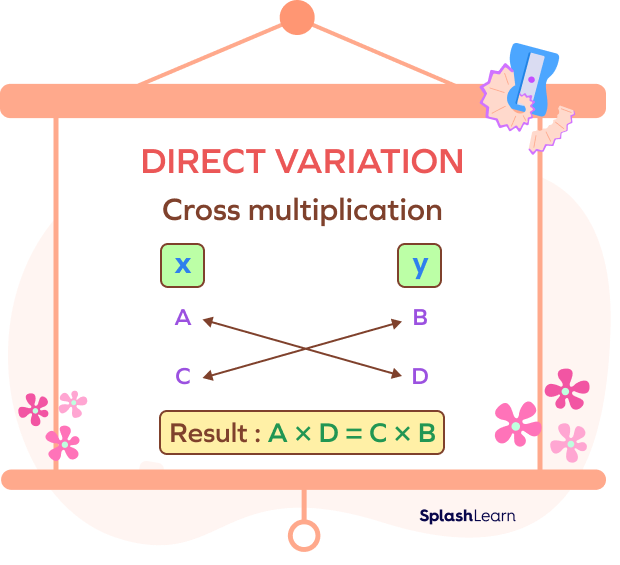
Cross Multiplication Method to Solve Direct Variation Problems

We can easily solve direct variation problems using the cross multiplication method. Consider two variables, x and y, in direct variation. 

Let y = B for x = A.

Let y = D for x = C.

Since x and y are in direct variation, we can write the proportion as

$\frac{A}{B} = \frac{C}{D}$ 

By cross multiplication, we get

Thus, $A \times D = B \times C$

We can find any missing value using this method.

In a direct variation, the variables change in proportion to each other, while in an inverse variation, the variables change in inverse proportion to each other.

See this comparison table that shows the difference between Direct and Inverse variations:

Facts on Direct Variation

• The constant of variation (k) is the fixed ratio that does not change even if the values of x and y change.
• The graph line passes through the origin (0,0) because the direct variation equation always includes the term y = 0 when x = 0.
• The constant of variation (k) gets bigger with a rise in the steepness of the slope of the line.
• A horizontal graph line indicates that the variable y is constant and does not change with x; hence, it does not have direct variation.
• A vertical graph line indicates that the variable x is constant and does not change with y; hence, it does not have direct variation.

Okay, so we now have a clear idea of the concepts relating to direct variation, including direct variation function, definition, graph, differences, and much more. Let us now look at some examples and practice problems to boost our understanding of the concept.

1. The cost of printing 100 pages is $50. What will be the cost of printing 150 pages?

Cost $\propto$ Number of pages

Cost $= k \times$ Number of pages

$k = \frac{y}{x} = \frac{cost}{Number \;of \;pages}$

$k = \frac{50}{100} = 0.5$

Now, the cost of 150 pages can be calculated by a direct variation equation.

Cost $= 0.5 \times $Number of pages

Cost $= 0.5 \times 150$

Cost $= 75$

Therefore, $\$75$ is the cost of printing 150 pages.

Another method:

$\$50 \times 150 = 100 \times$ ?

?$ = \frac{\$7500}{100}$

2. If the number and cost of notebooks have a direct variation, what will be the cost of 15 notebooks if 5 notebooks cost $\$10$ ?

As the cost varies directly with the number of notebooks, we can solve it by setting up the proportions.

5 notebooks cost $\$10$.

Let the cost of 15 notebooks to be x.

The proportion can be written as

$\frac{5}{10} = \frac{15}{x}$

Cross multiply.

$5 \times x = 10 \times 15$

Solve for x

Therefore, $\$30$ is the cost of 15 notebooks.

3. If a car covers 240 miles in 4 hours time. How many miles will it travel in 6 hours?

Solution:  

We know that the distance covered is directly proportional to the time taken. So, we can solve this question accordingly.

240 miles$\times 6 =$ ?$\times 4$ hours

?$= 360$ miles

Therefore, the car will cover 360 miles in 6 hours.

4. A company produces 100 units of a product per day. How many units will it produce in 5 days?

The number of units produced are directly proportional to the number of days.

Suppose that the company produces y units in 5 days.

$y = 100 \times 5$

Therefore, 500 units can be produced in 5 days.

5. Find the constant of direct variation where the cost of 4 dozen oranges is $\$24$ . Also, find the cost of 8 dozen oranges.

Assume the cost of 8 dozen oranges to be y. 

As we can see that the cost of oranges varies directly with the number of dozens. So, we can set up a proportion as

$\frac{4}{24} = 8y$

Isolate y on one side by cross-multiplying both sides

$4y = 24 \times 8$

Simplify it

Therefore, 8 dozen oranges will cost $48.

Now, let us find the constant of direct variation by using the equation y = kx

where 

y = the cost,

x = the number of dozens, and

k = the constant of variation

$k = \frac{1}{6}$

Therefore, $\frac{1}{6}$ or 0.1667 (approx) is the constant of direct variation.

Attend this quiz & Test your knowledge.

What will be the cost of 10 donuts if 4 donuts cost $\$2$?

If it takes 2 hours to mow a 1 acre lawn, how many hours will it take to mow a lawn that is $\frac{1}{4}$ an acre, if a car can go 30 miles with one gallon of gas, then how far can it go with 6 gallons of gas, 5 pounds of apples cost $\$10$. what will be the cost of 8.5 pounds of apples, which equation represents a direct variation.

Are the terms direct variation and direct proportion the same?

Yes, the terms direct variation and direct proportion are used interchangeably, but mean the same thing.

How can you identify direct variation?

In direct variation, the ratio of two quantities is always constant. As one variable increases, the other variable also increases. Also, if one variable decreases, the other variable also decreases.

Can the constant of proportionality be negative?

Yes, it can be positive or negative. It can never be 0. When we study the positive rate of change, we only consider positive values of k.

Are direct variations always linear?

We mostly study direct variations that are linear, but they do not have to be linear. We can say that linear equations are a specific type of direct variation, but not all direct variations follow a linear relationship. In direct variation, the ratio between the two variables remains constant, regardless of the type of relationship they exhibit.

RELATED POSTS

• Difference between Square and Rectangle – Definition, Examples, FAQs
• Onto Function: Definition, Formula, Properties, Graph, Examples
• Octagon Formula For Area and Perimeter With Derivation
• Area of Triangle in Determinant Form – Definition, Examples
• Convert MM to Inches Formula – Examples, FAQs, How to Convert

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Pre-Algebra >

Direct and Inverse Variation Worksheets

Direct and inverse variation worksheets are designed for high schoolers and are divided into subtopics like identifying the type of variation by observing equations, graphs and tables, finding the constant of variation, and much more. The worksheets provide dual levels, level 1 deals with direct and inverse variations, while level 2 deals with direct, inverse, joint and combined variation. A prior knowledge of proportions will definitely be an added advantage. Kick-start your practice with our free worksheets!

Recognize Direct and Inverse Variation

The quintet multiple response pdf worksheets have exercises for learners to observe equations, graphs and recognize the type of variation as direct (linear graph) or inverse (rectangular hyperbola).

• Download the set

Direct and Inverse Variation - Equation

Equations representing the direct variation are in the form y = kx and inverse variation is in the form xy = k. Identify the type of variation in the equations featured in these printable worksheets. Also, find the constant of variation (k).

Direct and Inverse Variation - Table

State whether the table represents a direct variation or inverse variation or neither of them. Find the constant of variation as well.

Constant of Variation - Equation

These high school pdf worksheets feature exercises on finding the constant of variation (k) from the given equations, packed into two levels for easier navigation.

Constant of Variation with the given Values

Find the constant of variation (k) based on the values of the variables in the given statement. Validate your responses with our answer keys.

Write the Equation

Find the constant of variations and translate the statements into equations.

Missing Values

Navigate through the printable worksheets here to formulate an equation relating the variables to find the value of the missing entity.

Complete the Table

This set of pdf worksheets consist of exercises in tabular format. Find the constant of variation (k) and complete the table.

Direct and Inverse Variation Word Problems

Find 70+ word problems, where the student learns to apply the concept of variation to real-life scenarios.

(15 Worksheets)

Related Worksheets

» Ratio Word Problems

» Solving Proportions

» Proportions

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

• IIT JEE Study Material

Direct and Inverse Variations

Direct variation means when one quantity changes, the other quantity also changes in direct proportion. Inverse variation is exactly the opposite of this. In this article, you will learn the definition of direct and inverse variations, along with some solved examples.

A few situations in life have either a direct or indirect relationship with each other:

• As the bill at the shopping centre increases, the amount to be paid also increases.
• As the speed of the car decreases, the time taken to reach the destination increases.

If the two values of the objects are related in such a way that an increase or decrease in the value of one object affects the value of the other, it is termed a variation. The two types of variation are as follows:

Direct Variation

The quantities are said to be in direct proportion if:

• An increase in quantity A leads to an increase in quantity B and vice versa, provided their respective ratios are the same.

The methods to solve direct variation problems are tabular and unitary methods.

Direct variation is represented as follows:

Y = KX, where K is the constant of proportionality.

The direct variation graph is a line through the origin.

Inverse Variation

The quantities are said to be in inverse proportion if,

• An increase in the quantity A leads to a decrease in quantity B and vice versa.

The graph of inverse variation is as follows:

Direct and Inverse Variation Problems

Example 1: A and B can do a particular work in 72 days, B and C in 120 days, and A and C in 90 days. In how many days can A alone do the work?

Let us say A, B, and C can respectively do work alone in x, y, and z days

Therefore, in 1 day, A, B, and C alone can work in 1 / x, 1 / y, and 1 / z days

⇒ (A + B) in 1 day can do 1 / x + 1 / y work

∴ (A + B) can do full work in 1 / ([1 / x] + [1 / y]) day

⇒1 / ([1 / x] + [1 / y]) = 72 i.e.,

1 / x + 1 / y = 1 / 72 ———— (1)

Similarly, 1 / y + 1 / z =1 / 120 ———- (2)

1 / z + 1 / x = 1 / 90 ——– (3)

From (1) – (2), 1 / x − 1 / z = 1 / 72 − 1 / 120 ——– (4)

1 / x + 1 / z = 1 / 92 ———– (5)

Adding IV and V, 2 / x = 1 / 72 − 1 / 120 + 1 / 90

= [5 − 3 + 4] / [360] = 6 / 360 = 1 / 60

Example 2: A and B undertake to do a piece of work for Rs. 600. A alone can do it in 6 days, while B alone can do it in 8 days but with the help of C, they can finish it in 3 days. Find the share of C.

A, B, and C can do (alone) work in 6 days, 8 days, and x days (assume), respectively.

∴ Together, they will do it in 1 / ([1 / 6] + [1 / 8] + [1 / x ]) days.

Now, 1 / [(1 / 6) + (1 / 8) + (1 / x)] = 3

⇒ (1 / 6) + (1 / 8) + (1 / x) = 1 / 3

⇒ 1 / x = 1 / 3 − 1 / 6 − 1 / 8 = 1 / 24

⇒ x = 24 days

Efficiency ratio of A : B : C = [1 / 6] : [1 / 8] : [1 / 24] = 4 : 3 : 1

Share of C = (1 / [4 + 3 + 1]) × 600 = Rs. 75.

Example 3: 45 men can complete a work in 16 days. Six days after they started working, 30 more men joined them. How many days will they now take to complete the remaining work?

45 men, 16 days ⇒ 1 work.

1 man, 1 day ⇒ 1 / [45 × 16] work

For the first 6 days: 45 men, 6 days ⇒ [45 × 16] / [45 × 16] work = 3/8 work

Work left = 1 − ⅜ = ⅝

Now, 45 + 30 = 75 men, 1 man, 1 day = 1 / [45 × 16] = work 75 men,

1 day = 75 / [45 × 16] work 75 men, x days = 75x / [45 × 16] work

But = 75x / [45 × 16] work = 5 / 8

⇒ x = 5 / 8 × [(45 × 16) / 75] = 6 days.

Example 4: Two pipes, A and B, can fill a tank in 24 minutes and 32 minutes, respectively. If both the pipes are opened together, after how much time should B be closed so that the tank is full in 18 minutes?

Let after ‘t’ minutes ‘B’ be closed

For first ‘t’ minutes part filled= t ∗ [1 / 24 + 1 / 32] = t ∗ 7 / 96

The part left = (1 − 7t / 96) ‘A’ filled 1 /24 part in 1 minutes ⇒ A fills = (1 − [7t / 96]) part in 24

= (1 − 7t / 96) minutes

Now, [t + 24] (1 − 7t / 96) = 18

⇒t + 24 − [7 t / 4] = 8

⇒6 = 3t / 4

Example 5: Twenty women can do work in sixteen days. Sixteen men can complete the same work in fifteen days. What is the ratio between the capacity of a man and a woman?

One woman can do work in 20 × 16 = 320 days

In 1 day, 1 woman can do (1 / 320) parts of the work

Similarly, 1 man can do work in 16 × 15 = 240 days

∴ In 1 day, one man can do 1 / 240 parts of the work

Capacity of man: woman = 1 / 240 : 1 / 320 = 1 / 3 : 1 / 4 = 4 : 3

Example 6: A pipe can fill a tank in 15 hours. Due to a leak in the bottom, it is filled in 20 hours. If the tank is full, how much time will the leak take to empty it?

Filling in 1 hr = [1 / 15] of the tank

Let emptying by leak in 1 hr = [1 / x] tank (where leak empties tank in ‘x’ hrs)

∴ Hours in which it fills along with leak also emptying is

⇒ 1 / ([1 / 15] − [1 / x]) = 20hrs

Example 7: A worker is paid Rs. 139.20 for 3 days.

(i) What will he get in the month of June (in Rs.)?

(ii) For how many days will he be working for Rs. 696?

Let Rs. x2 be paid in the month of June.

Since it is a case of direct proportion, 

[x1 / y1] = [x2 / y2]

⇒ [139.20 / 3] = [x2 / 30] 

⇒ x2 = [139.20 × 30] / 3

⇒ x2 = 1392. 

Thus, Rs. 1392 will be paid in the month of June. 

(ii) Let y2 be the number of days he will work for Rs. 696.

It is a case of direct proportion. 

∴ [139.20 / 3] = [696 / y2]

⇒ y2 = [696 × 3 × 10] / [1392] 

Thus, he will work for 15 days for Rs. 696.

Example 8:  Which of the following tables shows the inverse proportion?

A)  Only (i)

B)  Both (i) and (ii)

C)  Both (ii) and (iii)

D)  None of these

(i) For inverse proportion, xy = constant

Now, 6 × 250 = 1500, 12 × 125 = 1500, 30 × 50 = 1500 and 48 × 31.25 = 1500

∴ The data is in inverse proportion.

(ii) 115 × 615 = 70725, 130 × 600 = 78000

∴ The data is not in inverse proportion.

(iii) 50 × 300 = 15000, 100 × 150 = 15000, and 300 × 100 = 30000

Therefore, option A is the answer.

Example 9:  Match the following.

P. According to the question, [40 / 120] = [60 / y] or y = [60 × 120] / 40 = 180

Q. According to the question, [12 × 300] = [24 × y] or y = [12 × 300] / [24] = 150.

R. According to the question, [30 / 50] = [96 / y] or y = [96 × 50] / [30] = 160

S. According to the question, [20 × 650] = [100 × y] or y = [20 × 650] / [100] = 130

Arithmetic Progression for IIT JEE

Frequently Asked Questions

What do you mean by direct proportion.

Two quantities are said to be in direct proportion if an increase in one quantity leads to an increase in the other quantity or vice versa.

What do you mean by indirect proportion?

Two quantities are said to be in indirect proportion if an increase in one quantity leads to a decrease in the other quantity or vice versa.

Give an example of direct variation in real life.

The cost of the groceries is directly proportional to their weight.

Give an example of indirect variation in real life.

As the speed of a car increases, the time taken to reach the destination decreases.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.