how do you solve math problems with percentages

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Do Percentage Calculations? (+FREE Worksheet!)

Want to find a percent of a number? You can calculate percentages in a few simple and easy steps.

Related Topics

• How to Find Percent of Increase and Decrease
• How to Solve Percent Problems
• How to Find Discount, Tax, and Tip
• How to Solve Simple Interest Problems

Step by step guide to solving percentage problems

• Percent is a ratio of a number and \(100\). It always has the same denominator, \(100\). The percent symbol is \(\%\).
• Percent is another way to write decimals or fractions. For example: \(40\%=0.40=\frac{40}{100}=\frac{2}{5}\)
• Use the following formula to find part, whole, or percent: \(\color{blue}{part =\frac{percent}{100} \ × \ whole }\)

Percentage Calculations – Example 1:

What is \(15\%\) of \(50\)?

Use the this formula: \(\color{ blue }{part =\frac{percent}{100} \ × \ whole }\). \(part\) \(=\frac{15}{100} \ × \ 50 →\) \(part\) \(=\frac{15 \ × \ 50}{100}→\) \(part\) \(=\frac{75}{10}→\) \(part\) \(=7.5 \)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Percentage calculations – example 2:.

What is \(30\%\) of \(35\)?

Use the this formula: \(\color{ blue }{part =\frac{percent}{100} \ × \ whole }\). \(part\) \(=\frac{30}{100} \ × \ 35 →\) \(part\) \(=\frac{30 \ × \ 35}{100}→\) \(part\) \(=\frac{105}{10}→\) \(part\) \(=10.5 \)

Percentage Calculations – Example 3:

What is \(10\%\) of \(45\)?

Use the this formula: \(\color{ blue }{part =\frac{percent}{100} \ × \ whole }\). \(part\) \(=\frac{10}{100}×45 →part\)\(=\frac{1}{10}×45\)→\(part\) \(=\frac{45}{10}→\) \(part\) \(=4.5\)

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

Percentage calculations – example 4:.

What is \(15\%\) of \(24\)?

Use the percent formula: \(\color{ blue }{part =\frac{percent}{100} \ × \ whole }\). \(part\) \(=\frac{15}{100}×24 →\) \(part\) \(=\frac{15 \ × \ 24}{100}\)→ \(part\) \(=\frac{360}{100} →\) \(part\) \(=3.6 \)

Exercises for Doing Percentage Calculations

Calculate the percentages..

• \(\color{blue}{50\% \ of \ 25}\)
• \(\color{blue}{ 80\% \ of \ 15 }\)
• \(\color{blue}{ 30\% \ of \ 34 }\)
• \(\color{blue}{ 70\% \ of \ 45 }\)
• \(\color{blue}{ 10\% \ of \ 0 }\)
• \(\color{blue}{ 80\% \ of \ 22 }\)

Download Percentage Calculations Worksheet

• \(\color{blue}{12.5}\)
• \(\color{blue}{12}\)
• \(\color{blue}{10.2}\)
• \(\color{blue}{31.5}\)
• \(\color{blue}{0}\)
• \(\color{blue}{17.6}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• How to Calculate the Area, Perimeter, and Radius of Quarter Circles
• How to Instill in Your Child a Love of Math at School: Tips for Parents
• How to Apply for College: Complete Guide
• Tangible Learning: How to Represent Addition of Fractions with Unlike Denominators Using Everyday Objects
• How to Solve Measurement Word Problems
• What are the types of math?
• 5th Grade K-PREP Math Worksheets: FREE & Printable
• How to Get a GED Certificate?
• How to Solve a Quadratic Equation by Completing the Square?
• Top 10 Free Websites for ATI TEAS 7 Math Preparation

What people say about "How to Do Percentage Calculations? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Percent Maths Problems

• Math Article

In mathematics, a percentage is a number or ratio that can be expressed as a fraction of 100. If we have to  calculate percent of a number,  divide the number by the whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100 . It is represented by the symbol “%” . 

Examples of percentages are:

• 10% is equal to 1/10 fraction
• 20% is equivalent to ⅕ fraction
• 25% is equivalent to ¼ fraction
• 50% is equivalent to ½ fraction
• 75% is equivalent to ¾ fraction
• 90% is equivalent to 9/10 fraction

Percentages have no dimension. Hence it is called a dimensionless number. If we say, 50% of a number, then it means 50 per cent of its whole.

Percentages can also be represented in decimal or fraction form, such as 0.6%, 0.25%, etc. In academics, the marks obtained in any subject are calculated in terms of percentage. Like, Ram has got 78% of marks in his final exam. So, this percentage is calculated on account of the total marks obtained by Ram, in all subjects to the total marks.

Percentage Formula

To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100.

Percentage formula = (Value/Total value)  × 100

Example: 2/5  × 100 = 0.4 × 100 = 40 per cent

How to calculate the percentage of a number?

To calculate the percentage of a number, we need to use a different formula such as:

P% of Number = X

where X is the required percentage.

If we remove the % sign, then we need to express the above formulas as;

P/100 * Number = X

Example: Calculate 10% of 80.

Let 10% of 80 = X

10/100 * 80 = X

is what % of

  Also, try out: Percentage Calculator .

Percentage Difference Formula

If we are given with two values and we need to find the percentage difference between these two values, then it can be done using the formula:

\(\begin{array}{l}Percentage~Difference = \frac{\left|N_{1}-N_{2}\right|}{\left[\frac{\left(N_{1}+N_{2}\right)}{2}\right]} \times 100\end{array} \)

For example, if 20 and 30 are two different values, then the percentage difference between them will be:

% difference between 20 and 30 = \(\begin{array}{l}Percentage~Difference = \frac{\left|20-30\right|}{\left[\frac{\left(20+30\right)}{2}\right]} \times 100\end{array} \)

Percentage Increase and Decrease

The percentage increase is equal to the subtraction of the original number from a new number, divided by the original number and multiplied by 100.

% increase = [(New number – Original number)/Original number] x 100

increase in number = New number – original number

Similarly, a percentage decrease is equal to the subtraction of a new number from the original number, divided by the original number and multiplied by 100. 

% decrease = [(Original number – New number)/Original number] x 100

Where decrease in number = Original number – New number

So basically if the answer is negative then there is a percentage decrease.

Solved Example

Two quantities are generally expressed on the basis of their ratios. Here, let us understand the concepts of percentage through a few examples in a much better way.

Percentage Chart

The percentage chart is given here for fractions converted into percentages.

Converting Fractions to Percentage

A fraction can be represented by a/b .

Multiplying and dividing the fraction by 100, we have

From the definition of percentage, we have;

(1/100) = 1%

Thus, equation (i) can be written as:

(a/b)  × 100%

Therefore, a fraction can be converted to a percentage simply by multiplying the given fraction by 100. Also, read:  Ratio To Percentage

Percentage Questions

Q.1: If 16% of 40% of a number is 8, then find the number.

Let X be the required number.

Therefore, as per the given question, 

(16/100) × (40/100) × X = 8

So, X = (8 × 100 × 100) / (16 × 40)

Q.2: What percentage of 2/7 is 1/35 ?

Let X% of 2/7 is 1/35.

∴ [(2/7) / 100] × X = 1/35

⇒ X = (1/35) × (7/2) × 100 

Q.3: Which number is 40% less than 90?

Required number = 60% of 90

= (90 x 60)/100

Therefore, the number 54 is 40% less than 90.

Q.4: The sum of (16% of 24.2) and (10% of 2.42) is equal to what value?

As per the given question ,

Sum = (16% of 24.2) + (10% of 2.42)

= (24.2 × 16)/100 + (2.42 × 10)/100

= 3.872 + 0.242

Word Problems

Q.1: A fruit seller had some apples. He sells 40% apples and still has 420 apples. Originally, he had how many apples?

Let he had N apples, originally.

Now, as per the given question, we have;

(100 – 40)% of N = 420

⇒ (60/100) × N = 420

⇒ N = (420 × 100/60) = 700

Q.2: Out of two numbers, 40% of the greater number is equal to 60% of the smaller. If the sum of the numbers is 150, then the greater number is?

Let X be the greater number.

∴ Smaller number = 150 – X {given that the sum of two numbers is 150}

According to the question,

(40 × X)/100 = 60(150 – X)/100

⇒ 2p = 3 × 150 – 3X

⇒ 5X = 3 × 150

Difference between Percentage and Percent

The words percentage and percent are related closely to each other.

Percent ( or symbol %) is accompanied by a specific number.

E.g., More than 75% of the participants responded with a positive response to abjure.

The percentage is represented without a number.

E.g., The percentage of the population affected by malaria is between 60% and 65%.

Fractions, Ratios, Percents and Decimals are interrelated with each other. Let us look at the conversion of one form to another:

Percentage in Maths

Every percentage problem has three possible unknowns or variables :

In order to solve any percentage problem, you must be able to identify these variables.

Look at the following examples. All three variables are known:

Example 1: 70% of 30 is 21

70 is the percentage.

30 is the base.

21 is the part.

Example 2: 25% of 200 is 50

25 is the percent.

200 is the base.

50 is the part.

Example 3: 6 is 50% of 12

6 is the part.

50 is the percent.

12 is the base.

Percentage Tricks

To calculate the percentage, we can use the given below tricks.

Example- Prove that 10% of 30 is equal to 30% of 10.

Solution- 10% of 30 = 3

30% of 10 = 3

Therefore, they are equal i.e. x % of y = y % of x holds true.

Marks Percentage

Students get marks in exams, usually out of 100. The marks are calculated in terms of per cent. If a student has scored out of total marks, then we have to divide the scored marks by total marks and multiply by 100. Let us see some examples here:

Problems and Solutions

Frequently asked questions – faqs, what do you mean by percentage, what is the symbol of percentage, what is the percentage formula, what is the percentage of 45 out of 150, what is 40% of 120.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Very usefull app

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: Percents Problems and Applications of Percent

• Last updated
• Save as PDF
• Page ID 142718

• Morgan Chase
• Clackamas Community College via OpenOregon

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

You may use a calculator throughout this module.

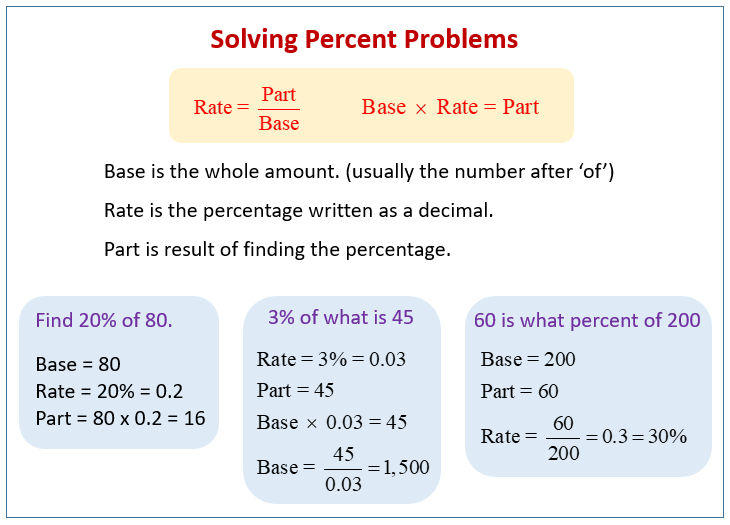
Recall: The amount is the answer we get after finding the percent of the original number. The base is the original number, the number we find the percent of. We can call the percent the rate.

When we looked at percents in a previous module, we focused on finding the amount. In this module, we will learn how to find the percentage rate and the base.

\(\text{Amount}=\text{Rate}\cdot\text{Base}\)

\(A=R\cdot{B}\)

We can translate from words into algebra.

• “is” means equals
• “of” means multiply
• “what” means a variable

Solving Percent Problems: Finding the Rate

Suppose you earned \(56\) points on a \(60\)-point quiz. To figure out your grade as a percent, you need to answer the question “\(56\) is what percent of \(60\)?” We can translate this sentence into the equation \(56=R\cdot60\).

Exercises \(\PageIndex{1}\)

1. \(56\) is what percent of \(60\)?

2. What percent of \(120\) is \(45\)?

1. \(93\%\) or \(93.3\%\)

2. \(37.5\%\)

Be aware that this method gives us the answer in decimal form and we must move the decimal point to convert the answer to a percent.

Also, if the instructions don’t explicitly tell you how to round your answer, use your best judgment: to the nearest whole percent or nearest tenth of a percent, to two or three significant figures, etc.

Solving Percent Problems: Finding the Base

Suppose you earn \(2\%\) cash rewards for the amount you charge on your credit card. If you want to earn $ \(50\) in cash rewards, how much do you need to charge on your card? To figure this out, you need to answer the question “\(50\) is \(2\%\) of what number?” We can translate this into the equation \(50=0.02\cdot{B}\).

3. $ \(50\) is \(2\%\) of what number?

4. \(5\%\) of what number is \(36\)?

3. $ \(2,500\)

5. An \(18\%\) tip will be added to a dinner that cost $ \(107.50\). What is the amount of the tip?

6. The University of Oregon women’s basketball team made \(13\) of the \(29\) three-points shots they attempted during a game against UNC. What percent of their three-point shots did the team make?

7. \(45\%\) of the people surveyed answered “yes” to a poll question. If \(180\) people answered “yes”, how many people were surveyed altogether?

5. $ \(19.35\)

6. \(44.8\%\) or \(45\%\)

7. \(400\) people were surveyed

Solving Percent Problems: Percent Increase

When a quantity changes, it is often useful to know by what percent it changed. If the price of a candy bar is increased by \(50\) cents, you might be annoyed because it’s it’s a relatively large percentage of the original price. If the price of a car is increased by \(50\) cents, though, you wouldn’t care because it’s such a small percentage of the original price.

To find the percent of increase:

• Subtract the two numbers to find the amount of increase.
• Using this result as the amount and the original number as the base, find the unknown percent.

Notice that we always use the original number for the base, the number that occurred earlier in time. In the case of a percent increase, this is the smaller of the two numbers.

8. The price of a candy bar increased from $ \(0.89\) to $ \(1.39\). By what percent did the price increase?

9. The population of Portland in 2010 was \(583,793\). The estimated population in 2019 was \(654,741\). Find the percent of increase in the population. [1]

8. \(56.2\%\) increase

9. \(12.2\%\) increase

Solving Percent Problems: Percent Decrease

Finding the percent decrease in a number is very similar.

To find the percent of decrease:

• Subtract the two numbers to find the amount of decrease.

Again, we always use the original number for the base, the number that occurred earlier in time. For a percent decrease, this is the larger of the two numbers.

10. During a sale, the price of a candy bar was reduced from $ \(1.39\) to $ \(0.89\). By what percent did the price decrease?

11. The number of students enrolled at Clackamas Community College decreased from \(7,439\) in Summer 2019 to \(4,781\) in Summer 2020. Find the percent of decrease in enrollment.

10. \(36.0\%\) decrease

11. \(35.7\%\) decrease

Relative Error

In an earlier module, we said that a measurement will always include some error, no matter how carefully we measure. It can be helpful to consider the size of the error relative to the size of what is being measured. As we saw in the examples above, a difference of \(50\) cents is important when we’re pricing candy bars but insignificant when we’re pricing cars. In the same way, an error of an eighth of an inch could be a deal-breaker when you’re trying to fit a screen into a window frame, but an eighth of an inch is insignificant when you’re measuring the length of your garage.

The expected outcome is what the number would be in a perfect world. If a window screen is supposed to be exactly \(25\) inches wide, we call this the expected outcome, and we treat it as though it has infinitely many significant digits. In theory, the expected outcome is \(25.000000...\)

To find the absolute error , we subtract the measurement and the expected outcome. Because we always treat the expected outcome as though it has unlimited significant figures, the absolute error should have the same precision (place value) as the measurement , not the expected outcome .

To find the relative error , we divide the absolute error by the expected outcome. We usually express the relative error as a percent. In fact, the procedure for finding the relative error is identical to the procedures for finding a percent increase or percent decrease!

To find the relative error:

• Subtract the two numbers to find the absolute error.
• Using the absolute error as the amount and the expected outcome as the base, find the unknown percent.

Exercisew \(\PageIndex{1}\)

12. A window screen is measured to be \(25\dfrac{3}{16}\) inches wide instead of the advertised \(25\) inches. Determine the relative error, rounded to the nearest tenth of a percent.

13. The contents of a box of cereal are supposed to weigh \(10.8\) ounces, but they are measured at \(10.67\) ounces. Determine the relative error, rounded to the nearest tenth of a percent.

12. \(0.1875\div25\approx0.8\%\)

13. \(0.13\div10.8\approx1.2\%\)

The tolerance is the maximum amount that a measurement is allowed to differ from the expected outcome. For example, the U.S. Mint needs its coins to have a consistent size and weight so that they will work in vending machines. A dime (10 cents) weighs \(2.268\) grams, with a tolerance of \(\pm0.091\) grams. [2] This tells us that the minimum acceptable weight is \(2.268-0.091=2.177\) grams, and the maximum acceptable weight is \(2.268+0.091=2.359\) grams. A dime with a weight outside of the range \(2.177\leq\text{weight}\leq2.359\) would be unacceptable.

A U.S. nickel (5 cents) weighs \(5.000\) grams with a tolerance of \(\pm0.194\) grams.

14. Determine the lowest acceptable weight and highest acceptable weight of a nickel.

15. Determine the relative error of a nickel that weighs \(5.21\) grams.

A U.S. quarter (25 cents) weighs \(5.670\) grams with a tolerance of \(\pm0.227\) grams.

16. Determine the lowest acceptable weight and highest acceptable weight of a quarter.

17. Determine the relative error of a quarter that weighs \(5.43\) grams.

14. \(4.806\) g; \(5.194\) g

15. \(0.21\div5.000=4.2\%\)

16. \(5.443\) g; \(5.897\) g

17. \(0.24\div5.670\approx4.2\%\)

• www.census.gov/quickfacts/fact/table/portlandcityoregon,OR,US/PST045219 ↵
• https://www.usmint.gov/learn/coin-and-medal-programs/coin-specifications and https://www.thesprucecrafts.com/how-much-do-coins-weigh-4171330 ↵

Solving Percent Problems

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

A free service from Mattecentrum

Solving problems with percentages

• Price difference I
• Price difference II
• How many students?

To solve problems with percent we use the percent proportion shown in "Proportions and percent".

$$\frac{a}{b}=\frac{x}{100}$$

$$\frac{a}{{\color{red} {b}}}\cdot {\color{red} {b}}=\frac{x}{100}\cdot b$$

$$a=\frac{x}{100}\cdot b$$

x/100 is called the rate.

$$a=r\cdot b\Rightarrow Percent=Rate\cdot Base$$

Where the base is the original value and the percentage is the new value.

47% of the students in a class of 34 students has glasses or contacts. How many students in the class have either glasses or contacts?

$$a=r\cdot b$$

$$47\%=0.47a$$

$$=0.47\cdot 34$$

$$a=15.98\approx 16$$

16 of the students wear either glasses or contacts.

We often get reports about how much something has increased or decreased as a percent of change. The percent of change tells us how much something has changed in comparison to the original number. There are two different methods that we can use to find the percent of change.

The Mathplanet school has increased its student body from 150 students to 240 from last year. How big is the increase in percent?

We begin by subtracting the smaller number (the old value) from the greater number (the new value) to find the amount of change.

$$240-150=90$$

Then we find out how many percent this change corresponds to when compared to the original number of students

$$90=r\cdot 150$$

$$\frac{90}{150}=r$$

$$0.6=r= 60\%$$

We begin by finding the ratio between the old value (the original value) and the new value

$$percent\:of\:change=\frac{new\:value}{old\:value}=\frac{240}{150}=1.6$$

As you might remember 100% = 1. Since we have a percent of change that is bigger than 1 we know that we have an increase. To find out how big of an increase we've got we subtract 1 from 1.6.

$$1.6-1=0.6$$

$$0.6=60\%$$

As you can see both methods gave us the same answer which is that the student body has increased by 60%

Video lessons

A skirt cost $35 regulary in a shop. At a sale the price of the skirtreduces with 30%. How much will the skirt cost after the discount?

Solve "54 is 25% of what number?"

• Pre-Algebra
• The mean, the median and the mode
• Stem-and-Leaf Plots and Box-and-Whiskers Plot
• Calculating the outcome
• Combinations and permutations
• Finding the odds
• Probability of events
• Geometry – fundamental statements
• Circle graphs
• Angles and parallel lines
• Quadrilaterals, polygons and transformations
• Measure areas
• Pyramids, prisms, cylinders and cones
• Square roots and real numbers
• The Pythagorean Theorem
• Trigonometry
• Algebra 1 Overview
• Algebra 2 Overview
• Geometry Overview
• SAT Overview
• ACT Overview

Real Life Problems on Percentage

Real life problems on percentage will help us to solve different types of problems related to the real-life situations. To understand the procedures follow step-by-step explanation so that you can solve any other similar type of percentage problems.

Solved real life problems on percentage:

1.  Mike needs 30% to pass. If he scored 212 marks and falls short by 13 marks, what was the maximum marks he could have got?

If Mike had scored 13 marks more, he could have scored 30%

Therefore, Mike required 212 + 13 = 225 marks

Let the maximum marks be m.

Then 30 % of m = 225

(30/100) × m = 225

m = (225 × 100)/30

m = 22500/30

2. A number is increased by 40 % and then decreased by 40 %. Find the net increase or decrease per cent.

Solution:            

Let the number be 100.

Increase in the number = 40 % = 40 % of 100

                               = (40/100 × 100)

                               = 40

Therefore, increased number = 100 + 40 = 140

This number is decreased by 40 %

Therefore, decrease in number = 40 % of 140

                                             = (40/100 × 140)

                                             = 5600/100

                                             = 56

Therefore, new number = 140 - 56 = 84

Thus, net decreases = 100 - 84 = 16

Hence, net percentage decrease = (16/100 × 100) %

                                               = (1600/100) %

                                               = 16 %

3. Max scored 6 marks more than what he did in the previous examination in which he scored 30. Maria scored 30 marks more than she did in the previous examination in which she scored 60. Who showed less improvement?

Max percentage improvement in the first exam = (6/30 × 100) %

                                                                     = (600/30) %

                                                                     = 20 %

Maria percentage improvement in the first exam = (30/60 × 100) %

                                                                       = (3000/60) %

                                                                       = 50 %

Hence, 20 % < 50 %

Therefore, Max showed less improvement.

Fraction into Percentage

Percentage into Fraction

Percentage into Ratio

Ratio into Percentage

Percentage into Decimal

Decimal into Percentage

Percentage of the given Quantity

How much Percentage One Quantity is of Another?

Percentage of a Number

Increase Percentage

Decrease Percentage

Basic Problems on Percentage

Solved Examples on Percentage

Problems on Percentage

Word Problems on Percentage

Application of Percentage

8th Grade Math Practice From Real Life Problems on Percentage to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Numbers | Notation | Numeration | Numeral | Estimation | Examples

May 12, 24 06:28 PM

Face Value and Place Value|Difference Between Place Value & Face Value

May 12, 24 06:23 PM

Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns

May 12, 24 06:09 PM

Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar

May 12, 24 04:59 PM

Worksheet on Pictographs | Picture Graph Worksheets | Pictograph Works

May 12, 24 04:31 PM

Worksheet on Fraction into Percentage

Worksheet on Percentage into Fraction

Worksheet on Percentage into Ratio

Worksheet on Ratio into Percentage

Worksheet on Percentage into Decimal

Worksheet on Percentage of a Number

Worksheet on Finding Percent

Worksheet on Finding Value of a Percentage

Worksheet on Percentage of a Given Quantity

Worksheet on Word Problems on Percentage

Worksheet on Increase Percentage

Worksheet on Decrease Percentage

Worksheet on increase and Decrease Percentage

Worksheet on Expressing Percent

Worksheet on Percent Problems

Worksheet on Finding Percentage

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Percentages, Ratios, and Proportions

Note : For more problems with percents and ratios, see the Algebra Word Problems section .

Percentages and Percent Changes

Percentages are something you are probably quite familiar with because of shopping; for example, when a store has everything $ 20\%$ off? The easiest example of percentages is $ 50\%$ off, which means that the item is half price.

Percentages really aren’t that difficult if you truly understand what they are. The word “percentage” comes from the word “per cent”, which means “per hundred” in Latin. Remember that “per” usually means “over”. So, “per cent” literally means “over $ 100$” or “divided by $ 100$”. And remember what “of” typically means in math? I’ll write it again, since it’s so important:

OF  =  TIMES

When we say “$ 20\%$ off  of something”, translate it to “$ 20$ over (or divided by) $ 100$ — then times the original price”, and that will be the amount to subtract from the original price.

Remember that we cannot use a percentage in math; we need to turn it into a decimal.   To turn a percentage into a decimal, move the decimal $ 2$ places to the left (to divide by $ 100$), and to turn a decimal back into a percentage, move the decimal $ 2$ places to the  right (to multiply by $ 100$). ( I like to think of it this way : when taking away the $ \%$, we are afraid of it, so we move $ 2$ decimal places away from it, or to the left . When we need to turn a number into a $ \%$, we like it, so we move $ 2$ decimals towards it, or to the right .)

Let’s get back to our percentage example.  If there’s an item we like for say $ \$50$ ,  and it’s $ 20\%$ off (“off” means take-away or minus!), we’ll do the math to figure out the sales price.  This is called a percent change   problem.

Amount of sale : $ \displaystyle 20\%\,\,\text{of }\,\$50=.2\times \$50=\$10.\,\,\,\,\$50-\$10=\$40$. The item would be $ \$40$. See how we had to turn the $ 20\%$ into a decimal by taking away the $ \%$ sign and moving $ 2$ decimals to the left, or away from it?

We could have also multiplied the original price by $ \displaystyle 80\%\,(100\%-20\%)$, or $ \displaystyle \frac{{80}}{{100}}$, since that’s what we’ll be paying if we get $ 20\%$ off ($ 100\%$ full price minus $ 20\%$ discount equals $ 80\%$ discounted price):

Price of discounted item : $ \displaystyle 80\%\,\,\text{of }\,\$50=.8\times \$50=\$40$. This method has fewer steps.

This shopping example is a percent decrease problem; the following is the formula for that. Make sure you relate this formula back to the example above.

$ \displaystyle \text{Newer}\,\,\text{lower}\,\,\text{price =}\,\,\text{original}\,\,\text{price}\,\,-\,\,\left( {\text{original}\,\,\text{price}\,\,\times \,\,\left. {\frac{{\text{percentage}\,\,\text{off}}}{{100}}} \right)} \right.$

$ \displaystyle \$50-\left( {\$50\,\,\times \,\,\left. {\frac{{20}}{{100}}} \right)} \right.\,\,=\,\,\$50-\$10=\$40$

Notice that we worked the math in the parentheses first (we will get to this in more detail later) .

Now let’s talk about a percent increase problem, which is also a percent change problem. A great example of a percent increase is the tax you pay on this item. Tax is typically a percentage that you add on to what you pay so we can continue driving on the streets free and going to public school “free”.

If we need to add on $ 8.25\%$ sales tax to the $ \$40$ that we are going to spend on the item, we’ll have to know the percent increase formula, but let’s first figure it out without the formula. Tax is the amount we have to add that is based on a percentage of the price that we’re paying for the item.

The tax is $ 8.25\%$ or $ .0825$ (remember – we don’t like the %, so we take it away and move away from it?) times the price of the item and then add it back to the price.

Total price with tax: $ \displaystyle \$50+(8.25\%\times 50)=\$50+(.0825\times 50)=\$50+\$4.125=\$54.125=\$54.13$.

Note that we rounded up to two decimal places, since we’re dealing with money. Note also that we did the math inside the parentheses first. The total price of the item is $ \$54.13$.

Here’s the formula:

$ \displaystyle \text{Price}\,\,\text{with}\,\,\text{tax}=\,\,\text{original}\,\,\text{price}+\,\,\left( {\text{original}\,\,\text{price}\,\,\times \,\,\left. {\frac{{\text{tax}\,\,\text{percentage}}}{{100}}} \right)} \right.$

$ \displaystyle \$50+\left( {\$50\,\,\times \,\,\left. {\frac{{8.25}}{{100}}} \right)} \right.=\$50+\left( {\$50\times \left. {.0825} \right)} \right.\,\,=\,\,\$50+\$4.125=\$54.125=\$54.13$

Another way we can figure percent increase is to multiply the original amount by $ 1$ plus the tax rate, so we include the original amount plus the tax:

$ \displaystyle \text{Price}\,\,\text{with}\,\,\text{tax}\text{=}\text{original}\,\,\text{price}\,\,\times \,\,\left( {1+\left. {\frac{{\text{tax}\,\,\text{percentage}}}{{100}}} \right)} \right.$

$ \displaystyle \$50\,\times \,\left( {1+\left. {\frac{{8.25}}{{100}}} \right)} \right.=\$50\,\times \,\left( {1+\left. {.0825} \right)} \right.=\$50\times 1.0825=\$54.125=\$54.13$

If we need to figure out the actual percent decrease or increase ( percent change ), we can use the following formulas:

$ \displaystyle \text{Percent Increase}=\frac{{\text{New Price}-\text{Old Price}}}{{\text{Old Price}}}\,\times 100$

$ \displaystyle \text{Percent Decrease}\,=\frac{{\text{Old Price}-\text{New Price}}}{{\text{Old Price}}}\,\,\times \,100$

For example, say we want to work backwards to get the percentage of sales tax that we pay (percent increase). If we know that the original (old) price is $ \$50$, and the price we pay (new price) is $ \$54.13$, we could get the $ \%$ we pay in tax this way (note that since we rounded to get the $ 54.13$, our answer is off a little):

$ \displaystyle \text{Percent Increase (Tax)}\,\,=\frac{{54.13-50}}{{50}}\,\,\times \,100\,=\,8.26%$

Sometimes we have to work a little backwards in the problem to get the right answer. For example, we may have a problem that says something like this:

Your favorite pair of shoes are on sale for $ 30\%$ off. The sale price is  $ \$62.30$. What was the original price?

Notice that if the shoes are on sale for $ 30\%$, we need to pay $ 70\%$ for them. Also remember that “ of = times ”. We can set it up this way:

$ \displaystyle \,\,.7\,\,\times \,\,?=\$62.30\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,? = \frac{{62.30}}{{.7}} = \$89$

The original price of the shoes would have been $ \$89$ before tax.

In the Algebra sections, we will address solving the following types of percentage problems, but I’ll briefly address them here if you need to do them now. If you don’t totally follow how to get the answers, don’t worry about it, since we’ll cover “ Algebra Word Problems ” later!

One other way to address percentages is the “$ \displaystyle \frac{{\text{is}}}{{\text{of}}}$” trick, which we’ll address below.

Ratios and Proportions

Ratios  are just a comparison of two numbers. They look a little scary since they involve fractions, but they really aren’t bad at all. Again, they are typically used when you are comparing two things — like cost of one pair of shoes to another pair, or maybe even the number of shirts you have compared to the number of jeans you have.

Let’s use that as an example. Let’s say you have about $ 5$ shirts for every $ 1$ pair of jeans you have, and you figure this same ratio is pretty typical among your friends. You can write your ratio in a fraction like $ \displaystyle \frac{5}{1}$, or you can use a colon in between the two numbers, like  $ 5:1$ (spoken as “$ 5$ to  $ 1$”).

The fractions over $ 1$ is actually a rate (this word is related to the word ratio!), for example, just like when you think of miles per hour. Our rate is shirts per one pair of jeans – $ 5$ shirts for every pair of jeans. Also note that this particular ratio is a unit rate , since the second number (denominator in the fraction) is $ 1$.

Here’s an example. Let’s say you know your friend Alicia has $ 7$ pairs of jeans and you’re wondering how many shirts she has, based on the ratio or rate of $ 5$ shirts to one pair of jeans.  We can do this with math quite easily by setting up the following proportion , which is an equation (setting two things equal to one another) with a ratio on each side:

How do we figure out how many shirts Alicia has? One way is just to think about reducing or expanding fractions. Let’s expand the fraction $ \displaystyle \frac{5}{1}$ to another fraction that has $ 7$ on the bottom:

$ \displaystyle \frac{{\text{shirts}}}{{\text{jeans}}}\,=\,\frac{5}{1}\,=\,\frac{5}{1}\,\times \,1\,=\frac{5}{1}\,\,\times \,\,\frac{7}{7}\,=\frac{{35}}{7}$             Alicia would have $ 35$ shirts.

I’m going to also show you a concept called cross-multiplying , which is very, very useful, even when we get into Algebra, Geometry and up through Calculus! This is a much easier way to do these types of problems.

Remember the “butterfly” concept when we’re comparing fractions, and remember how the fractions are equal when the “butterfly” products are equal?

We’re going to use this concept to set the fractions or ratios equal so we know how many shirts Alicia has:

We know that $ 5\times 7=35$, so we need to know what multiplied by $ 1$ will give us $ 35$. $ 35$!! Alicia has $ 35$ shirts!!! See how easy that was? If we didn’t have the $ 1$ as a factor to get to $ 35$, we’d have to divide $ 35$ by the number under the $ 5$ to get the answer. This is because dividing “undoes” multiplying.

There’s also something called a “ WON ” method for proportions. To do this, set up a table with WON at the top. “ W ” stands for Words , “ O ” stands for Original or Old , and “ N ” stands for New (in this example, for Alicia). Put the words and numbers in the table, and then cross multiply like we did earlier. Again, we get that Alicia has $ 35$ shirts , based on the proportion of $ 5$ shirts to every pair of jeans, and the fact that she has  $ 7$ pairs of jeans.

$ \require{cancel} \displaystyle \frac{{\text{teaspoons}}}{{\text{tablespoons}}}\,\,\,\,\,={}^{6}{{\xcancel{{\frac{3}{1}\,\,\,=\,\,\,\frac{?}{2}}}}^{6}}$

We know that $ 3\times 2=6$, so we need to know what multiplied by $ 1$ will give us $ 6$. We would need $ 6$ teaspoons for our $ 2$ tablespoons.

Now let’s go on to a more complicated example that relates back to converting numbers back and forth between the Metric System and our customary system here.

Let’s say we have $ 13$ meters of something and we want to know how many feet this is.  We can either look up how many feet are in $ 1$ meter, or how many meters are in $ 1$ foot – it really doesn’t matter – but we need a conversion number.

We find that $ 1$ meter equals approximately $ 3.28$ feet; it’s easier to deal with numbers over $ 1$, so this is the best conversion. Let’s set all this up in a proportion. Remember to keep the same unit either on the tops of the proportion, or on the sides; it works both ways:

$ \displaystyle \frac{{\text{meters}}}{{\text{meters}}}\,\,=\,\,\frac{{\text{feet}}}{{\text{feet}}}\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\,\frac{{\text{meters}}}{{\text{feet}}}\,\,=\,\,\frac{{\text{meters}}}{{\text{feet}}}\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\,\frac{{\text{feet}}}{{\text{meters}}}\,\,=\,\,\frac{{\text{feet}}}{{\text{meters}}}$

Let’s solve both two different ways to get the number of feet in $ 13$ meters. Notice that we can turn proportions sideways, with the “$ =$” sideways too; this is how we got from the first equation to the second above.

Here’s an example where we have to do some dividing with our cross multiplying. Try to really understand why we have to divide by $ 2$ to get the answer (it “undoes” the multiplying):

$ \displaystyle \frac{5}{2}\,=\,\frac{?}{9}\,\,\,\,\,\,\,\,\,\,\,\,\,5\,\,\times \,\,9\,=2\,\,\times \,\,?\,\,\,\,\,\,\,\,\,\,\,?\,=\,\frac{{5\,\,\times \,\,9}}{2}\,=\,\frac{{45}}{2}\,=\,\,22\frac{1}{2}$

Unit Multipliers

We can also use what we call unit multipliers to change numbers from one unit to another. The idea is to multiply fractions to get rid of the units we don’t want. This concept is also called Dimensional Analysis .

Let’s say we want to use unit multipliers to convert $ 58$ inches to yards.

Since we have inches and we want to end up with yards, we can multiply by ratios (fractions) that relate the units to each other. We are really multiplying by “$ 1$”, since the top and bottom amounts will be the same (just the units will be different). Start with the units we have, and end with the units we want, to see what we need to do in between. Make all the terms look like fractions:

$ \displaystyle \frac{{58\text{ inches}}}{1}\,\,\times \,\,\frac{?}{?}\,\,\times \,\,\frac{?}{?}\,\,\times …=\,\,\frac{{?\text{ yards}}}{1}$

We need to get rid of the inches unit on the top and somehow get the yards unit on the top; it’s easiest to include feet to do this and set up the units so the ones not needed can be crossed out:

$ \require{cancel} \displaystyle \frac{{58\text{ }\cancel{{\text{inches}}}}}{1}\,\times \,\frac{{?\text{ }\cancel{{\text{feet}}}}}{{?\text{ }\cancel{{\text{inches}}}}}\,\times \,\frac{{?\text{ }\,\text{yards}}}{{?\text{ }\cancel{{\text{feet}}}}}\,=\,\frac{{\text{? }\,\text{yards}}}{\text{1}}$

Now just fill in how many inches are in a foot, and how many feet are in a yard, and multiply across:

$ \displaystyle \frac{{58\text{ }\cancel{{\text{inches}}}}}{1}\,\times \,\frac{{1\text{ }\cancel{{\text{foot}}}}}{{12\text{ }\cancel{{\text{inches}}}}}\,\times \,\frac{{1\text{ yard}}}{{3\text{ }\cancel{{\text{feet}}}}}\,=\,\frac{{58\times 1\times 1\text{ yards}}}{{1\times 12\times 3}}\,=\,\frac{{58}}{{36}}\text{ }\,\text{yards}\,=\,\frac{{29}}{{18}}\text{ }\,\text{yards}$

Here’s another example where we use unit multipliers; notice how we can take care of the square kilometers by using the unit multiplier twice.

Use unit multipliers to convert $ 100$ square kilometers to square meters.

$ \displaystyle \frac{{100\text{ }\cancel{{\text{kilometers}}}\times \cancel{{\text{kilometers}}}}}{1}\,\times \,\frac{{1000\text{ meters}}}{{1\text{ }\cancel{{\text{kilometer}}}}}\,\times \,\frac{{1000\text{ meters}}}{{1\text{ }\cancel{{\text{kilometer}}}}}\,=\,100,000,000\,\, \text{meter}{{\text{s}}^{2}}$

Using Percentages with Ratios

Now let’s revisit percentages and show how proportions can help with them too! One trick to use is the $ \displaystyle \frac{{\text{is}}}{{\text{of}}}$ and $ \displaystyle \frac{{\text{part}}}{{\text{whole}}}$ tricks. You can remember these since the word that comes first in the alphabet (“is” and “part”) are on the top of the fractions. You can typically solve percentage problems by using the following formula:

$ \displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{\text{ }\!\!\%\!\!\text{ }}{{100}}$

What this means is that the number around the “is” in an equation is on top of the proportion, and the number that comes after the “of” in an equation is on bottom of the proportion, and the percentage is over the $ 100$.

You can also think of this as the following, but you have to remember that sometimes the part may be actually be bigger than the whole (if the percentage is greater than $ 100$):

$ \displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\text{ }\!\!\%\!\!\text{ }}{{100}}$

Here are some examples, using the same problems that we did above. (Later, in the Algebra Word Problems section , we’ll learn how to translate math word problems like these word-for-word from English to math.)

• What is $ 20\%$ of $ 100$? Since the $ 20$ is the $ \%$ part, put that over the $ 100$. The $ 100$ comes after the “of”, so put that on the bottom. We’re looking for the “part” of the “whole”.

$ \displaystyle \frac{{\text{is}}}{{\text{of}}}=\,\frac{\%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{?}{{100}}=\frac{{20}}{{100}}\,\,\,\,\,\,\,\,\,?=20$

• $ 100$ is what percentage of $ 200$? The $ 100$ is close to the “is”, so put that on the top. The $ 200$ comes after the “of”, so put that on the bottom. The $ 100$ is the “part” of the $ 200$ “whole”.

$ \displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{100}}{{200}}=\frac{{?\,\,\,\%}}{{100}}\,\,\,\,\,\,\,\,\,?=50$

• $ 200$ is $ 50\%$ of what number? The $ 200$ is close to the “is” and we don’t know what the “of” is. The $ 50$ is the percentage. The $ 200$ is the “part”, so we need to find the “whole”.

$ \displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{part}}}{{\text{whole}}}=\frac{%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{200}}{?}=\frac{{50}}{{100}}\,\,\,\,\,\,\,\,\,?=400$

Here are a few more problems on rates and percentages ; remember to cross-multiply to find the answers.

Remember also – if you’re not quite sure what you’re doing, think of the problems with easier numbers and see how you’re doing it! This can help a lot of the time. Learn these rules and practice, practice, practice!

Click on Submit (the arrow to the right of the problem) to solve this problem. You can also type in more problems, or click on the 3 dots in the upper right hand corner to drill down for example problems.

If you click on “Tap to view steps”, you will go to the  Mathway  site, where you can register for the  full version  (steps included) of the software.  You can even get math worksheets.

You can also go to the  Mathway  site here , where you can register, or just use the software for free without the detailed solutions.  There is even a Mathway App for your mobile device.  Enjoy!

On to Negative Numbers and Absolute Value   – you are ready!!

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

Stormy Daniels Takes the Stand

The porn star testified for eight hours at donald trump’s hush-money trial. this is how it went..

This transcript was created using speech recognition software. While it has been reviewed by human transcribers, it may contain errors. Please review the episode audio before quoting from this transcript and email [email protected] with any questions.

It’s 6:41 AM. I’m feeling a little stressed because I’m running late. It’s the fourth week of Donald J. Trump’s criminal trial. It’s a white collar trial. Most of the witnesses we’ve heard from have been, I think, typical white collar witnesses in terms of their professions.

We’ve got a former publisher, a lawyer, accountants. The witness today, a little less typical, Stormy Daniels, porn star in a New York criminal courtroom in front of a jury more accustomed to the types of witnesses they’ve already seen. There’s a lot that could go wrong.

From “The New York Times,” I’m Michael Barbaro. This is “The Daily.”

Today, what happened when Stormy Daniels took the stand for eight hours in the first criminal trial of Donald J. Trump. As before, my colleague Jonah Bromwich was inside the courtroom.

[MUSIC PLAYING]

It’s Friday, May 10th.

So it’s now day 14 of this trial. And I think it’s worth having you briefly, and in broad strokes, catch listeners up on the biggest developments that have occurred since you were last on, which was the day that opening arguments were made by both the defense and the prosecution. So just give us that brief recap.

Sure. It’s all been the prosecution’s case so far. And prosecutors have a saying, which is that the evidence is coming in great. And I think for this prosecution, which is trying to show that Trump falsified business records to cover up a sex scandal, to ease his way into the White House in 2016, the evidence has been coming in pretty well. It’s come in well through David Pecker, former publisher of The National Enquirer, who testified that he entered into a secret plot with Trump and Michael Cohen, his fixer at the time, to suppress negative stories about Trump, the candidate.

It came in pretty well through Keith Davidson, who was a lawyer to Stormy Daniels in 2016 and negotiated the hush money payment. And we’ve seen all these little bits and pieces of evidence that tell the story that prosecutors want to tell. And the case makes sense so far. We can’t tell what the jury is thinking, as we always say.

But we can tell that there’s a narrative that’s coherent and that matches up with the prosecution’s opening statement. Then we come to Tuesday. And that day really marks the first time that the prosecution’s strategy seems a little bit risky because that’s the day that Stormy Daniels gets called to the witness stand.

OK, well, just explain why the prosecution putting Stormy Daniels on the stand would be so risky. And I guess it makes sense to answer that in the context of why the prosecution is calling her as a witness at all.

Well, you can see why it makes sense to have her. The hush money payment was to her. The cover-up of the hush money payment, in some ways, concerns her. And so she’s this character who’s very much at the center of this story. But according to prosecutors, she’s not at the center of the crime. The prosecution is telling a story, and they hope a compelling one. And arguably, that story starts with Stormy Daniels. It starts in 2006, when Stormy Daniels says that she and Trump had sex, which is something that Trump has always denied.

So if prosecutors were to not call Stormy Daniels to the stand, you would have this big hole in the case. It would be like, effect, effect, effect. But where is the cause? Where is the person who set off this chain reaction? But Stormy Daniels is a porn star. She’s there to testify about sex. Sex and pornography are things that the jurors were not asked about during jury selection. And those are subjects that bring up all kinds of different complex reactions in people.

And so, when the prosecutors bring Stormy Daniels to the courtroom, it’s very difficult to know how the jurors will take it, particularly given that she’s about to describe a sexual episode that she says she had with the former president. Will the jurors think that makes sense, as they sit here and try to decide a falsifying business records case, or will they ask themselves, why are we hearing this?

So the reason why this is the first time that the prosecution’s strategy is, for journalists like you, a little bit confusing, is because it’s the first time that the prosecution seems to be taking a genuine risk in what they’re putting before these jurors. Everything else has been kind of cut and dry and a little bit more mechanical. This is just a wild card.

This is like live ammunition, to some extent. Everything else is settled and controlled. And they know what’s going to happen. With Stormy Daniels, that’s not the case.

OK, so walk us through the testimony. When the prosecution brings her to the stand, what actually happens?

It starts, as every witness does, with what’s called direct examination, which is a fancy word for saying prosecutors question Stormy Daniels. And they have her tell her story. First, they have her tell the jury about her education and where she grew up and her professional experience. And because of Stormy Daniels’s biography, that quickly goes into stripping, and then goes into making adult films.

And I thought the prosecutor who questioned her, Susan Hoffinger, had this nice touch in talking about that, because not only did she ask Daniels about acting in adult films. But she asked her about writing and directing them, too, emphasizing the more professional aspects of that work and giving a little more credit to the witness, as if to say, well, you may think this or you may think that. But this is a person with dignity who took what she did seriously. Got it.

What’s your first impression of Daniels as a witness?

It’s very clear that she’s nervous. She’s speaking fast. She’s laughing to herself and making small jokes. But the tension in the room is so serious from the beginning, from the moment she enters, that those jokes aren’t landing. So it just feels, like, really heavy and still and almost oppressive in there. So Daniels talking quickly, seeming nervous, giving more answers than are being asked of her by the prosecution, even before we get to the sexual encounter that she’s about to describe, all of that presents a really discomfiting impression, I would say.

And how does this move towards the encounter that Daniels ultimately has?

It starts at a golf tournament in 2006, in Lake Tahoe, Nevada. Daniels meets Trump there. There are other celebrities there, too. They chatted very briefly. And then she received a dinner invitation from him. She thought it over, she says. And she goes to have dinner with Trump, not at a restaurant, by the way. But she’s invited to join him in the hotel suite.

So she gets to the hotel suite. And his bodyguard is there. And the hotel door is cracked open. And the bodyguard greets her and says she looks nice, this and that. And she goes in. And there’s Donald Trump, just as expected. But what’s not expected, she says, is that he’s not wearing what you would wear to a dinner with a stranger, but instead, she says, silk or satin pajamas. She asked him to change, she says. And he obliges.

He goes, and he puts on a dress shirt and dress pants. And they sit down at the hotel suite’s dining room table. And they have a kind of bizarre dinner. Trump is asking her very personal questions about pornography and safe sex. And she testifies that she teased him about vain and pompous he is. And then at some point, she goes to the bathroom. And she sees that he has got his toiletries in there, his Old Spice, his gold tweezers.

Very specific details.

Yeah, we’re getting a ton of detail in this scene. And the reason we’re getting those is because prosecutors are trying to elicit those details to establish that this is a credible person, that this thing did happen, despite what Donald Trump and his lawyers say. And the reason you can know it happened, prosecutors seem to be saying, is because, look at all these details she can still summon up.

She comes out of the bathroom. And she says that Donald Trump is on the hotel bed. And what stands out to me there is what she describes as a very intense physical reaction. She says that she blacked out. And she quickly clarifies, she doesn’t mean from drugs or alcohol. She means that, she says, that the intensity of this experience was such that, suddenly, she can’t remember every detail. The prosecution asks a question that cuts directly to the sex. Essentially, did you start having sex with him? And Daniels says that she did. And she continues to provide more details than even, I think, the prosecution wanted.

And I think we don’t want to go chapter and verse through this claimed sexual encounter. But I wonder what details stand out and which details feel important, given the prosecution’s strategy here.

All the details stand out because it’s a story about having had sex with a former president. And the more salacious and more private the details feel, the more you’re going to remember them. So we’ll remember that Stormy Daniels said what position they had sex in. We’ll remember that she said he didn’t use a condom. Whether that’s important to the prosecution’s case, now, that’s a much harder question to answer, as we’ve been saying.

But what I can tell you is, as she’s describing having had sex with Donald Trump, and Donald Trump is sitting right there, and Eric Trump, his son, is sitting behind him, seeming to turn a different color as he hears this embarrassment of his father being described to a courtroom full of reporters at this trial, it’s hard to even describe the energy in that room. It was like nothing I had ever experienced. And it was just Daniels’s testimony and, seemingly, the former President’s emotions. And you almost felt like you were trapped in there with both of them as this description was happening.

Well, I think it’s important to try to understand why the prosecution is getting these details, these salacious, carnal, pick your word, graphic details about sex with Donald Trump. What is the value, if other details are clearly making the point that she’s recollecting something?

Well, I think, at this point, we can only speculate. But one thing we can say is, this was uncomfortable. This felt bad. And remember, prosecutor’s story is not about the sex. It’s about trying to hide the sex. So if you’re trying to show a jury why it might be worthwhile to hide a story, it might be worth —

Providing lots of salacious details that a person would want to hide.

— exposing them to how bad that story feels and reminding them that if they had been voters and they had heard that story, and, in fact, they asked Daniels this very question, if you hadn’t accepted hush money, if you hadn’t signed that NDA, is this the story you would have told? And she said, yes. And so where I think they’re going with this, but we can’t really be sure yet, is that they’re going to tell the jurors, hey, that story, you can see why he wanted to cover that up, can’t you?

You mentioned the hush money payments. What testimony does Daniels offer about that? And how does it advance the prosecution’s case of business fraud related to the hush money payments?

So little evidence that it’s almost laughable. She says that she received the hush money. But we actually already heard another witness, her lawyer at the time, Keith Davidson, testify that he had received the hush money payment on her behalf. And she testified about feeling as if she had to sell this story because the election was fast approaching, almost as if her leverage was slipping away because she knew this would be bad for Trump.

That feels important. But just help me understand why it’s important.

Well, what the prosecution has been arguing is that Trump covered up this hush money payment in order to conceal a different crime. And that crime, they say, was to promote his election to the presidency by illegal means.

Right, we’ve talked about this in the past.

So when Daniels ties her side of the payment into the election, it just reminds the jurors maybe, oh, right, this is what they’re arguing.

So how does the prosecution end this very dramatic, and from everything you’re saying, very tense questioning of Stormy Daniels about this encounter?

Well, before they can even end, the defense lawyers go and they consult among themselves. And then, with the jury out of the room, one of them stands up. And he says that the defense is moving for a mistrial.

On what terms?

He says that the testimony offered by Daniels that morning is so prejudicial, so damning to Trump in the eyes of the jury, that the trial can no longer be fair. Like, how could these jurors have heard these details and still be fair when they render their verdict? And he says a memorable expression. He says, you can’t un-ring that bell, meaning they heard it. They can’t un-hear it. It’s over. Throw out this trial. It should be done.

Wow. And what is the response from the judge?

So the judge, Juan Merchan, he hears them out. And he really hears them out. But at the end of their arguments, he says, I do think she went a little too far. He says that. He said, there were things that were better left unsaid.

By Stormy Daniels?

By Stormy Daniels. And he acknowledges that she is a difficult witness. But, he says, the remedy for that is not a mistrial, is not stopping the whole thing right now. The remedy for that is cross-examination. If the defense feels that there are issues with her story, issues with her credibility, they can ask her whatever they want. They can try to win the jury back over. If they think this jury has been poisoned by this witness, well, this is their time to provide the antidote. The antidote is cross-examination. And soon enough, cross-examination starts. And it is exactly as intense and combative as we expected.

We’ll be right back.

So, Jonah, how would you characterize the defense’s overall strategy in this intense cross-examination of Stormy Daniels?

People know the word impeach from presidential impeachments. But it has a meaning in law, too. You impeach a witness, and, specifically, their credibility. And that’s what the defense is going for here. They are going to try to make Stormy Daniels look like a liar, a fraud, an extortionist, a money-grubbing opportunist who wanted to take advantage of Trump and sought to do so by any means necessary.

And what did that impeachment strategy look like in the courtroom?

The defense lawyer who questions Stormy Daniels is a woman named Susan Necheles. She’s defended Trump before. And she’s a bit of a cross-examination specialist. We even saw her during jury selection bring up these past details to confront jurors who had said nasty things about Trump on social media with. And she wants to do the same thing with Daniels. She wants to bring up old interviews and old tweets and things that Daniels has said in the past that don’t match what Daniels is saying from the stand.

What’s a specific example? And do they land?

Some of them land. And some of them don’t. One specific example is that Necheles confronts Daniels with this old tweet, where Daniels says that she’s going to dance down the street if Trump goes to jail. And what she’s trying to show there is that Daniels is out for revenge, that she hates Trump, and that she wants to see him go to jail. And that’s why she’s testifying against him.

And Daniels is very interesting during the cross-examination. It’s almost as if she’s a different person. She kind of squares her shoulders. And she sits up a little straighter. And she leans forward. Daniels is ready to fight. But it doesn’t quite land. The tweet actually says, I’ll dance down the street when he’s selected to go to jail.

And Daniels goes off on this digression about how she knows that people don’t get selected to go to jail. That’s not how it works. But she can’t really unseat this argument, that she’s a political enemy of Donald Trump. So that one kind of sticks, I would say. But there are other moves that Necheles tries to pull that don’t stick.

So unlike the prosecution, which typically used words like adult, adult film, Necheles seems to be taking every chance she can get to say porn, or pornography, or porn star, to make it sound base or dirty. And so when she starts to ask Daniels about actually being in pornography, writing, acting, and directing sex films, she tries to land a punch line, Necheles does. She says, so you have a lot of experience making phony stories about sex appear to be real, right?

As if to say, perhaps this story you have told about entering Trump’s suite in Lake Tahoe and having sex with him was made up.

Just another one of your fictional stories about sex. But Daniels comes back and says, the sex in the films, it’s very much real, just like what happened to me in that room. And so, when you have this kind of combat of a lawyer cross-examining very aggressively and the witness fighting back, you can feel the energy in the room shift as one lands a blow or the other does. But here, Daniels lands one back. And the other issue that I think Susan Necheles runs into is, she tries to draw out disparities from interviews that Daniels gave, particularly to N-TOUCH, very early on once the story was out.

It’s kind of like a tabloid magazine?

But some of the disparities don’t seem to be landing quite like Necheles would want. So she tries to do this complicated thing about where the bodyguard was in the room when Daniels walked into the room, as described in an interview in a magazine. But in that magazine interview, as it turns out, Daniels mentioned that Trump was wearing pajamas. And so, if I’m a juror, I don’t care where the bodyguard is. I’m thinking about, oh, yeah, I remember that Stormy Daniels said now in 2024 that Trump was wearing pajamas.

I’m curious if, as somebody in the room, you felt that the defense was effective in undermining Stormy Daniels’s credibility? Because what I took from the earlier part of our conversation was that Stormy Daniels is in this courtroom on behalf of the prosecution to tell a story that’s uncomfortable and has the kind of details that Donald Trump would be motivated to try to hide. And therefore, this defense strategy is to say, those details about what Trump might want to hide, you can’t trust them. So does this back and forth effectively hurt Stormy Daniels’s credibility, in your estimation?

I don’t think that Stormy Daniels came off as perfectly credible about everything she testified about. There are incidents that were unclear or confusing. There were things she talked about that I found hard to believe, when she, for instance, denied that she had attacked Trump in a tweet or talked about her motivations. But about what prosecutors need, that central story, the story of having had sex with him, we can’t know whether it happened.

But there weren’t that many disparities in these accounts over the years. In terms of things that would make me doubt the story that Daniels was telling, details that don’t add up, those weren’t present. And you don’t have to take my word for that, nor should you. But the judge is in the room. And he says something very, very similar.

What does he say? And why does he say it?

Well, he does it when the defense, again, at the end of the day on Thursday, calls for a mistrial.

With a similar argument as before?

Not only with a similar argument as before, but, like, almost the exact same argument. And I would say that I was astonished to see them do this. But I wasn’t because I’ve covered other trials where Trump is the client. And in those trials, the lawyers, again and again, called for a mistrial.

And what does Judge Marchan say in response to this second effort to seek a mistrial?

Let me say, to this one, he seems a little less patient. He says that after the first mistrial ruling, two days before, he went into his chambers. And he read every decision he had made about the case. He took this moment to reflect on the first decision. And he found that he had, in his own estimation, which is all he has, been fair and not allowed evidence that was prejudicial to Trump into this trial. It could continue. And so he said that again. And then he really almost turned on the defense. And he said that the things that the defense was objecting to were things that the defense had made happen.

He says that in their opening statement, the defense could have taken issue with many elements of the case, about whether there were falsified business records, about any of the other things that prosecutors are saying happened. But instead, he says, they focused their energy on denying that Trump ever had sex with Daniels.

And so that was essentially an invitation to the prosecution to call Stormy Daniels as a witness and have her say from the stand, yes, I had this sexual encounter. The upshot of it is that the judge not only takes the defense to task. But he also just says that he finds Stormy Daniels’s narrative credible. He doesn’t see it as having changed so much from year to year.

Interesting. So in thinking back to our original question here, Jonah, about the idea that putting Stormy Daniels on the stand was risky, I wonder if, by the end of this entire journey, you’re reevaluating that idea because it doesn’t sound like it ended up being super risky. It sounded like it ended up working reasonably well for the prosecution.

Well, let me just assert that it doesn’t really matter what I think. The jury is going to decide this. There’s 12 people. And we can’t know what they’re thinking. But my impression was that, while she was being questioned by the prosecution for the prosecution’s case, Stormy Daniels was a real liability. She was a difficult witness for them.

And the judge said as much. But when the defense cross-examined her, Stormy Daniels became a better witness, in part because their struggles to discredit her may have actually ended up making her story look more credible and stronger. And the reason that matters is because, remember, we said that prosecutors are trying to fill this hole in their case. Well, now, they have. The jury has met Stormy Daniels. They’ve heard her account. They’ve made of it what they will. And now, the sequence of events that prosecutors are trying to line up as they seek prison time for the former President really makes a lot of sense.

It starts with what Stormy Daniels says with sex in a hotel suite in 2006. It picks up years later, as Donald Trump is trying to win an election and, prosecutors say, suppressing negative stories, including Stormy Daniels’s very negative story. And the story that prosecutors are telling ends with Donald Trump orchestrating the falsification of business records to keep that story concealed.

Well, Jonah, thank you very much. We appreciate it.

Of course, thanks for having me.

The prosecution’s next major witness will be Michael Cohen, the former Trump fixer who arranged for the hush money payment to Stormy Daniels. Cohen is expected to take the stand on Monday.

Here’s what else you need to know today. On Thursday, Israeli Prime Minister Benjamin Netanyahu issued a defiant response to warnings from the United States that it would stop supplying weapons to Israel if Israel invades the Southern Gaza City of Rafah. So far, Israel has carried out a limited incursion into the city where a million civilians are sheltering, but has threatened a full invasion. In a statement, Netanyahu said, quote, “if we need to stand alone, we will stand alone.”

Meanwhile, high level ceasefire negotiations between Israel and Hamas have been put on hold in part because of anger over Israel’s incursion into Rafah.

A reminder, tomorrow, we’ll be sharing the latest episode of our colleague’s new show, “The Interview” This week on “The Interview,” Lulu Garcia-Navarro talks with radio host Charlamagne Tha God about his frustrations with how Americans talk about politics.

If me as a Black man, if I criticize Democrats, then I’m supporting MAGA. But if I criticize, you know, Donald Trump and Republicans, then I’m a Democratic shill. Why can’t I just be a person who deals in nuance?

Today’s episode was produced by Olivia Natt and Michael Simon Johnson. It was edited by Lexie Diao, with help from Paige Cowett, contains original music by Will Reid and Marion Lozano, and was engineered by Alyssa Moxley. Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly.

That’s it for “The Daily.” I’m Michael Barbaro. See you on Monday.

• May 15, 2024   •   25:48 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India
• May 8, 2024   •   28:28 A Plan to Remake the Middle East
• May 7, 2024   •   27:43 How Changing Ocean Temperatures Could Upend Life on Earth
• May 6, 2024   •   29:23 R.F.K. Jr.’s Battle to Get on the Ballot
• May 3, 2024   •   25:33 The Protesters and the President
• May 2, 2024   •   29:13 Biden Loosens Up on Weed
• May 1, 2024   •   35:16 The New Abortion Fight Before the Supreme Court
• April 30, 2024   •   27:40 The Secret Push That Could Ban TikTok

Hosted by Michael Barbaro

Featuring Jonah E. Bromwich

Produced by Olivia Natt and Michael Simon Johnson

Edited by Lexie Diao

With Paige Cowett

Original music by Will Reid and Marion Lozano

Engineered by Alyssa Moxley

Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube

This episode contains descriptions of an alleged sexual liaison.

What happened when Stormy Daniels took the stand for eight hours in the first criminal trial of former President Donald J. Trump?

Jonah Bromwich, one of the lead reporters covering the trial for The Times, was in the room.

On today’s episode

Jonah E. Bromwich , who covers criminal justice in New York for The New York Times.

Background reading

In a second day of cross-examination, Stormy Daniels resisted the implication she had tried to shake down Donald J. Trump by selling her story of a sexual liaison.

Here are six takeaways from Ms. Daniels’s earlier testimony.

There are a lot of ways to listen to The Daily. Here’s how.

We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.

The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Dan Farrell, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.

Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Renan Borelli, Maddy Masiello, Isabella Anderson and Nina Lassam.

Jonah E. Bromwich covers criminal justice in New York, with a focus on the Manhattan district attorney’s office and state criminal courts in Manhattan. More about Jonah E. Bromwich

Advertisement