math problems to solve with programming

About Project Euler

What is Project Euler?

Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems. The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.

Who are the problems aimed at?

The intended audience include students for whom the basic curriculum is not feeding their hunger to learn, adults whose background was not primarily mathematics but had an interest in things mathematical, and professionals who want to keep their problem solving and mathematics on the cutting edge.

Currently we have 1292775 registered members who have solved at least one problem, representing 220 locations throughout the world, and collectively using 112 different programming languages to solve the problems.

Can anyone solve the problems?

The problems range in difficulty and for many the experience is inductive chain learning. That is, by solving one problem it will expose you to a new concept that allows you to undertake a previously inaccessible problem. So the determined participant will slowly but surely work his/her way through every problem.

In order to track your progress it is necessary to setup an account and have Cookies enabled.

If you already have an account, then Sign In . Otherwise, please Register – it's completely free!

However, as the problems are challenging, then you may wish to view the Problems before registering.

"Project Euler exists to encourage, challenge, and develop the skills and enjoyment of anyone with an interest in the fascinating world of mathematics."

The page has been left unattended for too long and that link/button is no longer active. Please refresh the page.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Mathematical Programming Tasks

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Computer Science Principles

Course: ap®︎/college computer science principles   >   unit 3, mathematical expressions.

• Mathematical procedures and constants

Arithmetic operators

Multiple operators, storing with variables, pseudocode for mathematical expressions, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

DEV Community

Posted on Nov 3, 2023 • Updated on Mar 15

Why we need MATH for Programming (10 math concepts)

Many people believe that you don't need to know any math to be a computer programmer. While that may be partially true, understanding some essential math concepts can make programming much more accessible and help you unlock the secrets of the digital world.

Now, let's explore the 10 math concepts that every programmer should be familiar with.

1. Boolean Algebra

Boolean algebra is a fundamental concept in programming. It deals with binary variables that can have only two values: true or false. We use three operators to work with Boolean values: AND , OR , and NOT .

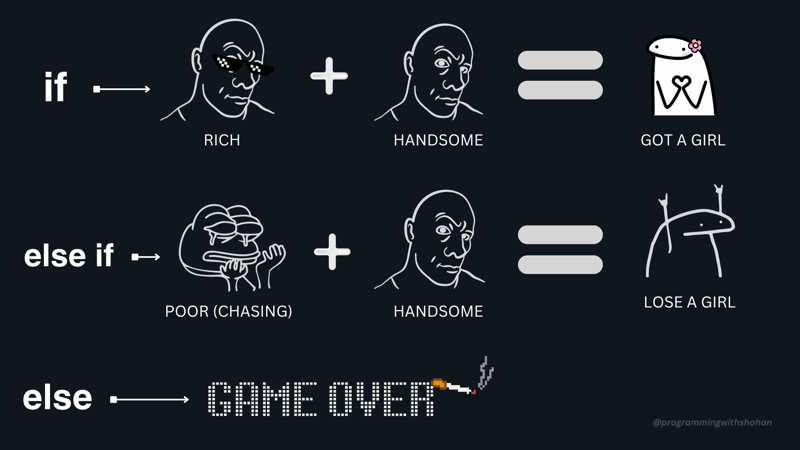
Imagine these as tools for making decisions. For example, if you want to know if someone is both rich and handsome to get a girl , Boolean variables can help you decide. If both conditions are met, he gets a girl. If not, he may have other options. You can represent this logic using if statements, Venn diagrams , or truth tables .

2. Numeral Systems

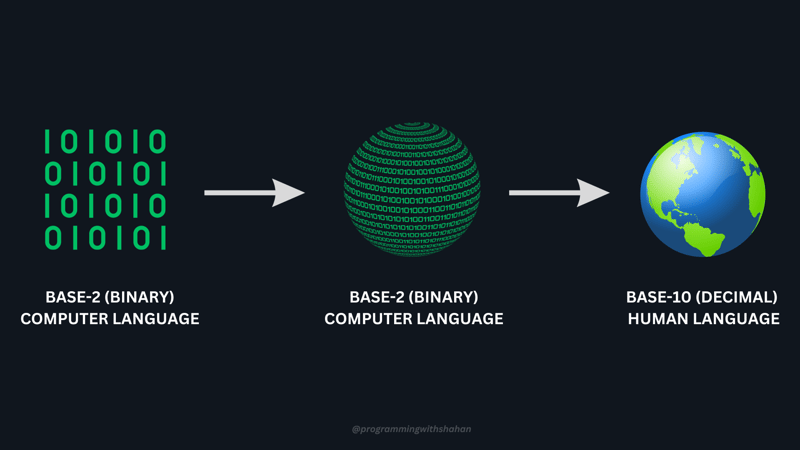
Computers use base-2 (binary) numeral systems, unlike humans who use base-10 (decimal) systems. In base-2, numbers are represented using only two symbols: 0 and 1. Understanding binary helps us work with other numeral systems like hexadecimal (base-16) and base-64, which are essential in programming, especially for encoding and representing data.

3. Floating Point Numbers

Floating point numbers are how computers represent real numbers. They are not always precise, which can lead to tiny errors in calculations. These numbers use scientific notation to handle large and small values efficiently. Knowing the limitations of floating point numbers is crucial for avoiding these errors in your code.

4. Logarithmic Functions

Logarithms help us understand how some natural phenomena work. Think of a logarithm as a way to measure how many times you need to cut a log to reach a specific length. In programming, logarithmic functions are used in algorithms like binary search. These functions play a vital role in various applications, from algorithms to scientific research.

5. Set Theory

The set theory deals with collections of unique values. In programming, this concept is used extensively, especially in databases, where tables are sets of unique rows. Joining sets, finding intersections, unions, and differences are common operations in this context. Understanding set theory is important for working with databases and data manipulation.

6. Combinatorics

Combinatorics is all about counting things and combinations. Whether you're developing algorithms for news apps or designing globally distributed databases, combinatorics helps you calculate all possible combinations or permutations efficiently. It's a valuable skill in programming.

7. Graph Theory

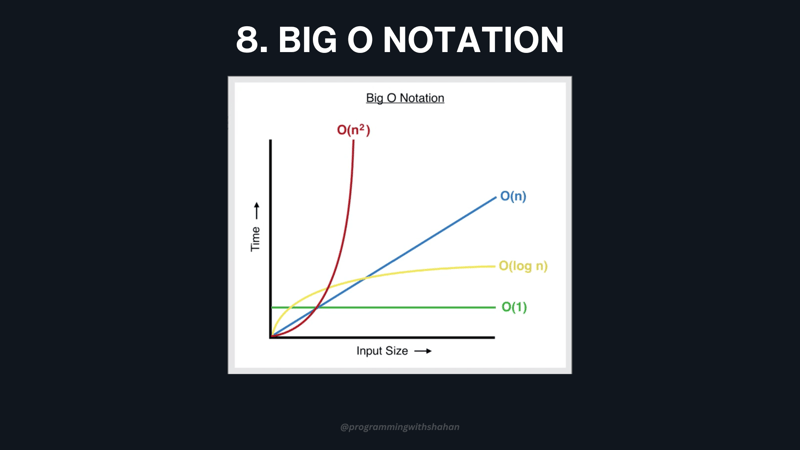
8. Complexity Theory (Big O Notation)

Complexity theory helps you analyze the efficiency of algorithms. Big O notation is a tool for expressing the time and memory complexity of algorithms. It helps you choose the most efficient solution for your programming tasks, a valuable skill for interviews and writing efficient code.

9. Statistics

Statistics is essential for various fields of programming, especially in artificial intelligence and machine learning. Understanding basic statistical concepts like mean, median, mode, and standard deviation is what makes you best at making predictions. It's the foundation for making predictions and decisions in data-driven applications .

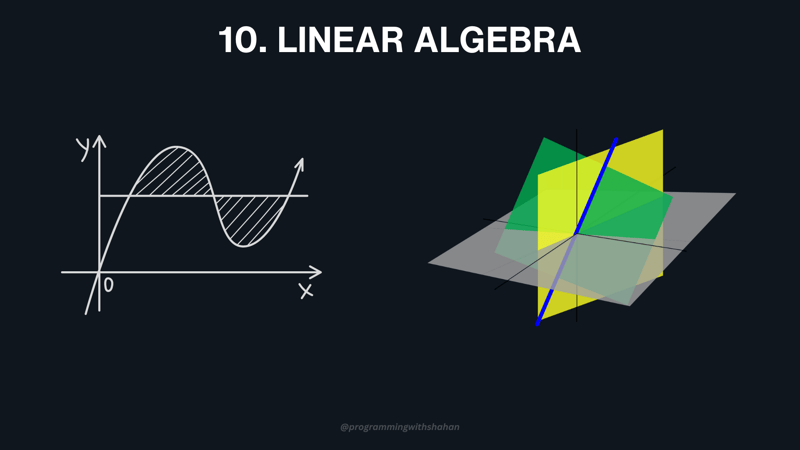
10. Linear Algebra

Linear algebra is essential in computer graphics, deep neural networks, and many other areas of programming. It involves scalars, vectors, and matrices to represent and manipulate data. If you want to work with 3D graphics, cryptography, and machine learning, then Linear Algebra come into play. You need to master Linear Algebra to tackle these.

🤖 Recommendation: Use Notion to boost productivity

Notion is a fantastic tool for developers! It supports syntax highlighting for over 60 programming languages. If your day-to-day involves reading coding docs, watching programming tutorials and tracking progress, taking notes, and writing content, Notion can make you more efficient.

Notion is more than just a note-taking app. As a developer, you can use Notion to track your freelance projects, organize your code snippets, collaborate with clients, keep track of jobs you're applying for, and integrate with third-party tools to boost your entire developer workflow 10x faster.

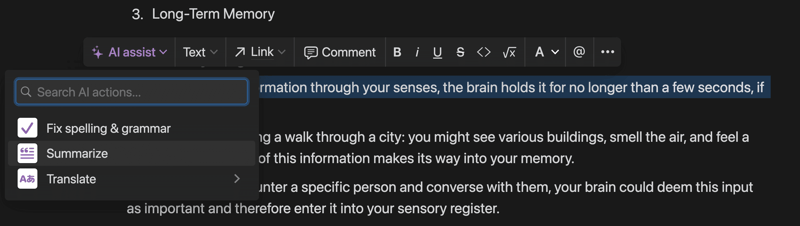
Notion AI has the capacity to generate code, equations, graphs, and even explanations for code snippets. It is the smartest AI assistant that helps you think bigger, work faster, and augment your creativity, right inside the functional notion workspace you're already familiar with.

It is available as an add-on to Notion plans , including Free Plans, for $10 per member, per month. This gives you access to all AI features in Notion. A 20% discount is available to all workspaces on any plan with annual billing .

Mathematics is a powerful tool in the world of programming, and these 10 concepts are just the beginning. They can help you develop more efficient code, solve complex problems, and unveil the magic behind the digital world. These math concepts will make you a better programmer, and you'll be well-equipped to conquer a wide range of challenges in the ever-evolving field of technology.

You can watch a short video of this article here:

Related articles: The Roadmap to Frontend Developer in 6 months

Stay tuned for more valuable content, and if you find it helpful, you may also like my YouTube channel .

You can follow me on X for latest tech updates.

Top comments (16)

Templates let you quickly answer FAQs or store snippets for re-use.

• Location Germany
• Work Flow specialist, IoT developer
• Joined May 24, 2021

Even if you have some knowlede about mathematical concepts, you will find that the implementation in a certain language often differs from the generalized concept:

• You know, what a floating point number is, but the implementation limits this to a certain number range.
• Numerical results have a limited accuracy giving you unexpected results: 14900*(10.8/100) = 1609.200000000003 (Javascript)
• Boolean knows True and False, but you can also write if (a > "0") ... The result will mainly depend on the language you use

So, even if you know the mathematical concept, this might not be enough to master a programming language.

If you are dealing with 3D-geometry and need to show some perspective projection, they are very efficient to calculate the image. But the best thing about Homogeneous coordinates is that they are able to accumulate a number of transformations in a single matrix. Usually your would apply a number of transformations one by one to show an object: Assume, A, B and C are matrices that apply a single tranformation to a point P, which is a vector. If you want to calculate the projected positions, you need to write:

Instead, with homogenuous coordinates you write:

Assume, there is not a single point, but millions of points to show. Instead of applying multiple vector multiplications, you just need to do one.

Mathematical concepts can be most helpful to programmers, but programming has it´s own rules. A good mathematician will not necessarily be a good programmer. And there are many mathematical disciplines, that apply mainly to solving programming problems. Computer geometry is one of them, discrete mathematics another one. Many programmers will not do much more mathematics than adding 1+1, but on certain fields it is good to know the mathematical concepts.

• Joined Jul 17, 2019

Eckehard, you will Always surprise me:-)

• Joined Oct 5, 2023

Wow! That’s a brilliant explanation. Exactly what I believe. Thanks for sharing this.

• Location Brazil
• Education M.E. in Computer Engineering
• Pronouns she/her
• Joined Oct 17, 2022

I agree that it's essential to have a solid grasp of the fundamentals and progressively deepen the knowledge as the need arises.

But when it comes to game development, the requirements often extend beyond the basics and may even demand an understanding of physics.

I'm not trying to discourage anyone, but it's good to be aware of this if you're interested in pursuing this career 😅

• Email [email protected]
• Location Sylhet, Bangladesh
• Joined Jun 3, 2021

Yep! I agree with that.

• Email [email protected]
• Education Mathematics, Ph.D
• Work Researcher, Developer
• Joined Jul 13, 2023

Hi. Thanks for your post. I totally agree that math is fundamental for being a nice programmer. Actually, I could added some topics to your list that are important to understand what programming really is.

• Formal systems : programming languages are particular examples of formal systems. Studying formal systems allow you to think about programming in a more formal way.
• Type Theory : any programming language that has data structures is a kind of type system. Studying type theory allow you to better understand what is the role that data structures play in a programming language.
• Category Theory : the topic above are about the syntax of programming languages. Category theory, on tge other hand, plays a fundamental role in the description of their semantics.

• Location Niš, Srbija
• Education BCS
• Work It Mrav
• Joined Aug 18, 2018

I like this kind of articles, right on the points. "Intuition" math is what most coders need, but in order to solve any complex problem math probably already has a solution that you only need to employ. Learn as you go and don't fear math it is 🌻

Exactly! Don't fear math. Learn when needed. This is how you can master programming as you go along.

• Joined Jan 19, 2023

Very Useful for **me **and my followers!

• Location Minneapolis, MN
• Education B.A. English (Creative Writing), Minnesota State University
• Pronouns he/him/dude
• Work Solutions Architect at Wings Financial Credit Union
• Joined Sep 30, 2021

I mean, other than that incel garbage in the first diagram, this was a pretty solid article.

• Joined Feb 25, 2024

Man I’ve been to interested in cryptography and learning algorithms and python man , I would really like to tap in with someone hands on

Hey jasaan, Thanks for sharing your interest. I would recommend you start with a programming language (python is most popular for beginners), then learn algorithms, cryptography and so on. You can always ask me questions on LinkedIn or Twitter .

• Location Norway
• Education Business School and IB School of Economics
• Work Private Investor and Volunteer DEV Mod
• Joined Oct 27, 2023

I have understood that basic math is what is needed for most programmers. For game programmers on the other hand, is knowledge of Vector Math in addition to basic math, important (which you already mentioned in 10. Linear Algebra).

Yes, it's true that basic math is enough for most programmers (e.g. web developers), as they usually don't need to be involved in complex tasks such as game development, competitive programming, and so on. But knowing them is super beneficial to sharpening your coding skills.

Again, I believe learning things when necessary is the best way to master programming. Learning lots of things without applying them is never going to be helpful. This is what I experienced after spending countless hours learning useless things that I didn't need. I rarely remember lots of programming concepts that I haven't used in the past few months.

• Joined Nov 13, 2023

You can take a look at AI-related analysis at bestaiproductlist.com/

Are you sure you want to hide this comment? It will become hidden in your post, but will still be visible via the comment's permalink .

Hide child comments as well

For further actions, you may consider blocking this person and/or reporting abuse

3075. Maximize Happiness of Selected Children

MD ARIFUL HAQUE - May 9

Building a Portfolio: Showcasing Your Projects and Skills to Stand Out in the Job Market

Syed Balkhi - May 4

Installing and Configuring MySQL on Arch Linux

tinApyp - May 5

Code Improvements

Walter Nascimento - May 8

We're a place where coders share, stay up-to-date and grow their careers.

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers
• Competitive Programming - A Complete Guide
• Competitive Programming (CP) Handbook with Complete Roadmap

Mathematics for Competitive Programming

Must do math for competitive programming.

• Pigeonhole Principle for CP | Identification, Approach & Problems
• Euler Totient for Competitive Programming
• Essential Maths for Competitive Programming Course By GeeksforGeeks

Number Theory for CP

• Binary Exponentiation for Competitive Programming
• GCD (Greatest Common Divisor) Practice Problems for Competitive Programming

Bit Manipulation for CP

• Bit Manipulation for Competitive Programming
• Bit Tricks for Competitive Programming
• Bitwise Hacks for Competitive Programming

Combinatorics for CP

• Inclusion Exclusion principle for Competitive Programming

Greedy for CP

• Binary Search on Answer Tutorial with Problems
• Ternary Search for Competitive Programming

Array based concepts for CP

• What are Online and Offline query-based questions in Competitive Programming
• Precomputation Techniques for Competitive Programming
• PreComputation Technique on Arrays
• Frequency Measuring Techniques for Competitive Programming

Dynamic Programming (DP) for CP

• DP on Trees for Competitive Programming
• Dynamic Programming in Game Theory for Competitive Programming

Game Theory for CP

• Interactive Problems in Competitive Programming
• Mastering Bracket Problems for Competitive Programming
• MEX (Minimum Excluded) in Competitive Programming

Graphs for CP

• BFS using STL for competitive coding

Advanced Data Structure

• Introduction to Heavy Light Decomposition
• Meet in the middle
• Policy based data structures in g++

Competitive Programming in Python

• Getting Started with Competitive Programming in Python
• Why is python best suited for Competitive Coding?
• Python in Competitive Programming
• Competitive Coding Setup for C++ and Python in VS Code using Python Script
• Python Input Methods for Competitive Programming
• Input/Output from external file in C/C++, Java and Python for Competitive Programming
• Fast I/O for Competitive Programming in Python
• Which Python Modules are useful for competitive programming?
• Python Tricks for Competitive Coding

Competitive Programming in C++

• Why C++ is best for Competitive Programming?
• Setting up a C++ Competitive Programming Environment
• How to setup Competitive Programming in Visual Studio Code for C++
• Setting up Sublime Text For Competitive Programming (C++) Using Fast Olympic Coding Plugin
• Setting Up Sublime Text For Competitive Coding in C++14 on Ubuntu
• Writing C/C++ code efficiently in Competitive programming
• Writing code faster during Competitive Programming in C++
• Which C++ libraries are useful for competitive programming?
• C++: Methods of code shortening in competitive programming
• Common mistakes to be avoided in Competitive Programming in C++ | Beginners
• C++ tricks for competitive programming (for C++ 11)

Competitive Programming in Java

• Setting up Java Competitive Programming Environment
• How to Setup IntelliJ IDEA For Java Competitive Programming Environment?
• Fast I/O in Java in Competitive Programming
• Efficiently Reading Input For Competitive Programming using Java 8
• Java tricks for competitive programming (for Java 8)
• Java Generics to Code Efficiently in Competitive Programming
• Java Competitive Programming Setup in VS Code with Fast I/O and Snippets
• Which Java libraries are useful for competitive programming?

Competitive Programming in JavaScript

• How to get started with Competitive Programming in JavaScript
• What is Competitive Programming/Coding and How to Prepare for It?
• Fast I/O for Competitive Programming
• Why Should You Do Competitive Programming?
• How to Get Started with Competitive Programming?
• How to begin with Competitive Programming?
• How to read Competitive Programming Questions?
• Top Programming Languages For Competitive Programming
• 5 Best Languages for Competitive Programming
• Competitive Programming - Myths and Mind Blowing Facts
• What are Ad Hoc Problems in Competitive Programming?
• Learning the art of Competitive Programming
• How to become a master in competitive programming?

Tips & Tricks for CP

• Tips and Tricks for Competitive Programmers | Set 1 (For Beginners)
• Most Critical Mistakes & Tips in Competitive Programming
• How To Make Competitive Programming Interesting?
• Some important shortcuts in Competitive Programming
• A Better Way To Approach Competitive Programming
• Knowing the complexity in competitive programming
• Logarithm tricks for Competitive Programming
• Importance of Testing In Competitive Programming
• Tips for testing code in Competitive programming

Resources for CP

• What Are The Best Resources For Competitive Programming?
• Top 10 Algorithms and Data Structures for Competitive Programming
• Can ChatGPT be used to solve Competitive Coding Problems?
• Top 15 Websites for Coding Challenges and Competitions
• 7 Best Books for Competitive Programming

Career with CP

• Companies that hire Interns through Competitive programming in India
• Competitive Programming vs Software Development - Where Should I Invest My Time?
• Is Competitive Programming Must For Software Development Roles?
• How can competitive programming help you get a job?
• Is Competitive Programming Must For Getting Jobs at Product-Based Companies?

C ompetitive P rogramming ( CP ) doesn’t typically require one to know high-level calculus or some rocket science. But there are some concepts and tricks which are sufficient most of the time. You can definitely start competitive coding without any mathematical background, but maths becomes essential as you dive deep into the world of CP.

A majority of the Competitive Coding problems that you’ll encounter will have some mathematical logic or trick. All the algorithms that we learn are derived from a mathematical point of view. Most of the time, maths helps us solve the question within the necessary time constraints.  All of the topics can’t be covered in a single article but we’ll be looking into some of the most common mathematical concepts in competitive coding. Some of these concepts might look too difficult at first sight but applying them to problems will ease them for you. 

1. BigInteger  

For e. g. Calculating factorials of large numbers (lets say 100) or taking large numbers of input around 100000 digits in length. In c++, it is not possible to store these numbers even if we use long long int. One way to take this kind of number is, taking them into an array more wisely use a vector … each number will hold an index of the array, if the number is 12345 then 12345%10=5 will in index[4], and the number now=12345/10=1234. now 1234%10=4 will be in [3] and so on to 1%10=1 is in [0], or you can use string too, it is easier since the char array only allow 1 byte for each index so you don’t need that modulation operation to fit number into the index.  Java provides Biginteger class to handle this.

2. GCD , LCM , Euclidean Algorithm, Extended Euclidean Algorithm  

• LCM(a, b) * GCD(a, b) = a*b, calculating GCD is equivalent to calculating LCM. 

Now, how do we calculate the GCD of two numbers?  We can of course find the factors of the two numbers and then determine the highest common factor. As the numbers get bigger though ( say 155566328819), factorization becomes ineffective.  This is where Euclid’s algorithm comes to our rescue. This algorithm uses the easy-to-prove fact gcd(a, b)=gcd(b, r), where r is the remainder when a is divided by b, or just a%b. 

Can we find the numbers (x, y) such that ux + vy = gcd(u, v)?. There exists infinitely many pairs – this is Bezout’s Lemma. The algorithm to generate such pairs is called Extended Euclidean Algorithm.

3. Sieve of Eratosthenes and Segmented Sieve  

Generating primes fast is very important in some problems. Let’s cut to the chase and introduce Eratosthenes’s Sieve . You can use the Sieve of Eratosthenes to find all the prime numbers that are less than or equal to a given number N or to find out whether a number is a prime number.  The basic idea behind the Sieve of Eratosthenes is that at each iteration one prime number is picked up and all its multiples are eliminated. After the elimination process is complete, all the unmarked numbers that remain are prime.

Suppose we want to find all primes between 2 and 50. Iterate from 2 to 50. We start with 2. Since it is not checked, it is a prime number. Now check all numbers that are multiple of except 2. Now we move on, to number 3. It’s not checked, so it is a prime number. Now check all numbers that are multiple of 3, except 3. Now move on to 4. We see that this is checked – this is a multiple of 2! So 4 is not a prime. We continue doing this. 

What if the number is large (say 10^16), in that case we require segmented sieve . The idea of segmented sieve is to divide the range [0..n-1] in different segments and compute primes in all segments one by one. This algorithm first uses Simple Sieve to find primes smaller than or equal to ?(n). Below are steps used in Segmented Sieve. 

• Use Simple Sieve to find all primes up to square root of ‘n’ and store these primes in an array “prime[]”. Store the found primes in an array ‘prime[]’. 
• We need all primes in range [0..n-1]. We divide this range in different segments such that size of every segment is at-most ?n 
• Create an array mark[high-low+1]. Here we need only O(x) space where x is number of elements in given range
• Iterate through all primes found in step 1. For every prime, mark its multiples in given range [low..high].  In Simple Sieve, we needed O(n) space which may not be feasible for large n. Here we need O(?n) space and we process smaller ranges at a time 

4. Modulo arithmetic, Modulo exponentiation and Modulo inverse  

When one number is divided by another, the modulo operation finds the remainder. It is denoted by the % symbol. Example  Assume that you have two numbers 10 and 3. 10%3 is 1 because when 10 is divided by 3, the remainder is 1. Properties : 1. (a+b)%c = ((a%c)+(b%c))%c  2. (a*b)%c = ((a%c)*(b%c))%c  3. (a-b)%c = ((a%c)-(b%c)+c)%c  4. (a/b)%c = ((a%c)?(b%c))%c 

When are these properties used?  Assume that a = 10^12, b = 10^12, and c = 10^9+7. You have to find (a*b)%c. When you multiply a with b, the answer is 10^24, which does not confirm with the standard integer data types. Therefore, to avoid this we used the properties. (a*b)%c = ((a%c)*(b%c))%c Fast Modulo exponentiation  Calculate a^b in modular m in O(log b),  It uses binary expansion of b, and is very straightforward. 

Now, let us talk about modular inverse . By using Extended Euclidean Algorithm, we can get the inverse of a modulo m. 

Fermat’s Little Theorem gives a^(p-1)==a (mod p) if gcd(a, p)=1, where p is a prime. Therefore, we can calculate the modular inverse of a as a^(p-2), by fast exponentiation also.

5. Lucas Theorem

We can calculate nCr in modulo p (p is a prime) very fast using Lucas’ Theorem. Lucas theorem basically suggests that the value of nCr can be computed by multiplying results of n(i)Cr(i) where n(i) and r(i) are individual same-positioned digits in base p representations of n and r respectively. This is very efficient when p is small and n, r is huge. We can precalculate the factorials and inverse of factorials modulo p by using the above code. 

6. Chinese Remainder Theorem<  

Two numbers (positive integers) a and b are relatively prime (prime to each other), if they have no common prime factors. The numbers m1, m2, ….mr, are pair wise relatively prime if any two distinct numbers in that collection, are relatively prime. Chinese remainder theorem says that given any r pair wise relatively prime numbers m1, m2, ….mr, and any numbers b1, b2, b3, ….br, we can always find a number M which leaves the remainders b1, b2, b3, ..br when it is divided by m1, m2, …mr respectively.  Let us solve x == r (mod mi), where mi are pairwise coprime.  (If they are not coprime, break them into prime powers, and if some are contradictory, there are no solutions.)

7. Series and Sequences  

You just need to know some basics like : 

• What is a series and does it converge to some value?
• Know about famous series like trigonometric, hyperbolic…etc.
• How to calculate the finite limit of famous series like ( geometric series, harmonic series) 

and basically the same thing for the sequences, you just need to know the basics. (Trick: use OEIS site)  We sometimes land up in a situation when various coding problems can be simplified to a mathematical formula but often finding that formula isn’t that straightforward .Here comes, OEIS for rescue. We can calculate the terms for initial indices i.e n=0, 1, 2, 3, …….. and then may use OEIS to find the mathematical expression.

8. Catalan Numbers  

Catalan numbers are a sequence of natural numbers that helps to solve many counting problem. Terms starting with n=0 are : 1, 1, 2, 5, 14, 42, 132, 429, 1430 ….and so on.  Questions based on catalan number may appear in many coding competitions. So it is always a plus point to know in depth about catalan number.  Catalan numbers find extensive applications in forming closed solutions to combinatorics problems. Some of the examples are: 

• The number of binary search trees that can be formed using ‘n’ nodes is the nth Catalan number. 
• The number of ways that a convex polygon of n+2 sides, can be cut into 2 or more triangles by joining any 2 edges is the nth Catalan number. 
• The closed solution to the number of possible parentheses matching given ‘n’ pairs is the nth Catalan number.

9. Pigeonhole Principle 

The pigeonhole principle is a powerful tool used in combinatorial maths. But the idea is simple and can be explained by the following peculiar problem. Imagine that 3 pigeons need to be placed into 2 pigeonholes. Can it be done? The answer is yes, but there is one catch. The catch is that no matter how the pigeons are placed, one of the pigeonholes must contain more than one pigeon.  The logic can be generalized for larger numbers.

The pigeonhole principle states that if more than n pigeons are placed into n pigeonholes, some pigeonhole must contain more than one pigeon. While the principle is evident, its implications are astounding.

For example consider this statement “If you pick five numbers from the integers 1 to 8, then two of them must add up to nine.”  Explanation: Every number can be paired with another to sum to nine. In all, there are four such pairs: the numbers 1 and 8, 2 and 7, 3 and 6, and lastly 4 and 5.Each of the five numbers belongs to one of those four pairs. By the pigeonhole principle, two of the numbers must be from the same pair–which by construction sums to 9.

10. Inclusion Exclusion Principle  

Inclusion Exclusion principle is a very basic theorem of counting and many problems in various programming contests are based on it, a formal explanation of inclusion exclusion principle goes as follows:  Consider A as a collection of objects and |A| as the number of objects in A and similarly for B, then the cardinality of collection of objects of both sets A and B ( when both A and B are disjoint) can be stated as (for 2 finite sets) : 

• |AUB| = |A| + |B| 

But what if the sets are not disjoint?  Then we need to subtract the common objects counted twice while calculating the cardinality of both A and B and new form will become: 

• AUB| = |A| + |B| – |A ∩ B| 

This is the most basic form of the inclusion-exclusion principle.  But what if there are more than 2 sets, let`s say n sets.  Then it can be stated as : 

(Include=add, exclude=subtract)  |A1 U A2 U A3 …..U AN| = (Include count of each set, Exclude count of pairwise set, Include count of triplet sets, exclude count of quadruplet sets……till nth tuple is included( if odd) or excluded( if even))  i. e., |A1 U A2 U A3 …..U AN| = (|A1| + |A2| + |A3| + |A4| … + |AN|) – ( |A1 ∩ A2| + |A1 ∩ A3| + |A1 ∩ A4|.. + all combinations) + (|A1 ∩ A2 ∩ A3| … all combinations)………. and so on.

This list is not exhaustive but the concepts will be very useful in contests in codeforces, codechef etc.. So grab your pen, paper and laptop and start practicing. Happy coding!  

Please Login to comment...

Similar reads.

• GBlog-Competitive-Programming
• Modular Arithmetic
• Competitive Programming
• Mathematical
• Write From Home

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.12: Linear Programming

• Last updated
• Save as PDF
• Page ID 129563

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

After completing this section, you should be able to:

• Compose an objective function to be minimized or maximized.
• Compose inequalities representing a system application.
• Apply linear programming to solve application problems.

Imagine you hear about some natural disaster striking a far-away country; it could be an earthquake, a fire, a tsunami, a tornado, a hurricane, or any other type of natural disaster. The survivors of this disaster need help—they especially need food, water, and medical supplies. You work for a company that has these supplies, and your company has decided to help by flying the needed supplies into the disaster area. They want to maximize the number of people they can help. However, there are practical constraints that need to be taken into consideration; the size of the airplanes, how much weight each airplane can carry, and so on. How do you solve this dilemma? This is where linear programming comes into play. Linear programming is a mathematical technique to solve problems involving finding maximums or minimums where a linear function is limited by various constraints.

As a field, linear programming began in the late 1930s and early 1940s. It was used by many countries during World War II; countries used linear programming to solve problems such as maximizing troop effectiveness, minimizing their own casualties, and maximizing the damage they could inflict upon the enemy. Later, businesses began to realize they could use the concept of linear programming to maximize output, minimize expenses, and so on. In short, linear programming is a method to solve problems that involve finding a maximum or minimum where a linear function is constrained by various factors.

A Mathematician Invents a “Tsunami Cannon”

On December 26, 2004, a massive earthquake occurred in the Indian Ocean. This earthquake, which scientists estimate had a magnitude of 9.0 or 9.1 on the Richter Scale, set off a wave of tsunamis across the Indian Ocean. The waves of the tsunami averaged over 30 feet (10 meters) high, and caused massive damage and loss of life across the coastal regions bordering the Indian Ocean.

Usama Kadri works as an applied mathematician at Cardiff University in Wales. His areas of research include fluid dynamics and non-linear phenomena. Lately, he has been focusing his research on the early detection and easing of the effects of tsunamis. One of his theories involves deploying a series of devices along coastlines which would fire acoustic-gravity waves (AGWs) into an oncoming tsunami, which in theory would lessen the force of the tsunami. Of course, this is all in theory, but Kadri believes it will work. There are issues with creating such a device: they would take a tremendous amount of electricity to generate an AGW, for instance, but if it would save lives, it may well be worth it.

Compose an Objective Function to Be Minimized or Maximized

An objective function is a linear function in two or more variables that describes the quantity that needs to be maximized or minimized.

Example 5.96

Composing an objective function for selling two products.

Miriam starts her own business, where she knits and sells scarves and sweaters out of high-quality wool. She can make a profit of $8 per scarf and $10 per sweater. Write an objective function that describes her profit.

Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. Let P P represent profit. Since each scarf has a profit of $8 and each sweater has a profit of $10, the objective function is P = 8 x + 10 y P = 8 x + 10 y .

Your Turn 5.96

Example 5.97, composing an objective function for production.

William’s factory produces two products, widgets and wadgets. It takes 24 minutes for his factory to make 1 widget, and 32 minutes for his factory to make 1 wadget. Write an objective function that describes the time it takes to make the products.

Let x x equal the number of widgets made; let y y equal the number of wadgets made; let T T represent total time. The objective function is T = 24 x + 32 y T = 24 x + 32 y .

Your Turn 5.97

Composing inequalities representing a system application.

For our two examples of profit and production, in an ideal world the profit a person makes and/or the number of products a company produces would have no restrictions. After all, who wouldn’t want to have an unrestricted profit? However in reality this is not the case; there are usually several variables that can restrict how much profit a person can make or how many products a company can produce. These restrictions are called constraints .

Many different variables can be constraints. When making or selling a product, the time available, the cost of manufacturing and the amount of raw materials are all constraints. In the opening scenario with the tsunami, the maximum weight on an airplane and the volume of cargo it can carry would be constraints. Constraints are expressed as linear inequalities; the list of constraints defined by the problem forms a system of linear inequalities that, along with the objective function, represent a system application.

Example 5.98

Representing the constraints for selling two products.

Two friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for profit and the two constraints.

Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. There are two constraints: the number of items the business can make in a day (a maximum of 8) and the number of bags of knitting wool they can use per day (a maximum of 27). The first constraint (total number of items in a day) is written as:

x + y ≤ 8 x + y ≤ 8

Since each scarf takes 3 bags of knitting wool and each sweater takes 4 bags of knitting wool, the second constraint, total bags of knitting wool per day, is written as:

3 x + 4 y ≤ 27 3 x + 4 y ≤ 27

In summary, here are the equations that represent the new business:

P = 8 x + 10 y P = 8 x + 10 y ; This is the profit equation: The business makes $8 per scarf and $10 per sweater.

x + y ≤ 8 3 x + 4 y ≤ 27 x + y ≤ 8 3 x + 4 y ≤ 27

Your Turn 5.98

Example 5.99, representing constraints for production.

A factory produces two products, widgets and wadgets. It takes 24 minutes for the factory to make 1 widget, and 32 minutes for the factory to make 1 wadget. Research indicates that long-term demand for products from the factory will result in average sales of 12 widgets per day and 10 wadgets per day. Because of limitations on storage at the factory, no more than 20 widgets or 17 wadgets can be made each day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for time and the two constraints.

Let x x equal the number of widgets made; let y y equal the number of wadgets made. Based on the long-term demand, we know the factory must produce a minimum of 12 widgets and 10 wadgets per day. We also know because of storage limitations, the factory cannot produce more than 20 widgets per day or 17 wadgets per day. Writing those as inequalities, we have:

x ≥ 12 x ≥ 12

y ≥ 10 y ≥ 10

x ≤ 20 x ≤ 20

y ≤ 17 y ≤ 17

The number of widgets made per day must be between 12 and 20, and the number of wadgets made per day must be between 10 and 17. Therefore, we have:

12 ≤ x ≤ 20 12 ≤ x ≤ 20

10 ≤ y ≤ 17 10 ≤ y ≤ 17

The system is:

T = 24 x + 32 y T = 24 x + 32 y

T T is the variable for time; it takes 24 minutes to make a widget and 32 minutes to make a wadget.

Your Turn 5.99

Applying linear programming to solve application problems.

There are four steps that need to be completed when solving a problem using linear programming. They are as follows:

Step 1: Compose an objective function to be minimized or maximized.

Step 2: Compose inequalities representing the constraints of the system.

Step 3: Graph the system of inequalities representing the constraints.

Step 4: Find the value of the objective function at each corner point of the graphed region.

The first two steps you have already learned. Let’s continue to use the same examples to illustrate Steps 3 and 4.

Example 5.100

Solving a linear programming problem for two products.

Three friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Determine the number of scarves and sweaters they should make each day to maximize their profit.

Step 1: Compose an objective function to be minimized or maximized. From Example 5.98, the objective function is P = 8 x + 10 y P = 8 x + 10 y .

Step 2: Compose inequalities representing the constraints of the system. From Example 5.98, the constraints are x + y ≤ 8 x + y ≤ 8 and 3 x + 4 y ≤ 27 3 x + 4 y ≤ 27 .

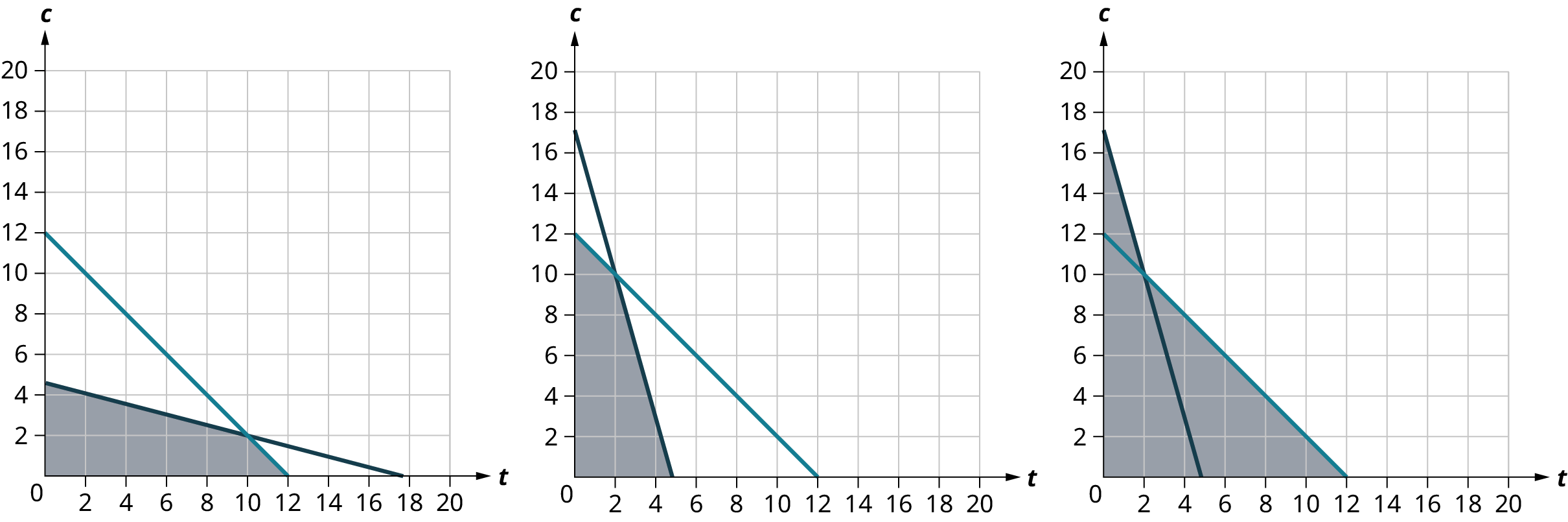
Step 3: Graph the system of inequalities representing the constraints. Using methods discussed in Graphing Linear Equations and Inequalities, the graphs of the constraints are shown below. Because the number of scarves ( x Figure 5.110 shows each constraint graphed on its own axes, while Figure 5.111 shows the graph of the system of inequalities (the two constraints graphed together). In Figure 5.111, the large shaded region represents the area where the two constraints intersect. If you are unsure how to graph these regions, refer back to Graphing Linear Equations and Inequalities.

Step 4: Find the value of the objective function at each corner point of the graphed region. The “graphed region” is the area where both of the regions intersect; in Figure 5.112, it is the large shaded area. The “corner points” refer to each vertex of the shaded area. Why the corner points? Because the maximum and minimum of every objective function will occur at one (or more) of the corner points. Figure 5.112 shows the location and coordinates of each corner point.

Three of the four points are readily found, as we used them to graph the regions; the fourth point, the intersection point of the two constraint lines, will have to be found using methods discussed in Systems of Linear Equations in Two Variables, either using substitution or elimination. As a reminder, set up the two equations of the constraint lines:

3 x + 4 y = 27 x + y = 8 3 x + 4 y = 27 x + y = 8

For this example, substitution will be used.

x + y = 8 y = 8 - x . x + y = 8 y = 8 - x .

Substituting 8 - x 8 - x into the first equation for y y , we have

3 x + 4 ( 8 − x ) = 27 3 x + 32 − 4 x = 27 − x = − 5 x = 5 3 x + 4 ( 8 − x ) = 27 3 x + 32 − 4 x = 27 − x = − 5 x = 5

Now, substituting the 5 in for x x in either equation to solve for y y . Choosing the second equation, we have:

5 + y = 8 y = 3 5 + y = 8 y = 3

Therefore, x = 5 x = 5 , and y = 3 y = 3 .

To find the value of the objective function, P = 8 x + 10 y P = 8 x + 10 y , put the coordinates for each corner point into the equation and solve. The largest solution found when doing this will be the maximum value, and thus will be the answer to the question originally posed: determining the number of scarves and sweaters the new business should make each day to maximize their profit.

The maximum value for the profit P P occurs when x = 5 x = 5 and y = 3 y = 3 . This means that to maximize their profit, the new business should make 5 scarves and 3 sweaters every day.

Your Turn 5.100

People in mathematics, leonid kantorovich.

Leonid Vitalyevich Kantorovich was born January 19, 1912, in St. Petersburg, Russia. Two major events affected young Leonid’s life: when he was five, the Russian Revolution began, making life in St. Petersburg very difficult; so much so that Leonid’s family fled to Belarus for a year. When Leonid was 10, his father died, leaving his mother to raise five children on her own.

Despite the hardships, Leonid showed incredible mathematical ability at a young age. When he was only 14, he enrolled in Leningrad State University to study mathematics. Four years later, at age 18, he graduated with what would be equivalent to a Ph.D. in mathematics.

Although his primary interests were in pure mathematics, in 1938 he began working on problems in economics. Supposedly, he was approached by a local plywood manufacturer with the following question: how to come up with a work schedule for eight lathes to maximize output, given the five different kinds of plywood they had at the factory. By July 1939, Leonid had come up with a solution, not only to the lathe scheduling problem but to other areas as well, such as an optimal crop rotation schedule for farmers, minimizing waste material in manufacturing, and finding optimal routes for transporting goods. The technique he discovered to solve these problems eventually became known as linear programming. He continued to use this technique for solving many other problems involving optimization, which resulted in the book The Best Use of Economic Resources , which was published in 1959. His continued work in linear programming would ultimately result in him winning the Nobel Prize of Economics in 1975.

Check Your Understanding

• /**/{P = 20t - 10c}/**/
• /**/{P = 20c + 10t}/**/
• /**/{P = 20t + 10c}/**/
• /**/{P = 20c - 10t}/**/
• /**/{P = 150w + 180b}/**/
• /**/{P = 150b + 180w}/**/
• /**/{P = 180w + 150b}/**/
• /**/{P = 150w - 180b}/**/
• /**/{P = 2.50f + 6.75c}/**/
• /**/{P = 2.50f + 6.75t}/**/
• /**/{P = 2.50t + 6.75f}/**/
• None of these
• /**/{20t + 10c \leq 70}/**/
• /**/{ t + c \leq 70}/**/
• /**/{ 15t + 4c \geq 70}/**/
• /**/{ 15t + 4c \leq 70}/**/
• /**/{t + c \leq 12}/**/
• /**/{ 20t + 10c \leq 12}/**/
• /**/{ 20t + 10c \geq 12}/**/
• /**/{ 20t + 10c \leq 70}/**/
• /**/{w + b \leq 945}/**/
• /**/{ 10w + 15b \geq 945}/**/
• /**/{ 10w + 15b \leq 945}/**/
• /**/{ 150w + 180w \leq 945}/**/
• /**/{150w + 180b \leq \text{1,635}}/**/
• /**/{25w + 30b \leq \text{1,635}}/**/
• /**/{w + b \leq \text{1,635}}/**/
• /**/{30w + 25b \leq \text{1,635}}/**/

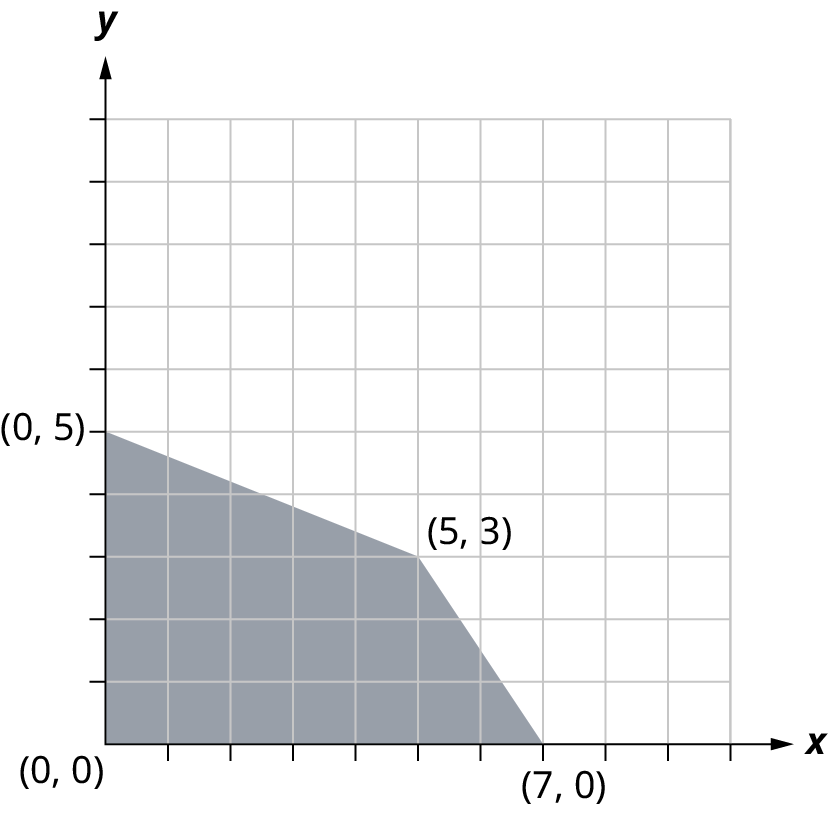
• /**/{(0, 0), (0, 12), (10, 2), (12, 0)}/**/
• /**/{(0, 0), (0, 12), (2, 10), (4\tfrac{2}{3} , 0)}/**/
• /**/{(0, 0), (17.5, 0), (2, 10), (12, 0)}/**/

Section 5.11 Exercises

Reset password New user? Sign up

Existing user? Log in

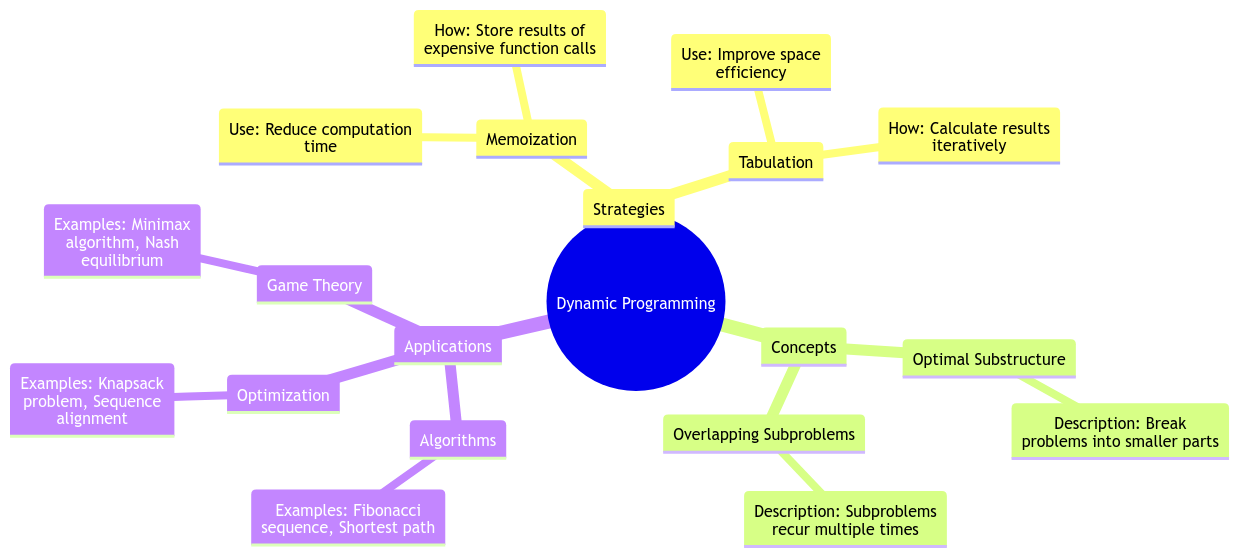
Dynamic Programming

Already have an account? Log in here.

• Karleigh Moore
• Norbert Madarász

Dynamic programming refers to a problem-solving approach, in which we precompute and store simpler, similar subproblems, in order to build up the solution to a complex problem. It is similar to recursion , in which calculating the base cases allows us to inductively determine the final value. This bottom-up approach works well when the new value depends only on previously calculated values.

An important property of a problem that is being solved through dynamic programming is that it should have overlapping subproblems. This is what distinguishes DP from divide and conquer in which storing the simpler values isn't necessary.

To show how powerful the technique can be, here are some of the most famous problems commonly approached through dynamic programming:

• Backpack Problem : Given a set of treasures with known values and weights, which of them should you pick to maximize your profit whilst not damaging your backpack which has a fixed capacity?
• Egg Dropping : What is the best way to drop \(n\) eggs from an \(m\)-floored building to figure out the lowest height from which the eggs when dropped crack?
• Longest Common Subsequence : Given two sequences, which is the longest subsequence common to both of them?
• Subset Sum Problem : Given a set and a value \(n,\) is there a subset the sum of whose elements is \(n?\)
• Fibonacci Numbers : Is there a better way to compute Fibonacci numbers than plain recursion?

In a contest environment, dynamic programming almost always comes up (and often in a surprising way, no matter how familiar the contestant is with it).

Motivational Example: Change of Coins

Recursion with memoization, bidimensional dynamic programming: example, example: maximum paths.

What is the minimum number of coins of values \(v_1,v_2, v_3, \ldots, v_n\) required to amount a total of \(V?\) You may use a denomination more than once.

Optimal Substructure

The most important aspect of this problem that encourages us to solve this through dynamic programming is that it can be simplified to smaller subproblems.

Let \(f(N)\) represent the minimum number of coins required for a value of \(N\).

Visualize \(f(N)\) as a stack of coins. What is the coin at the top of the stack? It could be any of \(v_1,v_2, v_3, \ldots, v_n\). In case it were \(v_1\), the rest of the stack would amount to \(N-v_1;\) or if it were \(v_2\), the rest of the stack would amount to \(N-v_2\), and so on.

How do we decide which is it? Sure enough, we do not know yet. We need to see which of them minimizes the number of coins required.

Going by the above argument, we could state the problem as follows:

\[f(V) = \min \Big( \big\{ 1 + f(V - v_1), 1 + f(V-v_2), \ldots, 1 + f(V-v_n) \big \} \Big). \]

Because the coin at the top of the stack also counts as one coin, and then we can look at the rest.

Overlapping Subproblems

It is easy to see that the subproblems could be overlapping.

For example, if we are trying to make a stack of $11 using $1, $2, and $5, our look-up pattern would be like this: \[\begin{align} f(11) &= \min \Big( \big\{ 1+f(10),\ 1+ f(9),\ 1 + f(6) \big\} \Big) \\ &= \min \Big ( \big \{ 1+ \min {\small \left ( \{ 1 + f(9), 1+ f(8), 1+ f(5) \} \right )},\ 1+ f(9),\ 1 + f(6) \big \} \Big ). \end{align} \] Clearly enough, we'll need to use the value of \(f(9)\) several times.

One of the most important aspects of optimizing our algorithms is that we do not recompute these values. To do this, we compute and store all the values of \(f\) from 1 onwards for potential future use.

The recursion has to bottom out somewhere, in other words, at a known value from which it can start.

For this problem, we need to take care of two things:

Zero : It is clear enough that \(f(0) = 0\) since we do not require any coins at all to make a stack amounting to 0.

Negative and Unreachable Values : One way of dealing with such values is to mark them with a sentinel value so that our code deals with them in a special way. A good choice of a sentinel is \(\infty\), since the minimum value between a reachable value and \(\infty\) could never be infinity.

The Algorithm

Let's sum up the ideas and see how we could implement this as an actual algorithm:

We have claimed that naive recursion is a bad way to solve problems with overlapping subproblems. Why is that? Mainly because of all the recomputations involved.

Another way to avoid this problem is to compute the data first time and store it as we go, in a top-down fashion.

Let's look at how one could potentially solve the previous coin change problem in the memoization way. 1 2 3 4 5 6 7 8 9 10 11 12 def coinsChange ( V , v ): memo = {} def Change ( V ): if V in memo : return memo [ V ] if V == 0 : return 0 if V < 0 : return float ( "inf" ) memo [ V ] = min ([ 1 + Change ( V - vi ) for vi in v ]) return memo [ V ] return Change ( V )

Dynamic Programming vs Recursion with Caching

There are \(k\) types of brackets each with its own opening bracket and closing bracket. We assume that the first pair is denoted by the numbers 1 and \(k+1,\) the second by 2 and \(k+2,\) and so on. Thus the opening brackets are denoted by \(1, 2, \ldots, k,\) and the corresponding closing brackets are denoted by \(k+1, k+2, \ldots, 2k,\) respectively.

Some sequences with elements from \(1, 2, \ldots, 2k\) form well-bracketed sequences while others don't. A sequence is well-bracketed if we can match or pair up opening brackets of the same type in such a way that the following holds:

• Every bracket is paired up.
• In each matched pair, the opening bracket occurs before the closing bracket.
• For a matched pair, any other matched pair lies either completely between them or outside them.

In this problem, you are given a sequence of brackets of length \(N\): \(B[1], \ldots, B[N]\), where each \(B[i]\) is one of the brackets. You are also given an array of Values: \(V[1],\ldots, V[N] \).

Among all the subsequences in the Values array, such that the corresponding bracket subsequence in the B Array is a well-bracketed sequence, you need to find the maximum sum.

Task: Solve the above problem for this input.

Input Format

One line, which contains \((2\times N + 2)\) space separate integers. The first integer denotes \(N.\) The next integer is \(k.\) The next \(N\) integers are \(V[1],..., V[N].\) The last \(N\) integers are \(B[1],..., B[N].\)

Constraints

• \(1 \leq k \leq 7\)
• \(-10^6 \leq V[i] \leq 10^6\), for all \(i\)
• \(1 \leq B[i] \leq 2k\), for all \(i\)

Illustrated Examples

For the examples discussed here, let us assume that \(k = 2\). The sequence 1, 1, 3 is not well-bracketed as one of the two 1's cannot be paired. The sequence 3, 1, 3, 1 is not well-bracketed as there is no way to match the second 1 to a closing bracket occurring after it. The sequence 1, 2, 3, 4 is not well-bracketed as the matched pair 2, 4 is neither completely between the matched pair 1, 3 nor completely outside of it. That is, the matched pairs cannot overlap. The sequence 1, 2, 4, 3, 1, 3 is well-bracketed. We match the first 1 with the first 3, the 2 with the 4, and the second 1 with the second 3, satisfying all the 3 conditions. If you rewrite these sequences using [, {, ], } instead of 1, 2, 3, 4 respectively, this will be quite clear.

Suppose \(N = 6, k = 3,\) and the values of \(V\) and \(B\) are as follows: Then, the brackets in positions 1, 3 form a well-bracketed sequence (1, 4) and the sum of the values in these positions is 2 (4 + (-2) =2). The brackets in positions 1, 3, 4, 5 form a well-bracketed sequence (1, 4, 2, 5) and the sum of the values in these positions is 4. Finally, the brackets in positions 2, 4, 5, 6 form a well-bracketed sequence (3, 2, 5, 6) and the sum of the values in these positions is 13. The sum of the values in positions 1, 2, 5, 6 is 16 but the brackets in these positions (1, 3, 5, 6) do not form a well-bracketed sequence. You can check the best sum from positions whose brackets form a well-bracketed sequence is 13.

We'll try to solve this problem with the help of a dynamic program, in which the state , or the parameters that describe the problem, consist of two variables.

First, we set up a two-dimensional array dp[start][end] where each entry solves the indicated problem for the part of the sequence between start and end inclusive.

We'll try to think what happens when we run across a new end value, and need to solve the new problem in terms of the previously solved subproblems. Here are all the possibilities:

• When end <= start , there are no valid subsequences.
• When b[end] <= k , i.e, the last entry is an open bracket, no valid subsequence can end with it. Effectively, the result is the same if we hadn't included the last entry at all.
• When b[end] > k , i.e, the last entry is a closing bracket, one has to find the best match for it, or simply ignore it, whichever maximizes the sum.

Can you use these ideas to solve the problem?

Very often, dynamic programming helps solve problems that ask us to find the most profitable (or least costly) path in an implicit graph setting. Let us try to illustrate this with an example.

You are supposed to start at the top of a number triangle and chose your passage all the way down by selecting between the numbers below you to the immediate left or right. Your goal is to maximize the sum of the elements lying in your path. For example, in the triangle below, the red path maximizes the sum.

To see the optimal substructures and the overlapping subproblems , notice that everytime we make a move from the top to the bottom right or the bottom left, we are still left with smaller number triangle, much like this:

We could break each of the sub-problems in a similar way until we reach an edge-case at the bottom:

In this case, the solution is a + max(b,c) .

A bottom-up dynamic programming solution is to allocate a number triangle that stores the maximum reachable sum if we were to start from that position . It is easy to compute the number triangles from the bottom row onward using the fact that the

\[\text{best from this point} = \text{this point} + \max(\text{best from the left, best from the right}).\]

Let me demonstrate this principle through the iterations. Iteration 1: 1 8 5 9 3 Iteration 2: 1 2 10 13 15 8 5 9 3 Iteration 3: 1 2 3 20 19 10 13 15 8 5 9 3 Iteration 4: 1 2 3 4 23 20 19 10 13 15 8 5 9 3 So, the effective best we could do from the top is 23, which is our answer.

Problem Loading...

Note Loading...

Set Loading...

eMathHelp Math Solver - Free Step-by-Step Calculator

Solve math problems step by step.

At eMathHelp, we provide a wealth of mathematical calculators designed to simplify your daily computations, whether you need to tackle complex equations or perform fundamental math operations.

Our Calculator Categories

Algebra calculator.

Explore our Algebra Calculator, designed to help solve equations, factor polynomials, and more, making algebra more accessible to you.

Geometry Calculator

Our Geometry Calculator is your handy tool for working with triangles.

Pre-Calculus Calculator

Solve pre-calculus problems with our specialized calculator, helping you master foundational math concepts before diving into advanced mathematics.

Calculus Calculator

Improve your calculus knowledge with our Calculus Calculator, which makes complex operations like derivatives, integrals, and differential equations easy.

Linear Algebra Calculator

Perform matrix operations and solve systems of linear equations with our Linear Algebra Calculator, essential for fields like physics and engineering.

Discrete Math Calculator

Tackle discrete mathematical problems confidently with our specialized calculator, ideal for computer science, cryptography, and more.

Probability and Statistics Calculator

Make data analysis a breeze with our Probability and Statistics Calculator, which helps you extract meaningful insights from your data.

Linear Programming Calculator

Optimize linear objective functions easily using our Linear Programming Calculator, which is valuable in resource allocation and economics.

Who Are We?

eMathHelp is a team of dedicated math enthusiasts who believe everyone should have access to powerful mathematical tools. Our mission is to make math more approachable and enjoyable for people of all ages and backgrounds.

Why Choose Our Calculators?

Versatility.

We offer a wide range of calculators for math, including algebraic and calculus tools, making it your one-stop destination for all your mathematical needs.

Our user-friendly interface ensures that even complex calculations can be performed effortlessly, making math accessible to everyone.

Our calculator is designed to provide precise results, helping you save time and eliminate errors.

Diverse Categories of Calculators

We cover various mathematical concepts and topics, from simple to complex.

Our Most Popular Math Calculators

Definite and improper integral calculator.

Solve complex integration problems, including improper integrals, quickly.

Efficiently optimize resources by solving linear programming problems.

Integral Calculator

Easily find antiderivatives by applying different techniques.

Function Calculator

Find the main properties of functions easily.

Discriminant Calculator

Quickly analyze quadratic equations.

What types of calculations can the online math calculator perform?

Our online math calculator offers a wide range of operations to perform. You can use it to solve equations, find derivatives, factor expressions, and more.

Are the online math calculators free to use?

Absolutely! We provide free calculators for math, ensuring you can access powerful mathematical tools without cost. No subscriptions or hidden fees.

How many online math calculators do you offer?

We offer a wide range of online math calculators covering a variety of math topics.

Do the calculators provide step-by-step solutions?

Many of our calculators provide detailed, step-by-step solutions. This will help you better understand the concepts that interest you.

Code With C

The Way to Programming

• C Tutorials
• Java Tutorials
• Python Tutorials
• PHP Tutorials
• Java Projects

Dynamic Programming: Strategies for Solving Complex Problems Efficiently

Dynamic Programming Demystified 🚀

Hey there, fellow tech enthusiasts! 🤖 Today, let’s delve into the fascinating world of Dynamic Programming 🌟. Don’t be scared off by the jargon; I’m here to break it down with a sprinkle of humor and a dollop of enthusiasm! So, grab your virtual seat and let’s dive right in! 💻

Understanding Dynamic Programming

So, what in the world is Dynamic Programming ? 🤔 Imagine you have this colossal problem to solve, and it’s so complex that you feel like pulling your hair out! Dynamic Programming swoops in like a superhero, offering you a strategy to break down this mammoth task into bite-sized, manageable chunks. Voila! Problem solved! 💪

Definition of Dynamic Programming

Dynamic Programming is like the master chef in the kitchen of algorithms . It’s a methodical way of solving complex problems by breaking them down into simpler subproblems. 🍳 Each subproblem’s solution is stored to avoid redundant calculations, making the overall process more efficient. Efficiency for the win! 🎉

Importance of Dynamic Programming

Picture this: You’re at a buffet, and you want to sample every dish. Dynamic Programming allows you to do just that in the realm of algorithms – optimize your solutions and tackle even the most intricate problems with finesse. It’s like having a secret recipe book for cracking challenging puzzles in record time! 🍽️

Basic Principles of Dynamic Programming

Let’s talk about the fundamental rules that make Dynamic Programming the rockstar of problem-solving techniques! 🌟

• Overlapping Subproblems : It’s like finding money in the pockets of your old jeans. Dynamic Programming identifies these recurring subproblems and saves their solutions for later use, eliminating unnecessary work. It’s all about efficiency, baby! 💸
• Optimal Substructure : This principle is like building a sturdy LEGO tower. Each piece (subproblem) fits perfectly to create the optimal solution . Dynamic Programming ensures that each subproblem’s solution contributes to the overall best answer. It’s all about that solid foundation! 🏗️

Strategies for Applying Dynamic Programming

Now that we’ve got the basics under our belt, let’s explore the two dynamic strategies that make the magic happen! 🎩✨

• Top-down Approach : Imagine you’re skydiving from the top. This approach starts with the main problem and recursively breaks it down into subproblems. It’s adventurous, exhilarating, and definitely keeps you on your toes! 🪂
• Bottom-up Approach : Ever built a tower from the ground up? That’s the bottom-up approach. You start with the smallest subproblems, gradually solving larger ones until you conquer the main problem like a champ. It’s a steady climb to success! 🗼

Applications of Dynamic Programming

Dynamic Programming isn’t just a fancy term; it’s the powerhouse behind some incredible real-world applications! 🌐 Let’s take a peek at a couple of them:

• Fibonacci Sequence : Ah, the Fibonacci sequence, nature’s favorite mathematical marvel ! Dynamic Programming nimbly calculates Fibonacci numbers faster than you can say “Golden Ratio.” It’s all about those efficient number-crunching skills! 🔢
• Shortest Path Algorithms : Navigating through a maze? Dynamic Programming has your back! It’s the GPS guiding you through the shortest route with speed and precision. Say goodbye to taking the long, scenic route! 🗺️

Challenges and Tips for Mastering Dynamic Programming

Ah, every hero has their kryptonite, right? Let’s uncover some challenges in mastering Dynamic Programming and how to conquer them like a pro! 🦸‍♂️

• Identifying Optimal Substructure : Sometimes the forest (complex problem) is so dense that you can’t see the trees (optimal substructure). Mastering Dynamic Programming involves honing your detective skills to spot these crucial patterns. Sherlock, who? 🕵️
• Handling State Transitions efficiently : It’s like switching gears in a Formula 1 race. Efficiently transitioning between states is key to zipping through problems with ease. Rev up those mental engines and zoom past any hurdles! 🏎️

Overall, Mastering Dynamic Programming Like a Pro! 🚀

So, there you have it, folks! Dynamic Programming, the unsung hero of problem-solving, ready to tackle any challenge with finesse. Remember, practice makes perfect, and with a dash of determination and a sprinkle of creativity, you’ll be mastering Dynamic Programming like a seasoned pro in no time! 💪

Thanks for tuning in, and remember: Keep coding, keep smiling, and embrace the dynamic journey ahead! 🌟

Stay Dynamically Awesome, Techies! 🚀👩‍💻

In closing, thanks a ton for joining me on this Dynamic Programming rollercoaster! 🎢 Keep shining bright and solving those tech puzzles like a boss! See you in the next coding adventure! ✨

Program Code – Dynamic Programming: Strategies for Solving Complex Problems Efficiently

Code Output: The 10th Fibonacci number is: 55

Code Explanation:

In the given dynamic programming example , we solve for the nth Fibonacci number, a popular problem showcasing the elegance and efficiency of the dynamic programming approach. The recursive nature of the Fibonacci sequence, where each number is the sum of the two preceding ones (excluding the first two numbers which are both considered as 1), makes it an ideal candidate for dynamic programming, particularly memoization.

The code defines a fibonacci function that takes two arguments: n , the position in the Fibonacci sequence whose value we want to find, and memo , a dictionary used as a cache to store the results of the Fibonacci numbers we’ve already computed.

At the function’s core, we employ a base case for when n is less than or equal to 2. For these cases, we simply return 1, as the first two Fibonacci numbers by definition are 1.

The true power and efficiency lie in the subsequent lines. Before plunging headlong into a recursive frenzy, we first check if our current n is in the memo . If it’s not, this means we haven’t computed it yet, and then we proceed to perform the recursive operations to calculate fibonacci(n-1) and fibonacci(n-2) . Crucially, we then store this computed value in memo[n] . This storage step is what saves us from the redundant work if we encounter the same n value again in our computations.

In essence, any subsequent calls for the same Fibonacci number won’t have to go through the recursion again; instead, they’ll directly fetch the result from our memo , dramatically reducing the time complexity from what would have been exponential in a naive recursive approach (O(2^n)) to O(n) in our dynamic programming approach.

Let’s not forget—the function concludes by returning the memoized or newly computed value of the nth Fibonacci number, giving us our desired result efficiently and elegantly. Dynamic programming, with its memoization strategy, thus transforms an otherwise computationally intensive problem into a tractable one, showcasing its power in optimizing the performance of algorithms dealing with overlapping subproblems.

Frequently Asked Questions (F&Q) on Dynamic Programming

What is dynamic programming and how does it work.

Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It involves solving each subproblem only once and storing the solution to avoid redundant calculations. This approach can significantly improve the efficiency of solving problems with overlapping subproblems.

When should I use dynamic programming to solve a problem?

Dynamic programming is most useful when a problem can be broken down into overlapping subproblems, and the optimal solution to the problem can be constructed from optimal solutions to its subproblems. It is commonly used in optimization problems, such as finding the shortest path or maximizing profit.

What are the key characteristics of problems that are suitable for dynamic programming?

Problems suitable for dynamic programming usually exhibit two key characteristics: optimal substructure and overlapping subproblems. Optimal substructure means that the optimal solution to the problem can be constructed from the optimal solutions to its subproblems. Overlapping subproblems refer to the fact that the same subproblems are solved multiple times in a recursive algorithm .

Can you provide an example of a problem that can be solved using dynamic programming?

One classic example of a problem solved using dynamic programming is the Fibonacci sequence. By storing the results of subproblems (calculating Fibonacci numbers for smaller indices), we can avoid redundant calculations and compute the nth Fibonacci number efficiently.

Are there different strategies or approaches to dynamic programming?

Yes, there are several strategies for approaching dynamic programming problems, such as top-down with memoization and bottom-up with tabulation. Top-down with memoization involves solving the problem recursively while storing the results of subproblems to avoid redundant calculations. Bottom-up with tabulation involves solving the problem iteratively, starting from the smallest subproblems and building up to the desired solution.

What are some common pitfalls to avoid when using dynamic programming?

One common pitfall when using dynamic programming is not recognizing the overlapping subproblems and failing to store and reuse intermediate results. It is essential to identify the repeating subproblems to benefit from the efficiency of dynamic programming . Additionally, starting with a brute-force approach before optimizing with dynamic programming can help in understanding the problem better.

How can I improve my skills in dynamic programming?

To improve your skills in dynamic programming, practice solving a variety of problems that can be optimized using dynamic programming techniques . Online coding platforms, coding contests, and algorithmic problem-solving websites offer a wide range of problems to help you sharpen your skills. Additionally, studying different dynamic programming patterns and approaches can enhance your problem-solving abilities.

What are some resources to learn more about dynamic programming?

There are plenty of resources available to deepen your understanding of dynamic programming, including online courses, textbooks, and tutorials. Websites like LeetCode, GeeksforGeeks, and CodeSignal offer practice problems and explanations related to dynamic programming. Additionally, joining online coding communities and forums can provide valuable insights and tips from experienced programmers in the field.

You Might Also Like

Binary decision diagrams: simplifying complex decision processes, optimizing data search in binary search trees, binary search tree: structure, operations, and applications, binary tree search: navigating trees for efficient data retrieval, searching in a binary search tree: algorithms and efficiency.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Latest Posts

Cutting-Edge Artificial Intelligence Project Unveiled in Machine Learning World

Enhancing Exams with Image Processing: E-Assessment Project

Cutting-Edge Blockchain Projects for Cryptocurrency Enthusiasts – Project

Artificial Intelligence Marvel: Cutting-Edge Machine Learning Project

Personalized Affective Feedback Project: Deep Learning Solutions for Student Frustration in IT

Privacy overview.

Sign in to your account

Username or Email Address

Remember Me

How Coding Can Improve Math Performance

• 11 Free STEM Activities for Kids
• Win a Drone for Your Class at TCEA 2018!

The conventional belief has always been that kids interested in coding should develop strong math skills. However, it turns out the reverse may also be true: coding can help children build math skills and make learning math more engaging and fun.

In the three years that Casita Center, a magnet elementary school in Southern California, has been teaching coding with Tynker, they’ve seen considerable improvements in their students’ math scores, outperforming virtually all California schools with similar demographics. Jenny Anderson, the school’s STEM specialist,  believes this improvement is due to the effectiveness of their CS program. When kids learn to code, they develop key skills like problem solving and practice algorithmic and computational thinking – and when they learn to code with Tynker, they have fun at the same time, so they’re more likely to stay engaged with the material. These broad skill sets and ways of breaking down and analyzing problems translate across the curriculum and are particularly helpful when it comes to math.

Whether kids are learning to code at school or at home, you may just see an impact on their overall academic performance! Here are a few ways that coding helps kids learn math:

Coding helps kids visualize abstract concepts

Grasping abstract math concepts can be a challenge to many kids and put them off the subject entirely. Parents, teachers, and technology specialists are using Tynker to help children visualize abstract concepts with math and coding .

“One of the most common cross curricular benefits of computer programming is that the kids have an easier time learning math skills,” says Michelle Lagos, a computer science teacher who uses Tynker in elementary classes at the American School in Tegucigalpa, Honduras. “When they have to work on long division, it is easier for them to visualize the numbers now instead of counting with their fingers. They visualize the equation and think of the best way to solve it.” Lagos reports that she has “seen kids in many grades improve their math skills” by using Tynker to learn coding.

Jesse Thorstad, Technology Coordinator for the Fergus Falls Public Schools district in Minnesota, has had a similar experience. “Tynker provides kids with a concrete example of the power of decimal places,” he says. “When studying decimals in math, the students experience a heartwarming ‘Ah-ha!’ moment when they see how moving a decimal coding block can affect the objects on the screen tenfold.”

Kids explore the real-world applications of math concepts

Repairing spaceships or saving puppies with Tynker is a great way for a child to see concrete applications of math for computer programming strategies. Tynker parent Sri Ramakrishnan points out that kids develop stronger math skills when applying concepts in a real-world context: “The computational thinking involved in computer programming involves logic, organizing and analyzing data, and breaking a problem into smaller and more manageable parts. Much of this is also required when solving math problems!”

Math can be used in creative coding projects

Kids who use Tynker see how math coding is inherently creative. Here is an example of math art that kids can create with Tynker:

10-year-old Jacob Myers, a big math buff who regularly competes in math contests, uses Tynker to make math art with spirals and triangles. Kids can also complete activities like Pattern Maker and Spin Draw to learn how to create art with coding and math!

Coding teaches problem-solving skills

Coding is a real-world way to teach mathematical thinking. When students create or debug a program, they practice solving problems. Math teachers find that Tynker’s beginning lessons are a great way to teach pattern identification as well. Teachers can assign activities like  Multiplication Escape or Analog Clock  and encourage students to find solutions with math.

How is Coding Used in Math?

Math and coding are like best friends! They team up to make math super easy and powerful. In coding, we use special computer languages such as Python or MATLAB to work on math problems. It’s like having a math wizard in your computer. We can use coding for math calculations, which means it helps us solve math puzzles and do math homework quickly. It’s like having a calculator on steroids!

Coding also helps us play with math symbols, such as x and +. This is important because it allows us to solve tricky equations and understand how things in math fit together. We use a special tool called SymPy to work with math symbols in coding. Additionally, coding helps us with data analysis in math. This means we can look at lots of numbers, like in surveys or experiments, and find out what those numbers mean. It’s like having a detective for math patterns!

But math and coding don’t stop there. They work together to create models and simulations for things like predicting disease outbreaks or understanding how rockets fly. It’s like building a virtual math world where we can experiment and learn how things work. So, math and coding are like a dynamic duo, helping us solve math mysteries, draw math pictures, and explore the fascinating world of numbers and shapes.

What is Coding in Math for Kids?

Coding in math for kids is a fun and creative way to use computer programming to explore mathematical concepts and solve math problems. It involves using special computer languages, often designed for children, to write code that can perform math-related tasks. Here are some ways coding can be used in math for kids:

1. Math Games: Kids can create their own math games using coding. For example, they can code a game that quizzes them on addition, subtraction, multiplication, or division, making learning math more enjoyable.

2. Math Visualizations: Coding allows kids to create colorful and interactive visualizations of math concepts. They can build graphs, charts, and geometric shapes to better understand math ideas.

3. Math Puzzles and Challenges: Kids can code programs to generate math puzzles and challenges. For instance, they can create a program that generates random math problems for them to solve.

5. Math Simulations: Coding can be used to simulate real-world math scenarios. For example, kids can create a program that simulates the growth of a population or the trajectory of a projectile.

6. Math Art: Coding can be a creative tool for making math-based art. Kids can write code to create symmetrical patterns, fractals, and other artistic representations of mathematical concepts.

7. Educational Tools: There are coding platforms and software specifically designed for math education. These tools provide interactive math lessons and exercises that make learning math more engaging and interactive.

8. Robotics and Math: In robotics programs for kids, coding is used to program robots to perform math-related tasks. This hands-on approach can make math more tangible and exciting.

Coding in math for kids is not just about solving equations; it’s about making math come to life through programming. It encourages problem-solving, critical thinking, and creativity while reinforcing math skills in a way that’s enjoyable and engaging for young learners.

What is an example of math in coding? 

An example of math in coding is writing a program to calculate the average (mean) of a list of numbers. Here’s a simple Python code snippet that demonstrates this:

# List of numbers numbers = [10, 15, 20, 25, 30]

# Calculate the sum of the numbers sum_of_numbers = sum(numbers)

# Calculate the average average = sum_of_numbers / len(numbers)

# Print the result print(“The average is:”, average)

• We start with a list of numbers [10, 15, 20, 25, 30] .
• We use the sum() function to calculate the sum of all the numbers in the list, which is 10 + 15 + 20 + 25 + 30 = 100 .
• We then calculate the average by dividing the sum ( 100 ) by the number of elements in the list (which is 5 ), giving us an average of 20 .
• Finally, we print out the result, which displays “The average is: 20” on the screen.

This is just one simple example, but math is used extensively in coding for a wide range of tasks, from basic arithmetic operations like addition and subtraction to more complex mathematical calculations, such as solving equations, working with matrices, and implementing algorithms for tasks like sorting and searching. Coding allows us to automate and efficiently perform mathematical operations in various applications and domains.

Coding makes math more fun

“My kids ask to program with Tynker because they enjoy it,” says Jennifer Apy, the parent of a 15-year-old, an 11-year-old, and an 8-year-old. “Without realizing it, my kids are identifying attributes and grouping variables, applying conditional logic, developing algorithmic functions, and calculating angles within geometric shapes. But most of all, they are patiently articulating hypotheses to solve problems, and boldly applying trial-and-error experimentation, strategies required by any field of study. And this is in addition to some of the coding that requires real math – to correctly calculate wait times, set score counters, calculate points, and time interactions between characters in their games.”

“If kids realize they are using math when programming Tynker games,” Apy says, “it could actually build their confidence with math and show them that mathematical thinking can be cool.”

Math is cool? What could be better than that?

Related Searches:

Coding for Kids

Elementary Math

Math in Tynker

About Tynker

Related articles.

Minecraft Starting Tips: Survive Your First Night & Thrive

Discover the best Python programming app in 2024

Top Minecraft Tips to Boost Your Survival Skills

Best App to Learn Programming in 2024: Top Picks

My coding path.

Take your child from novice to expert. Just follow the path.

Block Coding Courses

Apply your coding skills! Find your passion!

Other Advanced Tynker Courses

Graduate to Python and other text coding languages with Tynker’s advanced elective courses.

We use programing and math in much the same way to teach what I consider to be a fundamental skill; the ability to break a large problem down in to smaller problems. In life, you are often faced with problems that seem insurmountable when looked at as a whole. The ability to break those down into logical and manageable units is a skill that enables you do to huge things and not get stuck only facing problems that come to you as bite sized. When you focus math and programing teaching at that goal, the practical applications become much more clear even to those that don’t plan on using advanced math or programming in life. I completely agree, that the underlying skills that make you good at either of these things, will pay dividends long down the road even if you never write another line of code or solve for the area under a curve.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

linear programming calculator

• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

Help | Advanced Search

Mathematics > Optimization and Control

Title: addressing unboundedness in quadratically-constrained mixed-integer problems.

Abstract: Quadratically-constrained unbounded integer programs hold the distinction of being undecidable, suggesting a possible soft-spot for Mathematical Programming (MP) techniques, which otherwise constitute a good choice to treat integer or mixed-integer (MI) problems. We consider the challenge of minimizing MI convex quadratic objective functions subject to unbounded decision variables and quadratic constraints. Given the theoretical weakness of white-box MP solvers to handle such models, we turn to black-box meta-heuristics of the Evolution Strategies (ESs) family, and question their capacity to solve this challenge. Through an empirical assessment of quadratically-constrained quadratic objective functions, across varying Hessian forms and condition numbers, we compare the performance of the CPLEX solver to state-of-the-art MI ESs, which handle constraints by penalty. Our systematic investigation begins where the CPLEX solver encounters difficulties (timeouts as the search-space dimensionality increases, (D>=30), on which we report by means of detailed analyses. Overall, the empirical observations confirm that black-box and white-box solvers can be competitive, especially when the constraint function is separable, and that two common ESs' mutation operators can effectively handle the integer unboundedness. We also conclude that conditioning and separability are not intuitive factors in determining the complexity of this class of MI problems, where regular versus rough landscape structures can pose mirrored degrees of challenge for MP versus ESs.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

ChatGPT may be about to make your job way easier

• You'll soon be able to pull ChatGPT up on your screen and get real-time feedback on your work.
• ChatGPT was able to suggest fixes to errors in code in a live demo on Monday.
• OpenAI debuted the feature as part of GPT-4o, the latest model powering the AI tool.

The latest version of ChatGPT could turn the artificial-intelligence tool into a personal assistant — including at work .

Among the new features that OpenAI highlighted on Monday: You can pull up ChatGPT on your computer desktop or smartphone screen and show it whatever you're looking at, whether it's a math problem on a whiteboard or a screen full of code.

In one demo during OpenAI's presentation on its newest model powering the chatbot, GPT-4o (that's the letter O, not zero), ChatGPT suggested changes to code in real time on a user's computer.

At first, ChatGPT was known for its command-prompt-like interface, which allows users to type in questions or requests for images. Last fall, OpenAI added a voice mode, allowing users to ask questions like they would with Alexa or Siri — albeit with a more sophisticated model responding.

But with GPT-4o, users can now show ChatGPT what they're working on and get real-time feedback.

Related stories

In another example, ChatGPT gave a one-sentence summary of a line graph when an OpenAI employee pulled it up on his desktop.

Damn... the idea of being able to just share your screen natively using the new ChatGPT Mac app and have gpt work with you is freaking awesome 🤯 pic.twitter.com/mwZvZWVP1u — Josh Cohenzadeh (@jshchnz) May 13, 2024

With the GPT-4o/ChatGPT desktop app, you can have a coding buddy (black circle) that talks to you and sees what you see! #openai announcements thread! https://t.co/CpvCkjI0iA pic.twitter.com/Tfh81mBHCv — Andrew Gao (@itsandrewgao) May 13, 2024

For anyone who codes or handles data for a living, it's not hard to imagine how the latest version of ChatGPT could make work easier .

Holy shit ChatGPT can help you fix and write codes in real freaking time, it can see your screen and can talk to you in real time. I hope you got an idea about how crazy this shit is pic.twitter.com/ZxqsL2TOje — Kuldeep Lather (@Kullthegreat) May 13, 2024

ChatGPT can also give feedback on work in the real world. In Monday's demo, OpenAI employees showed the tool, via smartphone camera, a simple algebra problem written on a whiteboard.

Eventually, ChatGPT gave them hints on how to solve an unknown variable, giving them feedback at different stages.

GPT-4o marks "the first time that we are really making a huge step forward when it comes to the ease of use," OpenAI's chief technology officer, Mira Murati, told an audience at the company's offices as Monday's presentation kicked off.

Correction: May 13, 2024 — A previous version of this story referred to the latest version of ChatGPT by the wrong name. It is still called ChatGPT, not ChatGPT-4o. GPT-4o is the new model that powers the chatbot.

Axel Springer, Business Insider's parent company, has a global deal to allow OpenAI to train its models on its media brands' reporting.

Watch: What is ChatGPT, and should we be afraid of AI chatbots?

• Main content

Search form

You are here, aida khajavirad: minimizing trade-offs in mathematical optimization.

“My branch of research,” says Khajavirad, “deals with optimization problems with a nonconvex objective function and both continuous and integer variables.”

Khajavirad’s work revolves around making the solution of these optimization problems more tractable, particularly when dealing with nonconvex objectives and a mix of continuous and integer variables. “Although many real-word problems can naturally be formulated as MINLPs, solving such optimization problems is often very challenging,” she says.

Khajavirad recently secured a three-year, $389,000 grant from the Air Force Office of Scientific Research . In collaboration with Antonio De Rosa , an associate professor of mathematics at the University of Maryland, she will address complex MINLP problems in data science applications, where locally optimal solutions often overshadow globally optimal ones, leading to computational inefficiencies.

The goal is to develop novel linear programming relaxations and scalable optimization algorithms with theoretical guarantees. This dual-pronged approach aims to overcome the hurdles associated with locally optimal solutions and extensive computation times in solving large-scale MINLP problems in data science. 

Khajavirad’s approach puts the emphasis on providing both theoretical guarantees and reduced computation time. "To solve large-scale nonconvex problems in a reasonable time, existing methods either rely on heuristics, which provide good solutions but forego any guarantee on the quality of the solution, or use semi-definite programming relaxations, which do not scale well and are impractical for large-scale optimization.”

The applications of her research span many domains, including computer vision, medical imaging, and finance, to enhance the efficiency and accuracy of data-driven processes.

“A variety of applications in data science can naturally be formulated as large-scale MINLPs, such as data clustering, image matching, and sparse regression,” she says.

At a time when the demand for efficient and accurate data science processes is paramount, Khajavirad’s work is critical. 

“Many optimization experts believe that, in the case of nonconvex nonlinear problems, one must compromise either on the guarantee of solution quality or on the speed of solving the problems. My ultimate research goal is to minimize this trade-off by advancing the state-of-the-art in MINLP at theoretical, algorithmic, and software levels.”

The past year included a milestone for Khajavirad: She and University of Wisconsin–Madison professor Alberto Del Pia were awarded the 2023 INFORMS Computing Society Prize for their work on “convexifications for mixed-integer polynomial optimization” based on a series of seven papers. This was her second award from the Institute for Operations Research and the Management Sciences, having received an INFORMS Optimization Society Prize for Young Researchers in 2017.

Looking ahead, Khajavirad expects continued growth in research on nonconvex MINLP, and aims to address open questions and tackle applications where current methods fall short.

“My area of research is relatively new, and there are many open questions that I aspire to answer,” she says. “Research in nonconvex MINLP has witnessed significant growth at both theoretical and algorithmic levels over the last few years. While this class of problems has already made a remarkable impact on industrial and systems engineering, there are still numerous important applications that cannot be efficiently addressed using such a class, and these are the ones I want to work on.” 

As the landscape of data science continues to evolve, Khajavirad’s work pushes the boundaries of mathematical optimization while paving the way for more efficient and accurate data-driven solutions. Solutions that will ultimately facilitate the decision-making processes across a range of industries.

Resolve Magazine: Volume 1, 2024

More from This Volume

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Solve Max-Cut Problem Using QAOA

This example uses:

• MATLAB Support Package for Quantum Computing MATLAB Support Package for Quantum Computing
• Global Optimization Toolbox Global Optimization Toolbox
• Optimization Toolbox Optimization Toolbox

This example shows how to use the quantum approximate optimization algorithm (QAOA) to solve max-cut problems. The max-cut problem is a graph partitioning problem whose objective is to create two subsets of vertices that maximize the number of edges between the two groups. In this example, you first solve a max-cut problem classically by considering all graph partitions and then solve it using QAOA.

Set up Max-Cut Problem

Generally, the max-cut problem can be expressed as

max   ∑ i , j = 1 N w ij x i ( 1 - x j ) ,

where N is the number of nodes in the graph, x i denotes which node subset node i is in using 0 or 1, and w ij is the weight of the edge between nodes i and j .

Create and plot a four-node graph where all edges have unit weight 1.

Using the max-cut expression, the objective function to maximize for this graph is:

f = ∑ i , j = 1 4 w ij x i ( 1 - x j )     = ( x 1 ( 1 - x 2 ) + x 2 ( 1 - x 1 ) ) + ( x 1 ( 1 - x 4 ) + x 4 ( 1 - x 1 ) )           + ( x 2 ( 1 - x 3 ) + x 3 ( 1 - x 2 ) ) + ( x 3 ( 1 - x 4 ) + x 4 ( 1 - x 3 ) )

Solve Using Classical Approach

A graph with N nodes has 2 N possible solutions, or ways to partition the nodes into two subsets. For the four-node example, there are 2 4 , or 16, possible solutions. Use the objective function to calculate the solution for each partition and list them in a table. Each row of the allSols table represents a possible partition, and the table variable f represents the objective value for the corresponding partition, or how many edges are between the subsets.

Two solutions maximize the number of edges between the two subsets of nodes. In both solutions, the graph is partitioned so that nodes x 1 and x 3 are in one subset and nodes x 2 and x 4 are in the other subset. These partitions result in four edges between the two groups.

Set Up QAOA Approach

QAOA is a quantum-classical hybrid approach to solving optimization problems. In this hybrid approach, you create a quantum circuit that represents potential solutions to the problem, and a classical optimizer iteratively adjusts the angles in the circuit to improve the quality of the solution. For the max-cut problem, the QAOA approach has steps for initialization, optimization, and termination.

Initialization

Create a QAOA circuit that encodes the max-cut problem. This circuit is composed of Hadamard and rotation gates that are parameterized by the set of angles θ .

Define a set of initial angles θ 0 .

Optimization

Measure the QAOA circuit.

Calculate the expected objective value from the measurements.

Update the angles that are used in the QAOA circuit if the termination criteria is not met.

Termination

Measure the QAOA circuit at the set of angles θ that satisfy the termination criteria.

Return the final values.

This expectedObjectiveValue function implements the algorithm steps for the four-node example.

QAOA Circuit

The QAOA circuit for the max-cut problem uses a set of Hadamard gates, which place all gates in an equal superposition, and layers of cost and mixer gates, as seen in the circuit from [2] . The cost gates encode a Hamiltonian for the objective function of the optimization problem. The mixer gates, which allow the quantum state to transition between energy states, encode a simple Hamiltonian whose maximal state is + + + + . This maximal state is the equal superposition state generated by the initial Hadamard gates and the initial QAOA state.

Create the QAOA circuit for one layer of the max-cut problem using the qaoaCircuit helper function. Here, gamma and beta define the angle of the cost gate and the angle of the mixer gate, respectively. To view the code for this helper function, see Helper Function .

This circuit has four qubits, one for each node in the graph. Four Hadamard gates place all the qubits in an equal superposition and are followed by cost gates, composed of RZZ gates, and mixer gates, composed of RX gates. Each RZZ gate encodes an edge relationship in the original graph.

In general, the alternating cost and mixer gates approximately solve the problem because QAOA is a discretized example of adiabatic quantum computation (AQC), as described in [1] and [2] .

AQC uses a quantum system that combines a mixer Hamiltonian H M , which represents an energy state that is easy to prepare, and a cost Hamiltonian H C , which represents the energy state of the problem of interest. The adiabatic theorem states that if a quantum system starts in the given energy state of H M , then it will remain in that state while H M is evolved to H C , given that the change occurs at a sufficiently slow rate.

The Hamiltonian combination for the max-cut problem is

H ( t ) = t T H C + ( 1 - t T ) H M ,

where T is the total run time of the system. The solution to the Schrödinger equation for this circuit can be written using the Trotter-Suzuki approximation as a series of multiplications of cost and mixer gates.

Simulate Iterations of Max-Cut

Use surrogateopt (Global Optimization Toolbox) with the objective function to maximize the expected objective value. In this example, use two layers of cost-mixer gates and sample the circuit 1000 times each time the optimizer calculates the expected objective value. surrogateopt calculates a global minimum, so the negation of the expected objective value is minimized. Set the maximum number of objective function evaluations to 100.

The best function value is approximately 4. In other words, the maximum number of edges between two subsets of nodes is 4.

Construct the quantum circuit using the optimized angles, and simulate the circuit to see the expected probability distribution over qubit states. The 0101 and 1010 states appear with the highest probabilities, which were the two solutions found when calculating the expected values classically.

Run Final Iteration on QPU

Connect to an IonQ device using quantum.backend.QuantumDeviceAWS . Specify the region of the device and path to a bucket to store results.

Create a task to run the circuit with optimized angles on the QPU. Specify the number of shots as 1000.

Fetch the results and plot a histogram of the states.

The states 0101 and 1010 appear again as the states with the highest probabilities, so the QPU results agree with the local simulation of the circuit.

Helper Function

This code defines the qaoaCircuit helper function.

[1] J., Abhijith, Adetokunbo Adedoyin, John Ambrosiano, Petr Anisimov, William Casper, Gopinath Chennupati, Carleton Coffrin, et al. “Quantum Algorithm Implementations for Beginners.” ACM Transactions on Quantum Computing 3, no. 4 (December 31, 2022): 1–92. https://doi.org/10.1145/3517340 .

[2] Zhou, Leo, Sheng-Tao Wang, Soonwon Choi, Hannes Pichler, and Mikhail D. Lukin. “Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices.” Physical Review X 10, no. 2 (June 24, 2020): 021067. https://doi.org/10.1103/PhysRevX.10.021067 .

quantumCircuit

Related Topics

• Workflow for QUBO Problems

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Israel preparing for Rafah invasion in Gaza amid increasing tension with U.S.

60 Minutes Archive: Coverage of North Korea

Danish butter magnate's huge coin collection up for sale 100 year's after he died

How much does it cost to file for bankruptcy?

• The Inventory

Support Quartz

Fund next-gen business journalism with $10 a month

Free Newsletters

OpenAI's new ChatGPT can tell bedtime stories and solve math problems

Chatgpt-4o is the company's latest ai chatbot and will soon be available to all users.

OpenAI on Monday debuted a new chatbot with some impressive — or freaky, depending on your perspective — capabilities. With its ability to see, hear, and talk like a real person, OpenAI executives demonstrated how the latest ChatGPT can translate live conversations and tell bedtime stories in different voices.

Related Content

OpenAI’s head of frontiers research, Mark Chen, asked the chatbot to tell “a bedtime story about robots and love.”

“Oh, a bedtime story about robots and love? I got you covered!” an enthusiastic feminine voice responded immediately. “Once upon a time, in a world not too different from ours, there was a robot named Byte. Byte was a curious robot. Always exploring.”

Chen interrupted, “I want a little bit more emotion in your voice, a little bit more drama.”

“Got it. Let’s add some drama,” said ChatGPT-4o, beginning its story again, but this time in a deeper voice with more intrigue.

Chen interceded once more, “No, no, no, ChatGPT, I really want maximal emotion, like maximal expressiveness, much more than you were doing before.”

“Understood. Let’s amplify the drama,” it responded, again repeating its opening line in a much louder, even-more-dramatic voice. OpenAI chief of technology Mira Murati asked the chatbot to switch to the story in a robot voice; it obeyed. Then fellow researcher Barret Zoph interjected, asking for a singsong voice. ChatGPT sighed and began to sing.

Murati Chen, and Zoph showed how ChatGPT-4o can translate a live conversation between Italian and French and how it can listen to you breathe and walk you through breathing exercises. The chatbot is twice as fast as GPT-4 turbo and available to free users.

“For the past couple of years, we’ve been very focused on improving the intelligence of these models, and they’ve gotten pretty good, said Murati. “But this is the first time That we are really making a huge step forward when it comes to the ease of use.”

Perhaps even more impressive than its real-time conversation skills is ChatGPT’s visual capabilities. The chatbot can look at someone’s face through a phone camera and tell them how it thinks they’re feeling from their facial expressions. It can look at a user’s computer screen through screen share and help solve a math problem.

Safety concerns

Murati said the chatbot’s capabilities, while a major improvement, pose “new challenges for us when it comes to safety.”

“Our team has been hard at work figuring out how to build in mitigations against misuse,” she said, adding that OpenAI is working with governments and companies across “all industries” to work toward its goals. She did not give specifics about safety concerns, OpenAI’s plan, or the nature of its partnerships.

📬 Sign up for the Daily Brief

Our free, fast, and fun briefing on the global economy, delivered every weekday morning.