- - Google Chrome
Intended for healthcare professionals
- My email alerts
- BMA member login
- Username * Password * Forgot your log in details? Need to activate BMA Member Log In Log in via OpenAthens Log in via your institution


Search form
- Advanced search
- Search responses
- Search blogs
- Nested case-control...
Nested case-control studies: advantages and disadvantages
- Related content
- Peer review
- Philip Sedgwick , reader in medical statistics and medical education 1
- 1 Centre for Medical and Healthcare Education, St George’s, University of London, London, UK
- p.sedgwick{at}sgul.ac.uk
Researchers investigated whether antipsychotic drugs were associated with venous thromboembolism. A population based nested case-control study design was used. Data were taken from the UK QResearch primary care database consisting of 7 267 673 patients. Cases were adult patients with a first ever record of venous thromboembolism between 1 January 1996 and 1 July 2007. For each case, up to four controls were identified, matched by age, calendar time, sex, and practice. Exposure to antipsychotic drugs was assessed on the basis of prescriptions on, or during the 24 months before, the index date. 1
There were 25 532 eligible cases (15 975 with deep vein thrombosis and 9557 with pulmonary embolism) and 89 491 matched controls. The primary outcome was the odds ratios for venous thromboembolism associated with antipsychotic drugs adjusted for comorbidity and concomitant drug exposure. When adjusted using logistic regression to control for potential confounding, prescription of antipsychotic drugs in the previous 24 months was significantly associated with an increased occurrence of venous thromboembolism compared with non-use (odds ratio 1.32, 95% confidence interval 1.23 to 1.42). The researchers concluded that prescription of antipsychotic drugs was associated with venous thromboembolism in a large primary care population.
Which of the following statements, if any, are true?
a) The nested case-control study is a retrospective design
b) The study design minimised selection bias compared with a case-control study
c) Recall bias was minimised compared with a case-control study
d) Causality could be inferred from the association between prescription of antipsychotic drugs and venous thromboembolism
Statements a , b , and c are true, …
Log in using your username and password
BMA Member Log In
If you have a subscription to The BMJ, log in:
- Need to activate
- Log in via institution
- Log in via OpenAthens
Log in through your institution
Subscribe from £184 *.
Subscribe and get access to all BMJ articles, and much more.
* For online subscription
Access this article for 1 day for: £33 / $40 / €36 ( excludes VAT )
You can download a PDF version for your personal record.
Buy this article
- Subscribe to journal Subscribe
- Get new issue alerts Get alerts
Secondary Logo
Journal logo.
Colleague's E-mail is Invalid
Your message has been successfully sent to your colleague.
Save my selection
Bias in Full Cohort and Nested Case-Control Studies?
Wacholder, Sholom
From the Division of Cancer Epidemiology and Genetics, National Cancer Institute, Bethesda, Maryland.
Supported in part by the Intramural Research Program of the NIH, National Cancer Institute, Division of Cancer Epidemiology and Genetics.
Editors’ Note : Related articles appear on pages 321, 330, and 341.
Correspondence: Sholom Wacholder, Division of Cancer Epidemiology and Genetics, National Cancer Institute, Bethesda, MD 20892. E-mail: [email protected] .
In this issue, Langholz and Richardson 1 and Hein et al 2 address 2 recent articles by Deubner et al 3,4 about nested case-control studies. In 1 article, 3 Deubner et al called into question the fundamental validity of the nested case-control design. If their critique were compelling, it would raise doubts about the interpretation of hundreds of publications that report results from nested case-control studies. In another article, 4 the same authors suggested a restriction on control selection in nested case-control studies to make cases and controls more comparable.
Fundamentally, a properly executed case-control study nested in a cohort is valid if the corresponding analysis of the full cohort is valid. The mathematics of the likelihoods are the same for both, 5 as Langholz and Richardson 1 point out, and the same software procedures work for both. The only salient difference between the 2 designs is whether independent random samples or 100% samples are used in the conditional likelihood factor for each case. As Deubner et al 3 note, the design and analysis of nested case-control studies are complex, but no more so than the analysis of cohorts, which must consider issues including time scales, various measures of time-dependent variables, and possible censoring.
Generally, the only disadvantages to nested case-control studies are the reduced precision and power due to sampling of controls, and the possibility of flaws in the sampling design or its implementation. Therefore, any fundamental problem with nested case-control studies must also be a problem for full cohort analysis. Demonstration that the problem applies to both designs or an explanation of any discordance between designs would add to the credibility of the challenge.
The simulations by Deubner et al appear to show bias in nested case-control studies with lagged measures of exposure. Each step of the simulation seems reasonable. Simulated case-control studies assign case and control status to members of the cohort, preserving their age and work history information. In each simulation, the authors randomly assigned 142 of the cohort members to be cases, and took the end of their follow-up as the event or end point time. Controls matched to each case were selected from at-risk cohort members at the age of the case's event. A case's cumulative exposure was measured from time of entry into the cohort until event time. A control's cumulative exposure was measured from time of entry until the control reached the age at event of the index case to which the control was matched. Analysis was conducted by conditional logistic regression.
In fact, a subtle flaw in the design of these simulation studies renders them misleading. As Langholz and Richardson 1 point out, Deubner et al mistakenly chose cases as a random sample of all cohort members; in fact, as in Table 1 of the paper by Hein et al, 2 the average age-at-event in cases is less than the average age at the end of follow-up in comparable cohort members when censoring is not informative and the exposure has no effect on risk of the event or censoring. Why are cases younger at the event? It is because the cases’ age at end of follow-up has to be the minimum of (1) the age of death from lung cancer, (2) the age of death from other causes, or (3) the age at other causes of censoring—whereas controls are followed to the minimum of (2) and (3) only.
Further, controls’ follow-up time in the simulations tends to begin at an older age than cases'. This is because, to be chosen, controls must be followed at the age of the event in the case, and (as is standard) follow-up time is truncated when the control reaches the age of the index case. In the simulations, therefore, average follow-up time in controls will tend to be less than in cases, which are randomly selected from the cohort and have untruncated follow-up times. Similarly, all measures of exposure that depend on follow-up time (such as duration, average, and cumulative exposure) are distorted even when everyone receives the same level of exposure during follow-up. This phenomenon can be seen in the second row (and possibly the first row) of Table 2 of the paper by Deubner et al 3 where, in the absence of an exposure effect, the cumulative exposure of cases (proportional to follow-up time when exposure is constant) is greater than that of controls. In contrast, average cumulative exposure in cases and controls are similar when the hazard ratio is 1 in simulations that generate a random cohort (Table 1, rows 1 and 2). 2
So why does proportional hazards analysis truncate exposures for controls but not for cases? In proportional hazards analysis of full cohorts and nested case-control studies, the key calculation is the set of conditional probabilities that each case is the one who developed disease among all those in the cohort (or among the case and matched controls in the nested case-control study) under follow-up at case's age at event, given everyone's exposure through that age. Logically, any exposure in the case after the event cannot be related to risk at the time of event. Similarly, the other cohort members’ exposures subsequent to the index case's age at event also should not be allowed to affect the conditional probability of the event.
I do not agree with Deubner et al that lagging raises special concerns. A lagged measure of exposure with lag L bases risk at a given time point t only on exposure through time point t − L . Lagging is simply one way to measure exposure, and does not differ fundamentally from choosing other metrics such as average exposure, peak exposure, or cumulative exposure without lagging. 1 As long as exposure is measured only up to the time of the event, the particular choice of exposure summary cannot introduce bias in comparing cases and controls. 1
In their second paper, Deubner et al (this time with Levy as the first author 4 ) suggest the use of risk-set members’ age at the end of follow-up as a control selection criterion. Specifically, they advocate choosing only controls whose age at end of follow-up is close to the index case's age at death in order to avoid imbalance between cases and controls in age at start of follow-up or of first exposure and in age at censoring. Unfortunately, the use of risk set members’ age at end of follow-up as a control selection criterion generates nonrandom samples. As Lubin and Gail 6 state (and Levy et al 4 quote), it is essential to choose a random sample from the risk set. Indeed, Hein et al, 2 (Table 1, row 3) show that there is a bias generated from a nonrandom sample with controls who are younger at end of follow-up than the average in the risk set. The extra restriction proposed by Levy et al 4 can also cause another bias: if a time-independent exposure, one whose value is constant during follow-up, causes censoring due to death from another cause, the average exposure of cohort members in the risk set with follow-up even only slightly beyond the time of diagnosis of the case will tend to be less than the average in the risk set. Thus, the difference in exposure between cases and controls—and its estimated effect—will be exaggerated, even under the usual assumption of independent censoring. By contrast, the full cohort analysis will not have an analogous restriction and will be valid under independent censoring.
In my view, the 2 papers published in this issue 1,2 and the arguments offered here provide a persuasive defense of the standard analytic approach for nested case control designs. The arguments by Deubner et al 3,4 about lagged exposure do not in fact undermine the standard analysis. The setup of their simulation contains an error, and their results are not confirmed by others. These authors offer no explanation of why the bias with lagged exposures would be restricted to nested case-control studies and not be present in the full cohort analysis. Their suggestion of nonrandom selection of controls could itself induce bias. Taking all things into account, their critique is not a valid criticism of this familiar and useful epidemiologic approach. Even so, such challenges to the status quo as offered by Deubner et al are not without benefit—they push us to a better understanding of the fundamental principles that underlie our methods.
ACKNOWLEDGMENTS
I thank Kyle Steenland, Emory University, for help in preparation of this manuscript.
- + Favorites
- View in Gallery
- Research article
- Open access
- Published: 21 July 2008
Advantages of the nested case-control design in diagnostic research
- Cornelis J Biesheuvel 1 , 2 ,
- Yvonne Vergouwe 1 ,
- Ruud Oudega 1 ,
- Arno W Hoes 1 ,
- Diederick E Grobbee 1 &
- Karel GM Moons 1
BMC Medical Research Methodology volume 8 , Article number: 48 ( 2008 ) Cite this article
50k Accesses
95 Citations
2 Altmetric
Metrics details
Despite its benefits, it is uncommon to apply the nested case-control design in diagnostic research. We aim to show advantages of this design for diagnostic accuracy studies.
We used data from a full cross-sectional diagnostic study comprising a cohort of 1295 consecutive patients who were selected on their suspicion of having deep vein thrombosis (DVT). We draw nested case-control samples from the full study population with case:control ratios of 1:1, 1:2, 1:3 and 1:4 (per ratio 100 samples were taken). We calculated diagnostic accuracy estimates for two tests that are used to detect DVT in clinical practice.
Estimates of diagnostic accuracy in the nested case-control samples were very similar to those in the full study population. For example, for each case:control ratio, the positive predictive value of the D-dimer test was 0.30 in the full study population and 0.30 in the nested case-control samples (median of the 100 samples). As expected, variability of the estimates decreased with increasing sample size.
Our findings support the view that the nested case-control study is a valid and efficient design for diagnostic studies and should also be (re)appraised in current guidelines on diagnostic accuracy research.
Peer Review reports
In diagnostic research it is essential to determine the accuracy of a test to evaluate its value for medical practice [ 1 ]. Diagnostic test accuracy is assessed by comparing the results of the index test with the results of the reference standard in the same patients. Given the cross-sectional nature of a diagnostic accuracy question, the design may be referred to as a cross-sectional cohort design. The (cohort) characteristic by which the study subjects (cohort members) are selected is 'the suspicion of the target disease', defined by the presence of particular symptoms or signs [ 2 ]. The collected study data allow for calculation of all diagnostic accuracy parameters of the index test, such as sensitivity, specificity, odds ratio, receiver operating characteristic (ROC) curve and predictive values, i.e. the probabilities of presence and absence of the disease given the index test result(s).
Subjects are not always selected on their initial suspicion of having the disease but often on the true presence or absence of the disease among those who underwent the reference test in routine care practice, which merely reflects a cross-sectional case-control design [ 3 , 4 ]. Appraisal of such conventional case-control design in diagnostic accuracy research has been limited due to its problems related to the incorrect sampling of cases and controls [ 3 – 7 ]. These problems may be overcome by applying a nested (cross-sectional) case-control study design, which may be advantageous over a full (cross-sectional) cohort design. The rationale, strengths and limitations of a nested case-control approach in epidemiology studies have widely been discussed in the literature [ 8 – 11 ], but not so much in the context of diagnostic accuracy research [ 6 ].
We therefore aim to show advantages of the nested case-control design for addressing diagnostic accuracy questions and discuss its pros and cons in relation to a conventional case-control design and to the full (cross sectional) cohort design in this domain. We will illustrate this with data from a recently conducted diagnostic accuracy study.
Case-control versus nested case-control design
The essence of a case-control study is that cases with the condition under study arise in a source population and controls are a representative sample of this same source population. Not the entire population is studied, what would be a full cohort study or census approach, but rather a random sample from the source population [ 12 ]. A major flaw inherent to case-control studies, described as early as 1959 [ 13 ], is the difficulty to ensure that cases and controls are a representative sample of the same source population. In a nested case-control study the cases emerge from a well-defined source population and the controls are sampled from that same population. The main difference between a case-control and a nested case-control study is that in the former the cases and controls are sampled from a source population with unknown size, whereas the latter is 'nested' in an existing predefined source population with known sample size. This source population can be a group or cohort of subjects that is followed over time or not.
The term 'cohort' is commonly referred to a group of subjects followed over time in etiologic or prognostic research. But in essence, time is no prerequisite for the definition of a cohort. A cohort is a group of subjects that is defined by the same characteristic. This characteristic can be a particular birth year, a particular living area, and also the presence of a particular sign or symptom that makes them suspected of having a particular disease as in diagnostic research. Accordingly, a cross-sectional study can either be a cross-sectional case-control study or a cross-sectional cohort study.
Case-control and nested case-control design in diagnostic accuracy research
In diagnostic accuracy research the case-control design is incorrectly applied when subjects are selected from routine care databases. First, this design commonly leads to biased estimates of diagnostic accuracy of the index test due to referral or (partial) verification bias [ 4 , 14 – 18 ]. In routine care, physicians selectively refer patients for additional tests, including the reference test, based on previous test results. This is good clinical practice but a bad starting point for diagnostic research. As said, for diagnostic research purposes all subjects suspected of the target disease preferably undergo the index test(s) plus reference test irrespective of previous test results. Second, selection of patients with a negative reference test result as 'controls' may lead to inclusion of controls that correspond to a different clinical domain, i.e. patients who underwent the reference test but not necessarily because they were similarly suspected of the target condition [ 16 , 17 ]. A third disadvantage of such case-control design is that absolute probabilities of disease presence given the index test results, i.e. the predictive values or post-test probabilities, that are the desired parameters for patient care, cannot be obtained. Cases and controls are sampled from a source population of unknown size. The total number of patients that were initially suspected of the target disease based on the presence of symptoms or signs, i.e. the true source population, is commonly unknown as in routine care patients are hardly classified by their symptoms and signs at presentation [ 18 ]. Hence, the sampling fraction of cases and controls is unknown and valid estimates of the absolute probabilities of disease presence cannot be calculated [ 12 ].
A nested case-control study in diagnostic research includes the full population or cohort of patients suspected of the target disease. The 'true' disease status is obtained for all these patients with the reference standard. Hence, there is no referral or partial verification bias. The results of the index tests can then be obtained for all subjects with the target condition but only for a sample of the subjects without the target condition. Usually all patients with the target disease are included, but this could as well be a sample of the cases. Besides the absence of bias, all measures of diagnostic accuracy, including the positive and negative predictive values, can simply be obtained by weighing the controls with the case-control sampling fraction, as explained in Figure 1 .
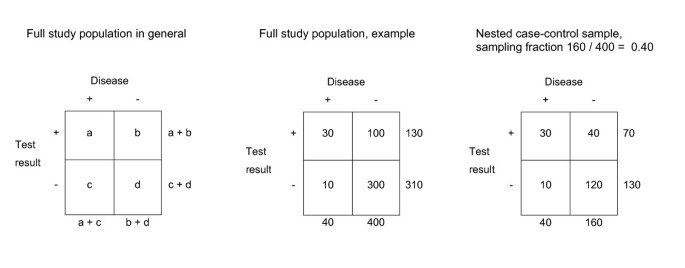
Theoretical example of a full study population and a nested case-control sample . The index test result and the outcome are obtained for all patients of the study population. The case-control ratio was 1:4 (sampling fraction (SF) = 160/400 = 0.40). Valid diagnostic accuracy measures can be obtained from the nested case-control sample, by multiplying the controls with 1/sampling fraction. For example, the positive predictive value (PPV) of a full study population can be calculated with a/(a + b), in this example 30/(30 + 100) = 0.23. In a nested case-control sample the PPV is calculated with a/(a + (1/SF)*b), in this example: 30/(30 + 2.5*40) = 0.23. In a case-control sample however, the controls are sampled from a source population with unknown size. Therefore, the sample fraction is unknown and valid estimate of the PPV cannot be calculated.
Potential advantages of a nested case-control design in diagnostic research
The nested case-control study design can be advantageous over a full cross-sectional cohort design when actual disease prevalence in subjects suspected of a target condition is low, the index test is costly to perform, or if the index test is invasive and may lead to side effects. Under these conditions, one limits patient burden and saves time and money as the index test is performed in only a sample of the control subjects.
Furthermore, the nested case-control design is of particular value when stored data (serum, images etc.) of an existing study population are re-analysed for diagnostic research purposes. Using a nested case-control design, only data of a sample of the full study population need to be retrieved and analysed without having to perform a new diagnostic study from the start. This may for example apply to evaluation of tumour markers to detect cancer, but also for imaging or electrophysiology tests.
Diagnostic accuracy estimates derived from a nested case-control study, should be virtually identical to a full cohort analysis. However, the variability of the accuracy estimates will increase with decreasing sample size. We illustrate this with data of a diagnostic study on a cohort of patients who were suspected of DVT.
A cross-sectional study was performed among a cohort of adult patients suspected of deep vein thrombosis (DVT) in primary care. This suspicion was primarily defined by the presence of a painful and swollen or red leg that existed no longer than 30 days. Details on the setting, data collection and main results have been described previously. [ 19 , 20 ] In brief, the full study population included 1295 consecutive patients who visited one of the participating primary care physicians with above symptoms and signs of DVT. Patients were excluded if pulmonary embolism was suspected. The general practitioner systematically documented information on patient history and physical examination. Patient history included information such as age, gender, history of malignancy, and recent surgery. Physical examination included swelling of the affected limb and difference in circumference of the calves calculated as the circumference (in centimetres) of affected limb minus circumference of unaffected limb, further referred to as calf difference test. Subsequently, all patients were referred to undergo D-dimer testing. In line with available guidelines and previous studies, the D-dimer test result was considered abnormal if the test yielded a D-dimer level ≥ 500 ng/ml. [ 21 , 22 ] Finally, they all underwent the reference test, i.e. repeated compression ultrasonography (CUS) of the lower extremities. In patients with a normal first CUS measurement, the CUS was repeated after seven days. DVT was considered present if one CUS measurement was abnormal. The echographist was blinded to the results of patient history, physical examination, and the D-dimer assay.
Nested case-control samples
Nested case-control samples were drawn from the full study population (n = 1295). In all samples, we included always all 289 cases with DVT. Controls were randomly sampled from the 1006 subjects without DVT. We applied four different and frequently used case-control ratios, i.e. one control for each case (1:1), two controls for each case (1:2), three controls for each case (1:3) and four controls for each case (1:4). For example, a sample with case-control ratio of 1:1 contained 289 cases and 289 random subjects out of 1006 controls (sampling fraction 289/1006 = 0.287). In the 1:4 approach, we sampled with replacement. For each case-control ratio, 100 nested case-control samples were drawn.
Statistical analysis
We focussed on two important diagnostic tests for DVT, i.e. the dichotomous D-dimer test and the continuous calf difference test. The latter was specifically chosen as it allowed for the estimation and thus comparison of the area under the ROC curve (ROC area). Diagnostic accuracy measures of both tests were estimated for the four case-control ratios and compared with those obtained from the full study population. Measures of diagnostic accuracy included sensitivity and specificity, positive and negative predictive values and the odds ratio (OR) for the D-dimer test, and the OR and the ROC area for the calf difference test.
In the analysis of the nested case-control samples, we multiplied control samples by [1/sample fraction] corresponding to the case-control ratio (1:1 = 3.48; 1:2 = 1.74; 1:3 = 1.16; 1:4 = 0.87). For each case-control ratio, the point estimates and variability were determined. The median estimate of the 100 samples was considered as the point estimate. Analyses were performed using SPSS version 12.0 and S-plus version 6.0.
In the full study population, the prevalence of DVT was 22% (n = 289), the D-dimer test was abnormal in 69% of the patients (n = 892) and the mean difference in calf circumference was 2.3 cm (Table 1 ). The prevalence of DVT was 50%, 33%, 25% and 20% in the nested case-control samples as a result of the sampling ratios (1:1, 1:2, 1:3 and 1:4, respectively). The distributions of the test characteristics in the control samples were similar as for the patients from the full study population without DVT (Table 1 ).
In the full study population the sensitivity and negative predictive value were high for the D-dimer test, 0.94 and 0.96, respectively (Table 2 ), whereas the specificity and positive predictive value were relatively low. The OR for the calf difference test was 1.44 and the ROC area was 0.69.
The average estimates of diagnostic accuracy for each of the four case-control ratios were similar to the corresponding estimates of the full study population (Figure 2 ). For example, the negative predictive value of the D-dimer test was 0.955 in both the full study population and for the four case-control ratios. The OR of the calf difference test was 1.44 in the full study population and the OR derived from the nested case-control samples were on average also 1.44.
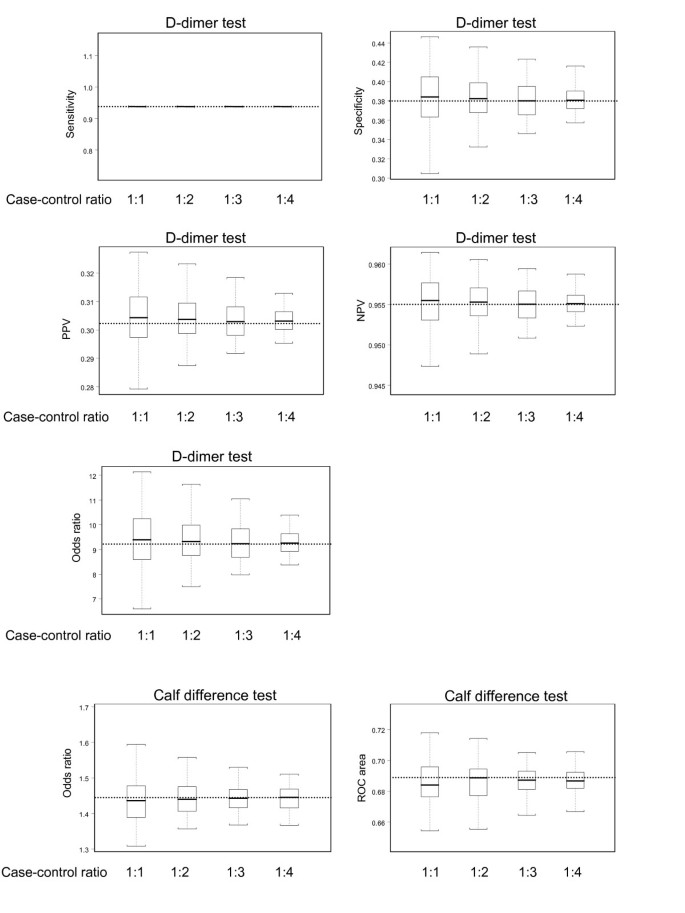
Estimates of diagnostic accuracy of the D-dimer test and calf difference test for the 100 nested case-control samples with case-control ratios ranging from 1:1 to 1:4 . The boxes indicate mean values and corresponding interquartile ranges (25 th and 75 th percentile). Whiskers indicate 2.5 th and 97.5 th percentiles. The dotted lines represent the values estimated in the full study population.
The use of (conventional) case-control studies in diagnostic research has often been associated with biased estimates of diagnostic accuracy, due to the incorrect sampling of subjects [ 3 – 6 , 18 ]. Moreover, this study design does not allow for the estimation of the desired absolute disease probabilities. We discussed and showed that a case-control study nested within a well defined cohort of subjects suspected of a particular target disease with known sample size can yield valid estimates of diagnostic accuracy of an index test, including the absolute probabilities of disease presence or absence. Diagnostic accuracy parameters derived from a full (cross-sectional) cohort of patients suspected of DVT were similar to the estimates derived from various nested case-control samples averaged over 100 simulations. Expectedly, the variability decreased with increasing number of controls, making the measures estimated in the larger case-control samples more precise.
As discussed, the number of subjects from which the index test results need to be retrieved can substantially be reduced with a nested case-control design. Hence, the nested case-control design is particularly advantageous when the prevalence of the target condition in the cohort of patients suspected of the target disease is rare, when the index test results are costly or difficult to collect and for re-analysing stored images or specimen. However, precision of the diagnostic accuracy measures will be hampered by increased variability when too little control patients are included.
Rutjes et al nicely discussed limitations of different study designs in diagnostic research [ 6 ]. They proposed the 'two-gate design with representative sampling' (which resembles the nested case-control design in this paper) as a valid design. We confirmed their proposition with a quantitative analysis of a diagnostic study. Rutjes et al suggested not to use the term 'nested case-control' to prevent confusion with etiologic studies where this design is commonly applied. Indeed, diagnostic and etiologic research differs fundamentally, first and foremost on the concept of time. Diagnostic accuracy studies are, in contrast to etiologic studies, typically cross-sectional in nature. Furthermore, diagnostic associations between index and reference tests are purely descriptive, whereas in etiologic studies causal associations and potential confounding are involved. Despite these major differences we believe there is no reason not to use the term nested case-control study in diagnostic research as well. The term inherently refers to the method of sampling of study subjects which can be the same in a diagnostic or etiologic setting, and has no direct bearing on the other issues typically related to etiologic case control studies.
Our findings support the view that the nested case-control study is a valid and efficient design for diagnostic studies. We believe that the nested case-control approach should be applied more often in diagnostic research, and also be (re)appraised in current guidelines on diagnostic methodology.
Knottnerus JA, van Weel C, Muris JW: Evaluation of diagnostic procedures. BMJ. 2002, 324 (7335): 477-480. 10.1136/bmj.324.7335.477.
Article PubMed PubMed Central Google Scholar
Knottnerus JA, Muris JW: Assessment of the accuracy of diagnostic tests: the cross-sectional study. J Clin Epidemiol. 2003, 56 (11): 1118-1128. 10.1016/S0895-4356(03)00206-3.
Article CAS PubMed Google Scholar
Lijmer JG, Mol BW, Heisterkamp S, Bonsel GJ, Prins MH, Meulen van der JHP, Bossuyt PMM: Empirical evidence of design-related bias in studies of diagnostic tests. JAMA. 1999, 282: 1061-1066. 10.1001/jama.282.11.1061.
Rutjes AW, Reitsma JB, Di Nisio M, Smidt N, van Rijn JC, Bossuyt PM: Evidence of bias and variation in diagnostic accuracy studies. CMAJ. 2006, 174 (4): 469-476.
Whiting P, Rutjes AW, Reitsma JB, Glas AS, Bossuyt PM, Kleijnen J: Sources of variation and bias in studies of diagnostic accuracy: a systematic review. Ann Intern Med. 2004, 140 (3): 189-202.
Article PubMed Google Scholar
Rutjes AW, Reitsma JB, Vandenbroucke JP, Glas AS, Bossuyt PM: Case-control and two-gate designs in diagnostic accuracy studies. Clin Chem. 2005, 51 (8): 1335-1341. 10.1373/clinchem.2005.048595.
Kraemer H: Evaluating Medical Tests. 1992, London, UK , Sage Publications
Google Scholar
Mantel N: Synthetic retrospective studies and related topics. Biometrics. 1973, 29 (3): 479-486. 10.2307/2529171.
Essebag V, Genest J, Suissa S, Pilote L: The nested case-control study in cardiology. Am Heart J. 2003, 146 (4): 581-590. 10.1016/S0002-8703(03)00512-X.
Ernster VL: Nested case-control studies. Prev Med. 1994, 23 (5): 587-590. 10.1006/pmed.1994.1093.
Langholz B: Case-Control Study, Nested. Encyclopedia of Biostatistics. Edited by: Armitage PCT. 2005, New York , John Wiley & Sons, 646-665. 2nd
Rothman KJ, Greenland S: Modern epidemiology. 1998, Philadelphia , Lincot-Raven Publishers, Second
Mantel N, Haenszel W: Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst. 1959, 22 (4): 719-748.
CAS PubMed Google Scholar
Ransohoff DF, Feinstein AR: Problems of spectrum and bias in evaluating the efficacy of diagnostic tests. N Engl J Med. 1978, 299 (17): 926-930.
Begg CB, Greenes RA: Assessment of diagnostic tests when disease verification is subject to selection bias. Biometrics. 1983, 39: 297-215. 10.2307/2530820.
Article Google Scholar
Knottnerus JA, Leffers JP: The influence of referral patterns on the characteristics of diagnostic tests. J Clin Epidemiol. 1992, 45: 1143-1154. 10.1016/0895-4356(92)90155-G.
van der Schouw YT, van Dijk R, Verbeek ALM: Problems in selecting the adequate patient population from existing data files for assessment studies of new diagnostic tests. J Clin Epidemiol. 1995, 48: 417-422. 10.1016/0895-4356(94)00144-F.
Oostenbrink R, Moons KG, Bleeker SE, Moll HA, Grobbee DE: Diagnostic research on routine care data: prospects and problems. J Clin Epidemiol. 2003, 56 (6): 501-506. 10.1016/S0895-4356(03)00080-5.
Oudega R, Hoes AW, Moons KG: The Wells rule does not adequately rule out deep venous thrombosis in primary care patients. Ann Intern Med. 2005, 143 (2): 100-107.
Oudega R, Moons KG, Hoes AW: Limited value of patient history and physical examination in diagnosing deep vein thrombosis in primary care. Fam Pract. 2005, 22 (1): 86-91. 10.1093/fampra/cmh718.
Perrier A, Desmarais S, Miron M, de Moerloose P, Lepage R, Slosman D, Didier D, Unger P, Patenaude J, Bounameaux H: Non-invasive diagnosis of venous thromboembolism in outpatients. Lancet. 1999, 353: 190-195. 10.1016/S0140-6736(98)05248-9.
Schutgens RE, Ackermark P, Haas FJ, Nieuwenhuis HK, Peltenburg HG, Pijlman AH, Pruijm M, Oltmans R, Kelder JC, Biesma DH: Combination of a normal D-dimer concentration and a non-high pretest clinical probability score is a safe strategy to exclude deep venous thrombosis. Circulation. 2003, 107 (4): 593-597. 10.1161/01.CIR.0000045670.12988.1E.
Pre-publication history
The pre-publication history for this paper can be accessed here: http://www.biomedcentral.com/1471-2288/8/48/prepub
Download references
Acknowledgements
For this research project we received financial support from the Netherlands Organization for Scientific Research, grant number: ZON-MW904-66-112. The funding source had no influence on the design, data analysis and report of this study.
Author information
Authors and affiliations.
Julius Center for Health Sciences and Primary Care, University Medical Center, Utrecht, The Netherlands
Cornelis J Biesheuvel, Yvonne Vergouwe, Ruud Oudega, Arno W Hoes, Diederick E Grobbee & Karel GM Moons
The Children's Hospital at Westmead, Sydney, Australia
Cornelis J Biesheuvel
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Karel GM Moons .
Additional information
Competing interests.
The authors declare that they have no competing interests.
Authors' contributions
All authors commented on the draft and the interpretation of the findings, read and approved the final manuscript. CJB was responsible for the design, statistical analysis and wrote the original manuscript. YV was responsible for the design and statistical analysis. RO was responsible for the data collection. AWH was responsible for expertise in case-control design. DEG and KGMM were responsible for conception and design of the study and coordination.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Authors’ original file for figure 1
Authors’ original file for figure 2, rights and permissions.
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Reprints and permissions
About this article
Cite this article.
Biesheuvel, C.J., Vergouwe, Y., Oudega, R. et al. Advantages of the nested case-control design in diagnostic research. BMC Med Res Methodol 8 , 48 (2008). https://doi.org/10.1186/1471-2288-8-48
Download citation
Received : 07 March 2008
Accepted : 21 July 2008
Published : 21 July 2008
DOI : https://doi.org/10.1186/1471-2288-8-48
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Diagnostic Accuracy
- Deep Vein Thrombosis
- Target Disease
- Diagnostic Accuracy Study
BMC Medical Research Methodology
ISSN: 1471-2288
- General enquiries: [email protected]
Help | Advanced Search
Computer Science > Machine Learning
Title: a rigorous machine learning analysis pipeline for biomedical binary classification: application in pancreatic cancer nested case-control studies with implications for bias assessments.
Abstract: Machine learning (ML) offers a collection of powerful approaches for detecting and modeling associations, often applied to data having a large number of features and/or complex associations. Currently, there are many tools to facilitate implementing custom ML analyses (e.g. scikit-learn). Interest is also increasing in automated ML packages, which can make it easier for non-experts to apply ML and have the potential to improve model performance. ML permeates most subfields of biomedical research with varying levels of rigor and correct usage. Tremendous opportunities offered by ML are frequently offset by the challenge of assembling comprehensive analysis pipelines, and the ease of ML misuse. In this work we have laid out and assembled a complete, rigorous ML analysis pipeline focused on binary classification (i.e. case/control prediction), and applied this pipeline to both simulated and real world data. At a high level, this 'automated' but customizable pipeline includes a) exploratory analysis, b) data cleaning and transformation, c) feature selection, d) model training with 9 established ML algorithms, each with hyperparameter optimization, and e) thorough evaluation, including appropriate metrics, statistical analyses, and novel visualizations. This pipeline organizes the many subtle complexities of ML pipeline assembly to illustrate best practices to avoid bias and ensure reproducibility. Additionally, this pipeline is the first to compare established ML algorithms to 'ExSTraCS', a rule-based ML algorithm with the unique capability of interpretably modeling heterogeneous patterns of association. While designed to be widely applicable we apply this pipeline to an epidemiological investigation of established and newly identified risk factors for pancreatic cancer to evaluate how different sources of bias might be handled by ML algorithms.
| Comments: | 22 pages, 12 figures |
| Subjects: | Machine Learning (cs.LG); Machine Learning (stat.ML) |
| Cite as: | [cs.LG] |
| (or [cs.LG] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
DBLP - CS Bibliography
Bibtex formatted citation.
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
- Introduction
- Conclusions
- Article Information
ADHD indicates attention-deficit/hyperactivity disorder; CVD, cardiovascular disease.
a Controls were derived from the same base cohort as the cases; thus, a case with a later date of CVD diagnosis could potentially serve as a control for another case in the study.
Crude odds ratios (ORs) were based on cases and controls matched on age, sex, and calendar time. Adjusted ORs (AORs) were based on cases and controls matched on age, sex, and calendar time and adjusted for country of birth, educational level, somatic comorbidities (type 2 diabetes, obesity, dyslipidemia, and sleep disorders), and psychiatric comorbidities (anxiety disorders, autism spectrum disorder, bipolar disorder, conduct disorder, depressive disorder, eating disorders, intellectual disability, personality disorders, schizophrenia, and substance use disorders).
The solid lines represent the adjusted odds ratios, and the shaded areas represent the 95% CIs. In restricted cubic splines analysis, knots were placed at the 10th, 50th, and 90th percentiles of ADHD medication use.
eTable 1. International Classification of Diseases (ICD) Codes from the Swedish National Inpatient Register
eTable 2. Type of Cardiovascular Disease in Cases
eTable 3. Risk of CVD Associated With ADHD Medication Use Across Different Average Defined Daily Doses
eTable 4. Risk of CVD Associated With Cumulative Duration of Use of Different Types of ADHD Medications
eTable 5. Sensitivity Analyses of CVD Risk Associated With Cumulative Use of ADHD Medications, Based On Different Cohort, Exposure, and Outcome Definitions
eFigure. Risk of CVD Associated With Cumulative Use of ADHD Medications, Stratified by Sex
Data Sharing Statement
- Long-Term ADHD Medications and Cardiovascular Disease Risk JAMA Medical News in Brief December 26, 2023 Emily Harris
- Long-Term Cardiovascular Effects of Medications for ADHD—Balancing Benefits and Risks of Treatment JAMA Psychiatry Editorial February 1, 2024 Samuele Cortese, MD, PhD; Cristiano Fava, MD, PhD
See More About
Select your interests.
Customize your JAMA Network experience by selecting one or more topics from the list below.
- Academic Medicine
- Acid Base, Electrolytes, Fluids
- Allergy and Clinical Immunology
- American Indian or Alaska Natives
- Anesthesiology
- Anticoagulation
- Art and Images in Psychiatry
- Artificial Intelligence
- Assisted Reproduction
- Bleeding and Transfusion
- Caring for the Critically Ill Patient
- Challenges in Clinical Electrocardiography
- Climate and Health
- Climate Change
- Clinical Challenge
- Clinical Decision Support
- Clinical Implications of Basic Neuroscience
- Clinical Pharmacy and Pharmacology
- Complementary and Alternative Medicine
- Consensus Statements
- Coronavirus (COVID-19)
- Critical Care Medicine
- Cultural Competency
- Dental Medicine
- Dermatology
- Diabetes and Endocrinology
- Diagnostic Test Interpretation
- Drug Development
- Electronic Health Records
- Emergency Medicine
- End of Life, Hospice, Palliative Care
- Environmental Health
- Equity, Diversity, and Inclusion
- Facial Plastic Surgery
- Gastroenterology and Hepatology
- Genetics and Genomics
- Genomics and Precision Health
- Global Health
- Guide to Statistics and Methods
- Hair Disorders
- Health Care Delivery Models
- Health Care Economics, Insurance, Payment
- Health Care Quality
- Health Care Reform
- Health Care Safety
- Health Care Workforce
- Health Disparities
- Health Inequities
- Health Policy
- Health Systems Science
- History of Medicine
- Hypertension
- Images in Neurology
- Implementation Science
- Infectious Diseases
- Innovations in Health Care Delivery
- JAMA Infographic
- Law and Medicine
- Leading Change
- Less is More
- LGBTQIA Medicine
- Lifestyle Behaviors
- Medical Coding
- Medical Devices and Equipment
- Medical Education
- Medical Education and Training
- Medical Journals and Publishing
- Mobile Health and Telemedicine
- Narrative Medicine
- Neuroscience and Psychiatry
- Notable Notes
- Nutrition, Obesity, Exercise
- Obstetrics and Gynecology
- Occupational Health
- Ophthalmology
- Orthopedics
- Otolaryngology
- Pain Medicine
- Palliative Care
- Pathology and Laboratory Medicine
- Patient Care
- Patient Information
- Performance Improvement
- Performance Measures
- Perioperative Care and Consultation
- Pharmacoeconomics
- Pharmacoepidemiology
- Pharmacogenetics
- Pharmacy and Clinical Pharmacology
- Physical Medicine and Rehabilitation
- Physical Therapy
- Physician Leadership
- Population Health
- Primary Care
- Professional Well-being
- Professionalism
- Psychiatry and Behavioral Health
- Public Health
- Pulmonary Medicine
- Regulatory Agencies
- Reproductive Health
- Research, Methods, Statistics
- Resuscitation
- Rheumatology
- Risk Management
- Scientific Discovery and the Future of Medicine
- Shared Decision Making and Communication
- Sleep Medicine
- Sports Medicine
- Stem Cell Transplantation
- Substance Use and Addiction Medicine
- Surgical Innovation
- Surgical Pearls
- Teachable Moment
- Technology and Finance
- The Art of JAMA
- The Arts and Medicine
- The Rational Clinical Examination
- Tobacco and e-Cigarettes
- Translational Medicine
- Trauma and Injury
- Treatment Adherence
- Ultrasonography
- Users' Guide to the Medical Literature
- Vaccination
- Venous Thromboembolism
- Veterans Health
- Women's Health
- Workflow and Process
- Wound Care, Infection, Healing
Others Also Liked
- Download PDF
- X Facebook More LinkedIn
Zhang L , Li L , Andell P, et al. Attention-Deficit/Hyperactivity Disorder Medications and Long-Term Risk of Cardiovascular Diseases. JAMA Psychiatry. 2024;81(2):178–187. doi:10.1001/jamapsychiatry.2023.4294
Manage citations:
© 2024
- Permissions
Attention-Deficit/Hyperactivity Disorder Medications and Long-Term Risk of Cardiovascular Diseases
- 1 Department of Medical Epidemiology and Biostatistics, Karolinska Institutet, Stockholm, Sweden
- 2 Unit of Cardiology, Heart and Vascular Division, Department of Medicine, Karolinska University Hospital, Karolinska Institutet, Stockholm, Sweden
- 3 School of Medical Sciences, Faculty of Medicine and Health, Örebro University, Örebro, Sweden
- 4 Department of Applied Health Science, School of Public Health, Indiana University, Bloomington
- 5 Department of Psychological and Brain Sciences, Indiana University, Bloomington
- Editorial Long-Term Cardiovascular Effects of Medications for ADHD—Balancing Benefits and Risks of Treatment Samuele Cortese, MD, PhD; Cristiano Fava, MD, PhD JAMA Psychiatry
- Medical News in Brief Long-Term ADHD Medications and Cardiovascular Disease Risk Emily Harris JAMA
Question Is long-term use of attention-deficit/hyperactivity disorder (ADHD) medication associated with an increased risk of cardiovascular disease (CVD)?
Findings In this case-control study of 278 027 individuals in Sweden aged 6 to 64 years who had an incident ADHD diagnosis or ADHD medication dispensation, longer cumulative duration of ADHD medication use was associated with an increased risk of CVD, particularly hypertension and arterial disease, compared with nonuse.
Meaning Findings of this study suggest that long-term exposure to ADHD medications was associated with an increased risk of CVD; therefore, the potential risks and benefits of long-term ADHD medication use should be carefully weighed.
Importance Use of attention-deficit/hyperactivity disorder (ADHD) medications has increased substantially over the past decades. However, the potential risk of cardiovascular disease (CVD) associated with long-term ADHD medication use remains unclear.
Objective To assess the association between long-term use of ADHD medication and the risk of CVD.
Design, Setting, and Participants This case-control study included individuals in Sweden aged 6 to 64 years who received an incident diagnosis of ADHD or ADHD medication dispensation between January 1, 2007, and December 31, 2020. Data on ADHD and CVD diagnoses and ADHD medication dispensation were obtained from the Swedish National Inpatient Register and the Swedish Prescribed Drug Register, respectively. Cases included individuals with ADHD and an incident CVD diagnosis (ischemic heart diseases, cerebrovascular diseases, hypertension, heart failure, arrhythmias, thromboembolic disease, arterial disease, and other forms of heart disease). Incidence density sampling was used to match cases with up to 5 controls without CVD based on age, sex, and calendar time. Cases and controls had the same duration of follow-up.
Exposure Cumulative duration of ADHD medication use up to 14 years.
Main Outcomes and Measures The primary outcome was incident CVD. The association between CVD and cumulative duration of ADHD medication use was measured using adjusted odds ratios (AORs) with 95% CIs.
Results Of 278 027 individuals with ADHD aged 6 to 64 years, 10 388 with CVD were identified (median [IQR] age, 34.6 [20.0-45.7] years; 6154 males [59.2%]) and matched with 51 672 control participants without CVD (median [IQR] age, 34.6 [19.8-45.6] years; 30 601 males [59.2%]). Median (IQR) follow-up time in both groups was 4.1 (1.9-6.8) years. Longer cumulative duration of ADHD medication use was associated with an increased risk of CVD compared with nonuse (0 to ≤1 year: AOR, 0.99 [95% CI, 0.93-1.06]; 1 to ≤2 years: AOR, 1.09 [95% CI, 1.01-1.18]; 2 to ≤3 years: AOR, 1.15 [95% CI, 1.05-1.25]; 3 to ≤5 years: AOR, 1.27 [95% CI, 1.17-1.39]; and >5 years: AOR, 1.23 [95% CI, 1.12-1.36]). Longer cumulative ADHD medication use was associated with an increased risk of hypertension (eg, 3 to ≤5 years: AOR, 1.72 [95% CI, 1.51-1.97] and >5 years: AOR, 1.80 [95% CI, 1.55-2.08]) and arterial disease (eg, 3 to ≤5 years: AOR, 1.65 [95% CI, 1.11-2.45] and >5 years: AOR, 1.49 [95% CI, 0.96-2.32]). Across the 14-year follow-up, each 1-year increase of ADHD medication use was associated with a 4% increased risk of CVD (AOR, 1.04 [95% CI, 1.03-1.05]), with a larger increase in risk in the first 3 years of cumulative use (AOR, 1.08 [95% CI, 1.04-1.11]) and stable risk over the remaining follow-up. Similar patterns were observed in children and youth (aged <25 years) and adults (aged ≥25 years).
Conclusions and Relevance This case-control study found that long-term exposure to ADHD medications was associated with an increased risk of CVDs, especially hypertension and arterial disease. These findings highlight the importance of carefully weighing potential benefits and risks when making treatment decisions about long-term ADHD medication use. Clinicians should regularly and consistently monitor cardiovascular signs and symptoms throughout the course of treatment.
Attention-deficit/hyperactivity disorder (ADHD) is a common psychiatric disorder characterized by developmentally inappropriate inattentiveness, impulsivity, and hyperactivity. 1 , 2 Pharmacological therapy, including both stimulants and nonstimulants, is recommended as the first-line treatment for ADHD in many countries. 1 , 3 The use of ADHD medication has increased greatly in both children and adults during the past decades. 4 Although the effectiveness of ADHD medications has been demonstrated in randomized clinical trials (RCTs) and other studies, 5 , 6 concerns remain regarding their potential cardiovascular safety. 7 Meta-analyses of RCTs have reported increases in heart rate and blood pressure associated with both stimulant and nonstimulant ADHD medications. 5 , 7 - 9
As RCTs typically evaluate short-term effects (average treatment duration of 75 days), 7 it remains uncertain whether and to what extent the increases in blood pressure and heart rate associated with ADHD medication lead to clinically significant cardiovascular disease (CVD) over time. Longitudinal observational studies 10 - 12 examining the association between ADHD medication use and serious cardiovascular outcomes have emerged in recent years, but the findings have been mixed. A meta-analysis 13 of observational studies found no statistically significant association between ADHD medication and risk of CVD. However, the possibility of a modest risk increase cannot be ruled out due to several methodological limitations in these studies, including confounding by indication, immortal time bias, and prevalent user bias. Additionally, most of these studies had an average follow-up time of no more than 2 years. 13 , 14 Thus, evidence regarding the long-term cardiovascular risk of ADHD medication use is still lacking.
Examining the long-term cardiovascular risk associated with ADHD medicine use is clinically important given that individuals with a diagnosis of ADHD, regardless of whether they receive treatment, face an elevated risk of CVD. 15 Additionally, a substantial proportion of young individuals with ADHD continues to have impairing symptoms in adulthood, 16 necessitating prolonged use of ADHD medication. Notably, studies have indicated a rising trend in the long-term use of ADHD medications, with approximately half of individuals using ADHD medication for over 5 years. 17 Furthermore, evidence is lacking regarding how cardiovascular risk may vary based on factors such as type of CVD, type of ADHD medication, age, and sex. 13 Therefore, there is a need for long-term follow-up studies to address these knowledge gaps and provide a more comprehensive understanding of the cardiovascular risks associated with ADHD medication use. This information is also crucial from a public health perspective, particularly due to the increasing number of individuals receiving ADHD medications worldwide. 4
This study aimed to assess the association between cumulative use of ADHD medication up to 14 years and the risk of CVD by using nationwide health registers in Sweden. We hypothesized that longer cumulative use of ADHD medication would be associated with increased CVD risk. In addition, we aimed to examine whether the associations differ across types of ADHD medication, types of CVD, sex, and age groups.
We used data from several Swedish nationwide registers linked through unique personal identification numbers. 18 Diagnoses were obtained from the National Inpatient Register, 19 which contains data on inpatient diagnoses since 1973 and outpatient diagnoses since 2001. Information on prescribed medications was retrieved from the Swedish Prescribed Drug Register, which contains all dispensed medications in Sweden since July 2005 and includes information on drug identity based on the Anatomical Therapeutic Chemical (ATC) classification, 20 dispensing dates, and free-text medication prescriptions. Socioeconomic factors were obtained from the Longitudinal Integrated Database for Health Insurance and Labour Market studies. 21 Information on death was retrieved from the Swedish Cause of Death Register, 22 which contains information on all deaths since 1952. The study was approved by the Swedish Ethical Review Authority. Informed patient consent is not required for register-based studies in Sweden. The study followed the Reporting of Studies Conducted Using Observational Routinely Collected Health Data–Pharmacoepidemiological Research ( RECORD-PE ) guideline. 23
We conducted a nested case-control study of all individuals residing in Sweden aged 6 to 64 years who received an incident diagnosis of ADHD or ADHD medication dispensation 15 between January 1, 2007, and December 31, 2020. The diagnosis of ADHD ( International Statistical Classification of Diseases and Related Health Problems, Tenth Revision [ ICD-10 ] code F90) was identified from the National Inpatient Register. Incident ADHD medication dispensation was identified from the Swedish Prescribed Drug Register and was defined as a dispensation after at least 18 months without any ADHD medication dispensation. 24 Baseline (ie, cohort entry) was defined as the date of incident ADHD diagnosis or ADHD medication dispensation, whichever came first. Individuals with ADHD medication prescriptions for indications other than ADHD 25 and individuals who emigrated, died, or had a history of CVD before baseline were excluded from the study. The cohort was followed until the case index date (ie, the date of CVD diagnosis), death, migration, or the study end date (December 31, 2020), whichever came first.
Within the study cohort, we identified cases as individuals with an incident diagnosis of any CVD (including ischemic heart diseases, cerebrovascular diseases, hypertension, heart failure, arrhythmias, thromboembolic disease, arterial disease, and other forms of heart disease; eTable 1 in Supplement 1 ) during follow-up. For each case, the date of their CVD diagnosis was assigned as the index date. Using incidence density sampling, 26 up to 5 controls without CVD were randomly selected for each case from the base cohort of individuals with ADHD. The matching criteria included age, sex, and calendar time, ensuring that cases and controls had the same duration of follow-up from baseline to index date. Controls were eligible for inclusion if they were alive, living in Sweden, and free of CVD at the time when their matched case received a diagnosis of CVD, with the index date set as the date of CVD diagnosis of the matched case ( Figure 1 ). Controls were derived from the same base cohort as the cases. Thus, a case with a later date of CVD diagnosis could potentially serve as a control for another case in the study. 26
The main exposure was cumulative duration of ADHD medication use, which included all ADHD medications approved in Sweden during the study period, including stimulants (methylphenidate [ATC code N06BA04], amphetamine [ATC code N06BA01], dexamphetamine [ATC code N06BA02], and lisdexamfetamine [ATC code N06BA12]) as well as nonstimulants (atomoxetine [ATC code N06BA09] and guanfacine [ATC code C02AC02]). Duration of ADHD medication use was derived from a validated algorithm that estimates treatment duration from free text in prescription records. 25 The cumulative duration of ADHD medication use was calculated by summing all days covered by ADHD medication between baseline and 3 months prior to the index date. The last 3 months before the index date were excluded to reduce reverse causation, as clinicians’ perception of potential cardiovascular risks may influence ADHD medication prescription. This time window was chosen because routine psychiatric practice in Sweden limits a prescription to a maximum 3 months at a time. 27 Individuals with follow-up of less than 3 months were excluded.
We conducted conditional logistic regression analyses to estimate odds ratios (ORs) for the associations between cumulative durations of ADHD medication use and incident CVD. Crude ORs were adjusted for all matching variables (age, sex, and calendar time) by design. Adjusted ORs (AORs) were additionally controlled for country of birth (Sweden vs other), highest educational level (primary or lower secondary, upper secondary, postsecondary or postgraduate, or unknown; individuals aged <16 years were included as a separate category), and diagnoses of somatic (type 2 diabetes, obesity, dyslipidemia, and sleep disorders) and psychiatric comorbidities (anxiety disorders, autism spectrum disorder, bipolar disorder, conduct disorder, depressive disorder, eating disorders, intellectual disability, personality disorders, schizophrenia, and substance use disorders; eTable 1 in Supplement 1 ) before baseline. The association between cumulative ADHD medication use and incident CVD was assessed using both continuous and categorical measures (no ADHD medication use, 0 to ≤1, 1 to ≤2, 2 to ≤3, 3 to ≤5, and >5 years). To capture potential nonlinear associations, we used restricted cubic splines to examine ADHD medication use as a continuous measure throughout follow-up. 28 The associations were examined in the full sample and stratified by age at baseline, that is, children or youth (<25 years old) and adults (≥25 years old). Furthermore, to evaluate the association with dosage of ADHD medication, we estimated the risk of CVD associated with each 1-year increase in use of ADHD medication across different dosage groups categorized by the average defined daily dose (DDD; for instance, 1 DDD of methylphenidate equals 30 mg) during follow-up. 29
In subgroup analyses, we examined the associations between ADHD medication use and specific CVDs, including arrhythmias, arterial disease, cerebrovascular disease, heart failure, hypertension, ischemic heart disease, and thromboembolic disease (eTable 1 in Supplement 1 ). Additionally, we investigated the associations with CVD risk for the most commonly prescribed ADHD medications in Sweden, ie, methylphenidate, lisdexamfetamine, and atomoxetine, while adjusting for other ADHD medication use. We also examined sex-specific associations.
To further examine the robustness of our findings, we conducted 4 sensitivity analyses. First, we restricted the sample to ever users of ADHD medication to reduce unmeasured confounding between ADHD medication users and nonusers. Second, we assessed ADHD medication exposure over the entire follow-up period without excluding the 3 months prior to the index date. Third, to capture fatal cardiovascular events, we additionally included death by CVD in the outcome definition. Finally, we constructed a conditional logistic regression model that adjusted for propensity scores of ADHD medication use. Data management was performed using SAS, version 9.4 (SAS Institute Inc) and all analyses were performed using R, version 4.2.3 (R Foundation for Statistical Computing).
The study cohort consisted of 278 027 individuals with ADHD aged 6 to 64 years. The incidence rate of CVD was 7.34 per 1000 person-years. After applying exclusion criteria and matching, the analysis included 10 388 cases (median [IQR] age at baseline, 34.6 (20.0-45.7) years; 6154 males [59.2%] and 4234 females [40.8%]) and 51 672 matched controls (median [IQR] age at baseline, 34.6 [19.8-45.6] years; 30 601 males [59.2%] and 21 071 females [40.8%]) ( Figure 1 and Table 1 ). Median (IQR) follow-up in both groups was 4.1 (1.9-6.8) years. Among the controls, 3363 had received a CVD diagnosis after their index dates. The most common types of CVD in cases were hypertension (4210 cases [40.5%]) and arrhythmias (1310 cases [12.6%]; eTable 2 in Supplement 1 ). Table 1 presents the sociodemographic information and somatic and psychiatric comorbidities in cases and controls. In general, cases had higher rates of somatic and psychiatric comorbidities and a lower level of educational attainment compared with controls.
A similar proportion of cases (83.9%) and controls (83.5%) used ADHD medication during follow-up, with methylphenidate being the most commonly dispensed type, followed by atomoxetine and lisdexamfetamine. Longer cumulative duration of ADHD medication use was associated with an increased risk of CVD compared with nonuse (0 to ≤1 year: AOR, 0.99 [95% CI, 0.93-1.06]; 1 to ≤2 years: AOR, 1.09 [95% CI, 1.01-1.18]; 2 to ≤3 years: AOR, 1.15 [95% CI, 1.05-1.25]; 3 to ≤5 years: AOR, 1.27 [95% CI, 1.17-1.39]; and >5 years: AOR, 1.23 [95% CI, 1.12-1.36]) ( Figure 2 ). The restricted cubic spline model suggested a nonlinear association, with the AORs increasing rapidly for the first 3 cumulative years of ADHD medication use and then becoming stable thereafter ( Figure 3 ). Throughout the entire follow-up, each 1-year increase in the use of ADHD medication was associated with a 4% increased risk of CVD (AOR, 1.04 [95% CI, 1.03-1.05]), and the corresponding increase for the first 3 years was 8% (AOR, 1.08 [95% CI, 1.04-1.11]). We observed similar results when examining children or youth and adults separately ( Figure 2 ). The restricted cubic spline model suggested a similar nonlinear association, with higher AORs in children or youth than in adults, but the 95% CIs largely overlapped ( Figure 3 ). Furthermore, similar associations were observed for females and males (eFigure in Supplement 1 ). The dosage analysis showed that the risk of CVD associated with each 1 year of ADHD medication use increased with higher average DDDs. The risk was found to be statistically significant only among individuals with a mean dose of at least 1.5 times the DDD (eTable 3 in Supplement 1 ). For example, among individuals with a mean DDD of 1.5 to 2 or less (eg, for methylphenidate, 45 to ≤60 mg), each 1-year increase in ADHD medication use was associated with a 4% increased risk of CVD (AOR, 1.04 [95% CI, 1.02-1.05]). Among individuals with a mean DDD >2 (eg, for methylphenidate >60 mg), each 1-year increase in ADHD medication use was associated with 5% increased risk of CVD (AOR, 1.05 [95% CI, 1.03-1.06]).
When examining the risk for specific CVDs, we found that long-term use of ADHD medication (compared with no use) was associated with an increased risk of hypertension (AOR, 1.72 [95% CI, 1.51-1.97] for 3 to ≤5 years; AOR, 1.80 [95% CI 1.55-2.08] for >5 years) ( Table 2 ), as well as arterial disease (AOR, 1.65 [95% CI, 1.11-2.45] for 3 to ≤5 years; AOR, 1.49 [95% CI 0.96-2.32] for >5 years). However, we did not observe any statistically significant increased risk for arrhythmias, heart failure, ischemic heart disease, thromboembolic disease, or cerebrovascular disease ( Table 2 ). Furthermore, long-term use of methylphenidate (compared with no use) was associated with an increased risk of CVD (AOR, 1.20 [95% CI, 1.10-1.31] for 3 to ≤5 years; AOR, 1.19 [95% CI, 1.08-1.31]) for >5 years; eTable 4 in Supplement 1 ). Compared with no use, lisdexamfetamine was also associated with an elevated risk of CVD (AOR, 1.23 [95% CI, 1.05-1.44] for 2 to ≤3 years; AOR, 1.17 [95% CI, 0.98-1.40] for >3 years), while the AOR for atomoxetine use was significant only for the first year of use (1.07 [95% CI 1.01-1.13]; eTable 4 in Supplement 1 ).
In sensitivity analyses, we observed a similar pattern of estimates when the analysis was restricted to ever users of ADHD medications. Significantly increased risk of CVD was found when comparing ADHD medication use for 1 year or less with use for 3 to 5 or less years (AOR, 1.28 (95% CI, 1.18-1.38) or for use for more than 5 years (AOR, 1.24 [95% CI, 1.13-1.36]) (eTable 5 in Supplement 1 ). When assessing ADHD medication use across the entire follow-up period, and compared with no use, the pattern of estimates was similar to the main analysis (3 to ≤5 years: AOR, 1.28 [95% CI, 1.18-1.39]; >5 years: AOR, 1.25 [95% CI, 1.14-1.37]) (eTable 5 in Supplement 1 ). The analysis that included cardiovascular death as a combined outcome also had results similar to the main analysis. Moreover, when adjusting for propensity scores of ADHD medication use, the findings remained consistent (eTable 5 in Supplement 1 ).
This large, nested case-control study found an increased risk of incident CVD associated with long-term ADHD medication use, and the risk increased with increasing duration of ADHD medication use. This association was statistically significant both for children and youth and for adults, as well as for females and males. The primary contributors to the association between long-term ADHD medication use and CVD risk was an increased risk of hypertension and arterial disease. Increased risk was also associated with stimulant medication use.
We found individuals with long-term ADHD medication use had an increased risk of incident CVD in a dose-response manner in the first 3 years of cumulative ADHD medication use. To our knowledge, few previous studies have investigated the association between long-term ADHD medication use and the risk of CVD with follow-up of more than 2 years. 13 The only 2 prior studies with long-term follow-up (median, 9.5 and 7.9 years 30 , 31 ) found an average 2-fold and 3-fold increased risk of CVD with ADHD medication use compared with nonuse during the study period, yet 1 of the studies 30 included only children, and participants in the other study 31 were not the general population of individuals with ADHD (including those with ADHD and long QT syndrome). Furthermore, both studies were subject to prevalent user bias. Results from the current study suggest that the CVD risk associated with ADHD medication use (23% increased risk for >5 years of ADHD medication use compared with nonuse) is lower than previously reported. 30 , 31 Furthermore, we observed that the increased risk stabilized after the first several years of medication use and persisted throughout the 14-year follow-up period.
The association between ADHD medication use and CVD was significant for hypertension and arterial disease, while no significant association was observed with other types of cardiovascular events. To our knowledge, only 1 previous study 12 has examined the association between ADHD medication use and clinically diagnosed hypertension, and it found an increased risk, although the increase was not statistically significant. Furthermore, increased blood pressure associated with ADHD medication use has been well documented. 7 , 9 One study 32 found that blood pressure was mainly elevated during the daytime, suggesting that the cardiovascular system may recover at night. However, the cross-sectional nature of that study cannot preclude a long-term risk of clinically diagnosed hypertension associated with ADHD medication use. We also identified an increased risk for arterial disease. To date, no previous study has explored the association between ADHD medication use and arterial disease. A few studies have reported that ADHD medication may be associated with changes in serum lipid profiles, but the results were not consistent. 33 , 34 Further research is needed on the potential implications of ADHD medications for individuals’ lipid profiles. We did not observe any association between ADHD medication use and the risk of arrhythmias. A recent systematic review of observational studies of ADHD medication use reported an elevated risk of arrhythmias, but the finding was not statistically significant. 13 A review of RCTs also found that the use of stimulants was associated with an average increase in heart rate of 5.7 beats/min, 9 but no evidence of prolonged QT interval or tachycardia was found based on electrocardiograms. 7 Additionally, it is worth noting that some individuals receiving ADHD medications might be prescribed antiarrhythmic β-blockers to alleviate palpitation symptoms, thus potentially attenuating an association between ADHD medications and arrhythmias. Nevertheless, the absence of an association between ADHD medication use and clinically diagnosed arrhythmias in the present study does not rule out an increased risk for mild arrhythmias or subclinical symptoms, as palpitations and sinus tachycardia are not routinely coded as arrhythmia diagnoses. Further research is necessary to replicate our findings.
Regarding types of ADHD medication, findings of the present study suggest that increasing cumulative durations of methylphenidate and lisdexamfetamine use were associated with incident CVD, while the associations for atomoxetine were statistically significant only for the first year of use. Previous RCTs have reported increased blood pressure and heart rate with methylphenidate, lisdexamfetamine, and atomoxetine, 5 , 35 , 36 but the mechanisms behind these adverse effects are still a topic of debate; there might be differences in cardiovascular adverse effects in stimulants vs nonstimulants. 37
We found that the association between cumulative duration of ADHD medication use and CVD was similar in females and males. Previous investigations exploring sex-specific association found higher point estimates in females, although the differences were not statistically significant. 13 Research has indicated that females diagnosed with ADHD may demonstrate different comorbidity patterns and potentially have different responses to stimulant medications compared with males. 38 - 40 Therefore, additional studies are needed to explore and better understand the potential sex-specific differences in cardiovascular responses to ADHD medications.
A strength of this study is that data on ADHD medication prescriptions and CVD diagnoses were recorded prospectively, so the results were not affected by recall bias. The findings should, however, be interpreted in the context of several limitations. First, our approach for identification of patients with CVD was based on recorded diagnoses and there could be under ascertainment of cardiovascular diagnoses in the registers used. This means that some controls may have had undiagnosed CVD that did not yet require medical care, which would tend to underestimate associations between ADHD medication use and CVD. Second, exposure misclassification may have occurred if patients did not take their medication as prescribed. This misclassification, if nondifferential, would tend to reduce ORs such that the estimates we observed were conservative. Third, while we accounted for a wide range of potential confounding variables, considering the observational nature of the study and the possibility of residual confounding, we could not prove causality. It is possible that the association observed might have been affected by time-varying confounders. For example, other psychotropic medications and lifestyle factors could have affected both ADHD medication use and the occurrence of cardiovascular events. 41 , 42 Confounding by ADHD severity is also a potential factor to consider, as individuals with more severe ADHD symptoms may have more comorbidities and a less healthy lifestyle, which could affect the risk of CVD. Fourth, the study did not examine the risk of CVD among individuals with preexisting CVD. Individuals with preexisting CVD represent a distinct clinical group that requires careful monitoring; thus, evaluating the risk among them necessitates a different study design that carefully considers the potential impact of prior knowledge and periodic monitoring. Finally, the results by type of ADHD medication and type of CVD need to be replicated by studies with larger sample sizes.
The results of this population-based case-control study with a longitudinal follow-up of 14 years suggested that long-term use of ADHD medication was associated with an increased risk of CVD, especially hypertension and arterial disease, and the risk was higher for stimulant medications. These findings highlight the importance of carefully weighing potential benefits and risks when making treatment decisions on long-term ADHD medication use. Clinicians should be vigilant in monitoring patients, particularly among those receiving higher doses, and consistently assess signs and symptoms of CVD throughout the course of treatment. Monitoring becomes even more crucial considering the increasing number of individuals engaging in long-term use of ADHD medication.
Accepted for Publication: August 29, 2023.
Published Online: November 22, 2023. doi:10.1001/jamapsychiatry.2023.4294
Open Access: This is an open access article distributed under the terms of the CC-BY License . © 2023 Zhang L et al. JAMA Psychiatry .
Corresponding Authors: Zheng Chang, PhD ( [email protected] ) and Le Zhang, PhD ( [email protected] ), Department of Medical Epidemiology and Biostatistics, Karolinska Institutet, Nobels väg 12A, 171 65 Stockholm, Sweden.
Author Contributions: Dr Zhang and Prof Chang had full access to all of the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis.
Concept and design: Zhang, Johnell, Larsson, Chang.
Acquisition, analysis, or interpretation of data: Zhang, Li, Andell, Garcia-Argibay, Quinn, D'Onofrio, Brikell, Kuja-Halkola, Lichtenstein, Johnell, Chang.
Drafting of the manuscript: Zhang.
Critical review of the manuscript for important intellectual content: All authors.
Statistical analysis: Zhang, Li.
Obtained funding: Larsson, Chang.
Administrative, technical, or material support: Garcia-Argibay, D'Onofrio, Kuja-Halkola, Lichtenstein, Chang.
Supervision: Andell, Lichtenstein, Johnell, Larsson, Chang.
Conflict of Interest Disclosures: Dr Larsson reported receiving grants from Takeda Pharmaceuticals and personal fees from Takeda Pharmaceuticals, Evolan, and Medici Medical Ltd outside the submitted work. No other disclosures were reported.
Funding/Support: This study was supported by grants from the Swedish Research Council for Health, Working Life, and Welfare (2019-01172 and 2022-01111) (Dr Chang) and the European Union’s Horizon 2020 research and innovation program under grant agreement 965381 (Dr Larsson).
Role of the Funder/Sponsor: The funders had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.
Data Sharing Statement: See Supplement 2 .
- Register for email alerts with links to free full-text articles
- Access PDFs of free articles
- Manage your interests
- Save searches and receive search alerts
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 18 June 2024
A matched case-control analysis of autonomous vs human-driven vehicle accidents
- Mohamed Abdel-Aty 1 &
- Shengxuan Ding ORCID: orcid.org/0009-0006-7690-9546 1
Nature Communications volume 15 , Article number: 4931 ( 2024 ) Cite this article
9272 Accesses
978 Altmetric
Metrics details
- Civil engineering
- Decision making
Despite the recent advancements that Autonomous Vehicles have shown in their potential to improve safety and operation, considering differences between Autonomous Vehicles and Human-Driven Vehicles in accidents remain unidentified due to the scarcity of real-world Autonomous Vehicles accident data. We investigated the difference in accident occurrence between Autonomous Vehicles’ levels and Human-Driven Vehicles by utilizing 2100 Advanced Driving Systems and Advanced Driver Assistance Systems and 35,113 Human-Driven Vehicles accident data. A matched case-control design was conducted to investigate the differential characteristics involving Autonomous’ versus Human-Driven Vehicles’ accidents. The analysis suggests that accidents of vehicles equipped with Advanced Driving Systems generally have a lower chance of occurring than Human-Driven Vehicles in most of the similar accident scenarios. However, accidents involving Advanced Driving Systems occur more frequently than Human-Driven Vehicle accidents under dawn/dusk or turning conditions, which is 5.25 and 1.98 times higher, respectively. Our research reveals the accident risk disparities between Autonomous Vehicles and Human-Driven Vehicles, informing future development in Autonomous technology and safety enhancements.
Similar content being viewed by others
Multiple vehicle cooperation and collision avoidance in automated vehicles: survey and an AI-enabled conceptual framework

The ironies of autonomy

The risk ethics of autonomous vehicles: an empirical approach
Introduction.
Automation of systems has been experiencing rapid development and has brought about a revolution in the transportation industry. The introduction of Autonomous Vehicles (AV) technology has made the vision of a safe transportation system with effortless driving seem attainable. It is anticipated that the automation of systems will significantly reduce the number of accidents, as human errors contribute up to 90% of accidents 1 . While smart transportation has showcased several benefits, these emerging technologies have also exhibited drawbacks, particularly regarding safety risks. Accidents of on-road testing have already been documented in limited testing data 2 .
According to findings from the RAND corporation 3 , a mere advancement in safety features in the initial release of AVs could yield significant life-saving results. The research suggests that if AVs were to be introduced with an average safety level ten percent higher than that of the typical human driver, approximately 600,000 fatalities could be averted in the United States over a span of 35 years. Nevertheless, it is crucial to acknowledge that between 2015 and 2022, there was a yearly rise in both the annual miles traveled by autonomous vehicles (AVMT) and the number of AV accidents on public roads in California, with the exception of a decline in 2020 attributable probably to the COVID-19 pandemic 4 . AV testing on California public roads is permitted by the California Department of Motor Vehicles (CADMV) 5 . Up until June 2023, we have identified and enriched with 598 Advanced Driving Systems (ADS (SAE Level 4)) accidents in California (AVOID dataset) 6 . These reports provide details about AV accidents and disengagements, which happen when the vehicle switches from autonomous mode due to technological issues or when the test driver or operator assumes manual control for safety purposes 7 . The detailed information included in these reports revealed various factors related to AV accidents. We further collected the corresponding reports of Human-Driven Vehicles (HDV) accidents to contrast the differences between AV and matched HDV accidents.
There are many potential benefits of AVs on traffic safety, such as a reduction in human error, reduced fatigue, and distraction. ADAS functions including Electronic Stability Control (ESC), Anti-Lock Braking (ABS), and Information and Communication Technology aids in ongoing driving tasks to prevent accidents 8 , 9 , 10 . For example, Tesla Autopilot consistently maintains a closer distance to the lane center than human drivers 11 . Additionally, Level 3 or higher levels of automation can further enhance traffic by reducing accidents 12 , 13 , improving mobility for the disabled and elderly, and minimizing traffic collisions through efficient driving and the reduction of human errors 14 . Koopman and Wagner highlighted the importance of understanding how AVs will interact with human drivers, pedestrians, and other road users 15 . Compared with HDV, accident avoidance features of AVs can reduce accidents and fatalities caused by distracted driving or human error by helping control the vehicle and alerting drivers to potential dangers 16 , 17 .
However, there are also some possible safety challenges that need to be addressed in AVs. Penmetsa et al. 18 identified several safety challenges that need to be addressed in the development of AV, such as the need for reliable sensing and perception, robust decision-making algorithms, and fail-safe mechanisms 18 . Kalra and Paddock presented a statistical methodology with 382 accidents per 100 million miles based on binomial and Poisson distributions for estimating the required mileage to establish the reliability of AVs, it shows that AVs would have to be driven hundreds of millions of miles and sometimes hundreds of billions of miles to demonstrate their reliability in terms of fatalities and injuries 19 . Some studies also have concentrated on analyzing the accident severity involving different types of AV 20 . Ding et al. 6 collected 1280 cases to compare factors related to injury severity between the ADAS and ADS accidents by random parameter multinomial logit models. Subject vehicle’s contact area, road and environment, and pre-accident movement, significantly impact accidents injury severity. ADS-equipped vehicles in work zones have a higher probability of being involved in minor and moderate/severe injury accidents 21 .
The comparison of safety performance between AV and HDV is a topic of debate, with conflicting viewpoints 22 . On one side, numerous studies support the view that AVs are generally safer than HDVs 23 . For instance, Dixit et al. 24 analyzed the statistical distribution of reports on 69 manual disengagements and accidents, they compared the accident rates of Google self-driving cars to those of human drivers and found that fatal accidents involving Google cars were lower than that of HDV, no fatalities occurred as compared to 1 death for every 108 million miles in California 24 . Additionally, from 2009 to 2015 in Mountain View, California, Google cars demonstrated a significantly lower rate of police-reportable accidents per million vehicle miles traveled (VMT) compared to human drivers (2.19 versus 6.06) 25 . On the other hand, some research challenges this view, suggesting that the safety of AVs may not always exceed that of HDVs. Schoettle and Sivak uncovered that AVs have a higher rate of accidents per million miles traveled compared to HDVs in limited (and generally less demanding) conditions (e.g., avoiding snowy areas) 26 . Favarò et al. 27 found that rear-end accidents were the most frequent type of AV accidents, with AVs being hit from behind by conventional vehicles at a rate twice that of rear-end accidents than rear-end “fender-benders” for conventional vehicles in California 2013 27 .
These studies offered significant insight into the factors that contribute to AV and HDV accidents, while earlier studies may not consider sufficient factors of road environment, accident outcome, pre-accident condition, and accident type for accident analysis due to a lack of matched AV and HDV data for identifying the characteristics of AV accidents and how they differ from regular HDV accidents 28 , 29 , 30 . The number of accidents of the relevant studies and their automation level are shown in Fig. 1 .
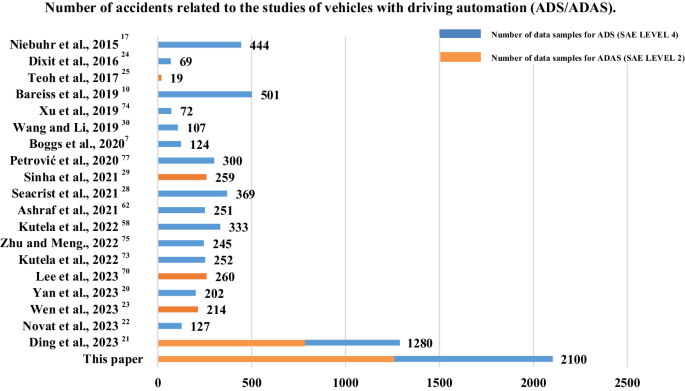
The blue line shows the number of ADS data samples, and the orange line shows the number of ADAS data samples used in related studies.
In this work, we examined a dataset comprising both AV and HDV accidents. The dataset utilized in this study was compiled from various sources and encompassed information on accident types, road and environmental conditions, pre-accident vehicle movements, and accident outcomes. We use a matched case-control logistic regression model. We further add the National Highway Traffic Safety Administration (NHTSA) AV database comprising an additional 495 ADS and 1001 Advanced driver assistance systems (ADAS (SAE Level 2)) accidents 31 . These findings illuminate the factors that contribute to accidents involving AVs vs. HDVs.
General trends in the full accident data
We first present general trends and comparisons between AV and HDV accidents of the full dataset. Figure 2a–d displays the distribution of factors affecting AV (2100), including SAE level 4 ADS (1099), level 2 ADAS (1001) and HDV accidents (35,133), respectively. Notably, vehicles make up 80% of participants in AV accidents, with pedestrians accounting for 3%. In contrast, for HDVs, pedestrians constitute 15% and vehicles 63% of accident participants, as depicted in Fig. 2a, b . When examining the outcomes of accidents, both AVs and HDVs lead to either no injuries or minor injuries occurring in 94%.
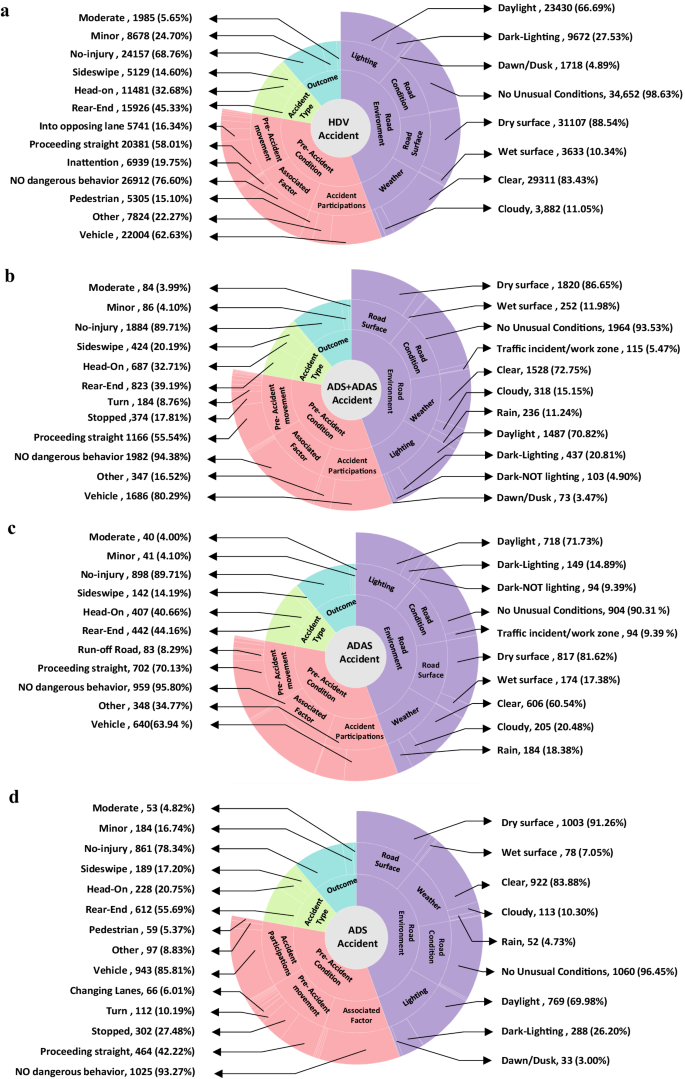
a HDV accidents with a sample of 35,133. b SAE level 4 ADS + SAE level 2 ADAS accidents with a sample of 2100. c SAE level 2 ADAS accidents with a sample of 1001. d SAE level 4 ADS accidents with a sample of 1099.
Significant disparities between AV and HDV accidents can be seen in work zones, traffic events, and pre-accident movements such as slowing down, proceeding straight, and moving into opposing lanes, with AVs exhibiting higher accident rates. For both AVs and HDVs, the most frequent pre-accident movement is proceeding straight. It is observed that 56% of AV accidents and 58% of HDV accidents occur under this specific condition. About 5% of AV accidents take place in locations impacted by previous traffic events or work zones, where normal traffic is disrupted by earlier incidents like disabled vehicles or spilled cargo. In comparison, just 1.3% of HDV accidents occur in similar settings. Analyzing the pre-accident scenario, a distinctive observation is that only 1.8% of AV accidents are attributed to inattention or poor driving behavior, in contrast to a much higher 19.8% for HDVs.
Evaluating environmental factors, the majority of accidents involving both AVs and HDVs tend to happen under clear weather conditions. Notably, accidents involving HDVs occur slightly more frequently under these conditions, at a rate of 83%, compared to 73% for AVs. However, AVs are more commonly involved in accidents during rainy conditions, accounting for 11% of such accidents, compared to HDVs which experience these conditions in only 5% of accidents. Dawn or dusk conditions experience 3.5% of AV accidents, which is lower than the 4.9% rate for HDVs.
In terms of accident type, rear-end accidents constitute a majority for both AVs and HDVs. Furthermore, we determine the accident type associated with AV and HDV based on the accident angle. Our data indicates that for HDVs, the rear-end stands at 45% (other vehicles hit HDV), while head-on accidents (HDV hit other vehicles) occur at a rate of 33%. In contrast, AVs have a slightly lower rear-end accidents (other vehicles hit AV) rate of 39%, but a similar head-on accidents (AV hit other vehicles) rate of 33%. This suggests that while AVs have a marginally lower percentage of being rear-ended compared to HDVs, their percentage of head-on accidents is almost the same.
Figure 3 describes two conditions related to ADS rear-end accidents: a: HDV has hit an ADS from behind (252) and b: an ADS has hit an HDV from behind (67). The left side of the diagram starts with two conditions of HDV hit ADS or ADS hit HDV. The middle section shows the movement of vehicle: Moving or Stopping. The right side categorizes the severity of the accidents: Minor, Moderate and Major. The numbers indicated in each section of the diagram correspond to the total count of each specific category. The width of each link connecting the sections of the diagrams represents the proportion of scenarios that fall into the subsequent category. For example, In Fig. 3a , which details accidents where a HDV hit an ADS, we see that for the accidents where the ADS was moving (middle section), 62 cases (57%) involved ADS in autonomous mode while 46 cases (43%) involved ADS in conventional mode (left section). Among the 108 accidents categorized under the ‘moving condition’, there were 2 cases (2%) that resulted in major injuries, 18 cases (17%) that led to moderate injuries, and the remaining 88 cases (81%) involved minor injuries.
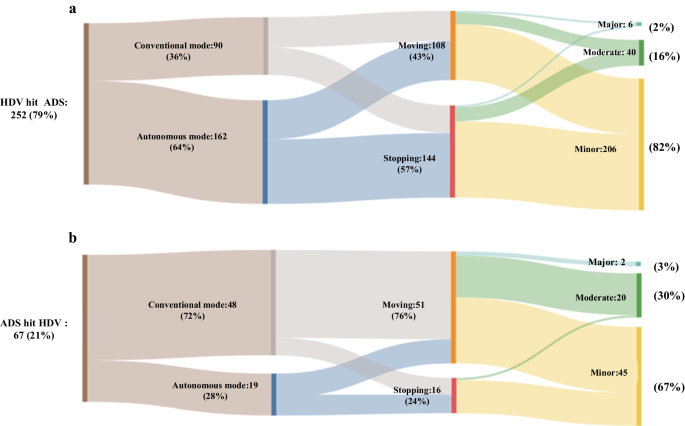
a Rear-end accidents that HDV hit an ADS from behind with a sample of 252. b Rear-end accidents that ADS hit an HDV from behind with a sample of 67.
The analysis reveals that 79% of rear-end accidents involve HDV hitting ADS, while 21% of rear-end accidents involve ADS hitting HDV. When the ADS hit HDV in conventional mode, most of the ADS are moving. We may conclude that compared with the autonomous mode, human drivers may not react as quickly or may not notice the object in time to take appropriate action. In terms of accident severity, 206 of accidents (82%) occur as minor injury when HDV hit ADS. This percentage is 67% when the ADS hit HDV. It is important to note that a majority of moderate and major accidents involving an ADS hitting an HDV occur when both vehicles are moving in the conventional mode. Notably, in cases where HDVs hit ADS, 64% of ADS are operating in autonomous mode. Conversely, when ADS are responsible for hitting HDVs, 72% of ADS are operating in the conventional mode. According to Dixit et al. in 2016, 56.1% of disengagements were attributed to system failures, 26.57% were initiated by the driver, and 9.89% were related to road infrastructure issues 24 . This observation suggests that conventional mode occurred more frequently than autonomous mode where ADS hit the HDV. This may be attributed to the advance autonomous mode of ADS. Autonomous mode uses advanced algorithms to detect and avoid obstacles and other vehicles in the path of the vehicle 32 .
We also contrast the ADS vs the ADAS, accidents related to ADAS and ADS display differences across various conditions, as shown in Fig. 2c, d . Regarding weather and road conditions, ADAS has 23.34% fewer accident number in clear skies but a 13.65% higher in rain compared to ADS. For road conditions, ADAS accidents experience a 7.48% higher accident number in traffic events or work zones and 10.33% higher accident number on wet roads than ADS. Analyzing pre-accident movements, ADAS indicate a 27.91% higher accident number for proceeding straight, while reporting 3.0% fewer turning accident numbers than ADS. In terms of accident types, ADAS is 3.0% higher accident number than ADS in broadside accidents and lags by 5.4% in sideswipe accidents. From an injury outcome perspective, ADAS accidents present a 11.37% higher accident number of no-injury but a 2.1% lower number in fatal injuries against ADS. To enhance the understanding of pre-accident speeds, heatmaps that visually represent these speed patterns for ADS and ADAS vehicles are shown in Fig. 4 . This chart offers a detailed comparison of how speeds vary across different days of the week and at various times of the day. This trend can be attributed to the fact that ADAS is primarily designed for highway use, leading to a higher average pre-accident speed when compared to ADS vehicles, which are designed for a complex urban driving scenario.
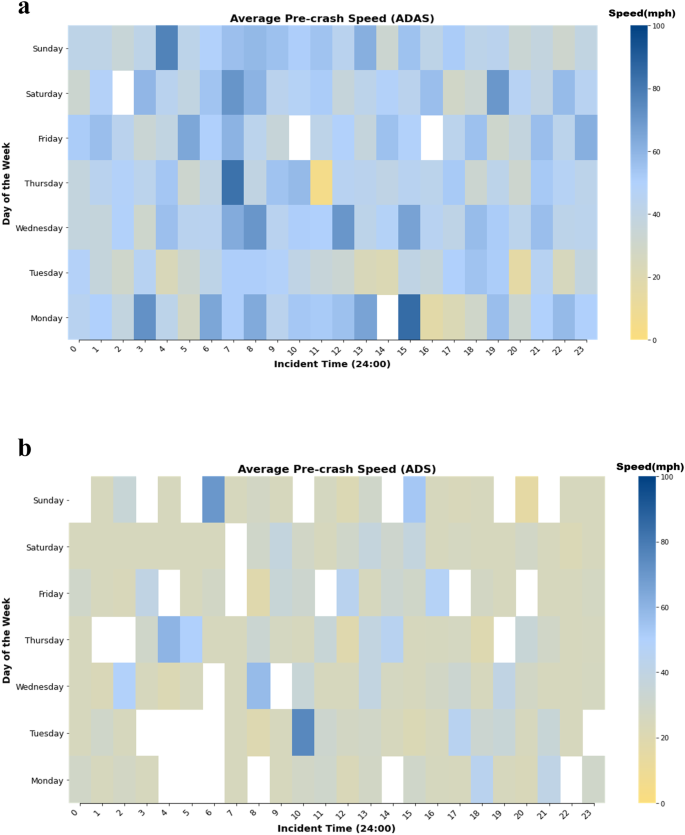
a ADAS Average Pre-accident Speed Heatmap. b ADS Average Pre-accident Speed Heatmap.
We have also analyzed the full data to identify the influence of roadway elements and factors related to time using a random parameter logit model 33 . Only a single random parameter “Day of the week” demonstrated a significant effect. Upon analyzing the model, we found that the dawn/dusk and turn conditions exhibit positive coefficients that are statistically significant at a 95% confidence level. This indicates a higher odd of an AV accident occurrence when these variables are significant in the random parameter logit model. Furthermore, we discovered that several variables demonstrate high significance and exhibit negative coefficients, suggesting a reduced likelihood of an accident when these factors are significant. These variables include the rain conditions, rear-end conditions, broadside conditions (a broadside condition is a car accident that occurs when the front of one vehicle slams into the side of another vehicle), moderate severity, proceeding straight, run-off road, backing, and entering traffic lane.
Findings of road, environment, and accident type
Based on the results of the matched case control logistic regression model, compared with HDV, the odds of an ADS accident occurring in rainy weather are 0.335 times. This indicates a lower likelihood of an ADS accident in rainy weather compared to an HDV accident. RADAR is capable of detecting objects at distances exceeding 150 m, even in adverse weather conditions such as fog or rain 34 . In contrast, human drivers may only be able to perceive objects up to approximately 10 meters away under similar circumstances 35 . Although adverse weather can increase the likelihood of potential failures or loss of sensors 36 , 37 , 38 , recent innovations in visual algorithms, coupled with the combined use of cameras, LIDAR, GNSS, and RADAR sensors 39 , 40 , are crafted to recognize pedestrians and vehicles under varying weather scenarios, such as cloudiness, snow, rain, and darkness 41 , 42 . This offers solutions to the challenges associated with driving in less-than-ideal conditions. In contrast, human drivers may have difficulties seeing through heavy rain or fog, leading to a delay in detecting potential hazards or reacting appropriately 40 .
Interestingly, the dawn/dusk odds ratio indicates a 5.250 higher probability of ADS accident than HDV accident. This could be attributed to the sensors and cameras used by AVs may not be able to quickly adapt to changes in lighting conditions, which could affect their ability to detect obstacles, pedestrians, and other vehicles 39 , 43 . At dawn and dusk, for instance, the sun’s shadows and reflections may confuse sensors, making it hard for them to distinguish between objects and identify potential hazards. Furthermore, the fluctuating light conditions can impact the accuracy of object detection and recognition algorithms used by AVs, which can result in false positives or negatives 35 , 44 .
Accident types related findings for ADS and HDVs are worth noting. Compared to HDV accidents, AVs experience relatively lower risks in rear-end and broadside accidents (0.457 times and 0.171 times, respectively). This finding indicates that AVs may detect and react to potential rear-end and sideswipe accident situations much faster than humans can. This is because they are equipped with advanced sensors and software that can quickly analyze the surrounding environment and make decisions based on the data received 45 . In addition, the kinematic method used by ACC system keeps track of and regulates the distance between vehicles, alerting drivers if this space becomes smaller than the safe limit, especially at highways 46 . By ensuring that vehicles keep a consistent speed and distance between vehicles, thus effectively reduces the risk of rear-end accidents 47 . Compared with ADS, HDVs tend to display greater velocity differences at larger spacing ranges 48 , a factor that significantly contributes to a higher incidence of rear-end and sideswipe accidents 49 .
Findings of pre-accident conditions and accident outcomes
In terms of pre-accident conditions, most of the pre-accident movements made by ADS reduce the probability of accidents from the results of the matched case control logistic regression, except for turning, which increases the likelihood of an accident by 1.988 times compared to HDVs. One possible reason is a lack of situational awareness. Situational awareness of AVs can be defined as the ability of these vehicles to perceive essential elements in their surroundings, understand the importance of these elements, and anticipate their future state or changes 50 . The complexity of turning in autonomous driving scenarios arises from three primary challenges: choosing the appropriate lane (target lane selection), devising and computing a safe and efficient path (trajectory planning and calculation), and executing the turn while adjusting to dynamic conditions (vehicle controlling and tracking) 51 . AVs rely on sensors and algorithms to perceive their surroundings and make driving decisions 45 . However, these systems may not detect all obstacles and hazards, particularly in complex and dynamic driving scenarios like turning at intersections 52 , 53 . It is a significant challenge to generate sufficient information and achieve comprehensive detection of the surrounding environment from a single independent source due to limited sensor ranges and limited coverage of the environment by sensors in AV 45 , 54 . Additionally, some AVs are programmed to follow predefined rules and scenarios, which may not encompass every possible driving situation 55 , 56 , 57 . The modifications of scenarios can present difficulty for AVs in perceiving and responding to them, thereby raising the risk of an accident 58 . Moreover, multiple oncoming HDVs and the complexity of such driving scenarios are a considerable challenge for AVs such as unprotected left turns at intersections 59 . These situations are complicated by factors like limited priority and variation in trajectories 60 . AVs tend to be overcautious (such as having a longer startup delay during the turning at intersections) 61 , which can lead to rear-end or sideswipe accidents with HDVs 62 . Furthermore, multi-interactions caused by mixed flows aggravate uncertainties in detection, such as the superposition of distance and angle measurement error 63 . Conversely, HDVs can adapt and modify their speed more seamlessly than AVs, highlighting the limitations of AVs in comparison to the adeptness of experienced drivers 64 . And AVs face difficulties with executing lane changes or turning in heavy traffic and lack psychological insight 65 , 66 . In addition, HDVs can predict pedestrian movements and exercise caution based on their driving experience, whereas AVs may struggle with recognizing pedestrians’ intentions, potentially leading to emergency braking or accidents due to a lack of understanding of social cues and psychological reasoning 65 , 67 , 68 .
ADS accidents are less likely to occur than HDV accidents in situations such as proceeding straight, run-off road (a vehicle leaves the designated roadway and travels onto an area that is not intended for regular traffic) and entering traffic lane conditions (a vehicle transitioning from a stationary or parked position to enter a traffic lane and become physically present within the flow of traffic). When considering the proceeding straight condition, it was found that AV accident resulted in a 0.299 lower probability of an HDV accident. Remarkably, ADS accident risk is 0.021 times as high as that of an HDV accident in run-off road condition, which can be explained by the faster reaction time of AVs 24 . AVs can detect these situations and apply corrective actions, such as adjusting the speed or steering angle 69 , 70 , more quickly and accurately than a human driver 71 , 72 . The result of matched-case control model revealed a significant correlation between the entering traffic lane condition of ADS accident, the risk of which is 0.267 times as high as HDV accident. According to the results of the matched case-control logistic regression, the impact of backing is noteworthy, which shows that the ADS is less likely to be affected than the HDV. According to the analysis, the model using accidents of AVs showed a decreased probability of accidents for moderate and fatal severity in comparison to HDV.
A comprehensive examination was performed using a dataset of AV and HDV accidents in this study. A total of 2100 AV accidents and 35,133 HDV accident records were collected, which accurately reflected the accident details. The analysis first dealt the whole available data that includes both ADS and ADAS (SAE levels 4 and 2, respectively) using general descriptive statistics, percentages, and a random parameter logit model (not shown in the paper for brevity and since results are almost consistent with the other matched model). The analysis considered four categories of variables, including accident type, road and environment, pre-accident movement, and accident outcomes.
The accident data of AV and HDV were compared using the matched case-control logistic regression. The impact of different variables on the potential of accidents in AV vs HDV was conducted using a matched case-control logistic regression model. Based on the model estimation results, it can be concluded that ADS in general are safer than HDVs in most accident scenarios for their object detection and avoidance, precision control, and better decision-making.
However, the odds ratio of an ADS accident happening under dawn/dusk or turning conditions is 5.250 and 1.988 times higher, respectively, than the probability of an HDV accident occurring under the same conditions. The possible reasons might be a lack of situational awareness in complex driving scenarios and limited driving experience of AVs 21 . Improving the safety of ADS under dawn/dusk or turning conditions necessitates a holistic approach that involves advanced sensors, robust algorithms, and smart design considerations. Key strategies include enhancing weather and lighting sensors, implementing redundancy measures, and integrating sensor data effectively. By focusing on these aspects, the safety of ADS can be significantly enhanced in challenging scenarios.
Compared with current studies that only focus on AV accidents 73 , 74 , 75 or analyze AV and HDV with limited samples 4 , 76 , 77 , this paper has analyzed the factors that contribute to AV in comparison to HDV accidents through the analysis of real-world accidents and multi-source data. Furthermore, this research encompassed both AV and HDV accidents, instead of solely concentrating on different levels of AV accidents without considering a comparison with HDV accidents. Moreover, this study addresses the issue of unbalanced data between AV and HDV accidents by employing a matched case-control study design. One of the constraints of this study is analyzing the detailed levels of AV and the specific activated ADAS or AV system in an accident. Understanding and modeling different classifications of AV versus HDV accidents can be challenging and may require more data. It would also be crucial in the future to incorporate data about right-of-way at intersections, encompassing yield signs, stop signs, priority signals, and traffic lights, to enhance the comparative analysis between AV and HDV. Future research could also benefit from consulting a group of AV experts to identify and report on the factors contributing to safety differences between HDVs and AVs. Reporting their responses could provide qualitative depth to the research findings.
Data preparation
The full AV data set includes 2100 (ADS + ADAS) accidents based on AVOID 6 (CADMV and NHTSA’s AV accident databases 31 ). Supplementary Table 3 presents the general descriptive statistics of the databases, and the description and explanation for the variables are given in Supplementary Table 4 . It provides a summary of the characteristics of the available variables that are classified into four major categories in the final data. The categories of variables include road and environmental characteristics (such as weather, road condition, road surface, and lighting conditions), pre-accident conditions (including vehicle manufacturers, AV driving modes, and pre-accident vehicle movement status), accident type, and accident outcome (accident severity), as shown in Supplementary Table 3 . Among this information, the day of week, time of day and road location are typical confounders relevant to the traffic accident risk 78 . To be specific, the risk of traffic accidents can vary by the day of the week and time of day due to differences in traffic volume and driver behavior (e.g., commuters mostly in peak periods). In addition, the road location can affect the risk of traffic accidents by influencing traffic volume, speed limits, and the presence of other risk factors such as road design factors, intersections, pedestrians, and bicyclists.
The second group of accidents data comprised information of HDV, which was gathered from the Statewide Integrated Traffic Records System (SWITRS) 79 . This format and structure of data can be matched with the AV data, we collected 35,113 cases of HDV accidents according to the year of AV accidents as the first step. The distributions of accident types (head-on, sideswipe, rear-end, broadside) for vehicle categories (HDV and ADS) are shown in Fig. 5 , which visually illustrates the frequency and proportion of each accident type in the respective locations by vehicle categories. For HDV accidents, intersections are the primary locations (significantly higher than other HDV accident location types with F = 5.1043 and p = 0.0166), where 61.5% of HDV intersection accidents are rear-end, making it the most common type. Urban streets are the second most common scenario, with head-on accounting for 48.0% of HDV street accidents. Conversely, ADS accidents occur more frequently on urban streets (significantly higher than other ADS accident location types with F = 10.4982 and p = 0.0011), where 45.6% of ADS street accidents were head-on. Accidents at intersections are the second most common for ADS, with rear-end making up 53.8% of these ADS intersection accidents.
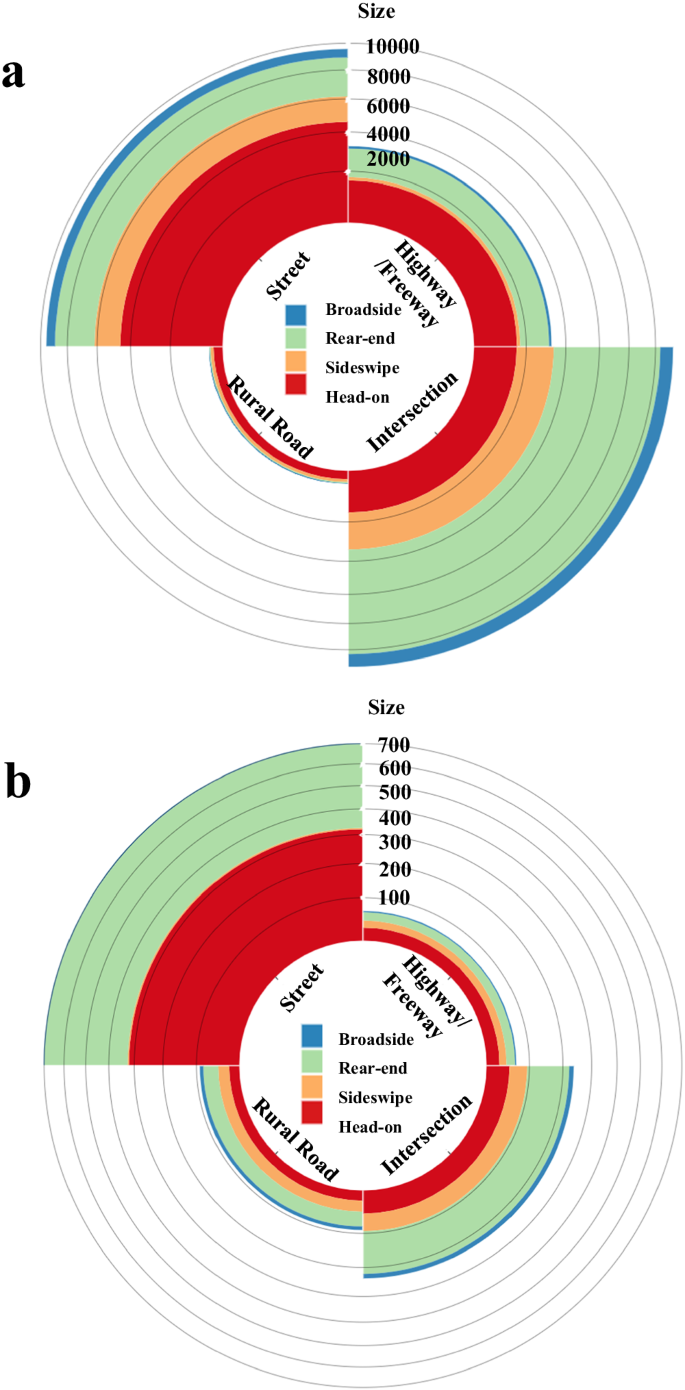
a HDV accidents with a sample of 35,113. b ADS accidents with a sample of 1099. The distributions of accident types (head-on, sideswipe, rear-end, broadside) for vehicle categories (HDV and ADS) illustrate the frequency and proportion of each accident type in the respective locations by vehicle categories.
A matched case-control logistic regression model
A matched case-control study is an observational study that involves comparing individuals who have a specific health outcome or disease (the cases) with individuals who do not have the health outcome or disease (the controls) 80 . The study design involves selecting cases and controls based on their exposure to a particular risk factor or characteristic, and then comparing the frequency of that exposure between the two groups. In the context of this paper, a matched case-control study could be used to investigate the relationship between accident-related risk factors 81 , 82 . Cases would be AVs involved in accidents, and controls would be HDVs involved in accidents.
A matched control study has been designed to investigate the impact of various factors on the likelihood of accidents in two specific scenarios: AV and HDV.
Conditional logistic regression is a variant of logistic regression that specifically tackles the issue of stratification within matched case-control studies 83 . In this research, there are N strata denoted by \(i={{{{\mathrm{1,2}}}}},\ldots \ldots,N\) . Each stratum has one AV accident case sample and k HDV accident control samples denoted by \(j={{{{\mathrm{1,2}}}}},\ldots \ldots,k\) . The conditional likelihood for the \({i\; th}\) strata depends on the probability of the total number of cases (AV accident case samples) and controls ( k HDV accident control samples) recorded in the stratum 84 . \({P}_{{ri}}\) ( \({x}_{{ji}}\) ) refers to the probability of the \({j\; th}\) samples in the \({i\; th}\) stratum is a AV accident where \({x}_{{ij}}=(\,{x}_{1{ij}},\,{x}_{2{ij}},\,{\ldots \ldots,\, x}_{{pij}})\) is determined by a vector of variables \((\,{x}_{1},\,{x}_{2},\,{\ldots \ldots,\, x}_{p})\) . A logistic regression model with linear parameters is employed to estimate the likelihood of an accident, as described by Abdel-Aty et al. 85 :
The controlled variables used to create strata are reflected in the intercept term. To incorporate the impact of stratification in the analysis, it is possible to construct a conditional log-likelihood. This log-likelihood function comprises multiple terms, each representing the conditional probability of an accident occurring within a specific stratum 86 . The following equation presents the formula for the conditional likelihood function, as stated by Abdel-Aty et al. 85 :
The coefficients’ estimates in Eq. ( 1 ) are identical to the maximum likelihood function values in Eq. ( 2 ). These estimates are log-odds ratios that can provide an approximation of the relative risk of an accident and are also referred to as hazard ratios (i.e., the ratio of odds for accident occurrence versus non-occurrence). The hazard ratio is calculated by raising the exponential value to the coefficient’s power. For a dummy variable, the odds ratio is a statistic defined as the ratio of the odds of the case. The odds ratio can be written as
where, \(Z\) represents the vector of explanatory variables excluding \({x}_{k}\) . \({\beta }_{k}\) is estimated coefficient for \({x}_{k}\) .
Matched case control study for ADS accidents
Our aim is to explore the differential characteristics of accidents involving AVs and HDVs, rather than comparing accidents and non-accidents. Direct comparisons between AV and HDV accidents are still not viable as the difference in exposure and number of vehicles of both types is extremely unbalanced. We incorporated Annual Average Daily Traffic (AADT) data of various road types from the California Traffic Census Program 87 , which is provided in the supplementary methods. HDVs show a higher incidence of accidents on highways, intersections, and streets, particularly on highways. For rural roads, HDVs and AVs exhibit almost similar accident rates. Across all road types, HDVs consistently record significantly higher accident figures than AVs. To examine the impact of exogenous variables on accident risk for different vehicle types, we conducted a matched case-control logistic regression model for AV (ADS) and HDV accidents. The coordinates of accidents are extracted by Google Map API, and then the type of road is identified to conduct matched case-control logistic regression. The distribution of AV accidents over various situations differs from the distribution of HDV accidents is concluded from the matched case-control study.
To overcome this challenge of variables that confound the relationship between risk factors and traffic accident outcomes, the first principle is to match cases and controls at the same location. In the case of a location that does not have enough controls, similar locations within a radius of 5 miles for intersections and urban segments were used, and the day of the week and time of day were controlled. We assumed that cases and controls were under similar traffic patterns based on the controlled time and space. Aside from intersections and streets, the location of each stratum for AV and HDV accidents is on the same highways and expressways. In addition, the same road type for each stratum is controlled to ensure similar geometric design. As the manual override and conventional modes of ADAS closely resemble HDV, we only focus on ADS cases from CA for the matched case-control study. Furthermore, some cases were removed due to difficulties in obtaining or imputing precise road types for matched case-control logistic regression.
We organized the data into N strata according to the occurrence of AV accidents. Each stratum consisted of one case and k corresponding controls. To ensure consistency across strata, we employed a matched case-control logistic regression by adjusting the number of control samples and assessed the resulting estimates for each model. Samples generally refer to the groups of accidents selected for comparison within each stratum. Case samples are specific accidents who have the outcome that is the focus of the study. Control samples are accidents who do not have the specific outcome being studied. In this study, ‘AV accident case sample’ consists of AV accidents within each stratum, and the ‘HDV accident control samples’ consist of the HDV accidents within the same stratum. The method begins by utilizing an initial equal proportion of AV accident case samples to HDV accident control samples (1:1) and progressively increasing the ratio (1:3, 1:5, 1:7, 1:9…) until the coefficients between consecutive models exhibit no significant change. From Fig. 6 , it is evident that there are no notable disparities between the models employing sample ratios of 1:5 and 1:6. As a result, we opt for the 1:5 ratio for our analysis. To further support our decision, we evaluate the improvement in log-likelihood across the models, aligning with our hypothesis of selecting an AV accident case sample to HDV-accident control sample ratio of 1:5.
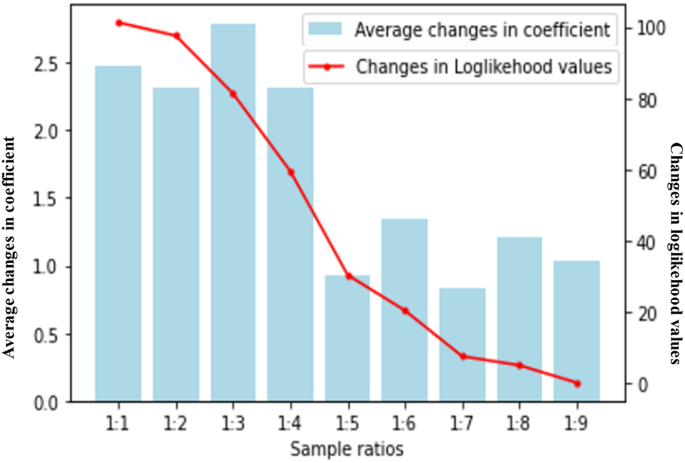
The blue column line indicates the average coefficient changes (left y-axis), and the red line shows the changes in loglikelihood values (right y-axis).
As a result, 548 ADS accident accidents were applied for the matched case-control design and are discussed in this paper. The sample of the data is shown in Fig. 7 . The estimation results and 95% confidence intervals of the odds ratio are presented in Table 1 , which was generated using the survival package in R programming 88 . A total of 11 significant variables were identified by combining road and environment, accident type, accident outcomes, and pre-accident conditions during the estimation process.
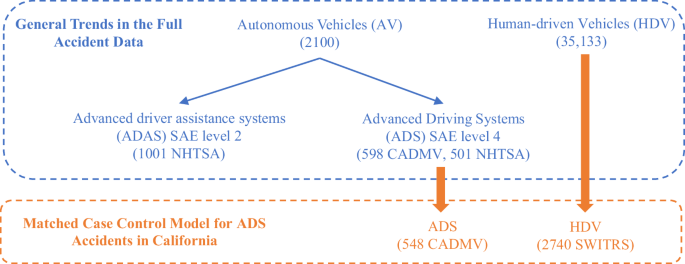
The blue fonts indicate general accident trends, while the orange fonts represent data for the matched case control model of ADS accidents in California. The HDV data is sourced from SWITRS 79 . The ADS (SAE Level 4) data is sourced from CADMV 5 and NHTSA 31 , while the ADAS (SAE Level 2) data is sourced from NHTSA 31 .
Data availability
The Human Driven-Vehicle (HDV) accidents dataset that we used to is publicly available at https://www.chp.ca.gov/programs-services/services-information/switrs-internet-statewide-integrated-traffic-records-system . The Autonomous Vehicle (AV) accidents dataset is available at https://github.com/UCF-SST-Lab/AVOID-Autonomous-Vehicle-Operation-Incident-Dataset/tree/main/asset . The Annual Average Daily Traffic (AADT) data of various road types from the California Traffic Census Program is available at https://dot.ca.gov/programs/traffic-operations/census . Source data for figures are provided with this paper. All other data used in this study are available from the corresponding authors upon request. Source data are provided with this paper.
Code availability
The codes for data validation and processing are available on Zenodo with a ( https://doi.org/10.5281/zenodo.11081206 ). The quick tutorial and README file are also included in the repository for reference. Python scripts for geospatial data processing are prepared with the OSMnX package and offered in the repository, which can be referred to in the file Address2OSM.ipynb under the folder of code. All other code used in this study are available from the corresponding authors upon request.
Fleetwood, J. Public health, ethics, and autonomous vehicles. Am. J. Public Health 107 , 532–537 (2017).
Article PubMed PubMed Central Google Scholar
Lee, D. & Hess, D. J. Regulations for on-road testing of connected and automated vehicles: Assessing the potential for global safety harmonization. Transp. Res. Part A 136 , 85–98 (2020).
Google Scholar
Zhang, L. Cruise’s Safety Record Over 1 Million Driverless Miles , https://getcruise.com/news/blog/2023/cruises-safety-record-over-one-million-driverless-miles (2023).
Liu, Q., Wang, X., Wu, X., Glaser, Y. & He, L. Crash comparison of autonomous and conventional vehicles using pre-crash scenario typology. Accid. Anal. Prev. 159 , 106281 (2021).
Article PubMed Google Scholar
DMV, C. Autonomous vehicle collision reports, https://www.dmv.ca.gov/portal/vehicle-industry-services/autonomous-vehicles/autonomous-vehicle-collision-reports/ (2023).
Zheng, O. et al. AVOID: Autonomous Vehicle Operation Incident Dataset Across the Globe. Preprint at https://arxiv.org/abs/2303.12889 (2023).
Boggs, A. M., Wali, B. & Khattak, A. J. Exploratory analysis of automated vehicle crashes in California: A text analytics & hierarchical Bayesian heterogeneity-based approach. Accid. Anal. Prev. 135 , 105354 (2020).
Scanlon, J. M. et al. Waymo simulated driving behavior in reconstructed fatal crashes within an autonomous vehicle operating domain. Accident. Anal. Prev. 163 , 106454 (2021).
Article Google Scholar
Ahangarnejad, A. H., Radmehr, A. & Ahmadian, M. A review of vehicle active safety control methods: From antilock brakes to semiautonomy. J. Vib. Control 27 , 1683–1712 (2021).
Article MathSciNet Google Scholar
Bareiss, M., Scanlon, J., Sherony, R. & Gabler, H. C. Crash and injury prevention estimates for intersection driver assistance systems in left turn across path/opposite direction crashes in the United States. Traffic Inj. Prev. 20 , S133–S138 (2019).
Gordon, T. J. & Lidberg, M. Automated driving and autonomous functions on road vehicles. Vehicle System Dynamics 53 , 958–994 (2015).
Milakis, D., Van Arem, B. & Van Wee, B. Policy and society related implications of automated driving: A review of literature and directions for future research. J. Intell. Transp. Syst. 21 , 324–348 (2017).
Yue, L., Abdel-Aty, M., Wu, Y. & Wang, L. Assessment of the safety benefits of vehicles’ advanced driver assistance, connectivity and low level automation systems. Accident . Anal. Prev. 117 , 55–64 (2018).
Chan, C.-Y. Advancements, prospects, and impacts of automated driving systems. Int. J. Transp. Sci. Technol. 6 , 208–216 (2017).
Koopman, P. & Wagner, M. Autonomous vehicle safety: An interdisciplinary challenge. IEEE Intell. Transp. Syst. Mag. 9 , 90–96 (2017).
Harper, C. D., Hendrickson, C. T. & Samaras, C. Cost and benefit estimates of partially-automated vehicle collision avoidance technologies. Accid. Anal. Prev. 95 , 104–115 (2016).
Niebuhr, T., Junge, M. & Achmus, S. Expanding pedestrian injury risk to the body region level: how to model passive safety systems in pedestrian injury risk functions. Traffic Inj. Prev. 16 , 519–531 (2015).
Penmetsa, P., Sheinidashtegol, P., Musaev, A., Adanu, E. K. & Hudnall, M. Effects of the autonomous vehicle crashes on public perception of the technology. IATSS Res. 45 , 485–492 (2021).
Kalra, N. & Paddock, S. M. Driving to safety: How many miles of driving would it take to demonstrate autonomous vehicle reliability? Transp. Res. Part A 94 , 182–193 (2016).
Yan, S., Huang, C. & He, D. A comparison of patterns and contributing factors of ADAS and ADS involved crashes. J. Transp. Saf. Sec. 15 , 1–28 (2023).
Ding, S. et al. Exploratory Analysis of the Crash Severity between Vehicular Automation (SAE L2-5) with Multi-Source Data. Preprint at https://arxiv.org/abs/2303.17788 (2023).
Norris, N., Emmanuel, K., Boniphace, K. & Angela, E. K. A comparative study of collision types between automated and conventional vehicles using Bayesian probabilistic inferences. J. Saf. Res. 84 , 251–260 (2023).
Wen, X., Huang, C., Jian, S. & He, D. Analysis of discretionary lane-changing behaviours of autonomous vehicles based on real-world data. Transportmetrica A: Transport Science 19 , 1–24 (2023).
Dixit, V. V., Chand, S. & Nair, D. J. Autonomous vehicles: disengagements, accidents and reaction times. PLoS One 11 , e0168054 (2016).
Teoh, E. R. & Kidd, D. G. Rage against the machine? Google’s self-driving cars versus human drivers. J. Saf. Res. 63 , 57–60 (2017).
Schoettle, B. & Sivak, M. A preliminary analysis of real-world crashes involving self-driving vehicles (University of Michigan Transportation Research Institute, 2015).
Favarò, F. M., Nader, N., Eurich, S. O., Tripp, M. & Varadaraju, N. Examining accident reports involving autonomous vehicles in California. PLoS One 12 , e0184952 (2017).
Seacrist, T. et al. In-depth analysis of crash contributing factors and potential ADAS interventions among at-risk drivers using the SHRP 2 naturalistic driving study. Traffic Inj. Prev. 22 , S68–S73 (2021).
Sinha, A., Vu, V., Chand, S., Wijayaratna, K. & Dixit, V. A crash injury model involving autonomous vehicle: Investigating of crash and disengagement reports. Sustainability 13 , 7938 (2021).
Wang, S. & Li, Z. Exploring the mechanism of crashes with automated vehicles using statistical modeling approaches. PloS One 14 , e0214550 (2019).
Article CAS PubMed PubMed Central Google Scholar
NHTSA. Standing General Order on Crash Reporting , https://www.nhtsa.gov/laws-regulations/standing-general-order-crash-reporting#data (2023).
Ahangar, M. N., Ahmed, Q. Z., Khan, F. A. & Hafeez, M. A survey of autonomous vehicles: Enabling communication technologies and challenges. Sensors 21 , 706 (2021).
Article ADS PubMed PubMed Central Google Scholar
Yuan, R., Ding, S., Fang, Z., Gu, X., & Xiang, Q. Investigating the spatial heterogeneity of factors influencing speeding-related crash severities using correlated random parameter order models with heterogeneity-in-means. Transp. Lett. 15 , 1−13 (2023).
Sun, Z., Bebis, G. & Miller, R. On-road vehicle detection: A review. IEEE Trans. Pattern Anal. Mach. Intell. 28 , 694–711 (2006).
Zang, S. et al. The impact of adverse weather conditions on autonomous vehicles: How rain, snow, fog, and hail affect the performance of a self-driving car. IEEE Vehicular Technol. Mag. 14 , 103–111 (2019).
Gehrig, S., Reznitskii, M., Schneider, N., Franke, U. & Weickert, J. Priors for stereo vision under adverse weather conditions. In Proceedings of the IEEE International Conference on Computer Vision Workshops . 238–245 (2013).
Cui, Z., Yang, S.-W. & Tsai, H.-M. A vision-based hierarchical framework for autonomous frontvehicle taillights detection and signal recognition. In 2015 IEEE 18th International Conference on Intelligent Transportation Systems . 931–937 (IEEE, 2015).
Hnewa, M. & Radha, H. Object detection under rainy conditions for autonomous vehicles: A review of state-of-the-art and emerging techniques. IEEE Signal Process. Mag. 38 , 53–67 (2020).
Vargas, J., Alsweiss, S., Toker, O., Razdan, R. & Santos, J. An Overview of Autonomous Vehicles Sensors and Their Vulnerability to Weather Conditions. Sensors 21 , 5397 (2021).
Van Brummelen, J., O’Brien, M., Gruyer, D. & Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C 89 , 384–406 (2018).
Radecki, P., Campbell, M. & Matzen, K. All weather perception: Joint data association, tracking, and classification for autonomous ground vehicles. Preprint at https://arxiv.org/abs/1605.02196 (2016).
Filgueira, A., González-Jorge, H., Lagüela, S., Díaz-Vilariño, L. & Arias, P. Quantifying the influence of rain in LiDAR performance. Measurement 95 , 143–148 (2017).
Article ADS Google Scholar
Parekh, D. et al. A review on autonomous vehicles: Progress, methods and challenges. Electronics 11 , 2162 (2022).
Khatab, E., Onsy, A., Varley, M. & Abouelfarag, A. Vulnerable objects detection for autonomous driving: A review. Integration 78 , 36–48 (2021).
Yeong, D. J., Velasco-Hernandez, G., Barry, J. & Walsh, J. Sensor and sensor fusion technology in autonomous vehicles: A review. Sensors 21 , 2140 (2021).
Alotibi, F. & Abdelhakim, M. Anomaly detection for cooperative adaptive cruise control in autonomous vehicles using statistical learning and kinematic model. IEEE Trans. Intell. Transp. Syst. 22 , 3468–3478 (2020).
Li, Y. et al. Evaluation of the impacts of cooperative adaptive cruise control on reducing rear-end collision risks on freeways. Accid. Anal. Prev. 98 , 87–95 (2017).
Article ADS PubMed Google Scholar
Adewale, A. & Lee, C. Prediction of car-following behavior of autonomous vehicle and human-driven vehicle based on drivers’ memory and cooperation with lead vehicle. Transp. Res. Record. , https://doi.org/10.1177/03611981231195051 (2023).
Li, Y., Wu, D., Lee, J., Yang, M. & Shi, Y. Analysis of the transition condition of rear-end collisions using time-to-collision index and vehicle trajectory data. Accid. Anal. Prev. 144 , 105676 (2020).
Endsley, M. R. Toward a theory of situation awareness in dynamic systems. Hum. factors 37 , 32–64 (1995).
Ding, Z., Sun, C., Zhou, M., Liu, Z. & Wu, C. Intersection vehicle turning control for fully autonomous driving scenarios. Sensors 21 , 3995 (2021).
Levin, M. W. & Boyles, S. D. Intersection auctions and reservation-based control in dynamic traffic assignment. Transp. Res. Rec. 2497 , 35–44 (2015).
Haris, M. & Hou, J. Obstacle detection and safely navigate the autonomous vehicle from unexpected obstacles on the driving lane. Sensors 20 , 4719 (2020).
Bhavsar, P., Das, P., Paugh, M., Dey, K. & Chowdhury, M. Risk analysis of autonomous vehicles in mixed traffic streams. Transp. Res. Rec. 2625 , 51–61 (2017).
Fagnant, D. J. & Kockelman, K. Preparing a nation for autonomous vehicles: opportunities, barriers and policy recommendations. Transp. Res. Part A 77 , 167–181 (2015).
Zhang, Q. et al. A systematic framework to identify violations of scenario-dependent driving rules in autonomous vehicle software. Proc. ACM Meas. Anal. Comput. Syst. 5 , 1–25 (2021).
CAS Google Scholar
Riedmaier, S., Ponn, T., Ludwig, D., Schick, B. & Diermeyer, F. Survey on scenario-based safety assessment of automated vehicles. IEEE Access 8 , 87456–87477 (2020).
Kutela, B., Avelar, R. E. & Bansal, P. Modeling automated vehicle crashes with a focus on vehicle at-fault, collision type, and injury outcome. J. Transp. Eng. Part A 148 , 04022024 (2022).
Zhou, D., Ma, Z., Zhang, X. & Sun, J. Autonomous vehicles’ intended cooperative motion planning for unprotected turning at intersections. IET Intell. Transp. Syst. 16 , 1058–1073 (2022).
Wael, K. M. A., Miho, A., Hideki, N. & Dang Minh, T. Stochastic approach for modeling the effects of intersection geometry on turning vehicle paths. Transp. Res. Part C. 32 , 179–192 (2013).
Noh, S. Decision-making framework for autonomous driving at road intersections: Safeguarding against collision, overly conservative behavior, and violation vehicles. IEEE Trans. Ind. Electron. 66 , 3275–3286 (2018).
Ashraf, M. T., Dey, K., Mishra, S. & Rahman, M. T. Extracting rules from autonomous-vehicle-involved crashes by applying decision tree and association rule methods. Transp. Res. Rec. 2675 , 522–533 (2021).
Zhou, D., Ma, Z. & Sun, J. Autonomous Vehicles’ Turning Motion Planning for Conflict Areas at Mixed-Flow Intersections. IEEE Trans. Intell. Veh. 5 , 204–216 (2020).
Grahn, H., Kujala, T., Silvennoinen, J., Leppänen, A. & Saariluoma, P. Expert drivers’ prospective thinking-aloud to enhance automated driving technologies–Investigating uncertainty and anticipation in traffic. Accid. Anal. Prev. 146 , 105717 (2020).
Lake, B. M., Ullman, T. D., Tenenbaum, J. B. & Gershman, S. J. Building machines that learn and think like people. Behav. Brain Sci. 40 , e253 (2017).
Zhang, Y., Wang, W., Zhou, X., Wang, Q. & Sun, X. Tactical-level explanation is not enough: Effect of explaining AV’s lane-changing decisions on drivers’ decision-making, trust, and emotional experience. Int. J. Hum. Comput. Interact. 39 , 1438–1454 (2023).
Rasouli, A. & Tsotsos, J. K. Autonomous vehicles that interact with pedestrians: A survey of theory and practice. IEEE Trans. Intell. Transp. Syst. 21 , 900–918 (2019).
Schwarting, W., Pierson, A., Alonso-Mora, J., Karaman, S. & Rus, D. Social behavior for autonomous vehicles. Proc. Natl Acad. Sci. 116 , 24972–24978 (2019).
Article ADS MathSciNet CAS PubMed PubMed Central Google Scholar
Raouf, I. et al. Sensor-based prognostic health management of advanced driver assistance system for autonomous vehicles: A recent survey. Mathematics 10 , 3233 (2022).
Lee, S., Arvin, R. & Khattak, A. J. Advancing investigation of automated vehicle crashes using text analytics of crash narratives and Bayesian analysis. Accid. Anal. Prev. 181 , 106932 (2023).
Cui, J., Sabaliauskaite, G., Liew, L. S., Zhou, F. & Zhang, B. Collaborative analysis framework of safety and security for autonomous vehicles. IEEE Access 7 , 148672–148683 (2019).
Sun, X., Cao, S. & Tang, P. Shaping driver-vehicle interaction in autonomous vehicles: How the new in-vehicle systems match the human needs. Appl. Ergonomics 90 , 103238 (2021).
Kutela, B., Das, S. & Dadashova, B. Mining patterns of autonomous vehicle crashes involving vulnerable road users to understand the associated factors. Accid. Anal. Prev. 165 , 106473 (2022).
Xu, C., Ding, Z., Wang, C. & Li, Z. Statistical analysis of the patterns and characteristics of connected and autonomous vehicle involved crashes. J. Saf. Res. 71 , 41–47 (2019).
Zhu, S. & Meng, Q. What can we learn from autonomous vehicle collision data on crash severity? A cost-sensitive CART approach. Accid. Anal. Prev. 174 , 106769 (2022).
Cascetta, E., Carteni, A. & Di Francesco, L. Do autonomous vehicles drive like humans? A Turing approach and an application to SAE automation Level 2 cars. Transp. Res. Part C. 134 , 103499 (2022).
Petrović, Đ., Mijailović, R. & Pešić, D. Traffic accidents with autonomous vehicles: type of collisions, manoeuvres and errors of conventional vehicles’ drivers. Transp. Res. Proc. 45 , 161–168 (2020).
Gross, F. & Jovanis, P. P. Estimation of the safety effectiveness of lane and shoulder width: Case-control approach. J. Transp. Eng. 133 , 362–369 (2007).
SWITRS. Statewide Integrated Traffic Records System , https://iswitrs.chp.ca.gov/Reports/jsp/index.jsp (2023).
Ingram, D., Sanders, K., Kolybaba, M. & Lopez, D. Case-control study of phyto-oestrogens and breast cancer. Lancet 350 , 990–994 (1997).
Article CAS PubMed Google Scholar
Abdel-Aty, M. A., Hassan, H. M., Ahmed, M. & Al-Ghamdi, A. S. Real-time prediction of visibility related crashes. Transp. Res. part C 24 , 288–298 (2012).
Ahmed, M. M., Abdel-Aty, M. & Yu, R. Bayesian updating approach for real-time safety evaluation with automatic vehicle identification data. Transp. Res. Rec. 2280 , 60–67 (2012).
Rahman, M. M. & Lamsal, B. P. Ultrasound‐assisted extraction and modification of plant‐based proteins: Impact on physicochemical, functional, and nutritional properties. Compr. Rev. Food Sci. Food Saf. 20 , 1457–1480 (2021).
Rahman, R., Bhowmik, T., Eluru, N. & Hasan, S. Assessing the crash risks of evacuation: A matched case-control approach applied over data collected during Hurricane Irma. Accid. Anal. Prev. 159 , 106260 (2021).
Abdel-Aty, M., Uddin, N., Pande, A., Abdalla, M. F. & Hsia, L. Predicting freeway crashes from loop detector data by matched case-control logistic regression. Transp. Res. Rec. 1897 , 88–95 (2004).
Peck, R. C., Gebers, M. A., Voas, R. B. & Romano, E. The relationship between blood alcohol concentration (BAC), age, and crash risk. J. Saf. Res. 39 , 311–319 (2008).
Program, T. C. Traffic Census Program , https://dot.ca.gov/programs/traffic-operations/census (2024).
Therneau, T. M., Lunley, T., Atkinson, E. & Crowson, C. survival: Survival analysis. https://cran.r-project.org/web/packages/survival/index.html (2024).
Download references
Acknowledgements
The authors wish to thank Dr. Ou Zheng for his role in creating the AVOID data used in this study.
Author information
Authors and affiliations.
Smart and Safe Transportation Lab (SST), Department of Civil, Environmental and Construction Engineering, University of Central Florida, 12800 Pegasus Dr, Orlando, FL, 32816, USA
Mohamed Abdel-Aty & Shengxuan Ding
You can also search for this author in PubMed Google Scholar
Contributions
M.A.A. and S.D. conceived the study. M.A.A. and S.D. wrote the manuscript. M.A.A. and S.D. estimated the models and conducted the analysis. M.A.A. supervised the analysis and edited the manuscript.
Corresponding author
Correspondence to Shengxuan Ding .
Ethics declarations
Competing interests.
The authors declare no competing interests.
Peer review
Peer review information.
Nature Communications thanks Yee Mun Lee and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information
Supplementary information, peer review file, source data, source data, rights and permissions.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Cite this article.
Abdel-Aty, M., Ding, S. A matched case-control analysis of autonomous vs human-driven vehicle accidents. Nat Commun 15 , 4931 (2024). https://doi.org/10.1038/s41467-024-48526-4
Download citation
Received : 30 September 2023
Accepted : 02 May 2024
Published : 18 June 2024
DOI : https://doi.org/10.1038/s41467-024-48526-4
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- My Bibliography
- Collections
- Citation manager
Save citation to file
Email citation, add to collections.
- Create a new collection
- Add to an existing collection
Add to My Bibliography
Your saved search, create a file for external citation management software, your rss feed.
- Search in PubMed
- Search in NLM Catalog
- Add to Search
Selective Serotonin Reuptake Inhibitors and Risk of Noncardioembolic Ischemic Stroke: A Nested Case-Control Study
Affiliations.
- 1 Unit of Epidemiology and Public Health. School of Medicine, University of Alcalá, Alcalá de Henares, Madrid, Spain (R.A.-F., F.B.).
- 2 Clinical Pharmacology Unit, University Hospital Príncipe de Asturias, Alcalá de Henares, Madrid, Spain (S.R.-M., D.B.-H., E.F.-A., A.R.M., F.J.d.A.).
- 3 Department of Biomedical Sciences (Pharmacology Sector), School of Medicine, University of Alcalá (IRYCIS), Alcalá de Henares, Madrid, Spain (S.R.-M., D.B.-H., E.F.-A., A.R.M., F.J.d.A.).
- 4 Stroke Unit, Department of Neurology, University Hospital Príncipe de Asturias, Alcalá de Henares, Madrid, Spain (L.I.-E.).
- 5 Division of Pharmacoepidemiology and Pharmacovigilance, Spanish Agency for Medicines and Medical Devices, Madrid, Spain (M.G., D.G.-B.).
- 6 Department of Cardiology, University Hospital Príncipe de Asturias, Alcalá de Henares, Madrid, Spain (A.G.-L.).
- 7 Department of Medicine, School of Medicine, University of Alcalá, Alcalá de Henares, Madrid, Spain (A.G.-L.).
- 8 Department of Epidemiology and Biostatistics, Graduate School of Public Health, City University of New York (F.B.).
- 9 CIBERESP, Spain (F.B.).
- PMID: 35109681
- DOI: 10.1161/STROKEAHA.121.036661
Background: Multiple studies have reported that the use of selective serotonin reuptake inhibitors (SSRIs) is associated with an increased risk of ischemic stroke; however, this finding may be the result of a confounding by indication. We examined the association using different approaches to minimize such potential bias.
Methods: A nested case-control study was carried out in a Spanish primary health-care database over the study period 2001 to 2015. Cases were patients sustaining an ischemic stroke with no sign of cardioembolic or unusual cause. For each case, up to 5 matched controls (for exact age, sex, and index date) were randomly selected. Antidepressants were divided in 6 pharmacological subgroups according to their mechanism of action. The current use of SSRIs (use within a 30-day window before index date) was compared with nonuse, past use (beyond 365 days) and current use of other antidepressants through a conditional logistic regression model to obtain adjusted odds ratios and 95% CI. Only initiators of SSRIs and other antidepressants were considered.
Results: A total of 8296 cases and 37 272 matched controls were included. Of them, 255 (3.07%) were current users of SSRIs among cases and 834 (2.24%) among controls, yielding an adjusted odds ratio of 1.14 (95% CI, 0.97-1.34) as compared with nonusers, 0.94 (95% CI, 0.77-1.13) as compared with past-users and 0.74 (95% CI, 0.58-0.93) as compared with current users of other antidepressants. No relevant differences were found by duration (≤1, >1 year), sex, age (<70, ≥70 years old) and background vascular risk.
Conclusions: The use of SSRIs was not associated with an increased risk of noncardioembolic ischemic stroke. On the contrary, as compared with other antidepressants, SSRIs appeared to be protective.
Keywords: depression; odds ratio; risk factor; serotonin uptake inhibitors.
PubMed Disclaimer
Similar articles
- Selective serotonin reuptake inhibitors (SSRIs) and serotonin-norepinephrine reuptake inhibitors (SNRIs) for the prevention of tension-type headache in adults. Banzi R, Cusi C, Randazzo C, Sterzi R, Tedesco D, Moja L. Banzi R, et al. Cochrane Database Syst Rev. 2015 May 1;2015(5):CD011681. doi: 10.1002/14651858.CD011681. Cochrane Database Syst Rev. 2015. PMID: 25931277 Free PMC article. Review.
- Use of selective serotonin reuptake inhibitors and risk of stroke: a systematic review and meta-analysis. Shin D, Oh YH, Eom CS, Park SM. Shin D, et al. J Neurol. 2014 Apr;261(4):686-95. doi: 10.1007/s00415-014-7251-9. Epub 2014 Jan 30. J Neurol. 2014. PMID: 24477492 Review.
- Risk of ischemic stroke associated with antidepressant drug use in elderly persons. Trifirò G, Dieleman J, Sen EF, Gambassi G, Sturkenboom MC. Trifirò G, et al. J Clin Psychopharmacol. 2010 Jun;30(3):252-8. doi: 10.1097/JCP.0b013e3181dca10a. J Clin Psychopharmacol. 2010. PMID: 20473059
- Selective serotonin reuptake inhibitors and the risk of stroke: a population-based case-control study. Bak S, Tsiropoulos I, Kjaersgaard JO, Andersen M, Mellerup E, Hallas J, García Rodríguez LA, Christensen K, Gaist D. Bak S, et al. Stroke. 2002 Jun;33(6):1465-73. doi: 10.1161/01.str.0000018589.56991.ba. Stroke. 2002. PMID: 12052976
- Intracranial haemorrhage and use of selective serotonin reuptake inhibitors. de Abajo FJ, Jick H, Derby L, Jick S, Schmitz S. de Abajo FJ, et al. Br J Clin Pharmacol. 2000 Jul;50(1):43-7. doi: 10.1046/j.1365-2125.2000.00216.x. Br J Clin Pharmacol. 2000. PMID: 10886117 Free PMC article.
- Selective serotonin reuptake inhibitor use, age-related neuropathology and cognition in late-life. Sood A, Wilson RS, Yu L, Wang T, Schneider JA, Honer WG, Bennett DA. Sood A, et al. Psychiatry Res. 2023 Oct;328:115471. doi: 10.1016/j.psychres.2023.115471. Epub 2023 Sep 9. Psychiatry Res. 2023. PMID: 37742529
- Risk of Ischemic Stroke Associated with Calcium Supplements and Interaction with Oral Bisphosphonates: A Nested Case-Control Study. Barreira-Hernández D, Rodríguez-Martín S, Gil M, Mazzucchelli R, Izquierdo-Esteban L, García-Lledó A, Pérez-Gómez A, Rodríguez-Miguel A, de Abajo FJ. Barreira-Hernández D, et al. J Clin Med. 2023 Aug 14;12(16):5294. doi: 10.3390/jcm12165294. J Clin Med. 2023. PMID: 37629338 Free PMC article.
- Association of oral bisphosphonates with cardioembolic ischemic stroke: a nested case-control study. Rodríguez-Martín S, Barreira-Hernández D, Mazzucchelli R, Gil M, García-Lledó A, Izquierdo-Esteban L, Pérez-Gómez A, Rodríguez-Miguel A, De Abajo FJ. Rodríguez-Martín S, et al. Front Pharmacol. 2023 May 26;14:1197238. doi: 10.3389/fphar.2023.1197238. eCollection 2023. Front Pharmacol. 2023. PMID: 37305544 Free PMC article.
- Confounding by Indication in Studies of Selective Serotonin Reuptake Inhibitors. Lee J, Chang SM. Lee J, et al. Psychiatry Investig. 2022 Nov;19(11):873-883. doi: 10.30773/pi.2022.0209. Epub 2022 Nov 23. Psychiatry Investig. 2022. PMID: 36444151 Free PMC article.
Publication types
- Search in MeSH
Related information
Linkout - more resources, full text sources.
- Ingenta plc
- Ovid Technologies, Inc.
- Wolters Kluwer
- Genetic Alliance
- MedlinePlus Health Information
Miscellaneous
- NCI CPTAC Assay Portal
- Citation Manager
NCBI Literature Resources
MeSH PMC Bookshelf Disclaimer
The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.
- Open access
- Published: 28 June 2024
Diagnostic accuracy of an automated microscope solution (miLab™) in detecting malaria parasites in symptomatic patients at point-of-care in Sudan: a case–control study
- Muzamil M. Abdel Hamid 1 ,
- Abdelrahim O. Mohamed 1 , 6 ,
- Fayad O. Mohammed 1 ,
- Arwa Elaagip 1 ,
- Sayed A. Mustafa 4 ,
- Tarig Elfaki 4 ,
- Waleed M. A. Jebreel 1 ,
- Musab M. Albsheer 1 , 5 ,
- Sabine Dittrich 2 ,
- Ewurama D. A. Owusu 2 , 3 &
- Seda Yerlikaya 2 , 7
Malaria Journal volume 23 , Article number: 200 ( 2024 ) Cite this article
162 Accesses
Metrics details
Microscopic detection of malaria parasites is labour-intensive, time-consuming, and expertise-demanding. Moreover, the slide interpretation is highly dependent on the staining technique and the technician’s expertise. Therefore, there is a growing interest in next-generation, fully- or semi-integrated microscopes that can improve slide preparation and examination. This study aimed to evaluate the clinical performance of miLab™ (Noul Inc., Republic of Korea), a fully-integrated automated microscopy device for the detection of malaria parasites in symptomatic patients at point-of-care in Sudan.
This was a prospective, case–control diagnostic accuracy study conducted in primary health care facilities in rural Khartoum, Sudan in 2020. According to the outcomes of routine on-site microscopy testing, 100 malaria-positive and 90 malaria-negative patients who presented at the health facility and were 5 years of age or older were enrolled consecutively. All consenting patients underwent miLab™ testing and received a negative or suspected result. For the primary analysis, the suspected results were regarded as positive (automated mode). For the secondary analysis, the operator reviewed the suspected results and categorized them as either negative or positive (corrected mode). Nested polymerase chain reaction (PCR) was used as the reference standard, and expert light microscopy as the comparator.
Out of the 190 patients, malaria diagnosis was confirmed by PCR in 112 and excluded in 78. The sensitivity of miLab™ was 91.1% (95% confidence interval [CI] 84.2–95.6%) and the specificity was 66.7% (95% Cl 55.1–67.7%) in the automated mode. The specificity increased to 96.2% (95% Cl 89.6–99.2%), with operator intervention in the corrected mode. Concordance of miLab with expert microscopy was substantial (kappa 0.65 [95% CI 0.54–0.76]) in the automated mode, but almost perfect (kappa 0.97 [95% CI 0.95–0.99]) in the corrected mode. A mean difference of 0.359 was found in the Bland–Altman analysis of the agreement between expert microscopy and miLab™ for quantifying parasite counts.
When used in a clinical context, miLab™ demonstrated high sensitivity but low specificity. Expert intervention was shown to be required to improve the device’s specificity in its current version. miLab™ in the corrected mode performed similar to expert microscopy. Before clinical application, more refinement is needed to ensure full workflow automation and eliminate human intervention.
Trial registration ClinicalTrials.gov: NCT04558515
Malaria remains a major health concern in the tropics, especially in sub-Saharan Africa, despite significant improvements in malaria control and management in recent decades [ 1 ]. In Sudan, malaria is a serious public health problem with loss of livelihood and economic impact [ 2 , 3 ]. Successful management of malaria in patients requires correct and timely diagnosis by detecting the malaria parasites in the blood smear and administering an effective treatment. Light microscopy has been the standard of reference for malaria diagnosis since the introduction of Giemsa stain in 1904 [ 4 ]. Main reasons behind its longstanding reign are its low direct cost and ability to detect, quantify, and differentiate malaria parasites. However, this major malaria diagnostic tool also has its well-recognized limitations; it is labour-intensive, time-consuming, and expertise-demanding [ 5 ]. Moreover, competence level of operators plays a decisive role in slide interpretation [ 6 ]. Efforts to standardize the quality have intensified within the last decade resulting in considerable improvements in parasitological diagnosis of malaria by microscopy [ 7 ]; however, these efforts also proved to be expensive and difficult to sustain, especially in settings where the number of malaria cases is in decline [ 4 ]. Besides, the quality of equipment and infrastructure used and the staining technique preferred often impact the results greatly, even with highly competent microscopists especially in detecting low parasitaemia [ 8 ].
With the aim of advancing the conventional microscopy by addressing its limitations, multiple developers have come up with innovative diagnostic solutions which combine features like automated smearing, staining, image acquisition, and/or analysis by artificial intelligence (AI)-based algorithms for the identification of Plasmodium parasites [ 9 , 10 , 11 ]; however, very few of these solutions propose a fully-integrated, sample-to-result approach. One such example is the Micro-Intelligent Laboratory (Noul Inc, Ltd., Republic of Korea), referred to as miLab™, a technology platform that provides rapid (< 30 min), automated, and standardized diagnosis for all human-infecting species of malaria [ 12 ]. The portable and battery-driven instrument automatically performs (i) sample preparation: peripheral thin blood smear, fixation, and staining using proprietary stamping technology using a disposable cartridge [ 13 ], (ii) digital imaging with high resolution and speed (500 × lenses and CMOS sensor) scanning all red blood cells (RBC) in 400 fields; and (iii) embedded AI-based analysis for parasite detection and quantification performed on a server-free central processing unit.
The current study aimed to perform a prospective validation of diagnostic accuracy of miLab™ in detecting malaria parasites in primary health care facilities in Sudan, as part of the Innovation Platform project of FIND, the global alliance for diagnostics [ 14 ].
Study design
This was a prospective, case–control diagnostic accuracy study. Both cases and controls were sampled from a single source population, patients with symptoms suggestive of malaria seeking clinical care in health facilities. A total of 100 malaria-positive and 90 malaria-negative patients based on the results of routine microscopy testing at the health care facility were screened for eligibility and enrolled consecutively.
Sample size
The sample size was calculated assuming miLab™ would have a sensitivity of 93.75% and a specificity of 95.65%, each with a 95% CI of ± 5%, based on preliminary data from the developer using PCR as the reference standard. Additionally, due to the higher sensitivity of molecular methods over microscopy, up to 30% of samples identified as negative by microscopy were expected to be false negatives when verified by PCR [ 15 ].
A total of 190 participants were enrolled in the study. It was estimated that 100 patients positive for malaria (cases) by routine microscopy would need to be recruited for the evaluation of miLab™ to obtain a reliable estimate of the expected sensitivity, with 95% power of obtaining a 95% confidence interval (CI) of ± 10% or less, while allowing for procedural errors in 10% of all cases. In addition, it was estimated that 90 patients negative for malaria (controls) by routine microscopy would need to be recruited for the evaluation of miLab™ to obtain a reliable estimate of the expected specificity with 95% power of obtaining a 95% CI of ± 10% or less, while allowing for procedural errors in 10% of all controls and a false-negativity rate of 30% among controls as determined by the reference standard. The formula used for sample size calculation can be found in [ 16 ].
Study participants were enrolled between October 2020 and December 2020 at two primary health care centers at Gezira Slanj (GS) and Alsororab (SOR) in rural Omdurman, 40–50 km north of Khartoum (Suppl. Fig. S1). Both sites are endemic for Plasmodium falciparum and Plasmodium vivax malaria [ 17 ]. Malaria transmission is seasonal, occurring twice a year. The first season occurs during the short rainy period, which peaks from July to September. The plantation irrigation in the area causes the second season, which runs from October through March.
Inclusion and exclusion criteria
Patients were included in the study if they were five years of age or older, had a malaria status (positive or negative) determined by routine microscopy at the health facility where they were presenting, freely agreed to participate by signing an informed consent form (adults aged 18 years and older and parent/legal guardian of a child) and providing assent (children aged 13–17 years), and were willing to provide a finger prick blood sample at enrollment. Severely ill patients as defined by WHO guidelines or patients who had received malaria treatment during the preceding four-week period were excluded from this study [ 18 , 19 ].
Specimen collection, handling, and storage
Capillary sampling was performed by trained laboratory personnel according to World Health Organization (WHO) guidelines on drawing blood [ 20 ]. A total of 120 µL fresh blood was collected from a finger prick: two microscopy slides with thin and thick blood smears were prepared using 15 µL, two dried blood spots (DBS) for DNA extraction were prepared using 100 µL, and 5 µL was used for miLab™ testing. Figure 1 describes the procedures that were performed during this study.

Flow chart of the study procedures
Index test (miLab™)
Storage, handling, and testing by miLab™ were performed in accordance with the manufacturer’s instructions. Five microlitres of fresh capillary blood were directly loaded onto a single-use cartridge (Model: MDX1000 I P/N CMAA); Lot number 200827210226) which was then inserted into the cartridge stage of the miLab™ device (Serial number: N203 DMLA20010601; N205 DMLA19122001) (Suppl Fig. S2). A plastic glass slide was applied on the plastic cartridge before insertion. The device automatically performed thin blood smearing, staining, and image acquisition within minutes. The cartridge was automatically expelled after testing completion. The result screen displayed acquired images of parasitized (suspected) and non-parasitized (negative) RBC, along with the number of parasites and parasite count per microliter (µL) (Suppl Fig. S2). The miLab™ algorithm detected ring and trophozoite forms of all Plasmodium species but could not differentiate between them. Finally, the cartridge and other disposals were disposed of according to local regulations.
The operators received online training on how to operate miLab™ and were blinded to the comparator and reference standard results. In the corrected mode, the same operators reviewed the suspected results and categorized them as negative or positive. Supplementary Fig. S3 A, B & C shows RBC with or without parasites in images captured by miLab™. The parasite count per µL of blood was calculated using the following formula embedded in the device: Parasitaemia (parasite [p]/µL) = [(Ring # + Trophozoites # + Gametocytes #) / Total Number of RBC] × 5.00 × 1,000,000.
Comparator test (microscopic examination)
As per standard protocols, thin and thick blood smears were stained with 3% freshly prepared Giemsa (RAL Diagnostics, France), and allowed to dry at room temperature for an hour [ 21 , 22 ]. Thick films were used for detection of Plasmodium parasites, whereas thin blood films enabled identification of infecting species.
On-site study microscopy was conducted at the two health facilities (GS and SOR) by trained microscopists. Expert microscopy reading was performed at the central laboratory at the Institute of Endemic Diseases (IEND) by a WHO-certified expert (level I) microscopist. The parasite density was estimated by counting the number of parasites against 200 or 500 leucocytes depending on parasite density and assuming a density of 8,000 leucocytes per µL. Obare method calculator [ 23 ] was used to determine whether the parasite number calculated by the site microscopists and the expert microscopists were discordant. A third WHO-certified microscopist (level I) was included for reading the slides when there was discordance between the first and second microscopists.
Reference standard (nested PCR)
DNA was extracted from a half piece of a DBS (25 µL) using QIAamp DNA extraction kit (Qiagen, Germany) following the manufacturer instructions. Nested PCR (PCR) for detection of Plasmodium parasite species was used as reference standard and performed at IEND following the protocols previously described [ 24 ]. Negative, no-template, and positive controls, which were kindly provided by the WHO malaria amplification test external quality assessment scheme (WHO-NAAT), were included in each assay. Nucleic acid extraction and subsequent PCR testing were carried out within three months of sample collection. Operators performing the reference test were blinded to the index test results.
Baseline data and statistical analysis
Demographic and clinical data were recorded on a case report form by qualified medical doctors. A unique participant identifier was assigned to each study subject.
OpenClinica database was used for study trial data entry and monitored externally by FIND while SPSS 21.0 and MedCal softwares were used for statistical analysis. Sensitivity, specificity, and accuracy were calculated, together with 95% confidence intervals (CI), using Wilson’s score methods [ 25 ]. In order to compare miLab™ and expert microscopy against the reference standard, Cohen’s kappa (κ), a measure of concordance, was computed along with 95% CI. The concordance interpretation was as follows: κ ≤ 0 as no agreement, 0.01–0.20 as none to slight, 0.21–0.40 as fair, 0.41–0.60 as moderate, 0.61–0.80 as substantial, and 0.81–1.00 as almost perfect agreement. Bland–Altman analysis was used to assess the agreement between miLab™ and expert microscopy in quantifying parasite counts [ 26 ]. All values were expressed in the logarithmic form.
General characteristics of study population
Table 1 provides a summary of the general characteristics of the study participants. All study participants, cases, and controls had median ages of 29 (range 5–75), 24 (range 5–75), and 33 (range 5–55) years, respectively. While more females were seen in the controls (N = 47; 52.2%), there were more males among the positive cases (N = 63; 63%). All participants presented with fever or a history of fever within the last 48 h. The geometric mean of parasite density among microscopy-positives as determined by expert microscopy was 17,657 parasites per µL of blood (p/µL) with a range from 351 to 192,560 p/µL (Table 1 ).
Parasite identification by microscopy, PCR, and miLab™
Ninety (47.4%) samples were found to be negative for any Plasmodium infection, while 100 (52.6%) samples were found to be infected with Plasmodium , containing 62 P. falciparum and 38 P. vivax , according to routine microscopy confirmed by the expert microscopist (Table 1 ). Species identification by expert microscopy was identical to that of routine microscopy (Table 1 ).
The reference PCR method detected 112 positives and 78 negatives for malaria (Table 1 , Additional file 1 : Figure S2). Twelve of the microscopy-negatives were found to be positive by PCR, while all of the positives by microscopy were also positive by PCR (Table 1 ). Sixty-two (55.3%) P. falciparum , 32 (28.6%) P. vivax , and 18 (16.1%) mixed infections were detected among the PCR-positives (Table 1 ).
miLab™ identified 128 as suspected and 62 as negative in its automated mode, whereas 104 malaria-positives and 86 malaria-negatives were identified when corrected by the operator (Table 1 ).
Diagnostic performance of miLab™ and expert microscopy in comparison to PCR
Table 2 displays the sensitivity, specificity, and accuracy of miLab™, routine microscopy, and expert microscopy compared to PCR. miLab™ demonstrated 91.1% (95% CI 84.19–95.64) sensitivity and 66.7% (95% CI 55.08–76.74) specificity when operating in automated mode. The specificity increased to 96.2% (95% CI 89.56–99.23%) in the corrected mode, but the sensitivity remained similar at 90.2% (95% CI 83.1–94.9). The accuracy of the device in the automated mode was 81.1% (95% CI 60.7–74.5) and 96.0% (95% CI 92.2–98.3) in the corrected mode.
Sensitivity, specificity, and accuracy of expert microscopy in comparison to PCR were 89.3% (95% CI 82–94.3), 100% (95% CI 95.4–100), and 99.5% (95% CI 97.1–99.9), respectively (Table 2 ).
Concordance of miLab™ with expert microscopy
The concordance between miLab™ and expert microscopy in the automated mode was substantial with a Cohen’s kappa of 0.65 (95% CI 0.54 to 0.76), while the concordance in the corrected mode was almost perfect with a kappa of 0.96 (95% CI 0.93 to 1.0).
Inter-rater agreement of parasite counts between miLab™ and expert microscopy
Bland–Altman analysis of the agreement between miLab™ and expert microscopy in quantifying parasite counts showed a mean difference of 0.359 with limits of agreement ranging from − 1.431 to 2.149 on a logarithmic scale (Fig. 2 ).

Bland–Altman plot for for parasite counts by miLab™ and expert microscopy (n = 112). The continuous line is theT log mean of differences of parasites counts while and dotted line is the limits of agreement with 95% confidence interval (dotted lines)
For proper treatment and efficient patient management, accurate diagnosis of malaria is crucial. Malaria diagnosis still relies heavily on microscopy in malaria-endemic settings; however, microscopy has significant drawbacks [ 27 , 28 ], which are being attempted to be overcome by novel tools by introducing automation in the slide preparation, staining, digital image production and/or analysis [ 29 , 30 ]. The current study aimed to assess the diagnostic accuracy of such a novel, fully-integrated, automated microscopy solution when used by intended end users at the point-of-care in a malaria-endemic setting. miLab™ demonstrated high sensitivity but low specificity at the manufacturer-specified threshold when compared to PCR. In its current fully-automated version, the concordance of miLab™ with expert microscopy was observed to be substantial. Overall, the parasite counts as determined by miLab™ and the expert microscopy differed by 2.3 fold.
Although numerous AI-based solutions for computer-aided reading of thick and/or thin films for the diagnosis of malaria have been proposed, these methods still call for manual slide preparation, and the high variability in slide quality in healthcare facilities is likely to have an impact on the final diagnosis' accuracy [ 31 , 32 , 33 ]. The use of datasets comprised of slides prepared in the field for the algorithm development may be able to address this [ 34 , 35 , 36 ]. Additionally, users of app-based solutions often have to manually move the objective in order to scan films and take pictures for analysis; as a result, the results are not significantly more rapid than those obtained through manual reading [ 37 ]. Alternatives exist, integrating automated reading, scanning, and analysis; however, manual slide preparation is still necessary. In a multi-center, diagnostic accuracy trial, one such example, the Motic EasyScan GO, demonstrated 91.1% sensitivity, and specificity 75.6% [ 11 , 38 ]. When evaluated using a set of WHO malaria microscopy evaluation slides, the same system achieved WHO Competence levels 1 in detection accuracy, 2 in species identification, and 1 in quantification [ 11 ]. In its current version, miLab™ showed comparable sensitivity to EasyScan GO in our study, but lower specificity. It is likely that further algorithm training with additional datasets will help resolve miLab™'s current specificity problem. An opportunity for algorithm development exists with the corrected mode. In contrast to EasyScan GO, miLab™ integrates slide preparation into its system, ensuring that slide quality is maintained regardless of the setting or operator training level [ 11 ]. The performance of miLab™ in a multi-centre diagnostic accuracy trial as well as on the WHO evaluation slide set will need to be evaluated in the next step for a more accurate comparison, though. Moreover, the device’s usability in clinical settings remains to be investigated. However, it is worth noting that the device produces high quality images which can be used for educational and research purposes.
While it is promising that the device is digitized and open to AI learning and performance enhancement [ 11 , 39 ], expert intervention remains necessary for acceptable performance in its current state. Nonetheless, with its shortened time to result (less than 30 min), the test still provides an alternative to conventional microscopic methods. Moreover, the parasite count generated by miLab™ did not correlate with that by expert microscopy, possibly due to differences in the mathematical models and the type of smears used for parasite quantification. The initial assumption made by microscopists about the number of white cells [ 40 , 41 ] and the dependence of the entire process on relativity may also lead to limitations in the parasite count by manual microscopy. Conversely, the inclusion of gametocytes in miLab™ formula might lead to overestimation.
A considerable percentage of P. falciparum submicroscopic infection were observed, with P. vivax appearing as mixed infection in the PCR results. A previous study showed a high prevalence of P. vivax, reaching up to 26% in central and eastern Sudan [ 42 ]. Additionally, the study reported a high level of mixed infections detected by PCR, but not by microscopy, indicating a high prevalence of submicroscopic infection of both P. falciparum and P. vivax in the study area, consistent with the findings reported in this study.
There is one major limitation to consider when interpreting the results of this study. This was a prospective case–control study, so there could have been bias in the selection of participants. However, samples of cases and controls were taken from a single source population in order to minimize spectrum bias and limited-challenge bias. Moreover, operators performing microscopy and PCR were blinded to miLab™ results in order to avoid diagnostic review bias. To reduce classification bias resulting from incorrect identification of the infecting species and the relatively low sensitivity of other detection techniques like microscopy, PCR was selected as the reference standard. To prevent bias resulting from varying reference test methodologies used across sites, reference testing was conducted in a centralized reference laboratory. Additionally, to further prevent bias in clinical performance estimates due to partial verification; all study participants who underwent testing using miLab™ also underwent testing using the reference and comparator tests.
In conclusion, the miLab™ platform demonstrated potential for high sensitivity automated microscopy analysis for malaria diagnosis; however, its low specificity necessitates additional refinement prior to clinical application. To completely automate the workflow and eliminate human intervention, this will also be essential.
Availability of data and materials
All relevant data are within the manuscript. The datasets used and analysed during the current study are available from the corresponding author upon reasonable request.
Abbreviations
- Artificial intelligence
Confidence interval
Dried blood spot
Deoxyribonucleic acid
Gezira Slanj
Institute of Endemic Diseases
Micro-Intelligent Laboratory
Nucleic acid amplification test
Polymerase chain reaction
Red blood cells
WHO. World malaria report 2023. Geneva, World Health Organization, 2023. https://www.who.int/publications/i/item/9789240086173 .
Malik E, Khalafalla O. Malaria in Sudan: past, present and the future. Gezira J Health Sci. 2004;1:47–53.
Google Scholar
Nur E. The impact of malaria on labour use and efficiency in the Sudan. Soc Sci Med. 1993;37:1115–9.
Article CAS PubMed Google Scholar
Fleischer B. 100 years ago: Giemsa’s solution for staining of plasmodia. Trop Med Int Health. 2004;9:755–6.
Article PubMed Google Scholar
Payne D. Use and limitations of light microscopy for diagnosing malaria at the primary health care level. Bull World Health Organ. 1988;66:621–6.
CAS PubMed PubMed Central Google Scholar
Zimmerman P, Howes R. Malaria diagnosis for malaria elimination. Curr Opin Infect Dis. 2015;28:446–54.
Tetteh M, Dwomoh D, Asamoah A, Kupeh E, Malm K, Nonvignon J. Impact of malaria diagnostic refresher training programme on competencies and skills in malaria diagnosis among medical laboratory professionals: evidence from Ghana 2015–2019. Malar J. 2021;20:255.
Article PubMed PubMed Central Google Scholar
Wongsrichanalai C, Barcus M, Muth S, Sutamihardja A, Wernsdorfer W. A review of malaria diagnostic tools: microscopy and rapid diagnostic test (RDT). Am J Trop Med Hyg. 2007;77(6 Suppl):119–27.
Maturana C, de Oliveira A, Nadal S, Bilalli B, Serrat F, Soley M, et al. Advances and challenges in automated malaria diagnosis using digital microscopy imaging with artificial intelligence tools: a review. Front Microbiol. 2022;13:1006659.
Das D, Mukherjee R, Chakraborty C. Computational microscopic imaging for malaria parasite detection: a systematic review. J Microsc. 2015;260:1–19.
Horning M, Delahunt C, Bachman C, Luchavez J, Luna C, Hu L, et al. Performance of a fully-automated system on a WHO malaria microscopy evaluation slide set. Malar J. 2021;20:110.
Decentralized Diagnostic Platform, miLab™ https://noul.kr/en/milab/
Choi J, Chin L, Woo B, Song Y, Seol M, Hong Y, et al. Hydrogel-based stamping technology for solution-free blood cell staining. ACS Appl Mater Interfaces. 2021;13:22124–30.
FIND Malaria Innovation Platform https://www.finddx.org/what-we-do/projects/malaria-innovation-platform/ Accessed March 10, 2024.
Vincent OO, Ikeh E, Obisakin F. Comparison of nested PCR and conventional analysis of Plasmodium parasites in Kano, Nigeria. Eur J Clin Biomed Sci. 2017;28(3):85.
Article Google Scholar
Zhou X, Obuchowski N, McClish D. Statistical methods in diagnostic medicine, 2nd Edn. Wiley Series in Probability and Statistics. Wiley, 2011. P 592.
Abdelwhab O, Elaagip A, Albsheer M, Ahmed A, Paganotti G, Abdel HM. Molecular and morphological identification of suspected Plasmodium vivax vectors in Central and Eastern Sudan. Malar J. 2021;20:132.
Article CAS PubMed PubMed Central Google Scholar
Al Khaja K, Sequeira R. Drug treatment and prevention of malaria in pregnancy: a critical review of the guidelines. Malar J. 2021;20:62.
WHO. Guidelines for malaria. Geneva: World Health Organization; 2022.
WHO. Guidelines on drawing blood: best practices in phlebotomy. Geneva: World Health Organization; 2010.
Makler M, Palmer C, Ager A. A review of practical techniques for the diagnosis of malaria. Ann Trop Med Parasitol. 1998;92:419–33.
WHO. Malaria microscopy quality assurance manual-version 2. Geneva: World Health Organization; 2016.
Torres K, Bachman C, Delahunt C, Alarcon Baldeon J, Alava F, Gamboa Vilela D, et al. Automated microscopy for routine malaria diagnosis: a field comparison on Giemsa-stained blood films in Peru. Malar J. 2018;17:339.
Snounou G, Singh B. Nested PCR analysis of Plasmodium parasites. Methods Mol Med. 2002;72:189–203.
CAS PubMed Google Scholar
Wilson E. Probable inference, the law of succession, and statistical inference. J Am Stat Assoc. 1927;22:209–12.
Giavarina D. Understanding Bland Altman analysis. Biochem Med (Zagreb). 2015;25:141–51.
Bailey J, Williams J, Bain B, Parker-Williams J, Chiodini P. General haematology task force of the British committee for standards in haematology. Guideline: the laboratory diagnosis of malaria. Br J Haematol. 2013;163:573–80.
Kahama-Maro J, D’Acremont V, Mtasiwa D, Genton B, Lengeler C. Low quality of routine microscopy for malaria at different levels of the health system in Dar es Salaam. Malar J. 2011;10:332.
Yoon J, Jang W, Nam J, Mihn D, Lim C. An automated microscopic malaria parasite detection system using digital image analysis. Diagnostics (Basel). 2021;11:527.
Pillay E, Khodaiji S, Bezuidenhout B, Litshie M, Coetzer T. Evaluation of automated malaria diagnosis using the Sysmex XN-30 analyser in a clinical setting. Malar J. 2019;18:15.
Jan Z, Khan A, Sajjad M, Muhammad K, Rho S, Mehmood I. A review on automated diagnosis of malaria parasite in microscopic blood smears images. Multimed Tools Appl. 2018;77:9801–26.
Poostchi M, Silamut K, Maude R, Jaeger S, Thoma G. Image analysis and machine learning for detecting malaria. Transl Res. 2018;194:36–55.
Vasiman A, Stothard J, Bogoch I. Mobile phone devices and handheld microscopes as diagnostic platforms for malaria and neglected tropical diseases (NTDs) in low-resource settings: a systematic review, historical perspective and future outlook. Adv Parasitol. 2019;103:151–73.
Harchut K, Standley C, Dobson A, Klaassen B, Rambaud-Althaus C, Althaus F, et al. Over-diagnosis of malaria by microscopy in the Kilombero Valley, Southern Tanzania: an evaluation of the utility and cost-effectiveness of rapid diagnostic tests. Malar J. 2013;12:159.
Delahunt C, Jaiswal M, Horning M, Janko S, Thompson C, Kulhare S, et al. Fully-automated patient-level malaria assessment on field-prepared thin blood film microscopy images. 2019 IEEE Global Humanitarian Technology Conference (GHTC). Seattle, WA, USA.
O’Meara W, McKenzie F, Magill A, Forney J, Permpanich B, Lucas C, et al. Sources of variability in determining malaria parasite density by microscopy. Am J Trop Med Hyg. 2005;73:593–8.
Yu H, Mohammed F, Abdel Hamid M, Yang F, Kassim Y, Mohamed A, et al. Patient-level performance evaluation of a smartphone-based malaria diagnostic application. Malar J. 2023;22:33.
Das D, Vongpromek R, Assawariyathipat T, Srinamon K, Kennon K, Stepniewska K, et al. Field evaluation of the diagnostic performance of EasyScan GO: a digital malaria microscopy device based on machine-learning. Malar J. 2022;21:122.
Toha S, Ngah U, editors. Computer aided medical diagnosis for the identification of malaria parasites. 2007 International conference on signal processing, communications and networking; 2007: IEEE.
Oliveira A, Prats C, Espasa M, Zarzuela Serrat F, Montañola Sales C, Silgado A, et al. The malaria system MicroApp: a new, mobile device-based tool for malaria diagnosis. JMIR Res Protoc. 2017;6: e70.
Dhorda M, Ba E, Kevin Baird J, Barnwell J, Bell D, Carter J, et al. Research Malaria Microscopy Working Group. Towards harmonization of microscopy methods for malaria clinical research studies. Malar J. 2020;19:324.
Elgoraish AG, Elzaki SEG, Ahmed RT, Ahmed AI, Fadlalmula HA, Abdalgader Mohamed S, et al. Epidemiology and distribution of Plasmodium vivax malaria in Sudan. Trans R Soc Trop Med Hyg. 2019;6(113):517–24.
Download references
Acknowledgements
The authors thank all the study participants. We also thank the directors and all staff at the two hospitals in GS and SOR for their assistance and collaboration in patient recruitment and performing on-site microscopy and miLab TM testing. We would like to acknowledge that this study was conducted independently of the product developer, Noul Inc., and their involvement was limited to providing the miLab™ device and cartridges for evaluation.
This study was funded by the Australian Government, Department for Foreign Affairs and Trade, as part of the FIND Malaria Innovation Platform Project.
Author information
Authors and affiliations.
Department of Parasitology and Medical Entomology, Institute of Endemic Diseases, University of Khartoum, Khartoum, Sudan
Muzamil M. Abdel Hamid, Abdelrahim O. Mohamed, Fayad O. Mohammed, Arwa Elaagip, Waleed M. A. Jebreel & Musab M. Albsheer
FIND, Geneva, Switzerland
Sabine Dittrich, Ewurama D. A. Owusu & Seda Yerlikaya
Department of Medical Laboratory Sciences, School of Biomedical and Allied Health Sciences, College of Health Sciences, University of Ghana, Accra, Ghana
Ewurama D. A. Owusu
Malaria Control Program, Federal Ministry of Health, Khartoum, Sudan
Sayed A. Mustafa & Tarig Elfaki
Faculty of Medical Laboratory Sciences, Sinnar University, Sinnar, Sudan
Musab M. Albsheer
Department of Biochemistry, Faculty of Medicine, University of Khartoum, Khartoum, Sudan
Abdelrahim O. Mohamed
Department of Infectious Disease and Tropical Medicine, Heidelberg University Hospital, 69120, Heidelberg, Germany
Seda Yerlikaya
You can also search for this author in PubMed Google Scholar
Contributions
SY and SD designed the FIND Innovation Platform project and SY implemented the project. SY, MMA, EO, SD, AOM: proposal development, study design and implementation of research. SY, MMA, WMA, AOM: supervision of sample collection, data analysis and interpretation, preparation of the draft and critically and appraisal and revision of final manuscript. FOM, MMA, AE: sample collection, data entry and performed PCR tests. SAM, TE: site supervision and performing expert microscopy. EO, MMA, AOM, AE, and SY reviewed the manuscript. All authors read and approved the final manuscript.
Corresponding author
Correspondence to Muzamil M. Abdel Hamid .
Ethics declarations
Ethics approval and consent to participate.
The study was conducted according to ICH-GCP E6 (R2) guidelines. The study protocol was reviewed and received ethical approval from the National Ethics Committee, Federal Ministry of Health, Sudan (Ref: FMoH/ERC ID 3-2-2020 dated 01/03/2020), and the Medical and Health Sciences Ethical Committee, University of Khartoum (REF: FM/DO/EC dated 22/01/2020 and FMoH/ERC ID 3-2-2020 dated 01/03/2020). A written informed consent was obtained from all participants aged 18 years old or older. For children aged 5 years and older but younger than 13 years, consent of the parent or legal guardian was sought. For children aged 13 years and older but younger than 18 years, assent from the child and consent of the parent or legal guardian were obtained.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Additional file 1: fig s1.
Map showing the study area. Fig S2 miLab™ platform and its display screen. Fig S3 Images of parasitized and non-parasitized red blood cells produced by miLab™.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
Reprints and permissions
About this article
Cite this article.
Hamid, M.M.A., Mohamed, A.O., Mohammed, F.O. et al. Diagnostic accuracy of an automated microscope solution (miLab™) in detecting malaria parasites in symptomatic patients at point-of-care in Sudan: a case–control study. Malar J 23 , 200 (2024). https://doi.org/10.1186/s12936-024-05029-3
Download citation
Received : 25 March 2024
Accepted : 26 June 2024
Published : 28 June 2024
DOI : https://doi.org/10.1186/s12936-024-05029-3
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Automated microscope
Malaria Journal
ISSN: 1475-2875
- Submission enquiries: [email protected]
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Wiley Open Access Collection

Comparing the cohort design and the nested case–control design in the presence of both time-invariant and time-dependent treatment and competing risks: bias and precision
Peter c austin.
1 Institute for Clinical Evaluative Sciences, Toronto, Ontario, Canada
2 Institute of Health Management, Policy and Evaluation, University of Toronto, Toronto, Ontario, Canada
3 Dalla Lana School of Public Health, University of Toronto, Toronto, Ontario, Canada
Geoffrey M Anderson
Candemir cigsar.
4 Women's College Research Institute, Toronto, Ontario, Canada
5 Department of Biostatistics, Princess Margaret Hospital, Toronto, Ontario, Canada
Andrea Gruneir
Observational studies using electronic administrative healthcare databases are often used to estimate the effects of treatments and exposures. Traditionally, a cohort design has been used to estimate these effects, but increasingly, studies are using a nested case–control (NCC) design. The relative statistical efficiency of these two designs has not been examined in detail.
We used Monte Carlo simulations to compare these two designs in terms of the bias and precision of effect estimates. We examined three different settings: (A) treatment occurred at baseline, and there was a single outcome of interest; (B) treatment was time varying, and there was a single outcome; and C treatment occurred at baseline, and there was a secondary event that competed with the primary event of interest. Comparisons were made of percentage bias, length of 95% confidence interval, and mean squared error (MSE) as a combined measure of bias and precision.
In Setting A, bias was similar between designs, but the cohort design was more precise and had a lower MSE in all scenarios. In Settings B and C, the cohort design was more precise and had a lower MSE in all scenarios. In both Settings B and C, the NCC design tended to result in estimates with greater bias compared with the cohort design.
Conclusions
We conclude that in a range of settings and scenarios, the cohort design is superior in terms of precision and MSE. Copyright © 2012 John Wiley & Sons, Ltd.
INTRODUCTION
There is an increasing interest in using large administrative healthcare databases for comparative effectiveness, epidemiological, and pharmacoepidemiological research. Advantages to the use of administrative healthcare databases include comprehensive coverage of entire populations, relatively low cost for the acquisition of data on outcomes and covariates, and the ability to examine the effects of treatments and interventions as they are applied outside of the tightly controlled confines of randomized controlled trials.
The traditional approach to the analysis of these large observational datasets is the retrospective cohort design. The treatment status of each subject is determined at the time of cohort entry or at some observable time subsequent to cohort entry. Subjects are followed over time for the occurrence of the outcome of interest. The incidence of the outcome is then compared between those who were treated and those who were untreated using the incidence rate ratio.
In observational studies, treatment assignment is not at random but is often influenced by subject characteristics. There are often systematic differences in baseline characteristics between treated and untreated subjects. Therefore, statistical methods must be used to reduce the bias in the estimate of association. For a cohort design with time-to-event data, this is often accomplished using the Cox proportional hazards model. 1 The estimated hazard ratio represents the adjusted incidence rate ratio.
There has been a recent increase in the use of the nested case–control (NCC) design in pharmacoepidemiological studies. 2 – 12 The NCC is a variant of the classic case–control design where cases and controls are sampled from a well-defined cohort. 13 – 17 The measure of association derived from any case–control study, the odds ratio, is mathematically equivalent to the incidence rate ratio derived from a cohort study given that the ratio of treated to untreated in the control series is equivalent to the ratio of the treated to untreated person-time in the source population. 18 Traditional arguments in favor of the case–control design focused primarily on its improved efficiency relative to the cohort design. In this context, efficiency was defined as the potential to reduce the costs and/or burden of data collection. This efficiency arises from the fact that, whereas in a cohort study, data on covariates must be collected from all subjects, in a case–control design, data on covariates are required from all cases, but from only a sample of those who do not experience the outcome (i.e., the controls). This is not relevant in studies using administrative or other secondary data where the marginal cost of data collection for covariates is close to zero. More recently, some authors have suggested that another form of efficiency relates to computational efficiency, in particular, where there may be some time-varying element to the treatment. 19 Given the ongoing increases in computational speed and processing power, this aspect of efficiency may be less relevant for many analyses.
Because identifying a well-defined cohort is the first step when using either a cohort or NCC design, it is possible to use either design to estimate treatment effects in the same set of subjects. Although both designs, given specific conditions, can result in unbiased treatment effects when the research question relates to a relatively simple treatment–outcome relationship, it is less clear how these designs compare when more complex treatment–outcome relationships are of interest. Understanding the implications of one design over the other is required for investigators to make informed decisions. One way to judge the comparative quality of the estimates of treatment effect produced by the two designs is the bias and precision of these estimates.
The objective of the current study was to compare estimates of treatment effect made from a cohort design with those from an NCC design in terms of bias and precision. We used a series of Monte Carlo simulations to examine these issues in three different settings that describe important treatment–outcome relationships in pharmacoepidemiology: Setting A, the least complex setting, in which there is a single event of interest and subjects are treated/exposed at baseline and treatment status remains fixed over the duration of follow-up time. Setting B introduces a variation in the definition of treatment, with treatment status being allowed to vary over time. However, there is still only one event of interest. Setting C introduces an issue related to the outcome by allowing there to be secondary outcomes or events, which compete with the primary event of interest. In each of the three settings, we examined several different scenarios defined by the magnitude of the true treatment effect, the proportion of subjects who were treated, and the proportion of subjects who experienced the event or outcome.
MONTE CARLO SIMULATIONS—DESIGN
The operational definition of exposure varies widely across studies that use the NCC design. We examined three simple settings that form a foundation for more complex definitions of exposure. First, we considered a setting in which exposure is applied at the time of cohort entry and remains fixed over the duration of follow-up. Examples of this include studies comparing the effect of different chemotherapy regimes on patients diagnosed with specific cancers. A second example is a study to examine serum levels of superoxide dismutase activity and the risk of cancer mortality, in which the base cohort was the Japan Collaborative Cohort Study. 20 Cases were subjects who died of cancer. Exposure was defined using blood serum donated close to the time of cohort entry. The second setting we considered involved a point exposure that was applied at some point during the duration of follow-up. Examples of this include studies in which vaccines may have been administered at some point after cohort entry. Another is an Australian study to examine the effect of anti-inflammatory drugs on the incidence of myocardial infarction and all-cause mortality in the Australian veteran community. 21 Cases were subjects who experienced myocardial infarction, heart failure, or death of any cause. In the first reported analysis, exposure was defined as any receipt of a nonsteroidal anti-inflammatory medication during the follow-up period. The third scenario that we considered is an adaption of the first scenario, but with the outcome being a nonmortality outcome that is subject to competing risks (e.g., hip fracture, hospitalizations, or occurrence of a specific disease).
Data-generating process
We used a series of Monte Carlo simulations to examine bias and precision of estimates from cohort designs with those from NCC designs. We examined the following three settings: Setting A: a binary treatment was assigned and fixed at baseline; Setting B: a binary treatment was assigned at some time during the duration of the follow-up; and Setting C: similar to Setting A, but there were competing events. The basic setup of the simulations was similar across the three settings. These settings are important because they form the basis for more complex methods of defining exposure.
For a given iteration of the Monte Carlo simulation, we simulated baseline covariates, treatment status, and an outcome for each of 5000 subjects. For each subject, we simulated six baseline covariates ( X 1 – X 6 ), the first three from independent Bernoulli distributions with parameter 0.5 and the last three from independent standard normal distributions.
In Settings A, B, and C, we determined a treatment status at baseline using a logistic regression model:

The values of β weak , β medium , and β strong were set to log(1.10), log(1.50), and log(2), respectively, to denote weak, medium, and strong treatment selection effects. The value of the intercept, β 0,treat , was selected so that the marginal probability of receipt of treatment would be fixed at the desired level (this was one of the factors of the Monte Carlo simulations). We then simulated a treatment status from a Bernoulli distribution with subject-specific parameter p i . For Settings A and C, treatment status was assigned at baseline and then fixed over the duration of follow-up. In Setting B, for those subjects who were assigned to receive treatment, time to receipt of treatment was randomly generated from a Weibull distribution with shape and scale parameters of 0.25 and 433.2097, respectively; thus, the median time to treatment would be 100 days. We thus generated a treatment status for each subject and in Setting B, a time at which treatment was to be received.
We then simulated a time-to-event outcome for each subject using a Cox–Weibull model. For Setting A, in which treatment selection was fixed at baseline, a previously described data-generating process 22 , 23 was used to simulate time-to-event outcomes from the following Cox model:

where h 0 ( t ) denotes the baseline hazard function, and z is an indicator variable denoting treatment status. The values of α weak , α medium , and α strong were set at log(1.25), log(2), and log(3), respectively, to denote weak, medium, and strong effects on the hazard of the outcome. The coefficient β treat , which denotes the log–hazard ratio for the effect of treatment on the hazard of the outcome, is one of the factors that will be varied in the Monte Carlo simulations. In each setting, we assumed a Weibull distribution for time-to-event outcomes, with shape and scale parameters of 0.45 and 0.01, respectively. If the entire population were untreated, this would result in a marginal distribution of event times with a median of approximately 1000 days and a 25th percentile of approximately 53 days.
In Setting B, in which treatment status was time dependent, a time-to-event outcome was simulated for each subject using a data-generating process described elsewhere. 24 The same shape and scale parameters were used as stated earlier so that the marginal distribution of event times under lack of treatment was the same as in Setting A. If subjects experienced the event of interest prior to the time of receipt of treatment, the subject was defined to have been untreated for the entire duration of follow-up.
In Setting C, in which there were competing risks, a time-to-event outcome was simulated for each subject using a data-generating process described by Beyersmann et al . 25 In this setting, we assumed that there were two competing events (the primary event of interest and a competing event). Furthermore, we assumed that each of these two events had the same hazard function (and that the hazard function for each event was the same as that from Setting A). Thus, the overall hazard function of either event occurring was twice the cause-specific hazard function of the primary event of interest. For each subject, using the approach described by Bender et al ., we simulated a time-to-event outcome by inverting the cumulative overall hazard function. Then, because the two event types had the same hazard function, using the approach described by Beyersmann et al ., we randomly selected which of the two types was the event type that occurred, with each event type having a probability of 0.5. We then followed a similar approach to the one given in Setting A.
Factors of the Monte Carlo simulations
In each of the three settings, we used a full factorial design in which we allowed the following factors to vary: the true hazard ratio for the effect of treatment on the hazard of the outcome; the prevalence of treatment (the percentage of subjects who were assigned to treatment); and the proportion of subjects for whom the event was observed to occur, with the remaining subjects being subject to censoring. When inducing censoring, an event time was initially simulated for all subjects as described in the previous section. We then determined the appropriate percentile of survival or event times. All subjects with event times that exceeded this percentile of event time were then treated as censored observations, with their observed survival time set to this percentile. In using this approach, we induce Type II censoring. 26 However, this will not induce any bias in estimating regression coefficients ( 26 ; Section III.2).
In each of the three settings, the hazard ratio was allowed to take on the following values: 1.25 and 2. The proportion of subjects who were treated took on the following values: 0.10, 0.25, and 0.50, whereas the proportion of subjects for whom the event was observed to have occurred was 0.05, 0.10, and 0.25. Thus, for each of the three settings, there were 18 different scenarios (2 hazard ratios × 3 proportion of subjects treated × 3 proportion of subjects who were censored). In each of these 18 different scenarios, 1000 datasets were simulated, each consisting of 5000 subjects. In Setting C, although the proportion of subjects for whom any event was observed to have occurred took the following values: 0.10, 0.20, and 0.50 (because half of the observed events would be the primary event, whereas the other half would be the competing event, this implies that the primary event would be observed to occur for 5%, 10%, and 25% of subjects).
Statistical analyses
In each simulated dataset, the following statistical analyses were conducted. First, an analysis based on a conventional cohort design was conducted. A Cox proportional hazards regression model was used to regress survival time on an indicator variable denoting treatment status and the six baseline covariates. In Setting A, a conventional Cox model with time-invariant covariates was fit to each simulated dataset. In Setting B, the Cox model accounted for the time-dependent nature of treatment status: For subjects who were assigned to receive the treatment, subjects were considered untreated until the time of receipt of treatment. In Setting C, a Cox model was used to model the cause-specific hazard of the primary event of interest, treating the occurrence of the competing event as a censoring event. 27 In each case, the log–hazard ratio for the treatment effect and its standard error were estimated, along with the 95% confidence interval for the estimated hazard ratio.
Second, an analysis based on the NCC design was used. Cases were defined to be subjects who experienced the event of interest. For each case, one or more controls were selected by simple random sampling without replacement from the subjects in the case's risk set. A case's risk set is the set of subjects who were still at risk of the event at the time at which the case experienced the event of interest. Thus, each case was matched to a subject who, at the time that the case experienced the event of interest, had not yet experienced the event of interest. In Setting A, we used both 1:1 and 5:1 matching. In 1:1 matching, pairs of cases and controls were formed, whereas with 5:1 matching, each case was matched to up to five controls. Thus, for 1:1 matching, from a case's risk set, one subject was selected at random for matching to the given case; for 5:1 matching, five subjects were selected at random from the case's risk set for matching to the case. For each case, the index date was defined to be the time of the occurrence of the event of interest, whereas for each control, the index date was the time at which the event occurred for the matched case. For each case and the matched controls, we determined whether they had been treated/exposed prior to the index date. Conditional logistic regression was then used to determine the association between exposure and the occurrence of the event of interest while adjusting for the six baseline covariates and accounting for matched sets. From the conditional logistic regression model, we estimated the adjusted log–odds ratio for exposure, the standard error of the adjusted log–odds ratio, and the 95% confidence interval for the adjusted odds ratio.

The simulations and statistical analyses were conducted in SAS v9.2 (SAS Institute Inc., Cary, NC) and R v2.11.1 (The R Foundation for Statistical Computing, Vienna, Austria).
MONTE CARLO SIMULATIONS—RESULTS
Setting a—fixed exposure.
Results for this setting are reported in Figures 1 and and2. 2 . Due to space constraints, we do not report detailed results for 1:1 matching in the NCC design; however, we summarize these results in the following two paragraphs. In Figure 1 , we report relative bias. Across the 18 scenarios, the median relative bias was 0.1% for the cohort design, whereas it was 0.2% and −0.7% for the NCC analyses with 1:1 and 5:1 matching, respectively. For the cohort design, the 25th and 75th percentiles of relative bias were −0.2% and 1.6%, respectively, whereas for the NCC design with 1:1 matching, the upper and lower quartiles of relative bias were −3.4% and 2.3%. With 5:1 matching, the 25th and 75th percentiles of relative bias were −4.0% and 1.5%, respectively. In examining Figure 1 , one observes that there was a trend, when using the NCC design, towards an increase in the magnitude of relative bias as the proportion of subjects for whom events were observed to have occurred increased. However, in all 18 scenarios, the relative bias tended to be small. When using the cohort design, the magnitude of relative bias tended to decrease as the proportion of subjects who were treated increased.

Percentage bias: fixed treatment

Precision/Relative efficiency and mean squared error: fixed treatment
In the top two panels of Figure 2 , we report the ratio of the mean length of the 95% confidence intervals for the NCC design with 5:1 matching to the mean length of the 95% confidence intervals for the cohort design. This is equivalent to the asymptotic relative efficiency—the ratio of the standard error of the estimate from the NCC design to the standard error of the estimate from the cohort design. The median ratio of widths of confidence intervals was 1.26 across the 18 scenarios, whereas the 25th and 75th percentiles were 1.19 and 1.32, respectively. When 1:1 matching was employed, the 25th, 50th, and 75th percentiles of this ratio were 1.60, 1.83, and 2.09, respectively. In 17 of the 18 scenarios, the empirical coverage rates from the cohort design and the NCC (with 5:1 matching) were not statistically significantly different from their advertized rates of 0.95. The inefficiency of the NCC design relative to the cohort design increased as the proportion of subjects who were treated decreased. Furthermore, the relative inefficiency of the NCC design decreased as the proportion of subjects for whom an event occurred increased.
The MSEs of the estimated treatment effects are reported in the lower two panels of Figure 2 . The MSE from the cohort design was always smaller than that from the NCC design. The median MSE from the former design was 0.0105, whereas it was 0.0307 for the NCC design with 1:1 matching and 0.0173 with 5:1 matching. The MSE of the estimated treatment effect decreased as the proportion of subjects for whom an event occurred increased.
Setting B—time-dependent treatment status
The relative bias is reported in Figure 3 . Across the 18 scenarios, the median relative bias was −1.1% and 8.9% for the cohort and NCC designs, respectively. For the cohort design, the 25th and 75th percentiles of relative bias were −4.4% and −0.5%, respectively, whereas for the NCC design, the upper and lower quartiles of relative bias were 3.9% and 17.4%. For the NCC design, the relative bias tended to increase as the proportion of subjects for whom an event was observed increased. When the percentage of subjects who experienced an event was low (5%) and the prevalence of treatment was either 5% or 25%, then the cohort design resulted in estimates with greater relative bias compared with the NCC design. However, in the remaining scenarios, the NCC design resulted in greater relative bias. Furthermore, relative bias tended to be greater when the true treatment hazard ratio was 1.25 compared with when it was 2. When the treatment hazard ratio was 1.25 and the event occurred for 25% of the subjects, then the relative bias could be substantial for the NCC design.

Percentage bias: time-varying treatment
In the upper two panels of Figure 4 , we report the ratio of the mean length of the 95% confidence intervals for the NCC design to the mean length of the 95% confidence intervals for the cohort design. This is equivalent to the relative efficiency of the two designs: the ratio of the standard error of the NCC design to that of the cohort design. The median ratio of widths of confidence intervals was 1.51 across the 18 scenarios, whereas the 25th and 75th percentiles were 1.44 and 1.60, respectively. In 2 of the 18 scenarios, the empirical coverage rates from the cohort design were statistically significantly different from their advertized rates of 0.95. However, in 8 of the 18 scenarios, the empirical coverage rates from the NCC design were statistically significantly different from their advertized rates of 0.95. The relative inefficiency of the NCC design decreased as the proportion of subjects who experienced an event increased. The relative inefficiency also decreased as the proportion of subjects who were treated increased.

Precision/Relative efficiency and mean squared error: Time-varying treatment
The MSEs of the estimated treatment effects are reported in the lower two panels of Figure 4 . The MSE from the cohort design was always smaller than that from the NCC design. The median MSE from the former design was 0.0255, whereas it was 0.0490 for the latter. Differences between the MSEs of the estimated treatment effects from the two designs tended to decrease as the proportion of subjects who experienced an event increased and as the proportion of subjects who were treated increased.
Setting C—competing risks
The relative bias is reported in Figure 5 . Across the 18 scenarios, the median relative bias was 0.2% and −4.2% for the cohort and NCC designs, respectively. For the cohort design, the 25th and 75th percentiles of relative bias were −0.8% and 1.5%, respectively, whereas for the NCC design, the upper and lower quartiles of relative bias were −13.0% and −0.4%. When 25% of subjects experienced the event, the relative bias of the NCC design was substantial. However, when the percentage of subjects who experienced the event was low (10%), then the magnitude of the relative bias was modestly greater for the cohort design than for the NCC design.

Percentage bias: competing risks
In the upper two panels of Figure 6 , we report the ratio of the mean length of the 95% confidence intervals for the NCC design to the mean length of the 95% confidence intervals for the cohort design. This is equivalent to the relative efficiency of the two designs: the ratio of the standard error of the NCC design to that of the cohort design. The median ratio of widths of confidence intervals was 1.21 across the 18 scenarios, whereas the 25th and 75th percentiles were 1.16 and 1.28, respectively. In none of the 18 scenarios was the empirical coverage rate of 95% confidence intervals from the cohort design statistically significantly different from the advertized rate of 0.95. However, in 5 of the 18 scenarios, the empirical coverage rates of the 95% confidence intervals from the NCC design were statistically significantly different from the advertized rate of 0.95. The relative inefficiency of the NCC design decreased as the proportion of subjects who experienced the event increased and as the proportion of subjects who were treated increased.

Precision/Relative efficiency and mean squared error: competing risks
The MSEs of the estimated treatment effects are reported in the lower two panels of Figure 6 . The MSE from the cohort design was always smaller than that from the NCC design. The median MSE from the former design was 0.0114, whereas it was 0.0208 for the latter.
We compared the estimation of treatment effects in cohort designs using the Cox proportional hazards model with estimation in NCC designs using conditional logistic regression. When exposure was applied at time of cohort entry and in the absence of competing risks, both designs resulted in approximately unbiased estimation of log–hazard ratios. However, the cohort design resulted in estimates with greater precision and lower MSE. Thus, the penalty for using an NCC design in this context is the decreased precision or diminished statistical efficiency: The treatment effect is estimated with less precision. Thus, associated confidence intervals will be wider than if a cohort design was used. When both events or outcomes were rare and treatment or exposure occurred infrequently, then, although negligible in magnitude, the cohort design resulted in modestly more bias than did the NCC design. However, this modest increase in bias was offset by greater precision. When treatment was time dependent, then the NCC design tended to result in estimates with greater bias than those arising from a cohort design. As mentioned, the cohort design resulted in estimates with greater precision and lower MSE. Finally, in the presence of competing risks, the use of an NCC design resulted in greater bias compared with the cohort design. As with the other two settings, the cohort design resulted in estimates with greater precision and lower MSE. Thus, the primary penalty for using an NCC design rather than a cohort design is the decreased statistical efficiency, with the attendant increase in the width of estimated confidence intervals. However, in some settings, there was also an increase in the magnitude of the relative bias of the estimated treatment effect.
Our findings on bias in the setting with an exposure fixed at baseline and with no competing risks should be of no surprise. The conditional likelihood of the conditional logistic regression model is of the same form as the partial likelihood used in the Cox proportional hazards model. 28 For this reason, one would expect the estimated log–hazard ratio and the log–odds ratio to coincide. We found that the use of a cohort design resulted in estimates of greater precision than those arising from the use of an NCC design. This is also expected, given that in the cohort design, all of the available data are used for estimation, whereas in the case–control design, only the data on cases and a sample of controls are used. When we extended our examination to settings in which time-dependent covariates and competing risks occur, we found that bias was introduced with the NCC design and that this design also resulted in estimates with less precision than that of the cohort design.
The primary rationale for conducting an NCC study even when a cohort has been assembled is to obtain additional data that would be prohibitive to collect on the full cohort ( 18 , p. 94). Thus, as noted by Rothman and Greenland, an NCC design is more efficient than a cohort study. However, it is important to note that they are using the term efficiency in an economic or expenditure of effort sense and not in a statistical perspective. They suggested that an NCC study may be substantially cheaper to conduct than a cohort study, with nearly the same level of precision (p. 90). In our simulations, we found that the cohort design resulted in estimates with moderately greater precision as evidenced by confidence intervals that were, on average, moderately narrower than those arising from NCC designs. Thus, the increased economic efficiency of the NCC design comes at the cost of decreased statistical efficiency.
Essebag and colleagues examined the relative computational efficiency of the NCC design and the cohort design with time-dependent exposures. 19 Using a single dataset, they compared the computing time required for cohort and NCC analyses with time-dependent exposures. Although the relative increase in computing time for the cohort analysis compared with the NCC analysis was substantial, the absolute differences in computing time were small. In today's era of fast and relatively inexpensive computing power, we speculate that in most settings, the choice between which design to use will not be based on computational demand. We suspect that in most settings that use administrative or other secondary data, the decreased statistical efficiency in the NCC design will result in the cohort analysis being the default approach.
In the current study, we have focused on relatively simple approaches to operationalizing exposure. In two of the three settings, exposure was fixed at baseline, whereas in the other setting, exposure was a binary exposure that occurred once over the course of follow-up. In the applied literature, there is a move to more complicated methods of operationalizing exposure, particularly in settings with time-varying exposures or looking at the recentness of exposure. In such settings, it may be reasonable to use the NCC design for ease of operationalizing exposure, analyzing the data, and interpreting the findings. However, we suspect that such an approach will be accompanied with a reduction in statistical efficiency compared with what would be possible with the conventional cohort design.
There are certain limitations to the current study that suggest directions for further research. First, in the current study, we selected controls from subjects who were in the risk set of the case at the time that the case experienced the event of interest. However, we did not examine the effect of additional matching on other risk factors or confounding variables. Subsequent work is needed to examine the impact of matching on additional sets of covariates. Second, in the current study, we have restricted our attention on NCC designs and have ignored other case-based designs such as the nested case–cohort design. 17 Subsequent research comparing the relative performance of the nested case–cohort design with that of the NCC design and the cohort design is merited. Langholz reviewed analytical approaches for the case–cohort design and discussed its advantages and disadvantages, including issues of statistical efficiency, in comparison with the NCC design. 29 Third, we have focused our attention on settings in which the values of confounding variables are fixed at baseline and do not vary over the duration of follow-up. We have not examined estimation of treatment effects in settings in which both treatment and confounding variables vary over time and in which time-varying confounding variables can be influenced by prior treatment or exposure. Marginal structural models have been developed for use in this context. 30 – 33 Consideration of these types of scenarios was beyond the scope of the current study. We also want to note that, although the most common NCC design is based on the simple random sampling of the controls, there are other sampling designs for the controls such as countermatching design, which is a stratified NCC design. 34 This design may provide improvement in statistical efficiency depending on the available additional information on cohort members and the type of the study. Other sampling designs for the controls are discussed by Langholz. 35
In conclusion, we found that, across a wide range of different settings and different scenarios, the use of a cohort design tended to result in estimates with lower bias and greater precision compared with the use of an NCC design.
CONFLICT OF INTEREST
The authors declare no conflict of interests.
Acknowledgments
This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results, and conclusions reported in this article are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. Dr Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation of Ontario. This study was supported in part by an operating grant from the Canadian Institutes of Health Research (CIHR) (Funding MOP 86508). Dr Gruneir receives salary support from the Team Grant (OTG-88591) from the CIHR Institute of Nutrition, Metabolism, and Diabetes. Dr Cigsar receives support from Cancer Care Ontario and the Ontario Institute for Cancer Research (through funding provided by the Ministry of Health and Long-Term Care and the Ministry of Research & Innovation of the Government of Ontario).
- The cohort design results in estimates with greater precision and lower mean squared error compared to estimates from a nested case-control design.
- In settings with competing risks or time-varying treatments, a simple nested case-control design can result in biased estimation compared to a cohort design.

IMAGES
VIDEO
COMMENTS
It has been recently asserted that the nested case-control study design, in which case-control sets are sampled from cohort risk sets, can introduce bias ("study design bias") when there are lagged exposures. The bases for this claim include a theoretic and an "empirical evaluation" argument. Both of these arguments are examined and ...
a) The nested case-control study is a retrospective design. b) The study design minimised selection bias compared with a case-control study. c) Recall bias was minimised compared with a case-control study. d) Causality could be inferred from the association between prescription of antipsychotic drugs and venous thromboembolism.
The bias is defined by the difference between the estimates from the nested case-control sample and the full cohort estimate. For the stratified model, I used histology ( x 1 ) as the only covariate, and tumor stage ( x 2 ), and the age at baseline ( x 3 ) as the stratification factors to allow different baseline hazard functions.
Fundamentally, a properly executed case-control study nested in a cohort is valid if the corresponding analysis of the full cohort is valid. The mathematics of the likelihoods are the same for both, 5 as Langholz and Richardson 1 point out, and the same software procedures work for both. The only salient difference between the two designs is ...
The nested case-control study (NCC) design within a prospective cohort study is used when outcome data are available for all subjects, but the exposure of interest has not been collected, and is difficult or prohibitively expensive to obtain for all subjects. A NCC analysis with good matching procedures yields estimates that are as efficient and unbiased as estimates from the full cohort study.
The nested case-control design is well established as an epidemiologic study design. Nonetheless, a number of articles and letters have appeared recently asserting that the nested case-control study design is susceptible to a form of study design bias. 1-5 Given the theoretical understanding of the validity of the standard nested case-control design, in which case-control sets consist of the ...
The main advantages of a nested case-control study are as follows: (1) cost reduction and effort minimization, as only a fraction of the parent cohort requires the necessary outcome assessment; (2) reduced selection bias, as both case and control subjects are sampled from the same population; and (3) flexibility in analysis by allowing testing ...
It has been recently asserted that the nested case-control study design, in which case-control sets are sampled from cohort risk sets, can introduce bias ("study design bias") when there are lagged exposures. The bases for this claim include a theoretical and an "empirical evaluation" argument. We examined both of these arguments and found them ...
The nested case-control (NCC) study design is another widely used approach to explore the association between drug exposure and the event of interest. ... especially when only a single control was matched to each case. The bias of NCC estimates increased with higher proportion of events, while estimates from the full cohort analysis remained ...
Fundamentally, a properly executed case-control study nested in a cohort is valid if the corresponding analysis of the full cohort is valid. The mathematics of the likelihoods are the same for both, 5 as Langholz and Richardson 1 point out, and the same software procedures work for both. The only salient difference between the 2 designs is ...
Our findings support the view that the nested case-control study is a valid and efficient design for diagnostic studies and should also be (re)appraised in current guidelines on diagnostic accuracy research. ... Reitsma JB, Glas AS, Bossuyt PM, Kleijnen J: Sources of variation and bias in studies of diagnostic accuracy: a systematic review. Ann ...
A nested case-control (NCC) study is a variation of a case-control study in which cases and controls are drawn from the population in a fully enumerated cohort. [1] Usually, the exposure of interest is only measured among the cases and the selected controls. Thus the nested case-control study is more efficient than the full cohort design.
The case-control study can be subcategorized into four different subtypes based on how the control group is selected and when the cases develop the disease of interest as described in the following sections. Nested Case-Control Study When a case-control study is performed within a cohort study, it is called a nested case-control study. In a nested
Bias introduced by case-control matching is an intentional selection bias. Over the past two decades, a consensus has emerged in epidemiology that causal reasoning, with the help of directed acyclic graphs, has improved our understanding of confounding and its control [5-10].When confounding is defined by characteristic structures among causal relationships in the source population, the ...
Abstract. The nested case-control study design (or the case-control in a cohort study) is described here and compared with other designs, including the classic case-control and cohort studies and the case-cohort study. In the nested case-control study, cases of a disease that occur in a defined cohort are identified and, for each, a specified ...
For identifying potential selection bias, information concerning all invited families in the case-control study was obtained from the baseline questionnaire. Results show that there are several possible biases due to self-selection involved in an extensive study on the impact of the home environment on asthma and allergy among children.
reduction in costs, data collection efforts, and analysis compared to a full study cohort approach. The nested case-control study achieves all this with a relatively minor loss in statistical efficiency. The nested case-control study minimises selection bias and recall bias (cases and controls may recall past exposure differently) in the study.
A nested case-control study design involves the selection of several healthy controls for each case, typically from those still under observation at the time when the case developed the disease [3]. However, nested case-control studies have some limitations: 1) Inefficiency due to the alignment of each selected control subject to its matched case.
• Nested Case-Control Studies (Prentice and Breslow, 1978; Langholz and Goldstein 1996) - Match controls to each case based on time (age) of onset for ... show bias in estimates for case control sampling - Chen and Lo, 1999 and Chen, 2001 modify methods for case-control if overall prevalence of cases in cohort is known.
View a PDF of the paper titled A Rigorous Machine Learning Analysis Pipeline for Biomedical Binary Classification: Application in Pancreatic Cancer Nested Case-control Studies with Implications for Bias Assessments, by Ryan J. Urbanowicz and Pranshu Suri and Yuhan Cui and Jason H. Moore and Karen Ruth and Rachael Stolzenberg-Solomon and Shannon M. Lynch
A nested case-control study in diagnostic research includes the full population or cohort of patients suspected of the target disease. The 'true' disease status is obtained for all these patients with the reference standard. Hence, there is no referral or partial verification bias.
This large, nested case-control study found an increased risk of incident CVD associated with long-term ADHD medication use, and the risk increased with increasing duration of ADHD medication use. This association was statistically significant both for children and youth and for adults, as well as for females and males.
A matched case-control study is an observational study that involves comparing individuals who have a specific health outcome or disease (the cases) with individuals who do not have the health ...
Background: Multiple studies have reported that the use of selective serotonin reuptake inhibitors (SSRIs) is associated with an increased risk of ischemic stroke; however, this finding may be the result of a confounding by indication. We examined the association using different approaches to minimize such potential bias. Methods: A nested case-control study was carried out in a Spanish ...
The nested case-control study design employs case-control methodology within an established prospective cohort study . It first emerged in the 1970-80s and was typically used when it was expensive or difficult to obtain data on a particular exposure for all members of the cohort; instead a subset of controls would be selected at random [ 2 ].
There is one major limitation to consider when interpreting the results of this study. This was a prospective case-control study, so there could have been bias in the selection of participants. However, samples of cases and controls were taken from a single source population in order to minimize spectrum bias and limited-challenge bias.
There has been a recent increase in the use of the nested case-control (NCC) design in pharmacoepidemiological studies. 2 - 12 The NCC is a variant of the classic case-control design where cases and controls are sampled from a well-defined cohort. 13 - 17 The measure of association derived from any case-control study, the odds ratio ...