solve for x fraction problems

Fractions Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step
• To enter a fraction, type a / in between the numerator and denominator. For example: 1/3
• Or click the example.

Example (Click to try)

Fractions video lesson.

• Khan Academy Video: Adding Fractions

Need more problem types? Try MathPapa Algebra Calculator

Clear Fractions Calculator »

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.26: Solving Fractional Equations

• Last updated
• Save as PDF
• Page ID 48329

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

A fractional equation is an equation involving fractions which has the unknown in the denominator of one or more of its terms.

Example 24.1

The following are examples of fractional equations:

a) \(\frac{3}{x}=\frac{9}{20}\)

b) \(\frac{x-2}{x+2}=\frac{3}{5}\)

c) \(\frac{3}{x-3}=\frac{4}{x-5}\)

d) \(\frac{3}{4}-\frac{1}{8 x}=0\)

e) \(\frac{x}{6}-\frac{2}{3 x}=\frac{2}{3}\)

The Cross-Product property can be used to solve fractional equations.

Cross-Product Property

If \(\frac{A}{B}=\frac{C}{D}\) then \(A \cdot D=B \cdot C\).

Using this property we can transform fractional equations into non-fractional ones. We must take care when applying this property and use it only when there is a single fraction on each side of the equation. So, fractional equations can be divided into two categories.

I. Single Fractions on Each Side of the Equation

Equations a), b) and c) in Example 24.1 fall into this category. We solve these equations here.

a) Solve \(\frac{3}{x}=\frac{9}{20}\)

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 20=9 \cdot x \\ \text{Linear Equation} & 60=9 x \\ \text{Divide by 9 both sides} & \frac{60}{9}=x \end{array}\nonumber\]

The solution is \(x=\frac{60}{9}=\frac{20}{3}\).

\[\begin{array}{ll} \text{Cross-Product} & 5 \cdot(x-2)=3 \cdot(x+2) \\ \text{Remove parentheses} & 5 x-10=3 x+6 \\ \text{Linear Equation: isolate the variable} & 5 x-3 x=10+6 \\ & 2 x=16 \\ \text{Divide by 2 both sides} & \frac{2 x}{2}=\frac{16}{2}\end{array}\nonumber\]

the solution is \(x=8\).

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot(x-5)=4 \cdot(x-3) \\ \text{Remove parentheses} & 3 x-15=4 x-12 \\ \text{Linear Equation: isolate the variable} & 3 x-4 x=15-12 \\ & -x=3 \\ \text{Divide by 2 both sides} & \frac{-x}{-1}=\frac{3}{-1}\end{array}\nonumber\]

The solution is \(x=-3\)

Note: If you have a fractional equation and one of the terms is not a fraction, you can always account for that by putting 1 in the denominator. For example:

\[\frac{3}{x}=15\nonumber\]

We re-write the equation so that all terms are fractions.

\[\frac{3}{x}=\frac{15}{1}\nonumber\]

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 1=15 \cdot x \\ \text{Linear Equation: isolate the variable} & 3=15 x \\ \text{Divide by 15 both sides} & \frac{3}{15}=\frac{15 x}{15} \end{array}\nonumber\]

The solution is \(x=\frac{3}{15}=\frac{3 \cdot 1}{3 \cdot 5}=\frac{1}{5}\).

II. Multiple Fractions on Either Side of the Equation

Equations d) and e) in Example 24.1 fall into this category. We solve these equations here.

We use the technique for combining rational expressions we learned in Chapter 23 to reduce our problem to a problem with a single fraction on each side of the equation.

d) Solve \(\frac{3}{4}-\frac{1}{8 x}=0\)

First we realize that there are two fractions on the LHS of the equation and thus we cannot use the Cross-Product property immediately. To combine the LHS into a single fraction we do the following:

\[\begin{array}{ll} \text{Find the LCM of the denominators} & 8 x \\ \text{Rewrite each fraction using the LCM} & \frac{3 \cdot 2 x}{8 x}-\frac{1}{8 x}=0 \\ \text{Combine into one fraction} & \frac{6 x-1}{8 x}=0 \\ \text{Re-write the equation so that all terms are fractions} & \frac{6 x-1}{8 x}=\frac{0}{1} \\ \text{Cross-Product} & (6 x-1) \cdot 1=8 x \cdot 0 \\ \text{Remove parentheses} & 6 x-1=0 \\\text{Linear Equation: isolate the variable} & 6 x=1 \\ \text{Divide by 6 both sides} & \frac{6 x}{6}=\frac{1}{6} \end{array}\nonumber\]

The solution is \(x=\frac{1}{6}\).

e) Solve \(\frac{x}{6}+\frac{2}{3 x}=\frac{2}{3}\)

\[\begin{array}{ll} \text{Find the LCM of the denominators of LHS} & 6x \\ \text{Rewrite each fraction on LHS using their LCM} & \frac{x \cdot x}{6 x}+\frac{2 \cdot 2}{6 x}=\frac{2}{3} \\ \frac{x^{2}+4}{6 x}=\frac{2}{3} \text{Combine into one fraction} & \left(x^{2}+4\right) \cdot 3=6 x \cdot 2 \\ \text{Cross-Product} & 3 x^{2}+12=12 x \\ \text{Remove parentheses} & 3 x^{2}-12 x+12=0 \\ \text{Quadratic Equation: Standard form} & 3 x^{2}-12 x+12=0 \\\text{Quadratic Equation: Factor} & 3 \cdot x^{2}-3 \cdot 4 x+3 \cdot 4=0 \\ & 3\left(x^{2}-4 x+4\right)=0 \\ & 3(x-2)(x-2)=0 \\ \text{Divide by 3 both sides} & \frac{3(x-2)(x-2)}{3}=\frac{0}{3} \\ & (x-2)(x-2)=0 \\ \text{Quadratic Equation: Zero-Product Property} & (x-2)=0 \text { or }(x-2)=0 \end{array}\nonumber\]

Since both factors are the same, then \(x-2=0\) gives \(x=2\). The solution is \(x=2\)

Note: There is another method to solve equations that have multiple fractions on either side. It uses the LCM of all denominators in the equation. We demonstrate it here to solve the following equation: \(\frac{3}{2}-\frac{9}{2 x}=\frac{3}{5}\)

\[\begin{array} \text{Find the LCM of all denominators in the equation} & 10x \\ \text{Multiply every fraction (both LHS and RHS) by the LCM} & 10 x \cdot \frac{3}{2}-10 x \cdot \frac{9}{2 x}=10 x \cdot \frac{3}{5} \\ & \frac{10 x \cdot 3}{2}-\frac{10 x \cdot 9}{2 x}=\frac{10 x \cdot 3}{5} \\ \text{Simplify every fraction} & \frac{5 x \cdot 3}{1}-\frac{5 \cdot 9}{1}=\frac{2 x \cdot 3}{1} \\ \text{See how all denominatiors are now 1, thus can be disregarded} & 5 x \cdot 3-5 \cdot 9=2 x \cdot 3 \\ \text{Solve like you would any other equation} & 15 x-45=6 x \\ \text{Linear equation: islolate the variable} & 15 x-6 x=45 \\ & 9 x=45 \\ & x=\frac{45}{9} \\ & x=5 \end{array} \nonumber\]

The solution is \(x=5\)

Exit Problem

Solve: \(\frac{2}{x}+\frac{1}{3}=\frac{1}{2}\)

Algebra: Fraction Problems

Related Topics: More Algebra Word Problems

In these lessons, we will learn how to solve fraction word problems that deal with fractions and algebra. Remember to read the question carefully to determine the numerator and denominator of the fraction.

We will also learn how to solve word problems that involve comparing fractions, adding mixed numbers, subtracting mixed numbers, multiplying fractions and dividing fractions.

Fraction Word Problems using Algebra

Example: 2/3 of a number is 14. What is the number?

Answer: The number is 21.

Example: The numerator of a fraction is 3 less than the denominator. When both the numerator and denominator are increased by 4, the fraction is increased by fraction.

Solution: Let the numerator be x, then the denominator is x + 3, and the fraction is \(\frac{x}{{x + 3}}\) When the numerator and denominator are increased by 4, the fraction is \(\frac{{x + 4}}{{x + 7}}\) \(\frac{{x + 4}}{{x + 7}} - \frac{x}{{x + 3}} = \frac{{12}}{{77}}\) 77(x + 4)(x + 3) – 77x(x+7) = 12(x + 7)(x + 3) 77x 2 + 539x + 924 – 77x 2 – 539x = 12x 2 + 120x + 252 12x 2 + 120x – 672 = 0 x 2 + 10x – 56 = 0 (x – 4)(x + 14) = 0 x = 4 (negative answer not applicable in this case)

How to solve Fraction Word Problems using Algebra? Examples: (1) The denominator of a fraction is 5 more than the numerator. If 1 is subtracted from the numerator, the resulting fraction is 1/3. Find the original fraction. (2) If 3 is subtracted from the numerator of a fraction, the value of the resulting fraction is 1/2. If 13 is added to the denominator of the original fraction, the value of the new fraction is 1/3. Find the original fraction. (3) A fraction has a value of 3/4. When 14 is added to the numerator, the resulting fraction has a value equal to the reciprocal of the original fraction, Find the original fraction.

Algebra Word Problems with Fractional Equations Solving a fraction equation that appears in a word problem Example: One third of a number is 6 more than one fourth of the number. Find the number.

Fraction and Decimal Word Problems How to solve algebra word problems with fractions and decimals? Examples: (1) If 1/2 of the cards had been sold and there were 172 cards left, how many cards were printed? (2) Only 1/3 of the university students wanted to become teachers. If 3,360 did not wan to become teachers, how many university were there? (3) Rodney guessed the total was 34.71, but this was 8.9 times the total. What was the total?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Inverse operations

Solve equations with fractions

Here you will learn about how to solve equations with fractions, including solving equations with one or more operations. You will also learn about solving equations with fractions where the unknown is the denominator of a fraction.

Students will first learn how to solve equations with fractions in 7th grade as part of their work with expressions and equations and expand that knowledge in 8th grade.

What are equations with fractions?

Equations with fractions involve solving equations where the unknown variable is part of the numerator and/or denominator of a fraction.

The numerator (top number) in a fraction is divided by the denominator (bottom number).

To solve equations with fractions, you will use the “balancing method” to apply the inverse operation to both sides of the equation in order to work out the value of the unknown variable.

The inverse operation of addition is subtraction.

The inverse operation of subtraction is addition.

The inverse operation of multiplication is division.

The inverse operation of division is multiplication.

For example,

\begin{aligned} \cfrac{2x+3}{5} \, &= 7\\ \colorbox{#cec8ef}{$\times \, 5$} \; & \;\; \colorbox{#cec8ef}{$\times \, 5$} \\\\ 2x+3&=35 \\ \colorbox{#cec8ef}{$-\,3$} \; & \;\; \colorbox{#cec8ef}{$- \, 3$} \\\\ 2x & = 32 \\ \colorbox{#cec8ef}{$\div \, 2$} & \; \; \; \colorbox{#cec8ef}{$\div \, 2$}\\\\ x & = 16 \end{aligned}

Common Core State Standards

How does this relate to 7th grade and 8th grade math?

• Grade 7: Expressions and Equations (7.EE.A.1) Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
• Grade 8: Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
• Grade 8: Expressions and Equations (8.EE.C.7b) Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.

How to solve equations with fractions

In order to solve equations with fractions:

Identify the operations that are being applied to the unknown variable.

• Apply the inverse operations, one at a time, to both sides of the equation .
• When you have the variable on one side, you have the final answer.
• Check the answer by substituting the answer back into the original equation .

[FREE] Solve Equations with Fractions Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations with fractions. 15 questions with answers to identify areas of strength and support!

Solve equations with fractions examples

Example 1: equations with one operation.

Solve for x \text{: } \cfrac{x}{5}=4 .

The unknown is x.

Looking at the left hand side of the equation, the x is divided by 5.

\cfrac{x}{5}

2 Apply the inverse operations, one at a time, to both sides of the equation.

The inverse of “dividing by 5 ” is “multiplying by 5 ”.

You will multiply both sides of the equation by 5.

3 When you have the variable on one side, you have the final answer.

The final answer is x=20.

4 Check the answer by substituting the answer back into the original equation.

You can check the answer by substituting the answer back into the original equation.

\cfrac{20}{5}=20\div5=4

Example 2: equations with one operation

Solve for x \text{: } \cfrac{x}{3}=8 .

Looking at the left hand side of the equation, the x is divided by 3.

\cfrac{x}{3}

Apply the inverse operations, one at a time, to both sides of the equation.

The inverse of “dividing by 3 ” is “multiplying by 3 ”.

You will multiply both sides of the equation by 3.

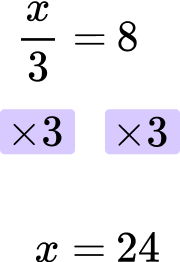
Write the final answer, checking that it is correct.

The final answer is x=24.

\cfrac{24}{3}=24\div3=8

Example 3: equations with two operations

Solve for x \text{: } \cfrac{x \, + \, 1}{2}=7 .

Looking at the left hand side of the equation, 1 is added to x and then divided by 2 (the denominator of the fraction).

\cfrac{x \, + \, 1}{2}

First, clear the fraction by multiplying both sides of the equation by 2.

Then, subtract 1 from both sides.

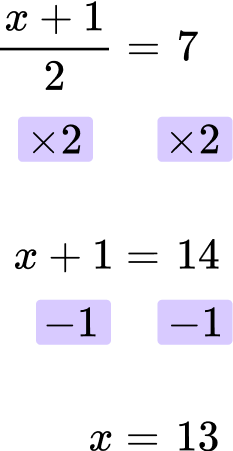
The final answer is x=13.

\cfrac{13 \, +1 \, }{2}=\cfrac{14}{2}=14\div2=7

Example 4: equations with two operations

Solve for x \text{: } \cfrac{x}{4}-2=3 .

Looking at the left hand side of the equation, x is divided by 4 and then 2 is subtracted.

\cfrac{x}{4}-2

First, add 2 to both sides of the equation.

Then, multiply both sides of the equation by 4.

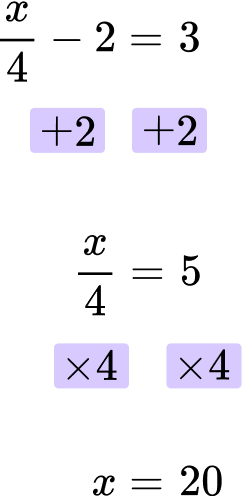
\cfrac{20}{4}-2=20\div4-2=5-2=3

Example 5: equations with three operations

Solve for x \text{: } \cfrac{3x}{5}+1=7 .

Looking at the left hand side of the equation, x is multiplied by 3, then divided by 5 , and then 1 is added.

\cfrac{3x}{5}+1

First, subtract 1 from both sides of the equation.

Then, multiply both sides of the equation by 5.

Finally, divide both sides by 3.

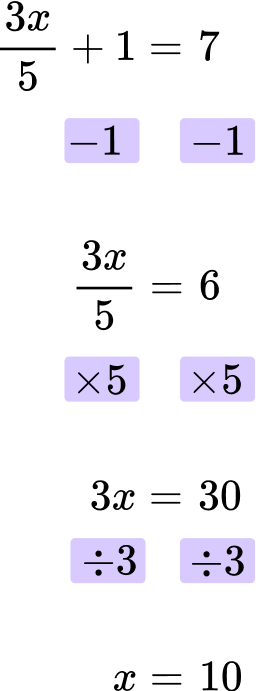
The final answer is x=10.

\cfrac{3 \, \times \, 10}{5}+1=\cfrac{30}{5}+1=6+1=7

Example 6: equations with three operations

Solve for x \text{: } \cfrac{2x-1}{7}=3 .

Looking at the left hand side of the equation, x is multiplied by 2, then 1 is subtracted, and the last operation is divided by 7 (the denominator).

\cfrac{2x-1}{7}

First, multiply both sides of the equation by 7.

Next, add 1 to both sides.

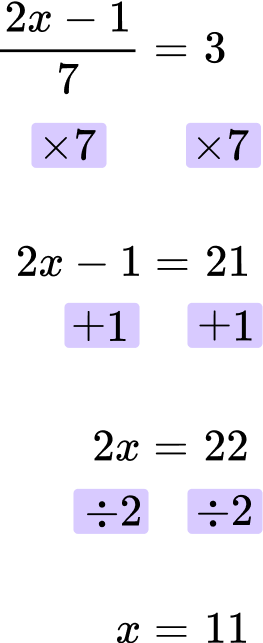
The final answer is x=11.

\cfrac{2 \, \times \, 11-1}{7}=\cfrac{22-1}{7}=\cfrac{21}{7}=3

Example 7: equations with the unknown as the denominator

Solve for x \text{: } \cfrac{24}{x}=6 .

Looking at the left hand side of the equation, x is the denominator. 24 is divided by x.

\cfrac{24}{x}

You need to multiply both sides of the equation by x.

Then, you can divide both sides by 6.

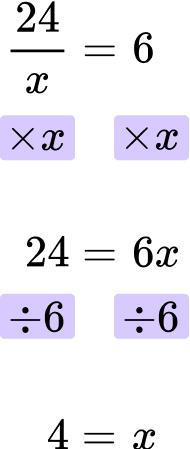
The final answer is x=4.

\cfrac{24}{4}=24\div4=6

Example 8: equations with the unknown as the denominator

Solve for x \text{: } \cfrac{18}{x}-6=3 .

Looking at the left hand side of the equation, x is the denominator. 18 is divided by x , and then 6 is subtracted.

\cfrac{18}{x}-6

First, add 6 to both sides of the equation.

Then, multiply both sides of the equation by x.

Finally, divide both sides by 9.

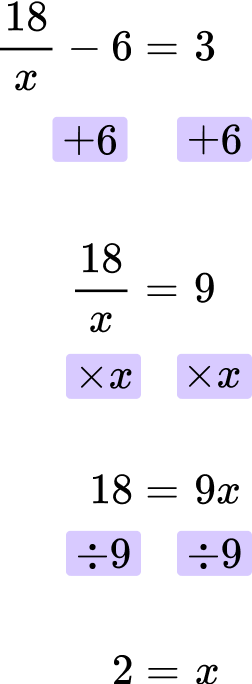
The final answer is x=2.

\cfrac{18}{2}-6=9-6=3

Teaching tips for solving equations with fractions

• When students first start working through practice problems and word problems, provide step-by-step instructions to assist them with solving linear equations.
• Introduce solving equations with fractions with one-step problems, then two-step problems, before introducing multi-step problems.
• Students will need lots of practice with solving linear equations. These standards provide the foundation for work with future linear equations in Algebra I and II.
• Provide opportunities for students to explain their thinking through writing. Ensure that they are using key vocabulary, such as, absolute value, coefficient, equation, common factors, inequalities, simplify, etc.

Easy mistakes to make

• The solution to an equation can be any type of number The unknowns do not have to be integers (whole numbers and their negative opposites). The solutions can be fractions or decimals. They can also be positive or negative numbers.
• The unknown of an equation can be on either side of the equation The unknown, represented by a letter, is often on the left hand side of the equations; however, it doesn’t have to be. It could also be on the right hand side of an equation.

• Lowest common denominator (LCD) It is common to get confused between solving equations involving fractions and adding and subtracting fractions. When adding and subtracting, you need to work out the lowest/least common denominator (sometimes called the least common multiple or LCM). When you solve equations involving fractions, multiply both sides of the equation by the denominator of the fraction.

Related math equations lessons

• Math equations
• Rearranging equations
• How to find the equation of a line
• Substitution
• Linear equations
• Writing linear equations
• Solving equations
• Identity math
• One step equations

Practice solve equations with fractions questions

1. Solve: \cfrac{x}{6}=3

You will multiply both sides of the equation by 6, because the inverse of “dividing by 6 ” is “multiplying by 6 ”.

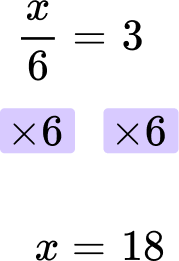
The final answer is x = 18.

\cfrac{18}{6}=18 \div 6=3

2. Solve: \cfrac{x \, + \, 4}{2}=7

Then subtract 4 from both sides.

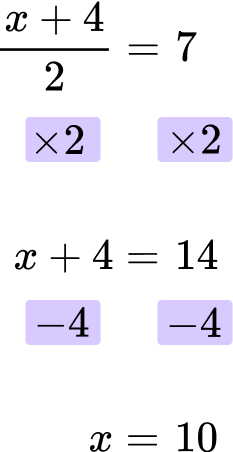
The final answer is x = 10.

\cfrac{10 \, + \, 4}{2}=\cfrac{14}{2}=14 \div 2=7

3. Solve: \cfrac{x}{8}-5=1

First, add 5 to both sides of the equation.

Then multiply both sides of the equation by 8.

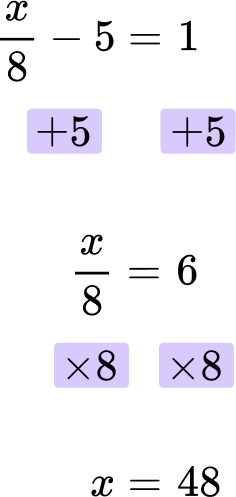
The final answer is x = 48.

\cfrac{48}{8}-5=48 \div 8-5=1

4. Solve: \cfrac{3x \, + \, 2}{4}=2

First, multiply both sides of the equation by 4.

Next, subtract 2 from both sides.

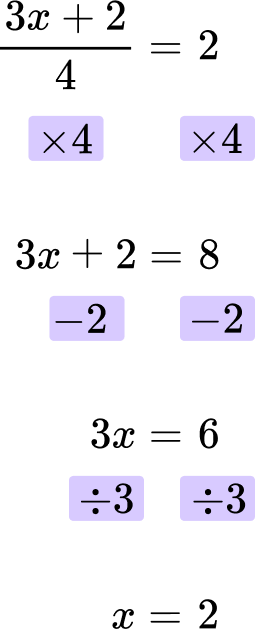
The final answer is x = 2.

\cfrac{3 \, \times \, 2+2}{4}=\cfrac{6 \, + \, 2}{4}=\cfrac{8}{4}=8 \div 4=2

5. Solve: \cfrac{4x}{7}-2=6

Then multiply both sides of the equation by 7.

Finally, divide both sides by 4.

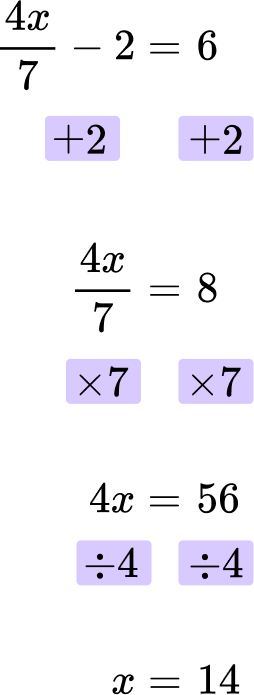
The final answer is x = 14.

\cfrac{4 \, \times \, 14}{7}-2=\cfrac{56}{7}-2=56 \div 7-2=6

6. Solve: \cfrac{42}{x}=7

Then you divide both sides by 7.

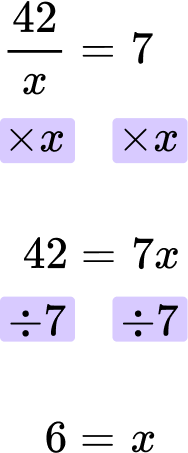
The final answer is x = 6.

\cfrac{42}{6}=42 \div 6=7

Solve equations with fractions FAQs

Yes, you still follow the order of operations when solving equations with fractions. You will start with any operations in the numerator and follow PEMDAS (parenthesis, exponents, multiply/divide, add/subtract), followed by any operations in the denominator. Then you will solve the rest of the equation as usual.

The next lessons are

• Inequalities
• Types of graphs
• Math formulas
• Coordinate plane
• Number patterns
• Algebraic expressions

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Solving equations & inequalities

About this unit.

There are lots of strategies we can use to solve equations. Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions.

Linear equations with variables on both sides

• Why we do the same thing to both sides: Variable on both sides (Opens a modal)
• Intro to equations with variables on both sides (Opens a modal)
• Equations with variables on both sides: 20-7x=6x-6 (Opens a modal)
• Equation with variables on both sides: fractions (Opens a modal)
• Equation with the variable in the denominator (Opens a modal)
• Equations with variables on both sides Get 3 of 4 questions to level up!
• Equations with variables on both sides: decimals & fractions Get 3 of 4 questions to level up!

Linear equations with parentheses

• Equations with parentheses (Opens a modal)
• Reasoning with linear equations (Opens a modal)
• Multi-step equations review (Opens a modal)
• Equations with parentheses Get 3 of 4 questions to level up!
• Equations with parentheses: decimals & fractions Get 3 of 4 questions to level up!
• Reasoning with linear equations Get 3 of 4 questions to level up!

Analyzing the number of solutions to linear equations

• Number of solutions to equations (Opens a modal)
• Worked example: number of solutions to equations (Opens a modal)
• Creating an equation with no solutions (Opens a modal)
• Creating an equation with infinitely many solutions (Opens a modal)
• Number of solutions to equations Get 3 of 4 questions to level up!
• Number of solutions to equations challenge Get 3 of 4 questions to level up!

Linear equations with unknown coefficients

• Linear equations with unknown coefficients (Opens a modal)
• Why is algebra important to learn? (Opens a modal)
• Linear equations with unknown coefficients Get 3 of 4 questions to level up!

Multi-step inequalities

• Inequalities with variables on both sides (Opens a modal)
• Inequalities with variables on both sides (with parentheses) (Opens a modal)
• Multi-step inequalities (Opens a modal)
• Using inequalities to solve problems (Opens a modal)
• Multi-step linear inequalities Get 3 of 4 questions to level up!
• Using inequalities to solve problems Get 3 of 4 questions to level up!

Compound inequalities

• Compound inequalities: OR (Opens a modal)
• Compound inequalities: AND (Opens a modal)
• A compound inequality with no solution (Opens a modal)
• Double inequalities (Opens a modal)
• Compound inequalities examples (Opens a modal)
• Compound inequalities review (Opens a modal)
• Solving equations & inequalities: FAQ (Opens a modal)
• Compound inequalities Get 3 of 4 questions to level up!

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Fraction Worksheets

Conversion :: Addition :: Subtraction :: Multiplication :: Division

Conversions

Fractions - addition, fractions - subtraction, fractions - multiplication, fractions - division.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve for X

Last Updated: May 3, 2024 Fact Checked

This article was co-authored by David Jia . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 812,583 times.

There are a number of ways to solve for x, whether you're working with exponents and radicals or if you just have to do some division or multiplication. No matter what process you use, you always have to find a way to isolate x on one side of the equation so you can find its value. Here's how to do it:

How do you solve for X in equations?

• For basic linear equations: Follow the order of operations (using PEMDAS) to resolve the equation.
• For exponents: Separate the exponent variable from the rest of the equation and find the square root of each side.
• For fractions: Cross-multiply to create a fraction-less equation, combine any like terms, and divide both sides by the x-value's coefficient.

Using a Basic Linear Equation

• 2 2 (x+3) + 9 - 5 = 32

• 4(x+3) + 9 - 5 = 32

• 4x + 12 + 9 - 5 = 32

• 4x+21-5 = 32
• 4x + 16 - 16 = 32 - 16

• 4x/4 = 16/4

Joseph Meyer

To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.

• 2 2 (x+3)+ 9 - 5 = 32
• 2 2 (4+3)+ 9 - 5 = 32
• 2 2 (7) + 9 - 5 = 32
• 4(7) + 9 - 5 = 32
• 28 + 9 - 5 = 32
• 37 - 5 = 32

With Exponents

• 2x 2 + 12 = 44

• 2x 2 +12-12 = 44-12

• (2x 2 )/2 = 32/2
• 4 Take the square root of each side of the equation. [6] X Research source Taking the square root of x 2 will cancel it out. So, take the square root of both sides. You'll get x left over on one side and plus or minus the square root of 16, 4, on the other side. Therefore, x = ±4.
• 2(4) 2 + 12 = 44
• 2(16) + 12 = 44
• 32 + 12 = 44

Using Fractions

• (x + 3)/6 = 2/3

• (x + 3) x 3 = 3x + 9
• 3x + 9 = 12

• 3x + 9 - 9 = 12 - 9

• (1 + 3)/6 = 2/3

Using Radical Signs

• √(2x+9) - 5 = 0

• √(2x+9) - 5 + 5 = 0 + 5
• √(2x+9) = 5

• (√(2x+9)) 2 = 5 2
• 2x + 9 = 25

• 2x + 9 - 9 = 25 - 9

• √(2(8)+9) - 5 = 0
• √(16+9) - 5 = 0
• √(25) - 5 = 0

Using Absolute Value

• |4x +2| - 6 = 8

• |4x +2| - 6 + 6 = 8 + 6
• |4x +2| = 14

• 4x + 2 = 14
• 4x + 2 - 2 = 14 -2

• 4x + 2 = -14
• 4x + 2 - 2 = -14 - 2
• 4x/4 = -16/4

• |4(3) +2| - 6 = 8
• |12 +2| - 6 = 8
• |14| - 6 = 8
• |4(-4) +2| - 6 = 8
• |-16 +2| - 6 = 8
• |-14| - 6 = 8

Practice Problems and Answers

Expert Q&A

• To check your work, plug the value of x back into the original equation and solve. Thanks Helpful 0 Not Helpful 1
• Radicals, or roots, are another way of representing exponents. The square root of x = x^1/2. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ David Jia. Academic Tutor. Expert Interview. 23 February 2021
• ↑ https://tutorial.math.lamar.edu/Classes/Alg/SolveLinearEqns.aspx
• ↑ https://www.purplemath.com/modules/solvelin.htm
• ↑ https://sciencing.com/tips-for-solving-algebraic-equations-13712207.html
• ↑ https://www.youtube.com/watch?v=LMS1NR4gZN8
• ↑ https://www.mathsisfun.com/algebra/fractions-algebra.html
• ↑ http://www.mathsisfun.com/algebra/radical-equations-solving.html
• ↑ http://www.sosmath.com/algebra/solve/solve0/solve0.html

About This Article

To solve for x in a basic linear equation, start by resolving the exponent using the order of operations. Then, isolate the variable to get your answer. To solve for x when the equation includes an exponent, start by isolating the term with the exponent. Then, isolate the variable with the exponent by dividing both sides by the coefficient of the x term to get your answer. If the equation has fractions, start by cross-multiplying the fractions. Then, combine like terms and isolate x by dividing each term by the x coefficient. If you want to learn how to solve for x if the equation has radicals or absolute values, keep reading the article! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Zukisa Buhle Denge

Jun 18, 2016

Did this article help you?

Mbali Palesa

Jul 25, 2020

Jun 6, 2016

Phumla Miya

Nov 18, 2018

Henry Statin

Jan 25, 2023

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Don’t miss out! Sign up for

wikiHow’s newsletter

Equation Solver

Enter the Equation you want to solve into the editor.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&