solve projectile motion problems calculator

Physics Problems with Solutions

Projectile motion calculator and solver.

An online calculator to calculate the maximum height, range, time of flight, initial angle and the path of a projectile. The projectile equations and parameters used in this calculator are decribed below.

1 - Projectile Motion Calculator and Solver Given Initial Velocity, Angle and Height

2 - projectile motion calculator and solver given range, initial velocity, and height, projectile equations used in the calculator and solver.

Horizontal Range = \( x(T_f) = V_0 cos(\theta) T_f \)

More References and Links

Popular pages.

• Privacy Policy

Projectile Motion Calculator

Kinematic equations, flight parameters at a given time, equations for projectile motion calculation.

Welcome to the projectile motion calculator , a kinematic tool that will help you to solve projectile equations in physics and calculate distance, maximum height, time of flight, and many more projectile parameters!

To learn more about the theory behind and solve the problems on your own, in the next section, we present the kinematic equations , which are the basis for the projectile equations such as the vertical velocity formula.

Click on the advanced mode to discover other additional parameters that could be useful.

🔎 With this tool, you can calculate the projectile motion parameters, but if you want to study the vertical position as a function of the horizontal displacement, use the trajectory calculator .

To understand the projectile equations, first, we must learn the equations used in kinematics calculations. Assuming constant acceleration:

• r = r 0 + V avg t
• V avg = (V 0 + V)/2 (for a = 0 )
• V= V 0 + r t
• r = r 0 + V 0 t + a t 2 /2
• V 2 = V 0 2 + 2a(r - r 0 )
• r — position at the time t ;
• r 0 — initial position;
• V — velocity at the time t ;
• v avg — average velocity;
• t — time; and
• a — acceleration

To apply the previous equations to the projectile motion calculation, we have to consider some aspects of this type of motion:

• The horizontal component of acceleration is zero ( a x = 0 )
• The vertical component equals the negative of the gravity acceleration ( a y = -g = -9.807 m/s 2 ), assuming positive is up.
• Assuming the air resistance is negligible, the horizontal component of velocity remains constant ( V x = V 0x )
• Horizontal velocity formula: V 0x = V 0 × cos(α)
• Vertical velocity formula: V 0y = V 0 × sin(α)

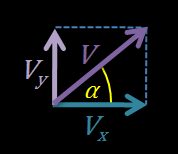
If the vertical velocity component is zero ( α = 0° ), then that's a case of horizontal projectile motion . If, on the other side, α = 90° , that's a case of free fall at zero initial velocity.

Considering the previous points, we can establish the flight parameters at a given time t :

Angle of launch: If we know the initial velocity and one of its components, we can also calculate the angle of launch:

• α = arccos(V 0x /V 0 ) = arcsin(V 0y /V 0 )

Maximum height: At this point, the projectile stops moving up and starts falling, so its vertical velocity component changes from positive to negative; therefore, V y =0 . For the time when V y =0 , we have:

• y max = y 0 + V 0y ²/(2g)

Horizontal distance traveled: if the problem you're solving in physics is calculating the distance traveled by the projectile, use the formula:

• d = V x t total = V 0x t total

Time of flight: Flight ends when the projectile hits the ground, which happens when y = 0 :

• t total = [V 0y + √(V 0y ² + 2gy 0 )]/g

Conservation of momentum

Schwarzschild radius.

• Astrophysics ( 17 )
• Atmospheric thermodynamics ( 11 )
• Continuum mechanics ( 21 )
• Conversion ( 15 )
• Dynamics ( 20 )
• Electrical energy ( 12 )
• Electromagnetism ( 18 )
• Electronics ( 34 )
• Fluid mechanics ( 29 )
• Kinematics ( 21 )
• Machines and mechanisms ( 20 )
• Math and statistics ( 34 )
• Optics ( 15 )
• Physical chemistry ( 15 )
• Quantum mechanics ( 14 )
• Relativity ( 9 )
• Rotational and periodic motion ( 17 )
• Thermodynamics ( 31 )
• Waves ( 14 )
• Other ( 33 )

Projectile Motion Calculator (+Horizontal Distance / Maximum Height)

Table of Contents

How to use the projectile motion calculator?

This projectile calculator makes your task easier as you don’t have to perform manual calculations with projectile motion equations to find the values for projectile motion. For this calculator, you need to know the 3 required values so you can enter them in the spaces provided. Here are the steps to follow when using this projectile motion calculator:

• First, enter the value of the Velocity then choose the unit of measurement from the drop-down menu.
• Then enter the value of the Angle of Launch and choose the unit of measurement from the drop-down menu.
• Finally, enter the value of the Initial Height then choose the unit of measurement from the drop-down menu.
• After entering all of these values, the projectile calculator automatically performs the calculation for you. It will generate the values for the Time of Flight, the Distance, and the Maximum Height.

How do you explain projectile motion?

The word “projectile” refers to any object that’s in flight after it gets projected or thrown. The projectile motion refers to the movement of the object. While in a projectile motion, there is only one type of acceleration working. This acceleration occurs in a vertical direction, and it occurs because of gravity or “g.” Therefore, you can apply projectile motion equations separately in y-axis and x-axis. Do this when you need to solve for unknown parameters.

Some examples of objects in projectile motion are a baseball, a football, a cricket ball, and any other object that’s either thrown or projected. Projectile motion has two main parts. The first one is horizontal motion where there’s no acceleration. The second is vertical motion which has constant acceleration because of gravity.

When a particle gets obliquely projected near the surface of the Earth, it moves in the vertical and horizontal directions simultaneously. This motion is also called projectile motion. When calculating projectile motion, you won’t take air resistance into account to make your calculations simpler.

Rather than using the projectile motion equations to find the projectile motion, you can use the projectile motion calculator which is also known as horizontal distance calculator, maximum height calculator or kinematic calculator. These provide you with the values needed without manual computation.

What is projectile motion equation?

When it comes to projectile motion, there are several equations to think about. This is why it’s easier and much more convenient to use the projectile motion calculator. But if you’d like to learn these equations to perform manual calculations, here they are:

• For the Horizontal Velocity variable, the formula is vx = v * cos(θ)
• For the Vertical Velocity variable, the formula is vy = v * sin(θ)
• For the Time of Flight, the formula is t = 2 * vy / g
• For the Range of the Projectile, the formula is R = 2* vx * vy / g
• For the Maximum Height, the formula is ymax = vy^2 / (2 * g)

When using these equations, keep these points in mind:

• The vectors vx, vy, and v all form a right triangle.
• You can express the horizontal distance traveled x = vx * t, where t refers to time.
• The formula for the vertical distance from the ground is y = vy * t – g * t^2 / 2, where g refers to the gravity acceleration.
• The horizontal acceleration is always equal to zero.
• The vertical acceleration is equal to -g since gravity is the only force which acts on the projectile.
• The time of flight ends as soon as the object in projectile motion hits the floor. This happens when the vertical distance is equal to zero or, when expressed as a formula: vy * t – g * t^2 / 2 = 0.
• The range of the projectile refers to the total distance traveled horizontally during the entire flight time.
• As soon as the projectile reaches its maximum height, its upward movement stops and it starts to fall. This means that the object’s vertical velocity shifts from positive to negative. In other words, the vertical velocity equals zero for a moment. Therefore, if vy – g * t(vy=0) = 0, you can modify the formula to t(vy=0) = vy / g.

What is projectile give example?

Try to think about how an archer sends one of his arrows in the air from his bow. The arrow starts its journey by moving forward and up at the same time with some inclination to the floor. The further the arrow flies, the slower it ascends. Finally, it starts to descend which means that its movement becomes forward and downward until it hits the floor.

If you trace the path of the arrow, you would have a curve or a “parabola.” Any other object which moves, in the same way, is in a projectile motion. There’s only one force which acts on a projectile motion and that’s the force of gravity. When it comes to projectile motion, you always omit or ignore air resistance.

When you think about it, projectile motion is a very logical concept. You can find projectile motion all around us. It’s a very common concept in physics and in other fields as well. Some good examples will help you understand the concept even better. Here are some examples of projectiles in the real world:

• When a football player kicks the ball during a game.
• When you fire a cannonball from a cannon.
• When you fire a bullet from a gun.
• When you throw a disc in the discus throw.
• When you hit a golf ball and it takes flight.
• When a jet or stream of water comes out of a hose.
• When cars and motorcycles jump during extreme sports.

Wolfram|Alpha Widgets Overview Tour Gallery Sign In

Share this page.

• StumbleUpon
• Google Buzz

Output Type

Output width, output height.

To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.

To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:

Save to My Widgets

Build a new widget.

We appreciate your interest in Wolfram|Alpha and will be in touch soon.

•  All online calculators
•  Suggest a calculator
•  Translation

PLANETCALC Online calculators

•  English

Projectile Motion Calculator

Calculation of Unknown Parameters of Projectile Motion

This calculator allows you to determine the unknown parameters of projectile motion using known values. The parameters involved in projectile motion include duration, maximum height, distance, initial velocity, and angle.

Projectile motion involves the motion of an object launched into the air at an angle. The main equations used in this calculator are derived from the principles of accelerated motion, considering that there is no acceleration along the x-axis and only the acceleration due to gravity "g" acts along the y-axis.

The known parameters can be any combination of distance (S), maximum height (h), flight duration (t), initial angle (\alpha), and initial velocity (v_0). The calculator can find the unknown parameters based on the provided known values.

For example, if you know the initial velocity and angle, the calculator can determine the flight duration, maximum height, and travel distance of the projectile. Conversely, if you know the initial angle and maximum height, the calculator can find the initial velocity, travel distance, and flight duration. Please note that it is not possible to determine the other parameters solely from the maximum height and flight duration.

By utilizing this calculator, you can easily compute the various parameters associated with projectile motion and gain insights into the behavior of projectiles in a given scenario.

Projectile Motion Equations

Similar calculators

• • Freefall distance problems solver
• • Angular velocity and linear velocity
• • Kinematic Equations for Constant Acceleration Calculator
• • Course angle and the distance between the two points on loxodrome (rhumb line).
• • Vertical Collision Kinematics Calculator
• • Physics section ( 66 calculators )

Share this page

• 1-800-234-2933
• [email protected]

Projectile Motion Calculator

Enter projectile motion problem

Solve the following projectile motion problem

Projectile motion equation:

h(t) = -16t 2 + vt + h where: h = height, v = velocity, and t = time

Plug in our numbers

h(t) = -16t 2 + ()t +

When does the object hit the ground:

Set h(t) = 0

-16t 2 + t + = 0

Evaluate the quadratic

Only take positive values since height cannot be negative

Quadratic Formula

Calculate -b, calculate the discriminant δ.

Δ = b 2 - 4ac:

Δ = 2 - 4 x -16 x

Δ = 0 - 0

Δ = 0 <--- Discriminant

Since Δ = 0, we expect one real root.

Take the square root of Δ

√ Δ = √ (0)

√ Δ = (0±√0)/

-b + Δ:

Numerator 1 = -b + √ Δ

Numerator 1 = 0 + √ 0

-b - Δ:

Numerator 2 = -b - √ Δ

Numerator 2 = 0 - √ 0

Calculate 2a

Denominator = 2 * a

Denominator = 2 * -16

Denominator = -32

Find Solutions

Solution 1 = -0

Solution 2 = -0

Solution Set

(Solution 1, Solution 2) = (-0, -0)

Prove our first answer

(-0) 2 (-0) ? 0

(0) + 00 ? 0

-0 + 00 ? 0

Prove our second answer

You have 2 free calculationss remaining, what is the answer, how does the projectile motion calculator work, what 1 formula is used for the projectile motion calculator, what 4 concepts are covered in the projectile motion calculator, example calculations for the projectile motion calculator.

• a ball is tossed into the air at 40 feet per second from a height of 5 feet. how long will it take the ball to reach the ground?
• projectile motion
• quadratic equation

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Subjects
• A.I. Training Data and Analytics
• Get Paid as an Affiliate

Top Categories

• Trigonometry
• Pre-Algebra
• Pre-Calculus
• Post a Math Problem

Projectile Motion Calculator

Welcome to the Projectile Motion Calculator! Enter 'n' for values you don't know. Also note that you must enter the launch angle.

Horizontal Motion

Solve for horizontal distance, solve for initial velocity, solve for horizontal velocity, solve for time, solve for angle, vertical motion, solve for final height, solve for inital height, solve for inital velocity, solve for inital vertical velocity, solve for final vertical velocity, solve for time, solve for angle.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Projectile Motion

• Last updated
• Save as PDF
• Page ID 14447

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Basic Equations and Parabolic Path

Projectile motion is a form of motion where an object moves in parabolic path; the path that the object follows is called its trajectory.

learning objectives

• Assess the effect of angle and velocity on the trajectory of the projectile; derive maximum height using displacement

Projectile Motion

Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In a previous atom we discussed what the various components of an object in projectile motion are. In this atom we will discuss the basic equations that go along with them in the special case in which the projectile initial positions are null (i.e. \(\mathrm{x_0=0}\) and \(\mathrm{y_0=0}\) ).

Initial Velocity

The initial velocity can be expressed as x components and y components:

\[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ} \end{align}\]

In this equation, \(\mathrm{u}\) stands for initial velocity magnitude and \(θ\) refers to projectile angle.

Time of Flight

The time of flight of a projectile motion is the time from when the object is projected to the time it reaches the surface. As we discussed previously, \(\mathrm{T}\) depends on the initial velocity magnitude and the angle of the projectile:

\[\begin{align} \mathrm{T} & \mathrm{=\dfrac{2⋅u_y}{g} } \\ \mathrm{T} & \mathrm{=\dfrac{2⋅u⋅\sin ⁡θ}{g}} \end{align}\]

Acceleration

In projectile motion, there is no acceleration in the horizontal direction. The acceleration, \(\mathrm{a}\), in the vertical direction is just due to gravity, also known as free fall:

\[\begin{align} \mathrm{a_x} & \mathrm{=0} \\ \mathrm{a_y} &\mathrm{=−g} \end{align}\]

The horizontal velocity remains constant, but the vertical velocity varies linearly, because the acceleration is constant. At any time, \(\mathrm{t}\), the velocity is:

\[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ−g⋅t} \end{align}\]

You can also use the Pythagorean Theorem to find velocity:

\[\mathrm{u=\sqrt{u_x^2+u_y^2}}\]

Displacement

At time, t, the displacement components are:

\[\begin{align} \mathrm{x} & \mathrm{=u⋅t⋅ \cos ⁡θ} \\ \mathrm{y} & \mathrm{=u⋅t⋅ \sin ⁡θ−\dfrac{1}{2}gt^2} \end{align}\]

The equation for the magnitude of the displacement is \(\mathrm{Δr=\sqrt{x^2+y^2}}\).

Parabolic Trajectory

We can use the displacement equations in the x and y direction to obtain an equation for the parabolic form of a projectile motion:

\[\mathrm{y=\tan θ⋅x−\dfrac{g}{2⋅u^2⋅ \cos ^2 θ}⋅x^2}\]

Maximum Height

The maximum height is reached when \(\mathrm{v_y=0}\). Using this we can rearrange the velocity equation to find the time it will take for the object to reach maximum height

\[\mathrm{t_h=\dfrac{u⋅\sin θ}{g}}\]

where \(\mathrm{t_h}\) stands for the time it takes to reach maximum height. From the displacement equation we can find the maximum height

\[\mathrm{h=\dfrac{u^2⋅ \sin ^2 ⁡θ}{2⋅g}}\]

The range of the motion is fixed by the condition \(\mathrm{y=0}\). Using this we can rearrange the parabolic motion equation to find the range of the motion:

\[\mathrm{R=\dfrac{u^2⋅ \sin ⁡2 θ}{g}.}\]

Range of Trajectory : The range of a trajectory is shown in this figure.

Projectiles at an Angle : This video gives a clear and simple explanation of how to solve a problem on Projectiles Launched at an Angle. I try to go step by step through this difficult problem to layout how to solve it in a super clear way. 2D kinematic problems take time to solve, take notes on the order of how I solved it. Best wishes. Tune into my other videos for more help. Peace.

Solving Problems

In projectile motion, an object moves in parabolic path; the path the object follows is called its trajectory.

• Identify which components are essential in determining projectile motion of an object

We have previously discussed projectile motion and its key components and basic equations. Using that information, we can solve many problems involving projectile motion. Before we do this, let’s review some of the key factors that will go into this problem-solving.

What is Projectile Motion?

Projectile motion is when an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning, after which the only influence on the trajectory is that of gravity.

What are the Key Components of Projectile Motion?

The key components that we need to remember in order to solve projectile motion problems are:

• Initial launch angle, \(\mathrm{θ}\)
• Initial velocity, \(\mathrm{u}\)
• Time of flight, \(\mathrm{T}\)
• Acceleration, \(\mathrm{a}\)
• Horizontal velocity, \(\mathrm{v_x}\)
• Vertical velocity, \(\mathrm{v_y}\)
• Displacement, \(\mathrm{d}\)
• Maximum height, \(\mathrm{H}\)
• Range, \(\mathrm{R}\)

How To Solve Any Projectile Motion Problem (The Toolbox Method) : Introducing the “Toolbox” method of solving projectile motion problems! Here we use kinematic equations and modify with initial conditions to generate a “toolbox” of equations with which to solve a classic three-part projectile motion problem.

Now, let’s look at two examples of problems involving projectile motion.

Example \(\PageIndex{1}\):

Let’s say you are given an object that needs to clear two posts of equal height separated by a specific distance. Refer to for this example. The projectile is thrown at \(\mathrm{25 \sqrt{2}}\) m/s at an angle of 45°. If the object is to clear both posts, each with a height of 30m, find the minimum: (a) position of the launch on the ground in relation to the posts and (b) the separation between the posts. For simplicity’s sake, use a gravity constant of 10. Problems of any type in physics are much easier to solve if you list the things that you know (the “givens”).

Diagram for Example 1 : Use this figure as a reference to solve example 1. The problem is to make sure the object is able to clear both posts.

Solution: The first thing we need to do is figure out at what time tt the object reaches the specified height. Since the motion is in a parabolic shape, this will occur twice: once when traveling upward, and again when the object is traveling downward. For this we can use the equation of displacement in the vertical direction, \(\mathrm{y−y_0}\) :

\[\mathrm{y−y_0=(v_y⋅t)−(\dfrac{1}{2}⋅g⋅t^2)}\]

We substitute in the appropriate variables:

\[\mathrm{v_y=u⋅ \sin θ=25 \sqrt{2} \dfrac{m}{s}⋅ \sin 45^{\circ}=25 \dfrac{m}{s}}\]

\[\mathrm{30m=25⋅t−\dfrac{1}{2}⋅10⋅t^2}\]

We can use the quadratic equation to find that the roots of this equation are 2s and 3s. This means that the projectile will reach 30m after 2s, on its way up, and after 3s, on its way down.

An object is launched from the base of an incline, which is at an angle of 30°. If the launch angle is 60° from the horizontal and the launch speed is 10 m/s, what is the total flight time? The following information is given: \(\mathrm{u=10 \frac{m}{s}; θ=60°; g=10 \frac{m}{s^2}}\).

Diagram for Example 2 : When dealing with an object in projectile motion on an incline, we first need to use the given information to reorient the coordinate system in order to have the object launch and fall on the same surface.

Solution: In order to account for the incline angle, we have to reorient the coordinate system so that the points of projection and return are on the same level. The angle of projection with respect to the \(\mathrm{x}\) direction is \(\mathrm{θ−α}\), and the acceleration in the \(\mathrm{y}\) direction is \(\mathrm{g⋅ \cos ⁡α}\). We replace \(\mathrm{θ}\) with \(\mathrm{θ−α}\) and \(\mathrm{g}\) with \(\mathrm{g⋅ \cos ⁡α}\):

\[\begin{align} \mathrm{T \; } & \mathrm{=\dfrac{2⋅u⋅ \sin (θ)}{g} = \dfrac{2⋅u⋅\sin (θ−α)}{g⋅ \cos (α)}=\dfrac{2⋅10⋅ \sin (60−30)}{10⋅\cos (30)} =\dfrac{20⋅ \sin (30)}{10⋅ \cos (30)} } \\ \mathrm{T \;} &\mathrm{=\dfrac{2}{\sqrt{3}}s} \end{align}\]

Zero Launch Angle

An object launched horizontally at a height \(\mathrm{H}\) travels a range \(\mathrm{v_0\sqrt{\frac{2H}{g}}}\) during a time of flight \(\mathrm{T=\sqrt{\frac{2H}{g}}}\).

• Explain the relationship between the range and the time of flight

Projectile motion is a form of motion where an object moves in a parabolic path. The path followed by the object is called its trajectory. Projectile motion occurs when a force is applied at the beginning of the trajectory for the launch (after this the projectile is subject only to the gravity).

One of the key components of the projectile motion, and the trajectory it follows, is the initial launch angle . The angle at which the object is launched dictates the range, height, and time of flight the object will experience while in projectile motion. shows different paths for the same object being launched at the same initial velocity and different launch angles. As illustrated by the figure, the larger the initial launch angle and maximum height, the longer the flight time of the object.

Projectile Trajectories : The launch angle determines the range and maximum height that an object will experience after being launched.This image shows that path of the same object being launched at the same speed but different angles.

We have previously discussed the effects of different launch angles on range, height, and time of flight. However, what happens if there is no angle, and the object is just launched horizontally? It makes sense that the object should be launched at a certain height (\(\mathrm{H}\)), otherwise it wouldn’t travel very far before hitting the ground. Let’s examine how an object launched horizontally at a height \(\mathrm{H}\) travels. In our case is when \(\mathrm{α}\) is 0.

Projectile motion : Projectile moving following a parabola.Initial launch angle is αα, and the velocity is \(\mathrm{v_0}\).

Duration of Flight

There is no vertical component in the initial velocity (\(\mathrm{v_0}\)) because the object is launched horizontally. Since the object travels distance \(\mathrm{H}\) in the vertical direction before it hits the ground, we can use the kinematic equation for the vertical motion:

\[\mathrm{(y−y_0)=−H=0⋅T−\dfrac{1}{2}gT^2}\]

Here, \(\mathrm{T}\) is the duration of the flight before the object its the ground. Therefore:

\[\mathrm{T=\sqrt{\dfrac{2H}{g}}}\]

In the horizontal direction, the object travels at a constant speed \(\mathrm{v_0}\) during the flight. Therefore, the range \(\mathrm{R}\) (in the horizontal direction) is given as:

\[\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\]

General Launch Angle

The initial launch angle (0-90 degrees) of an object in projectile motion dictates the range, height, and time of flight of that object.

• Choose the appropriate equation to find range, maximum height, and time of flight

Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning of the trajectory, after which the only interference is from gravity.

One of the key components of projectile motion and the trajectory that it follows is the initial launch angle. This angle can be anywhere from 0 to 90 degrees. The angle at which the object is launched dictates the range, height, and time of flight it will experience while in projectile motion. shows different paths for the same object launched at the same initial velocity at different launch angles. As you can see from the figure, the larger the initial launch angle, the closer the object comes to maximum height and the longer the flight time. The largest range will be experienced at a launch angle up to 45 degrees.

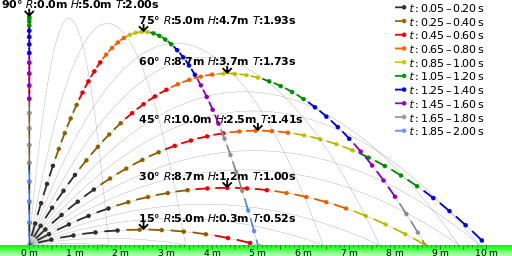
Launch Angle : The launch angle determines the range and maximum height that an object will experience after being launched. This image shows that path of the same object being launched at the same velocity but different angles.

The range, maximum height, and time of flight can be found if you know the initial launch angle and velocity, using the following equations:

\[\begin{align} \mathrm{R \;} & \mathrm{=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}} \\ \mathrm{h \;} & \mathrm{=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}} \\ \mathrm{T \;} & \mathrm{=\dfrac{2v_i \sin θ}{g}} \end{align}\]

Where R – Range, h – maximum height, T – time of flight, v i – initial velocity, θ i – initial launch angle, g – gravity.

Now that we understand how the launch angle plays a major role in many other components of the trajectory of an object in projectile motion, we can apply that knowledge to making an object land where we want it. If there is a certain distance, d, that you want your object to go and you know the initial velocity at which it will be launched, the initial launch angle required to get it that distance is called the angle of reach. It can be found using the following equation:

\[\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\]

Key Points: Range, Symmetry, Maximum Height

Projectile motion is a form of motion where an object moves in parabolic path. The path that the object follows is called its trajectory.

• Construct a model of projectile motion by including time of flight, maximum height, and range

What is Projectile Motion ?

Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In this atom we are going to discuss what the various components of an object in projectile motion are, we will discuss the basic equations that go along with them in another atom, “Basic Equations and Parabolic Path”

Key Components of Projectile Motion:

Time of flight, t:.

The time of flight of a projectile motion is exactly what it sounds like. It is the time from when the object is projected to the time it reaches the surface. The time of flight depends on the initial velocity of the object and the angle of the projection, θθ. When the point of projection and point of return are on the same horizontal plane, the net vertical displacement of the object is zero.

All projectile motion happens in a bilaterally symmetrical path, as long as the point of projection and return occur along the same horizontal surface. Bilateral symmetry means that the motion is symmetrical in the vertical plane. If you were to draw a straight vertical line from the maximum height of the trajectory, it would mirror itself along this line.

Maximum Height, H:

The maximum height of a object in a projectile trajectory occurs when the vertical component of velocity, vyvy, equals zero. As the projectile moves upwards it goes against gravity, and therefore the velocity begins to decelerate. Eventually the vertical velocity will reach zero, and the projectile is accelerated downward under gravity immediately. Once the projectile reaches its maximum height, it begins to accelerate downward. This is also the point where you would draw a vertical line of symmetry.

Range of the Projectile, R:

The range of the projectile is the displacement in the horizontal direction. There is no acceleration in this direction since gravity only acts vertically. shows the line of range. Like time of flight and maximum height, the range of the projectile is a function of initial speed.

Range : The range of a projectile motion, as seen in this image, is independent of the forces of gravity.

• Objects that are projected from, and land on the same horizontal surface will have a vertically symmetrical path.
• The time it takes from an object to be projected and land is called the time of flight. This depends on the initial velocity of the projectile and the angle of projection.
• When the projectile reaches a vertical velocity of zero, this is the maximum height of the projectile and then gravity will take over and accelerate the object downward.
• The horizontal displacement of the projectile is called the range of the projectile, and depends on the initial velocity of the object.
• When solving problems involving projectile motion, we must remember all the key components of the motion and the basic equations that go along with them.
• Using that information, we can solve many different types of problems as long as we can analyze the information we are given and use the basic equations to figure it out.
• To clear two posts of equal height, and to figure out what the distance between these posts is, we need to remember that the trajectory is a parabolic shape and that there are two different times at which the object will reach the height of the posts.
• When dealing with an object in projectile motion on an incline, we first need to use the given information to reorientate the coordinate system in order to have the object launch and fall on the same surface.
• For the zero launch angle, there is no vertical component in the initial velocity.
• The duration of the flight before the object hits the ground is given as \(\mathrm{T=\sqrt{\frac{2H}{g}}}\).
• In the horizontal direction, the object travels at a constant speed v 0 during the flight. The range R (in the horizontal direction) is given as: \(\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\).
• If the same object is launched at the same initial velocity, the height and time of flight will increase proportionally to the initial launch angle.
• An object launched into projectile motion will have an initial launch angle anywhere from 0 to 90 degrees.
• The range of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{R=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}}\).
• The maximum height of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{ｈ=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}}\).
• The time of flight of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{T=\dfrac{2v_i \sin θ}{g}}\) .
• The angle of reach is the angle the object must be launched at in order to achieve a specific distance: \(\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\).
• Objects that are projected from and land on the same horizontal surface will have a path symmetric about a vertical line through a point at the maximum height of the projectile.
• The time it takes from an object to be projected and land is called the time of flight. It depends on the initial velocity of the projectile and the angle of projection.
• The maximum height of the projectile is when the projectile reaches zero vertical velocity. From this point the vertical component of the velocity vector will point downwards.
• The horizontal displacement of the projectile is called the range of the projectile and depends on the initial velocity of the object.
• If an object is projected at the same initial speed, but two complementary angles of projection, the range of the projectile will be the same.
• trajectory : The path of a body as it travels through space.
• symmetrical : Exhibiting symmetry; having harmonious or proportionate arrangement of parts; having corresponding parts or relations.
• reorientate : to orientate anew; to cause to face a different direction
• gravity : Resultant force on Earth’s surface, of the attraction by the Earth’s masses, and the centrifugal pseudo-force caused by the Earth’s rotation.
• bilateral symmetry : the property of being symmetrical about a vertical plane

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• Sunil Kumar Singh, Features of Projectile Motion. September 18, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m13847/latest/ . License : CC BY: Attribution
• Projectile motion. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Projectile_motion . License : CC BY-SA: Attribution-ShareAlike
• trajectory. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/trajectory . License : CC BY-SA: Attribution-ShareAlike
• symmetrical. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/symmetrical . License : CC BY-SA: Attribution-ShareAlike
• Projectiles at an Angle. Located at : http://www.youtube.com/watch?v=4jNE3eTVEgo . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
• Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m13847/latest/ . License : CC BY: Attribution
• Sunil Kumar Singh, Projectile Motion on an Incline. September 18, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m14614/latest/ . License : CC BY: Attribution
• reorientate. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/reorientate . License : CC BY-SA: Attribution-ShareAlike
• Sunil Kumar Singh, Projectile Motion on an Incline. February 2, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m14614/latest/ . License : CC BY: Attribution
• How To Solve Any Projectile Motion Problem (The Toolbox Method). Located at : http://www.youtube.com/watch?v=M8xCj2VPHas . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
• Sunil Kumar Singh, Features of Projectile Motion. February 2, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m13847/latest/ . License : CC BY: Attribution
• Trajectory of a projectile. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Trajectory_of_a_projectile . License : CC BY-SA: Attribution-ShareAlike
• Trajectory. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Trajectory . License : CC BY-SA: Attribution-ShareAlike
• Ideal projectile motion for different angles. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg . License : CC BY-SA: Attribution-ShareAlike
• Ferde hajitas1. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Ferde_hajitas1.svg . License : CC BY-SA: Attribution-ShareAlike
• Sunil Kumar Singh, Features of Projectile Motion. September 17, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m13847/latest/ . License : CC BY: Attribution
• bilateral symmetry. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/bilateral_symmetry . License : CC BY-SA: Attribution-ShareAlike
• gravity. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/gravity . License : CC BY-SA: Attribution-ShareAlike
• trajectory. Provided by : Wiktionary. Located at : http://en.wiktionary.org/wiki/trajectory . License : CC BY-SA: Attribution-ShareAlike
• Ideal projectile motion for different angles. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg . License : CC BY-SA: Attribution-ShareAlike

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Classical Mechanics

How to Solve a Projectile Motion Problem

Last Updated: April 6, 2024

This article was co-authored by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 77,009 times.

Projectile motion is often one of the most difficult topics to understand in physics classes. Most of the time, there is not a direct way to get the answer; you need to solve for a few other variables to get the answer you are looking for. This means in order to find the distance an object traveled, you might first have to find the time it took or the initial velocity first. Just follow these steps and you should be able to fly through projectile motion problems!

• (1) an object is thrown off a higher ground than what it will land on.
• (2) the object starts on the ground, soars through the air, and then lands on the ground some distance away from where it started.

Community Q&A

You Might Also Like

About This Article

• Send fan mail to authors

Reader Success Stories

Feb 25, 2019

Did this article help you?

Cyril Shenouda

Feb 5, 2018

Nicholas Bunge

Aug 13, 2022

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Don’t miss out! Sign up for

wikiHow’s newsletter

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Horizontally Launched Projectile Problems
• What is a Projectile?
• Motion Characteristics of a Projectile
• Horizontal and Vertical Velocity
• Horizontal and Vertical Displacement
• Initial Velocity Components
• Non-Horizontally Launched Projectile Problems

There are two basic types of projectile problems that we will discuss in this course. While the general principles are the same for each type of problem, the approach will vary due to the fact the problems differ in terms of their initial conditions. The two types of problems are:

A projectile is launched with an initial horizontal velocity from an elevated position and follows a parabolic path to the ground. Predictable unknowns include the initial speed of the projectile, the initial height of the projectile, the time of flight, and the horizontal distance of the projectile.

Examples of this type of problem are

• A pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

A projectile is launched at an angle to the horizontal and rises upwards to a peak while moving horizontally. Upon reaching the peak, the projectile falls with a motion that is symmetrical to its path upwards to the peak. Predictable unknowns include the time of flight, the horizontal range, and the height of the projectile when it is at its peak.

• A football is kicked with an initial velocity of 25 m/s at an angle of 45-degrees with the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the football.
• A long jumper leaves the ground with an initial velocity of 12 m/s at an angle of 28-degrees above the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the long-jumper.

The second problem type will be the subject of the next part of Lesson 2 . In this part of Lesson 2, we will focus on the first type of problem - sometimes referred to as horizontally launched projectile problems. Three common kinematic equations that will be used for both type of problems include the following:

d = v i •t + 0.5*a*t 2 v f = v i + a•t v f 2  = v i 2  + 2*a•d  

Equations for the Horizontal Motion of a Projectile

The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions - both horizontally and vertically. Since these two components of motion are independent of each other, two distinctly separate sets of equations are needed - one for the projectile's horizontal motion and one for its vertical motion. Thus, the three equations above are transformed into two sets of three equations. For the horizontal components of motion, the equations are

x = v i x •t + 0.5*a x *t 2

v f x  = v i x  + a x •t

v f x 2  = v i x 2  + 2*a x •x

Of these three equations, the top equation is the most commonly used. An application of projectile concepts to each of these equations would also lead one to conclude that any term with a x in it would cancel out of the equation since a x = 0 m/s/s . Once this cancellation of ax terms is performed, the only equation of usefulness is:

x = v i x •t

Equations for the Vertical Motion of a Projectile

For the vertical components of motion, the three equations are

y = v iy •t + 0.5*a y *t 2

v fy  = v iy  + a y •t

v fy 2  = v iy 2  + 2*a y •y

In each of the above equations, the vertical acceleration of a projectile is known to be -9.8 m/s/s (the acceleration of gravity). Furthermore, for the special case of the first type of problem (horizontally launched projectile problems), v iy = 0 m/s. Thus, any term with v iy in it will cancel out of the equation.

The two sets of three equations above are the kinematic equations that will be used to solve projectile motion problems.

Solving Projectile Problems

To illustrate the usefulness of the above equations in making predictions about the motion of a projectile, consider the solution to the following problem.

The solution of this problem begins by equating the known or given values with the symbols of the kinematic equations - x, y, v ix , v iy , a x , a y , and t. Because horizontal and vertical information is used separately, it is a wise idea to organized the given information in two columns - one column for horizontal information and one column for vertical information. In this case, the following information is either given or implied in the problem statement:

As indicated in the table, the unknown quantity is the horizontal displacement (and the time of flight) of the pool ball. The solution of the problem now requires the selection of an appropriate strategy for using the kinematic equations and the known information to solve for the unknown quantities. It will almost always be the case that such a strategy demands that one of the vertical equations be used to determine the time of flight of the projectile and then one of the horizontal equations be used to find the other unknown quantities (or vice versa - first use the horizontal and then the vertical equation). An organized listing of known quantities (as in the table above) provides cues for the selection of the strategy. For example, the table above reveals that there are three quantities known about the vertical motion of the pool ball. Since each equation has four variables in it, knowledge of three of the variables allows one to calculate a fourth variable. Thus, it would be reasonable that a vertical equation is used with the vertical values to determine time and then the horizontal equations be used to determine the horizontal displacement (x). The first vertical equation (y = v iy •t +0.5•a y •t 2 ) will allow for the determination of the time. Once the appropriate equation has been selected, the physics problem becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

Since the first term on the right side of the equation reduces to 0, the equation can be simplified to

If both sides of the equation are divided by -5.0 m/s/s, the equation becomes

By taking the square root of both sides of the equation, the time of flight can then be determined .

Once the time has been determined, a horizontal equation can be used to determine the horizontal displacement of the pool ball. Recall from the given information , v ix = 2.4 m/s and a x = 0 m/s/s. The first horizontal equation (x = v ix •t + 0.5•a x •t 2 ) can then be used to solve for "x." With the equation selected, the physics problem once more becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

Since the second term on the right side of the equation reduces to 0, the equation can then be simplified to

The answer to the stated problem is that the pool ball is in the air for 0.35 seconds and lands a horizontal distance of 0.84 m from the edge of the pool table.

The following procedure summarizes the above problem-solving approach.

• Carefully read the problem and list known and unknown information in terms of the symbols of the kinematic equations. For convenience sake, make a table with horizontal information on one side and vertical information on the other side.
• Identify the unknown quantity that the problem requests you to solve for.
• Select either a horizontal or vertical equation to solve for the time of flight of the projectile.
• With the time determined, use one of the other equations to solve for the unknown. (Usually, if a horizontal equation is used to solve for time, then a vertical equation can be used to solve for the final unknown quantity.)

One caution is in order. The sole reliance upon 4- and 5-step procedures to solve physics problems is always a dangerous approach. Physics problems are usually just that - problems! While problems can often be simplified by the use of short procedures as the one above, not all problems can be solved with the above procedure. While steps 1 and 2 above are critical to your success in solving horizontally launched projectile problems, there will always be a problem that doesn't fit the mold . Problem solving is not like cooking; it is not a mere matter of following a recipe. Rather, problem solving requires careful reading, a firm grasp of conceptual physics, critical thought and analysis, and lots of disciplined practice. Never divorce conceptual understanding and critical thinking from your approach to solving problems.

Check Your Understanding

Use y = v iy • t + 0.5 • a y • t 2 to solve for time; the time of flight is 2.12 seconds.

Now use x = v ix • t + 0.5 • a x • t 2 to solve for v ix

Note that a x is 0 m/s/s so the last term on the right side of the equation cancels. By substituting 35.0 m for x and 2.12 s for t, the v ix can be found to be 16.5 m/s.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Projectile Motion & Quadratic Equations

Projectiles General Word Problems Max/Min Problems

Calculus involves lots of finding maximums, minimums, and zeroes. You will get a taste of that with quadratic word problems. In fact, if/when you reach calculus, you will discover that some of the homework exercises will be identical to those you're doing now; it's just that you'll have new tools for finding the answers.

Content Continues Below

MathHelp.com

A major category of quadratic-equation word problems relates to what is called projectile motion. For our purposes, a projectile is any object that is thrown, shot, or dropped. Almost always, in this context, the object is initially moving directly up or straight down. (If it starts by going up then, naturally, it will later be coming back down.) This initial movement speed is the velocity.

What does the velocity's sign say about the object?

The initial velocity of the object, in these exercises, tells us how the object was released. The initial value of the velocity will be either zero (so the object was just dropped), positive (so it was thrown or shot upward), or negative (so the object was thrown downward).

What does " g " stand for?

Advertisement

In projectile-motion exercises, the coefficient on the squared term is −½  g . The g stands for the constant of gravity (on Earth), which is −9.8 meters per second square (that is meters per second per second) in metric terms, or −32 feet per second squared in Imperial terms. The "minus" signs reflect the fact that Earth's gravity pulls us, and the object in question, downward.

What does "per second squared" mean?

Acceleration (being the change in speed, rather than the speed itself) is measured in terms of how much the velocity changes per unit time. So, if the velocity of an object is measured in feet per second, then that object's acceleration says how much that velocity changes per unit time; that is, acceleration measures how much the feet per second changes per second. And this duplicate "per second" is how we get "second squared". It's from the physics of the situation.

Which value should I use for gravity?

If a projectile-motion exercise is stated in terms of feet, miles, or some other Imperial unit, then use −32 for gravity; if the units are meters, centimeters, or some other metric unit, then use −9.8 for gravity.

What is the projectile-motion equation?

The projectile-motion equation is s ( t ) = −½  g x 2 +  v 0 x  +  h 0 , where g is the constant of gravity, v 0 is the initial velocity (that is, the velocity at time t  = 0 ), and h 0 is the initial height of the object (that is, the height at of the object at t  = 0 , the time of release).

Yes, you'll need to keep track of all of this stuff when working with projectile motion.

• An object is launched at 19.6 meters per second (m/s) from a 58.8 -meter tall platform. The equation for the object's height s at time t seconds after launch is s ( t ) = −4.9 t 2 + 19.6 t  + 58.8 , where s is in meters. When does the object strike the ground?

What is the height (above ground level) when the object smacks into the ground? Well, zero, obviously. So I'm looking for the time when the height is s  = 0 . I'll set s equal to zero, and solve:

0 = −4.9 t 2 + 19.6 t + 58.8 0 = t 2 − 4 t − 12 0 = ( t − 6)( t + 2)

Then t = 6 or t  = −2 . The second solution is from two seconds before launch, which doesn't make sense in this context. (It makes sense on the graph, because the line crosses the x -axis at −2 , but negative time won't work in this word problem.) So " t  = −2 " is an extraneous solution, and I'll ignore it.

Instead, my answer to this exercise (that is, the correct answer in context) is the other solution value. They asked me for the time, and time here is measured in seconds, so my answer is:

The object strikes the ground six seconds after launch.

Note the construction of the height equation in the problem above. (Yes, we went over this at the beginning, but you're really gonna need this info, so we're revisiting.)

The initial launch height was 58.8 meters, and the constant term was " 58.8 ". The initial velocity (or launch speed) was 19.6 m/s, and the coefficient on the linear term was " 19.6 ". This is always true for these up/down projectile motion problems. (If you have an exercise with sideways motion, the equation will have a different form, but they'll always give you that equation.) The initial velocity is the coefficient for the middle term, and the initial height is the constant term.

And the coefficient on the leading term comes from the force of gravity. This coefficient is negative, since gravity pulls downward, and the value will either be " −4.9 " (if your units are "meters") or " −16 " (if your units are "feet"). Yes, these values are half of the values listed for the gravity constant at the beginning of this page; they've had the ½ multiplied through.

In general, the projectile-motion equation's format is:

s ( t ) = − gt 2 + v 0 t + h 0

...where " g " here is the " 4.9 " or the " 16 " derived from the value of the force of gravity (technically, it's the force of gravity on Earth ), " v 0 " ("vee-naught", or "vee-sub-zero") is the initial velocity, and " h 0 " ("aitch-naught", or "aitch-sub-zero") is the initial height.

Memorize this equation (or at least its meaning), because you may need to know this on the test.

• An object in launched directly upward at 64 feet per second (ft/s) from a platform 80 feet high. What will be the object's maximum height? When will it attain this height?

Hmm... They didn't give me the equation this time. But that's okay, because I can create the equation from the information that they did give me. The initial height is 80 feet above ground and the initial speed is 64 ft/s upward. Since my units are feet, then the number for gravity will be −16 , and my equation is:

s ( t ) = −16 t 2 + 64 t + 80

They want me to find the maximum height. For a negative quadratic like this, the maximum will be at the vertex of the upside-down parabola. So they really want me to find the vertex. From graphing , I know how to find the vertex; in this case, the vertex is at ( h ,  k ) = (2, 144):

h = − b / 2 a = −(64)/2(−16) = −64/−32 = 2 k = s (2) = −16(2) 2 + 64(2) + 80 = −16(4) + 128 + 80 = 208 − 64 = 144

But what do the coordinates of this vertex tell me? According to my equation, I'm plugging in time values and extracting height values, so the input 2 was the time and the output 144 is the height.

It takes two seconds to reach the maximum height of 144 feet.

As long as you label clearly, you don't need a complete sentence (like I used above) for your hand-in answer. So you could also give you answer as, "time:  2  secs; height:  144  ft".

• An object is launched from ground level directly upward at 39.2 m/s. For how long is the object at or above a height of 34.3 meters?

My units this time are "meters", so the gravity number will be −4.9 . Since the object started at ground level, the initial height was 0 . Then my equation is:

s ( t ) = −4.9 t 2 + 39.2 t

Since this is a negative quadratic, the graph is an upside-down parabola. I can find the two times when the object is exactly 34.3 meters high, and I know that the object will be above 34.3 meters the whole time in between.

Why "two times", and how do I know that the time period is between those two times? Because the first time will be when the object passes a height of 34.3 meters on its way up to its maximum height, and the second time when be when it passes 34.3 meters as it is falling back down to the ground. So I have to solve the following:

−4.9 t 2 + 39.2 t = 34.3 t 2 − 8 t + 7 = 0 ( t − 7)( t − 1) = 0

The two solutions are at times t  = 1 and t  = 7 . So the object is at 34.3  meters at one second after launch (going up) and againt at seven seconds after launch (coming back down). Subtracting to find the difference, I find that:

The object is at or above 34.3  meters for six seconds.

Again, you don't technically need a complete sentence for your hand-in answer; saying " 6 secs" is probably good enough. But definitely do include the unit "seconds" on your answer.

Don't be surprised if many of your exercises work out as "neatly" as the above examples have. Many textbooks still engineer their exercises carefully, so that you can solve by factoring (that is, by quickly doing the algebra).

However (fair warning!), heavy dependence on calculators is leading more texts to create "interesting" (that is to say, needlessly complicated) exercises, so some (or all) of your exercises may involve much more messy computations than have been displayed here. If so, study these "neat" examples carefully, until you are quite sure you follow the reasoning.

• After the semester is over, you discover that the math department has changed textbooks (again) so the bookstore won't buy back your nearly-new book. You and your friend Herman decide to get creative. You go to the roof of a twelve-story building and look over the edge to the reflecting pool 160  feet below. You drop your book over the edge at the same instant that Herman chucks his book straight down at 48  feet per second. By how many seconds does his book beat yours into the water? (Round your answer to two decimal places.)

Our initial launch heights will be the same: we're both launching from 160  feet above ground. And the gravity number, since we're working in feet, will be −16 . My initial velocity is zero, since I just dropped my book, but my buddy Herman's velocity is a negative 48 , the negative coming from the fact that he chucked his book down rather than up. So our "height" equations are:

mine: s ( t ) = −16 t 2 + 160 his: s ( t ) = −16 t 2 − 48 t + 160

In each case, I need to find the time for the books to reach a height of zero (a height of zero being "ground level"), so:

mine: 0 = −16 t 2 + 160

t 2 − 10 = 0

his: 0 = −16 t 2 − 48 t + 160

t 2 + 3 t − 10 = 0

( t + 5)( t − 2) = 0

t = −5, +2

I will ignore the negative time values as being irrelevant in this context. (There may be a case, at some point, in some exercise, where a negative value does happen to be useful within a given context, so I do need to remember to think about the values and the context, rather than reflexively discarding any and all negative solutions.)

Herman's book hits the water about 1.16 seconds sooner than mine does.

Every once in a while, they'll get clever and put a "projectile" problem into a different environment. The equation will remain the same in structure, but you may have to account for a different value for gravity.

• The International Space Agency has finally landed a robotic explorer on an extra-solar planet. Some probes are extended from the lander's body to conduct various tests. To demonstrate the crushing weight of gravity on this planet, the lander's camera is aimed at a probe's ground-level ejection port, and the port launches a baseball directly upwards at 147 feet per second (ft/s), about the top speed of a professional pitcher. The force due to gravity on this planet is 98  ft/s 2 . Assuming no winds and that the probe can scurry out of the way in time, how long will it take for the ball to smack back into the surface?

To set up my equation for this exercise, I need to keep in mind that the value of the coefficient g from the projectile-motion equation above is one-half of the value of the force due to gravity in a given locale.

In physics, there is the "universal gravitational constant " G , being the gravitational pull inherent to our universe (or at least our region of it). Every object exerts its own gravitational force, which is related to its own mass and the universal constant G . In the "projectile motion" formula, the " g " is half of the value of the gravitational force for that particular body. For instance, the gravitational force on Earth is a downward 32 ft/s 2 , but we used 16 in the equation.

So g for my equation this time will by 98 ÷ 2 = 49 feet per second squared. Then:

s = −49 t 2 + 147 t 0 = −49 t 2 + 147 t 0 = t 2 − 3 t 0 = t  ( t − 3)

Then t = 0 or t = 3 . The first solution represents when the ball was launched, so the second solution is the one I want.

It takes three seconds for the ball to hit the ground.

Note: On Earth, it would take a little over nine seconds for the ball to fall back to the ground.

URL: https://www.purplemath.com/modules/quadprob.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Maximum Height Calculator – Projectile Motion

Table of contents

The maximum height calculator is a tool for finding the maximum vertical position of a launched object in projectile motion . Whether you need the max height formula for an object starting directly off the ground or from some initial elevation – we've got you covered. If you're still wondering how to find the maximum height of a projectile, read the two short paragraphs below, and everything should become clear.

How to find the maximum height of a projectile?

The maximum height of the object is the highest vertical position along its trajectory. The object is flying upwards before reaching the highest point – and it's falling after that point. It means that at the highest point of projectile motion, the vertical velocity is equal to 0 0 0 ( v y = 0 v_y = 0 v y ​ = 0 ).

From that equation we can find the time t h t_{\mathrm{h}} t h ​ needed to reach the maximum height h m a x h_{\mathrm{max}} h max ​ :

The formula describing vertical distance is:

So, given y = h m a x y = h_{\mathrm{max}} y = h max ​ and t = t h t = t_{\mathrm{h}} t = t h ​ , we can join those two equations together:

And what if we launch a projectile from some initial height h h h ? No worries! Apparently, the calculations are a piece of cake – all you need to do is add this initial elevation!

Let's discuss some special cases with changing angle of launch:

• If α = 90 ° \alpha = 90\degree α = 90° , then the formula simplifies to:

And the time of flight is the longest.

If, additionally, v y = 0 v_y = 0 v y ​ = 0 , then it's the case of free fall, which we detailed at the free fall calculator . Also, you may want to have a look at our even more accurate equivalent – the free fall with air resistance calculator .

• If α = 45 ° \alpha = 45\degree α = 45° , then the equation may be written as:

And in that case, the range is maximal if launching from the ground ( h = 0 h = 0 h = 0 ).

• If α = 0 ° \alpha = 0\degree α = 0° , then vertical velocity is equal to 0 0 0 ( v y = 0 v_y = 0 v y ​ = 0 ). In this case, we can calculate the horizontal projectile motion. As the sine of 0 ° 0\degree 0° is 0 0 0 , then the second part of the equation disappears, and we obtain:

The initial height from which we're launching the object is the maximum height in projectile motion.

Other tools related to projectiles' motion

The motion of a projectile is a classic problem in physics, and it has been analyzed in every possible aspect. The fact that we can easily reproduce it and observe it was a contributing factor. We decided to create a suit of tools related to the motion of a projectile:

The projectile motion calculator for a comprehensive analysis of the problem;

The trajectory calculator to analyze the problem as a geometric function; and

A set of specific tools:

• The projectile range calculator ;
• The time of flight calculator ; and
• The horizontal projectile motion calculator (for α = 0 \alpha=0 α = 0 ).

Maximum height calculator helps you find the answer

Just relax and look how easy-to-use this maximum height calculator is:

Choose the velocity of the projectile . Let's type 30   f t / s 30\ \mathrm{ft/s} 30   ft/s .

Enter the angle . Assume we're kicking a ball ⚽ at an angle of 70 ° 70\degree 70° .

Optionally, type the initial height . In our case, our starting position is the ground, so type in 0 0 0 . Can the ball fly over a 13   f t 13\ \mathrm{ft} 13   ft fence?

Here it is – maximum height calculator displayed the answer! It's 12.35   f t 12.35\ \mathrm{ft} 12.35   ft . So it will not fly over the mentioned barrier – throw it harder or increase the angle to reach your goal.

Just remember that we don't take air resistance into account!

How do I find the maximum height of a ball thrown up?

To find the maximum height of a ball thrown up, follow these steps:

• Write down the initial velocity of the ball, v₀ .
• Write down the initial height, h₀ .
• Replace both in the following formula: h_max = h₀ +(v₀)²/ 2g where g is the acceleration due to gravity, g ~ 9.8 m/s² .

What angle has the longest flight time?

90° . You can determine the flight time (t) with the formula t = 2 × V × sin(α) / g . For a given velocity V , this function reaches its maximum value when sin (α) = 1 , which occurs at α = 90° .

What factors affect projectile motion?

The main factor that could affect the motion of a projectile is friction. When air resistance is introduced, the friction opposes the direction of movement, decreasing the velocity components of the projectile.

Does the mass of the projectile affect maximum height?

No . The maximum height a projectile can reach after being thrown is only affected by the initial velocity and the launch angle. The mass of the projectile does not affect the maximum height.

Angle of launch

Angle between the velocity vector and the ground.

Initial height

.css-slt4t3.css-slt4t3{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-slt4t3.css-slt4t3:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-slt4t3 .js-external-link-button.link-like,.css-slt4t3 .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-slt4t3 .js-external-link-button.link-like:hover,.css-slt4t3 .js-external-link-anchor:hover,.css-slt4t3 .js-external-link-button.link-like:active,.css-slt4t3 .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-slt4t3 .js-external-link-button.link-like:focus-visible,.css-slt4t3 .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-slt4t3 p,.css-slt4t3 div{margin:0px;display:block;}.css-slt4t3 pre{margin:0px;display:block;}.css-slt4t3 pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-slt4t3 pre:not(:first-child){padding-top:8px;}.css-slt4t3 ul,.css-slt4t3 ol{display:block margin:0px;padding-left:20px;}.css-slt4t3 ul li,.css-slt4t3 ol li{padding-top:8px;}.css-slt4t3 ul ul,.css-slt4t3 ol ul,.css-slt4t3 ul ol,.css-slt4t3 ol ol{padding-top:0px;}.css-slt4t3 ul:not(:first-child),.css-slt4t3 ol:not(:first-child){padding-top:4px;} .css-4okk7a{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-4okk7a code,.css-4okk7a kbd,.css-4okk7a pre,.css-4okk7a samp{font-family:monospace;}.css-4okk7a code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-4okk7a figcaption,.css-4okk7a caption{text-align:center;}.css-4okk7a figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-4okk7a h3{font-size:1.75rem;}.css-4okk7a h4{font-size:1.5rem;}.css-4okk7a .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-4okk7a .mathBlock .katex{font-size:24px;text-align:left;}.css-4okk7a .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-4okk7a .videoBlock,.css-4okk7a .imageBlock{margin-bottom:16px;}.css-4okk7a .imageBlock__image-align--left,.css-4okk7a .videoBlock__video-align--left{float:left;}.css-4okk7a .imageBlock__image-align--right,.css-4okk7a .videoBlock__video-align--right{float:right;}.css-4okk7a .imageBlock__image-align--center,.css-4okk7a .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-4okk7a .imageBlock__image-align--none,.css-4okk7a .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-4okk7a .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-4okk7a .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-4okk7a .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-4okk7a .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-4okk7a .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-4okk7a .katex .katex-version::after{content:'0.13.13';}.css-4okk7a .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-4okk7a .katex .katex-html>.newline{display:block;}.css-4okk7a .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-4okk7a .katex .strut{display:inline-block;}.css-4okk7a .katex .textbf{font-weight:bold;}.css-4okk7a .katex .textit{font-style:italic;}.css-4okk7a .katex .textrm{font-family:KaTeX_Main;}.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .texttt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-4okk7a .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-4okk7a .katex .mathrm{font-style:normal;}.css-4okk7a .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-4okk7a .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-4okk7a .katex .amsrm{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathbb,.css-4okk7a .katex .textbb{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-4okk7a .katex .mathfrak,.css-4okk7a .katex .textfrak{font-family:KaTeX_Fraktur;}.css-4okk7a .katex .mathtt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathscr,.css-4okk7a .katex .textscr{font-family:KaTeX_Script;}.css-4okk7a .katex .mathsf,.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .mathboldsf,.css-4okk7a .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-4okk7a .katex .mathitsf,.css-4okk7a .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-4okk7a .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-4okk7a .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-4okk7a .katex .vlist-r{display:table-row;}.css-4okk7a .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-4okk7a .katex .vlist>span{display:block;height:0;position:relative;}.css-4okk7a .katex .vlist>span>span{display:inline-block;}.css-4okk7a .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-4okk7a .katex .vlist-t2{margin-right:-2px;}.css-4okk7a .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-4okk7a .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-4okk7a .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-4okk7a .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-4okk7a .katex .msupsub{text-align:left;}.css-4okk7a .katex .mfrac>span>span{text-align:center;}.css-4okk7a .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .mfrac .frac-line,.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline,.css-4okk7a .katex .hdashline,.css-4okk7a .katex .rule{min-height:1px;}.css-4okk7a .katex .mspace{display:inline-block;}.css-4okk7a .katex .llap,.css-4okk7a .katex .rlap,.css-4okk7a .katex .clap{width:0;position:relative;}.css-4okk7a .katex .llap>.inner,.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{position:absolute;}.css-4okk7a .katex .llap>.fix,.css-4okk7a .katex .rlap>.fix,.css-4okk7a .katex .clap>.fix{display:inline-block;}.css-4okk7a .katex .llap>.inner{right:0;}.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{left:0;}.css-4okk7a .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-4okk7a .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-4okk7a .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-4okk7a .katex .sizing.reset-size1.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-4okk7a .katex .sizing.reset-size1.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size1.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-4okk7a .katex .sizing.reset-size1.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size1.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size1.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-4okk7a .katex .sizing.reset-size1.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size1.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size1.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-4okk7a .katex .sizing.reset-size1.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-4okk7a .katex .sizing.reset-size1.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-4okk7a .katex .sizing.reset-size2.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size2.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-4okk7a .katex .sizing.reset-size2.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-4okk7a .katex .sizing.reset-size2.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size2.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size2.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-4okk7a .katex .sizing.reset-size2.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-4okk7a .katex .sizing.reset-size2.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size2.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size2.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-4okk7a .katex .sizing.reset-size2.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-4okk7a .katex .sizing.reset-size3.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-4okk7a .katex .sizing.reset-size3.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-4okk7a .katex .sizing.reset-size3.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-4okk7a .katex .sizing.reset-size3.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-4okk7a .katex .sizing.reset-size3.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-4okk7a .katex .sizing.reset-size3.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-4okk7a .katex .sizing.reset-size3.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-4okk7a .katex .sizing.reset-size3.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-4okk7a .katex .sizing.reset-size3.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-4okk7a .katex .sizing.reset-size4.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size4.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size4.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-4okk7a .katex .sizing.reset-size4.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-4okk7a .katex .sizing.reset-size4.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-4okk7a .katex .sizing.reset-size4.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-4okk7a .katex .sizing.reset-size4.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size4.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size4.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-4okk7a .katex .sizing.reset-size4.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-4okk7a .katex .sizing.reset-size4.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-4okk7a .katex .sizing.reset-size5.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size5.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size5.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-4okk7a .katex .sizing.reset-size5.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-4okk7a .katex .sizing.reset-size5.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-4okk7a .katex .sizing.reset-size5.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-4okk7a .katex .sizing.reset-size5.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size5.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size5.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-4okk7a .katex .sizing.reset-size5.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-4okk7a .katex .sizing.reset-size5.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-4okk7a .katex .sizing.reset-size6.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size6.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-4okk7a .katex .sizing.reset-size6.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-4okk7a .katex .sizing.reset-size6.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-4okk7a .katex .sizing.reset-size6.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-4okk7a .katex .sizing.reset-size6.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-4okk7a .katex .sizing.reset-size6.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size6.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size6.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-4okk7a .katex .sizing.reset-size6.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-4okk7a .katex .sizing.reset-size6.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-4okk7a .katex .sizing.reset-size7.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size7.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size7.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-4okk7a .katex .sizing.reset-size7.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size7.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size7.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size7.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-4okk7a .katex .sizing.reset-size7.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size7.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size7.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-4okk7a .katex .sizing.reset-size7.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-4okk7a .katex .sizing.reset-size8.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size8.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size8.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-4okk7a .katex .sizing.reset-size8.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size8.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size8.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size8.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size8.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-4okk7a .katex .sizing.reset-size8.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size8.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-4okk7a .katex .sizing.reset-size8.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-4okk7a .katex .sizing.reset-size9.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-4okk7a .katex .sizing.reset-size9.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size9.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-4okk7a .katex .sizing.reset-size9.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-4okk7a .katex .sizing.reset-size9.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-4okk7a .katex .sizing.reset-size9.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-4okk7a .katex .sizing.reset-size9.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size9.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size9.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-4okk7a .katex .sizing.reset-size9.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-4okk7a .katex .sizing.reset-size9.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-4okk7a .katex .sizing.reset-size10.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-4okk7a .katex .sizing.reset-size10.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-4okk7a .katex .sizing.reset-size10.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-4okk7a .katex .sizing.reset-size10.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-4okk7a .katex .sizing.reset-size10.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-4okk7a .katex .sizing.reset-size10.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-4okk7a .katex .sizing.reset-size10.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-4okk7a .katex .sizing.reset-size10.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-4okk7a .katex .sizing.reset-size10.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-4okk7a .katex .sizing.reset-size10.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-4okk7a .katex .sizing.reset-size10.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-4okk7a .katex .sizing.reset-size11.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-4okk7a .katex .sizing.reset-size11.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-4okk7a .katex .sizing.reset-size11.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-4okk7a .katex .sizing.reset-size11.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-4okk7a .katex .sizing.reset-size11.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-4okk7a .katex .sizing.reset-size11.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-4okk7a .katex .sizing.reset-size11.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-4okk7a .katex .sizing.reset-size11.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-4okk7a .katex .sizing.reset-size11.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-4okk7a .katex .sizing.reset-size11.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-4okk7a .katex .sizing.reset-size11.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-4okk7a .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-4okk7a .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-4okk7a .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-4okk7a .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-4okk7a .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-4okk7a .katex .delimcenter{position:relative;}.css-4okk7a .katex .op-symbol{position:relative;}.css-4okk7a .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-4okk7a .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-4okk7a .katex .op-limits>.vlist-t{text-align:center;}.css-4okk7a .katex .accent>.vlist-t{text-align:center;}.css-4okk7a .katex .accent .accent-body{position:relative;}.css-4okk7a .katex .accent .accent-body:not(.accent-full){width:0;}.css-4okk7a .katex .overlay{display:block;}.css-4okk7a .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-4okk7a .katex .mtable .arraycolsep{display:inline-block;}.css-4okk7a .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-4okk7a .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-4okk7a .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-4okk7a .katex .svg-align{text-align:left;}.css-4okk7a .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-4okk7a .katex svg path{stroke:none;}.css-4okk7a .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-4okk7a .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-4okk7a .katex .stretchy::before,.css-4okk7a .katex .stretchy::after{content:'';}.css-4okk7a .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-4okk7a .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-4okk7a .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .x-arrow-pad{padding:0 0.5em;}.css-4okk7a .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-4okk7a .katex .x-arrow,.css-4okk7a .katex .mover,.css-4okk7a .katex .munder{text-align:center;}.css-4okk7a .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-4okk7a .katex .fbox,.css-4okk7a .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-4okk7a .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-4okk7a .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-4okk7a .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-4okk7a .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-4okk7a .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-4okk7a .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-4okk7a .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-4okk7a .katex .mtr-glue{width:50%;}.css-4okk7a .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-4okk7a .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-4okk7a .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-4okk7a .katex-display{display:block;margin:1em 0;text-align:center;}.css-4okk7a .katex-display>.katex{display:block;white-space:nowrap;}.css-4okk7a .katex-display>.katex>.katex-html{display:block;position:relative;}.css-4okk7a .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-4okk7a .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-4okk7a .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-4okk7a body{counter-reset:katexEqnNo mmlEqnNo;}.css-4okk7a table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-4okk7a .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-4okk7a .tableBlock thead,.css-4okk7a .tableBlock thead th{border-bottom:1px solid #333!important;}.css-4okk7a .tableBlock th,.css-4okk7a .tableBlock td{padding:10px;text-align:left;}.css-4okk7a .tableBlock th{font-weight:bold!important;}.css-4okk7a .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-4okk7a .tableBlock caption>p{margin:0;}.css-4okk7a .tableBlock th>p,.css-4okk7a .tableBlock td>p{margin:0;}.css-4okk7a .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-4okk7a .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-4okk7a .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-4okk7a .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-4okk7a .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-4okk7a .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-4okk7a .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-4okk7a .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-4okk7a .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-4okk7a .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-4okk7a .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-4okk7a .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-4okk7a .tableBlock [data-text-align='center']{text-align:center;}.css-4okk7a .tableBlock [data-text-align='left']{text-align:left;}.css-4okk7a .tableBlock [data-text-align='right']{text-align:right;}.css-4okk7a .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-4okk7a .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-4okk7a .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-4okk7a .tableBlock__font-size--xxsmall{font-size:10px;}.css-4okk7a .tableBlock__font-size--xsmall{font-size:12px;}.css-4okk7a .tableBlock__font-size--small{font-size:14px;}.css-4okk7a .tableBlock__font-size--large{font-size:18px;}.css-4okk7a .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--bordered td,.css-4okk7a .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--borderless tbody+tbody,.css-4okk7a .tableBlock__border--borderless td,.css-4okk7a .tableBlock__border--borderless th,.css-4okk7a .tableBlock__border--borderless tr,.css-4okk7a .tableBlock__border--borderless thead,.css-4okk7a .tableBlock__border--borderless thead th{border:0!important;}.css-4okk7a .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-4okk7a .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-4okk7a .tableBlock__table-compactl th,.css-4okk7a .tableBlock__table-compact td{padding:3px!important;}.css-4okk7a .tableBlock__full-size{width:100%;}.css-4okk7a .textBlock{margin-bottom:16px;}.css-4okk7a .textBlock__text-formatting--finePrint{font-size:12px;}.css-4okk7a .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-4okk7a .textBlock__text-infoBox p{margin:0;}.css-4okk7a .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-4okk7a .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-4okk7a .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-4okk7a .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-4okk7a .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-4okk7a .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-4okk7a .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-4okk7a .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-4okk7a.css-4okk7a{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-4okk7a.css-4okk7a:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-4okk7a .js-external-link-button.link-like,.css-4okk7a .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-4okk7a .js-external-link-button.link-like:hover,.css-4okk7a .js-external-link-anchor:hover,.css-4okk7a .js-external-link-button.link-like:active,.css-4okk7a .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-4okk7a .js-external-link-button.link-like:focus-visible,.css-4okk7a .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-4okk7a p,.css-4okk7a div{margin:0px;display:block;}.css-4okk7a pre{margin:0px;display:block;}.css-4okk7a pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-4okk7a pre:not(:first-child){padding-top:8px;}.css-4okk7a ul,.css-4okk7a ol{display:block margin:0px;padding-left:20px;}.css-4okk7a ul li,.css-4okk7a ol li{padding-top:8px;}.css-4okk7a ul ul,.css-4okk7a ol ul,.css-4okk7a ul ol,.css-4okk7a ol ol{padding-top:0px;}.css-4okk7a ul:not(:first-child),.css-4okk7a ol:not(:first-child){padding-top:4px;} Specify horizontal and vertical velocity

Horizontal velocity

Velocity component parallel to the ground.

Vertical velocity

Velocity component perpendicular to the ground.

Maximum height