Calculate integrals online — with steps and graphing.
The Integral Calculator lets you calculate integrals and antiderivatives of functions online — for free!
Our calculator allows you to check your solutions to calculus exercises. It helps you practice by showing you the full working (step by step integration). All common integration techniques and even special functions are supported.
The Integral Calculator supports definite and indefinite integrals (antiderivatives) as well as integrating functions with many variables. You can also check your answers! Interactive graphs/plots help visualize and better understand the functions.
For more about how to use the Integral Calculator, go to " Help ". Also see " Examples ".
Enter the function you want to integrate into the Integral Calculator. Skip the f(x)= part and the differential dx ! The Integral Calculator will show you a graphical version of your input while you type. Make sure that it shows exactly what you want. Use parentheses, if necessary, e.g. a/(b+c) . Write decimal fractions with a period instead of a comma, e.g. 3.141 .
In " Examples " you will find some of the functions that are most frequently entered into the Integral Calculator.
When you're done entering your function, click " Go! ", and the Integral Calculator will show the result below.
In " Options ", you can set the variable of integration and the integration bounds . If you don't specify the bounds, only the antiderivative will be computed.
Click an example to enter it into the Integral Calculator (the current input will be deleted).
The practice problem generator allows you to generate as many random exercises as you want.
You find some configuration options and a proposed problem below. You can accept it (then it's input into the calculator) or generate a new one.
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Calculate the Integral of … Enter your own Answer:
This will be calculated:
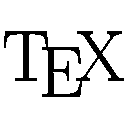
|
This will take a few seconds. |
Use parentheses, if necessary. Also see " Examples ". Change integration variable and order in " Options ".

How the Integral Calculator Works
For those with a technical background, the following section explains how the Integral Calculator works.
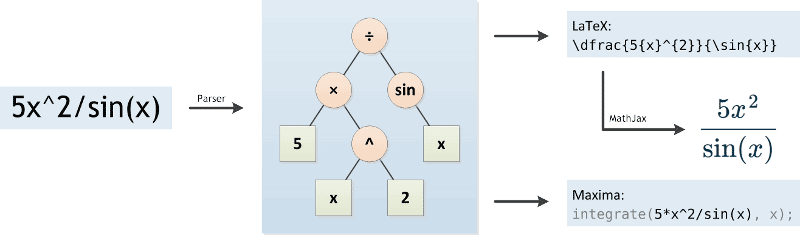
First, a parser analyzes the mathematical function. It transforms it into a form that is better understandable by a computer, namely a tree (see figure below). In doing this, the Integral Calculator has to respect the order of operations . A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write 5x instead of 5*x . The Integral Calculator has to detect these cases and insert the multiplication sign.
The parser is implemented in JavaScript , based on the Shunting-yard algorithm , and can run directly in the browser. This allows for quick feedback while typing by transforming the tree into LaTeX code. MathJax takes care of displaying it in the browser.
When the " Go! " button is clicked, the Integral Calculator sends the mathematical function and the settings (variable of integration and integration bounds) to the server, where it is analyzed again. This time, the function gets transformed into a form that can be understood by the computer algebra system Maxima .
Maxima takes care of actually computing the integral of the mathematical function. Maxima's output is transformed to LaTeX again and is then presented to the user. In many cases, the antiderivative is computed using the Risch algorithm , which is hard to understand for humans. That's why showing the steps of calculation is very challenging for integrals.
In order to show the steps, the calculator applies the same integration techniques that a human would apply. The program that does this has been developed over several years and is written in Maxima's own programming language. It consists of more than 17 000 lines of code. When the integrand matches a known form, it applies fixed rules to solve the integral (e.g. partial fraction decomposition for rational functions, trigonometric substitution for integrands involving the square roots of a quadratic polynomial or integration by parts for products of certain functions). Otherwise, it tries different substitutions and transformations until either the integral is solved, time runs out or there is nothing left to try. The calculator lacks the mathematical intuition that is very useful for finding an antiderivative, but on the other hand it can try a large number of possibilities within a short amount of time. The step by step antiderivatives are often much shorter and more elegant than those found by Maxima.
The "Check answer" feature has to solve the difficult task of determining whether two mathematical expressions are equivalent. Their difference is computed and simplified as far as possible using Maxima. For example, this involves writing trigonometric/hyperbolic functions in their exponential forms. If it can be shown that the difference simplifies to zero, the task is solved. Otherwise, a probabilistic algorithm is applied that evaluates and compares both functions at randomly chosen places. In the case of antiderivatives, the entire procedure is repeated with each function's derivative, since antiderivatives are allowed to differ by a constant.
The interactive function graphs are computed in the browser and displayed within a canvas element (HTML5) . For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph. While graphing, singularities (e.g. poles) are detected and treated specially. The gesture control is implemented using Hammer.js .
If you have any questions or ideas for improvements to the Integral Calculator, don't hesitate to write me an e-mail .
© David Scherfgen 2024 — all rights reserved.
Contact and Privacy

Online Integral Calculator
Solve integrals with wolfram|alpha.
More than just an online integral solver
Wolfram|Alpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals. The Wolfram|Alpha Integral Calculator also shows plots, alternate forms and other relevant information to enhance your mathematical intuition.
Learn more about:
Tips for entering queries
Use Math Input above or enter your integral calculator queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for an integral using plain English.
- integrate x/(x-1)
- integrate x sin(x^2)
- integrate x sqrt(1-sqrt(x))
- integrate x/(x+1)^3 from 0 to infinity
- integrate 1/(cos(x)+2) from 0 to 2pi
- integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi
- View more examples
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator
- Step-by-step solutions
- Wolfram Problem Generator
What are integrals?
Integration is an important tool in calculus that can give an antiderivative or represent area under a curve..
The indefinite integral of , denoted , is defined to be the antiderivative of . In other words, the derivative of is . Since the derivative of a constant is 0, indefinite integrals are defined only up to an arbitrary constant. For example, , since the derivative of is . The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to .
Both types of integrals are tied together by the fundamental theorem of calculus. This states that if is continuous on and is its continuous indefinite integral, then . This means . Sometimes an approximation to a definite integral is desired. A common way to do so is to place thin rectangles under the curve and add the signed areas together. Wolfram|Alpha can solve a broad range of integrals
How Wolfram|Alpha calculates integrals
Wolfram|Alpha computes integrals differently than people. It calls Mathematica's Integrate function, which represents a huge amount of mathematical and computational research. Integrate does not do integrals the way people do. Instead, it uses powerful, general algorithms that often involve very sophisticated math. There are a couple of approaches that it most commonly takes. One involves working out the general form for an integral, then differentiating this form and solving equations to match undetermined symbolic parameters. Even for quite simple integrands, the equations generated in this way can be highly complex and require Mathematica's strong algebraic computation capabilities to solve. Another approach that Mathematica uses in working out integrals is to convert them to generalized hypergeometric functions, then use collections of relations about these highly general mathematical functions.
While these powerful algorithms give Wolfram|Alpha the ability to compute integrals very quickly and handle a wide array of special functions, understanding how a human would integrate is important too. As a result, Wolfram|Alpha also has algorithms to perform integrations step by step. These use completely different integration techniques that mimic the way humans would approach an integral. This includes integration by substitution, integration by parts, trigonometric substitution and integration by partial fractions.
Integration Problems in Calculus | Examples & Solutions
Nereida Rondon has taught high school Geometry and AP Calculus AB for over 10 years. She holds a bachelor's degree in secondary Math education from Florida Southwestern State College.
Amy has a master's degree in secondary education and has been teaching math for over 9 years. Amy has worked with students at all levels from those with special needs to those that are gifted.
How does one solve a definite integral step by step?
To solve a definite integral, use the power rule to integrate and find the new equation. The constant of integration is not necessary since the limits of integration will be used to find a numerical value for the integral. After integrating the function using the power rule, plug in both limits of integration, one at a time. Subtract the results, the lower limit's result is subtracted from the upper limit's result. The final value is the solution to the integral.
How does one solve an integral problem?
Integrals are solved various ways depending on the function being evaluated. The most basic way is to use the power rule. If the integral is definite then the answer will be a numerical value. However, if the integral is indefinite, then the answer will be another function.
How does one solve an indefinite integration problem?
For indefinite integrals, a constant of integration must always be added to the solution because it is a part of the solution that is unknown. To solve an indefinite integral using the power rule, each term has to increase by one degree (or exponent has to increase by one power). Then divide the term by the new power.
Table of Contents
Integral calculus problems, integration problems, how to solve integration problems, integral practice problems, integration sums, lesson summary.
What is integral calculus? While differential calculus focuses on rates of change, integral calculus deals with totals of lengths, areas, and volumes. An integral is a numerical value equal to the area under a graph, but it could also be the equation of an original function that was derived. Recall that a function is an equation where every input has exactly one output. For example, {eq}f(x)=3x^2+4 {/eq} is a parabolic function, and the ordered pair {eq}(2, 16) {/eq} is one of many solutions to {eq}f(x){/eq}, but there are no other solutions that will have 2 as an input.
Integral calculus problems are used to undo derivatives, or work backward, starting from the differential equation towards finding the original function that was derived. The notation used to represent an integral involves an elongated S, {eq}\int {/eq}, called an integral sign followed by some type of function and then a variable of integration. Such as {eq}\int 4x\ dx {/eq}. Here {eq}4x {/eq} represents the function and {eq}dx {/eq} represents that the function is being integrated with respect to the variable {eq}x {/eq}. There are two types of integrals, definite and indefinite.
Definite Integrals
Definite integrals can be solved analytically or graphically. A definite integral will result in a numerical value and involves limits of integration within the notation. For example, {eq}\int_{0}^{2} 4x\ dx {/eq}. To break this down, the limits of integration are represented by the {eq}0 {/eq} (the lower limit) and the {eq}2 {/eq} (the upper limit). These endpoints are used to evaluate (or solve) the integral. What this means graphically is that the numerical value is a result of the area under the graph of {eq}f(x)=4x {/eq}, but strictly the region between {eq}x=0 {/eq} and {eq}x=2 {/eq}.
Graph of f(x)=4x with the area under the graph between x=0 and x=2 shaded in.
| |
The numerical value of {eq}\int_{0}^{2} 4x\ dx {/eq} is 8, because that is the calculated area found under the graph of {eq}f(x) {/eq} between {eq}x=0 {/eq} and {eq}x=2. {/eq} Looking at the graph of {eq}\int_{0}^{2} 4x\ dx {/eq}, the green region representing the area below the graph and above the x-axis is in the shape of a triangle. The area of a triangle can be found by using the formula {eq}A=\frac{1}{2}\cdot b\cdot h {/eq}. Since the triangle has a base length of {eq}2 {/eq} and a height of {eq}8 {/eq} units, the {eq}Area {/eq} is {eq}\frac{1}{2}\cdot 2\cdot 8 = \frac{1}{2}\cdot 16=8 {/eq}. Definite integrals can also be evaluated analytically (or algebraically). To evaluate integrals analytically, a specific set of rules are followed.
Indefinite Integrals
Finding indefinite integrals will result in an equation of a general function. This type of integral is less exact, or not definite, because a part of the function cannot be deduced so a constant of integration is used. The constant of integration , or {eq}+C {/eq}, is used for the portion of the function that is unknown. This term is a constant value. Since the constant could represent any number (even zero), {eq}+C {/eq} is used as a placeholder. For the most part, indefinite integrals are evaluated analytically.
For example: {eq}\int 4x\ dx {/eq} becomes {eq}2x^2+C {/eq}
To unlock this lesson you must be a Study.com Member. Create your account

An error occurred trying to load this video.
Try refreshing the page, or contact customer support.
You must c C reate an account to continue watching
Register to view this lesson.
As a member, you'll also get unlimited access to over 88,000 lessons in math, English, science, history, and more. Plus, get practice tests, quizzes, and personalized coaching to help you succeed.
Get unlimited access to over 88,000 lessons.
Already registered? Log in here for access
Resources created by teachers for teachers.
I would definitely recommend Study.com to my colleagues. It’s like a teacher waved a magic wand and did the work for me. I feel like it’s a lifeline.
You're on a roll. Keep up the good work!
Just checking in. are you still watching.
- 0:02 Integration Problems
- 0:36 Monomials
- 3:00 Reciprocals & Exponentials
- 4:06 Trigonometric Functions
- 4:32 Lesson Summary
Integration problems can involve different types of functions and different rules of integration. To evaluate integration problems, first identify the type of function. That will be useful to determine what rule to use. It is also important to have background knowledge on solving derivative problems since integration involves derivatives.
Recall that integration problems can be solved using the graphs of the functions and the area under the graph. However, the focus here will be how to solve integration problems algebraically. The most used rule will be the power rule , though there's also the constant rule , rules for reciprocal and exponential functions, the substitution rule for composite functions , and specific rules for trigonometric functions.
The most basic function is made up of a single term, for example {eq}f(x)=4x {/eq} only has one term, {eq}4x {/eq}. This single term is called a monomial . When integrating monomials, the degree of the function is used. The degree of the function is the highest power in the function. For {eq}f(x)=4x {/eq}, the {eq}x {/eq} has a power of one thus the function has a degree of one. To integrate this function the power rule is used. The power rule is as follows:
$$\int x^n\ dx = \frac{x^{n+1}}{n+1} +C,/ n\neq -1 $$
This means that the exponent of {eq}x {/eq} will increase by one degree and then the term will be divided by the new degree, {eq}n+1 {/eq}. Finally, since this is an indefinite integral , the constant of integration {eq}+C {/eq} is required. Notice how the exponent, {eq}n {/eq}, cannot be {eq}-1 {/eq} because then the denominator of the fraction created by the rule would be equal to zero. A fraction with a denominator of zero is {eq}undefined {/eq}. When {eq}n=-1 {/eq}, the power rule may not be used.
Using the power rule, here is how to integrate {eq}\int 4x\ dx {/eq} step by step. Add a degree to the exponent of x, then divide the term by that new exponent.
{eq}\begin{align*} \int 4x\ dx = \frac{4x^{1+1}}{1+1}+C \\\ =\frac{4x^{2}}{2}+C \\\ =2x^2+C \end{align*} {/eq}
Along with the power rule is the constant rule . The constant rules allows for a constant in an integral to be moved to the outer part of the integral to make it easier to solve the integral. For example, take the function from before {eq}f(x)=4x {/eq} when solving {eq}\int 4x\ dx {/eq}, the integral can be rewritten as {eq}4 \int x\ dx {/eq}. The integral would be solved with the power rule and the exponent would increase by one and the term {eq}x {/eq} would still be divided by the new exponent which is {eq}2 {/eq} but the {eq}4 {/eq} is multiplied back in after the power rule is used. The result is the same. The constant rule is helpful but not always necessary.
{eq}\begin{align*} \int 4x\ dx =4 \int x\ dx \\\ = 4\frac{x^{1+1}}{1+1}+C \\\ =\frac{4x^{2}}{2}+C \\\ =2x^2+C \end{align*} {/eq}
A monomial integral problem could also look like this: {eq}\int 5\ dx {/eq}. Whenever the integral problem is just a constant, then the solution will be {eq}5x+C {/eq}. Since no variable exists in this problem, imagine that {eq}x {/eq} simply has a power of zero, like this:
{eq}\begin{align*} \int 5\ dx = \int 5x^0\ dx \\\ = \frac{5x^{0+1}}{0+1}+C \\\ = 5x+C \end{align*} {/eq}
Here is another example of using the power rule to solve an indefinite integral involving a monomial:
{eq}\int 12x^3\ dx {/eq}, the solution to this integral is
{eq}\begin{align*} \int 12x^3\ dx= \frac{12x^{3+1}}{3+1}+C \\\ =\frac{12x^4}{4}+C \\\ =\frac{12}{4}x^4+C \\\ =3x^4+C \end{align*} {/eq}
As mentioned, definite integrals can also be solved algebraically but the result is a numerical value instead of an equation. Using the power rule, the integral {eq}\int_{0}^{6} \frac{1}{3}x^2\ dx {/eq} would be solved by evaluating the integral at the proposed limits of integration. First, use the power rule to find the new function, then take turns plugging in the limits of integration. Then finally subtract those values. The value from the lower limit must be subtracted from the value of the upper limit. Here is the step by step:
{eq}\begin{align*} \int_{0}^{3} \frac{1}{3} x^2\ dx =\frac{1}{3} \int_{0}^{3} x^2\ dx \\\ =\frac{1}{3} \cdot \frac{x^{2+1}}{2+1} \\\ =\frac{1}{3} \cdot \frac{x^3}{3} \\\ =\frac{1}{3} \cdot [ (\frac{3^3}{3}) - (\frac {0^3}{3})] \\\ =\frac{1}{3} \cdot [(\frac{27}{3})-(\frac {0}{3})] \\\ =\frac{1}{3} \cdot [9-0] \\\ =\frac{9}{3} \\\ =3 \end{align*} {/eq}
This is equivalent to graphing {eq}f(x)=\frac{1}{3}x^2 {/eq} and finding the area under the graph of {eq}f(x) {/eq}, between {eq}x=0 {/eq} and {eq}x=3. {/eq}
The graph of f(x)=1/3 x^2 with the area under the graph between x=0 and x=3 shaded in.
| |
Reciprocals
A reciprocal function looks like this {eq}f(x)=\frac{1}{x} {/eq}. This function, in particular, can be written as a negative exponent instead of as a fraction like so: {eq}f(x)=x^{-1} {/eq}. The power rule can not be used with this function because when the exponent is raised by one degree it becomes {eq}x^0 {/eq} and a fraction with a denominator of zero.
{eq}\begin{align*} \int \frac{1}{x}\ dx = \int x^{-1}\ dx \\\ =\frac{x^{-1+1}}{-1+1}+C \\\ =\frac{x^0}{0}+C \end{align*} {/eq}
This is a problem because fractions can not have a denominator of zero. This integral problem cannot be solved using the power rule is because it is related to the natural log function. Remember that derivatives are the prerequisite to integrals. The derivative of {eq}ln\ x {/eq} is {eq}\frac{1}{x} {/eq}.
{eq}\frac{d}{dx} [ln\ x]=\frac{1}{x} {/eq}
Which means that the integral of {eq}\frac{1}{x} {/eq} is {eq}ln\ x {/eq}
$$\begin{align*} \int \frac{1}{x}\ dx =ln\ |x| +C \end{align*} $$
The absolute value bars are necessary because {eq}ln\ x {/eq} is not defined for {eq}x<0 {/eq}.
The integral rule for {eq}ln\ x {/eq} is:
$$\int ln\ x\ dx=x(ln\ x-1)+C $$
Example: {eq}\begin{align*} \int 2\ ln\ x\ dx= 2\int ln\ x\ dx \\\ 2x \cdot (ln\ x-1)+C \end{align*} {/eq}
Here is an example of a reciprocal function that can be solved using the power rule:
{eq}\begin{align*} \int \frac{6}{x^3}\ dx = \int 6x^{-3}\ dx \\\ = 6\int x^{-3}\ dx \\\ =6\frac{x^{-3+1}}{-3+1}+C \\\ =6\frac{x^{-2}}{-2}+C \\\ =\frac{6}{-2}x^{-2}+C \\\ =-3x^{-2}+C \\\ =\frac{-3}{x^2}+C \end{align*} {/eq}
Exponentials
An exponential function is a function of the form {eq}f(x)=a^x {/eq} where a is a constant and {eq}a>0 {/eq} but {eq}a\neq 1 {/eq}. The most popular exponential function is {eq}e^x {/eq}.
The rules for integrating exponential functions are:
{eq}\begin{align*} \int a^x\ dx = \frac{a^x}{ln\ a}+C \end{align*} {/eq} and {eq}\begin{align*} \int e^x\ dx= e^x+C \end{align*} {/eq}.
Example: evaluate {eq}\int 5^x\ dx. {/eq}
{eq}\begin{align*} \int 5^x\ dx = \frac{5^x}{ln\ 5}+C \end{align*} {/eq}
Example: evaluate {eq}\int 2e^x\ dx. {/eq}
{eq}\begin{align*} \int 2e^x\ dx = 2\int e^x\ dx \\\ = 2e^x+C \end{align*} {/eq}
Example: evaluate {eq}\int 7e^{x+2}\ dx. {/eq}
{eq}\begin{align*} \int 7e^{x+2}\ dx = 7\int e^{x+2}\ dx \\\ = 7e^{x+2}+C \end{align*} {/eq}
Trigonometric Functions
Trigonometry is the branch of mathematics dealing with the relationship between the sides and angles of triangles. The ratios used to study this relationship are called trigonometric ratios. The six ratios are sine, cosine, tangent, cotangent, secant, and cosecant. These ratios are used in trigonometric functions . The integration rules for trigonometric functions are complicated due to them all being different. Once again, background knowledge in derivatives is helpful. By knowing the derivative rules for these trigonometric functions, it is easier to learn the integral rules.
{eq}\begin{align*} \int sin\ x\ dx= -cos\ x+C \\\ \int cos\ x\ dx= sin\ x+C \\\ \int sec^2\ x\ dx= tan\ x+C \\\ \int sec\ x\ tan\ x\ dx= sec\ x+C \\\ \int csc\ x\ cot\ x\ dx= -csc\ x+C \\\ \int csc^2\ x\ dx= -cot\ x+C \\\ \end{align*} {/eq}
Now here are some calculus example problems. Put all of these rules to work, solve the following indefinite integral problems.
{eq}\begin{align*} \int 45x^4\ dx \end{align*} {/eq}
{eq}\begin{align*} \int 3\ cos\ x\ dx \end{align*} {/eq}
{eq}\begin{align*} \int 2\ ln\ x\ dx \end{align*} {/eq}
{eq}\begin{align*} \int 7\ dx \end{align*} {/eq}
{eq}\begin{align*} \int \frac{3}{x+6}\ dx \end{align*} {/eq}
{eq}\begin{align*} \int 45x^4\ dx= \frac{45x^{4+1}}{4+1}+C \\\ =\frac{45x^5}{5}+C \\\ =\frac{45}{5}x^5+C \\\ =9x^5+C \end{align*} {/eq}
{eq}\begin{align*} \int 3\ cos\ x\ dx=3 \int cos\ x\ dx \\\ =3\ sin\ x+C \end{align*} {/eq}
{eq}\begin{align*} \int 2\ ln\ x\ dx= 2\int ln\ x\ dx \\\ =2x \cdot (ln\ x-1)+C \end{align*} {/eq}
{eq}\begin{align*} \int 7\ dx = \int 7x^0\ dx \\\ = \frac{7x^{0+1}}{0+1}+C \\\ = 7x+C \end{align*} {/eq}
{eq}\begin{align*} \int \frac{3}{x+6}\ dx = 3\int (x+6)^{-1}\ dx \\\ =3\ ln\ |x+6|+C \end{align*} {/eq}
The sum rule of integration problems is used when the integral problem is a made up of adding more than one function. It also looks like a bunch of monomials or a polynomial. To solve an integral problem with the sum rule, split the functions into separate integrals. For example:
{eq}\begin{align*} \int 5x^4+3\ dx = \int 5x^4\ dx + \int 3\ dx \\\ =\frac{5x^{4+1}}{4+1} + \frac{3x^{0+1}}{0+1} +C \\\ = \frac{5x^5}{5} + \frac{3x^1}{1} +C \\\ = \frac{5}{5} \cdot x^5 + \frac{3}{1} \cdot x +C \\\ = x^5 + 3x +C \end{align*} {/eq}
What is integral calculus? While differential calculus focuses on rates of change, integral calculus deals with totals of lengths, areas, and volumes. An integral is a numerical value equal to the area under a graph, but it could also be the equation of an original function that was derived. Recall that a function is an equation where every input has exactly one unique output. Integrals are the branch of calculus that deals with totals. There are two types of integrals, definite and indefinite . Definite integrals result in a numerical value. Indefinite integrals result in a new equation of a function. Definite integrals can be evaluated graphically or algebraically, whereas indefinite integrals are solved algebraically. To evaluate integrals algebraically, a specific set of rules are followed. The rule used depends on the function type. The rules covered in this lesson were the power rule and the constant rule . There are also specific rules that need to be followed for certain types of functions such as reciprocal functions , exponential functions , and trigonometric functions . Finally, the sum rule of integration is really solving a string of different functions all at once and can involve any of the rules, just working with one term at a time but integrating one function at a time.
For indefinite integrals, a constant of integration must always be added to the solution because it is a part of the solution that is unknown. To solve an indefinite integral using the power rule, each term has to increase by one degree (or exponent has to increase by one power). Then divide the term by the new power. For example, the function {eq}f(x)=6x^2 {/eq} has a degree (or exponent) of 2. Here is step by step of how the integral is solved:
{eq}\int 6x^2\ dx = \frac{6x^{2+1}}{2+1}+C=\frac{6x^3}{3}+C=2x^3+C. {/eq}
To solve a definite integral, use the power rule to find the new equation. The constant of integration is not necessary since the limits of integration will be used to find the value of the integral, like so:
{eq}\int_{1}^{2} 6x^2\ dx = 6\int_{1}^{2} x^2\ dx \\\ =6 \cdot \frac{x^{2+1}}{2+1} \\\ =6 \cdot \frac{x^3}{3} \\\ =\frac{6}{3} \cdot x^3 \\\ =2 \cdot x^3 {/eq}
plug in the limits of integration and subtract.
{eq}\\\ =2 \cdot [ (2^3) - (1^3)] \\\ =2 \cdot [8-1] \\\ =2 \cdot 7 \\\ =14 {/eq}
Video Transcript
Integrating various types of functions is not difficult. All you need to know are the rules that apply and how different functions integrate. You know the problem is an integration problem when you see the following symbol:
Remember, too, that your integration answer will always have a constant of integration, which means that you are going to add '+ C ' for all your answers. The various types of functions you will most commonly see are monomials, reciprocals, exponentials, and trigonometric functions. Certain rules like the constant rule and the power rule will also help you. Let's start with monomials.
Monomials are functions that have only one term. Some monomials are just constants, while others also involve variables. None of the variables have powers that are fractions; all the powers are whole integers. For example, f ( x ) = 6 is a constant monomial, while f ( x ) = x is a monomial with a variable.
When you see a constant monomial as your function, the answer when you integrate is our constant multiplied by the variable, plus our constant of integration. For example, if our function is f ( x ) = 6, then our answer will be the following:
We can write this in formula form as the following:
If our function is a monomial with variables like f ( x ) = x , then we will need the aid of the power rule which tells us the following:
The power rule tells us that if our function is a monomial involving variables, then our answer will be the variable raised to the current power plus 1, divided by our current power plus 1, plus our constant of integration. This is only if our current power is not -1. For example, if our function is f ( x ) = x , where our current power is 1, then our answer will be this:
Recall that if you don't see a power, it is always 1 because anything raised to the first power is itself.
Let's try another example. If our function is f ( x ) = x ^2, then our answer will be the following:
Whatever our current power is, our answer will be the variable raised to the next power divided by the next power. In the above example, our current power is 2, so our next power is 3. In our answer, we have a 3 for the variable's power and for the denominator following the power rule. If our monomial is a combination of a constant and a variable, we have the constant rule to help us. The constant rule looks like this:
The constant rule tells us to move the constant out of the integral and then to integrate the rest of the function. For example, if our function is f ( x ) = 6 x , then our integral and answer will be the following:
We've moved the 6 outside of the integral according to the constant rule, and then we integrated the x by itself using the power rule. For the answer, we simplified the 6 x ^2/2 to 3 x ^2 since 6 x divides evenly by 2.
Reciprocals and Exponentials
Another type of function we will deal with is the reciprocal. The integral of the reciprocal follows this formula:
The formula is telling us that when we integrate the reciprocal, the answer is the natural log of the absolute value of our variable plus our constant of integration. Exponential functions include the e ^ x function as well as the log( x ) function and these types of functions follow these formulas for integration:
The first formula tells us that when we have a function e ^ x , our answer for the integral will be e ^ x + C . The a in the middle integral formula stands for a constant. The middle formula tells us that when we have, for example, a function like 3^ x , then our answer after integrating will be 3^ x /log(3) + C . The integral formula tells us that the integral of the natural log of x function is x (log( x ) - 1) plus our constant of integration.
Our trigonometric functions include cosine, sine, and secant functions. They follow these formulas:
If you are integrating the cosine function, you will end up with the sine function plus the constant of integration. Integrating the sine function gives you the negative cosine function plus our constant of integration. If you see the secant function squared, your answer will be the tangent function plus our constant of integration.
Let's review. Integrating different functions involves referring to the formulas for each type of function along with applying the constant or power rule when necessary. The constant rule tells us to move the constant out of the integral and then to integrate the rest of the function. The power rule tells us that if our function is a monomial involving variables, then our answer will be the variable raised to the current power plus 1, divided by our current power plus 1, plus our constant of integration. Always remember your constant of integration when integrating.
Terms to Memorize
- Monomials : functions that have only one term
- Power rule : if the function is a monomial involving variables, then the answer will be the variable raised to the current power plus 1, divided by the current power plus 1, plus the constant of integration
- Constant rule : tells us to move the constant out of the integral and then to integrate the rest of the function
Learning Outcomes
As you move through the lesson, you could develop the capacity to:
- Determine whether a function is an integration problem
- Identify the formulas for reciprocals, trigonometric functions, exponentials and monomials
- Observe the power rule and constant rule
Unlock Your Education
See for yourself why 30 million people use study.com, become a study.com member and start learning now..
Already a member? Log In
Recommended Lessons and Courses for You
Related lessons, related courses, recommended lessons for you.

Integration Problems in Calculus | Examples & Solutions Related Study Materials
Browse by Courses
- High School Geometry: Tutoring Solution
- High School Trigonometry: Help and Review
- High School Trigonometry: Homework Help Resource
- CSET Math Subtest III (213) Prep
- Supplemental Math: Study Aid
- CLEP Precalculus Prep
- NY Regents Exam - Geometry: Help and Review
- NY Regents Exam - Geometry: Tutoring Solution
- NY Regents Exam - Integrated Algebra: Help and Review
- UExcel Statistics: Study Guide & Test Prep
- Calculus: Certificate Program
- Introduction to Statistics: Certificate Program
- College Algebra: Certificate Program
- CLEP Calculus Prep
- Precalculus: Tutoring Solution
Browse by Lessons
- Basic Calculus Types, Formulas & Rules
- Calculus Purpose & Applications in Real Life
- Calculus Definition, Branches & History
- Precalculus Assignment - Working with Polynomial Functions
- Polyhedron Project ideas
- Half Angle Formula | Quadrant Rule & Examples
- Perfect Parabola: Definition & Explanation
- Converse of a Theorem | Definition & Examples
- Identifying Lines in Space
- Polyhedron | Definition & Types
- Finding the Volume for a Sphere with a Radius of 4: How-To & Steps
- Converting 120 Degrees to Radians: How-To & Tutorial
- System of Equations Definition & Types
- Trigonometric Functions & Values | Overview & Examples
- Odd Functions | Overview, Examples & Graph
Create an account to start this course today Used by over 30 million students worldwide Create an account
Number Line
- \int e^x\cos(x)dx
- \int \cos^3(x)\sin (x)dx
- \int \frac{2x+1}{(x+5)^3}
- \int_{0}^{\pi}\sin(x)dx
- \int_{a}^{b} x^2dx
- \int_{0}^{2\pi}\cos^2(\theta)d\theta
- partial\:fractions\:\int_{0}^{1} \frac{32}{x^{2}-64}dx
- substitution\:\int\frac{e^{x}}{e^{x}+e^{-x}}dx,\:u=e^{x}
- What is the use of integration in real life?
- Integrations is used in various fields such as engineering to determine the shape and size of strcutures. In Physics to find the centre of gravity. In the field of graphical representation to build three-dimensional models.
- What is the best integral calculator?
- Symbolab is the best integral calculator solving indefinite integrals, definite integrals, improper integrals, double integrals, triple integrals, multiple integrals, antiderivatives, and more.
- What does to integrate mean?
- Integration is a way to sum up parts to find the whole. It is used to find the area under a curve by slicing it to small rectangles and summing up thier areas.
| 🌐 Languages | EN, ES, PT & more |
| 🏆 Practice | Improve your math skills |
|
| 😍 Step by step | In depth solution steps |
| ⭐️ Rating | based on 20924 reviews |
integral-calculator
- Advanced Math Solutions – Integral Calculator, common functions In the previous post we covered the basic integration rules (click here). Before we continue with more advanced...
Please add a message.
Message received. Thanks for the feedback.
Reset password New user? Sign up
Existing user? Log in
Integration Tricks
Already have an account? Log in here.
- Aareyan Manzoor
- Prasun Biswas
- Henry Maltby
- Christopher Williams
- Andrew Ellinor
- Mike Fuller
- Brandon Monsen
- Hua Zhi Vee
- Arjen Vreugdenhil
- Akeel Howell
- A Former Brilliant Member
- Aditya Khurmi
- Solden Stoll
- Enrique Mendez
- David Holcer
Many challenging integration problems can be solved surprisingly quickly by simply knowing the right technique to apply. While finding the right technique can be a matter of ingenuity, there are a dozen or so techniques that permit a more comprehensive approach to solving definite integrals.
Manipulations of definite integrals may rely upon specific limits for the integral, like with odd and even functions , or they may require directly changing the integrand itself, through some type of substitution . However, most integrals require a combination of techniques, and many of the more complicated approaches, like interpretation as a double integral , require multiple steps to reduce the expression.
Consider, for instance, the antiderivative
\[\displaystyle\int e^{- x^2} \, dx.\]
This is known as the Gaussian integral, after its usage in the Gaussian distribution , and it is well known to have no closed form. However, the improper integral
\[I = \int_0^\infty e^{- x^2} \, dx\]
may be evaluated precisely, using an integration trick . In fact, its value is given by the polar integral
\[I^2 = \int_0^\infty \int_0^\infty e^{-x^2} e^{-y^2} \, dy\, dx = \int_0^{\pi/2} \int_0^\infty r e^{-r^2} \, dr\, d\theta.\]
Without such a method for exact evaluation of the integral, the Gaussian (normal) distribution would be significantly more complicated. Such integrals appear throughout physics , statistics , and mathematics .
Odd and Even Functions
Reflections, cyclic points, inverse functions, integration by parts, trigonometric substitutions, weierstrass substitution, taylor series, differentiation under the integral sign, changing to a double integral, harmonic functions.
An odd function \(o(x)\) satisfies \(o(x) = - o(-x)\) for all \(x\). Therefore, for any finite \(t\),
\[\int_{-t}^t o(x) \, dx = 0.\]
An even function \(e(x)\) satisfies \(e(x) = e(-x)\) for all \(x\). Therefore, for any \(t\),
\[\int_{-t}^t e(x) \, dx = 2 \int_0^t e(x) \, dx.\]
Evaluate \[\int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx.\] Notice that the integrand is an odd function. So, \[\begin{align*} \int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx &= \int_{-1}^{1} \frac{(-x)^3-2(-x)}{\sqrt{(-x)^4+1}} \, d(-x) \\ &= - \int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx \\ &= 0. \end{align*}\] The final equivalence comes from the fact that the integral is equal to the negative of itself. Therefore, it is \(0\). \(_\square\)
\[ \large \int _{ -1 }^{ 1 }{ \frac { \sin { x } }{ 1+{ x }^{ 2 }+{ x }^{ 4 } } \, dx } = \, ? \]
A similar method to the above is to reverse the interval of integration: to "integrate backwards." For a function \(f\) and real numbers \(a < b\),
\[\int_a^b f(x) \, dx = \int_a^b f(a+b-x) \, dx.\]
Instead of the function being centered at \(0\), the function is now centered at \(\tfrac{a+b}{2}\). Then,
\[\int_a^b f(x) \, dx = \frac{1}{2} \int_a^b f(x) + f(a+b-x) \, dx.\]
Evaluate \[ \int_3^7 \frac{\ln(x+2)}{\ln\big(24+10x-x^2\big)} \, dx.\] We have \[\begin{align*} \int_3^7 \frac{\ln(x+2)}{\ln\big(24+10x-x^2\big)} \, dx &= \int_3^7 \frac{\ln(x+2)}{\ln(x+2) + \ln(12-x)} \, dx \\\\ &= \frac{1}{2} \int_3^7 \frac{\ln(12-x) + \ln(x+2)}{\ln(x+2) + \ln(12-x)} \, dx \\\\ &= 2.\ _\square \end{align*}\]
Let \(f(x)\) be a real-valued function continuous on \(\left[0,2\right]\) such that \(f(x)=f(2x)\) for all \(x\). If
\[\int_0^1 f(x) dx = 100,\]
then what is the value of
\[\int_0^2 f(x)dx ?\]
Suppose the function \(f\) has bounded antiderivative on \([0, \, \infty]\). Then, via the u-substitution \(x \mapsto \tfrac{1}{x}\),
\[\int_0^\infty f(x) \, dx = \frac{1}{2} \int_0^\infty f(x) + \frac{f\big(\frac{1}{x}\big)}{x^2} \, dx.\]
Evaluate \[ \int_0^\infty \frac{\ln (2x)}{1 + x^2} \, dx.\] We have \[\begin{align} \int_0^\infty \frac{\ln (2x)}{1 + x^2} \, dx &= \frac{1}{2} \int_0^\infty \frac{\ln(2x) + \ln\big(2x^{-1}\big)}{1 + x^2} \, dx \\\\ &= \frac{2\ln 2}{2} \int_0^\infty \frac{1}{1 + x^2} \, dx \\\\ &= \frac{\pi \ln 2}{2}.\ _\square \end{align}\]
Evaluate the integral \(\displaystyle \int_{0}^{\infty} \frac{\ln x}{x^2+2x+4} \, dx.\)
Round your answer to three decimal places.
This section is currently incomplete. Let's join hands to build this wiki. Feel free to add anything you know about this topic!
There are more transformations than simply reflections and inversions that maintain the interval of integration, but they are not as common.
Suppose the function \(f\) is one-to-one and increasing. Then, a geometric equivalence may be established:
\[\int_a^b f(x) \, dx + \int_{f(a)}^{f(b)} f^{-1}(x) \, dx = bf(b) - af(a).\]
Suppose the function \(f\) is one-to-one and decreasing. Then, another geometric equivalence may be established:
\[\int_a^b f(x) \, dx - \int_{f(b)}^{f(a)} f^{-1}(x) \, dx = (b-a)f(b) - a\big(f(a)-f(b)\big).\]
Let \(f(x)\) be a one-to-one continuous function such that \(f(1)=4\) and \(f(6)=2\), and assume \(\displaystyle \int_1^6 f(x) \, dx = 15\). Calculate \(\displaystyle \int_2^4 f^{-1}(x) \, dx\). The region bounded by \(f\), \(x = 1\), and \(y = 2\) must have area \(5\), implying the integral in question corresponds to the area \(5 + 1 \cdot (4 - 2) = \boxed{7}\). The above formula for decreasing functions provides the same answer. \(_\square\)
Integration by parts provides a way to change the integrand directly, and like the exploration of inverse functions, it is a geometric statement. However, this is a statement about the geometry of calculus operators, and any visualization of it would lie in an entirely different space. However, the same intuition can apply. Integration by parts is a very powerful tool, and many problems on this page could be solved by this (and more elementary methods) without the need for anything more complicated.
Integration by parts states that for any differentiable functions \(u(x)\) and \(v(x)\), the following equivalence holds:
\[ \int u(x) v'(x) \, dx = u(x) v(x) - \int v(x) u'(x) \, dx. \]
This can be thought of as a "backwards" application of the product rule .
Evaluate \[\int_1^7 \ln(1 + x) \, dx.\] Let \(u(x) = \ln(1 + x)\) and \(v(x) = x + 1\). Then, \[\begin{align} \int_1^7 \ln(1 + x) \, dx &= \big[(x+1)\ln(x+1)\big]_1^7 - \int_1^7 \frac{x+1}{x+1} \, dx \\ &= 8\ln 8 - 2\ln 2 - 6 \\ &= 22 \ln 2 - 6.\ _\square \end{align}\]
The (adjusted) beta function \(B(m, \, n)\) is defined for nonnegative integers \(m\) and \(n\) as \[B(m, \, n) = \int_0^1 x^{m}(1-x)^{n} \, dx.\] Find a closed form for \(B(m, \, n)\). Note that \(B(0, \, n) = \frac{1}{n+1}\). Now, suppose \(n\) is fixed, and note for \(m > 0\), \[\begin{align} B(m, \, n) &= \int_0^1 x^m (1-x)^n \, dx \\ &= 0 - \frac{m}{n+1} \int_0^1 x^{m-1} \cdot \left(-(1-x)^{n+1}\right) \, dx \\ &= \frac{m}{n+1} B(m-1, \, n+1). \end{align}\] Thus, \(B(m, \, n) = \frac{m}{n+1} \cdot \frac{m-1}{n+2} \cdots \frac{1}{n+m} B(0, n+m) = \frac{m! n!}{(m+n+1)!}.\) \(_\square\) Learn more about the beta function (with correctly off-set indices) here .
\[ \int_0^1 \left(1-x^2\right)^9 x^9 \, dx \]
Let \(I\) denote the value of the integral above. What is the sum of digits of \(I^{-1}?\)
When solving integrals with trigonometric functions, trigonometric identities create shortcuts! The Integration Of Trigonometric Functions wiki goes into this in detail, but below are a few examples.
The first identity is \(\sin^2x+\cos^2x=1.\)
We have \[\begin{align} \int(\sin x+\cos x)^2\, dx &=\int\left(\sin^2x+2\sin x\cos x+\cos^2x\right)\, dx\\ &=\int(1+\sin 2x)\, dx\\ &=x-\dfrac{1}{2}\cos 2x+C, \end{align}\] where \(C\) is the constant of integration.
Here is an example of a less obvious application of that identity:
We have \[\begin{align} \int_0^\frac{\pi}{2}\sin^5x\, dx &=\int_0^\frac{\pi}{2}\sin x\left(1-\cos^2x\right)^2\, dx\\ &=-\int_1^0\left(1-u^2\right)^2\, du\\ &=\int_0^1\left(1-u^2\right)^2\, du\\ &=\frac{8}{15}. \end{align}\]
Other examples that can be used are the double-angle formulas , which can be used in the integrals of \(\sin^2\theta\) and \(\cos^2\theta,\) as well as others.
We have \[\begin{align} \int\frac{\cos 2x}{\sin x+\cos x}\, dx &=\int\frac{\cos^2x-\sin^2x}{\sin x+\cos x}\, dx\\ &=\int(\cos x-\sin x)\, dx\\ &=\sin x+\cos x+C, \end{align}\] where \(C\) is the constant of integration.
Finally, the product-to-sum identities help to solve complex integrals.
We have \[\begin{align} \int\sin 2015x \sin 2016x \, dx &=\dfrac{1}{2}\int(\cos x-\cos 4031x)\, dx\\ &=\dfrac{\sin x}{2}-\dfrac{\sin 4031x}{8062}+C, \end{align}\] where \(C\) is the constant of integration.
One of the most powerful substitutions using trigonometric functions is the Weierstrass substitution of \(t=\tan\frac{\theta}{2}.\) This is most easily seen in rational functions involving trigonometric functions. Through trigonometric identities and manipulation \(\sin\theta=\frac{2t}{1+t^2},\) \(\cos\theta=\frac{1-t^2}{1+t^2},\) and \(d\theta=\frac{2\ dt}{1+t^2}.\) This can often transform the integral into the integral of a rational function, as seen in the following example:
Find the value of \(\displaystyle\int_0^\frac{\pi}{2}\frac{dx}{2+\cos x}.\) Use the Weierstrass substitution \(\cos x=\frac{1-t^2}{1+t^2}\) and \(dx=\frac{2dt}{1+t^2}:\) \[\int_0^\frac{\pi}{2}\frac{dx}{2+\cos x}\ =\int_0^1\frac{\frac{2dt}{1+t^2}}{2+\frac{1-t^2}{1+t^2}}=\int_0^1\frac{2}{t^2+3}dt.\] This integral can be finished by a \(u\)-substitution and application of the derivative of arctangent. \(_\square\)
The Weierstrass substitution can also be applied to a rather common integral, \(\displaystyle\int\csc x\ dx.\) A common method of solving this question is a "clever" multiplication by \(\frac{1}{1},\) but the Weierstrass substitution is easier to apply.
We have \[\int\csc \theta\, d\theta=\int\frac{d\theta}{\sin\theta}=\int\frac{\hspace{3mm} \frac{2dt}{1+t^2}\hspace{3mm} }{\frac{2t}{1+t^2}}=\int\frac{dt}{t}=\ln t+C,\] where \(C\) is the constant of integration. All that's needed is to re-substitute \(t=\tan\frac{\theta}{2}\) to obtain the final value of \[\ln\left(\tan\frac{\theta}{2}\right)+C=-\ln(\cot x+\csc x)+C=\ln\frac{\sin\theta}{\cos\theta+1}+C.\]
A final use of the Weierstrass substitution is the "reverse Weierstrass substitution," which involves simplifying the integral of a rational function with trigonometry.
Find the value of \(\displaystyle\int_0^1\dfrac{\arcsin\frac{2x}{1+x^2}}{1+x^2}\, dx\). Recall that in the Weierstrass substitution, \(\frac{2x}{1+x^2}=\sin\theta\) and \(\frac{2dx}{1+x^2}=d\theta.\) Then the above can be transformed to \[\displaystyle\int_0^\frac{\pi}{2}\frac{\sin^{-1}(\sin\theta)}{2}\, d\theta=\displaystyle\int_0^\frac{\pi}{2}\frac{\theta}{2}\, d\theta.\] This is the integral of a polynomial, which evaluates to \(\frac{\pi^2}{16}.\) \(_\square\)
\[\int_0^1\frac{x^4\left(1-x^2\right)^5}{\left(1+x^2\right)^{10}}\, dx=A\]
Given the above, find \(\frac{1}{A}.\)
Main article: Taylor Series
Some functions like \(\tfrac{1}{1-x}\), \(\ln(1 - x)\), \(\arctan x\), and \(e^x\) have nice Taylor expansions that, together with term-by-term integration, can lead to a closed-form answer. The monotone convergence theorem states that in most cases where the integral does exist (as should generally be the case when evaluating an integral), the summation and integral may be interchanged. For more information, see Double Integrals .
Evaluate \[ \int_0^1 \ln x \ln(1 - x) \, dx.\] Note \[ \int_0^1 \ln x \ln(1-x) \, dx = - \int_0^1 \sum_{k = 1}^\infty \frac{x^k \ln x}{k} \, dx.\] Since the monotone convergence theorem applies here, this is equal to \[\begin{align} - \sum_{k = 1}^\infty \int_0^1 \frac{x^k \ln x}{k} \, dx &= \sum_{k = 1}^\infty \frac{1}{k (k+1)^2} \\ &= \sum_{k = 1}^\infty \frac{1}{k(k + 1)} - \sum_{k = 1}^\infty \frac{1}{(k + 1)^2} \\ &= 2 - \frac{\pi^2}{6}.\ _\square \end{align}\]
Main article: Differentiation under the integral sign
Differentiating under the integral sign is a useful method for evaluating certain integrals which might be harder using other methods. This method of integrating was so frequently used by Richard Feynman that it is often referred to as Feynman's integration trick .
\[\dfrac{d}{dx} \displaystyle \int_{g(x)}^{h(x)} f(x,t)dt = f\big(x,h(x)\big)\dfrac{d}{dx}h(x) - f\big(x,g(x)\big)\dfrac{d}{dx}g(x) + \displaystyle \int_{g(x)}^{h(x)}\dfrac{\partial}{\partial x}f(x,t)dt. \]
Compute \[ \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-7x}}{x} \, dx. \] Let \( I(a) = \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-ax}}{x}\, dx.\) Upon differentiating under the integral sign, the equation becomes \[\begin{align} \dfrac{\partial I}{\partial a} &= \displaystyle \int_{0}^{\infty} \dfrac{\partial }{\partial a}\dfrac{e^{-5x} - e^{-ax}}{x}\, dx \\ &= \displaystyle \int_{0}^{\infty} \dfrac{0 -(-xe^{-ax})}{x}\, dx \\ &= \displaystyle \int_{0}^{\infty} e^{-ax}\, dx. \end{align}\] Now, integrating with respect to \(x\) yields the following: \[ \dfrac{\partial I}{\partial a} = \left[\dfrac{e^{-ax}}{a}\right]_{\infty}^{0} \implies \dfrac{\partial I}{\partial a} = \dfrac{1}{a} .\] Integrating both sides with respect to \(a,\) \[ I(a) = \displaystyle \int \dfrac{1}{a}\, da + C \Rightarrow I(a) = \ln a + C, \qquad (1) \] where \(C\) is the constant of integration. Notice that \( I(5) = \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-5x}}{x}\, dx = \int_{0}^{\infty} 0\, dx = 0. \) Substituting these values in \((1)\) gives \[ 0 = \ln 5 + C \implies C = -\ln 5 \implies I(a) = \ln\dfrac{a}{5}.\] To obtain the required integral, substitute \(a = 7\): \[ I(7) = \ln\dfrac{7}{5} \implies \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-7x}}{x}\, dx = \ln\dfrac{7}{5}. \ _\square\]
Compute \[ \displaystyle \int_{0}^{\infty} \dfrac{\sin x}{x}\, dx. \] Let \( I(a) = \displaystyle \int_{0}^{\infty} e^{-ax}\dfrac{\sin x}{x}\, dx. \) Then differentiating under the integral sign gives \[ \dfrac{\partial I(a)}{\partial a} = \displaystyle \int_{0}^{\infty} \dfrac{\partial}{\partial a} e^{-ax}\dfrac{\sin x}{x}\, dx= -\displaystyle \int_{0}^{\infty} e^{-ax}\sin x\, dx. \] Integrating with respect to \(x,\) \[ \dfrac{\partial I(a)}{\partial a} = \left[\dfrac{e^{-ax}\left(a\sin x + \cos x\right)}{a^{2}+1}\right]_{0}^{\infty} = -\dfrac{1}{1+a^{2}}. \] Integrating with respect to \(a,\) \[ I(a) = \displaystyle \int -\dfrac{1}{1+a^{2}}da = -\tan^{-1} a + C, \] where \(C\) is the constant of integration. Now, \[ \displaystyle \lim_{a\rightarrow \infty} = \displaystyle \int_{0}^{\infty} \displaystyle \lim_{a\rightarrow \infty} e^{-ax}\dfrac{\sin x}{x}dx = 0 .\] Using the above information, \[ 0 = -\displaystyle \lim_{a \rightarrow \infty} \tan^{-1} a + C \Rightarrow C = \dfrac{\pi}{2} \Rightarrow I(a) = \dfrac{\pi}{2} - \tan^{-1} a. \] To get our integral, we let \(a = 0\) to obtain \[ I(0) = \dfrac{\pi}{2} - \tan^{-1} 0 = \dfrac{\pi}{2}. \] Therefore, \( \displaystyle \int_{0}^{\infty} \dfrac{\sin x}{x}\, dx = \dfrac{\pi}{2} . \ _\square\)
\[ \int_0^1 x^{50} (\ln x)^{150} \, dx \]
If the value of the integral above is equal to
\[ \dfrac{A!}{B^C}, \]
where \(A,B,\) and \(C\) are positive integers, find the value of \(A+B+C\).
Bonus : Generalize \( \displaystyle \int_0^1 x^{m} (\ln x)^{n} \, dx \).
Find the value of the following integral:
\[ \displaystyle\int_{0}^{\infty} \dfrac{1}{x} \left(\tan^{-1} \pi x - \tan^{-1}x\right)\,dx.\]
Sometimes, the integrand looks like it has already been integrated. This may signal that the integral is better interpreted as a double integral . There are more possibilities for \(u\)-substitutions when two variables can be manipulated (polar, skewed, etc), and simply changing the order of integration may suffice to simplify the integral.
In many ways, this is a dual method to differentiation under the integral sign. The main difference is that the extra variable is interpreted inside of the variable rather than outside of it. In most cases where one works, both could work; in some cases, only one approach works nicely, so it is good to know both.
Suppose \(a\) and \(b\) are real numbers, \(f\) a function, and \(I = \int_a^b f(x) \, dx.\) If \(f(x) = g(x, s) - g(x, r)\) for some constants \(r\) and \( s\), then \[I = \int_a^b \int_r^s \frac{\partial}{\partial t} g(x,t) \, dt \, dx.\]
Supposing Fubini's theorem holds, the order of integration may be swapped or otherwise altered.
Evaluate \[\int_0^{\infty} \frac{e^{\pi x} - e^{x}}{x(e^{\pi x}+1)(e^{x}+1)} \, dx.\] We have \[ \begin{align*} \int_0^{\infty} \frac{e^{\pi x} - e^{x}}{x(e^{\pi x}+1)(e^{x}+1)} \, dx &= \int_0^\infty \frac{1}{x (e^x + 1)} - \frac{1}{x (e^{\pi x} + 1)} \, dx \\ &= \int_0^\infty \int_1^\pi \frac{e^{tx}}{(e^{tx} + 1)^2} \, dt \, dx \\ &= \int_1^\pi \int_0^\infty \frac{e^{tx}}{(e^{tx} + 1)^2} \, dx \, dt \\ &= \int_1^\pi \left[ - \frac{1}{t (e^{tx} + 1)} \right]_0^\infty \, dt \\ &= \int_1^\pi \frac{1}{(1 + 1)t} \, dt \\ &= \frac{\ln \pi}{2}.\ _\square \end{align*} \]
In complex analysis, a harmonic function is a real-valued function that is the real or imaginary part of a complex-differentiable function. In multivariable calculus, it is a function \(f(x, \, y)\) such that \(\left(\frac{\partial}{\partial x}\right)^2 f + \left( \frac{\partial}{\partial y}\right)^2f = 0.\) Generally, such facts from fields afar are not applicable to the evaluation of real integrals; however, the harmonic functions have a special property that greatly simplifies integration over circles .
Suppose \(f\) is a bivariate harmonic function, \((a, \, b)\) is a point in the plane, and \(r\) is a positive real number. Then, \[ \int_0^{2\pi} f(a + r\cos\theta, \, b + r\sin\theta) \, d\theta = 2\pi f(a, \, b).\]
Evaluate \[\int_0^{2\pi} e^{\cos x} \cos(\sin x) \, dx.\] Consider the function \(f(x, \, y) = e^x \cos y.\) Note that \[ \left(\frac{\partial}{\partial x}\right)^2 f + \left(\frac{\partial}{\partial y}\right)^2 f = e^x \cos y + e^x (- \cos y) = 0.\] Therefore, \(f\) is a harmonic function, and it follows that \[\int_0^{2\pi} e^{\cos x} \cos(\sin x) \, dx = 2\pi e^0 \cos(0) = 2\pi.\ _\square\]
Problem Loading...
Note Loading...
Set Loading...

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

7.6E: Exercises for Numerical Integration
- Last updated
- Save as PDF
- Page ID 24578

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
In exercises 1 - 5, approximate the following integrals using either the midpoint rule, trapezoidal rule, or Simpson’s rule as indicated. (Round answers to three decimal places.)
1) \( \displaystyle ∫^2_1\frac{dx}{x};\) trapezoidal rule; \( n=5\)
2) \( \displaystyle ∫^3_0\sqrt{4+x^3}\;dx;\) trapezoidal rule; \( n=6\)
3) \( \displaystyle ∫^3_0\sqrt{4+x^3}\;dx;\) Simpson’s rule; \( n=6\)
4) \( \displaystyle ∫^{12}_0x^2\;dx;\) midpoint rule; \( n=6\)
5) \( \displaystyle ∫^1_0\sin^2(\pi x)\;dx;\) midpoint rule; \( n=3\)
6) Use the midpoint rule with eight subdivisions to estimate \( \displaystyle ∫^4_2x^2\;dx.\)
7) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^4_2x^2\;dx.\)
8) Find the exact value of \( \displaystyle ∫^4_2x^2\;dx.\) Find the error of approximation between the exact value and the value calculated using the trapezoidal rule with four subdivisions. Draw a graph to illustrate.
Approximate the integral to four decimal places using the indicated rule.
9) \( \displaystyle ∫^1_0\sin^2(\pi x)\;dx;\) trapezoidal rule; \( n=6\)
10) \( \displaystyle ∫^3_0\frac{1}{1+x^3}\;dx;\) trapezoidal rule; \( n=6\)
11) \( \displaystyle ∫^3_0\frac{1}{1+x^3}\;dx;\) Simpson’s rule; \( n=6\)
12) \( \displaystyle ∫^{0.8}_0e^{−x^2}\;dx;\) trapezoidal rule; \( n=4\)
13) \( \displaystyle ∫^{0.8}_0e^{−x^2}\;dx;\) Simpson’s rule; \( n=4\)
14) \(\displaystyle ∫^{0.4}_0\sin(x^2)\;dx;\) trapezoidal rule; \( n=4\)
15) \(\displaystyle ∫^{0.4}_0\sin(x^2)\;dx;\) Simpson’s rule; \( n=4\)
16) \( \displaystyle ∫^{0.5}_{0.1}\frac{\cos x}{x}\;dx;\) trapezoidal rule; \(n=4\)
17) \( \displaystyle ∫^{0.5}_{0.1}\frac{\cos x}{x}\;dx;\) Simpson’s rule; \(n=4\)
18) Evaluate \( \displaystyle ∫^1_0\frac{dx}{1+x^2}\) exactly and show that the result is \( π/4\). Then, find the approximate value of the integral using the trapezoidal rule with \( n=4\) subdivisions. Use the result to approximate the value of \( π\).
19) Approximate \( \displaystyle ∫^4_2\frac{1}{\ln x}\;dx\) using the midpoint rule with four subdivisions to four decimal places.
20) Approximate \( \displaystyle ∫^4_2\frac{1}{\ln x}\;dx\) using the trapezoidal rule with eight subdivisions to four decimal places.
21) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^{0.8}_0x^3\;dx\) to four decimal places.
22) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^{0.8}_0x^3\;dx.\) Compare this value with the exact value and find the error estimate.
23) Using Simpson’s rule with four subdivisions, find \( \displaystyle ∫^{π/2}_0\cos(x)\;dx.\)
24) Show that the exact value of \( \displaystyle ∫^1_0xe^{−x}\;dx=1−\frac{2}{e}\). Find the absolute error if you approximate the integral using the midpoint rule with 16 subdivisions.
25) Given \( \displaystyle ∫^1_0xe^{−x}\;dx=1−\frac{2}{e},\) use the trapezoidal rule with 16 subdivisions to approximate the integral and find the absolute error.
26) Find an upper bound for the error in estimating \( \displaystyle ∫^3_0(5x+4)\;dx\) using the trapezoidal rule with six steps.
27) Find an upper bound for the error in estimating \( \displaystyle ∫^5_4\frac{1}{(x−1)^2}\;dx\) using the trapezoidal rule with seven subdivisions.
28) Find an upper bound for the error in estimating \( \displaystyle ∫^3_0(6x^2−1)\;dx\) using Simpson’s rule with \( n=10\) steps.
29) Find an upper bound for the error in estimating \( \displaystyle ∫^5_2\frac{1}{x−1}\;dx\) using Simpson’s rule with \( n=10\) steps.
30) Find an upper bound for the error in estimating \( \displaystyle ∫^π_02x\cos(x)\;dx\) using Simpson’s rule with four steps.
31) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^4_1(5x^2+8)\;dx\) with an error magnitude of less than 0.0001 using the trapezoidal rule.
32) Determine a value of n such that the trapezoidal rule will approximate \( \displaystyle ∫^1_0\sqrt{1+x^2}\;dx\) with an error of no more than 0.01.
33) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^3_2(2x^3+4x)\;dx\) with an error of magnitude less than 0.0001 using the trapezoidal rule.
34) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^4_3\frac{1}{(x−1)^2}\;dx\) with an error magnitude of less than 0.0001 using the trapezoidal rule.
35) Use Simpson’s rule with four subdivisions to approximate the area under the probability density function \( y=\frac{1}{\sqrt{2π}}e^{−x^2/2}\) from \( x=0\) to \( x=0.4\).
36) Use Simpson’s rule with \( n=14\) to approximate (to three decimal places) the area of the region bounded by the graphs of \( y=0, x=0,\) and \( x=π/2.\)
37) The length of one arch of the curve \( y=3\sin(2x)\) is given by \( L=∫^{π/2}_0\sqrt{1+36\cos^2(2x)}\;dx.\) Estimate L using the trapezoidal rule with \( n=6\).
38) The length of the ellipse \( x=a\cos(t),y=b\sin(t),0≤t≤2π\) is given by \( L=4a∫^{π/2}_0\sqrt{1−e^2\cos^2(t)}dt\), where e is the eccentricity of the ellipse. Use Simpson’s rule with \( n=6\) subdivisions to estimate the length of the ellipse when \( a=2\) and \( e=1/3.\)
39) Estimate the area of the surface generated by revolving the curve \( y=\cos(2x),0≤x≤\frac{π}{4}\) about the x-axis. Use the trapezoidal rule with six subdivisions.
40) Estimate the area of the surface generated by revolving the curve \( y=2x^2, 0≤x≤3\) about the x-axis. Use Simpson’s rule with \( n=6.\)
41) The growth rate of a certain tree (in feet) is given by \( y=\dfrac{2}{t+1}+e^{−t^2/2},\) where t is time in years. Estimate the growth of the tree through the end of the second year by using Simpson’s rule, using two subintervals. (Round the answer to the nearest hundredth.)
42) [T] Use a calculator to approximate \( \displaystyle ∫^1_0\sin(πx)\;dx\) using the midpoint rule with 25 subdivisions. Compute the relative error of approximation.
43) [T] Given \( \displaystyle ∫^5_1(3x^2−2x)\;dx=100,\) approximate the value of this integral using the midpoint rule with 16 subdivisions and determine the absolute error.
44) Given that we know the Fundamental Theorem of Calculus, why would we want to develop numerical methods for definite integrals?
45) The table represents the coordinates \( (x,y)\) that give the boundary of a lot. The units of measurement are meters. Use the trapezoidal rule to estimate the number of square meters of land that is in this lot.
| \( x\) | \( y\) | \( x\) | \( y\) |
| 0 | 125 | 600 | 95 |
| 100 | 125 | 700 | 88 |
| 200 | 120 | 800 | 75 |
| 300 | 112 | 900 | 35 |
| 400 | 90 | 1000 | 0 |
| 500 | 90 | | |
46) Choose the correct answer. When Simpson’s rule is used to approximate the definite integral, it is necessary that the number of partitions be____
a. an even number
b. odd number
c. either an even or an odd number
d. a multiple of 4
47) The “Simpson” sum is based on the area under a ____.
48) The error formula for Simpson’s rule depends on___.
a. \( f(x)\)
b. \( f′(x)\)
c. \( f^{(4)}(x)\)
d. the number of steps

- Derivation of Formulas
- Engineering Economy
- General Engineering
- Spherical Trigonometry
- Solid Geometry
- Analytic Geometry
Integral Calculus
- Differential Equations
- Advance Engineering Mathematics
- Strength of Materials
- Structural Analysis
- CE Board: Math
- CE Board: Hydro Geo
- CE Board: Design
- Timber Design
- Reinforced Concrete
- Geotechnical Engineering
- Basic Engineering Math
- General Discussions
Breadcrumbs
1. $\displaystyle \int du = u + C$
2. $\displaystyle \int a \, du = a\int du$
3. $\displaystyle \int (du + dv + ... + dz) = \int du + \int dv + ... + \int dz$
4. $\displaystyle \int f (x)\,dx = F(x) + C$
5. $\displaystyle \int_a^b f(x) \, dx = F(b) - F(a)$
6. $\displaystyle \int_a^b f(x) \, dx = -\int_b^a f(x) \, dx$
7. $\displaystyle \int_a^b f(x) \, dx = \int_a^c f(x) \, dx + \int_c^b f(x) \, dx$
8. $\displaystyle \int_a^b f(x) \, dx = \int_a^b f(z) \, dz$
9. $\displaystyle \int u^n \, du = \dfrac{u^{n + 1}}{n + 1} + C; \, n \neq -1$
10. $\displaystyle \int \dfrac{du}{u} = \ln u + C$
11. $\displaystyle \int a^u \, du = \dfrac{a^u}{\ln a} + C, \,\, a > 0, \,\, a \neq 1$
12. $\displaystyle \int e^u \, du = e^u + C$
13. $\displaystyle \int \sin u \, du = -\cos u + C$
14. $\displaystyle \int \cos u \, du = \sin u + C$
15. $\displaystyle \int \sec^2 u \, du = \tan u + C$
16. $\displaystyle \int \csc^2 u \, du = -\cot u + C$
17. $\displaystyle \int \sec u \, \tan u \, du = \sec u + C$
18. $\displaystyle \int \csc u \, \cot u \, du = -\csc u + C$
19. $\displaystyle \int \tan u \, du = \ln (\sec u) + C = -\ln (\cos u) + C$
20. $\displaystyle \int \cot u \, du = \ln (\sin u) + C$
21. $\displaystyle \int \sec u \, du = \ln (\sec u + \tan u) + C$
22. $\displaystyle \int \csc u \, du = \ln (\csc u - \cot u) + C = -\ln (\csc u + \cot u) + C$
23. $\displaystyle \int \dfrac{du}{\sqrt{a^2 - u^2}} = \arcsin \, \dfrac{u}{a} + C, \,\,\, a > 0$
24. $\displaystyle \int \dfrac{du}{a^2 + u^2} = \dfrac{1}{a}\arctan \, \dfrac{u}{a} + C$
25. $\displaystyle \int \dfrac{du}{u\sqrt{u^2 - a^2}} = \dfrac{1}{a} {\rm arcsec} \, \dfrac{u}{a} + C$
26. $\displaystyle \int u\,dv = uv - \int v\, du$
Book navigation
- Chapter 1 - Fundamental Theorems of Calculus
- Chapter 2 - Fundamental Integration Formulas
- Chapter 3 - Techniques of Integration
- Chapter 4 - Applications of Integration

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
Graph your math problems
Practice, practice, practice

Get math help in your language
- Skip to primary navigation
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Don't Miss a Post! Subscribe

- Educational AI
- Edtech Tools
- Edtech Apps
- Teacher Resources
- Special Education
- Edtech for Kids
- Buying Guides for Teachers

Educators Technology
Innovative EdTech for teachers, educators, parents, and students
Characteristics of The 21st Century Learning
By Med Kharbach, PhD | Last Update: May 9, 2024

Welcome back to our ongoing series on 21st-century education, where we delve into various themes that shape the educational landscape of our time. Drawing from my experience as an EdTech blogger and educator, I’ve been sharing insights and reflections on this dynamic and evolving field. In previous posts, we explored the characteristics of 21st-century teachers , characteristics of the 21st century classroom , and the traits of 21st-century learners . Today, we turn our focus to the characteristics of 21st-century learning itself.
To kick things off, we’ll start with a clear definition of what 21st-century learning entails, setting the stage for a deeper exploration of its features and implications.
It’s important to note that while technology undeniably plays a pivotal role in this discussion, it’s not the sole focus. Yes, technology is a critical medium that has transformed the educational landscape, but it’s the learning habits and skills that arise from this digital integration that truly define 21st-century learning.
We’re looking at a paradigm where technology is intertwined with critical thinking, creativity, collaboration, and other key skills, preparing learners not just to succeed academically but to thrive in life beyond the classroom. So, let’s dive in and unravel the layers of 21st-century learning, understanding its significance and how it shapes the learners of today and tomorrow.
What is 21st Century Learning
At its core, 21st-century learning is student-centered, focusing on developing essential life skills alongside academic knowledge. This modern educational paradigm is about nurturing essential life skills in tandem with academic knowledge, tailored to meet the demands of our rapidly evolving world. It’s a significant shift from the conventional models most of us were accustomed to, introducing new skill sets and learning players that are vital for success in today’s global landscape.
This approach isn’t just a slight deviation from past educational practices; it’s a comprehensive transformation. To say that ‘learning is just learning’ or to dismiss the 21st century as a mere label is to overlook the profound changes in how we perceive and engage with knowledge. The 21st-century learning model acknowledges the dynamic nature of the world we live in, focusing on developing skills that are crucial for navigating and thriving in it.
Key Components and Objectives of 21st-Century Learning
The key components of 21st century learning include:
- Critical Thinking and Problem Solving: Encouraging students to think deeply, question assumptions, and solve complex problems.
- Collaboration and Communication: Promoting teamwork and effective communication, both in person and through digital platforms.
- Creativity and Innovation: Fostering original thinking and the ability to generate new ideas and solutions.
- Digital Literacy: Equipping students with the skills to navigate and utilize technology effectively and responsibly.
- Global Awareness: Cultivating an understanding of global issues and diverse cultures, promoting empathy and open-mindedness.
- Lifelong Learning: Instilling a love for learning and the skills to continue learning independently throughout life.

Traditional Learning Models Vs 21st Century Learning Models
To better understand the nature of 21st century learning, we need to compare it to what is called, for a lack of a name, traditional learning (I am not fan of these labels). Indeed, the transition from traditional learning models to 21st-century approaches marks a significant shift in educational philosophy and practice. Traditional education often emphasizes rote memorization, standardized testing, and a one-size-fits-all teaching approach. In contrast, 21st-century learning is characterized by:
- Personalized and Adaptive Learning: Tailoring education to individual student needs, abilities, and interests.
- Project-Based and Experiential Learning: Engaging students in real-world projects and hands-on experiences that make learning relevant and exciting.
- Technological Integration: Using technology not just as a tool for teaching but as a part of the learning process itself, enabling new ways of learning, collaborating, and creating.
- Flexible and Dynamic Classrooms: Moving away from traditional classroom layouts to create spaces that accommodate various learning styles and activities.
- Teacher as Facilitator: Redefining the role of the teacher from a source of information to a facilitator of learning, guiding and supporting students in their educational journey.
Here is a table capturing what I think are some of the main differences between the two learning models:
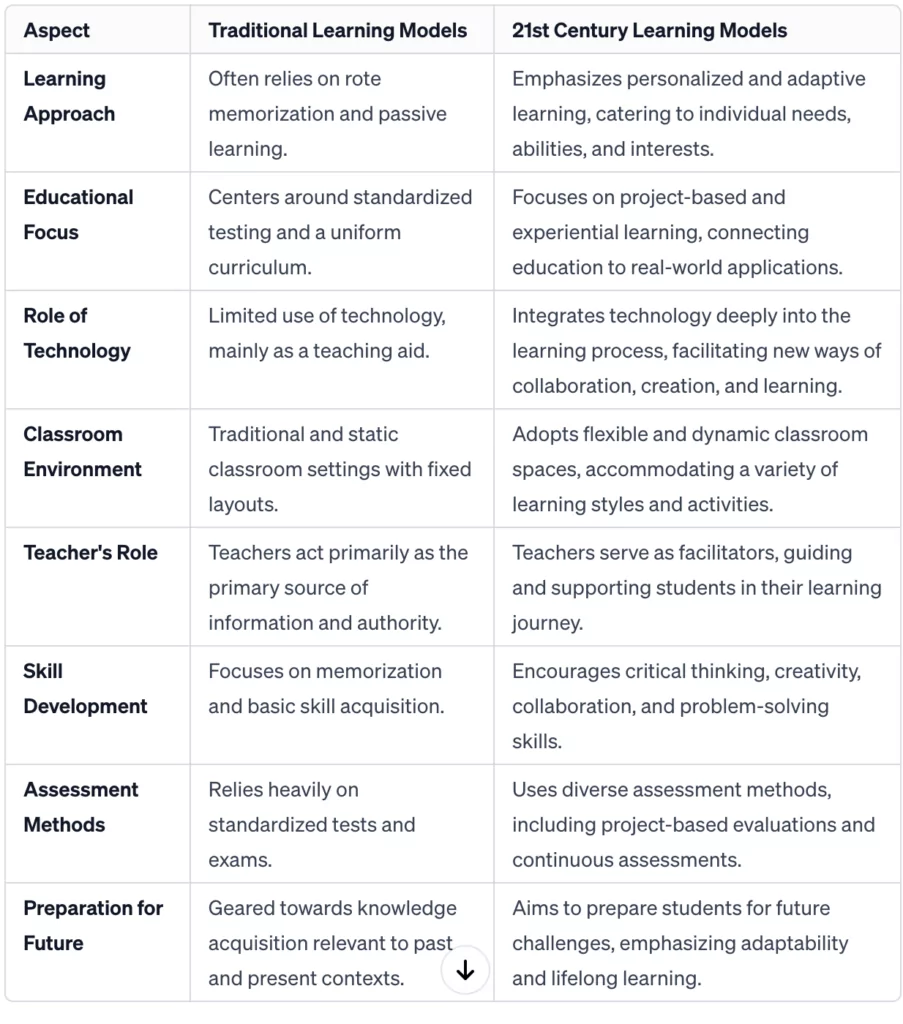
The important thing to bear in mind as we unravel the differences between these learning models is the understanding that education must be adaptable, forward-thinking, and aligned with the demands of the current world. In doing so, we inherently acknowledge that the skills needed today are different from those of the past and that our approach to education must evolve accordingly. Embracing these changes (and mindset) and integrating them into our teaching practices is crucial for preparing students for the realities of the modern world.
Let’s turn now to the characteristics of the 21st century learning. These are almost the same as the characteristics of 21st century learners I covered before but with slight differences.
1. Integration of Technology in Learning and Teaching
Whether we want it or not technology is now a central component of the pedagogical equation. The integration of technology in education has revolutionized how we teach and learn, making it a cornerstone of 21st century education. As NETP (2017) noted, “the conversation has shifted from whether technology should be used in learning to how it can improve learning to ensure that all students have access to high-quality educational experiences.” (p. 7)
Digital tools and resources have become integral, fundamentally altering the educational landscape. This integration ranges from the use of smartboards in classrooms to the use of educational apps and platforms that facilitate interactive learning.
In today’s classrooms, students are more likely to engage with digital textbooks , participate in online discussions , and submit assignments via learning management systems like Google Classroom or Moodle. The use of technology also extends to personalized learning, where adaptive learning technologies can cater to individual student needs, allowing for differentiation in teaching methods.
For instance, platforms like Khan Academy or Quizlet offer personalized learning paths based on student performance, ensuring that each student can learn at their own pace. Moreover, technology in education is not just a tool for learning; it’s also a subject of study in itself. Digital literacy – understanding how to use technology effectively and responsibly – has become a crucial part of the curriculum.
2. Collaborative and Interactive Learning
Another important characteristic of the 21st century learning is the shift towards collaborative and interactive learning. The ‘sage on the stage’ has become obsolete and cooperative learning methods have taken center stage.
Approaches such as project-based learning , problem-based learning, inquiry-based learning, among several others, have taken our classrooms from teacher-centered instruction to a more student-driven model where learners work together to solve problems, complete projects, and engage in discussions.
With collaborative learning comes the emphasis on teamwork, group projects, and learning environments that promote interactive (two-ways) learning. These interactive learning hubs draw on multimodal means of instruction that include the use of educational games , simulations, and virtual labs, which make learning more engaging and hands-on. These methods encourage active participation and allow students to apply what they’ve learned in practical, often real-world, scenarios.
Needless to mention that collaborative learning promotes a sense of accountability and responsibility among learners (Scager et al., 2016). In my own classroom, I’ve seen how group activities foster a sense of community and accountability among students. They learn to listen to different perspectives, articulate their own ideas, and work towards a common goal. This shift not only enhances the learning experience but also prepares students for a future where collaborative and interactive skills are highly valued.
3. Critical Thinking and Problem-Solving
We find ourselves in a remarkable era, one where the entirety of the world’s knowledge is accessible with a mere click. Today, anyone can effortlessly produce and share content, unhindered by paywalls or bureaucratic barriers. At first glance, this seems like an extraordinary advancement, a testament to the democratization of knowledge and information. However, a closer examination reveals a complex challenge: the onslaught of information overload. This deluge makes analytical and critical thinking skills more essential than ever.
In this digital age, our students are tasked with a formidable challenge. They must navigate through an immense sea of information, discerning the valuable from the trivial. They are required not only to gather and comprehend this information but also to critically evaluate its credibility and relevance .
This process is crucial in developing informed opinions and making sound decisions. The skills of critical thinking and problem-solving, therefore, become indispensable tools in their intellectual arsenal. They empower our students to adeptly sift through the vast array of information, enabling them to recognize and utilize knowledge that is both accurate and beneficial.
Critical Thinking Vs Problem Solving
Critical thinking, as Finn (2011) defines it, “is applied rationality…a set of skills that people can learn and apply in their everyday or professional lives.” (p. 69). Critical thinking skills involve analyzing and evaluating information or arguments in an objective and reflective manner.
Problem-solving, on the other hand, is about applying knowledge and critical thinking to find solutions to complex challenges. According to Martinez (1998), problem solving is “the process of moving toward a goal when the path to that goal is uncertain.
We solve problems every time we achieve something without having known beforehand how to do so” (p.605). For instance, problem solving is like figuring out how to fix a leaky faucet without previous plumbing experience, relying on trial and error, research, and reasoning to achieve the goal of repairing it.
Critical thinking and problem solving are closely intertwined yet distinct skills. Critical thinking primarily focuses on evaluating and analyzing information or arguments with an objective lens, emphasizing the understanding and assessment of different viewpoints.
In contrast, problem solving is more about applying these critical insights to create effective solutions to specific challenges or situations. While critical thinking lays the groundwork for understanding a problem deeply, problem solving is the next step, where this understanding is put into action to resolve the issue at hand.
Both critical thinking and problem solving are essential skills in today’s learning. In the classroom, fostering these skills can involve various strategies. For instance, project-based learning, where students tackle real-world problems, requires them to assess information, think logically, and devise practical solutions.
Inquiry-based learning, which encourages students to ask questions and explore answers, also nurtures critical thinking and problem solving. These approaches promote a deeper understanding of content, as students are actively engaged in the learning process, rather than passively receiving information.

4. Creativity and Innovation
Encouraging creativity and innovation in students is equally vital in today’s educational landscape. Creativity isn’t just about artistic expression; it’s a way of thinking that involves generating new and original ideas, while innovation is about implementing these creative ideas in practical ways.
Encouraging a creative atmosphere in your classroom is key to building innovative thinking habits, ones that can help students effectively address new challenges and opportunities. In his paper titled ‘ Teaching Creativit y’, Gary Davis (1967) explains how teachers can go about creating creative atmosphere in class.
Firstly, the teacher, as Davis pointed out, is encouraged to provide a broad range of sensory experiences, enabling students to engage with various instructional materials. This approach fosters an environment where exploration and experimentation are valued. Additionally, the emphasis should be on encouraging originality and creative expression in students, recognizing and nurturing any signs of creativity they show.
Davis also suggests that an essential aspect of a creative atmosphere involves helping students develop effective communication skills. This aspect is crucial because it allows students to articulate their ideas and thoughts clearly, which is a fundamental part of the creative process.
Furthermore, the teacher, as Davis explained, is advised to encourage empathetic understanding, which implies fostering a sense of connection and understanding among students, allowing them to appreciate and inspire each other’s creative endeavors.
These recommendations align beautifully with the idea of creating a classroom environment that doesn’t just teach content but also nurtures the creative and expressive abilities of students, making learning a more holistic and engaging experience.
Final thoughts
From integrating technology in meaningful ways to fostering critical thinking, creativity, and collaboration, 21st-century learning is about preparing students not just with knowledge, but with the skills and mindsets needed to navigate and contribute to a complex, interconnected world. As an EdTech blogger and educator, my experience has reinforced the belief that embracing these changes is not optional but essential for the holistic development of learners.
The journey through these various themes has not only been enlightening but also affirming. It underscores the importance of continual adaptation and growth, both for educators and students. As we move forward, it’s vital to keep the dialogue open, share best practices, and learn from each other. The landscape of education is ever-evolving, and by staying informed and flexible, we can ensure that our teaching methods and educational philosophies remain relevant and effective.
- Davis, G. A. (1967). Teaching Creativity. The Clearing House , 42(3), 162–166. https://doi.org/10.1080/00098655.1967.11477471
- Finn, P. (2011). Critical thinking: Knowledge and skills for evidence-based practice. Language, Speech & Hearing Services in Schools , 42(1), 69–72. https://doi.org/10.1044/0161-1461
- Martinez, M. E. (1998). What Is Problem Solving? The Phi Delta Kappan , 79(8), 605–609. http://www.jstor.org/stable/20439287
- National Education Technology Plan Update. (2017). Reimagining the Role of Technology in Education. U.S. Department of Education . Retrieved from: https://tech.ed.gov/files/2017/01/NETP17.pdf
- Scager, K., Boonstra, J., Peeters, T., Vulperhorst, J. & Wiegant, F. (2016). Collaborative learning in higher education: Evoking positive interdependence. CBE Life Sci Educ , 15(4):ar69. doi: 10.1187/cbe.16-07-0219 .

Join our mailing list
Never miss an EdTech beat! Subscribe now for exclusive insights and resources .

Meet Med Kharbach, PhD
Dr. Med Kharbach is an influential voice in the global educational technology landscape, with an extensive background in educational studies and a decade-long experience as a K-12 teacher. Holding a Ph.D. from Mount Saint Vincent University in Halifax, Canada, he brings a unique perspective to the educational world by integrating his profound academic knowledge with his hands-on teaching experience. Dr. Kharbach's academic pursuits encompass curriculum studies, discourse analysis, language learning/teaching, language and identity, emerging literacies, educational technology, and research methodologies. His work has been presented at numerous national and international conferences and published in various esteemed academic journals.

Join our email list for exclusive EdTech content.
Integration Rules

Integration rules: Integration is used to find many useful parameters or quantities like area, volumes, central points, etc., on a large scale. The most common application of integration is to find the area under the curve on a graph of a function.
To work out the integral of more complicated functions than just the known ones, we have some integration rules. These rules can be studied below. Apart from these rules, there are many integral formulas that substitute the integral form.
Integration Rules of Basic Functions
The integration rules are defined for different types of functions. Let us learn here the basic rules for integration of the some common functions, such as:
Integration of Constant
Integration of constant function say ‘a’ will result in:
∫a dx = ax + C
∫4 dx = 4x + C
Integration of Variable
If x is any variable then;
∫x dx = x 2 /2 + C
Integration of Square
If the given function is a square term, then;
∫x 2 dx = x 3 /3
Integration of Reciprocal
If 1/x is a reciprocal function of x, then the integration of this function is:
∫(1/x) dx = ln|x| + C (Natural log of x)
Integration of Exponential Function
The different rules for integration of exponential functions are:
- ∫e x dx = e x + C
- ∫a x dx = a x /ln(a) + C
- ∫ln(x) dx = x ln(x) − x + C
Integration of Trigonometric Function
- ∫cos(x) dx = sin(x) + C
- ∫sin(x) dx = -cos(x) + C
- ∫sec 2 (x) dx = tan(x) + C
Important Integration Rules
The important rules for integration are:
Multiplication by Constant
Power Rule of Integration
As per the power rule of integration, if we integrate x raised to the power n, then;
∫x n dx = (x n+1 /n+1) + C
By this rule the above integration of squared term is justified, i.e.∫x 2 dx. We can use this rule, for other exponents also.
Example: Integrate ∫x 3 dx.
∫x 3 dx = x (3+1) /(3+1) = x 4 /4
Sum Rule of Integration
The sum rule explains the integration of sum of two functions is equal to the sum of integral of each function.
∫(f + g) dx = ∫f dx + ∫g dx
Example: ∫(x + x 2 )dx
= ∫x dx + ∫x 2 dx
= x 2 /2 + x 3 /3 + C
Difference Rule of Integration
The difference rule of integration is similar to the sum rule.
∫(f – g) dx = ∫f dx – ∫g dx
Example: ∫(x – x 2 )dx
= ∫x dx – ∫x 2 dx
= x 2 /2 – x 3 /3 + C
If a function is multiplied by a constant then the integration of such function is given by:
∫cf(x) dx = c∫f(x) dx
Example: ∫2x.dx
=2 x 2 /2 + C
Apart from the above-given rules, there are two more integration rules:
Integration by parts
This rule is also called the product rule of integration. It is a special kind of integration method when two functions are multiplied together. The rule for integration by parts is:
∫ u v da = u∫ v da – ∫ u'(∫ v da)da
- u is the function of u(a)
- v is the function of v(a)
- u’ is the derivative of the function u(a)
Integration by Substitution
Integration by substitution is also known as “Reverse Chain Rule” or “u-substitution Method” to find an integral.
The first step in this method is to write the integral in the form:
∫ f(g(x))g'(x)dx
Now, we can do a substitution as follows:
g(x) = a and g'(a) = da
Now substitute the equivalent values in the above form:
Once you integrate the above form, finally substitute the original values.
Learn more about: Integration by substitution
Solved Examples
Question 1: What is ∫ 8 a 3 da?
Solution: We can take 8 out of integral,
∫ 8 a 3 da = 8 ∫ a 3 da
= 8 a 4 / 4 + C
= 2 a 4 + C
Question 2: What is ∫ 4 a 3 da?
Solution: We can take 4 out of integral,
∫ 4 a 3 da = 4 ∫ a 3 da
= 4 a 4 / 4 + C
Question 3: What is ∫ (Cos a + a) da ?
Solution: ∫ (Cos a + a) da = ∫ Cos a da + ∫ a da
= sin a + a 2 /2 + C
Question 4: What is ∫ (Sin a + a) da ?
Solution: ∫ (Sin a + a) da = ∫ Sin a da + ∫ a da
= – Cos a + a 2 /2 + C
Register at BYJU’S to learn more on other mathematical Rules.
Frequently Asked Questions – FAQs
What is the power rule of integration, what is the sum rule of integration, what is the product rule of integration, what is the value of integral of function when multiplied by a constant, what is the rule of integration for exponential function.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment

Thanks to solve my problem

Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Accessibility Policy
- Skip to content
- QUICK LINKS
- Oracle Cloud Infrastructure
- Oracle Fusion Cloud Applications
- Download Java
- Careers at Oracle

What Is Big Data?
Sherry Tiao | Senior Manager, AI & Analytics, Oracle | March 11, 2024

In This Article
Big Data Defined
The three “vs” of big data, the value—and truth—of big data, the history of big data, big data use cases, big data challenges, how big data works, big data best practices.
What exactly is big data?
The definition of big data is data that contains greater variety, arriving in increasing volumes and with more velocity. This is also known as the three “Vs.”
Put simply, big data is larger, more complex data sets, especially from new data sources. These data sets are so voluminous that traditional data processing software just can’t manage them. But these massive volumes of data can be used to address business problems you wouldn’t have been able to tackle before.
| Volume | The amount of data matters. With big data, you’ll have to process high volumes of low-density, unstructured data. This can be data of unknown value, such as X (formerly Twitter) data feeds, clickstreams on a web page or a mobile app, or sensor-enabled equipment. For some organizations, this might be tens of terabytes of data. For others, it may be hundreds of petabytes. |
| Velocity | Velocity is the fast rate at which data is received and (perhaps) acted on. Normally, the highest velocity of data streams directly into memory versus being written to disk. Some internet-enabled smart products operate in real time or near real time and will require real-time evaluation and action. |
| Variety | Variety refers to the many types of data that are available. Traditional data types were structured and fit neatly in a . With the rise of big data, data comes in new unstructured data types. Unstructured and semistructured data types, such as text, audio, and video, require additional preprocessing to derive meaning and support metadata. |
Two more Vs have emerged over the past few years: value and veracity . Data has intrinsic value. But it’s of no use until that value is discovered. Equally important: How truthful is your data—and how much can you rely on it?
Today, big data has become capital. Think of some of the world’s biggest tech companies. A large part of the value they offer comes from their data, which they’re constantly analyzing to produce more efficiency and develop new products.
Recent technological breakthroughs have exponentially reduced the cost of data storage and compute, making it easier and less expensive to store more data than ever before. With an increased volume of big data now cheaper and more accessible, you can make more accurate and precise business decisions.
Finding value in big data isn’t only about analyzing it (which is a whole other benefit). It’s an entire discovery process that requires insightful analysts, business users, and executives who ask the right questions, recognize patterns, make informed assumptions, and predict behavior.
But how did we get here?
Although the concept of big data itself is relatively new, the origins of large data sets go back to the 1960s and ‘70s when the world of data was just getting started with the first data centers and the development of the relational database.
Around 2005, people began to realize just how much data users generated through Facebook, YouTube, and other online services. Hadoop (an open source framework created specifically to store and analyze big data sets) was developed that same year. NoSQL also began to gain popularity during this time.
The development of open source frameworks, such as Hadoop (and more recently, Spark) was essential for the growth of big data because they make big data easier to work with and cheaper to store. In the years since then, the volume of big data has skyrocketed. Users are still generating huge amounts of data—but it’s not just humans who are doing it.
With the advent of the Internet of Things (IoT), more objects and devices are connected to the internet, gathering data on customer usage patterns and product performance. The emergence of machine learning has produced still more data.
While big data has come far, its usefulness is only just beginning. Cloud computing has expanded big data possibilities even further. The cloud offers truly elastic scalability, where developers can simply spin up ad hoc clusters to test a subset of data. And graph databases are becoming increasingly important as well, with their ability to display massive amounts of data in a way that makes analytics fast and comprehensive.

Discover the Insights in Your Data
- Who are the criminals passing dirty money around and committing financial services fraud?
- Who has been in contact with an infected person and needs to go into quarantine?
- How can feature engineering for data science be made simpler and more efficient?
Click below to access the 17 Use Cases for Graph Databases and Graph Analytics ebook.
Big Data Benefits
- Big data makes it possible for you to gain more complete answers because you have more information.
- More complete answers mean more confidence in the data—which means a completely different approach to tackling problems.
Big data can help you address a range of business activities, including customer experience and analytics. Here are just a few.
| Product development | Companies like Netflix and Procter & Gamble use big data to anticipate customer demand. They build predictive models for new products and services by classifying key attributes of past and current products or services and modeling the relationship between those attributes and the commercial success of the offerings. In addition, P&G uses data and analytics from focus groups, social media, test markets, and early store rollouts to plan, produce, and launch new products. |
| Predictive maintenance | Factors that can predict mechanical failures may be deeply buried in structured data, such as the year, make, and model of equipment, as well as in unstructured data that covers millions of log entries, sensor data, error messages, and engine temperature. By analyzing these indications of potential issues before the problems happen, organizations can deploy maintenance more cost effectively and maximize parts and equipment uptime. |
| Customer experience | The race for customers is on. A clearer view of customer experience is more possible now than ever before. Big data enables you to gather data from social media, web visits, call logs, and other sources to improve the interaction experience and maximize the value delivered. Start delivering personalized offers, reduce customer churn, and handle issues proactively. |
| Fraud and compliance | When it comes to security, it’s not just a few rogue hackers—you’re up against entire expert teams. Security landscapes and compliance requirements are constantly evolving. Big data helps you identify patterns in data that indicate fraud and aggregate large volumes of information to make regulatory reporting much faster. |
| Machine learning | Machine learning is a hot topic right now. And data—specifically big data—is one of the reasons why. We are now able to teach machines instead of program them. The availability of big data to train machine learning models makes that possible. |
| Operational efficiency | Operational efficiency may not always make the news, but it’s an area in which big data is having the most impact. With big data, you can analyze and assess production, customer feedback and returns, and other factors to reduce outages and anticipate future demands. Big data can also be used to improve decision-making in line with current market demand. |
| Drive innovation | Big data can help you innovate by studying interdependencies among humans, institutions, entities, and process and then determining new ways to use those insights. Use data insights to improve decisions about financial and planning considerations. Examine trends and what customers want to deliver new products and services. Implement dynamic pricing. There are endless possibilities. |

Download your free ebook to learn about:
- New ways you can use your data
- Ways the competition could be innovating
- Benefits and challenges of different use cases
While big data holds a lot of promise, it is not without its challenges.
First, big data is…big. Although new technologies have been developed for data storage, data volumes are doubling in size about every two years. Organizations still struggle to keep pace with their data and find ways to effectively store it.
But it’s not enough to just store the data. Data must be used to be valuable and that depends on curation. Clean data, or data that’s relevant to the client and organized in a way that enables meaningful analysis, requires a lot of work. Data scientists spend 50 to 80 percent of their time curating and preparing data before it can actually be used.
Finally, big data technology is changing at a rapid pace. A few years ago, Apache Hadoop was the popular technology used to handle big data. Then Apache Spark was introduced in 2014. Today, a combination of the two frameworks appears to be the best approach. Keeping up with big data technology is an ongoing challenge.
Discover more big data resources:
Big data gives you new insights that open up new opportunities and business models. Getting started involves three key actions:
1. Integrate Big data brings together data from many disparate sources and applications. Traditional data integration mechanisms, such as extract, transform, and load (ETL) generally aren’t up to the task. It requires new strategies and technologies to analyze big data sets at terabyte, or even petabyte, scale.
During integration, you need to bring in the data, process it, and make sure it’s formatted and available in a form that your business analysts can get started with.
2. Manage Big data requires storage. Your storage solution can be in the cloud, on premises, or both. You can store your data in any form you want and bring your desired processing requirements and necessary process engines to those data sets on an on-demand basis. Many people choose their storage solution according to where their data is currently residing. The cloud is gradually gaining popularity because it supports your current compute requirements and enables you to spin up resources as needed.
3. Analyze Your investment in big data pays off when you analyze and act on your data. Get new clarity with a visual analysis of your varied data sets. Explore the data further to make new discoveries. Share your findings with others. Build data models with machine learning and artificial intelligence. Put your data to work.
To help you on your big data journey, we’ve put together some key best practices for you to keep in mind. Here are our guidelines for building a successful big data foundation.
| Align big data with specific business goals | More extensive data sets enable you to make new discoveries. To that end, it is important to base new investments in skills, organization, or infrastructure with a strong business-driven context to guarantee ongoing project investments and funding. To determine if you are on the right track, ask how big data supports and enables your top business and IT priorities. Examples include understanding how to filter web logs to understand ecommerce behavior, deriving sentiment from social media and customer support interactions, and understanding statistical correlation methods and their relevance for customer, product, manufacturing, and engineering data. |
| Ease skills shortage with standards and governance | One of the biggest obstacles to benefiting from your investment in big data is a skills shortage. You can mitigate this risk by ensuring that big data technologies, considerations, and decisions are added to your IT governance program. Standardizing your approach will allow you to manage costs and leverage resources. Organizations implementing big data solutions and strategies should assess their skill requirements early and often and should proactively identify any potential skill gaps. These can be addressed by training/cross-training existing resources, hiring new resources, and leveraging consulting firms. |
| Optimize knowledge transfer with a center of excellence | Use a center of excellence approach to share knowledge, control oversight, and manage project communications. Whether big data is a new or expanding investment, the soft and hard costs can be shared across the enterprise. Leveraging this approach can help increase big data capabilities and overall information architecture maturity in a more structured and systematic way. |
| Top payoff is aligning unstructured with structured data | It is certainly valuable to analyze big data on its own. But you can bring even greater business insights by connecting and integrating low density big data with the structured data you are already using today. Whether you are capturing customer, product, equipment, or environmental big data, the goal is to add more relevant data points to your core master and analytical summaries, leading to better conclusions. For example, there is a difference in distinguishing all customer sentiment from that of only your best customers. Which is why many see big data as an integral extension of their existing business intelligence capabilities, data warehousing platform, and information architecture. Keep in mind that the big data analytical processes and models can be both human- and machine-based. Big data analytical capabilities include statistics, spatial analysis, semantics, interactive discovery, and visualization. Using analytical models, you can correlate different types and sources of data to make associations and meaningful discoveries. |
| Plan your discovery lab for performance | Discovering meaning in your data is not always straightforward. Sometimes we don’t even know what we’re looking for. That’s expected. Management and IT needs to support this “lack of direction” or “lack of clear requirement.” At the same time, it’s important for analysts and data scientists to work closely with the business to understand key business knowledge gaps and requirements. To accommodate the interactive exploration of data and the experimentation of statistical algorithms, you need high-performance work areas. Be sure that sandbox environments have the support they need—and are properly governed. |
| Align with the cloud operating model | Big data processes and users require access to a broad array of resources for both iterative experimentation and running production jobs. A big data solution includes all data realms including transactions, master data, reference data, and summarized data. Analytical sandboxes should be created on demand. Resource management is critical to ensure control of the entire data flow including pre- and post-processing, integration, in-database summarization, and analytical modeling. A well-planned private and public cloud provisioning and security strategy plays an integral role in supporting these changing requirements. |
Learn More About Big Data at Oracle
- Try a free big data workshop
- Infographic: How to Build Effective Data Lakes
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Calculus AB
Course: ap®︎/college calculus ab > unit 8.
- Area under rate function gives the net change
- Interpreting definite integral as net change
- Worked examples: interpreting definite integrals in context
- Interpreting definite integrals in context
- Analyzing problems involving definite integrals
Worked example: problem involving definite integral (algebraic)
- Problems involving definite integrals (algebraic)

Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page
Video transcript
SemiWiki: Arteris is Solving SoC Integration Challenges
by Mike Gianfagna, On Jun 06, 2024
The difficulty of SoC integration is clearly getting more demanding. Driven by process node density, multi-chip integration and seemingly never-ending demands for more performance at lower power, the hurdles continue to increase. When you consider these challenges in the context of Arteris, it’s natural to think about hardware integration and the benefits a network-on-chip (NoC) technology offers. But the problem is much bigger than hardware integration and so is the portfolio of solutions offered by Arteris. Managing all the information associated with a complex design and ensuring all teams are working off the same verified information is a daunting task. What you don’t know can hurt you. I recently had the opportunity to learn about the broader solution Arteris offers. Read on to see how Arteris is solving SoC integration challenges.
An Overview of the Problem
While most folks immediately think “NoC” when they hear Arteris, the company is assembling a much broader portfolio of solutions. The common thread is that they all facilitate more efficient and predictable connectivity and assembly of the design. At the highest level, the way I think about the company’s role is this – focus on your unique design idea and let Arteris help you put it all together.
I was able to spend some time recently with Insaf Meliane, Product Management & Marketing Manager at Arteris. Insaf has been with Arteris for three years. She came to Arteris through the company’s acquisition of Magillem, where she worked for four years prior to joining Arteris. She has a rich background in chip design from places such as NXP Semiconductors, ST Microelectronics and ST-Ericsson. Insaf was able to enlighten me about how Magillem’s technology helps Arteris deliver a holistic solution to the SoC integration problem. She began by describing the problem.
The information Insaf shared was, in part, based on actual customer discussions. She described SoC integration as a massive amount of hardware and software information each design creates and how that data interacts with the design flow and all the teams using it.
To read the full article on SemiWiki , click here .
Topics: Connected by Arteris
Arteris articles.
Discover news and articles about on-chip interconnects, SoC integration automation, and SoC design innovation across the semiconductor industry.
Subscribe to Arteris News
Recent articles.
All About Circuits: Speeding Derivative SoC Designs With Networks-on-Chips
Semiconductor Engineering: Turbocharging Cost-Conscious SoCs With Cache
Andes Technology and Arteris Partner To Accelerate RISC-V SoC Adoption
Electronic Design: Functional Safety for Control and Status Registers
Post By Topic
Post By Date
- June 2024 (2)
- May 2024 (3)
- April 2024 (6)
- March 2024 (10)
- February 2024 (6)
- January 2024 (7)
- December 2023 (4)
- November 2023 (8)
- October 2023 (7)
- September 2023 (4)
- August 2023 (4)
- July 2023 (7)
- June 2023 (3)
- May 2023 (6)
- April 2023 (3)
- March 2023 (7)
- February 2023 (5)
- January 2023 (5)
- December 2022 (2)
- November 2022 (3)
- October 2022 (1)
- September 2022 (3)
- August 2022 (1)
- July 2022 (2)
- June 2022 (1)
- May 2022 (2)
- April 2022 (3)
- March 2022 (5)
- February 2022 (2)
- January 2022 (6)
- December 2021 (4)
- November 2021 (6)
- October 2021 (6)
- September 2021 (9)
- August 2021 (8)
- July 2021 (4)
- June 2021 (6)
- May 2021 (8)
- April 2021 (8)
- March 2021 (6)
- February 2021 (9)
- January 2021 (8)
- December 2020 (2)
- November 2020 (4)
- October 2020 (8)
- September 2020 (8)
- August 2020 (6)
- July 2020 (4)
- June 2020 (7)
- May 2020 (10)
- April 2020 (5)
- March 2020 (6)
- February 2020 (2)
- January 2020 (3)
- December 2019 (1)
- November 2019 (3)
- October 2019 (1)
- September 2019 (4)
- August 2019 (3)
- July 2019 (2)
- June 2019 (6)
- May 2019 (7)
- April 2019 (10)
- March 2019 (11)
- February 2019 (8)
- January 2019 (7)
- December 2018 (2)
- November 2018 (1)
- October 2018 (8)
- September 2018 (2)
- August 2018 (2)
- July 2018 (12)
- June 2018 (8)
- May 2018 (2)
- April 2018 (4)
- March 2018 (6)
- February 2018 (5)
- January 2018 (4)
- December 2017 (1)
- November 2017 (3)
- October 2017 (3)
- September 2017 (4)
- June 2017 (2)
- May 2017 (1)
- April 2017 (2)
- March 2017 (5)
- February 2017 (2)
- January 2017 (1)
- November 2016 (3)
- October 2016 (4)
- September 2016 (4)
- August 2016 (1)
- July 2016 (2)
- June 2016 (2)
- May 2016 (9)
- April 2016 (2)
- March 2016 (1)
- February 2016 (4)
- January 2016 (3)
- December 2015 (1)
- November 2015 (4)
- September 2015 (1)
- August 2015 (1)
- July 2015 (1)
- June 2015 (1)
- May 2015 (1)
- April 2015 (2)
- March 2015 (3)
- February 2015 (4)
- January 2015 (1)
- December 2014 (1)
- November 2014 (2)
- October 2014 (3)
- September 2014 (3)
- July 2014 (4)
- June 2014 (1)
- April 2014 (1)
- March 2014 (2)
- February 2014 (4)
- January 2014 (1)
- December 2013 (1)
- November 2013 (3)
- October 2013 (4)
- September 2013 (1)
- August 2013 (4)
- July 2013 (1)
- June 2013 (3)
- May 2013 (2)
- April 2013 (5)
- March 2013 (1)
- February 2013 (3)
- January 2013 (2)
- November 2012 (1)
- October 2012 (3)
- September 2012 (3)
- August 2012 (2)
- July 2012 (1)
- May 2012 (3)
- April 2012 (2)
- March 2012 (1)
- February 2012 (6)
- January 2012 (5)
- December 2011 (1)
- November 2011 (3)
- October 2011 (1)
- August 2011 (1)
- July 2011 (4)
- June 2011 (3)
- April 2011 (2)
- March 2011 (5)
- February 2011 (2)
- January 2011 (4)
- December 2010 (1)
- November 2010 (3)
- October 2010 (2)
- September 2010 (1)
- July 2010 (2)
- June 2010 (1)
- May 2010 (1)
- April 2010 (1)
- March 2010 (1)
- December 2009 (1)
- June 2009 (1)
- January 2009 (1)
- October 2008 (1)
- August 2008 (1)
- May 2008 (1)
- February 2008 (1)
- January 2008 (1)
- November 2007 (1)

Understand millions of lines of code in minutes.
Senior Frontend Engineer

About the role
Job description.
We are seeking a skilled Senior Frontend Engineer to join our team at Driver AI. As a key member of our engineering team, you will play a crucial role in developing and enhancing our frontend web application using modern technologies such as Next.js, React, Vercel, and Tailwind CSS. Your contributions will directly impact the delivery of our product to our enterprise customers, ensuring a seamless and engaging user experience.
This role is a good fit if you are interested in being at a fast-paced, early-stage startup. You will work closely with the founders and small engineering team to rapidly iterate on tech and product foundations. We are a distributed team covering all time zones in the US.
Important cultural values at Driver include the concept of directly responsible individuals (DRIs), rapid iteration and experimentation, doing your homework to explain decisions with data, a culture of long-form documentation, prioritizing demos, asking questions, and open and respectful communication.
Responsibilities
- Lead the development of scalable and performant frontend systems using Next.js, React, and Tailwind CSS.
- Collaborate with backend and ML engineers to integrate with APIs and ensure smooth data flow between frontend and backend systems.
- Work closely with designers and product owners to implement intuitive and visually appealing user interfaces.
- Optimize frontend performance, ensuring fast load times and responsive interactions.
- Stay up-to-date with the latest frontend technologies and industry trends, and propose innovative solutions to enhance our product.
- Contribute to the overall engineering culture at Driver AI, promoting collaboration, documentation, and a focus on delivering high-quality software.
Skills and experience we’re seeking
- Strong knowledge of HTML, CSS, JavaScript/TypeScript, Node.js
- Experience with front-end frameworks and libraries, such as React, Angular.js, and Vue.js (we use React/Next.js)
- Experience interfacing with REST APIs and GraphQL End Points
- Experience with version control systems such as Git
- Excellent analytical and problem-solving skills
- Strong communication and collaboration abilities, especially written
- Understand database concepts and data modeling capabilities
- Development through all phases, from initial technical designs, implementation, and testing to production deployments
- Comfortable working with designers and tools such as Figma
- Experience with continuous integration and continuous deployment (CI/CD) pipelines for frontend applications
Preferred Qualifications
- Bachelor's degree or higher in Computer Science, Engineering, or a related field
- Experience with rich text editors like Tiptap or ProseMirror
- Experience with real-time collaboration applications
- Experience with B2B SaaS products
- Understanding of accessibility standards and best practices
- Previous experience in a startup environment, showcasing adaptability, creativity, and a proactive attitude
- Experienced deploying containerized solutions (e.g., Docker)
Driver AI is an equal opportunity employer. We celebrate diversity and are committed to creating an inclusive environment for all employees. We do not discriminate on the basis of race, religion, color, national origin, gender, sexual orientation, age, marital status, veteran status, or disability status.
- Competitive Compensation Packages - Cash & Equity
- Flexible Work Culture
- Unlimited Time Off + 12 Paid Company Holidays
- Insurance - Health, Dental, & Vision
- Life Insurance & FSA Accounts
- 401(k) Retirement Accounts - Traditional, Roth, or Both
- Quarterly Team Offsites
About Driver AI
Driver ai summary.
Driver AI is the new way to write technical documentation. It helps everyone in an organization write interactive documents to explain millions of lines of code in minutes instead of months.
WHO : Driver AI partners with chip manufacturing, enterprise IT, and software product development teams.
WHY : Traditionally, these teams spend millions and wait months (sometimes years) to understand their complex technology infrastructure well enough to build on top of it.
THE DRIVER DIFFERENCE: Instead, Driver AI is a tool that explains complex codebases in minutes vs. months. This enables teams to rapidly accelerate the technical discovery process and save significant resources.
HOW IT WORKS: Driver AI works by digesting a codebase, organizing it for analysis, and harnessing Large Language Models (LLMs) to generate interactive explanations for executives, product and technology leaders, and developers.
Working with Us
We are an ambitious early-stage enterprise SaaS company. We value a strong communications culture and are sales led whereby customer feedback flows from sales to product and design to engineering implementation.
We are building a world-class engineering team. We enjoy the challenge of navigating the delivery needs of an early startup with the importance of rigor in foundations, design, and culture. Exceptional hires, lean productive process, and an intrepid culture are our key ingredients.
On the technology side, we're building a powerful platform technology that includes a sophisticated frontend and UX experience, a wide ranging LLM content generation stack (compiler-inspired algorithms for traversal and processing of code with state-of-the-art RAG pipelines and agentic systems), and modern backend/cloud infra as a backbone.
Come join us and be a part of building something great!




































IMAGES
VIDEO
COMMENTS
Do you need to solve integrals and antiderivatives of functions online? Try the Integral Calculator, a free tool that shows you the step-by-step solution and graphs of your calculus problems. You can check your answers, learn integration techniques and explore special functions with the Integral Calculator.
The definite integral of a function gives us the area under the curve of that function. Another common interpretation is that the integral of a rate function describes the accumulation of the quantity whose rate is given. We can approximate integrals using Riemann sums, and we define definite integrals using limits of Riemann sums. The fundamental theorem of calculus ties integrals and ...
Is there a way to make sense out of the idea of adding infinitely many infinitely small things? Integral calculus gives us the tools to answer these questions and many more. Surprisingly, these questions are related to the derivative, and in some sense, the answer to each one is the opposite of the derivative. Start learning.
Free Online Integral Calculator allows you to solve definite and indefinite integration problems. Answers, graphs, alternate forms. Powered by Wolfram|Alpha. ... One involves working out the general form for an integral, then differentiating this form and solving equations to match undetermined symbolic parameters. Even for quite simple ...
Use the integration-by-parts formula to solve integration problems. Use the integration-by-parts formula for definite integrals. By now we have a fairly thorough procedure for how to evaluate many basic integrals. However, although we can integrate \(∫x \sin (x^2)\,dx\) by using the substitution, \(u=x^2\), something as simple looking as ...
Definite Integrals. Definite integrals can be solved analytically or graphically. A definite integral will result in a numerical value and involves limits of integration within the notation. For ...
Free integral calculator - solve indefinite, definite and multiple integrals with all the steps. Type in any integral to get the solution, steps and graph ... Integration is a way to sum up parts to find the whole. It is used to find the area under a curve by slicing it to small rectangles and summing up thier areas. ... Enter a problem ...
At time t equals zero, the depth of the water is 35 centimeters. What is the change in the water's depth during the fourth minute? So let's pause the video again and see if you can figure this out again, or figure out what expression can we use to solve the problem, the problem being what is the change in the water's depth during the fourth minute.
Accumulation problems are solved using definite integrals. Imagine we are given the following information: The temperature of a soup is increasing at a rate of r ( t) = 30 e − 0.3 t degrees Celsius per minute (where t is the time in minutes). At time t = 0 , the temperature of the soup is 23 degrees Celsius. And imagine we are asked to find ...
Practice Integration Math 120 Calculus I D Joyce, Fall 2013 This rst set of inde nite integrals, that is, an-tiderivatives, only depends on a few principles of integration, the rst being that integration is in-verse to di erentiation. Besides that, a few rules can be identi ed: a constant rule, a power rule,
Many challenging integration problems can be solved surprisingly quickly by simply knowing the right technique to apply. While finding the right technique can be a matter of ingenuity, there are a dozen or so techniques that permit a more comprehensive approach to solving definite integrals. Manipulations of definite integrals may rely upon specific limits for the integral, like with odd and ...
7.6E: Exercises for Numerical Integration. In exercises 1 - 5, approximate the following integrals using either the midpoint rule, trapezoidal rule, or Simpson's rule as indicated. (Round answers to three decimal places.) 1) ∫2 1dx x; trapezoidal rule; n = 5. 2) ∫3 0√4 + x3 dx; trapezoidal rule; n = 6.
Integration is an important topic for 11th and 12th standard students as these concepts are further covered in higher studies. The problems provided here are as per the CBSE board and NCERT curriculum. Exercising these questions will help students to solve the hard questions also and obtain more marks in the exam. Learn Integration Rules here.
Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration; Chapter 4 - Applications of Integration; Book traversal links for Integral Calculus. Chapter 1 - Fundamental Theorems of Calculus
4B-7 Solving for 2x 2in y = (x − 1) and y = (x + 1) gives the values a x a -x 2 2 2 top view slice a -x2 2 x = 1 ± √ y and x = −1 ± √ y The hard part is deciding which sign of the square root representing the endpoints of the square.-1 1 1 x = - + y 2 (x- y) 1 x = - y1 Method 1: The point (0, 1) has to be on the two curves.
In calculus, integration is defined as the inverse process of differentiation, and hence the evaluation of an integral is called an antiderivative. It is a process of the summation of a product if we have not said the summation is to be done from which point to which point. ... Solved Problems on Indefinite Integrals for JEE. Practice the below ...
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
The key components of 21st century learning include: Critical Thinking and Problem Solving: Encouraging students to think deeply, question assumptions, and solve complex problems. Collaboration and Communication: Promoting teamwork and effective communication, both in person and through digital platforms. Creativity and Innovation: Fostering ...
Integration Rules are the mathematical rules implemented to solve various integral problems. The integration rules are very important to find areas under the curve, volumes, etc., for a large scale. ... Integration by substitution. Solved Examples. Question 1: What is ∫ 8 a 3 da? Solution: We can take 8 out of integral, ∫ 8 a 3 da = 8 ∫ a ...
A big data solution includes all data realms including transactions, master data, reference data, and summarized data. Analytical sandboxes should be created on demand. Resource management is critical to ensure control of the entire data flow including pre- and post-processing, integration, in-database summarization, and analytical modeling.
Using definite integral to solve a word problem about the growth in the population of a town. Questions Tips & Thanks. ... Why does he not change the bounds of integration after the u-substitution? i.e. from t = [2, 5] to u = [2.4, 6] ? ... I solved using (e to the 1.2t power divided by 1.2) minus t squared from t = 2 to t= 5 and came up with ...
But the problem is much bigger than hardware integration and so is the portfolio of solutions offered by Arteris. Managing all the information associated with a complex design and ensuring all teams are working off the same verified information is a daunting task. ... Read on to see how Arteris is solving SoC integration challenges. An Overview ...
Job Description We are seeking a skilled Senior Frontend Engineer to join our team at Driver AI. As a key member of our engineering team, you will play a crucial role in developing and enhancing our frontend web application using modern technologies such as Next.js, React, Vercel, and Tailwind CSS. Your contributions will directly impact the delivery of our product to our enterprise customers ...