solving motion problems using parametric and vector valued functions

AP Calculus BC: 9.6 Solving Motion Problems Using Parametric and Vector- Valued Functions – Exam Style questions with Answer- FRQ

For time t ≥ 0, a particle moves in the xy-plane with position (x(t),  y(t)) , and velocity vector \(\left \langle (t-1)^{e^{t^{2}}}, sin \left ( t^{1.25} \right ) \right \rangle.\) At time t = 0 , the position of the particle is (−2, 5) . (a) Find the speed of the particle at time t = 1.2. Find the acceleration vector of the particle at time t = 1.2. (b) Find the total distance traveled by the particle over the time interval 0 ≤ t ≤ 1.2. (c) Find the coordinates of the point at which the particle is farthest to the left for t ≥ 0. Explain why there is no point at which the particle is farthest to the right for t ≥ 0.

\(Speed = \sqrt{(x'(t))^{2}+(y'(t))^{2}}\)

\(\sqrt{\left ( (1.2-1)e^{(1.2)^{2}} \right )^{2}+\left ( sin((1.2)^{1.25}) \right )^{2}}\)

Speed = 1.271                  \(accel: \left \langle (t-1)(2+e^{t2})+(1)(e^{t2}),cos (t^{1.25}\cdot 1.25t^{.25}) \right \rangle\)

of     t = 1.2

accel = < 6.247,   .405>

\(\int_{0}^{1.2}\sqrt{\left ( (t-1)e^{t2} \right )^{2}+\left ( sin(t^{1.25}) \right )^{2}}dt\)

x'(t) is negative on (0, 1) and is positive on (1, 0). x'(1) = 0 Since x'(t) goes from negative to positive at  t = 1 and x'(1) = 0, x(t) has a rel. minimum at  t=1, since x(t) decreases until t=1 and always increases afterwards, x(1) is on abs. min / that is the location of further to the left,   \(-2+\int_{0}^{1}(t-1)e^{t2}dt = x(1)\)

x(1) = -2.604

\(5+\int_{0}^{0}(sin (e^{1.25}))dt = y(1)\)

y (1) = 5.410

(-2.604, 5.410)

There is no point furthest to the right because x'(t) increases towards infinity on +20, meaning there is no abs max of x(t) (sint x(t) will thus be increasing towards ∝  on t > 1). This means the particle will continue to the right for t > 1, creating no furthest right point.

 There are two vectors 〈1, -4〉 and 〈2, k〉 where k is an unknown quantity. (A) Find a value of k such that the vectors are orthogonal. (B) Find a value of k such that the vectors are parallel. (C) If k = 6, find the angle between the two vectors. Round to the nearest tenth of a degree.

(A) If vectors are orthogonal, the angle between them is \(\frac{\pi }{2}\) so that their dot product is defined by \(r_{1}r_{2}\cos \Theta =0\) Then \(r_{1}r_{2}=x_{1}x_{2}+y_{1}y_{2}=\left \langle 1,-4 \right \rangle.\left \langle 2,k \right \rangle=1(2)+(-4)(k)=0\).Then \(-4k=-2\Rightarrow k=\frac{1}{2}\)

(B)If vectors are parallel, the angle between them is 0, where cos(0) = 1. You know that, in the case of parallel vectors,\(r_2=Cr_1\) , where C is a constant. In this case, the horizontal component of \(r_{2}\) differs from \(r_{1}\) by a factor of 2. Multiplying the y-component by the same factor, you get k = -8. You can get the same result by applying the equation \(\cos \Theta =\frac{r_{1}.r_{2}}{\left \| r_{1} \right \|\left \| r_{2} \right \|}=-1\). You find that \(\frac{2-4k}{(\sqrt{17})\sqrt{4+k^{2}}}=-1\). If you multiply through by the denominator and then square both sides, you find that \(4-16k+16k^{2}=17(4+k^{2})\) and, combining terms, you get \(k^{2}+16k+64=0\). You can then factor to find that (k + 8)(k + 8) = 0 or k = -8. (C) Find the angle between two vectors by applying the equation \(\Theta =\cos ^{-1}\frac{r_1.r_2}{\left \| r_{1} \right \|\left \| r_{2} \right \|}.\)Here,\(r_{1}.r_{2}=1(2)-4(6)=-22,\left \| r_{1} \right \|=\sqrt{1^{2}+4^{2}}=\sqrt{17}\)  and \( \left \| r_{2} \right \|=\sqrt{2^{2}+6^{2}}=\sqrt{40}=2\sqrt{10}.\)Substituting, we find that \(\Theta =-\frac{22}{2\sqrt{170}}\approx 147.5^{\circ}\)

 A force of 2 newtons is applied to the right side of an object. A force of 4 newtons is applied from below. A force of 8 newtons is applied to the left side of the object at an angle of \(\frac{\pi }{3}\) above the horizontal. (A) Find the resultant force vector being applied to the object. (B) Find an approximation (to the nearest hundredth) of the magnitude of the total force on the object. (C) What additional force vector would need to be applied to keep the object from moving?

 An object is moving on a path defined by the vector-valued function \(r(t)=\left \langle 2\cos t,2\sin t \right \rangle\).Find the following functions at time \(t=\frac{\pi }{4}\). (A) the velocity vector (B) the acceleration vector (C) the tangent vector (D) the normal vector.

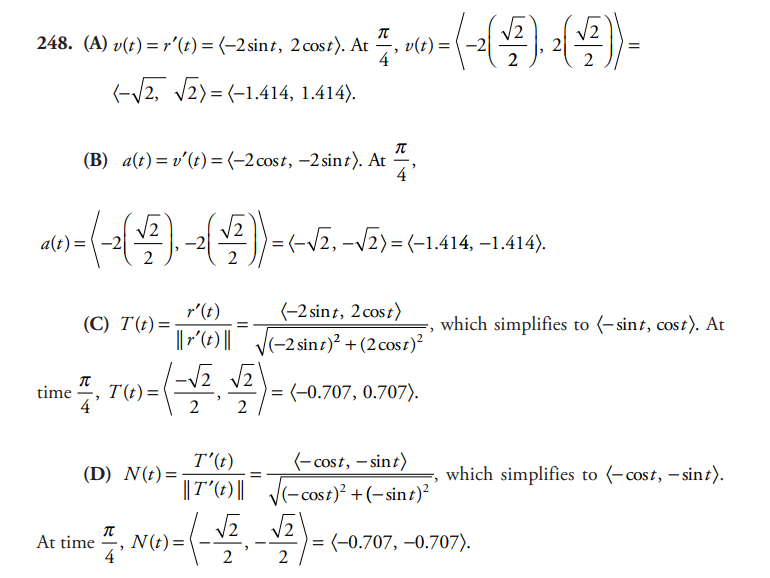
 A curve is defined by parametric equations \( x(t)=t^{3}-2t+1\) and \(y(t)=t^{2}-5t\). (A) Find an equation for the tangent line corresponding to t = 1. (B) For what value(s) of t is the tangent line horizontal? (C) For what value(s) of t is the tangent line vertical?

(A) The slope of the tangent line equals\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\frac{\mathrm{d} y}{\mathrm{d} t}}{\frac{\mathrm{d} x}{\mathrm{d} t}}=\frac{2t-5}{3t^{2}-2}-3\) at t=-1 Substituting t = 1 into the parametric equations gives us the coordinates (0, -4). Thus, the equation for the tangent line is y+4=-3(x-0)or,solving fory,y=-3x-4. (B) The tangent line is horizontal if \(\frac{\mathrm{d} y}{\mathrm{d} t}=0\).Thus 2t-5=0 and \(t=\frac{5}{2}\) (C) The tangent line is vertical if \(\frac{\mathrm{d} x}{\mathrm{d} t}=9.\)Thus \(3t^{2}-2=0\) and \(t=\pm \sqrt{\frac{2}{3}}\)

Find what you need to study

♾️ AP Calculus AB/BC

📌 exam date: may 13, 2024.

Cram Finales

Study Guides

Practice Questions

AP Cheatsheets

Study Plans

Attend a live cram event

Review all units live with expert teachers & students

AP Calc Unit 9 Study Guides

Unit 9 – parametric equations, polar coordinates, & vector-valued functions (bc only).

Unit 9 Overview: Parametric Equations, Polar Coordinates, and Vector-Valued Functions

written by Kashvi Panjolia

Defining and Differentiating Parametric Equations

written by Jed Quiaoit

Second Derivatives of Parametric Equations

Finding Arc Lengths of Curves Given by Parametric Equations

Defining and Differentiating Vector-Valued Functions

Integrating Vector-Valued Functions

Solving Motion Problems Using Parametric and Vector-Valued Functions

Defining Polar Coordinates and Differentiating in Polar Form

Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve

Finding the Area of the Region Bounded by Two Polar Curves

Additional Resources

Study tools.

2024 AP Calculus AB Exam Guide

21 min read

written by A Q

2024 AP Calculus BC Exam Guide

26 min read

Download AP Calculus Cheat Sheet PDF Cram Chart

Frequently Asked Questions

What is U-Sub and how do I use it?

What to Know Before Taking AP Calculus AB

written by Jenna Takach

What Calculator Functions Will Save Your Life?

written by Rupi Adhikary

Is AP Calculus AB/BC Hard? Is AP Calc Worth Taking?

written by Catherine Liu

What are Riemann Sums?

written by Dylan Black

How Can I Get a 5 in AP Calculus AB/BC?

Exam Skills

AP Calculus Multiple Choice Questions

written by Meghan Dwyer

AP Calculus AB/BC Multiple Choice Help (MCQ)

AP Calculus Free Response Question (FRQ) Overview

10 min read

written by Nick Molnar

Score Higher on AP Calculus 2024: MCQ Tips from Students

Score Higher on AP Calculus 2024: FRQ Tips from Students

2015 FRQ Review

streamed by Brandon Wu

AP Cram Sessions 2021

🌶️ AP Calc Cram Review: Unit 1: Limits and Continuity

streamed by Meghan Dwyer

AP Calc AB Cram Unit 1: Limits and Continuity

slides by Meghan Dwyer

AP Calc AB Cram Unit 2: Differentiation: Definition and Fundamental Properties

slides by Jamil Siddiqui

🌶️ AP Calc Cram Review: Unit 2: Differentiation: Definition and Fundamental Properties

streamed by Jamil Siddiqui

🌶️ AP Calc Cram Review: Unit 3: Differentiation: Composite, Implicit, and Inverse Functions

AP Calc AB Cram Unit 3: Differentiation: Composite, Implicit, and Inverse Functions

Live Cram Sessions 2020

Limits, Continuity & Differentiability

Finding Derivatives

Related Rates

Curve Sketching

Calc BC Tests for Series Convergence

The Fundamental Theorem of Calculus

Previous Exam Prep

Graphical Limits

Algebraic Limits

Helping Students Master Taking Derivatives Part I (for Teachers)

Limits @ Infinity and Horizontal Asymptotes

streamed by Suzanne Ferrell-Locke

Continuity Part I

Polar Coordinates and Calculus (for BC teachers)

Stay Connected

© 2024 Fiveable Inc. All rights reserved.

AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2: Vector-Valued Functions and Motion in Space

• Last updated
• Save as PDF
• Page ID 587

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

• 2.1: Vector Valued Functions A vector valued function is a function where the domain is a subset of the real numbers and the range is a vector. There is an equivalence between vector valued functions and parametric equations.
• 2.2: Arc Length in Space For this topic, we will be learning how to calculate the length of a curve in space. The ideas behind this topic are very similar to calculating arc length for a curve in with x and y components, but now, we are considering a third component, z.
• 2.3: Curvature and Normal Vectors of a Curve For a parametrically defined curve we had the definition of arc length. Since vector valued functions are parametrically defined curves in disguise, we have the same definition. We have the added benefit of notation with vector valued functions in that the square root of the sum of the squares of the derivatives is just the magnitude of the velocity vector.
• 2.4: The Unit Tangent and the Unit Normal Vectors The derivative of a vector valued function gives a new vector valued function that is tangent to the defined curve. The analog to the slope of the tangent line is the direction of the tangent line. Since a vector contains a magnitude and a direction, the velocity vector contains more information than we need. We can strip a vector of its magnitude by dividing by its magnitude.
• 2.5: Velocity and Acceleration In single variable calculus the velocity is defined as the derivative of the position function. For vector calculus, we make the same definition.
• 2.6: Tangential and Normal Components of Acceleration This section breaks down acceleration into two components called the tangential and normal components. Similar to how we break down all vectors into \(\hat{\textbf{i}}\), \( \hat{\textbf{j}} \), and \( \hat{\textbf{k}} \) components, we can do the same with acceleration. The addition of these two components will give us the overall acceleration.
• 2.7: Parametric Surfaces We have now seen many kinds of functions. When we talked about parametric curves, we defined them as functions from \(\mathbb{R}\) to \(\mathbb{R}^2\) (plane curves) or \(\mathbb{R}\) to \(\mathbb{R}^3\) (space curves). Because each of these has its domain \(\mathbb{R}\), they are one dimensional (you can only go forward or backward). In this section, we investigate how to parameterize two dimensional surfaces.