steps on how to solve word problems

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Introduction to Word Problems

Algebra topics  -, introduction to word problems, algebra topics introduction to word problems.

Algebra Topics: Introduction to Word Problems

Lesson 9: introduction to word problems.

/en/algebra-topics/solving-equations/content/

What are word problems?

A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you've ever taken a math class, you've probably solved a word problem. For instance, does this sound familiar?

Johnny has 12 apples. If he gives four to Susie, how many will he have left?

You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you're supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:

12 - 4 = 8 , so you know Johnny has 8 apples left.

Word problems in algebra

If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.

You can tackle any word problem by following these five steps:

• Read through the problem carefully, and figure out what it's about.
• Represent unknown numbers with variables.
• Translate the rest of the problem into a mathematical expression.
• Solve the problem.
• Check your work.

We'll work through an algebra word problem using these steps. Here's a typical problem:

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?

It might seem complicated at first glance, but we already have all of the information we need to solve it. Let's go through it step by step.

Step 1: Read through the problem carefully.

With any problem, start by reading through the problem. As you're reading, consider:

• What question is the problem asking?
• What information do you already have?

Let's take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?

There's only one question here. We're trying to find out how many miles Jada drove . Now we need to locate any information that will help us answer this question.

There are a few important things we know that will help us figure out the total mileage Jada drove:

• The van cost $30 per day.
• In addition to paying a daily charge, Jada paid $0.50 per mile.
• Jada had the van for 2 days.
• The total cost was $360 .

Step 2: Represent unknown numbers with variables.

In algebra, you represent unknown numbers with letters called variables . (To learn more about variables, see our lesson on reading algebraic expressions .) You can use a variable in the place of any amount you don't know. Looking at our problem, do you see a quantity we should represent with a variable? It's often the number we're trying to find out.

Since we're trying to find the total number of miles Jada drove, we'll represent that amount with a variable—at least until we know it. We'll use the variable m for miles . Of course, we could use any variable, but m should be easy to remember.

Step 3: Translate the rest of the problem.

Let's take another look at the problem, with the facts we'll use to solve it highlighted.

The rate to rent a small moving van is $30 per day , plus $0.50 per mile . Jada rented a van to drive to her new home. It took 2 days , and the van cost $360 . How many miles did she drive?

We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It's $30 per day, and $0.50 per mile. A simpler way to say this would be:

$30 per day plus $0.50 per mile is $360.

If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360 . The shorter version will be easier to translate into a mathematical expression.

Let's start by translating $30 per day . To calculate the cost of something that costs a certain amount per day, you'd multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅ days, or 30 times the number of days . (Not sure why you'd translate it this way? Check out our lesson on writing algebraic expressions .)

$30 per day and $.50 per mile is $360

$30 ⋅ day + $.50 ⋅ mile = $360

As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50 , $.50 per mile became $.50 ⋅ mile , and is became = .

Next, we'll add in the numbers and variables we already know. We already know the number of days Jada drove, 2 , so we can replace that. We've also already said we'll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.

30 ⋅ 2 + .5 ⋅ m = 360

Now we have our expression. All that's left to do is solve it.

Step 4: Solve the problem.

This problem will take a few steps to solve. (If you're not sure how to do the math in this section, you might want to review our lesson on simplifying expressions .) First, let's simplify the expression as much as possible. We can multiply 30 and 2, so let's go ahead and do that. We can also write .5 ⋅ m as 0.5 m .

60 + .5m = 360

Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we'll know what m is equal to—in other words, it will let us know the number of miles in our word problem.

We can start by getting rid of the 60 on the left side by subtracting it from both sides .

The only thing left to get rid of is .5 . Since it's being multiplied with m , we'll do the reverse and divide both sides of the equation with it.

.5 m / .5 is m and 300 / 0.50 is 600 , so m = 600 . In other words, the answer to our problem is 600 —we now know Jada drove 600 miles.

Step 5: Check the problem.

To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got— 600 —and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada's distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let's take another look at the problem.

According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:

$30 per day and $0.50 per mile

30 ⋅ day + .5 ⋅ mile

30 ⋅ 2 + .5 ⋅ 600

According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We're done!

While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.

Let's practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:

If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.

Try completing this problem on your own. When you're done, move on to the next page to check your answer and see an explanation of the steps.

A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?

Here's another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?

Problem 1 Answer

Here's Problem 1:

A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?

Answer: $29

Let's solve this problem step by step. We'll solve it the same way we solved the problem on page 1.

Step 1: Read through the problem carefully

The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it . Let's look at the problem again. The question is right there in plain sight:

So is the information we'll need to answer the question:

• A single ticket costs $8 .
• The family pass costs $25 more than half the price of the single ticket.

Step 2: Represent the unknown numbers with variables

The unknown number in this problem is the cost of the family pass . We'll represent it with the variable f .

Step 3: Translate the rest of the problem

Let's look at the problem again. This time, the important facts are highlighted.

A single ticket to the fair costs $8 . A family pass costs $25 more than half that . How much does a family pass cost?

In other words, we could say that the cost of a family pass equals half of $8, plus $25 . To turn this into a problem we can solve, we'll have to translate it into math. Here's how:

• First, replace the cost of a family pass with our variable f .

f equals half of $8 plus $25

• Next, take out the dollar signs and replace words like plus and equals with operators.

f = half of 8 + 25

• Finally, translate the rest of the problem. Half of can be written as 1/2 times , or 1/2 ⋅ :

f = 1/2 ⋅ 8 + 25

Step 4: Solve the problem

Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.

• f is already alone on the left side of the equation, so all we have to do is calculate the right side.
• First, multiply 1/2 by 8 . 1/2 ⋅ 8 is 4 .
• Next, add 4 and 25. 4 + 25 equals 29 .

That's it! f is equal to 29. In other words, the cost of a family pass is $29 .

Step 5: Check your work

Finally, let's check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let's look at the original problem again.

We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.

• We could translate this into this equation, with s standing for the cost of a single ticket.

1/2s = 29 - 25

• Let's work on the right side first. 29 - 25 is 4 .
• To find the value of s , we have to get it alone on the left side of the equation. This means getting rid of 1/2 . To do this, we'll multiply each side by the inverse of 1/2: 2 .

According to our math, s = 8 . In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that's correct!

So now we're sure about the answer to our problem: The cost of a family pass is $29 .

Problem 2 Answer

Here's Problem 2:

Answer: $70

Let's go through this problem one step at a time.

Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it . What's the question here?

To solve the problem, you'll have to find out how much money Mo gave to charity. All the important information you need is in the problem:

• The amount Flor donated is three times as much the amount Mo donated
• Flor and Mo's donations add up to $280 total

The unknown number we're trying to identify in this problem is Mo's donation . We'll represent it with the variable m .

Here's the problem again. This time, the important facts are highlighted.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo . Between the two of them, they donated $280 . How much money did Mo give?

The important facts of the problem could also be expressed this way:

Mo's donation plus Flor's donation equals $280

Because we know that Flor's donation is three times as much as Mo's donation, we could go even further and say:

Mo's donation plus three times Mo's donation equals $280

We can translate this into a math problem in only a few steps. Here's how:

• Because we've already said we'll represent the amount of Mo's donation with the variable m , let's start by replacing Mo's donation with m .

m plus three times m equals $280

• Next, we can put in mathematical operators in place of certain words. We'll also take out the dollar sign.

m + three times m = 280

• Finally, let's write three times mathematically. Three times m can also be written as 3 ⋅ m , or just 3 m .

m + 3m = 280

It will only take a few steps to solve this problem.

• To get the correct answer, we'll have to get m alone on one side of the equation.
• To start, let's add m and 3 m . That's 4 m .
• We can get rid of the 4 next to the m by dividing both sides by 4. 4 m / 4 is m , and 280 / 4 is 70 .

We've got our answer: m = 70 . In other words, Mo donated $70 .

The answer to our problem is $70 , but we should check just to be sure. Let's look at our problem again.

If our answer is correct, $70 and three times $70 should add up to $280 .

• We can write our new equation like this:

70 + 3 ⋅ 70 = 280

• The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.

70 + 210 = 280

• The last step is to add 70 and 210. 70 plus 210 equals 280 .

280 is the combined cost of the tickets in our original problem. Our answer is correct : Mo gave $70 to charity.

/en/algebra-topics/distance-word-problems/content/

Solving Word Questions

With LOTS of examples!

In Algebra we often have word questions like:

Example: Sam and Alex play tennis.

On the weekend Sam played 4 more games than Alex did, and together they played 12 games.

How many games did Alex play?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if possible
• Assign letters for the values
• Find or work out formulas

You should also write down what is actually being asked for , so you know where you are going and when you have arrived!

Also look for key words:

Thinking Clearly

Some wording can be tricky, making it hard to think "the right way around", such as:

Example: Sam has 2 dollars less than Alex. How do we write this as an equation?

• Let S = dollars Sam has
• Let A = dollars Alex has

Now ... is that: S − 2 = A

or should it be: S = A − 2

or should it be: S = 2 − A

The correct answer is S = A − 2

( S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")

Example: on our street there are twice as many dogs as cats. How do we write this as an equation?

• Let D = number of dogs
• Let C = number of cats

Now ... is that: 2D = C

or should it be: D = 2C

Think carefully now!

The correct answer is D = 2C

( 2D = C is a common mistake, as the question is written "twice ... dogs ... cats")

Let's start with a really simple example so we see how it's done:

Example: A rectangular garden is 12m by 5m, what is its area ?

Turn the English into Algebra:

• Use w for width of rectangle: w = 12m
• Use h for height of rectangle: h = 5m

Formula for Area of a Rectangle : A = w × h

We are being asked for the Area.

A = w × h = 12 × 5 = 60 m 2

The area is 60 square meters .

Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?

• Use S for how many games Sam played
• Use A for how many games Alex played

We know that Sam played 4 more games than Alex, so: S = A + 4

And we know that together they played 12 games: S + A = 12

We are being asked for how many games Alex played: A

Which means that Alex played 4 games of tennis.

Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!

A slightly harder example:

Example: Alex and Sam also build tables. Together they make 10 tables in 12 days. Alex working alone can make 10 in 30 days. How long would it take Sam working alone to make 10 tables?

• Use a for Alex's work rate
• Use s for Sam's work rate

12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10

30 days of Alex alone is also 10 tables: 30a = 10

We are being asked how long it would take Sam to make 10 tables.

30a = 10 , so Alex's rate (tables per day) is: a = 10/30 = 1/3

Which means that Sam's rate is half a table a day (faster than Alex!)

So 10 tables would take Sam just 20 days.

Should Sam be paid more I wonder?

And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games. She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days. She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?

• The number of "5 hour" days: d
• The number of "3 hour" days: e

We know there are seven days in the week, so: d + e = 7

And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27

We are being asked for how many days she trains for 5 hours: d

The number of "5 hour" days is 3

Check : She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.

3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours

Some examples from Geometry:

Example: A circle has an area of 12 mm 2 , what is its radius?

• Use A for Area: A = 12 mm 2
• Use r for radius

And the formula for Area is: A = π r 2

We are being asked for the radius.

We need to rearrange the formula to find the area

Example: A cube has a volume of 125 mm 3 , what is its surface area?

Make a quick sketch:

• Use V for Volume
• Use A for Area
• Use s for side length of cube
• Volume of a cube: V = s 3
• Surface area of a cube: A = 6s 2

We are being asked for the surface area.

First work out s using the volume formula:

Now we can calculate surface area:

An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate. One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?

• Joel's normal rate of pay: $N per hour
• Joel works for 40 hours at $N per hour = $40N
• When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
• Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
• And together he earned $660, so:

$40N + $(12 × 1¼N) = $660

We are being asked for Joel's normal rate of pay $N.

So Joel’s normal rate of pay is $12 per hour

Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660

More about Money, with these two examples involving Compound Interest

Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?

This is the compound interest formula:

So we will use these letters:

• Present Value PV = $2,000
• Interest Rate (as a decimal): r = 0.11
• Number of Periods: n = 3
• Future Value (the value we want): FV

We are being asked for the Future Value: FV

Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33 What was the annual rate of interest for the savings account?

The compound interest formula:

• Present Value PV = $1,000
• Interest Rate (the value we want): r
• Number of Periods: n = 9
• Future Value: FV = $1,551.33

We are being asked for the Interest Rate: r

So the annual rate of interest is 5%

Check : $1,000 × (1.05) 9 = $1,000 × 1.55133 = $1,551.33

And an example of a Ratio question:

Example: At the start of the year the ratio of boys to girls in a class is 2 : 1 But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3 How many students are there altogether now?

• Number of boys now: b
• Number of girls now: g

The current ratio is 4 : 3

Which can be rearranged to 3b = 4g

At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1

b + 4 g − 2 = 2 1

Which can be rearranged to b + 4 = 2(g − 2)

We are being asked for how many students there are altogether now: b + g

There are 12 girls !

And 3b = 4g , so b = 4g/3 = 4 × 12 / 3 = 16 , so there are 16 boys

So there are now 12 girls and 16 boys in the class, making 28 students altogether .

There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3 At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1

And now for some Quadratic Equations :

Example: The product of two consecutive even integers is 168. What are the integers?

Consecutive means one after the other. And they are even , so they could be 2 and 4, or 4 and 6, etc.

We will call the smaller integer n , and so the larger integer must be n+2

And we are told the product (what we get after multiplying) is 168, so we know:

n(n + 2) = 168

We are being asked for the integers

That is a Quadratic Equation , and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.

Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES

Check 12: 12(12 + 2) = 12×14 = 168 YES

So there are two solutions: −14 and −12 is one, 12 and 14 is the other.

Note: we could have also tried "guess and check":

• We could try, say, n=10: 10(12) = 120 NO (too small)
• Next we could try n=12: 12(14) = 168 YES

But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).

Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side. Your client has 56 square meters of beautiful marble tiles to cover the whole area. What should the length of the room be?

Let's first make a sketch so we get things right!:

• the length of the room: L
• the width of the room: W
• the total Area including veranda: A
• the width of the room is half its length: W = ½L
• the total area is the (room width + 3) times the length: A = (W+3) × L = 56

We are being asked for the length of the room: L

This is a quadratic equation , there are many ways to solve it, this time let's use factoring :

And so L = 8 or −14

There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!

So the length of the room is 8 m

L = 8, so W = ½L = 4

So the area of the rectangle = (W+3) × L = 7 × 8 = 56

There we are ...

... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?

• Math for Kids
• Parenting Resources
• ELA for Kids
• Teaching Resources

How to Teach Long Division to Kids in 6 Easy Steps

15 Famous Mathematicians in History That Kids Should Know

11 Best Multiplication Apps for Kids

How to Teach Number Formation in 5 Easy Steps

13 Best Resources for Math Videos for Kids: Math Made Fun

6 Best Alternatives to Public Schooling: A Guide for Parents

How to Cope With Test Anxiety in 12 Easy Ways

Developmental Milestones for 4 Year Olds: The Ultimate Guide

Simple & Stress-Free After School Schedule for Kids of All Ages

When Do Kids Start Preschool: Age & Readiness Skills

How to Teach Letter Recognition in 6 Easy Steps

20 Fun Limericks for Kids

How to Improve Reading Comprehension: Strategies & Tips

40 Best Summer Writing Prompts for Kids of All Ages

12 Best Ways to Teach Rhyming Words to Kids

12 Best Tips for Substitute Teachers

30 Best Classroom Reward Ideas for Elementary Students

12 Best Websites for English Teachers

10 Best Game-Based Learning Platforms for Kids

60 Fun Animal Facts for Kids

10 Best Strategies for Solving Math Word Problems

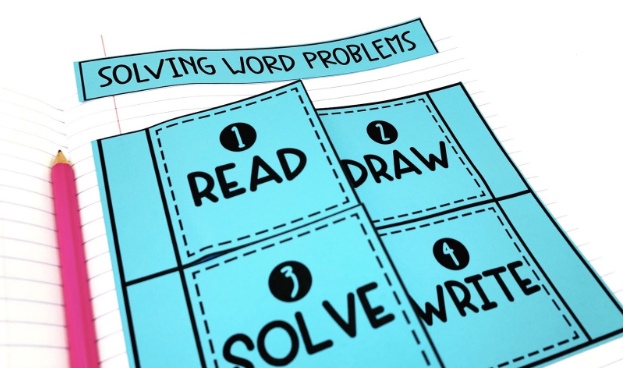
1. Understand the Problem by Paraphrasing

2. identify key information and variables, 3. translate words into mathematical symbols, 4. break down the problem into manageable parts, 5. draw diagrams or visual representations, 6. use estimation to predict answers, 7. apply logical reasoning for unknown variables, 8. leverage similar problems as templates, 9. check answers in the context of the problem, 10. reflect and learn from mistakes.

Have you ever observed the look of confusion on a student’s face when they encounter a math word problem ? It’s a common sight in classrooms worldwide, underscoring the need for effective strategies for solving math word problems . The main hurdle in solving math word problems is not just the math itself but understanding how to translate the words into mathematical equations that can be solved.

SplashLearn: Most Comprehensive Learning Program for PreK-5

SplashLearn inspires lifelong curiosity with its game-based PreK-5 learning program loved by over 40 million children. With over 4,000 fun games and activities, it’s the perfect balance of learning and play for your little one.

Generic advice like “read the problem carefully” or “practice more” often falls short in addressing students’ specific difficulties with word problems. Students need targeted math word problem strategies that address the root of their struggles head-on. 

A Guide on Steps to Solving Word Problems: 10 Strategies 

One of the first steps in tackling a math word problem is to make sure your students understand what the problem is asking. Encourage them to paraphrase the problem in their own words. This means they rewrite the problem using simpler language or break it down into more digestible parts. Paraphrasing helps students grasp the concept and focus on the problem’s core elements without getting lost in the complex wording.

Original Problem: “If a farmer has 15 apples and gives away 8, how many does he have left?”

Paraphrased: “A farmer had some apples. He gave some away. Now, how many apples does he have?”

This paraphrasing helps students identify the main action (giving away apples) and what they need to find out (how many apples are left).

Play these subtraction word problem games in the classroom for free:

Students often get overwhelmed by the details in word problems. Teach them to identify key information and variables essential for solving the problem. This includes numbers , operations ( addition , subtraction , multiplication , division ), and what the question is asking them to find. Highlighting or underlining can be very effective here. This visual differentiation can help students focus on what’s important, ignoring irrelevant details.

• Encourage students to underline numbers and circle keywords that indicate operations (like ‘total’ for addition and ‘left’ for subtraction).
• Teach them to write down what they’re solving for, such as “Find: Total apples left.”

Problem: “A classroom has 24 students. If 6 more students joined the class, how many students are there in total?”

Key Information:

• Original number of students (24)
• Students joined (6)
• Looking for the total number of students

Here are some fun addition word problems that your students can play for free:

The transition from the language of word problems to the language of mathematics is a critical skill. Teach your students to convert words into mathematical symbols and equations. This step is about recognizing keywords and phrases corresponding to mathematical operations and expressions .

Common Translations:

• “Total,” “sum,” “combined” → Addition (+)
• “Difference,” “less than,” “remain” → Subtraction (−)
• “Times,” “product of” → Multiplication (×)
• “Divided by,” “quotient of” → Division (÷)
• “Equals” → Equals sign (=)

Problem: “If one book costs $5, how much would 4 books cost?”

Translation: The word “costs” indicates a multiplication operation because we find the total cost of multiple items. Therefore, the equation is 4 × 5 = $20

Complex math word problems can often overwhelm students. Incorporating math strategies for problem solving, such as teaching them to break down the problem into smaller, more manageable parts, is a powerful approach to overcome this challenge. This means looking at the problem step by step rather than simultaneously trying to solve it. Breaking it down helps students focus on one aspect of the problem at a time, making finding the solution more straightforward.

Problem: “John has twice as many apples as Sarah. If Sarah has 5 apples, how many apples do they have together?”

Steps to Break Down the Problem:

Find out how many apples John has: Since John has twice as many apples as Sarah, and Sarah has 5, John has 5 × 2 = 10

Calculate the total number of apples: Add Sarah’s apples to John’s to find the total,  5 + 10 = 15

By splitting the problem into two parts, students can solve it without getting confused by all the details at once.

Explore these fun multiplication word problem games:

Diagrams and visual representations can be incredibly helpful for students, especially when dealing with spatial or quantity relationships in word problems. Encourage students to draw simple sketches or diagrams to represent the problem visually. This can include drawing bars for comparison, shapes for geometry problems, or even a simple distribution to better understand division or multiplication problems .

Problem: “A garden is 3 times as long as it is wide. If the width is 4 meters, how long is the garden?”

Visual Representation: Draw a rectangle and label the width as 4 meters. Then, sketch the length to represent it as three times the width visually, helping students see that the length is 4 × 3 = 12

Estimation is a valuable skill in solving math word problems, as it allows students to predict the answer’s ballpark figure before solving it precisely. Teaching students to use estimation can help them check their answers for reasonableness and avoid common mistakes.

Problem: “If a book costs $4.95 and you buy 3 books, approximately how much will you spend?”

Estimation Strategy: Round $4.95 to the nearest dollar ($5) and multiply by the number of books (3), so 5 × 3 = 15. Hence, the estimated total cost is about $15.

Estimation helps students understand whether their final answer is plausible, providing a quick way to check their work against a rough calculation.

Check out these fun estimation and prediction word problem worksheets that can be of great help:

When students encounter problems with unknown variables, it’s crucial to introduce them to logical reasoning. This strategy involves using the information in the problem to deduce the value of unknown variables logically. One of the most effective strategies for solving math word problems is working backward from the desired outcome. This means starting with the result and thinking about the steps leading to that result, which can be particularly useful in algebraic problems.

Problem: “A number added to three times itself equals 32. What is the number?”

Working Backward:

Let the unknown number be x.

The equation based on the problem is  x + 3x = 32

Solve for x by simplifying the equation to 4x=32, then dividing by 4 to find x=8.

By working backward, students can more easily connect the dots between the unknown variable and the information provided.

Practicing problems of similar structure can help students recognize patterns and apply known strategies to new situations. Encourage them to leverage similar problems as templates, analyzing how a solved problem’s strategy can apply to a new one. Creating a personal “problem bank”—a collection of solved problems—can be a valuable reference tool, helping students see the commonalities between different problems and reinforcing the strategies that work.

Suppose students have solved a problem about dividing a set of items among a group of people. In that case, they can use that strategy when encountering a similar problem, even if it’s about dividing money or sharing work equally.

It’s essential for students to learn the habit of checking their answers within the context of the problem to ensure their solutions make sense. This step involves going back to the original problem statement after solving it to verify that the answer fits logically with the given information. Providing a checklist for this process can help students systematically review their answers.

Checklist for Reviewing Answers:

• Re-read the problem: Ensure the question was understood correctly.
• Compare with the original problem: Does the answer make sense given the scenario?
• Use estimation: Does the precise answer align with an earlier estimation?
• Substitute back: If applicable, plug the answer into the problem to see if it works.

Problem: “If you divide 24 apples among 4 children, how many apples does each child get?”

After solving, students should check that they understood the problem (dividing apples equally).

Their answer (6 apples per child) fits logically with the number of apples and children.

Their estimation aligns with the actual calculation.

Substituting back 4×6=24 confirms the answer is correct.

Teaching students to apply logical reasoning, leverage solved problems as templates, and check their answers in context equips them with a robust toolkit for tackling math word problems efficiently and effectively.

One of the most effective ways for students to improve their problem-solving skills is by reflecting on their errors, especially with math word problems. Using word problem worksheets is one of the most effective strategies for solving word problems, and practicing word problems as it fosters a more thoughtful and reflective approach to problem-solving

These worksheets can provide a variety of problems that challenge students in different ways, allowing them to encounter and work through common pitfalls in a controlled setting. After completing a worksheet, students can review their answers, identify any mistakes, and then reflect on them in their mistake journal. This practice reinforces mathematical concepts and improves their math problem solving strategies over time.

3 Additional Tips for Enhancing Word Problem-Solving Skills

Before we dive into the importance of reflecting on mistakes, here are a few impactful tips to enhance students’ word problem-solving skills further:

1. Utilize Online Word Problem Games

Incorporate online games that focus on math word problems into your teaching. These interactive platforms make learning fun and engaging, allowing students to practice in a dynamic environment. Games can offer instant feedback and adaptive challenges, catering to individual learning speeds and styles.

Here are some word problem games that you can use for free:

2. Practice Regularly with Diverse Problems

Consistent practice with a wide range of word problems helps students become familiar with different questions and mathematical concepts. This exposure is crucial for building confidence and proficiency.

Start Practicing Word Problems with these Printable Word Problem Worksheets:

3. Encourage Group Work

Solving word problems in groups allows students to share strategies and learn from each other. A collaborative approach is one of the best strategies for solving math word problems that can unveil multiple methods for tackling the same problem, enriching students’ problem-solving toolkit.

Conclusion 

Mastering math word problems is a journey of small steps. Encourage your students to practice regularly, stay curious, and learn from their mistakes. These strategies for solving math word problems are stepping stones to turning challenges into achievements. Keep it simple, and watch your students grow their confidence and skills, one problem at a time.

Frequently Asked Questions (FAQs)

How can i help my students stay motivated when solving math word problems.

Encourage small victories and use engaging tools like online games to make practice fun and rewarding.

What's the best way to teach beginners word problems?

Begin with simple problems that integrate everyday scenarios to make the connection between math and real-life clear and relatable.

How often should students practice math word problems?

Regular, daily practice with various problems helps build confidence and problem-solving skills over time.

• Pre-Kindergarten
• Kindergarten

Most Popular

15 Best Report Card Comments Samples

117 Best Riddles for Kids (With Answers)

40 Best Good Vibes Quotes to Brighten Your Day

Recent posts.

15 Best Fourth of July Crafts for Preschoolers

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Watch your kids fall in love with math & reading through our scientifically designed curriculum.

Parents, try for free Teachers, use for free

• Games for Kids
• Worksheets for Kids
• Math Worksheets
• ELA Worksheets
• Math Vocabulary
• Number Games
• Addition Games
• Subtraction Games
• Multiplication Games
• Division Games
• Addition Worksheets
• Subtraction Worksheets
• Multiplication Worksheets
• Division Worksheets
• Times Tables Worksheets
• Reading Games
• Writing Games
• Phonics Games
• Sight Words Games
• Letter Tracing Games
• Reading Worksheets
• Writing Worksheets
• Phonics Worksheets
• Sight Words Worksheets
• Letter Tracing Worksheets
• Prime Number
• Order of Operations
• Long multiplication
• Place value
• Parallelogram
• SplashLearn Success Stories
• SplashLearn Apps
• [email protected]

© Copyright - SplashLearn

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

How do you solve word problems in math?

Master word problems with eight simple steps from a math tutor!

Author Amber Watkins

Published April 2024

• Key takeaways
• Students who struggle with reading, tend to struggle with understanding and solving word problems. So the best way to solve word problems in math is to become a better reader!
• Mastery of word problems relies on your child’s knowledge of keywords for word problems in math and knowing what to do with them.
• There are 8 simple steps each child can use to solve word problems- let’s go over these together.

Table of contents

• How to solve word problems

Lesson credits

As a tutor who has seen countless math worksheets in almost every grade – I’ll tell you this: every child is going to encounter word problems in math. The key to mastery lies in how you solve them! So then, how do you solve word problems in math?

In this guide, I’ll share eight steps to solving word problems in math.

How to solve word problems in math in 8 steps

Step 1: read the word problem aloud.

For a child to understand a word problem, it needs to be read with accuracy and fluency! That is why, when I tutor children with word problems, I always emphasize the importance of reading properly.

Mastering step 1 looks like this:

• Allow your child to read the word problem aloud to you. 
• Don’t let your child skip over or mispronounce any words. 
• If necessary, model how to read the word problem, then allow your child to read it again. Only after the word problem is read accurately, should you move on to step 2.

Step 2: Highlight the keywords in the word problem

The keywords for word problems in math indicate what math action should be taken. Teach your child to highlight or underline the keywords in every word problem. 

Here are some of the most common keywords in math word problems: 

• Subtraction words – less than, minus, take away
• Addition words – more than, altogether, plus, perimeter
• Multiplication words – Each, per person, per item, times, area 
• Division words – divided by, into
• Total words – in all, total, altogether

Let’s practice. Read the following word problem with your child and help them highlight or underline the main keyword, then decide which math action should be taken.

Michael has ten baseball cards. James has four baseball cards less than Michael. How many total baseball cards does James have? 

The words “less than” are the keywords and they tell us to use subtraction .

Step 3: Make math symbols above keywords to decode the word problem

As I help students with word problems, I write math symbols and numbers above the keywords. This helps them to understand what the word problem is asking.

Let’s practice. Observe what I write over the keywords in the following word problem and think about how you would create a math sentence using them:

Step 4: Create a math sentence to represent the word problem

Using the previous example, let’s write a math sentence. Looking at the math symbols and numbers written above the word problem, our math sentence should be: 10 – 5 = 5 ! 

Each time you practice a word problem with your child, highlight keywords and write the math symbols above them. Then have your child create a math sentence to solve. 

Step 5: Draw a picture to help illustrate the word problem

Pictures can be very helpful for problems that are more difficult to understand. They also are extremely helpful when the word problem involves calculating time , comparing fractions , or measurements . 

Step 6: Always show your work

Help your child get into the habit of always showing their work. As a tutor, I’ve found many reasons why having students show their work is helpful:

• By showing their work, they are writing the math steps repeatedly, which aids in memory
• If they make any mistakes they can track where they happened
• Their teacher can assess how much they understand by reviewing their work
• They can participate in class discussions about their work

Step 7: When solving word problems, make sure there is always a word in your answer!

If the word problem asks: How many peaches did Lisa buy? Your child’s answer should be: Lisa bought 10 peaches .

If the word problem asks: How far did Kyle run? Your child’s answer should be: Kyle ran 20 miles .

So how do you solve a word problem in math?

Together we reviewed the eight simple steps to solve word problems. These steps included identifying keywords for word problems in math, drawing pictures, and learning to explain our answers. 

Is your child ready to put these new skills to the test? Check out the best math app for some fun math word problem practice.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

Amber Watkins

Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring elementary through college level math. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

What we offer

Quick links

All rights reserved. 

Are you a parent, teacher or student?

Get started for free!

Maths information pack

We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.

Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack

We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.

DoodleMaths

DoodleTables

DoodleEnglish

DoodleSpell

If you’d like to use Doodle’s browser version, please visit this page on a desktop.

To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Word Problems in Algebra

Last Updated: December 19, 2022 Fact Checked

This article was co-authored by Daron Cam . Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 72,305 times.

You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don't know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.

Assessing the Problem

• For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
• In this problem, you are asked to find the price of the first book Jane purchased.

• For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don't know the price of the first book.

• Multiplication keywords include times, of, and f actor. [9] X Research source
• Division keywords include per, out of, and percent. [10] X Research source
• Addition keywords include some, more, and together. [11] X Research source
• Subtraction keywords include difference, fewer, and decreased. [12] X Research source

Finding the Solution

Completing a Sample Problem

• Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.

• Since you are combining their profits and tips, you will be adding two terms. So, x = __ + __.

Expert Q&A

• Word problems can have more than one unknown and more the one variable. Thanks Helpful 2 Not Helpful 1
• The number of variables is always equal to the number of unknowns. Thanks Helpful 1 Not Helpful 0
• While solving word problems you should always read every sentence carefully and try to extract all the numerical information. Thanks Helpful 1 Not Helpful 0

You Might Also Like

• ↑ Daron Cam. Academic Tutor. Expert Interview. 29 May 2020.
• ↑ http://www.purplemath.com/modules/translat.htm
• ↑ https://www.mathsisfun.com/algebra/word-questions-solving.html
• ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut8_probsol.htm
• ↑ http://www.virtualnerd.com/algebra-1/algebra-foundations/word-problem-equation-writing.php
• ↑ https://www.khanacademy.org/test-prep/praxis-math/praxis-math-lessons/praxis-math-algebra/a/gtp--praxis-math--article--algebraic-word-problems--lesson

About This Article

To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x - 10. To learn how to solve an equation with multiple variables, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

James Carson

Sep 13, 2019

Did this article help you?

Lee Broadway

Aug 26, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

5 Easy Steps to Solving Word Problems

Word problems strike fear into the hearts of many students, and the trauma can even carry into adulthood. This is why word problems are the topic of many education jokes.

“If two trains start at the same station and travel in opposite directions at the same speed, when will the bacon be ready for breakfast?”

This is obviously a silly scenario, but it shows how word problems are regarded by many: a mangle of confusion that doesn’t make sense and can’t be solved!

Why Are Word Problems Difficult for Children?

Why can word problems be so confusing and scary? There are a few possible reasons.

• Word problems are often introduced to us at an age before our skills of abstract thinking are fully developed. However, a student’s imagination is a great asset to use in understanding word problems!
• Word problems are sometimes simply included as the “harder problems” at the end of homework assignments and the student is never really taught how to approach them.
• It is sometimes ignored that a student’s math and reading ability come into play when word problems are assigned. But if the second grade math student is still only reading on a first-grade level, he will have difficulty solving word problems even if he is otherwise good at math! It can thus be helpful to assess both a student’s math and reading ability to set him up for success. The tutoring service provided by masterygenius.com is a great option since both math and reading skills can be addressed.

A quick tip before we get started…

Explain to students that the word “problem” really means “question.” A word problem is just asking a question to which the students must find an answer. Show them that you need to identify the question before you even worry about which math operations are going to be used. Word problems can be treated like mysteries: the students are the detectives that are going to use the clues in the question to find the answer!

So what are the five easy steps to solving word problems? Let’s take a look!

Five Easy Steps to Solving Word Problems (WASSP)

• Write (or draw) what you know.
• Ask the question.
• Set up a math problem that could answer the question.
• Solve the math problem to get an answer.
• Put the answer in a sentence to see if the answer makes sense!

Let’s look at an example word problem to demonstrate these steps.

Matt has twelve cookies he can give to his friends during lunchtime. If Matt has three friends sitting at his table, how many cookies can Matt give to each of his friends?

1. Write (or draw) what you know.

It is important to convince students that they do not have to immediately know what math operation is required to solve the problem. They first need only understand the scenario itself. In this example, the student could simply write down “12 cookies” and “3 friends,” or draw Matt with 12 cookies sitting at a table with three other children.

2. Ask the question.

Again, we don’t need to know what the math operation is yet! We just need to identify what is actually being asked. What do we NOT know?

The student could write, “How many cookies can each of Matt’s friends have?”

Alternatively, the student could draw a question mark over each friend’s head, maybe with a thought bubble of a cookie!

3. Set up a math problem that could answer the question.

• It can be a good idea to teach students “clue” words or phrases in problems which can identify what math operation may be needed. However, this should not be the student’s only skill for deciding what math operation to use, because these “clue” words can sometimes be confusing. For example, the phrases “how many in all” and “how many more” seem very similar to a student, but the first phrase indicates addition and the second phrase indicates subtraction!
• It is good for a student to also be able to reason what math operation is needed based on understanding the scenario itself (which is a better builder of true critical thinking skills). This is why the first two steps (write what you know and ask the question) are so important. The student that has a true understanding of the scenario will be better equipped to reason what math operation is needed.

In this example, the “clue” word (if you are using that method of reasoning) would be “each,” which indicates division. Or, the student could understand that Matt has to split, or divide, the cookies among his friends. Thus a division problem is needed!

Dividing 12 cookies among 3 friends means 12 is divided by 3.

4. Solve the problem.

It is important to note that using units can be a good idea . Otherwise, the answer could be misunderstood. Is it 4 cookies, or 4 friends, or something else?

12 cookies ÷ 3 friends = 4 cookies per friend

5. Put the answer in a sentence to see if the answer makes sense.

“Each of Matt’s friends can have four cookies.”

Does this answer make sense? It seems reasonable. How could this step help identify an incorrect answer?

What if the student had decided this was a multiplication problem?

12 cookies × 3 friends = 36 cookies per friend

If the student then writes a sentence using the answer, he may realize the answer can’t be right.

“Each of Matt’s friends can have 36 cookies.”

How would that be possible if Matt only had 12 cookies to start with? This must not be a multiplication problem. Let’s try again!

Practice the Five Easy Steps for Word-Problem Success!

Steps 1 and 2 ( Write what you know and Ask the question) help the student gain an understanding of the scenario.

Steps 3 and 4 ( Set up the math problem and Solve the problem) can be more easily navigated with critical thinking once the scenario is understood.

Step 5 ( Put the answer in a sentence) can help the student decide whether the answer makes sense.

Now your student is ready for word-problem success!

Make sure to start at the student’s level of understanding so he can experience success and build confidence, moving on to more challenging problems as appropriate. Customized curriculum is always best, which again makes masterygenius.com a great option if tutoring is needed. Students are assessed and then matched with a curriculum that strikes balance between building confidence and tackling challenges, leading to topic mastery.

How To Solve Algebra Word Problems?

Many students find solving algebra word problems difficult. The best way to approach word problems is to “divide and conquer”. Break the problem down into smaller bits and solve each bit at a time.

Related Pages Basic Algebra Combining Like Terms Solving Equations More Algebra Lessons

Step 1: Translate the problem into equations with variables

First, we need to translate the word problem into equation(s) with variables. Then, we need to solve the equation(s) to find the solution(s) to the word problems.

Translating words to equations

How to recognize some common types of algebra word problems and how to solve them step by step.

The following shows how to approach the common types of algebra word problems.

Age Problems usually compare the ages of people. They may involve a single person , comparing his/her age in the past, present or future. They may also compare the ages involving more than one person .

Average Problems involve the computations for arithmetic mean or weighted average of different quantities. Another common type of average problems is the average speed computation.

Coin Problems deal with items with denominated values. Similar word problems are Stamp Problems and Ticket Problems .

Consecutive Integer Problems deal with consecutive numbers. The number sequences may be Even or Odd , or some other simple number sequences.

Digit Problems involve the relationship and manipulation of digits in numbers.

Distance Problems involve the distance an object travels at a rate over a period of time. We can have objects that Travel at Different Rates , objects that Travel in Different Directions or we may need to find the distance Given the Total Time

Fraction Problems involve fractions or parts of a whole.

Geometry Word Problems deal with geometric figures and angles described in words. This include geometry word problems Involving Perimeters , Involving Areas and Involving Angles

Integer Problems involve numerical representations of word problems. The integer word problems may Involve 2 Unknowns or may Involve More Than 2 Unknowns

Interest Problems involve calculations of simple interest. Lever Problems deal with the lever principle described in word problems. Lever problem may involve 2 Objects or More than 2 Objects

Mixture Problems involve items or quantities of different values that are mixed together. This involve Adding to a Solution , Removing from a Solution , Replacing a Solution ,or Mixing Items of Different Values

Motion Word Problems are word problems that uses the distance, rate and time formula.

Number Sequence Problems use number sequences in the construction of word problems. You may be asked to find the Value of a Particular Term or the Pattern of a Sequence

Proportion Problems involve proportional and inversely proportional relationships of various quantities.

Ratio Problems require you to relate quantities of different items in certain known ratios, or work out the ratios given certain quantities. This could be Two-Term Ratios or Three-Term Ratios

Symbol Problems

Variation Word Problems may consist of Direct Variation Problems , Inverse Variation Problems or Joint Variation Problems

Work Problems involve different people doing work together at different rates. This may be for Two Persons , More Than Two Persons or Pipes Filling up a Tank

For more Algebra Word Problems and Algebra techniques, go to our Algebra page

Step 2: Solving the equations - finding the values of the variables for the equations

Simplifying the equation Isolate the variable (Transposition) Addition Method (Opposite-Coefficient Method) Substitution Method Factoring Quadratic Equations Quadratic Formula

Algebra Word Problems with examples, videos and step-by-step solutions

Age Problems Age Problems: Single Person More Than One Person Age Word Problems 1 Age Word Problems 2

Arithmetic Mean Weighted Average Average Speed

Problems involving Coins Stamp Problems Ticket Problems Coin Word Problems 1 Coin Word Problems 2

Consecutive Integers 1 Consecutive Integers 2 Consecutive Odd Integer Consecutive Even Integer Consecutive Integer Problems Even & Odd Word Problems

Simple Digit Problems Convert Digits to Numbers & Interchanging Digits Digits Word Problems

Distance Problems Travel at Different Rates Travel in Different Directions Given Total Time

Fraction Problems Percent Word Problems

Geometry Word Problems Involving Perimeters Involving Areas Involving Angles Angle Word Problems Perimeter Word Problems 1 Perimeter Word Problems 2 Perimeter Word Problems 3 Area Word Problems Area of Rectangle Word Problems Area of Triangle Word Problems Area of Parallelogram Word Problems Volume Word Problems Volume Word Problems Geometry Word Problems using Quadratic Equations Pythagorean Theorem Word Problems Trigonometry Word Problems

Involving 2 Unknowns More Than 2 Unknowns Integer Word Problems 1 Integer Word Problems 2

Interest Word Problems Simple Interest Word Problems Compound Interest Word Problems 1 Compound Interest Word Problems 2 Investment Word Problems

Involving 2 or More Objects

Mixture Problems Adding to a Solution Remove from a Solution Replace a Solution Mix Items of Different Values Algebra Mixture Problems 1 Algebra Mixture Problems 2 Algebra Mixture Problems 3

Money Word Problems

Rate, Time, Distance Problems 1 Rate, Time, Distance Problems 2 Rate, Time, Distance Problems 3 Motion Word Problems Motion Problems: Passing & Overtaking Wind & Current Problems

Number Sequence Problems Value of a Particular Term Pattern of a Sequence

Proportion Problems Directly Proportional Inversely Proportional Proportion Word Problems

Quadratic Word Problems Quadratic Equations Word Problems Quadratic Problems in Geometry Projectile Motion

Ratio Problems Two-Term Ratios Three-Term Ratios Ratio Word Problems

Direct Variation Problems Inverse Variation Problems Joint & Combined Variations Variation Word Problems

Work Problems Two Persons More Than Two Persons Pipes Filling up a Tank Algebra Work Problems 1 Algebra Work Problems 2

One Variable Word Problems Two-Variable Word Problems System of Equations Word Problems

Have a look at the following videos for some introduction of how to solve algebra problems:

Example: Angela sold eight more new cars this year than Carmen. If together they sold a total of 88 cars, how many cars did each of them sell?

Example: One number is 4 times as large as another. Their sum is 45. Find the numbers.

Example: Devon is going to make 3 shelves for her father. She has a piece of lumber 12 feet long. She wants the top shelf to be half a foot shorter than the middle, and the bottom shelf to be half a foot shorter than twice the length of the top shelf. How long will each shelf be if she uses the entire 12 feet of wood?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Grades 6-12
• School Leaders

Don't Miss the Grand Prize: A $2,500 Office Depot/OfficeMax Card!

14 Effective Ways to Help Your Students Conquer Math Word Problems

If a train leaving Minneapolis is traveling at 87 miles an hour…

Word problems can be tricky for a lot of students, but they’re incredibly important to master. After all, in the real world, most math is in the form of word problems. “If one gallon of paint covers 400 square feet, and my wall measures 34 feet by 8 feet, how many gallons do I need?” “This sweater costs $135, but it’s on sale for 35% off. So how much is that?” Here are the best teacher-tested ideas for helping kids get a handle on these problems.

1. Solve word problems regularly

This might be the most important tip of all. Word problems should be part of everyday math practice, especially for older kids. Whenever possible, use word problems every time you teach a new math skill. Even better: give students a daily word problem to solve so they’ll get comfortable with the process.

Learn more: Teaching With Jennifer Findlay

2. Teach problem-solving routines

There are a LOT of strategies out there for teaching kids how to solve word problems (keep reading to see some terrific examples). The important thing to remember is that what works for one student may not work for another. So introduce a basic routine like Plan-Solve-Check that every kid can use every time. You can expand on the Plan and Solve steps in a variety of ways, but this basic 3-step process ensures kids slow down and take their time.

Learn more: Word Problems Made Easy

[contextly_auto_sidebar]

3. Visualize or model the problem

Encourage students to think of word problems as an actual story or scenario. Try acting the problem out if possible, and draw pictures, diagrams, or models. Learn more about this method and get free printable templates at the link.

Learn more: Math Geek Mama

4. Make sure they identify the actual question

Educator Robert Kaplinsky asked 32 eighth grade students to answer this nonsensical word problem. Only 25% of them realized they didn’t have the right information to answer the actual question; the other 75% gave a variety of numerical answers that involved adding, subtracting, or dividing the two numbers. That tells us kids really need to be trained to identify the actual question being asked before they proceed. 

Learn more: Robert Kaplinsky

5. Remove the numbers

It seems counterintuitive … math without numbers? But this word problem strategy really forces kids to slow down and examine the problem itself, without focusing on numbers at first. If the numbers were removed from the sheep/shepherd problem above, students would have no choice but to slow down and read more carefully, rather than plowing ahead without thinking. 

Learn more: Where the Magic Happens Teaching

6. Try the CUBES method

This is a tried-and-true method for teaching word problems, and it’s really effective for kids who are prone to working too fast and missing details. By taking the time to circle, box, and underline important information, students are more likely to find the correct answer to the question actually being asked.

Learn more: Teaching With a Mountain View

7. Show word problems the LOVE

Here’s another fun acronym for tackling word problems: LOVE. Using this method, kids Label numbers and other key info, then explain Our thinking by writing the equation as a sentence. They use Visuals or models to help plan and list any and all Equations they’ll use. 

8. Consider teaching word problem key words

This is one of those methods that some teachers love and others hate. Those who like it feel it offers kids a simple tool for making sense of words and how they relate to math. Others feel it’s outdated, and prefer to teach word problems using context and situations instead (see below). You might just consider this one more trick to keep in your toolbox for students who need it.

Learn more: Book Units Teacher

9. Determine the operation for the situation

Instead of (or in addition to) key words, have kids really analyze the situation presented to determine the right operation(s) to use. Some key words, like “total,” can be pretty vague. It’s worth taking the time to dig deeper into what the problem is really asking. Get a free printable chart and learn how to use this method at the link.

Learn more: Solving Word Problems With Jennifer Findlay

10. Differentiate word problems to build skills

Sometimes students get so distracted by numbers that look big or scary that they give up right off the bat. For those cases, try working your way up to the skill at hand. For instance, instead of jumping right to subtracting 4 digit numbers, make the numbers smaller to start. Each successive problem can be a little more difficult, but kids will see they can use the same method regardless of the numbers themselves.

Learn more: Differentiating Math 

11. Ensure they can justify their answers

One of the quickest ways to find mistakes is to look closely at your answer and ensure it makes sense. If students can explain how they came to their conclusion, they’re much more likely to get the answer right. That’s why teachers have been asking students to “show their work” for decades now.

Learn more: Madly Learning

12. Write the answer in a sentence

When you think about it, this one makes so much sense. Word problems are presented in complete sentences, so the answers should be too. This helps students make certain they’re actually answering the question being asked… part of justifying their answer.

Learn more: Multi-Step Word Problems

13. Add rigor to your word problems

A smart way to help kids conquer word problems is to, well… give them better problems to conquer. A rich math word problem is accessible and feels real to students, like something that matters. It should allow for different ways to solve it and be open for discussion. A series of problems should be varied, using different operations and situations when possible, and even include multiple steps. Visit both of the links below for excellent tips on adding rigor to your math word problems.

Learn more: The Routty Math Teacher and Alyssa Teaches

14. Use a problem-solving rounds activity.

Put all those word problem strategies and skills together with this whole-class activity. Start by reading the problem as a group and sharing important information. Then, have students work with a partner to plan how they’ll solve it. In round three, kids use those plans to solve the problem individually. Finally, they share their answer and methods with their partner and the class. Be sure to recognize and respect all problem-solving strategies that lead to the correct answer.

Learn more: Teacher Trap

Like these word problem tips and tricks? Learn more about Why It’s Important to Honor All Math Strategies .

Plus, 60+ Awesome Websites For Teaching and Learning Math .

You Might Also Like

Digital Escape Rooms for Fun and Formative Assessment

Escape the monotony while racing the clock. Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

SOLVING WORD PROBLEMS: A VISUAL APPROACH: HOME

Step 1: Identify the given information in the problem.

Underline the information in your problem. Then create a checklist. As you use the information in your solution, make sure to check off each box.

Understanding a math word problem is 50% of the work. So give yourself a pat on the back when you’ve finished it! 

Step 2: Find the question in the passage and state it in your own words.

Underline the question with a different color than you used for the first step. After you have underlined the question, write the information out in your own words, so that you understand what is being asked. 

Step 3: Devise a strategy to solve the problem.

Now that you have collected the information you need to solve the problem, you need to come up with a strategy to conquer the problem.

Think about what’s being asked. Is there a formula you need to use? Do you need to calculate a percentage for your final answer? Write out the steps you need to use to solve the problem, so that you can carry out your plan.

THE STEPS TO SOLVING A WORD PROBLEM

• Identify the given information.
• Find the question and state it in your own words.
• Devise a strategy to solve the problem.
• Carry out your plan.

Use three different colored pencils/pens to separate each of the first three parts of the problem solving process.

Here are a few examples of how to use this process in solving a mathematical problem.

RATE THIS GUIDE

Ask the asc for help.

Need Academic Help? Contact the Academic Success Center (ASC)!

Step 4: Once you have created a plan, then you need to solve the problem. Make sure you have used all the given information in the problem, answered the question, and followed each step in your strategy.

Keep Calm.   Be confident.  You’ve got this! 

• Last Updated: Nov 22, 2017 12:17 PM
• URL: https://guides.kendall.edu/wordproblems

Strategies for Solving Math Word Problems

Math word problems can be tricky and often challenging to solve. Employing the SQRQCQ method can make solving math word problems easier and less intimidating.

The SQRQCQ method is particularly useful for children with learning disabilities and can be used effectively in special education programs. SQRQCQ is an abbreviation for Survey, Question, Read, Question, Compute, and Question.

Step 1 – SURVEY the Math Problem

The first step to solving a math word problem is to read the problem in its entirety to understand what you are being asked to solve. After you read it, you can decide the most relevant aspects of the problem that need to be solved and what aspects are not relevant to solving the problem. The idea here is to get a general understanding.

Step 2 – QUESTION

Once you have an idea of what you’re attempting to solve, you need to determine what formulas, steps, or equations should be utilized in order to find the correct answer. It is impossible to find an answer if you can’t determine what needs to be solved. Basically, what are the questions being asked by the problem?

Step 3 – REREAD

Now that you’ve determined what needs to be solved, reread the problem and pay close attention to specific details. Determine which aspects of the problem are interrelated. Identify all relevant facts and information needed to solve the problem. As you do, write them down.

Step 4 – QUESTION

Now that you’re familiar with specific details and how different facts and information within the problem are interrelated, determine what formulas or equations must be used to set up and solve the problem. Be sure to write down what steps or operations you will use for easy reference.

Step 5 – COMPUTE

Use the formulas and/or equations identified in the previous step to complete the calculations. Be sure to follow the steps you outlined while setting up an equation or using a formula. As you complete each step, check it off your list.

Step 6 – QUESTION

Once you’ve completed the calculations, review the final answer and make sure it is correct and accurate. If it does not appear logical, review the steps you took to find the answer and look for calculation or set-up errors. Recalculate the numbers or make other changes until you get an answer that makes sense.

How does SQRQCQ help students with learning disabilities?

Math word problems tend to be especially challenging for Learning Disabled (LD) students. LD students often lack “Concept Imagery”, or the ability to visualize the whole problem by creating a complete mental image. They often jump right into calculations and computations without understanding what the problem is asking or what they’re looking for.

LD students may also struggle to understand the words or wording within math word problems correctly. The inability to correctly interpret and understand wording greatly impacts their math reasoning skills and often leads them to making the wrong calculations and arriving incorrect conclusions.

Remembering and manipulating information and details in their working memory is another challenge some LD students face as they try to see the whole picture. Slow processing of information, followed by frustration and anxiety, will often lead LD students to try and get through math word problems as quickly as possible – which is why they often jump straight into computations in their attempt to make it to the finish line as quickly as possible.

SQRQCQ is a metacognitive guide that provides LD students with a logical order for solving math word problems. It provides just enough direction to guide them through the reasoning process without overwhelming them. SQRQCQ is also a mnemonic that is easy for students to remember and which they can fall back on when completing homework or taking tests.

Read also: – A Guide for St u dying Math

Similar Posts:

• Discover Your Learning Style – Comprehensive Guide on Different Learning Styles
• 15 Learning Theories in Education (A Complete Summary)
• 35 of the BEST Educational Apps for Teachers (Updated 2024)

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.

MAKE WAVES WITH THIS FREE WEEKLONG VOCABULARY UNIT!

Strategies for Solving Word Problems – Math

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.

The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!

How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.

Here are the seven strategies I use to help students solve word problems.

1. read the entire word problem.

Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.

2. Think About the Word Problem

Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.

Here are the questions:

A. what exactly is the question.

What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.

B. What do I need in order to find the answer?

Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.

This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined ), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better

Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.

One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.

If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?

This is where students will focus in on the numbers which will be used to solve the problem.

3. Write on the Word Problem

This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:

• Circle any numbers you’ll use.
• Lightly cross out any information you don’t need.
• Underline the phrase or sentence which tells exactly what you’ll need to find.

4. Draw a Simple Picture and Label It

Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.

For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!

5. Estimate the Answer Before Solving

Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.

6. Check Your Work When Done

This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable ? I want students to do more than to be number crunchers but to really think about what those numbers mean.

Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.

7. Practice Word Problems Often

Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.

When students practice word problems, often several things happen. Word problems become less scary (no, really).

They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.

If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.

This 3rd grade math task cards bundle has word problems in almost every one of its 30 task card sets..

There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.

CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.

CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.

CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?

3rd Grade: Rounding Whole Numbers Task Cards

4th Grade: Convert Fractions and Decimals Task Cards

5th Grade: Read, Write, and Compare Decimals Task Cards

Thanks so much for stopping by!

• Read more about: Math

You might also like...

Fraction Activities Students Love – Math

Fractions can be tough! While it takes time and repeated exposure with fractions for students to have a real understanding of them, there are lots

Math Games Using Dice

Games are an important part of math class, in my opinion. Not only are kids able to practice the skills that we have been focusing

Math Games Using Dominoes

Math games have always been part of our math time. I love the fact that any time I introduce a math game, I know I’ll

Hi, I’m Jenn, CEO and owner of The Teacher Next Door!

I know that you strive to be an effective upper elementary teacher while maintaining a healthy work-life balance.

In order to do that, you need resources that are impactful, yet simple .

The problem is that most resources and curriculums out there are far from simple. The pages upon pages of daily lesson plans are just plain overwhelming .

At TTND, we believe teachers should be living their lives outside of the classroom, and not spend hours lesson planning and searching for resources.

We understand that now, more than ever, teachers need space to be themselves which is why we create and support teachers with timesaving tips and standards-aligned resources.

Want access to TTND's Free Resource Library? Sign up for our newsletter and we'll email you the exclusive password!

Trending posts.

SEARCH BY TOPIC

• Classroom Ideas
• Holidays and Seasonal
• Mentor Texts
• Reading Block
• Uncategorized
• Writing & Grammar

POPULAR RESOURCES

Facebook Group

Teachers Pay Teachers

Free Resource Library

💌 Contact Us

Disclosures

Privacy Policy

Refund Policy

Purchase Orders

Your Downloads

Reward Points

©  The Teacher Next Door, LLC. All rights reserved.

* Please note: If your school has strong email filters, you may wish to use your personal email to ensure access.

3 Word Problem Solving Strategies To Improve Word Problem Performance

This post contains affiliate links. This means that when you make a purchase, at no additional cost to you, I will earn a small commission.

The ability to solve word problems doesn’t necessarily come easily to all students. We can improve our students’ ability to solve story problems with a few simple word problem-solving strategies. When it comes to comprehending, understanding, and solving word problems, sometimes it is helpful to move beyond traditional word problems and try a new word problem type that is designed to support students in tackling these tricky skills!

In order to solve word problems, students need to be able to:

• Comprehend the action or context of a word problem
• Understand the question or missing piece of information
• Develop a mathematically sound plan for solving for the missing information.
• Accurately calculate to find their solution.

It’s a balance between comprehension, an understanding of math concepts, and an ability to carry out math concepts. Identifying which of these steps are strengths or needs for your students can help you to choose a strategy that will best improve their word problem performance.

Word Problem Solving Strategy #1: Numberless Word Problems

Who is this strategy for? If your students are struggling to understand the action, context or question in a story problem, discussion and numberless word problems will be a word problem-solving strategy that can help your students tremendously! This strategy also helps your “number pluckers” who see numbers, pluck and add together regardless of context! Numberless word problems slow your students down!

Using a tool such as numberless word problems can help your students in their understanding precisely because the numberless word problem strategy emphasizes discussion every step of the way!

How do I use this strategy? As you solve numberless word problems you begin with a problem with no numbers at all and ask a variety of questions as you discuss and slowly add information back into the problem.

Reagan picked flowers for a bouquet! She picked both roses and carnations.

When you initially present the problem, ask your students questions such as

• Who is the story problem about?
• What is happening in this story?
• What are you wondering about?

Reagan picked flowers for a bouquet! She picked 7 roses and also some carnations.

• What new information do we have?
• What do you think we might learn next?
• What *could* be the number of carnations in the bouquet? What might make sense?

Reagan picked flowers for a bouquet! She picked 7 roses and 8 carnations.

• What new information do we know?
• What do you know about the story?
• What happened in the story?
• Could we draw a picture or diagram to match the story?
• What might we be wondering about the bouquet?
• What questions could we answer about the bouquet?

Reagan picked flowers for a bouquet! She picked 7 roses and 8 carnations. How many flowers are in the bouquet in all?

• What is the question wondering?
• Do we have enough information to answer that question?
• Where do we see the 7 roses in our diagram?
• Where do we see the 8 carnations in our diagram?
• How can we use the diagram to answer the question of how many flowers are in the bouquet in all?

DONE FOR YOU NUMBERLESS WORD PROBLEMS

Kindergarten | 1st Grade | 2nd Grade | 3rd Grade | 4th Grade

Word Problem Solving Strategy #2: Guided Visual Models

Who is this strategy for? Visual models help your students to organize the information they know as well as to visualize the missing piece of information. Drawing visual models helps lead your students to an equation. This strategy is ideal for students who understand what a word problem is asking but have difficulty connecting the action of a word problem to an equation.

A visual model might include:

• A math drawing (simple circles or an organic representation)
• A number bond (number bonds can be used beyond addition and subtraction! Adding more “parts” can help to visualize multiplication and division as well!)
• Tape diagrams

How can I use this strategy? As you are supporting your students in using these visual models, continually ask questions and draw connections between the word problem and their diagram.

Frank built a tower using 16 blocks. He took 7 blocks off of his tower and gave them to Declan so he could build a tower as well. How many blocks does Frank have left?

• Could you draw a picture that shows what happened?
• Frank had 16 blocks. Was that all of the blocks in the story or part of them? Where would we put the total in our number bond?
• Frank gave away 7 blocks. Was that all of the blocks or a part of the blocks? Where would we put the part in our number bond?
• And we’re wondering how many blocks Frank has left. Where is the missing part in our number bond? Could we write a question mark in that part?

If your students are familiar with number bonds or tape diagrams, knowing that they are missing a part will lead them to writing a subtraction equation or a missing addend addition equation to solve.

**If your students are not familiar with how to find a missing part or missing whole in an equation this is a topic that needs to be addressed as well! Your students are missing foundational math understandings that are critical to their word problem-solving strategy. Additional practice with both fact families and missing numbers in an equation will be helpful to your students!

Word Problem Strategy #3: Problem Sorts

Who is this strategy for? This strategy is for ALL students! When your students examine problems to help understand the underlying structures and problem types , solving word problems becomes easier.

If you were to be asked to cook dinner for a group of people at the drop of a hat, you would likely have a much easier time putting together a pizza than you would a complicated curry dish. You understand the underlying structure of a pizza- crust, sauce, cheese, toppings- and because you know this structure, given any different type of pizza (BBQ, Traditional, Garlic, Buffalo Chicken) you would be able to use the structure to come up with a recipe quickly and easily.

Understanding and recognizing problem types can do the same thing for our students! Understanding that in a “put together” problem there are going to be parts and that those parts can be put together using addition makes these problems much easier to solve!

How can I use this strategy? One way to help your students to recognize and understand problem types is to sort word problems. In a problem sort, you aren’t attending to the matter of solving the problem at all . Instead, you are reading the problems and sorting them based on whether the problem is missing a part or missing the total. If you are working on multiplication and division word problems you might sort based on whether the problem is missing the total , missing the number of groups or missing the group size. Other problem types will lend themselves to different sorting activities.

Additional Word Problem Resources

Using different types of word problem resources can help you to support your students in different ways.

Word Problem Sort Cards   can be a useful tool when you want your students to attend to the structure of math problems. Sort the cards based on problem type or based on the operation your students would use to solve. After sorting, solve the problems together. Reuse the sort as a math center!

Word Problem Notebooks  are a useful tool when you want your students to draw models and visual representations of word problems and to connect these models to an equation.

Numberless Word Problems   help get to the heart of the action or context of a word problem. Because you start with no numbers and employ a great deal of conversation these problems are simple to differentiate and give all students a point of access into the activity.

• Read more about: Uncategorized

You might also like...

Hands-On Fraction Materials

Simplifying Math Intervention Data

3 Engaging Ways to Anchor Your Math Intervention Lesson

Find it here.

Let's Connect

Search the site.

© The Math Spot • Website by KristenDoyle.co

Word Problem Calculator

Get detailed solutions to your math problems with our word problem step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems, are you struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Popular problems

Most popular problems solved with this calculator: