why is teaching problem solving an important part of mathematics

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Mathematics Through Problem Solving

What Is A ‘Problem-Solving Approach’?

• interactions between students/students and teacher/students (Van Zoest et al., 1994)
• mathematical dialogue and consensus between students (Van Zoest et al., 1994)
• teachers providing just enough information to establish background/intent of the problem, and students clarifing, interpreting, and attempting to construct one or more solution processes (Cobb et al., 1991)
• teachers accepting right/wrong answers in a non-evaluative way (Cobb et al., 1991)
• teachers guiding, coaching, asking insightful questions and sharing in the process of solving problems (Lester et al., 1994)
• teachers knowing when it is appropriate to intervene, and when to step back and let the pupils make their own way (Lester et al., 1994)
• A further characteristic is that a problem-solving approach can be used to encourage students to make generalisations about rules and concepts, a process which is central to mathematics (Evan and Lappin, 1994).

Schoenfeld (in Olkin and Schoenfeld, 1994, p.43) described the way in which the use of problem solving in his teaching has changed since the 1970s:

My early problem-solving courses focused on problems amenable to solutions by Polya-type heuristics: draw a diagram, examine special cases or analogies, specialize, generalize, and so on. Over the years the courses evolved to the point where they focused less on heuristics per se and more on introducing students to fundamental ideas: the importance of mathematical reasoning and proof…, for example, and of sustained mathematical investigations (where my problems served as starting points for serious explorations, rather than tasks to be completed).

Schoenfeld also suggested that a good problem should be one which can be extended to lead to mathematical explorations and generalisations. He described three characteristics of mathematical thinking:

• valuing the processes of mathematization and abstraction and having the predilection to apply them
• developing competence with the tools of the trade and using those tools in the service of the goal of understanding structure – mathematical sense-making (Schoenfeld, 1994, p.60).
• As Cobb et al. (1991) suggested, the purpose for engaging in problem solving is not just to solve specific problems, but to ‘encourage the interiorization and reorganization of the involved schemes as a result of the activity’ (p.187). Not only does this approach develop students’ confidence in their own ability to think mathematically (Schifter and Fosnot, 1993), it is a vehicle for students to construct, evaluate and refine their own theories about mathematics and the theories of others (NCTM, 1989). Because it has become so predominant a requirement of teaching, it is important to consider the processes themselves in more detail.

The Role of Problem Solving in Teaching Mathematics as a Process

Problem solving is an important component of mathematics education because it is the single vehicle which seems to be able to achieve at school level all three of the values of mathematics listed at the outset of this article: functional, logical and aesthetic. Let us consider how problem solving is a useful medium for each of these.

It has already been pointed out that mathematics is an essential discipline because of its practical role to the individual and society. Through a problem-solving approach, this aspect of mathematics can be developed. Presenting a problem and developing the skills needed to solve that problem is more motivational than teaching the skills without a context. Such motivation gives problem solving special value as a vehicle for learning new concepts and skills or the reinforcement of skills already acquired (Stanic and Kilpatrick, 1989, NCTM, 1989). Approaching mathematics through problem solving can create a context which simulates real life and therefore justifies the mathematics rather than treating it as an end in itself. The National Council of Teachers of Mathematics (NCTM, 1980) recommended that problem solving be the focus of mathematics teaching because, they say, it encompasses skills and functions which are an important part of everyday life. Furthermore it can help people to adapt to changes and unexpected problems in their careers and other aspects of their lives. More recently the Council endorsed this recommendation (NCTM, 1989) with the statement that problem solving should underly all aspects of mathematics teaching in order to give students experience of the power of mathematics in the world around them. They see problem solving as a vehicle for students to construct, evaluate and refine their own theories about mathematics and the theories of others.

According to Resnick (1987) a problem-solving approach contributes to the practical use of mathematics by helping people to develop the facility to be adaptable when, for instance, technology breaks down. It can thus also help people to transfer into new work environments at this time when most are likely to be faced with several career changes during a working lifetime (NCTM, 1989). Resnick expressed the belief that ‘school should focus its efforts on preparing people to be good adaptive learners, so that they can perform effectively when situations are unpredictable and task demands change’ (p.18). Cockcroft (1982) also advocated problem solving as a means of developing mathematical thinking as a tool for daily living, saying that problem-solving ability lies ‘at the heart of mathematics’ (p.73) because it is the means by which mathematics can be applied to a variety of unfamiliar situations.

Problem solving is, however, more than a vehicle for teaching and reinforcing mathematical knowledge and helping to meet everyday challenges. It is also a skill which can enhance logical reasoning. Individuals can no longer function optimally in society by just knowing the rules to follow to obtain a correct answer. They also need to be able to decide through a process of logical deduction what algorithm, if any, a situation requires, and sometimes need to be able to develop their own rules in a situation where an algorithm cannot be directly applied. For these reasons problem solving can be developed as a valuable skill in itself, a way of thinking (NCTM, 1989), rather than just as the means to an end of finding the correct answer.

Many writers have emphasised the importance of problem solving as a means of developing the logical thinking aspect of mathematics. ‘If education fails to contribute to the development of the intelligence, it is obviously incomplete. Yet intelligence is essentially the ability to solve problems: everyday problems, personal problems … ‘(Polya, 1980, p.1). Modern definitions of intelligence (Gardner, 1985) talk about practical intelligence which enables ‘the individual to resolve genuine problems or difficulties that he or she encounters’ (p.60) and also encourages the individual to find or create problems ‘thereby laying the groundwork for the acquisition of new knowledge’ (p.85). As was pointed out earlier, standard mathematics, with the emphasis on the acquisition of knowledge, does not necessarily cater for these needs. Resnick (1987) described the discrepancies which exist between the algorithmic approaches taught in schools and the ‘invented’ strategies which most people use in the workforce in order to solve practical problems which do not always fit neatly into a taught algorithm. As she says, most people have developed ‘rules of thumb’ for calculating, for example, quantities, discounts or the amount of change they should give, and these rarely involve standard algorithms. Training in problem-solving techniques equips people more readily with the ability to adapt to such situations.

A further reason why a problem-solving approach is valuable is as an aesthetic form. Problem solving allows the student to experience a range of emotions associated with various stages in the solution process. Mathematicians who successfully solve problems say that the experience of having done so contributes to an appreciation for the ‘power and beauty of mathematics’ (NCTM, 1989, p.77), the “joy of banging your head against a mathematical wall, and then discovering that there might be ways of either going around or over that wall” (Olkin and Schoenfeld, 1994, p.43). They also speak of the willingness or even desire to engage with a task for a length of time which causes the task to cease being a ‘puzzle’ and allows it to become a problem. However, although it is this engagement which initially motivates the solver to pursue a problem, it is still necessary for certain techniques to be available for the involvement to continue successfully. Hence more needs to be understood about what these techniques are and how they can best be made available.

In the past decade it has been suggested that problem-solving techniques can be made available most effectively through making problem solving the focus of the mathematics curriculum. Although mathematical problems have traditionally been a part of the mathematics curriculum, it has been only comparatively recently that problem solving has come to be regarded as an important medium for teaching and learning mathematics (Stanic and Kilpatrick, 1989). In the past problem solving had a place in the mathematics classroom, but it was usually used in a token way as a starting point to obtain a single correct answer, usually by following a single ‘correct’ procedure. More recently, however, professional organisations such as the National Council of Teachers of Mathematics (NCTM, 1980 and 1989) have recommended that the mathematics curriculum should be organized around problem solving, focusing on:

• developing skills and the ability to apply these skills to unfamiliar situations
• gathering, organising, interpreting and communicating information
• formulating key questions, analyzing and conceptualizing problems, defining problems and goals, discovering patterns and similarities, seeking out appropriate data, experimenting, transferring skills and strategies to new situations
• developing curiosity, confidence and open-mindedness (NCTM, 1980, pp.2-3).

One of the aims of teaching through problem solving is to encourage students to refine and build onto their own processes over a period of time as their experiences allow them to discard some ideas and become aware of further possibilities (Carpenter, 1989). As well as developing knowledge, the students are also developing an understanding of when it is appropriate to use particular strategies. Through using this approach the emphasis is on making the students more responsible for their own learning rather than letting them feel that the algorithms they use are the inventions of some external and unknown ‘expert’. There is considerable importance placed on exploratory activities, observation and discovery, and trial and error. Students need to develop their own theories, test them, test the theories of others, discard them if they are not consistent, and try something else (NCTM, 1989). Students can become even more involved in problem solving by formulating and solving their own problems, or by rewriting problems in their own words in order to facilitate understanding. It is of particular importance to note that they are encouraged to discuss the processes which they are undertaking, in order to improve understanding, gain new insights into the problem and communicate their ideas (Thompson, 1985, Stacey and Groves, 1985).

It has been suggested in this chapter that there are many reasons why a problem-solving approach can contribute significantly to the outcomes of a mathematics education. Not only is it a vehicle for developing logical thinking, it can provide students with a context for learning mathematical knowledge, it can enhance transfer of skills to unfamiliar situations and it is an aesthetic form in itself. A problem-solving approach can provide a vehicle for students to construct their own ideas about mathematics and to take responsibility for their own learning. There is little doubt that the mathematics program can be enhanced by the establishment of an environment in which students are exposed to teaching via problem solving, as opposed to more traditional models of teaching about problem solving. The challenge for teachers, at all levels, is to develop the process of mathematical thinking alongside the knowledge and to seek opportunities to present even routine mathematics tasks in problem-solving contexts.

Example #1 – Mathematical Treasure Hunt

Objective – The objective of this activity is to encourage students to apply their problem-solving skills while having fun exploring mathematical concepts in a real-world context.

Materials Needed

Paper and pencils for each student Treasure map (could be a printed map or drawn by hand) Clues (math-related questions or puzzles) Optional: Small prizes or rewards for completing the treasure hunt Instructions:

Introduction (5 minutes)

Begin by introducing the activity to the students. Explain that they will be going on a mathematical treasure hunt where they will solve math problems to uncover hidden clues leading them to the treasure. Emphasize that this activity will require their problem-solving skills and teamwork.

Setting Up the Treasure Hunt (10 minutes)

Prepare a treasure map with different locations marked on it. These locations could be scattered around the classroom, school, or any other designated area. Hide clues at each location that will lead the students to the next destination.

Creating Clues (15 minutes)

Create math-related clues or puzzles that the students will need to solve to uncover the next location on the treasure map. The clues should be age-appropriate and aligned with the students’ math skills. For example:

Solve the following addition problem to reveal the next clue: 15 + 27 – 9 = ?

Count the number of chairs in the classroom and multiply by 3 to find the next location.

Find the area of the square-shaped rug in the library to unlock the next clue.

Starting the Treasure Hunt (5 minutes)

Divide the students into small groups or pairs, depending on the class size. Provide each group with a treasure map and the first clue. Explain the rules of the treasure hunt and encourage students to work together to solve the clues.

Exploring and Solving Clues (30 minutes)

Allow the students to begin the treasure hunt. As they solve each clue, they will uncover the location of the next clue on the treasure map. Encourage them to discuss and collaborate on the solutions to the math problems. Circulate around the room to provide assistance and guidance as needed.

Finding the Treasure (10 minutes)

Once the students have solved all the clues and reached the final location on the treasure map, they will discover the hidden treasure.

Congratulate them on their problem-solving skills and teamwork. You can optionally reward the students with small prizes or certificates for completing the treasure hunt successfully.

Reflection and Discussion (10 minutes)

After the treasure hunt, gather the students together for a brief reflection and discussion. Ask them about their favorite part of the activity, the challenges they faced, and what they learned from solving the math problems. Encourage them to share their strategies and insights with the class.

Extension Ideas

Create themed treasure hunts based on specific mathematical concepts such as geometry, fractions, or measurement.

Invite students to design their own treasure hunts for their classmates, incorporating math problems and creative clues.

Integrate technology by using QR codes or digital maps to lead students to each clue location.

By engaging students in a fun and interactive math problem-solving activity like the “Mathematical Treasure Hunt,” educators can foster a positive attitude towards mathematics while strengthening students’ critical thinking and collaboration skills.

Example #2 – Math Maze Adventure

Objective – The objective of this activity is to challenge students’ problem-solving abilities while navigating through a maze filled with math-related obstacles and puzzles.

Large maze layout (could be drawn on a poster board or printed) Dice Game tokens or markers for each student Math problem cards (with varying difficulty levels) Stopwatch or timer Optional: Prizes or rewards for completing the maze within a certain time limit

Instructions

Begin by introducing the “Math Maze Adventure” to the students. Explain that they will embark on a thrilling journey through a maze filled with mathematical challenges that they must overcome using their problem-solving skills.

Setting Up the Maze (10 minutes)

Create a large maze layout on a poster board or print one from a maze generator website. Designate a starting point and an endpoint within the maze. Place obstacles and challenges throughout the maze, such as math problems, riddles, or puzzles.

Preparing Math Problem Cards (15 minutes)

Create a set of math problem cards with varying difficulty levels. These problems could involve arithmetic operations, geometry concepts, fractions, or any other relevant math topics. Write each problem on a separate card and mix them up.

Starting the Adventure (5 minutes)

Divide the students into small groups or pairs, depending on the class size. Provide each group with a game token or marker to represent their position in the maze. Explain the rules of the game and how to navigate through the maze.

Navigating the Maze (30 minutes)

Start the timer and allow the students to begin their “Math Maze Adventure.” They will roll the dice to determine how many spaces they can move in the maze. When they land on a space with a math problem, they must draw a problem card and solve it correctly to proceed.

Solving Math Problems (30 minutes)

As students encounter math problems in the maze, they will work together to solve them. Encourage them to discuss strategies, share ideas, and check each other’s work. If they solve the problem correctly, they can continue moving through the maze. If not, they must stay in place until they solve it.

Reaching the Endpoint (10 minutes)

The goal of the “Math Maze Adventure” is to reach the endpoint of the maze within a certain time limit. Students must use their problem-solving skills and teamwork to overcome obstacles and challenges along the way. If they reach the endpoint before time runs out, they win the game!

After completing the maze, gather the students together for a reflection and discussion. Ask them about their experience navigating through the maze, the math problems they encountered, and the strategies they used to solve them. Encourage them to share their insights and lessons learned.

Create multiple versions of the maze with different layouts and levels of difficulty to provide ongoing challenges for students.

Integrate storytelling elements into the maze adventure, with each space representing a different part of the story that unfolds as students progress.

Incorporate technology by using a digital maze app or online platform to create and navigate through virtual mazes with math challenges.

The “Math Maze Adventure” offers an exciting and interactive way for students to practice their problem-solving skills while embarking on a thrilling journey through a maze filled with mathematical challenges. Through teamwork, critical thinking, and perseverance, students will navigate their way to success!

Carpenter, T. P. (1989). ‘Teaching as problem solving’. In R.I.Charles and E.A. Silver (Eds), The Teaching and Assessing of Mathematical Problem Solving, (pp.187-202). USA: National Council of Teachers of Mathematics.

Clarke, D. and McDonough, A. (1989). ‘The problems of the problem solving classroom’, The Australian Mathematics Teacher, 45, 3, 20-24.

Cobb, P., Wood, T. and Yackel, E. (1991). ‘A constructivist approach to second grade mathematics’. In von Glaserfield, E. (Ed.), Radical Constructivism in Mathematics Education, pp. 157-176. Dordrecht, The Netherlands: Kluwer Academic Publishers.

Cockcroft, W.H. (Ed.) (1982). Mathematics Counts. Report of the Committee of Inquiry into the Teaching of Mathematics in Schools, London: Her Majesty’s Stationery Office.

Evan, R. and Lappin, G. (1994). ‘Constructing meaningful understanding of mathematics content’, in Aichele, D. and Coxford, A. (Eds.) Professional Development for Teachers of Mathematics , pp. 128-143. Reston, Virginia: NCTM.

Gardner, Howard (1985). Frames of Mind. N.Y: Basic Books.

Lester, F.K.Jr., Masingila, J.O., Mau, S.T., Lambdin, D.V., dos Santon, V.M. and Raymond, A.M. (1994). ‘Learning how to teach via problem solving’. in Aichele, D. and Coxford, A. (Eds.) Professional Development for Teachers of Mathematics , pp. 152-166. Reston, Virginia: NCTM.

National Council of Teachers of Mathematics (NCTM) (1980). An Agenda for Action: Recommendations for School Mathematics of the 1980s, Reston, Virginia: NCTM.

National Council of Teachers of Mathematics (NCTM) (1989). Curriculum and Evaluation Standards for School Mathematics, Reston, Virginia: NCTM.

Olkin, I. & Schoenfeld, A. (1994). A discussion of Bruce Reznick’s chapter. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 39-51). Hillsdale, NJ: Lawrence Erlbaum Associates.

Polya, G. (1980). ‘On solving mathematical problems in high school’. In S. Krulik (Ed). Problem Solving in School Mathematics, (pp.1-2). Reston, Virginia: NCTM.

Resnick, L. B. (1987). ‘Learning in school and out’, Educational Researcher, 16, 13-20..

Romberg, T. (1994). Classroom instruction that fosters mathematical thinking and problem solving: connections between theory and practice. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 287-304). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schifter, D. and Fosnot, C. (1993). Reconstructing Mathematics Education. NY: Teachers College Press.

Schoenfeld, A. (1994). Reflections on doing and teaching mathematics. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 53-69). Hillsdale, NJ: Lawrence Erlbaum Associates.

Stacey, K. and Groves, S. (1985). Strategies for Problem Solving, Melbourne, Victoria: VICTRACC.

Stanic, G. and Kilpatrick, J. (1989). ‘Historical perspectives on problem solving in the mathematics curriculum’. In R.I. Charles and E.A. Silver (Eds), The Teaching and Assessing of Mathematical Problem Solving, (pp.1-22). USA: National Council of Teachers of Mathematics.

Swafford, J.O. (1995). ‘Teacher preparation’. in Carl, I.M. (Ed.) Prospects for School Mathematics , pp. 157-174. Reston, Virginia: NCTM.

Thompson, P. W. (1985). ‘Experience, problem solving, and learning mathematics: considerations in developing mathematics curricula’. In E.A. Silver (Ed.), Teaching and Learning Mathematical Problem Solving: Multiple Research Perspectives, (pp.189-236). Hillsdale, N.J: Lawrence Erlbaum.

Van Zoest, L., Jones, G. and Thornton, C. (1994). ‘Beliefs about mathematics teaching held by pre-service teachers involved in a first grade mentorship program’. Mathematics Education Research Journal. 6(1): 37-55.

Related Article on Teaching Values  |  Other Articles

📬 Sign Up for Our Amazing Newsletter!

Writing result-oriented ad copy is difficult, as it must appeal to, entice, and convince consumers to take action.

Why It's So Important to Learn a Problem-Solving Approach to Mathematics

was invited to the Math Olympiad Summer Program (MOP) in the 10th grade. I went to MOP certain that I must really be good at math. But in my five weeks at MOP, I encountered over sixty problems on various tests and I didn’t solve a single one. That’s right—I was 0-for-60+. I came away no longer confident that I was good at math. I assumed that most of the other kids did better at MOP because they knew more tricks than I did. My formula sheets were pretty thorough, but perhaps they were missing something. By the end of MOP, I had learned a somewhat unsettling truth. The others knew fewer tricks than I did, not more. They didn’t even have formula sheets!

At another contest later that summer, a younger student, Alex, from another school asked me for my formula sheets. In my local and state circles, students’ formula sheets were the source of knowledge, the source of power that fueled the top students and the top schools. They were studied, memorized, revered. But most of all, they were not shared. But when Alex asked for my formula sheets I remembered my experience at MOP and I realized that formula sheets are not really math . Memorizing formulas is no more mathematics than memorizing dates is history or memorizing spelling words is literature. I gave him the formula sheets. (Alex must later have learned also that the formula sheets were fool’s gold—he became a Rhodes scholar.)

The difference between MOP and many of these state and local contests I participated in was the difference between problem solving and what many people call mathematics. For these people, math is a series of tricks to use on a series of specific problems. Trick A is for Problem A, Trick B for Problem B, and so on. In this vein, school can become a routine of learn tricks for a week, use tricks on a test, forget most tricks quickly. The tricks get forgotten quickly primarily because there are so many of them, and also because the students don’t see how these ‘tricks’ are just extensions of a few basic principles.

I had painfully learned at MOP that true mathematics is not a process of memorizing formulas and applying them to problems tailor-made for those formulas. Instead, the successful mathematician possesses fewer tools, but knows how to apply them to a much broader range of problems. We use the term problem solving to distinguish this approach to mathematics from the memorize, use, forget approach.

After MOP I relearned math throughout high school. I was unaware that I was learning much more. When I got to Princeton I enrolled in organic chemistry. There were over 200 students in the course, and we quickly separated into two groups. One group understood that all we would be taught could largely be derived from a very small number of basic principles. We loved the class—it was a year-long exploration of where these fundamental concepts could take us. The other, much larger, group saw each new destination not as the result of a path from the building blocks, but as yet another place whose coordinates had to be memorized if ever they were to visit again. Almost to a student, the difference between those in the happy group and those in the struggling group was how they learned mathematics. The class seemingly involved no math at all, but those who took a memorization approach to math were doomed to do it again in chemistry. The skills the problem solvers developed in math transferred, and these students flourished.

We use math to teach problem solving because it is the most fundamental logical discipline. Not only is it the foundation upon which sciences are built, it is the clearest way to learn and understand how to develop a rigorous logical argument. There are no loopholes, there are no half-truths. The language of mathematics is as precise as it is ‘right’ and ‘wrong’ (or ‘proven’ and ‘unproven’). Success and failure are immediate and indisputable; there isn’t room for subjectivity. This is not to say that those who cannot do math cannot solve problems. There are many paths to strong problem-solving skills. Mathematics is the shortest .

Problem solving is crucial in mathematics education because it transcends mathematics. By developing problem-solving skills, we learn not only how to tackle math problems, but also how to logically work our way through any problems we may face. The memorizer can only solve problems he has encountered already, but the problem solver can solve problems she’s never seen before. The problem solver is flexible; she can diversify. Above all, she can create .

Subscribe for news, tips and advice from AoPS

Richard rusczyk, related articles, resolve to problem solve: your new year's challenge, stop making silly mistakes, more articles, combating bias in big data, with cathy o'neil, the 12 days of x-math, education in the metaverse, with maaroof fakhri, aops summer mathwalk challenge, expanding diversity in stem, with meena boppana, raising problem solvers guidebook: how to support your advanced problem solver, more episodes, sapienship, with dr. jim clarke, wonder, with dr. frank keil, learning stem through fiction, with dr. pamela cosman, managing academic expectations, with charlene wang, edtech at-home, with monica burns, learned helplessness, with vida john, receive weekly podcast summaries right to your inbox, get weekly podcast summaries/takeaways.

By clicking this button, I consent to receiving AoPS communications, and confirm that I am over 13, or under 13 and already a member of the Art of Problem Solving community. View our Privacy Policy .

Aops programs

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2013 Revised 2019

Problem Solving and the New Curriculum

• seeking solutions not just memorising procedures
• exploring patterns not just memorising formulas
• formulating conjectures, not just doing exercises.

Noah watched the animals going into the ark. He was counting and by noon he got to $12$, but he was only counting the legs of the animals. How many creatures did he see? See if you can find other answers? Try to tell someone how you found these answers out?

Planning a School Trip

This activity is taken from the ATM publication "We Can Work It Out!", a book of collaborative problem solving activity cards by Anitra Vickery and Mike Spooner. It is available from The Association of Teachers of Mathematics https://www.atm.org.uk/Shop/Primary-Education/Primary-Education-Books/Books--Hardcopy/We-Can-Work-It-Out-1/act054

References Polya, G. 1945) How to Solve It. Princeton University Press Schoenfeld, A.H. (1992) Learning to think mathematically: problem solving, metacognition and sense-making in mathematics. In D.Grouws (ed) Handbook for Research on Mathematics Teaching and Learning (pp334-370) New York: MacMillan

Lampert m (1992) quoted in schoenfeld, above..

Making Sense of Mathematics

Teaching Mathematics through Problem Solving- An Upside-Down Approach

By inviting children to solve problems in their own ways, we are initiating them into the community of mathematicians who engage in structuring and modeling their “lived worlds” mathematically.

 Fosnot and Jacob, 2007

Teaching mathematics through problem solving requires you to think about the types of tasks you pose to students, how you facilitate discourse in your classroom, and how you support students use of a variety of representations as tools for problem solving, reasoning, and communication.

This is a different approach from “do-as-I-show-you” approach where the teacher shows all the mathematics, demonstrates strategies to solve a problem, and then students just have to practice that exact same skill/strategy, perhaps using a similar problem.

Teaching mathematics through problem solving means that students solve problems to learn new mathematics through real contexts, problems, situations, and strategies and models that allow them to build concept and make connections on their own.

The main difference between the traditional approach “I-do-you-do” and teaching through problem solving, is that the problem is presented at the beginning of the lesson, and the skills, strategies and ideas emerge when students are working on the problem. The teacher listens to students’ responses and examine their work, determining the moment to extend students’ thinking and providing targeted feedback.

Here are the 4 essential moves in a math lesson using a student-centered approach or problem-solving approach:

• Number Talk (5-8 min) (Connection)

The mini-lesson starts with a Number Talk. The main purpose of a Number Talk is:

*to build number sense, and 

*to provide opportunities for students to explain their thinking and respond to the mathematical thinking of others.

Please refer to the document Int§roducing Number Talks . Or watch this video with Sherry Parrish to gain understanding about how Number Talks can build fluency with your students.

Here are some videos of Number Talks so you can observe some of the main teaching moves.

The role of the teacher during a number talk is crucial. He/she needs to listen carefully to the way student is explaining his/her reasoning, then use a visual representation of what the student said. Other students also share their strategies, and the teacher represents those strategies as well. Students then can visualize a variety of strategies to solve a problem. They learn how to use numbers flexibly, there is not just one way to solve a problem. When students have a variety if strategies in their math tool box, they can solve any problem, they can make connections with mathematical concepts.

There are a variety of resources that can be used for Math Talks. Note : the main difference between Number Talks and Math Talks, is that one allows students to use numbers flexibly leading them to fluency, develop number sense, and opportunities to communicate and reason with mathematics; the other allows for communicating and reasoning, building arguments to critique the reasoning of others, the use of logical thinking, and the ability to recognize different attributes to shapes and other figures and make sense of the mathematics involved.

• 2. Using problems to teach (5-8 min) Mini Lesson

Problems that can serve as effective tasks or activities for students to solve have common features. Use the following points as a guide to assess if the problem/task has the potential to be a genuine problem:

*Problem should be appropriate to their current understanding, and yet still find it challenging and interesting.

*The main focus of the problem should allow students to do the mathematics they need to learn, the emphasis should be on making sense of the problem, and developing the understanding of the mathematics. Any context should not overshadow the mathematics to be learned.

*Problems must require justification, students explain why their solution makes sense. It is not enough when the teacher tells them their answer is correct.

*Ideally, a problem/task should have multiple entries. For example “find 3 factors whose product is 108”, instead of just “multiplying 3 numbers. “

The most important part of the mini-lesson is to avoid teaching tricks or shortcuts, or plain algorithms. Our goal is always to help guide students to understand why the math works (conceptual understanding). And most importantly how different mathematical concepts/ideas are connected! “Math is a connected subject”  Jo Boaler’s video

“Students can learn mathematics through exploring and solving contextual and mathematical problems vs. students can learn to apply mathematics only after they have mastered the basic skills.” By Steve Leinwand author of Principles to Action .

• 3. Active Engagement (20-30 min)

This is the opportunity for students to work with partners or independently on the problem, making connections of what they know, and trying to use the strategy that makes sense to them. Always making sure to represent the problem with a visual representation. It can be any model that helps student understand what the problem is about.

The job of the teacher during this time, is to walk around asking questions to students to guide them in the right direction, but without telling too much. Allowing students to come up with their own solutions and justifications.

• Teacher can clarify any questions around the problem, not the solution.
• Teacher emphasizes reasoning to make sense of the problem/task.
• Teacher encourages student-student dialogue to help build a sense of self.

Some lessons will include a rich task, or a project based learning, or a number problem (find 3 numbers whose product is 108). There are a variety of learning target tasks to choose from, for each grade level on the Assessment Live Binders website created by Erma Anderson and Project AERO.

Again, keep in mind that some lessons will follow a different structure depending on the learning target for that day. Regardless of instructional design, the teacher should not be doing the thinking, reasoning, and connection building; it must be the students who are engaged in these activities

• 4. Share (8-12 min) (Link)

The most crucial part of the lesson is here. This is where the teaching/learning happens, not only learning from teacher, but learning from peers reaching their unique “zone of proximal development” (Vygotsky, 1978).

We bring back our students to share how they solved their problem. Sometimes they share with a partner first, to make sure they are using the right vocabulary, and to make sure they make sense of their answer. Then a few of them can share with the rest of the class. But sharing with a partner first is helpful so everyone has the opportunity to share.

“Talk to each other and the teacher about ideas – Why did I choose this method? Does it work in other cases? How is the method similar or different to methods other people used?” Jo Boaler’s article “How Students Should Be Taught Mathematics.”

Students make sense of their solution. The teacher listens and makes connections between different strategies that students are sharing. Teacher paraphrases the strategy student described, perhaps linking it with an efficient strategy.

“It is a misperception that student-centered classrooms don’t include any lecturing. At times it’s essential the teacher share his or her expertise with the larger group. Students could drive the discussion and the teacher guides and facilitates the learning.” Trevor MacKenzie

If the target for today’s lesson was to introduce the use a number line, for example, this is where the teacher will share that strategy as another possible way to solve today’s problem!

This could also be a good time for any formative assessment, using See Saw, using exit slips, or any kind of evidence of what they learned today.

References.

“Teaching Student-Centered Mathematics” Table 2.1 page 26 , Van de Walle, Karp, Lovin, Bay-Williams

“Number Talks” , Sherry Parrish

“How Students Should be Taught Mathematics: Reflections from Research and Practice” Jo Boaler

“Erma Anderson, Project AERO Assessments live binders

“Principles to Action” , Steve Leinwand

“ Turning Teaching Upside Down “, by Cathy Seeley

“Four Inquiry Qualities At The Heart of Student-Centered Teaching”

By Trevor MacKenzie

“The Zone of Proximal Development” Vygotsky, 1978

*** Here is a link to my favorite places to plan Math padlet, you will find a variety of resources, videos, articles, etc. By Caty Romero

***One more padlet for many resources to plan, teach, and assess mathematics that make sense: Making Sense of Mathematics Padlet.

Share this:

• learning math
• making sense of math
• number sense

Published by Caty Romero - Math Specialist

Passionate about learning and making sense of mathematics. Teacher, Math Learning Specialist, K-8 Math Consultant, and Instructional Coach. Student-Centered-Learning is my approach! Contact me at [email protected] or follow me on Twitter @catyrmath View all posts by Caty Romero - Math Specialist

Leave a comment Cancel reply

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

Mathematics as a Complex Problem-Solving Activity

By jacob klerlein and sheena hervey, generation ready.

By the time young children enter school they are already well along the pathway to becoming problem solvers. From birth, children are learning how to learn: they respond to their environment and the reactions of others. This making sense of experience is an ongoing, recursive process. We have known for a long time that reading is a complex problem-solving activity. More recently, teachers have come to understand that becoming mathematically literate is also a complex problem-solving activity that increases in power and flexibility when practiced more often. A problem in mathematics is any situation that must be resolved using mathematical tools but for which there is no immediately obvious strategy. If the way forward is obvious, it’s not a problem—it is a straightforward application.

Mathematicians have always understood that problem-solving is central to their discipline because without a problem there is no mathematics. Problem-solving has played a central role in the thinking of educational theorists ever since the publication of Pólya’s book “How to Solve It,” in 1945. The National Council of Teachers of Mathematics (NCTM) has been consistently advocating for problem-solving for nearly 40 years, while international trends in mathematics teaching have shown an increased focus on problem-solving and mathematical modeling beginning in the early 1990s. As educators internationally became increasingly aware that providing problem-solving experiences is critical if students are to be able to use and apply mathematical knowledge in meaningful ways (Wu and Zhang 2006) little changed at the school level in the United States.

“Problem-solving is not only a goal of learning mathematics, but also a major means of doing so.”

(NCTM, 2000, p. 52)

In 2011 the Common Core State Standards incorporated the NCTM Process Standards of problem-solving, reasoning and proof, communication, representation, and connections into the Standards for Mathematical Practice. For many teachers of mathematics this was the first time they had been expected to incorporate student collaboration and discourse with problem-solving. This practice requires teaching in profoundly different ways as schools moved from a teacher-directed to a more dialogic approach to teaching and learning. The challenge for teachers is to teach students not only to solve problems but also to learn about mathematics through problem-solving. While many students may develop procedural fluency, they often lack the deep conceptual understanding necessary to solve new problems or make connections between mathematical ideas.

“A problem-solving curriculum, however, requires a different role from the teacher. Rather than directing a lesson, the teacher needs to provide time for students to grapple with problems, search for strategies and solutions on their own, and learn to evaluate their own results. Although the teacher needs to be very much present, the primary focus in the class needs to be on the students’ thinking processes.”

(Burns, 2000, p. 29)

Learning to problem solve

To understand how students become problem solvers we need to look at the theories that underpin learning in mathematics. These include recognition of the developmental aspects of learning and the essential fact that students actively engage in learning mathematics through “doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning” (Copley, 2000, p. 29). The concept of co-construction of learning is the basis for the theory. Moreover, we know that each student is on their unique path of development.

Beliefs underpinning effective teaching of mathematics

• Every student’s identity, language, and culture need to be respected and valued.
• Every student has the right to access effective mathematics education.
• Every student can become a successful learner of mathematics.

Children arrive at school with intuitive mathematical understandings. A teacher needs to connect with and build on those understandings through experiences that allow students to explore mathematics and to communicate their ideas in a meaningful dialogue with the teacher and their peers.

Learning takes place within social settings (Vygotsky, 1978). Students construct understandings through engagement with problems and interaction with others in these activities. Through these social interactions, students feel that they can take risks, try new strategies, and give and receive feedback. They learn cooperatively as they share a range of points of view or discuss ways of solving a problem. It is through talking about problems and discussing their ideas that children construct knowledge and acquire the language to make sense of experiences.

Students acquire their understanding of mathematics and develop problem-solving skills as a result of solving problems, rather than being taught something directly (Hiebert1997). The teacher’s role is to construct problems and present situations that provide a forum in which problem-solving can occur.

Why is problem-solving important?

Our students live in an information and technology-based society where they need to be able to think critically about complex issues, and “analyze and think logically about new situations, devise unspecified solution procedures, and communicate their solution clearly and convincingly to others” (Baroody, 1998). Mathematics education is important not only because of the “gatekeeping role that mathematics plays in students’ access to educational and economic opportunities,” but also because the problem-solving processes and the acquisition of problem-solving strategies equips students for life beyond school (Cobb, & Hodge, 2002).

The importance of problem-solving in learning mathematics comes from the belief that mathematics is primarily about reasoning, not memorization. Problem-solving allows students to develop understanding and explain the processes used to arrive at solutions, rather than remembering and applying a set of procedures. It is through problem-solving that students develop a deeper understanding of mathematical concepts, become more engaged, and appreciate the relevance and usefulness of mathematics (Wu and Zhang 2006). Problem-solving in mathematics supports the development of:

• The ability to think creatively, critically, and logically
• The ability to structure and organize
• The ability to process information
• Enjoyment of an intellectual challenge
• The skills to solve problems that help them to investigate and understand the world

Problem-solving should underlie all aspects of mathematics teaching in order to give students the experience of the power of mathematics in the world around them. This method allows students to see problem-solving as a vehicle to construct, evaluate, and refine their theories about mathematics and the theories of others.

Problems that are “Problematic”

The teacher’s expectations of the students are essential. Students only learn to handle complex problems by being exposed to them. Students need to have opportunities to work on complex tasks rather than a series of simple tasks devolved from a complex task. This is important for stimulating the students’ mathematical reasoning and building durable mathematical knowledge (Anthony and Walshaw, 2007). The challenge for teachers is ensuring the problems they set are designed to support mathematics learning and are appropriate and challenging for all students.  The problems need to be difficult enough to provide a challenge but not so difficult that students can’t succeed. Teachers who get this right create resilient problem solvers who know that with perseverance they can succeed. Problems need to be within the students’ “Zone of Proximal Development” (Vygotsky 1968). These types of complex problems will provide opportunities for discussion and learning.

Students will have opportunities to explain their ideas, respond to the ideas of others, and challenge their thinking. Those students who think math is all about the “correct” answer will need support and encouragement to take risks. Tolerance of difficulty is essential in a problem-solving disposition because being “stuck” is an inevitable stage in resolving just about any problem. Getting unstuck typically takes time and involves trying a variety of approaches. Students need to learn this experientially. Effective problems:

• Are accessible and extendable
• Allow individuals to make decisions
• Promote discussion and communication
• Encourage originality and invention
• Encourage “what if?” and “what if not?” questions
• Contain an element of surprise (Adapted from Ahmed, 1987)

“Students learn to problem solve in mathematics primarily through ‘doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning.”

(Copley, 2000, p. 29)

“…as learners investigate together. It becomes a mini- society – a community of learners engaged in mathematical activity, discourse and reflection. Learners must be given the opportunity to act as mathematicians by allowing, supporting and challenging their ‘mathematizing’ of particular situations. The community provides an environment in which individual mathematical ideas can be expressed and tested against others’ ideas.…This enables learners to become clearer and more confident about what they know and understand.”

(Fosnot, 2005, p. 10)

Research shows that ‘classrooms where the orientation consistently defines task outcomes in terms of the answers rather than the thinking processes entailed in reaching the answers negatively affects the thinking processes and mathematical identities of learners’ (Anthony and Walshaw, 2007, page 122).

Effective teachers model good problem-solving habits for their students. Their questions are designed to help children use a variety of strategies and materials to solve problems. Students often want to begin without a plan in mind. Through appropriate questions, the teacher gives students some structure for beginning the problem without telling them exactly what to do. In 1945 Pólya published the following four principles of problem-solving to support teachers with helping their students.

• Understand and explore the problem
• Find a strategy
• Use the strategy to solve the problem
• Look back and reflect on the solution

Problem-solving is not linear but rather a complex, interactive process. Students move backward and forward between and across Pólya’s phases. The Common Core State Standards describe the process as follows:

“Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary”. (New York State Next Generation Mathematics Learning Standards 2017).

Pólya’s Principals of Problem-Solving

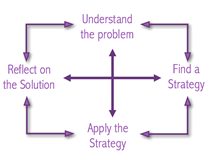
Students move forward and backward as they move through the problem-solving process.

The goal is for students to have a range of strategies they use to solve problems and understand that there may be more than one solution. It is important to realize that the process is just as important, if not more important, than arriving at a solution, for it is in the solution process that students uncover the mathematics. Arriving at an answer isn’t the end of the process. Reflecting on the strategies used to solve the problem provides additional learning experiences. Studying the approach used for one problem helps students become more comfortable with using that strategy in a variety of other situations.

When making sense of ideas, students need opportunities to work both independently and collaboratively. There will be times when students need to be able to work independently and other times when they will need to be able to work in small groups so that they can share ideas and learn with and from others.

Getting real

Effective teachers of mathematics create purposeful learning experiences for students through solving problems in relevant and meaningful contexts. While word problems are a way of putting mathematics into contexts, it doesn’t automatically make them real. The challenge for teachers is to provide students with problems that draw on their experience of reality, rather than asking them to suspend it. Realistic does not mean that problems necessarily involve real contexts, but rather they make students think in “real” ways.

Planning for talk

By planning for and promoting discourse, teachers can actively engage students in mathematical thinking. In discourse-rich mathematics classes, students explain and discuss the strategies and processes they use in solving mathematical problems, thereby connecting their everyday language with the specialized vocabulary of mathematics.

Students need to understand how to communicate mathematically, give sound mathematical explanations, and justify their solutions. Effective teachers encourage their students to communicate their ideas orally, in writing, and by using a variety of representations. Through listening to students, teachers can better understand what their students know and misconceptions they may have. It is the misconceptions that provide a window into the students’ learning process. Effective teachers view thinking as “the process of understanding,” they can use their students’ thinking as a resource for further learning. Such teachers are responsive both to their students and to the discipline of mathematics.

“Mathematics today requires not only computational skills but also the ability
to think and reason mathematically in order to solve the new problems and learn the new ideas that students will face in the future. Learning is enhanced in classrooms where students are required to evaluate their own ideas and those of others, are encouraged to make mathematical conjectures and test them, and are helped to develop their reasoning skills.”

(John Van De Walle)

“Equity. Excellence in mathematics education requires equity—high expectations and strong support for all students.”

How teachers organize classroom instruction is very much dependent on what they know and believe about mathematics and on what they understand about mathematics teaching and learning. Teachers need to recognize that problem-solving processes develop over time and are significantly improved by effective teaching practices. The teacher’s role begins with selecting rich problem-solving tasks that focus on the mathematics the teacher wants their students to explore. A problem-solving approach is not only a way for developing students’ thinking, but it also provides a context for learning mathematical concepts. Problem-solving allows students to transfer what they have already learned to unfamiliar situations. A problem-solving approach provides a way for students to actively construct their ideas about mathematics and to take responsibility for their learning. The challenge for mathematics teachers is to develop the students’ mathematical thinking process alongside the knowledge and to create opportunities to present even routine mathematics tasks in problem-solving contexts.

Given the efforts to date to include problem-solving as an integral component of the mathematics curriculum and the limited implementation in classrooms, it will take more than rhetoric to achieve this goal. While providing valuable professional learning, resources, and more time are essential steps, it is possible that problem-solving in mathematics will only become valued when high-stakes assessment reflects the importance of students’ solving of complex problems.

Why teachers are letting students solve math problems in lots of different ways

PhD student, Faculty of Education, York University, Canada

PhD student, Mathematics Education, Faculty of Education, York University, Canada

Disclosure statement

The authors do not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and have disclosed no relevant affiliations beyond their academic appointment.

York University provides funding as a member of The Conversation CA.

York University provides funding as a member of The Conversation CA-FR.

View all partners

Families might be wondering why their child’s math classroom looks so different from what they remember in school.

Why aren’t teachers putting students on the spot and getting them to prove that they know the math? Why are teachers letting students solve problems in lots of different ways instead of just telling them how to do it?

Teachers are moving beyond traditional ways of teaching math and shifting towards more evidence-based equitable teaching and assessment practices. This means every student is provided with what they need as opposed to being provided with the exact same resources and assessment practices.

For example, instead of giving all students in the classroom the exact same test, a student with test anxiety will be given an alternative format to showcase their learning.

Math is not ‘neutral’

Mathematics is not a “neutral” subject — biases in math exist that are grounded in colonial ideals.

For example, what is traditionally considered a standard measurement in a Canadian math curricula is only standard in western cultures.

Traditional mathematics teaching focuses on the teacher’s way of solving a problem as the right way. Students who might think about the problem in a different way are then at a disadvantage. In some cases, their cultural way of doing mathematics is then viewed as incorrect.

Many strategies can be used

One study examined the multiplication strategies Filipino immigrant children living in Japan used . In Japanese culture, children learn a formal multiplication method (kuku) that involves learning to recite times tables , whereas in the Philippines, it is common to use finger multiplication.

Read more: Indigenous basket-weaving makes an excellent digital math lesson

The study found that immigrant Filipino families only taught their children finger multiplication if they found that their child was struggling with multiplication. The children would hide this method from their teachers.

When only one strategy for math is taught as universally correct, this marginalizes students and compounds inequities.

Draw on existing knowledge

What are some signs teachers are practising equitable teaching in math ?

Teachers draw on students’ existing knowledge . In order to serve each student and their unique learning styles, teachers ideally get to know their students and how they learn best.

This means teachers view their students as having knowledge that can be shared within the learning community. This is in contrast to traditional teaching practices that work on the assumption that students are empty vessels to be filled with knowledge .

Peer collaboration

When you were in school, what did participating in classroom activities look like? Did you raise your hand? Did you turn to your elbow partner? Were you sitting in rows and expected to be quiet until you were called upon?

Equitable classrooms promote student voice and agency, peer collaboration and values learning from each other.

This creates an equitable learning environment because it provides all students with the platform to have their voices heard and validates students’ cultural ways of knowing math that may have otherwise been hidden.

An added bonus is that if all students have multiple ways to solve a problem, they have more strategies to rely on.

What an equitable math classroom looks like

Teachers get to know students through student interest surveys where students can explain what they like about math and what they need from their teachers to be successful in math.

Students can write narratives about their experiences with math to help identify students’ attitudes towards math (how they feel about themselves as a math learner, what they think math is about, whether they like math or not).

Teachers focus on how students solve problems and their solution strategies instead of just getting the right answer. Teachers allow students to show their thinking in a variety of ways (like in conversations and group work).

Instructional time (when the teacher is speaking about the ideas being taught) happens after students engage with their learning. This communicates to the students that they are capable of solving the problem, and that their ideas are both important and valuable.

There are a variety of strategies and solutions generated by the students.

Students have lots of choice about where they are working (standing at whiteboards, working collaboratively with peers or in groups, building hands-on models).

Instead of students only writing tests, the teacher is able to use diverse and different types of data to assess student learning (conversations, group work, models).

What an equitable math classroom sounds like

Teachers ask questions about what students are thinking, rather than giving them the answers.

Teachers wait for students to ask for help before assistance is offered to communicate that they are able to solve the problem (though adults can remind students they are there to help when students need it).

Students talk more than the teacher; these classrooms are loud with student talk.

Teachers ask questions about student thinking (“How do you know that’s the correct answer?”; “Can you tell me more about your thinking?”).

The teacher uses the students’ ideas to consolidate the learning after the students have worked with the problem.

What an equitable math classroom feels like

A safe space to showcase the voices and ideas of all people in the classroom.

Welcoming, fair and supportive.

Equitable math classrooms can be best realized when families, teachers and students support the importance and benefits of equitable classrooms.

• Mathematics
• Cultural bias
• Multiplication
• Peer support
• children's math

PhD Scholarship

Senior Lecturer, HRM or People Analytics

Senior Research Fellow - Neuromuscular Disorders and Gait Analysis

Centre Director, Transformative Media Technologies

Postdoctoral Research Fellowship

Teaching Mathematics Through Problem Solving

By Tom McDougal, Akihiko Takahashi

What do your students do when faced with a math problem they don't know how to solve? Most students give up pretty quickly. At best, they seek help from another student or the teacher. At worst, they shut down, seeing their failure as more evidence that they just aren't good at math. Neither of these behaviors will serve students in the long run. Inevitably, someday, every one of your students will encounter problems that they will not have explicitly studied in school and their ability to find a solution will have important consequences for them.

In the Common Core State Standards for Mathematics, the very first Standard for Mathematical Practice is that students should “understand problems and persevere in solving them.”1 Whether you are beholden to the Common Core or not, this is certainly something you would wish for your students. Indeed, the National Council of Teachers of Mathematics (NCTM) has been advocating for a central role for problem solving at least since the release of Agenda for Action in 1980, which said, “Problem solving [must] be the focus of school mathematics… .”2 

The common instructional model of “I do, we do, you do,” increases student dependence on the teacher and decreases students’ inclination to persevere. How, then, can teachers develop perseverance in problem solving in their students?

First we should clarify what we mean by “problem solving.” According to NCTM, “Problem solving means engaging in a task for which the solution is not known in advance.”3 A task does not have to be a word problem to qualify as a problem — it could be an equation or calculation that students have not previously learned to solve. Also, the same task can be a problem or not, depending on when it is given. Early in the year, before students learn a particular skill, the task could be a problem; later, it becomes an exercise, because now they know how to solve it.

In Japan, math educators have been thinking about how to develop problem solving for several decades. They studied George Polya's How to Solve It ,4 NCTM's Agenda for Action , and other documents, and together, using a process called lesson study , they began exploring what it would mean to make problem solving “the focus of school mathematics.” And they succeeded. Today, most elementary mathematics lessons in Japan are organized around the solving of one or a very few problems, using an approach known as “teaching through problem solving.”

“Teaching through problem solving” needs to be clearly distinguished from “teaching problem solving.” The latter, which is not uncommon in the United States, focuses on teaching certain strategies — guess-and-check, working backwards, drawing a diagram, and others. In a lesson about problem solving, students might work on a problem and then share with the class how using one of these strategies helped them solve the problem. Other students applaud, the students sit down, and the lesson ends. These lessons are usually outside the main flow of the curriculum; indeed, they are purposely independent of any curriculum.

In “teaching through problem solving,” on the other hand, the goal is for students to learn precisely that mathematical idea that the curriculum calls for them to learn next.

A “teaching through problem solving” lesson would begin with the teacher setting up the context and introducing the problem. Students then work on the problem for about 10 minutes while the teacher monitors their progress and notes which students are using which approaches. Then the teacher begins a whole-class discussion. Similar to a “teaching problem solving” lesson, the teacher may call on students to share their ideas, but, instead of ending the lesson there, the teacher will ask students to think about and compare the different ideas — which ideas are incorrect and why, which ideas are correct, which ones are similar to each other, which ones are more efficient or more elegant. Through this discussion, the lesson enables students to learn new mathematical ideas or procedures. This approach is represented in Figure 1.

Let's illustrate this with an example from a hypothetical fifth-grade lesson based on the most popular elementary mathematics textbook in Japan. (This textbook has been translated into English as Mathematics International and is available at http://GlobalEdResources.com . 5) During most Japanese lessons, the textbook is closed, but the textbook shows how the authors think the lesson might play out.

When the lesson begins, the blackboard is completely empty. The teacher starts by displaying, either with a poster or using a projector, the picture from the textbook of four different rabbit cages, shown in Figure 2 (it is not uncommon for Japanese elementary students to care for rabbits in several rabbit hutches, so this is a familiar context).

Figure 2 (Mathematics International, Grade 5, p. A93)

“What do you notice about the cages?” the teacher asks. Some students notice that some of the cages are different sizes. The teacher then asks, “Should each cage have the same number of rabbits?” No, say the students, smaller cages should have fewer rabbits, so the rabbits aren't too crowded.

The teacher then displays the pictures in Figure 3. “What do you think?” the teacher asks, as he puts them up one at a time for dramatic effect. “Are these equally crowded, or do you think some cages are more crowded than others?” There is some discussion about the rabbits in cage B, and students decide that just because they are bunched together right now, they probably won't stay that way. Students recognize that cages A and B are the same size, and since cage A has more rabbits (9 vs. 8), it is more crowded. The teacher writes that observation on the board: “When two cages are the same size, the one with more rabbits is more crowded.”

Figure 3 (Mathematics International, Grade 5, p. A93)

“What about the others?” he asks. “How can we decide which are more crowded?” This last question becomes the key mathematical question of the lesson, and the teacher writes it on the board: “Let's think about how to compare crowdedness.” Students copy this problem in their notebooks while he writes.

The teacher gives students a piece of paper with the pictures from Figure 3 to glue in their notebooks and gives them 5 minutes to think about the problem. Several students take a ruler and begin measuring. “Why are you doing that?” the teacher quietly asks one of them. “I want to figure out the area,” the student says. “Oh! You think the area might be important. Write that idea in your notebook.” Other students count the rabbits and decide that B and C are equally crowded because they look like they are the same size, but they are unsure about D.

The teacher stops the students and asks for ideas. He first calls on a student who thinks that B and C are the same size. He records her idea on the board: “Arthi says B and C look like they are the same size and have the same number of rabbits, so they are equally crowded.” A student who found the areas says that they are not. The teacher records this idea on the board: “Karen thinks you need to know the area.” He turns to the first student. “Arthi, what do you think?” he asks. She and other students agree. The teacher posts a table with the areas of the four cages (Figure 4). “Let's copy this table into our notebooks, and think about the problem some more.”

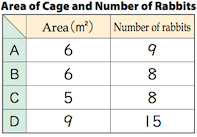
Figure 4 (Mathematics International, Grade 5, p. A94)

Students work independently for another 5 minutes while the teacher monitors their progress, encourages them to keep thinking, and reminds them to record their ideas in their notebook. He anticipates the following five ideas and notes which students are using them:

Idea 1: B and C have the same number of rabbits, but C has a smaller area, so C is more crowded. Unsure about A vs. C. 

Idea 2: If you make 5 copies of A and 6 copies of C, they would have the same area (30 m2). A would then have 45 rabbits while C would have 48 rabbits, so C is more crowded. 

Idea 3: If you make 8 copies of A and 9 copies of C, they would have the same number of rabbits (72). A would have an area of 48 m2 while C would have an area of 45 m2, so B is more crowded. 

Idea 4: Divide: (area) ÷ (# of rabbits) = amount of area per rabbit 

Idea 5: Divide: (# of rabbits) ÷ (area) = number of rabbits per unit area

The teacher invites students to explain their ideas to the class, selecting students based on the order above, while he records each idea on the blackboard. He asks students to compare Idea 1 to the thinking used to compare A and B. He writes on the board: “If either the area or the number of rabbits is the same, it's easy to compare.” The student with Idea 2 says, “I found a way to make the area the same,” and explains. This prompts the student with Idea 3 to say, “I used kind of the same approach to make the number of rabbits the same.”

When a student with Idea 4 comes up, she begins, “I decided to divide the area by the number of rabbits.” The teacher stops her. He writes: “(area) ÷ (# of rabbits).” Then he asks the class, “Why is she doing this? Who can explain her thinking?” Another student says, “That gives the amount of area for each rabbit.” He lets the student finish her idea:

A: 9÷6 = 1.5 C: 8÷5 = 1.6

The teacher asks the class to clarify what the 1.5 and 1.6 mean (m2 per rabbit) and what that says about the crowdedness of each cage.

He then invites a student to explain Idea 5: “I divided the other way…”

A: 6÷9 = 0.66… C: 5÷8 = 0.625

“Why is he doing this?” the teacher asks the class. “What does this 0.66… mean? What does 0.625 mean?” (“Rabbits per square meter,” the students answer.)

The teacher then asks the class to look for similarities across the five ideas, which are all visible on the blackboard. Some students note that Ideas 2 and 3 use multiplication while Ideas 4 and 5 use division, a superficial similarity. But some students notice the more significant connection that 2 and 5 are both about making the area the same, while 3 and 4 are both about making the number of rabbits the same.

“We haven't talked about cage D yet,” the teacher points out. “How shall we compare A, C, and D? Please try using one of these ideas.”

Students work in their notebooks for a few minutes. Students who try using multiplication (Idea 2 or 3) discover that the method is cumbersome. The teacher invites students who used Ideas 4 and 5 to share their calculations, adding them to the lists from before: Idea 4:

A: 9÷6 = 1.5 C: 8÷5 = 1.6 D: 15÷9 = 1.66… (m2/rabbit) Idea 5: A: 6÷9 = 0.66… C: 5÷8 = 0.625 D: 9÷15 = 0.6 (rabbits/m2)

“What do you think about these ideas?” asks the teacher, and students respond, “They are easy!” So the teacher writes a summary on the board, “Using division, it is easy to compare crowdedness.” He asks the students to write a reflection in their notebooks. One student who used multiplication writes, “I tried using multiplication, but dividing is easier. Next time I want to try that.” And the lesson ends.

In the students’ previous experience with comparing quantities, a single quantity was important, such as the number of apples or kilograms or square meters. Their prior experience with division was about finding a missing multiplier or multiplicand, which was itself a single quantity. This problem presented students for the first time with a situation in which two numbers needed to be considered. So by working on a problem about rabbits and cages, students learn that division can be used to compute a new type of quantity, a per unit quantity, that expresses the relationship between rabbits and area and can be used to compare crowdedness. In subsequent lessons, students will see how division can be used to compute other types of per unit quantities, such as the productivity of two farms in crops grown per acre of land or the cost per pencil.

What was the teacher's role in helping students learn this new mathematical idea? He never explained anything to the students, but the task had to be carefully constructed, and the teacher had to be very deliberate in how he directed the lesson, or the lesson wouldn't have worked.

The task was accessible to all students in the beginning by the fact that two cages had the same area (A and B) and two cages had the same number of rabbits (B and C), but since it wasn't clear whether B and C were the same size, students were pushed to think formally about area. And, while using multiplication was feasible for comparing cages A and C, the area of cage D was such that multiplication was cumbersome for comparing all three cages. Students who might have been happy with using multiplication and uncomfortable with the decimal values that result from division were pushed by cage D to appreciate the efficiency of using division.

The teacher's role in the lesson can be compared to the role of a film director, who carefully stages each scene and makes cuts between cameras to create the desired effect. Early in the lesson, the teacher highlighted the idea, raised by students, that equal areas or equal numbers of rabbits made comparisons easier. This was the foundation for the idea of dividing to find a “per unit quantity,” square meters per one rabbit or rabbits per one square meter. By starting with a discussion of incorrect or partially correct ideas and writing them on the board, the teacher valued those ideas. This encourages students to try: Even if they can’t solve the whole problem, they might come up with something to contribute. When a student first suggested the idea of dividing, the teacher asked other students to explain the thinking behind it. This enabled students who did not themselves think of dividing to make the idea their own. And by carefully organizing student ideas on the board (Figure 5), the teacher made it easier for students to compare those ideas with each other and to follow the flow of learning in the lesson.

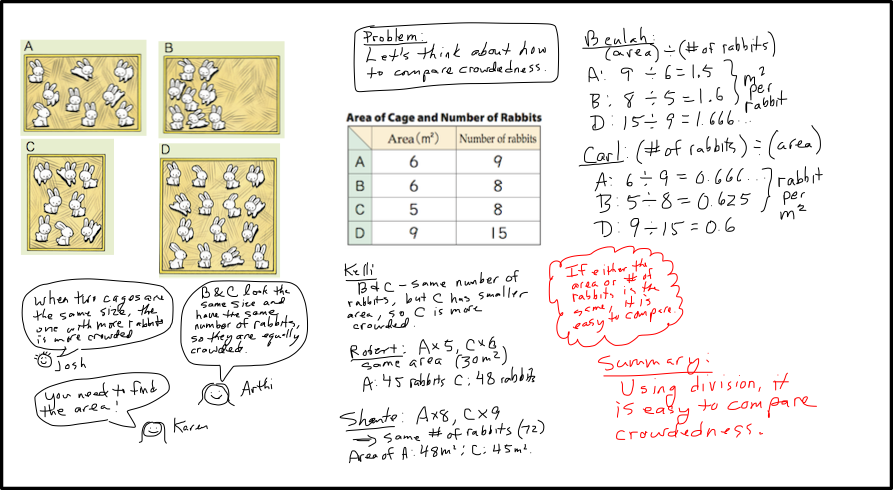
Figure 5 (includes items from Mathematics International, Grade 5, pp. A93-94)

Although the lesson vignette above is fictional, videos of lessons like it can be found at http://tinyurl.com/kuwb4bg . The grade 3 lesson “Multiplication Algorithm” and the grade 5 lesson “Do I Have a Window Seat or an Aisle Seat?” are particularly good, both for the quality of the lessons and for the quality of the videos themselves.

Japanese educators believe that regular lessons that teach through problem solving, interspersed with occasional practice days, help their students learn mathematics more thoroughly than didactic instruction coupled with a greater amount of practice. Certainly Japanese students have performed very well on the TIMSS and PISA international studies of mathematics achievement. But perhaps more important, teaching through problem solving habituates students to being confronted with unfamiliar problems, to struggling at length with those problems, and to learning from those problems. This is a way to cultivate perseverance in problem solving.

Reading this article and watching videos, however, will not equip most teachers to incorporate teaching through problem solving into their practice. The teacher who wishes to do so is faced with several challenges. The first challenge is that few curricula are designed to support such lessons; most are designed to support fairly direct instruction by the teacher. The second problem is that students are not used to learning this way and may resist. And the third problem is that teaching this way is hard. It requires ways of thinking about a lesson that are unfamiliar to almost all U.S. teachers. One needs to be absolutely clear about what the mathematical goal of the lesson is; that goal is never for students to simply solve a problem. One needs to anticipate the various solutions, correct and incorrect, that are likely to come from students, as well as the ways students will get stuck. One needs to plan how the discussion around the various student ideas will address misconceptions and build toward the mathematical goal of the lesson. One needs to think about how the ideas will be organized on the board so that students can easily compare them.

Japanese teachers certainly did not learn to teach this way by reading articles or watching videos. They learned it — and continue to learn it — by trying it, together, one lesson at a time through a process called lesson study .6,7 A full treatment of lesson study would be another article in itself, but U.S. teachers who are interested in learning to teach through problem solving can find more information about lesson study at http://LessonStudyGroup.net  and at http://LSAlliance.org . Lesson Study Alliance organizes the annual Chicago Lesson Study Conference, which features live lessons by teachers who are working to incorporate teaching through problem solving into their practice.

1. National Governors Association Center for Best Practices, Council of Chief State School Officers, Common Core State Standards for Mathematics (Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010); online at www.corestandards.org/math/ . 2. National Council of Teachers of Mathematics, An Agenda for Action: Recommendations for School Mathematics of the 1980s (Washington, DC: NCTM, 1980); online at www.nctm.org/standards/content.aspx?id=17278 .  3. National Council of Teachers of Mathematics, Principles and Standards for School Mathematics (Washington, DC: NCTM, 2000); online at http://www.nctm.org/standards/content.aspx?id=16909 . 4. George Polya, How to Solve It: A New Aspect of Mathematical Method (Princeton, NJ: Princeton University Press, 1945).  5. T. Fujii and S. Iitaka, Mathematics International , Grades 1-6 (Tokyo: Tokyo Shoseki Co., Ltd., 2012).  6. Akihiko Takahashi, “Implementing Lesson Study in North American Schools and School Districts” (no date); online at http://hrd.apec.org/images/a/ae/51.2.pdf .  7. Akihiko Takahashi and Makoto Yoshida, “Ideas for Establishing Lesson-Study Communities.” Teaching Children Mathematics , May 2004.

Tom McDougal is executive director of Lesson Study Alliance in Chicago, a nonprofit organization that promotes and supports Lesson Study. He taught middle and high school mathematics and was an elementary math specialist.

Akihiko Takahashi is associate professor of mathematics education at DePaul University in Chicago. He taught students in grades 1-6 for 19 years in Japan, where he helped lead the national shift to teaching mathematics through problem solving.

Why We Need to Expect More

A teacher reflects on what students need and want from adults—and why adults should expect more of themselves, too..

Read the Post

The home of mathematics education in New Zealand.

• Forgot password ?
• Teaching material
• Problem solving activities
• Problem Solving Information
• Why Teach Problem Solving?

Why teach problem solving?

Thanks for visiting NZMaths. We are preparing to close this site and currently expect this to be in June 2024 but we are reviewing this timing due to the large volume of content to move and improvements needed to make it easier to find different types of content on Tāhūrangi. We will update this message again shortly.

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

In this section we discuss "Why teach problem solving?" under two headings: benefits of problem solving, and difficulties of teaching problem solving.

Benefits of problem solving

Problem solving is the process part of mathematics that has often been overlooked in the past in favour of other skills (see What is problem solving? ). But there are other reasons for it to be included in your mathematics programme:

• It bases students’ mathematical development on their current knowledge
• It is an interesting and enjoyable way to learn mathematics
• It is a way to learn new mathematics with greater understanding
• It produces positive attitudes towards mathematics
• It makes the student a junior research mathematician
• It teaches thinking, flexibility and creativity
• It teaches general problem solving skills
• It encourages cooperative skills
• It is a useful way to practice mathematical skills learned by other means
• It is similar in approach to the way that other subjects are taught in primary school.

Based on current knowledge. A constructivist view of learning proposes that we construct our knowledge through our experience rather than absorbing what we are told. The constructivist views the student as an active learner. The more traditional approach to teaching mathematics sees the student as an empty vessel that has to be filled. Correspondingly we have two contrasting models of "the guide on the side", the coach trying to encourage the learner along, and  "the sage on the stage", the lecturer imparting knowledge. In actual fact, the best teaching approach is probably some combination of the two.

Most of the problems used in problem solving have more than one solution. So each of them can be approached in a variety of ways, some of which are sophisticated and some of which are less sophisticated. Hopefully, every student in your class can find one approach that they can use to solve the problems that you present. Over time, and from seeing what other students have done, you should be able to develop and extend the range of strategies that students have at their disposal.

Interesting and enjoyable. Problem solving seems to be implicitly interesting to students. This is partly because it does not involve a sequence of very similar questions that are designed to practice the same skill. The novelty of the problems seems to add to their interest.

Problem solving can be made even more engaging  if you personalise problems to include characters that the students in the class know. This also makes them more interesting and relevant to the students.

Then again the questions can be very interesting in themselves. This is partly because they involve some detective work, which most students enjoy. It’s also partly because we all enjoy getting the answer after having struggled with a problem. And it’s partly because students enjoy having "ownership" of the problem. The ownership issue is an important one. By working on a problem, students can get quite deeply involved with both the mathematics that is required to solve it, and the mathematics that may be required to solve it.

Greater understanding.  In the process of struggling with a problem, students can obtain a deep understanding of the mathematics surrounding the problem. This understanding is often enhanced, when, in a whole class setting, teachers draw together the various threads from all of the students in the class. (We say more about this in the 'Reporting Back' section of Organising the Teaching of Problem Solving .)

Positive attitudes.  Because students enjoy the problems it helps them to gain a positive attitude towards mathematics more generally. Some of them have even expressed the opinion that what they were doing was not mathematics and have asked to do more problem solving instead of mathematics! But we want them to see that problem solving is mathematics and that it is an enjoyable subject.

Junior research mathematician. The way that students tackle problems can be virtually the same as the way a research mathematician tackles research problems. Hence, through problem solving, students get a much better feel for what mathematics is actually about than they get in the more traditional type of teaching. Hopefully they begin to see that the subject is a live one, get some feeling for the way it is created, and see why certain things are done in certain ways. This then increases their insight into the subject as a whole and gives them a better feeling for what the subject is and what it is trying to do.

Flexibility and creativity. Problem solving provides an opportunity for students to explore ideas and gives them the chance to extend their creativity. Students are continually coming up with ways of tackling problems that we hadn’t thought of before. The interesting thing is that the students who are producing these ideas are not always the ones who we generally think of as being good at mathematics. Sometimes though, it can take a little work on the your part before the consequences of some ideas are seen.

General problem solving. It is important to point out at this stage, that though we are concentrating here on mathematical problem solving, many of the strategies and techniques that are used in mathematics are used in any type of problem. The four stages of problem solving described by Pólya (in What is Problem Solving? ) are quite general steps that can be applied to any problem whether mathematical or not.

Cooperative skills. Traditionally, mathematics has been taught to individuals working by themselves. Very little encouragement has been given to cooperation in the traditional didactic approach to teaching mathematics. There has not been the emphasis on students working together that there has been in other curriculum areas. But working in cooperative groups does have advantages. Discussing mathematics out loud helps learning and understanding, and it also helps many students produce original ideas. Emphasising group work in problem solving appears to increase not only enjoyment, but also learning and social skills such as communication.

To practice skills. Some teachers use problems to reinforce technical skills that may have been taught in other ways. Certain problems are chosen because they will use certain algorithmic skills. The divide by 2 or multiply by three and add 1 problem (in What is Problem Solving? ) is an example of this. To get a feel for this problem you have to do quite a bit of arithmetic. If you want to practice the 5 times table, then do the extension where the 3 is changed to a 5. This problem then gives some point to multiplication. Hopefully, after doing lots of examples, the students will start to see some patterns.  We have also mentioned the practising of skills under the strategy Think.  By choosing problems of this type the students have an opportunity to work on basic skills in an interesting situation.

Similar approach to other subjects. Approaching mathematics through a problem solving perspective puts the subject much more on a par with other subjects, especially those in the primary school. The general philosophy of the teacher as a facilitator helping the student to learn and understand, is much more akin to the philosophy adopted in other areas of the curriculum than it is in the more traditional approach to mathematics. We believe that problem solving may provide a way to teach mathematics that is more in sympathy with primary teachers’ approach to teaching generally.

Difficulties of teaching problem solving         

There are generally thought to be a number of disadvantages to the teaching of problem solving in class. We list and discuss some of these below.

• It produces teacher discomfort
• It produces student insecurity
• It puts constraints on the curriculum and takes too long to teach
• It is not possible with students of low ability
• It takes a lot of preparation.

Teacher discomfort.  The main cause of teacher discomfit regarding teaching problem solving is the worry that students will come up with ideas that they won’t understand. In a way this shouldn’t happen. In problem solving we expect students to be able to explain their methods. So you should be able to understand most of the ideas and solutions students produce because the students should be able to explain them. However, you can’t be expected to know everything about everything. So you shouldn’t feel embarrassed if you are not sure if the student's idea is a good one or not. There is nothing wrong with telling a student, class or group that you are not sure but will try to find out. Often things can be resolved by a quiet moment with a coffee, a paper and pencil or with a chat to colleagues in the staff room. However, as time goes by the answers to these unexpected ideas will mount, as will your strategies for dealing with them.

Student insecurity. This may occur because the students have never met open-ended problems before. Some teachers in mathematics have traditionally given students relatively closed tasks to work on. It is not surprising that in more open problem solving situations, some students will feel insecure. However, by careful handling and by introducing things gradually, students should be able to overcome their initial insecurity.

Curriculum constraints. Many teachers, especially initially, feel that problem solving takes a considerable amount of time. Hence they are concerned that parts of the mathematics curriculum at a given Level, will need to be omitted. Our experience is that teaching problem solving is time consuming initially . It does seem to take a while for both teachers and students to get the feel of how it works. But after this initial period, time can be actually gained. Many teachers find they are able to cover material more quickly than in previous years. They put this down partly to the fact that the students were looking for, and seeing, patterns and connections everywhere. This enables teachers to cover ideas more quickly.

There does seem to be another factor though. The time that students spend on problem solving seems to help them to come to grips with a topic - to own it. This produces greater understanding and provides a solid base for later learning.

Low ability students. There is some feeling that it is all right to undertake problem solving with bright students but it is of little value for lower ability students. Anecdotally however students of all abillities have been seen to make significant gains in mathematics after having problem solving lessons once a week for two terms. These gains are across the curriculum and not just confined to problem solving. 

But there is an issue regarding both students who are not good readers and ESOL students. Clearly these students may not be able to read the problem. Because it is the mathematics that is important, lack of reading ability should not be a barrier to these students.

All students will need to read the problem more than once. If you are starting students off with a problem from a whole class setting, then it will almost certainly be read more than once. You can assess whether or not all students have understood the problem by asking them to restate it in their own words. As you go around from group to group, you can also check that every student is working on the problem that you actually posed. With New Entrants students, you will probably do most of your problem solving starting in a whole class situation. During this time you can make sure that the problem is understood.

Preparation time. There is no doubt that this is a problem for teachers undertaking problem solving for the first time. The main difficulty is finding the right problem to use to introduce a given strategy or to fit in to a given Strand or Level. One of the points of this website is to provide problems that are easily accessible in Strand and Level format. On the other hand, time can certainly be saved if informal teacher networks are established. Then ideas and problems can be shared.

Why Is Math Important? 9 Reasons Why Math Skills Improve Quality of Life

Written by Ashley Crowe

• Parent Resources

Why is math so important in life?

• 9 Benefits of a great math education

Why students struggle to master certain math concepts

• Set your child’s math skills up for life with Prodigy Math

Math isn't just an important subject in school — it’s essential for many of your daily tasks. You likely use it every day to perform real-life skills, like grocery shopping, cooking and tracking your finances. 

What makes math special is that it’s a universal language — a powerful tool with the same meaning across the globe. Though languages divide our world, numbers unite us. Math allows us to work together towards new innovations and ideas. 

In this post, learn why math is important for kids and adults. Plus, find out why learning even the most basic math can significantly improve your family’s quality of life.

You simply can’t make it through a day without using some sort of basic math. Here’s why.

A person needs an understanding of math, measurements and fractions to cook and bake. Many people may also use math to count calories or nutrients as part of their diet or exercise routine. 

You also need math to calculate when you should leave your house to arrive on time, or how much paint you need to redo your bedroom walls. 

And then the big one, money. Financial literacy is an incredibly important skill for adults to master. It can help you budget, save and even help you make big decisions like changing careers or buying a home. 

Mathematical knowledge may even be connected to many other not-so-obvious benefits. A strong foundation in math can translate into increased understanding and regulation of your emotions, improved memory and better problem-solving skills.

The importance of math: 9 benefits of a great math education

Math offers more opportunities beyond grade school, middle school and high school. Its applications to real-life scenarios are vast. 

Though many students sit in math class wondering when they’ll ever use these things they’re learning, we know there are many times their math skills will be needed in adulthood. 

The importance of mathematics to your child’s success can’t be overstated. Basic math is a necessity, but even abstract math can help hone critical thinking skills — even if your child chooses not to pursue a STEM-style career. Math can help them succeed professionally, emotionally and cognitively. Here’s why.

1. Math promotes healthy brain function

“Use it or lose it.” We hear this said about many skills, and math is no exception. 

Solving math problems and improving our math skills gives our brain a good workout. And it improves our cognitive skills over time. Many studies have shown that routinely practicing math keeps our brain healthy and functioning well.

2. Math improves problem-solving skills

At first, classic math problems like Johnny bringing home 42 watermelons and returning 13 of them can just seem a silly exercise. But all those math word problems our children solve really do improve their problem solving skills. Word problems teach kids how to pull out the important information and then manipulate it to find a solution.

Later on, complex life problems take the place of workbooks, but problem-solving still happens the same way. When students understand algorithms and problems more deeply, they can decode the facts and more easily solve the issue. Real-life solutions are found with math and logic.

3. Math supports logical reasoning and analytical thinking

A strong understanding of math concepts means more than just number sense. It helps us see the pathways to a solution. Equations and word problems need to be examined before determining the best method for solving them. And in many cases, there’s more than one way to get to the right answer. 

It’s no surprise that logical reasoning and analytical thinking improve alongside math skills. Logic skills are necessary at all levels of mathematical education.

4. Math develops flexible thinking and creativity

Practicing math has been shown to improve investigative skills, resourcefulness and creativity.

This is because math problems often require us to bend our thinking and approach problems in more than one way. The first process we try might not work. We need flexibility and creativity to think of new pathways to the solution. And just like anything else, this way of thinking is strengthened with practice.

5. Math opens up many different career paths

There are many careers that use a large number of math concepts. These include architects, accountants, and scientists. 

But many other professionals use math skills every day to complete their jobs. CEOs use math to analyze financials. Mailmen use it to calculate how long it will take them to walk their new route. Graphic designers use math to figure out the appropriate scale and proportions in their designs. 

No matter what career path your child chooses, math skills will be beneficial.

Math skills might become even more important for today's kids!

Math can certainly open up a lot of opportunities for many of us. But did you know that careers which heavily use math are going to be among the fastest-growing jobs by the time kids today start their careers? These jobs include:

• Statisticians
• Data scientists
• Software developers
• Cybersecurity analysts

It's not just STEM jobs that will require math either. Other popular, high-growth careers like nursing and teaching now ask for a minimum knowledge of college-level math.

6. Math may boost emotional health

While this research is still in its early days, what we have seen is promising. 

The parts of the brain used to solve math problems seem to work together with the parts of the brain that regulate emotions. This suggests that math practice can actually help us cope with difficult situations. In these studies, the better someone was with numerical calculations, the better they were at regulating fear and anger. Strong math skills may even be able to help treat anxiety and depression.

7. Math improves financial literacy

Though kids may not be managing their finances now, there's going to be plenty of times where math skills are going to make a massive difference in their life as an adult.

Budgeting and saving is a big one. Where can they cut back on their spending? How will budgeting help them reach their financial goals? Can they afford this new purchase now? 

As they age into adulthood, It will benefit your child to understand how loans and interest work before purchasing a house or car. They should fully grasp profits and losses before investing in the stock market. And they will likely need to evaluate job salaries and benefits before choosing their first job.

8. Math sharpens your memory

Learning mental math starts in elementary school. Students learn addition tables, then subtraction, multiplication and division tables. As they master those skills, they’ll begin to memorize more tips and tricks, like adding a zero to the end when multiplying by 10. Students will memorize algorithms and processes throughout their education. 

Using your memory often keeps it sharp. As your child grows and continues to use math skills in adulthood, their memory will remain in tip top shape.

9. Math teaches perseverance

“I can do it!’ 

These are words heard often from our toddlers. This phrase is a marker of growth, and a point of pride. But as your child moves into elementary school, you may not hear these words as often or with as much confidence as before. 

Learning math is great for teaching perseverance. With the right math instruction, your child can see their progress and once again feel that “I can do it” attitude. The rush of excitement a child experiences when they master a new concept sticks in their memory. And they can reflect back on it when they’re struggling with a new, harder skill. 

Even when things get tough, they’ll know they can keep trying and eventually overcome it — because they’ve done it before.

Tip: Set goals to inspire and motivate your child to learn math

If your child has a  Prodigy Math Membership , you can use your parent account to set learning goals for them to achieve as they play our online math game.

The best bit? Every time they complete a goal, they'll also get a special in-game reward!

Many students experience roadblocks and hurdles throughout their math education. You might recognize some of these math struggles below in your child. But don’t worry! Any struggle is manageable with the right support and help. Together, you and your child can tackle anything. 

Here are some of the most common math struggles. 

• Increasing complexity

Sometimes the pace of class moves a bit faster than your child can keep up with. Or the concepts are just too abstract and difficult for them to wrap their mind around in one lesson. Some math ideas simply take more time to learn. 

• Wrong teaching style

A good teaching style with plenty of practice is essential to a high-quality math education. If the teacher’s style doesn’t mesh well with how your child learns, math class can be challenging. 

• Fear of failure  

Even as adults, we can feel scared to fail. It’s no surprise that our children experience this same same fear, especially with the many other pressures school can bring. 

• Lack of practice  

Sometimes, all your child needs is a little more practice. But this can be easier said than done. You can help by providing them with plenty of support and encouragement to help them get that practice time in.

• Math anxiety

Algorithms and complex problems can strike anxiety in the heart of any child (and many adults). Math anxiety is a common phenomenon. But with the right coping strategies it can be managed. 

Set your child’s math skills up for success with Prodigy Math

Now we've discovered just how important math is in both our everyday and life decisions, let's set the next generation up for success with the right tools that'll help them learn math.

Prodigy Math is a game-based, online learning platform that makes learning math fun for kids. As kids play and explore a safe, virtual world filled with fun characters and pets to collect, they'll answer math questions. These questions are curriculum-aligned and powered by an adaptive algorithm that can help them master math skills more quickly.

Plus, with a free parent account , you'll also get to be a big part of their math education without needing to be a math genius. You'll get to:

• Easily keep up with their math learning with a monthly Report Card
• See how they're doing in math class when their teacher uses Prodigy Math
• Send them motivational messages to encourage their perseverance in math

Want to play an even bigger role in helping your child master math? Try our optional Math Memberships for extra in-game content for your child to enjoy and get amazing parent tools like the ability to set in-game goals and rewards for them to achieve.

See why Prodigy can make math fun below!

ORIGINAL RESEARCH article

Mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Learning to Teach Mathematics Through Problem Solving

• Open access
• Published: 21 April 2022
• Volume 57 , pages 407–423, ( 2022 )

Cite this article

You have full access to this open access article

• Judy Bailey   ORCID: orcid.org/0000-0001-9610-9083 1  

5387 Accesses

2 Citations

1 Altmetric

Explore all metrics

While there has been much research focused on beginning teachers; and mathematical problem solving in the classroom, little is known about beginning primary teachers’ learning to teach mathematics through problem solving. This longitudinal study examined what supported beginning teachers to start and sustain teaching mathematics through problem solving in their first 2 years of teaching. Findings show ‘sustaining’ required a combination of three factors: (i) participation in professional development centred on problem solving (ii) attending subject-specific complementary professional development initiatives alongside colleagues from their school; and (iii) an in-school colleague who also teaches mathematics through problem solving. If only one factor is present, in this study attending the professional development focussed on problem solving, the result was little movement towards a problem solving based pedagogy. Recommendations for supporting beginning teachers to embed problem solving are included.

Similar content being viewed by others

Forging New Opportunities for Problem Solving in Australian Mathematics Classrooms through the First National Mathematics Curriculum

Mathematical knowledge for teaching teachers: knowledge used and developed by mathematics teacher educators in learning to teach via problem solving.

Part IV: Commentary – Characteristics of Mathematical Challenge in Problem-Based Approach to Teaching Mathematics

Avoid common mistakes on your manuscript.

Introduction

For many years curriculum documents worldwide have positioned mathematics as a problem solving endeavour (e.g., see Australian Curriculum, Assessment and Reporting Authority, 2018 ; Ministry of Education, 2007 ). There is evidence however that even with this prolonged emphasis, problem solving has not become a significant presence in many classrooms (Felmer et al., 2019 ). Research has reported on a multitude of potential barriers, even for experienced teachers (Clarke et al., 2007 ; Holton, 2009 ). At the same time it is widely recognised that beginning teachers encounter many challenges as they start their careers, and that these challenges are particularly compelling when seeking to implement ambitious methods of teaching, such as problem solving (Wood et al., 2012 ).

Problem solving has been central to mathematics knowledge construction from the beginning of human history (Felmer et al., 2019 ). Teaching and learning mathematics through problem solving supports learners’ development of deep and conceptual understandings (Inoue et al., 2019 ), and is regarded as an effective way of catering for diversity (Hunter et al., 2018 ). While the importance and challenge of mathematical problem solving in school classrooms is not questioned, the promotion and enabling of problem solving is a contentious endeavour (English & Gainsburg, 2016 ). One debate centres on whether to teach mathematics through problem solving or to teach problem solving in and of itself. Recent scholarship (and this research) leans towards teaching mathematics through problem solving as a means for students to learn mathematics and come to appreciate what it means to do mathematics (Schoenfeld, 2013 ).

Problem solving has been defined in a multitude of ways over the years. Of central importance to problem solving as it is explored in this research study is Schoenfeld’s ( 1985 ) proposition that, “if one has ready access to a solution schema for a mathematical task, that task is an exercise and not a problem” (p. 74). A more recent definition of what constitutes a mathematical problem from Mamona-Downs and Mamona ( 2013 ) also emphasises the centrality of the learner not knowing how to proceed, highlighting that problems cannot be solved by procedural effort alone. These are important distinctions because traditional school texts and programmes often position problems and problem solving as an ‘add-on’ providing a practice opportunity for a previously taught, specific procedure. Given the range of learners in any education setting an important point to also consider is that what constitutes a problem for some students may not be a problem for others (Schoenfeld, 2013 ).

A research focus exploring what supports beginning teachers’ learning about teaching mathematics through problem solving is particularly relevant at this time given calls for an increased curricular focus on mathematical practices such as problem solving (Grootenboer et al., 2021 ) and recent recommendations from an expert advisory panel on the English-medium Mathematics and Statistics curriculum in Aotearoa (Royal Society Te Apārangi, 2021 ). The ninth recommendation from this report advocates for the provision of sustained professional learning in mathematics and statistics for all teachers of Years 0–8. With regard to beginning primary teachers, the recommendation goes further suggesting that ‘mathematics and statistics professional learning’ (p. 36) be considered as compulsory in the first 2 years of teaching. This research explores what the nature of that professional learning might involve, with a focus on problem solving.

Scoping the Context for Learning and Sustaining Problem Solving

The literature reviewed for this study draws from two key fields: the nature of support and professional development effective for beginning teachers; and specialised supports helping teachers to employ problem solving pedagogies.

Beginning Teachers, Support and Professional Development

A teacher’s early years in the profession are regarded as critical in terms of constructing a professional practice (Feiman-Nemser, 2003 ) and avoiding high attrition (Karlberg & Bezzina, 2020 ). Research has established that beginning teachers need professional development opportunities geared specifically to their needs (Fantilli & McDougall, 2009 ) and their contexts (Gaikhorst, et al., 2017 ). Providing appropriate support is not an uncontentious matter with calls for institutions to come together and collaborate to provide adequate and ongoing support (Karlberg & Bezzina, 2020 ). The proposal is that support is needed from both within and beyond the beginning teacher’s school; and begins with effective pre-service teacher preparation (Keese et al., 2022 ).

Within schools where beginning teachers regard the support they receive positively, collaboration, encouragement and ‘involved colleagues’ are considered as vital; with the guidance of a 'buddy’ identified as some of the most valuable in-school support activities (Gaikhorst et al., 2014 ). Cameron et al.’s ( 2007 ) research in Aotearoa reports beginning teachers joining collaborative work cultures had greater opportunities to talk about teaching with their colleagues, share planning and resources, examine students’ work, and benefit from the collective expertise of team members.

Opportunities to participate in networks beyond the beginning teacher’s school have also been identified as being important for teacher induction (Akiri & Dori, 2021 ; Cameron et al., 2007 ). Fantilli & McDougall ( 2009 ) in their Canadian study found beginning teachers reported a need for many support and professional development opportunities including subject-specific (e.g., mathematics) workshops prior to and throughout the year. Akiri and Dori ( 2021 ) also refer to the need for specialised support from subject-specific mentors. This echoes the findings of Wood et al. ( 2012 ) who advocate that given the complexity of learning to teach mathematics, induction support specific to mathematics, and rich opportunities to learn are not only desirable but essential.

Akiri and Dori ( 2021 ) describe three levels of mentoring support for beginning teachers including individual mentoring, group mentoring and mentoring networks with all three facilitating substantive professional growth. Of relevance to this paper are individual and group mentoring. Individual mentoring involves pairing an experienced teacher with a beginning teacher, so that a beginning teacher’s learning is supported. Group mentoring involves a group of teachers working with one or more mentors, with participants receiving guidance from their mentor(s) (Akiri & Dori, 2021 ). Findings from Akiri and Dori suggest that of the varying forms of mentoring, individual mentoring contributes the most for beginning teachers’ professional learning.

Teachers Learning to Teach Mathematics Through Problem Solving

Learning to teach mathematics through problem solving begins in pre-service teacher education. It has been shown that providing pre-service teachers with opportunities to engage in problem solving as learners can be productive (Bailey, 2015 ). Opportunities to practise content-specific instructional strategies such as problem solving during student teaching has also been positively associated with first-year teachers’ enactment of problem solving (Youngs et al., 2022 ).

The move from pre-service teacher education to the classroom can be fraught for beginning teachers (Feiman-Nemser, 2003 ), and all the more so for beginning teachers attempting to teach mathematics through problem solving (Wood et al., 2012 ). In a recent study (Darragh & Radovic, 2019 ) it has been shown that an individual willingness to change to a problem-based pedagogy may not be enough to sustain a change in practice in the long term, particularly if there is a contradiction with the context and ‘norms’ (e.g., school curriculum) within which a teacher is working. Cady et al. ( 2006 ) explored the beliefs and practices of two teachers from pre-service teacher education through to becoming experienced teachers. One teacher who initially adopted reform practices reverted to traditional beliefs about the learning and teaching of mathematics. In contrast, the other teacher implemented new practices only after understanding these and gaining teaching experience. Participation in mathematically focused professional development and involvement in resource development were thought to favourably influence the second teacher.

Lesson structures have been found to support teachers learning to teach mathematics through problem solving. Sullivan et al. ( 2016 ) explored the use of a structure comprising four phases: launching, exploring, summarising and consolidating. Teachers in Australia and Aotearoa have reported the structure as productive and feasible (Ingram et al., 2019 ; Sullivan et al., 2016 ). Teaching using challenging tasks (such as in problem solving) and a structure have been shown to accommodate student diversity, a pressing concern for many teachers. Student diversity has often been managed by grouping students according to perceived levels of capability (called ability grouping). Research identifies this practice as problematic, excluding and marginalising disadvantaged groups of students (e.g., see Anthony & Hunter, 2017 ). The lesson structure explored by Sullivan et al. ( 2016 ) caters for diversity by deliberately differentiating tasks, providing enabling and extending prompts. Extending prompts are offered to students who finish an original task quickly and ideally elicit abstraction and generalisation. Enabling prompts involve reducing the number of steps, simplifying the numbers, and/or varying forms of representation for students who cannot initially proceed, with the explicit intention that students then return to the original task.

Recognising the established challenges teachers encounter when learning about teaching mathematics through problem solving, and the paucity of recent research focussing on beginning teachers learning about teaching mathematics in this way, this paper draws on data from a 2 year longitudinal study. The study was guided by the research question:

What supports beginning teachers’ implementation of a problem solving pedagogy for the teaching and learning of mathematics?

Research Methodology and Methods

Data were gathered from three beginning primary teachers who had completed a 1 year graduate diploma programme in primary teacher education the previous year. The beginning teachers had undertaken a course in mathematics education (taught by the author for half of the course) as part of the graduate diploma. An invitation to be involved in the research was sent to the graduate diploma cohort at the end of the programme. Three beginning teachers indicated their interest and remained involved for the 2 year research period. The teachers had all secured their first teaching positions, and were teaching at different year levels at three different schools. Julia (pseudonyms have been used for all names) was teaching year 0–2 (5–6 years) at a small rural school; Charlotte, year 5–6 (9–10 years) at a large urban city school; and Reine, year 7–8 (11–12 years), at another small rural school. All three beginning teachers taught at their respective schools, teaching the same year levels in both years of the study. Ethical approval was sought and given by the author’s university ethics committee. Informed consent was gained from the teachers, school principals and involved parents and children.

Participatory action research was selected as the approach in the study because of its emphasis on the participation and collaboration of all those involved (Townsend, 2013 ). Congruent with the principles of action research, activities and procedures were negotiated throughout both years in a responsive and emergent way. The author acted as a co-participant with the teachers, aiming to improve practice, to challenge and reorient thinking, and transform contexts for children’s learning (Locke et al., 2013 ). The author’s role included facilitating the research-based problem solving workshops (see below), contributing her experience as a mathematics educator and researcher. The beginning teachers were involved in making sense of their own practice related to their particular sites and context.

The first step in the research process was a focus group discussion before the beginning teachers commenced their first year of teaching. This discussion included reflecting on their learning about problem solving during the mathematics education course; and envisaging what would be helpful to support implementation. It was agreed that a series of workshops would be useful. Two were subsequently held in the first year of the study, each for three hours, at the end of terms one and two. Four workshops were held during the second year, one during each term. At the end of the first year the author suggested a small number of experienced teachers who teach mathematics through problem solving join the workshops for the second year. The presence of these teachers was envisaged to support the beginning teachers’ learning. The beginning teachers agreed, and an invitation was extended to four teachers from other schools whom the author knew (e.g., through professional subject associations). The focus of the research remained the same, namely exploring what supported beginning teachers to implement a problem solving pedagogy.

Each workshop began with sharing and oral reflections about recent problem solving experiences, including successes and challenges. Key workshop tasks included developing a shared understanding of what constitutes problem solving, participating in solving mathematical problems (modelled using a lesson structure (Sullivan et al., 2016 ), and learning techniques such as asking questions. A time for reflective writing was provided at the end of each workshop to record what had been learned and an opportunity to set goals.

During the first focus group discussion it was also decided the author would visit and observe the beginning teachers teaching a problem solving lesson (or two) in term three or four of each year. A semi-structured interview between the author and each beginning teacher took place following each observed lesson. The beginning teachers also had an opportunity to ask questions as they reflected on the lesson, and feedback was given as requested. A second focus group discussion was held at the end of the first year (an approximate midpoint in the research), and a final focus group discussion was held at the end of the second year.

All focus group discussions, problem solving workshops, observations and interviews were audio-recorded and transcribed. Field notes of workshops (recorded by the author), reflections from the beginning teachers (written at the end of each workshop), and lesson observation notes (recorded by the author) were also gathered. The final data collected included occasional emails between each beginning teacher and the author.

Data Analysis

The analysis reported in this paper drew on all data sets, primarily using inductive thematic analysis (Braun & Clarke, 2006 ). The research question guided the key question for analysis, namely: What supports beginning teachers’ implementation of a problem solving pedagogy for the teaching and learning of mathematics? Alongside this question, consideration was also given to the challenges beginning teachers encountered as they implemented a problem solving pedagogy. Data familiarisation was developed through reading and re-reading the whole body of data. This process informed data analysis and the content for each subsequent workshop and focus group discussions. Colour-coding and naming of themes included comparing and contrasting data from each beginning teacher and throughout the 2-year period. As a theme was constructed (Braun & Clarke, 2006 ) subsequent data was checked to ascertain whether the theme remained valid and/or whether it changed during the 2 years. Three key themes emerged revealing what supported the beginning teachers’ developing problem solving pedagogy, and these constitute the focus for this paper.

Mindful of the time pressures beginning teachers experience in their early years, the author undertook responsibility for data analysis. The author’s understanding of the unfolding ‘story’ of each beginning teacher’s experiences and the emerging themes were shared with the beginning teachers, usually at the beginning of a workshop, focus group discussion or observation. Through this process the author’s understandings were checked and clarified. This iterative process of member checking (Lincoln & Guba, 1985 ) began at a mid-point during the first year, once a significant body of data had been gathered. At a later point in the analysis and writing, the beginning teachers also had an opportunity to read, check and/or amend quotes chosen to exemplify their thinking and experiences.

Findings and Discussion

In this section the three beginning teachers’ experiences at the start of the 2 year research timeframe is briefly described, followed by the first theme centred on the use of a lesson structure including prompts for differentiation. The second and third themes are presented together, starting with a brief outline of each beginning teacher’s ‘story’ providing the context within which the themes emerged. Sharing the ‘story’ of each beginning teacher and including their ‘voice’ through quotes acknowledges them and their experiences as central to this research.

The beginning teachers’ pre-service teacher education set the scene for learning about teaching mathematics through problem solving. A detailed list brainstormed during the first focus group discussion suggested a developing understanding from their shared pre-service mathematics education course. In their first few weeks of teaching, all three beginning teachers implemented a few problems. It transpired however this inclusion of problem solving occurred only while children were being assessed and grouped. Following this, all three followed a traditional format of skill-based (with a focus on number) mathematics, taught using ability groups. The beginning teachers’ trajectories then varied with Julia and Reine both eventually adopting a pedagogy primarily based on problem solving, while Charlotte employed a traditional skill-based mathematics using a combination of whole class and small group teaching.

A Lesson Structure that Caters for Diversity Supports Early Efforts

Data show that developing familiarity with a lesson structure including prompts for differentiation supported the beginning teachers’ early efforts with a problem solving pedagogy. This addressed a key issue that emerged during the first workshop. During the workshop while a ‘list’ of ideas for teaching a problem solving lesson was co-constructed, considerable concern was expressed about catering for a range of learners when introducing and working with a problem. For example, Charlotte queried, “ Well, what happens when you are trying to do something more complicated, and we’re (referring to children) sitting here going, ‘I’ve no idea what you're talking about” ? Reine suggested keeping some children with the teacher, thinking he would say, “ If you’re unsure of any part stay behind” . He was unsure however about how he would then maintain the integrity of the problem.

It was in light of this discussion that a lesson structure with differentiated prompts (Sullivan et al., 2016 ) was introduced, experienced and reflected on during the second workshop. While the co-constructed list developed during the first workshop had included many components of Sullivan’s lesson structure, (e.g., a consideration of ‘extensions’) there had been no mention of ‘enabling prompts’. Now, with the inclusion of both enabling and extending prompts, the beginning teachers’ discussion revealed them starting to more fully envisage the possibilities of using a problem solving approach, and being able to cater for all children. Reine commented that, “… you can give the entire class a problem, you've just got to have a plan, [and] your enabling and extension prompts” . Charlotte was also now considering and valuing the possibility of having a whole class work on the same problem. She said, “I think … it’s important and it’s useful for your whole class to be working on the same thing. And … have enablers and extenders to make sure that everyone feels successful” . Julia also referred to the planning prompts. She thought it would be key to “plan it well so that we’ve got enabling and extending prompts” .

Successful Problem Solving Lessons

Following the second workshop all three beginning teachers were observed teaching a lesson using the structure. These lessons delighted the beginning teachers, with them noting prolonged engagement of children, the children’s learning and being able to cater for all learners. Reine commented on how excited and engaged the children were, saying they were, “ just so enthusiastic about it ”. In Charlotte’s words, “ it really worked ”, and Julia enthusiastically pondered this could be “ the only way you teach maths !”.

During the focus group discussion at the end of the first year, all three reflected on the value of the lesson structure. Reine called it a ‘framework’ commenting,

I like the framework. So from start to finish, how you go through that whole lesson. So how you set it up and then you go through the phases… I like the prompts that we went through…. knowing where you could go, if they’re like, ‘What do I do?’ And then if they get it too easy then ‘Where can you go?’ So you've got all these little avenues.

Charlotte also valued the lesson structure for the breadth of learning that could occur, explaining,

… it really helped, and really worked. So I found that useful for me and my class ‘cause they really understood. And I think also making sure that you know all the ins and outs of a problem. So where could they go? What do you need to know? What do they need to know?

While the beginning teachers’ pre-service teacher education and the subsequent research process, including the use of the lesson structure, supported the beginning teachers’ early efforts teaching mathematics through problem solving, two key factors further enabled two of the beginning teachers (Julia and Reine) to sustain a problem solving pedagogy. These were:

Being involved in complementary mathematics professional development alongside members of their respective school staff (a form of group mentoring); and

Having a colleague in the same school teaching mathematics through problem solving (a form of individual mentoring).

Charlotte did not have these opportunities and she indicated this limited her implementation. Data for these findings for each teacher are presented below.

Complementary Professional Development and Problem Solving Colleague in Same School

Julia began to significantly implement problem solving from the second term in the first year. This coincided with her attending a 2-day workshop (with staff from her school) that focused on the use of problem solving to support children who are not achieving at expected levels (see ALiM: Accelerated Learning in Maths—Ministry of Education, 2022 ). She explained, “ … I did the PD with (colleague’s name), which was really helpful. And we did lots of talking about rich learning tasks and problem solving tasks…. And what it means ”. Following this, Julia reported using rich tasks and problem solving in her mathematics teaching in a regular (at least weekly) and ongoing way.

During the observation in term three of the first year Julia again referred to the impact of having a colleague also teaching mathematics through problem solving. When asked what she believed had supported her to become a teacher who teaches mathematics in this way she firstly identified her involvement in the research project, and then spoke about her colleague. She said, “ I’m really lucky one of our other teachers is doing the ALiM project… So we’re kind of bouncing off each other a little bit with resources and activities, and things like that. So that’s been really good ”.

At the beginning of the second year, Julia reiterated this point again. On this occasion she said having a colleague teaching mathematics through problem solving, “ made a huge difference for me last year ”, explaining the value included having someone to talk with on a daily basis. Mid-way through the second year Julia repeated her opinion about the value of frequent contact with a practising problem solving colleague. Whereas her initial comments spoke of the impact in terms of being “ a little bit ”, later references recount these as ‘ huge ’ and ‘ enabling ’. She described:

a huge effect… it enabled me. Cause I mean these workshops are really helpful. But when it’s only once a term, having [colleague] there just enabled me to kind of bounce ideas off. And if I did a lesson that didn’t work very well, we could talk about why that was, and actually talk about what the learning was instead…. . It was being able to reflect together, but also share ideas. It was amazing.

Julia’s comments raise two points. It is likely that participating in the ALiM professional development (which could be conceived as a form of group mentoring) consolidated the learning she first encountered during pre-service teacher education and later extended through her involvement in the research. Having a colleague (in essence, an individual mentor) within the same school teaching mathematics through problem solving appears to be another factor that supported Julia to implement problem solving in a more sustained way. Julia’s comments allude to a number of reasons for this, including: (i) the more frequent discussion opportunities with a colleague who understands what it means for children to learn mathematics through problem solving; (ii) being able to share and plan suitable activities and resources; and (iii) as a means for reflection, particularly when challenges were encountered.

Reine’s mathematics programme throughout the first year was based on ability groups and could be described as traditional. He occasionally used some mathematical problems as ‘extension activities’ for ‘higher level’ children, or as ‘fillers’. In the second year, Reine moved to working with mixed ability groups (where students work together in small groups with varying levels of perceived capability) and initially implemented problem solving approximately once a fortnight. In thinking back to these lessons he commented, “ We weren’t really unpacking one problem properly, it was just lots of busy stuff ”. A significant shift occurred in Reine’s practice to teaching mathematics primarily by problem solving towards the last half of the second year. He explained, “ I really ramped up towards terms three and four, where it’s more picking one problem across the whole maths class but being really, really conscious of that problem. Low entry, high ceiling, and doing more of it too ”.

Reine attributed this change to a number of factors. In response to a question about what he considered led to the change he explained,

… having this, talking about this stuff, trialling it and then with our PD at school with the research into ability grouping... We’ve got a lot of PD saying why it can be harmful to group on ability, and that’s been that last little kick I needed, I think. And with other teachers trialling this as well. Our senior teacher has flipped her whole maths program and just does problem solving.

Like Julia, Reine firstly referred to his involvement in the research project including having opportunities to try problems in his class and discuss his experiences within the research group. He then told of a colleague teaching at his school leading school-wide professional development focussed on the pitfalls of ability grouping in mathematics (e.g., see Clarke, 2021 ) and instead using problem solving tasks. He also referred to having another teacher also teaching mathematics through problem solving. It is interesting to consider that having positive experiences in pre-service teacher education, the positive and encouraging support of colleagues (Reine’s principal and co-teacher in both years), regular participation in ongoing professional development (the problem solving workshops), and having a highly successful one-off problem solving teaching experience (the first year observation) were not enough for Reine to meaningfully sustain problem solving in his first year of teaching.

As for Julia, pivotal factors leading to a sustaining of problem solving teaching practice in the second year included complementary mathematics professional development (a form of group mentoring) and at least one other teacher (acting as an individual mentor) in the same school teaching mathematics through problem solving. It could be argued that pre-service teacher education and the problem solving workshops ‘paved the way’ for Julia and Reine to make a change. However, for both, the complementary professional development and presence of a colleague also teaching through problem solving were pivotal. It is also interesting to note that three of the four experienced teachers in the larger research group taught at the same level as Reine (see Table 1 below) yet he did not relate this to the significant change in his practice observed towards the end of the second year.

Charlotte’s mathematics programme during the first year was also traditional, teaching skill-based mathematics using ability groups. At the beginning of the second year Charlotte moved to teaching her class as a whole group, using flexible grouping as needed (children are grouped together in response to learning needs with regard to a specific idea at a point in time, rather than perceived notions of ability). She reported that she occasionally taught a lesson using problem solving in the first year, and approximately once or twice a term in the second year. Charlotte did not have opportunities for professional development in mathematics nor did she have a colleague in the same school teaching mathematics through problem solving. Pondering this, Charlotte said,

It would have been helpful if I had someone else in my school doing the same thing. I just thought about when you were saying the other lady was doing it [referring to Julia’s colleague]. You know, someone that you can just kind of back-and-forth like. I find with Science, I usually plan with this other lady, and we share ideas and plan together. We come up with some really cool stuff whereas I don’t really have the same thing for this.

Based on her experiences with teaching science it is clear Charlotte recognised the value of working alongside a colleague. In this, her view aligns with what Julia and Reine experienced.

Table 1 provides a summary of the variables for each beginning teacher, and whether a sustained implementation of teaching mathematics through problem solving occurred.

The table shows two variables common to Julia and Reine, the beginning teachers who began and sustained problem solving. They both participated in complementary professional development with colleagues from their school, and the presence of a colleague, also at their school, teaching mathematics through problem solving. Given that Julia was able to implement problem solving in the absence of a ‘research workshop colleague’ teaching at the same year level, and Reine’s lack of comment about the potential impact of this, suggests that this was not a key factor enabling a sustained implementation of problem solving.

Attributing the changes in Julia and Reine’s teaching practice primarily to their involvement in complementary professional development attended by members of their school staff, and the presence of at least one other teacher teaching mathematics through problem solving in their school, is further supported by a consideration of the timing of the changes. The data shows that while Julia could be considered an ‘early adopter’, Reine changed his practice reasonably late in the 2 year period. Julia’s early adoption of teaching mathematics through problem solving coincided with her involvement, early in the 2 years, in the professional development and opportunity to work alongside a problem solving practising colleague. Reine encountered these similar conditions towards the end of the 2 years and it is notable that this was the point at which he changed his practice. That problem solving did not become embedded or frequent within Charlotte’s mathematics programme tends to support the argument.

Understanding what supports primary teachers to teach mathematics through problem solving at the beginning of their careers is important because all students, including those taught by beginning teachers, need opportunities to develop high-level thinking, reasoning, and problem solving skills. It is also important in light of recent calls for mathematics curricula to include more emphasis on mathematical practices (such as problem solving) (e.g., see Grootenboer et al., 2021 ); and the Royal Society Te Apārangi report ( 2021 ). Findings from this research suggest that learning about problem solving during pre-service teacher education is enough for beginning teachers to trial teaching mathematics in this way. Early efforts were supported by gaining experience with a lesson structure that specifically attends to diversity. The lesson structure prompted the beginning teachers to anticipate different children’s responses, and consider how they would respond to these. An increased confidence and sense of security to trial teaching mathematics through problem solving was enabled, based on their more in-depth preparation. Beginning teachers finding the lesson structure useful extends the findings of Sullivan et al. ( 2016 ) in Australia and Ingram et al. ( 2019 ) in Aotearoa to include less experienced teachers.

In order for teaching mathematics through problem solving to be sustained however, a combination of three factors, subsequent to pre-service teacher education, was needed: (i) active participation in problem solving workshops (in this context provided by the research-based problem solving workshops); (ii) attending complementary professional development initiatives alongside colleagues from their school (a form of group mentoring); and (iii) the presence of an in-school colleague who also teaches mathematics through problem solving (a form of individual mentoring). It seems possible these three factors acted synergistically resulting in Julia and Reine being able to sustain implementation. If only one factor is present, in this study attending the problem solving workshops, and despite a genuine interest in using a problem based pedagogy, the result was limited movement towards this way of teaching.

Akiri and Dori ( 2021 ) have reported that individual mentoring contributes the most to beginning teachers’ professional growth. In a manner consistent with these findings, an in-school colleague (who in essence was acting as an individual mentor) played a critical role in supporting Reine and Julia. However, while Akiri and Dori, amongst others (e.g., Cameron et al., 2007 ; Karlberg & Bezzina, 2020 ), have identified the value of supportive, approachable colleagues, for both Julia and Reine it was important that their colleague was supportive and approachable, and actively engaged in teaching mathematics through problem solving. Having supportive and approachable colleagues, as Reine experienced in his first year, on their own were not enough to support a sustained problem solving pedagogy.

Implications for Productive Professional Learning and Development

This study sought to explore the conditions that supported problem solving for beginning teachers, each in their unique context and from their perspective. The research did not examine how the teaching of mathematics through problem solving affected children’s learning. However, multiple sets of data were collected and analysed over a 2-year period. While it is neither possible nor appropriate to make claims as to generalisability some suggestions for productive beginning teacher professional learning and development are offered.

Given the first years of teaching constitute a particular and critical phase of teacher learning (Karlberg & Bezzina, 2020 ) and the findings from this research, it is imperative that well-funded, subject-focussed support occurs throughout a beginning teacher’s first 2 years of teaching. This is consistent with the ninth recommendation in the Royal Society Te Apārangi report ( 2021 ) suggesting compulsory professional learning during the induction period (2 years in Aotearoa New Zealand). Participation in subject-specific professional development has been recognised to favourably influence new teachers’ efforts to adopt reform practices such as problem solving (Cady et al., 2006 ).

Findings from this study suggest professional development opportunities that complement each other support beginning teacher learning. In the first instance complementarity needs to be with what beginning teachers have learned during their pre-service teacher education. In this study, the research-based problem solving workshops served this role. Complementarity between varying forms of professional development also appears to be important. Furthermore, as indicated by Julia and Reine’s experiences, subsequent professional development need not be on exactly the same topic. Rather, it can be complementary in the sense that there is an underlying congruence in philosophy and/or focus on a particular issue. For example, it emerged in the problem solving workshops, that being able to cater for diversity was a central concern for the beginning teachers. Attending to this issue within the problem solving workshops via the introduction of a lesson structure that enabled differentiation, was congruent with the nature of the professional development in the two schools: ALiM in Julia’s school, and mixed ability grouping and teaching mathematics through problem solving in Reine’s school. All three of these settings were focussed on positively responding to diversity in learning needs.

The presence of a colleague within the same school teaching mathematics through problem solving also appears to be pivotal. This is consistent with Darragh and Radovic ( 2019 ) who have shown the significant impact a teacher’s school context has on their potential to sustain problem based pedagogies in mathematics. Given that problem solving is not prevalent in many primary classrooms, it would seem clear that colleagues who have yet to learn about teaching mathematics through problem solving, particularly those that have a role supporting beginning teachers, will also require access to professional development opportunities. It seems possible that beginning and experienced teachers learning together is a potential pathway forward. Finding such pathways will be critical if mathematical problem solving is to be consistently implemented in primary classrooms.

Finally, these implications together with calls for institutions to collaborate to provide adequate and ongoing support for new teachers (Karlberg & Bezzina, 2020 ) suggest there is a need for pre-service teacher educators, professional development providers and the Teaching Council of Aotearoa New Zealand to work together to support beginning teachers’ starting and sustaining teaching mathematics through problem solving pedagogies.

Akiri, E., & Dori, Y. (2021). Professional growth of novice and experienced STEM teachers. Journal of Science Education and Technology, 31 (1), 129–142.

Article   Google Scholar  

Anthony, G., & Hunter, R. (2017). Grouping practices in New Zealand mathematics classrooms: Where are we at and where should we be? New Zealand Journal of Educational Studies, 52 (1), 73–92.

Australian Curriculum, Assessment and Reporting Authority. (2018). F-10 curriculum: Mathematics . Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/ . Accessed 20 April 2022.

Bailey, J. (2015). Experiencing a mathematical problem solving teaching approach: Opportunity to identify ambitious teaching practices. Mathematics Teacher Education and Development, 17 (2), 111–124.

Google Scholar  

Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3 (2), 77–101.

Cady, J., Meier, S., & Lubinski, C. (2006). the mathematical tale of two teachers: A longitudinal study relating mathematics instructional practices to level of intellectual development. Mathematics Education Research Journal, 18 (1), 3–26.

Cameron, M., Lovett, S., & Garvey Berger, J. (2007). Starting out in teaching: Surviving or thriving as a new teacher. SET Research Information for Teachers, 3 , 32–37.

Clarke, D. (2021). Calling a spade a spade: The impact of within-class ability grouping on opportunity to learn mathematics in the primary school. Australian Primary Mathematics Classroom, 26 (1), 3–8.

Clarke, D., Goos, M., & Morony, W. (2007). Problem solving and working mathematically. ZDM Mathematics Education, 39 (5–6), 475–490.

Darragh, L., & Radovic, D. (2019). Chaos, control, and need: Success and sustainability of professional development in problem solving. In P. Felmer, P. Liljedahl, & B. Koichu (Eds.), Problem solving in mathematics instruction and teacher professional development (pp. 339–358). Springer. https://doi.org/10.1007/978-3-030-29215-7_18

Chapter   Google Scholar  

English, L., & Gainsburg, J. (2016). Problem solving in a 21st-century mathematics curriculum. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (pp. 313–335). Routledge.

Fantilli, R., & McDougall, D. (2009). A study of novice teachers: Challenges and supports in the first years. Teaching and Teacher Education, 25 (6), 814–825.

Feiman-Nemser, S. (2003). What new teachers need to learn. Educational Leadership, 60 (8), 25–29.

Felmer, P., Liljedahl, P., & Koichu, B. (Eds.). (2019). Problem solving in mathematics instruction and teacher professional development . Springer. https://doi.org/10.1007/978-3-030-29215-7_18

Book   Google Scholar  

Gaikhorst, L., Beishuizen, J., Korstjens, I., & Volman, M. (2014). Induction of beginning teachers in urban environments: An exploration of the support structure and culture for beginning teachers at primary schools needed to improve retention of primary school teachers. Teaching and Teacher Education, 42 , 23–33.

Gaikhorst, L., Beishuizen, J., Roosenboom, B., & Volman, M. (2017). The challenges of beginning teachers in urban primary schools. European Journal of Teacher Education , 40 (1), 46–61.

Grootenboer, P., Edwards-Groves, C., & Kemmis, S. (2021). A curriculum of mathematical practices. Pedagogy, Culture & Society. https://doi.org/10.1080/14681366.2021.1937678

Holton, D. (2009). Problem solving in the secondary school. In R. Averill & R. Harvey (Eds.), Teaching secondary school mathematics and statistics: Evidence-based practice (Vol. 1, pp. 37–53). NZCER Press.

Hunter, R., Hunter, J., Anthony, G., & McChesney, K. (2018). Developing mathematical inquiry communities: Enacting culturally responsive, culturally sustaining, ambitious mathematics teaching. SET Research Information for Teachers, 2 , 25–32.

Ingram, N., Holmes, M., Linsell, C., Livy, S., McCormick, M., & Sullivan, P. (2019). Exploring an innovative approach to teaching mathematics through the use of challenging tasks: A New Zealand perspective. Mathematics Education Research Journal . https://doi.org/10.1007/s13394-019-00266-1

Inoue, N., Asada, T., Maeda, N., & Nakamura, S. (2019). Deconstructing teacher expertise for inquiry-based teaching: Looking into consensus building pedagogy in Japanese classrooms. Teaching and Teacher Education, 77 , 366–377.

Karlberg, M., & Bezzina, C. (2020). The professional development needs of beginning and experienced teachers in four municipalities in Sweden. Professional Development in Education . https://doi.org/10.1080/19415257.2020.1712451

Keese, J., Waxman, H., Lobat, A., & Graham, M. (2022). Retention intention: Modeling the relationships between structures of preparation and support and novice teacher decisions to stay. Teaching and Teacher Education . https://doi.org/10.1016/j.tate.2021.103594

Locke, T., Alcorn, N., & O’Neill, J. (2013). Ethical issues in collaborative action research. Educational Action Research, 21 (1), 107–123.

Lincoln, Y., & Guba, E. (1985). Naturalistic Inquiry . Sage Publications.

Mamona-Downs, J., & Mamona, M. (2013). Problem solving and its elements in forming proof. The Mathematics Enthusiast, 10 (1–2), 137–162.

Ministry of Education. (2022). ALiM: Accelerated Learning in Maths. Retrieved from https://www.education.govt.nz/school/funding-and-financials/resourcing/school-funding-for-programmes-forstudents-pfs/#sh-ALiM . Accessed 20 April 2022.

Ministry of Education. (2007). The New Zealand Curriculum . Learning Media.

Royal Society Te Apārangi. (2021). Pāngarau Mathematics and Tauanga Statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum : Expert Advisory Panel. Publisher

Schoenfeld, A. (1985). Mathematical problem solving . Academic Press.

Schoenfeld, A. (2013). Reflections on problem solving theory and practice. The Mathematics Enthusiast, 10 (1/2), 9–34.

Sullivan, P., Borcek, C., Walker, N., & Rennie, M. (2016). Exploring a structure for mathematics lessons that initiate learning by activating cognition on challenging tasks. The Journal of Mathematical Behaviour, 41 , 159–170.

Townsend, A. (2013). Action research: The challenges of understanding and changing practice . Open University Press.

Wood, M., Jilk, L., & Paine, L. (2012). Moving beyond sinking or swimming: Reconceptualizing the needs of beginning mathematics teachers. Teachers College Record, 114 , 1–44.

Youngs, P., Molloy Elreda, L., Anagnostopoulos, D., Cohen, J., Drake, C., & Konstantopoulos, S. (2022). The development of ambitious instruction: How beginning elementary teachers’ preparation experiences are associated with their mathematics and English language arts instructional practices. Teaching and Teacher Education . https://doi.org/10.1016/j.tate.2021.103576

Download references

Open Access funding enabled and organized by CAUL and its Member Institutions.

Author information

Authors and affiliations.

University of Waikato, Hamilton, New Zealand

Judy Bailey

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Judy Bailey .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Bailey, J. Learning to Teach Mathematics Through Problem Solving. NZ J Educ Stud 57 , 407–423 (2022). https://doi.org/10.1007/s40841-022-00249-0

Download citation

Received : 17 January 2022

Accepted : 04 April 2022

Published : 21 April 2022

Issue Date : December 2022

DOI : https://doi.org/10.1007/s40841-022-00249-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Beginning teachers
• Mathematical problem solving
• Professional development
• Problem solving lesson structure
• Find a journal
• Publish with us
• Track your research

The Hechinger Report

Covering Innovation & Inequality in Education

Why schools are teaching math word problems all wrong

Share this:

• Click to share on LinkedIn (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to email a link to a friend (Opens in new window)

The Hechinger Report is a national nonprofit newsroom that reports on one topic: education. Sign up for our  weekly newsletters  to get stories like this delivered directly to your inbox. Consider supporting our stories and becoming  a member  today.

Get important education news and analysis delivered straight to your inbox

• Weekly Update
• Future of Learning
• Higher Education
• Early Childhood
• Proof Points

CENTRAL FALLS, R.I. — When Natalia Molina began teaching her second grade students word problems earlier this school year, every lesson felt difficult. Most students were stymied by problems such as: “Sally went shopping. She spent $86 on groceries and $39 on clothing. How much more did Sally spend on groceries than on clothing?”

Both Molina, a first-year teacher, and her students had been trained to tackle word problems by zeroing in on key words like “and,” “more” and “total”  — a simplistic approach that Molina said too often led her students astray. After recognizing the word “and,” for instance, they might mistakenly assume that they needed to add two nearby numbers together to arrive at an answer.

Some weaker readers, lost in a sea of text, couldn’t recognize any words at all.

“I saw how overwhelmed they would get,” said Molina, who teaches at Segue Institute for Learning, a predominantly Hispanic charter school in this small city just north of Providence.

So, with the help of a trainer doing work in Rhode Island through a state grant, Molina and some of her colleagues revamped their approach to teaching word problems this winter — an effort that they said is already paying off in terms of increased student confidence and ability. “It has been a game changer for them,” Molina said.

Perhaps no single educational task encompasses as many different skills as the word problem. Between reading, executive functioning, problem solving, computation and vocabulary, there are a lot of ways for students to go wrong. And for that reason, students perform significantly worse overall on word problems compared to questions more narrowly focused on computation or shapes (for example: “Solve 7 + _ = 22” or “What is 64 x 3?”).

If a student excels at word problems, it’s a good sign that they’re generally excelling at school. “Word-problem solving in lower grades is one of the better indicators of overall school success in K-12,” said Lynn Fuchs, a research professor at Vanderbilt University. In a large national survey , for instance, algebra teachers rated word-problem solving as the most important among 15 skills required to excel in the subject.

Teacher takeaways

• Don’t instruct students to focus mainly on “key words” in word problems such as “and” or “more” 
• Mix question types in any lesson so that students don’t assume they just apply the same operation (addition, subtraction) again and again
• Teach students the underlying structure — or schema — of the word problem

Yet most experts and many educators agree that too many schools are doing it wrong, particularly in the elementary grades. And in a small but growing number of classrooms, teachers like Molina are working to change that. “With word problems, there are more struggling learners than non-struggling learners” because they are taught so poorly, said Nicole Bucka, who works with teachers throughout Rhode Island to provide strategies for struggling learners.

Too many teachers, particularly in the early grades, rely on key words to introduce math problems. Posters displaying the terms — sum, minus, fewer, etc. — tied to operations including addition and subtraction are a staple in elementary school classrooms across the country.

Key words can be a convenient crutch for both students and teachers, but they become virtually meaningless as the problems become harder, according to researchers. Key words can help first graders figure out whether to add or subtract more than half of the time, but the strategy rarely works for the multi-step problems students encounter starting in second and third grade. “With multi-step problems, key words don’t work 90 percent of the time,” said Sarah Powell, a professor at the University of Texas in Austin who studies word problems and whose research has highlighted the inefficacy of key words . “But the average kindergarten teacher is not thinking about that; they are teaching 5-year-olds, not 9-year-olds.”

Many teachers in the youngest grades hand out worksheets featuring the same type of word problem repeated over and over again. That’s what Molina’s colleague, Cassandra Santiago, did sometimes last year when leading a classroom on her own for the first time. “It was a mistake,” the first grade teacher said. “It’s really important to mix them up. It makes them think more critically about the parts they have to solve.”

Another flaw with word problem instruction is that the overwhelming majority of questions are divorced from the actual problem-solving a child might have to do outside the classroom in their daily life — or ever, really. “I’ve seen questions about two trains going on the same track,” said William Schmidt, a University Distinguished Professor at Michigan State University. “First, why would they be going on the same track and, second, who cares?”

Schmidt worked on an analysis of about 8,000 word problems used in 23 textbooks in 19 countries. He found that less than one percent had “real world applications” and involved “higher order math applications .”

“That is one of the reasons why children have problems with mathematics,” he said. “They don’t see the connection to the real world … We’re at this point in math right now where we are just teaching students how to manipulate numbers.”

He said a question, aimed at middle schoolers, that does have real world connections and involves more than manipulating numbers, might be: “Shopping at the new store in town includes a 43% discount on all items which are priced the same at $2. The state you live in has a 7% sales tax. You want to buy many things but only have a total of $52 to spend. Describe in words how many things you could buy.”

Schmidt added that relevancy of word problems is one area where few, if any, countries excel. “No one was a shining star leading the way,” he said. 

In her brightly decorated classroom one Tuesday afternoon, Santiago, the first grade teacher, gave each student a set of animal-shaped objects and a sheet of blue paper (the water) and green (the grass). “We’re going to work on a number story,” she told them. “I want you to use your animals to tell me the story.”

“ Once upon a time,” the story began. In this tale, three animals played in the water, and two animals played in the grass. Santiago allowed some time for the ducks, pigs and bears to frolic in the wilds of each student’s desk before she asked the children to write a number sentence that would tell them how many animals they have altogether.

Some of the students relied more on pictorial representations (three dots on one side of a line and two dots on the other) and others on the number sentence (3+2 = 5) but all of them eventually got to five. And Santiago made sure that her next question mixed up the order of operations (so students didn’t incorrectly assume that all they ever have to do is add): “Some more animals came and now there are seven. So how many more came?”

One approach to early elementary word problems that is taking off in some schools, including Segue Institute, has its origins in a special education intervention for struggling math students. Teachers avoid emphasizing key words and ask students instead to identify first the conceptual type of word problem (or schema, as many practitioners and researchers refer to it) they are dealing with: “Total problems,” for instance, involve combining two parts to find a new amount; “change problems” involve increasing or decreasing the amount of something. Total problems do not necessarily involve adding, however.

“The schemas that students learn in kindergarten will continue with them throughout their whole career,” said Powell, the word-problem researcher, who regularly works with districts across the country to help implement the approach. 

In Olathe, Kansas — a district inspired by Powell’s work — teachers had struggled for years with word problems, said Kelly Ulmer, a math support specialist whose goal is to assist in closing academic gaps that resulted from lost instruction time during the pandemic. “We’ve all tried these traditional approaches that weren’t working,” she said. “Sometimes you get pushback on new initiatives from veteran teachers and one of the things that showed us how badly this was needed is that the veteran teachers were the most excited and engaged — they have tried so many things” that haven’t worked.

In Rhode Island, many elementary schools initially used the strategy with students who required extra help, including those in special education, but expanded this use to make it part of the core instruction for all, said Bucka. In some respects, it’s similar to the recent, well publicized evolution of reading instruction in which some special education interventions for struggling readers  — most notably, a greater reliance on phonics in the early grades — have gone mainstream.

There is an extensive research bas e showing that focusing on the different conceptual types of word problems is an effective way of teaching math, although much of the research focuses specifically on students experiencing difficulties in the subject. 

Molina has found asking students to identify word problems by type to be a useful tool with nearly all of her second graders; next school year she hopes to introduce the strategy much earlier.

One recent afternoon, a lesson on word problems started with everyone standing up and chanting in unison: “Part plus part equals total” (they brought two hands together). “Total minus part equals part ” (they took one hand away) .

It’s a way to help students remember different conceptual frameworks for word problems. And it’s especially effective for the students who learn well through listening and repeating. For visual learners, the different types of word problems were mapped out on individual dry erase mats.

The real work began when Molina passed out questions, and the students— organized into the Penguin, Flower Bloom, Red Panda and Marshmallow teams — had to figure out which framework they were dealing with on their own and then work toward an answer. A few months ago, many of them would have automatically shut down when they saw the text on the page, Molina said.

For the Red Pandas, the question under scrutiny was: “The clothing store had 47 shirts. They sold 21, how many do they have now?”

“It’s a total problem,” one student said.

“No, it’s not total,” responded another.

“I think it’s about change,” said a third.

None of the students seemed worried about their lack of consensus, however. And neither was Molina. A correct answer is always nice but those come more often now that most of the students have made a crucial leap. “I notice them thinking more and more,” she said, “about what the question is actually asking.”

This story about word problems was produced by The Hechinger Report , a nonprofit, independent news organization focused on inequality and innovation in education. Sign up for the Hechinger newsletter .

Related articles

The Hechinger Report provides in-depth, fact-based, unbiased reporting on education that is free to all readers. But that doesn't mean it's free to produce. Our work keeps educators and the public informed about pressing issues at schools and on campuses throughout the country. We tell the whole story, even when the details are inconvenient. Help us keep doing that.

Join us today.

Sarah Carr CONTRIBUTING EDITOR

Email:... More by Sarah Carr

Letters to the Editor

At The Hechinger Report, we publish thoughtful letters from readers that contribute to the ongoing discussion about the education topics we cover. Please read our guidelines for more information. We will not consider letters that do not contain a full name and valid email address. You may submit news tips or ideas here without a full name, but not letters.

By submitting your name, you grant us permission to publish it with your letter. We will never publish your email address. You must fill out all fields to submit a letter.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Sign me up for the newsletter!