word problems system of equations calculator

System of Equations Calculator

Step-by-step calculator for systems of equations.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to view)

• Enter your equations in the boxes above, and press Calculate!
• Or click the example.

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Solving Systems of Equations Real World Problems

Wow! You have learned many different strategies for solving systems of equations! First we started with Graphing Systems of Equations . Then we moved onto solving systems using the Substitution Method . In our last lesson we used the Linear Combinations or Addition Method to solve systems of equations.

Now we are ready to apply these strategies to solve real world problems! Are you ready? First let's look at some guidelines for solving real world problems and then we'll look at a few examples.

Steps For Solving Real World Problems

• Highlight the important information in the problem that will help write two equations.
• Define your variables
• Write two equations
• Use one of the methods for solving systems of equations to solve.
• Check your answers by substituting your ordered pair into the original equations.
• Answer the questions in the real world problems. Always write your answer in complete sentences!

Ok... let's look at a few examples. Follow along with me. (Having a calculator will make it easier for you to follow along.)

Example 1: Systems Word Problems

You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?

1.  Let's start by identifying the important information:

• hot dogs cost $1.50
• Sodas cost $0.50
• Made a total of $78.50
• Sold 87 hot dogs and sodas combined

2.  Define your variables.

• Ask yourself, "What am I trying to solve for? What don't I know?

In this problem, I don't know how many hot dogs or sodas were sold. So this is what each variable will stand for. (Usually the question at the end will give you this information).

Let x = the number of hot dogs sold

Let y = the number of sodas sold

3. Write two equations.

One equation will be related to the price and one equation will be related to the quantity (or number) of hot dogs and sodas sold.

1.50x + 0.50y = 78.50    (Equation related to cost)

 x + y = 87   (Equation related to the number sold)

4.  Solve! 

We can choose any method that we like to solve the system of equations. I am going to choose the substitution method since I can easily solve the 2nd equation for y.

5. Think about what this solution means.

x is the number of hot dogs and x = 35. That means that 35 hot dogs were sold.

y is the number of sodas and y = 52. That means that 52 sodas were sold.

6.  Write your answer in a complete sentence.

35 hot dogs were sold and 52 sodas were sold.

7.  Check your work by substituting.

1.50x + 0.50y = 78.50

1.50(35) + 0.50(52) = 78.50

52.50 + 26 = 78.50

35 + 52 = 87

Since both equations check properly, we know that our answers are correct!

That wasn't too bad, was it? The hardest part is writing the equations. From there you already know the strategies for solving. Think carefully about what's happening in the problem when trying to write the two equations.

Example 2: Another Word Problem

You and a friend go to Tacos Galore for lunch. You order three soft tacos and three burritos and your total bill is $11.25. Your friend's bill is $10.00 for four soft tacos and two burritos. How much do soft tacos cost? How much do burritos cost?

• 3 soft tacos + 3 burritos cost $11.25
• 4 soft tacos + 2 burritos cost $10.00

In this problem, I don't know the price of the soft tacos or the price of the burritos.

Let x = the price of 1 soft taco

Let y = the price of 1 burrito

One equation will be related your lunch and one equation will be related to your friend's lunch.

3x + 3y = 11.25  (Equation representing your lunch)

4x + 2y = 10   (Equation representing your friend's lunch)

We can choose any method that we like to solve the system of equations. I am going to choose the combinations method.

5. Think about what the solution means in context of the problem.

x = the price of 1 soft taco and x = 1.25.

That means that 1 soft tacos costs $1.25.

y = the price of 1 burrito and y = 2.5.

That means that 1 burrito costs $2.50.

Yes, I know that word problems can be intimidating, but this is the whole reason why we are learning these skills. You must be able to apply your knowledge!

If you have difficulty with real world problems, you can find more examples and practice problems in the Algebra Class E-course.

Take a look at the questions that other students have submitted:

Problem about the WNBA

Systems problem about ages

Problem about milk consumption in the U.S.

Vans and Buses? How many rode in each?

Telephone Plans problem

Systems problem about hats and scarves

Apples and guavas please!

How much did Alice spend on shoes?

All about stamps

Going to the movies

Small pitchers and large pitchers - how much will they hold?

Chickens and dogs in the farm yard

• System of Equations
• Systems Word Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

Online Systems of Equations Solver

Solve equations and systems of equations with wolfram|alpha, a powerful tool for finding solutions to systems of equations and constraints.

Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

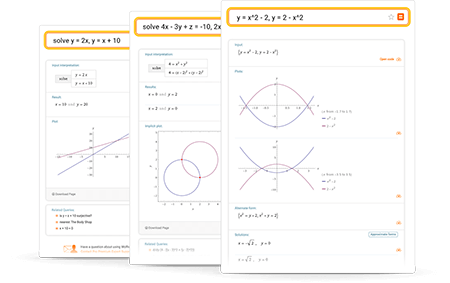
Learn more about:

• Systems of equations

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

• solve y = 2x, y = x + 10
• solve system of equations {y = 2x, y = x + 10, 2x = 5y}
• y = x^2 - 2, y = 2 - x^2
• solve 4x - 3y + z = -10, 2x + y + 3z = 0, -x + 2y - 5z = 17
• solve system {x + 2y - z = 4, 2x + y + z = -2, z + 2y + z = 2}
• solve 4 = x^2 + y^2, 4 = (x - 2)^2 + (y - 2)^2
• x^2 + y^2 = 4, y = x
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

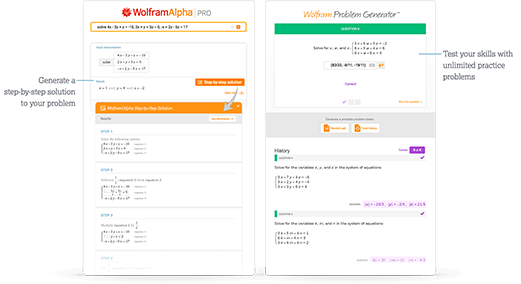
• Step-by-step solutions
• Wolfram Problem Generator

What are systems of equations?

A system of equations is a set of one or more equations involving a number of variables..

The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.

Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Systems of Equations Word Problems? (+FREE Worksheet!)

Learn how to create and solve systems of equations word problems by the elimination method.

Related Topics

• How to Solve One-Step Equations
• How to Solve One-Step Inequalities
• How to Solve Multi-Step Inequalities
• How to Solve Systems of Equations
• How to Graph Single–Variable Inequalities

Step by step guide to solve systems of equations word Problems

• Find the key information in the word problem that can help you define the variables.
• Define two variables: \(x\) and \(y\)
• Write two equations.
• Use the elimination method for solving systems of equations.
• Check the solution by substituting the ordered pair into the original equations.

The Absolute Perfect Practice Workbook for Algebra I

Algebra I for Beginners The Ultimate Step by Step Guide to Acing Algebra I

Systems of equations word problems – example 1:.

Tickets to a movie cost \($8\) for adults and \($5\) for students. A group of friends purchased \(20\) tickets for \($115.00\). How many adult tickets did they buy?

Let \(x\) be the number of adult tickets and \(y\) be the number of student tickets. There are \(20\) tickets. Then: \(x+y=20\). The cost of adults’ tickets is \($8\) and for students ticket is \($5\), and the total cost is \($115\). So, \(8x+5y=115\). Now, we have a system of equations: \(\begin{cases}x+y=20 \\ 8x+5y=115\end{cases}\) Multiply the first equation by \(-5\) and add to the second equation: \(-5(x+y= 20)=- \ 5x-5y=- \ 100\) \(8x+5y+(-5x-5y)=115-100→3x=15→x=5→5+y=20→y=15\). There are \(5\) adult tickets and \(15\) student tickets.

Exercises for Solving Systems of Equations Word Problems

• A farmhouse shelters \(10\) animals, some are pigs and some are ducks. Altogether there are \(36\) legs. How many of each animal are there?
• A class of \(195\) students went on a field trip. They took vehicles, some cars, and some buses. Find the number of cars and the number of buses they took if each car holds \(5\) students and each bus holds \(45\) students.
• The difference of two numbers is \(6\). Their sum is \(14\). Find the numbers.
• The sum of the digits of a certain two–digit number is \(7\). Reversing is increasing the number by \(9\). What is the number?
• The difference of two numbers is \(18\). Their sum is \(66\). Find the numbers.

Download Systems of Equations Word Problems Worksheet

• There are \(8\) pigs and \(2\) ducks.
• There are \(3\) cars and \(4\) buses.
• \(10\) and \(4\).
• \(24\) and \(42\).

The Best Books to Ace Algebra

Algebra I Practice Workbook The Most Comprehensive Review of Algebra 1

Algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra for beginners the ultimate step by step guide to preparing for the pre-algebra test, pre-algebra tutor everything you need to help achieve an excellent score.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• 10 Must-Have Math Teacher Supplies
• How to Discovering Patterns: Using Graphs to Find Rules
• The Ultimate TABE Math Course (+FREE Worksheets & Tests)
• Top 10 Free Websites for AFOQT Math Preparation
• How to Solve Word Problems of Subtracting Numbers Up to 7 Digits
• Your Coach’s Playbook: How to Understand Percent of Change
• Average Value of a Curve
• FREE 3rd Grade OST Math Practice Test
• Top 10 6th Grade STAAR Math Practice Questions
• The Ultimate 6th Grade North Carolina EOG Math Course (+FREE Worksheets)

What people say about "How to Solve Systems of Equations Word Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

• 1-800-234-2933
• [email protected]

Word Problems Calculators: (41) lessons

2 number word problems.

Free 2 number Word Problems Calculator - This calculator handles word problems in the format below: * Two numbers have a sum of 70 and a product of 1189 What are the numbers? * Two numbers have a sum of 70. Their difference 32

2 Unknown Word Problems

Free 2 Unknown Word Problems Calculator - Solves a word problem based on two unknown variables

Age Difference

Free Age Difference Calculator - Determines the ages for an age difference word problem.

Age Word Problems

Free Age Word Problems Calculator - Determines age in age word problems

Angle of Elevation

Free Angle of Elevation Calculator - Solves angle of elevation word problems

Free Break Even Calculator - Given a fixed cost, variable cost, and revenue function or value, this calculates the break-even point

Coin Combinations

Free Coin Combinations Calculator - Given a selection of coins and an amount, this determines the least amount of coins needed to reach that total.

Coin Total Word Problems

Free Coin Total Word Problems Calculator - This word problem lesson solves for a quantity of two coins totaling a certain value with a certain amount more or less of one coin than another

Coin Word Problems

Free Coin Word Problems Calculator - This word problem lesson solves for a quantity of two coins totaling a certain value

Collinear Points that form Unique Lines

Free Collinear Points that form Unique Lines Calculator - Solves the word problem, how many lines can be formed from (n) points no 3 of which are collinear.

Compare Raises

Free Compare Raises Calculator - Given two people with a salary and annual raise amount, this determines how long it takes for the person with the lower salary to catch the person with the higher salary.

Consecutive Integer Word Problems

Free Consecutive Integer Word Problems Calculator - Calculates the word problem for what two consecutive integers, if summed up or multiplied together, equal a number entered.

Cost Revenue Profit

Free Cost Revenue Profit Calculator - Given a total cost, variable cost, revenue amount, and profit unit measurement, this calculates profit for each profit unit

Free Decay Calculator - Determines decay based on an initial mass and decay percentage and time.

Distance Catch Up

Free Distance Catch Up Calculator - Calculates the amount of time that it takes for a person traveling at one speed to catch a person traveling at another speed when one person leaves at a later time.

Distance Rate and Time

Free Distance Rate and Time Calculator - Solves for distance, rate, or time in the equation d=rt based on 2 of the 3 variables being known.

Find two numbers word problems

Free Find two numbers word problems Calculator - Given two numbers with a sum of s where one number is n greater than another, this calculator determines both numbers.

Inclusive Number Word Problems

Free Inclusive Number Word Problems Calculator - Given an integer A and an integer B, this calculates the following inclusive word problem questions: 1) The Average of all numbers inclusive from A to B 2) The Count of all numbers inclusive from A to B 3) The Sum of all numbers inclusive from A to B

Free Map Scale Calculator - Solves map scale problems based on unit measurements

Markup Markdown

Free Markup Markdown Calculator - Given the 3 items of a markup word problem, cost, markup percentage, and sale price, this solves for any one of the three given two of the items. This works as a markup calculator, markdown calculator.

Numbers Word Problems

Free Numbers Word Problems Calculator - Solves various basic math and algebra word problems with numbers

Free Overtime Calculator - Solves overtime wage problems

Percent Off Problem

Free Percent Off Problem Calculator - Given the 3 items of a percent word problem, Reduced Price, percent off, and full price, this solves for any one of the three given two of the items.

Percentage of the Pie Word Problem

Free Percentage of the Pie Word Problem Calculator - This takes two or three fractions of ownership in some good or object, and figures out what remaining fraction is left over.

Percentage Word Problems

Free Percentage Word Problems Calculator - Solves percentage word problems

Population Doubling Time

Free Population Doubling Time Calculator - Determines population growth based on a doubling time.

Population Growth

Free Population Growth Calculator - Determines population growth based on an exponential growth model.

Product of Consecutive Numbers

Free Product of Consecutive Numbers Calculator - Finds the product of (n) consecutive integers, even or odd as well. Examples include: product of 2 consecutive integers product of 2 consecutive numbers product of 2 consecutive even integers product of 2 consecutive odd integers product of 2 consecutive even numbers product of 2 consecutive odd numbers product of two consecutive integers product of two consecutive odd integers product of two consecutive even integers product of two consecutive numbers product of two consecutive odd numbers product of two consecutive even numbers product of 3 consecutive integers product of 3 consecutive numbers product of 3 consecutive even integers product of 3 consecutive odd integers product of 3 consecutive even numbers product of 3 consecutive odd numbers product of three consecutive integers product of three consecutive odd integers product of three consecutive even integers product of three consecutive numbers product of three consecutive odd numbers product of three consecutive even numbers product of 4 consecutive integers product of 4 consecutive numbers product of 4 consecutive even integers product of 4 consecutive odd integers product of 4 consecutive even numbers product of 4 consecutive odd numbers product of four consecutive integers product of four consecutive odd integers product of four consecutive even integers product of four consecutive numbers product of four consecutive odd numbers product of four consecutive even numbers product of 5 consecutive integers product of 5 consecutive numbers product of 5 consecutive even integers product of 5 consecutive odd integers product of 5 consecutive even numbers product of 5 consecutive odd numbers product of five consecutive integers product of five consecutive odd integers product of five consecutive even integers product of five consecutive numbers product of five consecutive odd numbers product of five consecutive even numbers

Ratio Word Problems

Free Ratio Word Problems Calculator - Solves a ratio word problem using a given ratio of 2 items in proportion to a whole number.

Rebound Ratio

Free Rebound Ratio Calculator - Calculates a total downward distance traveled given an initial height of a drop and a rebound ratio percentage

Slope Word Problems

Free Slope Word Problems Calculator - Solves slope word problems

Solution Mixture

Free Solution Mixture Calculator - Determines a necessary amount of a Solution given two solution percentages and 1 solution amount.

Split Fund Interest

Free Split Fund Interest Calculator - Given an initial principal amount, interest rate on Fund 1, interest rate on Fund 2, and a total interest paid, calculates the amount invested in each fund.

Sum of Consecutive Numbers

Free Sum of Consecutive Numbers Calculator - Finds the sum of (n) consecutive integers, even or odd as well. Examples include: sum of 2 consecutive integers sum of 2 consecutive numbers sum of 2 consecutive even integers sum of 2 consecutive odd integers sum of 2 consecutive even numbers sum of 2 consecutive odd numbers sum of two consecutive integers sum of two consecutive odd integers sum of two consecutive even integers sum of two consecutive numbers sum of two consecutive odd numbers sum of two consecutive even numbers sum of 3 consecutive integers sum of 3 consecutive numbers sum of 3 consecutive even integers sum of 3 consecutive odd integers sum of 3 consecutive even numbers sum of 3 consecutive odd numbers sum of three consecutive integers sum of three consecutive odd integers sum of three consecutive even integers sum of three consecutive numbers sum of three consecutive odd numbers sum of three consecutive even numbers sum of 4 consecutive integers sum of 4 consecutive numbers sum of 4 consecutive even integers sum of 4 consecutive odd integers sum of 4 consecutive even numbers sum of 4 consecutive odd numbers sum of four consecutive integers sum of four consecutive odd integers sum of four consecutive even integers sum of four consecutive numbers sum of four consecutive odd numbers sum of four consecutive even numbers sum of 5 consecutive integers sum of 5 consecutive numbers sum of 5 consecutive even integers sum of 5 consecutive odd integers sum of 5 consecutive even numbers sum of 5 consecutive odd numbers sum of five consecutive integers sum of five consecutive odd integers sum of five consecutive even integers sum of five consecutive numbers sum of five consecutive odd numbers sum of five consecutive even numbers

Sum of Five Consecutive Integers

Free Sum of Five Consecutive Integers Calculator - Finds five consecutive integers, if applicable, who have a sum equal to a number. Sum of 5 consecutive integers

Sum of Four Consecutive Integers

Free Sum of Four Consecutive Integers Calculator - Finds four consecutive integers, if applicable, who have a sum equal to a number. Sum of 4 consecutive integers

Sum of the First (n) Numbers

Free Sum of the First (n) Numbers Calculator - Determines the sum of the first (n) * Whole Numbers * Natural Numbers * Even Numbers * Odd Numbers * Square Numbers * Cube Numbers * Fourth Power Numbers

Sum of Three Consecutive Integers

Free Sum of Three Consecutive Integers Calculator - Finds three consecutive integers, if applicable, who have a sum equal to a number. Sum of 3 consecutive integers

Free Sun Shadow Calculator - This solves for various components and scenarios of the sun shadow problem

Unit Savings

Free Unit Savings Calculator - A discount and savings word problem using 2 people and full prices versus discount prices.

Work Word Problems

Free Work Word Problems Calculator - Given Person or Object A doing a job in (r) units of time and Person or Object B doing a job in (s) units of time, this calculates how long it would take if they combined to do the job.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Subjects
• A.I. Training Data and Analytics
• Get Paid as an Affiliate

Top Categories

• Trigonometry
• Pre-Algebra
• Pre-Calculus
• Post a Math Problem

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 6

• Age word problem: Imran
• Age word problem: Ben & William
• Age word problem: Arman & Diya
• Age word problems
• System of equations word problem: walk & ride
• Systems of equations word problems
• System of equations word problem: no solution
• System of equations word problem: infinite solutions

Systems of equations word problems (with zero and infinite solutions)

• Systems of equations with elimination: TV & DVD
• Systems of equations with elimination: apples and oranges
• Systems of equations with substitution: coins
• Systems of equations with elimination: coffee and croissants
• Systems of equations: FAQ
• (Choice A)   There is not enough information to determine the exact cost of a notebook and a newspaper. A There is not enough information to determine the exact cost of a notebook and a newspaper.
• (Choice B)   The given information describes an impossible situation. B The given information describes an impossible situation.
• (Choice C)   A notebook costs $ 2.50 ‍   and a newspaper costs $ 1.50 ‍   . C A notebook costs $ 2.50 ‍   and a newspaper costs $ 1.50 ‍   .
• (Choice D)   A notebook costs $ 1.50 ‍   and a newspaper costs $ 2.50 ‍   . D A notebook costs $ 1.50 ‍   and a newspaper costs $ 2.50 ‍   .

Systems of Linear Equations and Word Problems

Note that we saw how to solve linear inequalities here in the Coordinate System and Graphing Lines section . Note also that we solve Algebra Word Problems without Systems here , and we solve systems using matrices in the Matrices and Solving Systems with Matrices  section here.

Introduction to Systems

“Systems of equations” just means that we are dealing with more than one equation and variable. So far, we’ve basically just played around with the equation for a line, which is $ y=mx+b$. Let’s say we have the following situation:

Now, you can always do “guess and check” to see what would work, but you might as well use algebra! It’s much better to learn the algebra way, because even though this problem is fairly simple to solve, the algebra way will let you solve any algebra problem – even the really complicated ones.

The first trick in problems like this is to figure out what we want to know. This will help us decide what variables (unknowns) to use. What we want to know is how many pairs of jeans we want to buy (let’s say “$ j$”) and how many dresses we want to buy (let’s say “$ d$”). Always write down what your variables will be:

Let $ j=$ the number of jeans you will buy Let $ d=$ the number of dresses you’ll buy

Like we did before, let’s translate word-for-word from math to English:

Now we have the 2 equations as shown below. Notice that the $ j$ variable is just like the $ x$ variable and the $ d$ variable is just like the $ y$. It’s easier to put in $ j$   and $ d$ so we can remember what they stand for when we get the answers.

This is what we call a system, since we have to solve for more than one variable – we have to solve for 2 here. The cool thing is to solve for 2   variables , you typically need 2   equations , to solve for 3   variables , you need 3   equations , and so on. That’s easy to remember, right?

We need to get an answer that works in both equations ; this is what we’re doing when we’re solving; this is called solving simultaneous systems , or solving system simultaneously . There are several ways to solve systems; we’ll talk about graphing first.

Solving Systems by Graphing

Remember that when you graph a line, you see all the different coordinates (or $ x/y$ combinations) that make the equation work. In systems, you have to make both equations work, so the intersection of the two lines shows the point that fits both equations (assuming the lines do in fact intersect; we’ll talk about that later).  The points of intersections satisfy both equations simultaneously. 

Put these equations into the $ y=mx+b$ ($ d=mj+b$) format, by solving for the $ d$ (which is like the $ y$):

$ \displaystyle j+d=6;\text{ }\,\text{ }\text{solve for }d:\text{ }d=-j+6\text{ }$

$ \displaystyle 25j+50d=200;\text{ }\,\,\text{solve for }d:\text{ }d=\frac{{200-25j}}{{50}}=-\frac{1}{2}j+4$

Now graph both lines:

Note that with non-linear equations, there will most likely be more than one intersection; an example of how to get more than one solution via the Graphing Calculator can be found in the  Exponents and Radicals in Algebra section. Also, t here are some examples of systems of inequality  here in the Coordinate System and Graphing Lines section .

Solving Systems with Substitution

Substitution is the favorite way to solve for many students! It involves exactly what it says: substituting one variable in another equation so that you only have one variable in that equation. Here is the same problem:

You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50 .  You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?

Below are our two equations, and let’s solve for “$ d$” in terms of “$ j$” in the first equation. Then, let’s substitute what we got for “$ d$” into the next equation. Even though it doesn’t matter which equation you start with, remember to always pick the “easiest” equation first (one that we can easily solve for a variable) to get a variable by itself.

We could buy 4 pairs of jeans and 2 dresses . Note that we could have also solved for “$ j$” first; it really doesn’t matter. You’ll want to pick the variable that’s most easily solved for. Let’s try another substitution problem that’s a little bit different:

Solving Systems with Linear Combination or Elimination

Probably the most useful way to solve systems is using linear combination, or linear elimination. The reason it’s most useful is that usually in real life we don’t have one variable in terms of another (in other words, a “$ y=$” situation).

The main purpose of the linear combination method is to add or subtract the equations so that one variable is eliminated. We can add, subtract, or multiply both sides of equations by the same numbers – let’s use real numbers as shown below. We are using the Additive Property of Equality , Subtraction Property of Equality , Multiplicative Property of Equality , and/or Division Property of Equality that we saw here in the Types of Numbers and Algebraic Properties section :

If we have a set of 2 equations with 2 unknowns, for example, we can manipulate them by adding, multiplying or subtracting (we usually prefer adding) so that we get one equation with one variable. Let’s use our previous problem:

We could buy 4 pairs of jeans and 2 dresses .

Here’s another example:

Types of equations

In the example above, we found one unique solution to the set of equations. Sometimes, however, for a set of equations, there are no solutions (when lines are parallel) or an infinite number of solutions or infinitely many solutions (when the two lines are actually the same line, and one is just a “multiple” of the other).

When there is at least one solution , the equations are consistent equations , since they have a solution. When there is only one solution, the system is called independent , since they cross at only one point. When equations have infinite solutions, they are the same equation, are consistent , and are called dependent or coincident (think of one just sitting on top of the other).

When equations have no solutions , they are called inconsistent equations , since we can never get a solution . 

Here are graphs of inconsistent and dependent equations that were created on a graphing calculator:

Systems with Three Equations

Let’s get a little more complicated with systems; in real life, we rarely just have two unknowns to solve for.

Let’s say at the same store, they also had pairs of shoes for $20 and we managed to get $60 more to spend! Now we have a new problem. To spend the even $260 , how many pairs of jeans, dresses, and pairs of shoes should we get if want, for example, exactly 10 total items (Remember that jeans cost $25 each and dresses cost $50 each).

Let’s let $ j=$ the number of pair of jeans, $ d=$ the number of dresses, and $ s=$ the number of pairs of shoes we should buy. So far, we’ll have the following equations:

$ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+\,20s=260\end{array}$

We’ll need another equation, since for three variables, we need three equations (otherwise, we theoretically might have infinite ways to solve the problem). In this type of problem, you would also need something like this: We want twice as many pairs of jeans as pairs of shoes . Now, since we have the same number of equations as variables , we can potentially get one solution for the system of equations. Here are the three equations:

We’ll learn later how to put these in our calculator to easily solve using matrices (see the  Matrices and Solving Systems with Matrices section). For now, we can use two equations at a time to eliminate a variable (using substitution and/or elimination), and keep doing this until we’ve solved for all variables. These can get really difficult to solve, but remember that in “real life”, there are computers to do all this work!

Remember again, that if we ever get to a point where we end up with something like this, it means there are an infinite number of solutions : $ 4=4$  (variables are gone and a number equals another number and they are the same). And if we up with something like this, it means there are no solutions : $ 5=2$ (variables are gone and two numbers are left and they don’t equal each other).

Let’s solve our system:      $ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+20s=260\\j=2s\end{array}$ :

We could buy 6 pairs of jeans, 1 dress, and 3 pairs of shoes .

Here’s one more example of a three-variable system of equations, where we’ll only use linear elimination:

$ \displaystyle \begin{align}5x-6y-\,7z\,&=\,7\\6x-4y+10z&=\,-34\\2x+4y-\,3z\,&=\,29\end{align}$

I know – this is really difficult stuff! But if you do it step-by-step and keep using the equations you need with the right variables, you can do it. Think of it like a puzzle – you may not know exactly where you’re going, but do what you can in baby steps, and you’ll get there (sort of like life sometimes, right?!). And we’ll learn much easier ways to do these types of problems.

Algebra Word Problems with Systems

Let’s do more word problems; you’ll notice that many of these are the same type that we did earlier in the Algebra Word Problems  section , but now we can use more than one variable. This will actually make the problems easier! Again, when doing these word problems:

• If you’re wondering what the variables (or unknowns) should be when working on a word problem, look at what the problem is asking. These are usually (but not always) what your variables are!
• If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!

Here are some problems:

Investment Word Problem

We also could have set up this problem with a table:

Mixture Word Problems

Here’s a mixture word problem . With mixture problems, remember if the problem calls for a pure solution or concentrate , use 100% (if the percentage is that solution) or 0% (if the percentage is another solution).

Let’s do the math (use substitution )!

$ \displaystyle \begin{array}{c}x\,\,+\,\,y=10\\.01x+.035y=10(.02)\end{array}$          $ \displaystyle \begin{array}{c}\,y=10-x\\.01x+.035(10-x)=.2\\.01x\,+\,.35\,\,-\,.035x=.2\\\,-.025x=-.15;\,\,\,\,\,x=6\\\,y=10-6=4\end{array}$

We would need 6 liters of the 1% milk, and 4 liters of the 3.5% milk.

Here’s another mixture problem:

$ \displaystyle \begin{array}{c}x+y=50\\8x+4y=50\left( {6.4} \right)\end{array}$                   $ \displaystyle \begin{array}{c}y=50-x\\8x+4\left( {50-x} \right)=320\\8x+200-4x=320\\4x=120\,;\,\,\,\,x=30\\y=50-30=20\\8x+4y=50(6.4)\end{array}$

We would need 30 pounds of the $8 coffee bean, and 20 pounds of the $4 coffee bean. See how similar this problem is to the one where we use percentages?

Distance Word Problem:

Here’s a distance word problem using systems ; distance problems have to do with an object’s speed, time, and distance. Note that, as well as the distance word problem here in the Algebra Word Problems section , there’s an example of a Parametric Distance Problem here in the Parametric Equations section .

Which Plumber Problem

Many word problems you’ll have to solve have to do with an initial charge or setup charge, and a charge or rate per time period. In these cases, the initial charge will be the $ \boldsymbol {y}$ -intercept , and the  rate will be the slope . Here is an example:

Geometry Word Problem:

Many times, we’ll have a geometry problem as an algebra word problem; these might involve perimeter, area, or sometimes angle measurements (so don’t forget these things!). Let’s do one involving angle measurements.

See – these are getting easier! Here’s one that’s a little tricky though:

Work Problem : 

Let’s do a “ work problem ” that is typically seen when studying Rational Equations (fraction with variables in them) and can be found here in the Rational Functions, E quations and Inequalities  section .

Note that there’s also a simpler version of this problem here in the Direct, Inverse, Joint and Combined Variation section .

Three Variable Word Problem:

Let’s do one more with three equations and three unknowns:

The “Candy” Problem

Sometimes we get lucky and can solve a system of equations where we have more unknowns (variables) then equations. (Actually, I think it’s not so much luck, but having good problem writers!) Here’s one like that:

There are more Systems Word Problems in the  Matrices and Solving Systems with Matrices section , Linear Programming section , and Right Triangle Trigonometry section .

Understand these problems, and practice, practice, practice!

For Practice : Use the Mathway  widget below to try a  Systems of Equations  problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve by Substitution or Solve by Addition/Elimination  to see the answer .

You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.

If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).

On to Algebraic Functions, including Domain and Range   – you’re ready! 

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Search IntMath
• Math interactives
• About (site info)
• Uses of Trignometry
• ASCIIMath input, KaTeX output
• ASCIIMath input, LaTeX and KaTeX output
• Send Math in emails
• Syntax for ASCIIMathML
• Math Display Experiments
• Scientific Notebook

Math Problem Solver

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.

Sign up for free here .

Problem Solver Subjects

Our math problem solver that lets you input a wide variety of math math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.

• Math Word Problems
• Pre-Algebra
• Geometry Graphing
• Trigonometry
• Precalculus
• Finite Math
• Linear Algebra

Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.

Basic Math Solutions

Below are examples of basic math problems that can be solved.

• Long Arithmetic
• Rational Numbers
• Operations with Fractions
• Ratios, Proportions, Percents
• Measurement, Area, and Volume
• Factors, Fractions, and Exponents
• Unit Conversions
• Data Measurement and Statistics
• Points and Line Segments

Math Word Problem Solutions

Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.

Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?

Simplified Equation: 17 - x = 8

Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?

Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)

Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}

Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?

Simplified: 40 - 10 - 5

Pre-Algebra Solutions

Below are examples of Pre-Algebra math problems that can be solved.

• Variables, Expressions, and Integers
• Simplifying and Evaluating Expressions
• Solving Equations
• Multi-Step Equations and Inequalities
• Ratios, Proportions, and Percents
• Linear Equations and Inequalities

Algebra Solutions

Below are examples of Algebra math problems that can be solved.

• Algebra Concepts and Expressions
• Points, Lines, and Line Segments
• Simplifying Polynomials
• Factoring Polynomials
• Linear Equations
• Absolute Value Expressions and Equations
• Radical Expressions and Equations
• Systems of Equations
• Quadratic Equations
• Inequalities
• Complex Numbers and Vector Analysis
• Logarithmic Expressions and Equations
• Exponential Expressions and Equations
• Conic Sections
• Vector Spaces
• 3d Coordinate System
• Eigenvalues and Eigenvectors
• Linear Transformations
• Number Sets
• Analytic Geometry

Trigonometry Solutions

Below are examples of Trigonometry math problems that can be solved.

• Algebra Concepts and Expressions Review
• Right Triangle Trigonometry
• Radian Measure and Circular Functions
• Graphing Trigonometric Functions
• Simplifying Trigonometric Expressions
• Verifying Trigonometric Identities
• Solving Trigonometric Equations
• Complex Numbers
• Analytic Geometry in Polar Coordinates
• Exponential and Logarithmic Functions
• Vector Arithmetic

Precalculus Solutions

Below are examples of Precalculus math problems that can be solved.

• Operations on Functions
• Rational Expressions and Equations
• Polynomial and Rational Functions
• Analytic Trigonometry
• Sequences and Series
• Analytic Geometry in Rectangular Coordinates
• Limits and an Introduction to Calculus

Calculus Solutions

Below are examples of Calculus math problems that can be solved.

• Evaluating Limits
• Derivatives
• Applications of Differentiation
• Applications of Integration
• Techniques of Integration
• Parametric Equations and Polar Coordinates
• Differential Equations

Statistics Solutions

Below are examples of Statistics problems that can be solved.

• Algebra Review
• Average Descriptive Statistics
• Dispersion Statistics
• Probability
• Probability Distributions
• Frequency Distribution
• Normal Distributions
• t-Distributions
• Hypothesis Testing
• Estimation and Sample Size
• Correlation and Regression

Finite Math Solutions

Below are examples of Finite Math problems that can be solved.

• Polynomials and Expressions
• Equations and Inequalities
• Linear Functions and Points
• Systems of Linear Equations
• Mathematics of Finance
• Statistical Distributions

Linear Algebra Solutions

Below are examples of Linear Algebra math problems that can be solved.

• Introduction to Matrices
• Linear Independence and Combinations

Chemistry Solutions

Below are examples of Chemistry problems that can be solved.

• Unit Conversion
• Atomic Structure
• Molecules and Compounds
• Chemical Equations and Reactions
• Behavior of Gases
• Solutions and Concentrations

Physics Solutions

Below are examples of Physics math problems that can be solved.

• Static Equilibrium
• Dynamic Equilibrium
• Kinematics Equations
• Electricity
• Thermodymanics

Geometry Graphing Solutions

Below are examples of Geometry and graphing math problems that can be solved.

• Step By Step Graphing
• Linear Equations and Functions
• Polar Equations

Looking for the old Mathway Calculator? We've moved it to here .

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• elimination\:x+y+z=25,\:5x+3y+2z=0,\:y-z=6
• elimination\:x+2y=2x-5,\:x-y=3
• elimination\:5x+3y=7,\:3x-5y=-23
• elimination\:x+z=1,\:x+2z=4

elimination-system-of-equations-calculator

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.