Number Line
- ax^2+bx+c=0
- x^2+2x+1=3x-10
- 2x^2+4x-6=0
- How do you calculate a quadratic equation?
- To solve a quadratic equation, use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / (2a).
- What is the quadratic formula?
- The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √(b^2 - 4ac)) / (2a)
- Does any quadratic equation have two solutions?
- There can be 0, 1 or 2 solutions to a quadratic equation. If the discriminant is positive there are two solutions, if negative there is no solution, if equlas 0 there is 1 solution.
- What is quadratic equation in math?
- In math, a quadratic equation is a second-order polynomial equation in a single variable. It is written in the form: ax^2 + bx + c = 0 where x is the variable, and a, b, and c are constants, a ≠ 0.
- How do you know if a quadratic equation has two solutions?
- A quadratic equation has two solutions if the discriminant b^2 - 4ac is positive.
quadratic-equation-calculator
- High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine. But what if the quadratic equation...
Please add a message.
Message received. Thanks for the feedback.

Quadratic equation
- 1 Factoring
- 2 Completing the square
- 3 Quadratic Formula
The purpose of factoring is to turn a general quadratic into a product of binomials . This is easier to illustrate than to describe.
Completing the square
Quadratic Formula
See Quadratic Formula .
- Discriminant
- Vieta's Formulas
- Quadratic Inequality
- Factoring Quadratics
- Quadratic equations
Something appears to not have loaded correctly.
Click to refresh .

Solving Quadratics by the Quadratic Formula
How to solve quadratic equations using the quadratic formula.
There are times when we are stuck solving a quadratic equation of the form [latex]a{x^2} + bx + c = 0[/latex] because the trinomial on the left side can’t be factored out easily. It doesn’t mean that the quadratic equation has no solution. At this point, we need to call upon the straightforward approach of the quadratic formula to find the solutions of the quadratic equation or put simply, determine the values of [latex]x[/latex] that can satisfy the equation.
In order use the quadratic formula, the quadratic equation that we are solving must be converted into the “standard form”, otherwise, all subsequent steps will not work. The goal is to transform the quadratic equation such that the quadratic expression is isolated on one side of the equation while the opposite side only contains the number zero, [latex]0[/latex].
Take a look at the diagram below.
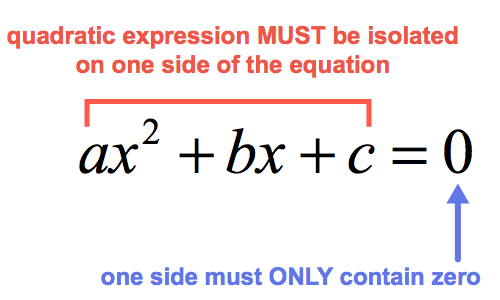
In this convenient format, the numerical values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easily identified! Upon knowing those values, we can now substitute them into the quadratic formula then solve for the values of [latex]x[/latex].
The Quadratic Formula
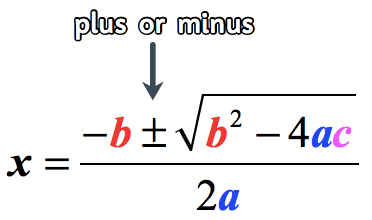
- Where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are the coefficients of an arbitrary quadratic equation in the standard form, [latex]a{x^2} + bx + c = 0[/latex].
Slow down if you need to. Be careful with every step while simplifying the expressions. This is where common mistakes usually happen because students tend to “relax” which results to errors that could have been prevented, such as in the addition, subtraction, multiplication and/or division of real numbers.
Examples of How to Solve Quadratic Equations by the Quadratic Formula
Example 1 : Solve the quadratic equation below using the Quadratic Formula.
By inspection, it’s obvious that the quadratic equation is in the standard form since the right side is just zero while the rest of the terms stay on the left side. In other words, we have something like this

This is great! What we need to do is simply identify the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] then substitute into the quadratic formula.
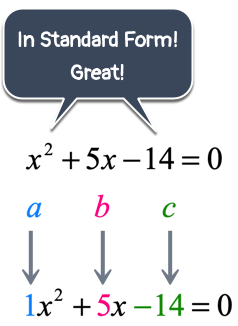
That’s it! Make it a habit to always check the solved values of [latex]x[/latex] back into the original equation to verify.
Example 2 : Solve the quadratic equation below using the Quadratic Formula.
This quadratic equation is absolutely not in the form that we want because the right side is NOT zero. I need to eliminate that [latex]7[/latex] on the right side by subtracting both sides by [latex]7[/latex]. That takes care of our problem. After doing so, solve for [latex]x[/latex] as usual.
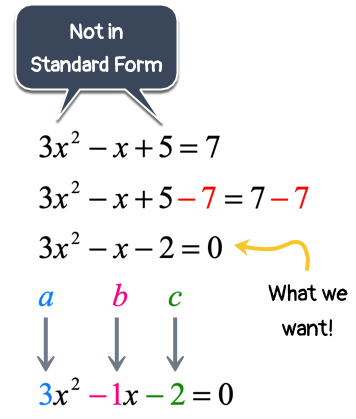
The final answers are [latex]{x_1} = 1[/latex] and [latex]{x_2} = – {2 \over 3}[/latex].
Example 3 : Solve the quadratic equation below using the Quadratic Formula.
This quadratic equation looks like a “mess”. I have variable [latex]x[/latex]’s and constants on both sides of the equation. If we are faced with something like this, always stick to what we know. Yes, it’s all about the Standard Form. We have to force the right side to be equal to zero. We can do just that in two steps.
I will first subtract both sides by [latex]5x[/latex], and followed by the addition of [latex]8[/latex].

Values we need:
[latex]a = – 1[/latex], [latex]b = – \,8[/latex], and [latex]c = 2[/latex]
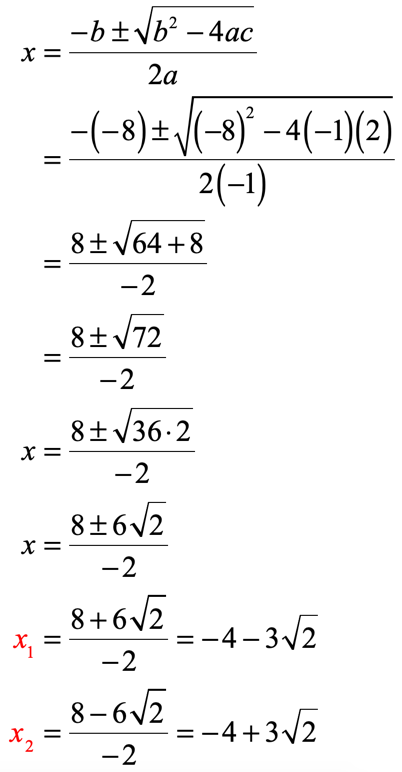
Example 4 : Solve the quadratic equation below using the Quadratic Formula.
Well, if you think that Example [latex]3[/latex] is a “mess” then this must be even “messier”. However, you’ll soon realize that they are really very similar.
We first need to perform some cleanup by converting this quadratic equation into standard form. Sounds familiar? Trust me, this problem is not as bad as it looks, as long as we know what to do.
Just to remind you, we want something like this

Therefore, we must do whatever it takes to make the right side of the equation equal to zero. Since we have three terms on the right side, it follows that three steps are required to make it zero.
The solution below starts by adding both sides by [latex]3{x^2}[/latex], followed by subtraction of [latex]3x[/latex], and finally the addition of [latex]5[/latex]. Done!
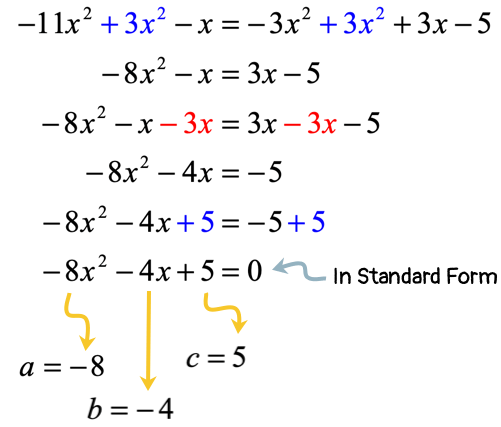
After making the right side equal to zero, the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easy to identify. Plug those values into the quadratic formula, and simplify to get the final answers!

Example 5 : Solve the quadratic equation below using the Quadratic Formula.
First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex].
- Eliminate the [latex]{x^2}[/latex] term on the right side.
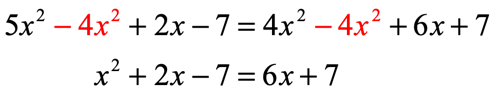
- Eliminate the [latex]x[/latex] term on the right side.
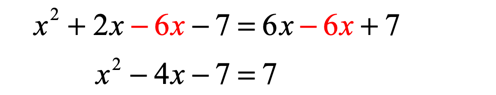
- Eliminate the constant on the right side.
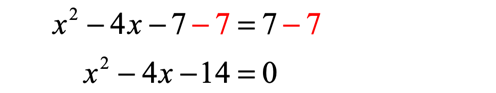
After getting the correct standard form in the previous step, it’s now time to plug the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] into the quadratic formula to solve for [latex]x[/latex].
- From the converted standard form, extract the required values.
[latex]a = 1[/latex], [latex]b = – \,4[/latex], and [latex]c = – \,14[/latex]
- Then evaluate these values into the quadratic formula.

You may also be interested in these related math lessons or tutorials:
Quadratic Formula Practice Problems with Answers
Solving Quadratic Equations by Square Root Method Solving Quadratic Equations by Factoring Method Solving Quadratic Equations by Completing the Square

- Math Forum/Help
- Problem Solver
- College Math
- Quadratic Equations

Quadratic Equations: Problems with Solutions

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Last modified on August 3rd, 2023
Quadratic Equation Word Problems
Here, we will solve different types of quadratic equation-based word problems. Use the appropriate method to solve them:
- By Completing the Square
- By Factoring
- By Quadratic Formula
- By graphing
For each process, follow the following typical steps:
- Make the equation
- Solve for the unknown variable using the appropriate method
- Interpret the result
The product of two consecutive integers is 462. Find the numbers?
Let the numbers be x and x + 1 According to the problem, x(x + 1) = 483 => x 2 + x – 483 = 0 => x 2 + 22x – 21x – 483 = 0 => x(x + 22) – 21(x + 22) = 0 => (x + 22)(x – 21) = 0 => x + 22 = 0 or x – 21 = 0 => x = {-22, 21} Thus, the two consecutive numbers are 21 and 22.
The product of two consecutive positive odd integers is 1 less than four times their sum. What are the two positive integers.
Let the numbers be n and n + 2 According to the problem, => n(n + 2) = 4[n + (n + 2)] – 1 => n 2 + 2n = 4[2n + 2] – 1 => n 2 + 2n = 8n + 7 => n 2 – 6n – 7 = 0 => n 2 -7n + n – 7 = 0 => n(n – 7) + 1(n – 7) = 0 => (n – 7) (n – 1) = 0 => n – 7 = 0 or n – 1 = 0 => n = {7, 1} If n = 7, then n + 2 = 9 If n = 1, then n + 1 = 2 Since 1 and 2 are not possible. The two numbers are 7 and 9
A projectile is launched vertically upwards with an initial velocity of 64 ft/s from a height of 96 feet tower. If height after t seconds is reprented by h(t) = -16t 2 + 64t + 96. Find the maximum height the projectile reaches. Also, find the time it takes to reach the highest point.
Since the graph of the given function is a parabola, it opens downward because the leading coefficient is negative. Thus, to get the maximum height, we have to find the vertex of this parabola. Given the function is in the standard form h(t) = a 2 x + bx + c, the formula to calculate the vertex is: Vertex (h, k) = ${\left\{ \left( \dfrac{-b}{2a}\right) ,h\left( -\dfrac{b}{2a}\right) \right\}}$ => ${\dfrac{-b}{2a}=\dfrac{-64}{2\times \left( -16\right) }}$ = 2 seconds Thus, the time the projectile takes to reach the highest point is 2 seconds ${h\left( \dfrac{-b}{2a}\right)}$ = h(2) = -16(2) 2 – 64(2) + 80 = 144 feet Thus, the maximum height the projectile reaches is 144 feet
The difference between the squares of two consecutive even integers is 68. Find the numbers.
Let the numbers be x and x + 2 According to the problem, (x + 2) 2 – x 2 = 68 => x 2 + 4x + 4 – x 2 = 68 => 4x + 4 = 68 => 4x = 68 – 4 => 4x = 64 => x = 16 Thus the two numbers are 16 and 18
The length of a rectangle is 5 units more than twice the number. The width is 4 unit less than the same number. Given the area of the rectangle is 15 sq. units, find the length and breadth of the rectangle.
Let the number be x Thus, Length = 2x + 5 Breadth = x – 4 According to the problem, (2x + 5)(x – 4) = 15 => 2x 2 – 8x + 5x – 20 – 15 = 0 => 2x 2 – 3x – 35 = 0 => 2x 2 – 10x + 7x – 35 = 0 => 2x(x – 5) + 7(x – 5) = 0 => (x – 5)(2x + 7) = 0 => x – 5 = 0 or 2x + 7 = 0 => x = {5, -7/2} Since we cannot have a negative measurement in mensuration, the number is 5 inches. Now, Length = 2x + 5 = 2(5) + 5 = 15 inches Breadth = x – 4 = 15 – 4 = 11 inches
A rectangular garden is 50 cm long and 34 cm wide, surrounded by a uniform boundary. Find the width of the boundary if the total area is 540 cm².
Given, Length of the garden = 50 cm Width of the garden = 34 cm Let the uniform width of the boundary be = x cm According to the problem, (50 + 2x)(34 + 2x) – 50 × 34 = 540 => 4x 2 + 168x – 540 = 0 => x 2 + 42x – 135 = 0 Since, this quadratic equation is in the standard form ax 2 + bx + c, we will use the quadratic formula, here a = 1, b = 42, c = -135 x = ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$ => ${\dfrac{-42\pm \sqrt{\left( 42\right) ^{2}-4\times 1\times \left( -135\right) }}{2\times 1}}$ => ${\dfrac{-42\pm \sqrt{1764+540}}{2}}$ => ${\dfrac{-42\pm \sqrt{2304}}{2}}$ => ${\dfrac{-42\pm 48}{2}}$ => ${\dfrac{-42+48}{2}}$ and ${\dfrac{-42-48}{2}}$ => x = {-45, 3} Since we cannot have a negative measurement in mensuration the width of the boundary is 3 cm
The hypotenuse of a right-angled triangle is 20 cm. The difference between its other two sides is 4 cm. Find the length of the sides.
Let the length of the other two sides be x and x + 4 According to the problem, (x + 4) 2 + x 2 = 20 2 => x 2 + 8x + 16 + x 2 = 400 => 2x 2 + 8x + 16 = 400 => 2x 2 + 8x – 384 = 0 => x 2 + 4x – 192 = 0 => x 2 + 16x – 12x – 192 = 0 => x(x + 16) – 12(x + 16) = 0 => (x + 16)(x – 12) = 0 => x + 16 = 0 and x – 12 = 0 => x = {-16, 12} Since we cannot have a negative measurement in mensuration, the lengths of the sides are 12 and 16
Jennifer jumped off a cliff into the swimming pool. The function h can express her height as a function of time (t) = -16t 2 +16t + 480, where t is the time in seconds and h is the height in feet. a) How long did it take for Jennifer to attain a maximum length. b) What was the highest point that Jennifer reached. c) Calculate the time when Jennifer hit the water?
Comparing the given function with the given function f(x) = ax 2 + bx + c, here a = -16, b = 16, c = 480 a) Finding the vertex will give us the time taken by Jennifer to reach her maximum height x = ${-\dfrac{b}{2a}}$ = ${\dfrac{-16}{2\left( -16\right) }}$ = 0.5 seconds Thus Jennifer took 0.5 seconds to reach her maximum height b) Putting the value of the vertex by substitution in the function, we get ${h\left( \dfrac{1}{2}\right) =-16\left( \dfrac{1}{2}\right) ^{2}+16\left( \dfrac{1}{2}\right) +480}$ => ${-16\left( \dfrac{1}{4}\right) +8+480}$ => 484 feet Thus the highest point that Jennifer reached was 484 feet c) When Jennifer hit the water, her height was 0 Thus, by substituting the value of the height in the function, we get -16t 2 +16t + 480 = 0 => -16(t 2 + t – 30) = 0 => t 2 + t – 30 = 0 => t 2 + 6t – 5t – 30 = 0 => t(t + 6) – 5(t + 6) = 0 => (t + 6)(t – 5) = 0 => t + 6 = 0 or t – 5 = 0 => x = {-6, 5} Since time cannot have any negative value, the time taken by Jennifer to hit the water is 5 seconds.
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
Quadratic Equation Solver
We can help you solve an equation of the form " ax 2 + bx + c = 0 " Just enter the values of a, b and c below :
Is it Quadratic?
Only if it can be put in the form ax 2 + bx + c = 0 , and a is not zero .
The name comes from "quad" meaning square, as the variable is squared (in other words x 2 ).
These are all quadratic equations in disguise:
| In disguise | In standard form | a, b and c |
|---|---|---|
| = 3x -1 | - 3x + 1 = 0 | a=1, b=-3, c=1 |
| - 2x) = 5 | - 4x - 5 = 0 | a=2, b=-4, c=-5 |
| - x - 3 = 0 | a=1, b=-1, c=-3 | |
| = 0 | + x - 1 = 0 | a=5, b=1, c=-1 |
How Does this Work?
The solution(s) to a quadratic equation can be calculated using the Quadratic Formula :
The "±" means we need to do a plus AND a minus, so there are normally TWO solutions !
The blue part ( b 2 - 4ac ) is called the "discriminant", because it can "discriminate" between the possible types of answer:
- when it is positive, we get two real solutions,
- when it is zero we get just ONE solution,
- when it is negative we get complex solutions.
Learn more at Quadratic Equations
Solving Quadratic Equations
Many word problems Involving unknown quantities can be translated for solving quadratic equations
Methods of solving quadratic equations are discussed here in the following steps.
Step I: Denote the unknown quantities by x, y etc.
Step II: use the conditions of the problem to establish in unknown quantities.
Step III: Use the equations to establish one quadratic equation in one unknown.
Step IV: Solve this equation to obtain the value of the unknown in the set to which it belongs.
Now we will learn how to frame the equations from word problem:
1. The product of two consecutive integers is 132. Frame an equation for the statement. What is the degree of the equation?
Method I: Using only one unknown
Let the two consecutive integers be x and x + 1
Form the equation, the product of x and x + 1 is 132.
Therefore, x(x + 1) = 132
⟹ x\(^{2}\) + x - 132 = 0, which is quadratic in x.
This is the equation of the statement, x denoting the smaller integer.
Method II: Using more than one unknown
Let the consecutive integers be x and y, x being the smaller integer.
As consecutive integers differ by 1, y - x = 1 ........................................... (i)
Again, from the question, the product of x and y is 132.
So, xy = 132 ........................................... (ii)
From (i), y = 1 + x.
Putting y = 1 + x in (ii),
x(1 + x) = 132
Solving the quadratic equation, we get the value of x. Then the value of y can be determined by substituting the value of x in y = 1 + x.
2. The length of a rectangle is greater than its breadth by 3m. If its area be 10 sq. m, find the perimeter.
Suppose, the breadth of the rectangle = x m.
Therefore, length of the rectangle = (x + 3) m.
So, area = (x + 3)x sq. m
Hence, by the condition of the problem
(x + 3)x = 10
⟹ x\(^{2}\) + 3x - 10 = 0
⟹ (x + 5)(x - 2) = 0
So, x = -5,2
But x = - 5 is not acceptable, since breadth cannot be negative.
Therefore x = 2
Hence, breadth = 2 m
and length = 5 m
Therefore, Perimeter = 2(2 + 5) m = 14 m.
x = -5 does not satisfy the conditions of the problem length or breadth can never be negative. Such a root is called an extraneous root. In solving a problem, each root of the quadratic equation is to be verified whether it satisfies the conditions of the given problem. An extraneous root is to be rejected.
Quadratic Equation
Introduction to Quadratic Equation
Formation of Quadratic Equation in One Variable
General Properties of Quadratic Equation
Methods of Solving Quadratic Equations
Roots of a Quadratic Equation
Examine the Roots of a Quadratic Equation
Problems on Quadratic Equations
Quadratic Equations by Factoring
Word Problems Using Quadratic Formula
Examples on Quadratic Equations
Word Problems on Quadratic Equations by Factoring
Worksheet on Formation of Quadratic Equation in One Variable
Worksheet on Quadratic Formula
Worksheet on Nature of the Roots of a Quadratic Equation
Worksheet on Word Problems on Quadratic Equations by Factoring
- 9th Grade Math
From Solving Quadratic Equations to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
|
What’s this? | Facebook X Pinterest WhatsApp Messenger |
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Types of quadrilaterals | properties of quadrilateral | parallelogram.
Jul 04, 24 12:43 AM
Worksheet on H.C.F. and L.C.M. | H.C.F. by Long Division Method | Ans
Jul 03, 24 07:08 AM

Different Types of Polygons | Triangle, Quadrilateral|Pentagon|Hexagon
Jul 03, 24 01:54 AM
Quadrilateral Worksheet |Different Types of Questions in Quadrilateral
Jul 03, 24 01:02 AM

Pairs of Angles | Complementary Angles | Supplementary Angles|Adjacent
Jul 02, 24 11:53 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

10 Quadratic Equations Word Problems
Quadratic equations word problems are math problems in which the equations are not given directly. These problems can be solved by using the given information to obtain a quadratic equation of the form $latex ax^2+bx+c$. We can then use the factoring method, the completing the square method or the quadratic formula to solve the equation.
Here, we will look at 10 quadratic equations word problems with answers. In addition, you will also be able to practice with 5 word problems to solve.
Relevant for …
Learning to solve word problems of quadratic equations.
See problems
10 quadratic equations word problems with answers
Quadratic equations word problems to solve.
The following problems are solved by forming a quadratic equation with the given word problem. Try to solve the problems yourself before looking at the solution.
If the sum of two numbers is equal to 17 and their product is equal to 60, what are the numbers?
We can use the letters X (smaller number) and Y (larger number) to represent both numbers. Then, from the statement, we can obtain the following equations:
$latex X+Y=17~~[1]$
$latex XY=60~~[2]$
Now, we can rearrange equation 1 to get $latex Y=17-X$. Substituting this expression into the second equation, we have:
$latex X(17-X)=60$
Expanding the parentheses and rearranging the equation, we have:
$latex 17X-X^2=60$
$latex X^2-17X+60=0$
Now, we can factor the equation to solve:
$latex (X-12)(X-5)=0$
$latex X-12=0~~$ or $latex ~~X-5=0$
$latex X=12~~$ or $latex ~~X=5$
Therefore, we have:
- If $latex X=5$, we have $latex Y=17-5=12$. This solution is correct because X<Y.
- If $latex X=12$, we have $latex Y=17-12=5$
The numbers are 12 and 5.
The difference between two numbers is equal to 5 and their product is equal to 126. What are these numbers?
Using the information in the statement and using the letters X (smaller number) and Y (larger number) to represent the numbers, we can obtain the following equations:
$latex Y-X=5 ~~[1]$
$latex XY=126~~[2]$
Now, we can write the first equation as $latex Y=5+X$ and substituting it into the second equation, we have:
$latex X(5+X)=126$
$latex 5X+X^2=126$
$latex X^2+5X-126=0$
Now, we can factor and solve:
$latex (X+13)(X-9)=0$
$latex X+13=0~~$ or $latex ~~X-9=0$
$latex X=-13~~$ or $latex ~~X=9$
- If $latex X=-13$, we have $latex Y=5-13=-8$
- If $latex X=9$, we have $latex Y=5+9=14$. This solution is correct because $latex XY=126$
If the area of a rectangle is 78 square units and its longest side is 7 units longer than its shortest side, what are the lengths of the sides?
We can represent the shorter side with x . This means that the longest side is equal to x +7.
Also, we remember that the area of a rectangle is equal to the product of its sides. Therefore, we can form the following equation:
$latex x(x+7)=78$
Expanding and writing the equation in the form $late ax^2+bx+c=0$, we have:
$latex x^2+7x-78=0$
Now, we can use factorization to solve:
$latex (x+13)(x-6)=0$
$latex x+13=0~~$ or $latex ~~x-6=0$
$latex x=-13~~$ or $latex ~~x=6$
Since we can’t have negative lengths, we have $latex x=6$, so the lengths are 6 and 13.
Find the lengths of the sides of a rectangle that has an area of 200 square units if the longer side is twice the length of the shorter side.
Using the letters X (short side) and Y (long side) to represent the sides, we can obtain the following equations using the given information:
$latex Y=2X~~[1]$
$latex XY=200~~[2]$
Now, we can substitute equation 1 into equation 2 and we have:
$latex X(2X)=200$
$latex 2X^2=200$
To solve this equation, we have to isolate X² completely and take the square root of both sides:
$latex X^2=100$
$latex X=\pm\sqrt{100}$
$latex X=\pm 10$
Since a length can’t be negative, we have $latex X=10$. Therefore, we have $latex Y=20$.
The difference between the squares of two consecutive odd numbers is equal to 48. Find both numbers.
Representing the first number with x , we can deduce that a consecutive odd number is equal to $latex x+2$. Therefore, using the information in the statement, we form an equation with the squares of the consecutive numbers:
$latex (x+2)^2-x^2=48$
Expanding, simplifying and solving, we have:
$latex x^2+4x+4-x^2=48$
$latex 4x+4=48$
$latex 4x=44$
$latex x=11$
The consecutive odd numbers are 11 and 13.
The sides of a right triangle have lengths x , x +2, and 10. If 10 is the hypotenuse of the triangle, find the value of x .
Since the triangle is a right triangle, we can use the Pythagorean theorem to find an equation for the lengths of the three sides of the triangle.
The statement tells us that 10 is the hypotenuse of the triangle. Therefore, we have:
$latex x^2+(x+2)^2=10^2$
Expanding and simplifying the equation, we have:
$latex x^2+x^2+4x+4=100$
$latex 2x^2+4x+4=100$
$latex 2x^2+4x-96=0$
Now, we can divide the entire equation by 2 to simplify it:
$latex x^2+2x-48=0$
Solving by factorization, we have:
$latex (x+8)(x-6)=0$
$latex x+8=0~~$ or $latex ~~x-6=0$
$latex x=-8~~$ or $latex ~~x=6$
Since we can’t have a negative length, the answer is $latex x=6$.
If the product of two numbers is equal to 48 and their average is equal to 7, find both numbers.
We can represent one of the numbers with x . This means that the other number is equal to 48/ x since their product is equal to 48.
Therefore, considering that the average of two numbers is equal to the sum of the numbers divided by 2, we have:
$latex \frac{x+48/x}{2}=7$
Simplifying, we have:
$latex x+\frac{48}{x}=14$
$latex x^2+48=14x$
$latex x^2-14x+48=0$
Now, we can solve by factorization:
$latex (x-8)(x-6)=0$
$latex x-8=0~~$ or $latex ~~x-6=0$
$latex x=8~~$ or $latex ~~x=6$
The numbers are 6 and 8.
If the side length of a square is increased by 4, its area is multiplied by 9. Find the side length of the original square.
In this problem, there are two areas that we need to consider, the area of the original square and the area of the larger square (length +4).
Using the x to represent the sides of the original square and remembering that the area of a square is equal to the length of one of the sides squared, we have:
Larger area = 9 × Original area
$latex (x+4)^2=9x^2$
Expanding and simplifying, we have:
$latex x^2+8x+16=9x^2$
$latex 8x^2-8x-16=0$
We can divide the entire equation by 8 and solving by factoring, we have:
$latex x^2-x-2=0$
$latex (x-2)(x+1)=0$
$latex x-2=0~~$ or $latex ~~x+1=0$
$latex x=2~~$ or $latex ~~x=-1$
Since a length cannot be negative, the answer is $latex x=2$.
The shortest side of a right triangle is 4 units less than its hypotenuse. The difference between the short side and the intermediate side is 2 units. If the shorter side is x -2, find the value of x .
From the statement, we can deduce the following lengths of the triangle:
- Short side = x -2
- Intermediate side = x (2 units difference with short side)
- Hypotenuse = x + 2 (4 units more than short side)
Now, we can use the Pythagorean theorem to write an equation for the three lengths:
$latex (x-2)^2+x^2=(x+2)^2$
$$x^2-4x+4+x^2=x^2+4x+4$$
$$x^2-4x+4+x^2-x^2-4x-4=0$$
$latex x^2-8x=0$
$latex x(x-8)=0$
$latex x=0~~$ or $latex ~~x=8$
Since the length cannot be 0, we have $latex x=8$.
PROBLEM 1 0
The figure below has an area of 100 square units. Find the value of x .
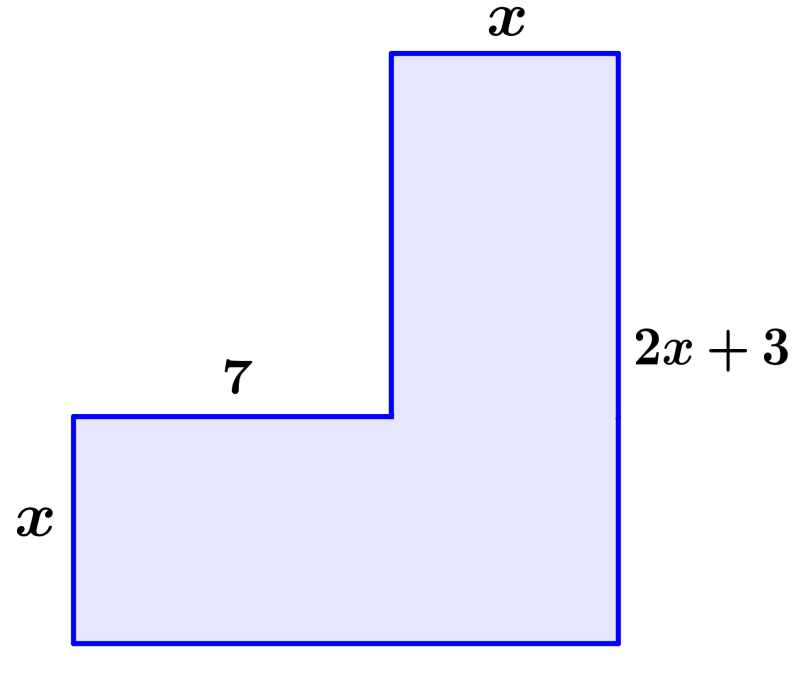
We can divide the figure into two rectangles, one rectangle has the area 7 x and the other rectangle has the area x (2 x +3). Adding these areas, we have:
$latex 7x+x(2x+3)=100$
$latex 7x+2x^2+3x=100$
$latex 2x^2+10x-100=0$
Now, we can divide the entire equation by 2 and solve by factoring:
$latex x^2+5x-50=0$
$latex (x+10)(x-5)=0$
$latex x=-10~~$ or $latex ~~x=5$
Since we can’t have a negative length, the answer is $latex x=5$.
Solve the following problems using any method of solving quadratic equations.
Find two numbers such that their sum equals 18 and their product equals 56.
Choose an answer
Find the length of the sides of a rectangle that has an area of 84 square units if the length of one side is 5 units longer than the other side.
The three sides of a right triangle are x, x+1, and 5. if the hypotenuse equals 5, what is the value of x, the difference of the squares of two consecutive even numbers is 68. find the two numbers., if the length of the sides of a square is increased by 6, its area is multiplied by 16. find the length of one of the sides of the original square..
Interested in learning more about quadratic equations? Take a look at these pages:
- Quadratic Equations Calculator
- Solving Quadratic Equations – Methods and Examples
- How to Solve Quadratic Equations? Step-by-Step
- 20 Quadratic Equation Examples with Answers

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.

INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Class 10 (Old)
Course: class 10 (old) > unit 4.
- Quadratic equations word problem: triangle dimensions
- Quadratic equations word problem: box dimensions
- Quadratic word problem: ball
- Word problems: Writing quadratic equations
Word problems: Solving quadratic equations
- Quadratic equations word problems (basic)
- Quadratic equations word problems (intermediate)
- Quadratic equations word problems (advanced)
- Your answer should be
- an integer, like 6
- a simplified proper fraction, like 3 / 5
- a simplified improper fraction, like 7 / 4
- a mixed number, like 1 3 / 4
- an exact decimal, like 0.75
- a multiple of pi, like 12 pi or 2 / 3 pi
- Math Lessons
- Math Formulas
- Calculators
Math Calculators, Lessons and Formulas
It is time to solve your math problem
- HW Help (paid service)
- Solving Equations
- Quadratic Equation Solver
Quadratic equation solver
This step-by-step calculator solves quadratic equations using three different methods: the quadratic formula method , completing the square , and the factoring method . Calculator shows all the work and provides detailed explanation on how to solve an equation.
| Factoring |
| Completing the square |
| Quadratic formula |
- Factoring Polynomials
- Polynomial Roots
- Synthetic Division
- Polynomial Operations
- Graphing Polynomials
- Simplify Polynomials
- Generate From Roots
- Simplify Expression
- Multiplication / Division
- Addition / Subtraction
- Rationalize Denominator
- Simplifying
- Quadratic Equations Solver
- Polynomial Equations
- Solving Equations - With Steps
- Solving (with steps)
- Quadratic Plotter
- Factoring Trinomials
- Equilateral Triangle
- Right Triangle
- Oblique Triangle
- Square Calculator
- Rectangle Calculator
- Circle Calculator
- Hexagon Calculator
- Rhombus Calculator
- Trapezoid Calculator
- Triangular Prism
- Distance calculator
- Midpoint Calculator
- Triangle Calculator
- Graphing Lines
- Lines Intersection
- Two Point Form
- Line-Point Distance
- Parallel/Perpendicular
- Circle Equation
- Circle From 3 Points
- Circle-line Intersection
- Modulus, inverse, polar form
- Vectors (2D & 3D)
- Add, Subtract, Multiply
- Determinant Calculator
- Matrix Inverse
- Characteristic Polynomial
- Eigenvalues
- Eigenvectors
- Matrix Decomposition
- Limit Calculator
- Derivative Calculator
- Integral Calculator
- Arithmetic Sequences
- Geometric Sequences
- Find n th Term
- Degrees to Radians
- Trig. Equations
- Long Division
- Evaluate Expressions
- Fraction Calculator
- Greatest Common Divisor GCD
- Least Common Multiple LCM
- Prime Factorization
- Scientific Notation
- Percentage Calculator
- Dec / Bin / Hex
- Probability Calculator
- Probability Distributions
- Descriptive Statistics
- Standard Deviation
- Z - score Calculator
- Normal Distribution
- T-Test Calculator
- Correlation & Regression
- Simple Interest
- Compound Interest
- Amortization Calculator
- Annuity Calculator
- Work Problems
Hire MATHPORTAL experts to do math homework for you.
Prices start at $3 per problem.
How to use this calculator
The most commonly used methods for solving quadratic equations are:
1 . Factoring method
2 . Solving quadratic equations by completing the square
3 . Using quadratic formula
In the following sections, we'll go over these methods.
Method 1A : Factoring method
If a quadratic trinomial can be factored, this is the best solving method.
We often use this method when the leading coefficient is equal to 1 or -1. If this is not the case, then it is better to use some other method.
Example 01: Solve $ x^2 \color{red}{-8}x \color{blue}{+ 15} = 0 $ by factoring.
Here we see that the leading coefficient is 1, so the factoring method is our first choice.
To factor this equation, we must find two numbers ( $ a $ and $ b $ ) with a sum is $ a + b = \color{red}{8} $ and a product of $ a \cdot b = \color{blue}{15} $.
After some trials and errors, we see that $ a = 3 $ and $ b = 5 $.
Now we use formula $ x^2 - 8x + 15 = (x - a)(x - b) $ to get factored form:
Divide the factored form into two linear equations to get solutions.
Method 1B : Factoring - special cases
Example 02: Solve $ x^2 -8x = 0 $ by factoring.
In this case, (when the coefficient c = 0 ) we can factor out $ \color{blue}{x} $ out of $ x^2 - 8x $.
Example 03: Solve $ x^2 - 16 = 0 $ by factoring.
In this case, ( when the middle term is equal 0) we can use the difference of squares formula.
Method 3 : Solve using quadratic formula
This method solves all types of quadratic equations. It works best when solutions contain some radicals or complex numbers.
Example 05: Solve equation $ 2x^2 + 3x - 2 = 0$ by using quadratic formula.
Step 1 : Read the values of $a$, $b$, and $c$ from the quadratic equation. ( $a$ is the number in front of $x^2$ , $b$ is the number in front of $x$ and $c$ is the number at the end)
Step 2 :Plug the values for a, b, and c into the quadratic formula and simplify.
Step 3 : Solve for $x_1$ and $x_2$
Method 2 : Completing the square
This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. The method involves seven steps.
Example 04: Solve equation $ 2x^2 + 8x - 10= 0$ by completing the square.
Step 1 : Divide the equation by the number in front of the square term.
Step 2 : move $-5$ to the right:
Step 3 : Take half of the x-term coefficient $ \color{blue}{\dfrac{4}{2}} $, square it $ \color{blue}{\left(\dfrac{4}{2} \right)^2} $ and add this value to both sides.
Step 4 : Simplify left and right side.
Step 5 : Write the perfect square on the left.
Step 6 : Take the square root of both sides.
Step 7 : Solve for $x_1$ and $x_2$ .
1. Quadratic Equation — step-by-step examples, video tutorials with worked examples.
2. Completing the Square — video on Khan Academy
3. Completing the Square — video on Khan Academy
4. Polynomial equation solver
Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .
If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]
Email (optional)

Snapsolve any problem by taking a picture. Try it in the Numerade app?
The Splitting Characteristic Finite Difference Domain Decomposition Scheme for Solving Time-Fractional MIM Nonlinear Advection–Diffusion Equations
- Published: 01 July 2024
- Volume 100 , article number 49 , ( 2024 )
Cite this article

- Zhongguo Zhou ORCID: orcid.org/0000-0001-9009-3404 1 ,
- Sihan Zhang 1 &
- Wanshan Li 2
Explore all metrics
In this paper, we develop a new splitting characteristic finite difference scheme for solving the time-fractional mobile-immobile nonlinear advection–diffusion equation by combining non-overlapping block-divided domain decomposition method, the operator splitting technique and the characteristic finite difference method. Over each sub-domain, the solutions and fluxes along x -direction in the interiors of sub-domains are computed by the implicit characteristic finite difference method while the intermediate fluxes on the interfaces of sub-domains are computed by local multi-point weighted average from the approximate solutions at characteristic tracking points which are solved by the quadratic interpolation. Secondly, the solutions and fluxes along y direction in the interiors of sub-domains are computed lastly by the implicit characteristic difference method while the time fractional derivative is approximated by L 1-format and the intermediate fluxes on the interfaces of sub-domains are computed by local multi-point weighted average from the approximate solutions at characteristic tracking points are solved by the quadratic interpolation. Applying Brouwer fixed point theorem, we prove strictly the existence and uniqueness of the proposed scheme. The conditional stability and convergence with \(O\left( {\varDelta t}+{\varDelta t}^{2-\alpha }+{h}^2+{H}^\frac{5}{2}\right) \) of the proposed scheme are given as well. Numerical experiments verify the theoretical results.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Similar content being viewed by others
The characteristic difference DDM for solving the time-fractional order convection–diffusion equations
An efficient conservative splitting characteristic difference method for solving 2-d space-fractional advection–diffusion equations

The conservative characteristic difference method and analysis for solving two-sided space-fractional advection-diffusion equations
Data availability.
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Alikhanov, A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280 , 424–438 (2015)
Article MathSciNet Google Scholar
Benson, D., Meerschaert, M.: A simple and efficient random walk solution of multi-rate mobile/immobile mass transport equations. Adv. Water Resour. 32 , 532–539 (2009)
Article Google Scholar
Chen, C., Liu, H., Zheng, X., Wang, H.: A two-grid MMOC finite element method for nonlinear variable-order time-fractional mobile–immobile advection–diffusion equations. Comput. Math. Appl. 79 , 2771–2783 (2020)
Cui, X., Yue, J., Yuan, G.: Nonlinear scheme with high accuracy for nonlinear coupled parabolic-hyperbolic system. J. Comput. Appl. Math. 235 , 3527–3540 (2011)
Cao, G., Sun, H., Sun, Z.: Stability and convergence of finite difference schemes for a class of time-fractional sub-diffusion equations based on certain superconvergence. J. Comput. Phys. 280 , 510–528 (2015)
Chen, M., Deng, W.: Fourth order accurate scheme for the space fractional diffusion equations. SIAM J. Numer. Anal. 52 , 1418–1438 (2014)
Deng, W., Li, B., Tian, W., Zhang, P.: Boundary problems for the fractional and tempered fractional operators. Multiscale Model. Simul. 16 , 125–149 (2018)
Deng, W., Wang, X., Zhang, P.: Anisotropic nonlocal diffusion operators for normal and anomalous dynamics. Multiscale Model. Simul. 18 , 415–443 (2020)
Ding, H., Li, C., Chen, Y.: High-order algorithms for Riesz derivative and their applications (II). J. Comput. Phys. 293 , 218–237 (2015)
Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 54 , 667–696 (2012)
Du, Q., Mu, M., Wu, Z.: Efficient parallel algorithms for parabolic problems. SIAM J. Numer. Anal. 39 , 1469–1487 (2001)
Fu, K., Liang, D.: The conservative characteristic FD methods for atmospheric aerosol transport problems. J. Comput. Phys. 305 , 494–520 (2016)
Fu, K., Liang, D.: The time second order mass conservative characteristic FDM for advection–diffusion equations in high dimensions. J. Sci. Comput. 73 , 26–49 (2017)
Fu, K., Liang, D.: A mass-conservative temporal second order and spatial fourth order characteristic finite volume method for atmosphertic pollution advection diffusion problems. SIAM J. Sci. Comput. 41 , 1178–1210 (2019)
Feng, L., Zhuang, P., Liu, F., Turner, I., Gu, Y.: Finite element method for space-time fractional diffusion equation. Numer. Algorithms 72 , 749–767 (2016)
Gao, G., Sun, Z., Zhang, H.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259 , 33–50 (2014)
Gong, Y., Yuan, G., Cui, X.: Existence of a fully implicit solution with second-order time evolution for strong nonlinear diffusion equation. Appl. Math. Letters 117 , 107091 (2021)
Hang, T., Zhou, Z., Pan, H., Wang, Y.: The conservative characteristic difference method and analysis for solving two-sided space-fractional advection-diffusion equations. Numer. Algorithms 92 , 1723–1755 (2023)
Jia, J., Wang, H.: A preconditioned fast finite volume scheme for a fractional differential equation discretized on a locally refined composite mesh. J. Comput. Phys. 299 , 842–862 (2015)
Jia, J., Wang, H.: A fast finite volume method for conservative space-fractional diffusion equations in convex domains. J. Comput. Phys. 310 , 63–84 (2016)
Li, R., Zhou, Z., Li, L., et al.: The mass-preserving domain decomposition scheme for solving three-dimensional convection-diffusion equations. Math. Comput. Simul. 177 , 527–555 (2020)
Li, X., Rui, H.: A two-grid block-centered finite difference method for the nonlinear time-fractional parabolic equation. J. Sci. Comput. 72 , 863–891 (2017)
Li, C., Yuan, Y.: A modified upwind difference domain decomposition method for convection–diffusion euqations. Appl. Numer. Math. 59 , 1584–1598 (2009)
Liu, Z., Li, X.: A parallel CGS block-centered finite difference method for nonlinear time-fractional parabolic equation. Comput. Methods Appl. Mech. Eng. 308 , 330–348 (2016)
Liu, F., Zhuang, P., Turner, I., Burrage, K., Anh, V.: A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 38 , 3871–3878 (2014)
Liu, Q., Liu, F., Turner, I., Anh, V., Gu, Y.: A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl. Math. Comput. 226 , 336–347 (2014)
MathSciNet Google Scholar
Liu, J., Fu, H.: An efficient QSC approximation of variable-order time-fractional mobile-immobile diffusion equations with variably diffusive coefficients. J. Sci. Comput. 93 , 44 (2022)
Ma, K., Sun, T.: A non-overlapping DDM combined with the characteristic method for optimal control problems governed by convection–diffusion equations. Comput. Optim. Appl. 71 , 273–306 (2018)
Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339 , 1–77 (2000)
Nie, D., Sun, J., Deng, W.: Numerical algorithm for the model describing anomalous diffusion in expanding media. ESAIM Math. Model. Numer. Anal. 54 , 2265–2294 (2020)
Roul, P., Rohil, V.: A novel high-order numerical scheme and its analysis for the two-dimensional time-fractional reaction–subdiffusion euqation. Numer. Algorithms 90 , 1357–1387 (2022)
Schumer, R., Benson, D., Meerschaert, M., Baeumer, B.: Fractal mobile/immobile solute transport. Water Resour. Res. 39 , 1–12 (2003)
Simmons, A., Yang, Q., Moroney, T.: A finite volume method for two-sided fractional diffusion equations on non-uniform meshes. J. Comput. Phys. 335 , 747–759 (2017)
Shi, H., Liao, H.: Unconditional stability of corrected explicit/implicit domain decomposition algorithms for parallel approximation of heat equations. SIAM J. Numer. Anal. 44 , 1584–1611 (2006)
Tian, W., Zhou, H., Deng, W.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84 , 1703–1727 (2015)
Vong, S., Lyu, P., Chen, X., et al.: High order finite difference method for time-space fractional differential equations with Caputo and Riemann–Liouville derivatives. Numer. Algorithms 72 , 195–210 (2015)
Wan, Z., Chen, G.: A second order difference scheme with nonuniform rectangular meshes for nonlinear parabolic system. Acta Math. Sin. 25 , 159–166 (2009)
Wang, H., Yang, D.: Wellposedness of variable-coefficient conservative fractional elliptic differential equations. SIAM J. Numer. Anal. 51 , 1088–1107 (2013)
Wang, H., Zheng, X.: Wellposedness and regularity of the variable-order time-fractional diffusion equations. J. Math. Anal. Appl. 475 , 1778–1802 (2019)
Wang, Y.: A high-order compact finite difference method and its extrapolation for fractional mobile/immobile convection–diffusion equations. Calcolo 54 , 733–768 (2017)
Wu, X., Deng, W., Barkai, E.: Tempered fractional Feynman–Kac equation: theory and examples. Phys. Rev. E 93 , 032151 (2016)
Yin, B., Liu, Y., Li, H.: A class of shifted high-order numerical methods for the fractional mobile/immobile transport equations. Appl. Math. Comput. 368 , 124799 (2020)
Yu, F., Chen, M.: Second-order error analysis for fractal mobile/immobile Allen–Cahn equation on graded meshes. J. Sci. Comput. 96 , 49 (2023)
Zhang, Y., Benson, D., Reeves, D.: Time and space nonlocalities underlying fractional-derivative models: distinction and literature review of field applications. Adv. Water Resour. 32 , 561–581 (2009)
Zhang, J., Yang, D., Guo, H., et al.: Parallel algorithm combined with mixed element procedure for compressible miscible displacement problem. Numer. Algorithms 76 , 1–27 (2017)
Zhang, J., Yang, D., Zhu, J.: Parallel characteristic mixed element method for saltwater intrusion problem. J. Comput. Appl. Math. 336 , 160–174 (2018)
Zhang, H., Liu, F., Phanikumar, M., Meerschaert, M.: A novel numerical method for the time variable fractional order mobile–immobile advection–dispersion model. Comput. Math. Appl. 66 , 693–701 (2013)
Zheng, Z., Wang, Y.: An averaged L1-type compact difference method for time-fractional mobile/immobile diffusion equations with weakly singular solutions. Appl. Math. Lett. 131 , 108076 (2022)
Zheng, Z., Wang, Y.: Fast high-order compact finite difference methods based on the averaged L1 formula for a time-fractional mobile–immobile diffusion problem. J. Sci. Comput. 99 , 43 (2024)
Zheng, H., Yuan, G., Cui, X.: A second-order space-time accurate scheme for nonlinear diffusion equation with general capacity term. Numer. Methods Partial Differ. Eq. 36 , 1845–1867 (2020)
Zhuang, Y., Sun, X.: Stabilitized explicit-implicit domain decomposition methods for the numerical solution of parabolic equations. SIAM J. Sci. Comput. 24 , 335–358 (2002)
Zhou, Z., Liang, D.: The mass-preserving and modified-upwind splitting DDM scheme for time-dependent convection diffusion equations. J. Comput. Appl. Math. 317 , 247–273 (2017)
Zhou, Z., Liang, D., Wong, Y.: The new mass-conserving S-DDM scheme for two-dimensional parabolic equations with variable coefficients. Appl. Math. Comput. 338 , 882–902 (2018)
Zhou, Z., Sun, X., Pan, H., Wang, Y.: An efficient characteristic finite difference S-DDM scheme for convection–diffusion equations. Comput. Math. Appl. 80 , 3044–3065 (2020)
Download references
Acknowledgements
We would like to thank two reviewers’ comments and suggestions on our manuscript which have helped to improve the paper greatly.
This work was supported by Natural Science Foundation of Shandong Government (Grant Nos. ZR2021MA002, ZR2022MF239), and National Natural Science Foundation of China (Grant No. 11701282).
Author information
Authors and affiliations.
School of Information Science and Engineering, Shandong Agricultural University, Taian, 271018, Shandong, China
Zhongguo Zhou & Sihan Zhang
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing, Jiangsu, 210094, China
You can also search for this author in PubMed Google Scholar
Corresponding authors
Correspondence to Zhongguo Zhou or Wanshan Li .
Ethics declarations
Conflict of interest.
The authors declare no Conflict of interest.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Zhou, Z., Zhang, S. & Li, W. The Splitting Characteristic Finite Difference Domain Decomposition Scheme for Solving Time-Fractional MIM Nonlinear Advection–Diffusion Equations. J Sci Comput 100 , 49 (2024). https://doi.org/10.1007/s10915-024-02603-4
Download citation
Received : 28 September 2023
Revised : 31 May 2024
Accepted : 17 June 2024
Published : 01 July 2024
DOI : https://doi.org/10.1007/s10915-024-02603-4
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Domain decomposition
- Nonlinear advection–diffusion
- Characteristic finite difference
- Convergence
- Find a journal
- Publish with us
- Track your research

IMAGES
VIDEO
COMMENTS
3w − 1 = the length of the rectangle. Step 4: Translate into an equation. We know the area. Write the formula for the area of a rectangle. Step 5: Solve the equation. Substitute in the values. Distribute. This is a quadratic equation; rewrite it in standard form. Solve the equation using the Quadratic Formula.
Problem. Solve. 6 + 2 x 2 − 3 x = 8 x 2 ... Worked example: quadratic formula (negative coefficients) Report a problem. Loading... Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class ...
Solve by completing the square: Non-integer solutions. Worked example: completing the square (leading coefficient ≠ 1) Solving quadratics by completing the square: no solution. Proof of the quadratic formula. Solving quadratics by completing the square. Completing the square review. Quadratic formula proof review.
The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √(b^2 - 4ac)) / (2a) Does any quadratic equation have two solutions? There can be 0, 1 or 2 solutions to a quadratic equation.
Solving quadratics by completing the square. Worked example: Completing the square (intro) Worked example: Rewriting expressions by completing the square. Worked example: Rewriting & solving equations by completing the square. Worked example: completing the square (leading coefficient ≠ 1) Solving quadratics by completing the square: no solution.
The more you use the formula to solve quadratic equations, the more you become expert at it! Use the illustration below as a guide. Notice that in order to apply the quadratic formula, we must transform the quadratic equation into the standard form, that is, [latex]a{x^2} + bx + c = 0[/latex] where [latex]a \ne 0[/latex].
Example 9.4.1 How to Solve a Quadratic Equation Using the Quadratic Formula. Solve by using the Quadratic Formula: 2x2 + 9x − 5 = 0. Solution: Step 1: Write the quadratic equation in standard form. Identify the a, b, c values. This equation is in standard form. ax2 + bx + c = 0 2x2 + 9x − 5 = 0 a = 2, b = 9, c = − 5.
A quadratic equation in one variable is an equation of the form , where , and are constants (that is, they do not depend on ) and is the unknown variable. Quadratic equations are solved using one of three main strategies: factoring, completing the square and the quadratic formula .
Example 5: Solve the quadratic equation below using the Quadratic Formula. First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex]. Eliminate the [latex]{x^2}[/latex] term on the right side. Eliminate the [latex]x[/latex] term on the right side. Eliminate the constant on the right side.
Problem 6. Solve the equation \displaystyle x^2-15x+26=0 x2 −15x+26 = 0 In the answer box, write the roots separated by a comma. Problem 7. Solve the quadratic equation \displaystyle x^2+14x+45=0 x2 +14x+45 = 0 In the answer box, write the roots separated by a comma. Problem 8. Solve the quadratic equation \displaystyle x^2+3x-70=0 x2 +3x− ...
Here, we will solve different types of quadratic equation-based word problems. Use the appropriate method to solve them: By Completing the Square; By Factoring; By Quadratic Formula; By graphing; For each process, follow the following typical steps: Make the equation; Solve for the unknown variable using the appropriate method; Interpret the result
The solutions to a quadratic equation of the form ax2 + bx + c = 0, a ≥ 0 are given by the formula: x = − b ± √b2 − 4ac 2a. To use the Quadratic Formula, we substitute the values of a, b, and c into the expression on the right side of the formula. Then, we do all the math to simplify the expression.
Also, learn Quadratic Formula here. Solving the problems based on quadratics will help students to understand the concept very well and also to score good marks in this section. All the questions are solved here step by step with a detailed explanation. ... Solve the quadratic equation 2x 2 + x - 528 = 0, using quadratic formula. Solution: If ...
Worked example. First we need to identify the values for a, b, and c (the coefficients). First step, make sure the equation is in the format from above, a x 2 + b x + c = 0 : is what makes it a quadratic). Then we plug a , b , and c into the formula: solving this looks like: Therefore x = 3 or x = − 7 .
A Quadratic Equation! Let us solve it using our Quadratic Equation Solver. Enter 1, −1 and −6; And you should get the answers −2 and 3; R 1 cannot be negative, so R 1 = 3 Ohms is the answer. The two resistors are 3 ohms and 6 ohms. Others. Quadratic Equations are useful in many other areas:
The solution (s) to a quadratic equation can be calculated using the Quadratic Formula: The "±" means we need to do a plus AND a minus, so there are normally TWO solutions ! The blue part ( b2 - 4ac) is called the "discriminant", because it can "discriminate" between the possible types of answer: when it is negative we get complex solutions.
Recall that quadratic equations are equations in which the variables have a maximum power of 2. These equations have the general form ax^2+bx+c=0 ax2 + bx+ c = 0. For example, the equations 4x^2+x+2=0 4x2 + x+ 2 = 0 and 2x^2-2x-3=0 2x2 − 2x− 3 = 0 are quadratic equations. There are several methods that we can use to solve quadratic ...
Methods of solving quadratic equations are discussed here in the following steps. Step I: Denote the unknown quantities by x, y etc. Step II: use the conditions of the problem to establish in unknown quantities. Step III: Use the equations to establish one quadratic equation in one unknown. Step IV: Solve this equation to obtain the value of ...
Quadratic equations word problems are math problems in which the equations are not given directly. These problems can be solved by using the given information to obtain a quadratic equation of the form ax^2+bx+c ax2 + bx+ c. We can then use the factoring method, the completing the square method or the quadratic formula to solve the equation.
Calculator Use. This online calculator is a quadratic equation solver that will solve a second-order polynomial equation such as ax 2 + bx + c = 0 for x, where a ≠ 0, using the quadratic formula. The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots.
Word problems: Solving quadratic equations. Cullen is 10 years younger than Ada. The product of their ages 2 years ago was 39 . Find Ada's present age. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a ...
Example 05: Solve equation 2x2 + 3x − 2 = 0 by using quadratic formula. Step 1: Read the values of a, b, and c from the quadratic equation. ( a is the number in front of x2 , b is the number in front of x and c is the number at the end) a = 2 b = 3 and c = −2. Step 2 :Plug the values for a, b, and c into the quadratic formula and simplify.
5. The x-intercepts of the graph can be found by setting \(y = 0\) and solving for \(x\). This gives us the roots of the quadratic equation, which are the points where the graph intersects the x-axis. By considering these points and the shape of the parabola, we can sketch the graph of the equation.
In this paper, we develop a new splitting characteristic finite difference scheme for solving the time-fractional mobile-immobile nonlinear advection-diffusion equation by combining non-overlapping block-divided domain decomposition method, the operator splitting technique and the characteristic finite difference method. Over each sub-domain, the solutions and fluxes along x-direction in the ...