solve initial value problem differential equations calculator

: a curve fitting program with Lorentzian, Sine, Exponential and Power series are available models to match your data.

: a Matched Filter program used to filter signals and slim pulses.

: options may be tested for an entire company, individual plant(s), or whole product lines. Imagine an increase in control settings from a 1 or 2 digits (i.e., a guess value) to an 8+ digit accuracy resulting from a Calculus programming calculation!

: via Arbitrary Equalization with Simple LC Structures to reduce errors.

: basically an electromagnetic transducer in which a coil placed in a magnetic pole gap experiences a force proportional to the current passing through the coil.

: find the transfer function's poles & zeros; H(s) = Y (s) / Y (s).

: Magnetic recording of transitions written onto a computer disc drive may produce an isolated pulse as shown.

: a simulation program for A.C. motor design that was reapplied as a constrained optimization problem with 12 unknown parameters and 7 constraints.

: an open-two- compartment model with first order absorption into elimination from central compartment is presented here.

Textbooks - Parameter Estimation 4 ODE/PDE - Signal Analysis / Spectral Estimation - Body Plasma - Solar Cell Increasing Productivity Examples: AC Motor Design - Matched Filters - Pulse Slimming / InterSymbol Interference - Pilot (safe) Ejection - PharmacoKinetics Simulation - Business Strategies & War Gaming - BVP - Implicit Equations

NOTE: It appears your browser does not support scripting (javascript) . Scripting is required to use this site. Please ensure scripting is enabled in your browser before continuing. Thanks, Optimal Designs Enterprise .

• Calculators
• Calculators: Differential Equations
• Calculus Calculator

Euler's Method Calculator

Apply the euler's method step by step.

The calculator will find the approximate solution of the first-order differential equation using the Euler's method, with steps shown.

Related calculators: Improved Euler (Heun's) Method Calculator , Modified Euler's Method Calculator

If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below.

Our Euler's Method Calculator is an excellent resource for solving differential equations using the Euler's Method. It promises accuracy with every use, and its in-depth, step-by-step solutions can enhance your understanding of the process.

How to Use the Euler's Method Calculator?

Begin by entering your differential equation into the specified field. Ensure it's correctly formatted to avoid any errors. Input the initial conditions. This would be a point $$$ \left(t_0,y_0\right) $$$ from where the computation starts. Determine and input the desired step size $$$ h $$$ . A smaller step size often leads to more accurate results but will require more computations.

Calculation

After ensuring all the inputs are correctly set, click the "Calculate" button.

The calculator will display the estimated value of the function at the specified point as well as intermediate steps.

What Is the Euler’s Method?

The Euler's Method is a straightforward numerical technique that approximates the solution of ordinary differential equations (ODE). Named after the Swiss mathematician Leonhard Euler, this method is precious for its simplicity and ease of understanding, especially for those new to differential equations.

The Euler's Method relies on using the derivative's value at a certain point to estimate the function's value at the next point. Essentially, it uses tangent lines to approximate the solution of the differential equation.

Mathematical Representation

Suppose we have the following differential equation:

with the initial condition $$$ y\left(t_0\right)=y_0 $$$ . The Euler's Method provides the approximate value of $$$ y $$$ at $$$ t_1=t_0+h $$$ (where $$$ h $$$ is a step size) using the following formula:

• $$$ y_1 $$$ is the function's new (approximated) value, the value at $$$ t=t_1 $$$ .
• $$$ y_0 $$$ is the known initial value.
• $$$ f\left(t_0,y_0\right) $$$ represents the value of the derivative at the initial point.
• $$$ h $$$ is the step size or the increment in the t-value.

Usage and Limitations

The Euler's Method is generally used when:

• The analytical (exact) solution of a differential equation is challenging to obtain.
• A quick approximation is sufficient.

However, it's essential to understand that the accuracy of the Euler's Method depends on step size. A smaller step size typically gives a more accurate approximation but requires more computational steps. Moreover, for some functions or over long intervals, the Euler's Method can't provide an accurate estimate, and other numerical methods might be more suitable.

Why Choose Our Euler's Method Calculator?

Our calculator is designed using advanced algorithms that closely approximate the exact solution of a differential equation. This guarantees accurate results.

User-Friendly Interface

The intuitive design means even those new to the Euler's Method can navigate and get results effortlessly. No need to do manual calculations.

Step-by-Step Solutions

Beyond providing the answer, our calculator breaks down the entire process, offering a detailed step-by-step explanation. This is invaluable for learners and professionals, aiding in comprehension and verification.

Versatility

Whether you're tackling simple or more complex differential equations, our tool can handle many problems.

Fast Computations

Our Euler's Method Calculator delivers results in seconds, simplifying the problem-solving process.

What is step size in the Euler’s Method?

Step size in the Euler’s method, often denoted as $$$ h $$$ , represents the interval or distance between consecutive points in the approximation. A smaller step size generally leads to a more accurate result but requires more computational steps, while a larger step size can speed up calculations but may sacrifice accuracy.

Can you use the Euler's Method in the opposite direction?

Yes, it's possible to use the Euler's Method in the opposite or backward direction. This method is known as the Backward Euler's Method. This approach uses the derivative at the next step rather than the current one, making it an implicit method.

Why is Euler more stable in the backward direction?

The Backward Euler's Method is more stable than the Forward Euler's Method, particularly for stiff differential equations. Its implicit nature allows for larger step sizes without sacrificing stability, making it ideal for stability-sensitive equations.

What are the disadvantages of the Euler’s Method?

While the Euler's Method is straightforward to understand, it has some drawbacks:

• The method may not be very accurate, especially with large step sizes.
• For some differential equations, especially when using a large step size, the method can produce unstable or divergent solutions.

•  All online calculators
•  Articles
•  Suggest a calculator
•  Calculator source code
•  Translation

PLANETCALC Online calculators

•  English

Euler method

This online calculator implements Euler's method, which is a first order numerical method to solve first degree differential equation with a given initial value.

Articles that describe this calculator

Calculators used by this calculator

• Mathematical calculator

Similar calculators

• • Mortgage loan early repayment date
• • Derivative
• • Math equation syntax
• • Linear Diophantine Equations Solver
• • Mortgage calculator
• • Math section ( 314 calculators )

Share this page

Informative

Conversion Calculator

menu_lang.Categorie

Follow Us On:

Euler's Method Calculator

Write down the first order function and required parameters in designated fields to calculate the solution by this Euler’s method calculator.

Add this calculator to your site

An online Euler’s method calculator helps you to estimate the solution of the first-order differential equation using the eulers method. Euler’s formula Calculator uses the initial values to solve the differential equation and substitute them into a table. Let's take a look at Euler's law and the modified method.

What is Euler's Method?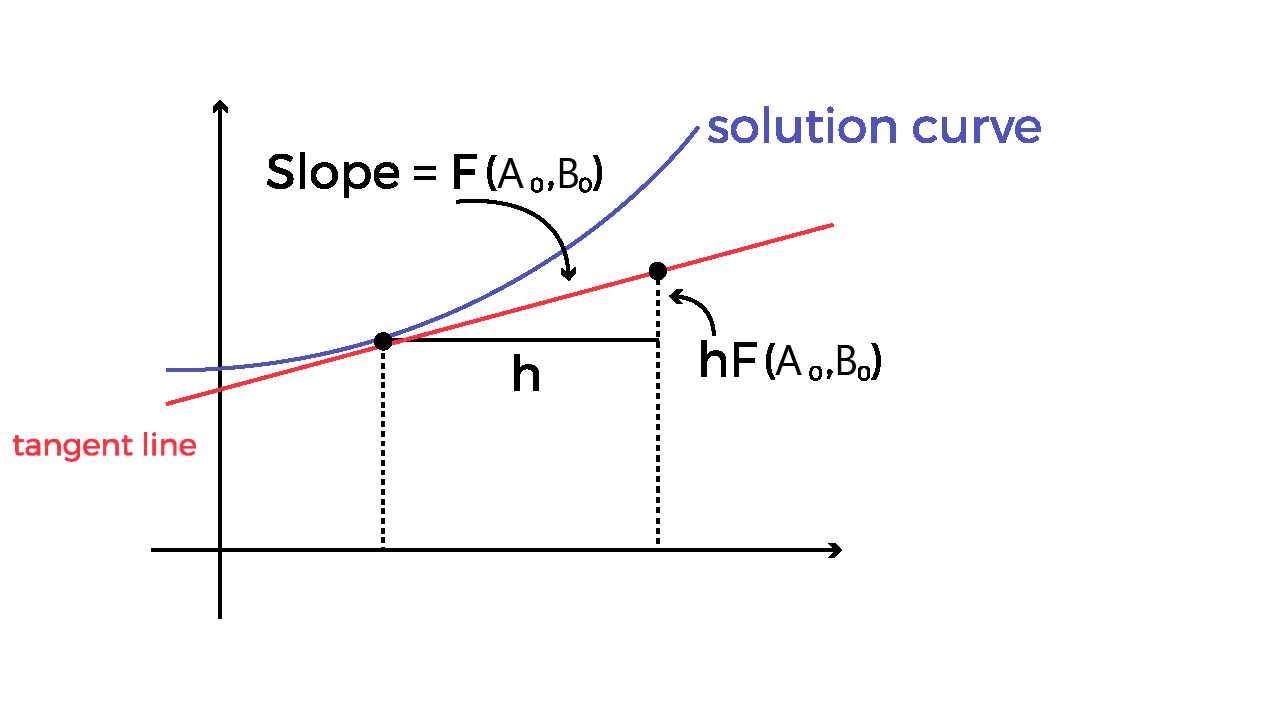

Euler's Method Formula:

Many different methods can be used to approximate the solution of differential equations. So, understand the Euler formula, which is used by Euler's method calculator, and this is one of the easiest and best ways to differentiate the equations. Curiously, this method and formula originally invented by Eulerian are called the Euler method. $$A_n = A_{n-1} + hA (B_{n-1}, A_{n-1})$$ Example: Given the initial value problem x'= x, x(0)=1, For four steps the Euler method to approximate x(4). Using step size which is equal to 1 (h = 1) The Euler’s method equation is \(x_{n+1} = x_n +hf(t_n,x_n)\), so first compute the \(f(t_{0},x_{0})\). Then, the function (f) is defined by f(t,x)=x: $$f(t_{0},x_{0})=f(0,1)=1.$$ The slope of the line, which is tangent to the curve at the points (0,1). So, the slope is the change in x divided by the change in t or Δx/Δt. multiply the above value with the step size h: $$f(x_0) = 1 . 1 = 1$$ Since the step is the change in the t, when multiplying the slope of the tangent and the step size, we get a change in x value. By substituting the initial x value in the euler method formula to find the next value. Also, you can find these values with euler’s method calculator. $$x_0 + hf(x_0) = x_1 = 1 + 1 . 1 = 2$$ By repeating the above steps to find x_{2},x_{3} and x_{4}. $$x_2 = x_1 + hf(x_1) = 2 + 1 . 2 = 4$$ $$x_3 = x_2 + hf(x_2) = 4 + 1 . 4 = 8$$ $$x_4 = x_3 + hf(x_3) = 8 + 1 . 8 = 16$$ Due to the repetitive nature of this eulers method, it can be helpful to organize all computation in an Euler's method table.

  Hence, the calculation is that x_{4}=16. The exact solution of this differential equation is: $$x(t)=e^{t}, so x(4)=e^{4} = 54.598$$ However, an Online Linear Approximation Calculator helps you to calculate the linear approximations of either parametric, polar, or explicit curves at any given point.

How Euler’s Method Calculator Works?

An online Euler method calculator solves ordinary differential equations and substitutes the obtained values in the table by following these simple instructions:

• Enter a function according to Euler's rule.
• Now, substitute the value of step size or the number of steps.
• Then, add the value for y and initial conditions.
• “Calculate”
• The Euler's method calculator provides the value of y and your input.
• It displays each step size calculation in a table and gives the step-by-step calculations using Euler's method formula.
• You can do these calculations quickly and numerous times by clicking on recalculate button.

FAQ for Euler Method:

What is the step size of euler's method.

Usually, Euler's method is the basis for creating more complex methods. Euler's method is based on the fact that near a point, the meaning of the function and its tangent is almost the same. Change the x coordinate, also known as the step size.

Can you use the Euler method in the opposite direction?

In numerical analysis and scientific calculations, the inverse Euler method (or implicit Euler method) is one of the most important numerical methods for solving ordinary differential equations. It is similar to the (standard) Euler method, but the difference is that it is an implicit method.

Why is Euler more stable in the backward direction?

The forward and backward Euler schemes have the same accuracy limits. However, the inverse Euler method is implicit, so it is a very stable method for most problems. Therefore, when solving linear equations (such as Fourier equations), the inverse Euler method is stable.

What are the disadvantages of Euler's method?

Euler's method makes the pendulum simple. Advantages: Euler's method is simple and straightforward. Can be used for non-linear IVP. Disadvantages: low accuracy and unstable value. The Euler's approximation error is proportional to the step size h.

Why is Runge-Kutta more accurate?

High-order RK methods are multi-level because they include multi-level slope calculations between the current value and the next discrete time value.

Conclusion:

Use this online Euler's method calculator to approximate the differential equations that display the size of each step and related values in a table using Euler's law.  Of course, manually it is difficult to solve the differential equations by using Euler's method, but it will become handy when the improved Euler method calculator is used.

From the source of Wikipedia: Euler method, Informal geometrical description, MATLAB code example, R code example, Using other step sizes, Local truncation error , Global truncation error, Numerical stability, Rounding errors, Modifications and extensions. From the source of Delta College: Summary of Euler's Method , A Preliminary Example, Applying the Method, The General Initial Value Problem. From the source of Brilliant: Euler's Method, The Method, Effects of Step Size , Subsequent Steps. From the source of Paul’s Notes: Intervals of Validity section, Uses of Euler’s Method , a bit of pseudo-code, Approximation methods.  

e Calculator

Linear Approximation Calculator

Inverse Function Calculator

Log and Antilog Calculator

Even or Odd Function Calculator

Standard Form Calculator

Scientific Notation Calculator

Put this calculator on your website to increase visitor engagement.

Just copy a given code & paste it right now into your website HTML (source) for suitable page.

Give Us Your Feedback

Get the ease of calculating anything from the source of calculator online

Email us at

© Copyrights 2024 by Calculator-Online.net

• Math calculators

Differential equation calculator with initial condition | Ordinary differential equations

Differential equation calculator.

The Ordinary Differential Equations Calculator that we are pleased to put in your hands is a very useful tool when it comes to studying and solving differential equations.

Its intuitive interface means that you can use it from the first moment without having to spend time reading the instructions for use. But so that you do not have any doubts about how to use the differential equation calculator, we will explain step by step how to use it below. In turn, after the introduction we will show you a brief introduction to the most relevant theoretical concepts in the world of ordinary differential equations.

Table of Contents

• 1 Differential equation calculator
• 2 Instructions for using the differential equation calculator
• 3 What are differential equations?
• 4 What is order of differential equation?
• 5 Degree of differential equation

Instructions for using the differential equation calculator

• The first step in using the calculator is to indicate the variables that define the function that will be obtained after solving the differential equation. To do so, the two fields at the top of the calculator will be used. For example, if you want to solve the second-order differential equation y”+4y’+ycos(x)=0, you must select the variables y , x as shown in the following image:

• In the second step, the differential equation to be solved is entered. To do this, you must write the expression in the main field of the calculator, either using the keyboard of the calculator itself or that of your device. Note that you must use single quotes, and’, to indicate the first derivative, two single quotes to indicate the second derivative, etc.

• If it is required to solve the differential equation from certain initial conditions, you must press the blue button below the keyboard. When doing so, a box will be displayed with those necessary to enter the initial conditions. It is important to note that you can enter them directly in the main field, separating each condition with a comma, for example: y”+4y’+ycos(x)=0, y(1)=2.
• Finally, you just have to press the «Calculate» button and a window with the solution will automatically be displayed, as shown below:

What are differential equations?

Differential equations are mathematical equations that describe how a quantity changes as a function of one or more (independent) variables, often over time or space. We can also define a differential equation as an equation composed of a function and its derivatives.

A differential equation is one that is written in the form y’ = ………. Some differential equations can be solved simply by performing integration, while others require much more complex mathematical processes.

What is order of differential equation?

The order of a differential equation is determined by the highest order derivative. The higher the order of the differential equation, the more arbitrary constants must be added to the general solution. A first-order equation will have one, a second-order equation will have two, and so on. A particular solution can be found by assigning values to the arbitrary constants to match any given constraint.

Degree of differential equation

The degree of a differential equation is determined by the highest power in one of its variables.

Wolfram|Alpha Widgets Overview Tour Gallery Sign In

Share this page.

• StumbleUpon
• Google Buzz

Output Type

Output width, output height.

To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.

To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:

Save to My Widgets

Build a new widget.

We appreciate your interest in Wolfram|Alpha and will be in touch soon.

Initial and Boundary Value Problems

Overview of Initial (IVPs) and Boundary Value Problems (BVPs)

DSolve can be used for finding the general solution to a differential equation or system of differential equations. The general solution gives information about the structure of the complete solution space for the problem. However, in practice, one is often interested only in particular solutions that satisfy some conditions related to the area of application. These conditions are usually of two types.

The symbolic solution of both IVPs and BVPs requires knowledge of the general solution for the problem. The final step, in which the particular solution is obtained using the initial or boundary values, involves mostly algebraic operations, and is similar for IVPs and for BVPs.

IVPs and BVPs for linear differential equations are solved rather easily since the final algebraic step involves the solution of linear equations. However, if the underlying equations are nonlinear , the solution could have several branches, or the arbitrary constants from the general solution could occur in different arguments of transcendental functions. As a result, it is not always possible to complete the final algebraic step for nonlinear problems. Finally, if the underlying equations have piecewise (that is, discontinuous) coefficients, an IVP naturally breaks up into simpler IVPs over the regions in which the coefficients are continuous.

Linear IVPs and BVPs

To begin, consider an initial value problem for a linear first-order ODE.

It should be noted that, in contrast to initial value problems, there are no general existence or uniqueness theorems when boundary values are prescribed, and there may be no solution in some cases.

The previous discussion of linear equations generalizes to the case of higher-order linear ODEs and linear systems of ODEs.

Nonlinear IVPs and BVPs

Many real-world applications require the solution of IVPs and BVPs for nonlinear ODEs. For example, consider the logistic equation, which occurs in population dynamics.

It may not always be possible to obtain a symbolic solution to an IVP or BVP for a nonlinear equation. Numerical methods may be necessary in such cases.

IVPs with Piecewise Coefficients

The differential equations that arise in modern applications often have discontinuous coefficients. DSolve can handle a wide variety of such ODEs with piecewise coefficients. Some of the functions used in these equations are UnitStep , Max , Min , Sign , and Abs . These functions and combinations of them can be converted into Piecewise objects.

A piecewise ODE can be thought of as a collection of ODEs over disjoint intervals such that the expressions for the coefficients and the boundary conditions change from one interval to another. Thus, different intervals have different solutions, and the final solution for the ODE is obtained by patching together the solutions over the different intervals.

If there are a large number of discontinuities in a problem, it is convenient to use Piecewise directly in the formulation of the problem.

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Solve differential equations online

Differential equation is called the equation which contains the unknown function and its derivatives of different orders:

F ( x , y ' , y '' , ... , y ( n ) ) = 0

The order of differential equation is called the order of its highest derivative. To solve differential equation, one need to find the unknown function , which converts this equation into correct identity. To do this, one should learn the theory of the differential equations or use our online calculator with step by step solution.

Our online calculator is able to find the general solution of differential equation as well as the particular one. To find particular solution, one needs to input initial conditions to the calculator. To find general solution, the initial conditions input field should be left blank.

Leave your comment:

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 24 June 2024

Laplace neural operator for solving differential equations

• Qianying Cao 1 ,
• Somdatta Goswami   ORCID: orcid.org/0000-0002-8255-9080 1 &
• George Em Karniadakis   ORCID: orcid.org/0000-0002-9713-7120 1 , 2  

Nature Machine Intelligence volume  6 ,  pages 631–640 ( 2024 ) Cite this article

1721 Accesses

Metrics details

• Applied mathematics
• Computational science

A preprint version of the article is available at arXiv.

Neural operators map multiple functions to different functions, possibly in different spaces, unlike standard neural networks. Hence, neural operators allow the solution of parametric ordinary differential equations (ODEs) and partial differential equations (PDEs) for a distribution of boundary or initial conditions and excitations, but can also be used for system identification as well as designing various components of digital twins. We introduce the Laplace neural operator (LNO), which incorporates the pole–residue relationship between input–output spaces, leading to better interpretability and generalization for certain classes of problems. The LNO is capable of processing non-periodic signals and transient responses resulting from simultaneously zero and non-zero initial conditions, which makes it achieve better approximation accuracy over other neural operators for extrapolation circumstances in solving several ODEs and PDEs. We also highlight the LNO’s good interpolation ability, from a low-resolution input to high-resolution outputs at arbitrary locations within the domain. To demonstrate the scalability of LNO, we conduct large-scale simulations of Rossby waves around the globe, employing millions of degrees of freedom. Taken together, our findings show that a pretrained LNO model offers an effective real-time solution for general ODEs and PDEs at scale and is an efficient alternative to existing neural operators.

This is a preview of subscription content, access via your institution

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 12 digital issues and online access to articles

111,21 € per year

only 9,27 € per issue

Buy this article

• Purchase on Springer Link
• Instant access to full article PDF

Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others

Machine-learning-based spectral methods for partial differential equations

Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators

Promising directions of machine learning for partial differential equations

Data availability.

The dataset generation scripts used for the problems studied in this work are available in a publicly available GitHub repository 39 .

Code availability

The code used in this study is released in a publicly available GitHub repository 39 .

Lu, L., Jin, P., Pang, G., Zhang, Z. & Karniadakis, G. E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Mach. Intell. 3 , 218–229 (2021).

Article   Google Scholar  

Li, Z. et al. Fourier neural operator for parametric partial differential equations. In Proc. 2021 International Conference on Learning Representation (ICLR, 2021).

Lu, L. et al. A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data. Comput. Methods Appl. Mech. Eng. 393 , 114778 (2022).

Article   MathSciNet   Google Scholar  

Kontolati, K., Goswami, S., Shields, M. D. & Karniadakis, G. E. On the influence of over-parameterization in manifold based surrogates and deep neural operators. J. Comput. Phys. 479 , 112008 (2023).

Cao, Q., Goswami, S., Tripura, T., Chakraborty, S. & Karniadakis, G. E. Deep neural operators can predict the real-time response of floating offshore structures under irregular waves. Comput. Struct. 291 , 107228 (2024).

Oommen, V., Shukla, K., Goswami, S., Dingreville, R. & Karniadakis, G. E. Learning two-phase microstructure evolution using neural operators and autoencoder architectures. npj Comput. Mater. 8 , 190 (2022).

Goswami, S. et al. Neural operator learning of heterogeneous mechanobiological insults contributing to aortic aneurysms. J. R. Soc. Interface 19 , 20220410 (2022).

Li, Z. et al. Neural operator: graph kernel network for partial differential equations. Preprint at arXiv:2003.03485 (2020).

Kovachki, N. et al. Neural operator: Learning maps between function spaces with applications to pdes. J. Mach. Learn. Res 24 , 1–97 (2023).

MathSciNet   Google Scholar  

Li, Z. et al. Multipole graph neural operator for parametric partial differential equations. Adv. Neural. Inf. Process. Syst. 33 , 6755–6766 (2020).

Google Scholar  

Tripura, T. & Chakraborty, S. Wavelet neural operator for solving parametric partial differential equations in computational mechanics problems. Comput. Methods Appl. Mech. Eng. 404 , 115783 (2023).

Bonev, B. et al. Spherical fourier neural operators: learning stable dynamics on the sphere. In International Conference on Machine Learning (ed. Lawrence, N.) 2806–2823 (PMLR, 2023).

Borrel-Jensen, N., Goswami, S., Engsig-Karup, A. P., Karniadakis, G. E. & Jeong, C. H. Sound propagation in realistic interactive 3D scenes with parameterized sources using deep neural operators. Proc. Natl Acad. Sci. USA 121 , e2312159120 (2024).

Maust, H. et al. Fourier continuation for exact derivative computation in physics-informed neural operators. Preprint at arXiv:2211.15960 (2022).

Li, Z. et al. Learning dissipative dynamics in chaotic systems. In Proc. 36th Conference on Neural Information Processing Systems 1220 (Curran Associates, 2022).

Wen, G., Li, Z., Azizzadenesheli, K., Anandkumar, A. & Benson, S. M. U-FNO—an enhanced Fourier neural operator-based deep-learning model for multiphase flow. Adv. Water Res. 163 , 104180 (2022).

Jiang, Z. et al. Fourier-MIONet: Fourier-enhanced multiple-input neural operators for multiphase modeling of geological carbon sequestration. Preprint at arXiv:2303.04778 (2023).

Gupta, J. K. & Brandstetter, J. Towards multi-spatiotemporal-scale generalized pde modeling. TMLR https://openreview.net/forum?id=dPSTDbGtBY (2023).

Raonic, B., Molinaro, R., Rohner, T., Mishra, S. & de Bezenac, E. Convolutional neural operators. In ICLR 2023 Workshop on Physics for Machine Learning (2023).

Bartolucci, F. et al. Are neural operators really neural operators? Frame theory meets operator learning. SAM Research Report (ETH Zuric, 2023).

Deka, S. A. & Dimarogonas, D. V. Supervised learning of Lyapunov functions using Laplace averages of approximate Koopman eigenfunctions. IEEE Control Syst. Lett. 7 , 3072–3077 (2023).

Mohr, R. & Mezić, I. Construction of eigenfunctions for scalar-type operators via Laplace averages with connections to the Koopman operator. Preprint at arXiv:1403.6559 (2014).

Brunton, S. L., Budišić, M., Kaiser, E. & Kutz, J. N. Modern Koopman theory for dynamical systems. SIAM Review 64 , 229–340 (2021).

Bevanda, P., Sosnowski, S. & Hirche, S. Koopman operator dynamical models: Learning, analysis and control. Ann. Rev. Control 52 , 197–212 (2021).

Lin, Y. K. M. Probabilistic Theory of Structural Dynamics. (Krieger Publishing Company, 1967).

Kreyszig, E. Advanced Engineering Mathematics Vol. 334 (John Wiley & Sons, 1972).

Hu, S. L. J., Yang, W. L. & Li, H. J. Signal decomposition and reconstruction using complex exponential models. Mech. Syst. Signal Process. 40 , 421–438 (2013).

Hu, S. L. J., Liu, F., Gao, B. & Li, H. Pole-residue method for numerical dynamic analysis. J. Eng. Mech. 142 , 04016045 (2016).

Cho, K. et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proc. 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) 1724–1734 (2014).

Ronneberger, O., Fischer, P. & Brox, T. U-net: convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-assisted Intervention – MICCAI 2015: 18th International Conference Part III (eds Navab, N. et al.) 234–241 (Springer International, 2015).

Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. Adv. Neural. Inf. Process. Syst. 32 , 1–12 (2019).

Agarwal, A. et al. Tensorflow: a system for large-scale machine learning. In Proc. of the 12th USENIX Conference on Operating Systems Design and Implementation 265–283 (USENIX Association, 2016).

Shi, Y. Analysis on Averaging Lorenz System and its Application to Climate. Doctoral dissertation, Univ. of Minnesota (2021).

Ahmed, N., Rafiq, M., Rehman, M. A., Iqbal, M. S. & Ali, M. Numerical modeling of three dimensional Brusselator reaction diffusion system. AIP Adv. 9 , 015205 (2019).

Xu, Y., Ma, J., Wang, H., Li, Y. & Kurths, J. Effects of combined harmonic and random excitations on a Brusselator model. Eur. Phys. J. B 90 , 194 (2017).

Behrens, J. Atmospheric and ocean modeling with an adaptive finite element solver for the shallow-water equations. Appl. Numer. Math. 26 , 217–226 (1998).

Kontolati, K., Goswami, S., Karniadakis, G. E. & Shields, M. D. Learning in latent spaces improves the predictive accuracy of deep neural operators. Preprint at arXiv:2304.07599 (2023).

Cao, Q., James Hu, S. L. & Li, H. Laplace-and frequency-domain methods on computing transient responses of oscillators with hysteretic dampings to deterministic loading. J. Eng. Mech. 149 , 04023005 (2023).

Cao, Q., Goswami, S. & Karniadakis, G. E. Code and data for Laplace neural operator for solving differential equations. Zenodo https://doi.org/10.5281/zenodo.11002002 (2024).

Download references

Acknowledgements

Q.C. acknowledges funding from the Dalian University of Technology for visiting Brown University, USA. Q.C., S.G. and G.E.K. acknowledge support by the DOE SEA-CROGS project (DE-SC0023191), the MURI-AFOSR FA9550-20-1-0358 project and the ONR Vannevar Bush Faculty Fellowship (N00014-22-1-2795). All authors acknowledge the computing support provided by the computational resources and services at the Center for Computation and Visualization (CCV), Brown University, where experiments were conducted.

Author information

Authors and affiliations.

Division of Applied Mathematics, Brown University, Providence, RI, USA

Qianying Cao, Somdatta Goswami & George Em Karniadakis

School of Engineering, Brown University, Providence, RI, USA

George Em Karniadakis

You can also search for this author in PubMed   Google Scholar

Contributions

Q.C. and G.E.K. were responsible for conceptualization. Q.C., S.G. and G.E.K. were responsible for data curation. Q.C. and S.G. were responsible for formal analysis, investigation, software, validation and visualization. Q.C. was responsible for the methodology. G.E.K. was responsible for funding acquisition, project administration, resources and supervision. All authors wrote the original draft, and reviewed and edited the manuscript.

Corresponding author

Correspondence to George Em Karniadakis .

Ethics declarations

Competing interests.

G.E.K. is one of the founders of Phinyx AI, a private start-up company developing AI software products for engineering. The remaining authors (Q.C. and S.G.) declare no competing interests.

Peer review

Peer review information.

Nature Machine Intelligence thanks David Ruhe and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information.

Additional results as well as details of the network architecture used in this work.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Cite this article.

Cao, Q., Goswami, S. & Karniadakis, G.E. Laplace neural operator for solving differential equations. Nat Mach Intell 6 , 631–640 (2024). https://doi.org/10.1038/s42256-024-00844-4

Download citation

Received : 07 July 2023

Accepted : 26 April 2024

Published : 24 June 2024

Issue Date : June 2024

DOI : https://doi.org/10.1038/s42256-024-00844-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Solving Differential Equations using Physics-Informed Deep Equilibrium Models

This paper introduces Physics-Informed Deep Equilibrium Models (PIDEQs) for solving initial value problems (IVPs) of ordinary differential equations (ODEs). Leveraging recent advancements in deep equilibrium models (DEQs) and physics-informed neural networks (PINNs), PIDEQs combine the implicit output representation of DEQs with physics-informed training techniques. Our validation of PIDEQs, using the Van der Pol oscillator as a benchmark problem, yielded compelling results, demonstrating their efficiency and effectiveness in solving IVPs. Our analysis includes key hyperparameter considerations for optimizing PIDEQ performance. By bridging deep learning and physics-based modeling, this work advances computational techniques for solving IVPs with implications for scientific computing and engineering applications.

I INTRODUCTION

The advent of deep learning has revolutionized various industries, demonstrating its prowess in tackling complex problems across domains ranging from image recognition to natural language processing. Despite the success of deep learning in various industries, applying this technology to solve initial value problems (IVPs) of differential equations presents a formidable challenge, primarily due to the data-driven nature of deep learning models. Gathering sufficient data from real-life dynamical systems can be prohibitively expensive, necessitating a novel approach to training deep learning models for such tasks.

The work by [ 1 ] introduced the approach of solving IVPs using deep learning models by optimizing a model’s dynamics rather than solely its outputs. This approach allows deep learning models to approximate the dynamics of a system, provided an accurate description of these dynamics is known, typically in the form of differential equations. Focusing on optimizing the dynamics allows the model to be trained with minimal data, covering only the initial and boundary conditions.

In parallel, [ 2 ] and [ 3 ] proposed an innovative approach to deep learning by implicitly defining a model’s output as a solution to an equilibrium equation. This methodology results in a model known as a Deep Equilibrium Model (DEQ), which exhibits an infinite-depth network structure with residual connections. This design offers significant representational power with relatively few parameters, widening the architectural possibilities for deep learning models.

The transition from PINNs to DEQs presents an opportunity to combine the strengths of both approaches. PINNs excel in incorporating physical laws into the learning process, reducing the dependency on extensive data. DEQs, with their implicit infinite-depth structure, offer a powerful framework for solving complex problems with fewer parameters. By integrating these methodologies, we can create a Physics-Informed Deep Equilibrium Model (PIDEQ) that leverages the physics-informed training techniques of PINNs within the robust and efficient framework of DEQs.

This paper explores this integration by studying, implementing, and validating PIDEQs as efficient and accurate solvers for IVPs. An efficient solver is characterized by its ability to operate with minimal data and computational resources. In contrast, an effective solver can provide accurate solutions across a vast domain of the independent variable. Our research is guided by three objectives: implementing a DEQ, designing and implementing a PINN training algorithm suitable for DEQs, and evaluating the performance of the physics-informed DEQ in solving IVPs. These objectives form the backbone of our study. More specifically, our contributions are:

A novel approach for training DEQs for solving IVPs using physics regularization, resulting in a physics-informed deep equilibrium model.

An experimental evaluation of PIDEQs as efficient and effective solvers for ordinary differential equations using the Van der Pol oscillator.

An analysis of the key hyperparameters that must be adjusted to develop PIDEQs effectively.

Through these efforts, we aim to provide insights into the suitability of DEQs, a cutting-edge deep learning architecture, for addressing the challenges posed by solving IVPs of ODEs, paving the way for their broader adoption in scientific computing and engineering applications.

II SOLVING IVPs USING DEEP LEARNING

Solving IVPs of differential equations using deep learning poses unique challenges. Unlike traditional deep learning tasks where input-output pairs are readily available, in IVPs, both the target function (solution to the IVP) and input-output pairs are unknown or too complex to be directly useful. This lack of information complicates the training process, as the conventional approach of constructing a dataset of input-output pairs becomes impractical or impossible.

II-A Problem Statement

Consider an IVP of an ODE with boundary conditions. Given a function 𝒩 : ℝ × ℝ m → ℝ m : 𝒩 → ℝ superscript ℝ 𝑚 superscript ℝ 𝑚 \mathcal{N}:\mathbb{R}\times\mathbb{R}^{m}\to\mathbb{R}^{m} caligraphic_N : blackboard_R × blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT and initial condition t 0 ∈ I ⊂ ℝ , 𝒚 0 ⊂ ℝ m formulae-sequence subscript 𝑡 0 𝐼 ℝ subscript 𝒚 0 superscript ℝ 𝑚 t_{0}\in I\subset\mathbb{R},\,\bm{y}_{0}\subset\mathbb{R}^{m} italic_t start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ∈ italic_I ⊂ blackboard_R , bold_italic_y start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ⊂ blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT , we aim to find a solution ϕ : I → ℝ m : bold-italic-ϕ → 𝐼 superscript ℝ 𝑚 \bm{\phi}:I\to\mathbb{R}^{m} bold_italic_ϕ : italic_I → blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT such that the differential equation

holds on the entirety of the interval I 𝐼 I italic_I .

Our objective is to train a deep learning model D θ : I → ℝ m : subscript 𝐷 𝜃 → 𝐼 superscript ℝ 𝑚 D_{\mathbf{\theta}}:I\to\mathbb{R}^{m} italic_D start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT : italic_I → blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT , parameterized by θ ∈ Θ 𝜃 Θ \mathbf{\theta}\in\Theta italic_θ ∈ roman_Θ , to approximate the solution function ϕ bold-italic-ϕ \bm{\phi} bold_italic_ϕ , satisfying the same conditions, i.e.,

II-B Physics Regularization

The conventional approach of constructing a dataset for training is inefficient in the context of IVPs, as it does not leverage the known dynamics represented by 𝒩 𝒩 \mathcal{N} caligraphic_N . To address this challenge, [ 1 ] proposed a physics-informed learning approach incorporating known dynamics into the training process.

The key idea is to train the model D θ subscript 𝐷 𝜃 D_{\mathbf{\theta}} italic_D start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT to approximate the solution ϕ bold-italic-ϕ \bm{\phi} bold_italic_ϕ at t 0 subscript 𝑡 0 t_{0} italic_t start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT , satisfying the initial condition constraint, and simultaneously train its Jacobian to approximate 𝒩 𝒩 \mathcal{N} caligraphic_N , ensuring that the dynamics are captured accurately.

To achieve this, the cost function is defined as

\lambda\in\mathbb{R}_{+} italic_λ ∈ blackboard_R start_POSTSUBSCRIPT + end_POSTSUBSCRIPT . By optimizing this cost function, the model is guided to simultaneously satisfy the initial condition and approximate the dynamics represented by 𝒩 𝒩 \mathcal{N} caligraphic_N .

The term J b ⁢ ( θ ) subscript 𝐽 𝑏 𝜃 J_{b}(\mathbf{\theta}) italic_J start_POSTSUBSCRIPT italic_b end_POSTSUBSCRIPT ( italic_θ ) is introduced to enforce the initial condition constraint. It is given by

using an ℓ 2 subscript ℓ 2 \ell_{2} roman_ℓ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT norm to penalize the deviation from the initial condition.

The term J 𝒩 ⁢ ( θ ) subscript 𝐽 𝒩 𝜃 J_{\mathcal{N}}(\mathbf{\theta}) italic_J start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT ( italic_θ ) plays a crucial role in ensuring that the model captures the underlying dynamics specified by 𝒩 𝒩 \mathcal{N} caligraphic_N . By regularizing the model’s Jacobian, this term forces the model to learn not just the solution at discrete points, but also how the solution evolves according to the differential equations. This is achieved by minimizing the difference between the model’s predicted derivative d d ⁢ t ⁢ D 𝜽 ⁢ ( t ) 𝑑 𝑑 𝑡 subscript 𝐷 𝜽 𝑡 \frac{d}{dt}D_{\bm{\theta}}(t) divide start_ARG italic_d end_ARG start_ARG italic_d italic_t end_ARG italic_D start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT ( italic_t ) and the true dynamics 𝒩 ⁢ ( t , D 𝜽 ⁢ ( t ) ) 𝒩 𝑡 subscript 𝐷 𝜽 𝑡 \mathcal{N}(t,D_{\bm{\theta}}(t)) caligraphic_N ( italic_t , italic_D start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT ( italic_t ) ) . For such, it is defined as

where 𝒰 ⁢ ( I ) 𝒰 𝐼 \mathcal{U}(I) caligraphic_U ( italic_I ) is a uniform distribution over the I 𝐼 I italic_I interval, i.e., the data is uniformly sampled from the domain 1 1 1 The sampling strategy can be considered a design choice. .

This approach eliminates the need for explicit knowledge of the target function ( ϕ bold-italic-ϕ \bm{\phi} bold_italic_ϕ ) and allows for efficient training using randomly constructed samples, making deep learning a viable option for solving IVPs.

III DEEP EQUILIBRIUM MODELS

This section introduces and defines DEQs and presents their combination with physics-informed training in the proposed PIDEQ framework. We follow the notation proposed by [ 2 ] and explore the foundational concepts and practical considerations that enable the introduction of our proposed approach.

III-A Introduction and Definition

Deep Learning models typically compose simple parametrized functions to capture complex features. While traditional architectures stack these functions in a sequential manner, in a DEQ, the architecture is based on an infinite stack of the same function. If this function is well-posed, i.e., it respects a Lipschitz-continuity condition  [ 3 ] , the infinite stack leads to an equilibrium point that serves as the model’s output.

III-B Forward Computation

Formally, a DEQ can be defined as the solution to an equilibrium equation. Let 𝒇 θ : ℝ n × ℝ m → ℝ m : subscript 𝒇 𝜃 → superscript ℝ 𝑛 superscript ℝ 𝑚 superscript ℝ 𝑚 \bm{f}_{\theta}:\mathbb{R}^{n}\times\mathbb{R}^{m}\to\mathbb{R}^{m} bold_italic_f start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT : blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT × blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_m end_POSTSUPERSCRIPT be the layer function. Then, the output of a DEQ can be described through the solution 𝒛 ⋆ superscript 𝒛 ⋆ \bm{z}^{\star} bold_italic_z start_POSTSUPERSCRIPT ⋆ end_POSTSUPERSCRIPT of the equilibrium equation

where 𝒙 𝒙 \bm{x} bold_italic_x is the model’s input. Fig.  1 illustrates the equilibrium equation inside a DEQ.

The simplest way to solve the equilibrium equation that defines the output of a DEQ is by iteratively applying the equilibrium function until convergence. Given an input 𝒙 𝒙 \bm{x} bold_italic_x and an initial guess 𝒛 [ 0 ] superscript 𝒛 delimited-[] 0 \bm{z}^{[0]} bold_italic_z start_POSTSUPERSCRIPT [ 0 ] end_POSTSUPERSCRIPT , the procedure updates the equilibrium guess 𝒛 [ i ] superscript 𝒛 delimited-[] 𝑖 \bm{z}^{[i]} bold_italic_z start_POSTSUPERSCRIPT [ italic_i ] end_POSTSUPERSCRIPT by

until | 𝒛 [ i ] − 𝒛 [ i − 1 ] | superscript 𝒛 delimited-[] 𝑖 superscript 𝒛 delimited-[] 𝑖 1 |\bm{z}^{[i]}-\bm{z}^{[i-1]}| | bold_italic_z start_POSTSUPERSCRIPT [ italic_i ] end_POSTSUPERSCRIPT - bold_italic_z start_POSTSUPERSCRIPT [ italic_i - 1 ] end_POSTSUPERSCRIPT | is sufficiently small. This approach, known as the simple iteration method, is intuitive but can be slow to converge and is sensitive to the starting point. Moreover, it only finds equilibrium of functions that are a contraction between the starting point and the equilibrium point  [ 4 ] . For example, the simple iteration method fails to find the equilibrium of f ⁢ ( z ) = 2 ⁢ z − 1 𝑓 𝑧 2 𝑧 1 f(z)=2z-1 italic_f ( italic_z ) = 2 italic_z - 1 starting from any point other than the equilibrium itself ( z = 1 𝑧 1 z=1 italic_z = 1 ).

To address these limitations, Newton’s method can be used. It updates the incumbent equilibrium point by

𝑖 1 superscript 𝒛 delimited-[] 𝑖 subscript 𝒇 𝜽 𝒙 superscript 𝒛 delimited-[] 𝑖 \frac{d\bm{f}_{\bm{\theta}}(\bm{x},\bm{z}^{[i]})}{d\bm{z}}\left(\bm{z}^{[i+1]}% -\bm{z}^{[i]}\right)=-\bm{f}_{\bm{\theta}}(\bm{x},\bm{z}^{[i]}) divide start_ARG italic_d bold_italic_f start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT ( bold_italic_x , bold_italic_z start_POSTSUPERSCRIPT [ italic_i ] end_POSTSUPERSCRIPT ) end_ARG start_ARG italic_d bold_italic_z end_ARG ( bold_italic_z start_POSTSUPERSCRIPT [ italic_i + 1 ] end_POSTSUPERSCRIPT - bold_italic_z start_POSTSUPERSCRIPT [ italic_i ] end_POSTSUPERSCRIPT ) = - bold_italic_f start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT ( bold_italic_x , bold_italic_z start_POSTSUPERSCRIPT [ italic_i ] end_POSTSUPERSCRIPT ) instead. .

Newton’s method converges much faster and is applicable to a broader class of functions compared to simple iteration  [ 4 ] . It offers a faster and more robust alternative by leveraging the Jacobian of f 𝜽 subscript 𝑓 𝜽 f_{\bm{\theta}} italic_f start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT . As the deep learning paradigm is to perform gradient-based optimization, the well-posedness of the Jacobian of the equilibrium function is already guaranteed. In other words, we can benefit from the fast convergence rate and broad applicability of Newton’s method. In fact, most modern root-finding algorithms can be used for computing the equilibrium, such as Anderson acceleration  [ 5 ] and Broyden’s Method  [ 6 ] .

III-C Backward Computation

Computing the gradient of the output of a DEQ with respect to its parameters is not straightforward. The approach of automatic-differentiation frameworks for deep learning is to backpropagate the loss at training time, differentiating every operation in the forward pass. Differentiating through modern root-finding algorithms is, at best, an intricate and costly operation. Even if the forward pass is done through the iterative process, its differentiation would require backpropagating through an unknown number of layers.

Luckily, we can exploit the fact that the output of a DEQ for an equilibrium function 𝒇 𝜽 ⁢ ( 𝒙 , 𝒛 ) subscript 𝒇 𝜽 𝒙 𝒛 \bm{f}_{\bm{\theta}}(\bm{x},\bm{z}) bold_italic_f start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT ( bold_italic_x , bold_italic_z ) defines a parametrization of 𝒛 𝒛 \bm{z} bold_italic_z with respect to 𝒙 𝒙 \bm{x} bold_italic_x . This allows us to apply the implicit function theorem to write the Jacobian of a DEQ as

Note that the Jacobian can be computed regardless of the operations applied during the forward pass . Furthermore, we do not need to compute the entire Jacobian matrix for gradient descent. We need to compute the gradient of a loss function ℒ ℒ \mathcal{L} caligraphic_L with respect to the model’s parameters. Such gradient can be written as

where d ⁢ ℒ d ⁢ y ^ 𝑑 ℒ 𝑑 ^ 𝑦 \frac{d\mathcal{L}}{d\hat{y}} divide start_ARG italic_d caligraphic_L end_ARG start_ARG italic_d over^ start_ARG italic_y end_ARG end_ARG is the gradient of the loss function and d ⁢ D 𝜽 E ⁢ Q d ⁢ 𝜽 𝑑 subscript superscript 𝐷 𝐸 𝑄 𝜽 𝑑 𝜽 \frac{dD^{EQ}_{\bm{\theta}}}{d\bm{\theta}} divide start_ARG italic_d italic_D start_POSTSUPERSCRIPT italic_E italic_Q end_POSTSUPERSCRIPT start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT end_ARG start_ARG italic_d bold_italic_θ end_ARG is the Jacobian of the DEQ with respect to its parameters. Note that the gradient requires us to compute two vector-matrix products, in which the result of − d ⁢ ℒ d ⁢ y ^ ⁢ [ d ⁢ 𝒇 𝜽 d ⁢ 𝒛 − I ] − 1 𝑑 ℒ 𝑑 ^ 𝑦 superscript delimited-[] 𝑑 subscript 𝒇 𝜽 𝑑 𝒛 𝐼 1 -\frac{d\mathcal{L}}{d\hat{y}}\left[\frac{d\bm{f}_{\bm{\theta}}}{d\bm{z}}-I% \right]^{-1} - divide start_ARG italic_d caligraphic_L end_ARG start_ARG italic_d over^ start_ARG italic_y end_ARG end_ARG [ divide start_ARG italic_d bold_italic_f start_POSTSUBSCRIPT bold_italic_θ end_POSTSUBSCRIPT end_ARG start_ARG italic_d bold_italic_z end_ARG - italic_I ] start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT can be computed through a root-finding algorithm, assuming that the gradient of the loss function is known. We refer the reader to [ 2 ] and [ 3 ] for further details.

III-D Physics-Informed Deep Equilibrium Model (PIDEQ)

A Physics-Informed Deep Equilibrium Model (PIDEQ) extends the principles of physics-informed learning to a DEQ. In summary, PIDEQs leverage the principles of physics-informed learning to enhance the capabilities of DEQs. By integrating physics-based constraints, PIDEQs deliver the architectural power of DEQs with robustness and accuracy in modeling physical systems.

The challenge in physics-informing a DEQ lies in optimizing a cost function on its derivatives. As exposed in Sec.  III-C , [ 2 ] proposed an efficient method to compute the first derivative of a DEQ with respect to either its parameters or the input, which, in the context of physics-informed learning, allows us to compute the loss function value. However, in computing the gradient of the loss function, we require second derivatives, which pose additional challenges as they imply differentiating the backward pass. Furthermore, to the best of our knowledge, higher-order derivatives of DEQs have not been investigated. To address this challenge, we limit ourselves to using solely differentiable operators in the backward pass. This way, automatic differentiation frameworks can automatically compute the second derivatives.

Finally, it has been shown that DEQs benefit significantly from penalizing the presence of large values in its Jacobian  [ 7 ] . This penalization can be achieved by adding the Frobenius norm of the Jacobian of the equilibrium function as a regularization term in the loss function, which was shown to reduce training and inference times.

Therefore, we propose the following loss function for training PIDEQs:

It combines a base loss term ( J b subscript 𝐽 𝑏 J_{b} italic_J start_POSTSUBSCRIPT italic_b end_POSTSUBSCRIPT ) with a physics-informed loss term ( J 𝒩 subscript 𝐽 𝒩 J_{\mathcal{N}} italic_J start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT ) and a regularization term based on the Frobenius norm of the Jacobian of the equilibrium function, weighed by a κ ≥ 0 𝜅 0 \kappa\geq 0 italic_κ ≥ 0 coefficient.

IV EXPERIMENTS

In this section, we conduct a series of experiments to evaluate the capacity of PIDEQs for solving differential equations. We use the Van der Pol oscillator as our benchmark IVP due to its well-documented complexity and lack of an analytical solution, which makes it an ideal candidate for testing the robustness of numerical solvers. We compare the PIDEQ approach with physic-informed neural networks (PINNs), a well-established deep learning technique for similar tasks  [ 1 , 8 ] .

IV-A Problem Definition

The Van der Pol oscillator system is chosen as the target ODE for our experiments due to its nonlinear dynamics and the absence of an analytical solution, providing a stringent test for our models. The system is a classic example in nonlinear dynamics and has been extensively studied, making it a reliable benchmark.

The dynamics of the oscillator are described as a system of first-order equations

We select a value of μ = 1 𝜇 1 \mu=1 italic_μ = 1 for the dampening coefficient and an initial condition 𝒚 ⁢ ( 0 ) = ( 0 , 0.1 ) 𝒚 0 0 0.1 \bm{y}(0)=(0,0.1) bold_italic_y ( 0 ) = ( 0 , 0.1 ) , i.e., a small perturbation around the unstable equilibrium at the origin, where 𝒚 𝒚 \bm{y} bold_italic_y represents the two states of the system. The desired solution is sought over a time horizon of 2 seconds, during which the system is expected to converge to a limit cycle  [ 9 ] , as illustrated in Fig.  2 .

IV-A 1 Evaluation Metrics

Since no analytical solution is available, we assess the performance of the models based on their approximation error compared to a reference solution obtained using the fourth-order Runge-Kutta (RK4) method. The Integral of the Absolute Error (IAE) is computed over 1000 equally time-spaced steps within the solution interval. We also consider the computational time required for training and inference as valuable metrics, especially for time-sensitive applications.

IV-B Training

In our experiments with the PIDEQ, we use an architecture similar to the one proposed by [ 3 ] , with an equilibrium function that provides as the output the (element-wise) hyperbolic tangent of an affine combination of its inputs, namely, the time value and the hidden states ( 𝒛 𝒛 \bm{z} bold_italic_z ). The model’s output is a linear combination of the equilibrium vector 𝒛 ⋆ superscript 𝒛 ⋆ \bm{z}^{\star} bold_italic_z start_POSTSUPERSCRIPT ⋆ end_POSTSUPERSCRIPT . Formally, we can write

where the vector parameter is simply a vectorized representation of all coefficients, i.e., 𝜽 = ( A , C , 𝒂 , 𝒃 ) 𝜽 𝐴 𝐶 𝒂 𝒃 \bm{\theta}=(A,C,\bm{a},\bm{b}) bold_italic_θ = ( italic_A , italic_C , bold_italic_a , bold_italic_b ) , and the input is 𝒙 = t 𝒙 𝑡 \bm{x}=t bold_italic_x = italic_t .

We use the Adam optimizer  [ 10 ] for training the PIDEQ. The cost function incorporates regularization terms to enforce physics-informed training, as detailed in Sec.  III-D . Our default hyperparameter configuration 3 3 3 Determined through early experimentation. was a learning rate of 10 − 3 superscript 10 3 10^{-3} 10 start_POSTSUPERSCRIPT - 3 end_POSTSUPERSCRIPT , λ = 0.1 𝜆 0.1 \lambda=0.1 italic_λ = 0.1 , κ = 1.0 𝜅 1.0 \kappa=1.0 italic_κ = 1.0 , and a budget of 50000 epochs. Our default solver for the forward pass was Anderson acceleration with a tolerance of 10 − 4 superscript 10 4 10^{-4} 10 start_POSTSUPERSCRIPT - 4 end_POSTSUPERSCRIPT , while the backward pass is always solved iteratively to ensure differentiability.

Nevertheless, the dimension of the hidden states ( | 𝒛 | 𝒛 |\bm{z}| | bold_italic_z | ), the solver tolerance, and the coefficient for the Jacobian regularization term ( κ 𝜅 \kappa italic_κ ) are all considered hyperparameters, and we measure their impacts empirically. We also consider as a hyperparameter the choice between Anderson acceleration, Broyden’s method, and the simple iteration procedure as the forward pass solver.

IV-C Experimental Results

All experiments reported below were performed on a high-end computer using an RTX 3060 GPU. Further implementation details can be seen in our code repository 4 4 4 https://github.com/brunompacheco/pideq . For every hyperparameter configuration, five models were trained with random initial values for the trainable parameters.

IV-C 1 Baseline

Our baseline PINN model follows the architecture proposed in [ 8 ] , with four layers of twenty nodes each. As a DEQ with as many states as there are hidden nodes in a deep feedforward network has at least as much representational power  [ 3 ] , we start with | 𝒛 | = 80 𝒛 80 |\bm{z}|=80 | bold_italic_z | = 80 hidden states. The results can be seen in Fig.  3 . Even though both models achieved low IAE values, the PINN presented better performance in terms of IAE and training time, converging in far fewer epochs.

IV-C 2 Hyperparameter Optimization

A deeper look at the baseline PIDEQ shows that the parameters converged to an A 𝐴 A italic_A matrix with many null rows. This indicates that the model could achieve similar performance with fewer hidden states. Such intuition proved truthful in our hyperparameter tuning experiments, as shown in Fig.  4 . We iteratively halved the number of states until the A 𝐴 A italic_A matrix had no more empty rows, which happened at | 𝒛 | = 5 𝒛 5 |\bm{z}|=5 | bold_italic_z | = 5 states. Then, we took one step further, reducing to | z | = 2 𝑧 2 |z|=2 | italic_z | = 2 states, but the results indicated that, indeed, 5 was the sweet spot, with faster convergence and lower final IAE. The following experiments are performed with PIDEQs with five hidden states.

We further investigate the importance of the regularization term on the Jacobian of the equilibrium function. Even though the Jacobian of the DEQ, in the context of physics-informed training, is directly learned, our experiments indicate that the presence of the regularization term is essential. Otherwise, the training took over 30 times longer and was very unstable. However, the magnitude of the κ 𝜅 \kappa italic_κ coefficient has little impact on the outcomes. Our results for different values of κ 𝜅 \kappa italic_κ (including 0) are illustrated in Fig.  5 .

Anderson acceleration, Broyden’s method, and the simple iteration procedure were evaluated as solvers for the forward pass. As the results illustrated in Fig.  6 show, Broyden’s method could provide a performance gain, but it came with a significant computational cost, as the epochs took over six times longer in comparison to using Anderson acceleration. At the same time, using the simple iteration procedure was three times faster than using Anderson acceleration. However, as discussed in Sec.  III-B , the theoretical limitation of the simple iterative procedure limits its reliability. We also evaluated the performance of PIDEQ under different values for the solver tolerance, but no performance gain was observed for values different than our default of 10 − 4 superscript 10 4 10^{-4} 10 start_POSTSUPERSCRIPT - 4 end_POSTSUPERSCRIPT .

IV-C 3 Results

The final PIDEQ, after hyperparameter tuning, achieves comparable results to the baseline PINN models. In terms of approximation performance, while the baseline PIDEQ achieved an IAE of 0.0082, our best PIDEQ achieved an IAE of 0.0018, and the baseline PINN achieved an IAE of 0.0002, which is seen through the last epochs in Fig.  8 . Fig.  7 illustrates how small the difference is between the two approaches, showing them in comparison to the solution computed using RK4. However, the greatest gain comes from the reduced training time, as the tuned PIDEQ converges much faster than the baseline PIDEQ.

The greatest performance gain came from reducing the number of hidden states, guided by the sparsity of the A 𝐴 A italic_A matrix. The smaller model size leads to improved memory efficiency and explainability. We also trained PINN models with two hidden layers of 5 nodes each, totaling 52 trainable parameters, the same number of parameters as the tuned PIDEQ. The results are shown in Fig.  8 . Note that both final models take around the same number of epochs to converge.

V CONCLUSIONS

This study explored two innovative approaches to deep learning: Physics-Informed Neural Networks (PINNs) and Deep Equilibrium Models (DEQs). While PINNs offer efficiency in training models for physical problems, DEQs promise greater representational power with fewer parameters. We introduced Physics-Informed Deep Equilibrium Models (PIDEQ), uniting the physics-regularization with the infinite-depth architecture.

Our experiments on the Van der Pol oscillator validated PIDEQs’ effectiveness in solving IVPs of ODEs, validating our proposed approach. However, comparisons with PINN models revealed mixed results. Although PIDEQs demonstrated the ability to solve IVPs, they exhibited slightly higher errors and slower training times compared to PINNs. This suggests that while DEQ structures offer theoretical advantages in representational power, these benefits may not translate into practical improvements for certain types of problems like the Van der Pol oscillator.

The strengths of PIDEQs lie in their potential for handling more complex problems, leveraging the implicit depth of DEQs. However, the current implementation’s reliance on simple iterative methods for the backward pass can be a limiting factor, especially for more challenging problems and partial differential equations (PDEs). This limitation points to a significant area for improvement.

Future research should focus on evaluating PIDEQs with more complex problems (e.g., higher-order ODEs and PDEs) to better understand their potential advantages. Additionally, exploring more sophisticated methods for the backward pass, such as implicit differentiation techniques, could enhance the training efficiency and accuracy of PIDEQs.

In conclusion, while PIDEQs present a promising direction for integrating physics-informed principles with advanced deep-learning architectures, further work is still necessary to fully realize their potential and address their current limitations compared to traditional PINNs. This future research could pave the way for more robust and versatile models capable of solving a wide range of complex dynamical systems, providing competitive solver alternatives.

Acknowledgment

This research was funded in part by Fundação de Amparo à Pesquisa e Inovação do Estado de Santa Catarina (FAPESC) under grant 2021TR2265, CNPq under grants 308624/2021-1 and 402099/2023-0, and CAPES under grant PROEX.

• [1] M. Raissi, P. Perdikaris, and G. Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” Journal of Computational Physics , vol. 378, pp. 686–707, 2019.
• [2] S. Bai, J. Z. Kolter, and V. Koltun, “Deep equilibrium models,” in Advances in Neural Information Processing Systems (H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, eds.), vol. 32, Curran Associates, Inc., 2019.
• [3] L. El Ghaoui, F. Gu, B. Travacca, A. Askari, and A. Tsai, “Implicit deep learning,” SIAM Journal on Mathematics of Data Science , vol. 3, p. 930–958, Jan. 2021.
• [4] E. Süli and D. F. Mayers, An Introduction to Numerical Analysis . Cambridge University Press, Aug. 2003.
• [5] H. F. Walker and P. Ni, “Anderson acceleration for fixed-point iterations,” SIAM Journal on Numerical Analysis , vol. 49, p. 1715–1735, Jan. 2011.
• [6] C. G. Broyden, “A class of methods for solving nonlinear simultaneous equations,” Mathematics of Computation , vol. 19, no. 92, p. 577–593, 1965.
• [7] S. Bai, V. Koltun, and Z. Kolter, “Stabilizing equilibrium models by Jacobian regularization,” in Proceedings of the 38th International Conference on Machine Learning (M. Meila and T. Zhang, eds.), vol. 139, pp. 554–565, PMLR, 18–24 Jul 2021.
• [8] E. A. Antonelo, E. Camponogara, L. O. Seman, E. R. de Souza, J. P. Jordanou, and J. F. Hübner, “Physics-informed neural nets for control of dynamical systems,” Neurocomputing , vol. 579, p. 127419, April 2024.
• [9] R. Grimshaw, Nonlinear Ordinary Differential Equations: Applied Mathematics and Engineering Science Texts . CRC Press, March 2017.
• [10] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” in 3rd International Conference on Learning Representations (ICLR) (Y. Bengio and Y. LeCun, eds.), (San Diego, CA, USA), 2015.

• Advanced Search

Numerical integration of stiff problems using a new time-efficient hybrid block solver based on collocation and interpolation techniques

New citation alert added.

This alert has been successfully added and will be sent to:

You will be notified whenever a record that you have chosen has been cited.

To manage your alert preferences, click on the button below.

New Citation Alert!

Please log in to your account

Information & Contributors

Bibliometrics & citations, view options, recommendations, semi-analytical time differencing methods for stiff problems.

A semi-analytical method is developed based on conventional integrating factor (IF) and exponential time differencing (ETD) schemes for stiff problems. The latter means that there exists a thin layer with a large variation in their solutions. The ...

Two classes of implicit-explicit multistep methods for nonlinear stiff initial-value problems

The initial value problems of nonlinear ordinary differential equations which contain stiff and nonstiff terms often arise from many applications. In order to reduce the computation cost, implicit-explicit (IMEX) methods are often applied to these ...

Continuous block backward differentiation formula for solving stiff ordinary differential equations

In this paper, we consider an implicit Continuous Block Backward Differentiation formula (CBBDF) for solving Ordinary Differential Equations (ODEs). A block of p new values at each step which simultaneously provide the approximate solutions for the ODEs ...

Information

Published in.

Elsevier Science Publishers B. V.

Netherlands

Publication History

Author tags.

• ℒ-stability
• Order stars
• Stiff problems
• Efficiency curves
• Research-article

Contributors

Other metrics, bibliometrics, article metrics.

• 0 Total Citations
• 0 Total Downloads
• Downloads (Last 12 months) 0
• Downloads (Last 6 weeks) 0

View options

Login options.

Check if you have access through your login credentials or your institution to get full access on this article.

Full Access

Share this publication link.

Copying failed.

Number Line

The Calculus Calculator is a powerful online tool designed to assist users in solving various calculus problems efficiently. Here's how to make the most of its capabilities:

• Begin by entering your mathematical expression into the above input field, or scanning it with your camera.
• Choose the specific calculus operation you want to perform, such as differentiation, integration, or finding limits.
• Once you've entered the function and selected the operation, click the 'Go' button to generate the result.
• The calculator will instantly provide the solution to your calculus problem, saving you time and effort.
• \lim_{x\to 3}(\frac{5x^2-8x-13}{x^2-5})
• \lim _{x\to \:0}(\frac{\sin (x)}{x})
• \int e^x\cos (x)dx
• \int \cos^3(x)\sin (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \frac{d}{dx}(\frac{3x+9}{2-x})
• \frac{d^2}{dx^2}(\frac{3x+9}{2-x})
• implicit\:derivative\:\frac{dy}{dx},\:(x-y)^2=x+y-1
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• tangent\:of\:f(x)=\frac{1}{x^2},\:(-1,\:1)

calculus-calculator

initial value problem

• High School Math Solutions – Derivative Calculator, the Basics Differentiation is a method to calculate the rate of change (or the slope at a point on the graph); we will not...

Please add a message.

Message received. Thanks for the feedback.