solve the initial value problem below using the method of laplace transforms

Browse Course Material

Course info, instructors.

• Prof. Arthur Mattuck
• Prof. Haynes Miller
• Dr. Jeremy Orloff
• Dr. John Lewis

Departments

• Mathematics

As Taught In

• Differential Equations
• Linear Algebra

Learning Resource Types

Laplace transform: solving initial value problems.

« Previous | Next »

Session Overview

Session activities.

Read the course notes:

• Laplace Transform: Solving Initial Value Problems: Introduction (PDF)
• Laplace Transform Table (PDF)
• Table Entries: Derivative Rules (PDF)
• Precise Definition of Laplace Inverse (PDF)
• Laplace: Solving Initial Value Problems (PDF)
• IVP’s and t-translation (PDF)
• IVP’s: Longer Examples (PDF)

Watch the problem solving video:

• Laplace: Solving ODE’s

Complete the practice problems:

• Practice Problems 29 (PDF)
• Practice Problems 29 Solutions (PDF)

Check Yourself

Complete the problem sets:

Problem Set Part I Problems (PDF)

Problem Set Part I Solutions (PDF)

Problem Set Part II Problems (PDF)

Problem Set Part II Solutions (PDF)

You are leaving MIT OpenCourseWare

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Differential equations

Course: differential equations   >   unit 3, laplace transform to solve an equation.

• Laplace transform solves an equation 2
• Using the Laplace transform to solve a nonhomogeneous eq
• Laplace/step function differential equation

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Table of Contents

Solve Differential Equations Using Laplace Transform

Examples of how to use Laplace transform to solve ordinary differential equations (ODE) are presented. One of the main advantages in using Laplace transform to solve differential equations is that the Laplace transform converts a differential equation into an algebraic equation. Heavy calculations involving decomposition into partial fractions are presented in the appendix at the bottom of the page.

Example 1 Use Laplace transform to solve the differential equation \[ - 2 y' + y = 0 \] with the initial conditions \( y(0) = 1 \) and \( y \) is a function of time \( t \). Solution to Example1 Let \( Y(s) \) be the Laplace transform of \( y(t) \) Take the Laplace transform of both sides of the given differential equation: \( \mathscr{L}\{ y(t) \} = Y(s) \) \( \mathscr{L}\{ -2 y' + y\} = \mathscr{L}\{0 \} \) Use linearity property of Laplace transform to rewrite the equation as \( - 2 \mathscr{L}\{ y'\} + \mathscr{L}\{ y\} = \mathscr{L}\{0 \} \) Use derivative property to rewrite the term \( \mathscr{L}\{ y'\} = (s Y(s) - y(0)) \). \( - 2 ( s Y(s) - y(0)) + Y(s) = 0 \) Expand the above as \( - 2 s Y(s) + 2 y(0) + Y(s) = 0 \) Substitute \( y(0) \) by its given numerical value \( - 2 s Y(s) + 2 + Y(s) = 0 \) Solve the above for \( Y(s) \) \( Y(s) (1 - 2 s) = -2 \) \( Y(s) = \dfrac{2}{2 s - 1} \) \( Y(s) = \dfrac{1}{ s - 1/2} \) We now use formula (3) in the table of formulas of Laplace transform to find the inverse Laplace transform of \( Y(s) \) obtained above as \( \displaystyle y(t) = e^{\frac{1}{2} t } \) Note: Check solution let's check that the solution obtained \( y(t) = e^{\frac{1}{2} t } \) satisfies the given differential equation \( - 2 y' + y = - 2 ( (1/2) e^{\frac{1}{2} t } ) + e^{\frac{1}{2} t } \) Simplify the above \( - e^{\frac{1}{2} t } + e^{\frac{1}{2} t } = 0 \) ; differential equation satisfied. \( y(0) = e^{\frac{1}{2} 0 } = e^0 = 1 \) ; initial value also satisfied.

Example 2 Use Laplace transform to solve the differential equation \[ y'' - 2 y' -3 y = 0 \] with the initial conditions \( y(0) = 2 \) and \( y'(0) = - 1 \) and \( y \) is a function of time \( t \). Solution to Example 2 Let \( Y(s) \) be the Laplace transform of \( y(t) \) Take the Laplace transform of both sides of the given differential equation \( \mathscr{L}\{ y'' - 2 y' -3 y \} = \mathscr{L}\{0 \} \) Use linearity property of Laplace transform to rewrite the equation as \( \mathscr{L}\{ y"\} - 2 \mathscr{L}\{ y'\} - 3 \mathscr{L}\{ y \} = \mathscr{L}\{0 \} \) Use first and second derivative properties to rewrite the terms \( \mathscr{L}\{ y"\} \) and \( \mathscr{L}\{ y'\} \) and simplify the right side. \( s^2 Y(s) - s y(0) - y'(0) - 2 (sY(s) - y(0)) - 3 Y(s) = 0 \) Substitute \( y(0) \) and \( y'(0) \) by their numerical values and expand \( s^2 Y(s) - 2 s + 1 - 2 s Y(s) + 4 - 3Y(s) = 0 \) Group like terms and keep terms with \( Y(s) \) on the left \( s^2 Y(s) - 2 s Y(s) - 3 Y(s) = 2 s - 5 \) Factor \( Y(s) \) out \( Y(s) (s^2 - 2 s - 3 ) = 2 s - 5 \) Solve the above for \( Y(s) \) \( Y(s) = \dfrac{2s - 5}{s^2 - 2 s - 3} \) Expand the right side into partial fractions (see details in Appendix A at the bottom of the page) \( Y(s) = \dfrac{7}{4\left(s+1\right)}+\dfrac{1}{4\left(s-3\right)} \) We now use formula (3) in the table of formulas of Laplace transform to find the inverse Laplace transform of \( Y(s) \) which is given by \( \displaystyle y(t) = \dfrac{7}{4} e^{- t } + \dfrac{1}{4} e^{3 t } \) You may check that the solution obtained satisfies the differential equation and the initial values given.

Example 3 Use Laplace transform to solve the differential equation \[ y'' + 2 y' + 2 y = 0 \] with the initial conditions \( y(0) = -1 \) and \( y'(0) = 2 \) and \( y \) is a function of time \( t \). Solution to Example 3 Let \( Y(s) \) be the Laplace transform of \( y(t) \) Take the Laplace transform of both sides of the given differential equation \( \mathscr{L}\{ y'' + 2 y' + 2 y \} = \mathscr{L}\{0 \} \) Use linearity property of Laplace transform to rewrite the equation as \( \mathscr{L}\{ y"\} + 2 \mathscr{L}\{ y'\} + 2 \mathscr{L}\{ y \} = \mathscr{L}\{0 \} \) Use first and second derivative properties to rewrite the terms \( \mathscr{L}\{ y"\} \) and \( \mathscr{L}\{ y'\} \) and simplify the right side. \( s^2 Y(s) - s y(0) - y'(0) + 2 (sY(s) - y(0)) + 2 Y(s) = 0 \) Substitute \( y(0) \) and \( y'(0) \) by their numerical values and expand \( s^2 Y(s) + s - 2 + 2 s Y(s) + 2 + 2 Y(s) = 0 \) Group like terms and keep terms with \( Y(s) \) on the left side of the equation \( s^2 Y(s) + 2 s Y(s) + 2 Y(s) = - s \) Factor \( Y(s) \) out \( Y(s) (s^2 + 2 s + 2 ) = - s \) Solve the above for \( Y(s) \) \( Y(s) = \dfrac{-s}{s^2 + 2 s + 2} \) Factor denominator over the complex numbers by first solving the equation \( s^2 + 2 s + 2 = 0 \) which gives two complex solutions \( S_1 = -1 + j \) and \( s_2 = -1 - j \) Factor \( Y(s) = \dfrac{-s}{(s - s_1)(s - s_2)} \) Expand the right side of the above into partial fractions (see Appendix B at the bottom of the page) \( \dfrac{-s}{(s - s_1)(s - s_2)} = \dfrac{A}{s-s_1} + \dfrac{B}{s-s_2} \) with \( A = \dfrac{-s_1}{s_1-s_2} = \dfrac{-(-1 + j)}{2 j} = -\dfrac{1}{2} - \dfrac{1}{2} j \) and \( B = \dfrac{-s_2}{s_2-s_1} = \dfrac{-(-1 - j)}{-2 j} = - \dfrac{1}{2} + \dfrac{1}{2} j \) Use formulas in the table of formulas to find the inverse Laplace transform of \( Y(s) = \dfrac{A}{s-s_1} + \dfrac{B}{s-s_2} \) which is given by \( y(t) = A e^{s_1 t} + B e^{s_2 t} \) Let us write \( A \) and \( B \) in exponential form \( A = -\dfrac{1}{2} - \dfrac{1}{2} j = \frac{\sqrt 2}{2} e^{ \frac{-3\pi}{4} j} \) \( B = -\dfrac{1}{2} + \dfrac{1}{2} j = \frac{\sqrt 2}{2} e^{ \frac{3\pi}{4} j} \) Substitute \( s_1 \), \( s_2 \), \( A \) and \( B \) by their values and rewrite \( y(t) \) as \( y(t) = (\frac{\sqrt 2}{2} e^{ \frac{-3\pi}{4} j}) e^{(-1 + j) t} + (\frac{\sqrt 2}{2} e^{ \frac{3\pi}{4} j}) e^{(-1 - j) t} \) Factor \( \dfrac{\sqrt 2}{2} e^{-t} \) out and group exponents \( y(t) = \dfrac{\sqrt 2}{2} e^{-t} \left[ e^{j t - \frac{3\pi}{4} j } + e^{-j t + \frac{3\pi}{4} j } \right] \) Use Euler formula ( \( e^jx = \cos x + j \sin x \) ) to simplify the terms inside the brackets \( y(t) = \dfrac{\sqrt 2}{2} e^{-t} \left[ \cos(t - \frac{3\pi}{4}) + j\sin(t - \frac{3\pi}{4}) + \cos(-t + \frac{3\pi}{4}) + j\sin(- t + \frac{3\pi}{4}) \right] \) which simplifies to \( y(t) = \sqrt 2 e^{-t} \cos(t - \frac{3\pi}{4}) \) You may check that the solution obtained satisfies the differential equation and the initial values given.

Example 4 Use Laplace transform to solve the differential equation \[ y'' - y' - 2 y = \sin(3t) \] with the initial conditions \( y(0) = 1 \) and \( y'(0) = -1 \). Solution to Example 4 Let \( Y(s) \) be the Laplace transform of \( y(t) \) Take the Laplace transform of both sides of the given differential equation \( \mathscr{L}\{ y'' - y' - 2 y \} = \mathscr{L}\{ \sin(3t) \} \) Use linearity property of Laplace transform to expand the left side and use table to evaluate the right side. \( \mathscr{L}\{ y"\} - \mathscr{L}\{ y'\} - 2 \mathscr{L}\{ y \} = \dfrac{3}{s^2+3^2} \) Use first and second derivative properties to rewrite the terms \( \mathscr{L}\{ y"\} \) and \( \mathscr{L}\{ y'\} \) and simplify the right side. \( s^2 Y(s) - s y(0) - y'(0) - (sY(s) - y(0)) + 2 Y(s) = \dfrac{3}{s^2+3^2} \) Substitute \( y(0) \) and \( y'(0) \) by their numerical values and expand \( s^2 Y(s) - s + 1 - s Y(s) + 1 - 2 Y(s) = \dfrac{3}{s^2+3^2} \) Group like terms and keep terms with \( Y(s) \) on the left side of the equation \( s^2 Y(s) - s Y(s) - 2 Y(s) = \dfrac{3}{s^2+3^2} + s - 2 \) Factor \( Y(s) \) out on the left side \( Y(s) (s^2 - s - 2 ) = \dfrac{3}{s^2+3^2} + s - 2 \) Solve the above for \( Y(s) \) \( Y(s) = \dfrac{3}{(s^2+3^2)(s^2 - s - 2)} + \dfrac{s-2}{s^2 - s - 2} \) Factor the term \( s^2 - s - 2 \) in the denominator \( Y(s) = \dfrac{3}{(s^2+3^2)(s-2)(s+1)} + \dfrac{s-2}{(s-2)(s+1)} \) which may be expanded in partial fractions as (see Appendix C at the bottom of the page for details). \( Y(s) = \dfrac{3s}{130(s^2+3^2)} - \dfrac{33}{130(s^2+3^2)} + \dfrac{9}{10(s+1)} + \dfrac{1}{13(s-2)} \) We now use formulas in the table of formulas of Laplace tranform to find the inverse Laplace transform of \( Y(s) \) which is given by \( y(t) = \dfrac{3}{130} \cos(3x) - \dfrac{11}{130} \sin(3x) + \dfrac{9}{10} e^{-x} +\dfrac{1}{13} e^{2x}\)

Partial fractions decomposition of example 2 Factor denominator \( \dfrac{2s - 5}{s^2 - 2 s - 3} = \dfrac{2s - 5}{(s-3)(s+1)} \) Expand into partial fractions \( \dfrac{2s - 5}{s^2 - 2 s - 3} = \dfrac{A}{s+1} + \dfrac{B}{s-3} \) Multiply all terms of the above by \( (s-3)(s+1) \) and simplify \( 2s - 5 = A(s-3) + B(s+1) \)      (1) Set \( s = 3 \) in equation (1) 2(3) - 5 = A(3 -3) + B(3+1) Simplify and solve for \( B \) \( B = 1/4 \) Set \( s = - 1 \) in equation (1) \( 2(-1) - 5 = A(-1-3) + B(-1+1) \) Simplify and solve for \( A \) \( A = \dfrac{7}{4} \)

Partial fractions decomposition of example 3 Partial fractions decomposition of \( \dfrac{-s}{(s - s_1)(s - s_2)} \) \( \dfrac{-s}{(s - s_1)(s - s_2)} = \dfrac{A}{s-s_1} + \dfrac{B}{s-s_2} \) Multiply all terms of the above by \( (s - s_1)(s - s_2) \) and simplify \( - s = A (s-s_2) + B(s - s_1) \)       (1) Evaluate the above at \(s=s_1 \) \( - s_1 = A (s_1-s_2) + B(s_1 - s_1) \) Simplify \( -s_1 = A (s_1-s_2) \) Solve for \( A \) \( A = \dfrac{-s_1}{s_1-s_2} = \dfrac{-(-1 + j)}{2 j} = -\dfrac{1}{2} - \dfrac{1}{2} j \) Evaluate both sides of eq equation (1) at \( S = s_2 \) and find \( B \) in a similar way as finding \( A \) above \( B = \dfrac{-s_2}{s_2-s_1} = \dfrac{-(-1 - j)}{-2 j} = - \dfrac{1}{2} + \dfrac{1}{2} j \)

Expand in partial fractions from example 4 \( \dfrac{3}{(s^2+3^2)(s^2 - s - 2)} + \dfrac{s-2}{s^2 - s - 2}\) Factor denominators \( \dfrac{3}{(s^2+3^2)(s-2)(s+1)} + \dfrac{s-2}{(s-2)(s+1)}\) Simplify the term on the right \( \dfrac{3}{(s^2+3^2)(s-2)(s+1)} + \dfrac{1}{s+1} \) Express into partial fractions \( \dfrac{3}{(s^2+3^2)(s-2)(s+1)} + \dfrac{1}{s+1} = \dfrac{As + B}{s^2+3^2} + \dfrac{C}{s+1} + \dfrac{D}{s-2} \) Multiply all terms of the above by the denominator \( (s^2+3^2)(s-2)(s+1) \) and simplify \( 3 + (s^2+3^2)(s-2) = (As + B)(s-2)(s+1) + C (s^2+3^2)(s-2) + D (s^2+3^2)(s+1) \)     (1) Select values of \( s \) that simplify calculations for the coefficients \( A, B, C \) and \( D \) Set \( s = 2 \) on both sides of equation (1) \( 3 + (2^2+3^2)(2-2) = (2 A + B)(2-2)(s+1) + C (2^2+3^2)(2-2) + D (2^2+3^2)(2+1) \) Simplify \( 3 = 39 D \) Solve for \( D \) \( D = \dfrac{1}{13} \) Set \( s = -1 \) on both sides of equation (1) \( 3 + ((-1)^2+3^2)(-1-2) = (-A + B)(-1-2)(-1+1) + C ((-1)^2+3^2)(-1-2) + D ((-1)^2+3^2)(-1+1) \) Simplify \( 3 - 30 = - 30 C \) Solve for \( C \) \( C = \dfrac{9}{10} \) Set \( s = 0 \) on both sides of equation (1) \( 3 +(0^2+3^2)(0-2) = (0 + B)(0-2)(0+1) + C (0^2+3^2)(0-2) + D (0^2+3^2)(0+1) \) Simplify \( 3 - 18 = -2 B - 19 C + 9D \) Substitute \( C \) and \( D \) by their numerical values obtained above and solve for B to obtain \( B = -\dfrac{33}{130} \) Set \( s = 1 \) on both sides of equation (1) \( 3 + (1^2+3^2)(1-2) = (A + B)(1-2)(1+1) + C (1^2+3^2)(1-2) + D (1^2+3^2)(1+1) \) Substitute \( B, C \) and \( D \) by their numerical values obtained above and solve for A to obtain \( A = \dfrac{3}{130} \) Hence \( \dfrac{3}{(s^2+3^2)(s^2 - s - 2)} + \dfrac{s-2}{s^2 - s - 2}\) \( \quad \quad = \dfrac{As}{s^2+3^2} + \dfrac{B}{s^2+3^2} + \dfrac{C}{s+1} + \dfrac{D}{s-2} \) \( \quad \quad = \dfrac{ 3s}{130(s^2+3^2)} - \dfrac{33}{130(s^2+3^2)} + \dfrac{9}{10(s+1)} + \dfrac{1}{13(s-2)} \)

More References and Links

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Introduction to the Laplace Transform

• Last updated
• Save as PDF
• Page ID 43322

• William F. Trench
• Trinity University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Definition of the Laplace Transform

To define the Laplace transform, we first recall the definition of an improper integral . If \(g\) is integrable over the interval \([a,T]\) for every \(T>a\), then the improper integral of \(g\) over \([a,\infty)\) is defined as

\[\label{eq:8.1.1} \int^\infty_a g(t)\,dt=\lim_{T\to\infty}\int^T_a g(t)\,dt.\]

We say that the improper integral converges if the limit in Equation \ref{eq:8.1.1} exists; otherwise, we say that the improper integral diverges or does not exist . Here’s the definition of the Laplace transform of a function \(f\).

Defintion 8.1.1 : Laplace Transform

Let \(f\) be defined for \(t\ge0\) and let \(s\) be a real number. Then the Laplace transform of \(f\) is the function \(F\) defined by

\[\label{eq:8.1.2} F(s)=\int_0^\infty e^{-st} f(t)\,dt,\]

for those values of \(s\) for which the improper integral converges.

It is important to keep in mind that the variable of integration in Equation \ref{eq:8.1.2} is \(t\), while \(s\) is a parameter independent of \(t\). We use \(t\) as the independent variable for \(f\) because in applications the Laplace transform is usually applied to functions of time.

The Laplace transform can be viewed as an operator \({\cal L}\) that transforms the function \(f=f(t)\) into the function \(F=F(s)\). Thus, Equation \ref{eq:8.1.2} can be expressed as

\[F={\cal L}(f).\nonumber \]

The functions \(f\) and \(F\) form a transform pair , which we’ll sometimes denote by

\[f(t)\leftrightarrow F(s).\nonumber\]

It can be shown that if \(F(s)\) is defined for \(s=s_0\) then it is defined for all \(s>s_0\) ( Exercise 8.1.14b ).

Computation of Some Simple Laplace Transforms

Example 8.1.1.

Find the Laplace transform of \(f(t)=1\).

From Equation \ref{eq:8.1.2} with \(f(t)=1\),

\[F(s)=\int_0^\infty e^{-st}\,dt=\lim_{T\to\infty}\int_0^T e^{-st}\, dt.\nonumber\]

If \(s\ne 0\) then

\[\label{eq:8.1.3} \int_0^T e^{-st}dt=-{1\over s}e^{-st}\Big|_0^T={1-e^{-sT}\over s}.\]

\[\label{eq:8.1.4} \lim_{T\to\infty}\int_0^T e^{-st}dt=\left\{\begin{array}{rr} {1\over s}, & s>0,\\ \infty, & s<0. \end{array}\right.\]

If \(s=0\) the integrand reduces to the constant \(1\), and

\[\lim_{T\to\infty}\int_0^T 1\,dt=\lim_{T\to\infty}\int_0^T 1\,dt= \lim_{T\to\infty}T=\infty.\nonumber\]

Therefore \(F(0)\) is undefined, and

\[F(s)=\int_0^\infty e^{-st}dt={1\over s},\quad s>0.\nonumber\]

This result can be written in operator notation as

\[{\cal L}(1)={1\over s},\quad s>0,\nonumber\]

or as the transform pair

\[1\leftrightarrow{1\over s},\quad s>0.\nonumber\]

It is convenient to combine the steps of integrating from \(0\) to \(T\) and letting \(T → ∞\). Therefore, instead of writing Equation \ref{eq:8.1.3} and \ref{eq:8.1.4} as separate steps we write

\[\int_{0}^{\infty} e^{-s t} d t=-\left.\frac{1}{s} e^{-s t}\right|_{0} ^{\infty}=\left\{\begin{array}{cl}{\frac{1}{s},} & {s>0} \\ {\infty,} & {s<0}\end{array}\right. \nonumber\]

We'll follow this practice throughout this chapter.

Example 8.1.2

Find the Laplace transform of \(f(t)=t\).

From Equation \ref{eq:8.1.2} with \(f(t)=t\),

\[\label{eq:8.1.5} F(s)=\int_0^\infty e^{-st}t\,dt.\]

If \(s\ne0\), integrating by parts yields

\[\begin{align*} \int_0^\infty e^{-st}t\,dt&=-{te^{-st}\over s}\bigg|_0^\infty +{1\over s}\int_0^\infty e^{-st}\,dt =-\left[{t\over s}+{1\over s^2}\right]e^{-st}\bigg|_0^\infty \\&=\left\{\begin{array}{rr} {1\over s^2},\quad s>0,\\ \infty,\,s<0.\end{array}\right.\end{align*}\nonumber\]

If \(s=0\), the integral in Equation \ref{eq:8.1.5} becomes

\[\int_0^\infty t\,dt={t^2\over2}\bigg|_0^\infty=\infty.\nonumber\]

Therefore \(F(0)\) is undefined and

\[F(s)={1\over s^2},\quad s>0.\nonumber\]

This result can also be written as

\[{\cal L}(t)={1\over s^2},\quad s>0,\nonumber\]

\[t\leftrightarrow{1\over s^2},\quad s>0.\nonumber\]

Example 8.1.3

Find the Laplace transform of \(f(t)=e^{at}\), where \(a\) is a constant.

From Equation \ref{eq:8.1.2} with \(f(t)=e^{at}\),

\[F(s)=\int_0^\infty e^{-st}e^{at}\,dt.\nonumber\]

Combining the exponentials yields

\[F(s)=\int_0^\infty e^{-(s-a)t}\,dt.\nonumber\]

However, we know from Example 8.1.1 that

\[\int_0^\infty e^{-st}\,dt={1\over s},\quad s>0.\nonumber\]

Replacing \(s\) by \(s-a\) here shows that

\[F(s)={1\over s-a},\quad s>a.\nonumber\]

This can also be written as

\[{\cal L}(e^{at})={1\over s-a},\quad s>a, \text{ or } e^{at}\leftrightarrow{1\over s-a},\quad s>a.\nonumber\]

Example 8.1.4

[ Find the Laplace transforms of \(f(t)=\sin\omega t\) and \(g(t)=\cos\omega t\), where \(\omega\) is a constant.

\[\label{eq:8.1.6} F(s)=\int_0^\infty e^{-st}\sin\omega t\,dt\]

\[\label{eq:8.1.7} G(s)=\int_0^\infty e^{-st}\cos\omega t\,dt.\]

If \(s>0\), integrating Equation \ref{eq:8.1.6} by parts yields

\[F(s)=-{e^{-st}\over s}\sin\omega t\Big|_0^\infty+{\omega\over s} \int_0^\infty e^{-st}\cos\omega t\,dt,\nonumber\]

\[\label{eq:8.1.8} F(s)={\omega\over s}G(s).\]

If \(s>0\), integrating Equation \ref{eq:8.1.7} by parts yields

\[G(s)=-{e^{-st}\cos\omega t\over s}\Big|_0^\infty - {\omega\over s} \int_0^\infty e^{-st}\sin\omega t\,dt,\nonumber\]

\[G(s)={1\over s} - {\omega\over s} F(s).\nonumber\]

Now substitute from Equation \ref{eq:8.1.8} into this to obtain

\[G(s)={1\over s} - {\omega^2\over s^2} G(s).\nonumber\]

Solving this for \(G(s)\) yields

\[G(s)={s\over s^2+\omega^2},\quad s>0.\nonumber\]

This and Equation \ref{eq:8.1.8} imply that

\[F(s)={\omega\over s^2+\omega^2},\quad s>0.\nonumber\]

Tables of Laplace Transforms

Extensive tables of Laplace transforms have been compiled and are commonly used in applications. The brief table of Laplace transforms in the Appendix will be adequate for our purposes.

Example 8.1.5

Use the table of Laplace transforms to find \({\cal L}(t^3e^{4t})\).

The table includes the transform pair

\[t^ne^{at}\leftrightarrow {n!\over(s-a)^{n+1}}.\nonumber\]

Setting \(n=3\) and \(a=4\) here yields

\[\cal L (t^3e^{4t})={3!\over(s-4)^4}={6\over(s-4)^4}.\nonumber\]

We’ll sometimes write Laplace transforms of specific functions without explicitly stating how they are obtained. In such cases you should refer to the table of Laplace transforms.

Linearity of the Laplace Transform

The next theorem presents an important property of the Laplace transform.

Theorem 8.1.2 Linearity Property

Suppose \({\cal L}(f_i)\) is defined for \(s>s_i,\) \(1\le i\le n).\) Let \(s_0\) be the largest of the numbers \(s_1\), \(s_{2},\) …,\(s_n,\) and let \(c_1\), \(c_2\),…, \(c_n\) be constants. Then

\[{\cal L}(c_1f_1+c_2f_2+\cdots+c_nf_n)=c_1{\cal L}(f_1)+c_2{\cal L}(f_2) +\cdots+c_n{\cal L}(f_n)\mbox{ for } s>s_0.\nonumber\]

We give the proof for the case where \(n=2\). If \(s>s_0\) then

\[\begin{aligned} {\cal L}(c_1f_1+c_2f_2)&= \int_0^\infty e^{-st}\left(c_1f_1(t)+c_2f_2(t))\right)\,dt\\ &= c_1\int_0^\infty e^{-st}f_1(t)\,dt+c_2\int_0^\infty e^{-st}f_2(t)\,dt\\ &= c_1{\cal L}(f_1)+c_2{\cal L}(f_2).\end{aligned}\nonumber\]

Example 8.1.6

Use Theorem 8.1.2 and the known Laplace transform

\[{\cal L}(e^{at})={1\over s-a} \nonumber\]

to find \({\cal L}(\cosh bt)\,(b\ne0)\).

By definition,

\[\cosh bt={e^{bt}+e^{-bt}\over 2}. \nonumber\]

\[\label{eq:8.1.9} \begin{array}{ccl} {\cal L}(\cosh bt)&=& {\cal L}\left( {1\over 2} e^{bt}+ {1\over 2}e^{-bt}\right)\\[4pt] &=& {1\over 2} {\cal L}(e^{bt}) + {1\over 2} {\cal L}(e^{-bt}) \qquad \hbox{(linearity property)}\\[4pt] &=& {1\over 2}\, {1\over s-b} + {1\over 2}\, {1\over s+b}, \end{array}\]

where the first transform on the right is defined for \(s>b\) and the second for \(s>-b\); hence, both are defined for \(s>|b|\). Simplifying the last expression in Equation \ref{eq:8.1.9} yields

\[{\cal L}(\cosh bt)={s\over s^2-b^2},\quad s>|b|.\nonumber\]

The next theorem enables us to start with known transform pairs and derive others. (For other results of this kind, see Exercises 8.1.6 and 8.1.13 .)

Theorem 8.1.3 First Shifting Theorem

\[\label{eq:8.1.10} F(s)=\int_0^\infty e^{-st} f(t)\,dt\]

is the Laplace transform of \(f(t)\) for \(s>s_0\), then \(F(s-a)\) is the Laplace transform of \(e^{at}f(t)\) for \(s >s_0+a\).

Replacing \(s\) by \(s-a\) in Equation \ref{eq:8.1.10} yields

\[\label{eq:8.1.11} F(s-a)=\int_0^\infty e^{-(s-a)t}f(t)\,dt\]

if \(s-a>s_0\); that is, if \(s>s_0+a\). However, Equation \ref{eq:8.1.11} can be rewritten as

\[F(s-a)=\int_0^\infty e^{-st}\left(e^{at}f(t)\right)\,dt,\nonumber\]

which implies the conclusion.

Example 8.1.7

Use Theorem 8.1.3 and the known Laplace transforms of \(1\), \(t\), \(\cos\omega t\), and \(\sin\omega t\) to find

\[{\cal L}(e^{at}),\quad {\cal L}(te^{at}),\quad {\cal L}(e^{\lambda t}\sin \omega t),\mbox{and } {\cal L}(e^{\lambda t}\cos\omega t).\nonumber\]

In the following table the known transform pairs are listed on the left and the required transform pairs listed on the right are obtained by applying Theorem 8.1.3 .

Existence of Laplace Transforms

Not every function has a Laplace transform. For example, it can be shown ( Exercise 8.1.3 ) that

\[\int_0^\infty e^{-st}e^{t^2} dt=\infty\nonumber\]

for every real number \(s\). Hence, the function \(f(t)=e^{t^2}\) does not have a Laplace transform.

Our next objective is to establish conditions that ensure the existence of the Laplace transform of a function. We first review some relevant definitions from calculus.

Recall that a limit

\[\lim_{t\to t_0} f(t)\nonumber\]

exists if and only if the one-sided limits

\[\lim_{t\to t_0-}f(t)\quad \text{and} \quad \lim_{t\to t_0+}f(t)\nonumber\]

both exist and are equal; in this case,

\[\lim_{t\to t_0}f(t)=\lim_{t\to t_0-}f(t)=\lim_{t\to t_0+}f(t) .\nonumber\]

Recall also that \(f\) is continuous at a point \(t_0\) in an open interval \((a,b)\) if and only if

\[\lim_{t\to t_0}f(t)=f(t_0),\nonumber\]

which is equivalent to

\[\label{eq:8.1.12} \lim_{t\to t_0+}f(t)=\lim_{t\to t_0-}f(t)=f(t_0).\]

For simplicity, we define

\[f(t_0+)=\lim_{t\to t_0+}f(t)\quad\hbox{and }\quad f(t_0-)=\lim_{t\to t_0-}f(t),\nonumber\]

so Equation \ref{eq:8.1.12} can be expressed as

\[f(t_0+)=f(t_0-)=f(t_0).\nonumber\]

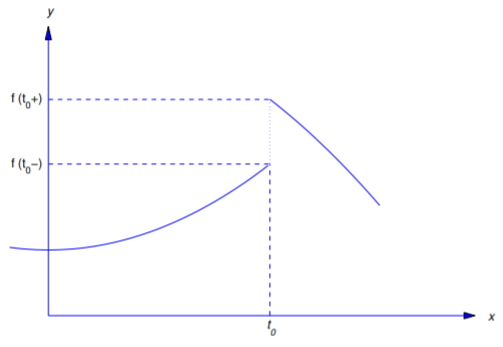
If \(f(t_0+)\) and \(f(t_0-)\) have finite but distinct values, we say that \(f\) has a jump discontinuity at \(t_0\), and

\[f(t_0+)-f(t_0-)\nonumber\]

is called the jump in \(f\) at \(t_0\) (Figure 8.1.1 ).

If \(f(t_0+)\) and \(f(t_0-)\) are finite and equal, but either \(f\) isn’t defined at \(t_0\) or it is defined but

\[f(t_0)\ne f(t_0+)=f(t_0-),\nonumber\]

we say that \(f\) has a removable discontinuity at \(t_0\) (Figure 8.1.2 ). This terminolgy is appropriate since a function \(f\) with a removable discontinuity at \(t_0\) can be made continuous at \(t_0\) by defining (or redefining)

\[f(t_0)=f(t_0+)=f(t_0-).\nonumber\]

We know from calculus that a definite integral isn’t affected by changing the values of its integrand at isolated points. Therefore, redefining a function f to make it continuous at removable discontinuities does not change \(\cal{L}(f)\).

Definition 8.1.4 : Piecewise Continuous

• A function \(f\) is said to be piecewise continuous on a finite closed interval \([0,T]\) if \(f(0+)\) and \(f(T-)\) are finite and \(f\) is continuous on the open interval \((0,T)\) except possibly at finitely many points, where \(f\) may have jump discontinuities or removable discontinuities.
• A function \(f\) is said to be piecewise continuous on the infinite interval \([0,\infty)\) if it is piecewise continuous on \([0,T]\) for every \(T>0\).

Figure 8.1.3 shows the graph of a typical piecewise continuous function.

It is shown in calculus that if a function is piecewise continuous on a finite closed interval then it is integrable on that interval. But if \(f\) is piecewise continuous on \([0,\infty)\), then so is \(e^{-st}f (t)\), and therefore

\[\int_0^T e^{-st}f(t)\,dt \nonumber\]

exists for every \(T>0\). However, piecewise continuity alone does not guarantee that the improper integral

\[\label{eq:8.1.13} \int_0^\infty e^{-st}f(t)\,dt=\lim_{T\to\infty}\int_0^T e^{-st}f(t)\, dt\]

converges for \(s\) in some interval \((s_0,\infty)\). For example, we noted earlier that Equation \ref{eq:8.1.13} diverges for all \(s\) if \(f(t)=e^{t^2}\). Stated informally, this occurs because \(e^{t^2}\) increases too rapidly as \(t\to\infty\). The next definition provides a constraint on the growth of a function that guarantees convergence of its Laplace transform for \(s\) in some interval \((s_0,\infty)\).

Definition 8.1.5 : of exponential order

A function \(f\) is said to be of exponential order \(s_0\) if there are constants \(M\) and \(t_0\) such that

\[\label{eq:8.1.14} |f(t)|\le Me^{s_0t},\quad t\ge t_0.\]

In situations where the specific value of \(s_0\) is irrelevant we say simply that \(f\) is of exponential order .

The next theorem gives useful sufficient conditions for a function \(f\) to have a Laplace transform. The proof is sketched in Exercise 8.1.10 .

Theorem 8.1.6

If \(f\) is piecewise continuous on \([0,\infty)\) and of exponential order \(s_0,\) then \({\cal L}(f)\) is defined for \(s>s_0\).

We emphasize that the conditions of Theorem 8.1.6 are sufficient, but not necessary , for \(f\) to have a Laplace transform. For example, Exercise 8.1.14(c) shows that \(f\) may have a Laplace transform even though \(f\) isn’t of exponential order

Example 8.1.8

If \(f\) is bounded on some interval \([t_0,\infty)\), say

\[|f(t)|\le M,\quad t\ge t_0,\nonumber\]

then Equation \ref{eq:8.1.14} holds with \(s_0=0\), so \(f\) is of exponential order zero. Thus, for example, \(\sin\omega t\) and \(\cos \omega t\) are of exponential order zero, and Theorem 8.1.6 implies that \({\cal L}(\sin\omega t)\) and \({\cal L}(\cos \omega t)\) exist for \(s>0\). This is consistent with the conclusion of Example 8.1.4 .

Example 8.1.9

It can be shown that if \(\lim_{t\to\infty}e^{-s_0t}f(t)\) exists and is finite then \(f\) is of exponential order \(s_0\) ( Exercise 8.1.9 ). If \(\alpha\) is any real number and \(s_0>0\) then \(f(t)=t^\alpha\) is of exponential order \(s_0\), since

\[\lim_{t\to\infty}e^{-s_0t}t^\alpha=0,\nonumber\]

by L’Hôpital’s rule. If \(\alpha\ge 0\), \(f\) is also continuous on \([0,\infty)\). Therefore Exercise 8.1.9 and Theorem 8.1.6 imply that \({\cal L}(t^\alpha)\) exists for \(s\ge s_0\). However, since \(s_0\) is an arbitrary positive number, this really implies that \({\cal L}(t^\alpha)\) exists for all \(s>0\). This is consistent with the results of Example 8.1.2 and Exercises 8.1.6 and 8.1.8 .

Example 8.1.10

Find the Laplace transform of the piecewise continuous function

\[f(t)=\left\{\begin{array}{cl} 1,&0\le t<1,\\ -3e^{-t},&t\ge 1.\end{array}\right.\nonumber\]

Since \(f\) is defined by different formulas on \([0,1)\) and \([1,\infty)\), we write

\[F(s)=\int_0^\infty e^{-st} f(t)\,dt =\int_0^1e^{-st}(1)\,dt+\int_1^\infty e^{-st}(-3e^{-t})\,dt.\nonumber\]

\[\int_{0}^{1}e^{-st}dt = \left\{\begin{array}{cl} {\frac{1-e^{-s}}{s}}&{s\neq 0} \\ {1}&{s=0} \end{array} \right. \nonumber \]

\[\int_1^\infty e^{-st}(-3e^{-t})\,dt=-3\int_1^\infty e^{-(s+1)t}\,dt=-{3e^{-(s+1)}\over s+1},\quad s>-1,\nonumber\]

it follows that

\[F(s) = \left\{\begin{array}{rl}{\frac{1-e^{-s}}{s}-3\frac{e^{-(s+1)}}{s+1}}&{s>-1, s\neq 0} \\ {1-\frac{3}{e}}&{s=0} \end{array} \right. \nonumber \]

This is consistent with Theorem 8.1.6 , since

\[|f(t)|\le 3e^{-t},\quad t\ge 1,\nonumber\]

and therefore \(f\) is of exponential order \(s_0=-1\).

In Section 8.4 we’ll develop a more efficient method for finding Laplace transforms of piecewise continuous functions.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• First Derivative
• Product Rule
• Quotient Rule
• Sum/Diff Rule
• Second Derivative
• Third Derivative
• Higher Order Derivatives
• Derivative at a point
• Partial Derivative
• Implicit Derivative
• Second Implicit Derivative
• Derivative using Definition
• Slope of Tangent
• Curved Line Slope
• Extreme Points
• Tangent to Conic
• Linear Approximation
• Difference Quotient
• Horizontal Tangent
• One Variable
• Multi Variable Limit
• At Infinity
• L'Hopital's Rule
• Squeeze Theorem
• Substitution
• Sandwich Theorem
• Indefinite Integrals
• Definite Integrals
• Partial Fractions
• U-Substitution
• Trigonometric Substitution
• Weierstrass Substitution
• Long Division
• Improper Integrals
• Antiderivatives
• Double Integrals
• Triple Integrals
• Multiple Integrals
• Limit of Sum
• Area under curve
• Area between curves
• Area under polar curve
• Volume of solid of revolution
• Function Average
• Riemann Sum
• Trapezoidal
• Simpson's Rule
• Midpoint Rule
• Geometric Series Test
• Telescoping Series Test
• Alternating Series Test
• P Series Test
• Divergence Test
• Comparison Test
• Limit Comparison Test
• Integral Test
• Absolute Convergence
• Radius of Convergence
• Interval of Convergence
• Linear First Order
• Linear w/constant coefficients
• Second Order
• Non Homogenous
• System of ODEs
• IVP using Laplace
• Series Solutions
• Method of Frobenius
• Gamma Function
• Taylor Series
• Maclaurin Series
• Fourier Series
• Fourier Transform
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• laplace\:e^{\frac{t}{2}}
• laplace\:e^{-2t}\sin^{2}(t)
• laplace\:8\pi
• laplace\:g(t)=3\sinh(2t)+3\sin(2t)
• inverse\:laplace\:\frac{s}{s^{2}+4s+5}
• inverse\:laplace\:\frac{1}{x^{\frac{3}{2}}}
• inverse\:laplace\:\frac{\sqrt{\pi}}{3x^{\frac{3}{2}}}
• inverse\:laplace\:\frac{5}{4x^2+1}+\frac{3}{x^3}-5\frac{3}{2x}
• How do you calculate the Laplace transform of a function?
• The Laplace transform of a function f(t) is given by: L(f(t)) = F(s) = ∫(f(t)e^-st)dt, where F(s) is the Laplace transform of f(t), s is the complex frequency variable, and t is the independent variable.
• What is mean by Laplace equation?
• The Laplace equation is a second-order partial differential equation that describes the distribution of a scalar quantity in a two-dimensional or three-dimensional space. The Laplace equation is given by: ∇^2u(x,y,z) = 0, where u(x,y,z) is the scalar function and ∇^2 is the Laplace operator.
• What kind of math is Laplace?
• Laplace transforms are a type of mathematical operation that is used to transform a function from the time domain to the frequency domain. They are a specific example of a class of mathematical operations called integral transforms.
• Why is it called Laplace?
• The Laplace equation is named after the discoverer Pierre-Simon Laplace, a French mathematician and physicist who made significant contributions to the field of mathematics and physics in the 18th and 19th centuries.
• What does the Laplace equation use for?
• The Laplace equations are used to describe the steady-state conduction heat transfer without any heat sources or sinks

laplace-calculator

• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.