solving algebraic equations fractions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.9: Solving Equations with Fractions

• Last updated
• Save as PDF
• Page ID 24084

• David Arnold
• College of the Redwoods

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Undoing Subtraction

We can still add the same amount to both sides of an equation without changing the solution.

Solve for x : \(x - \frac{5}{6} = \frac{1}{3}\).

To “undo” subtracting 5/6, add 5/6 to both sides of the equation and simplify.

\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - \frac{5}{6} + \frac{5}{6} = \frac{1}{3} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Add } \frac{5}{6} \text{ to both sides.}} \\ x = \frac{1 \cdot 2}{3 \cdot 2} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 6.}} \\ x = \frac{2}{6} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

It is perfectly acceptable to leave your answer as an improper fraction. If you desire, or if you are instructed to do so, you can change your answer to a mixed fraction (7 divided by 6 is 1 with a remainder of 1). That is \(x = 1 \frac{1}{6}\).

Checking the Solution

Substitute 7/6 for x in the original equation and simplify.

\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{7}{6} - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Substitute 7/6 for } x.} \\ \frac{2}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Subtract.}} \\ \frac{1}{3} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]

Because the last statement is true, we conclude that 7/6 is a solution of the equation x − 5/6 = 1/3.

Undoing Addition

You can still subtract the same amount from both sides of an equation without changing the solution.

Solve for x : \(x + \frac{2}{3} = - \frac{3}{5}\).

To “undo” adding 2/3, subtract 2/3 from both sides of the equation and simplify.

\[ \begin{aligned} x + \frac{2}{3} = - \frac{3}{5} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + \frac{2}{3} - \frac{2}{3} = - \frac{3}{5} - \frac{2}{3} ~ & \textcolor{red}{ \text{ Subtract } \frac{2}{3} \text{ from both sides.}} \\ x = - \frac{3 \cdot 3}{5 \cdot 3} - \frac{2 \cdot 5}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 15.}} \\ x = - \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = - \frac{19}{15} ~ & \textcolor{red}{ \text{ Subtract.}} \end{aligned}\nonumber \]

Readers are encouraged to check this solution in the original equation.

Solve for x : \(x + \frac{3}{4} = - \frac{1}{2}\)

Undoing Multiplication

We “undo” multiplication by dividing. For example, to solve the equation 2 x = 6, we would divide both sides of the equation by 2. In similar fashion, we could divide both sides of the equation

\[ \frac{3}{5} x = \frac{4}{10}\nonumber \]

by 3/5. However, it is more efficient to take advantage of reciprocals. For convenience, we remind readers of the Multiplicative Inverse Property .

Multiplicative Inverse Property

Let a / b be any fraction. The number b / a is called the multiplicative inverse or reciprocal of a / b . The product of reciprocals is 1.

\[ \frac{a}{b} \cdot \frac{b}{a} = 1.\nonumber \]

Let’s put our knowledge of reciprocals to work.

Solve for x : \(\frac{3}{5}x = \frac{4}{10}\).

To “undo” multiplying by 3/5, multiply both sides by the reciprocal 5/3 and simplify.

\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{5}{3} \left( \frac{3}{5} x \right) = \frac{5}{3} \left( \frac{4}{10} \right) & ~ \textcolor{red}{ \text{ Multiply both sides by 5/3.}} \\ \left( \frac{5}{3} \cdot \frac{3}{5} \right) x = \frac{20}{30} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, multiply.} \end{array}} \\ 1x = \frac{2}{3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } \frac{5}{3} \cdot \frac{3}{5} = 1. \\ \text{ On the right, reduce: } \frac{20}{30} = \frac{2}{3}. \end{array}} \\ x = \frac{2}{3} ~ & \textcolor{red}{ \text{ On the left, } 1x = x.} \end{aligned}\nonumber \]

Substitute 2/3 for x in the original equation and simplify.

\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3}{5} \left( \frac{2}{3} \right) = \frac{4}{10} ~ & \textcolor{red}{ \text{ Substitute 2/3 for }x.} \\ \frac{6}{15} = \frac{4}{10} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ \frac{2}{5} = \frac{2}{5} ~ & \textcolor{red}{ \text{ Reduce both sides to lowest terms.}} \end{aligned}\nonumber \]

Because this last statement is true, we conclude that 2/3 is a solution of the equation (3/5) x = 4/10.

Solve for y : \( \frac{2}{3} y = \frac{4}{5}\)

Solve for x : \(- \frac{8}{9} x = \frac{5}{18}\).

To “undo” multiplying by −8/9, multiply both sides by the reciprocal −9/8 and simplify.

\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ - \frac{9}{8} \left( - \frac{8}{9} x \right) = - \frac{9}{8} \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -9/8.} \\ \left[ - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) \right] x = - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, prime factor.} \end{array}} 1x = \frac{ \cancel{3} \cdot \cancel{3}}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot \cancel{3} \cdot \cancel{3}} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) = 1. \\ \text{ On the right, cancel common factors.} \end{array}} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ On the left, } 1x = x. \text{ Multiply on the right.}} \end{aligned}\nonumber \]

Solve for z: \(− \frac{2}{7} z = \frac{4}{21}\)

Clearing Fractions from the Equation

Although the technique demonstrated in the previous examples is a solid mathematical technique, working with fractions in an equation is not always the most efficient use of your time.

To clear all fractions from an equation, multiply both sides of the equation by the least common denominator of the fractions that appear in the equation.

Let’s put this idea to work.

In Example 1, we were asked to solve the following equation for x :

\[x - \frac{5}{6} = \frac{1}{3}.\nonumber \]

Take a moment to review the solution technique in Example 1. We will now solve this equation by first clearing all fractions from the equation.

Multiply both sides of the equation by the least common denominator for the fractions appearing in the equation.

\[ \begin{aligned} x - \frac{5}{6}= \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 6 \left( x - \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 6.}} \\ 6x - 6 \left( \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Distribute the 6.}} \\ 6x-5 = 2 ~ & \textcolor{red}{ \text{ On each side, multiply first.}} \\ ~ & \textcolor{red}{6 \left( \frac{5}{6} \right) = 5 \text{ and } 6 \left( \frac{1}{3} \right) = 2.} \end{aligned}\nonumber \]

Note that the equation is now entirely clear of fractions, making it a much simpler equation to solve.

\[ \begin{aligned} 6x - 5 + 5 = 2 + 5 ~ & \textcolor{red}{ \text{ Add 5 to both sides.}} \\ 6x = 7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{6x}{6} = \frac{7}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Note that this is the same solution found in Example 1.

Solve for t : \(t - \frac{2}{7} = - \frac{1}{4}\)

In Example 4, we were asked to solve the following equation for x .

\[- \frac{8}{9}x = \frac{5}{18}\nonumber \]

Take a moment to review the solution in Example 4. We will now solve this equation by first clearing all fractions from the equation.

Multiply both sides of the equation by the least common denominator for the fractions that appear in the equation.

\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 18 \left( - \frac{8}{9} x \right) = 18 \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 18.}} \\ -16x=5 ~ & \textcolor{red}{ \text{ On each side, cancel and multiply.}} \\ ~ & \textcolor{red}{ 18 \left( - \frac{8}{9} \right) = -16 \text{ and } 18 \left( \frac{5}{18} \right) = 5.} \end{aligned}\nonumber \]

Note that the equation is now entirely free of fractions. Continuing,

\[ \begin{aligned} \frac{-16x}{-16} = \frac{5}{-16} ~ & \textcolor{red}{ \text{ Divide both sides by } -16.} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Note that this is the same as the solution found in Example 4.

Solve for u :

\[ - \frac{7}{9} u = \frac{14}{27}\nonumber \]

Solve for x : \(\frac{2}{3}x + \frac{3}{4} = \frac{1}{2}\).

\[ \begin{aligned} \frac{2}{3} x + \frac{3}{4} = \frac{1}{2} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 12 \left( \frac{2}{3} x + \frac{3}{4} = \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 12.}} \\ 12 \left( \frac{2}{3}x \right) + 12 \left( \frac{3}{4} \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ On the left, distribute 12.}} \\ 8x + 9 = 6 ~ & \textcolor{red}{ \text{ Multiply: } 12 \left( \frac{2}{3} x \right) = 8x, ~ 12 \left( \frac{3}{4} \right) = 9,} \\ ~ & \textcolor{red}{ \text{ and } 12 \left( \frac{1}{2} \right) = 6.} \end{aligned}\nonumber \]

Note that the equation is now entirely free of fractions. We need to isolate the terms containing x on one side of the equation.

\[ \begin{aligned} 8x + 9 - 9 = 6 - 9 ~ & \textcolor{red}{ \text{ Subtract 9 from both sides.}} \\ 8x = - 3 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{8x}{8} = \frac{-3}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = - \frac{3}{8} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Solve for r : \(\frac{3}{4} r + \frac{2}{3} = \frac{1}{2}\)

Solve for x : \( \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8}.\)

Multiply both sides of the equation by the least common denominator for the fractions in the equation.

\[ \begin{aligned} \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 24 \left( \frac{2}{3} - \frac{3x}{4} \right) = 24 \left( \frac{x}{2} - \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 24.}} \\ 24 \left( \frac{2}{3} \right) - 24 \left( \frac{3x}{4} \right) = 24 \left( \frac{x}{2} \right) - 24 \left( \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ On both sides, distribute 24.}} \\ 16 - 18x = 12x - 3 ~ & \textcolor{red}{ \text{ Left: } 24 \left( \frac{2}{3} \right) = 16, ~ 24 \left( \frac{3x}{4} \right) = 18x.} \\ ~ & \textcolor{red}{ \text{ Right: } 24 \left( \frac{x}{2} \right) = 12x, ~ 24 \left( \frac{1}{8} \right) = 3.} \end{aligned}\nonumber \]

\[ \begin{aligned} 16 - 18x - 12x = 12x - 3 - 12x ~ & \textcolor{red}{ \text{ Subtract } 12x \text{ from both sides.}} \\ 16 - 30x = -3 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } -18x - 12x = -30x. \\ \text{ Right: } 12x - 12x = 0. \end{aligned}} \\ 16 - 30x - 16 = -3 - 16 ~ & \textcolor{red}{ \text{ Subtract 16 from both sides.}} \\ -30x = -19 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } 16-16=0. \\ \text{ Right: } -3 - 16 = -19. \end{aligned}} \\ \frac{-30x}{-30} = \frac{-19}{-30} ~ & \textcolor{red}{ \text{ Divide both sides by } -30.} \\ x = \frac{19}{30} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Solve for s : \( \frac{3}{2} - \frac{2s}{5} = \frac{s}{3} - \frac{1}{5}\).

Add texts here. Do not delete this text first.

Applications

Let’s look at some applications that involve equations containing fractions. For convenience, we repeat the Requirements for Word Problem Solutions .

Requirements for Word Problem Solutions

• Statements such as “Let P represent the perimeter of the rectangle.”
• Labeling unknown values with variables in a table.
• Labeling unknown quantities in a sketch or diagram.
• Set up an Equation . Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
• Solve the Equation . You must always solve the equation set up in the previous step.
• Answer the Question . This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units. 5. Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”

In the third quarter of a basketball game, announcers informed the crowd that attendance for the game was 12,250. If this is two-thirds of the capacity, find the full seating capacity for the basketball arena.

We follow the Requirements for Word Problem Solutions .

1. Set up a Variable Dictionary . Let F represent the full seating capacity. Note: It is much better to use a variable that “sounds like” the quantity that it represents. In this case, letting F represent the full seating capacity is much more descriptive than using x to represent the full seating capacity.

2. Set up an Equation . Two-thirds of the full seating capacity is 12,250.

\[ \begin{aligned} \colorbox{cyan}{Two-thirds} & \text{ of } & \colorbox{cyan}{Full Seating Capacity} & \text{ is } & 12,250 \\ \frac{2}{3} & \cdot & F & = & 12,250 \end{aligned}\nonumber \]

Hence, the equation is

\[ \frac{2}{3} F = 12250.\nonumber \]

3. Solve the Equation . Multiply both sides by 3 to clear fractions, then solve.

\[ \begin{aligned} \frac{2}{3} F = 12250 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 \left( \frac{2}{3} F \right) = 3(12250) ~ & \textcolor{red}{ \text{ Multiply both sides by 3.}} \\ 2F = 36750 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2F}{2} = \frac{36750}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ F = 18375 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

4. Answer the Question . The full seating capacity is 18,375.

5. Look Back . The words of the problem state that 2/3 of the seating capacity is 12,250. Let’s take two-thirds of our answer and see what we get.

\[ \begin{aligned} \frac{2}{3} \cdot 18375 & = \frac{2}{3} \cdot \frac{18375}{1} \\ & = \frac{2}{3} \cdot \frac{3 \cdot 6125}{1} \\ & = \frac{2}{ \cancel{3}} \cdot \frac{ \cancel{3} \cdot 6125}{1} \\ & = 12250 \end{aligned}\nonumber \]

This is the correct attendance, so our solution is correct.

Attendance for the Celtics game was 9,510. If this is 3/4 of capacity, what is the capacity of the Celtics’ arena?

The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.

1. Set up a Variable Dictionary . Our variable dictionary will take the form of a well labeled diagram.

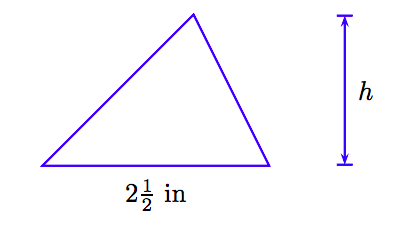
2. Set up an Equation . The area A of a triangle with base b and height h is

\[A = \frac{1}{2} bh.\nonumber \]

Substitute A = 20 and b = \(2 \frac{1}{2}\).

\[20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h.\nonumber \]

3. Solve the Equation . Change the mixed fraction to an improper fraction, then simplify.

\[ \begin{aligned} 20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h ~ & \textcolor{red}{ \text{ Original equation.}} \\ 20 = \frac{1}{2} \left( \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Mixed to improper: } 2 \frac{1}{2} = \frac{5}{2}.} \\ 20 = \left( \frac{1}{2} \cdot \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Associative property.}} \\ 20 = \frac{5}{4} h ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{2} \cdot \frac{5}{2} = \frac{5}{4}.} \end{aligned}\nonumber \]

Now, multiply both sides by 4/5 and solve.

\[ \begin{aligned} \frac{4}{5} (20) = \frac{4}{5} \left( \frac{5}{4} h \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 4/5.}} \\ 16 = h ~ & \textcolor{red}{ \text{ Simplify: } \frac{4}{5} (20) = 16} \\ ~ & \textcolor{red}{ \text{ and } \frac{4}{5} \cdot \frac{5}{4} = 1.} \end{aligned}\nonumber \]

4. Answer the Question . The height of the triangle is 16 inches.

5. Look Back . If the height is 16 inches and the base is \(2 \frac{1}{2}\) inches, then the area is

\[ \begin{aligned} A & = \frac{1}{2} \left( 2 \frac{1}{2} \right) (16) \\ & = \frac{1}{2} \cdot \frac{5}{2} \cdot \frac{16}{1} \\ & = \frac{5 \cdot 16}{2 \cdot 2} \\ & = \frac{(5) \cdot (2 \cdot 2 \cdot 2 \cdot 2)}{(2) \cdot (2)} \\ & = \frac{5 \cdot \cancel{2} \cdot \cancel{2} \cdot 2 \cot 2}{ \cancel{2} \cdot \cancel{2}} & = 20 \end{aligned}\nonumber \]

This is the correct area (20 square inches), so our solution is correct.

The area of a triangle is 161 square feet. If the base of the triangle measures \(40 \frac{1}{4}\) feet, find the height of the triangle.

1. Is 1/4 a solution of the equation \(x + \frac{5}{8} = \frac{5}{8}\)?

2. Is 1/4 a solution of the equation \(x + \frac{1}{3} = \frac{5}{12}\)?

3. Is −8/15 a solution of the equation \(\frac{1}{4} x = − \frac{1}{15}\)?

4. Is −18/7 a solution of the equation \(− \frac{3}{8} x = \frac{25}{28}\)?

5. Is 1/2 a solution of the equation \(x + \frac{4}{9} = \frac{17}{18}\)?

6. Is 1/3 a solution of the equation \(x + \frac{3}{4} = \frac{13}{12}\)?

7. Is 3/8 a solution of the equation \(x − \frac{5}{9} = − \frac{13}{72}\)?

8. Is 1/2 a solution of the equation \(x − \frac{3}{5} = − \frac{1}{10}\)?

9. Is 2/7 a solution of the equation \(x − \frac{4}{9} = − \frac{8}{63}\)?

10. Is 1/9 a solution of the equation \(x − \frac{4}{7} = − \frac{31}{63}\)?

11. Is 8/5 a solution of the equation \( \frac{11}{14}x = \frac{44}{35}\)?

12. Is 16/9 a solution of the equation \(\frac{13}{18} x = \frac{104}{81}\)?

In Exercises 13-24, solve the equation and simplify your answer.

13. \(2x − 3=6x + 7\)

14. \(9x − 8 = −9x − 3\)

15. \(−7x +4=3x\)

16. \(6x +9= −6x\)

17. \(−2x = 9x − 4\)

18. \(−6x = −9x + 8\)

19. \(−8x = 7x − 7\)

20. \(−6x = 5x + 4\)

21. \(−7x +8=2x\)

22. \(−x − 7=3x\)

23. \(−9x +4=4x − 6\)

24. \(−2x +4= x − 7\)

In Exercises 25-48, solve the equation and simplify your answer.

25. \(x + \frac{3}{2 = \frac{1}{2}\)

26. \(x − \frac{3}{4} = \frac{1}{4}\)

27. \(− \frac{9}{5} x = \frac{1}{2}\)

28. \(\frac{7}{3} x = − \frac{7}{2}\)

29. \(\frac{3}{8} x = \frac{8}{7}\)

30. \(− \frac{1}{9} x = − \frac{3}{5}\)

31. \(\frac{2}{5} x = − \frac{1}{6}\)

32. \(\frac{1}{6} x = \frac{2}{9}\)

33. \(− \frac{3}{2} x = \frac{8}{7}\)

34. \(− \frac{3}{2} x = − \frac{7}{5}\)

35. \(x + \frac{3}{4} = \frac{5}{9}\)

36. \(x − \frac{1}{9} = − \frac{3}{2}\)

37. \(x − \frac{4}{7} = \frac{7}{8}\)

38. \(x + \frac{4}{9} = − \frac{3}{4}\)

39. \(x + \frac{8}{9} = \frac{2}{3}\)

40. \(x − \frac{5}{6} = \frac{1}{4}\)

41. \(x + \frac{5}{2} = − \frac{9}{8}\)

42. \(x + \frac{1}{2} = \frac{5}{3}\)

43. \(− \frac{8}{5} x = \frac{7}{9}\)

44. \(− \frac{3}{2} x = − \frac{5}{9}\)

45. \(x − \frac{1}{4} = − \frac{1}{8}\)

46. \(x − \frac{9}{2} = − \frac{7}{2}\)

47. \(− \frac{1}{4} x = \frac{1}{2}\)

48. \(− \frac{8}{9} x = − \frac{8}{3}\)

In Exercises 49-72, solve the equation and simplify your answer.

49. \(− \frac{7}{3} x − \frac{2}{3} = \frac{3}{4} x + \frac{2}{3}\)

50. \(\frac{1}{2} x − \frac{1}{2} = \frac{3}{2} x + \frac{3}{4}\)

51. \(− \frac{7}{2} x − \frac{5}{4} = \frac{4}{5}\)

52. \(− \frac{7}{6} x + \frac{5}{6} = − \frac{8}{9}\)

53. \(− \frac{9}{7} x + \frac{9}{2} = − \frac{5}{2}\)

54. \(\frac{5}{9} x − \frac{7}{2} = \frac{1}{4}\)

55. \(\frac{1}{4} x − \frac{4}{3} = − \frac{2}{3}\)

56. \(\frac{8}{7} x + \frac{3}{7} = \frac{5}{3}\)

57. \(\frac{5}{3} x + \frac{3}{2} = − \frac{1}{4}\)

58. \(\frac{1}{2} x − \frac{8}{3} = − \frac{2}{5}\)

59. \(− \frac{1}{3} x + \frac{4}{5} = − \frac{9}{5} x − \frac{5}{6}\)

60. \(− \frac{2}{9} x − \frac{3}{5} = \frac{4}{5} x − \frac{3}{2}\)

61. \(− \frac{4}{9} x − \frac{8}{9} = \frac{1}{2} x − \frac{1}{2}\)

62. \(− \frac{5}{4} x − \frac{5}{3} = \frac{8}{7} x + \frac{7}{3}\)

63. \(\frac{1}{2} x − \frac{1}{8} = − \frac{1}{8} x + \frac{5}{7}\)

64. \(− \frac{3}{2} x + \frac{8}{3} = \frac{7}{9} x − \frac{1}{2}\)

65. \(− \frac{3}{7} x − \frac{1}{3} = − \frac{1}{9}\)

66. \(\frac{2}{3} x + \frac{2}{9} = − \frac{9}{5}\)

67. \(− \frac{3}{4} x + \frac{2}{7} = \frac{8}{7} x − \frac{1}{3}\)

68. \(\frac{1}{2} x + \frac{1}{3} = − \frac{5}{2} x − \frac{1}{4}\)

69. \(− \frac{3}{4} x − \frac{2}{3} = − \frac{2}{3} x − \frac{1}{2}\)

70. \(\frac{1}{3} x − \frac{5}{7} = \frac{3}{2} x + \frac{4}{3}\)

71. \(− \frac{5}{2} x + \frac{9}{5} = \frac{5}{8}\)

72. \(\frac{9}{4} x + \frac{4}{3} = − \frac{1}{6}\)

73. At a local soccer game, announcers informed the crowd that attendance for the game was 4,302. If this is 2/9 of the capacity, find the full seating capacity for the soccer stadium.

74. At a local basketball game, announcers informed the crowd that attendance for the game was 5,394. If this is 2/7 of the capacity, find the full seating capacity for the basketball stadium.

75. The area of a triangle is 51 square inches. If the length of the base is \(8 \frac{1}{2}\) inches, find the height (altitude) of the triangle.

76. The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.

77. The area of a triangle is 18 square inches. If the length of the base is \(4 \frac{1}{2}\) inches, find the height (altitude) of the triangle.

78. The area of a triangle is 44 square inches. If the length of the base is \(5 \frac{1}{2}\) inches, find the height (altitude) of the triangle.

79. At a local hockey game, announcers informed the crowd that attendance for the game was 4,536. If this is 2/11 of the capacity, find the full seating capacity for the hockey stadium.

80. At a local soccer game, announcers informed the crowd that attendance for the game was 6,970. If this is 2/7 of the capacity, find the full seating capacity for the soccer stadium.

81. Pirates . About one-third of the world’s pirate attacks in 2008 occurred off the Somali coast. If there were 111 pirate attacks off the Somali coast, estimate the number of pirate attacks worldwide in 2008.

82. Nuclear arsenal . The U.S. and Russia agreed to cut nuclear arsenals of long-range nuclear weapons by about a third, down to 1, 550. How many long-range nuclear weapons are there now? Associated Press-Times-Standard 04/04/10 Nuclear heartland anxious about missile cuts.

83. Seed vault . The Svalbard Global Seed Vault has amassed half a million seed samples, and now houses at least one-third of the world’s crop seeds. Estimate the total number of world’s crop seeds. Associated Press-Times-Standard 03/15/10 Norway doomsday seed vault hits half-million mark.

84. Freight train . The three and one-half mile long Union Pacific train is about 2 1 2 times the length of a typical freight train. How long is a typical freight train? Associated Press-Times-Standard 01/13/10 Unusally long train raises safety concerns.

13. \(− \frac{5}{2}\)

15. \(\frac{2}{5}\)

17. \(\frac{4}{11}\)

19. \(\frac{7}{15}\)

21. \(\frac{8}{9}\)

23. \(\frac{10}{13}\)

25. \(−1\)

27. \(− \frac{5}{18}\)

29. \(\frac{64}{21}\)

31. \(− \frac{5}{12}\)

33. \(− \frac{16}{21}\)

35. \(− \frac{7}{36}\)

37. \(\frac{81}{56}\)

39. \(− \frac{2}{9}\)

41. \(− \frac{29}{8}\)

43. \(− \frac{35}{72}\)

45. \(\frac{1}{8}\)

47. \(−2\)

49. \(− \frac{16}{37}\)

51. \(− \frac{41}{70}\)

53. \(\frac{49}{9}\)

55. \(\frac{8}{3}\)

57. \(− \frac{21}{20}\)

59. \(− \frac{49}{44}\)

61. \(− \frac{7}{17}\)

63. \(\frac{47}{35}\)

65. \(− \frac{14}{27}\)

67. \(\frac{52}{159}\)

69. \(− 2\)

71. \(\frac{47}{100}\)

81. There were about 333 pirate attacks worldwide.

83. 1,500,000

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Solving Equations with Fractions

I know fractions are difficult, but with these easy step-by step instructions you'll be solving equations with fractions in no time.

Do you start to get nervous when you see fractions? Do you have to stop and review all the rules for adding, subtracting, multiplying and dividing fractions?

If so, you are just like almost every other math student out there! But... I am going to make your life so much easier when it comes to solving equations with fractions!

Our first step when solving these equations is to get rid of the fractions because they are not easy to work with!

Let see what happens with a typical two-step equation with the distributive property.

In this problem, we would typically distribute the 3/4 throughout the parenthesis and then solve. Let's see what happens:

Yuck! That just made this problem worse! Now we have two fractions to contend with and that means subtracting fractions and multiplying fractions.

So... let's stop here and say,

We DO NOT want to do this! DO NOT distribute fractions.

We are going to learn how to get rid of the fractions and make this much more simple!

So... what do we do? We are going to get rid of just the denominator in the fraction, so we will be left with the numerator, or just an integer!

I know, easier said than done! It's really not hard, but before I get into it, I want to go over one algebra definition.

We need to discuss the word term.

In Algebra, each term within an equation is separated by a plus (+) sign, minus (-) sign or an equals sign (=). Variable or quantities that are multiplied or divided are considered the same term.

That last example is the most important to remember. If a quantity is in parentheses, it it considered one term!

Let's look at a few examples of how to solve these crazy looking problems!

Example 1 - Equations with Fractions

Take a look at this example on video if you are feeling overwhelmed.

Hopefully you were able to follow that example. I know it's tough, but if you can get rid of the fraction, it will make these problems so much easier. Keep going, you'll get the hang of it!

In the next example, you will see two fractions.  Since they have the same denominator, we will multiply by the denominator and get rid of both fractions.

Example 2 - Equations with Fractions with the Same Denominator

Did you notice how multiplying by 2 (the denominator of both fractions) allowed us to get rid of the fractions?  This is the best way to deal with equations that contain fractions.

In the next example, you will see what happens when you have 2 fractions that have different denominators. 

We still want to get rid of the fractions all in one step. Therefore, we need to multiply all terms by the least common multiple.  Remember how to find the LCM?  If not, check out the LCM lesson here .

Example 3 - Equations with Two Fractions with Different Denominators

Yes, the equations are getting harder, but if you take it step-by-step, you will arrive at the correct solution. Keep at it - I know you'll get it!

• Solving Equations
• Equations with Fractions

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Algebraic Fractions

Here we will learn about algebraic fractions , including operations with fractions, and solving linear and quadratic equations written in the form of algebraic fractions.

There are also algebraic fractions worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are algebraic fractions?

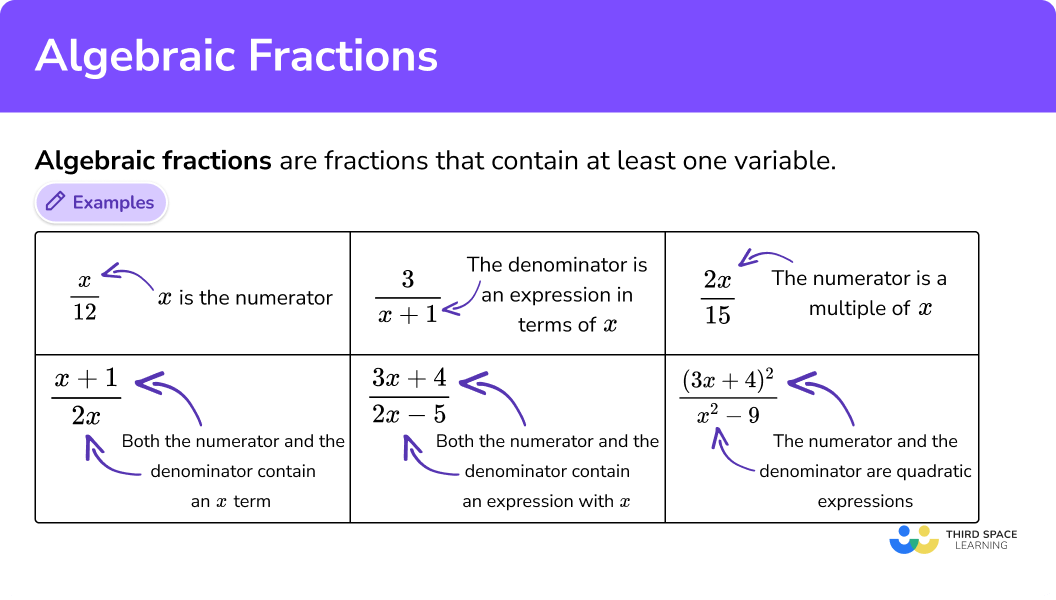
Algebraic fractions are fractions that contain at least one variable.

The following algebraic expressions are examples of algebraic fractions:

x is the numerator:       \quad \quad \quad \frac{x}{12}   Both the numerator and the denominator contain an x term:       \quad \quad \quad \frac{x+1}{2x}

   An expression in    terms of x is the    denominator:       \quad \quad \frac{3}{x+1}\      Both the numerator    and the    denominator    contain an    expression with x :       \quad \quad \frac{3x+4}{2x-5}

   The numerator is a multiple of x :           \quad\quad \quad \quad \frac{2x}{15}      The numerator and the denominator are    quadratic expressions:             \quad\quad \quad \quad \frac{(x+3)^{2}}{x^{2}-9}

The main aim of this lesson is to understand how to solve equations that include algebraic fractions.

All the examples above are expressions whereas the examples below are equations as we can find specific values for x for each example to solve the equation.

One step equation:     \quad \quad \frac{x}{12}=4   A separate constant term:   \quad \frac{x+1}{2x}+4=x

   A quadratic    equation:       \quad\frac{3}{x+1}=x+5      A linear equation:         \quad \frac{3x+4}{2x-5}=6

   A second fraction:         \quad \frac{2x}{15}=\frac{5x}{2}      Double brackets, difference of two    squares and simultaneous equations:       \quad \frac{(x+3)^{2}}{x^{2}-9}=2x-1

It is important to be able to simplify algebraic fractions into their simplest form. If you need to practice this or need a quick refresher, see the lesson on simplifying algebraic fractions for further information.

Step-by-step guide: Simplifying algebraic fractions

How to solve equations including algebraic fractions

We need to be able to solve equations including algebraic fractions. 

Let’s look at a simple example when \frac{8}{x}=2 .

Here, the denominator of the fraction contains the variable, so we first need to get the variable out of the denominator.

Rearranging the equation by multiplying both sides by x and then dividing by 2 , we get the value of x=4 .

We can substitute this into the original equation to prove that the answer is correct.

Here, \frac{8}{4}=2 so we have the correct answer.

We shall now consider more complicated cases when equations involve algebraic fractions.

In order to solve equations including algebraic fractions.

Convert each fraction so they all have a common denominator.

• Multiply the equation throughout by the common denominator.
• Solve the equation (linear or quadratic).

Explain how to solve equations including algebraic fractions

Algebraic fractions worksheet

Get your free algebraic fractions worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Algebraic fractions examples

Example 1: equation with one fraction.

Solve the equation

Here, we only have one fraction and so we do not need to convert any other term into a fraction.

2 Multiply the equation throughout by the common denominator .

Multiplying the equation throughout by 3 (the denominator of the fractional term), we get

Make sure that you multiply every term in the equation by 3 .

3 Solve the equation (linear or quadratic) .

You can check your solution by substituting the value for x into the original equation and evaluating it.

Example 2: Equation with two fractions

Here, we have the two fractions with the denominators of 2 and 5 . The lowest common multiple of 2 and 5 is 10 and so we can convert the two fractions so that they have the same denominator.

Remember to use brackets to ensure that you multiply the entire numerator by 5 .

Remember to use brackets to ensure that you multiply the entire numerator by 2 .

We now have the equation

Multiply the equation throughout by the common denominator .

Multiplying the equation throughout by 10 (the denominator of the fractional terms), we get

Solve the equation (linear or quadratic) .

Example 3: Equation with x in the denominator

Here, we have one fraction so we do not need to find a common denominator.

Multiplying the equation throughout by x + 1 (the denominator of the fractional terms), we get

Example 4: Equation with three fractions

Here, we need to find the lowest common multiple of x, 2x, and 3x . As x is the highest common factor, x \times 1 \times 2 \times 3 is the lowest common multiple, which is equal to 6x. .

So by multiplying the numerator and denominator of each fraction by a constant, we can convert each fraction to have the common denominator of 6x: .

We now have an equation which we can immediately simplify.

Multiplying the equation throughout by 6x (the denominator of the fractional terms), we get

Example 5: Denominators are expressions in terms of x

Here, we need to find a common denominator for (x + 2) and (x − 4) .

The easiest way to do this is to multiply the two expressions together.

Top tip: do not expand the brackets too soon as you may be able to simplify the fraction before solving the equation.

By multiplying each fraction by the denominator of the other fraction, we get

Multiplying the equation throughout by (x+2)(x-4) (the denominator of the fractional term), we get

Example 6: Equation including a quadratic

Here, we have a single fraction and so we do not need to find a common denominator.

Multiplying the equation throughout by x (the denominator of the fractional terms), we get

Here, we have two possible solutions for x so we can check both:

Common misconceptions

• Multiplying the numerator by the denominator

Let us look at example 2 . When multiplying throughout by 10 to remove the denominator from each fraction, the numerator has also been multiplied by 10 . This means that the fractions have been multiplied by 100 , instead of 10 , leaving the next line of work to be incorrect.

• Ignoring the denominators

When given an equation including an algebraic fraction, if the denominators are ignored the question will be answered incorrectly.

• Not multiplying all terms by the denominator

When rearranging an equation, the denominator is moved to the other side of the equals sign, instead of each term being multiplied by it. You must remember to multiply throughout by any value, not just the opposite side of the equals sign.

• Simplifying fractions incorrectly (1)

When adding two fractions, the denominator must be the same. A common misconception for adding two fractions is to add the numerators and the denominators together because this method is emphasised when looking at multiplying fractions.

• Simplifying fractions incorrectly (2)

Seeing the same term on the numerator and denominator allow the misconception that they can both be cancelled. 

Practice algebraic fractions questions

1. Solve the equation

2. Solve the equation

3. Solve the equation

4. Solve the equation

5. Solve the equation

6. Solve the equation

Algebraic fractions GCSE questions

1. Arron earns £40 per hour. One day, he receives a bonus of £5 . He shares this day’s earnings equally with his brother and sister. If he gives away £190 , how many hours did Arron work that day?

2. Use the quadratic formula to solve the equation

2x(x+2)+5x(x+3)=4(x+3)(x+2) or equivalent

x=3 or x=-\frac{8}{3}

3. Two shapes given below have the same area. Calculate the value for x .

Area of Triangle = \frac{2(x+8)}{2}=x+8

Area of Square = \left(\frac{3}{\sqrt{x}}\right)^{2}=\frac{9}{x}

x=1 or x=-9

Conclusion: x=1 only

Learning checklist

You have now learned how to:

• use algebraic methods to solve linear equations in 1 variable (including all forms that require rearrangement)
• simplify and manipulate algebraic fractions

The next lessons are

• Expanding brackets
• Factorising
• Solving equations

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Solving equations with fractions

Part of Maths Equations

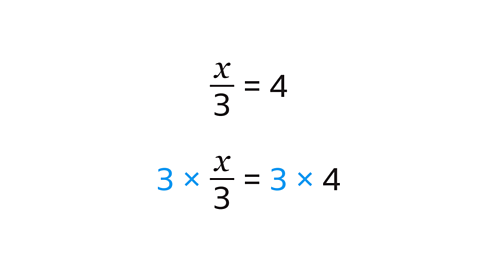
Equations involving one fraction

• If an equation has just one fraction, then the most common first step is to multiply both sides by the denominator close denominator Number written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3 of the fraction.
• Multiplying both sides of the equation will remove the fraction.
• The number of terms will be reduced and will lead to a new equation that is still balanced.
• The new equation will have just one unknown variable close variable A quantity that can take on a range of values. .
• Check your answer by substituting close substitute In algebra substitute means to replace a letter (or variable) with a number. the solution back into the original equation.

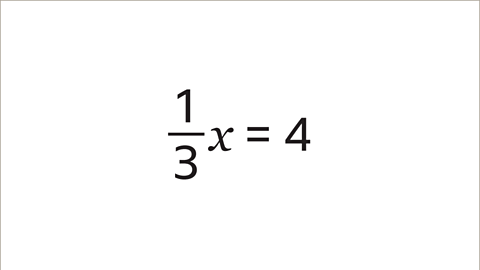
Solve the equation ⅓𝒙 = 4 by working out the value of 𝒙

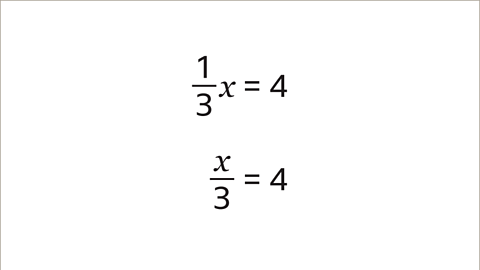
⅓𝒙 = 4 can be rewritten as 𝒙/3 = 4

Multiply both sides of the equation by the denominator (3) to keep the equation in balance.

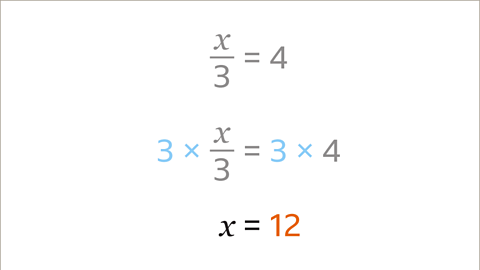
If both sides are multiplied by 3, the answer is 𝒙 = 12

It is important to check the answer. The original question stated that 𝒙/3 = 4. Substitute the value of 12 in place of the 𝒙 term.

If 𝒙 = 12, then 12 ÷ 3 = 4. When 𝒙 is 12 both sides of the equation are equal. This confirms the solution that 𝒙 = 12

Find the value of the unknown term \(x\) in this equation.

Solve the equation by working out the value of 𝒙.

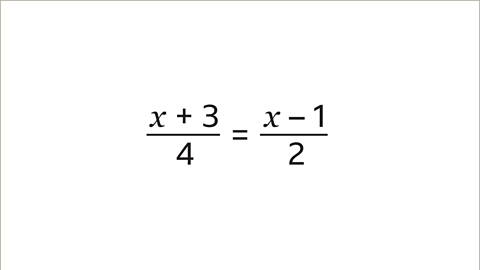
Both sides of the equation involve a fraction. Find the lowest common multiple (LCM) of the denominators (4 and 2).

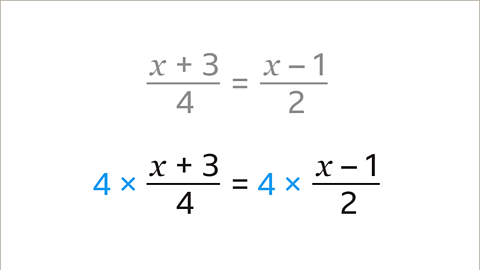
The lowest common multiple (LCM) is 4. Multiply both sides by 4

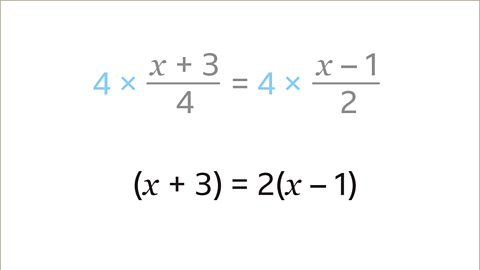
The fraction element of the equation has now been removed. This leaves a new equation that is still in balance.

Expand the brackets.

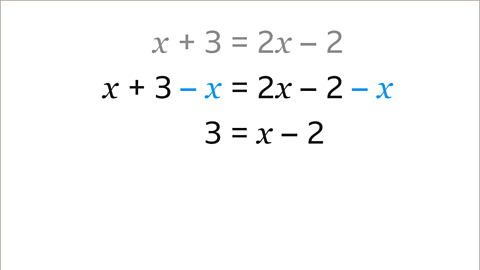
Subtract 𝒙 from both sides of the equation, 𝒙 + 3 – 𝒙 = 3 and 2𝒙 – 2 – 𝒙 = 𝒙 – 2

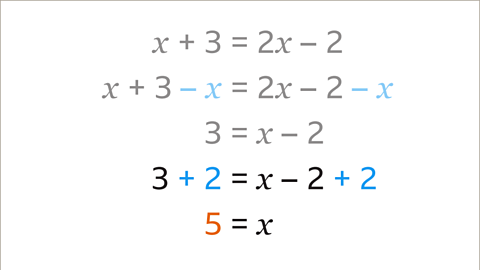
Add 2 to both sides of the equation. 3 + 2 = 5 and 𝒙 – 2 + 2 = 𝒙. The answer is 𝒙 = 5

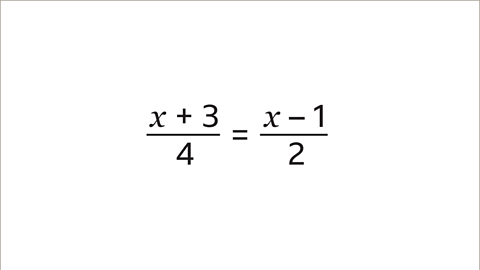
It is important to check the answer. The original question stated that 𝒙 + 3/4 = 𝒙 – 1/2. Substitute the value of 5 in place of the 𝒙 terms.

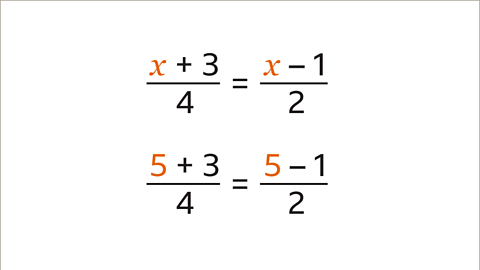
If 𝒙 = 5, then (5 + 3) ÷ 4 = 2 and (5 – 1) ÷ 2 = 2. When 𝒙 is 5 both sides of the equation are equal. This confirms the solution 𝒙 = 5

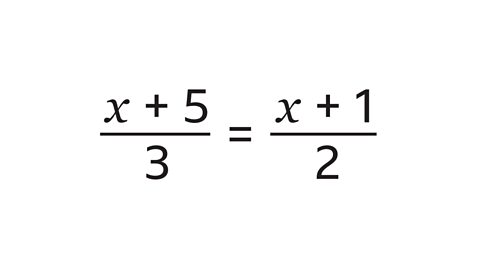
More on Equations

Find out more by working through a topic

Introduction to simultaneous equations

• count 5 of 7

Solving simultaneous equations graphically

• count 6 of 7

Calculating speed, distance and time

• count 7 of 7

Solving equations with 𝒙 on one side

• count 1 of 7

Solving Equations with Algebraic Fractions

Hello! Today we are going to take a look at how to solve equations that have algebraic fractions . But first, let’s review what algebraic fractions are. An algebraic fraction is any fraction that contains an algebraic expression. In other words, it’s a fraction that has a variable in it anywhere. For example,

\(\frac{5}{x}\), \(\frac{2x-9}{7}\), and \(\frac{3x}{2}\)

are all algebraic fractions.

So, now that we know what they are, let’s jump into a problem where we have to solve these. So we’re going to take a look at:

\(\frac{x}{8}=7\)

This is a nice and simple one. We know that in order to solve an equation, we need to isolate our variable. Here we can see that our variable, \(x\), is being divided by 8. So, to undo this division, we simply need to multiply both sides by 8.

\(8\cdot \frac{x}{8}=7\cdot 8\)

When we do that, our division is canceled out and we’re left with \(x\) on the left side, and \(7\times 8=56\), so:

Not too hard, right? Let’s try one that’s a little bit more complicated.

\(\frac{3x}{4}-\frac{2x}{12}=7\)

To solve this, I’m first going to simplify my fractions on the left side. To do this, I’ll need to convert \(\frac{3x}{4}\) to a fraction with a denominator of 12. I can do this by multiplying both the numerator and denominator by 3.

\(\frac{3x\cdot 3}{4\cdot 3}=\frac{9x}{12}\)

So that gives me the fraction, \(\frac{9x}{12}\). And then the rest of our equation is going to stay the same, so:

\(\frac{9x}{12}-\frac{2x}{12}=7\)

Since our denominators are the same, we can now subtract our numerators, so \(9x-2x=7x\).

\(\frac{7x}{12}=7\)

Another way we can write this is:

\(\frac{7}{12}\cdot x=7\)

So if we look at it this way, the way that we can get rid of this \(\frac{7}{12}\) over here is by multiplying by the reciprocal. So the reciprocal of \(\frac{7}{12}\), is \(\frac{12}{7}\), so we’ll multiply by that on both sides.

\(\frac{12}{7}\cdot \frac{7}{12}\cdot x=7\cdot \frac{12}{7}\)

When we do that, it cancels our fractions out over here, and we’re left with \(x\), which is what we want. And then if we do that over here, we can simplify first by doing \(7\div 7\), which gives us 1, and then do \(1\times 12\), which is 12.

So \(x=12\), which is our answer.

Let’s take a look at another problem.

\(\frac{4x}{5}=\frac{3x}{10}+9\)

This one we’re going to solve a little bit differently. For this problem, I’m going to solve for \(x\) by eliminating the fractions in our first step. To do this, we simply multiply the entire equation by the least common multiple of the denominators, of the fractions in the problem.

In this case, our denominators are 5 and 10, and the least common multiple of 5 and 10 is 10. So multiply the entire equation by 10.

\(10(\frac{4x}{5}=\frac{3x}{10}+9)\)

So that means we’re going to multiply each part of our equation by 10. So, \(10\cdot \frac{4x}{5}\). We can do \(10\div 5\) first, because remember it doesn’t matter if you multiply or divide first, multiplication and division can happen simultaneously. So for this, I’m going to divide \(10\div 5\) and get 2, and then multiply by \(4x\) to get \(8x\). If I multiply 10 by \(\frac{3x}{10}\), our 10s will cancel out and we’ll be left with \(3x\). And \(10\cdot 9=90\).

\(8x=3x+90\)

Now we can solve it like a normal algebra problem . So I’m going to subtract \(3x\) from both sides.

\(8x-3x=3x-3x+90\)

That gives us:

And then we divide both sides by 5.

\(\frac{5x}{5}=\frac{90}{5}\)

Either of these methods will help you get the right answer when solving equations with algebraic fractions, so feel free to use whichever one you feel most comfortable with.

Before we go, I want to show you one more problem you might come across.

\(\frac{x+17}{5}=21\)

So we have an expression in the numerator instead of just a variable, and maybe a number being multiplied by it, so it’s a little bit different than the ones we’ve looked at before. So, to solve problems like these, we first get rid of the fraction by multiplying by the denominator on both sides of the equation. So we’re going to multiply by 5 on both sides.

\(5\cdot \frac{x+17}{5}=21\cdot 5\)

That cancels out our denominator, so we no longer have a fraction, and we’re just left with the expression in the numerator: \(x+17\). And \(21\cdot 5=105\).

\(x+17=105\)

So now we’re going to solve it like normal. We’ll subtract 17 from both sides,

\(x+17-17=105-17\)   \(x=88\)

And that’s it! I hope this video helped you better understand how to solve equations with algebraic fractions. Thanks for watching, and happy studying!

Solving Equations with Algebraic Fractions Practice Questions

  Solve the equation: \(\frac{2x}{3}-\frac{4x}{9}=6\).

We can combine the fractions on the left side by converting \(\frac{2x}{3}\) to a fraction with a denominator of 9. To do so, multiply the first fraction by \(\frac{3}{3}\).

\(\frac{3}{3}\cdot\frac{2x}{3}-\frac{4x}{9}=6\)   \(\frac{6x}{9}-\frac{4x}{9}=6\)   \(\frac{2x}{9}=6\)

Now, multiply both sides by 9.

\(9\cdot\frac{2x}{9}=6\cdot9\)   \(2x=54\)

Finally, divide both sides by 2.

\(\frac{2x}{2}=\frac{54}{2}\)   \(x=27\)

  Solve the equation: \(\frac{5x}{6}=\frac{11x}{15}+2\).

We can multiply both sides of the equation by the least common multiple of the denominators. The least common multiple of 6 and 15 is 30, so multiply the entire equation by 30

\(30\left(\frac{5}{6}x=\frac{11}{15}x+2\right)\)   \(\frac{30\cdot5}{6}x=\frac{30\cdot11}{15}x+30\cdot2\)   \(25x=22x+60\)

To get the variable terms on the left side, subtract 22x from both sides of the equation.

\(25x-22x=22x+60-22x\)   \(3x=60\)

Now, divide both sides by 3.

\(\frac{3x}{3}=\frac{60}{3}\)   \(x=20\)

Solve the equation: \(2x+79=5\).

We can get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 9.

\(9\cdot \frac{2x+7}{9}=5\cdot9\)   \(2x+7=45\)

Now, subtract 7 from both sides.

\(2x+7-7=45-7\)   \(2x=38\)

Then, divide both sides by 2.

\(\frac{2x}{2}=\frac{38}{2}\)   \(x=19\)

  The quotient of thirteen less than a number and 7 equals twice the number. What is the number?

Let x be the number you are trying to find. Since quotient means to divide, we can write the quotient of thirteen less than a number and 7 as \(\frac{x-13}{7}\). Twice the number can be written as \(2x\). Set these two expressions equal to each other to get the equation:

\(\frac{x-13}{7}=2x\)

To solve for x, first, get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 7.

\(7\cdot\frac{x-13}{7}=2x\cdot7\)   \(x-13=14x\)

To get the variable terms on the left side, subtract \(14x\) from both sides of the equation.

\(x-13-14x=14x-14x\)   \(-13x-13=0\)

Now, add the constant of 13 to both sides.

\(-13x-13+13=0+13\)   \(-13x=13\)

Then, divide both sides by –13.

\(\frac{-13x}{-13}=\frac{13}{-13}\)   \(x=-1\)

So, the number is –1.

  You and a friend play on the same soccer team. Both of you decide to save money to buy a soccer goal to practice shooting. One-third of the money, in dollars, you and your friend have saved is $30 less than twice of what you have saved. If your friend has saved $25, how much money have you saved?

Let x be the amount of money you have saved. Since your friend has saved $25, we can write one-third of the money you and your friend have saved as \(\frac{x+25}{3}\). Thirty dollars less than twice of what you have saved can be written as \(2x-30\). Setting these two expressions equal to each other gives us the equation:

\(\frac{x+25}{3}=2x-30\)

To solve for x, first, get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 3.

\(3\cdot\frac{x+25}{3}=3(2x-30)\)   \(x+25=6x-90\)

To get the variable terms on the left side, subtract \(6x\) from both sides of the equation.

\(x+25-6x=6x-90-6x\)   \(-5x+25=-90\)

Now, subtract 25 from both sides.

\(-5x+25-25=-90-25\)   \(-5x=-115\)

Then, divide both sides by –5.

\(\frac{-5x}{-5}=\frac{115}{-5}\)   \(x=23\)

So, you have saved $23.

Return to Algebra I Videos

by Mometrix Test Preparation | This Page Last Updated: December 26, 2023

• International
• Schools directory
• Resources Jobs Schools directory News Search

Solving equations with algebraic fractions

Subject: Mathematics

Age range: 11 - 18

Resource type: Lesson (complete)

Last updated

26 September 2019

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

A FULL LESSON , which could definitely be used over 2 lessons for the right classes, on solving equations involving algebraic fractions.

Contents of download:

• Normal PowerPoint lesson with which you can use a clicker / mouse / keyboard to continue animations and show fully animated and worked solutions.
• Two worksheets printable for students with examples to speed up the lesson (no copying down questions etc). Worksheet can be used independent of the PowerPoint lesson!

We are learning about: Solving equations with algebraic fractions We are learning to: Solve equations involving algebraic fractions

Differentiated objectives:

• Developing learners will be able to solve equations involving algebraic fractions with numerical denominators.
• Secure learners will be able to solve equations involving algebraic fractions with algebraic denominators.
• Excelling learners will be able to solve unfamiliar problems involving solving equations with algebraic fractions.

Main: Walked through examples with binomial numerators, which lead on to practice exercises of similar question types. Further walked through examples with binomial denominators. This splits the lesson into two distinct parts (or 2 whole lessons for the appropriate classes). All solutions given on PPT.

Please do leave feedback!!

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

why are all algebraic fractions being added ? and never subtracted.

cparkinson3

You could always just change some to subtract?

Empty reply does not make any sense for the end user

jabbottdorcan

Very clear and easy to explain to students

Thank you. I hope it helps!

lucia_threadgill

Looks good but I can't seem to adapt the powerpoint. Is it protected?

It wasn’t when uploaded. But is a free resource as a singular lesson of my algebraic fractions collection. In my later releases free resources will be read only!

Thank you. Very Useful.

Thank you. I hope it helps

Especially for those very bright kids who need more challenge.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• calculators
• Algebraic Fractions

Algebraic Fractions Calculator

Get detailed solutions to your math problems with our algebraic fractions step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Here, we show you a step-by-step solved example of algebraic fractions. This solution was automatically generated by our smart calculator:

Divide $x^2$ by $x^2+1$

Resulting polynomial

 Final answer to the problem

Are you struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Popular problems

Most popular problems solved with this calculator:

Algebraic Fractions Practice Questions

Click here for questions, click here for answers.

adding, subtracting, dividing, multiplying, algebra, fractions

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Real World Examples of Quadratic Equations

A Quadratic Equation looks like this:

Quadratic equations pop up in many real world situations!

Here we have collected some examples for you, and solve each using different methods:

• Factoring Quadratics
• Completing the Square
• Graphing Quadratic Equations
• The Quadratic Formula
• Online Quadratic Equation Solver

Each example follows three general stages:

• Take the real world description and make some equations
• Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones

When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...

... and a Quadratic Equation tells you its position at all times!

Example: Throwing a Ball

A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.

Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)

Add them up and the height h at any time t is:

h = 3 + 14t − 5t 2

And the ball will hit the ground when the height is zero:

3 + 14t − 5t 2 = 0

Which is a Quadratic Equation !

In "Standard Form" it looks like:

−5t 2 + 14t + 3 = 0

It looks even better when we multiply all terms by −1 :

5t 2 − 14t − 3 = 0

Let us solve it ...

There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :

ac = −15 , and b = −14 .

The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15

By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)

The "t = −0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

Here is the graph of the Parabola h = −5t 2 + 14t + 3

It shows you the height of the ball vs time

Some interesting points:

(0,3) When t=0 (at the start) the ball is at 3 m

(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.

(3,0) says that at 3 seconds the ball is at ground level.

Also notice that the ball goes nearly 13 meters high.

Note: You can find exactly where the top point is!

The method is explained in Graphing Quadratic Equations , and has two steps:

Find where (along the horizontal axis) the top occurs using −b/2a :

• t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

Example: New Sports Bike

You have designed a new style of sports bicycle!

Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

Based on similar bikes, you can expect sales to follow this "Demand Curve":

Where "P" is the price.

For example, if you set the price:

• at $0, you just give away 70,000 bikes
• at $350, you won't sell any bikes at all
• at $300 you might sell 70,000 − 200×300 = 10,000 bikes

So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

Profit = −200P 2 + 92,000P − 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square .

Solve: −200P 2 + 92,000P − 8,400,000 = 0

Step 1 Divide all terms by -200

Step 2 Move the number term to the right side of the equation:

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900

Step 4 Take the square root on both sides of the equation:

Step 5 Subtract (-230) from both sides (in other words, add 230):

What does that tell us? It says that the profit is ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

It is exactly half way in-between! At $230

And here is the graph:

The best sale price is $230 , and you can expect:

• Unit Sales = 70,000 − 200 x 230 = 24,000
• Sales in Dollars = $230 x 24,000 = $5,520,000
• Costs = 700,000 + $110 x 24,000 = $3,340,000
• Profit = $5,520,000 − $3,340,000 = $2,180,000

A very profitable venture.

Example: Small Steel Frame

Your company is going to make frames as part of a new product they are launching.

The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2

The inside of the frame has to be 11 cm by 6 cm

What should the width x of the metal be?

Area of steel before cutting:

Area of steel after cutting out the 11 × 6 middle:

Let us solve this one graphically !

Here is the graph of 4x 2 + 34x :

The desired area of 28 is shown as a horizontal line.

The area equals 28 cm 2 when:

x is about −9.3 or 0.8

The negative value of x make no sense, so the answer is:

x = 0.8 cm (approx.)

Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.

There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:

• Let x = the boat's speed in the water (km/h)
• Let v = the speed relative to the land (km/h)

Because the river flows downstream at 2 km/h:

• when going upstream, v = x−2 (its speed is reduced by 2 km/h)
• when going downstream, v = x+2 (its speed is increased by 2 km/h)

We can turn those speeds into times using:

time = distance / speed

(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x−2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2) (x+2) :

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x 2 −4) = 15x+30 + 15x−30

Bring everything to the left and simplify:

3x 2 − 30x − 12 = 0

It is a Quadratic Equation!

Let us solve it using the Quadratic Formula :

Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0

Solve 3x 2 - 30x - 12 = 0

Answer: x = −0.39 or 10.39 (to 2 decimal places)

x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&