solving inelastic collision problems physics

Inelastic Collisions

Created by Csorensen6

Edited/Claimed by Jessica Ouyang, Fall 2018

Edited/Claimed by Vansh Kareer, Spring 2017

Edited/Claimed by Abigail Brady, Fall 2017

This topic covers the concept of inelastic collisions and the results of the collisions on the bodies involved. Included are the methods that can be applied to solve problems related to these types of collisions, along with worked examples.

1.1 Mathematical Model
1.2 Computational Model
2.2 Middling
2.3 Difficult
3 Connectedness
5.1 Further reading
5.2 External links
6 References

The Main Idea

There are two types of collisions: inelastic and elastic. The big identifying characteristics of inelastic collisions that distinguish them from elastic collisions is that in inelastic collisions, the momentum of the interacting bodies are conserved, but the kinetic energy is not. This change in kinetic energy from initial to final states is what differentiates inelastic collisions from elastic collisions. Generally, the forces involved in an inelastic collisions are so large relative to external forces that those external forces can be ignored. Consequently, given that [math]\displaystyle{ ΔP_{system} = F_{net,ext}ΔT }[/math] , if we approximate [math]\displaystyle{ F_{net,ext} }[/math] as zero, then [math]\displaystyle{ ΔP_{system} = 0 }[/math] , and [math]\displaystyle{ P_i = P_f }[/math] .

Because the final kinetic energy differs from the initial kinetic energy, inelastic collisions witness a change in the internal energy of the objects involved in the collision. A change in internal energy often manifests itself in the form of deformation, rotation, heat, vibration, explosions, or energy state excitation.

Types of Inelastic Collisions

One type of inelastic collisions is the maximally inelastic collision, also known as the perfectly inelastic collision, in which two objects collide and then remain connected for the duration of the observable interaction. This does not indicate an end to movement, as momentum must be conserved by the end of the interaction. See problem 1 for an example. More information about such problems can be found in the page Maximally Inelastic Collision .

Most inelastic collisions are considered partially inelastic collisions. In these types, two or more objects collide but do not stick together (unlike maximally inelastic collisions), but as a result of their collision, one or both begin to rotate, vibrate, deform, heat up, etc. In these problems, there is a positive ΔEint and a negative ΔK, and Ki > Kf. An example of a typically inelastic collision is a car crash.

Explosions are a somewhat special case of inelastic collisions. In these types of problems, an object bursts apart, and some of its internal energy is converted into kinetic energy. As a result, ΔK is actually positive and ΔEint is actually negative, in that internal energy is used up in the course of the explosion and causes an increase in the speed of the particles involved. This can be seen in the relation Ki < Kf, wherein the change in internal energy of the lends itself to the increase in kinetic energy from Ki to Kf, which directly correlates to an increase in particle speed in the explosion's aftermath.

solving inelastic collision problems physics

Mathematical Model

In inelastic collisions, the change in internal energy is equal to the negative change in kinetic energy. Based on these characteristics, and applying the momentum principle, a few basic equations can be set to outline an inelastic collision.

The picture below illustrates some characteristics of a typical, inelastic collision: a car crash.

In the car crash depicted above, there is a loss of kinetic energy, which is converted into internal energy in the form of produced heat and deformation of the car and the tree.

This is in accordance with the relation [math]\displaystyle{ ΔE_{internal} = -ΔK_{trans}=-0.5(mass)(Δvelocity)^2 }[/math] .

A very simple way to approach many inelastic collision problems is using the conservation of momentum principle. Since the two objects would not bounce and thus stick together- they become one object in terms of calculations. So the final equation would be: [math]\displaystyle{ m_1v_1 + m_2v_2 = (m_1 + m_2)v_f }[/math] .

Computational Model

Using the Collision Lab [1] , you can model different scenarios for the inelastic collision. Such as when the two bodies have the same mass, or when one is moving at a higher speed than the other. This simulation can help visualize inelastic collisions under different circumstances.

Typical Process for Solving

In such problems, it is often necessary to apply both the momentum principle and the energy principle.

Momentum Principle: [math]\displaystyle{ p_{1f} + p_{2f} = p_{1i} }[/math]

Energy Principle: [math]\displaystyle{ K_{1f} + K_{2f} + E_{int,f} = K_{1i} + E_{int,i} }[/math]

As shown above, the change in internal energy is directly related to the change in kinetic energy, in the Energy Principle.

The steps for solving inelastic collision problems are often as follows:

1) Draw a picture of the initial and final states.

2) Given that collisions involve extremely large forces acting over short time intervals, it is accurate to say that [math]\displaystyle{ F_{net,ext} = 0 }[/math] , because the external forces are typically much, much smaller than the internal forces involved in the collision.

3) Knowing that [math]\displaystyle{ F_{net,ext} = 0 }[/math] , this means that momentum is conserved and that [math]\displaystyle{ P_f = P_i }[/math] . This comes from the momentum principle, in that [math]\displaystyle{ ΔP_{system} = F_{net,ext}ΔT }[/math] , and if [math]\displaystyle{ F_{net,ext} }[/math] is zero, then the right side of that equation is also zero.

4) Next, knowing that [math]\displaystyle{ P_f = P_i }[/math] , you can solve for any unknown velocities of the objects involved via the momentum principle.

5) Having determined the velocity of each object, you can then determine the initial and final kinetic energies of the system using [math]\displaystyle{ K = (1/2)m|v|^2 }[/math] for each object.

6) Next, you can find the change in kinetic energy, or ΔK, and this will be equal to the negative change in the internal energy (whether it be heat, rotation, etc.) gained by the objects in the course of the collision. In other words [math]\displaystyle{ ΔE_{int} = -ΔK }[/math] .

Block A moves on a friction-less surface at a speed of 5 m/s towards block B. Block B is moving towards Block A at a speed of 2 m/s. Block A has a mass of 2 kg and block B has a mass of 1.5 kg. Assume the blocks are moving directly toward each other in the x direction and stick together on colliding. What is the speed of the blocks after the collision?

Using conservation of momentum, we can say that the momentum of the two blocks before the collision is equal to the momentum of the blocks after the collision.

[math]\displaystyle{ p_{1i} + p_{2i} = p_{f} }[/math]

[math]\displaystyle{ m_{A}v_{A,i} + m_{B}v_{B,i} = m_{f}v_{f} }[/math]

[math]\displaystyle{ (2)(5) + (1.5)(2) = (2 + 1.5)(v_f) }[/math]

[math]\displaystyle{ 10 + 3 = 3.5v_f }[/math]

[math]\displaystyle{ v_f = 3.714 m/s }[/math]

There are two hockey pucks traveling across the surface of a frozen pond. The first puck has a mass of 0.15 kg and is moving with a velocity of <2.5, 3.4, 0> m/s. The second puck has a mass of 0.13 kg and is moving with a velocity of <-3.1, 1.7, 0> m/s. After colliding, the first puck then has a velocity of <-1.9, 3.0, 0> m/s. (Reference the image below).

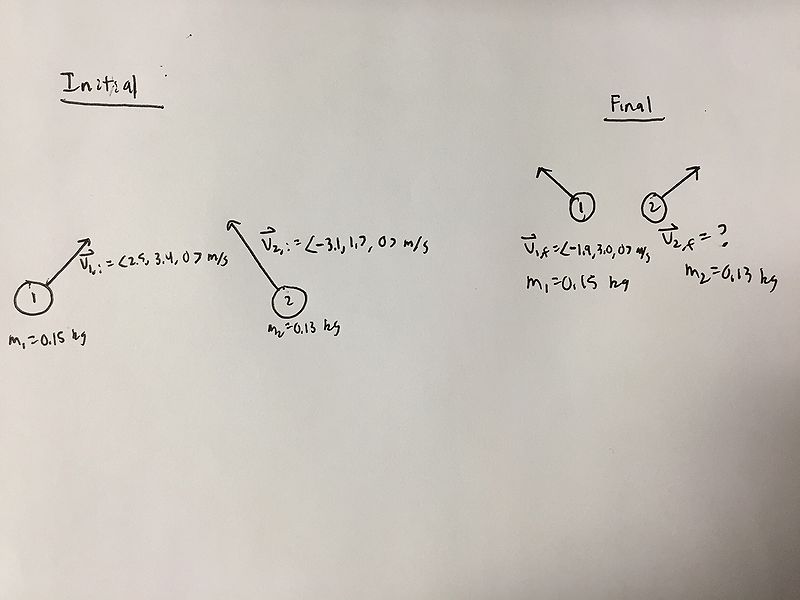
a) What is the velocity of the second puck after the collision?

b) What is the initial kinetic energy?

c) What is the final kinetic energy?

d) What is the change of the internal energy of the two pucks?

A bullet of mass 0.071 kg traveling horizontally at a speed of 100 m/s embeds itself in a block of mass 2 kg that is sitting at rest on a nearly frictionless surface.

(a) What is the speed of the block after the bullet embeds itself in the block?

(b) Calculate the kinetic energy of the bullet plus the block before the collision:

(d) Was this collision elastic or inelastic?

(e) Calculate the rise in thermal energy of the bullet plus block as a result of the collision:

(f) What was the transfer of energy Q (microscopic work) from the surroundings into the block+bullet system during the collision? (Remember that Q represents energy transfer due to a temperature difference between a system and its surroundings.)

A lit firework of mass 15 kg is launched into the sky with an initial velocity of <10,17,0> m/s. Eventually, its fuse burns up and the firework explodes, bursting into four parts. One piece has a mass of 3 kg and a velocity of <8,7,0> m/s. Another has a mass of 4 kg and a velocity of <15,0,0> m/s. The third has a mass of 3.5 kg and a velocity of <12,-5,0> m/s.

Reference the picture below.

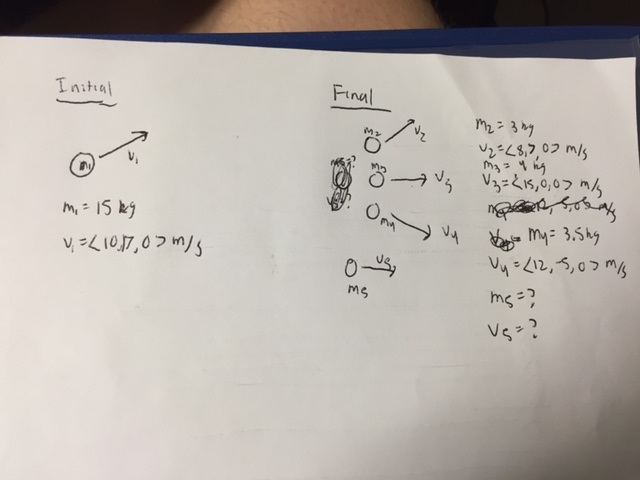
a) What is the mass of the fourth piece?

b) What is the momentum and velocity of that piece?

c) What is the change in internal energy?

d) Justify the sign of the answer found in part c).

Connectedness

The science of collisions and the study of momentum are especially prominent when it comes to the sport of football, and particularly in regards to concussions, or traumatic brain injuries sustained due to hard blows to the head. Significant research within the biomedical field is being conducted into how to reduce concussion frequency and severity, and this often entails specifically designing helmets to minimize the impact of high-speed, hard-hitting tackles. This research has come to greater prominence with the relatively recent discovery of the role football plays in the acquisition of CTE, a degenerative disease which slowly causes the loss of cognitive function, similar to dementia, and is especially prominent among football players and other athletes who suffer repeated head trauma.

The concepts presented through collisions are also the founding physics principles for studying car crashes, or car safety, as well as other real world events that contain collisions. By using the mathematical models introduced earlier, studies can be done to improve the user experience and overall safety of many things including vehicles.

The idea of inelastic collisions is rooted in the conservation of linear momentum, which is implied by Newton's Laws. Newton published his book, the Philosophiae Naturalis Principia Mathematica, in 1687. This book, commonly known as Principia, described Newton’s findings on collisions and laid a foundation for the different types of collisions we study today.

The history of collisions in modern physics starts with Rutherford’s Gold Foil experiment. He found that while they did not touch, the alpha particles and the gold nucleus collided elastically. It is essential that the collision was elastic, in that it gives us the famous scatting pattern and led to the discovery of the positively charged nucleus.

External links

A different explanation of inelastic collisions

A Khan Academy video on elastic and inelastic collisions

Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

7.3: Collisions

Last updated
Save as PDF
Page ID 14475

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Conservation of Energy and Momentum

In an inelastic collision the total kinetic energy after the collision is not equal to the total kinetic energy before the collision.

learning objectives

Assess the conservation of total momentum in an inelastic collision

At this point we will expand our discussion of inelastic collisions in one dimension to inelastic collisions in multiple dimensions. It is still true that the total kinetic energy after the collision is not equal to the total kinetic energy before the collision. While inelastic collisions may not conserve total kinetic energy, they do conserve total momentum.

We will consider an example problem in which one mass ($\mathrm{m_1}$) slides over a frictionless surface into another initially stationary mass ($\mathrm{m_2}$). Air resistance will be neglected. The following things are known:

\[\begin{align} \mathrm{m_1} & \mathrm{=0.250kg,} \\ \mathrm{m_2} & \mathrm{=0.400kg,} \\ \mathrm{v_1} & \mathrm{=2.00m/s,} \\ \mathrm{v_1′}& \mathrm{=1.50m/s,} \\ \mathrm{v_2}& \mathrm{=0m/s,} \\ \mathrm{θ_1′} & \mathrm{=45.0∘,} \end{align}\]

where $\mathrm{v_1}$ is the initial velocity of the first mass, $\mathrm{v_1′}$ is the final velocity of the first mass, $\mathrm{v_2}$ is the initial velocity of the second mass, and $\mathrm{θ_1′}$ is the angle between the velocity vector of the first mass and the x-axis.

The object is to calculate the magnitude and direction of the velocity of the second mass. After this, we will calculate whether this collision was inelastic or not.

Since there are no net forces at work (frictionless surface and negligible air resistance), there must be conservation of total momentum for the two masses. Momentum is equal to the product of mass and velocity. The initially stationary mass contributes no initial momentum. The components of velocities along the x-axis have the form $\mathrm{v⋅\cos θ}$, where θ is the angle between the velocity vector of the mass of interest and the x-axis.

Expressing these things mathematically:

\[\mathrm{m_1v_1=m_1v_1′ \cdot \cos (θ_1)+m_2v‘_2 \cdot \cos (θ_2). (Eq. 2)}\]

The components of velocities along the y-axis have the form $\mathrm{v \cdot \sin θ}$, where θ is the angle between the velocity vector of the mass of interest and the x-axis. By applying conservation of momentum in the y-direction we find:

\[\mathrm{0=m_1v_1′ \cdot \sin (θ_1)+m_2v‘_2 \cdot \sin (θ_2). (Eq. 3)}\]

If we divide Eq. 3 by Eq. 2, we will find:

\[\mathrm{ \tan θ_2=\dfrac{v_1′ \cdot \sin θ_1}{v_1′ \cos θθ_1−v_1} (Eq. 4) }\]

Eq. 4 can then be solved to find $\mathrm{θ_2}$approx. 312º.

Now let’ use Eq. 3 to solve for $\mathrm{v′_2}$. Re-arranging Eq. 3, we find:

\[\mathrm{v_2′=\dfrac{−m_1v_1′ \cdot \sin θ_1}{ m_2 \cdot \sin θ_2.}}\]

After plugging in our known values, we find that $\mathrm{v_2′=0.886m/s}$.

We can now calculate the initial and final kinetic energy of the system to see if it the same.

\[\begin{align} \mathrm{Initial \; Kinetic \; Energy} & \mathrm{ =\frac{1}{2}m_1 \cdot v_1^2+\frac{1}{2}m_2 \cdot v_2^2=0.5J.} \\ \mathrm{Final \; Kinetic \; Energy} & \mathrm{= \frac{1}{2}m_1 \cdot v_1′^2+\frac{1}{2}m_2 \cdot v_2′^2≈0.43J.} \end{align}\]

Since these values are not the same we know that it was an inelastic collision.

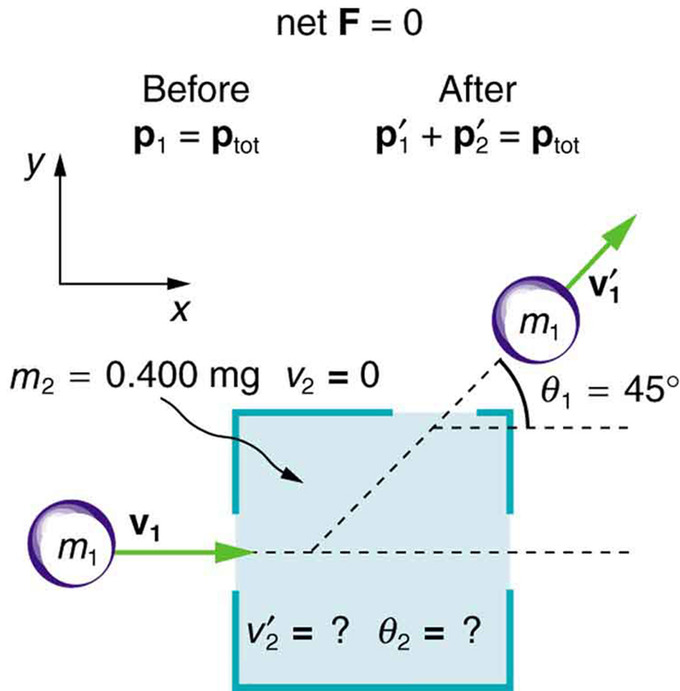
Collision Example : This illustrates the example problem in which one mass collides into another mass that is initially stationary.

Glancing Collisions

Glancing collision is a collision that takes place under a small angle, with the incident body being nearly parallel to the surface.

Identify necessary conditions for a “glancing collision”

A collision is short duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in velocity ). The magnitude of the velocity difference at impact is called the closing speed. All collisions conserve momentum. What distinguishes different types of collisions is whether they also conserve kinetic energy. Line of impact – It is the line which is common normal for surfaces are closest or in contact during impact. This is the line along which internal force of collision acts during impact and Newton’s coefficient of restitution is defined only along this line.

When dealing with an incident body that is nearly parallel to a surface, it is sometimes more useful to refer to the angle between the body and the surface, rather than that between the body and the surface normal (see ), in other words 90° minus the angle of incidence. This small angle is called a glancing angle. Collision at glancing angle is called “glancing collision”.

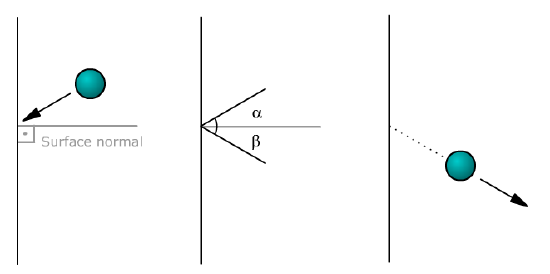
Collision : Object is deflected after the collision withthe surface. The angles between the body and the surface normal areindicated as α and β. The angles between the body and the surface are $\mathrm{90 – α}$ and $\mathrm{90 – β}$.

Collisions can either be elastic, meaning they conserve both momentum and kinetic energy, or inelastic, meaning they conserve momentum but not kinetic energy. An inelastic collision is sometimes also called a plastic collision.

A “perfectly-inelastic” collision (also called a “perfectly-plastic” collision) is a limiting case of inelastic collision in which the two bodies stick together after impact.

The degree to which a collision is elastic or inelastic is quantified by the coefficient of restitution, a value that generally ranges between zero and one. A perfectly elastic collision has a coefficient of restitution of one; a perfectly-inelastic collision has a coefficient of restitution of zero.

Elastic Collisions in One Dimension

An elastic collision is a collision between two or more bodies in which kinetic energy is conserved.

Assess the relationship among the collision equations to derive elasticity

An elastic collision is a collision between two or more bodies in which the total kinetic energy of the bodies before the collision is equal to the total kinetic energy of the bodies after the collision. An elastic collision will not occur if kinetic energy is converted into other forms of energy. It important to understand how elastic collisions work, because atoms often undergo essentially elastic collisions when they collide. On the other hand, molecules do not undergo elastic collisions when they collide. In this atom we will review case of collision between two bodies.

The mathematics of an elastic collision is best demonstrated through an example. Consider a first particle with mass $\mathrm{m_1}$ and velocity $\mathrm{v_{1i}}$ and a second particle with mass $\mathrm{m_2}$ and velocity $\mathrm{v_{2i}}$. If these two particles collide, there must be conservation of momentum before and after the collision. If we know that this is an elastic collision, there must be conservation of kinetic energy by definition. Therefore, the velocities of particles 1 and 2 after the collision ($\mathrm{v_{1f}}$ and $\mathrm{v_{2f}}$ respectively) will be related to the initial velocities by:

$\mathrm{\frac{1}{2}m_1 \cdot v_{1i}^2+\frac{1}{2} m_2 \cdot v_{2i}^2= \frac{1}{2}m_1 \cdot v_{1f}^2+\frac{1}{2}m_2 \cdot v_{2f}^2}$ (due to conservation of kinetic energy)

$\mathrm{m_1 \cdot v_{1i}+m_2 \cdot v_{2i}=m_1 \cdot v_{1f}+m_2 \cdot v_{2f}}$ (due to conservation of momentum).

Since we have two equations, we are able to solve for any two unknown variables. In our case, we will solve for the final velocities of the two particles.

By grouping like terms and canceling out the ½ terms, we can rewrite our conservation of kinetic energy equation as:

\[\mathrm{m_1 \cdot (v_{1i}^2−v_{1f}^2)=m_2 \cdot (v_{2f}^2−v_{2i}^2). (Eq.1)}\]

By grouping like terms from our conservation of momentum equation we can find:

\[\mathrm{m_1 \cdot (v_{1i}−v_{1f})=m_2 \cdot (v_{2f}−v_{2i}). (Eq. 2)}\]

If we then divide Eq. 1 by Eq. 2 and perform some cancelations we will find:

\[\mathrm{v_{1i}+v_{1f}=v_{2f}+v_{2i}. (Eq. 3)}\]

We can solve for $\mathrm{v_{1f}}$ as:

\[\mathrm{v_{1f}=v_{2f}+v_{2i}−v_{1i}. (Eq. 4)}\]

At this point we see that $\mathrm{v_{2f}}$ is still an unknown variable. So we can fix this by plugging Eq. 4 into our initial conservation of momentum equation. Our conservation of momentum equation with Eq. 4 substituted in looks like:

\[\mathrm{m_1 \cdot v_{1i}+m_2 \cdot v_{2i}=m_1 \cdot (v_{2f}+v_{2i}−v_{1i})+m_2 \cdot v_{2f}. (Eq.5)}\]

After doing a little bit of algebra on Eq. 5 we find:

\[\mathrm{v_{2f}=\dfrac{2 \cdot m_1}{(m_2+m_1)} v_{1i}+\dfrac{(m_2−m_1)}{(m_2+m_1)}v_{2i}. (Eq.6)}\]

At this point we have successfully solved for the final velocity of the second particle. We still need to solve for the velocity of the first particle, so let us do that by plugging Eq. 6 into Eq. 4.

\[\mathrm{v_{1f}=[\dfrac{2 \cdot m_1}{(m_2+m_1)}v_{1i}+\dfrac{(m_2−m_1)}{(m_2+m_1)}v_{2i}]+v_{2i}−v_{1i}. (Eq. 7)}\]

After performing some algebraic manipulation of Eq. 7, we finally find:

\[\mathrm{v_{1f}=\dfrac{(m_1−m_2)}{(m_2+m_1)} v_{1i}+\dfrac{2 \cdot m_2}{(m_2+m_1)} v_{2i}. (Eq. 8)}\]

Elastic Collision of Two Unequal Masses : In this animation, two unequal masses collide and recoil.

Elastic Collisions in Multiple Dimensions

To solve a two dimensional elastic collision problem, decompose the velocity components of the masses along perpendicular axes.

Construct an equation for elastic collision

As stated previously, there is conservation of total kinetic energy before and after an elastic collision. If an elastic collision occurs in two dimensions, the colliding masses can travel side to side after the collision (not just along the same line as in a one dimensional collision). The general approach to solving a two dimensional elastic collision problem is to choose a coordinate system in which the velocity components of the masses can be decomposed along perpendicular axes.

Collisions in Multiple Dimensions : A brief introduction to problem solving of collisions in two dimensions using the law of conservation of momentum.

Example $\PageIndex{1}$:

In this example, we consider only point masses. These are structure-less particles that cannot spin or rotate. We will consider a case in which no outside forces are acting on the system, meaning that momentum is conserved. We will consider a situation in which one particle is initially at rest. This situation is illustrated in.

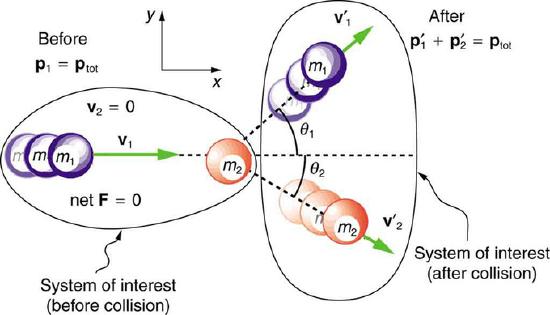
Illustration of Elastic Collision in Two Dimensions : In this illustration, we see the initial and final configurations of two masses that undergo an elastic collision in two dimensions.

By defining the x-axis to be along the direction of the incoming particle, we save ourselves time in breaking that velocity vector into its x- and y- components. Now let us consider conservation of momentum in the x direction:

\[\mathrm{p_{1x}+p_{2x}=p_{1x}′+p_{2x}′ (Eq. 1)}\]

In Eq. 1, the initial momentum of the incoming particle is represented by $\mathrm{p_{1x}}$ , the initial momentum of the stationary particle is represented by $\mathrm{p_{2x}}$ , the final momentum of the incoming particle is represented by $\mathrm{p_{1x}'}$ . and the final momentum of the initially stationary particle is represented by $\mathrm{p_{2x}'}$ .

We can expand Eq. 1 by taking into account that momentum is equal to the product of mass and velocity. Also, we know that $\mathrm{p_{2x} = 0}$ because the initial velocity of the stationary particle is 0.

The components of velocities along the x-axis have the form $\mathrm{v \cdot \cos θ}$, where θ is the angle between the velocity vector of the particle of interest and the x-axis.

\[\mathrm{m_1v_1=m_1v_1′ \cdot \cos (θ_1)+m_2v'_2 \cdot \cos (θ_2) (Eq. 2)}\]

The components of velocities along the y-axis have the form $\mathrm{v \cdot \sin θ}$, where θ is the angle between the velocity vector of the particle of interest (denoted in the following equations by subscript 1 or 2) and the x-axis. We can apply conservation of momentum in the y-direction in a similar way to yield:

\[\mathrm{0=m_1v_1' \cdot \sin (θ_1)+m_2v_2' \cdot \sin (θ_2) (Eq. 3)}\]

In finding Eq. 3, it was taken into consideration that the incoming particle had no component of velocity along the y-axis.

Solving for Two Unknowns

Now we have gotten to a point where we have two equations, this means that we can solve for any two unknowns that we want. We also know that because the collision is elastic that there must be conservation of kinetic energy before and after the collision. This means that we may also write Eq. 4, which gives us three equations to solve for three unknowns:

\[\mathrm{\dfrac{1}{2}m_1 \cdot v_1^2+\dfrac{1}{2}m_2 \cdot v_2^2=\dfrac{1}{2}m_1 \cdot v_1′^2+ \dfrac{1}{2}m_2 \cdot v_2′^2}\]

The general approach to finding the defining equations for an n-dimensional elastic collision problem is to apply conservation of momentum in each of the n- dimensions. You can generate an additional equation by utilizing conservation of kinetic energy.

Inelastic Collisions in One Dimension

Collisions may be classified as either inelastic or elastic collisions based on how energy is conserved in the collision.

Distinguish examples of inelastic collision from elastic collisions

In an inelastic collision the total kinetic energy after the collision is not equal to the total kinetic energy before the collision. This is in contrast to an elastic collision in which conservation of total kinetic energy applies. While inelastic collisions may not conserve total kinetic energy, they do conserve total momentum.

If two objects collide, there are many ways that kinetic energy can be transformed into other forms of energy. For example, in the collision of macroscopic bodies, some kinetic energy is turned into vibrational energy of the constituent atoms. This causes a heating effect and results in deformation of the bodies. Another example in which kinetic energy is transformed into another form of energy is when the molecules of a gas or liquid collide. When this happens, kinetic energy is often exchanged between the molecules’ translational motion and their internal degrees of freedom.

A perfectly inelastic collision happens when the maximum amount of kinetic energy in a system is lost. In such a collision, the colliding particles stick together. The kinetic energy is used on the bonding energy of the two bodies.

Sliding Block Example

Let us consider an example of a two-body sliding block system. The first block slides into the second (initially stationary block). In this perfectly inelastic collision, the first block bonds completely to the second block as shown. We assume that the surface over which the blocks slide has no friction. We also assume that there is no air resistance. If the surface had friction or if there was air resistance, one would have to account for the bodies’ momentum that would be transferred to the surface and/or air.

Inelastic Collision : In this animation, one mass collides into another initially stationary mass in a perfectly inelastic collision.

Writing about the equation for conservation of momentum, one finds:

\[\mathrm{m_au_a+m_bu_b=(m_a+m_b)v}\]

where m a is the mass of the incoming block, u a is the velocity of the incoming block, m b is the mass of the initially stationary block, u b is the velocity of initially stationary block (0 m/s), and v is the final velocity the two body system. Solving for the final velocity,

\[\mathrm{v=\dfrac{m_au_a+m_bu_b}{m_a+m_b}.}\]

Taking into account that the blocks have the same mass and that the one of the blocks is initially stationary, the expression for the final velocity of the system may be defined as:

\[\mathrm{v=\dfrac{u_a}{2}.}\]

Inelastic Collisions in Multiple Dimensions

While inelastic collisions may not conserve total kinetic energy, they do conserve total momentum.
Relate inelastic collision multiple dimension equations to the one dimension collisions you learned earlier

Example $\PageIndex{2}$:

Examples of Collisions

We will consider an example problem, illustrated in, in which one mass (m1m1) slides over a frictionless surface into another initially stationary mass (m2m2). Air resistance will be neglected. The following quantities are known:

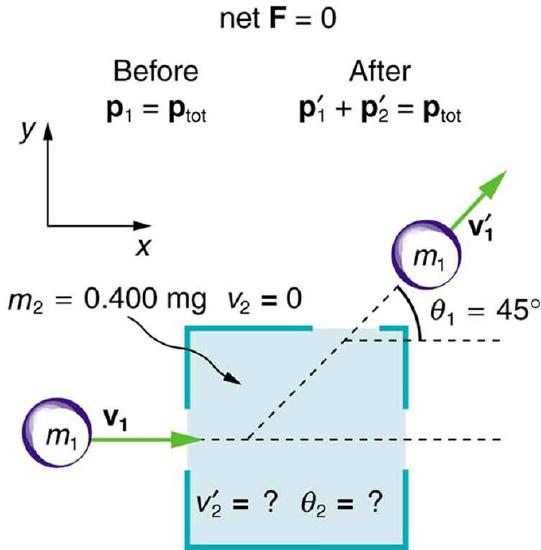
where v1v1 is the initial velocity of the first mass, v′1v1′ is the final velocity of the first mass, v2v2is the initial velocity of the second mass, and θ′1θ1′ is the angle between the velocity vector of the first mass and the x-axis.

Since there are no net forces at work (frictionless surface and negligible air resistance), there must be conservation of total momentum for the two masses. Momentum is equal to the product of mass and velocity. The (initially) stationary mass contributes no initial momentum. The components of velocities along the x-axis have the form v⋅cosθv⋅cosθ, where θ is the angle between the velocity vector of the mass of interest and the x-axis.

As these values are not the same, we know this was an inelastic collision.

If there are no net forces at work (collision takes place on a frictionless surface and there is negligible air resistance ), there must be conservation of total momentum for the two masses.
The variable θ is the angle between the velocity vector of the mass of interest and the x-axis in traditional Cartesian coordinate systems.
Collision is short duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this.
Collisions can either be elastic, meaning they conserve both momentum and kinetic energy, or inelastic, meaning they conserve momentum but not kinetic energy.
When dealing with an incident body that is nearly parallel to a surface, it is sometimes more useful to refer to the angle between the body and the surface, rather than that between the body and the surface normal.
An elastic collision will not occur if kinetic energy is converted into other forms of energy.
While molecules do not undergo elastic collisions, atoms often undergo elastic collisions when they collide.
If two particles are involved in an elastic collision, the velocity of the first particle after collision can be expressed as: $\mathrm{v_{1f}=\frac{(m_1−m_2)}{(m_2+m_1)}v_{1i}+ \frac{2 \cdot m_2}{(m_2+m_1)}v_{2i}.}$
If two particles are involved in an elastic collision, the velocity of the second particle after collision can be expressed as: $\mathrm{v_{2f}=\frac{2 \cdot m_1}{(m_2+m_1)}v_{1i}+\frac{(m_2−m_1)}{(m_2+m_1)}v_{2i}.}$
If an elastic collision occurs in two dimensions, the colliding masses can travel side to side after the collision.
By defining the x- axis to be along the direction of the incoming particle, we can simplify the defining equations.
In an inelastic collision, the total kinetic energy after the collision is not equal to the total kinetic energy before the collision.
A perfectly inelastic collision happens when the maximum amount of kinetic energy in a system is lost.
If there are no net forces at work (i.e., collision takes place on a frictionless surface and there is negligible air resistance ), there must be conservation of total momentum for the two masses.
kinetic energy : The energy possessed by an object because of its motion, equal to one half the mass of the body times the square of its velocity.
momentum : (of a body in motion) the product of its mass and velocity.
force : A physical quantity that denotes ability to push, pull, twist or accelerate a body which is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn)
elastic collision : An encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter. Elastic collisions occur only if there is no net conversion of kinetic energy into other forms.
dimension : A measure of spatial extent in a particular direction, such as height, width or breadth, or depth.
degrees of freedom : A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system. The set of all dimensions of a system is known as a phase space.
friction : A force that resists the relative motion or tendency to such motion of two bodies in contact.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

OpenStax College, College Physics. September 17, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42165/latest/?collection=col11406/latest . License : CC BY: Attribution
Inelastic collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Inelastic_collision . License : CC BY-SA: Attribution-ShareAlike
momentum. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/momentum . License : CC BY-SA: Attribution-ShareAlike
kinetic energy. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/kinetic%20energy . License : CC BY-SA: Attribution-ShareAlike
OpenStax College, College Physics. January 16, 2015. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42165/latest/?collection=col11406/latest . License : CC BY: Attribution
Conservation of Energy and Momentum. Located at : http://www.youtube.com/watch?v=meDqfux_zLU . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
Collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Collision . License : CC BY-SA: Attribution-ShareAlike
Angle of incidence. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Angle_of_incidence . License : CC BY-SA: Attribution-ShareAlike
force. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/force . License : CC BY-SA: Attribution-ShareAlike
Provided by : Wikimedia. Located at : http://upload.wikimedia.org/Wikipedia/commons/3/34/Deflection.png . License : CC BY-SA: Attribution-ShareAlike
Elastic collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Elastic_collision . License : CC BY-SA: Attribution-ShareAlike
elastic collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/elastic%20collision . License : CC BY-SA: Attribution-ShareAlike
Elastic collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Elastic_collision . License : CC BY: Attribution
dimension. Provided by : Wiktionary. Located at : http://en.wiktionary.org/wiki/dimension . License : CC BY-SA: Attribution-ShareAlike
OpenStax College, College Physics. February 10, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42165/latest/?collection=col11406/latest . License : CC BY: Attribution
Collisions in Multiple Dimensions. Located at : http://www.youtube.com/watch?v=0Yo7Izga1q8 . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
degrees of freedom. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/degrees_of_freedom . License : CC BY-SA: Attribution-ShareAlike
Inelastic collision. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Inelastic_collision . License : CC BY: Attribution
friction. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/friction . License : CC BY-SA: Attribution-ShareAlike
Elastic collision. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/Elastic_collision . License : CC BY: Attribution
Examples of Collisions. Located at : http://www.youtube.com/watch?v=1bxsUfurZMc . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license

Science Notes Posts
Contact Science Notes
Todd Helmenstine Biography
Anne Helmenstine Biography
Free Printable Periodic Tables (PDF and PNG)
Periodic Table Wallpapers
Interactive Periodic Table
Periodic Table Posters
How to Grow Crystals
Chemistry Projects
Fire and Flames Projects
Holiday Science
Chemistry Problems With Answers
Physics Problems
Unit Conversion Example Problems
Chemistry Worksheets
Biology Worksheets
Periodic Table Worksheets
Physical Science Worksheets
Science Lab Worksheets
My Amazon Books

Elastic Collision Example Problem – Physics Example Problems

Elastic collisions are collisions between objects where both momentum and kinetic energy are conserved. This elastic collision example problem will show how to find the final velocities of two bodies after an elastic collision.

Elastic Collision - Conservation of Momentum Example

This illustration shows a generic elastic collision between two masses A and B. The variables involved are

m A is the mass of the object A V Ai is the initial velocity of the object A V Af is the final velocity of the object A m B is the mass of the object B V Bi is the initial velocity of the object B and V Bf is the final velocity of the object B.

If the initial conditions are known, the total momentum of the system can be expressed as

total momentum before collision = total momentum after collision

m A V Ai + m B V Bi = m A V Af + m B V Bf

The kinetic energy of the system is

kinetic energy before collision = kinetic energy after collection

½m A V Ai 2 + ½m B V Bi 2 = ½m A V Af 2 + ½m B V Bf 2

These two equations can be solved for the final velocities as

If you’d like to see how to get to these equations, see Elastic Collision of Two Masses – It Can Be Shown Exercise for a step by step solution.

Elastic Collision Example Problem

A 10 kg mass traveling 2 m/s meets and collides elastically with a 2 kg mass traveling 4 m/s in the opposite direction. Find the final velocities of both objects.

First, visualize the problem. This illustration shows what we know of the conditions.

Elastic Collision Example Problem Illustration

The second step is to set your reference. Velocity is a vector quantity and we need to distinguish the direction of the velocity vectors. I’m going to choose from left to right as the “positive” direction. Any velocity moving from right to left will then contain a negative value.

Next, identify the known variables. We know the following:

m A = 10 kg V Ai 2 m/s m B = 2 kg V Bi = -4 m/s. The negative sign is because the velocity is in the negative direction.

Now we need to find V Af and V Bf . Use the equations from above. Let’s start with V Af .

Elastic Collision Final Velocity of Mass A Formula

Plug in our known values.

elastic collision example - final velocity of mass A step 1

V Af = 0 m/s

The final velocity of the larger mass is zero. The collision completely stopped this mass.

Now for V Bf

Elastic Collision Final Velocity of Mass B Formula

Plug in our known values

step 2 to find the final velocity of mass B

V Bf = 6 m/s

The second, smaller mass shoots off to the right (positive sign on the answer) at 6 m/s while the first, larger mass is stopped dead in space by the elastic collision.

Note: If you chose your frame of reference in the opposite direction in the second step, your final answer will be V Af = 0 m/s and V Bf = -6 m/s. The collision does not change, only the signs on your answers. Make sure the velocity values you use in your formulas match your frame of reference.

8.4 Elastic Collisions in One Dimension

Learning objectives.

By the end of this section, you will be able to:

Describe an elastic collision of two objects in one dimension.
Define internal kinetic energy.
Derive an expression for conservation of internal kinetic energy in a one dimensional collision.
Determine the final velocities in an elastic collision given masses and initial velocities.

Let us consider various types of two-object collisions. These collisions are the easiest to analyze, and they illustrate many of the physical principles involved in collisions. The conservation of momentum principle is very useful here, and it can be used whenever the net external force on a system is zero.

We start with the elastic collision of two objects moving along the same line—a one-dimensional problem. An elastic collision is one that also conserves internal kinetic energy. Internal kinetic energy is the sum of the kinetic energies of the objects in the system. Figure 8.6 illustrates an elastic collision in which internal kinetic energy and momentum are conserved.

Truly elastic collisions can only be achieved with subatomic particles, such as electrons striking nuclei. Macroscopic collisions can be very nearly, but not quite, elastic—some kinetic energy is always converted into other forms of energy such as heat transfer due to friction and sound. One macroscopic collision that is nearly elastic is that of two steel blocks on ice. Another nearly elastic collision is that between two carts with spring bumpers on an air track. Icy surfaces and air tracks are nearly frictionless, more readily allowing nearly elastic collisions on them.

Elastic Collision

An elastic collision is one that conserves internal kinetic energy.

Internal Kinetic Energy

Internal kinetic energy is the sum of the kinetic energies of the objects in the system.

Now, to solve problems involving one-dimensional elastic collisions between two objects we can use the equations for conservation of momentum and conservation of internal kinetic energy. First, the equation for conservation of momentum for two objects in a one-dimensional collision is

where the primes (') indicate values after the collision. By definition, an elastic collision conserves internal kinetic energy, and so the sum of kinetic energies before the collision equals the sum after the collision. Thus,

expresses the equation for conservation of internal kinetic energy in a one-dimensional collision.

Example 8.4

Calculating velocities following an elastic collision.

Calculate the velocities of two objects following an elastic collision, given that

Strategy and Concept

First, visualize what the initial conditions mean—a small object strikes a larger object that is initially at rest. This situation is slightly simpler than the situation shown in Figure 8.6 where both objects are initially moving. We are asked to find two unknowns (the final velocities v ′ 1 v ′ 1 and v ′ 2 v ′ 2 ). To find two unknowns, we must use two independent equations. Because this collision is elastic, we can use the above two equations. Both can be simplified by the fact that object 2 is initially at rest, and thus v 2 = 0 v 2 = 0 . Once we simplify these equations, we combine them algebraically to solve for the unknowns.

For this problem, note that v 2 = 0 v 2 = 0 and use conservation of momentum. Thus,

Using conservation of internal kinetic energy and that v 2 = 0 v 2 = 0 ,

Solving the first equation (momentum equation) for v ′ 2 v ′ 2 , we obtain

Substituting this expression into the second equation (internal kinetic energy equation) eliminates the variable v ′ 2 v ′ 2 , leaving only v ′ 1 v ′ 1 as an unknown (the algebra is left as an exercise for the reader). There are two solutions to any quadratic equation; in this example, they are

As noted when quadratic equations were encountered in earlier chapters, both solutions may or may not be meaningful. In this case, the first solution is the same as the initial condition. The first solution thus represents the situation before the collision and is discarded. The second solution ( v ′ 1 = − 3 . 00 m/s ) ( v ′ 1 = − 3 . 00 m/s ) is negative, meaning that the first object bounces backward. When this negative value of v ′ 1 v ′ 1 is used to find the velocity of the second object after the collision, we get

The result of this example is intuitively reasonable. A small object strikes a larger one at rest and bounces backward. The larger one is knocked forward, but with a low speed. (This is like a compact car bouncing backward off a full-size SUV that is initially at rest.) As a check, try calculating the internal kinetic energy before and after the collision. You will see that the internal kinetic energy is unchanged at 4.00 J. Also check the total momentum before and after the collision; you will find it, too, is unchanged.

The equations for conservation of momentum and internal kinetic energy as written above can be used to describe any one-dimensional elastic collision of two objects. These equations can be extended to more objects if needed.

Making Connections: Take-Home Investigation—Ice Cubes and Elastic Collision

Find a few ice cubes which are about the same size and a smooth kitchen tabletop or a table with a glass top. Place the ice cubes on the surface several centimeters away from each other. Flick one ice cube toward a stationary ice cube and observe the path and velocities of the ice cubes after the collision. Try to avoid edge-on collisions and collisions with rotating ice cubes. Have you created approximately elastic collisions? Explain the speeds and directions of the ice cubes using momentum.

PhET Explorations

Collision lab.

Investigate collisions on an air hockey table. Set up your own experiments: vary the number of discs, masses and initial conditions. Is momentum conserved? Is kinetic energy conserved? Vary the elasticity and see what happens.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

Authors: Paul Peter Urone, Roger Hinrichs
Publisher/website: OpenStax
Book title: College Physics 2e
Publication date: Jul 13, 2022
Location: Houston, Texas
Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
Section URL: https://openstax.org/books/college-physics-2e/pages/8-4-elastic-collisions-in-one-dimension

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Physics library

Course: physics library > unit 6.

Elastic and inelastic collisions
What are elastic and inelastic collisions?
Solving elastic collision problems the hard way

Deriving the shortcut to solve elastic collision problems

How to use the shortcut for solving elastic collisions

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

TPC and eLearning
What's NEW at TPC?
Read Watch Interact
Practice Review Test
Teacher-Tools
Subscription Selection
Seat Calculator
Ad Free Account
Edit Profile Settings
Classes (Version 2)
Student Progress Edit
Task Properties
Export Student Progress
Task, Activities, and Scores
Metric Conversions Questions
Metric System Questions
Metric Estimation Questions
Significant Digits Questions
Proportional Reasoning
Acceleration
Distance-Displacement
Dots and Graphs
Graph That Motion
Match That Graph
Name That Motion
Motion Diagrams
Pos'n Time Graphs Numerical
Pos'n Time Graphs Conceptual
Up And Down - Questions
Balanced vs. Unbalanced Forces
Change of State
Force and Motion
Mass and Weight
Match That Free-Body Diagram
Net Force (and Acceleration) Ranking Tasks
Newton's Second Law
Normal Force Card Sort
Recognizing Forces
Air Resistance and Skydiving
Solve It! with Newton's Second Law
Which One Doesn't Belong?
Component Addition Questions
Head-to-Tail Vector Addition
Projectile Mathematics
Trajectory - Angle Launched Projectiles
Trajectory - Horizontally Launched Projectiles
Vector Addition
Vector Direction
Which One Doesn't Belong? Projectile Motion
Forces in 2-Dimensions
Being Impulsive About Momentum
Explosions - Law Breakers
Hit and Stick Collisions - Law Breakers
Case Studies: Impulse and Force
Impulse-Momentum Change Table
Keeping Track of Momentum - Hit and Stick
Keeping Track of Momentum - Hit and Bounce
What's Up (and Down) with KE and PE?
Energy Conservation Questions
Energy Dissipation Questions
Energy Ranking Tasks
LOL Charts (a.k.a., Energy Bar Charts)
Match That Bar Chart
Words and Charts Questions
Name That Energy
Stepping Up with PE and KE Questions
Case Studies - Circular Motion
Circular Logic
Forces and Free-Body Diagrams in Circular Motion
Gravitational Field Strength
Universal Gravitation
Angular Position and Displacement
Linear and Angular Velocity
Angular Acceleration
Rotational Inertia
Balanced vs. Unbalanced Torques
Getting a Handle on Torque
Torque-ing About Rotation
Properties of Matter
Fluid Pressure
Buoyant Force
Sinking, Floating, and Hanging
Pascal's Principle
Flow Velocity
Bernoulli's Principle
Balloon Interactions
Charge and Charging
Charge Interactions
Charging by Induction
Conductors and Insulators
Coulombs Law
Electric Field
Electric Field Intensity
Polarization
Case Studies: Electric Power
Know Your Potential
Light Bulb Anatomy
I = ∆V/R Equations as a Guide to Thinking
Parallel Circuits - ∆V = I•R Calculations
Resistance Ranking Tasks
Series Circuits - ∆V = I•R Calculations
Series vs. Parallel Circuits
Equivalent Resistance
Period and Frequency of a Pendulum
Pendulum Motion: Velocity and Force
Energy of a Pendulum
Period and Frequency of a Mass on a Spring
Horizontal Springs: Velocity and Force
Vertical Springs: Velocity and Force
Energy of a Mass on a Spring
Decibel Scale
Frequency and Period
Closed-End Air Columns
Name That Harmonic: Strings
Rocking the Boat
Wave Basics
Matching Pairs: Wave Characteristics
Wave Interference
Waves - Case Studies
Color Addition and Subtraction
Color Filters
If This, Then That: Color Subtraction
Light Intensity
Color Pigments
Converging Lenses
Curved Mirror Images
Law of Reflection
Refraction and Lenses
Total Internal Reflection
Who Can See Who?
Formulas and Atom Counting
Atomic Models
Bond Polarity
Entropy Questions
Cell Voltage Questions
Heat of Formation Questions
Reduction Potential Questions
Oxidation States Questions
Measuring the Quantity of Heat
Hess's Law
Oxidation-Reduction Questions
Galvanic Cells Questions
Thermal Stoichiometry
Molecular Polarity
Quantum Mechanics
Balancing Chemical Equations
Bronsted-Lowry Model of Acids and Bases
Classification of Matter
Collision Model of Reaction Rates
Density Ranking Tasks
Dissociation Reactions
Complete Electron Configurations
Elemental Measures
Enthalpy Change Questions
Equilibrium Concept
Equilibrium Constant Expression
Equilibrium Calculations - Questions
Equilibrium ICE Table
Intermolecular Forces Questions
Ionic Bonding
Lewis Electron Dot Structures
Limiting Reactants
Line Spectra Questions
Mass Stoichiometry
Measurement and Numbers
Metals, Nonmetals, and Metalloids
Metric Estimations
Metric System
Molarity Ranking Tasks
Mole Conversions
Name That Element
Names to Formulas
Names to Formulas 2
Nuclear Decay
Particles, Words, and Formulas
Periodic Trends
Precipitation Reactions and Net Ionic Equations
Pressure Concepts
Pressure-Temperature Gas Law
Pressure-Volume Gas Law
Chemical Reaction Types
Significant Digits and Measurement
States Of Matter Exercise
Stoichiometry Law Breakers
Stoichiometry - Math Relationships
Subatomic Particles
Spontaneity and Driving Forces
Gibbs Free Energy
Volume-Temperature Gas Law
Acid-Base Properties
Energy and Chemical Reactions
Chemical and Physical Properties
Valence Shell Electron Pair Repulsion Theory
Writing Balanced Chemical Equations
Mission CG1
Mission CG10
Mission CG2
Mission CG3
Mission CG4
Mission CG5
Mission CG6
Mission CG7
Mission CG8
Mission CG9
Mission EC1
Mission EC10
Mission EC11
Mission EC12
Mission EC2
Mission EC3
Mission EC4
Mission EC5
Mission EC6
Mission EC7
Mission EC8
Mission EC9
Mission RL1
Mission RL2
Mission RL3
Mission RL4
Mission RL5
Mission RL6
Mission KG7
Mission RL8
Mission KG9
Mission RL10
Mission RL11
Mission RM1
Mission RM2
Mission RM3
Mission RM4
Mission RM5
Mission RM6
Mission RM8
Mission RM10
Mission LC1
Mission RM11
Mission LC2
Mission LC3
Mission LC4
Mission LC5
Mission LC6
Mission LC8
Mission SM1
Mission SM2
Mission SM3
Mission SM4
Mission SM5
Mission SM6
Mission SM8
Mission SM10
Mission KG10
Mission SM11
Mission KG2
Mission KG3
Mission KG4
Mission KG5
Mission KG6
Mission KG8
Mission KG11
Mission F2D1
Mission F2D2
Mission F2D3
Mission F2D4
Mission F2D5
Mission F2D6
Mission KC1
Mission KC2
Mission KC3
Mission KC4
Mission KC5
Mission KC6
Mission KC7
Mission KC8
Mission AAA
Mission SM9
Mission LC7
Mission LC9
Mission NL1
Mission NL2
Mission NL3
Mission NL4
Mission NL5
Mission NL6
Mission NL7
Mission NL8
Mission NL9
Mission NL10
Mission NL11
Mission NL12
Mission MC1
Mission MC10
Mission MC2
Mission MC3
Mission MC4
Mission MC5
Mission MC6
Mission MC7
Mission MC8
Mission MC9
Mission RM7
Mission RM9
Mission RL7
Mission RL9
Mission SM7
Mission SE1
Mission SE10
Mission SE11
Mission SE12
Mission SE2
Mission SE3
Mission SE4
Mission SE5
Mission SE6
Mission SE7
Mission SE8
Mission SE9
Mission VP1
Mission VP10
Mission VP2
Mission VP3
Mission VP4
Mission VP5
Mission VP6
Mission VP7
Mission VP8
Mission VP9
Mission WM1
Mission WM2
Mission WM3
Mission WM4
Mission WM5
Mission WM6
Mission WM7
Mission WM8
Mission WE1
Mission WE10
Mission WE2
Mission WE3
Mission WE4
Mission WE5
Mission WE6
Mission WE7
Mission WE8
Mission WE9
Vector Walk Interactive
Name That Motion Interactive
Kinematic Graphing 1 Concept Checker
Kinematic Graphing 2 Concept Checker
Graph That Motion Interactive
Two Stage Rocket Interactive
Rocket Sled Concept Checker
Force Concept Checker
Free-Body Diagrams Concept Checker
Free-Body Diagrams The Sequel Concept Checker
Skydiving Concept Checker
Elevator Ride Concept Checker
Vector Addition Concept Checker
Vector Walk in Two Dimensions Interactive
Name That Vector Interactive
River Boat Simulator Concept Checker
Projectile Simulator 2 Concept Checker
Projectile Simulator 3 Concept Checker
Hit the Target Interactive
Turd the Target 1 Interactive
Turd the Target 2 Interactive
Balance It Interactive
Go For The Gold Interactive
Egg Drop Concept Checker
Fish Catch Concept Checker
Exploding Carts Concept Checker
Collision Carts - Inelastic Collisions Concept Checker
Its All Uphill Concept Checker
Stopping Distance Concept Checker
Chart That Motion Interactive
Roller Coaster Model Concept Checker
Uniform Circular Motion Concept Checker
Horizontal Circle Simulation Concept Checker
Vertical Circle Simulation Concept Checker
Race Track Concept Checker
Gravitational Fields Concept Checker
Orbital Motion Concept Checker
Angular Acceleration Concept Checker
Balance Beam Concept Checker
Torque Balancer Concept Checker
Aluminum Can Polarization Concept Checker
Charging Concept Checker
Name That Charge Simulation
Coulomb's Law Concept Checker
Electric Field Lines Concept Checker
Put the Charge in the Goal Concept Checker
Circuit Builder Concept Checker (Series Circuits)
Circuit Builder Concept Checker (Parallel Circuits)
Circuit Builder Concept Checker (∆V-I-R)
Circuit Builder Concept Checker (Voltage Drop)
Equivalent Resistance Interactive
Pendulum Motion Simulation Concept Checker
Mass on a Spring Simulation Concept Checker
Particle Wave Simulation Concept Checker
Boundary Behavior Simulation Concept Checker
Slinky Wave Simulator Concept Checker
Simple Wave Simulator Concept Checker
Wave Addition Simulation Concept Checker
Standing Wave Maker Simulation Concept Checker
Color Addition Concept Checker
Painting With CMY Concept Checker
Stage Lighting Concept Checker
Filtering Away Concept Checker
InterferencePatterns Concept Checker
Young's Experiment Interactive
Plane Mirror Images Interactive
Who Can See Who Concept Checker
Optics Bench (Mirrors) Concept Checker
Name That Image (Mirrors) Interactive
Refraction Concept Checker
Total Internal Reflection Concept Checker
Optics Bench (Lenses) Concept Checker
Kinematics Preview
Velocity Time Graphs Preview
Moving Cart on an Inclined Plane Preview
Stopping Distance Preview
Cart, Bricks, and Bands Preview
Fan Cart Study Preview
Friction Preview
Coffee Filter Lab Preview
Friction, Speed, and Stopping Distance Preview
Up and Down Preview
Projectile Range Preview
Ballistics Preview
Juggling Preview
Marshmallow Launcher Preview
Air Bag Safety Preview
Colliding Carts Preview
Collisions Preview
Engineering Safer Helmets Preview
Push the Plow Preview
Its All Uphill Preview
Energy on an Incline Preview
Modeling Roller Coasters Preview
Hot Wheels Stopping Distance Preview
Ball Bat Collision Preview
Energy in Fields Preview
Weightlessness Training Preview
Roller Coaster Loops Preview
Universal Gravitation Preview
Keplers Laws Preview
Kepler's Third Law Preview
Charge Interactions Preview
Sticky Tape Experiments Preview
Wire Gauge Preview
Voltage, Current, and Resistance Preview
Light Bulb Resistance Preview
Series and Parallel Circuits Preview
Thermal Equilibrium Preview
Linear Expansion Preview
Heating Curves Preview
Electricity and Magnetism - Part 1 Preview
Electricity and Magnetism - Part 2 Preview
Vibrating Mass on a Spring Preview
Period of a Pendulum Preview
Wave Speed Preview
Slinky-Experiments Preview
Standing Waves in a Rope Preview
Sound as a Pressure Wave Preview
DeciBel Scale Preview
DeciBels, Phons, and Sones Preview
Sound of Music Preview
Shedding Light on Light Bulbs Preview
Models of Light Preview
Electromagnetic Radiation Preview
Electromagnetic Spectrum Preview
EM Wave Communication Preview
Digitized Data Preview
Light Intensity Preview
Concave Mirrors Preview
Object Image Relations Preview
Snells Law Preview
Reflection vs. Transmission Preview
Magnification Lab Preview
Reactivity Preview
Ions and the Periodic Table Preview
Periodic Trends Preview
Chemical Reactions Preview
Intermolecular Forces Preview
Melting Points and Boiling Points Preview
Bond Energy and Reactions Preview
Reaction Rates Preview
Ammonia Factory Preview
Stoichiometry Preview
Nuclear Chemistry Preview
Gaining Teacher Access
Tasks and Classes
Tasks - Classic
Subscription
Subscription Locator
1-D Kinematics
Newton's Laws
Vectors - Motion and Forces in Two Dimensions
Momentum and Its Conservation
Work and Energy
Circular Motion and Satellite Motion
Thermal Physics
Static Electricity
Electric Circuits
Vibrations and Waves
Sound Waves and Music
Light and Color
Reflection and Mirrors
About the Physics Interactives
Task Tracker
Usage Policy
Newtons Laws
Vectors and Projectiles
Forces in 2D
Momentum and Collisions
Circular and Satellite Motion
Balance and Rotation
Electromagnetism
Waves and Sound
Atomic Physics
Forces in Two Dimensions
Work, Energy, and Power
Circular Motion and Gravitation
Sound Waves
1-Dimensional Kinematics
Circular, Satellite, and Rotational Motion
Einstein's Theory of Special Relativity
Waves, Sound and Light
QuickTime Movies
About the Concept Builders
Pricing For Schools
Directions for Version 2
Measurement and Units
Relationships and Graphs
Rotation and Balance
Vibrational Motion
Reflection and Refraction
Teacher Accounts
Task Tracker Directions
Kinematic Concepts
Kinematic Graphing
Wave Motion
Sound and Music
About CalcPad
1D Kinematics
Vectors and Forces in 2D
Simple Harmonic Motion
Rotational Kinematics
Rotation and Torque
Rotational Dynamics
Electric Fields, Potential, and Capacitance
Transient RC Circuits
Light Waves
Units and Measurement
Stoichiometry
Molarity and Solutions
Thermal Chemistry
Acids and Bases
Kinetics and Equilibrium
Solution Equilibria
Oxidation-Reduction
Nuclear Chemistry
Newton's Laws of Motion
Work and Energy Packet
Static Electricity Review
NGSS Alignments
1D-Kinematics
Projectiles
Circular Motion
Magnetism and Electromagnetism
Graphing Practice
About the ACT
ACT Preparation
For Teachers
Other Resources
Solutions Guide
Solutions Guide Digital Download
Motion in One Dimension
Work, Energy and Power
Algebra Based Physics
Honors Physics
Other Tools
Frequently Asked Questions
Purchasing the Download
Purchasing the CD
Purchasing the Digital Download
About the NGSS Corner
NGSS Search
Force and Motion DCIs - High School
Energy DCIs - High School
Wave Applications DCIs - High School
Force and Motion PEs - High School
Energy PEs - High School
Wave Applications PEs - High School
Crosscutting Concepts
The Practices
Physics Topics
NGSS Corner: Activity List
NGSS Corner: Infographics
About the Toolkits
Position-Velocity-Acceleration
Position-Time Graphs
Velocity-Time Graphs
Newton's First Law
Newton's Second Law
Newton's Third Law
Terminal Velocity
Projectile Motion
Forces in 2 Dimensions
Impulse and Momentum Change
Momentum Conservation
Work-Energy Fundamentals
Work-Energy Relationship
Roller Coaster Physics
Satellite Motion
Electric Fields
Circuit Concepts
Series Circuits
Parallel Circuits
Describing-Waves
Wave Behavior Toolkit
Standing Wave Patterns
Resonating Air Columns
Wave Model of Light
Plane Mirrors
Curved Mirrors
Teacher Guide
Using Lab Notebooks
Current Electricity
Light Waves and Color
Reflection and Ray Model of Light
Refraction and Ray Model of Light
Classes (Legacy Version)
Teacher Resources
Subscriptions

Newton's Laws
Einstein's Theory of Special Relativity
About Concept Checkers
School Pricing
Newton's Laws of Motion
Newton's First Law
Newton's Third Law

Mechanics: Momentum and Collisions

Calculator pad, version 2, momentum and collisions: problem set.

Determine the momentum of …

a. … an electron (m= 9.1 x10 -31 kg) moving at 2.18 x 10 6 m/s (as if it were in a Bohr orbit in the H atom). b. … a 0.45 Caliber bullet (m = 0.162 kg) leaving the muzzle of a gun at 860 m/s. c. … a 110-kg professional fullback running across the line at 9.2 m/s. d. … a 360,000-kg passenger plane taxiing down a runway at 1.5 m/s

Audio Guided Solution
Show Answer

A bicycle has a momentum of 24 kg•m/s. What momentum would the bicycle have if it had …

a. … twice the mass and was moving at the same speed? b. … the same mass and was moving with twice the speed? c. … one-half the mass and was moving with twice the speed? d. … the same mass and was moving with one-half the speed? e. … three times the mass and was moving with one-half the speed? f. … three times the mass and was moving with twice the speed?

According to the Guinness Book of World Records, the fastest recorded baseball pitch was delivered by Nolan Ryan in 1974. The pitch was clocked at 100.9 mi/hr (45.0 m/s). Determine the impulse required to give a 0.145-kg baseball such a momentum.

Jerome plays middle linebacker for South's varsity football team. In a game against cross-town rival North, he delivered a hit to North's 82-kg running back, changing his eastward velocity of 5.6 m/s into a westward velocity of 2.5 m/s.

a. Determine the initial momentum of the running back. b. Determine the final momentum of the running back. c. Determine the momentum change of the running back. d. Determine the impulse delivered to the running back.

Kara Less was applying her makeup when she drove into South's busy parking lot last Friday morning. Unaware that Lisa Ford was stopped in her lane 30 feet ahead, Kara rear-ended Lisa's rented Taurus. Kara's 1300-kg car was moving at 11 m/s and stopped in 0.14 seconds.

a. Determine the momentum change of Kara's car. b. Determine the impulse experienced by Kara's car. c. Determine the magnitude of the force experienced by Kara's car.

An interesting story is often told of baseball star Johnny Bench when he was a rookie catcher in 1968. During a Spring Training game, he kept signaling to star pitcher Jim Maloney to throw a curve ball. Maloney continuously shook off Bench's signal, opting to throw fastballs instead. The rookie catcher walked to the mound and told the veteran Maloney that his fastball wasn't fast enough and that he should throw some curve balls. Bench again signaled for a curve. Maloney shook of the signal and threw a fastball. Before the ball reached the plate, Bench took off his glove; he then caught the pitch barehanded.

a. Determine the impulse required to stop a 0.145-kg baseball moving at 35.7 m/s (80.0 mi/hr). b. If this impulse is delivered to the ball in 0.020 seconds, then what is magnitude of the force acting between the bare hand and the ball?

While playing basketball in PE class, Logan lost his balance after making a lay-up and colliding with the padded wall behind the basket. His 74-kg body decelerated from 7.6 m/s to 0 m/s in 0.16 seconds.

a. Determine the force acting upon Logan's body. b. If Logan had hit the concrete wall moving at the same speed, his momentum would have been reduced to zero in 0.0080 seconds. Determine what the force on his body would have been for such an abrupt collision.

NASA's Langley Research Center has been experimenting with the use of air bags to soften the landings of crew exploration vehicles (CEV) on land. What stopping time will be required in order to safely stop a 7250 kg CEV moving at 7.65 m/s with an average force of 426000 N (an average force of 6 Gs)?

In a study conducted by a University of Illinois researcher, the football team at Unity High School in Tolono, IL was equipped for an entire season with helmets containing accelerometers. Information about every impact in practice and in games was sent to a computer present on the sidelines. The study found that the average force on a top of the head impact was 1770 N and endured for 7.78 milliseconds. Using a head mass of 5.20 kg and presuming the head to be a free body , determine the velocity change experienced in such an impact.

Problem 10:

Cassie has just finished her session on the trampoline during PE. As she prepares to exit the trampoline, her vertical momentum is reduced by a series of three resistive impulses with the bounce mat. Just prior to this series of impulses, her 48.5-kg body is moving downward at 8.20 m/s. On the first impulse, Cassie experiences an average upward force of 230 N for 0.65 seconds. The second impulse of 112 N•s lasts for 0.41 seconds. The last impulse involves an average upward force of 116 N which cases a 84 kg•m/s momentum change. What vertical velocity does Cassie have after these three impulses?

Problem 11:

Aaron Agin nodded off while driving home from play practice this past Sunday evening. His 1500-kg car hit a series of guardrails while moving at 19.8 m/s. The first guard rail delivered a resistive impulse of 5700 N•s. The second guard rail pushed against his car with a force of 79000 N for 0.12 seconds. The third guard rail collision lowered the car's velocity by 3.2 m/s. Determine the final velocity of the car.

Problem 12:

Mr. H ignites the enthusiasm of the class with a home-made cannon demonstration. The 1.27-kg cannon is loaded with a 54-gram tennis ball and placed on the floor. Mr. H adds the fuel, waits for its vapors to fill the reaction chamber and then brings a match nearby. The explosion stuns the crowd and propels the ball forward. A photogate measurement determines that the cannon recoiled backwards with a speed of 7.8 m/s. Determine the speed of the ball.

Problem 13:

An 82-kg male and a 48-kg female pair figure skating team are gliding across the ice at 7.4 m/s, preparing for a throw jump maneuver. The male skater tosses the female skater forward with a speed of 8.6 m/s. Determine the speed of the male skater immediately after the throw.

Problem 14:

A candy-filled piñata is hung from a tree for Matthew's birthday. During an unsuccessful attempt to break the 4.4-kg piñata, Hayden cracks it with a 0.54-kg stick moving at 4.8 m/s. The stick stops and the piñata undergoes a gentle swinging motion. Determine the swing speed of the piñata immediately after being cracked by the stick.

Problem 15:

During an in-class demonstration of momentum change and impulse, Mr. H asks Jerome (102 kg) and Michael (98 kg) to sit on a large 14-kg skate cart. Mr. H asks Suzie (44 kg) to sit on a second 14-kg skate cart. The two carts are placed on low friction boards in the hallway. Jerome pushes off of Suzie's cart. Measurements are made to determine that Suzie's cart acquired a post-impulse speed of 9.6 m/s. Determine the expected recoil speed of Jerome and Michael's cart.

Problem 16:

A 70.9-kg boy and a 43.2-kg girl, both wearing skates face each other at rest on a skating rink. The boy pushes the girl, sending her eastward with a speed of 4.64 m/s. Neglecting friction, determine the subsequent velocity of the boy.

Problem 17:

To Mr. H's disgust, a 450-g black crow is raiding the recently-filled bird feeder. As Mr. H runs out the back door with his broom in an effort to scare the crow away, it pushes off the 670-gram feeder with a takeoff speed of 1.5 m/s. Determine the speed at which the feeder initially recoils backwards.

Problem 18:

Jaclyn plays singles for South's varsity tennis team. During the match against North, Jaclyn won the sudden death tiebreaker point with a cross-court passing shot. The 57.5-gram ball hit her racket with a northward velocity of 26.7 m/s. Upon impact with her 331-gram racket, the ball rebounded in the exact opposite direction (and along the same general trajectory) with a speed of 29.5 m/s.

a. Determine the pre-collision momentum of the ball. b. Determine the post-collision momentum of the ball. c. Determine the momentum change of the ball. d. Determine the velocity change of the racket.

Problem 19:

Anna Litical and Noah Formula are doing The Cart and the Brick Lab. They drop a brick on a 2.6 kg cart moving at 28.2 cm/s. After the collision, the dropped brick and cart are moving together with a velocity of 15.7 cm/s. Determine the mass of the dropped brick.

Problem 20:

A Roller Derby exhibition recently came to town. They packed the gym for two consecutive weekend nights at South's field house. On Saturday evening, the 68-kg Anna Mosity was moving at 17 m/s when she collided with 76-kg Sandra Day O'Klobber who was moving forward at 12 m/s and directly in Anna's path. Anna jumped onto Sandra's back and the two continued moving together at the same speed. Determine their speed immediately after the collision.

Problem 21:

Ima Rilla Saari rushes to her car in order to hurry home and get dressed for work. Failing to realize the dangers of driving under slick and icy conditions, she collides her 940-kg Mazda Miata into the rear of a 2460-kg pick-up truck which was at rest at the light on Lake Avenue. Ima's pre-collision speed was 12.5 m/s. Determine the post-collision speed of the two entangled cars as they slide across the ice.

Problem 22:

In a goal line stand against New Greer Academy, South's linebackers Jerome (m=102 kg) and Michael (m=98 kg) meet the 84-kg halfback moving southward through the air at 6.4 m/s. Upon contact, Jerome and Michael are both moving at 3.6 m/s in the exact opposite direction. Determine the post-collision speed and direction of the collection of three players. Assume they move together after the collision.

Problem 23:

Hayden (m=24.3-kg) is gliding along the sidewalk on his skateboard at 8.6 ft/s. As he travels under a low-hanging branch of the tree where Matthew is sitting, he grabs the 4.5-kg bag of soccer balls from Matthew's hands. Determine the speed of Hayden immediately after grabbing the bag of soccer balls.

Problem 24:

Rex (m=86 kg) and Tex (92 kg) board the bumper cars at the local carnival. Rex is moving at a full speed of 2.05 m/s when he rear-ends Tex who is at rest in his path. Tex and his 125-kg car lunge forward at 1.40 m/s. Determine the post-collision speed of Rex and his 125-kg car.

Problem 25:

Abbey and Mia are in the basement playing pool. On Abbey's recent shot, the cue ball was moving east at 82 cm/s when it struck the slower 5-ball moving in the same direction at 24 cm/s. The 5-ball immediately speeds up to 52 cm/s. Determine the post-collision speed of the cue ball.

Problem 26:

Polly Ester and Ray Ahn are doing the Elastic Collision lab on a low-friction track. Cart A has a mass of 1.00 kg and is moving rightward at 27.6 cm/s prior to the collision with Cart B. Cart B has a mass of 0.50 kg and is moving leftward with a speed of 42.9 cm/s. After the magnetic repulsion of the two carts, Cart A is moving leftward at 10.1 cm/s. Determine the post-collision speed and direction of cart B.

Problem 27:

Bailey is on the tenth frame of her recent bowling competition and she needs to pick up the last pin for a spare and the first place trophy. She rolls the 7.05-kg ball down the lane and it hits the 1.52-kg pin head on. The ball was moving at 8.24 m/s before the collision. The pin went flying forward at 13.2 m/s. Determine the post-collision speed of the ball.

Problem 28:

Jack D. Ripper flipped out after missing a Must-Do-It question for the third time on his Minds On Physics assignment. Outraged by the futility of his efforts, he flings a 4.0-gram pencil across the room. The pencil lodges into a 221.0-gram Sponge Bob doll which is at rest on a countertop. Once in motion, the pencil/doll combination slide a distance of 11.9 cm across the countertop before stopping. The coefficient of friction between the doll and the countertop is 0.325. Determine the speed at which the pencil is moving prior to striking Sponge Bob.

Problem 29:

A physics student hurls a 315-gram ball directly into a 3.54-kg box which is at rest on a table top. The baseball strikes the box with a pre-impact speed of 54.1 m/s. The box is filled with towels to help absorb the blow and effectively catch the ball. The coefficient of friction between the box and the table is 0.714. Determine the distance which the ball and box slide across the table after the collision.

Problem 30:

A 72-kg boy and a 48-kg girl, both wearing ice skates face each other at rest on a skating rink. The boy pushes the girl, sending her eastward with a speed of 6.8 m/s. When the impulse is completed, the boy and girl are a distance of 1.4 meters apart. Determine the distance of separation between the boy and the girl 5.0 seconds after the impulse is completed.

Problem 31:

The city police are in pursuit of Robin Banks after his recent holdup at the savings and loan. The high speed police chase ends at an intersection as a 2080-kg Ford Explorer (driven by Robin) traveling north at 32.6 m/s collides with a 18400-kg garbage truck moving east at 12.4 m/s. The Explorer and the garbage truck entangle together in the middle of the intersection and move as a single object. Determine the post-collision speed and direction of the two entangled vehicles.

Problem 32:

A 92-kg fullback moving south with a speed of 5.8 m/s is tackled by a 110-kg lineman running west with a speed of 3.6 m/s. Assuming momentum conservation, determine the speed and direction of the two players immediately after the tackle.

Return to Overview

View Audio Guided Solution for Problem:

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32

JEE-IIT-NCERT Physics & Math

Widget atas posting, elastic collision problems and solutions.

Problem #1

MIT News | Massachusetts Institute of Technology

Machine learning
Social justice
Black holes
Classes and programs

Departments

Aeronautics and Astronautics
Brain and Cognitive Sciences
Architecture
Political Science
Mechanical Engineering

Centers, Labs, & Programs

Abdul Latif Jameel Poverty Action Lab (J-PAL)
Picower Institute for Learning and Memory
Lincoln Laboratory
School of Architecture + Planning
School of Engineering
School of Humanities, Arts, and Social Sciences
Sloan School of Management
School of Science
MIT Schwarzman College of Computing

Ten with MIT connections win 2024 Hertz Foundation Fellowships

Press contact :.

10 headshots of the 2024 Hertz Fellows with ties to MIT

Previous image Next image

The Fannie and John Hertz Foundation announced that it has awarded fellowships to 10 PhD students with ties to MIT. The prestigious award provides each recipient with five years of doctoral-level research funding (up to a total of $250,000), which allows them the flexibility and autonomy to pursue their own innovative ideas.

Fellows also receive lifelong access to Hertz Foundation programs, such as events, mentoring, and networking. They join the ranks of over 1,300 former Hertz Fellows who are leaders and scholars in a range of fields in science, engineering, and technology. Connections among fellows over the years have sparked collaborations in startups, research, and technology commercialization.

The 10 MIT recipients are among a total of 18 Hertz Foundation Fellows scholars selected this year from across the country. Five of them received their undergraduate degrees at the Institute and will pursue their PhDs at other schools. Two are current MIT graduate students, and four will begin their studies here in the fall.

“For more than 60 years, Hertz Fellows have led scientific and technical innovation in national security, applied biological sciences, materials research, artificial intelligence, space exploration, and more. Their contributions have been essential in advancing U.S. competitiveness,” says Stephen Fantone, chair of the Hertz Foundation board of directors and founder and president of Optikos Corp. “I’m excited to watch our newest Hertz Fellows as they pursue challenging research and continue the strong tradition of applying their work for the greater good.”

This year’s MIT-affiliated awardees are:

Owen Dugan ’24 graduated from MIT in just two-and-a-half years with a degree in physics, and he plans to pursue a PhD in computer science at Stanford University. His research interests lie at the intersection of AI and physics. As an undergraduate, he conducted research in a broad range of areas, including using physics concepts to enhance the speed of large language models and developing machine learning algorithms that automatically discover scientific theories. He was recognized with MIT’s Outstanding Undergraduate Research Award and is a U.S. Presidential Scholar, a Neo Scholar, and a Knight-Hennessy Scholar. Dugan holds multiple patents, co-developed an app to reduce food waste, and co-founded a startup that builds tools to verify the authenticity of digital images.

Kaylie Hausknecht will begin her physics doctorate at MIT in the fall, having completing her undergraduate degree in physics and astrophysics at Harvard University. While there, her undergraduate research focused on developing new machine learning techniques to solve problems in a range of fields, such as fluid dynamics, astrophysics, and condensed matter physics. She received the Hoopes Prize for her senior thesis, was inducted into Phi Beta Kappa as a junior, and won two major writing awards. In addition, she completed five NASA internships. As an intern, she helped identify 301 new exoplanets using archival data from the Kepler Space Telescope. Hausknecht served as the co-president of Harvard’s chapter of Science Club for Girls, which works to encourage girls from underrepresented backgrounds to pursue STEM.

Elijah Lew-Smith majored in physics at Brown University and plans to pursue a doctoral degree in physics at MIT. He is a theoretical physicist with broad intellectual interests in effective field theory (EFT), which is the study of systems with many interacting degrees of freedom. EFT reveals how to extract the relevant, long-distance behavior from complicated microscopic rules. In 2023, he received a national award to work on applying EFT systematically to non-equilibrium and active systems such as fluctuating hydrodynamics or flocking birds. In addition, Lew-Smith received a scholarship from the U.S. State Department to live for a year in Dakar, Senegal, and later studied at ’École Polytechnique in Paris, France.

Rupert Li ’24 earned his bachelor’s and master’s degrees at MIT in mathematics as well as computer science, data science, and economics, with a minor in business analytics.He was named a 2024 Marshall Scholar and will study abroad for a year at Cambridge University before matriculating at Stanford University for a mathematics doctorate. As an undergraduate, Li authored 12 math research articles, primarily in combinatorics, but also including discrete geometry, probability, and harmonic analysis. He was recognized for his work with a Barry Goldwater Scholarship and an honorable mention for the Morgan Prize, one of the highest undergraduate honors in mathematics.

Amani Maina-Kilaas is a first-year doctoral student at MIT in the Department of Brain and Cognitive Sciences, where he studies computational psycholinguistics. In particular, he is interested in using artificial intelligence as a scientific tool to study how the mind works, and using what we know about the mind to develop more cognitively realistic models. Maina-Kilaas earned his bachelor’s degree in computer science and mathematics from Harvey Mudd College. There, he conducted research regarding intention perception and theoretical machine learning, earning the Astronaut Scholarship and Computing Research Association’s Outstanding Undergraduate Researcher Award.

Zoë Marschner ’23 is a doctoral student at Carnegie Mellon University working on geometry processing, a subfield of computer graphics focused on how to represent and work with geometric data digitally; in her research, she aims to make these representations capable of enabling fundamentally better algorithms for solving geometric problems across science and engineering. As an undergraduate at MIT, she earned a bachelor’s degree in computer science and math and pursued research in geometry processing, including repairing hexahedral meshes and detecting intersections between high-order surfaces. She also interned at Walt Disney Animation Studios, where she worked on collision detection algorithms for simulation. Marschner is a recipient of the National Science Foundation’s Graduate Research Fellowship and the Goldwater Scholarship.

Zijian (William) Niu will start a doctoral program in computational and systems biology at MIT in the fall. He has a particular interest in developing new methods for imaging proteins and other biomolecules in their native cellular environments and using those data to build computational models for predicting their dynamics and molecular interactions. Niu received his bachelor’s degree in biochemistry, biophysics, and physics from the University of Pennsylvania. His undergraduate research involved developing novel computational methods for biological image analysis. He was awarded the Barry M. Goldwater Scholarship for creating a deep-learning algorithm for accurately detecting tiny diffraction-limited spots in fluorescence microscopy images that outperformed existing methods in quantifying spatial transcriptomics data.

James Roney received his bachelor’s and master’s degrees from Harvard University in computer science and statistics, respectively. He is currently working as a machine learning research engineer at D.E. Shaw Research. His past research has focused on interpreting the internal workings of AlphaFold and modeling cancer evolution. Roney plans to pursue a PhD in computational biology at MIT, with a specific interest in developing computational models of protein structure, function, and evolution and using those models to engineer novel proteins for applications in biotechnology.

Anna Sappington ’19 is a student in the Harvard University-MIT MD-PhD Program, currently in the first year of her doctoral program at MIT in electrical engineering and computer science. She is interested in building methods to predict evolutionary events, especially connections among machine learning, biology, and chemistry to develop reinforcement learning models inspired by evolutionary biology. Sappington graduated from MIT with a bachelor’s degree in computer science and molecular biology. As an undergraduate, she was awarded a 2018 Barry M. Goldwater Scholarship and selected as a Burchard Scholar and an Amgen Scholar. After graduating, she earned a master’s degree in genomic medicine from the University of Cambridge, where she studied as a Marshall Scholar, as well as a master’s degree in machine learning from University College London.

Jason Yang ’22 received his bachelor’s degree in biology with a minor in computer science from MIT and is currently a doctoral student in genetics at Stanford University. He is interested in understanding the biological processes that underlie human health and disease. At MIT, and subsequently at Massachusetts General Hospital, Yang worked on the mechanisms involved in neurodegeneration in repeat expansion diseases, uncovering a novel molecular consequence of repeat protein aggregation.

Share this news article on:

Six with MIT ties win 2023 Hertz Foundation Fellowships

Headshots of Roderick Bayliss III, David Li, Syamantak Payra, Scott Barrow Moroch, and Alexander Cohen

Five with MIT ties win 2022 Hertz Foundation Fellowships

Composite three-way photo featuring headshots of the three fellows

Three from MIT receive 2021 Hertz Foundation Fellowships

Previous item Next item

More MIT News

A rendering shows the MIT campus and Cambridge, with MIT buildings in red.

Students research pathways for MIT to reach decarbonization goals

Read full story →

Namrata Kala sits in glass-walled building

Improving working environments amid environmental distress

Ashesh Rambachan converses with a student in the front of a classroom.

A data-driven approach to making better choices

On the left, Erik Lin-Greenberg talks, smiling, with two graduate students in his office. On the right, Tracy Slatyer sits with two students on a staircase, conversing warmly.

Paying it forward

Portrait photo of John Fucillo posing on a indoor stairwell

John Fucillo: Laying foundations for MIT’s Department of Biology

Graphic of hand holding a glowing chip-based 3D printer

Researchers demonstrate the first chip-based 3D printer

More news on MIT News homepage →

Massachusetts Institute of Technology 77 Massachusetts Avenue, Cambridge, MA, USA

Map (opens in new window)
Events (opens in new window)
People (opens in new window)
Careers (opens in new window)
Accessibility
Social Media Hub
MIT on Facebook
MIT on YouTube
MIT on Instagram

IMAGES

Inelastic Collision: Definition, Formula, and Examples
How to Solve an Inelastic Collision Problem
Inelastic Collision Physics Problems In One Dimension
How to Solve for the Final Velocity of a Perfectly Inelastic 1D
Inelastic Collision Example Problem
How To Solve Collision Problems Physics

VIDEO

Phoenix 2.0: Physics Most Important Video for NEET 2025
Form 4 Physics
Physics Unit 6.3 Inelastic Collisions
SPH4U
An Inelastic Collision (Solved Problem)
super trick collision 💥#collision #elasticcollision #inelasticcollision #supertrick

COMMENTS

8.3 Elastic and Inelastic Collisions
This video reviews the definitions of momentum and impulse. It also covers an example of using conservation of momentum to solve a problem involving an inelastic collision between a car with constant velocity and a stationary truck. Note that Sal accidentally gives the unit for impulse as Joules; it is actually N ⋅ ⋅ s or k ⋅ ⋅ gm/s.
Collision Analysis and Momentum Problems
To determine v (the velocity of the truck), the sum of the individual after-collision momentum of the two objects is set equal to the total momentum. The following equation results: 3000*v + 15 000 = 30 000. 3000*v = 15 000. v = 5.0 m/s. Using algebra skills, it can be shown that v = 5.0 m/s.
Solving elastic collision problems the hard way
Solving elastic collision problems the hard way. In this video, David shows how to solve elastic problems the hard way. In other words, using conservation of momentum and conservation of kinetic energy, David substitutes one equation into the other and solves for the final velocities. Created by David SantoPietro.
Inelastic Collision Physics Problems In One Dimension
This physics video tutorial Explains how to solve inelastic collision problems in one dimension using the law of conservation of linear momentum. In an inel...
Inelastic Collisions
The steps for solving inelastic collision problems are often as follows: 1) Draw a picture of the initial and final states. ... The concepts presented through collisions are also the founding physics principles for studying car crashes, or car safety, as well as other real world events that contain collisions. By using the mathematical models ...
8.5: Inelastic Collisions in One Dimension
An inelastic collision is one in which the internal kinetic energy changes (it is not conserved). Figure 8.5.1 8.5. 1 shows an example of an inelastic collision. Two objects that have equal masses head toward one another at equal speeds and then stick together. Their total internal kinetic energy is initially.
Inelastic Collision Example Problem
Solution: Part A: To find the final velocity, remember momentum is conserved before and after the collision. total momentum before = total momentum after. m T v T + m C v C = (m T + m C )v Final. where. m T = mass of the truck = 3000 kg. m C = mass of the car = 1000 kg. v T = velocity of the truck = 50 km/hr. v C = velocity of the car = 0 km/hr.
7.3: Collisions
In an inelastic collision the total kinetic energy after the collision is not equal to the total kinetic energy before the collision. ... A brief introduction to problem solving of collisions in two dimensions using the law of conservation of momentum. ... College Physics. September 17, 2013. Provided by: ...
8.5 Inelastic Collisions in One Dimension
Define inelastic collision. Explain perfectly inelastic collision. Apply an understanding of collisions to sports. Determine recoil velocity and loss in kinetic energy given mass and initial velocity. We have seen that in an elastic collision, internal kinetic energy is conserved. An inelastic collision is one in which the internal kinetic ...
Elastic and inelastic collisions (video)
And for most inelastic collisions the initial total kinetic energy is greater than the final total kinetic energy. In other words, in an inelastic collision you'll lose some kinetic energy, some of this kinetic energy gets transformed into some other kind of energy and that energy is typically thermal energy. 'Cause think about it.
Inelastic Collision Problems
Inelastic Collision Problems. The law of conservation of momentum can be used to solve all types of collisions when there are no external forces involved. Inelastic collisions are collisions in which there is some loss of energy. In fact, almost all "real" collisions are inelastic because some energy is lost to sound or damage.
What are two dimensional collisions? (article)
For a collision where objects will be moving in 2 dimensions (e.g. x and y), the momentum will be conserved in each direction independently (as long as there's no external impulse in that direction). In other words, the total momentum in the x direction will be the same before and after the collision. Σ p x i = Σ p x f.
Physics
Tutorial on solving problems with inelastic collisions.
Inelastic collisions
Inelastic collisions, momentum conservation, friction; Reasoning: Board B and C collide inelastically. Board A slides over boards B and C, and we have sliding friction. Solve the problem in a inertial frame. Details of the calculation: After the collision boards B and C stick together and move with speed v/2 in the lab frame (momentum ...
Elastic Collision Example Problem
Elastic collisions are collisions between objects where both momentum and kinetic energy are conserved. This elastic collision example problem will show how to find the final velocities of two bodies after an elastic collision. This illustration shows a generic elastic collision between two masses A and B. The variables involved are. m A is the ...
Inelastic Collision Problems and Solutions
Initial: K i = K 1,i + K 2,i = ½m 1 v 1,i 2 + ½m 2 v 2,i2. Final : K f = K 1,f + K 2,f = ½ (m 1 + m 2) v f2. As you did in Sample Problem E, use the equation for a perfectly inelastic collision to calculate the final velocity. Substitute the values into the equation and solve: First, calculate the final velocity, which will be used in the ...
An Alternative Approach to Solving Collision Problems
Perfectly inelastic collision: ΔE=½μΔv². Semi-elastic collision: ΔE=½μΔv²(1-e²) Perfectly elastic collision: ΔE=0. The reader is encouraged to try out the above formulae to solve collision problems- they should be as widely applicable as are the principles of conservation of energy and momentum since that is their genesis!
8.4 Elastic Collisions in One Dimension
8.5 Inelastic Collisions in One Dimension; ... to solve problems involving one-dimensional elastic collisions between two objects we can use the equations for conservation of momentum and conservation of internal kinetic energy. First, the equation for conservation of momentum for two objects in a one-dimensional collision is ... //openstax.org ...
What are elastic and inelastic collisions?
An inelastic collision is a collision in which there is a loss of kinetic energy. While momentum of the system is conserved in an inelastic collision, kinetic energy is not. This is because some kinetic energy had been transferred to something else. Thermal energy, sound energy, and material deformation are likely culprits.
Deriving the shortcut to solve elastic collision problems
1. your way might be better to get a faster answer. 2. David's way better to grasp another intuition about an elastic collision. 3. perfectness must be assumed in both cases, i believe. otherwise, kinetic energy must be lost somewhere. then all of the equations here and in video might not work. ( 1 vote) Upvote.
Momentum and Collisions Problem Sets
Problem 24: Rex (m=86 kg) and Tex (92 kg) board the bumper cars at the local carnival. Rex is moving at a full speed of 2.05 m/s when he rear-ends Tex who is at rest in his path. Tex and his 125-kg car lunge forward at 1.40 m/s. Determine the post-collision speed of Rex and his 125-kg car. Audio Guided Solution.
Solving elastic collision problems the hard way
In this video, David shows how to solve elastic problems the hard way. In other words, using conservation of momentum and conservation of kinetic energy, Dav...
Elastic Collision Problems and Solutions
Elastic Collision Problems and Solutions. Post a Comment. Problem #1. A 0.015 kg marble moving to the right at 0.225 m/s makes an elastic head-on collision with a 0.030 kg shooter marble moving to the left at 0.180 m/s. After the collision, the smaller marble moves to the left at 0.315 m/s. Assume that neither marble rotates before or after the ...
Ten with MIT connections win 2024 Hertz Foundation Fellowships
While there, her undergraduate research focused on developing new machine learning techniques to solve problems in a range of fields, such as fluid dynamics, astrophysics, and condensed matter physics. She received the Hoopes Prize for her senior thesis, was inducted into Phi Beta Kappa as a junior, and won two major writing awards.
Reflecting on a Pivotal Physics Calculation
A Q&A with physicist David Politzer about solving the mystery of the strong force more than 50 years ago. When David Politzer, Caltech's Richard Chace Tolman Professor of Theoretical Physics, was a fourth-year graduate student at Harvard in 1973, he made an astounding discovery that would forever reshape the field of particle physics.He had been mulling over a physics problem and decided to do ...
Elastic Collisions In One Dimension Physics Problems
This physics video provides a basic introduction into elastic collisions. It explains how to solve one dimension elastic collision physics problems. In an ...