solving problems using exponential function

6.6 Exponential and Logarithmic Equations

Learning objectives.

In this section, you will:

• Use like bases to solve exponential equations.
• Use logarithms to solve exponential equations.
• Use the definition of a logarithm to solve logarithmic equations.
• Use the one-to-one property of logarithms to solve logarithmic equations.
• Solve applied problems involving exponential and logarithmic equations.

In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.

Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.

Using Like Bases to Solve Exponential Equations

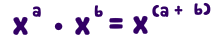
The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers b , b , S , S , and T , T , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 , b S = b T b S = b T if and only if S = T . S = T .

In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.

For example, consider the equation 3 4 x − 7 = 3 2 x 3 . 3 4 x − 7 = 3 2 x 3 . To solve for x , x , we use the division property of exponents to rewrite the right side so that both sides have the common base, 3. 3. Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for x x :

Using the One-to-One Property of Exponential Functions to Solve Exponential Equations

For any algebraic expressions S and  T , S and  T , and any positive real number b ≠ 1 , b ≠ 1 ,

Given an exponential equation with the form b S = b T , b S = b T , where S S and T T are algebraic expressions with an unknown, solve for the unknown.

• Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form b S = b T . b S = b T .
• Use the one-to-one property to set the exponents equal.
• Solve the resulting equation, S = T , S = T , for the unknown.

Solving an Exponential Equation with a Common Base

Solve 2 x − 1 = 2 2 x − 4 . 2 x − 1 = 2 2 x − 4 .

Solve 5 2 x = 5 3 x + 2 . 5 2 x = 5 3 x + 2 .

Rewriting Equations So All Powers Have the Same Base

Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.

For example, consider the equation 256 = 4 x − 5 . 256 = 4 x − 5 . We can rewrite both sides of this equation as a power of 2. 2. Then we apply the rules of exponents, along with the one-to-one property, to solve for x : x :

Given an exponential equation with unlike bases, use the one-to-one property to solve it.

• Rewrite each side in the equation as a power with a common base.

Solving Equations by Rewriting Them to Have a Common Base

Solve 8 x + 2 = 16 x + 1 . 8 x + 2 = 16 x + 1 .

Solve 5 2 x = 25 3 x + 2 . 5 2 x = 25 3 x + 2 .

Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base

Solve 2 5 x = 2 . 2 5 x = 2 .

Solve 5 x = 5 . 5 x = 5 .

Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?

No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.

Solving an Equation with Positive and Negative Powers

Solve 3 x + 1 = −2. 3 x + 1 = −2.

This equation has no solution. There is no real value of x x that will make the equation a true statement because any power of a positive number is positive.

Figure 2 shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.

Solve 2 x = −100. 2 x = −100.

Solving Exponential Equations Using Logarithms

Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since log ( a ) = log ( b ) log ( a ) = log ( b ) is equivalent to a = b , a = b , we may apply logarithms with the same base on both sides of an exponential equation.

Given an exponential equation in which a common base cannot be found, solve for the unknown.

• If one of the terms in the equation has base 10, use the common logarithm.
• If none of the terms in the equation has base 10, use the natural logarithm.
• Use the rules of logarithms to solve for the unknown.

Solving an Equation Containing Powers of Different Bases

Solve 5 x + 2 = 4 x . 5 x + 2 = 4 x .

Solve 2 x = 3 x + 1 . 2 x = 3 x + 1 .

Is there any way to solve 2 x = 3 x ? 2 x = 3 x ?

Yes. The solution is 0. 0.

Equations Containing e

One common type of exponential equations are those with base e . e . This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base e e on either side, we can use the natural logarithm to solve it.

Given an equation of the form y = A e k t , y = A e k t , solve for t . t .

• Divide both sides of the equation by A . A .
• Apply the natural logarithm of both sides of the equation.
• Divide both sides of the equation by k . k .

Solve an Equation of the Form y = Ae kt

Solve 100 = 20 e 2 t . 100 = 20 e 2 t .

Using laws of logs, we can also write this answer in the form t = ln 5 . t = ln 5 . If we want a decimal approximation of the answer, we use a calculator.

Solve 3 e 0.5 t = 11. 3 e 0.5 t = 11.

Does every equation of the form y = A e k t y = A e k t have a solution?

No. There is a solution when k ≠ 0 , k ≠ 0 , and when y y and A A are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is 2 = −3 e t . 2 = −3 e t .

Solving an Equation That Can Be Simplified to the Form y = Ae kt

Solve 4 e 2 x + 5 = 12. 4 e 2 x + 5 = 12.

Solve 3 + e 2 t = 7 e 2 t . 3 + e 2 t = 7 e 2 t .

Extraneous Solutions

Sometimes the methods used to solve an equation introduce an extraneous solution , which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.

Solving Exponential Functions in Quadratic Form

Solve e 2 x − e x = 56. e 2 x − e x = 56.

When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation e x = −7 e x = −7 because a positive number never equals a negative number. The solution ln ( −7 ) ln ( −7 ) is not a real number, and in the real number system this solution is rejected as an extraneous solution.

Solve e 2 x = e x + 2. e 2 x = e x + 2.

Does every logarithmic equation have a solution?

No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.

Using the Definition of a Logarithm to Solve Logarithmic Equations

We have already seen that every logarithmic equation log b ( x ) = y log b ( x ) = y is equivalent to the exponential equation b y = x . b y = x . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3.   log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3.   To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x : x :

For any algebraic expression S S and real numbers b b and c , c , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 ,

Using Algebra to Solve a Logarithmic Equation

Solve 2 ln x + 3 = 7. 2 ln x + 3 = 7.

Solve 6 + ln x = 10. 6 + ln x = 10.

Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve 2 ln ( 6 x ) = 7. 2 ln ( 6 x ) = 7.

Solve 2 ln ( x + 1 ) = 10. 2 ln ( x + 1 ) = 10.

Using a Graph to Understand the Solution to a Logarithmic Equation

Solve ln x = 3. ln x = 3.

Figure 3 represents the graph of the equation. On the graph, the x -coordinate of the point at which the two graphs intersect is close to 20. In other words e 3 ≈ 20. e 3 ≈ 20. A calculator gives a better approximation: e 3 ≈ 20.0855. e 3 ≈ 20.0855.

Use a graphing calculator to estimate the approximate solution to the logarithmic equation 2 x = 1000 2 x = 1000 to 2 decimal places.

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x > 0 , x > 0 , S > 0 , S > 0 , T > 0 T > 0 and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,

For example,

So, if x − 1 = 8 , x − 1 = 8 , then we can solve for x , x , and we get x = 9. x = 9. To check, we can substitute x = 9 x = 9 into the original equation: log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for x : x :

To check the result, substitute x = 10 x = 10 into log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) .

For any algebraic expressions S S and T T and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

Given an equation containing logarithms, solve it using the one-to-one property.

• Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form log b S = log b T . log b S = log b T .
• Use the one-to-one property to set the arguments equal.

Solving an Equation Using the One-to-One Property of Logarithms

Solve ln ( x 2 ) = ln ( 2 x + 3 ) . ln ( x 2 ) = ln ( 2 x + 3 ) .

There are two solutions: 3 3 or −1. −1. The solution −1 −1 is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.

Solve ln ( x 2 ) = ln 1. ln ( x 2 ) = ln 1.

Solving Applied Problems Using Exponential and Logarithmic Equations

In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.

One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life . Table 1 lists the half-life for several of the more common radioactive substances.

We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:

• A 0 A 0 is the amount initially present
• T T is the half-life of the substance
• t t is the time period over which the substance is studied
• A ( t ) A ( t ) is the amount of the substance present after time t t

Using the Formula for Radioactive Decay to Find the Quantity of a Substance

How long will it take for ten percent of a 1000-gram sample of uranium-235 to decay?

Ten percent of 1000 grams is 100 grams. If 100 grams decay, the amount of uranium-235 remaining is 900 grams.

How long will it take before twenty percent of our 1000-gram sample of uranium-235 has decayed?

Access these online resources for additional instruction and practice with exponential and logarithmic equations.

• Solving Logarithmic Equations
• Solving Exponential Equations with Logarithms

6.6 Section Exercises

How can an exponential equation be solved?

When does an extraneous solution occur? How can an extraneous solution be recognized?

When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?

For the following exercises, use like bases to solve the exponential equation.

4 − 3 v − 2 = 4 − v 4 − 3 v − 2 = 4 − v

64 ⋅ 4 3 x = 16 64 ⋅ 4 3 x = 16

3 2 x + 1 ⋅ 3 x = 243 3 2 x + 1 ⋅ 3 x = 243

2 − 3 n ⋅ 1 4 = 2 n + 2 2 − 3 n ⋅ 1 4 = 2 n + 2

625 ⋅ 5 3 x + 3 = 125 625 ⋅ 5 3 x + 3 = 125

36 3 b 36 2 b = 216 2 − b 36 3 b 36 2 b = 216 2 − b

( 1 64 ) 3 n ⋅ 8 = 2 6 ( 1 64 ) 3 n ⋅ 8 = 2 6

For the following exercises, use logarithms to solve.

9 x − 10 = 1 9 x − 10 = 1

2 e 6 x = 13 2 e 6 x = 13

e r + 10 − 10 = −42 e r + 10 − 10 = −42

2 ⋅ 10 9 a = 29 2 ⋅ 10 9 a = 29

− 8 ⋅ 10 p + 7 − 7 = −24 − 8 ⋅ 10 p + 7 − 7 = −24

7 e 3 n − 5 + 5 = −89 7 e 3 n − 5 + 5 = −89

e − 3 k + 6 = 44 e − 3 k + 6 = 44

− 5 e 9 x − 8 − 8 = −62 − 5 e 9 x − 8 − 8 = −62

− 6 e 9 x + 8 + 2 = −74 − 6 e 9 x + 8 + 2 = −74

2 x + 1 = 5 2 x − 1 2 x + 1 = 5 2 x − 1

e 2 x − e x − 132 = 0 e 2 x − e x − 132 = 0

7 e 8 x + 8 − 5 = −95 7 e 8 x + 8 − 5 = −95

10 e 8 x + 3 + 2 = 8 10 e 8 x + 3 + 2 = 8

4 e 3 x + 3 − 7 = 53 4 e 3 x + 3 − 7 = 53

8 e − 5 x − 2 − 4 = −90 8 e − 5 x − 2 − 4 = −90

3 2 x + 1 = 7 x − 2 3 2 x + 1 = 7 x − 2

e 2 x − e x − 6 = 0 e 2 x − e x − 6 = 0

3 e 3 − 3 x + 6 = −31 3 e 3 − 3 x + 6 = −31

For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.

log ( 1 100 ) = −2 log ( 1 100 ) = −2

log 324 ( 18 ) = 1 2 log 324 ( 18 ) = 1 2

For the following exercises, use the definition of a logarithm to solve the equation.

5 log 7 n = 10 5 log 7 n = 10

− 8 log 9 x = 16 − 8 log 9 x = 16

4 + log 2 ( 9 k ) = 2 4 + log 2 ( 9 k ) = 2

2 log ( 8 n + 4 ) + 6 = 10 2 log ( 8 n + 4 ) + 6 = 10

10 − 4 ln ( 9 − 8 x ) = 6 10 − 4 ln ( 9 − 8 x ) = 6

For the following exercises, use the one-to-one property of logarithms to solve.

ln ( 10 − 3 x ) = ln ( − 4 x ) ln ( 10 − 3 x ) = ln ( − 4 x )

log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n ) log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n )

log ( x + 3 ) − log ( x ) = log ( 74 ) log ( x + 3 ) − log ( x ) = log ( 74 )

ln ( − 3 x ) = ln ( x 2 − 6 x ) ln ( − 3 x ) = ln ( x 2 − 6 x )

log 4 ( 6 − m ) = log 4 3 m log 4 ( 6 − m ) = log 4 3 m

ln ( x − 2 ) − ln ( x ) = ln ( 54 ) ln ( x − 2 ) − ln ( x ) = ln ( 54 )

log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 ) log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 )

ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 ) ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 )

For the following exercises, solve each equation for x . x .

log ( x + 12 ) = log ( x ) + log ( 12 ) log ( x + 12 ) = log ( x ) + log ( 12 )

ln ( x ) + ln ( x − 3 ) = ln ( 7 x ) ln ( x ) + ln ( x − 3 ) = ln ( 7 x )

log 2 ( 7 x + 6 ) = 3 log 2 ( 7 x + 6 ) = 3

ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 ) ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 )

log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 ) log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 )

ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 ) ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 )

log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 ) log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 )

For the following exercises, solve the equation for x , x , if there is a solution . Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.

log 9 ( x ) − 5 = −4 log 9 ( x ) − 5 = −4

log 3 ( x ) + 3 = 2 log 3 ( x ) + 3 = 2

ln ( 3 x ) = 2 ln ( 3 x ) = 2

ln ( x − 5 ) = 1 ln ( x − 5 ) = 1

log ( 4 ) + log ( − 5 x ) = 2 log ( 4 ) + log ( − 5 x ) = 2

− 7 + log 3 ( 4 − x ) = −6 − 7 + log 3 ( 4 − x ) = −6

ln ( 4 x − 10 ) − 6 = − 5 ln ( 4 x − 10 ) − 6 = − 5

log ( 4 − 2 x ) = log ( − 4 x ) log ( 4 − 2 x ) = log ( − 4 x )

log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 ) log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 )

ln ( 2 x + 9 ) = ln ( − 5 x ) ln ( 2 x + 9 ) = ln ( − 5 x )

log 9 ( 3 − x ) = log 9 ( 4 x − 8 ) log 9 ( 3 − x ) = log 9 ( 4 x − 8 )

log ( x 2 + 13 ) = log ( 7 x + 3 ) log ( x 2 + 13 ) = log ( 7 x + 3 )

3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 ) 3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 )

ln ( x ) − ln ( x + 3 ) = ln ( 6 ) ln ( x ) − ln ( x + 3 ) = ln ( 6 )

For the following exercises, solve for the indicated value, and graph the situation showing the solution point.

An account with an initial deposit of   $6,500   $6,500 earns 7.25 %   7.25 %   annual interest, compounded continuously. How much will the account be worth after 20 years?

The formula for measuring sound intensity in decibels D D is defined by the equation D = 10 log ( I I 0 ) , D = 10 log ( I I 0 ) , where I I is the intensity of the sound in watts per square meter and I 0 = 10 − 12 I 0 = 10 − 12 is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of 8.3 ⋅ 10 2 8.3 ⋅ 10 2 watts per square meter?

The population of a small town is modeled by the equation P = 1650 e 0.5 t P = 1650 e 0.5 t where t t is measured in years. In approximately how many years will the town’s population reach 20,000? 20,000?

For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate the variable to 3 decimal places.

1000 ( 1.03 ) t = 5000 1000 ( 1.03 ) t = 5000 using the common log.

e 5 x = 17 e 5 x = 17 using the natural log

3 ( 1.04 ) 3 t = 8 3 ( 1.04 ) 3 t = 8 using the common log

3 4 x − 5 = 38 3 4 x − 5 = 38 using the common log

50 e − 0.12 t = 10 50 e − 0.12 t = 10 using the natural log

For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.

7 e 3 x − 5 + 7.9 = 47 7 e 3 x − 5 + 7.9 = 47

ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2 ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2

log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 ) log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 )

Atmospheric pressure P P in pounds per square inch is represented by the formula P = 14.7 e − 0.21 x , P = 14.7 e − 0.21 x , where x x is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of 8.369 8.369 pounds per square inch? ( Hint : there are 5280 feet in a mile)

The magnitude M of an earthquake is represented by the equation M = 2 3 log ( E E 0 ) M = 2 3 log ( E E 0 ) where E E is the amount of energy released by the earthquake in joules and E 0 = 10 4.4 E 0 = 10 4.4 is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing 1.4 ⋅ 10 13 1.4 ⋅ 10 13 joules of energy?

Use the definition of a logarithm along with the one-to-one property of logarithms to prove that b log b x = x . b log b x = x .

Recall the formula for continually compounding interest, y = A e k t . y = A e k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.

Recall the compound interest formula A = a ( 1 + r k ) k t . A = a ( 1 + r k ) k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t . t .

Newton’s Law of Cooling states that the temperature T T of an object at any time t can be described by the equation T = T s + ( T 0 − T s ) e − k t , T = T s + ( T 0 − T s ) e − k t , where T s T s is the temperature of the surrounding environment, T 0 T 0 is the initial temperature of the object, and k k is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/6-6-exponential-and-logarithmic-equations

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Reset password New user? Sign up

Existing user? Log in

Exponential Functions - Problem Solving

Already have an account? Log in here.

Recommended Course

Complex numbers.

The beauty of Algebra through complex numbers, fractals, and Euler’s formula.

• Andrew Hayes

An exponential function is a function of the form \(f(x)=a \cdot b^x,\) where \(a\) and \(b\) are real numbers and \(b\) is positive. Exponential functions are used to model relationships with exponential growth or decay. Exponential growth occurs when a function's rate of change is proportional to the function's current value. Whenever an exponential function is decreasing, this is often referred to as exponential decay .

To solve problems on this page, you should be familiar with

• rules of exponents - algebraic
• solving exponential equations
• graphs of exponential functions .

Growth and Decay

Problem solving - basic, problem solving - intermediate, problem solving - advanced.

Suppose that the population of rabbits increases by 1.5 times a month. When the initial population is 100, what is the approximate integer population after a year? The population after \(n\) months is given by \(100 \times 1.5^n.\) Therefore, the approximate population after a year is \[100 \times 1.5^{12} \approx 100 \times 129.75 = 12975. \ _\square \]

Suppose that the population of rabbits increases by 1.5 times a month. At the end of a month, 10 rabbits immigrate in. When the initial population is 100, what is the approximate integer population after a year? Let \(p(n)\) be the population after \(n\) months. Then \[p(n+2) = 1.5 p(n+1) + 10\] and \[p(n+1) = 1.5 p(n) + 10,\] from which we have \[p(n+2) - p(n+1) = 1.5 \big(p(n+1) - p(n)\big).\] Then the population after \(n\) months is given by \[p(0) + \big(p(1) - p(0)\big) \frac{1.5^{n} - 1}{1.5 - 1} .\] Therefore, the population after a year is given by \[\begin{align} 100 + (160 - 100) \frac{1.5^{12} - 1}{1.5 - 1} \approx& 100 + 60 \times 257.493 \\ \approx& 15550. \ _\square \end{align}\]

Suppose that the annual interest is 3 %. When the initial balance is 1,000 dollars, how many years would it take to have 10,000 dollars? The balance after \(n\) years is given by \(1000 \times 1.03^n.\) To have the balance 10,000 dollars, we need \[\begin{align} 1000 \times 1.03^n \ge& 10000 \\ 1.03^n \ge& 10\\ n \log_{10}{1.03} \ge& 1 \\ n \ge& 77.898\dots. \end{align}\] Therefore, it would take 78 years. \( _\square \)

The half-life of carbon-14 is approximately 5730 years. Humans began agriculture approximately ten thousand years ago. If we had 1 kg of carbon-14 at that moment, how much carbon-14 in grams would we have now? The weight of carbon-14 after \(n\) years is given by \(1000 \times \left( \frac{1}{2} \right)^{\frac{n}{5730}}\) in grams. Therefore, the weight after 10000 years is given by \[1000 \times \left( \frac{1}{2} \right)^{\frac{10000}{5730}} \approx 1000 \times 0.298 = 298.\] Therefore, we would have approximately 298 g. \( _\square \)

Given three numbers such that \( 0 < a < b < c < 1\), define

\[ A = a^{a}b^{b}c^{c}, \quad B = a^{a}b^{c}c^{b} , \quad C = a^{b}b^{c}c^{a}. \]

How do the values of \(A, B, C \) compare to each other?

\[\large 2^{x} = 3^{y} = 12^{z} \]

If the equation above is fulfilled for non-zero values of \(x,y,z,\) find the value of \(\frac { z(x+2y) }{ xy }\).

If \(5^x = 6^y = 30^7\), then what is the value of \( \frac{ xy}{x+y} \)?

If \(27^{x} = 64^{y} = 125^{z} = 60\), find the value of \(\large\frac{2013xyz}{xy+yz+xz}\).

\[\large f(x)=\frac{e^x+e^{-x}}{e^x-e^{-x}} \]

Suppose we define the function \(f(x) \) as above. If \(f(a)=\frac{5}{3}\) and \(f(b)=\frac{7}{5},\) what is the value of \(f(a+b)?\)

\[\large \left(1+\frac{1}{x}\right)^{x+1}=\left(1+\frac{1}{2000}\right)^{2000}\]

Given that \(x\) is an integer that satisfies the equation above, find the value of \(x\).

\[\Large a^{(a-1)^{(a-2)}} = a^{a^2-3a+2}\]

Find the sum of all positive integers \(a\) that satisfy the equation above.

Find the sum of all solutions to the equation

\[ \large (x^2+5x+5)^{x^2-10x+21}=1 .\]

\[\large |x|^{(x^2-x-2)} < 1 \]

If the solution to the inequality above is \(x\in (A,B) \), then find the value of \(A+B\).

Master concepts like these

Learn more in our Complex Numbers course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

Exponential Equations

Exponential equations , as the name suggests, involve exponents. We know that the exponent of a number (base) indicates the number of times the number (base) is multiplied. But, what happens if the power of a number is a variable? When the power is a variable and if it is a part of an equation, then it is called an exponential equation. We may need to use the connection between the exponents and logarithms to solve the exponential equations.

Let us learn the definition of exponential equations along with the process of solving them when the bases are the same and when the bases are not the same along with a few solved examples and practice questions.

What are Exponential Equations?

An exponential equation is an equation with exponents where the exponent (or) a part of the exponent is a variable . For example, 3 x = 81, 5 x - 3 = 625, 6 2y - 7 = 121, etc are some examples of exponential equations. We may come across the use of exponential equations when we are solving the problems of algebra, compound interest , exponential growth , exponential decay , etc.

Types of Exponential Equations

There are three types of exponential equations. They are as follows:

• Equations with the same bases on both sides. (Example: 4 x = 4 2 )
• Equations with different bases that can be made the same. (Example: 4 x = 16 which can be written as 4 x = 4 2 )
• Equations with different bases that cannot be made the same. (Example: 4 x = 15)

Equations with Exponents

The equations in algebra involving variable exponents are called equations with exponents or exponential equations. In other words, we can say that algebraic equations in which variables occur as exponents are known as the equations with exponents. Some of the examples of such an equation are, 3 x + 4  = 81, -2 3y-7  = -64, etc.  

Exponential Equations Formulas

While solving an exponential equation , the bases on both sides may be the same or may not be the same. Here are the formulas that are used in each of these cases, which we will learn in detail in the upcoming sections.

Property of Equality for Exponential Equations

This property is useful to solve an exponential equation with the same bases. It says when the bases on both sides of an exponential equation are equal, then the exponents must also be equal. i.e.,

a x = a y ⇔ x = y.

Exponential Equations to Logarithmic Form

We know that logarithms are nothing but exponents and vice versa. Hence an exponential equation can be converted into a logarithmic function . This helps in the process of solving an exponential equation with different bases. Here is the formula to convert exponential equations into logarithmic equations.

b x = a ⇔ log b a = x

Solving Exponential Equations With Same Bases

Sometimes, an exponential equation may have the same bases on both sides of the equation. For example, 5 x = 5 3 has the same base 5 on both sides. Sometimes, though the exponents on both sides are not the same, they can be made the same. For example, 5 x = 125. Though it doesn't have the same bases on both sides of the equation, they can be made the same by writing it as 5 x = 5 3 (as 125 = 5 3 ). To solve the exponential equations in each of these cases, we just apply the property of equality of exponential equations, using which, we set the exponents to be the same and solve for the variable.

Here is another example where the bases are not the same but can be made the same.

Example: Solve the exponential equation 7 y + 1 = 343 y .

We know that 343 = 7 3 . Using this, the given equation can be written as,

7 y + 1 = (7 3 ) y

7 y + 1 = 7 3y

Now the bases on both sides are the same. So we can set the exponents to be the same.

Subtracting y from both sides,

Dividing both sides by 2,

Solving Exponential Equations With Different Bases

Sometimes, the bases on both sides of an exponential equation may not be the same (or) cannot be made the same. We solve the exponential equations using logarithms when the bases are not the same on both sides of the equation. For example, 5 x = 3 neither has the same bases on both sides nor the bases can be made the same. In such cases, we can do one of the following things.

• Convert the exponential equation into the logarithmic form using the formula b x = a ⇔ log b a = x and solve for the variable.
• Apply logarithm (log) on both sides of the equation and solve for the variable. In this case, we will have to use a property of logarithm , log a m = m log a.

We will solve the equation 5 x = 3 in each of these methods.

We will convert 5 x = 3 into logarithmic form. Then we get,

log 5 3 = x

Using the change of base property ,

x = (log 3) / (log 5)

We will apply log on both sides of 5 x = 3. Then we get, log 5 x = log 3. Using the property log a m = m log a on the left side of the equation, we get, x log 5 = log 3. Dividing both sides by log 5,

Important Notes on Exponential Equations:

Here are some important notes with respect to the exponential equations.

• To solve the exponential equations of the same bases, just set the exponents equal.
• To solve the exponential equations of different bases, apply logarithm on both sides.
• The exponential equations with the same bases also can be solved using logarithms.
• If an exponential equation has 1 on any one side, then we can write it as 1 = a 0 , for any 'a'. For example, to solve 5 x = 1, we can write it as 5 x = 5 0 , then we get x = 0.
• To solve an exponential equation using logarithms, we can either apply "log" or apply "ln" on both sides.

Related Articles:

• Exponential Form
• Exponent Rules
• Exponential Functions
• Exponential Equation Calculator

Exponential Equations Examples

Example 1: Solve 27 / (3 -x ) = 3 6 .

We know that 27 = 3 3 . We can make the bases to be the same on both sides using this.

3 3 / (3 -x ) = 3 6

Using the quotient property of exponents, a m /a n = a m - n . Using this,

3 3 - (-x) = 3 6

3 3 + x = 3 6

Now the bases on both sides are the same. So we can set the exponents to be equal.

Subtracting 3 from both sides,

Therefore, the solution of the given exponential equation is x = 3.

Example 2: Solve the exponential equation 7 3x + 7 = 490.

490 cannot be written as a power of 7. So we cannot make the bases to be the same here. So we solve this exponential equation using logarithms.

Apply log on both sides of the given equation,

log 7 3x + 7 = log 490

Using a property of logarithms , log a m = m log a. Using this,

(3x + 7) log 7 = log 490 ... (1)

Here, 490 = 49 × 10 = 7 2 × 10.

So, log 490 = log (7 2 × 10)

= log 7 2 + log 10 (because log (mn) = log m + log n)

= 2 log 7 + 1 (because log a m = m log a and log 10 = 1)

Substituting this in (1),

(3x + 7) log 7 = 2 log 7 + 1

Dividing both sides by log 7,

3x + 7 = (2 log 7 + 1) / (log 7)

3x + 7 = 2 + (1 / log 7)

Subtracting 7 from both sides,

3x = -5 + (1 / log 7)

Dividing both sides by 3,

x = -5/3 + (1 / (3 log 7))

Answer: The solution of the given exponential equation is x = -5/3 + (1 / (3 log 7)).

Example 3: How long does it take for $20,000 to double if the amount is compounded annually at 8% annual interest? Round your answer to the nearest integer.

The principal amount, P = $20000.

The rate of interest is, r = 8% = 8/100 = 0.08.

The final amount is, A = 20000 x 2 = $40,000

Let us assume that the required time in years is t.

Using the compound interest formula when compounded annually,

A = P (1 + r) t

40000 = 20000 (1 + 0.08) t

Dividing both sides by 20000,

2 = (1.08) t

Taking log on both sides,

log 2 = log (1.08) t

log 2 = t log (1.08)

t = (log 2) / (log 1.08)

The final answer is rounded to the nearest integer.

Answer: It takes 9 years for $20,000 to double itself.

go to slide go to slide go to slide

Book a Free Trial Class

Exponential Equations Questions

go to slide go to slide

FAQs on Exponential Equations

What are exponential equations.

An exponential equation is an equation that has a variable in its exponent(s). For example, 5 2x - 3 = 125, 3 7 - 2x = 91, etc are exponential equations.

What Are Types of Exponential Equations?

There are three types of exponential equations. They are,

• The exponential equations with the same bases on both sides.
• The exponential equations with different bases on both sides that can be made the same.
• The exponential equations with different bases on both sides that cannot be made the same.

How To Solve Exponential Equations?

To solve the exponential equations of equal bases, we set the exponents equal whereas to solve the exponential equations of different bases, we apply logarithms on both sides.

How To Write Exponential Equation in Logarithmic Form?

Writing the exponential equation in the logarithmic form helps us to solve it. This can be done using the formula b x = a ⇔ log b a = x.

What Is the Property of Equality of Exponential Equations?

The equality property of exponential equations says to set the exponents equal whenever the bases on both sides of the equation are equal. i.e., a x = a y ⇔ x = y.

How To Solve Exponential Equations of Same bases?

When an exponential equation has the same bases on both sides, just set the exponents equal and solve for the variable. Here is an example, 4 2x - 1 = 4 1 - x . Here the bases on both sides are equal. So we can set the exponents equal. 2x - 1 = 1 - x 3x = 2 x = 2/3.

How To Solve Exponential Equations of Different bases?

When an exponential equation has different bases on both sides, apply log on both sides and solve for the variable. Here is an example, 4 x - 5 = 8. Taking log on both sides, log 4 x - 5 = log 8 (x - 5) log 4 = log 8 x - 5 = (log 8) / (log 4) x = [(log 8) / (log 4)] + 5.

How To Solve Exponential Equations Using Logarithms?

We solve exponential equations using logarithms in two ways.

• Convert the exponential equation into logarithmic equation using b x = a ⇔ log b a = x.
• Apply "log" or "ln" on both sides and solve.

Rules, Formulas and Practice Problems

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• 8^{x-2}=\sqrt{8}
• 10^{1-x}=10^4
• 6^{3x}=2^{2x-3}
• 3^x=9^{x+5}
• What is an exponential equation?
• An exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable.
• How do you solve exponential equations?
• To solve an exponential equation start by isolating the exponential expression on one side of the equation. Then, take the logarithm of both sides of the equation to convert the exponential equation into a logarithmic equation. The logarithm must have the same base as the exponential expression in the equation. Use logarithmic properties to simplify the logarithmic equation, and solve for the variable by isolating it on one side of the equation.
• What is an exponent?
• An exponent is a mathematical notation indicating the number of times a value is multiplied by itself.
• what is e in math?
• In mathematics, 'e' refers to the mathematical constant approximately equal to 2.71828. It is widely used in various mathematical and scientific fields, such as exponential and logarithmic functions.
• Is log the inverse of exponential?
• Logarithm and exponential are inverse functions. If y = b^x, where b is the base of the exponential, then x = logb(y).

exponential-equation-calculator

• High School Math Solutions – Radical Equation Calculator Radical equations are equations involving radicals of any order. We will show examples of square roots; higher...

Please add a message.

Message received. Thanks for the feedback.

Solving Partial Differential Problems with Tau Toolbox

• Open access
• Published: 22 May 2024
• Volume 18 , article number  8 , ( 2024 )

Cite this article

You have full access to this open access article

• Nilson J. Lima 1 ,
• José M. A. Matos 2 &
• Paulo B. Vasconcelos 3  

76 Accesses

Explore all metrics

This paper briefly examines how literature addresses the numerical solution of partial differential equations by the spectral Tau method. It discusses the implementation of such a numerical solution for PDE’s presenting the construction of the problem’s algebraic representation and exploring solution mechanisms with different orthogonal polynomial bases. It highlights contexts of opportunity and the advantages of exploring low-rank approximations and well-conditioned linear systems, despite the fact that spectral methods usually give rise to dense and ill-conditioned matrices. It presents Tau Toolbox , a Python numerical library for the solution of integro-differential problems. It shows numerical experiments illustrating the implementations’ accuracy and computational costs. Finally, it shows how simple and easy it is to use the Tau Toolbox to obtain approximate solutions to partial differential problems.

Similar content being viewed by others

Spectral Lanczos’ Tau Method for Systems of Nonlinear Integro-Differential Equations

Dealing with Functional Coefficients Within Tau Method

Exact solutions for nonlinear partial differential equations via a fusion of classical methods and innovative approaches

Avoid common mistakes on your manuscript.

1 Introduction

Solving partial differential equations is challenging due to the nonlinear, high-dimensional, and often non-analytical nature of the equations involved. Various numerical and analytical methods have been developed to address these challenges in recent years. Among those is the spectral Tau method that produces, from a truncated series expansion in a complete set of orthogonal functions, an approximate polynomial solution for differential problems. Although powerful it is not widely used due to the lack of automatic mechanisms to wrap the analytical problem in a numerical treatable form.

Previous numerical implementations are usually dedicated to the solution of a particular problem, and there is no mathematical library that solves differential problems in a general and automatic way. There are, however, a few mathematical libraries implementing the spectral Galerkin method, such as Shenfun  [ 1 ] and particularly the Chebfun project [ 2 , 3 ], but not the spectral Tau method. Contrary to the most common spectral Galerkin method, where the expansion functions must satisfy the boundary conditions, in the Tau method, the coefficients of the series are computed by forcing the differential problem to be exact in its spectral representation as far as possible. Additional conditions are set such that the initial/boundary conditions are exactly satisfied.

The spectral Tau method to approximate the solution of partial differential problems is implemented as part of the Tau Toolbox —a numerical library for the solution of integro-differential problems. This mathematical software provides a general framework for the solution of such problems, ensuring accurate and fast approximate solutions. It enables a symbolic syntax to be applied to objects to manipulate and solve differential problems with ease, high accuracy, and efficiency.

In this paper we discuss the implementation of such a numerical solution for partial differential equations, presenting the construction of the problem’s algebraic representation, specifying different procedure possibilities to tackle the linear systems involved, and exploring solution mechanisms with different orthogonal polynomial bases.

The paper is organized as follows. After the preliminary introduction, in Sect.  3 we present an implementation of the spectral Tau method, following the operational traditional approach [ 4 ], to solve partial differential problems and use examples to illustrate its efficiency. A tuned direct method is devised to ensure the solution is well adapted to the original Lanczos’ idea, following [ 5 ]. It can be used on problems set on n -dimensional spaces but it can be both resource and time-consuming. In Sect.  4 , we incorporate low-rank techniques [ 6 , 7 ] within the existing operational spectral Tau approach and devise an implementation that produces an approximate solution fast and with good accuracy for smooth functions [ 8 , 9 ]. This approach is only possible, for now, for bi-dimensional problems. An example of applying this low-rank implementation to numerically solve partial differential problems is given in the following section. We summarize our results in Sect.  5 .

2 Preliminaries

Let \(\Omega \subset \mathbb {R}^n\) be a compact domain, \(\mathbb {F}(\Omega )\) and \(\mathbb {G}(\Omega )\) spaces of functions defined on \(\Omega \) , and \(u(x_1, \dots , x_n) \in \mathbb {F}(\Omega )\) an unknown function, with independent variables \((x_1, \dots , x_n) \in \Omega \) . The problem can be formulated as

where \(\mathcal {D}\) , \(\mathcal {C}_i\) , \(i=1, \dots ,\nu \) , are given differential operators defined on \(\mathbb {F}(\Omega ) \rightarrow \mathbb {G}(\Omega )\) , and f and \(s_i\) are given functions belonging to \(\mathbb {G}(\Omega )\) .

Considering the inner products in the polynomial space \(\mathbb {P}(\Omega )\) , \(\langle .,. \rangle _i : \mathbb {P}_i^2([a_i, b_i])\rightarrow \mathbb {R}\) , the following sets of orthogonal polynomials

can be built.

Polynomial basis for \(\mathbb {P}(\Omega )\) are then constructed, \(\mathcal {P} = \mathcal {P}_1\otimes \mathcal {P}_2\dots \otimes \mathcal {P}_n =[P_0, P_1,\dots ]^T\) , where \(\otimes \) is the Kronecker product. The sought solution u can be expressed as a polynomial in this basis as

where \(\mathbb {N}_0\) is the set of nonnegative integers.

3 Traditional Tau Approach

3.1 tau method.

The Tau method consists in the truncation of u in the multi-order \(k=(k_1,\dots , k_n) \in \mathbb {N}^n_0\) , giving rise to

solution of the perturbed problem with the form

with \(\mathbb {J} \in \mathbb {N}^n_0\) .

The differential operator, being linear and of the form

with coefficients \( f_j\approx \sum _{\ell =0}^{d_j} f_{j,\ell }x^{\ell }, \; x\in \Omega ,\; \ell ,d_j\in \mathbb {N}^n_0\) , can be cast in matrix form \(\textsf{D}\) by

Likewise, the boundary conditions

are translated in terms of the coefficients of \(u_k\) by \(\textsf{C}=\left[ \textsf{C}_i \right] _{i=1}^{\nu }\) :

Finally, the Tau coefficient matrix is built

where the number of boundary rows is \(nbr=\sum _{j=1}^{\nu }\prod _{j\ne i=1}^{n} (k_i+1)\) , the number of rows is \(nr = nbr+\prod _{i=1}^{n} (k_i+h_i+1)\) and the number of columns is \(nc=\prod _{i=1}^{n} (k_i+1)\) , \(nr>nc\) . Note that \(h_i =\max \{h_{ij}\}\) , \(h_{i0}\) the height of D and \(h_{ij}\) the height of \(\mathcal {C}_i\) , in \(x_j\) , \(j=1,...,n\) .

Given f and \(s_i,\ i=1,\ldots \nu \) , the problem’s right-hand side, we define the coefficients vectors in the polynomial approximations

from which the Tau right-hand side vector

can be constructed.

The system \(\textsf{T}\textsf{a}=\textsf{b}\) is overdetermined and large dimensional. Different solvers may produce the usual Tau solution or a kind of weak form of it (e.g. linear least squares approach).

We provide an algorithm to solve the problem \(\textsf{T}\textsf{a}=\textsf{b}\) with a direct method ensuring a solution that fully satisfies the initial/boundary conditions and minimizes the error on the operator terms – Tau solution. This approach, drawn in Algorithm 1, is based on an adaptation of the LU factorization: a two-level approach. The pivoting process prioritizes two types of rows: (i) those that define boundary conditions, which impose a threshold on the growth factor, and (ii) those that specify terms of the operator with a lower degree.

solve \(\textsf{T}\textsf{a}=\textsf{b}\) with LU 2 special decomposition

3.2 Numerical Illustration

To illustrate the use of this approach, we solve Saint-Venant’s torsion problem for a prismatic bar with a square section

The analytic solution can be developed as

and we use a truncation of the series to evaluate the quality of the Tau approximate solution provided by Tau Toolbox using the traditional approach. Figure  1 shows, for problem ( 2 ), the difference surface between the truncated solution, using 99 terms, and the Tau approximation, for small polynomial degrees.

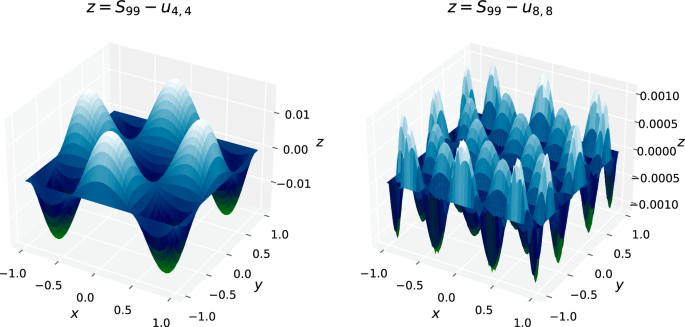
Difference surface (between the serie’s solution with 99 terms and the Tau approximation \(u_{m,n}\) , \(m,n=4\) , and \(m,n=8\) )

The results clearly evidence the quality of the approximation, bearing in mind the low polynomial degrees involved. Furthermore, they show a remarkable equioscillatory behavior [ 4 ].

On the other hand, the elapsed time to compute the approximation and memory resources are high whenever a moderate/high polynomial approximation is required. In Fig.  2 we depict the elapsed time required to compute a Tau approximate solution for the Saint-Venant’s problem using Algorithm 1 and a linear least squares approach. We report also on the time required to unpack the problem and build the linear system. Clearly, time increases exponentially with the polynomial degree.

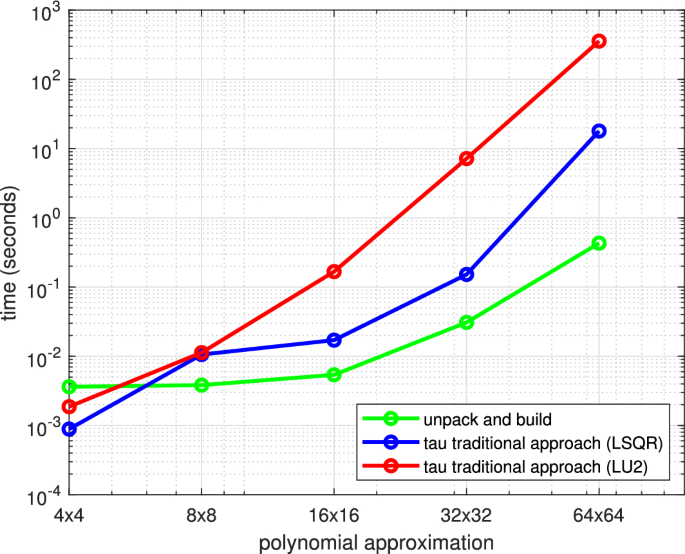
Computation time in seconds for the Tau approximation (logarithmic scale)

To overcome this limitation, a Gegenbauer-Tau implementation together low-rank approximation techniques are used, as explained in the next section.

4 A Gegenbauer-Tau Approach with Low-Rank Approximation

4.1 gegenbauer-tau approach.

Following the ideas in [ 9 ], formulating the Tau method in terms of Gegenbauer polynomials and their associated sparse matrices, can bring additional benefits in terms of computational efficiency and numerical stability.

First recall that Gegenbauer, also known as ultraspherical, polynomials \(C_j^{(\alpha )}\) , \(j\ge 0\) are orthogonal polynomials, belonging to the more general class of Jacobi polynomials, orthogonal on \([-1,1]\) with respect to the weight function \((1-x^2)^{\alpha -\frac{1}{2}}\) . Although they can be used with any real parameter \(\alpha > -\frac{1}{2}\) , three particular cases appear with special emphasis in applications: Legendre polynomials \(P_j(x)=C_j^{(\frac{1}{2})}(x)\) ; Chebyshev of second kind \(U_j(x)=C_j^{(1)}(x)\) and Chebyshev of first kind, the limit case, \(T_j(x)=\lim _{\alpha \mapsto 0^+} \frac{1}{2\alpha }C_{j}^{(\alpha )}(x)\) .

Of great relevance is that a Gegenbauer polynomial \(C_j^{(\alpha )}\) satisfies the property of derivatives [ 10 ]

And, applying \(\ell \) times the last relation, one gets

where \((\alpha )_\ell =\alpha (\alpha +1)\cdots (\alpha +\ell -1)\) is the raising factorial (or Pochhammer symbol).

Let, for \(\alpha >-\frac{1}{2}\) , \(\mathcal {C}^{(\alpha )}=[C_0^{(\alpha )}, C_1^{(\alpha )}, \ldots ]^T\) be a Gegenbauer polynomial basis, and

be a formal series represented by the coefficients vector \(\textsf{u}=[u_0,u_1,\ldots ]\) , then the \(\ell \) th derivative

is represented by a sparse matrix operator

is the shift operator.

However, since \(\textsf{N}_\ell \) takes coefficients in \(\mathcal {C}^{(\alpha )}\) into coefficients in \(\mathcal {C}^{(\ell +\alpha )}\) , all terms on the differential problem must be also translated into coefficients in \(\mathcal {C}^{(\ell +\alpha )}\) . This can be accomplished using the relation [ 10 ]

which can be applied via the following operator matrices

This is important to explore since spectral methods usually represent differential operators by dense matrices, even if there is some cost associated with the change in polynomial basis.

Finally, to have an operational formulation of the Tau method in terms of Gegenbauer polynomials, we have to represent the multiplication operation by an algebraic operator. This can be done from the three-term characteristic recurrence relation [ 10 ]

with \(C_{-1}^{(\alpha )}=0\) and \(C_{0}^{(\alpha )}=1\) . This can be written in matrix form using matrices

So, if \(u=\textsf{u}\mathcal {C}^{(\alpha )}\) ( 3 ) and \(D=\sum _{\ell =0}^{\nu } f_\ell \dfrac{d^\ell }{dx^\ell }\) is a differential operator with coefficients \(f_\ell =\sum _{i=0}^{n_\ell } f_{\ell ,i} x^i\) , then

The resulting linear system, \(\textsf{T}\textsf{a}=\textsf{b}\) has the usual trapezoidal shape and can be solved by LU factorization, where

Using Gegenbauer polynomials, matrix \(\textsf{T}\) is well-conditioned [ 11 ].

Another possibility is to use QR factorization, following Algorithm 2, which works on a triangular matrix similar to \(\textsf{T}\) .

solve \(\textsf{T}\textsf{a}=\textsf{b}\) with QR special decomposition

4.2 Low-Rank Implementation

In this subsection, we succinctly summarize the inclusion of low rank approximations in the resolution of partial differential problems. Indeed, partial differentiation can be adapted to the use of low-rank approximations since it can be represented by a tensor product of univariate differentiation. For the moment, only the bidimensional case is treated.

Let us consider the two-dimensional partial differential problem from ( 1 )

for \(\Omega \subset \mathbb {R}^2\) , \(u(x, y) \in \mathbb {F}(\Omega )\) , and

a linear operator, where \(\nu _1\) is the differential order of \(\mathcal {D}\) in the x variable and \(\nu _2\) in the y variable, and \(p_{i,j}(x,y)\) are functions defined on \(\Omega \) . A low-rank approximation for a bivariate function \(p_{i,j}\) ( tau.Polynomial2 ) can be expressed by a sum of outer products of univariate polynomials ( tau.Polynomial1 ):

with \(0\le i \le \nu _2\) and \(0 \le j \le \nu _1\) . As a consequence, the partial differential operator \(\mathcal {D}\) can be expressed by a low-rank representation of rank k as

where \(c_j(y)\) and \(r_j(x)\) belong to the tau.Polynomial1 class.

Thus, a sum of tensor products of linear ordinary differential operators is built from a separable representation of a partial differential operator. Then the ordinary differential operator is tackled with the Gegenbauer-Tau spectral approach, and finally a \(\nu _2 \times \nu _1\) discretized generalized Sylvester matrix equation is solved to provide an approximate solution to the problem. A detailed explanation on these steps can be found in [ 9 , 11 ]. This set of actions brings benefits in terms of computational efficiency and numerical stability.

4.3 Numerical Illustration

We begin by illustrating the Saint-Venant problem using the Tau Toolbox :

The writing of the code is intuitive and self-explanatory. The problem is set in the library by calling | tau.Problem2|. By default, \([-1,1]\) is the domain, and ChebyshevT is the basis for all variables. The result is a Tau object | u| computed via the | solve| functionality of Tau Toolbox :

The computations were carried out using a low-approximation factorization of rank 33, even if the discretization involved a \(257\times 257\) matrix. The approximate solution and the error are depicted in Fig.  3 .

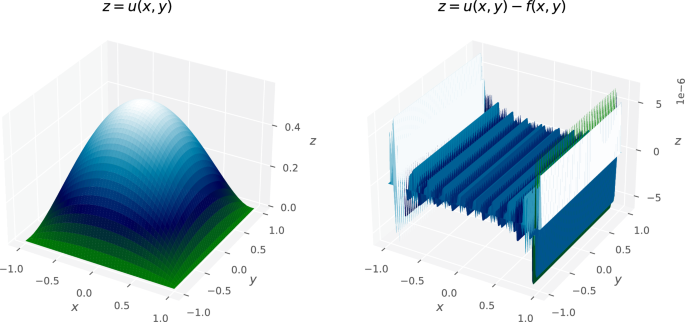
Approximate solution and difference surface (between an approximate solution f ( x ,  y ) sum of the first 99 terms and the Gegenbauer-Tau approximation \(u_{256,256}\) )

In Fig.  4 we show the performance achieved in the computation of the low-rank approximate solution with Gegenbauer-Tau approach. For very large polynomial degree approximation, there is no gain to achieve since the rank of the problem stays unchanged. As expected, the computation time increases with the degree of the approximation but is much less than the traditional approach.

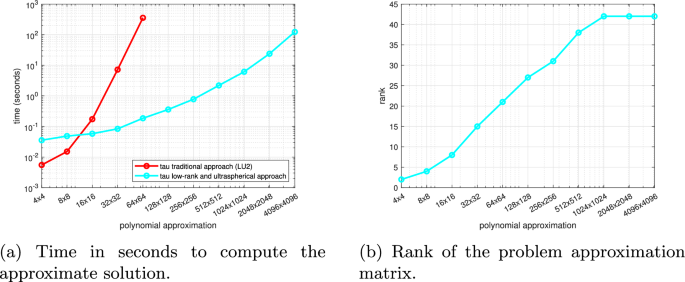
Performance of the Gegenbauer-Tau approach with low-rank approximations

Another example is the partial differential problem

with exact solution given by \(u(x,t)=e^{tx} \cos (x + t)\) . The excerpt of the code to solve the problem follows:

Approximate solution and difference surface (between the exact solution f ( x ,  t ) and the approximation \(u_{33,33}\) ) provided by Tau Toolbox

The solution of problem ( 5 ) is computed to almost machine precision (see Fig.  5 ), working on matrix structures with rank 12 to approximate the operators:

5 Conclusion

In this work we have introduced the Tau Toolbox —a MATLAB / Python toolbox for the solution of integro-differential problems, presented implementation details on how to solve bidimensional PDEs making use of low-rank approximations and Gegenbauer polynomials, and illustrated the simplicity of use of Tau Toolbox in the solution of PDEs as well as the efficiency of the implemented approach.

Mortensen, M.: Shenfun: high performance spectral Galerkin computing platform. J. Open Source Softw. 3 (31), 1071 (2018)

Article   Google Scholar  

Trefethen, L.N.: Computing numerically with functions instead of numbers. Math. Comput. Sci. 1 , 9–19 (2007)

Article   MathSciNet   Google Scholar  

Driscoll, T.A., Hale, N., Trefethen, L.N.: Chebfun Guide. Pafnuty Publications, Oxford (2014)

Google Scholar  

Ortiz, E.L., Samara, H.: Numerical solution of partial differential equations with variable coefficients with an operational approach to the tau method. Comput. Math. Appl. 10 (1), 5–13 (1984)

Matos, J., Rodrigues, M.J., Vasconcelos, P.B.: New implementation of the Tau method for PDEs. J. Comput. Appl. Math. 164 , 555–567 (2004)

Bebendorf, M.: Adaptive cross approximation of multivariate functions. Constr. Approx. 34 , 149–179 (2011)

Hackbusch, W.: Hierarchical Matrices: Algorithms and Analysis. Springer, Berlin (2015)

Book   Google Scholar  

Townsend, A., Trefethen, L.N.: An extension of Chebfun to two dimensions. SIAM J. Sci. Comput. 35 (6), 495–518 (2013)

Olver, S., Townsend, A.: A fast and well-conditioned spectral method. SIAM Rev. 55 (3), 462–489 (2013)

Olver, F.W.: NIST Handbook of Mathematical Functions Hardback and CD-ROM. Cambridge University Press, Cambridge (2010)

Townsend, A., Olver, S.: The automatic solution of partial differential equations using a global spectral method. J. Comput. Phys. 299 , 106–123 (2015)

Download references

Acknowledgements

The authors were partially supported by CMUP, member of LASI, which is financed by national funds through FCT – Fundação para a Ciência e a Tecnologia, I.P., under the projects with reference UIDB/00144/2020 and UIDP/00144/2020.

Open access funding provided by FCT|FCCN (b-on).

Author information

Authors and affiliations.

CMUP, Departamento de Matemática, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre s/n, 4169-007, Porto, Portugal

Nilson J. Lima

CMUP, Departamento de Matemática, Faculdade de Ciências, Instituto Superior de Engenharia, Instituto Politécnico do Porto, Rua do Campo Alegre s/n, 4169-007, Porto, Portugal

José M. A. Matos

CMUP, Departamento de Matemática, Faculdade de Ciências, Faculdade de Economia, Universidade do Porto, Rua Dr. Roberto Frias s/n, 4200-464, Porto, Portugal

Paulo B. Vasconcelos

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Paulo B. Vasconcelos .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Lima, N.J., Matos, J.M.A. & Vasconcelos, P.B. Solving Partial Differential Problems with Tau Toolbox. Math.Comput.Sci. 18 , 8 (2024). https://doi.org/10.1007/s11786-024-00580-3

Download citation

Received : 27 July 2023

Revised : 24 February 2024

Accepted : 15 March 2024

Published : 22 May 2024

DOI : https://doi.org/10.1007/s11786-024-00580-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Spectral methods
• Partial differential problems
• Orthogonal polynomials

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.6: Application Problems with Exponential and Logarithmic Functions

• Last updated
• Save as PDF
• Page ID 38600

• Rupinder Sekhon and Roberta Bloom
• De Anza College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

In this section, you will:

• review strategies for solving equations arising from exponential formulas
• solve application problems involving exponential functions and logarithmic functions

STRATEGIES FOR SOLVING EQUATIONS THAT CONTAIN EXPONENTS

When solving application problems that involve exponential and logarithmic functions, we need to pay close attention to the position of the variable in the equation to determine the proper way solve the equation we investigate solving equations that contain exponents.

Suppose we have an equation in the form : value = coefficient(base) exponent

We consider four strategies for solving the equation:

STRATEGY A : If the coefficient, base, and exponent are all known, we only need to evaluate the expression for coefficient(base) exponent to evaluate its value.

STRATEGY B: If the variable is the coefficient, evaluate the expression for (base) exponent . Then it becomes a linear equation which we solve by dividing to isolate the variable.

STRATEGY C : If the variable is in the exponent, use logarithms to solve the equation.

STRATEGY D: If the variable is not in the exponent, but is in the base, use roots to solve the equation.

Below we examine each strategy with one or two examples of its use.

Example \(\PageIndex{1}\)

Suppose that a stock’s price is rising at the rate of 7% per year, and that it continues to increase at this rate. If the value of one share of this stock is $43 now, find the value of one share of this stock three years from now.

The problem tells us that \(a\) = 43 and \(r\) = 0.07, so \(b = 1+ r = 1+ 0.07 = 1.07\)

Therefore, function is \(y = 43(1.07)^t\).

In this case we know that \(t\) = 3 years, and we need to evaluate \(y\) when \(t\) = 3.

At the end of 3 years, the value of this one share of this stock will be

\[y=43(1.07)^{3}=\$ 52.68 \nonumber \]

Example \(\PageIndex{2}\)

The value of a new car depreciates (decreases) after it is purchased. Suppose that the value of the car depreciates according to an exponential decay model. Suppose that the value of the car is $12000 at the end of 5 years and that its value has been decreasing at the rate of 9% per year. Find the value of the car when it was new.

The function is \(y = a(0.91)^t\)

In this case we know that when \(t\) = 5, then \(y\) = 12000; substituting these values gives

\[12000 = a(0.91)^5 \nonumber \]

We need to solve for the initial value a, the purchase price of the car when new.

First evaluate (0.91) 5 ; then solve the resulting linear equation to find \(a\).

\[ 1200 = a(0.624) \nonumber \]

\(a=\frac{12000}{0.624} = \$ 19,230.77\); The car's value was $19,230.77 when it was new.

Example \(\PageIndex{3}\)

A national park has a population of 5000 deer in the year 2016. Conservationists are concerned because the deer population is decreasing at the rate of 7% per year. If the population continues to decrease at this rate, how long will it take until the population is only 3000 deer?

\(r\) = -0.07 and \(b = 1+r = 1+(-0.07) = 0.93\) and the initial population is \(a\) = 5000

The exponential decay function is \(y = 5000(0.93)^t\)

To find when the population will be 3000, substitute \(y\) = 3000

\[ 3000 = 5000(0.93)^t \nonumber \]

Next, divide both sides by 5000 to isolate the exponential expression

\[\begin{array}{l} \frac{3000}{5000}=\frac{5000}{5000}(0.93)^{2} \\ 0.6=0.93^{t} \end{array} \nonumber \]

Rewrite the equation in logarithmic form; then use the change of base formula to evaluate.

\[t=\log _{0.93}(0.6) \nonumber \]

\(t = \frac{\ln(0.6)}{\ln(0.93)}=7.039\) years; After 7.039 years, there are 3000 deer.

Note: In Example \(\PageIndex{3}\), we needed to state the answer to several decimal places of precision to remain accurate. Evaluating the original function using a rounded value of \(t\) = 7 years gives a value that is close to 3000, but not exactly 3000.

\[y=5000(0.93)^{7}=3008.5 \text { deer } \nonumber \]

However using \(t\) = 7.039 years produces a value of 3000 for the population of deer

\[ y=5000(0.93)^{7.039}=3000.0016 \approx 3000 \text { deer } \nonumber \]

Example \(\PageIndex{4}\)

A video posted on YouTube initially had 80 views as soon as it was posted. The total number of views to date has been increasing exponentially according to the exponential growth function \(y = 80e^{0.2t}\), where \(t\) represents time measured in days since the video was posted. How many days does it take until 2500 people have viewed this video?

Let \(y\) be the total number of views \(t\) days after the video is initially posted. We are given that the exponential growth function is \(y = 80e^{0.2t}\) and we want to find the value of \(t\) for which \(y\) = 2500. Substitute \(y\) = 2500 into the equation and use natural log to solve for \(t\).

\[2500 = 80e^{0.12t} \nonumber \]

Divide both sides by the coefficient, 80, to isolate the exponential expression.

\[\begin{array}{c} \frac{2500}{80}=\frac{80}{80} e^{0.12 t} \\ 31.25=e^{0.12 t} \end{array} \nonumber \]

Rewrite the equation in logarithmic form

\[ 0.12t = \ln(31.25) \nonumber \]

Divide both sides by 0.04 to isolate \(t\); then use your calculator and its natural log function to evaluate the expression and solve for \(t\).

\[\begin{array}{l} \mathrm{t}=\frac{\ln (31.25)}{0.12} \\ \mathrm{t}=\frac{3.442}{0.12} \\ \mathrm{t} \approx 28.7 \text { days } \end{array} \nonumber \]

This video will have 2500 total views approximately 28.7 days after it was posted.

STRATEGY D: If the variable is not in the exponent, but is in the base, we use roots to solve the equation. It is important to remember that we only use logarithms when the variable is in the exponent.

Example \(\PageIndex{5}\)

A statistician creates a website to analyze sports statistics. His business plan states that his goal is to accumulate 50,000 followers by the end of 2 years (24 months from now). He hopes that if he achieves this goal his site will be purchased by a sports news outlet. The initial user base of people signed up as a result of pre-launch advertising is 400 people. Find the monthly growth rate needed if the user base is to accumulate to 50,000 users at the end of 24 months.

Let \(y\) be the total user base \(t\) months after the site is launched.

The growth function for this site is \(y = 400(1+r)^t\);

We don’t know the growth rate \(r\). We do know that when \(t\) = 24 months, then \(y\) = 50000.

Substitute the values of \(y\) and \(t\); then we need to solve for \(r\).

\[5000 = 400(1+r)^{24} \nonumber \]

Divide both sides by 400 to isolate (1+r) 24 on one side of the equation

\[\begin{array}{l} \frac{50000}{400}=\frac{400}{400}(1+r)^{24} \\ 125=(1+r)^{24} \end{array} \nonumber \]

Because the variable in this equation is in the base, we use roots:

\[\begin{array}{l} \sqrt[24]{125}=1+r \\ 125^{1 / 24}=1+r \\ 1.2228 \approx 1+r \\ 0.2228 \approx r \end{array} \nonumber \]

The website’s user base needs to increase at the rate of 22.28% per month in order to accumulate 50,000 users by the end of 24 months.

Example \(\PageIndex{6}\)

A fact sheet on caffeine dependence from Johns Hopkins Medical Center states that the half life of caffeine in the body is between 4 and 6 hours. Assuming that the typical half life of caffeine in the body is 5 hours for the average person and that a typical cup of coffee has 120 mg of caffeine.

• Write the decay function.
• Find the hourly rate at which caffeine leaves the body.
• How long does it take until only 20 mg of caffiene is still in the body? www.hopkinsmedicine.org/psyc...fact_sheet.pdf

a. Let \(y\) be the total amount of caffeine in the body \(t\) hours after drinking the coffee.

Exponential decay function \(y = ab^t\) models this situation.

The initial amount of caffeine is \(a\) = 120.

We don’t know \(b\) or \(r\), but we know that the half- life of caffeine in the body is 5 hours. This tells us that when \(t\) = 5, then there is half the initial amount of caffeine remaining in the body.

\[\begin{array}{l} y=120 b^{t} \\ \frac{1}{2}(120)=120 b^{5} \\ 60=120 b^{5} \end{array} \nonumber \]

Divide both sides by 120 to isolate the expression \(b^5\) that contains the variable.

\[\begin{array}{l} \frac{60}{120}=\frac{120}{120} \mathrm{b}^{5} \\ 0.5=\mathrm{b}^{5} \end{array} \nonumber \]

The variable is in the base and the exponent is a number. Use roots to solve for \(b\):

\[\begin{array}{l} \sqrt[5]{0.5}=\mathrm{b} \\ 0.5^{1 / 5}=\mathrm{b} \\ 0.87=\mathrm{b} \end{array} \nonumber \]

We can now write the decay function for the amount of caffeine (in mg.) remaining in the body \(t\) hours after drinking a cup of coffee with 120 mg of caffeine

\[y=f(t)=120(0.87)^{t} \nonumber \]

b. Use \(b = 1 + r\) to find the decay rate \(r\). Because \(b = 0.87 < 1\) and the amount of caffeine in the body is decreasing over time, the value of \(r\) will be negative.

\[\begin{array}{l} 0.87=1+r \\ r=-0.13 \end{array} \nonumber \]

The decay rate is 13%; the amount of caffeine in the body decreases by 13% per hour.

c. To find the time at which only 20 mg of caffeine remains in the body, substitute \(y\) = 20 and solve for the corresponding value of \(t\).

\[\begin{array}{l} y=120(.87)^{t} \\ 20=120(.87)^{t} \end{array} \nonumber \]

Divide both sides by 120 to isolate the exponential expression.

\[\begin{array}{l} \frac{20}{120}=\frac{120}{120}\left(0.87^{t}\right) \\ 0.1667=0.87^{t} \end{array} \nonumber \]

Rewrite the expression in logarithmic form and use the change of base formula

\[\begin{array}{l} t=\log _{0.87}(0.1667) \\ t=\frac{\ln (0.1667)}{\ln (0.87)} \approx 12.9 \text { hours } \end{array} \nonumber \]

After 12.9 hours, 20 mg of caffeine remains in the body.

EXPRESSING EXPONENTIAL FUNCTIONS IN THE FORMS y = ab t and y = ae kt

Now that we’ve developed our equation solving skills, we revisit the question of expressing exponential functions equivalently in the forms \(y = ab^t\) and \(y = ae^{kt}\)

We’ve already determined that if given the form \(y = ae^{kt}\), it is straightforward to find \(b\).

Example \(\PageIndex{7}\)

For the following examples, assume \(t\) is measured in years.

• Express \(y = 3500e^{0.25t}\) in form \(y = ab^t\) and find the annual percentage growth rate.
• Express \(y = 28000e^{-0.32t}\) in form \(y = ab^t\) and find the annual percentage decay rate.

a. Express \(y = 3500e^{0.25t}\) in the form \(y = ab^t\)

\[\begin{array}{l} y=a e^{k t}=a b^{t} \\ a\left(e^{k}\right)^{t}=a b^{t} \end{array} \nonumber \]

Thus \(e^k=b\)

In this example \(b=e^{0.25} \approx 1.284\)

We rewrite the growth function as y = 3500(1.284 t )

To find \(r\), recall that \(b = 1+r\) \[\begin{aligned} &1.284=1+r\\ &0.284=\mathrm{r} \end{aligned} \nonumber \]

The continuous growth rate is \(k\) = 0.25 and the annual percentage growth rate is 28.4% per year.

b. Express \(y = 28000e^{-0.32t}\) in the form \(y = ab^t\)

In this example \(\mathrm{b}=e^{-0.32} \approx 0.7261\)

We rewrite the growth function as y = 28000(0.7261 t )

To find \(r\), recall that \(b = 1+r\) \[\begin{array}{l} 0.7261=1+r \\ 0.2739=r \end{array} \nonumber \]

The continuous decay rate is \(k\) = -0.32 and the annual percentage decay rate is 27.39% per year.

In the sentence, we omit the negative sign when stating the annual percentage decay rate because we have used the word “decay” to indicate that r is negative.

Example \(\PageIndex{8}\)

• Express \(y = 4200 (1.078)^t\) in the form \(y =ae^{kt}\)
• Express \(y = 150 (0.73)^t\) in the form \(y =ae^{kt}\)

a. Express \(y = 4200 (1.078)^t\) in the form \(y =ae^{kt}\)

\[\begin{array}{l} \mathrm{y}=\mathrm{a} e^{\mathrm{k} t}=\mathrm{ab}^{\mathrm{t}} \\ \mathrm{a}\left(e^{\mathrm{k}}\right)^{\mathrm{t}}=\mathrm{ab}^{\mathrm{t}} \\ e^{\mathrm{k}}=\mathrm{b} \\ e^{k}=1.078 \end{array} \nonumber \]

Therefore \(\mathrm{k}=\ln 1.078 \approx 0.0751\)

We rewrite the growth function as \(y = 3500e^{0.0751t}\)

b. Express \(y =150 (0.73)^t\) in the form \(y = ae^{kt}\)

\[\begin{array}{l} y=a e^{k t}=a b^{t} \\ a\left(e^{k}\right)^{t}=a b^{t} \\ e^{k}=b \\ e^{k}=0.73 \end{array} \nonumber \]

Therefore \(\mathrm{k}=\ln 0.73 \approx-0.3147\)

We rewrite the growth function as \(y = 150e^{-0.3147t}\)

AN APPLICATION OF A LOGARITHMIC FUNCTON

Suppose we invest $10,000 today and want to know how long it will take to accumulate to a specified amount, such as $15,000. The time \(t\) needed to reach a future value \(y\) is a logarithmic function of the future value: \(t = g(y)\)

Example \(\PageIndex{9}\)

Suppose that Vinh invests $10000 in an investment earning 5% per year. He wants to know how long it would take his investment to accumulate to $12000, and how long it would take to accumulate to $15000.

We start by writing the exponential growth function that models the value of this investment as a function of the time since the $10000 is initially invested

\[y=10000(1.05)^{t} \nonumber \]

We divide both sides by 10000 to isolate the exponential expression on one side.

\[\frac{y}{10000}=1.05^{t} \nonumber \]

Next we rewrite this in logarithmic form to express time as a function of the accumulated future value. We’ll use function notation and call this function \(g(y)\).

\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\log _{1.05}\left(\frac{\mathrm{y}}{10000}\right) \nonumber \]

Use the change of base formula to express \(t\) as a function of \(y\) using natural logarithm:

\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)} \nonumber \]

We can now use this function to answer Vinh’s questions.

To find the number of years until the value of this investment is $12,000, we substitute \(y\) = $12,000 into function \(g\) and evaluate \(t\):

\[\mathrm{t}=\mathrm{g}(12000)=\frac{\ln \left(\frac{12000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.2)}{\ln (1.05)}=3.74 \text { years } \nonumber \]

To find the number of years until the value of this investment is $15,000, we substitute \(y\) = $15,000 into function \(g\) and evaluate \(t\):

\[\mathrm{t}=\mathrm{g}(15000)=\frac{\ln \left(\frac{15000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.5)}{\ln (1.05)}=8.31 \text { years } \nonumber \]

Before ending this section, we investigate the graph of the function \(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\). We see that the function has the general shape of logarithmic functions that we examined in section 5.5. From the points plotted on the graph, we see that function \(g\) is an increasing function but it increases very slowly.

If we consider just the function \(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\), then the domain of function would be \(y > 0\), all positive real numbers, and the range for \(t\) would be all real numbers.

In the context of this investment problem, the initial investment at time \(t\) = 0 is \(y\) =$10,000. Negative values for time do not make sense. Values of the investment that are lower than the initial amount of $10,000 also do not make sense for an investment that is increasing in value.

Therefore the function and graph as it pertains to this problem concerning investments has domain \(y ≥ 10,000\) and range \(t ≥ 0\).

The graph below is restricted to the domain and range that make practical sense for the investment in this problem.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 12

• Exponential expressions word problems (numerical)
• Initial value & common ratio of exponential functions

Exponential expressions word problems (algebraic)

• Interpreting exponential expression word problem
• Interpret exponential expressions word problems