solving systems of equations by graphing online practice

5.1 Solve Systems of Equations by Graphing

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Determine the number of solutions of linear system
• Solve applications of systems of equations by graphing

Be Prepared 5.1

Before you get started, take this readiness quiz.

• For the equation y = 2 3 x − 4 y = 2 3 x − 4 ⓐ is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 2.1 .
• Find the slope and y -intercept of the line 3 x − y = 12 3 x − y = 12 . If you missed this problem, review Example 4.42 .
• Find the x - and y -intercepts of the line 2 x − 3 y = 12 2 x − 3 y = 12 . If you missed this problem, review Example 4.21 .

Determine Whether an Ordered Pair is a Solution of a System of Equations

In Solving Linear Equations and Inequalities we learned how to solve linear equations with one variable. Remember that the solution of an equation is a value of the variable that makes a true statement when substituted into the equation.

Now we will work with systems of linear equations , two or more linear equations grouped together.

System of Linear Equations

When two or more linear equations are grouped together, they form a system of linear equations.

We will focus our work here on systems of two linear equations in two unknowns. Later, you may solve larger systems of equations.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

A linear equation in two variables, like 2 x + y = 7, has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) that make both equations true. These are called the solutions to a system of equations .

Solutions of a System of Equations

Solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ).

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Let’s consider the system below:

Is the ordered pair ( 2 , −1 ) ( 2 , −1 ) a solution?

The ordered pair (2, −1) made both equations true. Therefore (2, −1) is a solution to this system.

Let’s try another ordered pair. Is the ordered pair (3, 2) a solution?

The ordered pair (3, 2) made one equation true, but it made the other equation false. Since it is not a solution to both equations, it is not a solution to this system.

Example 5.1

Determine whether the ordered pair is a solution to the system: { x − y = −1 2 x − y = −5 { x − y = −1 2 x − y = −5

ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )

Determine whether the ordered pair is a solution to the system: { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .

ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )

Determine whether the ordered pair is a solution to the system: { x − 3 y = −8 −3 x − y = 4 . { x − 3 y = −8 −3 x − y = 4 .

ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )

Solve a System of Linear Equations by Graphing

In this chapter we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown in Figure 5.2 :

For the first example of solving a system of linear equations in this section and in the next two sections, we will solve the same system of two linear equations. But we’ll use a different method in each section. After seeing the third method, you’ll decide which method was the most convenient way to solve this system.

Example 5.2

How to solve a system of linear equations by graphing.

Solve the system by graphing: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Solve each system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .

Solve each system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .

The steps to use to solve a system of linear equations by graphing are shown below.

To solve a system of linear equations by graphing.

• Step 1. Graph the first equation.
• Step 2. Graph the second equation on the same rectangular coordinate system.
• Step 3. Determine whether the lines intersect, are parallel, or are the same line.
• If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.
• If the lines are parallel, the system has no solution.
• If the lines are the same, the system has an infinite number of solutions.

Example 5.3

Solve the system by graphing: { y = 2 x + 1 y = 4 x − 1 . { y = 2 x + 1 y = 4 x − 1 .

Both of the equations in this system are in slope-intercept form, so we will use their slopes and y -intercepts to graph them. { y = 2 x + 1 y = 4 x − 1 { y = 2 x + 1 y = 4 x − 1

Solve each system by graphing: { y = 2 x + 2 y = − x − 4 . { y = 2 x + 2 y = − x − 4 .

Solve each system by graphing: { y = 3 x + 3 y = − x + 7 . { y = 3 x + 3 y = − x + 7 .

Both equations in Example 5.3 were given in slope–intercept form. This made it easy for us to quickly graph the lines. In the next example, we’ll first re-write the equations into slope–intercept form.

Example 5.4

Solve the system by graphing: { 3 x + y = −1 2 x + y = 0 . { 3 x + y = −1 2 x + y = 0 .

We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts. { 3 x + y = −1 2 x + y = 0 { 3 x + y = −1 2 x + y = 0

Solve each system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .

Solve each system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .

Usually when equations are given in standard form, the most convenient way to graph them is by using the intercepts. We’ll do this in Example 5.5 .

Example 5.5

Solve the system by graphing: { x + y = 2 x − y = 4 . { x + y = 2 x − y = 4 .

We will find the x - and y -intercepts of both equations and use them to graph the lines.

Solve each system by graphing: { x + y = 6 x − y = 2 . { x + y = 6 x − y = 2 .

Try It 5.10

Solve each system by graphing: { x + y = 2 x − y = −8 . { x + y = 2 x − y = −8 .

Do you remember how to graph a linear equation with just one variable? It will be either a vertical or a horizontal line.

Example 5.6

Solve the system by graphing: { y = 6 2 x + 3 y = 12 . { y = 6 2 x + 3 y = 12 .

Try It 5.11

Solve each system by graphing: { y = −1 x + 3 y = 6 . { y = −1 x + 3 y = 6 .

Try It 5.12

Solve each system by graphing: { x = 4 3 x − 2 y = 24 . { x = 4 3 x − 2 y = 24 .

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example 5.7

Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .

Try It 5.13

Solve each system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .

Try It 5.14

Solve each system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .

Example 5.8

Solve the system by graphing: { y = 2 x − 3 −6 x + 3 y = − 9 . { y = 2 x − 3 −6 x + 3 y = − 9 .

Try It 5.15

Solve each system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .

Try It 5.16

Solve each system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .

If you write the second equation in Example 5.8 in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident. Coincident lines have the same slope and same y -intercept.

Coincident Lines

Coincident lines have the same slope and same y -intercept.

Determine the Number of Solutions of a Linear System

There will be times when we will want to know how many solutions there will be to a system of linear equations, but we might not actually have to find the solution. It will be helpful to determine this without graphing.

We have seen that two lines in the same plane must either intersect or are parallel. The systems of equations in Example 5.2 through Example 5.6 all had two intersecting lines. Each system had one solution.

A system with parallel lines, like Example 5.7 , has no solution. What happened in Example 5.8 ? The equations have coincident lines , and so the system had infinitely many solutions.

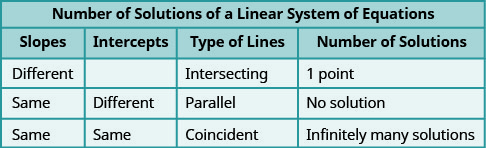
We’ll organize these results in Figure 5.3 below:

Parallel lines have the same slope but different y -intercepts. So, if we write both equations in a system of linear equations in slope–intercept form, we can see how many solutions there will be without graphing! Look at the system we solved in Example 5.7 .

The two lines have the same slope but different y -intercepts. They are parallel lines.

Figure 5.4 shows how to determine the number of solutions of a linear system by looking at the slopes and intercepts.

Let’s take one more look at our equations in Example 5.7 that gave us parallel lines.

When both lines were in slope-intercept form we had:

Do you recognize that it is impossible to have a single ordered pair ( x , y ) ( x , y ) that is a solution to both of those equations?

We call a system of equations like this an inconsistent system . It has no solution.

A system of equations that has at least one solution is called a consistent system .

Consistent and Inconsistent Systems

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent equations , they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations , we get coincident lines.

Independent and Dependent Equations

Two equations are independent if they have different solutions.

Two equations are dependent if all the solutions of one equation are also solutions of the other equation.

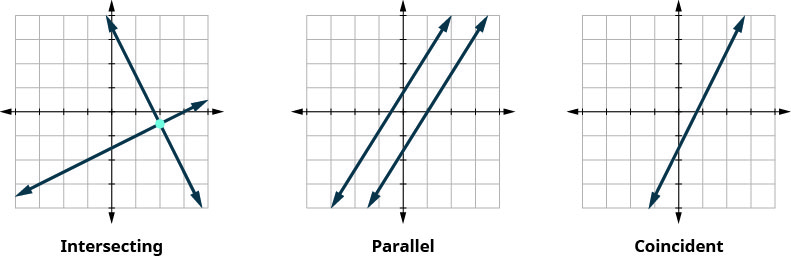
Let’s sum this up by looking at the graphs of the three types of systems. See Figure 5.5 and Figure 5.6 .

Example 5.9

Without graphing, determine the number of solutions and then classify the system of equations: { y = 3 x − 1 6 x − 2 y = 12 . { y = 3 x − 1 6 x − 2 y = 12 .

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

Try It 5.17

Without graphing, determine the number of solutions and then classify the system of equations.

{ y = − 2 x − 4 4 x + 2 y = 9 { y = − 2 x − 4 4 x + 2 y = 9

Try It 5.18

{ y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6

Example 5.10

Without graphing, determine the number of solutions and then classify the system of equations: { 2 x + y = − 3 x − 5 y = 5 . { 2 x + y = − 3 x − 5 y = 5 .

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

Try It 5.19

{ 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1

Try It 5.20

{ x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3

Example 5.11

Without graphing, determine the number of solutions and then classify the system of equations. { 3 x − 2 y = 4 y = 3 2 x − 2 { 3 x − 2 y = 4 y = 3 2 x − 2

A system of equations whose graphs are coincident lines has infinitely many solutions and is consistent and dependent.

Try It 5.21

{ 4 x − 5 y = 20 y = 4 5 x − 4 { 4 x − 5 y = 20 y = 4 5 x − 4

Try It 5.22

{ −2 x − 4 y = 8 y = − 1 2 x − 2 { −2 x − 4 y = 8 y = − 1 2 x − 2

Solve Applications of Systems of Equations by Graphing

We will use the same problem solving strategy we used in Math Models to set up and solve applications of systems of linear equations. We’ll modify the strategy slightly here to make it appropriate for systems of equations.

Use a problem solving strategy for systems of linear equations.

• Step 1. Read the problem. Make sure all the words and ideas are understood.

Step 2. Identify what we are looking for.

Step 3. Name what we are looking for. Choose variables to represent those quantities.

Step 4. Translate into a system of equations.

Step 5. Solve the system of equations using good algebra techniques.

Step 6. Check the answer in the problem and make sure it makes sense.

Step 7. Answer the question with a complete sentence.

Step 5 is where we will use the method introduced in this section. We will graph the equations and find the solution.

Example 5.12

Sondra is making 10 quarts of punch from fruit juice and club soda. The number of quarts of fruit juice is 4 times the number of quarts of club soda. How many quarts of fruit juice and how many quarts of club soda does Sondra need?

Step 1. Read the problem.

We are looking for the number of quarts of fruit juice and the number of quarts of club soda that Sondra will need.

  Let f = f = number of quarts of fruit juice.      c = c = number of quarts of club soda

We now have the system. { f + c = 10 f = 4 c { f + c = 10 f = 4 c

The point of intersection (2, 8) is the solution. This means Sondra needs 2 quarts of club soda and 8 quarts of fruit juice.

Does this make sense in the problem?

Yes, the number of quarts of fruit juice, 8 is 4 times the number of quarts of club soda, 2.

Yes, 10 quarts of punch is 8 quarts of fruit juice plus 2 quarts of club soda.

Sondra needs 8 quarts of fruit juice and 2 quarts of soda.

Try It 5.23

Manny is making 12 quarts of orange juice from concentrate and water. The number of quarts of water is 3 times the number of quarts of concentrate. How many quarts of concentrate and how many quarts of water does Manny need?

Try It 5.24

Alisha is making an 18 ounce coffee beverage that is made from brewed coffee and milk. The number of ounces of brewed coffee is 5 times greater than the number of ounces of milk. How many ounces of coffee and how many ounces of milk does Alisha need?

Access these online resources for additional instruction and practice with solving systems of equations by graphing.

• Instructional Video Solving Linear Systems by Graphing
• Instructional Video Solve by Graphing

Section 5.1 Exercises

Practice makes perfect.

Determine Whether an Ordered Pair is a Solution of a System of Equations . In the following exercises, determine if the following points are solutions to the given system of equations.

{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5

ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

{ 7 x − 4 y = −1 −3 x − 2 y = 1 { 7 x − 4 y = −1 −3 x − 2 y = 1

ⓐ   ⓑ ( 1 , −2 ) ( 1 , −2 )

{ 2 x + y = 5 x + y = 1 { 2 x + y = 5 x + y = 1

ⓐ ( 4 , −3 ) ( 4 , −3 ) ⓑ ( 2 , 0 ) ( 2 , 0 )

{ −3 x + y = 8 − x + 2 y = −9 { −3 x + y = 8 − x + 2 y = −9

ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )

{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x

ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )

{ x + y = 1 y = 2 5 x { x + y = 1 y = 2 5 x

ⓐ ( 5 7 , 2 7 ) ( 5 7 , 2 7 ) ⓑ ( 5 , 2 ) ( 5 , 2 )

{ x + 5 y = 10 y = 3 5 x + 1 { x + 5 y = 10 y = 3 5 x + 1

ⓐ ( −10 , 4 ) ( −10 , 4 ) ⓑ ( 5 4 , 7 4 ) ( 5 4 , 7 4 )

{ x + 3 y = 9 y = 2 3 x − 2 { x + 3 y = 9 y = 2 3 x − 2

ⓐ ( −6 , 5 ) ( −6 , 5 ) ⓑ ( 5 , 4 3 ) ( 5 , 4 3 )

Solve a System of Linear Equations by Graphing In the following exercises, solve the following systems of equations by graphing.

{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5

{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4

{ −3 x + y = −1 2 x + y = 4 { −3 x + y = −1 2 x + y = 4

{ −2 x + 3 y = −3 x + y = 4 { −2 x + 3 y = −3 x + y = 4

{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2

{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2

{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5

{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5

{ − x + y = −3 4 x + 4 y = 4 { − x + y = −3 4 x + 4 y = 4

{ x − y = 3 2 x − y = 4 { x − y = 3 2 x − y = 4

{ −3 x + y = −2 4 x − 2 y = 6 { −3 x + y = −2 4 x − 2 y = 6

{ x + y = 5 2 x − y = 4 { x + y = 5 2 x − y = 4

{ x − y = 2 2 x − y = 6 { x − y = 2 2 x − y = 6

{ x + y = 2 x − y = 0 { x + y = 2 x − y = 0

{ x + y = 6 x − y = −8 { x + y = 6 x − y = −8

{ x + y = −5 x − y = 3 { x + y = −5 x − y = 3

{ x + y = 4 x − y = 0 { x + y = 4 x − y = 0

{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2

{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3

{ −2 x + 3 y = 3 x + 3 y = 12 { −2 x + 3 y = 3 x + 3 y = 12

{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12

{ 2 x + 3 y = 6 y = −2 { 2 x + 3 y = 6 y = −2

{ −2 x + y = 2 y = 4 { −2 x + y = 2 y = 4

{ x − 3 y = −3 y = 2 { x − 3 y = −3 y = 2

{ 2 x − 2 y = 8 y = −3 { 2 x − 2 y = 8 y = −3

{ 2 x − y = −1 x = 1 { 2 x − y = −1 x = 1

{ x + 2 y = 2 x = −2 { x + 2 y = 2 x = −2

{ x − 3 y = −6 x = −3 { x − 3 y = −6 x = −3

{ x + y = 4 x = 1 { x + y = 4 x = 1

{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14

{ x + 3 y = 4 −2 x − 6 y = 3 { x + 3 y = 4 −2 x − 6 y = 3

{ −2 x + 4 y = 4 y = 1 2 x { −2 x + 4 y = 4 y = 1 2 x

{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1

{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8

{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14

{ 2 x + y = 6 −8 x − 4 y = −24 { 2 x + y = 6 −8 x − 4 y = −24

{ 5 x + 2 y = 7 −10 x − 4 y = −14 { 5 x + 2 y = 7 −10 x − 4 y = −14

{ x + 3 y = −6 4 y = − 4 3 x − 8 { x + 3 y = −6 4 y = − 4 3 x − 8

{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1

{ −3 x + 2 y = −2 y = − x + 4 { −3 x + 2 y = −2 y = − x + 4

{ − x + 2 y = −2 y = − x − 1 { − x + 2 y = −2 y = − x − 1

Determine the Number of Solutions of a Linear System Without graphing the following systems of equations, determine the number of solutions and then classify the system of equations.

{ y = 2 3 x + 1 −2 x + 3 y = 5 { y = 2 3 x + 1 −2 x + 3 y = 5

{ y = 1 3 x + 2 x − 3 y = 9 { y = 1 3 x + 2 x − 3 y = 9

{ y = −2 x + 1 4 x + 2 y = 8 { y = −2 x + 1 4 x + 2 y = 8

{ y = 3 x + 4 9 x − 3 y = 18 { y = 3 x + 4 9 x − 3 y = 18

{ y = 2 3 x + 1 2 x − 3 y = 7 { y = 2 3 x + 1 2 x − 3 y = 7

{ 3 x + 4 y = 12 y = −3 x − 1 { 3 x + 4 y = 12 y = −3 x − 1

{ 4 x + 2 y = 10 4 x − 2 y = −6 { 4 x + 2 y = 10 4 x − 2 y = −6

{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5

{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10

{ y = x + 1 − x + y = 1 { y = x + 1 − x + y = 1

{ y = 2 x + 3 2 x − y = −3 { y = 2 x + 3 2 x − y = −3

{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5

Solve Applications of Systems of Equations by Graphing In the following exercises, solve.

Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?

Jamal is making a snack mix that contains only pretzels and nuts. For every ounce of nuts, he will use 2 ounces of pretzels. How many ounces of pretzels and how many ounces of nuts does he need to make 45 ounces of snack mix?

Enrique is making a party mix that contains raisins and nuts. For each ounce of nuts, he uses twice the amount of raisins. How many ounces of nuts and how many ounces of raisins does he need to make 24 ounces of party mix?

Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?

Everyday Math

Leo is planning his spring flower garden. He wants to plant tulip and daffodil bulbs. He will plant 6 times as many daffodil bulbs as tulip bulbs. If he wants to plant 350 bulbs, how many tulip bulbs and how many daffodil bulbs should he plant?

A marketing company surveys 1,200 people. They surveyed twice as many females as males. How many males and females did they survey?

Writing Exercises

In a system of linear equations, the two equations have the same slope. Describe the possible solutions to the system.

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith
• Publisher/website: OpenStax
• Book title: Elementary Algebra
• Publication date: Feb 22, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra/pages/5-1-solve-systems-of-equations-by-graphing

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

How to solve systems of equations by Graphing

Step by step tutorial for systems of linear equations (in 2 variables)

Video on Solving by Graphing

The Graph Method

What is the solution of the following system of equations?

$$ y = x + 1 \\ y = 2x $$

Graph both equations

On the right, the graph of the two lines

The solution of the system is the point of intersection : (1, 2)

Practice Problems

Use the graph method to solve the system of equations below

$$ y = 2x +1 \\ y = 4x -1 $$

The solution of this system is the point of intersection : (1,3).

Solve the following system of linear equations by graphing .

$$ \text{ A) } 2y = 4x + 2 \\ \text{ B) }2y = -x + 7 $$

Rewrite each equation in slope intercept form

$$ \text{ A) } 2y = 4x + 2 \\ \frac{1}{2} 2y = \frac{1}{2}(4x+2) \\ y = 2x +1 $$

$$ \text{ B) } 2y = 8x - 2 \\ \frac{1}{2} 2y = \frac{1}{2}( 8x - 2) \\ y = 4x +1 $$

This system of lines is the same system that we looked at in the last example.

Graph each equation to find the point of intersection --which is the solution. (same as earlier problem)

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

4. Systems of Equations

4.1 Solve Systems of Equations by Graphing

Lynn Marecek and MaryAnne Anthony-Smith

Learning Objectives

By the end of this section it is expected that you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Determine the number of solutions of linear system
• Solve applications of systems of equations by graphing

Determine Whether an Ordered Pair is a Solution of a System of Equations

 We learned before how to solve linear equations with one variable. Now we will work with systems of linear equations , two or more linear equations grouped together, witch is known as a system of linear equations.

System of Linear Equations

When two or more linear equations are grouped together, they form a system of linear equations.

We will focus our work here on systems of two linear equations in two unknowns. Later, you may solve larger systems of equations.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

A linear equation in two variables, like 2 x + y = 7, has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) that make both equations true. These are called the solutions to a system of equations .

Solutions of a System of Equations

Solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ).

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Let’s consider the system below:

The ordered pair (2, −1) made both equations true. Therefore (2, −1) is a solution to this system.

Let’s try another ordered pair. Is the ordered pair (3, 2) a solution?

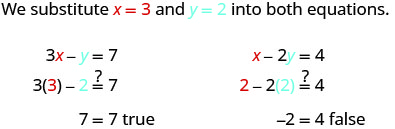
The ordered pair (3, 2) made one equation true, but it made the other equation false. Since it is not a solution to both equations, it is not a solution to this system.

• a) yes b) no

Equations by Graphing

In this chapter we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown in (Figure 1) :

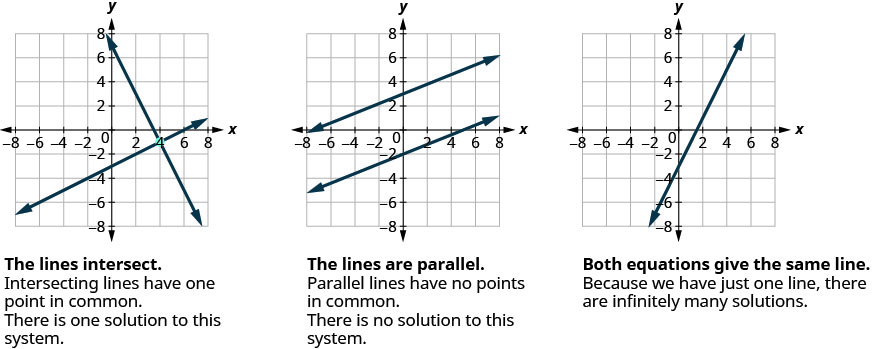
For the first example of solving a system of linear equations in this section and in the next two sections, we will solve the same system of two linear equations. But we’ll use a different method in each section. After seeing the third method, you’ll decide which method was the most convenient way to solve this system.

The steps to use to solve a system of linear equations by graphing are shown below

To solve a system of linear equations by graphing.

• Graph the first equation.
• Graph the second equation on the same rectangular coordinate system.
• Determine whether the lines intersect, are parallel, or are the same line.
• If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.
• If the lines are parallel, the system has no solution.
• If the lines are the same, the system has an infinite number of solutions.

Usually when equations are given in standard form, the most convenient way to graph them is by using the intercepts. We’ll do this in the next example.

We will find the x – and y -intercepts of both equations and use them to graph the lines.

Do you remember how to graph a linear equation with just one variable? It will be either a vertical or a horizontal line.

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

• no solution

• infinitely many solutions

If you write the second equation in Example 8 in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident. Coincident lines have the same slope and same y -intercept.

Coincident Lines

Coincident lines have the same slope and same y -intercept.

Determine the Number of Solutions of a Linear System

There will be times when we will want to know how many solutions there will be to a system of linear equations, but we might not actually have to find the solution. It will be helpful to determine this without graphing.

We have seen that two lines in the same plane must either intersect or are parallel. The systems of equations in Example 2 through Example 6 all had two intersecting lines. Each system had one solution.

A system with parallel lines, like Example 7, has no solution. What happened in Example 8? The equations have coincident lines , and so the system had infinitely many solutions.

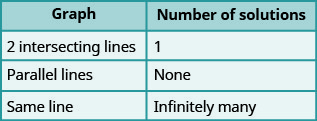
We’ll organize these results in (Table 1) below:

Parallel lines have the same slope but different y -intercepts. So, if we write both equations in a system of linear equations in slope–intercept form, we can see how many solutions there will be without graphing! Look at the system we solved in Example 7.

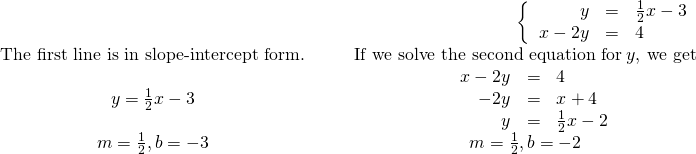
The two lines have the same slope but different y -intercepts. They are parallel lines.

(Table 2) shows how to determine the number of solutions of a linear system by looking at the slopes and intercepts.

Let’s take one more look at our equations in (Example 7) that gave us parallel lines.

When both lines were in slope-intercept form we had:

We call a system of equations like this an inconsistent system . It has no solution.

A system of equations that has at least one solution is called a consistent system .

Consistent and Inconsistent Systems

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent equations , they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations , we get coincident lines.

Independent and Dependent Equations

Two equations are independent if they have different solutions.

Two equations are dependent if all the solutions of one equation are also solutions of the other equation.

Let’s sum this up by looking at the graphs of the three types of systems. See (Figure 3) and (Table 3) .

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

Without graphing, determine the number of solutions and then classify the system of equations.

no solution, inconsistent, independent

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

one solution, consistent, independent

A system of equations whose graphs are coincident lines has infinitely many solutions and is consistent and dependent.

infinitely many solutions, consistent, dependent

Solve Applications of Systems of Equations by Graphing

We will modify the  problem solving strategy slightly to set up and solve applications of systems of linear equations.

How to use a problem solving strategy for systems of linear equations.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose variables to represent those quantities.
• Translate into a system of equations.
• Solve the system of equations using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Step 5 is where we will use the method introduced in this section. We will graph the equations and find the solution.

Sondra is making 10 quarts of punch from fruit juice and club soda. The number of quarts of fruit juice is 4 times the number of quarts of club soda. How many quarts of fruit juice and how many quarts of club soda does Sondra need?

Step 1. Read the problem.

Step 2. Identify what we are looking for.

We are looking for the number of quarts of fruit juice and the number of quarts of club soda that Sondra will need.

Step 3. Name what we are looking for. Choose variables to represent those quantities.

Step 4. Translate into a system of equations.

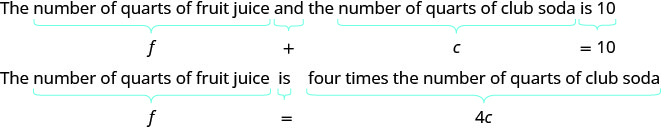
Step 5. Solve the system of equations using good algebra techniques.

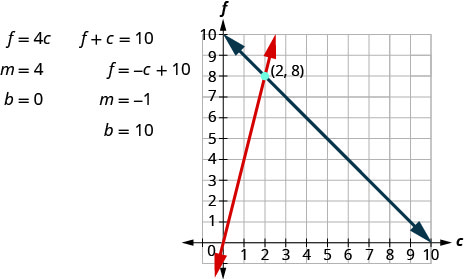
The point of intersection (2, 8) is the solution. This means Sondra needs 2 quarts of club soda and 8 quarts of fruit juice.

Step 6. Check the answer in the problem and make sure it makes sense.

Does this make sense in the problem?

Yes, the number of quarts of fruit juice, 8 is 4 times the number of quarts of club soda, 2.

Yes, 10 quarts of punch is 8 quarts of fruit juice plus 2 quarts of club soda.

Step 7. Answer the question with a complete sentence.

Sondra needs 8 quarts of fruit juice and 2 quarts of soda.

Manu is making 12 quarts of orange juice from concentrate and water. The number of quarts of water is 3 times the number of quarts of concentrate. How many quarts of concentrate and how many quarts of water does Manu need?

Manu needs 3 quarts juice concentrate and 9 quarts water.

Access these online resources for additional instruction and practice with solving systems of equations by graphing.

• Instructional Video Solving Linear Systems by Graphing
• Instructional Video Solve by Graphing

Key Concepts

4.1 exercise set.

In the following exercises, determine if the following points are solutions to the given system of equations.

• (\left(\frac{5}{4},\frac{7}{4}\right)\)

In the following exercises, solve the following systems of equations by graphing.

Without graphing the following systems of equations, determine the number of solutions and then classify the system of equations.

In the following exercises, solve.

• Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?
• Enrique is making a party mix that contains raisins and nuts. For each ounce of nuts, he uses twice the amount of raisins. How many ounces of nuts and how many ounces of raisins does he need to make 24 ounces of party mix?
• Leo is planning his spring flower garden. He wants to plant tulip and daffodil bulbs. He will plant 6 times as many daffodil bulbs as tulip bulbs. If he wants to plant 350 bulbs, how many tulip bulbs and how many daffodil bulbs should he plant?
• a) no b) yes

• no solutions
• no solutions, inconsistent, independent
• consistent, 1 solution
• Molly needs 16 ounces of strawberry juice and 48 ounces of water.
• Enrique needs 8 ounces of nuts and 16 ounces of water.
• Leo should plant 50 tulips and 300 daffodils.

Business/Technical Mathematics Copyright © 2021 by Lynn Marecek and MaryAnne Anthony-Smith is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.2: Solve Systems of Equations by Substitution

• Last updated
• Save as PDF
• Page ID 15152

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve a system of equations by substitution
• Solve applications of systems of equations by substitution

Before you get started, take this readiness quiz.

• Simplify −5(3−x). If you missed this problem, review Example 1.10.43 .
• Simplify 4−2(n+5). If you missed this problem, review Example 1.10.49 .
• Solve for y. 8y−8=32−2y If you missed this problem, review Example 2.3.22 .
• Solve for x. 3x−9y=−3 If you missed this problem, review Example 2.6.22 .

Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.

In this section, we will solve systems of linear equations by the substitution method.

Solve a System of Equations by Substitution

We will use the same system we used first for graphing.

\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.

We’ll fill in all these steps now in Example \(\PageIndex{1}\).

Example \(\PageIndex{1}\): How to Solve a System of Equations by Substitution

Solve the system by substitution. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

Try It \(\PageIndex{2}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)

Try It \(\PageIndex{3}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)

SOLVE A SYSTEM OF EQUATIONS BY SUBSTITUTION.

• Solve one of the equations for either variable.
• Substitute the expression from Step 1 into the other equation.
• Solve the resulting equation.
• Substitute the solution in Step 3 into one of the original equations to find the other variable.
• Write the solution as an ordered pair.
• Check that the ordered pair is a solution to both original equations.

If one of the equations in the system is given in slope–intercept form, Step 1 is already done! We’ll see this in Example \(\PageIndex{4}\).

Example \(\PageIndex{4}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)

The second equation is already solved for y . We will substitute the expression in place of y in the first equation.

Try It \(\PageIndex{5}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)

Try It \(\PageIndex{6}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)

(−1,−3)

If the equations are given in standard form, we’ll need to start by solving for one of the variables. In this next example, we’ll solve the first equation for y .

Example \(\PageIndex{7}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)

We need to solve one equation for one variable. Then we will substitute that expression into the other equation.

Try It \(\PageIndex{8}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)

(1,−2)

Try It \(\PageIndex{9}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)

In Example \(\PageIndex{7}\) it was easiest to solve for y in the first equation because it had a coefficient of 1. In Example \(\PageIndex{10}\) it will be easier to solve for x .

Example \(\PageIndex{10}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)

We will solve the first equation for \(x\) and then substitute the expression into the second equation.

Try It \(\PageIndex{11}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)

(−2,−3)

Try It \(\PageIndex{12}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)

When both equations are already solved for the same variable, it is easy to substitute!

Example \(\PageIndex{13}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)

Since both equations are solved for y , we can substitute one into the other.

Try It \(\PageIndex{14}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)

Try It \(\PageIndex{15}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)

Be very careful with the signs in the next example.

Example \(\PageIndex{16}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)

We need to solve one equation for one variable. We will solve the first equation for y .

Try It \(\PageIndex{17}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)

\((2,\frac{3}{2})\)

Try It \(\PageIndex{18}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)

\((−\frac{1}{2},−2)\)

In Example , it will take a little more work to solve one equation for x or y .

Example \(\PageIndex{19}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)

We need to solve one equation for one variable. We will solve the first equation for x .

Try It \(\PageIndex{20}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)

infinitely many solutions

Try It \(\PageIndex{21}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)

Look back at the equations in Example \(\PageIndex{22}\). Is there any way to recognize that they are the same line?

Let’s see what happens in the next example.

Example \(\PageIndex{22}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)

The second equation is already solved for y , so we can substitute for y in the first equation.

Try It \(\PageIndex{23}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)

no solution

Try It \(\PageIndex{24}\)

Solve the system by substitution. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)

Solve Applications of Systems of Equations by Substitution

We’ll copy here the problem solving strategy we used in the Solving Systems of Equations by Graphing section for solving systems of equations. Now that we know how to solve systems by substitution, that’s what we’ll do in Step 5.

HOW TO USE A PROBLEM SOLVING STRATEGY FOR SYSTEMS OF LINEAR EQUATIONS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose variables to represent those quantities.
• Translate into a system of equations.
• Solve the system of equations using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Some people find setting up word problems with two variables easier than setting them up with just one variable. Choosing the variable names is easier when all you need to do is write down two letters. Think about this in the next example—how would you have done it with just one variable?

Example \(\PageIndex{25}\)

The sum of two numbers is zero. One number is nine less than the other. Find the numbers.

Try It \(\PageIndex{26}\)

The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.

The numbers are 3 and 7.

Try It \(\PageIndex{27}\)

The sum of two number is −6. One number is 10 less than the other. Find the numbers.

The numbers are 2 and −8.

In the Example \(\PageIndex{28}\), we’ll use the formula for the perimeter of a rectangle, P = 2 L + 2 W .

Example \(\PageIndex{28}\)

The perimeter of a rectangle is 88. The length is five more than twice the width. Find the length and width of the rectangle.

Try It \(\PageIndex{29}\)

The perimeter of a rectangle is 40. The length is 4 more than the width. Find the length and width of the rectangle.

The length is 12 and the width is 8.

Try It \(\PageIndex{30}\)

The perimeter of a rectangle is 58. The length is 5 more than three times the width. Find the length and width of the rectangle.

The length is 23 and the width is 6.

For Example \(\PageIndex{31}\) we need to remember that the sum of the measures of the angles of a triangle is 180 degrees and that a right triangle has one 90 degree angle.

Example \(\PageIndex{31}\)

The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.

We will draw and label a figure.

Try It \(\PageIndex{32}\)

The measure of one of the small angles of a right triangle is 2 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of the angles are 22 degrees and 68 degrees.

Try It \(\PageIndex{33}\)

The measure of one of the small angles of a right triangle is 18 less than twice the measure of the other small angle. Find the measure of both angles.

The measure of the angles are 36 degrees and 54 degrees.

Example \(\PageIndex{34}\)

Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 plus $15 for each training session. Option B would pay her $10,000 + $40 for each training session. How many training sessions would make the salary options equal?

Try It \(\PageIndex{35}\)

Geraldine has been offered positions by two insurance companies. The first company pays a salary of $12,000 plus a commission of $100 for each policy sold. The second pays a salary of $20,000 plus a commission of $50 for each policy sold. How many policies would need to be sold to make the total pay the same?

There would need to be 160 policies sold to make the total pay the same.

Try It \(\PageIndex{36}\)

Kenneth currently sells suits for company A at a salary of $22,000 plus a $10 commission for each suit sold. Company B offers him a position with a salary of $28,000 plus a $4 commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?

Kenneth would need to sell 1,000 suits.

Access these online resources for additional instruction and practice with solving systems of equations by substitution.

• Instructional Video-Solve Linear Systems by Substitution
• Instructional Video-Solve by Substitution

Number Line

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.

system-of-linear-equations-calculator

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 6

• Systems of equations with substitution: potato chips
• Systems of equations with substitution: -3x-4y=-2 & y=2x-5

Systems of equations with substitution

• Substitution method review (systems of equations)

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍