examples of problem solving mathematics

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Free Mathematics Tutorials, Problems and Worksheets

Thousands of math problems and questions with solutions and detailed explanations are included. Free math tutorials and problems to help you explore and gain deep understanding of math topics such as: Algebra and graphing   ,   Precalculus   ,   Practice tests and worksheets   ,   Calculus   ,   Linear Algebra   ,   Geometry   ,   Trigonometry   ,   Math Videos   ,   Math From Grade 4 to Grade 12   ,   Statistics and Probabilities   ,   Applied Math   ,   Engineering Mathematics   ,   More Math Resources   ,   Math Pages in Different languages and Analyzemath.com in Different Languages

ALGEBRA AND GRAPHING

• Algebra Questions and Problems
• Fractions Questions and Problems with Solutions
• Solving Equation and Inequalities
• Find Domain and Range of Functions
• Complex Numbers
• Step by Step Maths Worksheets Solvers
• Free Graph Paper
• Online Step by Step Algebra Calculators and Solvers

PRECALCULUS

• Graphs of Functions, Equations, and Algebra
• Analytical Tutorials
• Math Problems
• Online Math Calculators and Solvers
• Math Software

PRACTICE TESTS AND WORKSHEETS

• Free Practice for SAT, ACT and Compass Math tests
• Free Practice for quantitative GRE Maths Tests
• Free Math Worksheets to Download
• Differentiation and Derivatives Questions and Problems with Solutions
• Integrals Questions and Problems in Calculus
• Calculus Problem Solving and Applications
• Calculus Tutorials and Problems
• Calculus Questions With Answers
• AP Calculus Questions With Solutions
• Online Step by Step Calculus Calculators and Solvers
• Free Calculus Worksheets to Download

LINEAR ALGEBRA

• Linear Algebra - Questions with Solutions
• Geometry Tutorials and Problems
• Online Geometry Calculators and Solvers
• Online 3D Geometry Calculators and Solvers
• Free Geometry Worksheets to Download

TRIGONOMETRY

• Trigonometry Tutorials and Problems for Self Tests
• Free Trigonometry Questions with Answers
• Free Trigonometry Worksheets to Download
• Online Trigonometry Calculators and Solvers
• Vectors Calculators and Solvers

STATISTICS AND PROBABILITIES

• Elementary Statistics and Probability Tutorials and Problems
• Probabilities
• Statistics Calculators, Solvers and Graphers
• Probability Calculators
• Google Sheets in Math, Statistics and Probabilities

MATH FROM GRADE 4 TO GRADE 12

• Grade 12 Math Problems with Solutions.
• Grade 11 Math Problems with Solutions.
• Grade 10 Math Problems with Solutions.
• Grade 9 Math Problems with Solutions.
• Grade 8 Math Problems with Solutions.
• Grade 7 Math Problems with Solutions.
• Grade 6 Math Problems with Solutions.
• Grade 5 Math Problems with Solutions.
• Grade 4 Math Problems with Solutions.
• High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
• Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
• Primary Math (grades 4 and 5) - Free Questions and Problems With Answers
• Units Conversion and Calculators
• Convert Units of Measurements

APPLIED MATH

• The Applications of Mathematics in Physics and Engineering
• Linear Programming
• Mathematics for Machine Learning
• Mathematical Finance

MORE MATH RESOURCES

• Math Formulas for Mobile Devices
• Engineering Mathematics
• Understanding, Teaching and Learning Mathematics
• HTML5 Applets for iPads
• Math Videos

MATH PAGES IN DIFFERENT LANGUAGES

• Analyzemath.com in Different Languages
• Exercises de Mathematiques Utilisant les Applets
• Mathematics pages in French

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• Converting Cubic Meters to Liters
• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• The Frayer Model for Math
• How to Use Math Journals in Class
• Algorithms in Mathematics and Beyond
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Christmas Word Problem Worksheets
• Graphic Organizers in Math
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Critical Thinking Definition, Skills, and Examples
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created on May 19, 2022

Updated on January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

1:1 Math Lessons

Want to raise a genius? Start learning Math with Brighterly

Guess and check.

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

As adults, we take numbers for granted, but preschoolers and kindergartners have no idea what these symbols mean. Yet, we often demand instant understanding and flawless performance when we start teaching numbers to our children. If you don’t have a clue about how to teach numbers for kids, browse no more. You will get four […]

May 19, 2022

Teaching children is a complex process because they require more attention than an adult person. You may need to employ different teaching strategies when teaching kids. But what are teaching strategies? Teaching strategies are the methods to ensure your kids or students learn efficiently. But not all strategies yield similarly, and if the one you […]

Book 1 to 1 Math Lesson

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

After-School Math Program

Related posts.

Culturally Responsive Teaching Strategies

Teaching and learning have and will continue to undergo many changes. With technological advancement, teachers have more options for incorporating interactive and engaging instructional methods that promote easy learning and student retention in their classes. One of the approaches to follow is culturally responsive teaching which helps handle the diversity of cultures and learning styles […]

Jun 03, 2022

Teach Your Children How to Read Time: A Comprehensive Teaching Guide

As we age, we see time as an inherent and integral component of our everyday existence. However, kids often find this idea complex. Generally, it takes children a few years to master essential time-telling skills, let alone make precise forecasts and projections. In this article, you will learn all about teaching kids how to read […]

Apr 05, 2022

Common Core Math and Its Difference from Traditional Math

Math requires you to dig deeper into the understanding of why problems exist. And in that process, you find multiple solutions to the problems. After decades of solving math problems a certain way, teachers now use a new and improved method to teach math to kids. Although some parents may find this common core math […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Ratio problem solving

Here you will learn about ratio problem solving, including how to set up and solve problems. You will also look at real life ratio word problems.

Students will first learn about ratio problem solving as part of ratio and proportion in 6 th grade and 7 th grade.

What is ratio problem solving?

Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities. They are usually written in the form a : b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are:

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that you can use to help you find an answer.

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods you can use when given certain pieces of information.

When solving ratio word problems, it is very important that you are able to use ratios. This includes being able to use ratio notation.

For example, Charlie and David share some sweets in the ratio of 3 : 5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

You use the ratio to divide 40 sweets into 8 equal parts.

40 \div 8=5

Then you multiply each part of the ratio by 5.

3\times 5:5\times 5=15 : 25

This means that Charlie will get 15 sweets and David will get 25 sweets.

There can be ratio word problems involving different operations and types of numbers.

Here are some examples of different types of ratio word problems:

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

• Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
• Grade 7 – Ratio and Proportional Relationships (7.RP.A.2) Recognize and represent proportional relationships between quantities.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

[FREE] Ratio Problem Solving Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of ratio problem solving. 15 questions with answers to identify areas of strength and support!

Ratio problem solving examples

Example 1: part:part ratio.

Within a school, the total number of students who have school lunches to packed lunches is 5 : 7. If 465 students have a school lunch, how many students have a packed lunch?

Within a school, the number of students who have school lunches to packed lunches is \textbf{5 : 7} . If \textbf{465} students have a school lunch, how many students have a packed lunch?

Here you can see that the ratio is 5 : 7, where the first part of the ratio represents school lunches (S) and the second part of the ratio represents packed lunches (P).

You could write this as:

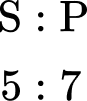
Where the letter above each part of the ratio links to the question.

You know that 465 students have school lunch.

2 Know what you are trying to calculate.

From the question, you need to calculate the number of students that have a packed lunch, so you can now write a ratio below the ratio 5 : 7 that shows that you have 465 students who have school lunches, and p students who have a packed lunch.

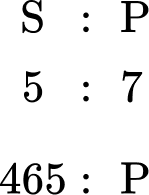
You need to find the value of p.

3 Use prior knowledge to structure a solution.

You are looking for an equivalent ratio to 5 : 7. So you need to calculate the multiplier.

You do this by dividing the known values on the same side of the ratio by each other.

465\div 5 = 93

This means to create an equivalent ratio, you can multiply both sides by 93.

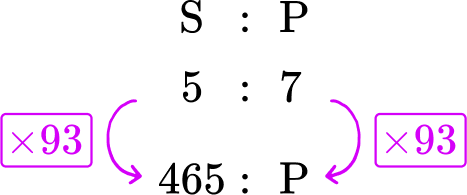
So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

Use the table above to convert £520 \; (GBP) to Euros € \; (EUR).

Use the table above to convert \bf{￡520} \textbf{ (GBP)} to Euros \textbf{€ } \textbf{(EUR)}.

The two values in the table that are important are \text{GBP} and EUR. Writing this as a ratio, you can state,

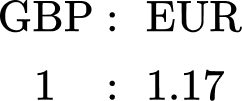
You know that you have £520.

You need to convert GBP to EUR and so you are looking for an equivalent ratio with GBP=£520 and EUR=E.

To get from 1 to 520, you multiply by 520 and so to calculate the number of Euros for £520, you need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520=€608.40.

Example 3: writing a ratio 1 : n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500 \, ml of concentrated plant food must be diluted into 2 \, l of water. Express the ratio of plant food to water, respectively, in the ratio 1 : n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500 \, ml} of concentrated plant food must be diluted into \bf{2 \, l} of water. Express the ratio of plant food to water respectively as a ratio in the form 1 : n.

Using the information in the question, you can now state the ratio of plant food to water as 500 \, ml : 2 \, l. As you can convert liters into milliliters, you could convert 2 \, l into milliliters by multiplying it by 1000.

2 \, l=2000 \, ml

So you can also express the ratio as 500 : 2000 which will help you in later steps.

You want to simplify the ratio 500 : 2000 into the form 1:n.

You need to find an equivalent ratio where the first part of the ratio is equal to 1. You can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

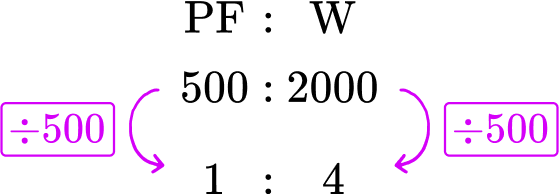
So the ratio of plant food to water in the form 1 : n is 1 : 4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives \$ 8 allowance, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their ages. Kieran is \bf{3} years older than Josh. Luke is twice Josh’s age. If Luke receives \bf{\$ 8} allowance, how much money do the three siblings receive in total?

You can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, you have:

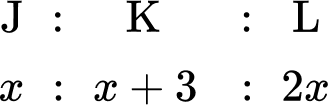
You also know that Luke receives \$ 8.

You want to calculate the total amount of allowance for the three siblings.

You need to find the value of x first. As Luke receives \$ 8, you can state the equation 2x=8 and so x=4.

Now you know the value of x, you can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

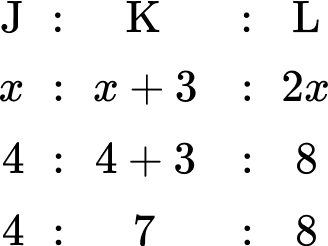
The total amount of allowance is therefore 4+7+8=\$ 19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colors of counters in a bag.

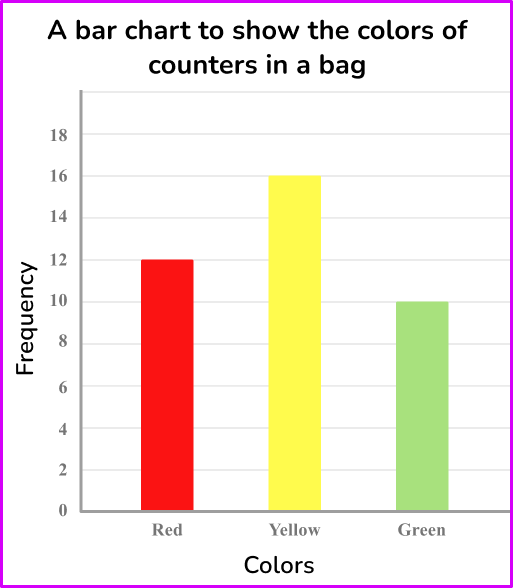
Express this data as a ratio in its simplest form.

From the bar chart, you can read the frequencies to create the ratio.

You need to simplify this ratio.

To simplify a ratio, you need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} & 12 = 1, {\color{red}2}, 3, 4, 6, 12 \\\\ & 16 = 1, {\color{red}2}, 4, 8, 16 \\\\ & 10 = 1, {\color{red}2}, 5, 10 \end{aligned}

HCF(12,16,10) = 2

Dividing all the parts of the ratio by 2, you get

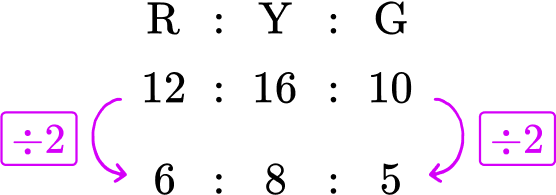
Our solution is 6 : 8 : 5.

Example 6: combining two ratios

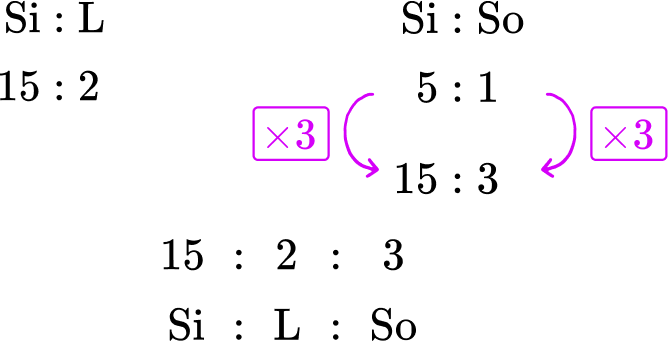
Glass is made from silica, lime and soda. The ratio of silica to lime is 15 : 2. The ratio of silica to soda is 5 : 1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15 : 2}. The ratio of silica to soda is \bf{5 : 1}. State the ratio of silica:lime:soda.

You know the two ratios

You are trying to find the ratio of all 3 components: silica, lime and soda.

Using equivalent ratios you can say that the ratio of Silica:Soda is equivalent to 15 : 3 by multiplying the ratio by 3.

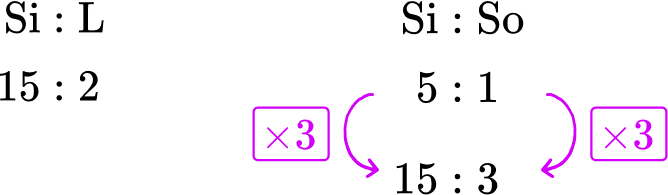
You now have the same amount of silica in both ratios and so you can now combine them to get the ratio 15 : 2 : 3.

Example 7: using bar modeling

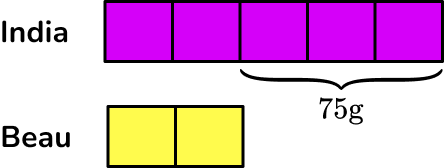
India and Beau share some popcorn in the ratio of 5 : 2. If India has 75 \, g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5 : 2} . If India has \bf{75 \, g} more popcorn than Beau, what was the original quantity?

You know that the initial ratio is 5 : 2 and that India has three more parts than Beau.

You want to find the original quantity.

Drawing a bar model of this problem, you have:

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if you can find out this value, you can then find the total quantity.

From the question, India’s share is 75 \, g more than Beau’s share so you can write this on the bar model.

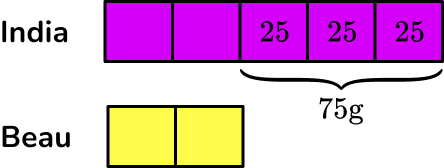
You can find the value of one share by working out 75 \div 3=25 \, g.

You can fill in each share to be 25 \, g.

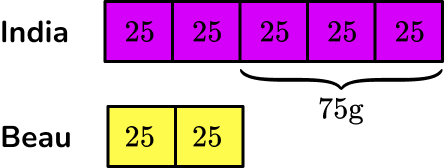
Adding up each share, you get

India=5 \times 25=125 \, g

Beau=2 \times 25=50 \, g

The total amount of popcorn was 125+50=175 \, g.

Teaching tips for ratio problem solving

• Continue to remind students that when solving ratio word problems, it’s important to identify the quantities being compared and express the ratio in its simplest form.
• Create practice problems for students using the information in your classroom. For example, ask students to find the ratio of boys to the ratio of girls using the total number of students in your classroom, then the school.
• To find more practice questions, utilize educational websites and apps instead of worksheets. Some of these may also provide tutorials for struggling students. These can also be helpful for test prep as they are more engaging for students.
• Use a variety of numbers in your ratio word problems – whole numbers, fractions, decimals, and mixed numbers – to give students a variety of practice.
• Provide students with a step-by-step process for problem solving, like the one shown above, that can be applied to every ratio word problem.

Easy mistakes to make

• Mixing units Make sure that all the units in the ratio are the same. For example, in example 6, all the units in the ratio were in milliliters. You did not mix ml and l in the ratio.
• Writing ratios in the wrong order For example, the number of dogs to cats is given as the ratio 12 : 13 but the solution is written as 13 : 12.

• Counting the number of parts in the ratio, not the total number of shares For example, the ratio 5 : 4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
• Ratios of the form \bf{1 : \textbf{n}} The assumption can be incorrectly made that n must be greater than 1, but n can be any number, including a decimal.

Related ratio lessons

• Unit rate math
• Simplifying ratios
• Ratio to fraction
• How to calculate exchange rates
• Ratio to percent
• How to write a ratio
• Dividing ratios
• How to find the unit rate
• Ratio scale
• Constant of proportionality

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3 : 8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The ratio of prime numbers to non-prime numbers from 1-200 is 45 : 155. Express this as a ratio in the form 1 : n.

You need to simplify the ratio so that the first number is 1. That means you need to divide each number in the ratio by 45.

45 \div 45=1

155\div{45}=3\cfrac{4}{9}

3. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2 : 3 and the ratio of cloud to rain was 9 : 11. State the ratio that compares sunshine:cloud:rain for the month.

3 \times S : C=6 : 9

4. The angles in a triangle are written as the ratio x : 2x : 3x. Calculate the size of each angle.

You should know that the 3 angles in a triangle always equal 180^{\circ}.

\begin{aligned} & x+2 x+3 x=180 \\\\ & 6 x=180 \\\\ & x=30^{\circ} \\\\ & 2 x=60^{\circ} \\\\ & 3 x=90^{\circ} \end{aligned}

5. A clothing company has a sale on tops, dresses and shoes. \cfrac{1}{3} of sales were for tops, \cfrac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

\cfrac{1}{3}+\cfrac{1}{5}=\cfrac{5+3}{15}=\cfrac{8}{15}

1-\cfrac{8}{15}=\cfrac{7}{15}

6. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75 \, l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

The given ratio in the word problem is 2. 75 \mathrm{~L}: 18^{\circ} \mathrm{K}

Divide 45 by 18 to see the relationship between the two temperatures.

45 \div 18=2.5

45 is 2.5 times greater than 18. So we multiply 2.75 by 2.5 to get the amount of gas.

2.75 \times 2.5=6.875 \mathrm{~l}

Ratio problem solving FAQs

A ratio is a comparison of two or more quantities. It shows how much one quantity is related to another.

A recipe calls for 2 cups of flour and 1 cup of sugar. What is the ratio of flour to sugar? (2 : 1)

In middle school ( 7 th grade and 8 th grade), students transition from understanding basic ratios to working with more complex and real-life applications of ratios and proportions. They gain a deeper understanding of how ratios relate to different mathematical concepts, making them more prepared for higher-level math topics in high school.

The next lessons are

• Converting fractions, decimals and percentages

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Problem Solving Skills: Meaning, Examples & Techniques

Table of Contents

26 January 2021

Reading Time: 2 minutes

Do your children have trouble solving their Maths homework?

Or, do they struggle to maintain friendships at school?

If your answer is ‘Yes,’ the issue might be related to your child’s problem-solving abilities. Whether your child often forgets his/her lunch at school or is lagging in his/her class, good problem-solving skills can be a major tool to help them manage their lives better.

Children need to learn to solve problems on their own. Whether it is about dealing with academic difficulties or peer issues when children are equipped with necessary problem-solving skills they gain confidence and learn to make healthy decisions for themselves. So let us look at what is problem-solving, its benefits, and how to encourage your child to inculcate problem-solving abilities

Problem-solving skills can be defined as the ability to identify a problem, determine its cause, and figure out all possible solutions to solve the problem.

• Trigonometric Problems

What is problem-solving, then? Problem-solving is the ability to use appropriate methods to tackle unexpected challenges in an organized manner. The ability to solve problems is considered a soft skill, meaning that it’s more of a personality trait than a skill you’ve learned at school, on-the-job, or through technical training. While your natural ability to tackle problems and solve them is something you were born with or began to hone early on, it doesn’t mean that you can’t work on it. This is a skill that can be cultivated and nurtured so you can become better at dealing with problems over time.

Problem Solving Skills: Meaning, Examples & Techniques are mentioned below in the Downloadable PDF. 

Benefits of learning problem-solving skills  

Promotes creative thinking and thinking outside the box.

Improves decision-making abilities.

Builds solid communication skills.

Develop the ability to learn from mistakes and avoid the repetition of mistakes.

Problem Solving as an ability is a life skill desired by everyone, as it is essential to manage our day-to-day lives. Whether you are at home, school, or work, life throws us curve balls at every single step of the way. And how do we resolve those? You guessed it right – Problem Solving.

Strengthening and nurturing problem-solving skills helps children cope with challenges and obstacles as they come. They can face and resolve a wide variety of problems efficiently and effectively without having a breakdown. Nurturing good problem-solving skills develop your child’s independence, allowing them to grow into confident, responsible adults. 

Children enjoy experimenting with a wide variety of situations as they develop their problem-solving skills through trial and error. A child’s action of sprinkling and pouring sand on their hands while playing in the ground, then finally mixing it all to eliminate the stickiness shows how fast their little minds work.

Sometimes children become frustrated when an idea doesn't work according to their expectations, they may even walk away from their project. They often become focused on one particular solution, which may or may not work.

However, they can be encouraged to try other methods of problem-solving when given support by an adult. The adult may give hints or ask questions in ways that help the kids to formulate their solutions. 

Encouraging Problem-Solving Skills in Kids

Practice problem solving through games.

Exposing kids to various riddles, mysteries, and treasure hunts, puzzles, and games not only enhances their critical thinking but is also an excellent bonding experience to create a lifetime of memories.

Create a safe environment for brainstorming

Welcome, all the ideas your child brings up to you. Children learn how to work together to solve a problem collectively when given the freedom and flexibility to come up with their solutions. This bout of encouragement instills in them the confidence to face obstacles bravely.

Invite children to expand their Learning capabilities

 Whenever children experiment with an idea or problem, they test out their solutions in different settings. They apply their teachings to new situations and effectively receive and communicate ideas. They learn the ability to think abstractly and can learn to tackle any obstacle whether it is finding solutions to a math problem or navigating social interactions.

Problem-solving is the act of finding answers and solutions to complicated problems. 

Developing problem-solving skills from an early age helps kids to navigate their life problems, whether academic or social more effectively and avoid mental and emotional turmoil.

Children learn to develop a future-oriented approach and view problems as challenges that can be easily overcome by exploring solutions. 

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular  Online Classes  for academics and skill-development, and their Mental Math App, on both  iOS  and  Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial.

Frequently Asked Questions (FAQs)

How do you teach problem-solving skills.

Model a useful problem-solving method. Problem solving can be difficult and sometimes tedious. ... 1. Teach within a specific context. ... 2. Help students understand the problem. ... 3. Take enough time. ... 4. Ask questions and make suggestions. ... 5. Link errors to misconceptions.

What makes a good problem solver?

Excellent problem solvers build networks and know how to collaborate with other people and teams. They are skilled in bringing people together and sharing knowledge and information. A key skill for great problem solvers is that they are trusted by others.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 1: Algebra foundations

Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Simple Algebra Problems – Easy Exercises with Solutions for Beginners

JUMP TO TOPIC

Understanding Algebraic Expressions

Breaking down algebra problems, solving algebraic equations, tackling algebra word problems, types of algebraic equations, algebra for different grades.

For instance, solving the equation (3x = 7) for (x) helps us understand how to isolate the variable to find its value.

I always find it fascinating how algebra serves as the foundation for more advanced topics in mathematics and science. Starting with basic problems such as ( $(x-1)^2 = [4\sqrt{(x-4)}]^2$ ) allows us to grasp key concepts and build the skills necessary for tackling more complex challenges.

So whether you’re refreshing your algebra skills or just beginning to explore this mathematical language, let’s dive into some examples and solutions to demystify the subject. Trust me, with a bit of practice, you’ll see algebra not just as a series of problems, but as a powerful tool that helps us solve everyday puzzles.

Simple Algebra Problems and Strategies

When I approach simple algebra problems, one of the first things I do is identify the variable.

The variable is like a placeholder for a number that I’m trying to find—a mystery I’m keen to solve. Typically represented by letters like ( x ) or ( y ), variables allow me to translate real-world situations into algebraic expressions and equations.

An algebraic expression is a mathematical phrase that can contain ordinary numbers, variables (like ( x ) or ( y )), and operators (like add, subtract, multiply, and divide). For example, ( 4x + 7 ) is an algebraic expression where ( x ) is the variable and the numbers ( 4 ) and ( 7 ) are terms. It’s important to manipulate these properly to maintain the equation’s balance.

Solving algebra problems often starts with simplifying expressions. Here’s a simple method to follow:

• Combine like terms : Terms that have the same variable can be combined. For instance, ( 3x + 4x = 7x ).
• Isolate the variable : Move the variable to one side of the equation. If the equation is ( 2x + 5 = 13 ), my job is to get ( x ) by itself by subtracting ( 5 ) from both sides, giving me ( 2x = 8 ).

With algebraic equations, the goal is to solve for the variable by performing the same operation on both sides. Here’s a table with an example:

Algebra word problems require translating sentences into equations. If a word problem says “I have six less than twice the number of apples than Bob,” and Bob has ( b ) apples, then I’d write the expression as ( 2b – 6 ).

Understanding these strategies helps me tackle basic algebra problems efficiently. Remember, practice makes perfect, and each problem is an opportunity to improve.

In algebra, we encounter a variety of equation types and each serves a unique role in problem-solving. Here, I’ll brief you about some typical forms.

Linear Equations : These are the simplest form, where the highest power of the variable is one. They take the general form ( ax + b = 0 ), where ( a ) and ( b ) are constants, and ( x ) is the variable. For example, ( 2x + 3 = 0 ) is a linear equation.

Polynomial Equations : Unlike for linear equations, polynomial equations can have variables raised to higher powers. The general form of a polynomial equation is ( $a_nx^n + a_{n-1}x^{n-1} + … + a_2x^2 + a_1x + a_0 = 0$ ). In this equation, ( n ) is the highest power, and ( $a_n$ ), ( $a_{n-1} $), …, ( $a_0$ ) represent the coefficients which can be any real number.

• Binomial Equations : They are a specific type of polynomial where there are exactly two terms. Like ($ x^2 – 4 $), which is also the difference of squares, a common format encountered in factoring.

To understand how equations can be solved by factoring, consider the quadratic equation ( $x^2$ – 5x + 6 = 0 ). I can factor this into ( (x-2)(x-3) = 0 ), which allows me to find the roots of the equation.

Here’s how some equations look when classified by degree:

Remember, identification and proper handling of these equations are essential in algebra as they form the basis for complex problem-solving.

In my experience with algebra, I’ve found that the journey begins as early as the 6th grade, where students get their first taste of this fascinating subject with the introduction of variables representing an unknown quantity.

I’ve created worksheets and activities aimed specifically at making this early transition engaging and educational.

6th Grade :

Moving forward, the complexity of algebraic problems increases:

7th and 8th Grades :

• Mastery of negative numbers: students practice operations like ( -3 – 4 ) or ( -5 $\times$ 2 ).
• Exploring the rules of basic arithmetic operations with negative numbers.
• Worksheets often contain numeric and literal expressions that help solidify their concepts.

Advanced topics like linear algebra are typically reserved for higher education. However, the solid foundation set in these early grades is crucial. I’ve developed materials to encourage students to understand and enjoy algebra’s logic and structure.

Remember, algebra is a tool that helps us quantify and solve problems, both numerical and abstract. My goal is to make learning these concepts, from numbers to numeric operations, as accessible as possible, while always maintaining a friendly approach to education.

I’ve walked through various simple algebra problems to help establish a foundational understanding of algebraic concepts. Through practice, you’ll find that these problems become more intuitive, allowing you to tackle more complex equations with confidence.

Remember, the key steps in solving any algebra problem include:

• Identifying variables and what they represent.
• Setting up the equation that reflects the problem statement.
• Applying algebraic rules such as the distributive property ($a(b + c) = ab + ac$), combining like terms, and inverse operations.
• Checking your solutions by substituting them back into the original equations to ensure they work.

As you continue to engage with algebra, consistently revisiting these steps will deepen your understanding and increase your proficiency. Don’t get discouraged by mistakes; they’re an important part of the learning process.

I hope that the straightforward problems I’ve presented have made algebra feel more manageable and a little less daunting. Happy solving!

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

• Prodigy Math
• Prodigy English
• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

120 Math Word Problems To Challenge Students Grades 1 to 8

Written by Marcus Guido

Hey teachers! 👋

Use Prodigy to spark a love for math in your students – including when solving word problems!

• Teaching Tools
• Subtraction
• Multiplication
• Mixed operations
• Ordering and number sense
• Comparing and sequencing
• Physical measurement
• Ratios and percentages
• Probability and data relationships

You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.

A jolt of creativity would help. But it doesn’t come.

Whether you’re a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.

This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes.

There are 120 examples in total.

The list of examples is supplemented by tips to create engaging and challenging math word problems.

120 Math word problems, categorized by skill

Addition word problems.

Best for: 1st grade, 2nd grade

1. Adding to 10: Ariel was playing basketball. 1 of her shots went in the hoop. 2 of her shots did not go in the hoop. How many shots were there in total?

2. Adding to 20: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store to get 3 more pieces of gum. How many pieces of gum does Adrianna have now?

3. Adding to 100: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store and got 70 pieces of strawberry gum and 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

4. Adding Slightly over 100: The restaurant has 175 normal chairs and 20 chairs for babies. How many chairs does the restaurant have in total?

5. Adding to 1,000: How many cookies did you sell if you sold 320 chocolate cookies and 270 vanilla cookies?

6. Adding to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In June, the hobby store sold 15,498 more trading cards than normal. In total, how many trading cards did the hobby store sell in June?

7. Adding 3 Numbers: Billy had 2 books at home. He went to the library to take out 2 more books. He then bought 1 book. How many books does Billy have now?

8. Adding 3 Numbers to and over 100: Ashley bought a big bag of candy. The bag had 102 blue candies, 100 red candies and 94 green candies. How many candies were there in total?

Subtraction word problems

Best for: 1st grade, second grade

9. Subtracting to 10: There were 3 pizzas in total at the pizza shop. A customer bought 1 pizza. How many pizzas are left?

10. Subtracting to 20: Your friend said she had 11 stickers. When you helped her clean her desk, she only had a total of 10 stickers. How many stickers are missing?

11. Subtracting to 100: Adrianna has 100 pieces of gum to share with her friends. When she went to the park, she shared 10 pieces of strawberry gum. When she left the park, Adrianna shared another 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

Practice math word problems with Prodigy Math

Join millions of teachers using Prodigy to make learning fun and differentiate instruction as they answer in-game questions, including math word problems from 1st to 8th grade!

12. Subtracting Slightly over 100: Your team scored a total of 123 points. 67 points were scored in the first half. How many were scored in the second half?

13. Subtracting to 1,000: Nathan has a big ant farm. He decided to sell some of his ants. He started with 965 ants. He sold 213. How many ants does he have now?

14. Subtracting to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In July, the hobby store sold a total of 20,777 trading cards. How many more trading cards did the hobby store sell in July compared with a normal month?

15. Subtracting 3 Numbers: Charlene had a pack of 35 pencil crayons. She gave 6 to her friend Theresa. She gave 3 to her friend Mandy. How many pencil crayons does Charlene have left?

16. Subtracting 3 Numbers to and over 100: Ashley bought a big bag of candy to share with her friends. In total, there were 296 candies. She gave 105 candies to Marissa. She also gave 86 candies to Kayla. How many candies were left?

Multiplication word problems

Best for: 2nd grade, 3rd grade

17. Multiplying 1-Digit Integers: Adrianna needs to cut a pan of brownies into pieces. She cuts 6 even columns and 3 even rows into the pan. How many brownies does she have?

18. Multiplying 2-Digit Integers: A movie theatre has 25 rows of seats with 20 seats in each row. How many seats are there in total?

19. Multiplying Integers Ending with 0: A clothing company has 4 different kinds of sweatshirts. Each year, the company makes 60,000 of each kind of sweatshirt. How many sweatshirts does the company make each year?

20. Multiplying 3 Integers: A bricklayer stacks bricks in 2 rows, with 10 bricks in each row. On top of each row, there is a stack of 6 bricks. How many bricks are there in total?

21. Multiplying 4 Integers: Cayley earns $5 an hour by delivering newspapers. She delivers newspapers 3 days each week, for 4 hours at a time. After delivering newspapers for 8 weeks, how much money will Cayley earn?

Division word problems

Best for: 3rd grade, 4th grade, 5th grade

22. Dividing 1-Digit Integers: If you have 4 pieces of candy split evenly into 2 bags, how many pieces of candy are in each bag?

23. Dividing 2-Digit Integers: If you have 80 tickets for the fair and each ride costs 5 tickets, how many rides can you go on?

24. Dividing Numbers Ending with 0: The school has $20,000 to buy new computer equipment. If each piece of equipment costs $50, how many pieces can the school buy in total?

25. Dividing 3 Integers: Melissa buys 2 packs of tennis balls for $12 in total. All together, there are 6 tennis balls. How much does 1 pack of tennis balls cost? How much does 1 tennis ball cost?

26. Interpreting Remainders: An Italian restaurant receives a shipment of 86 veal cutlets. If it takes 3 cutlets to make a dish, how many cutlets will the restaurant have left over after making as many dishes as possible?

Mixed operations word problems

27. Mixing Addition and Subtraction: There are 235 books in a library. On Monday, 123 books are taken out. On Tuesday, 56 books are brought back. How many books are there now?

28. Mixing Multiplication and Division: There is a group of 10 people who are ordering pizza. If each person gets 2 slices and each pizza has 4 slices, how many pizzas should they order?

29. Mixing Multiplication, Addition and Subtraction: Lana has 2 bags with 2 marbles in each bag. Markus has 2 bags with 3 marbles in each bag. How many more marbles does Markus have?

30. Mixing Division, Addition and Subtraction: Lana has 3 bags with the same amount of marbles in them, totaling 12 marbles. Markus has 3 bags with the same amount of marbles in them, totaling 18 marbles. How many more marbles does Markus have in each bag?

Ordering and number sense word problems

31. Counting to Preview Multiplication: There are 2 chalkboards in your classroom. If each chalkboard needs 2 pieces of chalk, how many pieces do you need in total?

32. Counting to Preview Division: There are 3 chalkboards in your classroom. Each chalkboard has 2 pieces of chalk. This means there are 6 pieces of chalk in total. If you take 1 piece of chalk away from each chalkboard, how many will there be in total?

33. Composing Numbers: What number is 6 tens and 10 ones?

34. Guessing Numbers: I have a 7 in the tens place. I have an even number in the ones place. I am lower than 74. What number am I?

35. Finding the Order: In the hockey game, Mitchell scored more points than William but fewer points than Auston. Who scored the most points? Who scored the fewest points?

Fractions word problems

Best for: 3rd grade, 4th grade, 5th grade, 6th grade

36. Finding Fractions of a Group: Julia went to 10 houses on her street for Halloween. 5 of the houses gave her a chocolate bar. What fraction of houses on Julia’s street gave her a chocolate bar?

37. Finding Unit Fractions: Heather is painting a portrait of her best friend, Lisa. To make it easier, she divides the portrait into 6 equal parts. What fraction represents each part of the portrait?

38. Adding Fractions with Like Denominators: Noah walks ⅓ of a kilometre to school each day. He also walks ⅓ of a kilometre to get home after school. How many kilometres does he walk in total?

39. Subtracting Fractions with Like Denominators: Last week, Whitney counted the number of juice boxes she had for school lunches. She had ⅗ of a case. This week, it’s down to ⅕ of a case. How much of the case did Whitney drink?

40. Adding Whole Numbers and Fractions with Like Denominators: At lunchtime, an ice cream parlor served 6 ¼ scoops of chocolate ice cream, 5 ¾ scoops of vanilla and 2 ¾ scoops of strawberry. How many scoops of ice cream did the parlor serve in total?

41. Subtracting Whole Numbers and Fractions with Like Denominators: For a party, Jaime had 5 ⅓ bottles of cola for her friends to drink. She drank ⅓ of a bottle herself. Her friends drank 3 ⅓. How many bottles of cola does Jaime have left?

42. Adding Fractions with Unlike Denominators: Kevin completed ½ of an assignment at school. When he was home that evening, he completed ⅚ of another assignment. How many assignments did Kevin complete?

43. Subtracting Fractions with Unlike Denominators: Packing school lunches for her kids, Patty used ⅞ of a package of ham. She also used ½ of a package of turkey. How much more ham than turkey did Patty use?

44. Multiplying Fractions: During gym class on Wednesday, the students ran for ¼ of a kilometre. On Thursday, they ran ½ as many kilometres as on Wednesday. How many kilometres did the students run on Thursday? Write your answer as a fraction.

45. Dividing Fractions: A clothing manufacturer uses ⅕ of a bottle of colour dye to make one pair of pants. The manufacturer used ⅘ of a bottle yesterday. How many pairs of pants did the manufacturer make?

46. Multiplying Fractions with Whole Numbers: Mark drank ⅚ of a carton of milk this week. Frank drank 7 times more milk than Mark. How many cartons of milk did Frank drink? Write your answer as a fraction, or as a whole or mixed number.

Decimals word problems

Best for: 4th grade, 5th grade

47. Adding Decimals: You have 2.6 grams of yogurt in your bowl and you add another spoonful of 1.3 grams. How much yogurt do you have in total?

48. Subtracting Decimals: Gemma had 25.75 grams of frosting to make a cake. She decided to use only 15.5 grams of the frosting. How much frosting does Gemma have left?

49. Multiplying Decimals with Whole Numbers: Marshall walks a total of 0.9 kilometres to and from school each day. After 4 days, how many kilometres will he have walked?

50. Dividing Decimals by Whole Numbers: To make the Leaning Tower of Pisa from spaghetti, Mrs. Robinson bought 2.5 kilograms of spaghetti. Her students were able to make 10 leaning towers in total. How many kilograms of spaghetti does it take to make 1 leaning tower?

51. Mixing Addition and Subtraction of Decimals: Rocco has 1.5 litres of orange soda and 2.25 litres of grape soda in his fridge. Antonio has 1.15 litres of orange soda and 0.62 litres of grape soda. How much more soda does Rocco have than Angelo?

52. Mixing Multiplication and Division of Decimals: 4 days a week, Laura practices martial arts for 1.5 hours. Considering a week is 7 days, what is her average practice time per day each week?

Comparing and sequencing word problems

Best for: Kindergarten, 1st grade, 2nd grade

53. Comparing 1-Digit Integers: You have 3 apples and your friend has 5 apples. Who has more?

54. Comparing 2-Digit Integers: You have 50 candies and your friend has 75 candies. Who has more?

55. Comparing Different Variables: There are 5 basketballs on the playground. There are 7 footballs on the playground. Are there more basketballs or footballs?

56. Sequencing 1-Digit Integers: Erik has 0 stickers. Every day he gets 1 more sticker. How many days until he gets 3 stickers?

57. Skip-Counting by Odd Numbers: Natalie began at 5. She skip-counted by fives. Could she have said the number 20?

58. Skip-Counting by Even Numbers: Natasha began at 0. She skip-counted by eights. Could she have said the number 36?

59. Sequencing 2-Digit Numbers: Each month, Jeremy adds the same number of cards to his baseball card collection. In January, he had 36. 48 in February. 60 in March. How many baseball cards will Jeremy have in April?

Time word problems

66. Converting Hours into Minutes: Jeremy helped his mom for 1 hour. For how many minutes was he helping her?

69. Adding Time: If you wake up at 7:00 a.m. and it takes you 1 hour and 30 minutes to get ready and walk to school, at what time will you get to school?

70. Subtracting Time: If a train departs at 2:00 p.m. and arrives at 4:00 p.m., how long were passengers on the train for?

71. Finding Start and End Times: Rebecca left her dad’s store to go home at twenty to seven in the evening. Forty minutes later, she was home. What time was it when she arrived home?

Money word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade, 5th grade

60. Adding Money: Thomas and Matthew are saving up money to buy a video game together. Thomas has saved $30. Matthew has saved $35. How much money have they saved up together in total?

61. Subtracting Money: Thomas has $80 saved up. He uses his money to buy a video game. The video game costs $67. How much money does he have left?

62. Multiplying Money: Tim gets $5 for delivering the paper. How much money will he have after delivering the paper 3 times?

63. Dividing Money: Robert spent $184.59 to buy 3 hockey sticks. If each hockey stick was the same price, how much did 1 cost?

64. Adding Money with Decimals: You went to the store and bought gum for $1.25 and a sucker for $0.50. How much was your total?

65. Subtracting Money with Decimals: You went to the store with $5.50. You bought gum for $1.25, a chocolate bar for $1.15 and a sucker for $0.50. How much money do you have left?

67. Applying Proportional Relationships to Money: Jakob wants to invite 20 friends to his birthday, which will cost his parents $250. If he decides to invite 15 friends instead, how much money will it cost his parents? Assume the relationship is directly proportional.

68. Applying Percentages to Money: Retta put $100.00 in a bank account that gains 20% interest annually. How much interest will be accumulated in 1 year? And if she makes no withdrawals, how much money will be in the account after 1 year?

Physical measurement word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade

72. Comparing Measurements: Cassandra’s ruler is 22 centimetres long. April’s ruler is 30 centimetres long. How many centimetres longer is April’s ruler?

73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?

74. Adding Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Micha’s dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?

75. Subtracting Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Micha’s dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?

76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?

77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?

78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?

79. Converting Volume: Shad has a lemonade stand and sold 20 cups of lemonade. Each cup was 500 millilitres. How many litres did Shad sell in total?

80. Converting Length: Stacy and Milda are comparing their heights. Stacy is 1.5 meters tall. Milda is 10 centimetres taller than Stacy. What is Milda’s height in centimetres?

81. Understanding Distance and Direction: A bus leaves the school to take students on a field trip. The bus travels 10 kilometres south, 10 kilometres west, another 5 kilometres south and 15 kilometres north. To return to the school, in which direction does the bus have to travel? How many kilometres must it travel in that direction?

Ratios and percentages word problems

Best for: 4th grade, 5th grade, 6th grade

82. Finding a Missing Number: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?

83. Finding Missing Numbers: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. The difference between the numbers is 12. What are the numbers?

84. Comparing Ratios: The school’s junior band has 10 saxophone players and 20 trumpet players. The school’s senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?

85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?

86. Determining Percent of Change: A decade ago, Oakville’s population was 67,624 people. Now, it is 190% larger. What is Oakville’s current population?

87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?

88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?

Probability and data relationships word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade

89. Understanding the Premise of Probability: John wants to know his class’s favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?

90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?

91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.

92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?

93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Maurita’s 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felice’s 4 tests: 3, 3, 3. If Maurita’s mean for the 4 tests is 1 point higher than Felice’s, what’s the score of Felice’s 4th test?

94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?

95. Writing Equations for Proportional Relationships: Lionel loves soccer, but has trouble motivating himself to practice. So, he incentivizes himself through video games. There is a proportional relationship between the amount of drills Lionel completes, in x , and for how many hours he plays video games, in y . When Lionel completes 10 drills, he plays video games for 30 minutes. Write the equation for the relationship between x and y .

Geometry word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade, 8th grade

96. Introducing Perimeter:  The theatre has 4 chairs in a row. There are 5 rows. Using rows as your unit of measurement, what is the perimeter?

97. Introducing Area: The theatre has 4 chairs in a row. There are 5 rows. How many chairs are there in total?

98. Introducing Volume: Aaron wants to know how much candy his container can hold. The container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. What is the container’s volume?

99. Understanding 2D Shapes: Kevin draws a shape with 4 equal sides. What shape did he draw?

100. Finding the Perimeter of 2D Shapes: Mitchell wrote his homework questions on a piece of square paper. Each side of the paper is 8 centimetres. What is the perimeter?

101. Determining the Area of 2D Shapes: A single trading card is 9 centimetres long by 6 centimetres wide. What is its area?

102. Understanding 3D Shapes: Martha draws a shape that has 6 square faces. What shape did she draw?

103. Determining the Surface Area of 3D Shapes: What is the surface area of a cube that has a width of 2cm, height of 2 cm and length of 2 cm?

104. Determining the Volume of 3D Shapes: Aaron’s candy container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. Bruce’s container is 25 centimetres tall, 9 centimetres long and 9 centimetres wide. Find the volume of each container. Based on volume, whose container can hold more candy?

105. Identifying Right-Angled Triangles: A triangle has the following side lengths: 3 cm, 4 cm and 5 cm. Is this triangle a right-angled triangle?

106. Identifying Equilateral Triangles: A triangle has the following side lengths: 4 cm, 4 cm and 4 cm. What kind of triangle is it?

107. Identifying Isosceles Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 5 cm. What kind of triangle is it?

108. Identifying Scalene Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 6 cm. What kind of triangle is it?

109. Finding the Perimeter of Triangles: Luigi built a tent in the shape of an equilateral triangle. The perimeter is 21 metres. What is the length of each of the tent’s sides?

110. Determining the Area of Triangles: What is the area of a triangle with a base of 2 units and a height of 3 units?

111. Applying Pythagorean Theorem: A right triangle has one non-hypotenuse side length of 3 inches and the hypotenuse measures 5 inches. What is the length of the other non-hypotenuse side?

112. Finding a Circle’s Diameter: Jasmin bought a new round backpack. Its area is 370 square centimetres. What is the round backpack’s diameter?

113. Finding a Circle's Area: Captain America’s circular shield has a diameter of 76.2 centimetres. What is the area of his shield?

114. Finding a Circle’s Radius: Skylar lives on a farm, where his dad keeps a circular corn maze. The corn maze has a diameter of 2 kilometres. What is the maze’s radius?

Variables word problems

Best for: 6th grade, 7th grade, 8th grade

115. Identifying Independent and Dependent Variables: Victoria is baking muffins for her class. The number of muffins she makes is based on how many classmates she has. For this equation, m is the number of muffins and c is the number of classmates. Which variable is independent and which variable is dependent?

116. Writing Variable Expressions for Addition: Last soccer season, Trish scored g goals. Alexa scored 4 more goals than Trish. Write an expression that shows how many goals Alexa scored.

117. Writing Variable Expressions for Subtraction: Elizabeth eats a healthy, balanced breakfast b times a week. Madison sometimes skips breakfast. In total, Madison eats 3 fewer breakfasts a week than Elizabeth. Write an expression that shows how many times a week Madison eats breakfast.

118. Writing Variable Expressions for Multiplication: Last hockey season, Jack scored g goals. Patrik scored twice as many goals than Jack. Write an expression that shows how many goals Patrik scored.

119. Writing Variable Expressions for Division: Amanda has c chocolate bars. She wants to distribute the chocolate bars evenly among 3 friends. Write an expression that shows how many chocolate bars 1 of her friends will receive.

120. Solving Two-Variable Equations: This equation shows how the amount Lucas earns from his after-school job depends on how many hours he works: e = 12h . The variable h represents how many hours he works. The variable e represents how much money he earns. How much money will Lucas earn after working for 6 hours?

How to easily make your own math word problems & word problems worksheets

Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:

• Link to Student Interests:  By framing your word problems with student interests, you’ll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
• Make Questions Topical:  Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
• Include Student Names:  Naming a question’s characters after your students is an easy way make subject matter relatable, helping them work through the problem.
• Be Explicit:  Repeating keywords distills the question, helping students focus on the core problem.
• Test Reading Comprehension:  Flowery word choice and long sentences can hide a question’s key elements. Instead, use concise phrasing and grade-level vocabulary.
• Focus on Similar Interests:  Framing too many questions with related interests -- such as football and basketball -- can alienate or disengage some students.
• Feature Red Herrings:  Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.

A key to differentiated instruction , word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.

Final thoughts about math word problems

You’ll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, they’ll be more relevant to -- and engaging for -- your students.

Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.

The result?

A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.

• Spencer Greenberg
• 14 min read

Problem-Solving Techniques That Work For All Types of Challenges

Essay by Spencer Greenberg, Clearer Thinking founder

A lot of people don’t realize that there are general purpose problem solving techniques that cut across domains. They can help you deal with thorny challenges in work, your personal life, startups, or even if you’re trying to prove a new theorem in math.

Below are the 26 general purpose problem solving techniques that I like best, along with a one-word name I picked for each, and hypothetical examples to illustrate what sort of strategy I’m referring to.

Consider opening up this list whenever you’re stuck solving a challenging problem. It’s likely that one or more of these techniques can help!

1. Clarifying

Try to define the problem you are facing as precisely as you can, maybe by writing down a detailed description of exactly what the problem is and what constraints exist for a solution, or by describing it in detail to another person. This may lead to you realizing the problem is not quite what you had thought, or that it has a more obvious solution than you thought.

Life Example

“I thought that I needed to find a new job, but when I thought really carefully about what I don’t like about my current job, I realized that I could likely fix those things by talking to my boss or even, potentially, just by thinking about them differently.”

Startup Example

“we thought we had a problem with users not wanting to sign up for the product, but when we carefully investigated what the problem really was, we discovered it was actually more of a problem of users wanting the product but then growing frustrated because of bad interface design.”

2. Subdividing

Break the problem down into smaller problems in such a way that if you solve each of the small problems, you will have solved the entire problem. Once a problem is subdivided it can also sometimes be parallelized (e.g., by involving different people to work on the different components).

“My goal is to get company Z to become a partner with my company, and that seems hard, so let me break that goal into the steps of (a) listing the ways that company Z would benefit from becoming a partner with us, (b) finding an employee at company Z who would be responsive to hearing about these benefits, and (c) tracking down someone who can introduce me to that employee.”

Math Example

“I want to prove that a certain property applies to all functions of a specific type, so I start by (a) showing that every function of that type can be written as a sum of a more specific type of function, then I show that (b) the property applies to each function of the more specific type, and finally I show that (c) if the property applies to each function in a set of functions then it applies to arbitrary sums of those functions as well.”

3. Simplifying

Think of the simplest variation of the problem that you expect you can solve that shares important features in common with your problem, and see if solving this simpler problem gives you ideas for how to solve the more difficult version.

“I don’t know how to hire a CTO, but I do know how to hire a software engineer because I’ve done it many times, and good CTOs will often themselves be good software engineers, so how can I tweak my software engineer hiring to make it appropriate for hiring a CTO?”

“I don’t know how to calculate this integral as it is, but if I remove one of the free parameters, I actually do know how to calculate it, and maybe doing that calculation will give me insight into the solution of the more complex integral.”

4. Crowd-sourcing 

Use suggestions from multiple people to gain insight into how to solve the problem, for instance by posting on Facebook or Twitter requesting people’s help, or by posting to a Q&A site like Quora, or by sending emails to 10 people you know explaining the problem and requesting assistance.

Business Example

“Do you have experience outsourcing manufacturing to China? If so, I’d appreciate hearing your thoughts about how to approach choosing a vendor.”

Health Example

“I have trouble getting myself to stick to doing exercise daily. If you also used to have trouble getting yourself to exercise but don’t anymore, I’d love to know what worked to make it easier for you.”

5. Splintering

If the problem you are trying to solve has special cases that a solution to the general problem would also apply to, consider just one or two of these special cases as examples and solve the problem just for those cases first. Then see if a solution to one of those special cases helps you solve the problem in general.

“I want to figure out how to improve employee retention in general, let me examine how I could have improved retention in the case of the last three people that quit.”

“I want to figure out how to convince a large number of people to become customers, let me first figure out how to convince just Bill and John to become customers since they seem like the sort of customer I want to attract, and see what general lessons I learn from doing that.”

Read the books or textbooks that seem most related to the topic, and see whether they provide a solution to the problem, or teach you enough related information that you can now solve it yourself.

Economics Example

“Economists probably have already figured out reasonable ways to estimate demand elasticity, let’s see what an econometrics textbook says rather than trying to invent a technique from scratch.”

Mental Health Example

“I’ve been feeling depressed for a long time, maybe I should read some well-liked books about depression.”

7. Searching

Think of a similar problem that you think practitioners, bloggers or academics might have already solved and search online (e.g., via google, Q&A sites, or google scholar academic paper search) to see if anyone has done a write-up about how they solved it.

Advertising Example

“I’m having trouble figuring out the right advertising keywords to bid on for my specific product, I bet someone has a blog post describing how to approach choosing keywords for other related products.”

Machine Learning Example

“I can’t get this neural network to train properly in my specific case, I wonder if someone has written a tutorial about how to apply neural networks to related problems.”

8. Unconstraining

List all the constraints of the problem, then temporarily ignore one or more of the constraints that make the problem especially hard, and try to solve it without those constraints. If you can, then see if you can modify that unconstrained solution until it becomes a solution for the fully constrained problem.

“I need to hire someone who can do work at the intersection of machine learning and cryptography, let me drop the constraint of having cryptography experience and recruit machine learning people, then pick from among them a person that seems both generally capable and well positioned to learn the necessary cryptography.”

Computer Science Example

“I need to implement a certain algorithm, and it needs to be efficient, but that seems very difficult, so let me first figure out how to implement an inefficient version of the algorithm (i.e., drop the efficiency constraint), then at the end I will try to figure out how to optimize that algorithm for efficiency.”

9. Distracting

Fill your mind with everything you know about the problem, including facts, constraints, challenges, considerations, etc. and then stop thinking about the problem, and go and do a relaxing activity that requires little focus, such as walking, swimming, cooking, napping or taking a bath to see if new ideas or potential solutions pop into your mind unexpectedly as your subconscious continues to work on the problem without your attention.

“For three days, I’ve been trying to solve this problem at work, but the solution only came to me when I was strolling in the woods and not even thinking about it.”

Example from mathematician Henri Poincaré

“The incidents of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go someplace or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuchsian functions were identical with those of non-Euclidean geometry.”

10. Reexamining

Write down all the assumptions you’ve been making about the problem or about what a solution should I look like (yes – make an actual list). Then start challenging them one by one to see if they are actually needed or whether some may be unnecessary or mistaken.

Psychology Example

“We were assuming in our lab experiments that when people get angry they have some underlying reason behind it, but there may be some anger that is better modeled as a chemical fluctuation that is only loosely related to what happens in the lab, such as when people are quick to anger because they are hungry.”

“I need to construct a function that has this strange property, and so far I’ve assumed that the function must be smooth, but if it doesn’t actually need to be then perhaps I can construct just such a function out of simple linear pieces that are glued together.”

11. Reframing

Try to see the problem differently. For instance, by flipping the default, analyzing the inverse of the problem instead, thinking about how you would achieve the opposite of what you want, or shifting to an opposing perspective.

If we were building this company over again completely from scratch, what would we do differently in the design of our product, and can we pivot the product in that direction right now?”

“Should move to New York to take a job that pays $20,000 more per year? Well, if I already lived in New York, the decision to stay there rather than taking a $20,000 pay cut to move here would be an easy one. So maybe I’m overly focused on the current default of not being in New York and the short term unpleasantness of relocating.”

Marketing Example

“If I were one of our typical potential customers, what would I do to try to find a product like ours?”

12. Brainstorming

Set a timer for at least 5 minutes, and generate as many plausible solutions or ideas that you can without worrying about quality at all. Evaluate the ideas only at the end after the timer goes off.

“I’m going to set a timer for 5 minutes and come up with at least three new ways I could go about looking for a co-founder.”

“I’m going to set a timer for 20 minutes and come up with at least five possible explanations for why I’ve been feeling so anxious lately.”

13. Experting

Find an expert (or someone highly knowledgeable) in the topic area and ask their opinion about the best way to solve the problem.

“Why do you think most attempts at creating digital medical records failed, and what would someone have to do differently to have a reasonable chance at success?”

“What sort of optimization algorithm would be most efficient for minimizing the objective functions of this type?”

14. Eggheading

Ask the smartest person you know how they would solve the problem. Be sure to send an email in advance, describing the details so that this person has time to deeply consider the problem before you discuss it.

“Given the information I sent you about our competitors and the interviews we’ve done with potential customers, in which direction would you pivot our product if you were me (and why)?”

Research Example

“Given the information I sent you about our goals and the fact that our previous research attempts have gotten nowhere, how would you approach researching this topic to find the answer we need?”

15. Guessing

Start with a guess for what the solution could be, now check if it actually works and if not, start tweaking that guess to see if you can morph it into something that could work.

“I don’t know what price to use for the product we’re selling, so let me start with an initial guess and then begin trying to sell the thing, and tweak the price down if it seems to be a sticking point for customers, and tweak the price up if the customers don’t seem to pay much attention to the price.”

“My off the cuff intuition says that this differential equation might have a solution of the form x^a * e^(b x)for some a or b, let me plug it into the equation to see if indeed it satisfies the equation for any choice of a and b, and if not, let me see if I can tweak it to make something similar work.”

“I don’t know what the most effective diet for me would be, so I’ll just use my intuition to ban from my diet some foods that seem both unhealthy and addictive, and see if that helps.”

16. Comparing

Think of similar domains you already understand or similar problems you have already solved in the past, and see whether your knowledge of those domains or solutions to those similar problems may work as a complete or partial solution here.

“I don’t know how to find someone to fix things in my apartment, but I have found a good house cleaner before by asking a few friends who they use, so maybe I can simply use the same approach for finding a person to fix things.”

“This equation I’m trying to simplify reminds me of work I’m familiar with related to Kullback-Leibler divergence, I wonder if results from information theory could be applied in this case.”

17. Outsourcing

Consider whether you can hire someone to solve this problem, instead of figuring out how to solve it yourself.

“I don’t really understand how to get media attention for my company, so let me hire a public relations firm and let them handle the process.”

“I have no fashion sense, but I’d like to look better. Maybe I should hire someone fashionable who works in apparel to go shopping with me and help me choose what I should wear.”

18. Experimenting

Rapidly develop possible solutions and test them out (in sequence, or in parallel) by applying cheap and fast experiments. Discard those that don’t work, or iterate on them to improve them based on what you learn from the experiments.

“We don’t know if people will like a product like the one we have in mind, but we can put together a functioning prototype quickly, show five people that seem like they could be potential users, and iterate or create an entirely new design based on how they respond.”

“I don’t know if cutting out sugar will help improve my energy levels, but I can try it for two weeks and see if I notice any differences.”

19. Generalizing

Consider the more general case of the specific problem you are trying to solve, and then work on solving the general version instead. Paradoxically, it is sometimes easier to make progress on the general case rather than a specific one because it increases your focus on the structure of the problem rather than unimportant details.

“I want to figure out how to get this particular key employee more motivated to do good work, let me construct a model of what makes employees motivated to do good work in general, then I’ll apply it to this case.”

“I want to solve this specific differential equation, but it’s clearly a special case of a more general class of differential equations, let me study the general class and see what I can learn about them first and then apply what I learn to the specific case.”

20. Approximating

Consider whether a partial or approximate solution would be acceptable and, if so, aim for that instead of a full or exact solution.

“Our goal is to figure out which truck to send out for which delivery, which theoretically depends on many factors such as current location, traffic conditions, truck capacity, fuel efficiency, how many hours the driver has been on duty, the number of people manning each truck, the hourly rate we pay each driver, etc. etc. Maybe if we focus on just the three variables that we think are most important, we can find a good enough solution.”

“Finding a solution to this equation seems difficult, but if I approximate one of the terms linearly it becomes much easier, and maybe for the range of values we’re interested in, that’s close enough to an exact solution!”

21. Annihilating

Try to prove that the problem you are attempting to solve is actually impossible. If you succeed, you may save yourself a lot of time working on something impossible. Furthermore, in attempting to prove that the problem is impossible, you may gain insight into what makes it actually possible to solve, or if it turns out to truly be impossible, figure out how you could tweak the problem to make it solvable.

“I’m struggling to find a design for a theoretical voting system that has properties X, Y, and Z, let me see if I can instead prove that no such voting system with these three properties could possibly exist.”

“My goal has been to prove that this property always applies to this class of functions, let me see if I can generate a counterexample to prove that this goal is actually impossible.”

Physics Example

“I was trying to design a physical system with certain properties, but I now realize that if such a system could be realized, then it would allow for perpetual motion, and therefore it is impossible to build the sort of system I had in mind.”

22. Modeling

Try to build an explicit model of the situation, including what elements there are and how they related to each other. For instance, try drawing a diagram or flow chart that encapsulates your understanding of all the important information that relates to the problem.

“I’ve noticed that there are certain situations that cause me to freak out that would not bother other people. So what are the common elements when this happens, and how do they seem to relate to each other and to the way I end up feeling? Let me see if I can draw a diagram of this on paper.”

“What are all the different groups (e.g., providers, payers, patients) involved in the healthcare system, and if we diagram how they interact with each other, will that give us ideas for how we can sell our healthcare product?”

23. Brute forcing

One-by-one, consider every possible solution to the problem until you’ve found a good one or exhausted them all.

Startup example

“We’re not sure the order that these four parts of the user registration process should go in, so let’s make a list of all 24 possible orderings, and examine them one by one to see which makes the most sense.”

“It’s not clear how to pick which of these machine learning methods to use on this problem, but since we have lots of data, we can just try each of the algorithms and see which makes the most accurate predictions on data we’ve held to the side for testing.”

24. Refocusing

Forget about trying to solve the problem, and instead consider why you are trying to solve it. Then consider if there is a different problem you can work on that is aimed at producing the same sort of value in a different way.

Startup Example 1

“Maybe instead of trying increasingly hard to figure out how to get this type of consumer to buy, we need to switch our focus to the problem of how to sell to businesses, since what we actually care about is selling it, not selling it to one particular group.”

Startup Example 2

“I’ve been banging my head against the wall trying to implement this extremely complex feature, but there are lots of features that users would find just as valuable that are much easier to implement, maybe I should focus on those instead.”

25. Sidestepping

Consider whether you really want to spend more time trying to solve this problem and whether you can avoid the problem by instead working on totally different problems that you also care about.

“We’ve tried selling our solution to replace Excel for 12 months without much success, maybe we should go back to the drawing board and consider designing a totally new product. Our assumptions about customer needs seem to simply have been wrong.”

“I’ve spent six months on this math problem with little progress, but there are two other math problems I’m equally excited about, so maybe I should spend some time investigating whether one of those may be more tractable.”

26. Aggregating

Consider whether multiple problems you’re now experiencing might, in fact, be caused by the same source of difficulty, rather than being independent problems.

“I seem to be having conflict with a few different friends right now – could it be that I’m doing something without realizing it that is increasing my chance of conflict with all of them?”

“Three employees have quit in the last month. Perhaps the primary problem isn’t really about convincing this one important employee to stay, which is how I was framing it, but rather, about identifying why people keep leaving more generally.”

Recent Posts

We're launching a scientific test of astrology, and anyone can participate!

Remembering Daniel Kahneman: 7 theories that can help you understand how you think

Test how well you understand human psychology with our new quiz

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Sample Problems and Solutions
• Kinematic Equations Introduction
• Solving Problems with Kinematic Equations
• Kinematic Equations and Free Fall
• Kinematic Equations and Kinematic Graphs

Check Your Understanding

Answer: d = 1720 m

Answer: a = 8.10 m/s/s

Answers: d = 33.1 m and v f = 25.5 m/s

Answers: a = 11.2 m/s/s and d = 79.8 m

Answer: t = 1.29 s

Answers: a = 243 m/s/s

Answer: a = 0.712 m/s/s

Answer: d = 704 m

Answer: d = 28.6 m

Answer: v i = 7.17 m/s

Answer: v i = 5.03 m/s and hang time = 1.03 s (except for in sports commericals)

Answer: a = 1.62*10 5 m/s/s

Answer: d = 48.0 m

Answer: t = 8.69 s

Answer: a = -1.08*10^6 m/s/s

Answer: d = -57.0 m (57.0 meters deep) 

Answer: v i = 47.6 m/s

Answer: a = 2.86 m/s/s and t = 30. 8 s

Answer: a = 15.8 m/s/s

Answer: v i = 94.4 mi/hr

Solutions to Above Problems

d = (0 m/s)*(32.8 s)+ 0.5*(3.20 m/s 2 )*(32.8 s) 2

Return to Problem 1

110 m = (0 m/s)*(5.21 s)+ 0.5*(a)*(5.21 s) 2

110 m = (13.57 s 2 )*a

a = (110 m)/(13.57 s 2 )

a = 8.10 m/ s 2

Return to Problem 2

d = (0 m/s)*(2.60 s)+ 0.5*(-9.8 m/s 2 )*(2.60 s) 2

d = -33.1 m (- indicates direction)

v f = v i + a*t

v f = 0 + (-9.8 m/s 2 )*(2.60 s)

v f = -25.5 m/s (- indicates direction)

Return to Problem 3

a = (46.1 m/s - 18.5 m/s)/(2.47 s)

a = 11.2 m/s 2

d = v i *t + 0.5*a*t 2

d = (18.5 m/s)*(2.47 s)+ 0.5*(11.2 m/s 2 )*(2.47 s) 2

d = 45.7 m + 34.1 m

(Note: the d can also be calculated using the equation v f 2 = v i 2 + 2*a*d)

Return to Problem 4

-1.40 m = (0 m/s)*(t)+ 0.5*(-1.67 m/s 2 )*(t) 2

-1.40 m = 0+ (-0.835 m/s 2 )*(t) 2

(-1.40 m)/(-0.835 m/s 2 ) = t 2

1.68 s 2 = t 2

Return to Problem 5

a = (444 m/s - 0 m/s)/(1.83 s)

a = 243 m/s 2

d = (0 m/s)*(1.83 s)+ 0.5*(243 m/s 2 )*(1.83 s) 2

d = 0 m + 406 m

Return to Problem 6

(7.10 m/s) 2 = (0 m/s) 2 + 2*(a)*(35.4 m)

50.4 m 2 /s 2 = (0 m/s) 2 + (70.8 m)*a

(50.4 m 2 /s 2 )/(70.8 m) = a

a = 0.712 m/s 2

Return to Problem 7

(65 m/s) 2 = (0 m/s) 2 + 2*(3 m/s 2 )*d

4225 m 2 /s 2 = (0 m/s) 2 + (6 m/s 2 )*d

(4225 m 2 /s 2 )/(6 m/s 2 ) = d

Return to Problem 8

d = (22.4 m/s + 0 m/s)/2 *2.55 s

d = (11.2 m/s)*2.55 s

Return to Problem 9

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(2.62 m)

0 m 2 /s 2 = v i 2 - 51.35 m 2 /s 2

51.35 m 2 /s 2 = v i 2

v i = 7.17 m/s

Return to Problem 10

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(1.29 m)

0 m 2 /s 2 = v i 2 - 25.28 m 2 /s 2

25.28 m 2 /s 2 = v i 2

v i = 5.03 m/s

To find hang time, find the time to the peak and then double it.

0 m/s = 5.03 m/s + (-9.8 m/s 2 )*t up

-5.03 m/s = (-9.8 m/s 2 )*t up

(-5.03 m/s)/(-9.8 m/s 2 ) = t up

t up = 0.513 s

hang time = 1.03 s

Return to Problem 11

(521 m/s) 2 = (0 m/s) 2 + 2*(a)*(0.840 m)

271441 m 2 /s 2 = (0 m/s) 2 + (1.68 m)*a

(271441 m 2 /s 2 )/(1.68 m) = a

a = 1.62*10 5 m /s 2

Return to Problem 12

• (NOTE: the time required to move to the peak of the trajectory is one-half the total hang time - 3.125 s.)

First use:  v f  = v i  + a*t

0 m/s = v i  + (-9.8  m/s 2 )*(3.13 s)

0 m/s = v i  - 30.7 m/s

v i  = 30.7 m/s  (30.674 m/s)

Now use:  v f 2  = v i 2  + 2*a*d

(0 m/s) 2  = (30.7 m/s) 2  + 2*(-9.8  m/s 2 )*(d)

0 m 2 /s 2  = (940 m 2 /s 2 ) + (-19.6  m/s 2 )*d

-940  m 2 /s 2  = (-19.6  m/s 2 )*d

(-940  m 2 /s 2 )/(-19.6  m/s 2 ) = d

Return to Problem 13

-370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s 2 )*(t) 2

-370 m = 0+ (-4.9 m/s 2 )*(t) 2

(-370 m)/(-4.9 m/s 2 ) = t 2

75.5 s 2 = t 2

Return to Problem 14

(0 m/s) 2 = (367 m/s) 2 + 2*(a)*(0.0621 m)

0 m 2 /s 2 = (134689 m 2 /s 2 ) + (0.1242 m)*a

-134689 m 2 /s 2 = (0.1242 m)*a

(-134689 m 2 /s 2 )/(0.1242 m) = a

a = -1.08*10 6 m /s 2

(The - sign indicates that the bullet slowed down.)

Return to Problem 15

d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s 2 )*(3.41 s) 2

d = 0 m+ 0.5*(-9.8 m/s 2 )*(11.63 s 2 )

d = -57.0 m

(NOTE: the - sign indicates direction)

Return to Problem 16

(0 m/s) 2 = v i 2 + 2*(- 3.90 m/s 2 )*(290 m)

0 m 2 /s 2 = v i 2 - 2262 m 2 /s 2

2262 m 2 /s 2 = v i 2

v i = 47.6 m /s

Return to Problem 17

( 88.3 m/s) 2 = (0 m/s) 2 + 2*(a)*(1365 m)

7797 m 2 /s 2 = (0 m 2 /s 2 ) + (2730 m)*a

7797 m 2 /s 2 = (2730 m)*a

(7797 m 2 /s 2 )/(2730 m) = a

a = 2.86 m/s 2

88.3 m/s = 0 m/s + (2.86 m/s 2 )*t

(88.3 m/s)/(2.86 m/s 2 ) = t

t = 30. 8 s

Return to Problem 18

( 112 m/s) 2 = (0 m/s) 2 + 2*(a)*(398 m)

12544 m 2 /s 2 = 0 m 2 /s 2 + (796 m)*a

12544 m 2 /s 2 = (796 m)*a

(12544 m 2 /s 2 )/(796 m) = a

a = 15.8 m/s 2

Return to Problem 19

v f 2 = v i 2 + 2*a*d

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(91.5 m)

0 m 2 /s 2 = v i 2 - 1793 m 2 /s 2

1793 m 2 /s 2 = v i 2

v i = 42.3 m/s

Now convert from m/s to mi/hr:

v i = 42.3 m/s * (2.23 mi/hr)/(1 m/s)

v i = 94.4 mi/hr

Return to Problem 20

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

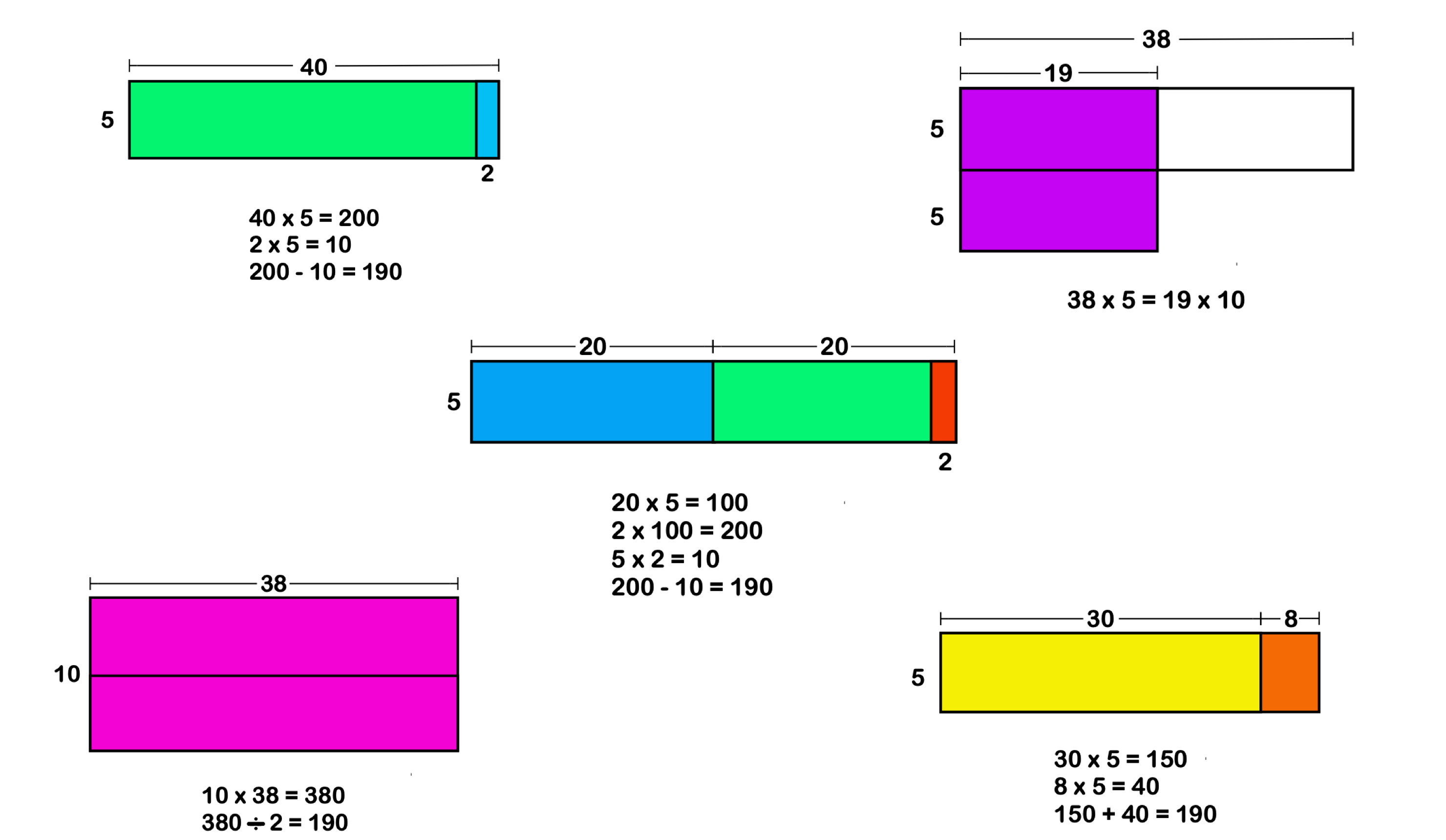
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Game Central

Similar problems from web search.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Problem Solving and Estimating

• Last updated
• Save as PDF
• Page ID 34173

• David Lippman
• Pierce College via The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Finally, we will bring together the mathematical tools we’ve reviewed, and use them to approach more complex problems. In many problems, it is tempting to take the given information, plug it into whatever formulas you have handy, and hope that the result is what you were supposed to find. Chances are, this approach has served you well in other math classes.

This approach does not work well with real life problems. Instead, problem solving is best approached by first starting at the end: identifying exactly what you are looking for. From there, you then work backwards, asking “what information and procedures will I need to find this?” Very few interesting questions can be answered in one mathematical step; often times you will need to chain together a solution pathway, a series of steps that will allow you to answer the question.

Problem Solving Process

• Identify the question you’re trying to answer.
• Work backwards, identifying the information you will need and the relationships you will use to answer that question.
• Continue working backwards, creating a solution pathway.
• If you are missing necessary information, look it up or estimate it. If you have unnecessary information, ignore it.
• Solve the problem, following your solution pathway.

In most problems we work, we will be approximating a solution, because we will not have perfect information. We will begin with a few examples where we will be able to approximate the solution using basic knowledge from our lives.

How many times does your heart beat in a year?

This question is asking for the rate of heart beats per year. Since a year is a long time to measure heart beats for, if we knew the rate of heart beats per minute, we could scale that quantity up to a year. So the information we need to answer this question is heart beats per minute. This is something you can easily measure by counting your pulse while watching a clock for a minute.

Suppose you count 80 beats in a minute. To convert this beats per year:

\(\frac{80 \text { beats }}{1 \text { minute }} \cdot \frac{60 \text { minutes }}{1 \text { hour }} \cdot \frac{24 \text { hours }}{1 \text { day }} \cdot \frac{365 \text { days }}{1 \text { year }}=42,048,000\) beats per year

How thick is a single sheet of paper? How much does it weigh?

While you might have a sheet of paper handy, trying to measure it would be tricky. Instead we might imagine a stack of paper, and then scale the thickness and weight to a single sheet. If you’ve ever bought paper for a printer or copier, you probably bought a ream, which contains 500 sheets. We could estimate that a ream of paper is about 2 inches thick and weighs about 5 pounds. Scaling these down,

\(\frac{2 \text { inches }}{\text { ream }} \cdot \frac{1 \text { ream }}{500 \text { pages }}=0.004\) inches per sheet

\(\frac{5 \text { pounds }}{\text { ream }} \cdot \frac{1 \text { ream }}{500 \text { pages }}=0.01\) pounds per sheet, or 0.16 ounces per sheet.

A recipe for zucchini muffins states that it yields 12 muffins, with 250 calories per muffin. You instead decide to make mini-muffins, and the recipe yields 20 muffins. If you eat 4, how many calories will you consume?

There are several possible solution pathways to answer this question. We will explore one.

To answer the question of how many calories 4 mini-muffins will contain, we would want to know the number of calories in each mini-muffin. To find the calories in each mini-muffin, we could first find the total calories for the entire recipe, then divide it by the number of mini-muffins produced. To find the total calories for the recipe, we could multiply the calories per standard muffin by the number per muffin. Notice that this produces a multi-step solution pathway. It is often easier to solve a problem in small steps, rather than trying to find a way to jump directly from the given information to the solution.

We can now execute our plan:

\(12 \text{muffins} $\cdot \frac{250 \text { calories }}{\text { muffin }}=3000$\) calories for the whole recipe

\(\frac{3000 \text { calories }}{20 \text { mini }-\text { muffins }}\) gives 150 calories per mini-muffin

\(4\text{ mini muffins } \cdot \frac{150 \text { calories }}{\text { mini - muffin }}\) totals 600 calories consumed.

You need to replace the boards on your deck. About how much will the materials cost?

There are two approaches we could take to this problem: 1) estimate the number of boards we will need and find the cost per board, or 2) estimate the area of the deck and find the approximate cost per square foot for deck boards. We will take the latter approach.

For this solution pathway, we will be able to answer the question if we know the cost per square foot for decking boards and the square footage of the deck. To find the cost per square foot for decking boards, we could compute the area of a single board, and divide it into the cost for that board. We can compute the square footage of the deck using geometric formulas. So first we need information: the dimensions of the deck, and the cost and dimensions of a single deck board.

Suppose that measuring the deck, it is rectangular, measuring 16 ft by 24 ft, for a total area of \(384 \mathrm{ft}^{2}\).

From a visit to the local home store, you find that an 8 foot by 4 inch cedar deck board costs about $7.50. The area of this board, doing the necessary conversion from inches to feet, is:

\(8 \text { feet } \cdot 4 \text { inches } \cdot \frac{1 \text { foot }}{12 \text { inches }}=2.667 \mathrm{ft}^{2}\). The cost per square foot is then

\(\frac{\$ 7.50}{2.667 \mathrm{ft}^{2}}=\$ 2.8125 \text { per } \mathrm{ft}^{2}\).

This will allow us to estimate the material cost for the whole \(384 \mathrm{ft}^{2}\) deck

\(\$ 384 \mathrm{ft}^{2} \cdot \frac{\$ 2.8125}{\mathrm{ft}^{2}}=\$ 1080\) total cost.

Of course, this cost estimate assumes that there is no waste, which is rarely the case. It is common to add at least 10% to the cost estimate to account for waste.

Is it worth buying a Hyundai Sonata hybrid instead the regular Hyundai Sonata?

To make this decision, we must first decide what our basis for comparison will be. For the purposes of this example, we’ll focus on fuel and purchase costs, but environmental impacts and maintenance costs are other factors a buyer might consider.

It might be interesting to compare the cost of gas to run both cars for a year. To determine this, we will need to know the miles per gallon both cars get, as well as the number of miles we expect to drive in a year. From that information, we can find the number of gallons required from a year. Using the price of gas per gallon, we can find the running cost.

From Hyundai’s website, the 2013 Sonata will get 24 miles per gallon (mpg) in the city, and 35 mpg on the highway. The hybrid will get 35 mpg in the city, and 40 mpg on the highway.

An average driver drives about 12,000 miles a year. Suppose that you expect to drive about 75% of that in the city, so 9,000 city miles a year, and 3,000 highway miles a year.

We can then find the number of gallons each car would require for the year.

\(9000\text{ city miles } \cdot \frac{1 \text { gallon }}{24 \text { city miles }}+3000\text{ hightway miles}. \frac{1 \text { gallon }}{35 \text { highway miles }}=460.7\text{ gallons}\)

\(9000\text{ city miles }\cdot \frac{1 \text { gallon }}{35 \text { city miles }}+3000\text{ hightway miles}. \frac{1 \text { gallon }}{40 \text { highway miles }}=332.1\text{ gallons}\)

If gas in your area averages about $3.50 per gallon, we can use that to find the running cost:

Sonata: \(460.7 \text { gallons } \cdot \frac{\$ 3.50}{\text { gallon }}=\$ 1612.45\)

Hybrid: \(\text { 332.1 gallons } \cdot \frac{\$ 3.50}{\text { gallon }}=\$ 1162.35\)

The hybrid will save $450.10 a year. The gas costs for the hybrid are about \(\frac{\$ 450.10}{\$ 1612.45} = 0.279 = 27.9\%\) lower than the costs for the standard Sonata.

While both the absolute and relative comparisons are useful here, they still make it hard to answer the original question, since “is it worth it” implies there is some tradeoff for the gas savings. Indeed, the hybrid Sonata costs about $25,850, compared to the base model for the regular Sonata, at $20,895.

To better answer the “is it worth it” question, we might explore how long it will take the gas savings to make up for the additional initial cost. The hybrid costs $4965 more. With gas savings of $451.10 a year, it will take about 11 years for the gas savings to make up for the higher initial costs.

We can conclude that if you expect to own the car 11 years, the hybrid is indeed worth it. If you plan to own the car for less than 11 years, it may still be worth it, since the resale value of the hybrid may be higher, or for other non-monetary reasons. This is a case where math can help guide your decision, but it can’t make it for you.

Try it Now 6

If traveling from Seattle, WA to Spokane WA for a three-day conference, does it make more sense to drive or fly?

There is not enough information provided to answer the question, so we will have to make some assumptions, and look up some values.

Assumptions:

a) We own a car. Suppose it gets 24 miles to the gallon. We will only consider gas cost.

b) We will not need to rent a car in Spokane, but will need to get a taxi from the airport to the conference hotel downtown and back.

c) We can get someone to drop us off at the airport, so we don’t need to consider airport parking.

d) We will not consider whether we will lose money by having to take time off work to drive.

Values looked up (your values may be different)

a) Flight cost: \(\$184\)

b) Taxi cost: \(\$25\) each way (estimate, according to hotel website)

c) Driving distance: \(280\) miles each way

d) Gas cost: \(\$3.79\) a gallon

Cost for flying: \(\$184\text{ flight cost }+ \$50\text{ in taxi fares }= \$234\).

Cost for driving: \(560\) miles round trip will require 23.3 gallons of gas, costing \(\$88.31\).

Based on these assumptions, driving is cheaper. However, our assumption that we only include gas cost may not be a good one. Tax law allows you deduct \(\$0.55\) (in 2012) for each mile driven, a value that accounts for gas as well as a portion of the car cost, insurance, maintenance, etc. Based on this number, the cost of driving would be \(\$319\).

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center