steps in solving problems involving rational functions

Chapter 5 Polynomial and Rational Functions

5.6 Rational Functions

Learning objectives.

In this section, you will:

• Use arrow notation.
• Solve applied problems involving rational functions.
• Find the domains of rational functions.
• Identify vertical asymptotes.
• Identify horizontal asymptotes.
• Graph rational functions.

Suppose we know that the cost of making a product is dependent on the number of items,[latex]\,x,\,[/latex]produced. This is given by the equation [latex]\,C\left(x\right)=15,000x-0.1{x}^{2}+1000.\,[/latex]If we want to know the average cost for producing[latex]\,x\,[/latex]items, we would divide the cost function by the number of items,[latex]\,x.[/latex]

The average cost function, which yields the average cost per item for[latex]\,x\,[/latex]items produced, is

Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.

In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.

Using Arrow Notation

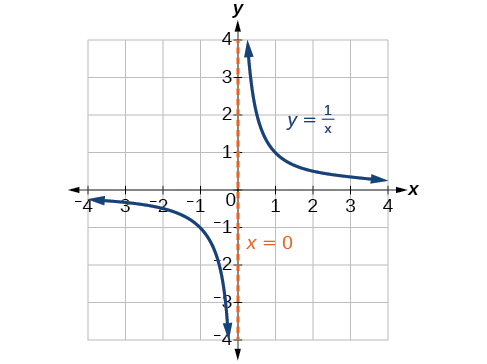
We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Examine these graphs, as shown in Figure 1, and notice some of their features.

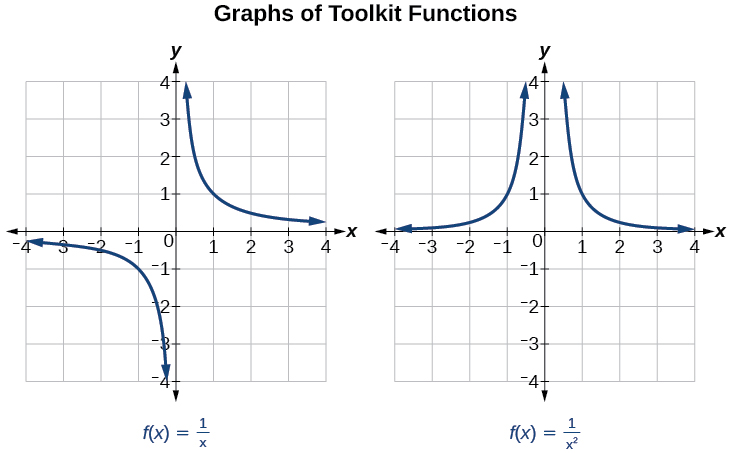
Several things are apparent if we examine the graph of[latex]\,f\left(x\right)=\frac{1}{x}.[/latex]

• On the left branch of the graph, the curve approaches the x -axis[latex]\,\left(y=0\right) \text{as } x\to –\infty .[/latex]
• As the graph approaches[latex]\,x=0\,[/latex]from the left, the curve drops, but as we approach zero from the right, the curve rises.
• Finally, on the right branch of the graph, the curves approaches the x- axis[latex]\,\left(y=0\right) \text{as } x\to \infty .[/latex]

To summarize, we use arrow notation to show that[latex]\,x\,[/latex]or[latex]\,f\left(x\right)\,[/latex]is approaching a particular value. See the table below.

Local Behavior of[latex]\,f\left(x\right)=\frac{1}{x}[/latex]

Let’s begin by looking at the reciprocal function,[latex]\,f\left(x\right)=\frac{1}{x}.\,[/latex]We cannot divide by zero, which means the function is undefined at[latex]\,x=0;\,[/latex]so zero is not in the domain . As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in the following table.

We write in arrow notation

As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). We can see this behavior in the table below.

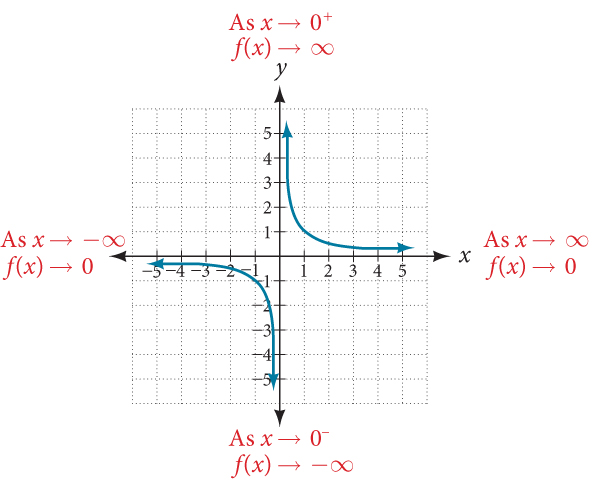
This behavior creates a vertical asymptote , which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line[latex]\,x=0\,[/latex]as the input becomes close to zero. See Figure 3.

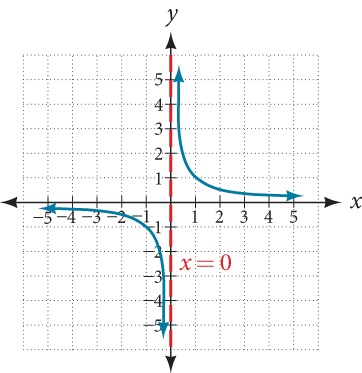
Vertical Asymptote

A vertical asymptote of a graph is a vertical line[latex]\,x=a\,[/latex]where the graph tends toward positive or negative infinity as the inputs approach[latex]\,a.\,[/latex]We write

End Behavior of[latex]\,f\left(x\right)=\frac{1}{x}[/latex]

As the values of[latex]\,x\,[/latex]approach infinity, the function values approach 0. As the values of[latex]\,x\,[/latex]approach negative infinity, the function values approach 0. See Figure 4. Symbolically, using arrow notation

[latex]\text {As }x\to \infty ,f\left(x\right)\to 0,\text{and as }x\to -\infty ,f\left(x\right)\to 0.[/latex]

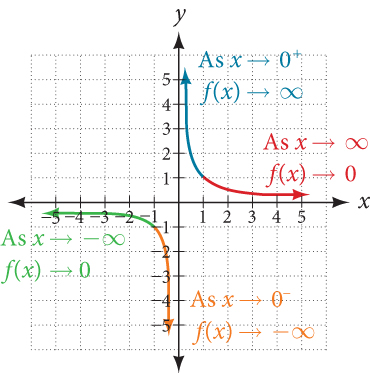
Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. This behavior creates a horizontal asymptote , a horizontal line that the graph approaches as the input increases or decreases without bound. In this case, the graph is approaching the horizontal line[latex]\,y=0.\,[/latex]See Figure 5 .

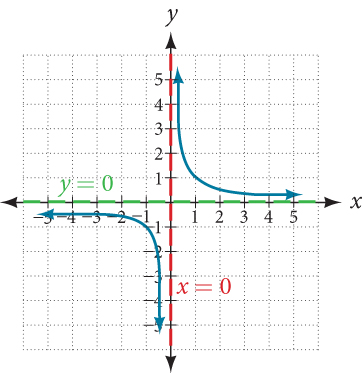
Horizontal Asymptote

A horizontal asymptote of a graph is a horizontal line[latex]\,y=b\,[/latex]where the graph approaches the line as the inputs increase or decrease without bound. We write

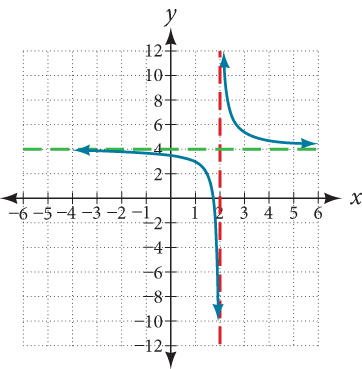
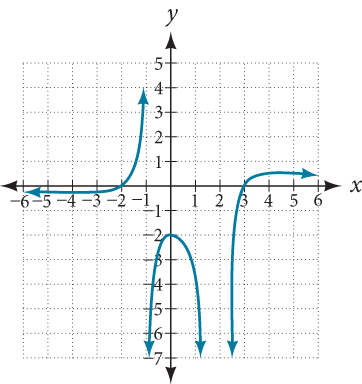
Use arrow notation to describe the end behavior and local behavior of the function graphed in Figure 6.

Notice that the graph is showing a vertical asymptote at[latex]\,x=2,\,[/latex]which tells us that the function is undefined at[latex]\,x=2.[/latex]

And as the inputs decrease without bound, the graph appears to be leveling off at output values of 4, indicating a horizontal asymptote at[latex]\,y=4.\,[/latex]As the inputs increase without bound, the graph levels off at 4.

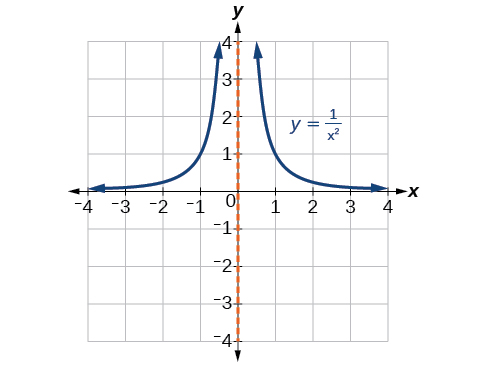
Use arrow notation to describe the end behavior and local behavior for the reciprocal squared function.

End behavior: as[latex]\,x\to ±\infty , f\left(x\right)\to 0;\,[/latex]Local behavior: as[latex]\,x\to 0, f\left(x\right)\to \infty \,[/latex](there are no x – or y -intercepts)

Using Transformations to Graph a Rational Function

Sketch a graph of the reciprocal function shifted two units to the left and up three units. Identify the horizontal and vertical asymptotes of the graph, if any.

Shifting the graph left 2 and up 3 would result in the function

or equivalently, by giving the terms a common denominator,

The graph of the shifted function is displayed in Figure 7.

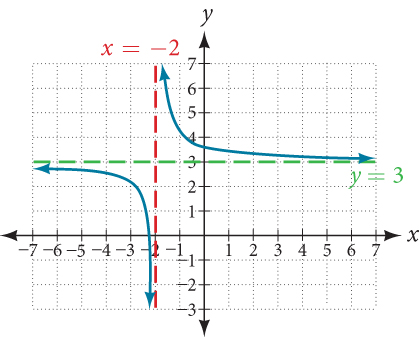
Notice that this function is undefined at[latex]\,x=-2,\,[/latex]and the graph also is showing a vertical asymptote at[latex]\,x=-2.[/latex]

As the inputs increase and decrease without bound, the graph appears to be leveling off at output values of 3, indicating a horizontal asymptote at[latex]\,y=3.[/latex]

Notice that horizontal and vertical asymptotes are shifted left 2 and up 3 along with the function.

Sketch the graph, and find the horizontal and vertical asymptotes of the reciprocal squared function that has been shifted right 3 units and down 4 units.

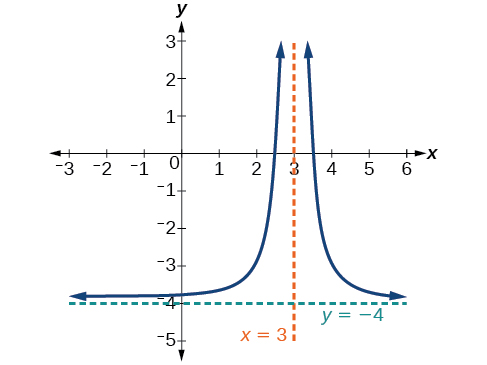
The function and the asymptotes are shifted 3 units right and 4 units down. As[latex]\,x\to 3,f\left(x\right)\to \infty ,\,[/latex]and as[latex]\,x\to ±\infty ,f\left(x\right)\to -4.[/latex]

The function is[latex]\,f\left(x\right)=\frac{1}{{\left(x-3\right)}^{2}}-4.[/latex]

Solving Applied Problems Involving Rational Functions

In Figure 7, we shifted a toolkit function in a way that resulted in the function [latex]\,f\left(x\right)=\frac{3x+7}{x+2}.\,[/latex] This is an example of a rational function. A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.

Rational Function

A rational function is a function that can be written as the quotient of two polynomial functions[latex]\,P\left(x\right) \text{and } Q\left(x\right).[/latex]

Solving an Applied Problem Involving a Rational Function

A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the ratio of sugar to water, in pounds per gallon in the tank after 12 minutes. Is that a greater ratio of sugar to water, in pounds per gallon than at the beginning?

Let[latex]\,t\,[/latex]be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:

The ratio of sugar to water, in pounds per gallon,[latex]\,C\,[/latex], will be the ratio of pounds of sugar to gallons of water

The ratio of sugar to water, in pounds per gallon after 12 minutes is given by evaluating[latex]\,C\left(t\right)\,[/latex]at[latex]\,t=\text{ }12.[/latex]

This means the ratio of sugar to water, in pounds per gallon is 17 pounds of sugar to 220 gallons of water.

At the beginning, the ratio of sugar to water, in pounds per gallon is

Since[latex]\,\frac{17}{220}\approx 0.08>\frac{1}{20}=0.05,\,[/latex]the ratio of sugar to water, in pounds per gallon is greater after 12 minutes than at the beginning.

There are 1,200 freshmen and 1,500 sophomores at a prep rally at noon. After 12 p.m., 20 freshmen arrive at the rally every five minutes while 15 sophomores leave the rally. Find the ratio of freshmen to sophomores at 1 p.m.

[latex]\frac{12}{11}[/latex]

Finding the Domains of Rational Functions

A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

Domain of a Rational Function

• The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

Given a rational function, find the domain.

• Set the denominator equal to zero.
• Solve to find the x -values that cause the denominator to equal zero.
• The domain is all real numbers except those found in Step 2.

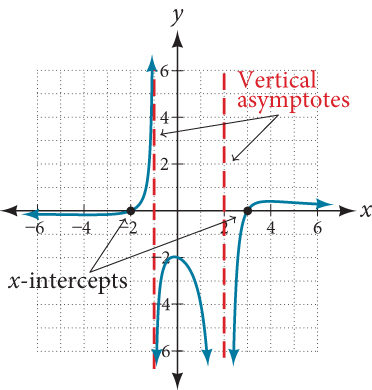
Finding the Domain of a Rational Function

Find the domain of[latex]\,f\left(x\right)=\frac{x+3}{{x}^{2}-9}.[/latex]

Begin by setting the denominator equal to zero and solving.

The denominator is equal to zero when[latex]\,x=±3.\,[/latex]The domain of the function is all real numbers except[latex]\,x=±3.[/latex]

A graph of this function, as shown in Figure 8, confirms that the function is not defined when[latex]\,x=±3.[/latex]

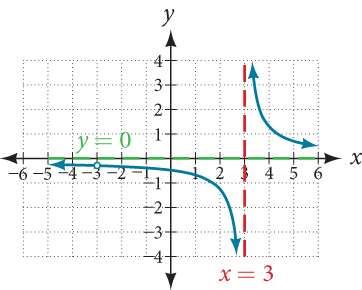
There is a vertical asymptote at[latex]\,x=3\,[/latex]and a hole in the graph at[latex]\,x=-3.\,[/latex]We will discuss these types of holes in greater detail later in this section.

Find the domain of[latex]\,f\left(x\right)=\frac{4x}{5\left(x-1\right)\left(x-5\right)}.[/latex]

The domain is all real numbers except[latex]\,x=1\,[/latex]and[latex]\,x=5.[/latex]

Identifying Vertical Asymptotes of Rational Functions

By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.

Vertical Asymptotes

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

Given a rational function, identify any vertical asymptotes of its graph.

• Factor the numerator and denominator.
• Note any restrictions in the domain of the function.
• Reduce the expression by canceling common factors in the numerator and the denominator.
• Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
• Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities, or “holes.”

Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of[latex]\,k\left(x\right)=\frac{5+2{x}^{2}}{2-x-{x}^{2}}.[/latex]

First, factor the numerator and denominator.

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

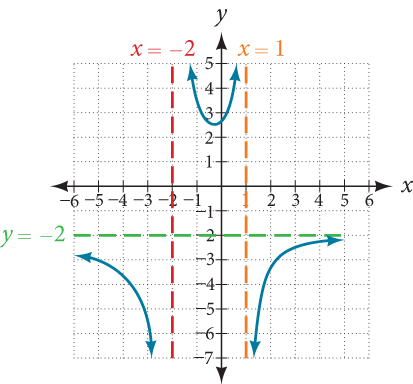
Neither[latex]\,x=–2\,[/latex]nor[latex]\,x=1\,[/latex]are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph in Figure 9 confirms the location of the two vertical asymptotes.

Removable Discontinuities

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.

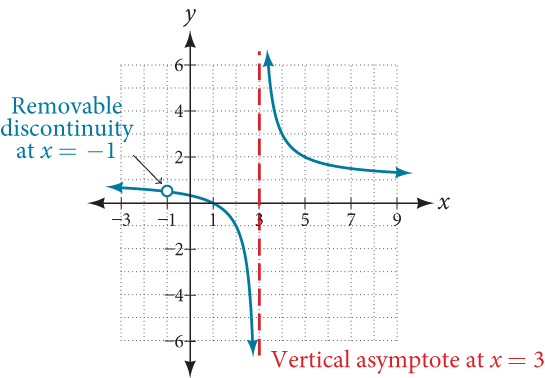
For example, the function[latex]\,f\left(x\right)=\frac{{x}^{2}-1}{{x}^{2}-2x-3}\,[/latex]may be re-written by factoring the numerator and the denominator.

Notice that[latex]\,x+1\,[/latex]is a common factor to the numerator and the denominator. The zero of this factor,[latex]\,x=-1,\,[/latex]is the location of the removable discontinuity. Notice also that[latex]\,x–3\,[/latex]is not a factor in both the numerator and denominator. The zero of this factor,[latex]\,x=3,\,[/latex]is the vertical asymptote. See Figure 10. [Note that removable discontinuities may not be visible when we use a graphing calculator, depending upon the window selected.]

Key Takeaways

Removable discontinuities of rational functions.

A removable discontinuity occurs in the graph of a rational function at[latex]\,x=a\,[/latex]if[latex]\,a\,[/latex]is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of[latex]\,k\left(x\right)=\frac{x-2}{{x}^{2}-4}.[/latex]

Factor the numerator and the denominator.

Notice that there is a common factor in the numerator and the denominator,[latex]\,x–2.\,[/latex]The zero for this factor is[latex]\,x=2.\,[/latex]This is the location of the removable discontinuity.

Notice that there is a factor in the denominator that is not in the numerator,[latex]\,x+2.\,[/latex]The zero for this factor is[latex]\,x=-2.\,[/latex]The vertical asymptote is[latex]\,x=-2.\,[/latex] See Figure 11.

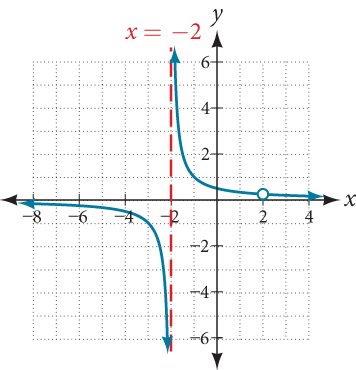
The graph of this function will have the vertical asymptote at[latex]\,x=-2,\,[/latex]but at[latex]\,x=2\,[/latex]the graph will have a hole.

Find the vertical asymptotes and removable discontinuities of the graph of[latex]\,f\left(x\right)=\frac{{x}^{2}-25}{{x}^{3}-6{x}^{2}+5x}.[/latex]

Removable discontinuity at[latex]\,x=5.\,[/latex]Vertical asymptotes:[latex]\,x=0,\text{ }x=1.[/latex]

Identifying Horizontal Asymptotes of Rational Functions

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms.

There are three distinct outcomes when checking for horizontal asymptotes:

Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at[latex]\,y=0.[/latex]

In this case, the end behavior is[latex]\,f\left(x\right)\approx \frac{4x}{{x}^{2}}=\frac{4}{x}.\,[/latex]This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function[latex]\,g\left(x\right)=\frac{4}{x},\,[/latex]and the outputs will approach zero, resulting in a horizontal asymptote at[latex]\,y=0.\,[/latex]See Figure 12. Note that this graph crosses the horizontal asymptote.

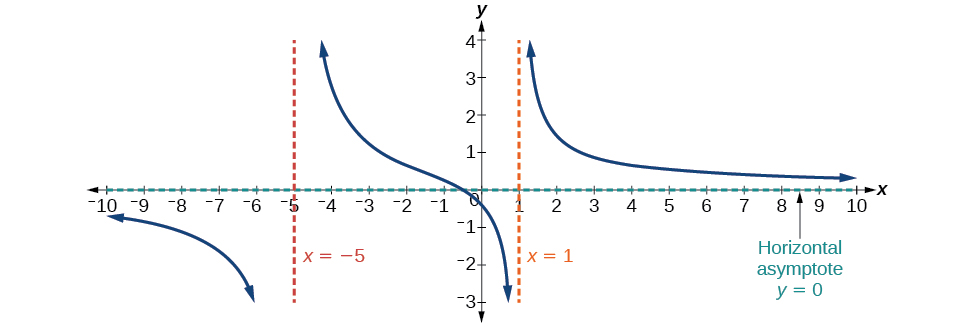
Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.

In this case, the end behavior is[latex]\,f\left(x\right)\approx \frac{3{x}^{2}}{x}=3x.\,[/latex]This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function[latex]\,g\left(x\right)=3x.\,[/latex]As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of[latex]\,g\left(x\right)=3x\,[/latex]looks like a diagonal line, and since[latex]\,f\,[/latex]will behave similarly to[latex]\,g,\,[/latex]it will approach a line close to[latex]\,y=3x.\,[/latex]This line is a slant asymptote.

To find the equation of the slant asymptote, divide[latex]\,\frac{3{x}^{2}-2x+1}{x-1}.\,[/latex]The quotient is[latex]\,3x+1,\,[/latex]and the remainder is 2. The slant asymptote is the graph of the line[latex]\,g\left(x\right)=3x+1.\,[/latex]See Figure 13.

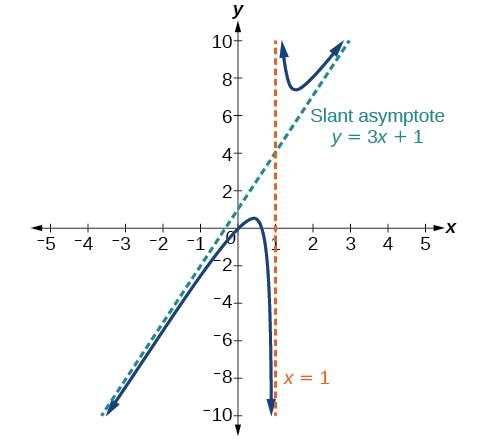
Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at[latex]\,y=\frac{{a}_{n}}{{b}_{n}},\,[/latex]where[latex]\,{a}_{n}\,[/latex]and[latex]\,{b}_{n}\,[/latex]are the leading coefficients of[latex]\,p\left(x\right)\,[/latex]and[latex]\,q\left(x\right)\,[/latex]for[latex]\,f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0.[/latex]

In this case, the end behavior is[latex]\,f\left(x\right)\approx \frac{3{x}^{2}}{{x}^{2}}=3.\,[/latex]This tells us that as the inputs grow large, this function will behave like the function[latex]\,g\left(x\right)=3,\,[/latex]which is a horizontal line. As[latex]\,x\to ±\infty ,f\left(x\right)\to 3,\,[/latex]resulting in a horizontal asymptote at[latex]\,y=3.\,[/latex]See Figure 14. Note that this graph crosses the horizontal asymptote.

Notice that, while the graph of a rational function will never cross a vertical asymptote , the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.

It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

with end behavior

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

• Degree of numerator is less than degree of denominator: horizontal asymptote at[latex]\,y=0.[/latex]
• Degree of numerator is greater than degree of denominator by one : no horizontal asymptote; slant asymptote.
• Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Identifying Horizontal and Slant Asymptotes

For the functions listed, identify the horizontal or slant asymptote.

• [latex]g\left(x\right)=\frac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}[/latex]
• [latex]h\left(x\right)=\frac{{x}^{2}-4x+1}{x+2}[/latex]
• [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{3}-8}[/latex]

For these solutions, we will use[latex]\,f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}, q\left(x\right)\ne 0.[/latex]

• [latex]g\left(x\right)=\frac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}:\,[/latex]The degree of[latex]\,p=\text{degree of } q=3,\,[/latex]so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at[latex]\,y=\frac{6}{2}\,[/latex]or[latex]\,y=3.[/latex]

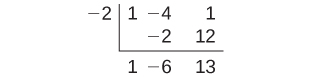
The quotient is[latex]\,x–6\,[/latex]and the remainder is 13. There is a slant asymptote at[latex]\,y=x–6.[/latex]

• [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{3}-8}:\,[/latex]The degree of[latex]\,p=2\text{ }\,[/latex]degree of[latex]\,q=3,\,[/latex]so there is a horizontal asymptote[latex]\,y=0.[/latex]

Identifying Horizontal Asymptotes

In the sugar concentration problem earlier, we created the equation[latex]\,C\left(t\right)=\frac{5+t}{100+10t}.[/latex]

Find the horizontal asymptote and interpret it in context of the problem.

Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is[latex]\,t,\,[/latex]with coefficient 1. In the denominator, the leading term is[latex]\,10t,\,[/latex]with coefficient 10. The horizontal asymptote will be at the ratio of these values:

This function will have a horizontal asymptote at[latex]\,y=\frac{1}{10}.[/latex]

This tells us that as the values of t increase, the values of[latex]\,C\,[/latex]will approach[latex]\,\frac{1}{10}.\,[/latex]In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or[latex]\,\frac{1}{10}\,[/latex]pounds per gallon.

Identifying Horizontal and Vertical Asymptotes

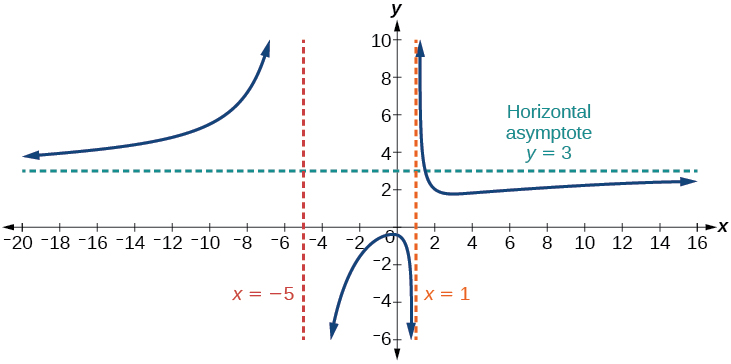
Find the horizontal and vertical asymptotes of the function

First, note that this function has no common factors, so there are no potential removable discontinuities.

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at[latex]\,x=1,–2,\text{and }5,\,[/latex]indicating vertical asymptotes at these values.

The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as[latex]\,x\to ±\infty , f\left(x\right)\to 0.\,[/latex]This function will have a horizontal asymptote at[latex]\,y=0.\,[/latex]See Figure 15.

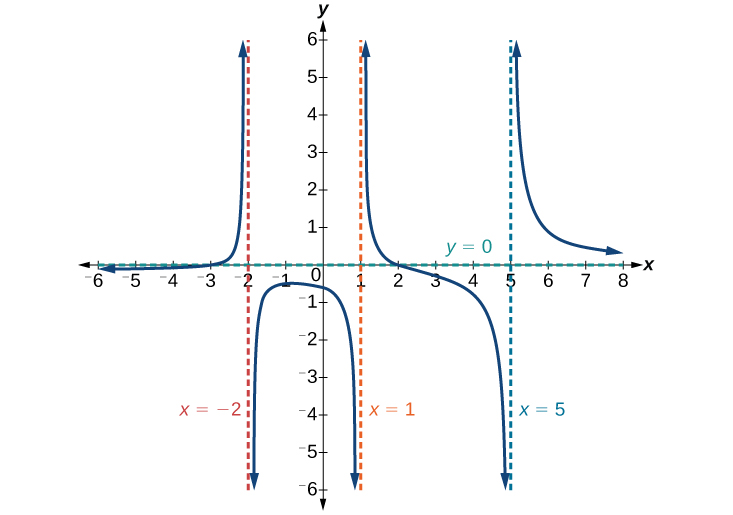
Find the vertical and horizontal asymptotes of the function:

[latex]f\left(x\right)=\frac{\left(2x-1\right)\left(2x+1\right)}{\left(x-2\right)\left(x+3\right)}[/latex]

Vertical asymptotes at[latex]\,x=2\,[/latex]and[latex]\,x=–3;\,[/latex]horizontal asymptote at[latex]\,y=4.[/latex]

Intercepts of Rational Functions

A rational function will have a y -intercept at[latex]\,f\left(0\right)[/latex], if the function is defined at zero. A rational function will not have a y -intercept if the function is not defined at zero.

Likewise, a rational function will have x -intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x -intercepts can only occur when the numerator of the rational function is equal to zero.

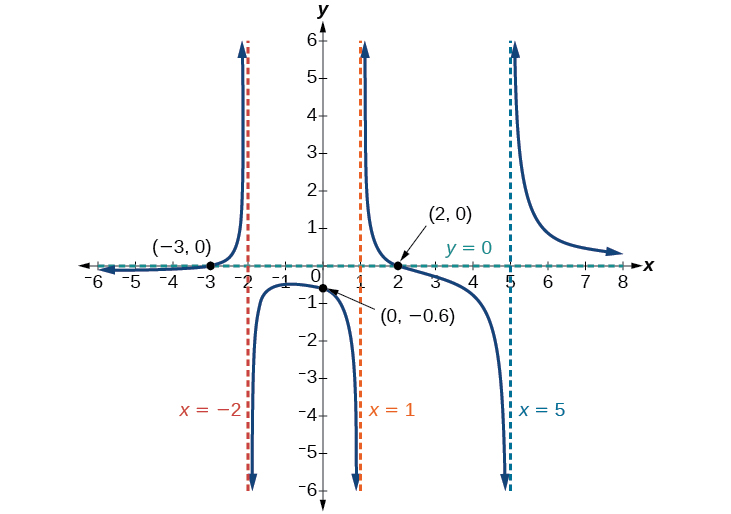
Finding the Intercepts of a Rational Function

Find the intercepts of[latex]\,f\left(x\right)=\frac{\left(x-2\right)\left(x+3\right)}{\left(x-1\right)\left(x+2\right)\left(x-5\right)}.[/latex]

We can find the y -intercept by evaluating the function at zero

The x -intercepts will occur when the numerator of the function is equal to zero:

The y -intercept is[latex]\,\left(0,–0.6\right),\,[/latex]the x -intercepts are[latex]\,\left(2,0\right)\,[/latex]and[latex]\,\left(–3,0\right).\,[/latex]See Figure 16.

Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x – and y -intercepts and the horizontal and vertical asymptotes.

For the transformed reciprocal squared function, we find the rational form.[latex]\,f\left(x\right)=\frac{1}{{\left(x-3\right)}^{2}}-4=\frac{1-4{\left(x-3\right)}^{2}}{{\left(x-3\right)}^{2}}=\frac{1-4\left({x}^{2}-6x+9\right)}{\left(x-3\right)\left(x-3\right)}=\frac{-4{x}^{2}+24x-35}{{x}^{2}-6x+9}[/latex]

Because the numerator is the same degree as the denominator we know that as[latex]\,x\to ±\infty , f\left(x\right)\to -4; \text{so} y=–4\,[/latex]is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is[latex]\,x=3,\,[/latex]because as[latex]\,x\to 3,f\left(x\right)\to \infty .\,[/latex]We then set the numerator equal to 0 and find the x -intercepts are at[latex]\,\left(2.5,0\right)\,[/latex]and[latex]\,\left(3.5,0\right).\,[/latex]Finally, we evaluate the function at 0 and find the y -intercept to be at[latex]\,\left(0,\frac{-35}{9}\right).[/latex]

Graphing Rational Functions

We have learned that the numerator of a rational function reveals the x -intercepts of the graph, whereas the denominator reveals the vertical asymptotes of the graph. As with polynomials, factors of the numerator may have integer powers greater than one. Fortunately, the effect on the shape of the graph at those intercepts is the same as we saw with polynomials.

The vertical asymptotes associated with the factors of the denominator will mirror one of the two toolkit reciprocal functions. When the degree of the factor in the denominator is odd, the distinguishing characteristic is that on one side of the vertical asymptote the graph heads towards positive infinity, and on the other side the graph heads towards negative infinity. See Figure 17.

When the degree of the factor in the denominator is even, the distinguishing characteristic is that the graph either heads toward positive infinity on both sides of the vertical asymptote or heads toward negative infinity on both sides. See Figure 18.

For example, the graph of[latex]\,f\left(x\right)=\frac{{\left(x+1\right)}^{2}\left(x-3\right)}{{\left(x+3\right)}^{2}\left(x-2\right)}\,[/latex]is shown in Figure 19.

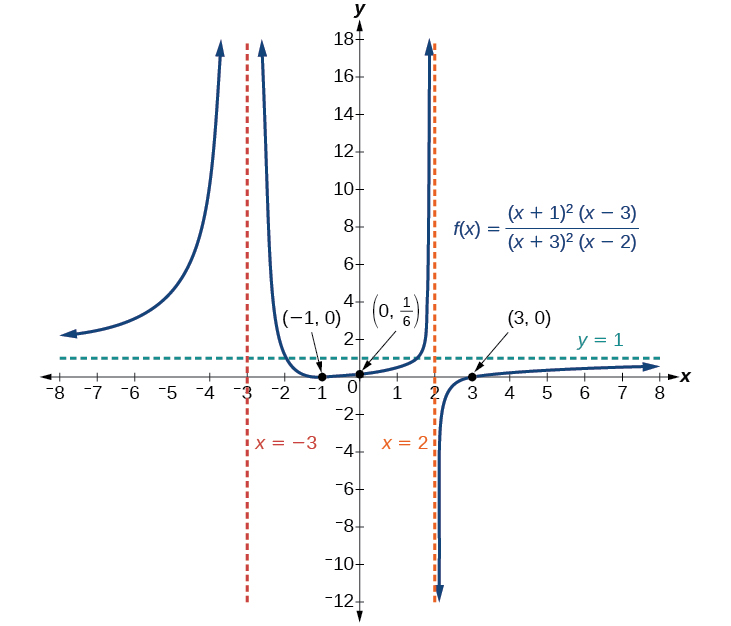
• At the x -intercept[latex]\,x=-1\,[/latex]corresponding to the[latex]\,{\left(x+1\right)}^{2}\,[/latex]factor of the numerator, the graph “bounces”, consistent with the quadratic nature of the factor.
• At the x -intercept[latex]\,x=3\,[/latex]corresponding to the[latex]\,\left(x-3\right)\,[/latex]factor of the numerator, the graph passes through the axis as we would expect from a linear factor.
• At the vertical asymptote[latex]\,x=-3\,[/latex]corresponding to the[latex]\,{\left(x+3\right)}^{2}\,[/latex]factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function[latex]\,f\left(x\right)=\frac{1}{{x}^{2}}.[/latex]
• At the vertical asymptote[latex]\,x=2,\,[/latex]corresponding to the[latex]\,\left(x-2\right)\,[/latex]factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side, consistent with the behavior of the function[latex]\,f\left(x\right)=\frac{1}{x}.[/latex]

Given a rational function, sketch a graph.

• Evaluate the function at 0 to find the y -intercept.
• For factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the x -intercepts.
• Find the multiplicities of the x -intercepts to determine the behavior of the graph at those points.
• For factors in the denominator, note the multiplicities of the zeros to determine the local behavior. For those factors not common to the numerator, find the vertical asymptotes by setting those factors equal to zero and then solve.
• For factors in the denominator common to factors in the numerator, find the removable discontinuities by setting those factors equal to 0 and then solve.
• Compare the degrees of the numerator and the denominator to determine the horizontal or slant asymptotes.
• Sketch the graph.

Graphing a Rational Function

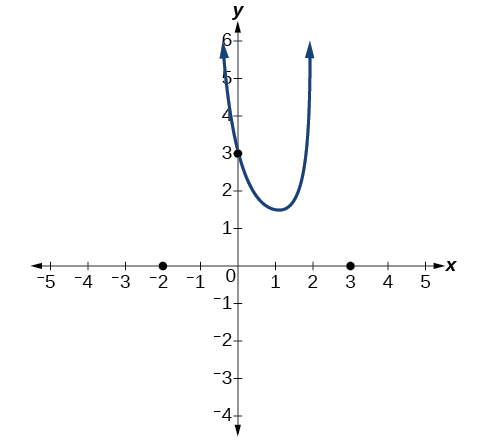
Sketch a graph of[latex]\,f\left(x\right)=\frac{\left(x+2\right)\left(x-3\right)}{{\left(x+1\right)}^{2}\left(x-2\right)}.[/latex]

We can start by noting that the function is already factored, saving us a step.

Next, we will find the intercepts. Evaluating the function at zero gives the y -intercept:

To find the x -intercepts, we determine when the numerator of the function is zero. Setting each factor equal to zero, we find x -intercepts at[latex]\,x=–2\,[/latex]and[latex]\,x=3.\,[/latex]At each, the behavior will be linear (multiplicity 1), with the graph passing through the intercept.

We have a y -intercept at[latex]\,\left(0,3\right)\,[/latex]and x -intercepts at[latex]\,\left(–2,0\right)\,[/latex]and[latex]\,\left(3,0\right).[/latex]

To find the vertical asymptotes, we determine when the denominator is equal to zero. This occurs when[latex]\,x+1=0\,[/latex]and when[latex]\,x–2=0,\,[/latex]giving us vertical asymptotes at[latex]\,x=–1\,[/latex]and[latex]\,x=2.[/latex]

There are no common factors in the numerator and denominator. This means there are no removable discontinuities.

Finally, the degree of denominator is larger than the degree of the numerator, telling us this graph has a horizontal asymptote at[latex]\,y=0.[/latex]

To sketch the graph, we might start by plotting the three intercepts. Since the graph has no x -intercepts between the vertical asymptotes, and the y -intercept is positive, we know the function must remain positive between the asymptotes, letting us fill in the middle portion of the graph as shown in Figure 20.

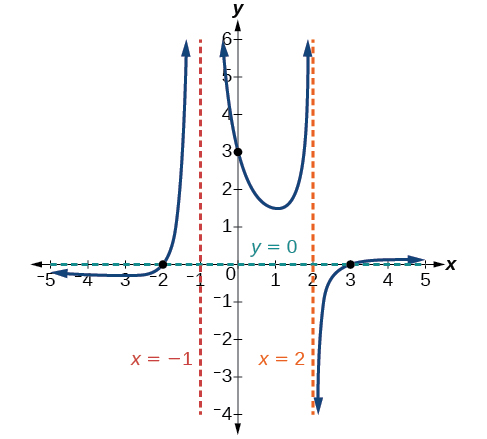
The factor associated with the vertical asymptote at[latex]\,x=-1\,[/latex]was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.

For the vertical asymptote at[latex]\,x=2,\,[/latex]the factor was not squared, so the graph will have opposite behavior on either side of the asymptote. See Figure 21. After passing through the x -intercepts, the graph will then level off toward an output of zero, as indicated by the horizontal asymptote.

Given the function[latex]\,f\left(x\right)=\frac{{\left(x+2\right)}^{2}\left(x-2\right)}{2{\left(x-1\right)}^{2}\left(x-3\right)},\,[/latex]use the characteristics of polynomials and rational functions to describe its behavior and sketch the function.

Horizontal asymptote at[latex]\,y=\frac{1}{2}.\,[/latex]Vertical asymptotes at[latex]\,x=1 \text{ and } x=3.\,[/latex] y -intercept at[latex]\,\left(0,\frac{4}{3}.\right)[/latex]

x -intercepts at[latex]\,\left(2,0\right) \text{ and }\left(–2,0\right).\,[/latex][latex]\left(–2,0\right)\,[/latex]is a zero with multiplicity 2, and the graph bounces off the x -axis at this point.[latex]\,\left(2,0\right)\,[/latex]is a single zero and the graph crosses the axis at this point.

Writing Rational Functions

Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x -intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x -intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.

Writing Rational Functions from Intercepts and Asymptotes

If a rational function has x -intercepts at[latex]\,x={x}_{1},{x}_{2},...,{x}_{n},\,[/latex]vertical asymptotes at[latex]\,x={v}_{1},{v}_{2},\dots ,{v}_{m},\,[/latex]and no[latex]\,{x}_{i}=\text{any }{v}_{j},\,[/latex]then the function can be written in the form:

where the powers[latex]\,{p}_{i}\,[/latex]or[latex]\,{q}_{i}\,[/latex]on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor[latex]\,a\,[/latex]can be determined given a value of the function other than the x -intercept or by the horizontal asymptote if it is nonzero.

Given a graph of a rational function, write the function.

• Determine the factors of the numerator. Examine the behavior of the graph at the x -intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the “simplest” function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
• Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
• Use any clear point on the graph to find the stretch factor.

Writing a Rational Function from Intercepts and Asymptotes

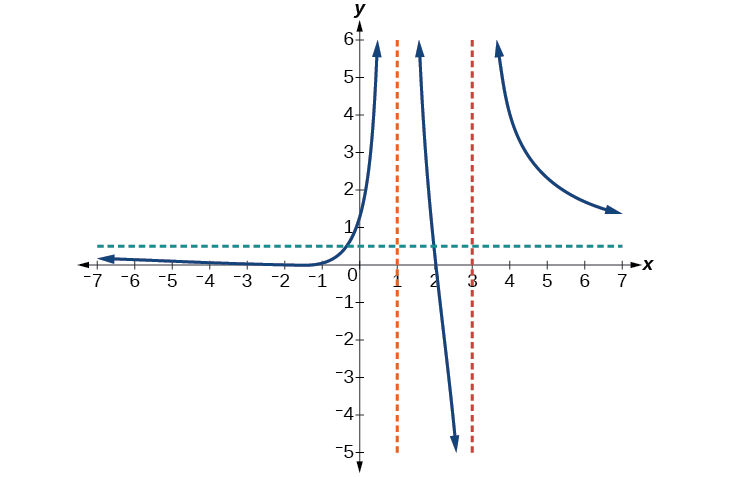
Write an equation for the rational function shown in Figure 22.

The graph appears to have x -intercepts at[latex]\,x=–2\,[/latex]and[latex]\,x=3.\,[/latex]At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at[latex]\,x=–1\,[/latex]seems to exhibit the basic behavior similar to[latex]\,\frac{1}{x},\,[/latex]with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at[latex]\,x=2\,[/latex]is exhibiting a behavior similar to[latex]\,\frac{1}{{x}^{2}},\,[/latex]with the graph heading toward negative infinity on both sides of the asymptote. See Figure 23.

We can use this information to write a function of the form

To find the stretch factor, we can use another clear point on the graph, such as the y -intercept[latex]\,\left(0,–2\right).[/latex]

This gives us a final function of[latex]\,f\left(x\right)=\frac{4\left(x+2\right)\left(x-3\right)}{3\left(x+1\right){\left(x-2\right)}^{2}}.[/latex]

Key Equations

Key concepts.

• We can use arrow notation to describe local behavior and end behavior of the toolkit functions[latex]\,f\left(x\right)=\frac{1}{x}\,[/latex]and[latex]\,f\left(x\right)=\frac{1}{{x}^{2}}.\,[/latex]
• A function that levels off at a horizontal value has a horizontal asymptote. A function can have more than one vertical asymptote.
• Application problems involving rates and concentrations often involve rational functions.
• The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
• A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero.
• A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
• Graph rational functions by finding the intercepts, behavior at the intercepts and asymptotes, and end behavior.
• If a rational function has x -intercepts at[latex]\,x={x}_{1},{x}_{2},\dots ,{x}_{n},\,[/latex]vertical asymptotes at[latex]\,x={v}_{1},{v}_{2},\dots ,{v}_{m},\,[/latex]and no[latex]\,{x}_{i}=\text{any }{v}_{j},\,[/latex]then the function can be written in the form

Section Exercises

1. What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?

The rational function will be represented by a quotient of polynomial functions.

2. What is the fundamental difference in the graphs of polynomial functions and rational functions?

3. If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?

The numerator and denominator must have a common factor.

4. Can a graph of a rational function have no vertical asymptote? If so, how?

5. Can a graph of a rational function have no x -intercepts? If so, how?

Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator.

For the following exercises, find the domain of the rational functions.

6. [latex]f\left(x\right)=\frac{x-1}{x+2}[/latex]

[latex]\text{All reals }x\ne –1, 1[/latex]

8. [latex]f\left(x\right)=\frac{{x}^{2}+4}{{x}^{2}-2x-8}[/latex]

9. [latex]f\left(x\right)=\frac{{x}^{2}+4x-3}{{x}^{4}-5{x}^{2}+4}[/latex]

[latex]\text{All reals }x\ne –1, –2, 1, 2[/latex]

For the following exercises, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.

10. [latex]f\left(x\right)=\frac{4}{x-1}[/latex]

11. [latex]f\left(x\right)=\frac{2}{5x+2}[/latex]

V.A. at[latex]\,x=–\frac{2}{5};\,[/latex]H.A. at[latex]\,y=0;\,[/latex]Domain is all reals[latex]\,x\ne –\frac{2}{5}[/latex]

12. [latex]f\left(x\right)=\frac{x}{{x}^{2}-9}[/latex]

13. [latex]f\left(x\right)=\frac{x}{{x}^{2}+5x-36}[/latex]

V.A. at[latex]\,x=4, –9;\,[/latex]H.A. at[latex]\,y=0;\,[/latex]Domain is all reals[latex]\,x\ne 4, –9[/latex]

14. [latex]f\left(x\right)=\frac{3+x}{{x}^{3}-27}[/latex]

15. [latex]f\left(x\right)=\frac{3x-4}{{x}^{3}-16x}[/latex]

V.A. at[latex]\,x=0, 4, -4;\,[/latex]H.A. at[latex]\,y=0;[/latex]Domain is all reals[latex]\,x\ne 0,4, –4[/latex]

16. [latex]f\left(x\right)=\frac{{x}^{2}-1}{{x}^{3}+9{x}^{2}+14x}[/latex]

17. [latex]f\left(x\right)=\frac{x+5}{{x}^{2}-25}[/latex]

V.A. at[latex]\,x=-5;\,[/latex]H.A. at[latex]\,y=0;\,[/latex]Domain is all reals[latex]\,x\ne 5,-5[/latex]

18. [latex]f\left(x\right)=\frac{x-4}{x-6}[/latex]

19. [latex]f\left(x\right)=\frac{4-2x}{3x-1}[/latex]

V.A. at[latex]\,x=\frac{1}{3};\,[/latex]H.A. at[latex]\,y=-\frac{2}{3};\,[/latex]Domain is all reals[latex]\,x\ne \frac{1}{3}.[/latex]

For the following exercises, find the x – and y -intercepts for the functions.

20. [latex]f\left(x\right)=\frac{x+5}{{x}^{2}+4}[/latex]

21. [latex]f\left(x\right)=\frac{x}{{x}^{2}-x}[/latex]

22. [latex]f\left(x\right)=\frac{{x}^{2}+8x+7}{{x}^{2}+11x+30}[/latex]

23. [latex]f\left(x\right)=\frac{{x}^{2}+x+6}{{x}^{2}-10x+24}[/latex]

[latex]x\text{-intercepts none, }y\text{-intercept }\left(0,\frac{1}{4}\right)[/latex]

24. [latex]f\left(x\right)=\frac{94-2{x}^{2}}{3{x}^{2}-12}[/latex]

For the following exercises, describe the local and end behavior of the functions.

25. [latex]f\left(x\right)=\frac{x}{2x+1}[/latex]

Local behavior:[latex]\,x\to -{\frac{1}{2}}^{+},f\left(x\right)\to -\infty ,x\to -{\frac{1}{2}}^{-},f\left(x\right)\to \infty \,[/latex]

End behavior:[latex]\,x\to ±\infty ,f\left(x\right)\to \frac{1}{2}[/latex]

26. [latex]f\left(x\right)=\frac{2x}{x-6}[/latex]

27. [latex]f\left(x\right)=\frac{-2x}{x-6}[/latex]

Local behavior:[latex]\,x\to {6}^{+},f\left(x\right)\to -\infty ,x\to {6}^{-},f\left(x\right)\to \infty ,\,[/latex]End behavior:[latex]\,x\to ±\infty ,f\left(x\right)\to -2[/latex]

28. [latex]f\left(x\right)=\frac{{x}^{2}-4x+3}{{x}^{2}-4x-5}[/latex]

29. [latex]f\left(x\right)=\frac{2{x}^{2}-32}{6{x}^{2}+13x-5}[/latex]

Local behavior:[latex]\,x\to -{\frac{1}{3}}^{+},f\left(x\right)\to \infty ,x\to -{\frac{1}{3}}^{-},\,[/latex][latex]f\left(x\right)\to -\infty ,x\to {\frac{5}{2}}^{-},f\left(x\right)\to \infty ,x\to {\frac{5}{2}}^{+},f\left(x\right)\to -\infty[/latex]

End behavior: [latex]x\to ±\infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to \frac{1}{3}[/latex]

For the following exercises, find the slant asymptote of the functions.

30. [latex]f\left(x\right)=\frac{24{x}^{2}+6x}{2x+1}[/latex]

[latex]y=2x+4[/latex]

32. [latex]f\left(x\right)=\frac{81{x}^{2}-18}{3x-2}[/latex]

33. [latex]f\left(x\right)=\frac{6{x}^{3}-5x}{3{x}^{2}+4}[/latex]

[latex]y=2x[/latex]

34. [latex]f\left(x\right)=\frac{{x}^{2}+5x+4}{x-1}[/latex]

For the following exercises, use the given transformation to graph the function. Note the vertical and horizontal asymptotes.

35. The reciprocal function shifted up two units.

[latex]V.A.\text{ }x=0,H.A.\text{ }y=2[/latex]

36. The reciprocal function shifted down one unit and left three units.

37. The reciprocal squared function shifted to the right 2 units.

[latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0[/latex]

38. The reciprocal squared function shifted down 2 units and right 1 unit.

For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.

[latex]V.A.\text{ }x=-4,\text{ }H.A.\text{ }y=2;\left(\frac{3}{2},0\right);\left(0,-\frac{3}{4}\right)[/latex]

40. [latex]q\left(x\right)=\frac{x-5}{3x-1}[/latex]

[latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0,\text{ }\left(0,1\right)[/latex]

42. [latex]r\left(x\right)=\frac{5}{{\left(x+1\right)}^{2}}[/latex]

43. [latex]f\left(x\right)=\frac{3{x}^{2}-14x-5}{3{x}^{2}+8x-16}[/latex]

[latex]V.A.\text{ }x=-4,\text{ }x=\frac{4}{3},\text{ }H.A.\text{ }y=1;\left(5,0\right);\left(-\frac{1}{3},0\right);\left(0,\frac{5}{16}\right)[/latex]

44. [latex]g\left(x\right)=\frac{2{x}^{2}+7x-15}{3{x}^{2}-14x+15}[/latex]

45. [latex]a\left(x\right)=\frac{{x}^{2}+2x-3}{{x}^{2}-1}[/latex]

[latex]V.A.\text{ }x=-1,\text{ }H.A.\text{ }y=1;\left(-3,0\right);\left(0,3\right)[/latex]

46. [latex]b\left(x\right)=\frac{{x}^{2}-x-6}{{x}^{2}-4}[/latex]

47. [latex]h\left(x\right)=\frac{2{x}^{2}+ x-1}{x-4}[/latex]

[latex]V.A.\text{ }x=4,\text{ }S.A.\text{ }y=2x+9;\left(-1,0\right);\left(\frac{1}{2},0\right);\left(0,\frac{1}{4}\right)[/latex]

48. [latex]k\left(x\right)=\frac{2{x}^{2}-3x-20}{x-5}[/latex]

49. [latex]w\left(x\right)=\frac{\left(x-1\right)\left(x+3\right)\left(x-5\right)}{{\left(x+2\right)}^{2}\left(x-4\right)}[/latex]

[latex]V.A.\text{ }x=-2,\text{ }x=4,\text{ }H.A.\text{ }y=1,\left(1,0\right);\left(5,0\right);\left(-3,0\right);\left(0,-\frac{15}{16}\right)[/latex]

50. [latex]z\left(x\right)=\frac{{\left(x+2\right)}^{2}\left(x-5\right)}{\left(x-3\right)\left(x+1\right)\left(x+4\right)}[/latex]

For the following exercises, write an equation for a rational function with the given characteristics.

51. Vertical asymptotes at[latex]\,x=5\,[/latex]and[latex]\,x=-5,\,[/latex] x -intercepts at[latex]\,\left(2,0\right)\,[/latex]and[latex]\,\left(-1,0\right),\,[/latex] y -intercept at[latex]\,\left(0,4\right)[/latex]

[latex]y=50\frac{{x}^{2}-x-2}{{x}^{2}-25}[/latex]

52. Vertical asymptotes at[latex]\,x=-4\,[/latex]and[latex]\,x=-1,\,[/latex] x- intercepts at[latex]\,\left(1,0\right)\,[/latex]and[latex]\,\left(5,0\right),\,[/latex] y- intercept at[latex]\,\left(0,7\right)[/latex]

53. Vertical asymptotes at[latex]\,x=-4\,[/latex]and[latex]\,x=-5,\,[/latex] x -intercepts at[latex]\,\left(4,0\right)\,[/latex]and[latex]\,\left(-6,0\right),\,[/latex]Horizontal asymptote at[latex]\,y=7[/latex]

[latex]y=7\frac{{x}^{2}+2x-24}{{x}^{2}+9x+20}[/latex]

54. Vertical asymptotes at[latex]\,x=-3\,[/latex]and[latex]\,x=6,\,[/latex] x -intercepts at[latex]\,\left(-2,0\right)\,[/latex]and[latex]\,\left(1,0\right),\,[/latex]Horizontal asymptote at[latex]\,y=-2[/latex]

55. Vertical asymptote at[latex]\,x=-1,\,[/latex]Double zero at[latex]\,x=2,\,[/latex] y -intercept at[latex]\,\left(0,2\right)[/latex]

[latex]y=\frac{1}{2}\frac{{x}^{2}-4x+4}{x+1}[/latex]

56. Vertical asymptote at[latex]\,x=3,\,[/latex]Double zero at[latex]\,x=1,\,[/latex] y -intercept at[latex]\,\left(0,4\right)[/latex]

For the following exercises, use the graphs to write an equation for the function.

57. Write the equation.

[latex]y=4\frac{x-3}{{x}^{2}-x-12}[/latex]

[latex]y=-9\frac{x-2}{{x}^{2}-9}[/latex]

[latex]y=\frac{1}{3}\frac{{x}^{2}+x-6}{x-1}[/latex]

[latex]y=-6\frac{{\left(x-1\right)}^{2}}{\left(x+3\right){\left(x-2\right)}^{2}}[/latex]

For the following exercises, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote

65. [latex]f\left(x\right)=\frac{1}{x-2}[/latex]

Vertical asymptote[latex]\,x=2,\,[/latex]Horizontal asymptote[latex]\,y=0[/latex]

67. [latex]f\left(x\right)=\frac{2x}{x+4}[/latex]

Vertical asymptote[latex]\,x=-4,\,[/latex]Horizontal asymptote[latex]\,y=2[/latex]

68. [latex]f\left(x\right)=\frac{2x}{{\left(x-3\right)}^{2}}[/latex]

69. [latex]f\left(x\right)=\frac{{x}^{2}}{{x}^{2}+2x+1}[/latex]

Vertical asymptote[latex]\,x=-1,\,[/latex]Horizontal asymptote[latex]\,y=1[/latex]

For the following exercises, use a calculator to graph[latex]\,f\left(x\right).\,[/latex]Use the graph to solve[latex]\,f\left(x\right)>0.[/latex]

70. [latex]f\left(x\right)=\frac{2}{x+1}[/latex]

71. [latex]f\left(x\right)=\frac{4}{2x-3}[/latex]

[latex]\left(\frac{3}{2},\infty \right)[/latex]

72. [latex]f\left(x\right)=\frac{2}{\left(x-1\right)\left(x+2\right)}[/latex]

73. [latex]f\left(x\right)=\frac{x+2}{\left(x-1\right)\left(x-4\right)}[/latex]

[latex]\left(-2,1\right)\cup \left(4,\infty \right)[/latex]

74. [latex]f\left(x\right)=\frac{{\left(x+3\right)}^{2}}{{\left(x-1\right)}^{2}\left(x+1\right)}[/latex]

For the following exercises, identify the removable discontinuity.

75. [latex]f\left(x\right)=\frac{{x}^{2}-4}{x-2}[/latex]

[latex]\left(2,4\right)[/latex]

76. [latex]f\left(x\right)=\frac{{x}^{3}+1}{x+1}[/latex]

77. [latex]f\left(x\right)=\frac{{x}^{2}+x-6}{x-2}[/latex]

[latex]\left(2,5\right)[/latex]

78. [latex]f\left(x\right)=\frac{2{x}^{2}+5x-3}{x+3}[/latex]

79. [latex]f\left(x\right)=\frac{{x}^{3}+{x}^{2}}{x+1}[/latex]

[latex]\left(–1,\text{1}\right)[/latex]

Real-World Applications

For the following exercises, express a rational function that describes the situation.

80. A large mixing tank currently contains 200 gallons of water, into which 10 pounds of sugar have been mixed. A tap will open, pouring 10 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 3 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after[latex]\,t\,[/latex]minutes.

81. A large mixing tank currently contains 300 gallons of water, into which 8 pounds of sugar have been mixed. A tap will open, pouring 20 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 2 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after[latex]\,t\,[/latex]minutes.

[latex]C\left(t\right)=\frac{8+2t}{300+20t}[/latex]

For the following exercises, use the given rational function to answer the question.

82. The concentration[latex]\,C\,[/latex]of a drug in a patient’s bloodstream[latex]\,t\,[/latex]hours after injection in given by[latex]\,C\left(t\right)=\frac{2t}{3+{t}^{2}}.\,[/latex]What happens to the concentration of the drug as[latex]\,t\,[/latex]increases?

83. The concentration[latex]\,C\,[/latex]of a drug in a patient’s bloodstream [latex]\,t\,[/latex] hours after injection is given by[latex]\,C\left(t\right)=\frac{100t}{2{t}^{2}+75}.\,[/latex]Use a calculator to approximate the time when the concentration is highest.

After about 6.12 hours.

For the following exercises, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.

84. An open box with a square base is to have a volume of 108 cubic inches. Find the dimensions of the box that will have minimum surface area. Let[latex]\,x\,[/latex]= length of the side of the base.

85. A rectangular box with a square base is to have a volume of 20 cubic feet. The material for the base costs 30 cents/ square foot. The material for the sides costs 10 cents/square foot. The material for the top costs 20 cents/square foot. Determine the dimensions that will yield minimum cost. Let[latex]\,x\,[/latex]= length of the side of the base.

[latex]A\left(x\right)=50{x}^{2}+\frac{800}{x}.\,[/latex]2 by 2 by 5 feet.

86. A right circular cylinder has volume of 100 cubic inches. Find the radius and height that will yield minimum surface area. Let[latex]\,x\,[/latex]= radius.

87. A right circular cylinder with no top has a volume of 50 cubic meters. Find the radius that will yield minimum surface area. Let[latex]\,x\,[/latex]= radius.

[latex]A\left(x\right)=\pi {x}^{2}+\frac{100}{x}.\,[/latex]Radius = 2.52 meters.

88. A right circular cylinder is to have a volume of 40 cubic inches. It costs 4 cents/square inch to construct the top and bottom and 1 cent/square inch to construct the rest of the cylinder. Find the radius to yield minimum cost. Let[latex]\,x\,[/latex]= radius.

Media Attributions

• 5.6 Fig 1 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 2 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 3 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 4 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 5 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 6 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 7 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 “Try It 2” solution © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 8 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 9 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 10 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 11 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 12 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 13 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 14 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Synthetic Division chart © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 15 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 16 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 17 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 18 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 19 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 20 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 21 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Try It Solution B 8 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 22 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 5.6 Fig 23 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Rational Functions

Introduction to rational functions, learning objectives.

By the end of this lesson, you will be able to:

• Use arrow notation.
• Solve applied problems involving rational functions.
• Find the domains of rational functions.
• Identify vertical asymptotes.
• Identify horizontal asymptotes.
• Graph rational functions.

Suppose we know that the cost of making a product is dependent on the number of items, x , produced. This is given by the equation [latex]C\left(x\right)=15,000x - 0.1{x}^{2}+1000[/latex]. If we want to know the average cost for producing x  items, we would divide the cost function by the number of items, x .

The average cost function, which yields the average cost per item for x  items produced, is

Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.

In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.

• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

3.7 Rational Functions

Learning objectives.

In this section, you will:

• Use arrow notation.
• Solve applied problems involving rational functions.
• Find the domains of rational functions.
• Identify vertical asymptotes.
• Identify horizontal asymptotes.
• Graph rational functions.

Suppose we know that the cost of making a product is dependent on the number of items, x , x , produced. This is given by the equation C ( x ) = 15,000 x − 0.1 x 2 + 1000. C ( x ) = 15,000 x − 0.1 x 2 + 1000. If we want to know the average cost for producing x x items, we would divide the cost function by the number of items, x . x .

The average cost function, which yields the average cost per item for x x items produced, is

Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.

In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.

Using Arrow Notation

We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Examine these graphs, as shown in Figure 1 , and notice some of their features.

Several things are apparent if we examine the graph of f ( x ) = 1 x . f ( x ) = 1 x .

• On the left branch of the graph, the curve approaches the x -axis ( y = 0 ) as x → – ∞ . ( y = 0 ) as x → – ∞ .
• As the graph approaches x = 0 x = 0 from the left, the curve drops, but as we approach zero from the right, the curve rises.
• Finally, on the right branch of the graph, the curves approaches the x- axis ( y = 0 ) as x → ∞ . ( y = 0 ) as x → ∞ .

To summarize, we use arrow notation to show that x x or f ( x ) f ( x ) is approaching a particular value. See Table 1 .

Local Behavior of f ( x ) = 1 x f ( x ) = 1 x

Let’s begin by looking at the reciprocal function, f ( x ) = 1 x . f ( x ) = 1 x . We cannot divide by zero, which means the function is undefined at x = 0 ; x = 0 ; so zero is not in the domain . As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in Table 2 .

We write in arrow notation

As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). We can see this behavior in Table 3 .

See Figure 2 .

This behavior creates a vertical asymptote , which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line x = 0 x = 0 as the input becomes close to zero. See Figure 3 .

Vertical Asymptote

A vertical asymptote of a graph is a vertical line x = a x = a where the graph tends toward positive or negative infinity as the input approaches a a from either the left or the right. We write

End Behavior of f ( x ) = 1 x f ( x ) = 1 x

As the values of x x approach infinity, the function values approach 0. As the values of x x approach negative infinity, the function values approach 0. See Figure 4 . Symbolically, using arrow notation

As  x → ∞ , f ( x ) → 0 , and as  x → − ∞ , f ( x ) → 0. As  x → ∞ , f ( x ) → 0 , and as  x → − ∞ , f ( x ) → 0.

Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. This behavior creates a horizontal asymptote , a horizontal line that the graph approaches as the input increases or decreases without bound. In this case, the graph is approaching the horizontal line y = 0. y = 0. See Figure 5 .

Horizontal Asymptote

A horizontal asymptote of a graph is a horizontal line y = b y = b where the graph approaches the line as the inputs increase or decrease without bound. We write

Use arrow notation to describe the end behavior and local behavior of the function graphed in Figure 6 .

Notice that the graph is showing a vertical asymptote at x = 2 , x = 2 , which tells us that the function is undefined at x = 2. x = 2.

And as the inputs decrease without bound, the graph appears to be leveling off at output values of 4, indicating a horizontal asymptote at y = 4. y = 4. As the inputs increase without bound, the graph levels off at 4.

Use arrow notation to describe the end behavior and local behavior for the reciprocal squared function.

Using Transformations to Graph a Rational Function

Sketch a graph of the reciprocal function shifted two units to the left and up three units. Identify the horizontal and vertical asymptotes of the graph, if any.

Shifting the graph left 2 and up 3 would result in the function

or equivalently, by giving the terms a common denominator,

The graph of the shifted function is displayed in Figure 7 .

Notice that this function is undefined at x = − 2 , x = − 2 , and the graph also is showing a vertical asymptote at x = − 2. x = − 2.

As the inputs increase and decrease without bound, the graph appears to be leveling off at output values of 3, indicating a horizontal asymptote at y = 3. y = 3.

Notice that horizontal and vertical asymptotes are shifted left 2 and up 3 along with the function.

Sketch the graph, and find the horizontal and vertical asymptotes of the reciprocal squared function that has been shifted right 3 units and down 4 units.

Solving Applied Problems Involving Rational Functions

In Example 2 , we shifted a toolkit function in a way that resulted in the function f ( x ) = 3 x + 7 x + 2 . f ( x ) = 3 x + 7 x + 2 . This is an example of a rational function. A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.

Rational Function

A rational function is a function that can be written as the quotient of two polynomial functions P ( x ) and Q ( x ) . P ( x ) and Q ( x ) .

Solving an Applied Problem Involving a Rational Function

After running out of pre-packaged supplies, a nurse in a refugee camp is preparing an intravenous sugar solution for patients in the camp hospital. A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of distilled water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration (pounds per gallon) of sugar in the tank after 12 minutes. Is that a greater concentration than at the beginning?

Let t t be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:

The concentration, C , C , will be the ratio of pounds of sugar to gallons of water

The concentration after 12 minutes is given by evaluating C ( t ) C ( t ) at t = 12. t = 12.

This means the concentration is 17 pounds of sugar to 220 gallons of water.

At the beginning, the concentration is

Since 17 220 ≈ 0.08 > 1 20 = 0.05 , 17 220 ≈ 0.08 > 1 20 = 0.05 , the concentration is greater after 12 minutes than at the beginning.

To find the horizontal asymptote, divide the leading coefficient in the numerator by the leading coefficient in the denominator:

Notice the horizontal asymptote is y = 0.1. y = 0.1. This means the concentration, C , C , the ratio of pounds of sugar to gallons of water, will approach 0.1 in the long term.

There are 1,200 first-year and 1,500 second-year students at a rally at noon. After 12 p.m., 20 first-year students arrive at the rally every five minutes while 15 second-year students leave the rally. Find the ratio of first-year to second-year students at 1 p.m.

Finding the Domains of Rational Functions

A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

Domain of a Rational Function

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

Given a rational function, find the domain.

• Set the denominator equal to zero.
• Solve to find the x -values that cause the denominator to equal zero.
• The domain is all real numbers except those found in Step 2.

Finding the Domain of a Rational Function

Find the domain of f ( x ) = x + 3 x 2 − 9 . f ( x ) = x + 3 x 2 − 9 .

Begin by setting the denominator equal to zero and solving.

The denominator is equal to zero when x = ± 3. x = ± 3. The domain of the function is all real numbers except x = ± 3. x = ± 3.

A graph of this function, as shown in Figure 8 , confirms that the function is not defined when x = ± 3. x = ± 3.

There is a vertical asymptote at x = 3 x = 3 and a hole in the graph at x = − 3. x = − 3. We will discuss these types of holes in greater detail later in this section.

Find the domain of f ( x ) = 4 x 5 ( x − 1 ) ( x − 5 ) . f ( x ) = 4 x 5 ( x − 1 ) ( x − 5 ) .

Identifying Vertical Asymptotes of Rational Functions

By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.

Vertical Asymptotes

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

Given a rational function, identify any vertical asymptotes of its graph.

• Factor the numerator and denominator.
• Note any restrictions in the domain of the function.
• Reduce the expression by canceling common factors in the numerator and the denominator.
• Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
• Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities.

Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of k ( x ) = 5 + 2 x 2 2 − x − x 2 . k ( x ) = 5 + 2 x 2 2 − x − x 2 .

First, factor the numerator and denominator.

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

Neither x = – 2 x = – 2 nor x = 1 x = 1 are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph in Figure 9 confirms the location of the two vertical asymptotes.

Removable Discontinuities

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity .

For example, the function f ( x ) = x 2 − 1 x 2 − 2 x − 3 f ( x ) = x 2 − 1 x 2 − 2 x − 3 may be re-written by factoring the numerator and the denominator.

Notice that x + 1 x + 1 is a common factor to the numerator and the denominator. The zero of this factor, x = − 1 , x = − 1 , is the location of the removable discontinuity. Notice also that x – 3 x – 3 is not a factor in both the numerator and denominator. The zero of this factor, x = 3 , x = 3 , is the vertical asymptote. See Figure 10 .

Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at x = a x = a if a a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of k ( x ) = x − 2 x 2 − 4 . k ( x ) = x − 2 x 2 − 4 .

Factor the numerator and the denominator.

Notice that there is a common factor in the numerator and the denominator, x – 2. x – 2. The zero for this factor is x = 2. x = 2. This is the location of the removable discontinuity.

Notice that there is a factor in the denominator that is not in the numerator, x + 2. x + 2. The zero for this factor is x = − 2. x = − 2. The vertical asymptote is x = − 2. x = − 2. See Figure 11 .

The graph of this function will have the vertical asymptote at x = −2 , x = −2 , but at x = 2 x = 2 the graph will have a hole.

Find the vertical asymptotes and removable discontinuities of the graph of f ( x ) = x 2 − 25 x 3 − 6 x 2 + 5 x . f ( x ) = x 2 − 25 x 3 − 6 x 2 + 5 x .

Identifying Horizontal Asymptotes of Rational Functions

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.

There are three distinct outcomes when checking for horizontal asymptotes:

Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y = 0. y = 0.

In this case, the end behavior is f ( x ) ≈ 4 x x 2 = 4 x . f ( x ) ≈ 4 x x 2 = 4 x . This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function g ( x ) = 4 x , g ( x ) = 4 x , and the outputs will approach zero, resulting in a horizontal asymptote at y = 0. y = 0. See Figure 12 . Note that this graph crosses the horizontal asymptote.

Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.

In this case, the end behavior is f ( x ) ≈ 3 x 2 x = 3 x . f ( x ) ≈ 3 x 2 x = 3 x . This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function g ( x ) = 3 x . g ( x ) = 3 x . As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of g ( x ) = 3 x g ( x ) = 3 x looks like a diagonal line, and since f f will behave similarly to g , g , it will approach a line close to y = 3 x . y = 3 x . This line is a slant asymptote.

To find the equation of the slant asymptote, divide 3 x 2 − 2 x + 1 x − 1 . 3 x 2 − 2 x + 1 x − 1 . The quotient is 3 x + 1 , 3 x + 1 , and the remainder is 2. The slant asymptote is the graph of the line g ( x ) = 3 x + 1. g ( x ) = 3 x + 1. See Figure 13 .

Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at y = a n b n , y = a n b n , where a n a n and b n b n are the leading coefficients of p ( x ) p ( x ) and q ( x ) q ( x ) for f ( x ) = p ( x ) q ( x ) , q ( x ) ≠ 0. f ( x ) = p ( x ) q ( x ) , q ( x ) ≠ 0.

In this case, the end behavior is f ( x ) ≈ 3 x 2 x 2 = 3. f ( x ) ≈ 3 x 2 x 2 = 3. This tells us that as the inputs grow large, this function will behave like the function g ( x ) = 3 , g ( x ) = 3 , which is a horizontal line. As x → ± ∞ , f ( x ) → 3 , x → ± ∞ , f ( x ) → 3 , resulting in a horizontal asymptote at y = 3. y = 3. See Figure 14 . Note that this graph crosses the horizontal asymptote.

Notice that, while the graph of a rational function will never cross a vertical asymptote , the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.

It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

with end behavior

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

• Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0. y = 0.
• Degree of numerator is greater than degree of denominator by one : no horizontal asymptote; slant asymptote.
• Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Identifying Horizontal and Slant Asymptotes

For the functions below, identify the horizontal or slant asymptote.

• ⓐ g ( x ) = 6 x 3 − 10 x 2 x 3 + 5 x 2 g ( x ) = 6 x 3 − 10 x 2 x 3 + 5 x 2
• ⓑ h ( x ) = x 2 − 4 x + 1 x + 2 h ( x ) = x 2 − 4 x + 1 x + 2
• ⓒ k ( x ) = x 2 + 4 x x 3 − 8 k ( x ) = x 2 + 4 x x 3 − 8

For these solutions, we will use f ( x ) = p ( x ) q ( x ) , q ( x ) ≠ 0. f ( x ) = p ( x ) q ( x ) , q ( x ) ≠ 0.

• ⓐ g ( x ) = 6 x 3 − 10 x 2 x 3 + 5 x 2 : g ( x ) = 6 x 3 − 10 x 2 x 3 + 5 x 2 : The degree of p = degree of q = 3 , p = degree of q = 3 , so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at y = 6 2 y = 6 2 or y = 3. y = 3.

The quotient is x – 6 x – 6 and the remainder is 13. There is a slant asymptote at y = x – 6. y = x – 6.

• ⓒ k ( x ) = x 2 + 4 x x 3 − 8 : k ( x ) = x 2 + 4 x x 3 − 8 : The degree of p = 2 < p = 2 < degree of q = 3 , q = 3 , so there is a horizontal asymptote y = 0. y = 0.

Identifying Horizontal Asymptotes

In the sugar concentration problem earlier, we created the equation C ( t ) = 5 + t 100 + 10 t . C ( t ) = 5 + t 100 + 10 t .

Find the horizontal asymptote and interpret it in context of the problem.

Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is t , t , with coefficient 1. In the denominator, the leading term is 10 t , 10 t , with coefficient 10. The horizontal asymptote will be at the ratio of these values:

This function will have a horizontal asymptote at y = 1 10 . y = 1 10 .

This tells us that as the values of t increase, the values of C C will approach 1 10 . 1 10 . In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or 1 10 1 10 pounds per gallon.

Identifying Horizontal and Vertical Asymptotes

Find the horizontal and vertical asymptotes of the function

First, note that this function has no common factors, so there are no potential removable discontinuities.

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at x = 1 , – 2 , and  5 , x = 1 , – 2 , and  5 , indicating vertical asymptotes at these values.

The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as x → ± ∞ , f ( x ) → 0. x → ± ∞ , f ( x ) → 0. This function will have a horizontal asymptote at y = 0. y = 0. See Figure 15 .

Find the vertical and horizontal asymptotes of the function:

f ( x ) = ( 2 x − 1 ) ( 2 x + 1 ) ( x − 2 ) ( x + 3 ) f ( x ) = ( 2 x − 1 ) ( 2 x + 1 ) ( x − 2 ) ( x + 3 )

Intercepts of Rational Functions

A rational function will have a y -intercept when the input is zero, if the function is defined at zero. A rational function will not have a y -intercept if the function is not defined at zero.

Likewise, a rational function will have x -intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x -intercepts can only occur when the numerator of the rational function is equal to zero.

Finding the Intercepts of a Rational Function

Find the intercepts of f ( x ) = ( x − 2 ) ( x + 3 ) ( x − 1 ) ( x + 2 ) ( x − 5 ) . f ( x ) = ( x − 2 ) ( x + 3 ) ( x − 1 ) ( x + 2 ) ( x − 5 ) .

We can find the y -intercept by evaluating the function at zero

The x -intercepts will occur when the function is equal to zero:

The y -intercept is ( 0 , –0.6 ) , ( 0 , –0.6 ) , the x -intercepts are ( 2 , 0 ) ( 2 , 0 ) and ( –3 , 0 ) . ( –3 , 0 ) . See Figure 16 .

Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x - and y -intercepts and the horizontal and vertical asymptotes.

• Graphing Rational Functions

In Example 9 , we see that the numerator of a rational function reveals the x -intercepts of the graph, whereas the denominator reveals the vertical asymptotes of the graph. As with polynomials, factors of the numerator may have integer powers greater than one. Fortunately, the effect on the shape of the graph at those intercepts is the same as we saw with polynomials.

The vertical asymptotes associated with the factors of the denominator will mirror one of the two toolkit reciprocal functions. When the degree of the factor in the denominator is odd, the distinguishing characteristic is that on one side of the vertical asymptote the graph heads towards positive infinity, and on the other side the graph heads towards negative infinity. See Figure 17 .

When the degree of the factor in the denominator is even, the distinguishing characteristic is that the graph either heads toward positive infinity on both sides of the vertical asymptote or heads toward negative infinity on both sides. See Figure 18 .

For example, the graph of f ( x ) = ( x + 1 ) 2 ( x − 3 ) ( x + 3 ) 2 ( x − 2 ) f ( x ) = ( x + 1 ) 2 ( x − 3 ) ( x + 3 ) 2 ( x − 2 ) is shown in Figure 19 .

• At the x -intercept x = − 1 x = − 1 corresponding to the ( x + 1 ) 2 ( x + 1 ) 2 factor of the numerator, the graph bounces, consistent with the quadratic nature of the factor.
• At the x -intercept x = 3 x = 3 corresponding to the ( x − 3 ) ( x − 3 ) factor of the numerator, the graph passes through the axis as we would expect from a linear factor.
• At the vertical asymptote x = − 3 x = − 3 corresponding to the ( x + 3 ) 2 ( x + 3 ) 2 factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function f ( x ) = 1 x 2 . f ( x ) = 1 x 2 .
• At the vertical asymptote x = 2 , x = 2 , corresponding to the ( x − 2 ) ( x − 2 ) factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side.

Given a rational function, sketch a graph.

• Evaluate the function at 0 to find the y -intercept.
• For factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the x -intercepts.
• Find the multiplicities of the x -intercepts to determine the behavior of the graph at those points.
• For factors in the denominator, note the multiplicities of the zeros to determine the local behavior. For those factors not common to the numerator, find the vertical asymptotes by setting those factors equal to zero and then solve.
• For factors in the denominator common to factors in the numerator, find the removable discontinuities by setting those factors equal to 0 and then solve.
• Compare the degrees of the numerator and the denominator to determine the horizontal or slant asymptotes.
• Sketch the graph.

Graphing a Rational Function

Sketch a graph of f ( x ) = ( x + 2 ) ( x − 3 ) ( x + 1 ) 2 ( x − 2 ) . f ( x ) = ( x + 2 ) ( x − 3 ) ( x + 1 ) 2 ( x − 2 ) .

We can start by noting that the function is already factored, saving us a step.

Next, we will find the intercepts. Evaluating the function at zero gives the y -intercept:

To find the x -intercepts, we determine when the numerator of the function is zero. Setting each factor equal to zero, we find x -intercepts at x = –2 x = –2 and x = 3. x = 3. At each, the behavior will be linear (multiplicity 1), with the graph passing through the intercept.

We have a y -intercept at ( 0 , 3 ) ( 0 , 3 ) and x -intercepts at ( –2 , 0 ) ( –2 , 0 ) and ( 3 , 0 ) . ( 3 , 0 ) .

To find the vertical asymptotes, we determine when the denominator is equal to zero. This occurs when x + 1 = 0 x + 1 = 0 and when x – 2 = 0 , x – 2 = 0 , giving us vertical asymptotes at x = –1 x = –1 and x = 2. x = 2.

There are no common factors in the numerator and denominator. This means there are no removable discontinuities.

Finally, the degree of denominator is larger than the degree of the numerator, telling us this graph has a horizontal asymptote at y = 0. y = 0.

To sketch the graph, we might start by plotting the three intercepts. Since the graph has no x -intercepts between the vertical asymptotes, and the y -intercept is positive, we know the function must remain positive between the asymptotes, letting us fill in the middle portion of the graph as shown in Figure 20 .

The factor associated with the vertical asymptote at x = −1 x = −1 was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.

For the vertical asymptote at x = 2 , x = 2 , the factor was not squared, so the graph will have opposite behavior on either side of the asymptote. See Figure 21 . After passing through the x -intercepts, the graph will then level off toward an output of zero, as indicated by the horizontal asymptote.

Given the function f ( x ) = ( x + 2 ) 2 ( x − 2 ) 2 ( x − 1 ) 2 ( x − 3 ) , f ( x ) = ( x + 2 ) 2 ( x − 2 ) 2 ( x − 1 ) 2 ( x − 3 ) , use the characteristics of polynomials and rational functions to describe its behavior and sketch the function.

Writing Rational Functions

Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x -intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x -intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.

Writing Rational Functions from Intercepts and Asymptotes

If a rational function has x -intercepts at x = x 1 , x 2 , ... , x n , x = x 1 , x 2 , ... , x n , vertical asymptotes at x = v 1 , v 2 , … , v m , x = v 1 , v 2 , … , v m , and no x i = any  v j , x i = any  v j , then the function can be written in the form:

where the powers p i p i or q i q i on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor a a can be determined given a value of the function other than the x -intercept or by the horizontal asymptote if it is nonzero.

Given a graph of a rational function, write the function.

• Determine the factors of the numerator. Examine the behavior of the graph at the x -intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the “simplest” function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
• Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
• Use any clear point on the graph to find the stretch factor.

Writing a Rational Function from Intercepts and Asymptotes

Write an equation for the rational function shown in Figure 22 .

The graph appears to have x -intercepts at x = – 2 x = – 2 and x = 3. x = 3. At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at x = – 1 x = – 1 seems to exhibit the basic behavior similar to 1 x , 1 x , with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at x = 2 x = 2 is exhibiting a behavior similar to 1 x 2 , 1 x 2 , with the graph heading toward negative infinity on both sides of the asymptote. See Figure 23 .

We can use this information to write a function of the form

To find the stretch factor, we can use another clear point on the graph, such as the y -intercept ( 0 , –2 ) . ( 0 , –2 ) .

This gives us a final function of f ( x ) = 4 ( x + 2 ) ( x − 3 ) 3 ( x + 1 ) ( x − 2 ) 2 . f ( x ) = 4 ( x + 2 ) ( x − 3 ) 3 ( x + 1 ) ( x − 2 ) 2 .

Access these online resources for additional instruction and practice with rational functions.

• Find the Equation of a Rational Function
• Determining Vertical and Horizontal Asymptotes
• Find the Intercepts, Asymptotes, and Hole of a Rational Function

3.7 Section Exercises

What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?

What is the fundamental difference in the graphs of polynomial functions and rational functions?

If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?

Can a graph of a rational function have no vertical asymptote? If so, how?

Can a graph of a rational function have no x -intercepts? If so, how?

For the following exercises, find the domain of the rational functions.

f ( x ) = x − 1 x + 2 f ( x ) = x − 1 x + 2

f ( x ) = x + 1 x 2 − 1 f ( x ) = x + 1 x 2 − 1

f ( x ) = x 2 + 4 x 2 − 2 x − 8 f ( x ) = x 2 + 4 x 2 − 2 x − 8

f ( x ) = x 2 + 4 x − 3 x 4 − 5 x 2 + 4 f ( x ) = x 2 + 4 x − 3 x 4 − 5 x 2 + 4

For the following exercises, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.

f ( x ) = 4 x − 1 f ( x ) = 4 x − 1

f ( x ) = 2 5 x + 2 f ( x ) = 2 5 x + 2

f ( x ) = x x 2 − 9 f ( x ) = x x 2 − 9

f ( x ) = x x 2 + 5 x − 36 f ( x ) = x x 2 + 5 x − 36

f ( x ) = 3 + x x 3 − 27 f ( x ) = 3 + x x 3 − 27

f ( x ) = 3 x − 4 x 3 − 16 x f ( x ) = 3 x − 4 x 3 − 16 x

f ( x ) = x 2 − 1 x 3 + 9 x 2 + 14 x f ( x ) = x 2 − 1 x 3 + 9 x 2 + 14 x

f ( x ) = x + 5 x 2 − 25 f ( x ) = x + 5 x 2 − 25

f ( x ) = x − 4 x − 6 f ( x ) = x − 4 x − 6

f ( x ) = 4 − 2 x 3 x − 1 f ( x ) = 4 − 2 x 3 x − 1

For the following exercises, find the x - and y -intercepts for the functions.

f ( x ) = x + 5 x 2 + 4 f ( x ) = x + 5 x 2 + 4

f ( x ) = x x 2 − x f ( x ) = x x 2 − x

f ( x ) = x 2 + 8 x + 7 x 2 + 11 x + 30 f ( x ) = x 2 + 8 x + 7 x 2 + 11 x + 30

f ( x ) = x 2 + x + 6 x 2 − 10 x + 24 f ( x ) = x 2 + x + 6 x 2 − 10 x + 24

f ( x ) = 94 − 2 x 2 3 x 2 − 12 f ( x ) = 94 − 2 x 2 3 x 2 − 12

For the following exercises, describe the local and end behavior of the functions.

f ( x ) = x 2 x + 1 f ( x ) = x 2 x + 1

f ( x ) = 2 x x − 6 f ( x ) = 2 x x − 6

f ( x ) = − 2 x x − 6 f ( x ) = − 2 x x − 6

f ( x ) = x 2 − 4 x + 3 x 2 − 4 x − 5 f ( x ) = x 2 − 4 x + 3 x 2 − 4 x − 5

f ( x ) = 2 x 2 − 32 6 x 2 + 13 x − 5 f ( x ) = 2 x 2 − 32 6 x 2 + 13 x − 5

For the following exercises, find the slant asymptote of the functions.

f ( x ) = 24 x 2 + 6 x 2 x + 1 f ( x ) = 24 x 2 + 6 x 2 x + 1

f ( x ) = 4 x 2 − 10 2 x − 4 f ( x ) = 4 x 2 − 10 2 x − 4

f ( x ) = 81 x 2 − 18 3 x − 2 f ( x ) = 81 x 2 − 18 3 x − 2

f ( x ) = 6 x 3 − 5 x 3 x 2 + 4 f ( x ) = 6 x 3 − 5 x 3 x 2 + 4

f ( x ) = x 2 + 5 x + 4 x − 1 f ( x ) = x 2 + 5 x + 4 x − 1

For the following exercises, use the given transformation to graph the function. Note the vertical and horizontal asymptotes.

The reciprocal function shifted up two units.

The reciprocal function shifted down one unit and left three units.

The reciprocal squared function shifted to the right 2 units.

The reciprocal squared function shifted down 2 units and right 1 unit.

For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.

p ( x ) = 2 x − 3 x + 4 p ( x ) = 2 x − 3 x + 4

q ( x ) = x − 5 3 x − 1 q ( x ) = x − 5 3 x − 1

s ( x ) = 4 ( x − 2 ) 2 s ( x ) = 4 ( x − 2 ) 2

r ( x ) = 5 ( x + 1 ) 2 r ( x ) = 5 ( x + 1 ) 2

f ( x ) = 3 x 2 − 14 x − 5 3 x 2 + 8 x − 16 f ( x ) = 3 x 2 − 14 x − 5 3 x 2 + 8 x − 16

g ( x ) = 2 x 2 + 7 x − 15 3 x 2 − 14 x + 15 g ( x ) = 2 x 2 + 7 x − 15 3 x 2 − 14 x + 15

a ( x ) = x 2 + 2 x − 3 x 2 − 1 a ( x ) = x 2 + 2 x − 3 x 2 − 1

b ( x ) = x 2 − x − 6 x 2 − 4 b ( x ) = x 2 − x − 6 x 2 − 4

h ( x ) = 2 x 2 + x − 1 x − 4 h ( x ) = 2 x 2 + x − 1 x − 4

k ( x ) = 2 x 2 − 3 x − 20 x − 5 k ( x ) = 2 x 2 − 3 x − 20 x − 5

w ( x ) = ( x − 1 ) ( x + 3 ) ( x − 5 ) ( x + 2 ) 2 ( x − 4 ) w ( x ) = ( x − 1 ) ( x + 3 ) ( x − 5 ) ( x + 2 ) 2 ( x − 4 )

z ( x ) = ( x + 2 ) 2 ( x − 5 ) ( x − 3 ) ( x + 1 ) ( x + 4 ) z ( x ) = ( x + 2 ) 2 ( x − 5 ) ( x − 3 ) ( x + 1 ) ( x + 4 )

For the following exercises, write an equation for a rational function with the given characteristics.

Vertical asymptotes at x = 5 x = 5 and x = − 5 , x = − 5 , x -intercepts at ( 2 , 0 ) ( 2 , 0 ) and ( − 1 , 0 ) , ( − 1 , 0 ) , y -intercept at ( 0 , 4 ) ( 0 , 4 )

Vertical asymptotes at x = − 4 x = − 4 and x = − 1 , x = − 1 , x- intercepts at ( 1 , 0 ) ( 1 , 0 ) and ( 5 , 0 ) , ( 5 , 0 ) , y- intercept at ( 0 , 7 ) ( 0 , 7 )

Vertical asymptotes at x = − 4 x = − 4 and x = − 5 , x = − 5 , x -intercepts at ( 4 , 0 ) ( 4 , 0 ) and ( − 6 , 0 ) , ( − 6 , 0 ) , Horizontal asymptote at y = 7 y = 7

Vertical asymptotes at x = − 3 x = − 3 and x = 6 , x = 6 , x -intercepts at ( − 2 , 0 ) ( − 2 , 0 ) and ( 1 , 0 ) , ( 1 , 0 ) , Horizontal asymptote at y = − 2 y = − 2

Vertical asymptote at x = − 1 , x = − 1 , Double zero at x = 2 , x = 2 , y -intercept at ( 0 , 2 ) ( 0 , 2 )

Vertical asymptote at x = 3 , x = 3 , Double zero at x = 1 , x = 1 , y -intercept at ( 0 , 4 ) ( 0 , 4 )

For the following exercises, use the graphs to write an equation for the function.

For the following exercises, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote

f ( x ) = 1 x − 2 f ( x ) = 1 x − 2

f ( x ) = x x − 3 f ( x ) = x x − 3

f ( x ) = 2 x x + 4 f ( x ) = 2 x x + 4

f ( x ) = 2 x ( x − 3 ) 2 f ( x ) = 2 x ( x − 3 ) 2

f ( x ) = x 2 x 2 + 2 x + 1 f ( x ) = x 2 x 2 + 2 x + 1

For the following exercises, use a calculator to graph f ( x ) . f ( x ) . Use the graph to solve f ( x ) > 0. f ( x ) > 0.

f ( x ) = 2 x + 1 f ( x ) = 2 x + 1

f ( x ) = 4 2 x − 3 f ( x ) = 4 2 x − 3

f ( x ) = 2 ( x − 1 ) ( x + 2 ) f ( x ) = 2 ( x − 1 ) ( x + 2 )

f ( x ) = x + 2 ( x − 1 ) ( x − 4 ) f ( x ) = x + 2 ( x − 1 ) ( x − 4 )

f ( x ) = ( x + 3 ) 2 ( x − 1 ) 2 ( x + 1 ) f ( x ) = ( x + 3 ) 2 ( x − 1 ) 2 ( x + 1 )

For the following exercises, identify the removable discontinuity.

f ( x ) = x 2 − 4 x − 2 f ( x ) = x 2 − 4 x − 2

f ( x ) = x 3 + 1 x + 1 f ( x ) = x 3 + 1 x + 1

f ( x ) = x 2 + x − 6 x − 2 f ( x ) = x 2 + x − 6 x − 2

f ( x ) = 2 x 2 + 5 x − 3 x + 3 f ( x ) = 2 x 2 + 5 x − 3 x + 3

f ( x ) = x 3 + x 2 x + 1 f ( x ) = x 3 + x 2 x + 1

Real-World Applications

For the following exercises, express a rational function that describes the situation.

In the refugee camp hospital, a large mixing tank currently contains 200 gallons of water, into which 10 pounds of sugar have been mixed. A tap will open, pouring 10 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 3 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after t t minutes.

In the refugee camp hospital, a large mixing tank currently contains 300 gallons of water, into which 8 pounds of sugar have been mixed. A tap will open, pouring 20 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 2 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after t t minutes.

For the following exercises, use the given rational function to answer the question.

The concentration C C of a drug in a patient’s bloodstream t t hours after injection in given by C ( t ) = 2 t 3 + t 2 . C ( t ) = 2 t 3 + t 2 . What happens to the concentration of the drug as t t increases?

The concentration C C of a drug in a patient’s bloodstream t t hours after injection is given by C ( t ) = 100 t 2 t 2 + 75 . C ( t ) = 100 t 2 t 2 + 75 . Use a calculator to approximate the time when the concentration is highest.

For the following exercises, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.

An open box with a square base is to have a volume of 108 cubic inches. Find the dimensions of the box that will have minimum surface area. Let x x = length of the side of the base.

A rectangular box with a square base is to have a volume of 20 cubic feet. The material for the base costs 30 cents/ square foot. The material for the sides costs 10 cents/square foot. The material for the top costs 20 cents/square foot. Determine the dimensions that will yield minimum cost. Let x x = length of the side of the base.

A right circular cylinder has volume of 100 cubic inches. Find the radius and height that will yield minimum surface area. Let x x = radius.

A right circular cylinder with no top has a volume of 50 cubic meters. Find the radius that will yield minimum surface area. Let x x = radius.

A right circular cylinder is to have a volume of 40 cubic inches. It costs 4 cents/square inch to construct the top and bottom and 1 cent/square inch to construct the rest of the cylinder. Find the radius to yield minimum cost. Let x x = radius.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Precalculus 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions
• Section URL: https://openstax.org/books/precalculus-2e/pages/3-7-rational-functions

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Rational Function Problems

These lessons are compiled to help PreCalculus students learn about rational function problems and applications.

Related Pages Simplifying Rational Expressions Graphing Rational Functions PreCalculus Lessons

The following figure shows how to solve rational equations . Scroll down the page for examples and solutions on how to solve rational function problems and applications.

Rational Function Problems - Work And Tank

The video explains application problems that use rational equations. Part 1 of 2.

• Martin can pour a concrete walkway in 6 hours working alone. Victor has more experience and can pour the same walkway in 4 hours working alone. How long will it take both people to pour the concrete walkway working together?
• An inlet pipe can fill a water tank in 12 hours. An outlet pipe can drain the tank in 20 hours. If both pipes are mistakenly left open, how long will it take to fill the tank?

Rational Function Applications - Work And Rate

The video explains application problems that use rational equations. Part 2 of 2.

• One person can complete a task 8 hours sooner than another person. Working together, both people can perform the task in 3 hours. How many hours does it take each person to complete the task working alone?
• The speed of a passenger train is 12 mph faster than the speed of the freight train. The passenger train travels 330 miles in the same time it takes the freight train to travel 270 miles. Find the speed of each train.

Rational Functions Word Problems - Work, Tank And Pipe

Here are a few examples of work problems that are solved with rational equations.

• Sam can paint a house in 5 hours. Gary can do it in 4 hours. How long will it take the two working together?
• Joy can file 100 claims in 5 hours. Stephen can file 100 claims in 8 hours. If they work together, how long will it take to file 100 claims?
• A water tank is emptied through two drains in 50 minutes. If only the larger drain is used, the tank will empty in 85 minutes. How long would it take to empty if only the smaller drain is used?
• One computer can run a sorting algorithm in 24 minutes. If a second computer is used together with the first, it takes 13 minutes. How long would it take the second computer alone?
• Two pipes are filling a tank. One pipe fills three times as fast as the other. With both pipes working, the tank fills in 84 minutes. How long would each pipe take working alone?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Solving Rational Equations and Applications

Learning Objective(s)

·          Solve rational equations.

·          Check for extraneous solutions.

·          Solve application problems involving rational equations.

Introduction

You can solve these equations using the techniques for performing operations with rational expressions and the procedures for solving algebraic equations. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing distance-speed-time relationships and for modeling work problems that involve more than one person.

Solving Rational Equations

One method for solving rational equations is to rewrite the rational expressions in terms of a common denominator. Then, since you know the numerators are equal, you can solve for the variable. To illustrate this, let’s look at a very simple equation.

Since the denominator of each expression is the same, the numerators must be equivalent. This means that x = 2.

This is true for rational equations with polynomials too.

Since the denominators of each rational expression are the same, x + 4, the numerators must be equivalent for the equation to be true. So, x – 5 = 11 and x = 16.

Just as with other algebraic equations, you can check your solution in the original rational equation by substituting the value for the variable back into the equation and simplifying.

When the terms in a rational equation have unlike denominators, solving the equation will involve some extra steps. One way of solving rational equations with unlike denominators is to multiply both sides of the equation by the least common multiple of the denominators of all the fractions contained in the equation. This eliminates the denominators and turns the rational equation into a polynomial equation. Here’s an example.

Another way to solve a rational equation with unlike denominators is to rewrite each term with a common denominator and then just create an equation from the numerators. This works because if the denominators are the same, the numerators must be equal. The next example shows this approach with the same equation you just solved:

In some instances, you’ll need to take some additional steps in finding a common denominator. Consider the example below, which illustrates using what you know about denominators to rewrite one of the expressions in the equation.

You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.

Excluded Values and Extraneous Solutions

Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values . Let’s look at an example.

Let’s look at an example with a more complicated denominator.

You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions . That's why it is always important to check all solutions in the original equations—you may find that they yield untrue statements or produce undefined expressions.

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for m.

-4 is excluded because

it leads to division by 0.

Check the solutions in the original equation.

Since m = −4 leads to division by 0, it is an extraneous solution.

Solving Application Problems

A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, W = rt . (Notice that the work formula is very similar to the relationship between distance, rate, and time, or d = rt .) The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). The work formula has 3 versions.

Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.

Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.

The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t , set it equal to the amount of work done, and solve the rational equation.

You can solve rational equations by finding a common denominator. By rewriting the equation so that all terms have the common denominator, you can solve for the variable using just the numerators. Or, you can multiply both sides of the equation by the least common multiple of the denominators so that all terms become polynomials instead of rational expressions. Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.

An important step in solving rational equations is to reject any extraneous solutions from the final answer. Extraneous solutions are solutions that don't satisfy the original form of the equation because they produce untrue statements or are excluded values that make a denominator equal to 0.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

15.2.1: Solving Rational Equations and Applications

• Last updated
• Save as PDF
• Page ID 72095

• The NROC Project

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve rational equations.
• Check for extraneous solutions.
• Solve application problems involving rational equations.

Introduction

Equations that contain rational expressions are called rational equations . For example, \(\ \frac{2 x+1}{4}=\frac{x}{3}\) is a rational equation.

You can solve these equations using the techniques for performing operations with rational expressions and the procedures for solving algebraic equations. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing distance-speed-time relationships and for modeling work problems that involve more than one person.

Solving Rational Equations

One method for solving rational equations is to rewrite the rational expressions in terms of a common denominator. Then, since you know the numerators are equal, you can solve for the variable. To illustrate this, let’s look at a very simple equation.

\(\ \frac{2}{5}=\frac{x}{5}\)

Since the denominator of each expression is the same, the numerators must be equivalent. This means that \(\ x=2\).

This is true for rational equations with polynomials too.

\(\ \frac{x-5}{x+4}=\frac{11}{x+4}\)

Since the denominators of each rational expression are the same, \(\ x+4\), the numerators must be equivalent for the equation to be true. So, \(\ x-5=11\) and \(\ x=16\).

Just as with other algebraic equations, you can check your solution in the original rational equation by substituting the value for the variable back into the equation and simplifying.

\(\ \begin{array}{c} \frac{16-5}{16+4}=\frac{11}{16+4} \\ \frac{11}{20}=\frac{11}{20} \end{array}\)

When the terms in a rational equation have unlike denominators, solving the equation will involve some extra steps. One way of solving rational equations with unlike denominators is to multiply both sides of the equation by the least common multiple of the denominators of all the fractions contained in the equation. This eliminates the denominators and turns the rational equation into a polynomial equation. Here’s an example.

Solve the equation \(\ \frac{x+5}{8}=\frac{7}{4}\)

Another way to solve a rational equation with unlike denominators is to rewrite each term with a common denominator and then just create an equation from the numerators. This works because if the denominators are the same, the numerators must be equal. The next example shows this approach with the same equation you just solved:

Solve the equation \(\ \frac{x+5}{8}=\frac{7}{4}\).

In some instances, you’ll need to take some additional steps in finding a common denominator. Consider the example below, which illustrates using what you know about denominators to rewrite one of the expressions in the equation.

Solve the equation \(\ \frac{x}{3}+1=\frac{4}{3}\).

You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.

Excluded Values and Extraneous Solutions

Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values . Let’s look at an example.

Solve the equation \(\ \frac{2 x-5}{x-5}=\frac{15}{x-5}\).

Give the excluded values for \(\ \frac{7}{p+2}+\frac{5}{p-2}=\frac{10 p-2}{p^{2}-4}\). Do not solve.

• \(\ \frac{2}{10}\)
• \(\ -2,2,4\)
• Incorrect. Excluded values are those values of the variable which result in a 0 in the denominator, not in the numerator. The correct answer is \(\ -2,2\).
• Incorrect. 2 is an excluded value, but -2 also results in a 0 in the denominator. The correct answer is \(\ -2,2\).
• Correct. -2 and 2, when substituted into the equation, result in a 0 in the denominator. Since division by 0 is undefined, both of these values are excluded from the solution.
• Incorrect. While -2 and 2 are excluded, 4 is not excluded because it does not cause the denominator to be 0. The correct answer is -2, 2.

Let’s look at an example with a more complicated denominator.

Solve the equation \(\ \frac{x}{x^{2}-9}+\frac{3}{x-3}=\frac{3}{x+3}\).

\(\ x=-18\)

Solve the equation: \(\ \frac{4}{m}=\frac{3}{m-2}, m \neq 0 \text { or } 2\)

• no solution
• Incorrect. You probably found the common denominator correctly, but forgot to distribute when you were simplifying. You also forgot to check your solution or note the excluded values; \(\ m \neq 2\) because it makes the expression on the right side undefined. Multiplying both sides by the common denominator gives \(\ \frac{4}{m} \cdot m(m-2)=\frac{3}{m-2} \cdot m(m-2)\), so \(\ 4 m-8=3 m\). The correct answer is \(\ m=8\).
• Incorrect. \(\ \frac{4}{m} \cdot m(m-2)=\frac{3}{m-2} \cdot m(m-2)\), so \(\ 4 m-8=3 m\). The solution, 8, is not an excluded value. The correct answer is \(\ m=8\).
• Correct. Multiplying both sides of the equation by the common denominator gives \(\ \frac{4}{m} \cdot m(m-2)=\frac{3}{m-2} \cdot m(m-2)\), so \(\ 4 m-8=3 m\). The correct answer is \(\ m=8\).

You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions . That's why it is always important to check all solutions in the original equations: you may find that they yield untrue statements or produce undefined expressions.

Solve the equation \(\ \frac{16}{m+4}=\frac{m^{2}}{m+4}\).

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \frac{5}{x-7}=\frac{2}{x-2}
• \frac{7x+5}{x-4}-\frac{6x-1}{x-3}-\frac{1}{x^{2}-7x+12}=1
• \frac{7}{x-3}-\frac{10}{x-2}-\frac{6}{x-1}=0
• \frac{x-3}{3-x}=2

rational-equation-calculator

• High School Math Solutions – Radical Equation Calculator Radical equations are equations involving radicals of any order. We will show examples of square roots; higher...

Please add a message.

Message received. Thanks for the feedback.