kinematics problem solving

• Exam Center
• Ticket Center
• Flash Cards
• Straight Line Motion

Kinematics Practice Problems with Answers

Are you struggling with kinematics problems? Do you want to understand the principles of motion in a clear, concise manner? Look no further! Our comprehensive guide on “Kinematics Problems” is here to help.

Whether you’re studying for an exam or working on homework, these solutions offer a practical approach to understanding and applying kinematics equations.

All kinematics equations are summarized in the following expressions: \begin{gather*} \Delta x=\frac{v_1+v_2}{2}\times \Delta t \\\\ v=v_0+at \\\\ \Delta x=\frac 12 at^2+v_0t \\\\ v^2-v_0^2=2a\Delta x \end{gather*} In the rest of this long article, you will see how to apply these equations in the given problems.

By the way, if you’re preparing for the AP Physics 1 exam , feel free to download this comprehensive AP formula sheet . It’s the ultimate resource you need!

Kinematics Practice Problems:

Problem (1): A car slows down its motion from 10 m/s to 6 m/s in 2 seconds under constant acceleration.  (a) What is its acceleration? (b) How far did the car travel during this time interval?

Solution : This is a basic kinematics problem, so we will explain the steps in detail.

Step 1: Since all these problems are in one dimension, draw a horizontal axis (like the positive $x$ axis), and place the object on it, so that its motion matches the direction of the axis. 

Step 2:  Specify the known and wanted information. Here, in the elapsed time interval $2\,{\rm s}$, the initial and final velocities of the car are given as $v_i=10\,{\rm m/s}$ and $v_f=6\,{\rm m/s}$. The wanted quantity is the constant acceleration of the object (car), $a=?$. 

Step 3: Apply the kinematics equation that is appropriate for this situation. 

(a) To find the acceleration in this problem, we are given the time, initial, and final velocity. The kinematics equation $v=v_0+at$ is suitable for this situation, as the only unknown variable is the acceleration $a$. By rearranging the equation, we get \begin{gather*} v=v_0+at\\\\ 6=10+a(2) \\\\ 6-10=2a \\\\\Rightarrow \quad a=\frac{6-10}{2}=-2\quad {\rm \frac{m}{s^2}}\end{gather*} Since the problem states that the acceleration is constant, we could also use any of the other constant acceleration kinematics equations. The negative sign of the acceleration indicates that it is directed toward the negative $x$ axis.

(b)  "How far'' indeed refers to the distance traveled, denoted by $x$ in the kinematics equations. 

Here, the best equation that relates the known and unknown information is $x=\frac 12 at^2+v_0t$ or $v^2-v_0^2=2ax$. We choose the first, so \begin{align*} x&=\frac 12 at^2+v_0t \\\\&=\frac 12 (-2)(2)^2+(10)(2) \\\\&=16\quad {\rm m}\end{align*} 

Our journey is taking us to the US, and we’re counting on your generosity ( here ) to help us maintain and enhance our website during this transition.

Problem (2): A moving object slows down from $12\,{\rm m/s}$ to rest at a distance of 20 m. Find the acceleration of the object (assumed constant).

Solution : In the diagram below, all known information along with the direction of the uniform motion is shown. 

A common phrase in kinematics problems is “ending or coming to a rest”, which means the final velocity of the object in the time interval we are considering is zero, $v_f=0$.

The kinematics equation that suits this problem is $v^2-v_0^2=2a(x-x_0)$, where the only unknown variable is the acceleration $a$. 

For simplicity, we can assume the initial position of the motion $x_0$ is zero in all kinematics problems, $x_0$. \begin{gather*} v^2-v_0^2=2ax\\\\0^2-(12)^2 =2a(20) \\\\ \rightarrow a=\frac{-144}{2\times 20}\\\\\Rightarrow \boxed{a=-3.6\quad {\rm \frac{m}{s^2}}}\end{gather*} As before, the negative sign indicates of the acceleration indicates that it is directed to the left .

Problem (3): A bullet leaves the muzzle of an 84-cm rifle with a speed of 521 m/s. Find the magnitude of the bullet's acceleration by assuming it is constant inside the barrel of the rifle.

Solution : The bullet accelerates from rest to a speed of 521 m/s over a distance of 0.84 meters. We have the following known quantities: the initial velocity $v_0$, ​ the final velocity $v$, and the displacement $x-x_0$. The unknown is acceleration $a$. The perfect kinematics equation that relates all these variables is $v^2-v_0^2=2a(x-x_0)$. Solving for $a$, we have: \begin{gather*}v^2-v_0^2=2a(x-x_0)\\\\ (521)^2-0=2(a)(0.84-0) \\\\ \Rightarrow \boxed{a=1.62\times 10^5\quad {\rm m/s^2}}\end{gather*} This calculation results in a very large acceleration. 

Problem (4): A car starts its motion from rest and uniformly accelerates at a rate of $4\,{\rm m/s^2}$ for 2 seconds in a straight line.  (a) How far did the car travel during those 2 seconds?  (b) What is the car's velocity at the end of that time interval?

Solution : "Start from rest'' means the initial object's velocity is zero, $v_0=0$. The known information are $a=4\,{\rm m/s^2}$, $t=2\,{\rm s}$ and wants the distance traveled $x=?$. 

(a) The kinematics equation that relates the given information is $x=\frac 12 at^2+v_0 t+x_0$ since the only unknown quantity is $x$. Given the known data, we can calculate $x$ as follows: \begin{align*} x&=\frac 12 at^2+v_0 t+x_0 \\\\&=\frac 12 (4)(2)^2+(0)(2) \\\\&=\boxed{8\quad {\rm m}}\end{align*} As before, we set $x_0=0$. 

(b) Now that we know the distance traveled by car in that time interval, we can use the following kinematics equation to find the car's final velocity $v$: \begin{align*} v^2-v_0^2 &=2a(x-x_0) \\\\v^2-(0)^2&=2(4)(8-0) \\\\v^2&=64\end{align*} Taking the square root, we get $v$: \[v=\sqrt{64}=\pm 8\quad {\rm \frac ms}\] We know that velocity is a vector quantity in physics and has both a direction and a magnitude. 

The magnitude of the velocity (speed) was obtained as 8 m/s, but in what direction? Or which sign should we choose? Because the car is uniformly accelerating without stopping in the positive $x$ axis, the correct sign for velocity is positive. 

Therefore, the car's final velocity is $\boxed{v_f=+8\,{\rm m/s}}$. 

Problem (5): We aim to design an airport runway with the following specifications: The lowest acceleration of a plane should be $4\,{\rm m/s^2}$, and its take-off speed should be 75 m/s. How long would the runway have to be to allow the planes to accelerate through it? 

Solution: The known quantities are acceleration $a=4\,{\rm m/s^2}$, and final velocity $v=75\,{\rm m/s}$. The wanted quantity is the runway length $\Delta x=x-x_0$. The ideal kinematics equation that relates these variables is $v^2-v_0^2=2a(x-x_0)$. \begin{align*} v^2-v_0^2&=2a\Delta x\\\\ (75)^2-0&=2(4) \Delta x\\\\ \Rightarrow \Delta x&=\boxed{703\quad {\rm m}}\end{align*} Thus, for the runway to be effective, its length must be at least approximately 703 meters.

Problem (6): A stone is dropped vertically from a high cliff. After 3.55 seconds, it hits the ground. How high is the cliff? 

Solution : There is another type of kinematics problem in one dimension but in the vertical direction. In such problems, the constant acceleration is that of free falling, $a=g=-10\,{\rm m/s^2}$.  

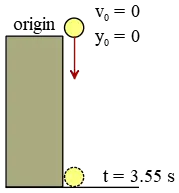
"Dropped'' or "released'' in free-falling problems means the initial velocity is zero, $v_0=0$.  In addition, it is always better to consider the point of release as the origin of the coordinate, so $y_0=0$. 

The most relevant kinematics equation for these known and wanted quantities is $y=-\frac 12 gt^2+v_0t+y_0$ \begin{align*} y&=-\frac 12 gt^2+v_0t+y_0 \\\\&=-\frac 12 (9.8)(3.55)^2+0+0\\\\&=\boxed{-61.8\quad {\rm m}}\end{align*} The negative indicates that the impact point is below our chosen origin . 

Problem (7): A car slows down uniformly from $45\,\rm m/s$ to rest in $10\,\rm s$. How far did it travel in this time interval?

Solution : List the data known as follows: initial speed $v_0=45\,\rm m/s$, final speed $v=0$, and the total time duration that this happened is $t=10\,\rm s$. The unknown is also the amount of displacement, $\Delta x$. 

The only kinematics equation that relates these together is $\Delta x=\frac{v_1+v_2}{2}\times \Delta t$, where $v_1$ and $v_2$ are the velocities at the beginning and end of that time interval. \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\times \Delta t \\\\ &=\frac{45+0}{2}\times 10 \\\\ &=\boxed{225\,\rm m}\end{align*} Keep in mind that we use this formula when the object slows down uniformly, or, in other words when the object's acceleration is constant.

Problem (8):  A ball is thrown into the air vertically from the ground level with an initial speed of 20 m/s.  (a) How long is the ball in the air? (b) At what height does the ball reach?

Solution : The throwing point is considered to be the origin of our coordinate system, so $y_0=0$. Given the initial velocity $v_0=+20\,{\rm m/s}$ and the gravitational acceleration $a=g=-9.8\,{\rm m/s^2}$. The wanted time is how long it takes the ball to reach the ground again.

To solve this free-fall problem , it is necessary to know some notes about free-falling objects. 

Note (1): Because the air resistance is neglected, the time the ball is going up is half the time it is going down.  

Note (2): At the highest point of the path, the velocity of the object is zero. 

(a) By applying the kinematics equation $v=v_0+at$ between the initial and the highest ($v=0$) points of the vertical path, we can find the going up time. \begin{align*} v&=v_0+at \\0&=20+(-9.8)t\\\Rightarrow t&=2.04\quad {\rm s}\end{align*} The total flight time is twice this time \[t_{tot}=2t=2(2.04)=4.1\,{\rm s}\] Hence, the ball takes about 4 seconds to reach the ground. 

(b) The kinematics equation $v^2-v_0^2=2a(y-y_0)$ is best for this part. \begin{align*} v^2-v_0^2&=2a(y-y_0) \\0-20^2&=2(-9.8)(y-0) \\ \Rightarrow y&=\boxed{20\quad {\rm m}}\end{align*} Hence, the ball goes up to a height of about 20 meters.

Problem (9): An object moving in a straight line with constant acceleration, has a velocity of $v=+10\,{\rm m/s}$ when it is at position $x=+6\,{\rm m}$ and of $v=+15\,{\rm m/s}$ when it is at $x=10\,{\rm m}$. Find the acceleration of the object.

Solution : Draw a diagram, put all known data into it, and find a relevant kinematics equation that relates them together. 

We want to analyze the motion in a distance interval of $\Delta x=x_2-x_1=10-6=4\,{\rm m}$, thus, we can consider the velocity at position $x_1=6\,{\rm m}$ as the initial velocity and at $x_2=10\,{\rm m}$ as the final velocity. 

The most relevant kinematics equation that relates these known quantities to the wanted acceleration $a$ is $v^2-v_0^2=2a(x-x_0)$, where $x-x_0$ is the same given distance interval. Thus, \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\ (15)^2-(10)^2&=2(a)(4) \\\\225-100&=8a\\\\\Rightarrow a&=\frac{125}{8}\\\\&=15.6\,{\rm m/s^2}\end{align*} 

Problem (10): A moving object accelerates uniformly from 75 m/s at time $t=0$ to 135 m/s at $t=10\,{\rm s}$. How far did it move at the time interval $t=2\,{\rm s}$ to $t=4\,{\rm s}$? 

Solution : Draw a diagram and implement all known data in it as below. 

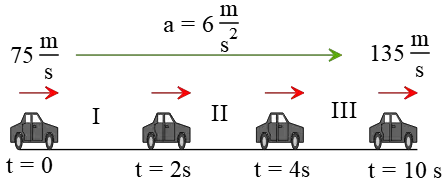
Because the problem tells us that the object accelerates uniformly, we can infer that its acceleration is constant throughout its entire path. 

Given the initial and final velocities of the moving object, we can determine its acceleration using the definition of instantaneous acceleration as follows: \[a=\frac{v_2-v_1}{t_2-t_1}=\frac{135-75}{10}=6\,{\rm m/s^2}\] To analyze the motion between the requested times (referred to as stage II in the figure), we need some information for that time interval, such as their velocities or the distance between them. 

As you can see in the figure, the initial velocity of stage II is the final velocity of stage I. By using a relevant kinematics equation that relates these data to each other, we find that \begin{align*} v&=v_0+at\\\\&=75+(6)(2) \\\\&=87\,{\rm m/s}\end{align*} This velocity will be the initial velocity for stage II of the motion. Now, all the known information for stage II is as follows: initial velocity $v_0=87\,{\rm m/s}$, acceleration $a=6\,{\rm m/s^2}$, and time interval $\Delta t=2\,{\rm s}$. The unknown is the distance traveled, denoted by $x=?$

The appropriate equation that relates all these variables is $x=\frac 12 at^2+v_0t+x_0$. Substituting the known values, we get \begin{align*}x&=\frac 12 at^2+v_0t+x_0\\\\&=\frac 12 (6)(2)^2+(87)(2)+0\\\\&=186\quad {\rm m}\end{align*} Hence, our moving object travels a distance of 186 m between the instances of 2 s and 4 s. 

Problem (11): A fast car starts from rest and accelerates at a uniform rate of $1.5\,{\rm m/s^2}$ for 4 seconds. After a while, the driver applies the brakes for 3 seconds, causing the car to uniformly slow down (decelerate) at a rate of $-2\,{\rm m/s^2}$.  (a) How fast is the car at the end of the braking period? (b) How far has the car traveled after the braking period?

Solution : This motion is divided into two parts. First, draw a diagram and specify each section's known kinematics quantities. 

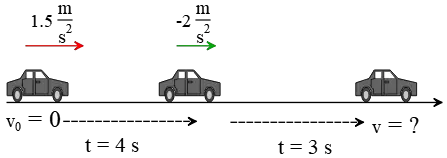
(a) In the first part, given the acceleration, initial velocity, and time interval, we can calculate the final velocity at the end of 4 seconds. \begin{align*} v&=v_0+at\\&=0+(1.5)(4) \\&=6\quad {\rm m/s}\end{align*} This velocity is considered as the initial velocity for the second part, where we want to find the final velocity.

In the next part, given the magnitude of acceleration and braking time interval, we can calculate the final velocity as follows: \begin{align*} v&=v_0+at\\&=6+(-2)(3) \\&=0\end{align*} The zero velocity here indicates that the car comes to a stop after the braking period.

(b) The distance traveled in the second part can now be calculated using the kinematics equation $x=\frac 12 at^2+v_0t+x_0$, because the only unknown quantity is distance $x$. \begin{align*} x&=\frac 12 at^2+v_0t+x_0\\\\&=\frac 12 (-2)(3)^2+(6)(3)+0\\\\&=+9\quad {\rm m}\end{align*} Therefore, after braking, the car travels a distance of 9 meters before coming to a stopped. 

Problem (12): A car moves at a speed of 20 m/s down a straight path. Suddenly, the driver sees an obstacle in front of him and applies the brakes. Before the car reaches a stop, it experiences an acceleration of $-10\,{\rm m/s^2}$.  (a) After applying the brakes, how far did it travel before stopping?  (b) How long does it take the car to reach a stop? 

Solution : As always, the first and most important step in solving a kinematics problem is to draw a diagram and input all known values into it, as shown below.

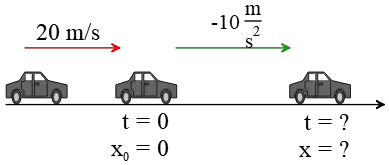
(a) The kinematics equation $v^2-v_0^2=2a(x-x_0)$ is the perfect equation to use here, as the only unknown quantity in it is the distance traveled, denoted by $x$. Thus, \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\ 0^2-(20)^2&=2(-10)(x-0) \\\\\Rightarrow \quad x&=\frac {-400}{-20}\\\\&=20\quad {\rm m}\end{align*} (b)  The phrase "How long does it take'' asks us to find the time interval. The initial and final velocities, as well as acceleration, are known, so the only relevant kinematics equation is $v=v_0+at$. Thus, \begin{align*} v&=v_0+at\\\\0&=20+(-10)t\\\\\Rightarrow t&=\frac{-20}{-10}\\\\&=2\quad {\rm s}\end{align*} Therefore, after braking, the car moves for 2 seconds before coming to a stop.

Problem (13): A sports car moves a distance of 100 m in 5 seconds with a uniform speed. Then, the driver brakes, and the car, comes to a stop after 4 seconds. Find the magnitude and direction of its acceleration (assumed constant). 

Solution : uniform speed means constant speed or zero acceleration for the motion before braking. Thus, we can use the definition of average velocity to find its speed just before braking as below \begin{align*} \bar{v}&=\frac{\Delta x}{\Delta t}\\\\&=\frac{100}{5}\\\\&=20\quad {\rm m/s}\end{align*} Now, we know the initial and final velocities of the car in the braking stage. Since the acceleration is assumed to be constant, by applying the definition of average acceleration, we would have \begin{align*} \bar{a}&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{0-20}{4}\\\\&=-5\quad {\rm m/s^2}\end{align*} The negative shows the direction of the acceleration, which is toward the negative $x$-axis. 

Hence, the car's acceleration has a magnitude of $5\,{\rm m/s^2}$ in the negative $x$ direction. 

Problem (14): A race car accelerates from rest at a constant rate of $2\,{\rm m/s^2}$ in 15 seconds. It then travels at a constant speed for 20 seconds, and after that, it comes to a stop with an acceleration of $2\,{\rm m/s^2}$.  (a) What is the total distance traveled by car? (b) What is its average velocity over the entire path?

Solution : To solve this kinematics question, we divided the entire path into three parts. 

Part I: "From rest'' means the initial velocity is zero. Thus, given the acceleration and time interval, we can use the kinematics equation $v=v_0+at$ to calculate the distance traveled by the car at the end of 15 seconds for the first part of the path. \begin{align*} x&=\frac{1}{2}at^2 +v_0 t+x_0\\\\&=\frac 12 (2)(15)^2 +(0)(15)+0\\\\&=\boxed{125\quad{\rm m}}\end{align*}   As a side calculation, we find the final velocity for this part as below \begin{align*}v&=v_0+at\\\\&=0+(2) (15) \\\\&=30\quad {\rm m/s}\end{align*} Part II: the speed in this part is the final speed in the first part because the car continues moving at this constant speed after that moment. 

The constant speed means we are facing zero acceleration. As a result, it is preferable to use the average velocity definition rather than the kinematics equations for constant (uniform) acceleration.

The distance traveled for this part, which takes 20 seconds at a constant speed of 30 m/s, is computed by the definition of average velocity as below \begin{align*} \bar{v}&=\frac{\Delta x}{\Delta t}\\\\30&=\frac{\Delta x}{20}\end{align*} Thus, we find the distance traveled as $\boxed{x=600\,{\rm m}}$. 

Part III: In this part, the car comes to a stop, $v=0$, so its acceleration must be a negative value as $a=-2\,{\rm m/s^2}$. Here, the final velocity is also zero. Its initial velocity is the same as in the previous part. 

Consequently, the best kinematics equation that relates those known to the wanted distance traveled $x$, is $v^2-v_0^2=2a(x-x_0)$. \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\0^2-(30)^2&=2(-2)(x-0) \\\\ \Rightarrow \quad x&=\boxed{225\quad {\rm m}}\end{align*} The total distance traveled by car for the entire path is the sum of the above distances \[D=125+600+225=\boxed{950\quad {\rm m}}\]

Problem (15): A ball is dropped vertically downward from a tall building of 30-m-height with an initial speed of 8 m/s. After what time interval does the ball strike the ground? (take $g=-10\,{\rm m/s^2}$.)

Solution : This is a free-falling kinematics problem. As always, choose a coordinate system along with the motion and the origin as the starting point. 

Here, the dropping point is considered the origin, so in all kinematics equations, we set $y_0=0$. By this choice, the striking point is 30 meters below the origin, so in equations, we also set $y=-30\,{\rm m}$. 

Remember that velocity is a vector in physics whose magnitude is called speed. In this problem, the initial speed is 8 m/s downward. This means that the velocity vector is written as $v=-8\,{\rm m/s}$. 

Now that all necessary quantities are ready, we can use the kinematics equation $y=\frac 12 at^2+v_0t+y_0$, to find the wanted time that the ball strikes the ground. \begin{align*} y&=\frac 12 at^2+v_0t+y_0\\\\-30&=\frac 12 (-10)t^2+(-8)t+0\end{align*} After rearranging, a quadratic equation like $5t^2+8t-30=0$ is obtained, whose solutions are given as below: \begin{gather*} t=\frac{-8\pm\sqrt{8^2-4(5)(-30)}}{2(5)}\\\\ \boxed{t_1=1.77\,{\rm s}} \quad , \quad t_2=-3.37\,{\rm s}\end{gather*} $t_1$ is the accepted time because the other is negative, which is not acceptable in kinematics. Therefore, the ball takes about 1.7 seconds to hit the ground. 

Note: The solutions of a quadratic equation like $at^2+bt+c=0$, where $a,b,c$ are some constants, are found by the following formula: \[t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] 

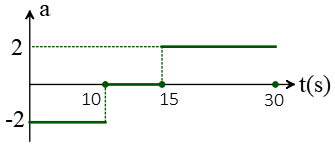
Problem (16): The acceleration versus time graph for an object that moves at a constant speed of 30 m/s is shown in the figure below. Find the object's average velocity between instances $t_1=10\,{\rm s}$ and $t_2=30\,{\rm s}$. 

Solution : The best and shortest approach to solving such a kinematics problem is to first draw its velocity-vs-time graph. Next, the area under the obtained graph gives us the total displacement, which is divided by the total time interval to yield the average velocity.

The path consists of three parts with different accelerations. 

In the first part, the object slows down its motion at a constant rate of $-2\,{\rm m/s^2}$ in 10 seconds. Its initial velocity is also 30 m/s. With these known quantities in hand, the kinematics equation $v=v_0+at$ gives us the velocity at the end of this time interval. \begin{align*} v&=v_0+at\\&=30+(-2)(10) \\&=10\quad {\rm m/s}\end{align*} This calculation corresponds to a straight line between the points $(v=30\,{\rm m/s},t=0)$ and $(v=10\,{\rm m/s},t=10\,{\rm s})$ on the $v-t$ graph as shown below.

Next, the object moves with zero acceleration for 5 seconds, which means the velocity does not change during this time interval. This implies that we must draw a horizontal line in the $v-t$ graph.

In the last part, the object accelerates from 10 m/s with a constant rate of $+2\,{\rm m/s^2}$ in 15 seconds. Thus, its final velocity at the end of this time interval is determined as below \begin{align*} v&=v_0+at\\&=10+(2)(15) \\&=40\quad {\rm m/s}\end{align*} Now, it's time to draw the velocity-vs-time graph. As an important point, note that all these motions have a constant acceleration, so all parts of a velocity-time graph, are composed of straight-line segments with different slopes.

For part I, we must draw a straight-line segment between the velocities of 30 m/s and 10 m/s. 

Part II is a horizontal line since its velocities are constant during that time interval, and finally, in Part III, there is a straight line between velocities of 10 m/s and 40 m/s. 

All these verbal phrases are illustrated in the following velocity-vs-time graph . 

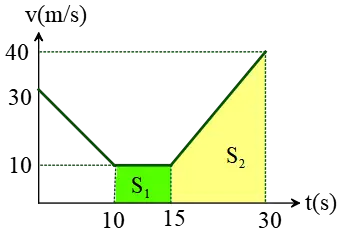
Recall that the area under a velocity vs. time graph always gives the displacement. Hence, the area under the $v-t$ graph between 10 s and 30 s gives the displacement. Therefore, the areas of rectangle $S_1$ and trapezoid $S_2$ are calculated as below \begin{gather*} S_1 =10\times 5=50\quad {\rm m} \\\\S_2=\frac{10+40}{2}\times 15=375\quad {\rm m}\end{gather*} Therefore, the total displacement in the time interval $[15,30]$ is \[D=S_{tot}=S_1+S_2=425\,{\rm m}\] From the definition of average velocity, we have \[\bar{v}=\frac{displacement}{time}=\frac{425}{20}=21.25\,{\rm m/s}\] 

Challenging Kinematics Problems

In the following, some challenging kinematics problems are presented for homework.

A driver is moving along at $45\,\rm m/s$ when she suddenly notices a roadblock $100\,\rm m$ ahead. Can the driver stop the vehicle in time to avoid colliding with the obstruction if her reaction time is assumed to be $0.5\,\rm s$ and her car's maximum deceleration is $5\,\rm m/s^2$?

Solution : The time between seeing the obstacle and taking action, such as slamming on the brake, is defined as the reaction time. During this time interval, the moving object travels at a constant speed. 

Thus, in all such questions, we have two phases. One is constant speed, and the other is accelerating with negative acceleration (deceleration). 

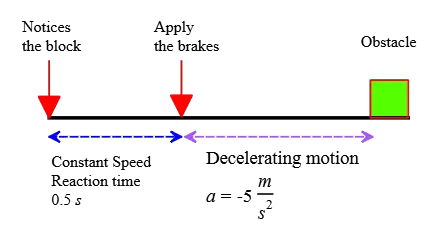
Here, between the time of seeing the barrier and the time of braking, the driver covers a distance of \begin{align*} x_1&=vt_{reac} \\\\ &=25\times 0.5 \\\\ &=12.5\,\rm m\end{align*} In the decelerating phase, the car moves a distance, which is obtained using the following kinematics equation: \begin{gather*} v^2-v_0^2=2ax_2 \\\\ (0)^2-(25)^2=2(-5) x_2 \\\\ \Rightarrow x_2=62.5\,\rm m\end{gather*} Summing these two distances gives a total distance that is a good indication of whether the moving object hits the obstacle or not. \begin{gather*} \Delta x_{actual}=x_1+x_2=75\,\rm m \\\\ \Rightarrow \Delta x_{covered}<\Delta x_{actual} \end{gather*} As a result, because the distance covered by the car is less than the actual distance between the time of seeing the barrier and the obstacle itself, the driver has sufficient time to stop the car in time to avoid a collision.

For a moving car at a constant speed of $90\,\rm km/h$ and a human reaction time of $0.3\,\rm s$; find the stopping distance if it slows down at a rate of $a=3\,\rm m/s^2$. 

Solution : We use SI units, so first convert the given speed in these units as below \begin{align*} v&=90\,\rm km/h \\\\ &=\rm 90\times \left(\frac{1000\,m}{3600\,s}\right) \\\\ &=25\,\rm m/s\end{align*} As we said previously, during the reaction time, your car moves at a constant speed and covers a distance of \begin{align*} x_1&=vt_{react} \\\\ &=(25)(0.3) \\\\ &=7.5\,\rm m \end{align*} Deceleration means the moving object slows down, or a decrease per second in the velocity of the car occurs. In this case, we must put the acceleration with a negative sign in the kinematics equations. 

During the second phase, your car has negative acceleration and wants to be stopped. Thus, the distance covered during this time interval is found as follows \begin{align*} v^2-v_0^2=2a\Delta x \\\\ (0)^2-(25)^2=2(3)\Delta x \\\\ \Rightarrow \quad \boxed{\Delta x=104.17\,\rm m}\end{align*} 

Assume you are traveling $35\,\rm m/s$ when suddenly you see red light traffic $50\,\rm m$ ahead. If it takes you $0.456\,\rm s$ to apply the brakes and the maximum deceleration of the car is $4.5\,\rm m/s^2$,  (a) Will you be able to stop the car in time?  (b) How far from the time of seeing the red light will you be? 

Solution : When you see the red light until you apply the brakes, your car is moving at a constant speed. This time interval is defined as the reaction time, $\Delta t_{react}=0.456\,\rm s$. After you get the brakes on, the car starts to decelerate at a constant rate, $a=-4.5\,\rm m/s^2$. Pay attention to the negative signs of such problems. The negative tells us that the car is decreasing its speed. 

(a) In the first phase, the car moves a distance of \begin{align*} x_1&=v\Delta t_{react} \\\\ &=35\times 0.455 \\\\ &=15.96\,\rm m\end{align*} In the phase of deceleration, the car is moving a distance whose magnitude is found using the time-independent kinematics equation as below \begin{gather*} v^2-v_0^2=2ax_2 \\\\ (0)^2-(35)^2=2(4.5)x_2 \\\\ \Rightarrow \quad x_2=136.11\,\rm m\end{gather*} The sum of these two distances traveled gives us the total distance covered by the car from the time of seeing the red traffic light to the moment of a complete stop. \[x_{tot}=x_1+x_2=152.07\,\rm m \] Because the total distance traveled is greater than the actual distance to the red light, the driver will not be able to stop the car in time. 

(b) As previously calculated, the total distance traveled by the car is nearly $152\,\rm m$ or the car is about $102\,\rm m$ past the red light traffic. 

A person stands on the edge of a $60-\,\rm m$-high cliff and throws two stones vertically downward, $1$ second apart, and sees they both reach the water simultaneously. The first stone had an initial speed of $4\,\rm m/s$.  (a) How long after dropping the first stone does the second stone hit the water? (b) How fast was the second stone released? (c) What is the speed of each stone at the instant of hitting the water?

Solution:  Because all quantities appearing in the kinematics equation are vectors, we must first choose a positive direction. Here, we take up as a positive $y$ direction.

Both stones arrived in the water at the same time. Thus, calculate the time the first stone was in the air. Next,  use the time interval between the two drops to find the duration the second stone was in the air. (a) The first stone is released downward at a speed of $4\,\rm m/s$, thus, its initial velocity is $v_0=-4\,\rm m/s$. The minus sign is for moving in the opposite direction of the chosen direction. 

The only relevant kinematics equation that relates this known information is $\Delta y=-\frac 12 gt^2+v_0t$, where $\Delta y=-60\,\rm m$ is the vertical displacement, and the negative indicates that the stone hit a point below the chosen origin. Substituting the numerical values into this and solving for the time duration $t$ gives \begin{gather*} \Delta y=-\frac 12 gt^2+v_0t \\\\ -60=-\frac 12 (10)t^2+(-4)t \\\\ 5t^2+4t-60=0 \\\\ \Rightarrow \boxed{t=3.0\,\rm s} \, , \, t'=-3.8\,\rm s \end{gather*} The second answer is not acceptable. 

(b) The second stone was released $1$ second after throwing the first one and arrived at the same time as the first stone. Therefore, the time interval that the second stone was in the air is found to be \begin{align*} t_2&=t_1-1 \\ &=3.0-1\\ &=2\,\rm s\end{align*} 

(c) It is better to apply the time-independent kinematics equation $v^2-v_0^2=-2g\Delta y$ to find the stone's velocity at the moment it hit the water. For the first stone, we have \begin{gather*} v^2-v_0^2=-2g\Delta y \\\\ v^2-(-4)^2=-2(10)(-60) \\\\ \Rightarrow \quad \boxed{v=34.8\,\rm m/s} \end{gather*} The second stone's velocity is left to you as an exercise.

In a tennis game, the ball leaves the racket at a speed of $75\,\rm m/s$ whereas it is in contact with the racket for $25\,\rm ms$, and starts at rest. Assume the ball experiences constant acceleration.  (a) What was the ball's acceleration during this serve? (b) How far has the ball traveled on this serve?

Solution : In this question, we are asked to find the ball's acceleration and distance traveled during that pretty small time interval.  (a) In a time interval of $\Delta t=25\times 10^{-3}\,\rm s$, we are given the beginning velocity $v_1=0$ and the end velocity $v_2=85\,\rm m/s$. Because it is assumed the acceleration is constant, the average acceleration definition, $a=\frac{\Delta v}{\Delta t}$, is best suited for these known quantities. \begin{align*} a&=\frac{v_2-v_1}{\Delta t} \\\\ &=\frac{75-0}{25\times 10^{-3}} \\\\ &=3000\,\rm m/s^2 \end{align*} A huge acceleration is given to the tennis ball.  (b) Here, we are asked to find the amount of distance traveled by the ball during the time the ball was in contact with the racket. Because we have a constant acceleration motion, it is best to use the following equation to find the distance traveled. \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\times \Delta t \\\\ &=\frac{0+75}{2}\times (25\times 10^{-3}) \\\\ &=937.5\times 10^{-3}\,\rm m\end{align*} In millimeters, $\Delta x=937.5\,\rm mm$, and in centimeters $\Delta x=93.75\,\rm cm$. Therefore, during this incredibly short time interval, the ball moves about $94\,\rm cm$ along with the racket.

Starting from rest and ending at rest, a car travels a distance of $1500\,\rm m$ along the $x$-axis. During the first quarter of the distance, it accelerates at a rate of $+1.75\,\rm m/s^2$, while for the remaining distance, its acceleration is $-0.450\,\rm m/s^2$.  (a) What is the time travel of the whole path?  (b) What is the maximum speed of the car over this distance?

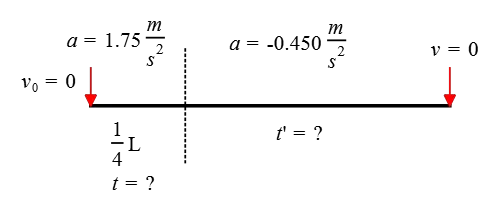
None of the time-dependent kinematics equations give us the time travel $t'$ without knowing the initial speed at the instant of the start of this second path. 

We can find it using the equation $v^2-v_0^2=2a\Delta x$, setting $v=0$ at the end of the path, and solving for $v_0$ \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ (0)^2-v_0^2=2(-0.450)(1125) \\\\ v_0=\sqrt{2\times 0.45\times 1125} \\\\ \Rightarrow v_0=31.82\,\rm m/s\end{gather*} Given that, one can use the simple equation $v=v_0+at$ and solve for the time travel in this part of the path. \begin{gather*} v=v_0+at \\\\ 0=31.82+(-0.450)t' \\\\ \Rightarrow t'=70.71\,\rm s\end{gather*} Therefore, the total time traveled over the entire path is the sum of these two times. \begin{align*} T&=t+t' \\\\ &=20.70+70.71 \\\\ &=\boxed{91.41\,\rm s} \end{align*}

A train that is $75$ meters long starts accelerating uniformly from rest. When the front of the train reaches a railway worker who is standing $150$ meters away from where the train started, it is traveling at a speed of $20\,\rm m/s$. What will be the speed of the last car as it passes the worker?

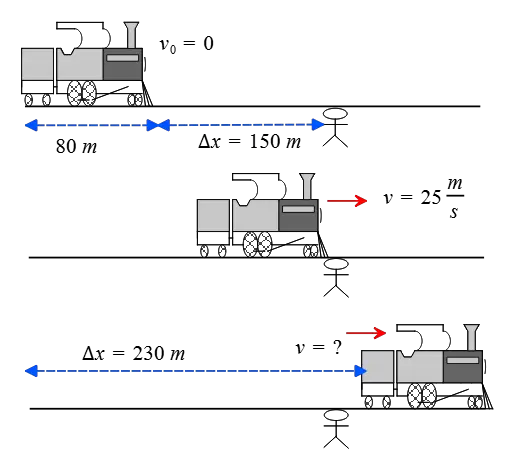
Solution : The front of the train is initially $150\,\rm m$ away from the worker, and when it passes him, it has a speed of $25\,\rm m/s$. From this data, we can find the acceleration of the front of the train (which is the same acceleration as the whole train) by applying the following kinematics equation \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ (25)^2-(0)^2=2a\times 150 \\\\ \Rightarrow \quad a=2.08\,\rm m/s^2\end{gather*} Given the train's acceleration, now focus on the last car.

The last car is initially at rest and placed at a distance of $150+80=230\,\rm m$ away from the person. When it passes the person, it has traveled $\Delta x= 230\,\rm m$ and its speed is determined simply as below \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ v^2-(0)^2=2(2.08)(230) \\\\ \Rightarrow \quad \boxed{v=30.93\,\rm m/s}\end{gather*}

A wildcat moving with constant acceleration covers a distance of $100\,\rm m$ apart in $8\,\rm s$. Assuming that its speed at the second point is $20\,\rm m/s$,  (a) What was its speed in the first place?  (b) At what rate does its speed change over this distance? 

Solution : First of all, list all known data given to us. Time interval $\Delta t=8\,\rm s$, the horizontal displacement $\Delta x=100\,\rm m$, speed at second point $v_2=20\,\rm m/s$. 

We are asked to find the speed at the second point. To solve this kinematics problem, we use the following kinematics equation because the acceleration is constant and this is the most relevant equation that relates the known to the unknown quantities. \begin{gather*} \Delta x=\frac{v_1+v_2}{2}\times \Delta t \\\\ 100=\frac{v_1+20}{2}\times 8 \\\\ \Rightarrow \quad \boxed{v_1=5\,\rm m/s} \end{gather*} Therefore, the wildcat's speed in the first place is $5\,\rm m/s$. 

In this part, we should find the wildcat's acceleration because acceleration is defined as the time rate of change of the speed of a moving object. Given the first place speed, $v_1=5\,\rm m/s$, found in the preceding part, we can use the following time-independent kinematics equation to find the wanted unknown. \begin{gather*} v_2^2-v_1^2=2a\Delta x \\\\ (20)^2-(5)^2=2a(100) \\\\ \Rightarrow  \quad \boxed{a=1.875\,\rm m/s^2}\end{gather*}

In this tutorial, all concepts about kinematics equations are taught in a problem-solution strategy. 

We can also find these kinematic variables using a position-time  or velocity-time graph. Because slopes in those graphs represent velocity and acceleration, respectively, and the concavity of a curve in a position vs. time graph shows the sign of its acceleration in an x-t graph  as well.

These multiple-choice questions on kinematics for AP Physics 1 are also available to review for students enrolled in AP Physics courses.

Author : Dr. Ali Nemati Date published : 8-7-2021 Updated : June 12, 2023

© 2015 All rights reserved. by Physexams.com

Kinematic Equations: Explanation, Review, and Examples

• The Albert Team
• Last Updated On: April 29, 2022

Now that you’ve learned about displacement, velocity, and acceleration, you’re well on your way to being able to describe just about any motion you could observe around you with physics. All that’s left is to learn how these values really play into each other. We know a few ways to move between them, but they’re all pretty limited. What happens if you need to find displacement, but only know acceleration and time? We don’t have a way to combine all of those values yet. Enter the four kinematic equations. 

What We Review

The Kinematic Equations

The following four kinematic equations come up throughout physics from the earliest high school class to the highest level college course:

Don’t let all of these numbers and symbols intimidate you. We’ll talk through each one – what they mean and when we use them. By the end of this post, you’ll be a master of understanding and implementing each of these physics equations. Let’s start with defining what all of those symbols mean. 

The First Kinematic Equation

This physics equation would be read as “the final velocity is equal to the initial velocity plus acceleration times time”. All it means is that if you have constant acceleration for some amount of time, you can find the final velocity. You’ll use this one whenever you’re looking at changing velocities with a constant acceleration.

The Second Kinematic Equation

This one is read as “displacement equals final velocity plus initial velocity divided by two times time”. You’ll use this one whenever you don’t have an acceleration to work with but you need to relate a changing velocity to a displacement.

The Third Kinematic Equation

This one may look a bit scarier as it is longer than the others, but it is read as “displacement equals initial velocity times time plus one half acceleration times time squared”. All it means is that our displacement can be related to our initial velocity and a constant acceleration without having to find the final velocity. You’ll use this one when final velocity is the only value you don’t know yet.

It is worth noting that this kinematic equation has another popular form: x=x_{0}+v_{0}t+\frac{1}{2}at^{2} . While that may seem even more intimidating, it’s actually exactly the same. The only difference here is that we have split up \Delta x into x-x_{0} and then solved to get x on its own. This version can be particularly helpful if you’re looking specifically for a final or initial position rather than just an overall displacement.

The Fourth Kinematic Equation

Our last kinematic equation is read as “final velocity squared equals initial velocity squared plus two times acceleration times displacement”. It’s worth noting that this is the only kinematic equation without time in it. Many starting physicists have been stumped by reaching a problem without a value for time. While staring at an equation sheet riddled with letters and numbers can be overwhelming, remembering you have this one equation without time will come up again and again throughout your physics career.

It may be worth noting that all of these are kinematic equations for constant acceleration. While this may seem like a limitation, we learned before that high school physics courses generally utilize constant acceleration so we don’t need to worry about it changing yet. If you do find yourself in a more advanced course, new physics equations will be introduced at the appropriate times.

How to Approach a Kinematics Problem

So now that we have all of these different kinematic equations, how do we know when to use them? How can we look at a physics word problem and know which of these equations to apply? You must use problem-solving steps. Follow these few steps when trying to solve any complex problems, and you won’t have a problem.

Step 1: Identify What You Know

This one probably seems obvious, but skipping it can be disastrous to any problem-solving endeavor. In physics problems, this just means pulling out values and directions. If you can add the symbol to go with the value (writing t=5\text{ s} instead of just 5\text{ s} , for example), even better. It’ll save time and make future steps even easier.

Step 2: Identify the Goal

In physics, this means figuring out what question you’re actually being asked. Does the question want you to find the displacement? The acceleration? How long did the movement take? Figure out what you’re being asked to do and then write down the symbol of the value you’re solving for with a question mark next to it ( t=\text{?} , for example). Again, this feels obvious, but it’s also a vital step.

Step 3: Gather Your Tools

Generally, this means a calculator and an equation. You’ll want to look at all of the symbols you wrote down and pick the physics equation for all of them, including the unknown value. Writing everything down beforehand will make it easier to pull a relevant equation than having to remember what values you need while searching for the right equation. You can use the latter method, but you’re far more likely to make a mistake and feel frustrated that way.

Step 4: Put it all Together

Plug your values into your equation and solve for the unknown value. This will usually be your last step, though you may find yourself having to repeat it a few times for exceptionally complex problems. That probably won’t come up for quite a while, though. After you’ve found your answer, it’s generally a good idea to circle it to make it obvious. That way, whoever is grading you can find it easily and you can easily keep track of which problems you’ve already completed while flipping through your work.

Kinematic Equation 1: Review and Examples

To learn how to solve problems with these new, longer equations, we’ll start with v=v_{0}+at . This kinematic equation shows a relationship between final velocity, initial velocity, constant acceleration, and time. We will explore this equation as it relates to physics word problems. This equation is set up to solve for velocity, but it can be rearranged to solve for any of the values it contains. For this physics equation and the ones following, we will look at one example finding the variable that has already been isolated and one where a new variable needs to be isolated using the steps we just outlined. So, let’s jump into applying this kinematic equation to a real-world problem.

A car sits at rest waiting to merge onto a highway. When they have a chance, they accelerate at 4\text{ m/s}^2 for 7\text{ s} . What is the car’s final velocity?

We have a clearly stated acceleration and time, but there’s no clearly defined initial velocity here. Instead, we have to take this from context. We know that the car “sits at rest” before it starts moving. This means that our initial velocity in this situation is zero. Other context clues for an object starting at rest is if it is “dropped” or if it “falls”. Our other known values will be even easier to pull as we were actually given numerical values. Now it’s time to put everything into a list.

• v_{0}=0\text{ m/s}
• a=4\text{ m/s}^2
• t=7\text{ s}

Our goal here was clearly stated: find the final velocity. We’ll still want to list that out so we can see exactly what symbols we have to work with on this problem.

We already know which of the kinematic equations we’re using, but if we didn’t, this would be where we search our equation sheet for the right one. Regardless, we’ll want to write that down too.

Step 4: Put it All Together

At this point, we’ll plug all of our values into our kinematic equation. If you’re working on paper, there’s no need to repeat anything we’ve put above. That being said, for the purposes of digital organization and so you can see the full problem in one spot, we will be rewriting things here.

Now let’s get a bit trickier with a problem that will require us to rearrange our kinematic equation.

A ball rolls toward a hill at 3\text{ m/s} . It rolls down the hill for 5\text{ s} and has a final velocity of 18\text{ m/s} . What was the ball’s acceleration as it rolled down the hill?

Just like before, we’ll make a list of our known values:

• v_{0}=3\text{ m/s}
• t=5\text{ s}
• v=18\text{ m/s}

Again, our goal was clearly stated, so let’s add it to our list:

We already know which equation we’re using, but let’s pretend we didn’t. We know that we need to solve for acceleration, but if you look at our original list of kinematic equations, there isn’t one that’s set up to solve for acceleration:

This begs the question, how to find acceleration (or any value) that hasn’t already been solved for? The answer is to rearrange an equation. First, though, we need to pick the right one. We start by getting rid of the second equation in this list as it doesn’t contain acceleration at all. Our options are now:

• \Delta x=v_{0}t+\dfrac{1}{2}at^{2}
• v^{2}=v_{0}^{2}+2a\Delta x

Now we’ll need to look at the first list we made of what we know. We know the initial velocity, time, and final velocity. There’s only one equation that has all the values we’re looking for and all of the values we know with none that we don’t. This is the first kinematic equation:

In this case, we knew the kinematic equation coming in so this process of elimination wasn’t necessary, but that won’t often be the case in the future. You’ll likely have to find the correct equation far more often than you’ll have it handed to you. It’s best to practice finding it now while we only have a few equations to work with.

Like before, we’ll be rewriting all of our relevant information below, but you won’t need to if you’re working on paper.

Although you can plug in values before rearranging the equation, in physics, you’ll usually see the equation be rearranged before values are added. This is mainly done to help keep units where they’re supposed to be and to avoid any mistakes that could come from moving numbers and units rather than just a variable. We’ll be taking the latter approach here. Follow the standard PEMDAS rules for rearranging the equation and then write it with the variable we’ve isolated on the left. While that last part isn’t necessary, it is a helpful organizational practice:

For a review of solving literal equations, visit this post ! Now we can plug in those known values and solve:

Kinematic Equation 2: Review and Examples

Next up in our four kinematics equations is \Delta x=\dfrac{v+v_{0}}{2} t . This one relates an object’s displacement to its average velocity and time. The right-hand side shows the final velocity plus the initial velocity divided by two – the sum of some values divided by the number of values, or the average. Although this equation doesn’t directly show a constant acceleration, it still assumes it. Applying this equation when acceleration isn’t constant can result in some error so best not to apply it if a changing acceleration is mentioned.

A car starts out moving at 10\text{ m/s} and accelerates to a velocity of 24\text{ m/s} . What displacement does the car cover during this velocity change if it occurs over 10\text{ s} ?

• v_{0}=10\text{ m/s}
• v=24\text{ m/s}
• t=10\text{ s}
• \Delta x=\text{?}
• \Delta x=\dfrac{v+v_{0}}{2} t

This time around we won’t repeat everything here. Instead, We’ll jump straight into plugging in our values and solving our problem:

A ball slows down from 15\text{ m/s} to 3\text{ m/s} over a distance of 36\text{ m} . How long did this take?

• v_{0}=15\text{ m/s}
• v=3\text{ m/s}
• \Delta x=36\text{ m}

We don’t have a kinematic equation for time specifically, but we learned before that we can rearrange certain equations to solve for different variables. So, we’ll pull the equation that has all of the values we need and isolate the variable we want later:

Again, we won’t be rewriting anything, but we will begin by rearranging our equation to solve for time:

Now we can plug in our known values and solve for time.

Kinematic Equation 3: Review and Examples

Our next kinematic equation is \Delta x=v_{0}t+\frac{1}{2}at^{2} . This time we are relating our displacement to our initial velocity, time, and acceleration. The only odd thing you may notice is that it doesn’t include our final velocity, only the initial. This equation will come in handy when you don’t have a final velocity that was stated either directly as a number or by a phrase indicating the object came to rest. Just like before, we’ll use this equation first to find a displacement, and then we’ll rearrange it to find a different value.

A rocket is cruising through space with a velocity of 50\text{ m/s} and burns some fuel to create a constant acceleration of 10\text{ m/s}^2 . How far will it have traveled after 5\text{ s} ?

• v_{0}=50\text{ m/s}
• a=10\text{ m/s}^2
• \Delta x=v_{0}t+\frac{1}{2}at^{2}

At this point, it appears that these problems seem to be quite long and take several steps. While that is an inherent part of physics in many ways, it will start to seem simpler as time goes on. This problem presents the perfect example. While it may have been easy to combine lines 4 and 5 mathematically, they were shown separately here to make sure the process was as clear as possible. While you should always show all of the major steps of your problem-solving process, you may find that you are able to combine some of the smaller steps after some time of working with these kinematic equations.

Later in its journey, the rocket is moving along at 20\text{ m/s} when it has to fire its thrusters again. This time it covers a distance of 500\text{ m} in 10\text{ s} . What was the rocket’s acceleration during this thruster burn?

• v_{0}=20\text{ m/s}
• \Delta x=500\text{ m}

As usual, we’ll begin by rearranging the equation, this time to solve for acceleration.

Now we can plug in our known values to find the value of our acceleration.

Kinematic Equation 4: Review and Examples

The last of the kinematic equations that we will look at is v^{2}=v_{0}^{2}+2a\Delta x . This one is generally the most complicated looking, but it’s also incredibly important as it is our only kinematic equation that does not involve time. It relates final velocity, initial velocity, acceleration, and displacement without needing a time over which a given motion occurred. For this equation, as with the others, let’s solve it as is and then rearrange it to solve for a different variable.

A car exiting the highway begins with a speed of 25\text{ m/s} and travels down a 100\text{ m} long exit ramp with a deceleration (negative acceleration) of 3\text{ m/s}^2 . What is the car’s velocity at the end of the exit ramp?

• v_{0}=25\text{ m/s}
• \Delta x=100\text{ m}
• a=-3\text{ m/s}^2

Note that our acceleration here is a negative value. That is because our problem statement gave us a deceleration instead of an acceleration. Whenever you have a deceleration, you’ll make the value negative to use it as an acceleration in your problem-solving. This also tells us that our final velocity should be less than our initial velocity so we can add that to the list of what we know as well.

• Final velocity will be less than initial.

Being able to know something to help check your answer at the end is what makes this subject a bit easier than mathematics for some students.

While we generally try to not have any operations going on for the isolated variable, sometimes it’s actually easier that way. Having your isolated variable raised to a power is generally a time to solve before simplifying. This may seem like an arbitrary rule, and in some ways it is, but as you continue through your physics journey you’ll come up with your own practices for making problem-solving easier.

Now that we have both sides simplified, we’ll take the square root to eliminate the exponent on the left-hand side:

If we remember back at the beginning, we said that our final velocity would have to be less than our initial velocity because the problem statement told us that we were decelerating. Our initial velocity was 25\text{ m/s} which is, indeed, greater than 5\text{ m/s} so our answer checks out.

A ghost is sliding a wrench across a table to terrify the mortal onlooker. The wrench starts with a velocity of 2\text{ m/s} and accelerates to a velocity of 5\text{ m/s} over a distance of 7\text{ m} . What acceleration did the ghost move the wrench with?

• v_{0}=2\text{ m/s}
• v=5\text{ m/s}
• \Delta x=7\text{ m}

We can also make an inference about our acceleration here – that it will be positive. Not every problem will tell you clearly the direction of the acceleration, but if your final velocity is greater than your initial velocity, you can be sure that your acceleration will be positive.

• Positive acceleration

You’ll get better at picking up on subtle hints like this as you continue your physics journey and your brain starts naturally picking up on some patterns. You’ll likely find this skill more and more helpful as it develops and as problems get more difficult.

We’ll start by rearranging our equation to solve for acceleration.

As usual, now that we’ve rearranged our equation, we can plug in our values.

Again, we can go back to the beginning when we said our acceleration would be a positive number and confirm that it is. 

Problem-Solving Strategies

At this point, you’re likely getting the sense that physics will be a lot of complex problem-solving. If so, your senses are correct. In many ways, physics is the science of explaining nature with mathematical equations. There’s a lot that goes into developing and applying these equations, but at this point in your physics career, you’ll find that the majority of your time will likely be spent on applying equations to word problems. If you feel that your problem-solving skills could still use some honing, check out more examples and strategies from this post by the Physics Classroom or through this video-guided tutorial from Khan Academy.

That was a lot of equations and examples to take in. Eventually, whether you’re figuring out how to find a constant acceleration or how to solve velocity when you don’t have a value for time, you’ll know exactly which of the four kinematic equations to apply and how. Just keep the problem-solving steps we’ve used here in mind, and you’ll be able to get through your physics course without any unsolvable problems.

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

UP Class 11 Physics

Course: up class 11 physics   >   unit 3.

• Choosing kinematic equations
• Choosing the best kinematic equation
• Using equations of motion (1 step numerical)
• Using equations of motion (2 steps numerical)
• Kinematic equations: calculations
• Free fall - 2 body solved numerical

Solving freefall problems using kinematic formulas

• Your answer should be
• an exact decimal, like 0.75 ‍  

PHYS101: Introduction to Mechanics

Problem-Solving Basics for One-Dimensional Kinematics

Read this text for a step-by-step guide on how to solve problems of constant acceleration using kinematic equations.

Problem-Solving Steps

While there is no simple step-by-step method that works for every problem, the following general procedures facilitate problem solving and make it more meaningful. A certain amount of creativity and insight is required as well.

Examine the situation to determine which physical principles are involved. It often helps to draw a simple sketch at the outset. You will also need to decide which direction is positive and note that on your sketch. Once you have identified the physical principles, it is much easier to find and apply the equations representing those principles.

Although finding the correct equation is essential, keep in mind that equations represent physical principles, laws of nature, and relationships among physical quantities. Without a conceptual understanding of a problem, a numerical solution is meaningless.

Make a list of what is given or can be inferred from the problem as stated (identify the knowns). Many problems are stated very succinctly and require some inspection to determine what is known. A sketch can also be very useful at this point. Formally identifying the knowns is of particular importance in applying physics to real-world situations. Remember, "stopped" means velocity is zero, and we often can take initial time and position as zero.

Identify exactly what needs to be determined in the problem (identify the unknowns). In complex problems, especially, it is not always obvious what needs to be found or in what sequence. Making a list can help.

Find an equation or set of equations that can help you solve the problem. Your list of knowns and unknowns can help here. It is easiest if you can find equations that contain only one unknown - that is, all of the other variables are known, so you can easily solve for the unknown.

If the equation contains more than one unknown, then an additional equation is needed to solve the problem. In some problems, several unknowns must be determined to get at the one needed most. In such problems it is especially important to keep physical principles in mind to avoid going astray in a sea of equations. You may have to use two (or more) different equations to get the final answer.

Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units. This step produces the numerical answer; it also provides a check on units that can help you find errors. If the units of the answer are incorrect, then an error has been made. However, be warned that correct units do not guarantee that the numerical part of the answer is also correct.

Check the answer to see if it is reasonable: Does it make sense? This final step is extremely important - the goal of physics is to accurately describe nature. To see if the answer is reasonable, check both its magnitude and its sign, in addition to its units.

Your judgment will improve as you solve more and more physics problems, and it will become possible for you to make finer and finer judgments regarding whether nature is adequately described by the answer to a problem. This step brings the problem back to its conceptual meaning. If you can judge whether the answer is reasonable, you have a deeper understanding of physics than just being able to mechanically solve a problem.

When solving problems, we often perform these steps in different order, and we also tend to do several steps simultaneously. There is no rigid procedure that will work every time. Creativity and insight grow with experience, and the basics of problem solving become almost automatic.

One way to get practice is to work out the text's examples for yourself as you read. Another is to work as many end-of-section problems as possible, starting with the easiest to build confidence and progressing to the more difficult. Once you become involved in physics, you will see it all around you, and you can begin to apply it to situations you encounter outside the classroom, just as is done in many of the applications in this text.

10.2 Kinematics of Rotational Motion

Learning objectives.

By the end of this section, you will be able to:

• Observe the kinematics of rotational motion.
• Derive rotational kinematic equations.
• Evaluate problem solving strategies for rotational kinematics.

Just by using our intuition, we can begin to see how rotational quantities like θ θ , ω ω , and α α are related to one another. For example, if a motorcycle wheel has a large angular acceleration for a fairly long time, it ends up spinning rapidly and rotates through many revolutions. In more technical terms, if the wheel’s angular acceleration α α is large for a long period of time t t , then the final angular velocity ω ω and angle of rotation θ θ are large. The wheel’s rotational motion is exactly analogous to the fact that the motorcycle’s large translational acceleration produces a large final velocity, and the distance traveled will also be large.

Kinematics is the description of motion. The kinematics of rotational motion describes the relationships among rotation angle, angular velocity, angular acceleration, and time. Let us start by finding an equation relating ω ω , α α , and t t . To determine this equation, we recall a familiar kinematic equation for translational, or straight-line, motion:

Note that in rotational motion a = a t a = a t , and we shall use the symbol a a for tangential or linear acceleration from now on. As in linear kinematics, we assume a a is constant, which means that angular acceleration α α is also a constant, because a = rα a = rα . Now, let us substitute v = rω v = rω and a = rα a = rα into the linear equation above:

The radius r r cancels in the equation, yielding

where ω 0 ω 0 is the initial angular velocity. This last equation is a kinematic relationship among ω ω , α α , and t t —that is, it describes their relationship without reference to forces or masses that may affect rotation. It is also precisely analogous in form to its translational counterpart.

Making Connections

Kinematics for rotational motion is completely analogous to translational kinematics, first presented in One-Dimensional Kinematics . Kinematics is concerned with the description of motion without regard to force or mass. We will find that translational kinematic quantities, such as displacement, velocity, and acceleration have direct analogs in rotational motion.

Starting with the four kinematic equations we developed in One-Dimensional Kinematics , we can derive the following four rotational kinematic equations (presented together with their translational counterparts):

In these equations, the subscript 0 denotes initial values ( θ 0 θ 0 , x 0 x 0 , and t 0 t 0 are initial values), and the average angular velocity ω - ω - and average velocity v - v - are defined as follows:

The equations given above in Table 10.2 can be used to solve any rotational or translational kinematics problem in which a a and α α are constant.

Problem-Solving Strategy for Rotational Kinematics

• Examine the situation to determine that rotational kinematics (rotational motion) is involved . Rotation must be involved, but without the need to consider forces or masses that affect the motion.
• Identify exactly what needs to be determined in the problem (identify the unknowns) . A sketch of the situation is useful.
• Make a list of what is given or can be inferred from the problem as stated (identify the knowns) .
• Solve the appropriate equation or equations for the quantity to be determined (the unknown) . It can be useful to think in terms of a translational analog because by now you are familiar with such motion.
• Substitute the known values along with their units into the appropriate equation, and obtain numerical solutions complete with units . Be sure to use units of radians for angles.
• Check your answer to see if it is reasonable: Does your answer make sense ?

Example 10.3

Calculating the acceleration of a fishing reel.

A deep-sea fisherman hooks a big fish that swims away from the boat pulling the fishing line from his fishing reel. The whole system is initially at rest and the fishing line unwinds from the reel at a radius of 4.50 cm from its axis of rotation. The reel is given an angular acceleration of 110 rad/s 2 110 rad/s 2 for 2.00 s as seen in Figure 10.7 .

(a) What is the final angular velocity of the reel?

(b) At what speed is fishing line leaving the reel after 2.00 s elapses?

(c) How many revolutions does the reel make?

(d) How many meters of fishing line come off the reel in this time?

In each part of this example, the strategy is the same as it was for solving problems in linear kinematics. In particular, known values are identified and a relationship is then sought that can be used to solve for the unknown.

Solution for (a)

Here α α and t t are given and ω ω needs to be determined. The most straightforward equation to use is ω = ω 0 + αt ω = ω 0 + αt because the unknown is already on one side and all other terms are known. That equation states that

We are also given that ω 0 = 0 ω 0 = 0 (it starts from rest), so that

Solution for (b)

Now that ω ω is known, the speed v v can most easily be found using the relationship

where the radius r r of the reel is given to be 4.50 cm; thus,

Note again that radians must always be used in any calculation relating linear and angular quantities. Also, because radians are dimensionless, we have m × rad = m m × rad = m .

Solution for (c)

Here, we are asked to find the number of revolutions. Because 1 rev = 2π rad 1 rev = 2π rad , we can find the number of revolutions by finding θ θ in radians. We are given α α and t t , and we know ω 0 ω 0 is zero, so that θ θ can be obtained using θ = ω 0 t + 1 2 αt 2 θ = ω 0 t + 1 2 αt 2 .

Converting radians to revolutions gives

Solution for (d)

The number of meters of fishing line is x x , which can be obtained through its relationship with θ θ :

This example illustrates that relationships among rotational quantities are highly analogous to those among linear quantities. We also see in this example how linear and rotational quantities are connected. The answers to the questions are realistic. After unwinding for two seconds, the reel is found to spin at 220 rad/s, which is 2100 rpm. (No wonder reels sometimes make high-pitched sounds.) The amount of fishing line played out is 9.90 m, about right for when the big fish bites.

Example 10.4

Calculating the duration when the fishing reel slows down and stops.

Now let us consider what happens if the fisherman applies a brake to the spinning reel, achieving an angular acceleration of – 300 rad/s 2 – 300 rad/s 2 . How long does it take the reel to come to a stop?

We are asked to find the time t t for the reel to come to a stop. The initial and final conditions are different from those in the previous problem, which involved the same fishing reel. Now we see that the initial angular velocity is ω 0 = 220 rad/s ω 0 = 220 rad/s and the final angular velocity ω ω is zero. The angular acceleration is given to be α = − 300 rad/s 2 α = − 300 rad/s 2 . Examining the available equations, we see all quantities but t are known in ω = ω 0 + αt , ω = ω 0 + αt , making it easiest to use this equation.

The equation states

We solve the equation algebraically for t , and then substitute the known values as usual, yielding

Note that care must be taken with the signs that indicate the directions of various quantities. Also, note that the time to stop the reel is fairly small because the acceleration is rather large. Fishing lines sometimes snap because of the accelerations involved, and fishermen often let the fish swim for a while before applying brakes on the reel. A tired fish will be slower, requiring a smaller acceleration.

Example 10.5

Calculating the slow acceleration of trains and their wheels.

Large freight trains accelerate very slowly. Suppose one such train accelerates from rest, giving its 0.350-m-radius wheels an angular acceleration of 0 . 250 rad/s 2 0 . 250 rad/s 2 . After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the track? (b) What are the final angular velocity of the wheels and the linear velocity of the train?

In part (a), we are asked to find x x , and in (b) we are asked to find ω ω and v v . We are given the number of revolutions θ θ , the radius of the wheels r r , and the angular acceleration α α .

The distance x x is very easily found from the relationship between distance and rotation angle:

Solving this equation for x x yields

Before using this equation, we must convert the number of revolutions into radians, because we are dealing with a relationship between linear and rotational quantities:

Now we can substitute the known values into x = rθ x = rθ to find the distance the train moved down the track:

We cannot use any equation that incorporates t t to find ω ω , because the equation would have at least two unknown values. The equation ω 2 = ω 0 2 + 2 αθ ω 2 = ω 0 2 + 2 αθ will work, because we know the values for all variables except ω ω :

Taking the square root of this equation and entering the known values gives

We can find the linear velocity of the train, v v , through its relationship to ω ω :

The distance traveled is fairly large and the final velocity is fairly slow (just under 32 km/h).

There is translational motion even for something spinning in place, as the following example illustrates. Figure 10.8 shows a fly on the edge of a rotating microwave oven plate. The example below calculates the total distance it travels.

Example 10.6

Calculating the distance traveled by a fly on the edge of a microwave oven plate.

A person decides to use a microwave oven to reheat some lunch. In the process, a fly accidentally flies into the microwave and lands on the outer edge of the rotating plate and remains there. If the plate has a radius of 0.15 m and rotates at 6.0 rpm, calculate the total distance traveled by the fly during a 2.0-min cooking period. (Ignore the start-up and slow-down times.)

First, find the total number of revolutions θ θ , and then the linear distance x x traveled. θ = ω ¯ t θ = ω ¯ t can be used to find θ θ because ω - ω - is given to be 6.0 rpm.

Entering known values into θ = ω ¯ t θ = ω ¯ t gives

As always, it is necessary to convert revolutions to radians before calculating a linear quantity like x x from an angular quantity like θ θ :

Now, using the relationship between x x and θ θ , we can determine the distance traveled:

Quite a trip (if it survives)! Note that this distance is the total distance traveled by the fly. Displacement is actually zero for complete revolutions because they bring the fly back to its original position. The distinction between total distance traveled and displacement was first noted in One-Dimensional Kinematics .

Check Your Understanding

Rotational kinematics has many useful relationships, often expressed in equation form. Are these relationships laws of physics or are they simply descriptive? (Hint: the same question applies to linear kinematics.)

Rotational kinematics (just like linear kinematics) is descriptive and does not represent laws of nature. With kinematics, we can describe many things to great precision but kinematics does not consider causes. For example, a large angular acceleration describes a very rapid change in angular velocity without any consideration of its cause.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/10-2-kinematics-of-rotational-motion

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Kinematic Equations and Free Fall
• Kinematic Equations Introduction
• Solving Problems with Kinematic Equations
• Sample Problems and Solutions
• Kinematic Equations and Kinematic Graphs

Like any moving object, the motion of an object in free fall can be described by four kinematic equations. The kinematic equations that describe any object's motion are:

The symbols in the above equation have a specific meaning: the symbol d stands for the displacement ; the symbol t stands for the time ; the symbol a stands for the acceleration of the object; the symbol v i stands for the initial velocity value; and the symbol v f stands for the final velocity .

Applying Free Fall Concepts to Problem-Solving

There are a few conceptual characteristics of free fall motion that will be of value when using the equations to analyze free fall motion. These concepts are described as follows:

• An object in free fall experiences an acceleration of -9.8 m/s/s. (The - sign indicates a downward acceleration.) Whether explicitly stated or not, the value of the acceleration in the kinematic equations is -9.8 m/s/s for any freely falling object.
• If an object is merely dropped (as opposed to being thrown) from an elevated height, then the initial velocity of the object is 0 m/s.
• If an object is projected upwards in a perfectly vertical direction, then it will slow down as it rises upward. The instant at which it reaches the peak of its trajectory, its velocity is 0 m/s. This value can be used as one of the motion parameters in the kinematic equations; for example, the final velocity ( v f ) after traveling to the peak would be assigned a value of 0 m/s.
• If an object is projected upwards in a perfectly vertical direction, then the velocity at which it is projected is equal in magnitude and opposite in sign to the velocity that it has when it returns to the same height. That is, a ball projected vertically with an upward velocity of +30 m/s will have a downward velocity of -30 m/s when it returns to the same height.

These four principles and the four kinematic equations can be combined to solve problems involving the motion of free falling objects. The two examples below illustrate application of free fall principles to kinematic problem-solving. In each example, the problem solving strategy that was introduced earlier in this lesson will be utilized.  

Example Problem A

Luke Autbeloe drops a pile of roof shingles from the top of a roof located 8.52 meters above the ground. Determine the time required for the shingles to reach the ground.

The solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step involves the identification and listing of known information in variable form. You might note that in the statement of the problem, there is only one piece of numerical information explicitly stated: 8.52 meters. The displacement ( d ) of the shingles is -8.52 m. (The - sign indicates that the displacement is downward). The remaining information must be extracted from the problem statement based upon your understanding of the above principles . For example, the v i value can be inferred to be 0 m/s since the shingles are dropped (released from rest; see note above ). And the acceleration ( a ) of the shingles can be inferred to be -9.8 m/s 2 since the shingles are free-falling ( see note above ). (Always pay careful attention to the + and - signs for the given quantities.) The next step of the solution involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the time of fall. So t is the unknown quantity. The results of the first three steps are shown in the table below.

The next step involves identifying a kinematic equation that allows you to determine the unknown quantity. There are four kinematic equations to choose from. In general, you will always choose the equation that contains the three known and the one unknown variable. In this specific case, the three known variables and the one unknown variable are d , v i , a , and t . Thus, you will look for an equation that has these four variables listed in it. An inspection of the four equations above reveals that the equation on the top left contains all four variables.

Once the equation is identified and written down, the next step involves substituting known values into the equation and using proper algebraic steps to solve for the unknown information. This step is shown below.

-8.52 m = (0 m/s) • (t) + ½ • (-9.8 m/s 2 ) • (t) 2

-8.52 m = (0 m) *(t) + (-4.9 m/s 2 ) • (t) 2

-8.52 m = (-4.9 m/s 2 ) • (t) 2

(-8.52 m)/(-4.9 m/s 2 ) = t 2

1.739 s 2 = t 2

The solution above reveals that the shingles will fall for a time of 1.32 seconds before hitting the ground. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. The shingles are falling a distance of approximately 10 yards (1 meter is pretty close to 1 yard); it seems that an answer between 1 and 2 seconds would be highly reasonable. The calculated time easily falls within this range of reasonability. Checking for accuracy involves substituting the calculated value back into the equation for time and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!  

Example Problem B

Rex Things throws his mother's crystal vase vertically upwards with an initial velocity of 26.2 m/s. Determine the height to which the vase will rise above its initial height.

Once more, the solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step involves the identification and listing of known information in variable form. You might note that in the statement of the problem, there is only one piece of numerical information explicitly stated: 26.2 m/s. The initial velocity ( v i ) of the vase is +26.2 m/s. (The + sign indicates that the initial velocity is an upwards velocity). The remaining information must be extracted from the problem statement based upon your understanding of the above principles . Note that the v f value can be inferred to be 0 m/s since the final state of the vase is the peak of its trajectory ( see note above ). The acceleration ( a ) of the vase is -9.8 m/s 2 ( see note above ). The next step involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the displacement of the vase (the height to which it rises above its starting height). So d is the unknown information. The results of the first three steps are shown in the table below.

The next step involves identifying a kinematic equation that would allow you to determine the unknown quantity. There are four kinematic equations to choose from. Again, you will always search for an equation that contains the three known variables and the one unknown variable. In this specific case, the three known variables and the one unknown variable are v i , v f , a , and d . An inspection of the four equations above reveals that the equation on the top right contains all four variables.

v f 2 = v i 2 + 2 • a • d

(0 m/s) 2 = (26.2 m/s) 2 + 2 •(-9.8m/s 2 ) •d

0 m 2 /s 2 = 686.44 m 2 /s 2 + (-19.6 m/s 2 ) •d

(-19.6 m/s 2 ) • d = 0 m 2 /s 2 -686.44 m 2 /s 2

(-19.6 m/s 2 ) • d = -686.44 m 2 /s 2

d = (-686.44 m 2 /s 2 )/ (-19.6 m/s 2 )

The solution above reveals that the vase will travel upwards for a displacement of 35.0 meters before reaching its peak. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. The vase is thrown with a speed of approximately 50 mi/hr (merely approximate 1 m/s to be equivalent to 2 mi/hr). Such a throw will never make it further than one football field in height (approximately 100 m), yet will surely make it past the 10-yard line (approximately 10 meters). The calculated answer certainly falls within this range of reasonability. Checking for accuracy involves substituting the calculated value back into the equation for displacement and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!

Kinematic equations provide a useful means of determining the value of an unknown motion parameter if three motion parameters are known. In the case of a free-fall motion, the acceleration is often known. And in many cases, another motion parameter can be inferred through a solid knowledge of some basic kinematic principles . The next part of Lesson 6 provides a wealth of practice problems with answers and solutions.  

Reset password New user? Sign up

Existing user? Log in

Angular Kinematics

Already have an account? Log in here.

Angular kinematics is the study of rotational motion in the absence of forces. The equations of angular kinematics are extremely similar to the usual equations of kinematics , with quantities like displacements replaced by angular displacements and velocities replaced by angular velocities. Just as kinematics is routinely used to describe the trajectory of almost any physical system moving linearly, the equations of angular kinematics are relevant to most rotating physical systems.

Basic Equations of Angular Kinematics

Derivation of equations of angular kinematics, rotating systems in physics.

In purely rotational (circular) motion, the equations of angular kinematics are:

\[v = r\omega, \qquad a_c = -r\omega^2, \qquad a = r\alpha\]

The tangential velocity \(v\) describes the velocity of an object tangent to its path in rotational motion at angular frequency \(\omega\) and radius \(r\). This is the velocity an object would follow if it suddenly broke free of rotational motion and traveled along a straight line. The rate of change of this velocity is the tangential acceleration \(a\). The centripetal acceleration \(a_c\) is a second acceleration experienced by rotating objects, because changing the direction of a velocity vector requires an acceleration. Since the direction of the velocity vector changes constantly in rotational motion, rotating objects must be continuously accelerated towards the axis of rotation by some force providing a centripetal acceleration.

From the above equations, the usual kinematic equations hold in angular form. If an object undergoes constant angular acceleration \(\alpha\), the total angular displacement is:

\[\theta - \theta_0 = \omega_0 t + \frac12 \alpha t^2\]

where \(\theta_0\) is the initial angle and \(\omega_0\) is the initial angular velocity. Similarly, the angular velocity changes according to:

\[\omega^2 = \omega_0^2 + 2\alpha (\theta - \theta_0)\]

in terms of the angular displacement, or

\[\omega = \omega_0 + \alpha t\]

in terms of time.

Though the above derivation gives the magnitudes of angular quantities correctly, it does not capture the fact that angular quantities are also vector quantities . The direction in which the angular velocity points can be found from the right-hand rule: curving the fingers of your right hand along the direction of rotation, your thumb points in the direction of the angular velocity vector, along the axis of rotation. This is true by definition; although it seems strange since the vector is perpendicular to the rotation, this definition turns out to be the only way to formulate a consistent vector theory of rotational forces.

A turntable is spun from rest with a constant angular acceleration of \(\frac{\pi}{2} \text{ rad}/\text{s}^2\). After completing six full revolutions, what is its angular velocity in \(\text{rad}/\text{s}\)?

A merry-go-round has a radius of about \(8 \text{ m}\). A child sitting on a horse on the outer edge sees his parents, standing still at the entrance, every \(20 \text{ s}\). If the child's horse could break free of its merry-go-round restraints and continue forward tangentially without accelerating, how fast would it be traveling in \(\text{m}/\text{s}\)?

In a rotating frame of reference, it is often more convenient to use polar coordinates than Cartesian coordinates. Similarly, for vectors it is more convenient to use the radial and tangential vectors \(\hat{r}\) and \(\hat{\theta}\) in place of the usual Cartesian basis vectors \(\hat{x}\) and \(\hat{y}\). The radial vector to an object is defined so that it always points towards the object:

\[\hat{r} = \cos \theta\, \hat{x} + \sin \theta\, \hat{y}.\]

Note that the \(x\) and \(y\) components of the radial vector are just the usual polar coordinates, normalized to one. Similarly, the tangential vector \(\hat{\theta}\) is defined so that it is always orthogonal to the radial vector and tangent to the circle on which the radial vector lies:

\[\hat{\theta} = -\sin \theta\,\hat{x} + \cos \theta\, \hat{y}.\]

The polar basis vectors \(\hat{r}\) and \(\hat{\theta}\) explained graphically.

Show that \(\frac{d\hat{r}}{dt} = \dot{\theta} \hat{\theta}\) and \(\frac{d\hat{\theta}}{dt} = -\dot{\theta} \hat{r}\), where dots indicate time derivatives. Solution: Note that in Cartesian coordinates, the derivatives of the basis vectors \(\hat{x}\), \(\hat{y}\), etc. always vanish, because these basis vectors are fixed. The polar basis vectors, however, rotate in time so that they are always pointing radially and tangentially along some trajectory. Computing the derivative from the definitions above using the chain rule: \[ \begin{align} \frac{d\hat{r}}{dt} &= \frac{d}{dt} \left( \cos \theta\, \hat{x} + \sin \theta\, \hat{y}\right) = -\dot{\theta} \sin \theta\,\hat{x} + \dot{\theta} \cos \theta\,\hat{y} = \dot{\theta} \hat{\theta} \\ \frac{d\hat{\theta}}{dt} &= \frac{d}{dt} \left( -\sin \theta\, \hat{x} + \cos \theta\, \hat{y}\right) = -\dot{\theta} \cos \theta\,\hat{x} - \dot{\theta} \sin \theta\,\hat{y} = -\dot{\theta} \hat{r} \end{align} \] as claimed.

From the definitions above, all of the laws of angular kinematics are straightforward to derive. Suppose that the vector pointing to some rotating object is \(\vec{r} = r\hat{r}\) in polar coordinates, where \(r\) is the magnitude of the distance from the origin. The velocity of the object is then:

\[\frac{d\vec{r}}{dt} = \dot{r} \hat{r} +r\dot{\theta} \hat{\theta}.\]

The velocity has two components, as can be seen above. The first term, \(\dot{r} \hat{r}\), describes the radial velocity of the object away from the origin. The second term is the tangential velocity. Denoting \(\dot{\theta} = \omega\) as the angular velocity , the tangential velocity is just \(v = r\omega\).

Taking another derivative allows identification of the different terms contributing to the acceleration of the object:

\[ \begin{align} \frac{d^2 \vec{r}}{dt} &= \frac{d}{dt} \frac{d\vec{r}}{dt} = \frac{d}{dt} \left( \dot{r} \hat{r} +r\dot{\theta} \hat{\theta} \right) \\ &=(\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r} \dot{\theta}) \hat{\theta} \end{align} \]

The radial terms \(\ddot{r}\) and \(r\dot{\theta}^2 = r\omega^2\) describe the radial acceleration outward from the origin and the centripetal acceleration towards the origin, respectively. The tangential terms are the tangential acceleration \(a = r\ddot{\theta} = r\alpha\), where \(\alpha = \dot{\omega}\) is the angular acceleration , and \(2\dot{r} \dot{\theta} = 2\dot{r} \omega\), the Coriolis acceleration .

A straight line in an inertial frame becomes a curved line in the rotating frame when there is no force to provide Coriolis acceleration [2].

Remarkably, this derivation proves without reference to any forces at all that an object in circular motion with angular velocity \(\omega\) must accelerate radially inward with the centripetal acceleration \(a_c\) given above.

Countless rotating systems in physics can be analyzed using the laws of angular kinematics; a few are explored in the following examples.

As most kids learn, if you quickly rotate a tube containing a ball, the ball can be made to "slingshot" out the end at very high speeds. The same effect is visible in rotating a rod with a bead around it and many other physical scenarios. How fast does the velocity of the ball/bead increase if the tube/rod is rotated at constant angular velocity \(\omega\)? Solution: Since there is no radial force on the ball/bead, the total radial acceleration is zero according to Newton's second law. In polar coordinates this means that: \[\ddot{r} - r\omega^2 = 0.\] This differential equation in \(r\) is solved by: \[r(t) = Ae^{\omega t} + Be^{-\omega t},\] for some constants \(A\) and \(B\) depending on initial conditions. If the ball/bead starts from rest at radius \(r_0\), these constants are fixed to be: \[A = B = \frac{r_0}{2},\] so the solution for the velocity of the ball/bead is found by differentiating to be: \[\dot{r}(t) = \frac{r_0 \omega}{2} e^{\omega t} - \frac{r_0 \omega}{2} e^{-\omega t}.\] The velocity of the ball/bead grows exponentially, since the second term damps to zero quickly.

A bead is lodged in a wheel that rolls without slipping with constant velocity \(V\). Show that the trajectory of the bead traces a cycloid in the lab frame. Solution: In the wheel reference frame, the bead is in uniform circular motion. If the wheel is of radius \(r\), the bead has coordinates and velocity with respect to the center of the wheel: \[ \begin{align} \vec{r} &= r\hat{r} \\ \vec{v} &= r \omega \hat{\theta} = V \hat{\theta} \end{align} \] In the lab reference frame, the center of the wheel moves with velocity \(V\), so it is located at: \[\vec{R} = Vt \hat{x} + r\hat{y} = r\omega t \hat{x} + r\hat{y},\] keeping in mind that the center of the wheel is a height \(r\) above the ground. The position of the bead in the lab frame is therefore: \[\vec{R} + \vec{r} = r\omega t \hat{x} + r\hat{y} + r\hat{r}\] Now if the wheel rolls clockwise (i.e., to the right) without slipping, the angle the bead has traveled is: \[\theta(t) = -\omega t\] assuming the bead starts at \(\theta = 0\). So the position of the bead is: \[ r\omega t \hat{x} + r\hat{y} + r\hat{r} = r(\omega t +\cos (\omega t)) \hat{x} + r(1-\sin (\omega t)) \hat{y}.\] Below is a plot of the position above for \(r = \omega = 1\) to verify that it is indeed a cycloid: Cycloidal motion of a bead at the edge of a wheel. :

The fact that the Earth rotates means that everywhere on the surface of the earth is a rotating reference frame. This has observable effects from the Coriolis acceleration, most notably in the precession of the axis of rotation of a sufficiently large pendulum. This experimental apparatus is usually called a Foucault pendulum . Precession of the axis of rotation of a Foucault pendulum [3]. Derive the precession of the Foucault pendulum assuming the Earth rotates with angular frequency \(\Omega\). Solution: The precession results from the fact that the plane in which the pendulum oscillates rotates with the rotation of the Earth. However, at higher latitudes \(\varphi\), this precession is slower than at the equator. In two dimensions, the Coriolis acceleration is then: \[ \begin{align} \ddot{x} &= \Omega \sin \varphi \dot{y} \\ \ddot{y} &= \Omega \sin \varphi \dot{x} \end{align} \] Small oscillations of a pendulum at frequency \(\omega\) obey Hooke's law . Using this fact and Newton's second law gives the following equations of motion: \[ \begin{align} \ddot{x} &= -\omega^2 x + 2\Omega \sin \varphi \dot{y} \\ \ddot{y} &= -\omega^2 y - 2\Omega \sin \varphi \dot{x} \end{align} \] The solution for the complex coordinate \(z= x+iy\) can be found by matrix ODE methods to be: \[z = e^{-i\Omega \sin \varphi t} \left(A e^{i\omega t} + Be^{-i \omega t} \right).\] for some constants \(A\) and \(B\) to be determined by initial conditions. The leading prefactor \(e^{-i\Omega \sin \varphi t}\) describes the \(z\) coordinate as rotating over time. Since \(z = x+iy\), the axis of the pendulum thus rotates in the \(x,y\) plane with frequency \(\Omega \sin \varphi\). Since \(\Omega = 2\pi \text{ rads}/\text{day}\), over the course of a single day, the pendulum oscillation precesses by an angle \(-2\pi \sin \varphi\).

[1] D. Kleppner and R. Kolenkow, An Introduction to Mechanics . McGraw-Hill, 1973.

[2] Image from https://en.wikipedia.org/wiki/Coriolis_force#/media/File:Corioliskraftanimation.gif under Creative Commons licensing for reuse with modification.

[3] Image from https://en.wikipedia.org/wiki/Foucault_pendulum#/media/File:Foucault-rotz.gif under Creative Commons licensing for reuse with modification.

Problem Loading...

Note Loading...

Set Loading...

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.8: Problem Solving

• Last updated
• Save as PDF
• Page ID 15514

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

learning objectives

• Develop and apply a strong problem-solving strategy for rotational kinematics

Problem-Solving Strategy For Rotational Kinematics

When solving problems on rotational kinematics:

• Examine the situation to determine that rotational kinematics (rotational motion) is involved. Rotation must be involved, but without the need to consider forces or masses that affect the motion.
• Identify exactly what needs to be determined in the problem (identify the unknowns). A sketch of the situation is useful.
• Make a list of what is given or can be inferred from the problem as stated (identify the knowns).
• Solve the appropriate equation or equations for the quantity to be determined (the unknown). It can be useful to think in terms of a translational analog because by now you are familiar with such motion.
• Substitute the known values along with their units into the appropriate equation, and obtain numerical solutions complete with units. Be sure to use units of radians for angles.
• Check your answer to see if it is reasonable: Does your answer make sense?

Example \(\PageIndex{1}\):

Suppose a large freight train accelerates from rest, giving its 0.350 m radius wheels an angular acceleration of 0.250 rad/s 2 . After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the track? (b) What are the final angular velocity of the wheels and the linear velocity of the train?

In part (a), we are asked to find x, and in (b) we are asked to find ω and v. We are given the number of revolutions θ, the radius of the wheels r, and the angular acceleration α.

The distance x is very easily found from the relationship between distance and rotation angle: \(\mathrm{θ=\frac{x}{r}}\).

Solving this equation for x yields \(\mathrm{x=rθ}\).

Before using this equation, we must convert the number of revolutions into radians, because we are dealing with a relationship between linear and rotational quantities:

\[\mathrm{θ=(200 rev)(\dfrac{2π \; rad}{1 \; rev})=1257 \; rad.}\]

Substitute the known values into \(\mathrm{x=rθ}\) to find the distance the train moved down the track:

\[\mathrm{x=rθ=(0.350 \;m)(1257 \; rad)=440 \; m.}\]

We cannot use any equation that incorporates t to find ω, because the equation would have at least two unknown values. The equation \(\mathrm{ω^2=ω_0^2+2 \alpha \theta}\) will work, because we know the values for all variables except ω. Taking the square root of this equation and entering the known values gives

\[\begin{align} \mathrm{ω} & \mathrm{=\sqrt{0+2(0.250 \; rad/s^2)(1257 \; rad)}} \\ & \mathrm{=25.1 \; rad/s} \end{align}\]

One may find the linear velocity of the train, v, through its relationship to ω:

\[\mathrm{v=rω=(0.350 \; m)(25.1 \; rad/s)=8.77 \; m/s}\]

Rotational motion : Part of a series of videos on physics problem-solving. The problems are taken from “The Joy of Physics. ” This one deals with angular motion. The viewer is urged to pause the video at the problem statement and work the problem before watching the rest of the video.

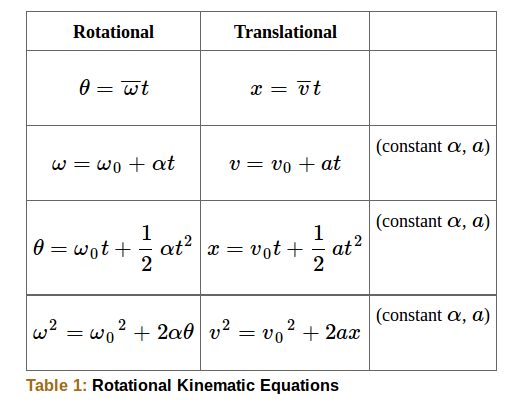
Equation list : Rotational and translational kinematic equations.

• Examine the situation to determine that rotational kinematics (rotational motion ) is involved, and identify exactly what needs to be determined.
• Make a list of what is given or can be inferred from the problem as stated and solve the appropriate equations.
• Substitute the known values along with their units into the appropriate equation, and obtain numerical solutions complete with units.
• kinematics : The branch of mechanics concerned with objects in motion, but not with the forces involved.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• OpenStax College, Kinematics of Rotational Motion. September 17, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42178/latest/ . License : CC BY: Attribution
• kinematics. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/kinematics . License : CC BY-SA: Attribution-ShareAlike
• Rotational motion. Located at : http://www.youtube.com/watch?v=FZ8U_3qZQqs . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
• OpenStax College, Kinematics of Rotational Motion. February 8, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42178/latest/ . License : CC BY: Attribution