linear equations examples grade 7

LetsPlayMaths.Com

Class vii math, class-7 linear equations in one variable, linear equations, rules to solve linear equation, rules of transposition, procedure to solve linear equation, linear equation word problem, linear equation test, linear equation worksheet, answer sheet.

An equation containing only one variable having power 1 is known as linear equation. Let's see some examples. 2p + 4 = 8, 5 − 3y = -7, 2a ⁄ 5 − 4 = 6 All the above 3 linear equations are having only one variable and having power 1.

• We can add same number to both sides of an equation
• We can subtract same number from both sides of an equation
• We can multiply same nonzero number to both sides of an equation
• We can divide same nonzero to both sides of an equation

A term can be transposed from one side of the equation to the other side by changing its sign. Let's see some examples.

Example 1. 5b − 3 = 12 The above linear equation can be written as         => 5b = 12 + 3 Transposing −3 from LHS to RHS by changing it's sign to +3.

Example 2. 5q + 5 = 19 − 2q The above linear equation can be written as         => 5q + 2q = 19 − 5 Here we have transpose 5 from LHS to RHS by changing it's sign to −5. Similarly, we have transpose -2q from RHS to LHS by changing it's sign to +2q.

• Simplify both sides by removing group symbols and collecting like terms
• Remove fractions by multiplying both sides by appropriate factor
• Arrange all the variable terms on one side and all constant terms on the other side
• Make the coefficient of the variable as 1

Example 1. Solve 3m + 5 = 25 − 2m. Solution. 3m + 5 = 25 − 2m         => 3m + 2m = 25 − 5         => 5m = 20         => m = 20 ÷ 5         => m = 4

Example 2. Solve 2(p − 1) = p + 12. Solution. 2(p − 1) = p + 12         => 2p − 2 = p + 12         => 2p − p = 12 + 2         => p = 14

Example 3. Solve 5n − 4 ⁄ 5 = 20. Solution. 5n − 4 ⁄ 5 = 20 Multiply both sides by 5.         => 25n − 4 = 100         => 25n = 100 + 4         => 25n = 104         => n = 104 ÷ 25         => n = 20 4 ⁄ 5

Problem stated in words are known as word problems. Solving word problem consists two steps. First step is translating the words of the problem into an algebraic equation. Second step is solving the equation. Let's see some examples.

Example 1. If 7 is added to three times of a number, then the result is 28. Find the number. Solution. Let's assume the number is p. As per the word problem given, linear equation will be         3p + 7 = 28         => 3p = 28 − 7         => 3p = 21         => p = 21 ÷ 3         => p = 7 Hence, the number is 7.

Example 2. Find the three consecutive odd numbers whose sum is 105. Solution. Let's consider the smallest, odd number is equal to m. Next two odd numbers are m+2 and m+4. According to the given word problem following linear equation can be formed.         m + m + 2 + m + 4 = 105         => 3m + 4 = 105         => 3m = 99         => m = 99 ÷ 3         => m = 33 Hence, the required consecutive odd numbers are 33, 35 and 37.

Example 3. The cost of 3 notebooks and 5 similar pens is Rs. 460. If the notebook cost is Rs. 20 more than the pen, then find the cost of each. Solution. Let's consider cost of the pen = q Then, cost of the notebook = q + 20 So, the linear equation will be         3(q + 20) + 5q = 460         => 3q + 60 + 5q = 460         => 8q + 60 = 460         => 8q = 400         => q = 400 ÷ 8         => q = 50 Hence, cost of the pen and notebook is Rs. 50 and Rs. 70 respectively.

Linear Equation - 1

Linear Equation - 2

Linear Equation Worksheet - 1

Linear Equation Worksheet - 2

Linear Equation Worksheet - 3

Linear-Equation-Answer Download the pdf

Copyright © 2024 LetsPlayMaths.com. All Rights Reserved. Email: [email protected]

• Join for FREE
• Printable Worksheets
• Online Lessons
• Test Maker™
• Printable Games
• Worksheet Generator
• Plans & Pricing

Printable & online resources for educators

• Test Maker TM
• Browse All Questions
• Questions With Images
• Advanced Search

Share/Like This Page

Filter by grade.

You are browsing Grade 7 questions. View questions in All Grades .

Grade 5 Grade 6 Grade 7 Grade 8 Grade 9 Grade 10 Grade 11

Browse Questions

• All Subjects w/ Images (7032)
• By ELA/Literacy Standard
• By Math Standard
• All Subjects (20661)
• English Language Arts (6182)
• English as a Second Language ESL (4512)
• Health and Medicine (452)
• Life Skills (110)

Arithmetic and Number Concepts

Function and algebra concepts, absolute value, algebraic expressions, functions and relations, inequalities, linear equations, literal equations, number properties, polynomials and rational expressions, sequences and series, geometry and measurement, mathematical process, statistics and probability concepts.

• Physical Education (419)
• Science (5451)
• Social Studies (3531)
• Study Skills and Strategies (37)
• Technology (78)
• Vocational Education (2)

Seventh Grade (Grade 7) Linear Equations Questions

You can create printable tests and worksheets from these Grade 7 Linear Equations questions! Select one or more questions using the checkboxes above each question. Then click the add selected questions to a test button before moving to another page.

• [math]x=9[/math]
• [math]x=14[/math]
• [math]x=4[/math]
• [math]x=2[/math]
• [math]x=-3[/math]
• [math]x=-20[/math]
• [math]x=-56[/math]
• [math]x=-96[/math]
• [math]t+5=11[/math]
• [math]3-t=-3[/math]
• [math]7t=42[/math]
• [math]24/t=3[/math]
• [math]c = 55m[/math]
• [math]c = 30.25m[/math]
• [math]c = 30 + 0.25m[/math]
• [math]c = 0.25 + 30m[/math]
• [math]2/3[/math]
• [math]-2/3[/math]
• [math]3/2[/math]
• [math]-3/2[/math]
• [math]x=1 2/3[/math]
• [math]x=5[/math]
• [math]x=15[/math]
• [math]x=30[/math]
• [math]10(1.35)=x[/math]
• [math]10-x=1.35[/math]
• [math]1.35+10=x[/math]
• [math]10=1.35x[/math]
• expression.
• Divide 3 from both sides, then subtract 8 from both sides.
• Subtract 8 from both sides, then divide both sides by 3.
• Subtract 17 from both sides, then divide both sides by 8.
• Multiply both sides by 3, then subtract 8 from both sides.
• Privacy Policy
• Terms of Use
• FREE Printable Worksheets
• Common Core ELA Worksheets
• Common Core Math Worksheets

Free Printable Linear Equations Worksheets for 7th Grade

Linear Equations: Discover a vast collection of free printable worksheets for Grade 7 Math teachers, focusing on solving and graphing linear equations to enhance students' learning experience.

Recommended Topics for you

• Slope-Intercept Form
• Slope of a Line

Explore Linear Equations Worksheets by Grades

• kindergarten

Explore Linear Equations Worksheets for grade 7 by Topic

Explore other subject worksheets for grade 7.

• Social studies
• Social emotional
• Foreign language
• Reading & Writing

Explore printable Linear Equations worksheets for 7th Grade

Linear Equations worksheets for Grade 7 are an essential resource for teachers looking to help their students master the fundamental concepts of algebra. These worksheets provide a variety of problems that challenge students to apply their knowledge of math and algebra to solve linear equations. With a range of difficulty levels, these worksheets cater to the diverse needs of students in a Grade 7 classroom. Teachers can use these worksheets to supplement their lesson plans, provide extra practice for struggling students, or as a review before assessments. By incorporating Linear Equations worksheets for Grade 7 into their curriculum, teachers can ensure that their students build a strong foundation in algebra, setting them up for success in future math courses.

Quizizz is an excellent platform for teachers to access a wide variety of resources, including Linear Equations worksheets for Grade 7, math games, and other engaging activities. This platform allows teachers to create customized quizzes and assignments, making it easy to tailor the content to the specific needs of their students. In addition to worksheets, Quizizz offers interactive games and challenges that help students develop their problem-solving skills while having fun. Teachers can also track their students' progress and identify areas where they may need additional support. By incorporating Quizizz into their lesson plans, teachers can provide a dynamic and engaging learning experience for their Grade 7 students, ensuring that they develop a strong understanding of algebra and other essential math concepts.

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Worksheets for simplifying expressions

Worksheets for evaluating expressions with variables

Worksheets for writing expressions with variables from verbal expressions

Worksheets for linear inequalities

Key to Algebra Workbooks

Key to Algebra offers a unique, proven way to introduce algebra to your students. New concepts are explained in simple language, and examples are easy to follow. Word problems relate algebra to familiar situations, helping students to understand abstract concepts. Students develop understanding by solving equations and inequalities intuitively before formal solutions are introduced. Students begin their study of algebra in Books 1-4 using only integers. Books 5-7 introduce rational numbers and expressions. Books 8-10 extend coverage to the real number system.

Linear Equation Worksheets (Distributive Property)

Related Topics: More Math Worksheets More Grade 7 Math Lessons Grade 7 Math Worksheets

There are five sets of solving linear equation worksheets:

• Solve linear equations (1-step equations)
• Solve linear equations (2-step equations)
• Solve linear equations (combine like terms)
• Solve linear equations (distributive property & combine like terms)
• Solve linear equations (fractions)

Examples, solutions, videos, and worksheets to help Grade 6 and Grade 7 students learn how to solve linear equations by using the distributive property and combining like terms.

How to solve linear equations (distributive property & combining like terms)?

There are three sets of solving linear equations worksheets using distributive property & combining like terms.

• Solve linear equations (variables on one side, positive coefficients).
• Solve linear equations (variables on one side, negative coefficients).
• Solve linear equations (variables on both sides).

You can follow these steps to solve a linear equation:

• Use the distributive property and combine like terms, if applicable.
• Multiply each term inside the parentheses by the number or variable outside the parentheses.
• Combine the like terms that were created by the distribution.
• Isolate the variable term. Perform inverse operations to move all other terms to the opposite side of the equation.
• Simplify the equation further, if necessary, until you have the variable term isolated on one side of the equation.
• Solve for the variable by performing the necessary operations to isolate it.
• Check your solution by substituting the value you found back into the original equation and verifying that both sides are equal.

For example, 3x + 3(2x + 3) = 54 3x + 6x + 9 = 54 9x + 9 = 54 9x = 54 x = 5

Click on the following worksheet to get a printable pdf document. Scroll down the page for more Linear Equations Worksheets .

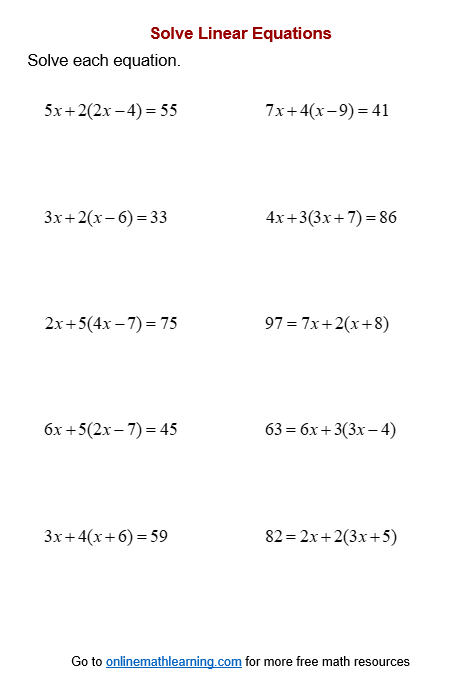
More Linear Equation Worksheets (Distributive Property & Combine Like Terms)

Printable (Answers on the second page.) Linear Equations Worksheet #1 (variables on one side, positive coefficients) Linear Equations Worksheet #2 (variables on one side, negative coefficients) Linear Equations Worksheet #3 (variables on both sides)

Online or Generated Combine like Terms (Sprint) Solve by Combining Like Terms Solve Equations with the Variable on Both Sides Solve Equations by Distributive Property Solve Multi-Step Equations 1 Solve Multi-Step Equations 2 Solve Word Problems using Algebra

Related Lessons & Worksheets

Solve Linear Equations

More Printable Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Systems of Linear Equations

A linear equation is not always in the form y = 3.5 − 0.5x ,

It can also be like y = 0.5(7 − x)

Or like y + 0.5x = 3.5

Or like y + 0.5x − 3.5 = 0 and more.

(Note: those are all the same linear equation!)

A System of Linear Equations is when we have two or more linear equations working together.

Example: Here are two linear equations:

Together they are a system of linear equations.

Can you discover the values of x and y yourself? (Just have a go, play with them a bit.)

Let's try to build and solve a real world example:

Example: You versus Horse

It's a race!

You can run 0.2 km every minute.

The Horse can run 0.5 km every minute. But it takes 6 minutes to saddle the horse.

How far can you get before the horse catches you?

We can make two equations ( d =distance in km, t =time in minutes)

• You run at 0.2km every minute, so d = 0.2t
• The horse runs at 0.5 km per minute, but we take 6 off its time: d = 0.5(t−6)

So we have a system of equations (that are linear ):

• d = 0.5(t−6)

We can solve it on a graph:

Do you see how the horse starts at 6 minutes, but then runs faster?

It seems you get caught after 10 minutes ... you only got 2 km away.

Run faster next time.

So now you know what a System of Linear Equations is.

Let us continue to find out more about them ....

There can be many ways to solve linear equations!

Let us see another example:

Example: Solve these two equations:

• −3x + y = 2

The two equations are shown on this graph:

Our task is to find where the two lines cross.

Well, we can see where they cross, so it is already solved graphically.

But now let's solve it using Algebra!

Hmmm ... how to solve this? There can be many ways! In this case both equations have "y" so let's try subtracting the whole second equation from the first:

Now let us simplify it:

So now we know the lines cross at x=1 .

And we can find the matching value of y using either of the two original equations (because we know they have the same value at x=1). Let's use the first one (you can try the second one yourself):

And the solution is:

x = 1 and y = 5

And the graph shows us we are right!

Linear Equations

Only simple variables are allowed in linear equations. No x 2 , y 3 , √x, etc :

Common Variables

Equations that "work together" share one or more variables:

A System of Equations has two or more equations in one or more variables

Many Variables

So a System of Equations could have many equations and many variables.

Example: 3 equations in 3 variables

There can be any combination:

• 2 equations in 3 variables,
• 6 equations in 4 variables,
• 9,000 equations in 567 variables,

When the number of equations is the same as the number of variables there is likely to be a solution. Not guaranteed, but likely.

In fact there are only three possible cases:

• No solution
• One solution
• Infinitely many solutions

When there is no solution the equations are called "inconsistent" .

One or infinitely many solutions are called "consistent"

Here is a diagram for 2 equations in 2 variables :

Independent

"Independent" means that each equation gives new information. Otherwise they are "Dependent" .

Also called "Linear Independence" and "Linear Dependence"

• 2x + 2y = 6

Those equations are "Dependent" , because they are really the same equation , just multiplied by 2.

So the second equation gave no new information .

Where the Equations are True

The trick is to find where all equations are true at the same time .

True? What does that mean?

The "you" line is true all along its length (but nowhere else).

Anywhere on that line d is equal to 0.2t

• at t=5 and d=1, the equation is true (Is d = 0.2t? Yes, as 1 = 0.2×5 is true)
• at t=5 and d=3, the equation is not true (Is d = 0.2t? No, as 3 = 0.2×5 is not true )

Likewise the "horse" line is also true all along its length (but nowhere else).

But only at the point where they cross (at t=10, d=2) are they both true .

So they have to be true simultaneously ...

... that is why some people call them "Simultaneous Linear Equations"

Solve Using Algebra

It is common to use Algebra to solve them.

Here is the "Horse" example solved using Algebra:

The system of equations is:

In this case it seems easiest to set them equal to each other:

d = 0.2t = 0.5(t−6)

Now we know when you get caught!

And our solution is:

t = 10 minutes and d = 2 km

Algebra vs Graphs

Why use Algebra when graphs are so easy? Because:

More than 2 variables can't be solved by a simple graph.

So Algebra comes to the rescue with two popular methods:

Solving By Substitution

Solving by elimination.

We will see each one, with examples in 2 variables, and in 3 variables. Here goes ...

These are the steps:

• Write one of the equations so it is in the style "variable = ..."
• Replace (i.e. substitute) that variable in the other equation(s).
• Solve the other equation(s)
• (Repeat as necessary)

Here is an example with 2 equations in 2 variables :

• 3x + 2y = 19

We can start with any equation and any variable .

Let's use the second equation and the variable "y" (it looks the simplest equation).

Write one of the equations so it is in the style "variable = ...":

We can subtract x from both sides of x + y = 8 to get y = 8 − x . Now our equations look like this:

Now replace "y" with "8 − x" in the other equation:

• 3x + 2 (8 − x) = 19

Solve using the usual algebra methods:

Expand 2(8−x) :

• 3x + 16 − 2x = 19

Then 3x−2x = x :

• x + 16 = 19

And lastly 19−16=3

Now we know what x is, we can put it in the y = 8 − x equation:

• y = 8 − 3 = 5

And the answer is:

x = 3 y = 5

Note: because there is a solution the equations are "consistent"

Check: why don't you check to see if x = 3 and y = 5 works in both equations?

Solving By Substitution: 3 equations in 3 variables

OK! Let's move to a longer example: 3 equations in 3 variables .

This is not hard to do... it just takes a long time !

• 2x + y + 3z = 15

We should line up the variables neatly, or we may lose track of what we are doing:

We can start with any equation and any variable. Let's use the first equation and the variable "x".

Now replace "x" with "6 − z" in the other equations:

(Luckily there is only one other equation with x in it)

2(6−z) + y + 3z = 15 simplifies to y + z = 3 :

Good. We have made some progress, but not there yet.

Now repeat the process , but just for the last 2 equations.

Let's choose the last equation and the variable z:

Now replace "z" with "3 − y" in the other equation:

−3y + (3−y) = 7 simplifies to −4y = 4 , or in other words y = −1

Almost Done!

Knowing that y = −1 we can calculate that z = 3−y = 4 :

And knowing that z = 4 we can calculate that x = 6−z = 2 :

x = 2 y = −1 z = 4

Check: please check this yourself.

We can use this method for 4 or more equations and variables... just do the same steps again and again until it is solved.

Conclusion: Substitution works nicely, but does take a long time to do.

Elimination can be faster ... but needs to be kept neat.

"Eliminate" means to remove : this method works by removing variables until there is just one left.

The idea is that we can safely :

• multiply an equation by a constant (except zero),
• add (or subtract) an equation on to another equation

Like in these two examples:

CAN we safely add equations to each other?

Yes, because we are "keeping the balance".

Imagine two really simple equations:

x − 5 = 3 5 = 5

We can add the "5 = 5" to "x − 5 = 3":

x − 5 + 5 = 3 + 5 x = 8

Try that yourself but use 5 = 3+2 as the 2nd equation

It works just fine, because both sides are equal (that is what the = is for)

We can also swap equations around, so the 1st could become the 2nd, etc, if that helps.

OK, time for a full example. Let's use the 2 equations in 2 variables example from before:

Very important to keep things neat:

Now ... our aim is to eliminate a variable from an equation.

First we see there is a "2y" and a "y", so let's work on that.

Multiply the second equation by 2:

Subtract the second equation from the first equation:

Yay! Now we know what x is!

Next we see the 2nd equation has "2x", so let's halve it, and then subtract "x":

Multiply the second equation by ½ (i.e. divide by 2):

Subtract the first equation from the second equation:

x = 3 and y = 5

And here is the graph:

The blue line is where 3x + 2y = 19 is true

The red line is where x + y = 8 is true

At x=3, y=5 (where the lines cross) they are both true. That is the answer.

Here is another example:

• 6x − 3y = 3

Lay it out neatly:

Multiply the first equation by 3:

0 − 0 = 9 ???

What is going on here?

Quite simply, there is no solution.

And lastly:

• 6x − 3y = 12

Well, that is actually TRUE! Zero does equal zero ...

... that is because they are really the same equation ...

... so there are an Infinite Number of Solutions

And so now we have seen an example of each of the three possible cases:

Solving By Elimination: 3 equations in 3 variables

Before we start on the next example, let's look at an improved way to do things.

Follow this method and we are less likely to make a mistake.

First of all, eliminate the variables in order :

• Eliminate x s first (from equation 2 and 3, in order)
• then eliminate y (from equation 3)

Start with:

Eliminate in this order:

We then have this "triangle shape":

Now start at the bottom and work back up (called "Back-Substitution") (put in z to find y , then z and y to find x ):

And we are solved:

ALSO, it is easier to do some of the calculations in our head, or on scratch paper, instead of always working within the set of equations:

• x + y + z = 6
• 2y + 5z = −4
• 2x + 5y − z = 27

Written neatly:

First, eliminate x from 2nd and 3rd equation.

There is no x in the 2nd equation ... move on to the 3rd equation:

Subtract 2 times the 1st equation from the 3rd equation (just do this in your head or on scratch paper):

And we get:

Next, eliminate y from 3rd equation.

We could subtract 1½ times the 2nd equation from the 3rd equation (because 1½ times 2 is 3) ...

... but we can avoid fractions if we:

• multiply the 3rd equation by 2 and
• multiply the 2nd equation by 3

and then do the subtraction ... like this:

And we end up with:

We now have that "triangle shape"!

Now go back up again "back-substituting":

We know z , so 2y+5z=−4 becomes 2y−10=−4 , then 2y=6 , so y=3 :

Then x+y+z=6 becomes x+3−2=6 , so x=6−3+2=5

x = 5 y = 3 z = −2

Please check this for yourself, it is good practice.

General Advice

Once you get used to the Elimination Method it becomes easier than Substitution, because you just follow the steps and the answers appear.

But sometimes Substitution can give a quicker result.

• Substitution is often easier for small cases (like 2 equations, or sometimes 3 equations)
• Elimination is easier for larger cases

And it always pays to look over the equations first, to see if there is an easy shortcut ... so experience helps ... so get experience!

• RD Sharma Solutions
• Chapter 8 Linear Equations In One Variable

RD Sharma Solutions for Class 7 Maths Chapter - 8 Linear Equations in One Variable

RD Sharma Solutions for Class 7 Maths Chapter 8 Linear Equation in One Variable are the best study materials for those students who find difficulties in solving Maths problems. Students can download the PDF of RD Sharma Solutions Maths Chapter 8 Linear Equations in One Variable from the links available here. These exercise problems are solved by our subject experts in Maths to help students prepare well for the annual exam.

Chapter 8, Linear Equations in One Variable, contains four exercises. RD Sharma Solutions for Class 7 , given here, contain the answers to all the questions present in these exercises. Let us have a look at some of the concepts discussed in this chapter.

• Equation – A statement of equality which involves one or more literal
• Linear equations – An equation in which the highest power of the variables involved is 1
• The solution of an equation in the trial and error method
• Systematic method
• Equations involving addition
• Equations involving subtraction
• Equations involving multiplication
• Equations involving division
• Transposition method
• Applications of linear equations to practical problems
• RD Sharma Solutions Class 7 Maths Chapter 1 Integers
• RD Sharma Solutions Class 7 Maths Chapter 2 Fractions
• RD Sharma Solutions Class 7 Maths Chapter 3 Decimals
• RD Sharma Solutions Class 7 Maths Chapter 4 Rational Numbers
• RD Sharma Solutions Class 7 Maths Chapter 5 Operations on Rational Numbers
• RD Sharma Solutions Class 7 Maths Chapter 6 Exponents
• RD Sharma Solutions Class 7 Maths Chapter 7 Algebraic Expressions
• RD Sharma Solutions Class 7 Maths Chapter 8 Linear Equations in One Variable
• RD Sharma Solutions Class 7 Maths Chapter 9 Ratio and Proportion
• RD Sharma Solutions Class 7 Maths Chapter 10 Unitary Method
• RD Sharma Solutions Class 7 Maths Chapter 11 Percentage
• RD Sharma Solutions Class 7 Maths Chapter 12 Profit and Loss
• RD Sharma Solutions Class 7 Maths Chapter 13 Simple Interest
• RD Sharma Solutions Class 7 Maths Chapter 14 Lines and Angles
• RD Sharma Solutions Class 7 Maths Chapter 15 Properties of Triangles
• RD Sharma Solutions Class 7 Maths Chapter 16 Congruence
• RD Sharma Solutions Class 7 Maths Chapter 17 Constructions
• RD Sharma Solutions Class 7 Maths Chapter 18 Symmetry
• RD Sharma Solutions Class 7 Maths Chapter 19 Visualising Solid Shapes
• RD Sharma Solutions Class 7 Maths Chapter 20 Mensuration I (Perimeter and Area of Rectilinear Figures)
• RD Sharma Solutions Class 7 Maths Chapter 21 Mensuration II (Area of Circle)
• RD Sharma Solutions Class 7 Maths Chapter 22 Data Handling I (Collection and Organisation of Data)
• RD Sharma Solutions Class 7 Maths Chapter 23 Data Handling II (Central Values)
• RD Sharma Solutions Class 7 Maths Chapter 24 Data Handling III (Constructions of Bar Graphs)
• RD Sharma Solutions Class 7 Maths Chapter 25 Data Handling IV (Probability)
• Exercise 8.1 Chapter 8 Linear Equations in One Variable
• Exercise 8.2 Chapter 8 Linear Equations in One Variable
• Exercise 8.3 Chapter 8 Linear Equations in One Variable
• Exercise 8.4 Chapter 8 Linear Equations in One Variable

RD Sharma Solutions for Class 7 Maths Chapter 8 Linear Equations in One Variable

carouselExampleControls111

Previous Next

Access answers to Maths RD Sharma Solutions for Class 7 Chapter 8 – Linear Equations in One Variable

Exercise 8.1 Page No: 8.6

1. Verify by substitution that:

(i) x = 4 is the root of 3x – 5 = 7

(ii) x = 3 is the root of 5 + 3x = 14

(iii) x = 2 is the root of 3x – 2 = 8x – 12

(iv) x = 4 is the root of (3x/2) = 6

(v) y = 2 is the root of y – 3 = 2y – 5

(vi) x = 8 is the root of (1/2)x + 7 = 11

(i) Given x = 4 is the root of 3x – 5 = 7

Now, substituting x = 4 in place of ‘x’ in the given equation, we get

= 3(4) – 5 = 7

= 12 – 5 = 7

Since, LHS = RHS

Hence, x = 4 is the root of 3x – 5 = 7.

(ii) Given x = 3 is the root of 5 + 3x = 14.

Now, substituting x = 3 in place of ‘x’ in the given equation, we get

= 5 + 3(3) = 14

= 5 + 9 = 14

Hence, x = 3 is the root of 5 + 3x = 14.

(iii) Given x = 2 is the root of 3x – 2 = 8x – 12.

Now, substituting x = 2 in place of ‘x’ in the given equation, we get

= 3(2) – 2 = 8(2) – 12

= 6 – 2 = 16 – 12

Hence, x = 2 is the root of 3x – 2 = 8x – 12.

(iv) Given x = 4 is the root of 3x/2 = 6.

= (3 × 4)/2 = 6

= (12/2) = 6

Hence, x = 4 is the root of (3x/2) = 6.

(v) Given y = 2 is the root of y – 3 = 2y – 5.

Now, substituting y = 2 in place of ‘y’ in the given equation, we get

= 2 – 3 = 2(2) – 5

= -1 = 4 – 5

Hence, y = 2 is the root of y – 3 = 2y – 5.

(vi) Given x = 8 is the root of (1/2)x + 7 = 11.

Now, substituting x = 8 in place of ‘x’ in the given equation, we get

= (1/2) (8) + 7 =11

= 4 + 7 = 11

Hence, x = 8 is the root of 12x + 7 = 11.

2. Solve each of the following equations by trial – and – error method:

(i) x + 3 =12

(ii) x -7 = 10

(iii) 4x = 28

(iv) (x/2) + 7 = 11

(v) 2x + 4 = 3x

(vi) (x/4) = 12

(vii) (15/x) = 3

(vii) (x/18) = 20

(i) Given x + 3 =12

Here LHS = x +3 and RHS = 12

Therefore, if x = 9, LHS = RHS.

Hence, x = 9 is the solution to this equation.

(ii) Given x -7 = 10

Here LHS = x -7 and RHS = 10

Therefore if x = 17, LHS = RHS

Hence, x = 17 is the solution to this equation.

(iii) Given 4x = 28

Here LHS = 4x and RHS = 28

Therefore if x = 7, LHS = RHS

Hence, x = 7 is the solution to this equation.

(iv) Given (x/2) + 7 = 11

Here LHS = (x/2) + 7 and RHS = 11

Since RHS is a natural number, (x/2) must also be a natural number, so we must substitute values of x that are multiples of 2.

Therefore if x = 8, LHS = RHS

Hence, x = 8 is the solution to this equation.

(v) Given 2x + 4 = 3x

Here LHS = 2x + 4 and RHS = 3x

Therefore if x = 4, LHS = RHS

Hence, x = 4 is the solution to this equation.

(vi) Given (x/4) = 12

Here LHS = (x/4) and RHS = 12

Since RHS is a natural number, x/4 must also be a natural number, so we must substitute values of x that are multiples of 4.

Therefore if x = 48, LHS = RHS

Hence, x = 48 is the solution to this equation.

(vii) Given (15/x) = 3

Here LHS = (15/x) and RHS = 3

Since RHS is a natural number, 15x must also be a natural number, so we must substitute values of x that are factors of 15.

Therefore if x = 5, LHS = RHS

Hence, x = 5 is the solution to this equation.

(viii) Given (x/18) = 20

Here LHS = (x/18) and RHS = 20

Since RHS is a natural number, (x/18) must also be a natural number, so we must substitute values of x that are multiples of 18.

Therefore if x = 360, LHS = RHS

Hence, x = 360 is the solution to this equation.

Exercise 8.2 Page No: 8.12

Solve each of the following equations and check your answers:

1. x – 3 = 5

Given x – 3 = 5

Adding 3 to both sides, we get,

x – 3 + 3 = 5 + 3

Verification:

Substituting x = 8 in LHS, we get

LHS = x – 3 and RHS = 5

LHS = 8 – 3 = 5 and RHS = 5

Hence, verified.

2. x + 9 = 13

Given x + 9 = 13

Subtracting 9 from both sides, i.e., LHS and RHS, we get

x + 9 – 9 = 13 – 9

Substituting x = 4 on LHS, we get

LHS = 4 + 9 = 13 = RHS

3. x – (3/5) = (7/5)

Given x – (3/5) = (7/5)

Add (3/5) to both sides, we get

x – (3/5) + (3/5) = (7/5) + (3/5)

x = (7/5) + (3/5)

Substitute x = 2 in LHS of given equation, then we get

2 – (3/5) = (7/5)

(10 – 3)/5 = (7/5)

(7/5) = (7/5)

Hence, verified

Given 3x = 0

On dividing both sides by 3 we get,

(3x/3) = (0/3)

Substituting x = 0 in LHS, we get

And RHS = 0

Therefore LHS = RHS

5. (x/2) = 0

Given x/2   = 0

Multiplying both sides by 2, we get

(x/2) × 2 = 0 × 2

LHS = 0/2 = 0 and RHS = 0

LHS = 0 and RHS = 0

6. x – (1/3) = (2/3)

Given x – (1/3) = (2/3)

Adding (1/3) to both sides, we get

x – (1/3) + (1/3) = (2/3) + (1/3)

x = (2 + 1)/3

Substituting x = 1 in LHS, we get

1 – (1/3) = (2/3)

(3 – 1)/3 = (2/3)

(2/3) = (2/3)

7. x + (1/2) = (7/2)

Given x + (1/2) = (7/2)

Subtracting (1/2) from both sides, we get

x + (1/2) – (1/2) = (7/2) – (1/2)

x = (7 – 1)/2

Substituting x = 3 in LHS, we get

3 + (1/2) = (7/2)

(6 + 1)/2 = (7/2)

(7/2) = (7/2)

8. 10 – y = 6

Given 10 – y = 6

Subtracting 10 from both sides, we get

10 – y – 10 = 6 – 10

Multiplying both sides by -1, we get

-y × -1 = – 4 × – 1

Substituting y = 4 in LHS, we get

10 – y = 10 – 4 = 6 and RHS = 6

9. 7 + 4y = -5

Given 7 + 4y = -5

Subtracting 7 from both sides, we get

7 + 4y – 7 = -5 -7

Dividing both sides by 4, we get

Substituting y = -3 in LHS, we get

7 + 4y = 7 + 4(-3) = 7 – 12 = -5, and RHS = -5

10. (4/5) – x = (3/5)

Given (4/5) – x = (3/5)

Subtracting (4/5) from both sides, we get

(4/5) – x – (4/5) = (3/5) – (4/5)

– x = (3 -4)/5

– x = (-1/5)

Substituting x = (1/5) in LHS, we get

(4/5) – (1/5) = (3/5)

(4 -1)/5 = (3/5)

(3/5) = (3/5)

Therefore LHS =RHS

11. 2y – (1/2) = (-1/3)

Given 2y – (1/2) = (-1/3)

Adding (1/2) from both the sides, we get

2y – (1/2) + (1/2) = (-1/3) + (1/2)

2y = (-1/3) + (1/2)

2y = (-2 + 3)/6 [LCM of 3 and 2 is 6]

Now divide both the side by 2, we get

Substituting y = (1/12) in LHS we get

2 (1/12) – (1/2) = (-1/3)

(1/6) – (1/2) = (-1/3)

(2 – 6)/12 = (-1/3) [LCM of 6 and 2 is 12]

(-4/12) = (-1/3)

(-1/3) = (-1/3)

12. 14 = (7x/10) – 8

Given 14 = (7x/10) – 8

Adding 8 to both sides we get,

14 + 8 = (7x/10) – 8 + 8

22 = (7x/10)

Multiply both sides by 10 we get,

x = (220/7)

Substituting x = (220/7) in RHS we get,

14 = (7/10) × (220/7) – 8

Therefore LHS = RHS.

13. 3 (x + 2) = 15

Given 3 (x + 2) = 15

Dividing both sides by 3 we get,

3 (x + 2)/3 = (15/3)

(x + 2) = 5

Now subtracting 2 by both sides, we get

x + 2 -2 = 5 -2

Substituting x =3 in LHS we get,

3 (3 + 2) = 15

14. (x/4) = (7/8)

Given (x/4) = (7/8)

Multiply both sides by 4 we get,

(x/4) × 4 = (7/8) × 4

Substituting x = (7/2) in LHS we get,

(7/2)/4 = (7/8)

(7/8) = (7/8)

15. (1/3) – 2x = 0

Given (1/3) – 2x = 0

Subtract (1/3) from both sides we get,

(1/3) – 2x – (1/3) = 0 – (1/3)

– 2x = – (1/3)

Divide both side by 2 we get,

2x/2 = (1/3)/2

Substituting x = (1/6) in LHS we get,

(1/3) – 2 (1/6) = 0

(1/3) – (1/3) = 0

16. 3 (x + 6) = 24

Given 3 (x + 6) = 24

Divide both the sides by 3 we get,

3 (x + 6)/3 = (24/3)

(x + 6) = 8

Now subtract 6 from both sides we get,

x + 6 – 6 = 8 – 6

Substituting x = 2 in LHS we get,

3 (2 + 6) = 24

17. 3 (x + 2) – 2 (x – 1) = 7

Given 3 (x + 2) – 2 (x – 1) = 7

On simplifying the brackets, we get

3 × x + 3 × 2 – 2 × x + 2 × 1 = 7

3x + 6 – 2x + 2 = 7

3x – 2x + 6 + 2 = 7

Subtracting 8 from both sides, we get

x + 8 – 8 = 7 – 8

Substituting x = -1 in LHS, we get

3 (x + 2) -2(x -1) = 7

3 (-1 + 2) -2(-1-1) = 7

(3×1) – (2×-2) = 7

18. 8 (2x – 5) – 6(3x – 7) = 1

Given 8 (2x – 5) – 6(3x – 7) = 1

(8 × 2x) – (8 × 5) – (6 × 3x) + (-6) × (-7) = 1

16x – 40 – 18x + 42 = 1

16x – 18x + 42 – 40 = 1

-2x + 2 = 1

Subtracting 2 from both sides, we get

-2x+ 2 – 2 = 1 -2

-2x × (-1) = -1× (-1)

Dividing both sides by 2, we get

2x/2 = (1/2)

Substituting x = (1/2) in LHS we get,

(8 × (2 × (1/2)–5) – (6 × (3 × (1/2)-7) = 1

8(1 – 5) – 6(3/2 – 7) = 1

8× (-4) – (6 × 3/2) + (6 × 7) = 1

– 32 – 9 + 42 = 1

– 41 + 42 = 1

19. 6 (1 – 4x) + 7 (2 + 5x) = 53

Given 6 (1 – 4x) + 7 (2 + 5x) = 53

(6 ×1) – (6 × 4x) + (7 × 2) + (7 × 5x) = 53

6 – 24x + 14 + 35x = 53

6 + 14 + 35x – 24x = 53

20 + 11x = 53

Subtracting 20 from both sides, we get 20 + 11x – 20 = 53 – 20

Dividing both sides by 11, we get

11x/11 = 33/11

6(1 – 4 × 3) + 7(2 + 5 × 3) = 53

6(1 – 12) + 7(2 + 15) = 53

6(-11) + 7(17) = 53

– 66 + 119 = 53

20. 5 (2 – 3x) -17 (2x -5) = 16

Given 5 (2 – 3x) -17 (2x – 5) = 16

On expanding the brackets, we get

(5 × 2) – (5 × 3x) – (17 × 2x) + (17 × 5) = 16

10 – 15x – 34x + 85 = 16

10 + 85 – 34x – 15x = 16

95 – 49x = 16

Subtracting 95 from both sides, we get

– 49x + 95 – 95 = 16 – 95

– 49x = -79

Dividing both sides by – 49, we get

– 49x/ -49 = -79/-49

Substituting x = (79/49) in LHS we get,

5 (2 – 3 × (79/49) – 17 (2 × (79/49) – 5) = 16

(5 × 2) – (5 × 3 × (79/49)) – (17 × 2 × (79/49)) + (17 × 5) = 16

10 – (1185/49) – (2686/49) + 85 = 16

(490 – 1185 – 2686 + 4165)/49 = 16

784/49 = 16

21. (x – 3)/5 -2 = -1

Given ((x – 3)/5) -2 = -1

Adding 2 to both sides we get,

((x -3)/5) – 2 + 2 = -1 + 2

(x -3)/5 = 1

Multiply both sides by 5 we get

(x – 3)/ 5 × 5 = 1 × 5

x – 3 = 5

Now add 3 to both sides we get,

Substituting x = 8 in LHS we get,

((8 – 3)/5) -2 = -1

(5/5) – 2 = -1

22. 5 (x – 2) + 3 (x +1) = 25

Given 5 (x – 2) + 3 (x +1) = 25

(5 × x) – (5 × 2) +3 × x + 3× 1 = 25

5x – 10 + 3x + 3 = 25

5x + 3x – 10 + 3 = 25

8x – 7 = 25

Adding 7 to both sides, we get

8x – 7 + 7 = 25 + 7

Dividing both sides by 8, we get

8x/8 = 32/8

Substituting x = 4 in LHS, we get

5(4 – 2) + 3(4 + 1) = 25

5(2) + 3(5) = 25

10 + 15 = 25

Exercise 8.3 Page No: 8.19

Solve each of the following equations. Also, verify the result in each case.

1. 6x + 5 = 2x + 17

Given 6x + 5 = 2x + 17

Transposing 2x to LHS and 5 to RHS, we get

6x – 2x = 17 – 5

4x/4 = 12/4

Substituting x = 3 in the given equation, we get

6 × 3 + 5 = 2 × 3 + 17

18 + 5 = 6 + 17

2. 2 (5x – 3) – 3 (2x – 1) = 9

Given 2 (5x – 3) – 3 (2x – 1) = 9

Simplifying the brackets, we get

2 × 5x – 2 × 3 – 3 × 2x + 3 × 1 = 9

10x – 6 – 6x + 3 = 9

10x – 6x – 6 + 3 = 9

4x – 3 = 9

Adding 3 to both sides, we get

4x – 3 + 3 = 9 + 3

Therefore x = 3.

2(5 × 3 – 3) – 3(2 × 3 – 1) = 9

2 × 12 – 3 × 5 = 9

24 – 15 = 9

Thus, LHS = RHS

3. (x/2) = (x/3) + 1

Given (x/2) = (x/3) + 1

Transposing (x/3) to LHS we get

(x/2) – (x/3) = 1

(3x – 2x)/6 = 1 [LCM of 3 and 2 is 6]

Multiplying 6 to both sides we get,

Substituting x = 6 in given equation we get

(6/2) = (6/3) + 1

Thus LHS = RHS

4. (x/2) + (3/2) = (2x/5) – 1

Given (x/2) + (3/2) = (2x/5) – 1

Transposing (2x/5) to LHS and (3/2) to RHS, then we get

(x/2) – (2x/5) = – 1 – (3/2)

(5x -4x)/10 = (-2 – 3)/2 [LCM of 5 and 2 is 10]

x/10 = -5/2

Multiplying both sides by 10 we get,

x/10 × 10 = (-5/2) × 10

x = (-50/2)

Substituting x = -25 in given equation we get

(-25/2) + (3/2) = (-50/5) – 1

(-25 + 3)/2 = -10 – 1

(-22/2) = -11

5. (3/4) (x -1) = (x – 3)

Given (3/4) (x -1) = (x – 3)

On simplifying the brackets both sides we get,

(3/4) x – (3/4) = (x – 3)

Now transposing (3/4) to RHS and (x – 3) to LHs

(3/4) x – x = (3/4) – 3

(3x – 4x)/4 = (3 – 12)/4

-x/4 = (-9/4)

Multiply both sides by -4 we get

-x/4 × -4 = (-9/4) × -4

Substituting x = 9 in the given equation:

(3/4) (9 – 1) = (9 -3)

(3/4) (8) = 6

3 × 2 = 6

6. 3 (x – 3) = 5 (2x + 1)

Given 3 (x – 3) = 5 (2x + 1)

On simplifying the brackets we get,

3x – 9 = 10x + 5

Now transposing 10x to LHS and 9 to RHs

3x – 10x = 5 + 9

Now dividing both sides by -7 we get

-7x/-7 = 14/-7

Substituting x = -2 in the given equation we get

3 (-2 – 3) = 5 (-4 + 1)

3 (-5) = 5 (-3)

-15 = – 15

7. 3x – 2 (2x -5) = 2 (x + 3) – 8

Given 3x – 2 (2x -5) = 2 (x + 3) – 8

On simplifying the brackets on both sides, we get

3x – 2 × 2x + 2 × 5 = 2 × x + 2 × 3 – 8

3x – 4x + 10 = 2x + 6 – 8

-x + 10 = 2x – 2

Transposing x to RHS and 2 to LHS, we get

10 + 2 = 2x + x

Dividing both sides by 3, we get

3x/3 = 12/3

Substituting x = 4 on both sides, we get

3(4) – 2{2(4) – 5} = 2(4 + 3) – 8

12 – 2(8 – 5) = 14 – 8

12 – 6 = 6

8. x – (x/4) – (1/2) = 3 + (x/4)

Given x – (x/4) – (1/2) = 3 + (x/4)

Transposing (x/4) to LHS and (1/2) to RHS

x – (x/4) – (x/4) = 3 + (1/2)

(4x – x – x)/4 = (6 + 1)/2

Substituting x = 7 in the given equation we get

7 – (7/4) – (1/2) = 3 + (7/4)

(28 – 7 – 2)/4 = (12 + 7)/4

19/4 = 19/4

9. (6x – 2)/9 + (3x + 5)/18 = (1/3)

Given (6x – 2)/9 + (3x + 5)/18 = (1/3)

(6x (2) – 2 (2) + 3x + 5)/18 = (1/3)

(12x – 4 + 3x + 5)/18 = (1/3)

(15x + 1)/ 18 = (1/3)

Multiplying both sides by 18 we get

(15x + 1)/18 × 18 = (1/3) × 18

15x + 1 = 6

Transposing 1 to RHS, we get

= 15x = 6 – 1

Dividing both sides by 15, we get

= 15x/15 = 5/15

Substituting x = 1/3 both sides, we get

(6 (1/3) – 2)/9 + (3 (1/3) + 5)/18 = (1/3)

(2 – 2)/9 + (1 + 5)/ 18 = 1/3

(6/18) = (1/3)

(1/3) = (1/3)

10. m – (m – 1)/2 = 1 – (m – 2)/3

Given m – (m – 1)/2 = 1 – (m – 2)/3

(2m – m + 1)/2 = (3 – m + 2)/3

(m + 1)/2 = (5 – m)/3

(m + 1)/2 = (5/3) – (m/3)

(m/2) + (1/2) = (5/3) – (m/3)

Transposing (m/3) to LHS and (1/2) to RHS

(m/2) + (m/3) = (5/3) – (1/2)

(3m + 2m)/6 = (10 – 3)/6

5m/6 = (7/6)

Dividing both sides by 5, we get

Substituting m = 7/5 on both sides, we get

(7/5) – (7 – 5)/10 = 1 – (7 – 10)/15

(7/5) – (2/10) = (15 + 3)/15

(14 – 2)/10 = (15 + 3)/15

12/10 = 18/15

(6/5) = (6/5)

11. (5x – 1)/3 – (2x – 2)/3 = 1

Given (5x – 1)/3 – (2x – 2)/3 = 1

(5x – 1 – 2x + 2)/3 = 1

(3x + 1)/3 = 1

Multiplying both sides by 3 we get

(3x + 1)/3 × 3 = 1 × 3

(3x + 1) = 3

Subtracting 1 from both sides we get

3x + 1 – 1 = 3 – 1

3x/3 = 2/3

Substituting x = 2/3 in LHS, we get

(5 (2/3) – 1)/3 – (2 (2/3) – 2)/3 = 1

(10/3 -1)/3 – (4/3 – 2)/3 = 1

(7/3)/3 – (-2/3)/3 = 1

(7/9) + (2/9) = 1

12. 0.6x + 4/5 = 0.28x + 1.16

Given 0.6x + 4/5 = 0.28x + 1.16

Transposing 0.28x to LHS and 45 to RHS, we get

0.6x – 0.28x = 1.16 – 45

0.32x = 1.16 – 0.8

0.32x = 0.36

Dividing both sides by 0.32, we get

0.32 x 0.32 = 0.360.32

Substituting x = 9/8 on both sides, we get

0.6(9/8) + 45 = 0.28(9/8) + 1.16

5.4/8 + 4/5 = 2.52/8 + 1.16

0.675 + 0.8 = 0.315 + 1.16

1.475 = 1.475

13. 0.5x + (x/3) = 0.25x + 7

Given 0.5x + (x/3) = 0.25x + 7

(5/10) x + (x/3) = (25x/100) + 7

(x/2) + (x/3) = (x/4) + 7

Transposing (x/4) to LHS we get

(x/2) + (x/3) – (x/4) = 7

(6x + 4x – 3x)/12 = 7

(7x/12) = 7

Multiplying both sides by 12 we get

(7x/12) × 12 = 7 × 12

Dividing both sides by 7 we get

(7x/7) = (84/7)

Substituting x = 12 in given equation we get

0.5 (12) + (12/3) = 0.25 (12) + 7

6 + 4 = 3 + 7

Exercise 8.4 Page No: 8.26

1. If 5 is subtracted from three times a number, the result is 16. Find the number.

Let the required number be x.

Then, given that 5 subtracted from 3 times x i.e. 3x – 5

⇒ 3x – 5 = 16

Adding 5 to both sides, we get

⇒ 3x – 5 + 5 = 16 + 5

⇒ 3x = 21

⇒ 3x/3 = 21/3

⇒ x = 7

Thus, the required number is x = 7.

2. Find the number which when multiplied by 7 is increased by 78.

Given that, when multiplied by 7, it gives 7x, and x increases by 78.

According to the question we can write as 7x = x + 78

Transposing x to LHS, we get

⇒ 7x – x = 78

⇒ 6x = 78

Dividing both sides by 6, we get

⇒ 6x/6 = 78/6

⇒ x =13

Thus, the required number is x = 13.

3. Find three consecutive natural numbers such that the sum of the first and second is 15 more than the third.

Let first number be x.

According to the question second number is x + 1 and the third is x + 2

Sum of first and second numbers = (x) + (x + 1).

According to question:

⇒ (x) + (x + 1) = 15 + (x + 2)

⇒ 2x + 1 = 17 + x

Transposing x to LHS and 1 to RHS, we get

⇒2x – x = 17 – 1

⇒ x = 16

So, first number = x = 16,

Second number = x + 1 = 16 + 1 = 17

And third number = x + 2 = 16 + 2 = 18

Thus, the required consecutive natural numbers are 16, 17 and 18.

4. The difference between two numbers is 7. Six times the smaller plus the larger is 77. Find the numbers.

Let the smaller number be ‘x’.

So, the larger number = x + 7.

⇒ 6x + (x + 7) = 77

⇒ 6x + x + 7 = 77

On simplifying we get

⇒ 7x + 7 = 77

⇒ 7x + 7 – 7 = 77 – 7

⇒ 7x = 70

Dividing both sides by 7, we get

⇒ 7x/7 = 70/7

⇒ x = 10

Thus, the smaller number = x = 10

And the larger number = x + 7 = 10 + 7 = 17.

The two required numbers are 10 and 17.

5. A man says, “I am thinking of a number. When I divide it by 3 and then add 5, my answer is twice the number I thought of”. Find the number.

So, according to question:

⇒ x/3 + 5 = 2x

Transposing x/3 to RHS, we get

⇒ 5 = 2x – (x/3)

⇒ 5 = (6x – x)/3

⇒ 5 = (5x/3)

Multiplying both sides by 3 we get,

⇒ 5 × 3 = (5x/3) × 3

⇒ 15 = 5x

Dividing both sides by 5 we get

⇒ 15/5 = 5x/5

⇒ 3 = x

Thus the number thought of by the man is 3.

6. If a number is tripled and the result is increased by 5, we get 50. Find the number.

Let the required number be ‘x’.

⇒ 3x + 5 = 50

Subtracting 5 from both sides, we get

⇒ 3x + 5 – 5 = 50 – 5

⇒ 3x = 45

⇒ 3x/3 = 45/3

⇒ x = 15

Therefore, the required number is 15.

7. Shikha is 3 years younger to her brother Ravish. If the sum of their ages 37 years, what are their present age?

Let the present age of Shikha be x years.

Therefore, the present age of Shikha’s brother Ravish = (x + 3) years.

So, sum of their ages = x + (x+ 3)

⇒ x +(x + 3) = 37

⇒ 2x + 3 = 37

Subtracting 3 from both sides, we get

⇒ 2x+ 3 – 3 = 37 – 3

⇒ 2x = 34

⇒ 2x/2 = 34/2

⇒ x = 17

Therefore, the present age of Shikha = 17 years,

And the present age of Ravish = x + 3 = 17 + 3 = 20 years.

8. Mrs Jain is 27 years older than her daughter Nilu. After 8 years she will be twice as old as Nilu. Find their present ages?

Let the present age of Nilu be x years

Therefore the present age of Nilu’s mother = (x + 27) years

So, after 8 years,

Nilu’s age = (x + 8), and Mrs Jain’s age = (x + 27 + 8) = (x + 35) years

⇒ x + 35 = 2(x + 8)

Expanding the brackets, we get

⇒ x + 35 = 2x + 16

Transposing x to RHS and 16 to LHS, we get

⇒ 35 – 16 = 2x – x

⇒ x = 19

So, the present age of Nilu = x = 19 years,

And the present age of Nilu’s mother that is Mrs Jain = x+ 27 = 19 + 27 = 46 years.

9. A man 4 times as old as his son. After 16 years, he will be only twice as old as his son. Find their present ages.

Let the present age of the son = x years.

Therefore, the present age of his father = 4x years.

So, after 16 years,

Son’s age = (x + 16) and father’s age = (4x + 16) years

⇒ 4x + 16 = 2(x + 16)

⇒ 4x + 16 = 2x + 32

Transposing 2x to LHS and 16 to RHS, we get

⇒ 4x – 2x = 32 – 16

⇒ 2x = 16

⇒ 2x/2 = 16/2

⇒ x = 8

So, the present age of the son = x = 8 years,

And the present age of the father = 4x = 4(8) = 32 years.

10. The difference in age between a girl and her younger sister is 4 years. The younger sister in turn is 4 years older than her brother. The sum of the ages of the younger sister and her brother is 16. How old are the three children?

Let the age of the girl = x years.

So, the age of her younger sister = (x – 4) years.

Thus, the age of the brother = (x – 4 – 4) years = (x – 8) years.

⇒ (x – 4) + (x – 8) = 16

⇒ x + x – 4 – 8 = 16

⇒ 2x – 12 = 16

Adding 12 to both sides, we get

⇒ 2x – 12 + 12 = 16 + 12

⇒ 2x = 28

⇒ 2x/2 = 28/2

⇒ x = 14

Thus, the age of the girl = x = 14 years,

The age of the younger sister = x – 4 = 14 – 4 = 10 years,

The age of the younger brother = x – 8 = 14 – 8 = 6 years.

11. One day, during their vacation at beach resort, Shella found twice as many sea shells as Anita and Anita found 5 shells more than sandy. Together sandy and Shella found 16 sea shells. How many did each of them find?

Let the number of sea shells found by sandy = x

So, the number of sea shells found by Anita = (x + 5).

The number of sea shells found by Shella = 2 (x + 5).

According to the question,

⇒ x + 2(x + 5) = 16

⇒ x + 2x +10 = 16

⇒ 3x + 10 = 16

⇒ 3x + 10 – 10 = 16 – 10

⇒ 3x = 6

⇒ 3x/3 = 6/3

⇒ x = 2

Thus, the number of sea shells found by Sandy = x = 2,

The number of sea shells found by Anita = x + 5 = 2 + 5 = 7,

The number of sea shells found by Shelia = 2 (x + 5) = 2 (2 + 5) = 2(7) = 14.

12. Andy has twice as many marbles as Pandy, and Sandy has half as many has Andy and Pandy put together. If Andy has 75 marbles more than Sandy. How many does each of them have?

Let the number of marbles with Pandy = x

So, the number of marbles with Andy = 2x

Thus, the number of marbles with Sandy = (x/2) + (2x/2) = (3x/2)

According to the question:

⇒ 2x = (3x/2) + 75

By transposing we get

⇒2x – (3x/2) = 75

⇒ (4x – 3x)/2 = 75

⇒ (x/2) = 75

⇒ x = 150

Since number of marbles cannot be negative

Therefore x = 150

So, Pandy has 150 marbles,

Andy has 2x = 2 (150) = 300 marbles,

Sandy has 3x/2 = 225 marbles.

13. A bag contains 25 paise and 50 paise coins whose total value is Rs 30. If the number of 25 paise coins is four times that of 50 paise coins, find the number of each type of coins.

Let the number of 50 paise coins = x

So, the money value contribution of 50 paise coins in bag = 0.5x.

The number of 25 paise coins in bag = 4x

The money value contribution of 25 paise coins in bag = 0.25 (4x) = x.

⇒ 0.5x + x = 30

⇒ 1.5x = 30

Dividing both sides by 1.5, we get

⇒ 1.5x/1.5= 30/1.5

⇒ x = 20

Thus, the number of 50 paise coins = x = 20,

The number of 25 paise coins = 4x = 4 (20) = 80.

14. The length of a rectangular field is twice its breadth. If the perimeter of the field is 228 meters, find the dimensions of the field.

Let the breadth of the rectangle = x metres.

Length of the rectangle = 2x metres

Perimeter of a rectangle = 2 (length + breadth)

So, 2 (2x + x) = 228

⇒ 2 (3x) = 228

⇒ 6x = 228

⇒ 6x/6 = 228/6

⇒ x = 38

So, the breadth of the rectangle = x = 38 metres,

The length of the rectangle = 2x = 2(38) = 76 metres.

15. There are only 25 paise coins in a purse. The value of money in the purse is Rs 17.50. Find the number of coins in the purse.

Let the number of 25-paise coins in the purse be x

So, the value of money in the purse = 0.25x.

But 0.25x = 17.50.

Dividing both sides by 0.25, we get

⇒ 0.25x/0.25 = 17.5/0.25

⇒ x = 70

Thus, the number of 25 paise coins in the purse = 70.

16. In a hostel mess, 50kg rice are consumed every day. If each student gets 400gm of rice per day, find the number of students who take meals in the hostel mess.

Let the number of students in the hostel be x

Quantity of rice consumed by each student = 400 gm.

So, daily rice consumption in the hostel mess = 400 (x).

But, daily rice consumption = 50 kg = 50 × 1000 = 50000gm [since 1 kg = 1000gm].

⇒ 400x = 50000

Dividing both sides by 400, we get

⇒ 400 x/400 = 50000/400

⇒ x = 125

Thus, 125 students have their meals in the hostel mess.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Solving Linear Equations

Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When we are given two or more such linear equations, we can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let us discuss each of these methods in detail.

Solving Linear Equations in One Variable

A linear equation in one variable is an equation of degree one and has only one variable term. It is of the form 'ax+b = 0', where 'a' is a non zero number and 'x' is a variable. By solving linear equations in one variable, we get only one solution for the given variable. An example for this is 3x - 6 = 0. The variable 'x' has only one solution, which is calculated as 3x - 6 = 0 3x = 6 x = 6/3 x = 2

For solving linear equations with one variable, simplify the equation such that all the variable terms are brought to one side and the constant value is brought to the other side. If there are any fractional terms then find the LCM ( Least Common Multiple ) and simplify them such that the variable terms are on one side and the constant terms are on the other side. Let us work out a small example to understand this.

4x + 8 = 8x - 10. To find the value of 'x', let us simplify and bring the 'x' terms to one side and the constant terms to another side.

4x - 8x = -10 - 8 -4x = -18 4x = 18 x = 18/4 On simplifying, we get x = 9/2.

Solving Linear Equations by Substitution Method

The substitution method is one of the methods of solving linear equations. In the substitution method , we rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has only one variable, we can solve it and find the value of that variable. In the two given equations, any equation can be taken and the value of a variable can be found and substituted in another equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let us understand this with an example of solving the following system of linear equations. x + y = 6 --------------(1) 2x + 4y = 20 -----------(2)

Step 1: Find the value of one of the variables using any one of the equations. In this case, let us find the value of 'x' from equation (1). x + y = 6 ---------(1) x = 6 - y Step 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, let us substitute the value of 'x' in the second equation 2x + 4y = 20.

x = 6 - y Substituting the value of 'x' in 2x + 4y = 20, we get,

2(6 - y) + 4y = 20 12 - 2y + 4y = 20 12 + 2y = 20 2y = 20 - 12 2y = 8 y = 8/2 y = 4 Step 3: Now substitute the value of 'y' in either equation (1) or (2). Let us substitute the value of 'y' in equation (1).

x + y = 6 x + 4 = 6 x = 6 - 4 x = 2 Therefore, by substitution method, the linear equations are solved, and the value of x is 2 and y is 4.

Solving Linear Equations by Elimination Method

The elimination method is another way to solve a system of linear equations. Here we make an attempt to multiply either the 'x' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let us understand the steps of solving linear equations by elimination method . Consider the given linear equations: 2x + y = 11 ----------- (1) x + 3y = 18 ---------- (2) Step 1: Check whether the terms are arranged in a way such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the constant term should be present. The given set of linear equations are already arranged in the correct way which is ax+by=c or ax+by-c=0.

Step 2: The next step is to multiply either one or both the equations by a constant value such that it will make either the 'x' terms or the 'y' terms cancel out which would help us find the value of the other variable. Now in equation (2), let us multiply every term by the number 2 to make the coefficients of x the same in both the equations. x + 3y = 18 ---------- (2) Multiplying all the terms in equation (2) by 2, we get,

2(x) + 2(3y) = 2(18). Now equation (2) becomes, 2x + 6y = 36 -----------(2)

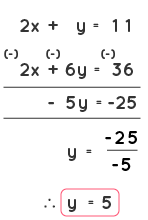
Therefore, y = 5. Step 4: Using the value obtained in step 3, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (1). We get, 2x + y = 11 2x + 5 = 11 2x = 11 - 5 2x = 6 x = 6/2 x = 3

Therefore, by solving linear equations, we get the value of x = 3 and y = 5.

Graphical Method of Solving Linear Equations

Another method for solving linear equations is by using the graph. When we are given a system of linear equations, we graph both the equations by finding values for 'y' for different values of 'x' in the coordinate system. Once it is done, we find the point of intersection of these two lines. The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method.

x + y = 8 -------(1)

y = x + 2 --------(2)

Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.

Let us take some values for 'x' and find the values for 'y' in the equation y = x + 2.

Plotting these points on the coordinate plane, we get a graph like this.

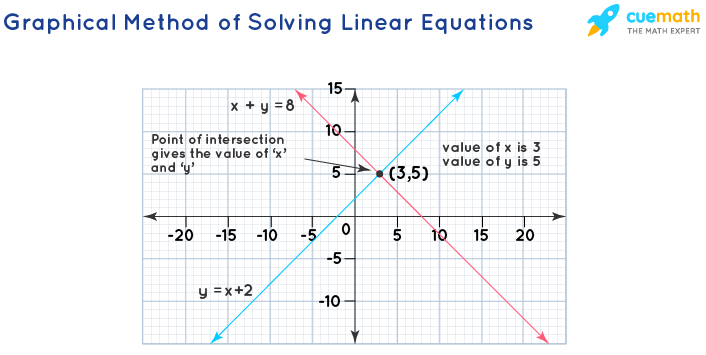
Now, we find the point of intersection of these lines to find the values of 'x' and 'y'. The two lines intersect at the point (3,5). Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations .

This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.

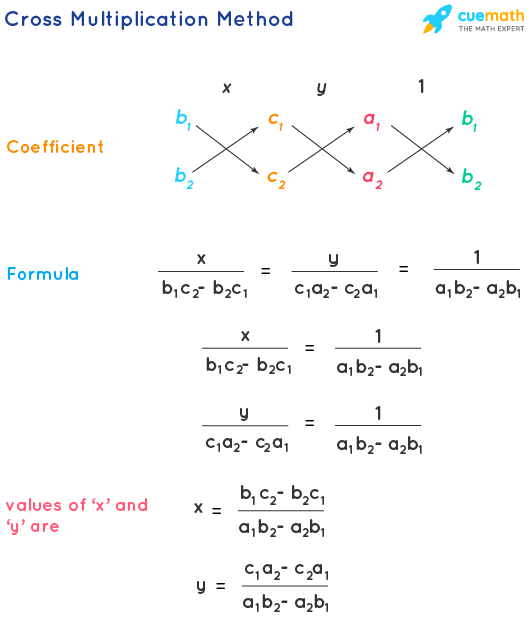
Cross Multiplication Method of Solving Linear Equations

The cross multiplication method enables us to solve linear equations by picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.

Topics Related to Solving Linear Equations

Check the given articles related to solving linear equations.

• Linear Equations
• Application of Linear Equations
• Two-Variable Linear Equations
• Linear Equations and Half Planes
• One Variable Linear Equations and Inequations

Solving Linear Equations Examples

Example 1: Solve the following linear equations by the substitution method.

3x + y = 13 --------- (1) 2x + 3y = 18 -------- (2)

By using the substitution method of solving linear equations, let us take the first equation and find the value of 'y' and substitute it in the second equation.

From equation (1), y = 13-3x. Now, substituting the value of 'y' in equation (2), we get, 2x + 3 (13 - 3x) = 18 2x + 39 - 9x = 18 -7x + 39 = 18 -7x = 18 - 39 -7x = -21 x = -21/-7 x = 3 Now, let us substitute the value of 'x = 3' in equation (1) and find the value of 'y'. 3x + y = 13 ------- (1) 3(3) + y = 13 9 + y = 13 y = 13 - 9 y = 4

Therefore, by the substitution method, the value of x is 3 and y is 4.

Example 2: Using the elimination method of solving linear equations find the values of 'x' and 'y'.

3x + y = 21 ------ (1) 2x + 3y = 28 -------- (2)

By using the elimination method, let us make the 'y' variable to be the same in both the equations (1) and (2). To do this let us multiply all the terms of the first equation by 3. Therefore equation (1) becomes,

3(3x) + 3(y) = 63 9x + 3y = 63 ---------- (3) The second equation is, 2x + 3y = 28 Now let us cancel the 'y' terms and find the value of 'x' by subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (2).

Example 3: Using the cross multiplication method of solving linear equations, solve the following equations.

x + 2y - 16 = 0 --------- (1) 4x - y - 10 = 0 ---------- (2)

Compare the given equation with \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)x+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,

\(a_{1}\) = 1, \(a_{2}\) = 4, \(b_{1}\) = 2, \(b_{2}\) = -1, \(c_{1}\) = -16, and \(c_{2}\) = -10.

By cross multiplication method,

x = \(b_{1}\)\(c_{2}\) - \(b_{2}\)\(c_{1}\)/\(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\) y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)

Substituting the values in the formula we get,

x = ((2)(-10)) - ((-1)(-16)) / ((1)(-1)) - ((4)(2)) x = (-20-16)/(-1-8) x = -36/-9 x = 36/9 x = 4 y = ((-16)(4)) - ((-10)(1)) / ((1)(-1)) - ((4)(2)) y = (-64 + 10) / (-1 - 8) y = -54 / -9 y = 54/9 y = 6 Therefore, by the cross multiplication method, the value of x is 4 and y is 6.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Solving Linear Equations

Faqs on solving linear equations, what does it mean by solving linear equations.

An equation that has a degree of 1 is called a linear equation. We can have one variable linear equations , two-variable linear equations , linear equations with three variables, and more depending on the number of variables in it. Solving linear equations means finding the values of all the variables present in the equation. This can be done by substitution method, elimination method, graphical method, and the cross multiplication method . All these methods are different ways of finding the values of the variables.

How to Use the Substitution Method for Solving Linear Equations?

The substitution method of solving equations states that for a given system of linear equations, find the value of either 'x' or 'y' from any of the given equations and then substitute the value found of 'x' or 'y' in another equation so that the other unknown value can be found.

How to Use the Elimination Method for Solving Linear Equations?

In the elimination method of solving linear equations, we multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the same. Then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'x' or 'y'). After finding one of the values, we substitute the value in one of the equations and find the other unknown value.

What is the Graphical Method of Solving Linear Equations?

In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of x as 0, 1, 2, 3, and so on, and plot a graph in the coordinate system for the line for various values of 'x' for both the system of linear equations. We will see that these two lines intersect at a point. This point is the solution for the given system of linear equations. If there is no intersection point between two lines, then we consider them as parallel lines , and if we found that both the lines lie on each other, those are known as coincident lines and have infinitely many solutions.

What are the Steps of Solving Linear Equations that has One Variable?

A linear equation is an equation with degree 1. To solve a linear equation that has one variable we bring the variable to one side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with one variable will be of the form 'x - 4 = 2'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.

What are the Steps of Solving Linear Equations having Three Variables?

To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we have two linear equations with two variables, we can use the substitution method or elimination method, or any other method to solve the values of two unknown variables. After finding these two variables, we substitute them in any of the three equations to find the third unknown variable.

What are the 4 Methods of Solving Linear Equations?

The methods for solving linear equations are given below:

• Substitution method
• Elimination method
• Cross multiplication method
• Graphical method

Solving Linear Equations

Worked-out examples on solving linear equations are given below. Instructions are given step-by-step with detailed explanation by using addition, subtraction, multiplication and division for solving linear equations.

Examples on Solving Linear Equations:

1.  Solve: (2x + 5)/(x + 4) = 1 Solution: (2x + 5)/(x + 4) = 1

⇒ 2x + 5 = 1(x + 4) 

⇒ 2x + 5 = x + 4 

⇒ 2x - x = 4 - 5    (Transferring positive x to the left hand side changes to negative x and again, positive 5 changes to negative 5)   ⇒ x = -1 

Therefore, x = - 1 is the required solution of the equation (2x + 5)/(x + 4) = 1 

2. Solve: 6x - 19 = 3x - 10

Solution: 6x - 19 = 3x - 10

⇒ 6x - 3x = - 10 + 19   (Transferring 3x to L.H.S changes to negative 3x and -19 to R.H.S. changes to positive 19) ⇒ 3x = 9

⇒ 3x/3 = 9/3   (Dividing both sides by 3)

3. Solve: 5 - 2(x - 1) = 4(3 - x) - 2x. Solution: 5 - 2(x - 1) = 4(3 - x) - 2x

⇒ 5 - 2x + 2 = 12 - 4x - 2x   (Removing the brackets and then simplify) ⇒ 7 - 2x = 12 - 6x   (Transferring -6x to L.H.S. changes to positive 6x and 7 to R.H.S. changes to negative 7) ⇒ -2x + 6x = 12 - 7

⇒ 4x/4 = 5/4

4. x/2 + x/3 = x - 7 Solution: x/2 + x/3 = x - 7

Least common multiple of2 and 3 is 6

⇒ (x/2 × 3/3) + (x/3 × 2/2) = x - 7

⇒ 3x/6 + 2x/6 = x - 7

⇒ (3x + 2x)/6 = x - 7

⇒ 5x/6 = x - 7

⇒ 5x = 6(x - 7)

⇒ 5x = 6x - 42   (Transferring 6x to L.H.S. changes to negative 6x) ⇒ 5x - 6x = -42

5. 2/(x + 3) = 3/(5 - x) Solution: 2/(x + 3) = 3/(5 - x)

⇒ 3(x + 3) = 2(5 - x)   (cross multiply and then remove the brackets) ⇒ 3x + 9 = 10 - 2x   (Transferring -2x to L.H.S. changes to positive 2x and 9 to R.H.S. changes to -9) ⇒ 3x + 2x = 10 - 9

⇒ 5x/5 = 1/5   (Dividing both sides by 5)

●   Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Linear Equations

Practice Test on Word Problems on Linear Equations

●   Equations - Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

7th Grade Math Problems   8th Grade Math Practice   From Solving Linear Equations to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

International Place-value Chart | International Place-value System

May 20, 24 06:48 PM

Reading and Writing Large Numbers | Large Numbers in Words in Billion

May 20, 24 06:41 PM

Worksheet on Formation of Numbers | Questions on Formation of Numbers

May 20, 24 12:43 PM

Worksheet on Forming Numbers with Digits | Smallest & Greatest Numbers

May 20, 24 02:06 AM

Shifting of Digits in a Number |Exchanging the Digits to Another Place

May 19, 24 06:35 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

New content!

Review articles, unit 1: proportional relationships, unit 2: rates and percentages, unit 3: integers: addition and subtraction, unit 4: rational numbers: addition and subtraction, unit 5: negative numbers: multiplication and division, unit 6: expressions, equations, & inequalities, unit 7: statistics and probability, unit 8: scale copies, unit 9: geometry.