problem solving angle of depression

• Math Article
• Angle Of Depression

Angle of Depression

The angle of depression is formed when the observer is higher than the object he/she is looking at. When an observer looks at an object that is situated at a distance lower than the observer, an angle is formed below the horizontal line drawn with the level of the eye of the observer and line joining object with the observer’s eye. Whereas the angle of elevation is the angle formed if a person stands on the ground and looks on the object kept above the ground at a height above the height of the person. This is the basic difference between the two angles. Both the angles are calculated by using the concept of trigonometry.

What is Angle of Depression?

The angle of depression is defined as an angle constructed by a horizontal line and the line joining the object and observer’s eye. This angle is dependent on two factors, i.e., height and distance. Let us learn about its definition, formula and real-life problems based on it.

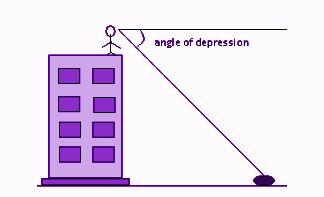
Angle of Depression Definition

The angle of depression is the angle between the horizontal line and the observation of the object from the horizontal line. It is basically used to get the distance of the two objects where the angles and an object’s distance from the ground are known to us. Its an angle that is formed with the horizontal line if the line of sight is downward from the horizontal line.

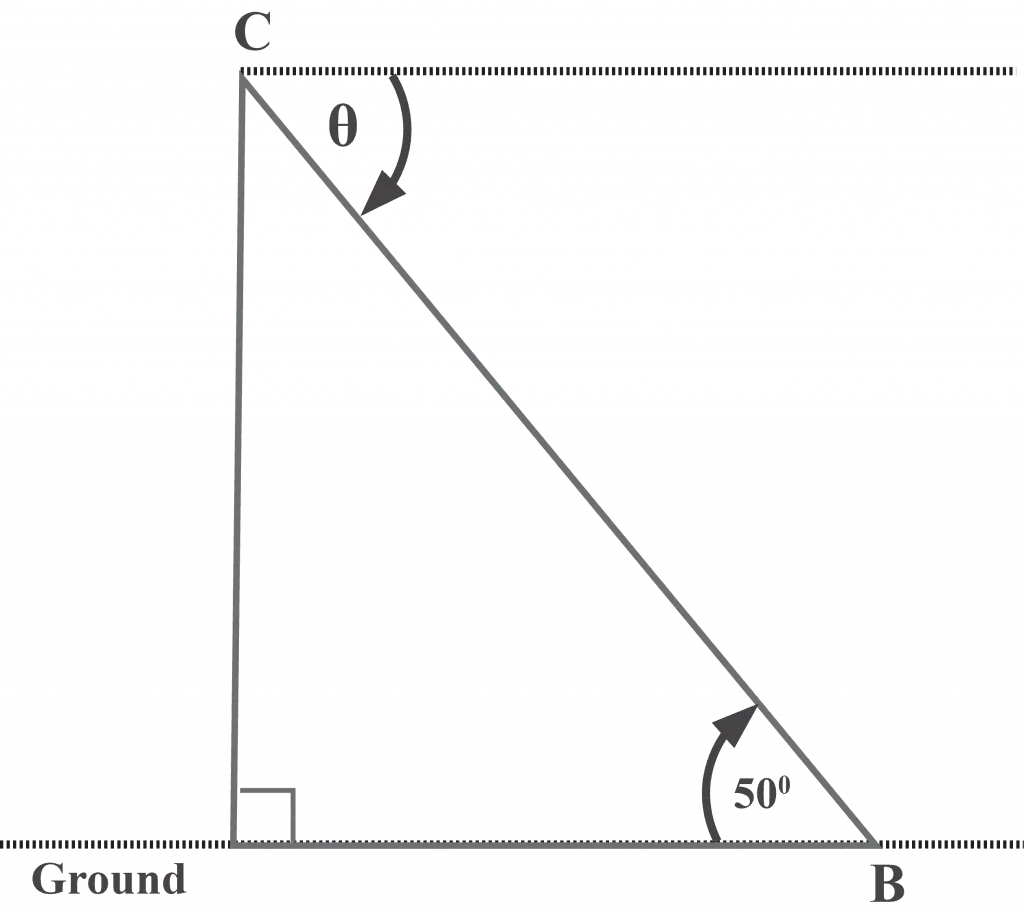
If the object observed by the observer is below the level of the observer, then the angle formed between the horizontal line and the observer’s line of sight is called the angle of depression. In the below figure, θ is the angle of depression.

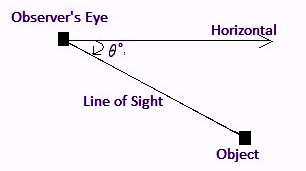
Angle of Depression Formula

With angles of elevation, if two of the sides of the right triangle are known, then the formula for the angle of depression is given as below:

Tan θ = Opposite Side/Adjacent Side

θ = tan -1 (Opposite Side/Adjacent Side)

See the below diagram, where θ is the angle of inclination, such as,

∠ ABO = Angle of elevation

∠O = Angle of depression

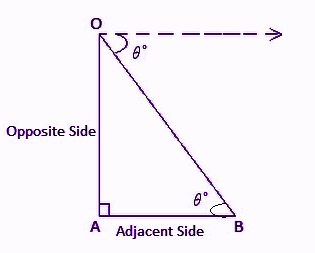
Hence, ∠ABO = ∠O = θ

Angle of Depression and Elevation comparison

The angle of elevation is just opposite to the angle of depression. The angle of elevation is formed when it is between the line of sight and the horizontal line. If the line of sight is above to the horizontal line, the angle formed is known as the angle of elevation. But in the angle of depression, the line of sight is downwards to the horizontal line. The figure that represents the angle of elevation is given below:

Angle of Depression Examples

The angle of depression of a vehicle from the top of a tower on the ground is 60. If the vehicle is away from the building at a distance of 100 meters, find the height of the tower.

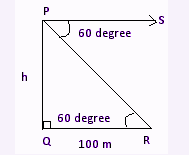
In the above figure,

R is a vehicle

PQ is the height of the tower

RQ is the distance between the tower and the vehicle

PS is the line of sight.

The angle of depression, ∠ SPR = 60°

The angle of elevation, ∠ QRP = Angle of depression, ∠ SPR = 60°.

Now, in right triangle PQR,

PQ = h (in m)

Let ∠ R = θ = 60°

tan θ = (Opposite Side/Adjacent Side)

Tan 60 = PQ/RQ = h/100

h = √3 x 100

h = 173.20 m

Hence, the height of the tower is 173.20 meters.

The angle of depression of a stone from the top of a tower on the ground is 45. If the stone is away from the building at a distance of 120 meters, find the height of the tower.

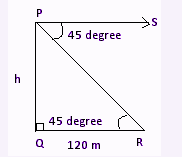
R is a stone.

PQ is the height of the tower.

RQ is the distance between the tower and the stone.

Given, Angle of depression, ∠ SPR = 45°.

As we know,

Angle of elevation, ∠ QRP = Angle of depression, ∠ SPR = 45°.

Now, in right-angled triangle PQR, we know that;

Let ∠ R = θ = 45°

We know that,

tanθ = Opposite side/Adjacent side

tan 45° = PQ/RQ = h/120

On cross multiplying, we get;

h = 120 x tan 45°

Since, tan 45 = 1

Therefore, h = 120 meters.

To learn more Mathematical concepts, register with BYJU’S – The Learning App and download the app today!

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Angle of Depression

The angle of depression is formed when an observer looks down at an object. It is the angle formed between the horizontal line which is straight to the observer's eye and the line of sight. Let us learn more about the angle of depression in this article.

What is Angle of Depression?

The angle of depression is "an angle formed between the horizontal line and the line of sight when an observer looks downwards at an object is known as an angle of depression". It measures the change of angle of our sight when we look down. Suppose you are standing in your kitchen and looking straight, and suddenly you spot an insect crawling on the floor. So, that immediate change in the angle of your sight from straight to downwards is the angle of depression.

Angle of Depression Terminology

The angle of depression involves the following terminology:

• Observer (the person who observes)
• Object (the object that is being observed by the observer)
• Horizontal line (a horizontal ray that starts from the observer)
• Line of sight (the line that connects the observer and the object)

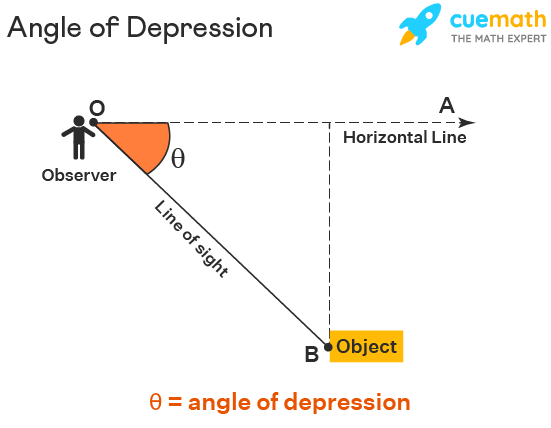
The angle of depression is the angle between the horizontal line and the line of sight. In the following figure, the observer is at 'O' and the object is at 'B'. Let OA be the horizontal line and OB be the line of sight. So, the angle formed between these two, i.e angle AOB is the angle of depression.

Angle of Depression Formula

The formula for the angle of depression is the same as basic trigonometric ratios formulae. If any two sides of the right triangle formed are known, then we can easily find the required angle by using the angle of depression formulas, that are given below.

Angle of Depression Vs Angle of Elevation

The angle of depression and angle of elevation are opposites of each other. In the angle of depression, the object is placed below the observer, while in the case of the angle of elevation, it is placed above the observer. If you are standing at your terrace and looking at the sun, then the angle of elevation will be formed. On the other hand, if you will look at the dog standing on the road from your terrace, then the angle of depression will be formed. In both cases, we use trigonometry angles to find the heights and distances . Let us understand the difference between the angle of depression and elevation from the image given below.

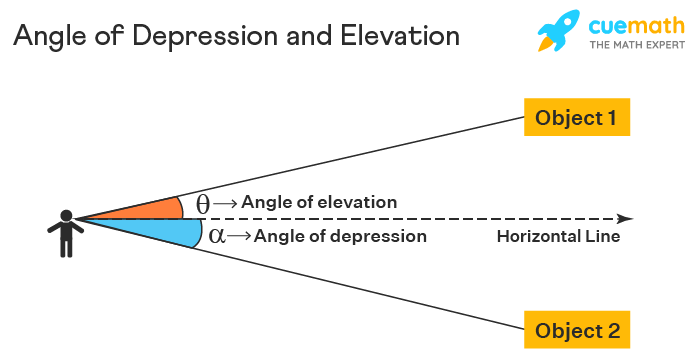
In the above image, θ is the angle of elevation and α is the angle of depression.

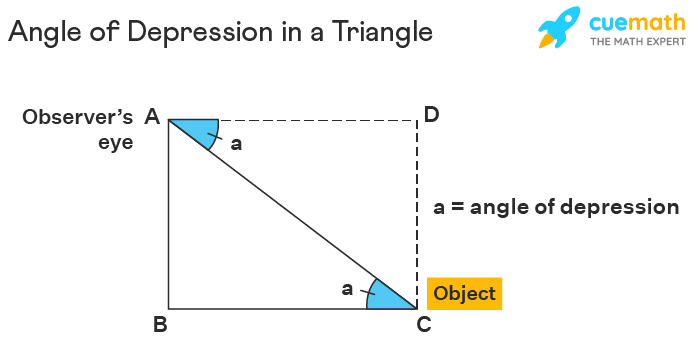
Angle of Depression in a Triangle

In a right-angled triangle, the angle of depression is formed at the top of the perpendicular line segment. It is originally at the outside of the triangle , but we use the alternate interior angles theorem to find its alternate angle inside the triangle. For example, in the image given below, if an observer is standing at point A looking down at point C then the angle of depression 'a' is formed with respect to the horizontal axis AD. But, ∠DAC = ∠ACB (by using alternate angles theorem). So, now in the triangle, ABC, the angle of depression is ∠ACB which can be used to find measure the missing side of the triangle.

☛ Related Topics:

Check these interesting articles to know more about the concept of the angle of depression and its related topics.

• Trigonometric Chart
• Trigonometry Calculator

Angle of Depression Examples

Example 1: If a person standing at the top of the building of height 50 ft is looking at her daughter standing at a distance of 30 ft away from the building, what will be the angle of depression formed?

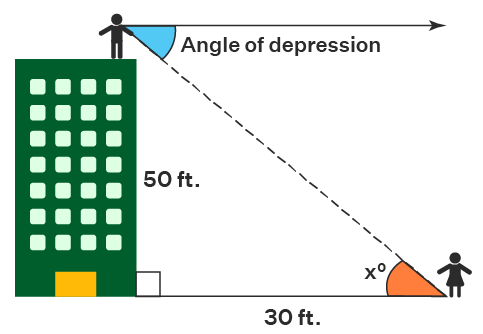
Solution: It is given that the height of the building is 50 ft, and the distance between the building and the girl is 30 ft. Now, in the given figure, the angle of depression is denoted by x° (as the angle of depression and angle x are the same by using alternate interior angles theorem). By using the formula for finding the angle of depression, we get tan x = 50/30.

⇒ tan x = 5/3

⇒ x = tan -1 (5/3)

Answer: Therefore, the angle of depression is tan -1 (5/3).

Example 2: Find the value of x in the given figure.

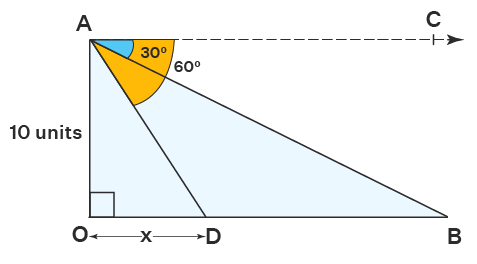
Solution: In the figure given above, there are two angles of depression formed from point A, which are ∠BAC=30° and ∠DAC=60°. We know that, ∠DAC=∠ADO (by using alternate interior angles theorem ). So, ∠ADO=60°. By applying the angle of depression formula in △AOD, we get tan 60° = AO/OD.

⇒ √3 = 10/x

⇒ x = 10/√3 units

Answer: Therefore, the value of x is 10/√3 units.

Example 3: From a hot air balloon that is flying at a height of 100 ft, the angle of depression of a person on the ground is 30 degrees. Find the length of the rope that is tied from the person on the ground to the balloon.

Let the length of the rope be x (in ft).

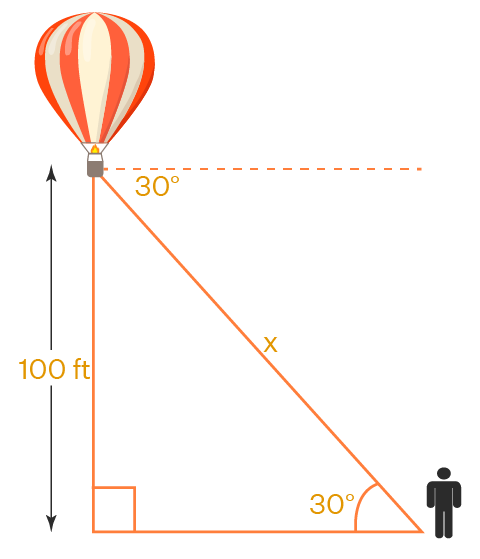
Here, we have written the angle at the person to be 30 degrees by the alternate interior angle theorem.

Now, apply sine for the triangle,

sin 30 = 100/x

x = 100/(sin 30) = 100 / (1/2) = 200 ft

Answer: The length of the rope = 200 ft.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Angle of Depression

go to slide go to slide

FAQs on Angle of Depression

What is the definition of angle of depression in trigonometry.

In trigonometry, the angle of depression is the angle formed between the horizontal line and the line of sight when we look downwards at an object. In this angle, the object at which we look is always placed below the horizontal axis or line.

What is the Angle of Elevation and the Angle of Depression?

The angle of elevation and depression are formed on either side of the horizontal line which is the straight line forming an angle of 90 degrees with the object. When we look upwards, the angle of elevation is formed and when we look down at some object, the angle of depression is formed. Both are important in order to find the heights and distances of large structures.

What is the Formula for Angle of Depression?

The formula of the angle of depression is the same as the basic trigonometric ratios formulae, which are given below:

• sin x = perpendicular / hypotenuse
• cos x = base/hypotenuse
• tan x = perpendicular/base

These three formulas can be used to find the angle of depression, based on which two sides of the right triangle are given.

How to Calculate Angle of Depression?

The angle of depression is the angle formed between the horizontal line and the line of sight which is below the horizontal line. It always forms a right-angled triangle between the observer, line, and the object. To calculate the angle of depression, we can use any of the basic trigonometric formulas of sine, cosine, and tangent , depending on which two sides of the triangle are given.

How to Find Distance with Angle of Depression?

To find distance with the angle of depression, we can use trigonometric formulas for calculations. Suppose, a girl is standing at the top of a 10 meters long tower making an angle of depression of 45 degrees with a bicycle standing on the road. Then the distance between the bicycle and the tower can be found by using the tangent formula which is tan 45° = 10/distance. Now, tan 45°=1, so, 1 = 10/distance, which means distance is equal to 10 units.

Is Angle of Depression and Inclination the Same?

The angle of inclination is the angle that forms above the horizontal axis. It is the same as the angle of elevation . The angle of depression is the same as the angle of declination as both are formed below the horizontal axis with a downward slope .

How is Angle of Depression Related to Real Life?

The angle of depression is used to measure heights and distances involving large calculations. It is used in architecture, engineering, science, etc.

How Do You Find Angle of Elevation and Depression?

Angle of elevation is the angle between a horizontal line of sight and the object when a person is looking up at an object. Whereas the angle of depression is the angle between the horizontal line of sight and the object when a person is looking down at an object.

What is the Importance of Angle of Elevation and Depression?

One of the main aspects of using the angle of elevation and depression is that it is used mostly in word problems in trigonometry when there are is a line of sight involved. These angles are used in solving trigonometric problems such as sine, cosine, and tangent along with inverse trigonometric functions .

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Angle of Depression – Detailed Explanation and Examples

JUMP TO TOPIC

How To Find the Angle of Depression

Practice questions, angle of depression – explanation & examples.

When you look at an item below you, you can easily measure the angle of depression formed by your line of sight with the horizontal line. Just imagine you are standing at the top of the Tower of Pisa and looking at an infinite horizon to enjoy the beautiful weather on a great rainy day. Suddenly your friend on the ground accidentally sees you and screams to say “Hi.” You  lower  your eyes to look at your friend. You must realize that you created a certain angle as you look downwards toward your friend. This angle is called the angle of depression . 

The angle of depression is basically the measure of an angle between the horizontal line and line of sight of a person’s eyes to any item below . The angle of elevation depends upon the movement of your eyes.  

After this lesson, we expect you to learn the concepts of the angle of depression and be able to confidently explain what it is.

What Is an Angle of Depression?

When an observer is looking down at an object below him, the angle established by the line of sight with the horizontal line is called the  angle of depression .

Let us consider a vertical wall with its base fixed to the ground as shown in Figure 12-1. Let’s say a man is standing some distance away from the wall and looking straight at it. The line drawn from the man’s perspective to the far point where the man is staring is known as the  line of sight . Since this line is parallel to the ground, we call it the horizontal line of sight — or simply a  horizontal line .

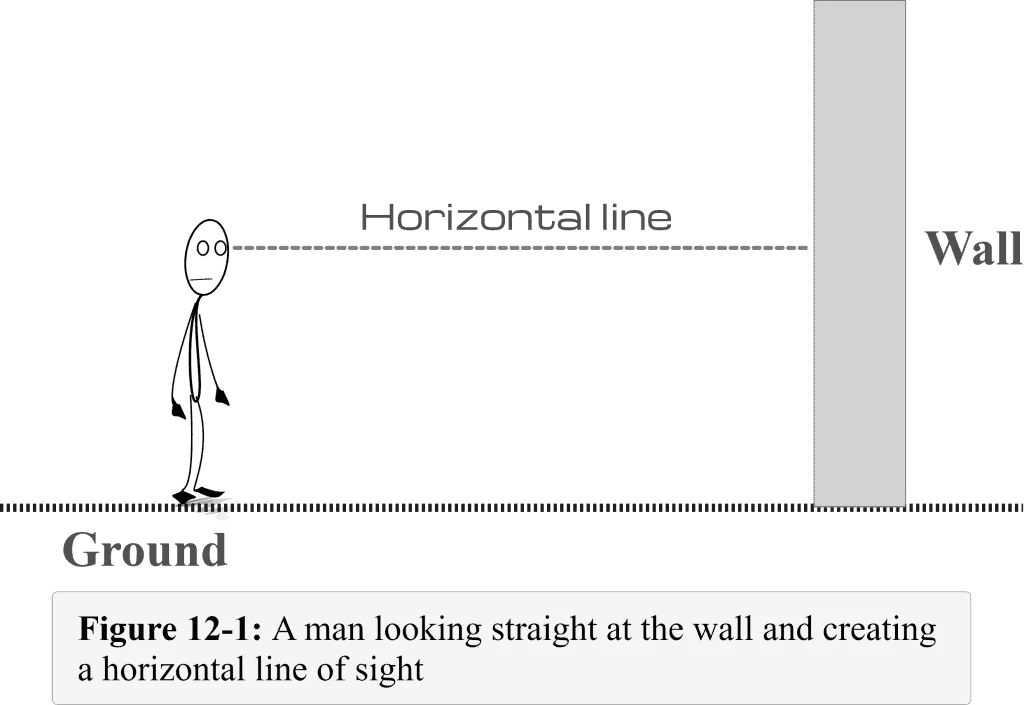
Now if the man is looking at the base of the wall, what should be the line of sight?

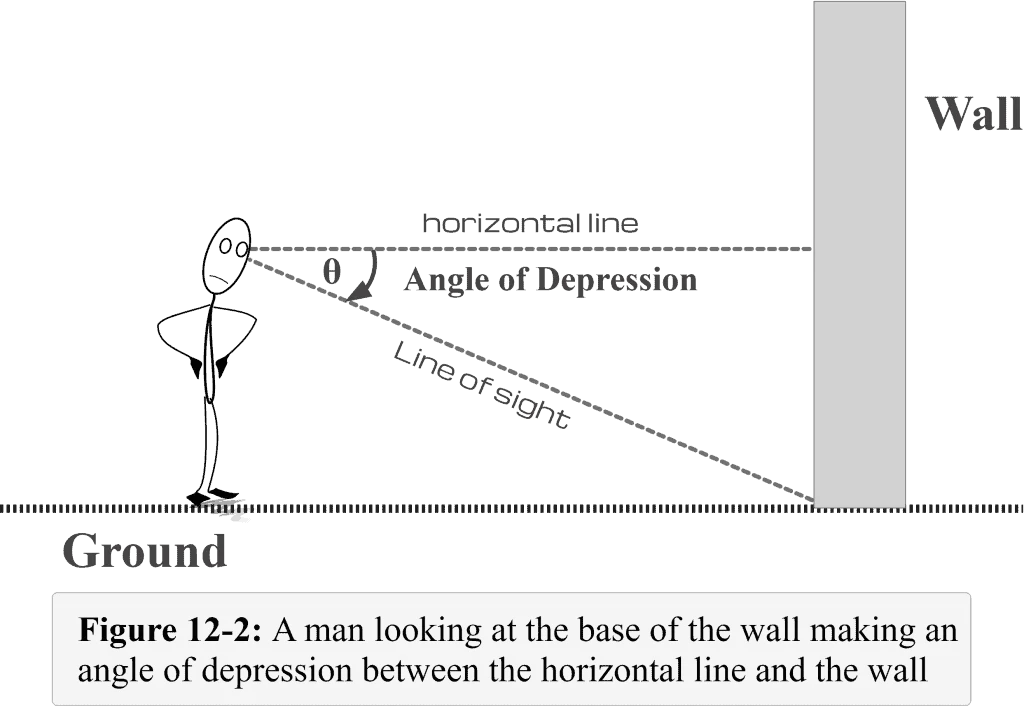
The above Figure 11-2 shows that the line drawn from the eye to the base of the wall would be the line of sight. We can easily observe that this line of sight (when looking down) makes an angle with the horizontal line. This angle is called the  angle of depression . You need to ponder that the line of sight is below the horizontal line.

Looking at Figure 11-2, the angle $\theta$   represents the angle of depression.

In Figure 11-3, Mr. Toni, from the top of the building, is seeing his friend lying on the ground to take a rest. The height of the building is $70$ m. His friend is $70$ m from the building. Let us determine the angle of depression between Toni’s line of sight (when looking downward) to his friend and the horizontal line drawn from Toni’s eyes.

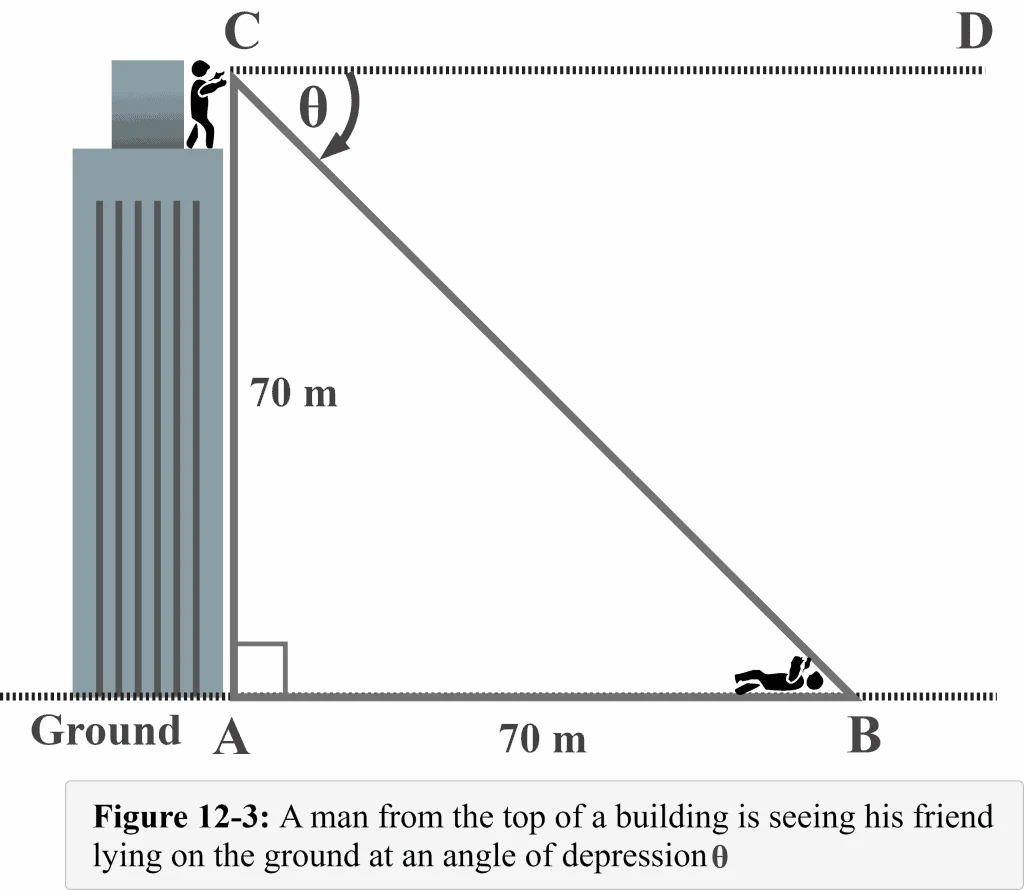
In this example, the angle $\theta$   represents the angle of depression between Mr. Toni’s line of sight (when looking downward) to his friend and the horizontal line. Note that the angle of depression is outside of the triangle and measured from the top, which is the ceiling. Also, the horizontal line is parallel to the ground surface.

Similarly, note that $∠CBA$ is an angle of elevation (discussed in our previous lesson) as it is measured from the ground, the angle with which Toni’s friend will be looking at him from the ground surface (another horizontal line).

Now, we have:

• Two parallel lines $CD$ and $AB$
• A line of sight $BC$ is the transversal

We must recall the geometry rule that when two parallel lines $AB$ and $CD$ are cut by a transversal line $BC$, we get the alternate interior angles which are angle $\theta$ (angle of depression) and $∠CBA$ (angle of elevation) in our case. We know that alternate interior angles are congruent . Thus,

Angle of depression $\theta =$ Angle of elevation $∠CBA$

Now utilizing this fact, we need to label $∠CBA$ as $\theta$ inside the triangle, as shown in Figure 12-4 below.

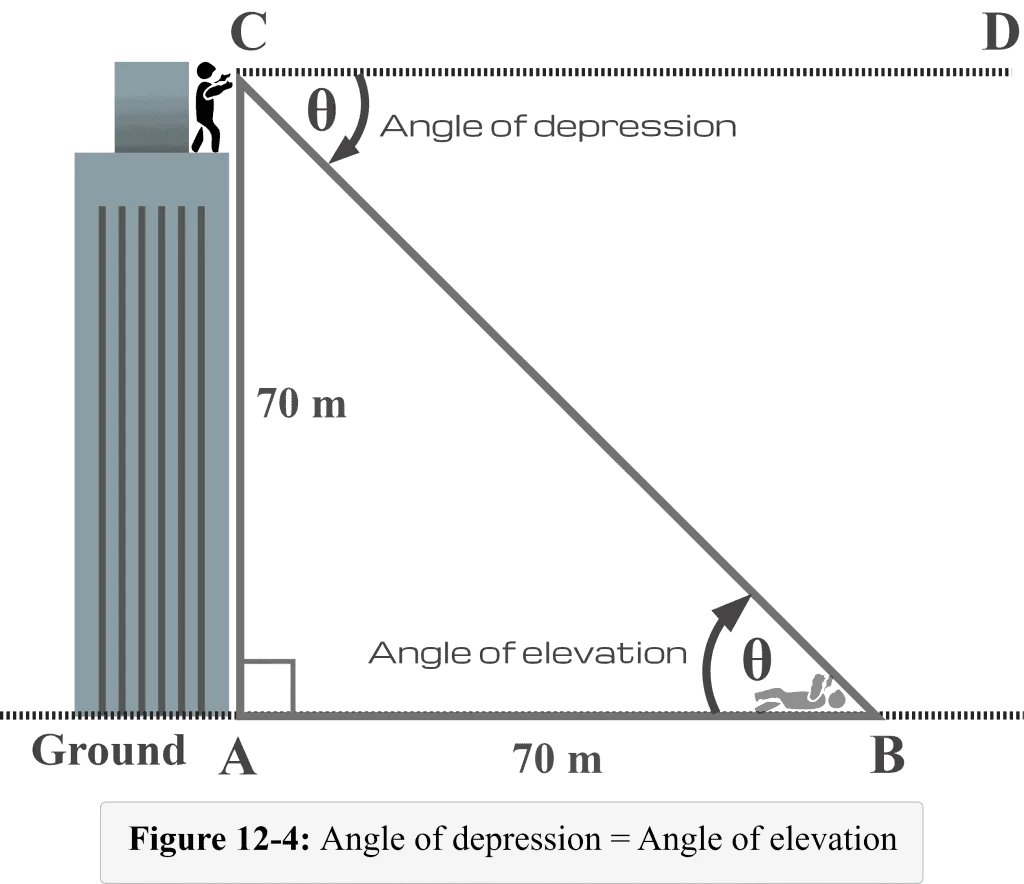
Now from the perspective of $m∠B = \theta$, we observe that:

Opposite side $AC = 70$ m

Adjacent side $AB = 70$ m

Using the formula of the tangent function

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite $= 70$, and adjacent $= 70$ in the formula

${\displaystyle \tan \theta ={\frac {70}{70}}}$

$\tan \theta = 1$

solving the equation

$\theta =\tan^{-1}(1)$

$\theta = 45^{\circ }$

We know that the angle of depression is equal to the angle of elevation.

Therefore, the measure of the required angle of depression θ is $\theta = 45^{\circ }$.

Figure 12-5 also illustrates the relationship between the angle of depression and the angle of elevation.

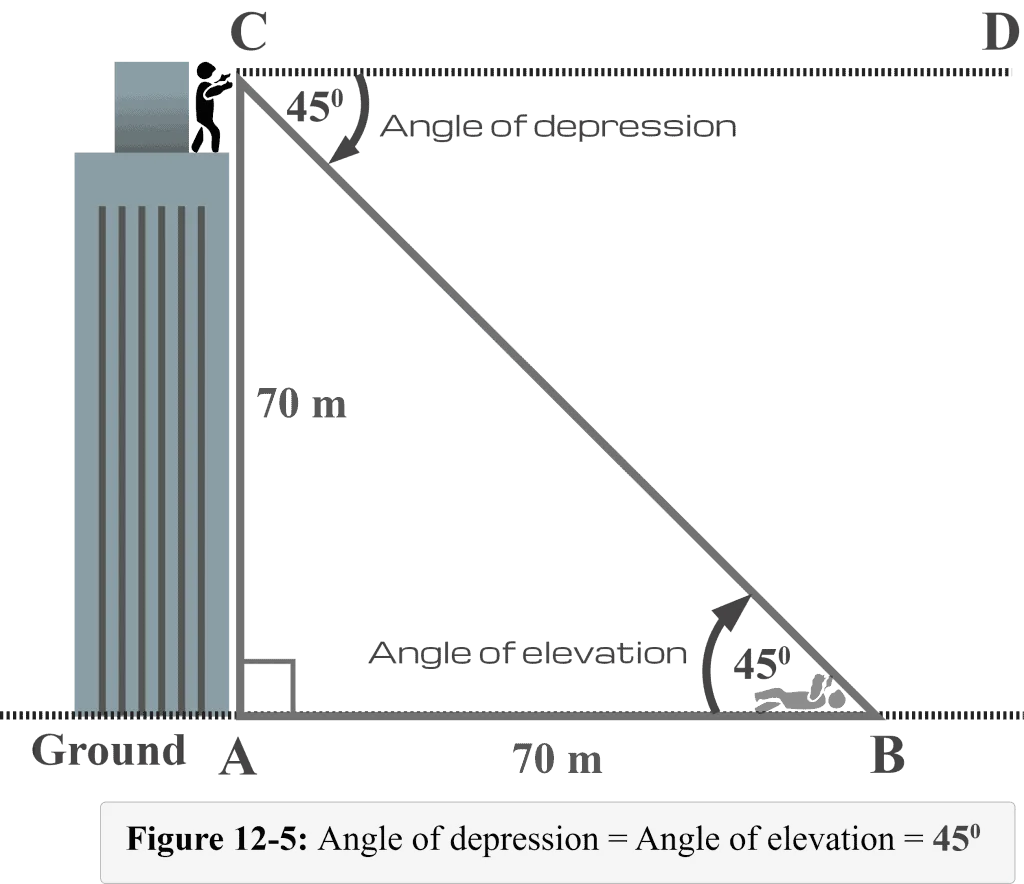
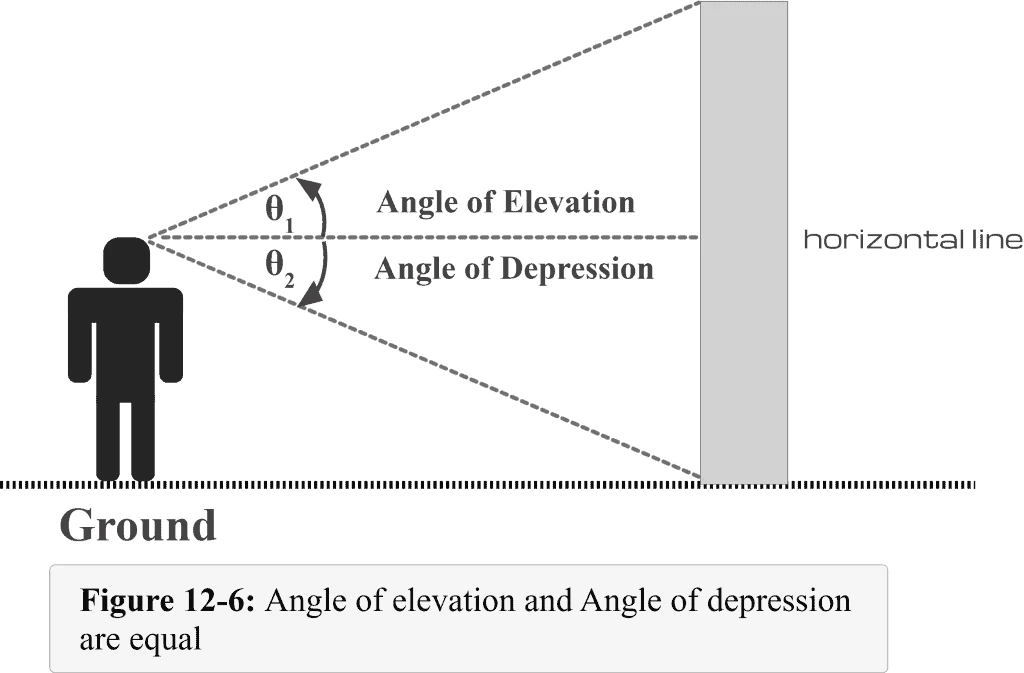
Figure 12-6 illustrates the summary of what we have discussed so far.

• When the light of sight is above the horizontal line, an angle of elevation is formed. 
• When the light of sight is below the horizontal line, an angle of depression is formed. 
• Angle of depression $\theta$ 1 = Angle of elevation $\theta$ 2

From the top of a palm tree of length $18$ m, Mr. Toni observes the base of the building on the ground. If the building is at a distance of $20$ meters from the tree, what is the angle of depression of the building on the ground from the top of the tree? Assume that the tree is vertical.

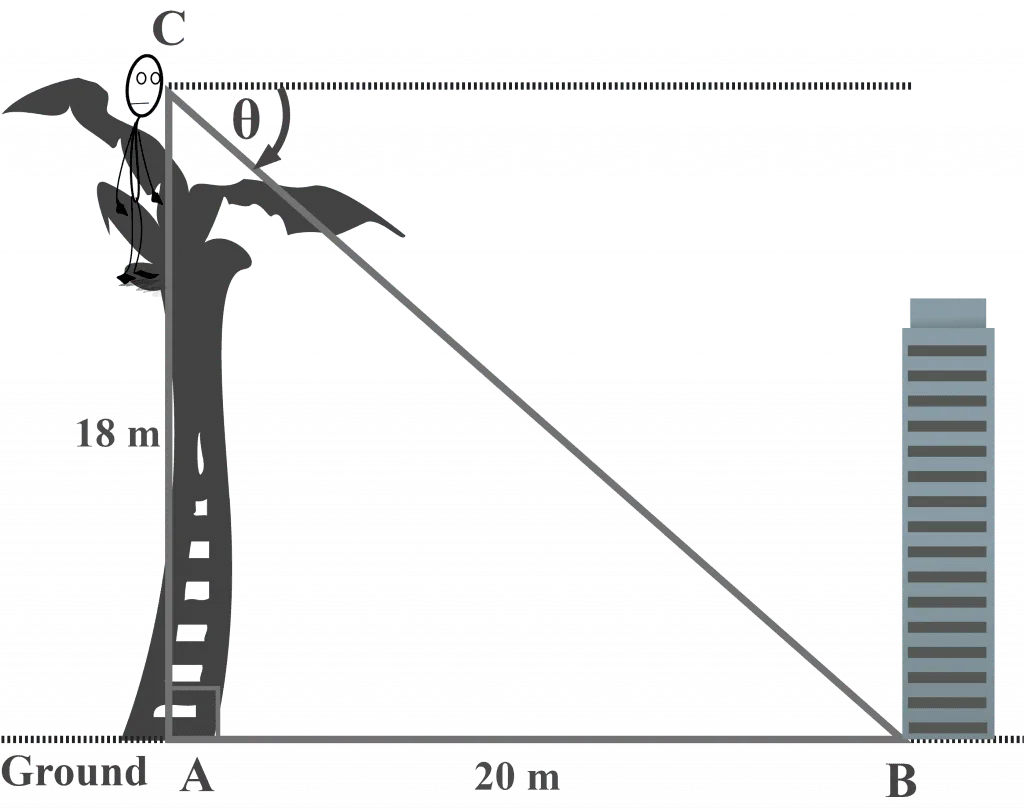
In this diagram, $\theta$ represents the angle of depression of the building on the ground from the top of the tree.

Take note that the horizontal line in the angle of the depression diagram is parallel to the ground surface, establishing the fact that alternate interior angles are congruent. Thus, the measure of the angle $\theta$ is equal to $m∠CBA$. In other words,

$m∠B = \theta$

The tree is vertical, making it perpendicular to the ground, so looking at the diagram, it is clear that a right triangle $ΔCAB$ is formed.

From the perspective of $m∠B = \theta$, we observe that:

Opposite side $AC = 18$ m

Adjacent side $AB = 20$ m

Using the formula of the tangent function:

substitute opposite = $18$, and adjacent = $20$ in the formula

${\displaystyle \tan \theta = {\frac {{18}}{20}}}$

$\tan \theta = 0.9$

$\theta =\tan^{-1}(0.9)$

$\theta = 41.9872125^{\circ }$

$\theta ≈ 42^{\circ }$ (Rounded to the whole number)

Therefore, the measure of the required angle of depression θ is approximately $42^{\circ }$.

From the top of the building, Mr. Robertson sees his two friends, Friend $A$ and Friend $B$, on the ground at an angle of depression of $60^{\circ }$ and $30^{\circ }$, respectively, on the opposite sides of the building. The height of the building is $100$ m. Determine the distance between Friend A and Friend B.

First, create a simple labeled diagram showing the known measurements and depicting the scenario as shown below.

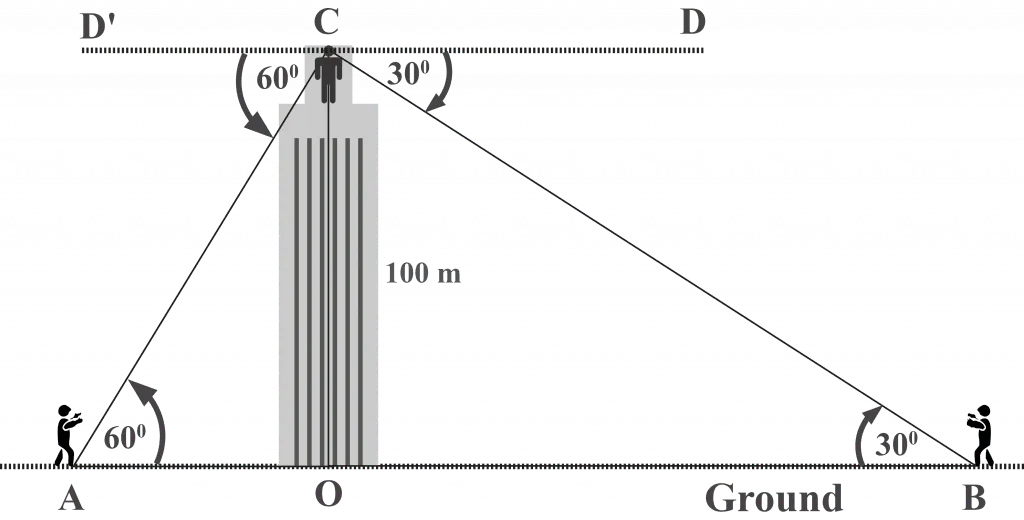
Looking at the diagram, we can observe that:

$CO =$ Height of the building $= 100$ m

Friend $A$ is at position $A$, and friend $B$ is at position $B$.

The angle of depression $m∠DCB = 30^{\circ }$ and $m∠D’CA = 60^{\circ }$

In geometry, alternate interior angles are congruent.

$∠DCB ≅ ∠CBO$

$∠D’CA ≅ ∠CAO$

$m∠CBO = 30^{\circ }$

$m∠CAO = 60^{\circ }$

The distance $AB$ between Friend $A$ and Friend $B = AO + BO$

In the right-angled triangle $⊿COA$,

${\displaystyle \tan 60^{\circ } = {\frac {{CO}}{AO}}}$

$\sqrt{3} = {\frac {{100}}{AO}}$

$AO = {\frac {{100}}{\sqrt{3}}}$

In the right-angled triangle $⊿COB$,

${\displaystyle \tan 30^{\circ } = {\frac {{CO}}{BO}}}$

${\frac {{1}}{\sqrt{3}}} = {\frac {{100}}{BO}}$

$BO = 100\sqrt{3}$

                                                                                           $= {\frac {{100}}{\sqrt{3}}} + 100\sqrt{3}$

                                                                                           $= {\frac {{100+300}}{\sqrt{3}}}$

                                                                                            $= {\frac {{400}}{\sqrt{3}}}$

                                                                                            $= {\frac {{400}}{1.73205}}$

                                                                                            $≈ 230.9$ m (Rounded to the nearest $0.01$)

Therefore, the distance between Friend $A$ and Friend $B$ is approximately $230.9$ m.

From the top of a larger building, Mr. Jordan observes the top and the base of the smaller building at the angle of depression of $30^{\circ }$ and $60^{\circ }$, respectively. The height of the larger building is $60$ m. What is the height of the smaller building?

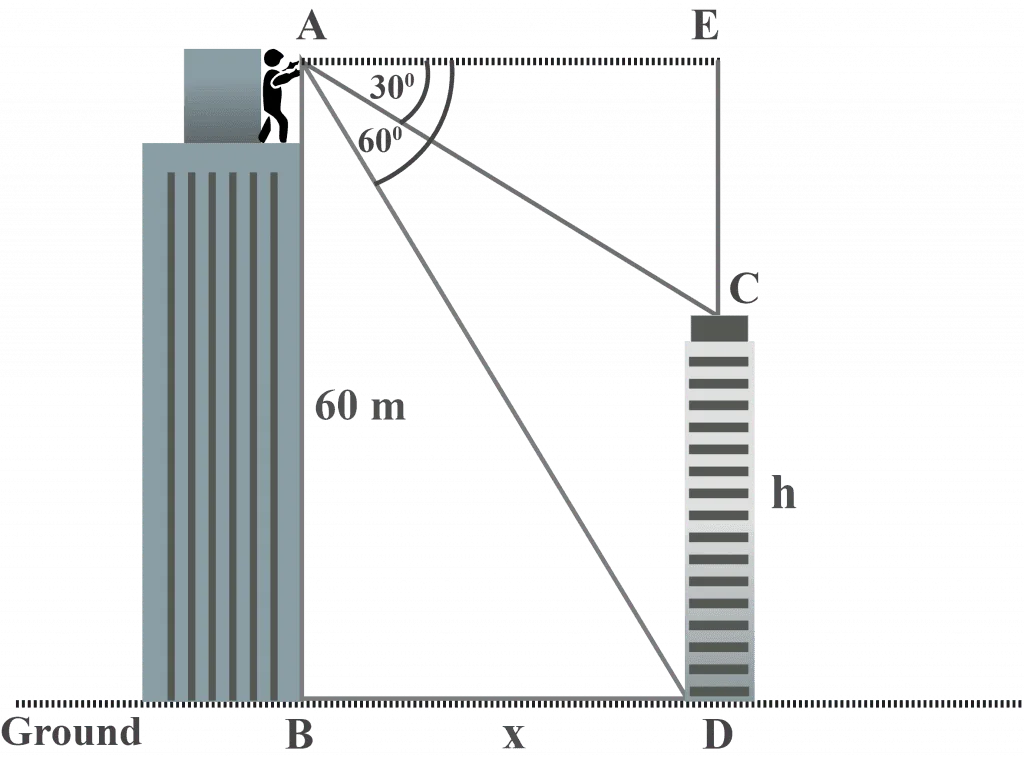
Looking at the diagram, we observe that:

Height of the larger building $AB = 60$ m

The angle of depression of the top of the smaller building is $30^{\circ }$, as observed from the top of the larger building.

$m∠EAC = 30^{\circ }$

The angle of depression of the base/foot of the smaller building is $60^{\circ }$, as observed from the top of the larger building.

$m∠EAD = 60^{\circ }$

$AB = ED = 60$ m

Let the height of smaller building $CD = h$

$CE = 60 – h%%EDITORCONTENT%%nbsp;        ∵ $AB = ED = 60$ and $ED = CD + CE$

As $AE$ is parallel and equal to $BD$

In the triangle $△EAC$,

${\displaystyle \tan 30^{\circ } = {\frac {{CE}}{AE}}}$

${\frac {{1}}{\sqrt{3}}} = {\frac {{(60-h)}}{x}}%%EDITORCONTENT%%nbsp;   — $[1]$

In the triangle $△EAD$,

${\displaystyle \tan 60^{\circ } = {\frac {{ED}}{AE}}}$

$\sqrt{3} = {\frac {{60}}{x}}%%EDITORCONTENT%%nbsp;   — $[2]$

Dividing equation $1$ by $2$, we get

$\frac{\frac{\left(60-h\right)}{x}}{\frac{60}{x}}=\frac{\frac{1}{\sqrt{3}}}{\sqrt{3}}$

$\frac{\left(60\:-\:h\right)}{60}\:=\:\frac{1}{3}$

$3\left(60\:-\:h\right)=60$

$180\:-\:3h\:=\:60$

$3h=180-60$

Divide both sides of the equation by $3$

Therefore, the height of the smaller building is $40$ m.

Previous Lesson  |  Main Page | Next Lesson

Angles of Elevation and Angles of Depression Word Problems

Angles of elevation and angles of depression word problems are some of the most common problems in studies of trigonometry. These types of problems are famous for requiring the use of trigonometric ratios to relate a given angle and side length to find an unknown side length.

Whether it is the base of the cliff or the height of the lamp post, understanding how to solve angles of elevation and angles of depression word problems is an essential problem solving skill! 

So let’s dig into it! It’s time to …  elevate …  your understanding!

What are Angles of Depression and Elevation?

Picture standing at the top of a tower and looking straight ahead along an imaginary horizontal line of sight. Suddenly, someone at ground level calls your name! You tilt your head downward from the imaginary horizontal line toward the ground through some angle. 

As it turns out, this angle is the  angle of depression!  This angle is sometimes referred to as the angle of declination since there is a “decline” between the horizontal line of sight and the object being observed. An angle of depression must always be an acute angle.

Now, imagine that you are the person shouting up toward the top of the tower. You begin by looking straight ahead at the base of the tower, and tilt your head from ground level up toward the top of the tower.

The angle that you are tilting your head through is the  angle of elevation.  This angle is sometimes referred to as the angle of inclination since there is an “incline” between the horizontal line of sight and the top of the object. An angle of elevation must also always be an acute angle.

There are many famous angle theorems that can help us solve problems involving triangles. However, if you think back to your understanding of alternate interior angles , you should be able to see that these two angles are actually equal! This is because the line of sight and the ground are parallel lines.

Since we have a “Z-pattern”, we know that the angle of depression is equal to the angle of elevation ! This is an important piece of knowledge that is going to help you solve any given angles of elevation or angles of depression word problems that you come across! 

Before we take a look at the first example, watch this short video for an excellent visual representation of angles of elevation and angles of depression. I promise you won’t forget the difference after watching this video!

Solving Angles of Elevation and Angles of Depression Word Problems

When it comes to solving angles of elevation and angles of depression word problems, the first step is to always start with a diagram to visualize the problem. Look for key phrases that give you hints about what specific angles and side lengths might be involved. Phrases such as  the height of the first building  give you an indication that that particular building will be important in your calculation.

From here, think about what trigonometric ratios will be involved. For example, the tangent ratio is used when you are relating the angle, the opposite, and the adjacent sides.

Let’s take a look at a few examples!

Example #1: Angles of Depression Word Problems

You are looking out a window at the very top of a tower. The height of the tower is known to be 50 feet. From the top of the building, you measure the angle of depression of a car to be 30 degrees. How far is the car from the building to the nearest foot?

To begin, we draw a diagram to help us visualize this scenario. The most important pieces of information given in this problem are the height of the tower (one of the sides of the right triangle) and the angle of depression of the car. Remember, since we are working with a building, we know that we have a right angle between the building and the ground.

The key trick to most angles of depression word problems is using your knowledge of alternate interior angles. This works since our line of sight and the ground are parallel lines!

We can use our understanding of alternate interior angles to show that the angle of depression from the top of the building is actually equal to the angle of elevation from the car up toward the tower!

Therefore, each of these angles are now known to be 30 degrees.

Looking at this new angle, we have the length of the side  opposite  to the angle (the height of the building) and we want to solve for length of the side  adjacent to the angle   (the distance from the car to the base of the tower). The trigonometric ratio relating the opposite and adjacent side lengths is the tangent ratio!

Setting up this ratio and solving for  x  results in:

$$ \begin{split} tan30^\circ &= \frac{50}{x} \\ \\ x &= \frac{50}{tan30^\circ} \\ \\ x &= 86.6 \\ \end{split} $$

Therefore, the car is 87 feet away from the base of the tower (rounded to the nearest foot).

Example #2: Angles of Elevation Word Problems

You are standing on the ground and see two buildings in front of you that are the same distance away from you. You measure the angle of elevation to the top of the first building to be 45 degrees, and the angle of elevation to the top of the second building to be 60 degrees. You know that the height of the first building is 40 feet. What is the height of the second building to the nearest foot?

Just like the last problem, we start by sketching a diagram to help visualize this scenario. This scenario is slightly more complex since we are working with two buildings, so a diagram is important!

As it stands, the problem has not given us enough information to solve for the height of the second building, h . In order to solve the problem, we first need to determine the horizontal distance, d , between you and the base of the buildings. Once we have determined this horizontal distance, we can use it to solve for the height of the second building!

We use the height of the first building and the 45 degree angle (the angle of elevation) to set up a tangent ratio:

$$ \begin{split} tan45^\circ &= \frac{40}{d} \\ \\ d &= \frac{40}{tan45^\circ} \\ \\ d &= 40 \\ \end{split} $$

So we know the horizontal distance, d , is also 40 feet. From here, we can use the horizontal distance and the 60 degree angle of elevation to find the height of the second building!

$$ \begin{split} tan60^\circ &= \frac{h}{40} \\ \\ 40 \times tan60^\circ &= h \\ \\ h &= 69.28 \\ \end{split} $$

Therefore, the height of the second building is 69 feet!

Review: Solving Angles of Elevation and Depression Word Problems

Each angle of elevation or depression problem that you encounter will have similarities. You will always have to use the information given and a vertical line formed by some object to find the height of the tree, building, or tower.

If you aren’t give one, drawing a diagram should always be your first step. This is important to help you visualize the angles of elevation or depression that you are given. And as you have seen, having a good understanding of alternate interior angles and trigonometric ratios is also important!

For more practice on solving these types of problems, check out this angles elevation and angle of depression word problems worksheet !

My hope is that these examples have helped you understand the difference between angles of elevation and angles of depression. With this knowledge and a little practice, you will be able to solve any related problem that you come across!

Did you find this overview of angles of elevation and depression helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Examples of One Solution Equations, Zero, and Infinite

Linear Equations Word Problems Worksheet with Solutions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.2.7: Angles of Elevation and Depression

• Last updated
• Save as PDF
• Page ID 14950

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Angles going up or down from a horizontal line of sight.

Angles of Elevation and Depression

You have decided to go camping with some friends. While out on a hike, you reach the top of a ridge and look down at the trail behind you. In the distance, you can see your camp. You're thinking about how far you've traveled, and wonder if there is a way to determine it.

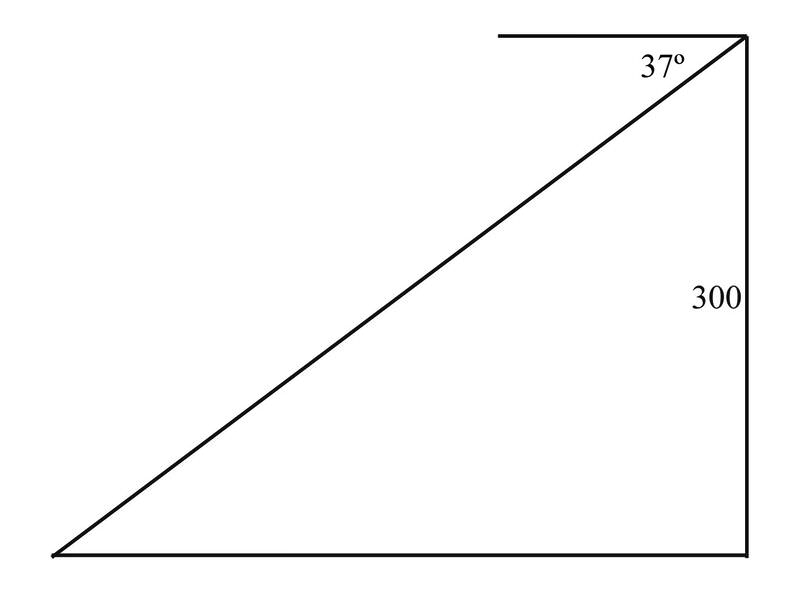
By using a small device called a clinometer, you're able to measure the angle between your horizontal line of sight and the camp as \(37^{\circ}\), and you know that the hill you just hiked up has a height of 300 m. Is it possible to find out how far away your camp is using this information? (Assume that the trail you hiked is slanted like the side of a triangle.)

You can use right triangles to find distances, if you know an angle of elevation or an angle of depression .

The figure below shows each of these kinds of angles.

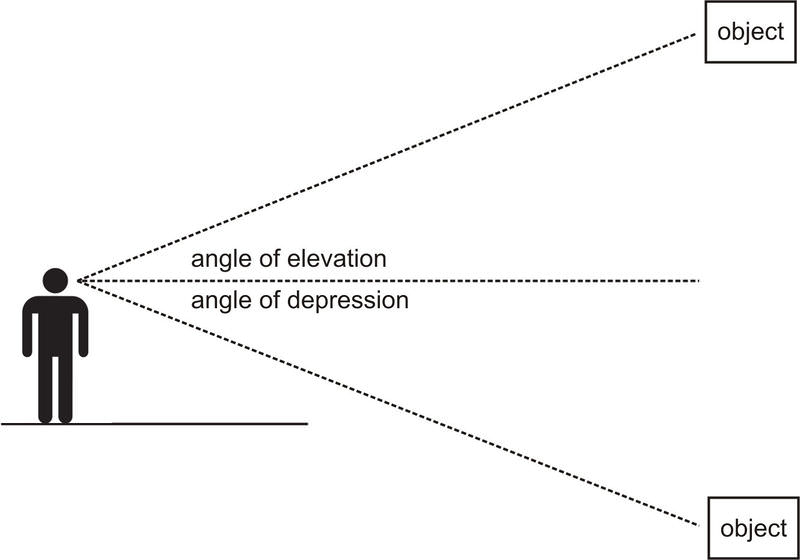
The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. For example, if you are standing on the ground looking up at the top of a mountain, you could measure the angle of elevation. The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. For example, if you were standing on top of a hill or a building, looking down at an object, you could measure the angle of depression. You can measure these angles using a clinometer or a theodolite. People tend to use clinometers or theodolites to measure the height of trees and other tall objects. Here we will solve several problems involving these angles and distances.

Finding the angle of elevation

You are standing 20 feet away from a tree, and you measure the angle of elevation to be \(38^{\circ}\). How tall is the tree?

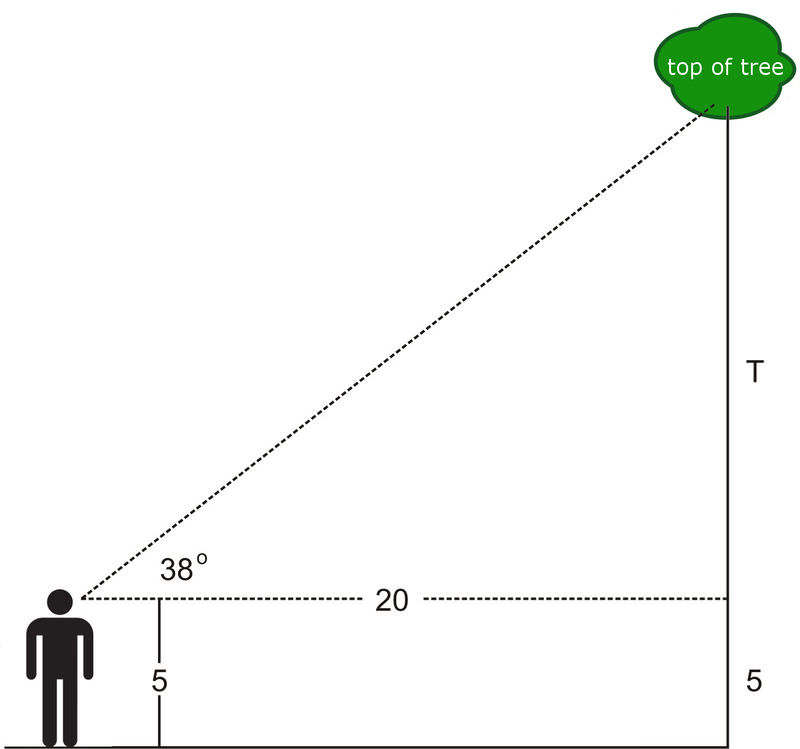
The solution depends on your height, as you measure the angle of elevation from your line of sight. Assume that you are 5 feet tall.

The figure shows us that once we find the value of \(T\), we have to add 5 feet to this value to find the total height of the triangle. To find \(T\), we should use the tangent value:

\(\begin{aligned} tan38^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{T}{20} \\ tan38^{\circ}&=\dfrac{T}{20}\\ T&=20tan38^{\circ}\approx 15.63\\ \text{Height of tree}&\approx 20.63 \text{ ft}\end{aligned}\)

You are standing on top of a building, looking at a park in the distance. The angle of depression is 53^{\circ} . If the building you are standing on is 100 feet tall, how far away is the park? Does your height matter?

Finding the angle of depression

If we ignore the height of the person, we solve the following triangle:

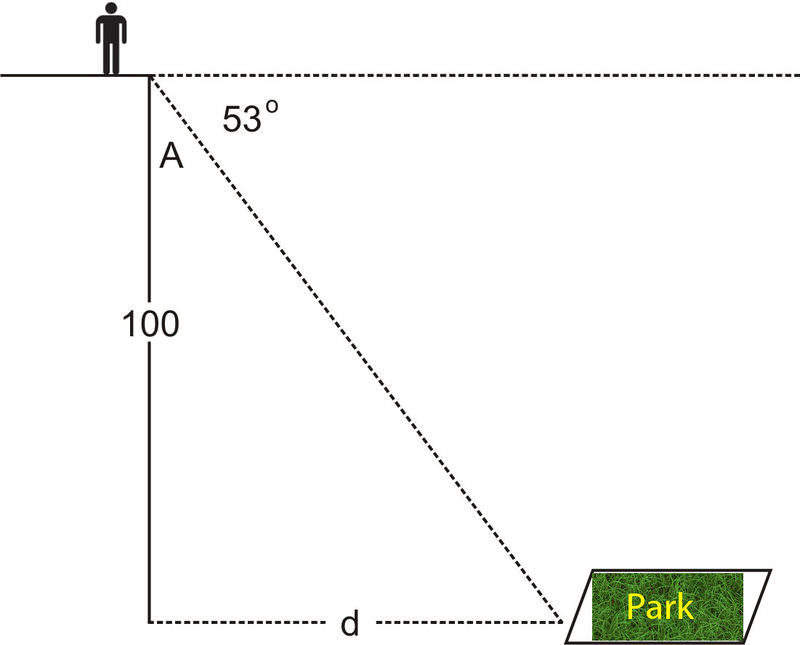
Given the angle of depression is \(53^{\circ}\), \(\angle A\) in the figure above is \(37^{\circ}\). We can use the tangent function to find the distance from the building to the park:

\(\begin{aligned} tan 37^{\circ}=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{100}\\ tan37^{\circ} &=\dfrac{d}{100}\\d&=100 tan37^{\circ} \approx 75.36\text{ ft} \end{aligned}\)

If we take into account the height if the person, this will change the value of the adjacent side. For example, if the person is 5 feet tall, we have a different triangle:

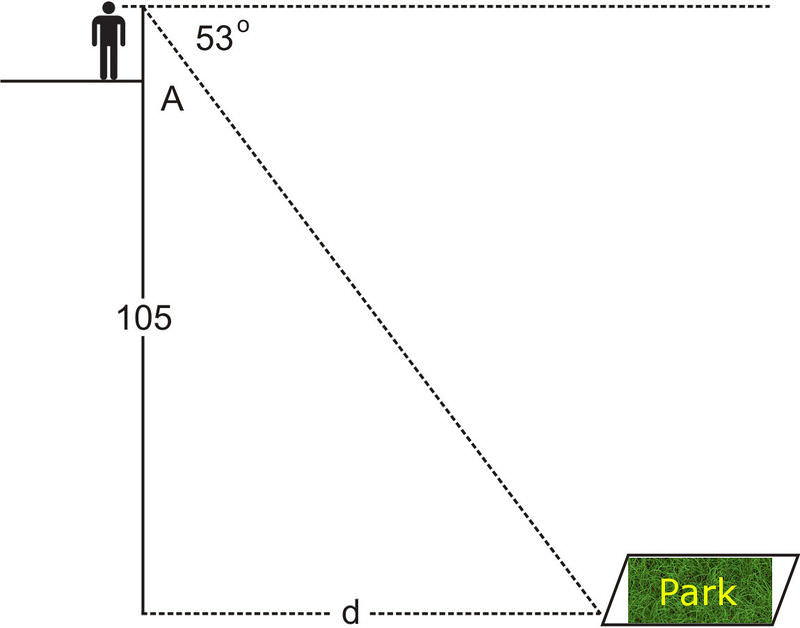
\(\begin{aligned} tan37^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{105} \\ tan37^{\circ} &=\dfrac{d}{105} \\ d&=105{tan37^{\circ} \approx 79.12\text{ ft}\end{aligned}\)

If you are only looking to estimate a distance, then you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller. For example, the height of the person will influence the result more in the tree height problem than in the building problem, as the tree is closer in height to the person than the building is.

Real-World Application: The Horizon

You are on a long trip through the desert. In the distance you can see mountains, and a quick measurement tells you that the angle between the mountaintop and the ground is \(13.4^{\circ}\). From your studies, you know that one way to define a mountain is as a pile of land having a height of at least 2,500 meters . If you assume the mountain is the minimum possible height, how far are you away from the center of the mountain?

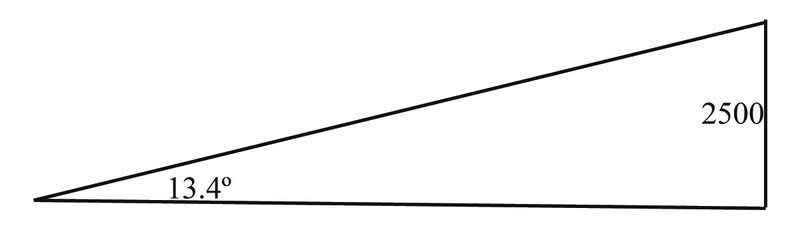
\(\begin{aligned} tan 13.4^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{2500}{d}\\ tan 13.4^{\circ} &=\dfrac{2500}{d} \\ d&=\dfrac{2500}{tan13.4^{\circ}} \approx 10,494 meters \end{aligned}\)

Example \(\PageIndex{1}\)

Earlier, you were asked if it was possible to find out how far away your camp is using the information given.

Since you know the angle of depression is \(37^{\circ}\), you can use this information, along with the height of the hill, to create a trigonometric relationship:

Since the unknown side of the triangle is the hypotenuse, and you know the opposite side, you should use the sine relationship to solve the problem:

\(\begin{aligned} sin37^{\circ}&=\dfrac{300}{hypotenuse} \\ hypotenuse&=\dfrac{300}{sin37^{\circ} }\\ hypotenuse &\approx 498.5\end{aligned}\)

You have traveled approximately 498.5 meters up the hill.

Example \(\PageIndex{2}\)

You are six feet tall and measure the angle between the horizontal and a bird in the sky to be 40^{\circ} . You can see that the shadow of the bird is directly beneath the bird, and 200 feet away from you on the ground. How high is the bird in the sky?

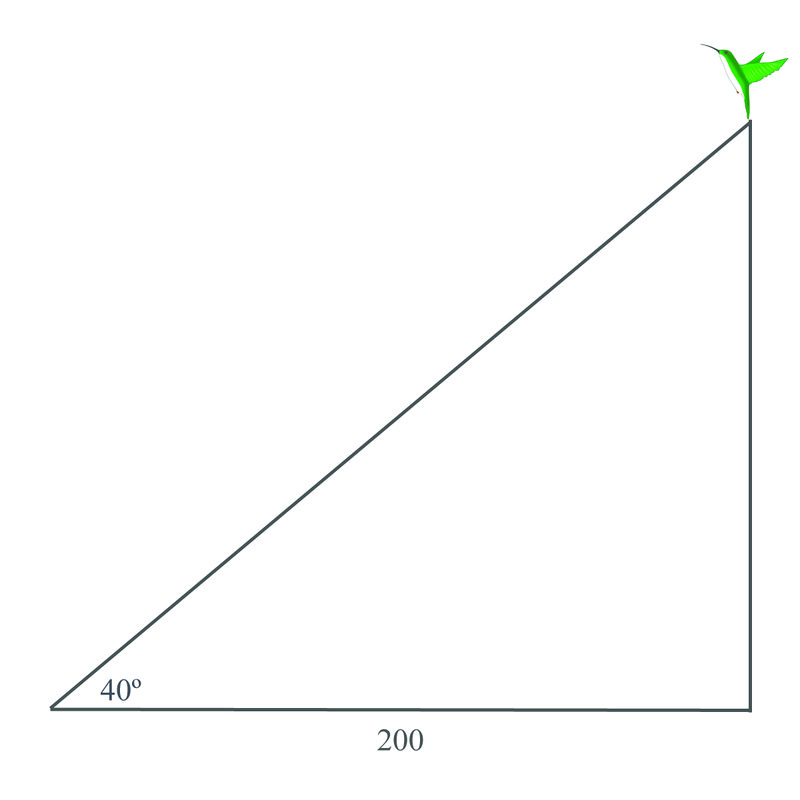
We can use the tangent function to find out how high the bird is in the sky:

\(\begin{aligned} tan40^{\circ} =\dfrac{height}{200} \\ height&=200 tan40^{\circ} \\ height&=(200)(.839) \\height&=167.8\end{aligned}\)

We then need to add your height to the solution for the triangle. Since you are six feet tall, the total height of the bird in the sky is 173.8 feet.

Example \(\PageIndex{3}\)

While out swimming one day you spot a coin at the bottom of the pool. The pool is ten feet deep, and the angle between the top of the water and the coin is \(15^{\circ}\). How far away is the coin from you along the bottom of the pool?

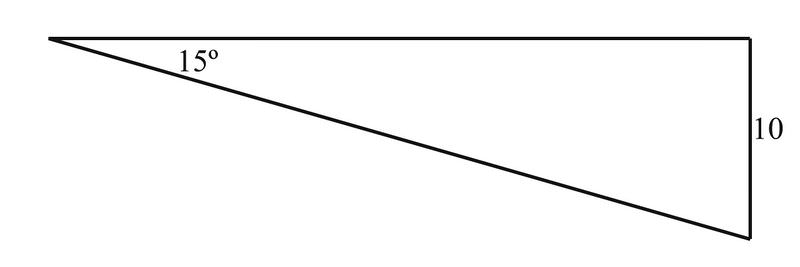
Since the distance along the bottom of the pool to the coin is the same as the distance along the top of the pool to the coin, we can use the tangent function to solve for the distance to the coin:

\(\begin{aligned} tan15^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}} \\ tan 15^{\circ} =\dfrac{10}{x} \\ x&=\dfrac{10}{tan15^{\circ}} \\ x&\approx 37.32^{\circ}\end{aligned}\)

Example \(\PageIndex{4}\)

You are hiking and come to a cliff at the edge of a ravine. In the distance you can see your campsite at the base of the cliff, on the other side of the ravine. You know that the distance across the ravine is 500 meters , and the angle between your horizontal line of sight and your campsite is \(25^{\circ}\). How high is the cliff? (Assume you are five feet tall.)

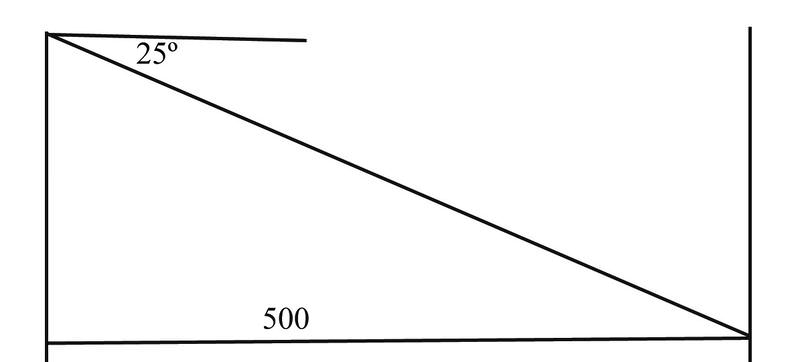
Using the information given, we can construct a solution:

\(\begin{aligned} tan 25^{\circ} =\dfrac{\text{opposite}}{\text{adjacent}}\\ tan25^{\circ}&=\dfrac{height}{500} \\ height&=\dfrac{500}{tan25^{\circ}}\\ height&=(500)(.466) \\ height&=233\text{ meters}\end{aligned}\)

This is the total height from the bottom of the ravine to your horizontal line of sight. Therefore, to get the height of the ravine, you should take away five feet for your height, which gives an answer of 228 meters.

• A 70 foot building casts an 50 foot shadow. What is the angle that the sun hits the building?
• You are standing 10 feet away from a tree, and you measure the angle of elevation to be \(65^{\circ}\). How tall is the tree? Assume you are 5 feet tall up to your eyes.
• Kaitlyn is swimming in the ocean and notices a coral reef below her. The angle of depression is \(35^{\circ}\) and the depth of the ocean, at that point is 350 feet. How far away is she from the reef?
• The angle of depression from the top of a building to the base of a car is \(60^{\circ}\). If the building is 78 ft tall, how far away is the car?
• The Leaning Tower of Pisa currently “leans” at a \(4^{\circ}\) angle and has a vertical height of 55.86 meters. How tall was the tower when it was originally built?
• The angle of depression from the top of an apartment building to the base of a fountain in a nearby park is \(72^{\circ}\). If the building is 78 ft tall, how far away is the fountain?
• You are standing 15 feet away from a tree, and you measure the angle of elevation to be \(35^{\circ}\). How tall is the tree? Assume you are 5 feet tall up to your eyes.
• Bill spots a tree directly across the river from where he is standing. He then walks 18 ft upstream and determines that the angle between his previous position and the tree on the other side of the river is \(55^{\circ}\). How wide is the river?
• A 50 foot building casts an 50 foot shadow. What is the angle that the sun hits the building?
• Eric is flying his kite one afternoon and notices that he has let out the entire 100 ft of string. The angle his string makes with the ground is \(60^{\circ}\). How high is his kite at this time?
• A tree struck by lightning in a storm breaks and falls over to form a triangle with the ground. The tip of the tree makes a \(36^{\circ}\) angle with the ground 25 ft from the base of the tree. What was the height of the tree to the nearest foot?
• Upon descent an airplane is 15,000 ft above the ground. The air traffic control tower is 200 ft tall. It is determined that the angle of elevation from the top of the tower to the plane is \(15^{\circ}\). To the nearest mile, find the ground distance from the airplane to the tower.
• Tara is trying to determine the angle at which to aim her sprinkler nozzle to water the top of a 10 ft bush in her yard. Assuming the water takes a straight path and the sprinkler is on the ground 4 ft from the tree, at what angle of inclination should she set it?
• Over 3 miles (horizontal), a road rises 1000 feet (vertical). What is the angle of elevation?
• Over 4 miles (horizontal), a road rises 1000 feet (vertical). What is the angle of elevation?

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.13.

Additional Resources

Interactive element.

Video: Example: Determine What Trig Function Relates Specific Sides of a Right Triangle

Practice: Angles of Elevation and Depression

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

Angle of Depression – Formula, Definition With Examples

Created on Jan 03, 2024

Updated on January 5, 2024

Welcome to Brighterly, a comprehensive online math program for kids. Today, we’re focusing on a key concept in geometry: the angle of depression. This topic is not just a part of our math for kids curriculum but is also crucial for developing problem-solving skills. Understanding the angle of depression helps in various real-world applications, making it a fascinating and practical area of study in our math tutoring for kids.

What is Angle of Depression?

In geometry, the angle of depression is measured when an observer looks at a point below their horizontal line of sight. Here’s a straightforward explanation:

Observer’s Position: The observer is at a higher elevation than the point they are looking at. This could be someone standing at the top of a building, hill, or any elevated position.

Horizontal Line: Imagine a straight line extending outwards from the observer’s eyes, parallel to the ground. This is the horizontal reference line.

Line of Sight: This is a straight line from the observer’s eyes to the point of interest below them.

Angle of Depression: The angle of depression is the angle formed between the horizontal line and the line of sight. It is always measured downwards from the horizontal line.

This concept is particularly important in real-world applications like determining the height of an object or distance from a point when direct measurement is not feasible. In mathematical problems, it is often used alongside trigonometric ratios to calculate distances and heights.

Detailed Definition of Angle of Depression

When teaching math for kids, it’s important to explain concepts clearly. The angle of depression occurs when an observer looks down from a higher point to a lower point. For instance, if a child is looking down from the top of a slide to their friend below, the angle between their line of sight and the imaginary horizontal line from their eyes is the angle of depression. This concept is a cornerstone in Brighterly’s.

Formula for Calculating Angle of Depression

In our online math tutoring for kids, we emphasize the importance of formulas. The angle of depression can be calculated using the formula: Angle of Depression=(1/tan)*(Opposite Side/Adjacent Side)

This formula is crucial in trigonometry, a key part of our math program for kids, allowing them to calculate distances and heights in real-life situations.

Angle of Depression Vs Angle of Elevation

In geometry, it’s essential to distinguish between the angle of depression and the angle of elevation. These concepts are foundational in our math curriculum, especially for visualizing and solving real-world problems. Let’s clarify these terms:

Angle of Elevation: This angle is formed when you look up from a lower point to a higher point. For example, if you’re standing on the ground and looking up at the top of a building, the angle your line of sight makes with the horizontal line is the angle of elevation.

Angle of Depression: Conversely, the angle of depression occurs when you look down from a higher point to a lower point. If you’re at the top of the building looking down at a point on the ground, the angle between your line of sight and the horizontal line is the angle of depression.

Naming Angles Worksheet

Naming Angles Worksheet PDF

Classifying Angles Worksheet

Classifying Angles Worksheet PDF

Application of Angle of Depression in Triangles

Triangles, especially right-angled ones, are a mainstay in geometry and crucial in our math for kids program. The angle of depression helps in solving problems involving heights and distances. For instance, calculating the height of a tree from a certain distance can be solved using the angle of depression, a practical and engaging method in our online math program for kids.

Examples of Angle of Depression

Practice questions on angle of depression:.

From a 50-meter-high tower, if the angle of depression to a point on the ground is 30 degrees, find the distance from the base of the tower to that point.

Solution: Using the formula for the angle of depression, calculate the horizontal distance.

A bird is flying at a height of 150 meters, and the angle of depression to a fish in the water is 45 degrees. Determine the horizontal distance between the bird and the fish.

Solution: Apply the formula, using the height as the opposite side, to find the horizontal distance.

Classify Angles Worksheet

Identifying Types Of Angles Worksheet

FAQs on Angle of Depression

How does understanding the angle of depression benefit kids in real life.

It helps in practical applications like determining the height of objects, which is a part of our math lessons for kids.

Why is the angle of depression important in Brighterly’s math program for kids?

It lays the foundation for understanding trigonometry and geometry, essential in our comprehensive math curriculum for kids.

Can the angle of depression be the same as the angle of elevation?

Yes, in cases where two observers are at different heights, their angles of depression and elevation can be congruent.

How does Brighterly make learning angles engaging for kids?

We use interactive tools, real-life examples, and clear explanations to make geometry fun and engaging in our online math tutor program for kids.

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.

Book 1 to 1 Math Lesson

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

After-School Math Program

Related math, significant figures – definition, examples, rules, rounding.

Welcome to another exciting journey into the vibrant world of mathematics brought to you by Brighterly! At Brighterly, our mission is to illuminate the path of learning for children, breaking down complex mathematical concepts into comprehensible and engaging chunks. Today, we turn our spotlight on a fascinating yet often misunderstood topic: significant figures. Understanding significant […]

41 in Words

The number 41 is expressed in words as “forty-one”. It is one more than forty. Imagine having forty-one pencils; it means you have forty pencils and then add one more. Tens Ones 4 1 How to Write 41 in Words? Writing 41 in words is straightforward. It consists of a ‘4’ in the tens place […]

Remainder Theorem and Polynomials – Definition With Examples

Welcome to another thrilling exploration with Brighterly, where we bring the universe of mathematics closer to the brilliant minds of our young readers. Today, we’re delving into the mesmerizing world of Remainder Theorem and Polynomials. Polynomials are like the building blocks of mathematics, and the Remainder Theorem is one of those intriguing tools that make […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

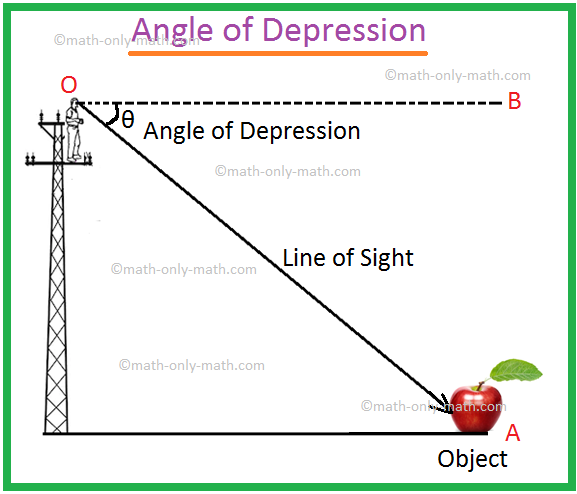
Angle of Depression

Let O be the eye of an observer and A be an object below the level of the eye. The ray OA is called the line of sight. Let OB be the horizontal line through O. Then the angle BOA is called the angle of depression of the object A as seen from O.

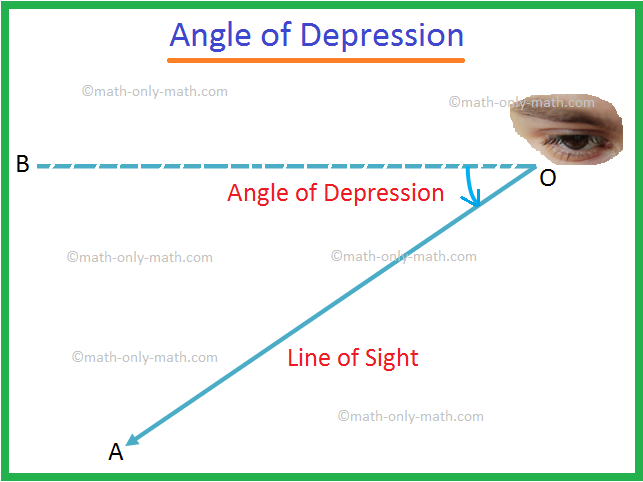
It may so happen that a man climbs up the pole, keeps his eyes at a point O and see the object placed at the point A is the angle of depression of the point A with respect to the point O.

 How can we get the angle of depression?

We shall have to imagine a straight line OB parallel to the straight line CA. The measure of the angle of depression will be ∠BOA.

It is clear from the figure below that the angle of elevation of A as seen from B = the angle of depression of B as seen from A.

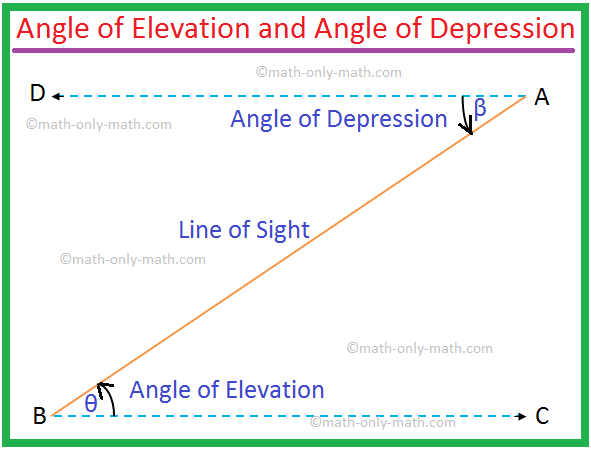
Therefore, ∠θ = ∠β.

Note: 1. Here, BC ∥ DA and AB is the transversal. So the angle of elevation ∠ABC = the angle of depression ∠BAD. But even then they are to be indicated to solve problems.

2. The observer is taken as a point unless the height of the observer is given.

3. √3 = 1.732 (Approximately).

10th Grade Heights and Distances

Solved Examples on Angle of Depression:

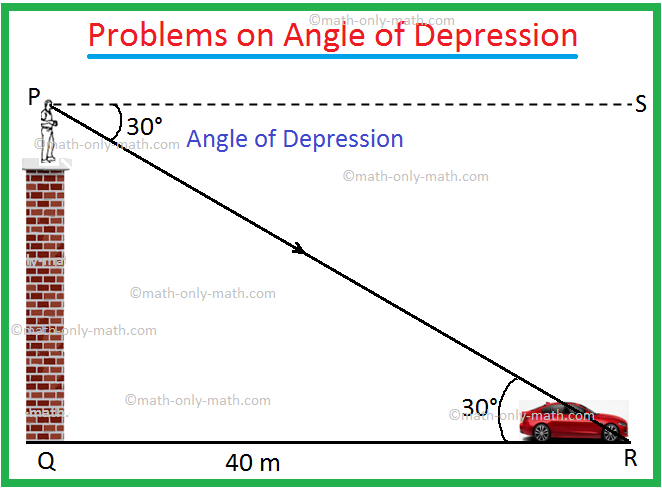
1. From the top of a tower, a man finds that the angle of depression of a car on the ground is 30°. If the car is at a distance 40 metres from the tower, find the height of the tower.

Let PQ be the tower and the car is at R. 

The angle of depression = ∠SPR = 30° and QR = 40 m.

From geometry, ∠PRQ = ∠SPR = 30°.

In the right-angled ∆PQR, 

                           tan  30° = \(\frac{PQ}{QR}\)

                       ⟹ \(\frac{1}{√3}\) = \(\frac{PQ}{40 m}\)

                       ⟹ √3PQ = 40m

                       ⟹ PQ = \(\frac{40}{√3}\) m

                       ⟹ PQ = \(\frac{40√3}{3}\) m

                       ⟹ PQ = \(\frac{40 × 1.732}{3}\) m

                       ⟹ PQ = 23 m (Approx.).

Therefore, the height of the tower is 23 m (Approx.).

Angle of Depression Example 

2. From the top of a cliff 200 m height, the angles of depression of two places A and B on the ground and on the opposite sides of the cliff are 60° and 30°. Find the distance between M and N.

Let TO be the cliff, and given that TO = 200 m.

M and N are the two points.

The angle of depression ∠X'TM = 60° and ∠XTN = 30°.

By geometry, ∠TMO = 60° and ∠TNO = 30°.

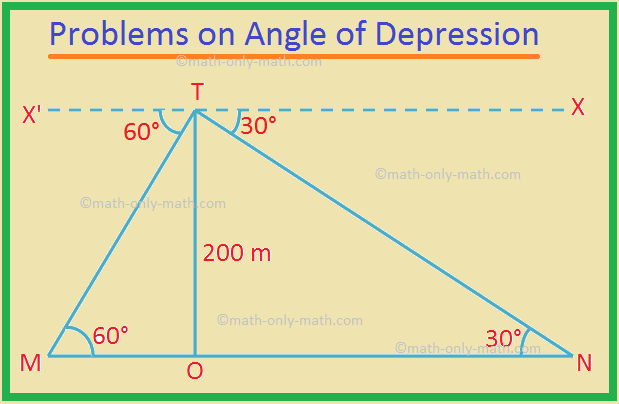
In the right-angled ∆TOM, 

                                 tan 60° = \(\frac{TO}{MO}\)

                            ⟹       √3  = \(\frac{200 m}{MO}\)

                            ⟹       MO  = \(\frac{200 m}{√3}\)

In the right-angled ∆TON, 

                                 tan 30° = \(\frac{TO}{NO}\)

                            ⟹       \(\frac{40}{√3}\) = \(\frac{200 m}{NO}\)

                            ⟹       NO  = 200√3 m.

Therefore, the required distance MN = MO + NO 

                                                     = \(\frac{200 m}{√3}\) + 200√3 m.

                                                     = \(\frac{200 + 600}{√3}\) m

                                                     = \(\frac{800}{√3}\) m

                                                     = \(\frac{800√3}{3}\) m

                                                     = \(\frac{800 × 1.732}{3}\) m

                                                     = 461.89 m (Approx.)

Word problems on Angle of Depression:

3. A building stands on the bank of a river. A man observes from a corner of the roof of the building, the foot of a electric post just on the opposite bank. If the angle of depression of the foot of the light post at your eye is 30° and the height of the building is 12 meters, what is the width of the river?

Let P is the roof of the building, Q is the foot of the building vertically below the corner point and R is the foot of the light post just on the opposite of the bank of the river. A right-angled triangle PQR is formed by joining these points.

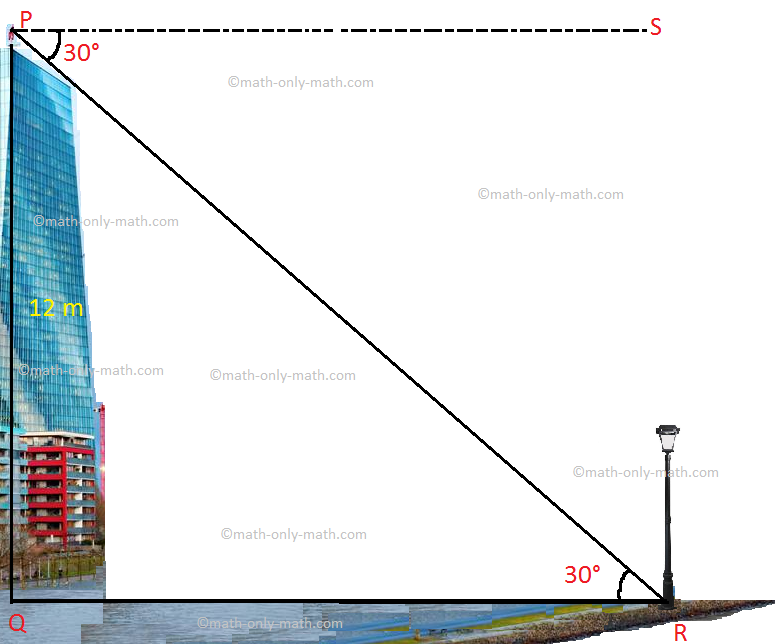
Let PS be the horizontal line through P.

∠SPR, the angle of depression = ∠PRQ = 30°, and with respect to this angle perpendicular PQ = 12 metres and base QR = width of the river = h metres.

From right-angled triangle PQR,

\(\frac{PQ}{QR}\) = tan 30°

\(\frac{12}{h}\) = \(\frac{1}{√3}\)

⟹ h = 12 × √3

⟹ h = 12 × 1.732

⟹ h = 20.784 (Approximately)

Therefore, the width of the river is 20.784 meters (Approximately).

Angle of Depression Problem:

4. From the top of a building, the angle of depression of the top and the foof of a lamp post are 30° and 60° respectively. What is the height of the lamp post?

According to the problem, the height of the building PQ = 12 m.

Let height of the lamp post RS.

Angle of depression of the top of a lamp post is 30°

Therefore, ∠TPR = 30°.

again, Angle of depression of the foot of a lamp post is 60°

Therefore, ∠TPS = 60°.

PQ = TS = 12 m.

Let the height of the lamp post RS = h m.

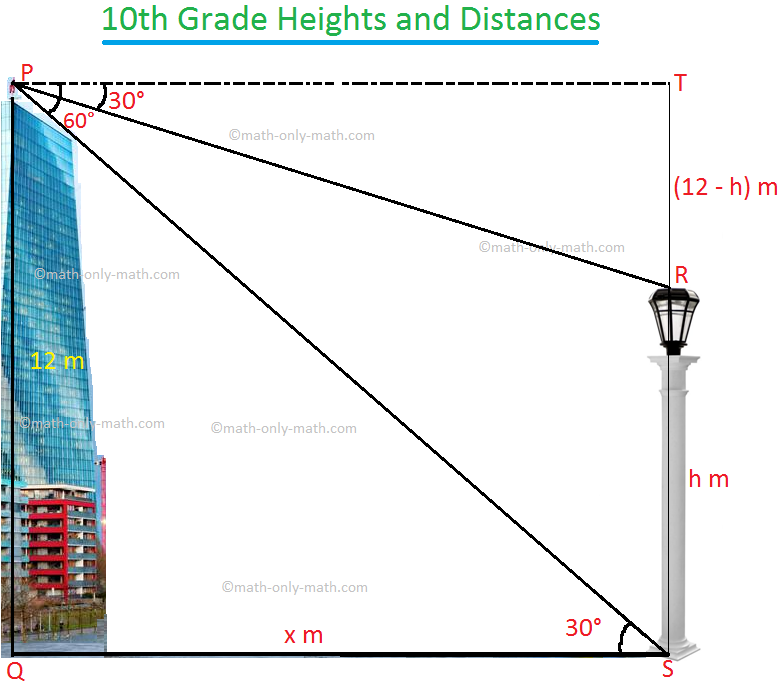
Therefore, 

TR = (12 - h) m.

Also, let PT = x m

Now tan ∠TPR = \(\frac{TR}{PT}\) = tan 30°

Therefore, \(\frac{12 - h}{x}\) = \(\frac{1}{√3}\) ........... (i)

Again, tan ∠TPS = \(\frac{TS}{PT}\) = tan 60°

Therefore, \(\frac{12}{x}\) = √3 ........... (ii)

Dividing (i) by (ii), we get

\(\frac{12 - h}{12}\) = \(\frac{1}{3}\)

⟹ 36 - 3h = 12

⟹ 3h = 36- 12

⟹ h = \(\frac{24}{3}\)

Therefore, height of the lamp post is 8 metres.

• 10th Grade Math

From Angle of Depression to HOME

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Worksheet on Formation of Numbers | Questions on Formation of Numbers

May 20, 24 12:43 PM

Worksheet on Forming Numbers with Digits | Smallest & Greatest Numbers

May 20, 24 02:06 AM

Shifting of Digits in a Number |Exchanging the Digits to Another Place

May 19, 24 06:35 PM

Formation of Greatest and Smallest Numbers | Arranging the Numbers

May 19, 24 03:36 PM

Formation of Numbers with the Given Digits |Making Numbers with Digits

May 19, 24 03:19 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school geometry

Course: high school geometry   >   unit 5.

• Right triangle word problem

Angles of elevation and depression

• Right triangle trigonometry word problems
• Right triangle trigonometry review
• Right triangles and trigonometry FAQ

Practice problem

• (Choice A)   ∠ 1 ‍   A ∠ 1 ‍  
• (Choice B)   ∠ 2 ‍   B ∠ 2 ‍  
• (Choice C)   ∠ 3 ‍   C ∠ 3 ‍  
• (Choice D)   ∠ 4 ‍   D ∠ 4 ‍  

When are these terms useful?

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Helping with Math

Angle of Depression

Introduction

Trigonometry has applications in both mathematics and physics. Applications of trigonometry include calculating height, distances, angles of elevation , and angles of depression.

Let’s say, for instance, that an observer on the roof of a building is looking at a car on the road; from the observer’s point of view, there is an angle of depression generated toward the car. Using trigonometric ratios like sine, cosine, and tangent, the angle of depression helps in the computation of distances.

The angle of depression associated terminologies and calculation process will all be covered in this article.

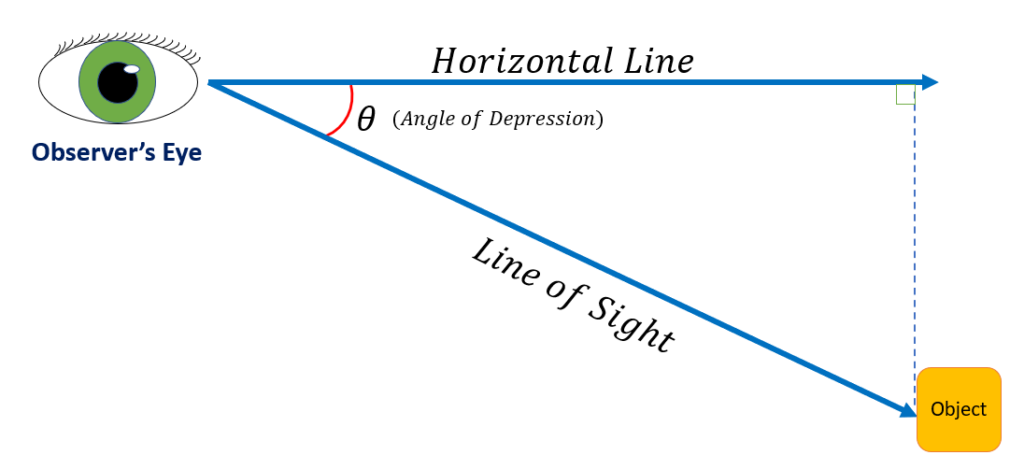
The angle of depression is formed by the line drawn between an object below the observer’s eye and a horizontal line or plane. The line that the observer’s eye is on is called the line of sight. The angle of depression is therefore constructed such that, as the name implies, it is below the observer’s eye.

For instance, as seen in the figure below, an observer focuses on an object. The angle of depression is represented by θ. 

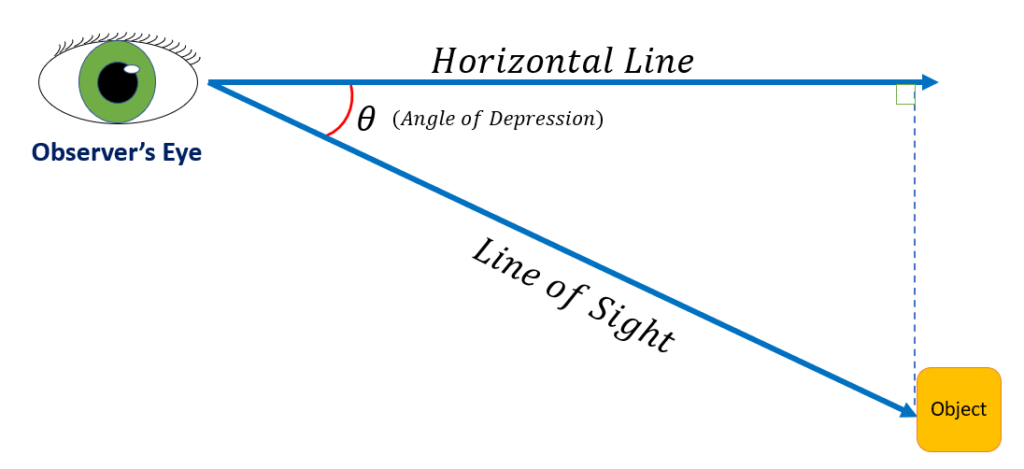
If we join the horizontal line and the object vertically, in this case, we get a right-angle triangle. So, we can calculate the observer’s distance from the object using trigonometry . The height of the object will be viewed as the opposite side of θ of the constructed triangle, and the horizontal line will be considered the adjacent side of the triangle.

Keywords Associated with Angle of Depression

These are the terms we must be familiar with when dealing with the angle of depression.

When two straight rays or lines meet at a single point, an angle is created. Degrees are used to express angles.

Line of Sight

The line of sight is the line drawn from the observer’s eye to the object being viewed. It is an oblique line which is therefore not horizontal nor vertical. The line of sight, together with the horizontal line , forms the angle of depression. 

Horizontal Line

The horizontal line is a straight line on a flat surface. In a coordinate system, a horizontal line has points with the same y-coordinate. The line of sight, together with the horizontal line, forms the angle of depression. 

Observer’s Eye

The observer’s eye is the position where the line of sight and the horizontal line meet.

The Angle of Depression vs. Angle of Elevation

The opposite of an elevation angle is the angle of depression. The object is placed at an angle of elevation above the observer, as opposed to being placed at an angle of depression below the observer. If you are standing and staring at something on a rooftop, you will generate an angle of elevation. However, if you look at the plants on the ground, an angle of depression is created. The heights and distances in both scenarios can be determined using trigonometric concepts.

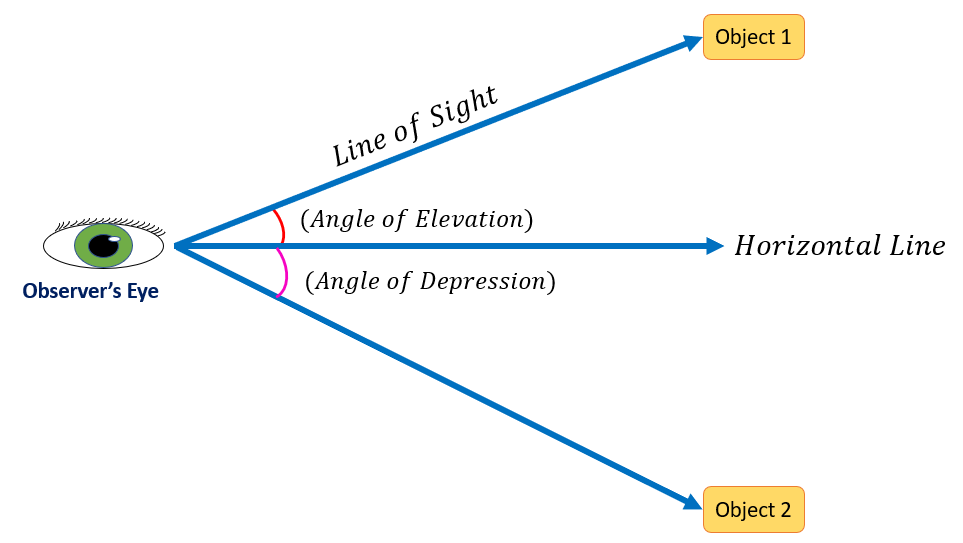
The table below shows the difference between the angle of elevation and depression.

The Angle of Depression Formulas

Some formulas are used to calculate the angle of depression.

Let’s use the illustration below to demonstrate how we apply the formulas. Recall that a right-angle triangle will be constructed if an imaginary vertical line is drawn between the object to the end of the horizontal line. Therefore, we may use the idea of trigonometry to calculate how far the observer is from the object. The position of the object will be viewed as the opposite side of θ, and the horizontal line will be considered the adjacent side of the created triangle .

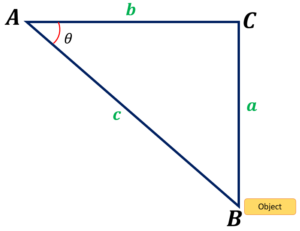
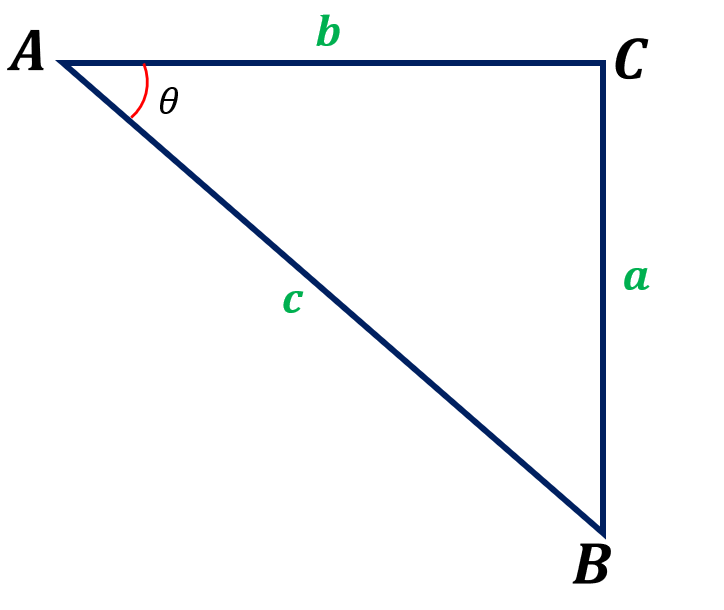
In the figure, side a is the opposite side of , side b is the adjacent side, and side c is the hypotenuse or length of the line of sight.

To determine the angle of depression, we can use the formulas below, provided we know the angles’ two sides. 

If we must calculate the angle of depression given the line of sight and the vertical distance of the object from the horizontal line, we can use the sine formula θ = ($\frac{a}{c}$). 

If we must calculate the angle of depression given the hypotenuse or the line of sight and the adjacent side of , we can use the cosine formula θ = ($\frac{b}{c}$).

If we must calculate the angle of depression given the opposite side of and the adjacent side of , we can use the tangent formula θ = ($\frac{a}{b}$).

For example, in the figure below, we must calculate the length of segment BC.

In the given triangle ABC, ∠A is the angle of depression, side AC is the adjacent side, and side BC is the opposite of the angle θ. Since we know two sides of the triangle, opposite and the adjacent sides of the angle , we must use the formula for the tangent. 

AC ( adjacent side ) = 50 meters

BC ( opposite side ) = 29 meters

Thus, we have,

tan tanθ=$\frac{opposite\: side}{adjacent\: side}$

tan tanθ=$\frac{29\: meters}{50\: meters}$  

tan tanθ=0.58  

Therefore, θ=( 0.58 )

Hence, the value of θ ≈ 30°.

Find the value of the angle of depression ( θ ) in each of the given figures.

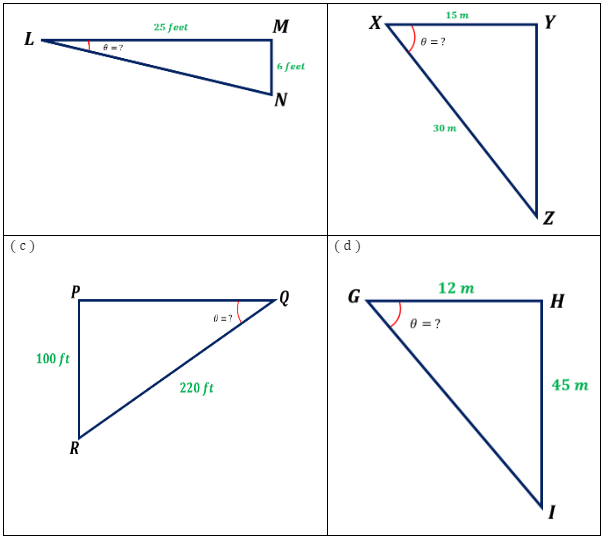
( a ) In the given triangle LMN, ∠L is the angle of depression, side MN is the opposite side, and side LM is the adjacent side of the angle θ. Since we know two sides of the triangle, opposite and the adjacent sides of the angle , we must use the formula for the tangent. 

MN (opposite side ) = 6 ft

LM ( adjacent side ) = 25 ft

tan tanθ=$\frac{6\: ft}{25\: ft}$  

tan tanθ=0.24  

Therefore, θ=( 0.24 )

Hence, the value of θ ≈ 13.50°.

( b ) In the given triangle XYZ, ∠Y is the angle of depression, side XZ is the length of the line of sight or the hypotenuse of the triangle, while side XY is the adjacent side of the angle θ. Since we know the lengths of the hypotenuse and the adjacent side of the angle , we must use the formula for cosine. 

XZ ( hypotenuse side ) = 30 m

XY ( adjacent side ) = 15 m

cos cosθ=$\frac{adjacent\: side}{hypotenuse\: side}$  

cos cosθ=$\frac{15\: m}{30\: m}$  

cos cosθ=0.50

Therefore, θ=( 0.50 )

Hence, the value of θ = 60°.

( c ) In the given triangle PQR, ∠Q is the angle of depression, side QR is the length of the line of sight or the hypotenuse of the triangle, while side PR is the opposite side of the angle θ. Since we know two sides of the triangle, hypotenuse and the opposite side of the angle , we must use the formula for sine. 

QR (hypotenuse side ) = 220 ft

PR ( opposite side ) = 100 ft

sin sinθ=$\frac{opposite\: side}{hypotenuse\: side}$  

sin sinθ=$\frac{100\: ft}{220\: ft}$  

sin sinθ=0.45  

Therefore, θ=( 0.45 )

Hence, the value of θ ≈ 27°.

( d ) In the given triangle GHI, ∠H is the angle of depression, side HI is the opposite side of , while side GH is the adjacent side of the angle θ. Since we know two sides of the triangle, the adjacent and the opposite side of the angle , we must use the formula for the tangent. 

HI ( opposite side ) = 45 m

GH ( adjacent side ) = 12 m

tan tanθ=$\frac{45\: m}{12\: m}$  

tan tanθ≈3.75  

Therefore, θ=( 3.75 )

Hence, the value of θ ≈ 75°.

When looking down from a tower’s top, the angle of depression of a car is at a 30-degree angle. Determine the tower’s height if the car is 150 meters from the building.

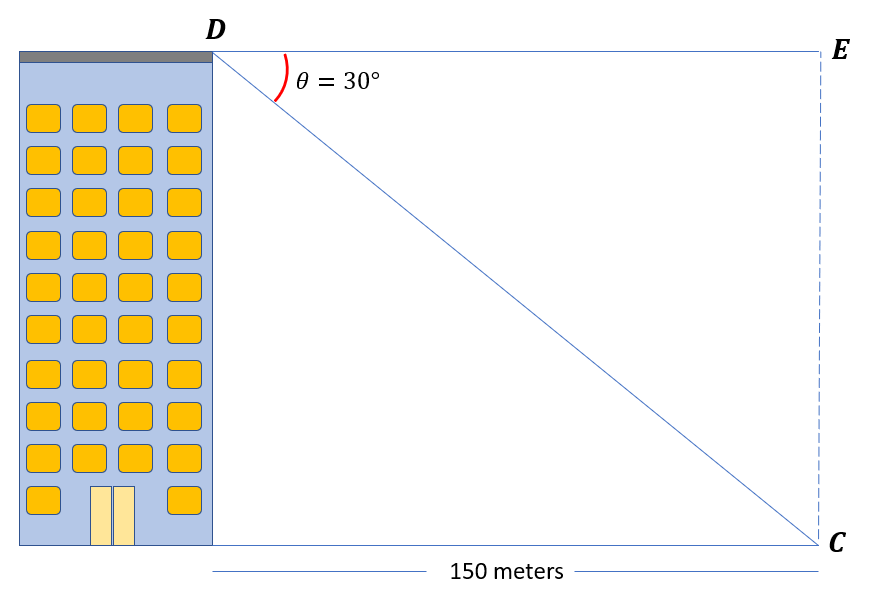
In the figure above, ∠D is the angle of depression that measures 30°, and C is the car. The car’s distance from the tower is the same as the length of the line segment DE. The line segment QC is the line of sight, while line segment CE is the tower’s height. 

The opposite side of angle θ is the height of the tower. Let us use the formula for tangent since the problem involves the triangle’s opposite and adjacent sides. Thus, we have,

tan tan30°=$\frac{height\: of\: the\: tower}{150\: m}$  

tan tan30° ( 150 m ) = height of the tower

86.60 m ≈ height of the tower

height of the tower ≈ 86.60 m

Hence, the height of the tower is approximately 86.60 m.

From a cliff, the angle of depression of a boat is °50. Find the boat’s horizontal distance from the cliff if the line of sight or hypotenuse is 75 feet long, as indicated in the image below.

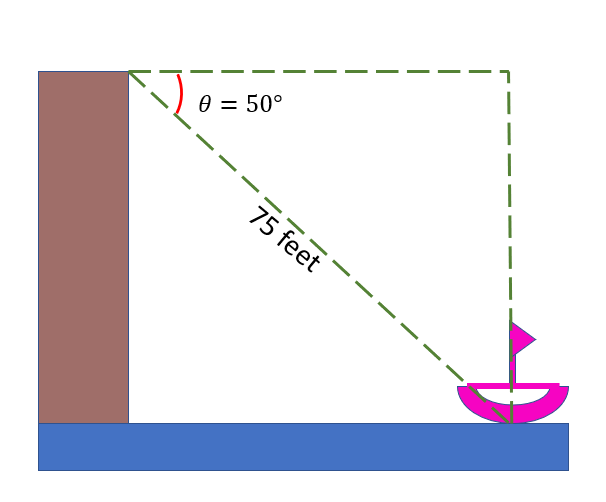
Let us label the vertices of the triangle formed in the given figure. 

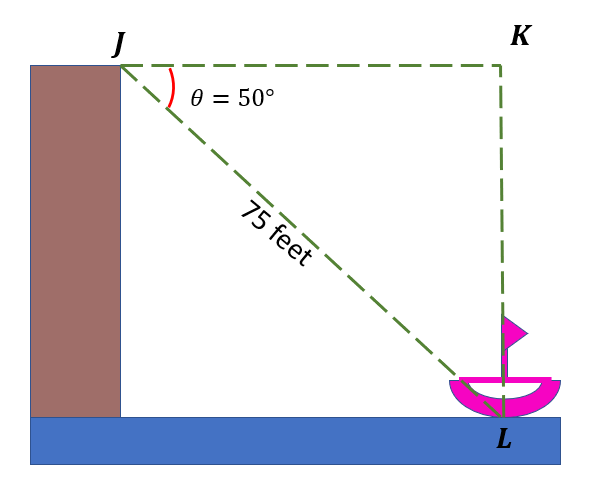
Here, we have ∠J as the angle of depression, and the line segment JL measures 75 feet. Since we must calculate the horizontal distance of the boat from the cliff, it is getting the length of the line segment JK.

We will use the cosine formula since we know and the hypotenuse of the triangle. Hence we have, 

JL ( hypotenuse side ) = 75 feet

cos cosθ=$\frac{adjacent\: side}{hypotenuse\: side}$

cos cos50°=$\frac{adjacent\: side}{75\: feet}$  

cos cos50° ( 75 feet ) = adjacent side

48.21 ≈ adjacent side

Hence, the distance of the boat from the cliff is 48.21 feet.

If we must calculate the angle of depression given the line of sight and the vertical distance of the object from the horizontal line, we can use the sine formula θ = ( $\frac{a}{c}$ ). 

If we must calculate the angle of depression given the hypotenuse or the line of sight and the adjacent side of , we can use the cosine formula θ = ( $\frac{b}{c}$ ).

If we must calculate the angle of depression given the opposite side of and the adjacent side of , we can use the tangent formula θ = ( $\frac{a}{b}$ ).

Frequently Asked Questions on Angle of Depression ( FAQs )

What is meant by the angle of depression, what are the terms associated with the angle of depression.

Angle, line of sight, horizontal line, and the observer’s eye are the terms we must be familiar with when dealing with the angle of depression.

The line of sight is the line drawn from the observer’s eye to the object being viewed. It is an oblique line which is therefore not horizontal nor vertical. The line of sight, together with the horizontal line, forms the angle of depression. 

What distinguishes the angle of elevation from the angle of depression?

How do we calculate the angle of depression.

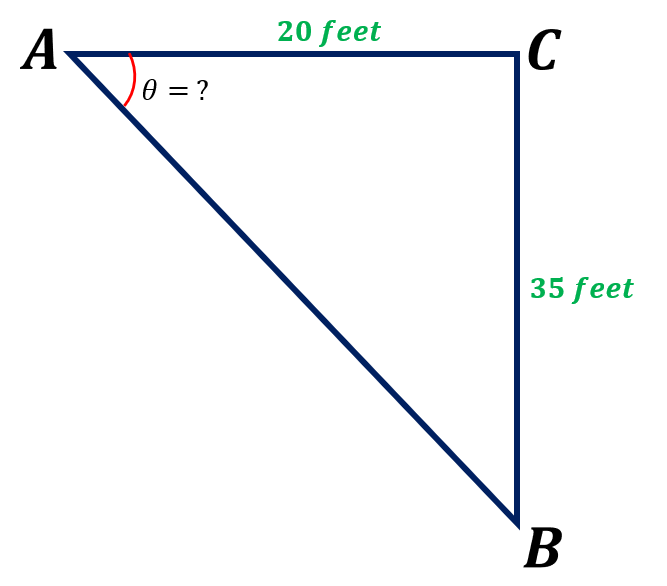
AC ( adjacent side ) = 20 feet

BC ( opposite side ) = 35 feet

tan tanθ=$\frac{35\: feet}{20\: feet}$  

tan tanθ=1.75  

Therefore, θ=( 1.75 )

Hence, the value of θ ≈ 60.26°.

In a right triangle, how do you calculate distance using the angle of depression?

As an illustration, let us use the triangle below with vertices ZBC and θ as the given angle of depression.

Let us say we want to calculate the distance or length of each side, a, b, and c. 

To calculate side a, we will use the cosine formula which involves the adjacent side b and the hypotenuse side c. Hence we have,

cos cosθ=$\frac{adjacent\: side}{hypotenuse}$

cos cosθ=$\frac{b}{c}$

Adjacent side of = ( cos θ ) ( c )

Therefore, the adjacent side is the product of the hypotenuse and cosine θ.

To calculate side b, we will use the sine formula which involves the opposite side a and the hypotenuse side c. Hence we have,

sin sinθ=$\frac{opposite\: side}{hypotenuse}$

sin sinθ=$\frac{a}{c}$

( sin θ ) ( c ) = a 

The opposite side of = ( sin θ ) ( c )

Therefore, the opposite side of θ is the product of the hypotenuse and sine θ.

To calculate side c, we will use the sine or the cosine formula. Hence, we have,

What is the importance of the angle of depression and angle of elevation?

Mathematical and physical uses of trigonometry exist. Calculating height, distance, angles of elevation, and angles of depression are all applications of trigonometry. As a result, it is crucial to learn and comprehend the angle of elevation and depression as they are both used in several applications that entail measurements, especially when precision is crucial.

Recommended Worksheets

Spatial Skills: Angles (Human Rights Day Themed) Math Worksheets Horizontal and Vertical Line (Women’s History Month Themed) Math Worksheets Parallel and Perpendicular Lines (Songkran Festival Themed) Math Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

<a href="https://helpingwithmath.com/angle-of-depression/">Angle of Depression</a>

"Angle of Depression". Helping with Math . Accessed on May 20, 2024. https://helpingwithmath.com/angle-of-depression/.

"Angle of Depression". Helping with Math , https://helpingwithmath.com/angle-of-depression/. Accessed 20 May, 2024.

Additional Geometry Theory:

Latest worksheets.

The worksheets below are the mostly recently added to the site.

Comparing Data Using “Less” and “More” 1st Grade Math Worksheets

Representing Data using Table and Charts 1st Grade Math Worksheets

Solving Word Problems involving Addition and Subtraction of numbers within 120 1st Grade Math Worksheets

Understanding Commutative and Associative Property of Addition 1st Grade Math Worksheets

Determining the Unknown Whole Number in an Addition or Subtraction Equation 1st Grade Math Worksheets

Translation of the Coordinate Plane (School Fair Themed) Math Worksheets

Classifying Shapes by Lines and Angles 4th Grade Math Worksheets

Understanding Number and Shape Patterns 4th Grade Math Worksheets

Prime and Composite Numbers 4th Grade Math Worksheets

Comparing Multi-digit Numbers 4th Grade Math Worksheets

Solved Example Problems | Trigonometry | Mathematics - Problems involving Angle of Depression | 10th Mathematics : UNIT 6 : Trigonometry

Chapter: 10th mathematics : unit 6 : trigonometry.

Problems involving Angle of Depression

In  this section, we try to solve problems when Angles of depression are given. 

Angle of Depression and Angle of Elevation are equal become they are alternative angles. 

Example 6.26

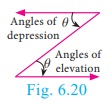
A player sitting on the top of a tower of height 20 m observes the angle of epression of a ball lying on the ground as 60 ° . Find the distance between the foot of the tower and the ball. (√3 = 1.732)

Let BC be the height of the tower and A be the position of the ball lying on the ground. Then,

BC = 20 m and ∠ XCA = 60° = ∠ CAB

Let AB = x metres.

In right triangle ABC ,

tan 60° = BC/AB

Hence, the distance between the foot of the tower and the ball is 11.54 m.

Example 6.27

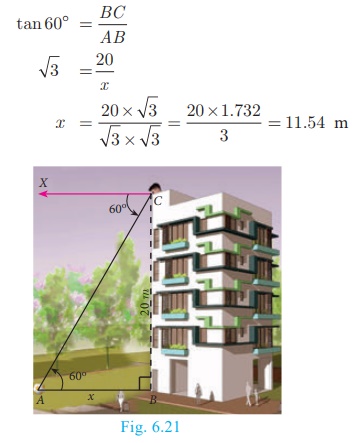
The horizontal distance between two buildings is 140 m. The angle of depression of the top of the first building when seen from the top of the second building is 30 ° . If the height of the first building is 60 m, find the height of the second building. (√3 = 1.732)

The height of the first building AB = 60 m. Now, AB = MD = 60 m Let the height of the second building CD = h . Distance BD = 140 m 

Now, AM = BD = 140 m

From the diagram,

∠ XCA = 30° = ∠ CAM

Now, h = CD = CM + MD = 80.78+60 = 140.78

Therefore the height of the second building is 140.78 m

Example 6.28

From the top of a tower 50 m high, the angles of depression of the top and bottom of a tree are observed to be 30 ° and 45 ° respectively. Find the height of the tree. (√3 = 1.732)

The height of the tower AB = 50 m

Let the height of the tree CD = y and BD = x

From the diagram, ∠ XAC = 30° = ∠ ACM and ∠ XAD = 45° = ∠ ADB

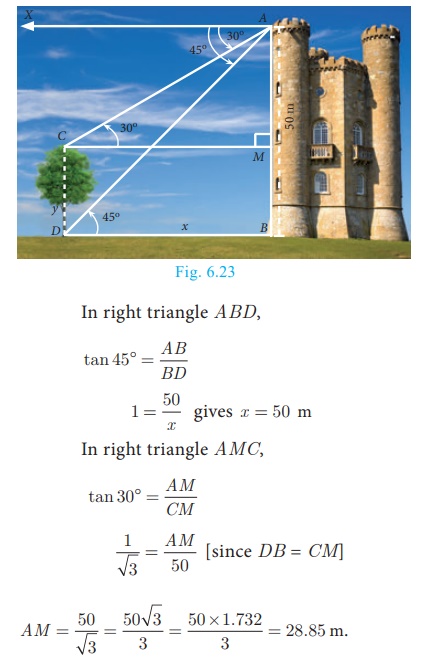
Therefore, height of the tree = CD = MB = AB − AM = 50 −28. 85 = 21. 15 m

Example 6.29

As observed from the top of a 60 m high light house from the sea level, the angles of depression of two ships are 28 ° and 45 ° . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. (tan 28 ° =0.5317)

Let the observer on the lighthouse CD be at D .

Height of the lighthouse CD = 60 m

∠ XDA = 28° = ∠ DAC and

∠ XDB = 45° = ∠ DBC

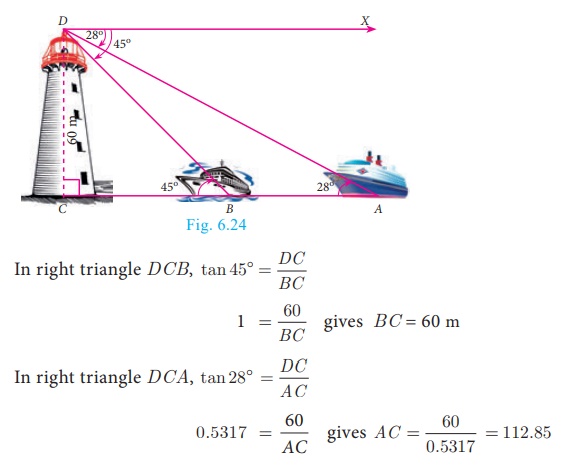
Distance between the two ships AB = AC − BC = 52.85 m

Example 6.30

A man is watching a boat speeding away from the top of a tower. The boat makes an angle of depression of 60° with the man’s eye when at a distance of 200 m from the tower. After 10 seconds, the angle of depression becomes 45°. What is the approximate speed of the boat (in km / hr), assuming that it is sailing in still water? (√3 = 1.732)

Let AB be the tower.

Let C and D be the positions of the boat.

∠ XAC = 60° = ∠ ACB and

∠ XAD = 45° = ∠ ADB , BC = 200 m

In right triangle ABC , tan 60° = AB/BC

gives √3 = AB /200

 we get AB = 200√3 ...(1)

In right triangle ABD , tan 45° = AB/BD

Gives 1 = 200√3 / BD      [by (1) ]

we get, BD = 200√3

Now, CD =  BD − BC

 CD = 200√3 − 200 = − 200(√3 – 1) = 146 4.

It is given that the distance CD is covered in 10 seconds.

That is, the distance of 146.4 m is covered in 10 seconds.

Therefore, speed of the boat = distance / time

= 146.4 / 10  = 14. 64 m/s gives 14. 64 × (3600/1000) km/hr = 52. 704 km/hr

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Angles Of Elevation And Depression

In these lessons, we will study how to find the angles of elevation and depression using trigonometry.

Related Pages Angles Of Elevation And Depression Angles Trigonometry More Geometry Lessons

What Is Angle Of Elevation And Depression?

The angle of elevation is the angle between a horizontal line and the line joining the observer’s eye to some object above the horizontal line.

The angle of depression is the angle between a horizontal line and the line joining the observer’s eye to some object beneath the horizontal line.

In real world situations, we often discuss the angles of elevation and depression. The angles of elevation and depression is used often in word problems, especially those involving a person’s line of sight as they look up at an object.

This video will explain what is the angle of elevation and what is the angle of depression. It will also give some examples of how to use the angles of elevation and angles of depression.

Angle of Elevation/Depression Story Problems

Examples: The angle of elevation from point A to the top of a cliff is 38 degrees. If point A is 80 feet from the base of the cliff, how high is the cliff? Let x be the height of the cliff.

• From the top of the tower, the angle of depression to a stake on the ground is 72 degrees. The top of the tower is 80 feet above the ground. How far is the stake from the foot of the tower?
• A tree 40 feet high casts a shadow 58 feet long. Find the measure of elevation of the sun.
• A ladder leaning against a house makes an angle of 60 degrees with the ground. The foot of the ladder is 7 feet from the foundation of the house. How long is the ladder?
• A balloon on a 40-foot string makes an angle of 50 degrees with the ground. How high above the ground is the balloon if the hand of the person holding the balloon is 6 feet above the ground?

Angles of Elevation and Depression

This video goes through three word problems that require trigonometry to calculate side lengths or angle measures in right triangles.

• A salvage ship uses sonar to determine that the angle of depression to the wreck on the ocean floor is 13.25 degrees. The depth chart shows that the ocean floor is 40 meters below the surface. How far must the diver lowered from the salvage ship walk along the ocean floor to reach the wreck?
• Find the angle of elevation of the sun when a 7.6 m flag pole casts a 18.2 m shadow.
• Olivia is in a lighthouse on a cliff. The top of the cliff is 110 feet above the water and Olivia is in a place in the lighthouse 85 feet above the top of the cliff. She observes two sailboats due east of the lighthouse. The angle of depression to the two boats are 33 degrees and 57 degrees. Find the distance between the two boats.

How to solve application problems using angles of depression and elevation?

• A homeowner is to construct a ramp to his front door to make it wheelchair-accessible. How long is the ramp if the door is 4ft above the ground level and the angle of elevation is 20°
• For a laser light show at an amusement park, the laser beam directed from the top of a 30 ft building is to reflect from an object that is 100 ft away from a point directly below the location of the laser. What is the angle of depression from the laser to the reflecting object?

Angle of Elevation/Angle of Depression Problems

• An observer standing on the top of a vertical cliff spots a house in the adjacent valley at an angle of depression of 12°. The cliff is 60m tall. How far is the house from the base of the cliff?
• Buildings A and B are across the street from each other, 35m apart. From a point on the roof of Building A, the angle of elevation of the roof of Building B is 24°, and the angle of depression of the base of Building B is 34°. How tall is each building?

Angle of elevation part 1

Examples: The passengers on a ship, 3700 m from the base of a 1800 m high cliff are able to see the Byron Bay lighthouse on top of a cliff. Find the angle of elevation from the ship to the top of the cliff.

Angle of elevation part 2

Determining the Angle of Elevation

How to determine the angle of elevation?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Angles of Inclination / Declination

What is an angle of elevation / inclination.

An angle of elevation (also called an angle of inclination) is an angle that goes above the horizontal from whatever is the vantage point. For instance, suppose you are standing on the sidewalk looking up at the top of the chimney on the house across the street.

Content Continues Below

MathHelp.com

Angles of Elevation and Depression

If there were a plank between where you're standing and that chimney's top, walking that plank would involve hiking up an incline. You must elevate your eyes (above the horizontal) to focus on that chimney. The angle above the horizontal that corresponds to your line of sight above the street between you and that house's chimney would be the angle of inclination (also called the angle of elevation).

Advertisement

What is an angle of depression / declination?

An angle of declination (also called the angle of depression) is an angle that goes below the horizontal from whatever is the vantage point. For instance, suppose you are standing on the balcony of your third-floor apartment and are wondering how far down the sidewalk is. The angle between the horizontal (being you looking across the parking lot to your friend on her third-floor deck in the next building over) and the sidewalk would be the angle of depression (also called the angle of declination).

What is the difference between angles of inclination/elevation and angles of declination/depression?

Angles of elevation/inclination are angles above the horizontal; angles of depression/declination are angles below the horizontal.

Whenever you have one of these angles, you should immediately start picturing how a right triangle will fit into the description.

• Driving along a straight flat stretch of Arizona highway, you spot a particularly tall saguaro ("suh-WAHR-oh") cactus right next to a mile marker. Watching your odometer, you pull over exactly two-tenths of a mile down the road. Retrieving your son's theodolite from the trunk, you measure the angle of elevation from your position to the top of the saguaro as 2.4° . Accurate to the nearest foot, how tall is the cactus?

Two-tenths of a mile is 0.2 × 5280  feet = 1056  feet, so this is my horizontal distance. I need to find the height h of the cactus. So I draw a right triangle and label everything I know:

The scale is not important; I'm not bothering to draw the angles or distances accurately. I'm just using the drawing as a placeholder — that is, as a way to keep track of information; the particular size is irrelevant.

What is relevant is that I have "opposite" and "adjacent" and an angle measure. This means I can create and solve an equation using the tangent ratio:

h /1056 = tan(2.4°)

h = 1056 × tan(2.4°) = 44.25951345...

Checking the exercise statement, I am reminded that my unit is feet, and that I'm supposed to round. Then, to the nearest foot, the saguaro is:

44 feet tall

• You were flying a kite from the top of a bluff, but you managed somehow to dump your kite into the lake below. You know that you've given out 325 feet of string. A surveyor on his lunch break wanders over and tells you that the angle of declination from your position to the kite is 15° . How high is the bluff where you and the surveyor are standing? (Round your answer to the nearest whole number.)

First, I draw my triangle:

The horizontal line across the top is the line from which the angle of depression is measured. But by nature of parallel lines, the same angle is in the bottom triangle. I can see the trig ratios more easily in the bottom triangle, and the height is a bit more obvious. So I'll use this part of the drawing.

I have opposite, hypotenuse, and an angle, so I'll use the sine ratio to find the height.

h /325 = sin(15°) h = 325×sin(15°) = 84.11618966...

Checking the exercise statement, I am reminded that my units are feet and that I'm supposed to round. Then the bluff stands above the lake at a height of:

about 84 ft

• A lighthouse stands on a hill 100  m above sea level, as shown in the graphic below. If ∠ACD measures 60° and ∠BCD is 30 °, find the height of the lighthouse, to the nearest whole meter.

The first thing I notice is that, even without rounding, my answer can only be approximate, because lighthouses taper a bit as they go up. So the outer point of the lighthouse's base is not directly below the outer point of the top.

(But this is math, not real life, so it's okay to ignore this and just work from the picture they've given me.)

The second thing I notice is that I'm going to have to work this exercise in steps. I can't find the height of the tower, AB , until I have the length of the base CD . I will move the point D to the right, to meet the continuation downward of the height-line AB , forming a right triangle, as shown in my edited picture below:

Now I have two right triangles: triangle CAD and triangle CBD. I can work with this.

For my first computation to find the length of side CD , I'll use the height of the hill for the length of the opposite side of triangle CBD .

100/|CD| = tan(30°) 100/tan(30°) = |CD| = 173.2050808...

(To minimize round-off error, I'll use all the digits from my calculator in my computations, and try to carry the computations in my calculator the whole way.)

Now that I have the length of the base of triangle CBD (and thus for triangle CAD), I can find the total height of the hill-plus-lighthouse (that is, of the segment |AD|) by using the angle that measures the elevation from sea level to the top of the tower.

h /173.2050808 = tan(60°) h = 173.2050808×tan(60°) = 300

Excellent! By keeping all the digits and carrying the computations in my calculator, I got an exact answer. No rounding! But I do need to subtract, because " 300 " is the height from the water to the top of the tower. The first hundred meters of this total height is hill, so the tower is actually only:

200 meters tall

What are the steps for angles of inclincation/declination?

To sum up, the method for solving inclination/declination exercises is this:

• By definition, an angle of inclination or declination is measured with respect to some horizontal line. Draw that line, and the angle with respect to it.
• By definition, an angle of inclination or declination is relating that angle to the height (or depth) that an object is above (or below) the horizontal. Draw that height line. You should now have a right angle.
• The line-of-sight will be the hypotenuse of the right triangle. Draw this line.
• Solve the right triangle for the required information.

URL: https://www.purplemath.com/modules/incldecl.htm

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Angle of Depression

The "downwards" angle from the horizontal to a line of sight from the observer to some point of interest.

If the angle goes "upwards" it is called an Angle of Elevation.

TRIGONOMETRY WORD PROBLEMS WITH ANGLE OF DEPRESSION

Angle of Depression :

The angle of depression is an angle formed by the line of sight with the horizontal when the point is below the horizontal level. That is, the case when we lower our head to look at the point being viewed.

Problem 1 :

From the top of a rock 50 √ 3 m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock.

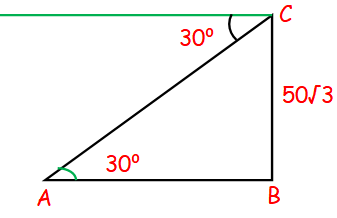
BC = Rock, 

Car in the position A.

tan θ  =  Opposite side / Adjacent side 

tan 30  =  BC/AB

1/ √ 3  =  50 √ 3/AB

AB  =  50 √ 3( √ 3)

AB  =  50(3)

AB  =  150 m

The distance of the car from the rock is 150 m.

Problem 2 :

The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building.

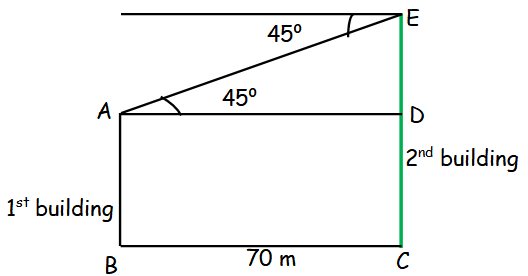
CE  =  120 m

BC   =  DC  =  70 m

In triangle ADE,

tan 45  =  DE/AD

1  =  (120 - x)/70

70  =  120 - x

x  =  120 - 70

x  =  50 m

So, the height of the 1 st building is 50 m

Problem 3 :

From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post. (tan 38° = 0.7813,  √ 3 = 1.732)

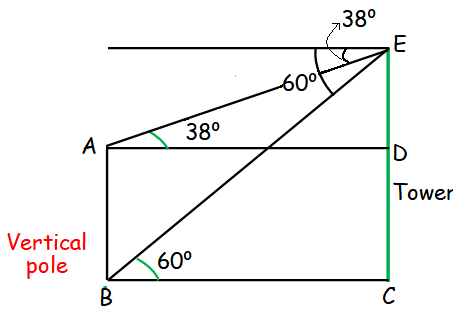
Height of tower  =  60 m

Let DC = x, ED  =  60 - x

tan 38  =  DE/AD

0.7813  =  (60 - x)/AD

AD  =  (60 - x)/ 0.7813 ---(1)

In triangle BEC,

tan 60  =  EC/BC

√3  =  60/BC

BC  =  60/√3 

BC  =  20√3 ------(2)

(1)  =  (2)

(60 - x)/0.7813  =  20√3

60 - x  =  20(0.7813)(1.732)

60 - x  =  34.64(0.7813)

60 - x  =  27.06

x  =  60 - 27.06

x  =  32.94

So, the height of the vertical lamp post is 32.94 m

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM