solving problems on force

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• TaskTracker
• Other Tools
• Algebra Based Physics
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Mechanics: Vectors and Forces in Two-Dimensions

Calculator pad, version 2, vectors and forces in 2-d: problem set.

For each collection of listed forces, determine the vector sum or the net force.

• Audio Guided Solution
• Show Answer

Hector is walking his dog (Fido) around the neighborhood. Upon arriving at Fidella's house (a friend of Fido's), Fido turns part mule and refuses to continue on the walk. Hector yanks on the chain with a 67.0 N force at an angle of 30.0° above the horizontal. Determine the horizontal and vertical components of the tension force.

Helen is parasailing. She sits in a seat harness which is attached by a tow rope to a speedboat. The rope makes an angle of 51° with the horizontal and has a tension of 350 N. Determine the horizontal and vertical components of the tension force.

At one moment during a walk around the block, there are four forces exerted upon Fido - a 10.0 kg dog. The forces are:

F app = 67.0 N at 30.0° above the horizontal (rightward and upward) F norm = 64.5 N, up F frict = 27.6 N, left F grav = 98 N, down

Resolve the applied force (F app ) into horizontal and vertical components, then add the forces up as vectors to determine the net force.

Jerome and Michael, linebackers for South’s varsity football team, delivered a big hit to the halfback in last weekend’s game. Striking the halfback simultaneously from different directions with the following forces:

F Jerome = 1230 N at 53° F Michael = 1450 at 107°

Determine the resultant force applied by Jerome and Michael to the halfback. (The directions of the two forces are stated as counter-clockwise angles of rotation with East.)

A pack of three Artic wolves are fighting over the carcass of a dead polar bear. A top view of the magnitude and direction of the three forces is shown in the diagram to the right.

a. Determine the resultant or net force acting upon the carcass. b. Determine the acceleration of the 750-kg polar bear carcass.

Lee Mealone is sledding with his friends. Disgruntled by a coarse comment, he decides to separate from the group. He momentarily exerts a 31 N force on the rope which is attached to his 2.5-kg sled. The rope makes an angle of 22° with the nearly frictionless surface. Use the structure provided below to determine the net force on and acceleration of the sled.

Renee is on Spring Break and pulling her 21-kg suitcase through the airport at a constant speed of 0.47 m/s. She pulls on the strap with 120 N of force at an angle of 38° above the horizontal. Determine the normal force and the total resistance force (friction and air resistance) experienced by the suitcase.

Ben Laborin works for the South bookstore during the summer months to help prepare for Fall sales. Books from one supplier are shipped to the school in large crates equipped with rope handles on all sides. On one occasion, Ben momentarily pulled with a force of 692 N at an angle of 36.0° above the horizontal to accelerate a 112-kg crate of books. The coefficient of friction between the crates and the vinyl floor is 0.548. Determine the acceleration experienced by the crate. (Suggestion: Begin with a free body diagram.)

Problem 10:

A fire breaks out on a high rise building and a rescue helicopter is called to the scene. The helicopter is equipped with a rescue basket attached by a strong cable to a winch on the helicopter. The rescue basket is lowered to the roof and some occupants of the top floor escape to the roof and enter the basket. As the helicopter takes off, the cable momentarily makes a 78.2° angle to the horizontal, imparting a slight horizontal acceleration to the 621-kg basket and occupants across the roof top. The coefficient of friction between the basket and the roof top is 0.568 and the tension in the cable is 4980 N. Determine the acceleration of the basket and occupants. (Suggestion: Begin with a free body diagram.)

Problem 11:

The custodians clean the field house gym floor between games at the annual Holiday Basketball Classic. Chuck exerts a force on a 1.1-kg push broom as he walks across the floor at a constant speed. The coefficient of friction between the floor and the broom is 0.45 and the broom handle makes an angle of 41° with the horizontal. Determine the amount of force with which Chuck pushes downward (along the handle of the broom) in order to achieve this constant speed motion. (Suggestion: Begin with a free body diagram.)

Problem 12:

Lon Mauer is cleaning up the driveway after mowing the grass. He exerts a sudden downward force of 56.8 N at a constant angle of 54.7° below the horizontal in order to accelerate his 1.05-kg broom from rest. The coefficient of friction between the broom bristles and the driveway is 0.567. Determine the rate of acceleration of the broom. (Suggestion: Begin with a free body diagram.)

Problem 13:

South still displays with great pride the large sign boasting of their 1996 State Championship Girl’s Basketball Team. The 43.1-kg sign hangs from two cables which make an angle of 34.5° with the horizontal. Determine the tension in each of the cables.

Problem 14:

A massive light hangs over the table in Jeremy's dining room. The light is supported by four strong chains which make an angle of 75.0° with the horizontal. The force in each chain is 35.8 N.

a. Determine the force with which a single chain pulls horizontally and vertically upon the light. b. Determine the mass of the light.

Problem 15:

Troy Ginometri, owner of the local floral shop, displays the sale of the month in the front window of his shop. The 5.6-kg flower pot is suspended by three chains from the ceiling. The chains make an angle of 25° with the vertical. Determine the tension in one of the chains.

Problem 16:

The historic Stanley Center for the Arts in Utica, New York is the proud owner of the world’s largest LED chandelier. The chandelier is 35 feet wide, 17 feet tall and has a mass of 2900 kg. It is directly supported by four cables which make an angle of 63° with the horizontal. Determine the tension in the cables.

Problem 17:

Xavier went rock climbing this past weekend. During one climb through a narrow vertical chimney, he supported his weight by leaning with his back against one wall of the chimney and pushing off the opposite wall with his legs. His left leg made a 26° angle with the horizontal. The coefficient of frcition between his back and the chimney wall is 0.508. Determine the minimum amount of tension which would be required to support the weight of his 86-kg body.

a. Determine the tension in his left leg. b. Determine the normal force of the chimney wall pushing upon his back.

Problem 18:

Charles Blondin is famous for having crossed the Niagra Falls on an 1100-foot long tight-rope at a height of 160 feet above the gorge. He accomplished the feet several times in a variety of ways – blindfolded, in a sack, carrying his manager on his shoulders, pushing a wheelbarrow and walking on stilts. Suppose the 65-kg Blondin is at the midpoint of the tight-rope and has stopped to cook and eat an omelet. If the tightrope makes an angle of 5° with the horizontal, determine the tension in the rope.

Problem 19:

Mom and Dad have tied a rope to Matthew’s sled and are momentarily pulling him through the snow. Dad is pulling with force A and Mom with force B.

A: 54 N at 65° north of east B: 130 N at 22° south of east

a. Determine the resultant force of A and B. b. Determine the acceleration that these momentary forces would create for a 39-kg sled and child (assuming negligible friction).

Problem 20:

A local automobile dealership has chosen to hang a car outside the entry to their showroom. The car has been modified so that its mass is 645 kg. The car's weight will be supported by a heavy-duty chain which pulls upwards and leftwards. A beam will push outward to balance the wallward pull of the chain. The manufacturer of the chain claims it has a breaking strength of 17400 Newtons. Village code requires that there be a safety factor of 2.20. That is, the actual tension in the chain must be no more than 1/2.20 of the breaking strength. What is the minimum angle (between the chain and the horizontal ) at which the dealership can hang the car?

Problem 21:

Lab partners Anna Litical and Noah Formula placed a 0.500-kg glider on their air track and inclined the track at 15.0° above the horizontal. Determine the net force and acceleration of the glider along the frictionless track. Use the structure provided with the free body diagram shown below.

Problem 22:

Anna Litical and Noah Formula now place a 1.38-kg brick on a wooden board and incline the board at 24.0° above the horizontal. The coefficient of friction between the brick and the board is 0. 328. Determine the net force and the acceleration of the brick. Use the structure provided with the free body diagram shown below.

Problem 23:

Ben Laborin exerts a force on an 86-kg crate of books to push it up the ramp of the loading dock at a constant speed of 24 cm/s. The ramp makes an angle of 12° with the horizontal. The coefficient of friction between the crate and the ramp is 0.74. Assuming that Ben is pushing parallel to the inclined plane, determine the force with which he is pushing. (Suggestion: Begin with a free body diagram.)

Problem 24:

The infamous Lombard Street in San Francisco has an abnormally steep block which consists of several tight hairpin turns. On average, the roadway on this block of the street is inclined at 16°. Determine the force which would be required to pull a 23-kg wagon and child up the hill at constant speed. Assume the force is exerted parallel to the road and that friction is negligible.

Problem 25:

In an effort to determine the coefficient of friction between a wood block and a metal track, Anna Litical and Noah Formula place the block on the track and slowly elevate one of its ends until the block finally budges from rest and slides down the incline. Anna and Noah repeat several trials and determine that the block accelerates from its rest position when the track makes an angle of 38° above the horizontal. Use this angle value to determine the coefficient of friction. (Suggestion: Begin with a free body diagram.)

Problem 26:

The Splash Mountain flume ride at Walt Disney World's Magic Kingdom in Orlando, Florida boasts one of the steepest flume rides in the world. The boats plunge 52 feet down a 43-degree incline near the final stage of the ride. Assuming a coefficient of friction of 0.12, determine the acceleration of the boat and riders. (Suggestion: Begin with a free body diagram.)

Problem 27:

Ethan recently found out that the sledding hill on the west side of Lake Bluebird is more of a shredding hill than a sledding hill. He boarded his 60-inch sled and descended the steepest section near the tall trees. Before his ride ended at the location of a tree stump buried a few inches below the snow, he was accelerating at 2.5 m/s/s down the 19° incline. Determine the coefficient of friction between the sled and the snow. (Suggestion: Begin with a free body diagram.)

Return to Overview

View Audio Guided Solution for Problem:

Physics Problems with Solutions

Forces in physics, tutorials and problems with solutions.

Free tutorials on forces with questions and problems with detailed solutions and examples. The concepts of forces, friction forces, action and reaction forces, free body diagrams, tension of string, inclined planes, etc. are discussed and through examples, questions with solutions and clear and self explanatory diagrams. Questions to practice for the SAT Physics test on forces are also included with their detailed solutions. The discussions of applications of forces engineering system are also included.

Forces: Tutorials with Examples and Detailed Solutions

• Forces in Physics .
• Components of a Force in a System of Coordinates .
• Free Body Diagrams, Tutorials with Examples and Explanations .
• Forces of Friction .
• Addition of Forces .
• What is the Tension of a String or rope? .
• Newton's Laws in Physics .
• Hooke's Law, Examples with solutions .

Problems on Forces with Detailed Solutions

• Inclined Planes Problems in Physics with Solutions .
• Tension, String, Forces Problems with Solutions .

SAT Questions on Forces with Solutions

• Physics Practice Questions with Solutions on Forces and Newton's Laws .

Formulas and Constants

• Physics Formulas Reference
• SI Prefixes Used with Units in Physics, Chemistry and Engineering
• Constants in Physics, Chemistry and Engineering

Popular Pages

• Privacy Policy

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

High School Physics : Calculating Force

Study concepts, example questions & explanations for high school physics, all high school physics resources, example questions, example question #1 : net force.

Plug these into the equation to solve for acceleration.

Example Question #2 : Calculating Force

Plug in the values given to us and solve for the force.

Example Question #1 : Calculating Force

Plug in the given values to solve for the mass.

(Assume the only two forces acting on the object are friction and Derek).

Plug in the information we've been given so far to find the force of friction.

Friction will be negative because it acts in the direction opposite to the force of Derek.

Newton's third law states that when one object exerts a force on a second object, the second object exerts a force equal in size, but opposite in direction to the first. That means that the force of the hammer on the nail and the nail on the hammer will be equal in size, but opposite in direction.

Example Question #6 : Calculating Force

We can find the net force by adding the individual force together.

Example Question #7 : Calculating Force

If the object has a constant velocity, that means that the net acceleration must be zero.

In conjunction with Newton's second law, we can see that the net force is also zero. If there is no net acceleration, then there is no net force.

Since Franklin is lifting the weight vertically, that means there will be two force acting upon the weight: his lifting force and gravity. The net force will be equal to the sum of the forces acting on the weight.

We know the mass of the weight and we know the acceleration, so we can solve for the lifting force.

We are given the mass, but we will need to calculate the acceleration to use in the formula.

Plug in our given values and solve for acceleration.

Now we know both the acceleration and the mass, allowing us to solve for the force.

Example Question #9 : Calculating Force

We can calculate the gravitational force using the mass.

Example Question #10 : Calculating Force

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

6.1 Solving Problems with Newton’s Laws

Learning objectives.

By the end of this section, you will be able to:

• Apply problem-solving techniques to solve for quantities in more complex systems of forces
• Use concepts from kinematics to solve problems using Newton’s laws of motion
• Solve more complex equilibrium problems
• Solve more complex acceleration problems
• Apply calculus to more advanced dynamics problems

Success in problem solving is necessary to understand and apply physical principles. We developed a pattern of analyzing and setting up the solutions to problems involving Newton’s laws in Newton’s Laws of Motion ; in this chapter, we continue to discuss these strategies and apply a step-by-step process.

Problem-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, but we emphasize specific strategies that are useful in applying Newton’s laws of motion . Once you identify the physical principles involved in the problem and determine that they include Newton’s laws of motion, you can apply these steps to find a solution. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy

Applying newton’s laws of motion.

• Identify the physical principles involved by listing the givens and the quantities to be calculated.
• Sketch the situation, using arrows to represent all forces.
• Determine the system of interest. The result is a free-body diagram that is essential to solving the problem.
• Apply Newton’s second law to solve the problem. If necessary, apply appropriate kinematic equations from the chapter on motion along a straight line.
• Check the solution to see whether it is reasonable.

Let’s apply this problem-solving strategy to the challenge of lifting a grand piano into a second-story apartment. Once we have determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation. Such a sketch is shown in Figure 6.2 (a). Then, as in Figure 6.2 (b), we can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

As with most problems, we next need to identify what needs to be determined and what is known or can be inferred from the problem as stated, that is, make a list of knowns and unknowns. It is particularly crucial to identify the system of interest, since Newton’s second law involves only external forces. We can then determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure 6.2 (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton’s Laws of Motion , the system of interest depends on the question we need to answer. Only forces are shown in free-body diagrams, not acceleration or velocity. We have drawn several free-body diagrams in previous worked examples. Figure 6.2 (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is drawn, we apply Newton’s second law. This is done in Figure 6.2 (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. We do this by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known. Generally, just write Newton’s second law in components along the different directions. Then, you have the following equations:

(If, for example, the system is accelerating horizontally, then you can then set a y = 0 . a y = 0 . ) We need this information to determine unknown forces acting on a system.

As always, we must check the solution. In some cases, it is easy to tell whether the solution is reasonable. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an answer is reasonable. Another way to check a solution is to check the units. If we are solving for force and end up with units of millimeters per second, then we have made a mistake.

There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills. We look first at problems involving particle equilibrium, which make use of Newton’s first law, and then consider particle acceleration, which involves Newton’s second law.

Particle Equilibrium

Recall that a particle in equilibrium is one for which the external forces are balanced. Static equilibrium involves objects at rest, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these conditions are relative. For example, an object may be at rest when viewed from our frame of reference, but the same object would appear to be in motion when viewed by someone moving at a constant velocity. We now make use of the knowledge attained in Newton’s Laws of Motion , regarding the different types of forces and the use of free-body diagrams, to solve additional problems in particle equilibrium .

Example 6.1

Different tensions at different angles.

Thus, as you might expect,

This gives us the following relationship:

Note that T 1 T 1 and T 2 T 2 are not equal in this case because the angles on either side are not equal. It is reasonable that T 2 T 2 ends up being greater than T 1 T 1 because it is exerted more vertically than T 1 . T 1 .

Now consider the force components along the vertical or y -axis:

This implies

Substituting the expressions for the vertical components gives

There are two unknowns in this equation, but substituting the expression for T 2 T 2 in terms of T 1 T 1 reduces this to one equation with one unknown:

which yields

Solving this last equation gives the magnitude of T 1 T 1 to be

Finally, we find the magnitude of T 2 T 2 by using the relationship between them, T 2 = 1.225 T 1 T 2 = 1.225 T 1 , found above. Thus we obtain

Significance

Particle acceleration.

We have given a variety of examples of particles in equilibrium. We now turn our attention to particle acceleration problems, which are the result of a nonzero net force. Refer again to the steps given at the beginning of this section, and notice how they are applied to the following examples.

Example 6.2

Drag force on a barge.

The drag of the water F → D F → D is in the direction opposite to the direction of motion of the boat; this force thus works against F → app , F → app , as shown in the free-body diagram in Figure 6.4 (b). The system of interest here is the barge, since the forces on it are given as well as its acceleration. Because the applied forces are perpendicular, the x - and y -axes are in the same direction as F → 1 F → 1 and F → 2 . F → 2 . The problem quickly becomes a one-dimensional problem along the direction of F → app F → app , since friction is in the direction opposite to F → app . F → app . Our strategy is to find the magnitude and direction of the net applied force F → app F → app and then apply Newton’s second law to solve for the drag force F → D . F → D .

The angle is given by

From Newton’s first law, we know this is the same direction as the acceleration. We also know that F → D F → D is in the opposite direction of F → app , F → app , since it acts to slow down the acceleration. Therefore, the net external force is in the same direction as F → app , F → app , but its magnitude is slightly less than F → app . F → app . The problem is now one-dimensional. From the free-body diagram, we can see that

However, Newton’s second law states that

This can be solved for the magnitude of the drag force of the water F D F D in terms of known quantities:

Substituting known values gives

The direction of F → D F → D has already been determined to be in the direction opposite to F → app , F → app , or at an angle of 53 ° 53 ° south of west.

In Newton’s Laws of Motion , we discussed the normal force , which is a contact force that acts normal to the surface so that an object does not have an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride? Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed? Take a guess before reading the next example.

Example 6.3

What does the bathroom scale read in an elevator.

From the free-body diagram, we see that F → net = F → s − w → , F → net = F → s − w → , so we have

Solving for F s F s gives us an equation with only one unknown:

or, because w = m g , w = m g , simply

No assumptions were made about the acceleration, so this solution should be valid for a variety of accelerations in addition to those in this situation. ( Note: We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton’s second law becomes F s − w = − m a . F s − w = − m a . )

• We have a = 1.20 m/s 2 , a = 1.20 m/s 2 , so that F s = ( 75.0 kg ) ( 9.80 m/s 2 ) + ( 75.0 kg ) ( 1.20 m/s 2 ) F s = ( 75.0 kg ) ( 9.80 m/s 2 ) + ( 75.0 kg ) ( 1.20 m/s 2 ) yielding F s = 825 N . F s = 825 N .
• Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more than his weight? For any constant velocity—up, down, or stationary—acceleration is zero because a = Δ v Δ t a = Δ v Δ t and Δ v = 0 . Δ v = 0 . Thus, F s = m a + m g = 0 + m g F s = m a + m g = 0 + m g or F s = ( 75.0 kg ) ( 9.80 m/s 2 ) , F s = ( 75.0 kg ) ( 9.80 m/s 2 ) , which gives F s = 735 N . F s = 735 N .

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In Figure 6.5 (b), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

Check Your Understanding 6.1

Now calculate the scale reading when the elevator accelerates downward at a rate of 1.20 m/s 2 . 1.20 m/s 2 .

The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person’s weight. If the elevator is in free fall and accelerating downward at g , then the scale reading is zero and the person appears to be weightless.

Example 6.4

Two attached blocks.

For block 1: T → + w → 1 + N → = m 1 a → 1 T → + w → 1 + N → = m 1 a → 1

For block 2: T → + w → 2 = m 2 a → 2 . T → + w → 2 = m 2 a → 2 .

Notice that T → T → is the same for both blocks. Since the string and the pulley have negligible mass, and since there is no friction in the pulley, the tension is the same throughout the string. We can now write component equations for each block. All forces are either horizontal or vertical, so we can use the same horizontal/vertical coordinate system for both objects

When block 1 moves to the right, block 2 travels an equal distance downward; thus, a 1 x = − a 2 y . a 1 x = − a 2 y . Writing the common acceleration of the blocks as a = a 1 x = − a 2 y , a = a 1 x = − a 2 y , we now have

From these two equations, we can express a and T in terms of the masses m 1 and m 2 , and g : m 1 and m 2 , and g :

Check Your Understanding 6.2

Calculate the acceleration of the system, and the tension in the string, when the masses are m 1 = 5.00 kg m 1 = 5.00 kg and m 2 = 3.00 kg . m 2 = 3.00 kg .

Example 6.5

Atwood machine.

• We have For m 1 , ∑ F y = T − m 1 g = m 1 a . For m 2 , ∑ F y = T − m 2 g = − m 2 a . For m 1 , ∑ F y = T − m 1 g = m 1 a . For m 2 , ∑ F y = T − m 2 g = − m 2 a . (The negative sign in front of m 2 a m 2 a indicates that m 2 m 2 accelerates downward; both blocks accelerate at the same rate, but in opposite directions.) Solve the two equations simultaneously (subtract them) and the result is ( m 2 − m 1 ) g = ( m 1 + m 2 ) a . ( m 2 − m 1 ) g = ( m 1 + m 2 ) a . Solving for a : a = m 2 − m 1 m 1 + m 2 g = 4 kg − 2 kg 4 kg + 2 kg ( 9.8 m/s 2 ) = 3.27 m/s 2 . a = m 2 − m 1 m 1 + m 2 g = 4 kg − 2 kg 4 kg + 2 kg ( 9.8 m/s 2 ) = 3.27 m/s 2 .
• Observing the first block, we see that T − m 1 g = m 1 a T = m 1 ( g + a ) = ( 2 kg ) ( 9.8 m/s 2 + 3.27 m/s 2 ) = 26.1 N . T − m 1 g = m 1 a T = m 1 ( g + a ) = ( 2 kg ) ( 9.8 m/s 2 + 3.27 m/s 2 ) = 26.1 N .

Check Your Understanding 6.3

Determine a general formula in terms of m 1 , m 2 m 1 , m 2 and g for calculating the tension in the string for the Atwood machine shown above.

Newton’s Laws of Motion and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics , and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, acceleration, velocity, and/or position, listing the givens and the quantities to be calculated will allow you to identify the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the problem-solving strategy given earlier in this chapter, as well as strategies presented in other chapters, is applied to an integrated concept problem.

Example 6.6

What force must a soccer player exert to reach top speed.

• We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is Δ v = 8.00 m/s Δ v = 8.00 m/s . We are given the elapsed time, so Δ t = 2.50 s . Δ t = 2.50 s . The unknown is acceleration, which can be found from its definition: a = Δ v Δ t . a = Δ v Δ t . Substituting the known values yields a = 8.00 m/s 2.50 s = 3.20 m/s 2 . a = 8.00 m/s 2.50 s = 3.20 m/s 2 .
• Here we are asked to find the average force the ground exerts on the runner to produce this acceleration. (Remember that we are dealing with the force or forces acting on the object of interest.) This is the reaction force to that exerted by the player backward against the ground, by Newton’s third law. Neglecting air resistance, this would be equal in magnitude to the net external force on the player, since this force causes her acceleration. Since we now know the player’s acceleration and are given her mass, we can use Newton’s second law to find the force exerted. That is, F net = m a . F net = m a . Substituting the known values of m and a gives F net = ( 70.0 kg ) ( 3.20 m/s 2 ) = 224 N . F net = ( 70.0 kg ) ( 3.20 m/s 2 ) = 224 N .

This is a reasonable result: The acceleration is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

Check Your Understanding 6.4

The soccer player stops after completing the play described above, but now notices that the ball is in position to be stolen. If she now experiences a force of 126 N to attempt to steal the ball, which is 2.00 m away from her, how long will it take her to get to the ball?

Example 6.7

What force acts on a model helicopter.

The magnitude of the force is now easily found:

Check Your Understanding 6.5

Find the direction of the resultant for the 1.50-kg model helicopter.

Example 6.8

Baggage tractor.

• ∑ F x = m system a x ∑ F x = m system a x and ∑ F x = 820.0 t , ∑ F x = 820.0 t , so 820.0 t = ( 650.0 + 250.0 + 150.0 ) a a = 0.7809 t . 820.0 t = ( 650.0 + 250.0 + 150.0 ) a a = 0.7809 t . Since acceleration is a function of time, we can determine the velocity of the tractor by using a = d v d t a = d v d t with the initial condition that v 0 = 0 v 0 = 0 at t = 0 . t = 0 . We integrate from t = 0 t = 0 to t = 3 : t = 3 : d v = a d t , ∫ 0 3 d v = ∫ 0 3.00 a d t = ∫ 0 3.00 0.7809 t d t , v = 0.3905 t 2 ] 0 3.00 = 3.51 m/s . d v = a d t , ∫ 0 3 d v = ∫ 0 3.00 a d t = ∫ 0 3.00 0.7809 t d t , v = 0.3905 t 2 ] 0 3.00 = 3.51 m/s .
• Refer to the free-body diagram in Figure 6.8 (b). ∑ F x = m tractor a x 820.0 t − T = m tractor ( 0.7805 ) t ( 820.0 ) ( 3.00 ) − T = ( 650.0 ) ( 0.7805 ) ( 3.00 ) T = 938 N . ∑ F x = m tractor a x 820.0 t − T = m tractor ( 0.7805 ) t ( 820.0 ) ( 3.00 ) − T = ( 650.0 ) ( 0.7805 ) ( 3.00 ) T = 938 N .

Recall that v = d s d t v = d s d t and a = d v d t a = d v d t . If acceleration is a function of time, we can use the calculus forms developed in Motion Along a Straight Line , as shown in this example. However, sometimes acceleration is a function of displacement. In this case, we can derive an important result from these calculus relations. Solving for dt in each, we have d t = d s v d t = d s v and d t = d v a . d t = d v a . Now, equating these expressions, we have d s v = d v a . d s v = d v a . We can rearrange this to obtain a d s = v d v . a d s = v d v .

Example 6.9

Motion of a projectile fired vertically.

The acceleration depends on v and is therefore variable. Since a = f ( v ) , a = f ( v ) , we can relate a to v using the rearrangement described above,

We replace ds with dy because we are dealing with the vertical direction,

We now separate the variables ( v ’s and dv ’s on one side; dy on the other):

Thus, h = 114 m . h = 114 m .

Check Your Understanding 6.6

If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

Interactive

Explore the forces at work in this simulation when you try to push a filing cabinet. Create an applied force and see the resulting frictional force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/6-1-solving-problems-with-newtons-laws

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

About me and why I created this physics website.

Force Problems

• Search Website

Real World Applications — for high school level and above

• Amusement Parks
• Battle & Weapons
• Engineering
• Miscellaneous

Education & Theory — for high school level and above

• Useful Formulas
• Physics Questions
• Example Mechanics Problems
• Learn Physics Compendium

Kids Section

• Physics For Kids
• Science Experiments
• Science Fair Ideas
• Science Quiz
• Science Toys
• Teacher Resources
• Commercial Disclosure
• Privacy Policy

© Copyright 2009-2024 real-world-physics-problems.com

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 3: Forces and Newton's laws of motion

About this unit.

This unit is part of the Physics library. Browse videos, articles, and exercises by topic.

Newton's laws of motion

• Newton's first law of motion introduction (Opens a modal)
• Newton's first law of motion (Opens a modal)
• Applying Newton's first law of motion (Opens a modal)
• What is Newton's first law? (Opens a modal)
• Newton's second law of motion (Opens a modal)
• More on Newton's second law (Opens a modal)
• What is Newton's second law? (Opens a modal)
• Newton's third law of motion (Opens a modal)
• More on Newton's third law (Opens a modal)
• What is Newton's third law? (Opens a modal)
• Newton's first law Get 5 of 7 questions to level up!
• Newton's third law of motion Get 5 of 7 questions to level up!
• All of Newton's laws of motion Get 5 of 7 questions to level up!

Normal force and contact force

• Normal force and contact force (Opens a modal)
• What is weight? (Opens a modal)
• Normal force in an elevator (Opens a modal)
• More on Normal force (shoe on floor) (Opens a modal)
• More on Normal force (shoe on wall) (Opens a modal)
• What is normal force? (Opens a modal)

Balanced and unbalanced forces

• Balanced and unbalanced forces (Opens a modal)
• Unbalanced forces and motion (Opens a modal)

Slow sock on Lubricon VI

• Slow sock on Lubricon VI (Opens a modal)
• Normal forces on Lubricon VI (Opens a modal)

Inclined planes and friction

• Inclined plane force components (Opens a modal)
• Ice accelerating down an incline (Opens a modal)
• Force of friction keeping the block stationary (Opens a modal)
• Correction to force of friction keeping the block stationary (Opens a modal)
• Force of friction keeping velocity constant (Opens a modal)
• Intuition on static and kinetic friction comparisons (Opens a modal)
• Static and kinetic friction example (Opens a modal)
• What is friction? (Opens a modal)
• What are inclines? (Opens a modal)
• The force of tension (Opens a modal)
• Mild and medium tension (Opens a modal)
• Super hot tension (Opens a modal)
• What is tension? (Opens a modal)
• Introduction to tension (Opens a modal)
• Introduction to tension (part 2) (Opens a modal)
• Tension in an accelerating system and pie in the face (Opens a modal)

Treating systems

• Treating systems (the hard way) (Opens a modal)
• Treating systems (the easy way) (Opens a modal)
• Two masses hanging from a pulley (Opens a modal)
• Three box system problem (Opens a modal)
• Masses on incline system problem (Opens a modal)

Physics Made Easy

How to solve physics problems with Forces

Get ready to see your understanding of dynamics skyrocket , have you ever been stuck when trying to answer a high school physics question where forces are involved, maybe you are clueless on how to begin, or you often get stuck at a certain point, well, this course is there to solve that problem.

Structure of the course 

This course is structured in 3 sections..

The first three episodes  contain a summary of the 5 steps and 2 solved examples. The goal of this first section is to for you to get an overview of the technique before diving into the details.

The second section consists in 6 lesson videos.  The process of applying each step is presented in detail and in various situation. The conceptual and mathematical tools required to carry out each single step are also presented (1 step = 1 video + 1 extra video about the manipulation of vectors). You will learn here how to draw a free body diagram, how to express a resultant force mathematically, how to manipulate vectors, when and how to apply Newton’s Laws etc…

The third section is your play-ground!  You will find 8 exercises for you to train your skills in applying the 5-step technique to solve physics problems. After giving you a chance to solve each question yourself, the presenter carries out a detailed correction on the white board. This section also contains a video lesson about mechanical friction forces.

What you will gain by taking this course

If you follow this class till the end, and carry out all the exercises diligently, you will gain more than just the ability to solve mechanics problems.

By doing so, you will realize that Physics is actually pretty easy to handle: the patterns of thinking presented in this course are commonly used in many areas of physics, and could be very useful to you in your studies.

Level of this course

The level of this course corresponds to the last years of High School Physics Programs. This makes it an ideal tool as support for the lessons you get at school, and to prepare any High School Diplomas in Physics, like for example IB Physics, A-Level Physics, AP Physics etc.

It is also a great tool for University students and engineers to revisit the vary basics of mechanics. As a researcher myself, I realized that refreshing the basics does bring new perspectives!

Detailed content

Section 1: the 5-step technique to solve physics problems with forces (introduction).

• Episode 1: The 5-step technique in a nutshell
• Episode 2: Solved example in 1 dimension
• Episode 3: Solved example in 2 dimensions

Section 2: The 5 steps in detail (Lesson Videos)

• Episode 4: Free Body Diagrams (Step 1)
• Episode 5: Defining the Axes (Step 2)
• Episode 6: Manipulating Vectors
• Episode 7: Expressing the Net Force (Step 3)
• Episode 8: Applying Newton’s Laws (Step 4)
• Episode 9: Solving the Problem

Section 3: Applying the 5-step technique (Exercise Videos)

• Episode 10: Tensions & Ropes (Exercise 1)
• Episode 11: Connected Blocks (Exercise 2)
• Episode 12: A Block on a Slope (Exercise 3)
• Episode 13: Understanding Friction (Lesson Video)
• Episode 13B: Friction on an inclined plane (Exercise 4)
• Episode 14: The Elevator (Exercise 5)
• Episode 15: The Crate and the Pit (Exercise 6)
• Episode 16: The Flea Jump (Exercise 7)
• Episode 17: The Asymmetric Rope (Exercise 8)

Master the manipulations of Forces and finally get your grips on Mechanics

Beef up your skills at solving physics problems, take the course now.

• › Force and Motion
• › This article

Solving problems which involve forces, friction, and Newton's Laws: A step-by-step guide

This step-by-step guide is meant to show you how to approach problems where you have to deal with moving objects subject to friction and other forces, and you need to apply Newton's Laws. We will go through many problems, so you can have a clear idea of the process involved in solving them.

The problems we will examine include objects that

• are pushed/pulled horizontally with an angle
• move up or down an incline
• hang from ropes attached to the ceiling
• hang from ropes that run over pulleys
• move connected by a string
• are pushed in contact with each other (Coming soon!)
• Box pulled at an angle over a horizontal surface
• Block pushed over the floor with a downward and forward force
• Object moving at constant velocity over a horizontal surface
• Block pushed up a frictionless ramp
• Mass pulled up an incline with friction
• A mass hanging from two ropes
• Two hanging objects connected by a rope
• Two masses on a pulley
• Two blocks connected by a string are pulled horizontally

Forces in Two Dimensions

Practice problem 1.

• the magnitude of the acceleration of the human cannonball inside the barrel
• the net force on the human cannonball inside the barrel
• the weight of the human cannonball
• the components of her weight that are parallel and perpendicular to the barrel of the cannon
• the force on the feet of the human cannonball while she is being launched
• the magnitude and direction of the acceleration of the human cannonball in flight
• the horizontal and vertical components of her initial velocity
• the time she spends in the air
• the distance from the mouth of the cannon to the center of a properly placed net
• her maximum height above the mouth of the cannon

Use one of the equations of motion to find the acceleration of the human cannonball inside the cannon. I recommend the one traditionally known as the third.

Use Newton's second law of motion to get the net force on the human cannonball inside the cannon. Use the acceleration we just calculated.

Use the appropriate equation for the weight of the human cannonball.

Make a drawing so you can see which trig function to use for which component of her weight.

Make another drawing showing how the forces work when the human cannonball is on her way out.

The component of her weight and the normal that is perpendicular to the barrel cancel out. Nothing's happening in that direction. The component of her weight and the normal force that is parallel to the barrel must not cancel since she is accelerating in that direction. The normal force must be greater than the parallel component of her weight by an amount equal to the net force.

This is roughly 4½ times her weight. Being a human cannonball requires a lot of strength.

Once she leaves the barrel of the cannon, the human cannonball is an object in free fall. Her acceleration is the acceleration due to gravity on Earth — 9.8 m/s 2 down .

Make another drawing so you can see which trig function to use for which component of her velocity.

At the highest point in her trajectory, the human cannonball's vertical velocity is zero. Use this to find the time it takes her to get to this point. We'll call this the half time. I recommend the definition of acceleration as the equation of choice. (Negative numbers were substituted since her velocity at this time and in this direction is decreasing.)

Save this number because we'll need it later. Double it for now to get the number this part of the question asked for.

t  =  3.18 s

The distance to the net is a horizontal measurement. Use the horizontal component of her velocity with the time we just calculated and the definition of speed. There is no acceleration in this direction, so her speed is a constant value.

Maximum height is a vertical measurement. Use the vertical component of her initial velocity with the acceleration due to gravity and the half time we calculated earlier. These numbers work with the second equation of motion. Watch the signs. Let's let up be positive.

We could also use the third equation of motion. This has the benefit of not relying on the half time we calculated earlier.

practice problem 2

• Draw a free body diagram of the crate.
• the component of the crate's weight that is perpendicular to the ramp
• the component of the crate's weight that is parallel to the ramp
• the normal force between the crate and the ramp
• the static friction force between the crate and the ramp
• At what angle will the crate just begin to slip?
• the kinetic friction force between the crate and the ramp
• the net force on the crate
• the acceleration of the crate

This is an example of a classic physics problem that students have been solving since the 17th century. It starts as an equilibrium problem, since the crate isn't going anywhere.

The component of the crate's weight perpendicular to the ramp is found using the cosine function. An object's weight is entirely pushing into a surface when the surface is level (a 0° angle of inclination). None of that weight is pushing into the surface when the surface is vertical, like a wall (a 90° angle of inclination). Cosine is a maximum when the angle is zero and zero when the angle is 90°. This is how the perpendicular component works.

The component of the crate's weight parallel to the ramp is found using the sine function. An object's weight has no sideways component on a level floor (a floor with no inclination). An object's weight is entirely parallel to a wall (a floor with a 90° inclination, in a sense). Sine is zero when the angle is zero and a maximum when the angle is 90°. This is how the parallel component works.

Normal forces are normal — that is, perpendicular to a tangent drawn to a curve or surface. This crate isn't currently going anywhere, so all the forces perpendicular to the incline must cancel. For a static crate on an incline, the force normal to the incline equals the perpendicular component of its weight.

Friction is a sideways, lateral, or tangential force — that is, parallel to a tangent drawn to a curve or surface. I'll say it again, this crate isn't going anywhere, so all the forces parallel to the incline should cancel. For a static crate on an incline, the static friction force equals the parallel component of the crate's weight.

The component of the crate's weight parallel to the incline pulls the crate down the incline while the frictional force tries to keep it in place. Since nothing is going anywhere, these two forces must balance each other.

As the angle of inclination increases, so to does the static friction, but it can't keep doing this forever. At some angle, the parallel component of the weight will equal the maximum static friction. Friction won't be strong enough and the crate will slip.

Cancel the weight.

μ s  cos θ = sin θ

Do some trig.

tan θ = μ s

Enter numbers.

tan θ =  0.28

Compute. The angle at which the crate just begins to slip is…

θ =  16°

This number is known as the critical angle (because it marks a critical value separating two types of behavior — sticking vs. sliding), angle of friction (because you gotta call it something), angle of repose (because granular materials will settle, or repose, in conical piles with this angle), or critical angle of repose (because adding grains to a pile with this angle will make it slump ).

The second part of this problem may or may not describe an object in equilibrium. We'll have to see.

The perpendicular component follows the sames rules it did in part a. Use cosine here.

The parallel component of the weight still uses the sine function.

There is no way for the crate to move perpendicular to the ramp in this scenario. The normal force must therefore equal the perpendicular component of the crate's weight.

The angle of inclination in part d is greater than the critical angle calculated in part c. Friction is no longer strong enough to keep the crate in place. The kinetic friction in this part of the problem is now really a function of the material surfaces (the coefficient of friction) and the contact forces (the normal force).

The forces perpendicular to the surface cancel out. The forces parallel to the surface do not. One is greater than the other. The parallel component of the weight is greater than the kinetic friction force. The difference of these two is the net force, and it drags the crate down the ramp.

Net force and mass determine acceleration. The three quantities are related by Newton's second law of motion.

practice problem 3

• the laboratory cart
• the lead weight
• the weight of the lead weight
• the weight of the laboratory cart
• the components of the cart's weight parallel and perpendicular to the track
• the normal force of the cart on the track
• the net force acting on the system
• the acceleration of the system
• the tension in the string

The challenge in this problem is keeping track of the different objects. Sometimes we're dealing with the lab cart (identified by a subscripted 1), sometimes we're dealing with the lead weight (identified by a subscripted 2), and sometimes we're dealing with the whole system — the cart and weight connected by a string (identified by the lack of a subscript). This level of detail is not necessary for your own personal work, but it is a good idea for me to do it so that my work is less ambiguous to you.

Why make two diagrams when you can make one?

Lab cart on the left, lead weight on the right.

Weight is mass times gravity. The SI unit of force is the newton, which is based on the kilogram and the meter per second squared. Be sure you're using the right units.

Repeat the steps above with a different mass.

Use sine for the component parallel to the track and cosine for the component perpendicular to the track.

Normal equals the perpendicular component of the weight on an inclined surface like the one described above.

N 1  =  W 1⟂ N 1  =  4.84 N

Normal and the perpendicular component of the weight cancel out on the track. Tension is an internal force for the cart-weight system. The net force is whatever's left over — the lead weight's weight minus the parallel component of the cart's weight.

∑ F  =  W 2  −  W 1∥ ∑ F  =  0.980 N − 0.767 N ∑ F  =  0.213 N

Use Newton's second law of motion to determine the acceleration of the system. The mass that's being accelerated is the mass of the cart plus the weight.

Note that this is less than the acceleration due to gravity, which is as it should be. The system is not in free fall.

Tension is an internal force for the system as a whole, but tension minus the parallel component of the cart's weight is the net force acting on the cart. Apply Newton's second law to the cart by itself. (Let right be the positive direction since that's the direction the cart is accelerating.)

Tension is also one of two forces acting on the suspended weight. The other is the weight of the weight. The difference in these two is the net force on the lead weight. Use this information and Newton's second law to find the tension. (Let down be the positive direction since that's the direction the weight is accelerating.)

Two methods give the same answer, so all is well. The lab cart and the lead weight experience the same tension (same magnitude, different directions).

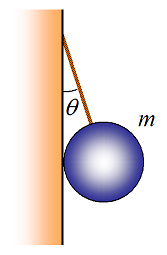
practice problem 4

• Draw a free body diagram for the pendulum bob.
• Derive an equation for acceleration of the vehicle in terms of the quantities given and known constants.

The pendulum bob swings in the direction opposite the acceleration. In a sense, the bob is trying to catch up to the moving vehicle when it speeds up and is overrunning the vehicle when it slows down. Inertia in action.

Start with a free body diagram. We have weight down and tension at an angle. Break the tension up into components in the traditional directions of horizontal and vertical.

Apply Newton's second law of motion…

∑ F  =  m a

but do it twice. (Let up and forward be the positive directions.)

In the horizontal direction, the horizontal component of the tension is unbalanced. It is the net force.

In the vertical direction, we assume there is no acceleration. The upward component of the tension should balance the downward weight of the pendulum bob.

Divide these two equations.

Simplify using algebra and trig identities.

a  =  g  tan θ

Test the equation with a few representative values. A 0° angle indicates no acceleration, since tan 0° = 0; a 45° angle corresponds to a horizontal acceleration of 1 g, since tan 45° = 1; and a 90° angle is impossible, since tan 90° = ∞.

Although the idea of using a pendulum to measure horizontal accelerations is a simple one, there really was no need to make one until people regularly started to move at speeds faster than a fast horse. The first pendulum accelerometer was built in 1889 by the British mechanical engineer Frederick Lanchester (1868–1946). A pencil was attached to the pendulum bob so that it could automatically draw an acceleration-time graph on a piece of paper.

Lanchester was interested in the smoothness of braking systems on trains. In particular, he was curious about the cause of the sudden change in motion that happens right before a braking train comes to rest.

It has been remarked that a characteristic feature of brake diagrams is the suddenness of the drop at the instant of stopping. This is a very interesting and important point, inasmuch as it is the cause of the "jerk" nearly always experienced just as a train comes to rest; it was in fact in investigating this jerk in 1888 that the idea of the pendulum accelerometer occurred to the writer. At that time it was currently supposed that the jerk was the effect of the recoil of the buffer springs after stopping; whereas a very little consideration shows that it is in reality sudden change of acceleration [emphasis original] that we recognize physiologically as "jerk," that is df / dt [for some odd reason, he chose to use f for acceleration], and not change in the direction of motion. It suggests itself in fact that the term "jerk" might well be given a scientific meaning and be defined as d 3 s / dt 3 . Frederick Lanchester, 1905

The suggestion stuck.

Force Vector Problems: Exploring the Dynamics of Motion

Force vector problems are a fundamental concept in physics and engineering that involve the analysis and manipulation of forces acting on objects. Understanding force vectors is crucial for solving problems related to motion, equilibrium, and the interaction between objects. In these problems , forces are represented as vectors, which have both magnitude and direction. By applying principles of vector addition and subtraction, we can determine the net force acting on an object and predict its resulting motion . Key takeaways from force vector problems include the ability to break down forces into their components, understanding the concept of equilibrium, and using vector diagrams to visualize and solve problems.

Understanding Force Vectors

Definition of force vectors.

In physics, force is defined as a push or pull that can cause an object to accelerate or deform. A force vector is a mathematical representation of a force, which includes both its magnitude and direction. It is represented by an arrow , where the length of the arrow represents the magnitude of the force and the direction of the arrow represents the direction of the force.

Force vectors are an essential concept in physics, particularly when dealing with vector problems and force analysis. They allow us to understand and predict the motion of objects by considering the forces acting upon them.

Why is Force Considered a Vector?

Force is considered a vector quantity because it has both magnitude and direction. Magnitude refers to the strength or intensity of the force, while direction indicates the line along which the force acts. These two components of a force vector are crucial in understanding how forces interact with each other and how they affect the motion of objects.

By considering force as a vector , we can apply vector addition and vector subtraction to determine the resultant force acting on an object. This allows us to analyze complex systems where multiple forces are acting simultaneously.

Force Vectors in Physics

Force vectors play a fundamental role in various areas of physics, including mechanics, dynamics, and statics. They are used to describe and analyze the forces acting on objects in different situations .

Resolving Forces

One common application of force vectors is resolving forces into their components. This involves breaking down a force vector into two or more vectors that are perpendicular to each other. By doing so, we can analyze the effect s of the force in different directions and determine how it contributes to the overall motion of an object.

Force Diagrams

Force diagrams , also known as free-body diagrams , are graphical representations of force vectors. They are used to visually represent the forces acting on an object and their directions. By drawing force diagrams, we can simplify complex systems and analyze the equilibrium of forces, which is crucial in understanding the motion of objects.

Vector Addition and Subtraction

Vector addition and subtraction are essential operations when dealing with force vectors. By adding or subtracting force vectors , we can determine the resultant force acting on an object. This resultant force represents the combined effect of all the individual forces and determines the resulting motion of the object.

Force Equilibrium

Force equilibrium occurs when the net force acting on an object is zero. In other words , the forces are balanced, and there is no acceleration . Understanding force vectors allows us to analyze and determine the conditions for force equilibrium, which is essential in statics and structural analysis .

Distinguishing Between Vector and Scalar Quantities

Is force a vector or scalar.

When it comes to distinguishing between vector and scalar quantities , one common question that arises is whether force is a vector or scalar quantity. The answer is clear: force is a vector quantity.

In physics, a vector quantity is defined as a quantity that has both magnitude and direction. On the other hand, a scalar quantity only has magnitude. Force, being a vector quantity, possesses both magnitude and direction.

Why is Force a Vector Quantity?

To understand why force is considered a vector quantity, let’s take a closer look at what force represents. Force is defined as an external influence that can cause an object to accelerate or deform. When we apply a force to an object, we not only need to consider the magnitude of the force but also its direction.

For example, imagine pushing a box across a table . The force you apply to the box has a specific magnitude , but it also has a direction – the direction in which you push the box. If you were to push the box with the same magnitude of force but in a different direction , the resulting motion of the box would be different. This is why force is considered a vector quantity.

Vector Addition and Subtraction in Force Analysis

In force analysis, vector addition and subtraction are essential tools for understanding the overall effect of multiple forces acting on an object. By breaking down forces into their vector components , we can analyze how they contribute to the resultant force.

When adding vectors, we consider both their magnitudes and directions. The resultant force is obtained by adding the individual force vectors together. On the other hand, when subtracting vectors, we subtract the magnitude and direction of one vector from another.

Resolving Forces and Vector Components

Resolving forces involves breaking down a force vector into its horizontal and vertical components . This allows us to analyze the effect of the force in different directions. By using trigonometry, we can determine the magnitude and direction of each component .

The process of resolving forces is particularly useful when dealing with forces acting at angles. By breaking down the forces into their components, we can simplify the analysis and determine the overall effect on an object.

Force Diagrams and Equilibrium of Forces

Force diagrams , also known as free-body diagrams , are graphical representations that show the forces acting on an object. These diagrams help us visualize the forces and their directions, making it easier to analyze the overall effect.

In the context of force analysis, equilibrium refers to a state where the net force acting on an object is zero. In other words , the forces are balanced, and there is no acceleration . By applying the principles of vector addition and subtraction, we can determine whether an object is in equilibrium or not.

Calculating Force Vectors

Force Vector Equation

When it comes to analyzing forces in physics, one of the fundamental concepts is the use of force vectors. A force vector represents both the magnitude and direction of a force. By understanding how to calculate force vectors, we can solve various vector problems and gain insights into force analysis.

To calculate a force vector, we need to consider two main components : magnitude and direction. The magnitude of a force vector represents the strength or intensity of the force, while the direction indicates the line along which the force acts. Combining these two aspects allows us to fully describe a force in a vector form.

The force vector equation can be expressed as:

Here, (\vec{F}) represents the force vector, (F_x), (F_y), and (F_z) are the components of the force vector in the x, y, and z directions respectively, and (\hat{i}), (\hat{j}), and (\hat{k}) are the unit vectors in the x, y, and z directions respectively.

How to Calculate Vector Force

To calculate a vector force, we need to follow a system atic approach that involves vector addition and subtraction. Let’s break down the steps :

Identify the Forces: Begin by identifying all the forces acting on an object. These forces can be represented by arrows, with the length of the arrow indicating the magnitude and the direction indicating the direction of the force.

Resolve the Forces: Resolve each force into its components along the x, y, and z directions. This step involves breaking down the forces into their respective x , y, and z components using trigonometry.

Perform Vector Addition or Subtraction: Once the forces are resolved into their components, we can perform vector addition or subtraction to find the resultant force. Vector addition involves adding the corresponding components of the forces, while vector subtraction involves subtracting the components.

Determine the Resultant Force: After performing the vector addition or subtraction, we obtain the resultant force vector . The resultant force represents the combined effect of all the forces acting on the object.

Check for Equilibrium: Finally, we can check if the object is in equilibrium by analyzing the resultant force. If the resultant force is zero, the object is in equilibrium, meaning the forces are balanced. If the resultant force is non-zero, the object is not in equilibrium, indicating an unbalanced force .

By following these steps , we can effectively calculate vector forces and gain a deeper understanding of force analysis. It is important to note that vector components and vector resolution play a crucial role in this process , allowing us to break down forces into manageable parts and analyze their effects .

To visualize the forces and their components, a force diagram can be used. A force diagram is a graphical representation that shows the forces acting on an object, their directions, and their magnitudes . This visual aid helps in understanding the force equilibrium and the overall force vector analysis .

Practical Applications of Force Vectors

Force vectors are a fundamental concept in physics and engineering, and they have numerous practical applications in real-world scenarios . By understanding force vectors, we can analyze and solve problems related to forces acting on objects in various situations . Let’s explore some practical applications of force vectors.

Force Vector Word Problems

One common application of force vectors is in solving word problems that involve forces acting on objects. These problems often require us to determine the magnitude and direction of the resultant force or find the equilibrium of forces. By representing forces as vectors, we can apply vector addition and subtraction to solve these problems .

For example, consider a scenario where two forces are acting on an object at different angles . We can represent each force as a vector and then use vector addition to find the resultant force. By analyzing the magnitudes and directions of the forces, we can determine the net effect on the object.

Force Vector Practice Problems

To further enhance our understanding of force vectors, it is essential to practice solving problems that involve force analysis. These practice problems allow us to apply the principles of vector addition, subtraction, and resolution to real-world scenarios .

For instance, imagine a situation where an object is subjected to multiple forces acting in different directions. By resolving these forces into their components, we can determine the individual effects of each force and then use vector addition to find the resultant force. This process helps us analyze complex force systems and predict the resulting motion or equilibrium of the object.

Force Vector Problems and Solutions

In addition to word problems and practice exercises , studying force vector problems and their solutions can provide valuable insights into the application of force vectors. These problems often involve analyzing force diagrams, resolving forces, and determining the equilibrium of forces.

For example, let’s consider a scenario where an object is in equilibrium, meaning the net force acting on it is zero. By analyzing the force diagram and resolving the forces into their components, we can determine the necessary conditions for force equilibrium. This understanding is crucial in designing structures or systems that require balanced forces .

By studying and solving force vector problems, we can develop a strong foundation in force analysis and vector manipulation . These skills are essential in various fields , including physics, engineering, and mechanics.

Examples of Force Vectors

Force vectors are a fundamental concept in physics and engineering. They represent the magnitude and direction of a force acting on an object. Understanding force vectors is crucial for analyzing and solving problems related to forces. Let’s explore some examples of force vectors and how they can be analyzed.

Force Vectors Examples

Example 1: force analysis.

Consider a box being pushed with a force of 50 Newtons at an angle of 30 degrees above the horizontal . To analyze this force vector , we can break it down into its horizontal and vertical components . Using trigonometry, we can determine that the horizontal component is 50 * cos(30° ) = 43.3 N and the vertical component is 50 * sin(30° ) = 25 N. By resolving the force vector into its components, we can better understand how it affects the motion of the box.

Example 2: Vector Addition

Suppose two forces are acting on an object: a force of 30 Newtons directed to the right and a force of 20 Newtons directed upwards. To find the resultant force, we can use vector addition. By adding the horizontal component s (30 N) and the vertical component s (20 N), we can determine that the resultant force is the square root of (30^2 + 20^2) = 36.06 N. The direction of the resultant force can be found using trigonometry, giving us an angle of arctan(20/30) = 33.69 degrees above the horizontal .

Example 3: Equilibrium of Forces

In a system where forces are in equilibrium, the net force acting on the object is zero. Consider a box on a flat surface with two forces acting on it: a force of 40 Newtons directed to the right and a force of 40 Newtons directed to the left . Since the magnitudes of the forces are equal, the net force is zero, and the box remains in equilibrium. This concept is crucial for understanding the stability of structures and objects.

Force Vector Questions and Answers

Q: how do you resolve forces into their components.

A: To resolve a force vector into its components, you can use trigonometry. By determining the angle of the force vector with respect to a reference axis , you can calculate the horizontal and vertical components using the formulas : horizontal component = force magnitude * cos(angle) and vertical component = force magnitude * sin(angle).

Q: What is the difference between vector addition and vector subtraction?

A: Vector addition involves combining two or more force vectors to find their resultant force . It is represented by adding the magnitudes and directions of the vectors . On the other hand, vector subtraction involves finding the difference between two force vectors . It is represented by subtracting the magnitudes and directions of the vectors .

Q: How can force vectors be used to analyze the equilibrium of forces?

A: Force vectors can be used to analyze the equilibrium of forces by considering the net force acting on an object. In equilibrium, the net force is zero, which means the sum of all forces in one direction is equal to the sum of all forces in the opposite direction . By analyzing the forces acting on an object and ensuring they balance each other, we can determine if the object is in equilibrium.

The Impact of Force on Velocity

Does force affect velocity.

When it comes to understanding the relationship between force and velocity, it is important to consider the principles of physics. Force, which is a vector quantity, has the ability to influence the velocity of an object. In this section , we will explore how force affects velocity and the various factors that come into play.

Force Vector and Velocity

To begin, let’s discuss the concept of a force vector. A force vector represents both the magnitude and direction of a force. It is important to note that force is a vector quantity because it has both magnitude and direction. On the other hand, velocity is also a vector quantity that represents the rate at which an object changes its position .

When a force is applied to an object, it can cause a change in its velocity . This change can occur in two ways : by changing the magnitude of the velocity or by changing its direction. The effect of force on velocity depends on the direction and magnitude of the force vector.

In order to understand how force affects velocity, it is crucial to grasp the concept of vector addition and subtraction. When multiple forces act on an object, they can be combined using vector addition. This allows us to determine the resultant force, which is the net force acting on the object. The resultant force will determine the change in velocity of the object.

On the other hand, vector subtraction is used when forces act in opposite directions . By subtracting one force vector from another, we can determine the net force acting on the object. This net force will also affect the object’s velocity.

Resolving Forces and Equilibrium

Resolving forces is another important concept when analyzing the impact of force on velocity. It involves breaking down a force vector into its components along different axes . By doing so, we can determine the effect of each component on the object’s velocity.

When multiple forces acting on an object are in equilibrium, the net force is zero. In this case , the object’s velocity remains constant. However, if the forces are unbalanced, the object will experience a change in velocity.

Force Diagrams and Analysis

To better understand the impact of force on velocity, force diagrams are often used. These diagrams visually represent the forces acting on an object, including their magnitudes and directions. By analyzing these force diagrams , we can determine the resultant force and its effect on the object’s velocity.

Force analysis involves applying the principles of vector addition, subtraction, and resolution to determine the net force acting on an object. By considering the forces at play, their magnitudes , and directions, we can predict how the object’s velocity will change.

How can force vector problems be interpreted using force graph visualizations and analysis?

‘Interpreting force graph visualizations and analysis’ is a crucial aspect when addressing force vector problems. By employing force graph visualizations and analysis, we can gain a deeper understanding of the forces at play within a system. These visualizations provide a graphical representation of the forces and their magnitudes, allowing us to identify patterns and relationships that may not be immediately apparent from numerical data alone. Additionally, by analyzing the force graph, we can uncover insights about the interactions between objects and how they affect the overall system dynamics. For a more comprehensive exploration of this topic, refer to the article on Interpreting force graph visualizations and analysis.

Frequently Asked Questions

1. Is force a vector or scalar?

Force is a vector quantity.

2. Why is force considered a vector quantity?

Force is considered a vector quantity because it has both magnitude and direction.

3. What is vector force in physics?

Vector force in physics refers to the representation of force as a vector quantity, taking into account both its magnitude and direction.

4. How do you calculate vector force?

Vector force can be calculated by using vector addition or subtraction, depending on the situation . The resultant force is determined by combining the individual forces using appropriate vector operations .

5. What are some examples of force vectors?

Examples of force vectors include the force exerted by a person pushing a box, the gravitational force acting on an object, and the tension in a rope .

6. Does force affect velocity?

Yes, force can affect the velocity of an object. According to Newton’s second law of motion, the acceleration of an object is directly proportional to the net force acting on it.

7. What is force vector analysis?

Force vector analysis involves breaking down a force into its components and analyzing their effects on an object. This analysis helps determine the resultant force and its direction.

8. How do you resolve forces into their vector components?

Forces can be resolved into their vector components by using trigonometry. The magnitude and direction of the force can be determined by calculating the horizontal and vertical components of the force.

9. What is force equilibrium and how does it relate to vectors?

Force equilibrium refers to a state where the net force acting on an object is zero. In vector terms , this means that the sum of all forces acting on the object is zero, taking into account both magnitude and direction.

10. What is a force diagram and how does it help with vector analysis?

A force diagram is a visual representation of the forces acting on an object, typically shown as arrows indicating the direction and magnitude of each force. It helps in analyzing vector forces by providing a clear visual representation of the forces involved.

• Force in artificial gravity
• Force due to neutrinos
• Force in globular clusters
• How to find the force of a magnet
• Force on different surfaces
• How to find force in microgravity
• How to find force balance in astrophysics
• How to find force in a cosmic microwave background observation
• Calculating force in fluids
• When did force theories evolve

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.

2.7: Two-Dimensional Force System: Problem Solving

Chapter 0: physics basics, chapter 1: an introduction to statics, chapter 2: force vectors, chapter 3: equilibrium of a particle, chapter 4: force system resultants, chapter 5: equilibrium of a rigid body, chapter 6: structural analysis, chapter 7: internal forces, chapter 8: friction, chapter 9: center of gravity and centroid, chapter 10: moment of inertia, chapter 11: virtual work, chapter 12: kinematics of a particle, chapter 13: kinetics of a particle: force and acceleration, chapter 14: kinetics of a particle: impulse and momentum, chapter 15: planar kinematics of a rigid body, chapter 16: 3-dimensional kinetics of a rigid body, chapter 17: concept of stress, chapter 18: stress and strain - axial loading.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

Consider a wiper inclined at an angle of 25 degrees to the baseline 's' in a two-dimensional system. A force acting on the handle, pivoted to the center of the wiper, makes an angle of 20 degrees with the reference line 'c', which is parallel to baseline 's.'

If the force component along the a-axis is 65 Newtons, determine the magnitude of the force and its component along the b-axis.

Here, considering alternate angles, coa‘ becomes 25 degrees, while angle Foc is 20 degrees. So, the angle made by the force vector with the a-axis is determined by adding the two angles and is equal to 45 degrees.

As the force component along the a-axis is known, the magnitude of a force is estimated by the ratio of the a component of the force to the cosine of 45 degrees.

Now, the b component of the force is expressed as the product of the magnitude of the force and sine of 45 degrees. It is negative since it is along the negative b-axis.

Solving problems related to two-dimensional force systems is an essential aspect of mechanics and engineering. By applying the principles of vector analysis and force equilibrium, one can determine the effect of multiple forces acting on an object in a two-dimensional space.

The first step to solving a two-dimensional force system problem is to draw a free-body diagram of the object under consideration. This diagram helps identify all the external forces acting on the object, including their magnitudes, directions, and point of application.

Next, one needs to resolve the forces into their components in the x and y directions using the principles of vector analysis. This step helps convert the given forces into their Cartesian vector form, enabling easy representation and analysis. The components can be resolved using trigonometric functions, such as the sine and cosine of the given angles.

After breaking forces into components, the next step is determining the net force in each direction. This is done by adding up all of the forces in each direction. After that, the resultant force and its direction are determined using the Pythagorean theorem and trigonometry. If the net force is zero, the object is in equilibrium and not accelerating. If the net force is non-zero, then the object is accelerating in the direction of the net force. The principle of force equilibrium states that the sum of all external forces acting on the element must be equal to zero in both the x and y directions. This allows us to determine the unknown forces acting on the object, such as tension or compression in a member.

In some cases, the moment equilibrium principle is also used to determine the effect of external forces on the object. This principle states that the sum of all external moments acting on the element must equal zero. This step helps determine the values and directions of moments acting on the object.

• Beer, F.P.; Johnston, E.R.; Mazurek, D.F; Cromwell, P.J. and Self, B.P. (2019). Vector Mechanics for Engineers ‒ Statics and Dynamics. New York: McGraw-Hill. pp 29-33
• Hibbeler, R.C. (2016). Engineering Mechanics ‒ Statics and Dynamics. Hoboken, New Jersey: Pearson Prentice Hall. pp 33 ‒ 35.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

• Exam Center
• Ticket Center
• Flash Cards

Buoyant Force Formula with Solved Examples

In this tutorial, we will explore the buoyant force formula through a problem-solving approach .

You may have seen a ship or a boat floating on water. But what makes some objects float or sink in fluids?

Let’s try an experiment.

Attach a dense object to a spring scale and measure its weight. Then, immerse it in water and measure its weight again. You will notice that the scale reading in water is lower than that in air.

Why is that?

We can infer that there is an upward force acting on the object in the fluid (for example, water) that counteracts the downward gravitational force (weight) resulting in a lower weight, called apparent weight , in the fluid.

This is a common phenomenon that happens in all fluids when an object with a different density is submerged in it.

The force exerted by a fluid on an object that is completely or partially submerged in it is called buoyant force and its magnitude is equal to the weight of the fluid displaced by the object.

This upward force, which is called the buoyant force, is not a new type of force.

It arises from the pressure difference between the upper and lower surfaces of a submerged object in a fluid.

Origin of the buoyant force formula: 

Consider a body submerged (say, a cube) in a fluid. The fluid exerts forces on all sides of the cube.

The forces in the horizontal direction are equal and opposite, so they cancel out. (This is because they are at the same depth from the fluid surface, so the pressure is the same.)

The forces in the vertical direction are different because the top and bottom sides are at different depths of the fluid.

We know that the pressure increases with depth, so the force on the bottom side is larger than the force on the top side. This results in a net upward force, which is called the buoyant force.

But how is the buoyancy force formula derived? 

To find the buoyant force, let’s simplify the problem by considering a cube of height $h$ and base area $A$ that is completely submerged in a fluid with density $\rho_f$.

As shown in the figure, the fluid exerts vertical forces on the cube due to the water pressure at different depths. The force $F_1$​ acts downward on the top surface of the cube, while the force $F_2$​ acts upward on the bottom surface of the cube.

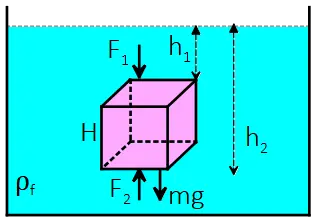
These are the only vertical forces that the fluid applies to the cube.

The horizontal forces cancel out since they are equal and opposite. 

By adding the vertical forces, we get a net upward force, which is the buoyant force. We can derive the formula for the buoyant force as follows: \begin{align*} F_{net} &= F_2-F_1\\ \\&=P_2A-P_1A\\ \\&=(\rho_f gh_2)A-(\rho_g g h_1)A\\ \\&=\rho_f g(h_2-h_1)A\\ \\&=\rho_f V_{dis}g \end{align*} In the above derivation, we used the following facts: the pressure at a depth $h$ below the fluid surface is $P=P_0+\rho_f gh$ where $P_0$ is the surface pressure.

Therefore, the  buoyant force formula is the product of the fluid density $\rho_f$, the displaced fluid volume $V_{dis}$, and the gravitational constant $g$. \[F_b=\rho_f V_{dis} g\]

We can also use the definition of density as the ratio of mass to volume, $\rho=\frac mV$, to find another useful equation for buoyant force as \[F_b=m_f g\] where, in this version, $m_f$ is the mass of the fluid displaced by the object submerged in it. 

Example (1): A solid cylinder with base area $A=20\,{\rm cm^2}$ is placed completely underwater as shown in the figure. Calculate the difference between the forces exerted by the water on the upper and lower bases of the cylinder. ($g=10\,{\rm m/s^2}$ and $\rho_{water}=1\,{\rm g/cm^3}$).

Solution : The water exerts two forces $F_1=P_1 A$ and $F_2=P_2 A$ on the upper and lower bases of the cylinder, respectively. The pressure at depth $h$ of a fluid with density $\rho$ is given by $P=\rho gh$.

The upper base is at depth $h_1=0.1\,{\rm m}$, so the pressure at that depth is $P_1=1000\times 10\times 0.1=1000\,{\rm Pa}$. 

The lower base is at depth $h_2=0.5\,{\rm m}$, so the pressure at that depth is $P_2=1000\times 10\times 0.5=5000\,{\rm Pa}$. 

The difference in forces is the upward buoyant force exerted on the cylinder by the water. $\Delta F=F_2-F_1=(P_2-P_1)A$, so we have \begin{align*}\Delta F&=F_2-F_1=(P_2-P_1)A\\&=(5000-1000)20\times(0.01)^2 \\&=8\quad {\rm N}\end{align*}

We can also find it using the buoyant force equation as $F_b=\rho_{water}V_{body}g$, where $V_{body}$ is the volume of the cylinder submerged in the water (here, the whole cylinder is submerged). \begin{align*}F_b&=\rho_{water}V_{body}g\\ &=(1000)(40\times 20)\times 10^{-5}\times 10\\&=8\quad {\rm N}\end{align*} The volume of the cylinder is the product of the base area ($A=20\,{\rm cm^2}$) and the height ($h=40\,{\rm cm}$). 

The buoyant force formula was derived for a simple shape, a cube, but it can be shown that it is valid for any shape.

Key points about the buoyant force formula:

• The mass in the formula is the mass of the  fluid  that is displaced by the object, not the mass of the object itself.
• The formula works for any shape, because any shape can be broken down into many tiny cubes, and the formula applies to each cube.
• The buoyant force only depends on the density of the fluid $\rho_f$, not the density of the object. It does not matter what material the object is made of, whether it is wood or iron. The buoyant force is the same as long as the object displaces the same amount of fluid.

The example below shows what is meant by displaced volume in the buoyancy force equation.

Example (2): A rectangular container of ethanol with density $\rho_{eth}=800\,{\rm kg/m^3}$ floats in the liquid of density $\rho_{f}=1200\,{\rm kg/m^3}$. Height and base of the container are $H=6\,{\rm cm}$ and $A=20\,{\rm cm^2}$, respectively. $h=4\,{\rm cm}$ of its height is in the fluid. Find the buoyancy force exerted on the container. 

Solution : The buoyant force is the weight of the fluid that is displaced by an object submerged in it. We can write it as $F_b=m_f g$ or $F_b=\rho_f V_{dis}g$, where $m_f$ is the mass of the displaced fluid, and $V_{dis}$ is the volume of the object under the fluid surface.

In this problem, the volume of the object under the fluid surface is $V_{dis}=A\times h$, where $A$ is the base area and $h$ is the height of the object. Substituting this into the buoyant force formula, we get \begin{align*}F_b&=\rho_{f}V_{dis}g\\&=\rho_f \times (Ah)g\\&=(1200)(20\times 4)\times 10^{-5}\times 10\\&=9.6\quad {\rm N}\end{align*}

This is the buoyant force that acts upward on the object. The buoyant force is based on  Archimedes' principle , which states that: 

Any object that is wholly or partially submerged in a fluid experiences a buoyant force equal to the weight of the fluid displaced by the object.

Example(3): A piece of wood with density $\rho_{wood}=0.6\,{\rm g/cm^3}$ floats on the surface of the water. What is the ratio of the portion of the wood submerged in the water to that of outside the water? ($\rho_{water}=1\,{\rm g/cm^3}$) 

Solution : The wood floats on water because its density is lower than that of water. The weight of the wood is balanced by the upward buoyant force exerted by the water. Using the buoyant force formula and the weight formula, we get: \begin{align*} \text{buoyant force}&=\text{weight}\\ \\ \rho_{fluid}V_{dis}g&=\rho_{body}V_{body}g\\ \\ \Rightarrow \frac{V_{dis}}{V_{body}}&=\frac{\rho_{body}}{\rho_{fluid}}\\ \\ &=\frac{0.6}{1}\\ \\ \Rightarrow V_{fluid}&=0.6\, V_{body}\end{align*} Here, $V_{dis}$ is the volume of the water displaced by the wood, and $V_{body}$ is the total volume of the wood.

To find the volume of the wood that is above the water, we can use the following equation: \begin{align*} V_{wood}&=V_{wood-in}+V_{wood-out}\\ \\V&=0.6V+V_{wood-out} \\ \\\Rightarrow& V_{wood-out}=0.4V\end{align*} Here, $V_{out}$​ is the volume of the wood that is outside the water.

Therefore, the volume of the wood that is inside the water is $V_{wood-in}=0.6V$ and the volume of the wood that is outside the water is $V_{wood-out}=0.4V$. Their ratio is $\frac 32$.

The buoyancy formula can be used to find the density of a fluid if we know the density of an object that floats in it. For example, consider the following problem:

Example (4): A piece of wood floats in water so that two-thirds of its volume $V$ is beneath the water level. When the same piece of wood is placed in oil, the submerged volume is $0.8V$. Find the density of (a) the wood and (b) the oil. 

Solution : The object floats on the fluids (water and oil) so the downward gravitation force and upward buoyant force must balance each other.

Recall that the buoyancy force formula is the fluid density times the volume of the part of the object beneath the fluid level times the gravitational constant, i.e., $F_b=\rho_f V_{dis}g$. 

In the case of water, the volume of the fluid displaced by the wood is, i.e., $V_{dis}=2/3 V$, since two-thirds of the wood's volume is submerged.  Therefore, equating the weight and the buoyant force, we get: \begin{align*} F_b&=mg\\ \rho_{water}V_{dis}g&=\rho_{wood}Vg\\ (1000)(2/3 V)&=\rho_{wood}\times V\\ \Rightarrow \rho_{wood}&=\frac{2000}{3}\quad{\rm \frac{kg}{m^3}}\end{align*}

In the case of oil, the volume of the fluid displaced by the wood is $V_{dis}=0.8 V$, since $80\%$ of the wood's volume is submerged. Using the same logic, we get: \begin{align*} F_b&=mg\\ \rho_{oil}V_{dis}g&=\rho_{wood}Vg\\ \\\rho_{oil}(0.8 V)&=\underbrace{\rho_{wood}}_{2000/3}\times V\\ \\ \Rightarrow \rho_{oil}&=834  \quad{\rm \frac{kg}{m^3}}\end{align*} Therefore, the density of the wood is $\frac{2000}{3}\,\rm kg/m^3$ and the density of the oil is $834\,\rm kg/m^3$.

Another application of the buoyant force equation is to find the apparent weight of objects in fluids. Consider the following example:

Example (5): An iron object has a density of $7.8\,{\rm g/cm^3}$ and appears 200 N lighter in water than in air. 

(a) What is the volume of the object? (b) How much does it weigh in the air?

Solution : Since the body has become lighter in water, there must be an upward force acting on the object, which cancels some downward weight force. In fluids, this force is called floating or buoyancy force.

Note:  200 N is the  buoyant force  that acts on the iron object when it is submerged in water. It is the force that makes the object appear lighter in water than in air. You can find this force by using Archimedes’ principle.

(a) According to Archimedes’ principle, the buoyant force is equal to the weight of the fluid displaced by the object. Therefore, we can use the following equation to find the volume of the object: \begin{align*} F_b &= \rho_{water} \times V_{object} \times g \\ \\ 200&=1000\times V_{object}\times 10 \\ \\ \Rightarrow V_{object}&=\frac{2}{100}\quad {\rm m^3}\end{align*} Note that $V_{object}$ is volume of the water displaced by the iron or explicitly, part of the iron underwater (All of it). 

(b) The weight of the object in air is given by the product of its mass and gravity. We can find its mass by multiplying its density and volume: \[W=\rho Vg=(7800)\left(\frac{2}{100}\right)(10)=1560\,{\rm N}\] where, here, $V$ is the actual volume of the object.

Example (6): An object with a mass of 150 kg is thrown into the water and displaces a volume of 100 liters of water. Will the object sink or float? 

Solution : To see what happens after throwing, we need to calculate the forces acting on the object in the water: the upward buoyant force and the downward weight .

We know that the buoyant force is equal to the weight of the fluid displaced by the object. Here, the volume displaced by the object is $100$ liters, which we need to convert to SI units of volume, $m^3$, as $1\,{\rm L}=10^{-3}\,m^3$.

Using the buoyant force formula, we get \begin{align*} F_b&=\rho_{water}\times V_{dis}\times g\\&=(1000)(100\times 10^{-3})(10)\\&=1000\quad {\rm N}\end{align*} The weight of the object, directed downward, is given by $W=mg=1500\,{\rm N}$. Applying Newton’s second law, we find the net force on the object: \[F_{net}=1000\uparrow-1500\downarrow=-500\downarrow\,{\rm N}\] Since weight is greater than the upward buoyant force, the object will sink.

Example (7): A raft has a volume of 6 cubic meters and two-thirds of its volume is submerged in seawater with a density of $1025\,{\rm kg/m^3}$. What is the buoyant force on the raft?

Solution : We can use the buoyant force equation $F_B=\rho V_{dis}g$, where $V_{dis}$ is the amount of the volume of the object under the fluid's level and $\rho$ is the density of the surrounding fluid. \begin{align*} F_B&=\rho V_{dis} g\\ &=(1025)\left(\frac {2}{3} 6\right)(9.8)\\&=40180\quad {\rm N}\end{align*}

This article explained how to use the buoyant force equation, which states that the buoyant force is equal to the weight of the fluid displaced by the object.

The article also provided examples of how to apply the equation to different situations, such as finding the volume, weight, or net force of an object in a fluid.

The article used a problem-solving approach to illustrate the steps and calculations involved in each example.

Author: Ali Nemati Page Created: 1/31/2021 Last Update: Feb 2, 2024

© 2015 All rights reserved. by Physexams.com

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Israel preparing for Rafah invasion in Gaza amid increasing tension with U.S.

60 Minutes Archive: Coverage of North Korea

As a Social Security cut looms, should seniors buy long-term care insurance now?

How a group of veterans helped a U.S. service member's mother get out of war-torn Gaza

Two-week 'Robin Sage' Special Forces training to begin Friday, 26 NC counties participating

Hurricanes expect 'dogfight' in Game 5 vs. Rangers, Kuznetsov says

Buescher confronts reddick after another near-miss nascar loss at darlington raceway, rory mcilroy rallies to win record 4th wells fargo championship title, lowe homer completes comeback bulls win on mother's day 8-7, usga opens new headquarters in pinehurst, showcasing historic golf artifacts.

WRAL Late News

WRAL WeatherCenter Forecast

Remembering heroes: 23 fallen officers honored in Raleigh

NC votes Tuesday. Races on the ballot, what to bring

Sky 5 flies over Atlantic Avenue crash

• Share full article

Advertisement

Supported by

The Architects of Hades Strive to Bewitch Gamers Again

Supergiant Games, a small independent studio, had always tackled new projects. Then its dungeon crawler featuring the Greek pantheon became an enormous success.

By Brian X. Chen

Brian X. Chen, The Times’s personal tech columnist, reported from San Francisco. His favorite weapon in Hades was the rail gun.

When Supergiant Games was wrapping up Hades, a mythologically rich hack-and-slash dungeon crawler it had spent more than three years developing, the studio concluded it was not quite done. The game’s premise of being trapped in hell, which particularly resonated during the pandemic , had opened paths to untold stories about Greek lore.

It needed a sequel.

This was a plot twist for the small independent studio, which had always pursued new ideas — even after its debut game, Bastion, was an immediate hit that ultimately sold millions of copies. Although Hades won numerous industry accolades and prestigious Hugo and Nebula Awards, the decision to make Hades II was a hard one.

“Making a sequel to us, as well, was unexpected,” Greg Kasavin, the creative director of Supergiant, said at the company’s chic studio space in San Francisco ahead of the early access release of Hades II this month.

“We think they’re really quite tough,” he added. “To be able to surprise and delight the audience in the same way is quite a challenge.”

For big-budget triumphs like Mass Effect and Red Dead Redemption, a new installment is an obvious step toward building a lucrative franchise. But although some popular indie games, like Spelunky and Slay the Spire , have pursued sequels, it is a much less frequent route for smaller game makers. Rather than making decisions for shareholders, they often prioritize artists and designers who are eager to express their creativity.

Indie hits also face distinct constraints. They often stand out because of a novel element — like the ability to rewind time in Braid — and that buzz does not always carry into a sequel, said Jesper Juul, an associate professor at the Royal Danish Academy of Architecture, Design and Conservation in Copenhagen.

“The first time people will tweet and post about it and say, ‘Wow, that’s amazing,’” said Juul, who wrote a book about independent games . “The second time it doesn’t have that novelty value.”

Supergiant was founded in 2009 by Amir Rao and Gavin Simon, who had worked on the real-time strategy Command & Conquer franchise at Electronic Arts, a giant corporation responsible for franchises such as The Sims and Madden.

Rao and Simon had noticed that several best-selling games, like Plants vs. Zombies and Castle Crashers, were coming from small studios. So they decided to form their own, initially setting up shop at a vacant house owned by Rao’s father in San Jose, Calif. Kasavin, a former video games journalist who also worked at Electronic Arts, joined them.

Kasavin said Supergiant had been tempted to create a sequel after the positive reception of Bastion (2011), in which a child collects powerful shards in a hostile environment that unfolds as a narrator provides commentary. But the team of seven at the time decided to explore other ideas, including science fiction, instead.

That led to Supergiant’s second game, Transistor (2014), about a famous singer who battles robots in a futuristic city. Its third project, the role-playing game Pyre (2017), features a band of exiles seeking freedom from purgatory.

By the time the studio, which now has 25 employees, released an early-access version of Hades in 2018, it had unintentionally created a perception that it was anti-sequel. Yet Supergiant is anything but: Among the games that employees list as their favorites are classic sequels, including Diablo II, Street Fighter II and Warcraft II.

Hades follows the journey of Zagreus, who in some versions of Greek mythology is considered the son of the god of the dead. As he ventures upward through the layers of hell with hopes of visiting his mother on the surface world, Zagreus fights monsters (including his father) with the help of other gods.

The idea of a sequel clicked when Supergiant realized that the god Hades also had daughters. Melinoë, a witch, created the opportunity to dive deep on the connection between Greek mythology and witchcraft.

Hades II has been in the works for more than three years, and not a single member of the team was against pursuing it, Kasavin said.

“We’re too small for that to be an acceptable starting point,” he said. “It’s only going to get tougher from there if you don’t have the raw excitement at the beginning.”

The long development process of Hades underscores one way that games are trying to optimize their odds of success . An incomplete version of the role-playing game Baldur’s Gate 3 was available to players for nearly three years before it was officially released in August to universal acclaim.

The early access version of Hades was made available in December 2018 with the hopes of receiving player input; the game that was officially released in September 2020 was the result of revisions based on thousands of pieces of feedback.

Supergiant is repeating this approach for the sequel. Hades II was released in early access on Steam and the Epic Games Store last week, and the studio said it expected to keep refining it through at least the end of this year.

Rao, who works on the game’s design and mechanics, said player feedback was crucial to the success of Hades. “We will absolutely need that for Hades II,” he said.

In its current state, Hades II is much more polished than the original Hades was at the same point. (A year before Hades was released in early access, it was a game that involved exploring a minotaur’s labyrinth.) But the sequel will still benefit from crowdsourced feedback, Rao said, because it is much larger in scope.

Unlike Zagreus’s singular path in the first Hades, Melinoë will be able to explore two main routes, which essentially makes the sequel at least double the size. Option A is a path down into the underworld to fight Chronos, the god of time, who has usurped her father’s throne. Option B, which opens up later in the game, is a path upward to defend Mount Olympus, the home of the gods, which is under siege by Chronos.

Much of what made the original game addictive remains intact. Hades II is part of the roguelite genre, where players incrementally progress by starting out weak, failing, trying again and applying what they have learned or unlocked to eventually beat the main boss.

To get stronger, Melinoë picks up artifacts known as boons that contain powers shared by gods such as Aphrodite, Hermes and Zeus. The average player will probably die dozens of times before snowballing into an unstoppable force to defeat Chronos.

Sequels can have particular pitfalls. Sitara Shefta, the head of studio at No Brakes Games, said it had been a challenge to expand on Human Fall Flat — a physics-based puzzle game that involves controlling a character named Bob through a dreamy landscape — while preserving what people loved about it.

The original game, by a solo developer, sold 50 million copies. A team of about 35 is working on the sequel, focusing on adding levels and improving the graphics.

“What we don’t want to do is dilute it,” Shefta said. “It’s a physics game where so many people can express themselves in different ways.”

Juul, the video game scholar, said successful independent game makers often faced an innovator’s dilemma. As teams grow larger, he said, they can lose nimbleness and begin playing it safe in response to external demands.

Supergiant said it got no such pressure to make a sequel from partners, including Netflix, which recently published Hades as a mobile game . The studio declined to share sales numbers, saying only that Hades outperformed Bastion, which sold 3 million copies by 2015 .

Days before Supergiant released the early access version of Hades II, a small cluster of employees worked in its small studio space, which has an open floor design embellished with orange and crimson accents reminiscent of the original game’s color palette.

The team was eager to reveal how Melinoë’s role as a witch added new dimensions to the gameplay. Zagreus’s punches and sword swings were conducive to rapid button mashing, but Melinoë’s spell-casting staff and other magic weapons require careful timing and precision. With one of her combat moves, she projects a force field that traps surrounding enemies.

Rao said Supergiant would study player feedback through the studio’s Discord channel, web forums, livestreams and social media. The studio also logs some important data — if most players are not picking a certain weapon, for instance, that can serve as a suggestion for designers to make it more fun to use.

The iterative process of learning from mistakes to improve Hades and Hades II is essentially a rogue game in and of itself. Supergiant has been immersed in Greek mythology for nearly seven years, so it is easy for Kasavin to draw a comparison: Sisyphus pushing a boulder for eternity.

Brian X. Chen is the lead consumer technology writer for The Times. He reviews products and writes Tech Fix , a column about the social implications of the tech we use. More about Brian X. Chen

Inside the World of Video Games

What to Play Next?: For inspiration, read what our critics thought about the newest titles , as well as which games our journalists have been enjoying .

Influencers Dying to Go Viral:  The horror video game Content Warning, a surprise hit , lets players microdose as momentary celebrities on the fictional website SpookTube.

No Rest for the Wicked:  The studio behind Ori and the Blind Forest has pivoted into dark fantasy , inspired by Dark Souls, Diablo and “Game of Thrones.”

Difficult but Accessible: Games like Another Crab’s Treasure  are questioning whether fiendish challenges are an intrinsic feature of the Soulslike genre.

Vibrant African Myths: Tales of Kenzera: Zau  is both a paean to one son’s paternal memories and an engrossing Metroidvania, our critic says.

• Campus Crime Stats
• Scholarship First Agenda
• Our Achievements
• Our Community

Our Leadership

• Board of Supervisors
• Administration

Our Commitment

• Division of Engagement, Civil Rights & Title IX

Our Campuses

• Baton Rouge
• Pennington Biomedical
• LSU Health New Orleans
• LSU Health Shreveport

Programs & Information

• Certificate Programs
• Academic Programs Abroad
• Academic Calendar
• General Catalog

Academic Offices

• Academic Affairs
• University Registrar
• International Programs

Colleges & Schools

• College of Agriculture
• College of Art & Design
• E. J. Ourso College of Business
• College of Coast & Environment
• College of Human Sciences & Education
• College of Humanities & Social Sciences
• Manship School of Mass Communication
• College of Music & Dramatic Arts
• College of Engineering
• School of Veterinary Medicine
• Roger Hadfield Ogden Honors College
• University College
• LSU Paul M. Hebert Law Center
• Pinkie Gordon Lane Graduate School
• College of Science
• An Elite and Historic University
• Academic Excellence
• A Vibrant Community
• Lots of Ways to Get Involved
• Help When You Need It
• Financial Aid & Scholarships

Ready to Apply?

• Undergraduate Admissions
• Honors College
• Graduate School Admissions
• Professional Schools
• Request More Information
• Plan a Visit
• Estimated Cost

• Student Affairs
• Center for Advising & Counseling
• Disability Services
• Student Health Center
• Student Financial Management Center
• Campus Safety
• Code of Student Conduct
• Campus Life
• Residential Life
• University Recreation
• Campus Dining
• Events Calendar
• Orientation
• Center for Freshman Year
• Campus Bookstore
• Center for Academic Success
• Geaux Communicate
• Olinde Career Center
• Office of Retention & Student Success
• Student Engagement & Impact

Get Involved

• How to Do LSU
• Organizations
• Student Government
• Research & Economic Development
• Industry & Business
• LSU Innovation
• LSU Discover
• GeauxGrants

Initiatives

• Artificial Intelligence
• Cybersecurity
• Energy Innovation

Communications

• Latest News
• Working for Louisiana
• Research Highlights
• Research Magazine
• LSU Science Café

Online Degrees

• Discover LSU Online
• Master's Degrees
• Graduate Certificates
• Bachelor's Degrees
• Associate Degrees

More Information

• Online Certificates / MicroCreds®
• Professional Development
• Online Distance Learning
• Pre-College Programs

LSU Shreveport Students with Math, Computer Skills to Help Air Force Tackle Real-Life Problems

May 08, 2024

LSU Shreveport students Eliana Gafford and Joseph Barnes sign fellowship papers.

Two LSU Shreveport students will assist the Air Force in generating solutions to real-world problems as part of the National Security Fellowship Program with the Air Force Global Strike Command on Barksdale Air Force Base.

Eliana Gafford and Joseph Barnes, who both have strong family ties to the military, are the first LSUS students selected for the year-long program , which targets students with skills in computer science, mathematics, and other related fields.

“I wanted to work with (Barksdale AFB) to help airmen and help my country,” said Gafford, a computer science junior whose father served in the Army. “I wanted to serve my country, and I’m happy to help in any way, shape or form that I can.” 

Barnes is a mathematics major with computer science interest whose brother is serving overseas in the Air Force. “(Airmen) out there have it really rough, and I’d love to have a hand in using technology to assist them and make their lives a little bit easier,” he said.

The National Security Fellowship begins June 3 with the students working full-time this summer and then part-time as they resume classes in the fall and spring semesters. The AFGSC, headquartered in Barksdale, is responsible for two-thirds of the United States’ nuclear arsenal with the intercontinental ballistic missile wings and the Air Force’s entire bomber force.

LSU's Scholarship First Agenda is helping achieve health, prosperity, and security for Louisiana and the world.

POPULAR SEARCHES:

Video Modal

What a lovely hat

Is it made out of tin foil , paper 2024/712, quantum nv sieve on grover for solving shortest vector problem.

Quantum computers can efficiently model and solve several challenging problems for classical computers, raising concerns about potential security reductions in cryptography. NIST is already considering potential quantum attacks in the development of post-quantum cryptography by estimating the quantum resources required for such quantum attacks. In this paper, we present quantum circuits for the NV sieve algorithm to solve the Shortest Vector Problem (SVP), which serves as the security foundation for lattice-based cryptography, achieving a quantum speedup of the square root. Although there has been extensive research on the application of quantum algorithms for lattice-based problems at the theoretical level, specific quantum circuit implementations for them have not been presented yet. Notably, this work demonstrates that the required quantum complexity for the SVP in the lattice of rank 70 and dimension 70 is $2^{43}$ (a product of the total gate count and the total depth) with our optimized quantum implementation of the NV sieve algorithm. This complexity is significantly lower than the NIST post-quantum security standard, where level 1 is $2^{157}$, corresponding to the complexity of Grover's key search for AES-128.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

18.1: Solving Problems with Newton's Laws (Part 1)

• Last updated
• Save as PDF
• Page ID 85846

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Success in problem solving is necessary to understand and apply physical principles. We developed a pattern of analyzing and setting up the solutions to problems involving Newton’s laws in Newton’s Laws of Motion ; in this chapter, we continue to discuss these strategies and apply a step-by-step process.

Problem-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, but we emphasize specific strategies that are useful in applying Newton’s laws of motion. Once you identify the physical principles involved in the problem and determine that they include Newton’s laws of motion, you can apply these steps to find a solution. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy: Applying Newton’s Laws of Motion

• Identify the physical principles involved by listing the givens and the quantities to be calculated.
• Sketch the situation, using arrows to represent all forces.
• Determine the system of interest, and draw a free body diagram.
• Apply Newton’s second law to solve the problem. If necessary, apply appropriate kinematic equations from the chapter on motion along a straight line.
• Check the solution to see whether it is reasonable.

Let’s apply this problem-solving strategy to the challenge of lifting a grand piano into a second-story apartment. Once we have determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation. Such a sketch is shown in Figure \(\PageIndex{1a}\). Then, as in Figure \(\PageIndex{1b}\), we can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

Figure \(\PageIndex{1}\): (a) A grand piano is being lifted to a second-story apartment. (b) Arrows are used to represent all forces: \(\vec{T}\) is the tension in the rope above the piano, \(\vec{F}_{T}\) is the force that the piano exerts on the rope, and \(\vec{w}\) is the weight of the piano. All other forces, such as the nudge of a breeze, are assumed to be negligible. (c) Suppose we are given the piano’s mass and asked to find the tension in the rope. We then define the system of interest as shown and draw a free-body diagram. Now \(\vec{F}_{T}\) is no longer shown, because it is not a force acting on the system of interest; rather, \(\vec{F}_{T}\) acts on the outside world. (d) Showing only the arrows, the head-to-tail method of addition is used. It is apparent that if the piano is stationary, \(\vec{T}\) = \(- \vec{w}\).

As with most problems, we next need to identify what needs to be determined and what is known or can be inferred from the problem as stated, that is, make a list of knowns and unknowns. It is particularly crucial to identify the system of interest, since Newton’s second law involves only external forces. We can then determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure \(\PageIndex{1c}\).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton’s Laws of Motion , the system of interest depends on the question we need to answer. Only forces are shown in free-body diagrams, not acceleration or velocity. We have drawn several free-body diagrams in previous worked examples. Figure \(\PageIndex{1c}\) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is drawn, we apply Newton’s second law. This is done in Figure \(\PageIndex{1d}\) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. We do this by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known. Generally, just write Newton’s second law in components along the different directions. Then, you have the following equations:

\[\sum F_{x} = m a_{x}, \quad \sum F_{y} = m a_{y}\ldotp\]

(If, for example, the system is accelerating horizontally, then you can then set ay = 0.) We need this information to determine unknown forces acting on a system.

As always, we must check the solution. In some cases, it is easy to tell whether the solution is reasonable. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an answer is reasonable. Another way to check a solution is to check the units. If we are solving for force and end up with units of millimeters per second, then we have made a mistake.

There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills. We look first at problems involving particle equilibrium, which make use of Newton’s first law, and then consider particle acceleration, which involves Newton’s second law.

Particle Equilibrium

Recall that a particle in equilibrium is one for which the external forces are balanced. Static equilibrium involves objects at rest, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these conditions are relative. For example, an object may be at rest when viewed from our frame of reference, but the same object would appear to be in motion when viewed by someone moving at a constant velocity. We now make use of the knowledge attained in Newton’s Laws of Motion , regarding the different types of forces and the use of free-body diagrams, to solve additional problems in particle equilibrium.

Example \(\PageIndex{1}\): Different Tensions at Different Angles

Consider the traffic light (mass of 15.0 kg) suspended from two wires as shown in Figure \(\PageIndex{2}\). Find the tension in each wire, neglecting the masses of the wires.

Figure \(\PageIndex{2}\): A traffic light is suspended from two wires. (b) Some of the forces involved. (c) Only forces acting on the system are shown here. The free-body diagram for the traffic light is also shown. (d) The forces projected onto vertical (y) and horizontal (x) axes. The horizontal components of the tensions must cancel, and the sum of the vertical components of the tensions must equal the weight of the traffic light. (e) The free-body diagram shows the vertical and horizontal forces acting on the traffic light.

The system of interest is the traffic light, and its free-body diagram is shown in Figure \(\PageIndex{2c}\). The three forces involved are not parallel, and so they must be projected onto a coordinate system. The most convenient coordinate system has one axis vertical and one horizontal, and the vector projections on it are shown in Figure \(\PageIndex{2d}\). There are two unknowns in this problem (T 1 and T 2 ), so two equations are needed to find them. These two equations come from applying Newton’s second law along the vertical and horizontal axes, noting that the net external force is zero along each axis because acceleration is zero.

First consider the horizontal or x-axis:

\[F_{net x} = T_{2x} - T_{1x} = 0 \ldotp\]

Thus, as you might expect,

\[T_{1x} = T_{2x} \ldotp\]

This give us the following relationship:

\[T_{1} \cos 30^{o} = T_{2} \cos 45^{o} \ldotp\]

\[T_{2} = 1.225 T_{1} \ldotp\]

Note that T 1 and T 2 are not equal in this case because the angles on either side are not equal. It is reasonable that T 2 ends up being greater than T 1 because it is exerted more vertically than T 1 .

Now consider the force components along the vertical or y-axis:

\[F_{net y} = T_{1y} + T_{1x} - w = 0 \ldotp\]

This implies

\[T_{1y} + T_{2y} = w \ldotp\]

Substituting the expressions for the vertical components gives

\[T_{1} \sin 30^{o} + T_{2} \sin 45^{o} = w \ldotp\]

There are two unknowns in this equation, but substituting the expression for T 2 in terms of T 1 reduces this to one equation with one unknown:

\[T_{1} (0.500) + (1.225 T_{1})(0.707) = w = mg,\]

which yields

\[1.366 T_{1} = (15.0\; kg)(9.80\; m/s^{2}) \ldotp\]

Solving this last equation gives the magnitude of T 1 to be

\[T_{1} = 108\; N \ldotp\]

Finally, we find the magnitude of T 2 by using the relationship between them, T 2 = 1.225 T 1 , found above. Thus we obtain

\[T_{2} = 132\; N \ldotp\]

Significance

Both tensions would be larger if both wires were more horizontal, and they will be equal if and only if the angles on either side are the same (as they were in the earlier example of a tightrope walker in Newton’s Laws of Motion .)

Example \(\PageIndex{2}\): Drag Force on a Barge

Two tugboats push on a barge at different angles (Figure \(\PageIndex{3}\)). The first tugboat exerts a force of 2.7 x 10 5 N in the x-direction, and the second tugboat exerts a force of 3.6 x 10 5 N in the y-direction. The mass of the barge is 5.0 × 10 6 kg and its acceleration is observed to be 7.5 x 10 −2 m/s 2 in the direction shown. What is the drag force of the water on the barge resisting the motion? ( Note : Drag force is a frictional force exerted by fluids, such as air or water. The drag force opposes the motion of the object. Since the barge is flat bottomed, we can assume that the drag force is in the direction opposite of motion of the barge.)

Figure \(\PageIndex{3}\): (a) A view from above of two tugboats pushing on a barge. (b) The free-body diagram for the ship contains only forces acting in the plane of the water. It omits the two vertical forces—the weight of the barge and the buoyant force of the water supporting it cancel and are not shown. Note that \(\vec{F}_{app}\) is the total applied force of the tugboats.

The directions and magnitudes of acceleration and the applied forces are given in Figure \(\PageIndex{3a}\). We define the total force of the tugboats on the barge as \(\vec{F}_{app}\) so that

\[\vec{F}_{app} = \vec{F}_{1} + \vec{F}_{2} \ldotp\]

The drag of the water \(\vec{F}_{D}\) is in the direction opposite to the direction of motion of the boat; this force thus works against \(\vec{F}_{app}\), as shown in the free-body diagram in Figure \(\PageIndex{3b}\). The system of interest here is the barge, since the forces on it are given as well as its acceleration. Because the applied forces are perpendicular, the x- and y-axes are in the same direction as \(\vec{F}_{1}\) and \(\vec{F}_{2}\). The problem quickly becomes a one-dimensional problem along the direction of \(\vec{F}_{app}\), since friction is in the direction opposite to \(\vec{F}_{app}\). Our strategy is to find the magnitude and direction of the net applied force \(\vec{F}_{app}\) and then apply Newton’s second law to solve for the drag force \(\vec{F}_{D}\).

Since F x and F y are perpendicular, we can find the magnitude and direction of \(\vec{F}_{app}\) directly. First, the resultant magnitude is given by the Pythagorean theorem:

\[ \vec{F}_{app} = \sqrt{F_{1}^{2} + F_{2}^{2}} = \sqrt{(2.7 \times 10^{5}\; N)^{2} + (3.6 \times 10^{5}\; N)^{2}} = 4.5 \times 10^{5} \; N \ldotp\]

The angle is given by

\[\theta = \tan^{-1} \left(\dfrac{F_{2}}{F_{1}}\right) = \tan^{-1} \left(\dfrac{3.6 \times 10^{5}\; N}{2.7 \times 10^{5}\; N}\right) = 53.1^{o} \ldotp\]

From Newton’s first law, we know this is the same direction as the acceleration. We also know that \(\vec{F}_{D}\) is in the opposite direction of \(\vec{F}_{app}\), since it acts to slow down the acceleration. Therefore, the net external force is in the same direction as \(\vec{F}_{app}\), but its magnitude is slightly less than \(\vec{F}_{app}\). The problem is now one-dimensional. From the free-body diagram, we can see that

\[F_{net} = F_{app} - F_{D} \ldotp\]

However, Newton's second law states that

\[F_{net} = ma \ldotp\]

\[F_{app} - F_{D} = ma \ldotp\]

This can be solved for the magnitude of the drag force of the water F D in terms of known quantities:

\[F_{D} = F_{app} - ma \ldotp\]

Substituting known values gives

\[F_{D} = (4.5 \times 10^{5}\; N) - (5.0 \times 10^{6}\; kg)(7.5 \times 10^{-2}\; m/s^{2}) = 7.5 \times 10^{4}\; N \ldotp\]

The direction of \(\vec{F}_{D}\) has already been determined to be in the direction opposite to \(\vec{F}_{app}\), or at an angle of 53° south of west.

The numbers used in this example are reasonable for a moderately large barge. It is certainly difficult to obtain larger accelerations with tugboats, and small speeds are desirable to avoid running the barge into the docks. Drag is relatively small for a well-designed hull at low speeds, consistent with the answer to this example, where F D is less than 1/600th of the weight of the ship.

In Newton’s Laws of Motion , we discussed the normal force, which is a contact force that acts normal to the surface so that an object does not have an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride?

Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed? Take a guess before reading the next example.

Example \(\PageIndex{3}\): What does the Bathroom Scale Read in an Elevator?

Figure \(\PageIndex{4}\) shows a 75.0-kg man (weight of about 165 lb.) standing on a bathroom scale in an elevator. Calculate the scale reading: (a) if the elevator accelerates upward at a rate of 1.20 m/s 2 , and (b) if the elevator moves upward at a constant speed of 1 m/s.

Figure \(\PageIndex{4}\): (a) The various forces acting when a person stands on a bathroom scale in an elevator. The arrows are approximately correct for when the elevator is accelerating upward—broken arrows represent forces too large to be drawn to scale. \(\vec{T}\) is the tension in the supporting cable, \(\vec{w}\) is the weight of the person, \(\vec{w}_{s}\) is the weight of the scale, \(\vec{w}_{e}\) is the weight of the elevator, \(\vec{F}_{s}\) is the force of the scale on the person, \(\vec{F}_{p}\) is the force of the person on the scale, \(\vec{F}_{t}\) is the force of the scale on the floor of the elevator, and \(\vec{N}\) is the force of the floor upward on the scale. (b) The free-body diagram shows only the external forces acting on the designated system of interest—the person—and is the diagram we use for the solution of the problem.

If the scale at rest is accurate, its reading equals \(\vec{F}_{p}\), the magnitude of the force the person exerts downward on it. Figure \(\PageIndex{4a}\) shows the numerous forces acting on the elevator, scale, and person. It makes this one-dimensional problem look much more formidable than if the person is chosen to be the system of interest and a free-body diagram is drawn, as in Figure \(\PageIndex{4b}\). Analysis of the free-body diagram using Newton’s laws can produce answers to both Figure \(\PageIndex{4a}\) and (b) of this example, as well as some other questions that might arise. The only forces acting on the person are his weight \(\vec{w}\) and the upward force of the scale \(\vec{F}_{s}\). According to Newton’s third law, \(\vec{F}_{p}\) and \(\vec{F}_{s}\) are equal in magnitude and opposite in direction, so that we need to find F s in order to find what the scale reads. We can do this, as usual, by applying Newton’s second law,

\[\vec{F}_{net} = m \vec{a} \ldotp\]

From the free-body diagram, we see that \(\vec{F}_{net} = \vec{F}_{s} - \vec{w}\), so we have

\[F_{s} - w = ma \ldotp\]

Solving for F s gives us an equation with only one unknown:

\[F_{s} = ma + w,\]

or, because w = mg, simply

\[F_{s} = ma + mg \ldotp\]

No assumptions were made about the acceleration, so this solution should be valid for a variety of accelerations in addition to those in this situation. ( Note : We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton’s second law becomes F s − w = −ma.)

• We have a = 1.20 m/s 2 , so that $F_{s} = (75.0\; kg)(9.80\; m/s^{2}) + (75.0\; kg)(1.20\; m/s^{2})$yielding $F_{s} = 825\; N \ldotp$
• Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more than his weight? For any constant velocity—up, down, or stationary—acceleration is zero because \(a = \frac{\Delta v}{\Delta t}\) and \(\Delta v = 0\). Thus, $F_{s} = ma + mg = 0 + mg$or $F_{s} = (75.0\; kg)(9.80\; m/s^{2}),$which gives $F_{s} = 735\; N \ldotp$

The scale reading in Figure \(\PageIndex{4a}\) is about 185 lb. What would the scale have read if he were stationary? Since his acceleration would be zero, the force of the scale would be equal to his weight:

\[F_{net} = ma = 0 = F_{s} − w\]

\[F_{s} = w = mg\]

\[F_{s} = (75.0\; kg)(9.80\; m/s^{2}) = 735\; N \ldotp\]

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward.

Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In Figure \(\PageIndex{4b}\), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

Exercise \(\PageIndex{4}\)

Now calculate the scale reading when the elevator accelerates downward at a rate of 1.20 m/s 2 .

The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person’s weight. If the elevator is in free fall and accelerating downward at g, then the scale reading is zero and the person appears to be weightless.

Example \(\PageIndex{5}\): Two Attached Blocks

Figure \(\PageIndex{5}\) shows a block of mass m 1 on a frictionless, horizontal surface. It is pulled by a light string that passes over a frictionless and massless pulley. The other end of the string is connected to a block of mass m 2 . Find the acceleration of the blocks and the tension in the string in terms of m 1 , m 2 , and g.

Figure \(\PageIndex{5}\): (a) Block 1 is connected by a light string to block 2. (b) The free-body diagrams of the blocks.

We draw a free-body diagram for each mass separately, as shown in Figure \(\PageIndex{5}\). Then we analyze each one to find the required unknowns. The forces on block 1 are the gravitational force, the contact force of the surface, and the tension in the string. Block 2 is subjected to the gravitational force and the string tension. Newton’s second law applies to each, so we write two vector equations:

For block 1: \(\vec{T} + \vec{w}_{1} + \vec{N} = m_{1} \vec{a}_{1}\)

For block 2: \(\vec{T} + \vec{w}_{2} = m_{2} \vec{a}_{2}\).

Notice that \(\vec{T}\) is the same for both blocks. Since the string and the pulley have negligible mass, and since there is no friction in the pulley, the tension is the same throughout the string. We can now write component equations for each block. All forces are either horizontal or vertical, so we can use the same horizontal/vertical coordinate system for both objects.

The component equations follow from the vector equations above. We see that block 1 has the vertical forces balanced, so we ignore them and write an equation relating the x-components. There are no horizontal forces on block 2, so only the y-equation is written. We obtain these results:

When block 1 moves to the right, block 2 travels an equal distance downward; thus, a 1x = −a 2y . Writing the common acceleration of the blocks as a = a 1x = −a 2y , we now have

\[T = m_{1}a\]

\[T − m_{2}g = −m_{2}a \ldotp\]

From these two equations, we can express a and T in terms of the masses m 1 and m 2 , and g:

\[a = \frac{m_{2}}{m_{1} + m_{2}}g\]

\[T = \frac{m_{1} m_{2}}{m_{1} + m_{2}} g \ldotp\]

Notice that the tension in the string is less than the weight of the block hanging from the end of it. A common error in problems like this is to set T = m 2 g. You can see from the free-body diagram of block 2 that cannot be correct if the block is accelerating.

Check Your Understanding \(\PageIndex{6}\)

Calculate the acceleration of the system, and the tension in the string, when the masses are m 1 = 5.00 kg and m 2 = 3.00 kg.

Example \(\PageIndex{7}\): Atwood Machine

A classic problem in physics, similar to the one we just solved, is that of the Atwood machine, which consists of a rope running over a pulley, with two objects of different mass attached. It is particularly useful in understanding the connection between force and motion. In Figure \(\PageIndex{6}\), m 1 = 2.00 kg and m 2 = 4.00 kg. Consider the pulley to be frictionless. (a) If m 2 is released, what will its acceleration be? (b) What is the tension in the string?

Figure \(\PageIndex{6}\): An Atwood machine and free-body diagrams for each of the two blocks.

We draw a free-body diagram for each mass separately, as shown in the figure. Then we analyze each diagram to find the required unknowns. This may involve the solution of simultaneous equations. It is also important to note the similarity with the previous example. As block 2 accelerates with acceleration a 2 in the downward direction, block 1 accelerates upward with acceleration a 1 . Thus, a = a 1 = −a 2 .

• We have $For\; m_{1}, \sum F_{y} = T − m_{1}g = m_{1}a \ldotp \quad For\; m_{2}, \sum F_{y} = T − m_{2}g = −m_{2}a \ldotp$(The negative sign in front of m 2 a indicates that m 2 accelerates downward; both blocks accelerate at the same rate, but in opposite directions.) Solve the two equations simultaneously (subtract them) and the result is $(m_{2} - m_{1})g = (m_{1} + m_{2})a \ldotp$Solving for a: $a = \frac{m_{2} - m_{1}}{m_{1} + m_{2}}g = \frac{4\; kg - 2\; kg}{4\; kg + 2\; kg} (9.8\; m/s^{2}) = 3.27\; m/s^{2} \ldotp$
• Observing the first block, we see that $T − m_{1}g = m_{1}a$ $T = m_{1}(g + a) = (2\; kg)(9.8\; m/s^{2} + 3.27\; m/s^{2}) = 26.1\; N \ldotp$

The result for the acceleration given in the solution can be interpreted as the ratio of the unbalanced force on the system, (m 2 − m 1 )g, to the total mass of the system, m 1 + m 2 . We can also use the Atwood machine to measure local gravitational field strength.

Exercise 6.3

Determine a general formula in terms of m 1 , m 2 and g for calculating the tension in the string for the Atwood machine shown above.