what are the steps in solving problems on direct proportion

Direct & Inverse Proportions/Variations

In these lessons, we will learn how to solve direct proportions (variations) and inverse proportions (inverse variations) problems. (Note: Some texts may refer to inverse proportions/variations as indirect proportions/variations.)

Related Pages: Direct Variations Proportion Word Problems More Algebra Lessons

The following diagram gives the steps to solve ratios and direct proportion word problems. Scroll down the page for examples and step-by-step solutions.

Direct Proportions/Variations

Knowing that the ratio does not change allows you to form an equation to find the value of an unknown variable.

Example : If two pencils cost $1.50, how many pencils can you buy with $9.00?

How To Solve Directly Proportional Questions?

Example 1: F is directly proportional to x. When F is 6, x is 4. Find the value of F when x is 5. Example 2: A is directly proportional to the square of B. When A is 10, B is 2. Find the value of A when B is 3.

How To Use Direct Proportion?

How To Solve Word Problems Using Proportions?

This video shows how to solve word problems by writing a proportion and solving 1. A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour, how much sugar do I use? 2. A syrup is made by dissolving 2 cups of sugar in 2/3 cups of boiling water. How many cups of sugar should be used for 2 cups of boiling water? 3. A school buys 8 gallons of juice for 100 kids. how many gallons do they need for 175 kids?

Solving More Word Problems Using Proportions

1. On a map, two cities are 2 5/8 inches apart. If 3/8 inches on the map represents 25 miles, how far apart are the cities (in miles)? 2. Solve for the sides of similar triangles using proportions

Inverse Proportions/Variations Or Indirect Proportions

Two values x and y are inversely proportional to each other when their product xy is a constant (always remains the same). This means that when x increases y will decrease, and vice versa, by an amount such that xy remains the same.

Knowing that the product does not change also allows you to form an equation to find the value of an unknown variable

Example : It takes 4 men 6 hours to repair a road. How long will it take 8 men to do the job if they work at the same rate?

Solution : The number of men is inversely proportional to the time taken to do the job. Let t be the time taken for the 8 men to finish the job. 4 × 6 = 8 × t 24 = 8t t = 3 hours

Usually, you will be able to decide from the question whether the values are directly proportional or inversely proportional.

How To Solve Inverse Proportion Questions?

This video shows how to solve inverse proportion questions. It goes through a couple of examples and ends with some practice questions Example 1: A is inversely proportional to B. When A is 10, B is 2. Find the value of A when B is 8 Example 2: F is inversely proportional to the square of x. When A is 20, B is 3. Find the value of F when x is 5.

How To Use Inverse Proportion To Work Out Problems?

How to use a more advanced form of inverse proportion where the use of square numbers is involved.

More examples to explain direct proportions / variations and inverse proportions / variations

How to solve Inverse Proportion Math Problems on pressure and volume?

In math, an inverse proportion is when an increase in one quantity results in a decrease in another quantity. This video will show how to solve an inverse proportion math problem. Example : The pressure in a piston is 2.0 atm at 25°C and the volume is 4.0L. If the pressure is increased to 6.0 atm at the same temperature, what will be the volume?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Direct Proportion

Direct proportion is a mathematical comparison between two numbers where the ratio of the two numbers is equal to a constant value. The proportion definition says that when two ratios are equivalent, they are in proportion. The symbol used to relate the proportions is "∝". Let us learn more about direct proportion in this article.

Direct Proportion Definition

The definition of direct proportion states that "When the relationship between two quantities is such that if we increase one, the other will also increase, and if we decrease one the other quantity will also decrease, then the two quantities are said to be in a direct proportion". For example, if there are two quantities x and y where x = number of candies and y = total money spent. If we buy more candies, we will have to pay more money, and we buy fewer candies then we will be paying less money. So, here we can say that x and y are directly proportional to each other. It is represented as x ∝ y. Direct proportion is also known as direct variation.

Some real-life examples of direct proportionality are given below:

• The number of food items is directly proportional to the total money spent.
• Work done is directly proportional to the number of workers.
• Speed is in direct proportion to the distance w.r.t a fixed time.

Direct Proportion Formula

The direct proportion formula says if the quantity y is in direct proportion to quantity x, then we can say y = kx, for a constant k. y = kx is also the general form of the direct proportion equation.

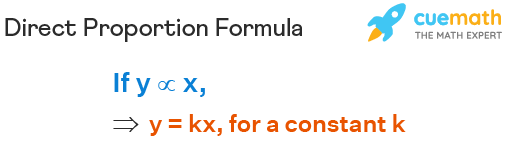
• k is the constant of proportionality .
• y increases as x increases.
• y decreases as x decreases.

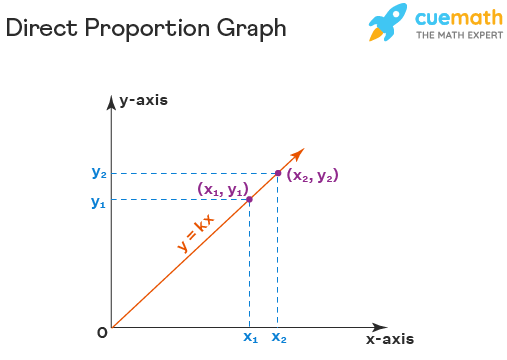
Direct Proportion Graph

The graph of direct proportion is a straight line with an upward slope . Look at the image given below. There are two points marked on the x-axis and two on the y-axis, where (x) 1 < (x) 2 and (y) 2 < (y) 2 . If we increase the value of x from (x) 1 to (x) 2 , we observe that the value of y is also increased from (y) 1 to (y) 2 . Thus, the line y=kx represents direct proportionality graphically.

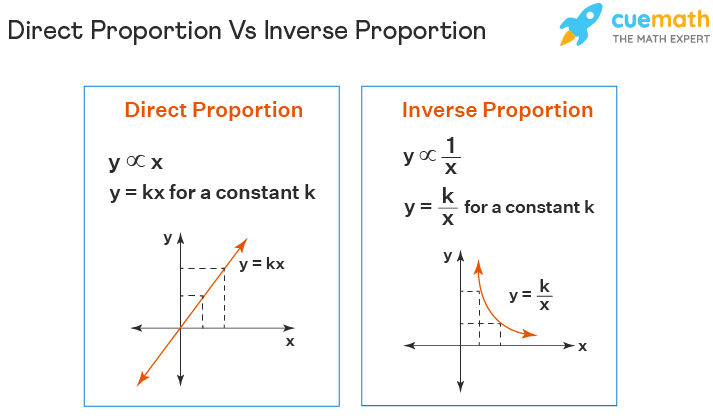
Direct Proportion Vs Inverse Proportion

There are two types of proportionality that can be established based on the relation between the two given quantities. Those are direct proportion and inverse proportional. Two quantities are directly proportional to each other when an increase or decrease in one leads to an increase or decrease in the other. While on the other hand, two quantities are said to be in inverse proportion if an increase in one quantity leads to a decrease in the other, and vice-versa. The graph of direct proportion is a straight line while the inverse proportion graph is a curve. Look at the image given below to understand the difference between direct proportion and inverse proportion.

Topics Related to Direct Proportion

Check these interesting articles related to the concept of direct proportion.

• Constant of Proportionality
• Inversely Proportional
• Percent Proportion

Direct Proportion Examples

Example 1: Let us assume that y varies directly with x, and y = 36 when x = 6. Using the direct proportion formula, find the value of y when x = 80?

Using the direct proportion formula, y = kx Substitute the given x and y values, and solve for k. 36 = k × 6 k = 36/6 = 6 The direct proportion equation is: y = 6x Now, substitute x = 80 and find y. y = 6 × 80 = 480

Answer: The value of y is 480.

Example 2: If the cost of 8 pounds of apples is $10, what will be the cost of 32 pounds of apples?

It is given that, Weight of apples = 8 lb Cost of 8 lb apples = $10 Let us consider the weight by x parameter and cost by y parameter. To find the cost of 32 lb apples, we will use the direct proportion formula. y=kx 10 = k × 8 (on substituting the values) k = 5/4 Now putting the value of k = 5/4 when x = 32 we have, The cost of 32 lb apples = 5/4 × 32 y =5×8 y = 40

Answer: The cost of 32 lb apples is $40 .

Example 3: Henry gets $300 for 50 hours of work. How many hours has he worked if he got $258?

Solution: Let the amount received by Henry be treated as y and the number of hours he worked as x. Substitute the given x and y values in the direct proportion formula, we get, 300 = k × 50

⇒ k=300/50 k = 6 The equation is: y = 6x. Now, substitute y = 258 and find x. 258 = 6 × x

⇒ x = 258/6 = 43 hours Therefore, if Henry got $258, he worked for 43 hours.

go to slide go to slide go to slide

Book a Free Trial Class

Direct Proportion Practice Questions

go to slide go to slide

FAQs on Direct Proportion

What is direct proportion in maths.

Two quantities are said to be in direct proportion if an increase in one also leads to an increase in the other quantity, and vice-versa. For example, if a ∝ b, this implies if 'a' increases, 'b' will also increase, and if 'a' decreases, 'b' will also decrease.

What Is the Symbol ∝ Denotes in Direct Proportion Formula?

In the direct proportion formula, the proportionate symbol ∝ denotes the relationship between two quantities. It is expressed as y ∝ x, and can be written in an equation as y = kx, for a constant k.

What is Direct Proportion and Inverse Proportion?

Direct proportion, as the name suggests, indicates that an increase in one quantity will also increase the value of the other quantity and a decrease in one quantity will also decrease the value of the other quantity. While inverse proportion shows an inverse relationship between the two given quantities. It means an increase in one will decrease the value of the other quantity and vice-versa.

How do you Represent the Direct Proportional Formula?

The direct proportional formula depicts the relationship between two quantities and can be understood by the steps given below:

• Identify the two quantities which vary in the given problem.
• Identify the variation as the direct variation .
• Direct proportion formula: y ∝ kx.

What is a Direct Proportion Equation?

The equation of direct proportionality is y = kx, where x and y are the given quantities and k is any constant value. Some examples of direct proportional equations are y = 3x, m = 10n, 10p = q, etc.

How to Solve Direct Proportion Problems?

To solve direct proportion word problems, follow the steps given below:

• Make sure that the variation is directly proportional.
• Form an equation in terms of y = kx and find the value of k base on the given values of x and y.
• Find the unknown value by putting the values of x and the known variable.

How to Show Relationship Between Two Quantities Using Direct Proportion Formula?

The directly proportional relationship between two quantities can figure out using the following key points.

• Identify the two quantities given in the problem.
• If x/y is constant then the quantities have a directly proportional relationship.

Direct Proportion: Definition, Formula, Symbol, Examples, FAQs

What is direct proportion in math, difference between direct proportion and inverse proportion, how to use direct proportion to solve problems, solved examples of direct proportion, practice problems on direct proportion, frequently asked questions about direct proportion.

Direct proportion or direct variation is a type of proportion in which the ratio of two quantities stays constant. 

Suppose a variable y varies directly with x, then it means that if x increases, y increases by the same factor. If x decreases, then there is a proportionate decrease in y also.

Direct Proportion Example: 

The cost of the candy increases as the number of the same increases.

Direct Proportion Symbol

The “directly proportional symbol” or “direct proportional symbol” is $\propto$. 

We read x ∝ y as “x is directly proportional to y.” 

It means that x is dependent on y.

We read y ∝ x as “y is directly proportional to x.” 

It means that y is dependent on x.

Direct Proportion Formula

If y is directly proportional to x, then the direct proportion formula or the direct proportion equation is given by y=kx, where k is a constant of proportionality.

Constant of Proportionality

From the direct proportion formula, we have y = kx.

The fixed value $k = \frac{y}{x}$ is called the constant of proportionality and it represents the constant ratio between the two quantities that are in direct proportion. k can be any non-zero real number.

Direct Proportion Graph

If you construct a graph of a direct proportion, it always comes out to be a straight line passing through the origin (0, 0).

The slope of this line is k.

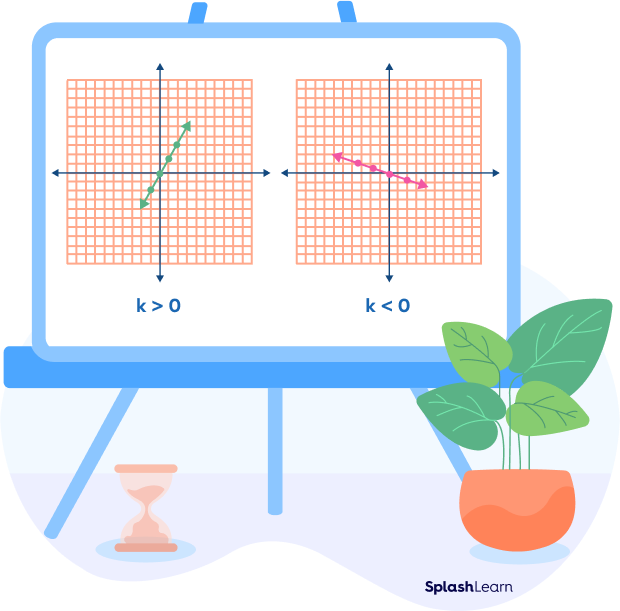
• If k is negative, the line goes down from left to right.
• If k is positive, the line rises from left to right.

Direct proportion and inverse proportion are two kinds of proportional relationships in math describing the relation between two variables. Here are their key differences in the table below:

Let’s understand this with the help of an example.

Example: If 20 pens cost $25, what would be the cost of 100 pens?

Here, the cost of pens is directly proportional to the number of pens.

Note down the given values of x and y. 

Since the quantities are in direct proportion, their ratio is constant.

$\frac{20}{25} = \frac{100}{?}$

By cross multiplying, we get

$20 \times ?= 100 \times 25$

? $= \$125$

100 pens will cost $\$125$.

Facts about Direct Proportion

• Prior to $\propto$ (symbol), a double colon (::) was used.
• The proportionality symbol $(\propto)$ was used by William Emerson (London, 1768) for the first time.
• The link between the two variables is no longer a direct proportion if the proportionality ratio changes.

In this article, we learned about direct proportion, its graph, formula, equation, and examples. Let’s solve a few examples and practice problems to understand the concept better.

1. If 8 rooms are required for 24 guests, how many rooms would be required to accommodate 12 guests?

Here, $\frac{24}{8} = \frac{w}{12}$

Cross-multiply:

$w \times 8 = 12 \times 24$

Therefore, for 12 guests, a total of 36 rooms will be required. 

2. If 4 tasks take 8 hours for completion, how many tasks can be completed in 20 hours?

Let’s write the constant ratios.

$\frac{4}{8} = \frac{n}{20}$

In 20 hours, 10 tasks can be completed.

3. What will 10 movie tickets cost if the price of 6 tickets is $\$36$ ?

6 tickets cost $\$36$.

Let 10 movie tickets cost $y.

$\frac{6}{36} = \frac{10}{6}$

$y \times 6 = 36 \times 10$

4. If a task is completed in 20 days by 5 workers, how long will it take 10 workers to perform the same task?

Solution:  

This problem can again be solved using the direct proportion formula.

Let the number of days for 10 workers to complete the task be x.

$\frac{5}{10} = \frac{20}{x}$

Cross-multiply

$5x = 10 \times 20$

$x = \frac{(10 \times 20)}{5}$

Therefore, 10 workers will require 40 days to complete the same task.

5. How far can John run in 60 minutes if he can cover 9 miles in 90?

Solution: 

Use the direct proportion formula for this problem.

Let the distance John covers in 60 minutes be x.

$\frac{9}{90} = \frac{x}{60}$

Cross-multiply.

$\frac{9 \times 60} = 90x$

$x = \frac{(9 \times 60)}{90}$

Therefore, John can run 6 miles in an hour.

Attend this quiz & Test your knowledge.

If x is directly proportional to y, we write it as

If a car travels 75 miles on 3 gallons of gas, how many miles can it travel on 5 gas gallons, the graph for direct proportionality is, on the graph of a direct proportion, the constant of proportionality represents the.

Is y being inversely proportional to x the same thing as y being directly proportional to $\frac{1}{x}$ ?

Yes, y being inversely proportional to x the same thing as y being directly proportional to the reciprocal of x, which is $\frac{1}{x}$.

How do we know whether any two variables are directly proportional or not?

We can confirm the direct proportionality of any two variables if their ratio remains constant. This is expressed mathematically as $\frac{y}{x} = k$. Here, k is the constant of proportionality.

What are the uses of direct proportion?

Direct proportion is a universal concept profoundly used in different fields to explain and predict relationships between variables. The direct proportion has multiple practical uses in various fields, including mathematics, science, engineering, finance, art, population rates, and many others.

What is an independent variable and dependent variable in direct proportion?

For given two quantities, the cause and effect relationship decides the independent variable and the dependent variable. The independent variable is the cause, and the dependent variable is the variable whose value depends on the independent variable. We can define them based on the context.

is $x \propto y$ same as $y \propto x$ ?

No, these two statements are not the same. 

$x \propto y$ means that x is directly proportional to y.

$y \propto x$ means that y is directly proportional to x.

RELATED POSTS

• Average Speed Formula: Definition, Examples, Facts,  FAQs
• Decimal to Octal: Steps, Methods, Conversion Table
• Relatively Prime
• Meters to Yards Conversion – Definition, Formula, Steps, Examples
• How to Calculate Percent Difference – Definition, Formula, Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Directly Proportional and Inversely Proportional

Directly proportional: as one amount increases, another amount increases at the same rate.

Example: you are paid $20 an hour

How much you earn is directly proportional to how many hours you work

Work more hours, get more pay; in direct proportion.

This could be written:

Earnings ∝ Hours worked

• If you work 2 hours you get paid $40
• If you work 3 hours you get paid $60

Constant of Proportionality

The "constant of proportionality" is the value that relates the two amounts

Example: you are paid $20 an hour (continued)

The constant of proportionality is 20 because:

Earnings = 20 × Hours worked

This can be written:

Where k is the constant of proportionality

Example: y is directly proportional to x, and when x=3 then y=15. What is the constant of proportionality?

They are directly proportional, so:

Put in what we know (y=15 and x=3):

Solve (by dividing both sides by 3):

The constant of proportionality is 5:

When we know the constant of proportionality we can then answer other questions

Example: (continued)

What is the value of y when x = 9?

What is the value of x when y = 2?

Inversely Proportional

Example: speed and travel time.

Speed and travel time are Inversely Proportional because the faster we go the shorter the time.

• As speed goes up, travel time goes down
• And as speed goes down, travel time goes up

Example: 4 people can paint a fence in 3 hours. How long will it take 6 people to paint it? (Assume everyone works at the same rate)

It is an Inverse Proportion:

• As the number of people goes up, the painting time goes down.
• As the number of people goes down, the painting time goes up.

We can use:

• t = number of hours
• k = constant of proportionality
• n = number of people

"4 people can paint a fence in 3 hours" means that t = 3 when n = 4

So now we know:

And when n = 6:

So 6 people will take 2 hours to paint the fence.

How many people are needed to complete the job in half an hour?

So it needs 24 people to complete the job in half an hour. (Assuming they don't all get in each other's way!)

Proportional to ...

It is also possible to be proportional to a square, a cube, an exponential, or other function!

Example: Proportional to x 2

A stone is dropped from the top of a high tower.

The distance it falls is proportional to the square of the time of fall.

The stone falls 19.6 m after 2 seconds, how far does it fall after 3 seconds?

• d is the distance fallen and
• t is the time of fall

When d = 19.6 then t = 2

And when t = 3:

So it has fallen 44.1 m after 3 seconds.

Inverse Square

Inverse Square : when one value decreases as the square of the other value.

Example: light and distance

The further away we are from a light, the less bright it is.

In fact the brightness decreases as the square of the distance. Because the light is spreading out in all directions.

So a brightness of "1" at 1 meter is only "0.25" at 2 meters (double the distance leads to a quarter of the brightness), and so on.

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Direct And Indirect Proportion

Here we will learn about direct and indirect proportion, including what direct proportion is and what indirect proportion is. We will look at solving some real life word problems involving these different proportional relationships. We will also look at some GCSE maths revision and exam style questions (which are also in the IGCSE).

There are also direct and indirect proportion worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are direct and indirect proportion?

Direct and indirect proportion are two different proportional relationships. They are two ways in which quantities are related to each other.

• Direct proportion is a relationship between two quantities where as one quantity increases, so does the other quantity. 

For example,

The cost of a banana is 70p. As the number of bananas increases, so does the cost; 3 bananas would cost 3 times the cost of one banana (£2.10).

If y is directly proportional to x \ (y\propto{x}), then y=kx where k is the constant of proportionality.

Step-by-step guide: Direct proportion

• Indirect proportion (inverse proportion) is a relationship between two quantities where as one quantity increases, the other quantity decreases and vice-versa.

For example, it takes 1 worker 9 hours to dig a hole. As the number of workers increases, the number of hours it takes to dig the same hole decreases. 3 workers would take a third of the time ( 3 hours).

To calculate indirect proportion problems we need to appreciate that multiplication and division are inverse operations of each other.

Indirect proportion is sometimes known as inverse variation.

If y is indirectly proportional to x \ (y\propto\frac{1}{x}), then y=\frac{k}{x} where k is the constant of proportionality.

Step-by-step guide: Inverse proportion

How to use direct and indirect proportion

In order to answer word problems involving direct and inverse proportion:

Determine the type of proportionality relationship between the two quantities.

Calculate the constant of proportionality, k.

Calculate the unknown value.

Write the solution.

Direct and inverse proportion worksheet

Get your free direct and inverse proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Direct and indirect proportion examples

Example 1: direct proportion.

A t-shirt costs £4. How much do 5 t-shirts cost?

As the number of t-shirts increases, so does the cost. This is a direct proportion problem.

2 Calculate the constant of proportionality, k.

For direct proportion, the constant of proportionality k is the cost of one t-shirt. As this is already given (a t-shirt costs £4 ) we can say k=4 and so y=4x where y would be the total cost of x number of t-shirts.

3 Calculate the unknown value.

Substituting x=5 into y=4x, we have

4 Write the solution.

The cost of 5 t-shirts is £20.

Example 2: direct proportion

7 bags of sweets weigh 350 grams. How much do 10 bags of sweets weigh?

As the number of bags of sweets increases, so does the weight. This is a direct proportion problem.

For direct proportion, the constant of proportionality k is the weight of one bag of sweets.

Using k=\frac{y}{x} where y is the weight of a bag of sweets and x is the number of bags of sweets, we can calculate the value of k.

k=\frac{350}{7}=50

k=50 and so a bag of sweets weighs 50g and we can say y=50x.

Substituting x=10 into y=50x, we have

y=50\times{10}=500.

The weight of 10 bags of sweets is 500g.

Example 3: direct proportion

8 laps of a race track has a total of 12 \ km. What would the distance be for 20 laps of the race track?

As the number of laps of the track increases, so does the total distance. This is a direct proportion problem.

For direct proportion, the constant of proportionality k is the distance of one lap of the track.

Using k=\frac{y}{x} where y is the distance travelled and x is the number of laps, we can calculate the value of k.

k=\frac{12}{8}=1.5

k=1.5 and so one lap of the track is 1.5 \ km and we can say y=1.5x.

Substituting x=20 into y=1.5x, we have

y=1.5\times{20}=30.

The distance covered in 20 laps is 30 \ km.

Example 4: indirect proportion

A worker takes 10 days to fit a bathroom. How long would it take 2 workers to fit a bathroom?

As the number of workers increases, the time taken to fit a bathroom decreases. This is an indirect proportion problem.

For indirect proportion, the constant of proportionality k is the time it takes one person to fit a bathroom.

As one worker takes 10 days to fit a bathroom, we can say that k=10 and so we have the equation y=\frac{10}{x} where y is the time taken for x number of workers to complete a bathroom.

Substituting x=2 into y=\frac{10}{x}, we have

y=10\div{2}=5.

It takes 2 workers 5 days to complete a bathroom.

Example 5: indirect proportion

An oil tank takes 25 hours to be filled by 3 hose pipes. How long does it take 5 hose pipes to fill the same oil tank?

As the number of hose pipes increases, the time taken to fill the oil tank decreases. This is an indirect proportion problem.

For indirect proportion, the constant of proportionality k is the time it takes one hose to fill the oil tank.

Using k=xy where x is the number of hoses and y is the time taken to fill the oil tank, we can calculate the value of k.

k=3\times{25}=75

k=75 and so one hose would take 75 hours to fill the oil tank and we can say y=\frac{75}{x}.

Substituting x=5 into y=\frac{75}{x}, we have

y=75\div{5}=15.

It takes 5 hoses 15 hours to fill an oil tank.

Example 6: indirect proportion

10 computers can do a task in 15 minutes. How long does it take 3 computers to do the same task?

As the number of computers increases, the time taken to do a task decreases. This is an indirect proportion problem.

For indirect proportion, the constant of proportionality k is the time it takes one computer to complete a task.

Using k=xy where x is the number of computers and y is the time taken to complete the task, we can calculate the value of k.

k=10\times{15}=150

k=150 and so one computer would take 150 hours to complete a task and we can say y=\frac{150}{x}.

Substituting x=3 into y=\frac{150}{x}, we have

y=150\div{3}=50.

It takes 3 computers 50 hours to complete a task.

Common misconceptions

• Modelling assumption

Whenever you solve word problems for proportion you assume everything has the same value. If the question involves the costs of pencils, we assume each pencil costs the same. If the question involves the number of people working, we assume all the workers work at the same rate.

• Indirect proportion has a negative rate of change

Direct proportion is referred to as “as one value increases, so does the other”. Indirect proportion is therefore considered to be the opposite where “as one value decreases, so does the other”. This is not true. An indirectly proportional relationship shows that when one value increases, the other decreases. As a graph, this would look like a reciprocal graph.

• Indirect proportion is treated as direct proportion

For example, if 3 people take 12 hours to build a wall, 6 people take 24 hours to build the same size wall. This is not true as we assume everyone works at the same rate and so the wall should be built in less time if more people are building it. As the number of people increases, the time taken to build the wall decreases and so if we have 6 builders (double the original amount), the time it takes to build the wall should be 6 hours (half of the original amount). The type of proportion must be determined for every proportionality question.

• There may be several ways to solve problems involving proportion

There may be several ways to get the correct answer for proportion questions. Some ways are more efficient than others depending on the numbers involved.

• Take care with writing money

Money is used in some proportional word problems. If an answer is 4.1 you may be tempted to write it as £4.1, but the correct way of writing it would be £4.10.

• Take care with writing time

Time is used in some proportional word problems. If an answer is 7.25 you may be tempted to write it as 7 hours 25 minutes, but it would be 7 hours 15 minutes. (Remember there are 60 minutes in an hour).

Related lessons on direct and indirect proportion

Direct and indirect proportion is part of our series of lessons to support revision on proportion . You may find it helpful to start with the main proportion lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Directly proportional graph / inversely proportional graph
• Direct proportion
• Direct proportion formula
• Inverse proportion
• Inverse proportion formula

Practice direct and indirect proportion questions

1. One tennis ball weighs 57 grams. Find the weight of 4 tennis balls.

14.25 grams

k=57 and y=kx where y is the weight of x number of tennis balls. This means that y=57x. When x=4 ,

2. One worker takes 30 hours to build a wall. Find the time it would take 5 workers to build a similar wall.

k=30 and y=\frac{k}{x} where y is the time taken to build a wall with x number of people. This means that y=\frac{30}{x}. When x=5,

y=30\div{5}=6 hours.

3. 4 computer games cost £18. Find the cost of 5 computer games.

If 4 computer games cost £18 , 1 computer game will cost £4.50 .

k=4.5 and y=kx where y is the cost of x number of computer games. This means that y=4.5x. When x=5 ,

4. 7 workers take 20 weeks to build a house. How long would it take 10 workers to build the same house?

k=xy. When x=7, \ y=20 and so k=7 \times 20=140. This means that it would take 1 person 140 weeks to build the house and so y=\frac{140}{x}.

y=140 \div 10=14 weeks.

5. 5 pens cost 65p. Find the cost of 8 pens.

k=\frac{y}{x}. When x=5, \ y=65 and so k=65 \div 5=13. This means that 1 pen costs £0.13 and so y=0.13x.

6. 4 machines take 15 hours to complete a job. Find how long it would take 3 machines to complete the same job.

k=xy. When x=4, \ y=15 and so k=4 \times 15=60. This means that it would take 1 machine 60 hours to complete the job and so y=\frac{60}{x}.

y=60\div{3}=20 hours.

Direct and indirect proportion GCSE questions

1. 5 sacks of potatoes cost £40.

Find the cost of 7 sacks of potatoes.

2. A small town has four rubbish trucks to collect its rubbish.

It takes four trucks 18 hours to collect the rubbish.

One of the trucks breaks down.

Find how long it would take 3 trucks to collect the rubbish in the town.

3. A recipe for lemon cheesecake needs 250 grams of soft cheese.

The lemon cheesecake will have 6 proportions.

Soft cheese is sold in 300 gram packets.

The packets cost £1.25 each.

Samir wants to make enough lemon cheesecake for 15 portions.

Calculate the cost of soft cheese for Samir to make 15 portions of cheese cake.

625\div{300}=2.08\dot{3} and 3 packets.

Learning checklist

You have now learned how to:

• Solve problems involving direct and inverse proportion, including algebraic representations

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Direct and Inverse Proportion

Revision Notes

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Proportions

• Last updated
• Save as PDF
• Page ID 130921

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In the previous section, we learned that a ratio is a comparison of two quantities. However, many of the problems we solved involved comparing multiple ratios, and often required finding an equality between two ratios. These sorts of problems are most easily solved using proportions , which are the subject of this section.

In this section, you will learn to:

• Recognize and set up proportion problems
• Apply the Cross Multiplication and Division undoes Multiplication methods to solve proportion problems
• Use the Compare to the Whole method to solve problems involving proportions

Proportions: Definition and Basic Methods

Let's recall our starting example from the previous section, in which we had a recipe that called for \(2\) cups of flour and \(1\) cup of sugar. We asked the question: if we wanted to make a larger version of the same recipe using \(3\) cups of sugar, how much flour should we use?

We know now that ratios can be expressed as fractions, and whenever ratios are equivalent, the fractional representations of those ratios are equal. So, let's call the number of cups of flour \(x\) and set up the following equality:

\[\frac{2 \text{ cups of flour}}{1 \text{ cup of sugar}} = \frac{x \text{ cups of flour}}{3 \text{ cups of sugar}}\]

We need to figure out the value of \(x\) that makes this equation true. That is, what number can be substituted in place of \(x\) so that these fractions truly are equal? In this case, the easiest way is to guess-and-check, which is a perfectly valid solution method with small numbers. If you just try some small numbers, you can find that \(x = 6\) is the solution, because \(\frac{6}{3}\) reduces to \(\frac{2}{1}\), and thus \(\frac{6}{3}\) and \(\frac{2}{1}\)are equivalent ratios.

In this chapter, we'll learn how to solve problems like this generally, including those that can't be solved using guess-and-check. Our primary tool will be a proportion.

Definition: Proportion

A proportion is an equality between ratios.

This means that, in a strictly mathematical sense, a proportion is an equation. For example,

\[\frac{5}{2} = \frac{40}{16}\]

is a proportion, because it contains two ratios that are equal to one another. You may have heard the word proportion used in other ways, and that's because the word "proportion" has a different mathematical meaning than its typical English usage. That doesn't mean either usage is wrong; rather, it is dependent upon context. In this book, we will use the word proportion to mean any equation that looks like this:

\[\frac{a}{b} = \frac{c}{d}\]

where \(a, b, c\), and \(d\) will usually be numbers or variables.

The reasons we care about proportions is that they give us a way to find an unknown part of one of the ratios involved . Recall the following example, which we saw in the Ratios section:

Example \(\PageIndex{1}\)

On the Western Oregon University website , the total enrollment is listed as \(3752\) students, and the student-faculty ratio is listed as \(13 \colon 1\). You want to know how many faculty there are at WOU. How might you find this out, and how do you explain your answer?

In solving this problem before, we set up two ratios

\[3752 \colon x \quad \text{and} \quad 13 \colon 1 \]

Why did we do this? Well, it turns out that all proportion problems can be solved using a method from algebra known as cross multiplication . While this text mostly stays away from algebra, this procedure is essential. The good news is that it works the same way every time, and it's not very complicated.

Cross Multiplication

If you have a proportion of the form:

then "cross multiplication" refers to rewriting the equation in the following equivalent way:

\[c \times b= a \times d\]

In other words, we are "crossing" from \(a\) to \(d\) in the \(\searrow\) direction and from \(c\) to \(b\) in the \(\swarrow\) direction.

A quick mathematical note: what we're really doing is multiplying both sides by \(b\) and \(d\), and then canceling common factors -- but calling it cross multiplication seems to make it easier for students to understand and remember.

Let's practice cross multiplying in our example. We had the proportion:

\[\frac{3752}{x} = \frac{13}{1}\]

Cross multiplying this gives us the following equation:

\[13 \times x = 3752 \times 1\]

What good did that do? Well, note that we can simplify a little bit. It's typical to omit the \(\times\) when a variable is multiplied by a number, so we can rewrite \(13x\) for \(13 \times x\). We also know that \(3752 \times 1 = 3752\). So our equation becomes

\[13x = 3752\]

Now what? We've eliminated the fractions, but we can't yet say what \(x\) is. In order to find \(x\), we need one more algebra procedure, which we will call Division undoes Multiplication.

Division undoes Multiplication

Given an equation of the form \[Ax = B\] where \(A\) and \(B\) are numbers, we can find the value of \(x\) by dividing both sides by \(A\). That is, \[x = \frac{B}{A} = B \div A\]

Once again, we are using properties of fractions here: mathematically, we are dividing both sides by \(A\) and then reducing:

\[\begin{align*} Ax & = B\\ \frac{Ax}{A} & = \frac{B}{A} \\ \frac{\cancel{A}x}{\cancel{A}} & = \frac{B}{A} \\ x & = \frac{B}{A} \\ \end{align*} \]

But this is another procedure used so frequently that it's worth giving it a name.

Back to our example: we had the equation \[13x = 3752\]

We now have a tool to find \(x\) -- the fact that Division undoes Multiplication ! Using this procedure, we have \[x = \frac{3752}{13} = 3752 \div 13 \approx 288.6\]

This is the same answer we found before, but we used a slightly different method. And keep in mind that, just as the previous section, we would need to round this answer to \(289\) faculty to make sense in context. That said; the main point is now we now have a fool-proof way to solve this type of equation! 

While this may seem more complicated at first, you'll find that the following sequence of steps will always work to solve proportions:

Solving Proportions

• Set up the proportion with exactly one unknown value, called \(x\).
• Apply the Cross Multiplication.
• Apply Division undoes Multiplication.

We will get lots of practice with this procedure in the exercises for this section. Once you practice with the procedures above, you'll find that it's not too bad. The hardest part is often the first step — setting up the proportion correctly. That's the part that depends on reading the question very carefully! In general, the way to set up a proportion involves keeping track of units. Let's see an example to understand.

Example \(\PageIndex{2}\)

In an office supply store, \(8\) markers cost a total of \(\$12.00\). Assuming all markers are equally priced, how much would 6 markers cost?

This is a problem that is suitable to be solved using proportions because the markers are all equally priced, meaning that the ratio of total cost : number of markers purchased will be the same, no matter how many markers are purchased. That means we can set up the following proportion:

\[\frac{12 \text{ dollars}}{8 \text{ markers}} = \frac{x \text{ dollars}}{6 \text{ markers}}\]

Notice how, in the equation above, we are labeling the units of all quantities involved. Moreover, the units on each side match: dollars are on top, markers are on bottom, and the corresponding quantities are grouped on each side of the equation -- \(\$12\) for \(8\) markers, and \(\$x\) for 6 markers. Labeling your units in this way will help you avoid mistakes with units!

Now that we've gotten our proportion set up correctly, we can rewrite it without labels: \[\frac{12}{8} = \frac{x}{6}\]

From here, we'll follow the last two steps: cross multiply, and then use division to find \(x\). Using Cross Multiplication, we have \[x \times 8 = 12 \times 6 \]

On the left, we can rewrite \(x \times 8\) as \(8 x\), since multiplication can always switch orders. Then we can simplify to get \[8x = 72\]

Now we can use Division undoes Multiplication to get

\[x = \frac{72}{8} = 72 \div 8 = 9\]

Therefore, \(x = 9\). Now, we want to make sure our answer actually means something. What are the units on \(x\)? Well, if we look back at our original proportion,

we see that \(x\) is a number of dollars. Thus, we can say that \(x = \$9\), which means that 6 markers will cost \(\$9\).

You may be thinking: there is a much faster way to do that! And that may be true for you. Once again, the point is not to mimic a particular method for problem solving here — these notes will show some good ways of solving a problem, but they cannot cover every good solution. They are intended to highlight themes and strategies that will work for many types of situations. Other ways you may have solved the problem above include:

• Calculate the cost per marker to be \(\$1.50\), and multiply that number by 6 markers to get \(\$9\).
• Calculate that \(6\) is \(\frac{3}{4}\) of \(8\), so the cost of \(6\) markers would be \(\frac{3}{4}\) the cost of \(8\) markers, and \(\frac{3}{4}\) of \(\$12\) is \(\$9\).
• Set up a different initial proportion, such as \(\frac{12 \text{ dollars}}{x \text{ dollars}} = \frac{8 \text{ markers}}{6 \text{ markers}}\) or \(\frac{8 \text{ markers}}{12 \text{ dollars}} = \frac{6 \text{ markers}}{x \text{ dollars}}\) and then solved that proportion.

What's amazing about the last point above is that both of those proportions — which were different than the method used in the solution above — still give the same answer! This shows that there are many  different ways of approaching the same problem. All you need to do is find the one that works for you, and be able to explain your work.

Comparing to the Whole

Sometimes a problem involving proportions will be less straightforward. For example, consider the following:

Example \(\PageIndex{3}\)

In a rainforest in Panama, the ratio of two-toed sloths to three-toed sloths is \(10 \colon 3\). There are \(741\) total sloths in the rainforest. How many of them are two-toed?

In the problem above, we are given one ratio that compares the quantity of two-toed versus three-toed sloths. However, we are not given any information about the actual numbers of either two- or three-toed sloths. We simply know the comparison between them. Instead, we are just given the total number of sloths, but no actual breakdown into how many fall into each category. How are we supposed to find the number of two-toed sloths from just this information? We can't readily write down a proportion like we were able to in the previous example, because the units would be wrong; we need to compare like quantities. This situation calls for one more procedure.

Compare to the Whole

Assume there are two quantities, \(x\) and \(y\), neither of which you know. However, you know two things about them

• The total \(x + y\) (the total number of both quantities)
• The ratio of quantity \(x\) to quantity \(y\) is \(a \colon b\)

Then you can use the Compare to the Whole method. This says that, to find quantity \(x\), you use the proportion \[\frac{a}{a+b} = \frac{x}{x+y}\] and then find \(x\). Note: you already know \(x+y\), since it is the total number of both quantities.

Let's see how this procedure can be applied to the sloth example.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

direct proportions

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Direct and Inverse Proportion Practice Questions

Click here for questions, click here for answers .

variation, proportionality

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 1

Intro to proportional relationships.

• Proportional relationships: movie tickets
• Proportional relationships: bananas
• Proportional relationships: spaghetti
• Identify proportional relationships
• Proportional relationships
• Is side length & area proportional?
• Is side length & perimeter proportional?

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Proportions

Last Updated: March 26, 2024

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 95,984 times.

What is the "vertical" way to solve a proportion?

How can I solve a proportion with the "horizontal" method?

How do I solve a proportion step by step by cross-multiplying?

How do you find the missing value in a proportion with a table of ratios?

• Each column in this table represents a fraction. All of the fractions in this table are equal to each other.

• The two answers are the same, which means your answer is correct.

How do you solve percent proportions?

How do you solve proportions algebraically?

• You can change the left hand side of the equation, as long as you do the same math to the right hand side.

• To get rid of the fraction on the left, multiply both sides by 27:

How do you solve a proportion with a variable on both sides?

• Warning : This is a difficult example. If you haven't learned about quadratic equations yet, you might want to skip this part.

• You can now solve this as a quadratic equation , using any method that you've learned.

Proportions Calculator, Practice Problems, and Answers

Community Q&A

• The algebraic method above works with any proportion. But for a specific proportion, there is often a faster way to use algebra to find the answer. As you learn more algebra, this will get easier. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ http://www.mathvillage.info/node/72
• ↑ https://www.youtube.com/watch?v=nwsDiID7UtQ
• ↑ https://www.youtube.com/watch?v=Uo8HgcyfRFI
• ↑ https://www.purplemath.com/modules/ratio2.htm

About This Article

To solve proportions, start by taking the numerator, or top number, of the fraction you know and multiplying it with the denominator, or bottom number, of the fraction you don’t know. Next, take that number and divide it by the denominator of the fraction you know. Now you can replace x with this final number. For example, to figure out “x” in the problem 3/4 = x/8, multiply 3 x 8 to get 24, then divide 24 / 4 to get 6, or the value of x. To learn how to use proportions to determine percentages, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

John Almacen

Nov 10, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

Direct Proportion Questions

Students can quickly understand the concept of “Direct Proportion” by using the direct proportion questions and answers. The questions provided here can help students grasp the concept more quickly. To help them comprehend more clearly, we have also included some practice questions. Additionally, you may double-check your answers with comprehensive explanations provided on our page for each question. To learn more about direct proportion, click here .

Direct Proportion Questions with Solutions

1. Determine whether the following quantities vary directly or inversely with each other?

(i) Number of books purchased (a) and their price (b).

(ii) Area of land (x) and the cost of the land (y).

(i) The number of books purchased (a) and their price (b)

As we know, if the number of books purchased increases, their price will also increase. Similarly, if we purchase fewer books, their price will decrease. Hence, the number of books purchased and their price are directly proportional.

Thus, a ∝ b.

(ii) Area of land (x) and the cost of the land (y) .

The cost of the land will be more if its area increases. Similarly, the cost of land will be lesser if its area decreases. Hence, the area of land and the cost of the land is directly proportional.

Therefore, x ∝ y.

2. Given that both x and y vary directly from each other. If x = 10 and y = 15, which of the following pairs is not possible with respect to the value of x and y?

• x = 2 and y = 3
• x = 8 and y = 12
• x = 15 and y = 20
• x = 25 and y = 37.5

Given that x and y are directly proportional.

Hence, x/y = k(constant)

So, x/y = 10/15 = 2/3 …(1)

Now, check with the options provided here.

(a) x = 2 and y = 3

x/y = 2/3 …(2)

Hence, (1) = (2)

(b) x = 8 and y = 12

x/y = 8/12 = 2/3 …(3)

Hence, (1) = (3)

(c) x = 15 and y = 20

x/y = 15/20 = 3/4 …(4)

Hence, (1) ≠ (4)

(d) x = 25 and y = 37.5

x/y = 25/37.5 = 2/3 …(5)

Hence, (1) = (5)

Therefore, option (c) x = 15 and y = 20 should not be a possible pair with respect to the values x and y.

3. Check whether the values “x” and “y” given the table are directly proportional.

In the given table, the value of y is three times the value of x.

Hence, in all columns, we can observe that y = 3x, which is equal to y/x = 3

y/x = 21/7 = 3

y/x = 27/9 = 3

x/y = 39/13 = 3

x/y = 63/21 = 3

x/y = 75/25 = 3

Hence, the values “x” and “y” presented in the table are directly proportional.

4. If “a” varies directly as “b”, then find the value of “k” in the following table.

Given that “a” and “b” are directly proportional.

Hence, a/b = k (constant)

From the given table,

a/b = 12/48 = 1/4.

Similarly in second column,

a/b = 6/k = 1/4.

Hence, the value of k is 24.

5. Fill in the missing values in the table, such that “a” is directly proportional to “b”.

Given that, “a” and “b” are directly proportional.

Let the unknown values be “x” and “y”

From the given table, we can write

a/b = 3/x = 5/20 = 7/28 = 9/y

Now, compare 3/x = 5/20

Cross multiplying the above equation, we get

3(20) = 5(x)

x = 60/5 = 12.

Similarly, compare 7/28 = 9/y.

So, we get 7y = 28(9)

Hence, y = 252/7

Hence, the unknown values are x = 12 and y = 36.

Also, read: Direct and Inverse Proportion .

6. Ramya purchased 97 meters of cloth that cost Rs. 242.50. What will the length of the cloth be if she purchased it for Rs. 302.50.

As we know, the length of the cloth and its costs are directly proportional. Because if we purchase more, the cost will be higher. Similarly, if we purchase less, the cost will decrease.

Hence, we get

Now, we have to find the value of “x”.

Since the length and cost of cloth are directly proportional, we can write

97/242.50 = x/302.50

Now, cross multiply the above equation, we get

242.50x = 97(302.50)

242.50x = 29342.5

Hence, x = 29342.5 / 242.50 = 121.

Hence, the length of the cloth is 121 meters, if she purchased it for Rs. 302.50.

7. The area occupied by 10 postal stamps is 50 square centimeters. Hence, find the total area occupied by 100 such postal stamps.

Given that,

The area occupied by 10 postal stamps = 50 cm 2

Hence, the area occupied by 1 postal stamp = 50/10 = 5 cm 2 .

Therefore, the area occupied by 100 postal stamps = 100 × 5 = 500 cm 2 .

8. State whether the given statement is true or false:

‘If “a” and “b” are in direct proportion, then (a – 1) and (b – 1) are also in direct proportion”.

The given statement is “ False ”

Justification:

We know that, if “a” and “b” are in direct proportion, we can write

Let us assume that a = 2 and b = 4

Hence, a/b = 2/4 = 1/2 …(1)

So, (a – 1) / (b – 1) = (2 – 1) / (4 – 1) = 1/3 …(2)

Thus, (1) ≠ (2)

Hence, the given statement “If ‘a’ and ‘b’ are in direct proportion, then (a – 1) and (b – 1) are also in direct proportion” is false.

9. A housemaid is paid Rs. 800 for 8 days. If she works for 25 days, how much will she get?

According to the given question, we get the following:

Here, we have taken the unknown income to be “x”.

If the housemaid works for many days, her income will be more. Similarly, if she works for fewer days, she will get less income.

Hence, the number of days worked and income is directly proportional.

Therefore, we can write

8/800 = 25/x

1/100 = 25/x

Hence, x = 25(100)

Therefore, if she works for 25 days, she will get Rs. 2500.

10. If a woman earns Rs. 805 per week, how much will she earn in 16 days?

Solution: Rs. 1840

As we know, 1 week = 7 days.

Thus, the income of a woman in 7 days = 805.

Hence, the income of a woman in 1 day = 805/7 = 115.

So, the income of a woman in 16 days = 16 × 115 = 1840.

Therefore, a woman will earn Rs. 1840 in 16 days.

Explore More Articles

• Divisibility Rules Questions
• Direct and Inverse Proportion Questions
• Class 11 Maths Questions
• Volume Questions
• Area Questions
• Perimeter Questions

Practice Questions

Solve the following direct proportion questions:

1. If the cost of 18 dolls is Rs. 630, how many dolls can be purchased for Rs. 455?

2. Find the missing values in the below-given table, if p is directly proportional to q.

3. Fill in the blanks in each of the given statements, such that the statement becomes true.

• If x = 3y, then x and y vary ___ with each other.
• If “a” and “b” are said to vary directly with each other, then ____ = k, where “k” is a positive number.

4. Rahul purchased 12 books for Rs. 156. Then find the cost of 7 such books.

5. If 2 kg sugar contains 7 × 10 6 crystals, then find how many sugar crystals are present in 4 kg of sugar?

Keep visiting BYJU’S – The Learning App and download the app to quickly learn all Maths-related concepts.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.