- Privacy Policy

Mathematical Reasoning: A Complete Guide

Mathematical Reasoning is the foundation of problem-solving and critical thinking in mathematics. It involves the ability to analyze, deduce, and draw conclusions from mathematical concepts, principles, and relationships. In this guide, we will explore the key aspects of mathematical reasoning, provide examples to illustrate its application, and discuss effective methods for developing strong mathematical reasoning skills.
Key Aspects of Mathematical Reasoning
Logical deduction :.
Mathematical reasoning involves using logical deduction to arrive at conclusions based on given information or premises. It requires the ability to follow a chain of reasoning step by step, ensuring that each step is based on sound logic.
Pattern Recognition :
Recognizing patterns and relationships is crucial for mathematical reasoning. Identifying trends and regularities helps in making conjectures and predictions, and aids in solving problems efficiently.
Abstraction :
Abstraction involves generalizing specific cases into broader concepts. It allows us to work with generalized properties rather than specific instances, making problem-solving more versatile.
Inductive and Deductive Reasoning :
Inductive reasoning involves making generalizations based on a set of specific observations, while deductive reasoning uses established principles to draw specific conclusions. Both are important for mathematical reasoning.
Counter examples :
Counterexamples are instances that disprove a conjecture or statement. Considering counterexamples is crucial to test the validity of a mathematical claim.
Mathematical proofs are rigorous arguments that establish the truth of a statement or proposition. Constructing and understanding proofs is a fundamental aspect of mathematical reasoning.
Examples Illustrating Mathematical Reasoning
Example: fibonacci numbers.
Consider the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, ..
By observing the pattern, we notice that each term is the sum of the previous two terms. This pattern leads to a conjecture: the nth term is the sum of the (n-1)th and (n-2)th terms. We can prove this by mathematical induction.
Example: Prime Numbers
Prime numbers are positive integers greater than 1 that have no divisors other than 1 and themselves. By using deductive reasoning, we can prove that there are infinitely many prime numbers. Suppose there are only finitely many primes. We can then consider the number obtained by multiplying all existing primes and adding 1. This number is either prime itself (contradicting the assumption) or has a prime factor that is not in our list, leading to a contradiction.
Example: Pythagorean Theorem
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides.
Mathematical Reasoning: One way to prove this theorem is using geometric reasoning. Consider a square with side lengths a + b, where a and b are the lengths of the triangle’s legs. The square can be divided into smaller squares and
rearranged to show that the area of the large square is equal to the sum of the areas of the two smaller squares.
Methods for Developing Strong Mathematical Reasoning Skills
Practice Problem-Solving:
Regularly solve a variety of mathematical problems. Start with simpler problems and gradually work your way up to more complex ones. This will help you develop pattern recognition and logical deduction skills.
Analyze Proofs:
Study different types of mathematical proofs. Understand the structure of a proof, from the assumptions to the conclusion. This will enhance your ability to construct rigorous arguments.
Explore Counterexamples :
When encountering a new conjecture, try to find counterexamples that might disprove it. This practice will help you refine your reasoning skills and think critically about mathematical statements.
Work Collaboratively :
Discuss mathematical problems and concepts with peers or mentors. Explaining your reasoning to others and listening to their perspectives can provide new insights and broaden your understanding.
Engage with Mathematical Literature :
Read mathematical books, papers, and articles. Exposing yourself to various mathematical ideas and approaches will expand your toolkit for reasoning.
Participate in Math Competitions:
Joining math competitions or problem-solving clubs can challenge you to think creatively and critically under time constraints.
Mathematical Reasoning is a fundamental skill that underlies all branches of mathematics. It involves logical deduction, pattern recognition, abstraction, and the ability to construct and understand proofs. By engaging with examples and following effective methods, you can develop strong mathematical reasoning skills that will serve you well in both academic and real-world problem-solving scenarios. Regular practice, thoughtful analysis, and a curious mindset are key to mastering this essential skill. Visit maths.ai to help in solving maths problems.
Related Posts

Integral Calculus: Examples and Methods

Understanding Vector: A Complete Guide

Mastering Algebra: An In-Depth Manual
Leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Is mathematical reasoning important to study?
Table of Contents
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. |
January 18, 2021
Reading Time: 9 minutes
Introduction
The purpose of mathematics is not just to earn grades. Students who wish to aim high in life need to figure out their purpose. Broadly speaking, Mathematics is implemented in every sphere of life. Nowadays, organizations require measurable input and output for performance assessment, and career outcomes are not based on qualitative or verbal feedback.
Students need to gear up and prepare for a future that will depend solely on mathematics. The evolution of newer technologies like data science will bring a renewed emphasis on Mathematics.

Mathematical reasoning, on the other hand, helps individuals build mathematical critical thinking and logical reasoning. A lack of mathematical reasoning skills may reflect not just in mathematics performance but also in Physics, Chemistry, or Economics.
In the subsequent sections, we will try to understand What is Mathematical reasoning and what are the basic terms used in mathematical reasoning. We will also have a look at different types of mathematical reasoning and go through mathematical reasoning questions and answers.
Later in the article, we will look at a few Frequently Asked Questions with solutions to solidify the idea behind learning mathematical reasoning.
- The importance of developing mathematical thinking in children
- Logical Reasoning: Topics, Examples, Syllabus, Questions
- Slow Learners
Here is a downloadable PDF. After downloading, you will be able to read 'Mathematical Reasoning’ offline at your convenience and as many times as you want. Click on the download button to explore them.
| 📥 |
|
What is Mathematical Reasoning?
Mathematical reasoning is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman's words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs require a factual and scientific basis.
Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.
When we learn literature, we follow certain rules of grammar. Likewise, there are certain rules and parts of a scientific hypothesis. It is important to note that most books and texts written on mathematical reasoning follow scientific grammar or relevant terminologies and notations.
What are the basic terms used in Mathematical Reasoning?
In this section, the basic terminologies associated with Mathematical reasoning are discussed.
Any sentence in mathematics which follows the following rules is a statement.
A sentence needs to be either true or false but not both to be considered a mathematically accepted statement.
Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement.
A Sentence containing one or many variables is termed an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values
Example: The distance from the center of a circle to any point on the circumference of the circle is equal.
Conjunction and Disjunction
Whenever statements are joined to make a new statement and all the conditions need to be fulfilled, it is a Conjunction. ‘And’, ‘with’ are commonly used to join such statements.
Whenever statements are joined to make a new statement and only one of the conditions needs to be fulfilled, it is a Disjunction. ‘Or’, ‘But’ are commonly used to join such statements.
The conjunction is true only if the original statements are found to be true. The conjunction is false if the original statement or statements are found to be false.
The conjunction is true if only one statement is found to be true. The conjunction is false if none of the original statements are found to be true.
Example: Square is a polygon and a parallelogram can also be a square.
These are a few mathematical terminologies that will help you comprehend and apply mathematical reasoning. These terms will also help you solve and understand reasoning questions.
What are the types of mathematical reasoning?
Inductive reasoning.
Inductive reasoning is based on observations and not any hypothesis. If any phenomena are observed for n number of times, it can be generalized. This generalization is based on observation and therefore it may be false. Inductive reasoning is a logical guess which can be backed up by using valid reasons.

This type of reasoning is not used in geometry, for instance, one may observe a few right triangles and conclude all triangles to be right triangles. Therefore, other mathematical tools are used to prove geometrical results. An example of inductive reasoning will help elucidate the concept.
Example of Inductive Reasoning:
Statement: I picked a ball from the bag and it happens to be a red ball. I picked a second red ball. A third ball from the bag is also red. Therefore, all the balls in the bag are red.
Reasoning : All the balls picked up from the bag are red. Therefore, we can say all the balls are red. This is an example of inductive reasoning where existing data is analyzed to come to a general conclusion.
Deductive Reasoning
Deductive reasoning is based on the exact opposite principles of induction. Unlike Inductive reasoning, Deductive reasoning is not based on simple generalizations. A Hypothesis is required or a statement that has to be true under specified conditions for deductive reasoning to be valid. In the case of Inductive reasoning, the conclusion may be false but Deductive reasoning is true in all cases.
Therefore, Deductive reading is used for geometrical and mathematical proofs. The following example will simplify the concepts discussed in this section.
Example of Deductive Reasoning:
Statement: The sum of angles in a triangle is always equal to 180° and ABC is a Triangle.
Reasoning: Here in the given statement we are considering two hypotheses, where the sum of angles in a triangle is said to be 180° and ABC is a triangle. Based on the given hypotheses we deduce that the sum of angles of ABC is 180°.
Abductive Reasoning
Abductive reasoning is a modified version of Inductive Reasoning and takes a more practical approach. In the case of inductive reasoning, the data or observation is complete but in real situations, most of the data is not available at the time of making a decision.

So based on the data and its availability, the conclusion may vary and reasoning may change.
Example of Abductive Reasoning:
Statement: The heights of four students studying in a class were found to be 160cm, 162cm, 163 cm, 167 cm respectively. The measuring scale available had the least count of 1cm.
Reasoning : As per the data and hypotheses available at the time of observation, the average height comes out to be 163cm. But once a new measuring scale was installed the least count was found to be 0.1 cm and the recorded height of students changed. This also impacted the Average height which came to be 63.8 cm.
As discussed in this section, reasoning techniques are categorized in three major sections. An understanding of Inductive, Abductive and Deductive reasoning will help you solve any reasoning question. It is important to identify the reasoning technique which has to be used to solve a question from examination point of view.
What are the types of reasoning statements?
Reasoning statements in mathematics are broadly classified into three types:
Simple Statements
Compound Statements
If-Then Statements
We will look into each type of reasoning statement along with their examples.
If the truth value of a statement or proposition does not directly depend on another statement, it is a simple statement. In other words, a simple statement should not be composed of simpler statements.
Therefore a simple statement can never be broken down into simpler statements. It is easiest to work with simple statements and direct reasoning approach can be implemented. A few examples have been provided to clear the concept of simple statements.
Example 1: Square is a parallelogram.
Reasoning: There are no modifiers in the given statement. Therefore we can say that the given statement is simple.
Compound Statement
In simple words, the combination of simple statements is a compound statement. Therefore, such statements are made of either two or more simple statements joined together by connectives like 'and', 'or'.
A variety of connectives can be used instead of the two connectives as mentioned. These statements are crucial for Deduction reasoning in Mathematics. Have a look at the detailed example below for a better understanding:
Example 1: We have taken two simple statements that can be joined together by the use of a connector.
Statement 1: Parallel lines do not intersect.
Statement 2: Transversal lines make equal alternate angles with parallel lines
Compound Statement: Parallel lines do not intersect and Transversal lines make equal alternate angles with parallel lines.
Example 2: In this example, a compound statement is being dissected into its simple statement components.
Compound Statement: Triangle has three sides and the square has four sides.
The Simple Statements for this statement is:
Statement 1: Triangle has three sides.
Statement 2: The square has four sides.
If-then Statement
Conditional statements where a hypothesis is followed by a conclusion are known as the If-then statement. If the hypothesis is true and the conclusion is false then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false.
Example 1: If 40% population is female then 60% population is male.
Reasoning: Here the 40% female is the hypothesis and if that condition is met then the conclusion is satisfying.
Sample Mathematical Reasoning Questions With Answers
Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth.
Q1. Look at this series: 12, 10, 13, 11, 14, 12, … What number should come next?
A. 15 B. 16 C. 13 D. 10
Answer: Option D.
Explanation: First, 2 is subtracted, then 3 is added therefore when 3 is added to 12 it becomes 15. This is an example of an alternating number of subtraction series.
Q2. SQUARE:PERIMETER::CIRCLE :?
A.RADIUS B. CHORD C. SECTOR D. CIRCUMFERENCE
Answer: D.CIRCUMFERENCE.
Explanation: The boundary of a square is given by its perimeter just as the boundary of a circle is given by circumference.
Most kids study mathematics for the sake of grades. That will improve grades temporarily but cause great damage in the longer run. Kids need to ask questions to understand how a particular concept is being used. If children do not understand the concepts in their initial days, they will struggle at a later stage.
Practice Proofs
Proofs will help Children Ideate their own set of techniques to understand complex problems. Students need to focus on Geometry Proofs, results, and maths reasoning questions.
Cuemath Activities
Some kids do need additional support and tools. Sometimes kids underperform in mathematics due to stress and fear of bad grades. Such kids are unable to ask questions in class and eventually start lagging. Cuemath provides a customized learning journey for such kids.
The most basic concepts are cleared and corrected. Individual attention by professional Mathematics Teachers helps them cope better. Once a child gains confidence, mathematics is a cakewalk.
Begin teaching mathematical reasoning at an early age to avoid struggling with it at a later stage. Children need to understand the principles of mathematics rather than mugging up proofs and theorems.
This will help them solve higher-order problems and develop mathematical aptitude. Over time you will find your child solving complex problems on their own without much intervention or assistance.
About Cuemath
Cuemath, a student-friendly mathematics and coding platform, conducts regular Online Classes for academics and skill-development, and their Mental Math App, on both iOS and Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath fee structure and sign up for a free trial.
Frequently asked questions (FAQs)
What is a fallacy in mathematical reasoning.
Fallacy refers to errors in hypotheses caused due to logical inaccuracy.
Why is mathematical reasoning important?
Students have the potential to solve higher-order thinking questions which are frequently asked in competitive examinations. But a lack of mathematical reasoning skills may render their potential. Encouragement is needed to develop a student's natural inclination to strive for purpose and meaning.
The reasoning is the most fundamental and essential tool of mathematics. It helps one understand and justify mathematical theorems. A good grip in reasoning will help students apply the concepts they learn in the classroom.
What are the two types of fallacy?
The two types of fallacies are as follows:
Formal fallacy: When the relationship between premises and conclusion is not valid or when premises are unsound, Formal fallacies are created.
Informal Fallacy: Misuse of language and evidence is classified as an Informal fallacy.
Reasoning Skills
Developing opportunities and ensuring progression in the development of reasoning skills
Achieving the aims of the new National Curriculum:
Developing opportunities and ensuring progression in the development of reasoning skills.
The aims of the National Curriculum are to develop fluency and the ability to reason mathematically and solve problems. Reasoning is not only important in its own right but impacts on the other two aims. Reasoning about what is already known in order to work out what is unknown will improve fluency; for example if I know what 12 × 12 is, I can apply reasoning to work out 12 × 13. The ability to reason also supports the application of mathematics and an ability to solve problems set in unfamiliar contexts.
Research by Nunes (2009) identified the ability to reason mathematically as the most important factor in a pupil’s success in mathematics. It is therefore crucial that opportunities to develop mathematical reasoning skills are integrated fully into the curriculum. Such skills support deep and sustainable learning and enable pupils to make connections in mathematics.
This resource is designed to highlight opportunities and strategies that develop aspects of reasoning throughout the National Curriculum programmes of study. The intention is to offer suggestions of how to enable pupils to become more proficient at reasoning throughout all of their mathematics learning rather than just at the end of a particular unit or topic.
We take the Progression Map for each of the National Curriculum topics, and augment it with a variety of reasoning activities (shaded sections) underneath the relevant programme of study statements for each year group. The overall aim is to support progression in reasoning skills. The activities also offer the opportunity for children to demonstrate depth of understanding, and you might choose to use them for assessment purposes as well as regular classroom activities.
Place Value Reasoning
Addition and subtraction reasoning, multiplication and division reasoning, fractions reasoning, ratio and proportion reasoning, measurement reasoning, geometry - properties of shapes reasoning, geometry - position direction and movement reasoning, statistics reasoning, algebra reasoning.
The strategies embedded in the activities are easily adaptable and can be integrated into your classroom routines. They have been gathered from a range of sources including real lessons, past questions, children’s work and other classroom practice.
Strategies include:
- Spot the mistake / Which is correct?
- True or false?
- What comes next?
- Do, then explain
- Make up an example / Write more statements / Create a question / Another and another
- Possible answers / Other possibilities
- What do you notice?
- Continue the pattern
- Missing numbers / Missing symbols / Missing information/Connected calculations
- Working backwards / Use the inverse / Undoing / Unpicking
- Hard and easy questions
- What else do you know? / Use a fact
- Fact families
- Convince me / Prove it / Generalising / Explain thinking
- Make an estimate / Size of an answer
- Always, sometimes, never
- Making links / Application
- Can you find?
- What’s the same, what’s different?
- Odd one out
- Complete the pattern / Continue the pattern
- Another and another
- Testing conditions
- The answer is…
- Visualising
These strategies are a very powerful way of developing pupils’ reasoning skills and can be used flexibly. Many are transferable to different areas of mathematics and can be differentiated through the choice of different numbers and examples.
Nunes, T. (2009) Development of maths capabilities and confidence in primary school, Research Report DCSF-RR118 (PDF)
Is there anything wrong with this page?
Subscribe to our newsletter

The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning.
This brief lesson is designed to lead students into thinking about how to solve mathematical problems. It features ideas of strategies to use, clear steps to follow and plenty of opportunities for discussion.

The PixiMaths problem solving booklets are aimed at "crossover" marks (questions that will be on both higher and foundation) so will be accessed by most students. The booklets are collated Edexcel exam questions; you may well recognise them from elsewhere. Each booklet has 70 marks worth of questions and will probably last two lessons, including time to go through answers with your students. There is one for each area of the new GCSE specification and they are designed to complement the PixiMaths year 11 SOL.
These problem solving starter packs are great to support students with problem solving skills. I've used them this year for two out of four lessons each week, then used Numeracy Ninjas as starters for the other two lessons. When I first introduced the booklets, I encouraged my students to use scaffolds like those mentioned here , then gradually weaned them off the scaffolds. I give students some time to work independently, then time to discuss with their peers, then we go through it as a class. The levels correspond very roughly to the new GCSE grades.
Some of my favourite websites have plenty of other excellent resources to support you and your students in these assessment objectives.
@TessMaths has written some great stuff for BBC Bitesize.
There are some intersting though-provoking problems at Open Middle.
I'm sure you've seen it before, but if not, check it out now! Nrich is where it's at if your want to provide enrichment and problem solving in your lessons.
MathsBot by @StudyMaths has everything, and if you scroll to the bottom of the homepage you'll find puzzles and problem solving too.
I may be a little biased because I love Edexcel, but these question packs are really useful.
The UKMT has a mentoring scheme that provides fantastic problem solving resources , all complete with answers.
I have only recently been shown Maths Problem Solving and it is awesome - there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring!

Or search by topic
Number and algebra
- The Number System and Place Value
- Calculations and Numerical Methods
- Fractions, Decimals, Percentages, Ratio and Proportion
- Properties of Numbers
- Patterns, Sequences and Structure
- Algebraic expressions, equations and formulae
- Coordinates, Functions and Graphs
Geometry and measure
- Angles, Polygons, and Geometrical Proof
- 3D Geometry, Shape and Space
- Measuring and calculating with units
- Transformations and constructions
- Pythagoras and Trigonometry
- Vectors and Matrices
Probability and statistics
- Handling, Processing and Representing Data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
- Cross-curricular contexts
- Physical and digital manipulatives
For younger learners
- Early Years Foundation Stage
Advanced mathematics
- Decision Mathematics and Combinatorics
- Advanced Probability and Statistics
Published 2014 Revised 2024
Using NRICH Tasks to Develop Key Problem-solving Skills
In her article Developing Excellence in Problem Solving with Young Learners , Jennie Pennant suggests that as teachers we can help children get better at problem solving in three main ways, one of which is through 'explicitly and repeatedly providing children with opportunities to develop key problem-solving skills'. This article builds on Jennie's. In particular, it explains what we mean by 'problem-solving skills' and aims to give further guidance on how we can help learners to develop these skills by highlighting relevant NRICH tasks.
What do we mean by 'problem-solving skills'?
In the aforementioned article, Jennie outlines four stages of the problem-solving process:
By explicitly drawing children's attention to these four stages, and by spending time on them in turn, we can help children become more confident problem solvers. Jennie outlines different ways in which learners might get started on a task (stage 1), but it is once they have got going and are working on the problem (stage 2) that children will be making use of their problem-solving skills. Here are some useful problem-solving skills:
- Trial and improvement
- Working systematically (and remember there will be more that one way of doing this: not just the one that is obvious to you!)
- Pattern spotting
- Working backwards
- Reasoning logically
- Visualising
- Conjecturing
The first two in this list are perhaps particularly helpful. As learners progress towards a solution, they may take the mathematics further (stage 3) and two more problem-solving skills become important:
- Generalising
Having reached a solution, stage 4 of the process then involves children explaining their findings and reflecting on different methods used. For the purposes of this article, we will think of 'problem-solving skills' as those skills that learners need in order to work on the mathematics of a task, during stages 2 and 3 of the problem-solving process.
How can we help children get better at these problem-solving skills?

Mathematical Reasoning & Problem Solving
In this lesson, we’ll discuss mathematical reasoning and methods of problem solving with an eye toward helping your students make the best use of their reasoning skills when it comes to tackling complex problems.
Previously Covered:
- Over the course of the previous lesson, we reviewed some basics about chance and probability, as well as some basics about sampling, surveys, etc. We also covered some ideas about data sets, how they’re represented, and how to interpret the results.
Approaches to Problem Solving
When solving a mathematical problem, it is very common for a student to feel overwhelmed by the information or lack a clear idea about how to get started.
To help the students with their problem-solving “problem,” let’s look at some examples of mathematical problems and some general methods for solving problems:
Identify the following four-digit number when presented with the following information:
- One of the four digits is a 1.
- The digit in the hundreds place is three times the digit in the thousands place.
- The digit in the ones place is four times the digit in the ten’s place.
- The sum of all four digits is 13.
- The digit 2 is in the thousands place.
Help your students identify and prioritize the information presented.
In this particular example, we want to look for concrete information. Clue #1 tells us that one digit is a 1, but we’re not sure of its location, so we see if we can find a clue with more concrete information.
We can see that clue #5 gives us that kind of information and is the only clue that does, so we start from there.
Because this clue tells us that the thousands place digit is 2, we search for clues relevant to this clue. Clue #2 tells us that the digit in the hundreds place is three times that of the thousands place digit, so it is 6.
So now we need to find the tens and ones place digits, and see that clue #3 tells us that the digit in the ones place is four times the digit in the tens place. But we remember that clue #1 tells us that there’s a one somewhere, and since one is not four times any digit, we see that the one must be in the tens place, which leads us to the conclusion that the digit in the ones place is four. So then we conclude that our number is:
If you were following closely, you would notice that clue #4 was never used. It is a nice way to check our answer, since the digits of 2614 do indeed add up to be thirteen, but we did not need this clue to solve the problem.
Recall that the clues’ relevance were identified and prioritized as follows:
- clue #3 and clue #1
By identifying and prioritizing information, we were able to make the information given in the problem seem less overwhelming. We ordered the clues by relevance, with the most relevant clue providing us with a starting point to solve the problem. This method also utilized the more general method of breaking a problem into smaller and simpler parts to make it easier to solve.
Now let’s look at another mathematical problem and another general problem-solving method to help us solve it:
Two trees with heights of 20 m and 30 m respectively have ropes running from the top of each tree to the bottom of the other tree. The trees are 40 meters apart. We’ll assume that the ropes are pulled tight enough that we can ignore any bending or drooping. How high above the ground do the ropes intersect?
Let’s solve this problem by representing it in a visual way , in this case, a diagram:
You can see that we have a much simpler problem on our hands after drawing the diagram. A, B, C, D, E, and F are vertices of the triangles in the diagram. Now also notice that:
b = the base of triangle EFA
h = the height of triangle EFA and the height above the ground at which the ropes intersect
If we had not drawn this diagram, it would have been very hard to solve this problem, since we need the triangles and their properties to solve for h. Also, this diagram allows us to see that triangle BCA is similar to triangle EFC, and triangle DCA is similar to triangle EFA. Solving for h shows that the ropes intersect twelve meters above the ground.
Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods , such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by making it more concrete and approachable.
Let’s try another one.
Given a pickle jar filled with marbles, about how many marbles does the jar contain?
Problems like this one require the student to make and use estimations . In this case, an estimation is all that is required, although, in more complex problems, estimates may help the student arrive at the final answer.
How would a student do this? A good estimation can be found by counting how many marbles are on the base of the jar and multiplying that by the number of marbles that make up the height of the marbles in the jar.
Now to make sure that we understand when and how to use these methods, let’s solve a problem on our own:
How many more faces does a cube have than a square pyramid?
Reveal Answer
The answer is B. To see how many more faces a cube has than a square pyramid, it is best to draw a diagram of a square pyramid and a cube:
From the diagrams above, we can see that the square pyramid has five faces and the cube has six. Therefore, the cube has one more face, so the answer is B.
Before we start having the same problem our model student in the beginning did—that is, being overwhelmed with too much information—let’s have a quick review of all the problem-solving methods we’ve discussed so far:
- Sort and prioritize relevant and irrelevant information.
- Represent a problem in different ways, such as words, symbols, concrete models, and diagrams.
- Generate and use estimations to find solutions to mathematical problems.
Mathematical Mistakes
Along with learning methods and tools for solving mathematical problems, it is important to recognize and avoid ways to make mathematical errors. This section will review some common errors.
Circular Arguments
These involve drawing a conclusion from a premise that is itself dependent on the conclusion. In other words, you are not actually proving anything. Circular reasoning often looks like deductive reasoning, but a quick examination will reveal that it’s far from it. Consider the following argument:
- Premise: Only an untrustworthy man would become an insurance salesman; the fact that insurance salesmen cannot be trusted is proof of this.
- Conclusion: Therefore, insurance salesmen cannot be trusted.
While this may be a simplistic example, you can see that there’s no logical procession in a circular argument.
Assuming the Truth of the Converse
Simply put: The fact that A implies B doesn’t not necessarily mean that B implies A. For example, “All dogs are mammals; therefore, all mammals are dogs.”
Assuming the Truth of the Inverse
Watch out for this one. You cannot automatically assume the inverse of a given statement is true. Consider the following true statement:
If you grew up in Minnesota , you’ve seen snow.
Now, notice that the inverse of this statement is not necessarily true:
If you didn’t grow up in Minnesota , you’ve never seen snow.
Faulty Generalizations
This mistake (also known as inductive fallacy) can take many forms, the most common being assuming a general rule based on a specific instance: (“Bridge is a hard game; therefore, all card games are difficult.”) Be aware of more subtle forms of faulty generalizations.
Faulty Analogies
It’s a mistake to assume that because two things are alike in one respect that they are necessarily alike in other ways too. Consider the faulty analogy below:
People who absolutely have to have a cup of coffee in the morning to get going are as bad as alcoholics who can’t cope without drinking.
False (or tenuous) analogies are often used in persuasive arguments.
Now that we’ve gone over some common mathematical mistakes, let’s look at some correct and effective ways to use mathematical reasoning.
Let’s look at basic logic, its operations, some fundamental laws, and the rules of logic that help us prove statements and deduce the truth. First off, there are two different styles of proofs: direct and indirect .
Whether it’s a direct or indirect proof, the engine that drives the proof is the if-then structure of a logical statement. In formal logic, you’ll see the format using the letters p and q, representing statements, as in:
If p, then q
An arrow is used to indicate that q is derived from p, like this:
This would be the general form of many types of logical statements that would be similar to: “if Joe has 5 cents, then Joe has a nickel or Joe has 5 pennies “. Basically, a proof is a flow of implications starting with the statement p and ending with the statement q. The stepping stones we use to link these statements in a logical proof on the way are called axioms or postulates , which are accepted logical tools.
A direct proof will attempt to lay out the shortest number of steps between p and q.
The goal of an indirect proof is exactly the same—it wants to show that q follows from p; however, it goes about it in a different manner. An indirect proof also goes by the names “proof by contradiction” or reductio ad absurdum . This type of proof assumes that the opposite of what you want to prove is true, and then shows that this is untenable or absurd, so, in fact, your original statement must be true.
Let’s see how this works using the isosceles triangle below. The indirect proof assumption is in bold.
Given: Triangle ABC is isosceles with B marking the vertex
Prove: Angles A and C are congruent.
Now, let’s work through this, matching our statements with our reasons.
- Triangle ABC is isosceles . . . . . . . . . . . . Given
- Angle A is the vertex . . . . . . . . . . . . . . . . Given
- Angles A and C are not congruent . . Indirect proof assumption
- Line AB is equal to line BC . . . . . . . . . . . Legs of an isosceles triangle are congruent
- Angles A and C are congruent . . . . . . . . The angles opposite congruent sides of a triangle are congruent
- Contradiction . . . . . . . . . . . . . . . . . . . . . . Angles can’t be congruent and incongruent
- Angles A and C are indeed congruent . . . The indirect proof assumption (step 3) is wrong
- Therefore, if angles A and C are not incongruent, they are congruent.
“Always, Sometimes, and Never”
Some math problems work on the mechanics that statements are “always”, “sometimes” and “never” true.
Example: x < x 2 for all real numbers x
We may be tempted to say that this statement is “always” true, because by choosing different values of x, like -2 and 3, we see that:
Example: For all primes x ≥ 3, x is odd.
This statement is “always” true. The only prime that is not odd is two. If we had a prime x ≥ 3 that is not odd, it would be divisible by two, which would make x not prime.
- Know and be able to identify common mathematical errors, such as circular arguments, assuming the truth of the converse, assuming the truth of the inverse, making faulty generalizations, and faulty use of analogical reasoning.
- Be familiar with direct proofs and indirect proofs (proof by contradiction).
- Be able to work with problems to identify “always,” “sometimes,” and “never” statements.
- International
- Education Jobs
- Schools directory
- Resources Education Jobs Schools directory News Search

Reasoning and Problem Solving Questions Collection - KS1 and KS2
Subject: Mathematics
Age range: 5-7
Resource type: Worksheet/Activity
Last updated
10 March 2023
- Share through email
- Share through twitter
- Share through linkedin
- Share through facebook
- Share through pinterest

These booklets each contain over 40 reasoning and problem solving questions suitable for KS1, KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS.
The answers are provided with some simple notes at the back of the booklet and for some problems supplementary questions and variation has been provided.
As always we welcome any feedback on the work we are doing and the materials that we are releasing. Thank you for taking an interest in our work. The White Rose Maths Hub Team
Creative Commons "Sharealike"
Your rating is required to reflect your happiness.
It's good to leave some feedback.
Something went wrong, please try again later.

TES Resource Team
We are pleased to let you know that your resource Reasoning and Problem Solving Questions Collection - KS1 and KS2, has been hand-picked by the Tes resources content team to be featured in https://www.tes.com/teaching-resources/blog/fluency-reasoning-and-problem-solving-primary-maths in April 2024 on https://www.tes.com/teaching-resources/blog. Congratulations on your resource being chosen and thank you for your ongoing contributions to the Tes Resources marketplace.
Empty reply does not make any sense for the end user
graceamfo18
A very good and engaging way to teach mastery of maths. Thank you for sharing
thank you for sharing, this is really good
Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.
Not quite what you were looking for? Search by keyword to find the right resource:
Cookie Consent
We use cookies to help provide a better website experience for you, and help us to understand how people use our website. Our partners will also collect data and use cookies for ad personalisation and measurement.
Clicking "Accept" will allow us and our partners to use cookies, learn more in our cookie policy or to change your cookie preferences, click "Manage".
To find out more about cookies and the types of cookies we are setting please visit our cookie policy .
If you'd prefer that certain types of cookie are not saved on your browser when visiting our website, use the toggles below to adjust those preferences and click "Save choices".
Strictly Necessary
These cookies are necessary for the website to function and without them you would not be able to reliably use the website. For example, logging into your account or completing forms.
Analytics Cookies
A series of cookies that collect anonymised data on how users interact with our website. This anonymous data helps us improve the website with a focus on its users, for example, ensuring the most popular content is easier to access.
View associated providers +
Marketing Cookies
These cookies track your online activity to help advertisers deliver more relevant and personalised advertising or to limit how many times you see an ad. These cookies can share that information with other organisations or advertisers.
- +91-9818737605
- [email protected]

How to Develop Critical Thinking Skills in Class 8 Maths
- Aspirations Institute
- July 9, 2024

Welcome to our blog post on developing critical thinking skills in Class 8 Maths. In this article, we will explore the importance of critical thinking in Math, strategies to develop these skills, and the long-term benefits for students. By fostering critical thinking, students can become better problem solvers and develop a deeper understanding of mathematical concepts.
Understanding Critical Thinking in Class 8 Maths:
Critical thinking is a fundamental skill that plays a vital role in the field of mathematics. It involves the ability to analyze, evaluate, and solve problems using logical reasoning and evidence-based thinking. For Class 8 students, developing critical thinking skills in Maths is essential as it helps them go beyond memorization and rote learning, enabling them to understand and apply mathematical concepts effectively.
At Aspirations Institute, we recognize the significance of critical thinking in Class 8 Maths education. Our goal is to nurture students’ critical thinking abilities, allowing them to become proficient problem solvers and independent thinkers. By fostering a deep understanding of mathematical concepts and encouraging students to think critically, we prepare them for success not only in Class 8 but also in higher-level math and real-life situations.
Understanding critical thinking in Class 8 Maths involves the following aspects:
A. Definition of Critical Thinking: We define critical thinking as the ability to analyze and evaluate mathematical problems, concepts, and arguments through logical reasoning, evidence-based thinking, and problem-solving skills. It entails questioning assumptions, examining multiple perspectives, and applying appropriate strategies to solve complex mathematical problems.
B. Relevance of Critical Thinking in Solving Mathematical Problems: Critical thinking is highly relevant in solving mathematical problems as it helps students approach problems with a deeper understanding and the ability to think flexibly. It enables them to break down complex problems into manageable steps, identify patterns, and apply appropriate problem-solving strategies. By developing critical thinking skills, students become more confident and efficient in tackling challenging math concepts and real-world applications.
C. Difference Between Rote Learning and Critical Thinking in Math: Rote learning, often associated with memorization, involves repetitive practice and recall of facts and formulas. While rote learning has its place in building foundational knowledge, it falls short in developing critical thinking skills. Critical thinking, on the other hand, goes beyond memorization and encourages students to understand the underlying concepts, think critically, and apply their knowledge to solve problems creatively.
At Aspirations Institute, we emphasize the importance of moving beyond rote learning in Class 8 Maths. Our experienced faculty members guide students to think critically and develop a deep understanding of mathematical concepts. Through engaging teaching methodologies, interactive discussions, and problem-solving activities, we encourage students to question, analyze, and apply their knowledge in practical ways.
We believe that understanding critical thinking in Class 8 Maths is crucial for students’ overall academic growth and success. By instilling critical thinking skills, we empower students to become independent learners, confident problem solvers, and analytical thinkers. At Aspirations Institute, we are committed to providing a supportive and nurturing learning environment that fosters critical thinking in Class 8 Maths and equips students with the skills they need to excel academically and beyond.
Strategies to Develop Critical Thinking Skills in Class 8 Maths:
Developing critical thinking skills in Class 8 Maths is essential for students to become proficient problem solvers, analytical thinkers, and independent learners. At Aspirations Institute, we employ various strategies to foster the development of critical thinking skills among our students. These strategies encourage students to think critically, analyze problems from different angles, and apply logical reasoning to solve mathematical challenges. Here are some effective strategies we implement:
A. Encouraging Problem-Solving Approaches:
- Introduction to Real-Life Problem-Solving Scenarios: We present students with real-life scenarios that require mathematical problem-solving skills. This approach helps students understand the practical application of math and encourages them to think critically about how to solve problems in real-world contexts.
- Use of Open-Ended Questions and Puzzles: Open-ended questions and puzzles stimulate critical thinking by requiring students to analyze, reason, and come up with creative solutions. These activities promote exploration, experimentation, and problem-solving strategies beyond the traditional textbook approach.
- Emphasis on Logical Reasoning and Analysis: We guide students to analyze problems logically, identify patterns, and make connections between different mathematical concepts. This approach cultivates their ability to think critically, recognize relationships, and apply logical reasoning to arrive at solutions.
B. Promoting Mathematical Reasoning:
- Introduction to Different Problem-Solving Strategies: We expose students to various problem-solving strategies such as working backward, using models/diagrams, and breaking down complex problems into smaller, more manageable parts. This helps students develop a toolkit of problem-solving techniques that they can apply in different scenarios.
- Encouraging Students to Explain Their Thought Processes: We create a supportive environment where students are encouraged to explain their thinking while solving math problems. Articulating their thought processes helps students develop metacognitive skills and gain a deeper understanding of their own reasoning, enabling them to identify areas for improvement and refine their critical thinking skills.
- Using Visual Representations and Manipulatives: Visual aids, such as diagrams, charts, and manipulatives, help students visualize mathematical concepts and relationships. These visual representations aid in the development of critical thinking skills by enabling students to analyze, compare, and draw conclusions based on visual data.
C. Fostering Creativity in Math:
- Incorporating Creative Tasks and Projects: We integrate creative tasks and projects that require students to think outside the box, generate alternative solutions, and apply critical thinking skills. This approach encourages students to explore different approaches, consider multiple perspectives, and develop their unique problem-solving strategies.
- Encouraging Students to Explore Multiple Solution Methods: We promote an open-minded approach to problem-solving, encouraging students to explore various solution methods and evaluate their effectiveness. By considering multiple solutions, students develop a deeper understanding of the underlying concepts and enhance their critical thinking abilities.
- Allowing for Trial and Error and Learning from Mistakes: We create a safe space for students to take risks, make mistakes, and learn from them. This approach fosters resilience, perseverance, and critical thinking skills as students analyze their mistakes, identify areas for improvement, and develop alternative strategies to solve problems.
D. Developing Critical Thinking Through Collaborative Learning:
- Group Discussions and Cooperative Problem-Solving Activities: We facilitate group discussions and cooperative problem-solving activities where students can share their perspectives, exchange ideas, and collaborate to find solutions. This approach enhances critical thinking skills by exposing students to diverse perspectives and encouraging them to consider alternative viewpoints.
- Peer-to-Peer Learning and Sharing of Multiple Perspectives: We encourage students to learn from their peers by sharing their approaches, discussing problem-solving strategies, and challenging each other’s thinking. This peer-to-peer interaction promotes critical thinking by stimulating intellectual discourse and fostering a culture of collaborative learning.
- Engaging in Debates and Discussions on Mathematical Concepts: We organize debates and discussions on mathematical concepts, encouraging students to present arguments, defend their reasoning, and critically evaluate opposing viewpoints. These activities enhance critical thinking skills by promoting analysis, evaluation, and logical reasoning in a structured and engaging manner.
E. Utilizing Technology for Critical Thinking in Math:
- Introduction to Interactive Online Resources and Tools: We incorporate interactive online resources and tools that engage students in problem-solving activities, simulations, and virtual manipulatives. These digital resources provide opportunities for students to think critically, explore mathematical concepts, and apply their knowledge in interactive and engaging ways.
- Using Educational Apps and Software for Problem-Solving: We leverage educational apps and software that offer gamified problem-solving experiences. These tools enhance critical thinking skills by presenting math problems in interactive and engaging formats, encouraging students to think critically, and providing immediate feedback on their solutions.
- Incorporating Online Simulations and Virtual Manipulatives: Online simulations and virtual manipulatives provide students with hands-on experiences and visual representations of mathematical concepts. These interactive tools promote critical thinking by allowing students to explore, manipulate, and analyze mathematical relationships in a dynamic and interactive virtual environment.
At Aspirations Institute, we believe that incorporating these strategies into Class 8 Maths education helps students develop critical thinking skills that extend beyond the classroom. By nurturing their ability to think critically, analyze problems, and apply logical reasoning, we empower students to become confident problem solvers and lifelong learners in mathematics and beyond.
Assessing Critical Thinking Skills in Class 8 Maths:
Assessing and monitoring critical thinking skills in Class 8 Maths is crucial to measure students’ progress, identify areas for improvement, and provide targeted feedback. At Aspirations Institute, we employ various assessment methods to evaluate students’ critical thinking abilities and track their growth over time. These assessments provide valuable insights into students’ problem-solving strategies, analytical thinking, and application of mathematical concepts. Here are some approaches we use to assess and monitor critical thinking skills in Class 8 Maths:
Assessments to Evaluate Critical Thinking Skills:
- Problem-Solving Tasks : We design problem-solving tasks that require students to apply critical thinking skills to analyze, evaluate, and solve mathematical problems. These tasks assess students’ ability to think critically, make connections, and apply appropriate problem-solving strategies.
- Open-Ended Questions : Open-ended questions allow students to demonstrate their critical thinking skills by requiring them to provide detailed explanations, justifications, and alternative approaches to solving math problems. This type of assessment encourages students to think critically, articulate their reasoning, and communicate their thought processes effectively.
- Group Projects and Presentations: Group projects and presentations provide opportunities for students to collaborate, think critically, and communicate their mathematical understanding. These assessments evaluate students’ ability to analyze problems, work collaboratively, and present their findings, fostering critical thinking and communication skills.
- Performance-Based Assessments: Performance-based assessments involve real-life scenarios or simulations where students apply critical thinking skills to solve authentic math problems. These assessments assess students’ ability to analyze, reason, and utilize mathematical concepts in practical situations, reflecting real-world problem-solving skills.
In conclusion, developing critical thinking skills in Class 8 Maths is crucial for students’ overall growth and success in mathematics. By implementing the strategies discussed in this article, students can become proficient problem solvers and develop a deeper understanding of mathematical concepts. Encourage your child to think critically and embrace the challenges that Class 8 Maths presents. With practice and guidance, they will excel in their mathematical journey.
Remember, critical thinking takes time and practice. Encourage students to embrace challenges, ask questions, and explore multiple solution methods. By fostering critical thinking skills, we are empowering students to become lifelong learners and adaptable thinkers.
- Tags: Analytical Thinking , Creative Thinking , Critical Thinking Skills , Effective Teaching Strategies , Logical Reasoning , Problem Solving
- Class 7 Maths Tuition
- Class 7 Science Tuition
- Class 8 Maths Tuition
- Class 8 Science Tuition
- Class 9 Maths Tuition
- Class 9 Science Tuition
- Class 9 SST Tuition
- Class 10 Maths Tuition
- Class 10 Science Tuition
- Class 10 SST Tuition
- Class 11 Physics Tuition
- Class 11 Chemistry Tuition
- Class 11 Maths Tuition
- Class 11 Accountancy Tuition
- Class 11 Economics Tuition
- Class 11 Applied Maths Tuition
- Class 12 Physics Tuition
- Class 12 Chemistry Tuition
- Class 12 Maths Tuition
- Class 12 Accountancy Tuition
- Class 12 Economics Tuition
- Economics Club
- Class TImetable
- Career Counselling
- CBSE Syllabus
- Dwarka School Directory
Our Results

Socialize with us
Worried about cbse exam preparation, learn anytime, anywhere with the aspirations institute's online mcq tests.

- B-185, Palam Extention, Near Ramphal Chowk, Sector 7, Dwarka, New Delhi-110075, India.
- +91-9818737605, +91-9868326454
CBSE Tuition for Classes 8 to 10
- 8 Maths & Science
- 9 Social Science (SST)
- 10 Sci Tuition
- 10 Social Science (SST)
CBSE Tuition for Class 11 & 12
- 11 Chemistry
- 11 Accountancy
- 11 Economics
- 12 Chemistry
- 12 Accountancy
- 12 Economics
Useful Links
- Classes Schedule
- Testimonials
- Free Downloads
- List of Schools in Dwarka
July 1, 2024
The Biggest Problem in Mathematics Is Finally a Step Closer to Being Solved
Number theorists have been trying to prove a conjecture about the distribution of prime numbers for more than 160 years
By Manon Bischoff

Weiquan Lin/Getty Images
The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in mathematician David Hilbert’s groundbreaking speech from 1900 and among the “Millennium Problems” formulated a century later. The person who solves it will win a million-dollar prize.
But the Riemann hypothesis is a tough nut to crack. Despite decades of effort, the interest of many experts and the cash reward, there has been little progress. Now mathematicians Larry Guth of the Massachusetts Institute of Technology and James Maynard of the University of Oxford have posted a sensational new finding on the preprint server arXiv.org. In the paper, “the authors improve a result that seemed insurmountable for more than 50 years,” says number theorist Valentin Blomer of the University of Bonn in Germany.
Other experts agree. The work is “a remarkable breakthrough,” mathematician and Fields Medalist Terence Tao wrote on Mastodon , “though still very far from fully resolving this conjecture.”
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The Riemann hypothesis concerns the basic building blocks of natural numbers: prime numbers, values only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, 13, and so on.
Every other number, such as 15, can be clearly broken down into a product of prime numbers: 15 = 3 x 5. The problem is that the prime numbers do not seem to follow a simple pattern and instead appear randomly among the natural numbers. Nineteenth-century German mathematician Bernhard Riemann proposed a way to deal with this peculiarity that explains how prime numbers are distributed on the number line—at least from a statistical point of view.
A Periodic Table for Numbers
Proving this conjecture would provide mathematicians with nothing less than a kind of “periodic table of numbers.” Just as the basic building blocks of matter (such as quarks, electrons and photons) help us to understand the universe and our world, prime numbers also play an important role, not just in number theory but in almost all areas of mathematics.
There are now numerous theorems based on the Riemann conjecture. Proof of this conjecture would prove many other theorems as well—yet another incentive to tackle this stubborn problem.
Interest in prime numbers goes back thousands of years. Euclid proved as early as 300 B.C.E. that there are an infinite number of prime numbers. And although interest in prime numbers persisted, it was not until the 18th century that any further significant findings were made about these basic building blocks.
As a 15-year-old, physicist Carl Friedrich Gauss realized that the number of prime numbers decreases along the number line. His so-called prime number theorem (not proven until 100 years later) states that approximately n / ln( n ) prime numbers appear in the interval from 0 to n . In other words, the prime number theorem offers mathematicians a way of estimating the typical distribution of primes along a chunk of the number line.
The exact number of prime numbers may differ from the estimate given by the theorem, however. For example: According to the prime number theorem, there are approximately 100 / ln(100) ≈ 22 prime numbers in the interval between 1 and 100. But in reality there are 25. There is therefore a deviation of 3. This is where the Riemann hypothesis comes in. This hypothesis gives mathematicians a way to estimate the deviation. More specifically, it states that this deviation cannot become arbitrarily large but instead must scale at most with the square root of n , the length of the interval under consideration.
The Riemann hypothesis therefore does not predict exactly where prime numbers are located but posits that their appearance on the number line follows certain rules. According to the Riemann hypothesis, the density of primes decreases according to the prime number theorem, and the primes are evenly distributed according to this density. This means that there are no large areas in which there are no prime numbers at all, while others are full of them.
You can also imagine this idea by thinking about the distribution of molecules in the air of a room: the overall density on the floor is somewhat higher than on the ceiling, but the particles—following this density distribution—are nonetheless evenly scattered, and there is no vacuum anywhere.
A Strange Connection
Riemann formulated the conjecture named after him in 1859, in a slim, six-page publication (his only contribution to the field of number theory). At first glance, however, his work has little to do with prime numbers.
He dealt with a specific function, the so-called zeta function ζ( s ), an infinitely long sum that adds the reciprocal values of natural numbers that are raised to the power of s :

Even before Riemann’s work, experts knew that such zeta functions are related to prime numbers. Thus, the zeta function can also be expressed as a function of all prime numbers p as follows:
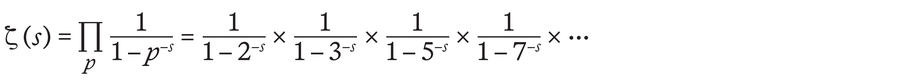
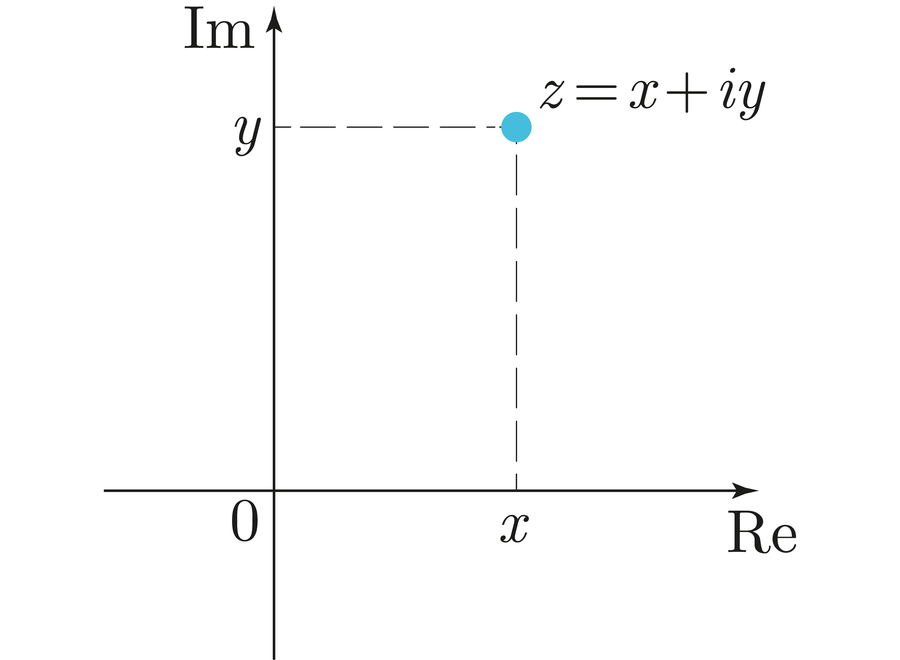
Riemann recognized the full significance of this connection with prime numbers when he used not only real values for s but also complex numbers. These numbers contain both a real part and roots from negative numbers, the so-called imaginary part.
You can imagine complex numbers as a two-dimensional construct. Rather than mark a point on the number line, they instead lie on the plane. The x coordinate corresponds to the real part and the y coordinate to the imaginary part:
Никита Воробьев/Wikimedia
The complex zeta function that Riemann investigated can be visualized as a landscape above the plane. As it turns out, there are certain points amid the mountains and valleys that play an important role in relation to prime numbers. These are the points at which the zeta function becomes zero (so-called zeros), where the landscape sinks to sea level, so to speak.
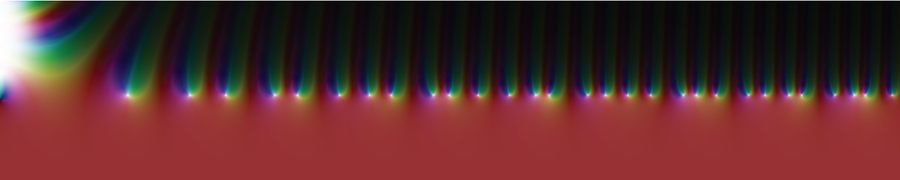
The colors represent the values of the complex zeta function, with the white dots indicating its zeros.
Jan Homann/Wikimedia
Riemann quickly found that the zeta function has no zeros if the real part is greater than 1. This means that the area of the landscape to the right of the straight line x = 1 never sinks to sea level. The zeros of the zeta function are also known for negative values of the real part. They lie on the real axis at x = –2, –4, –6, and so on. But what really interested Riemann—and all mathematicians since—were the zeros of the zeta function in the “critical strip” between 0 ≤ x ≤ 1.
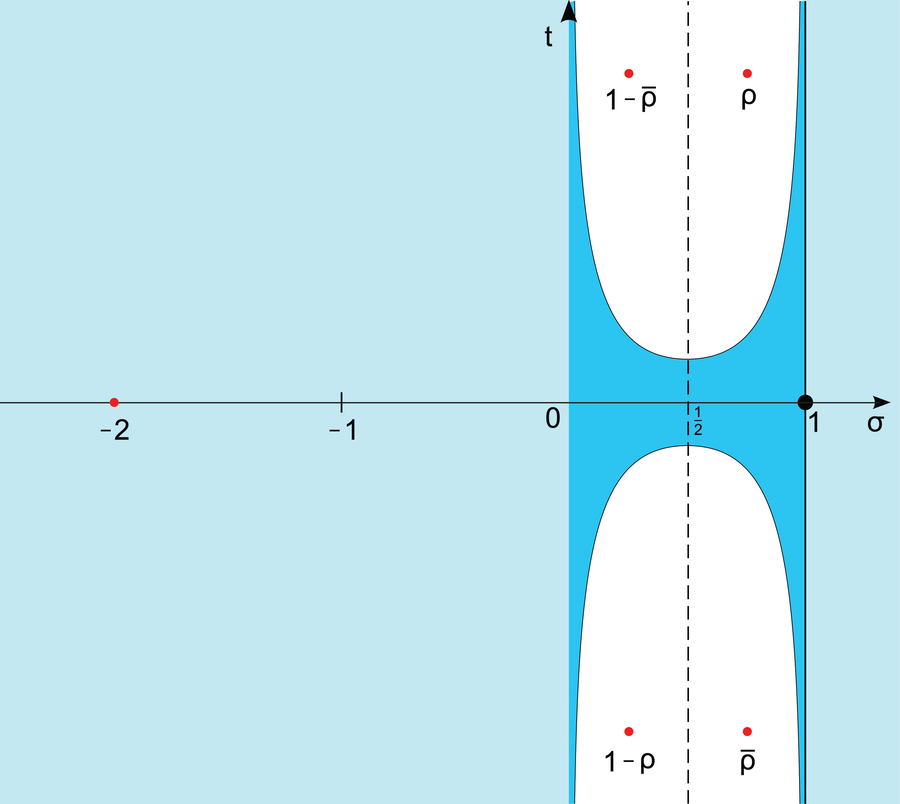
In the critical strip (dark blue), the Riemann zeta function can have “nontrivial” zeros. The Riemann conjecture states that these are located exclusively on the line x = 1/2 (dashed line).
LoStrangolatore/Wikimedia ( CC BY-SA 3.0 )
Riemann knew that the zeta function has an infinite number of zeros within the critical strip. But interestingly, all appear to lie on the straight line x = 1 / 2 . Thus Riemann hypothesized that all zeros of the zeta function within the critical strip have a real part of x = 1 / 2 . That statement is actually at the crux of understanding the distribution of prime numbers. If correct, then the placement of prime numbers along the number line never deviates too much from the prime number set.
On the Hunt for Zeros
To date, billions and billions of zeta function zeros have now been examined— more than 10 13 of them —and all lie on the straight line x = 1 / 2 .
But that alone is not a valid proof. You would only have to find a single zero that deviates from this scheme to disprove the Riemann hypothesis. Therefore we are looking for a proof that clearly demonstrates that there are no zeros outside x = 1 / 2 in the critical strip.
Thus far, such a proof has been out of reach, so researchers took a different approach. They tried to show that there is, at most, a certain number N of zeros outside this straight line x = 1 / 2 . The hope is to reduce N until N = 0 at some point, thereby proving the Riemann conjecture. Unfortunately, this path also turns out to be extremely difficult. In 1940 mathematician Albert Ingham was able to show that between 0.75 ≤ x ≤ 1 there are at most y 3/5+ c zeros with an imaginary part of at most y , where c is a constant between 0 and 9.
In the following 80 years, this estimation barely improved. The last notable progress came from mathematician Martin Huxley in 1972 . “This has limited us from doing many things in analytic number theory,” Tao wrote in his social media post . For example, if you wanted to apply the prime number theorem to short intervals of the type [ x , x + x θ ], you were limited by Ingham’s estimate to θ > 1 / 6 .
Yet if Riemann’s conjecture is true, then the prime number theorem applies to any interval (or θ = 0), no matter how small (because [ x , x + x θ ] = [ x , x + 1] applies to θ = 0).
Now Maynard, who was awarded the prestigious Fields Medal in 2022 , and Guth have succeeded in significantly improving Ingham’s estimate for the first time. According to their work, the zeta function in the range 0.75 ≤ x ≤ 1 has at most y (13/25)+ c zeros with an imaginary part of at most y . What does that mean exactly? Blomer explains: “The authors show in a quantitative sense that zeros of the Riemann zeta function become rarer the further away they are from the critical straight line. In other words, the worse the possible violations of the Riemann conjecture are, the more rarely they would occur.”
“This propagates to many corresponding improvements in analytic number theory,” Tao wrote . It makes it possible to reduce the size of the intervals for which the prime number theorem applies. The theorem is valid for [ x , x + x 2/15 ], so θ > 1 / 6 = 0.166... becomes θ > 2 ⁄ 15 = 0.133...
For this advance, Maynard and Guth initially used well-known methods from Fourier analysis for their result. These are similar techniques to what is used to break down a sound into its overtones. “The first few steps are standard, and many analytic number theorists, including myself, who have attempted to break the Ingham bound, will recognize them,” Tao explained . From there, however, Maynard and Guth “do a number of clever and unexpected maneuvers,” Tao wrote.
Blomer agrees. “The work provides a whole new set of ideas that—as the authors rightly say—can probably be applied to other problems. From a research point of view, that’s the most decisive contribution of the work,” he says.
So even if Maynard and Guth have not solved Riemann’s conjecture, they have at least provided new food for thought to tackle the 160-year-old puzzle. And who knows—perhaps their efforts hold the key to finally cracking the conjecture.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
We-Math: Does Your Large Multimodal Model Achieve Human-like Mathematical Reasoning?
- Qiao, Runqi
- Dong, Guanting
- Song, Xiaoshuai
- GongQue, Zhuoma
- Lei, Shanglin
- Zhang, Miaoxuan
- Qiao, Runfeng
- Zhang, Yifan
- Bao, Zhimin
- Zhang, Honggang
Visual mathematical reasoning, as a fundamental visual reasoning ability, has received widespread attention from the Large Multimodal Models (LMMs) community. Existing benchmarks, such as MathVista and MathVerse, focus more on the result-oriented performance but neglect the underlying principles in knowledge acquisition and generalization. Inspired by human-like mathematical reasoning, we introduce WE-MATH, the first benchmark specifically designed to explore the problem-solving principles beyond end-to-end performance. We meticulously collect and categorize 6.5K visual math problems, spanning 67 hierarchical knowledge concepts and five layers of knowledge granularity. We decompose composite problems into sub-problems according to the required knowledge concepts and introduce a novel four-dimensional metric, namely Insufficient Knowledge (IK), Inadequate Generalization (IG), Complete Mastery (CM), and Rote Memorization (RM), to hierarchically assess inherent issues in LMMs' reasoning process. With WE-MATH, we conduct a thorough evaluation of existing LMMs in visual mathematical reasoning and reveal a negative correlation between solving steps and problem-specific performance. We confirm the IK issue of LMMs can be effectively improved via knowledge augmentation strategies. More notably, the primary challenge of GPT-4o has significantly transitioned from IK to IG, establishing it as the first LMM advancing towards the knowledge generalization stage. In contrast, other LMMs exhibit a marked inclination towards Rote Memorization - they correctly solve composite problems involving multiple knowledge concepts yet fail to answer sub-problems. We anticipate that WE-MATH will open new pathways for advancements in visual mathematical reasoning for LMMs. The WE-MATH data and evaluation code are available at https://github.com/We-Math/We-Math.
- Computer Science - Artificial Intelligence;
- Computer Science - Computation and Language;
- Computer Science - Computer Vision and Pattern Recognition;
- Computer Science - Machine Learning;
- Computer Science - Symbolic Computation
Help | Advanced Search
Computer Science > Artificial Intelligence
Title: smart vision-language reasoners.
Abstract: In this article, we investigate vision-language models (VLM) as reasoners. The ability to form abstractions underlies mathematical reasoning, problem-solving, and other Math AI tasks. Several formalisms have been given to these underlying abstractions and skills utilized by humans and intelligent systems for reasoning. Furthermore, human reasoning is inherently multimodal, and as such, we focus our investigations on multimodal AI. In this article, we employ the abstractions given in the SMART task (Simple Multimodal Algorithmic Reasoning Task) introduced in \cite{cherian2022deep} as meta-reasoning and problem-solving skills along eight axes: math, counting, path, measure, logic, spatial, and pattern. We investigate the ability of vision-language models to reason along these axes and seek avenues of improvement. Including composite representations with vision-language cross-attention enabled learning multimodal representations adaptively from fused frozen pretrained backbones for better visual grounding. Furthermore, proper hyperparameter and other training choices led to strong improvements (up to $48\%$ gain in accuracy) on the SMART task, further underscoring the power of deep multimodal learning. The smartest VLM, which includes a novel QF multimodal layer, improves upon the best previous baselines in every one of the eight fundamental reasoning skills. End-to-end code is available at this https URL .
| Comments: | Accepted in ICML 2024 MATH AI Workshop |
| Subjects: | Artificial Intelligence (cs.AI) |
| Cite as: | [cs.AI] |
| (or [cs.AI] for this version) |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
Mastery-Aligned Maths Tutoring
“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."
FREE daily maths challenges
A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

Developing Maths Reasoning in KS2: The Mathematical Skills Required And How To Teach Them
Developing maths reasoning skills at and before KS2 is crucial to succeeding in the new curriculum and its maths mastery approach to learning.
Moreover, as the results of the KS2 SATs , with their focus on maths reasoning questions have shown us, pupils need strong applied reasoning with their maths facts to be able to succeed.
My approach to primary school mathematics teaching and learning is that it should be about exploring, reasoning and challenging thinking rather than learning rote/abstract rules for calculations and facts.
Though I recognise that fluency in maths and memorising key number facts is essential in Key Stage 1 and Key Stage 2 mathematics, to acquire the basics, these skills ought to be used and applied in real life contexts.
The questions from the KS2 SATs Papers 2019 seem to align with my belief. To succeed in the national curriculum tests, it is clear that children require deep knowledge of facts and mathematical concepts. Moreover, they need to be able to use and apply these facts to a range of contexts, and different types of word problems , including the more complex multi-step and two-step word problems
What is reasoning in maths?
Let’s start with the definition of maths reasoning. Reasoning in maths is the process of applying logical and critical thinking to a mathematical problem in order to work out the correct strategy to use (and as importantly, not to use) in reaching a solution.
Reasoning is sometimes seen as the glue that bonds pupils’ mathematical skills together; it’s also seen as bridging the gap between fluency and problem solving, allowing pupils to use their fluency to accurately carry out problem solving.
In my opinion it is only when we teach children to reason and give them the freedom to look for different strategies when faced with an unfamiliar context that we are really teaching mathematics in primary school.
Why focus teaching and learning on reasoning?
Logical reasoning requires metacognition (thinking about thinking) . It influences behaviour and attitudes through greater engagement, requesting appropriate help (self-regulation) and seeking conceptual understanding.
Reasoning promotes these traits because it requires children to use their mathematical vocabulary . In short, reasoning requires a lot of active talk.
It is worth mentioning that with reasoning, active listening is equally important and if done right can also ensure increased learning autonomy for pupils.

The Ultimate Guide to Problem Solving Techniques
9 ready-to-go problem solving techniques with accompanying tasks to get KS2 reasoning independently
The theory behind mathematical reasoning at KS1 & KS2
The infographic (below) from Helen Drury cleverly details what should underpin mathematics teaching and learning. It’s a good starting point when you’re thinking about your mathematics curriculum in the context of fluency reasoning and problem solving .
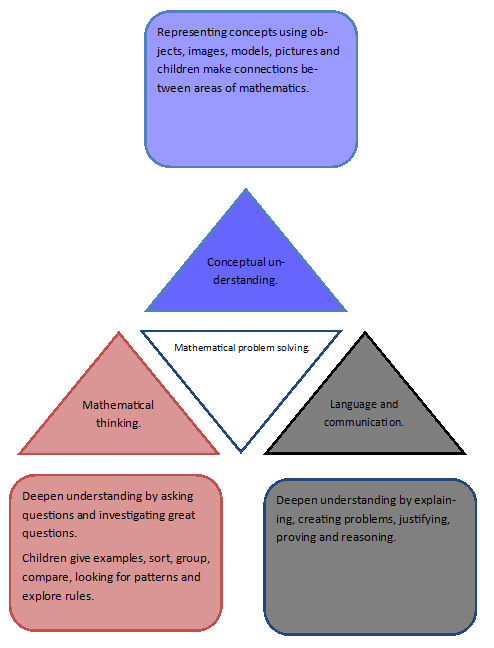
I’ve also been very influenced by the Five Principles of Extraordinary Math Teaching by Dan Finkel
These are as follows, and are a great starting point to developing maths reasoning at KS2
1. Start mathematics lessons with a question 2. Students need to wonder and struggle 3. You are not the answer key 4. Say yes to your students original ideas (but not yes to methodical answers) 5. Play!
See also this free guide to KS2 maths problem solving and reasoning techniques .
How to make reasoning central to Maths lessons in KS2
Pose lesson objectives as a question to ks1 & ks2 children.
A ‘light bulb’ idea from my own teaching and learning was to redesign learning objectives, fashioning them into a question for learning. Instead of ‘to identify multiples of a number’, for example, I’ll use ‘why is a square number a square number?’.
Phrasing LOs as a question instantly engages and enthuses children, they wonder what the answer is. It also ensures that they show their reasoning in a model or image when they answer.
In this instance – interestingly – children knew the process to calculate square numbers but could not articulate or mathematically reason why it worked until after the session.
It seems denying children answers allows them time to think, struggle and learn.
Ban the word ‘yes’ in Maths lessons
One of the simplest strategies I have found to make reasoning inseparable from mathematical learning is to ban the word ‘yes’ from the classroom.
Instead, asking children to reason their thoughts and explain why they think they are right can allow for greater learning gains and depth of understanding. Admittedly, this is still a work in progress and easier said than done.
To facilitate this, I always tell my children that I am not the answer key.
Using my example of square numbers, I allowed children time to struggle and wrestle with my question without providing an answer or giving hints. Instead, I questioned to unpick understanding at the beginning of the lesson and brought together mathematical ideas during a whole class discussion.
After a short discussion on how children might show or visualize a square number we began to show a model using arrays, like below:
The children working at greater depth were encouraged to consider cubed numbers and show how they might be represented using multi-link cubes without any input from me. This made sure links were made between mathematical knowledge, mathematical vocabulary, and learning.
Use ‘sometimes, always, never’ classroom activities
A ‘sometimes, always, never’ activity is another great way to foster reasoning and problem-solving skills. Take the image below:

Here, children are first required to sort the statement into always, sometimes or never being true. The next day, they are moved on to the lesson with the title phrased as a question. So Not ‘to identify patterns’, but ‘how does this pattern work?’ with a pattern already presented on the board.
The children, instantly engaged, begin conjecturing, making predictions and thinking about the next patterns in the sequence (this lesson was actually inspired by an Nrich activity) .
5 tips for developing mathematical reasoning in the KS2 classroom
While small changes will not provide the framework you need to properly embed reasoning in the classroom when implemented alongside ideas such as those mentioned above. These tips can help instil greater depth in maths in your class for all ability levels.
1. Start lessons with a question.
2. Start lessons with a provocative mathematical statement and challenge your class to provide the mathematical proof: “ N will always = N” or “Multiples of 9 always have the digital sum of 9”.
3. Present answers to SATs question as a puzzle to generate discussion. When framed like this, children like to ‘come up’ with what the question could be:
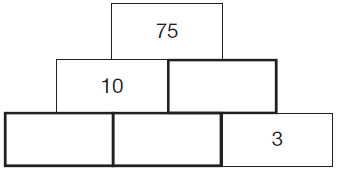
or
4. Grouping children in threes is the magic number when working through problems. Child one talks through the problem. Child two writes down everybody’s reasoning. Child three actively listens and watches.
5. Include reasoning prompting posters around the classroom. The image below, for example, can be useful to children who are starting to formulate thoughts, predictions and assertions.
As the most recent KS2 Maths SATs tests proved, your pupils will need an in-depth understanding of facts and concepts to truly succeed. Plus, they will need to be able to use and apply that knowledge to a range of contexts. As such, it’s clear that we need to provide them with a strong foundation of reasoning skills to give them their very best shot at the assessments they must face.
- Maths Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
- Get to Grips with Maths Problem Solving KS2
- 21 Maths Challenges To Really Stretch Your More Able Pupils
- Maths Reasoning and Problem Solving CPD Powerpoint
- 20 Maths Strategies KS2 That Guarantee Progress
- Why You Should Be Incorporating Stem Sentences Into Your Primary Maths Teaching
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils
What Is Numicon? Explained For Primary School Teachers, Parents And Pupils
FREE Guide to Maths Mastery
All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.
Ideal for running staff meetings on mastery or sense checking your own approach to mastery.
Privacy Overview
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- TECHNOLOGY FEATURE
- 03 July 2024
Inside the maths that drives AI
- Michael Brooks 0
Michael Brooks is a science writer in Lewes, UK.
You can also search for this author in PubMed Google Scholar
Credit: Getty
People usually talk about the race to the bottom in artificial intelligence as a bad thing. But it’s different when you’re discussing loss functions.
Loss functions are a crucial but frequently overlooked component of useful artificial intelligence (AI), and they’re all about getting to the bottom — albeit of a literal curve on a graph — as quickly as possible. When training an algorithm to automate tedious data analysis, such as looking for specific features in millions of photographs, you need a way of measuring its performance. That’s the ‘loss function’: it measures an algorithm’s error relative to the ‘ground truth’ of the data — information that is known to be real or true. Then you adjust the algorithm’s parameters, rinse and repeat, and hope the error is smaller next time. “You’re trying to find a minimum: the point where the error is as small as possible — hopefully zero,” says Anna Bosman, a computational-intelligence researcher at the University of Pretoria.
Dozens of off-the-shelf loss functions have been written. But choose the wrong one, or just handle it badly, and the algorithm can lead you astray. It could blatantly contradict human observations, make random fluctuations (known as experimental noise) look like data, or even obscure the central results of an experiment. “There are lots of things that can go wrong,” Bosman says. And worst of all, the opacity of AI means you might not even know that you’ve been misled.
That’s why a growing number of scientists are abandoning ready-made loss functions and constructing their own. But how do they get it right? How do you make a home-made loss function your go-to tool and not a time-swallowing mistake?
Error assessment
Machine-learning algorithms are generally trained on annotated data, or by being told when they get the answer wrong. Loss functions provide a mathematical measure of wrongness, but there are multiple ways to quantify that.
‘Absolute error’ functions, for example, report the difference between the algorithm’s prediction and the target value. Then there’s mean squared error: square the differences between your predictions and the ground truth, and then average them out across the whole data set.
Mean squared error is a simple, straightforward and proven approach that works well when errors are relatively small and consistent. But it can be problematic if your data are full of outliers, because the algorithm amplifies their impact. A loss function called pseudo-Huber (a smooth approximation of an approach called the Huber loss function) considers whether each data point’s error is large or small, providing a compromise between the mean squared error and absolute error loss functions.
Absolute error, mean squared error and Huber are most useful for regression analysis, which uses past data on continuous variables such as height or weight in a population to predict what shape future data sets will take (see ‘Quantifying loss’). Classification tasks, by contrast, answer questions such as what type of object something is and how many of them are in the data set. In this case, the machine-learning algorithm determines the probability that an object belongs to a particular class — how likely it is that a particular collection of pixels represents a dog, for example. The most useful loss functions include cross entropy, a measure that compares probability distributions related to the model’s output and the real-world value (also known as maximum likelihood), and hinge loss. The latter finds the curve that is the farthest possible distance from every data point, providing the cleanest possible decision about which category a data point falls into.
These generalized loss functions are not always the best option, however. Take Arjun Raj’s experience, for example.
A geneticist at the University of Pennsylvania in Philadelphia, Raj uses fluorescence microscopy to quantify gene expression in single cells. In these experiments, each RNA transcript is a discrete spot in an image: the trick is to count the spots and assign them to the correct cell. Finding the spots — which are two or three pixels across — is trivial for a human. “One summer, I had a high-school student working with me who had never seen these images, and I was able to teach him how to perfectly annotate the images within two minutes,” says William Niu, a former undergraduate student in Raj’s laboratory.
Unfortunately, the lab generates data sets that might represent thousands of fluorescent spots in millions of cells, too many to analyse by hand. Even more unfortunately, the analysis is much harder for machines than it is for humans. When Raj and his colleagues tried to automate the process, they found that no known loss function could return a reliable result.
The problem mainly came down to ‘class imbalance’, Raj says: when spots are few and far between, the algorithm might think that it is performing well if it simply labels every pixel as ‘not-spot’. But that gives a catastrophically high false-negative rate. “You could make a really ‘good’ classifier that just said there’s no spots in this image because 99.9% of the time, there are no spots,” Raj says. “It’s very, very accurate in some sense, even though it’s basically doing nothing useful at all.”

AI and science: what 1,600 researchers think
Niu, Raj and others in their lab worked together to translate their understanding of the issues into a loss function called SmoothF1 1 . F1 is a metric that balances false negatives against false positives. However, the mathematical function behind F1 cannot be differentiated, which means it can’t be used to train a neural network, because it lacks a way to minimize the algorithm’s error. SmoothF1 approximates the F1 score in a way that compensates for class imbalance while allowing the algorithm to find its way to the bottom of the error slope. The team then used this function to drive a spot-detection algorithm called Piscis.
The work Niu did “made a huge difference to our lab”, Raj says. “It has allowed us to power through analyses with much higher throughput.” But Piscis should be useful for a range of applications, Niu says. “Theoretically, our method should be able to get better performance on any type of object in which the objects that you’re looking for occupy less than, say, 5% of the image,” he says.
Pedro Seber, a chemical-engineering student at the Massachusetts Institute of Technology in Cambridge, created his own loss function to teach a machine-learning algorithm to predict sites of glycosylation — sugar chain addition — in mammalian proteins. Such a task is potentially useful in understanding the pathways of diseases, including cancer 2 .
Seber didn’t set out to delve into the machine-learning side of his research — he was trying to train his model using a loss function based on cross entropy, but this impaired the model’s performance. “Sometimes, the model with the lowest cross entropy was not necessarily the model with the best metrics,” Seber says. Digging deeper, he found that this was because the cross entropy didn’t actually relate to the prediction task. “It was optimizing something that I didn’t really care about,” he explains.

How to spice up your bioinformatics skill set with AI
Seber decided to create a bespoke loss function that focused on something he did care about: a tweaked version of the Matthews correlation coefficient (MCC), a function similar to F1 that provides a metric for training an algorithm. It might not have the snappiest name, but Seber’s ‘weighted focal differentiable MCC loss function’ boosted MCC performance by about 10%. That’s not very high, he acknowledges, “but at that point, every improvement counts”. Seber says that even this improvement is enough to achieve state-of-the-art performance — a highly desirable outcome because glycosylation sites represent potential targets for drug and biotherapeutic development.
Not every venture into creating loss functions will be a huge success, warns Andrew Engel, a data scientist at the Pacific Northwest National Laboratory in Richland, Washington. Engel has had mixed results, for instance, with a loss function designed to help neural networks assess the redshift of galaxies in telescope images 3 — a measure used to derive the distance of objects from Earth.
Engel had wondered whether supplementing an existing loss function with astronomical knowledge might improve its performance. To his surprise, it didn’t, probably because the new information he was feeding the algorithm was effectively reiterating what it already knew. But at least he didn’t waste a lot of time: training the model wasn’t particularly time-consuming, meaning he could test different approaches — to “fail quickly”, as Engel puts it. “The nice thing about this field is we get constant feedback on whether our idea is working or not.”
What to measure?
That said, researchers can’t always articulate what their loss function should be measuring. You want the AI to do better, but in what way? “There’s always going to be some barrier in translating what your desires are to what it means mathematically,” Niu says.
That view is supported by a study 4 published in 2023 by engineering researchers Hansol Ryu and Manoj Srinivasan at the Ohio State University in Columbus. Ryu and Srinivasan asked scientists and engineers to manually perform the work of a loss function, fitting curves to a variety of data sets by eye. To the team’s surprise, each individual’s approach varied from data set to data set and person to person.
AI under the microscope: the algorithms powering the search for cells
“Humans are a lot more variable than computer algorithms,” Ryu says. For instance, many of those who said they were trying to visualize mean-squared error were subconsciously using a different method — one that involved finding the most frequently occurring value, called the mode of the data set, instead of the mean. What’s more, researchers were inconsistent in how they handled outliers, and they seemed to reject outliers more as the amount of data increased.
Complicating matters, training an AI is about more than minimizing error. Researchers must also avoid ‘overfitting’, in which the training has been too narrow to allow the model to work with real-world data — creating a loss function that is extremely efficient, but not in a good way. “If your model is overly complex, then you might have an extremely complex [function] that crosses every single point in your data set,” Bosman says. “On paper, it looks like your model is absolutely great, but if you try to apply it to some real points, the output will be absolutely horrendous and the predictions will be completely wrong.”
However, Bosman’s main advice is: know your noise. “In the real world, data is very, very messy,” she points out. A generic loss function makes assumptions — which might not necessarily apply to your data. Mean squared error, the most common loss function for regression problems, assumes a normal distribution of data points, for example. But your data might conform better to a different shape. Bosman is part of a team that has investigated loss functions that use the Cauchy distribution for such data. This distribution looks similar to a normal distribution but has heavier tails — that is, more of the data lie outside the most common values. Cauchy-based loss functions can give a better performance when there is noise in the data that doesn’t conform to a normal distribution, she says.
Choose your function
It’s hard to overstate the importance of such considerations, says Jonathan Wilton, a machine-learning graduate student at the University of Queensland in Brisbane, Australia. “If you’re in a situation where you believe that there are probably errors or problems with your data … then it’s probably a good idea to consider using a loss function that’s not so standard,” he says.
Working with Nan Ye, a statistics, data-science and machine-learning researcher at the University of Queensland, Wilton constructed a framework for creating loss functions that are robust against noise in classification tasks 5 . Here, the problem can be summed up as mislabelling: training data that has a dog incorrectly labelled as a cat, for example. That’s a common problem in machine learning, Ye says. “If your loss function is not robust to that kind of noise, then you might end up encouraging the model to fit the noise, not the regularities in the data.”
To create his function, Wilton started with a loss function for a machine-learning architecture called a decision tree — something that might analyse a slew of highly disparate medical information to make a disease diagnosis, for example. Now, Wilton is trying to develop an equivalent function for neural-net architectures. Decision trees, he explains, are “really versatile”. “But neural nets are particularly useful in situations where you collect very large data sets, in the order of hundreds of thousands or millions of examples, all of a similar type.” So far, he says, the results are promising.
Beyond knowing your noise, one crucial thing specialists advise is incorporating ‘domain knowledge’: seek to create a loss function that reflects what a real-world practitioner knows about the system. The reason Niu’s loss function was so successful, Raj says, is that Niu “really paid attention to what real users needed and how to make it work best for them”.
Engel agrees. “I see many new AI scientists being deployed to problems or data sets where they lack domain knowledge,” he says. “In those cases, they should sit down with a domain expert for a long time to really ingest and jargon-bust that field.” It might take a few iterations to apply that knowledge successfully, he says, but it’s worth the effort.

NatureTech hub
That said, as the pool of available loss functions grows larger, picking the right function will only grow more complex. Programming libraries such as PyTorch and scikit-learn allow researchers to swap loss functions fairly easily, and Bosman suggests playing around with several functions to see what works. “My recommendation is usually to try [a couple of options], train for 30 times with each, and then we have a statistical sample and we can figure out if one is statistically better on average than the other,” she says.
The problem could get easier soon, however. Wilton, who is curating a library of loss functions for decision trees, says one possibility is a unification of loss functions — an overarching method that will work broadly across many kinds of data and problem. Another option is a machine-learning algorithm that chooses and optimizes its own loss function, or what Bosman calls a ‘meta-model’ that could recommend the best loss function for your problem from a list of available options.
Niu imagines an even more radical idea: you just tell a generative AI about your research, and it will recommend the right tool. “A generative AI model might just give you this for free,” he suggests.
Some researchers are already doing this. Machine-learning researcher Juan Terven at the National Polytechnic Institute in Mexico City regularly converses with the chatbot ChatGPT about his loss function requirements. “You need to specify the nature of your problem and the nature of your data, but it will give you a list of things to try,” he says. Last year, Terven and his colleagues conducted an extensive review of loss functions and their applications 6 and is impressed by ChatGPT’s ability to select the right ones.
In the end, says Ye, finding the best loss function for your problem “is both a science and an art”. A science, because loss functions can be quantified and compared; and an art, because the blending of maths and domain knowledge often requires creative thinking. But whether art or science, loss functions deserve your attention. Ignore them, and AI will remain a black, and sometimes befuddling, box.
Nature 631 , 244-246 (2024)
doi: https://doi.org/10.1038/d41586-024-02185-z
Niu, Z. et al. Preprint at bioRxiv https://doi.org/10.1101/2024.01.31.578123 (2024).
Seber, P. Preprint at arXiv https://doi.org/10.48550/arXiv.2402.17131 (2024).
Engel, A. & Strube, J. Preprint at arXiv https://doi.org/10.48550/arXiv.2310.13624 (2023).
Ryu, H. X. & Srinivasan, M. Preprint at bioRxiv https://doi.org/10.1101/2023.09.19.558376 (2023).
Wilton, J. & Ye, N. Preprint at arXiv https://doi.org/10.48550/arXiv.2312.12937 (2024).
Terven, J., Cordova-Esparza, D. M., Ramirez-Pedraza, A. & Chavez-Urbiola, E. A. Preprint at arXiv https://doi.org/10.48550/arXiv.2307.02694 (2023).
Download references
Related Articles

- Machine learning
- Computer science
Ex-Meta scientists debut gigantic AI protein design model
News 08 JUL 24
Streamlined collaboration can boost CRISPR gene therapies for rare diseases
Correspondence 02 JUL 24

Bionic leg moves like a natural limb — without conscious thought
News 01 JUL 24
AI machine translation tools must be taught cultural differences too
Correspondence 25 JUN 24

‘Fighting fire with fire’ — using LLMs to combat LLM hallucinations
News & Views 19 JUN 24

Not all ‘open source’ AI models are actually open: here’s a ranking
News 19 JUN 24

Can AI be superhuman? Flaws in top gaming bot cast doubt

How I’m using AI tools to help universities maximize research impacts
World View 26 JUN 24
Al Medical Engineering at School of Biomedical Engineering
Tsinghua BME offers faculty positions in the emerging research direction of AI Medical Engineering
Beijing, China
Tsinghua University
Shanghai Jiao Tong University Global Recruitment
Interested applicants can send CV to the relevant department/school.
Shanghai, China
Shanghai Jiao Tong University
Faculty Positions in School of Engineering, Westlake University
The School of Engineering (SOE) at Westlake University is seeking to fill multiple tenured or tenure-track faculty positions in all ranks.
Hangzhou, Zhejiang, China
Westlake University
Postdoctoral Fellow – Thoracic and Head & Neck Medical Oncology
Postdoctoral Fellow – Thoracic and Head &Neck Medical Oncology – KRAS-mutant non-small cell lung cancer (NSCLC)
Houston, Texas (US)
The University of Texas MD Anderson Cancer Center
Postdoctoral Fellow - Biostatistics
Memphis, Tennessee
The University of Tennessee Health Science Center (UTHSC)
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies

IMAGES
VIDEO
COMMENTS
Fluency, reasoning and problem solving are central strands of mathematical competency, as recognized by the National Council of Teachers of Mathematics (NCTM) and the National Research Council's report 'Adding It Up'. They are key components to the Standards of Mathematical Practice, standards that are interwoven into every mathematics ...
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
Mathematical Reasoning is the foundation of problem-solving and critical thinking in mathematics. It involves the ability to analyze, deduce, and draw conclusions from mathematical concepts, principles, and relationships. In this guide, we will explore the key aspects of mathematical reasoning, provide examples to illustrate its application ...
Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth. Q1. Look at this series: 12, 10, 13, 11, 14, 12, ….
This is an essential element of mastering mathematics. As well as being part of the problem-solving process, we suggest that being able to prove is also the highest step on the reasoning journey (see our Reasoning Feature and particularly our article Reasoning: the Journey from Novice to Expert), following
translate problems in mathematical or non-mathematical contexts into a process or a series of mathematical processes. make and use connections between different parts of mathematics. interpret results in the context of the given problem. evaluate methods used and results obtained. evaluate solutions to identify how they may have been affected ...
Developing Excellence in Problem Solving with Young Learners. Age 5 to 11. Becoming confident and competent as a problem solver is a complex process that requires a range of skills and experience. In this article, Jennie suggests that we can support this process in three principal ways. Using NRICH Tasks to Develop Key Problem-solving Skills.
The ability to reason also supports the application of mathematics and an ability to solve problems set in unfamiliar contexts. Research by Nunes (2009) identified the ability to reason mathematically as the most important factor in a pupil's success in mathematics. It is therefore crucial that opportunities to develop mathematical reasoning ...
Professional mathematicians think a certain way to solve real problems, problems that can arise from the everyday world, or from science, or from within mathematics itself. The key to success in school math is to learn to think inside-the-box. In contrast, a key feature of mathematical thinking is thinking outside-the-box - a valuable ability ...
The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning. ... there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring! KS2 - KS4 Teaching Resources Index. KS5 Teaching Resources Index.
Pattern spotting. Working backwards. Reasoning logically. Visualising. Conjecturing. The first two in this list are perhaps particularly helpful. As learners progress towards a solution, they may take the mathematics further (stage 3) and two more problem-solving skills become important: Generalising. Proving.
The perspective on teaching and learning through problem solving that is taken here emphasizes the complexity of simultaneously learning mathematics and the broad domains of the language of mathematics. Problem solving is one way that students are accorded opportunities to develop deep understandings of mathematical concepts; to acquire the ...
Mathematics provides a systematic and logical framework for problem-solving and critical thinking. The study of math helps to develop analytical skills, logical reasoning, and problem-solving abilities that can be applied to many areas of life.By using critical thinking skills to solve math problems, we can develop a deeper understanding of concepts, enhance our problem-solving skills, and ...
Develop fluency, reasoning and problem solving in Maths with the mastery approach. The skills of fluency, reasoning and problem solving are well-known to all primary Maths teachers, and in mastery teaching they play an essential role. To help you develop your mastery approach, we have hand-picked this selection of Maths resources, with ...
Fluency reasoning and problem solving have been central to the new maths national curriculum for primary schools introduced in 2014. Here we look at how these three approaches or elements of maths can be interwoven in a child's maths education through KS1 and KS2.
This booklet contains over 40 reasoning and problem solving questions suitable for KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS. The answers are provided with some simple notes at the ... The White Rose Maths Hub Team . KS2
Reasoning in maths is the exciting bridge that allows students to come up with a reasonable strategy to solve a problem, and explain how and why they have worked the way they have. Working with reasoning in mind helps to develop a deeper level of mathematical understanding. Instead of simply 'doing what miss says' and mindlessly following a set ...
These are as follows, and are a great starting point to developing math reasoning at the elementary school level. 1. Start math lessons with a question. 2. Students need to wonder and struggle. 3. You are not the answer key. 4. Say yes to your students original ideas (but not yes to methodical answers)
Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods, such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by ...
Tip # 1: Read the question thoroughly and understand the meaning of all the symbols given in the question to solve problem solving reasoning based questions easily. Tip # 2: Problem based questions are mathematics related, so it requires a lot of calculation.
pptx, 2.35 MB. pdf, 3.51 MB. These booklets each contain over 40 reasoning and problem solving questions suitable for KS1, KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS. The answers are provided with some simple notes at the back of the booklet and for some ...
By explicitly teaching Polya's problem-solving process, the students cultivated valuable skills that extend beyond maths problems. Some of the key benefits observed were: Mathematical Reasoning: Polya's process promotes the development of mathematical reasoning skills. Students analysed problems, explored different strategies, and apply logical ...
Please check back soon, or follow our social media accounts for updates. Our maths problems of the day provide four problems across KS1, KS2 and Lower KS3 for pupils to solve. View our Maths resources from White Rose Maths.
A. Encouraging Problem-Solving Approaches: Introduction to Real-Life Problem-Solving Scenarios: We present students with real-life scenarios that require mathematical problem-solving skills. This approach helps students understand the practical application of math and encourages them to think critically about how to solve problems in real-world ...
The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in ...
Inspired by human-like mathematical reasoning, we introduce WE-MATH, the first benchmark specifically designed to explore the problem-solving principles beyond end-to-end performance. We meticulously collect and categorize 6.5K visual math problems, spanning 67 hierarchical knowledge concepts and five layers of knowledge granularity.
In this article, we investigate vision-language models (VLM) as reasoners. The ability to form abstractions underlies mathematical reasoning, problem-solving, and other Math AI tasks. Several formalisms have been given to these underlying abstractions and skills utilized by humans and intelligent systems for reasoning. Furthermore, human reasoning is inherently multimodal, and as such, we ...
These tips can help instil greater depth in maths in your class for all ability levels. 1. Start lessons with a question. 2. Start lessons with a provocative mathematical statement and challenge your class to provide the mathematical proof: " N will always = N" or "Multiples of 9 always have the digital sum of 9". 3.
Here, the problem can be summed up as mislabelling: training data that has a dog incorrectly labelled as a cat, for example. That's a common problem in machine learning, Ye says.
(Develop Problem Solving, Critical Thinking, Analytical & STEM Skills in Kids Ages 4, 5, 6.) PDF My First Logic Workbook for Gritty Kids: Spatial Reasoning, Math Puzzles, Logic Problems, Focus Activities. (Develop Problem Solving, Critical Thinking, Analytical & STEM Skills in Kids Ages 4, 5, 6.) DOWNLOAD OR READ this book by click link below: