how to solve grid problems programming

Ensure that you are logged in and have the required permissions to access the test.

A server error has occurred. Please refresh the page or try after some time.

An error has occurred. Please refresh the page or try after some time.

Signup and get free access to 100+ Tutorials and Practice Problems Start Now

1. Introduction

There are many problems in online coding contests which involve finding a minimum-cost path in a grid, finding the number of ways to reach a particular position from a given starting point in a 2-D grid and so on. This post attempts to look at the dynamic programming approach to solve those problems. The problems which will be discussed here are :

Finding the Minimum Cost Path in a Grid when a Cost Matrix is given. Finding the number of ways to reach from a starting position to an ending position travelling in specified directions only. Finding the number of ways to reach a particular position in a grid from a starting position (given some cells which are blocked)

2. Finding Minimum-Cost Path in a 2-D Matrix

Problem Statement : Given a cost matrix Cost[][] where Cost[i][j] denotes the Cost of visiting cell with coordinates (i,j), find a min-cost path to reach a cell (x,y) from cell (0,0) under the condition that you can only travel one step right or one step down. (We assume that all costs are positive integers)

Solution : It is very easy to note that if you reach a position (i,j) in the grid, you must have come from one cell higher, i.e. (i-1,j) or from one cell to your left , i.e. (i,j-1). This means that the cost of visiting cell (i,j) will come from the following recurrence relation:

The above statement means that to reach cell (i,j) wit minimum cost, first reach either cell(i-1,j) or cell (i,j-1) in as minimum cost as possible. From there, jump to cell (i,j). This brings us to the two important conditions which need to be satisfied for a dynamic programming problem:

Optimal Sub-structure :- Optimal solution to a problem involves optimal solutions to sub-problems. Overlapping Sub-problems :- Subproblems once computed can be stored in a table for further use. This saves the time needed to compute the same sub-problems again and again.

(You can google the above two terms for more details)

The problem of finding the min-Cost Path is now almost solved. We now compute the values of the base cases: the topmost row and the leftmost column. For the topmost row, a cell can be reached only from the cell on the left of it. Assuming zero-based index,

i.e. cost of reaching cell (0,j) = Cost of reaching cell (0,j-1) + Cost of visiting cell (0,j) Similarly,

i.e. cost of reaching cell (i,0) = Cost of reaching cell (i-1,0) + Cost of visiting cell (i,0)

Other values can be computed from them. See the code below for more understanding.

Another variant of this problem includes another direction of motion, i.e. one is also allowed to move diagonally lower from cell (i,j) to cell (i+1,j+1). This question can also be solved easily using a slight modification in the recurrence relation. To reach (i,j), we must first reach either (i-1,j), (i,j-1) or (i-1,j-1).

2. Finding the number of ways to reach from a starting position to an ending position travelling in specified directions only.

Problem Statement : Given a 2-D matrix with M rows and N columns, find the number of ways to reach cell with coordinates (i,j) from starting cell (0,0) under the condition that you can only travel one step right or one step down.

Solution : This problem is very similar to the previous one. To reach a cell (i,j), one must first reach either the cell (i-1,j) or the cell (i,j-1) and then move one step down or to the right respectively to reach cell (i,j). After convincing yourself that this problem indeed satisfies the optimal sub-structure and overlapping subproblems properties, we try to formulate a bottom-up dynamic programming solution.

We first need to identify the states on which the solution will depend. To find the number of ways to reach to a position, what are the variables on which my answer depends? Here, we need the row and column number to uniquely identify a position. For more details on how to decide the state of a dynamic programming solution, see this : How can one start solving Dynamic Programming problems? Therefore, let NumWays(i,j) be the number of ways to reach position (i,j). As stated above, number of ways to reach cell (i,j) will be equal to the sum of number of ways of reaching (i-1,j) and number of ways of reaching (i,j-1). Thus, we have our recurrence relation as :

Now, all you need to do is take care of the base cases and the recurrence relation will calculate the rest for you. :)

The base case, as in the previous question, are the topmost row and leftmost column. Here, each cell in topmost row can be visited in only one way, i.e. from the left cell. Similar is the case for the leftmost column. Hence the code is:

3. Finding the number of ways to reach a particular position in a grid from a starting position (given some cells which are blocked)

Problem Statement : You can read the problem statement here: Robots and Paths Input is three integers M, N and P denoting the number of rows, number of columns and number of blocked cells respectively. In the next P lines, each line has exactly 2 integers i and j denoting that the cell (i, j) is blocked.

Solution : The code below explains how to proceed with the solution. The problem is same as the previous one, except for few extra checks(due to blocked cells.)

Another variant

Finally, we discuss another variant of problems involving grids. You can see the problem here. Working Out A short description of the problem is:

Problem Statement : You are given a 2-D matrix A of n rows and m columns where A[i][j] denotes the calories burnt. Two persons, a boy and a girl, start from two corners of this matrix. The boy starts from cell (1,1) and needs to reach cell (n,m). On the other hand, the girl starts from cell (n,1) and needs to reach (1,m). The boy can move right and down. The girl can move right and up. As they visit a cell, the amount in the cell A[i][j] is added to their total of calories burnt. You have to maximize the sum of total calories burnt by both of them under the condition that they shall meet only in one cell and the cost of this cell shall not be included in either of their total.

Solution : Let us analyse this problem in steps:

The boy can meet the girl in only one cell.

So, let us assume they meet at cell (i,j).

Boy can come in from left or the top, i.e. (i,j-1) or (i-1,j). Now he can move right or down.That is, the sequence for the boy can be:

Similarly, the girl can come in from the left or bottom, i.e. (i,j-1) or (i+1,j) and she can go up or right. The sequence for girl's movement can be:

Comparing the 4 sequences of the boy and the girl, the boy and girl meet only at one position (i,j), iff

Convince yourself that in no other case will they meet at only one position.

Now, we can solve the problem by creating 4 tables:

Boy's journey from start (1,1) to meeting cell (i,j)
Boy's journey from meeting cell (i,j) to end (n,m)
Girl's journey from start (n,1) to meeting cell (i,j)
Girl's journey from meeting cell (i,j) to end (1,n)

The meeting cell can range from 2<= i <= n-1 and 2 <= j <= m-1

See the code below for more details:

Thanks for reading. :) I hope it was helpful!

An alphabet
A special character
Minimum 8 characters

A password reset link will be sent to the following email id

Navigate a Grid Using Combinations And Permutations

Puzzles can help develop your intuition -- figuring how to navigate a grid helped me understand combinations and permutations.

Suppose you're on a 4 × 6 grid, and want to go from the bottom left to the top right. How many different paths can you take? Avoid backtracking -- you can only move right or up.

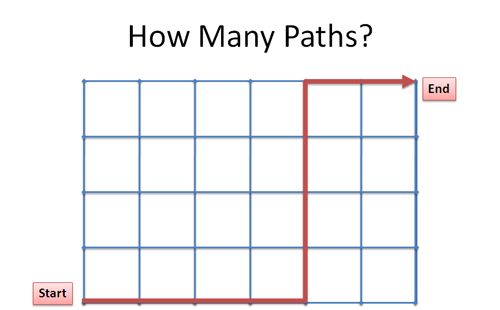
Spend a few seconds thinking about how you'd figure it out.

Insight: Convert Pictures To Text

When considering the possible paths (tracing them out with your finger), you might whisper "Up, right, up, right...".

Why not write those thoughts down? Using "u" and "r" we can write out a path:

That is, go all the way right (6 r's), then all the way up (4 u's). The path in the diagram would be:

Using the text interpretation, the question becomes "How many ways can we re-arrange the letters rrrrrruuuu ?"

Ah, the ubiquitous combination/permutation problem -- never thought it'd be useful, eh?

Understanding Combinations And Permutations

There's several ways to see combination and permutation problems. Once the first explanation clicks, we can go back and see it a different way. When trying to build math intuition for a problem, I imagine several mental models circling a core idea. Starting with one insight, I work around to the others.

Approach 1: Start The Same

Instead of having 6 rights at 4 ups, imagine we start with 10 rights ( r r r r r r r r r r ).

Clearly this won't do: we need to change 4 of those rights into ups. How many ways can we pick 4 rights to change?

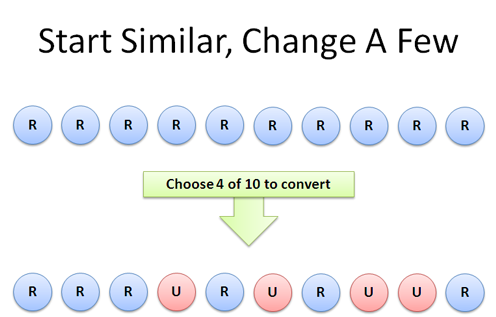
Well, we have 10 choices for the first 'right' to convert (see the combinations article ). And 9 for the second, 8 for the third, and 7 choices for the final right-to-up conversion. There are 10 * 9 * 8 * 7 = 10!/6! = 5040 possibilities.

But, wait! We need to remove the redundancies: after all, converting moves #1 #2 #3 and #4 (in that order) is the same as converting #4 #3 #2 #1. We have 4! (4 * 3 * 2 * 1 = 24) ways to rearrange the ups we picked, so we finally get:

$\displaystyle{\frac{(10!/6!)}{4!} = \frac{5040}{24} = 210 }$

We're just picking the items to convert (10!/6!) and dividing out the redundancies (4!).

Approach 2: Just Use the Combination Formula

Halfway through that explanation, you might have realized we were recreating the combination formula:

$\displaystyle{C(10,4) = 210}$

That's the shortcut when you know order doesn't matter. However, sometimes I'm not sure whether I need a permutation or combination from the outset. While saying "Just use C(10,4)" may be accurate, it's not helpful as a teaching tool. Sometimes it helps to re-create the situation on your own.

Approach 3: Start Different

Here's another approach: instead of letting each r and u be interchangeable, label the 'right' moves r1 to r6, and the 'up' moves u1 to u4. How many ways can we re-arrange these 10 items?

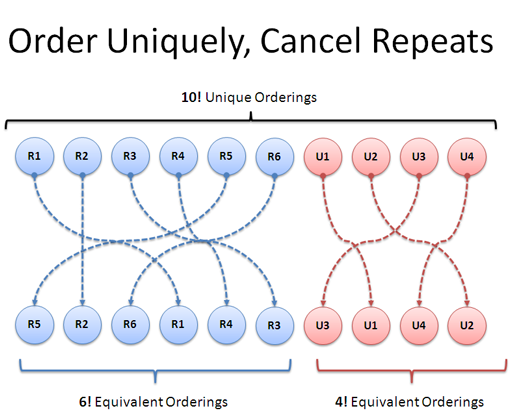
This question is easy: 10! = 3,628,800 (wow, big number). We have 10 choices for the 1st move, 9 for the second, and so on, until we have 2 choices for the 9th and only 1 for the last. Cool.

Of course, we know that "r1 r2 u1 u2" is the same path as "r2 r1 u2 u1". We can shuffle the r's and u's in their own subgroups and the path will stay the same.

How many ways can we shuffle all 10? 10! = 3,628,800
How many ways can we shuffle 6 r's? 6! = 720
How many ways can we shuffle 4 u's? 4! = 24

So, we start with the total number of possibilities (10! = 3,628,800) and divide out the cases where we shuffle the r's (6! = 720) and the u's (4! = 24):

$\displaystyle{10! / 6! / 4! = 10! / (6! \cdot 4!) = 210}$

Neat! It's cool seeing the same set of multiplications and divisions in different ways, just by regrouping them.

Why is this useful?

One goal is to learn how problems can be transformed. Remember that painting of the old lady & young woman?

Do you see both? Can you switch between them? Isn't that cool?

Part of the fun of the grid-path puzzle is seeing how to look at a problem using a visual or text metaphor. The more math you learn, the more models you have available, and you can turn problems into each other.

This doesn't have to be "practical" -- it's fun to see how listing out paths can be be done simply using letters on paper.

In math lingo, problems which can be converted to each other are "isomorphic". Mathematically, they may be the same -- but from a human perspective, one may be easier than the other (like seeing the old woman or young woman first).

For the grid puzzle, we used each perspective where comfortable:

Visualizing the grid to understand the general problem and see a single path.
Write the paths as text to see the general format of all paths & an easy method to enumerate them

And that's the key lesson: It's completely fine to use one model to understand the idea, and another to work out the details. Math becomes difficult when we think there's only one way to approach it.

Variations and Extensions

Now that we've been building our mental models, let's tackle some harder problems.

Imagine your "grid" is actually in 3 dimensions. This is harder to draw, but the text representation keeps on working. Let's say we have a cube (x, y and z dimensions) that is 5 units long on each side. How many paths are there from one corner to its opposite?

Hrm. In this case, I might try the second approach, where we listed out all the possibilities. Assume we label each move differently: we have 5 uniquely-labeled moves of each type (x1-x5, y1-y5, z1-z5). We can arrange these in 15! ways (it's huge: 1.3 trillion). But, we need to remember to divide out the redundancies for each dimension.

There are 5! ways to rearrange the 5 identical motions in each direction, and we divide them out:

$\displaystyle{15! / 5! / 5! / 5! = 15!/(5!\cdot 5!\cdot 5!) = 756,756}$

Wow, that's huge number of paths on a small cube! Earlier today you'd have trouble with the question -- I know I would have. But starting with the grid example and converting it to text, we've beefed up our model to handle 3 dimensions. Paths in four, five or 10-d should be no problem.

Redefining The Problem

Here's the fun part: instead of changing how we see the solution, why not change the problem ? What else could "Find paths on a grid" represent?

Trap platform : Let's say you're making a set of trapdoors 4 × 6, with only 1 real path through (the others drop you into a volcano). What are the chances someone randomly walks through? With a 4×6 it's 210, as before. With a 12×12 grid it's 24!/12!12! = 2.7 million paths, with only 1 correct one.

Order of operations : Suppose you have 10 sets of exercises to do: 4 identical leg exercises, and 6 identical arm exercises. How many different routines can you pick? This is the same as navigating the path, except the axis labels are "legs" and "arms" instead of "right" and "up".

Random walk . Suppose we know an object moves randomly up or right. What's the chance it hits our desired endpoint after 10 steps? Well, there are 2^10 = 1024 ways to move up or right (pick "u" or "r" 10 times), and 210 ways to get to our exact destination. Therefore, you can expect to hit our spot 210 / 1024 = 20.5% of the time!

Here's a calculator to play with a few variations:

Onward and Upward

Puzzles are a fun way to learn new mental models, and deepen your understanding for the ones you're familiar with. While I might "know" combinations and permutations, it's not until I recognize them in the wild do I feel really comfortable. Ideas do no good sitting inside your head like artifacts in a museum -- they need to be taken out and played with. Happy math.

Topic Reference

Combination.

Permutation

Join 450k Monthly Readers

Dynamic programming approach in action

Level up your tech skills and advance your career with Hyperskill

“It has all the necessary theory, lots of practice, and projects of different levels. I haven't skipped any of the 3000+ coding exercises.“

Hyperskill graduate

This topic will show you how to apply the dynamic programming approach to find a solution for the classic grid walk problem . This problem or, more precisely, this type of problem, requires counting all possible ways to walk across a grid of an arbitrary size subject to certain conditions. The techniques you will learn in this topic will grant you hands-on experience in solving similar dynamic programming problems.

Problem description

Consider a rectangular grid of a certain width and height. The starting point is in the top left corner of the grid and the destination point is in the bottom right corner. The goal is to find all possible paths to walk across the grid provided that you may move either to the right or down from the cell you are currently in:

Let's think about the problem and try to find a possible solution step by step. The first thing to keep in mind is that from any given cell you can move in exactly two directions. Second, you can never re-visit any already visited cell, which means you don't have to worry about tracking the cells you have visited. Another important thing is that whenever you take a step you find yourself in a situation very similar to the one you had in the previous step. You will have a grid to walk across but its height or width will be lesser by one than in the previous step, depending on which direction you chose.

This means that you have the same problem as at the beginning of the walk but with different starting conditions and this new problem is a subset of the initial problem. So you can try to solve the sub-problems first and then somehow combine the solutions of all sub-problems to get the solution of the whole problem. Dynamic programming suggests solving each sub-problem only once and reusing the solution but now we are going to divide the problem into sub-problems and deal with the reusability later.

Dividing the problem

Since each sub-problem is of the same type as the initial problem, you can try applying recursion.

In the first approximation, the solution is going to be a function that accepts a grid and returns the number of paths found. First, you should decide how you want to represent the grid. Are you going to use a class or an array, or some other data structure? To make a decision, let's explore how to track the current position in the grid. Take a closer look at this image:

tracking the current position in the grid

Do you really need to track your coordinates? Probably no. You can pretend that when you take each step you create a new grid with one side lesser by 1 than the previous grid. This leads to a solution where you may pass only the grid's width and height as the arguments:

Let's figure out the base conditions for this recursion. When can you say that you've reached the finish point? When you hit the bottom right cell, you have nowhere to go because the available grid is the size of one cell:

In this case, countPaths should return 1 because you reached the finish and found a new path.

What if you reach a border row or column in the grid? If you take a step outside the grid, you won't reach the finish anymore. So you should either avoid exiting the grid or detect that you have exited it and discontinue the walk. For example, if the current width is 1 you should not go to the right and if the current height is 1 you should not go downwards:

Another, and maybe an easier way is to detect a situation when the current position is outside the grid, that is when either width or height is less than 1 . If you detect that you stepped out of the grid, countPaths should return 0 . This means that you took a path and failed to reach the finish:

So far, only the recursion part remains. As you may choose only two directions, you need to sum the number of paths found in both directions and return that number:

Did we miss anything? Probably not. Let's test this solution on a few small grids where we can count all possible paths manually:

Here is the output:

Are you excited to count the number of paths for a really big grid? Say, 30 x 40 ? Let's run it and see if we are going to have an overflow. Seems like the program takes too long to run. Let's investigate the reasons and find a solution.

Bad performance

First, it is worth measuring the execution time. For this, let's refactor the code and wrap the path counting method with a method that calculates its execution time:

And then check the execution time for a series of grid sizes:

The execution time is growing extremely fast:

Why is it happening? To understand it, take a look at the execution of the recursive method for a small grid ( 3 x 2 ):

The numbers in the rectangles indicate the current grid size, the words down and right show the chosen direction and the numbers near the lines are the values returned by countPaths for the given grid size.

1. The execution starts when the grid is 3 x 2 .

2. If the downward path is taken, the grid size becomes 3 x 1 .

3. If the downward path is taken again, we step out of the grid ( 3 x 0 ). At this point, countPaths returns 0 .

4. If at step 3 we choose another direction, the grid size becomes equal to 2 x 1 .

5. If the right path is taken, we reach the finish and countPaths returns 1 .

6. If the downwards path is chosen at step 5, we again step outside the grid and countPaths returns 0 .

7. At this point, the method at step 5 receives two results from invoked countPaths , 1 and 0 , and returns their sum to the method invoked at step 2 which in its turn adds the value produced at step 3 and returns the sum to the caller method.

The same applies to the right part of the execution tree. If you look closely, you will notice that there are steps with the same input arguments and the same returned values. This is where countPaths does some extra work, and the higher the tree, the more extra work happens. It's time to find a way to solve each sub-problem only once and reuse the solutions.

Memoization

Memoization is a technique that helps reuse solutions calculated for sub-problems. You can associate the current position in the grid with the found number of paths available for that position and store such information in an appropriate data structure. Let's write a new version of countPaths that uses memoization:

Let's run the performance test for the new method:

You will see that memoization improves its performance tremendously:

For a grid as big as 60 x 60 , the execution time is a few milliseconds, and even a 300 x 300 grid takes a fraction of a second to calculate.

In this topic, we applied dynamic programming to solve a grid walk problem. We took a close look at the problem's description to get a better comprehension and find a suitable solution. In the process, we found a pitfall associated with recursion and successfully bypassed it using the memoization technique. The use of appropriate data structures and the standard library helped with implementing a reliable solution. We hope that this topic will help you efficiently deal with similar tasks and real-life problems!

DEV Community

Posted on Jan 19, 2021 • Originally published at yourdevopsguy.com

6 Hard Dynamic Programming Problems Made Easy

In this article , I gave you an introduction to Dynamic Programming with several examples. Here I will solve 6 harder Dynamic Programming problems to show you how to approach them.

Unique Paths

A robot is located at the top-left corner of a m x n grid

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid.

How many possible unique paths are there?

Given that the robot can only move to the right or down, we can reach the position {m,n} (bottom-right corner) in two different ways:

Going to the right from (m, n -1)
Going down from (m -1, n)

Therefore, the total number of paths to (m, n) will be the number of paths to (m, n-1) plus the number of paths to (m-1, n). These two new problems are just instances of the original problem. Therefore we can use recursion to generate a solution.

Let's call f(m,n) the number of ways to reach the position (m, n).

Recursive solution

Line 5 represents the number of paths to reach any position in the first column or row of the grid (we can only reach them by going all the way right or down, therefore we return 1).

We can improve upon this if we notice that many problems will be computed more than once:

To compute f(m,n) we need f(m-1, n) and f(m, n-1).
For f(m-1, n) we need f(m-2, n) and f(m-1, n-1) .
For f(m, n-1) we need f(m, n-2) and f(m-1, n-1) .

If you suspect a problem might be solved via Dynamic Programming problems, I recommend drawing a tree with all possible paths to see if there are repeated subproblems. If you can derive a recursion and prove that there are repeated subproblems and optimal substructure, you can apply Dynamic Programming.

Top-down Dynamic Programming

Going from the recursive solution to a top-down DP solution is very straightforward. We just need to:

Check if the results are already in our cache. If so, we return them.
If they're not, cache them before we return.

In line 8, I check if (-1 == dp[n]) to avoid bugs like if(dp[n] = -1) .

Bottoum-up Dynamic Programming

Now, let's take a different look at the problem. From (0,0) we can go right to (0,1), (0,2), etc. There is only one way to reach these positions. Similarly, there is only one way to reach all the positions in the first column: going down from (0,0). We can start building a table with this information:

This approach will build the full m*n table with all possible results. We return the one we are interested in: the most bottom-right position.

Computing the complexity of the bottom-up approach is trivial. There are two nested loops in which the amount of work is constant, giving an overall time complexity of O( mn ). The space complexity is O(m*n*) as well.

For the top-down, it seems a bit trickier, but the logic is the same. We do constant work for every call (because we cache results) and there are O(mn) calls. Therefore, the time complexity is O( mn ).

This problem can be solved in O(m+n) using basic mathematics. You have m rows, n columns and you can only move to the right and down (states). You can code a path using R to symbolize right and D for down. Then, for m rows and n columns you need to generate a string of (m-1) + (n-1) elements that have 2 states: R or D. In this string, there will be m-1 Ds and n-1 Rs. This problem is equivalent to find all permutations of an array of m+n-2 elements (taking into account all the repetitions):

Unique Paths 2

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and space is marked as 1 and 0 respectively in the grid.

Try to solve this one without looking at my solution. The code (for any of the approaches I described for the previous problem) is almost the same. You only need to take into account that cells have values and some of them can be blocked. If a cell is blocked, the robot cannot visit it and therefore there are 0 ways in which the robot can reach, from a cell where the is an obstacle, the cell to its right or down.

To avoid duplication, here is the code only for the bottom-up approach.

Coin Change

You are given coins of different denominations and a total amount of money amount . Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1 .

You may assume that you have an infinite number of each kind of coin.

Imagine you need to solve this problem by hand. At every step, you have an amount of money and a few coins to choose from. Let's say the coins are 1,2 and 5, and the amount is 11. You can take three different paths:

Take the coin with value 1. You're facing now with the problem of computing the fewest number of coins that you need to get to 10 .
Choose the coin with value 2. You're facing now with the problem of computing the fewest number of coins that you need to get to 9 .
Take the coin with value 5. You're facing now with the problem of computing the fewest number of coins that you need to get to 6 .

Which one will produce the desired output (minimum number of coins)? At this stage, we don't know. We need to explore each path in full and return the minimum.

It is pretty obvious now that we can use recursion to solve this. It should look something like this, with f(n) representing the minimum number of coins to reach n

From this it is trivial to get a top-down solution. You only need to add a cache, as we did in the previous problem:

Bottom-up Dynamic Programming

The bottom-up solution takes a different path. The idea is to fill a table with the minimum amount of coins needed to generate the values [0, amount], starting from the "initial conditions":

From 0, we can use one coin to get to all the values in the array coins . We initialize them to 1.

Important note:

You may have noticed that I have created arrays that seem to have an extra element. The entry sol[0] represents the problem of reaching the amount 0. This is why it seems there is an offset of 1 in the code (we return sol[amount] instead of sol[amount -- 1] because indices represent quantities). You will see this pattern in more places in this article.

Variation :

How would you solve this problem if there there wasn't an infinite number of each kind of coin.

Coin Change 2

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount.

You may assume that you have infinite number of each kind of coin.

Let's review our previous example: amount = 11 and coins = [1,2,5]. Again, we have the same three choices.

In this case, instead of getting the minimum of the three, we return the sum of the three paths. If we arrive to an instance where amount = 0, we return 1 (it is a solution we need to count). If amount is negative, that path doesn't lead to a solution and we return 0.

Since this is just a variation on the previous problem, I will only write the C++ implementation of the bottom-up approach. You have the tools to generate recursive and top-down solutions.

Edit Distance

Given two strings word1 and word2 , return the minimum number of operations required to convert word1 to word2 .

You have the following three operations permitted on a word:

Insert a character
Delete a character
Replace a character
Input: word1 = "horse", word2 = "ros"

This problem seems tricky at first, so we need to be systematic and try to work our way into a solution from a good example. Let's take "horse" and "ros", and focus on the last character of each word:

If "e" and "s" were the same, we could "forget about them" and keep working with "hors" and "ro"
Replace "e" with "s" (or "s" with "e"), and now they're the same
Delete "e" (or "s") and see and continue with the rest of the string "hors" and "ros" to see
Insert a character ("s" or "e" respectively) to make the last characters equal

Each possibility will generate another subproblem of smaller size, therefore we can code this recursively. We need to find the minimum of these 3 branches and return it (plus 1, since taking any of these paths indicates that there is at least one edit operation ).

If you play around with this example you'll see that this problem has optimal substructure, so I'll just show you the code for the solution top-down here:

And bottom-up here:

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

The same word in the dictionary may be reused multiple times in the segmentation.
You may assume the dictionary does not contain duplicate words.
Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true

This problem has a relatively straightforward solution. If we were to solve this by hand, we would start taking prefixes of our input and see if they belong to our dictionary. As soon as we find one, we repeat the process with the remaining of the string. In other words, we solve a smaller instance of the same problem. Let's try to define the recursion first and later see if there are overlapping subproblems.

Let's use the following example to illustrate this algorithm:

We start taking prefixes of s until we find one that belongs to dict. In this case, the first prefix that meets this condition is dog .
Our new string s' is "andcats". Repeating 1 we get to sand.
Now, s" is "cats". The prefix cats belongs to the dictionary.
Since s"' is empty, we return true.

This snippet of code solves this problem recursively:

Coming back to the example, you can see that bot "dogs" + "and" and "dog" + "sand" produce the same suffix: "cat". There are overlapping subproblems and we can use memoization .

The bottom-up approach builds a table, where the empty string is initialized to true and every other entry to false. From there, the logic is the same:

We build the solution for all the substrings of s, from length 0 to the length of s. This is why we have a loop in the range 1,n and another internal loop in the range [i-1,0] to move around all prefixes for that length
If the problem has a solution for the prefix s 0,j , we "follow the recursion" on the suffix s[j+1,:): if this is a valid word, there is a solution for the problem represented by dp[i]

This is harder to explain in words than in code, so here it is:

Conclusions

As we have seen, dynamic programming problems can be solved in a systematic way:

Start with small examples and see if their solution can be derived from smaller instances of the same problem. If so, recursion is a natural choice.
Draw a tree with the possible paths you can take depending on the available choices. If you reach the same parameters more than once, you can improve your solution using a cache.
From the recursion, arriving at a top-down solution is mechanical: you just need to add a cache.
The bottom-up approach generates a table based on "the initial conditions" for the recursion.

I hope you found this article helpful. I recommend sharing it with a friend or the rest of the community because you could help someone pass their exams or their next job interview.

For more content, visit my blog , and connect with me on Twitter .

Top comments (0)

Templates let you quickly answer FAQs or store snippets for re-use.

Are you sure you want to hide this comment? It will become hidden in your post, but will still be visible via the comment's permalink .

Hide child comments as well

For further actions, you may consider blocking this person and/or reporting abuse

"Top Linux Interview Questions and Answers for Aspiring System Administrators"

Nikhil Soman Sahu - May 23

Non Executable Files in Unix Like Systems

\144\150\162\165\166(dhruv) - Apr 23

nameof vs + operater

Ahmed Shah - Apr 23

131. Palindrome Partitioning

MD ARIFUL HAQUE - May 22

We're a place where coders share, stay up-to-date and grow their careers.

Louis Raymond

Full Stack Developer, Physics and Philosophy graduate. Music enthusiast.

Custom Social Profile Link

Dynamic Programming: Finding Optimal Paths

November 29, 2018 8 minute read

Yesterday, I sat through a code challenge comprised of three questions. After having some success with the first two- the third problem in the test had me somewhat stumped, an (extremely) analogous problem is written below:

The Problem

A grid of size N*M (i.e. N rows and M columns) is given. Each square of the grid can be indexed using a pair of integers (A,B) where 0≤A < N and 0≤B < M. A machine is located initially at field (0, 0). It can perform two kinds of moves: Move from the field (A,B) to field (A+1,B) or Move from the field (A,B) to field (A,B+1) During its movement across the grid, it collects all the coins from the square it lands on. Write a function that, given a matrix of size N M describing the number of coins lying on each square of a N M-sized grid, returns the maximal number of coins the machine can collect while moving from the square (0, 0) to the square (N−1, M−1) in the manner specified above.

My Initial Attempt

While I don’t have the code for my initial attempt, something similar (with less consideration for edge cases and the like) to my work might look something like this:

There are edge cases to consider (such as behaviour when x and y are at the edges of our grid)- but it’s not too important here for demonstration, you can see the crux of this approach from the above code: Take the best next step available.

Why This Is A Poor Solution

This solution uses what is known as a greedy algorithm . The algorithm makes the optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem. Greedy algorithms can be quite successful, but they have some significant flaws.

For instance- since a greedy algorithm tries to find a path by selecting the highest number of coins available at each step- it can miss out on the largest sum, as shown in the animation below. A greedy algorithm’s weakness is that it makes decisions without regard for the overall problem.

On the plus side, the time complexity here has been kept nice and low. But, while this method has the merit of being efficient-it doesn’t entirely compensate for its propensity to produce incorrect results.

A Recursive Method

Why i avoided using recursion in the test.

During the test, it was emphasised that the algorithm I designed ought to be as efficient as possible, and it occurred to me that opting for a strategy involving recursion would lead to exponential time complexity, as every case would have to be recomputed. Additionally, the size of the call stack would be massive (just take a moment to imagine a tree-like diagram of all the cases that would have to be covered for a large matrix, each one calling the function again)

Believing there to be a choice between the above approach and the following, I opted to write code similar to that already discussed. However, If I did want to write a recursive solution- I imagine I would have written something similar to the snippet below:

What’s Going On Here

Here, I am recursively calculating the minimum path for each square in the matrix. This is covered again below- the difference being that in the above function, every value that has already been found is recomputed every time the function is called.

There was, however, a third approach- which I was unaware of. After the code challenge finished- I had a look online to see if anyone had solved a similar problem. Eventually, I stumbled across a lecture on Dynamic Programming from MIT OCW . This promised to provide some of the answers I was looking for.

Solving the Problem with Dynamic Programming

What is dynamic programming.

Fun Fact: Dynamic Programming got its name because the man who came up with it (Richard Bellman) just thought it sounded cool

Richard Bellman

In Brief, Dynamic Programming is a general, powerful algorithm design technique (for things like shortest path problems). You can also think of dynamic programming as a kind of exhaustive search. Ordinarily, this is a terrible idea, as an exhaustive search (usually) produces exponential time complexity. However, If you “brute force” carefully- you can get your algorithm down from exponential time to polynomial time- just like our greedy algorithm from earlier.

This technique involves “ memoization ’ (keeping a record/memo of relevant computations). The idea here is a bit like having a scratch pad. You write down and reuse the solutions you have already computed. The solutions on your scratch pad are not problems you ultimately care about for their own sake. Rather, They are the sub-problems you would previously have solved through recursion.

A Simple Example: The Fibonacci Sequence

When I first began learning to code, the first article I wrote for Medium was about recursion. Within it, I demonstrated a recursive method for finding the nth term in the series. Here, we will begin discussing a more efficient way to complete the same task to warm up before tackling our (slightly more complex) problem.

The above code works by establishing a known base case, here that if n=0 or n=1, your first term is 1. The known results are stored in our array . Then the process starts…

If the nth term is in our array (serving as our memo ), just return that.
Otherwise, compute the next term in the sequence and add to our memo.
Repeat step 1

This means that we compute each result ONCE , rather than potentially running the same computation many times over as before. Massively reducing the time complexity of the problem at hand.

While we could use recursion to “boot” the process where (by starting with an empty memo, and calling the function after computing and recording the first computation, meaning the function would be called twice)- we can avoid its main drawbacks.

Considering Our Two Dimensional Matrix

So, how does this apply to our coin-filled matrix? Well, notice that the problem has a point where we know on inspection what the answer would be if the machine stopped there. If the machine stayed on the first square [0][0] and never moved at all, it would collect A[0][0] squares (A[i][j] is our matrix).

In English, this means that we know the maximum number of coins you can collect without moving is the number of coins on the first square

So, We have our base case.

Next, we need to see if the problem can be broken down into smaller sub-problems. We already did this when working with recursion, If we know how many coins you would have at maximum without taking any steps, you can compute the maximum you can have after taking one step.

The maximum number of coins for any square will be equal to the number of coins on the square itself plus the maximum for the most profitable adjacent square.

To illustrate this, I’ve drawn a few diagrams:

The bottom left square is (0,0) and the top left is (2,2)

A “grid” with a number of coins on each square

The first entry on our memo

If we start at the bottom left corner and want to travel to the top right in the way prescribed, it’s apparent on inspection that before our first move (while we still stand at 0,0) We would have 1 coin.

Let’s record that on a memo, here that is going to take the form of another matrix which records the maximum possible number of coins for each square.

Now we have our base case, and we know the number of coins on each square- we can proceed by working out the maximums for the bottom row and column (moving in the required way, there is only one path to get to these squares)

For the bottom row, we move sideways- collecting 2 coins and then 3 coins:

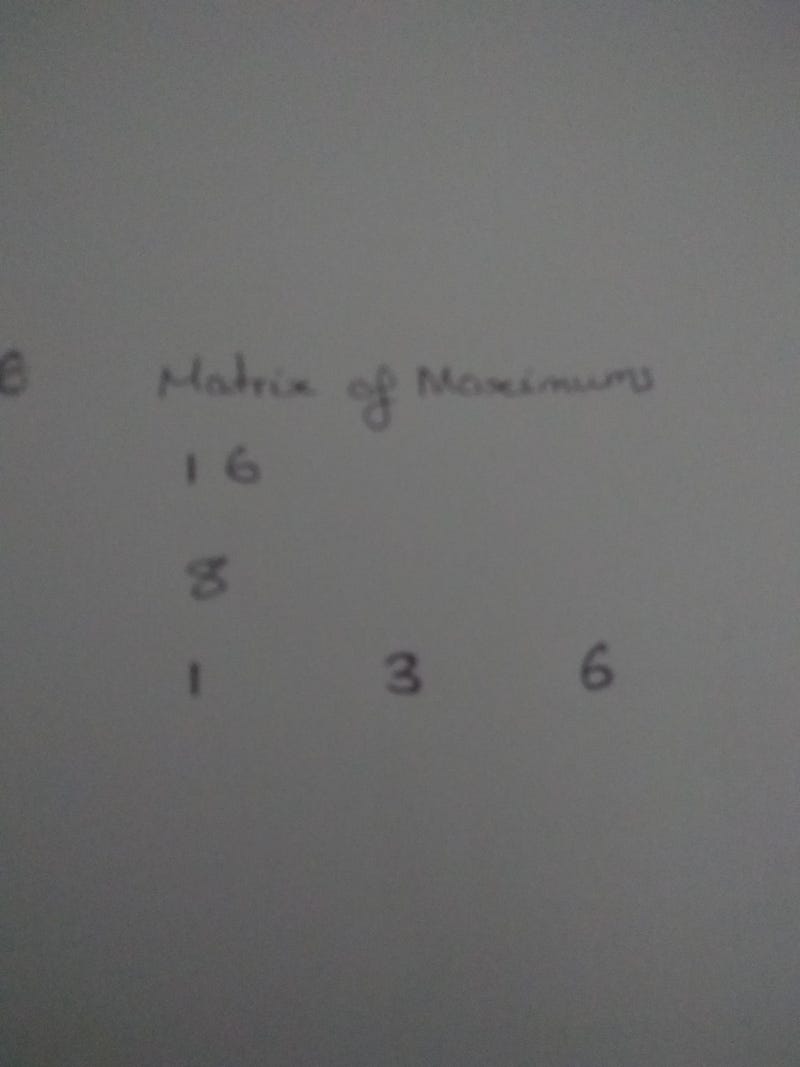
Matrix of maximums: Note that the maximum for a square is the highest maximum for a square prior, plus the number of coins on the square in question

We repeat this process with the first column then we fill in the middle to get the following complete matrix

We can then see that the maximum number of coins is 27. We did this without recursion because we never recomputed our old results.

Now, to do this with code:

This returns 27 as expected.

At the time, working through a problem under time pressure without knowing how to solve it was tough. However, After working out how a solution could be arrived upon, and having had a look at how this method works — overall, this has been a gratifying, and educational experience. I learned something new, that I can take with me into code challenges (and, perhaps, real enterprise code) in the future.

You May Also Enjoy

Ruby Blocks Give You Wings

July 10, 2020 6 minute read

Exploring scoping, bindings and closures in Ruby

Getting to Grips with Grep!

June 25, 2020 7 minute read

A staple of Linux administration, and a powerful tool that you can use to improve your efficiency.

An Introduction To CI

June 20, 2020 6 minute read

Introduction

Web Hosting Explained

June 14, 2020 6 minute read

Giga thoughts …

Insights into technology

Using Reinforcement Learning to solve Gridworld

“Take up one idea. Make that one idea your life — think of it, dream of it, live on that idea. Let the brain, muscles, nerves, every part of your body, be full of that idea, and just leave every other idea alone. This is the way to success.”

– Swami Vivekananda

“Be the change you want to see in the world”

– Mahatma Gandhi

“If you want to shine like the sun, first burn like the sun”

-Shri A.P.J Abdul Kalam

Reinforcement Learning

Reinforcement Learning (RL) involves decision making under uncertainty which tries to maximize return over successive states.There are four main elements of a Reinforcement Learning system: a policy, a reward signal, a value function. The policy is a mapping from the states to actions or a probability distribution of actions. Every action the agent takes results in a numerical reward. The agent’s sole purpose is to maximize the reward in the long run.

Reinforcement Learning is very different from Supervised, Unsupervised and Semi-supervised learning where the data is either labeled, unlabeled or partially labeled and the learning algorithm tries to learn the target values from the input features which is then used either for inference or prediction. In unsupervised the intention is to extract patterns from the data. In Reinforcement Learning the agent/robot takes action in each state based on the reward it would get for a particular action in a specific state with the goal of maximizing the reward. In many ways Reinforcement Learning is similar to how human beings and animals learn. Every action we take is with the goal of increasing our overall happiness, contentment, money,fame, power over the opposite!

RL has been used very effectively in many situations, the most famous is AlphaGo from Deep Mind, the first computer program to defeat a professional Go player in the Go game, which is supposed to be extremely complex. Also AlphaZero, from DeepMind has a higher ELO rating than that of Stockfish and was able to beat Stockfish 800+ times in 1000 chess matches. Take a look at DeepMind

In this post, I use some of the basic concepts of Reinforcment Learning to solve Grids (mazes). With this we can solve mazes, with arbitrary size, shape and complexity fairly easily. The RL algorithm can find the optimal path through the maze. Incidentally, I recollect recursive algorithms in Data Structures book which take a much more complex route with a lot of back tracking to solve maze problems

Reinforcement Learning involves decision making under uncertainty which tries to maximize return over successive states.There are four main elements of a Reinforcement Learning system: a policy, a reward signal, a value function. The policy is a mapping from the states to actions or a probability distribution of actions. Every action the agent takes results in a numerical reward. The agent’s sole purpose is to maximize the reward in the long run.

The reward indicates the immediate return, a value function specifies the return in the long run. Value of a state is the expected reward that an agent can accrue.

This can be written as

$v_{\pi}(s) = E_{\pi}[G_{t} |S_{t}=s] = E_{\pi}[\sum_{k=0}^{k=Inf} \gamma^{k}R_{t+k+1}|S_{t}=s]$

These are Bellman’s equation for the state value function

The Bellman equations give the equation for each of the state

The Bellman optimality equations give the optimal policy of choosing specific actions in specific states to achieve the maximum reward and reach the goal efficiently. They are given as

$v_{*}(s)=max_{a}\sum_{s',r} p(s',r|s,a)[r+\gamma*v_{*}(s')]$

The Bellman equations cannot be used directly in goal directed problems and dynamic programming is used instead where the value functions are computed iteratively

n this post I solve Grids using Reinforcement Learning. In the problem below the Maze has 2 end states as shown in the corner. There are four possible actions in each state up, down, right and left. If an action in a state takes it out of the grid then the agent remains in the same state. All actions have a reward of -1 while the end states have a reward of 0

This is shown as

where the reward for any transition is R t = − 1 Rt=−1 except the transition to the end states at the corner which have a reward of 0. The policy is a uniform policy with all actions being equi-probable with a probability of 1/4 or 0.25

1. Gridworld-1

The action value provides the next state for a given action in a state and the accrued reward

1a. Bellman Update

The valueMap is the result of several sweeps through all the states. It can be seen that the cells in the corner state have a higher value. We can start on any cell in the grid and move in the direction which is greater than the current state and we will reach the end state

1b. Greedify

The previous alogirthm while it works is somewhat inefficient as we have to sweep over the states to compute the state value function. The approach below works on the same problem but after each computation of the value function, a greedifications takes place to ensure that the action with the highest return is selected after which the policy π π is followed

To make the transitions clearer I also create another grid which shows the path from any cell to the end states as

‘u’ – up

‘d’ – down

‘r’ – right

‘l’ – left

Important note: If there are several alternative actions with equal value then the algorithm will break the tie randomly

From the above valueMap we can see that greedification solves this much faster as below

1c. Bellman Optimality update

The Bellman optimality update directly updates the value state function for the action that results in the maximum return in a state

The above valueMap shows the optimal path from any state

2.Gridworld 2

To make the problem more interesting, I created a 2nd grid which has more interesting structure as shown below <img src=”fig5.png”

The end state is the grey cell. Transitions to the black cells have a negative reward of -10. All other transitions have a reward of -1, while the end state has a reward of 0

##2a. Bellman Update

2b. greedify, 2c. bellman optimality update.

3. Another maze

This is the third grid world which I create where the green cell is the end state and has a reward of 0. Transitions to the black cell will receive a reward of -10 and all other transitions will receive a reward of -1

3a. Bellman Update

3b. greedify, 3c. bellman optimality update.

We can see that the Bellman Optimality Update correctly finds the path the to end node which we can see from the valueMap1 above which is

Conclusion:

We can see how with the Bellman equations implemented iteratively with dynamic programming we can solve mazes of arbitrary shapes and complexities as long as we correctly choose the reward for the transitions

References 1. Reinforcement learning – An introduction by Richard S. Sutton and Andrew G Barto 2. Reinforcement learning (RL) 101 with Python Blog by Gerard Martinez 3. Reinforcement Learning Demystified: Solving MDPs with Dynamic Programming Blog by Mohammed Ashraf

Published by Tinniam V Ganesh

Visionary, thought leader and pioneer with 27+ years of experience in the software industry. View all posts by Tinniam V Ganesh

14 thoughts on “ Using Reinforcement Learning to solve Gridworld ”

Pingback: Ranking T20 players in Intl T20, IPL, BBL and Natwest using yorkpy – Giga thoughts …
Pingback: Deconstructing Convolutional Neural Networks with Tensorflow and Keras – Giga thoughts …
Pingback: yorkr rocks women’s One Day International (ODI) and International T20!! – Giga thoughts …
Pingback: GooglyPlusPlus2021 enhanced with drill-down batsman, bowler analytics – Giga thoughts …
Pingback: GooglyPlusPlus2021 now with power play, middle and death over analysis – Giga thoughts …
Pingback: Analyzing player performance with animated charts! – Giga thoughts …
Pingback: Near Real-time Analytics of ICC Men’s T20 World Cup with GooglyPlusPlus – Giga thoughts …
Pingback: Using embeddings, collaborative filtering with Deep Learning to analyse T20 players – Giga thoughts …
Pingback: Boosting Win Probability accuracy with player embeddings – Giga thoughts …
Pingback: T20 Win Probability using CTGANs, synthetic data – Giga thoughts …
Pingback: IPL 2023:GooglyPlusPlus now with by AI/ML models, near real-time analytics! – Giga thoughts …
Pingback: IPL 2023:GooglyPlusPlus now with by AI/ML models, near real-time analytics! – Data Science Austria
Pingback: Computing IPL player similarity using Embeddings, Deep Learning – Giga thoughts …
Pingback: Identifying cricketing shots using AI – Giga thoughts …

Navigating in Gridworld using Policy and Value Iteration

Learn how to use policy evaluation, policy iteration, and value iteration to find the shortest path in gridworld.

In reinforcement learning, we are interested in identifying a policy that maximizes the obtained reward. Assuming a perfect model of the environment as a Markov decision process (MDPs), we can apply dynamic programming methods to solve reinforcement learning problems.

In this post, I present three dynamic programming algorithms that can be used in the context of MDPs. To make these concepts more understandable, I implemented the algorithms in the context of a gridworld, which is a popular example for demonstrating reinforcement learning.

Before we being with the application, I would like to quickly provide the theoretical background that is required for the following work on the gridworld.

Key Reinforcement Learning Terms for MDPs

The following sections explain the key terms of reinforcement learning, namely:

Policy: Which actions the agent should execute in which state
State-value function: The expected value of each state with regard to future rewards
Action-value function: The expected value of performing a specific action in a specific state with regard to future rewards
Transition probability: The probability to transition from one state to another
Reward function: The reward that the agent obtains when transitioning between states

A policy, π ( s , a ) , determines the probability of executing action a in state s . In deterministic environments, a policy directly maps from states to actions.

State-Value Function

Given a policy π , the state-value function V π ( s ) maps each state s to the expected return that the agent can obtain in this state:

V π ( s ) = E π { R t | s t = s } = E π { ∞ ∑ k = 0 γ k r t + k + 1 | s t = s }

In the formula, s t indicates the state at time t . The parameter γ ∈ [ 0 , 1 ] is called the discount factor . It determines the impact of rewards in the future. If we set γ = 1 , this indicates that we are sure about the future because we do not have to discount future rewards. For γ < 1 , we take the uncertainty about the future into account and give greater weight to more recently earned rewards.

Action-Value Function

Given a policy π , the action-value function Q π ( s , a ) determines the expected reward when executing action a in state s :

Q π ( s , a ) = E π { R t | s t = s , a t = a } = E π { ∞ ∑ k = 0 γ k r t + k + 1 | s t = s , a t = a }

Transition Probability

Executing an action a in state s may transition the agent to state s ′ . The probability that this transition takes place is described by P a s s ′ .

Reward Function

The reward function, R a s s ′ , specifies the reward that is obtained when the agent transitions from state s to state s ′ via action a .

Demonstration of Three Basic MDP Algorithms in Gridworld

In this post, you will learn how to apply three algorithms for MDPs in a gridworld:

Policy Evaluation: Given a policy π , what is the value function associated with π ?
Policy Iteration: Given a policy π , how can we find the optimal policy π ∗ ?
Value Iteration: How can we find an optimal policy π ∗ from scratch?

In gridworld, the goal of the agent is to reach a specified location in the grid. The agent can either go north, go east, go south, or go west. These actions are represented by the set : { N , E , S , W } . Note that the agent knows the state (i.e. its location in the grid) at all times.

To make life a bit harder, there are walls in the grid through which the agent cannot pass. Rather, when trying to move through a wall, the agent remains in its position. For example, when the agent chooses action N and there is a wall to the north of the agent, the agent will remain in its place.

Basic Gridworld Implementation

I’ve implemented the gridworld in an object-oriented manner. The following sections describe how I designed the code for the map and the policy entities.

Representing the Gridworld Map

To implement gridworld, the first thing I started with was a class for representing the map. I defined the following format to represent individual grid cells:

# indicate walls
X indicates the goal
Blanks indicate empty tiles

Relying on these symbols, I constructed the following map , which is used in the following work:

The map-related entities of the code are structured like this:

I implemented MapParser , which generates a Map object . The map object controls the access to the cells of the gridworld. Individual cell subclasses define the behavior of specific cells such as empty cells, walls, and the goal cell. Each cell can be identified using its row and column index.

With this setup, a map can be conveniently loaded:

Loading a Policy

For reinforcement learning, we need to be able to deal with a policy, π ( s , a ) . In gridworld, each state s represents a position of the agent. The actions move the agent one step into one of the four geographic directions. We will use the following symbols to map a policy onto a map:

N for the action GO_NORTH
E for the action GO_EAST
S for the action GO_SOUTH
W for the action GO_WEST

Unknown symbols are mapped to a NONE action in order to obtain a complete policy.

Using these definitions, I defined the following policy :

Note that the policy file retains the walls and the goal cell for better readability. The policy was written with two goals in mind:

The agent should be able to reach the goal. With a policy where this property is not fulfilled, policy evaluation will not give a reasonable result because the reward at the goal will never be earned.
The policy should be suboptimal . This means that there are states where the agent doesn’t take the shortest path to the goal. Such a policy allows us to see the effect of algorithms that try to improve upon the initial policy.

To load the policy, I implemented a policy parser , which stores the policy as a policy object . Using these objects, we can load our initial policy like so:

The policy object has a function for modeling π ( s , a ) :

Preparations for Reinforcement Learning

To prepare the implementation of the reinforcement learning algorithms, we still need to provide a transition and a reward function.

Transition Function

To define the transition function P a s s ′ , we first need to to differentiate between illegal and legal actions. In gridworld, there are two ways that an action can be illegal:

If the action would take the agent off the grid
If the action would move the agent into a wall

The gives us the first rule for the transition function:

Additionally, we must also require:

So what about legal actions? Of course, state transition must be valid with regard to the chosen action. Since each action moves the agent only a single position, a proposed state s ′ must have the agent in a cell that is adjacent to the one in state s :

For this rule, we assume that there is a predicate a d j ( s , s ′ ) to indicate whether the agent’s transition from s to s ′ involved adjacent cells.

Finally, once we have reached the goal state, s ∗ , we don’t want the agent to move away again. To stipulate this, we introduce the final rule:

Based on these four rules, we can define the transition function as follows:

P a s s ′ = { 1 ∀ illegal action with s = s ′ Rule 1 0 ∀ illegal action with s ≠ s ′ Rule 2 1 ∀ legal action with adj(s,s') Rule 3 0 ∀ if s = s ∗ Rule 4

The Python implementation provided by getTransitionProbability is a not as clear-cut as the mathematical formulation, but I will provide it nonetheless:

Note that proposeMove simulates the successful execution of an action and returns the new grid cell of the agent.

In gridworld, we want to find the shortest path to the terminal state. We want to maximize the obtained rewards, so the reward at the goal state, s ∗ should be higher than the reward at the other states. For the gridworld, we will use the following simple function:

R a s s ′ = { − 1 ∀ s ′ ≠ s ∗ 0 ∀ s ′ = s ∗

The Python implementation is given by

Policy Evaluation

The goal of the policy evaluation algorithm is to evaluate a policy π ( s , a ) , that is, to determine the value of all states in terms of V ( s ) ∀ s . The algorithm is based on the Bellman equation: V k + 1 ( s ) = ∑ a π ( s , a ) ∑ s ′ P a s s ′ [ R a s s ′ + γ V π k ( s ′ ) ] For iteration k + 1 , the equation yields the value of state s via:

π ( s , a ) : the probability of choosing action a in state s
P a s s ′ : the probability of transitioning from state s to state s ′ using action a
R a s s ′ : the expected reward when transitioning from state s to state s ′ using action a
γ : the discount rate
V π k ( s ′ ) : the value of state s ′ in step k , given the policy π

For a better understanding of the equations, let’s consider it piece by piece, in the context of gridworld:

π ( s , a ) : Since we’re in a deterministic environment, a policy only specifies a single action, a , with π ( s , a ) = 1 , while all other actions, a ′ , have π ( s , a ′ ) = 0 . So, the multiplication by π ( s , a ) just selects the action that is specified by the policy.
∑ s ′ : This sum is over all states, s ′ , that can be reached from the current state s . In gridworld, we merely need to consider adjacent cells and the current cell itself, i.e. s ′ ∈ { x | a d j ( x , s ) ∨ x = s } .
P a s s ′ : This is the probability of transitioning from state s to s ′ via action a .
R a s s ′ : This is the reward for the transition from s to s ′ via a . Note that in gridworld, the reward is merely determined by the next state, s ′ .
γ : The discounting factor modulates the impact of the expected reward.
V k ( s ′ ) : The expected reward at the proposed state, s ′ . The presence of this term is why policy evaluation is dynamic programming: we are using previously computed values to update the current value.

We will use γ = 1 because we are in an episodic setting where learning episodes stop when we reach the goal state. Because of this, the value function represents the length of the shortest path to the goal cell. More, precisely, let d ( s , s ∗ ) indicate the shortest path from state s to the goal. Then, V π ( s ) = − d ( s , s ∗ ) + 1 for s ≠ s ∗ .

To implement policy evaluation, we will typically perform multiple sweeps of the state space. Each sweep requires the value function from the previous iteration. The difference between the new and old value function is often used as a stopping criterion for the algorithm:

The function determines the indices of grid cells whose value function difference was less than θ . When the values of all states have converged to a stable value, we can stop. Since this is not always the case (e.g. if the policy specifies states with actions that do not lead to the goal or when the transition probabilities/rewards are configured inappropriately), we also specify a maximal number of iterations.

Once the stopping criterion is reached, evaluatePolicy returns the latest state-value function:

Once sweep of policy evaluation is performed by the evaluatePolicySweep function. The function iterates over all cells in the grid and determines the new value of the state:

Note that the ignoreCellIndices parameter represents the indices of cells for which subsequent sweeps didn’t change the value function. These cells are ignored in further iterations to improve the performance. This is fine for our gridworld example because we are just interested in finding the shortest path. So, the first time that a state’s value function doesn’t change, this is its optimal value.

The value of a state is computed using the evaluatePolicyForState function. At its core, the function implements the equations from Bellman that we talked about earlier. An important idea for this function is that we do not want to scan all states s ′ when computing the value function for state s . This is why the state generator generates only those states that can actually occur (i.e. have a transition probability greater than zero).

Results from Policy Evaluation

With the implementation in place, we can find the state-value function of our policy by executing:

To draw the value function together with the policy, we can use pyplot from matplotlib after converting the 1-D array that is used to represent the map to a 2D-array:

Using the function, we can visualize the state-value function of our policy:

For non-goal cells, the plot is annotated with the actions specified by the policy. The goal in the upmost right cell is indicated by the X label. Walls (infinite value) are shown in white.

The value of the others cells is indicated by color. The worst states (with the lowest reward) are shown in purple, bad states in blue, intermediate states in turquois, good states in green, and very good states (with the highest reward) are shown in yellow.

Looking at the values, we can see that the results match the actions that are dictated by the policy. For example, the state directly to the west of the goal has a very low value because this state’s action ( GO_WEST ) leads to a long detour. The cell directly south of the goal has a very high value because its action ( GO_NORTH ) leads directly to the goal.

Note that, for our future work, the performance of evaluatePolicy is of critical concern because we will call it many times. For the computed example, the function requires 61 iterations, which translates to roughly half a second on my laptop. Note that the policy evaluation will require fewer iterations for policies that are closer to the optimal policy because values will propagate faster.

Being able to determine the state-value function is nice - now we can quantify the merit of a proposed policy is. However, we haven’t yet dealt with the problem of finding an optimal policy. This is where policy iteration comes into play.

Policy Iteration

Now that we are able to compute the state-value function, we should be able to improve an existing policy . A simple strategy for this is a greedy algorithm that iterates over all the cells in the grid and then chooses the action that maximizes the expected reward according to the value function.

This approach implicitly determines the action-value function, which is defined as

Q π ( s , a ) = ∑ s ′ P a s s ′ [ R a s s ′ + γ V π ( s ′ ) ]

The improvePolicy function determines the value function of a policy (if it’s not available yet) and then calls findGreedyPolicy to identify the optimal action for every state:

What findGreedyPolicy does is to consider each cell and to select that action maximizing its expected reward, thereby constructing an improved version of the input policy. For example, after executing improvePolicy once and re-evaluating the policy, we obtain the following result:

In comparison to the original value function, all cells next to the goal are giving us a high reward now because the actions have been optimized. However, we can see that these improvements are merely local. So, how can we obtain an optimal policy?

The idea of the policy iteration algorithm is that we can find the optimal policy by iteratively evaluating the state-value function of the new policy and to improve this policy using the greedy algorithm until we’ve reached the optimum:

Results from Policy Iteration

Running the algorithm on the gridworld leads to the optimal solution within 20 iterations - about 4,5 seconds on my notebook. The termination after 20 iterations doesn’t come as a surprise: the width of the gridworld map is 19. So we need 19 iterations to optimize the values of the horizontal corridor. Then, we need one additional iteration to determine that the algorithm can terminate because the policy hasn’t changed.

A great tool for understanding policy iteration is by visualizing each iteration:

The following figure shows the optimal value function that has been constructed using policy iteration:

Visual inspection shows that the value function is correct, as it chooses the shortest path for each cell in the grid.

Value Iteration

With the tools we have explored until now, a new question arises: why do we need to consider an initial policy at all? The idea of the value iteration algorithm is that we can compute the value function without a policy. Instead of letting the policy, π , dictate which actions are selected, we will select those actions that maximize the expected reward:

V k + 1 ( s ) = max a ∑ s ′ P a s s ′ [ R a s s ′ + γ V k ( s ′ ) ]

Because the computations for value iteration are very similar to policy evaluation, I have already implemented the functionality for doing value iteration into the evaluatePolicyForState method that I defined earlier. I marked the relevant lines with > :

This function performs the value iteration algorithm as long as no policy is available. In this case, len(self.policy) will be zero such that pi always returns a value of one and such that V is determined as the maximum over the expected rewards for all actions.

So, to implement value iteration, we don’t have to do a lot of coding. We just have to iteratively call the evaluatePolicySweep function on a Policy object whose value function is unknown until the procedure gives us the optimal result. Then, to determine the corresponding policy, we merely call the findGreedyPolicy function that we’ve defined earlier:

Results from Value Iteration

How does value iteration perform? For our gridworld example, only 25 iterations are necessary and the result is available within less than half a second. Remember that this is roughly the same time that was needed to do a single run of evaluatePolicy for our badly designed initial policy. The reason why value iteration is much faster than policy iteration is that we immediately select the optimal action rather than cycling between the policy evaluation and policy improvement steps.

When performing value iteration, the reward (high: yellow, low: dark) spreads from the terminal state at the goal (top right X ) to the other states:

We have seen how reinforcement learning can be applied in the context of MDPs. We worked under the assumption that we have total knowledge of the environment and that the agent is fully aware of the environment. Based on this, we were able to facilitate dynamic programming to solve three problems. First, we used policy evaluation to determine the state-value function for a given policy. Next, we applied the policy iteration algorithm to optimize an existing policy. Third, we applied value iteration to find an optimal policy from scratch.

Since these algorithms require perfect knowledge of the environment, it’s not necessary for the agent to actually interact with the environment. Instead, we were able to precompute the optimal value function, which is also known as planning . Still, it is crucial to understand these concepts in order to understand reinforcement learning in settings with greater uncertainty, which will be the topic of another blog post.

There aren't any comments yet. Be the first to comment!

Your comment has been submitted and will be published once it has been approved.

Your post has not been submitted. Please return to the form and make sure that all fields are entered. Thank You!

Data Structures
Linked List
Binary Tree
Binary Search Tree
Segment Tree
Disjoint Set Union
Fenwick Tree
Red-Black Tree
Advanced Data Structures

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Member-only story

A Guide to Important Graph Algorithms for Competitive Programming

And how you can use dfs and bfs.

Siddhant Dubey

If you’ve read an Introduction to Competitive Programming , then you’re probably familiar with why Competitive Programming is important. For those of you who haven’t, I believe that Competitive Programming is important because it helps you build your problem-solving skills and your technical knowledge of data structures and algorithms.

One of the biggest parts of Competitive Programming is learning the algorithms you need to succeed. I’ll be covering a large number of those algorithms in this post, specifically all the graph algorithms you’ll need to be successful in solving graph problems in Competitive Programming contests. Of course, just knowing the algorithms isn’t enough and you will have to complete a lot of practice problems on sites like Codeforces . However, this article will present you with the tools you need to master important graph algorithms.

What is a Graph?

In theoretical computer science, graphs are different from what you learned about in middle school. They are not bar charts.

Graphs in theoretical Computer Science and Discrete Mathematics are an abstract way of representing various types of relationships such as roads connecting cities and other types of networks. Graphs are made up of two components: edges and vertices. A vertex is a point on a graph and an edge is what connects two points on a graph.

Graph problems in competitive programming will usually be talking about things like networks and grids in the problem statement.

Here’s a list of all the graph terminology you need to know:

Path: A sequence of edges which joins a sequence of distinct (different) vertices.
Walk: Walks are paths, but they don’t require a sequence of distinct vertices.
Cycle: A group of vertices linked together in a closed chain. In the picture above, [1,2,4] is a cycle.
Connected Graph: A graph where any pair of vertices have a path between them.
Tree: A connected graph that does not contain a cycle.
Undirected Graph: A graph where the edges have no direction, the picture above shows an undirected graph. In an undirected graph, you can travel in any direction along an edge.
Directed Graph: A graph where the edges have directions, the directions are represented by arrows. In a directed graph, you can only travel along an edge in the direction it goes.

Representing Graphs in Code

Before we’re able to code up any graph algorithms, you will need to know how to represent graphs in code. All of the following code will be in C++ since that is my favorite language for competitive programming due to its speed and built-in functions that make it easy to write up solutions to problems.

I’ll be showing you two ways to represent graphs: Adjacency Matrices and Adjacency Lists. Most of the time you’ll be using the Adjacency List representation.

Adjacency Matrices:

An Adjacency Matrix represents a graph as a 2D matrix with dimensions V x V where V is the number of vertices of the graph. Adjacency matrices are best to use when V² roughly equals E (number of edges), that is when the graph is dense. Entry a_ij represents how many edges connect vertex i and vertex j.

The following code constructs an adjacency matrix for an undirected graph. To modify it to construct an adjacency matrix for a directed graph, change the add_edge function by removing the second line within it: matrix[v][u] = 1;

Adjacency Lists

The other common way to represent graphs in code is through Adjacency Lists. Essentially, you create lists of neighbors for each vertex and then put all of those lists inside of another list. These are good to use when you have a small number of edges in your graph, i.e. when your graph is sparse. If you are representing a weighted graph, where each edge has some value, the list will contain pairs of (neighbor, weight) for the edges instead.

Depth First Search

Now that we’ve learned how to represent Graphs in code, we can begin learning some graph algorithms! We will begin with Depth First Search (DFS) and finish out with Breadth-First Search (BFS), for the sake of brevity, pathfinding algorithms will not be included in this article.

Depth First search is one of the most basic graph algorithms and it is used to find the distance from one vertex to other vertices in a graph. It is a traversal algorithm.

DFS will put each vertex in a graph into one of two labels: visited or not visited. The algorithm marks each vertex as visited while avoiding cycles. It works as follows:

Put any one of the graph’s vertices at the top of a stack.
Take the item at the top of the stack and add it to the visited list.
Create a list of that vertex’s neighbors. Add the ones which are not in the visited list to the top of the stack.
Repeat steps 2 and 3 until the stack is empty.

Breadth-First Search

Breadth-First Search is also a graph traversal algorithm and along with DFS will be a big chunk of your Competitive Programming journey, at least when it comes to graphs.

Just like Depth First Search, BFS puts each vertex in a graph into one of two categories, visited or not visited. The purpose for the algorithm is also the same, to mark each vertex in a graph as visited while avoiding cycles. It works as follows:

Put any vertex in the graph at the back of a queue.
Take the item at the front of the queue and add it to the visited list.
Create a list of that vertex’s neighbors. Add the ones which are not visited to the back of the queue.
Repeat 2 and 3 until the queue is empty.

As you can see the algorithm is very similar to DFS. However, instead of going down a branch of a graph or tree like DFS does, BFS goes through each level.

Now that you know the theory behind two of the most important graph traversal algorithms (BFS and DFS), you’ll need to practice your skills to actually be able to use these algorithms in contests. I would suggest going to Codeforces and doing problems tagged with bfs and dfs with a rating under 1400, to begin with. Once you solve those regularly, you can increase the difficulty of the problems.

Practicing your algorithmic problem-solving skills, especially graph algorithms will help you excel in programming contests and technical interviews. Now get out there and start practicing, good luck!

If you enjoyed this, consider signing up for my newsletter to receive similar works every sunday: https://mailchi.mp/35c069691d2c/newsletter-signup .

Written by Siddhant Dubey

HS Senior @NCSSM. siddcodes.com

More from Siddhant Dubey and codeburst

5 Things Machine Learning is Not

Machine learning is one of the hottest buzzwords of the modern day. people love to chuck it in to describe their product or they love to….

How To Create Horizontal Scrolling Containers

As a front end developer, more and more frequently i am given designs that include a horizontal scrolling component. this has become….

Top 50 Java Interview Questions for Beginners and Junior Developers

How I Used a Convolutional Neural Network to Classify Cricket Shots

I have recently delved into the world of deep learning, more specifically, image classification. after completing the first lecture in the…, recommended from medium.

Benoit Ruiz

Advice From a Software Engineer With 8 Years of Experience

Practical tips for those who want to advance in their careers.

Arslan Ahmad

Level Up Coding

Don’t Just LeetCode; Follow the Coding Patterns Instead

What if you don’t like to practice 100s of coding questions before the interview.

General Coding Knowledge

Stories to Help You Grow as a Software Developer

Coding & Development

ChatGPT prompts

Benedict Neo

bitgrit Data Science Publication

Roadmap to Learn AI in 2024

A free curriculum for hackers and programmers to learn ai.

Alexander obidiegwu

50 Coding Laws That Would Make You A Decent Programmer.

Follow these laws or get fired..

Gautam Sharma

Depth First Search explained from scratch using Python | Coding Interview Series

Dfs traversal.

I Solved 300+ Leetcode problems , Here is what I learnt.

Text to speech

Solving Dynamic Programming Problems on a Computational Grid

Published: 02 February 2014
Volume 45 , pages 261–284, ( 2015 )

Cite this article

Yongyang Cai 1 , 2 ,
Kenneth L. Judd 3 ,
Greg Thain 4 &
Stephen J. Wright 4

934 Accesses

18 Citations

Explore all metrics

We implement a dynamic programming algorithm on a computational grid consisting of loosely coupled processors, possibly including clusters and individual workstations. The grid changes dynamically during the computation, as processors enter and leave the pool of workstations. The algorithm is implemented using the Master–Worker library running on the HTCondor grid computing platform, which can be deployed on many networks. We implement value function iteration for large dynamic programming problems of two kinds: optimal growth problems and dynamic portfolio problems. We present examples that solve in hours on HTCondor but would take weeks if executed on a single workstation. The cost of using HTCondor is small because it uses CPU resources that otherwise would be idle. The use of HTCondor can increase a researcher’s computational productivity by at least two orders of magnitude.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Distributionally robust stochastic programs with side information based on trimmings

Existence and Uniqueness of Quasi-stationary Distributions for Symmetric Markov Processes with Tightness Property

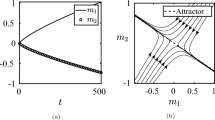
Asymmetric Replicator Dynamics on Polish Spaces: Invariance, Stability, and Convergence

Parallelization does not reduce total CPU time. In fact, parallelization will create overhead costs that do not arise with serial computation. The benefit of parallelization is that the user will receive results sooner. The focus in parallel computing is to economize on human time and other resources, not on total CPU time.

After this work was completed, the NSF launched the XSEDE project ( https://www.xsede.org/ ), which makes it far easier to access high power computing resources. Some of the machines available through XSEDE use HTCondor, making the software we describe in this paper useful in XSEDE projects.

The previous name was Condor.

The ideas presented in this paper can be implemented using other tools. For example, Matlab has a Parallel Computing Toolbox. While this permits some parallel computing, its value is limited because most machines using this toolbox have a small number of cores. We will provide examples where we use up to 200 CPUs.

Since checkpointing services have not been supported on Windows platforms, it will usually have better performance during the night than during the day.

The pool has machines of different characteristics, but a typical machine has eight cores and 8 GB memory, uses the Intel(R) Xeon(R) CPU E5345 @ 2.33GHz with 1 Gbps (Gigabit per second) Ethernet.

Abdelkhalek, A., Bilas, A., & Michaelides, A. (2001). Parallelization, optimization and performance analysis of portfolio choice models. In Proceedings of the 2001 international conference on parallel processing (ICPP01) (pp. 277–286).

Aldrich, E. M., Fernandez-Villaverde, J., Gallant, A. R., & Rubio-Ramrez, J. F. (2011). Tapping the supercomputer under your desk: Solving dynamic equilibrium models with graphics processors. Journal of Economic Dynamics and Control , 35 , 386–393.

Article Google Scholar

Bellman, R. (1957). Dynamic programming . Princeton: Princeton University Press.

Google Scholar

Cai, Y. (2010). Dynamic programming and its application in economics and finance . PhD thesis, Stanford University.

Cai, Y., & Judd, K. L. (2010). Stable and efficient computational methods for dynamic programming. Journal of the European Economic Association , 8 (2–3), 626–634.

Cai, Y., & Judd, K. L. (2012a). Dynamic programming with shape-preserving rational spline Hermite interpolation. Economics Letters , 117 (1), 161–164.

Cai, Y., & Judd, K. L. (2012b). Dynamic programming with Hermite approximation. NBER Working Paper No. w18540.

Cai, Y., & Judd, K. L. (2013). Shape-preserving dynamic programming. Mathematical Methods of Operations Research , 77 (3), 407–421.

Cai, Y., Judd, K. L., Lontzek, T. S., Michelangeli, V., & Su, C.-L. (2013a). Nonlinear programming method for dynamic programming. NBER Working Paper No. w19034.

Cai, Y., Judd, K. L., & Xu, R. (2013b). Numerical solutions of dynamic portfolio optimization with transaction costs. NBER Working Paper No. w18709.

Chung, S. L., Hanson, F. B., & Xu, H. H. (1992). Parallel stochastic dynamic programming: Finite element methods. Linear Algebra and Its Applications , 172 , 197–218.

Coleman, W. J. (1992). Solving nonlinear dynamic models on parallel computers. Discussion Paper 66, Institute for Empirical Macroeconomics, Federal Reserve Bank of Minneapolis.

Creel, M. (2005). User-friendly parallel computations with econometric examples. Computational Economics , 26 (2), 107–128.

Creel, M., & Goffe, W. L. (2008). Multi-core CPUs, clusters, and grid computing: A tutorial. Computational Economics , 32 (4), 353–382.

Den Haan, W. J., Judd, K. L., & Juillard, M. (2011). Computational suite of models with heterogeneous agents II: Multi-country real business cycle models. Journal of Economic Dynamics & Control , 35 , 175–177.

Gill, P., Murray, W., Saunders, M. A., & Wright, M. H. (1994). User’s guide for NPSOL 5.0: A Fortran package for nonlinear programming. Technical Report, SOL, Stanford University.

Griebel, M., & Wozniakowski, H. (2006). On the optimal convergence rate of universal and nonuniversal algorithms for multivariate integration and approximation. Mathematics of Computation , 75 (255), 1259–1286.

Judd, K. L. (1998). Numerical methods in economics . Cambridge, MA: The MIT Press.

Juillard, M., & Villemot, S. (2011). Multi-country real business cycle models: Accuracy tests and test bench. Journal of Economic Dynamics & Control , 35 , 178–185.

Morozov, S., & Mathur, S. (2012). Massively parallel computation using graphics processors with application to optimal experimentation in dynamic control. Computational Economics , 40 (2), 151–182.

Pflug, G. C., & Swietanowski, A. (2000). Selected parallel optimization methods for financial management under uncertainty. Parallel Computing , 26 (1), 3–25.

Rust, J. (1987). Optimal replacement of GMC bus engines: An empirical model of Harold Zurcher. Econometrica , 55 (5), 999–1033.

Rust, J. (1997). Using randomization to break the curse of dimensionality. Econometrica , 65 (3), 487–516.

Rust, J. (2008). Dynamic programming. In S. N. Durlauf & E. Blume (Eds.), New Palgrave dictionary of economics (2nd ed.). Basingstoke: Palgrave Macmillan.

Rust, J., Traub, J. F., & Wozniakowski, H. (2002). Is there a curse of dimensionality for contraction fixed points in the worst case? Econometrica , 70 (1), 285–329.

Stroud, A., & Secrest, D. (1966). Gaussian quadrature formulas . Englewood Cliffs, NJ: Prentice Hall.

Thain, D., Tannenbaum, T., & Livny, M. (2005). Distributed computing in practice: The condor experience. Concurrency and Computation: Practice and Experience , 17 (2–4), 323–356.

Zenios, S. A. (1999). High-performance computing in finance: The last 10 years and the next. Parallel Computing , 25 (13–14), 2149–2175.

Download references

Acknowledgments

We are grateful to the editor and anonymous reviewers for their insightful comments and suggestions. Cai and Judd gratefully acknowledge National Science Foundation support (SES-0951576). We also thank Miron Livny for his generous support and access to the HTCondor cluster at the University of Wisconsin-Madison.

Author information

Authors and affiliations.

Hoover Institution, Stanford University, Stanford, CA, USA

Yongyang Cai

Becker Friedman Institute, University of Chicago, Chicago, IL, USA

Hoover Institution, Stanford University & NBER, Stanford, CA, USA

Kenneth L. Judd

Computer Science Department, University of Wisconsin, Madison, WI , 53706, USA

Greg Thain & Stephen J. Wright

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongyang Cai .

Rights and permissions

Reprints and permissions

About this article

Cai, Y., Judd, K.L., Thain, G. et al. Solving Dynamic Programming Problems on a Computational Grid. Comput Econ 45 , 261–284 (2015). https://doi.org/10.1007/s10614-014-9419-x

Download citation

Accepted : 20 January 2014

Published : 02 February 2014

Issue Date : February 2015

DOI : https://doi.org/10.1007/s10614-014-9419-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Numerical dynamic programming
Parallel computing
Grid computing
Value function iteration
Dynamic portfolio optimization
Multi-country optimal growth

JEL Classification

Find a journal
Publish with us
Track your research

How to think like a programmer — lessons in problem solving

by Richard Reis

If you’re interested in programming, you may well have seen this quote before:

“Everyone in this country should learn to program a computer, because it teaches you to think.” — Steve Jobs

You probably also wondered what does it mean, exactly, to think like a programmer? And how do you do it??

Essentially, it’s all about a more effective way for problem solving .

In this post, my goal is to teach you that way.

By the end of it, you’ll know exactly what steps to take to be a better problem-solver.

Why is this important?

Problem solving is the meta-skill.

We all have problems. Big and small. How we deal with them is sometimes, well…pretty random.

Unless you have a system, this is probably how you “solve” problems (which is what I did when I started coding):

Try a solution.
If that doesn’t work, try another one.
If that doesn’t work, repeat step 2 until you luck out.

Look, sometimes you luck out. But that is the worst way to solve problems! And it’s a huge, huge waste of time.

The best way involves a) having a framework and b) practicing it.

“Almost all employers prioritize problem-solving skills first.

Problem-solving skills are almost unanimously the most important qualification that employers look for….more than programming languages proficiency, debugging, and system design.

Demonstrating computational thinking or the ability to break down large, complex problems is just as valuable (if not more so) than the baseline technical skills required for a job.” — Hacker Rank ( 2018 Developer Skills Report )

Have a framework

To find the right framework, I followed the advice in Tim Ferriss’ book on learning, “ The 4-Hour Chef ”.

It led me to interview two really impressive people: C. Jordan Ball (ranked 1st or 2nd out of 65,000+ users on Coderbyte ), and V. Anton Spraul (author of the book “ Think Like a Programmer: An Introduction to Creative Problem Solving ”).

I asked them the same questions, and guess what? Their answers were pretty similar!

Soon, you too will know them.

Sidenote: this doesn’t mean they did everything the same way. Everyone is different. You’ll be different. But if you start with principles we all agree are good, you’ll get a lot further a lot quicker.

“The biggest mistake I see new programmers make is focusing on learning syntax instead of learning how to solve problems.” — V. Anton Spraul

So, what should you do when you encounter a new problem?

Here are the steps:

1. Understand

Know exactly what is being asked. Most hard problems are hard because you don’t understand them (hence why this is the first step).

How to know when you understand a problem? When you can explain it in plain English.

Do you remember being stuck on a problem, you start explaining it, and you instantly see holes in the logic you didn’t see before?

Most programmers know this feeling.

This is why you should write down your problem, doodle a diagram, or tell someone else about it (or thing… some people use a rubber duck ).

“If you can’t explain something in simple terms, you don’t understand it.” — Richard Feynman

Don’t dive right into solving without a plan (and somehow hope you can muddle your way through). Plan your solution!

Nothing can help you if you can’t write down the exact steps.

In programming, this means don’t start hacking straight away. Give your brain time to analyze the problem and process the information.

To get a good plan, answer this question:

“Given input X, what are the steps necessary to return output Y?”

Sidenote: Programmers have a great tool to help them with this… Comments!

Pay attention. This is the most important step of all.

Do not try to solve one big problem. You will cry.

Instead, break it into sub-problems. These sub-problems are much easier to solve.

Then, solve each sub-problem one by one. Begin with the simplest. Simplest means you know the answer (or are closer to that answer).

After that, simplest means this sub-problem being solved doesn’t depend on others being solved.

Once you solved every sub-problem, connect the dots.

Connecting all your “sub-solutions” will give you the solution to the original problem. Congratulations!

This technique is a cornerstone of problem-solving. Remember it (read this step again, if you must).

“If I could teach every beginning programmer one problem-solving skill, it would be the ‘reduce the problem technique.’

For example, suppose you’re a new programmer and you’re asked to write a program that reads ten numbers and figures out which number is the third highest. For a brand-new programmer, that can be a tough assignment, even though it only requires basic programming syntax.

If you’re stuck, you should reduce the problem to something simpler. Instead of the third-highest number, what about finding the highest overall? Still too tough? What about finding the largest of just three numbers? Or the larger of two?

Reduce the problem to the point where you know how to solve it and write the solution. Then expand the problem slightly and rewrite the solution to match, and keep going until you are back where you started.” — V. Anton Spraul

By now, you’re probably sitting there thinking “Hey Richard... That’s cool and all, but what if I’m stuck and can’t even solve a sub-problem??”

First off, take a deep breath. Second, that’s fair.

Don’t worry though, friend. This happens to everyone!

The difference is the best programmers/problem-solvers are more curious about bugs/errors than irritated.

In fact, here are three things to try when facing a whammy:

Debug: Go step by step through your solution trying to find where you went wrong. Programmers call this debugging (in fact, this is all a debugger does).

“The art of debugging is figuring out what you really told your program to do rather than what you thought you told it to do.”” — Andrew Singer

Reassess: Take a step back. Look at the problem from another perspective. Is there anything that can be abstracted to a more general approach?

“Sometimes we get so lost in the details of a problem that we overlook general principles that would solve the problem at a more general level. […]

The classic example of this, of course, is the summation of a long list of consecutive integers, 1 + 2 + 3 + … + n, which a very young Gauss quickly recognized was simply n(n+1)/2, thus avoiding the effort of having to do the addition.” — C. Jordan Ball

Sidenote: Another way of reassessing is starting anew. Delete everything and begin again with fresh eyes. I’m serious. You’ll be dumbfounded at how effective this is.

Research: Ahh, good ol’ Google. You read that right. No matter what problem you have, someone has probably solved it. Find that person/ solution. In fact, do this even if you solved the problem! (You can learn a lot from other people’s solutions).

Caveat: Don’t look for a solution to the big problem. Only look for solutions to sub-problems. Why? Because unless you struggle (even a little bit), you won’t learn anything. If you don’t learn anything, you wasted your time.

Don’t expect to be great after just one week. If you want to be a good problem-solver, solve a lot of problems!

Practice. Practice. Practice. It’ll only be a matter of time before you recognize that “this problem could easily be solved with <insert concept here>.”

How to practice? There are options out the wazoo!

Chess puzzles, math problems, Sudoku, Go, Monopoly, video-games, cryptokitties, bla… bla… bla….

In fact, a common pattern amongst successful people is their habit of practicing “micro problem-solving.” For example, Peter Thiel plays chess, and Elon Musk plays video-games.

“Byron Reeves said ‘If you want to see what business leadership may look like in three to five years, look at what’s happening in online games.’

Fast-forward to today. Elon [Musk], Reid [Hoffman], Mark Zuckerberg and many others say that games have been foundational to their success in building their companies.” — Mary Meeker ( 2017 internet trends report )

Does this mean you should just play video-games? Not at all.

But what are video-games all about? That’s right, problem-solving!

So, what you should do is find an outlet to practice. Something that allows you to solve many micro-problems (ideally, something you enjoy).

For example, I enjoy coding challenges. Every day, I try to solve at least one challenge (usually on Coderbyte ).

Like I said, all problems share similar patterns.

That’s all folks!

Now, you know better what it means to “think like a programmer.”

You also know that problem-solving is an incredible skill to cultivate (the meta-skill).

As if that wasn’t enough, notice how you also know what to do to practice your problem-solving skills!

Phew… Pretty cool right?

Finally, I wish you encounter many problems.

You read that right. At least now you know how to solve them! (also, you’ll learn that with every solution, you improve).

“Just when you think you’ve successfully navigated one obstacle, another emerges. But that’s what keeps life interesting.[…]

Life is a process of breaking through these impediments — a series of fortified lines that we must break through.

Each time, you’ll learn something.

Each time, you’ll develop strength, wisdom, and perspective.

Each time, a little more of the competition falls away. Until all that is left is you: the best version of you.” — Ryan Holiday ( The Obstacle is the Way )

Now, go solve some problems!

And best of luck ?

Special thanks to C. Jordan Ball and V. Anton Spraul . All the good advice here came from them.

Thanks for reading! If you enjoyed it, test how many times can you hit in 5 seconds. It’s great cardio for your fingers AND will help other people see the story.

If this article was helpful, share it .

Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

How a simple fix could double the size of the U.S. electricity grid

Rewiring miles of power lines could make space for data centers, AI and a boom in renewables.

Key takeaways

Summary is AI-generated, newsroom-reviewed.

Upgrading existing high-voltage lines could double the flow of power through the electricity grid.
The limitations of the grid are slowing the transition to clean energy.
This work has been slow because utilities profit more from building new lines than upgrading them.

Did our AI help? Share your thoughts.

There is one big thing holding the United States back from a pollution-free electricity grid running on wind, solar and battery power: not enough power lines.

As developers rush to install wind farms and solar plants to power data centers, artificial intelligence systems and electric vehicles, the nation’s sagging, out-of-date power lines are being overwhelmed — slowing the transition to clean energy and the fight against climate change.

But experts say that there is a remarkably simple fix: installing new wires on the high-voltage lines that already carry power hundreds of miles across the United States. Just upgrading those wires, new reports show , could double the amount of power that can flow through America’s electricity grid.

“This is something that could be a triple win,” said Brian Deese, an innovation fellow at the Massachusetts Institute of Technology who headed the White House National Economic Council under President Biden until early last year. “A win for the electricity system, a win for utilities and a win for consumers.”

Since Biden signed the Inflation Reduction Act in August 2022 — pouring hundreds of billions of dollars toward the build-out of clean energy — experts have warned that without a dramatic increase in the size of the electricity grid, most of those new wind and solar farms won’t be able to plug in.

Many renewables are stuck in the “ interconnection queue ,” a long line of projects waiting to get connected to the grid. According to Lawrence Berkeley National Laboratory, more than 1,500 gigawatts of power , mostly renewables, are waiting for approval to connect. (That’s more than one-third of all the power produced in the United States.)

One of the main reasons for that long wait is that the nation builds transmission lines — those giant, high-voltage wires that carry power across large distances — extremely slowly. The average transmission line takes about 10 years to complete, and the country has been building even fewer lines recently than it did a decade ago.

Without enough power lines, there is nowhere for new solar, wind and battery power to go.

“We have to be able to integrate all this low-cost, renewable energy fast,” said Amol Phadke, a scientist at the University of California at Berkeley and Lawrence Berkeley National Laboratory.

That’s where replacing the country’s power lines — or “reconductoring,” as engineers call it — comes in.

Most of America’s lines are wired with a technology that has been around since the early 1900s — a core steel wire surrounded by strands of aluminum. When those old wires heat up — whether from power passing through them or warm outdoor temperatures — they sag. Too much sag in a transmission line can be dangerous, causing fires or outages. As a result, grid operators have to be careful not to allow too much power through the lines.

But a couple of decades ago, engineers designed a new type of wire: a core made of carbon fiber, surrounded by trapezoidal pieces of aluminum. Those new, carbon-fiber wires don’t sag as much in the heat. That means that they can take up to double the amount of power as the old lines.

According to the recent study from researchers at UC-Berkeley and GridLab, replacing these older steel wires could provide up to 80 percent of the new transmission needed on the electricity grid — without building anything new. It could also cost half as much as building an entirely new line and avoid the headaches of trying to get every state, city and even landowner along the route to agree to a new project.

“You’re not acquiring a new right of way; you’re not building new towers,” Phadke said. “So it can be done much faster.”

If stringing new lines is so easy — and cheap — why hasn’t it been done already? Part of the problem, experts say, is that utilities profit more from big infrastructure projects. Routine maintenance or larger-scale upgrades of the electricity grid don’t help utilities make a lot of cash compared with building new transmission lines.

Deese compares it to having leaky pipes in a building — building managers don’t get rewarded for fixing all of a building’s problems, but rather for just keeping things running as long as possible on a limited budget. “You patch and plug rather than thinking systematically,” Deese said.

Duncan Callaway, a professor of energy and resources at UC-Berkeley and one of the authors of the recent study, said that many transmission engineers are not used to thinking of rewiring as one of their tools. “But it’s a much faster way,” he said.

Some changes are already underway to encourage this approach. For a long time, utilities had to undergo lengthy environmental reviews if they were rewiring a line longer than 20 miles. Earlier this month, the Federal Energy Regulatory Commission announced that those would no longer be necessary if utilities are simply replacing wires.

And last month, the Biden administration announced a goal to upgrade 100,000 miles of transmission line over the next five years — which could include rewiring the lines.

“We actually need stuff that can cook right now, right away,” Ali Zaidi, the White House national climate adviser, said Tuesday at a White House summit on grid modernization. “And the way to do that is by deploying grid-enhancing technologies, by reconductoring the lines that we have already strung up or buried across the country.”

This doesn’t mean that new lines don’t need to be built. “In the longer run, newer lines will play an important role,” Phadke said. But as new demand surges onto the grid in the short term, upgrading the nation’s wires could help keep clean energy flowing until those new lines can be built.

“We have the potential to achieve all of these things with just taking new technology and running it through old lines,” Deese said. “It’s pretty cool.”

Notification: View the latest site access restrictions, updates, and resources related to the coronavirus (COVID-19) »

5G and Microgrids Might Be a Great Match

Nrel explores setup and security of 5g for microgrids with a 5g sandbox.

Whether it is coincidence or careful planning, the infrastructures of both power systems and telecommunications are heading in a similar direction: toward the edge. Solar panels on a roof are like 5G towers in a neighborhood—in both cases, distributed assets increasingly underpin these important systems.

To study the newest generation of wireless communications and what it offers power systems, the National Renewable Energy Laboratory (NREL) built a 5G research platform inside a replicated military microgrid and put it through resilience scenarios and cyberattacks, publishing their results in a report titled “ 5G Securely Energized and Resilient .” They found that 5G features can support distributed controls and configurable security and resilience for power systems.

The project was funded by the U.S. Department of Defense (DOD) Office of the Under Secretary of Defense for Research and Engineering as part of the FutureG program , which aims to ready the nation for next-generation telecommunications platforms, especially for the security, automation, and resilience aspects. But the results go well beyond defense: NREL showed how utilities might use 5G to the benefit of network security, recovery, and costs. And now with a realistic communications testing ground at NREL, partners can ensure utilities will function when most needed in contested environments.

No Wires, No Problem

A little lag is annoying during a stream, but it can be debilitating during critical energy operations. The target speed for autonomous power restoration is eight milliseconds—that is extremely fast. Hardwired fiber optics are the go-to alternative, but with such growth in distributed energy devices, laying fiber throughout a microgrid quickly becomes cost prohibitive. Instead, the project team explored how 5G ultralow latency might fill the gap.

“From a grid integration standpoint, many devices will need low latency and high reliability to successfully coordinate,” said Tony Markel, an NREL senior researcher and project lead. “A fundamental difference between 4G and 5G is the way the data moves; data resources can be closer to the edge. What if we harness the power of edge compute and reduced latency to make the grid components a more effective system?”

NREL researchers achieved some of 5G’s effectiveness by designing the microgrid to maintain power to both communications and critical loads. This included a layer of resilience that was added by using edge controllers to maintain microgrid component operation, even if some communications were unavailable.

With resilience and energy management both critical to NREL and DOD missions, this work found the combination of 5G, distributed controls, and a renewables-based microgrid to be a powerful combination.

Network Resilience, Priority Traffic, and Private Slicing: Some 5G Benefits

To evaluate 5G in credible operating conditions, NREL modeled its microgrid to reflect a military base in California. Identical solar arrays, battery systems, vehicle chargers, and protection equipment were modeled with interfaces via the 5G network. Many scenarios were tested including grid outages and various cyber intrusions.

“Our test scenarios were not only about controlling the power grid and microgrids for resilience but also about powering the 5G network itself. If we can keep the grid running for resilient power, that in turn keeps the communications network operational,” said Brian Miller, electric power systems engineering lead.

The scenarios included failure of a cell tower, a microgrid controller crash and recovery, unsecure foreign-operated network traffic, and congestion from other network devices.

“Edge computing, network traffic prioritization, and private slicing all worked out,” Miller said, discussing 5G features that they implemented in the test microgrid. “We could operate flawlessly with this network; for example, prioritization allowed us to preempt even when communication traffic was maxed out, so that it’s like having dedicated access to critical systems.”

Latency, however, was less impressive. Perhaps with millimeter wave 5G bands the researchers would achieve significantly faster exchanges of data, but the geographically dispersed microgrid required the longer range of sub-6-GHz bands. Latency was low, but not ultralow enough to smoothly coordinate power restoration without even a blip in power, as a battery backup unit would typically provide.

With regards to security, researchers focused on each 5G component and found many ways to make the network more secure against attackers with a foothold. As 5G is built on commodity server hardware and virtualized tools and functions, each component requires a thorough cyber assessment and tuning to prevent threat actors changing data or reading parameters of energy systems. Knowing that the network components and data flows are secure is step one in being able to trust 5G for future uses with distributed assets.

A New Lab Capability

This 5G lab capability exemplifies collaboration across government agencies for a technology that achieves mutual resilience. 5G has special importance to DOD with its possibility to support numerous rapid deployment scenarios such as expeditionary air base operations, agile combat employment, and more. With further testing, these results will serve as a foundation for military services to enhance infrastructure. In the broader picture, 5G research contributes to resilient homeland electrical grids and U.S. innovation.

“We plan to use this project as a development platform for research capabilities that can be replicated in the Advanced Research on Integrated Energy Systems (ARIES) Cyber Range,” Markel said. “The 5G core, multi-access edge compute, private slices—provides the foundation for research plans in large-scale secure integration of renewables.”

ARIES is the ideal research environment for utilities, device developers, energy service providers, and any grid researcher to stage their own systems and validate 5G solutions without the limitations of doing tests directly on the public grid.

“Industry led these efforts by planning a modular and open 5G architecture, and we are researching new ways to use its features in the electricity grid,” Markel said. “Millions of energy devices will become interconnected, and our research is showing the path to distributed, resilient, secure, and energy-efficient operations building on the 5G foundation.”

Learn about NREL job opportunities in 5G for cybersecurity .

COMMENTS

Dynamic Programming
This post attempts to look at the dynamic programming approach to solve those problems. The problems which will be discussed here are : Finding the Minimum Cost Path in a Grid when a Cost Matrix is given. Finding the number of ways to reach from a starting position to an ending position travelling in specified directions only.
Tutorial on Path Problems in a Grid, Maze, or Matrix
A grid or a maze is generally represented as a 2D array or matrix consisting of rows and columns. Each cell is a intersection of a particular row and column and it represents a location in the grid. The cells in the grid may be open for traversal or may be blocked by an obstacle. If a cell is blocked by an obstacle that cell cannot be visited.
Dynamic Programming (DP) on Grids
Grid problems involve a 2D grid of cells, often representing a map or graph. We can apply Dynamic Programming on Grids when the solution for a cell is dependent on solutions of previously traversed cells like to find a path or count number of paths or solve an optimization problem across the grid, with certain constraints on movement or cost. In this article we are going to discuss about the ...
DP-8 Grid Problems in Dynamic Programming
In this video we have discussed how to solve Grid Problems related to Dynamic Programming. We have also covered the solution of the 6th problem from the CSES...
Unique paths in a Grid with Obstacles
Unique paths in a Grid with Obstacles using Space Optimization of Dynamic Programming solution: In this method, we will use the given 'A' 2D matrix to store the previous answer using the bottom-up approach. Approach. Start traversing through the given 'A' 2D matrix row-wise and fill the values in it.
Dynamic Programming for Beginners
In this course you will learn to use Dynamic Programming strategies to solve programming challenges such as: Calculating the 40th number of the Fibonacci sequence. Counting the number of different ways to move through a 6x9 grid. Given a set of coins, how can you make 27 cents in the least number of coins. This course uses images and animations ...
Reinforcement Learning
8. When you try to get your hands on reinforcement learning, it's likely that Grid World Game is the very first problem you meet with. It is the most basic as well as classic problem in reinforcement learning and by implementing it on your own, I believe, is the best way to understand the basis of reinforcement learning.
Finding the Minimum Path Sum in a Grid with Dynamic Programming
The first thing I'll do is initiate a few variables that represent the rows and columns of the inputted grid. function minPathSum(grid) { const m = grid.length; const n = grid[0].length; //... Now, I want to create a new array called pathChange. The purpose of pathChange is to store the minimum sum path at each point in the inputted grid.
Navigate a Grid Using Combinations And Permutations
Visualizing the grid to understand the general problem and see a single path. Write the paths as text to see the general format of all paths & an easy method to enumerate them And that's the key lesson: It's completely fine to use one model to understand the idea, and another to work out the details.
Dynamic programming approach in action · Hyperskill
In this topic, we applied dynamic programming to solve a grid walk problem. We took a close look at the problem's description to get a better comprehension and find a suitable solution. In the process, we found a pitfall associated with recursion and successfully bypassed it using the memoization technique. The use of appropriate data ...
6 Hard Dynamic Programming Problems Made Easy
Here I will solve 6 harder Dynamic Programming problems to show you how to approach them. Unique Paths. A robot is located at the top-left corner of a m x n grid. The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid.
Applying Reinforcement Learning Algorithms to solve Gridworld Problems
1. Introduction. In a grid world problem, an agent is placed on an M X N rectangular array. The cells of the grid correspond to the states of the environment. At each cell, four actions are ...
dynamic programming grid problem approach solving using BFS
The grid has some blocked blocks on which Bob can not travel. Write a function that returns on how many possible positions Bob can move. Solve this problem using BFS and submit the executable code in any programming language. In the following image example, Bob's positioning is at 9,3, and it can visit the places where Y is marked; hence your ...
Dynamic Programming: Finding Optimal Paths
Solving the Problem with Dynamic Programming. What Is Dynamic Programming? A Simple Example: The Fibonacci Sequence; ... analogous problem is written below: The Problem. A grid of size N*M (i.e. N rows and M columns) is given. Each square of the grid can be indexed using a pair of integers (A,B) where 0≤A < N and 0≤B < M. ...
Grid Problems 1 [Programming Competition Problems]
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright ...
algorithm
I'm trying to solve the following problem from Skiena's Algorithm Design Manual: 8-16 Consider a city whose streets are defined by an X x Y grid. We are interested in walking from the upper left-hand corner of the grid to the lower right-hand corner. Unfortunately, the city has bad neighborhoods, whose intersections we do not want to walk in.
Using Reinforcement Learning to solve Gridworld
The Bellman equations cannot be used directly in goal directed problems and dynamic programming is used instead where the value functions are computed iteratively. n this post I solve Grids using Reinforcement Learning. In the problem below the Maze has 2 end states as shown in the corner. There are four possible actions in each state up, down ...
Navigating in Gridworld using Policy and Value Iteration
In reinforcement learning, we are interested in identifying a policy that maximizes the obtained reward. Assuming a perfect model of the environment as a Markov decision process (MDPs), we can apply dynamic programming methods to solve reinforcement learning problems.. In this post, I present three dynamic programming algorithms that can be used in the context of MDPs.
Top 50 Problems on Matrix/Grid Data Structure asked in ...
Given below are the most frequently asked interview questions on Matrix: Easy Level Problems on Matrix/Grid Data Structure. Rotate Matrix Elements. Sort the given matrix. Turn an image by 90-degree. Program to multiply two matrices. Find maximum element of each row in a matrix. Count all sorted rows in a matrix.
A Guide to Important Graph Algorithms for Competitive Programming
Put any one of the graph's vertices at the top of a stack. Take the item at the top of the stack and add it to the visited list. Create a list of that vertex's neighbors. Add the ones which are not in the visited list to the top of the stack. Repeat steps 2 and 3 until the stack is empty. An animation of DFS.
Solving Dynamic Programming Problems on a Computational Grid
We implement a dynamic programming algorithm on a computational grid consisting of loosely coupled processors, possibly including clusters and individual workstations. The grid changes dynamically during the computation, as processors enter and leave the pool of workstations. The algorithm is implemented using the Master-Worker library running on the HTCondor grid computing platform, which ...
How to think like a programmer
Simplest means you know the answer (or are closer to that answer). After that, simplest means this sub-problem being solved doesn't depend on others being solved. Once you solved every sub-problem, connect the dots. Connecting all your "sub-solutions" will give you the solution to the original problem. Congratulations!
Reinforcement Learning : Solving MDPs using Dynamic Programming (Part 3)
Bellman Equation. Remember what the Bellman Equation said, that the value of a state is equal to the immediate reward our agent gets leaving the state plus the value of the next state. So, the equation is breaking down the process of finding the value function of a state by dividing it into sub-problems.. Secondly, for overlapping sub-problems, we have Value functions.
White House announces actions to modernize America's electrical grid
It will compel utilities and grid operators to proactively plan to build regional electrical transmission and is a step toward solving the problem of vast amounts of clean energy being stuck in a ...
How a simple fix could double the size of the U.S. electricity grid
How a simple fix could double the size of the U.S. electricity grid. Rewiring miles of power lines could make space for data centers, AI and a boom in renewables. High voltage power transmission ...
5G and Microgrids Might Be a Great Match
The 5G microgrid setup at NREL is reconfigurable to support experiments involving microgrids and edge controllers. Photo by Brian Miller, NREL. NREL researchers achieved some of 5G's effectiveness by designing the microgrid to maintain power to both communications and critical loads. This included a layer of resilience that was added by using ...
ARIA
ARIA 0.1. The initial evaluation (ARIA 0.1) will be conducted as a pilot effort to fully exercise the NIST ARIA test environment. ARIA 0.1 will focus on risks and impacts associated with large language models (LLMs). Future iterations of ARIA may consider other types of generative AI technologies such as text-to-image models, or other forms of AI such as recommender systems or decision support ...