how to solve problems related to exponential functions equations and inequalities

Reset password New user? Sign up

Existing user? Log in

Exponential Inequalities

Already have an account? Log in here.

Exponential inequalities are inequalities in which one (or both) sides involve a variable exponent . They are useful in situations involving repeated multiplication, especially when being compared to a constant value, such as in the case of interest . For instance, exponential inequalities can be used to determine how long it will take to double ones money based on a certain rate of interest; e.g. money will take approximately 12 years to double at a constant interest rate of 6%.

Introduction

Exponential inequalities - same base, exponential inequalities - base less than 1, exponential inequalities - similar base, exponential inequalities - different base, exponential inequalities - multiple terms, exponential inequalities - problem solving.

The key to working with exponential inequalities is the following fact:

If \(a>1\) and \(x>y\), then \(a^x>a^y\). Otherwise, if \(0<a<1\), then \(a^x<a^y\).

Of course, if \(a=1\), then \(1^x=1\) for any \(x\), and similarly if \(a=0\), then \(0^x=0\) for any positive \(x\). More importantly, the converse is true as well:

If \(a>1\) and \(a^x>a^y\), then \(x>y\). Otherwise, if \(0<a<1\) and \(a^x>a^y\), then \(x<y\).

In more formal terms, the exponential function \(f(x)=a^x\) is monotonically increasing \(\big(\)increasing \(x\) always increases \(f(x)\big)\) for \(a>1\), and monotonically decreasing \(\big(\)increasing \(x\) always decreases \(f(x)\big)\) for \(0<a<1\).

Fortunately, both of these facts are quite intuitive: when the base is greater than 1, the side with the larger exponent will be the greater one, and the opposite is true when the base is less than 1. For instance, without any knowledge of the facts formalized above, one would intuitively expect \(2^{100}\) to be larger than \(2^{95}\).

If \(\big(\frac{1}{2}\big)^x > \big(\frac{1}{2}\big)^y,\) which of the following must be true about \(x\) and \(y?\)

When both sides of an inequality have the same base, the key facts from the introduction can be applied directly. For example,

What values of \(x\) satisfy the following inequality: \[2^{2x+3}>2^{3x}?\] Since the base is 2, which is greater than 1, the fact that \(2^{2x+3}>2^{3x}\) implies that \(2x+3>3x\). Subtracting \(2x\) from both sides gives \(3>x\), so all \(x\) less than \(3\) satisfy the inequality. \(_\square\)

This concept can also be applied to larger "stacks" of exponents:

What values of \(x\) satisfy the following inequality: \[\large 2^{3^{4x+1}}>2^{3^{2x+3}}?\] Since the base is 2, which is greater than 1, the given inequality implies \(3^{4x+1} > 3^{2x+3}\). This further implies that \(4x+1>2x+3\), or that \(2x>2 \implies x>1\). Therefore, all \(x\) greater than 1 satisfy the original inequality. \(_\square\)

In the case where the base is less than 1, the previous intuition is essentially reversed: the larger side is now the one with the smaller exponent.

What values of \(x\) satisfy the following inequality: \[\left(\frac{1}{2}\right)^{3x}>\left(\frac{1}{2}\right)^{2x+3}?\] Since the base is \(\frac{1}{2}\), which is less than 1, the given inequality implies \(3x<2x+3\). Then \(x<3\), so all \(x\) less than 3 satisfy the original inequality. \(_\square\)

In many inequalities, the bases are different but can be rewritten in terms of the same base. For example,

What values of \(x\) satisfy the following inequality: \[4^{x+2}>8^{2x}?\] Here, the bases are different, but they are related by the facts \(4=2^2, 8=2^3\). Rewriting the inequality to use 2 as a base gives \[2^{2(x+2)}>2^{3(2x)} \implies 2^{2x+4}>2^{6x},\] so \(2x+4>6x\), implying that \(4>4x\) and \(1>x\). Hence, all \(x\) less than 1 satisfy the original inequality. \(_\square\)

Suppose that \(\alpha < x< \beta\) is the solution to the following inequality: \[\left(\frac{1}{3}\right)^{x^2+1} > \left(\frac{1}{9}\right)^{x+2}.\] Then what is the value of \( \beta - \alpha ?\)

The same concept can be applied when there are several terms:

What values of \(x\) satisfy the following inequality: \[16^x>2^2 \cdot 4^3 \cdot 8^4?\] Writing all the bases as powers of 2 gives \[\big(2^4\big)^x>2^2 \cdot \big(2^2\big)^3 \cdot \big(2^3\big)^4 \implies 2^{4x}>2^2 \cdot 2^6 \cdot 2^{12}=2^{20}.\] Therefore, \(4x>20\implies x>5\). So, all \(x\) greater than 5 satisfy the original inequality. \(_\square\)

How many integer values of \(x\) satisfy the inequality \[\frac{32}{243} < \left( \frac{2}{3} \right)^{x^2} < \frac{9}{4} \cdot \left( \frac{8}{27} \right)^x ?\]

When the two bases are different and not related by a common base (as in the previous section), the use of logarithms becomes necessary. Fortunately, logarithms satisfy essentially the same properties as exponents do:

If \(a>1\) and \(x>y\), then \(\log_ax>\log_ay\). Otherwise, if \(0<a<1\), then \(\log_ax<\log_ay\).

The converse is also true:

If \(a>1\) and \(\log_ax>\log_ay\), then \(x>y\). Otherwise, if \(0<a<1\), then \(x<y\).

The application is generally a matter of straightforward algebra:

What values of \(x\) satisfy the following inequality: \[2^{5x}>5^{8-5x}?\] Taking the (base 10) logarithm of both sides gives \[\log 2^{5x} > \log 5^{8-5x} \implies 5x\log 2>(8-5x)\log 5,\] so \(5x\log 2>8\log 5-5x\log 5.\) Rearranging gives \(5x(\log 2+\log 5)>8\log 5.\) Since \(\log 2+\log 5=\log 10=1,\) this is equivalent to \(5x>8\log 5,\) so \(x>\frac{8}{5}\log 5.\) \(_\square\)

In the case of multiple terms, it is generally worth assigning another variable to an exponential term, solving the resulting inequality, and then working with the single-term inequality. For example,

What values of \(x\) satisfy the following inequality: \[2^x+4^x>6?\] Let \(y=2^x\), so that \(y+y^2>6\). This can be rearranged as \(y^2+y-6=(y-2)(y+3)>0\), which is true when \(y>2\) or \(y<-3\). Since \(2^x\) cannot be negative, this implies \(y>2 \implies 2^x>2^1\), which implies \(x>1\). Thus, all \(x\) greater than 1 satisfy the original inequality. \(_\square\)

In the case of an inequality chain, it is usually appropriate to treat each inequality separately, then combine the results. For example,

What values of \(x\) satisfy the following inequality: \[\left(\frac{1}{2}\right)^{x+2}<8<\left(\frac{1}{4}\right)^{2x}?\] The first inequality is \(\left(\frac{1}{2}\right)^{x+2}<8\), or \(\left(\frac{1}{2}\right)^{x+2}<\left(\frac{1}{2}\right)^{-3}\). Since \(\frac{1}{2}\) is less than 1, this implies that \(x+2>-3\), or that \(x>-5\). The second inequality is \(8<\left(\frac{1}{4}\right)^{2x}\), or \(\left(\frac{1}{2}\right)^{-3}<\left(\frac{1}{2}\right)^{4x}\). This implies that \(-3>4x\), or that \(-\frac{3}{4}>x\). Putting the two inequalities together, the solution set is \(-5<x<-\frac{3}{4}\). \(_\square\)

Let \(a\) and \(b\) be the minimum and maximum values of \(x\), respectively, that satisfy the inequality \[ 2 ^x (2 \cdot 2 ^x + 8) \leq 8 ^x (5 - 2 ^x). \] What is the value of \( a + b? \)

A key strategy is raising both sides of an inequality to the same exponent (usually some fractional exponent, which is the same as taking some root of both sides) in order to simplify the problem:

Find the greatest integer \(x\) for which \[3^{20}>32^x.\] Since \(32=2^5\), the inequality can be written as \(3^{20}>2^{5x}\implies \big(3^4\big)^5>\big(2^x\big)^5\). This means that \(3^4>2^x\), by taking the \(\frac{1}{5}\) power of both sides of the inequality. Since \(3^4=81\), the largest possible integer is \(6\). Alternatively, \(3^4>2^x\) implies that \(\log_2(3^4)>x \implies 4\log_23>x\), and since \(4\log_23 \approx 6.34\), the largest possible integer value of \(x\) is 6. \(_\square\)

What is the total number of integer solutions \(x\) such that \(5^{21} + 1 < x^7 < 2^{49} - 1?\)

Recall that negative bases only tend to work well with integer exponents; otherwise, the result is usually complex. Therefore, any value that makes a base negative should also make the exponent an integer in order for the expression to remain well-defined.

Solve the inequality \[(x^2+x-2)^{x^2-x-2}>0.\] We split into cases depending on the value of the base, \( x^2 + x - 2 \). Case 1: If \(x^2+x-2\) is positive, then the inequality is true whatever the exponent is, so the first case to solve is \[x^2+x-2>0 \implies (x+2)(x-1)>0 \implies x>1 \text{ or } x<-2.\] Case 2: If \( x^2 + x -2 \) equal 0, then the expression cannot be positive. So there are no solutions. Case 3: If \(x^2+x-2\) is negative, then \( x \in (-2, 1 ) \). For \((x^2+x-2)^{x^2-x-2}\) to be positive, \(x^2-x-2\) must be an even integer. The values of \( x^2 - x - 2 \) on the restricted domain of \( x \in ( -2, 1 ) \) is \( [ - \frac{9}{4} , 4) \). So the only possible values for \( x^2 - x - 2 \) to be an even integer are when it equals \( -2, 0,\) or \( 2. \). If \(x^2-x-2=-2\), then \(x^2-x=0 \implies x=0,1\). Since \( 0, 1 \in [ -2, 1 ] \), these are valid solutions. If \(x^2-x-2=0\), then \((x-2)(x+1)=0 \implies x=-1, 2\). Only \( -1 \in [ -2, 1 ] \), so this is the only solution in this subcase. If \(x^2-x-2=2\), then \(x^2-x-4=0 \implies x=\frac{1 \pm \sqrt{17}}{2}\). Only \(\frac{1-\sqrt{17}}{2} \in [ -2, 1 ] \), so this is the only solution in this subcase. Combining across the cases, the solution set is \[x<-2,\ x=\frac{1-\sqrt{17}}{2},\ x=-1,\ x=0,\ x>1.\ _\square\]

• Rules of Exponents
• Logarithmic Inequalities

Problem Loading...

Note Loading...

Set Loading...

Solving Exponential and Logarithmic Inequalities Lesson

• Demonstrate an understanding of how to solve exponential equations
• Demonstrate an understanding of how to solve logarithmic equations
• Learn how to solve exponential and logarithmic inequalities

How to Solve Exponential and Logarithmic Inequalities

General method for solving an exponential or logarithmic inequality.

• Remember that the argument for a logarithm is a positive real number
• Use the addition property of inequality to change the right side into 0 and then simplify the left side of the inequality as much as possible
• Replace the inequality symbol with an equality symbol and solve the resulting equation
• These critical values are where the function changes sign
• Critical values also occur where the function is undefined, found in step 1
• Solution(s) to our related equation
• Any undefined points
• Use a sign chart to keep track of the sign of the function
• Consider the critical values separately
• The solution is the union of all intervals where the function is positive or negative, depending on the inequality sign given in the problem

Number Line

• 1<e^{3x-1}<2
• How do you solve exponential inequalities?
• To solve exponential inequalities, write the inequality in the form of a single exponential function with a positive base. Take the logarithm of both sides of the inequality. Simplify the logarithmic expression to isolate the variable. Solve the inequality for the variable. Check the solution by plugging it back into the original inequality.
• What is exponential inequality?
• An exponential inequality is an inequality that involves one or more exponents.
• How do you solve exponential inequalities with fractions?
• To solve exponential inequalities with fractions, first convert the fractions to powers of the base using the properties of exponents. Then, apply the usual methods for solving exponential inequalities.

exponential-inequalities-calculator

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• About Varsity Tutors

Precalculus : Exponential Equations and Inequalities

Study concepts, example questions & explanations for precalculus, all precalculus resources, example questions, example question #1 : use logarithms to solve exponential equations and inequalities.

Solving an exponential equation.

We recall the property:

Example Question #132 : Exponential And Logarithmic Functions

Expanding the logarithms into sums of logarithms will cancel out the first two x terms, resulting in the equation:

Combining the first and second terms, then subtracting the new term over will allow you to isolate the variable term.

Divide both sides of the equation by 2, then exponentiate with 3.

Evaluating this term numerically will give the correct answer.

Solve the following equation:

To solve this equation, recall the following property:

Evaluate with your calculator to get

Example Question #141 : Exponential And Logarithmic Functions

After using the division rule to simplify the left hand side you can take the natural log of both sides.

If you then combine like terms you get a quadratic equation which factors to,

Example Question #1 : Exponential Equations And Inequalities

Example Question #2 : Use Logarithms To Solve Exponential Equations And Inequalities

Example Question #3 : Use Logarithms To Solve Exponential Equations And Inequalities

Example Question #4 : Use Logarithms To Solve Exponential Equations And Inequalities

Cannot be simplified any further

The logarithmic expression is as simplified as can be. 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

• Unit Conversions
• Sets and Types of Numbers
• Common Multiple and Divisor
• Fractions and Decimals
• Algebraic Expressions and Polynomials
• Linear Equations and Inequalities
• Systems of Equations and Inequalities
• Quadratic Equations and Inequalities
• Irrational Equations and Inequalities
• Exponential Equations and Inequalities
• Logarithmic Equations and Inequalities
• Trigonometric Equations and Inequalities
• Equation Word Problems
• Inequality Word Problems
• Sequences and Series
• Combinatorics
• Probability and Statistics
• Stereometry
• Analytical Geometry
• Limits, Derivatives, Integrals
• Analysis of Functions
• Trig table and chart

• Link Partners
• Privacy Policy

Copyright © 2015-2023 math-exercises.com - All rights reserved. Any use of website content without written permission is prohibited.

General Mathematics Quarter 1 – Module 18: Solving Exponential Equations and Inequalities

This module was designed and written with you in mind. It is here to help you master how to solve exponential equation and inequality. The scope of this module permits it to be used in many different learning situations. The language used recognizes the diverse vocabulary level of students. The lessons are arranged to follow the standard sequence of the course. But the order in which you read them can be changed to correspond with the textbook you are now using.

After going through this module, you are expected to:

1. explain how to apply the properties in solving exponential equations and inequalities; and

2. solve exponential equations and inequalities.

Can't Find What You'RE Looking For?

We are here to help - please use the search box below.

Leave a Comment Cancel reply

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.3: Exponential Equations and Inequalities

• Last updated
• Save as PDF
• Page ID 119170

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Math 370 Learning Objectives

• Briefly review solving exponential equations using logarithms.
• Optional: Solve exponential inequalities.
• Optional: Find the inverse when given an equation involving several exponential functions.

Solving Exponential Equations

In this section we will develop techniques for solving equations involving exponential functions. Suppose, for instance, we wanted to solve the equation \(2^{x} = 128\). After a moment’s calculation, we find \(128 = 2^{7}\), so we have \(2^{x} = 2^{7}\). The one-to-one property of exponential functions, detailed in Theorem 6.2.2 , tells us that \(2^{x} = 2^{7}\) if and only if \(x=7\). This means that not only is \(x=7\) a solution to \(2^{x} = 2^{7}\), it is the only solution.

Now suppose we change the problem ever so slightly to \(2^{x} = 129\). We could use one of the inverse properties of exponentials and logarithms to write \(129 = 2^{\log_{2}(129)}\). We’d then have \(2^{x} = 2^{\log_{2}(129)}\), which means our solution is \(x = \log_{2}(129)\). This makes sense because, after all, the definition of \(\log_{2}(129)\) is "the exponent we put on \(2\) to get \(129\)." Indeed we could have obtained this solution directly by rewriting the equation \(2^{x} = 129\) in its logarithmic form \(\log_{2}(129) = x\). Either way, in order to get a reasonable decimal approximation to this number, we’d use the Change of Base Formula  to give us something more calculator friendly, 1  say \(\log_{2}(129) = \frac{\ln(129)}{\ln(2)}\). Another way to arrive at this answer is as follows

\[\begin{array}{rclr} 2^{x} & = & 129 & \\ \ln\left(2^{x}\right) & = & \ln(129) & \left(\text{Take the natural log of both sides} \right) \\ x \ln(2) & = & \ln(129) & \left(\text{Power Rule of Logarithmic Functions}\right) \\ x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{array}\nonumber\]

"Taking the natural log" of both sides is akin to squaring both sides: since \(f(x) = \ln(x)\) is a function , as long as two quantities are equal, their natural logs are equal. 2  Also note that we treat \(\ln(2)\) as any other non-zero real number and divide it through 3  to isolate the variable \(x\).

Example \( \PageIndex{1} \)

Solve the following equations. Check your answer graphically using a calculator.

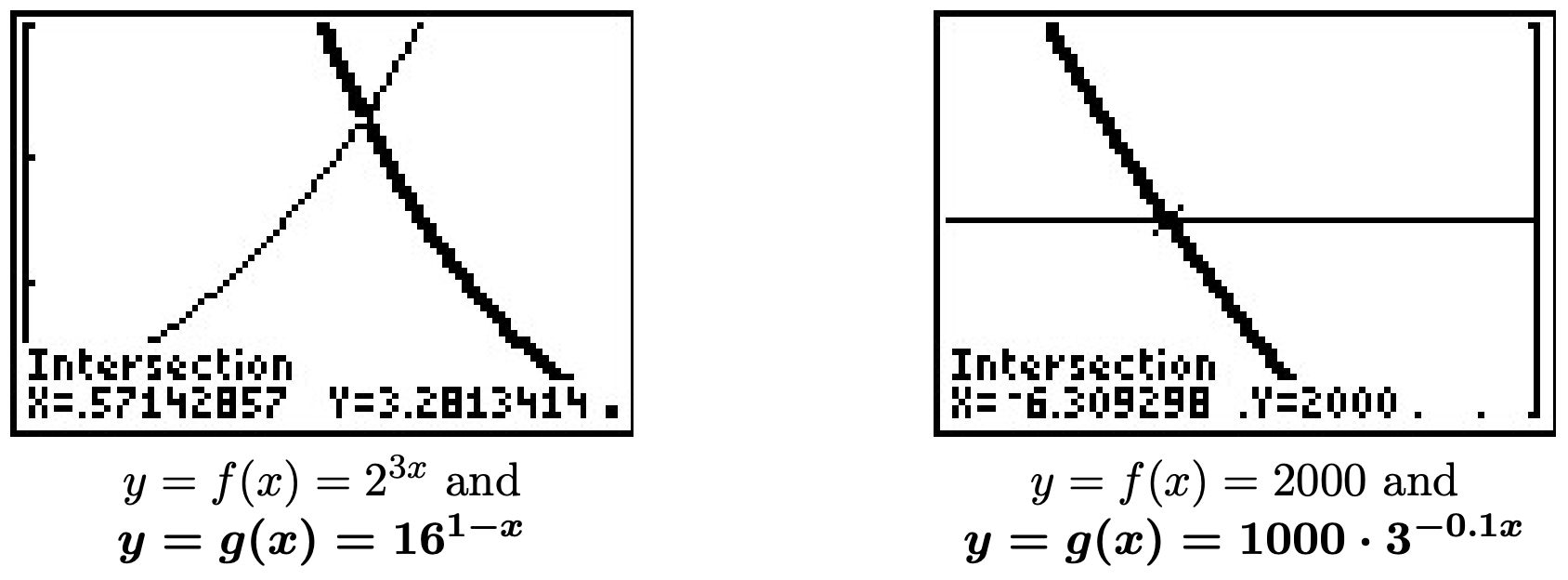
• \(2^{3x} = 16^{1-x}\)
• \(2000 = 1000 \cdot 3^{-0.1 t}\)
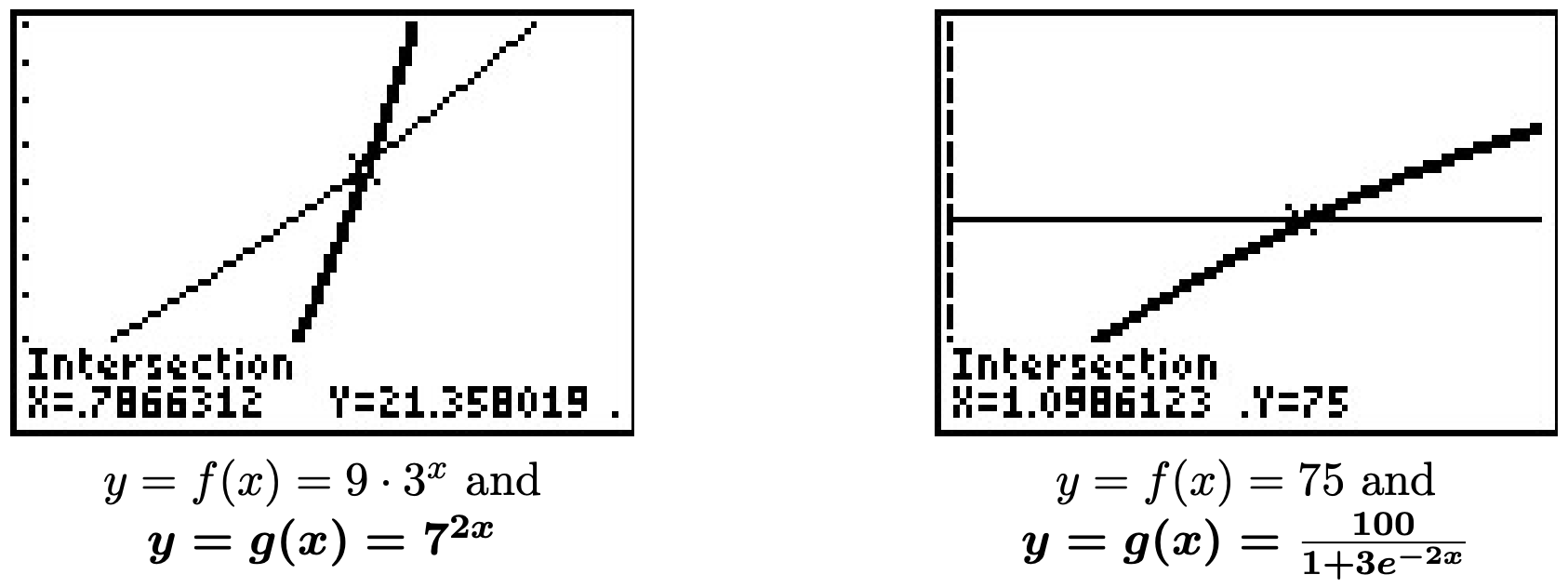
• \(9 \cdot 3^{x} = 7^{2x}\)
• \(75 = \frac{100}{1 + 3e^{-2t}}\)
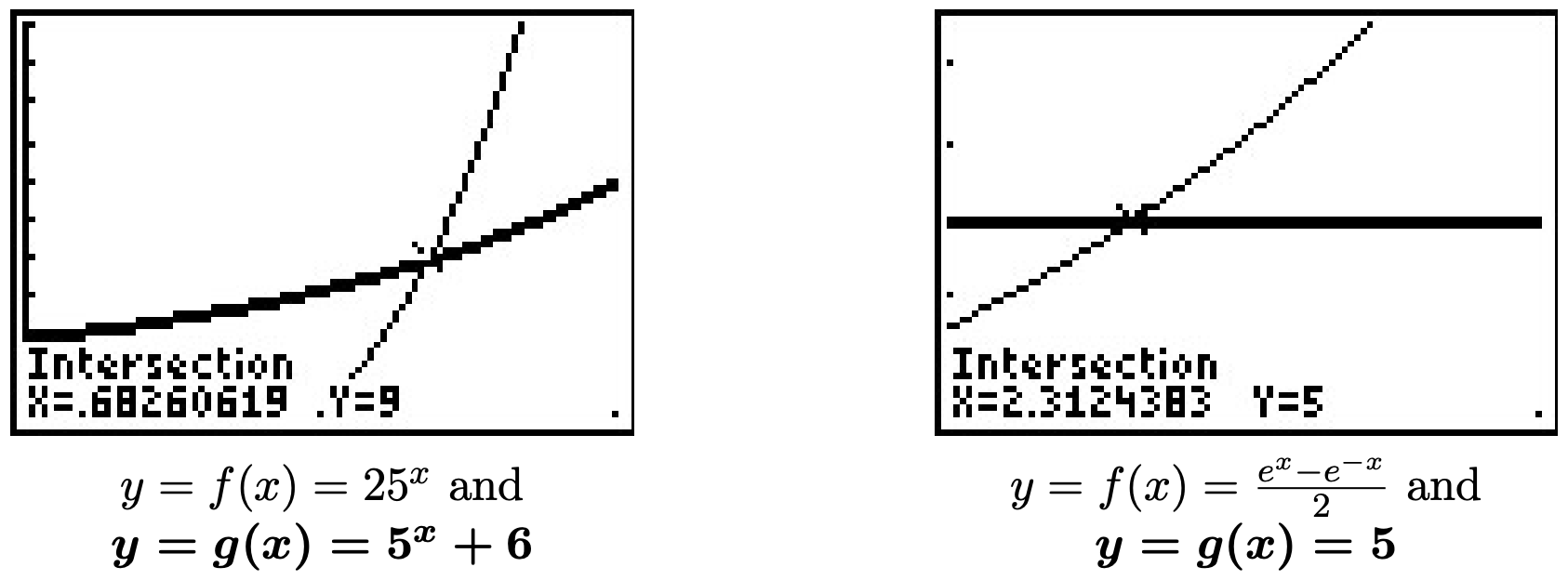
• \(25^{x} = 5^{x} + 6\)
• \(\frac{e^{x} - e^{-x}}{2} = 5\)
• Since \(16\) is a power of \(2\), we can rewrite \(2^{3x} = 16^{1-x}\) as \(2^{3x} = \left(2^4\right)^{1-x}\). Using properties of exponents, we get \(2^{3x} = 2^{4(1-x)}\). Using the one-to-one property of exponential functions, we get \(3x = 4(1-x)\) which gives \(x=\frac{4}{7}\). To check graphically, we set \(f(x) = 2^{3x}\) and \(g(x) = 16^{1-x}\) and see that they intersect at \(x=\frac{4}{7} \approx 0.5714\).

• We first note that we can rewrite the equation \(9 \cdot 3^{x} = 7^{2x}\) as \(3^2 \cdot 3^x = 7^{2x}\) to obtain \(3^{x+2} = 7^{2x}\). Since it is not convenient to express both sides as a power of \(3\) (or \(7\) for that matter) we use the natural log: \(\ln\left(3^{x+2}\right) = \ln\left(7^{2x}\right)\). The Power Rule of Logarithmic Functions gives \((x+2) \ln(3) = 2x \ln(7)\). Even though this equation appears very complicated, keep in mind that \(\ln(3)\) and \(\ln(7)\) are just constants. The equation \((x+2) \ln(3) = 2x \ln(7)\) is actually a linear equation and as such we gather all of the terms with \(x\) on one side, and the constants on the other. We then divide both sides by the coefficient of \(x\), which we obtain by factoring.\[\begin{array}{rclr} (x+2) \ln(3) & = & 2x \ln(7) & \\ x \ln(3) + 2 \ln(3) & = & 2x \ln(7) & \\ 2 \ln(3) & = & 2x \ln(7) - x \ln(3) & \\ 2 \ln(3) & = & x (2 \ln(7) - \ln(3)) & \left(\text{Factor}\right) \\ x & = & \dfrac{2 \ln(3)}{2\ln(7) - \ln(3)} & \\ \end{array}\nonumber\]Graphing \(f(x) = 9 \cdot 3^{x}\) and \(g(x) = 7^{2x}\) on the calculator, we see that these two graphs intersect at \(x = \frac{2 \ln(3)}{2\ln(7) - \ln(3)} \approx 0.7866\).

• We start solving \(25^{x} = 5^{x} + 6\) by rewriting \(25 = 5^2\) so that we have \(\left(5^2\right)^{x} = 5^{x} + 6\), or \(5^{2x} = 5^{x} + 6\). Even though we have a common base, having two terms on the right hand side of the equation foils our plan of equating exponents or taking logs. If we stare at this long enough, we notice that we have three terms with the exponent on one term exactly twice that of another. To our surprise and delight, we have a "quadratic in disguise." Letting \(u = 5^{x}\), we have \(u^2 = \left(5^{x}\right)^2 = 5^{2x}\) so the equation \(5^{2x} = 5^{x} + 6\) becomes \(u^2 = u + 6\). Solving this as \(u^2 - u - 6=0\) gives \(u = -2\) or \(u = 3\). Since \(u = 5^{x}\), we have \(5^{x} = -2\) or \(5^{x} = 3\). Since \(5^{x} = -2\) has no real solution, (Why not?) we focus on \(5^{x} = 3\). Since it isn’t convenient to express \(3\) as a power of \(5\), we take natural logs and get \(\ln\left(5^{x}\right) = \ln(3)\) so that \(x \ln(5) = \ln(3)\) or \(x = \frac{\ln(3)}{\ln(5)}\). On the calculator, we see the graphs of \(f(x) = 25^{x}\) and \(g(x) = 5^{x} + 6\) intersect at \(x=\frac{\ln(3)}{\ln(5)} \approx 0.6826\).

​The authors would be remiss not to mention that Example \( \PageIndex{1} \) holds great educational value. Much can be learned about logarithms and exponentials by verifying the solutions obtained in Example \( \PageIndex{1} \) analytically. For example, to verify our solution to \(2000 = 1000 \cdot 3^{-0.1 t}\), we substitute \(t = -\frac{10\ln(2)}{\ln(3)}\) and obtain

\[\begin{array}{rclr} 2000 & \stackrel{?}{=} & 1000 \cdot 3^{-0.1 \left(-\dfrac{10\ln(2)}{\ln(3)}\right)} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\dfrac{\ln(2)}{\ln(3)}} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\log_{3}(2)} & \left(\text{Change of Base}\right) \\ 2000 & \stackrel{?}{=} & 1000 \cdot 2 & \left(\text{Inverse Property}\right) \\ 2000 & \stackrel{\checkmark}{=} & 2000 & \\ \end{array}\nonumber\]

The other solutions can be verified by using a combination of log and inverse properties. Some fall out quite quickly, while others are more involved. We leave them to the reader.

Subsection Footnotes

1  You can use natural logs or common logs. We choose natural logs. (In Calculus, you’ll learn these are the most "mathy" of the logarithms.)

2  This is also the "if" part of the statement \(\log _{b}(u)=\log _{b}(w)\) if and only if \(u = w\) in Theorem 6.2.2 .

3  Please resist the temptation to divide both sides by "\(\ln{}\)" instead of \(\ln(2)\). Just like it wouldn’t make sense to divide both sides by the square root symbol "\(\sqrt{\quad} \)" when solving \(x \sqrt{2}=5\), it makes no sense to divide by "\(\ln{}\)".

Solving Exponential Inequalities

Since exponential functions are continuous on their domains, the Intermediate Value Theorem  applies. As with the algebraic functions in Section 5.3 , this allows us to solve inequalities using sign diagrams as demonstrated below.

Example \( \PageIndex{2} \)

Solve the following inequalities. Check your answer graphically using a calculator.

• \(2^{x^2-3x} - 16 \geq 0\)
• \(\frac{e^{x}}{e^{x}-4} \leq 3\)
• \(x e^{2x} < 4x\)

Example \( \PageIndex{3} \)

Recall from Example 6.1.2 that the temperature of coffee \(T\) (in degrees Fahrenheit) \(t\) minutes after it is served can be modeled by \(T(t) = 70 + 90 e^{-0.1 t}\). When will the coffee be warmer than \(100^{\circ}\mbox{F}\)?

We need to find when \(T(t) > 100\), or in other words, we need to solve the inequality \(70 + 90 e^{-0.1 t} > 100\). Getting \(0\) on one side of the inequality, we have \(90 e^{-0.1 t} - 30 > 0\), and we set \(r(t) = 90 e^{-0.1 t} - 30\). The domain of \(r\) is artificially restricted due to the context of the problem to \([0, \infty)\), so we proceed to find the zeros of \(r\). Solving \(90 e^{-0.1 t} - 30=0\) results in \(e^{-0.1t} = \frac{1}{3}\) so that \(t = -10\ln\left(\frac{1}{3}\right)\) which, after a quick application of the Power Rule of Logarithmic Functions leaves us with \(t = 10 \ln(3)\). If we wish to avoid using the calculator to choose test values, we note that since \(1 < 3\), \(0 = \ln(1) < \ln(3)\) so that \(10\ln(3) > 0\). So we choose \(t = 0\) as a test value in \([0, 10 \ln(3))\). Since \(3 < 4\), \(10 \ln(3) < 10 \ln(4)\), so the latter is our choice of a test value for the interval \((10 \ln(3), \infty)\). Our sign diagram is below, and next to it is our graph of \(y=T(t)\) from Example 6.1.2 with the horizontal line \(y = 100\).

In order to interpret what this means in the context of the real world, we need a reasonable approximation of the number \(10 \ln(3) \approx 10.986\). This means it takes approximately \(11\) minutes for the coffee to cool to \(100^{\circ}\mbox{F}\). Until then, the coffee is warmer than that. 8

4  This is because the base of \(\ln (x)\) is \(e>1\). If the base \(b\) were in the interval \(0<b<1\), then \(\log _{b}(x)\) would decreasing.

5  We could, of course, use the calculator, but what fun would that be?

6  A calculator can be used at this point. As usual, we proceed without apologies, with the analytical method.

7  Note: \(\ln (2) \approx 0.693\).

8  Critics may point out that since we needed to use the calculator to interpret our answer anyway, why not use it earlier to simplify the computations? It is a fair question which we answer unfairly: it’s our book.

Finding the Inverse When Given an Equation Involving Exponentials

We close this section by finding the inverse of a function which is a composition of a rational function with an exponential function.

Example \( \PageIndex{4} \)

The function \(f(x) = \frac{5e^{x}}{e^{x}+1}\) is one-to-one. Find a formula for \(f^{-1}(x)\) and check your answer graphically using your calculator.

We start by writing \(y=f(x)\), and interchange the roles of \(x\) and \(y\). To solve for \(y\), we first clear denominators and then isolate the exponential function.

\[\begin{array}{rclr} y & = & \dfrac{5e^{x}}{e^{x}+1} & \\   x & = & \dfrac{5e^{y}}{e^{y}+1} & \left(\text{Switch }x\text{ and }y\right) \\   x \left(e^{y}+1\right) & = & 5e^{y} & \\  x e^{y}+x & = & 5e^{y} & \\  x & = & 5e^{y} - x e^{y} & \\  x & = & e^{y}(5 - x) & \\  e^{y}& = & \dfrac{x}{5-x} & \\ \ln\left(e^{y}\right) & = & \ln\left(\dfrac{x}{5-x}\right) & \\  y & = & \ln\left(\dfrac{x}{5-x}\right) & \\ \end{array}\nonumber\]

We claim \(f^{-1}(x) = \ln\left(\frac{x}{5-x}\right)\). To verify this analytically, we would need to verify the compositions \(\left(f^{-1} \circ f\right)(x) = x\) for all \(x\) in the domain of \(f\) and that \(\left(f \circ f^{-1}\right)(x) = x\) for all \(x\) in the domain of \(f^{-1}\). We leave this to the reader. To verify our solution graphically, we graph \(y = f(x) = \frac{5e^{x}}{e^{x}+1}\) and \(y = g(x) = \ln\left(\frac{x}{5-x}\right)\) on the same set of axes and observe the symmetry about the line \(y=x\). Note the domain of \(f\) is the range of \(g\) and vice-versa.