how to solve ratio problems with fractions

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Ratio Problem Solving

Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.

There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio problem solving?

Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer. 

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods we can use when given certain pieces of information.

When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation. 

For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

We use the ratio to divide 40 sweets into 8 equal parts. 

Then we multiply each part of the ratio by 5.

3 x 5:5 x 5 = 15:25

This means that Charlie will get 15 sweets and David will get 25 sweets.

• Dividing ratios

Step-by-step guide: Dividing ratios (coming soon)

Ratios and fractions (proportion problems)

We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.

Simplifying and equivalent ratios

• Simplifying ratios

Equivalent ratios

Units and conversions ratio questions

Units and conversions are usually equivalent ratio problems (see above).

• If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
• The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.

Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.

Top tip: if you are converting units, always write the units in your ratio.

Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .

Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Explain how to do ratio problem solving

Ratio problem solving worksheet

Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on ratio

Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• How to work out ratio  
• Ratio to fraction
• Ratio scale
• Ratio to percentage

Ratio problem solving examples

Example 1: part:part ratio.

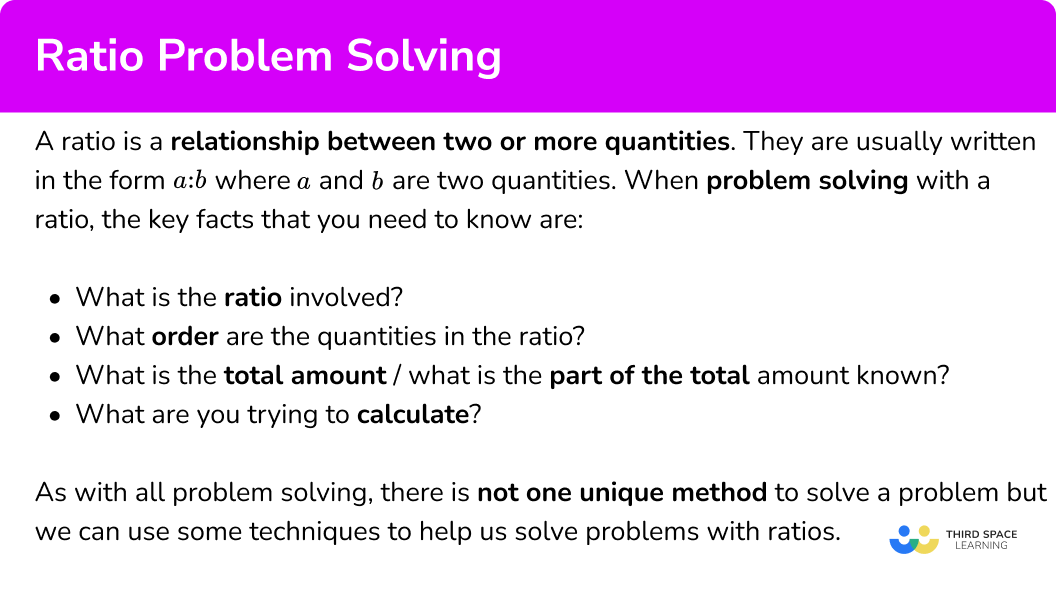
Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?

Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?

Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).

We could write this as

Where the letter above each part of the ratio links to the question.

We know that 465 students have school dinner.

2 Know what you are trying to calculate.

From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.

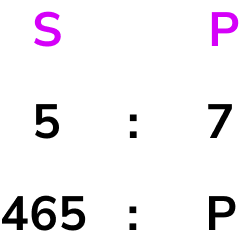
We need to find the value of p.

3 Use prior knowledge to structure a solution.

We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.

So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

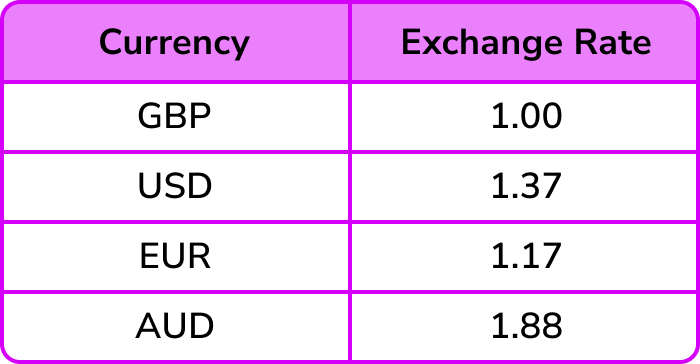
Use the table above to convert £520 (GBP) to Euros € (EUR).

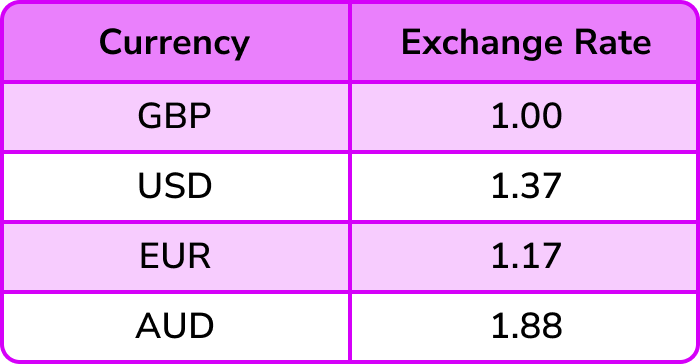
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).

The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state

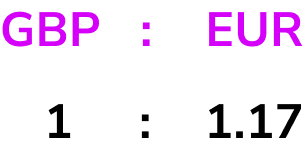
We know that we have £520.

We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520 = €608.40.

Example 3: writing a ratio 1:n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.

Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.

2l = 2000ml

So we can also express the ratio as 500:2000 which will help us in later steps.

We want to simplify the ratio 500:2000 into the form 1:n.

We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

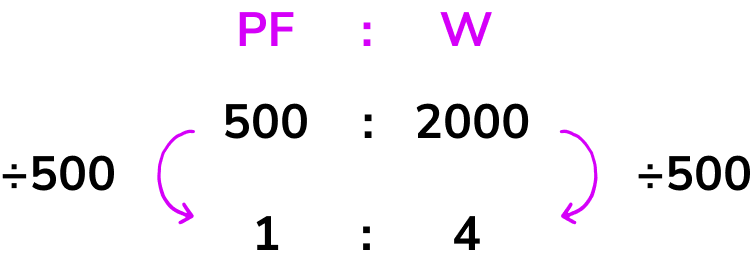
So the ratio of plant food to water in the form 1:n is 1:4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?

We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have

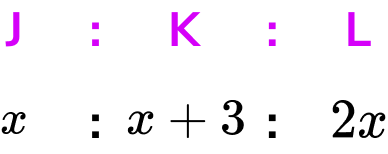
We also know that Luke receives £8.

We want to calculate the total amount of pocket money for the three siblings.

We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.

Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

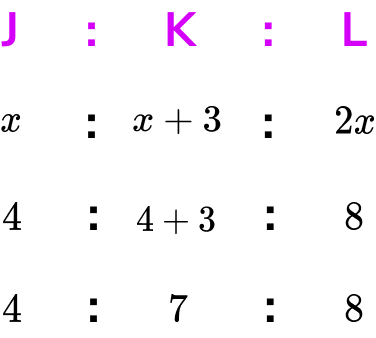
The total amount of pocket money is therefore 4+7+8=£19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colours of counters in a bag.

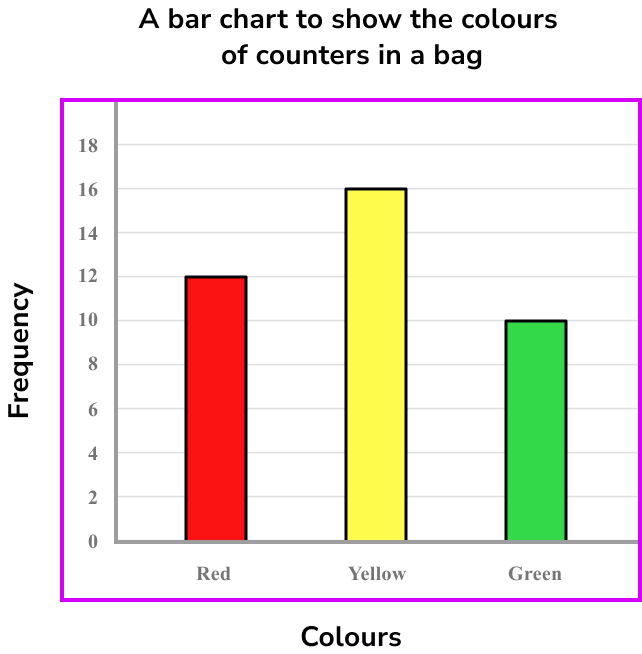
Express this data as a ratio in its simplest form.

From the bar chart, we can read the frequencies to create the ratio.

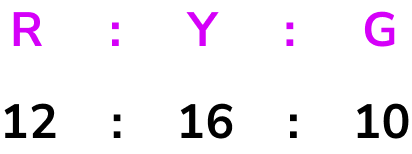
We need to simplify this ratio.

To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}

HCF (12,16,10) = 2

Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .

Example 6: combining two ratios

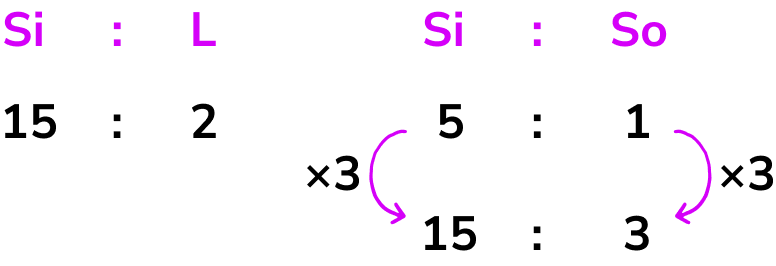
Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .

We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.

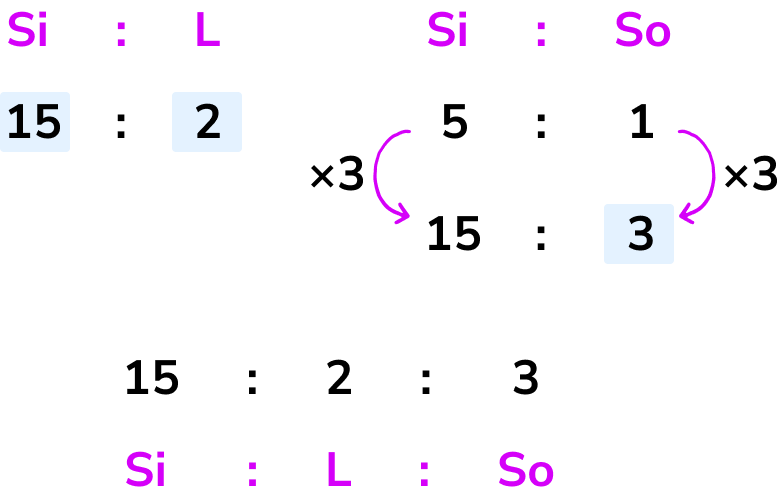
Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.

We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.

Example 7: using bar modelling

India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?

We know that the initial ratio is 5:2 and that India has three more parts than Beau.

We want to find the original quantity.

Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if we can find out this value, we can then find the total quantity.

From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.

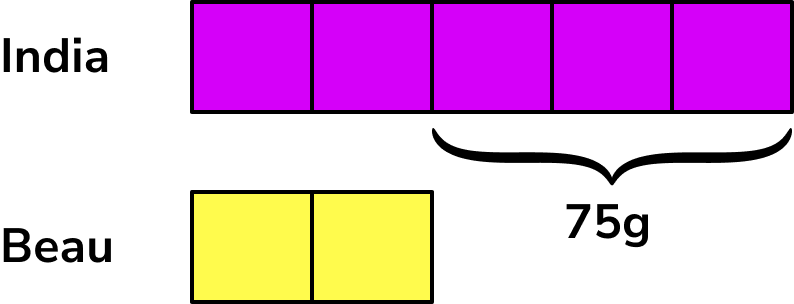
We can find the value of one share by working out 75 \div 3=25g.

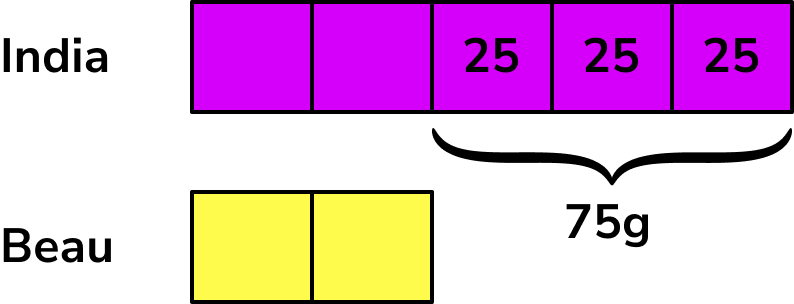
We can fill in each share to be 25g.

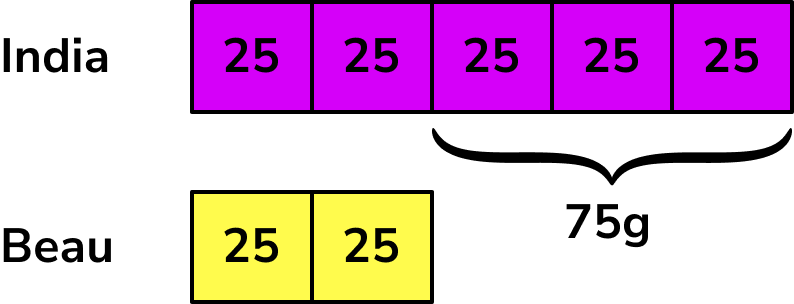
Adding up each share, we get

India = 5 \times 25=125g

Beau = 2 \times 25=50g

The total amount of popcorn was 125+50=175g.

Common misconceptions

• Mixing units

Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.

• Ratio written in the wrong order

For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.

• Ratios and fractions confusion

Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

• Counting the number of parts in the ratio, not the total number of shares

For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.

• Ratios of the form \bf{1:n}

The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.

4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.

5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.

Ratio problem solving GCSE questions

1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.

Write this in the form 1gram:n where n represents the number of water molecules in standard form.

2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.

Calculate the length of the plank of wood.

5-3=2 \ parts = 36cm so 1 \ part = 18cm

3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.

(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.

Learning checklist

You have now learned how to:

• Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
• Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
• Make and use connections between different parts of mathematics to solve problems

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Get 25% off all test packages.

Get 25% off all test packages!

Click below to get 25% off all test packages.

How To Simplify Ratios With Fractions

Simplifying ratios that involve fractions.

Ratios are used as a way of comparing values. Typically expressed in the form A:B, they tell us how much of one thing we have compared to another. For example, if we have a bowl of fruit containing two apples and six oranges, we can express this as 2:6.

Ratios are useful because they allow us to easily scale values and express quantities in a way that is simple to understand. As such, you’ll find them used in everything from official statistics to grocery store labels.

When ratios appear in an everyday context, they are usually given in their lowest form. In a numerical reasoning test , you may be required to simplify a ratio. This process is straightforward enough when working with whole numbers, but is complicated when working with ratios that involve fractions.

Take, for example, the ratio 1 5/12:7/3. As each side, or term, of the ratio is a fraction, we first need to manipulate these and identify a common denominator that will allow us to find the ratio’s lowest form. We’ll walk through this process below.

A step-by-step guide to simplifying ratios with fractions

Taking the example above of the ratio 1 5/12:7/3, there are four steps we need to work through to express this in its simplest form.

Step 1: Convert mixed fractions to improper fractions

In our example, the antecedent term of the ratio is the mixed fraction 1 5/12, so we first need to convert this to an improper fraction (if there are no mixed fractions in the ratio, you can skip this step).

To do this, we first multiply the whole number by the denominator of the fractional part; in this case, 1 x 12 = 12.

We then add this result to the numerator of the fractional part, so 12 + 5 = 17. This number now becomes our new numerator, which we place above our original denominator, giving us the improper fraction 17/12.

Step 2: Convert both fractions using the lowest common denominator

Our ratio is now 17/12:7/30, so our next task is to find the lowest common denominator of our two fractions.

By listing multiples of both 12 and 30, we find the lowest common denominator is 60.

To keep the values of our fractions the same, we need to multiply both the numerator and the denominator by the same amount. So:

12 x 5 = 60 and 17 x 5 = 85, giving us 85/60

30 x 2 = 60 and 7 x 2 = 14, giving us 14/60

Step 3: Write the numerators as a ratio

Now we have a common denominator, we can omit this and write out our ratio using the numerators.

This gives us the ratio 85:14

Step 4: Simplify the ratio

The final step is to simplify the ratio by dividing both sides by the highest common factor.

In our example, the highest common factor is 1, so the ratio is already in its lowest form.

We can therefore say that 1 5/12:7/30 = 85:14.

Example question 1

Simplify the ratio 12/17:15/68

Here we have two proper fractions, so we can move straight onto step two and find the lowest common denominator. Since 68 is a multiple of 17, this is our answer:

17 x 4 = 68

Now multiply the numerator by the same amount to keep the value of the fraction:

12 x 4 = 48

This leaves us with 48/68:15/68.

We can omit the common denominator and write our ratio using both numerators:

Now look for the highest common factor, in this case 3, and divide both terms of the ratio to simplify:

Answer: 12/17:15/68 = 16:5

Example question 2

Simplify the ratio 3 2/9:5/18

Here we have a mixed fraction, so we first need to convert this to an improper fraction. Multiply the whole number by the denominator of the fractional part:

Add this to the numerator:

27 + 2 = 29

Place this over the original denominator, giving you the ratio 29/9:5/18.

Now find the lowest common denominator of the two fractions, in this case, 18. Keep the value of the fractions by multiplying both numerator and denominator by the same amount:

9 x 2 - 18 and 29 x 2 = 59

This gives us 58/18:5/18

Omit the denominators and write out the ratio using the numerators:

The highest common factor here is 1, so we cannot simply any further.

Answer: 3 2/9:5/18 = 58:5

Tips for simplifying ratios that include fractions

Practise simplifying ratios with whole numbers.

Before you start working with ratios that involve fractions, first master the art of simplifying ratios with whole numbers .

You’ll need to understand this process to express a ratio in its lowest form, so make this the starting point of your revision. You need to work at speed in a numerical reasoning test, and the quicker you are at this process, the faster you’ll be overall.

Learn to convert mixed fractions

A ratio containing both mixed and proper fractions can be intimidating, causing you to draw a blank and eating into your time allowance.

This is easily avoidable if you’re confident in converting mixed fractions to improper fractions. All you need to remember are two simple rules: multiply the whole by the denominator, and add to the numerator.

Know your times tables

Quick multiplication is key when looking for a lowest common denominator. Knowing your times tables is also useful for identifying the highest common factor across the terms of a ratio.

Pay attention to detail

Always ensure you understand the question and watch out for costly mistakes. If your question is presented as a word problem, write it out as a numerical equation, checking each part of the ratio is placed correctly.

For example, ‘what is 3/6 to 5/8 in its simplest form?’ should be written 3/6:5/8, with the first figure mentioned as the antecedent term.

Equally, when converting fractions, double-check your numerators and denominators and, when writing your final answer, ensure the terms of your ratio are consistent with the question.

Enjoy what you’ve read? Let others know!

• Share on whatsapp
• Share on linkedin
• Share on twitter
• Share on facebook
• Share via email

By using our website you agree with our Cookie Policy.

Maths with Mum

Be your child's best tutor

Solving Ratio Problems

• We add the parts of the ratio to find the total number of parts.
• There are 2 + 3 = 5 parts in the ratio in total.
• To find the value of one part we divide the total amount by the total number of parts.
• 50 ÷ 5 = 10.
• We multiply the ratio by the value of each part.
• 2:3 multiplied by 10 gives us 20:30.
• The 50 counters are shared into 20 counters to 30 counters.

• 2 + 3 = 5 and so there are 5 parts in the ratio in total.
• We divide by this total number of parts to find the value of each part.
• We multiply the original ratio by the value of each part.
• We have 20:30.

• Sharing in a Ratio: Part 1

Ratio Problems: Worksheets and Answers

How to Solve Ratio Problems

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to print (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Telegram (Opens in new window)
• Click to share on Skype (Opens in new window)

Algebra: Ratio Word Problems

Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Algebra Lessons

In these lessons, we will learn how to solve ratio word problems that have two-term ratios or three-term ratios.

Ratio problems are word problems that use ratios to relate the different items in the question.

The main things to be aware about for ratio problems are:

• Change the quantities to the same unit if necessary.
• Write the items in the ratio as a fraction .
• Make sure that you have the same items in the numerator and denominator.

Ratio Problems: Two-Term Ratios

Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?

Solution: Step 1: Assign variables: Let x = number of red sweets.

Step 2: Solve the equation. Cross Multiply 3 × 120 = 4 × x 360 = 4 x

Answer: There are 90 red sweets.

Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?

Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = number of blue marbles for Jane 20 – x = number red marbles for Jane

Step 2: Solve the equation

Cross Multiply 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x

John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.

Answer: John has 4 more blue marbles than Jane.

How To Solve Word Problems Using Proportions?

This is another word problem that involves ratio or proportion.

Example: A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?

How To Solve Proportion Word Problems?

When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.

• Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
• Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank? 3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?

Ratio problems: Three-term Ratios

Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?

Solution: Step 1: Assign variables: Let x = amount of corn

Step 2: Solve the equation Cross Multiply 2 × x = 3 × 5 2 x = 15

Answer: The mixture contains 7.5 pounds of corn.

Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?

Solution: Step 1: Assign variables: Let x = number of red shirts and y = number of green shirts

Step 2: Solve the equation Cross Multiply 3 × 20 = x × 4 60 = 4 x x = 15

5 × 20 = y × 4 100 = 4 y y = 25

The total number of shirts would be 15 + 25 + 20 = 60

Answer: There are 60 shirts.

Algebra And Ratios With Three Terms

Let’s study how algebra can help us think about ratios with more than two terms.

Example: There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

A ratio compares values .

A ratio says how much of one thing there is compared to another thing.

Ratios can be shown in different ways:

A ratio can be scaled up:

Try it Yourself

Using ratios.

The trick with ratios is to always multiply or divide the numbers by the same value .

Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk.

So the ratio of flour to milk is 3 : 2

To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4:

3 ×4 : 2 ×4 = 12 : 8

In other words, 12 cups of flour and 8 cups of milk .

The ratio is still the same, so the pancakes should be just as yummy.

"Part-to-Part" and "Part-to-Whole" Ratios

The examples so far have been "part-to-part" (comparing one part to another part).

But a ratio can also show a part compared to the whole lot .

Example: There are 5 pups, 2 are boys, and 3 are girls

Part-to-Part:

The ratio of boys to girls is 2:3 or 2 / 3

The ratio of girls to boys is 3:2 or 3 / 2

Part-to-Whole:

The ratio of boys to all pups is 2:5 or 2 / 5

The ratio of girls to all pups is 3:5 or 3 / 5

Try It Yourself

We can use ratios to scale drawings up or down (by multiplying or dividing).

Example: To draw a horse at 1/10th normal size, multiply all sizes by 1/10th

This horse in real life is 1500 mm high and 2000 mm long, so the ratio of its height to length is

1500 : 2000

What is that ratio when we draw it at 1/10th normal size?

We can make any reduction/enlargement we want that way.

"I must have big feet, my foot is nearly as long as my Mom's!"

But then she thought to measure heights, and found she is 133cm tall, and her Mom is 152cm tall.

In a table this is:

The "foot-to-height" ratio in fraction style is:

We can simplify those fractions like this:

And we get this (please check that the calcs are correct):

"Oh!" she said, "the Ratios are the same".

"So my foot is only as big as it should be for my height, and is not really too big."

You can practice your ratio skills by Making Some Chocolate Crispies

How do we solve ratio problems?

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Fraction Questions in Math

Last Updated: April 14, 2024 Fact Checked

This article was co-authored by Mario Banuelos, PhD and by wikiHow staff writer, Sophia Latorre . Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,199,654 times.

Fraction questions can look tricky at first, but they become easier with practice and know-how. Start by learning the terminology and fundamentals, then pratice adding, subtracting, multiplying, and dividing fractions. [1] X Research source Once you understand what fractions are and how to manipulate them, you'll be breezing through fraction problems in no time.

Doing Calculations with Fractions

• For instance, to solve 5/9 + 1/9, just add 5 + 1, which equals 6. The answer, then, is 6/9 which can be reduced to 2/3.

• For instance, to solve 6/8 - 2/8, all you do is take away 2 from 6. The answer is 4/8, which can be reduced to 1/2.

• For example, if you need to add 1/2 and 2/3, start by determining a common multiple. In this case, the common multiple is 6 since both 2 and 3 can be converted to 6. To turn 1/2 into a fraction with a denominator of 6, multiply both the numerator and denominator by 3: 1 x 3 = 3 and 2 x 3 = 6, so the new fraction is 3/6. To turn 2/3 into a fraction with a denominator of 6, multiply both the numerator and denominator by 2: 2 x 2 = 4 and 3 x 2 = 6, so the new fraction is 4/6. Now, you can add the numerators: 3/6 + 4/6 = 7/6. Since this is an improper fraction, you can convert it to the mixed number 1 1/6.
• On the other hand, say you're working on the problem 7/10 - 1/5. The common multiple in this case is 10, since 1/5 can be converted into a fraction with a denominator of 10 by multiplying it by 2: 1 x 2 = 2 and 5 x 2 = 10, so the new fraction is 2/10. You don't need to convert the other fraction at all. Just subtract 2 from 7, which is 5. The answer is 5/10, which can also be reduced to 1/2.

• For instance, to multiply 2/3 and 7/8, find the new numerator by multiplying 2 by 7, which is 14. Then, multiply 3 by 8, which is 24. Therefore, the answer is 14/24, which can be reduced to 7/12 by dividing both the numerator and denominator by 2.

• For example, to solve 1/2 ÷ 1/6, flip 1/6 upside down so it becomes 6/1. Then just multiply 1 x 6 to find the numerator (which is 6) and 2 x 1 to find the denominator (which is 2). So, the answer is 6/2 which is equal to 3.

Joseph Meyer

Think about fractions as portions of a whole. Imagine dividing objects like pizzas or cakes into equal parts. Visualizing fractions this way improves comprehension, compared to relying solely on memorization. This approach can be helpful when adding, subtracting, and comparing fractions.

Practicing the Basics

• For instance, in 3/5, 3 is the numerator so there are 3 parts and 5 is the denominator so there are 5 total parts. In 7/8, 7 is the numerator and 8 is the denominator.

• If you need to turn 7 into a fraction, for instance, write it as 7/1.

• For example, if you have the fraction 15/45, the greatest common factor is 15, since both 15 and 45 can be divided by 15. Divide 15 by 15, which is 1, so that's your new numerator. Divide 45 by 15, which is 3, so that's your new denominator. This means that 15/45 can be reduced to 1/3.

• Say you have the mixed number 1 2/3. Stary by multiplying 3 by 1, which is 3. Add 3 to 2, the existing numerator. The new numerator is 5, so the mixed fraction is 5/3.

Tip: Typically, you'll need to convert mixed numbers to improper fractions if you're multiplying or dividing them.

• Say that you have the improper fraction 17/4. Set up the problem as 17 ÷ 4. The number 4 goes into 17 a total of 4 times, so the whole number is 4. Then, multiply 4 by 4, which is equal to 16. Subtract 16 from 17, which is equal to 1, so that's the remainder. This means that 17/4 is the same as 4 1/4.

Fraction Calculator, Practice Problems, and Answers

Community Q&A

• Check with your teacher to find out if you need to convert improper fractions into mixed numbers and/or reduce fractions to their lowest terms to get full marks. Thanks Helpful 2 Not Helpful 1
• Take the time to carefully read through the problem at least twice so you can be sure you know what it's asking you to do. Thanks Helpful 2 Not Helpful 2
• To take the reciprocal of a whole number, just put a 1 over it. For example, 5 becomes 1/5. Thanks Helpful 1 Not Helpful 1

You Might Also Like

• ↑ https://www.sparknotes.com/math/prealgebra/fractions/terms/
• ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
• ↑ https://www.mathsisfun.com/fractions_multiplication.html
• ↑ https://www.mathsisfun.com/fractions_division.html
• ↑ https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
• ↑ https://www.youtube.com/watch?v=PcEwj5_v75g
• ↑ https://sciencing.com/solve-math-problems-fractions-7964895.html

About This Article

To solve a fraction multiplication question in math, line up the 2 fractions next to each other. Multiply the top of the left fraction by the top of the right fraction and write that answer on top, then multiply the bottom of each fraction and write that answer on the bottom. Simplify the new fraction as much as possible. To divide fractions, flip one of the fractions upside-down and multiply them the same way. If you need to add or subtract fractions, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Sebastian Maxwell

Jun 1, 2017

Did this article help you?

Jul 19, 2017

Sep 16, 2017

Kamaria Albert

Feb 28, 2017

Oct 17, 2016

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

ACT Math: How to Solve Ratio Problems

There are a few key concepts to get down in order to ace ACT Math ratios. Let’s go right into how the ACT will test you on ratios and break it down for you.

Ratio Basics

A ratio tells you the proportional quantity of one thing relative to another.

Make sure not to get ratios confused with fractions. Fractions tell you the proportional quantity of something relative to its whole. Ratios expressed as fractions do not tell you the whole. One instance where you need to use the concept of ratios involves baking. If you want to make double the amount of cookies that a recipe will yield, then you need to double the quantity of each ingredient.

ACT Math: Dealing With Ratios

You might see ACT ratios written in fraction form, colon form, or in plain English. Whatever the case may be, you can treat them all the same way. In the case of the fraction form, do not get it confused with a regular fraction! The denominator of a ratio is not necessarily equivalent to the denominator of a ratio.

For example, the ratio 12/8, 12:8, and 12 to 8 are all the same. Like fractions, you should reduce ratios down to simplest terms – in this case, it is 3/2. Keep your numbers manageable, especially when you need to look for the lowest common multiple later on in the multi-step ratio section.

On the test, ratios will be clearly spelled out for you. If you are looking at a ratio problem, you’ll know it because the test makers will make it obvious.

The important part lies in knowing how to manipulate ratios to get to your answer. The two main things you need to know are proportions and multi-step ratios.

Proportions

You’ll find that these are very common on the ACT. Thankfully, they are also easy to solve.

You will usually be given a ratio along with a hypothetical quantity of one of the things on the original ratio. The key is to set up two ratios and cross-multiply as you would two fractions to solve for the missing fourth quantity.

If you have a ratio of 3 cats to 2 dogs, how many cats do you have if you have 20 dogs? You could use mental math or set up two fractions to get 30 cats as your answer.

Multi-Step Ratios

These are a little bit more involved, but shouldn’t pose much of a threat to your ACT Math score one you learn about how to go about solving them.

Here you’ll be given two ratios and three different types of quantities: a, b, and c. The two ratios given compare a to b and b to c. You’ll then be asked to figure out the ratio of a to c.

In order to solve, you need to figure out the least common multiple of the two b’s and multiply the respective a’s accordingly. Now with your b’s equal to each other, simply take the values of your a and c and create a new ratio.

For example, if a:b is 2:3 and b:c is 6:9, then what is a:c? Here we need to multiply our first ratio by 2 in order to get 4:6. Since our b from the first and second ratio match, we can take our a and c and form a new ratio.

Our answer is 4:9.

Minh’s passion for helping students succeed grew during his time as a career counselor at the University of California, Irvine. Now, he’s helping students all over the world by spilling SAT/ACT secrets through blog posts on Magoosh. When he’s not busy tutoring or writing, he enjoys playing guitar, traveling, and talking about himself in third-person.

View all posts

More from Magoosh

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 1

• Ratio tables
• Solving ratio problems with tables
• Equivalent ratios
• Equivalent ratios: recipe

Equivalent ratio word problems

• Understanding equivalent ratios
• Equivalent ratios in the real world
• Interpreting unequal ratios
• Understand equivalent ratios in the real world