how to solve the travelling salesman problem

Learning center series

Travelling salesman problem explained

• Published on April 26, 2024
• by Oguzhan Uyar
• Last updated: 3 days ago

Revolutionize your understanding of the Travelling Salesman Problem (TSP); a mind-boggling conundrum that has compelled academia and industry alike. In the upcoming lines, we decode the key concepts, algorithms, and anticipated solutions for 2024 to this age-old dilemma.

Now, picture the TSP as a globetrotting traveling salesman who’s whirlwind journey. He must stop at every city once, only the origin city once, and find the quickest shortest possible route back home. If daunting to visualize, consider this: the possible number of routes in the problem concerning just 20 cities exceeds the number of atoms in the observable universe.

Fathom the sheer magnitude?

So, what is the Travelling Salesman Problem, and why has it remained unsolved for years? Let’s snap together the puzzle of this notorious problem that spans mathematics, computer science, and beyond. Welcome to an insightful voyage into the astonishing world of the TSP.

Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms

Defining the travelling salesman problem: a comprehensive overview.

The Travelling Salesman Problem, often abbreviated as TSP, has a strong footing in the realm of computer science. To the untrained eye, it presents itself as a puzzle: a salesperson or traveling salesman must traverse through a number of specific cities before an ending point and return to their ending point as of origin, managing to do so in the shortest possible distance. But this problem is not simply a conundrum for those fond of riddles; it holds immense significance in the broad field of computer science and optimization. Optimizing travel routes is the key to solving the Travelling Salesman Problem efficiently, ensuring the shortest and most cost-effective journey for salespeople or travelers.

The sheer computational complexity of TSP is what sets it apart, and incidentally, why it is considered a challenging problem to solve. Its complexity derives from the factorial nature of the problem: whenever a new city is added, the total number of possibilities increases exponentially. Thus, as the problem scope enlarges, it swiftly becomes computationally prohibitive to simply calculate all possible solutions to identify an optimal shortest route through. Consequently, developing effective and efficient algorithms to solve the TSP has become a priority in the world of computational complexity.

Polynomial Time Solution: The TSP can be solved by a deterministic Turing machine in polynomial time, which means that the number of steps to solve the problem can be at most 1.5 times the optimal global solution.

One such algorithm is the dynamic programming approach that can solve TSP problems in polynomial time. The approach uses a recursive formula to compute the shortest possible route that visits all other nodes in the cities exactly once and ends at all nodes in the starting point or city. Moreover, linear programming and approximation algorithms have also been used to find near-optimal solutions.

Unraveling TSP Algorithms: From Brute Force to Heuristics

A multitude of algorithms have been developed to contend with the TSP. The brute force method, for example, entails considering the shortest distance for all possible permutations of cities, calculating the total distance for six cities along each route, and selecting the shortest distance for one. While brute force promises an optimal solution, it suffers from exponential computational complexity, rendering it unfeasible for large datasets.

TSP Complexity: A TSP with just 10 cities has 362,880 possible routes , making brute force infeasible for larger instances.

On the other hand, we have heuristic algorithms that generate good, albeit non-optimal, solutions in reasonable timeframes. The greedy algorithm, for instance, initiates from a starting city and looks for the shortest distance from other nodes to the next node minimizes the distance, and guarantees speed but is not necessarily an optimal solution.

Algorithmic Potential: Local Solutions 4/3 Times Optimal Global: The theoretical conjecture suggests an algorithm that can provide a local solution within 4/3 times the optimal global solution.

Record Local TSP Solution: The record for a local solution to the Traveling Salesman Problem (TSP) is 1.4 times the optimal global solution, achieved in September 2012 by Andr´as Seb˝o and Jens Vygen.

Exploring further, we encounter more refined heuristic solutions such as the genetic algorithm and simulated annealing algorithm. These algorithms deploy probabilistic rules, with the former incorporating principles of natural evolution and the latter being inspired by the cooling process in metallurgy. They differ significantly from each other in terms of how they search for solutions, but when compared to brute force, they often offer a promising trade-off between quality and computational effort.

Certainly, the TSP is far more than a problem to puzzle over during a Sunday afternoon tea. It’s a complex computational task with real-world implications, and unraveling it requires more than brute force; it demands the application of sophisticated algorithms designed to balance efficiency and quality of results. Nevertheless, with a better understanding of the problem statement and its dynamics, you can unlock the potential to not just solve problems faster, but to do so more intelligently.

Practical Solutions to the Travelling Salesman Problem

Implementing tsp solutions: a step-by-step guide, a comprehensive process for implementing tsp solutions.

Developing complete, practical solutions for the Travelling Salesman Problem (TSP) requires a good grasp of specific algorithms. Visual aids, for example, such as finding all the edges leading out of a given city, can help to simplify the process. Enhance your ability to solve the Travelling Salesman Problem by mastering route optimization with Google Maps , streamlining your path and saving significant time on the go.

TSP's Computer Science Quest for Shortest Routes: The TSP involves finding the shortest route to visit a set of cities exactly once before returning to the starting city, aiming to minimize travel distance.

One popular approach to TSP problem solving is the dynamic programming approach, which involves breaking down the problem into smaller sub-problems and recursively solving them. Other approaches include approximation algorithms, which generate near-optimal solutions to small problems in polynomial time, and bound algorithms, which aim to find an upper bound on the optimal solution given graph top.

TSP Variants: ASTP and STSP The TSP can be divided into two types: the asymmetric traveling salesman problem (ASTP) and the symmetric traveling salesman problem (STSP)

Practical code implementation

Before diving into code manipulations, it’s worth noting that practical implementation varies based on the specifics of the problem and the chosen algorithm. Let’s further deconstruct these notions by examining the steps for code implementation for a pre-determined shortest path first. It’s crucial to efficiently concede each point of the shortest path, call other nodes, connect each node, and conclude each route. Hereby, I shall delve into the practicalities of coding from an output standpoint, concentrating on readability, scalability, and execution efficiency.

TSP Instance Size: The size of the TSP instances used in the studies is 100 nodes.

Cluster Quantity in TSP Instances: The number of clusters in the TSP instances used in the studies is 10 .

The Quantity of Instances per Cluster in Studies: The number of instances in each cluster used in the studies is 100.

Optimizing TSP Solutions: Tips and Tricks

Tsp solutions optimization techniques.

An optimized solution for the TSP is often accomplished using advanced algorithms and techniques. Optimization techniques allow professionals to solve more intricate problems, rendering them invaluable tools when handling large datasets and attempting to achieve the best possible solution. Several approaches can be taken, such as heuristic and metaheuristic approaches, that can provide near-optimal solutions with less use of resources.

Expert Advice for Maximum Efficiency Minimum Cost

Even the most proficient problem solvers can gain from learning expert tips and tricks. These nuggets of wisdom often provide the breakthrough needed to turn a good solution into a great one. The TSP is no exception. Peering into the realm of experts can provide novel and creative ways to save time, increase computation speed, manage datasets, and achieve the most efficient shortest route around.

By comprehending and implementing these solutions to the Travelling Salesman Problem, one can unravel the complex web of nodes and paths. This equips any problem-solver with invaluable insights that make navigating through real-world TSP applications much more manageable. By adopting sophisticated routing planner software , businesses can significantly streamline their delivery operations, ensuring a more predictable and cost-effective way of dealing with the challenges presented by the Travelling Salesman Problem.

Real-World Applications of the Travelling Salesman Problem

Tsp in logistics and supply chain management.

The Travelling Salesman Problem (TSP) is not confined to theoretical mathematics or theoretical computer science either, it shines in real-world applications too. One of its most potent applications resides in the field of logistics and supply chain management. Explore how the latest gratis route planning applications can revolutionize logistics and supply chain efficiency by uncovering the top 10 free software tools for 2024.

With globalization, the importance of more efficient routes for logistics and supply chain operations has risen dramatically. Optimizing routes and decreasing costs hold the key to success in this arena. Here’s where TSP comes into play. Discover how Planning for Multiple Stops can revolutionize your logistics, ensuring the most efficient paths are taken. Dive into our post to see how it streamlines operations and reduces expenses.

In the vast complexity of supply chain networks, routing can be a colossal task. TSP algorithms bring clarity to the chaos, eliminating redundant paths and pointing to the optimal route covering the most distance, shortest path, and least distance between all the necessary points—leading to a drastic dip in transportation costs and delivery times. Uncover how optimizing delivery routes can revolutionize your logistics, ensuring efficiency and cost-effectiveness in your delivery operations.

Real-World Examples

Consider the case of UPS – the multinational package delivery company. They’ve reportedly saved hundreds of millions of dollars yearly by implementing route optimization algorithms originating from the Travelling Salesman Problem. The solution, named ORION, helped UPS reduce the distance driven by their drivers roughly by 100 million miles annually.

TSP in GIS and Urban Planning: Optimal Route

TSP’s contributions to cities aren’t confined to logistics; it is invaluable in Geographic Information Systems (GIS) and urban planning as well. A city’s efficiency revolves around transportation. The better the transport networks and systems, the higher the city’s productivity. And as city authorities continuously strive to upgrade transportation systems, they find an ally in TSP. Discover how TSP enhances road architecture by integrating specialized truck routing solutions , elevating urban transport strategies.

Advanced GIS systems apply TSP to design more efficient routes and routing systems for public transportation. The aim of the route is to reach maximum locations with the least travel time and least distance, ensuring essential amenities are accessible to everyone in the city.

The city of Singapore, known for its efficient public transportation system, owes part of its success to similar routing algorithms. The Land Transport Authority uses TSP-related solutions to plan bus routes, reducing travel durations and enhancing accessibility across the city.

Delving Deeper: The Complexity and History of the Travelling Salesman Problem

Understanding the complexity of tsp.

TSP is fascinating not just for its inherent practicality but also for the complexity it brings along. TSP belongs to a class of problems known as NP-hard, a category that houses some of the most complex problems in computer science. But what makes TSP so gnarled?

Unravel the Intricacies: Why is TSP complex?

TSP is a combinatorial optimization problem, which simply means that it’s all about figuring out the most often optimal solution among a vast number of possible solutions or combinations of approximate solutions. The real challenge comes from an innocent-sounding feature of TSP: As the number of cities (we call them nodes) increases, the complexity heightens exponentially, not linearly. The number of possible routes takes a dramatic upward turn as you add more nodes, clearly exemplifying why TSP is no walk-in-the-park problem.

NP-hard and TSP: A Connection Explored

In computer science, we use the terms P and NP for classifying problems. P stands for problems where a solution can be found in ‘polynomial time’. NP stands for ‘nondeterministic polynomial time’, which includes problems where a solution can be verified in polynomial time. The concept of ‘NP-hardness’ applies to TSP. Any problem that can be ‘reduced’ to an NP problem in polynomial time is described as NP-hard. In simpler terms, it’s harder than the hardest problems of NP. TSP holds a famed position in this class, making it a noteworthy example of an NP-hard problem. Discovering efficient solutions for the Traveling Salesman Problem (TSP) exemplifies how optimizing routes can streamline complex logistical challenges, showcasing the practical impact of advancements in algorithmic route optimization.

A Look Back: The History of the Travelling Salesman Problem

TSP is not a new kid on the block. Its roots can be traced back to the 1800s, and the journey since then has been nothing short of a compelling tale of mathematical and computational advancements.

The Origins and Evolution of TSP

Believe it or not, the Travelling Salesman Problem was first formulated as a mathematical problem in the 1800s. This was way before the advent of modern computers. Mathematicians and logisticians were intrigued by the problem and its implications. However, it wasn’t until the mid-20th century that the problem started to gain more widespread attention. Over the years, the TSP has transformed from a theoretical model to a practical problem that helps solve real-world issues.

A Classic Shortest Route Problem Since 1930s: The TSP is a classic optimization problem within the field of operations research, first studied during the 1930s.

Milestones in TSP Research

Looking at all the cities and milestones in TSP research, the story is truly impressive. From some of the initial heuristic algorithms to solve smaller instances of TSP, to geometric methods and then approximation algorithms, TSP research has seen a lot. More recently, we have also seen practical solutions to TSP using quantum computing — a testament to how far we’ve come. Each of these milestones signifies an innovative shift in how we understand and solve TSP. Discovering the top delivery route planning software in 2024, we navigated through the advancements in TSP solutions to identify which applications excel in streamlining delivery logistics.

Wrapping Up The Journey With Algorithms and Solutions

The Travelling Salesman Problem (TSP) remains a complex enigma of business logistics, yet, the advent of sophisticated algorithms and innovative solutions are paving avenues to optimize routing, reduce travel costs further, and enhance customer interactions.

Navigating the TSP intricacies is no longer a daunting challenge but a worthwhile investment in refining operational efficiency and delivering unparalleled customer experiences. With advanced toolsets and intelligent systems, businesses are closer to making more informed, strategic decisions.

Now, it’s your turn. Reflect on your current logistics complexities. How can your business benefit from implementing these key concepts and algorithms? Consider where you could incorporate these practices to streamline and revolutionize your daily operations.

Remember, in the world of dynamic business operations, mastering the TSP is not just an option, but a strategic imperative. As you move forward into 2024, embrace the art of solving the TSP. Unravel the potential, decipher the complexities, and unlock new horizons for your business.

Ready for the challenge?

What is route optimization?

7 reasons for delivery route optimization

What is multi-stop route planning and why is it important?

How to optimize routes with Google Maps

7 benefits of using route scheduling software

Truck route planning vs common route planning

Best delivery route planning software for 2024

Top 10 free route planning software of 2024

‟3 Metrobi Drivers together completed more than 170 deliveries for us.”

Diamond Bakery

‟I am able to do twice as many orders because I don't spend time delivering”

‟Great service and support from Metrobi”

Anna’s Taqueria

‟My favorite drivers are there for me”

Field Trip Flowers

Success Stories

Jacobson Floral

Quinlan-Wasserman

Dorchester Brewing Company

Secret Garden Rose

Hanato Floral Design

Flamingo Estate

DELIVER WITH METROBI

Grow with confidence

• 55 Court St floor 2, Boston, MA 02108
• [email protected]
• Team Metrobi
• Privacy policy
• Terms of service
• Write for us

Refer us to a company, you earn $250 and they earn $250. Learn more

• Shopify Delivery Planner App
• Delivery Management Software
• Atlanta courier service
• Boston courier service
• Chicago courier service
• Denver courier service
• Miami courier service
• New York City courier service
• Los Angeles courier service
• Philadelphia courier service
• San Francisco courier service
• Washington DC courier service
• See all locations
• Bulk Order Delivery Service
• Express Urgent Delivery Service
• Fixed Route Delivery Service
• On Demand Delivery Service
• Overnight Delivery Service
• Same Day Delivery Service
• Scheduled Delivery Service
• Wholesale Delivery Service
• See all delivery services
• Metrobi vs. Onfleet
• Metrobi vs. Roadie
• Metrobi vs. Roadie Support
• Artisan Food
• Food Producers

Want to access our large pool of drivers?

We started Metrobi to take operations off your plate. We provide drivers (rated 4.97/5), dedicated operation managers (70% cheaper), and routing software with a receiver notification system.

• Travelling salesman problem

The travelling salesman problem (often abbreviated to TSP) is a classic problem in graph theory . It has many applications, in many fields. It also has quite a few different solutions.

The problem

The problem is usually stated in terms of a salesman who needs to visit several towns before eventually returning to the starting point. There are various routes he could take, visiting the different towns in different orders. Here is an example:

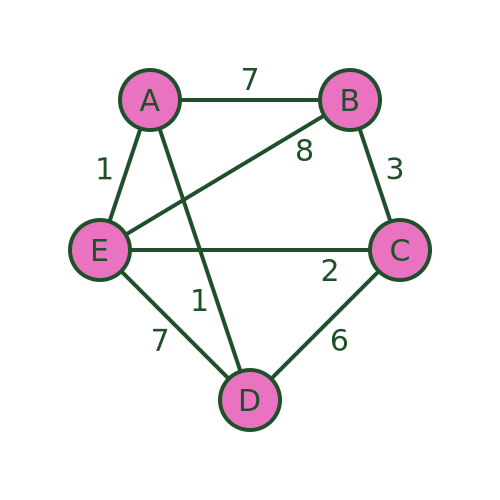
There are several different routes that will visit every town. For example, we could visit the towns in the order A , B , C , D , E , then back to A . Or we could use the route A , D , C , E , B then back to A .

But not all routes are possible. For example, we cannot use a route A , D , E , B , C and then back to A , because there is no road from C to A .

The aim is to find the route that visits all the towns with the minimum cost . The cost is shown as the weight of each edge in the graph. This might be the distance between the towns, or it might be some other measure. For example, it might be the time taken to travel between the towns, which might not be proportionate to the distance because some roads have lower speed limits or are more congested. Or, if the salesman was travelling by train, it might be the price of the tickets.

The salesman can decide to optimise for whatever measure he considers to be most important.

Alternative applications and variants

TSP applies to any problem that involves visiting various places in sequence. One example is a warehouse, where various items need to be fetched from different parts of a warehouse to collect the items for an order. In the simplest case, where one person fetches all the items for a single order and then packs and dispatches the items, a TSP algorithm can be used. Of course, a different route would be required for each order, which would be generated by the ordering system.

Another interesting example is printed circuit board (PCB) drilling. A PCB is the circuit board you will find inside any computer or other electronic device. They often need holes drilled in them, including mounting holes where the board is attached to the case and holes where component wires need to pass through the board. These holes are usually drilled by a robot drill that moves across the board to drill each hole in the correct place. TSP can be used to calculate the optimum drilling order.

The TSP algorithm can be applied to directed graphs (where the distance from A to B might be different to the distance from B to A ). Directed graphs can represent things like one-way streets (where the distance might not be the same in both directions) or flight costs (where the price of a single airline ticket might not be the same in both directions).

There are some variants of the TSP scenario. The mTSP problem covers the situation where there are several salesmen and exactly one salesman must visit each city. This applies to delivery vans, where there might be several delivery vans. The problem is to decide which parcels to place on each van and also to decide the route of each van.

The travelling purchaser problem is another variant. In that case, a purchaser needs to buy several items that are being sold in different places, potentially at different prices. The task is to purchase all the items, minimising the total cost (the cost of the items and the cost of travel). A simple approach would be to buy each item from the place where it is cheapest, in which case this becomes a simple TSP. However, it is not always worth buying every item from the cheapest place because sometimes the travel cost might outweigh the price difference.

In this article, we will only look at the basic TSP case.

Brute force algorithm

We will look at 3 potential algorithms here. There are many others. The first, and simplest, is the brute force approach.

We will assume that we start at vertex A . Since we intend to make a tour of the vertices (ie visit every vertex once and return to the original vertex) it doesn't matter which vertex we start at, the shortest loop will still be the same.

So we will start at A , visit nodes B , C , D , and E in some particular order, then return to A .

To find the shortest route, we will try every possible ordering of vertices B , C , D , E , and record the cost of each one. Then we can find the shortest.

For example, the ordering ABCDEA has a total cost of 7+3+6+7+1 = 24.

The ordering ABCEDA (i.e. swapping D and E ) has a total cost of 7+3+2+7+1 = 20.

Some routes, such as ADEBCA are impossible because a required road doesn't exist. We can just ignore those routes.

After evaluating every possible route, we are certain to find the shortest route (or routes, as several different routes may happen to have the same length that also happens to be the shortest length). In this case, the shortest route is AECBDA with a total length of 1+8+3+6+1 = 19.

The main problem with this algorithm is that it is very inefficient. In this example, since we have already decided that A is the start/end point, we must work out the visiting order for the 4 towns BCDE . We have 4 choices of the first town, 3 choices for the second town, 2 choices for the third town, and 1 choice for the fourth town. So there are 4! (factorial) combinations. That is only 24 combinations, which is no problem, you could even do it by hand.

If we had 10 towns (in addition to the home town) there would be 10! combinations, which is 3628800. Far too many to do by hand, but a modern PC might be able to do that in a fraction of a second if the algorithm was implemented efficiently.

If we had 20 towns, then the number of combinations would be of order 10 to the power 18. If we assume a computer that could evaluate a billion routes per second (which a typical PC would struggle to do, at least at the time of writing), that would take a billion seconds, which is several decades.

Of course, there are more powerful computers available, and maybe quantum computing will come into play soon, but that is only 20 towns. If we had 100 towns, the number of combinations would be around 10 to the power 157, and 1000 towns 10 to the power 2568. For some applications, it would be quite normal to have hundreds of vertices. The brute force method is impractical for all but the most trivial scenarios.

Nearest neighbour algorithm

The nearest neighbour algorithm is what we might call a naive attempt to find a good route with very little computation. The algorithm is quite simple and obvious, and it might seem like a good idea to someone who hasn't put very much thought into it. You start by visiting whichever town is closest to the starting point. Then each time you want to visit the next town, you look at the map and pick the closest town to wherever you happen to be (of course, you will ignore any towns that you have visited already). What could possibly go wrong?

Starting at A , we visit the nearest town that we haven't visited yet. In this case D and E are both distance 1 from A . We will (completely arbitrarily) always prioritise the connections in alphabetical order. So we pick D .

As an aside, if we had picked E instead we would get a different result. It might be better, but it is just as likely to be worse, so there is no reason to chose one over the other.

From D , the closest town is C with a distance of 6 (we can't pick A because we have already been there).

From C the closest town is E with distance 2. From E we have to go to B because we have already visited every other town - that is a distance of 8. And from B we must return to A with a distance of 7.

The final path is ADCEBA and the total distance is 1+6+2+8+7 = 24.

The path isn't the best, but it isn't terrible. This algorithm will often find a reasonable path, particularly if there is a natural shortest path. However, it can sometimes go badly wrong.

The basic problem is that the algorithm doesn't take account of the big picture. It just blindly stumbles from one town to whichever next town is closest.

In particular, the algorithm implicitly decides that the final step will be B to A . It does this based on the other distances, but without taking the distance BA into account. But what if, for example, there is a big lake between B and A that you have to drive all the way around? This might make the driving distance BA very large. A more sensible algorithm would avoid that road at all costs, but the nearest neighbour algorithm just blindly leads us there.

We can see this with this revised graph where BA has a distance of 50:

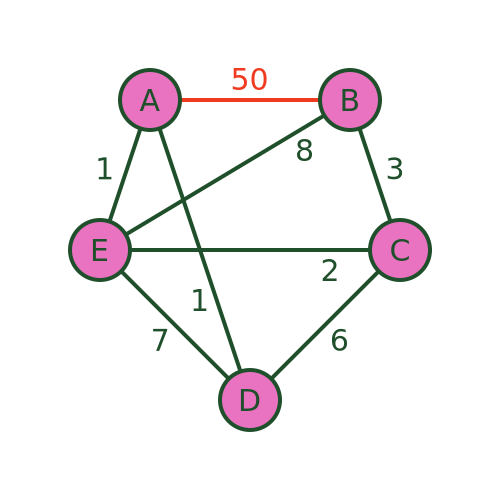
The algorithm will still recommend the same path because it never takes the distance BA into account. The path is still ADCEBA but the total distance is now 1+6+2+8+50 = 67. There are much better routes that avoid BA .

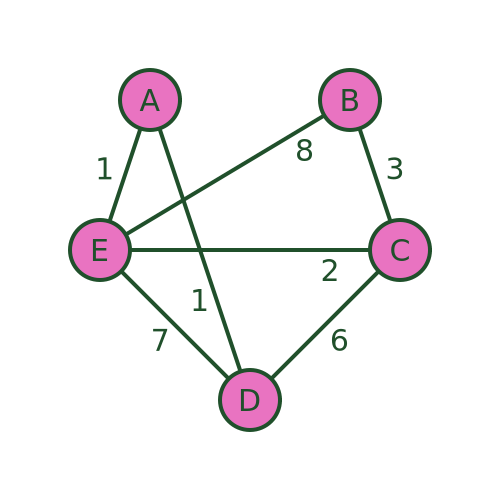
An even worse problem can occur if there is no road at all from B to A . The algorithm would still guide us to town B as the final visit. But in that case, it is impossible to get from B to A to complete the journey:

Bellman–Held–Karp algorithm

The Bellman–Held–Karp algorithm is a dynamic programming algorithm for solving TSP more efficiently than brute force. It is sometimes called the Held–Karp algorithm because it was discovered by Michael Held and Richard Karp, but it was also discovered independently by Richard Bellman at about the same time.

The algorithm assumes a complete graph (ie a graph where every vertex is connected to every other). However, it can be used with an incomplete graph like the one we have been using. To do this, we simply add extra the missing connections (shown below in grey) and assign them a very large distance (for example 1000). This ensures that the missing connections will never form part of the shortest path:

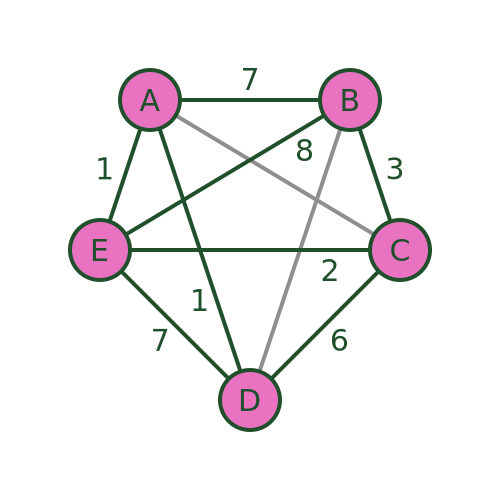
The technique works by incrementally calculating the shortest path for every possible set of 3 towns (starting from A ), then for every possible set of 4 towns, and so on until it eventually calculates the shortest path that goes from A via every other town and back to A .

Because the algorithm stores its intermediate calculations and discards non-optimal paths as early as possible, it is much more efficient than brute force.

We will use the following notation. We will use this to indicate the distance between towns A and B :

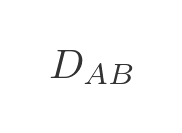
And we will use this to indicate the cost (ie the total distance) from A to C via B :

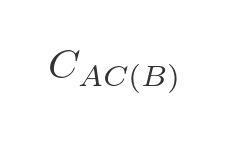
Here are some examples:

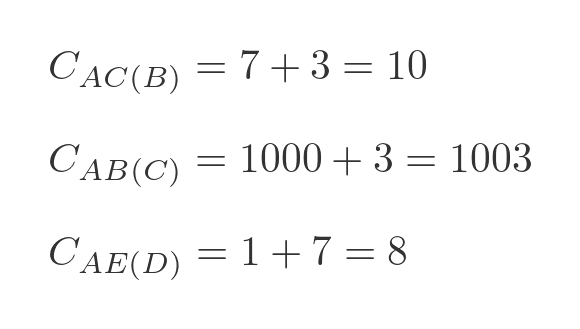
The first example is calculated by adding the distance AB to BC , which gives 10. The second example is calculated by adding AC to CB . But since there is no road from A to C , we give that a large dummy distance of 1000, so that total cost is 1003, which means it is never going to form a part of the shortest route. The third example is calculated by adding the distance AD to DE , which gives 8.

In the first step, we will calculate the value of every possible combination of 2 towns starting from A . There are 12 combinations: AB(C) , AB(D) , AB(E) , AC(B) , AC(D) , AC(E) , AD(B) , AD(C) , AD(E) , AE(B) , AE(C) , AE(D) .

These values will be stored for later use.

For step 2 we need to extend our notation slightly. We will use this to indicate the lowest cost from A to D via B and C (in either order):

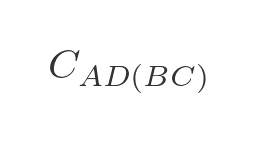
To be clear, this could represent one of two paths - ABCD or ACBD whichever is shorter. We can express this as a minimum of two values:

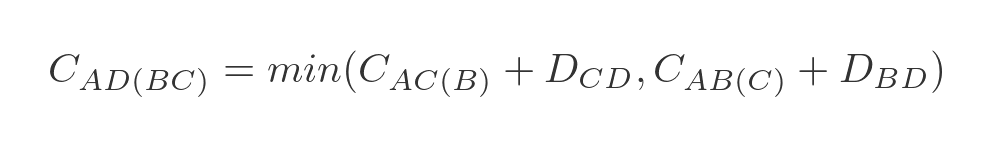
This represents the 2 ways to get from A to D via B and C :

• We can travel from A to C via B , and then from C to D .
• We can travel from A to B via C , and then from B to D .

We have already calculated A to C via B (and all the other combinations) in step 1, so all we need to do is add the values and find the smallest. In this case:

• A to C via B is 10, C to D is 6, so the total is 16.
• A to B via C is 1003, B to D is 1000, so the total is 2003.

Clearly, ABCD is the best route.

We need to repeat this for every possible combination of travelling from A to x via y and z . There are, again, 12 combinations: AB(CD) , AB(CE) , AB(DE) , AC(BD) , AC(BE) , AC(DE) , AD(BC) , AD(BE) , AD(CE) , AE(BC) , AE(BD) , AE(CD) .

We store these values, along with the optimal path, for later use.

In the next step, we calculate the optimal route for travelling from A to any other town via 3 intermediate towns. For example, travelling from A to E via B , C , and D (in the optimal order) is written as:

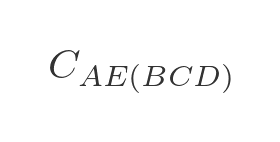
There are 3 paths to do this:

• A to D via B and C , then from D to E .
• A to C via B and D , then from C to E .
• A to B via C and D , then from B to E .

We will choose the shortest of these three paths:

Again we have already calculated all the optimal intermediate paths. This time there are only 4 combinations we need to calculate: AB(CDE) , AC(BDE) , AD(BCE) , and AE(BCD) .

We are now in a position to calculate the optimal route for travelling from A back to A via all 4 other towns:

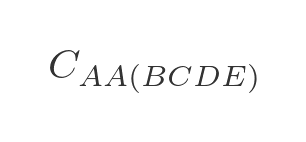
We need to evaluate each of the 4 options in step 3, adding on the extra distance to get back to A :

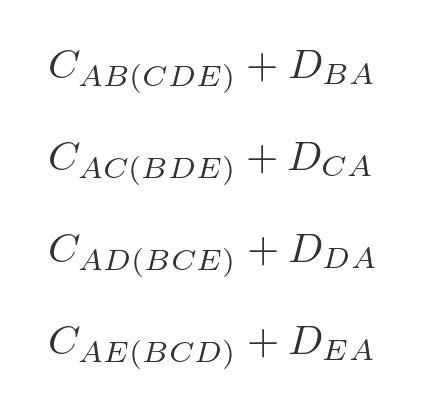
We can then choose the option that has the lowest total cost, and that will be the optimal route.

Performance

The performance of the Bellman–Held–Karp algorithm can be expressed in big-O notations as:

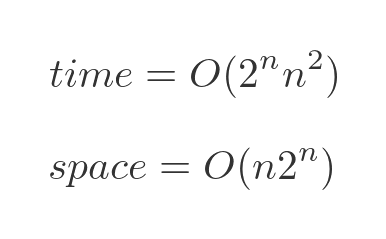
The time performance is approximately exponential. As the number of towns increases, the time taken will go up exponentially - each time an extra town is added, the time taken will double. We are ignoring the term in n squared because the exponential term is the most significant part.

Exponential growth is still quite bad, but it is far better than the factorial growth of the brute-force algorithm.

It is also important to notice that the algorithm requires memory to store the intermediate results, which also goes up approximately exponentially. The brute force algorithm doesn't have any significant memory requirements. However, that is usually an acceptable trade-off for a much better time performance.

The stages above describe how the algorithm works at a high level. We haven't gone into great detail about exactly how the algorithm keeps track of the various stages. Over the years since its discovery, a lot of work has been put into optimising the implementation. Optimising the implementation won't change the time complexity, which will still be roughly exponential. However, it might make the algorithm run several times faster than a poor implementation.

We won't cover this in detail, but if you ever need to use this algorithm for a serious purpose, it is worth considering using an existing, well-optimised implementation rather than trying to write it yourself. Unless you are just doing it for fun!

Other algorithms

Even the Bellman–Held–Karp algorithm has poor performance for modestly large numbers of towns. 100 towns, for example, would be well beyond the capabilities of a modern PC.

There are various heuristic algorithms that are capable of finding a good solution, but not necessarily the best possible solution, in a reasonable amount of time. I hope to cover these in a future article.

• Adjacency matrices
• The seven bridges of Königsberg
• Permutation matrices and graphs
• Dijkstra's algorithm

Join the GraphicMaths Newletter

Sign up using this form to receive an email when new content is added:

Popular tags

adder adjacency matrix alu and gate angle area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle eulers formula exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule pythagoras proof quadrilateral radians radius rectangle regular polygon rhombus root set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume of revolution xnor gate xor gate

• Graph theory
• 7 bridges of Königsberg
• Binary numbers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.10: Traveling Salesperson Problem

• Last updated
• Save as PDF
• Page ID 129677

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

After completing this section, you should be able to:

• Distinguish between brute force algorithms and greedy algorithms.
• List all distinct Hamilton cycles of a complete graph.
• Apply brute force method to solve traveling salesperson applications.
• Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths. In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

• Design of fiber optic networks
• Minimizing fuel expenses for repositioning satellites
• Development of semi-conductors for microchips
• A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

An algorithm is a sequence of steps that can be used to solve a particular problem. We have solved many problems in this chapter, and the procedures that we used were different types of algorithms. In this section, we will use two common types of algorithms, a brute force algorithm and a greedy algorithm . A brute force algorithm begins by listing every possible solution and applying each one until the best solution is found. A greedy algorithm approaches a problem in stages, making the apparent best choice at each stage, then linking the choices together into an overall solution which may or may not be the best solution.

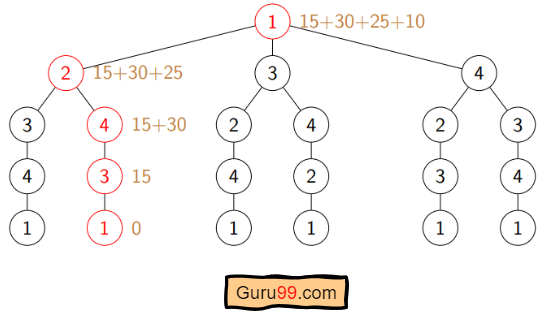
To understand the difference between these two algorithms, consider the tree diagram in Figure 12.214. Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

After phase 2, based on the information you have, you will choose the branch with 10, 7 and 4. Now, you are following a different branch than before, but it is the best choice based on the information you have. Let’s look at the last phase.

After phase 3, you will choose branch G which has a sum of 32.

The process of adding the values on each branch and selecting the highest sum is an example of a brute force algorithm because all options were explored in detail. The process of choosing the branch in phases, based on the best choice at each phase is a greedy algorithm. Although a brute force algorithm gives us the ideal solution, it can take a very long time to implement. Imagine a tree diagram with thousands or even millions of branches. It might not be possible to check all the sums. A greedy algorithm, on the other hand, can be completed in a relatively short time, and generally leads to good solutions, but not necessarily the ideal solution.

Example 12.42

Distinguishing between brute force and greedy algorithms.

A cashier rings up a sale for $4.63 cents in U.S. currency. The customer pays with a $5 bill. The cashier would like to give the customer $0.37 in change using the fewest coins possible. The coins that can be used are quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). The cashier starts by selecting the coin of highest value less than or equal to $0.37, which is a quarter. This leaves $ 0.37 − $ 0.25 = $ 0.12 $ 0.37 − $ 0.25 = $ 0.12 . The cashier selects the coin of highest value less than or equal to $0.12, which is a dime. This leaves $ 0.12 − $ 0.10 = $ 0.02 $ 0.12 − $ 0.10 = $ 0.02 . The cashier selects the coin of highest value less than or equal to $0.02, which is a penny. This leaves $ 0.02 − $ 0.01 = $ 0.01 $ 0.02 − $ 0.01 = $ 0.01 . The cashier selects the coin of highest value less than or equal to $0.01, which is a penny. This leaves no remainder. The cashier used one quarter, one dime, and two pennies, which is four coins. Use this information to answer the following questions.

• Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
• The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
• The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
• Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Now let’s focus our attention on the graph theory application known as the traveling salesperson problem (TSP) in which we must find the shortest route to visit a number of locations and return to the starting point.

Recall from Hamilton Cycles, the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.219 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

Any route that visits each base and returns to the start would be a Hamilton cycle on the graph. If the officer wants to travel the shortest distance, this will correspond to a Hamilton cycle of lowest weight. We saw in Table 12.11 that there are six distinct Hamilton cycles (directed cycles) in a complete graph with four vertices, but some lie on the same cycle (undirected cycle) in the graph.

a → b → c → d → a

a → b → d → c → a

a → c → b → d → a

a → d → c → b → a

a → c → d → b → a

a → d → b → c → a

Since the distance between bases is the same in either direction, it does not matter if the officer travels clockwise or counterclockwise. So, there are really only three possible distances as shown in Figure 12.220.

The possible distances are:

396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148 396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

Notice that we listed all of the Hamilton cycles and found their weights when we solved the TSP about the officer from Vandenberg. This is a skill you will need to practice. To make sure you don't miss any, you can calculate the number of possible Hamilton cycles in a complete graph. It is also helpful to know that half of the directed cycles in a complete graph are the same cycle in reverse direction, so, you only have to calculate half the number of possible weights, and the rest are duplicates.

In a complete graph with n n vertices,

• The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
• There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

TIP! When listing all the distinct Hamilton cycles in a complete graph, you can start them all at any vertex you choose. Remember, the cycle a → b → c → a is the same cycle as b → c → a → b so there is no need to list both.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

• Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
• Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
• Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
• Which pairs of cycles must have the same weights? How do you know?
• There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
• Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
• Yes, they are all distinct cycles and there are 6 of them.
• Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

TIP! When listing the possible cycles, ignore the vertex where the cycle begins and ends and focus on the ways to arrange the letters that represent the vertices in the middle. Using a systematic approach is best; for example, if you must arrange the letters M, O, and P, first list all those arrangements beginning with M, then beginning with O, and then beginning with P, as we did in Example 12.42.

Your Turn 12.43

The brute force method.

The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method . The steps in the brute force method are:

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

On the next assignment, the air force officer must leave from Travis Air Force base, visit Beal, Edwards, and Vandenberg Air Force bases each exactly once and return to Travis Air Force base. There is no need to visit Los Angeles Air Force base. Use Figure 12.221 to find the shortest route.

Step 1: Since there are 4 vertices, there will be ( 4 − 1 ) ! = 3 ! = 6 ( 4 − 1 ) ! = 3 ! = 6 cycles, but half of them will be the reverse of the others; so, there will be ( 4 − 1 ) ! 2 = 6 2 = 3 ( 4 − 1 ) ! 2 = 6 2 = 3 possible distances.

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.222.

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

The second path, T → B → V → E → T , and its reverse, T → E → V → B → T , have the least weight. The solution is that the officer should travel from Travis Air Force base to Beal Air Force Base, to Vandenberg Air Force base, to Edwards Air Force base, and return to Travis Air Force base, or the same route in reverse.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.221. There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

When the brute force method is impractical for solving a traveling salesperson problem, an alternative is a greedy algorithm known as the nearest neighbor method , which always visit the closest or least costly place first. This method finds a Hamilton cycle of relatively low weight in a complete graph in which, at each phase, the next vertex is chosen by comparing the edges between the current vertex and the remaining vertices to find the lowest weight. Since the nearest neighbor method is a greedy algorithm, it usually doesn’t give the best solution, but it usually gives a solution that is "good enough." Most importantly, the number of steps will be the number of vertices. That’s right! A problem with 10 vertices requires 10 steps, not 362,880. Let’s look at an example to see how it works.

Suppose that a candidate for governor wants to hold rallies around the state. They plan to leave their home in city A , visit cities B, C, D, E , and F each once, and return home. The airfare between cities is indicated in the graph in Figure 12.223.

Let’s help the candidate keep costs of travel down by applying the nearest neighbor method to find a Hamilton cycle that has a reasonably low weight. Begin by marking starting vertex as V 1 Figure 12.224. The lowest of these is $100, which is the edge between A and F .

Mark F as V 2 Figure 12.225. The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 Figure 12.226. The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 Figure 12.227. The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 Figure 12.228. Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

The Hamilton cycle we found is A → F → D → B → E → C → A . The weight of the circuit is $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 . This may or may not be the route with the lowest cost, but there is a good chance it is very close since the weights are most of the lowest weights on the graph and we found it in six steps instead of finding 120 different Hamilton cycles and calculating 60 weights. Let’s summarize the procedure that we used.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 2: Label the vertex at the end of the edge of lowest weight that you found in previous step as V n V n where the subscript n indicates the order the vertex is visited. Identify the edge of lowest weight between V n V n and the vertices that remain to be visited.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.229. Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Step 3: A Hamilton cycle of low weight is A → D → F → C → B → E → A . So, a route of relatively low travel time is A to D to F to C to B to E and back to A . The total travel time of this route is: 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min

Your Turn 12.45

Check your understanding, section 12.9 exercises.

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

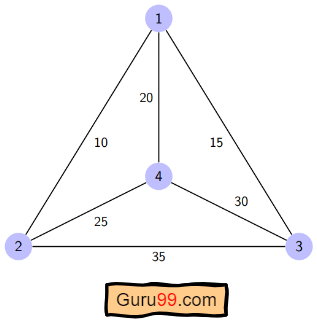
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

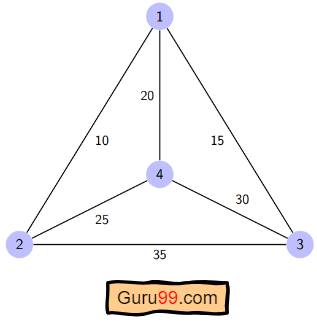
For the given figure, the adjacency matrix would be the following:

Let’s see how our algorithm works:

Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)
• Kadence’s Algorithm: Largest Sum Contiguous Subarray
• Radix Sort Algorithm in Data Structure
• Doubly Linked List: C++, Python (Code Example)
• Singly Linked List in Data Structures
• Adjacency List and Matrix Representation of Graph

Open Access is an initiative that aims to make scientific research freely available to all. To date our community has made over 100 million downloads. It’s based on principles of collaboration, unobstructed discovery, and, most importantly, scientific progression. As PhD students, we found it difficult to access the research we needed, so we decided to create a new Open Access publisher that levels the playing field for scientists across the world. How? By making research easy to access, and puts the academic needs of the researchers before the business interests of publishers.

We are a community of more than 103,000 authors and editors from 3,291 institutions spanning 160 countries, including Nobel Prize winners and some of the world’s most-cited researchers. Publishing on IntechOpen allows authors to earn citations and find new collaborators, meaning more people see your work not only from your own field of study, but from other related fields too.

Brief introduction to this section that descibes Open Access especially from an IntechOpen perspective

Want to get in touch? Contact our London head office or media team here

Our team is growing all the time, so we’re always on the lookout for smart people who want to help us reshape the world of scientific publishing.

Home > Books > Theory of Complexity - Definitions, Models, and Applications

How to Solve the Traveling Salesman Problem

Submitted: 23 September 2020 Reviewed: 20 January 2021 Published: 09 February 2021

DOI: 10.5772/intechopen.96129

Cite this chapter

There are two ways to cite this chapter:

From the Edited Volume

Theory of Complexity - Definitions, Models, and Applications

Edited by Ricardo López-Ruiz

To purchase hard copies of this book, please contact the representative in India: CBS Publishers & Distributors Pvt. Ltd. www.cbspd.com | [email protected]

Chapter metrics overview

812 Chapter Downloads

Impact of this chapter

Total Chapter Downloads on intechopen.com

Total Chapter Views on intechopen.com

The Traveling Salesman Problem (TSP) is believed to be an intractable problem and have no practically efficient algorithm to solve it. The intrinsic difficulty of the TSP is associated with the combinatorial explosion of potential solutions in the solution space. When a TSP instance is large, the number of possible solutions in the solution space is so large as to forbid an exhaustive search for the optimal solutions. The seemingly “limitless” increase of computational power will not resolve its genuine intractability. Do we need to explore all the possibilities in the solution space to find the optimal solutions? This chapter offers a novel perspective trying to overcome the combinatorial complexity of the TSP. When we design an algorithm to solve an optimization problem, we usually ask the critical question: “How can we find all exact optimal solutions and how do we know that they are optimal in the solution space?” This chapter introduces the Attractor-Based Search System (ABSS) that is specifically designed for the TSP. This chapter explains how the ABSS answer this critical question. The computing complexity of the ABSS is also discussed.

• combinatorial optimization
• global optimization
• heuristic local search
• computational complexity
• traveling salesman problem
• multimodal optimization
• dynamical systems

Author Information

• School of Management, University of Michigan-Flint, Flint, USA

*Address all correspondence to: [email protected]

1. Introduction

The TSP is one of the most intensively investigated optimization problems and often treated as the prototypical combinatorial optimization problem that has provided much motivation for design of new search algorithms, development of complexity theory, and analysis of solution space and search space [ 1 , 2 ]. The TSP is defined as a complete graph Q = V E C , where V = v i : i = 1 2 … n is a set of n nodes, E = e i j : i j = 1 2 … n i ≠ j n × n is an edge matrix containing the set of edges that connects the n nodes, and C = c i j : i j = 1 2 … n i ≠ j n × n is a cost matrix holding a set of traveling costs associated with the set of edges. The solution space S contains a finite set of all feasible tours that a salesman may traverse. A tour s ∈ S is a closed route that visits every node exactly once and returns to the starting node at the end. Like many real-world optimization problems, the TSP is inherently multimodal; that is, it may contain multiple optimal tours in its solution space. We assume that a TSP instance Q contains h ≥ 1 optimal tours in S . We denote f ( s ) as the objective function, s ∗ = min s ∈ S f s as an optimal tour and S ∗ as the set of h optimal tours. The objective of the TSP is to find all h optimal tours in the solution space, that is, S ∗ ⊂ S . Therefore, the argument is

Under this definition, the salesman wants to know what all best alternative tours are available. Finding all optimal solutions is the essential requirement for an optimization search algorithm. In practice, knowledge of multiple optimal solutions is extremely helpful, providing the decision-maker with multiple options, especially when the sensitivity of the objective function to small changes in its variables may be different at the alternative optimal points. Obviously, this TSP definition is elegantly simple but full of challenge to the optimization researchers and practitioners.

Optimization has been a fundamental tool in all scientific and engineering areas. The goal of optimization is to find the best set of the admissible conditions to achieve our objective in our decision-making process. Therefore, the fundamental requirement for an optimization search algorithm is to find all optimal solutions within a reasonable amount of computing time . The focus of computational complexity theory is to analyze the intrinsic difficulty of an optimization problem and the asymptotic property of a search algorithm to solve it. The complexity theory attempts to address this question: “How efficient is a search algorithm for a particular optimization problem, as the number of variables gets large?”

The TSP is known to be NP-hard [ 2 , 3 ]. The problems in NP-hard class are said to be intractable because these problems have no asymptotically efficient algorithm, even the seemingly “limitless” increase of computational power will not resolve their genuine intractability. The intrinsic difficulty of the TSP is that the solution space increases exponentially as the problem size increases, which makes the exhaustive search infeasible. When a TSP instance is large, the number of possible tours in the solution space is so large to forbid an exhaustive search for the optimal tours. A feasible search algorithm for the TSP is one that comes with a guarantee to find all best tours in time at most proportional to n k for some power k .

Do we need to explore all the possibilities in the solution space to find the optimal solutions? Imagine that searching for the optimal solution in the solution space is like treasure hunting. We are trying to hunt for a hidden treasure in the whole world. If we are “blindfolded” without any guidance, it is a silly idea to search every single square inch of the extremely large space. We may have to perform a random search process, which is usually not effective. However, if we are able to use various clues to locate the small village where the treasure was placed, we will then directly go to that village and search every corner of the village to find the hidden treasure. The philosophy behind this treasure-hunting case for optimization is that: if we do not know where the optimal point is in the solution space, we can try to identify the small region that contains the optimal point and then search that small region thoroughly to find that optimal point.

Optimization researchers have developed many optimization algorithms to solve the TSP. Deterministic approaches such as exhaustive enumeration and branch-and-bound can find exact optimal solutions, but they are very expensive from the computational point of view. Stochastic optimization algorithms, such as simple heuristic local search, Evolutionary Algorithms, Particle Swarm Optimization and many other metaheuristics, can find hopefully a good solution to the TSP [ 1 , 4 , 5 , 6 , 7 ]. The stochastic search algorithms trade in guaranteed correctness of the optimal solution for a shorter computing time. In practice, most stochastic search algorithms are based on the heuristic local search technique [ 8 ]. Heuristics are functions that help us decide which one of a set of possible solutions is to be selected next [ 9 ]. A local search algorithm iteratively explores the neighborhoods of solutions trying to improve the current solution by a local change. However, the scope of local search is limited by the neighborhood definition. Therefore, heuristic local search algorithms are locally convergent. The final solution may deviate from the optimal solution. Such a final solution is called a locally optimal solution , denoted as s ′ in this chapter. To distinguish from locally optimal solutions, the optimal solution s ∗ in the solution space is usually called the globally optimal solution .

This chapter studies the TSP from a novel perspective and presents a new search algorithm for the TSP. This chapter is organized in the following sections. Section 2 presents the ABSS algorithm for the TSP. Section 3 describes the important data structure that is a critical player in solving the TSP. Section 4 discusses the nature of heuristic local search algorithm and introduces the concept of solution attractor. Section 5 describes the global optimization features of the ABSS. Section 6 discusses the computational complexity of the ABSS. Section 7 concludes this chapter.

2. The attractor-based search system for the TSP

Figure 1 presents the Attractor-Based Search System (ABSS) for the TSP. In this algorithm, Q is a TSP instance with the edge matrix E and cost matrix C . At beginning of search, the matrix E is initialized by assigning zeros to all elements of E . The function InitialTour() constructs an initial tour s i using any tour-construction technique. The function LocalSearch() takes s i as an input, performs local search using any type of local search technique, and returns a locally optimal tour s j . The function UpdateE() updates the matrix E by recording the edge configuration of tour s j into the matrix. K is the number of search trajectories. After the edge configurations of K locally optimal tours are stored in the matrix E , the function ExhaustedSearch() searches E completely using the depth-first tree search technique, which is a simple recursive search method that traverses a directed graph starting from a node and then searches adjacent nodes recursively. Finally, the ABSS outputs a set of all best tours S ∗ found in the edge configuration of E . The search strategy in the ABSS is straightforward: generating K locally optimal tours, storing their edge configurations in the matrix E , and then identifying the best tours by evaluating all tours represented by the edge configuration of E . The ABSS is a simple and efficient computer program that can solve the TSP effectively. This search algorithm shows strong features of effectiveness, flexibility, adaptability, scalability and efficiency. The computational model of the ABSS is inherently parallel, facilitating implementation on concurrent processors. It can be implemented in many different ways: series, parallel, distributed, or hybrid.

The ABSS algorithm for the TSP.

Figure 2 uses a 10-node instance as an example to illustrate how the ABSS works. We randomly generate K = 6 n = 60 initial tours, which edge configurations hit all elements of the matrix E (marked as black color), as shown in Figure 2(a) . It means that these 60 random tours hit all 45 edges that represent all 181440 tours in the solution space. We let each of the search trajectories run 5000 iterations and obtain 60 locally optimal tours. However, due to the small size of the instance, most locally optimal tours have identical edge configurations. Among the 60 locally optimal tours, we find only four distinct locally optimal tours as shown in Figure 2(b) . Figure 2(c) shows the union of the edge configurations of the 60 locally optimal tours, in which 18 edges are hit. Then we use the depth-first tree search, as illustrated in Figure 2(d) , to identify all five tours in the edge configuration of E , which are listed in Figure 2(e) . In fact, one of the five tours is the globally optimal tour. This simple example indicates that (1) local search trajectories converge to small set of edges, and (2) the union of the edge configurations of K locally optimal tours is not just a countable union of the edge configurations of the these tours, but also include the edge configurations of other locally optimal tours. The ABSS consists of two search phases: local search phase and exhaustive search phase. The task of the local search phase is to identify the region that globally optimal tour is located (i.e. the village hiding the treasure), and the task of the exhaustive search phase is to find the globally optimal tour (i.e. find the hidden treasure). The remaining sections will briefly explain the features of the ABSS.

A simple example of the ABSS algorithm. (a) Union of the edge configurations of 60 random initial tours, (b) four distinct locally optimal tours, (c) union of the edge configurations of the 60 locally optimal tours, (d) the depth-first tree search on the edge configuration of E , and (e) five tours found in E .

In all experiments mentioned in the chapter, we generate symmetric TSP instances with n nodes. The element c i j of the cost matrix C is assigned a random integer independently drawn from a uniform distribution of the range [1, 1000]. The triangle inequality c i j + c j k ≥ c i k is not assumed in the instances. Although this type of problem instances is application-free, it is mathematically significant. A TSP instance without triangle inequality cannot be approximated within any constant factor. A heuristic local search algorithm usually performs much worse for this type of TSP instances, which offers a strikingly challenge to solving them [ 2 , 3 , 6 , 10 , 11 ]. We use the 2-opt local search technique in the local search phase. The 2-opt neighborhood can be characterized as the neighborhood that induces the greatest correlation between function values of neighboring tours, because neighboring tours differ in the minimum possible four edges. Along the same reasoning line, the 2-opt may have the smallest expected number of locally optimal points [ 12 ]. The local search process randomly selects a solution in the neighborhood of the current solution. A move that gives the first improvement is chosen. The great advantage of the first-improvement pivoting rule is to produce randomized locally optimal points. The software program written for the experiments use several different programming languages and are run in PCs with different versions of Window operating system.

3. The edge matrix E

Usually the edge matrix E is not necessary to be included in the TSP definition because the TSP is a complete graph. However, the edge matrix E is an effective data structure that can help us understand the search behavior of a local search system. General local search algorithm may not require much problem-specific knowledge in order to generate good solutions. However, it may be unreasonable to expect a search algorithm to be able to solve any problem without taking into account the data structure and properties of the problem at hand.

To solve a problem, the first step is to create a manipulatable description of the problem itself. For many problems, the choice of data structure for representing a solution plays a critical role in the analysis of search behavior and design of new search algorithm. For the TSP, a tour can be represented by an ordered list of nodes or an edge configuration of a tour in the edge matrix E , as illustrated in Figure 3 . The improvement of the current tour represents the change in the order of the nodes or the edge configuration of a tour.

Two representations of a tour: an ordered list of nodes and an edge configuration of a tour.

Observing the behavior of search trajectories in a local search system can be quite challenging. The edge matrix E is a natural data structure that can help us trace the search trajectories and understand the dynamics of a local search system. An edge e i j is the most basic element of a tour, but contains a piece of information about each of n − 2 ! tours that go through it. Essentially, the nature of local search for the TSP is an edge-selection process: preservation of good edges and rejection of bad edges according to the objective function f s . Each edge has an implicit probability to be selected by a locally optimal tour. A better edge has higher probability to be included in a locally optimal tour. Therefore, the edges in E can be divided into three groups: globally superior edges, G -edges, and bad edges. A globally superior edge is the edge that occurs in many or all locally optimal tours. Although each of these locally optimal tours selects this edge based on its own search trajectory, the edge is globally superior since the edge is selected by these individual tours from different search trajectories going through different search regions. The globally superior edges have higher probability to be selected by a locally optimal tour. A G -edge is the edge that is included in a globally optimal tour. All G -edges are globally superior edges and can be treated as a special subset of the globally superior edges. The edges that are discarded by all search trajectories or selected by only few locally optimal tours are bad edges. A bad edge is impossible to be included in a globally optimal tour. A locally optimal tour usually consists of some G -edges, some globally superior edges and a few bad edges.

The changes of the edge configuration of the matrix E represent the transformations of the search trajectories in a local search system. When all search trajectories reach their end points, the final edge configuration of E represents the final state of the local search system. For a tour s k , we define an element e i j of E as

Then the hit-frequency value e ij in the element e i j is defined as the number of occurrence of the element in K tours, that is

When K search trajectories reach their end points, the value e ij + e ji / K can represent the probability of the edge e i j being hit by a locally optimal tour. We can use graphical technique to observe the convergent behavior of the search trajectories through the matrix E . The hit-frequency value e ij can be easily converted into a unit of half-tone information in a computer, a value that we interpret as a number H ij somewhere between 0 and 1. The value 1 corresponds to black color, 0 to white color, and any value in between to a gray level. Let K be the number of search trajectories, the half-tone information H ij on a computer screen can be represented by the hit-frequency e ij in the element e i j of E :

Figure 4 illustrates a simple example of visualization showing the convergent behavior of 100 search trajectories for a 50-node instance. Figure 4(a) shows the image of the edge configurations of 100 random initial tours. Since each element of E has equal chance to be hit by these initial tours, almost all elements are hit by these initial tours, and all elements have very low H ij values, ranging from 0.00 to 0.02. When the local search system starts searching, the search trajectories constantly change their edge configurations, and therefore the colors in the elements of E are changed accordingly. As the search continues, more and more elements become white (i.e. they are discarded by all search trajectories) and other elements become darker (i.e. they are selected by more search trajectories). When all search trajectories reach their end points, the colored elements represent the final edge configuration of the search system. Figure 4(b) and (c) show the images of edge configuration of E when all search trajectories completed 2000 iterations and 5000 iterations, respectively. At 5000th iteration, the range of H ij values in the elements of E is from 0.00 to 0.42. The value 0.42 means that 42% of the search trajectories select this element. Majority of the elements of E become white color.

Visualization of the convergent dynamics of local search system. (a) the image of the edge configurations of 100 initial tours, (b) and (c) the images of edge configurations when the search trajectories are at 2000th and 5000th iteration, respectively.

This simple example has great explanatory power about the global dynamics of the local search system for the TSP. As search trajectories continue searching, the number of edges hit by them becomes smaller and smaller, and better edges are hit by more and more search trajectories. This edge-convergence phenomenon means that all search trajectories are moving closer and closer to each other, and their edge configurations become increasingly similar. This phenomenon describes the globally asymptotic behavior of the local search system.

It is easily verified that under certain conditons, a local search system is able to find the set of the globally optimal tours S ∗ when the number of search trajectories is unlimited, i.e.

However, the required search effort may be very huge – equivalent to enumerating all tours in the solution space. Now one question for the ABSS is “How many search trajectories in the search system do we need to find all globally optimal tours?” The matrix E consists of n n − 1 elements (excluding the diagonal elements). When we randomly construct a tour and record its edge configuration in E , n elements of E will be hit by this tour. If we construct more random tours and record their edge configurations in E , more elements will be hit. We define K as the number of randomly-constructed initial tours, whose edge configurations together will hit all elements of E . We know that all elements of E represent all combinatorial possibilities in the solution space. Therefore, K is the number of search trajectories such that the union of edge configurations of ther initial tours covers the entire solution space. In our experiments, we found that the edge configurations of at most 6 n randomly-constructed tours can guarantee to hit all elements of E . From the tour perspective, K = 6 n random tours represent only a small set of the tours in the solution space. However, from the view of edge-configuration, the union of the edge configurations of 6 n random tours represents the edge configurations of all tours in the solution space. It reveals an amazing fact: the union of the edge configurations of only 6 n random tours contains the edge configurations of all n n − 1 ! / 2 tours in the solution space. It reflects the combinatorial nature of the TSP: the tours in the solution space are formed by different combinations of the edges. The union of the edge configurations of a set of tours contains information about many other tours because one tour shares its edges with many other tours. One fundamental theory that can help us explain this phenomenon is the information theory [ 13 ]. According to the information theory, each solution point contains some information about its neighboring solutions that can be modeled as a function, called information function or influence function . The influence function of the i th solution point in the solution space S is defined as a function Ω i : S → R , such that Ω i is a decreasing function of the distance from a solution point to the i th solution point. The notion of influence function has been extensively used in datamining, data clustering, and pattern recognition.

4. The nature of heuristic local search

Heuristic local search is based on the concept of neighborhood search. A neighborhood of a solution s i , denoted as N s i , is a set of solutions that are in some sense close to s i . For the TSP, a neighborhood of a tour s i is defined as a set of tours that can be reached from s i in one single transition. From edge-configuration perspective, all tours in N s i are very similar because they share significant number of edges with s i . The basic operation of local search is iterative improvement, which starts with an initial tour and searches the neighborhood of the current tour for a better tour. If such a tour is found, it replaces the current tour and the search continues until no improvement can be made. The local search algorithm returns a locally optimal tour.

The behavior of a local search trajectory can be understood as a process of iterating a search function g s . We denote s 0 as an initial point of search and g t s as the t th iteration of the search function g s . A search trajectory s 0 , g s 0 , g 2 s 0 , … , g t s 0 , … converges to a locally optimal point s ′ as its limit, that is,

Therefore, a search trajectory will reach an end point (a locally optimal point) and will stays at this point forever.

In a heuristic local search algorithm, there is a great variety of ways to construct initial tour, choose candidate moves, and define criteria for accepting candidate moves. Most heuristic local search algorithms are based on randomization. In this sense, a heuristic local search algoorithm is a randomized system. There are no two search trajectories that are exactly alike in such a search system. Different search trajectories explore different regions of the solution space and stop at different final points. Therefore, local optimality depends on the initial points, the neighborhood function, randomness in the search process, and time spent on search process. On the other hand, however, a local search algorithm essentially is deterministic and not random in nature. If we observe the motion of all search trajectories, we will see that the search trajectories go towards the same direction, move closer to each other, and eventually converge into a small region in the solution space.

Heuristic local search algorithms are essentially in the domain of dynamical systems. A heuristic local search algorithm is a discrete dynamical system, which has a solution space S (the state space), a set of times T (search iterations), and a search function g : S × T → S that gives the consequents to a solution s ∈ S in the form of s t + 1 = g s t . A search trajectory is the sequence of states of a single search process at successive time-steps, which represents the part of the solution space searched by this search trajectory. The questions about the behavior of a local search system over time are actually the questions about its search trajectories. The most basic question about the search trajectories is “Where do they go in the solution space and what do they do when they get there?”

The attractor theory of dynamical systems is a natural paradigm that can be used to describe the search behavior of a heuristic local search system. The theory of dynamical systems is an extremely broad area of study. A dynamical system is a model of describing the temporal evolution of a system in its state space. The goal of dynamical system analysis is to capture the distinctive properties of certain points or regions in the state space of a given dynamical system. The theory of dynamical systems has discovered that many dynamical systems exhibt attracting behavior in the state space [ 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 ]. In such a system, all initial states tend to evolve towards a single final point or a set of points. The term attractor is used to describe this single point or the set of points in the state space. The attractor theory of dynamical systems describes the asymptotic behavior of typical trajectories in the dynamical system. Therefore, the attractor theory provides the theoretical foundation to study the search behavior of a heuristic lcoal search system.

In a local search system for the TSP, no matter where we start a search trajectory in the solution space, all search trajectories will converge to a small region in the solution space for a unimodal TSP instance or h small regions for a h -model TSP. We call this small region a solution attractor of the local search system for a given TSP instance, denoted as A . Therefore, the solution attractor of a local search system for the TSP can be defined as an invariant set A ⊂ S consisting of all locally optimal tours and the globally optimal tours. A single search trajectory typically converges to either one of the points in the solution attractor. A search trajectory that is in the solution attractor will remain within the solution attractor forward in time. Because a globally optimal tour s ∗ is a special case of locally optimal tours, it is undoubtedly embodied in the solutioin attractor, that is, s ∗ ∈ A . For a h -modal TSP instance, a local search system will generate h solution attractors A 1 A 2 … A h that attract all search trajectories. Each of the solution attractors has its own set of locally optimal tours, surrounding a globally optimal tour s i ∗ i = 1 2 … h . A particular search trajectory will converge into one of the h solution attractors. All locally optimal tours will be distributed to these solution attractors. According to dynamical systems theory [ 20 ], the closure of an arbitrary union of attractors is still an attractor. Therefore, the solution attractor A of a local search system for a h -modal TSP is a complete collection of h solution attractors A = A 1 ∪ A 2 ∪ … ∪ A h .

Convexity , i.e. ∀ s i ∈ S , g t s i ∈ A for sufficient long t ;

Centrality , i.e. the globally optimal tour s i ∗ is located centrally with respect to the other locally optimal tours in A i i = 1 2 … h ;

Invariance , i.e. ∀ s ′ ∈ A , g t s ′ = s ′ and g t A = A for all time t ;

Inreducibility , i.e. the solution attractor A contains a limit number of invariant locally optimal tours.

Illustration of the concepts of serch trajectories and solution attractors in a local search system for a multimodal optimization problem.

A search trajectory in a local search system changes its edge configuration during the search according to the objective function f s and its neighborhood structure. The matrix E can follow the “footprints” of search trajectories to capture the dynamics of the local search system. When all search trajectories reach their end points – the locally optimal tours, the edge configuration of the matrix E will become fixed, which is the edge configuration of the solution attractor A . This fixed edge configuration contains two groups of edges: the edges that are not hit by any of locally optimal tours (non-hit edges) and the edges that are hit by at least one of the locally optimal tours (hit edges). Figure 6 shows the edge grouping in the edge configuration of E when all search trajectories stop at their final points.

The grouping of the edges in E when all search trajectories reach their end points.

In the ABSS, we use K search trajectories in the local search phase. Different sets of K search trajectories will generate different final edge configuration of E . Suppose that, we start the local search from a set of K initial points and obtain a edge configuration M a in E when the local search phase is terminated. Then we start the local search process again from a different set of K initial points and obtains a little different edge configuration M b in E . Which edge configuration truly describes the edge configuration of the real solution attractor? Actually, M a and M b are structurally equivalent because they are different only in the set of bad edges, thus M a precisely replicates the dynamical properties of M b . The final edge configuration of the constructed solution attractor generated from K search trajectories is not sensitive to the selection of K search trajectories. This property indicates that a heuristic local search system actually is a deterministic system: although a single search trajectory appears stochastic, all search trajectories from differeitn initial points will be always trapped into the same small region in the solution space and the final edge configuration of E will always converge to the same set of the globally optimal edges.

The convergence of the search trajectories can be measured by the change in the edge configuration of the matrix E . In the local search process, search trajectories collect all available topology information about the quality of the edges from their search experience and record such information in the matrix E . The changes in the edge configuration of E fully reflects the real search evolution of the search system. A state of convergence is achieved once no any more local search trajectory can change the edge configuration of E . For a set of search trajectories to be converging, they must be getting closer and closer to each other, that is, their edge configurations become increasingly similar. As a result, the edge configurations of the search trajectories converge to a small set of edges that contains all globally superior edges and some bad edges. Let W denote total number of edges in E , α t the number of the edges that are hit by all search trajectories at time t , β t the number of the edges that are hit by one or some of the search trajectories, and γ t the number of edges that have no hit at all, then at any time t , we have

For a given TSP instance, W is a constant value W = n n − 1 / 2 for a symmetric instance or W = n n − 1 for an asymmetric instance. During the local search process, the values for α t and γ t will increase and the value for β t will decrease. However, these values cannot increase or decrease foreover. At certain point of time, they will become constant values, that is,

Our experiments confirmed this inference about α t , β t and γ t . Figure 7 illustrates the patterns of α t , β t and γ t curves generated in our experiments. Our experiments also found that, for unimodal TSP instances, the ratio γ t / W could approach to 0.70 quickly for different sizes of TSP instances. For multimodal TSP instances, this ratio depends on the number of the globally optimal points. However, the set of hit edges is still very small.

The α t , β t and γ t curves with search iterations.

It contains all locally optimal tours;

It contains a complete collection of solution attractors, i.e. A = A 1 ∪ A 2 ∪ … ∪ A h ;

It contains a complete collection of G -edges, i.e. G = G 1 ∪ G 2 ∪ … ∪ G h .

From this analysis, we can see that the edge matrix E is an extremely useful data structure that not only collcets the information about search trajectories, but also convert local search behavor of individual search trajectories into global search behavor of the search system. The global convergence and deterministic property of the search trajectories make the local search system always converge to the same solution attractors and the edge configurations of the search trajectories always converge to the same set of globally superior edges. The matrix E shows us clearly where the search trajectories go and where all locally optimal points are located. We found the village! However, it is still difficult to identify all G -edges among the globally superior edges. The ABSS uses the exhaustive search phase to find all tours in the solution attractor. Since the local search phase has significantly reduced the size of the search space for the exhaustive search phase, the complete search in the solution attractor becomes feasible.

5. Global optimization feature of the ABSS

The search system should be globally convergent.

The search system should be deterministic and have a rigorous guarantee for finding all globally optimal solutions without excessive computational burden.

The optimality criterion in the system must be based on information on the global behavior of the search system.

The ABSS combines beautifully two crucial aspects in search: exploration and exploitation. In the local search phase, K search trajectories explore the full solution space to identify the globally superior edges, which form the edge configuration of the solution attractor. These K search trajectories are independently and invidually executed, and therefore they create and maintain diversity from beginning to the end. The local search phase is a randomized process due to randomization in the local search function g s . In this sense, the K search trajectories actually perform the Monte Carlo simulation to sample locally optimal tours. The essential idea of Monte Carlo method is using randomness to solve problems that might be deterministic in principle [ 26 ]. In the ABSS, K search trajectories start a sample of initial points from a uniform distribution over the solution space S , and, through the randomized local search process, generate a sample of locally optimal points uniformly distributed in the solution attractor A . The edge configuration of E is actually constructed through this Monte Carlo sampling process.

Each of the K search trajectories passes through many neighborhoods on its way to the final point. For any tour s i , the size of N s i is greater than n 2 ! [ 12 ]. Let N s i ′ denote the neighborhood of the final point s i ′ of the i th search trajectory and Ω N s tran i as the union of the neighborhoods of all transition points of the search trajectory, then we can believe that the search space covered by K search trajectories is

That is, the solution attractor A is formed through the entire solution space S . The solution attractor A contains h unique minimal “convex” sets A i i = 1 2 … h . Each A i has a unique best tour s i ∗ surrounded by a set of locally optimal tours. The tour s i ∗ in A i satisfies f s i ∗ < f s for all s ∈ A i and f s 1 ∗ = f s 2 ∗ = … = f s h ∗ .

We see that the matrix E plays a critical role to transform local search process of the individual search trajectories into a collective global search process of the system. Each time when a local search trajectory finds a better tour and updates the edge configuraton of E , the conditional distribution on the edges are updated. More values are attached to the globally superior edges, and bad edges are discarded. Let W be the complete set of the edges in E and W A the set of edges in the edge configuration of the solution attractor A such that g W is contained in the interior of W . Then the intersection W A of the nested sequence of sets is

and lim t → ∞ g t W A = W A . As a result, the edge configurations of K search trajectories converge to a small set of edges.

∀ s ∈ A i , f s i ∗ < f s

f s 1 ∗ = f s 2 ∗ = … = f s h ∗

min s ∈ A f s = min s ∈ S f s

Therefore the global convergence and deterministic property of the search trajectories in the local search phase make the ABSS always find the same set of globally optimal tours. We conducted several experiments to confirm this argument empirically. In our experiments, for a given TSP instance, the ABSS performed the same search process on the instance several times, each time using a different set of K search trajectories. The ABSS outputed the same set of the best tours in all trials.

Table 1 shows the results of two experiments. One experiment generated n = 1000 instance Q 1000 , the other generated n = 10000 instance Q 10000 . We conducted 10 trials on each of the instances respectively. In each trial, the ABSS used K = 6 n search trajectories. Each search trajectory stopped when no improvement was made during 10 n iterations. The matrix E stored the edge configurations of the K final tours and then was searched completely using the depth-first tree search process. Table 1 lists the number of tours found in the constructed solution attractor A , the cost range of these tours, and the number of the best tours found in the constructed solution attractor. For instance, in trial 1 for Q 1000 , the ABSS found 6475824 tours with the cost range [3241, 4136] in the constructed solution attractor. There was a single best tour in the solution attractor. The ABSS found the same best tour in all 10 trials. For the instance Q 10000 , the ABSS found the same set of four best tours in all 10 trials. These four best tours have the same cost value, but with different edge configurations. If any trial had generated a different set of the best tours, we could immediately make a conclusion that the best tours in the constructed solution attractor may not be the globally optimal tours. From practical perspective, the fact that the same set of the best tours was detected in all trials provides an empirical evidence of the global optimality of these tours. The fact also indicates that the ABSS converges in solution. Convergence in solution means that the search system can identify all optimal solutions repeatedly. Always finding the same set of optimal solutions actually is the fundamental requirement for global optimization systems.

Tours in constructed solution attractor A for Q 1000 and Q 10000 .

6. Computing complexity of the ABSS

With current search technology, the TSP is an infeasible problem because it is not solvable in a reasonable amount of time. Faster computers will not help. A feasible search algorithm for the TSP is one that comes with a guarantee to find all best tours in time at most proportional to n k for some power k . The ABSS can guarantee to find all globally optimal tours for the TSP. Now the question is how efficient it is?

The core idea of the ABSS is that, if we have to use exhaustive search to confirm the globally optimal points, we should first find a way to quickly reduce the effective search space for the exhaustive search. When a local search trajectory finds a better tour, we can say that the local search trajectory finds some better edges. It is an inclusive view. We also can say that the local search trajectory discards some bad edges. It is an exclusive view. The ABSS uses the exclusive strategy to conquer the TSP. The local search phase in the ABSS quickly prunes out large number of edges that cannot possibly be included in any of the globally optimal tours. Thus, a large useless area of the solution space is excluded. When the first edge is discarded by all K search trajectories, n − 2 ! tours that go through that edge are removed from the search space for the exhaustive search phase. Each time when an edge is removed, large number of tours are removed from the search space. Although the complexity of finding a true locally optimal tour is still open, and we even do not know any nontrivial upper bounds on the number of iterations that may be needed to reach local optimality [ 27 , 28 ], decades of empirical evidence and practical research have found that heuristic local search converges quickly, within low order polynomial time [ 1 , 8 , 27 , 29 ]. In practice, we are rarely able to find perfect locally optimal tour because we simply do not allow the local search process to run enough long time. Usually we let a local search process run a predefined number of iterations, accept whatever tour it generates, and treat it as a locally optimal tour. Therefore, the size of the constructed solution attractor depends not only on the problem structure and the neighborhood function, but also on the amount of search time invested in the local search process. As we increase local search time, we will constructe a smaller and stronger solution attractor. The local search phase in the ABSS can significantly reduce the search space for the exhaustive search phase by excluding a large number of edges. Usually the local search phase can remove about 60% of edges of the matrix E in O n 2 .

Now an essential question is naturally raised: What is the relationship between the size of the constructed solution attractor and the size of the problem instance? Unfortunately, there is no theoretical analysis tool available in the literature that can be used to answer this question. We have to depend on empirical results to lend some insights. We conducted several experiments to observe the relationship between the size of the constructed solution attractor and the TSP instance size. Figures 8 – 10 show the results of one of our experiments. All other similar experiments reveal the same pattern. In this experiment, we generated 10 unimodal TSP instances in the size from 1000 to 10000 nodes with 1000-node increment. For each instance, the ABSS generated K = 6 n search trajectories. We first let each search trajectory stop when no tour improvement was made during 10000 iterations regardless of the size of the instance (named “fixed search time”). Then we did the same search procedures on these instances again. This time we made each search trajectory stop when no improvement was made during 10 n iterations (named “varied search time 1”) and 100 n iterations (named “varied search time 2”) respectively. Figure 8 shows the number of the edges that were discarded at the end of local search phase. Figure 9 shows the number of tours in the constructed solution attractor for each instance, and Figure 10 shows the effective branching factors in the exhaustive search phase.

The number of discarded edges at the end of local search phase.

Relationship between the size of the constructed solution attractor and instance size.

The b ∗ values for different instance size n in our experiment.

In Figure 8 , we can see that the search trajectories can quickly converge to a small set of edges. In the fixed-search-time case, about 60% of the edges were discarded by search trajectories for the 1000-node instance, but this percentage decreases as instance size increases. For the 10000-node instance, only about 46% of the edges are discarded. However, if we increase the local search time linearly when the instance size increases, we can keep the same percentage of discarded-edge for all instance sizes. In the varied-search-time-1 case, about 60% of the edges are abandoned for all different instance sizes. In the varied-search-time-2 case, this percentage increases to 68% for all instances. Higher percentage of abandoned edges means that majority of the branches are removed from the search tree.

Figure 9 shows the number of tours exist in the constructed solution attractor for these instances. All curves in the chart appear to be linear relationship between the size of constructed solution attractor and the size of the problem instance, and the varied-search-time curves have much flatter slope because longer local search time makes a smaller constructed solution attractor. Figures 8 and 9 indicate that the search trajectories in the local search phase can effectively and efficiently reduce the search space for the exhaustive search, and the size of the solution attractor increases linearly as the size of the problem instance increases. Therefore, the local search phase in the ABSS is an efficiently asymptotical search process that produces an extremely small search space for further exhaustive search.

The completely searching of the constructed solution attractor is delegated to the exhaustive search phase. This phase may still need to examine tens or hundreds of millions of tours but nothing a computer processor cannot handle, as opposed to the huge number of total possibilities in the solution space. The exhaustive search phase can find the exact globally optimal tours for the problem instance after a limited number of search steps.

The exhaustive search phase can use any enumerative technique. However, the edge configuration of E can be easily searched by the depth-first tree search algorithm. One of the advantages of depth-first tree search is less memory requirement since only the nodes on the current path are stored. When using tree-search algorithm, we usually use branching factor, average branching factor, or effective branching factor to measure the computing complexity of the algorithm [ 30 , 31 , 32 , 33 ]. In the data structure of search tree, the branching factor is the number of successors generated by a given node. If this value is not uniform, an average branching factor can be calculated. An effective branching factor b ∗ is the number of sucessors generated by a typical node for a given tree-search problem. We use the following definition to calculate effective brancing factor b ∗ for the exhaustive search phase:

where n is the size of the TSP instance, representing the depth of the tree, and N is total number of nodes generated in the tree from the origin node. In our experiments, the tree-search process always starts from node 1 (the first row of E ). N is total number of nodes that are processed to construct all valid tours and incomplete (therefore abandoned) tours in E . N does not count the node 1 (the origin node), but includes the node 1 as the end node of a valid tour. We use Figure 2(d) as an example. The depth-first search process searches the edge configuration of E and will generate N = 58 nodes. Therefore, b ∗ ≈ 1.3080 , that is, 58 ≈ 1.3080 + 1.3080 2 + … + 1.3080 10 . Figure 10 shows the effective branching factor b ∗ in our experiment. The low values of b ∗ indicates that the edge configuration of the solution attractor represents a tree with extremely sparse branches, and the degree of sparseness does not changes as the problem size increase if we linearly increase local search time in the local search phase for a large instance. The search time in the exhaustive search phase is probably in O n 2 since the size of the constructed solution attractor might be linearly increased with the problem size n and the number of edges in E is polynomially increased with the problem size. Our experiments shows that the ABSS can significantly reduce the computational complexity for the TSP and solve the TSP efficiently with global optimality guarantee.

Therefore, the ABSS is a simple algorithm that increases in computational difficulty polynomially with the size of the TSP. In the ABSS, the objective pursued by the local search phase is “quickly eliminating unnecessary search space as much as possible.” It can provide an answer to the question “In which small region of the solution space is the optimal solution located?” in time of O n 2 . The objective of the exhaustive search phase is “identifying the best tour in the remaining search space.” It can provide an anwer to the question “Which is the best tour in this small region?” in time of O n 2 . All together, the ABSS can answer the question “Is this tour the best tour in the solution space?” in time of O n 2 . Therefore, the ABSS is probably with computing complexity of O n 2 and memory space requirement of O n 2 . This suggests that the TSP might not be as complex as we might have expected.

7. Conclusion

Advances in computational techniques on the determination of the global optimum for an optimization problem can have great impact on many scientific and engineering fields. Although both the TSP and heuristic local search algorithms have huge literature, there is still a variety of open problems. Numerous experts have made huge advance on the TSP research, but two fundamental questions of the TSP remain essentially open: “How can we find the optimal tours in the solution space, and how do we know they are optimal?”

The P-vs-NP problem is about how fast we can search through a huge number of solutions in the solution space [ 34 ]. Do we ever need to explore all the possibilities of the problem to find the optimal one? Actually, the P-vs-NP problem asks whether, in general, we can find a method that completely searches only the region where the optimal points are located [ 34 , 35 , 36 ]. Most people believe P ≠ NP because we have made little fundamental progress in the area of exhaustive search. Modern computers can greatly speed up the search, but the extremely large solution space would still require geologic search time to find the exact optimal solution on the fastest machines imaginable. A new point of view is needed to improve our capacity to tackle these difficulty problems. This paper describe a new idea: using efficient local search process to effectively reduce the search space for exhaustive search. The concept of solution attractor in heuristic local search systems may change the way we think about both local search and exhaustive search. Heuristic local search is an efficient search system, while exhaustive search is an effective search system. The key is how we combines these two systems into one system beautifully to conquer the fundamental issues of the hard optimization problems. In the TSP case, the edge matrix E , a problem-specific data structure, plays a critical role of reducing the search space and transforming local search to global search.

The ABSS is designed for the TSP. However, the concepts and formulation behind the search algorithm can be used for any combinatorial optimization problem requiring the search of a node permutation in a graph.

• 1. Applegate DL, Bixby RE, Chaátal V, Cook WJ. The Traveling Salesman Problem: A Computational Study. Princeton: Princeton University Press; 2006
• 2. Papadimitriou CH, Steiglitz K. Combinatorial Optimization: Algorithms and Complexity. New York: Dover Publications; 1998
• 3. Papadimitriou CH, Steiglitz K. On the complexity of local search for the traveling salesman problem. SIAM Journal on Computing. 1977:6:76–83
• 4. Gomey J. Stochastic global optimization algorithms: a systematic formal approach. Information Science. 2019:472:53–76
• 5. Korte B, Vygen J. Combinatorial Optimization: Theory and Algorithms. New York: Springer; 2007
• 6. Rego C, Gamboa D, Glover F, Osterman C. Traveling salesman problem heuristics: leading methods, implementations and latest advances. European Journal of Operational Research. 2011:211:427–411
• 7. Zhigliavsky A, Zillinakas A. Stochastic Global Optimization. New York: Springer; 2008
• 8. Aart E, Lenstra JK. Local Search in Combinatorial Optimization. Princeton: Princeton University Press; 2003
• 9. Michalewicz Z, Fogel DB. How to Solve It: Modern Heuristics. Berlin: Springer; 2002
• 10. Sahni S, Gonzales T. P-complete approximation problem. Journal of the ACM. 1976:23:555–565
• 11. Sourlas N. Statistical mechanics and the traveling salesman problem. Europhysics Letters. 1986:2:919–923
• 12. Savage SL. Some theoretical implications of local optimality. Mathematical Programming. 1976:10:354–366
• 13. Shammon CE. A mathematical theory of communication. Bell System Technical Journal. 1948:27:379–423&623–656
• 14. Alligood KT, Sauer TD, York JA. Chaos: Introduction to Dynamical System. New York: Springer; 1997
• 15. Auslander J, Bhatia NP, Seibert P. Attractors in dynamical systems. NASA Technical Report NASA-CR-59858; 1964
• 16. Brin M, Stuck G. Introduction to Dynamical Systems. Cambridge: Cambridge University Press
• 17. Brown R. A Modern Introduction to Dynamical Systems. New York: Oxford University Press
• 18. Denes A, Makey G. Attractors and basis of dynamical systems. Electronic Journal of Qualitative Theory of Differential Equations. 2011:20(20):1–11
• 19. Fogedby H. On the phase space approach to complexity. Journal of Statistical Physics. 1992:69:411–425
• 20. Milnor J. On the concept of attractor. Communications in Mathematical Physics. 1985:99(2):177–195
• 21. Milnor J. Collected Papers of John Milnor VI: Dynamical Systems (1953–2000). American Mathematical Society; 2010
• 22. Ruelle D. Small random perturbations of dynamical systems and the definition of attractor. Communications in Mathematical Physics. 1981:82:137–151
• 23. Li W. Dynamics of local search trajectory in traveling salesman problem. Journal of Heuristics. 2005:11:507–524
• 24. Li W, Feng M. Solution attractor of local search in traveling salesman problem: concepts, construction and application. International Journal of Metaheuristics. 2013:2(3):201–233
• 25. Li W, Li X. Solution attractor of local search in traveling salesman problem: computational study. International Journal of Metaheuristics. 2019:7(2):93–126
• 26. Kroese DP, Taimre T, Botev ZI. Handbook of Monte Carlo Methods. New York: John Wiley & Sons; 2011
• 27. Fischer ST. A note on the complexity of local search problems. Information Processing Letters. 1995:53(2):69–75
• 28. Chandra B, Karloff HJ, Tovey CA. New results on the old-opt algorithm for the traveling salesman problem. SIAM Journal on Computing. 1999:28(6):1998–2029
• 29. Grover, LK. Local search and the local structure of NP-complete problems. Operations Research Letters. 1992:12(4):235–243
• 30. Baudet GM. On the branching factor of the alpha-beta pruning algorithm. Artificial Intelligence. 1978:10(23):173–199
• 31. Edelkamp S, Korf RE. The branching factor of regular search space. Proceedings of the 15 th National Conference on Artificial Intelligence. 1998:292–304
• 32. Korf RE. Depth-first iterative deepening: an optimal admissible tree search. Artificial Intelligence. 1985:27:97–109
• 33. Pearl J. The solution for the branching factor of the alpha-beta pruning algorithm and its optimality. Communication of the ACM. 1982:25(8):559–564
• 34. Fortnow L. The Golden Ticket – P, NP, and the Search for the Impossible. Princeton: Princeton University Press; 2013
• 35. Fortnow L. The status of the P versus NP problem. Communication of the ACM. 2009:52(9):78–86
• 36. Sipser M. The history of status of the P verses NP question. Proceedings of 24 th Annual ACM Symposium on Theory of Computing. 1992:603–618

© 2021 The Author(s). Licensee IntechOpen. This chapter is distributed under the terms of the Creative Commons Attribution 3.0 License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Continue reading from the same book

Theory of complexity.

Published: 30 June 2021

By Rafael Prieto Curiel

436 downloads

By Michael J. Droboniku, Heidi Kloos, Dieter Vanderel...

371 downloads

By Sérgio Henrique Vannucchi Leme de Mattos, Luiz Edu...

562 downloads

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

• The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
• The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

• The number of rows of the distance matrix, which is the number of locations (including the depot).
• The number of vehicles in the problem.
• The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices, from_index and to_index , and returns the corresponding entry of the distance matrix.

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

Scientists Solve Most Complex Traveling Salesman Problem Ever

See how they cracked the deceptively simple—but brutally tough—problem for 22 "cities."

• The traveling salesman is an age-old exercise in optimization , studied in school and relevant to "real life."
• Rearranging how data feeds through the processor allows more than one thread to compute at a time.

Scientists in Japan have solved a more complex traveling salesman problem than ever before. The previous standard for instant solving was 16 “cities,” and these scientists have used a new kind of processor to solve 22 cities. They say it would have taken a traditional von Neumann CPU 1,200 years to do the same task.

The traveling salesman problem is centuries old, and it asks a deceptively simple question: For a salesman with a map of, say, 10 cities with given distances apart and roads connecting them, what’s the shortest path for the salesman to travel to every city and return home? The “deceptive” part is that the math to support the problem quickly grows overwhelmingly complex.

Each leg of the journey has a different length. Not all the cities connect to each other to form an ideal full star topology. And segments that connect, say, five cities have to somehow be compared to segments that connect three or eight. It’s just too variable, in both the proverbial and literal senses. A computer processor must calculate one full route at a time while storing the order of the points touched and the length of each leg of the journey.

The problem combines graph theory (the “map” of points with weighted legs between them) with combinatorics (the different ways you can count through a graph, in this case) and optimization (choosing the best, shortest route from a given graph). Because of this robust subject appeal, it’s been a favorite exercise in math and computer science classes of all kinds for many, many years.

The secret to these researchers’ success with the traveling salesman problem is in the special circuit they designed to calculate the routes. In a traditional computer processor, the routes must be arranged and then calculated and all passed through the processor one point at a time—the system is linear.

In most computing applications, we don’t notice that processing happens this way because the calculations are so rapid that they basically appear simultaneous. But the traveling salesman problem clogs the works because the number of calculations required is so huge. Adding more points on the map only increases the complexity. (Honestly, this news itself underlines how complicated the problem is: It’s major news to be able to solve just 22 cities instead of just 16!)

The researchers took a traditional circuit architecture and changed one critical thing: They rearranged special “spin cells” representing all the graph points so that the spin cells could all communicate with each other, not just the immediate surroundings connected by lines on the graph. This new arrangement allows routes to be made using multiple points at a time instead of just one, with fewer bottlenecks in the computational process.

The potential applications of a more powerful salesman solver are myriad. The abstract problem is infamous because it’s so widely studied and difficult, but its roots are still as an abstraction of a real person’s dilemma: How do I do my job the most efficient way? Every day, taxi and Uber drivers must consider the best route to find the most passengers. Delivery drivers must arrange their addresses in an efficient way. And these applications don’t just involve minimizing distance—fresh food or the value of a fare add even more complexity.

Suddenly, the 22nd address on the route is going to receive a much hotter pizza.

Caroline Delbert is a writer, avid reader, and contributing editor at Pop Mech. She's also an enthusiast of just about everything. Her favorite topics include nuclear energy, cosmology, math of everyday things, and the philosophy of it all. 

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Science .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

Ancient Collision May Have Created Plate Tectonics

ChatGPT Just Passed the Moral Turing Test

Is Memory the Key to Understanding Consciousness?

Simulations Warn of Earth Turning Inhospitable

The Source of All Consciousness May Be Black Holes

Ancient Human Lava Tube Habitation Discovered

Kitchen Renovation Yields 17th Century Coin Hoard

Discovery May Create New Breed of Capacitors

Tungsten Tokamak Breaks Another Fusion Record

A 152-Year-Old Shipwreck Found While Fishing

Meet the Taam Ja': The World's Largest Blue Hole

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

• Check the length of every possible route, one route at a time.
• Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
• After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

• Visit every city.
• The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
• After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

In addition to using a greedy algorithm to solve the Traveling Salesman Problem, there are also other algorithms that can find approximations to the shortest route.

These algorithms are popular because they are much more effective than to actually check all possible solutions, but as with the greedy algorithm above, they do not find the overall shortest route.

Algorithms used to find a near-optimal solution to the Traveling Salesman Problem include:

• 2-opt Heuristic: An algorithm that improves the solution step-by-step, in each step removing two edges and reconnecting the two paths in a different way to reduce the total path length.
• Genetic Algorithm: This is a type of algorithm inspired by the process of natural selection and use techniques such as selection, mutation, and crossover to evolve solutions to problems, including the TSP.
• Simulated Annealing: This method is inspired by the process of annealing in metallurgy. It involves heating and then slowly cooling a material to decrease defects. In the context of TSP, it's used to find a near-optimal solution by exploring the solution space in a way that allows for occasional moves to worse solutions, which helps to avoid getting stuck in local minima.
• Ant Colony Optimization: This algorithm is inspired by the behavior of ants in finding paths from the colony to food sources. It's a more complex probabilistic technique for solving computational problems which can be mapped to finding good paths through graphs.

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

• Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
• Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
• Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
• Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
• Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

What is a Travelling Salesman Problem (TSP)? Explained!

• Author: Diksha Bhandari
• Read Time: 9 min
• Published: September 14, 2023
• Last Update: November 8th, 2023

Table of Contents

• Video telematics
• TrackoField Industries
• Route Planning
• Driver Behaviour
• Last Mile Delivery
• Asset Tracking
• Dispatch Management
• Fuel Management
• Route Optimisation
• Electric Vehicle
• Roster Management
• Vehicle Tracking
• TrackoMile Industries
• TrackoBit Industries
• Sensor Integration
• GPS Trackers and Hardware
• Tech and Beyond
• TrackoField
• What's New
• Employee Management
• Field Sales And Service
• Task and Workflow
• GPS Software
• Lead Management
• Fleet Management
• Leave And Attendance

Want to know what a travelling salesman problem (TSP) is? Need solutions to real-life TSP challenges. Learn here. 

Do you also look for the shortest route on Google Maps before embarking on a trip?

I am sure, you know multiple routes to reach the office, the mall, or your desired location, but checking on the internet before leaving home has become a ritual. It becomes all the more important to refer to maps when you have to pick up friends or colleagues along the way.

‘ADD STOPS’

Yes, you are right! 💯

That’s what solving the TSP challenge using software means!

What is a Travelling Salesman Problem (TSP)?

The traveling salesman problem is the popular combinatorial optimisation challenge in mathematics and computer science. The prime objective of the problem is to determine the shortest possible route a salesperson must take to cover a set of locations in one go and then return to the starting point.

Addressing travelling salesman challenges and their optimisation are more relevant in this time and age, especially in the supply chain, logistics and delivery space.

TSP may result in delayed deliveries and slimming profits as it’s not easy for delivery agents to choose the most viable and cost-effective route in real-time.

What are Traveling Salesman Problem Challenges to Solve?

When a salesperson is in the field hopping from one client site to another, finding out the best and the shortest route is an added pressure on the agent. In today’s day and age, distance isn’t the only factor that defines efficiency. There are several factors, such as time, fuel consumption, capacity, etc. that together define efficiency.

However, addressing the travelling salesman challenges involves mitigating a few unavoidable challenges along the way that field agents face themselves.

1. Time Constraints

Sales agents often have a tight schedule with multiple deliveries to make with a short TAT. Similarly, in TSP, optimising routes to minimise travel time is a fundamental challenge.

2. Last-minute Changes

Eleventh-hour changes are not a new concept for salespeople. They encounter urgent visits and last-minute cancellations a lot. Similarly, TSP solutions must be adaptable to handle dynamic scenarios and route modifications.

3. Resource Efficiency

Just as salespersons aim at reducing fuel costs and ensuring on-time deliveries, TSP solutions such as TrackoMile must strive for resource optimisation by reducing travel distances and delivery TAT.

4. Objective Diversification

While solving the travelling salesman problem (TSP) , optimising multiple objectives such as cost, time, and environmental factors adds complexity as solutions need to balance conflicting goals.

5. Combinatorial Complexity

TSP is a combinatorial optimisation problem, which means it involves complicated mathematical calculations with numerous variables. Sometimes, complex scenarios get further intricate as multiple variables are involved.

6. Adaptability and Scalability

Similarly, how sales agents adjust to the routes on the fly, the route algorithm must be flexible and responsive to real-time changes such as spiking volumes, vehicle breakdown or traffic slow down. A TSP solution must have a good appetite to handle large datasets and complex networks.

Also Read 4 Key Solutions for Fuel Management System 2023

Top 5 Solutions to The Travelling Salesman Problem

The traveling salesman problem solutions offer various trade-offs between computational intricacies and the quality of the resolution, allowing practitioners to choose the best-suited approach based on their needs and problems.

Here are the Top 5 solutions to the Traveling Salesman Problem (TSP) :

1. Brute Force Algorithm

The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all. While it guarantees an optimal solution, its downside lies in its major time complexity, making it practical only for small TSP challenges.

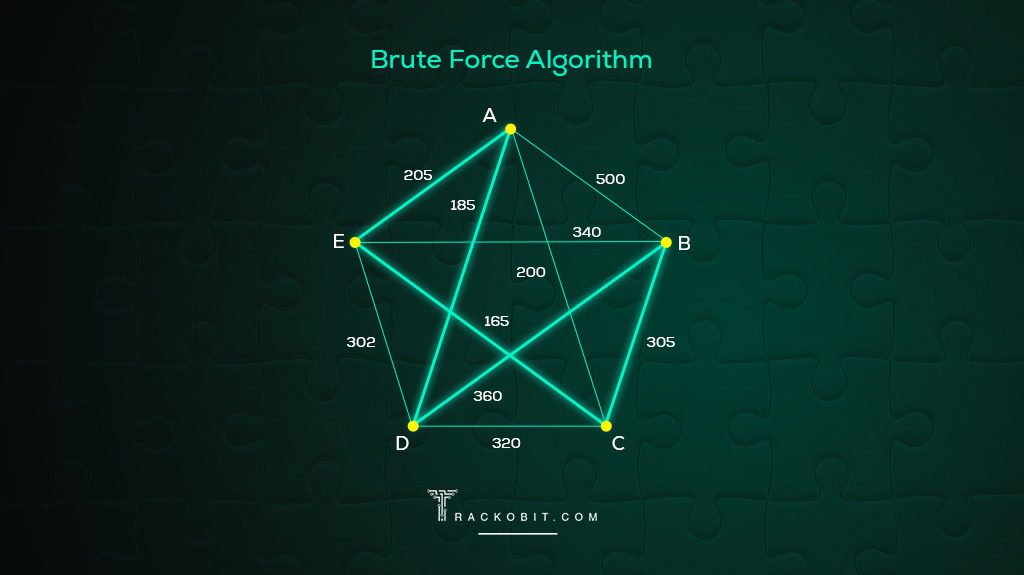
2. Nearest Neighbour Algorithm

The Nearest Neighbour method is the simplest heuristic for the TSP. It starts from the first location and repeatedly selects the closest unvisited location to form a tour. Although it is quick to implement this method, it may always yield the optimal solution for it prioritises proximity over other factors.

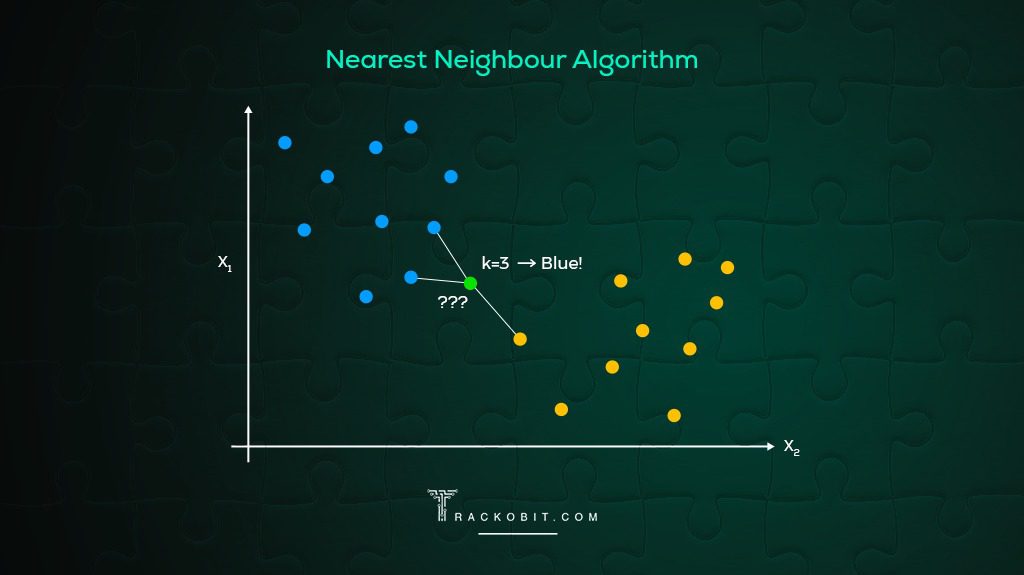
3. Genetic Algorithm

This technique or method draws inspiration from nature itself. They evolve TSP solutions through selection, crossovers and mutation. They pick the best routes and mix them up. This creates new routes that might be even better. Then, they keep the best ones and repeat the mixing and picking process. Survival of the fittest in the true sense.

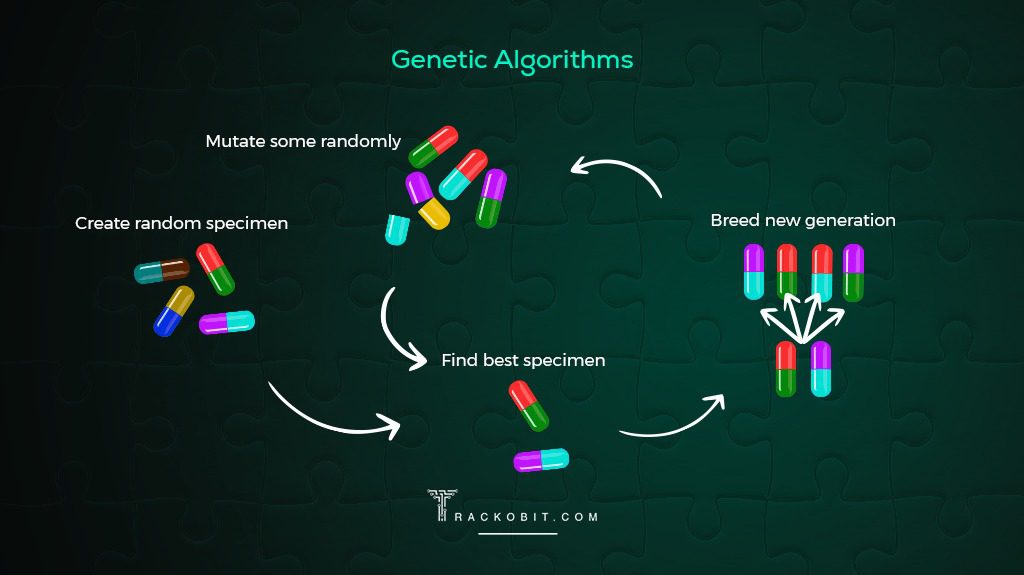
4. Ant Colony Optimisation (ACO)

Ants have a tendency to leave pheromones on the shorter routes they find, calling fellow ants on the same route. They keep leaving more pheromones on the shorter routes they find. Over time, the collective behaviour of the ants causes them to converge on the shortest route. Inspired by the nature of ants, ACO finds the shortest route by analysing the trails of data left by artificial ants based on the strength of these data trails.

5. Dynamic Programming

Dynamic Programming is like solving a puzzle, step-by-step, by breaking it into smaller pieces. In TSP challenges, it finds the best route to visit all locations. It begins with figuring out the shortest route between two locations; then it builds on that to find ways to more locations. It’s a smart TSP solution for small scenarios but may require significant memory resources for larger and more complex problems.

What Are Real-world Travelling Salesman Problem Applications?

The Traveling Salesman Problem (TSP) has a wide array of applications across various domains due to its relevance in optimising routes and sequences. Here are several crucial real-word TSP applications and implementations in the real world.

1. TSP implementation in Logistics and Delivery Services

The logistics and supply chain sectors have the widest TSP applications.

• Courier, Express & Parcel : Companies like FedEx, UPS, and DHL rely on TSP algorithms to optimise delivery routes for their fleet of delivery trucks. By finding the most efficient sequence of stops, they minimise fuel consumption , reduce delivery TAT, and save on operational overheads too.
• On-demand Delivery : Food delivery companies, instant grocery delivery apps and at-home appointment platforms like Swiggy, BlinkIt and UrbanCompany, respectively, leverage TSP solutions to ensure timely delivery. Enhancing the customer experience and increasing the number of deliveries each rider can make.

2. TSP Applications in Transportation and Urban Planning Waste collection routes, Traffic light synchronisation, optic cable installation, etc. are some areas where TSP Solutions works like a knight in shining armour. Other real-world TSP applications include

• Public Transport : City planners and public transport agencies use TSP principles to design bus, tram and train routes that reduce travel for passengers.
• Emergency Service Dispatch : Ambulance services, Police PCR vans employ TSP algorithms to dispatch vehicles quickly and efficiently in response to emergency calls. Finding the shortest route to reach the incident location can save lives.
• Urban Mobility Solution : In the era of ride-sharing and on-demand mobility apps like Uber, Ola, Lyft, etc., real-world TSP applications become prominent. TSP solutions optimise the route to destinations, ensuring quick and cost-effective transportation.

Other significant real-life applications of the Travelling Salesman Problem are

• TSP in Healthcare and Medical Research – for DNA sequencing and understanding genetic patterns and diseases.
• TSP in Manufacturing and Production – In circuit board manufacturing and job scheduling of technicians.
• TSP in Robotics and Autonomous Vehicles -Self-driving cars and drones use TSP-like algorithms for efficient navigation.

Solving the Travelling Salesman Problem – Last Mile Delivery Route Optimisation

Route optimisation is the key to efficient last-mile delivery . In order to attain flawless route optimisation, the software must solve the traveling salesman problem every step of the way.

Why it’s essential to solve TSP for Last Mile Delivery?

In simple and minimal words, solving TSP problems helps in many ways:

• Saves Time : It makes deliveries faster, so your customers get orders sooner.
• Customer Satisfaction : Fast deliveries give you an edge over the competition and enhance customer experience too.
• Saves Money : It reduces fuel wastage and vehicle wear, making deliveries cheaper.
• Environment Friendly : It lowers pollution by using fewer vehicles and shorter routes.
• Happy Staff: Drivers and dispatchers have less stress and can finish their work faster.

How do we solve the travelling salesman problem for last-mile delivery?

Solving TSP challenges for Last-mile delivery is like solving a big jigsaw puzzle. There are a hundred thousand addresses to visit daily. The software must find the shortest and most optimised route to them and come back to the starting point at the end.

• Our route optimisation software , TrackoMile, leverages capacity management , routing algorithms and robust rule engines to present the most optimal combination of delivery addresses. Thereby giving the most optimally planned routes or trips.
• All delivery managers have to do is upload the CSV file of the addresses or integrate TrackoMile to their CRM to fetch the delivery addresses. Now trip allocation, route optimisation, dispatch and everything else happen in a few clicks.
• ETA when the delivery is en route, POD when the order is delivered successfully, and trip analysis, are added features to simplify overall operations.

The Vehicle Routing Problem is very similar to TSP, with wide applications in logistics, delivery services and transportation. While TSP focuses on finding the shortest route for a single traveller visiting various locations, VRP deals with multiple vehicles serving multiple customers, considering added constraints like vehicle capacity, TATs and more.

How Can AI Help in Solving Traveling Salesman Problem (TSP)?

AI or Artificial Intelligence are becoming the driving force for business growth across various industrial sectors. AI particularly aids in solving the Traveling Salesman Problem(TSP) in the logistics and delivery sector by employing advanced algorithms and techniques. What are a few tricks up AI’s sleeves that help in automating TSP resolution? Let’s find out!

1. Advanced Algorithms

AI algorithms such as Genetic Algorithms, ACO, simulated annealing and a few others mentioned above, tackle complex Travelling Salesman Problem scenarios.

2. Machine Learning

Gathering information from historical data and optimising routes based on real-time insights is what AI is best for. Machine learning models are trained to adapt to changing conditions, like traffic, weather and delivery constraints, to provide a more accurate plan of action.

3. Parallel Computing

AIi enables the use of a parallel computing process, which means solving multiple segments of TSP simultaneously. This accelerates the problem-solving process for large-scale challenges.

4. Heuristic Improvement

TSP Heuristics powered by AI can groom initial solutions, gradually improving their results over time. These heuristics can be applied iteratively by AI to reach better results.

5. Hybrid Approaches

Applying hybrid algorithms is not a new technique to refine techniques and produce more accurate results. AI on top of it singles out data-oriented combinations that work the best in varied use cases.

Wrapping Up!

The travelling salesman problem’s importance lies in its real-world applications. Whether optimising delivery routes, planning manufacturing processes or organising circuit board drilling, finding the most efficient way to cover multiple locations is crucial to minimise costs and save time.

The TSP problems have evolved over the years, and so have TSP algorithms, heuristics and solutions. With the advent of advanced technologies such as GPS and machine learning, TSP continues to adapt and find new applications in emerging fields, cementing its status as a fundamental problem in optimization theory and a valuable tool for various industries. Mobility automation software like Trackobit, TrackoMile and TrackoField resort to TSP heuristics to solve challenges along the way.

Read Blog – Best Delivery Route Planner Apps for 2023

Traveling Salesman Problem FAQs

What is tsp.

TSP is an abbreviation for Traveling Salesman Problem. It’s the routing problem that deals with finding the shortest route to travel to a combination of locations in the most optimal manner.

Is Travelling Salesman Problem Solvable?

Yes, the Traveling Salesman Problem (TSP) is solvable, but the time to find the solution can grow proportionately with an increase in the number of locations. With the evolution of travelling salesman problem applications, various TSP algorithms and heuristics, their hybrids have also emerged.

Wh at is the objective of TSP?

The objective of the Traveling Salesman Problem (TSP) is to find the shortest possible route that covers all given locations or waypoints and comes back to the starting point with the least resource utilisation.

Diksha Bhandari

Currently creating SaaSy content strategies for TrackoBit and TrackoField, this content professional has dedicated a decade of her life to enriching her portfolio and continues to do so. In addition to playing with words and spilling SaaS, she has a passion for traveling to the mountains and sipping on adrak wali chai.

• Author Showcase
• All Blog Post

Never Miss a Beat

Related Blog

Top 12 Google Map Alternatives – Offering Precise Navigation

Explore our best picks for 12 free Google map alternatives that offer accurate and secure location and navigational solutions. 

Food Delivery Trends to Watch in 2024 & Beyond

Food and technology are both revolving along with consumer demands. Here are some of the food delivery trends to watch in 2024.

Biofuel – An Alternative to Fossil Fuels in Transportation | G20

Transportation industries are moving towards a greener future through the sustainable use of biofuels like Ethanol — discussed in the G20 2023 summit.

Top 10 Navigation Apps for Android and iOS | 2024

Discover the 10 best navigation apps in 2024 that offer personalised navigation just like Sherpas (experienced guides of Himalayan terrain) do.

Stay Updated on tech, telematics and mobility. Don't miss out on the latest in the industry.

Thank you for reaching out! We'll speak to you soon.

In the meantime, why not find out more about us, explore our products, or visit our blog?

Cookie Consent

We use cookies to enhance and personalize your browsing experience. By continuing to use our website, you agree to our Privacy Policy.

Algorithms for the Travelling Salesman Problem

Printables.com

• The Travelling Salesman Problem (TSP) is a classic algorithmic problem in the field of computer science and operations research, focusing on optimization. It seeks the shortest possible route that visits every point in a set of locations just once.
• The TSP problem is highly applicable in the logistics sector , particularly in route planning and optimization for delivery services. TSP solving algorithms help to reduce travel costs and time.
• Real-world applications often require adaptations because they involve additional constraints like time windows, vehicle capacity, and customer preferences.
• Advances in technology and algorithms have led to more practical solutions for real-world routing problems. These include heuristic and metaheuristic approaches that provide good solutions quickly.
• Tools like Routific use sophisticated algorithms and artificial intelligence to solve TSP and other complex routing problems, transforming theoretical solutions into practical business applications.

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest possible route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one — the one that will require the least distance or cost — is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem in graph theory. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm for solving travelling salesman problems in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

The main problem can be solved by calculating every permutation using a brute force approach, and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially, soon surpassing the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

TThe brute-force approach, also known as the naive approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the brute-force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one — this is the optimal solution. 

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route beyond the first pair of cities, one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the traveling salesman problem.

3. The nearest neighbor method

To implement the nearest neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the nearest neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the nearest neighbor algorithm serves as a good starting point for tackling the traveling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition. ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

• Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
• Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP. 
• Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization. 
• Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used. 
• Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II. 
• Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource. 

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, approximate solutions — often produced using artificial intelligence and machine learning — are useful in all verticals.

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.

Minimizing costs in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

What is a hamiltonian cycle, and why is it important in solving the travelling salesman problem.

A Hamiltonian cycle is a complete loop that visits every vertex in a graph exactly once before returning to the starting vertex. It's crucial for the TSP because the problem essentially seeks to find the shortest Hamiltonian cycle that minimizes travel distance or time.

What role does linear programming play in solving the Travelling Salesman Problem?

Linear programming (LP) is a mathematical method used to optimize a linear objective function, subject to linear equality and inequality constraints. In the context of TSP, LP can help in formulating and solving relaxation of the problem to find bounds or approximate solutions, often by ignoring the integer constraints (integer programming being a subset of LP) to simplify the problem.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion involves a function calling itself to solve smaller sub-problems of the same type as the larger problem. In TSP, recursion is used in methods like the "Divide and Conquer" strategy, breaking down the problem into smaller, manageable subsets, which can be particularly useful in dynamic programming solutions. It reduces redundancy and computation time, making the problem more manageable.

Why is understanding time complexity important when studying the Travelling Salesman Problem?

Time complexity refers to the computational complexity that describes the amount of computer time it takes to solve a problem. For TSP, understanding time complexity is crucial because it helps predict the performance of different algorithms, especially given that TSP is NP-hard and solutions can become impractically slow as the number of cities increases.

Related articles

Liked this article? See below for more recommended reading!

Solving the Vehicle Routing Problem (2024)

How To Optimize Multi-Stop Routes With Google Maps (2024)

How Route Optimization Impacts Our Earth

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Dynamic Approach)

Travelling salesman dynamic programming algorithm, implementation.

Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.

However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.

Let us consider a graph G = (V,E) , where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v) , which should be non-negative.

Suppose we have started at city 1 and after visiting some cities now we are in city j . Hence, this is a partial tour. We certainly need to know j , since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.

For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1 , and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j .

When |S|> 1 , we define 𝑪 C(S,1)= $\propto$ since the path cannot start and end at 1.

Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j . We should select the next city in such a way that

$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$

There are at the most 2 n .n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2 n .n 2 ) .

In the following example, we will illustrate the steps to solve the travelling salesman problem.

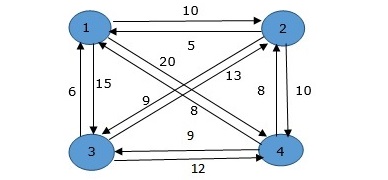
From the above graph, the following table is prepared.

$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$

$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$

$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$

$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$

$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$

$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$

$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$

$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$

$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$

$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$

The minimum cost path is 35.

Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.

When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Following are the implementations of the above approach in various programming languages −

To Continue Learning Please Login

Two-Stage Attention Model to Solve Large-Scale Traveling Salesman Problems

• Conference paper
• First Online: 15 November 2023
• Cite this conference paper

• Feng Wang 12 &
• Jingge Song 13  

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 14448))

Included in the following conference series:

• International Conference on Neural Information Processing

604 Accesses

The Traveling Salesman Problem (TSP) widely exists in real-world scenarios. Various methods, such as exact methods, heuristic methods, and deep learning-based methods, can solve TSPs efficiently. However, as the size of the problems increases, these methods become increasingly time-consuming due to the high complexity of large-scale TSPs. This paper proposes a two-stage attention model (TSAM) that incorporates the divide-and-conquer strategy and attention model to solve large-scale TSPs efficiently. Experimental results demonstrate that TSAM can rapidly produce promising solutions for TSP instances ranging from 500 to 10,000 nodes.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Applegate, D., Bixby, R., Chvatal, V., Cook, W.: Concorde tsp solver (2006)

Google Scholar  

Applegate, D.L., et al.: Certification of an optimal tsp tour through 85,900 cities. In: Operations Research Letters, pp. 11–15 (2009)

Helsgaun, K.: General k-opt submoves for the lin-kernighan tsp heuristic. Math. Program. Comput. 1 , 119–163 (2009). https://doi.org/10.1007/s12532-009-0004-6

Helsgaun, K.: An Extension of the lin-kernighan-helsgaun TSP Solver for Constrained Traveling Salesman and Vehicle Routing Problems, Roskilde University, Roskilde, pp. 1–60 (2017)

Kool, W., van Hoof, H., Welling, M.: Attention, learn to solve routing problems! In: Proceedings of the 7th International Conference on Learning Representations, pp. 1–25 (2019)

Taillard, É. D., Helsgaun, K.: Popmusic for the travelling salesman problem. Eur. J. Oper. Res. 272 , 420–429 (2019)

Vinyals, O., Fortunato, M., Jaitly, N.: Pointer networks. In: Proceedings of the 28th International Conference on Neural Information Processing Systems, pp. 2692–2700 (2015)

Bello, I., Pham, H., Le, Q.V., Norouzi, M., Bengio, S.: Neural combinatorial optimization with reinforcement learning, arXiv preprint arXiv:1611.09940 (2016)

Mnih, V., et al.: Asynchronous methods for deep reinforcement learning. In: International Conference on Machine Learning, pp. 1928–1937 (2016)

Deudon, Michel, Cournut, Pierre, Lacoste, Alexandre, Adulyasak, Yossiri, Rousseau, Louis-Martin.: Learning heuristics for the TSP by policy gradient. In: van Hoeve, Willem-Jan. (ed.) CPAIOR 2018. LNCS, vol. 10848, pp. 170–181. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93031-2_12

Chapter   Google Scholar  

Vaswani, A., et al.: Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, pp. 6000–6010 (2017)

Kwon, Y.D., Choo, J., Kim, B., Yoon, I., Gwon, Y., Min, S.: Pomo: policy optimization with multiple optima for reinforcement learning. In: Proceedings of the 34th Conference on Neural Information Processing Systems, pp. 21 188–21 198 (2020)

Gidaris, S., Singh, P., Komodakis, N.: Unsupervised representation learning by predicting image rotations, arXiv preprint arXiv:1803.07728 (2018)

Kim, M., Park, J., Park, J.: Sym-NCO: leveraging symmetricity for neural combinatorial optimization. In: Proceedings of the 36th Conference on Neural Information Processing Systems, pp. 1936–1949 (2022)

Joshi, C.K., Laurent, T., Bresson, X.: An efficient graph convolutional network technique for the travelling salesman problem, arXiv preprint arXiv:1906.01227 (2019)

Wu, Y., Song, W., Cao, Z., Zhang, J., Lim, A.: Learning improvement heuristics for solving routing problems. IEEE Trans. Neural Netw. Learn. Syst. 33 (9), 5057–5069 (2021)

Article   MathSciNet   Google Scholar  

d O Costa, P.R., Rhuggenaath, J., Zhang, Y., Akcay, A.: Learning 2-opt heuristics for the traveling salesman problem via deep reinforcement learning. In: Asian Conference on Machine Learning, pp. 465–480 (2020)

Ma, Y., Li, J., Cao, Z., Song, W., Zhang, L., Chen, Z., Tang, J.: Learning to iteratively solve routing problems with dual-aspect collaborative transformer. In: Proceedings of the 35th International Conference on Neural Information Processing Systems, pp. 11 096–11 107 (2021)

Chen, X., Tian, Y.: Learning to perform local rewriting for combinatorial optimization. In: Proceedings of the 33rd International Conference on Neural Information Processing Systems, pp. 6281–6292 (2019)

Gao, L., Chen, M., Chen, Q., Luo, G., Zhu, N., Liu, Z.: Learn to design the heuristics for vehicle routing problem, arXiv preprint arXiv:2002.08539 (2020)

Lu, H., Zhang, X., Yang, S.: A learning-based iterative method for solving vehicle routing problems. In: Proceedings of the 8th International Conference on Learning Representations, pp. 1–15 (2020)

Xin, L., Song, W., Cao, Z., Zhang, J.: Neurolkh: combining deep learning model with lin-kernighan-helsgaun heuristic for solving the traveling salesman problem. In: Proceedings of the 35th International Conference on Neural Information Processing Systems, pp. 7472–7483 (2021)

Kool, W., van Hoof, H., Gromicho, J., Welling, M.: Deep policy dynamic programming for vehicle routing problems. In: Proceedings of Integration of Constraint Programming, Artificial Intelligence, and Operations Research: 19th International Conference, pp. 190–213 (2022)

Fu, Z.-H., Qiu, K.-B., Zha, H.: Generalize a small pre-trained model to arbitrarily large tsp instances. In: Proceedings of the AAAI Conference on Artificial Intelligence, pp. 7474–7482 (2021)

Chaslot, G. M. J.-B. C.: Monte-carlo tree search (2010)

Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., Bengio, Y.: Graph attention networks. In: Proceedings of the 6th International Conference on Learning Representations, pp. 1–12 (2018)

He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778 (2016)

Ioffe, S., Szegedy, C.: Batch normalization: accelerating deep network training by reducing internal covariate shift. In: Proceedings of the International Conference on Machine Learning, pp. 448–456 (2015)

Download references

Acknowledgment

This work is supported by the National Nature Science Foundation of China [Grant Nos. 62173258, 61773296].

Author information

Authors and affiliations.

School of Computer Science, Wuhan University, Wuhan, China

Qi He & Feng Wang

Hongyi Honor College, Wuhan University, Wuhan, China

Jingge Song

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Feng Wang .

Editor information

Editors and affiliations.

Central South University, Changsha, China

Chinese Academy of Sciences, Beijing, China

Zhejiang University, Hangzhou, China

Zheng-Guang Wu

Guangdong University of Technology, Guangzhou, China

UNSW Sydney, Sydney, NSW, Australia

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Cite this paper.

He, Q., Wang, F., Song, J. (2024). Two-Stage Attention Model to Solve Large-Scale Traveling Salesman Problems. In: Luo, B., Cheng, L., Wu, ZG., Li, H., Li, C. (eds) Neural Information Processing. ICONIP 2023. Lecture Notes in Computer Science, vol 14448. Springer, Singapore. https://doi.org/10.1007/978-981-99-8082-6_10

Download citation

DOI : https://doi.org/10.1007/978-981-99-8082-6_10

Published : 15 November 2023

Publisher Name : Springer, Singapore

Print ISBN : 978-981-99-8081-9

Online ISBN : 978-981-99-8082-6

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications

A program written in Rust to explore Combinatorics using a Brute Force Algorithm to solve the TSP (Travelling Salesman Problem)

hgi0100/bruteforce

Folders and files, repository files navigation.

• Rust 100.0%

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Traveling Salesman Problem using Genetic Algorithm

• Travelling Salesman Problem using Hungarian method
• Traveling Salesman Problem using Branch And Bound
• Bitonic Travelling Salesman Problem
• Traveling Salesman Problem (TSP) Implementation
• Travelling Salesman Problem implementation using BackTracking
• Travelling Salesman Problem | Greedy Approach
• Travelling Salesman Problem using Dynamic Programming
• Travelling Salesman Problem (TSP) using Reduced Matrix Method
• Approximate solution for Travelling Salesman Problem using MST
• Proof that traveling salesman problem is NP Hard
• Bitmasking and Dynamic Programming | Travelling Salesman Problem
• Mutation Algorithms for String Manipulation (GA)
• How to implement Genetic Algorithm using PyTorch
• Steady State Genetic Algorithm (SSGA)
• Java Program to Solve Travelling Salesman Problem Using Incremental Insertion Method
• Simple Genetic Algorithm (SGA)
• Algorithms | Dynamic Programming | Question 7
• Python | Single Point Crossover in Genetic Algorithm
• Crossover in Genetic Algorithm

AuPrerequisites: Genetic Algorithm , Travelling Salesman Problem In this article, a genetic algorithm is proposed to solve the travelling salesman problem .  Genetic algorithms are heuristic search algorithms inspired by the process that supports the evolution of life. The algorithm is designed to replicate the natural selection process to carry generation, i.e. survival of the fittest of beings. Standard genetic algorithms are divided into five phases which are:   

• Creating initial population.
• Calculating fitness.
• Selecting the best genes.
• Crossing over.
• Mutating to introduce variations.

These algorithms can be implemented to find a solution to the optimization problems of various types. One such problem is the Traveling Salesman Problem . The problem says that a salesman is given a set of cities, he has to find the shortest route to as to visit each city exactly once and return to the starting city.  Approach: In the following implementation, cities are taken as genes, string generated using these characters is called a chromosome, while a fitness score which is equal to the path length of all the cities mentioned, is used to target a population. Fitness Score is defined as the length of the path described by the gene. Lesser the path length fitter is the gene. The fittest of all the genes in the gene pool survive the population test and move to the next iteration. The number of iterations depends upon the value of a cooling variable. The value of the cooling variable keeps on decreasing with each iteration and reaches a threshold after a certain number of iterations. Algorithm:    

Pseudo-code    

How the mutation works? Suppose there are 5 cities: 0, 1, 2, 3, 4. The salesman is in city 0 and he has to find the shortest route to travel through all the cities back to the city 0. A chromosome representing the path chosen can be represented as:   

This chromosome undergoes mutation. During mutation, the position of two cities in the chromosome is swapped to form a new configuration, except the first and the last cell, as they represent the start and endpoint.   

Original chromosome had a path length equal to INT_MAX , according to the input defined below, since the path between city 1 and city 4 didn’t exist. After mutation, the new child formed has a path length equal to 21 , which is a much-optimized answer than the original assumption. This is how the genetic algorithm optimizes solutions to hard problems.  

Below is the implementation of the above approach:  

Time complexity:  O(n^2) as it uses nested loops to calculate the fitness value of each gnome in the population.  Auxiliary Space : O(n)

Please Login to comment...

Similar reads.

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

A deep reinforcement learning algorithm framework for solving multi-objective traveling salesman problem based on feature transformation

Affiliations.

• 1 School of Mechatronic Engineering and Automation, Shanghai University, 99 Shangda Road, Shanghai 200444, China. Electronic address: [email protected].
• 2 School of Mechatronic Engineering and Automation, Shanghai University, 99 Shangda Road, Shanghai 200444, China. Electronic address: [email protected].
• PMID: 38733797
• DOI: 10.1016/j.neunet.2024.106359

As a special type of multi-objective combinatorial optimization problems (MOCOPs), the multi-objective traveling salesman problem (MOTSP) plays an important role in practical fields such as transportation and robot control. However, due to the complexity of its solution space and the conflicts between different objectives, it is difficult to obtain satisfactory solutions in a short time. This paper proposes an end-to-end algorithm framework for solving MOTSP based on deep reinforcement learning (DRL). By decomposing strategies, solving MOTSP is transformed into solving multiple single-objective optimization subproblems. Through linear transformation, the features of the MOTSP are combined with the weights of the objective function. Subsequently, a modified graph pointer network (GPN) model is used to solve the decomposed subproblems. Compared with the previous DRL model, the proposed algorithm can solve all the subproblems using only one model without adding weight information as input features. Furthermore, our algorithm can output a corresponding solution for each weight, which increases the diversity of solutions. In order to verify the performance of our proposed algorithm, it is compared with four classical evolutionary algorithms and two DRL algorithms on several MOTSP instances. The comparison shows that our proposed algorithm outperforms the compared algorithms both in terms of training time and the quality of the resulting solutions.

Keywords: Deep reinforcement learning; Feature transformation; Graph pointer network; Multi-objective traveling salesman problem.

Copyright © 2024 Elsevier Ltd. All rights reserved.