solving problems using algebra

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.7: Solving Linear Equations

• Last updated
• Save as PDF
• Page ID 6392

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Use the properties of equality to solve basic linear equations.
• Identify and solve conditional linear equations, identities, and contradictions.
• Clear fractions from equations.
• Set up and solve linear equations.

Solving Basic Linear Equations

An equation 129 is a statement indicating that two algebraic expressions are equal. A linear equation with one variable 130 , \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\). For example

\(3 x - 12 = 0\)

A solution 131 to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation \(3x − 12 = 0\) is \(x\) and the solution is \(x = 4\). To verify this, substitute the value \(4\) in for \(x\) and check that you obtain a true statement.

\(\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}\)

Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”

Example \(\PageIndex{1}\):

Is \(a=−\frac{1}{2}\) a solution to \(−10a+5=25\)?

Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.

\(- 10 a + 5 = - 10 ( \color{Cerulean}{- \frac { 1 } { 2 }} \color{Black}{ ) +} 5 = 5 + 5 = 10 \neq 25\:\: \color{red}{✗}\)  

No, \(a=−\frac{1}{2}\) does not satisfy the equation.

Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equations 132 as equations with the same solution set.

\(\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}\)

Here we can see that the three linear equations are equivalent because they share the same solution set, namely, \(\{7\}\). To obtain equivalent equations, use the following properties of equality 133 . Given algebraic expressions \(A\) and \(B\), where \(c\) is a nonzero number:

Multiplying or dividing both sides of an equation by \(0\) is carefully avoided. Dividing by \(0\) is undefined and multiplying both sides by \(0\) results in the equation \(0 = 0\).

We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form \(ax + b = c\), then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.

Example \(\PageIndex{2}\):

Solve: \(7x − 2 = 19\).

\(\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} \quad Add\: 2\: to\: both\: sides. \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } \quad \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}\)

The solution is \(3\).

Example \(\PageIndex{3}\):

Solve: \(56 = 8 + 12y\).

When no sign precedes the term, it is understood to be positive. In other words, think of this as \(56 = +8 + 12y\). Therefore, we begin by subtracting \(8\) on both sides of the equal sign.

\(\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}\)

It does not matter on which side we choose to isolate the variable because the symmetric property 134 states that \(4 = y\) is equivalent to \(y = 4\).

The solution is \(4\).

Example \(\PageIndex{4}\):

Solve: \(\frac { 5 } { 3 } x + 2 = - 8\).

Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient \(\frac{5}{3}\).

\begin{aligned} \frac { 5 } { 3 } x + 2 & = - 8 \\ \frac { 5 } { 3 } x + 2 \color{Cerulean}{- 2} & = - 8 \color{Cerulean}{- 2}\quad \color{Cerulean}{Subtract\: 2\: on\: both\: sides.} \\ \frac { 5 } { 3 } x & = - 10 \\ \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{ \cdot} \frac { 5 } { 3 } x & = \color{Cerulean}{\frac { 3 } { \cancel{5} }} \color{Black}{\cdot} ( \overset{-2}{\cancel{-10}} )\quad \color{Cerulean}{Multiply \:both \:sides\: by\: \frac{3}{5}.} \\ 1x & = 3 \cdot ( - 2 ) \\ x & = - 6 \end{aligned}

The solution is \(−6\).

In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation.

Exercise \(\PageIndex{1}\)

Solve: \(\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }\).

www.youtube.com/v/cQwqXs9AD6M

General Guidelines for Solving Linear Equations

Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:

• Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
• Step 2: Use the appropriate properties of equality to combine like terms on opposite sides of the equal sign. The goal is to obtain the variable term on one side of the equation and the constant term on the other.
• Step 3: Divide or multiply as needed to isolate the variable.
• Step 4: Check to see if the answer solves the original equation.

We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.

At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.

Example \(\PageIndex{5}\):

Solve: \(- 4 a + 2 - a = 1\).

First combine the like terms on the left side of the equal sign.

\(\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}\)

Always use the original equation to check to see if the solution is correct.

\(\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}\)

The solution is \(\frac{1}{5}\).

Given a linear equation in the form \(ax + b = cx + d\), we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.

Example \(\PageIndex{6}\):

Solve: \(−2y − 3 = 5y + 11\).

Subtract \(5y\) on both sides so that we can combine the terms involving y on the left side.

\(\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}\)

From here, solve using the techniques developed previously.

\(\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}\)

The solution is \(−2\).

Solving will often require the application of the distributive property.

Example \(\PageIndex{7}\):

Solve: \(- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )\).

Simplify the linear expressions on either side of the equal sign first.

\(\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}\)

The solution is \(\frac{1}{3}\).

Example \(\PageIndex{8}\):

Solve: \(5(3−a)−2(5−2a)=3\).

Begin by applying the distributive property.

\(\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}\)

Here we point out that \(−a\) is equivalent to \(−1a\); therefore, we choose to divide both sides of the equation by \(−1\).

\(\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}\)

Alternatively, we can multiply both sides of \(−a=−2\) by negative one and achieve the same result.

\(\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}\)

The solution is \(2\).

Exercise \(\PageIndex{2}\)

Solve: \(6 - 3 ( 4 x - 1 ) = 4 x - 7\).

www.youtube.com/v/NAIAZrFjU-o

There are three different types of equations. Up to this point, we have been solving conditional equations 135 . These are equations that are true for particular values. An identity 136 is an equation that is true for all possible values of the variable. For example,

\(x = x \quad\color{Cerulean}{Identity}\)

has a solution set consisting of all real numbers, \(ℝ\). A contradiction 137 is an equation that is never true and thus has no solutions. For example,

\(x+1=x\quad\color{Cerulean}{Contradiction}\)

has no solution. We use the empty set, \(Ø\), to indicate that there are no solutions.

If the end result of solving an equation is a true statement, like \(0 = 0\), then the equation is an identity and any real number is a solution. If solving results in a false statement, like \(0 = 1\), then the equation is a contradiction and there is no solution.

Example \(\PageIndex{9}\):

Solve: \(4 (x + 5) + 6 = 2 (2x + 3)\).

\(\begin{aligned} 4 ( x + 5 ) + 6 & = 2 ( 2 x + 3 ) \\ 4 x + 20 + 6 & = 4 x + 6 \\ 4 x + 26 & = 4 x + 6 \\ 26 & = 6\:\: \color{red}{✗} \end{aligned}\)

Solving leads to a false statement; therefore, the equation is a contradiction and there is no solution.

\(Ø\)

Example \(\PageIndex{10}\):

Solve: \(3 (3y + 5) + 5 = 10 (y + 2) − y\).

\(\begin{aligned} 3 ( 3 y + 5 ) + 5 & = 10 ( y + 2 ) - y \\ 9 y + 15 + 5 & = 10 y + 20 - y \\ 9 y + 20 & = 9 y + 20 \\ 9 y & = 9 y \\ 0 & = 0 \:\:\color{Cerulean}{✓} \end{aligned}\)

Solving leads to a true statement; therefore, the equation is an identity and any real number is a solution.

\(ℝ\)

The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).

Example \(\PageIndex{11}\):

Solve: \(\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1\).

Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the \(LCD (3, 5) = 15\).

\(\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}\)

The solution is \(−9\).

It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:

We simplify expressions and solve equations. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by \(6\), you obtain an equivalent equation.

Applications Involving Linear Equations

Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.

When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “ let x represent… ” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.

Example \(\PageIndex{12}\):

When \(6\) is subtracted from twice the sum of a number and \(8\) the result is \(5\). Find the number.

Let n represent the unknown number.

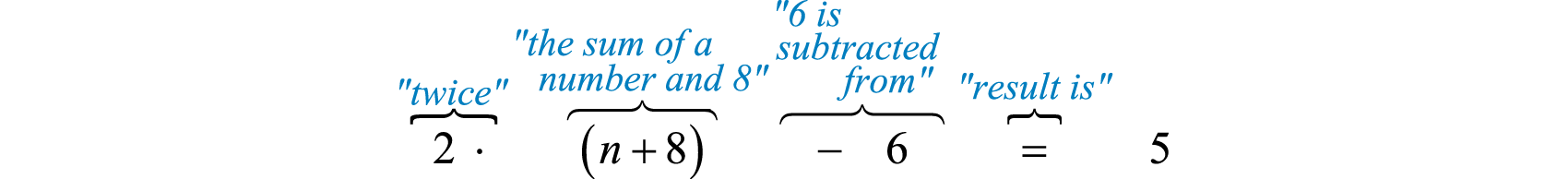
To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:

The key was to focus on the phrase “ twice the sum ,” this prompted us to group the sum within parentheses and then multiply by \(2\). After translating the sentence into a mathematical statement we then solve.

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}\)

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}\)       

The number is \(−\frac{5}{2}\).

General guidelines for setting up and solving word problems follow.

• Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
• Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
• Step 3: Translate and set up an algebraic equation that models the problem.
• Step 4: Solve the resulting algebraic equation.
• Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).

For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.

Example \(\PageIndex{13}\):

A rectangle has a perimeter measuring \(92\) meters. The length is \(2\) meters less than \(3\) times the width. Find the dimensions of the rectangle.

The sentence “ The length is 2 meters less than 3 times the width ,” gives us the relationship between the two variables.

Let \(w\) represent the width of the rectangle.

Let \(3w−2\) represent the length.

The sentence “ A rectangle has a perimeter measuring 92 meters ” suggests an algebraic set up. Substitute \(92\) for the perimeter and the expression \(3w−2\) for the length into the appropriate formula as follows:

\(P = \quad2 l\:\:\:\:\: +\:\:\: 2 w\)

\(\color{Cerulean}{\downarrow} \quad\:\:\:\quad \color{Cerulean}{\downarrow}\quad\quad\quad\quad\)

\(\color{OliveGreen}{92}\color{Black}{ =} 2 (\color{OliveGreen}{ 3 w - 2}\color{Black}{ )} + 2 w\)

Once you have set up an algebraic equation with one variable, solve for the width, \(w\).

\(\begin{array} { l } { 92 = 2 ( 3 w - 2 ) + 2 w \color{Cerulean}{ Distribute. } } \\ { 92 = 6 w - 4 + 2 w \quad\: \color{Cerulean} { Combine\: like\: terms. } } \\ { 92 = 8 w - 4 \quad\quad\quad\:\:\:\color{Cerulean} { Solve\: for\: w. } } \\ { 96 = 8 w } \\ { 12 = w } \end{array}\)

Use \(3w−2\) to find the length.

\(l = 3 w - 2 = 3 ( \color{OliveGreen}{12}\color{Black}{ )} - 2 = 36 - 2 = 34\)

To check, make sure the perimeter is \(92\) meters.

\(\begin{aligned} P & = 2 l + 2 w \\ & = 2 ( 34 ) + 2 ( 12 ) \\ & = 68 + 24 \\ & = 92 \end{aligned}\)

The rectangle measures \(12\) meters by \(34\) meters.

Example \(\PageIndex{14}\):

Given a \(4 \frac{3}{8}\)% annual interest rate, how long will it take \($2,500\) to yield \($437.50\) in simple interest?

Let t represent the time needed to earn \($437.50\) at \(4 \frac{3}{8}\)%. Organize the information needed to use the formula for simple interest, \(I=prt\).

Next, substitute all of the known quantities into the formula and then solve for the only unknown, t .

\(\begin{aligned} I & = p r t \\ \color{OliveGreen}{437.50} & \color{Black}{=} \color{OliveGreen}{2500}\color{Black}{ (}\color{OliveGreen}{ 0.04375}\color{Black}{ )} t \\ 437.50 & = 109.375 t \\ \frac{437.50}{\color{Cerulean}{109.375}} & \color{Black}{=} \frac { 109.375 t } { \color{Cerulean}{109.375} } \\ 4 & = t \end{aligned}\)

It takes \(4\) years for \($2,500\) invested at \(4 \frac{3}{8}\)% to earn \($437.50\) in simple interest.

Example \(\PageIndex{15}\):

Susan invested her total savings of \($12,500\) in two accounts earning simple interest. Her mutual fund account earned \(7\)% last year and her CD earned \(4.5\)%. If her total interest for the year was \($670\), how much was in each account?

The relationship between the two unknowns is that they total \($12,500\). When a total is involved, a common technique used to avoid two variables is to represent the second unknown as the difference of the total and the first unknown.

Let \(x\) represent the amount invested in the mutual fund.

Let \(12,500 − x\) represent the remaining amount invested in the CD.

Organize the data.

The total interest is the sum of the interest earned from each account.

\(\color{Cerulean}{mutual fund interest        +            CD  interest          =     total interest}\)

\( 0.07x         +        0.045(12,500−x)       =           670\)

This equation models the problem with one variable. Solve for \( x\) .

\(\begin{aligned} 0.07 x + 0.045 ( 12,500 - x ) & = 670 \\ 0.07 x + 562.5 - 0.045 x & = 670 \\ 0.025 x + 562.5 & = 670 \\ 0.025 x & = 107.5 \\ x & = \frac { 107.5 } { 0.025 } \\ x & = 4,300 \end{aligned}\)

Use \(12,500−x\) to find the amount in the CD.

\(12,500−x=12,500−\color{OliveGreen}{4,300}\color{Black}{=}8,200\)

Susan invested \($4,300\) at \(7\)% in a mutual fund and \($8,200\) at \(4.5\)% in a CD.

Key Takeaways

• Solving general linear equations involves isolating the variable, with coefficient \(1\), on one side of the equal sign. To do this, first use the appropriate equality property of addition or subtraction to isolate the variable term on one side of the equal sign. Next, isolate the variable using the equality property of multiplication or division. Finally, check to verify that your solution solves the original equation.
• If solving a linear equation leads to a true statement like \(0 = 0\), then the equation is an identity and the solution set consists of all real numbers, \(ℝ\).
• If solving a linear equation leads to a false statement like \(0 = 5\), then the equation is a contradiction and there is no solution, \(Ø\).
• Clear fractions by multiplying both sides of an equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
• Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.

Exercise \(\PageIndex{3}\)

Determine whether or not the given value is a solution.

• \(−5x + 4 = −1 ; x = −1\)
• \(4x − 3 = −7 ; x = −1\)
• \(3y − 4 = 5; y = \frac{9}{3}\)
• \(−2y + 7 = 12 ; y = −\frac{5}{2}\)
• \(3a − 6 = 18 − a; a = −3\)
• \(5 (2t − 1) = 2 − t; t = 2\)
• \(ax − b = 0; x = \frac{b}{a}\)
• \(ax + b = 2b; x = \frac{b}{a}\)

Exercise \(\PageIndex{4}\)

• \(5x − 3 = 27\)
• \(6x − 7 = 47\)
• \(4x + 13 = 35\)
• \(6x − 9 = 18\)
• \(9a + 10 = 10\)
• \(5 − 3a = 5\)
• \(−8t + 5 = 15\)
• \(−9t + 12 = 33\)
• \(\frac{2}{3} x + \frac{1}{2} = 1\)
• \(\frac{3}{8} x + \frac{5}{4} = \frac{3}{2}\)
• \(\frac{1 − 3y}{5} = 2\)
• \(\frac{2 − 5y}{6} = −8\)
• \(7 − y = 22\)
• \(6 − y = 12\)
• Solve for \(x: ax − b = c\)
• Solve for \(x: ax + b = 0\)

3. \(\frac{11}{2}\)

7. \(−\frac{5}{4}\)

9. \(\frac{3}{4}\)

11. \(−3\)

13. \(−15\)

15. \(x = \frac{b+c}{a}\)

Exercise \(\PageIndex{5}\)

• \(6x − 5 + 2x = 19\)
• \(7 − 2x + 9 = 24\)
• \(12x − 2 − 9x = 5x + 8\)
• \(16 − 3x − 22 = 8 − 4x\)
• \(5y − 6 − 9y = 3 − 2y + 8\)
• \(7 − 9y + 12 = 3y + 11 − 11y\)
• \(3 + 3a − 11 = 5a − 8 − 2a\)
• \(2 − 3a = 5a + 7 − 8a\)
• \(\frac{1}{3} x −\frac{3}{2} + \frac{5}{2} x = \frac{5}{6} x + \frac{1}{4}\)
• \(\frac{5}{8} + \frac{1}{5} x −\frac{3}{4} = \frac{3}{10} x − \frac{1}{4}\)
• \(1.2x − 0.5 − 2.6x = 2 − 2.4x\)
• \(1.59 − 3.87x = 3.48 − 4.1x − 0.51\)
• \(5 − 10x = 2x + 8 − 12x\)
• \(8x − 3 − 3x = 5x − 3\)
• \(5 (y + 2) = 3 (2y − 1) + 10\)
• \(7 (y − 3) = 4 (2y + 1) − 21\)
• \(7 − 5 (3t − 9) = 22\)
• \(10 − 5 (3t + 7) = 20\)
• \(5 − 2x = 4 − 2 (x − 4)\)
• \(2 (4x − 5) + 7x = 5 (3x − 2)\)
• \(4 (4a − 1) = 5 (a − 3) + 2 (a − 2)\)
• \(6 (2b − 1) + 24b = 8 (3b − 1)\)
• \(\frac{2}{3} (x + 18) + 2 = \frac{1}{3} x − 13\)
• \(\frac{2}{5} x − \frac{1}{2} (6x − 3) = \frac{4}{3}\)
• \(1.2 (2x + 1) + 0.6x = 4x\)
• \(6 + 0.5 (7x − 5) = 2.5x + 0.3\)
• \(5 (y + 3) = 15 (y + 1) − 10y\)
• \(3 (4 − y) − 2 (y + 7) = −5y\)
• \(\frac{1}{5} (2a + 3) −\frac{1}{2} = \frac{1}{3} a + \frac{1}{10}\)
• \(\frac{3}{2} a = \frac{3}{4} (1 + 2a) −\frac{1}{5} (a + 5)\)
• \(6 − 3 (7x + 1) = 7 (4 − 3x)\)
• \(6 (x − 6) − 3 (2x − 9) = −9\)
• \(\frac{3}{4} (y − 2) + \frac{2}{3} (2y + 3) = 3\)
• \(\frac{5}{4} − \frac{1}{2} (4y − 3) = \frac{2}{5} (y − 1)\)
• \(−2 (3x + 1) − (x − 3) = −7x + 1\)
• \(6 (2x + 1) − (10x + 9) = 0\)
• Solve for \(w: P = 2l + 2w\)
• Solve for \(a: P = a + b + c\)
• Solve for \(t: D = rt\)
• Solve for \(w: V = lwh\)
• Solve for \(b: A = \frac{1}{2} bh\)
• Solve for \(a:s = \frac{1}{2}at^{2}\)
• Solve for \(a: A = \frac{1}{2}h (a + b)\)
• Solve for \(h: V = \frac{1}{3}πr^{2}h\)
• Solve for \(F: C = \frac{5}{9} (F − 32)\)
• Solve for \(x: ax + b = c\)

3. \(−5\)

5. \(−\frac{17}{2}\)

7. \(ℝ\)

9. \(\frac{7}{8}\)

11. \(2.5\)

13. \(Ø\)

19. \(Ø\)

21. \(−\frac{5}{3}\)

23. \(−81\)

25. \(1.2\)

27. \(ℝ\)

31. \(Ø\)

33. \(\frac{6}{5}\)

35. \(ℝ\)

37. \(w = \frac{P − 2l}{2}\)

39. \(t = \frac{D}{r}\)

41. \(b = \frac{2A}{h}\)

43. \(a = \frac{2A}{h} − b\)

45. \(F = \frac{9}{5} C + 32\)

Exercise \(\PageIndex{6}\)

Set up an algebraic equation then solve.

Number Problems

• When \(3\) is subtracted from the sum of a number and \(10\) the result is \(2\). Find the number.
• The sum of \(3\) times a number and \(12\) is equal to \(3\). Find the number.
• Three times the sum of a number and \(6\) is equal to \(5\) times the number. Find the number.
• Twice the sum of a number and \(4\) is equal to \(3\) times the sum of the number and \(1\). Find the number.
• A larger integer is \(1\) more than \(3\) times another integer. If the sum of the integers is \(57\), find the integers.
• A larger integer is \(5\) more than twice another integer. If the sum of the integers is \(83\), find the integers.
• One integer is \(3\) less than twice another integer. Find the integers if their sum is \(135\).
• One integer is \(10\) less than \(4\) times another integer. Find the integers if their sum is \(100\).
• The sum of three consecutive integers is \(339\). Find the integers.
• The sum of four consecutive integers is \(130\). Find the integers.
• The sum of three consecutive even integers is \(174\). Find the integers.
• The sum of four consecutive even integers is \(116\). Find the integers.
• The sum of three consecutive odd integers is \(81\). Find the integers.
• The sum of four consecutive odd integers is \(176\). Find the integers.

1. \(−5\)

5. \(14, 43\)

7. \(46, 89\)

9. \(112, 113, 114\)

11. \(56, 58, 60\)

13. \(25, 27, 29\)

Exercise \(\PageIndex{7}\)

Geometry Problems

• The length of a rectangle is \(5\) centimeters less than twice its width. If the perimeter is \(134\) centimeters, find the length and width.
• The length of a rectangle is \(4\) centimeters more than \(3\) times its width. If the perimeter is \(64\) centimeters, find the length and width.
• The width of a rectangle is one-half that of its length. If the perimeter measures \(36\) inches, find the dimensions of the rectangle.
• The width of a rectangle is \(4\) inches less than its length. If the perimeter measures \(72\) inches, find the dimensions of the rectangle.
• The perimeter of a square is \(48\) inches. Find the length of each side.
• The perimeter of an equilateral triangle is \(96\) inches. Find the length of each side.
• The circumference of a circle measures \(80π\) units. Find the radius.
• The circumference of a circle measures \(25\) centimeters. Find the radius rounded off to the nearest hundredth.

1. Width: \(24\) centimeters; length: \(43\) centimeters

3. Width: \(6\) inches; length: \(12\) inches

5. \(12\) inches

7. \(40\) units

Exercise \(\PageIndex{8}\)

Simple Interest Problems

• For how many years must \($1,000\) be invested at \(5\frac{1}{2}\) % to earn \($165\) in simple interest?
• For how many years must \($20,000\) be invested at \(6\frac{1}{4}\) % to earn \($3,125\) in simple interest?
• At what annual interest rate must \($6500\) be invested for \(2\) years to yield \($1,040\) in simple interest?
• At what annual interest rate must \($5,750\) be invested for \(1\) year to yield \($333.50\) in simple interest?
• If the simple interest earned for \(5\) years was \($1,860\) and the annual interest rate was \(6\)%, what was the principal?
• If the simple interest earned for \(2\) years was \($543.75\) and the annual interest rate was \(3\frac{3}{4}\) %, what was the principal?
• How many years will it take \($600\) to double earning simple interest at a \(5\)% annual rate? (Hint: To double, the investment must earn \($600\) in simple interest.)
• How many years will it take \($10,000\) to double earning simple interest at a \(5\)% annual rate? (Hint: To double, the investment must earn \($10,000\) in simple interest.)
• Jim invested \($4,200\) in two accounts. One account earns \(3\)% simple interest and the other earns \(6\)%. If the interest after \(1\) year was \($159\), how much did he invest in each account?
• Jane has her \($6,500\) savings invested in two accounts. She has part of it in a CD at \(5\)% annual interest and the rest in a savings account that earns \(4\)% annual interest. If the simple interest earned from both accounts is \($303\) for the year, then how much does she have in each account?
• Jose put last year’s bonus of \($8,400\) into two accounts. He invested part in a CD with \(2.5\)% annual interest and the rest in a money market fund with \(1.5\)% annual interest. His total interest for the year was \($198\). How much did he invest in each account?
• Mary invested her total savings of \($3,300\) in two accounts. Her mutual fund account earned \(6.2\)% last year and her CD earned \(2.4\)%. If her total interest for the year was \($124.80\), how much was in each account?
• Alice invests money into two accounts, one with \(3\)% annual interest and another with \(5\)% annual interest. She invests \(3\) times as much in the higher yielding account as she does in the lower yielding account. If her total interest for the year is \($126\), how much did she invest in each account?
• James invested an inheritance in two separate banks. One bank offered \(5\frac{1}{2}\) % annual interest rate and the other \(6\frac{1}{4}\)%. He invested twice as much in the higher yielding bank account than he did in the other. If his total simple interest for \(1\) year was \($5,760\), then what was the amount of his inheritance?

1. \(3\) years

5. \($6,200\)

7. \(20\) years

9. He invested \($3,100\) at \(3\)% and \($1,100\) at \(6\)%.

11. Jose invested \($7,200\) in the CD and \($1,200\) in the money market fund.

13. Alice invested \($700\) at \(3\)% and \($2,100\) at \(5\)%.

Exercise \(\PageIndex{9}\)

Uniform Motion Problems

• If it takes Jim \(1 \frac{1}{4}\) hours to drive the \(40\) miles to work, then what is Jim’s average speed?
• It took Jill \(3 \frac{1}{2}\) hours to drive the \(189\) miles home from college. What was her average speed?
• At what speed should Jim drive if he wishes to travel \(176\) miles in \(2 \frac{3}{4}\) hours?
• James and Martin were able to drive the \(1,140\) miles from Los Angeles to Seattle. If the total trip took \(19\) hours, then what was their average speed?

1. \(32\) miles per hour

3. \(64\) miles per hour

Exercise \(\PageIndex{10}\)

• What is regarded as the main business of algebra? Explain.
• What is the origin of the word algebra ?
• Create an identity or contradiction of your own and share it on the discussion board. Provide a solution and explain how you found it.
• Post something you found particularly useful or interesting in this section. Explain why.
• Conduct a web search for “solving linear equations.” Share a link to website or video tutorial that you think is helpful.

1. Answer may vary

3. Answer may vary

5. Answer may vary

129 Statement indicating that two algebraic expressions are equal.

130 An equation that can be written in the standard form \(ax + b = 0\), where \(a\) and \(b\) are real numbers and \(a ≠ 0\).

131 Any value that can replace the variable in an equation to produce a true statement.

132 Equations with the same solution set.

133 Properties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.

134 Allows you to solve for the variable on either side of the equal sign, because \(x = 5\) is equivalent to \(5 = x\).

135 Equations that are true for particular values.

136 An equation that is true for all possible values.

137 An equation that is never true and has no solution.

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Solving equations

Here you will learn about solving equations, including linear and quadratic algebraic equations, and how to solve them.

Students will first learn about solving equations in grade 8 as a part of expressions and equations, and again in high school as a part of reasoning with equations and inequalities.

What is solving an equation?

Solving equations is a step-by-step process to find the value of the variable. A variable is the unknown part of an equation, either on the left or right side of the equals sign. Sometimes, you need to solve multi-step equations which contain algebraic expressions.

To do this, you must use the order of operations, which is a systematic approach to equation solving. When you use the order of operations, you first solve any part of an equation located within parentheses. An equation is a mathematical expression that contains an equals sign.

For example,

\begin{aligned}y+6&=11\\\\ 3(x-3)&=12\\\\ \cfrac{2x+2}{4}&=\cfrac{x-3}{3}\\\\ 2x^{2}+3&x-2=0\end{aligned}

There are two sides to an equation, with the left side being equal to the right side. Equations will often involve algebra and contain unknowns, or variables, which you often represent with letters such as x or y.

You can solve simple equations and more complicated equations to work out the value of these unknowns. They could involve fractions, decimals or integers.

Common Core State Standards

How does this relate to 8 th grade and high school math?

• Grade 8 – Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
• High school – Reasoning with Equations and Inequalities (HSA.REI.B.3) Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.

[FREE] Solving Equations Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations. 15 questions with answers to identify areas of strength and support!

How to solve equations

In order to solve equations, you need to work out the value of the unknown variable by adding, subtracting, multiplying or dividing both sides of the equation by the same value.

• Combine like terms .
• Simplify the equation by using the opposite operation to both sides.
• Isolate the variable on one side of the equation.

Solving equations examples

Example 1: solve equations involving like terms.

Solve for x.

Combine like terms.

Combine the q terms on the left side of the equation. To do this, subtract 4q from both sides.

The goal is to simplify the equation by combining like terms. Subtracting 4q from both sides helps achieve this.

After you combine like terms, you are left with q=9-4q.

2 Simplify the equation by using the opposite operation on both sides.

Add 4q to both sides to isolate q to one side of the equation.

The objective is to have all the q terms on one side. Adding 4q to both sides accomplishes this.

After you move the variable to one side of the equation, you are left with 5q=9.

3 Isolate the variable on one side of the equation.

Divide both sides of the equation by 5 to solve for q.

Dividing by 5 allows you to isolate q to one side of the equation in order to find the solution. After dividing both sides of the equation by 5, you are left with q=1 \cfrac{4}{5} \, .

Example 2: solve equations with variables on both sides

Combine the v terms on the same side of the equation. To do this, add 8v to both sides.

7v+8v=8-8v+8v

After combining like terms, you are left with the equation 15v=8.

Simplify the equation by using the opposite operation on both sides and isolate the variable to one side.

Divide both sides of the equation by 15 to solve for v. This step will isolate v to one side of the equation and allow you to solve.

15v \div 15=8 \div 15

The final solution to the equation 7v=8-8v is \cfrac{8}{15} \, .

Example 3: solve equations with the distributive property

Combine like terms by using the distributive property.

The 3 outside the parentheses needs to be multiplied by both terms inside the parentheses. This is called the distributive property.

\begin{aligned}& 3 \times c=3 c \\\\ & 3 \times(-5)=-15 \\\\ &3 c-15-4=2\end{aligned}

Once the 3 is distributed on the left side, rewrite the equation and combine like terms. In this case, the like terms are the constants on the left, –15 and –4. Subtract –4 from –15 to get –19.

Simplify the equation by using the opposite operation on both sides.

The goal is to isolate the variable, c, on one side of the equation. By adding 19 to both sides, you move the constant term to the other side.

\begin{aligned}& 3 c-19+19=2+19 \\\\ & 3 c=21\end{aligned}

Isolate the variable to one side of the equation.

To solve for c, you want to get c by itself.

Dividing both sides by 3 accomplishes this.

On the left side, \cfrac{3c}{3} simplifies to c, and on the right, \cfrac{21}{3} simplifies to 7.

The final solution is c=7.

As an additional step, you can plug 7 back into the original equation to check your work.

Example 4: solve linear equations

Combine like terms by simplifying.

Using steps to solve, you know that the goal is to isolate x to one side of the equation. In order to do this, you must begin by subtracting from both sides of the equation.

\begin{aligned} & 2x+5=15 \\\\ & 2x+5-5=15-5 \\\\ & 2x=10 \end{aligned}

Continue to simplify the equation by using the opposite operation on both sides.

Continuing with steps to solve, you must divide both sides of the equation by 2 to isolate x to one side.

\begin{aligned} & 2x \div 2=10 \div 2 \\\\ & x= 5 \end{aligned}

Isolate the variable to one side of the equation and check your work.

Plugging in 5 for x in the original equation and making sure both sides are equal is an easy way to check your work. If the equation is not equal, you must check your steps.

\begin{aligned}& 2(5)+5=15 \\\\ & 10+5=15 \\\\ & 15=15\end{aligned}

Example 5: solve equations by factoring

Solve the following equation by factoring.

Combine like terms by factoring the equation by grouping.

Multiply the coefficient of the quadratic term by the constant term.

2 x (-20) = -40

Look for two numbers that multiply to give you –40 and add up to the coefficient of 3. In this case, the numbers are 8 and –5 because 8 x -5=–40, and 8+–5=3.

Split the middle term using those two numbers, 8 and –5. Rewrite the middle term using the numbers 8 and –5.

2x^2+8x-5x-20=0

Group the terms in pairs and factor out the common factors.

2x^2+8x-5x-20=2x(x + 4)-5(x+4)=0

Now, you’ve factored the equation and are left with the following simpler equations 2x-5 and x+4.

This step relies on understanding the zero product property, which states that if two numbers multiply to give zero, then at least one of those numbers must equal zero.

Let’s relate this back to the factored equation (2x-5)(x+4)=0

Because of this property, either (2x-5)=0 or (x+4)=0

Isolate the variable for each equation and solve.

When solving these simpler equations, remember that you must apply each step to both sides of the equation to maintain balance.

\begin{aligned}& 2 x-5=0 \\\\ & 2 x-5+5=0+5 \\\\ & 2 x=5 \\\\ & 2 x \div 2=5 \div 2 \\\\ & x=\cfrac{5}{2} \end{aligned}

\begin{aligned}& x+4=0 \\\\ & x+4-4=0-4 \\\\ & x=-4\end{aligned}

The solution to this equation is x=\cfrac{5}{2} and x=-4.

Example 6: solve quadratic equations

Solve the following quadratic equation.

Combine like terms by factoring the quadratic equation when terms are isolated to one side.

To factorize a quadratic expression like this, you need to find two numbers that multiply to give -5 (the constant term) and add to give +2 (the coefficient of the x term).

The two numbers that satisfy this are -1 and +5.

So you can split the middle term 2x into -1x+5x: x^2-1x+5x-5-1x+5x

Now you can take out common factors x(x-1)+5(x-1).

And since you have a common factor of (x-1), you can simplify to (x+5)(x-1).

The numbers -1 and 5 allow you to split the middle term into two terms that give you common factors, allowing you to simplify into the form (x+5)(x-1).

Let’s relate this back to the factored equation (x+5)(x-1)=0.

Because of this property, either (x+5)=0 or (x-1)=0.

Now, you can solve the simple equations resulting from the zero product property.

\begin{aligned}& x+5=0 \\\\ & x+5-5=0-5 \\\\ & x=-5 \\\\\\ & x-1=0 \\\\ & x-1+1=0+1 \\\\ & x=1\end{aligned}

The solutions to this quadratic equation are x=1 and x=-5.

Teaching tips for solving equations

• Use physical manipulatives like balance scales as a visual aid. Show how you need to keep both sides of the equation balanced, like a scale. Add or subtract the same thing from both sides to keep it balanced when solving. Use this method to practice various types of equations.
• Emphasize the importance of undoing steps to isolate the variable. If you are solving for x and 3 is added to x, subtracting 3 undoes that step and isolates the variable x.
• Relate equations to real-world, relevant examples for students. For example, word problems about tickets for sports games, cell phone plans, pizza parties, etc. can make the concepts click better.
• Allow time for peer teaching and collaborative problem solving. Having students explain concepts to each other, work through examples on whiteboards, etc. reinforces the process and allows peers to ask clarifying questions. This type of scaffolding would be beneficial for all students, especially English-Language Learners. Provide supervision and feedback during the peer interactions.

Easy mistakes to make

• Forgetting to distribute or combine like terms One common mistake is neglecting to distribute a number across parentheses or combine like terms before isolating the variable. This error can lead to an incorrect simplified form of the equation.
• Misapplying the distributive property Incorrectly distributing a number across terms inside parentheses can result in errors. Students may forget to multiply each term within the parentheses by the distributing number, leading to an inaccurate equation.
• Failing to perform the same operation on both sides It’s crucial to perform the same operation on both sides of the equation to maintain balance. Forgetting this can result in an imbalanced equation and incorrect solutions.
• Making calculation errors Simple arithmetic mistakes, such as addition, subtraction, multiplication, or division errors, can occur during the solution process. Checking calculations is essential to avoid errors that may propagate through the steps.
• Ignoring fractions or misapplying operations When fractions are involved, students may forget to multiply or divide by the common denominator to eliminate them. Misapplying operations on fractions can lead to incorrect solutions or complications in the final answer.

Related math equations lessons

• Math equations
• Rearranging equations
• How to find the equation of a line
• Solve equations with fractions
• Linear equations
• Writing linear equations
• Substitution
• Identity math
• One step equation

Practice solving equations questions

1. Solve 4x-2=14.

Add 2 to both sides.

Divide both sides by 4.

2. Solve 3x-8=x+6.

Add 8 to both sides.

Subtract x from both sides.

Divide both sides by 2.

3. Solve 3(x+3)=2(x-2).

Expanding the parentheses.

Subtract 9 from both sides.

Subtract 2x from both sides.

4. Solve \cfrac{2 x+2}{3}=\cfrac{x-3}{2}.

Multiply by 6 (the lowest common denominator) and simplify.

Expand the parentheses.

Subtract 4 from both sides.

Subtract 3x from both sides.

5. Solve \cfrac{3 x^{2}}{2}=24.

Multiply both sides by 2.

Divide both sides by 3.

Square root both sides.

6. Solve by factoring:

Use factoring to find simpler equations.

Set each set of parentheses equal to zero and solve.

x=3 or x=10

Solving equations FAQs

The first step in solving a simple linear equation is to simplify both sides by combining like terms. This involves adding or subtracting terms to isolate the variable on one side of the equation.

Performing the same operation on both sides of the equation maintains the equality. This ensures that any change made to one side is also made to the other, keeping the equation balanced and preserving the solutions.

To handle variables on both sides of the equation, start by combining like terms on each side. Then, move all terms involving the variable to one side by adding or subtracting, and simplify to isolate the variable. Finally, perform any necessary operations to solve for the variable.

To deal with fractions in an equation, aim to eliminate them by multiplying both sides of the equation by the least common denominator. This helps simplify the equation and make it easier to isolate the variable. Afterward, proceed with the regular steps of solving the equation.

The next lessons are

• Inequalities
• Types of graph
• Math formulas
• Coordinate plane

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

• Add to Home
• TigerMilk.Education GmbH
• Privacy policy
• Terms of service

Copyright Ⓒ 2013-2024 tiger-algebra.com

• Arabic | اللغة العربية
• Spanish | Español
• French | Français
• German | Deutsch
• Hebrew | עִברִית
• Italian | Italiano
• Indonesian | Bahasa Indonesia
• Portuguese | Português
• Russian | Русский
• Serbian | Srpski
• Vietnamese | Tiếng Việt
• Chinese | 中文
• Hindi | हिंदी
• Bengali | বাংলা
• Filipino | Filipino
• Korean | 한국인
• Marathi | मराठी
• Tamil | தமிழ்
• Telugu | తెలుగు
• Turkish | Türkçe
• Japanese | 日本語

This site is best viewed with Javascript. If you are unable to turn on Javascript, please click here .

Tiger Algebra Calculator

Absolute value.

• Absolute value equations
• Absolute value inequalities
• Absolute value problems made easy
• Absolute value equations with two term

Basic Techniques

• Canceling out
• Identifying perfect cubes
• Pulling out like terms
• Reducing fractions to lowest terms
• Simplifying radicals
• Square root of fraction or number by prime factorization
• Graphing an ordered pair on a coordinate plane
• Long addition
• Long division
• Unit converter
• Long multiplication
• Long substraction
• Solving word problems by rewriting information as equations

Calculators

• Basic complex operations
• Find prime factors
• Greatest common factor
• Least common multiple (LCM)
• Order of operations
• Square root simplifier
• Finding a molecular mass

Coming Soon

• Converting weights using mass
• Properties of parabolas
• Formatting guide
• Dividing exponents
• Exponential equations
• Multiplying exponents
• Powers of i
• Raising to a power
• Scientific notation
• Operations with numbers in scientific notation

Factorization

• Factoring binomials as difference of squares
• Factoring binomials as sum or difference of cubes
• Factoring multivariable polynomials
• Factoring polynomials with four or more terms
• Factor trinomials
• Other factorizations
• Polynomial long division
• Polynomial root calculator
• Dividing fractions
• Multiplying fractions
• Operations with fractions
• Circle from equation
• Properties of circles
• Distance between two points
• Find area of triangle given by its 3 sides
• Finding a perpendicular line
• Line Equation From Point And Slope
• Midpoint of two points
• Trigonometry
• Finding a parallel line
• Properties of ellipses
• Circles from Equations
• Perpendicular lines with point-slope intercept mode
• Parallel lines with point-slope intercept mode

Nonlinear Equations and Approximation and Inequalities

• Approximation
• De Moivre formula
• Linear inequalities
• Nonlinear equations
• Solving radical equations

Quadratic Equations

• Equations which are reducible to quadratic
• Parabola finding vertex and X intercepts
• Quadratic Inequalities
• Solving quadratic equations by completing the square
• Solving quadratic equations using the quadratic formula
• Solving quadratic equations by factoring
• Quadratic equations by completing the square

Series and Progressions

• Arithmetic sequences
• Domain range and relation from ordered pairs
• Geometric Sequences
• Geometric series
• Ordered pairs

Sets of Linear Equations

• Linear equations with four unknowns
• Linear equations with one unknown
• Linear equations with three unknowns
• Linear equations with two unknowns
• Properties of a straight lines
• Solving linear equations by substitution
• Systems of linear equations
• Combination
• Combinations and Permutations
• Percentages
• Statistical measures
• Summarizing data
• Normal and standard normal distributions

Latest Solved

• 3 x − 5 = 25 − 3 x
• 2 x 2 + 55 x − 87 = 0
• graph of a circle with radius 10 and center at (15,-3)
• 2 , 9 , 16 , 23 , 30
• 0.15 ( y − 0.2 ) = 2 − 0.5 ( 1 − y )
• find the midpoint of the points (1,2) and (3,-4)
• find the domain and range of (7,3),(-2,-2),(4,1),(4,1),(-9,0)(0,7)
• 7 , 15 , 23 , 31 , 39 , 47 , 55 , 63
• 0.003234 to scientific
• 1 , 7 , 13 , 19 , 25 , 31 , 37 , 43
• lcm(26,14,91)
• d i s tan c e ( − 3 , 8 ) ( − 5 , 1 )
• 5280ft to mi
• sin ( 120 )
• ( 1.2 x 10 − 14 ) − ( 1.59 x 10 − 9 )
• ( x - 1 ) 2 / 4 + ( y + 2 ) 2 / 9 = 1
• y = 2 / 3 x - 3 , ( 4 , - 1 )
• p ( 0.15 < z < 2.92 )

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

Solving Equations Using Algebra Calculator

Example problem, how to solve the equation in algebra calculator, clickable demo.

More Examples

• Solve 2a+4=12: 2a+4=12
• Solve b+1=-2b: b+1=-2b

Related Articles

• Algebra Calculator Tutorial

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Introduction to Word Problems

Algebra topics  -, introduction to word problems, algebra topics introduction to word problems.

Algebra Topics: Introduction to Word Problems

Lesson 9: introduction to word problems.

/en/algebra-topics/solving-equations/content/

What are word problems?

A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you've ever taken a math class, you've probably solved a word problem. For instance, does this sound familiar?

Johnny has 12 apples. If he gives four to Susie, how many will he have left?

You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you're supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:

12 - 4 = 8 , so you know Johnny has 8 apples left.

Word problems in algebra

If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.

You can tackle any word problem by following these five steps:

• Read through the problem carefully, and figure out what it's about.
• Represent unknown numbers with variables.
• Translate the rest of the problem into a mathematical expression.
• Solve the problem.
• Check your work.

We'll work through an algebra word problem using these steps. Here's a typical problem:

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?

It might seem complicated at first glance, but we already have all of the information we need to solve it. Let's go through it step by step.

Step 1: Read through the problem carefully.

With any problem, start by reading through the problem. As you're reading, consider:

• What question is the problem asking?
• What information do you already have?

Let's take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?

There's only one question here. We're trying to find out how many miles Jada drove . Now we need to locate any information that will help us answer this question.

There are a few important things we know that will help us figure out the total mileage Jada drove:

• The van cost $30 per day.
• In addition to paying a daily charge, Jada paid $0.50 per mile.
• Jada had the van for 2 days.
• The total cost was $360 .

Step 2: Represent unknown numbers with variables.

In algebra, you represent unknown numbers with letters called variables . (To learn more about variables, see our lesson on reading algebraic expressions .) You can use a variable in the place of any amount you don't know. Looking at our problem, do you see a quantity we should represent with a variable? It's often the number we're trying to find out.

Since we're trying to find the total number of miles Jada drove, we'll represent that amount with a variable—at least until we know it. We'll use the variable m for miles . Of course, we could use any variable, but m should be easy to remember.

Step 3: Translate the rest of the problem.

Let's take another look at the problem, with the facts we'll use to solve it highlighted.

The rate to rent a small moving van is $30 per day , plus $0.50 per mile . Jada rented a van to drive to her new home. It took 2 days , and the van cost $360 . How many miles did she drive?

We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It's $30 per day, and $0.50 per mile. A simpler way to say this would be:

$30 per day plus $0.50 per mile is $360.

If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360 . The shorter version will be easier to translate into a mathematical expression.

Let's start by translating $30 per day . To calculate the cost of something that costs a certain amount per day, you'd multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅ days, or 30 times the number of days . (Not sure why you'd translate it this way? Check out our lesson on writing algebraic expressions .)

$30 per day and $.50 per mile is $360

$30 ⋅ day + $.50 ⋅ mile = $360

As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50 , $.50 per mile became $.50 ⋅ mile , and is became = .

Next, we'll add in the numbers and variables we already know. We already know the number of days Jada drove, 2 , so we can replace that. We've also already said we'll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.

30 ⋅ 2 + .5 ⋅ m = 360

Now we have our expression. All that's left to do is solve it.

Step 4: Solve the problem.

This problem will take a few steps to solve. (If you're not sure how to do the math in this section, you might want to review our lesson on simplifying expressions .) First, let's simplify the expression as much as possible. We can multiply 30 and 2, so let's go ahead and do that. We can also write .5 ⋅ m as 0.5 m .

60 + .5m = 360

Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we'll know what m is equal to—in other words, it will let us know the number of miles in our word problem.

We can start by getting rid of the 60 on the left side by subtracting it from both sides .

The only thing left to get rid of is .5 . Since it's being multiplied with m , we'll do the reverse and divide both sides of the equation with it.

.5 m / .5 is m and 300 / 0.50 is 600 , so m = 600 . In other words, the answer to our problem is 600 —we now know Jada drove 600 miles.

Step 5: Check the problem.

To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got— 600 —and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada's distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let's take another look at the problem.

According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:

$30 per day and $0.50 per mile

30 ⋅ day + .5 ⋅ mile

30 ⋅ 2 + .5 ⋅ 600

According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We're done!

While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.

Let's practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:

If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.

Try completing this problem on your own. When you're done, move on to the next page to check your answer and see an explanation of the steps.

A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?

Here's another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?

Problem 1 Answer

Here's Problem 1:

A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?

Answer: $29

Let's solve this problem step by step. We'll solve it the same way we solved the problem on page 1.

Step 1: Read through the problem carefully

The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it . Let's look at the problem again. The question is right there in plain sight:

So is the information we'll need to answer the question:

• A single ticket costs $8 .
• The family pass costs $25 more than half the price of the single ticket.

Step 2: Represent the unknown numbers with variables

The unknown number in this problem is the cost of the family pass . We'll represent it with the variable f .

Step 3: Translate the rest of the problem

Let's look at the problem again. This time, the important facts are highlighted.

A single ticket to the fair costs $8 . A family pass costs $25 more than half that . How much does a family pass cost?

In other words, we could say that the cost of a family pass equals half of $8, plus $25 . To turn this into a problem we can solve, we'll have to translate it into math. Here's how:

• First, replace the cost of a family pass with our variable f .

f equals half of $8 plus $25

• Next, take out the dollar signs and replace words like plus and equals with operators.

f = half of 8 + 25

• Finally, translate the rest of the problem. Half of can be written as 1/2 times , or 1/2 ⋅ :

f = 1/2 ⋅ 8 + 25

Step 4: Solve the problem

Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.

• f is already alone on the left side of the equation, so all we have to do is calculate the right side.
• First, multiply 1/2 by 8 . 1/2 ⋅ 8 is 4 .
• Next, add 4 and 25. 4 + 25 equals 29 .

That's it! f is equal to 29. In other words, the cost of a family pass is $29 .

Step 5: Check your work

Finally, let's check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let's look at the original problem again.

We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.

• We could translate this into this equation, with s standing for the cost of a single ticket.

1/2s = 29 - 25

• Let's work on the right side first. 29 - 25 is 4 .
• To find the value of s , we have to get it alone on the left side of the equation. This means getting rid of 1/2 . To do this, we'll multiply each side by the inverse of 1/2: 2 .

According to our math, s = 8 . In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that's correct!

So now we're sure about the answer to our problem: The cost of a family pass is $29 .

Problem 2 Answer

Here's Problem 2:

Answer: $70

Let's go through this problem one step at a time.

Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it . What's the question here?

To solve the problem, you'll have to find out how much money Mo gave to charity. All the important information you need is in the problem:

• The amount Flor donated is three times as much the amount Mo donated
• Flor and Mo's donations add up to $280 total

The unknown number we're trying to identify in this problem is Mo's donation . We'll represent it with the variable m .

Here's the problem again. This time, the important facts are highlighted.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo . Between the two of them, they donated $280 . How much money did Mo give?

The important facts of the problem could also be expressed this way:

Mo's donation plus Flor's donation equals $280

Because we know that Flor's donation is three times as much as Mo's donation, we could go even further and say:

Mo's donation plus three times Mo's donation equals $280

We can translate this into a math problem in only a few steps. Here's how:

• Because we've already said we'll represent the amount of Mo's donation with the variable m , let's start by replacing Mo's donation with m .

m plus three times m equals $280

• Next, we can put in mathematical operators in place of certain words. We'll also take out the dollar sign.

m + three times m = 280

• Finally, let's write three times mathematically. Three times m can also be written as 3 ⋅ m , or just 3 m .

m + 3m = 280

It will only take a few steps to solve this problem.

• To get the correct answer, we'll have to get m alone on one side of the equation.
• To start, let's add m and 3 m . That's 4 m .
• We can get rid of the 4 next to the m by dividing both sides by 4. 4 m / 4 is m , and 280 / 4 is 70 .

We've got our answer: m = 70 . In other words, Mo donated $70 .

The answer to our problem is $70 , but we should check just to be sure. Let's look at our problem again.

If our answer is correct, $70 and three times $70 should add up to $280 .

• We can write our new equation like this:

70 + 3 ⋅ 70 = 280

• The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.

70 + 210 = 280

• The last step is to add 70 and 210. 70 plus 210 equals 280 .

280 is the combined cost of the tickets in our original problem. Our answer is correct : Mo gave $70 to charity.

/en/algebra-topics/distance-word-problems/content/

Solving Word Problems Using Algebra (Worksheet)

Related Topics & Worksheets: Algebra Worksheets Evaluate Algebraic Expressions by Substitution Worksheet

Objective: I know how to solve word problems using algebra.

Solve the following word problems: a) When 9 is subtracted from a number and then divided by 2, the answer is 4. What is the number? The number is b) The length of a rectangle is twice that of the width. The perimeter of the rectangle is 24 cm. What is the width of the rectangle? The width of the rectangle is cm c) Marcus, Sally and Sammy decided to share 20 sweets. Marcus took 8 sweets and Sally took three times as many as Sammy. How many sweets did Sammy receive? Sammy received sweets. d) If the sum of three consecutive numbers is 72, what is the largest number? The largest number is e) Andy is 2 times younger than his sister and his father is 25 years older than him. If the total of their ages is 53 years, what is Andy’s age and his father’s age? Andy is years old and his father is years old. f) The length and width of a rectangle are 7 cm and (x - 8) cm respectively. Find the value of x if the area of the rectangle is 42 cm2. The value of x is cm g) Carol is y years old and her daughter is 25 years younger. Find Carol’s present age if the sum of their ages in 6 years’ time is 75 years Carol’s age is h) Diana buys 20 apples at x cents each and 40 oranges at x + 10 cents. She packs them into bags containing 5 apples and 10 oranges and sells the bags for 20x cents each. Find out the amount that Diana paid for each apple if she obtained a total of $24 from selling all the fruits. The apple cost cents each

We hope that the free math worksheets have been helpful. We encourage parents and teachers to select the topics according to the needs of the child. For more difficult questions, the child may be encouraged to work out the problem on a piece of paper before entering the solution. We hope that the kids will also love the fun stuff and puzzles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Praxis Core Math

Course: praxis core math   >   unit 1.

• Algebraic properties | Lesson
• Algebraic properties | Worked example
• Solution procedures | Lesson
• Solution procedures | Worked example
• Equivalent expressions | Lesson
• Equivalent expressions | Worked example
• Creating expressions and equations | Lesson
• Creating expressions and equations | Worked example

Algebraic word problems | Lesson

• Algebraic word problems | Worked example
• Linear equations | Lesson
• Linear equations | Worked example
• Quadratic equations | Lesson
• Quadratic equations | Worked example

What are algebraic word problems?

What skills are needed.

• Translating sentences to equations
• Solving linear equations with one variable
• Evaluating algebraic expressions
• Solving problems using Venn diagrams

How do we solve algebraic word problems?

• Define a variable.
• Write an equation using the variable.
• Solve the equation.
• If the variable is not the answer to the word problem, use the variable to calculate the answer.

What's a Venn diagram?

• 7 + 10 − 13 = 4 ‍   brought both food and drinks.
• 7 − 4 = 3 ‍   brought only food.
• 10 − 4 = 6 ‍   brought only drinks.
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  
• (Choice A)   $ 4 ‍   A $ 4 ‍  
• (Choice B)   $ 5 ‍   B $ 5 ‍  
• (Choice C)   $ 9 ‍   C $ 9 ‍  
• (Choice D)   $ 14 ‍   D $ 14 ‍  
• (Choice E)   $ 20 ‍   E $ 20 ‍  
• (Choice A)   10 ‍   A 10 ‍  
• (Choice B)   12 ‍   B 12 ‍  
• (Choice C)   24 ‍   C 24 ‍  
• (Choice D)   30 ‍   D 30 ‍  
• (Choice E)   32 ‍   E 32 ‍  
• (Choice A)   4 ‍   A 4 ‍  
• (Choice B)   10 ‍   B 10 ‍  
• (Choice C)   14 ‍   C 14 ‍  
• (Choice D)   18 ‍   D 18 ‍  
• (Choice E)   22 ‍   E 22 ‍  

Things to remember

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

The Algebra Problem: How Middle School Math Became a National Flashpoint

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Sign up for The Morning newsletter from the New York Times

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system.

Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly 4 in 5 poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class.

San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’ administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12% of Black and Latino eighth graders do, compared with roughly 24% of white pupils, a federal report found.

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research. A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Massachusetts, the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80% from 60%. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100%, yes,” he added. “That was not something that I could live with.”

c.2024 The New York Times Company

Recommended Stories

Bulls' lonzo ball reveals he underwent rare meniscus transplant procedure on left knee.

Ball's plan is to be ready at the start of next season.

Reports: Colorado S Shilo Sanders, Deion's son, facing NIL questions after filing for bankruptcy, $12 million assault lawsuit

A high school security guard won $12 million judgement after alleging Shilo Sanders broke his neck in 2015.

Doctor Who: 73 Yards review: Don’t stand so close to me

'73 Yards' offers a darker twist on the Doctor-lite episode.

This $13 outlet extender solves the problem of 'too many devices, not enough space' — it's over 30% off

It's a no-brainer in a tech-heavy household, plus it has a 12-month replacement period.

Quiz: Scarlett Johansson takes on OpenAI, Ben Affleck and Jennifer Lopez make headlines, Elvis's home dodges foreclosure attempt

Test your knowledge about this week's entertainment headlines.

Unlike the Fitbit, this popular smartwatch tracks your blood pressure — and it's only $22 for Memorial Day

The budget-friendly gizmo also monitors calories burned, steps walked, heart rate and even how well you slept.

The UK passes its version of the EU's Digital Markets Act

The UK has passed its version of the European Union's Digital Markets Act (DMA). The Digital Markets, Competition and Consumers Bill aims to keep major companies, including in tech, in check.

The best Memorial Day deals over 50% off — save hundreds at Target, Wayfair, Macy's and more

Adidas, All-Clad, Coach, Staub: Get deep discounts on sneakers, kitchen gear, luggage, patio furniture and tech from all your favorite retailers.

Don't miss Dick's Sporting Goods' Memorial Day sale: Save up to 50% on Nike, Yeti, Solo Stove and more

From a $7 logo chair to a North Face duffel bag that's over $50 off, these 10 deals are worth checking out.

'Less hair is going in the trash': The detangling brush loved by over 59,000 shoppers is on sale for as low as $10

The secret to a tangle-free mane — grab it while it's 50% off.

Smelly fridge? This deodorizer can keep it fresh for 10 years — and it's on sale for just $20

'I've tried many, many baking soda boxes over the years … and this little gem is it!' says one fan.

Russia can reportedly jam Ukraine’s access to Starlink at will

Russia has reportedly found new, more effective ways to knock out Ukraine’s Starlink service. The increased interference has disrupted communications at critical moments and is posing “a major threat to Ukraine.”

AEW Double or Nothing predictions, preview: Mercedes Moné says 'I'm ready to go' ahead of in-ring debut for Tony Khan's company

Mercedes Moné will make her AEW in-ring debut at 'Double or Nothing.' It's also her first match since suffering a severe ankle injury in 2023.

The 'Doge' dog has died

The Dogecoin dog has passed away. Kabosu, an adorable shiba inu, was likely around 18 years old.

Women in AI: Chinasa T. Okolo researches AI's impact on the Global South

To give AI-focused women academics and others their well-deserved — and overdue — time in the spotlight, TechCrunch has been publishing a series of interviews focused on remarkable women who’ve contributed to the AI revolution. Chinasa T. Okolo is a fellow at the Brookings Instutition in the Center of Technology Innovation's Governance Studies program. Before that, she served on the ethics and social impact committee that helped develop Nigeria's National Artificial Intelligence Strategy and has served as an AI policy and ethics advisor for various organizations, including the Africa Union Development Agency and the Quebec Artificial Intelligence Institute.

Nintendo is finally opening a second US store

Nintendo is opening its second official US store in San Francisco next year. The original New York location opened all the way back in 2005.

2024 Kicker rankings for fantasy football

The Yahoo Fantasy football analysts reveal their first kicker rankings for the 2024 NFL season.

This luxe Intex float has a removable canopy and it's over 25% off: 'An absolute dream'

Here's your ticket to idyllic idling! There's room for two ... but we say this baby's all for you: 'Like a little vacay.'

I cover fashion for a living — these are the best Memorial Day sales I've found at Amazon, Walmart, Hoka and more

Save up to 70% on staples like flattering swimsuits, fan-favorite shorts, top-selling sneakers and a breezy cooling bra.

I run hotter than Hades, but this neck fan kept me cool during a Disney heat wave — it's just $26 at Amazon

Over 32,000 five-star reviewers agree — this handy rechargeable cooling gadget is a hot weather must-have.

Man explains why we learn complex math problems that we'll never use in our lifetime

Usually, when asked about one subject that is the most complicated or least favorite, many people would instantly answer, "Mathematics." It is a common argument among many students that how learning math is pointless because they never use it in their future jobs. To some extent, it might be true. Unless our job demands us to solve mathematical problems, we never even have to think about calculus, algebra, trigonometry and other concepts we learned in school. However, this math enthusiast Hamza Alsamraee, a Stanford alumnus who majored in the subject, provided an answer for this argument through his LinkedIn post .

Being a math major, Alsamraee  agreed with  many who say they would never be solving elaborate problems at work. "I'll never solve a partial differential equation for work. But why is that the standard we judge the value of learning by?" he wrote. To this Stanford alumnus, saying that the college math we learned was "inapplicable in the real world" seemed silly. "College isn't a vocational training program. It's meant to provoke your curiosity, to expand your horizons," pointed out Alsamraee. Also, for those who think that college should only teach things that are accurately applicable to real-world jobs, he wrote, "If you want 'real world' learning, go to a boot camp/trade school, etc. There's nothing wrong with that. But trying to turn college into trade school is stupid ."

Alsamraee, the founder of a tech company called NewForm , also emphasized that the "useless" math concepts are the ones that  help us learn how to think. "How to analyze problems. How to weigh different perspectives. It's not a surprise the smartest people I've met in business also happen to have a lot of 'useless' knowledge," he wrote. As per the math enthusiast, "Curiosity shouldn't be constrained by capitalist pursuit." He mentioned that if people let capitalism control what we learn, we would end up being a "noninteresting person with little ability to think laterally" and that an AI agent will be outperforming us soon. "Go read about philosophy, math, history, whatever intrigues you. Who cares if it makes you money? It'll make you human," he concluded.

Men over forty share 10 valuable tips for men in their 30s and it's good advice

His post went viral, garnering over 15K on the platform. Later, Maheshwari Peri ( @maheshperi) shared it on X (previously Twitter), where it gained over 172K views after a student asked them why they had to learn trigonometry as it doesn't have real-life applicability. Not long after, people started sharing their views. "The response makes sense. Learning new unknown things opens up avenues and triggers curiosity. However, Trigonometry has real-life uses too. Without knowing Pythagoras's theorem, one might always take longer routes while they can reach their destination diagonally," commented @maddyb65 .

"It's laughable when someone says Trignometry and PDE have no real-world applicability. Just because students are not taught 'direct application' in class, does not mean there is no application in the world," wrote  @shivakjolad . "He's articulated his argument so well. Now we need systems of education and evaluation that force us to think and question," commented  @sammoorthy21 .

Speaking of college-level math, a Harvard math entrance exam from 1869 has been making its rounds on the internet. A Canadian mathematician and professor, Anthony Bonato ( @Anthony_Bonato ), shared those math questions pointing out that the calculator was not allowed back then. This left the internet flabbergasted, with many feeling lucky they now have access to calculators during math exams.

People share 10 common things from 50 years ago that only rich people can afford in today's time

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Ireland, Spain and Norway recognizing a Palestinian state

Antarctica's "doomsday glacier" undergoing "vigorous ice melt," study finds

Man finds ancient mammoth bones in his wine cellar

Uvalde victims' families sue Meta, video game company and gun manufacturer

To revisit this article, visit My Profile, then View saved stories .

• Backchannel
• Newsletters
• WIRED Insider
• WIRED Consulting

Julian Chokkattu

With Gemini on Android, Google Points to Mobile Computing’s Future—and Past

Nearly a decade ago, Google showed off a feature called Now on Tap in Android Marshmallow—tap and hold the home button and Google will surface helpful contextual information related to what’s on the screen. Talking about a movie with a friend over text? Now on Tap could get you details about the title without having to leave the messaging app. Looking at a restaurant in Yelp? The phone could surface OpenTable recommendations with just a tap.

I was fresh out of college, and these improvements felt exciting and magical—its ability to understand what was on the screen and predict the actions you might want to take felt future-facing. It was one of my favorite Android features. It slowly morphed into Google Assistant, which was great in its own right, but not quite the same.

Today, at Google’s I/O developer conference in Mountain View, California, the new features Google is touting in its Android operating system feel like the Now on Tap of old—allowing you to harness contextual information around you to make using your phone a bit easier. Except this time, these features are powered by a decade’s worth of advancements in large language models.

“I think what’s exciting is we now have the technology to build really exciting assistants,” Dave Burke, vice president of engineering on Android, tells me over a Google Meet video call. “We need to be able to have a computer system that understands what it sees and I don't think we had the technology back then to do it well. Now we do.”

I got a chance to speak with Burke and Sameer Samat, president of the Android ecosystem at Google, about what's new in the world of Android, the company's new AI assistant Gemini , and what it all holds for the future of the OS. Samat referred to these updates as a “once-in-a-generational opportunity to reimagine what the phone can do, and to rethink all of Android.”

Circle to Search … Your Homework

The upgraded Circle to Search in action.

It starts with Circle to Search, which is Google’s new way of approaching Search on mobile. Much like the experience of Now on Tap, Circle to Search—which the company debuted a few months ago—is more interactive than just typing into a search box. (You literally circle what you want to search on the screen.) Burke says, “It’s a very visceral, fun, and modern way to search … It skews younger as well because it’s so fun to use.”

Samat claims Google has received positive feedback from consumers, but Circle to Search’s latest feature hails specifically from student feedback. Circle to Search can now be used on physics and math problems when a user circles them—Google will spit out step-by-step instructions on completing the problems without the user leaving the syllabus app.

Samat made it clear Gemini wasn't just providing answers but was showing students how to solve the problems. Later this year, Circle to Search will be able to solve more complex problems like diagrams and graphs. This is all powered by Google's LearnLM models, which are fine-tuned for education.

Gemini Gets More Contextual on Android

Gemini is Google’s AI assistant that is in many ways eclipsing Google Assistant. Really—when you fire up Google Assistant on most Android phones these days, there's an option to replace it with Gemini instead. So naturally, I asked Burke and Samat whether this meant Assistant was heading to the Google Graveyard .

“The way to look at it is that Gemini is an opt-in experience on the phone,” Samat says. “I think obviously over time Gemini is becoming more advanced and is evolving. We don’t have anything to announce today, but there is a choice for consumers if they want to opt into this new AI-powered assistant. They can try it out and we are seeing that people are doing that and we're getting a lot of great feedback.”

By Carlton Reid

By David Nield

By Scott Gilbertson

By Boone Ashworth

With a coming update, you'll be able to drag AI-generated images into emails and messages.

At I/O, the updates to Gemini on Android are to make it more contextually aware, just like Now on Tap nearly a decade ago. Later this year, you’ll be able to generate images with Gemini and drag and drop them into apps like Gmail or Google Messages. Burke showed me an example of Gemini generating an image of tennis with pickles; he was responding to someone's text about playing pickleball . He hailed Gemini—which popped up as an overlay over the messaging app—asked it to generate the image, and then dragged one and dropped it in the chat.

You'll be able to ask Gemini to pull specific bits of information out of a video.

He then pulled up a YouTube video on pickleball rules. Call up Gemini while watching and you'll see a prompt to “Ask this video.” This lets you employ Gemini to find specific information in the video without scrubbing through the whole thing yourself. (Who has time for that?) Burke asked about a specific pickleball rule, and Gemini quickly spat out an answer based on the video. This “summarize” functionality has been the hallmark of many AI tools—summarizing PDFs, videos, memos, and news stories (yay).

Text summaries of videos may prove helpful.

Speaking of PDFs, you’ll soon be able to attach a PDF to Gemini (there will be a prompt for “Ask this PDF”) and Gemini can deliver specific information, saving you the need to scroll through several pages. Burke says these features are rolling out to millions of devices over the next few months, though the PDF feature will only be available for Gemini Advanced users—folks paying for the $20 per month subscription to access the cutting-edge capabilities of Google's AI models.

Gemini in general will show more “dynamic suggestions” based on what’s happening on the screen. These will pop up right above the Gemini overlay when you activate the assistant.

Gemini Nano Gets an Upgrade

Gemini Nano is Google’s large language model powering select on-device features on certain phones, like the Pixel 8 series , Samsung Galaxy S24 range , and even the new Pixel 8A . Running these as on-device features means data does not need to be sent to the cloud, making the features more private. They can even work offline too.

Nano currently powers features like Summarize in Google’s Recorder app, which summarizes transcriptions, and Smart Reply in select messaging apps, which offers more contextual auto-replies to messages. Google's newer version of the model—Gemini Nano with Multimodality—will arrive this year, starting with Pixel phones. It’s a bit of a mouthful, but it more or less means Gemini Nano will be able to do more than just process text.

“It's a 3.8 billion parameter model and it's multimodal—this is the first on-device built-in multimodal model,” Burke says. “It's very powerful. It hits, on academic benchmarks, around 80 percent of Gemini 1.0, which is pretty amazing for a small model.”

Google's screen reader will get an upgrade to better understand and describe images.

This model will now power Google’s existing TalkBack screen reader feature on Android, which helps blind and low-vision users understand what’s on the screen. Gemini Nano will purportedly offer richer and more precise descriptions of what’s in each image. Google says on average, TalkBalk users see “90 unlabeled images per day,” but Gemini can fill the gap as it’ll be able to visualize and understand the images on the screen and describe them even when the user is offline.

Google has poured many of its AI smarts over the past few years into improving its call screening technology to limit robocalls, and Gemini Nano with Multimodality will soon help you avoid phone scams—in real time. A new feature called Scam Detection will have Gemini listening in your phone calls, and if it picks up on certain phrases or requests from the person on the other end, it will issue an alert that you’re likely in the middle of a scam call. Burke says this model was trained on data from websites like BanksNeverAskThat.com to learn what a bank wouldn’t ask you—and the types of things scammers typically ask for. He says all of this listening and detection happens on-device, so it’s private. We'll hear more about this “opt-in feature” later this year.

Unusually, Google says it will be unveiling a few new Android features tomorrow rather than compressing all of the new stuff into today’s announcements, so stay tuned for more. (Update: The rest of those new Android features have been unveiled; here's a roundup .)

With the rise of AI hardware gadgets vying to replace your smartphone—and the talk of app-less generative interfaces —I asked Samat how he sees Android changing in the next five years. He's excited to see the innovation from new and existing companies trying new things—and that Google is “trying a lot of things internally” too. But he boiled things down to an analogy with the automotive space.

If you buy a car, you've come to expect certain standard features, like a steering wheel. But with AI, one giant leap would be to take away those features—no steering wheel, no interfaces. “Some people would be excited by that, some people would not be excited by that.” He believes certain functions we do on our phones will be more assistive than ever with the help of AI—and we can expect some features to be replaced in that way.

“As that continues, what we will find—and we’re already seeing this in our own testing—is there are opportunities to fundamentally transform the UI in certain areas where it tips over from the point of, ‘OK, that’s really assistive,’ to ‘Actually, there should be an entirely new way of doing this.’ That’s what’s fun and exciting about right now. It’s an amazing time to be working on this technology.”

You Might Also Like …

In your inbox: Will Knight's Fast Forward explores advances in AI

Indian voters are being bombarded with millions of deepfakes

They bought tablets in prison —and found a broken promise

The one thing that’s holding back the heat pump

It's always sunny: Here are the best sunglasses for every adventure

Boone Ashworth

Lauren Goode

David Nield

Michael Calore

Matt Burgess

WIRED COUPONS

Extra 20% Off Select Dyson Technology With Owner Rewards

Capture More Savings: up to 15% off GoPro cameras

Get Up To Extra 45% Off - May Secret Sale

5% Off Everything With Dell Coupon Code

VistaPrint Coupon Code: 20% Off Select Signage

Newegg Coupon - 10% Off