how to solve a problem with x and y

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

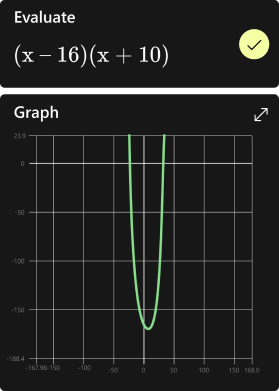
Graph your math problems

Practice, practice, practice

Get math help in your language

Game Central

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Online Equation Solver

Solve linear, quadratic and polynomial systems of equations with wolfram|alpha.

• Natural Language

More than just an online equation solver

Wolfram|Alpha is a great tool for finding polynomial roots and solving systems of equations. It also factors polynomials, plots polynomial solution sets and inequalities and more.

Learn more about:

• Equation solving

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to formulate queries.

• find roots to quadratic x^2-7x+12
• plot inequality x^2-7x+12<=0
• solve {3x-5y==2,x+2y==-1}
• plot inequality 3x-5y>=2 and x+2y<=-1
• solve 3x^2-y^2==2 and x+2y^2==5
• plot 3x^2-y^2>=2 and x+2y^2<=5
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

About solving equations

A value is said to be a root of a polynomial if ..

The largest exponent of appearing in is called the degree of . If has degree , then it is well known that there are roots, once one takes into account multiplicity. To understand what is meant by multiplicity, take, for example, . This polynomial is considered to have two roots, both equal to 3.

One learns about the "factor theorem," typically in a second course on algebra, as a way to find all roots that are rational numbers. One also learns how to find roots of all quadratic polynomials, using square roots (arising from the discriminant) when necessary. There are more advanced formulas for expressing roots of cubic and quartic polynomials, and also a number of numeric methods for approximating roots of arbitrary polynomials. These use methods from complex analysis as well as sophisticated numerical algorithms, and indeed, this is an area of ongoing research and development.

Systems of linear equations are often solved using Gaussian elimination or related methods. This too is typically encountered in secondary or college math curricula. More advanced methods are needed to find roots of simultaneous systems of nonlinear equations. Similar remarks hold for working with systems of inequalities: the linear case can be handled using methods covered in linear algebra courses, whereas higher-degree polynomial systems typically require more sophisticated computational tools.

How Wolfram|Alpha solves equations

For equation solving, Wolfram|Alpha calls the Wolfram Language's Solve and Reduce functions, which contain a broad range of methods for all kinds of algebra, from basic linear and quadratic equations to multivariate nonlinear systems. In some cases, linear algebra methods such as Gaussian elimination are used, with optimizations to increase speed and reliability. Other operations rely on theorems and algorithms from number theory, abstract algebra and other advanced fields to compute results. These methods are carefully designed and chosen to enable Wolfram|Alpha to solve the greatest variety of problems while also minimizing computation time.

Although such methods are useful for direct solutions, it is also important for the system to understand how a human would solve the same problem. As a result, Wolfram|Alpha also has separate algorithms to show algebraic operations step by step using classic techniques that are easy for humans to recognize and follow. This includes elimination, substitution, the quadratic formula, Cramer's rule and many more.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Systems of Algebraic Equations Containing Two Variables

Last Updated: July 30, 2023 Fact Checked

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,068,906 times.

In a "system of equations," you are asked to solve two or more equations at the same time. When these have two different variables in them, such as x and y, or a and b, it can be tricky at first glance to see how to solve them. [1] X Research source Fortunately, once you know what to do, all you need is basic algebra skills (and sometimes some knowledge of fractions) to solve the problem. If you are a visual learner or if your teacher requires it, learn how to graph the equations as well. Graphing can be useful to "see what's going on" or to check your work, but it can be slower than the other methods, and doesn't work well for all systems of equations.

Using the Substitution Method

• This method often uses fractions later on. You can try the elimination method below instead if you don't like fractions.

• 4x = 8 - 2y
• (4x)/4 = (8/4) - (2y/4)

• You know that x = 2 - ½y .
• Your second equation, that you haven't yet altered, is 5x + 3y = 9 .
• In the second equation, replace x with "2 - ½y": 5(2 - ½y) + 3y = 9 .

• 5(2 - ½y) + 3y = 9
• 10 – (5/2)y + 3y = 9
• 10 – (5/2)y + (6/2)y = 9 (If you don't understand this step, learn how to add fractions . This is often, but not always, necessary for this method.)
• 10 + ½y = 9

• You know that y = -2
• One of the original equations is 4x + 2y = 8 . (You can use either equation for this step.)
• Plug in -2 instead of y: 4x + 2(-2) = 8 .

• If you end up with an equation that has no variables and isn't true (for instance, 3 = 5), the problem has no solution . (If you graphed both of the equations, you'd see they were parallel and never intersect.)
• If you end up with an equation without variables that is true (such as 3 = 3), the problem has infinite solutions . The two equations are exactly equal to each other. (If you graphed the two equations, you'd see they were the same line.)

Using the Elimination Method

• You have the system of equations 3x - y = 3 and -x + 2y = 4 .
• Let's change the first equation so that the y variable will cancel out. (You can choose x instead, and you'll get the same answer in the end.)
• The - y on the first equation needs to cancel with the + 2y in the second equation. We can make this happen by multiplying - y by 2.
• Multiply both sides of the first equation by 2, like this: 2(3x - y)=2(3) , so 6x - 2y = 6 . Now the - 2y will cancel out with the +2y in the second equation.

• Your equations are 6x - 2y = 6 and -x + 2y = 4 .
• Combine the left sides: 6x - 2y - x + 2y = ?
• Combine the right sides: 6x - 2y - x + 2y = 6 + 4 .

• You have 6x - 2y - x + 2y = 6 + 4 .
• Group the x and y variables together: 6x - x - 2y + 2y = 6 + 4 .
• Simplify: 5x = 10
• Solve for x: (5x)/5 = 10/5 , so x = 2 .

• You know that x = 2 , and one of your original equations is 3x - y = 3 .
• Plug in 2 instead of x: 3(2) - y = 3 .
• Solve for y in the equation: 6 - y = 3
• 6 - y + y = 3 + y , so 6 = 3 + y

• If your combined equation has no variables and is not true (like 2 = 7), there is no solution that will work on both equations. (If you graph both equations, you'll see they're parallel and never cross.)
• If your combined equation has no variables and is true (like 0 = 0), there are infinite solutions . The two equations are actually identical. (If you graph them, you'll see that they're the same line.)

Graphing the Equations

• The basic idea is to graph both equations, and find the point where they intersect. The x and y values at this point will give us the value of x and the value of y in the system of equations.

• Your first equation is 2x + y = 5 . Change this to y = -2x + 5 .
• Your second equation is -3x + 6y = 0 . Change this to 6y = 3x + 0 , then simplify to y = ½x + 0 .
• If both equations are identical , the entire line will be an "intersection". Write infinite solutions .

• If you don't have graph paper, use a ruler to make sure the numbers are spaced precisely apart.
• If you are using large numbers or decimals, you may need to scale your graph differently. (For example, 10, 20, 30 or 0.1, 0.2, 0.3 instead of 1, 2, 3).

• In our examples from earlier, one line ( y = -2x + 5 ) intercepts the y-axis at 5 . The other ( y = ½x + 0 ) intercepts at 0 . (These are points (0,5) and (0,0) on the graph.)
• Use different colored pens or pencils if possible for the two lines.

• In our example, the line y = -2x + 5 has a slope of -2 . At x = 1, the line moves down 2 from the point at x = 0. Draw the line segment between (0,5) and (1,3).
• The line y = ½x + 0 has a slope of ½ . At x = 1, the line moves up ½ from the point at x=0. Draw the line segment between (0,0) and (1,½).
• If the lines have the same slope , the lines will never intersect, so there is no answer to the system of equations. Write no solution .

• If the lines are moving toward each other, keep plotting points in that direction.
• If the lines are moving away from each other, move back and plot points in the other direction, starting at x = -1.
• If the lines are nowhere near each other, try jumping ahead and plotting more distant points, such as at x = 10.

Practice Problems and Answers

Community Q&A

• You can check your work by plugging the answers back into the original equations. If the equations end up true (for instance, 3 = 3), your answer is correct. Thanks Helpful 3 Not Helpful 1
• In the elimination method, you will sometimes have to multiply one equation by a negative number in order to get a variable to cancel out. Thanks Helpful 1 Not Helpful 1

• These methods cannot be used if there is a variable raised to an exponent, such as x 2 . For more information on equations of this type, look up a guide to factoring quadratics with two variables. [11] X Research source Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ https://www.mathsisfun.com/definitions/system-of-equations.html
• ↑ https://calcworkshop.com/systems-equations/substitution-method/
• ↑ https://www.cuemath.com/algebra/substitution-method/
• ↑ https://tutorial.math.lamar.edu/Classes/Alg/SystemsTwoVrble.aspx
• ↑ http://www.purplemath.com/modules/systlin2.htm
• ↑ http://www.virtualnerd.com/algebra-2/linear-systems/graphing/solve-by-graphing/equations-solution-by-graphing
• ↑ https://www.khanacademy.org/math/algebra/multiplying-factoring-expression/factoring-quadratics-in-two-vari/v/factoring-quadratics-with-two-variables

About This Article

To solve systems of algebraic equations containing two variables, start by moving the variables to different sides of the equation. Then, divide both sides of the equation by one of the variables to solve for that variable. Next, take that number and plug it into the formula to solve for the other variable. Finally, take your answer and plug it into the original equation to solve for the other variable. To learn how to solve systems of algebraic equations using the elimination method, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Jan 8, 2018

Did this article help you?

Jul 24, 2017

Kaurovandu Uozondo

Apr 19, 2018

Nahid Shafreen Shareef

Feb 12, 2018

May 15, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 5

• Intro to slope-intercept form

Slope and y-intercept from equation

• Worked examples: slope-intercept intro
• Slope-intercept intro
• Linear equation word problems
• Linear equations word problems

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Solve for x

Solve for x is all related to finding the value of x in an equation of one variable that is x or with different variables like finding x in terms of y. When we find the value of x and substitute it in the equation, we should get L.H.S = R.H.S.

What Does Solve for x Mean?

Solve for x means finding the value of x for which the equation holds true. i.e when we find the value of x and substitute in the equation, we should get L.H.S = R.H.S If I ask you to solve the equation 'x + 1 = 2' that would mean finding some value for x that satisfies the equation. Do you think x = 1 is the solution to this equation? Substitute it in the equation and see. 1 + 1 = 2 2 = 2 L.H.S = R.H.S That’s what solving for x is all about.

How Do You Solve for x?

To solve for x, bring the variable to one side, and bring all the remaining values to the other side by applying arithmetic operations on both sides of the equation. Simplify the values to find the result. Let’s start with a simple equation as, x + 2 = 7 How do you get x by itself? Subtract 2 from both sides ⇒ x + 2 - 2 = 7 - 2 ⇒ x = 5 Now, check the answer, x = 5 by substituting it back into the equation. We get 5 + 2= 7. L.H.S = R.H.S

Solve for x in the Triangle

Solve for x" the unknown side or angle in a triangle we can use properties of triangle or the Pythagorean theorem.

Let us understand solve for x in a triangle with the help of an example.

△ ABC is right-angled at B with two of its legs measuring 7 units and 24 units. Find the hypotenuse x.

In △ABC by using the Pythagorean theorem,

we get AC 2 = AB 2 + BC 2

⇒ x 2 = 7 2 + 24 2

⇒ x 2 = 49 + 576

⇒ x 2 = 625

⇒ x = 25 units

Solve for x to find Missing Angle of Triangle

Suppose angle A = 50°, angle B = 60°, and angle C = x are the angles of a triangle. ABC. By using the angle sum property we can find the value of x.

angle A + angle B + angle C = 180 degrees.

50° + 60° + x° = 180° ⇒ x = 70°

Solve for x in Fractions

Solve for x in fractions , we simply do the cross multiplication and simplify the equation to find x.

For example: Solve for x for equation ⇒ 2/5 = x/10.

Cross multiply the fractions ⇒ 2 × 10 = 5 × x Solve the equation for x ⇒ x = 20 / 5 Simplify for x ⇒ x = 4 To verify the x value put the result, 4 back into the given equation ⇒ 2/5 = 4/10 Cross multiply the fractions ⇒ 2 × 10 = 4 × 5 ⇒ 20 = 20 L.H.S = R.H.S

Solve for x Equations

We can use a system of equations solver to find the value of x when we have equations with different variables.

We solve one of the equations for the x variable (solve for x in terms of y) and then substitute it in the second equation, and then solve for the y variable.

Finally, we substitute the value of the x variable that we found in one of the equations and solve for the other variable.

Let us understand solve for x and y with the help of an example.

For example, Solve for x: 2x - y = 5, 3x + 2y = 11

⇒ 2x - y = 5

Adding y on both sides we get,

⇒ 2x - y + y = 5 + y

⇒ 2x = 5 + y

⇒ x = (5 + y) / 2

Above equation is known as x in terms of y.

Substitute x = (5 + y) / 2 in second equation 3(5 + y) / 2 + 2y = 11

⇒ (15 + 3y) / 2 + 2y = 11

⇒ (15 + 3y + 4y) / 2 = 11

⇒ (15 + 7y) / 2 = 11

⇒15 +7y = 22

⇒ 7y = 22 - 15

Now, substitute y = 1 in x = (5+y) / 2

⇒ x = (5 + 1) / 2

⇒ 6 / 2 = 3

Thus, the solution of the given system of equations is x = 3 and y = 1.

Important Notes on Solve for x

• To solve for x (the unknown variable in the equation), apply arithmetic operations to isolate the variable.
• For solving 'x' number of equations we need exactly 'x' number of variables.
• Solve for x and y can be done by the substitution method, elimination method, cross-multiplication method, etc.

☛ Related Articles

Here is a solve for x calculator for you to get your answers quickly. Try now. Also, check out these interesting articles to know more about solve for x.

• System of Equations Solver
• Polynomial Equations
• Linear Equations
• Linear Equations in Two Variables

Solve for x Examples

Example1: Solve for x: 2 ( 3x + 1 ) + 3 ( 5x + 2 ) = x - 1

Solution: 2 (3x + 1) + 3 (5x + 2) = x - 1

⇒ 6x + 2 + 15x + 6 = x - 1

⇒ 8 + 21x = x - 1

⇒ x = -9/20

Example 2: It is given that x is the one side of the chessboard and it is smaller than its perimeter by 18 inches. Form an equation and solve for x?

Solution: The side of chessboard = 'x' inches

Since the chessboard is square (all sides are equal), therefore its perimeter will be '4x' inches

According to the given condition,

Perimeter = x + 18

⇒ 4x = x + 18

⇒ 4x - x = 18

The side of the chessboard is 6 inches.

Example 3: The ages of Roony and Herald are 5x and 7x. If four years later, the sum of their ages will be 56 years, then form an equation and solve for x.

Solution: The Rooney and Herald's age is 5x and 7x.

The sum of their ages after 4 years = 56

According to given condition,

⇒ (5x+4) + (7x+4) = 56

⇒ 5x + 7x + 4 + 4 = 56

⇒ 12x + 8 = 56

⇒ 12x = 56 - 8

⇒ x = 48/12

⇒ x = 4 The age of Roony = 5 × 4 = 20 years The age of Herald = 7× 4 = 28 years

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions

go to slide go to slide

FAQs on Solve For x

How do you solve for x in a bracket.

To solve for x in a bracket we use distributive law and remove the bracket, move all the x terms to one side and constant to the other side and find the unknown x. For example, 2(x−3) = 4 By using distributive law, 2x - 6 = 4 ⇒ 2x = 4 + 6 ⇒ 2x = 10 ⇒ x = 10/2 ⇒ x = 5

How Do You Solve for x in a Fraction?

To solve for x in fractions we have to eliminate the denominator by cross multiplication and then solve for x. For example, x/4 + 1/2 = 5/2 ⇒ (2x+4)/8 = 5/2 By doing cross multiplication we get, 2(2x + 4) = 8(5) ⇒ 4x + 8 = 40 ⇒ 4x = 40 - 8 ⇒ 4x = 32 ⇒ x = 32 / 4 ⇒ x = 8

How Do You Solve for x for the Equation 4x + 2 = -8?

To solve for x follow the points.

• Start with 4x + 2 = -8
• Subtract 2 from both sides: 4x = -8 - 2 = -10
• Divide by 4: x = -10 ÷ 4 = -5/2

How Do You Solve for x for the Equation 3x - 7 = 26?

• Start with 3x - 7 = 26
• Add 7 to both sides: 3x - 7 + 7 = 26 + 7
• Calculate: 3x = 33
• Divide by 3: x = 33 ÷ 3

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.