how to solve sat math problems

Choose Your Test

Sat / act prep online guides and tips, the complete guide to sat math word problems.

About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.

This post will be your complete guide to SAT Math word problems. We'll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.

Feature Image: Antonio Litterio /Wikimedia

What Are SAT Math Word Problems?

A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.

You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.

Secondly, these types of questions allow test makers to ask questions that'd be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it'd be difficult to demonstrate and ask this with only a diagram.

Translating Math Word Problems Into Equations or Drawings

In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.

For instance, the word "sum" means the value when two or more items are added together. So if you need to find the sum of a and b , you’ll need to set up your equation like this: a+b.

Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.

Here is a chart with all the key terms and symbols you should know for SAT Math word problems:

Now, let's look at these math terms in action using a few official examples:

We can solve this problem by translating the information we're given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let's write this out in algebraic form.

We'll say that the number of salads sold = S , and the number of drinks sold = D . The problem tells us that 209 salads and drinks have been sold, which we can think of as this:

S + D = 209

Finally, we've been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don't know the exact numbers of S and D , but we do know how much each unit costs. Therefore, we can write this equation:

6.50 S + 2 D = 836.5

We now have two equations with the same variables ( S and D ). Since we want to know how many salads were sold, we'll need to solve for D so that we can use this information to solve for S . The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S :

Now, just subtract S from both sides to get what D equals:

D = 209 − S

Finally, plug this expression in for D into our other equation, and then solve for S :

6.50 S + 2(209 − S ) = 836.5

6.50 S + 418 − 2 S = 836.5

6.50 S − 2 S = 418.5

4.5 S = 418.5

The correct answer choice is (B) 93.

This word problem asks us to solve for one possible solution (it asks for "a possible amount"), so we know right away that there will be multiple correct answers.

Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.

If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.

Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.

Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.

Typical SAT Word Problems

Word problems on the SAT can be grouped into three major categories:

• Word problems for which you must simply set up an equation
• Word problems for which you must solve for a specific value
• Word problems for which you must define the meaning of a value or variable

Below, we look at each world problem type and give you examples.

Word Problem Type 1: Setting Up an Equation

This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You'll also most likely see it first on the section.

For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.

Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.

To solve this problem, we'll need to know both Armand's and Tyrone's situations, so let's look at them separately:

Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m —the number of texts he sent per hour multiplied by the total number of hours he texted.

Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4 p —the number of texts he sent per hour multiplied by the total number of hours he texted.

We now know that Armand's situation can be written algebraically as 5m , and Tyrone's can be written as 4 p . Since we're being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:

The correct answer is choice (C) 5m + 4 p

Word Problem Type 2: Solving for a Missing Value

The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.

Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics , such as averages , single-variable equations , and ratios . You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.

Let's try to think about this problem in terms of x . If Type A trees produced 20% more pears than Type B did, we can write this as an expression:

x + 0.2 x = 1.2 x = # of pears produced by Type A

In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2 x ) to x , we get the number of pears produced by Type A trees.

The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2 x is equal to the number of pears produced by Type A, we can write the following equation:

1.2 x = 144

Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:

x = 144 / 1.2

The correct answer choice is (B) 120.

You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math . )

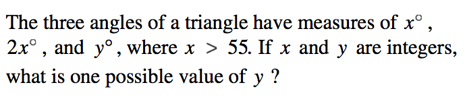
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.

Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it's the smallest integer larger than 55. Basically, it's a safe bet!)

Now, because x = 56, the next angle in the triangle—2 x —must measure the following:

Let's make a rough (not to scale) sketch of what we know so far:

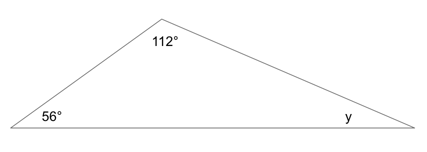
Now, we know that there are 180° in a triangle , so we can find the value of y by saying this:

y = 180 − 112 − 56

One possible value for y is 12. (Other possible values are 3, 6, and 9. )

Word Problem Type 3: Explaining the Meaning of a Variable or Value

This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.

This question might sound tricky at first, but it's actually quite simple.

We know tha t P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she's worked 0 days (i.e., if we plug 0 into the equation), here's what we get:

P = 108 − 23(0)

This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.

To help juggle all the various SAT word problems, let's look at the math strategies and tips at our disposal.

SAT Math Strategies for Word Problems

Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.

#1: Draw It Out

Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you're working with. For instance, let's look at how a picture can help you solve a word problem about a circle (specifically, a pizza):

If you often have trouble visualizing problems such as these, draw it out. We know that we're dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.

Because we'll need to solve the weight of each slice in ounces, let's first convert the total weight of our pizza from pounds into ounces. We're given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:

3 * 16 = 48 ounces (for whole pizza)

Now, let's draw a picture. First, the pizza is divided in half (not drawn to scale):

We now have two equal-sized pieces. Let's continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):

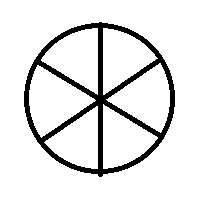
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:

48 / 6 = 8 ounces per piece

The correct answer choice is (C) 8.

As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.

#2: Memorize Key Terms

If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.

There are free SAT Math questions available online , so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.

#3: Underline and/or Write Out Important Information

The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.

One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.

#4: Pay Close Attention to What's Being Asked

It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.

Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?

It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.

#5: Brush Up on Any Specific Math Topic You Feel Weak In

You're likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.

For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!

Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now's a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!

All set? Let's go!

Test Your SAT Math Word Problem Knowledge

Finally, it's time to test your word problem know-how against real SAT Math problems:

Word Problems

1. No Calculator

2. Calculator OK

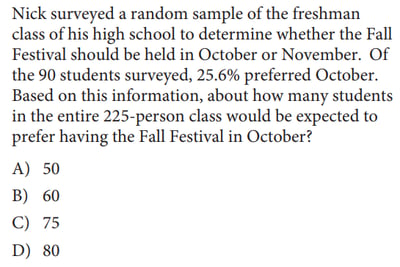
3. Calculator OK

4. Calculator OK

Answers: C, B, A, 1160

Answer Explanations

1. For this problem, we have to use the information we're given to set up an equation.

We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:

Ken and Paul split the bill evenly. This means that we'll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken's sandwich cost x dollars and Paul's cost x + 1, here's what our equation looks like when we combine the two expressions:

Now, we can divide this expression by 2 to get the price each person paid:

(2 x + 1) / 2

But we're not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:

( x + 0.5) + 0.2( x + 0.5)

x + 0.5 + 0.2 x + 0.1

1.2 x + 0.6

The correct answer choice is (C) 1.2 x + 0.6

2. You'll have to be familiar with statistics in order to understand what this question is asking.

Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.

Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:

225 * 0.256 = 57.6

Since the question is asking "about how many students"—and since we obviously can't have a fraction of a person!—we'll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).

3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don't be scared—it's actually not as difficult as it appears!

First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here's what happens to the equation when we plug in 0 for t :

h (0) = -16(0)2 + 110(0) + 72

h (0) = 0 + 0 + 72

As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).

4. You might be tempted to draw a diagram for this problem since it's talking about a pool (rectangle), but it's actually quicker to just look at the numbers given and work from there.

We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.

To find the amount of water in the pool now, we'll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:

8 * 70 = 560 gallons

This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:

560 + 600 = 1160

The correct answer is 1160.

Aaaaaaaaaaand time for a nap.

Key Takeaways: Making Sense of SAT Math Word Problems

Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.

Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.

Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.

What’s Next?

Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math . From polygons and slopes to probabilities and sequences , we've got you covered!

Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score .

Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.

Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math , written by a perfect scorer.

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

12 Classic SAT Math Questions You Must Know How to Solve

Most tests you take in your average math class are straightforward and obvious. As long as you’ve studied the concepts, you know what to do when you encounter a problem. You know what to expect.

On the SAT, however, even great math students may not know where to begin. Even if you know all the concepts, you won’t always know which ones to apply and how. To answer the tough questions, you need a combination of experience and a willingness to try things out.

I always warn new students that the SAT Math is unlike most tests they’ve done in school. But when they ask how it’s different, I usually have to resort to vague terms like "problem-solving, creative thinking, and word questions."

So here are 12 SAT questions that illustrate frequently tested ideas and ways of thinking that go beyond standard school material. I’ve included questions across all test topics—from algebra to geometry to logic.

All of them are tough! Try them on your own. Hints are available at the bottom and answers will be available in another post.

The Questions

• If \(2^x + 2^x + 2^x + 2^x = 2^{16}\), what is the value of \(x\)?
• The lengths of two sides of a triangle are \(4\) and \(9\). What is the greatest possible integer length of the third side?
• A car traveled \(10\) miles at an average speed of \(30\) miles per hour and then traveled the next \(10\) miles at an average speed of \(50\) miles per hour. What was the average speed, in miles per hour, of the car for the \(20\) miles?
• The average (arithmetic mean) age of a group of \(15\) teachers is \(40\) years. If \(6\) additional teachers are added to the group, then the average age of the \(21\) teachers is \(44\) years. What is the average age of the \(6\) additional teachers?
• Let the function \(f\) be defined by \(f(x) = x^2 + 18\). If \(a\) is a positive number such that \(f(2a) = 3f(a)\), what is the value of \(a\)?
• A tech company bought a number of computers for its employees: \(6\) costing \(\$1600\) each, \(4\) costing \(\$1200\) each, and \(y\) costing \(\$900\) each, where \(y\) is a positive odd integer. If the median price for all the computers purchased by the company was \(\$1200,\) what is the greatest possible value of \(y\)?

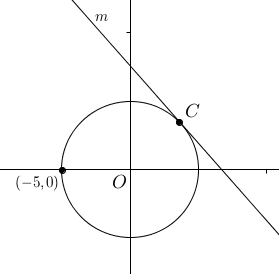
• If \(0\leq a \leq b\) and \((a + b)^2 - (a-b)^2 \geq 9\), what is the least possible value of \(b\)?
• In triangle \(ABC\), the measure of angle \(A\) is equal to \(2x^\circ + 20^\circ\) and the measure of angle \(B\) is equal to \(x^\circ + 46^\circ\). If \(\sin\angle A = \cos\angle B\), what is the value of \(x\)?
• \[f(t) = 800(1,000)^{\frac{t}{27}}\] The function \(f\) above represents the current total population of sand sharks off the coast of Greenland \(t\) years after 1980. To the nearest year, how many years did (or will) it take for the population to be 10 times larger than it was in 1980?
• In order to fulfill a prescription for 200 milliliters (mL) of a medication at a 55% solution, a pharmacist must mix \(x\) mL of a 40% solution with \(y\) mL of a 60% solution. What is the value of \(x\)?
• The answer is NOT 4. You can only add exponents when the terms are being multiplied. Think about how many \(2^{x}\)s there are.
• The answer is NOT "as big as you want." Look up the Triangle Inequality Theorem.
• The answer is NOT 40. This is much harder than that. Remember that distance \(=\) rate \(\times\) time
• Think about the sums of all the ages.
• No hint for this one. If you truly understand functions, you'll get this.
• No hint for this one either.
• What is the slope of \(\overline{OC}\)?
• Know your special triangles (30-60-90 and 45-45-90).
• First, expand (FOIL) and simply. Now how do the values of \(a\) and \(b\) affect each other when they are increased or decreased?
• You'll have to use a certain trigonometric identity.
• Use the fact that \(1,000 = 10^3\)
• 200 milliliters of a 55% solution contains how many milliliters of the actual medication?

I'm not going to post answer explanations (at least for now), because I want you to figure these out on your own. What I will do is post the answers, so you can check/review your work.

• \(\frac{75}{2}\) or \(37.5\)
• \(-\frac{3}{4}\)
• \(\frac{3}{2}\) or \(1.5\)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 11: Advanced: Problem solving and data analysis

About this unit.

Ready for a challenge? This unit covers the hardest problem solving and data analysis questions on the SAT Math test. Work through each skill, taking quizzes and the unit test to level up your mastery progress.

Ratios, rates, and proportions: advanced

• Ratios, rates, and proportions | SAT lesson (Opens a modal)
• Ratios, rates, and proportions — Basic example (Opens a modal)
• Ratios, rates, and proportions — Harder example (Opens a modal)
• Ratios, rates, and proportions: advanced Get 3 of 4 questions to level up!

Unit conversion: advanced

• Unit conversion | Lesson (Opens a modal)
• Units — Basic example (Opens a modal)
• Units — Harder example (Opens a modal)
• Unit conversion: advanced Get 3 of 4 questions to level up!

Percentages: advanced

• Percentages | Lesson (Opens a modal)
• Percents — Basic example (Opens a modal)
• Percents — Harder example (Opens a modal)
• Percentages: advanced Get 3 of 4 questions to level up!

Center, spread, and shape of distributions: advanced

• Center, spread, and shape of distributions | Lesson (Opens a modal)
• Center, spread, and shape of distributions — Basic example (Opens a modal)
• Center, spread, and shape of distributions — Harder example (Opens a modal)
• Center, spread, and shape of distributions: advanced Get 3 of 4 questions to level up!

Data representations: advanced

• Data representations | Lesson (Opens a modal)
• Key features of graphs — Basic example (Opens a modal)
• Key features of graphs — Harder example (Opens a modal)
• Data representations: advanced Get 3 of 4 questions to level up!

Scatterplots: advanced

• Scatterplots | Lesson (Opens a modal)
• Scatterplots — Basic example (Opens a modal)
• Scatterplots — Harder example (Opens a modal)
• Scatterplots: advanced Get 3 of 4 questions to level up!

Linear and exponential growth: advanced

• Linear and exponential growth | Lesson (Opens a modal)
• Linear and exponential growth — Basic example (Opens a modal)
• Linear and exponential growth — Harder example (Opens a modal)
• Linear and exponential growth: advanced Get 3 of 4 questions to level up!

Probability and relative frequency: advanced

• Probability and relative frequency | Lesson (Opens a modal)
• Table data — Basic example (Opens a modal)
• Table data — Harder example (Opens a modal)
• Probability and relative frequency: advanced Get 3 of 4 questions to level up!

Data inferences: advanced

• Data inferences | Lesson (Opens a modal)
• Data inferences — Basic example (Opens a modal)
• Data inferences — Harder example (Opens a modal)
• Data inferences: advanced Get 3 of 4 questions to level up!

Evaluating statistical claims: advanced

• Evaluating statistical claims | Lesson (Opens a modal)
• Data collection and conclusions — Basic example (Opens a modal)
• Data collection and conclusions — Harder example (Opens a modal)
• Evaluating statistical claims: advanced Get 3 of 4 questions to level up!

Reset password New user? Sign up

Existing user? Log in

SAT Algebra Word Problems

Already have an account? Log in here.

To solve SAT algebra word problems, you need to know:

• how to translate words into math
• manipulate algebraic expressions
• work with fractions and decimals
• how to work with ratios, proportions, and percents

SAT Tips for Algebra Word Problems

A fruit basket contains the same number of apples and pears. If Eric eats 5 apples and 1 pear, there will be twice as many pears as apples. How many pears remain in the basket? (A) \(\ \ 4\) (B) \(\ \ 8\) (C) \(\ \ 9\) (D) \(\ \ 10\) (E) \(\ \ 11\) Correct Answer: B Solution 1: Let \(x\) be the number of apples and the number of pears in the basket. Eric eats 5 apples, and therefore there are \(x-5\) apples remaining. He also eats 1 pear, and therefore there are \(x-1\) pears remaining. We're told that after Eric eats there are twice as many pears as apples in the basket. We set up an equation. \[\begin{array}{l c l l} 2(x-5) &=& x-1 &\quad \text{create equation} &(1)\\ 2x-10 &=& x-1 &\quad \text{use distributive property} &(2)\\ x-10 &=& -1 &\quad \text{subtract}\ x\ \text{from both sides} &(3)\\ x &=& 9 &\quad \text{add}\ 10\ \text{to both sides} &(4)\\ \end{array}\] We're looking for the number of pears remaining in the basket, but \(x=9\) is the original number of pears. Since he ate \(1\) pear, there are \(8\) pears remaining. Solution 2: Here, for each answer choice, we work our way backwards. We compute, based on how many pears are left, how many pears and apples there were to start with. Remember that there was the same number of apples and pears before Eric ate. (A) If 4 pears are left, then there were 4+1=5 pears to start with. Since there are twice as many pears remaining as apples, then there are \(\frac{4}{2}=2\) apples left, and there were 2+5=7 apples to start with. But \(5\neq 7.\) This is the wrong choice. (B) If 8 pears are left, then there were 8+1=9 pears to start with. Since there are twice as many pears remaining as apples, then there are \(\frac{8}{2}=4\) apples left, and there were 4+5=9 apples to start with. \(9=9\) and therefore this is the correct answer. (C) If 9 pears are left, then there were 9+1=10 pears to start with. Since there are twice as many pears remaining as apples, then there are \(\frac{9}{2}=4.5\) apples left, and there were 4.5+5=9.5 apples to start with. But \(9 \neq 9.5.\) This is the wrong choice. (D) If 10 pears are left, then there were 10+1=11 pears to start with. Since there are twice as many pears remaining as apples, then there are \(\frac{10}{2}=5\) apples left, and there were 5+5=10 apples to start with. But \(10\neq 11\). This is the wrong choice. (E) If 11 pears are left, then there were 11+1=12 pears to start with. Since there are twice as many pears remaining as apples, then there are \(\frac{11}{2}=5.5\) apples left, and there were 5.5+5=10.5 apples to start with. \(10.5\neq 12.\) This is the wrong choice. Incorrect Choices: If you got this problem wrong, you should review SAT Translating Word Problems . (A) This wrong choice is the number of apples that remain in the basket. (C) If you solve for the original number of pears, you will get this wrong answer. (D) When accounting for the pear Eric ate, if instead of subtracting 1 from the original number of pears, you add 1, you will get this wrong answer. (E) When finding how many apples remain in the basket after Eric consumed 5 of them, if you add 5 to \(x\) instead of subtract 5 from it, you will get \[\begin{array}{l c l l} 2(x\fbox{+}5) &=& x-1 &\quad \text{mistake: added}\ 5\ \text{to}\ x &(1)\\ \end{array}\] Or, you may get this wrong answer if in step (3) of the solution you subtract 10 from both sides and you ignore the negative signs.

Katie and Beth had the same number of marbles on January 1st. By the end of the year, Katie's collection of marbles increased by \(25\%\) and Beth's decreased by \(75\%\). On December 31st, the number of marbles Beth owned was what percent of the number of marbles Katie owned?

(A) \(\ \ 18.75\%\) (B) \(\ \ 20\%\) (C) \(\ \ 33.33\%\) (D) \(\ \ 75\%\) (E) \(\ \ 100\%\)

At 2:00 P.M. a train A leaves a station traveling at 100 mi/hr. At 4:30 P.M. train B leaves the station on a parallel route and traveling at 150 mi/hr. How far away from the station will the second train overtake the first train? (A) \(\ \ 250\) mi (B) \(\ \ 500\) mi (C) \(\ \ 750\) mi (D) \(\ \ 800\) mi (E) \(\ \ 1500\) mi Correct Answer: C Solution: Tip: Distance = Rate \(\times\) Time. Between 2:00 P.M. and 4:30 P.M. there are 2.5 hours. This means that train A travels 2.5 hrs more than train B. If \(t\) denotes the hours train B travels, then train A travels \((t+2.5)\) hrs. Let the distance the two trains travel be denoted by \(d\). Using \(d=rt\) we create an equation representing the distance each train traveled. \[\begin{array}{l l c l l} d&=&100(t+2.5) &\quad \text{train A} &(1)\\ d&=&150t &\quad \text{train B} &(2)\\ \end{array}\] Since the distance the two trains traveled is the same, we set \((1)\) equal to \((2).\) \[\begin{array}{r c l} 150t&=&100(t+2.5) &\quad (1) = (2) \\ 150t &=& 100t + 250 &\quad \text{use distributive property}\\ 50t &=& 250 &\quad \text{subtract}\ 100t\ \text{from both sides}\\ t&=&5\ \text{hrs} &\quad \text{divide both sides by}\ 25\\ \end{array}\] So, train B travel 5 hours before it catches up with train A. But we are looking for the distance the trains have traveled when train B takes over train A. Plugging \(t=5\) into \((2)\), we get \(5 \times 150 = 750\) miles. Incorrect Choices: (A) This is just the sum of the speeds of the two trains. (B) If you find the distance train A travels from 4:30 P.M. till train B overtakes it, you will get this wrong answer. (D) If you think the difference between 2:00 P.M. and 4:30 P.M. is 2 hrs, you will get this wrong answer. (E) If you find the combined distance the trains traveled, you will get this wrong answer.

If you thought these examples difficult and you need to review the material, these links will help:

• Fractions-Word Problems
• Decimals-Word Problems
• Percents-Word Problems
• Ratio and Proportion Word Problem
• Systems of Linear Equations Word Problems-Easy
• Linear Equations Word Problems
• Linear Inequalities Word Problems
• Convert Percentages, Fractions, and Decimals
• Percentage Change
• SAT Translating Word Problems
• SAT Fractions and Decimals
• SAT Direct and Inverse Variation

Read the entire question carefully. Distance = Rate \(\times\) Time. Know the Properties of Proportions. Replace variables with numbers. Pay attention to units. SAT General Tips

Problem Loading...

Note Loading...

Set Loading...

How to Analyze an SAT Math Problem:

Let’s learn some basic techniques for solving math problems on standardized math exams like the SAT or PSAT. Every student should know the following approaches and understand the weaknesses of each. 

Methods to Solve SAT Math Problems

Start to train your abstract brain, develop a process, understanding methods and strategies to solve math problems.

Look at the answer choices (The vertical scan):

a. Backsolving – This approach entails plugging the different answer options back into the formula or conditions of the question prompt to determine which answer satisfies the question conditions. Example:

Find the greatest common factor (GCF) between 150, 225, and 750.

A. 15 B. 25 C. 75 D. 125

One formal, robust method to solve this problem is to calculate the prime factorizations of all three numbers and take the product of only the common prime factors to each. On the other hand, some students will look at the answer options and, starting with the greatest, plug each back in to check for divisibility, which will determine if the answer is a factor. 125 does not divide into 150, so that is incorrect. Moving to the next largest answer option, 75 divides into 150, 225, and 750. It must be the correct answer. Time is saved, possible calculation errors are avoided, and the student can be confident they have the correct answer. This approach works well when the calculations required to test answer choices are simple and can be limited. An example where this approach will not work too well is the following.

The average of 15, 23, x and 8, 14, 22, and 2x are the same. What is the value of x?

A. 5 B. 8 C. 10 D. 12

 In this example, the calculation required for each answer is more complicated. It is easier to set up the equation and solve for x.

b. Trial and Error (Guess and Check) – In many cases the answer options include variables. In these cases, guessing a reasonable value for the variable(s) and checking the results for each answer choice can be effective. Example:

If R + S is even and S – T is odd, then which of the following must be odd?

A. R B. S C. R + T D. S – R

In lieu of general scenario analysis, students might guess numbers for each variable. Suppose R = 1. A guess of S = 3 would satisfy the first condition: 3 + 1 = 4 — an even result. Turning to the second condition, the student might guess T = 2 because S – T = 3 – 2 = 1 — an odd result. Once the conditions are satisfied, the student can check the answer choices. S – R = 3 – 1 = 2 — an even result. Option D is not always odd. On the other hand, R + T = 1 + 2 = 3 — an odd number. Option C works, and it is the correct answer.

The problem with substituting guessed values is the potential for false positives. For example, if the student checked option A or B, they would realize either of those is an odd result also based on the guessed numbers. R = 1 is odd. S = 3 is odd. Could those also be correct answers? In this case, option A and B are not because we could have just as easily chosen each variable to be even. In fact, the student must run a second scenario substituting an even value for R, like R = 4, to be completely confident option C is the correct answer.

c.  Estimates – The ability to round numbers and make effective estimates can help students solve some questions rapidly and accurately. Example:

Which of the following is closer to 0.19?

The shortcoming of this strategy is that easy estimates are not always available and often not accurate enough to differentiate some or all of the answer options, but the method can be useful w here it applies.

d. Reasonableness Test/Common Sense Checks – In many problems it is useful to assess the scale or range of values to determine which answers can be quickly eliminated. Example:

A. 11 B. 100 C. 101 D. 1010

The correct answer is approximately 7,000 ÷ 7 = 100. Students can quickly eliminate 11 and 1,010 because they are off by factors of 10. Note, both answers are traps designed to catch students who make typical long division mistakes. 11 results when students fail to insert a 0 for the ten’s place in the long division and 1,010 results when students divide by 7 rather than 70. The correct answer must be option B or option C, but the estimate of 100, in this case, must be low because the calculation above rounded 7,070 down to 7,000. Hence, the correct answer can only be option C, 101.

The method is not always effective at eliminating all wrong answers, which means other approaches and calculations must still be made in many cases.

e. Patterns – SAT math answer options frequently demonstrate patterns by design, and these patterns can often be used to help students more carefully or more quickly determine the correct answer. Typical patterns include a) multiples b) opposites c) imitations of the correct answer and more. Multiples, for example, often present answers that are doubled and halved from one another, which indicates the answer depends on doubling or halving a certain value and students must make sure they do that the correct number of times. Likewise, opposites present a positive and negative option for the same value(s), which should alert students to pay careful attention to signs. Also, many answers try to imitate the correct answer. For example, x 2 may be an expected part of the result, so that term appears in several answer choices. Test takers must take care that the other parts of their calculation are correct. Example:

 5×6×7×8 is divisible by which of the following?

A. 2 4 B. 2 5 C. 2 6 D. 2 7

Note the pattern among the answer choices. That can help students resolve the problem. Let’s look at a few possible approaches. The first approach is to complete the multiplication calculations and try to backsolve. The product in the question is 1,660. Divide that value by each of 16, 32, 64, and 256 to see which results in a whole number quotient. This solution, using backsolving, may be the longest and result in the most calculations and possibilities for errors. Another simpler approach is to take advantage of the fact that all the answers are in a particular pattern — they are all powers of 2. Some students might count the factors of 2 in the numbers included in the question prompt to see how many powers of 2 are in the product. Six has one factor of 2 — 2 × 3. 8 has three factors of 2 — 2 × 2 × 2. In all, that amounts to 4 factors of 2 in the product, so the correct answer must be option A, 2 4 . No multiplication calculations were required. In this approach, the student is leveraging their knowledge of factors and the pattern of answer choices to find the correct answer—an abstraction. There is no limit to the potential abstractions students can make to find faster, easier solutions. The SAT math sections are designed to reward this informal creative thinking.

The SAT rewards abstract solutions in math that prove to be faster and more effective. These solutions are abstract because they result from test takers observing some aspect of the problem that is tangentially related; the methodologies are not the direct solutions made by the conventional methods. For example, the idea that every squared real number must also be positive helped to solve a problem in the last chapter. Practice and familiarity will improve these insights. Let’s begin to train your abstract brain.

• If a + b = 9, then what is the value of 3a + 3b?

Resist the temptation to solve every equation for a single variable like you have done hundreds of times over in math class. That won’t work in this case because there are two variables and only one equation. You cannot know the value of a and the value for b individually, but that is okay because the question does not ask for the value of a or the value of b. Trained test takers will make certain they are answering the question asked. In this case, the goal is to express the desired result, 3a + 3b, in terms of the known value, a + b. As you probably already surmised, the expressions look alike, so the solution might come easily as it often does on SAT math problems. The desired expression to answer the question is just three times the known expression, so it must also be three times the known value: 3a + 3b = 3(a + b) = 3(9) = 27. Let’s look at a slightly more complicated variation.

• If a + 2b = 9 and 2a + b =15, then what is the value of a + b?

In this case, it is possible to find a value for a and b individually by solving the system of two equations. However, it is a lot easier if you recognize this is similar to the previous problem in reverse. Add the two equations to get 3a + 3b = 24. Extract the common factor 3(a + b) = 24 and solve: a + b = 8. There is no need to find a or b individually even if you can. The effort will only take more time and take more calculations, which translates into more opportunities to make a mistake. Let’s take things a step further.

• If 15x – 15 = 99, then what is 30x + 40?

The goal is to manipulate one expression to look like another, not solve for the variable. You could solve for x, but x is not even an integer, so that solution gets messy. It is easier to recognize the similarities between the expressions and utilize that observation. The second expression looks similar to twice the first. 2(15x – 15) = 30x – 30. In fact, the second expression in the question prompt is +40 – (-30) = 70 more. 3x + 40 = (3x – 30) + 70. Add 70 to twice the known expression value. 3x + 40 = 2(99) + 70 = 198 + 70 = 268. Math becomes more fun when you can make it easier. Try another.

• If a + 2b + 3c = 25 and 3a + 2b + c = 35, what is the value of a + b + c?

Many students begin with an explanation why this problem cannot be solved. Recall, the goal is not to solve for a single variable. Add the equations again. 4a + 4b + 4c = 60. 4(a + b + c) = 60. a + b + c = 15. The answer to the question is not only possible; it is quick. Let’s shift gears and look at a word problem, a large percentage of the question formats on the exam.

• If 3 hamburgers and 2 orders of fries cost $5.80, and 2 hamburgers and 3 french fries cost $4.30, then how much more do hamburgers cost?

An insightful student might realize one more hamburger less one more french fries order is equivalent to the difference between $5.80 and $4.30. In other words, hamburgers cost $1.50 more, which answers the question. Set up the equivalent equations to see this example is much like the previous problems. 3H + 2F = 5.80 and 2H + 3F = 4.30 where H and F are the prices of one hamburger and one order of french fries respectively. Similar to before, subtract one equation from the other. 1H – 1F = 5.80 – 4.30 = 1.50. Another example follows.

• If three-quarters of a house gets c ompleted in 60 days, then how many more days will it take to finish the house?

• If five machines produce five widgets in five minutes, then how long will it take for 100 machines to make 100 widgets?

The corresponding proportion equation for this work problem is a little trickier, so many students will fall back on their pattern recognition skills and assume 5-5-5 corresponds to 100-100-100. Unfortunately, 100 minutes is wrong, and that is the wrong easy approach – something to keep in mind when attempting abstract methods. The logic must be sound. In this case, it appears the per unit rate is 1 machine makes 1 widget every 5 minutes. That is the same as 5 machines make 5 widgets in 5 minutes. At that rate, any N machines will make N widgets in just 5 minutes. There are just more of them producing more overall in the same time frame. As a result, the correct answer is 5 minutes. 100 machines make 100 widgets in the same 5 minutes. Once you begin thinking more abstractly, it may be true you will find the abstract wording of problems easier to translate.

• If X widgets can be purchased for Y dollars, then what is the cost of Z widgets?

• What is the greatest common factor between every two-digit number decreased by the sum of its digits?

What does this question mean? Where do we begin? There are 90 two-digit numbers. How can we easily find the GCF?  Think about what is going on. Try an example: the lowest two-digit number 10. The number minus the sum of digits is 10 – 1 – 0 = 9. Increase the value by one. 11 – 1 – 1 = 9. The result is still 9 because every time the number increases by one the units digit that is subtracted increases by one to offset the change. When the tens digit increases by one the number still goes up by one, but the subtracted digits decrease by 9 – 1 = 8. The result is one more multiple of 9: 20 – 2 – 0 = 18. Thinking in the abstract frame of mind as the above problems, the expression to calculate for 20 is two times the expression for 10. It should be no surprise the answer is two times the value as well. In all cases, the result will be divisible by 9, so that must be the greatest common factor. Try this question.

• The sum of an odd number of even numbers must be

…a headache. Just kidding. A trained test taker will actually say, “An easy correct answer!” Try an example of an even number, 2. An odd number of those might be three 2s. The sum of three 2s is 2 + 2 + 2 = 6. Change the numbers, but the result will still be an even integer multiplied by an odd integer, which must be even. Abstract approaches are not limited to word problems or ratios. Let’s see an example in geometry.

• If the sides of a triangle with area A are doubled, then what is the new area?

The new triangle area is 4 times the old area, and there is no need to know the particular details. Trained test takers will know the area is always the square of lengths, so if the lengths are scaled by a factor, F, then the area will be scaled by F 2 . It does not matter what the shape is. Likewise, double the sides for a three-dimensional shape, a nd the new volume will be F 3 = 2 3 = 8 times the original volume.

These are but a few examples of abstract approaches that are limited only by your creativity and experience. Hopefully, they serve as a warm-up for your brain as we progress forward to gain more experience.  

How to Analyze an SAT Math Problem – The 7 Step Process

• Read the question carefully, and consider all the words in the question; this is the most important step.
• Assess what information is given including diagrams and charts.
• Look at the answer choices to identify any relationships or patterns that may be useful.
• Determine which math topic(s) will help solve the problem. In this effort, diagram the problem to help visualize the problem or guess a value that may be appropriate. Action, not inaction, helps more often than not at this stage.
• Can you find a solution that would take about 30 seconds? If you cannot find it in 30 seconds, then you may want to skip the problem and return in a later pass.
• Execute your solution.
• Before marking your answer, check that you are answering the exact question asked. Too often careless errors — answering the wrong questions or using intermediate solutions by mistake — are the downfall of test takers.

All Past SHSAT Student Handbooks SHSATAcademy Materials SHSATAcademy Tutoring SHSAT Free Course Pricing FAQ

Contact Us [email protected] External Links NYC DOE Inside Schools.org PassNYC.org

• Membership Account
• Academy Pro Content
• Content & Features
• Membership Levels
• SAT Student Dashboard
• SAT Question Bank – RW
• SAT Math Practice
• Student Dashboard BCA
• Why SAT Universal?
• Why SHSAT Academy Pro
• Why TestPrepSHSAT Tutoring

• SAT BootCamp
• SAT MasterClass
• SAT Private Tutoring
• SAT Proctored Practice Test
• ACT Private Tutoring
• Academic Subjects
• College Essay Workshop
• Academic Writing Workshop
• AP English FRQ BootCamp
• 1:1 College Essay Help
• Online Instruction
• Free Resources

Hardest SAT Math Problems (updated for Digital SAT)

Bonus Material: The Hardest SAT Math Problems Quiz

Aiming for a really great score on the SAT? Wondering if your math skills are up to the challenge of the hardest problems?

If you want to be able to get a perfect score, you have to be able to solve the hardest SAT math problems.

We used our extensive test-prep experience to find the questions that many students miss. The examples below are real problems from past official SATs. 

Give each of these 16 hard math problems a try, then read our step-by-step explanations to see if you’re solving them correctly.

If you’re thinking about getting SAT tutoring to help you tackle problems like these on the real SAT, be sure to check out our list of the 15 best SAT Tutoring Services

Then, download this quiz with 20 more of the hardest real SAT problems ever to see if you’re on track for a perfect score! 

Bonus Material: 20 of the All-Time Hardest SAT Math Problems

Math on the SAT

Math accounts for half of your Total SAT Score, regardless of whether you’re taking the old paper SAT or the new Digital SAT.

On the traditional, paper SAT (which will be phased out in early 2024), the Math section comprises section 3, which contains 20 questions, is 25 minutes long and does not allow you to use a calculator; and section 4, which contains 38 questions, is 55 minutes long and does allow a calculator.

On the upcoming digital SAT (which will come into place in spring of 2024), the format is considerably different. You’ll be given two 35-minute “modules” with 22 questions in each, with the difficulty level of the second one depending on your performance on the first one. In other words, if you do really poorly on the first set of 22 questions, the second set will be easier–but your overall math score will be negatively affected. You can use your calculator on both.

Every SAT covers the following math material:

Heart of Algebra: 33% of test . Linear equations and inequalities and their graphs and systems.

Problem Solving and Data Analysis: 29% of test . Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics.

Passport to Advanced Math: 28% of test . Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs.

Additional Topics in Math: 10% of test . A wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers.

On the old SAT , open-ended questions came at the end of each Math section. Many students find them harder because you can’t guess or work backwards from multiple-choice options.

However, what many students don’t know is that the first 1–3 of these grid-in questions will actually be easier than the last few multiple-choice questions. 

That’s because the math questions on the SAT get increasingly difficult over the course of each section, but the difficulty level starts over again with the grid-in questions.

The savvy student will know this and skip the harder multiple-choice questions to go answer the easier grid-in questions first. Of course, if you’re aiming for a perfect score, (on most tests) you’ll have to answer every question correctly . 

But on the new Digital SAT, these open-ended questions will pop up at different points throughout both modules. You may see them in the beginning, the middle, or the end: there’s no set place for these to appear. Nor is there a set difficulty: generally, we’ve seen these questions be slightly on the easier side, but this varies significantly from test to test.

Because there’s obviously no bubble sheet on the digital SAT, you’ll simply type your answer into the text box. Be sure to look for instructions in the question about how they want the answer formatted!

To work with us for one-on-one tutoring or for our group SAT classes, schedule a free consultation with our team .

Why these problems are essential if you’re aiming at a top school

A perfect score on the SAT Math is 800. The only way to get this score is to answer every question correctly . 

In order to score a 750, you can only miss 2 or 3 questions across both math sections .

A 750 Math SAT may sound like a very high score—and it is! It’s a very high score.

But at the very best schools in the US, three quarters of the students scored a 750 Math or better.

In fact, at the Ivy League and other top schools, at least a quarter of the students had a perfect score!

The average math scores are even higher at the top engineering schools. Three quarters of the students at CalTech had a 790 or 800, and three quarters of the students at MIT had at least a 780.

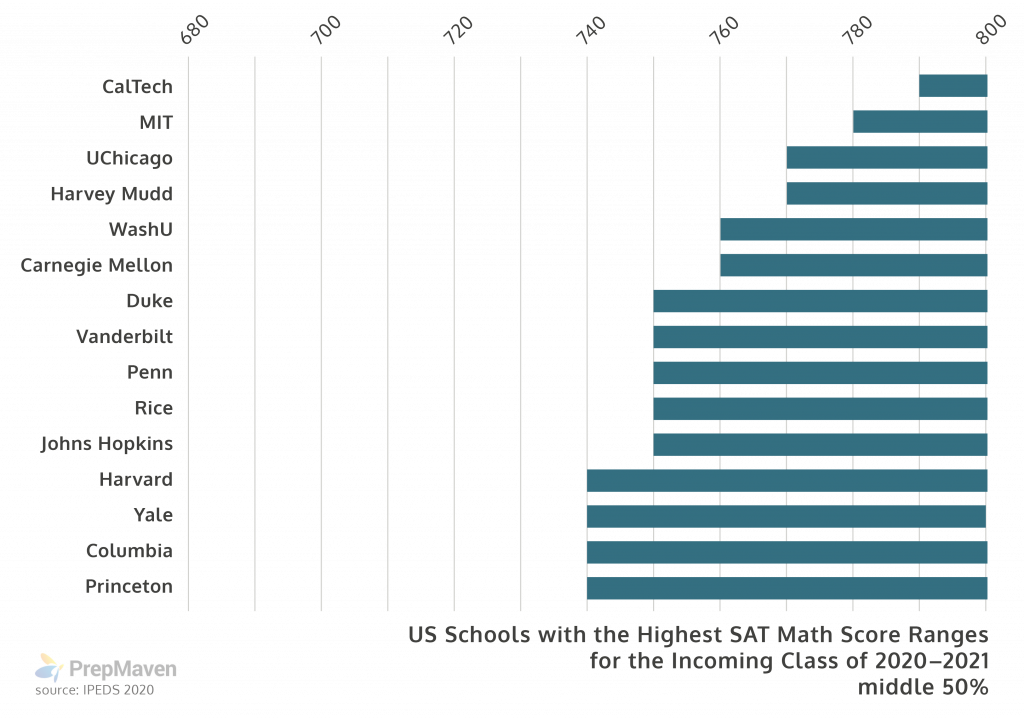
In order to be a competitive applicant to these schools, your SAT Math score should be within the “middle 50%” of the students at that school—in other words, more or less an average score for that school.

So if you’re aiming at an Ivy or one of the other top schools, you can only miss 2 or 3 questions out of the 58 math questions on the whole SAT.

If that’s your goal, make sure that you understand the problems explained below, and then try our quiz of 20 more real SAT questions that rank among the hardest questions ever.

SAT Problem #1

At first glance, this looks like a geometry question, since it talks about planes and lines and points . But this is actually an algebra question, dressed up with some geometric trappings. 

The key is to realize: 

1) We don’t need to solve for p and r individually. We just need to solve for (r/p) . 

2) The points themselves (p,r) and (2p, 5r) represent X and Y values on the line itself. (For example if p = 2 and r = 3 then that’s the same thing as an x-coordinate of 2 and a y-coordinate of 3.)

So let’s take a look at it. 

First, let’s plug in the p and r points for the x and y values to see what equations we end up with. 

y = x + b becomes r = p + b

y = 2x + b becomes 5r = 2(2p) + b or 5r = 4p + b

At this point we might get a little anxious because we have three variables. 

But we have to remember we don’t need to get the value of the individual letters, just the value of the relationship between r and p. 

That’s where b actually becomes helpful. Because we can now set both equations equal to b , plug in, and then see if we can manipulate the r and p to get them to express the same relationship we want. 

So, first set both equations equal to b to get: 

b = r – p

b = 5r – 4p

And since, obviously b = b … 

r – p = 5r – 4p

Let’s now use some basic algebra to put the like variables together, so:

Now we’re nearly home. All we have to do is manipulate the problem so r/p .

So, divide both sides by  3p :

4r / 3p = 1

Then multiply both sides by 3: 

And finally divide by 4, which gives us: 

CHOICE B  

Download the Hard SAT Math Problems quiz

SAT Problem #2

This is a question that can cause all sorts of problems if you forget your exponent rules—but it’s otherwise very straightforward. 

So let’s go over a few of those rules, just to get comfortable . . . and notice a pattern. I’ve included three below:

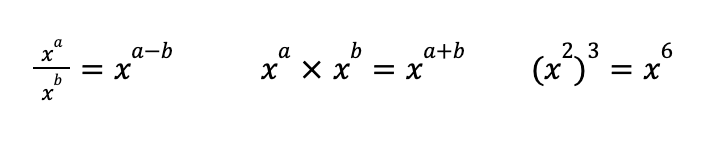
Two things to pay attention to:

First, when we divide variables with exponents, we keep the base and subtract the exponent. When we multiply variables with exponents, we keep the base and add the exponents. When we take a variable with an exponent to an additional power, we multiply the exponents. 

Second, in order to use the first two of these rules, the two numbers must have the same base . 

There is a base x on both the top and bottom of that fraction or the left and right side of that multiplication sign. 

So how does that help us here? 

Let’s forget the first half of the problem and look at the second:

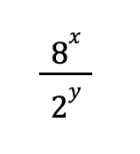
We might look back at these exponent rules and throw our hands up—the top and bottom parts of this fraction don’t have the same base, so what am I supposed to do here? 

Except… 

8 and 2 actually DO have the same base. Base 2. 

Isn’t 2^3 equal to 8? 

So if we re-write the problem, plugging in 2^3 for 8, and thinking about that third exponent rule I gave you above, the equation will look like this: 

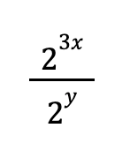
Now let’s go back to our exponent rules once more, and look at the first one. 

Because that tells us that… 

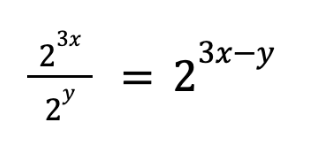
Well, hold on a second! 

We know the value of 3x – y . 

The problem tells us it’s 12.  

So we just plug in and get our answer… 

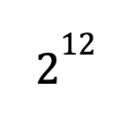
Which is CHOICE A. 

Keep up the practice! If you’d like help honing your skills, reach out to us for a free test prep consultation. All of our tutors are top 1% scorers who attended top-tier schools like Harvard and Princeton. That makes them uniquely qualified to help high-scoring students improve.

SAT Problem #3

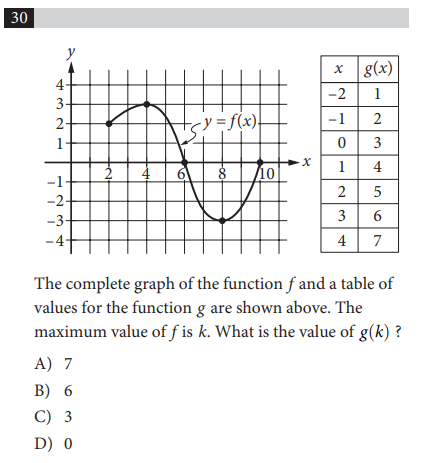
A question like this confuses a lot of students because they either forget how minimums and maximums work or find it hard to keep track of which numbers they are plugging in and where. 

In order to solve it, it’s helpful to think of a function as a machine . We enter an input into the machine (an x value)—it acts on it—and then it gives us an output (a y value). 

Let’s also remember that when we’re talking about minimum and maximums we’re talking about the y value when the function is at its highest and lowest point . 

With these two facts in mind, the problem is going to be much simpler, so let’s take it on in parts…

Since the question is asking us for g(k) and k represents the maximum value of f , it’s going to be helpful to first… 

Find k .  

So what is the maximum value of f , the graphed function? Well, the maximum value (as we realized earlier) is the y value when the function is at its highest. 

Looking at the graph, it looks the function is at highest when x = 4 , and more importantly, when 

Therefore, k = 3 .

Now let’s consider our functions as machines. 

When the problem asks us for g(k) , it’s telling us that k is going to act as the input (the x value for the function). So g(k) , the value after the machine acts upon the function, is going to be the output , or the y value . 

So, g(k) is the same as g(x) , except we’re plugging in our value of k , which is 3, for our x value. 

The rest is very simple. 

We go to the table and find where x = 3 , then move our finger across to see the output for that value, which is 6.

CHOICE B. 

Test your SAT math knowledge with our quiz

SAT Problem #4

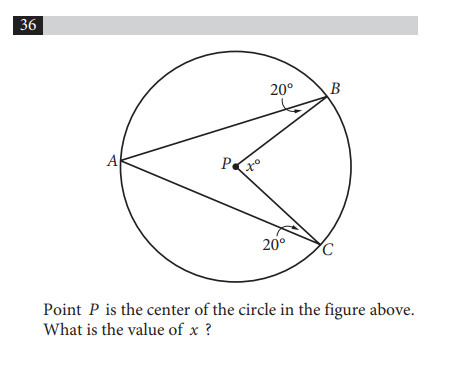
A version of this question has appeared on the SAT multiple times in recent years, and it often stumps students!

Here we have something that resembles a rotated version of the logo from Star Trek, and we’re asked to find the value of a degree inside the circle, between two points of the pointed figure.

We’re given a point that represents the center of the circle, along with two degree measurements inside the triangle-like figure. 

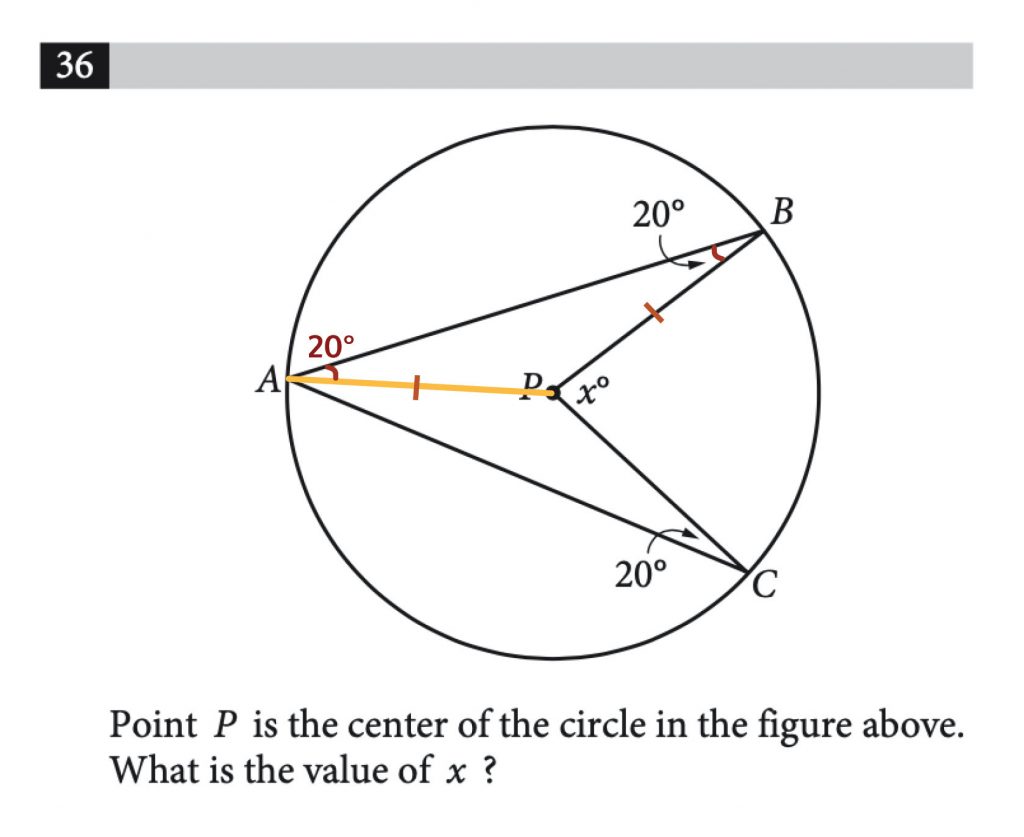
Generally, when we’re given a figure that looks unfamiliar to us—like the figure inside the circle— it can be extremely helpful to find a way to fix it (or cut it up) so that it’s made up of parts of shapes that are more familiar . 

So looking inside this circle, how might we “fix” this figure so that it becomes a little friendlier. 

Well, if we draw a line to the center of the circle ( P ) from the edge of the circle ( A ), then this unfamiliar figure suddenly becomes two triangles. 

And with triangles, unlike the figure we were originally given, we can apply some rules . 

Rules, for example, that dictate opposite sides of the triangle that have the same length will have the same opposite angles. 

And if we look at our drawing we see that two sides of our triangle are the same length because they’re both the radius …

And so we also know that the opposite angles of those sides will be the same… 

And we’ve been given one of those angles! 

Therefore, angles ⦣ABP and ⦣PAB will be the same—both 20 degrees. Let’s fill that in. 

Now again—because we have a triangle—we can apply another rule as well. 

We know that degrees of a triangle will add up to 180 degrees. 

So if we know one of the inner degrees of the triangle is 20, and the other is 20—the remaining angle has to be 140 degrees. (Because 180 – 40 = 140. )

We have two of these triangles, so we know the larger inner angles of both add up to 280. 

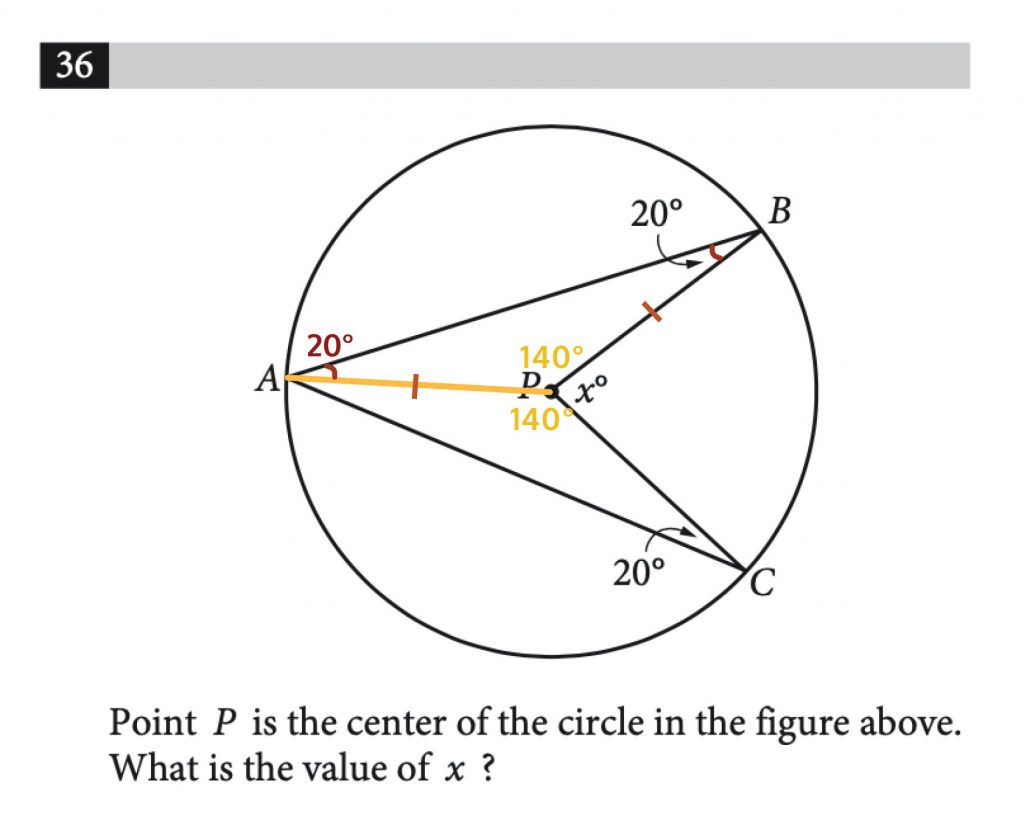
Because a circle is 360 degrees, the number of degrees “left over” when 280 is subtracted from 360 is 80. 

So X equals 80. 

There is actually a second clever way to solve this problem, involving arc measures. Can you spot it? (If not, don’t worry! Ask us how we did it here .)

SAT Problem #5

Here we have a problem that looks quite complicated—and one I find students often waste a lot of time on. They either try to plug in answers and work backwards… 

…or they waste time trying to combine the two terms on the right side of the equation and simplifying. 

It turns out the easiest way to solve this problem is by polynomial division , because we’ve already been given the answer! It’s the right-hand side of the equation: (-8x – 3) – (53 / (ax – 2)) .

That means that this is our answer to when (24x^2 + 25x – 47) is divided by ax – 2 .

So how does that help us get a value for a ? 

Well, let’s set this up as a polynomial division problem.

We’d write it as follows: 

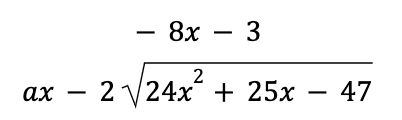
(I’m not putting the second half of the right side of the equation on top because that’s going to be our remainder.) 

So now we have a simple question. What number divided into 24 , gives me -8 ? 

Well, that’s easy. It’s -3 , right? 

Because -3 * -8 gives me 24 . 

So a equals -3 ,   CHOICE B .

Now, you could spend time plugging in -3 for a and dividing through the rest of the problem to make sure your answer matches the one on the exam—but generally on a timed test you really shouldn’t do more work than necessary. 

In fact, by setting this up as a polynomial division problem, we’ve saved time precisely because we don’t have to complete all the work . . . just enough to get us our answer. 

Try the quiz

SAT Problem #6

Because the SAT is a timed test, “difficult” includes not only questions that are hard to solve, but also those that—if a few wrong decisions are made—take a long time to solve. 

Sure, you may get the right answer, but those extra seconds or minutes wasted will inevitably cost you on other questions later on the exam.

Generally speaking, you should be able to answer each question in about a minute. If you spend more than 60 seconds on a single question, you should put down your best guess and move on (and hope that you have extra time at the end to return to this question).

To that end, let’s look at this question. You’re asked to find the value of 3x – 2 , and you’re given this equation:

(⅔)(9x – 6) – 4 = (9x – 6)

Many students will immediately think: “This is totally straightforward: Solve for x and plug it back into the equation.” 

They’ll distribute the ⅔ and end up with something like this: 

6x – 4 – 4 = 9x – 6

and then go through all the algebra from there, to get… 3x = -2 . 

These students will then find that x = (-⅔) . 

A few unlucky students will then forget that they have to plug in, and they’ll choose the trap answer C. 

The lucky ones will plug the (-⅔) back into 3x – 2 and get the correct answer, -4 , A . 

However, it turns out there is actually a much quicker way to solve this problem! 

We can solve it without ever having to plug into a second equation. 

If we simply subtract (⅔)(9x-6) from both sides, we end up with… 

-4 = (⅓)(9x-6) . 

We can realize that (⅓) of 9x-6 is the same as 3x-2 . 

And, what do you know… 

-4 = 3x – 2 . 

Ready to try some of these problems on your own? Try our quiz with 20 more of the hardest real SAT problems ever to see if you could get a perfect score on the SAT Math!

SAT Problem #7

This is a question you could muscle through, but it’s going to be a lot easier if we find a few shortcuts and work from there. Remember, a hard question isn’t necessarily difficult because of the conceptual and mathematical effort it asks from you but also because of the time it might require.

So how do we save ourselves some time? 

First, let’s notice that in the answer choices none of these numbers repeat . There are eight distinct numbers in the answer choices. Therefore, if we were pressed for time we only really have to find one of the values of c , choose the corresponding answer choice, and then move on. 

Second, let’s look at the other piece of information this problem gives us besides the quadratic. 

It tell us that a + b = 8.

This should be especially helpful because we know from FOIL (and what the rest of the problem gives us) that a * b = 15 , because abx^2 is going to be equal to 15x^2. 

Because a + b = 8 and ab = 15 , we know that the values of a and b are going to be 3 and 5. 

(We don’t know which one is which, and that’s precisely why this problem has two possible values for c .)

At this point we’ve done most of the “hard” work to save time in this problem, and it hasn’t even been particularly hard!

Now all we have to do is assign one of 3 or 5 to a , assign the other to b , FOIL out the problem, and pick whichever choice corresponds to one of the values of c . 

Let’s say a = 3 and b = 5 .

It will work like this: 

(3x + 2)(5x + 7) = 15x^2 + 21x + 10x + 14 .

Which simplifies to… 

15x^2 + 31x + 14 .

Which means c = 31 .

31 only appears once in our answer choices, so the answer must be CHOICE D.  

SAT Problem #8

When you’re faced with one of these more difficult system-of-equations problems—specifically the ones that ask you for no solutions or infinite solutions —it’s going to be much, much easier to think about the problems geometrically. 

In other words, as two line equations. 

So what does it mean for two lines to have no solutions ?

Well, for two lines to have no solutions, they’d have to never intersect , correct? 

(Just like if one of these problems asks you about two lines with infinite solutions , they’re saying that the lines are the same . They’re laid on top of each other. )

In other words, they’d have to be… parallel lines . 

And parallel lines have the same… slope! 

So this question is asking you to find the correct value for the variable that gives these lines the equivalent slope . 

Obviously, the first step is to put both of these equations in slope-intercept form. We’d end up with:

y = (-a/2)x + 2

Now the rest is very simple. All we need is a value of a that makes the slopes equal, so that it solves the equation (-a/2) = 3 .

With some basic algebra, we end up with -a = 6 . This is the same as a = -6 .

So the answer is CHOICE A, -6. 

Are these problems feeling super hard for you? Want to work on more similar problems? Check out our one-on-one tutoring with Ivy-League instructors. A great experienced tutor can help you focus on the concepts that are the hardest for you until you understand them thoroughly.

SAT Problem 9

This is another type of problem that students often have conceptual difficulty with, causing them to waste much more time than they should. 

(Remember, basically every problem in the SAT math section is designed to be solved in a minute and half or less. If you’re taking three or four minutes on a math problem, you’ve probably made a mistake!)

Some students will see that (u-t) is defined but not u or t individually, so they’ll try either solving for u in terms of t (or vice versa), or they’ll try squaring (u-t) to get a solution. (Which is closer to the correct way to solve the problem, but still incorrect). 

Instead, to solve this problem we need to remember the difference of squares . 

Remember, that the difference of squares states the following… 

(x+y)(x-y) = x^2 – xy + xy – y^2 .

Which means… 

(x+y)(x-y) = x^2 – y^2 .

And doesn’t that look awfully familiar to… u^2 – t^2 ?

In fact, we can now replace  u^2 – t^2 with (u + t)(u – t) .

So the whole problem would now read: (u + t)(u – t)(u – t) . Since we know the value of (u + t) and (u – t) , this would simply be the same as (2)(5)(2) .

Which equals our answer… 

Ready to see how you’re doing? Download the quiz

SAT Problem #10

What makes this question confusing is that students often get thrown off by the repetition of the (⅓). 

They forget that when the ⅓ gets factored out of the parenthesis like that, it means it’s going to apply to the whole equation: both the  x^2 AND the -2 . 

Once we remember that, we can solve this problem by difference of squares . This will save us the time of having to brute force the answer choices and FOIL each one through for the different values of k. 

We’ll simply square k and subtract it from the  x^2 for each choice. 

That will give us the following four choices: 

(⅓)(x^2  – 4)

(⅓)(x^2 – 36)

(⅓)(x^2 – 2)

(⅓) (x^2 – 6)

A student might rush to choose the third answer choice, since it appears to look like the expression at the beginning of the problem, but remember what I told you at the beginning: 

We’re going to apply that ⅓ to both the x^2 AND the k ! 

If we multiply that ⅓ through, the choices suddenly look like this…  

(⅓)(x^2) – (4/3)

(⅓)(x^2) –  (12)

(⅓)(x^2) – (⅔)

(⅓)(x^2) – (2)

. . . and so the correct answer is actually the fourth choice, CHOICE D . 

Ready to try more hard problems on your own? Download our free quiz to try 20 more of the hardest ever (real) SAT problems.

SAT Problem #11

There are not many problems on the SAT that involve knowing the equation for a circle—in fact, circle equation problems don’t show up on every test—but that’s precisely why students often find a problem like this more difficult. 

First, let’s do a quick refresher on what the numbers in the equation of a circle mean. 

Any equation for a circle is going to be in this form: 

(x – h)^2 + (y – k)^2 = r^2

Where h and k represent the coordinates of the center and r is the radius. 

Let’s apply that to our problem here… 

(x + 3)^2 + (y – 1)^2 = 25.

Remember: because in the form of the circle equation the numbers inside the parenthesis are subtracted from x and y , when they appear inside the parenthesis as positives , that indicates the coordinate point will be negative. 

Therefore the center of this circle is at point (-3, 1) .

Because the radius is expressed as r^2 , then the 25 indicates the radius will be 5 . 

So we have a circle centered on the point (-3,1) and with a radius of 5 . 

So… now what? 

How do we figure out which of these points is not inside the circle? 

First, let’s draw the circle itself and look at it. On the SAT itself, you won’t have graph paper, so just draw a rough sketch!

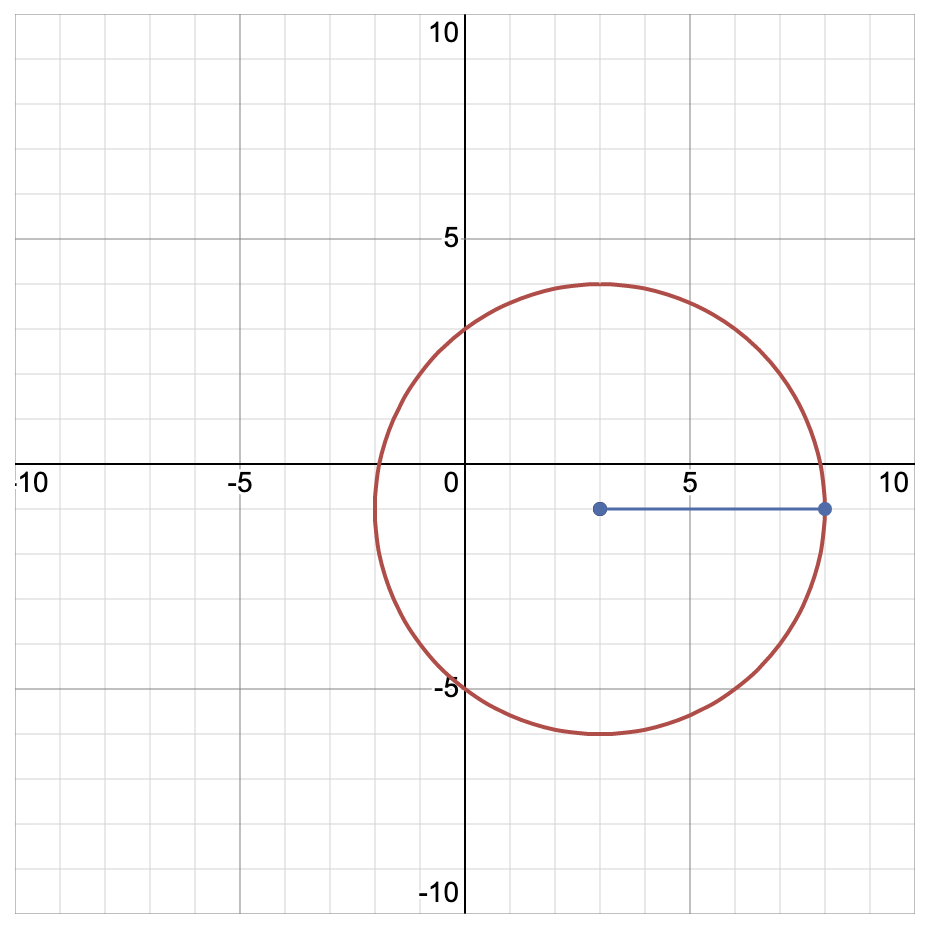
Of course if we’re truly flummoxed we could graph the points, eliminate what we can . . . and guess. 

But that’s not ideal, obviously! 

Instead, let’s think about what the radius means. 

The radius demarcates the boundaries of the circle from the center. 

In other words, any points with a distance less-than-the-radius away from the center will lie within the circle. 

And any points more-than-the-radius distance from the center will lie outside of it. 

(Any points exactly-the-radius distance from the center will lie on the circle itself.) 

So all we have to do is find the point that is more than 5 units away from our center, and that will be our answer. 

To do this requires the distance formula. 

Remember, the distance formula is

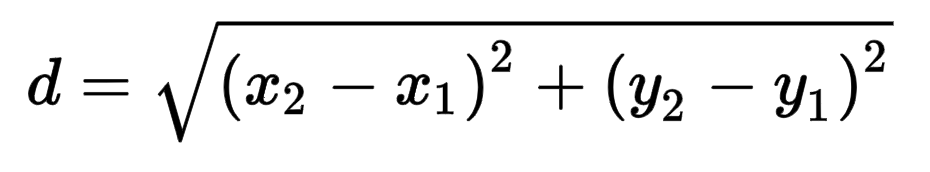
A quick note: if you ever forget the distance formula, simply plot the two points on a graph, make a triangle with the distance between the two points and the hypotenuse, and use the Pythagorean Theorem to find the length of the hypotenuse, like this: 

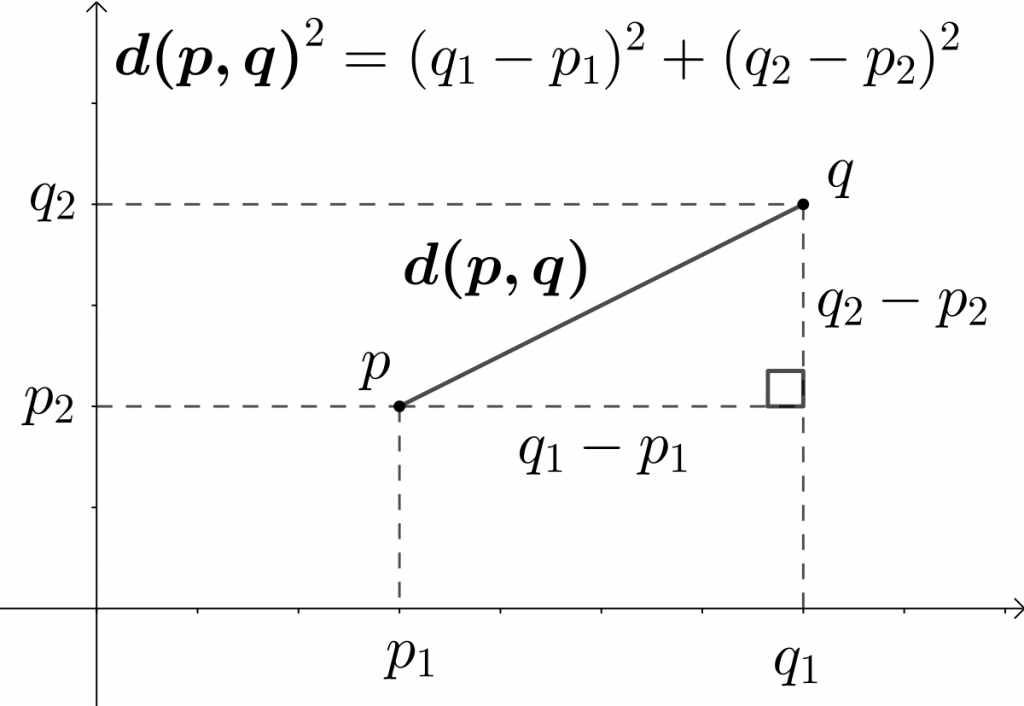
Going back to our problem, let’s plug each of the points in along with our radius to the equation. (I’ll include the second point here, although since that’s our center we need not actually bother with it when we’re going through the problem.) We end up with: 

√(-3 – (-7))^2 +(1-(3))^2) = √20

√(-3 – (-3))^2 +(1-(1))^2) = √0

√(-3 – (0))^2 +(1-(0))^2) = √10

√(-3 – (3))^2 +(1-(2))^2) = √37

Only the square root of 37—choice D—is an answer that is larger than five. 

So that’s our correct choice, D . 

Want more hand-picked problems? Get the quiz

SAT Problem #12

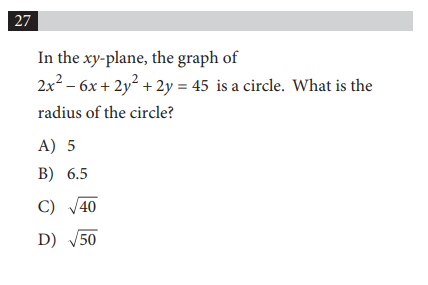
More circles! Let’s recall how the equation for a circle looked. It’s… 

(x – h)^2 + (y – k)^2 = r^2 

What the problem gives us, unfortunately, does not resemble that equation… 

…so our goal is to get the equation in the problem to look like a normal equation for a circle. 

Once we do this, we’ll just have to take the square root of whatever is on the right side of the equation, and that will give us our answer.

But how? 

We need to do something called completing the square . 

For the SAT, this concept is slightly obscure—it’s one you may see only once (or not at all) on a given exam. It makes the question a bit more difficult. 

Completing the square is normally a process reserved for solving a quadratic equation, but if you look closely at the way this problem is set up – 

2x^2 – 6x + 2y^2 + 2y = 45

we see that what we really have here are two quadratic equations, so we just have to complete the square twice. 

First we have to get rid of the coefficient in front of the x and y squared, so we have to divide through by 2 . 

This gives us  x^2 – 3x + y^2 + y = 22.5 .

Now we’re reading to complete the square!

Let’s deal with the x terms first. We have to think of what number, if we had it here in the equation, would allow us to factor x^2 – 3x into something of the form (x – z)^2 , where z is a constant. If we think about it, we realize that z has to be half of b . In this case, that means half of -3 , so -1.5 .

When we pop that into our setup, we get (x – 1.5)^2 . If we FOIL this out, however, we see that we get x^2 – 3x + 2.25 .

So it turns out that in order to be able to rewrite our expression in the form we want, we need to add 2.25 to our equation. As always in algebra, we do the same thing to both sides, so now we have:

x^2 – 3x + 2.25 + y^2 + y = 22.5 + 2.25.

Now we do the same thing for the y terms! Again, we need to add something to the equation so that we could rewrite the y part of the expression in the form (y – z)^2 . To get this number, we take half of the b term and square it: 1 divided by 2 , then squared, so 0.5^2 or 0.25.

Again, we have to add this number to both sides of the equation. Now we’ve got:

x^2 – 3x + 2.25 + y^2 + y + 0.25 = 22.5 + 2.25 + 0.25.

We can factor and rewrite this like:

( x – 1.5)^2 + (y + 0.5)^2 = 25.

Alright, now this is finally in the right format for the equation for a circle!

The final step is to use this equation to find the radius.

We know that the equation for a circle is (x – h)^2 + (y – k)^2 = r^2  . Fortunately this works out really nicely, since 25 is just 5^2. The radius must be 5, CHOICE A .

We’ve tutored thousands of students and used that experience to assemble a list of 20 more problems that students frequently miss. Can you answer them correctly? Download the quiz now to find out!

SAT Problem #13

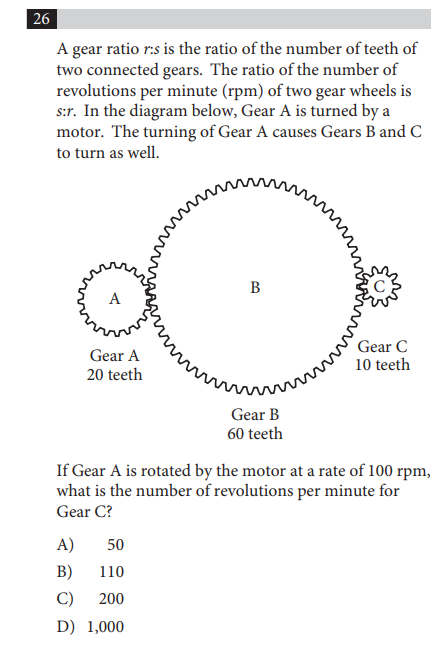
This question involves a number of moving parts and thus can be a little overwhelming for students to follow. 

It asks us to find, based on the rotation of the first gear, the rotation of the third. 

I find many students trip up on this problem by making two errors that are simple to fix, but relatively common. They fail to take the problem step by step… and they fail to write down their work as they track through the material. 

With that in mind, let’s work through the problem. 

Because gears A and C do not connect directly, but instead through gear B, we should first try to figure out the rotational relationship between A and B (at 100 rpm) before applying that to B and C. 

Because B is larger than A (and has more gears), A is going to rotate fully multiple times before B rotates once. 

How many times? Here it’s helpful to consider a ratio. 

A has 20 gears. 

B has 60 gears. 

So A is going to have to rotate three times before B rotates once . (20 goes into 60 three times.) 

Therefore, the ratio of rotation between A and B is 3 : 1 . 

Let’s write that down and then apply the same method to figure out the ratio between B and C. 

C has 10 gears. 

Here B only has to rotate a sixth of its distance for C to rotate once, so the ratio of rotation between B and C is 1 : 6 .

Now we take the number of RPMs the problem gives us, start with the gear on the left and multiply through with our ratios. 

So if Gear A rotates 100 times RPMS per minute, Gear B will rotate a third of that distance… 

So we divide 100 by 3. 

Because we know Gear C rotates six times as fast as Gear B, we then take our answer and multiply it by 6. 

So we get (100)(⅓)(6) . 

Which gives us 200 rpm. 

CHOICE C. 

SAT Problem #14

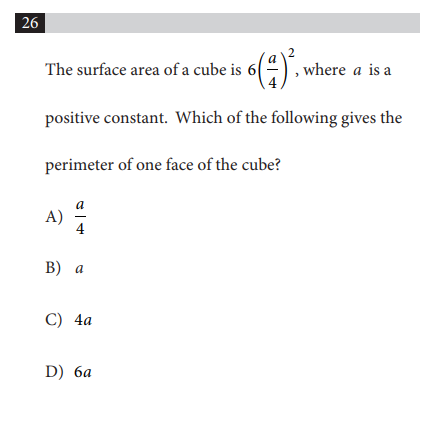
This question appears complicated—and students often get tripped up trying to either plug in numbers (which can be time consuming) or by searching for an equation that explains the relationship between the surface area and perimeter of the cube itself. 

This is especially tempting because while the question gives us the equation for the entire surface area of the cube, it only asks for the perimeter of one of the cube’s faces. 

However… 

If we think about the properties of a cube, this question actually becomes quite simple. 

First, let’s draw a cube.  

Again, the equation the problem gives us is for the entire surface area of the cube: 6(a/4)^2 .

But when we look at the cube, we may notice that it has, in fact, six faces. 

Therefore, each face would have one sixth of the surface area of the entire cube. 

So by dividing the equation by six, we get the surface area for one face of the cube, which is: 

But the question asks for the perimeter of one face of the cube. 

Let’s examine the drawing of the cube one more time. 

What shape is each cube face? It’s a square. 

And because each side of a square (let’s call each side x ) is equal to the other, the area of the square is going to be x^2, or the length of the side times itself. 

Well, wait a moment… 

If we go back to our equation for the surface area of ONE face of the cube, (a/4)^2 , we might notice that it’s in the same form as the equation for area of the square, except instead of x being squared, it’s (a/4) . 

And if we replace the x with (a/4) , we find that each side of the square is equivalent to (a/4) . 

Which makes finding the perimeter of this square quite simple, because it has four sides. 

So we merely add the four sides together: 

(a/4) + (a/4) + (a/4) + (a/4) . . .

which equals a . 

Which in this case is CHOICE B . 

Want more practice? We collected 20 more of the hardest SAT math problems. Download the quiz and take it with a 25-minute timer to mimic the real test!

SAT Problem #15

We have a lot of variables in this question, so it’s easiest to try to incorporate the extra piece of information we’re given, b = c – (½) , as best we can and then try to simplify the problem and solve from there. 

So how can we do that? 

The problem tells us b = c – (½) , which can also be expressed as b – c = -(½) .

(Once we put the b and c together on one side, it becomes easier to replace them together with a number). 

So what’s the best way to manipulate these two equations so that we’ll have b – c , which we can then replace with the (-½) and be left with x and y ? 

Because let’s remember that the problem does not ask us to solve for x and y individually. 

Just their relationship. 

So once we’re left with x and y as our only two variables, we should be able to make good progress. 

Anyhow, looking back over these two equations it seems the easiest way to be left with b – c is to… 

…subtract the bottom equation from the top one. 

When we do so, we’re left with the following: 

(3x – 3y) + (b – c) = (5x – 5y) + (-7 – (-7))

We replace b – c with -½  

And then combine like terms to get… 

(-½) = (5x – 3x) – (5y + 3y)

(-½) = 2x – 2y

Divide through by 2 … 

-¼ = x – y

Or x = y – (¼)

So our an answer is x = y – ¼ , CHOICE A .

Download 20 more of the hardest problems ever

SAT Problem #16

There are a few ways to solve this problem. The easiest one is simply to know the “remainder theorem.”

I don’t want to get too sidetracked with details, but remainder theorem states that when polynomial g(x) is divided by (x – a) , the remainder is g(a) .

In other words, when p(x) is divided by  (x-3) here, the remainder would be p(3) , which, according to the information we’re given, is -2 . 

That leads to CHOICE D . 

But what if, like many students, you don’t know the remainder theorem? (It’s pretty obscure and there’s a good chance you won’t see a problem about it on the entire exam.) 

Let’s look at an alternative way to solve the problem. 

If p(3) equals -2 , let’s imagine a function where that might be the case. 

We could do as simple one, like y = 3x – 11 , or a more complex one, like y = x^2 + 3x – 20 .

Either way, if I plug 3 into either of these functions for x , I get -2 as a y value. 

I should also notice immediately that (x – 5) , (x – 2) , and (x + 2) are not factors of either of them.

Clearly choices A, B, and C are not things that must be true. 

This also, by process of elimination, leads to CHOICE D. 

But just to check, let’s divide x – 3 into one of these functions – say 3x – 11 – and see what happens: 

The x goes into 3x three times – and three times (x-3) equals 3x – 9 .

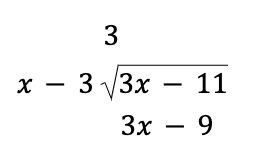
When I subtract 3x – 9 from 3x – 11 , I get -2 , which is my remainder. 

Which points us, again, to CHOICE D .

Test your knowledge with 20 more problems

If these problems feel really hard, don’t panic—you can still do well on the SAT without answering every question correctly. 

The average SAT Math score for US students in 2022 was 52 8, and you have to answer about 32 out of 58 math questions correctly to get this score. That’s only a little over half of the questions!

However, if you want a high score—or a perfect score—you’ll have to be able to answer tough questions like these. You’ll need a very high score to be a competitive applicant for Harvard, Stanford, MIT, or other highly competitive schools.

The good news is that it’s very possible to raise your math score! 

In fact, it’s typically easier to improve your SAT Math score than your Reading & Writing score. Good preparation (on your own or with a tutor ) will fill in the knowledge gaps for any concepts that might be shaky and then practice the most common problem types until they feel easy.

We’ve worked with students who were able to see a 200-point increase on the Math section alone, through lots of hard work and practice.

To see how your math skills stack up against the toughest parts of the SAT, download our quiz with 20 more of the hardest SAT math questions, taken from real tests administered in recent years.

Once you know where you stand, keep up the practice!

If you’re interested in customized one-on-one tutoring support from an expert SAT tutor who can help you understand these tough problems, schedule a free consultation with Jessica or one of our founders . Our Ivy-League tutors are top scorers themselves who can help you with these more advanced concepts and strategies.

Bonus Material: Quiz: 20 of the All-Time Hardest SAT Math Problems

Emily graduated  summa cum laude  from Princeton University and holds an MA from the University of Notre Dame. She was a National Merit Scholar and has won numerous academic prizes and fellowships. A veteran of the publishing industry, she has helped professors at Harvard, Yale, and Princeton revise their books and articles. Over the last decade, Emily has successfully mentored hundreds of students in all aspects of the college admissions process, including the SAT, ACT, and college application essay. 

CHECK OUT THESE RELATED POSTS

15 College Essays That Worked

May 13, 2024

In this regularly updated post, we share the college essays that helped students get into their dream schools -- including Ivy Leagues.

SSAT Score Release Dates – When You’ll Get That Score Report

May 2, 2024

You've studied hard. You've taken the SSAT. Now when will you get that score report? Find SSAT score release dates and more in this regularly updated post.

SSAT Prep Resources: Your Guide

Preparing to take the SSAT? What SSAT prep resources should you be utilizing? We weigh in on the best SSAT test prep tools in this post.

Scoring on the SSAT: Your 2024 Guide

Understanding your SSAT score report can be challenging. With this detailed breakdown of SSAT scores, you'll have a firm grasp on what to expect in no time!

What is a Good SSAT Score for 2024?

What is a good SSAT score? What percentile ranking do you need to get into the school of your dreams? Find out more in this comprehensive post.

Princeton Review vs Kaplan: Which SAT Prep Service is Better?

April 29, 2024

Princeton Review and Kaplan are two of the biggest test prep services, but which one is better? Detailed review of pricing, course materials, instructor qualifications, and customer service. Choose the best SAT prep to help you raise your score…

Kaplan SAT Prep Review: Rating All of Kaplan’s SAT Prep Options

Comprehensive review of Kaplan's SAT prep services: pricing, instructor qualifications, online platform, customer service, and educational quality.

Princeton Review vs Kaplan: Which ACT Prep Service is Better?

Princeton Review and Kaplan are two of the biggest test prep services, but which one is better? Detailed review of pricing, course materials, instructor qualifications, and customer service. Choose the best ACT prep to help you raise your score…

Kaplan ACT Prep Review: Rating All of Kaplan’s ACT Prep Options

Comprehensive review of Kaplan's ACT prep services: pricing, instructor qualifications, online platform, customer service, and educational quality.

15 Best Online Writing Tutoring Services for 2024 (50 Tutoring Services Reviewed)

A list of the 15 best online writing tutoring services, reviewed and ranked. Compare prices & writing tutor qualifications. Best overall: PrepMaven’s writing tutoring ($66–349/hr). Best on a budget: Wyzant ($20–600/hr). Best…

Privacy Preference Center

Privacy preferences.

What are your chances of acceptance?

Calculate for all schools, your chance of acceptance.

Your chancing factors

Extracurriculars.

SAT Math: How to Tackle Word Problems

When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.

For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.

Types of Math Word Problems on the SAT

You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.

Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.

Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.

Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.

Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!

How to Approach SAT Math Word Problems

For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.

The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:

Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:

Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.

When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.

Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.

Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.

Examples of SAT Math Word Problems

The following example problems come from the College Board’s free SAT practice tests .

Example of Creating an Equation/Formula

How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.

Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.

Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.

Example of Solving for a Value

How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.

Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.

Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.

Example of Defining/Interpreting

How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.

Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.

How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.

In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.

SAT Math Word Problems Tips

As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:

For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.

Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.

In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!

For more information about preparing for the SAT, check out these posts below:

30 SAT Math Formulas You Need to Know

25 Tips and Tricks for the SAT

5 Common SAT Math Mistakes to Avoid

Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!

Related CollegeVine Blog Posts

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

How To Improve SAT Math Score: 6 SAT Math Tips

reviewed by Jessica Kaminski

Created on May 23, 2024

Updated on May 23, 2024

Is your high school graduate wondering how to get a good score on the SAT? For many, it is a challenging, thought-provoking exam. But no worries, with some solid preparation, your schooler is good to go.

So how should they prepare? In this guide, we’re about to decipher a good SAT math score code.

How to get a high SAT score?

To get a high SAT score, a graduate should:

• Set distinct goals
• Prepare & register

Review & master PSAT-related assessments

Participate in challenging courses, make preparation & practice a top priority.

• Eventually, do their best to pass the test

As you can see, your graduate has to go a long way to succeed. And, indeed, it’s easier to prepare when there’s someone to guide and help. Luckily, there are many online platforms like Brighterly , where professional tutors can consult students whenever they need help.

Here are the benefits of such curated preparation:

• No blind memorizing — tutors encourage students to understand what they study;
• Online accessibility at any convenient time;
• Personalized learning plan and tailored approach;
• Interactive math classes that guarantee a no-stress environment;
• 1:1 format, which means that all attention is devoted to your graduate. 

Sure, the benefits of online tutoring are undeniable. But let’s explore some other SAT test- taking strategies to boost your schooler’s score. These are the core things to consider.

Find the homework support your child needs

Top math tutors for middle and high school students here.

Set distinct SAT score goals

Even before starting their preparation, students should understand the minimum score they need to get. It’s pretty easy to define. They must consider the average SAT range of their dream college. Alternatively, they can review the participation requirements for a scholarship. 

Prepare & register for the SAT

Choosing the date to pass the SAT is paramount (and it’s not only about superstitions). First, the day should leave enough time for preparation. Second, it should correspond to the application deadline at a chosen college. But note that some days are highly sought after so be sure to register for them beforehand.

If you wonder how to boost the SAT score, a good idea is to train with PSAT-related assessments like PSAT 8/9™, PSAT 10, and PSAT/NMSQT. All of these offer a good sense of the exam environment. Reviewing them helps define areas for improvement and outline a clear study plan.

Students should be attentive to their daily classes to get a higher SAT score. The reason is simple — at its core, the SAT contains the knowledge they receive in classrooms; nothing extraordinary here. Thus, an excellent way to get better at SAT math is by taking more challenging advanced courses, like Statistics, AP Calculus AB, or AP Calculus BC.

The best way to study for SAT math is to develop a clear plan and adjust it as a student progresses in some math areas. It allows for the maximum benefits with minimum time expenditures. But how do students know that they advanced in some topics? It’s where the sample assessments we’ve just discussed come into play!

Pass the SAT test

Your graduate should be 100% concentrated on the day X. Students usually get better SAT scores if they get a good night’s sleep, arrive on time, have a good meal, and minimize stress before the test.

SAT Math Tips 

The core SAT math tips for high school graduates are the following:

• Familiarize yourself with the subject and its areas
• Try to memorize essential formulas
• Practice your skills at demo tests
• Identify your weak areas and work on them
• Devote most of your time to challenging topics
• Ask for help

Remember that your schooler’s SAT math scores reflect how well they prepared. So, here are the tips for SAT math that will help them excel.

SAT Math Tip #1. Know the subject

All the best SAT tips and tricks to help you prepare for your SAT end up here — you must know what to study. It might seem obvious, but many students fail because they didn’t clarify the exact list of topics covered on the test. Here’s a cheat sheet:

• Manipulating & Solving Equations
• Exponents & Radicals
• Systems of Equations
• Exponential Vs. Linear Growth
• Word Problems 
• Expressions
• Quadratics 
• Trigonometry 
• Probability 

See? The list is even shorter than you might have thought. And many of these topics are regularly practiced in classrooms.

SAT Math Tip #2. Memorize the formulas

Did you know that most students ignore formulas? They usually say that the SAT provides a reference sheet, so there is no need to memorize each formula. But let’s be sincere: scrolling or flipping back and forth wastes time. Besides, the test won’t give every formula needed. So don’t let your high school graduate repeat that common mistake!

Here is a short list of 15 SAT formulas that students have consistently used during recent tests (and your graduate will most likely need, too).

1) Slope-Intercept Form of a Line

2) Vertex Form of a Parabola

3) Distance Formula

4) Quadratic Formula

5) Exponent Rule (Multiplication)

6) Exponent Rule (Division)

7) Complex Conjugate

8) Simple interest

9) Compound interest

10) Area of an Equilateral Triangle

11) Equation of a Circle

11) Pythagorean Theorem

12) Regular Polygon Interior Angle

13) Length of Arc in a Circle

14) Area of Sector in a Circle

SAT Math Tip #3. Practice at demo tests

Practice tests are a must. They show the weak points and topics that need further studies. But one demo won’t be enough to improve the SAT math score. Let’s clarify: each test is a training, and the more training a student gets, the better their result.

And one more pro tip: it’s a good idea to retake those demo tests regularly, say, once every two weeks. Just to see the progress.

SAT Math Tip #4. Identify weak areas

All the most popular SAT tips and tricks won’t work if a student can’t analyze their weaknesses. In fact, knowing weak areas is half a battle. They should devote time after each demo test to review mistakes. This way, graduates will turn their weaknesses into strengths. And that’s where we approach the next discussion point.

SAT Math Tip #5. Work on your weaknesses

All the SAT strategies math teach students to spend their time reasonably! If they know some math topics well (especially if they cover them at school), why spend that valuable time honing them at home? Instead, graduates should focus on what they struggle with. Yes, those topics may seem daunting or depressing. But if your schooler wants to increase SAT score, they must do it.

SAT Math Tip #6. Ask for help

But how to raise the SAT score if your graduate is on the humanitarian team? In most cases, experienced tutors can help. Those people are professionals in SAT preparation and can explain complex math concepts even to the biggest humanities-minded people. You can find such tutors on verified platforms like Brighterly and start studying online in a comfy setting. Sounds ideal, right? 

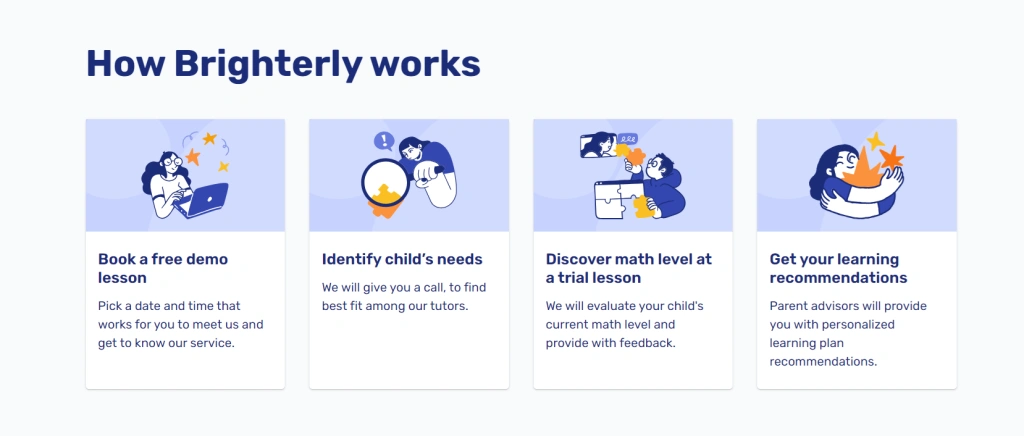
Hard to tackle those complicated math concepts?

Brighterly’s tutors can help your kids with that.

The best ways to improve the SAT score 

The best ways to improve SAT scores are to take practical demo exams, study effectively, use preparation materials, understand and memorize formulas, find a study group, and address a tutor. Overall, the SAT is the test of skills and nerve, so make sure your graduate trains both. Thus, they stay consistent and concentrated throughout the exam.

SAT test tips and tricks to use during the exam

Here are the best SAT math tricks to employ during the exam: 

• Answer the easiest questions first;
• Use the same letter for each answer;
• Don’t postpone grid-in tasks till the last minute;
• Carefully read the questions & answers.

Now, let’s take a closer look at these top SAT tips and tricks from our experts to help your high schooler shine bright during the test.

Answer the easiest questions first

All questions are worth the same points, no matter their complexity. So, first, check out those that require less time to understand and complete — it’s the quickest way to raise the SAT score.

Use the same letter for each answer

If your schooler is up for a guessing game, choosing the same letter each time is the best option. The thing is that each answer choice (A, B, C, or D) is correct in about 25% of cases. So, if they pick only As, for instance, they’ll guarantee about 25% of the score.

Don’t postpone grid-in tasks till the last minute

The logic of any test is this: easier questions go at the beginning. It’s also the logic that graduates should follow in their answers. Firstly, they should solve multiple-choice questions.

Once those tasks get too complex, it’s time to move to grid-in tasks. The easiest grid-ins will go at the beginning, remember? Once they get too complicated, switch back to multiple choices. This strategy also saves time, as students can play that guessing game with multiple-choice questions but cannot pick their answers randomly for grid-ins.

Carefully read the questions & answers

Students often complain that they didn’t understand a question or were tangled by the answers provided. Thus, it is vital to keep a keen eye for detail and do everything possible to understand the task correctly.

SAT may be a complex exam that tests students’ skills, knowledge, and endurance. However, if there’s one sure way to increase the SAT score, it’s the proper preparation. So, why not help your high school graduate with that? Ensure they have an exact study plan, train regularly, and concentrate mainly on their weakest topics. 

And maybe if they need extra help, is it time to book a lesson at Brighterly? Here, you can be sure that your schooler works with professionals.

Rachelle Bencio Yu is a qualified tutor with more than 15 years of experience teaching math to children from Pre-K to 12th grade. Currently, she is one of the best teachers at Brighterly educational platform and an author of educational content on the Brighterly blog.

What kind of math is used in computer science? Generally, computer scientists need to be comfortable with binary mathematics, linear algebra, calculus, discrete math, and statistics.  Computer science is a broad field. The type of math needed depends on the specific career path.  Let’s see how math is involved in computer science. How it helps […]

May 22, 2024

If your kid has difficulties grasping math or struggles with any calculations, your child may have dyscalculia. The good news is that they can still thrive in STEM subjects with the proper support. Check this article to find out the most effective teaching strategies for dyscalculia kids. You can overcome math challenges and develop a […]

May 23, 2024

Book 1 to 1 Math Lesson

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

Want your kid to excel in math?

Brighterly’s math tutors make it easy!

After-School Math Program

Related posts.

How to Find a Math Tutor for Your Child

The first step when you want to find a math tutor is to ask yourself a number of questions – What kind of classes will be most convenient for my child and me, where can I find a teacher that will help my child make the most progress, how can I choose the best teacher […]

Mar 28, 2024

Top Ten Educational Preschool Philosophy Models

When choosing a school for their children, parents often give serious thought to the preschool philosophy of an institution. This is because goals and student-teacher relationships are intrinsically related to ideologies. Accordingly, the strategy a school uses significantly impacts the quality of the preschool setting. Ten Preschool Philosophies  Parents are in dire need of guidance […]

Jun 27, 2022

30 Basic Classroom Rules For Kids

Picture this: you’re in the middle of explaining trigonometry, working hard to keep everyone engaged, when suddenly, Casey decides to break Mason’s ruler. Chaos ensues, and before you know it, your entire class is fixated on this mini-drama, forgetting all about trigonometry. This is just one example, but let’s be honest; there are plenty more […]

Nov 06, 2023

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 23, 2024   •   34:24 I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders
• May 22, 2024   •   23:20 Biden’s Open War on Hidden Fees
• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India

The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’

The answer involves a remarkable — and lucrative, and ridiculous — scheme to game the way we find music today..

By Brett Martin

Read by Eric Jason Martin

Produced by Adrienne Hurst and Aaron Esposito

Narration produced by Tanya Pérez and Krish Seenivasan

Edited by John Woo

Original music by Aaron Esposito

Engineered by Sophia Lanman and Devin Murphy

Listen and follow The Daily Apple Podcasts | Spotify

Have you heard the song “Brett Martin, You a Nice Man, Yes”?

Probably not. On Spotify, “Brett Martin, You a Nice Man, Yes” has not yet accumulated enough streams to even register a tally. Even Brett Martin, a contributing writer for The New York Times Magazine and the titular Nice Man, didn’t hear the 1 minute 14 second song until last summer, a full 11 years after it was uploaded by an artist credited as Papa Razzi and the Photogs.

When Martin stumbled on “Brett Martin, You a Nice Man, Yes,” he naturally assumed it was about a different, more famous Brett Martin: perhaps Brett Martin, the left-handed reliever who until recently played for the Texas Rangers; or Brett Martin, the legendary Australian squash player; or even Clara Brett Martin, the Canadian who in 1897 became the British Empire’s first female lawyer. Only when the singer began referencing details of stories that he made for public radio’s “This American Life” almost 20 years ago did he realize the song was actually about him. The song ended, “I really like you/Will you be my friend?/Will you call me on the phone?” Then it gave a phone number, with a New Hampshire area code.

So, he called.

There are a lot of ways to listen to ‘The Daily.’ Here’s how.

We want to hear from you. Tune in, and tell us what you think. Email us at [email protected] . Follow Michael Barbaro on X: @mikiebarb . And if you’re interested in advertising with The Daily, write to us at [email protected] .

Additional production for The Sunday Read was contributed by Isabella Anderson, Anna Diamond, Sarah Diamond, Elena Hecht, Emma Kehlbeck, Tanya Pérez, Frannie Carr Toth and Krish Seenivasan.

Advertisement