jump strategy problem solving

Addition Jump Strategy

Welcome, teachers and homeschoolers! We have an exciting resource to share with you that will enhance your students' understanding of addition using the jump strategy in mathematics. We are thrilled to introduce the "Addition Jump Strategy" worksheet, designed specifically for grade 1 and grade 2 students.

To get started, simply click on the button at the bottom of this page to download the worksheet. It's absolutely free, and we believe it will make learning

math both engaging and effective for your young learners.

This worksheet focuses on honing students' skills in using the jump strategy to solve addition problems with two-digit numbers. By utilising a number line, students will gain a visual representation of the process, enabling them to grasp the concept more effectively.

The worksheet consists of eight questions, each carefully crafted to gradually increase in difficulty. The first four questions provide scaffolding, with the jumps by tens and ones already completed on the number line. Students only need to fill in the missing numbers on the number line to find the answer to the addition question.

This initial section of the worksheet allows students to become familiar with the jump strategy in a guided manner. They will gain confidence as they observe the pattern and begin to develop a deeper understanding of how numbers interact when using the jump strategy.

The next four questions, however, offer less scaffolding. Here, students are presented with two-digit addition questions, and the number line is left blank. It's their opportunity to apply what they've learned independently. They must determine the appropriate jumps and fill in the missing numbers on the number line to find the correct answer.

This section encourages students to think critically and apply their knowledge of the jump strategy in a more autonomous manner. It fosters problem-solving skills, mathematical reasoning, and strengthens their ability to visualize and manipulate numbers on the number line effectively.

By utilising this worksheet, you are providing your students with an interactive and hands-on approach to learning addition. The jump strategy offers a foundation for mental math and lays the groundwork for more complex mathematical concepts in the future.

We encourage you to download the "Addition Jump Strategy" worksheet today and incorporate it into your lesson plans. Watch your students' confidence soar as they navigate the number line and uncover the solutions to their addition problems.

Remember, education is a journey, and we are here to support you every step of the way. Happy teaching and learning!

Jump Strategy

Jumping by parts of a number to solve a calculation.

For example: 4 + 12 = 4 + 10 + 1 + 1 = 16

Understanding Addition & Subtraction Strategies

• Differentiation , Math , Planning , Strategies

When Common Core stated that we needed to teach addition and subtraction strategies based on place value, properties of operations, and/or the relationship between addition and subtraction, I will admit I was at a loss for a long time. When I was growing up, the only thing I had learned was the standard algorithm. It was step-by-step do this, not that. Get it down, do it right! Over and over.

I had to do a lot of research to figure out what that standard was talking about. I’ll be honest: Since Common Core came out, I think I have done more research and critical thinking than in college AND than my own students! HA! (I kid…kind of.)  But, I now understand, and I figured I could not have possibly been the only one with my head tilted like a cute doggy going, “Whaaaaaaaaaaat?”

Understanding the Standard for Addition and Subtraction Strategies

A while back I explained the differences between teaching the standard algorithm and teaching strategies in the classroom in my post, Which is Better in Math: Standard Algorithm or Invented Strategies? along with my opinion of which was better to implement. When I started researching actual strategies for addition and subtraction, I was stunned to find so many different types. Which strategies were best to teach my students? Which were easier for them to learn and manage?

According to the standards, I had to make sure students were using strategies that were based on place value, the properties of addition, and the relationship between addition and subtraction. I was finding strategies called expanded form, partial sums, decomposition, compensation, number line, split, shortcut, jump, counting on, counting back, and friendly numbers, just to name a few! And I’m sorry, but I didn’t have that much time to teach all those strategies in the classroom – and realistically, wouldn’t students get confused with too many?

I turned to my trusty friends John Van De Walle and Marilyn Burns. No, I’m not really friends with them, but I have many of their books, and I dug in deep. What did I find out? Those strategies above? They are all pretty much the same thing – synonyms. You’ll see. Read on.

The Addition and Subtraction Strategies

The Split Strategy (AKA:  Partial Sums, Expanded Form, Decomposition):  In this strategy, students are breaking apart a number based on its place value and then adding or subtracting each individual place to find the answer. Once each individual place is found, then the expanded form is returned back to the standard form.

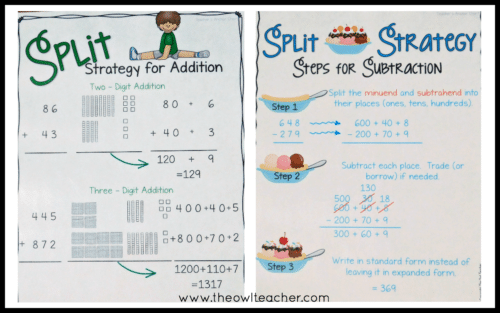
The Jump Strategy (AKA:  Counting On, Counting Back, Number Line):  In this strategy students are using a number line to add or subtract. Students break their numbers up into friendlier numbers based on place value as they move along the number line to find the answer. What’s great about this strategy is that it is also based on the relationship between addition and subtraction (in the subtraction). If you look closely in the (poor quality?) image below, I demonstrate this by making my students think of the inverse operation of 287 + ____ = 524. That is basing it on the relationship. I love when I hit two at once!

The Shortcut Strategy (AKA:  Friendly Numbers, Compensation):  In this strategy students are changing one of the numbers to a friendlier number by adding to it. In addition, a friendly number is a multiple of 10. In subtraction, a friendly number is one that ends in 9. Then, students change the bottom number according to the strategy and then finish the operation with the new set of numbers. This is also based on place value . Of the three strategies, this one can be the trickiest, because it is different between addition and subtraction.

When we think about the properties of addition , Common Core is referring mostly to the commutative property, where students remind themselves, for example, if they know that 10 + 80 is 90, then 80 + 10 is also 90.

Through all my research, I came to realize that it was not about a specific strategy that students had to learn  but rather how to use strategies and to rely on them , instead of simply using memorization and algorithms to arrive at an answer. Students need to understand that with mathematics there is more than one way to solve an equation. Mathematicians utilize methods that are most meaningful, efficient, and faster for them – whether that is through the use of an algorithm or an alternative strategy. Strategies are often meaningful to those who use them and are often faster and less susceptible to error.

When you are teaching addition and subtraction strategies, remind yourself that you are not teaching each of these strategies to mastery but instead are providing tools for the student to try and to find which works best for him or her. When assessing students, instead you should be providing them with an addition or subtraction problem and asking the student to solve it using at least two different approaches. Then, students should explain their thinking using mathematical vocabulary and by showing their work through the use of numbers and pictures.

My hope is that this (long!) post has helped you understand the addition and subtraction strategies a bit more and removed any frustration they may have caused you. Now head over to my Teaching Addition and Subtraction Strategies blog post to learn how I teach each of these strategies in my classroom. You can also get a freebie!

• Addition , Math Workshop , Strategies , Subtraction

FIND IT NOW!

Check me out on tpt.

CHECK THESE OUT

Three Types of Rocks and Minerals with Rock Cycle Circle Book

Partitioning Shapes Equal Share Fractions Halves, Thirds, Fourths Math Puzzles

Want to save time?

COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds

BOGO on EVERYTHING!

Resources teachers, parents and learners can use!

Grade 3 Mathematics Lesson Plan: Exploring the Jump Strategy

Objective: Learners will understand and apply the Jump Strategy for solving addition and subtraction problems. They will practice making “jumps” on a number line to break down and solve arithmetic problems, enhancing their mental math skills and number sense.

Materials Needed:

• Number line posters or individual number line handouts
• Flashcards with addition and subtraction problems
• Blank paper and markers or crayons for creating personal number lines
• Worksheets with exercises tailored to practicing the Jump Strategy

Lesson Structure:

• Begin with a discussion on different strategies for solving addition and subtraction problems, emphasizing the importance of mental math.
• Introduce the Jump Strategy, explaining how it uses “jumps” on a number line to simplify arithmetic operations.
• Using a number line poster, demonstrate how to apply the Jump Strategy for both addition and subtraction. Show how to make “jumps” to break down each problem into simpler steps.
• Use simple examples to start and gradually increase the complexity as learners become more comfortable with the strategy.
• Distribute blank paper and markers or crayons for learners to create their own number lines.
• Give learners flashcards with addition and subtraction problems. Ask them to use their personal number lines and apply the Jump Strategy to solve the problems. Circulate to offer guidance and support as needed.
• Provide worksheets with a variety of problems suitable for the Jump Strategy. Include a mix of addition and subtraction questions that learners can solve individually.
• Encourage learners to visualize the jumps on a number line even if they’re working directly on the worksheet, reinforcing the mental math aspect of the strategy.
• Invite learners to share their solutions and how they applied the Jump Strategy to solve different problems. Discuss any challenges they faced and how they overcame them.
• Review the correct solutions to worksheet problems as a class, highlighting effective uses of the strategy.

Assessment and Feedback:

• Assess learners through observation during hands-on practice and their ability to correctly apply the Jump Strategy on the worksheet activities.
• Provide individual feedback, praising successful application of the strategy and offering additional support where necessary to ensure understanding.

TEACHING NOTES:

This lesson is designed to build upon Grade 3 learners’ foundational arithmetic skills by introducing them to the Jump Strategy as a practical tool for mental math. The emphasis on visualizing and making “jumps” on a number line not only aids in simplifying addition and subtraction problems but also enhances learners’ number sense and mental calculation abilities. By engaging learners in both the creation of their own number lines and the practical application of the strategy through varied exercises, the lesson caters to diverse learning styles and encourages active participation. The structured progression from demonstration to hands-on practice and individual work ensures learners have a clear understanding of the Jump Strategy and feel confident in applying it to solve problems. This approach fosters a supportive learning environment where learners are encouraged to explore mathematical concepts creatively and independently.

This plan is adaptable to the needs of the learners and can be expanded to include more complex problems or other arithmetic strategies as appropriate.

You may also be interested in these posts

• International
• Schools directory
• Resources Jobs Schools directory News Search

Jump Strategy

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

22 February 2018

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

• Technical Support
• Find My Rep

You are here

Daily Routines to Jump-Start Problem Solving, Grades K-8

• John J. SanGiovanni - Howard Public School System
• Description

Finally! A book that helps solve the problem of teaching problem solving!

Learning to be a problem solver is hard. Teaching students how to be problem solvers themselves can be even harder. Some students may learn to mimic procedures to come up with correct answers, but are they really learning to solve problems? To become independent problem solvers, students need to practice exploring, tinkering, and, most important, thinking!!

The bite-size routines in this guide are perfect for teachers looking for the interesting, engaging, and doable practice students need to become problem-solving masters. These flexible, modifiable bursts of quality practice are designed to get students to look at problems at different ways, sparking discussion, making connections, and boosting mathematics achievement. This collection addresses the common challenges students and teachers face when learning to problem solve by offering guidance on

• Developing students’ mathematical reasoning and conceptual understanding
• Building students’ skills with various problem-solving strategies
• Nurturing mathematical confidence and improving identity and agency

Fortified with standards for math practices and processes, the ideas in this guide develop the reasoning and critical-thinking skills needed to become independent problem-solvers for life!

See what’s new to this edition by selecting the Features tab on this page. Should you need additional information or have questions regarding the HEOA information provided for this title, including what is new to this edition, please email [email protected] . Please include your name, contact information, and the name of the title for which you would like more information. For information on the HEOA, please go to http://ed.gov/policy/highered/leg/hea08/index.html .

For assistance with your order: Please email us at [email protected] or connect with your SAGE representative.

SAGE 2455 Teller Road Thousand Oaks, CA 91320 www.sagepub.com

Problem solving has long been a challenge for students—until now! This book provides teachers with a bank of routines to engage students in thinking, reasoning, and sense making. Everything you need to teach students to be effective problem solvers is in your hands right now!

John J. SanGiovanni has written yet another masterful book on routines focused on problem solving. My mentor once told me the way you get better at solving math problems is making sense and solving more math problems. Many students typically shy away from problem solving, yet in this book SanGiovanni has developed culturally relevant problems students can engage in to help build their problem solving skills. He has brilliantly put together a book of problem-solving routines to help all students be more successful. If we want equitable mathematics classrooms, ALL students must be engaged in daily problem solving and Daily Routines to Jump-Start Problem Solving is a resource to ensure that!

I have been using resources from John J. SanGiovanni since 2018! His strategies have helped propel thinking and student engagement in my classroom as well as classrooms across my district. His activities and routines have increased students’ enjoyment of mathematics concepts, which has led to higher scores across the district.

Teachers often say, “My students can solve math equations, but not word problems.” With SanGiovanni’s Daily Routines to Jump-Start Problem Solving , teachers can ensure students develop the confidence to solve word problems without using hazardous tricks and gimmicks. Students will be encouraged to think about the mathematics behind the problem. The ideas in this book should be part of every mathematics class.

Instead of “cookbook” problem-solving prompts, SanGiovanni provides teachers with step-by-step guidance on implementing problem solving through the use of classroom-ready instructional routines that allow students to engage in rich problem-solving experiences and promote reasoning. Additionally, this book encourages productive discourse, facilitates “just in time” scaffolds, and supports existing high-quality curriculum materials.

The routines in this book are easy to follow and help set the stage to spark student engagement and discourse in any math class. As a math coach, I am always looking for ways to support teachers in helping students to be better thinkers and to reason with math, and these quick bursts of quality practice are an amazing resource. The graphic organizers provided to support the routines help ensure all students have an entry point to problem solving.

Daily Routines to Jump-Start for Problem Solving offers a plethora of problem-solving routines to promote reasoning and critical thinking skills. A resource for administrators, instructional coaches, and math teachers, each protocol has a “Something to Think About” section, images and examples that encourage productive discussions, and variations of each routine to meet all students’ needs.

Daily Routines to Jump-Start Problem Solving is truly a game changer for K–8 educators. Every problemsolving situation embodies critical thinking and comprehension, thus building student self-efficacy. SanGiovanni provides practical tools and support to breathe new life into math language routines, promoting equitable problem solving for all students. Routines showcased in this book allow students to take the driver’s seat as they engage in real-world problem solving.

As math educators and leaders, we have all been waiting for a book like this to aid in facilitating rich discussions centered on problem-solving, all in the first few minutes of daily instruction! SanGiovanni provides 20 research-based strategies to help students become problem-posers and problem-solvers while building their confidence, agency, and identity. This book is truly a gift to the math education community.

SanGiovanni shares a creative collection of quick, high-quality practice opportunities that will help students sharpen their problem-solving skills. Teachers have been longing for purposeful activities like these to engage their students in thinking and sense-making as they strive to develop confident problem solvers in mathematics. This book will become one of teachers’ best-loved instructional resources!

Preview this book

For instructors, select a purchasing option.