solving quadratic equations by factoring examples with answers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.3: Solving Quadratic Equations by Factoring

• Last updated
• Save as PDF
• Page ID 49403

• Denny Burzynski & Wade Ellis, Jr.
• College of Southern Nevada via OpenStax CNX

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Factoring Method

To solve quadratic equations by factoring, we must make use of the zero-factor property.

• Set the equation equal to zero, that is, get all the nonzero terms on one side of the equal sign and 0 on the other. \(ax^2 + bx + c = 0\)
• Factor the quadratic expression. \(()() = 0\)
• By the zero-factor property, at least one of the factors must be zero, so, set each of the factors equal to 0 and solve for the variable.

Sample Set A

Solve the following quadratic equations. (We will show the check for problem 1.)

Example \(\PageIndex{1}\)

\(\begin{array}{flushleft} x^2 - 7x + 12 &= 0 & & & \text{The equation is already set equal to } 0\\ (x-3)(x-4) &= 0 & & & \text{Factor. Set each factor equal to } 0.\\ x-3 &= 0 & \text{ or } x - 4 &= 0\\ x &= 3 & \text{ or } x &= 4 \end{array}\)

If \(x = 3, x^2 - 7x + 12 = 0\)

\(\begin{array}{flushleft} 3^2 - 7 \cdot 3 + 12 & = 0 & \text{Is this correct?}\\ 9 - 21 + 12 &= 0 & \text{Is this correct?}\\ 0 &= 0 & \text{Yes, this is correct?} \end{array}\)

Check: If \(x = 4, x^2 - 7x + 12 = 0\)

\(\begin{array}{flushleft} 4^2 - 7 \cdot 4 + 12 &= 0 & \text{Is this correct?}\\ 16 - 28 + 12 &= 0 & \text{Is this correct?}\\ 0 &= 0 & \text{Yes, this is correct} \end{array}\)

Thus, the solutions to this equation are \(x = 3, 4\).

Example \(\PageIndex{2}\)

\(\begin{array}{flushleft} x^2 &= 25 & \text{Set the equation equal to } 0\\ x^2 - 25 &= 0 & \text{Factor.}\\ (x+5)(x-5) &= 0 & \text{Set each factor equal to } 0\\ x+5=0 & \text{ or } & x - 5 = 0\\ x = -5 & \text{ or } & x=5\\ \end{array}\)

Thus, the solutions to this equation are \(x = 5, -5\).

Example \(\PageIndex{3}\)

\(\begin{array}{flushleft} x^2 &= 2x & \text{Set the equation equal to } 0\\ x^2 - 2x &= 0 & \text{Factor.}\\ x(x-2) && \text{Set each factor equal to} 0\\ x=0 & \text{ or } & x-2=0\\ && x=2 \end{array}\)

Thus, the solutions to this equation are \(x = 0, 2\)

Example \(\PageIndex{4}\)

\(\begin{array}{flushleft} 2x^2 + 7x - 15 &= 0 & \text{Factor.}\\ (2x - 3)(x+5) &= 0 & \text{Set each factor equal to } 0\\ 2x-3=0 & \text{ or } & x + 5 = 0\\ 2x=3 & \text{ or } & x=-5\\ x=\dfrac{3}{2} \end{array}\)

Thus, the solutions to this equation are \(x = \dfrac{3}{2}, -5\).

Example \(\PageIndex{5}\)

\(63x^2 = 13x + 6\)

\(\begin{array}{flushleft} 63x^2 - 13x - 6 &= 0\\ (9x + 2)(7x - 3) &= 0\\ 9x + 2 = 0 & \text{ or } & 7x - 3 = 0\\ 9x = -2 & \text{ or } & 7x = 3\\ x=\dfrac{-2}{9} & \text{ or } & x = \dfrac{3}{7} \end{array}\)

Thus, the solutions to this equiation are \(x = \dfrac{-2}{9}, \dfrac{3}{7}\)

Practice Set A

Solve the following equations, if possible.

Practice Problem \(\PageIndex{1}\)

\((x−7)(x+4)=0\)

\(x=7, −4\)

Practice Problem \(\PageIndex{2}\)

\((2x+5)(5x−7)=0\)

\(x = \dfrac{-5}{2}, \dfrac{7}{5}\)

Practice Problem \(\PageIndex{3}\)

\(x^2 + 2x - 24 = 0\)

\(x=4, −6\)

Practice Problem \(\PageIndex{4}\)

\(6x^2 + 13x - 5 = 0\)

\(x = \dfrac{1}{3}, \dfrac{-5}{2}\)

Practice Problem \(\PageIndex{5}\)

\(5y^2 + 2y = 3\)

\(y = \dfrac{3}{5}, -1\)

Practice Problem \(\PageIndex{6}\)

\(m(2m - 11) = 0\)

\(m = 0, \dfrac{11}{2}\)

Practice Problem \(\PageIndex{7}\)

\(6p^2 = -(5p + 1)\)

\(p = \dfrac{-1}{3}, \dfrac{-1}{2}\)

Practice Problem \(\PageIndex{8}\)

\(r^2 - 49 = 0\)

\(r=7,−7\)

Solving Mentally After Factoring

Let's consider problems 4 and 5 of Sample Set A in more detail. Let's look particularly at the factorizations \((2x-3)(x + 5) = 0\) and \((9x + 2)(7x - 3) = 0\)/ The next step is to set each factor equal to zero and solve. We can solve mentally if we understand how to solve linear equations: we transpose the constant from the variable term and then divide by the coefficient of the variable.

Sample Set B

Example \(\pageindex{6}\).

Solve the following equation mentally.

\((2x - 3)(x + 5) = 0\)

\(\begin{array}{flushleft} 2x - 3 &= 0 & \text{Mentally add } 3 \text{ to both sides. The constant changes sign.}\\ 2x &= 3 & \text{Divide by } 2 \text{ the coefficient of } x \text{. The } 2 \text{ divides the cosntant } 3 \text{ into } \dfrac{3}{2}\\ & & \text{The coefficient becomes the denominator.}\\ x &= \dfrac{3}{2}\\ x + 5 &= 0 & \text{ Mentally subtract } 5 \text{ from both sides. The constant changes sign.}\\ x &= -5 & \text{Divide by the coefficient of } x, 1. \text{ The coefficient becomes the denominator}\\ x = \dfrac{-5}{1} &= -5\\ x &= -5 \end{array}\)

Now, we can immediately write the solution to the equation after factoring by looking at each factor, changing the sign of the constant, then divide by the coefficient.

Practice Set B

Practice problem \(\pageindex{9}\).

Solve \((9x + 2)(7x - 3) = 0\) using this mental method.

\(x = -\dfrac{2}{9}, \dfrac{3}{7}\)

For the following problems, solve the equations, if possible.

Exercise \(\PageIndex{1}\)

\((x+1)(x+3)=0\)

\(x=−1, −3\)

Exercise \(\PageIndex{2}\)

\((x+4)(x+9)=0\)

Exercise \(\PageIndex{3}\)

\((x−5)(x−1)=0\)

\(x=1,  5\)

Exercise \(\PageIndex{4}\)

\((x−6)(x−3)=0\)

Exercise \(\PageIndex{5}\)

\((x−4)(x+2)=0\)

\(x=−2, 4\)

Exercise \(\PageIndex{6}\)

\((x+6)(x−1)=0\)

Exercise \(\PageIndex{7}\)

\((2x+1)(x−7)=0\)

\(x = -\dfrac{1}{2}, 7\)

Exercise \(\PageIndex{8}\)

\((3x+2)(x−1)=0\)

Exercise \(\PageIndex{9}\)

\((4x+3)(3x−2)=0\)

\(x = -\dfrac{3}{4}, \dfrac{2}{3}\)

Exercise \(\PageIndex{10}\)

\((5x−1)(4x+7)=0\)

Exercise \(\PageIndex{11}\)

\((6x+5)(9x−4)=0\)

\(x = -\dfrac{5}{6}, \dfrac{4}{9}\)

Exercise \(\PageIndex{12}\)

\((3a+1)(3a−1)=0\)

Exercise \(\PageIndex{13}\)

\(x(x+4)=0\)

\(x=−4, 0\)

Exercise \(\PageIndex{14}\)

\(y(y−5)=0\)

Exercise \(\PageIndex{15}\)

\(y(3y−4)=0\)

\(y = 0, \dfrac{4}{3}\)

Exercise \(\PageIndex{16}\)

\(b(4b+5)=0\)

Exercise \(\PageIndex{17}\)

\(x(2x+1)(2x+8)=0\)

\(x = -4, -\dfrac{1}{2}, 0\)

Exercise \(\PageIndex{18}\)

\(y(5y+2)(2y−1)=0\)

Exercise \(\PageIndex{19}\)

\((x-8)^2 = 0\)

Exercise \(\PageIndex{20}\)

\((x-2)^2 = 0\)

Exercise \(\PageIndex{21}\)

\((b + 7)^2 = 0\)

\(b=−7\)

Exercise \(\PageIndex{22}\)

\((a + 1)^2\)

Exercise \(\PageIndex{23}\)

\((x(x-4)^2 = 0\)

Exercise \(\PageIndex{24}\)

\(y(y + 9)^2 = 0\)

Exercise \(\PageIndex{25}\)

\(y(y-7)^2 = 0\)

Exercise \(\PageIndex{26}\)

\(y(y + 5)^2 = 0\)

Exercise \(\PageIndex{27}\)

\(x^2 - 4 = 0\)

\(x=−2, 2\)

Exercise \(\PageIndex{28}\)

\(x^2 + 9 = 0\)

Exercise \(\PageIndex{29}\)

\(x^2 + 36\)

no solution

Exercise \(\PageIndex{30}\)

\(x^2 - 25 = 0\)

Exercise \(\PageIndex{31}\)

\(a^2 - 100 = 0\)

\(a=−10, 10\)

Exercise \(\PageIndex{32}\)

\(a^2 - 81 = 0\)

Exercise \(\PageIndex{33}\)

\(b^2 - 49 = 0\)

\(b=7, −7\)

Exercise \(\PageIndex{34}\)

\(y^2 - 1 = 0\)

Exercise \(\PageIndex{35}\)

\(3a^2 - 75 = 0\)

\(a=5, −5\)

Exercise \(\PageIndex{36}\)

\(5b^2 - 20 = 0\)

Exercise \(\PageIndex{37}\)

\(y^3 - y = 0\)

\(y=0, 1, −1\)

Exercise \(\PageIndex{38}\)

\(a^2 = 9\)

Exercise \(\PageIndex{39}\)

\(b^2 = 4\)

\(b=2, −2\)

Exercise \(\PageIndex{40}\)

\(b^2 = 1\)

Exercise \(\PageIndex{41}\)

\(a^2 = 36\)

\(a=6, −6\)

Exercise \(\PageIndex{42}\)

\(3a^2 = 12\)

Exercise \(\PageIndex{43}\)

\(-2x^2 = -4\)

\(x = \sqrt{2}, -\sqrt{2}\)

Exercise \(\PageIndex{44}\)

\(-2a^2 = -50\)

Exercise \(\PageIndex{45}\)

\(-7b^2 = -63\)

\(b=3,  −3\)

Exercise \(\PageIndex{46}\)

\(-2x^2 = -32\)

Exercise \(\PageIndex{47}\)

\(3b^2 = 48\)

\(b=4, −4\)

Exercise \(\PageIndex{48}\)

\(a^2 - 8a + 16 = 0\)

Exercise \(\PageIndex{49}\)

\(y^2 + 10y + 25 = 0\)

\(y=−5\)

Exercise \(\PageIndex{50}\)

\(y^2 + 9y + 16 = 0\)

Exercise \(\PageIndex{51}\)

\(x^2 - 2x - 1 = 0\)

Exercise \(\PageIndex{52}\)

\(a^2 + 6a + 9 = 0\)

Exercise \(\PageIndex{53}\)

\(a^2 + 4a + 4 = 0\)

\(a=−2\)

Exercise \(\PageIndex{54}\)

\(x^2 + 12x = -36\)

Exercise \(\PageIndex{55}\)

\(b^2 - 14b = -49\)

Exercise \(\PageIndex{56}\)

\(3a^2 + 18a + 27 = 0\)

Exercise \(\PageIndex{57}\)

\(2m^3 + 4m^2 + 2m = 0\)

\(m=0, −1\)

Exercise \(\PageIndex{58}\)

\(3mn^2 - 36mn + 36m = 0\)

Exercise \(\PageIndex{59}\)

\(a^2 + 2a - 3 = 0\)

\(a=−3, 1\)

Exercise \(\PageIndex{60}\)

\(a^2 + 3a - 10 = 0\)

Exercise \(\PageIndex{61}\)

\(x^2 + 9x + 14 = 0\)

\(x=−7, −2\)

Exercise \(\PageIndex{62}\)

\(x^2 - 7x + 12 = 3\)

Exercise \(\PageIndex{63}\)

\(b^2 + 12b + 27 = 0\)

\(b=−9,  −3\)

Exercise \(\PageIndex{64}\)

\(b^2 - 3b + 2 = 0\)

Exercise \(\PageIndex{65}\)

\(x^2 - 13x = -42\)

Exercise \(\PageIndex{66}\)

\(a^3 = -8a^2 - 15a\)

Exercise \(\PageIndex{67}\)

\(6a^2 + 13a + 5 = 0\)

\(a = -\dfrac{5}{3}, -\dfrac{1}{2}\)

Exercise \(\PageIndex{68}\)

\(6x^2 - 4x - 2 = 0\)

Exercise \(\PageIndex{69}\)

\(12a^2 + 15a + 3 = 0\)

\(a = -\dfrac{1}{4}, -1\)

Exercise \(\PageIndex{70}\)

\(18b^2 + 24b + 6 = 0\)

Exercise \(\PageIndex{71}\)

\(12a^2 + 24a + 12 = 0\)

\(a=−1\)

Exercise \(\PageIndex{72}\)

\(4x^2 - 4x = -1\)

Exercise \(\PageIndex{73}\)

\(2x^2 = x + 15\)

\(x = -\dfrac{5}{2}, 3\)

Exercise \(\PageIndex{74}\)

\(4a^2 = 4a + 3\)

Exercise \(\PageIndex{75}\)

\(4y^2 = -4y - 2\)

Exercise \(\PageIndex{76}\)

\(9y^2 = 9y + 18\)

Exercises For Review

Exercise \(\pageindex{77}\).

Simplify \((x^4y^3)^2(xy^2)^4\)

\(x^{12}y^{14}\)

Exercise \(\PageIndex{78}\)

Write \((x^{-2}y^3w^4)^{-2}\) so that only positive exponents appear.

Exercise \(\PageIndex{79}\)

Find the sum: \(\dfrac{x}{x^2 - x - 2} + \dfrac{1}{x^2 - 3x + 2}\)

\(\dfrac{x^2 + 1}{(x+1)(x-1)(x-2)}\)

Exercise \(\PageIndex{80}\)

Simplify \(\dfrac{\dfrac{1}{a} + \dfrac{1}{b}}{\dfrac{1}{a} - \dfrac{1}{b}}\)

Exercise \(\PageIndex{81}\)

Solve \((x + 4)(3x + 1) = 0\)

\(x = -4, \dfrac{-1}{3}\)

Factoring Quadratics

"Factoring" (or "Factorising" in the UK) a Quadratic is:

finding what to multiply to get the Quadratic

It is called "Factoring" because we find the factors (a factor is something we multiply by)

Example: (x+4) and (x−1) are factors of x 2 + 3x − 4

Let us "expand" (x+4) and (x−1) to be sure:

Yes, (x+4) and (x−1) are definitely factors of x 2 + 3x − 4

Did you see that Expanding and Factoring are opposites?

Expanding is usually easy, but Factoring can often be tricky .

OK, let's try an example where we don't know the factors yet:

Common Factor

First we can check for any common factors .

Example: what are the factors of 6x 2 − 2x = 0 ?

6 and 2 have a common factor of 2 :

2(3x 2 − x) = 0

And x 2 and x have a common factor of x :

2x(3x − 1) = 0

And we have done it! The factors are 2x and 3x − 1 ,

We can now also find the roots (where it equals zero):

• 2x is 0 when x = 0
• 3x − 1 is zero when x = 1 3

And this is the graph (see how it is zero at x=0 and x= 1 3 ):

But it is not always that easy ...

Guess and Check

Example: what are the factors of 2x 2 + 7x + 3 .

No common factors.

Maybe we can guess an answer? Then check if we are right ... we may get lucky!

Let's guess (2x+3)(x+1):

(2x+3)(x+1) = 2x 2 + 2x + 3x + 3 = 2x 2 + 5x + 3 (Close but WRONG )

How about (2x+7)(x−1):

(2x+7)(x−1) = 2x 2 − 2x + 7x − 7 = 2x 2 + 5x − 7 (WRONG AGAIN)

OK, how about (2x+9)(x−1):

(2x+9)(x−1) = 2x 2 − 2x + 9x − 9 = 2x 2 + 7x − 9 (WRONG AGAIN!)

We could be guessing for a long time before we get lucky.

That is not a very good method. So let us try something else.

A Method For Simple Cases

There is a method for simple cases.

With the quadratic equation in this form:

Step 1 : Find two numbers that multiply to give ac (in other words a times c), and add to give b .

Example: 2x 2 + 7x + 3

ac is 2×3 = 6 and b is 7

So we want two numbers that multiply together to make 6, and add up to 7

In fact 6 and 1 do that (6×1=6, and 6+1=7)

How do we find 6 and 1?

It helps to list the factors of ac= 6 , and then try adding some to get b= 7 .

Factors of 6 include 1, 2, 3 and 6.

Aha! 1 and 6 add to 7, and 6×1=6.

Step 2 : Rewrite the middle with those numbers:

Rewrite 7x with 6 x and 1 x:

2x 2 + 6x + x + 3

Step 3 : Factor the first two and last two terms separately:

The first two terms 2x 2 + 6x factor into 2x(x+3)

The last two terms x+3 don't actually change in this case

2x(x+3) + (x+3)

Step 4 : If we've done this correctly, our two new terms should have a clearly visible common factor.

In this case we can see that (x+3) is common to both terms, so we can go:

Check: (2x+1)(x+3) = 2x 2 + 6x + x + 3 = 2x 2 + 7x + 3 (Yes)

Let's see Steps 1 to 4 again, in one go :

OK, let us try another example:

Example: 6x 2 + 5x − 6.

Step 1 : ac is 6×(−6) = −36 , and b is 5

List the positive factors of ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36

One of the numbers has to be negative to make −36, so by playing with a few different numbers I find that −4 and 9 work nicely:

−4×9 = −36 and −4+9 = 5

Step 2 : Rewrite 5x with −4x and 9x:

6x 2 − 4x + 9x − 6

Step 3 : Factor first two and last two:

2x(3x − 2) + 3(3x − 2)

Step 4 : Common Factor is (3x − 2):

(2x+3)(3x − 2)

Check: (2x+3)(3x − 2) = 6x 2 − 4x + 9x − 6 = 6x 2 + 5x − 6 (Yes)

Finding Those Numbers

The hardest part is finding two numbers that multiply to give ac , and add to give b .

It is partly guesswork, and it helps to list out all the factors .

Here is another example to help you:

Example: ac = −120 and b = 7

What two numbers multiply to −120 and add to 7 ?

The factors of 120 are (plus and minus):

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120

We can try pairs of factors (start near the middle!) and see if they add to 7:

• −10 x 12 = −120, and −10+12 = 2 (no)
• −8 x 15 = −120 and −8+15 = 7 (YES!)

Get Some Practice

You can practice simple quadratic factoring .

Why Factor?

Well, one of the big benefits of factoring is that we can find the roots of the quadratic equation (where the equation is zero).

All we need to do (after factoring) is find where each of the two factors becomes zero

Example: what are the roots (zeros) of 6x 2 + 5x − 6 ?

We already know (from above) the factors are

(2x + 3)(3x − 2)

And we can figure out that

(2x + 3) is zero when x = −3/2

(3x − 2) is zero when x = 2/3

So the roots of 6x 2 + 5x − 6 are:

−3/2 and 2/3

Here is a plot of 6x 2 + 5x − 6 , can you see where it equals zero?

We can also check it using a bit of arithmetic:

At x = −3 2 : 6( −3 2 ) 2 + 5( −3 2 ) − 6 = 6×( 9 4 ) − 15 2 − 6 = 54 4 − 15 2 - 6 = 0

At x = 2 3 : 6( 2 3 ) 2 + 5( 2 3 ) − 6 = 6×( 4 9 ) + 10 3 − 6 = 24 9 + 10 3 - 6 = 0

We can also try graphing the quadratic equation . Seeing where it equals zero can give us clues.

Example: (continued)

Starting with 6x 2 + 5x − 6 and just this plot:

The roots are around x = −1.5 and x = +0.67, so we can guess the roots are:

Which can help us work out the factors 2x + 3 and 3x − 2

Always check though! The graph value of +0.67 might not really be 2/3

General Solution

Quadratic equations have symmetry, the left and right are like mirror images:

The midline is at −b/2 , and we can calculate the value w with these steps:

• First, "a" must be 1, if not then divide b and c by a:
• b = b/a, c = c/a
• w = √(mid 2 − c)
• roots are at mid−w and mid+w

Example: x 2 + 3x − 4

a = 1, b = 3 and c = −4

• a= 1, so we can go to next step
• mid = − 3 2
• w = √[( 3 2 ) 2 − (−4)] = √( 9 4 + 4) = √ 25 4 = 5 2
• roots are at  − 3 2 − 5 2 = −4 and − 3 2 + 5 2 = 1  

So we can factor x 2 + 3x − 4 into (x + 4)(x − 1) 

Quadratic formula

We can also use the quadratic formula :

We get two answers x + and x − (one is for the "+" case, and the other is for the "−" case in the "±") that gets us this factoring:

a(x − x + )(x − x − )

Example: what are the roots of 6x 2 + 5x − 6 ?

Substitute a=6, b=5 and c=−6 into the formula:

x = −b ± √(b 2 − 4ac) 2a

= −5 ± √(5 2 − 4×6×(−6)) 2×6

= −5 ± √(25 + 144) 12

= −5 ± √169 12

= −5 ± 13 12

So the two roots are:

x + = (−5 + 13) / 12 = 8/12 = 2/3,

x − = (−5 − 13) / 12 = −18/12 = −3/2

(Notice that we get the same answer as when we did the factoring earlier.)

Now put those values into a(x − x + )(x − x − ) :

6(x − 2/3)(x + 3/2)

We can rearrange that a little to simplify it:

3(x − 2/3) × 2(x + 3/2) = (3x − 2)(2x + 3)

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Quadratic Equations

1. Solving Quadratic Equations by Factoring

• 2. Completing the Square
• 3. The Quadratic Formula
• Sum and product of the roots of a quadratic equation
• 4. The Graph of the Quadratic Function
• Interactive Quadratic Function Graph
• 5. Equations in Quadratic Form

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Online Algebra Solver

Solve your algebra problem step by step!

IntMath Forum

Get help with your math queries:

The general form of a quadratic equation is

ax 2 + bx + c = 0

where x is the variable and a , b & c are constants

Examples of Quadratic Equations

(a) 5 x 2 − 3 x − 1 = 0 is a quadratic equation in quadratic form where

`a = 5`, `b = -3`, `c = -1`

(b) 5 + 3 t − 4.9 t 2 = 0 is a quadratic equation in quadratic form.

Here, `a = -4.9`, `b = 3`, `c = 5` [This equation arose from finding the time when a projectile, being acted on by gravity, hits the ground.]

(c) ( x + 1) 2 = 4 is a quadratic equation but not in quadratic form.

It has to be expanded and simplified to:

x 2 + 2 x − 3 = 0

In general, a quadratic equation:

• must contain an x 2 term
• must NOT contain terms with degrees higher than x 2 eg. x 3 , x 4 etc

Examples of NON-quadratic Equations

• bx − 6 = 0 is NOT a quadratic equation because there is no x 2 term.
• x 3 − x 2 − 5 = 0 is NOT a quadratic equation because there is an x 3 term (not allowed in quadratic equations).

Solutions of a Quadratic Equation

The solution of an equation consists of all numbers (roots) which make the equation true .

All quadratic equations have 2 solutions (ie. 2 roots). They can be:

• real and distinct
• real and equal
• imaginary (complex)

The quadratic equation x 2 − 7 x + 10 = 0 has roots of

`x = 2` and `x = 5`. (We'll show below how to find these roots.)

This can be seen by substituting in the equation:

When x = 2,

x 2 − 7 x + 10

= (2) 2 − 7(2) + 10 = 4 − 14 + 10 = 0

(This can be shown similarly for x = 5). In this example, the roots are real and distinct .

The quadratic equation x 2 − 6 x + 9 = 0 has double roots of x = 3 (both roots are the same)

This can be seen by substituting x = 3 in the equation:

x 2 − 6 x + 9

= (3) 2 − 6(3) + 9 = 9 − 18 + 9 = 0

The quadratic equation

x 2 + 9 = 0

has imaginary roots of

`x=sqrt(-9)` or `-sqrt(-9)`

Learn more about imaginary numbers .

Solving a Quadratic Equation by Factoring

For the time being, we shall deal only with quadratic equations that can be factored (factorised).

If you need a reminder on how to factor, go back to the section on:

Factoring Trinomials .

Using the fact that a product is zero if any of its factors is zero we follow these steps:

(i) Bring all terms to the left and simplify, leaving zero on the right side.

(ii) Factorise the quadratic expression

(iii) Set each factor equal to zero

(iv) Solve the resulting linear equations

(v) Check the solutions in the original equation

Solve x 2 − 2 x − 15 = 0

x 2 − 2 x − 15 = 0

Factoring gives:

( x − 5)( x + 3) = 0

Now, if either of the terms ( x − 5) or ( x + 3) is 0, the product is zero. So we conclude:

( x − 5) = 0 , therefore x = 5

( x + 3) = 0 , therefore x = − 3

Hence the roots are x = 5 and x = − 3 .

Are we correct?

We check the roots in the original equation by substitution.

When x = 5 :

x 2 − 2 x − 15

= (5) 2 − 10 − 15 = 25 − 10 − 15 = 0

(Similarly, when we substitute `x = -3`, we also get `0`.)

Alternate method (Po-Shen Loh's approach)

We could have proceded as follows to solve this quadratic equation. The following approach takes the guesswork out of the factoring step, and is similar to what we'll be doing next, in Completing the Square .

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × (−2) = 1`

Step 2: Expand `(1 − u)(1 + u) = 1 − u^2`

Step 3: Set that expansion equal to the constant term: `1 - u^2 = -15`

Step 4: Solve for `u`:

`1 - u^2 = -15` `u^2 = 16` `u= +-4`

Step 5: Substitute either value (we'll use `+4`) into the `u` bracket expressions, giving us the same roots of the quadratic equation that we found above:

`x=(1-u)=1-4 = -3,` or

`x=(1+u)=1+4 = 5`

For more on this approach, see: A Different Way to Solve Quadratic Equations (video by Po-Shen Loh).

`9x^2+ 6x + 1 = 0`

9 x 2 + 6 x + 1 = 0

(3 x + 1)(3 x + 1) = 0

So we conclude:

(3 x + 1) = 0 ,

We say there is a double root of `x = -1/3`.

We first need to re-express the quadratic with a `1` as the coefficient of `x^2.`

`x^2+ 2/3x + 1/9 = 0`

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × 2/3 = -1/3`

Step 2: Expand `(-1/3 − u)(-1/3 + u) = 1/9 − u^2`

Step 3: Set that expansion equal to the constant term: `1/9 - u^2 = 1/9`

`1/9 - u^2 = 1/9` `u^2 = 0` `u= 0`

Step 5: Substitute `u=0` into the `u` bracket expressions, giving us the same (repeated) root for the quadratic equation that we found above:

`x=-1/3-0 = -1/3,` or `x=-1/3+0 = -1/3`

Example 6 (involving fractions)

`2-1/x=3/(x+2)`

Multiply throughout by `x(x+2)` to remove the denominators (bottoms) of the fractions:

`2x(x+2)-(x(x+2))/x=(3(x)(x+2))/(x+2)`

Cancelling gives:

`2x(x+2)-(x+2)=3x`

Expanding the brackets:

`2x^2+4x-x-2=3x`

`(x+1)(x-1)=0`

So `x = -1` or `x = 1`.

CHECK: Substituting `x = -1` into both the left hand side and right hand side of the question gives:

`"LHS"=2-1/x=2-1/-1=3`

`"RHS"=3/(x+2)=3/(-1+2)=3="LHS" `

Likewise, for `x = +1`,

LHS `= 2 - 1 = 1` RHS `= 3/3 = 1 =` LHS

• Determine if the following are quadratic equations. If so, determine a , b , and c.

a. 5 x 2 = 9 − x b. (3 x − 2) 2 = 2

Q1a    `5x^2= 9 − x`

`5x^2+ x − 9 = 0`

So, yes, it is a quadratic equation with

`a = 5`, `b = 1`, `c = -9`

Q1b    `(3x − 2)^2= 2`

`9x^2− 12x + 4 = 2` `9x^2− 12x + 2 = 0`

`a = 9`, `b = -12`, `c = 2`

• Solve for x :

2 x 2 − 7 x + 6 = 3

2 x 2 − 7 x + 3 = 0 (2 x − 1)( x − 3) = 0

`x=1/2` or `x=3`.

Once again, we first need to re-express the quadratic with a `1` as the coefficient of `x^2.`

`x^2- 7/2x + 3/2 = 0`

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × (-7/2) = 7/4`

Step 2: Expand `(7/4 − u)(7/4 + u) = 49/16 − u^2`

Step 3: Set that expansion equal to the constant term: `49/16 - u^2 = 3/2`

`49/16 - u^2 = 3/2` `u^2 = 49/16 - 24/16 = 25/16` `u= +-5/4`

Step 5: Substitute either value (we'll use `+5/4`) into the `u` bracket expressions, giving us the same roots of the quadratic equation that we found above:

`x=7/4-5/4 = 1/2,` or `x=7/4+5/4 = 3`

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

Factoring Quadratics

Factoring quadratics is a method of expressing the polynomial as a product of its linear factors. It is a process that allows us to simplify quadratic expressions, find their roots and solve equations. A quadratic polynomial is of the form ax 2 + bx + c, where a, b, c are real numbers. Factoring quadratics is a method that helps us to find the zeros of the quadratic equation ax 2 + bx + c = 0.

In this mini-lesson, let us learn about the fascinating concept of factoring quadratics, the formula for factorization of quadratic equations along some solved examples for a better understanding.

What Is Factoring Quadratics?

Factoring quadratics is a method of expressing the quadratic equation ax 2 + bx + c = 0 as a product of its linear factors as (x - k)(x - h), where h, k are the roots of the quadratic equation ax 2 + bx + c = 0. This method is also is called the method of factorization of quadratic equations. Factorization of quadratic equations can be done using different methods such as splitting the middle term, using the quadratic formula, completing the squares, etc.

Factoring Quadratics Meaning

The factor theorem relates the linear factors and the zeros of any polynomial. Every quadratic equation has two roots, say \(\alpha\) and \(\beta\). They are the zeros of the quadratic equation. Consider a quadratic equation f(x) = 0, where f(x) is a polynomial of degree 2. Suppose that x = \(\alpha\) is one root of this equation. This means that x = \(\alpha\) is a zero of the quadratic expression f(x). Thus, (x - \(\alpha\)) should be a factor of f(x).

Similarly, if x = \(\beta\) is the second root of f(x) = 0, then x = \(\beta\) is a zero of f(x). Thus, (x - \(\beta\)) should be a factor of f(x). Hence, factoring quadratics is a method of expressing the quadratic equations as a product of its linear factors, that is, f(x) = (x - \(\alpha\))(x - \(\beta\)). Let us go through some examples of factoring quadratics:

Examples of Factoring Quadratics

1. Consider the quadratic equation x 2 + 5x + 6 = 0

-3 and -2 are the roots of the equation. Verify by substituting the roots in the given equation and check if the value equals 0.

Factor 1: (x + 3)

LHS = x 2 + 5x + 6 = (-3) 2 + 5 × -3 + 6 = 9 -15 + 6 = 0 = RHS

Factor 2: (x + 2)

LHS = x 2 + 5x + 6 = (-2) 2 + 5 × -2 + 6 = 4 -10 + 6 = 0 = RHS

Thus the equation has 2 factors (x + 3) and (x + 2)

2. Consider x 2 - 9 = 0

3 and -3 are the two roots of the equation. Verify by substituting the roots in the given equation and check if the value equals 0.

3 2 - 9 = 9 - 9 = 0

(-3) 2 - 9 = 9 - 9 = 0

Thus the equation has 2 factors (x+3) and (x-3)

Methods of Factoring Quadratics

Factoring quadratics gives us the roots of the quadratic equation. There are different methods that can be used for factoring quadratic equations. Factoring quadratics is done in 4 ways:

• Factoring out the GCD
• Splitting the middle term
• Using Algebraic Identities (Completing the Squares)
• Using Quadratic formula

Factoring Quadratics by Taking Out The GCD

Factoring quadratics can be done by finding the common numeric factor and the algebraic factors shared by the terms in the quadratic equation and then take them out. Let us solve an example to understand the factoring quadratic equations by taking the GCD out.

Consider this quadratic equation: 3x 2 + 6x = 0

• The numerical factor is 3 (coefficient of x 2 ) in both terms.
• The algebraic common factor is x in both terms.
• The common factors are 3 and x. Hence we take them out.
• Thus 3x 2 + 6x = 0 is factorized as 3x(x + 2) = 0

Splitting the Middle Term for Factoring Quadratics

• The sum of the roots of the quadratic equation ax 2 + bx + c = 0 is given by \(\alpha + \beta\) = -b/a
• The product of the roots in the quadratic equation ax 2 + bx + c = 0 is given by \(\alpha\beta\) = c/a

We split the middle term b of the quadratic equation ax 2 + bx + c = 0 when we try to factorize quadratic equations. We determine the factor pairs of the product of a and c such that their sum is equal to b.

Example: f(x) = x 2 + 8x + 12

Split the middle term 8x in such a way that the factors of the product of 1 and 12 add up to make 8. Factor pairs of 12 are (1, 12), (2, 6), (3, 4). Now, we can see that the factor pair (2, 6) satisfies our purpose as the sum of 6 and 2 is 8 and the product is 12. Hence, we split the middle term and write the quadratic equation as:

x 2 + 8x + 12 = 0

⇒ x 2 + 6x + 2x + 12 = 0

Now, club the terms in pairs as:

(x 2 + 6x) + (2x + 12) = 0

⇒ x(x + 6) + 2(x + 6) = 0

Taking the common factor (x + 6) out, we have

(x + 2) (x + 6) = 0

Thus, (x + 2) and (x + 6) are the factors of x 2 + 8x + 12 = 0

Identities for Factoring Quadratics

The process of factoring quadratics can be done by completing the squares which require the use of algebraic identities. The main algebraic identities which are used for completing the squares are:

• (a + b) 2 = a 2 + 2ab + b 2
• (a - b) 2 = a 2 - 2ab + b 2

Steps to factorize quadratic equation ax 2 + bx + c = 0 using completeing the squares method are:

• Step 1: Divide both the sides of quadratic equation ax 2 + bx + c = 0 by a. Now, the obtained equation is x 2 + (b/a) x + c/a = 0
• Step 2: Subtract c/a from both the sides of quadratic equation x 2 + (b/a) x + c/a = 0. Obtained equation is x 2 + (b/a) x = -c/a
• Step 3: Add the square of (b/2a) to both the sides of quadratic equation x 2 + (b/a) x = -c/a. Obtained equation is x 2 + (b/a) x + (b/2a) 2 = -c/a + (b/2a) 2
• Step 4: Now the LHS of the quadratic equation x 2 + (b/a) x + (b/2a) 2 = -c/a + (b/2a) 2 can be written as a complete square and simplify the RHS, if necessary. Obtained equation is (x + b/2a) 2 = -c/a + (b/2a) 2
• Step 5: The roots of the given quadratic equation can be obtained and hence, we can form the factors of the equation.

Another algebraic identity which is used for factoring quadratics is a 2 - b 2 = (a + b)(a - b). Let us see an example to understand.

Example 1: f(x) = 9x 2 - 4 (difference of 2 perfect squares)

9x 2 - 4 = (3x) 2 - 2 2

We notice that this is of the form, a 2 - b 2 = (a + b)(a - b)

Hence we factorize the equation 9x 2 - 4 = 0 as (3x+2) (3x-2)

9x 2 - 4 = (3x+2) (3x-2)

Example 2: f(x) = 4x 2 + 12x + 9

4x 2 + 12x + 9 = (2x) 2 + 2(2x)(3) + (3) 2 We notice that this is of the form (a+b) 2 = a 2 + 2ab + b 2 (2x) 2 + 2(2x)(3) + (3) 2 = (2x + 3) 2 Hence we have (2x + 3), (2x + 3) as the linear factors of f(x) = 4x 2 + 12x + 9

Formula for Factoring Quadratics

Factoring quadratics is also done by using a formula that gives us the roots of the quadratic equation and hence, the factors of the equation. If ax 2 + bx + c = 0 is a quadratic equation, a is the coefficient of x 2 , b is the coefficient of x and c is the constant term. Then we find the value of x by using the formula:

\(x= \dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)

Consider, the quadratic equation x 2 + 5x + 4 = 0. It is of the form ax 2 + bx + c = 0. Here a =1, b = 5, c = 4

Substituting the values of a, b and c in the quadratic formula formula, we get

\[\begin{align}x&= \dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\\\\x &= \dfrac{-5\pm \sqrt{5^2-4\times 1 \times 4}}{2\times 1}\\\\&= \dfrac{-5\pm \sqrt{25 -16}}{2}\\\\&= \dfrac{-5\pm \sqrt{9}}{2}\\\\&= \dfrac{-5\pm 3}{2}\\&= \dfrac{-5+3}{2}\text{ and } \dfrac{-5-3}{2}\\\\&=\dfrac{-2}{2}\text{ and }\dfrac{-8}{2}\\\\x &=(-1)\text{ and} (-4)\end{align}\]

Thus, the factors are (x + 1) and (x + 4).

Related Topics on Factoring Quadratics

• Factor Theorem
• Factoring Methods

Important Notes on Factoring Quadratics

• Linear factors are of the form ax + b and they cannot be factored further.
• A quadratic polynomial is a polynomial of degree 2.

Factoring Quadratics Examples

Example 1: Verify if (2x+3) and (x+3) are the linear factors of the quadratic equation f(x) = 2x 2 + 9x + 9.

Solution: To verify if (2x+3) and (x+3) are the linear factors of the quadratic equation f(x) = 2x 2 + 9x + 9, we will multiply the factors.

(2x + 3)(x + 3) = 2x 2 + 3x + 6x + 9 = 2x 2 + 9x + 9.

Answer: Hence, (2x+3) and (x+3) are the linear factors of the quadratic equation f(x) = 2x 2 + 9x + 9.

Example 2: Find the factors of the quadratic equation x 2 + x - 12 = 0 using the factoring quadratics method.

Solution: We will split the middle term of the quadratic equation x 2 + x - 12 = 0 to determine its factors.

x 2 + x - 12 = 0

⇒ x 2 + 4x - 3x - 12 = 0

⇒ x(x + 4) - 3(x + 4) = 0

⇒ (x - 3)(x + 4) = 0

Answer: Hence the factors of x 2 + x - 12 = 0 are (x - 3) and (x + 4).

go to slide go to slide

Book a Free Trial Class

Practice Questions on Factoring Quadratics

Faqs on factoring quadratics, what is factoring quadratics in algebra.

Factoring quadratics is a method of expressing the polynomial as a product of its linear factors. It is a process that allows us to simplify quadratic expressions, find their roots and solve equations.

How to Solve Quadratic Equations by Factoring Quadratics?

By determining the factors, we can get the roots of the quadratic equation and hence the solution.

What are the Methods used for Factorization of Quadratic Equations?

The methods to factorize quadratic equations are splitting the middle term, using algebraic identities, using the quadratic formula, and factoring the GCD out.

What is the Method of Factoring Quadratic Equations?

Splitting the middle term and using the quadratic formula are the most efficient methods for factoring quadratic equations.

Is Factoring Quadratics the Same as Solving it?

When we factorize a quadratic equation , we get linear factors that divide the quadratic polynomial evenly. The next step is finding the zeros of the equation by equating the factors with zero.

What is the Shortest Way to Factor any Quadratic Equation?

Using the quadratic formula is the shortest way of factoring quadratics.

What Are Some Tricks for Factoring Quadratics?

Find the sum of the roots and the product of the roots or by identifying any known algebraic identity, we can factorize the quadratic equations.

What is Quadratic Equation Factored Form?

(x - \(\alpha\)) (x - \(\beta\)) is the factored form of quadratic equation, where \(\alpha\) and \(\beta\) are the roots of the quadratic equation.

How to Solve a Quadratic Equation?

There are different methods that can be used for factoring quadratic equations and solving the quadratic equations. Factoring quadratics is done in 4 ways:

How Can you Factorize Quadratic Equations Easily?

We split the middle term b of the quadratic equation ax 2 + bx + c = 0 when we try to factorize quadratic equations. We determine the factor pairs of the product of a and c such that their sum is equal to b. Taking the common factors out, we can factorize quadratic equations easily.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Factoring Quadratic Equations – Methods & Examples

JUMP TO TOPIC

How to Factor a Quadratic Equation?

Factoring when the coefficient of x 2 is greater than 1, practice questions, factoring quadratic equations – methods & examples.

First of all, let’s take a quick review of the quadratic equation . A quadratic equation is a polynomial of a second degree, usually in the form of f(x) = ax 2 + bx + c where a, b, c, ∈ R, and a ≠ 0. The term ‘a’ is referred to as the leading coefficient, while ‘c’ is the absolute term of f (x).

Every quadratic equation has two values of the unknown variable, usually known as the roots of the equation (α, β). We can obtain the roots of a quadratic equation by factoring the equation.

For this reason, factorization is a fundamental step towards solving any equation in mathematics. Let’s find out.

Factoring a quadratic equation can be defined as the process of breaking the equation into the product of its factors. In other words, we can also say that factorization is the reverse of multiplying out.

To solve the quadratic equation ax 2  + bx + c = 0 by factorization, the following steps are used:

• Expand the expression and clear all fractions if necessary.
• Move all terms to the left-hand side of the equal to sign.
• Factorize the equation by breaking down the middle term.
• Equate each factor to zero and solve the linear equations

Solve: 2(x 2  + 1) = 5x

Expand the equation and move all the terms to the left of the equal sign.

⟹ 2x 2  – 5x + 2 = 0

⟹ 2x 2  – 4x – x + 2 = 0

⟹ 2x (x – 2) – 1(x – 2) = 0

⟹ (x – 2) (2x – 1) = 0

Equate each factor equal to zero and solve

⟹ x – 2 = 0 or 2x – 1 = 0

⟹ x = 2 or x = 1212

Therefore, the solutions are x = 2, 1/2.

Solve 3x 2 – 8x – 3 = 0

3x 2  – 9x + x – 3 = 0

⟹ 3x (x – 3) + 1(x – 3) = 0

⟹ (x – 3) (3x + 1) = 0

⟹ x = 3 or x = -13

Solve the following quadratic equation (2x – 3) 2  = 25

Expand the equation (2x – 3) 2  = 25 to get;

⟹ 4x 2 – 12x + 9 – 25 = 0

⟹ 4x 2  – 12x – 16 = 0

Divide each term by 4 to get;

⟹ x 2  – 3x – 4 = 0

⟹ (x – 4) (x + 1) = 0

⟹ x = 4 or x = -1

The are many methods of factorizing quadratic equations. In this article, our emphasis will be based on how to factor quadratic equations, in which the coefficient of x 2  is either 1 or greater than 1.

Therefore, we will use the trial and error method to get the right factors for the given quadratic equation.

Factoring when the Coefficient of x 2 is 1

To factorize a quadratic equation of the form x 2 + bx + c, the leading coefficient is 1. You need to identify two numbers whose product and sum are c and b, respectively.

CASE 1: When b and c are both positive

Solve the quadratic equation: x 2  + 7x + 10 = 0

List down the factors of 10:

1 × 10, 2 × 5

Identify two factors with a product of 10 and a sum of 7:

1 + 10 ≠ 7 2 + 5 = 7.

Verify the factors using the distributive property of multiplication.

(x + 2) (x + 5) = x 2  + 5x + 2x + 10 = x 2  + 7x + 10

The factors of the quadratic equation are:(x + 2) (x + 5)

Equating each factor to zero gives;

x + 2 = 0 ⟹x= -2

x + 5 = 0 ⟹ x = -5

Therefore, the solution is x = – 2, x = – 5

x 2 + 10x + 25.

Identify two factors with the product of 25 and sum of 10.

5 × 5 = 25, and 5 + 5 = 10

Verify the factors.

x 2 + 10x + 25 = x 2 + 5x + 5x + 25

= x (x + 5) + 5x + 25

= x (x + 5) + 5(x + 5)

= (x + 5) (x + 5)

Therefore, x = -5 is the answer.

CASE 2: When b is positive and c is negative

Solve x 2  + 4x – 5 = 0

Write the factors of -5.

1 × –5, –1 × 5

Identify the factors whose product is – 5 and sum is 4.

1 – 5 ≠ 4 –1 + 5 = 4

Verify the factors using the distributive property.

(x – 1) (x + 5) = x 2  + 5x – x – 5 = x 2  + 4x – 5 (x – 1) (x + 5) = 0

x – 1 = 0 ⇒ x = 1, or x + 5 = 0 ⇒ x = -5

Therefore, x = 1, x = -5 are the solutions.

CASE 3: When b and c are both negative

x 2  – 5x – 6

Write down the factors of – 6:

1 × –6, –1 × 6, 2 × –3, –2 × 3

Now identify factors whose product is -6 and sum is –5:

1 + (–6) = –5

Check the factors using the distributive property.

(x + 1) (x – 6) = x 2  – 6 x + x – 6 = x 2  – 5x – 6

Equate each factor to zero and solve to get; (x + 1) (x – 6) = 0

x + 1 = 0 ⇒ x = -1, or x – 6 = 0 ⇒ x = 6

Therefore, the solution is x=6, x = -1

CASE 4: When b is negative and c is positive

x 2  – 6x + 8 = 0

Write down all factors of 8.

–1 × – 8, –2 × –4

Identify factors whose product is 8 and sum is -6 –1 + (–8) ≠ –6 –2 + (–4) = –6

(x – 2) (x – 4) = x 2  – 4 x – 2x + 8 = x 2  – 6x + 8

Now equate each factor to zero and solve the expression to get;

(x – 2) (x – 4) = 0

x – 2 = 0 ⇒ x = 2, or x – 4 = 0 ⇒ x = 4

Factorize x 2 +8x+12.

Write down the factors of 12;

12 = 2 × 6 or = 4 × 3 Find factors whose sum is 8:

2 + 6 = 8 2 × 6 ≠ 8

Use distributive property to check the factors;

= x 2 + 6x +2x + 12 = (x 2 + 6x) +(2x + 12) = x(x+6) +2(x+6)

= x (x + 6) +2 (x + 6) = (x + 6) (x + 2)

Equate each factor to zero to get;

(x + 6) (x + 2)

Sometimes, the leading coefficient of a quadratic equation may be greater than 1. In this case, we can not solve the quadratic equation by the use of common factors.

Therefore, we need to consider the coefficient of x 2 and the factors of c to find numbers whose sum is b.

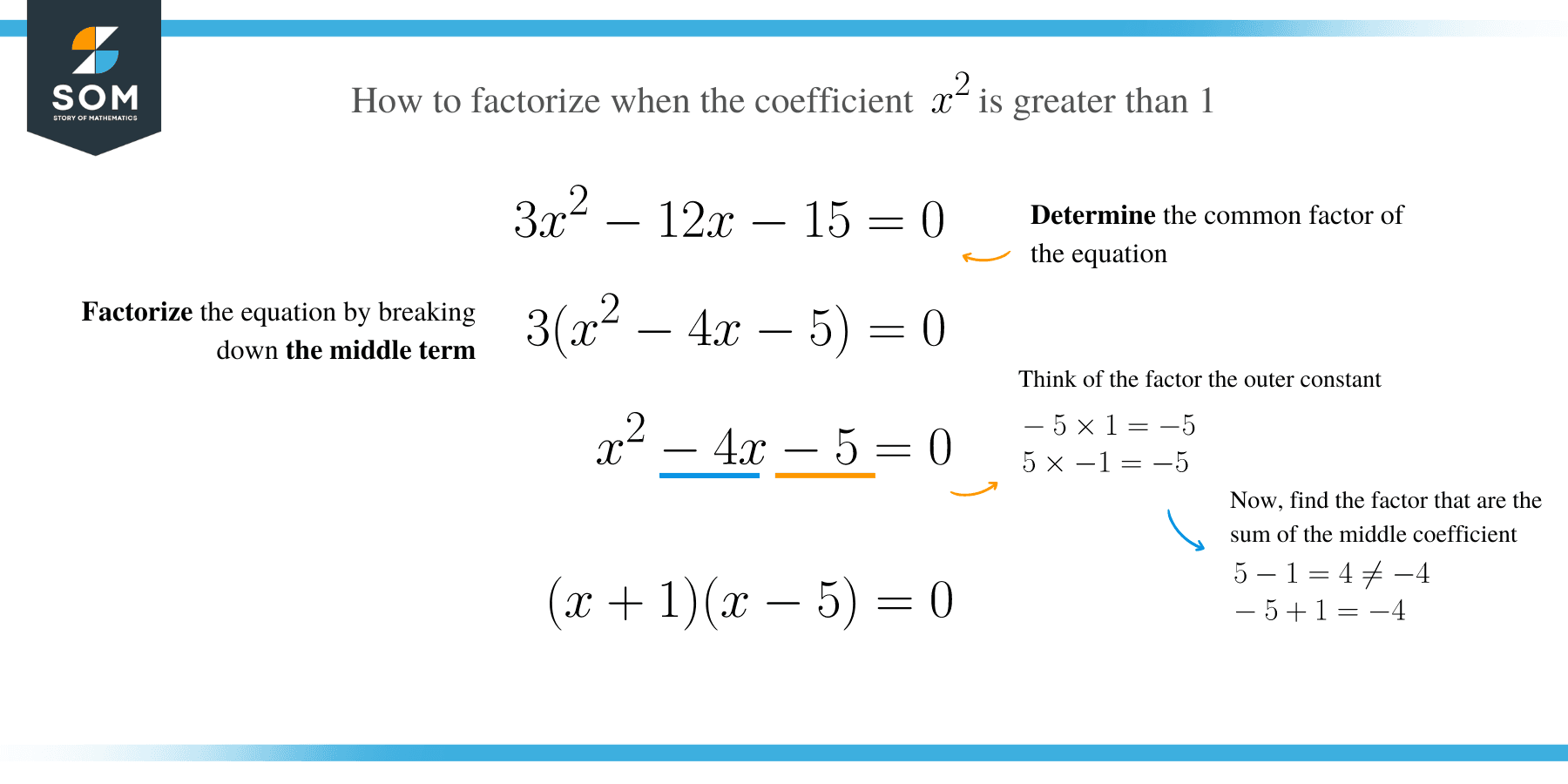
Solve 2x 2  – 14x + 20 = 0

Determine the common factors of the equation.

2x 2  – 14x + 20 ⇒ 2(x 2  – 7x + 10)

Now we can find the factors of (x 2  – 7x + 10). Therefore, write down factors of 10:

–1 × –10, –2 × –5

Identify factors whose sum is – 7:

1 + (–10) ≠ –7 –2 + (–5) = –7

Check the factors by applying distributive property.

2(x – 2) (x – 5) = 2(x 2  – 5 x – 2x + 10) = 2(x 2  – 7x + 10) = 2x 2  – 14x + 20

Equate each factor to zero and solve; 2(x – 2) (x – 5) = 0

x – 2 = 0 ⇒ x = 2, or x – 5 = 0 ⇒ x = 5

Solve 7x 2  + 18x + 11 = 0

Write down the factors of both 7 and 11.

11 = 1 × 11

Apply distributive property to check the factors as shown below:

(7x + 1) (x + 11) ≠ 7x 2  + 18x + 11

(7x + 11) (x + 1) = 7x 2  + 7x + 11x + 11 = 7x 2  + 18x + 11

Now equate each factor to zero and solve to get;

7x 2  + 18x + 11= 0 (7x + 11) (x + 1) = 0

x = -1, -11/7

Solve 2x 2  − 7x + 6 = 3

2x 2  − 7x + 3 = 0

(2x − 1) (x − 3) = 0

x=1/2​ or x=3

Solve 9x 2 +6x+1=0

Factorize to give:

(3x + 1) (3x + 1) = 0

(3x + 1) = 0,

Therefore, x = −1​/3

Factorize 6x 2 – 7x + 2 = 0

6x 2  – 4x – 3x + 2 = 0

Factorize the expression;

⟹ 2x (3x – 2) – 1(3x – 2) = 0

⟹ (3x – 2) (2x – 1) = 0

⟹ 3x – 2 = 0 or 2x – 1 = 0

⟹ 3x = 2 or 2x = 1

⟹ x = 2/3 or x = ½

Factorize x 2  + (4 – 3y) x – 12y = 0

Expand the equation;

x 2  + 4x – 3xy – 12y = 0

⟹ x (x + 4) – 3y (x + 4) = 0

x + 4) (x – 3y) = 0

⟹ x + 4 = 0 or x – 3y = 0

⟹ x = -4 or x = 3y

Thus, x = -4 or x = 3y

Quadratic Equations Factoring Worksheets

Quadratic equations, factoring: monic, factoring: non-monic.

Please add a message.

Message received. Thanks for the feedback.

Solve Quadratic Equation by Factoring Worksheets

Related Topics: More Math Worksheets More Grade 7 Math Lessons Grade 7 Math Worksheets

There are two sets of solving quadratic equation worksheets:

• Solve Quadratic Equation (use factoring)
• Solve Quadratic Equation (use quadratic formula)

Examples, solutions, videos, and worksheets to help Grade 7 and Grade 8 students learn how to solve quadratic equations by factoring.

How to solve quadratic equations using factoring?

There are four sets of solving equations using factoring worksheets.

• Solve Quadratic Equation by Factoring (use zero product property).
• Solve Quadratic Equation by Factoring (factor & solve, a = 1).
• Solve Quadratic Equation by Factoring (factor & solve, a ≠ 1).
• Solve Quadratic Equation by Factoring (rearrange, factor & solve).

These are the steps to solve a quadratic equation by factoring:

• Write the quadratic equation in the form: ax 2 +bx+c=0, where a, b, and c are constants.
• Factor the quadratic expression. Look for two binomials whose product gives you the original quadratic expression.
• Set each of the binomial factors equal to zero. This will give you two separate linear equations to solve.
• Solve each linear equation for x. These solutions are the roots or solutions of the quadratic equation.
• Check if the solutions obtained in step 4 satisfy the original quadratic equation.

Example: Solve the quadratic equation x 2 − 5x = -6.

• Rewrite down the equation as: x 2 − 5x + 6 = 0.
• Factor the quadratic expression: x 2 − 5x + 6 = 0 (x − 2)(x − 3) = 0
• Set each factor equal to zero: x − 2 = 0 or x − 3 = 0
• Solve for x For x − 2 = 0 x = 2 For x − 3 = 0 x = 3
• Check solutions: Substitute x = 2 and x = 3 back into the original equation. 2 2 − 5(2) + 6 = 0 (True) 3 2 − 5(3) + 6 = 0 (True)

Remember that not all quadratic equations can be easily factored. Some may require more complex factoring methods, or you may need to use the quadratic formula or completing the square to find the solutions.

Click on the following worksheet to get a printable pdf document. Scroll down the page for more Solve Quadratic Equation by Factoring Worksheets .

More Solve Quadratic Equation by Factoring Worksheets

Printable (Answers on the second page.) Solve Quadratic Equation by Factoring Worksheet #1 (use zero product property) Solve Quadratic Equation by Factoring Worksheet #2 (factor & solve, a = 1) Solve Quadratic Equation by Factoring Worksheet #3 (factor & solve, a ≠ 1) Solve Quadratic Equation by Factoring Worksheet #4 (rearrange, factor & solve)

Online or Generated Factor Binomials by Difference of Squares Factor Perfect Square Trinomials Factor Trinomials or Quadratic Equations Factor Different Types of Trinomials 1 Factor Different Types of Trinomials 2 Solve Trinomials using Quadratic Formula Find Discriminants of Quadratic Polynomials

Related Lessons & Worksheets

Solve Quadratic Equation by Factoring (a > 1) Solve Quadratic Equation by Factoring (common factors)

More Printable Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Algebra >
• Equations >
• Quadratic Equations >
• Factoring Method

Solving Quadratic Equations by Factoring Worksheets

Catapult to new heights your ability to solve a quadratic equation by factoring, with this assortment of printable worksheets. Backed by three distinct levels of practice, high school students master every important aspect of factoring quadratics. The quadratic equations in these exercise pdfs have real as well as complex roots. Keep to the standard form of a quadratic equation: ax 2 + bx + c = 0, where x is the unknown, and a ≠ 0, b, and c are numerical coefficients. Either the given equations are already in this form, or you need to rearrange them to arrive at this form. You can also use algebraic identities at this stage if the equation permits. Once you are here, follow these steps to a tee and you will progress your way to the roots with ease. Step 1 : Find the product of a and c. Step 2 : Determine the two factors of this product that add up to 'b'. Step 3 : Use these factors and rewrite the equation in the factored form. Step 4 : Equate each factor to zero and figure out the roots upon simplification. Now, you're all set to go! And our free worksheet is sure to give you a flying start!

Solve Quadratic Equations - Zero Product Property

Triumph in your quadratic equations like never before! The zero-product property signifies that when the product of any two factors is zero, one of the factors must be zero. Implement this rule, and solve the quadratic equations offered in factored form. Set each factor equal to zero, and reach to the roots.

• Download the set

Solve Quadratic Equations by Factoring - Easy

Kick-start your quadratic practice with this easy set where each pdf worksheet presents 10 equations with the coefficient of the leading term being 1 in each case. Factorize the constant term in such a way that its factors give the middle-term coefficient when added, and apply the zero-product rule to obtain the real roots.

Solve Quadratic Equations by Factoring - Moderate

Upgrade your skills with these moderate handouts rendering quadratic equations that have real and imaginary roots. High school students are supposed to rewrite the equation in the standard form and then proceed with the usual factoring and solving steps. Your quadratic learning will now take off!

Solve Quadratic Equations by Factoring - Difficult

Progress to the next level of difficulty by solving the complicated quadratic equations here! Because they have an expression in place of the unknown, these equations are called disguised quadratic equations. Make an appropriate substitution, convert the equation to general form, and solve for the roots.

Related Worksheets

» Solving Quadratic Equations | Square Root

» Solving Equations | Completing the Squares

» Solving Equations | Quadratic Formula

» Factoring Polynomials

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

• Solving quadratics by factoring
• Quadratics by factoring (intro)
• Solving quadratics by factoring: leading coefficient ≠ 1

Quadratics by factoring

• Solving quadratics using structure
• Solve equations using structure
• Quadratic equations word problem: triangle dimensions
• Quadratic equations word problem: box dimensions
• Solving quadratics by factoring review
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

The Quadratic Formula Explained

Quadratic Formula Discriminant Disc. & Graphs

When would I use the Quadratic Formula?

You can use the Quadratic Formula any time you're trying to solve a quadratic equation — as long as that equation is in the form "(a quadratic expression) that is set equal to zero".

Often, the simplest way to solve " ax 2 + bx + c = 0 " for the value of x is to factor the quadratic , set each factor equal to zero, and then solve each factor. But sometimes the quadratic is too messy, or it doesn't factor at all, or, heck, maybe you just don't feel like factoring. While factoring is not always going to be successful, the Quadratic Formula can always find the answers for you.

Content Continues Below

MathHelp.com

Practice The Quadratic Formula

The Quadratic Formula uses the " a ", " b ", and " c " from " ax 2 + bx + c ", where " a ", " b ", and " c " are just numbers; they are the "numerical coefficients" of the quadratic equation they've given you to solve.

The Quadratic Formula is derived from the process of completing the square, and is formally stated as:

What is the Quadratic Formula?

The Quadratic Formula is a rule that says that, in any equation of the form ax 2 + bx + c = 0 , the solution x -values of the equation are given by:

How do I use the Quadratic Formula?

To use the Quadratic Formula, you must:

Arrange your equation into the form "(quadratic) = 0 ".

Arrange the terms in the (equation) in decreasing order (so squared term first, then the x -term, and finally the linear term).

Pull out the numerical parts of each of these terms, which are the " a ", " b ", and " c " of the Formula.

Plug these numbers into the formula.

Simplify to get your answers.

Advisories: The " 2 a " in the denominator of the Formula is underneath everything above, not just the square root. And it's a " 2 a " under there, not just a plain " 2 ". Make sure that you are careful not to drop the square root or the "plus/minus" in the middle of your calculations, or I can guarantee that you will forget to "put them back in" on your test, and you'll mess yourself up. Remember that " b 2 " means "the square of ALL of b , including its sign", so don't leave b 2 being negative, even if b is negative, because the square of a negative is a positive.

In other words, don't be sloppy and don't try to take shortcuts, because it will only hurt you in the long run. Trust me on this!

What is an example of using the Quadratic Formula?

Solve x 2 + 3 x − 4 = 0.

This quadratic happens to factor, which I can use to confirm what I get from the Quadratic Formula. The Formula should give me the same answers.

x 2 + 3 x − 4 = ( x + 4)( x − 1) = 0

...so I already know that the solutions are x = −4 and x = 1 .

Now, what would my solution look like in the Quadratic Formula? Using a = 1 , b = 3 , and c = −4 , my solution process looks like this:

So, as expected, the solution is x = −4 , x = 1 .

For this particular quadratic equation, factoring would probably be the faster method. But the Quadratic Formula is a plug-n-chug method that will always work. Having "brain freeze" on a test and can't factor worth a darn? Use the plug-n-chug Formula; it'll always take care of you!

How does the Quadratic Formula relate to x -intercepts?

The solutions to the quadratic equation, as provided by the Quadratic Formula, are the x -intercepts of the corresponding graphed parabola.

How? Well, when y = 0 , you're on the x -axis. The x -intercepts of the graph are where the parabola crosses the x -axis. You're applying the Quadratic Formula to the equation ax 2 + bx + c = y , where y is set equal to zero.

Looking at the above example, there were two solutions for the equation x 2 + 3 x − 4 = 0 . This tells us that there must then be two x -intercepts on the graph. Graphing, we get the curve below:

Advertisement

As you can see, the x -intercepts (the red dots above) match the solutions, crossing the x -axis at x = −4 and x = 1 . This shows the connection between graphing and solving: When you are solving "(quadratic) = 0 ", you are finding the x -intercepts of the graph. This can be useful if you have a graphing calculator, because you can use the Quadratic Formula (when necessary) to solve a quadratic, and then use your graphing calculator to make sure that the displayed x -intercepts have the same decimal values as do the solutions provided by the Quadratic Formula.

Note, however, that the calculator's display of the graph will probably have some pixel-related round-off error, so you'd be checking to see that the computed and graphed values were reasonably close; don't expect an exact match.

Solve 2 x 2 − 4 x − 3 = 0 . Round your answer to two decimal places, if necessary.

There are no factors of (2)(−3) = −6 that add up to −4 , so I know that this quadratic cannot be factored . I will apply the Quadratic Formula. In this case, a = 2, b = −4 , and c = −3 :

Then the answer is x = −0.58, x = 2.58 , rounded to two decimal places.

Can I round my answers from the Quadratic Formula?

In general, no, you really shouldn't; the "solution" or "roots" or "zeroes" of a quadratic are usually required to be in the "exact" form of the answer. You can use the rounded form when graphing (if necessary), but "the answer(s)" from the Quadratic Formula should be written out in the (often messy) "exact" form.

In the example above, the exact form is the one with the square roots of ten in it. If you're wanting to graph the x -intercepts or needing to simplify the final answer in a word problem to be of a practical ("real world") form, then you can use the calculator's approximation. But unless you have a good reason to think that the answer is supposed to be a rounded answer, always go with the exact form.

Reinforcing the concept: Compare the solutions we found above for the equation 2 x 2 − 4 x − 3 = 0 with the x -intercepts of the graph:

Page 1 Page 2 Page 3

URL: https://www.purplemath.com/modules/quadform.htm

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles