visual math problem solving

Fun teaching resources & tips to help you teach math with confidence

Making Math Visual & Hands On & Why It Matters

Learn how to make math visual to enhance and deepen student understanding (hint: it’s about more than drawing pictures!) Plus, learn the science behind why this matters and ways to make the math topics you teach and explore more visual for your students.

Why Does Math Need to Be Visual?

Recent brain research has been able to show us what activity goes on in the brain when we solve a math problem. The results are amazing! 5 different processors “light up” with activity and talk to each other when we work on math and play with numbers.

Of those 5, 2 are visual processors .

That means we need to provide visuals to aid our brain in making sense of the problem, connecting it to other parts of the brain and to move it from our short term memory to our long term memory!

So even for those kids (and adults) who don’t consider themselves to be “visual learners,” we now know that’s just not true. Everyone needs visual tools to understand math deeply. Some might just have stronger visual processors than others.

Those who think they’re not “visual learners” need visual models and tools even more to strengthen those weaker parts of the brain.

What Does it Mean to Make Math Visual?

So making math visual is about so much more than drawing a picture to solve a word problem. Making math visual means giving our brains something to “hold on to” as we make sense of new concepts, think through word problems, visualize fractions and all the other math we want our kids to learn.

Making math visual means our brain is able to form connections between visual representations and more abstract representations or computations.

This might mean drawing a picture for a word problem.

It might mean using hands on manipulatives to represent the situation and help kids to “see” it.

But more often than not, it simple means using a visual math tool to represent the situation or a diagram to show our brains the information in a different format.

Visual or Hands On Math Representations Might Include:

• Base ten blocks
• Number bonds
• Number lines & open number lines
• Tables, charts or graphs
• Hundreds charts
• Area models or grids
• Arrays of objects
• Fraction bars

Or any other visual your kids come up with to show their thinking about a particular math problem.

Ideas for Making Math Instruction Visual & Hands On:

One of the easiest way to encourage your kids to visualize the math they’re learning and exploring is to use a graphic organizer . Although you could probably find various graphic organizers around the web, this can be as easy as folding a piece of paper into fourths.

Then give your students a math problem (computation or word problem) and ask them to solve it 4 different ways .

You might require things like solve it with the algorithm, solve it using place value, solve it on a number line, solve it with a number bond, solve it by drawing a picture, etc.

One especially helpful tip for getting kids to think deeply and visualize a problem is to make one of the boxes “ Write a story problem to match the problem ,” when you give them a computation problem.

For example, if the given problem is 24 – 8 , a student might solve by drawing a picture, using an open number line, with the regrouping algorithm and finally by writing a story problem such as, “I have 24 crayons. 8 are broken. How many are not broken?”

This allows them to think about, explore and visualize subtraction in a variety of ways, and sometimes discover meaningful strategies for solving that they had not been familiar with (or comfortable using) previously.

You might also like these posts with ideas for hands on math instruction:

• Ultimate Guide to Hands On Math
• My Top 5 Essential Math Manipulative Choices

Find More Visual Math Games & Hands On Resources for Your Classroom:

If you’re looking for quick and easy and done for you visual or hands on math activities, games and math tasks , check out the ever-growing list of resources below.

Simply click on the different graphics to learn more about each activity and grab the FREE download that you can use right away!

Find More Resources To Help Make Math Engaging!

Join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

• Our Mission

The Power of Visualization in Math

Creating visual representations for math students can open up understanding. We have resources you can use in class tomorrow.

When do you know it’s time to try something different in your math lesson?

For me, I knew the moment I read this word problem to my fifth-grade summer school students: “On average, the sun’s energy density reaching Earth’s upper atmosphere is 1,350 watts per square meter. Assume the incident, monochromatic light has a wavelength of 800 nanometers (each photon has an energy of 2.48 × 10 -19 joules at this wavelength). How many photons are incident on the Earth’s upper atmosphere in one second?”

My students couldn’t get past the language, the sizes of the different numbers, or the science concepts addressed in the question. In short, I had effectively shut them down, and I needed a new approach to bring them back to their learning. So I started drawing on the whiteboard and created something with a little whimsy, a cartoon photon asking how much energy a photon has.

Immediately, students started yelling out, “2.48 × 10 -19 joules,” and they could even cite the text where they had learned the information. I knew I was on to something, so the next thing I drew was a series of boxes with our friend the photon.

If all of the photons in the image below were to hit in one second, how much energy is represented in the drawing?

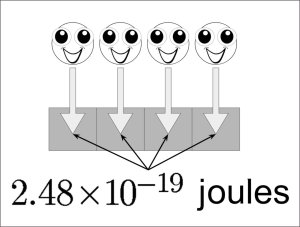
Students realized that we were just adding up all the individual energy from each photon and then quickly realized that this was multiplication. And then they knew that the question we were trying to answer was just figuring out the number of photons, and since we knew the total energy in one second, we could compute the number of photons by division.

The point being, we reached a place where my students were able to process the learning. The power of the visual representation made all the difference for these students, and being able to sequence through the problem using the visual supports completely changed the interactions they were having with the problem.

If you’re like me, you’re thinking, “So the visual representations worked with this problem, but what about other types of problems? Surely there isn’t a visual model for every problem!”

The power of this moment, the change in the learning environment, and the excitement of my fifth graders as they could not only understand but explain to others what the problem was about convinced me it was worth the effort to pursue visualization and try to answer these questions: Is there a process to unlock visualizations in math? And are there resources already available to help make mathematics visual?

I realized that the first step in unlocking visualization as a scaffold for students was to change the kind of question I was asking myself. A powerful question to start with is: “How might I represent this learning target in a visual way?” This reframing opens a world of possible representations that we might not otherwise have considered. Thinking about many possible visual representations is the first step in creating a good one for students.

The Progressions published in tandem with the Common Core State Standards for mathematics are one resource for finding specific visual models based on grade level and standard. In my fifth-grade example, what I constructed was a sequenced process to develop a tape diagram—a type of visual model that uses rectangles to represent the parts of a ratio. I didn’t realize it, but to unlock my thinking I had to commit to finding a way to represent the problem in a visual way. Asking yourself a very simple series of questions leads you down a variety of learning paths, and primes you for the next step in the sequence—finding the right resources to complete your visualization journey.

Posing the question of visualization readies your brain to identify the right tool for the desired learning target and your students. That is, you’ll more readily know when you’ve identified the right tool for the job for your students. There are many, many resources available to help make this process even easier, and I’ve created a matrix of clickable tools, articles, and resources .

The process to visualize your math instruction is summarized at the top of my Visualizing Math graphic; below that is a mix of visualization strategies and resources you can use tomorrow in your classroom.

Our job as educators is to set a stage that maximizes the amount of learning done by our students, and teaching students mathematics in this visual way provides a powerful pathway for us to do our job well. The process of visualizing mathematics tests your abilities at first, and you’ll find that it makes both you and your students learn.

• Math Activities
• Math Lessons Online
• Math Tutorial

Visual Math Learning: A New Perspective on Mathematical Education

Mathematics is a subject that often intimidates students and is regarded as challenging and abstract. However, a new approach to learning math has emerged, one that leverages the power of visualizations to make mathematical concepts more accessible and engaging. Visual maths learning provides students with a new perspective, enabling them to grasp complex mathematical ideas more easily. The benefits of studying arithmetic with visual assistance and how it can change math instruction will be covered in this article.

The Power of Visuals in Education

Visuals have long been recognized as effective tools in educational settings. They can simplify complex information, aid understanding, and enhance memory retention. Visuals can include images, diagrams, graphs, videos, and interactive simulations. When applied to mathematics education, they can transform how students perceive and interact with mathematical concepts.

The Concept of Visual Maths Learning

Visual maths learning is an approach that integrates visual elements into mathematics education. It involves using visual aids, such as diagrams, charts, and interactive models, to represent mathematical concepts and problem-solving processes. Students can better understand abstract mathematical ideas and their real-world applications by presenting information visually.

Benefits of Visual Maths Learning

Enhances comprehension and retention.

Visuals provide a tangible representation of abstract mathematical concepts, making them easier to comprehend. By visualizing mathematical ideas, students can see patterns, relationships, and connections that might be challenging to grasp through traditional methods alone. This enhanced comprehension leads to better retention of the material.

Fosters Creativity and Critical Thinking

Visual maths learning encourages students to think creatively and critically. When presented with visual problems, students are prompted to analyze and interpret the information before formulating a solution. This process enhances their problem-solving skills and nurtures their ability to think outside the box.

Promotes Real-World Application

Mathematics often appears disconnected from the real world, leading to the common question, “When will I ever use this?” Visual maths learning bridges this gap by showcasing practical applications of mathematical concepts. Students can see how math is relevant to everyday life, fostering a deeper appreciation.

Increases Engagement and Motivation

Traditional methods of teaching mathematics can be monotonous and disengaging for many students. Visual maths learning brings a dynamic and interactive element to the classroom, making learning more enjoyable and captivating. This increased engagement leads to higher motivation and a willingness to explore math further.

Implementing Visual Maths Learning Strategies

Educators can use various tools and techniques to effectively implement visual maths learning strategies. Here are some examples:

Interactive Whiteboards and Visual Presentations

Interactive whiteboards allow teachers to present mathematical concepts using visuals, animations, and interactive activities. By manipulating things and investigating various circumstances, students can actively engage in the learning process and improve their understanding.

Manipulatives and Physical Models

Manipulatives, such as blocks, counters, or geometric shapes, provide a hands-on experience that helps students visualize mathematical concepts. Physical models can aid in understanding spatial relationships, volume, and geometry.

Graphs, Diagrams, and Infographics

Graphs, diagrams, and infographics are powerful visual tools that simplify complex data and present it in a visually appealing manner. They are particularly effective for illustrating trends, patterns, and statistical information.

Virtual Reality and Augmented Reality

The immersive experiences of virtual reality (VR) and augmented reality (AR) technology allow students to study mathematical ideas in hypothetical settings.

Overcoming Challenges in Visual Maths Learning

Visual maths learning offers many advantages, but it is crucial to acknowledge and tackle the potential challenges that may arise. Some students might encounter difficulties translating visual representations into mathematical language or face difficulty interpreting visual information accurately. Educators should provide clear explanations, offer guidance, and create a supportive learning environment to ensure all students can effectively utilize visual tools in their mathematical education.

One significant challenge in visual maths learning is bridging the gap between visual representations and mathematical language. While visuals can enhance understanding and facilitate problem-solving, students may need help connecting the visual elements to the appropriate mathematical concepts. To address this challenge, educators should explicitly demonstrate the relationship between the visual representation and the corresponding mathematical notation or terminology. By providing clear explanations and examples, students can gradually develop the ability to express visual information in mathematical language and vice versa.

One possible difficulty students might face when learning math through visual aids is accurately interpreting visual information. Visual graphs, diagrams, or geometric figures convey mathematical concepts visually. Still, students might need help to extract the necessary information or discern relevant details. Educators can employ guided visualization or step-by-step analysis strategies to help students break down the visual information into manageable components. By systematically examining the visual elements and discussing their significance, students can develop stronger skills in interpreting visual data accurately.

Visual maths learning presents a revolutionary approach to teaching and learning mathematics. By incorporating visuals into the curriculum, students can overcome the barriers that abstract concepts often pose. The benefits of visual maths learning include enhanced comprehension, increased creativity and critical thinking, real-world application, and heightened engagement. By leveraging visual tools and techniques, educators can create a stimulating and effective learning environment that empowers students to excel in mathematics.

• Is visual maths learning suitable for all age groups?  Yes, visual maths learning can be adapted for learners of all ages, from early childhood to adulthood. The level of complexity and the choice of visual tools may vary based on the learners’ developmental stage.
• Can visual maths learning be applied to advanced mathematical concepts?  Absolutely! Visual tools can aid in understanding complex mathematical ideas, including calculus, geometry, and algebra. They provide visual representations that make abstract concepts more accessible.
• How can I incorporate visual maths learning at home?  Parents can use educational apps, online tutorials , and physical manipulatives to support visual maths learning. Exploring real-world examples and discussing everyday math applications can also enhance visual comprehension.
• Are there any research studies supporting the effectiveness of visual maths learning?  Numerous research has shown how beneficial visual tools are for teaching maths. Research indicates that visual representations improve conceptual understanding, problem-solving skills, and overall academic performance in mathematics.
• Where can I find resources for visual maths learning?  Various online platforms, educational websites, and books are dedicated to visual maths learning. Additionally, many educational institutions offer training programs and workshops for teachers and parents interested in implementing visual strategies in math education.

In conclusion, visual maths learning offers a transformative way to teach and learn mathematics. By harnessing the power of visuals, students can overcome the challenges associated with abstract concepts and develop a deep understanding of mathematical principles. Educators can create engaging learning environments that foster creativity, critical thinking, and real-world application by integrating visual tools and techniques. Embracing visual maths learning opens up exciting possibilities for students to excel in mathematics and appreciate its relevance.

• Grade 1 Lessons
• Grade 2 Lessons
• Grade 3 Lessons
• Grade 4 Lessons
• Grade 5 Lessons
• Grade 6 Lessons
• Grade 7 Lessons
• Grade 8 Lessons
• Kindergarten
• Multiplication
• Subtraction
• #basic mathematic
• #Basic Mathematical Operation
• #best math online math tutor
• #Best Math OnlineTutor
• #dividing fractions
• #effective teaching
• #grade 8 math lessons
• #linear equation
• #Math Online Blog
• #mathematical rule
• #mutiplying fractions
• #odd and even numbers
• #Online Math Tutor
• #online teaching
• #order of math operations
• #pemdas rule
• #Point-Slope Form
• #Precalculus
• #Slope-Intercept Form
• #Tutoring Kids

Thank you for signing up!

GET IN TOUCH WITH US

Maths Tips From Maths Insider

Quick tips and practical advice to help you guide your child to maths success.

• Maths Insider Amazon Store
• Free FB Group

Hear It, See It, Feel It – 24 Math Strategies for Your Auditory, Visual or Tactile Learner

Many children have a dominant learning style, so every parent should have some tricks up their sleeve to address these different styles.   Each parent needs to be flexible when dealing with different learning strategies.  Drilling can work, but we can’t just rely on the drill method with math worksheets and flashcards. When children are taught with the process that suits them best, their performance can improve dramatically.

Here are 24 ideas to use with the visual, tactile, or auditory learner in your home.

For visual math learners

1. Have visual learners write down explanations.  Writing and seeing are powerful for visual learners.

2. Have your child make and use flashcards. The act of writing the cards and viewing them will increase comprehension.

3. Ensure visual learners organize their notes.  Organization will make it easier to remember the information.

4. Encourage your child to take notes while listening in class.  To take notes, a student must either look at what you’re writing/presenting or visualize the material.  Either way requires visual processing.

5. Use visual analogies and metaphors to associate information.  Anything that encourages the student to develop a mental image will be beneficial.

6. Use a computer with your child to organize material, create graphs, tables, charts, and spreadsheets. The act of creating and reviewing visual representations can be powerful for visual learners.

7. Look for graphs, charts and diagrams that demonstrate key points. Presenting the information visually is critical to this type of learner.

8. Encourage your child to use color-coded highlighting in their notes. Differentiating information visually will assist in organizing the material in the student’s mind.

For tactile math learners:

1. Suggest to your tactile learner’s teacher that they sit near the front of the classroom and take notes. This will help them remain focused.

2. When revising for tests, have your make flashcards for each step in a process and put the cards in order until the sequence becomes automatic. Use the technique repeatedly with concepts and processes. Sticky notes come in handy here.

3. Use hands-on experiences whenever possible.  Use manipulatives. Marshmallows and individually wrapped candy comes in handy here. Solving problems with pencil and paper or calculator in hand will be most give this group of learners confidence.

4. Get your child to make diagrams and mind-maps of concepts and problem-solving processes.

5. Help them learn how to use calculators and computers to solve complex math problems.

6. Find educational computer games that require a great deal of mouse movement. This works great with these learners.

7. Help them prepare a multimedia project related to their maths project work.

8. Experiment with having your child working in a standing position.  By standing, your child’s balance and equilibrium are stimulated; this can be beneficial for many tactile learners.

For auditory math learners:

1. Pair up with your auditory learner and explain mathematical concepts to each other.

2. Have your child write a sequence of steps in sentence form and then read them out loud.  Actually hearing the problem-solving process will help to solidify it.

3. Encourage tour child to reason through solutions out loud.  Anything that stimulates the hearing process can be helpful.

4. Use mnemonics and word links for important math concepts or problem-solving processes.  Rhyming is helpful when possible.

5. Ask your child’s teacher if they allow students to record math lectures and review them or provide recordings of classes online.

6. When reviewing new information, encourage your child to repeat the most important information out loud.

7. Encourage your child to also use these strategies at school.

8. It’s important to maintain order in the classroom.  Any activities that encourage talking will have a tendency to lead to talking that is unrelated to math.

Visual, tactile and auditory learners have differing requirements to learn optimally, so it’s important to teach them with a variety of techniques.  Use the above ideas but also develop your own.  However, mixing things up a bit can also be beneficial to the your child and their enjoyment, participation, and learning will improve.

Author Bio:

Please note: I reserve the right to delete comments that are offensive or off-topic.

3 thoughts on “ Hear It, See It, Feel It – 24 Math Strategies for Your Auditory, Visual or Tactile Learner ”

This is great advice. I was definitely a sight oriented in learning especially math so those suggestions would have really done me good. I appreciate your love of your craft. Have a great day.

Great post, Caroline! I think that these are some great ideas to get people started in the world of math. I know a lot of people who get intimidated by math, but I think that a lot of these ideas will help people who’ve had those problems relate to math in a way that makes it easy to understand.

Great post! I does provide good teaching strategy for teacherd and parents alike. I’ll share the link with our school teacher.

Comments are closed.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 7

• Same thing to both sides of equations
• Representing a relationship with an equation
• Dividing both sides of an equation
• One-step equations intuition
• Identify equations from visual models (tape diagrams)

Identify equations from visual models (hanger diagrams)

• Solve equations from visual models
• (Choice A)   2 + k = 18 ‍   A 2 + k = 18 ‍  
• (Choice B)   2 k = 18 ‍   B 2 k = 18 ‍  
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• The LD@school Team
• Collaborate with Us
• Terms Of Use
• Mathematics
• Mental Health
• Executive Functions
• Social-Emotional Development
• What are Non-verbal Learning Disabilities?
• Accommodations, Modifications & Alternative Skill Areas
• Glossary of Terms
• Resources |
• Learning Modules |
• Educators’ Institute |
• Document Library |

Visual Representation in Mathematics

Print Resource

by Ian Matheson and Nancy Hutchinson 

Mathematics is a subject that deals with abstract ideas in order to solve problems. Information can be represented with numbers, words, and other types of symbols. Representing information with symbols can be a difficult practice for students with learning disabilities (LDs) to understand, and eventually begin to use themselves.

Information is often represented visually in mathematics as a method of organizing, extending, or replacing other methods of presentation. Visual representation in mathematics involves creating and forming models that reflect mathematical information (van Garderen & Montague, 2003).

LDs and Problem-Solving

Although there are a number of problem solving strategies that students use in mathematics, good problem solvers usually construct a representation of the problem to help them comprehend it (van Garderen & Montague, 2003). Students with LDs can have an especially challenging experience solving problems in math, and research suggests that their use of visual representation strategies differs from their typically-achieving peers in:

• frequency of use (Montague, 1997),
• type of visual representations used (van Garderen & Montague, 2003), and
• quality of visual representations (van Garderen, Scheuermann, & Jackson, 2012b).

Creating a visual representation to solve a problem in mathematics is a process that involves:

• processing the information in the problem,
• selecting important information, and
• identifying the goal of the problem.

Students with LDs struggle with visual representation in mathematics because they typically have difficulties processing information (Swanson, Lussier, & Orosco, 2013).

Visual representation is an important skill because higher-level math and science courses increasingly draw on visualization and spatial reasoning skills to solve problems (Zhang, Ding, Stegall, & Mo, 2012). Additionally, it is simply another strategy that students can use when they are thinking of the best way to answer a problem in mathematics.

The Importance of Explicit Instruction

Perhaps the most consistent message in the literature about visual representation in mathematics is that it needs to be explicitly taught to students. Representing information visually is not a skill that comes naturally to students, and so it must be taught and practiced.

When first introducing a new skill to students, it is important to model the skill in order for them to see how it is used followed by opportunity for students to try it themselves.

Click here to access the article  Explicit Instruction: A Teaching Strategy in Reading, Writing, and Mathematics for Students with Learning Disabilities .

The concrete-representational-abstract (CRA) approach to instructing students is a method of explicit instruction that is supported by research as being effective for students with LDs (Doabler, Fien, Nelson-Walker, & Baker, 2012; Mancl, Miller, & Kennedy, 2012). The concrete level involves the use of objects to represent mathematical information (e.g., counters, cubes); the representational level involves the drawing of pictures to represent the objects that were used in the previous level; and the abstract level replaces pictures of objects with mathematical symbols and numbers.

Click here to access the article Concrete-Representational-Abstract: And Instructional Strategy for Math .

Scaffolding is another approach to teaching visual representation to students with LDs that is supported by research (van Garderen, Scheuermann, & Jackson, 2012a). Scaffolding involves the use of temporary supports during the learning process as needed by the student. Providing a student with an incomplete diagram and having them finish it and then use it to solve a problem is an example of a scaffolding technique.

Types of Visual Representation

When you are talking about visual representation in mathematics, you may be talking about representing information on a page with a diagram or chart , or representing information in your head with an image . Fortunately, researchers have focussed on helping students improve their visual representation both externally (e.g., van Garderen, 2007) and internally (e.g., Zhang et al., 2012). Developing both external and internal visual representation strategies is important for students as both help support student learning in mathematics for different types of problems.

In addition to the distinction between internal and external visual representations, researchers have also outlined differences in visual imagery based on the purpose. Pictorial imagery is used for representing the visual appearance of objects or information. Schematic imagery is used for representing the spatial relationships between objects or information. While both can be used to help students learn and solve problems in mathematics, schematic imagery is more effective as a method for supporting problem solving. Students with LDs are more likely to use pictorial imagery when solving problems in math (van Garderen & Montague, 2003).

External Visual Representation

Diagrams and graphic organizers are two types of external visual representations that are used in mathematics, and both are supported by research for use with students with LDs. This is a type of visual representation that can be modelled to students as it is something that can be seen on a page or on the board at the front of the class.

Diagrams are visual displays that use the important information in mathematical problems. They are typically used to demonstrate how the important information is related , and can be used to organize information as well as to compute the answer to a problem. A common type of diagram might be a drawing that a student creates to represent the objects within a word problem.

Individuals with LDs may have a poorer understanding of what a diagram is, as well as when and how to use it (van Garderen et al., 2012b). Diagrams are effective for students with LDs as they can help highlight essential information and leave out information that is not necessary for solving a problem. This can simplify the problem-solving process (Kolloffel et al., 2009).

Distinctions can be made between pictorial diagrams and schematic diagrams . An example of a pictorial diagram would be a drawing of the important objects within a word problem, while a schematic diagram would be a drawing that includes the spatial relationships between the objects. As mentioned earlier, schematic diagrams are more useful for students and typically result in more success with problem solving (van Garderen & Montague, 2003).

Tree Diagrams

A tree diagram is a method of representing independent events or conditions related to an action, and it is often used to teach students probability theory.

This type of diagram might be used to teach students about probability through coin flipping or through drawing from a deck of cards. It is considered a powerful method of teaching probability in math, and is a great example of a visual representation that is a diagram (Kolloffel, Eysink, de Jong, & Wilhelm, 2009).

Number Lines

A number line is another type of diagram that is being used increasingly by mathematicians (Gersten et al., 2009). A number line consists of a straight line that has equally spaced numbers along it on points, and can be easily drawn by students for use when solving problems.

Number lines are often used for the teaching of integers , as well as for simple addition and subtraction problems, as they provide students with a visual that they can touch to keep track of their place .

Graphic Organizers

A graphic organizer is another type of external visual representation that is often used in mathematics. There are many types of graphic organizers and each have situations that they are best used for. While graphic organizers are often thought of simply as organizational tools , they can be used to make rapid inferences to solve different types of problems.

Research supports the idea that students with language disorders may benefit from learning and instruction using nonverbal information such as a graphic organizer (Ives, 2007).  Additionally, the use of graphic organizers to support learning has been found to improve the comprehension of facts and text for students with LDs at all ages (Dexter & Hughes, 2011), as well as enhancing conceptual understanding in mathematics (Ives, 2007).

Graphic organizers may be a great support for students with LDs because they take some of the organizational pressure off these individuals who may have difficulty sorting through information and seeing the relationships between different mathematical objects or concepts (Ives, 2007).

Four main types of graphic organizers can be used in mathematics:

1. Semantic Maps

A semantic map is one type of graphic organizer that can be used to support learning in mathematics. This type of graphic organizer is mainly used to relate conceptual information , and could be used to support conceptual learning in mathematics.

One example might be to use a semantic map to help young students who are learning to classify shapes into different categories. While shapes might be the main heading, students might organize shapes into further sub-heading such as round, symmetrical, right-angle, etc.

2. Semantic Feature Analysis

A semantic feature analysis is another type of graphic organizer. This graphic organizer is characterized by a matrix format , where features or characteristics of objects or concepts are displayed. A semantic feature analysis might be used to compare shapes in geometry, where comparisons could be made between number of sides, vertices, types of angles, etc.

3. Syntactic/Semantic Feature Analysis

A syntactic/semantic feature analysis is similar to the semantic feature analysis, but sentences are added in to help students identify specific features about each object.

An example sentence that might follow the matrix is “ A ________ has the most sides of all of the shapes we have looked at. ”

4. Visual Displays

Selecting the Appropriate Graphic Organizer

Though each type of graphic organizer can be used for learning mathematics by individuals with LDs, the differences in their design suggest that they may be best used in specific situations.

• Semantic maps and Semantic feature analyses are considered to be better for recalling facts though they are more difficult to understand and to learn how to use (Dexter & Hughes, 2011).
• Syntactic/semantic feature analyses and visual displays are considered to be more efficient for making computations to solve problems, and for recalling the information within these types of graphic organizers (Dexter & Hughes, 2011).

The advantages to each type of graphic organizer suggest that initial instruction of a mathematical concept may be best with more complicated graphic organizers, and that independent review and studying could be done with less complicated graphic organizers to improve recall of information for students with LDs (Dexter & Hughes, 2011).

Explicit Instruction of External Visual Representation

It is important to remember that explicit instruction is necessary for both diagrams and graphic organizers. This instruction should highlight the purpose of each type of external visual representation, as well as when and how to use them .  Both types of external visual representations can be easily modelled for students as educators can physically construct them and explain their thinking as they do so in front of students.

In a study conducted by van Garderen (2007), the researcher examined the effectiveness of a three-phase instructional strategy for teaching students with LDs to use diagrams in mathematics:

• The first phase involved explicit instruction about what diagrams are, as well as how and when they are used.
• The second phase connected the use of diagrams to one-step word problems , where students created diagrams that represented the information that they knew and the information that they did not know.
• The third phase was focused on two-step word problems which have more than one unknown piece of information, and students used diagrams to determine the ultimate goal of the problem, as well as the secondary pieces of information that they would need to find in order to compute the ultimate goal.

Teaching students with LDs to use diagrams with this sequence of explicit instruction resulted in improved performance , satisfaction of the students, and students were also more likely to use diagrams with other types of problems.

Internal Visual Representation

While external visual representation can be easy to model and teach explicitly to students, internal visual representation is not as easy to show students as it is a mental exercise. A visual schematic representation involves the creation or recall of visual imagery to represent information.

Students are often asked to visualize the problem in order to better understand it and solve it. This can be a difficult task for students and it should not be assumed that this is a skill that all students already possess .

To create a mental picture when solving a word problem in math, students must combine information from the problem with their prior knowledge of the topic. While students cannot see the mental images that their teachers create, it is still possible to walk students through the process of creating the mental image as a verbal model , or even to draw images of what they are seeing in their head to make it more explicit.

Click here to access the article Verbalization in Math Problem-Solving .

A group of researchers (Krawec, Huang, Montague, Kressler, Melia de Alba, 2012) developed an intervention to support students with LDs as they solve problems in mathematics. The intervention was aimed at explicitly instructing students about the cognitive processes that proficient problem solvers use in math, including visualization . The intervention was delivered by teachers who were trained to follow a sequence of instruction that included teaching visualizing to the students. The intervention involved the teachers “ thinking aloud ” as they progressed through the stages of the problem solving process. Students who were a part of the intervention reported using more strategies when solving problems in math, including the strategy of visualizing the problem (Krawec et al., 2012).

Visual-Chunking

One strategy that teachers can use to support their students with LDs in creating internal visual representations is known as visual-chunking representation .  Chunking is the practice of combining bits of information that are related in some way in order to reduce the overall amount of information for easier processing.  For students with LDs, a reduction in the amount of information to be processed can make exercises such as math problem solving much easier.

A group of researchers examined one method of visual-chunking for students with difficulties in math, where students were working with geometric shapes and transformations (Zhang et al., 2012). One group received series of nets of geometric shapes, while another group received the same nets, though sections had been shaded or “chunked” in an effort to see if it made a difference in their transformations. The group that received the visual-chunking support performed better than the other group, and found the exercise to be easier when provided with the visual-chunking support (Zhang et al., 2012).

Visual Schematic Representations

Visual schematic representations have been shown to be effective for individuals with specific difficulties in math, which can include LDs (Swanson et al., 2013). Instructing students about how to create internal visual representations can be difficult as it does not easily lend itself to explicit instructional techniques . Despite this challenge, teachers can still support the development of this skill by creating diagrams of their mental images as well as by thinking aloud as they are visualizing while problem solving.

The use of visual representation during instruction and learning tends to be an effective practice across a number of subjects , including mathematics (Gersten et al., 2009). While using visual representation alone as a teaching method does produce significant learning improvements for students in mathematics, these improvements are even greater when other teaching methods are used as well (Gersten et al., 2009).

Having students represent mathematical information verbally and in written form along with visual representation is encouraged. For students with LD, both receiving instruction and solving problems in a number of ways will help support their deeper understanding of concepts and operations in mathematics (Suh & Moyer, 2007).

The importance of using explicit instruction to teach students how to make visual representations cannot be overstated. The CRA method is an example of an effective sequence of explicitly instructing students with LD to use visual representation as a step towards the use of mathematical symbols exclusively (Mancl et al., 2012).

There are many types of diagrams (Kolloffel et al., 2009) and graphic organizers (Dexter & Hughes, 2011) that can be effectively used support students with LD in mathematics. While internal visual representation can be difficult to model, strategies do exist that can support students with LD as they develop this skill (Zhang et al., 2012).  Educators are encouraged to use a combination of external and internal visual representation strategies in their instruction to students in the interest of helping students develop both types of skills.

Related Resources on the LD@school Website

Click here to access the article Mind Maps .

Click here to access the article LDs in Mathematics: Evidence-Based Interventions, Strategies, and Resources .

Dexter, D. D., & Hughes, C. A. (2011). Graphic organizers and students with learning disabilities: A meta-analysis. Learning Disability Quarterly, 34 , 51-72.

Doabler, C. T., Fien, H., Nelson-Walker, N. J., & Baker, S. K. (2012). Evaluating three elementary mathematics programs for presence of eight research-based instructional design principles. Learning Disability Quarterly, 35 , 200-211.

Gersten, R., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79 , 1202-1242.

Ives, B. (2007). Graphics organizers applied to secondary algebra instruction for students with learning disorders. Learning Disabilities Research & Practice, 22 , 110-118.

Kolloffel, B., Eysink, T. H., de Jong, T., & Wilhelm, P. (2009). The effects of representational format on learning combinatorics from an interactive computer simulation. Instructional Science, 37 , 503-517.

Krawec, J., Huang, J., Montague, M., Kressler, B., Melia de Alba, A. (2012). The effects of cognitive strategy instruction on knowledge of math problem-solving processes of middle school students with learning disabilities. Learning Disabilities Quarterly, 36 , 80-92.

Mancl, D. B., Miller, S. P., & Kennedy, M. (2012). Using the concrete-representational-abstract sequence with integrated strategy instruction to teach subtraction with regrouping to students with learning disabilities. Learning Disabilities Research & Practice, 27 , 152-166.

Montague, M. (1997). Cognitive strategy instruction in mathematics for students with learning disabilities. Journal of Learning Disabilities, 30 , 164–177.

Suh, J., & Moyer, P. S. (2007). Developing students’ representational fluency using virtual and physical algebra balances. Journal of Computers in Mathematics and Science Teaching, 26 , 155-173.

Swanson, H. L., Lussier, C., & Orosco, M. (2013). Effects of cognitive strategy interventions and cognitive moderators on word problem solving in children at risk for problem solving difficulties. Learning Disabilities Research & Practice, 28 , 170-183.

van Garderen, D. (2007). Teaching students with LD to use diagrams to solve mathematical word problems. Journal of Learning Disabilities, 40 , 540-553.

van Garderen, D., & Montague, M. (2003). Visual-spatial representation, mathematical problem solving, and students of varying abilities. Learning Disabilities Research & Practice, 18 , 246-254.

van Garderen, D., Scheuermann, A., & Jackson, C. (2012a). Developing representational ability in mathematics for students with learning disabilities: A content analysis of grades 6 and 7 textbooks. Learning Disability Quarterly, 35 , 24-38.

van Garderen, D., Scheuermann, A., & Jackson, C. (2012b). Examining how students with diverse abilities use diagrams to solve mathematics word problems. Learning Disabilities Quarterly, 36 , 145-160.

Zhang, D., Ding, Y., Stegall, J., & Mo, L. (2012). The effect of visual-chunking-representation accommodation on geometry testing for students with math disabilities. Learning Disabilities Research & Practice, 27 , 167-177.

Searches were conducted of the literature for content appropriate for this topic that was published in scientific journals and other academic sources. The search included online database searches (ERIC, PsycINFO, Queen’s Summons, and Google Scholar). The gathered materials were checked for relevance by analysing data in this hierarchical order: (a) titles; (b) abstracts; (c) method; and (d) entire text.

Relevant journals’ archives were also hand-searched between issues from 2010 and the most recent issues. These journals included Learning Disability Quarterly, Journal of Learning Disabilities, and Learning Disabilities Research & Practice.

Nancy L. Hutchinson is a professor of Cognitive Studies in the Faculty of Education at Queen’s University. Her research has focused on teaching students with learning disabilities (e.g., math and career development) and on enhancing workplace learning and co-operative education for students with disabilities and those at risk of dropping out of school. In the past five years, in addition to her research on transition out of school, Nancy has worked with a collaborative research group involving researchers from Ontario, Quebec, and Nova Scotia on transition into school of children with severe disabilities. She teaches courses on inclusive education in the preservice teacher education program as well as doctoral seminars on social cognition and master’s courses on topics including learning disabilities, inclusion, and qualitative research. She has published six editions of a textbook on teaching students with disabilities in the regular classroom and two editions of a companion casebook.

Share This Story, Choose Your Platform!

Related articles.

Signup for our Newsletter

Get notified when new resources are posted on the website!

Sign up to receive our electronic newsletter!

Recent Posts

• Free Upcoming Webinar: Where Evidence-Based Literacy meets Differentiation- Supporting students in tiers 2 & 3
• Webinar Recording: Leading and Staying on Track – Leveraging Data to Monitor and Implement Informed Programs That Make an Impact
• Working with SLPs to Support Communication and Literacy

• Jul 16, 2021

Visuals That Work for Word Problems

Updated: Mar 6, 2023

Bar models are probably one of the most popular things people hear about when they research a Singapore-based math education. They may have seen some models used and are curious about how they help students make sense of word problems. As someone who didn't jump on the bar model band wagon willingly, I wanted to share my experience.

If you know my story, you know I loved math growing up. I loved the rules and the way things worked. However, in complete transparency, I had no idea what I was doing. I realize now that I was just following the procedures set in front of me. I was really good at memorizing and could just follow the steps to get an answer. I had no idea why that answer worked, but I had awesome grades.

Then, I began teaching and realized I couldn't break it down for my students. They would ask some great questions, and I did not know how to answer them. I began learning and studying all that I could, because I wanted to be there for my students.

One year, my principal decided we were going to start bar modeling. We were going to use this method to solve word problems. She sent me to my first training where I was a HORRIBLE participant. I just didn't see the point of solving using a bar model when I could use algebra. I feel so sorry for the presenter, because I was not an easy participant.

But I give her credit, because she made me a believer. She put a problem on the board that was really hard. I couldn't figure out how to use my rules to solve it. She drew a model and then, it totally made sense. The answer was obvious! She then explained it was a third grade problem, and my mind was blown! Third graders are solving these types of problems?! No way!

I realized the bar models were a great way to help students visualize and problem-solve. I also realized this was not a "math" issue but a "mindset" issue. Do I believe math is a series of following rules or a process to be understood? When I believed math was about following rules, bar models didn't make sense. If I believe that our ultimate goal is to become problem solvers, bar models are great visual tools to build a foundation of understanding of operations.

When we begin teaching these models in 2nd grade, we show students that one unit can represent a quantity. They move from one-to-one correspondence in Grade 1 to seeing that it's not always efficient to draw each one. Instead rectangles can be used to show a part-whole, comparison or equal groups relationship. Once I see the relationship, I can determine what operation to use.

Part of learning to use bar models is the ability to understand when to use each model. Reviewing the models can help students to think about the problems that can be asked with each model. That's where these bar model posters come in. Post these around the room and encourage students to consider when they should use each model. Encourage students to look at the model and create their own word problems. Ask students to reflect on which models they feel confident using.

If you need more support with bar models and word problems, don't forget to check out my two Problem Solving Handbooks. These books walk students through each model with concrete, pictorial and then abstract quantities. Each problem includes a video to help model the strategies and lead to mastery. There's also some great practice and challenge problems to extend our learners. You can grab them in the SHOP with digital, printable and teaching options.

In the meantime, begin exploring bar models with these posters and put them up in your classroom. Feel free to share your experience in the comments below!

Download your free bar model posters here:

• K-2 Free Math Resources
• Grades 3-6 Free Math Resources

Recent Posts

Great Big List of Math Literature

Math Literature: Goodnight Numbers and a Digital Freebie

Math Literature: The Action of Subtraction

Thanks for submitting!

Upload a screenshot and solve any math, physics, or accounting problem instantly with MathGPT!

Drag & drop an image file here, or click to select an image.

Visual representation in solving mathematics problems

[email protected]

[email protected]

• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Mohamad Rif'at , Nilamsari Kusumastuti , Nurfadilah Siregar; Visual representation in solving mathematics problems. AIP Conf. Proc. 13 July 2022; 2577 (1): 020055. https://doi.org/10.1063/5.0096126

Download citation file:

• Ris (Zotero)
• Reference Manager

It explores an experimental design that implemented teaching and learning based on visual thinking to solve math problems. There are three treatments in solving the problems: picturing, expressing the algebraic relationship, and constructing ide from the visual representation. There is no difference in students' performance in visualizing, but significantly different after the last two actions. That is 1) Visual thinking used for reasoning in constructing algebraic expression; 2) The visual and algebraic thinking applied alternately; 3) The two kinds of thinking are not hierarchical, but inadequate relation; 4) Solving the problem always start from visual thinking, and then thinking algebraically; 5) Visual construction is a mental process, as an abstraction of systematic reflective visualization. The recommendations are 1) In teaching and learning, mathematics should be by using visual representation; 2) The mathematics content knowledge by visualizing is an integrated learning activity. The orientation is in developing creativity and thinking alternatively.

Sign in via your Institution

Citing articles via, publish with us - request a quote.

Sign up for alerts

• Online ISSN 1551-7616
• Print ISSN 0094-243X
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

• Member Home
• My Bookmarks

Visual Models for Problem Solving in 1st Grade

May 10, 2020

As students enter 1st grade, they continue to work on math comprehension using early structures, like the Kindergarten journal we introduced last week, but now we begin to add visual models to the mix!

Let’s recap a child’s developmental journey through problem solving:

• In the early childhood years, a child needs lots of developmentally appropriate experience interacting with real objects in a physical world . 
• The physical world is captured in a quantitative picture , which young children observe and use as a springboard for mathematical conversations.
• We transition into a more structured math work mat to help young students be able to connect numbers to words and words to numbers, still using familiar situations from real life.
• The math work mat gives way to a formal math journal in Kindergarten that makes use of math comprehension skills. It provides a structure for students to explain their understanding of numbers within real world situations that will carry on throughout elementary school. 

Each of the stages of development builds on the skills developed in the previous step, so it is important that students aren’t rushed through these stages. The goal is to teach students the why behind the how so they aren’t just memorizing procedures but truly understand what is happening as they solve problems.

This 1st grade year is the last stage in the Math4Littles progression , in my opinion. After this, there isn’t much scaffolding, so we really want to carefully implement all the previous stages of problem solving before we turn the students loose, because we don’t want them to start guessing and checking. In taking students on this developmental journey, we are trying to build them a solid foundation for visual models to help them to understand problem solving. 

How We Used to Teach Problem Solving

When I was teaching 1st grade, I remember a strategy that we used for problem solving called the C.U.B.S. method. Each of those letters stood for a step in the problem solving process so students could remember what to do: C – circle the numbers, U – underline the word, B – box the operation, S – solve the problem. Seems like a simple process that gives kids a really great structure to start to understand what words problems are asking, right? But what I realized is that this strategy doesn’t hold up long term.

“Shannon has 5 lollipop and Scott has 4 more lollipops than Shannon. How many do they have all together?” 

I watched students follow that procedure with this type of problem. They circled the 4 and 5, underlined important information and put a box around the words all together , which means add because we’ve all seen the T-charts of addition/subtraction vocabulary – it says difference , it means we’re going to subtract, if you see all together , we’re going to add. But that strategy gives me 4, 5, and all together . If you go back to the question, you’ll realize the answer isn’t 9.

As I often do, I asked myself why ? Why isn’t it 9? A little more reading comprehension is required to decode that answer. The problem says I had 5 lollipops. Scott had 4 more than me, which means he also had 5. Adding that up, he had 9 and I had 5, so there were 14 all together.  

Why are we teaching kids procedures with concepts they don’t understand? Sometimes the strategies that we teach in math are conditional, meaning they only work for a certain amount of kids or a certain length of time. Then you have to worry about teaching them when to apply it and the rules for applying it, and what was meant to make things easier for students ends up being more complicated.

When we start working with strategies, I want to be able to find that vertical zip, meaning if I show you how this strategy might work in first grade, it has to work as the child gets older too so that they don’t have to learn a whole new set of strategies every year because every teacher teaches it differently. Honestly, the CUBS method would probably work for 75% of the problems in first grade. Students are doing more advanced part-whole addition problems, part-whole subtraction, part-whole missing addends, and they’ll start doing a few multi-step problems, all of which fit in the part-whole family, for which the CUBS method works well. But when you move out of that genre of problems, it falls apart. 

In the Kindergarten journal, we featured part-whole addition, part-whole subtraction, part-whole missing addend, a few problems with teen numbers, and a mixed review. The journal is very structured because it is intended to start students thinking about what they’re reading in the story problem: We have a story, a sentence form, a quick draw area, a number bond, a 10-frame, and a computation area. As they transition to 1st grade, how do we remove some of that scaffolding while still keeping it developmentally appropriate?

We have to be really careful with the way we make this transition, because very quickly, students can jump to the “circle the numbers, box the word” strategy and many times they just appeal to us because they don’t know what to do. It’s a word problem and it’s confusing, so they just add because we’re talking about adding that week. 

Additive Comparison Problems 

Additive comparison problems, where I have an amount and you have the same amount but you may have more or less than I do, are introduced after students have spent some time working on multi-step part-whole problems.

This type of problem is really a play on language, in my opinion, which makes it really confusing for kids to understand exactly what it is asking. So, we really want kids to take a step back to understand the additive comparison problems, which are coded AC in our journals. I find that building these problems with unfix cubes is a good way to start.

Let’s take this problem: Shannon has 10 pet rocks and Sherry has 4 pet rocks. How many more rocks does Shannon have than Sherry?

In some ways it seems like this might be a missing addend problem, but in fact we’re really comparing my pet rocks to Sherry’s pet rocks and we’re asking how many more does one have than the other. This really requires students to take it to the concrete level and make a bar model with unifix cubes.

I put 10 cubes to represent Shannon’s pet rocks, and then I’ll use different color cubes to show Sherry’s 4. Then, I want to compare the lengths of those two bars and figure out what the problem is really asking, which is the gap between where Sherry’s bar stops and Shannon’s bar stops. The question mark is asking for how many more does Shannon have? 

Sometimes, the language of an additive comparison problem might be reversed and say how many less does Sherry have? Since it is a play on words, which sometimes becomes confusing for students, we really need to put thought into how we go about teaching kids to do a problem like this.

Visual Models for Additive Comparison Problems

If I were to line up all the programs we work with, every one of them has bit of a different name for visual models: model drawings, tape diagrams, bar models, unit bars. We’re going to universally call them visual models for word problems. 

These aren’t the little quick draws we’ve been doing in Kindergarten because, as students get older and the problems get more complex, I’m not going to be able to draw 13 ducks and then 9 more because it will take too long! Instead, I want to put it into a visual model that has these units.

This first grade year is a transitional time where kids are going from the quick draw to what I’m going to call proportional bars, which have a length of individual cubes that are representative of the quantities we’re talking about in the problem.

I just was working with a first grade teacher last week on a Zoom call, and this teacher had not been able to attend our workshop on their campus about visual models. She, like most teachers I work with, didn’t understand why visual models were so important. She thought her students should be able to do quick draws and didn’t understand why they had to do boxes. She told me she was a big proponent of encouraging students to solve problems in different ways, so why would she possibly want to teach students a procedure like this and make them solve word problems in this way. 

After I took her through the same progression of problem solving we’ve been going through in our blog the past few weeks, she was sold! I took her up through fifth grade to help her see why it is that, in 1st grade, we’re asking students to stop doing quick draws and start to use a visual model that has a unit bar with different pieces. This proportional model is also a great transition into using a non-proportional bar.

Let’s say I had 92 pet rocks and Sherry has 45 pet rocks. A quick draw clearly won’t work for this problem, and I don’t have enough room on my paper to draw a proportional model for those numbers. But I can draw a longer bar that represents Shannon’s rocks, write in 92 rocks, and draw a shorter bar to show Sherry’s 45 rocks so I could see the proportionality. 

The hardest thing to remember when we do visual models for word problems is that it actually has nothing to do with math! We’re not actually solving the problem on the model; we are solely using a reading comprehension strategy.  

One of the biggest misconceptions we addressed when we started rolling out the 1st grade journal samples that I’ll be using in this video, was that the total doesn’t go on the line. If the problem asks for a total, we represent that in the visual model with a question mark. 

We also want to make sure that we label the visual model. For example, putting a B above the books that Erin had and an L above the books she got at the library. 

The whole point of this process is to provide a systematic way for students to work through problems that doesn’t stop working after 1st grade or when you start working on a different type of story problem. In fact, this strategy carries through multiplicative comparison problems and fractions, all the way into ratios and proportions in middle school. 

Step-by-Step Problem Solving

Read the problem. Then, have someone read it and repeat it, and every time a new piece of math information is presented, we’re going to put a chunk. So, as kids are reading the problem, they start to learn how to dissect what’s being asked. 

Not all first grade students will be able to read the story problem, but this process is modeled day after day after day in the first grade classroom, so eventually the child will become independent. 

I’m going to read a story problem: Mark has 9 strawberries, 6 of them are small. The rest are large. How many strawberries are large? 

Then, I’ll go back and read it in chunks: Mark has 9 strawberries . This is a new piece of mathematical information, so students will repeat that statement back and highlight or put a line there. The students also like to say chunk! Then we continue reading: Six of them were small. I’ll stop, repeat it, and the students say chunk! as they mark that chunk in their journals. Now we have two pieces of mathematical information. Let’s continue: The rest were large . Repeat and then chunk! So, we’ve got three sections of information that the problem has given us that we need to replicate in our visual model.  Finally, How many strawberries are large? Repeat that and then chunk!

By going through the problem slowly and methodically, students can really see these sections that they’re reading, and, as they’re going on to the subsequent steps of solving the problem, they can actually check off that they’ve included all the chunks of information in their visual model. 

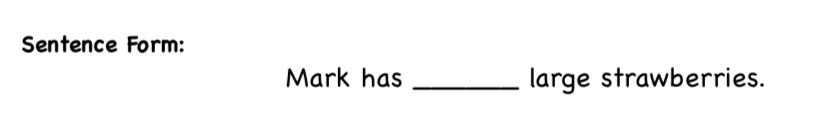
In our problem, it asked me how many strawberries are large? To put it in a sentence form, I would say: Mark has ____ large strawberries. I like to say Hmm for the ____  as we’re reading it out loud.

In Kindergarten, we provide the sentence for students, leaving the blank space for their answer. But in 1st grade, we take some of the scaffolding away. It might say “There were _____ large ____” and the students have to fill in the blanks.

The sentence form is a great way to make sure that kids are comprehending what they’re reading. Generally, students in first grade have a difficult time trying to create a sentence form, because they aren’t yet developmentally ready to give you a complete answer in reading. But students will be required to do a sentence form in 2nd through 5th grade so we can be sure they understand the problems being asked, so it’s really great practice to start in 1st grade with the scaffolding.

Proportional model. We start the 1st grade year with a proportional model. We may scaffold here for the who or the what, and students will eventually start to learn what goes in that visual model. In this case, we’re talking about all of Mark’s strawberries, even though the question itself is only asking about how many of them are large.

In a proportional model, you might see the 9 squares. This is a missing addend problem so that title is going to have PWMA at the top, and there will be exactly nine squares. Some people might think that’s giving it away, but remember the goal of visual models? It’s not to solve the problem but understand what’s going on in the problem, so we’re more concerned about whether or not the student can label the drawing correctly. 

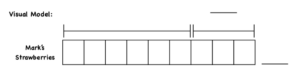
In this example, the student would total the bar at 9 and check off the first chunk of the problem that we read earlier –  Mark has nine strawberries.

The next part says “6 of them are small.” In 6 of my boxes, I’ll make six Xs, or I might make small circles, and at the top I can either write small or abbreviate with an s . 

Then it says “the rest are big.” I could label that other section of the boxes B for big, or write the whole word if I wanted. Then,  I need to put a question mark above that section between 9 (the total number of strawberries) and 6 (the number of small strawberries). That section represents the large strawberries, which is what my sentence form reminds me that I’m looking for. 

Technically, a student could just look at this easy proportional model and say there are 3 large strawberries because it’s right there in front of them. So some people might think this journal is just too easy, but at the end of the day, students are solidifying the process. They’re going back up to the problem and putting a check when they add Xs or circles for the six small strawberries. They’re putting in a check when they’ve talked about putting in the large strawberries. Then they put a question mark to show what we’re looking for. There’s a lot of detail that we’re looking for kids to have to interact with the text in math to show the comprehension. 

In some of our schools, we will do a unit bar at the bottom of the page. In the 1st grade journal we’ve created for Math4Littles, we’re going to leave the bar off and introduce the non-proportional bar a little bit later in the year. There is nothing wrong with having a model of the proportional bar and then underneath it having the non-proportional bar. In our journal, we plan to show the proportional bar, and then bring in both types of bars so that kids could see the relationship between the two. If where about this non proportional bar, where would I slice it to put the nine in? And then where’s my question mark? is it labeled? etc. 

The integral parts of visual models are: labelling the who or what, taking the bar and adjusting it based on the information that’s given, and writing in their question mark. Then it’s time to solve!

Computation. Although this step might not seem necessary because our sample problem is so simple, and to first graders after they do so many, it seems simple and both teachers and students might wonder why they’re even doing it, but I can promise that these problems will become more complex, very quickly. In our 1st grade journal, we will feature this look at the proportional bar, and then transition to having proportional and non proportional models, and then eventually just leaving it blank and having the student put in a non proportional bar to see that they can develop this progression. 

1st Grade Goals

The goal is, by the end of their first grade year, students should be able to solve problems with larger numbers and a non-proportional bar. You certainly don’t want to rush that progression. 1st grade is a really nice scaffold for students to get to that point of independence, because when we get to 2nd grade, we don’t do a whole lot of scaffolding. There are more open-ended sentences, more blanks, and students are doing more of the work.

Additionally, we want to mix up the types of problems we’re solving, give students time to understand them. You might do three days of part-whole addition to see if they can get it under their belt. Then do some part-whole subtraction, then mix the two to see if students are just following a pattern where we’re adding today or subtracting today. We want to know that they can really apply what they’re learning. Multi-step problems, where students have to add and then subtract, or vice versa, are next. Give students lots of good practice, and then mix it up again to see if they’re really following the words, or if they’re just learning a procedure. The last type of problem that we would integrate in the first grade is additive comparisons. 

Video Tutorials

In the video tutorials, you’ll see aspects of four different problems being displayed. Some will have the proportional bar, some will have the proportional and the non proportional and some just won’t have it just so you can get an overall idea of what this looks like as we go.

[yotuwp type=”playlist” id=”PL76vNL0J-a405ysBIwEwXfaMp5883yGh4″ ]

As you watch the videos, think about how you could set this up in your classroom, starting with some of the sample problems that we’re offering as a free download today. We will be releasing a full 1st grade journal soon, so stay tuned! 

Join us next week for problem solving in 2nd grade: What are the different problems that 2nd grade is going to encounter? How are journals coded?  As we start to look at how journals are coded, which you certainly could use these tutorial videos right away in your classroom or in your distance learning by thinking about story problems in a different way.

*Addition , *Subtraction , *Word Problems , Audience - Lower Elementary (K-2) , Series - Math4Littles | 0 comments

Related Posts

Screening for Numeracy Development

Dec 5, 2022

Ever feel like the years are flying by and standing still at the same time? Usually, it’s children that help us feel this odd sensation, but I also can’t believe it’s been TEN years since I first created my numeracy screeners!Ten years ago, I developed a set of...

Rekenrek Activities for Numeracy Development

Feb 28, 2022

This little-known math tool, the rekenrek, is a star when it comes to numeracy development!

Using Place Value Discs in the Math Classroom

Jan 27, 2022

I have all these place value discs - How am I supposed to use them across different areas of my mathematical instruction?? This is a question that we get from a lot of teachers and we know that having a Math Salad Bar full of tools but not knowing how to implement...

Evaluating Math Reasoning in Visual Contexts -->

Introduction

Large Language Models (LLMs) and Large Multimodal Models (LMMs) exhibit impressive problem-solving skills in many tasks and domains, but their ability in mathematical reasoning in visual contexts has not been systematically studied.

Leaderboard on testmini

🚨 To submit your results to the leaderboard, please send to this email with your result json files.

Leaderboard on test

🚨 For more submission details, please refer to this link and this link .

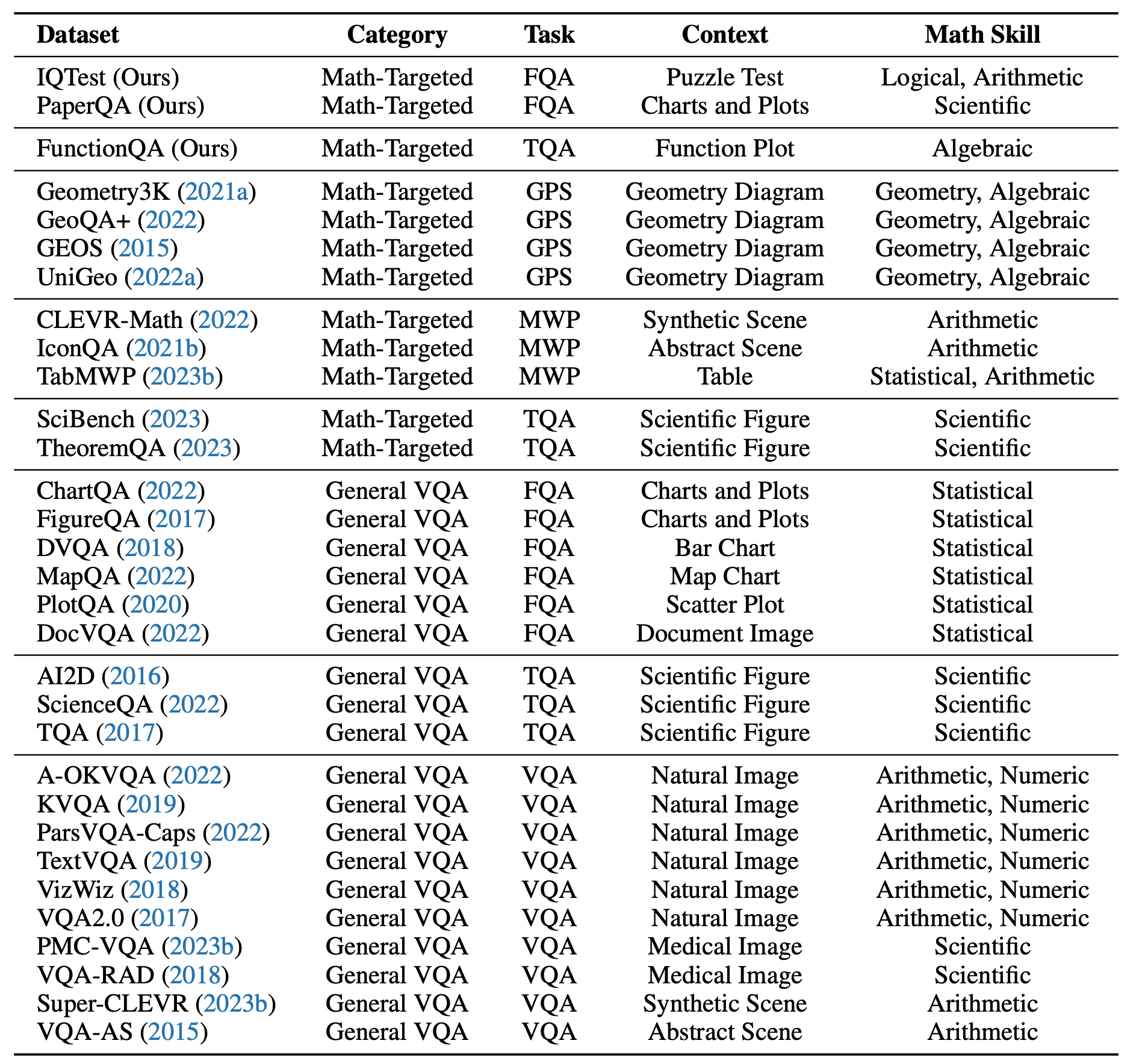
MathVista Dataset

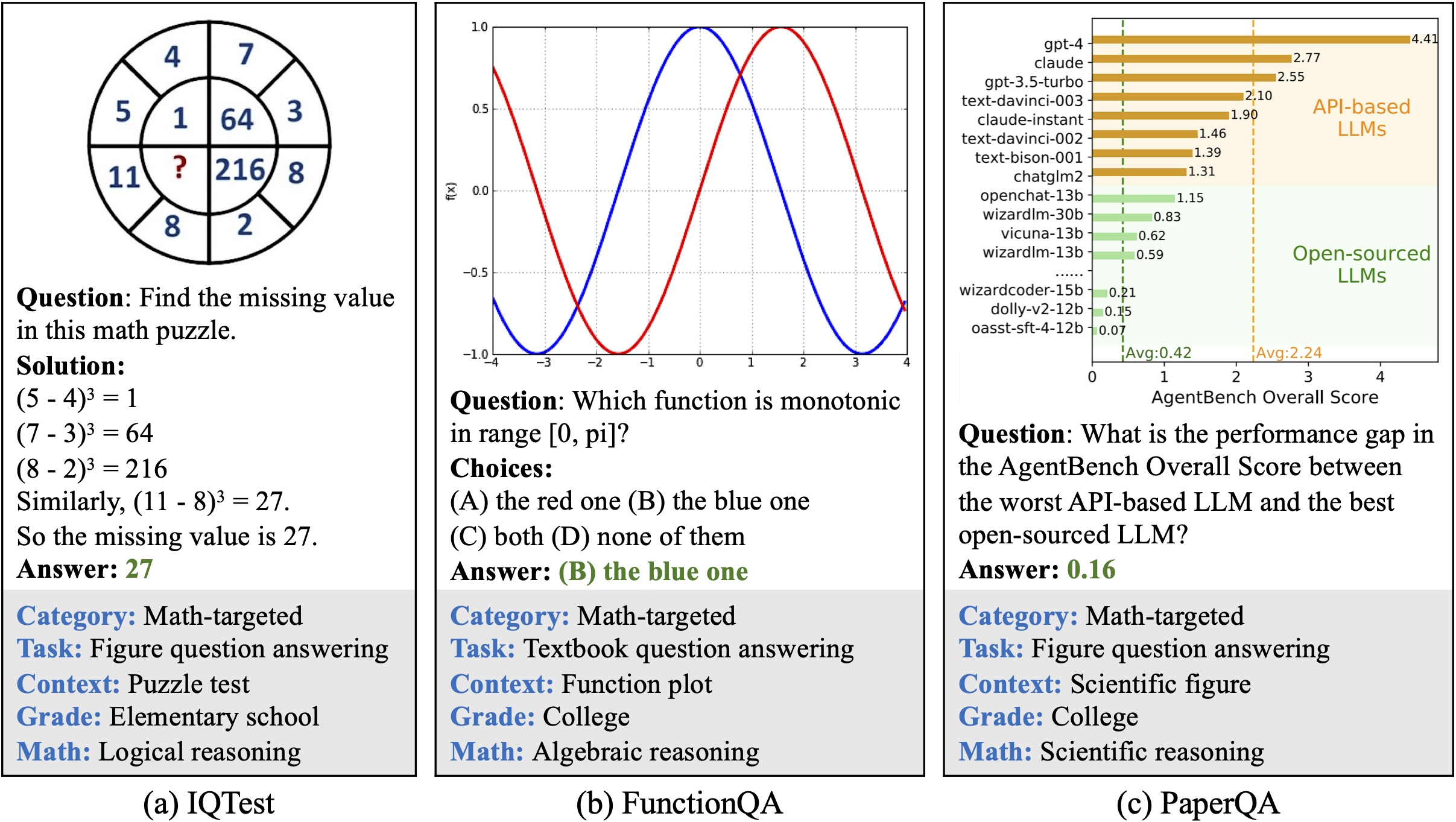
Examples of our newly annotated datasets: IQTest, FunctionQA, and PaperQA.

• testmini : 1,000 examples used for model development, validation, or for those with limited computing resources.
• test : 5,141 examples for standard evaluation. Notably, the answer labels for test will NOT be publicly released.

Arithmetic Reasoning

Algebraic Reasoning

Geometric Reasoning

Logical Reasoning

Numeric Reasoning

Statistical Reasoning

Scientific Reasoning

Geometry Diagram

Synthetic Scene

Natural Image

Scientific Figure

Function Plot

Abstract Scene

Puzzle Test

Scatter Plot

Document Image

Medical Image

Visualization

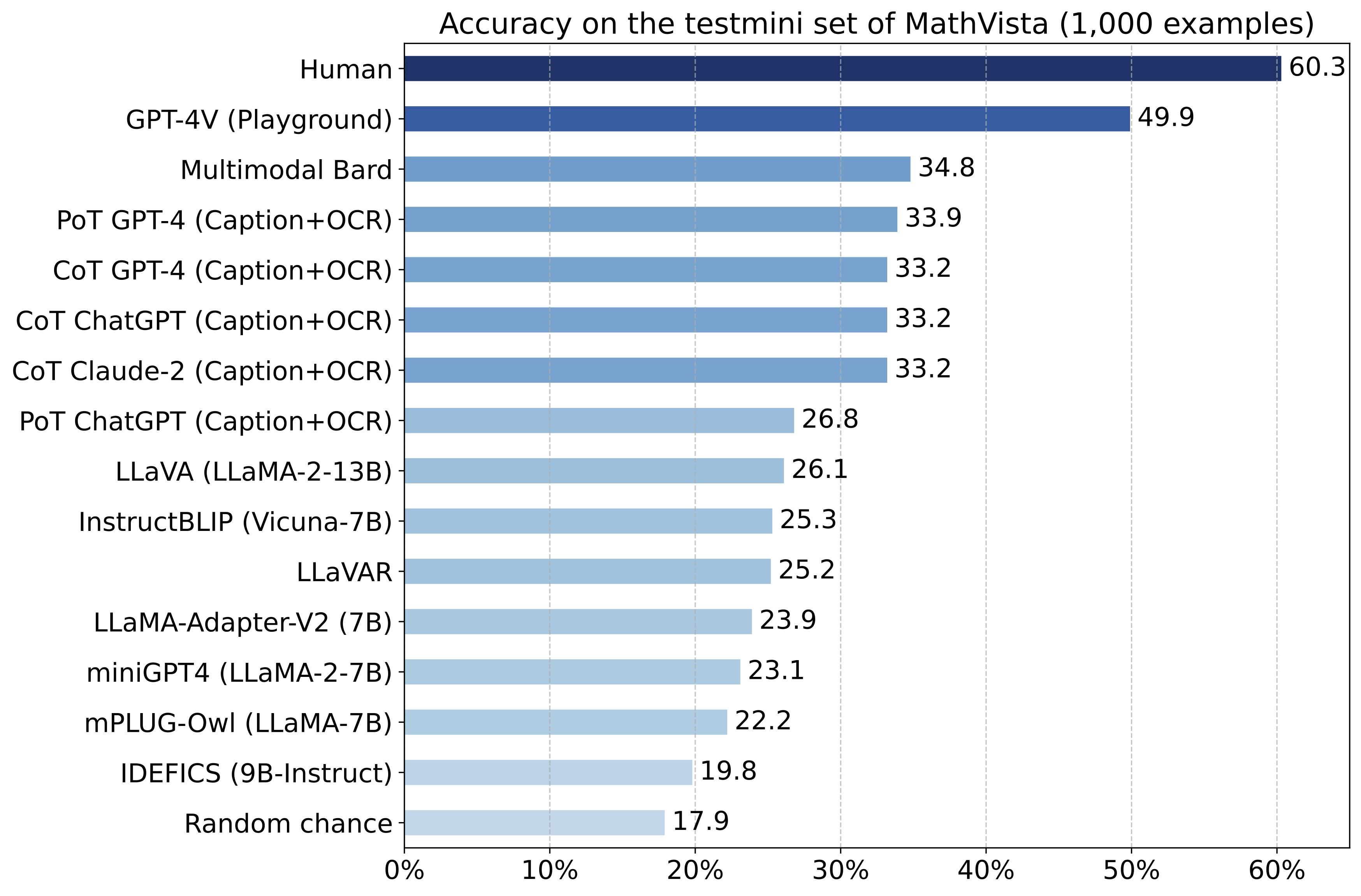
Experiment results, results on existing foundation models.

One example for each reasoning skill required in MathVista

Error analysis of Bard results: (a) presents errors in answers and explanations; (b) delves into the details of wrong explanations. Notations: “Answer” is “Ans.”, “Explanation” is “Exp.”, “Partially Correct” is “Partial”, and “Not applicable” refers to unanswerable or indeterminate cases.

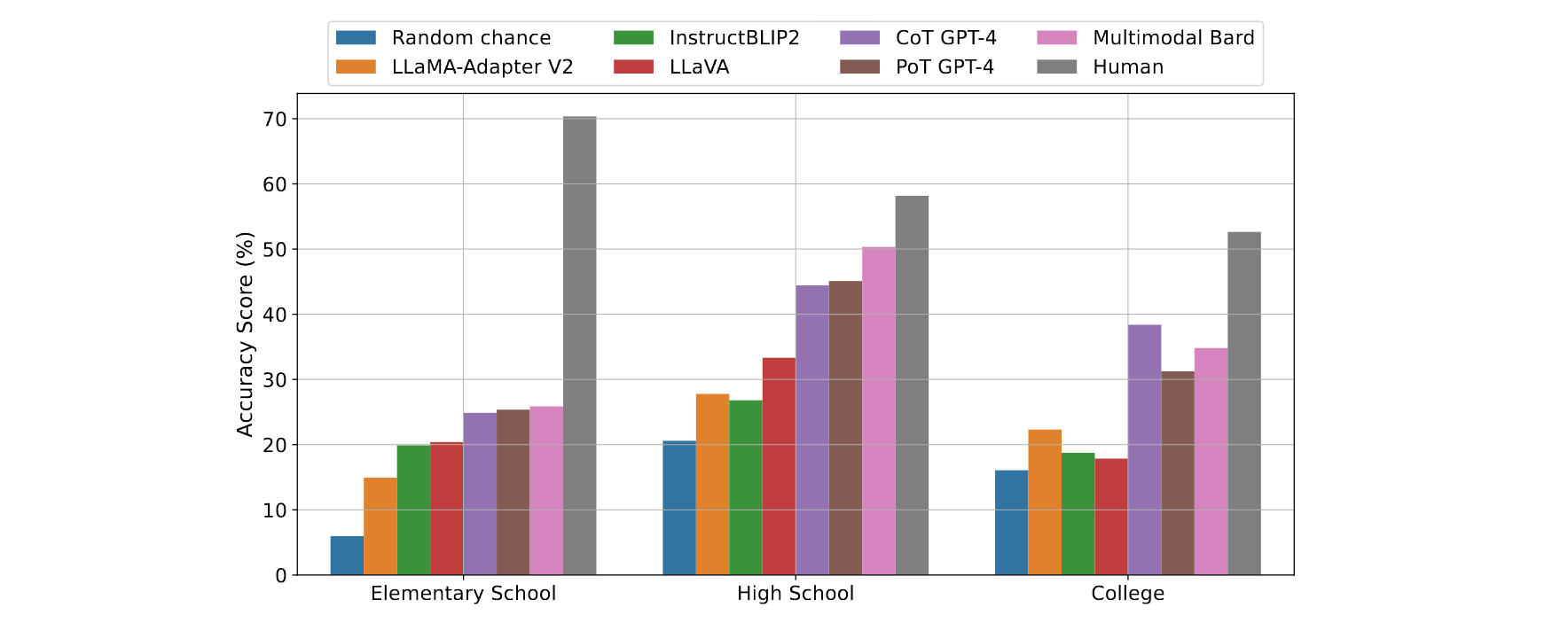
Average accuracy scores across different grade levels for leading foundation models

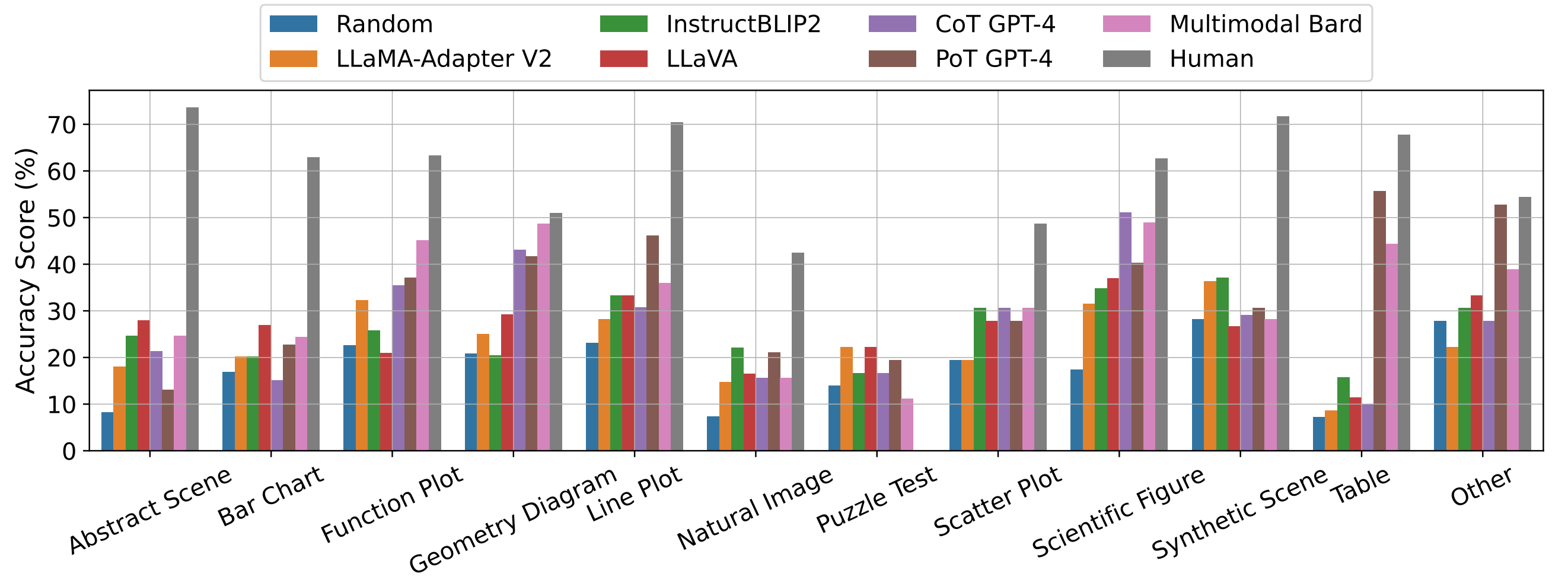
Accuracy scores of leading baselines across various visual contexts

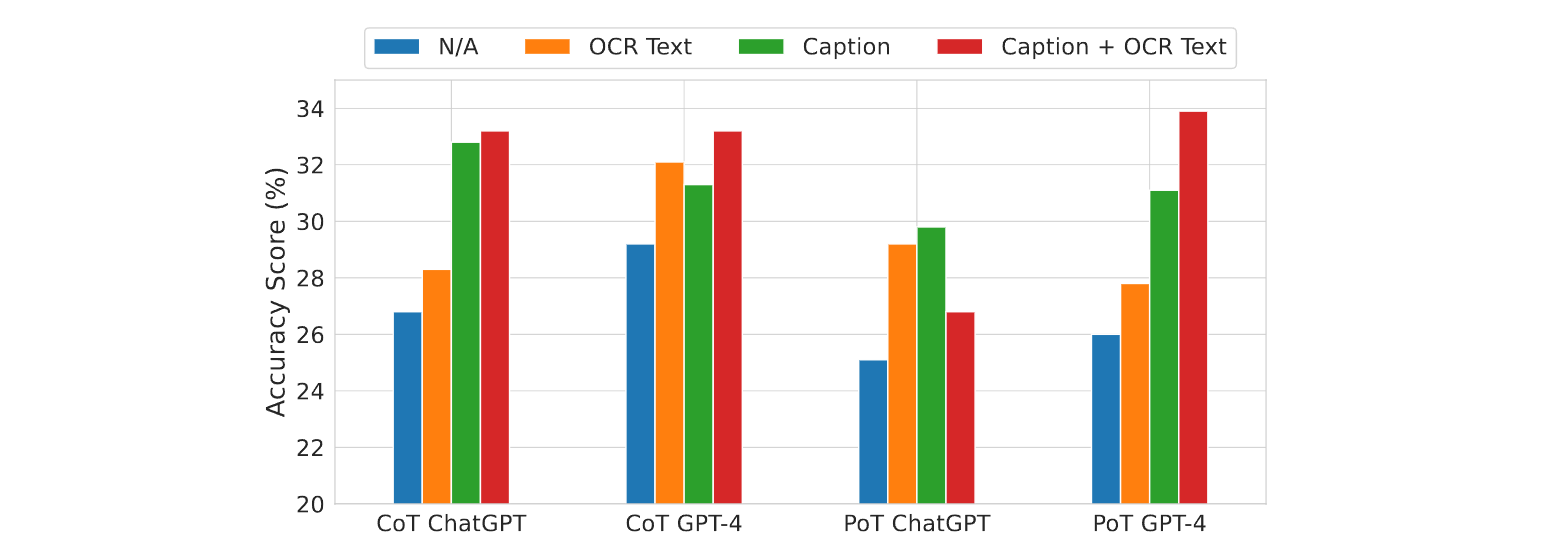
Average accuracy scores of LLM baselines under various visual inputs

Visualization Examples

Refresh Question

Multimodal Bard

CoT GPT4 (Caption+OCR)

Help | Advanced Search

Computer Science > Computer Vision and Pattern Recognition

Title: visiongraph: leveraging large multimodal models for graph theory problems in visual context.

Abstract: Large Multimodal Models (LMMs) have achieved impressive success in visual understanding and reasoning, remarkably improving the performance of mathematical reasoning in a visual context. Yet, a challenging type of visual math lies in the multimodal graph theory problem, which demands that LMMs understand the graphical structures accurately and perform multi-step reasoning on the visual graph. Additionally, exploring multimodal graph theory problems will lead to more effective strategies in fields like biology, transportation, and robotics planning. To step forward in this direction, we are the first to design a benchmark named VisionGraph, used to explore the capabilities of advanced LMMs in solving multimodal graph theory problems. It encompasses eight complex graph problem tasks, from connectivity to shortest path problems. Subsequently, we present a Description-Program-Reasoning (DPR) chain to enhance the logical accuracy of reasoning processes through graphical structure description generation and algorithm-aware multi-step reasoning. Our extensive study shows that 1) GPT-4V outperforms Gemini Pro in multi-step graph reasoning; 2) All LMMs exhibit inferior perception accuracy for graphical structures, whether in zero/few-shot settings or with supervised fine-tuning (SFT), which further affects problem-solving performance; 3) DPR significantly improves the multi-step graph reasoning capabilities of LMMs and the GPT-4V (DPR) agent achieves SOTA performance.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial
• 10 Best AI Tools to Boost Productivity in 2024
• 10 Best ChatGPT Prompts to Solve Complex Math Problems
• How to Use Algorithms to Solve Problems?
• How to use Chat-GPT to solve Coding Problems?
• Top 12 AI Tools for Remote Learning and Online Education
• 12 Best AI Tools for People with Disabilities [Latest 2024]
• 7 Best AI Tools for Healthcare Professionals free in 2024
• What are Mathematical Puzzles and How to solve them?
• 7 AI Tools You Can Use to Make Money Online
• Top 10 AI Poster Making Tools To Be Used in 2024
• 10 Best AI Tools for Lawyers (Free + Paid)
• 7 Best AI Tools for IT Professionals (2024)
• Top 15 Artificial Intelligence(AI) Tools List
• 10 Best AI SEO Tools to Boost Your Rankings in 2024
• 10 Best AI Search Engines To Try in 2024
• Problems on Ages - Aptitude Questions and Answers
• Top 12 AI Testing Tools for Test Automation in 2024
• Reasoning Tricks to Solve Coding -Decoding and Calendar Problems
• 10 AI Tools Under US $10 Per Month Worth Investing

10 Best Math AI Solvers to Solve Math Problems Online

Tackling challenging math problems can be a time-consuming endeavor. Math AI solvers make learning math simple. These AI-powered tools use machine learning and advanced algorithms to rapidly analyze math problems at all grade levels. Whether you’re a high school student or at the college level, an AI math problem solver can help save you time, ensure accuracy, and boost your school success.

With 24/7 convenience, they can be used anytime to get instant help with confusing math problems. When curating our list of top 10 best math AI solvers, we looked at several important factors, such as pricing, features, strengths, and weaknesses. Let’s explore these tools and learn in which areas they excel:

Mathful – Best Overall Math AI Solver to Solve Math Problems

Mathful is a valuable AI math solver often used by students to get help with complicated math problems. It delivers step-by-step guidance that breaks down the problem to make it easier to digest. The tool also provides the final answer to allow students to verify their solutions and gain confidence in their math skills.

Mathful is available 24/7, making it a convenient tool for students to get instant help with their math homework. Mathful acts as the ultimate solution for boosting academic success at all math levels. 

• Helps students gain a deeper understanding of math concepts with step-by-step guidance.
• Serves as a verification tool where students can check their work without costing a dime. 
• Enables students to complete their math homework with just one click. 
• Cannot be used to supplement a real classroom education. 

Solve Math Problems Instantly with Mathful’s AI Math Solver >>>

AI Math – Best AI Math Solver for All Grade Levels

AI Math is an innovative math AI solver designed to solve a wide range of mathematical problems, ranging from basic math concepts to more challenging equations. 

The way this unique tool works is by analyzing the math problem, finding potential solutions, validating those solutions, and returning the best possible results for the given problem.

While some math AI tools are only capable of solving basic math problems, AI Math is more diverse. Use it to solve math problems at all grade levels, from elementary to university and beyond. AI Math is trained on an extensive database of mathematical information and can guarantee 98% accuracy.

• Generates solutions to math problems with a high rate of accuracy.
• Designed to provide almost instant results for efficiency. 
• Covers all types of math and homework at all grade levels. 
• Requires a subscription after the initial trial period.

HIX Tutor – Best AI Math Solver for High Accuracy

HIX Tutor provides students with the solutions they need to understand and solve their math problems. 

With this powerful math solver AI tool, users can type in a math question or upload a document or image of the question. Using this input, Math AI Solver uses machine learning technology to perform dynamic calculations and give users the correct answer. 

HIX Tutor can provide solutions for math homework problems at all levels with a 98% accuracy rate. However, the tool goes beyond mere problem-solving by offering comprehensive calculations on how to solve the problem from start to finish. 

• Provides step-by-step solutions to math problems.
• Is less expensive than hiring a math tutor.
• Can type in math questions or upload documents or images of the problem.
• May have difficulty recognizing documents with messy handwriting.

HomeworkAI – Best All-in-One Solution for Homework Help

HomeworkAI is the ultimate homework assistant that can be used to get answers to any homework question, from math and science to history and geography. Its math AI solver acts as your personal AI tutor by providing comprehensive solutions to math problems that help students better understand the material.

This unique AI tool is available 24/7, making it a convenient and accessible resource for students who need immediate help with their homework. As the tool is free to try, students can get started right away by asking a math question that they’re struggling with. HomeworkAI can also help students prepare for important tests or exams by providing step-by-step instructions on how to work through certain math questions.

• Covers all school subjects, including math.
• Provides step-by-step explanations for each math problem.
• Supports multiple math problem input methods. 
• Some math solutions may be difficult to understand. 

Question AI – Best Homework AI Tool for Greater Academic Success

Question AI is a leading homework helper that uses powerful AI technology to instantly help with any school subject. Question AI is often used for any math problems, covering algebra, geometry, calculus, arithmetic, and trigonometry. Students often waste hours struggling with challenging homework questions they simply don’t understand. Question AI simplifies the homework process by breaking down the question to make it easier to learn. The math AI solver also promises a 99% accurate answer to the math question, allowing students to verify their own work.

Question AI serves as an innovative all-in-one product for AI homework help. It is a highly effective tool for helping students reach greater academic achievement.

• Covers all homework subjects, including all branches of mathematics. 
• Boosts student grades.
• Supports many different languages.
• Accuracy may be limited beyond core math subjects.
• The mobile app is not yet available. 
• Costs money after the free trial. 

QuickMath – Best Math AI Solver for High School and College Students

QuickMath is designed to automatically answer common math problems in algebra, calculus, and equations. The tool offers several options for solving math problems, including solving an equation, inequality, or a system. It can also simplify an expression, factor an expression, or expand a product or power. The diverse AI math solver can also graph, find the greatest common factor, and the least common measure. Advanced math solvers are also available for more complex math problems.

QuickMath is geared toward high school and college-level students. The tool’s features and capabilities are always being improved to ensure that users have access to the most comprehensive AI math tools available. 

• Offers a wide range of standard and advanced math solvers.
• Available to download on the App Store and Google Play.
• Quick-solve tutorials are available to help users learn math concepts. 
• Math problems must be typed in and cannot be uploaded. 
• Not suitable for grade levels lower than high school.
• Some users may receive Timeout messages due to 15-second CPU time rules.

Smodin – Best AI Math Solver for Acing Math Exams

Smodin Math AI Homework Solver offers a fast and effective way to prepare for difficult math exams. The versatile homework helper uses machine learning and advanced algorithms to help students learn core math concepts and boost their grades in school. Simply input a question or assignment and Smodin instantly generates step-by-step solutions.  The math solver AI tool consists of a simple interface that allows students to enter a question to solve. At the click of a button, the tool starts working to analyze the problem and present the best answer based on the equation. 

While Smodin Math AI Homework Solver does lack advanced features and capabilities, it can be a useful tool for students who want to study before a big math test.

• Provides in-depth answers to math questions to help students ace math exams.
• Users are given 3 free credits a day to ask math questions. 
• The clean interface makes it easy to enter math questions to solve. 
• Offers no advanced math features or capabilities.
• Users must pay for a subscription after reaching the daily credit limit. 

StudyMonkey – Best AI Math Problem Solver for Personalized Learning

StudyMonkey is a diverse homework helper for students that uses complex machine learning capabilities to provide step-by-step guidance on many school subjects, including math.  The innovative math AI solver can be used by learners of all backgrounds and ages to improve their understanding of math concepts and enhance their academic success. With round-the-clock availability, this unique tool can save students significant time when completing homework assignments.

• Students can personalize their output based on the subject and grade level. 
• There is a free plan for users that only requires occasional homework help.
• Users can see a history of past questions and answers. 
• Users must purchase a paid plan to ask more than 3 questions daily.
• Answers to more complex math questions may not be as accurate. 
• Must upgrade to the $8 plan to use the Advanced AI Model. 

Interactive Mathematics – Best Math AI Tool for Solving Word Problems

Interactive Mathematics claims to be more accurate than ChatGPT, faster than a math tutor, and more powerful than a math calculator. The advanced AI math problem solver has been trained in a wide array of math subjects, such as basic algebra, advanced algebra, trigonometry, geometry, calculus, advanced calculus, physics, and more. It is also highly effective at solving math word problems with step-by-step solutions. 

With Interactive Mathematics, users can type in their math problems or copy and paste a photo. The tool then analyzes the problem and delivers near-instant results. 

• Efficient at solving math word problems.
• Optimized for mobile phones and tablet use.
• A subscription comes with additional discounts and bonuses. 
• Users can only ask 3 questions before having to upgrade to the paid version. 
• No app is yet available. 
• Pushes tutoring services when the tool is unable to give an accurate answer. 

SnapXam – Best AI Math Solver for On-the-Go

SnapXam is an AI-powered math tutor that can help students better understand different types of math, from calculus to trigonometry.  After entering the math problem, the tool quickly presents the final answer, as well as a step-by-step solution that shows how to work out the problem.

The unique AI math problem solver also provides access to informative YouTube videos that students can watch to learn more about different concepts in math. 

Upgrading to a Premium account can give students access to even more features and perks, including no ads, support for more than 100 math topics, and premium access to the iOS and Android apps.

• Students can get AI math help with only access to a smartphone. 
• Offers multiple solving methods.
• Covers more than 100 different math topics. 
• An ad-free environment is only available with the premium version.
• Geared toward older students. 
• Accuracy issues may occur with advanced math problems.

Completing math assignments can be a long and tedious process. Having access to the best math AI tools can help eliminate the stress and frustration that come with not understanding math problems. For convenience, efficiency, and unmatched accuracy, try some of the top math AI tools like Mathful for free today!

This is a guest post, created for informational purposes only, and should not be considered as professional advice. Readers are encouraged to conduct their own research and consult with relevant experts before making any financial or investment decisions.

Please Login to comment...

Similar reads, improve your coding skills with practice.

What kind of Experience do you want to share?

No videos yet!

Click on "Watch later" to put videos here

Playlist - Solving Equations

Using division to solve one-step equations.

Visual math talk prompts highlighting the relationship between multiplication and division to solve one-step algebraic equations.

Representing Ratios As Percentages

Visual math talk prompts with context used to help emerge the writing and solving of one-step algebraic equations.

Using Division to Solve One-Step Equations – Part 2

Visual math talk prompts highlighting the relationship between multiplication and quotative division to solve one-step algebraic equations.

Solving One-Step Equations With Context

Solving two-step equations with context [part 2].

Visual math talk prompts with context used to help emerge the writing and solving of two-step algebraic equations involving partitive division.

Two-Step Equations With Partitive and Quotative Division

Visual math talk prompts used to help emerge the writing and solving of two-step algebraic equations involving both types of division.

• Data Literacy 1
• Data Management & Statistics 7
• Fractions 2
• Linear Relations 1
• Measurement 13
• Number Sense 83
• Patterning 7
• Quadratics 1
• Data Literacy
• Data Management & Statistics
• Linear Relations
• Measurement
• Number Sense

News, Views & Insights

• Best of Blog (70)
• Astronomy (28)
• Computational Thinking (64)
• Current Events (36)
• Data Analysis and Visualization (138)
• Data Repository (11)
• Design (24)
• Developer Insights (76)
• Digital Humanities (7)
• Education (194)
• Events (44)
• Finance (24)
• Function Repository (12)
• Geosciences (12)
• High-Performance Computing (12)
• History (18)
• Image Processing (48)
• Machine Learning (16)
• Mathematica News (112)
• Mathematica Q&A (13)
• Mathematics (129)
• New Technology (41)
• Other Application Areas (136)
• Raspberry Pi (18)
• Recreational Computation (163)
• Software Development (35)
• System Modeler (49)
• Uncategorized (1)
• Wolfram Cloud (24)
• Wolfram Community (19)
• Wolfram Demonstrations Project (31)
• Wolfram Language (297)
• Wolfram News (278)
• Wolfram Notebooks (37)
• Wolfram U (29)
• Wolfram|Alpha (48)
• Wolfram|One (7)

Marking a Milestone: Four Years of Daily Study Groups

From data to discovery: studying computational biology with wolfram, navigating quantum computing: accelerating next-generation innovation, unlock innovative problem-solving skills with creative computation.

As computers continue to perform an increasing number of tasks for us, it’s never been more important to learn how to use computers in creative ways. Creative computing, an interdisciplinary subject combining coding with artistic expression, allows us to blend technology with human experiences. Learning to create in this way can help you unlock your innovative problem-solving skills. By mastering creative computation, you can create interactive artwork, design immersive experiences and develop creative solutions to real-world challenges.

Wolfram U ’s new Creative Computation course combines an introduction to Wolfram Language coding with a project-based exploration of various art forms, like visual art, poetry, audio and video game design. If you’ve never coded in Wolfram Language before, this course is a fantastic introduction to applied computing and will help you learn the language for any project. If you’ve already mastered the basics of coding, this course will help you apply your skills to fascinating new problems and projects.

We would love for you to join us in this interactive course as we explore what it means to work creatively with coding.

Motivation from History

Creative computing is a relatively new subject, but people have been using technology to make art for centuries. From the loom to the printing press or Walkman to Atari, technology has been part of art for as long as both have existed.

We now have a variety of exciting and creative ways to engage with computers, from AI-generated images to immersive virtual realities.

In this course, you will learn how to use Wolfram Language to create various forms of art. There are four main sections to the course: Computational Art, Computational Strings, Sound and Game Development. In each section, there are lessons teaching Wolfram Language skills, with associated exercises, and at the end of each section, there is a larger project. The projects are designed for you to stretch your creative muscles and use your new coding skills to create art. You’ll learn how to create visual art using images, how to write poetry using string manipulation, how to visualize audio and how to make text-based and graphics-based video games, all while learning how to code in Wolfram Language.

Here is a sneak peek at some of the topics in the course (shown in the left-hand column):

With 16 lessons, five quizzes and four projects, this course should take around five hours to complete. We recommend doing all the activities and projects to maximize your understanding and explore your new skills.

There is no background required to participate in this course. We will teach you all the coding skills you need to make the projects, so all that is required is your excitement and creativity.

Let’s explore what’s in the course.

There are 16 lessons in this course spread out over the five total sections (Computational Thinking and Coding, Computational Art, Computational Strings, Sound and Game Development). In each lesson, you will explore a different aspect of coding through a short video. You’ll start off by exploring the concept of computational thinking: how to translate your thoughts and your creativity into something the computer can understand and how to work with a computer to build creative artifacts. Here is a short excerpt from the video for this lesson:

Each lesson teaches a specific coding skill, with lots of examples and exploration of key concepts. In the Computational Art section, the goal is to use images and graphics to create a piece of art. In order to do that, we need to learn skills like variables, functions, lists, the Table and Map functions, colors, graphics and randomness, and image manipulation. Each skill is taught with an interactive video lesson in conjunction with exercises, before you use the project to test your knowledge.

The video lessons range from 5–13 minutes in length, and each video is accompanied by a transcript notebook displayed on the right-hand side of the screen. You can copy and paste Wolfram Language input directly from the transcript notebook to the embedded scratch notebook to try the examples for yourself.

Each lesson has a set of exercises to review the concepts covered during the lesson. Since this course is designed for independent study, a detailed solution is given for all exercises. Each exercise will help you practice a specific skill you’ve learned so that you are ready to use that skill in the project. Here is an example of an exercise from lesson 6 on image manipulation:

The exercise notebooks are interactive, so you can try variations of each problem in the Wolfram Cloud . You’re encouraged to blend skills together as you learn them. For example, for the aforementioned exercise, you could use the skills you just learned about randomness to replace the dominant colors in the image of the wolf with random colors, or you could import images to do the same exercise with a different image. When you’ve gotten further in the course, you could come back and build your own function that can do this to any two images.

Each section of the course includes a short project, and the Game Development section has two longer projects. In each case, you’ll use the skills you learned in that section to build something creative. In the first three sections, we provide detailed solutions and walk you though our processes, but in the Game Development section, we encourage you to build something unique.

In the Computational Art section, you’ll make art using images and shapes. In Computational Strings, you’ll write a Mad Libs haiku. In Sound, you’ll make an audio visualizer. In Game Development, you’ll make a text adventure game and a graphics-based Pac-Man –style game.

These projects will allow you to celebrate your successes and practice your new coding skills while cementing your understanding of creative computation.

Each section of the course ends with a short quiz, which allows you to demonstrate your understanding:

You will get instant feedback on your solutions, and you’re encouraged to try out the code.

Course Certificate

You are encouraged to watch all the lessons and attempt the projects and quizzes in the recommended sequence, since each topic in the course relies on earlier concepts and techniques. When you watch all 16 lesson videos and pass the five course quizzes, you will earn a certificate of course completion. The Track My Progress status bar in the course helps you to chart your progress, showing you where you left off from your previous course session. While you don’t have to submit projects to earn a certificate, they are a fundamental part of gaining computational skills, and we look forward to connecting with course users about their projects on Wolfram Community . Your course certificate represents completion of the basic course requirements, demonstrates your interest in exploring the latest technology and in building new computational skills, and it will add value to your resume or social media profile.

You are also encouraged to use the skills you learn in this course to go on to earn Level 1 certification for Wolfram Language proficiency . While the course does not require the same level of mathematics as the Level 1 certification exam, it will prepare you well for accomplishing the range of computational tasks that are required for Level 1 certification.

A Building Block for Success

A mastery of the fundamental concepts of creative computing will prepare you for working with computers to innovatively solve problems. Whether you’re interested in creating art or you’re interested in developing your coding skills, this course will provide a detailed foundation in both. Learning Wolfram Language is a valuable pursuit regardless of your career aspirations, as you can use the skills you learn in this course in any field.

Acknowledgements

I would like to thank my coauthor Eryn Gillam for their major contributions to the development of this course, as well as others who helped this course come together, including (but not limited to) Anisha Basil, Abrita Chakravarty, Cassidy Hinkle, Joyce Tracewell, Arben Kalziqi, Isabel Skidmore, Zach Shelton, Simeon Buttery, Ryan Domier and Eder Ordonez.

! Please enter your comment (at least 5 characters).

! Please enter your name.

! Please enter a valid email address.

Related Posts

After being asked to be punchy, direct and describe everything in their line of vision, the models took turns describing a man who was “sleek and stylish with their black leather jacket and light colored shirt” sitting in a room with “natural and artificial” lighting that was “dramatic and modern” and featuring a plant in the background that added “a touch of green to the space.” 

When a second person entered to give bunny ears to the first, GPT-4o was asked to sing a song based on what happened — and it did, crooning, “surprise guests with a playful streak.” 

In other videos, the model laughs at dad jokes (“that’s perfectly hilarious”) performs real-time translation of Spanish to English and vice versa, sings in a lullaby about “majestic potatoes” (first replying to the prompt, “now that’s what I call a mashup”), emulates a sarcastic voice much like the droll MTV cartoon character “Daria,” correctly identifies winners of rock-paper-scissors and recognizes that it’s someone’s birthday based on the presence of a piece of cake with a candle in it. 

It also interacts with puppies — replying in a sing-songy tone in the manner people talk to dogs, “well hello there cutie, what’s your name little fluff ball?” (it was Bowser by the way) — and guided a blind man through London, identifying through video input that the King was in residence based on the presence of the Royal Standard flag and described ducks “gently gliding across the water, moving in a fairly relaxed manner, not in a hurry.”

Additionally, GPT-4o can teach math; in one video it walks a young man through a problem based on an image of a triangle. The model asked the student to identify which sides of the triangle were the opposite adjacent and hypotenuse, relative to angle alpha. When he deduced that alpha equaled 7 over 25, the female voice praised: “You did a great job identifying the sides.”

GPT-4o can give fashion advice, too. In yet another video the LLM helped a mussy-haired job candidate wearing a slouchy T-shirt determine whether he looked presentable enough for an interview. 

A female voice chuckled and advised him to run a hand through his hair. The model also remarked drolly, “You definitely have the ‘I’ve been coding all night’ look down, which actually might work in your favor.” 

Winning the internet — or an underwhelming disappointment

Not surprisingly given the diversity of the AI community, the response, at least on social media, has been all over the place. 

Some are saying that it “wins the internet,” taking ChatGPT capabilities to whole new levels (and that it quickly rival Google Translate). One user called the video of AI teaching math “insane,” adding “The future is so, so bright.” 

This demo is insane. A student shares their iPad screen with the new ChatGPT + GPT-4o, and the AI speaks with them and helps them learn in *realtime*. Imagine giving this to every student in the world. The future is so, so bright. pic.twitter.com/t14M4fDjwV — Mckay Wrigley (@mckaywrigley) May 13, 2024

Nvidia senior research scientist Jim Fan — among others — noted how the assistant was “lively and even a bit flirty,” calling back to the 2013 sci-fi movie “Her.”

I know your timeline is flooded now with word salads of "insane, HER, 10 features you missed, we're so back". Sit down. Chill. <gasp> Take a deep breath like Mark does in the demo </gasp>. Let's think step by step: – Technique-wise, OpenAI has figured out a way to map audio to… pic.twitter.com/3fL9n8Mtch — Jim Fan (@DrJimFan) May 13, 2024

Still others called it “by far the most underrated OpenAI event ever.” 

this will prove to be in retrospect by far the most underrated openai event ever openai casually dropping text to 3d rendering in gpt4o and not even mentioning it (more ??) pic.twitter.com/dQ6bq3cV4J — Siqi Chen (@blader) May 13, 2024

My level of excitement for the new OpenAI chatbot launch. pic.twitter.com/mdFHLveC69 — Ted Gioia (@tedgioia) May 13, 2024

Ultimately, AI advisor and investor Allie K. Miller commented, “The super techies are disappointed that they don’t have some holographic laser beam that shoots out of their phone and reads their minds, and the wider business population didn’t seem to watch and weigh in.”

113,000 people joined live to watch the OpenAI new spring release livestream. Now, I’ll tell you right off the bat, the social media response (based on MY feed) is mixed. The super techies are disappointed that they don’t have some holographic laser beam that shoots out of their… — Allie K. Miller (@alliekmiller) May 13, 2024

But this is just day one reaction — it’ll be interesting to see and hear response once people have the chance to experiment with GPT-4o.

Stay in the know! Get the latest news in your inbox daily

By subscribing, you agree to VentureBeat's Terms of Service.

Thanks for subscribing. Check out more VB newsletters here .

An error occured.

What Can OpenAI’s GPT-4o Do?

O penAI on Monday revealed its latest flagship model called GPT-4o (“o” for “omni”), and it’s seemingly the closest we have gotten to having an intelligent assistant as the “Jarvis” in the Iron Man movie. 

The selling point is that ChatGPT-4o can handle different modalities, which most of the existing AI models cannot do. What this means is that GPT-4o can accept and generate any combination of text, audio, and image requests.

The staged demo presented by the team on X (formerly Twitter) was so impressive that many people hyped it up. One big feat is that GPT-4o responds to audio inputs in as little as 232 milliseconds, which is similar to human response time during conversation.

“It feels like AI from the movies; and it’s still a bit surprising to me that it’s real,” OpenAI’s CEO Sam Altman wrote in a blog post Monday. “Getting to human-level response times and expressiveness turns out to be a big change.”

OpenAI has started rolling out GPT-4o’s text and image features to users. In the coming weeks, the audio and video capabilities will be released to “a small group of trusted partners in the API,” the company said. 

Notwithstanding, here are some of the things you can do with the ChatGPT-4o model. 

Things You Can Do With GPT-4o

Create images with legible texts.

Up until now, some AI image generators like Midjourney still struggle to make images with readable texts. OpenAI said GPT-4o now understands text descriptions much better and can make legible texts on images. 

Real-Time Translation

In a situation where a translator is needed, GPT-4o can act as one. In a video demonstration, OpenAI’s team showed that GPT-4o could repeat something said in English in Spanish, perhaps other languages, and back from Spanish to English.

Look and Tell

For people who are visually impaired, or just for the fun of it, ChatGPT-4o can look and tell what is happening around your surroundings through the phone camera. In one case, the model was able to tell someone was having a birthday celebration when it noticed a cake and candle in the room.

Solve Math Problems

GPT-4o can also look at math problems on a paper sheet or display screen and give the answer to them. Not just that, it can also tutor and guide you to learn how to solve the problem.

AI in Visual Meeting

GPT-4o can join visual meetings and hold conservations with participants. It can also help users prepare for job interview meetings. 

site categories

Renate reinsve on her return to cannes with ‘armand’, “the hardest thing i’ve ever done”.

‘I’m A Virgo’ Star Jharrel Jerome, Team On Magic Of Illusion And Solving Math Problems

“Definitely the most challenging thing I’ve had to do thus far as an actor, a lot of mental gymnastics involved,” Jharrel Jerome admits about the uniqueness of his role in the Boots Riley -created absurdist series I’m A Virgo , on which he plays a previously extremely sheltered 13-foot-tall Oakland teen. “At no point do I look my scene partners in the eye, and as an actor that’s so critical, you know, as connection.”

Related Stories

2024 Premiere Dates For New & Returning Series On Broadcast, Cable & Streaming

Garth Brooks On Trisha Yearwood's Greatness, His Amazon Live Concert & Treating People Right

Watch the interview here and see photos from the event below.

Launched in June 2023 with all seven episodes, the small-screen debut of Coup frontman and Sorry to Bother You director Riley is a true display of originality in an analogue and Situationist spirit that “never turns away from what it is to be young and Black in the Land of the Free and Home of the Brave,” as I said in my review of the Prime Video series last year.

“I think the magic of what really brought me to this project was the idea of not using CGI or special effects, because that in itself is requiring a lot for the actor,” Jerome says. “And there’s no rulebook on it, right, there’s no way to do it right. There was, we were all running on the set.

“Honestly, after this everything’s going be easy,” the actor and executive producer adds to laughter from his colleagues.

Olivia Washington, Deirdra E. Govan, Boots Riley, Walton Goggins and Jharrel Jerome

Boots Riley and Jharrel Jerome

Michael Buckner for Deadline

Walton Goggins

Olivia Washington and Deirdra E. Govan

Amidst the political and social aspects of I’m a Virgo , which was tied for my top show of 2023 with the final season of Reservation Dogs , the power of illusion and visual reality was in many ways a character unto itself — especially Govan’s costume design.

“Spending time with the actors in the fitting room is my process,” said Govan, whose credits include Sorry to Bother You and Harlem . “That is my time to not only gain their trust, but also really listen to what they are tapping into and how they’re going to inhabit the skin of these characters.”

“What we should know is that the clothes were a big part of the effects,” Riley says of the pivotal role the costumes played in enabling the sense of scale, both for Jerome’s character Cootie as well as everyone else in I’m a Virgo ‘s world. “It’s half the trick of what’s happening on screen.”

Along with Jerome, Washington and Goggins (who also stars in Prime Video ‘s Fallout ), I’m a Virgo features two-time Tony nominee Kara Young, Carmen Ejogo, Mike Epps, Brett Gray and Kendrick Sampson. Elijah Wood makes a guest appearance as do the voices of Danny Glover, Joel Edgerton, Juliette Lewis and philosopher/cultural theorist Slavoj Žižek.

For more Deadline Studio at Prime Experience content, click  here .

Must Read Stories

‘kinds of kindness’ review + red carpet photos; coppola on movie biz & trump.

Hollywood Mourns Prolific ‘9 To 5’, ‘Tootsie’ & ‘WarGames’ Actor

Sony & paramount sign nda allowing talks to start, but it’s not a $26b bid anymore, josh brolin talks brando, day-lewis, disco & more: the film that lit my fuse.

Subscribe to Deadline Breaking News Alerts and keep your inbox happy.

Read More About:

No comments.

Deadline is a part of Penske Media Corporation. © 2024 Deadline Hollywood, LLC. All Rights Reserved.