how to do half life problems in chemistry

7.2 / 2.4 = 3 half-lives (1/2) 3 = 0.125 (the amount remaining after 3 half-lives) 100.0 g x 0.125 = 12.5 g remaining

20.0 / 3.6 = 5.56 half-lives (1/2) 5.56 = 0.0213 (the decimal fraction remaining after 5.56 half-lives) (6.02 x 10 23 ) (0.0213) = 1.28 x 10 22 atoms remain

(1/2) 3 = 0.125 (the amount remaining after 3 half-lives) 10.0 g x 0.125 = 1.25 g remain 10.0 g − 1.25 g = 8.75 g have decayed Note that the length of the half-life played no role in this calculation. In addition, note that the question asked for the amount that decayed, not the amount that remaning.

2.00 mg / 128.0 mg = 0.015625

(1/2) n = 0.015625 n log 0.5 = log 0.015625 n = log 0.5 / log 0.015625 n = 6

24 days / 6 half-lives = 4.00 days

17/32 = 0.53125 (this is the decimal amount that remains) (1/2) n = 0.53125 n log 0.5 = log 0.53125 n = 0.91254 (this is how many half-lives have elapsed) 60 min / 0.91254 = 65.75 min n = 66 min (to two sig figs)

(1/2) n = 0.01 n log 0.5 = log 0.01 n = 6.64 6.64 x 8.040 days = 53.4 days

0.334 x 10 = 3.34 seconds

24.0 hr / 23.9 hr/half-life = 1.0042 half-lives One day = one half-life; (1/2) 1.0042 = 0.4985465 remaining = 4.98 g Two days = two half-lives; (1/2) 2.0084 = 0.2485486 remaining = 2.48 g Seven days = 7 half-lives; (1/2) 7.0294 = 0.0076549 remaining = 0.0765 g

5.00 / 100.0 = 0.05 (decimal fraction remaining) (1/2) n = 0.05 n log 0.5 = log 0.05 n = 4.32 half-lives 36.0 hours x 4.32 = 155.6 hours

If you lose 75%, then 25% remains. Use 0.25 rather than 25%. (1/2) n = 0.25 n = 2 (remember (1/2) 2 = 1/4 and 1/4 = 0.25) 12.26 x 2 = 24.52 years

(1/2) n = 0.25 n log 0.5 = log 0.25 n = log 0.25 / log 0.5 n = 2

Core Concepts

In this article, you will learn what a half-life is, in 0th. 1st, and 2nd order reactions. You will also learn what the half-life formula is and how to use it to find the age of a substance.

Topics Covered in Other Articles

• Marie Curie and Radioactivity
• Radioactive Decay
• Alpha, Beta, and Gamma Decay
• Nuclear Processes
• Reaction Order – First & Second Order

What is a Half-Life?

A half-life (t 1/2 ) is the time it takes half the concentration of a sample to decay. For example, if the starting concentration of a sample is 1M, then the half-life will be the time it takes for the concentration of the sample to decay to 0.5M.

First Order Half-Life

First-order reactions, including radioactive decay, are reactions where the rate of reaction is only dependent on the concentration of one reactant. First-order reactions have constant half-lives. We can prove this using the integrated first-order rate law:

[A] is the concentration of a reactant at time t, [A]₀ is the initial concentration of the reactant, and k is the rate constant. Here, we can move all the natural logs to the left side of the equation:

Since we are trying to find the half-life of the reactant, we can set t as the half-life and [A] as half of the initial concentration:

Substituting those values into the equation gives us the following:

Finally, dividing the k and the negative gives us an equation for the half-life of a first-order reaction:

Second Order Half-Life

Second-order reactions are reactions where the rate of reaction is dependent on the concentrations of 2 reactants. The half-lives of second-order reactions depend on the reactant’s initial concentration. The integrated rate law for second-order reactions is as follows:

We can then isolate the t to solve for the half-life of a second-order reaction:

Zero Order Half-Life

In zero-order reactions, the rate of reaction does not depend on the reactant’s concentration. The half-lives of zero-order reactions, however, do depend on the initial concentration of the reactant. The integrated rate law for zero-order reactions is as follows:

We can then isolate the t to solve for the half-life of a zero-order reaction:

Practice Problems

• The half-life for a first-order reaction is 2768 years. Starting with a concentration of 0.345M, what will the concentration be after 11072 years?
• What is the half-life of a compound if 75 percent of a given sample of the compound decomposes in 60 min? Assume first-order kinetics.
• A substance hydrolyzes in water with a rate constant of 2.0 × 10 −3  min −1 . Calculate the t 1/2 for the hydrolysis reaction. Assume first-order kinetics.
• 0.0216M. First, find out how many half-lives have passed. By dividing 11072 by 2768, we find that 4 half-lives have passed. Therefore, we can find the final concentration by dividing 0.345M by 2 four times. This leaves us with 0.0216M.
• 30 mins. 25 percent of the sample is left, meaning 2 half-lives have passed. 60 mins divided by 2 is 30 mins, which is the half-life.

Further Reading

• The Element Radium
• The Element Radon
• What is an isotope?
• Cations and Anions

Half-Life Calculator

Table of contents

The half-life calculator is a tool that helps you understand the principles of radioactive decay. You can use it to not only learn how to calculate half-life, but also as a way of finding the initial and final quantity of a substance or its decay constant. This article will also present you with the half-life definition and the most common half-life formula.

Half-life definition

Each radioactive material contains stable and unstable nuclei. Stable nuclei don't change, but unstable nuclei undergo a type of radioactive decay , emitting alpha particles, beta particles, or gamma rays and eventually decaying into stable nuclei. Half-life is defined as the time required for half of the unstable nuclei to undergo their decay process.

Each substance has a different half-life. For example, carbon-10 has a half-life of only 19 seconds, making it impossible for this isotope to be encountered in nature. Uranium-233, on the other hand, has a half-life of about 160 000 years.

This term can also be used more generally to describe any kind of exponential decay - for example, the biological half-life of metabolites.

Half-life is a probabilistic measure - it doesn't mean that exactly half of the substance will have decayed after the time of the half-life has elapsed. Nevertheless, it is an approximation that gets very accurate when a sufficient number of nuclei are present.

🙋 One of the applications of knowing half-life is radiocarbon dating. Learn more about that by checking out our Radiocarbon dating calculator .

Half-life formula

We can determine the number of unstable nuclei remaining after time t t t using this equation:

• N ( t ) N(t) N ( t ) – Remaining quantity of a substance after time t t t has elapsed;
• N ( 0 ) N(0) N ( 0 ) – Initial quantity of this substance; and
• T T T – half-life.

It is also possible to determine the remaining quantity of a substance using a few other parameters:

• τ \tau τ – mean lifetime - the average amount of time a nucleus remains intact; and
• λ \lambda λ – decay constant (rate of decay).

All three of the parameters characterizing a substance's radioactivity are related in the following way:

How to calculate the half-life

• Determine the initial amount of a substance. For example, N ( 0 ) = 2.5  kg \small N(0) = 2.5\ \text{kg} N ( 0 ) = 2.5   kg .
• Determine the final amount of a substance - for instance, N ( t ) = 2.1  kg \small N(t) = 2.1\ \text{kg} N ( t ) = 2.1   kg .
• Measure how long it took for that amount of material to decay. In our experiment, we observed that it took 5 minutes.
• Input these values into our half-life calculator. It will compute a result for you instantaneously - in this case, the half-life is equal to 19.88  minutes \small 19.88\ \text{minutes} 19.88   minutes .
• If you are not certain that our calculator returned the correct result, you can always check it using the half-life formula.

Confused by exponential formulas? Try our exponent calculator .

Half-life is a similar concept to doubling time in biology. Check our generation time calculator to learn how exponential growth is both useful and a problem in laboratories! Also, we use a similar concept in pharmacology, and we call it the "drug half-life". Find out more about that in our drug half-life calculator .

What is half life?

Half-life is defined as the time taken by a substance to lose half of its quantity. This term should not be confused with mean lifetime , which is the average time a nucleus remains intact.

How to calculate half life?

To find half-life:

• Find the substance's decay constant.
• Divide the natural logarithm of 2 or ln(2) by the decay constant of the substance.
• Alternatively, you can multiply ln(2) by the mean lifetime.

What is the half life of radium?

The half-life of radium-218 is 25.2 x 10 -6 seconds . On the other hand, one of the most common radium isotopes is radium-226, with a half-life of 1600 years!

What is the half life of carbon?

The half-life of carbon-14 is 5730 years . This means that after 5730 years have elapsed, half of an initial quantity of carbon-14 would have disintegrated.

What is the half life of uranium?

The half-life of uranium-238 is 4.5 billion years . It is one of the three natural occurring uranium isotopes, along with uranium-235 (700 million years), and uranium-234 (246,000 years).

Initial quantity (N(0))

Half-life time (T)

Total time (t)

Remaining quantity (N(t))

Decay constant (λ)

Mean lifetime (τ)

An average length of time before an element decays.

Chapter 15. Nuclear Chemistry

Learning objectives.

• Define half-life .
• Determine the amount of radioactive substance remaining after a given number of half-lives.

Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is half-life , which is the amount of time it takes for one-half of a radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.

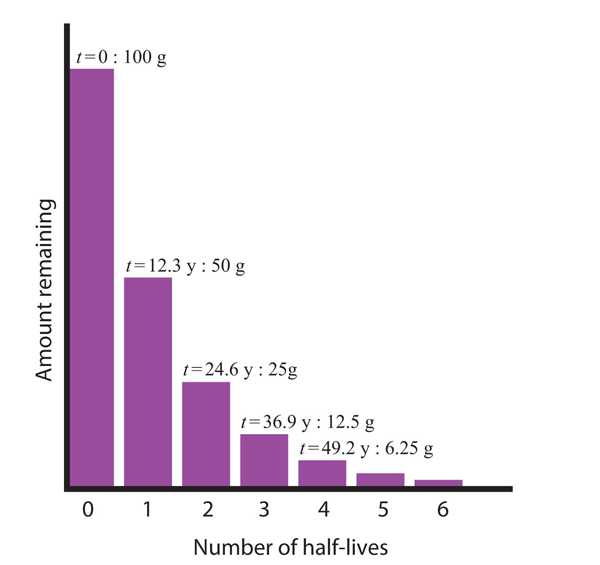
Consider the following example. Suppose we have 100.0 g of tritium (a radioactive isotope of hydrogen). It has a half-life of 12.3 y. After 12.3 y, half of the sample will have decayed from hydrogen-3 to helium-3 by emitting a beta particle, so that only 50.0 g of the original tritium remains. After another 12.3 y—making a total of 24.6 y—another half of the remaining tritium will have decayed, leaving 25.0 g of tritium. After another 12.3 y—now a total of 36.9 y—another half of the remaining tritium will have decayed, leaving 12.5 g. This sequence of events is illustrated in Figure 15.1 “Radioactive Decay” .

Figure 15.1 Radioactive Decay

During each successive half-life, half of the initial amount will radioactively decay.

We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:

where n is the number of half-lives. This expression works even if the number of half-lives is not a whole number.

The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 44.0 s?

If we compare the time that has passed to the isotope’s half-life, we note that 44.0 s is exactly 4 half-lives, so using the previous expression, n = 4. Substituting and solving results in the following:

Less than one-third of a gram of fluorine-20 remains.

Test Yourself

The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 240.0 y?

Half-lives of isotopes range from fractions of a microsecond to billions of years. Table 15.2 “Half-Lives of Various Isotopes” lists the half-lives of some isotopes.

Table 15.2 Half-Lives of Various Isotopes

Chemistry Is Everywhere: Radioactive Elements in the Body

You may not think of yourself as radioactive, but you are. A small portion of certain elements in the human body are radioactive and constantly undergo decay. The following table summarizes radioactivity in the normal human body.

The average human body experiences about 8,000 radioactive decays/s.

Most of the radioactivity in the human body comes from potassium-40 and carbon-14. Potassium and carbon are two elements that we absolutely cannot live without, so unless we can remove all the radioactive isotopes of these elements, there is no way to escape at least some radioactivity. There is debate about which radioactive element is more problematic. There is more potassium-40 in the body than carbon-14, and it has a much longer half-life. Potassium-40 also decays with about 10 times more energy than carbon-14, making each decay potentially more problematic. However, carbon is the element that makes up the backbone of most living molecules, making carbon-14 more likely to be present around important molecules, such as proteins and DNA molecules. Most experts agree that while it is foolhardy to expect absolutely no exposure to radioactivity, we can and should minimize exposure to excess radioactivity.

What if the elapsed time is not an exact number of half-lives? We can still calculate the amount of material we have left, but the equation is more complicated. The equation is

where e is the base of natural logarithms (2.71828182…), t is the elapsed time, and t 1/2 is the half-life of the radioactive isotope. The variables t and t 1/2 should have the same units of time, and you may need to make sure you know how to evaluate natural-logarithm powers on your calculator (for many calculators, there is an “inverse logarithm” function that you can use; consult your instructor if you are not sure how to use your calculator). Although this is a more complicated formula, the length of time t need not be an exact multiple of half-lives.

The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 60.0 s?

Although similar to Example 3, the amount of time is not an exact multiple of a half-life. Here we identify the initial amount as 5.00 g, t = 60.0 s, and t 1/2 = 11.0 s. Substituting into the equation:

amount remaining = (5.00 g) × e −(0.693)(60.0 s)/11.0 s

Evaluating the exponent (and noting that the s units cancel), we get

amount remaining = (5.00 g) × e −3.78

Solving, the amount remaining is 0.114 g. (You may want to verify this answer to confirm that you are using your calculator properly.)

The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 100.0 y?

Key Takeaways

• Natural radioactive processes are characterized by a half-life, the time it takes for half of the material to decay radioactively.
• The amount of material left over after a certain number of half-lives can be easily calculated.

Do all isotopes have a half-life? Explain your answer.

Which is more radioactive—an isotope with a long half-life or an isotope with a short half-life?

How long does it take for 1.00 g of palladium-103 to decay to 0.125 g if its half-life is 17.0 d?

How long does it take for 2.00 g of niobium-94 to decay to 0.0625 g if its half-life is 20,000 y?

It took 75 y for 10.0 g of a radioactive isotope to decay to 1.25 g. What is the half-life of this isotope?

It took 49.2 s for 3.000 g of a radioactive isotope to decay to 0.1875 g. What is the half-life of this isotope?

The half-live of americium-241 is 432 y. If 0.0002 g of americium-241 is present in a smoke detector at the date of manufacture, what mass of americium-241 is present after 100.0 y? After 1,000.0 y?

If the half-life of tritium (hydrogen-3) is 12.3 y, how much of a 0.00444 g sample of tritium is present after 5.0 y? After 250.0 y?

Explain why the amount left after 1,000.0 y in Exercise 7 is not one-tenth of the amount present after 100.0 y, despite the fact that the amount of time elapsed is 10 times as long.

Explain why the amount left after 250.0 y in Exercise 8 is not one-fiftieth of the amount present after 5.0 y, despite the fact that the amount of time elapsed is 50 times as long.

An artifact containing carbon-14 contains 8.4 × 10 −9 g of carbon-14 in it. If the age of the artifact is 10,670 y, how much carbon-14 did it have originally? The half-life of carbon-14 is 5,730 y.

Carbon-11 is a radioactive isotope used in positron emission tomography (PET) scans for medical diagnosis. Positron emission is another, though rare, type of radioactivity. The half-life of carbon-11 is 20.3 min. If 4.23 × 10 −6 g of carbon-11 is left in the body after 4.00 h, what mass of carbon-11 was present initially?

Only radioactive isotopes have a half-life.

0.000170 g; 0.0000402 g

Radioactive decay is an exponential process, not a linear process.

3.1 × 10 −8 g

• Introductory Chemistry- 1st Canadian Edition . Authored by : Jessie A. Key and David W. Ball. Provided by : BCCampus. Located at : https://opentextbc.ca/introductorychemistry/ . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Download this book for free at http://open.bccampus.ca

Privacy Policy

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications

How to Calculate Half Life

Last Updated: May 26, 2023 References

Understanding Half-Life

Learning the half-life equation, calculating from a graph, using a calculator, example problems, calculator, practice problems, and answers, expert q&a.

This article was co-authored by Meredith Juncker, PhD and by wikiHow staff writer, Hannah Madden . Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases. There are 11 references cited in this article, which can be found at the bottom of the page. This article has been viewed 1,162,777 times.

The half-life of a substance undergoing decay is the time it takes for the amount of the substance to decrease by half. It was originally used to describe the decay of radioactive elements like uranium or plutonium, but it can be used for any substance which undergoes decay along a set, or exponential, rate. You can calculate the half-life of any substance, given the rate of decay, which is the initial quantity of the substance and the quantity remaining after a measured period of time. [1] X Research source

• Elements like uranium and plutonium are most often studied with half-life in mind.

• Therefore, you can calculate the half-life for a particular element and know for certain how quickly it will break down no matter what.

• Technically, there are 2 types of carbon: carbon-14, which decays, and carbon-12, which stays constant.

• Simply replacing the variable doesn't tell us everything, though. We still have to account for the actual half-life, which is, for our purposes, a constant.

• On half-life graphs, the x-axis will usually show the timeline, while the y-axis usually shows the rate of decay.

• For example, if the starting point is 1,640, divide 1,640 / 2 to get 820.
• If you are working with a semi log  plot, meaning the count rate is not evenly spaced, you’ll have to take the logarithm of any number from the vertical axis. [11] X Research source

• If you know the half-life but you don’t know the initial quantity, you can input the half-life, the quantity that remains, and the time that has passed. As long as you know 3 of the 4 values, you’ll be able to use a half-life calculator.

• If you don’t know the half-life but you do know the decay constant and the mean lifetime, you can input those instead. Just like the initial equation, you only need to know 2 of the 3 values to get the third one.

• This is a helpful visual, and it can be useful if you don’t want to do all of the equation work.

• Check to see if the solution makes sense. Since 112 g is less than half of 300 g, at least one half-life must have elapsed. Our answer checks out.

• Substitute and evaluate.

• Remember to check your solution intuitively to see if it makes sense.

• For this particular equation, the actual length of the half-life did not play a role.

You Might Also Like

• ↑ https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/Reaction_Rates/Half-lives_and_Pharmacokinetics
• ↑ https://chem.libretexts.org/Courses/Furman_University/CHM101%3A_Chemistry_and_Global_Awareness_(Gordon)/05%3A_Basics_of_Nuclear_Science/5.07%3A_Calculating_Half-Life
• ↑ https://atomic.lindahall.org/what-is-meant-by-half-life.html
• ↑ http://faculty.bard.edu/belk/math213/ExponentialDecay.pdf
• ↑ https://www.ausetute.com.au/halflife.html
• ↑ https://socratic.org/chemistry/nuclear-chemistry/nuclear-half-life-calculations
• ↑ https://www.khanacademy.org/test-prep/mcat/physical-processes/atomic-nucleus/a/decay-graphs-and-half-lives-article
• ↑ https://www.gcsescience.com/prad17-measuring-half-life.htm
• ↑ https://www.calculator.net/half-life-calculator.html
• ↑ https://www.youtube.com/watch?v=5mKrIv1lo1E&feature=youtu.be&t=163
• ↑ https://www.chemteam.info/Radioactivity/Radioactivity-Half-Life-probs1-10.html

About This Article

To find the half life of a substance, or the time it takes for a substance to decrease by half, you’ll be using a variation of the exponential decay formula. Plug in ½ for a, use the time for x, and multiply the left side by the initial quantity of the substance. Rearrange the equation so that you’re solving for what the problem asks for, whether that’s half life, mass, or another value. Plug in the values you have and solve, writing the answer in seconds, days, or years. To see the half life equation and look at examples, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Georgy Komissarov

Mar 14, 2018

Did this article help you?

Feb 7, 2017

Jun 16, 2018

Christopher Emmanuel

Jan 31, 2017

Howard Farmer

Apr 19, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 15. Nuclear Chemistry

Learning Objectives

• Define half-life .
• Determine the amount of radioactive substance remaining after a given number of half-lives.

Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is half-life , which is the amount of time it takes for one-half of a radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.

Consider the following example. Suppose we have 100.0 g of tritium (a radioactive isotope of hydrogen). It has a half-life of 12.3 y. After 12.3 y, half of the sample will have decayed from hydrogen-3 to helium-3 by emitting a beta particle, so that only 50.0 g of the original tritium remains. After another 12.3 y — making a total of 24.6 y — another half of the remaining tritium will have decayed, leaving 25.0 g of tritium. After another 12.3 y — now a total of 36.9 y — another half of the remaining tritium will have decayed, leaving 12.5 g. This sequence of events is illustrated in Figure 15.4 “Radioactive Decay”.

We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:

where n is the number of half-lives. This expression works best when the number of half-lives is a whole number.

Example 15.3

The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 44.0 s?

Solution If we compare the time that has passed to the isotope’s half-life, we note that 44.0 s is exactly 4 half-lives, so using the previous expression, n = 4. Substituting and solving results in the following:

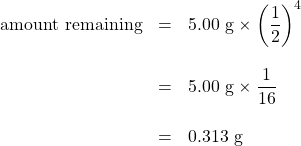
Less than one-third of a gram of fluorine-20 remains.

Test Yourself The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 240.0 y?

Answer 0.0375 g

Half-lives of isotopes range from fractions of a microsecond to billions of years. Table 15.4 “Half-Lives of Various Isotopes” lists the half-lives of some isotopes.

Chemistry Is Everywhere: Radioactive Elements in the Body

You may not think of yourself as radioactive, but you are. A small portion of certain elements in the human body are radioactive and constantly undergo decay. The following table summarizes radioactivity in the normal human body.

The average human body experiences about 8,000 radioactive decays/s.

Most of the radioactivity in the human body comes from potassium-40 and carbon-14. Potassium and carbon are two elements that we absolutely cannot live without, so unless we can remove all the radioactive isotopes of these elements, there is no way to escape at least some radioactivity. There is debate about which radioactive element is more problematic. There is more potassium-40 in the body than carbon-14, and it has a much longer half-life. Potassium-40 also decays with about 10 times more energy than carbon-14, making each decay potentially more problematic. However, carbon is the element that makes up the backbone of most living molecules, making carbon-14 more likely to be present around important molecules, such as proteins and DNA molecules. Most experts agree that while it is foolhardy to expect absolutely no exposure to radioactivity, we can and should minimize exposure to excess radioactivity.

What if the elapsed time is not an exact number of half-lives? We can still calculate the amount of material we have left, but the equation is more complicated. The equation is:

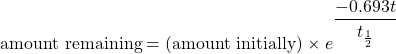
where e is the base of natural logarithms (2.71828182…), t is the elapsed time, and t ½ is the half-life of the radioactive isotope. The variables t and t ½ should have the same units of time, and you may need to make sure you know how to evaluate natural-logarithm powers on your calculator (for many calculators, there is an “inverse logarithm” function that you can use; consult your instructor if you are not sure how to use your calculator). Although this is a more complicated formula, the length of time t need not be an exact multiple of half-lives.

Example 15.4

The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 60.0 s?

Solution Although similar to Example 15.3, the amount of time is not an exact multiple of a half-life. Here we identify the initial amount as 5.00 g, t = 60.0 s, and t ½ = 11.0 s. Substituting into the equation:

Evaluating the exponent (and noting that the s units cancel), we get:

Solving, the amount remaining is 0.114 g. (You may want to verify this answer to confirm that you are using your calculator properly.)

Test Yourself The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 100.0 y?

Answer 0.189 g

Key Takeaways

• Natural radioactive processes are characterized by a half-life, the time it takes for half of the material to decay radioactively.
• The amount of material left over after a certain number of half-lives can be easily calculated.
• Do all isotopes have a half-life? Explain your answer.
• Which is more radioactive — an isotope with a long half-life or an isotope with a short half-life?
• How long does it take for 1.00 g of palladium-103 to decay to 0.125 g if its half-life is 17.0 d?
• How long does it take for 2.00 g of niobium-94 to decay to 0.0625 g if its half-life is 20,000 y?
• It took 75 y for 10.0 g of a radioactive isotope to decay to 1.25 g. What is the half-life of this isotope?
• It took 49.2 s for 3.000 g of a radioactive isotope to decay to 0.1875 g. What is the half-life of this isotope?
• The half-live of americium-241 is 432 y. If 0.0002 g of americium-241 is present in a smoke detector at the date of manufacture, what mass of americium-241 is present after 100.0 y? After 1,000.0 y?
• If the half-life of tritium (hydrogen-3) is 12.3 y, how much of a 0.00444 g sample of tritium is present after 5.0 y? After 250.0 y?
• Explain why the amount left after 1,000.0 y in Exercise 7 is not one-tenth of the amount present after 100.0 y, despite the fact that the amount of time elapsed is 10 times as long.
• Explain why the amount left after 250.0 y in Exercise 8 is not one-fiftieth of the amount present after 5.0 y, despite the fact that the amount of time elapsed is 50 times as long.
• An artifact containing carbon-14 contains 8.4 × 10 −9 g of carbon-14 in it. If the age of the artifact is 10,670 y, how much carbon-14 did it have originally? The half-life of carbon-14 is 5,730 y.
• Carbon-11 is a radioactive isotope used in positron emission tomography (PET) scans for medical diagnosis. Positron emission is another, though rare, type of radioactivity. The half-life of carbon-11 is 20.3 min. If 4.23 × 10 −6 g of carbon-11 is left in the body after 4.00 h, what mass of carbon-11 was present initially?
• Only radioactive isotopes have a half-life.
• 0.000170 g; 0.0000402 g
• Radioactive decay is an exponential process, not a linear process.
• 3.1 × 10 −8 g

Introductory Chemistry - 1st Canadian Edition Copyright © 2014 by Jessie A. Key is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Equations for half lives
• Determining a half life
• Converting a half life to a rate constant
• Graphical relations and half lives

t ½ =  [A o ] / 2k

t ½ = 0.693 / k

t ½ = 1 / k [A o ]

• The order of the reaction or enough information to determine it.
• The rate constant, k, for the reaction or enough information to determine it.
• In some cases, we need to know the initial concentration, [A o ]
• The half life of the reaction, t ½ .
• For a zero order reaction (Half life decreases with decreasing concentration.)
• For a 1st order reaction (Half life is constant.)
• For a second order reaction (Half life increases with decreasing concentration.)

Half Life Formula

The half-life formula is used to find the half-life of a substance that is decaying or reducing in quantity. A substance that is decaying has a different rate of decay for different quantities of the substance. As the quantity of the substance reduces the rate of decay also slows down, and hence it is very difficult to find the life of a decaying substance. Therefore the half-life formula is used to provide the right metrics to define the life of decaying material. In this section, let us learn more about the half life formula and solve a few examples .

What is Half Life Formula?

Half-life refers to the amount of time it takes for half of a particular sample to react i.e it refers to the time that a particular quantity requires to reduce its initial value to half. The half-life formula is commonly used in nuclear physics where it describes the speed at which an atom undergoes radioactive decay. The formula for the half-life is obtained by dividing  0.693 by the constant  λ. Here λ is called the disintegration or decay constant. Hence the formula to calculate the half-life of a substance is:

\(t_{\frac{1}{2}} = \dfrac{0.693}{\lambda} \)

\(t_{\frac{1}{2}}\) = half-life

λ = constant

Let N be the size of the population of the radioactive atoms at a given time t, dN be the amount by which it decreases in time dt. The rate of change is given as dN/d t = -λN, where λ is the decay constant.

On integrating this equation, we get N = \(N_0\)e -λt  , where \(N_0\) = the size of the initial population of radioactive atoms at t = 0. This shows that the population decays exponentially at a rate that depends on λ. The time taken for half of the original population of radioactive atoms to decay is called the half-life. This relationship between half-life, the time period, t 1/2 , and the decay constant λ is given by   \(t_{\frac{1}{2}} = \dfrac{0.693}{\lambda} \).

Book a Free Trial Class

Examples Using Half Life Formula

Example 1: The decay constant of a substance is 0.84 s -1 . Find the half life of the substance.

Given decay constant λ = 0.84  The half life formula can be used to find the half life of the substance. \(t_{\frac{1}{2}}\)   = 0.693/ λ

= 0.693/0.84

= 0.825 Therefore, the half life of the substance is 0.8 seconds.

Example 2: Find the value of the decay constant of a radioactive substance having a half-life of 0.04 seconds.

Solution: Given half life of the substance is \(t_{\frac{1}{2}}\)= 0.04 The half life formula can be used to find the half life of the substance. \(t_{\frac{1}{2}}\)   = 0.693/ λ

λ = 0.693/0.04

= 17.325 Therefore, the decay constant of the radioactive substance is 17.325 s -1 .

Example 3: Calculate the half-life of a radioactive substance whose disintegration constant happens to be 0.004 1/years?

The quantities available here are,

λ = 0.004  1/years

Using the half life formula, 

\(t_{\frac{1}{2}}\)   = 0.693/ λ

=0.693/0.004

Hence, the half-life of this particular radioactive substance is 173.25 years.

FAQs on Half Life Formula

What is meant by half life formula .

Half-life refers to the amount of time it takes for half of a particular sample to react i.e it refers to the time that a particular quantity requires to reduce its initial value to half. The half-life formula is commonly used in nuclear physics where it describes the speed at which an atom undergoes radioactive decay. The formula is \(t_{\frac{1}{2}}\)= 0.693/ λ

What is the Formula to Find the Half Life of a Substance?

 The formula for the half-life is obtained by dividing 0.693 by the constant λ . Here λ is called the disintegration or decay constant. Hence the formula to calculate the half-life of a value is:

Are the Number Positive or Negative in the Half Life Formula?

Both the time and  λ are positive numbers, where the time shows the time taken for decaying quantity and the  λ is the decay constant of the decaying quantity. 

Using the Half Life Formula, Find the Half Life of a Substance with Disintegration Constant happens to be 0.008 1/years?

λ = 0.008  1/years

= 0.693/0.008

Hence, the half-life of this particular radioactive substance is 86.625 years.

• Chemistry Concept Questions and Answers
• Half Life Questions

Half-Life Questions

Half-Life or previously known as the Half-Life Period is one of the common terminologies used in Science to describe the radioactive decay of a particular sample or element within a certain period of time.

However, this concept is also widely used to describe various types of decay processes, especially exponential and non-exponential decay. Apart from science, the term is used in medical sciences to represent the biological half-life of certain chemicals in the human body or in drugs.

Half-Life Chemistry Questions with Solutions

Q1. An isotope of caesium (Cs-137) has a half-life of 30 years. If 1.0g of Cs-137 disintegrates over a period of 90 years, how many grams of Cs-137 would remain?

b.) 0.125 g

c.) 0.00125 g

Correct Answer- (b.) 0.125 g

Q2. Selenium-83 has a half-life of 25.0 minutes. How many minutes would it take for a 10.0 mg sample to decay and only have 1.25 mg of it remain?

a.) 75 minutes

b.) 75 days

c.) 75 seconds

d.) 75 hours

Correct Answer- (a.) 75 minutes

Q3. How long does it take a 100.00g sample of As-81, with a half-life of 33 seconds, to decay to 6.25g?

a.) 122 seconds

b.) 101 seconds

c.) 132 seconds

d.) 22 seconds

Correct Answer – (c.) 132 seconds

Q4. What is the half-life of a radioactive isotope if a 500.0g sample decays to 62.5g in 24.3 hours?

a.) 8.1 hours

b.) 6.1 hours

c.) 5 hours

d.) 24 hours

Correct Answer- (a.) 8.1 hours

Q5. What is the half-life of Polonium-214 if, after 820 seconds, a 1.0g sample decays to 0.03125g?

a.) 164 minutes

b.) 164 seconds

c.) 64 seconds

d.) 160 minutes

Correct Answer- (b.) 164 seconds

Q6. The half-life of Zn-71 is 2.4 minutes. If one had 100.0 g at the beginning, how many grams would be left after 7.2 minutes have elapsed?

To begin, we’ll count the number of half-lives that have passed. This can be obtained by doing the following:

Half-life (t½) = 2.4 mins

Time (t) = 7.2 mins

Number of half-lives

n = 7.2/2.4 = 3

Thus, three half-lives have passed.

Finally, we will calculate the remaining amount. This can be obtained by doing the following:

N 0 (original amount) = 100 g

(n) = number of half-lives

Amount remaining (N) =?

N = 100 / 2 3

N = 100 / 8

As a result, the amount of Zn-71 remaining after 7.2 minutes is 12.5 g.

Q7. Pd-100 has a half-life of 3.6 days. If one had 6.02 x 10 23 atoms at the start, how many atoms would be present after 20.0 days?

Half-life = 3.6 days

Initial atoms = 6.02 ×10 23 atoms

Time = 20days

To calculate the atoms present after 20 days, we use the formula below.

Thus, the number of atoms available is 1.28 × 10 22 atoms.

Q8. Os-182 has a half-life of 21.5 hours. How many grams of a 10.0 gram sample would have decayed after exactly three half-lives?

Answer. The amount of the radioactive substance that will remain after 3- half- lives=(½) 3 × a,

where a = initial concentration of the radioactive element.

So, amount of the radioactive substance that remains aftet 3- half-lives=( ½)³x10 = 10/8= 1.25 g.

Therefore, the number of grams of the radioactive substance that decayed in 3 half-lives = (10 – 1.25) g

Q9. After 24.0 days, 2.00 milligrams of an original 128.0 milligram sample remain. What is the half-life of the sample?

Answer. The remaining decimal fraction is:

2.00 mg / 128.0 mg = 0.015625

The half-lives that must have expired to get to 0.015625?

(½) n = 0.015625

n log 0.5 = 0.015625

n = log 0.5 / 0.015625 n = 6

Calculation of the half-life:

24 days divided by 6 half-lives equals 4.00 days

Q10. A radioactive isotope decayed to 17/32 of its original mass after 60 minutes. Find the half-life of this radioisotope.

Answer. The amount that remains

17/32 = 0.53125

(1/2) n = 0.53125

n log 0.5 = log 0.53125

n = 0.91254

Half-lives that have elapsed are therefore, n = 0.9125

60 minutes divided by 0.91254 equals 65.75 minutes.

Therefore, n = 66 minutes

Q11. How long will it take for a 40 gram sample of I-131 (half-life = 8.040 days) to decay to 1/100 of its original mass?

Answer. (1/2) n = 0.01

n log 0.5 = log 0.01

6.64 x 8.040 days = 53.4 days

Therefore, it will take 53.4 days to decay to 1/100 of its original mass.

Q12. At time zero, there are 10.0 grams of W-187. If the half-life is 23.9 hours, how much will be present at the end of one day? Two days? Seven days?

24.0 hr / 23.9 hr/half-life = 1.0042 half-lives

One day = one half-life; (1/2) 1.0042 = 0.4985465 remaining = 4.98 g

Two days = two half-lives; (1/2) 2.0084 = 0.2485486 remaining = 2.48 g

Seven days = 7 half-lives; (1/2) 7.0234 = 0.0076549 remaining = 0.0765 g

Q13. 100.0 grams of an isotope with a half-life of 36.0 hours is present at time zero. How much time will have elapsed when 5.00 grams remains?

The afraction amount remaining will be-

5.00 / 100.0 = 0.05

(1/2) n = 0.05

n log 0.5 = log 0.05

n = 4.32 half-lives

36.0 hours x 4.32 = 155.6 hours

Q14. How much time will be required for a sample of H-3 to lose 75% of its radioactivity? The half-life of tritium is 12.26 years.

If you lose 75%, then 25% remains.

(1/2) n = 0.25

n = 2 (Since, (1/2) 2 = 1/4 and 1/4 = 0.25)

12.26 x 2 = 24.52 years

Therefore, 24.52 years of time will be required for a sample of H-3 to lose 75% of its radioactivity

Q15. The half-life for the radioactive decay of 14 C is 5730 years. An archaeological artifact containing wood had only 80% of the 14 C found in a living tree. Estimate the age of the sample.

Answer. Decay constant, k = 0.693/t 1/2 = 0.693/5730 years = 1/209 × 10 –4 /year

= 1846 years (approx)

Practise Questions on Half-Life

Q1. A newly prepared radioactive nuclide has a decay constant λ of 10 –6 s –1 . What is the approximate half-life of the nuclide?

d.) 1 month

Q2. If the decay constant of a radioactive nuclide is 6.93 x 10 –3 sec –1 , its half-life in minutes is:

Q3. A first-order reaction takes 40 min for 30% decomposition. Calculate t 1/2 .

Q4. What will be the time for 50% completion of a first-order reaction if it takes 72 min for 75% completion?

Q5. How much time will it take for 90% completion of a reaction if 80% of a first-order reaction was completed in 70 min?

Click the PDF to check the answers for Practice Questions. Download PDF

Recommended Videos

Zero order reaction.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: First Order Reaction Half-Life

• Last updated
• Save as PDF
• Page ID 164750

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• To know how to use half-lives to describe the rates of first-order reactions

Another approach to describing reaction rates is based on the time required for the concentration of a reactant to decrease to one-half its initial value. This period of time is called the half-life of the reaction, written as t 1 /2 . Thus the half-life of a reaction is the time required for the reactant concentration to decrease from [A] 0 to [A] 0/2 . If two reactions have the same order, the faster reaction will have a shorter half-life, and the slower reaction will have a longer half-life.

The half-life of a first-order reaction under a given set of reaction conditions is a constant. This is not true for zeroth- and second-order reactions. The half-life of a first-order reaction is independent of the concentration of the reactants. This becomes evident when we rearrange the integrated rate law for a first-order reaction to produce the following equation:

Substituting [A] 0/2 for [A] and t 1 /2 for t (to indicate a half-life) into Equation \(\ref{21.4.1}\) gives

Substituting \(\ln{2} \approx 0.693\) into the equation results in the expression for the half-life of a first-order reaction:

\[t_{1/2}=\dfrac{0.693}{k} \label{21.4.2}\]

Thus, for a first-order reaction, each successive half-life is the same length of time, as shown in Figure \(\PageIndex{1}\) , and is independent of [A].

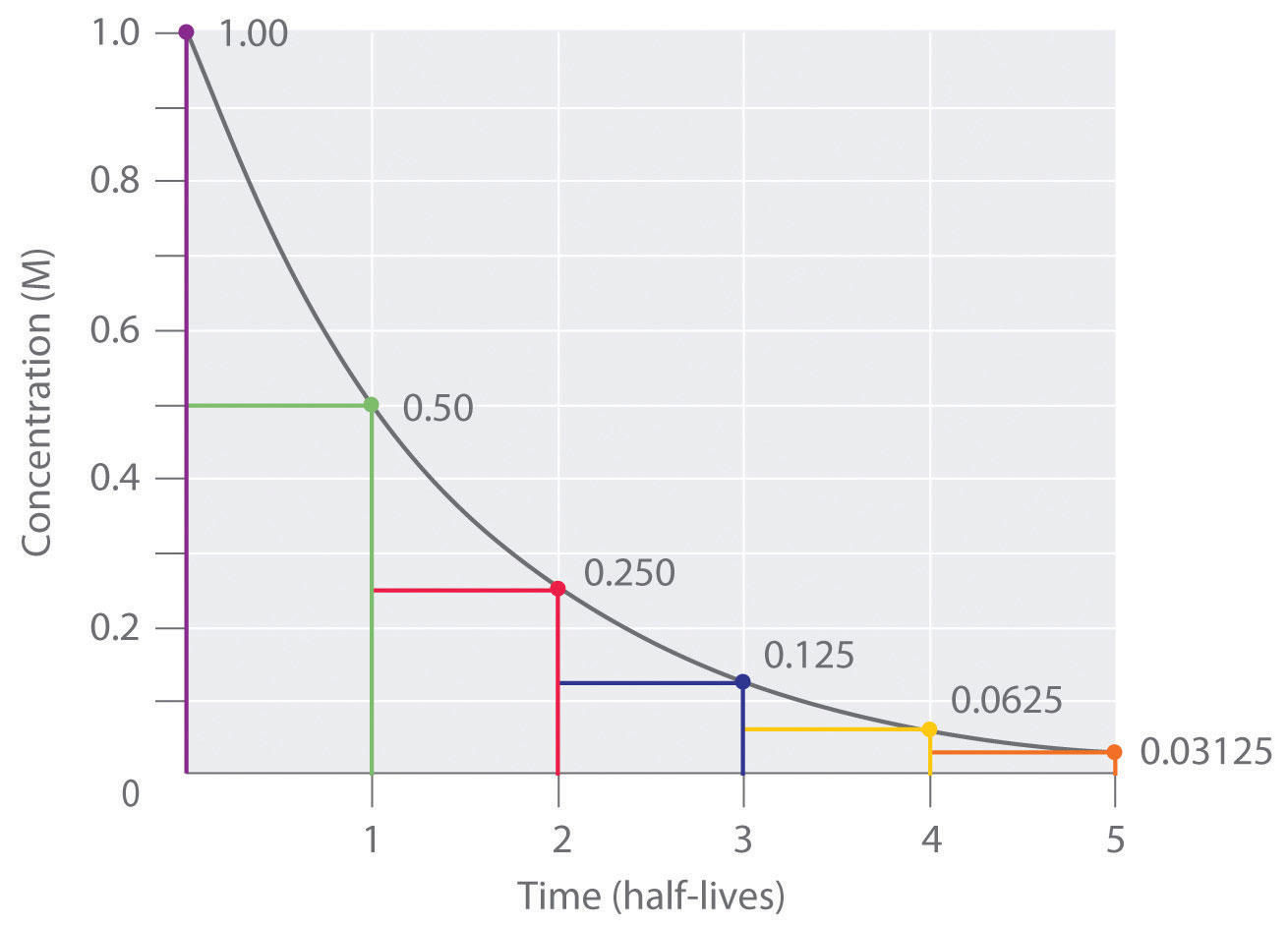
If we know the rate constant for a first-order reaction, then we can use half-lives to predict how much time is needed for the reaction to reach a certain percent completion.

As you can see from this table, the amount of reactant left after n half-lives of a first-order reaction is (1/2) n times the initial concentration.

For a first-order reaction, the concentration of the reactant decreases by a constant with each half-life and is independent of [A].

Example \(\PageIndex{1}\)

The anticancer drug cis-platin hydrolyzes in water with a rate constant of 1.5 × 10 −3 min −1 at pH 7.0 and 25°C. Calculate the half-life for the hydrolysis reaction under these conditions. If a freshly prepared solution of cis-platin has a concentration of 0.053 M, what will be the concentration of cis-platin after 5 half-lives? after 10 half-lives? What is the percent completion of the reaction after 5 half-lives? after 10 half-lives?

Given: rate constant, initial concentration, and number of half-lives

Asked for: half-life, final concentrations, and percent completion

• Use Equation \(\ref{21.4.2}\) to calculate the half-life of the reaction.
• Multiply the initial concentration by 1/2 to the power corresponding to the number of half-lives to obtain the remaining concentrations after those half-lives.
• Subtract the remaining concentration from the initial concentration. Then divide by the initial concentration, multiplying the fraction by 100 to obtain the percent completion.

A We can calculate the half-life of the reaction using Equation \(\ref{21.4.2}\) :

\(t_{1/2}=\dfrac{0.693}{k}=\dfrac{0.693}{1.5\times10^{-3}\textrm{ min}^{-1}}=4.6\times10^2\textrm{ min}\)

Thus it takes almost 8 h for half of the cis-platin to hydrolyze.

B After 5 half-lives (about 38 h), the remaining concentration of cis-platin will be as follows:

After 10 half-lives (77 h), the remaining concentration of cis-platin will be as follows:

C The percent completion after 5 half-lives will be as follows:

The percent completion after 10 half-lives will be as follows:

Thus a first-order chemical reaction is 97% complete after 5 half-lives and 100% complete after 10 half-lives.

Exercise \(\PageIndex{1}\)

Ethyl chloride decomposes to ethylene and HCl in a first-order reaction that has a rate constant of 1.6 × 10 −6 s −1 at 650°C.

• What is the half-life for the reaction under these conditions?
• If a flask that originally contains 0.077 M ethyl chloride is heated at 650°C, what is the concentration of ethyl chloride after 4 half-lives?

4.3 × 10 5 s = 120 h = 5.0 days;

4.8 × 10 −3 M

Radioactive Decay Rates

Radioactivity, or radioactive decay, is the emission of a particle or a photon that results from the spontaneous decomposition of the unstable nucleus of an atom. The rate of radioactive decay is an intrinsic property of each radioactive isotope that is independent of the chemical and physical form of the radioactive isotope. The rate is also independent of temperature. In this section, we will describe radioactive decay rates and how half-lives can be used to monitor radioactive decay processes.

In any sample of a given radioactive substance, the number of atoms of the radioactive isotope must decrease with time as their nuclei decay to nuclei of a more stable isotope. Using N to represent the number of atoms of the radioactive isotope, we can define the rate of decay of the sample, which is also called its activity ( A ) as the decrease in the number of the radioisotope’s nuclei per unit time:

Activity is usually measured in disintegrations per second (dps) or disintegrations per minute (dpm).

The activity of a sample is directly proportional to the number of atoms of the radioactive isotope in the sample:

\[A = kN \label{21.4.4}\]

Here, the symbol k is the radioactive decay constant, which has units of inverse time (e.g., s −1 , yr −1 ) and a characteristic value for each radioactive isotope. If we combine Equation \(\ref{21.4.3}\) and Equation \(\ref{21.4.4}\) , we obtain the relationship between the number of decays per unit time and the number of atoms of the isotope in a sample:

Equation \(\ref{21.4.5}\) is the same as the equation for the reaction rate of a first-order reaction, except that it uses numbers of atoms instead of concentrations. In fact, radioactive decay is a first-order process and can be described in terms of either the differential rate law ( Equation \(\ref{21.4.5}\) ) or the integrated rate law:

\[N = N_0e^{−kt} \]

\[\ln \dfrac{N}{N_0}=-kt \label{21.4.6}\]

Because radioactive decay is a first-order process, the time required for half of the nuclei in any sample of a radioactive isotope to decay is a constant, called the half-life of the isotope. The half-life tells us how radioactive an isotope is (the number of decays per unit time); thus it is the most commonly cited property of any radioisotope. For a given number of atoms, isotopes with shorter half-lives decay more rapidly, undergoing a greater number of radioactive decays per unit time than do isotopes with longer half-lives. The half-lives of several isotopes are listed in Table 14.6 , along with some of their applications.

Radioactive decay is a first-order process.

Radioisotope Dating Techniques

In our earlier discussion, we used the half-life of a first-order reaction to calculate how long the reaction had been occurring. Because nuclear decay reactions follow first-order kinetics and have a rate constant that is independent of temperature and the chemical or physical environment, we can perform similar calculations using the half-lives of isotopes to estimate the ages of geological and archaeological artifacts. The techniques that have been developed for this application are known as radioisotope dating techniques.

The most common method for measuring the age of ancient objects is carbon-14 dating. The carbon-14 isotope, created continuously in the upper regions of Earth’s atmosphere, reacts with atmospheric oxygen or ozone to form 14 CO 2 . As a result, the CO 2 that plants use as a carbon source for synthesizing organic compounds always includes a certain proportion of 14 CO 2 molecules as well as nonradioactive 12 CO 2 and 13 CO 2 . Any animal that eats a plant ingests a mixture of organic compounds that contains approximately the same proportions of carbon isotopes as those in the atmosphere. When the animal or plant dies, the carbon-14 nuclei in its tissues decay to nitrogen-14 nuclei by a radioactive process known as beta decay, which releases low-energy electrons (β particles) that can be detected and measured:

\[ \ce{^{14}C \rightarrow ^{14}N + \beta^{−}} \label{21.4.7}\]

The half-life for this reaction is 5700 ± 30 yr.

The 14 C/ 12 C ratio in living organisms is 1.3 × 10 −12 , with a decay rate of 15 dpm/g of carbon ( Figure \(\PageIndex{2}\) ). Comparing the disintegrations per minute per gram of carbon from an archaeological sample with those from a recently living sample enables scientists to estimate the age of the artifact, as illustrated in Example 11.Using this method implicitly assumes that the 14 CO 2 / 12 CO 2 ratio in the atmosphere is constant, which is not strictly correct. Other methods, such as tree-ring dating, have been used to calibrate the dates obtained by radiocarbon dating, and all radiocarbon dates reported are now corrected for minor changes in the 14 CO 2 / 12 CO 2 ratio over time.

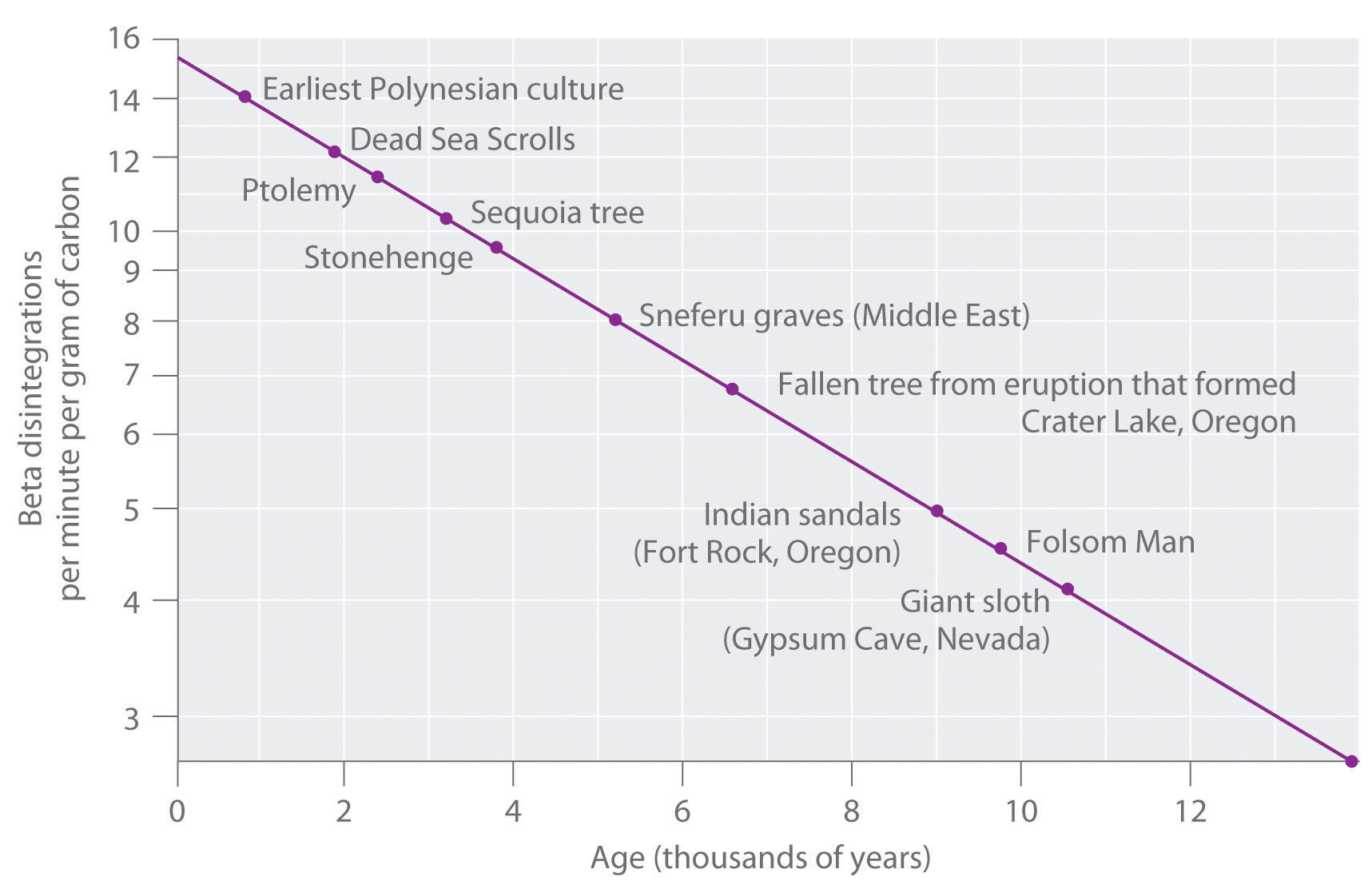
Example \(\PageIndex{2}\)

In 1990, the remains of an apparently prehistoric man were found in a melting glacier in the Italian Alps. Analysis of the 14 C content of samples of wood from his tools gave a decay rate of 8.0 dpm/g carbon. How long ago did the man die?

Given: isotope and final activity

Asked for: elapsed time

A Use Equation \(\ref{21.4.4}\) to calculate N 0 / N . Then substitute the value for the half-life of 14 C into Equation \(\ref{21.4.2}\) to find the rate constant for the reaction.

B Using the values obtained for N 0 / N and the rate constant, solve Equation \(\ref{21.4.6}\) to obtain the elapsed time.

We know the initial activity from the isotope’s identity (15 dpm/g), the final activity (8.0 dpm/g), and the half-life, so we can use the integrated rate law for a first-order nuclear reaction ( Equation \(\ref{21.4.6}\) ) to calculate the elapsed time (the amount of time elapsed since the wood for the tools was cut and began to decay).

A From Equation \(\ref{21.4.4}\) , we know that A = kN . We can therefore use the initial and final activities ( A 0 = 15 dpm and A = 8.0 dpm) to calculate N 0 / N :

Now we need only calculate the rate constant for the reaction from its half-life (5730 yr) using Equation \(\ref{21.4.2}\) :

This equation can be rearranged as follows:

B Substituting into the equation for t ,

From our calculations, the man died 5200 yr ago.

Exercise \(\PageIndex{2}\)

It is believed that humans first arrived in the Western Hemisphere during the last Ice Age, presumably by traveling over an exposed land bridge between Siberia and Alaska. Archaeologists have estimated that this occurred about 11,000 yr ago, but some argue that recent discoveries in several sites in North and South America suggest a much earlier arrival. Analysis of a sample of charcoal from a fire in one such site gave a 14 C decay rate of 0.4 dpm/g of carbon. What is the approximate age of the sample?

• The half-life of a first-order reaction is independent of the concentration of the reactants.
• The half-lives of radioactive isotopes can be used to date objects.

The half-life of a reaction is the time required for the reactant concentration to decrease to one-half its initial value. The half-life of a first-order reaction is a constant that is related to the rate constant for the reaction: t 1 /2 = 0.693/ k . Radioactive decay reactions are first-order reactions. The rate of decay, or activity, of a sample of a radioactive substance is the decrease in the number of radioactive nuclei per unit time.