how to solve absolute value equations on both sides

SOLVING EQUATIONS WITH ABSOLUTE VALUES ON BOTH SIDES

The picture shown below explains how to solve the equations in which we have absolute value sign on both sides.

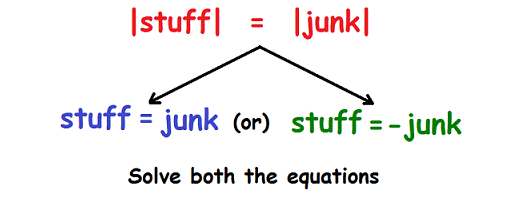
Example 1 :

Solve for x :

|x - 3| = |3x + 2|

Based on the idea given above, we have

x - 3 = (3x + 2) 

x - 3 = 3x + 2

x - 3 = -(3x + 2) 

x - 3 = - 3x - 2

Justify and evaluation :

Substitute x = -5/2 and x = 1/4 in the given absolute value equation. 

|-5/2 - 3| = |3(-5/2) + 2|

|-11/2| = |-15/2 + 2|

|-11/2| = |-11/2|

11/2 = 11/2

|1/4 - 3| = |3(1/4) + 2|

|-11/4| = |3/4 + 2|

|11/4| = |11/4|

11/4 = 11/4

Substituting x = -5/2 and x = 1/4 into the original equation results in true  statements.

Both the answers x = -5/2 and x = 1/4 are correct and acceptable.

Problem 2 :

|x - 7| = |2x - 2|

x - 7 = 2x - 2

x - 7 = - (2x - 2) 

x - 7 = -2x + 2

Substitute x = -5 and x = 3 in the given absolute value equation.

|-5 - 7| = |2(-5) - 2|

|-12| = |-10 - 2|

|-12| = |-12|

|3 - 7| = |2(3) - 2|

|-4| = |6 - 2|

Substituting x = -5 and x = 3 into the original equation results in true  statements.

Both the answers x = -5 and x = 3 are correct and acceptable.

Problem 3 :

Solve for z :

|2z + 5| = |2z - 1|

2z + 5 = 2z - 1

The above statement is false. 

No solution here.

2z + 5 = - (2z - 1) 

2z + 5 = -2z + 1

Substitute z = -1 in the given absolute value equation.

|2(-1) + 5| = |2(-1) - 1|

|-2 + 5| = |-2 - 1|

Substituting z = -1 into the original equation results in true  statement. 

So, the answer z  = -1 is correct and acceptable.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Converting Between Polar and Rectangular Coordinates

May 12, 24 01:14 PM

Trigonometry Sum and Difference Identities

May 07, 24 09:17 AM

Trigonometry Even and Odd Iidentities

May 05, 24 12:25 AM

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Algebra 2 (FL B.E.S.T.)

Course: algebra 2 (fl b.e.s.t.)   >   unit 2.

• Intro to absolute value equations and graphs

Solving absolute value equations

• Absolute value equations
• Worked example: absolute value equation with two solutions
• Worked example: absolute value equations with one solution
• Worked example: absolute value equations with no solution
• Solve absolute value equations

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

How to solve absolute value equations

|x + 5| = 3.

Worksheet on Abs Val Equations Abs Val Eqn Solver

The General Steps to solve an absolute value equation are:

• Rewrite the absolute value equation as two separate equations, one positive and the other negative
• Solve each equation separately
• After solving, substitute your answers back into original equation to verify that you solutions are valid
• Write out the final solution or graph it as needed

It's always easiest to understand a math concept by looking at some examples so, check outthe many examples and practice problems below.

You can always check your work with our Absolute value equations solver too

Practice Problems

Example equation.

Solve the equation: | X + 5| = 3

Click here to practice more problems like this one , questions that involve variables on 1 side of the equation.

Some absolute value equations have variables both sides of the equation. However, that will not change the steps we're going to follow to solve the problem as the example below shows:

Solve the equation: |3 X | = X − 21

Solve the following absolute value equation: | 5X +20| = 80

Solve the following absolute value equation: | X | + 3 = 2 X

This first set of problems involves absolute values with x on just 1 side of the equation (like problem 2 ).

Solve the following absolute value equation: |3 X −6 | = 21

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.6: Solving Absolute Value Equations and Inequalities

• Last updated
• Save as PDF
• Page ID 6238

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Review the definition of absolute value.
• Solve absolute value equations.
• Solve absolute value inequalities.

Absolute Value Equations

Recall that the absolute value 63 of a real number \(a\), denoted \(|a|\), is defined as the distance between zero (the origin) and the graph of that real number on the number line. For example, \(|−3|=3\) and \(|3|=3\).

In addition, the absolute value of a real number can be defined algebraically as a piecewise function.

\(| a | = \left\{ \begin{array} { l } { a \text { if } a \geq 0 } \\ { - a \text { if } a < 0 } \end{array} \right.\)

Given this definition, \(|3| = 3\) and \(|−3| = − (−3) = 3\).Therefore, the equation \(|x| = 3\) has two solutions for \(x\), namely \(\{±3\}\). In general, given any algebraic expression \(X\) and any positive number \(p\):

\(\text{If}\: | X | = p \text { then } X = - p \text { or } X = p\)

In other words, the argument of the absolute value 64 \(X\) can be either positive or negative \(p\). Use this theorem to solve absolute value equations algebraically.

Example \(\PageIndex{1}\):

Solve: \(|x+2|=3\).

In this case, the argument of the absolute value is \(x+2\) and must be equal to \(3\) or \(−3\).

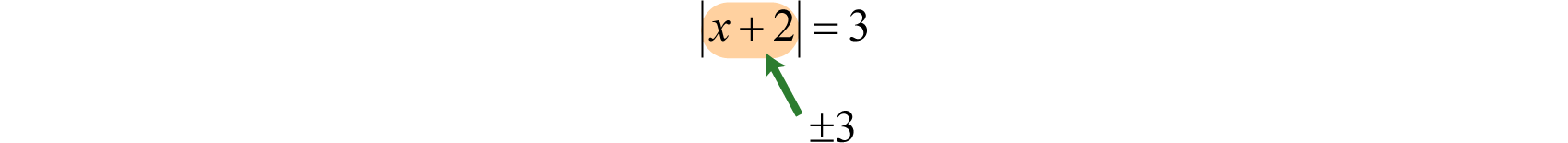
Therefore, to solve this absolute value equation, set \(x+2\) equal to \(±3\) and solve each linear equation as usual.

\(\begin{array} { c } { | x + 2 | = 3 } \\ { x + 2 = - 3 \quad \quad\text { or } \quad\quad x + 2 = 3 } \\ { x = - 5 \quad\quad\quad\quad\quad\quad\quad x = 1 } \end{array}\)

The solutions are \(−5\) and \(1\).

To visualize these solutions, graph the functions on either side of the equal sign on the same set of coordinate axes. In this case, \(f (x) = |x + 2|\) is an absolute value function shifted two units horizontally to the left, and \(g (x) = 3\) is a constant function whose graph is a horizontal line. Determine the \(x\)-values where \(f (x) = g (x)\).

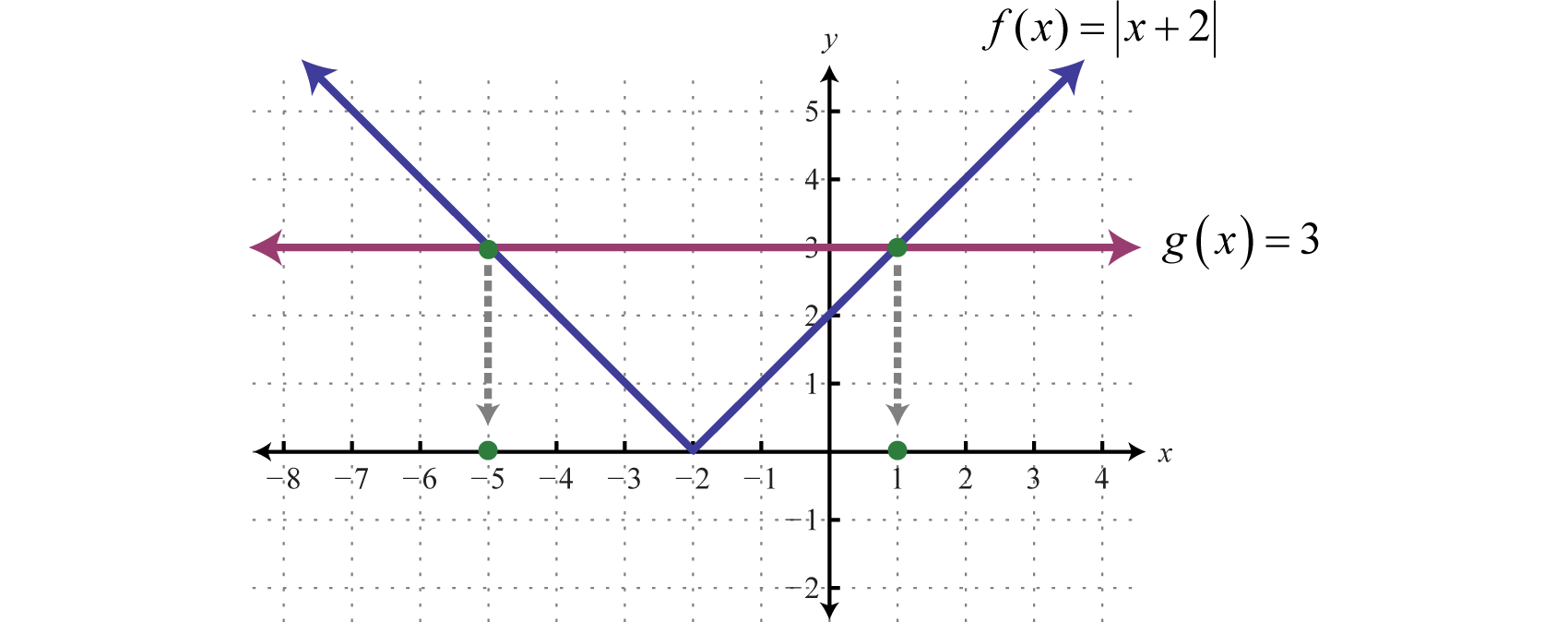
From the graph we can see that both functions coincide where \(x = −5\) and \(x = 1\). The solutions correspond to the points of intersection.

Example \(\PageIndex{2}\):

Solve: \(| 2 x + 3 | = 4\).

Here the argument of the absolute value is \(2x+3\) and can be equal to \(-4\) or \(4\).

\(\begin{array} { r l } { | 2 x + 3 | } & { = \quad 4 } \\ { 2 x + 3 = - 4 } & { \text { or }\quad 2 x + 3 = 4 } \\ { 2 x = - 7 } & \quad\quad\:\: { 2 x = 1 } \\ { x = - \frac { 7 } { 2 } } & \quad\quad\:\: { x = \frac { 1 } { 2 } } \end{array}\)

Check to see if these solutions satisfy the original equation.

The solutions are \(-\frac{7}{2}\) and \(\frac{1}{2}\).

To apply the theorem, the absolute value must be isolated. The general steps for solving absolute value equations are outlined in the following example.

Example \(\PageIndex{3}\):

Solve: \(2 |5x − 1| − 3 = 9\).

Step 1 : Isolate the absolute value to obtain the form \(|X| = p\).

\(\begin{aligned} 2 | 5 x - 1 | - 3 & = 9 \:\:\:\color{Cerulean} { Add\: 3\: to\: both\: sides. } \\ 2 | 5 x - 1 | & = 12 \:\:\color{Cerulean} { Divide\: both\: sides\: by\: 2 } \\ | 5 x - 1 | & = 6 \end{aligned}\)

Step 2 : Set the argument of the absolute value equal to \(±p\). Here the argument is \(5x − 1\) and \(p = 6\).

\(5 x - 1 = - 6 \text { or } 5 x - 1 = 6\)

Step 3 : Solve each of the resulting linear equations.

\(\begin{array} { r l } { 5 x - 1 = - 6 \quad\:\:\text { or } \quad\quad5 x - 1 } & { \:\:\:\:\:\:= 6 } \\ { 5 x = - 5 }\quad\:\quad\quad\quad\quad\quad\quad\: & { 5 x = 7 } \\ { x = - 1 } \quad\quad\quad\quad\quad\quad\quad\:\:& { x = \frac { 7 } { 5 } } \end{array}\)

Step 4 : Verify the solutions in the original equation.

The solutions are \(-1\) and \(\frac{7}{5}\)

Exercise \(\PageIndex{1}\)

Solve: \(2 - 7 | x + 4 | = - 12\).

www.youtube.com/v/G0EjbqreYmU

Not all absolute value equations will have two solutions.

Example \(\PageIndex{4}\):

Solve: \(| 7 x - 6 | + 3 = 3\).

Begin by isolating the absolute value.

\(\begin{array} { l } { | 7 x - 6 | + 3 = 3 \:\:\:\color{Cerulean} { Subtract\: 3\: on\: both\: sides.} } \\ { \quad | 7 x - 6 | = 0 } \end{array}\)

Only zero has the absolute value of zero, \(|0| = 0\). In other words, \(|X| = 0\) has one solution, namely \(X = 0\). Therefore, set the argument \(7x − 6\) equal to zero and then solve for \(x\).

\(\begin{aligned} 7 x - 6 & = 0 \\ 7 x & = 6 \\ x & = \frac { 6 } { 7 } \end{aligned}\)

Geometrically, one solution corresponds to one point of intersection.

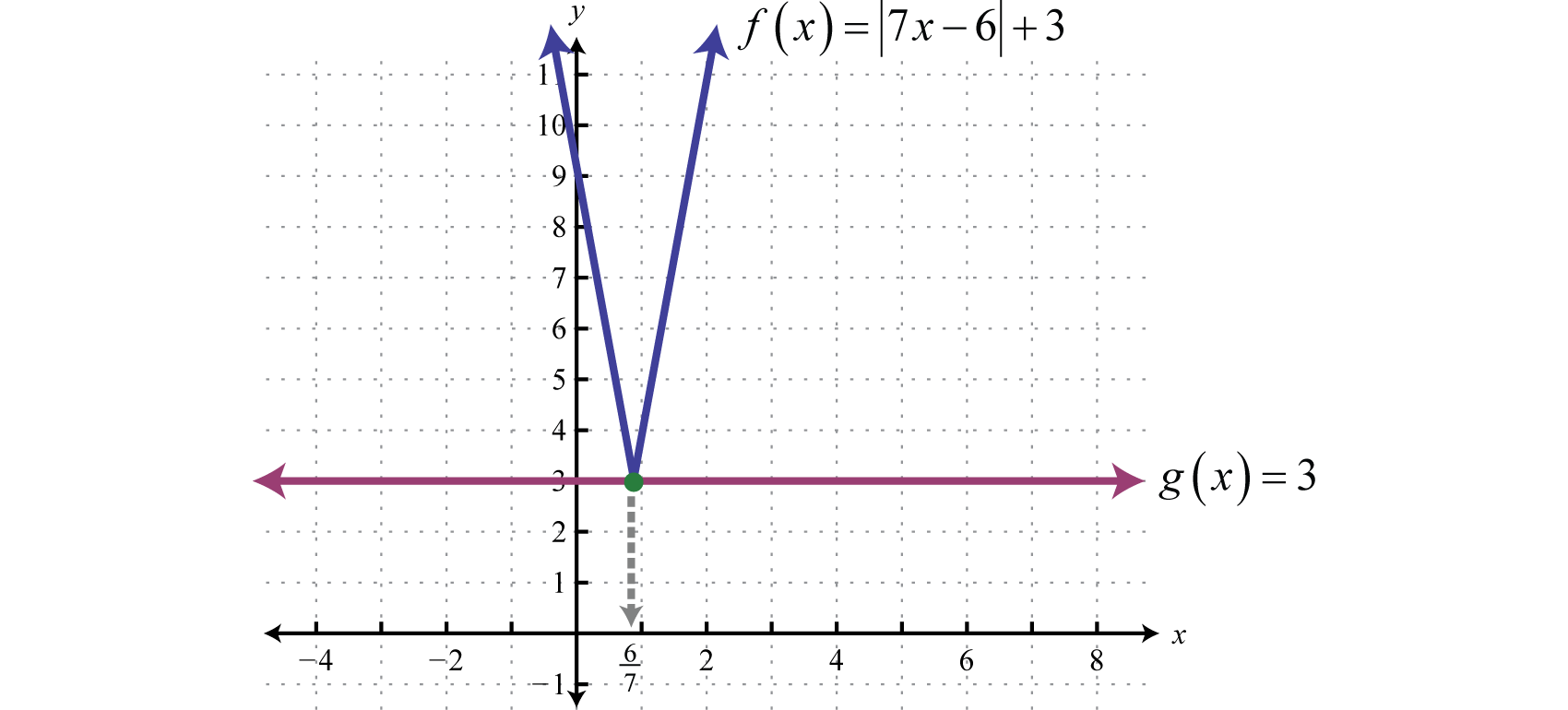
The solution is \(\frac{6}{7}\).

Example \(\PageIndex{5}\):

Solve: \(|x+7|+5=4\).

\(\begin{aligned} | x + 7 | + 5 & = 4 \:\:\color{Cerulean} { Subtract \: 5\: on\: both\: sides.} \\ | x + 7 | & = - 1 \end{aligned}\)

In this case, we can see that the isolated absolute value is equal to a negative number. Recall that the absolute value will always be positive. Therefore, we conclude that there is no solution. Geometrically, there is no point of intersection.

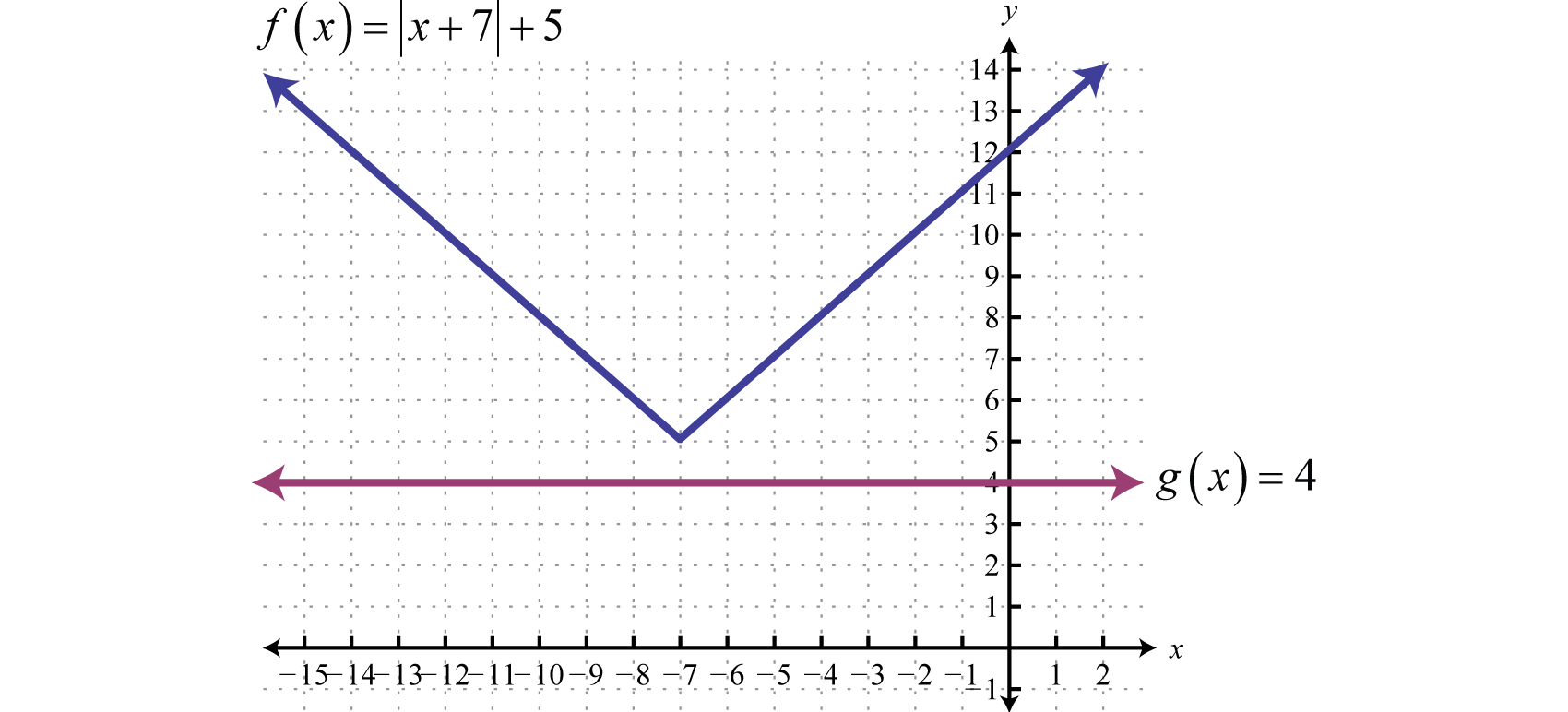
There is no solution, \(Ø\).

If given an equation with two absolute values of the form \(| a | = | b |\), then \(b\) must be the same as \(a\) or opposite. For example, if \(a=5\), then \(b = \pm 5\) and we have:

\(| 5 | = | - 5 | \text { or } | 5 | = | + 5 |\)

In general, given algebraic expressions \(X\) and \(Y\):

\(\text{If} | X | = | Y | \text { then } X = - Y \text { or } X = Y\).

In other words, if two absolute value expressions are equal, then the arguments can be the same or opposite.

Example \(\PageIndex{6}\):

Solve: \(| 2 x - 5 | = | x - 4 |\).

Set \(2x-5\) equal to \(\pm ( x - 4 )\) and then solve each linear equation.

\(\begin{array} { c } { | 2 x - 5 | = | x - 4 | } \\ { 2 x - 5 = - ( x - 4 ) \:\: \text { or }\:\: 2 x - 5 = + ( x - 4 ) } \\ { 2 x - 5 = - x + 4 }\quad\quad\quad 2x-5=x-4 \\ { 3 x = 9 }\quad\quad\quad\quad\quad\quad \quad\quad x=1 \\ { x = 3 \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:} \end{array}\)

To check, we substitute these values into the original equation.

As an exercise, use a graphing utility to graph both \(f(x)= |2x-5|\) and \(g(x)=|x-4|\) on the same set of axes. Verify that the graphs intersect where \(x\) is equal to \(1\) and \(3\).

The solutions are \(1\) and \(3\).

Exercise \(\PageIndex{2}\)

Solve: \(| x + 10 | = | 3 x - 2 |\).

www.youtube.com/v/CskWmsQCBMU

Absolute Value Inequalities

We begin by examining the solutions to the following inequality:

\(| x | \leq 3\)

The absolute value of a number represents the distance from the origin. Therefore, this equation describes all numbers whose distance from zero is less than or equal to \(3\). We can graph this solution set by shading all such numbers.

Certainly we can see that there are infinitely many solutions to \(|x|≤3\) bounded by \(−3\) and \(3\). Express this solution set using set notation or interval notation as follows:

\(\begin{array} { c } { \{ x | - 3 \leq x \leq 3 \} \color{Cerulean} { Set\: Notation } } \\ { [ - 3,3 ] \quad \color{Cerulean}{ Interval \:Notation } } \end{array}\)

In this text, we will choose to express solutions in interval notation. In general, given any algebraic expression \(X\) and any positive number \(p\):

\(\text{If} | X | \leq p \text { then } - p \leq X \leq p\).

This theorem holds true for strict inequalities as well. In other words, we can convert any absolute value inequality involving " less than " into a compound inequality which can be solved as usual.

Example \(\PageIndex{7}\):

Solve and graph the solution set: \(|x+2|<3\).

Bound the argument \(x+2\) by \(−3\) and \(3\) and solve.

\(\begin{array} { c } { | x + 2 | < 3 } \\ { - 3 < x + 2 < 3 } \\ { - 3 \color{Cerulean}{- 2}\color{Black}{ <} x + 2 \color{Cerulean}{- 2}\color{Black}{ <} 3 \color{Cerulean}{- 2} } \\ { - 5 < x < 1 } \end{array}\)

Here we use open dots to indicate strict inequalities on the graph as follows.

Using interval notation, \((−5,1)\).

The solution to \(| x + 2 | < 3\) can be interpreted graphically if we let \(f ( x ) = | x + 2 |\) and \(g(x)=3\) and then determine where \(f ( x ) < g ( x )\) by graphing both \(f\) and \(g\) on the same set of axes.

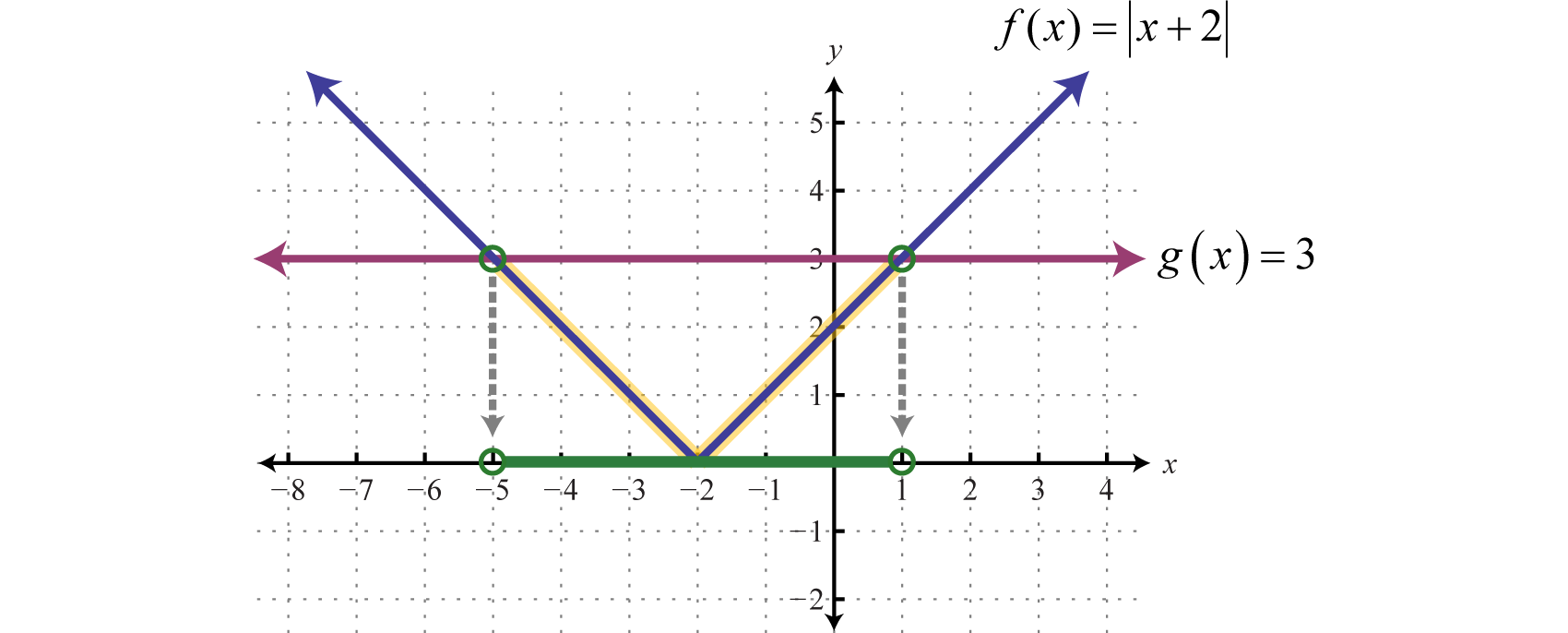
The solution consists of all \(x\)-values where the graph of \(f\) is below the graph of \(g\). In this case, we can see that \(|x + 2| < 3\) where the \(x\)-values are between \(−5\) and \(1\). To apply the theorem, we must first isolate the absolute value.

Example \(\PageIndex{8}\):

Solve: \(4 |x + 3| − 7 ≤ 5\).

\(\begin{array} { c } { 4 | x + 3 | - 7 \leq 5 } \\ { 4 | x + 3 | \leq 12 } \\ { | x + 3 | \leq 3 } \end{array}\)

Next, apply the theorem and rewrite the absolute value inequality as a compound inequality.

\(\begin{array} { c } { | x + 3 | \leq 3 } \\ { - 3 \leq x + 3 \leq 3 } \end{array}\)

\(\begin{aligned} - 3 \leq x + 3 \leq & 3 \\ - 3 \color{Cerulean}{- 3} \color{Black}{ \leq} x + 3 \color{Cerulean}{- 3} & \color{Black}{ \leq} 3 \color{Cerulean}{- 3} \\ - 6 \leq x \leq 0 \end{aligned}\)

Shade the solutions on a number line and present the answer in interval notation. Here we use closed dots to indicate inclusive inequalities on the graph as follows:

Using interval notation, \([−6,0]\)

Exercise \(\PageIndex{3}\)

Solve and graph the solution set: \(3 + | 4 x - 5 | < 8\).

Interval notation: \((0, \frac{5}{2})\)

www.youtube.com/v/sX6ppL2Fbq0

Next, we examine the solutions to an inequality that involves " greater than ," as in the following example:

\(| x | \geq 3\)

This inequality describes all numbers whose distance from the origin is greater than or equal to \(3\). On a graph, we can shade all such numbers.

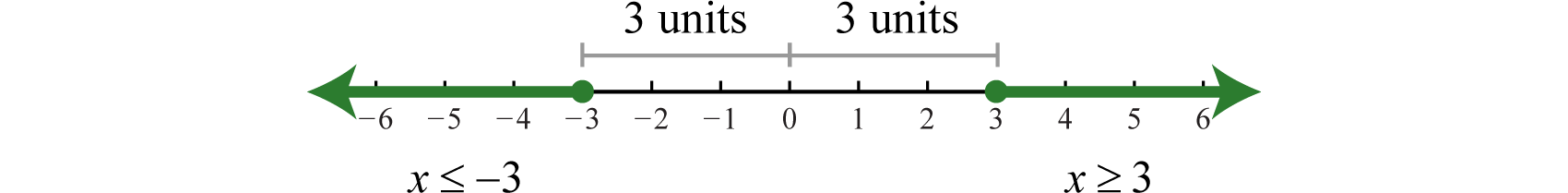
There are infinitely many solutions that can be expressed using set notation and interval notation as follows:

\(\begin{array} { l } { \{ x | x \leq - 3 \text { or } x \geq 3 \} \:\:\color{Cerulean} { Set\: Notation } } \\ { ( - \infty , - 3 ] \cup [ 3 , \infty ) \:\:\color{Cerulean} { Interval\: Notation } } \end{array}\)

In general, given any algebraic expression \(X\) and any positive number \(p\):

\(\text{If} | X | \geq p \text { then } X \leq - p \text { or } X \geq p\).

The theorem holds true for strict inequalities as well. In other words, we can convert any absolute value inequality involving “ greater than ” into a compound inequality that describes two intervals.

Example \(\PageIndex{9}\):

Solve and graph the solution set: \(|x+2|>3\).

The argument \(x+2\) must be less than \(−3\) or greater than \(3\).

\(\begin{array} { c } { | x + 2 | > 3 } \\ { x + 2 < - 3 \quad \text { or } \quad x + 2 > 3 } \\ { x < - 5 }\quad\quad\quad\quad\quad\: x>1 \end{array}\)

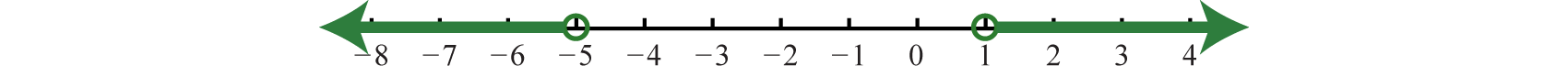
Using interval notation, \((−∞,−5)∪(1,∞)\).

The solution to \(|x + 2| > 3\) can be interpreted graphically if we let \(f (x) = |x + 2|\) and \(g (x) = 3\) and then determine where \(f(x) > g (x)\) by graphing both \(f\) and \(g\) on the same set of axes.

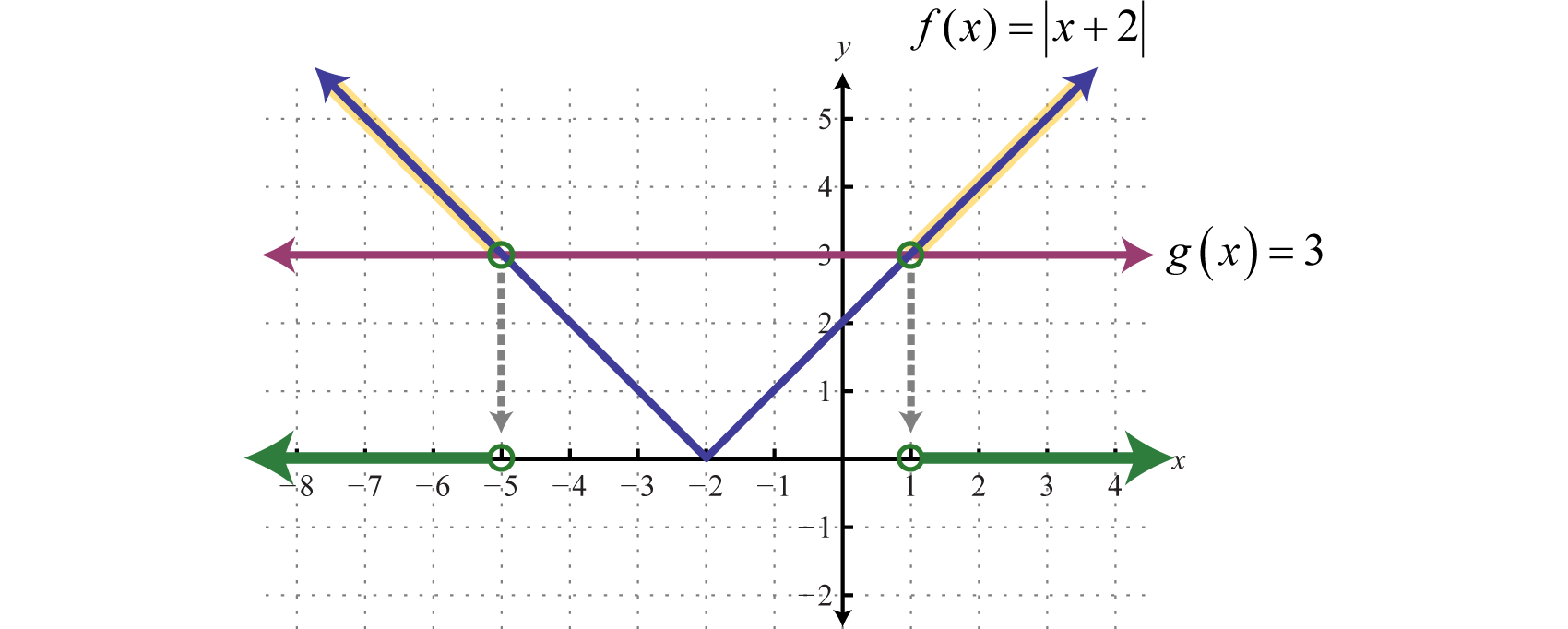
The solution consists of all \(x\)-values where the graph of \(f\) is above the graph of \(g\). In this case, we can see that \(|x + 2| > 3\) where the \(x\)-values are less than \(−5\) or are greater than \(1\). To apply the theorem we must first isolate the absolute value.

Example \(\PageIndex{10}\):

Solve: \(3 + 2 |4x − 7| ≥ 13\).

\(\begin{array} { r } { 3 + 2 | 4 x - 7 | \geq 13 } \\ { 2 | 4 x - 7 | \geq 10 } \\ { | 4 x - 7 | \geq 5 } \end{array}\)

\(\begin{array} &\quad\quad\quad\quad\:\:\:|4x-7|\geq 5 \\ 4 x - 7 \leq - 5 \quad \text { or } \quad 4 x - 7 \geq 5 \end{array}\)

\(\begin{array} { l } { 4 x - 7 \leq - 5 \text { or } 4 x - 7 \geq 5 } \\ \quad\:\:\:\:{ 4 x \leq 2 } \quad\quad\quad\:\:\: 4x\geq 12\\ \quad\:\:\:\:{ x \leq \frac { 2 } { 4 } } \quad\quad\quad\quad x\geq 3 \\ \quad\quad{ x \leq \frac { 1 } { 2 } } \end{array}\)

Shade the solutions on a number line and present the answer using interval notation.

Using interval notation, \((−∞,\frac { 1 } { 2 }]∪[3,∞)\)

Exercise \(\PageIndex{4}\)

Solve and graph: \(3 | 6 x + 5 | - 2 > 13\).

Using interval notation, \(\left( - \infty , - \frac { 5 } { 3 } \right) \cup ( 0 , \infty )\)

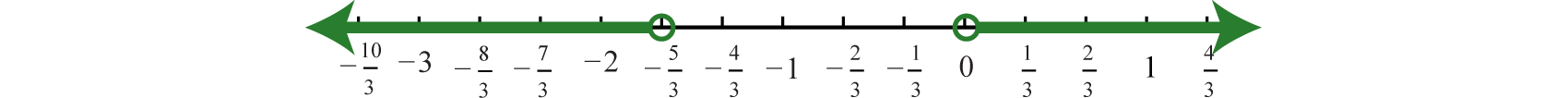
www.youtube.com/v/P6HjRz6W4F4

Up to this point, the solution sets of linear absolute value inequalities have consisted of a single bounded interval or two unbounded intervals. This is not always the case.

Example \(\PageIndex{11}\):

Solve and graph: \(|2x−1|+5>2\).

\(\begin{array} { c } { | 2 x - 1 | + 5 > 2 } \\ { | 2 x - 1 | > - 3 } \end{array}\)

Notice that we have an absolute value greater than a negative number. For any real number x the absolute value of the argument will always be positive. Hence, any real number will solve this inequality.

Geometrically, we can see that \(f(x)=|2x−1|+5\) is always greater than \(g(x)=2\).

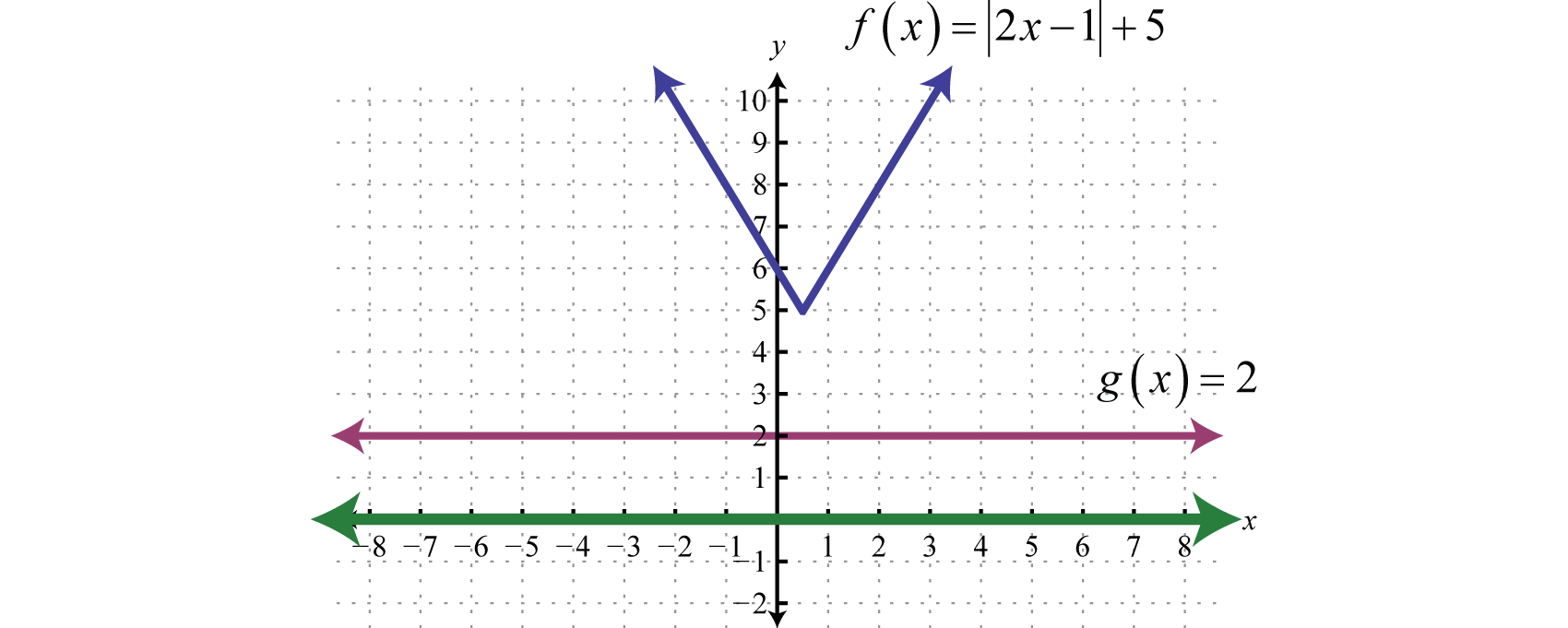
All real numbers, \(ℝ\).

Example \(\PageIndex{12}\):

Solve and graph: \(|x+1|+4≤3\).

\(\begin{array} { l } { | x + 1 | + 4 \leq 3 } \\ { | x + 1 | \leq - 1 } \end{array}\)

In this case, we can see that the isolated absolute value is to be less than or equal to a negative number. Again, the absolute value will always be positive; hence, we can conclude that there is no solution.

Geometrically, we can see that \(f(x)=|x+1|+4\) is never less than \(g(x)=3\).

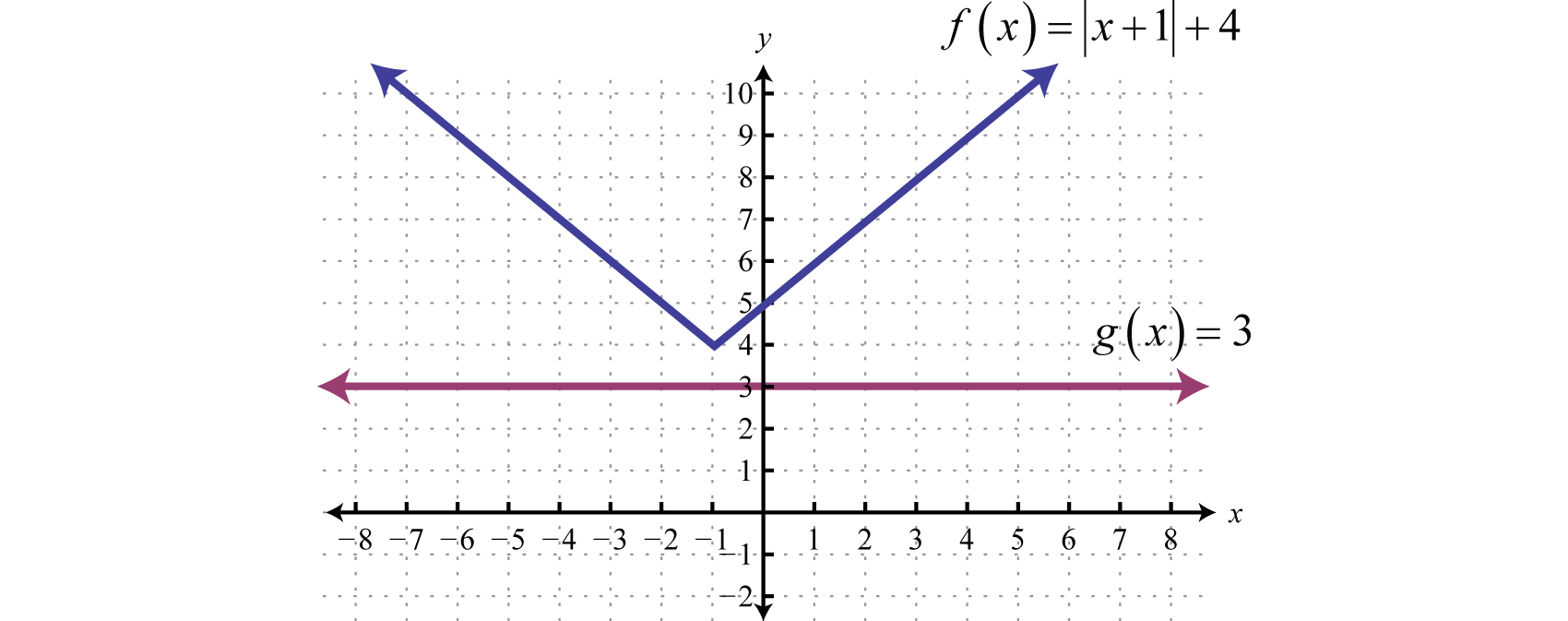
Answer : \(Ø\)

In summary, there are three cases for absolute value equations and inequalities. The relations \(=, <, \leq, > \) and \(≥\) determine which theorem to apply.

Case 1: An absolute value equation:

Case 2: an absolute value inequality involving " less than .", case 3: an absolute value inequality involving " greater than .", key takeaways.

• To solve an absolute value equation, such as \(|X| = p\), replace it with the two equations \(X = −p\) and \(X = p\) and then solve each as usual. Absolute value equations can have up to two solutions.
• To solve an absolute value inequality involving “less than,” such as \(|X| ≤ p\), replace it with the compound inequality \(−p ≤ X ≤ p\) and then solve as usual.
• To solve an absolute value inequality involving “greater than,” such as \(|X| ≥ p\), replace it with the compound inequality \(X ≤ −p\) or \(X ≥ p\) and then solve as usual.
• Remember to isolate the absolute value before applying these theorems.

Exercise \(\PageIndex{5}\)

• \(|x| = 9\)
• \(|x| = 1\)
• \(|x − 7| = 3\)
• \(|x − 2| = 5\)
• \(|x + 12| = 0\)
• \(|x + 8| = 0\)
• \(|x + 6| = −1\)
• \(|x − 2| = −5\)
• \(|2y − 1| = 13\)
• \(|3y − 5| = 16\)
• \(|−5t + 1| = 6\)
• \(|−6t + 2| = 8\)
• \(\left| \frac { 1 } { 2 } x - \frac { 2 } { 3 } \right| = \frac { 1 } { 6 }\)
• \(\left| \frac { 2 } { 3 } x + \frac { 1 } { 4 } \right| = \frac { 5 } { 12 }\)
• \(|0.2x + 1.6| = 3.6\)
• \(|0.3x − 1.2| = 2.7\)
• \(| 5 (y − 4) + 5| = 15\)
• \(| 2 (y − 1) − 3y| = 4\)
• \(|5x − 7| + 3 = 10\)
• \(|3x − 8| − 2 = 6\)
• \(9 + |7x + 1| = 9\)
• \(4 − |2x − 3| = 4\)
• \(3 |x − 8| + 4 = 25\)
• \(2 |x + 6| − 3 = 17\)
• \(9 + 5 |x − 1| = 4\)
• \(11 + 6 |x − 4| = 5\)
• \(8 − 2 |x + 1| = 4\)
• \(12 − 5 |x − 2| = 2\)
• \(\frac{1}{2} |x − 5| − \frac{2}{3} = −\frac{1}{6}\)
• \(\frac { 1 } { 3 } \left| x + \frac { 1 } { 2 } \right| + 1 = \frac { 3 } { 2 }\)
• \(−2 |7x + 1| − 4 = 2\)
• \(−3 |5x − 3| + 2 = 5\)
• \(1.2 |t − 2.8| − 4.8 = 1.2\)
• \(3.6 | t + 1.8| − 2.6 = 8.2\)
• \(\frac{1}{2} |2 (3x − 1) − 3| + 1 = 4\)
• \(\frac{2}{3} |4 (3x + 1) − 1| − 5 = 3\)
• \(|5x − 7| = |4x − 2|\)
• \(|8x − 3| = |7x − 12|\)
• \(|5y + 8| = |2y + 3|\)
• \(|7y + 2| = |5y − 2|\)
• \(|5 (x − 2)| = |3x|\)
• \(|3 (x + 1)| = |7x|\)
• \(\left| \frac { 2 } { 3 } x + \frac { 1 } { 2 } \right| = \left| \frac { 3 } { 2 } x - \frac { 1 } { 3 } \right|\)
• \(\left| \frac { 3 } { 5 } x - \frac { 5 } { 2 } \right| = \left| \frac { 1 } { 2 } x + \frac { 2 } { 5 } \right|\)
• \(|1.5t − 3.5| = |2.5t + 0.5|\)
• \(|3.2t − 1.4| = |1.8t + 2.8|\)
• \(|5 − 3 (2x + 1)| = |5x + 2|\)
• \(|3 − 2 (3x − 2)| = |4x − 1|\)

1. \(−9, 9\)

3. \(4, 10\)

5. \(−12\)

7. \(Ø\)

9. \(−6, 7\)

11. \(−1, \frac{7}{5}\)

13. \(1, \frac{5}{3}\)

15. \(−26, 10\)

17. \(0, 6\)

19. \(0, \frac{14}{5}\)

21. \(−\frac{1}{7}\)

23. \(1, 15\)

25. \(Ø\)

27. \(−3, 1\)

29. \(4, 6\)

31. \(Ø\)

33. \(−2.2, 7.8\)

35. \(−\frac{1}{6}, \frac{11}{6}\)

37. \(1, 5\)

39. \(−\frac{5}{3}, −\frac{11}{7}\)

41. \(\frac{5}{4} , 5\)

43. \(−\frac{1}{13} , 1\)

45. \(−4, 0.75\)

47. \(0, 4\)

Exercise \(\PageIndex{6}\)

Solve and graph the solution set. In addition, give the solution set in interval notation.

• Solve for \(x: p |ax + b| − q = 0\)
• Solve for \(x: |ax + b| = |p + q|\)

1. \(x = \frac { - b q \pm q } { a p }\)

Exercise \(\PageIndex{7}\)

• \(|x| < 5\)
• \(|x| ≤ 2\)
• \(|x + 3| ≤ 1\)
• \(|x − 7| < 8\)
• \(|x − 5| < 0\)
• \(|x + 8| < −7\)
• \(|2x − 3| ≤ 5\)
• \(|3x − 9| < 27\)
• \(|5x − 3| ≤ 0\)
• \(|10x + 5| < 25\)
• \(\left| \frac { 1 } { 3 } x - \frac { 2 } { 3 } \right| \leq 1\)
• \(\left| \frac { 1 } { 12 } x - \frac { 1 } { 2 } \right| \leq \frac { 3 } { 2 }\)
• \(|x| ≥ 5\)
• \(|x| > 1\)
• \(|x + 2| > 8\)
• \(|x − 7| ≥ 11\)
• \(|x + 5| ≥ 0\)
• \(|x − 12| > −4\)
• \(|2x − 5| ≥ 9\)
• \(|2x + 3| ≥ 15\)
• \(|4x − 3| > 9\)
• \(|3x − 7| ≥ 2\)
• \(\left| \frac { 1 } { 7 } x - \frac { 3 } { 14 } \right| > \frac { 1 } { 2 }\)
• \(\left| \frac { 1 } { 2 } x + \frac { 5 } { 4 } \right| > \frac { 3 } { 4 }\)

1. \(( - 5,5 )\);

3. \([ - 4 , - 2 ]\);

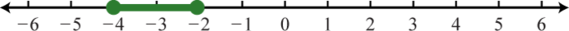
5. \(\emptyset\);

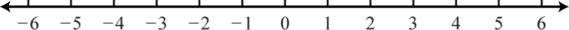
7. \([ - 1,4 ]\);

9. \(\left\{ \frac { 3 } { 5 } \right\}\);

11. \([ - 1,5 ]\);

13. \(( - \infty , - 5 ] \cup [ 5 , \infty )\);

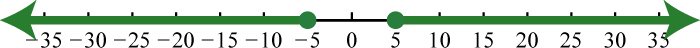
15. \(( - \infty , - 10 ) \cup ( 6 , \infty )\);

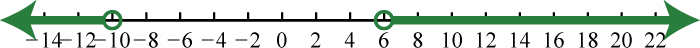
17. \(\mathbb { R }\);

19. \(( - \infty , - 2 ] \cup [ 7 , \infty )\);

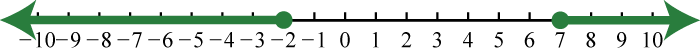
21. \(\left( - \infty , - \frac { 3 } { 2 } \right) \cup ( 3 , \infty )\);

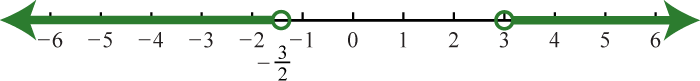
23. \(( - \infty , - 2 ) \cup ( 5 , \infty )\);

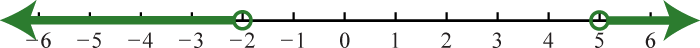
Exercise \(\PageIndex{8}\)

Solve and graph the solution set.

• \(|3 (2x − 1)| > 15\)
• \(|3 (x − 3)| ≤ 21\)
• \(−5 |x − 4| > −15\)
• \(−3 |x + 8| ≤ −18\)
• \(6 − 3 |x − 4| < 3\)
• \(5 − 2 |x + 4| ≤ −7\)
• \(6 − |2x + 5| < −5\)
• \(25 − |3x − 7| ≥ 18\)
• \(|2x + 25| − 4 ≥ 9\)
• \(|3 (x − 3)| − 8 < −2\)
• \(2 |9x + 5| + 8 > 6\)
• \(3 |4x − 9| + 4 < −1\)
• \(5 |4 − 3x| − 10 ≤ 0\)
• \(6 |1 − 4x| − 24 ≥ 0\)
• \(3 − 2 |x + 7| > −7\)
• \(9 − 7 |x − 4| < −12\)
• \(|5 (x − 4) + 5| > 15\)
• \(|3 (x − 9) + 6| ≤ 3\)
• \(\left| \frac { 1 } { 3 } ( x + 2 ) - \frac { 7 } { 6 } \right| - \frac { 2 } { 3 } \leq - \frac { 1 } { 6 }\)
• \(\left| \frac { 1 } { 10 } ( x + 3 ) - \frac { 1 } { 2 } \right| + \frac { 3 } { 20 } > \frac { 1 } { 4 }\)
• \(12 + 4 |2x − 1| ≤ 12\)
• \(3 − 6 |3x − 2| ≥ 3\)
• \(\frac{1}{2} |2x − 1| + 3 < 4\)
• 2 |\frac{1}{2} x + \frac{2}{3} | − 3 ≤ −1\)
• \(7 − |−4 + 2 (3 − 4x)| > 5\)
• \(9 − |6 + 3 (2x − 1)| ≥ 8\)
• \(\frac { 3 } { 2 } - \left| 2 - \frac { 1 } { 3 } x \right| < \frac { 1 } { 2 }\)
• \(\frac { 5 } { 4 } - \left| \frac { 1 } { 2 } - \frac { 1 } { 4 } x \right| < \frac { 3 } { 8 }\)

1. \(( - \infty , - 2 ) \cup ( 3 , \infty )\);

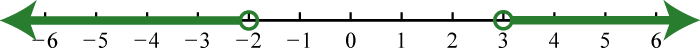
3. \(( 1,7 )\);

5. \(( - \infty , 3 ) \cup ( 5 , \infty )\);

7. \(( - \infty , - 8 ) \cup ( 3 , \infty )\);

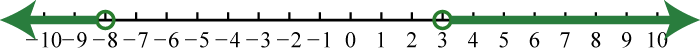
9. \(( - \infty , - 19 ] \cup [ - 6 , \infty )\);

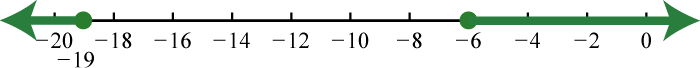
11. \(\mathbb { R }\);

13. \(\left[ \frac { 2 } { 3 } , 2 \right]\);

15. \(( - 12 , - 2 )\);

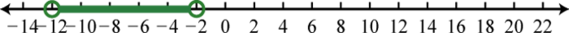
17. \(( - \infty , 0 ) \cup ( 6 , \infty )\);

19. \([ 0,3 ]\);

21. \(\frac { 1 } { 2 }\);

23. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 2 } \right)\);

25. \(\left( 0 , \frac { 1 } { 2 } \right)\);

27. \(( - \infty , 3 ) \cup ( 9 , \infty )\);

Exercise \(\PageIndex{9}\)

Assume all variables in the denominator are nonzero.

• Solve for \(x\) where \(a, p > 0: p |ax + b| − q ≤ 0\)
• Solve for \(x\) where \(a, p > 0: p |ax + b| − q ≥ 0\)

1. \(\frac { - q - b p } { a p } \leq x \leq \frac { q - b p } { a p }\)

Exercise \(\PageIndex{10}\)

Given the graph of \(f\) and \(g\), determine the \(x\)-values where:

(a) \(f ( x ) = g ( x )\)

(b) \(f ( x ) > g ( x )\)

(c) \(f ( x ) < g ( x )\)

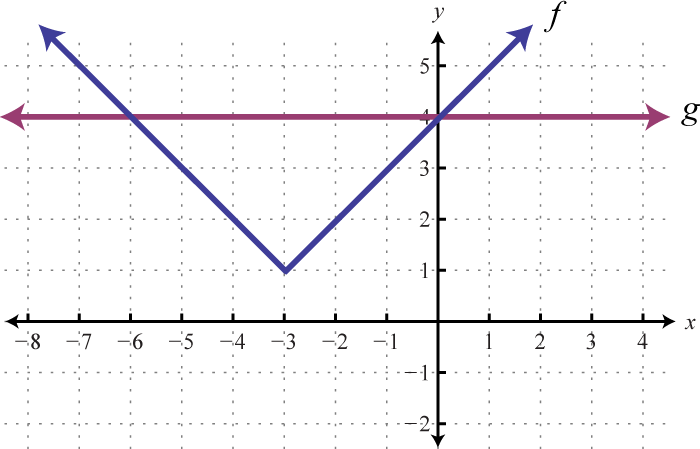
1. (a) \(−6, 0\); (b) \((−∞, −6) ∪ (0, ∞)\); (c) \((−6, 0)\)

3. (a) \(Ø\); (b) \(ℝ\); (c) \(Ø\)

Exercise \(\PageIndex{11}\)

• Make three note cards, one for each of the three cases described in this section. On one side write the theorem, and on the other write a complete solution to a representative example. Share your strategy for identifying and solving absolute value equations and inequalities on the discussion board.
• Make your own examples of absolute value equations and inequalities that have no solution, at least one for each case described in this section. Illustrate your examples with a graph.

1. Answer may vary

63 The distance from the graph of a number \(a\) to zero on a number line, denoted \(|a|\).

64 The number or expression inside the absolute value.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Solving Absolute Value Equations – Methods & Examples

JUMP TO TOPIC

What is Absolute Value?

Practice questions, solving absolute value equations – methods & examples.

Solving equations containing an absolute value is as simple as working with regular linear equations . Before we can embark on solving absolute value equations, let’s take a review of what the word absolute value means.

In mathematics, the absolute value of a number refers to the distance of a number from zero, regardless of direction. The absolute value of a number x is generally represented as | x | = a, which implies that, x = + a and -a.

We say that the absolute value of a given number is the positive version of that number . For example, the absolute value of negative 5 is positive 5, and this can be written as: | − 5 | = 5.

Other examples of absolute values of numbers include:  |− 9| = 9, |0| = 0, − |−12| = −12 etc. From these examples of absolute values, we simply define absolute value equations as equations containing expressions with absolute value functions.

How to Solve Absolute Value Equations?

The following are the general steps for solving equations containing absolute value functions:

• Isolate the expression containing the absolute value function.
• Get rid of the absolute value notation by setting up the two equations so that in the first equation, the quantity inside absolute notation is positive. In the second equation, it is negative. You will remove the absolute notation and write the quantity with its suitable sign.
• Calculate the unknown value for the positive version of the equation.
• Solve for the negative version of the equation, in which you will first multiply the value on the other side of the equal sign by -1, and then solve.

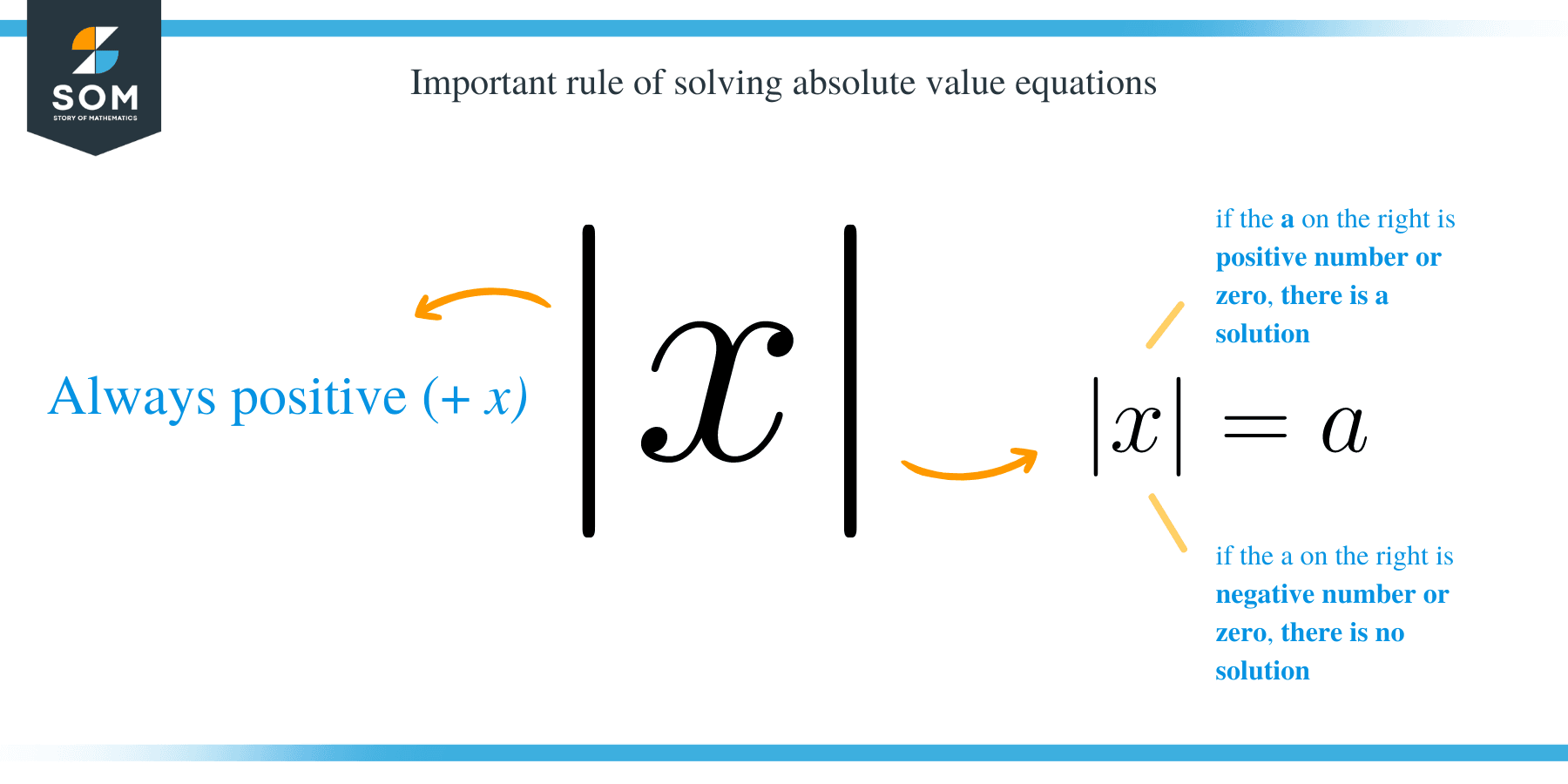
In addition to the above steps, there are other important rules you should keep in mind when solving absolute value equations.

• The ∣x∣is always positive: ∣x∣ → +x.
• In | x| = a, if the  a on the right is a positive number or zero, then there is a solution.

Solve the equation for x: |3 + x| − 5 = 4.

• Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain;

| 3 + x | − 5 + 5 = 4 + 5

| 3 + x |= 9

• Calculate for the positive version of the equation. Solve the equation by assuming the absolute value symbols.

| 3 +  x  | = 9 → 3 +  x  = 9

Subtract 3 from both sides of the equation.

3 – 3 + x = 9 -3

• Now calculate for the negative version of the equation by multiplying 9 by -1.

3 +  x  | = 9 → 3 +  x  = 9 × ( −1)

Also subtract 3 from both side to isolate x.

3 -3 + x = – 9 -3

Therefore 6 and -12 are the solutions.

Solve for all real values of x such that | 3x – 4 | – 2 = 3.

• Isolate the equation with absolute function by add 2 to both sides.

= | 3x – 4 | – 2 + 2 = 3 + 2

= | 3x – 4 |= 5

Assume the absolute signs and solve for the positive version of the equation.

| 3x – 4 |= 5→3x – 4 = 5

Add 4 to both sides of the equation.

3x – 4 + 4 = 5 + 4

Divide: 3x/3 =9/3

Now solve for the negative version by multiplying 5 by -1.

3x – 4 = 5→3x – 4 = -1(5)

3x – 4 = -5

3x – 4 + 4 = – 5 + 4

Divide by 3 on both sides.

Therefore, 3 and 1/3 are the solutions.

Solve for all real values of x: Solve | 2 x  – 3 | – 4 = 3

Add 4 to both sides.

| 2 x  – 3 | -4 = 3 →| 2 x  – 3 | = 7

Assume the absolute symbols and solve for the positive version of x.

2 x  – 3 = 7

2x – 3 + 3 = 7 + 3

Now solve for the negative version of x by multiplying 7 by -1

2 x  – 3 = 7→2 x  – 3 = -1(7)

Add 3 to both sides.

2x – 3 + 3 = – 7 + 3

x = – 2

Therefore, x  = –2, 5

Solve for all real numbers of x: | x + 2 | = 7

Already the absolute value expression is isolated, therefore assume the absolute symbols and solve.

| x + 2 | = 7 → x + 2 = 7

Subtract 2 from both sides.

x + 2 – 2 = 7 -2

Multiply 7 by -1 to solve for the negative version of the equation.

x + 2 = -1(7) → x + 2 = -7

Subtract by 2 on both sides.

x + 2 – 2 = – 7 – 2

Therefore, x = -9, 5

Previous Lesson  |  Main Page | Next Lesson

• EXPLORE Random Article

How to Solve Absolute Value Equations

Last Updated: January 31, 2023 References

This article was co-authored by wikiHow Staff . Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 23,120 times.

Setting up the Problem

• For example, |9| = 9; |-9| = -(-9) = 9.

Calculating the Values

Check Your Work

Expert Q&A

• Remember that absolute value bars are distinct from parentheses and function differently. Thanks Helpful 0 Not Helpful 0
• Once you've solved for any variables, remember to simplify absolute values accordingly. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ http://tutorial.math.lamar.edu/Classes/Alg/SolveAbsValueEqns.aspx
• ↑ https://www.mathsisfun.com/numbers/absolute-value.html
• ↑ http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations
• ↑ http://www.purplemath.com/modules/solveabs.htm
• ↑ https://www.khanacademy.org/math/algebra/absolute-value-equations-functions/absolute-value-equations/v/absolute-value-equations

About this article

To solve absolute value equations, first isolate the absolute value terms by moving anything outside of the vertical bars to the other side of the equation. Next, solve for the positive value of the equation by isolating the variable. Since the absolute variable can represent 2 numbers, then solve for the negative value by putting a negative sign outside the vertical bars. Then, move the negative by dividing both sides by -1 and solve for the variable. If you want to learn how to check your answers for an absolute value equation, keep reading the article! Did this summary help you? Yes No

Did this article help you?

• About wikiHow
• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

MathBootCamps

Absolute value equations.

Solving absolute value equations is based on the idea that absolute value represents the distance between a point on the number line and zero. In this lesson, we will look at a few examples to understand how to solve these equations and also take a bit of a look at this idea of distance as it relates to solving absolute value equations. Table of Contents

Steps for solving absolute value equations

• Step-by-step examples
• Absolute value equations with no solutions or one solution
• Why does our method work?

Another perspective

[adsenseWide]

When given an absolute value equation, you will first need to isolate the absolute value part of the equation. Then, you will write two equations based on the definition of absolute value (though sometimes, there will end up only being one equation). This sounds complicated, but it is only a step or two more than solving the typical linear equation.

Let’s try these steps out with some examples!

In this first example, the absolute value part of the equation is already isolated, so only step two will apply. Whether or not this first step applies or not, you will always have zero, one, or two solutions to any absolute value equation.

Solve the equation: \(|5x – 2| = 13\)

As mentioned, the absolute value part is already isolated. Therefore, we will solve two equations without the absolute value: one where the 13 is positive and one where 13 is negative.

Equation 1:

\(\begin{align}5x – 2 &= 13\\ 5x &= 15\\ x &= 3\end{align}\)

Equation 2:

\(\begin{align}5x – 2 &= -13\\ 5x &= -11 \\ x &= -\dfrac{11}{5}\end{align}\)

So, there are two solutions to this equation: \(x = \bbox[border: 1px solid black; padding: 2px]{3, -\dfrac{11}{5}}\)

In this next example, there will be a little more work since the absolute value part of the equation is not isolated. In this situation, you will always need to isolate this term before you write your two equations, or you will end up with incorrect answers.

Solve the equation: \(4 + 3|x – 5| = 16\)

Your first step here is to use algebra to isolate the absolute value part of the equation.

\(4 + 3|x – 5| = 16\)

Subtract 4 from both sides.

\(3|x – 5| = 12\)

Divide both sides by 3.

\(|x – 5| = 4\)

Now you can write and solve two equations, one where the 4 is negative and one where the 4 is positive. Remember to drop the absolute value symbol at this step.

\(\begin{align}x – 5 &= 4\\ x &= 9\end{align}\)

\(\begin{align}x – 5 &= -4\\ x &= 1\end{align}\)

Once again, there are two solutions to the equation: \(x = \bbox[border: 1px solid black; padding: 2px]{1, 9}\)

Absolute value equations with one solution or no solutions

In both of our examples above, there were two solutions so you may think that this is always the case. While this is often right, there are cases where there is only one solution and even when there are none. The next two examples will show when this happens.

Example – one solution

Solve the equation: \(6|x – 2| – 1 = -1\)

As usual, we will first isolate the absolute value equation.

\(6|x – 2| – 1 = -1\)

Add 1 to both sides.

\(6|x – 2| = 0\)

Divide both sides by 6.

\(|x – 2| = 0\)

Normally at this stage, we would write two equations without the absolute value bars, but writing 0 with a positive or negative is the same thing. So we only have one equation:

\(x – 2 = 0\)

Adding 2 to both sides then gives the only solution.

\(x = \bbox[border: 1px solid black; padding: 2px]{2}\)

We will look more closely at why this happens, but first let’s look at how you might end up with no solutions.

Example – no solutions

Solve the equation: \(|10x – 1| + 3 = -8\)

To isolate the absolute value, subtract 3 from both sides.

\(|10x – 1| = -11\)

At this step, it can be determined that there are no solutions to the equation. Why? The absolute value of any number is positive. Here, we have the absolute value of something is negative. This is not possible so there are no possible x-values that make this equation true. Therefore, you can write:

Answer : No solutions

The absolute value of any number is always positive. Use this to determine when there are no solutions to an absolute value equation.

Notice that in both examples, the steps were the same as before. You will always follow those two steps when solving any absolute value equation.

Why does this work?

You can think of the absolute value of any number as representing how far it is from zero on the number line. Consider \(|3|\) and \(|–3|\) below.

This is why the absolute value is always positive – it is representing a distance. Now think of an equation where the absolute value part is isolated, such as \(|5x + 1| = 2\). Is the absolute value is 2, then all you know is that \(5x + 1\) is 2 units from zero on the number line. This gives two possibilities:

So this is why we end up with two different equations. In the case of only one solution, you end up with an absolute value expression equal to zero. Since this means that the distance from zero on the number line is zero, you end up with only one equation.

When you study the graphs of absolute value equations, you can see the three cases of one solution, no solution, and two solutions graphically. This is due to the shape of the graph of the absolute value function. This is a bit beyond the scope of this lesson, but in the graph below, you can see the graph of \(y = |x – 1|\) and \(y = 2\). Notice that the two graphs intersect at two points. These represent the two solutions to the equation \(|x – 1| = 2\).

You can probably see how a horizontal line might cross the graph at exactly one point (one solution) or at no points (no solutions). This would be just changing the number on the right hand side of the equation.

Absolute value equations are always solved with the same steps: isolate the absolute value term and then write equations based on the definition of the absolute value. There may end up being two solutions, one solution, or no solutions. To catch when there is no solution, always remember that absolute values must be positive, but remember to apply this idea only after the absolute value term has been isolated.

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

What do you do when you have absolute values on both sides of the equations?

Explanation:

#" "# When we have absolute values on both sides of the equations,

we must consider both possibilities for acceptable solutions - positive and negative absolute value expressions.

We will look at an example first to understand:

Solve for #color(red)(x# :

#color(blue)(|2x-1|=|4x+9|#

Both sides of the equation contain absolute values .

Find solutions as shown below:

#color(red)((2x-1)=-(4x+9)# .. Exp.1

#color(blue)(OR#

#color(red)((2x-1)=(4x+9)# ...Exp.2

#color(green)(Case.1# :

Consider ... Exp.1 first and solve for #color(red)(x#

#color(red)((2x-1)=-(4x+9)#

#rArr 2x-1=-4x-9#

Add #color(red)(4x# to both sides of the equation.

#rArr 2x-1+4x=-4x-9+4x#

#rArr 2x-1+4x=-cancel (4x)-9+cancel(4x)#

#rArr 6x-1=-9#

Add #color(re)(1# to both sides of the equation.

#rArr 6x-1+1=-9+1#

#rArr 6x-cancel 1+cancel 1=-9+1#

#rArr 6x=-8#

Divide both sides by #color(red)(2#

#rArr (6x)/2=-8/2#

#rArr 3x=-4#

#color(blue)(rArr x = (-4/3)# ... Sol.1

#color(green)(Case.2# :

Consider ... Exp.2 next and solve for #color(red)(x#

#color(red)((2x-1)=(4x+9)#

#rArr 2x-1=4x+9#

Subtract #color(red)((4x)# from both sides of the equation.

#rArr 2x-1-4x=4x+9-4x#

#rArr 2x-1-4x=cancel(4x)+9-cancel(4x)#

#rArr -2x-1=9#

Add #color(red)(1# to both sdies of the equation.

#rArr -2x-1+1=9+1#

#rArr -2x-cancel 1+cancel 1=9+1#

#rArr -2x=10#

Divide both sides of the equation by #color(red)(2#

#rArr (-2x)/2=10/2#

#rArr -x=5#

#color(blue)(rArr x=-5# ... Sol.2

Hence, there are two solutions for the absolute value equation:

If you so wish, you can substitute these values of #color(red)(x# in both #color(green)(Case.1# and #color(green)(Case.2# to verify the accuracy.

We will work on Example.2 in my next answer.

Hope it helps.

#" "# Example.2 is given here.

#" "# This is a continuation of my solution given earlier.

We worked on Example.1 in that solution.

Please refer to that solution first, before reading this solution.

Let us consider a second example:

#color(red)(5|x+3|-4=8|x+3|-4#

Subtract #color(blue)(8|x+3|# and add #color(blue)(4# on both sides:

#rArr 5|x+3|-4-8|x+3|+4=8|x+3|-4-8|x+3|+4#

#rArr 5|x+3|-cancel 4-8|x+3|+cancel 4=cancel(8|x+3|)-4-cancel(8|x+3|)+4#

#rArr 5|x+3|-8|x+3|=-4+4#

#rArr -3|x+3|=0#

Divide both sides by #color(red)((-3)#

#rArr [(-3)(|x+3|)]/((-3))=0/((-3)#

#rArr [cancel (-3)(|x+3|)]/(cancel (-3))=0#

#rArr |x+3|=0#

#rArr x+3=0#

Subtract #color(red)(3# from both sides

#rArr x+3-3=0-3#

#rArr x+cancel 3-cancel 3=-3#

#rArr x=-3#

Hence, we conclude that

#color(blue)(x=-3# is the ONLY Solution for this example.

Related questions

• How can an absolute value equation have no solution?
• How can an absolute value equation have one solution?
• How do you solve absolute value equations?
• How do you solve #|x - 5| = 10#?
• How do you solve #8=3+|10y+5|#?
• How do you solve #8|x+6|=-48#?
• Can an absolute value equation ever have and infinite amount of solutions?
• How do you solve for m given #|\frac{m}{8}|=1#?
• How do you solve #3abs(-9 x-7)-2=13#?
• How do you solve #abs(x + 1)=abs(-4 x + 3)#?

Impact of this question