how to solve probability problems

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics
• Probability and Statistics

How to Calculate Probability

Last Updated: July 31, 2023 Fact Checked

This article was co-authored by Mario Banuelos, PhD . Mario Banuelos is an Associate Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 3,450,844 times.

Chances are (pun intended) you've encountered probability by now, but what exactly is probability, and how do you calculate it? Probability is the likelihood of a specific event happening, like winning the lottery or rolling a 6 on a die. Finding probability is easy using the probability formula (the number of favorable outcomes divided by the total number of outcomes). In this article, we'll walk you through exactly how to use the probability formula step by step, plus show you some examples of the probability formula in action.

Finding the Probability of a Single Random Event

Example: It would be impossible to calculate the probability of an event phrased as: “Both a 5 and a 6 will come up on a single roll of a die.”

• Example 1 : What is the likelihood of choosing a day that falls on the weekend when randomly picking a day of the week? "Choosing a day that falls on the weekend" is our event, and the number of outcomes is the total number of days in a week: 7.
• Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If a marble is drawn from the jar at random, what is the probability that this marble is red? "Choosing a red marble" is our event, and the number of outcomes is the total number of marbles in the jar, 20.

• Example 1 : What is the likelihood of choosing a day that falls on the weekend when randomly picking a day of the week? The number of events is 2 (since 2 days out of the week are weekends), and the number of outcomes is 7. The probability is 2 ÷ 7 = 2/7. You could also express this as 0.285 or 28.5%.
• Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If a marble is drawn from the jar at random, what is the probability that this marble is red? The number of events is 5 (since there are 5 red marbles), and the number of outcomes is 20. The probability is 5 ÷ 20 = 1/4. You could also express this as 0.25 or 25%.

• For example, the likelihood of rolling a 3 on a 6-sided die is 1/6. But the probability of rolling all five other numbers on a die is also 1/6. 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6 , which = 100%.

Note: If you had, for example, forgotten about the number 4 on the dice, adding up the probabilities would only reach 5/6 or 83%, indicating a problem.

• For example, if you were to calculate the probability of the Easter holiday falling on a Monday in the year 2020, the probability would be 0 because Easter is always on a Sunday.

Calculating the Probability of Multiple Random Events

Note: The probability of the 5s being rolled are called independent events, because what you roll the first time does not affect what happens the second time.

• Now, the likelihood that the second card is a club is 12/51, since 1 club will have already been removed. This is because what you do the first time affects the second. If you draw a 3 of clubs and don't put it back, there will be one less club and one less card in the deck (51 instead of 52).
• The probability that the first marble is red is 5/20, or 1/4. The probability of the second marble being blue is 4/19, since we have 1 less marble, but not 1 less blue marble. And the probability that the third marble is white is 11/18, because we’ve already chosen 2 marbles.

• Example 1 : Two cards are drawn randomly from a deck of cards. What is the likelihood that both cards are clubs? The probability of the first event happening is 13/52. The probability of the second event happening is 12/51. The probability is 13/52 x 12/51 = 12/204 = 1/17. You could also express this as 0.058 or 5.8%.
• Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If three marbles are drawn from the jar at random, what is the probability that the first marble is red, the second marble is blue, and the third is white? The probability of the first event is 5/20. The probability of the second event is 4/19. And the probability of the third event is 11/18. The probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032. You could also express this as 3.2%.

Converting Odds to Probabilities

• The number 11 represents the likelihood of choosing a white marble and the number 9 represents the likelihood of choosing a marble of a different color.
• So, odds are that you will draw a white marble.

• The event that you’ll draw a white marble is 11; the event another color will be drawn is 9. The total number of outcomes is 11 + 9, or 20.

• So, in our example, the probability of drawing a white marble is 11/20. Divide this out: 11 ÷ 20 = 0.55 or 55%.

Probability Cheat Sheets

Expert Q&A

• Mathematicians typically use the term “relative probability” to refer to the chances of an event happening. They insert the word "relative" since no outcome is 100% guaranteed. For example, if you flip a coin 100 times, you probably won't get exactly 50 heads and 50 tails. Relative probability takes this caveat into account. [10] X Research source Thanks Helpful 1 Not Helpful 2
• You may need to know that that in sports betting and bookmaking, odds are expressed as “odds against,” which means that the odds of an event happening are written first, and the odds of an event not happening come second. Although it can be confusing, it's important to know this if you’re planning to bet on a sporting event. Thanks Helpful 13 Not Helpful 4
• The most common ways of writing down probabilities include putting them as fractions, as decimals, as percentages, or on a 1–10 scale. Thanks Helpful 8 Not Helpful 5

You Might Also Like

• ↑ https://www.theproblemsite.com/reference/mathematics/probability/mutually-exclusive-outcomes
• ↑ Mario Banuelos, PhD. Associate Professor of Mathematics. Expert Interview. 11 December 2021.
• ↑ https://www.mathplanet.com/education/pre-algebra/probability-and-statistic/probability-of-events
• ↑ https://www.mathsisfun.com/probability_line.html
• ↑ https://www.probabilisticworld.com/not-all-zero-probabilities/
• ↑ https://www.khanacademy.org/math/ap-statistics/probability-ap/stats-conditional-probability/e/calculating-conditional-probability
• ↑ https://www.mathsisfun.com/data/probability.html
• ↑ https://www.mathsisfun.com/data/probability-events-types.html

About This Article

Probability is the likelihood that a specific event will occur. To calculate probability, first define the number of possible outcomes that can occur. For example, if someone asks, “What is the probability of choosing a day that falls on the weekend when randomly picking a day of the week,” the number of possible outcomes when choosing a random day of the week is 7, since there are 7 days of the week. Now define the number of events. In this example, the number of events is 2 since 2 days out of the week fall on the weekend. Finally, divide the number of events by the number of outcomes to get the probability. In our example, we would divide 2, the number of events, by 7, the number of outcomes, and get 2/7, or 0.28. You could also express the answer as a percentage, or 28.5%. Therefore, there’s a 28.5% probability that you would choose a day that falls on the weekend when randomly picking a day of the week. To learn how to calculate the probability of multiple events happening in a row, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Nathalie Ricardo

May 11, 2022

Did this article help you?

Jan 28, 2023

Jan 15, 2019

Victoria Dobson

May 24, 2017

Krishna Mitra

Nov 25, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

Reset password New user? Sign up

Existing user? Log in

Probability - Problem Solving

Already have an account? Log in here.

• Geoff Pilling
• Sandeep Bhardwaj

To solve problems on this page, you should be familiar with

• Uniform Probability
• Probability - By Outcomes
• Probability - Rule of Sum
• Probability - Rule of Product
• Probability - By Complement
• Probability - Independent Events
• Conditional Probability

Problem Solving - Basic

Problem solving - intermediate, problem solving - difficult.

If I throw 2 standard 5-sided dice, what is the probability that the sum of their top faces equals to 10? Assume both throws are independent to each other. Solution : The only way to obtain a sum of 10 from two 5-sided dice is that both die shows 5 face up. Therefore, the probability is simply \( \frac15 \times \frac15 = \frac1{25} = .04\)

If from each of the three boxes containing \(3\) white and \(1\) black, \(2\) white and \(2\) black, \(1\) white and \(3\) black balls, one ball is drawn at random. Then the probability that \(2\) white and \(1\) black balls will be drawn is?

2 fair 6-sided dice are rolled. What is the probability that the sum of these dice is \(10\)? Solution : The event for which I obtain a sum of 10 is \(\{(4,6),(6,4),(5,5) \}\). And there is a total of \(6^2 = 36\) possible outcomes. Thus the probability is simply \( \frac3{36} = \frac1{12} \approx 0.0833\)

If a fair 6-sided dice is rolled 3 times, what is the probability that we will get at least 1 even number and at least 1 odd number?

Three fair cubical dice are thrown. If the probability that the product of the scores on the three dice is \(90\) is \(\dfrac{a}{b}\), where \(a,b\) are positive coprime integers, then find the value of \((b-a)\).

You can try my other Probability problems by clicking here

Suppose a jar contains 15 red marbles, 20 blue marbles, 5 green marbles, and 16 yellow marbles. If you randomly select one marble from the jar, what is the probability that you will have a red or green marble? First, we can solve this by thinking in terms of outcomes. You could draw a red, blue, green, or yellow marble. The probability that you will draw a green or a red marble is \(\frac{5 + 15}{5+15+16+20}\). We can also solve this problem by thinking in terms of probability by complement. We know that the marble we draw must be blue, red, green, or yellow. In other words, there is a probability of 1 that we will draw a blue, red, green, or yellow marble. We want to know the probability that we will draw a green or red marble. The probability that the marble is blue or yellow is \(\frac{16 + 20}{5+15+16+20}\). , Using the following formula \(P(\text{red or green}) = 1 - P(\text{blue or yellow})\), we can determine that \(P(\text{red or green}) = 1 - \frac{16 + 20}{5+15+16+20} = \frac{5 + 15}{5+15+16+20}\).

Two players, Nihar and I, are playing a game in which we alternate tossing a fair coin and the first player to get a head wins. Given that I toss first, the probability that Nihar wins the game is \(\dfrac{\alpha}{\beta}\), where \(\alpha\) and \(\beta\) are coprime positive integers.

Find \(\alpha + \beta\).

If I throw 3 fair 5-sided dice, what is the probability that the sum of their top faces equals 10? Solution : We want to find the total integer solution for which \(a +b+c=10 \) with integers \(1\leq a,b,c \leq5 \). Without loss of generality, let \(a\leq b \leq c\). We list out the integer solutions: \[ (1,4,5),(2,3,5), (2,4,4), (3,3,4) \] When relaxing the constraint of \(a\leq b \leq c\), we have a total of \(3! + 3! + \frac{3!}{2!} + \frac{3!}{2!} = 18 \) solutions. Because there's a total of \(5^3 = 125\) possible combinations, the probability is \( \frac{18}{125} = 14.4\%. \ \square\)

Suppose you and 5 of your friends each brought a hat to a party. The hats are then put into a large box for a random-hat-draw. What is the probability that nobody selects his or her own hat?

How many ways are there to choose exactly two pets from a store with 8 dogs and 12 cats? Since we haven't specified what kind of pets we pick, we can choose any animal for our first pick, which gives us \( 8+12=20\) options. For our second choice, we have 19 animals left to choose from. Thus, by the rule of product, there are \( 20 \times 19 = 380 \) possible ways to choose exactly two pets. However, we have counted every pet combination twice. For example, (A,B) and (B,A) are counted as two different choices even when we have selected the same two pets. Therefore, the correct number of possible ways are \( {380 \over 2} = 190 \)

A bag contains blue and green marbles. If 5 green marbles are removed from the bag, the probability of drawing a green marble from the remaining marbles would be 75/83 . If instead 7 blue marbles are added to the bag, the probability of drawing a blue marble would be 3/19 . What was the number of blue marbles in the bag before any changes were made?

Bob wants to keep a good-streak on Brilliant, so he logs in each day to Brilliant in the month of June. But he doesn't have much time, so he selects the first problem he sees, answers it randomly and logs out, despite whether it is correct or incorrect.

Assume that Bob answers all problems with \(\frac{7}{13}\) probability of being correct. He gets only 10 problems correct, surprisingly in a row, out of the 30 he solves. If the probability that happens is \(\frac{p}{q}\), where \(p\) and \(q\) are coprime positive integers, find the last \(3\) digits of \(p+q\).

Out of 10001 tickets numbered consecutively, 3 are drawn at random .

Find the chance that the numbers on them are in Arithmetic Progression .

The answer is of the form \( \frac{l}{k} \) .

Find \( k - l \) where \(k\) and \(l\) are co-prime integers.

HINT : You might consider solving for \(2n + 1\) tickets .

You can try more of my Questions here .

A bag contains a blue ball, some red balls, and some green balls. You reach into​ the bag and pull out three balls at random. The probability you pull out one of each color is exactly 3%. How many balls were initially in the bag?

More probability questions

Photo credit: www.figurerealm.com

Amanda decides to practice shooting hoops from the free throw line. She decides to take 100 shots before dinner.

Her first shot has a 50% chance of going in.

But for Amanda, every time she makes a shot, it builds her confidence, so the probability of making the next shot goes up, But every time she misses, she gets discouraged so the probability of her making her next shot goes down.

In fact, after \(n\) shots, the probability of her making her next shot is given by \(P = \dfrac{b+1}{n+2}\), where \(b\) is the number of shots she has made so far (as opposed to ones she has missed).

So, after she has completed 100 shots, if the probability she has made exactly 83 of them is \(\dfrac ab\), where \(a\) and \(b\) are coprime positive integers, what is \(a+b\)?

Photo credit: http://polymathprogrammer.com/

Problem Loading...

Note Loading...

Set Loading...

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Probability Problems? (+FREE Worksheet!)

Do you want to know how to solve Probability Problems? Here you learn how to solve probability word problems.

Related Topics

• How to Interpret Histogram
• How to Interpret Pie Graphs
• How to Solve Permutations and Combinations
• How to Find Mean, Median, Mode, and Range of the Given Data

Step by step guide to solve Probability Problems

• Probability is the likelihood of something happening in the future. It is expressed as a number between zero (can never happen) to \(1\) (will always happen).
• Probability can be expressed as a fraction, a decimal, or a percent.
• To solve a probability problem identify the event, find the number of outcomes of the event, then use probability law: \(\frac{number\ of \ favorable \ outcome}{total \ number \ of \ possible \ outcomes}\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Probability problems – example 1:.

If there are \(8\) red balls and \(12\) blue balls in a basket, what is the probability that John will pick out a red ball from the basket?

There are \(8\) red balls and \(20\) a total number of balls. Therefore, the probability that John will pick out a red ball from the basket is \(8\) out of \(20\) or \(\frac{8}{8+12}=\frac{8}{20}=\frac{2}{5}\).

Probability Problems – Example 2:

A bag contains \(18\) balls: two green, five black, eight blue, a brown, a red, and one white. If \(17\) balls are removed from the bag at random, what is the probability that a brown ball has been removed?

If \(17\) balls are removed from the bag at random, there will be one ball in the bag. The probability of choosing a brown ball is \(1\) out of \(18\). Therefore, the probability of not choosing a brown ball is \(17\) out of \(18\) and the probability of having not a brown ball after removing \(17\) balls is the same.

Exercises for Solving Probability Problems

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting a \(4\) or smaller.
• A number is chosen at random from \(1\) to \(50\). Find the probability of selecting multiples of \(10\).
• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting of \(4\) and factors of \(6\).
• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting a multiple of \(3\).
• A number is chosen at random from \(1\) to \(50\). Find the probability of selecting prime numbers.
• A number is chosen at random from \(1\) to \(25\). Find the probability of not selecting a composite number.

Download Probability Problems Worksheet

• \(\color{blue}{\frac{2}{5}}\)
• \(\color{blue}{\frac{1}{10}}\)
• \(\color{blue}{\frac{1}{2}}\)
• \(\color{blue}{\frac{3}{10}}\)
• \(\color{blue}{\frac{9}{25}}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• How to Unlock the Secrets: “SIFT Math for Beginners” Solution Manual
• How to Find Transformation: Rotations, Reflections, and Translations?
• Top 10 3rd Grade FSA Math Practice Questions
• Overview of the CHSPE Mathematics Test
• 8th Grade NYSE Math Practice Test Questions
• How is the ParaPro Test Scored?
• 8th Grade Common Core Math Worksheets: FREE & Printable
• Dollars and Sense: How to Tackle Money Word Problems with Confidence
• Top 10 Tips to Create a CHSPE Math Study Plan
• 3rd Grade PEAKS Math Worksheets: FREE & Printable

What people say about "How to Solve Probability Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Probability Word Problems

In these lessons, we will learn how to solve a variety of probability problems.

Related Pages Probability Tree Diagrams Probability Without Replacement Theoretical vs. Experimental Probability More Lessons On Probability

Here we shall be looking into solving probability word problems involving:

• Probability and Sample Space
• Probability and Frequency Table
• Probability and Area
• Probability of Simple Events
• Probability and Permutations
• Probability and Combinations
• Probability of Independent Events

We will now look at some examples of probability problems.

Example: At a car park there are 100 vehicles, 60 of which are cars, 30 are vans and the remainder are lorries. If every vehicle is equally likely to leave, find the probability of: a) a van leaving first. b) a lorry leaving first. c) a car leaving second if either a lorry or van had left first.

Solution: a) Let S be the sample space and A be the event of a van leaving first. n(S) = 100 n(A) = 30

c) If either a lorry or van had left first, then there would be 99 vehicles remaining, 60 of which are cars. Let T be the sample space and C be the event of a car leaving. n(T) = 99 n(C) = 60

Example: A survey was taken on 30 classes at a school to find the total number of left-handed students in each class. The table below shows the results:

A class was selected at random. a) Find the probability that the class has 2 left-handed students. b) What is the probability that the class has at least 3 left-handed students? c) Given that the total number of students in the 30 classes is 960, find the probability that a student randomly chosen from these 30 classes is left-handed.

a) Let S be the sample space and A be the event of a class having 2 left-handed students. n(S) = 30 n(A) = 5

b) Let B be the event of a class having at least 3 left-handed students. n(B) = 12 + 8 + 2 = 22

c) First find the total number of left-handed students:

Total no. of left-handed students = 2 + 10 + 36 + 32 + 10 = 90

Here, the sample space is the total number of students in the 30 classes, which was given as 960.

Let T be the sample space and C be the event that a student is left-handed. n(T) = 960 n(C) = 90

Probability And Area

Example: ABCD is a square. M is the midpoint of BC and N is the midpoint of CD. A point is selected at random in the square. Calculate the probability that it lies in the triangle MCN.

Area of square = 2x × 2x = 4x 2

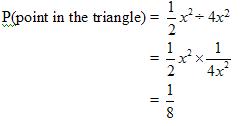
This video shows some examples of probability based on area.

Probability Of Simple Events

The following video shows some examples of probability problems. A few examples of calculating the probability of simple events.

• What is the probability of the next person you meeting having a phone number that ends in 5?
• What is the probability of getting all heads if you flip 3 coins?
• What is the probability that the person you meet next has a birthday in February? (Non-leap year)

This video introduces probability and gives many examples to determine the probability of basic events.

A bag contains 8 marbles numbered 1 to 8 a. What is the probability of selecting a 2 from the bag? b. What is the probability of selecting an odd number? c. What is the probability of selecting a number greater than 6?

Using a standard deck of cards, determine each probability. a. P(face card) b. P(5) c. P(non face card)

Using Permutations To Solve Probability Problems

This video shows how to evaluate factorials, how to use permutations to solve probability problems, and how to determine the number of permutations with indistinguishable items.

A permutation is an arrangement or ordering. For a permutation, the order matters.

• If a class has 28 students, how many different arrangements can 5 students give a presentation to the class?
• How many ways can the letters of the word PHEONIX be arranged?
• How many ways can you order 3 blue marbles, 4 red marbles and 5 green marbles? Marbles of the same color look identical.

Using Combinations To Solve Probability Problems

This video shows how to evaluate combinations and how to use combinations to solve probability problems.

A combination is a grouping or subset of items. For a combination, the order does not matter.

• The soccer team has 20 players. There are always 11 players on the field. How many different groups of players can be in the field at the same time?
• A student needs 8 more classes to complete her degree. If she has met the prerequisites for all the courses, how many ways can she take 4 class next semester?
• There are 4 men and 5 women in a small office. The customer wants a site visit from a group of 2 men and 2 women. How many different groups van be formed from the office?

How To Find The Probability Of Different Events?

This video explains how to determine the probability of different events. This can be found that can be found using combinations and basic probability.

• The probability of drawing 2 cards that are both face cards.
• The probability of drawing 2 cards that are both aces.
• The probability of drawing 4 cards all from the same suite.

A group of 10 students made up of 6 females and 4 males form a committee of 4. What is the probability the committee is all male? What is the probability that the committee is all female? What is the probability the committee is made up of 2 females and 2 males?

How To Find The Probability Of Multiple Independent Events?

This video explains the counting principle and how to determine the number of ways multiple independent events can occur.

• How many ways can students answer a 3-question true of false quiz?
• How many passwords using 6 digits where the first digit must be letters and the last four digits must be numbers?
• A restaurant offers a dinner special in which you get to pick 1 item from 4 different categories. How many different meals are possible?
• A door lock on a classroom requires entry of 4 digits. All digits must be numbers, but the digits can not be repeated. How many unique codes are possible?

How To Find The Probability Of A Union Of Two Events?

This video shows how to determine the probability of a union of two events.

• If you roll 2 dice at the same time, what is the probability the sum is 6 or a pair of odd numbers?
• What is the probability of selecting 1 card that is red or a face card?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin

When a coin is tossed, there are two possible outcomes:

Heads (H) or Tails (T)

• the probability of the coin landing H is ½
• the probability of the coin landing T is ½

Throwing Dice

When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6 .

The probability of any one of them is 1 6

In general:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 1 6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 4 5 = 0.8

Probability Line

We can show probability on a Probability Line :

Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we can expect 50 Heads .

But when we actually try it we might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index .

Some words have special meaning in Probability:

Experiment : a repeatable procedure with a set of possible results.

Example: Throwing dice

We can throw the dice again and again, so it is repeatable.

The set of possible results from any single throw is {1, 2, 3, 4, 5, 6}

Outcome: A possible result.

Example: "6" is one of the outcomes of a throw of a die.

Trial: A single performance of an experiment.

Example: I conducted a coin toss experiment. After 4 trials I got these results:

Three trials had the outcome "Head", and one trial had the outcome "Tail"

Sample Space: all the possible outcomes of an experiment.

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)

So the Sample Space is all 52 possible cards : {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

• the 5 of Clubs is a sample point
• the King of Hearts is a sample point

"King" is not a sample point. There are 4 Kings, so that is 4 different sample points.

There are 6 different sample points in that sample space.

Event: one or more outcomes of an experiment

Example Events:

An event can be just one outcome:

• Getting a Tail when tossing a coin
• Rolling a "5"

An event can include more than one outcome:

• Choosing a "King" from a deck of cards (any of the 4 Kings)
• Rolling an "even number" (2, 4 or 6)

Hey, let's use those words, so you get used to them:

Example: Alex wants to see how many times a "double" comes up when throwing 2 dice.

The Sample Space is all possible Outcomes (36 Sample Points):

{1,1} {1,2} {1,3} {1,4} ... ... ... {6,3} {6,4} {6,5} {6,6}

The Event Alex is looking for is a "double", where both dice have the same number. It is made up of these 6 Sample Points :

{1,1} {2,2} {3,3} {4,4} {5,5} and {6,6}

These are Alex's Results:

 After 100 Trials , Alex has 19 "double" Events ... is that close to what you would expect?

Probability

Probability defines the likelihood of occurrence of an event. There are many real-life situations in which we may have to predict the outcome of an event. We may be sure or not sure of the results of an event. In such cases, we say that there is a probability of this event to occur or not occur. Probability generally has great applications in games, in business to make predictions, and also it has extensive applications in this new area of artificial intelligence.

The probability of an event can be calculated by the probability formula by simply dividing the favourable number of outcomes by the total number of possible outcomes. The value of the probability of an event happening can lie between 0 and 1 because the favourable number of outcomes can never be more than the total number of outcomes. Also, the favorable number of outcomes cannot be negative. Let us discuss the basics of probability in detail in the following sections.

What is Probability?

Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event. For an experiment having 'n' number of outcomes, the number of favorable outcomes can be denoted by x. The formula to calculate the probability of an event is as follows.

Probability(Event) = Favorable Outcomes/Total Outcomes = x/n

Probability is used to predict the outcomes for the tossing of coins, rolling of dice, or drawing a card from a pack of playing cards. The probability is classified into two types:

• Theoretical probability
• Experimental probability

To understand each of these types, click on the respective links.

Terminology of Probability Theory

The following terms in probability theorey help in a better understanding of the concepts of probability.

Experiment: A trial or an operation conducted to produce an outcome is called an experiment.

Sample Space: All the possible outcomes of an experiment together constitute a sample space . For example, the sample space of tossing a coin is {head, tail}.

Favorable Outcome: An event that has produced the desired result or expected event is called a favorable outcome. For example, when we roll two dice, the possible/favorable outcomes of getting the sum of numbers on the two dice as 4 are (1,3), (2,2), and (3,1).

Trial: A trial denotes doing a random experiment.

Random Experiment: An experiment that has a well-defined set of outcomes is called a random experiment . For example, when we toss a coin, we know that we would get ahead or tail, but we are not sure which one will appear.

Event: The total number of outcomes of a random experiment is called an event .

Equally Likely Events: Events that have the same chances or probability of occurring are called equally likely events. The outcome of one event is independent of the other. For example, when we toss a coin, there are equal chances of getting a head or a tail.

Exhaustive Events: When the set of all outcomes of an event is equal to the sample space, we call it an exhaustive event .

Mutually Exclusive Events: Events that cannot happen simultaneously are called mutually exclusive events . For example, the climate can be either hot or cold. We cannot experience the same weather simultaneously.

Events in Probability

In probability theory, an event is a set of outcomes of an experiment or a subset of the sample space. If P(E) represents the probability of an event E, then, we have,

• P(E) = 0 if and only if E is an impossible event.
• P(E) = 1 if and only if E is a certain event.
• 0 ≤ P(E) ≤ 1.

Suppose, we are given two events, "A" and "B", then the probability of event A, P(A) > P(B) if and only if event "A" is more likely to occur than the event "B". Sample space(S) is the set of all of the possible outcomes of an experiment and n(S) represents the number of outcomes in the sample space.

P(E) = n(E)/n(S)

P(E’) = (n(S) - n(E))/n(S) = 1 - (n(E)/n(S))

E’ represents that the event will not occur.

Therefore, now we can also conclude that, P(E) + P(E’) = 1

Probability Formula

The probability equation defines the likelihood of the happening of an event. It is the ratio of favorable outcomes to the total favorable outcomes. The probability formula can be expressed as,

i.e., P(A) = n(A)/n(S)

• P(A) is the probability of an event 'B'.
• n(A) is the number of favorable outcomes of an event 'B'.
• n(S) is the total number of events occurring in a sample space.

Different Probability Formulas

Probability formula with addition rule : Whenever an event is the union of two other events, say A and B, then P(A or B) = P(A) + P(B) - P(A∩B) P(A ∪ B) = P(A) + P(B) - P(A∩B)

Probability formula with the complementary rule: Whenever an event is the complement of another event, specifically, if A is an event, then P(not A) = 1 - P(A) or P(A') = 1 - P(A). P(A) + P(A′) = 1.

Probability formula with the conditional rule : When event A is already known to have occurred, the probability of event B is known as conditional probability and is given by: P(B∣A) = P(A∩B)/P(A)

Probability formula with multiplication rule : Whenever an event is the intersection of two other events, that is, events A and B need to occur simultaneously. Then

• P(A ∩ B) = P(A)⋅P(B) (in case of independent events )
• P(A∩B) = P(A)⋅P(B∣A) (in case of dependent events )

Calculating Probability

In an experiment, the probability of an event is the possibility of that event occurring. The probability of any event is a value between (and including) "0" and "1". Follow the steps below for calculating probability of an event A:

• Step 1: Find the sample space of the experiment and count the elements. Denote it by n(S).
• Step 2: Find the number of favorable outcomes and denote it by n(A).
• Step 3: To find probability, divide n(A) by n(S). i.e., P(A) = n(A)/n(S).

Here are some examples that well describe the process of finding probability.

Example 1 : Find the probability of getting a number less than 5 when a dice is rolled by using the probability formula.

To find: Probability of getting a number less than 5 Given: Sample space, S = {1,2,3,4,5,6} Therefore, n(S) = 6

Let A be the event of getting a number less than 5. Then A = {1,2,3,4} So, n(A) = 4

Using the probability equation, P(A) = (n(A))/(n(s)) p(A) = 4/6 m = 2/3

Answer: The probability of getting a number less than 5 is 2/3.

Example 2: What is the probability of getting a sum of 9 when two dice are thrown?

There is a total of 36 possibilities when we throw two dice. To get the desired outcome i.e., 9, we can have the following favorable outcomes. (4,5),(5,4),(6,3)(3,6). There are 4 favorable outcomes. Probability of an event P(E) = (Number of favorable outcomes) ÷ (Total outcomes in a sample space) Probability of getting number 9 = 4 ÷ 36 = 1/9

Answer: Therefore the probability of getting a sum of 9 is 1/9.

Probability Tree Diagram

A tree diagram in probability is a visual representation that helps in finding the possible outcomes or the probability of any event occurring or not occurring. The tree diagram for the toss of a coin given below helps in understanding the possible outcomes when a coin is tossed. Each branch of the tree is associated with the respective probability (just like how 0.5 is written on each brack in the figure below). Remember that the sum of probabilities of all branches that start from the same point is always 1 (here, 0.5 + 0.5 = 1).

Types of Probability

There can be different perspectives or types of probabilities based on the nature of the outcome or the approach followed while finding probability of an event happening. The four types of probabilities are,

Classical Probability

Empirical probability, subjective probability, axiomatic probability.

Classical probability, often referred to as the "priori" or "theoretical probability", states that in an experiment where there are B equally likely outcomes, and event X has exactly A of these outcomes, then the probability of X is A/B, or P(X) = A/B. For example, when a fair die is rolled, there are six possible outcomes that are equally likely. That means, there is a 1/6 probability of rolling each number on the die.

The empirical probability or the experimental perspective evaluates probability through thought experiments. For example, if a weighted die is rolled, such that we don't know which side has the weight, then we can get an idea for the probability of each outcome by rolling the die number of times and calculating the proportion of times the die gives that outcome and thus find the probability of that outcome.

Subjective probability considers an individual's own belief of an event occurring. For example, the probability of a particular team winning a football match on a fan's opinion is more dependent upon their own belief and feeling and not on a formal mathematical calculation.

In axiomatic probability, a set of rules or axioms by Kolmogorov are applied to all the types. The chances of occurrence or non-occurrence of any event can be quantified by the applications of these axioms, given as,

• The smallest possible probability is zero, and the largest is one.
• An event that is certain has a probability equal to one.
• Any two mutually exclusive events cannot occur simultaneously, while the union of events says only one of them can occur.

Coin Toss Probability

Let us now look into the probability of tossing a coin . Quite often in games like cricket, for making a decision as to who would bowl or bat first, we sometimes use the tossing of a coin and decide based on the outcome of the toss. Let us check how we can use the concept of probability in the tossing of a single coin. Further, we shall also look into the tossing of two and three coins.

Tossing a Coin

A single coin on tossing has two outcomes, a head, and a tail. The concept of probability which is the ratio of favorable outcomes to the total number of outcomes can be used in finding probability of getting the head and the probability of getting a tail.

Total number of possible outcomes = 2; Sample Space = {H, T}; H: Head, T: Tail

• P(H) = Number of heads/Total outcomes = 1/2
• P(T)= Number of Tails/ Total outcomes = 1/2

Tossing Two Coins

In the process of tossing two coins, we have a total of four (= 2 2 ) outcomes. The probability formula can be used to find the probability of two heads, one head, no head, and a similar probability can be calculated for the number of tails. The probability calculations for the two heads are as follows.

Total number of outcomes = 4; Sample Space = {(H, H), (H, T), (T, H), (T, T)}

• P(2H) = P(0 T) = Number of outcome with two heads/Total Outcomes = 1/4
• P(1H) = P(1T) = Number of outcomes with only one head/Total Outcomes = 2/4 = 1/2
• P(0H) = (2T) = Number of outcome with two heads/Total Outcomes = 1/4

Tossing Three Coins

The number of total outcomes on tossing three coins simultaneously is equal to 2 3 = 8. For these outcomes, we can find the probability of getting one head, two heads, three heads, and no head. A similar probability can also be calculated for the number of tails.

Total number of outcomes = 2 3 = 8 Sample Space = {(H, H, H), (H, H, T), (H, T, H), (T, H, H), (T, T, H), (T, H, T), (H, T, T), (T, T, T)}

• P(0H) = P(3T) = Number of outcomes with no heads/Total Outcomes = 1/8
• P(1H) = P(2T) = Number of Outcomes with one head/Total Outcomes = 3/8
• P(2H) = P(1T) = Number of outcomes with two heads /Total Outcomes = 3/8
• P(3H) = P(0T) = Number of outcomes with three heads/Total Outcomes = 1/8

Dice Roll Probability

Many games use dice to decide the moves of players across the games. A dice has six possible outcomes and the outcomes of a dice is a game of chance and can be obtained by using the concepts of probability. Some games also use two dice, and there are numerous probabilities that can be calculated for outcomes using two dice. Let us now check the outcomes, their probabilities for one dice and two dice respectively.

Rolling One Dice

The total number of outcomes on rolling a die is 6, and the sample space is {1, 2, 3, 4, 5, 6}. Here we shall compute the following few probabilities to help in better understanding the concept of probability on rolling one dice.

• P( Even Number ) = Number of even number outcomes/Total Outcomes = 3/6 = 1/2
• P( Odd Number ) = Number of odd number outcomes/Total Outcomes = 3/6 = 1/2
• P( Prime Number ) = Number of prime number outcomes/Total Outcomes = 3/6 = 1/2

Rolling Two Dice

The total number of outcomes on rolling two dice is 6 2 = 36. The following image shows the sample space of 36 outcomes on rolling two dice.

Let us check a few probabilities of the outcomes from two dice. The probabilities are as follows.

• Probability of getting a doublet(Same number) = 6/36 = 1/6
• Probability of getting a number 3 on at least one dice = 11/36
• Probability of getting a sum of 7 = 6/36 = 1/6

As we see, when we roll a single die, there are 6 possibilities. When we roll two dice, there are 36 (= 6 2 ) possibilities. When we roll 3 dice we get 216 (= 6 3 ) possibilities. So a general formula to represent the number of outcomes on rolling 'n' dice is 6 n .

Probability of Drawing Cards

A deck containing 52 cards is grouped into four suits of clubs, diamonds, hearts, and spades. Each of the clubs, diamonds, hearts, and spades have 13 cards each, which sum up to 52. Now let us discuss the probability of drawing cards from a pack. The symbols on the cards are shown below. Spades and clubs are black cards. Hearts and diamonds are red cards.

The 13 cards in each suit are ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, king. In these, the jack, the queen, and the king are called face cards. We can understand the card probability from the following examples.

• The probability of drawing a black card is P(Black card) = 26/52 = 1/2
• The probability of drawing a hearts card is P(Hearts) = 13/52 = 1/4
• The probability of drawing a face card is P(Face card) = 12/52 = 3/13
• The probability of drawing a card numbered 4 is P(4) = 4/52 = 1/13
• The probability of drawing a red card numbered 4 is P(4 Red) = 2/52 = 1/26

Probability Theorems

The following theorems of probability are helpful to understand the applications of probability and also perform the numerous calculations involving probability.

Theorem 1: The sum of the probability of happening of an event and not happening of an event is equal to 1. P(A) + P(A') = 1.

Theorem 2: The probability of an impossible event or the probability of an event not happening is always equal to 0. P(ϕ) = 0.

Theorem 3: The probability of a sure event is always equal to 1. P(A) = 1

Theorem 4: The probability of happening of any event always lies between 0 and 1. 0 < P(A) < 1

Theorem 5: If there are two events A and B, we can apply the formula of the union of two sets and we can derive the formula for the probability of happening of event A or event B as follows.

P(A∪B) = P(A) + P(B) - P(A∩B)

Also for two mutually exclusive events A and B, we have P( A U B) = P(A) + P(B)

Bayes' Theorem on Conditional Probability

Bayes' theorem describes the probability of an event based on the condition of occurrence of other events. It is also called conditional probability . It helps in calculating the probability of happening of one event based on the condition of happening of another event.

For example, let us assume that there are three bags with each bag containing some blue, green, and yellow balls. What is the probability of picking a yellow ball from the third bag? Since there are blue and green colored balls also, we can arrive at the probability based on these conditions also. Such a probability is called conditional probability.

The formula for Bayes' theorem is \(\begin{align}P(A|B) = \dfrac{ P(B|A)·P(A)} {P(B)}\end{align}\)

where, \(\begin{align}P(A|B) \end{align}\) denotes how often event A happens on a condition that B happens.

where, \(\begin{align}P(B|A) \end{align}\) denotes how often event B happens on a condition that A happens.

\(\begin{align}P(A) \end{align}\) the likelihood of occurrence of event A.

\(\begin{align}P(B) \end{align}\) the likelihood of occurrence of event B.

Law of Total Probability

If there are n number of events in an experiment, then the sum of the probabilities of those n events is always equal to 1.

P(A 1 ) + P(A 2 ) + P(A 3 ) + … + P(A n ) = 1

Important Notes on Probability:

• Probability is a measure of how likely an event is to happen.
• Probability is represented as a fraction and always lies between 0 and 1.
• An event can be defined as a subset of sample space.
• The sample of throwing a coin is {head, tail} and the sample space of throwing dice is {1, 2, 3, 4, 5, 6}.
• A random experiment cannot predict the exact outcomes but only some probable outcomes.

☛ Related Articles:

• Event Probability Calculator
• Probability and Statistics
• Probability Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Probability Examples

Example 1: What is the probability of getting a sum of 10 when two dice are thrown?

There are 36 possibilities when we throw two dice.

The desired outcome is 10. To get 10, we can have three favorable outcomes.

{(4,6),(6,4),(5,5)}

Probability of an event = number of favorable outcomes/ sample space

Probability of getting number 10 = 3/36 =1/12

Answer: Therefore the probability of getting a sum of 10 is 1/12.

Example 2: In a bag, there are 6 blue balls and 8 yellow balls. One ball is selected randomly from the bag. Find the probability of getting a blue ball.

Let us assume the probability of drawing a blue ball to be P(B)

Number of favorable outcomes to get a blue ball = 6

Total number of balls in the bag = 14

P(B) = Number of favorable outcomes/Total number of outcomes = 6/14 = 3/7

Answer: Therefore the probability of drawing a blue ball is 3/7.

Example 3: There are 5 cards numbered: 2, 3, 4, 5, 6. Find the probability of picking a prime number, and putting it back, you pick a composite number.

The two events are independent. Thus we use the product of the probability of the events.

P(getting a prime) = n(favorable events)/ n(sample space) = {2, 3, 5}/{2, 3, 4, 5, 6} = 3/5

p(getting a composite) = n(favorable events)/ n(sample space) = {4, 6}/{2, 3, 4, 5, 6}= 2/5

Thus the total probability of the two independent events = P(prime) × P(composite)

= 3/5 × (2/5)

Answer: Therefore the probability of picking a prime number and a prime number again is 6/25.

Example 4: Find the probability of getting a face card from a standard deck of cards using the probability equation.

Solution: To find: Probability of getting a face card Given: Total number of cards = 52 Number of face cards = Favorable outcomes = 12 Using the probability formula, Probability = (Favorable Outcomes)÷(Total Favourable Outcomes) P(face card) = 12/52 m = 3/13

Answer: The probability of getting a face card is 3/13

go to slide go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Probability

go to slide go to slide

FAQs on Probability

What is the meaning of probability in statistics.

Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. Probability measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty.

How to Find Probability?

The probability can be found by first knowing the sample space of the outcomes of an experiment. A probability is generally calculated for an event (x) within the sample space. The probability of an event happening is obtained by dividing the number of outcomes of an event by the total number of possible outcomes or sample space.

What are the Three Types of Probability?

The three types of probabilities are theoretical probability, experimental probability, and axiomatic probability. The theoretical probability calculates the probability based on formulas and input values. The experimental probability gives a realistic value and is based on the experimental values for calculation. Quite often the theoretical and experimental probability differ in their results. And the axiomatic probability is based on the axioms which govern the concepts of probability.

How To Calculate Probability?

The probability of any event depends upon the number of favorable outcomes and the total outcomes. Finding probability is finding the ratio of the number of favorable outcomes to the total outcomes in that sample space. It is expressed as, Probability of an event P(E) = (Number of favorable outcomes) ÷ (Number of Elements in Sample space).

What is Conditional Probability?

The conditional probability predicts the happening of one event based on the happening of another event. If there are two events A and B, conditional probability is a chance of occurrence of event B provided the event A has already occurred. The formula for the conditional probability of happening of event B, given that event A, has happened is P(B/A) = P(A ∩ B)/P(A).

What is Experimental Probability?

The experimental probability is based on the results and the values obtained from the probability experiments. Experimental probability is defined as the ratio of the total number of times an event has occurred to the total number of trials conducted. The results of the experimental probability are based on real-life instances and may differ in values from theoretical probability.

What is a Probability Distribution?

The two important probability distributions are binomial distribution and Poisson distribution. The binomial distribution is defined for events with two probability outcomes and for events with a multiple number of times of such events. The Poisson distribution is based on the numerous probability outcomes in a limited space of time, distance, sample space. An example of the binomial distribution is the tossing of a coin with two outcomes, and for conducting such a tossing experiment with n number of coins. A Poisson distribution is for events such as antigen detection in a plasma sample, where the probabilities are numerous.

How are Probability and Statistics Related?

The probability calculates the happening of an experiment and it calculates the happening of a particular event with respect to the entire set of events. For simple events of a few numbers of events, it is easy to calculate the probability. But for calculating probabilities involving numerous events and to manage huge data relating to those events we need the help of statistics . Statistics helps in rightly analyzing

How Probability is Used in Real Life?

Probability has huge applications in games and analysis. Also in real life and industry areas where it is about prediction we make use of probability. The prediction of the price of a stock, or the performance of a team in cricket requires the use of probability concepts. Further, the new technology field of artificial intelligence is extensively based on probability.

Where Do We Use the Probability Formula In Our Real Life?

The following activities in our real-life tend to follow the probability equation:

• Weather forecasting
• Playing cards
• Voting strategy in politics
• Rolling a dice.
• Pulling out the exact matching socks of the same color
• Chances of winning or losing in any sports.

How was Probability Discovered?

The use of the word "probable" started first in the seventeenth century when it was referred to actions or opinions which were held by sensible people. Further, the word probable in the legal content was referred to a proposition that had tangible proof. The field of permutations and combinations, statistical inference, cryptoanalysis, frequency analysis have altogether contributed to this current field of probability.

What is the Conditional Probability Formula?

The conditional probability depends upon the happening of one event based on the happening of another event. The conditional probability formula of happening of event B, given that event A, has already happened is expressed as P(B/A) = P(A ∩ B)/P(A).

Teach yourself statistics

ProbabilityTutorial

Applied researchers make decisions under uncertainty. Probability theory makes it possible for researchers to quantify the extent of uncertainty inherent in their conclusions and inferences.

About the Tutorial

This tutorial covers the essence of probabilty theory clearly and simply in just a few short lessons. The tutorial focuses on six topics:

• Probability basics. To solve probability problems, it helps to know about sets, subsets, and statistical experiments.
• Probability problems. To solve probability problems, you need to understand the rules of probability; and you need to know how to count data points.
• Poker probability. To compute probabilities for poker hands, you rely on fundamental principles in probability. It's a great way to build analytical skill, and it's fun.
• Random variables. Random variables are at the heart of probability. They can be characterized by central tendency, variability, and a probability distribution.
• Discrete probability distributions. How to work with binomial, hypergeometric, multinomial, negative binomial, and Poisson distributions.
• Continuous probability distributions. How to work with normal, standard normal, chi-square, t-, and f-distributions.

This tutorial is designed for students and researchers who have some familiarity with introductory statistics (e.g., a high school statistics course or Advanced Placement Statistics ).

How to Use This Tutorial

Individual lessons are accessible through the table of contents, which can be found in the vertical column on the left side of the page. You should work through lessons in the order in which they appear; because some lessons build on previous lessons.

Individual lessons are accessible through the table of contents, which can be accessed by tapping the "Probability: Table of Contents" button at the top of the page. You should work through lessons in the order in which they appear; because some lessons build on previous lessons.

Additional Helpful Resources

As you progress through the tutorial, take advantage of the following helpful resources.

• Analytical tools . Stat Trek provides a variety of analytical tools - online statistical tables, calculators, problem solvers - to take the drudgery out of computations. The tutorial will alert you to these tools, all of which are free.
• Sample problems . Most of the lessons include sample problems. The sample problems help you test your knowledge. They also illustrate shortcuts and solutions to common statistics problems.
• Jargon interpreter . Stat Trek's online Statistics Dictionary takes the mystery out of statistical jargon. If any term or concept is unclear, visit the dictionary for additional explanation.

Note : The dictionary can be accessed by clicking the Help tab in the main menu (located at the top of this web page).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.2: Combining Probabilities with “And” and “Or”

• Last updated
• Save as PDF
• Page ID 22318

• Maxie Inigo, Jennifer Jameson, Kathryn Kozak, Maya Lanzetta, & Kim Sonier
• Coconino Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Many probabilities in real life involve more than one outcome. If we draw a single card from a deck we might want to know the probability that it is either red or a jack. If we look at a group of students, we might want to know the probability that a single student has brown hair and blue eyes. When we combine two outcomes to make a single event we connect the outcomes with the word “and” or the word “or.” It is very important in probability to pay attention to the words “and” and “or” if they appear in a problem. The word “and” restricts the field of possible outcomes to only those outcomes that simultaneously satisfy more than one event. The word “or” broadens the field of possible outcomes to those that satisfy one or more events.

Example \(\PageIndex{1}\): Counting Students

Suppose a teacher wants to know the probability that a single student in her class of 30 students is taking either Art or English. She asks the class to raise their hands if they are taking Art and counts 13 hands. Then she asks the class to raise their hands if they are taking English and counts 21 hands. The teacher then calculates

\[P(\text{Art or English}) = \dfrac{13+21}{30} = \dfrac{33}{30} \nonumber \]

The teacher knows that this is wrong because probabilities must be between zero and one, inclusive. After thinking about it she remembers that nine students are taking both Art and English. These students raised their hands each time she counted, so the teacher counted them twice. When we calculate probabilities we have to be careful to count each outcome only once.

Mutually Exclusive Events

An experiment consists of drawing one card from a well shuffled deck of 52 cards. Consider the events E : the card is red, F : the card is a five, and G : the card is a spade. It is possible for a card to be both red and a five at the same time but it is not possible for a card to be both red and a spade at the same time. It would be easy to accidentally count a red five twice by mistake. It is not possible to count a red spade twice.

Definition: Mutually Exclusive

Two events are mutually exclusive if they have no outcomes in common.

Example \(\PageIndex{2}\): Mutually Exclusive with Dice

Two fair dice are tossed and different events are recorded. Let the events E , F and G be as follows:

• E = {the sum is five} = {(1, 4), (2, 3), (3, 2), (4, 1)}
• F = {both numbers are even} = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
• G = {both numbers are less than five} = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4,1), (4, 2), (4, 3), (4,4)}
• Are events E and F mutually exclusive?

Yes. E and F are mutually exclusive because they have no outcomes in common. It is not possible to add two even numbers to get a sum of five.

• Are events E and G mutually exclusive?

No. E and G are not mutually exclusive because they have some outcomes in common. The pairs (1, 4), (2, 3), (3, 2) and (4, 1) all have sums of 5 and both numbers are less than five.

• Are events F and G mutually exclusive?

No. F and G are not mutually exclusive because they have some outcomes in common. The pairs (2, 2), (2, 4), (4, 2) and (4, 4) all have two even numbers that are less than five.

Addition Rule for “Or” Probabilities

The addition rule for probabilities is used when the events are connected by the word “or”. Remember our teacher in Example \(\PageIndex{1}\) at the beginning of the section? She wanted to know the probability that her students were taking either art or English. Her problem was that she counted some students twice. She needed to add the number of students taking art to the number of students taking English and then subtract the number of students she counted twice. After dividing the result by the total number of students she will find the desired probability. The calculation is as follows:

\[ \begin{align*} P(\text{art or English}) &= \dfrac{\# \text{ taking art + } \# \text{ taking English - } \# \text{ taking both}}{\text{total number of students}} \\[4pt] &= \dfrac{13+21-9}{30} \\[4pt] &= \dfrac{25}{30} \approx {0.833} \end{align*} \nonumber \]

The probability that a student is taking art or English is 0.833 or 83.3%.

When we calculate the probability for compound events connected by the word “or” we need to be careful not to count the same thing twice. If we want the probability of drawing a red card or a five we cannot count the red fives twice. If we want the probability a person is blonde-haired or blue-eyed we cannot count the blue-eyed blondes twice. The addition rule for probabilities adds the number of blonde-haired people to the number of blue-eyed people then subtracts the number of people we counted twice.

If A and B are any events then

\[P(A\, \text{or}\, B) = P(A) + P(B) – P(A \,\text{and}\, B). \nonumber \]

If A and B are mutually exclusive events then \(P(A \,\text{and}\, B) = 0\), so then

\[P(A \, \text{or}\, B) = P(A) + P(B). \nonumber \]

Example \(\PageIndex{3}\): Additional Rule for Drawing Cards

A single card is drawn from a well shuffled deck of 52 cards. Find the probability that the card is a club or a face card.

There are 13 cards that are clubs, 12 face cards (J, Q, K in each suit) and 3 face cards that are clubs.

\[ \begin{align*} P(\text{club or face card}) &= P(\text{club}) + P(\text{face card}) - P(\text{club and face card}) \\[4pt] &= \dfrac{13}{52} + \dfrac{12}{52} - \dfrac{3}{52} \\[4pt] &= \dfrac{22}{52} = \dfrac{11}{26} \approx {0.423} \end{align*} \nonumber \]

The probability that the card is a club or a face card is approximately 0.423 or 42.3%.

Example \(\PageIndex{4}\): Addition Rule for Tossing a Coin and Rolling a Die

An experiment consists of tossing a coin then rolling a die. Find the probability that the coin lands heads up or the number is five.

Let H represent heads up and T represent tails up. The sample space for this experiment is S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}.

• There are six ways the coin can land heads up, {H1, H2, H3, H4, H5, H6}.
• There are two ways the die can land on five, {H5, T5}.
• There is one way for the coin to land heads up and the die to land on five, {H5}.

\[ \begin{align*} P(\text{heads or five}) &= P(\text{heads}) + P(\text{five}) - P(\text{both heads and five}) \\[4pt] &= \dfrac{6}{12} + \dfrac{2}{12} - \dfrac{1}{12} \\[4pt] &= \dfrac{7}{12} = \approx {0.583} \end{align*} \nonumber \]

The probability that the coin lands heads up or the number is five is approximately 0.583 or 58.3%.

Example \(\PageIndex{5}\): Addition Rule for Satisfaction of Car Buyers

Two hundred fifty people who recently purchased a car were questioned and the results are summarized in the following table.

Find the probability that a person bought a new car or was not satisfied.

\[\begin{align*} P(\text{new car or not satisfied}) &= P(\text{new car}) + P(\text{not satisfied}) - P(\text{new car and not satisfied}) \\[4pt] &= \dfrac{120}{250} + \dfrac{75}{250} - \dfrac{28}{250} = \dfrac{167}{250} \approx 0.668 \end{align*} \nonumber \]

The probability that a person bought a new car or was not satisfied is approximately 0.668 or 66.8%.

Independent Events

Sometimes we need to calculate probabilities for compound events that are connected by the word “and.” We have two methods to choose from, independent events or conditional probabilities (Section 3.3). Tossing a coin multiple times or rolling dice are independent events. Each time you toss a fair coin the probability of getting heads is ½. It does not matter what happened the last time you tossed the coin. It’s similar for dice. If you rolled double sixes last time that does not change the probability that you will roll double sixes this time. Drawing two cards without replacement is not an independent event. When you draw the first card and set it aside, the probability for the second card is now out of 51 cards not 52 cards.

Definition: Independent Events

Two events are independent events if the occurrence of one event has no effect on the probability of the occurrence of the other event.

Multiplication Rule for “And” Probabilities: Independent Events

If events A and B are independent events, then \( P(\text{A and B}) = P(A) \cdot P(B)\).

Example \(\PageIndex{6}\): Independent Events for Tossing Coins

Suppose a fair coin is tossed four times. What is the probability that all four tosses land heads up?

The tosses of the coins are independent events. Knowing a head was tossed on the first trial does not change the probability of tossing a head on the second trial.

\(P(\text{four heads in a row}) = P(\text{1st heads and 2nd heads and 3rd heads and 4th heads})\)

\( = P(\text{1st heads}) \cdot P(\text{2nd heads}) \cdot P(\text{3rd heads}) \cdot P(\text{4th heads})\)

\( = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}\)

\( = \dfrac{1}{16}\)

The probability that all four tosses land heads up is \(\dfrac{1}{16}\).

Example \(\PageIndex{7}\): Independent Events for Drawing Marbles

A bag contains five red and four white marbles. A marble is drawn from the bag, its color recorded and the marble is returned to the bag. A second marble is then drawn. What is the probability that the first marble is red and the second marble is white?

Since the first marble is put back in the bag before the second marble is drawn these are independent events.

\[\begin{align*} P(\text{1st red and 2nd white}) &= P(\text{1st red}) \cdot P(\text{2nd white}) \\[4pt] &= \dfrac{5}{9} \cdot \dfrac{4}{9} = \dfrac{20}{81}\end{align*} \nonumber \]

The probability that the first marble is red and the second marble is white is \(\dfrac{20}{81}\).

Example \(\PageIndex{8}\): Independent Events for Faulty Alarm Clocks

Abby has an important meeting in the morning. She sets three battery-powered alarm clocks just to be safe. If each alarm clock has a 0.03 probability of malfunctioning, what is the probability that all three alarm clocks fail at the same time?

Since the clocks are battery powered we can assume that one failing will have no effect on the operation of the other two clocks. The functioning of the clocks is independent.

\[\begin{align*} P(\text{all three fail}) &= P(\text{first fails}) \cdot P(\text{second fails})\cdot P(\text{third fails}) \\[4pt] &= (0.03)(0.03)(0.03) \\[4pt] &= 2.7 \times 10^{-5} \end{align*} \nonumber \]

The probability that all three clocks will fail is approximately 0.000027 or 0.0027%. It is very unlikely that all three alarm clocks will fail.

At Least Once Rule for Independent Events

Many times we need to calculate the probability that an event will happen at least once in many trials. The calculation can get quite complicated if there are more than a couple of trials. Using the complement to calculate the probability can simplify the problem considerably. The following example will help you understand the formula.

Example \(\PageIndex{9}\): At Least Once Rule

The probability that a child forgets her homework on a given day is 0.15. What is the probability that she will forget her homework at least once in the next five days?

Assume that whether she forgets or not one day has no effect on whether she forgets or not the second day.

If P (forgets) = 0.15, then P (not forgets) = 0.85.

\[\begin{align*} P(\text{forgets at least once in 5 tries}) &= P(\text{forgets 1, 2, 3, 4 or 5 times in 5 tries}) \\[4pt] & = 1 - P(\text{forgets 0 times in 5 tries}) \\[4pt] &= 1 - P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \\[4pt] &= 1 - (0.85)(0.85)(0.85)(0.85)(0.85) \\[4pt] & = 1 - (0.85)^{5} = 0.556 \end{align*} \nonumber \]

The probability that the child will forget her homework at least one day in the next five days is 0.556 or 55.6%

The idea in Example \(\PageIndex{9}\) can be generalized to get the At Least Once Rule.

Definition: At Least Once Rule

If an experiment is repeated n times, the n trials are independent and the probability of event A occurring one time is P(A) then the probability that A occurs at least one time is: \(P(\text{A occurs at least once in n trials}) = 1 - P(\overline{A})^{n}\)

Example \(\PageIndex{10}\): At Least Once Rule for Bird Watching

The probability of seeing a falcon near the lake during a day of bird watching is 0.21. What is the probability that a birdwatcher will see a falcon at least once in eight trips to the lake?

Let A be the event that he sees a falcon so P(A) = 0.21. Then, \(P(\overline{A}) = 1 - 0.21 = 0.79\).

\(P(\text{at least once in eight tries}) = 1 - P(\overline{A})^{8}\)

\( = 1 - (0.79)^{8}\)

\( = 1 - (0.152) = 0.848\)

The probability of seeing a falcon at least once in eight trips to the lake is approximately 0.848 or 84.8%.

Example \(\PageIndex{11}\): At Least Once Rule for Guessing on Multiple Choice Tests

A multiple choice test consists of six questions. Each question has four choices for answers, only one of which is correct. A student guesses on all six questions. What is the probability that he gets at least one answer correct?

Let A be the event that the answer to a question is correct. Since each question has four choices and only one correct choice, \(P(\text{correct}) = \dfrac{1}{4}\).

That means \(P(\text{not correct}) =1 - \dfrac{1}{4} = \dfrac{3}{4}\).

\[ \begin{align*} P(\text{at least one correct in six trials}) &= 1 - P(\text{not correct})^{6} \\[4pt] &= 1 - \left(\dfrac{3}{4}\right)^{6} \\[4pt] &= 1 - (0.178) = 0.822 \end{align*} \nonumber \]

The probability that he gets at least one answer correct is 0.822 or 82.2%.

“And” Probabilities from Two-Way Tables

“And” probabilities are usually done by one of two methods. If you know the events are independent you can use the rule \(P(A \text{and } B) = P(A) \cdot P(B)\). If the events are not independent you can use the conditional probabilities in Section 3.3. There is an exception when we have data given in a two-way table. We can calculate “and” probabilities without knowing if the events are independent or not.

Example \(\PageIndex{12}\): “And” Probability from a Two-Way Table

Continuation of Example \(\PageIndex{5}\):

A person is chosen at random. Find the probability that the person:

• bought a new car and was satisfied.

\[\begin{align*} P(\text{new car and satisfied}) &= \dfrac{\text{number of new car and satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{92}{250} = 0.368 = 36.8 \% \end{align*} \nonumber \]

• bought a used car and was not satisfied.

\[\begin{align*} P(\text{used car and not satisfied}) &= \dfrac{\text{number of used and not satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{47}{250} = 0.188 = 18.8 \% \end{align*} \nonumber \]

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

15 Probability Questions And Practice Problems for Middle and High School: Harder Exam Style Questions Included

Beki Christian

Probability questions and probability problems require students to work out how likely it is that something is to happen. Probabilities can be described using words or numbers. Probabilities range from 0 to 1 and can be written as fractions, decimals or percentages .

Here you’ll find a selection of probability questions of varying difficulty showing the variety you are likely to encounter in middle school and high school, including several harder exam style questions.

What are some real life examples of probability?

The more likely something is to happen, the higher its probability. We think about probabilities all the time.

For example, you may have seen that there is a 20% chance of rain on a certain day or thought about how likely you are to roll a 6 when playing a game, or to win in a raffle when you buy a ticket.

15 Probability Questions Worksheet

Get this 15 probability questions for your middle and high school students. Allows students tackle problems at their own pace and includes an answer key!

How to calculate probabilities

The probability of something happening is given by:

We can also use the following formula to help us calculate probabilities and solve problems:

• Probability of something not occuring = 1 – probability of if occurring P(not\;A) = 1 - P(A)
• For mutually exclusive events: Probability of event A OR event B occurring = Probability of event A + Probability of event B P(A\;or\;B) = P(A)+P(B)
• For independent events: Probability of event A AND event B occurring = Probability of event A times probability of event B P(A\;and\;B) = P(A) × P(B)

Probability question: A worked example

Question: What is the probability of getting heads three times in a row when flipping a coin?

When flipping a coin, there are two possible outcomes – heads or tails. Each of these options has the same probability of occurring during each flip. The probability of either heads or tails on a single coin flip is ½.

Since there are only two possible outcomes and they have the same probability of occurring, this is called a binomial distribution.

Let’s look at the possible outcomes if we flipped a coin three times.

Let H=heads and T=tails.

The possible outcomes are: HHH, THH, THT, HTT, HHT, HTH, TTH, TTT

Each of these outcomes has a probability of ⅛.

Therefore, the probability of flipping a coin three times in a row and having it land on heads all three times is ⅛.

Middle school probability questions

In middle school, probability questions introduce the idea of the probability scale and the fact that probabilities sum to one. We look at theoretical and experimental probability as well as learning about sample space diagrams and venn diagrams.

6th grade probability questions

1. Which number could be added to this spinner to make it more likely that the spinner will land on an odd number than a prime number?

Currently there are two odd numbers and two prime numbers so the chances of landing on an odd number or a prime number are the same. By adding 3, 5 or 11 you would be adding one prime number and one odd number so the chances would remain equal.

By adding 9 you would be adding an odd number but not a prime number. There would be three odd numbers and two prime numbers so the spinner would be more likely to land on an odd number than a prime number.

2. Ifan rolls a fair dice, with sides labeled A, B, C, D, E and F. What is the probability that the dice lands on a vowel?

A and E are vowels so there are 2 outcomes that are vowels out of 6 outcomes altogether.

Therefore the probability is   \frac{2}{6} which can be simplified to \frac{1}{3} .

7th grade probability questions

3. Max tested a coin to see whether it was fair. The table shows the results of his coin toss experiment:

Heads          Tails

    26                  41

What is the relative frequency of the coin landing on heads?

Max tossed the coin 67 times and it landed on heads 26 times.

\text{Relative frequency (experimental probability) } = \frac{\text{number of successful trials}}{\text{total number of trials}} = \frac{26}{67}

4. Grace rolled two dice. She then did something with the two numbers shown. Here is a sample space diagram showing all the possible outcomes:

What did Grace do with the two numbers shown on the dice?

Add them together

Subtract the number on dice 2 from the number on dice 1

Multiply them

Subtract the smaller number from the bigger number

For each pair of numbers, Grace subtracted the smaller number from the bigger number.

For example, if she rolled a 2 and a 5, she did 5 − 2 = 3.

8th grade probability questions

5. Alice has some red balls and some black balls in a bag. Altogether she has 25 balls. Alice picks one ball from the bag. The probability that Alice picks a red ball is x and the probability that Alice picks a black ball is 4x. Work out how many black balls are in the bag.

Since the probability of mutually exclusive events add to 1:  

\begin{aligned} x+4x&=1\\\\ 5x&=1\\\\ x&=\frac{1}{5} \end{aligned}

\frac{1}{5} of the balls are red and \frac{4}{5} of the balls are blue.

6. Arthur asked the students in his class whether they like math and whether they like science. He recorded his results in the venn diagram below.

How many students don’t like science?

We need to look at the numbers that are not in the ‘Like science’ circle. In this case it is 9 + 7 = 16.

High school probability questions

In high school, probability questions involve more problem solving to make predictions about the probability of an event. We also learn about probability tree diagrams, which can be used to represent multiple events, and conditional probability.

9th grade probability questions

7. A restaurant offers the following options:

Starter – soup or salad

Main – chicken, fish or vegetarian

Dessert – ice cream or cake

How many possible different combinations of starter, main and dessert are there?

The number of different combinations is 2 × 3 × 2 = 12.

8. There are 18 girls and 12 boys in a class. \frac{2}{9} of the girls and \frac{1}{4} of the boys walk to school. One of the students who walks to school is chosen at random. Find the probability that the student is a boy. 

First we need to work out how many students walk to school:

\frac{2}{9} \text{ of } 18 = 4

\frac{1}{4} \text{ of } 12 = 3

7 students walk to school. 4 are girls and 3 are boys. So the probability the student is a boy is \frac{3}{7} .

9. Rachel flips a biased coin. The probability that she gets two heads is 0.16. What is the probability that she gets two tails?

We have been given the probability of getting two heads. We need to calculate the probability of getting a head on each flip.

Let’s call the probability of getting a head p.

The probability p, of getting a head AND getting another head is 0.16.

Therefore to find p:

The probability of getting a head is 0.4 so the probability of getting a tail is 0.6.

The probability of getting two tails is 0.6 × 0.6 = 0.36 .

10th grade probability questions

10. I have a big tub of jelly beans. The probability of picking each different color of jelly bean is shown below:

If I were to pick 60 jelly beans from the tub, how many orange jelly beans would I expect to pick?

First we need to calculate the probability of picking an orange. Probabilities sum to 1 so 1 − (0.2 + 0.15 + 0.1 + 0.3) = 0.25.

The probability of picking an orange is 0.25.

The number of times I would expect to pick an orange jelly bean is 0.25 × 60 = 15 .

11. Dexter runs a game at a fair. To play the game, you must roll a dice and pick a card from a deck of cards.

To win the game you must roll an odd number and pick a picture card. The game can be represented by the tree diagram below.

Dexter charges players $1 to play and gives $3 to any winners. If 260 people play the game, how much profit would Dexter expect to make?

Completing the tree diagram:

Probability of winning is \frac{1}{2} \times \frac{4}{13} = \frac{4}{26}

If 260 play the game, Dexter would receive $260.

The expected number of winners would be \frac{4}{26} \times 260 = 40

Dexter would need to give away 40 × $3 = $120 .

Therefore Dexter’s profit would be $260 − $120 = $140.

12. A fair coin is tossed three times. Work out the probability of getting two heads and one tail.

There are three ways of getting two heads and one tail: HHT, HTH or THH.

The probability of each is \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} 

Therefore the total probability is \frac{1}{8} +\frac{1}{8} + \frac{1}{8} = \frac{3}{8}

11th/12th grade probability questions

13. 200 people were asked about which athletic event they thought was the most exciting to watch. The results are shown in the table below.

A person is chosen at random. Given that that person chose 100m, what is the probability that the person was female?

Since we know that the person chose 100m, we need to include the people in that column only.

In total 88 people chose 100m so the probability the person was female is \frac{32}{88}   .

14.   Sam asked 50 people whether they like vegetable pizza or pepperoni pizza.

37 people like vegetable pizza. 

25 people like both. 

3 people like neither.

Sam picked one of the 50 people at random. Given that the person he chose likes pepperoni pizza, find the probability that they don’t like vegetable pizza.

We need to draw a venn diagram to work this out.

We start by putting the 25 who like both in the middle section. The 37 people who like vegetable pizza includes the 25 who like both, so 12 more people must like vegetable pizza. 3 don’t like either. We have 50 – 12 – 25 – 3 = 10 people left so this is the number that must like only pepperoni.

There are 35 people altogether who like pepperoni pizza. Of these, 10 do not like vegetable pizza. The probability is   \frac{10}{35} .

15. There are 12 marbles in a bag. There are n red marbles and the rest are blue marbles. Nico takes 2 marbles from the bag. Write an expression involving n for the probability that Nico takes one red marble and one blue marble.

We need to think about this using a tree diagram. If there are 12 marbles altogether and n are red then 12-n are blue.

To get one red and one blue, Nico could choose red then blue or blue then red so the probability is:

Looking for more middle school and high school probability math questions?

• Ratio questions
• Algebra questions
• Trigonometry questions
• Venn diagram questions
• Long division questions
• Pythagorean theorem questions

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.

Related articles

15 Venn Diagram Questions And Practice Problems (Middle & High School): Exam Style Questions Included

9 Algebra Questions And Practice Problems To Do With Your Middle Schoolers

15 Trigonometry Questions And Practice Problems To Do With High Schoolers

Ratio Questions And Practice Problems: Differentiated Practice Questions Included

Solving Inequalities Questions [FREE]

Downloadable skills and applied questions about solving inequalities.

Includes 10 skills questions, 5 applied questions and an answer key. Print and share with your classes to support their learning.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• A\:fair\:coin\:is\:tossed\:four\:times\:what\:is\:the\:probability\:of\:obtaining\:at\:least\:three\:heads
• What\:is\:the\:probability\:of\:rolling\:2\:standard\:dice\:which\:sum\:to\:11
• One\:card\:is\:selected\:at\:random\:from\:a\:deck\:of\:cards.\:Determine\:the\:probability\:that\:the\:card\:selected\:is\:a\:9?

probability-problems-calculator

• Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 8: Counting, permutations, and combinations

About this unit.

How many outfits can you make from the shirts, pants, and socks in your closet? Address this question and more as you explore methods for counting how many possible outcomes there are in various situations. Learn about factorial, permutations, and combinations, and look at how to use these ideas to find probabilities.

Counting principle and factorial

• Count outcomes using tree diagram (Opens a modal)
• Counting outcomes: flower pots (Opens a modal)
• The counting principle Get 3 of 4 questions to level up!

Permutations

• Permutation formula (Opens a modal)
• Zero factorial or 0! (Opens a modal)
• Factorial and counting seat arrangements (Opens a modal)
• Possible three letter words (Opens a modal)
• Ways to arrange colors (Opens a modal)
• Ways to pick officers (Opens a modal)
• Permutations Get 3 of 4 questions to level up!

Combinations

• Intro to combinations (Opens a modal)
• Combination formula (Opens a modal)
• Handshaking combinations (Opens a modal)
• Combination example: 9 card hands (Opens a modal)
• Combinations Get 3 of 4 questions to level up!
• Permutations & combinations Get 5 of 7 questions to level up!

Combinatorics and probability

• Probability using combinations (Opens a modal)
• Probability & combinations (2 of 2) (Opens a modal)
• Example: Different ways to pick officers (Opens a modal)
• Example: Combinatorics and probability (Opens a modal)
• Getting exactly two heads (combinatorics) (Opens a modal)
• Exactly three heads in five flips (Opens a modal)
• Generalizing with binomial coefficients (bit advanced) (Opens a modal)
• Example: Lottery probability (Opens a modal)
• Conditional probability and combinations (Opens a modal)
• Mega millions jackpot probability (Opens a modal)
• Birthday probability problem (Opens a modal)
• Probability with permutations and combinations Get 3 of 4 questions to level up!