linear equations sat practice

SAT Math: Guide to Linear Equations

tl;dr: Learn how to solve Linear Equations in the SAT Math section with sample practice problems, solutions and advice. The main takeaways are that you need to be able to demonstrate your understanding of linear equations and their applications, convert between graphical and algebraic representations, analyze word problems, define and isolate key variables, write expressions, equations, and inequalities, and solve them.

‍ The SAT Math section contains approximately 60 questions, separated into:

• No-Calculator Section
• 15 Multiple Choice
• Calculator Section
• 30 Multiple Choice
• Total Time: 80 Minutes

These questions (both with-calculator and no-calculator) test on four major content areas : the Heart of Algebra , Problem Solving , Data Analysis , and the Passport to Advanced Math .

Linear Equations fall under the Heart of Algebra content section.

Topics Related to “Linear Equations”

• Systems of Linear Equations
• Linear Functions
• Linear Inequalities
• Graphical & Algebraic Manipulation
• Linear & Algebraic Reasoning

What You Have to Do

• Convey a thorough understanding of critical thinking, and multiple core concepts in Algebra, specifically:
• Linear Equations
• Demonstrate that you can convert between graphical representations of linear equations and their algebraic representations (and vice versa)
• Analyze word problems to manipulate and create linear equations to solve for different variables
• Be able to define and isolate key variables
• Be able to write expressions, equations, and inequalities
• Be able to solve linear equations and interpret the solution to apply it to the context of the problem

Sample Problem Section 📚

Non-calculator practice problems �

General directions for this section you should expect to see:

• The use of a calculator is not permitted.
• All variables and expressions used represent real numbers unless otherwise indicated.
• Figures provided in this test are drawn to scale unless otherwise indicated.
• All figures lie in a plane unless otherwise indicated.

1. In 2014, County X had 783 miles of paved roads. Starting in 2015, the county has been building 8 miles of new paved roads each year. At this rate, how many miles of paved road will County X have in 2030? (Assume that no paved roads go out of service.)

The correct answer is B.

AP College Board SAT Practice Problems

Solution & Advice 🚧

• Let’s break down this linear equation-based word problem and start with what we know!
• Our first step is to conclude which variables we need to define (also referred to as the variable we need to solve for!). Since this problem asks how many miles of paved road the county will have in 2030, our unknown variable will be the number of years after 2014!
• Our second step is to write our linear equation.

Let’s Break it Down!

⇒ Each year after 2014 (where the number of miles of paved roads has already been determined) can be represented with the variable x.

⇒ Since we already have 783 miles, the number of miles of paved roads in 2030 can be represented by 783 + 8*x , but what is x?

⇒ Glad you asked! Since x is the number of years after 2014, a quick calculation of 2030 (the year of interest) - 2014 (the current year), tells us that x = 16.

⇒ From here, we can plug this value into our linear expression!

⇒ 783 + 8(16) = 783 + 128 = 911 miles of paved roads in 2030.

Feeling good? Let’s try another one!

2. In 2014, County X had 783 miles of paved roads. Starting in 2015, the county has been building 8 miles of new paved roads each year. At this rate, in which year will County X have at least 1,000 miles of paved roads? (Assume that no paved roads go out of service.)

The correct answer is C.

Solution & Advice 🛣️

• Let’s break down this linear equation-based word problem and start off with what we know!
• Before we get started, let’s recognize a keyword-phrase hint: “At least.”
• Typically, the phrase “at least” indicates that you’ll be utilizing an inequality rather than an expression or equation.
• This question tests your ability to write linear expressions, differentiate between equations and inequalities, and translate word problems into equations.
• Just like in Equation 1, let’s let x represent the number of years after 2014.

⇒ Since we start with 783 miles, x is the number of years after 2014, and the rate of paving is 8 miles a year, our expression can be represented as 783 + 8n

⇒ This question asks when there'll be at least 1,000 miles of total paved roads in County X (not when an additional 1,000 miles will be paved).

⇒ Our inequality can be written as 783 + 8n >= 1000

⇒ Why isn’t it <, <=, or >? We aren’t looking for when the amount of total miles will be less than 1,000, and at least indicates that we can include 1,000 ; therefore it’s >=

⇒ 783 + 8n >=1000

⇒ 8n >= 217

⇒ n >= 27.125

⇒ Once we add 27.125 to 2014, we get 2041.125, which does not make sense in the context of the question. In the year 2041, only 999 miles of paved road exist in the county. Therefore, we need to round up to 2042 to have at least 1,000 miles of paved roads total!

Onto Question 3!

3. To edit a manuscript, Miguel charges $50 for the first 2 hours and $20 per hour after the first 2 hours. Which of the following expresses the amount, C, in dollars, Miguel charges if it takes him x hours to edit a manuscript, where x>2?

• C = 20x + 10
• C = 20x + 50
• C = 20x + 90

Solution & Advice 📝

• Miguel charges $50 for the first 2 hours and $20 only after the first 2 hours.
• Therefore, the remaining time can be represented by x-2 (since the first two hours are $50)
• Therefore, our equation is C = 50 + 20(x-2)

⇒ C = 50 + 20(x-2)

⇒ C = 50 + 20x - 40

⇒ C = 10 + 20x

⇒ C = 20x + 10, which is option B

Let’s try one more!

• -2x = 4y + 6

2(2y + 3) = 3x - 5

What is the solution (x,y) to the system of equations above?

Solution & Advice 🤝

• Let’s break down this system of linear equations and start off with what we know!
• This system of linear equations can be solved via substitution.
• Substitution is a method of solutions through isolating for one variable and plugging that answer into another equation
• Let’s start off with -2x = 4y + 6

⇒ -2x = 4y + 6 ⇒ let’s simplify this and divide all terms by 2!

⇒ -x = 2y + 3

⇒ x = -2y - 3

⇒ Now that we’ve isolated for x, we can plug this into the second equation and solve!

⇒ 2(2y + 3) = 3x - 5

⇒ 2(2y + 3) = 3(-2y - 3) - 5 ⇒ Since x = -2y - 3, we plugged in -2y - 3 in place of x

⇒ 4y + 6 = -6y - 9 - 5

⇒ 4y + 6 = -6y - 14

⇒ 10y = - 20

⇒ Now that we’ve solved for y, we can plug this back into our first equation!

⇒ -2x = 4y + 6

⇒ -2x = 4(-2) + 6

⇒ -2x = -8 + 6

⇒ Since x = 1 and y = -2, our answer is (1, -2)

TIP: Always plug your answer back into either the first or second equation (or both) to make sure they work! If your solution is correct, both sides of the equation should be equal

Excellent work!

Congratulations! You’ve made it to the end of this prep activity 🙌 You learned about “SAT Math: Linear Equations ” You should have a better understanding of the Math sections for the SAT© , topic highlights, what you will have to be able to do in order to succeed, as well as have seen some practice questions that put the concepts in action. Good luck studying for the SAT Math section 👏

Need more resources? Check out our complete SAT Math Study Guide w/ Practice Problems . You got this 🥳.

Guide Outline

Related content, sat math: guide to quadratic equations & radicals, sat math: how to use your calculator, sat reading: guide to the social science passage, how to study for the sat/psat english sections, sat language: guide to word choice & passive flow.

Stay Connected

Mastering Linear Equations in One Variable Questions on the SAT

Linear function questions demands a deep understanding of real-world scenarios, variable definition and complex function setups, but we will show you a fool-proof way to tackle these problems.

Algebra problems comprise ~35% of the questions on the SAT math section, and one of the most common types of algebra questions is linear equations in one variable. At their core, these equations are simple enough, structured around the basic principle of finding the value of a single variable, usually denoted as x x x .

However, the simplicity is deceptive. These equations can easily become complex, involving fractions and parentheses and requiring numerous steps to solve. The difficulty escalates when equations are compounded with extraneous terms or require manipulations that aren’t immediately apparent.

Solving single-variable linear equation problems isn't just about finding the right answer; it's about understanding the logical process that leads to that answer. By following our 4-step process below, you will learn to systematically solve these problems every time, no matter how complex they seem.

How to solve linear equations in one variable problems

• Simplify Each Side of the Equation
• Get the Variable on One Side
• Simplify the Equation Again
• Check Your Solution

Step 1: Simplify Each Side of the Equation

The first step is to streamline the equation by reducing complexity through algebraic manipulations, such as combining similar terms and resolving parentheses, which is crucial for making the equation more manageable and clearer to solve.

Combine Like Terms

Add or subtract terms with the same variable simplify the equation.

For example: 5 x + 3 − 2 x + 4 = 10 5x + 3 - 2x + 4 = 10 5 x + 3 − 2 x + 4 = 10 simplifies to 3 x + 7 = 10 3x + 7 = 10 3 x + 7 = 10

Eliminate Parentheses

Use the distributive property to multiply terms outside the parentheses with those inside, simplifying the equation further.

For instance: 2 ( 3 x + 4 ) − 5 = 11 2(3x + 4) - 5 = 11 2 ( 3 x + 4 ) − 5 = 11 becomes 6 x + 8 − 5 = 11 6x + 8 - 5 = 11 6 x + 8 − 5 = 11 and further simplifies to 6 x + 3 = 11 6x + 3 = 11 6 x + 3 = 11

Simplify Complex Fractions

By finding a common denominator and multiplying all terms by it, you can eliminate fractions and make the equation more straightforward.

An example is: x 4 + 3 6 = 2 3 \frac{x}{4} + \frac{3}{6} = \frac{2}{3} 4 x ​ + 6 3 ​ = 3 2 ​ which simplifies to 3 x + 6 = 8 3x + 6 = 8 3 x + 6 = 8

Rearrange the Equation

Organize the equation for clarity, often by moving all terms with the variable to one side and constants to the other.

For example: x + 5 = 3 x − 7 x + 5 = 3x - 7 x + 5 = 3 x − 7 rearranges to − 2 x = − 12 -2x = -12 − 2 x = − 12

Deal with Special Cases

Address unique situations like products equalling zero or variables in denominators, which require specific approaches.

For example: x ( x − 5 ) = 0 x(x - 5) = 0 x ( x − 5 ) = 0 leads to solutions x = 0 x = 0 x = 0 or x = 5 x = 5 x = 5 . Another example is 1 x + 2 = 5 \frac{1}{x} + 2 = 5 x 1 ​ + 2 = 5 which simplifies to 1 + 2 x = 5 x 1 + 2x = 5x 1 + 2 x = 5 x

Complete Example

Let's take an equation and apply the simplification steps:

3 ( x + 2 ) − 2 x = 5 + x − 1 3(x + 2) - 2x = 5 + x - 1 3 ( x + 2 ) − 2 x = 5 + x − 1

First, eliminate the parentheses and combine like terms:

3 x + 6 − 2 x = 5 + x − 1 3x + 6 - 2x = 5 + x - 1 3 x + 6 − 2 x = 5 + x − 1

Then, simplify the equation further by combining all like terms:

3 x − 2 x − x = 5 − 1 − 6 3x - 2x - x = 5 - 1 - 6 3 x − 2 x − x = 5 − 1 − 6

The equation becomes:

− x = − 2 -x = -2 − x = − 2

Step 2: Get the Variable on One Side

This step involves manipulating the equation to isolate the variable on one side, which is key to solving the equation and finding the value of the variable.

Isolate the Variable

Use addition, subtraction, multiplication, or division to get the variable by itself on one side of the equation.

For example: 5 x − 3 = 12 5x - 3 = 12 5 x − 3 = 12 can be simplified by adding 3 to both sides, resulting in 5 x = 15 5x = 15 5 x = 15

Undo Addition or Subtraction

If there’s a number added or subtracted from the variable, do the opposite operation on both sides of the equation to isolate the variable.

For example: x + 4 = 9 x + 4 = 9 x + 4 = 9 becomes x = 9 − 4 x = 9 - 4 x = 9 − 4 , which simplifies to x = 5 x = 5 x = 5

Undo Multiplication or Division

If the variable is multiplied or divided by a number, reverse the operation on both sides of the equation to get the variable alone.

For instance: 4 x = 20 4x = 20 4 x = 20 can be simplified by dividing both sides by 4, leading to x = 20 4 x = \frac{20}{4} x = 4 20 ​ , which simplifies to x = 5 x = 5 x = 5

Let’s apply these steps to another equation:

3 x + 7 = 10 3x + 7 = 10 3 x + 7 = 10

First, undo the addition by subtracting 7 from both sides:

3 x = 10 − 7 3x = 10 - 7 3 x = 10 − 7

Then, undo the multiplication by dividing each side by 3:

x = 3 3 x = \frac{3}{3} x = 3 3 ​

The equation simplifies to:

x = 1 x = 1 x = 1

Step 3: Simplify the Equation Again

After isolating the variable, this step involves further simplification to ensure the equation is in its simplest form, facilitating an easier and more accurate solution.

Further Simplification

Check if the equation can be simplified further by combining like terms or performing basic arithmetic operations.

For example: 2 x + 3 x = 10 2x + 3x = 10 2 x + 3 x = 10 can be simplified to 5 x = 10 5x = 10 5 x = 10

Reduce Fractions

If your solution is a fraction, reduce it to its simplest form.

For instance: 8 4 = x \frac{8}{4} = x 4 8 ​ = x simplifies to 2 = x 2 = x 2 = x

Decimal and Percentage Conversion

Convert decimals to fractions or percentages if it makes the equation simpler or more understandable.

Example: x = 0.75 x = 0.75 x = 0.75 can be expressed as x = 3 4 x = \frac{3}{4} x = 4 3 ​ or x = 75 % x = 75\% x = 75%

Let’s apply these steps to simplify an equation:

4 x + 2 x − x = 12 4x + 2x - x = 12 4 x + 2 x − x = 12

Combine like terms:

5 x = 12 5x = 12 5 x = 12

If possible, reduce to simpler form:

x = 12 5 x = \frac{12}{5} x = 5 12 ​

Step 4: Check Your Solution

This crucial step ensures that the solution you've found actually satisfies the original equation, verifying the accuracy of your work.

Substitute the Solution Back Into the Original Equation

Replace the variable with your solution in the original equation to see if the equation holds true.

For example, if the solution is x = 3 x = 3 x = 3 for the equation 2 x + 4 = 10 2x + 4 = 10 2 x + 4 = 10 , substitute ‘3’ for ‘x’ to check: 2 ( 3 ) + 4 = 10 2(3) + 4 = 10 2 ( 3 ) + 4 = 10

Verify the Equality

Perform the necessary arithmetic to confirm that both sides of the equation are equal after the substitution.

Continuing the example: 6 + 4 = 10 6 + 4 = 10 6 + 4 = 10 confirms that the solution is correct.

Let's verify the solution for the equation:

3 x + 4 = 13 3x + 4 = 13 3 x + 4 = 13 , where we found x = 3 x = 3 x = 3 as the solution.

Substitute '3' for 'x' in the original equation:

3 ( 3 ) + 4 = 13 3(3) + 4 = 13 3 ( 3 ) + 4 = 13

Perform the arithmetic:

9 + 4 = 13 9 + 4 = 13 9 + 4 = 13 shows that the solution is indeed correct.

How to Solve Linear Equations on the SAT

Remember when you realized that math wasn’t just numbers? Suddenly letters were involved, too? It’s at that point that you started to learn algebra. Depending on how long ago your memory is drifting back to, you might be rusty on this whole basic algebra thing.

On the SAT Math section, there’s a set of questions called The Heart of Algebra . Essentially, this is all about the fundamentals of algebra. And, at the very beginning of all algebra concepts is linear equations.

Kickstart Your SAT Prep with Test Geek’s Free SAT Study Guide.

What are linear equations.

Linear equations make straight lines on graphs.

Makes sense, right? Linear = straight.

The reason linear equations make straight lines when graphed is because they don’t have exponents. No exponents mean we’re always going to have a straight line.

On a real SAT, you’ll likely find 2-4 questions that test how to solve linear equations. They could be:

• Linear equations in one variable – a linear equation that contains one variable (something like x or y)
• Linear equations in two variables – a linear equation that contains two different variables (something like x and y)
• Word problems that involve linear equations

This makes linear equations a frequently tested topic on the SAT. You should be able to identify linear equations and be able to consistently solve linear equations of both one and two variables.

We’ll start with linear equations in one variable.

Linear Equations in One Variable

First, you need to be able to identify linear equations in one variable. This is important because the SAT isn’t going to tell you what skill is required on a particular question. It’s your responsibility to know (a) what type of question you’re working with and (b) how to solve it.

What would 200 EXTRA POINTS do for you? Boost Your SAT Score with Test Geek SAT prep.

How to identify a linear equation in one variable on the sat.

Linear equations in one variable will contain:

• A single variable
• No exponents

Let’s do a knowledge check

Which of these are linear equations in one variable?

Now that we know how to identify linear equations in one variable, we can talk about how to solve these linear equations.

How to Solve Linear Equations in One Variable

The key to solving linear equations in one variable is isolating the variable. In other words, we want to get our variable all by itself.

Rule: Whenever you do something to one side of an equation, you must do it to the other side as well.

Remember this rule and you’ll be a whiz at linear equations in no time.

Let’s look at an example.

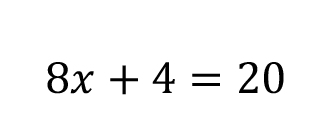
Ask yourself, “how would you isolate x?”

There are several paths you can take here, but I’m always looking for the simplest (and fastest) path on the SAT. Don’t waste any time!

We can start to get x by itself by getting rid of the 4 that’s on the left side. We can subtract this 4 from the left side, but we’ll also need to subtract 4 from the right side. Remember that rule! What you do to one side, you must also do to the other side.

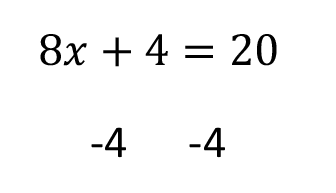
Great! We’re getting closer. Now, we need to get rid of that 8 attached to our x. It’s important to note that when you have a number right next to a variable like that, it’s being multiplied.

So, if you want to get rid of the 8, we need to divide both sides by 8.

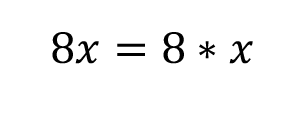
Look at that! We’ve isolated our variable. That’s our answer.

In order to start isolating our variable, we need to get rid of that 4. 6x is being divided by 4. The opposite of division is multiplication. So, we are going to multiply both sides by 4.

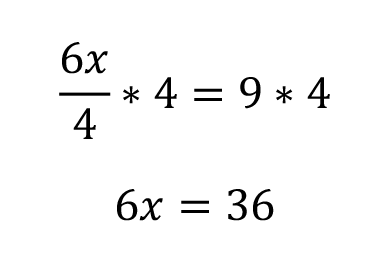
Now it looks like Example 1. To isolate x, we divide both sides by 6.

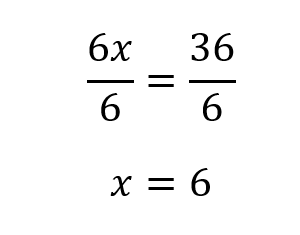
And, we have our answer.

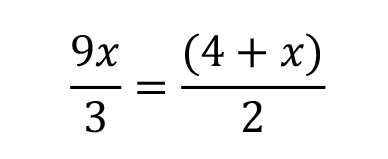
Time for another practice question.

Tip: Any time you see one fraction that is set equal to another fraction, you should be thinking multiply and divide. Or, you may be more familiar with the term cross multiply and divide.

Recall that a fraction is

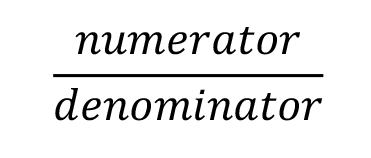
To multiply and divide , use this formula:

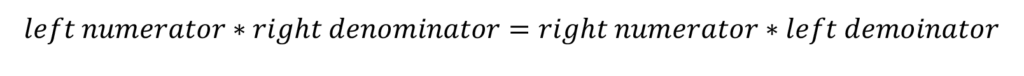
Plug in to the multiply and divide formula.

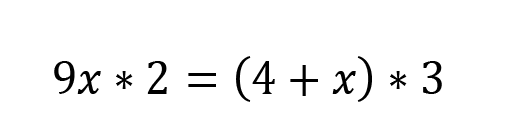
Multiply out to help simplify. To perform multiplication on the right side, you need to distribute that 3 into every term inside the parentheses.

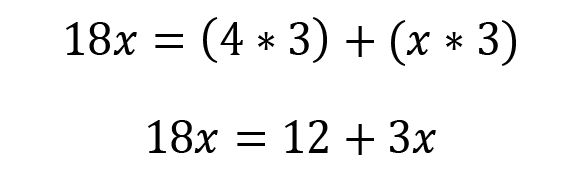
Combine like terms. Subtract the 3x from both sides.

Sometimes SAT linear equation questions won’t be so straightforward, though.

Linear Equation in One Variable – Word Problems

Occasionally SAT linear equation questions are in the form of word problems. I know, I know. Word problems probably aren’t your favorite, but don’t be tempted to just skip these questions because there’s lots to read. They’re actually pretty simple.

When we have a word problem, we need to translate the words into a mathematical equation. Then, we can solve it just like we’ve done previously. Don’t let wordiness on the SAT trip you up.

Rule : “Is” in a word problem can be translated as “=”

Now we need to translate “10 more than 14.” We can think about “more” as “+.”

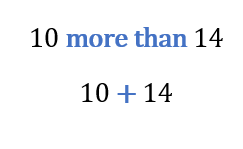
Let’s put it all together.

Simplify the right side.

Now it looks just like the simple linear equations we’ve been working with. Let’s isolate that variable.

Start by subtracting 16 from both sides.

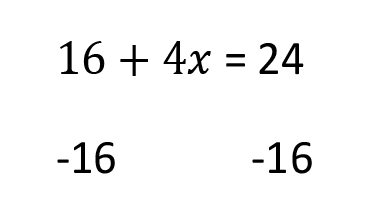
Now we divide both sides by 4.

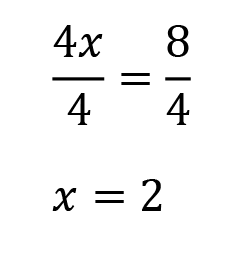
We have our answer! Right? …..right? Nope. We always need to circle back up to the original question and make sure we are truly answering the SAT’s question.

Let’s take a look.

In this case, the SAT is asking us for the value of 8x. So, we need to multiply the x value we found by 8 to get the final answer.

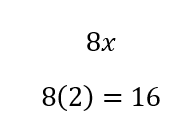
The answer is C.

The equation above relates the number of minutes, x, Eli spends running each day and the number of minutes, y, he spends skateboarding each day. In the equation, what does the number 45 represent?

A) The number of minutes spent running each day

B) The number of minutes spent skateboarding each day

C) The total number of minutes spent running and skateboarding each day

D) The number of minutes spent skateboarding for each minute spent running

This question is testing your understanding of the relationship between a real-word concept and algebraic expression. We need to reason through what the equation represents in order to solve this correctly.

If x represents the number of minutes spent running and y represents the number of minutes spent skateboarding, and we add those two numbers together what do we get? We should get the total number of minutes Eli spent doing these two things. This makes our answer C.

Linear Equations in Two Variables

Let’s move on to linear equations in two variables. Linear equations in two variables have multiple variables.

Rule: We need one distinct equation for each variable.

If we have two variables (x and y), we need two equations in order to solve for x and y. If we have three variables (ex. a, b, c), we need three equations in order to solve for a, b and c.

How to Identify a Linear Equation in Two Variables on the SAT

Check if both are true:

• More than one variable
• No variables have exponents.

Let’s do a knowledge check.

How to Solve Linear Equations in Two Variables: 2 Methods

There are two main ways to solve linear equations in two variables:

• Substitution
• Elimination

Typically, both methods are possible , but usually only one is optimal. One method may be much quicker than the other. That should be your goal: to quickly assess which method will get you to the answer more quickly. It’s important you understand how to use both methods, so you can choose the best one for the given question.

Substitution Method

The process for using substitution to solve linear equations is 4 basic steps:

• Identify an equation to start with. (You choose which equation)
• Solve the chosen equation for one of the variables. (You choose which variable)
• Plug in to your second equation to find variable #1.
• Plug variable #1 in to either equation to solve for variable #2.

It’ll make more sense as we walk through an example.

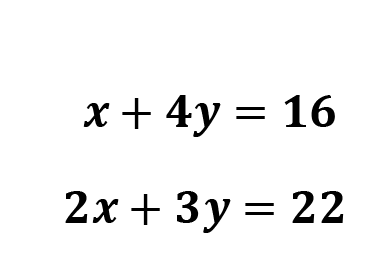
• Identify an equation to start with.

You can choose whichever equation you’d like. You’ll get the same results either way, but the goal is to make this as easy as possible, so I’m going to choose the first equation. I notice that the first equation has a variable, x, that doesn’t have a coefficient, so this will make it very easy to work with

2. Solve the chosen equation for one of the variables. (You choose which variable)

I could solve for y here, but it would be a little messier since I would have to do division. Because the x doesn’t have any coefficient, it’ll be easier to solve for x.

Subtract 4y from both sides.

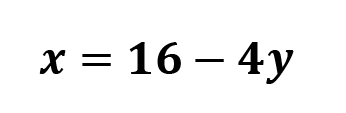
3. Plug in to your second equation to find variable #1.

Now, we can plug in 16 -4y wherever we see x in our second equation.

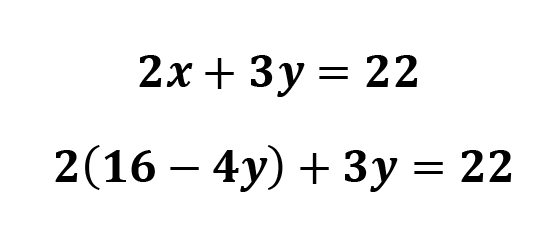
Multiply out the left side.

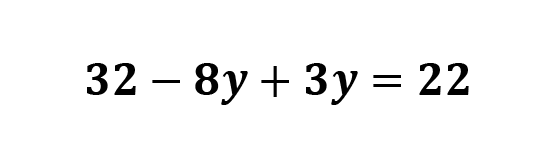
We’re working with a single variable linear equation now, so use the methods I shared in the single variable linear equation section to isolate the variable y.

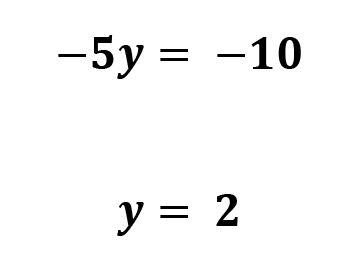
4. Plug variable #1 in to either equation to solve for variable #2.

You can plug y= 2 into either equation to solve for x. Focus on choosing the one that will be quicker. In this case, I think it’ll be quicker to plug into the first equation.

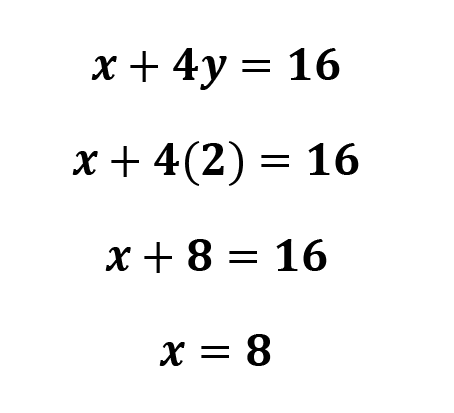
Elimination Method

Sometimes elimination will be the quicker path to solve a system of linear equations. As you do more practice, you’ll start to see patterns that will help you make the decision.

The process for using elimination is three steps:

• Choose a variable to eliminate. Perform any multiplication or division needed.
• Add or subtract the equations to remove one of the variables and solve for the other variable.
• Plug in to solve for the remaining variable.

Let’s walk through an example.

Solve for x and y.

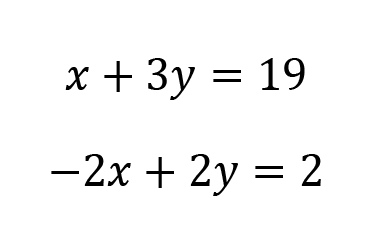
The trick here is to identify the variable that will be easy to eliminate. To eliminate a variable, we need the coefficients to be opposite. For example, -4a and 4a would cancel out. Or 3x and -3x would also work.

When I look at this system of equations, I notice that the x variables are already opposite in sign. The first equation has a positive x and the second has a negative x. So, it’d be pretty simple for me to multiply the first equation by 2 to get a pair that would cancel out (be eliminated) in my next step.

Feeling Overwhelmed? Get 1-on-1 SAT Help from a Test Geek Tutor.

Let’s multiply the first equation by 2. Remember, what we do to one side, we must do to the other, so we’re going to multiply the left and right side by 2.

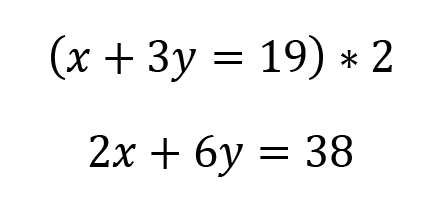
2. Add or subtract the equations to remove one of the variables and solve for the other variable.

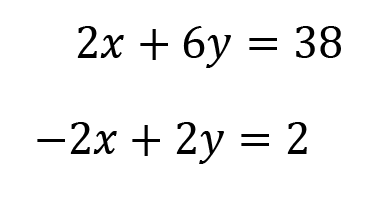
Because of what we did in step 1, we can now add these two equations together and our x variables will be eliminated.

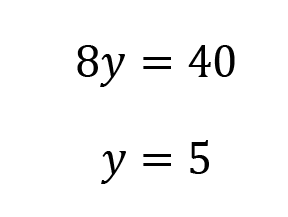
3. Plug in to solve for the remaining variable.

We can choose either equation to plug in y=5. Choose the one that will be quicker to solve. I’ll use the first equation.

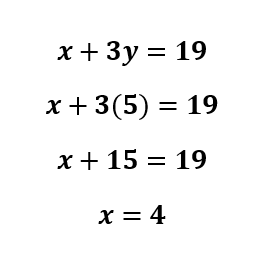
It’s important to note here that this system of equations could have been solved with either elimination or substitution. Focus on asking yourself which method will be quicker, or which method will require less steps to get to the end solution. The more practice you do, the easier it will be to determine which method works better.

Let’s work through some practice questions.

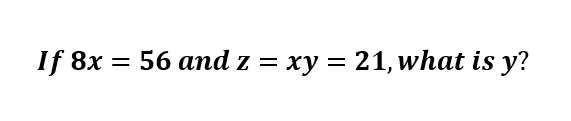
We know this is a multi-variable linear equation because we have, you guessed it, multiple variables and none of our variables have exponents. We must have two distinct equations (which we do in this case) because we have two variables: x and y.

First step is to determine if we should use elimination or substitution.

In this case, substitution will be the better option because our first equation can quickly be solved for x. Then, we can plug it in to our second equation and solve for y.

Divide both sides by 8.

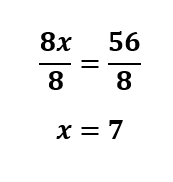
Plug in x=7  to xy=21 .

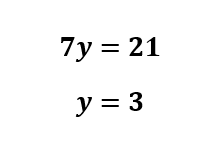
Try another practice question.

Notice this question has 3 variables and 3 equations. Substitution is going to make the most sense, because, like Example 5, one equation only has one variable. We can start there and then move forward with substitution.

Solve for z.

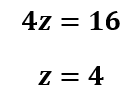
Plug z into the second equation.

One more variable to solve for. Let’s use the final equation to solve for x by plugging in y=1 .

Nice work. Let’s do one final practice question.

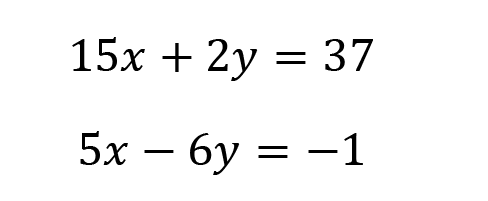
This is a great candidate for elimination. If we multiply the second equation by -3, we could eliminate 15x and -15x.

Multiply the second equation by -3.

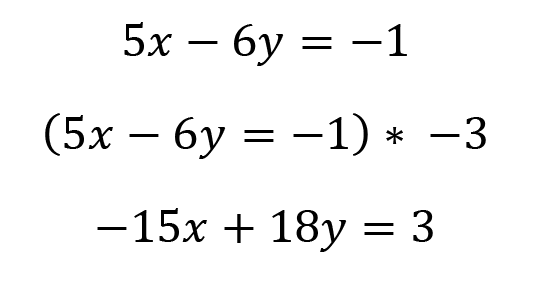
Add the equations together, eliminating x.

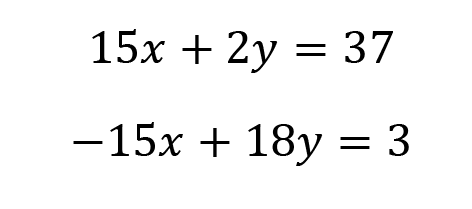
Plug y=2  into either equation to solve for x. I’ll use the second equation.

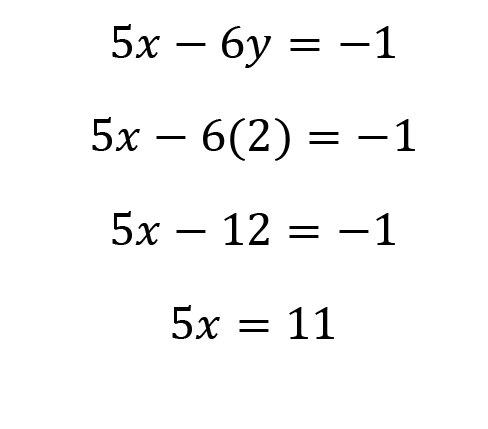
Divide by 5, and we have our answer.

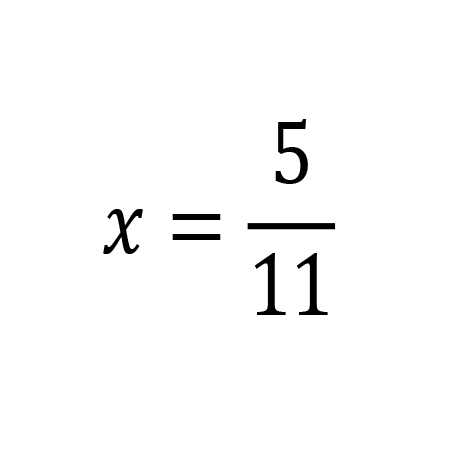
Final Thoughts

Solving linear equations is a must-know skill for the SAT Math section. Understanding how to identify linear equations in both one and two variables is the first steps to success. From there, you should use the methods I’ve laid out to solve.

What Does it Mean if My SAT Score is Under Review?

Sat math heart of algebra ultimate guide [updated for 2022], you may also like, state of texas average act score – class of 2021.

State of Georgia Average SAT Score – Class of 2021

State of Illinois Average SAT Score – Class of 2021

State of Texas Average SAT Score – Class of 2021

Comments are closed.

More in ACT

How to Send ACT Scores to Colleges

When is the Next ACT Test?

ACT Dates in Kansas City

How to Cancel Your ACT Test

SUBSCRIBE TO THE TEST GEEK BLOG

Get expert SAT & ACT tips delivered

Recent posts, when are sat scores released, must know formulas for the act, your sat question and answer service questions, answered, how many questions are on the sat.

• ACT English
• ACT General
• ACT Reading
• ACT Science
• College Admissions
• General ACT & SAT
• SAT General
• SAT Reading
• SAT Writing

Lost your password?

• 1-on-1 SAT Tutoring
• 1-on-1 ACT Tutoring
• Online SAT Tutoring (1-on-1)
• Online SAT Group
• Online ACT Tutoring (1-on-1)
• Online ACT Group
• SAT vs. ACT
• Parent Guide
• 2022 SAT Test Dates
• 2022 ACT Test Dates
• SAT Scores Guide
• ACT Scores Guide
• Resources for Schools
• About Test Geek
• Our Methods & Curriculum
• Colorado Springs
• Dallas-Plano-Frisco
• Kansas City
• Oklahoma City
• Phoenix-Scottsdale
• San Antonio

Linear Equations and Inequalities

Linear equations and inequalities are fundamental concepts in algebra, and they are also an important part of the SAT Math section. Linear equations represent straight lines on a graph and can be used to model many real-world situations, such as the growth of a population or the depreciation of an asset over time. Inequalities, on the other hand, represent a range of possible values and are often used to express constraints or limitations in a given situation.

On the SAT, linear equations and inequalities are tested in a variety of ways, including solving equations for a given variable, graphing equations and inequalities, and using equations to solve word problems. By mastering these concepts, you'll be better equipped to tackle the SAT Math section and succeed in your college admissions journey.

To help you prepare for the SAT Math section, we've created a practice test for linear equations and inequalities. This test will give you the opportunity to practice solving problems similar to those you'll encounter on the SAT. As always, should you have any trouble with the questions on this test, don't hesitate to reach out for personalized SAT tutoring to help you ace this section. 

1. Solve for x:

2. solve for y:.

2y + 5 = 15

3. Solve the inequality:

-3x + 4 > 10

4. Solve the inequality:

4 - 5y ≤ 19

5. Solve the system of linear equations:

6. which of the following is the graph of the equation y = -2x + 3.

A line with a positive slope

A line with a negative slope

A horizontal line

A vertical line

7. What is the slope of the line represented by the equation 3x - 4y = 12?

8. solve the inequality:.

2x - 3 ≤ 3x + 2

9. What is the y-intercept of the line represented by the equation 6x - 3y = 9?

10. solve the system of linear inequalities:.

x + y > 4

x > 4, y > 0

x > 2, y < 3

x ≤ 4, y > 0

x ≤ 2, y < 3

Click here to have your paper evaluated by Brian

Try our other test papers:

• Systems of Linear Equations & Inequalities
• Interpretation of Linear Functions in Context

Master the the SATs and ACTs with the best examination prep experience anywhere. One-on-One sessions with Brian Leaf. The best-selling author of 10 SAT/ACT prep books.

Information

• About Brian
• Consulting Sessions

Top 50 Skills

• ACT English, Reading, Science
• SAT Critical Reading, Writing

Subscribe to my newsletter

• SAT and ACT Prep Courses
• Stress Management Sessions
• Defining Breaking Dawn
• Defining Eclipse
• Defining New Moon
• Defining Twilight
• Name That Movie: Comedy & Action Edition
• Name That Movie: Romantic Comedy & Drama Edition
• ACT English, Reading, and Science
• SAT Critical Reading and Writing
• Linear Equations & Inequalities
• Practice Test 1
• Critical Reading 1
• Critical Reading 2

SAT Math Practice Test 88: Systems of Linear Equations

Test information.

See All test questions

SAT Math Multiple-Choice Tests

• SAT Math Multiple-Choice Test 1
• SAT Math Multiple-Choice Test 2
• SAT Math Multiple-Choice Test 3
• SAT Math Multiple-Choice Test 4
• SAT Math Multiple-Choice Test 5
• SAT Math Multiple-Choice Test 6
• SAT Math Multiple-Choice Test 7
• SAT Math Multiple-Choice Test 8
• SAT Math Multiple-Choice Test 9
• SAT Math Multiple-Choice Test 10
• SAT Math Multiple-Choice Test 11
• SAT Math Multiple-Choice Test 12
• SAT Math Multiple-Choice Test 13
• SAT Math Multiple-Choice Test 14
• SAT Math Multiple-Choice Test 15
• SAT Math Multiple-Choice Test 16
• SAT Math Multiple-Choice Test 17
• SAT Math Multiple-Choice Test 18
• SAT Math Multiple-Choice Test 19
• SAT Math Multiple-Choice Test 20
• SAT Math Multiple-Choice Test 21
• SAT Math Multiple-Choice Test 22
• SAT Math Multiple-Choice Test 23
• SAT Math Multiple-Choice Test 24
• SAT Math Multiple-Choice Test 25

- 2 x + 9 y = 25 3 x + 6 y = 21

Which of the following ordered pairs ( x , y ) is a solution to the system of equations above?

5 x - 2 y = - 12 2 x + 3 y = - 1

If ( x , y ) is a solution to the system of equations above, what is the value of x + y ?

3. A nursery sells fertilizer in 25-pound and 100-pound bags. If Juliet bought 13 bags of fertilizer for her landscaping business that contained 775 pounds of fertilizer, how many 100-pound bags did she buy?

4. Line l has a slope of 1 2 and an x -axis intercept of-4. Line m is perpendicular to line l. The two lines intersect on the y -axis. Which of the following is the equation of line m ?

14 x - a y = - 9 2 7 2 x - y = - 1 4

If a is a constant for the given system of equations above, for what value of a will the system of equations have no solution?

6. Due to train schedules, it takes Yvette longer to return from work to her home in the evening than it takes for her to get from home to work in the morning. If Yvette's average total daily commuting time was 1 hour 12 minutes and her average morning commuting time was 8 minutes less than her evening average, what was her average commuting time returning home?

7. A pet supplies store maintains an inventory of a certain brand of dog food in 15-pound and 30-pound bags. The store pays $0.60 per pound for the 15-pound bags and $0.50 per pound for the 30-pound bags. The store's current inventory of this product is 32 bags of this dog food for which it paid $408. Which of the following systems of equations can be used to determine the number of 15-pound bags, s, and the number of 30-pound bags, b ?

y = b + 5 y = m x 2

For which of the following values of m and b does the system of equations above have exactly two real solutions?

9. The 8 soup cans in Carlos's pantry contain either 8 or 12 ounces each. Carlos has 4 ounces more soup in 8-ounce cans than in 12-ounce cans. How many 12-ounce cans of soup are in his pantry?

y = a ( x 2 + b ) y = 3 x + 14

The lines for the two equations above are parallel and separated by a vertical distance of 2 when graphed in the xy -plane. Which of the following could be the value of b ?

a x - b y = 5 3 x - 4 y = 15

The system of equations above has infinitely many solutions. What is the value of a b ?

New SAT Math: How to Solve Linear Equations

Knowing how to solve linear equations is key for success on the SAT Math section . Linear equations are equations that consist of variables raised to the power of 1. When graphed, these equations produce a straight line.

Solving Linear Equations With One Variable

These are simple to solve once you get the hang of it.

1. For linear equations that consist of only one variable, the key is to isolate the variable on one side.

2. Next, get all the constants to the other side of the equation.

3. Lastly, simplify both sides of the equation until you get to the answer.

New SAT Math: Linear Equation Example

Let’s take a look at a common question type that the new SAT test makers will throw at you.

If 6x = 42 and xk = 2, what is the value of k?
 A. 2/7 B. 1/6 C. 7 D. 1/7

Let’s take a look at both equations and think about it for a second. In the first equation, there is only one variable, and it is raised to the power of 1. Since there is more than one variable in the second equation (x and k), we can’t know for sure what k is unless we solve for x first.

We should go ahead and solve the first equation for x before moving on to the next equation.

1. In order to isolate the variable on one side, we need to divide both sides by 6. That yields x = 7.

2. Now we can plug in x = 7 into the second equation. This gives us 7k = 2.

3. In order to isolate the k on one side, divide both sides by 7. This leaves us with k = 2/7.

In this case, the answer is A.

New SAT Math: Linear Equation Example #2

James is budgeting his time to think about the number of classes c he will take this year. For every class that he takes, he believes that he’ll spend 2 1/2 hours each week working on homework. He believes that he’ll spend an additional 6 1/2 hours each week completing the reading work for all of his classes together. If James has 19 hours free every week to finish homework and reading work for his classes, which equation best models this situation?

A. 2.5c – 6.5 = 19 B. 2.5c + 6.5 = 19 C. 6.5c – 2.5 = 19 D. 6.5c + 2.5 = 19

This type of question looks much more involved than the first one, but don’t worry! The key here is to circle keywords so that we can construct an equation quickly and move on to the next question without getting bogged down too much from all the reading we have to do.

1. Circle all the keywords – the variables involved and the numbers that we have to work with. In this case, we have 2.5 hours per class per week, 6.5 hours for reading work per week, and 19 hours of free time.

2. Look at what the question is asking for. Here we want to figure out how many classes James can take in a week given his time constraint (19 hours per week).

3. Put the numbers together and create the equation. We don’t know how many classes James is going to take each week, so we should put a variable after 2.5 to indicate the unknown number. In this case, c = the number of classes.

Since James believes that he will spend 6.5 hours total each week for reading work regardless of the number of classes taken, we should add that to 2.5x to represent the total number of hours spent on homework and reading work.

James has 19 hours total to complete all of his work, so let’s set 2.5x + 6.5 equal to 19 to figure out the maximum number of classes he can take.

2.5c + 6.5 = 19

Choice B matches our answer! A job well done.  

Minh’s passion for helping students succeed grew during his time as a career counselor at the University of California, Irvine. Now, he’s helping students all over the world by spilling SAT/ACT secrets through blog posts on Magoosh. When he’s not busy tutoring or writing, he enjoys playing guitar, traveling, and talking about himself in third-person.

View all posts

More from Magoosh

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Choose Your Test

Sat / act prep online guides and tips, systems of equations in sat math: algebra prep and practice.

Sure, you've done your paces on single variable equations and now they're no problem, but what do you do when presented with multiple equations and multiple variables at once? These are what we call “systems of equations” and, luckily for us, they are extremely predictable types of problems with multiple methods for solving them. Depending on how you like to work best, you can basically choose your own adventure when it comes to system of equation problems.

But before you choose the method that suits you (or the individual problem) best, let's look at all the various options you have available as well as the types of questions you'll see come test day. These questions will always show up once or twice on any given test, so it's best to understand all the strategies you have at your disposal. 

This will be your complete guide to systems of equations questions —what they are, the many different ways for solving them, and how you'll see them on the SAT.

What Are Systems of Equations?

Systems of equations are a set of two (or more) equations which have two (or more) variables. The equations rely on each other and can be solved only with the information that each provides.

The majority of the time on the SAT, you will see a system of equations that involves two equations and two variables, but it is certainly not unheard of that you will see three equations and/or a three variables, in any number of combinations.

Systems of equations can also be solved in a multitude of ways. As always with the SAT, how you chose to solve your problems mostly depends on how you like to work best as well as the time you have available to dedicate to the problem.

The three methods to solve a system of equations problem are:

#1 : Graphing #2 : Substitution #3 : Subtraction

Let us look at each method and see them in action by using the same system of equations as an example.

For the sake of our example, let us say that our given system of equations is:

$$2y + 3x = 38$$

$$y - 2x = 12$$

Solving Method 1: Graphing

There will only ever be  one  solution for the system of equations, and that one solution will be the intersection of the two lines. In order to graph our equations, we must first put each equation into slope-intercept form. If you are familiar with lines and slopes , you know that slope intercept-form looks like:

$y = mx + b$

So let us put our two equations into slope-intercept form.

$2y + 3x = 38$

$2y = -3x + 38$

$y = {-3/2}x + 19$

$y - 2x = 12$

$y = 2x + 12$

Now let us graph each equation in order to find their point of intersection.

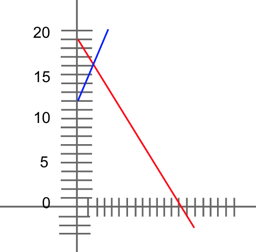
Once we graphed our equation, we can see that the intersection is at (2, 16).

So our final results are: $x = 2$ and $y = 16$

Solving Method 2: Substitution

In order to solve our system of equations through substitution, we must isolate one variable in one of the equations and then use that found variable for the second equation in order to solve for the remaining variable.

For example, we have two equations,

So let us select just one of the equations and then isolate one of the variables.

In this case, let us chose the second equation and isolate our $y$ value.

Next, we must plug that found variable into the second equation. (In this case, because we used the second equation to isolate our $y$, we need to plug in that $y$ value into the first equation.)

$2(2x + 12) + 3x = 38$

$4x + 24 + 3x = 38$

$24 + 7x = 38$

And finally, you can find the numerical value for your first variable ($y$) by plugging in the numerical value for your second variable ($x$) into either equation.

$2y + 3(2) = 38$

$2y + 6 = 38$

$y - 2(2) = 12$

$y - 4 = 12$

Either way, you have found the value of both your $x$ and $y$.

Again, $x = 2$ and $y = 16$

Solving Method 3: Subtraction

As the last method for solving systems of equations, you can subtract one of the variables completely in order to find the value of the second variable. We do this by subtracting one of the entire equations from the other, complete, equation.

Do take note that you can only do this if the variables in question (the one you wish to eliminate) are exactly the same . If they are NOT the same, then we must first multiply the entire equation by the necessary amount in order to make them the same.

In the case of our two equations, none of our variables are equal.

In this case, let us decide to subtract our $y$ values and cancel them out. This means that we must first make them equal by multiplying our second equation by 2, so that both $y$ values match.

$2y + 3x = 38$ (This first equation remains unchanged)

$2(y - 2x = 12)$ => $2y - 4x = 24$ (The entire equation is multiplied by 2)

And now we can cancel out our $y$ values by subtracting the entire second equation from the first.

$2y - 4x = 24$

--------------------

$3x - -4x = 14$

Now that we have isolated our $x$ value, we can plug it into either of our two equations to find our $y$ value.  

Our final results are, once again, $x = 2$ and $y = 16$.

Though there are many ways to solve your problems, don't let this knowledge overwhelm you; with practice, you'll find the best solving method for you.

No matter which method we use to solve our problems, a system of equations will either have one solution —meaning that each variable will have a numerical value attached— no solution, or infinite solutions .

In order for a system of equations to have infinite solutions , each system is actually identical. This means that they are the same line.

In order for a system of equations to have no solution , the $x$ values will be equal when the $y$ values are set to 1 (which means that both variables—$x$ and $y$—will be equal). The reason this is true is that it will result in two parallel lines, as the lines will have the same slope . The system has no solution because the two lines will never meet and therefore have no point of intersection.

For instance,

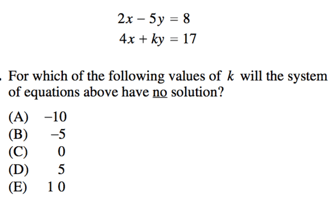
Because our system will have no solution when both our $y$ values and our $x$ values are equal , this means that there will be no solution where we have eliminated both our variables by canceling them out.

In this case, the most expedient solution to this problem will be subtraction. Why? We can see this because the two $x$ values ($2x$ and $4x$) are multiples of one another, so we can easily multiply one equation in order to equal them out.

$2x - 5y = 8$

$4x + ky = 17$

Now, let us multiply the top equation in order to equal out our $x$ values. So the system pair,

$2(2x - 5y = 8)$

$4x - 10y = 16)$

----------------------

$-10y - ky = -1$

In order to have NO solution, our two $y$ values must balance out to zero. So let us set our two $y$ values equal to one another:

$-10y - ky = 0$

$-ky = 10y$

Our $k$ value  must be -10 in order for our system of equations to have no solution.

Our final answer is A , -10.

[Note: don't fall for the bait answer of +10! You are still subtracting your system of equations, so keep close track of your negatives.]

Also, if it is frustrating or confusing to you to try to decide which of the three solving methods “best” fits the particular problem, don't worry about it! You will almost always be able to solve your systems of equations problems no matter which method you choose.

For instance, you could have also chosen to graph this question. If you had done so, you would first have to put each equation into slope-intercept form:

$-5y = -2x + 8$

$y = 2/5(x) + 8$

$ky = -4x + 17$

$y = {-4/k}(x) + 17$

Now, we know a system of equations will have no solution only when each variable balances out to zero, so let us equate our two $x$ variables in order to solve for $k$.

$2/5(x) = {-4/k}(x)$

$2/5 = {-4}/k$

${2k}/5 = -4$

Again, our $k$ value is -10.

As you can see, there is never any “best” method to solve a system of equations question, only the solving method that appeals to you the most.

All roads lead to Rome, so don't stress yourself by trying to find the "right" solving method for your systems problems.

Typical Systems of Equations Questions

Most systems of equations questions on the SAT will let you know that it IS a systems of equations by explicitly using the words “systems of equations” in the question itself.

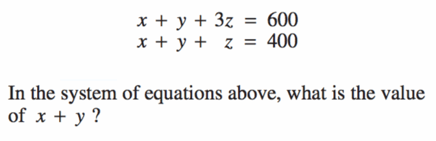
(We will walk through how to solve this question later in the guide)

Other problems will simply present you with multiple equations with variables in common and ask you to find the value of a one of the variables, or even a combination of the variables (such as the value of $x + y$ or $x - y$).

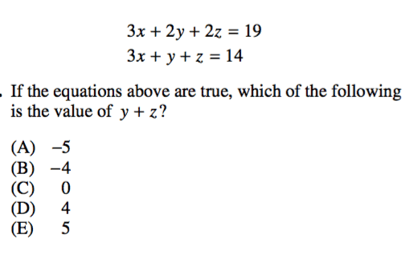
And finally, the last type of systems of equation question will ask you to find the numerical value of a variable in which there is NO solution, as with the example from earlier.

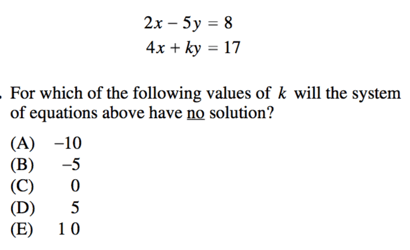
Strategies for Solving Systems of Equations Questions

All systems of equations questions can be solved through the same methods that we outlined above, but there are additional strategies you can use to solve your questions most accurately and expediently.

#1: To begin, find the variable that is already the most isolated

The ultimate goal is the find the value of all the variables, but we can only do this by finding one variable to start with. The easiest way to solve for this one variable isolate (or eliminate) the variable that has the fewest coefficients or is seemingly the most isolated.

$5x - 3y = -13$

$2x + y = 19$

If we are using substitution, it is easiest for us to first isolate the $y$ value in our second equation. It is already the most isolated variable, as it does not have any coefficients, and so we will not have to deal with fractions once we replace its value in the first equation. 

If, on the other hand, we were using subtraction, it is still best to target and eliminate our $y$ values. Why? Because we have $3y$ and $y$, which means that we only have to multiply the second equation by 3 in order to match up our $y$ values. If we were to target and eliminate our $x$ values, we would have to multiply both equations—the first by 2 and the second by 5—in order to make our $x$ values match. 

Though you can always find your solutions no matter which variables you choose to isolate or eliminate, it's always nice to save yourself the time, energy, and hassle (not to mention avoid possible mistakes) by going for the easy pickings first. 

#2: Practice all three solving methods to see which one is most comfortable to you

The best way to decide which system of equation solving method suits you the best is by practicing on multiple problems (though it will help your flexibility if you can become comfortable using all the solving methods available, even if one or two suit you better than the other(s)).

When you test yourself on systems questions, try to solve each one using more than one method in order to see which one is most comfortable for you personally.

#3: Use subtraction for questions that require finding more than just one variable

Most “multiple variable solve” systems of equations questions will ask you to find $x + y$ or $x - y$, which will almost always be most easily found via the subtraction method.

It is also most useful to use the method of subtraction when we have three or more variables, especially when it is a combination of multiple variables AND three or more variables.

We will see this kind of problem in action in the next section.

Test Your Knowledge

Now let us test your system of equation knowledge on real SAT math questions.

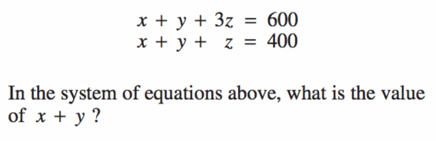
Answers: 300, E, 12

Answer Explanations:

1. As we outlined in our strategy section, it is almost always easiest to find the value of multiple variables by using the method of subtraction (though, again, it is not the only way).

We are restricted somewhat, though, as we have three variables and only two equations. Why is this important? Well, we can find the individual values for each variable if we have the same number of equations as we have variables, but in this case we do not. This means we need to use a solution that will give us $x + y$, since we cannot find the value of $x$ or $y$ alone. 

So let us use subtraction.

To do this, we must subtract like variables and, luckily for us, both equations have a single $x + y$ value. This means we can isolate our variable $z$.

$x + y + 3z = 600$

$x + y + z = 400$

So let us subtract them.

-------------------------

Now that we have the value of $z$, we can replace it in either of the equations in order to find the value of $x + y$.

Because it is always easiest to use the most isolated variable (less math involved for us!), let us our second equation to plug in our $z$ value into.

$x + y + 100 = 400$

$x + y = 300$

Our final answer for the value of $x + y$  is 300.

Do note, however, that if you would much prefer to use substitution, you can definitely do so.

Because we are trying to find $x + y$, let us isolate it as our wanted variable in one of our equations.  

Let us use our first equation.

$x + y = 600 - 3z$

And now we can substitute our $x + y$ value into our second equation.

$(600 - 3z) + z = 400$

$600 - 2z = 400$

$-2z = -200$

Now that we have found our value for $z$, we can plug it into either equation to find the numerical value for our $x + y$.

Let us use the second equation to do so. Why the second? Because each value is already the most isolated and so will be easiest to work with, but each question will work either way.

Again, our final answer is $x + y = 300$

As you can see, any method will suit you—it just depends on how you like to work.

2. Again, though not the only way to solve our problem, it is easiest to use subtraction when we have three or more variables in our equations or we are trying to find a combination of variables (in this case, the value of $y + z$). In this case, we have both, so let us use subtraction.

$3x + 2y + 2z = 19$

$3x + y + z = 14$

Our $x$ values are identical, so let us simply subtract the second equation from the first.

---------------------------

$y + z = 5$

Our final answer is E , $y + z = 5$

3. In this case, let us use the method of substitution in order to isolate one of our values and plug it into one of the other equations in our system.

The equations we are given are:

$v$ is already isolated, so let us plug it back into our first equation.

$x = 3(4t)$

Now, we are also told that $x = pt$, so we can equate the two expressions.

Because 12 and $p$ both act as coefficients (numbers before a variable) for $t$, we can see that they are equal.

This means that $p = 12$

Our final answer is 12.

The Take-Aways

As you can see, systems of equations are some of the most versatile problems when it comes to methods for solving them (though the problems themselves are not terribly varied). Though you can solve many problems on the SAT in a variety of ways, most are not quite so flexible, so take heart that you have many choices for how to proceed for your systems of equations questions.

Once you practice and familiarize yourself with these types of questions, you'll find the best method for you—your strengths, and your timing—for taking the test. And pretty soon, you'll be able to knock out systems of equations questions in multiple ways, blindfolded, and with hands behind your back (though why you would want to is, frankly, anyone's guess).

What's Next?

Systems were a snap, you say? You're ready for math problems, you say? Well lucky you! We have more math guides than you can shake a stick at, all of which cover crucial aspects of the SAT math section . Lines and angles , polygons , integers , ratios ...any topic you need to brush up on is at your fingertips, so make the best of your study time and energy and target any of your known problem areas before test day.

Want to know the most valuable strategies for SAT math problems? Check out our guides on plugging in answers and plugging in numbers to help finesse the vast majority of your SAT math questions.

Looking to get a perfect score? Look no further than our guide to getting a perfect 800 on the SAT math section, written by a perfect-scorer.

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• About Varsity Tutors

SAT Math : Systems of Equations

Study concepts, example questions & explanations for sat math, all sat math resources, example questions, example question #1 : systems of equations.

If 7 x + y = 25 and 6 x + y = 23, what is the value of x ?

You can subtract the second equation from the first equation to eliminate y :

7 x + y = 25 – 6 x + y = 23: 7 x  – 6 x = x ; y  –  y = 0; 25 – 23 = 2

You could also solve one equation for y and substitute that value in for y in the other equation:

6 x + y = 23 → y = 23 – 6 x .

7 x + y = 25 → 7 x + (23 – 6 x ) = 25 → x + 23 = 25 → x = 2

Example Question #2 : Systems Of Equations

7x + 3y = 20 and –4x – 6y = 11. Find the value of 3x – 3y

We can add these equations to one another.

(7x + 3y = 20) + (–4x – 6y = 11) = (3x – 3y = 31)

Example Question #3 : Systems Of Equations

Consider the three lines given by the following equations:

4x - 3y = 2

What is the value of the x-coordinate of the point of intersection that is common to ALL three lines?

If the point of intersection lies on all three lines, then we should be able to select any two lines, find their point of intersection, and come up with the same point of intersection each time. In other words, the point of intersection of the first two lines must be the point of intersection of the second and third lines. 

Let's consider the first and second lines. We can solve the system of equations by substituting the value of y from the second equation into the first.

x + 2(2x + 3) = 1

x + 4x + 6 = 1

y = 2(-1) + 3 = 1

The point of intersection of the first two lines is (-1,1).

Now we can find the point of intersection of the second and third lines. Again, we can substitute the value of y from the second equation into the third.

4x - 3(2x + 3) = 2

4x -6x - 9 = 2

y = 2(-11/2)+3 = -8

Thus, the second and third lines intersect at (-11/2,-8).

Because the point of intersection between the first and second line does not coincide with the point of intersection between the second and third, there is no point that is common to ALL three lines. Thus, there is no point of intersection.

Each sheep has 4 legs and each chicken has 2 legs. If a farm boy counts 50 heads and 140 feet, how many sheep are there?

Set x as the number of sheep and y as the number of chicken. This gives us x+y=50 and 4x+2y=140. We want to solve for x. Solving the first equation we get y=50-x. Substitute that into the second you have 4x+2(50-x)=140. Multiplying it out gives 4x+100-2x=140. So 2x+100=140. 2x=40, x=20. Giving 20 sheep.

Example Question #1 : How To Find The Solution For A System Of Equations

If 8x – 9 is 10 less than 5, what is the value of 4x?

The first thing to do is to write an algebrai equation for the problem:

8x – 9 = 5 – 10

8x – 9 = –5

Thus, 4 * x = 2

4x - 5y = 12

6y - 3x = -6

Quantity A: x + y

Quantity B: 6

Quantity B is greater

Quantity A is greater

The relationship cannot be determined from the information given

The two quantities are equal

Add the two equations:

4x - 5y = 12 plus

6y - 3x = -6:

4x - 5y + (6y - 3x) = 12 + (-6)

4x - 3x + 6y - 5y = 12 - 6

• A charity organization is signing up volunteers to prepare for a fundraiser.  Each volunteer can either help setup tables or auction galleries.  A volunteer can setup 6 tables per hour or 2 auction galleries per hour.  There are 180 tables to be setup as well as 12 auction galleries.  If the volunteers will have 3 hours to prepare, how many volunteers must be signed up?

Find out how much a volunteer can produce in 3 hours.

6 tables/hour * 3 hours = 18 tables/hour

180 table need to be setup.  If one volunteer can setup 18 in 3 hours, then 10 volunteers will take care of the 180 tables.

2 auction galleries/hour * 3 hours = 6 galleries/hour

2 volunteers will be able to complete 12 auction galleries

10 + 2 = 12 volunteers

Example Question #8 : Systems Of Equations

If  x + 12 = 28, what is the value of (3x + 2) * (–x + 10)?

Solve for x, then plug into the formula to find the value.  x = 28 – 12 = 16

(3 * 16 + 2) * (–16 +10) = –300

Joey has $1.50. If he only has quarters and nickels and he has 14 coins total, how many nickels does he have?

Setting x and the number of quarters he has and y as the numbver of nickels. x + y = 14 (total coins), 0.25x + 0.05y = 1.50 (total amount). Substituting x = 14 – y from the first equation into the second, we get y = 10. Therefore Joey has 10 nickels.

A soccer player kicks a ball at 8m/s. A player runs to receive it as soon as the ball as kicked at a speed of 4m/s. If the receiving player starts 12m ahead of the ball, how far does he travel before he gets the ball?

Setting t as the time elapsed we need to find when 8t = 12 + 4t (this is the distance traveled by the ball compared to the distance traveled by the player+difference from origin). Solving for t we get a travel time of 3 seconds. If the player runs for 3 seconds at 4m/s, the player travels 12m before receiving the ball.

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

The Best SAT Math Worksheets: FREE & Printable

Looking for FREE printable SAT Math worksheets to help you or your students prepare for the SAT Math test? If so, you are in the right place.

Here’s a collection of FREE downloadable PDF Math worksheets for all SAT Math topics.

These worksheets can help your students succeed on the SAT Math test.

This is a comprehensive and perfect collection of everything on the SAT Math that a test taker needs to learn before the test day.

Download our free Math worksheets for SAT Mathematics and learn how to ACE the test!

There is alos a FREE SAT Mathematics Practice Test   Hope you enjoy it!

IMPORTANT: COPYRIGHT TERMS: These worksheets are for personal use. Worksheets may not be uploaded to the internet, including classroom/personal websites or network drives. You can download the worksheets and print as many as you need. You can distribute the printed copies to your students, teachers, tutors, and friends. 

You Do NOT have permission to send these worksheets to anyone in any way (via email, text messages, or other ways). They MUST download the worksheets themselves. You can send the address of this page to your students, tutors, friends, etc.

The Absolute Best Book to Ace the SAT Math Test

SAT Math for Beginners 2024 The Ultimate Step by Step Guide to Preparing for the SAT Math Test

Sat math topics, fractions and decimals.

• Simplifying Fractions
• Adding and Subtracting Fractions
• Multiplying and Dividing Fractions
• Adding and Subtracting Mixed Numbers
• Multiplying and Dividing Mixed Numbers
• Adding and Subtracting Decimals
• Multiplying and Dividing Decimals
• Comparing Decimals
• Rounding Decimals
• Factoring Numbers
• Greatest Common Factor
• Least Common Multiple

Real Numbers and Integers

• Adding and Subtracting Integers
• Multiplying and Dividing Integers
• Order of Operations
• Ordering Integers and Numbers
• Integers and Absolute Value

Proportions, Ratios, and Percent

• Simplifying Ratios
• Proportional Ratios
• Similarity and Ratios
• Ratio and Rates Word Problems
• Percentage Calculations
• Percent Problems
• Discount, Tax and Tip
• Percent of Change
• Simple Interest

Algebraic Expressions

• Simplifying Variable Expressions
• Simplifying Polynomial Expressions
• Translate Phrases into an Algebraic Statement
• The Distributive Property
• Evaluating One Variable Expressions
• Evaluating Two Variables Expressions
• Combining like Terms

Equations and Inequalities

• One-Step Equations
• Multi-Step Equations
• Graphing Single–Variable Inequalities
• One-Step Inequalities
• Multi-Step Inequalities

Systems of Equations

• Systems of Equations Word Problems
• Quadratic Equation

Linear Functions

• Finding Slope
• Graphing Lines Using Line Equation
• Writing Linear Equations
• Graphing Linear Inequalities
• Finding Midpoint
• Finding Distance of Two Points

The Best Study Guide to Ace the SAT Math Test

SAT Math Test Prep Bundle Study Guide + Practice Workbook + Practice Tests

Exponents and radicals.

• Multiplication Property of Exponents
• Zero and Negative Exponents
• Division Property of Exponents
• Powers of Products and Quotients
• Negative Exponents and Negative Bases
• Scientific Notation
• Square Roots

Polynomials

• Writing Polynomials in Standard Form
• Simplifying Polynomials
• Adding and Subtracting Polynomials
• Multiplying Monomials
• Multiplying and Dividing Monomials
• Multiplying a Polynomial and a Monomial
• Multiplying Binomials
• Factoring Trinomials
• Operations with Polynomials

Geometry and Solid Figures

• Pythagorean Relationship
• Rectangular Prism
• Pyramids and Cone

Statistics and Probability

• Mean and Median
• Mode and Range
• Stem–and–Leaf Plot
• Probability Problems
• Combinations and Permutations
• Solving a Quadratic Equation
• Quadratic Formula and the Discriminant
• Graphing Quadratic Functions
• Solving Quadratic Inequalities

Complex Numbers

• Adding and Subtracting Complex Numbers
• Multiplying and Dividing Complex Numbers
• Rationalizing Imaginary Denominators
• Function Notation
• Adding and Subtracting Functions
• Multiplying and Dividing Functions
• Composition of Functions

Trigonometric Functions

• Trig Ratios of General Angles
• Angles and Angle Measure
• Evaluating Trigonometric Function
• Arc Length and Sector Area

Take a FREE SAT Mathematics Practice Test  

A Perfect SAT Math Prep Book to Help You Prepare for the SAT Math Test!

SAT Math Full Study Guide Comprehensive Review + Practice Tests + Online Resources

Sat math exercises, proportions and ratios, solid figures, function operations, quadratic functions, college entrance tests.

Looking for the best resource to help you or your student succeed on the SAT Math test?

The Best Books to Ace the SAT Math Test

SAT Math in 10 Days The Most Effective SAT Math Crash Course

Sat math exercise book a comprehensive workbook + sat math practice tests, sat math test prep the ultimate guide to sat math + 2 full-length practice tests, sat math study guide step-by-step guide to preparing for the sat math test.

by: Effortless Math Team about 4 years ago (category: Blog , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• FREE HiSET Math Practice Test
• 4th Grade IAR Math FREE Sample Practice Questions
• SHSAT Math Worksheets: FREE & Printable
• What is the Relationship between Dilations and Angles in Geometry
• The College Mathematics Exam Overview
• FREE 4th Grade PARCC Math Practice Test
• Area of a Parallelogram
• Top 10 PSAT / NMSQT Prep Books (Our 2023 Favorite Picks)
• How to Find Midpoint? (+FREE Worksheet!)
• SSAT Middle-Level Math Worksheets: FREE & Printable

What people say about "The Best SAT Math Worksheets: FREE & Printable - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

SAT Math in 30 Days The Most Effective SAT Math Crash Course

Sat math practice workbook 2024 the most comprehensive review for the math section of the sat test.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 49 %

It was $69.99 now it is $35.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.