the optimal solution of the linear programming problem is located

Reset password New user? Sign up

Existing user? Log in

Linear Programming

Already have an account? Log in here.

• Andrew Hayes

Linear programming is an optimization technique for a system of linear constraints and a linear objective function. An objective function defines the quantity to be optimized, and the goal of linear programming is to find the values of the variables that maximize or minimize the objective function.

A factory manufactures doodads and whirligigs. It costs $2 and takes 3 hours to produce a doodad. It costs $4 and takes 2 hours to produce a whirligig. The factory has $220 and 150 hours this week to produce these products. If each doodad sells for $6 and each whirligig sells for $7, then how many of each product should be manufactured this week in order to maximize profit? This kind of problem is perfect to use linear programming techniques on. All of the quantifiable relationships in the problem are linear. The values of variables are constrained in some way. The goal is to find values of the variables that will maximize some quantity.

Linear programming is useful for many problems that require an optimization of resources. It could be applied to manufacturing, to calculate how to assign labor and machinery to minimize cost of operations. It could be applied in high-level business operations, to decide which products to sell and in what quantity in order to maximize profit. It could also be applied in logistics, to decide how to apply resources to get a job done in the minimum amount of time.

When to use Linear Programming

Linear programming in two variables, simplex algorithm, special cases of simplex algorithm, big-m method.

Linear programming can be used to solve a problem when the goal of the problem is to maximize some value and there is a linear system of inequalities that defines the constraints on the problem.

A constraint is an inequality that defines how the values of the variables in a problem are limited. In order for linear programming techniques to work, all constraints should be linear inequalities.

Returning to the example in the introduction:

Note that there is a cost associated with producing each part. Each doodad costs $2 to make and each whirligig costs $4 to make. The factory only has $220 available to spend on these costs, so the production is limited by cost. Let \(x\) be the number of doodads produced, and let \(y\) be the number of whirligigs produced. Then this constraint can be written as an inequality: \[2x+4y \le 220.\] There is also the limitation on how much time the factory has to produce these parts. Each doodad requires 3 hours to make and each whirligig requires 2 hours to make. The factory only has 150 hours available this week, so production is also limited by time. This constraint can be written as an inequality: \[3x+2y \le 150.\] In addition to these constraints, there is also a couple of "common sense" constraints. It's not possible to produce less than 0 of any part, so these constraints are also written: \[\begin{align} x &\ge 0 \\ y &\ge 0. \end{align}\] These are called non-negative constraints . Altogether, the constraints form a system of inequalities: \[\begin{cases}\begin{align} 2x+4y &\le 220 \\ 3x+2y &\le 150 \\ x &\ge 0 \\ y &\ge 0. \end{align}\end{cases}\]

Graphing these inequalities in the coordinate plane creates a polygon shape.

Graph the system of constraints \[\begin{cases}\begin{align} 2x+4y &\le 220 \\ 3x+2y &\le 150 \\ x &\ge 0 \\ y &\ge 0. \end{align}\end{cases}\]

The shaded region above is the feasible region of this problem.

The region that is bound by the system of constraints is called the feasible region . It represents the possible values of the variables that satisfy all of the constraints. In order for linear programming techniques to work, it should be a convex polytope (in 2 dimensions, a convex polygon; in 3 dimensions, a convex polyhedron; and so on).

Finding the feasible region is only sufficient to give the possible solutions of a problem. The goal of linear programming is to find the best solution to a problem. This is done by maximizing or minimizing the objective function .

The objective function is a function that defines some quantity that should be minimized or maximized. The arguments of the objective function are the same variables that are used in the constraints. In order for linear programming techniques to work, the objective function should be linear.

Each doodad costs $2 to make and sells for $6. This gives a profit of $4 per doodad. Each whirligig costs $4 to make and sells for $7. This gives a profit of $3 per whirligig. The profit function can be defined as \[p(x,y)=4x+3y.\] This is the objective function of this problem, and the goal is to maximize it.

It seems like the strategy now would be to test ordered pairs in the feasible region until a maximum profit is found. However, a more efficient method is available.

Let \(P\) be the maximum profit in the feasible region: \[P=4x+3y.\] Solve for y: \[y=-\frac{4}{3}x+\frac{P}{3}.\] This maximum profit gives an equation of a line, and whatever point in the feasible region passes through this line is the optimal solution. The \(y\)-intercept of this line is \(\frac{P}{3}.\) Since \(P\) is maximized, this \(y\)-intercept should be maximized as well. Graph several lines with the same slope of \(-\frac{4}{3}.\) The line that maximizes the \(y\)-intercept is the one that passes through the vertex at \((20,45),\) the intersection of the first two constraints. All other higher lines do not pass through the feasible region. All other lower lines pass through more than one point in the feasible region, and do not maximize the \(y\)-intercept of the line. Therefore, the factory should produce 20 doodads and 45 whirligigs. This will give a profit of \($215.\) \(_\square\)

In the previous example, it was shown that the optimal solution was on a vertex of the feasible region. This is true for all linear programming problems.

Given a convex polygonal feasible region and a linear objective function, the solution that maximizes or minimizes the objective function will be located on one of the vertices of the feasible region.

Let the objective function be \(f(x,y)=ax+by.\) Let the maximum value of this function be \(P,\) and let the minimum value of this function be \(Q.\) There exist lines which intersect each of the optimal solutions, \((x,y)\): \[\begin{align} ax+by &= P &&\qquad (1) \\ ax+by &= Q &&\qquad (2) \\\\ \Rightarrow y &= -\frac{a}{b}x + \frac{P}{b} &&\qquad (1) \\ y &= -\frac{a}{b}x + \frac{Q}{b}. &&\qquad (2) \end{align}\] Since \(P\) is the maximum value of the objective function, \((1)\) has the maximum \(y\)-intercept of a line with slope \(-\frac{a}{b}\) that passes through the feasible region. Likewise, \((2)\) has the minimum \(y\)-intercept of a line with slope \(-\frac{a}{b}\) that passes through the feasible region. Suppose that \((1)\) or \((2)\) passes through a point that is not one of the vertices of the feasible region. Case 1. The intersection point is on a side of the feasible region that is parallel to lines \((1)\) and \((2).\) If this is the case, then line \((1)\) or \((2)\) also contains a vertex of the feasible region, so this cannot be so. Case 2. The intersection point is somewhere else within the feasible region. The line will intersect more than one point in the feasible region. Then there will exist another point within the feasible region, either higher or lower, that a line with a parallel slope intersects. This cannot be true if line \((1)\) or \((2)\) has the maximum or minimum \(y\)-intercept of a line that passes through the feasible region. Hence, \((1)\) and \((2)\) must intersect a vertex of the feasible region. Each optimal solution is located at a vertex of the feasible region. \(_\square\)

This theorem gives a simple method for finding the optimal solution to a linear programming problem in two variables.

Process for finding the optimal solution of a linear programming problem in two variables Confirm that the feasible region is a convex polygon and the objective function is linear. Find the ordered pair of each vertex of the feasible region. Substitute each ordered pair into the objective function to find the solution that maximizes or minimizes the objective function.

A farmer feeds his cows a feed mix to supplement their foraging. The farmer uses two types of feed for the mix. Corn feed contains 100 g protein per kg and 750 g starch per kg. Wheat feed contains 150 g protein per kg and 700 g starch per kg. Each cow should be fed at most 7 kg of feed per day. The farmer would like each cow to receive at least 650 g protein and 4000 g starch per day. If corn feed costs $0.40/kg and wheat costs $0.45/kg, then what is the optimal feed mix that minimizes cost? Round your answers to the nearest gram. Let \(c\) be the kilograms of corn feed per cow per day, and let \(w\) be the kilograms of wheat feed per cow per day. The system of constraints can be written: \[\begin{cases} \begin{align} 0.1c+0.15w &\ge 0.65 \\ 0.75c+0.7w &\ge 4 \\ c+w &\le 7 \\ c &\ge 0 \\ w &\ge 0. \end{align} \end{cases}\] The objective function is \[\text{Minimize:} \ f(c,w)=0.40c+0.45w.\] Graphing the system of constraints gives an idea of where the vertices of the feasible region are, and which lines intersect to form them: Solve for each vertex of the feasible region by solving each pair of intersecting lines as a system of equations. For example, to solve for the vertex within the \(1^\text{st}\) quadrant, solve the system of equations \[\begin{cases} \begin{align} 0.1c+0.15w &= 0.65 \\ 0.75c +0.7w &= 4. \end{align} \end{cases}\] Solving this system gives \(c \approx 3.411\) and \(w \approx 2.059.\) These values can be substituted into the objective function to obtain the cost of this mix: \[f(3.411,2.059) = \$2.29.\] Note that it is not necessary to solve for every vertex. Since the problem requires a minimum and the objective function line has a negative slope, the optimal solution must be on the underside of the feasible region. Solve for these vertices: \[\begin{cases} \begin{align} 0.75c +0.7w &= 4 \\ c &= 0 \end{align} \end{cases} \implies c=0, w \approx 5.714 \implies f(0,5.714)=\$2.57 \] \[\begin{cases} \begin{align} 0.1c+0.15w &= 0.65 \\ w &= 0 \end{align} \end{cases} \implies c=6.5, w=0 \implies f(6.5,0)=\$2.60. \] The feed mix that minimizes cost contains 3411 g corn and 2059 g wheat. It costs $2.29 per cow. \(_\square\)

A manufacturer has 750 meters of cotton and 1000 meters of polyester. Production of a sweatshirt requires 1 meter of cotton and 2 meters of polyester, while production of a shirt requires 1.5 meters of cotton and 1 meter of polyester. The sale prices of a sweatshirt and a shirt are 30 € and 24 €, respectively. What are the number of sweatshirts \((S)\) and the number of shirts \((C)\) that maximize total sales?

Submit \(S + C.\)

Jordan has $100 to buy some comic books. He really likes the Star Wars books which cost $12 each, but he could also buy the Marvels books which cost $5 each. If he has to buy at least 12 books, what is the maximum number of the Star Wars books that he can buy?

An amateur bodybuilder is looking for supplement protein bars to build his muscle fast, and there are 2 available products: protein bar A and protein bar B.

Each protein bar A contains 15 g of protein and 30 g of carbohydrates and has total 200 calories. On the other hand, each protein bar B contains 30 g of protein and 20 g of carbohydrates and has total 240 calories.

According to his nutritional plan, this bodybuilder needs at least 20,000 calories from these supplements over the month, which must comprise of at least 1,800 g of protein and at least 2,200 g of carbohydrates.

If each protein bar A costs $3 and each protein bar B costs $4, what is the least possible amount of money (in $) he can spend to meet all his one-month requirements?

This kind of method would also work for linear optimization problems in more than two variables. However, these kinds of problems are more challenging to visualize with a coordinate graph, and there can be many more vertices to check for the optimal solution. The simplex algorithm was developed as an efficient method to solve these kinds of problems.

The simplex algorithm is a method to obtain the optimal solution of a linear system of constraints, given a linear objective function. It works by beginning at a basic vertex of the feasible region, and then iteratively moving to adjacent vertices, improving upon the solution each time until the optimal solution is found.

The simplex algorithm has many steps and rules, so it is helpful to understand the logic behind these steps and rules with a simple example before proceeding with the formal algorithm.

Given the system of constraints \[\begin{cases} \begin{align} 2x+3y &\le 90 \\ 3x+2y &\le 120 \\ x & \ge 0 \\ y & \ge 0, \end{align} \end{cases}\] maximize the objective function \[f(x,y)=7x+5y.\] The simplex algorithm begins by converting the constraints and objective functions into a system of equations. This is done by introducing new variables called slack variables . Slack variables represent the positive difference, or slack , between the left hand side of an inequality and the right hand side of that inequality. The inequality \[2x+3y \le 90\] becomes \[2x+3y+s_1=90.\] Likewise, the inequality \[3x+2y \le 120\] becomes \[3x+2y+s_2 = 120.\] In addition to the slack variables, a variable \(z\) is introduced to represent the value of the objective function. This gives the equation \[z-7x-5y=0.\] These equations give the system of equations \[\begin{cases} \begin{array}{cccccccccccc} z & - & 7x & - & 5y & & & & & = & 0 && (0) \\ & & 2x & + & 3y & + & s_1 & & & = & 90 && (1) \\ & & 3x & + & 2y & & & + & s_2 & = & 120. && (2) \end{array} \end{cases}\] In augmented matrix form, this is \[\left[\begin{array}{ccccc|c} 1 & -7 & -5 & 0 & 0 & 0 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] It is implied that all variables in this system (including \(s_1,\) \(s_2,\) and \(z\)) are greater than or equal to 0. The variables \(s_1\) and \(s_2\) have zero coefficients in row \((0)\) and are called basic variables . The variables \(x\) and \(y\) have non-zero coefficients in row \((0)\) and are called non-basic variables . At any point in this process, the basic solution is given by setting the non-basic variables to 0. Currently, the basic solution is \[x=0, \quad y=0, \quad s_1=90, \quad s_2=120, \quad z=0.\] Consider what effect increasing the values of the non-basic variables would have on the value of \(z.\) Increasing either \(x\) or \(y\) would cause \(z\) to also increase, because \(x\) and \(y\) have negative coefficients in row \((0).\) Thus, this is not the optimal solution. The iterations of the simplex algorithm involve exchanging basic variables and non-basic variables by using matrix row operations. At each step of the process, a non-basic variable in row \((0)\) is eliminated, leading another basic variable to take its place as a non-basic variable. This is called a pivot . Suppose \(x\) were to be eliminated in row \((0).\) This can be done with either row \((1)\) or row \((2).\) Case 1. Eliminating \(x\) in row \((0)\) with row \((1)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}\] During this pivot, the variable \(x\) entered as a basic variable, and the variable \(s_1\) left to become a non-basic variable. Now eliminate \(x\) in row \((2)\): \[\left[\begin{array}{ccccc|c} 1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 0 & -\frac{5}{2} & -\frac{3}{2} & 1 & -15 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \end{array}\] This gives the basic solution \[x=45, \quad y=0, \quad s_1=0, \quad s_2=-15, \quad z=315.\] This solution is impossible, because it leads to one of the variables being negative. Case 2. Eliminating \(x\) in row \((0)\) with row \((2)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}\] During this pivot, the variable \(x\) entered as a basic variable, and the variable \(s_2\) left to become a non-basic variable. Now eliminate \(x\) in row \((1)\): \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] This gives the basic solution \[x=40, \quad y=0, \quad s_1=10, \quad s_2=0, \quad z=280.\] This solution is possible, but it is not optimal, because there is a negative coefficient in row \((0).\) This implies that \(z\) can be increased further by increasing \(y.\) Another pivot will be needed to find the optimal solution. It is a fair amount of work to perform a pivot, only to find that it gives an infeasible solution. Fortunately, one can anticipate which pivot will result in a feasible solution by observing the ratio of the element in the right part of the augmented matrix to the coefficient of the entering variable. Consider \(y\) as the entering variable, and calculate these ratios: \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & {\color{red}\frac{5}{3}} & 1 & -\frac{2}{3} & {\color{red}10} \\ 0 & 3 & {\color{blue}2} & 0 & 1 & {\color{blue}120} \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] For entering variable \(y,\) this ratio is \(10\div \frac{5}{3}=6\) for row \((1)\) and \(\frac{120}{2}=60\) for row \((2).\) Selecting the row that minimizes this ratio will ensure that the pivot results in a feasible solution. Thus, row \((1)\) should be selected as the pivot row. Eliminating \(y\) in row \((0)\) with row \((1)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] Then eliminating \(y\) in row \((2)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 0 & -\frac{6}{5} & \frac{9}{5} & 108 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2)\vphantom{\frac{1}{2}} \end{array}\] This gives the basic solution \[x=36, \quad y=6, \quad s_1=0, \quad s_2=0, \quad z=282.\] This solution must be optimal, because any increase in the non-basic variables \(s_1\) and \(s_2\) will cause a decrease in \(z.\) Thus, the maximum value of the objective function is \[f(36,6)=282.\ _\square\]

Simplex Algorithm for Maximization This version of the simplex algorithm is valid for a maximization problem with all constraints (except for the non-negative constraints) giving maximum values (using the \(\le\) symbol). In matrix form, the requirements are \[\begin{array}{ll} \text{Maximize:} & \textbf{c}^\text{T} \cdot \textbf{x} \\ \text{Subject to:} & \textbf{A}\textbf{x} \le \textbf{b}, \ \ x_i \ge 0, \end{array}\] where \(\textbf{c}\) is a vector containing the coefficients of the objective function, \(\textbf{x}\) is a vector containing the variables of the problem, \(\textbf{A}\) is a matrix containing the constraint coefficients, and \(\textbf{b}\) is a vector containing the maximum values of those constraints. Convert the constraints and objective function into a system of equations by introducing slack variables and the \(z\) variable. Put the system of equations into augmented matrix form. The objective function equation should go in row \((0).\) Select one of the non-basic variables to be the entering variable. Select the pivot row by computing the ratio \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}}\) for each row. The correct pivot row minimizes this ratio. However, this ratio must be positive. If all coefficients of non-basic variables in row \((0)\) are positive, then you have the optimal solution. Otherwise, select a non-basic variable that has a negative coefficient in row \((0)\) to be the next entering variable, then pivot again to find another feasible solution. Continue pivoting until the optimal solution is found.

A toy factory manufactures three kinds of toys: cars, motorcycles, and boats. One toy car makes $20 profit, one toy motorcycle makes $15 profit, and one toy boat makes $25 profit. There are three departments of labour: casting, which has 8 workers; assembly, which has 12 workers; quality control, which has 10 workers.

Every day, the labour is allocated as follows: a toy car requires 2 casting, 2 assembly, 2 quality control; a toy motorcycles requires 1 casting, 2 assembly, 1 quality control; a toy boat requires 2 casting, 3 assembly, 3 quality control.

What is the maximum profit per day (in dollars) the toy company can achieve?

The simplex algorithm for minimization problems works by converting the problem to a maximization problem. This concept that every maximization problem has a corresponding minimization problem is formalized with the von Neumann duality principle .

Given the system of constraints \[\begin{cases}\begin{align} 4x+3y+5z &\ge 65 \\ x+3y+2z &\ge 38 \\ 2x+3y+4z &\ge 52 \\ x,y,z &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y,z)=12x+3y+10z.\] This problem could be put into the form shown in the maximization examples above, but an issue would occur with finding the first basic solution: setting the \(x,\) \(y,\) and \(z,\) variables to \(0\) would give an infeasible solution with the slack variables taking on negative values. The simplex algorithm needs to start with a feasible solution, so this would not work. The Big-M method gives a workaround to this problem, but there is a much simpler method for this problem. A "dual" of this problem can be written by transposing the coefficients. Place the coefficients of the constraints into an augmented matrix. Place the coefficients of the objective function into the bottom row, with a 0 in the right part: \[\left[\begin{array}{ccc|c} \color{green}4 & \color{red}3 & \color{blue}5 & \color{orange}65 \\ \color{green}1 & \color{red}3 & \color{blue}2 & \color{orange}38 \\ \color{green}2 & \color{red}3 & \color{blue}4 & \color{orange}52 \\ \hline \color{green}12 & \color{red}3 & \color{blue}10 & \color{orange}0 \end{array}\right].\] Transpose the elements of the matrix: \[\left[\begin{array}{ccc|c} \color{green}4 & \color{green}1 & \color{green}2 & \color{green}12 \\ \color{red}3 & \color{red}3 & \color{red}3 & \color{red}3 \\ \color{blue}5 & \color{blue}2 & \color{blue}4 & \color{blue}10 \\ \hline \color{orange}65 & \color{orange}38 & \color{orange}52 & \color{orange}0 \end{array}\right].\] Note: It's tempting to divide out the 3 in the second row of this matrix, but this will break the symmetry that is required to return to the original problem. This gives a new system of constraints and an objective function to be maximized: Given the system of constraints \[\begin{cases}\begin{align} 4u+v+2w &\le 12 \\ 3u+3v+3w &\le 3 \\ 2u+3v+4w &\le 52 \\ u,v,w &\ge 0, \end{align}\end{cases}\] maximize the function \[g(u,v,w)=65u+38v+52w.\] Now the simplex algorithm can be applied to find the optimal solution \[\left[\begin{array}{ccccccc|c} 1 & -65 & -38 & -52 & 0 & 0 & 0 & 0 \\ 0 & 4 & 1 & 2 & 1 & 0 & 0 & 12 \\ 0 & 3 & 3 & 3 & 0 & 1 & 0 & 3 \\ 0 & 2 & 3 & 4 & 0 & 0 & 1 & 52 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] Enter \(u\) with row \((2)\): \[\left[\begin{array}{ccccccc|c} 1 & 0 & 27 & 13 & 0 & \frac{65}{3} & 0 & 65 \\ 0 & 0 & -3 & -2 & 1 & -4 & 0 & 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 & 0 & 1 & 2 & 0 & -2 & 1 & 50 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{array}\] All coefficients in row \((0)\) are positive, so this is the optimal solution. The maximum value in the top right of the matrix, \(65,\) is the same as the minimum value for the original problem. However, the variables \(u,\) \(v,\) and \(w\) are not the same as the variables in the original problem. Fortunately, the values of the variables that minimize the original problem correspond to the coefficients of the slack variables in row \((0).\) \[\left[\begin{array}{ccccccc|c} 1 & 0 & 27 & 13 & \color{red}0 & \color{red}\frac{65}{3} & \color{red}0 & 65 \\ 0 & 0 & -3 & -2 & 1 & -4 & 0 & 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 & 0 & 1 & 2 & 0 & -2 & 1 & 50 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{array}\] Thus, the values of the original problem that minimize the objective function are \[x=0, \quad y=\frac{65}{3}, \quad z=0.\ _\square\]

Simplex Algorithm for Minimization This version of the simplex algorithm is valid for a minimization problem with all constraints giving minimum values (using the \(\ge\) symbol). In matrix form, the requirements are: \[\begin{array}{ll} \text{Minimize:} & \textbf{c}^\text{T} \cdot \textbf{x} \\ \text{Subject to:} & \textbf{A}\textbf{x} \ge \textbf{b}\, \quad x_i \ge 0 \end{array}\] where \(\textbf{c}\) is a vector containing the coefficients of the objective function, \(\textbf{x}\) is a vector containing the variables of the problem, \(\textbf{A}\) is a matrix containing the constraint coefficients, and \(\textbf{b}\) is a vector containing the minimum values of those constraints. Place the coefficients of the constraints and objective function into an augmented matrix. The coefficients of the objective function should go into the bottom row. Transpose this matrix. This new matrix represents the dual maximization problem. Write the new system of constraints and objective function. This problem has different variables than the original problem. Use the simplex algorithm for maximization to obtain the maximum value. This maximum value is the same as the minimum value for the original problem. The coefficients of the slack variables in row \((0)\) correspond to the values of the variables in the original problem.

The simplex algorithm can sometimes lead to some surprising results. It is possible that a linear programming problem has infinite solutions or no solutions. These special cases are explored here.

As was stated earlier, a linear programming problem that has minimum constraints does not work with the simplex algorithm. The reason for this is that the initial basic solution is infeasible.

Given the system of constraints \[\begin{cases}\begin{align} 2x+3y &\ge 10 \\ 3x+y &\ge 8 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=5x+10y.\] Show that this cannot be done using the normal simplex algorithm. This problem could be solved with a dual or by simply testing the vertices of the feasible region, but consider solving it with the simplex algorithm. Because the constraints are minimum constraints, the slack variables need to have negative coefficients. In addition, the objective function is a minimization. This can be accounted for by treating the problem as a maximization of \(-z.\) Applying the simplex algorithm, this gives the initial matrix \[\left[ \begin{array}{ccccc|c} -1 & 5 & 10 & 0 & 0 & 0 \\ 0 & 2 & 3 & -1 & 0 & 10 \\ 0 & 3 & 1 & 0 & -1 & 8 \\ \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] This initial matrix implies an infeasible solution of \(s_1=-10,\ s_2=-8.\) The simplex algorithm will not produce a meaningful result if the initial basic solution is infeasible. \(_\square\)

It is sometimes possible to solve the problem with its dual, but this is not the case if a problem mixes minimum constraints with maximum constraints.

Given the system of constraints \[\begin{cases}\begin{align} -x+5y &\le 25 \\ 6x+5y &\le 60 \\ x+y &\ge 2 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=x-10y.\] Show that this cannot be done using the normal simplex algorithm or the dual method. Putting this problem into a simplex matrix would give an initial basic solution that is infeasible: \[\left [ \begin{array}{cccccc|c} -1 & 1 & -10 & 0 & 0 & 0 & 0 \\ 0 & -1 & 5 & 1 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 2 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[\begin{array}{ccc} s_1 = 25, & s_2 = 60, & s_3 = -2. \end{array}\] Putting the problem's dual into a simplex matrix would also yield an infeasible initial basic solution: \[\left [ \begin{array}{cccccc|c} 1 & -25 & -60 & 2 & 0 & 0 & 0\\ 0 & 1 & -6 & 1 & 1 & 0 & 1 \\ 0 & -5 & -5 & 1 & 0 & 1 & -10 \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] \[\begin{array}{cc} s_1 = 1, & s_2 = -10.\ _\square \end{array}\]

The Big-M method can be used when an initial basic solution is infeasible. The idea behind this method is to introduce artificial variables to the problem in order to move the solution into the feasible region. Unlike slack variables, these artificial variables must have a value of zero in the final solution.

Given the system of constraints \[\begin{cases}\begin{align} -x+5y &\le 25 \\ 6x+5y &\le 60 \\ x+y &\ge 2 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=x-10y.\] From the previous example, it is known that the third constraint produces an infeasible \(s_3=-2.\) To compensate for this, an artificial variable, \(a_1,\) is introduced to this constraint and the objective function. In the objective function, this variable has a coefficient of \(M.\) \(M\) represents an arbitrarily large constant amount. The new constraints and objective function are \[\begin{cases}\begin{array}{ccccccccccccccc} -z & + & x & - & 10y & & & & & & & + & Ma_1 & = & 0 \\ & - & x & + & 5y & + & s_1 & & & & & & & = & 25 \\ & & 6x & + & 5y & & & + & s_2 & & & & & = & 60 \\ & & x & + & y & & & & & - & s_3 & + & a_1 & = & 2. \end{array}\end{cases} \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] In matrix form, \[\left [ \begin{array}{ccccccc|c} -1 & 1 & -10 & 0 & 0 & 0 & M & 0 \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \end{array} \right ]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] The first goal with the Big-M method is to move the problem into the feasible region. Recall that the current basic solution has \(s_3=-2.\) This variable will be the leaving variable, with the artificial variable, \(a_1,\) being the entering variable: \[\left [ \begin{array}{ccccccc|c} -1 & 1-M & -10-M & 0 & 0 & M & 0 & -2M \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \\ \end{array} \right ]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] The current solution is now in the feasible region, with all basic variables positive: \[s_1 = 25, \quad s_2 = 60, \quad a_1 = 2.\] This solution is clearly not correct, because it contains a non-zero artificial variable in the solution. Furthermore, there are negative coefficients in row \((0)\). The Big-M method now proceeds just as the simplex algorithm. The new goal is to enter variables with negative coefficients in row \((0)\). Since \(y\) has the most negative coefficient in the row \((0)\), that variable will be entered first. The row that minimizes the ratio of the right hand side and the coefficient is \((3)\), so \(y\) will be entered through this row: \[\left [ \begin{array}{ccccccc|c} -1 & 11 & 0 & 0 & 0 & -10 & 10+M & 20 \\ 0 & -6 & 0 & 1 & 0 & 5 & -5 & 15 \\ 0 & 1 & 0 & 0 & 1 & 5 & -5 & 50 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[y=2, \quad s_1=15, \quad s_2=50.\] This solution no longer contains the artificial variable, but it is not yet optimal due to the negative coefficient in row \((0).\) \(s_3\) must be the next variable to enter. The minimum positive ratio for this variable is in row \((1)\): \[\left [ \begin{array}{ccccccc|c} -1 & -1 & 0 & 2 & 0 & 0 & M & 50 \\ 0 & -6 & 0 & 1 & 0 & 5 & -5 & 15 \\ 0 & 7 & 0 & -1 & 1 & 0 & 0 & 35 \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[y = 5, \quad s_2 = 35, \quad s_3 = 3.\] Now \(x\) must be the entering variable, and the only row with a positive ratio is \((2)\): \[\left [ \begin{array}{ccccccc|c} -1 & 0 & 0 & \frac{15}{7} & \frac{1}{7} & 0 & M & 55 \\ 0 & 0 & 0 & \frac{1}{7} & \frac{6}{7} & 5 & -5 & 45 \\ 0 & 7 & 0 & -1 & 1 & 0 & 0 & 35 \\ 0 & 0 & 5 & \frac{6}{7} & \frac{1}{7} & 0 & 0 & 30 \\ \end{array} \right ]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{7}} \\ (1)\vphantom{\frac{1}{7}} \\ (2) \\ (3)\vphantom{\frac{1}{7}} \end{array}\] Now it is clear that this gives the optimal solution: \[x=5, y=6, s_3=9\implies f(5,6)=-55.\ _\square\]

Big M Simplex Method This method is viable for any linear programming problem that does not match the forms of the previous section . It is also required for problems which contain equality constraints. Assign slack variables and the \(z\) variable as with the basic simplex algorithm, and create a simplex matrix. For each slack variable that has a negative value in the initial basic solution, add a distinct artificial variable to that constraint. Also add a distinct artificial variable to each equality constraint. Artificial variables begin with a coefficient of \(1\) in each constraint row. In the objective function row, every artificial variable begins with the same coefficient, \(M.\) This represents an arbitrarily large positive constant amount. If the problem is a minimization, then the coefficients of the objective function row are negated, and the goal is to maximize \(-z.\) Move the solution into the feasible region by performing pivots with a negative slack variable as the leaving variable and an artificial variable as the entering variable. Once the basic solution is in the feasible region, proceed with the simplex algorithm as before. While performing the simplex algorithm, ensure that the elements in the right side of the matrix are positive. If an element in the right side is not positive, multiply that row by \(-1\) to make it positive. If an element in the right side of the matrix is \(0,\) then ensure that the coefficient of the basic variable in that row is positive. Choose the entering variable by observing the coefficient in row \((0)\) that is the most negative. Choose pivot rows by selecting the row that minimizes the ratio \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}}.\) The ratio must be non-negative, and the coefficient of the entering variable in the pivot row must be positive. An optimal solution cannot contain any artificial variables. If row \((0)\) of the matrix contains no negative coefficients, and the solution contains an artificial variable, then the problem has no solution.

Vanessa is scheduling her employees for the upcoming week. When on the assembly line, Darren assembles 5 units per hour, and when on the packaging line, he packages 10 units per hour. Lori only works on the assembly line, and she assembles 4 units per hour. Darren's pay is $12 per hour and Lori's pay is $9 per hour Vanessa needs to have at least 200 units assembled and packaged by the end of the week. She can assign each worker a maximum of 40 hours. How should Vanessa schedule her employees to minimize payroll? This problem can be solved with simpler methods, but is solved here with the Big M method as a demonstration of how to deal with different types of constraints with the Big M method. Let \(m_d\) and \(m_l\) be the number of hours that Darren and Lori work on the assembly line, respectively. Let \(p_d\) be the number of hours that Darren and Lori work on the packaging line, respectively. Each worker can work a maximum of 40 hours. This gives the constraints \[\begin{align} m_d+p_d &\le 40 \\ m_l &\le 40. \end{align}\] Vanessa would not want to waste hours on packaging if there are no assembled units to package. Therefore, the number of units assembled should equal the number of units packaged. This can be expressed with the equation \[5m_d+4m_l=10p_d.\] The number of units assembled and packaged should be at least 200. This can be expressed with the constraint \[\begin{align} 10p_d &\ge 200 \\ p_d &\ge 20. \end{align}\] This gives the following system of constraints: \[\begin{cases} \begin{array}{ccccccc} m_d & & & + & p_d & \le & 40 \\ & & m_l & & & \le & 40 \\ & & & & p_d & \ge & 20 \\ 5m_d & + & 4m_l & - & 10p_d & = & 0 \\ m_d, & & m_l, & & p_d & \ge & 0. \end{array} \end{cases}\] The objective function is \[f(m_d,m_l,p_d)=12m_d+9m_l+12p_d.\] Converting the system of constraints and objective function to a simplex matrix, \[\left[\begin{array}{ccccccc|c} -1 & 12 & 9 & 12 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 \\ \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] The basic solution is currently infeasible: \[m_d=0, \quad m_l=0, \quad p_d=0, \quad s_1 = 40, \quad s_2=40, \quad s_3=-20.\] Since \(s_3\) has an infeasible value, the row that contains it requires an artificial variable. The equality constraint row also requires an artificial variable. These artificial variables are given the coefficient \(M\) in row \((0):\) \[\left[\begin{array}{ccccccccc|c} -1 & 12 & 9 & 12 & 0 & 0 & 0 & M & M & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] To move the solution into the feasible region, \(s_3\) will be the leaving variable and \(a_1\) will be the entering variable. The pivot will be performed with row \((3):\) \[\left[\begin{array}{ccccccccc|c} -1 & 12 & 9 & 12-M & 0 & 0 & M & 0 & M & -20M \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] The other artificial variable must be moved into the basic solution as well: \[\left[\begin{array}{ccccccccc|c} -1 & 12-5M & 9-4M & 12+9M & 0 & 0 & M & 0 & 0 & -20M \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now the algorithm proceeds as the usual simplex algorithm. The goal is to eliminate the negative coefficients in row \((0).\) Since \(M\) is an arbitrarily large positive constant value, \(12-5M\) is the most negative coefficient in row \((0).\) Therefore, \(m_d\) will be the entering variable. The selection of the pivot row is slightly more challenging than the usual simplex algorithm. Observe that every value in the right-hand side of the constraint rows is positive except for the value in row \((4).\) In this row, the right-hand side is \(0,\) and the basic variable contained in this row, \(a_2,\) has a positive coefficient. It is important to maintain these two things: values in the right-hand sides of the constraint rows are positive, or if the value in the right hand side is \(0,\) then the coefficient of the basic variable in that row is positive. Maintaining this will ensure the correct selection of the pivot row. The pivot row is selected by choosing the row that minimizes the ratio of \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}},\) provided that the coefficient of the entering variable is positive . Thus, the minimum ratio for the entering variable is \(\frac{0}{5}\) from row \((4).\) This will be the pivot row: \[\left[\begin{array}{ccccccccc|c} -1 & 0 & -\frac{3}{5} & 36-M & 0 & 0 & M & 0 & M-\frac{12}{5} & -20M \\ 0 & 0 & -4 & 15 & 5 & 0 & 0 & 0 & -1 & 200 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(36-M\) is the most negative coefficient in row \((0).\) Thus, \(p_d\) will be the entering variable. Row \((4)\) will not be chosen as the pivot row again, as it has a negative coefficient for this variable. The row that minimizes the ratio is \(\frac{200}{15}\) from row \((1):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 9-\frac{4}{15}M & 0 & \frac{1}{3}M-12 & 0 & M & 0 & \frac{14}{15}M & -\frac{20}{3}M-480 \\ 0 & 0 & -4 & 15 & 5 & 0 & 0 & 0 & -1 & 200 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 4 & 0 & -5 & 0 & -15 & 15 & 1 & 100 \\ 0 & 15 & 4 & 0 & 10 & 0 & 0 & 0 & 1 & 400 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(9-\frac{4}{15}M\) is the most negative coefficient in row \((0).\) \(m_l\) will be the entering variable and the minimizing ratio is \(\frac{100}{4}\) in row \((3):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 0 & 0 & -\frac{3}{4} & 0 & \frac{135}{4} & M-\frac{135}{4} & M-\frac{9}{4} & -705 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 0 & 0 & 0 & 5 & 4 & 15 & -15 & -1 & 60 \\ 0 & 0 & 4 & 0 & -5 & 0 & -15 & 15 & 1 & 100 \\ 0 & 1 & 0 & 0 & 1 & 0 & 1 & -1 & 0 & 20 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(-\frac{3}{4}\) is the most negative coefficient in row \((0).\) \(s_1\) will be the entering variable and the minimizing ratio is \(\frac{60}{5}\) in row \((2):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 0 & 0 & 0 & \frac{3}{5} & 36 & M-36 & M-\frac{12}{5} & -696 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 0 & 0 & 0 & 5 & 4 & 15 & -15 & -1 & 60 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 5 & 0 & 0 & 0 & -4 & -10 & 10 & 1 & 40 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] With all coefficients in row \((0)\) positive and no artificial variables in the solution, the solution is optimal. The solution is \[m_d=8, \quad m_l=40, \quad p_d=20, \quad z=696.\] Vanessa should put Darren on the assembly line for 8 hours and on the packaging line for 20 hours. She should put Lori on the assembly line for 40 hours. This will put payroll at $696 for the week. \(_\square\)

Problem Loading...

Note Loading...

Set Loading...

Learn maths at home

Linear Programming: How to Find the Optimal Solution

Linear programming video lessons, how to do linear programming, linear programming with multiple solutions, linear programming with infinite solutions, linear programming with integer solutions, what is linear programming.

Linear programming is an algebraic method for finding an optimal value in a situation in which there are constraints. The process involves forming constraint equations, graphing the feasible region and substituting vertices into the objective function to find a minimum or maximum value.

• Constraint equations are found for each category. The amounts used in each category are compared to the total amount of each that is available or required.
• The feasible region is the shaded region between the constraint equations. All combinations of coordinates within this region satisfy the requirements of the problem.
• The vertices are the corners of the feasible region. These are the most extreme cases of the solutions found in the feasible region and therefore, the optimal solution is found at one or more of these vertices.
• The objective function is the equation which we want to maximise or minimise.

This process of testing the vertices in the objective function to find the optimal solution is known as the simplex method.

Linear programming is used in a variety of real life contexts such as:

• Manufacturing: Maximising profits by finding the optimal combination of products to manufacture.
• Engineering: Minimising wastage in a design whilst still meeting structural requirements.
• Business: Allocating resources and budgets to complete a project with minimal cost.
• Transportation: Minimising travel time when subject to limited resources or work force.
• Finance: Maximising profit or minimising risk of investments made in a portfolio.
• Scheduling: Minimising project completion time or constructing timetables.

How to Do Linear Programming to Find an Optimal Solution

• Form the constraint equations.
• Sketch the constraint equations.
• Find the vertices of the feasible region.
• Substitute the coordinates of the vertices into the objective function.
• The optimal solution is the vertex at which the maximum or minimum value is obtained.

Linear Programming: How to Find a Minimum

• The optimal solution is the vertex at which the minimum value is obtained.

A minimisation problem will involve searching for the feasible solution that minimises the objective function.

Typical minimisation problems involve the minimisation of cost, weight or time.

Here is an example of a minimisation problem in linear programming.

An athlete desires to have at least 60g of carbohydrates, 100g of protein and no more that 80g of fat each day.

He considers two different supplements to meet this requirement.

• Tins of supplement A cost $20 and contain 20g of carbohydrates, 25g of protein and 10g of fat.
• Tins of supplement B cost $30 and contain 20g of carbohydrates, 50g of protein and 20g of fat.

Find the combination of supplements that will meet his needs in the cheapest way.

In linear programming, it is helpful to write a paragraph of text as a table of ordered information as this allows the constraint equations to be found more easily.

Label each row of the table with the two items which we want to optimise.

In this example, that is supplement A and supplement B.

Label each column of the table with the categories that the two items contain.

In this example, each supplement contains carbohydrates, protein, fat and they have a cost. Therefore these are the names of each column.

The constraints are written by finding the total amount of each category that is available or required.

In this example, the athlete has a daily requirement for each of carbohydrate, protein and fat.

Since he requires at least 60g of carbohydrates, we write ≥ 60.

The amount of carbohydrates must be at least 60. This means it can be equal to 60 or greater but it cannot be less than 60.

Since he requires at least 100g of protein, we write ≥ 100. This means his total daily protein must be greater than or equal to 100.

However, since he must have no more than 80g of fat, he must have equal to 80g of fat or less than this. He cannot have more than 80g of fat. Therefore we write ≤ 80.

Step 1. Find the Constraint Equations

• Label the amount of the two items as x and y respectively.
• For each category, multiply the number each item contains by x or y respectively.
• Write the sum of these terms ≤ the total maximum limit or ≥ the total minimum requirement.

Here are some common meanings of the inequality signs.

In linear programming, when there is a minimum requirement for a particular resource we use the ≥ symbol.

When there is a fixed total maximum limit of a resource that is available, we use the ≤ symbol.

We will look at the constraint equation for each category individually.

Considering the carbohydrates constraint:

Supplement A (which we will label as x) contains 20g of carbohydrate.

So the total carbohydrate from A is equal to 20x.

Supplement B (which we will label as y) contains 20g of carbohydrate.

So the total carbohydrate from supplement B is equal to 20y.

The total carbohydrate from both supplements is therefore 20x + 20y.

In total, at least 60g of carbohydrate is required so we write ≥ 60.

Therefore, the constraint equation for carbohydrate is 20x + 20y ≥ 60.

This equation can be simplified easily by dividing all terms by 10 to obtain 2x + 2y ≥ 6.

It could also be simplified further by halving each term to obtain x + y ≥ 3 if needed.

The simplification of the constraint equations is not a necessary step.

Considering the protein constraint:

Each tin of supplement A contains 25g of protein, so the total protein from all of supplement A is 25x.

Each tin of supplement B contains 50g of protein, so the total protein from all of supplement B is 50y.

The total protein from both supplements is therefore 25x + 50y.

The athlete requires at least 100g of protein each day, so we write ≥100.

Therefore the constraint equation is 25x + 50y ≥ 100.

This can be simplified by dividing each term by 25 to obtain x + 2y ≥ 4.

Considering the fat constraint:

Each tin of supplement A contains 10g of fat, so the total fat from all of supplement A is 10x.

Each tin of supplement B contains 20g of fat, so the total fat from all of supplement B is 20y.

The athlete must have no more than 80g of fat in total so we write ≤ 80.

The inequality is now less than or equal to as the total fat must be less than or equal to 80.

The constraint is 10x + 20y ≤ 80.

This can be simplified by dividing each term by 10 to obtain x + 2y ≤ 8.

How to Find the Objective Function

The objective function is the equation that is to be maximised or minimised. It is of the form O = p x+ q y where x and y are the number of the two items being used and p and q are the constraints.

• If the cost is being minimised then p and q are the costs of x and y respectively.
• If the profit is being maximised then p and q are the profits from x and y respectively.
• If the weight is being minimised then p and q are the weights of x and y respectively.
• If the time is being minimised then p and q are the times of x and y respectively.
• If the volume is being maximised then p and q are the volumes of x and y respectively.

In this example, we are maximising cost. Therefore p and q are the costs of x and y respectively.

We write C = 20x + 30y.

Step 2. Sketch the Constraint Equations and Feasible Region

• Substitute x = 0 and solve for y to find the y-intercept.
• Substitute y = 0 and solve for x to find the x-intercept.
• Draw the line between the intercepts.
• Draw a horizontal line if the constraint is of the form y=a and a vertical line if it is of the form x=b.
• Shade below the line if y , left of the line if x .

A summary of where to shade for each given inequality is shown below.

If the constraint is of the form:

• x≤a then shade left of the line.
• x≥a then shade right of the line.
• y≤a then shade below the line.
• y≥a then shade above the line.
• x+y≤ a then shade below the line.
• x+y≥a then shade above the line.

Note that if the coefficients of x or y are negative, then the opposite will apply.

The first constraint to draw is 2x + 2y ≥ 6.

The x intercept is found by substituting y=0 into 2x + 2y = 6.

We obtain 2x = 6 and so, x = 3.

The y intercept is found by substituting x=0 into 2x + 2y = 6.

We obtain 2y = 6 and so, y = 3.

We connect the x and y intercepts with a straight line as shown below.

Since the equation contains a greater than or equal to sign (≥), we shade above the line.

The next constraint to draw is x + 2y ≥ 4.

The x intercept is found by substituting y=0 into x + 2y = 4.

We obtain x = 4 and so, x = 4.

The y intercept is found by substituting x=0 into x + 2y = 4.

We obtain 2y = 4 and so, y = 2.

The final constraint to draw is x + 2y ≤ 8.

The x intercept is found by substituting y=0 into x + 2y = 8.

We obtain x = 8.

The y intercept is found by substituting x=0 into x + 2y = 8.

We obtain 2y = 8 and so, y = 4.

Since the equation contains a greater than or equal to sign (≤), we shade below the line.

The feasible region is the region that satisfies all of the constraint equations. To graph the feasible region, shade above lines containing ‘≥’ and below lines containing ‘ ≤ ‘. If the coefficients of x or y are negative, the opposite applies.

In this example, we shade where the previously drawn lines are all pointing.

That is, above 2x+2y≥6. above x+2y≥4 and below x+2y≤8.

Step 3. Find the vertices of the feasible region.

The vertices of the feasible region are the corners of the shaded region. They are found wherever two or more constraint lines intersect. The optimal solution will be found at one or more of these vertices.

The vertices of this feasible region are:

(0,3) (0,4) (2,1) (4,0) and (8,0).

Step 4. Substitute the coordinates of the vertices into the objective function.

The vertices made up of a pair of coordinates (x, y) and are found at the corners of the feasible region. Substitute the values of x and y from these coordinates into the objective function to find the optimal solution.

We will do this ‘simplex process’ for each of the vertices.

The objective function is C = 20x + 30y.

Step 5. The optimal solution is the vertex at which the minimum value is obtained

In linear programming, the optimal solution is the maximum or minimum value of the objective function. This is always found at one of the vertices of the feasible region.

In this example, we wish to find the combination of supplements that meet the athlete’s needs at the cheapest cost.

The cheapest combination was the value which minimised the cost equation.

This was at the vertex (2, 1) with a cost of $70.

The vertex (2, 1) means that x=2 and y=1.

x is the number of supplement A that should be used.

y is the number of supplement B that should be used.

Therefore, the athlete should use 2 tins of supplement A and 1 tin of supplement B at a total cost of $70.

Linear Programming: How to Find a Maximum

• The optimal solution is the vertex at which the maxmimum value is obtained.

Here is an example of maximising an objective function using linear programming.

A restaurant produces two different breakfast options, small and large. Each day there are only 20 eggs and 12 tomatoes available to use in these breakfasts.

The small breakfast sells for $10 profit and contains 2 eggs and 1 tomato.

The large breakfast sells for $15 profit and contains 2 eggs and 2 tomatoes.

No more than 4 large breakfasts can be produced each day.

Find the number of each breakfast that should be made to maximise profit.

Step 1. Form the constraint equations.

We will let x be the number of small breakfasts produced each day.

We will let y be the number of large breakfasts produced each day.

Considering the eggs constraint:

The total eggs used in small breakfasts is 2x.

The total eggs used in large breakfasts is 2y.

There are only 20 eggs available therefore the total eggs used in all breakfasts must be less than or equal to 20.

2x + 2y ≤ 20.

We can simplify this by dividing each term by 2 to obtain x + y ≤ 10.

Considering the tomatoes constraint:

The number of tomatoes in the small breakfasts is just x.

The number of tomatoes in the large breakfasts is 2y.

There are only 12 tomatoes available so the total tomatoes must be less than or equal to 12.

x + 2y ≤ 12.

Considering that no more than 4 large breakfasts can be produced:

y is the number of large breakfasts. From this constraint, the number of large breakfasts must be less than or equal to 4.

Therefore y ≤ 4.

The objective function is the profit since we wish to maximise this.

The profit from the small breakfasts is 10x and the profit from the large breakfasts is 15y.

Therefore the objective function is P = 10x + 15y.

Considering the non-negative constraints:

We know that it is impossible to produce less than 0 of each type of breakfast, therefore the number of each type of breakfast must be greater than or equal to zero.

In linear programming, the non-negative constraints are x≥0 and y≥0. This means that the problem is confined to the positive quadrant involving only positive values of x and y.

They are included whenever the quantities being optimised cannot be negative, which is the case in the production or consumption found in real life problems.

Step 2. Graph the Constraint Equations

The non-negative constraints require us to only consider the top right quadrant with positive x and y values. The feasible region will be above the x-axis and to the right of the y-axis.

We have the three constraints x+y≤10, x+2y≤12 and y≤4.

Considering x+y≤10 :

The x-intercept is found by substituting y=0 into x+y=10. We obtain x=10.

The y-intercept is found by substituting x=0 into x+y=10. We obtain y=10.

We then connect these intercepts to find the line.

We shade below the line since the inequality in the constraint is ‘≤’.

Considering x+2y≤12 :

The x-intercept is found by substituting y=0 into x+2y=12. We obtain x=12.

The y-intercept is found by substituting x=0 into x+2y=12. We obtain 2y=12 and y = 6.

Considering y≤4 :

y=4 is a horizontal line at a height of y=4.

Step 3. Find the Vertices of the Feasible Region

The feasible region is found below all three of the given constraint equations.

This is the shaded region shown below.

The vertices of this region are: (0,4), (4, 4), (8, 2) and (10,0). There is also (0,0) but producing zero of each breakfast option will certainly not result in the optimal profit.

The objective function to be maximised is P = 10x + 15y.

Step 5. The optimal solution is the vertex at which the maximum value is obtained.

The optimal solution is produced from the vertex which maximises the profit.

This is found at (8, 2) where $110 profit is made.

This is the largest profit result produced.

Therefore 8 small breakfasts and 2 large breakfasts should be produced to maximise the profit and make $110.

How to Find Vertices in Linear Programming

The vertices can be observed by looking at the corners of the feasible region. Where the coordinates are not clear, vertices can be calculated accurately by solving the simultaneous equations formed by the two constraint equations that intersect at that particular point.

For example, consider the feasible region given by the constraints:

From the graph below it can be seen that the vertex lies at the coordinate (5, 3). This is where x=5 and y=3.

However, if we were not sure of this, we could find the coordinate of the vertex by solving the two constraint equations simultaneously.

To solve these equations simultaneously, we will multiply the equations so that there is a common term in both.

Multiplying equation (1) by 2, we obtain:

Multiplying equation (2) by 5, we obtain:

We write the equations above one another like so:

We subtract the top equation from the bottom equation to obtain:

Therefore, we obtain (5, 3) as the vertex.

Linear Programming with Multiple Optimal Solutions

Multiple optimal solutions occur if two or more vertices result in the same optimal solution. All points between these vertices will be optimal solutions too. Multiple solutions occur when the slope of the objective function is parallel to the constraint line connecting the multiple optimal solutions.

Here is an example of linear programming in which multiple optimal solutions occur.

A car manufacturer has access to 16 exhausts, 36 metal panels and 14 gearboxes.

He is able to manufacture 2 different models of car: Car model A and Car model B.

Car model A costs $20 000 and it requires 1 exhaust, 1 metal panel and 1 gearbox.

Car model B costs $40 000 and it requires 2 exhausts, 6 metal panels and 1 gearbox.

They wish to decide on the number of each car model to make to maximise their profits.

Since the total number of exhausts used must be less than or equal to 16, we obtain:

Since the total number of metal panels used must be less than or equal to 36, we obtain:

Since the total number of gearboxes used must be less than or equal to 14, we obtain:

The objective function to be maximised is the cost.

The constraints are drawn resulting in the feasible region shown below.

The vertices of the feasible region are: (0, 6), (6, 5), (12, 2) and (14, 0).

Substituting these into the objective function results in two maximum values.

Both (6, 5) and (12, 2) result in the objective function maximised at 320.

Since both (6, 5) and (12, 2) provide the optimal solution, we must also look at all solutions that lie on the line connecting these two points.

Since we are considering how many of each car model to manufacture, the solutions must be whole numbers rather than decimals.

So along with (6, 5) and (12, 2), we also have (8, 4) and (10, 3) as shown below.

Therefore the optimal solutions are (6, 5), (8, 4), (10, 3) and (12, 2).

All of these solutions will result in the same optimal objective function of 320.

This means that we should produce either of the following combinations to make a profit of $320 000:

6 of Car A, 5 of Car B

8 of Car A, 4 of Car B

10 of Car A, 3 of Car B

12 of Car A, 2 of Car B.

We will now look algebraically how multiple optimal solutions can be identified.

Multiple optimal solutions will be present when the objective function is parallel to a constraint of the feasible region. That is, the objective function will be a multiple of one of the constraint equations.

Therefore if the objective function is a multiple of one of the constraint equations, it will be parallel to it and multiple optimal solutions will lie on this line.

Therefore the optimised value of the objective function is 320.

The optimised value of the objective function is the value that the objective function is equal to so that when graphed, the objective function line lies on the boundary of the feasible region.

Infinite Solutions in Linear Programming

Linear programming problems can have infinite optimal solutions if two vertices result in the same optimised value of the objective function and the solutions can take non-integer values. The infinite solutions are found between the values of the two vertices.

Here is an example of a linear programming problem with infinite solutions.

A company has 18kg of gravel, 21kg of cement, 4kg of sand with which it can make two different concrete mixes.

Concrete A costs $2000 and it requires 3kg of gravel, 7kg of cement and 1kg of sand.

Concrete B costs $2000 and it requires 6kg of gravel, 3kg of cement and 1kg of sand.

The company can produce concrete in any measure quantity and wish to maximise their profits.

The constraint equations are given by:

The objective function is the cost of purchase, which we wish to maximise.

The feasible region is shown below all three of the constraint lines.

The vertices of the feasible region are: (0, 3), (2, 2), (2.25, 1.75) and (3,0).

Substituting these vertices into the objective function, we obtain two optimal answers of $8000 found at both (2,2) and (2.25, 1.75).

Since the concrete can be produced in any given quantity, the optimal solution does not need to take integer solutions and so, (2.25, 1.75) is a valid solution.

It simply means 2.25kg of concrete A and 1.75kg of concrete B.

Since there are two vertices which maximise the objective function, we have multiple solutions.

When two vertices optimise the objective function, they are both solutions and all points between these two points are also solutions.

Since the concrete does not need to take only integer values, it can take all decimal values between the points of (2,2) and (2.25, 1.75).

There are an infinite number of different decimal numbers this could be and therefore there are infinite solutions to this linear programming problem.

Whenever a linear problem has multiple solutions and can take non-integer values, there are an infinite number of solutions.

The green line below shows the range where the infinite solutions take place. All of these combinations of concrete result in a cost of purchase of $8000.

Integer Solutions to Linear Programming

If a linear programming solution can only take integer (whole number) values then also consider integer solutions inside the feasible region that are close to any decimal vertices and substitute these into the objective function as well.

Many linear programming problems deal with quantities that must take integer values.

Integers are whole numbers.

Only linear programming involving continuously measured quantities will permit non-integer solutions. Examples where non-integer solutions are allowed include problems involving weight, volume, capacity, area and length.

Here is an example in which only integer solutions are permitted.

A construction needs to be able to support at least 4 units of lateral load and at least 10 units of vertical load.

Steel beams weigh 50kg and support 1 unit of lateral load and 5 units of vertical load.

Wooden beams weigh 30kg and support 2 units of lateral load and 2 units of vertical load.

Find the optimal combination of beams that support the required loads but minimise the weight.

Since we cannot use fractional amounts of each beam, we can only use whole numbers in our solution. We can only take integer solutions.

The two constraint equations are shown graphed on the axes below.

We shade above both lines.

The vertices of the feasible region are (0, 5), (4,0) and (1.5, 1.25).

At (0,5) we the value of the objective function is 150 and at (4, 0) the value of the objective function is 200.

We do cannot use the third vertex of (1.5, 1.25) as it does not contain only whole numbers. We cannot use 1.5 or 1.25 of a beam in this problem.

Therefore we must look at whole number points that are inside the feasible region, near to this decimal vertex of (1.5, 1.25).

The closest whole number solutions are shown below with red coordinates.

We can look at (2, 2), (3, 1) and (1, 3).

We see that (2, 2) gives an objective function result of 160, (3, 1) results in 180 and (1, 3) results in 140.

Therefore the weight is minimised at (1, 3) with a weight of 140kg.

It is important to notice that the optimal solution in this example was found at (1, 3) which was not a vertex of the feasible region.

In all other instances, the optimal solution is always found at a vertex.

However, if one vertex is a decimal, it is possible that the optimal solution may be found inside the feasible region, nearby to it.

Linear Programming Without Graphing

Linear programming can be solved algebraically without graphing. Whilst graphing is often a faster process that assists the visualisation of the solution, it may not be practical for problems involving more constraints and linear programming can be solved in an algebraic manner or using a computer.

• Find the point of intersection for each of the possible different pairs of constraint equations.
• Substitute these points into the other constraint inequalities.
• Remove any points that fail the constraint inequalities.
• Substitute the remaining points into the objective function to find the optimal solution.

Here is an example of solving a linear programming constraint problem without graphing.

Step 1. Find the point of intersection for each of the possible different pairs of constraint equations

This results in a vertex at (2, 1).

This results in a vertex of (-2, 5).

There is no solution to this pair of equations.

We now continue by considering the solutions found by the following pairs of constraints.

The final list of vertices is therefore:

(0, 3), (0, 4), (2, 1), (4, 0), (8, 0).

These are then all substituted into the objective function to find the optimal result.

Linear Programming with 3 Variables

Linear programming problems with 3 variables can be solved graphically in 3 dimensions. 3D software is beneficial. Alternatively, it can be easier to solve linear programming with 3 or more variables computationally.

Here is an example in which a linear program problem involving 3 variables will be solved graphically.

We will see how linear programming constraint equations will be created in 3 variables: x, y and z.

A tour operator offers three different tours each day.

The City Tour requires 1 bus, 3 tour guides and 2 microphones. It makes $1000 profit.

The Country Tour requires 3 buses, 4 tour guides and 3 microphones. It makes $3000 profit.

The Scenic Tour requires 2 buses, 6 tour guides and 6 microphones. It makes $2500 in profit.

In total the tour operator has 20 buses, 50 tour guides and 42 microphones available to allocate.

The information is laid out as in the table above for clarity.

With linear programming with 3 variables 3 dimensions are considered in which each constraint equation forms a plane rather than a line.

The three constraint equations are depicted below as planes. The feasible region is bounded below each of these planes and the x, y and z axes.

The vertices of the feasible region can be found where each plane intersects the axes and also where the three planes intersect.

The vertices of this feasible region are where the three planes intersect and also where the planes intersect each axis.

The vertices of the feasible region are (16.67, 0, 0), (0, 0, 7), (0, 6.67, 0), (6, 2, 4), (0, 3, 5.5) and (8, 0, 4.33).

Substituting these values into the objective function, it is maximised at (0, 3, 5.5).

However since we cannot use decimal solutions (we cannot have 5.5 of a tour), we must search nearby to this vertex for other optimal solutions.

Instead the optimal solution is (1, 3, 5) which results in a profit of $22 500.

Linear Programming

Linear programming is a process that is used to determine the best outcome of a linear function. It is the best method to perform linear optimization by making a few simple assumptions. The linear function is known as the objective function. Real-world relationships can be extremely complicated. However, linear programming can be used to depict such relationships, thus, making it easier to analyze them.

Linear programming is used in many industries such as energy, telecommunication, transportation, and manufacturing. This article sheds light on the various aspects of linear programming such as the definition, formula, methods to solve problems using this technique, and associated linear programming examples.

What is Linear Programming?

Linear programming, also abbreviated as LP, is a simple method that is used to depict complicated real-world relationships by using a linear function . The elements in the mathematical model so obtained have a linear relationship with each other. Linear programming is used to perform linear optimization so as to achieve the best outcome.

Linear Programming Definition

Linear programming can be defined as a technique that is used for optimizing a linear function in order to reach the best outcome. This linear function or objective function consists of linear equality and inequality constraints. We obtain the best outcome by minimizing or maximizing the objective function .

Linear Programming Examples

Suppose a postman has to deliver 6 letters in a day from the post office (located at A) to different houses (U, V, W, Y, Z). The distance between the houses is indicated on the lines as given in the image. If the postman wants to find the shortest route that will enable him to deliver the letters as well as save on fuel then it becomes a linear programming problem. Thus, LP will be used to get the optimal solution which will be the shortest route in this example.

Linear Programming Formula

A linear programming problem will consist of decision variables , an objective function, constraints, and non-negative restrictions. The decision variables, x, and y, decide the output of the LP problem and represent the final solution. The objective function, Z, is the linear function that needs to be optimized (maximized or minimized) to get the solution. The constraints are the restrictions that are imposed on the decision variables to limit their value. The decision variables must always have a non-negative value which is given by the non-negative restrictions. The general formula of a linear programming problem is given below:

• Objective Function: Z = ax + by
• Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
• Non-negative restrictions: x ≥ 0, y ≥ 0

How to Solve Linear Programming Problems?

The most important part of solving linear programming problem is to first formulate the problem using the given data. The steps to solve linear programming problems are given below:

• Step 1: Identify the decision variables.
• Step 2: Formulate the objective function. Check whether the function needs to be minimized or maximized.
• Step 3: Write down the constraints.
• Step 4: Ensure that the decision variables are greater than or equal to 0. (Non-negative restraint)
• Step 5: Solve the linear programming problem using either the simplex or graphical method.

Let us study about these methods in detail in the following sections.

Linear Programming Methods

There are two main methods available for solving linear programming problem. These are the simplex method and the graphical method. Given below are the steps to solve a linear programming problem using both methods.

Linear Programming by Simplex Method

The simplex method in lpp can be applied to problems with two or more decision variables. Suppose the objective function Z = 40\(x_{1}\) + 30\(x_{2}\) needs to be maximized and the constraints are given as follows:

\(x_{1}\) + \(x_{2}\) ≤ 12

2\(x_{1}\) + \(x_{2}\) ≤ 16

\(x_{1}\) ≥ 0, \(x_{2}\) ≥ 0

Step 1: Add another variable, known as the slack variable, to convert the inequalities into equations. Also, rewrite the objective function as an equation .

- 40\(x_{1}\) - 30\(x_{2}\) + Z = 0

\(x_{1}\) + \(x_{2}\) + \(y_{1}\) =12

2\(x_{1}\) + \(x_{2}\) + \(y_{2}\) =16

\(y_{1}\) and \(y_{2}\) are the slack variables.

Step 2: Construct the initial simplex matrix as follows:

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 2& 1 & 0& 1 & 0 & 16 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Step 3: Identify the column with the highest negative entry. This is called the pivot column. As -40 is the highest negative entry, thus, column 1 will be the pivot column.

Step 4: Divide the entries in the rightmost column by the entries in the pivot column. We exclude the entries in the bottom-most row.

12 / 1 = 12

The row containing the smallest quotient is identified to get the pivot row. As 8 is the smaller quotient as compared to 12 thus, row 2 becomes the pivot row. The intersection of the pivot row and the pivot column gives the pivot element.

Thus, pivot element = 2.

Step 5: With the help of the pivot element perform pivoting, using matrix properties , to make all other entries in the pivot column 0.

Using the elementary operations divide row 2 by 2 (\(R_{2}\) / 2)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Now apply \(R_{1}\) = \(R_{1}\) - \(R_{2}\)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Finally \(R_{3}\) = \(R_{3}\) + 40\(R_{2}\) to get the required matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ 0&-10&0&20&1&320 \end{bmatrix}\)

Step 6: Check if the bottom-most row has negative entries. If no, then the optimal solution has been determined. If yes, then go back to step 3 and repeat the process. -10 is a negative entry in the matrix thus, the process needs to be repeated. We get the following matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1 &2 &-1 &0 &8 \\ 1& 0 & -1& 1 & 0 & 4 \\ 0&0&20&10&1&400 \end{bmatrix}\)

Writing the bottom row in the form of an equation we get Z = 400 - 20\(y_{1}\) - 10\(y_{2}\). Thus, 400 is the highest value that Z can achieve when both \(y_{1}\) and \(y_{2}\) are 0.

Also, when \(x_{1}\) = 4 and \(x_{2}\) = 8 then value of Z = 400

Thus, \(x_{1}\) = 4 and \(x_{2}\) = 8 are the optimal points and the solution to our linear programming problem.

Linear Programming by Graphical Method

If there are two decision variables in a linear programming problem then the graphical method can be used to solve such a problem easily.

Suppose we have to maximize Z = 2x + 5y.

The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9

where, x ≥ 0 and y ≥ 0.

To solve this problem using the graphical method the steps are as follows.

Step 1: Write all inequality constraints in the form of equations.

x + 4y = 24

3x + y = 21

Step 2: Plot these lines on a graph by identifying test points.

x + 4y = 24 is a line passing through (0, 6) and (24, 0). [By substituting x = 0 the point (0, 6) is obtained. Similarly, when y = 0 the point (24, 0) is determined.]

3x + y = 21 passes through (0, 21) and (7, 0).

x + y = 9 passes through (9, 0) and (0, 9).

Step 3: Identify the feasible region. The feasible region can be defined as the area that is bounded by a set of coordinates that can satisfy some particular system of inequalities.

Any point that lies on or below the line x + 4y = 24 will satisfy the constraint x + 4y ≤ 24.

Similarly, a point that lies on or below 3x + y = 21 satisfies 3x + y ≤ 21.

Also, a point lying on or below the line x + y = 9 satisfies x + y ≤ 9.

The feasible region is represented by OABCD as it satisfies all the above-mentioned three restrictions.

Step 4: Determine the coordinates of the corner points. The corner points are the vertices of the feasible region.

B = (6, 3). B is the intersection of the two lines 3x + y = 21 and x + y = 9. Thus, by substituting y = 9 - x in 3x + y = 21 we can determine the point of intersection.

C = (4, 5) formed by the intersection of x + 4y = 24 and x + y = 9

Step 5: Substitute each corner point in the objective function. The point that gives the greatest (maximizing) or smallest (minimizing) value of the objective function will be the optimal point.

33 is the maximum value of Z and it occurs at C. Thus, the solution is x = 4 and y = 5.

Applications of Linear Programming

Linear programming is used in several real-world applications. It is used as the basis for creating mathematical models to denote real-world relationships. Some applications of LP are listed below:

• Manufacturing companies make widespread use of linear programming to plan and schedule production.
• Delivery services use linear programming to decide the shortest route in order to minimize time and fuel consumption.
• Financial institutions use linear programming to determine the portfolio of financial products that can be offered to clients.

Related Articles:

• Introduction to Graphing
• Linear Equations in Two Variables
• Solutions of a Linear Equation
• Mathematical Induction

Important Notes on Linear Programming

• Linear programming is a technique that is used to determine the optimal solution of a linear objective function.
• The simplex method in lpp and the graphical method can be used to solve a linear programming problem.
• In a linear programming problem, the variables will always be greater than or equal to 0.

As the minimum value of Z is 127, thus, B (3, 28) gives the optimal solution. Answer: The minimum value of Z is 127 and the optimal solution is (3, 28)

• Example 3: Using the simplex method in lpp solve the linear programming problem Minimize Z = \(x_{1}\) + 2\(x_{2}\) + 3\(x_{3}\) \(x_{1}\) + \(x_{2}\) + \(x_{3}\) ≤ 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) ≤ 18 \(x_{1}\), \(x_{2}\), \(x_{3}\) ≥ 0 Solution: Convert all inequalities to equations by introducing slack variables. -\(x_{1}\) - 2\(x_{2}\) - 3\(x_{3}\) + Z = 0 \(x_{1}\) + \(x_{2}\) + \(x_{3}\) + \(y_{1}\) = 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) + \(y_{2}\) = 18 Expressing this as a matrix we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 1 & 1 & 1 & 1 & 0 & 0 & 12\\ 2 & 1 & 3 & 0 & 1 & 0 & 18\\ -1 & -2 & -3 & 0 & 0 & 1 & 0 \end{bmatrix}\) As -3 is the greatest negative value thus, column 3 is the pivot column. 12 / 1 = 12 18 / 3 = 6 As 6 is the smaller quotient thus, row 2 is the pivot row and 3 is the pivot element. By applying matrix operations we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.33 & 0.667 & 0 & 1 & -0.33 & 0 & 6\\ 0.667 & 0.33 & 1 & 0 & 0.33 & 0 & 6\\ 1 & -1 & 0 & 0 & 1 & 1 & 18 \end{bmatrix}\) Now -1 needs to be eliminated. Thus, by repreating the steps the matrix so obtained is as follows \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.5 & 1 & 0 & 1.5 & 0.5 & 0 & 9\\ 0.5 & 0 & 1 & -0.5 & 0.5 & 0 & 3\\ 1.5 & 0 & 0 & 1.5 & 0.5 & 1 & 27 \end{bmatrix}\) We get the maximum value of Z = 27 at \(x_{1}\) = 0, \(x_{2}\) = 9 \(x_{3}\) = 3 Answer: Maximum value of Z = 27 and optimal solution (0, 9, 3)

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Programming

go to slide go to slide

FAQs on Linear Programming

What is meant by linear programming.

Linear programming is a technique that is used to identify the optimal solution of a function wherein the elements have a linear relationship.

What is Linear Programming Formula?

The general formula for a linear programming problem is given as follows:

What is the Objective Function in Linear Programming Problems?

The objective function is the linear function that needs to be maximized or minimized and is subject to certain constraints. It is of the form Z = ax + by.

How to Formulate a Linear Programming Model?

The steps to formulate a linear programming model are given as follows:

• Identify the decision variables.
• Formulate the objective function.
• Identify the constraints.
• Solve the obtained model using the simplex or the graphical method.

How to Find Optimal Solution in Linear Programming?

We can find the optimal solution in a linear programming problem by using either the simplex method or the graphical method. The simplex method in lpp can be applied to problems with two or more variables while the graphical method can be applied to problems containing 2 variables only.

How to Find Feasible Region in Linear Programming?

To find the feasible region in a linear programming problem the steps are as follows:

• Draw the straight lines of the linear inequalities of the constraints.
• Use the "≤" and "≥" signs to denote the feasible region of each constraint.
• The region common to all constraints will be the feasible region for the linear programming problem.

What are Linear Programming Uses?

Linear programming is widely used in many industries such as delivery services, transportation industries, manufacturing companies, and financial institutions. The linear program is solved through linear optimization method, and it is used to determine the best outcome in a given scenerio.

• School Guide
• Class 12 Syllabus
• Class 12 Revision Notes
• Maths Notes Class 12
• Physics Notes Class 12
• Chemistry Notes Class 12
• Biology Notes Class 12
• NCERT Solutions Class 12 Maths
• RD Sharma Solutions Class 12
• Graphical Solution of Linear Programming Problems
• Linear Programming
• Solving Linear Inequalities Word Problems
• Stars and Bars Algorithms for Competitive Programming
• Python | Linear search on list or tuples
• Top 50 Dynamic Programming Coding Problems for Interviews
• Dynamic Programming (DP) Tutorial with Problems
• Program to find all types of Matrix
• Dynamic Programming | High-effort vs. Low-effort Tasks Problem
• Python | Linear Programming in Pulp
• C++ Program for the Fractional Knapsack Problem
• Transportation Problem | Set 1 (Introduction)
• Algorithms | Dynamic Programming | Question 7
• Algorithms | Dynamic Programming | Question 4
• Algorithms | Dynamic Programming | Question 3
• Algorithms | Dynamic Programming | Question 2
• How to begin with Competitive Programming?
• Dynamic Programming (DP) on Grids
• Knuth's Optimization in Dynamic Programming

Types of Linear Programming Problems

Linear programming is a mathematical technique for optimizing operations under a given set of constraints. The basic goal of linear programming is to maximize or minimize the total numerical value. It is regarded as one of the most essential strategies for determining optimum resource utilization. Linear programming challenges include a variety of problems involving cost minimization and profit maximization, among others. They will be briefly discussed in this article.

The purpose of this article is to provide students with a comprehensive understanding of the different types of linear programming problems and their solutions.

What is Linear Programming?

Linear programming (LP) is a mathematical optimization technique used to maximize or minimize a linear objective function, subject to a set of linear equality and inequality constraints. It is widely used in various fields such as economics, engineering, operations research, and management science to find the best possible outcome given limited resources.

Components of Linear Programming

Components of linear programming include:

• Objective Function: This is a linear function that needs to be optimized (maximized or minimized). It represents the quantity to be maximized or minimized, such as profit, cost, time, etc.
• Decision Variables: These are the variables that represent the choices or decisions to be made. They are the unknown quantities that the optimization process seeks to determine. Decision variables must be continuous and can take any real value within a specified range.
• Constraints: These are restrictions or limitations on the decision variables that must be satisfied. Constraints can be expressed as linear equations or inequalities. They represent the limitations imposed by available resources, capacity constraints, demand requirements, etc.
• Feasible Region: The feasible region is the set of all possible combinations of decision variables that satisfy all constraints. It is defined by the intersection of the constraint boundaries.
• Optimal Solution: This is the best possible solution that maximizes or minimizes the objective function while satisfying all constraints. In graphical terms, it is the point within the feasible region that maximizes or minimizes the objective function.

Linear programming provides a systematic and efficient approach to decision-making in situations where resources are limited and objectives need to be optimized.

Different Types of Linear Programming Problems

The following are the types of linear programming problems:

• Manufacturing problems
• Diet problems
• Transportation problems
• Optimal alignment problem

Let’s discuss more about each of them.

Manufacturing Problems

In these problems, we evaluate the number of units of various items that should be produced and sold by a company when each product requires a given number of workforce, machine hours, labour hours per unit of product, warehouse space per unit of output, and so on, to maximize profit.

Manufacturing problems involve maximizing the production rate or net profits of manufactured products, which might measure the available workspace, the number of workers, machine hours, packing materials used, raw materials required, the product’s market value, and other factors. These are commonly used in the industrial sector to anticipate a company’s future capital increase over time.

Diet Problems

In these challenges, we assess how many components or nutrients a diet should contain in order to lower the cost of the desired diet while guaranteeing the minimal amount of each vitamin.

As the name suggests, diet-related problems can be resolved by eating more particular foods that are rich in essential nutrients and can support the adoption of a particular diet plan. Finding a set of meals that will satisfy a set of daily nutritional demands for the least amount of money is the aim of a diet problem.

Transportation Problems

In these problems , we create a transportation schedule to discover the most cost-effective method of carrying a product from various plants/factories to various markets.

The study of transportation routes or how items from diverse production sources are transported to various markets to minimize the total transportation cost is linked to transportation difficulties. Analyzing such challenges is crucial for large firms with several production units and a broad customer base.

Optimal Assignment Problems

This problem addresses a company’s completion of a given task/assignment by selecting a specific number of employees to complete the assignment within the required timeframe, assuming that each person works on only one job. Event planning and management in major organizations, for example, are examples of such problems.

Constraints and Objective Function of Each Linear Programming Problem

Steps for solving linear programming problems.

Step 1: Identify the decision variables : The first step is to determine which choice factors control the behaviour of the objective function. A function that needs to be optimised is an objective function. Determine the decision variables and designate them with X, Y, and Z symbols.

Step 2: Form an objective function : Using the decision variables, write out an algebraic expression that displays the quantity we aim to maximize.

Step 3: Identify the constraints : Choose and write the given linear inequalities from the data.

Step 4: Draw the graph for the given data : Construct the graph by using constraints for solving the linear programming problem.

Step 5: Draw the feasible region : Every constraint on the problem is satisfied by this portion of the graph. Anywhere in the feasible zone is a viable solution for the objective function.

Step 6: Choosing the optimal point : Choose the point for which the given function has maximum or minimum values.

Solved Problems of Linear Programming Problems

Question 1. A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?

We define our unknowns:

Let the number of regular gadgets manufactured each day = x

and the number of premium gadgets manufactured each day = y

The objective function is

P = 20x + 30y

We now write the constraints. The fourth sentence states that the company can make at most 7 gadgets a day. This translates as

Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get

x + 2y ≤ 12

Similarly, the regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.

2x + y ≤ 12

The fact that x and y can never be negative is represented by the following two constraints:

x ≥ 0, and y ≥ 0.

We have formulated the problem as follows :

Maximize P=20x + 30y Subject to : x + y ≤ 7, x + 2y ≤ 122, x + y ≤ 12, x ≥ 0, y ≥ 0

In order to solve the problem, we next graph the constraints and feasible region.

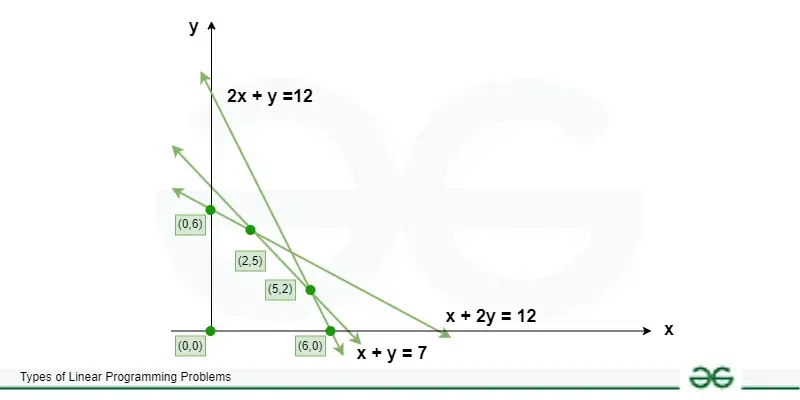
Again, we have shaded the feasible region, where all constraints are satisfied.

Since the extreme value of the objective function always takes place at the vertices of the feasible region, we identify all the critical points. They are listed as (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0). To maximize profit, we will substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.

FAQ on Linear programming

How many methods are there in lpp.

There are different methods to solve a linear programming problem. Such as Graphical method, Simplex method, Ellipsoid method, Interior point methods.

What are the four 4 special cases in linear programming?

Four special cases and difficulties arise at times when using the graphical approach to solving LP problems: (1) infeasibility, (2) unboundedness, (3) redundancy, and (4) alternate optimal solutions.

What are the 3 components of linear programming?

The basic components of the LP are as follows: Decision Variables. Constraints. Objective Functions.

What are the applications of LPP?

LPP applications may include production scheduling, inventory policies, investment portfolio, allocation of advertising budget, construction of warehouses, etc.

What are the limitations of LPP?

Constraints (limitations) should be expressed in mathematical form. Relationships between two or more variables should be linear. The values of the variables should always be non-negative or zero. There should always be finite and infinite inputs and output numbers.

Please Login to comment...

Similar reads.

• Maths-Class-12
• Mathematics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.6: Integer Solutions of Linear Programming Problems

• Last updated
• Save as PDF
• Page ID 97954

• Mitchel T. Keller & William T. Trotter
• Georgia Tech & Morningside College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

A linear programming problem is an optimization problem that can be stated in the following form: Find the maximum value of a linear function

\(c_1x_1+c_2x_2+c_3x_3+ \cdot \cdot \cdot +c_nx_n\)

subject to \(m\) constraints \(C_1\), \(C_2\),…,\(C_m\), where each constraint \(C_i\) is a linear equation of the form:

\(C_i\): \(a_{i1}x_1+a_{i2}x_2+a_{i3}x_3+ \cdot \cdot \cdot +a_{in}x_n=b_i\)

where all coefficients and constants are real numbers.

While the general subject of linear programming is far too broad for this course, we would be remiss if we didn't point out that:

• Linear programming problems are a very important class of optimization problems and they have many applications in engineering, science, and industrial settings.
• There are relatively efficient algorithms for finding solutions to linear programming problems.
• A linear programming problem posed with rational coefficients and constants has an optimal solution with rational values—if it has an optimal solution at all.
• A linear programming problem posed with integer coefficients and constants need not have an optimal solution with integer values—even when it has an optimal solution with rational values.
• A very important theme in operations research is to determine when a linear programming problem posed in integers has an optimal solution with integer values. This is a subtle and often very difficult problem.
• The problem of finding a maximum flow in a network is a special case of a linear programming problem.
• A network flow problem in which all capacities are integers has a maximum flow in which the flow on every edge is an integer. The Ford-Fulkerson labeling algorithm guarantees this!
• In general, linear programming algorithms are not used on networks. Instead, special purpose algorithms, such as Ford-Fulkerson, have proven to be more efficient in practice.

Linear Programming Subject to Max-Product Fuzzy Relation Inequalities with Discrete Variables

• Conference paper
• First Online: 11 May 2024
• Cite this conference paper

• Chang-xin Zhu 7 &
• Zejian Qin   ORCID: orcid.org/0000-0003-2903-0249 8  

Part of the book series: Lecture Notes on Data Engineering and Communications Technologies ((LNDECT,volume 207))

Included in the following conference series:

• International Conference on Fuzzy Information & Engineering

In this paper, we introduced the linear programming subject to max-product fuzzy relation inequalities with discrete variables to denote the optimization management model of physical distribution. It is shown that the inequalities constraints can be transformed into the problem of finding the all the potential minimal solution, and expressed by 2 m linear equations in 0-1 mixed variables and mn inequalities. Then the original problem can converted into a 0-1 mixed-integer linear programming problem and then adopt to the branch-and-bound scheme to find optimal solution.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Sanchez, E.: Equations de Relations Flous. These Biologie Humaine, France (1972)

Google Scholar  

Sanchez, E.: Resolutions in fuzzy relation equations. Inf. Control 30 , 38–48 (1976)

Sanchez, E.: Solution in composite fuzzy relation equations: application to medical diagnosis in Brouwerian logic. In: Gupta, M.M., Saridis, G.N., Gaines, B.R. (eds.) Fuzzy Automata and Decision Processes, pp 221–234. North-Holland, Amsterdam (1993)

Nola, A.D., Sessa, S., Pedrycz, W., Sanchez, E.: Fuzzy Relational Equations and Their Applications in Knowledge Engineering. Kluwer Academic Press, Dordrecht (1989)

Yang, X.-P., Zheng, G.-Z., Zhou, X.-G., Cao, B.-Y.: Lexicography minimum solution of fuzzy relation inequalities: applied to optimal control in P2P file sharing system. Int. J. Mach. Learn. Cybern. (2016)

Yang, X.-P., Zhou, X.-G., Cao, B.-Y.: Multi-level linear programming subject to addition-min fuzzy relation inequalities with application in Peer-to-Peer file sharing system. J. Intell. Fuzzy Syst. 28 , 2679–2689 (2015)

Yang, X.-P., Zhou, X.-G., Cao, B.-Y.: Latticized linear programming subject to max-product fuzzy relation inequalities with application in wireless. Inf. Sci. 358–359 , 44–55 (2016)

Yang, X.-P., Zhou, X.-G., Cao, B.-Y.: Singal variable term semi-latticized fuzzy relation geomtric programming with max-product operator. Inf. Sci. 325 , 271–287 (2015)

Yang, X.-P., Zhou, X.-G., Cao, B.-Y.: Min-max programming problem subject to addition-min fuzzy relation inequalities. IEE Trans. Fuzzy Syst. 24 , 111–119 (2016)

Drewniak, J., Matusiewicz, Z.: Properties of max-* relation equations. Soft Comput. 14 , 1037–1041 (2010)

Li, P., Fang, S.-C.: A survey on fuzzy relational equations, part I: classification and solvability. Fuzzy Optim. Decis. Making 8 , 179–229 (2009)

Li, P., Fang, S.-C.: On the resolution and optimization of a system of fuzzy relation equations with sup-T composition. Fuzzy Optim. Decis. Making 7 , 169–214 (2008)

Li, H.-L., Huang, Y.-H., Fang, S.-C.: A logarithmic for reducing binary variables and inequalitiy constraints in solving task assignment problems. INFORMS J. Comput. 25 (4), 643–653 (2013)

Li, H.-L., Huang, Y.-H., Fang, S.-C.: Linear reformulation of polynomial discrete programming for fast computation. INFORMS J. Comput. 29 (1), 108–122 (2017)

Fang, S.-C., Li, G.-Z.: Solving fuzzy relation equations with a linear objective function. Fuzzy Sets Syst. 103 , 107–113 (1999)

Molai, A.A.: Fuzzy linear objective function optimization with fuzzy valued max-product fuzzy relation inequality constraints. Math. Comput. Model. 5 , 1240–1250 (2010)

Li, H.-L., Lu, H.-C.: Global optimization for generalized geometric programs with mixed free-sign variables. Oper. Res. 57 (3), 701–713 (2009)

Li, H.-L., Hao-chun, L., Huang, C.-H., Nian-Ze, H.: A superior representation method for piecewise linear functions. INFORMS J. Comput. 21 (2), 314–321 (2009)

Article   MathSciNet   Google Scholar  

Loetamonphong, J., Fang, S.-S.: Optimization of fuzzy relation equations with max-product composition. Fuzzy Sets Syst. 118 , 509–517 (2001)

Wang, P.Z., Wang, D.Z., Sanchez, E., Li, E.S.: Latticized linear programming and fuzzy relation inequalities. J. Math. Anal. Appl. 159 , 72–87 (1991)

Zhang, H.T., Dong, H.M., Ren, R.H.: Programming problem with fuzzy relation inequality constraints. J. Liaoning Normal Univ. 3 , 231–233 (2003)

Ghodousian, A., Khorram, E.: An algorithm for optimizing the linear function with fuzzy relation equation constraints regarding max-prod composition. Appl. Math. Comput. 178 , 502–509 (2006)

Ghodousian, A., Khorram, E.: Fuzzy linear optimization in the presence of the fuzzy relation inequality constraints with max-min composition. Inf. Sci. 178 , 501–519 (2008)

Guo, F.-F., Xia, Z.-Q.: An algorithm for solving optimization problems with one linear objective function and finitely many constraints of fuzzy relation inequalities. Fuzzy Optim. Decis. Mak. 5 , 33–47 (2006)

Guu, S.-M., Wu, Y.-K.: Minimizing a linear objective function with fuzzy relation equation constraints. Fuzzy Optim. Decis. Mak. 1 (4), 347–360 (2002)

Guu, S.-M., Wu, Y.-K.: Minimizing a linear objective function under a max-t-norm fuzzy relational equation constraint. Fuzzy Sets Syst. 161 , 285–297 (2010)

Wu, Y.-K., Guu, S.-M., Liu, J.Y.-C.: An accelerated approach for solving fuzzy relation equations with a linear objective function. IEEE Trans. Fuzzy Syst. 10 , 552–558 (2002)

Wu, Y.-K., Guu, S.-M.: Minimizing a linear function under a fuzzy max-min relational equation constraint. Fuzzy Sets Syst. 150 , 147–162 (2005)

Wu, Y.-K., Guu, S.-M.: A note on fuzzy relation programming problems with max-strict-t-norm composition. Fuzzy Optim. Decis. Mak. 3 , 271–278 (2004)

Pandey, D.: On the optimization of fuzzy relation equations with continuous t-norm and with linear objective function. In: Proceedings of the Second Asian Applied Computing Conference, AACC 2004, Kathmandu, Nepal, pp. 41–51 (2004)

Shivanian, E., Khorram, E.: Monomial geometric programming with fuzzy relation inequality constraints with max-product composition. Comput. Indust. Eng. 56 , 1386–1392 (2009)

Article   Google Scholar  

Thole, U., Zimmermann, H.-J., Zysno, P.: On the suitability of minimum and product operators for intersection of fuzzy sets. Fuzzy Sets Syst. 2 , 167–180 (1979)

Download references

Acknowledgements

The authors declare that they have no competing interests.

Author information

Authors and affiliations.

Human Resources Office, Guangzhou Vocational and Technical University of Science and Technology, Guangzhou, 510550, Guangdong, China

Department of Basic Course, Guangzhou Vocational and Technical University of Science and Technology, Guangzhou, 510550, China

Chang-xin Zhu

Department of Applied Mathematics, Guangdong University of Finance, Guangzhou, 510521, China

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Zejian Qin .

Editor information

Editors and affiliations.

School of Mathematics and Information Sciences, Guangzhou University, Guangzhou, Guangdong, China

Bing-Yuan Cao

Pearl River Delta Regional Logistics Research Center, Guangdong Baiyun University, Guangzhou, China

Shu-Feng Wang

Department of Applied Mathematics, University of Mazandaran, Bābolsar, Iran

Hadi Nasseri

Yu-Bin Zhong

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Cite this paper.

Fu, X., Zhu, Cx., Qin, Z. (2024). Linear Programming Subject to Max-Product Fuzzy Relation Inequalities with Discrete Variables. In: Cao, BY., Wang, SF., Nasseri, H., Zhong, YB. (eds) Intelligent Systems and Computing. ICFIE 2022. Lecture Notes on Data Engineering and Communications Technologies, vol 207. Springer, Singapore. https://doi.org/10.1007/978-981-97-2891-6_3

Download citation

DOI : https://doi.org/10.1007/978-981-97-2891-6_3

Published : 11 May 2024

Publisher Name : Springer, Singapore

Print ISBN : 978-981-97-2890-9

Online ISBN : 978-981-97-2891-6

eBook Packages : Engineering Engineering (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research