
- Math Forum/Help
- Problem Solver
- College Math
- Quadratic Equations


Quadratic Equations: Difficult Problems with Solutions
After 65 Years, Supercomputers Finally Solve This Unsolvable Math Problem
Piece of cake.

- Called the " summing of three cubes ," the challenge is to find x, y, and z.
- It took over a million computing hours to find the solution.
For decades, a math puzzle has stumped the smartest mathematicians in the world. x 3 +y 3 +z 3 =k , with k being all the numbers from one to 100, is a Diophantine equation that's sometimes known as "summing of three cubes."
When there are two or more unknowns, as is the case here, only the integers are studied. The trick is finding integers that work for all equations, or the numbers for x, y, and z that will all equal k. Over the years, scientists have solved for nearly every integer between 0 and 100. The last two that remained were 33 and 42.
Here's a Numberphile video explaining why this problem has proved to be so tricky:
Earlier this year, Andrew Booker of the University of Bristol spent weeks with a supercomputer to finally arrive at a solution for 33 . But 42, which by coincidence is a well-known number in pop culture , proved to be much more difficult.
So Booker turned to MIT math professor Andrew Sutherland, and Sutherland in turn enlisted the help of Charity Engine , which utilizes idle, unused computing power from over 500,000 home PCs to create a crowdsourced and environmentally conscious supercomputer.
The answers took over a million hours to compute. Without further ado, they are:
X = -80538738812075974, Y = 80435758145817515, and Z = 12602123297335631.
Well, obviously .
"I feel relieved," Booker says of breaking the 65-year old puzzle first set down at Cambridge in a press statement . "In this game it's impossible to be sure that you'll find something. It's a bit like trying to predict earthquakes, in that we have only rough probabilities to go by. So, we might find what we're looking for with a few months of searching, or it might be that the solution isn't found for another century."
David Grossman is a staff writer for PopularMechanics.com. He's previously written for The Verge, Rolling Stone, The New Republic and several other publications. He's based out of Brooklyn.

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Math .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

A Wonder Clock Has Rocked the Scientific World

Machines About to Tackle Fermat’s Last Theorem

Can AI Help Solve Math’s Thorniest Mysteries?

The History of Pi

Experts Discovered the Secret Geometry of Life

Scientists Solved a 141-Year-Old Problem

The Perfect Table Size for Your Jigsaw Puzzle

Breaking the 1880s Silk Dress Cryptogram

10 of the Hardest Math Problems Ever Solved

Solution to Riddle of the Week #12: Licking Frogs

Solution to Riddle of the Week #8

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
Hard Algebra Questions – Challenging Problems and Step-by-Step Solutions
JUMP TO TOPIC
Understanding the Fundamentals of Algebra
Solving algebraic operations, linear equations and their graphs, solving quadratic equations, systems of equations, applications of algebra.

Algebra is a fundamental branch of mathematics that deals with symbols and the rules for manipulating these symbols . In its most basic form, it is about finding the unknowns or the variables within equations.
As a student progresses, the questions in algebra can evolve from simple linear equations to more complex problems involving multiple steps, functions, or advanced concepts. Advanced algebra questions often probe one’s understanding of concepts like polynomial functions, rational expressions, exponents, and logarithms.
Navigating the web for reliable and challenging algebra problems and solutions I’ve found to be quite a task, but essential for anyone looking to master the subject. Websites and apps aimed at providing mathematics resources offer a range of problems, from basic to complex, helping learners tackle various topics effectively.
Engaging with these platforms allows for practice and reinforcement of algebraic concepts, which is crucial for solidifying one’s understanding and proficiency in mathematics.
I have to admit, that algebra can sometimes seem like a puzzle with a missing piece. But it’s that moment of clarity when the pieces fall into place that makes solving algebra questions incredibly rewarding. Stick around as we explore some hard algebra questions along with their solutions – the satisfaction of cracking them is just around the corner.
Algebra can seem challenging, but by grasping some key concepts, I can work through even the tough problems.

The backbone of algebra is the equation, which is a statement that two expressions are equal, often containing an unknown quantity, usually represented by a letter like ( x ) or ( y ).
For instance, in the equation ( x + 3 = 7 ), my goal is to find the value of ( x ) that makes this statement true. To do this, I simplify the equation to find ( x ). Simplification might involve combining like terms or using inverse operations. So, in this case, I subtract 3 from both sides to isolate ( x ), yielding ( x = 4 ).
Inequalities are like equations, but instead of equality, they express a relation where one value is larger or smaller than another. This can be represented by symbols such as “>,” “<,” “≤,” or “≥.” For example, if I have ( x – 5 > 10 ), I’m looking for all values of ( x ) that make this inequality true.
Solving this, I add 5 to both sides to get ( x > 15 ).
Here’s a simple way to visualize the process of solving an inequality :
| Steps | Example |
|---|---|
| Write down the inequality | ( x – 5 > 10 ) |
| Perform the same operation on both sides | ( x – 5 + 5 > 10 + 5 ) |
| Simplify to find the solution | ( x > 15 ) |
Remember, if I multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign flips. So, if I had ( -2x < 8 ), by dividing both sides by -2, it becomes ( x > -4 ).
Understanding the foundation allows me to simplify and solve equations and inequalities, providing the confidence to tackle more complex algebraic questions.
When I approach algebraic operations, I prioritize understanding the core concepts—exponents, factoring, complex numbers, and simplification.

These elements are the building blocks to solving more intricate algebra problems.
For exponents , remember that the base raised to the power of an exponent reflects how many times the base is multiplied by itself. For instance, $3^4$ means $3 \times 3 \times 3 \times 3$. When dealing with exponents, it’s essential to be familiar with the laws of exponents for simplification purposes.
| Law | Equation |
|---|---|
| Product of Powers | $a^m \cdot a^n = a^{m+n}$ |
| Quotient of Powers | $\frac{a^m}{a^n} = a^{m-n}$ |
| Power of a Power | $(a^m)^n = a^{m \cdot n}$ |
| Power of a Product | $(ab)^n = a^n \cdot b^n$ |
Next is factoring . I look for the greatest common factor (GCF) or use techniques like the difference of squares, and the quadratic formula for trinomials. For example, factoring $x^2 – 9$ would yield $(x + 3)(x – 3)$ because it is the difference of squares.
When it comes to complex numbers , which are in the form $a + bi$, where $i$ is the imaginary unit $(i^2 = -1)$, I remember that these numbers can be added, subtracted, and multiplied just like real numbers, with special attention to the property of $i$.
Finally, simplification is a matter of combining like terms and using the distributive property where necessary. For instance, to simplify the expression $2(x + 3) + x$, I first distribute the $2$ to get $2x + 6 + x$ and combine like terms to get $3x + 6$.
By mastering these components, I set a strong foundation for tackling hard algebra questions effectively.
Solving Advanced Algebraic Equations
Advanced algebra often serves as the foundation for calculus, statistics, and even programming. Let’s take a look at some of the core types of equations and how to approach them, including linear, quadratic, and systems of equations.
I’ll start by discussing linear equations , characterized by their straight-line graphs. A basic form of a linear equation is the slope-intercept form, expressed as ( y = mx + b ), where ( m ) is the slope and ( b ) is the y-intercept. Converting to standard form , ( Ax + By = C ), may be necessary for some applications. To graph these equations, I find two points by plugging in values for ( x ) and then plotting those points. Connecting these will give me a straight line.
Moving on to quadratic equations , these are typically presented in the general form ( a$x^2$ + bx + c = 0 ). These equations form parabolas when graphed.
I can solve quadratic equations using methods such as factoring, completing the square, or using the quadratic formula, ( x = $\frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$ ). Each method has its own use cases; for example, factoring is efficient when the equation easily decomposes into binomials.
Lastly, I’ll tackle systems of equations , where I have to find the solution set of two or more equations. When solving linear systems , I can use methods such as substitution, elimination, or graphing.
Substitution involves solving one equation for a variable and then substituting that expression into the other equation, while elimination adds or subtracts equations to eliminate a variable. Graphing requires drawing lines of each equation to find their point of intersection.
| Method | When to Use It |
|---|---|
| Substitution | One variable is easily isolated |
| Elimination | Equations can be easily summed or subtracted to cancel out a variable |
| Graphing | Ideal for visual learners and small systems |
These are standard approaches that I often use to find the solutions to various types of algebraic equations.
Algebra has countless applications in the real world, and one of the most practical applications is in calculating areas and perimeters of geometric shapes. Let me guide you through some examples:
Area of a Rectangle : To find the area of a rectangle, I use the formula:
$$ A = l \times w $$
where ( A ) represents the area, ( l ) is the length, and ( w ) is the width.
Perimeter of a Rectangle : Similarly, finding the perimeter is just as straightforward with the equation:
$$ P = 2(l + w) $$
where ( P ) stands for the perimeter.
Area of a Circle : When I look at circles, the area is found using:
$$ A = \pi r^2 $$
Here, ( A ) is the area and ( r ) is the radius of the circle.
Circumference of a Circle: And for the circumference, which is the perimeter of a circle, the formula is:
$$ C = 2\pi r $$
where ( C ) is the circumference.
| Shape | Formula for Area | Formula for Perimeter/Circumference |
|---|---|---|
| Rectangle | ( A = l \times w ) | ( P = 2(l + w) ) |
| Circle | ( A = $\pi r^2$ ) | ( C = 2$\pi$ r ) |
Understanding these formulas allows me to solve real-life problems, such as calculating the amount of paint needed to cover a wall or the fencing required for a circular garden.
With the help of algebra, I can create equations from word problems and solve them; the results help me make informed decisions and solve practical problems efficiently.
In our exploration of challenging algebra questions , I’ve presented a range of problems that test our understanding and application of algebraic concepts. From the intricacies of trigonometric equations to the puzzles of algebraic word problems, the journey through these issues illuminates the beauty of mathematics.
I sincerely hope that the solutions and strategies discussed have helped shed light on the complexity and elegance of algebra. Remember, practicing these tough problems not only sharpens your skills but also prepares you for more advanced mathematical challenges.
Whether you’re preparing for exams or simply indulging in the joy of problem-solving, the resilience and adaptability gained here are invaluable.
Algebra does not always yield its secrets easily, but patience and persistence in working through these tough problems can be immensely rewarding. Keep this momentum going, continue nurturing your mathematical curiosity, and let your confidence grow with each equation you solve.
- Pre Calculus
- Probability
- Sets & Set Theory
- Trigonometry
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

Multi-Step Equations Exercises
Multi-step equations practice problems with answers.
For this exercise, I have prepared seven (7) multi-step equations for you to practice. If you feel the need to review the techniques involved in solving multi-step equations, take a short detour to review my other lesson about it. Click the link below to take you there!

Solving Multi-Step Equations
1) Solve the multi-step equation for [latex]\large{c}[/latex].
[latex]c – 20 = 4 – 3c[/latex]
Add both sides by [latex]20[/latex]. Next, add [latex]3c[/latex] to both sides. Finally, divide both sides by the coefficient of [latex]4c[/latex] which is [latex]4[/latex] to get [latex]c=6[/latex].
2) Solve the multi-step equation for [latex]\large{n}[/latex].
[latex] – \,4\left( { – 3n – 8} \right) = 10n + 20[/latex]
- Remember to always perform the same operation on both sides of the equation.
- Subtract by [latex]32[/latex].
- Subtract by [latex]10n[/latex].
- Divide by [latex]2[/latex]
- The final solution is [latex]n=-6[/latex].
3) Solve the multi-step equation for [latex]\large{y}[/latex].
[latex]2\left( {4 – y} \right) – 3\left( {y + 3} \right) = – 11[/latex]
Apply twice the Distributive Property of Multiplication over Addition to the left side of the equation. Then combine like terms . Add both sides by [latex]1[/latex] followed by dividing both sides of the equation by [latex]-5[/latex].
4) Solve the multi-step equation for [latex]\large{k}[/latex].
[latex]{\Large{{6k + 4} \over 2}} = 2k – 11[/latex]
Multiply both sides by [latex]2[/latex]. Next, subtract [latex]4[/latex] to both sides. Then, subtract [latex]4k[/latex]. Finally, divide by [latex]2[/latex] to obtain the value of [latex]k[/latex] which is [latex]-13[/latex].
5) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex] – \left( { – 8 – 3x} \right) = – 2\left( {1 – x} \right) + 6x[/latex]
Apply the Distributive Property on both sides of the equation. Be careful when multiplying expressions with the same or different signs . Next, add [latex]2[/latex] to both sides, then subtract [latex]3x[/latex], and finally finish it off by dividing [latex]5[/latex] to both sides.
6) Solve the multi-step equation for [latex]\large{m}[/latex].
[latex]{\large{3 \over 4}}m – 2\left( {m – 1} \right) = {\large{1 \over 4}}m + 5[/latex]
7) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex]3\left( {3x – 8} \right) – 5\left( {3x – 8} \right) = 4\left( {x – 2} \right) – 6\left( {x – 2} \right)[/latex]
You may also be interested in these related math lessons or tutorials:
Two-Step Equations Practice Problems with Answers
Solving Equations
What is an equation.
An equation says that two things are equal. It will have an equals sign "=" like this:
That equations says:
what is on the left (x − 2) equals what is on the right (4)
So an equation is like a statement " this equals that "
What is a Solution?
A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .
Example: x − 2 = 4
When we put 6 in place of x we get:
which is true
So x = 6 is a solution.
How about other values for x ?
- For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
- For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .
In this case x = 6 is the only solution.
You might like to practice solving some animated equations .
More Than One Solution
There can be more than one solution.
Example: (x−3)(x−2) = 0
When x is 3 we get:
(3−3)(3−2) = 0 × 1 = 0
And when x is 2 we get:
(2−3)(2−2) = (−1) × 0 = 0
which is also true
So the solutions are:
x = 3 , or x = 2
When we gather all solutions together it is called a Solution Set
The above solution set is: {2, 3}
Solutions Everywhere!
Some equations are true for all allowed values and are then called Identities
Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities
Let's try θ = 30°:
sin(−30°) = −0.5 and
−sin(30°) = −0.5
So it is true for θ = 30°
Let's try θ = 90°:
sin(−90°) = −1 and
−sin(90°) = −1
So it is also true for θ = 90°
Is it true for all values of θ ? Try some values for yourself!
How to Solve an Equation
There is no "one perfect way" to solve all equations.
A Useful Goal
But we often get success when our goal is to end up with:
x = something
In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.
Example: Solve 3x−6 = 9
Now we have x = something ,
and a short calculation reveals that x = 5
Like a Puzzle
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.
Here are some things we can do:
- Add or Subtract the same value from both sides
- Clear out any fractions by Multiplying every term by the bottom parts
- Divide every term by the same nonzero value
- Combine Like Terms
- Expanding (the opposite of factoring) may also help
- Recognizing a pattern, such as the difference of squares
- Sometimes we can apply a function to both sides (e.g. square both sides)
Example: Solve √(x/2) = 3
And the more "tricks" and techniques you learn the better you will get.
Special Equations
There are special ways of solving some types of equations. Learn how to ...
- solve Quadratic Equations
- solve Radical Equations
- solve Equations with Sine, Cosine and Tangent
Check Your Solutions
You should always check that your "solution" really is a solution.
How To Check
Take the solution(s) and put them in the original equation to see if they really work.
Example: solve for x:
2x x − 3 + 3 = 6 x − 3 (x≠3)
We have said x≠3 to avoid a division by zero.
Let's multiply through by (x − 3) :
2x + 3(x−3) = 6
Bring the 6 to the left:
2x + 3(x−3) − 6 = 0
Expand and solve:
2x + 3x − 9 − 6 = 0
5x − 15 = 0
5(x − 3) = 0
Which can be solved by having x=3
Let us check x=3 using the original question:
2 × 3 3 − 3 + 3 = 6 3 − 3
Hang On: 3 − 3 = 0 That means dividing by Zero!
And anyway, we said at the top that x≠3 , so ...
x = 3 does not actually work, and so:
There is No Solution!
That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!
This gives us a moral lesson:
"Solving" only gives us possible solutions, they need to be checked!
- Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
- Show all the steps , so it can be checked later (by you or someone else)
- SAT BootCamp
- SAT MasterClass
- SAT Private Tutoring
- SAT Proctored Practice Test
- ACT Private Tutoring
- Academic Subjects
- College Essay Workshop
- Academic Writing Workshop
- AP English FRQ BootCamp
- 1:1 College Essay Help
- Online Instruction
- Free Resources
Hardest SAT Math Problems (updated for Digital SAT)
Bonus Material: The Hardest SAT Math Problems Quiz
Aiming for a really great score on the SAT? Wondering if your math skills are up to the challenge of the hardest problems?
If you want to be able to get a perfect score, you have to be able to solve the hardest SAT math problems.
We used our extensive test-prep experience to find the questions that many students miss. The examples below are real problems from past official SATs.
Give each of these 16 hard math problems a try, then read our step-by-step explanations to see if you’re solving them correctly.
If you’re thinking about getting SAT tutoring to help you tackle problems like these on the real SAT, be sure to check out our list of the 15 best SAT Tutoring Services
Then, download this quiz with 20 more of the hardest real SAT problems ever to see if you’re on track for a perfect score!

Bonus Material: 20 of the All-Time Hardest SAT Math Problems
Math on the SAT
Math accounts for half of your Total SAT Score, regardless of whether you’re taking the old paper SAT or the new Digital SAT.
On the traditional, paper SAT (which will be phased out in early 2024), the Math section comprises section 3, which contains 20 questions, is 25 minutes long and does not allow you to use a calculator; and section 4, which contains 38 questions, is 55 minutes long and does allow a calculator.
On the upcoming digital SAT (which will come into place in spring of 2024), the format is considerably different. You’ll be given two 35-minute “modules” with 22 questions in each, with the difficulty level of the second one depending on your performance on the first one. In other words, if you do really poorly on the first set of 22 questions, the second set will be easier–but your overall math score will be negatively affected. You can use your calculator on both.
Every SAT covers the following math material:
Heart of Algebra: 33% of test . Linear equations and inequalities and their graphs and systems.
Problem Solving and Data Analysis: 29% of test . Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics.
Passport to Advanced Math: 28% of test . Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs.
Additional Topics in Math: 10% of test . A wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers.

On the old SAT , open-ended questions came at the end of each Math section. Many students find them harder because you can’t guess or work backwards from multiple-choice options.
However, what many students don’t know is that the first 1–3 of these grid-in questions will actually be easier than the last few multiple-choice questions.
That’s because the math questions on the SAT get increasingly difficult over the course of each section, but the difficulty level starts over again with the grid-in questions.
The savvy student will know this and skip the harder multiple-choice questions to go answer the easier grid-in questions first. Of course, if you’re aiming for a perfect score, (on most tests) you’ll have to answer every question correctly .
But on the new Digital SAT, these open-ended questions will pop up at different points throughout both modules. You may see them in the beginning, the middle, or the end: there’s no set place for these to appear. Nor is there a set difficulty: generally, we’ve seen these questions be slightly on the easier side, but this varies significantly from test to test.
Because there’s obviously no bubble sheet on the digital SAT, you’ll simply type your answer into the text box. Be sure to look for instructions in the question about how they want the answer formatted!
To work with us for one-on-one tutoring or for our group SAT classes, schedule a free consultation with our team .
Why these problems are essential if you’re aiming at a top school
A perfect score on the SAT Math is 800. The only way to get this score is to answer every question correctly .
In order to score a 750, you can only miss 2 or 3 questions across both math sections .
A 750 Math SAT may sound like a very high score—and it is! It’s a very high score.

But at the very best schools in the US, three quarters of the students scored a 750 Math or better.
In fact, at the Ivy League and other top schools, at least a quarter of the students had a perfect score!
The average math scores are even higher at the top engineering schools. Three quarters of the students at CalTech had a 790 or 800, and three quarters of the students at MIT had at least a 780.
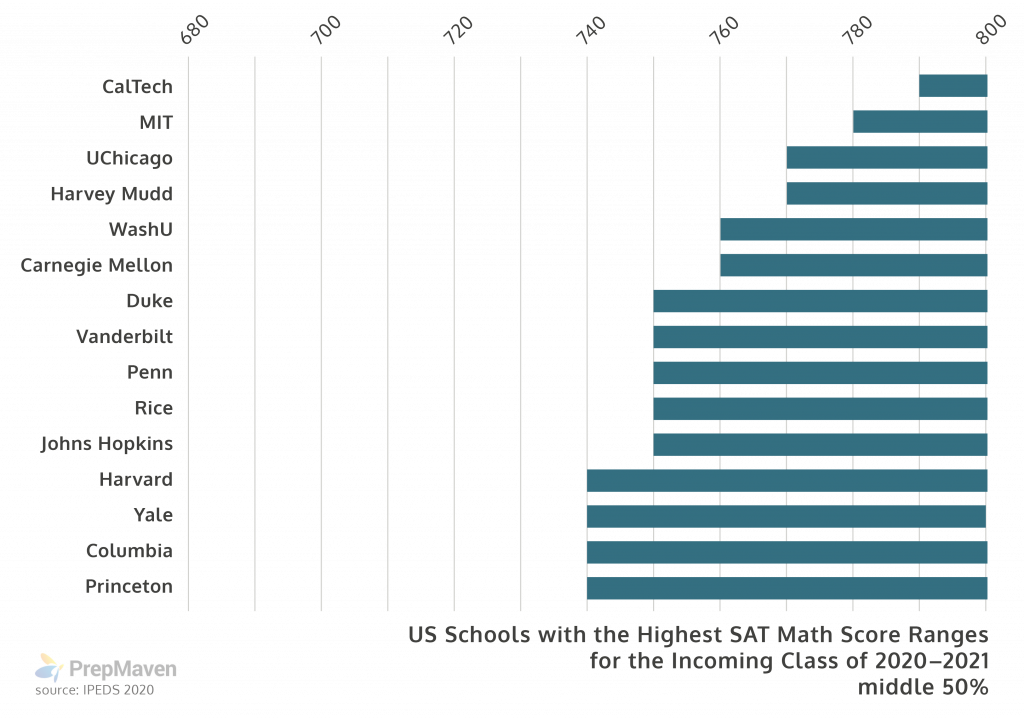
In order to be a competitive applicant to these schools, your SAT Math score should be within the “middle 50%” of the students at that school—in other words, more or less an average score for that school.
So if you’re aiming at an Ivy or one of the other top schools, you can only miss 2 or 3 questions out of the 58 math questions on the whole SAT.
If that’s your goal, make sure that you understand the problems explained below, and then try our quiz of 20 more real SAT questions that rank among the hardest questions ever.
SAT Problem #1

At first glance, this looks like a geometry question, since it talks about planes and lines and points . But this is actually an algebra question, dressed up with some geometric trappings.
The key is to realize:
1) We don’t need to solve for p and r individually. We just need to solve for (r/p) .
2) The points themselves (p,r) and (2p, 5r) represent X and Y values on the line itself. (For example if p = 2 and r = 3 then that’s the same thing as an x-coordinate of 2 and a y-coordinate of 3.)
So let’s take a look at it.
First, let’s plug in the p and r points for the x and y values to see what equations we end up with.
y = x + b becomes r = p + b
y = 2x + b becomes 5r = 2(2p) + b or 5r = 4p + b
At this point we might get a little anxious because we have three variables.
But we have to remember we don’t need to get the value of the individual letters, just the value of the relationship between r and p.
That’s where b actually becomes helpful. Because we can now set both equations equal to b , plug in, and then see if we can manipulate the r and p to get them to express the same relationship we want.

So, first set both equations equal to b to get:
b = r – p
b = 5r – 4p
And since, obviously b = b …
r – p = 5r – 4p
Let’s now use some basic algebra to put the like variables together, so:
Now we’re nearly home. All we have to do is manipulate the problem so r/p .
So, divide both sides by 3p :
4r / 3p = 1
Then multiply both sides by 3:
And finally divide by 4, which gives us:
CHOICE B
Download the Hard SAT Math Problems quiz
SAT Problem #2

This is a question that can cause all sorts of problems if you forget your exponent rules—but it’s otherwise very straightforward.
So let’s go over a few of those rules, just to get comfortable . . . and notice a pattern. I’ve included three below:
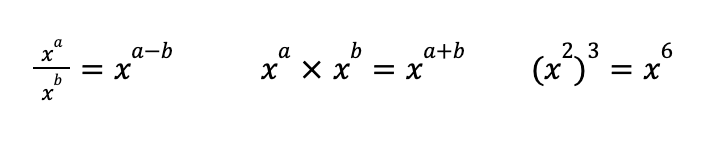
Two things to pay attention to:
First, when we divide variables with exponents, we keep the base and subtract the exponent. When we multiply variables with exponents, we keep the base and add the exponents. When we take a variable with an exponent to an additional power, we multiply the exponents.
Second, in order to use the first two of these rules, the two numbers must have the same base .
There is a base x on both the top and bottom of that fraction or the left and right side of that multiplication sign.
So how does that help us here?
Let’s forget the first half of the problem and look at the second:
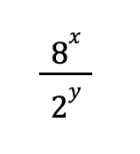
We might look back at these exponent rules and throw our hands up—the top and bottom parts of this fraction don’t have the same base, so what am I supposed to do here?
Except…
8 and 2 actually DO have the same base. Base 2.
Isn’t 2^3 equal to 8?
So if we re-write the problem, plugging in 2^3 for 8, and thinking about that third exponent rule I gave you above, the equation will look like this:
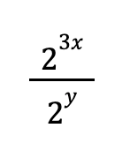
Now let’s go back to our exponent rules once more, and look at the first one.
Because that tells us that…
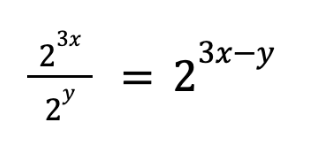
Well, hold on a second!
We know the value of 3x – y .
The problem tells us it’s 12.
So we just plug in and get our answer…
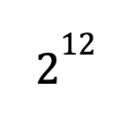
Which is CHOICE A.

Keep up the practice! If you’d like help honing your skills, reach out to us for a free test prep consultation. All of our tutors are top 1% scorers who attended top-tier schools like Harvard and Princeton. That makes them uniquely qualified to help high-scoring students improve.
SAT Problem #3
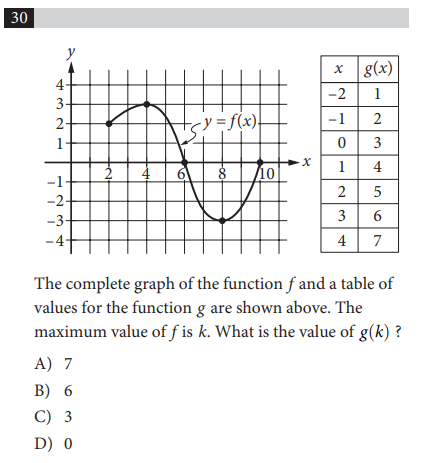
A question like this confuses a lot of students because they either forget how minimums and maximums work or find it hard to keep track of which numbers they are plugging in and where.
In order to solve it, it’s helpful to think of a function as a machine . We enter an input into the machine (an x value)—it acts on it—and then it gives us an output (a y value).
Let’s also remember that when we’re talking about minimum and maximums we’re talking about the y value when the function is at its highest and lowest point .
With these two facts in mind, the problem is going to be much simpler, so let’s take it on in parts…
Since the question is asking us for g(k) and k represents the maximum value of f , it’s going to be helpful to first…
Find k .
So what is the maximum value of f , the graphed function? Well, the maximum value (as we realized earlier) is the y value when the function is at its highest.
Looking at the graph, it looks the function is at highest when x = 4 , and more importantly, when
Therefore, k = 3 .

Now let’s consider our functions as machines.
When the problem asks us for g(k) , it’s telling us that k is going to act as the input (the x value for the function). So g(k) , the value after the machine acts upon the function, is going to be the output , or the y value .
So, g(k) is the same as g(x) , except we’re plugging in our value of k , which is 3, for our x value.
The rest is very simple.
We go to the table and find where x = 3 , then move our finger across to see the output for that value, which is 6.
CHOICE B.
Test your SAT math knowledge with our quiz
SAT Problem #4
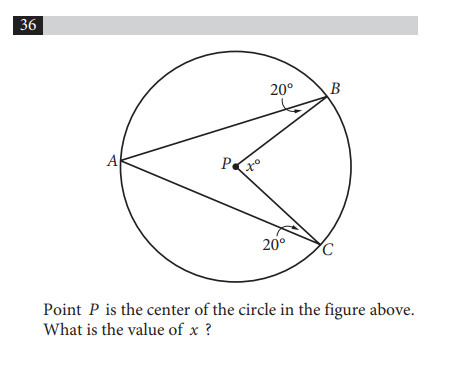
A version of this question has appeared on the SAT multiple times in recent years, and it often stumps students!
Here we have something that resembles a rotated version of the logo from Star Trek, and we’re asked to find the value of a degree inside the circle, between two points of the pointed figure.
We’re given a point that represents the center of the circle, along with two degree measurements inside the triangle-like figure.
Generally, when we’re given a figure that looks unfamiliar to us—like the figure inside the circle— it can be extremely helpful to find a way to fix it (or cut it up) so that it’s made up of parts of shapes that are more familiar .
So looking inside this circle, how might we “fix” this figure so that it becomes a little friendlier.

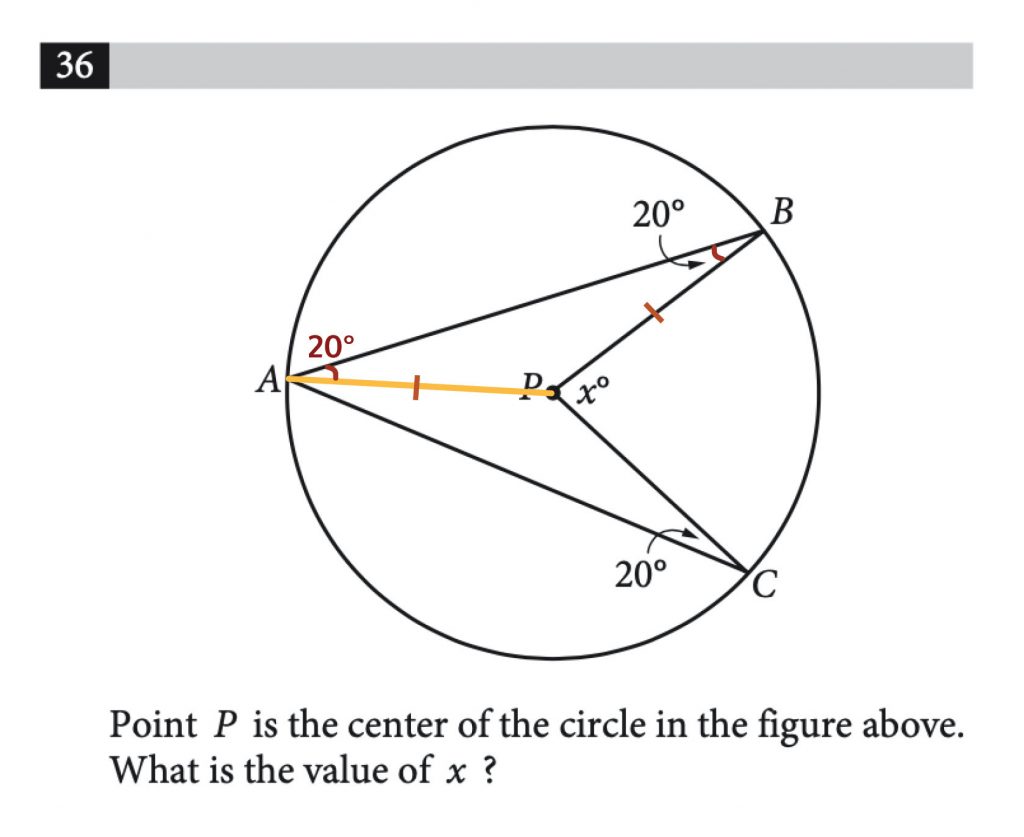
Well, if we draw a line to the center of the circle ( P ) from the edge of the circle ( A ), then this unfamiliar figure suddenly becomes two triangles.
And with triangles, unlike the figure we were originally given, we can apply some rules .
Rules, for example, that dictate opposite sides of the triangle that have the same length will have the same opposite angles.
And if we look at our drawing we see that two sides of our triangle are the same length because they’re both the radius …
And so we also know that the opposite angles of those sides will be the same…
And we’ve been given one of those angles!
Therefore, angles ⦣ABP and ⦣PAB will be the same—both 20 degrees. Let’s fill that in.
Now again—because we have a triangle—we can apply another rule as well.
We know that degrees of a triangle will add up to 180 degrees.
So if we know one of the inner degrees of the triangle is 20, and the other is 20—the remaining angle has to be 140 degrees. (Because 180 – 40 = 140. )
We have two of these triangles, so we know the larger inner angles of both add up to 280.
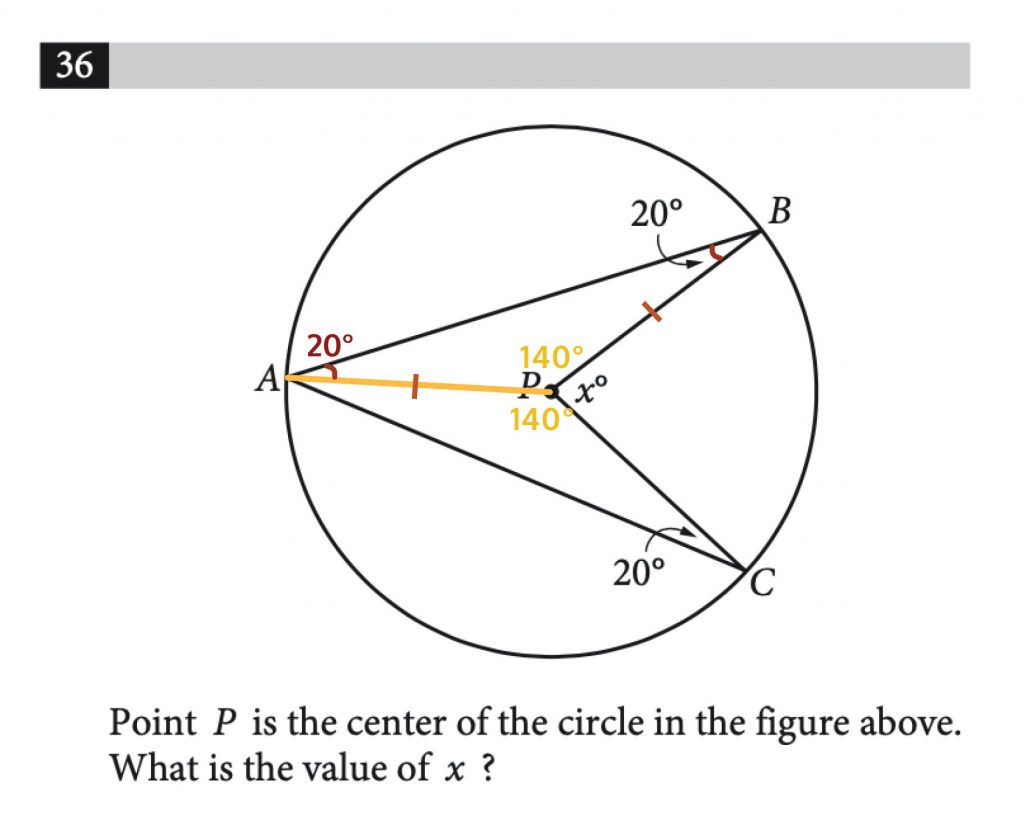
Because a circle is 360 degrees, the number of degrees “left over” when 280 is subtracted from 360 is 80.
So X equals 80.

There is actually a second clever way to solve this problem, involving arc measures. Can you spot it? (If not, don’t worry! Ask us how we did it here .)
SAT Problem #5

Here we have a problem that looks quite complicated—and one I find students often waste a lot of time on. They either try to plug in answers and work backwards…
…or they waste time trying to combine the two terms on the right side of the equation and simplifying.
It turns out the easiest way to solve this problem is by polynomial division , because we’ve already been given the answer! It’s the right-hand side of the equation: (-8x – 3) – (53 / (ax – 2)) .
That means that this is our answer to when (24x^2 + 25x – 47) is divided by ax – 2 .
So how does that help us get a value for a ?
Well, let’s set this up as a polynomial division problem.
We’d write it as follows:
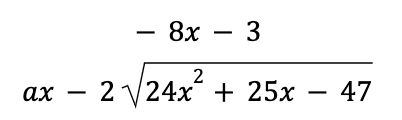
(I’m not putting the second half of the right side of the equation on top because that’s going to be our remainder.)
So now we have a simple question. What number divided into 24 , gives me -8 ?
Well, that’s easy. It’s -3 , right?
Because -3 * -8 gives me 24 .
So a equals -3 , CHOICE B .
Now, you could spend time plugging in -3 for a and dividing through the rest of the problem to make sure your answer matches the one on the exam—but generally on a timed test you really shouldn’t do more work than necessary.
In fact, by setting this up as a polynomial division problem, we’ve saved time precisely because we don’t have to complete all the work . . . just enough to get us our answer.
Try the quiz
SAT Problem #6

Because the SAT is a timed test, “difficult” includes not only questions that are hard to solve, but also those that—if a few wrong decisions are made—take a long time to solve.
Sure, you may get the right answer, but those extra seconds or minutes wasted will inevitably cost you on other questions later on the exam.
Generally speaking, you should be able to answer each question in about a minute. If you spend more than 60 seconds on a single question, you should put down your best guess and move on (and hope that you have extra time at the end to return to this question).
To that end, let’s look at this question. You’re asked to find the value of 3x – 2 , and you’re given this equation:
(⅔)(9x – 6) – 4 = (9x – 6)
Many students will immediately think: “This is totally straightforward: Solve for x and plug it back into the equation.”
They’ll distribute the ⅔ and end up with something like this:
6x – 4 – 4 = 9x – 6
and then go through all the algebra from there, to get… 3x = -2 .
These students will then find that x = (-⅔) .
A few unlucky students will then forget that they have to plug in, and they’ll choose the trap answer C.
The lucky ones will plug the (-⅔) back into 3x – 2 and get the correct answer, -4 , A .
However, it turns out there is actually a much quicker way to solve this problem!
We can solve it without ever having to plug into a second equation.
If we simply subtract (⅔)(9x-6) from both sides, we end up with…
-4 = (⅓)(9x-6) .
We can realize that (⅓) of 9x-6 is the same as 3x-2 .
And, what do you know…
-4 = 3x – 2 .

Ready to try some of these problems on your own? Try our quiz with 20 more of the hardest real SAT problems ever to see if you could get a perfect score on the SAT Math!
SAT Problem #7

This is a question you could muscle through, but it’s going to be a lot easier if we find a few shortcuts and work from there. Remember, a hard question isn’t necessarily difficult because of the conceptual and mathematical effort it asks from you but also because of the time it might require.
So how do we save ourselves some time?
First, let’s notice that in the answer choices none of these numbers repeat . There are eight distinct numbers in the answer choices. Therefore, if we were pressed for time we only really have to find one of the values of c , choose the corresponding answer choice, and then move on.
Second, let’s look at the other piece of information this problem gives us besides the quadratic.
It tell us that a + b = 8.
This should be especially helpful because we know from FOIL (and what the rest of the problem gives us) that a * b = 15 , because abx^2 is going to be equal to 15x^2.
Because a + b = 8 and ab = 15 , we know that the values of a and b are going to be 3 and 5.
(We don’t know which one is which, and that’s precisely why this problem has two possible values for c .)
At this point we’ve done most of the “hard” work to save time in this problem, and it hasn’t even been particularly hard!
Now all we have to do is assign one of 3 or 5 to a , assign the other to b , FOIL out the problem, and pick whichever choice corresponds to one of the values of c .
Let’s say a = 3 and b = 5 .
It will work like this:
(3x + 2)(5x + 7) = 15x^2 + 21x + 10x + 14 .
Which simplifies to…
15x^2 + 31x + 14 .
Which means c = 31 .
31 only appears once in our answer choices, so the answer must be CHOICE D.
SAT Problem #8

When you’re faced with one of these more difficult system-of-equations problems—specifically the ones that ask you for no solutions or infinite solutions —it’s going to be much, much easier to think about the problems geometrically.
In other words, as two line equations.
So what does it mean for two lines to have no solutions ?
Well, for two lines to have no solutions, they’d have to never intersect , correct?
(Just like if one of these problems asks you about two lines with infinite solutions , they’re saying that the lines are the same . They’re laid on top of each other. )
In other words, they’d have to be… parallel lines .
And parallel lines have the same… slope!
So this question is asking you to find the correct value for the variable that gives these lines the equivalent slope .
Obviously, the first step is to put both of these equations in slope-intercept form. We’d end up with:
y = (-a/2)x + 2
Now the rest is very simple. All we need is a value of a that makes the slopes equal, so that it solves the equation (-a/2) = 3 .
With some basic algebra, we end up with -a = 6 . This is the same as a = -6 .
So the answer is CHOICE A, -6.

Are these problems feeling super hard for you? Want to work on more similar problems? Check out our one-on-one tutoring with Ivy-League instructors. A great experienced tutor can help you focus on the concepts that are the hardest for you until you understand them thoroughly.
SAT Problem 9

This is another type of problem that students often have conceptual difficulty with, causing them to waste much more time than they should.
(Remember, basically every problem in the SAT math section is designed to be solved in a minute and half or less. If you’re taking three or four minutes on a math problem, you’ve probably made a mistake!)
Some students will see that (u-t) is defined but not u or t individually, so they’ll try either solving for u in terms of t (or vice versa), or they’ll try squaring (u-t) to get a solution. (Which is closer to the correct way to solve the problem, but still incorrect).
Instead, to solve this problem we need to remember the difference of squares .
Remember, that the difference of squares states the following…
(x+y)(x-y) = x^2 – xy + xy – y^2 .
Which means…
(x+y)(x-y) = x^2 – y^2 .
And doesn’t that look awfully familiar to… u^2 – t^2 ?
In fact, we can now replace u^2 – t^2 with (u + t)(u – t) .
So the whole problem would now read: (u + t)(u – t)(u – t) . Since we know the value of (u + t) and (u – t) , this would simply be the same as (2)(5)(2) .
Which equals our answer…
Ready to see how you’re doing? Download the quiz
SAT Problem #10

What makes this question confusing is that students often get thrown off by the repetition of the (⅓).
They forget that when the ⅓ gets factored out of the parenthesis like that, it means it’s going to apply to the whole equation: both the x^2 AND the -2 .
Once we remember that, we can solve this problem by difference of squares . This will save us the time of having to brute force the answer choices and FOIL each one through for the different values of k.
We’ll simply square k and subtract it from the x^2 for each choice.
That will give us the following four choices:
(⅓)(x^2 – 4)
(⅓)(x^2 – 36)
(⅓)(x^2 – 2)
(⅓) (x^2 – 6)
A student might rush to choose the third answer choice, since it appears to look like the expression at the beginning of the problem, but remember what I told you at the beginning:
We’re going to apply that ⅓ to both the x^2 AND the k !
If we multiply that ⅓ through, the choices suddenly look like this…
(⅓)(x^2) – (4/3)
(⅓)(x^2) – (12)
(⅓)(x^2) – (⅔)
(⅓)(x^2) – (2)
. . . and so the correct answer is actually the fourth choice, CHOICE D .

Ready to try more hard problems on your own? Download our free quiz to try 20 more of the hardest ever (real) SAT problems.
SAT Problem #11

There are not many problems on the SAT that involve knowing the equation for a circle—in fact, circle equation problems don’t show up on every test—but that’s precisely why students often find a problem like this more difficult.
First, let’s do a quick refresher on what the numbers in the equation of a circle mean.
Any equation for a circle is going to be in this form:
(x – h)^2 + (y – k)^2 = r^2
Where h and k represent the coordinates of the center and r is the radius.
Let’s apply that to our problem here…
(x + 3)^2 + (y – 1)^2 = 25.
Remember: because in the form of the circle equation the numbers inside the parenthesis are subtracted from x and y , when they appear inside the parenthesis as positives , that indicates the coordinate point will be negative.
Therefore the center of this circle is at point (-3, 1) .
Because the radius is expressed as r^2 , then the 25 indicates the radius will be 5 .
So we have a circle centered on the point (-3,1) and with a radius of 5 .
So… now what?
How do we figure out which of these points is not inside the circle?
First, let’s draw the circle itself and look at it. On the SAT itself, you won’t have graph paper, so just draw a rough sketch!
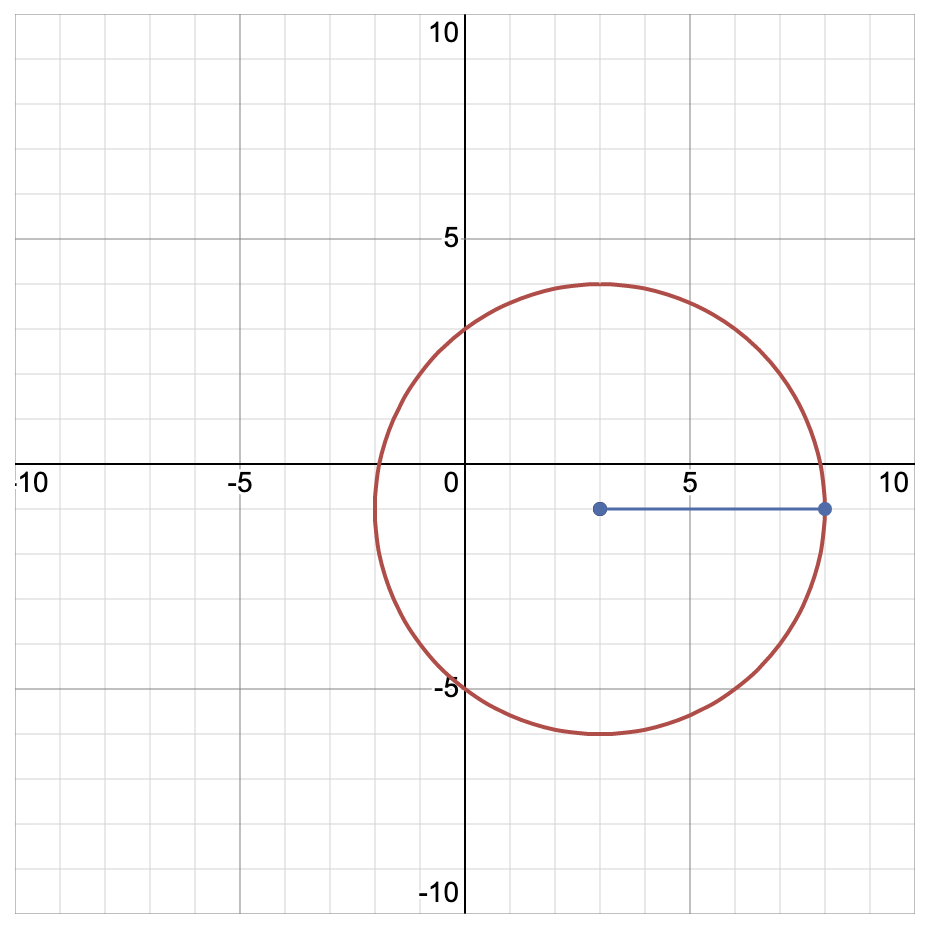
Of course if we’re truly flummoxed we could graph the points, eliminate what we can . . . and guess.
But that’s not ideal, obviously!
Instead, let’s think about what the radius means.
The radius demarcates the boundaries of the circle from the center.
In other words, any points with a distance less-than-the-radius away from the center will lie within the circle.
And any points more-than-the-radius distance from the center will lie outside of it.
(Any points exactly-the-radius distance from the center will lie on the circle itself.)
So all we have to do is find the point that is more than 5 units away from our center, and that will be our answer.
To do this requires the distance formula.
Remember, the distance formula is
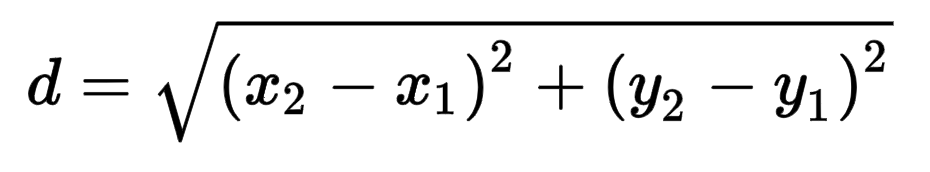
A quick note: if you ever forget the distance formula, simply plot the two points on a graph, make a triangle with the distance between the two points and the hypotenuse, and use the Pythagorean Theorem to find the length of the hypotenuse, like this:
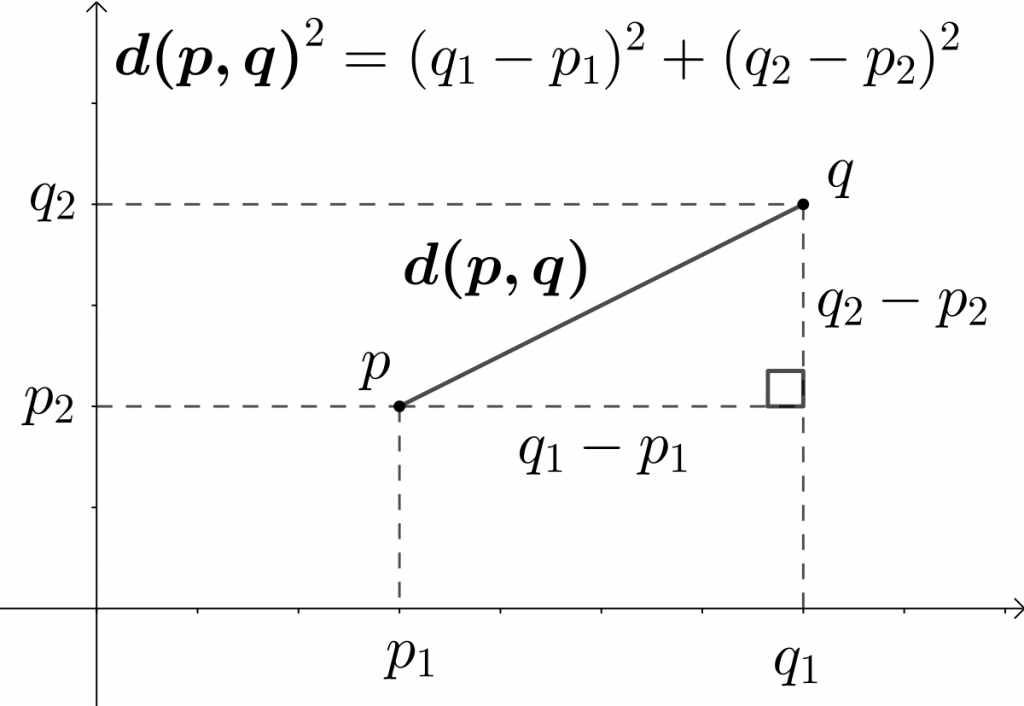
Going back to our problem, let’s plug each of the points in along with our radius to the equation. (I’ll include the second point here, although since that’s our center we need not actually bother with it when we’re going through the problem.) We end up with:
√(-3 – (-7))^2 +(1-(3))^2) = √20
√(-3 – (-3))^2 +(1-(1))^2) = √0
√(-3 – (0))^2 +(1-(0))^2) = √10
√(-3 – (3))^2 +(1-(2))^2) = √37
Only the square root of 37—choice D—is an answer that is larger than five.
So that’s our correct choice, D .
Want more hand-picked problems? Get the quiz
SAT Problem #12
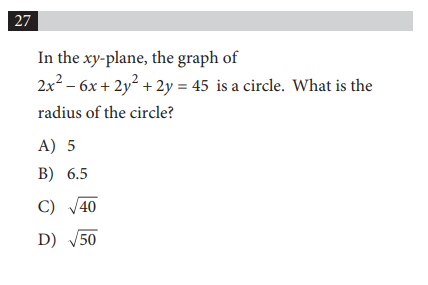
More circles! Let’s recall how the equation for a circle looked. It’s…
(x – h)^2 + (y – k)^2 = r^2
What the problem gives us, unfortunately, does not resemble that equation…
…so our goal is to get the equation in the problem to look like a normal equation for a circle.
Once we do this, we’ll just have to take the square root of whatever is on the right side of the equation, and that will give us our answer.
But how?
We need to do something called completing the square .
For the SAT, this concept is slightly obscure—it’s one you may see only once (or not at all) on a given exam. It makes the question a bit more difficult.
Completing the square is normally a process reserved for solving a quadratic equation, but if you look closely at the way this problem is set up –
2x^2 – 6x + 2y^2 + 2y = 45
we see that what we really have here are two quadratic equations, so we just have to complete the square twice.
First we have to get rid of the coefficient in front of the x and y squared, so we have to divide through by 2 .
This gives us x^2 – 3x + y^2 + y = 22.5 .
Now we’re reading to complete the square!
Let’s deal with the x terms first. We have to think of what number, if we had it here in the equation, would allow us to factor x^2 – 3x into something of the form (x – z)^2 , where z is a constant. If we think about it, we realize that z has to be half of b . In this case, that means half of -3 , so -1.5 .
When we pop that into our setup, we get (x – 1.5)^2 . If we FOIL this out, however, we see that we get x^2 – 3x + 2.25 .
So it turns out that in order to be able to rewrite our expression in the form we want, we need to add 2.25 to our equation. As always in algebra, we do the same thing to both sides, so now we have:
x^2 – 3x + 2.25 + y^2 + y = 22.5 + 2.25.
Now we do the same thing for the y terms! Again, we need to add something to the equation so that we could rewrite the y part of the expression in the form (y – z)^2 . To get this number, we take half of the b term and square it: 1 divided by 2 , then squared, so 0.5^2 or 0.25.
Again, we have to add this number to both sides of the equation. Now we’ve got:
x^2 – 3x + 2.25 + y^2 + y + 0.25 = 22.5 + 2.25 + 0.25.
We can factor and rewrite this like:
( x – 1.5)^2 + (y + 0.5)^2 = 25.
Alright, now this is finally in the right format for the equation for a circle!
The final step is to use this equation to find the radius.
We know that the equation for a circle is (x – h)^2 + (y – k)^2 = r^2 . Fortunately this works out really nicely, since 25 is just 5^2. The radius must be 5, CHOICE A .

We’ve tutored thousands of students and used that experience to assemble a list of 20 more problems that students frequently miss. Can you answer them correctly? Download the quiz now to find out!
SAT Problem #13
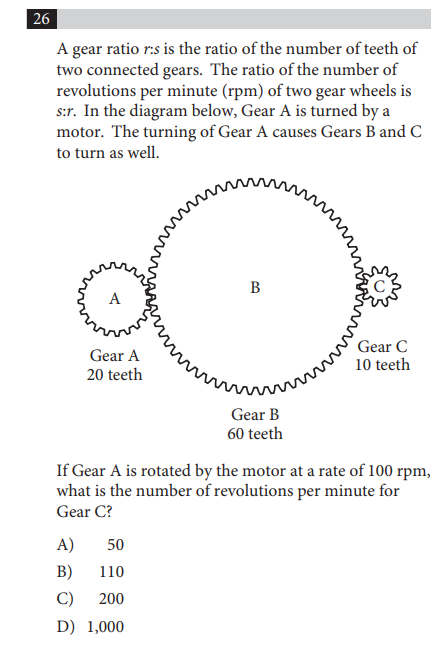
This question involves a number of moving parts and thus can be a little overwhelming for students to follow.
It asks us to find, based on the rotation of the first gear, the rotation of the third.
I find many students trip up on this problem by making two errors that are simple to fix, but relatively common. They fail to take the problem step by step… and they fail to write down their work as they track through the material.
With that in mind, let’s work through the problem.
Because gears A and C do not connect directly, but instead through gear B, we should first try to figure out the rotational relationship between A and B (at 100 rpm) before applying that to B and C.
Because B is larger than A (and has more gears), A is going to rotate fully multiple times before B rotates once.
How many times? Here it’s helpful to consider a ratio.
A has 20 gears.
B has 60 gears.
So A is going to have to rotate three times before B rotates once . (20 goes into 60 three times.)
Therefore, the ratio of rotation between A and B is 3 : 1 .
Let’s write that down and then apply the same method to figure out the ratio between B and C.
C has 10 gears.
Here B only has to rotate a sixth of its distance for C to rotate once, so the ratio of rotation between B and C is 1 : 6 .
Now we take the number of RPMs the problem gives us, start with the gear on the left and multiply through with our ratios.
So if Gear A rotates 100 times RPMS per minute, Gear B will rotate a third of that distance…
So we divide 100 by 3.
Because we know Gear C rotates six times as fast as Gear B, we then take our answer and multiply it by 6.
So we get (100)(⅓)(6) .
Which gives us 200 rpm.
CHOICE C.
SAT Problem #14
This question appears complicated—and students often get tripped up trying to either plug in numbers (which can be time consuming) or by searching for an equation that explains the relationship between the surface area and perimeter of the cube itself.
This is especially tempting because while the question gives us the equation for the entire surface area of the cube, it only asks for the perimeter of one of the cube’s faces.
However…
If we think about the properties of a cube, this question actually becomes quite simple.
First, let’s draw a cube.
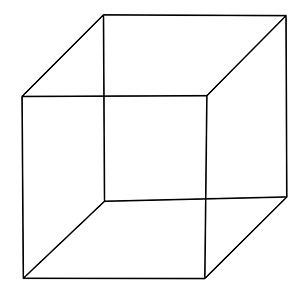
Again, the equation the problem gives us is for the entire surface area of the cube: 6(a/4)^2 .
But when we look at the cube, we may notice that it has, in fact, six faces.
Therefore, each face would have one sixth of the surface area of the entire cube.
So by dividing the equation by six, we get the surface area for one face of the cube, which is:
But the question asks for the perimeter of one face of the cube.
Let’s examine the drawing of the cube one more time.
What shape is each cube face? It’s a square.
And because each side of a square (let’s call each side x ) is equal to the other, the area of the square is going to be x^2, or the length of the side times itself.
Well, wait a moment…
If we go back to our equation for the surface area of ONE face of the cube, (a/4)^2 , we might notice that it’s in the same form as the equation for area of the square, except instead of x being squared, it’s (a/4) .
And if we replace the x with (a/4) , we find that each side of the square is equivalent to (a/4) .
Which makes finding the perimeter of this square quite simple, because it has four sides.
So we merely add the four sides together:
(a/4) + (a/4) + (a/4) + (a/4) . . .
which equals a .
Which in this case is CHOICE B .

Want more practice? We collected 20 more of the hardest SAT math problems. Download the quiz and take it with a 25-minute timer to mimic the real test!
SAT Problem #15

We have a lot of variables in this question, so it’s easiest to try to incorporate the extra piece of information we’re given, b = c – (½) , as best we can and then try to simplify the problem and solve from there.
So how can we do that?
The problem tells us b = c – (½) , which can also be expressed as b – c = -(½) .
(Once we put the b and c together on one side, it becomes easier to replace them together with a number).
So what’s the best way to manipulate these two equations so that we’ll have b – c , which we can then replace with the (-½) and be left with x and y ?
Because let’s remember that the problem does not ask us to solve for x and y individually.
Just their relationship.
So once we’re left with x and y as our only two variables, we should be able to make good progress.
Anyhow, looking back over these two equations it seems the easiest way to be left with b – c is to…
…subtract the bottom equation from the top one.
When we do so, we’re left with the following:
(3x – 3y) + (b – c) = (5x – 5y) + (-7 – (-7))
We replace b – c with -½
And then combine like terms to get…
(-½) = (5x – 3x) – (5y + 3y)
(-½) = 2x – 2y
Divide through by 2 …
-¼ = x – y
Or x = y – (¼)
So our an answer is x = y – ¼ , CHOICE A .
Download 20 more of the hardest problems ever
SAT Problem #16

There are a few ways to solve this problem. The easiest one is simply to know the “remainder theorem.”
I don’t want to get too sidetracked with details, but remainder theorem states that when polynomial g(x) is divided by (x – a) , the remainder is g(a) .
In other words, when p(x) is divided by (x-3) here, the remainder would be p(3) , which, according to the information we’re given, is -2 .
That leads to CHOICE D .
But what if, like many students, you don’t know the remainder theorem? (It’s pretty obscure and there’s a good chance you won’t see a problem about it on the entire exam.)
Let’s look at an alternative way to solve the problem.
If p(3) equals -2 , let’s imagine a function where that might be the case.
We could do as simple one, like y = 3x – 11 , or a more complex one, like y = x^2 + 3x – 20 .
Either way, if I plug 3 into either of these functions for x , I get -2 as a y value.
I should also notice immediately that (x – 5) , (x – 2) , and (x + 2) are not factors of either of them.
Clearly choices A, B, and C are not things that must be true.
This also, by process of elimination, leads to CHOICE D.
But just to check, let’s divide x – 3 into one of these functions – say 3x – 11 – and see what happens:
The x goes into 3x three times – and three times (x-3) equals 3x – 9 .
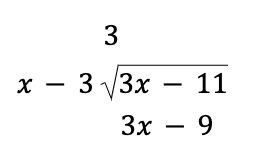
When I subtract 3x – 9 from 3x – 11 , I get -2 , which is my remainder.
Which points us, again, to CHOICE D .
Test your knowledge with 20 more problems
If these problems feel really hard, don’t panic—you can still do well on the SAT without answering every question correctly.
The average SAT Math score for US students in 2022 was 52 8, and you have to answer about 32 out of 58 math questions correctly to get this score. That’s only a little over half of the questions!

However, if you want a high score—or a perfect score—you’ll have to be able to answer tough questions like these. You’ll need a very high score to be a competitive applicant for Harvard, Stanford, MIT, or other highly competitive schools.
The good news is that it’s very possible to raise your math score!
In fact, it’s typically easier to improve your SAT Math score than your Reading & Writing score. Good preparation (on your own or with a tutor ) will fill in the knowledge gaps for any concepts that might be shaky and then practice the most common problem types until they feel easy.
We’ve worked with students who were able to see a 200-point increase on the Math section alone, through lots of hard work and practice.
To see how your math skills stack up against the toughest parts of the SAT, download our quiz with 20 more of the hardest SAT math questions, taken from real tests administered in recent years.
Once you know where you stand, keep up the practice!
If you’re interested in customized one-on-one tutoring support from an expert SAT tutor who can help you understand these tough problems, schedule a free consultation with Jessica or one of our founders . Our Ivy-League tutors are top scorers themselves who can help you with these more advanced concepts and strategies.
Bonus Material: Quiz: 20 of the All-Time Hardest SAT Math Problems

Emily graduated summa cum laude from Princeton University and holds an MA from the University of Notre Dame. She was a National Merit Scholar and has won numerous academic prizes and fellowships. A veteran of the publishing industry, she has helped professors at Harvard, Yale, and Princeton revise their books and articles. Over the last decade, Emily has successfully mentored hundreds of students in all aspects of the college admissions process, including the SAT, ACT, and college application essay.
CHECK OUT THESE RELATED POSTS

Registering for the SSAT
June 28, 2024
Registering for the SSAT is generally a simple process, but there’s still some important information you need to remember. First, be mindful of the registration deadlines, testing formats, and …

SSAT Test Dates for 2024-2025
June 25, 2024
Wondering what dates the SSAT is offered? SSAT test dates are updated each year in August, and you can expect the SSAT to be offered on …

What is the SSAT?
An integral part of the private school admissions process, the SSAT is a standardized test unlike any you’ve seen. With the SSAT, you can be expected to be tested on you knowledge of math skills, analogies, and…

How Long is the SSAT?
June 20, 2024
Wondering about the SSAT’s timing and length? While the format differs slightly between elementary, middle, and upper level SSATs, you can expect the test to take …

How many times should you take the SSAT?
Retaking the SSAT is a good move for almost everyone, but how many times will depend on your specific testing situation, as well as what test formats you’re mostly comfortable with. Students rarely see their top score on a first attempt, so…

Your Guide to the SSAT’s Format
June 3, 2024
Wondering about SSAT format, length, or content? In this post, we cover everything you need to know about the structure of this high stakes test so that you can prepare for …

6 SSAT Reading Strategies From the Experts
May 29, 2024
With these 6 SSAT Reading strategies, you'll be prepared to maximize your raw score on this difficult section.

15 College Essays That Worked
May 13, 2024
In this regularly updated post, we share the college essays that helped students get into their dream schools -- including Ivy Leagues.

SSAT Score Release Dates – When You’ll Get That Score Report
May 2, 2024
You've studied hard. You've taken the SSAT. Now when will you get that score report? Find SSAT score release dates and more in this regularly updated post.

SSAT Prep Resources: Your Guide
Preparing to take the SSAT? What SSAT prep resources should you be utilizing? We weigh in on the best SSAT test prep tools in this post.
Privacy Preference Center
Privacy preferences.
Challenging Algebra Questions
Challenging algebra questions are presented along with their detailed solutions. These questions needs the basic algebra rules, exponents, complex numbers, factoring, ... , thinking and some patience. Do not give up quickly; you will be learning a lot while you are looking for the solution.
Questions with Solutions
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
📬 Sign Up for Our Amazing Newsletter!
Writing result-oriented ad copy is difficult, as it must appeal to, entice, and convince consumers to take action.
How to Work Through Hard Math Problems
parent of one of our students wrote today about his daughter’s occasional frustration with the difficulty of some of the problems in our courses. She does fantastic work in our courses , and was easily among the very top students in the class she took with me, and yet she still occasionally hits problems that she can’t solve.
Moreover, she has access to an excellent math teacher in her school who sometimes can’t help her get past these problems, either. (This is no slight to him—I have students bring me problems I can’t solve, too!) Her question: “Why does it have to be so hard?”

The Case for Doing Hard Things
We ask hard questions because so many of the problems worth solving in life are hard. If they were easy, someone else would have solved them before you got to them. This is why college classes at top-tier universities have tests on which nearly no one clears 70%, much less gets a perfect score. They’re training future researchers, and the whole point of research is to find and answer questions that have never been solved. You can’t learn how to do that without fighting with problems you can’t solve. If you are consistently getting every problem in a class correct, you shouldn’t be too happy — it means you aren’t learning efficiently enough. You need to find a harder class.
The problem with not being challenged sufficiently goes well beyond not learning math (or whatever) as quickly as you can. I think a lot of what we do at AoPS is preparing students for challenges well outside mathematics. The same sort of strategies that go into solving very difficult math problems can be used to tackle a great many problems. I believe we’re teaching students how to think, how to approach difficult problems, and that math happens to be the best way to do so for many people.
The first step in dealing with difficult problems is to accept and understand their importance. Don’t duck them. They will teach you a lot more than a worksheet full of easy problems. Brilliant “Aha!” moments almost always spring from minds cultivated by long periods of frustration. But without that frustration, those brilliant ideas never arise.
Strategies for Difficult Math Problems — and Beyond
Here are a few strategies for dealing with hard problems, and the frustration that comes with them:
Do something . Yeah, the problem is hard. Yeah, you have no idea what to do to solve it. At some point you have to stop staring and start trying stuff. Most of it won’t work. Accept that a lot of your effort will appear to have been wasted. But there’s a chance that one of your stabs will hit something, and even if it doesn’t, the effort may prepare your mind for the winning idea when the time comes.
We started developing an elementary school curriculum months and months before we had the idea that became Beast Academy . Our lead curriculum developer wrote 100–200 pages of content, dreaming up lots of different styles and approaches we might use. Not a one of those pages will be in the final work, but they spurred a great many ideas for content we will use. Perhaps more importantly, it prepared us so that when we finally hit upon the Beast Academy idea, we were confident enough to pursue it.
Simplify the problem . Try smaller numbers and special cases. Remove restrictions. Or add restrictions. Set your sights a little lower, then raise them once you tackle the simpler problem.
Reflect on successes . You’ve solved lots of problems. Some of them were even hard problems! How did you do it? Start with problems that are similar to the one you face, but also think about others that have nothing to do with your current problem. Think about the strategies you used to solve those problems, and you might just stumble on the solution.
A few months ago, I was playing around with some Project Euler problems, and I came upon a problem that (eventually) boiled down to generating integer solutions to c ² = a ² + b ² + ab in an efficient manner. Number theory is not my strength, but my path to the solution was to recall first the method for generating Pythagorean triples. Then, I thought about how to generate that method, and the path to the solution became clear. (I’m guessing some of our more mathematically advanced readers have so internalized the solution process for this type of Diophantine equation that you don’t have to travel with Pythagoras to get there!)
Focus on what you haven’t used yet . Many problems (particularly geometry problems) have a lot of moving parts. Look back at the problem, and the discoveries you have made so far and ask yourself: “What haven’t I used yet in any constructive way?” The answer to that question is often the key to your next step.
Work backwards . This is particularly useful when trying to discover proofs. Instead of starting from what you know and working towards what you want, start from what you want, and ask yourself what you need to get there.
Ask for help . This is hard for many outstanding students. You’re so used to getting everything right, to being the one everyone else asks, that it’s hard to admit you need help. When I first got to the Mathematical Olympiad Program (MOP) my sophomore year, I was in way over my head. I understood very little of anything that happened in class. I asked for help from the professor once — it was very hard to get up the courage to do so. I didn’t understand anything he told me during the 15 minutes he worked privately with me. I just couldn’t admit it and ask for more help, so I stopped asking. I could have learned much, much more had I just been more willing to admit to people that I just didn’t understand. (This is part of why our classes now have a feature that allows students to ask questions anonymously.) Get over it. You will get stuck. You will need help. And if you ask for it, you’ll get much farther than if you don’t.
Start early . This doesn’t help much with timed tests, but with the longer-range assignments that are parts of college and of life, it’s essential. Don’t wait until the last minute — hard problems are hard enough without having to deal with time pressure. Moreover, complex ideas take a long time to understand fully. The people you know who seem wicked smart, and who seem to come up with ideas much faster than you possibly could, are often people who have simply thought about the issues for much longer than you have. I used this strategy throughout college to great success — in the first few weeks of each semester, I worked far ahead in all of my classes. Therefore, by the end of the semester, I had been thinking about the key ideas for a lot longer than most of my classmates, making the exams and such at the end of the course a lot easier.
Take a break . Get away from the problem for a bit. When you come back to it, you may find that you haven’t entirely gotten away from the problem at all — the background processes of your brain have continued plugging away, and you’ll find yourself a lot closer to the solution. Of course, it’s a lot easier to take a break if you start early.
Start over . Put all your earlier work aside, get a fresh sheet of paper, and try to start from scratch. Your other work will still be there if you want to draw from it later, and it may have prepared you to take advantage of insights you make in your second go-round.
Give up . You won’t solve them all. At some point, it’s time to cut your losses and move on. This is especially true when you’re in training, and trying to learn new things. A single difficult problem is usually going to teach you more in the first hour or two than it will in the next six, and there are a lot more problems to learn from. So, set yourself a time limit, and if you’re still hopelessly stuck at the end of it, then read the solutions and move on.
Be introspective . If you do give up and read the solution, then read it actively, not passively. As you read it, think about what clues in the problem could have led you to this solution. Think about what you did wrong in your investigation. If there are math facts in the solution that you don’t understand, then go investigate. I was completely befuddled the first time I saw a bunch of stuff about “mod”s in an olympiad solution — we didn’t have the internet then, so I couldn’t easily find out how straightforward modular arithmetic is! You have the internet now, so you have no excuse. If you did solve the problem, don’t just pat yourself on the back. Think about the key steps you made, and what the signs were to try them. Think about the blind alleys you explored en route to the solution, and how you could have avoided them. Those lessons will serve you well later.
Come back . If you gave up and looked at the solutions, then come back and try the problem again a few weeks later. If you don’t have any solutions to look at, keep the problem alive. Store it away on paper or in your mind.
Richard Feynman once wrote that he would keep four or five problems active in the back of his mind. Whenever he heard a new strategy or technique, he would quickly run through his problems and see if he could use it to solve one of his problems. He credits this practice for some of the anecdotes that gave Feynman such a reputation for being a genius. It’s further evidence that being a genius is an awful lot about effort, preparation, and being comfortable with challenges.
Subscribe for news, tips and advice from AoPS
Richard rusczyk, related articles, a problem-solving approach to language arts, resolve to problem solve: your new year's challenge, more articles, how improv can train innovators, with deana criess, why it's so important to learn a problem-solving approach to mathematics, embedding stem into your every day, with emily hunt, in the media: "keeping the gifted alive" by richard rusczyk, farther in space, further in time: what the james webb space telescope will show us, more episodes, sapienship, with dr. jim clarke, wonder, with dr. frank keil, learning stem through fiction, with dr. pamela cosman, managing academic expectations, with charlene wang, edtech at-home, with monica burns, learned helplessness, with vida john, receive weekly podcast summaries right to your inbox, get weekly podcast summaries/takeaways.
By clicking this button, I consent to receiving AoPS communications, and confirm that I am over 13, or under 13 and already a member of the Art of Problem Solving community. View our Privacy Policy .

Aops programs

Choose Your Test
Sat / act prep online guides and tips, the 15 hardest sat math questions ever.

Want to test yourself against the most difficult SAT math questions? Want to know what makes these questions so difficult and how best to solve them? If you're ready to really sink your teeth into the SAT math section and have your sights set on that perfect score, then this is the guide for you.
We've put together what we believe to be the 15 most difficult questions for the current SAT , with strategies and answer explanations for each. These are all hard SAT Math questions from College Board SAT practice tests, which means understanding them is one of the best ways to study for those of you aiming for perfection.
Image: Sonia Sevilla /Wikimedia
Brief Overview of SAT Math
The third and fourth sections of the SAT will always be math sections . The first math subsection (labeled "3") does not allow you to use a calculator, while the second math subsection (labeled as "4") does allow the use of a calculator. Don't worry too much about the no-calculator section, though: if you're not allowed to use a calculator on a question, it means you don't need a calculator to answer it.
Each math subsection is arranged in order of ascending difficulty (where the longer it takes to solve a problem and the fewer people who answer it correctly, the more difficult it is). On each subsection, question 1 will be "easy" and question 15 will be considered "difficult." However, the ascending difficulty resets from easy to hard on the grid-ins.
Hence, multiple choice questions are arranged in increasing difficulty (questions 1 and 2 will be the easiest, questions 14 and 15 will be the hardest), but the difficulty level resets for the grid-in section (meaning questions 16 and 17 will again be "easy" and questions 19 and 20 will be very difficult).
With very few exceptions, then, the most difficult SAT math problems will be clustered at the end of the multiple choice segments or the second half of the grid-in questions. In addition to their placement on the test, though, these questions also share a few other commonalities. In a minute, we'll look at example questions and how to solve them, then analyze them to figure out what these types of questions have in common.
But First: Should You Be Focusing on the Hardest Math Questions Right Now?
If you're just getting started in your study prep (or if you've simply skipped this first, crucial step), definitely stop and take a full practice test to gauge your current scoring level. Check out our guide to all the free SAT practice tests available online and then sit down to take a test all at once.
The absolute best way to assess your current level is to simply take the SAT practice test as if it were real , keeping strict timing and working straight through with only the allowed breaks (we know—probably not your favorite way to spend a Saturday). Once you've got a good idea of your current level and percentile ranking, you can set milestones and goals for your ultimate SAT Math score.
If you're currently scoring in the 200-400 or the 400-600 range on SAT Math, your best bet is first to check out our guide to improving your math score to be consistently at or over a 600 before you start in trying to tackle the most difficult math problems on the test.
If, however, you're already scoring above a 600 on the Math section and want to test your mettle for the real SAT, then definitely proceed to the rest of this guide. If you're aiming for perfect (or close to) , then you'll need to know what the most difficult SAT math questions look like and how to solve them. And luckily, that's exactly what we'll do.
WARNING: Since there are a limited number of official SAT practice tests , you may want to wait to read this article until you've attempted all or most of the first four official practice tests (since most of the questions below were taken from those tests). If you're worried about spoiling those tests, stop reading this guide now; come back and read it when you've completed them.

Now let's get to our list of questions (whoo)!
Image: Niytx /DeviantArt
The 15 Hardest SAT Math Questions
Now that you're sure you should be attempting these questions, let's dive right in! We've curated 15 of the most difficult SAT Math questions for you to try below, along with walkthroughs of how to get the answer (if you're stumped).
No Calculator SAT Math Questions
$$C=5/9(F-32)$$
The equation above shows how temperature $F$, measured in degrees Fahrenheit, relates to a temperature $C$, measured in degrees Celsius. Based on the equation, which of the following must be true?
- A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of $5/9$ degree Celsius.
- A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
- A temperature increase of $5/9$ degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only B) II only C) III only D) I and II only
ANSWER EXPLANATION: Think of the equation as an equation for a line
where in this case
$$C= {5}/{9} (F−32)$$
$$C={5}/{9}F −{5}/{9}(32)$$
You can see the slope of the graph is ${5}/{9}$, which means that for an increase of 1 degree Fahrenheit, the increase is ${5}/{9}$ of 1 degree Celsius.
$$C= {5}/{9} (F)$$
$$C= {5}/{9} (1)= {5}/{9}$$
Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of ${9}/{5}$ degrees Fahrenheit.
$$1= {5}/{9} (F)$$
$$(F)={9}/{5}$$
Since ${9}/{5}$ = 1.8, statement II is true.
The only answer that has both statement I and statement II as true is D , but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of ${5}/{9}$ degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:
$$C= {5}/{9} ({5}/{9})$$
$$C= {25} /{81} (\which \is ≠ 1)$$
An increase of $5/9$ degree Fahrenheit leads to an increase of ${25}/{81}$, not 1 degree, Celsius, and so Statement III is not true.
The final answer is D.
The equation ${24x^2 + 25x -47}/{ax-2} = -8x-3-{53/{ax-2}}$ is true for all values of $x≠2/a$, where $a$ is a constant.
What is the value of $a$?
A) -16 B) -3 C) 3 D) 16
ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by $ax-2$ (so you can get rid of the fraction). When you multiply each side by $ax-2$, you should have:
$$24x^2 + 25x - 47 = (-8x-3)(ax-2) - 53$$
You should then multiply $(-8x-3)$ and $(ax-2)$ using FOIL.
$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x + 6 - 53$$
Then, reduce on the right side of the equation
$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x - 47$$
Since the coefficients of the $x^2$-term have to be equal on both sides of the equation, $−8a = 24$, or $a = −3$.
The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.
The final answer is B.
If $3x-y = 12$, what is the value of ${8^x}/{2^y}$?
A) $2^{12}$ B) $4^4$ C) $8^2$ D) The value cannot be determined from the information given.
ANSWER EXPLANATION: One approach is to express
$${8^x}/{2^y}$$
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting $2^3$ for 8 in the numerator of ${8^x}/{2^y}$ gives
$${(2^3)^x}/{2^y}$$
which can be rewritten
$${2^3x}/{2^y}$$
Since the numerator and denominator of have a common base, this expression can be rewritten as $2^(3x−y)$. In the question, it states that $3x − y = 12$, so one can substitute 12 for the exponent, $3x − y$, which means that
$${8^x}/{2^y}= 2^12$$
The final answer is A.
Points A and B lie on a circle with radius 1, and arc ${AB}↖⌢$ has a length of $π/3$. What fraction of the circumference of the circle is the length of arc ${AB}↖⌢$?
ANSWER EXPLANATION: To figure out the answer to this question, you'll first need to know the formula for finding the circumference of a circle.
The circumference, $C$, of a circle is $C = 2πr$, where $r$ is the radius of the circle. For the given circle with a radius of 1, the circumference is $C = 2(π)(1)$, or $C = 2π$.
To find what fraction of the circumference the length of ${AB}↖⌢$ is, divide the length of the arc by the circumference, which gives $π/3 ÷ 2π$. This division can be represented by $π/3 * {1/2}π = 1/6$.
The fraction $1/6$ can also be rewritten as $0.166$ or $0.167$.
The final answer is $1/6$, $0.166$, or $0.167$.
$${8-i}/{3-2i}$$
If the expression above is rewritten in the form $a+bi$, where $a$ and $b$ are real numbers, what is the value of $a$? (Note: $i=√{-1}$)
ANSWER EXPLANATION: To rewrite ${8-i}/{3-2i}$ in the standard form $a + bi$, you need to multiply the numerator and denominator of ${8-i}/{3-2i}$ by the conjugate, $3 + 2i$. This equals
$$({8-i}/{3-2i})({3+2i}/{3+2i})={24+16i-3+(-i)(2i)}/{(3^2)-(2i)^2}$$
Since $i^2=-1$, this last fraction can be reduced simplified to
$$ {24+16i-3i+2}/{9-(-4)}={26+13i}/{13}$$
which simplifies further to $2 + i$. Therefore, when ${8-i}/{3-2i}$ is rewritten in the standard form a + bi, the value of a is 2.
In triangle $ABC$, the measure of $∠B$ is 90°, $BC=16$, and $AC$=20. Triangle $DEF$ is similar to triangle $ABC$, where vertices $D$, $E$, and $F$ correspond to vertices $A$, $B$, and $C$, respectively, and each side of triangle $DEF$ is $1/3$ the length of the corresponding side of triangle $ABC$. What is the value of $sinF$?
ANSWER EXPLANATION: Triangle ABC is a right triangle with its right angle at B. Therefore, $\ov {AC}$ is the hypotenuse of right triangle ABC, and $\ov {AB}$ and $\ov {BC}$ are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB =√{20^2-16^2}=√{400-256}=√{144}=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of $\angle ∠ {F}$ equals the measure of $\angle ∠ {C}$. Therefore, $sin F = sin C$. From the side lengths of triangle ABC,
$$sinF ={\opposite \side}/{\hypotenuse}={AB}/{AC}={12}/{20}={3}/{5}$$
Therefore, $sinF ={3}/{5}$.
The final answer is ${3}/{5}$ or 0.6.
Calculator-Allowed SAT Math Questions
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)
A) 0.410 B) 0.357 C) 0.333 D) 0.250
ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables ($x$ and $y$) and the information you're given. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be $5x$ and the number of right-handed male students will be $9y$. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:
$$x + y = 18$$
$$5x + 9y = 122$$
When you solve this system of equations, you get $x = 10$ and $y = 8$. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is ${50}/{122}$, which to the nearest thousandth is 0.410.
Questions 8 & 9
Use the following information for both question 7 and question 8.
If shoppers enter a store at an average rate of $r$ shoppers per minute and each stays in the store for average time of $T$ minutes, the average number of shoppers in the store, $N$, at any one time is given by the formula $N=rT$. This relationship is known as Little's law.
The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little's law to estimate that there are 45 shoppers in the store at any time.
Little's law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
ANSWER EXPLANATION: Since the question states that Little's law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, $N$, in the checkout line at any time is $N = rT$, where $r$ is the number of shoppers entering the checkout line per minute and $T$ is the average number of minutes each shopper spends in the checkout line.
Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with $T = 5$). Since there are 60 minutes in one hour, the rate is ${84 \shoppers \per \hour}/{60 \minutes} = 1.4$ shoppers per minute. Using the given formula with $r = 1.4$ and $T = 5$ yields
$$N = rt = (1.4)(5) = 7$$
Therefore, the average number of shoppers, $N$, in the checkout line at any time during business hours is 7.
The final answer is 7.
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little's law, there are, on average, $N = rT = (1.5)(12) = 18$ shoppers in the new store at any time. This is
$${45-18}/{45} * 100 = 60$$
percent less than the average number of shoppers in the original store at any time.
The final answer is 60.
Question 10
In the $xy$-plane, the point $(p,r)$ lies on the line with equation $y=x+b$, where $b$ is a constant. The point with coordinates $(2p, 5r)$ lies on the line with equation $y=2x+b$. If $p≠0$, what is the value of $r/p$?
ANSWER EXPLANATION: Since the point $(p,r)$ lies on the line with equation $y=x+b$, the point must satisfy the equation. Substituting $p$ for $x$ and $r$ for $y$ in the equation $y=x+b$ gives $r=p+b$, or $\bi b$ = $\bi r-\bi p$.
Similarly, since the point $(2p,5r)$ lies on the line with the equation $y=2x+b$, the point must satisfy the equation. Substituting $2p$ for $x$ and $5r$ for $y$ in the equation $y=2x+b$ gives:
$5r=2(2p)+b$
$\bi b$ = $\bo 5 \bi r-\bo 4\bi p$.
Next, we can set the two equations equal to $b$ equal to each other and simplify:
$b=r-p=5r-4p$
Finally, to find $r/p$, we need to divide both sides of the equation by $p$ and by $4$:
The correct answer is B , $3/4$.
If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point $(2p, 5r)$. If you picked Choice C, you may have confused $r$ and $p$.
Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!

Question 11
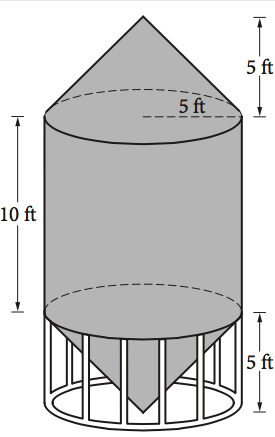
A) 261.8 B) 785.4 C) 916.3 D) 1047.2
ANSWER EXPLANATION: The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:
Volume of a Cone
$$V={1}/{3}πr^2h$$
Volume of a Cylinder
$$V=πr^2h$$
can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by
$$V_{silo}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250)π$$
which is approximately equal to 1,047.2 cubic feet.
Question 12
If $x$ is the average (arithmetic mean) of $m$ and $9$, $y$ is the average of $2m$ and $15$, and $z$ is the average of $3m$ and $18$, what is the average of $x$, $y$, and $z$ in terms of $m$?
A) $m+6$ B) $m+7$ C) $2m+14$ D) $3m + 21$
ANSWER EXPLANATION: Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations $x={m+9}/{2}$, $y={2m+15}/{2}$, $z={3m+18}/{2}$are true. The average of $x$, $y$, and $z$ is given by ${x + y + z}/{3}$. Substituting the expressions in m for each variable ($x$, $y$, $z$) gives
$$[{m+9}/{2}+{2m+15}/{2}+{3m+18}/{2}]/3$$
This fraction can be simplified to $m + 7$.
Question 13
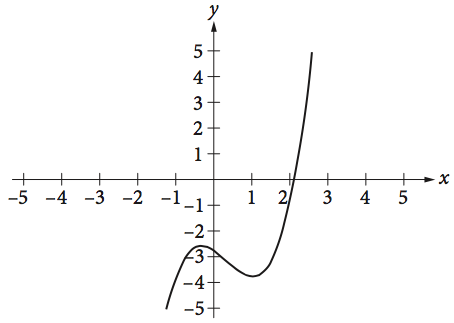
The function $f(x)=x^3-x^2-x-{11/4}$ is graphed in the $xy$-plane above. If $k$ is a constant such that the equation $f(x)=k$ has three real solutions, which of the following could be the value of $k$?
ANSWER EXPLANATION: The equation $f(x) = k$ gives the solutions to the system of equations
$$y = f(x) = x^3-x^2-x-{11}/{4}$$
A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the $xy$-plane.
The graph of $y = k$ is a horizontal line that contains the point $(0, k)$ and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation $y = −3$, or $f(x) = −3$. Therefore, $k$ is $-3$.
Question 14
$$q={1/2}nv^2$$
The dynamic pressure $q$ generated by a fluid moving with velocity $v$ can be found using the formula above, where $n$ is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity $v$ and the same fluid moving with velocity 1.5$v$. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
ANSWER EXPLANATION: To solve this problem, you need to set up to equations with variables. Let $q_1$ be the dynamic pressure of the slower fluid moving with velocity $v_1$, and let $q_2$ be the dynamic pressure of the faster fluid moving with velocity $v_2$. Then
$$v_2 =1.5v_1$$
Given the equation $q = {1}/{2}nv^2$, substituting the dynamic pressure and velocity of the faster fluid gives $q_2 = {1}/{2}n(v_2)^2$. Since $v_2 =1.5v_1$, the expression $1.5v_1$ can be substituted for $v_2$ in this equation, giving $q_2 = {1}/{2}n(1.5v_1)^2$. By squaring $1.5$, you can rewrite the previous equation as
$$q_2 = (2.25)({1}/{2})n(v_1)^2 = (2.25)q_1$$
Therefore, the ratio of the dynamic pressure of the faster fluid is
$${q2}/{q1} = {2.25 q_1}/{q_1}= 2.25$$
The final answer is 2.25 or 9/4.
Question 15
For a polynomial $p(x)$, the value of $p(3)$ is $-2$. Which of the following must be true about $p(x)$?
A) $x-5$ is a factor of $p(x)$. B) $x-2$ is a factor of $p(x)$. C) $x+2$ is a factor of $p(x)$. D) The remainder when $p(x)$ is divided by $x-3$ is $-2$.
ANSWER EXPLANATION: If the polynomial $p(x)$ is divided by a polynomial of the form $x+k$ (which accounts for all of the possible answer choices in this question), the result can be written as
$${p(x)}/{x+k}=q(x)+{r}/{x+k}$$
where $q(x)$ is a polynomial and $r$ is the remainder. Since $x + k$ is a degree-1 polynomial (meaning it only includes $x^1$ and no higher exponents), the remainder is a real number.
Therefore, $p(x)$ can be rewritten as $p(x) = (x + k)q(x) + r$, where $r$ is a real number.
The question states that $p(3) = -2$, so it must be true that
$$-2 = p(3) = (3 + k)q(3) + r$$
Now we can plug in all the possible answers. If the answer is A, B, or C, $r$ will be $0$, while if the answer is D, $r$ will be $-2$.
A. $-2 = p(3) = (3 + (-5))q(3) + 0$ $-2=(3-5)q(3)$ $-2=(-2)q(3)$
This could be true, but only if $q(3)=1$
B. $-2 = p(3) = (3 + (-2))q(3) + 0$ $-2 = (3-2)q(3)$ $-2 = (-1)q(3)$
This could be true, but only if $q(3)=2$
C. $-2 = p(3) = (3 + 2)q(3) + 0$ $-2 = (5)q(3)$
This could be true, but only if $q(3)={-2}/{5}$
D. $-2 = p(3) = (3 + (-3))q(3) + (-2)$ $-2 = (3 - 3)q(3) + (-2)$ $-2 = (0)q(3) + (-2)$
This will always be true no matter what $q(3)$ is.
Of the answer choices, the only one that must be true about $p(x)$ is D, that the remainder when $p(x)$ is divided by $x-3$ is -2.

You deserve all the naps after running through those questions.
What Do the Hardest SAT Math Questions Have in Common?
It's important to understand what makes these hard questions "hard." By doing so, you'll be able to both understand and solve similar questions when you see them on test day, as well as have a better strategy for identifying and correcting your previous SAT math errors.
In this section, we'll look at what these questions have in common and give examples of each type. Some of the reasons why the hardest math questions are the hardest math questions is because they:
#1: Test Several Mathematical Concepts at Once

Here, we must deal with imaginary numbers and fractions all at once.
Secret to success: Think of what applicable math you could use to solve the problem, do one step at a time, and try each technique until you find one that works!
#2: Involve a Lot of Steps
Remember: the more steps you need to take, the easier to mess up somewhere along the line!
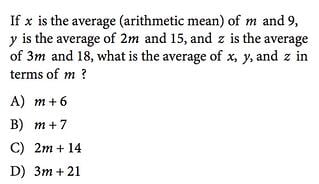
We must solve this problem in steps (doing several averages) to unlock the rest of the answers in a domino effect. This can get confusing, especially if you're stressed or running out of time.
Secret to success: Take it slow, take it step by step, and double-check your work so you don't make mistakes!
#3: Test Concepts That You Have Limited Familiarity With
For example, many students are less familiar with functions than they are with fractions and percentages, so most function questions are considered "high difficulty" problems.
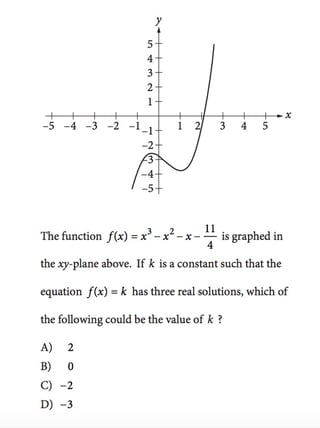
If you don't know your way around functions , this would be a tricky problem.
Secret to success: Review math concepts that you don't have as much familiarity with such as functions . We suggest using our great free SAT Math review guides .
#4: Are Worded in Unusual or Convoluted Ways
It can be difficult to figure out exactly what some questions are asking , much less figure out how to solve them. This is especially true when the question is located at the end of the section, and you are running out of time.

Because this question provides so much information without a diagram, it can be difficult to puzzle through in the limited time allowed.
Secret to success: Take your time, analyze what is being asked of you, and draw a diagram if it's helpful to you.
#5: Use Many Different Variables

With so many different variables in play, it is quite easy to get confused.
Secret to success: Take your time, analyze what is being asked of you, and consider if plugging in numbers is a good strategy to solve the problem (it wouldn't be for the question above, but would be for many other SAT variable questions).
The Take-Aways
The SAT is a marathon and the better prepared you are for it, the better you'll feel on test day. Knowing how to handle the hardest questions the test can throw at you will make taking the real SAT seem a lot less daunting.
If you felt that these questions were easy, make sure not underestimate the effect of adrenaline and fatigue on your ability to solve problems. As you continue to study, always adhere to the proper timing guidelines and try to take full tests whenever possible. This is the best way to recreate the actual testing environment so that you can prepare for the real deal.
If you felt these questions were challenging, be sure to strengthen your math knowledge by checking out our individual math topic guides for the SAT . There, you'll see more detailed explanations of the topics in question as well as more detailed answer breakdowns.
What's Next?
Felt that these questions were harder than you were expecting? Take a look at all the topics covered in the SAT math section and then note which sections were particular difficulty for you. Next, take a gander at our individual math guides to help you shore up any of those weak areas.
Running out of time on the SAT math section? Our guide will help you beat the clock and maximize your score .
Aiming for a perfect score? Check out our guide on how to get a perfect 800 on the SAT math section , written by a perfect-scorer.
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
Ask a Question Below
Have any questions about this article or other topics? Ask below and we'll reply!
Improve With Our Famous Guides
- For All Students
The 5 Strategies You Must Be Using to Improve 160+ SAT Points
How to Get a Perfect 1600, by a Perfect Scorer
Series: How to Get 800 on Each SAT Section:
Score 800 on SAT Math
Score 800 on SAT Reading
Score 800 on SAT Writing
Series: How to Get to 600 on Each SAT Section:
Score 600 on SAT Math
Score 600 on SAT Reading
Score 600 on SAT Writing
Free Complete Official SAT Practice Tests
What SAT Target Score Should You Be Aiming For?
15 Strategies to Improve Your SAT Essay
The 5 Strategies You Must Be Using to Improve 4+ ACT Points
How to Get a Perfect 36 ACT, by a Perfect Scorer
Series: How to Get 36 on Each ACT Section:
36 on ACT English
36 on ACT Math
36 on ACT Reading
36 on ACT Science
Series: How to Get to 24 on Each ACT Section:
24 on ACT English
24 on ACT Math
24 on ACT Reading
24 on ACT Science
What ACT target score should you be aiming for?
ACT Vocabulary You Must Know
ACT Writing: 15 Tips to Raise Your Essay Score
How to Get Into Harvard and the Ivy League
How to Get a Perfect 4.0 GPA
How to Write an Amazing College Essay
What Exactly Are Colleges Looking For?
Is the ACT easier than the SAT? A Comprehensive Guide
Should you retake your SAT or ACT?
When should you take the SAT or ACT?
Stay Informed
Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?
Check out our top-rated graduate blogs here:
GRE Online Prep Blog
GMAT Online Prep Blog
TOEFL Online Prep Blog
Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”
7 of the hardest problems in mathematics that have been solved
Mathematics is full of problems, some of which have been solved and others that haven’t. here, we focus on 7 of the hardest problems that have been solved..
Tejasri Gururaj

What are the hardest problems in math that have already been solved?
intararit
- Some problems in mathematics have taken centuries to be solved, due to their complexity.
- Although there are some complex math problems that still elude solutions, others have now been solved.
- Here are 7 of the hardest math problems ever solved.
Some mathematical problems are challenging even for the most accomplished mathematicians.
From the Poincaré conjecture to Fermat’s last theorem , here we take a look at some of the most challenging math problems ever solved.
1. Poincaré conjecture
Salix alba
The Poincaré conjecture is a famous problem in topology, initially proposed by French mathematician and theoretical physicist Henri Poincaré in 1904. It asserts that every simply connected, closed 3-manifold is topologically homeomorphic (a function that is a one-to-one mapping between sets such that both the function and its inverse are continuous) to a 3-dimensional sphere.
In simpler terms, the conjecture asserts that a particular group of three-dimensional shapes can be continuously transformed into a sphere without any gaps or holes.
The problem was solved by the reclusive Russian mathematician Grigori Perelman in 2003. He built upon the work of American mathematician Richard S. Hamilton’s program involving the Ricci flow.
What makes this achievement even more remarkable is that Perelman declined the prestigious Fields Medal and the Clay Millennium Prize reward that came with it. He chose to stay away from the spotlight and mathematical acclaim, but his proof withstood rigorous scrutiny from the mathematical community.
The resolution of the Poincaré conjecture confirmed the fundamental role of topology in understanding the shape and structure of spaces, impacting fields like geometry and manifold theory.
2. The prime number theorem
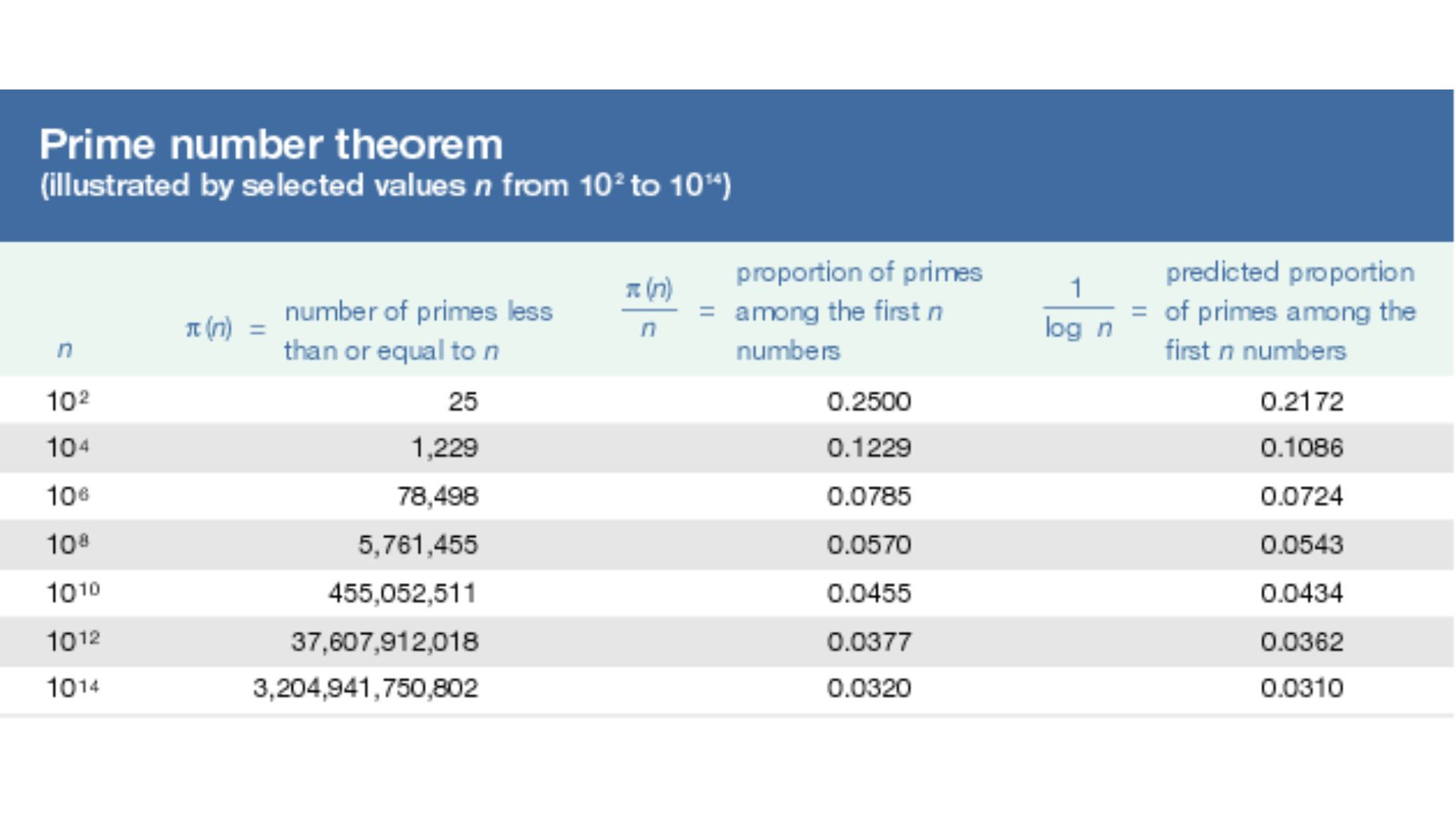
Britannica
The prime number theorem long stood as one of the fundamental questions in number theory. At its core, this problem is concerned with unraveling the distribution of prime numbers.
The question at hand revolves around the distribution pattern of these primes within the realm of natural numbers. Are there any discernible patterns governing the distribution of prime numbers, or do they appear to be entirely random? The theorem states that for large values of x, π(x) is approximately equal to x/ln(x).
The breakthrough in solving this theorem came in the late 19th century, thanks to the independent work of two mathematicians, Jacques Hadamard and Charles de la Vallée-Poussin. In 1896, both mathematicians presented their proofs of the theorem.
Their work demonstrated that prime numbers exhibit a remarkable, asymptotic distribution pattern . Their solution produced the insight that, as one considers larger and larger numbers, the density of prime numbers diminishes.
The theorem precisely characterized the rate of this decrease, showing that prime numbers become less frequent as we move along the number line. It’s as if they gradually thin out, although they never entirely vanish.
The prime number theorem was a turning point in the study of number theory . It provided profound insights into the distribution of prime numbers and put to rest the notion that there might exist a formula predicting each prime number.
Instead, it proposed a probabilistic approach to understanding the distribution of prime numbers. The theorem’s significance extends into various mathematical fields, especially in cryptography, where the properties of prime numbers play a pivotal role in securing communications.
3. Fermat’s last theorem
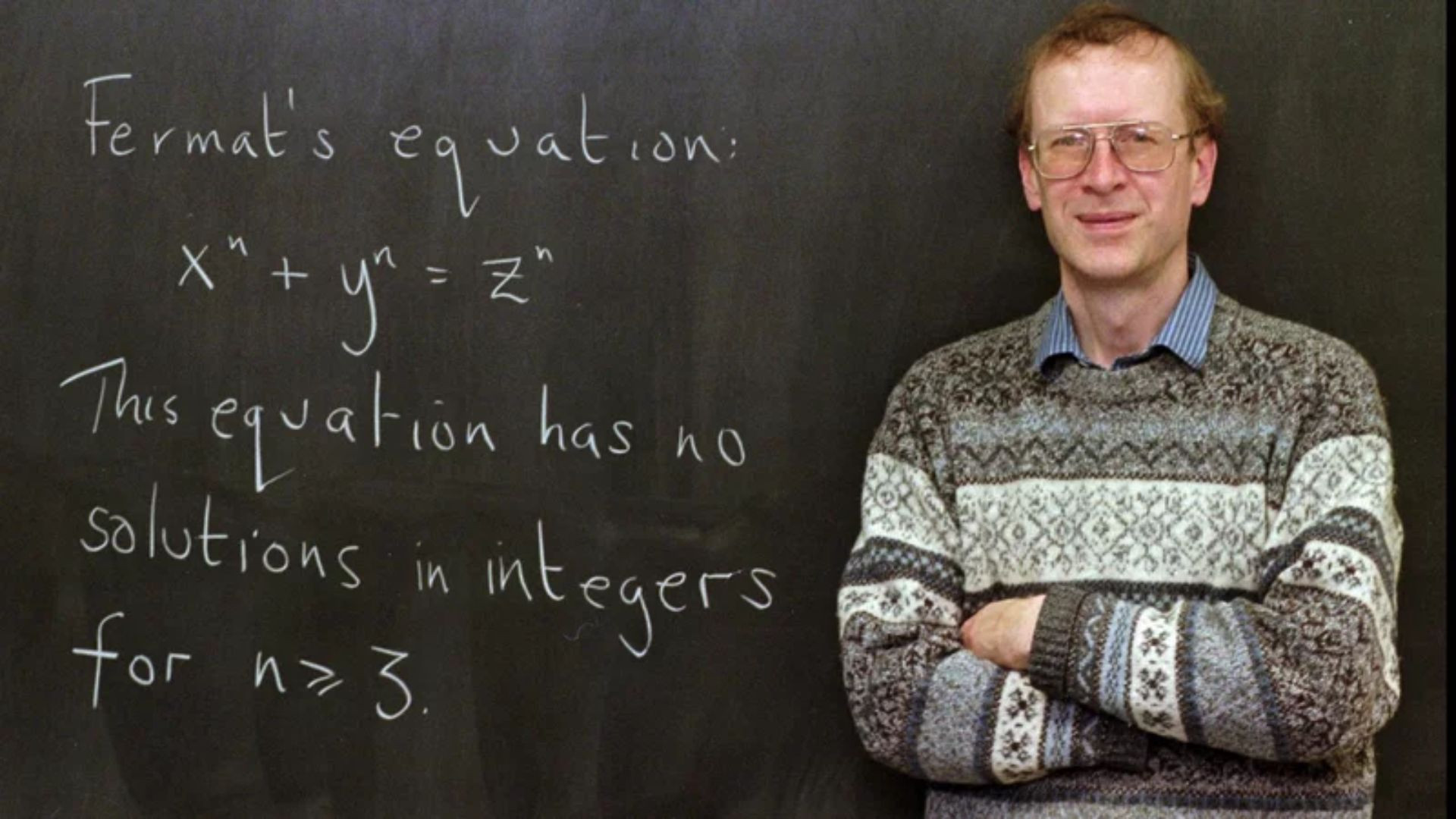
Charles Rex Arbogast/AP via NPR
Fermat’s last theorem is one of the problems on this list many people are most likely to have heard of. The conjecture, proposed by French mathematician Pierre de Fermat in the 17th century, states that it’s impossible to find three positive integers, a, b, and c, that can satisfy the equation a n + b n = c n for any integer value of n greater than 2.
For instance, there are no whole number values of a, b, and c that can make 3 3 + 4 3 = 5 3 true.
This problem remained unsolved for centuries and became one of the most challenging problems in mathematics. It was made more enticing because Fermat apparently wrote a note in his copy of the Arithmetica by Diophantus of Alexandria, saying, “I have discovered a truly remarkable proof [of this theorem], but this margin is too small to contain it.”
Numerous mathematicians attempted to prove or disprove Fermat’s conjecture, but it wasn’t until 1994 that the breakthrough came.
The solution was achieved by British mathematician Andrew Wiles, who built upon the work of many other mathematicians who had contributed to the field of number theory. Wiles’ proof was extraordinarily complex and required intricate mathematical concepts and theorems, particularly those related to elliptic curves and modular forms.
Wiles’ remarkable proof of Fermat’s last theorem confirmed that the conjecture was indeed true. Having taken more than three centuries to be solved, it had a profound impact on the world of mathematics, demonstrating the power of advanced mathematical techniques in solving long-standing problems.

Z. Ziegler, M. Ondrachek
Before Wiles presented its proof, it was in the Guinness Book of World Records as the “most difficult mathematical problem,” in part because the theorem has seen the greatest number of unsuccessful proofs.
4. Classification of finite simple groups
Jakob.scholbach/Pbroks13
This one is a bit different from the others on the list. The classification of finite simple groups , also known as the “enormous theorem,” set out to classify all finite simple groups, which are the fundamental building blocks of group theory.
Finite simple groups are those groups that cannot be divided into smaller non-trivial normal subgroups. The goal was to understand and categorize all the different types of finite simple groups that exist.
The solution to this problem is not straightforward. The proof is a collaborative effort by hundreds of mathematicians covering tens of thousands of pages in hundreds of journal articles published between 1955 and 2004.
It is one of the most extensive mathematical proofs ever produced and marks a monumental achievement in group theory.
The proof outlines the structure of finite simple groups and demonstrates that they can be classified into several specific categories. This achievement paved the way for a deeper understanding of group theory and its applications in various mathematical fields.
5. The four color theorem

Inductiveload
The four color theorem tackles an intriguing question related to topology and stands as one of the first significant theorems proved by a computer.
It states that any map in a plane can be colored using four colors so that no two adjacent regions share the same color while using the fewest possible colors. Adjacent, in this context, means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet.
The theorem doesn’t focus on the artistic aspect of map coloring but rather on the fundamental mathematical principles that underlie it.
The solution to this theorem arrived in 1976, thanks to the combined efforts of mathematicians Kenneth Appel and Wolfgang Haken. However, the proof was not widely accepted due to the infeasibility of checking it by hand.
Appel and Haken’s achievement confirmed that any map, regardless of its complexity, can be colored with just four colors such that no two neighboring regions share the same color. While the idea seems simple, proving it rigorously was complex and time-consuming.
To address any lingering skepticism about the Appel–Haken proof, a more accessible proof using similar principles and still utilizing computer assistance was presented in 1997 by Robertson, Sanders, Seymour, and Thomas.
Additionally, in 2005, Georges Gonthier achieved a proof of the theorem using general-purpose theorem-proving software, reinforcing the credibility of the four color theorem.
This theorem is not actually used in map-making but has far-reaching implications in various fields, from graph theory to computer science, where it finds applications in scheduling, circuit design, and optimization problems.
6. Gödel’s incompleteness theorems

Andrew Das Arulsamy/Research Gate
Gödel’s incompleteness theorems , formulated by Austrian mathematician Kurt Gödel in the 20th century, delve into the mysteries of formal systems and their inherent limitations.
In mathematics, a formal system has a structured and well-defined framework or language that comprises a set of symbols, rules, and axioms employed for representing and manipulating mathematical or logical expressions.
Gödel’s first incompleteness theorem explores a fundamental question: In any consistent formal system, are there true mathematical statements that are undecidable within that system? In other words, do statements exist that cannot be proven as either true or false using the rules and axioms of that system?
The second incompleteness theorem takes this further: Can any consistent formal system prove its own consistency?
Gödel not only posed these questions but also provided the answers. He established, through rigorous mathematical proofs , that there exist true statements within formal systems that cannot be proven within those very systems.
In essence, the first theorem asserts that there are statements that cannot be proven as either true or false using the rules and axioms of a system. The second theorem demonstrates that no consistent formal system can prove its own consistency.
Gödel’s theorems introduced a profound paradox within the realm of mathematical logic: There are truths that exist beyond the reach of formal proofs, and there are limits to what can be achieved through mathematical systems alone.
Gödel’s contributions to mathematical logic influenced the philosophy of mathematics and our understanding of the inherent limits of formal systems.
7. The goat problem
Mnchnstnr
The goat problem is a much more recently solved mathematical problem. It involves calculating the grazing area for a tethered goat. Despite its initial simplicity, mathematicians have pondered this problem for over a century.
In its basic form, a goat on a rope can graze in a semicircle with an area of A = 1/2πr 2 , where r is the rope’s length. However, the problem becomes more complex when you change the shape of the area the goat can access.
For instance, when tethered to a square barn, the goat can access more than just a semicircle. The goat can also go around the corners of the barn, creating additional quarter circles.
Mathematician Ingo Ullisch recently unraveled the goat grazing problem, introducing complex analysis into the equation. However, the solution is far from elementary.
It involves intricate calculations, relying on the ratio of contour integral expressions and involves numerous trigonometric terms . Although the solution may not offer a practical guide for goat owners, it represents a significant achievement in the world of mathematics.
RECOMMENDED ARTICLES
What makes the goat problem truly fascinating is its capacity to act as a mathematical Rosetta stone , transcending boundaries between various fields and serving as a versatile challenge for experts from diverse disciplines.
From age-old conundrums that took centuries to crack to enigmas that continue to elude solutions, mathematical mysteries remind us that the pursuit of knowledge is an ever-evolving journey.
So, the next time you find yourself pondering a difficult math problem, remember that you are in good company, following in the footsteps of the greatest mathematical explorers!
The Blueprint Daily
Stay up-to-date on engineering, tech, space, and science news with The Blueprint.
By clicking sign up, you confirm that you accept this site's Terms of Use and Privacy Policy
ABOUT THE EDITOR
Tejasri Gururaj Tejasri is a versatile Science Writer & Communicator, leveraging her expertise from an MS in Physics to make science accessible to all. In her spare time, she enjoys spending quality time with her cats, indulging in TV shows, and rejuvenating through naps.
POPULAR ARTICLES
Australia: humpback whale stuck in 1760 pounds of rope set free by rescuers, ‘nightmare’ peleliu: us to rebuild wwii runway in pacific to counter china, detroit rejects face recognition after grainy video got wrong man arrested, caribbean alert: hurricane beryl, 1st ever category 4 storm recorded in june, related articles.

Powerful US SeaGuardian drone to get NEW weapons for long-range attacks

US builds world’s most accurate atomic clock ever to boost space science

Feel the beat: MIT’s brain-powered bionic leg lets amputees dance again

150 mph roof-ripping winds hit Caribbean: Hurricane Beryl declared Category 5
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions
In order to continue enjoying our site, we ask you enter in the text you see in the image below so we can confirm your identity as a human. Thank you very much for your cooperation.
© 2003 - 2024 All other trademarks and copyrights are the property of their respective owners. All rights reserved.

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
Graph your math problems
Practice, practice, practice

Get math help in your language
What are your chances of acceptance?
Calculate for all schools, your chance of acceptance.
Your chancing factors
Extracurriculars.
15 Hardest SAT Math Questions

Is your SAT score enough to get you into your dream school?
Our free chancing engine takes into consideration your SAT score, in addition to other profile factors, such as GPA and extracurriculars. Create a free account to discover your chances at hundreds of different schools.
Students often want to prepare for the toughest questions they’ll see on the SAT so they can feel confident on test day. We’ve rounded up some of the hardest questions and we’re going to show you how to solve them.
These questions come from the free SAT practice tests because we wanted to make sure that we show you questions representative of those you’ll see on the real test. We’ve chosen a variety of question types, but this isn’t an exhaustive representation of all the math topics or types of questions on the SAT.
“Hard” is a little subjective; we think these questions are difficult based on working with many students, but you may find some of them easy. In general, you can expect to find harder questions in the second half of each SAT math section, as the questions generally increase in difficulty.
For each question below, we’ve identified the key concepts being tested and whether a calculator is allowed. We suggest you try solving these on your own before looking at the answer and our suggested solution. Remember: we’ve given you just one way to solve the problem. Most problems can be solved in a variety of ways!
Want to know your chances at the schools you’re applying for based on your SAT? Calculate your admissions chances right now and understand your odds before applying.
Math Topics on the SAT
Before we go into the questions, we want you to understand the terms that the College Board uses to categorize the topics. We’ve also included how many questions fall under each category, so if you’re self-studying, you can prioritize the types of questions that appear more often.
Heart of Algebra: 33% of test, 19 questions
Linear equations and inequalities and their graphs and systems.
Problem Solving and Data Analysis: 29% of test, 17 questions
Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics.
Passport to Advanced Math: 28% of test, 16 questions
Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs.
Additional Topics in Math: 10% of test, 6 questions total
This is the only category without a corresponding subscore, but it has a wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers.
Grid-in Questions
A grid-in question can test any of the topics above and is found at the end of each portion of the math test, both no-calculator and calculator. Most students find grid-in questions harder than the multiple-choice because some test tactics—like substituting answer choices into the problem—don’t work. You’ll need to find the correct solution without any help from answer choices. If you develop your math skills, however, then these questions won’t be that much more difficult for you.
Now grab a calculator, a pencil and a piece of paper, and let’s review the hardest SAT math questions!
Question 1: Calculator permitted, grid-in response

Answer: 750
Category: Heart of Algebra—systems of linear inequalities
Here’s how to solve it:
- In this question, we’re told coordinates \((a,b)\) lies in the solution set of these equations, and we want to know a maximum possible value. With inequalities, the graph will be shaded to include the set of values that satisfy the inequality, so \((a,b)\) lies in this overlapping region. Because it’s a grid-in response (only real numbers can be the answer to the grid-in questions—there is no option to bubble in infinity) we know that the value of \(b\) must be limited by the point of intersection. Since the inequalities are both less than or equal to , we know that the lines (and the point of intersection) are included in the solution set. If there were only less/greater than symbols, the lines would not be included in the solution set.
- This means we can find the point of intersection to find a maximum value of \(b\) and solve it just like a system of equations using the substitution method. This gives us the inequality \(5x\:\leq\:-15x+3000\). In this case, \(x\) is equivalent to \(a\), and the y-value is equivalent to \(b\).
- Move the variables to the same side by adding \(15x\) to both sides. \(20x\leq3000\).
- Divide both sides by \(20\) to find out what \(x\) is. \(x\:\leq\:150\). Many students might stop here, but remember we want coordinate \(b\) in \((a,b)\), or the y-value.
- We can plug \(x\) into either equation to find the value of \(b\). We picked the second one since it’s simpler: \(5\:\cdot\:150=750\). That’s our answer!
Question 2: Calculator permitted, multiple choice

Category: Problem-solving and data analysis—analyzing graphical data, probability
- With problems like these, it’s important that you pay attention to the wording of the question so that you know exactly what you’re being asked. Once you understand that, the math needed is not necessarily complex. The question asks: “If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y?” It can help to rewrite the question in your own words. Here’s a possible rewrite: “Out of all the people who remembered at least 1 dream, what fraction were in Group Y?”
- We need to know the total number of people who remembered at least one dream—to do this, we add \(28+57+11+68=164\).
- Next, we need to know how many of the people who remembered at least one dream were in Group Y. Add \(11+68=79\).
- We can now see that the chance of selecting a person from Group Y out of all the people who remembered at least \(1\) dream is \(79\) out of \(164\), or \(\frac{79}{164}\), which is C .
Question 3: Calculator not permitted, multiple choice

Category: Passport to Advanced Math—exponents
- To solve this problem, you’ll need to know exponent rules. Here are some of the ones you should know for the SAT and many other standardized tests:
- \(b^mb^n=b^{m+n}\)
- \(\frac{b^m}{b^n}=b^{m-n}\)
- \((b^m)^n=b^{m\:\cdot\:n}\)
- \(b^mc^m=(bc)^m\)
- \(\frac{b^m}{c^m}=(\frac{b}{c})^m\)
- Since we know that it’s likely that we’ll need exponent rules, we can see if we might be able to rewrite the expression \(\frac{8^x}{2^y}\) to fit one of the existing exponent rules. In fact, we can rewrite \(8=2^3\), so we have \(8^x=(2^3)^x=2^{3x}\).
- Substituting \(2^{3x}\) for \(8^x\), we can see that the expression can be rewritten using the second rule above: \(\frac{2^{3x}}{2^y}=2^{3x-y}\).
- Since we’ve been given the information that \(3x-y=12\) we can substitute \(12\) into the expression and get our answer: \(2^{3x-y}=2^{12}\).
Question 4: Calculator not-permitted, multiple choice
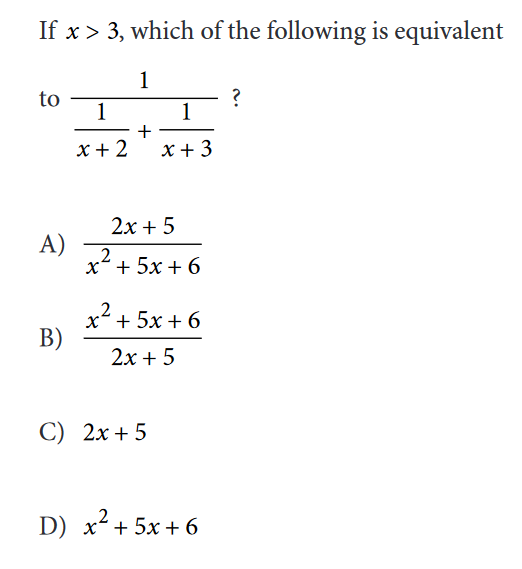
Category: Passport to Advanced Math—rational equations
- Students are sometimes intimidated by large fractions like this, but if you get comfortable manipulating fractions and variables across operations then you can handle any question like this. To start, we’ll want to add those two fractions in the denominator, and to do that, we need to find a common denominator. The common denominator in this case is \((x+2)(x+3)\).
- To convert each of those fractions in the denominator to ones we can easily add, we need to find equivalent fractions. You can multiply any fraction by \(1\) without changing its value, and so we can use fractions like \(\frac{2}{2}\), etc. We’re going to multiply the first fraction by \(\frac{x+3}{x+3}\) and the second fraction by \(\frac{x+2}{x+2}\). This gives us the following in the denominator: \(\frac{x+3}{(x+2)(x+3)}+\frac{x+2}{(x+2)(x+3)}\)
- Now we can add the numerators: \((x+3)+(x+2)\). Combine like terms in the numerator to get \(2x+5\).
- We now have a single fraction in the denominator, and we can proceed with fraction division. When dividing by a fraction, we multiply by its reciprocal , and we can find the reciprocal by switching the positions of the numerator and the denominator. We get:
\(\frac{1}{\frac{2x+5}{(x+2)(x+3)}}=1\:\cdot\:\frac{(x+2)(x+3)}{2x+5}=\frac{(x+2)(x+3)}{2x+5}\)
- Multiplying the numerator out, we can rewrite the expression as \((x+2)(x+3)=x^2+5x+6\). This gives us our answer: \(\frac{x^2+5x+6}{2x+5}\)
Question 5: Calculator permitted, grid-in response (see note)

Note: This is a two-part question, but we left out the first part to focus on the second one. The first question asked for the value of \(x\) in the expression. Because her bank account earns \(2\%\) interest compounded annually, we can convert \(2\%\) to a decimal, giving us \(.02\). We then add \(1\) to this so that we don’t lose the initial deposit. The answer is \(x=1.02\), which you need to know to solve the question above.
Answer: 6.11
Category: Passport to Advanced Math—exponential functions and equations (interest)
Here’s how you solve it:
- Given that Jessica uses the expression \(\$100(1.02)^t\) to find the value of her account after \(t\) years, we can create a similar expression to model Tyshaun’s account. This will be \(\$100(1.025)^t\).
- Now we can plug \(10\) in for \(t\) into both of the expressions. Jessica’s account will have \(\$100(1.02)^{10}\approx\$121.899\). Tyshaun’s account will have \(\$100(1.025)^{10}\approx\$128.008\).
- Now that we know how much money each account will have in 10 years, we can subtract the amount of money that Jessica’s account has from the amount of money that Tyshaun’s account has to find our answer. \(\$128.008-\$121.899=\$6.109\). Pay close attention to how problems ask for the answer: we need to round to the nearest cent and ignore the dollar sign, so the answer is \(6.11\).
Is your SAT score enough to get accepted to your dream school? Find out with CollegeVine’s free chancing calculator.
Question 6: Calculator not-permitted, multiple choice

Additional Topics in Math—complex numbers
- There’s usually at least one question on the SAT involving complex numbers, so it’s helpful to know how to add, subtract, and multiply them together. A complex number in standard form is written \(a+bi\), where \(a\) is a real number and \(bi\) is the imaginary part. In this question, we’ll want to use the conjugate form of \(a+bi\) which is \(a-bi\). This is because when we multiply complex conjugates, we get a real number: \((a+bi)(a-bi)=a^2-abi+abi-b^2i^2=a^2-b^2i^2\). However, because \(i=\sqrt{-1}\), that means that \(i^2=-1\). We can thus simplify \(a^2-b^2i^2=a^2+b^2\).
- Taking a hint from the answer choices, which only have real numbers in the first term, we can multiply the fraction above by the conjugate of the denominator like so:
\(\frac{3-5i}{8+2i}\cdot\frac{8-2i}{8-2i}=\frac{(3-5i)(8-2i)}{(8+2i)(8-2i)}\)
- We can quickly figure out the denominator given the information about conjugates above. \(8^2+2^2=64+4=68\).
- Multiplying complex numbers is just like multiplying binomials, keeping in mind that \(i^2=-1\) and we’ll need to simplify that out at the end.
\((3-5i)(8-2i)=24-6i-40i+10i^2=24-46i-10=14-46i\).
- Our new fraction is this: \(\frac{14-46i}{68}\). We can rewrite it so that the real part and the imaginary part of the complex numerator are separated and then simplify to get our answer.
\(\frac{14-46i}{68}=\frac{14}{68}-\frac{46i}{68}=\frac{7}{34}-\frac{23i}{34}\)
Question 7: Calculator permitted, multiple choice
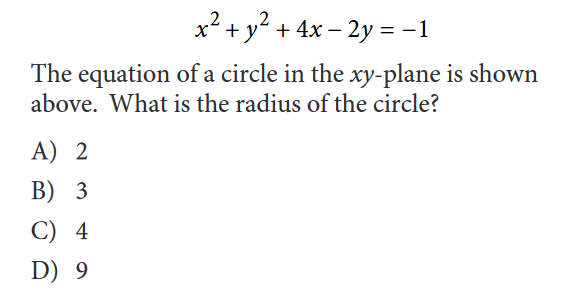
Category: Additional Topics in Math—Circles and their equations
- Like complex numbers, there’s usually at least one question involved the equation of a circle. This equation is not in the standard form of the equation of a circle, which is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center of the circle and \(r\) is the radius. We’ll need to rewrite this equation into standard form to easily find the radius.
- To begin rewriting the equation, we will need to complete the square twice, once for \(x\) and once for \(y\).
\(x^2+4x+y^2-2y=-1\)
\((x+2)^2-4+(y-1)^2-1= -1\)
- As you can see, we halved the absolute value of the \(x\) and \(y\) coefficients to find the constant to complete the square, then subtracted the squared constants to keep the equation the same. Now we need to move our constants to the other side by adding and we’ll have our equation in standard form.
\((x+2)^2+(y-1)^2=-1+1+4\)
\((x+2)^2+(y-1)^2=4\)
- We now see that \(r^2=4\), so the radius is \(\sqrt4=2\). That’s our answer!

Discover how your SAT score affects your chances
As part of our free guidance platform, our Admissions Assessment tells you what schools you need to improve your SAT score for and by how much. Sign up to get started today.
[amp-cta id='9353']
Question 8: Calculator not-permitted, multiple choice

Category: Passport to Advanced Math—rewriting equations in terms of another variable
1. Students get intimidated by questions that have only variables. Remember to use what you know about manipulating equations—such as whatever you do to one side you must do to the other—to handle these problems.
2. We want to rewrite the equation in terms of \(F\). To start, we’ll want to get rid of the \(F\) in the denominator of the equation above by multiplying both sides by \(N+F\) like so:
\(R(N+F)=\frac{F(N+F)}{(N+F)}\)
\(R(N+F)=F\)
3. Distribute the \(R\) on the left-hand side, and then move all the F ‘s to the same side.
\(RN+RF=F\)
\(F-RF=RN\)
4. Next, we can factor out the \(F\) on the left-hand side and divide both sides by the remaining factor to isolate \(F\) and get our answer.
\(F(1-R)=RN\)
\(F=\frac{RN}{1-R}\)
Question 9: Calculator permitted, multiple choice
Category: Problem Solving and Data Analysis—standard deviation, range, analyzing graphical data
Here’s how you solve it :
1. You won’t have to calculate standard deviation on the SAT, but you will need to know what it means and what affects it. Standard deviation is a measure of spread in a data set, specifically how far the points in the data set are from the mean value. A larger standard deviation means that the points in the data set are more spread out from the mean value, and a smaller one means that the points in the data set are close to the mean value. Likewise, you’ll need to know what is meant by range. Range refers to the difference between the highest and lowest values in a data set. The SAT may require you to calculate the range for a data set.
2. Let’s first determine the standard deviations of each data set relative to each other. In the first data set, most of the data points are clustered around each other, which makes it likely that the mean is somewhere around \(72\) (even though there are two outliers, they are equidistant from \(72\) so they will balance each other out when determining the mean). In contrast, the second data set is more spread out, so we can conclude that the standard deviation of the first set is smaller than the standard deviation of the second. We can eliminate choices A and C .
3. Now let’s look at the range for each set. We can subtract the highest and lowest values for each set to find the range. For the first set, \(88-56 = 32\). For the second set, \(112-80 = 32\). The ranges of each set are equivalent. This leaves us with choice D as our answer.
Question 10: Calculator not-permitted, multiple choice
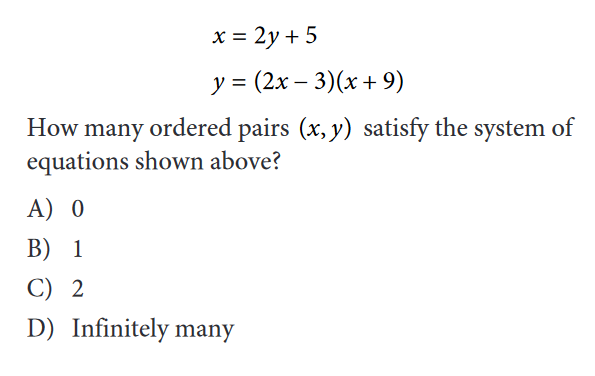
Category: Passport to Advanced Math—quadratic and algebraic functions and their graphs
1. We can solve this using substitution. Substitute the second equation into the first and expand the quadratic:
\(x=2[(2x-3)(x+9)]+5\)
\(x=2(2x^2+15x-27)+5\)
\(x=4x^2+30x-49\)
2. Next, move the x from the left-hand side over to the right. The roots of this quadratic will give us the solution to the system of equations above.
\(0=4x^2+29x-49\)
3. Since the roots of the above quadratic will give us the solution to the system of equations above, we can use the discriminant of the quadratic formula to find out how many solutions there are. The discriminant is the part of the quadratic formula under the radical, or \(b^2-4ac\). If the discriminant is positive, there are 2 solutions; if the discriminant is 0, there is 1 real solution (or a repeated solution); if the discriminant is negative, there are no real solutions. Substituting the numbers from the equation into the discriminant formula gives us \(29^2-4(4)(49)=841-784=57\). This is a positive number, which means there are 2 solutions to the system of equations.
How do your SAT and SAT Subject test scores influence your chances of admission? Calculate your chances with CollegeVine’s free admissions calculator.
Question 11: Calculator permitted, grid-in response

Answer: 2.25 or 9/4
Category: Passport to Advanced Math—determining effect of one variable on another
1. This is similar to the earlier problem where there are only variables, but if we proceed step-by-step and manipulate the equation carefully, we can find the solution. In this problem, we have two fluids, and one of them is moving at a velocity of \(1\) and the other at \(1.5\). We can substitute the \(1.5\) into the equation to see how it might affect \(q\), or the dynamic pressure.
\(q=\frac{1}{2}n(1.5v)^2\)
2. Using exponent rules (from Question 3 above) we can rewrite \((1.5v)^2=1.5^2v^2\) . Squaring \(1.5\) gives us \(2.25\).
3. For our fluid moving at a velocity of \(1.5\), we thus have: \(q=\frac{1}{2}n(2.25)v^2\). For our fluid moving at a velocity of \(1\), we have \(q=\frac{1}{2}n(1)v^2\). We can thus see that the dynamic pressure of the faster fluid will be \(2.25\) times that of the slower fluid.
Question 12: Calculator not-permitted, grid-in response

Answer: 3/5 or .6
Category: Additional Topics in Math—trigonometry
1. If you’re given a word problem that involves geometry or trigonometry and no diagram, you should draw yourself a diagram and label the information. This often makes it very clear how to find the answer. Here’s our diagram:
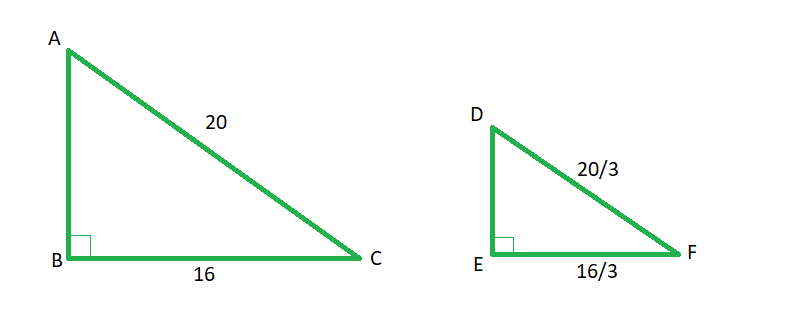
2. Many students know about the 30-60-90 and the 45-45-90 right triangles, and information about these triangles is included on the first page of each SAT math portion. However, you should also be on the lookout for the 3-4-5 and 5-12-13 right triangles. College Board likes to use these triangles and their similar counterparts because they have nice, whole-number sides that make calculations easy. Knowing this, we can see that Triangle ABC is similar to the 3-4-5 triangle, each side of ABC 4 times the length of the 3-4-5 triangle.
3. Knowing that triangle ABC is similar to a 3-4-5 triangle, and that triangle DEF is also similar to a 3-4-5 triangle, we can find \(sin\:F\) by substituting 3-4-5 for the sides of DEF and using the definition of sine: \(sin\:\theta\:=\frac{opposite}{hypotenuse}\)
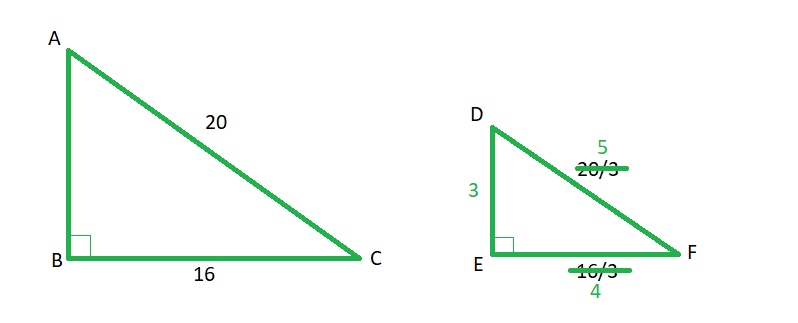
4. With respect to \(F\), the opposite side is \(3\) and the hypotenuse is \(5\). This means that \(sin\:F=\frac{3}{5}\), or \(0.6\).
Question 13: Calculator permitted, multiple choice

Category: Heart of Algebra—linear equations and inequalities in context
1. You’ll need to be able to write equations that reflect the context described in a word problem for several questions on the SAT, both linear context and non-linear contexts. If you have trouble “translating” word problems into math, this is a skill you’ll want to work on! Rewriting word problems to include words like equal to, less than, more than, sum, and so on can help you easily translate the problem into equations and inequalities.
2. We’re told that Roberto wanted to sell \(57\) insurance policies but he didn’t meet his goal, which means that he sold less than \(57\) insurance policies. Given that \(x\) represents the number of \(\$50,000\) policies sold and \(y\) represents the number of \(\$100,000\) policies sold, the sum of these two numbers is less than \(57\). This is represented as \(x+y\:\lt\:57\). We can eliminate choices B and D .
3. Next, we’re told that the value of all the policies sold was more than \(\$3,000,000\). We need to multiply the value of the policy by the number of that type of policy, which gives us \(50,000x+100,000y\:\gt\:3,000,000\). Choice C is the only answer that reflects Roberto’s insurance policy sales.
Question 14: Calculator permitted, multiple choice

Category: Problem Solving and Data Analysis—Statistics
1. These kinds of problems can surprise students because there isn’t any obvious calculation or “math” to do. Instead, you’re being asked to interpret the results based on given information, and you’ll need to know statistics to correctly interpret these types of problems. In this case, you’ll want to draw upon knowledge of population parameters, random sampling, and random assignment:
- A population parameter is a numerical value describing a characteristic of a population. For example, we’re told that the population targeted by this treatment are “people with poor eyesight.” While not given a number, any conclusion we draw can only be made regarding people who fall under this parameter.
- Random sampling means that the subjects in the sample were selected at random (without bias) from the entire population in question. If random sampling is used, the results can be generalized to the entire population.
- Random assignment means that subjects in the sample were assigned to a treatment at random (without bias). If random assignment is used, it might be appropriate to make conclusions regarding cause and effect.
2 . The SAT is very particular when including statistical clues and knowing the definitions of statistics. For example, if random sampling is not mentioned in a problem, then the results cannot be generalized to the entire population. Knowing the above, we can see that random sampling and random assignment are explicitly mentioned in this case. We can reasonably conclude cause and effect to be generalized to the population in question, or that it’s likely that Treatment X will improve the eyesight of people who have poor eyesight. The other choices are either too confident in their conclusion or do not specify the population in question.
Question 15: Calculator not-permitted, grid-in response
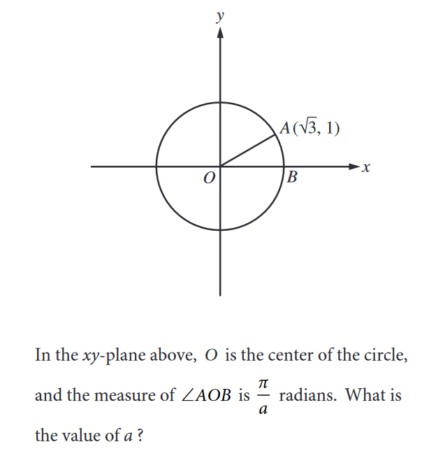
Category: Additional Topics in Math—Radians
1. The point \(A\) is \((3,1)\). We can create a triangle to find the degree measure of \(\angle{AOB}\). When we do this, we can use the information the SAT provides to see that this is a 30-60-90 triangle and that the hypotenuse (or the radius of the circle) is \(2\).
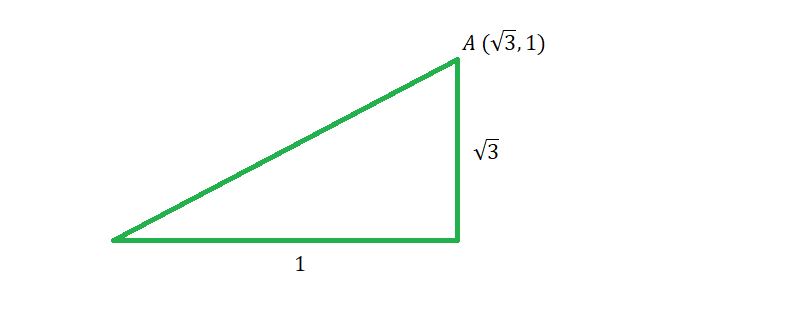
3. Since \(a\) is the denominator, the answer is \(6\).
We hope that you have a good sense of the type of questions that you might see on the SAT, but just remember that these questions aren’t a complete representation of the topics you could be tested on. Review the questions above and ask yourself: which ones were the most challenging to you? Which topics do you need to brush up on?
Check out our free guide with our top 8 tips for mastering the SAT.
Want to know how your SAT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
To learn more about how to do well on the SAT, check out these other posts:
- How to Get a Perfect 1600 Score on the SAT
- Ultimate Guide to the New SAT Reading Test
- Ultimate Guide to the New SAT Writing and Language Test
- Ultimate Guide to the New SAT Math Test
- Links to Every SAT Practice Test + Other Free Resources
Related CollegeVine Blog Posts

Student Question Bank: Math Questions
Because each question on the Math section deals with different numbers and mathematical scenarios, it's not as simple as the Reading and Writing section to identify exactly what each question stem will look like. You can still use the descriptions in this section to determine which math domains and skills you want to focus on in the Student Question Bank.
Math Questions
Related topics.
- Comment Comments
- Save Article Read Later Read Later
AI Reveals New Possibilities in Matrix Multiplication
November 23, 2022
Matrix multiplication is not unlike solving an unthinkably large Rubik’s Cube.
Mahmet Emin Güzel for Quanta Magazine
Introduction
Mathematicians love a good puzzle. Even something as abstract as multiplying matrices (two-dimensional tables of numbers) can feel like a game when you try to find the most efficient way to do it. It’s a little like trying to solve a Rubik’s Cube in as few moves as possible — challenging, but alluring. Except that for a Rubik’s Cube, the number of possible moves at each step is 18; for matrix multiplication, even in relatively simple cases, every step can present more than 10 12 options.
Over the past 50 years, researchers have approached this problem in many ways, all based on computer searches aided by human intuition. Last month, a team at the artificial intelligence company DeepMind showed how to tackle the problem from a new direction, reporting in a paper in Nature that they’d successfully trained a neural network to discover new fast algorithms for matrix multiplication. It was as if the AI had found an unknown strategy for solving a monstrously complex Rubik’s Cube.
“It’s a very neat result,” said Josh Alman , a computer scientist at Columbia University. But he and other matrix multiplication specialists also emphasized that such AI assistance will complement rather than replace existing methods — at least in the near term. “It’s like a proof of concept for something that could become a breakthrough,” Alman said. The result will simply help researchers on their quest.
As if to prove the point, three days after the Nature paper came out, a pair of Austrian researchers illustrated how new and old methods might complement each other. They used a conventional computer-aided search to further improve one of the algorithms that the neural network had discovered.
The results suggest that, like the process of solving a Rubik’s Cube, the path to better algorithms will be full of twists and turns.

Video : DeepMind researchers trained an AI system called AlphaTensor to find new, faster algorithms for matrix multiplication. AlphaTensor quickly rediscovered — and surpassed, for some cases — the reigning algorithm discovered by German mathematician Volker Strassen in 1969.
Christopher Webb Young/ Quanta Magazine ; Emily Zhang for Quanta Magazine
Multiplying Matrices
Matrix multiplication is one of the most fundamental and ubiquitous operations in all of mathematics. To multiply a pair of n -by- n matrices, each with n 2 elements, you multiply and add these elements together in particular combinations to generate the product, a third n -by- n matrix. The standard recipe for multiplying two n -by- n matrices requires n 3 multiplication operations, so a 2-by-2 matrix, for example, requires eight multiplications.
For larger matrices, with thousands of rows and columns, this process quickly becomes cumbersome. But in 1969, the mathematician Volker Strassen discovered a procedure for multiplying a pair of 2-by-2 matrices using seven rather than eight multiplication steps, at the cost of introducing more addition steps.
Strassen’s algorithm is needlessly convoluted if you just want to multiply a pair of 2-by-2 matrices. But he realized it would also work for bigger matrices. That’s because the elements of a matrix can themselves be matrices. For example, a matrix with 20,000 rows and 20,000 columns can be reimagined as a 2-by-2 matrix whose four elements are each 10,000-by-10,000 matrices. Each of these matrices can then be subdivided into four 5,000-by-5,000 blocks, and so on. Strassen could apply his method to multiply 2-by-2 matrices at each level of this nested hierarchy. As the matrix size increases, the savings from fewer multiplications grows.
Strassen’s discovery led to a search for efficient algorithms for matrix multiplication, which has since inspired two distinct subfields. One focuses on a question of principle: If you imagine multiplying two n -by- n matrices and let n run toward infinity, how does the number of multiplication steps in the fastest possible algorithm scale with n ? The current record for the best scaling, n 2.3728596 , belongs to Alman and Virginia Vassilevska Williams , a computer scientist at the Massachusetts Institute of Technology. (A recent unpublished preprint reported a tiny improvement using a new technique.) But these algorithms are of purely theoretical interest, winning out over methods like Strassen’s only for absurdly large matrices.
The second subfield thinks on a smaller scale. Soon after Strassen’s work, the Israeli American computer scientist Shmuel Winograd showed that Strassen had reached a theoretical limit: It’s not possible to multiply 2-by-2 matrices with fewer than seven multiplication steps. But for all other matrix sizes, the minimum number of required multiplications remains an open question. And fast algorithms for small matrices could have an outsize impact, since repeated iterations of such an algorithm might beat Strassen’s algorithm when reasonably sized matrices are being multiplied.
Unfortunately, the sheer number of possibilities is huge. Even for 3-by-3 matrices, “the number of possible algorithms exceeds the number of atoms in the universe,” said Alhussein Fawzi , a DeepMind researcher and one of the leaders of the new work.
Faced with this dizzying menu of options, researchers have made progress by transforming matrix multiplication into what seems like a totally different math problem — one that is easier for computers to handle. It’s possible to represent the abstract task of multiplying two matrices as a specific kind of mathematical object: a three-dimensional array of numbers called a tensor. Researchers can then break this tensor up into a sum of elementary components, called “rank-1” tensors; each of these will represent a different step in the corresponding matrix multiplication algorithm. That means that finding an efficient multiplication algorithm amounts to minimizing the number of terms in a tensor decomposition — the fewer the terms, the fewer the steps involved.
In this way, researchers have discovered new algorithms that multiply n -by- n matrices using fewer than the standard n 3 multiplication steps for many small matrix sizes. But algorithms that outperform not only the standard but also Strassen’s algorithm for small matrices have remained out of reach — until now.
The DeepMind team approached the problem by turning tensor decomposition into a single-player game. They started with a deep learning algorithm descended from AlphaGo — another DeepMind AI that in 2016 learned to play the board game Go well enough to beat the top human players.
All deep learning algorithms are built around neural networks: webs of artificial neurons sorted into layers, with connections that can vary in strength representing how much each neuron influences those in the next layer. The strength of these connections is tweaked over many iterations of a training procedure, during which the neural network learns to transform each input it receives into an output that helps the algorithm accomplish its overall goal.
In DeepMind’s new algorithm, dubbed AlphaTensor, the inputs represent steps along the way to a valid matrix multiplication scheme. The first input to the neural network is the original matrix multiplication tensor, and its output is the rank-1 tensor that AlphaTensor has chosen for its first move. The algorithm subtracts this rank-1 tensor from the initial input, yielding an updated tensor that is fed back into the network as a new input. The process repeats until eventually every element in the starting tensor has been reduced to zero, meaning there are no more rank-1 tensors to take out.
At that point, the neural network has discovered a valid tensor decomposition, since it’s mathematically guaranteed that the sum of all the rank-1 tensors is exactly equal to the starting tensor. And the steps it took to get there can be translated back into steps of the corresponding matrix multiplication algorithm.
Here’s the game: AlphaTensor repeatedly decomposes a tensor to a set of rank-1 components. Each time, AlphaTensor gets rewarded if it finds a way to reduce the number of steps. But shortcuts to victory are not at all intuitive, just as you sometimes must scramble a perfectly ordered face on a Rubik’s Cube before you can solve the whole thing.
The team now had an algorithm that could, theoretically, solve their problem. They just had to train it first.
Like all neural networks, AlphaTensor needs a lot of data to train on, but tensor decomposition is a notoriously hard problem. There were few examples of efficient decompositions that the researchers could feed the network. Instead, they helped the algorithm get started by training it on the much easier inverse problem: adding up a bunch of randomly generated rank-1 tensors.
“They’re using the easy problem to produce more data for the hard problem,” said Michael Littman , a computer scientist at Brown University. Combining this backward training procedure with reinforcement learning, wherein AlphaTensor generated its own training data as it blundered around looking for efficient decompositions, worked much better than either training method on its own.
The DeepMind team trained AlphaTensor to decompose tensors representing the multiplication of matrices up to 12-by-12. It sought fast algorithms for multiplying matrices of ordinary real numbers and also algorithms specific to a more constrained setting known as modulo 2 arithmetic. (This is math based on only two numbers, so matrix elements can only be 0 or 1, and 1 + 1 = 0.) Researchers often start with this more restricted but still vast space, in hopes that algorithms discovered here can be adapted to work on matrices of real numbers.
After training, AlphaTensor rediscovered Strassen’s algorithm within minutes. It then discovered up to thousands of new fast algorithms for each matrix size. These were different from the best-known algorithms but had the same number of multiplication steps.
In a few cases, AlphaTensor even beat existing records. Its most surprising discoveries happened in modulo 2 arithmetic, where it found a new algorithm for multiplying 4-by-4 matrices in 47 multiplication steps, an improvement over the 49 steps required for two iterations of Strassen’s algorithm. It also beat the best-known algorithm for 5-by-5 modulo 2 matrices, reducing the number of required multiplications from the previous record of 98 to 96. (But this new record still lags behind the 91 steps that would be required to beat Strassen’s algorithm using 5-by-5 matrices.)
The new high-profile result created a lot of excitement, with some researchers heaping praise on the AI-based improvement on the status quo. But not everyone in the matrix multiplication community was so impressed. “I felt like it was a little overhyped,” said Vassilevska Williams. “It’s another tool. It’s not like, ‘Oh, the computers beat the humans,’ you know?”
Researchers also emphasized that immediate applications of the record-breaking 4-by-4 algorithm would be limited: Not only is it valid only in modulo 2 arithmetic, but in real life there are important considerations besides speed.
Fawzi agreed that really, this is just the beginning. “There is a lot of room for improvement and research, and that’s a good thing,” he said.
A Final Twist
AlphaTensor’s greatest strength relative to well-established computer search methods is also its greatest weakness: It’s not constrained by human intuition about what good algorithms look like, so it can’t explain its choices. That makes it difficult for researchers to learn from its achievements.
But this may not be as big a drawback as it seems. A few days after the AlphaTensor result, the mathematician Manuel Kauers and his graduate student Jakob Moosbauer , both of Johannes Kepler University Linz in Austria, reported another step forward.

Manuel Kauers tweaked the DeepMind approach to generate further improvements.
Jakob Moosbauer
When the DeepMind paper came out, Kauers and Moosbauer were in the process of searching for new multiplication algorithms using a conventional computer-aided search. But unlike most such searches, which start afresh with a new guiding principle, their method works by repeatedly tweaking an existing algorithm in hopes of squeezing more multiplication savings out of it. Taking AlphaTensor’s algorithm for 5-by-5 modulo 2 matrices as a starting point, they were surprised to find that their method reduced the number of multiplication steps from 96 to 95 after just a few seconds of computation.
AlphaTensor also helped them make another improvement indirectly. Previously, Kauers and Moosbauer hadn’t bothered to explore the space of 4-by-4 matrices, believing that it would not be possible to beat two iterations of Strassen’s algorithm. The AlphaTensor result prompted them to reconsider, and after a week of computation time starting from scratch, their method turned up another 47-step algorithm unrelated to the one AlphaTensor had discovered. “If somebody had told us that there is something to discover for 4-by-4, we could have done that earlier,” said Kauers. “But OK, well, that’s how it works.”
Littman expects more such surprises, likening the situation to the first time a runner finished a mile in under four minutes, a feat that had widely been considered impossible. “People were like, ‘Oh, wait, we can do this,’ and now lots of people can do it,” he said.
Looking forward, Fawzi hopes to generalize AlphaTensor to tackle a broader range of mathematical and computational tasks, just as its ancestor AlphaGo eventually branched out into other games.
Kauers sees this as the true litmus test for the application of machine learning to discovering new algorithms. He points out that the quest for fast matrix multiplication algorithms is a combinatorial problem to which computer searches, with or without human assistance, are well suited. But not all mathematical problems are so easy to pin down. If machine learning can discover a qualitatively new algorithmic idea, he said, “this would then be a game changer.”
Get highlights of the most important news delivered to your email inbox
Comment on this article
Quanta Magazine moderates comments to facilitate an informed, substantive, civil conversation. Abusive, profane, self-promotional, misleading, incoherent or off-topic comments will be rejected. Moderators are staffed during regular business hours (New York time) and can only accept comments written in English.

Next article
- Share full article
For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.
Will Biden Withdraw?
Democratic worries about the president’s age have surged after thursday’s debate..
This transcript was created using speech recognition software. While it has been reviewed by human transcribers, it may contain errors. Please review the episode audio before quoting from this transcript and email [email protected] with any questions.
From “The New York Times,” I’m Natalie Kitroeff. This is “The Daily.”
[MUSIC PLAYING]
President Joe Biden’s disastrous debate performance last week set off a furious discussion among Democratic officials, donors, and strategists about whether and how to replace him as their party’s nominee. Today, chief White House correspondent Peter Baker takes us inside those discussions and Biden’s effort to shut that conversation down.
It’s Monday, July 1.
Peter, you’ve been reporting on what I think can be best described as the great Democratic freakout that started basically from the moment the debate began at 9:00 PM on Thursday night. Tell us about the aftermath.
Yeah, I’ve been covering politics for 38 years, and I’ve never seen a political panic like we saw after that debate. It was like a run on the bank. Everybody in the Democratic Party was suddenly confronted with what they didn’t want to admit up until then, which is that they have an 81-year-old candidate who would be 86 at the end of his second term. And it’s very possible that he was not capable of completing this campaign in a vigorous and competitive way against Donald Trump. That’s what really it comes down to for many Democrats. Can Joe Biden take the campaign to Donald Trump and stop what they think is an existential threat to the country?
I want to know more about who you were hearing from. Who are the people that are calling you? What are the big questions they’re asking? What are they struggling with?
Yeah, I don’t want to get into too many names. A lot of people don’t want to be out front. But you did see even publicly, people like Senator Claire McCaskill.
Joe Biden had one thing he had to do tonight and he didn’t do it.
The former Senator from Missouri, red state Democrat, was on MSNBC just minutes after the debate.
He had one thing he had to accomplish, and that was reassure America that he was up to the job at his age. And he failed at that tonight.
She talked about this was a crisis, that her phone was blowing up with a lot of Democrats. And she was very forthright about it. It was very striking that she said that.
I think there’s a lot of people who are going to want to see him consider taking a different course now,
People like van Jones, who was on CNN, he used to work in the Obama White House.
We’re still far from our convention. And there is time for this party to figure out a different way forward, if you will allow us to do that.
He very candidly talked about how this was going to raise questions about whether the President should continue as the candidate.
Some Democrats are calling for Biden to step down. Andrew Yang —
Andrew Yang, who ran against Biden in 2020 for the Democratic nomination, popular with some younger voters, he said on social media it was time for Biden to step aside. Those are some of the public people. And obviously, in the hours and days that followed, more came out and said, well, this is something we need to think about.
But the people I was talking to were people behind the scenes, people who have run White Houses before, people who work for President Biden in this administration. I heard words like, “He can’t win.” “This is a disaster.”
“This is a nightmare.” And they were very, very concerned that he could not beat Donald Trump.
Right. And you saw these really prominent media figures, outlets, “The Times” as an actor in this situation calling for Biden to step aside. Our editorial board did this. We should say this is entirely separate from our newsroom from the show, but there was this real crescendo. And there was a sense that this was a turning point, right?
Absolutely. But it’s not just the media. I think what the Biden campaign would like it to be is about the media. It’s just that the media tends to be more out front and say things more openly than Democrats were saying. It really was rank and file Democrats. It really was high ranking Democrats, and they were absolutely flipped out.
Right. These doubts are coming from all over, from many corners. Take me through, Peter, the argument for why this poor performance meant that Biden should be replaced. How do they explain that thinking?
Well, look, a lot of people who defended President Biden will say is that incumbent presidents don’t do well in their first debate, and that is true. Historically, that’s been true. Ronald Reagan, George W. Bush, Barack Obama, Donald Trump all lost, arguably, their first debate when they were running for re-election.
But the difference is, if Obama doesn’t register a good performance against Mitt Romney, first of all, nobody thought that Obama wasn’t capable of being president as a result. And second of all, he had another debate about a week or two later in order to try to recover. Neither of those factors works here.
Biden’s problem from this debate is much more existential. It’s much more profound because it’s about whether he is able to perform the office of president, not just for the next few months, but for the next 4 and 1/2 years. And there’s not going to be another debate until September. So he doesn’t have another big audience opportunity to change people’s minds, to show that, in fact, he does still have it and can run the country. And that’s a real problem for him.
And there’s this broader context here, right. Voters have been telling pollsters for a year now that Biden’s age is a major concern for them. We’ve seen Biden’s age before our very eyes. We’ve seen him stumble in speeches, in public appearances. And, Peter, we had talked to you about this very issue a few months ago after a special counsel investigating Biden’s son, Hunter, issued this report focusing on Biden’s mental state, in part, saying that the president was, quote, a “well-meaning elderly man with a poor memory” and had, quote, “diminished faculties in advancing age.”
But at the time, the White House dismissed that report as a partisan hit job. So in a sense, this debate performance was the capstone of something that’s been in the air for a very long time. It’s just that this time, it was undeniable. There was no spinning it.
Well, I think that’s exactly right. There was no spinning it. One Democrat put it to me. He said, for a long time, the fear of Trump stifled Democratic criticism of Biden. People didn’t want to criticize him because they desperately want to beat Trump.
But now, that same fear, he said to me, now meant that they could no longer stand behind Biden, that they worried that he had been diminishing over a period of time and that his staff and the people around him had hidden that from the public. There’s a real anger out there among some Democrats. Now, what the Biden circle would tell you is, no, we didn’t hide anything from you.
Yes, he does have moments where he is not as lucid as you would want him to be, but that, broadly speaking, when they see him operate, when they’re sitting with him in the Oval Office or in the situation room, he is sharp. He asks good questions. He understands and grasps the issues that he is confronting.
And I mean, we all have good days and bad days. But when you’re 81, your good days and bad days may be more pronounced.
And if he has good days and bad days, well, Thursday night was a very bad night.
Peter, I want to ask you about that, about your view on all of this, because I do think all this has raised this fundamental question for a lot of Democrats, for a lot of journalists, for voters, which is what you’re getting at. Was what we saw on the debate stage the real Biden? And had the White House been hiding him from us? Or were the people around him just unable to recognize the perils of this themselves? Like, have they been gaslighting us all, or are they in denial?
Yeah, it’s a good question. That’s the question in some ways, right. I think that people who work closely with the president and like him, admire him, respect him want to see the best in him and want everybody else to see the best in him. And they have been unwilling to admit whether or not he has slipped in the last 3 and 1/2 years.
And part of it may be strategic. They recognize in their view that he is the president. They’ve got to build him u and make him as successful as possible. And they have shielded him as much as possible from public scrutiny.
He hasn’t give as many interviews or as many press conferences as any of his predecessors going back to Reagan. He’s never getting interview to “The New York Times,” or “The Washington Post,” or “The Wall Street Journal,” or the “LA Times,” or any other newspaper, which is, I think, the first president, certainly in my lifetime, who hasn’t done that. And that’s been part of a pattern of them trying to protect him. And I think there’s kind of a reckoning right now among other Democrats, wondering whether they went too far.
OK. So we have this huge reaction to this moment, the debate from the Democrats in the news media. Can you walk us through how the Biden team responds to the full-blown panic?
His campaign was thrown into full-blown damage control over the weekend. And the President himself set out to do two things. First, privately, he met with donors and assured them, yes, he’s still a viable candidate and that they should still support him.
And then publicly, he went on a campaign blitz, traveling to seven events in four states. And his first stop on Friday, in fact, was at a rally in Raleigh, North Carolina.
[CROWD CHEERING]
Hello, hello, hello.
This was already scheduled before the debate, but it gave him an opportunity to both show that he can do the job —
Thank you, North Carolina.
— to demonstrate vigor and vitality —
I don’t know what you did last night, but I spent 90 days and 90 minutes on the stage debating the guy who has the morals of an alley cat.
— and to address his own performance.
I know I’m not a young man. State the obvious. Well, I know.
And he says pretty candidly, he says, yeah, I’m not a young man.
I don’t walk as easy as I used to. I don’t speak as smoothly as I used to. I don’t debate as well as I used to.
But he goes on.
Well, I know what I do know. I know how to tell the truth.
And I know how to tell right from wrong.
And I know how to do this job. I know how to get things done. And I know, like millions of Americans know, when you get knocked down, you get back up.
And, you know, he comes across as pretty vigorous, pretty energetic. Of course, he’s reading from a teleprompter. Always a lot easier to read from a teleprompter. But I think more important than that was the body language and the spirit that he brought to the moment.
It sounds like teleprompter, not the Biden who appears at the rally is meaningfully different, at least in style from the President that we saw on the debate stage. I’m wondering if you think this has changed anything. Has the conversation changed?
No, not fundamentally. I think fundamentally that people still recognize that there’s an issue here. Now, there was pushback among Democrats saying, OK, take a breath. Get a hold of yourself. He’s not dropping out.
I don’t think you judge a person’s — the body of their work on one night. They don’t always go the way you want to. I have confidence in the President because he’s delivered.
And I understand that he had a raspy voice. But like I’ve told folks, who cares? We have a choice this November between someone that’s a good person, a good president with a real record of results, and someone that has brought shame on the presidency.
Don’t let 90 minutes define a career of a president who’s been in office for 3 and 1/2 years, been in politics for 50 years, and overshadow the important issues that he stands for. And so you heard that line of thinking in the spin room and on TV.
Look, I think Joe Biden had a bad debate night, but it doesn’t change the fact that Donald Trump was a bad president.
And by the way, Trump did terribly, too, which is a fair point. Trump may have been more lucid in the sense that he sounded stronger. But if you actually looked at what he said, listen to what he said, he said so many things that were just not true. And it helped Biden that former President Barack Obama put out a statement saying, hey, guys, I’ve seen bad debates. It’s fine. Don’t freak out, in effect, is what he said.
And Jim Clyburn —
And if he asked my opinion, I would give it, as I always do —
— who is his very close ally in Congress from South Carolina, the Congressman who helped get him the nomination in the first place, said, stay the course.
He should stay in this race. He should demonstrate going forward his capacity to lead the country.
So it was important to have those voices out there among prominent Democrats trying to calm the waters. But it only went so far because the waters are still churning underneath.
Peter, I’m curious how his donors are reacting to all this. I mean, you mentioned that part of his full court press is to reassure them that he’s got the mental acuity to run. How successful has he been at that?
Yeah, I think that there are certainly some donors who are resigned. They feel like there’s not much choice. But there are others who actually are considering jumping off the boat. Jumping on what Mika Brzezinski on “Morning Joe” called the hysteria train. And I think that it’s an open question.
But part of the thing is, of course, they’re waiting to see how the polls really shake out. The initial polls after any debate are often not really representative of how an event settles into the political narrative. And the polling and data so far have been kind of contradictory. On the one hand, it shows that Trump clearly beat Biden. Biden clearly lost, and that Biden has only reinforced the doubts that most voters have about his age and mental capacity. That’s absolutely true.
At the same time, there’s some polling showing that the overall horse race number, who are you going to vote for, hasn’t moved dramatically yet, if it does at all, and that it’s possible this is baked in that people who were going to vote against him are still going to vote against him. The people who would vote for him, holding their nose, may not be happy about it, may still be voting for him.
But there’s a tell. The tell was from the Biden campaign. When they put out a memo by Jen O’Malley Dillon, who was his top political person at the campaign, and she says if you see polls go down in the next few days or weeks, what’s telling is that she is, in fact, anticipating that polls would be bad for them and trying to set expectations for supporters and voters and donors saying, don’t let that panic you any further. That’s normal, and we’ll get past that just as we have other bumps in the road.
It seems like the Biden effort over the weekend has, in some sense, quieted some public doubts from key Democrats, right? There’s not a — we didn’t see a deluge of senior lawmakers going on Sunday talk shows and saying, Mr. President, step aside. But from what you’re saying and based on the reporting that we’ve seen from our colleagues, the effort has not, by any means, ended the discussion about replacing Biden. That is very much still happening under the surface.
Yeah. That discussion is very much alive among Democrats. Will Biden and should Biden remain as the candidate? And the question then becomes is if he doesn’t, what then?
We’ll be right back.
Peter, given that this discussion of Biden stepping aside is still, as you said, very much alive, what would it look like for someone to replace him on the presidential ticket at this point in the campaign just a few months before election day? It sounds like it would be pretty daunting.
Yeah. I mean, look, we have never had a situation like this, not certainly in modern times. No president has ever dropped out of the race so late in the cycle. And you have to remember a couple of things.
First of all, the Democratic National Convention, which would anoint a new nominee, is in late August. But they’re actually scheduled to take a roll call vote before the convention begins on August 7. So that means we have five weeks between now and when the roll call is scheduled to be held to decide a nominee.
If the president were to drop out, that would create this truncated, incredibly intense, incredibly wide open, incredibly volatile, short campaign to figure out who would be the nominee. And it’s complicated logistically. It’s complicated politically, it’s complicated in all sorts of ways. And we don’t really know what’s going to happen or how it would happen because we’ve never seen it before.
But it is conceivable. It is possible. The President has to decide that he’s not going to run. If that doesn’t happen, then there’s no contest. There’s no way anybody sees a forcing him off the ballot if he chooses to continue to run. That doesn’t seem to be any appetite for trying to find a way to undo his nomination other than with his consent.
He controls the 3,900 delegates that are going to be at the convention. They’re obligated to vote for him on the first ballot. So it has to be first, his decision on whether he continues to run. If he does, then that’s it. That’s the end of that question. But if he doesn’t, then it’s jump ball.
Would his replacement automatically be Kamala Harris as the vice president?
No, not at all. If it were after the convention and they were both nominated, and then he stepped aside at the last minute, then they probably would simply go to Kamala Harris because she had been ratified by the convention as the vice presidential candidate. That’s possible. But if we’re talking about a situation before the convention, it’s anybody’s guess. There’s about a dozen other prominent Democrats out there who are looking at jumping in if suddenly, the nomination is up for grabs.
But so who are we talking about? What are some of the most prominent names that have come up?
Well, other than Kamala Harris, you have a number of governors, particularly Gavin Newsom of California, Gretchen Whitmer of Michigan, J.B. Pritzker of Illinois. There are, of course, those who ran last time who might jump back in, in theory. Senator Cory Booker, Senator Amy Klobuchar, potentially even maybe Pete Buttigieg, who is currently the transportation Secretary.
But the ones who are going to have the best chance are those who have an apparatus already, who have a set of donors and fundraisers who can raise money instantly, and who have the ability to get on TV and get media attention without having to work as hard for it. And that does suggest, obviously, a sitting vice president or a sitting governor.
Basically hitting reset on the whole nomination process requires embracing a moment of genuine political chaos. I mean, that’s the theoretical downside of this. But of course, I mean, there’s also a potential upside, right? Massive media attention potentially for whoever the replacement Democrat is, the possibility that that replacement could energize a lot of Democratic voters and independents, and even potentially moderate Republicans out there who dislike Trump but just couldn’t get excited about Biden.
Yeah, absolutely. Whoever emerges will have a certain advantage of freshness, right. And that person will have a generational argument to make against Trump because whoever it would be would be younger than Trump. And suddenly, Trump is then the old candidate. He’s 78.
And that new Democratic candidate would be able to say, I’m the next generation. This guy is also too old to be president. And if you’re concerned about our guy was, can he make it through four years, then you should be picking me because the other guy can’t make it either through four years.
Now, the downside, of course, is these are people who are largely untested on a national stage, at least in this kind of an environment. And you don’t know how people will do once they actually jump in. They didn’t have the advantage of a year-long primary contest to prove themselves.
Before you jump into a race, you can look really attractive. Look at Ron DeSantis. Before he jumped in to the Republican primaries, on the Republican side, they all thought, wow, he’s really great. Didn’t turn out to be so great once he got on the campaign trail. The magic didn’t actually appear. So that’s the danger here, is we don’t know which of these Democrats, if any, would have the ability to shine when the big giant klieg lights are on them.
And we’re clearly in a delicate moment right now. But are any of these potential contenders trying to signal interest at this point? I mean, what does that look like? It sort of seems like the art of raising your hand for something but not wanting it to publicly.
Yeah, it’s a really good question because you obviously can’t do anything that seems disloyal to Biden, right. Nobody’s willing to take on Biden directly and say, I’m now running, and you should take him down. So the trick here is you have to be loyal, loyal, loyal right up to the minute that Biden says he’s not running, at which point then suddenly you’re off to the races.
And doing that from a standing start is not a good idea for any campaign. So they have to find ways of talking to their people, lining up donors, thinking about what kind of a campaign would look like, who might be their strategist, without letting anybody know that they’re doing that, or at least not let anybody in our business know that because it would obviously backlash on them. And that’s a very hard thing to do. I mean, I heard that there are people out there making phone calls who want to run, but nobody’s going to admit that outright because it would be damaging to them.
And in terms of logistics here — I know this is all very hypothetical — but if a new candidate were to become the nominee, do they get all the money Biden raised? Do they get his campaign team, or are they literally creating a presidential campaign from scratch with four months to go?
I mean, presumably, they would adopt a lot of Biden’s apparatus. As for the money, a lot of the money these days is in kind of superpacs and these sort of amorphous structures that can go immediately to a different candidate. And everybody who contributed to Biden can now contribute to the new candidate. And then Biden can still spend his money as he chooses in support of whoever the candidate is.
So there’s that advantage in a way it could actually increase some fundraising. But you’re right, they would be starting from scratch in a lot of ways, at least in terms of a national organization.
And obviously, for this to even happen, it relies on Biden stepping aside here, as you said. Everything you’ve laid out so far suggests that he is, for now at least, closed off to this suggestion. And I have to ask what you think from your reporting would change that.
Well, President Biden is a proud man. He’s a stubborn man. As a lot of people of any age are, he is reluctant to confront and face his own weaknesses, and he’s not going to be talked out of running by a bunch of media chattering class, pundits, and junior Democrats. I mean, think about it. He’s been running for president since 1987. And the idea that he is now in office and running the country and as he thinks it, running it pretty well, that he’s going to simply step aside because a bunch of people tell him he should, he reacts viscerally to that. Of course, he doesn’t want to do that.
In fact, when you talk to Democrats, they’re very conscious of not trying to push him because it could have the opposite reaction. It could trigger him to want to stay even more. The people who have influence with him, not that many people.
I mean, at this point, he’s been in politics since 1972 when he was elected to the Senate. And the people he considers his peers, most of them are gone. He’s not surrounded by people whose opinion he truly respects.
Obama and Clinton, the only two former presidents out there other than Jimmy Carter, who are Democrats, I don’t know that if they told him it was time to pull the plug, that he would listen to that. In fact, he might, again, do the opposite. He still resents Obama for discouraging from running in 2016.
Obviously, congressional leaders like Chuck Schumer, Nancy Pelosi, Hakeem Jeffries, Jim Clyburn, people like that, could have an influence if they were to go as a group to him in a way like the Republicans went to Nixon in 1974 and said that he wasn’t going to survive. Maybe that might influence him. But I don’t think they’re likely to do it. It doesn’t look like they’re likely to do that.
Who does have his ear? I mean, who does he really listen to? Who do we know he’s going to be listening to in this moment?
Well, the real people he listens to the most are his family. He’s a very family-oriented guy. Remember, he went home to Wilmington almost every night when he was a Senator. Even now as president, he flies home to Wilmington most every weekend.
And he’s at Camp David this weekend with his family. They’re there because they had already planned to be together for a photo shoot, ironically, with Annie Leibovitz. So the family was already gathering at Camp David —
— gives him an opportunity. Right. And it gives him an opportunity to have a heart-to-heart conversation with the people who mean the most to him, in particular, Jill Biden, of course, the first lady and his sister, Valerie, the kids, and the grandkids. We don’t know what that conversation looks like.
I mean, that’s as private as it comes. Someday they’ll be histories written and memoirs written. And I’m fascinated to read what’s happening this weekend at Camp David, because I think it’s kind of pivotal. But what we do know is that up until now, at least, Jill has been all in.
She’s been encouraging him to run. And it sounds like she’s been encouraging him to stay in. And a lot of people think her voice is the most important voice in this.
And just to pause on this for a second, Peter, it sounds like you’re saying something pretty remarkable, actually, which is that this very small handful of people have influence over what is going to be a massive decision that affects hundreds of millions of Americans and really the entire world.
Well, don’t underplay it. But yeah, that’s exactly right. And you’re right to point out the stakes here, because it’s not just about Joe Biden and his future. It is about this presidential race. And it is about whether you want Donald Trump back in office. That’s the way most Democrats look at it. And the difference between a Biden presidency and a Trump presidency is about as stark as you can imagine. And this will have consequences that will ripple out for years to come.
Peter, I kind of want to end where we began this conversation, which is with this question of Democrats’ mindset right now, post-debate, and the question of what’s motivating them in this moment. Privately, they’re talking about replacing Biden. They seem too scared to do that publicly for all the reasons we’ve discussed, including that the White House is basically telling them to stop talking about it and that Biden probably won’t step aside anyway. So all of this may just be useless hand-wringing.
And all of that raises a pretty essential question for me, which is, are Democrats about to recommit to a damaged nominee who had a disastrous debate, who may only get worse over time out of loyalty to President Biden? Or do you think on some level they really believe this is all just overblown, that it’s one debate, everybody has bad days, and Biden really can recover from all this?
I think there’s a lot of doubt in the party that he can really recover from. This is the argument obviously the Biden campaign is making. And it’s really the only argument they have available to them to say, look, don’t overreact here. It’s just the media hyperventilating. We will recover like we’ve recovered before.
And it is what they have to say because they don’t have anything else that they can say. But almost every Democrat outside of the inner circle that I talk to says this was a complete disaster. They are not sugarcoating it. They saw what they saw with their own eyes, and they think that it’s not tenable for the campaign to pretend otherwise.
And it’s particularly devastating because the weakness of the Biden campaign has always been concerns about his age. People have expressed that to pollsters and in interviews with reporters going back more than a year. And now they just saw it for themselves on TV, in their living rooms, more than 50 million of them. And to convince them not to believe what they saw with their own eyes is just a monumental task politically.
So for Biden’s team and for the Democrats, it’s a big roll of the dice. Do you stick with him and try to correct the damage in the four months you have? Or do you say, it’s time for somebody else, which is going to be a roll of the dice itself?
And assuming Biden continues, Peter, it sounds like we won’t know if that bet, that bet that he’s the only one that ever beat him. He’s the only guy that can get this done, if that was solid or diluted thinking until November 5.
On November 5, or whatever day of the election is resolved, we will know how history judges this. And maybe everybody looks back on this and says, well, that was close, but they were right to stick it out because they won. Or in fact, it was a disastrous decision, and they wasted an opportunity to fix campaign that was already having trouble. Hindsight will be perfect, but there’s no question that this weekend will be remembered as perhaps the most decisive of this campaign.
Peter, thanks for coming on.
Thanks for having me.
After we spoke with Peter, “The New York Times” reported that while at Camp David, Biden’s family urged the president to stay in the race, arguing that, yes, he could still show voters he’s capable of serving another four years.
Here’s what else you need to know today. Early projections show that France’s far-right national rally party won a decisive victory in the first round of voting for the country’s national assembly on Sunday. National rally, an anti-immigrant party long on the fringes of the French political scene, captured about a third of the vote, according to polls, and now appears poised to become the largest force in the lower house of parliament.
The results dealt a blow to French president Emmanuel Macron, who took a gamble by dissolving parliament last month and calling for snap elections. But his bet that the far right wouldn’t repeat its recent success in European parliament elections backfired. A run-off election between the leading parties will be held on July 7.
Today’s episode was produced by Asthaa Chaturvedi, Rachelle Bonja, Will Reid, and Rob Szypko, with help from Olivia Natt and Lynsea Garrison. It was edited by Lexie Diao, with help from Ben Calhoun, Paige Cowett, and Mike Benoist. And special thanks to Michael Barbaro.
Contains original music by Dan Powell, Marion Lozano, and was engineered by Chris Wood. Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly.
That’s it for “The Daily.” I’m Natalie Kitroeff. See you tomorrow.

- Apple Podcasts
- Google Podcasts

Hosted by Natalie Kitroeff
Featuring Peter Baker
Produced by Rachelle Bonja , Will Reid and Rob Szypko
With Olivia Natt and Lynsea Garrison
Edited by Lexie Diao , Ben Calhoun , Paige Cowett and Mike Benoist
Original music by Dan Powell and Marion Lozano
Engineered by Chris Wood
Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube
President Biden’s disastrous debate performance last week set off a furious discussion among Democratic officials, donors and strategists about whether and how to replace him as the party’s nominee.
Peter Baker, who is the chief White House correspondent for The Times, takes us inside those discussions and Biden’s effort to shut them down.
On today’s episode

Peter Baker , the chief White House correspondent for The New York Times.

Background reading
President Biden’s allies can no longer wave away concerns about his capacity after his unsteady performance at Thursday’s debate.
Mr. Biden’s family is urging him to keep fighting .
There are a lot of ways to listen to The Daily. Here’s how.
We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.
Special thanks to Michael Barbaro .
The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.
Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Maddy Masiello, Isabella Anderson, Nina Lassam and Nick Pitman.
Natalie Kitroeff is the Mexico City bureau chief for The Times, leading coverage of Mexico, Central America and the Caribbean. More about Natalie Kitroeff
Peter Baker is the chief White House correspondent for The Times. He has covered the last five presidents and sometimes writes analytical pieces that place presidents and their administrations in a larger context and historical framework. More about Peter Baker
Advertisement

IMAGES
VIDEO
COMMENTS
Quadratic Equations: Very Difficult Problems with Solutions. Problem 1. Solve the equation \displaystyle \frac {5} {2-x}+\frac {x-5} {x+2}+\frac {3x+8} {x^2-4}=0 2−x5 + x+2x−5 + x2 −43x+8 = 0. In the answer box, write the roots separated by a comma. Problem 2. If \displaystyle x^2-2ax+a^2=0 x2 −2ax+a2 = 0, find the value of ...
Solve the quadratic equation [tex]x^2-20x-69=0[/tex] In the answer box, write the roots separated by a comma.
Unit test. Level up on all the skills in this unit and collect up to 1,100 Mastery points! There are lots of strategies we can use to solve equations. Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions.
In 2019, mathematicians finally solved one of the hardest math problems —one that had stumped them for decades. It's called a Diophantine Equation, and it's sometimes known as the "summing ...
The answers took over a million hours to compute. Without further ado, they are: X = -80538738812075974, Y = 80435758145817515, and Z = 12602123297335631. Well, obviously. "I feel relieved ...
Use the illustration below as a guide. Notice that in order to apply the quadratic formula, we must transform the quadratic equation into the standard form, that is, [latex]a{x^2} + bx + c = 0[/latex] where [latex]a \ne 0[/latex]. The problems below have varying levels of difficulty. I encourage you to try them all. Believe me, they are ...
Steps. Example. Write down the inequality. ( x - 5 > 10 ) Perform the same operation on both sides. ( x - 5 + 5 > 10 + 5 ) Simplify to find the solution. ( x > 15 ) Remember, if I multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign flips.
Unit test. Level up on all the skills in this unit and collect up to 800 Mastery points! Start Unit test. Ready for a challenge? This unit covers the hardest algebra questions on the SAT Math test. Work through each skill, taking quizzes and the unit test to level up your mastery progress.
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
Multi-Step Equations Practice Problems with Answers. For this exercise, I have prepared seven (7) multi-step equations for you to practice. If you feel the need to review the techniques involved in solving multi-step equations, take a short detour to review my other lesson about it. Click the link below to take you there!
2x + 3(x−3) − 6 = 0. Expand and solve: 2x + 3x − 9 − 6 = 0. 5x − 15 = 0. 5(x − 3) = 0. x − 3 = 0. Which can be solved by having x=3. Let us check x=3 using the original question: 2 × 3 3 − 3 + 3 = 6 3 − 3. Hang On: 3 − 3 = 0 That means dividing by Zero! And anyway, we said at the top that x≠3, so ... x = 3 does not ...
SAT Problem #1. Test #8, section 4. At first glance, this looks like a geometry question, since it talks about planes and lines and points. But this is actually an algebra question, dressed up with some geometric trappings. The key is to realize: 1) We don't need to solve for p and r individually.
Questions with Solutions. If x2 + 1 x2 = 10 x 2 + 1 x 2 = 10 , then what is the exact value of x5 + 1 x5 x 5 + 1 x 5 for x ≥ 0 x ≥ 0 ? solutions. Write the complex number (1 − i)1+i ( 1 − i) 1 + i in standard form a + ib a + i b where i = −1−−−√ i = − 1 is the imaginary unit. solutions. Solve the trigonometric equation given ...
Khan Academy's 100,000+ free practice questions give instant feedback, don't need to be graded, and don't require a printer. Math Worksheets. Khan Academy. Math worksheets take forever to hunt down across the internet. Khan Academy is your one-stop-shop for practice from arithmetic to calculus. Math worksheets can vary in quality from ...
Strategies for Difficult Math Problems — and Beyond. Here are a few strategies for dealing with hard problems, and the frustration that comes with them: Do something. Yeah, the problem is hard. Yeah, you have no idea what to do to solve it. At some point you have to stop staring and start trying stuff. Most of it won't work.
B) x − 2 is a factor of p ( x). C) x + 2 is a factor of p ( x). D) The remainder when p ( x) is divided by x − 3 is − 2. ANSWER EXPLANATION: If the polynomial p ( x) is divided by a polynomial of the form x + k (which accounts for all of the possible answer choices in this question), the result can be written as.
intararit. Some problems in mathematics have taken centuries to be solved, due to their complexity. Although there are some complex math problems that still elude solutions, others have now been ...
Free math problem solver answers your algebra homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store. Take a photo of your math problem on the app. get Go. Algebra. Basic Math.
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
One example of a problem you might see in pre-algebra is 4 + 3x = 2. In this problem, the letter x is the variable. You can solve this problem by isolating the variable, like this: 4 + 3x = 2 First, subtract four from both sides. 4 - 4+ 3x = 2 - 4 3x = -2 Now, divide both sides by three to isolate the variable. 3x ÷ 3 = -2 ÷ 3 x = -2/3 ...
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Answer: A. Category: Passport to Advanced Math—exponents. Here's how to solve it: To solve this problem, you'll need to know exponent rules. Here are some of the ones you should know for the SAT and many other standardized tests: b m b n = b m + n. b m b n = b m − n. ( b m) n = b m ⋅ n. b m c m = ( b c) m.
Hello My Dears and Sweet Family 🥰🥰I Hope You all are Doing Well👍👍you are reading this ️In this YouTube video, we tackle one of the hardest math problems...
Solve problems using definitions, properties, and theorems relating to circles, radii, diameters, tangents, angles, arc lengths, and sector areas. This skill may include working with ordered pairs, converting angle measures between degrees and radians, creating and interpreting graphs of circles, using the distance formula, using the unit ...
The team now had an algorithm that could, theoretically, solve their problem. They just had to train it first. New Paths. Like all neural networks, AlphaTensor needs a lot of data to train on, but tensor decomposition is a notoriously hard problem. There were few examples of efficient decompositions that the researchers could feed the network.
President Biden's disastrous debate performance last week set off a furious discussion among Democratic officials, donors and strategists about whether and how to replace him as the party's ...