word problems absolute value inequalities

Word Problems with Absolute Value Inequalities - Expii

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Last modified on April 17th, 2024

Inequality Word Problems

Inequalities are common in our everyday life. They help us express relationships between quantities that are unequal. Writing and solving word problems involving them helps develop our problem-solving approach, understanding, logical reasoning, and analytical skills.

Here are the 4 main keywords commonly used to write mathematical expressions involving inequalities.   

• At least →  ‘greater than or equal to’
• More than → ‘greater than’
• No more than or at most → ‘less than or equal to’
• Less than → ‘less than’

To participate in the annual sports day, Mr. Adams would like to have nine students in each group. But fewer than 54 students are in class today, so Mr. Adams is unable to make as many full groups as he wants. How many full groups can Mr. Adams make? Write the inequality that describes the situation.

Let ‘x’ be the total number of groups Mr. Adams can make. Since each group has 9 students, the total number of students in ‘x’ groups is 9x As we know, fewer than 54 students are in a class today. Thus, the inequality that represents the situation is: 9x < 54 On dividing both sides by 9, the maximum number of groups Mr. Adams can make is  x < 6 Thus, Mr. Adams can make a maximum of 6 full groups.

 Bruce needs at least \$561 to buy a new tablet. He has already saved \$121 and earns \$44 per month as a part-timer in a company. Write the inequality and determine how long he has to work to buy the tablet.

Let ‘x’ be the number of months Bruce needs to work. As we know,  The amount already saved by Bruce is \$121 He earns \$44 per month The cost of the tablet is at least \$561 After ‘x’ months of work, Bruce will have \$(121 + 44x) Now, the inequality representing the situation is: 121 + 44x ≥ 561 On subtracting 121 from both sides, 121 + 44x – 121 ≥ 561 – 121 ⇒ 44x ≥ 440 On dividing both sides by 44, x ≥ 10 Thus, Bruce needs to work for at least 10 months to buy the new tablet.

A store is offering a \$26 discount on all women’s clothes. Ava is looking at clothes originally priced between \$199 and \$299. How much can she expect to spend after the discount?

Let ‘x’ be the original price of the clothes Ava chooses. As we know, the original price range is 199 ≤ x ≤ 299, and the discount is \$26 Now, Ava pays \$(x – 26) after the discount. Thus, the inequality is: 199 – 26 ≤ x – 26 ≤ 299 – 26 ⇒ 173 ≤ x – 26 ≤ 273 Thus, she can expect to spend between \$173 and \$273 after the discount.

A florist makes a profit of \$6.25 per plant. If the store wants to profit at least \$4225, how many plants does it need to sell?

Let ‘P’ be the profit, ‘p’ be the profit per plant, and ‘n’ be the number of plants.  As we know, the store wants a profit of at least \$4225, and the florist makes a profit of \$6.25 per plant. Here, P ≥ 4225 and p = 6.25 …..(i) Also, P = p × n Substituting the values of (i), we get 6.25 × n ≥ 4225 On dividing both sides by 6.25, we get ${n\geq \dfrac{4225}{6\cdot 25}}$ ⇒ ${n\geq 676}$ Thus, the store needs to sell at least 676 plants to make a profit of \$4225.

Daniel had \$1200 in his savings account at the start of the year, but he withdraws \$60 each month to spend on transportation. He wants to have at least \$300 in the account at the end of the year. How many months can Daniel withdraw money from the account?

As we know, Daniel had \$1200 in his savings account at the start of the year, but he withdrew \$60 for transportation each month.  Thus, after ‘n’ months, he will have \$(1200−60n) left in his account. Also, Daniel wants to have at least \$300 in the account at the end of the year.  Here, the inequality is: 1200 – 60n ≥ 300 ⇒ 1200 – 60n – 1200 ≥ 300 – 1200 (by subtraction property) ⇒ -60n ≥ -900 ⇒ 60n ≤ 900 (by inversion property) ⇒ n ≤ ${\dfrac{900}{60}}$ ⇒ n ≤ 15 Thus, Daniel can withdraw money from the account for at most 15 months.

Anne is a model trying to lose weight for an upcoming beauty pageant. She currently weighs 165 lb. If she cuts 2 lb per week, how long will it take her to weigh less than 155 lb?

Let ‘t’ be the number of weeks to weigh less than 155 lb. As we know, Anne initially weighs 165 lb After ‘t’ weeks of cutting 2 lb per week, her weight will be 165 – 2t Now, Anne’s weight will be less than 155 lb Here, the inequality from the given word problem is: 165 – 2t < 155 On subtracting 165 from both sides, we get 165 – 2t – 165 < 155 – 165 ⇒ – 2t < -10 On dividing by -2, the inequality sign is reversed. ${\dfrac{-2t}{-2} >\dfrac{-10}{-2}}$ ⇒ t > 5

Rory and Cinder are on the same debate team. In one topic, Rory scored 5 points more than Cinder, but they scored less than 19 together. What are the possible points Rory scored?

Let Rory’s score be ‘r,’ and Cinder’s score be ‘c.’ As we know, Rory scored 5 points more than Cinder. Thus, Rory’s score is r = c + 5 …..(i) Also, their scores sum up to less than 19 points. Thus, the inequality is: r + c < 19 …..(ii) Substituting (i) in (ii), we get (c + 5) + c < 19 ⇒ 2c + 5 < 19 On subtracting 5 from both sides, we get 2c + 5 – 5 < 19 – 5 ⇒ 2c < 14 On dividing both sides by 2, we get ${\dfrac{2c}{2} >\dfrac{14}{2}}$ ⇒ c < 7 means Cinder’s score is less than 7 points. Now, from (i), r = c + 5 ⇒ c = r – 5 Thus, c < 7 ⇒ r – 5 < 7 On adding 5 to both sides, we get r – 5 + 5 < 7 + 5 ⇒ r < 12 means Rory’s score is less than 12 points. Hence, Rory’s scores can be 6, 7, 8, 9, 10, or 11 points.

An average carton of juice cans contains 74 pieces, but the number can vary by 4. Find out the maximum and minimum number of cans that can be present in a carton.

Let ‘c’ be the number of juice cans in a carton. As we know, the average number of cans in a carton is 74, and it varies by 4 cans. Thus, the required inequality is |c – 74| ≤ 4 ⇒ -4 ≤ c – 74 ≤ 4 On adding 74 to each side, we get -4 + 74 ≤ c – 74 + 74 ≤ 4 + 74 ⇒ 70 ≤ c ≤ 78 Hence, the minimum number of cans in a carton is 70, and the maximum number is 78.

 Layla rehearses singing for at least 12 hours per week, for three-fourths of an hour each session. If she has already sung 3 hours this week, how many more sessions remain for her to exceed her weekly practice goal?

Let ‘p’ be Layla’s total hours of practice in a week, and ‘s’ be the number of sessions she needs to complete. As we know, Layla has already rehearsed 3 hours, then her remaining rehearsal time is (p – 3) Each session lasts for three-fourths of an hour. Thus, we have the inequality: ${\dfrac{3}{4}s >p-3}$ …..(i) As we know, Layla rehearses for at least 12 hours, which means p ≥ 12 …..(ii) From (i), ${\dfrac{3}{4}s >p-3}$ ⇒ ${s >\dfrac{4}{3}\left( p-3\right)}$ From (ii), substituting the value p = 12 in (i), we get ${s >\dfrac{4}{3}\left( 12-3\right)}$ ⇒ ${s >\dfrac{4}{3}\cdot 9}$ ⇒ s > 12 Thus, Layla must complete more than 12 sessions to exceed her weekly rehearsal goal.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Absolute Value Inequalities

Solving absolute value inequalities.

In this lesson, we are going to learn how to solve absolute value inequalities using the standard approach usually taught in an algebra class. That is, learn the rules and apply them correctly. There are four cases involved when solving absolute value inequalities.

CAUTION: In all cases, the assumption is that the value of “[latex]a[/latex]” is positive, that is, [latex]a > 0[/latex].

Four (4) Cases to Consider When Solving Absolute Value Inequalities

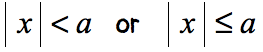
The absolute value of any number is either zero [latex](0)[/latex] or positive which can never be less than or equal to a negative number.

The answer to this case is always no solution .

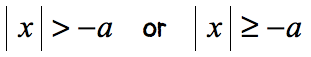
The absolute value of any number is either zero [latex](0)[/latex] or positive. It makes sense that it must always be greater than any negative number.

The answer to this case is always all real numbers

Examples of How to Solve Absolute Value Inequalities

Example 1 : Solve the absolute value inequality.

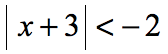
If you’re not familiar yet with the different cases, I suggest that you keep a copy of the list of cases above as a reference. This will definitely help you solve the problems easily.

The problem suggests that there exists a value of “[latex]x[/latex]” that can make the statement true. Well, the absolute value of something is always zero or positive which is never less than a negative number. This statement must be false, therefore, there is no solution . This is an example of case 3 .

Pick some test values to verify:

• If [latex]x[/latex] is positive, say, [latex]x = 5[/latex];

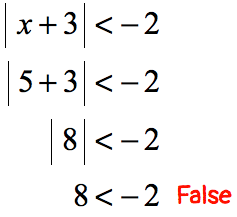
• If [latex]x[/latex] is zero;

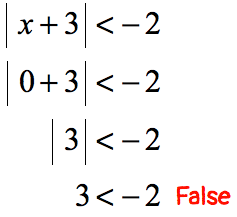
• If [latex]x[/latex] is negative, say, [latex]x = -5[/latex];

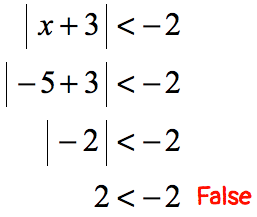
Example 2 : Solve the absolute value inequality.

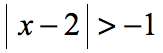
If you think about it, any values of “[latex]x[/latex]” can make the statement true. Test some numbers including zero, and any negative or positive number. What do you get?

Remember, the absolute value expression will yield a zero or positive answer which is always greater than a negative number. Therefore, the answer is all real numbers . This is case 4 .

Example 3 : Solve the absolute value inequality.

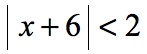
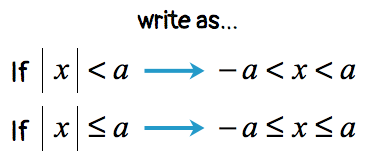
This is a “less than” absolute value inequality which is an example of case 1 . Get rid of the absolute value symbol by applying the rule. Then solve the linear inequality that arises.

The goal is to isolate the variable “[latex]x[/latex]” in the middle. To do that, we subtract the left, middle, and right parts of the inequality by [latex]6[/latex].

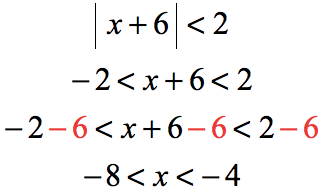
The answer in the form of the inequality symbol states that the solutions are all the values of [latex]x[/latex] between [latex]-8[/latex] and [latex]-4[/latex] but not including [latex]-8[/latex] and [latex]-4[/latex] themselves.

We can also write the answer in interval notation using parenthesis to denote that [latex]-8[/latex] and [latex]-4[/latex] are not part of the solutions.

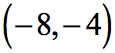
Or, write the answer on a number line where we use open circles to exclude [latex]-8[/latex] and [latex]-4[/latex] from the solution.

Example 4 : Solve the absolute value inequality.

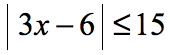
This is a “less than or equal to” absolute value inequality which still falls under case 1 . Clear out the absolute value symbol using the rule and solve the linear inequality.

Isolate the variable “[latex]x[/latex]” in the middle by adding all sides by [latex]6[/latex] and then dividing by [latex]3[/latex] (coefficient of [latex]x[/latex]).

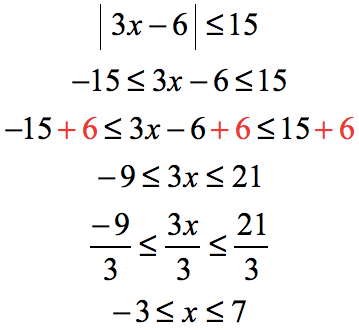
The inequality symbol suggests that the solution are all values of [latex]x[/latex] between [latex]-3[/latex] and [latex]7[/latex], and also including the endpoints [latex]-3[/latex] and [latex]7[/latex]. We include the endpoints because we are using the symbol “[latex]≤[/latex]”.

To write the answer in interval notation, we will utilize the square brackets instead of the regular parenthesis to denote that [latex]-3[/latex] and [latex]7[/latex] are part of the solution.

And finally, we will use closed or shaded circles to show that [latex]-3[/latex] and [latex]7[/latex] are included.

Example 5 : Solve the absolute value inequality.

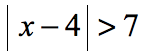
This is an example of a “greater than” absolute value inequality which is an example of case 2 . Let’s eliminate the absolute value expression using the rule below.

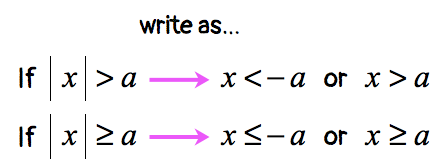
As you can see, we are solving two separate linear inequalities.

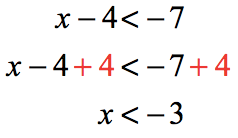
In interval notation, the word “ or ” is replaced by the symbol “[latex] \cup [/latex]” to mean “ union “. The union of sets means that we are putting together the non-overlapping elements of two or more sets of solutions.

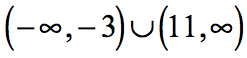
The answer in interval notation makes more sense if you see how it looks on the number line. In case 2, the arrows will always be in opposite directions. The open circles imply that [latex]-3[/latex] and [latex]7[/latex] are not included in the solutions which are the consequence of the symbol “[latex]>[/latex]”.

Example 6 : Solve the absolute value inequality.

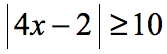
Break this up into two linear inequalities, and then solve each separately. Here’s the rule for case 2 .

Here’s the solution.

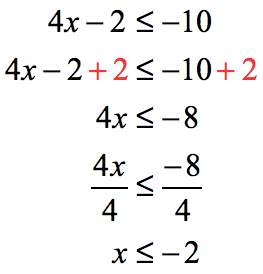
For the interval notation, we use the square brackets to include [latex]-2[/latex] and [latex]3[/latex] in the solution.

The shaded or closed circles signify that [latex]-2[/latex] and [latex]3[/latex] are part of the solution. In case 2, the arrows will always point to opposite directions.

You may also be interested in these related math lessons or tutorials:

Solving Absolute Value Equations

Graphing Absolute Value Functions

Absolute Value Inequality

How to solve absolute value inequalities, general formula.

In the picture below, you can see generalized example of absolute value equation and also the topic of this web page: absolute value inequalities .

The diagram below illustrated the difference between an absolute value equation and two absolute value inequalities

Absolute Value Inequality Calculator

Enter any values for A,b and c for any absolute value equation |A x + b| = c into the text boxes below and this solver will calculate your answer and show all of the steps!

Practice Problems

Solve the absolute value inequality below: $$| x -1 | \ge 2 $$

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Inequalities with Absolute Value – Examples and Practice Problems

Inequalities with absolute value follow the same rules as an absolute value in numbers; the difference is that in inequalities we have a variable. In this article, we will look at a brief introduction to inequalities with absolute value and we will learn a method for solving problems related to inequalities with absolute value.

Finally, we will look at some examples with answers to improve our understanding of the concepts.

Relevant for …

Solving exercises of inequalities with absolute value.

See process

What are inequalities with absolute value

How to solve inequalities with absolute value, inequalities with absolute value – examples with answers, inequalities with absolute value – practice problems.

Before we analyze inequalities with absolute value, let’s start by looking at a brief summary of the absolute value of a number.

Let’s start with the definition: the absolute value of a number is the distance of a value from the origin regardless of direction. The absolute value is denoted by two vertical lines that enclose the number or expression.

For example, the absolute value of  x  is expressed as $latex |x|=a$, which means that $latex x=+a$ and $latex x=-a$. Now, let’s see what inequalities with absolute value mean.

An inequality with absolute value is an expression that contains the absolute value function, as well as the absolute value signs. For example, the expression $latex | x +5|> 2$ is an inequality with an absolute value that contains a “greater than” sign.

We have four different inequality symbols: greater than (>), less than (<), greater than or equal to (≥), and less than or equal to (≤).

The following are inequalities with absolute value:

• $latex \left| x+1\right|<3$
• $latex \left| x-2\right|≥5$
• $latex \left| x+5\right|>1$

The steps to solve inequalities with absolute value are similar to the steps to solve equations, with the difference that we have to take into account a little extra information to solve the inequalities.

The following steps are general rules that can be followed to solve these types of algebraic problems:

Step 1:  Completely isolate the expression with the absolute value.

Step 2:  Solve the positive and negative versions of the absolute value inequalities.

• When the number on the other side of the inequality sign is negative, we conclude that either all real numbers are solutions or that the inequality has no solution.
• When the number on the other side is positive, we proceed to form a compound inequality by removing the bars from the absolute value.

Step 3:  The type of inequality sign determines the format of the compound inequality to be formed.

• If a problem contains greater than or greater/equal than signs, form a compound inequality as follows:

(values ​​within the absolute value sign)  < – (the number on the other side) or (values ​​within the absolute value sign) >  (the number on the other side)

• In the same way, if a problem contains less than or less/equal than signs, it forms an inequality composed of three parts as follows:

 (the number on the other side of the sign) < (values ​​within the absolute value sign) < (the number on the other side of the sign)

Step 4:  Solve the inequalities.

Solve the inequality $latex |x+4|-6<9$.

Step 1:  Solve for the absolute value:

$latex |x+4|-6<9$

$latex |x+4|<9+6$

$latex |x+4|<15$

Step 2:  Is the number on the other side negative? No, it is a positive number, 15. We move on to step 3.

Step 3:  Form a compound inequality: The inequality sign in this problem is a less than sign, so we form a three-part inequality:

$latex -15<x+4<15$

Step 4:  Solve the inequality:

$latex -15-4<x<15-4$

$latex -19<x<11$

Solve the inequality $latex |2x-1|-7≥-3$.

$latex |2x-1|-7≥-3$

$latex |2x-1|≥-3+7$

$latex |2x-1|≥4$

Step 2:  Is the number on the other side negative? No, it is a positive number, 4. We move on to step 3.

Step 3:  Form a compound inequality: The inequality sign in this problem is a greater/equal than sign, so we form a compound inequality with the word “or”:

$latex 2x-1≤-4$   o   $latex 2x-1≥4$

Step 4: : Solve the inequalities:

$latex 2x-1≤-4$   or   $latex 2x-1≥4$

$latex 2x≤-3$   or   $latex 2x≥5$

$latex x\le -\frac{3}{2}$  or  $latex x\ge \frac{5}{2}$

Solve the inequality $latex |5x+6|+4<1$.

$latex |5x+6|+4<1$

$latex |5x+6|<1-4$

$latex |5x+6|<-3$

Step 2:  Is the number on the other side negative? Yes, it is a negative number, -3. We will look at the signs on each side of the inequality to determine the solution to the problem:

positive $latex <$ negative

This statement is never true, so the problem has no solution.

Solve the inequality $latex |3x-4|+9>5$.

$latex |3x-4|+9>5$

$latex |3x-4|>5-9$

$latex |3x-4|>-4$

Step 2:  Is the number on the other side negative? Yes, it is a negative number, -4. Let’s look at the signs on each side of the inequality to determine the solution to the problem:

positive $latex >$ negative

This statement is always true, so the solution to the problem is all real numbers.

Solve the inequality $latex |2x-4|\leq 6$.

Choose an answer

Solve the inequality $latex 9-2|4x+1|>3$.

Solve the inequality $latex |2-6x|>10$..

Interested in learning more about absolute value? Take a look at these pages:

• Characteristics of Absolute Value Functions
• Absolute Value – Definition and Applications

Jefferson Huera Guzman

Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas

All rights reserved.

INFORMATION

Terms and Conditions

Privacy Policy

About Neurochispas

About the Author

Absolute Value Word Problems Worksheets

Health Word Problems

Gift Giving

Planet Math

Growing Plants

Fairy Tales

Comic Characters

About These 15 Worksheets

Absolute value word problems worksheets are  designed to teach and practice the concept of absolute value in the context of real-world situations. Absolute value is a mathematical term that represents the distance of a number from zero on the number line, regardless of direction, so it is always a non-negative value. These worksheets typically include word problems that require students to think about and apply absolute value in various scenarios.

Types of problems you might expect to see on such worksheets include:

Comparisons of Measurements – Problems where students must find the absolute difference between two measurements, such as heights, distances, temperatures, or weights.

Financial Situations – Scenarios involving profit and loss, price differences, or account balance changes.

Sports Statistics – Situations comparing scores, times, or points between players or teams.

Scientific Data – Problems involving pH levels, altitude changes, or temperature variations where students determine the absolute change. Here’s an example of an absolute value word problem:

Problem: During a week of fundraising, the school’s soccer team raised $350 on Monday. Due to some unforeseen expenses, they ended up using $150 of the raised funds on Tuesday. What is the absolute value of the difference in the soccer team’s funds from Monday to Tuesday?

Solution: To find the absolute value of the difference in the team’s funds, we subtract the smaller number from the larger number and ignore the sign of the result:

Absolute Difference = |$350 – (-$150)| = |$350 + $150| = |$500| = $500

So, the absolute value of the difference in the soccer team’s funds from Monday to Tuesday is $500.

What Are Absolute Value Word Problems?

Absolute value word problems involve using the concept of absolute value to solve real-life situations or scenarios. Absolute value represents the distance of a number from zero on a number line, regardless of its direction. In word problems, absolute value is often used to represent a magnitude or a distance, and it is denoted by vertical bars (| |).

Absolute value word problems can cover various topics and contexts, such as distances, temperatures, time intervals, financial transactions, and more. These problems typically require determining the absolute value of a quantity or comparing absolute values to find a solution.

For example, here’s a simple absolute value word problem:

Problem: A football team gains or loses yardage on each play. On one play, the team loses 12 yards. On the next play, they gain 8 yards. What is the total yardage change?

Solution: To find the total yardage change, we need to calculate the absolute value of the sum of the yardage gained and lost. In this case, the team lost 12 yards and gained 8 yards. So, the total yardage change is |(-12) + 8| = |-4| = 4 yards. Therefore, the total yardage change is 4 yards.

Absolute value word problems can become more complex, involving multiple quantities, comparisons, or inequalities. However, the underlying principle remains the same—finding the absolute value of a quantity to represent a magnitude or distance in the problem context.

How to Solve These Types of Problems

Solving absolute value word problems involves understanding the concept of absolute value and applying it to real-life scenarios. Here’s a step-by-step guide to help you solve absolute value word problems:

Begin by thoroughly understanding the problem statement. Identify the information provided and what you’re being asked to find. Pay attention to keywords and phrases that indicate the use of absolute value, such as “distance,” “deviation,” or “magnitude.”

Identify the absolute value expression – Look for the specific quantity or expression within the problem that is enclosed within absolute value symbols (| |). This expression represents the magnitude or distance from zero.

Set up the equation – Create an equation based on the information provided in the problem. Consider two scenarios – one where the absolute value expression is positive and another where it is negative. Set up the equation accordingly.

Solve for both cases – Solve the equation for each case you identified in the previous step. Remove the absolute value symbols and isolate the variable to find its possible values.

Check your solutions – Substitute the potential solutions back into the original problem and evaluate if they satisfy the given conditions. For absolute value problems involving distances, ensure that the solutions make sense within the context of the problem. State the final solution or solutions based on the context of the problem. Depending on the problem, you may need to provide a single answer, a range of values, or a set of possible solutions.

Check for extraneous solutions – Sometimes, when solving absolute value equations, extraneous solutions may arise. These are solutions that do not satisfy the original problem conditions. Double-check your solutions and ensure they are valid.

This Skill In The Real World

Here are a few examples of situations where absolute value is used:

Distance and Displacement – Absolute value is commonly used to represent distances or displacements. For instance, if you are calculating the distance between two cities or the displacement of an object from its initial position, you would use absolute value to ensure the result is positive.

Temperature – Absolute value can be used in temperature-related problems. For example, if you need to determine the difference in temperature between two points, you would take the absolute value to obtain a positive value regardless of whether one temperature is higher or lower than the other.

Finance and Economics – Absolute value is relevant in finance and economics when dealing with measures of deviation or error. For instance, calculating the absolute value of the difference between an actual value and an expected value can help determine the magnitude of the deviation or error.

Optimization and Constraints – In optimization problems, where you aim to maximize or minimize a certain quantity, absolute value can be used to express constraints. For example, if you have a constraint that the difference between two variables must be less than a certain value, you would use absolute value to formulate the constraint.

Physics and Science – Absolute value is frequently used in physics and other sciences. It can represent quantities like velocity, acceleration, force, or electric charge, where direction may not be relevant, and only the magnitude matters.

What Types of Jobs and Careers Use This Skill?

Several professions and fields require regularly solving absolute value word problems as part of their job responsibilities. Here are a few careers where the use of absolute value is common:

• Mathematics and Statistics – Mathematicians and statisticians often encounter absolute value word problems in their work. They use absolute value to analyze data, measure distances, calculate deviations, and solve various mathematical equations and inequalities.
• Physics and Engineering – Professionals in physics and engineering regularly work with absolute value concepts. They apply absolute value when dealing with measurements, vectors, forces, distances, and deviations in various physical phenomena.
• Economics and Finance – Economists and financial analysts frequently use absolute value in their work. They apply it to analyze deviations, calculate errors, measure differences, and determine the magnitude of changes in economic indicators, financial data, or investment returns.
• Operations Research and Optimization – Professionals in operations research and optimization use absolute value to formulate constraints and objective functions in mathematical models. They often encounter absolute value word problems when optimizing processes, resource allocation, scheduling, or decision-making.
• Data Analysis and Machine Learning – Data analysts and machine learning specialists encounter absolute value problems when working with datasets. They use absolute value to calculate error metrics, evaluate model performance, handle outliers, or measure distances between data points.
• Geography and Navigation – Geographers, cartographers, and navigation experts may use absolute value when calculating distances between locations or analyzing spatial data. Absolute value helps measure the magnitude of differences or deviations in geographic coordinates.
• Transportation and Logistics – Professionals in transportation and logistics rely on absolute value to solve problems related to routes, distances, and delivery times. They may use it to minimize deviations, calculate optimal paths, or evaluate the efficiency of transportation networks.

Have an account?

Absolute Value Inequalities and Word Pro...

9th - 12th grade, mathematics.

Absolute Value Inequalities and Word Problems

10 questions

Introducing new   Paper mode

No student devices needed.   Know more

• 4. Multiple Choice Edit 15 minutes 1 pt The radius of the gears produced at a factory must be 6 inches in length with a tolerance of 0.1 inches. The gears with radius beyond the tolerated lengths will be thrown away. Which of the following inequalities can be used to assess which gears are eligible? (x is the length of the radius) |x – 6| ≤ 0.1 |x – 6| ≥ 0.1 |x – 0.1| ≤ 6 |x – 0.1| ≥ 6
• 5. Multiple Choice Edit 15 minutes 1 pt Your have money in your wallet, but you don't know the exact amount. When a friend asks you, you say that you have 50 dollars give or take 15. Write an absolute value equation to model this situation. |x-50|=15 |x+15|=50 |50+x|=15 No Solution
• 6. Multiple Choice Edit 15 minutes 1 pt A company sells 20-ounce bottles of sports drink. The actual volume of liquid in the bottle must be within 0.03 ounces. What equation can be solved to find the minimum and maximum volume of liquid in a bottle. |v|-20=0.03 |v-20|=0.03 |v|-0.03=20 |v-0.03|=20

The street built in the city must be 25 feet in width with a tolerance of 0.5 feet. Streets that are not within the tolerated widths must be repaired. Which street width below would NOT have to be repaired?

24 feet, 10 inches

24 feet, 3 inches

25 feet, 7 inches

25 feet, 11 inches

• 8. Multiple Choice Edit 15 minutes 1 pt John is looking for a job after graduation. The salary which he is satisfied with must be $3000 with a tolerance of $500. Choose the salary John would accept. $3,478 $3,792 $2,489 $2,256
• 9. Multiple Choice Edit 2 minutes 1 pt Solve: 3 | 2x + 7| - 7 < -4 x < -3 and x > -5/3 x < -3 and x > -4 all real numbers no solution
• 10. Multiple Choice Edit 5 minutes 1 pt Solve. |d + ⅔| + ¾ = 0 no solution d = -9 or ½ d = -¾ or d = 9 d = -1/12 or d = -7/12

Explore all questions with a free account

Continue with email

Continue with phone

How Do You Solve a Word Problem Using an AND Absolute Value Inequality?

Word problems allow you to see math in action! This tutorial shows you how to translate a word problem to an absolute value inequality. Then see how to solve for the answer, write it in set builder notation, and graph it on a number line. Learn all about it in this tutorial!

• word problem
• translate words to algebra
• absolute value
• compound inequality
• set builder notation
• number line
• graph on number line
• absolute value inequality

Background Tutorials

Evaluating expressions.

What is a Variable?

You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!

Working with Integers

What's an Inequality?

Inequalities come up all the time when you're working algebra problems. In this tutorial you'll learn what an inequality is, and you'll see all the common inequality symbols that you're likely to see :)

Absolute Value

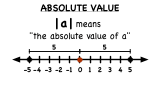
What Does Absolute Value Mean?

In this tutorial you'll see how you can think of absolute value in a very intuitive way. Let us know if you have any questions about it!

Compound Inequalities

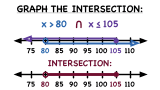
How Do You Graph the Intersection of Two Inequalities?

Number lines help make graphing the intersection of two inequalities a breeze! This tutorial shows you how to graph two inequalities on the same number line and then find the intersection. Take a look!

Solving Absolute Value Inequalities

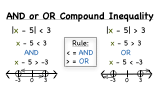
How Do You Figure Out if an Absolute Value Inequality is an AND or OR Compound Inequality?

When does an absolute value inequality represent an AND compound inequality? When does it represent an OR compound inequality? This tutorial will give you the answer and show you using examples on a number line!

Graphs of Inequalities

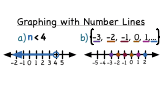
How Do You Graph an Inequality or an Infinite Set on a Number Line?

Number lines are really useful in visualizing an inequality or a set. In this tutorial, you'll see how to graph both. Take a look!

Solving Multi-Step Inequalities

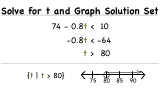
How Do You Solve and Graph a Two-Step Inequality?

Solving an inequality for a variable? Just perform the order of operations in reverse! Don't forget that if you multiply or divide by a negative number, you MUST flip the sign of the inequality! That's one of the big differences between solving equalities and solving inequalities.

Further Exploration

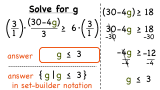
How Do You Solve a Multi-Step Inequality Using Reverse Order of Operations?

• Terms of Use

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Solving absolute value inequalities

When solving absolute value inequalities, the process is very similar to solving absolute value equations . You should review the latter before studying this lesson.

Solving absolute value inequalities using the definition of absolute value.

Notice that the smaller sign (<) was switched to a bigger sign (>). This happens whenever you divide or multiply inequalities by a negative number.

Absolute value

How to solve absolute value equations

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

absolute value inequalities word problems,, which sign to use

I have the below absolute value inequalities word problem, I was able to get the answer but had to solve it by trying both <= and >= and then working out which one was correct. But the videos I see online for example, the authors seem to know the sign right away, without having to try both way. Could someone explain how to get the sign without working out the problem, also is it always <= as everything I see online it's always <=.

Here is the problem: The height of the plan must be within 2 inches of the standard 13-inch show size

|h - 13| ≤ 2

was the solution. Reading the problem, I know it's either 11 or 15.

When I solved it I tried both |height of the plan - 13| ≤ 2 and |height of the plan - 13| ≥ 2

worked them out to see the possible values to get ≤ as the correct sign, since the values can be 11 or 15.

• absolute-value
• word-problem

You can break up one absolute value inequality into two simultaneous inequalities.

$|h-13|\le 2 \iff -2 \le h-13\le 2 \implies 11 \le h \le 15. $

• $\begingroup$ seeing it that way helps, does that mean when we solve these types of problems, it's always ≤ ? or can it ever be ≥? Word problems where they mention a range, like here where it's either 11 or 15. if a range is there is it always ≤ $\endgroup$ –  Paritosh Commented Oct 26, 2023 at 0:09
• $\begingroup$ You can use either so long as you don't accidently switch them. I think $\le$ is recommended though, just be sure you always but the lesser term on the left. Makes calculations easier with consistency and lots of text seem to go that route. $\endgroup$ –  TurlocTheRed Commented Oct 26, 2023 at 4:40

You must log in to answer this question.

Not the answer you're looking for browse other questions tagged inequality absolute-value word-problem ..

• Featured on Meta
• We spent a sprint addressing your requests — here’s how it went
• Upcoming initiatives on Stack Overflow and across the Stack Exchange network...

Hot Network Questions

• Should you use __pc fields in all cases for Person Accounts?
• 为什么字形不同的两个字「骨」的编码相同（从而是一个字）？
• im2double and im2uint8 Functions Implementation for Image in C++
• Minimum number of select-all/copy/paste steps for a string containing n copies of the original
• Any alternative to lockdown browser?
• Zener behaving strangely
• Segments of a string, doubling in length
• Seeing perfectly camouflaged objects
• Could two moons orbit each other around a planet?
• Sum of the vectors to each of the vertices of the polygon
• Control Blending Mode of the Color Mix node through the custom driver
• Do you always experience the gravitational influence of other mass as you see them in your frame?
• Converting cif file with powdll, plotting cif file in excel
• Why was this a draw?
• Two definitions of a monad on an ∞-category
• Can you be charged with breaking and entering if the door was open, and the owner of the property is deceased?
• Gradual light transition
• Plane to train in Copenhagen
• Are directed graphs with out-degree exactly 2 strongly connected with probability 1?
• Measure by mass vs. 'Spooned and Leveled'
• flalign's odd behavior with double ampersands (&&)
• Why does independent research from people without formal academic qualifications generally turn out to be a complete waste of time?
• Cliffhanger ending?
• Why are responses to an attack in a cycling race immediate?