problem solving involving polynomial equation

Polynomial Equation Word Problems (Mixed Operations)

These lessons help Algebra students learn how to write and solve polynomial equations for algebra word problems.

Related Pages Solving Challenging Word Problems Math Word Problems More Algebra Lessons

How To Solve Polynomial Equation Word Problem?

Example: A tree is supported by a wire anchored in the ground 5 feet from its base. The wire is 1 foot longer than the height that it reaches on the tree. Find the length of the wire.

Polynomial Equation Word Problem

Example: A gymnast dismounts the uneven parallel bars. Her height, h, depends on the time, t, that she is in the air as follows: h = -16t 2 + 8t + 8 a) How long will it take the gymnast to reach the ground? b) When will the gymnast be 8 feet above the ground?

How To Solve Word Problems With Polynomial Equations?

The sum of a number and its square is 72. Find the number.
The area of a triangle is 44m 2 . Find the lengths of the legs if one of the legs is 3m longer than the other leg.
The top of a 15-foot ladder is 3 feet farther up a wall than the foo is from the bottom of the wall. How far is the ladder from the bottom of the wall?
A projectile is launched upward from ground level with an initial speed of 98m/s. How high will it go? When will it return to the ground?

How To Write Polynomials For Word Problems?

Learn to write a polynomial for Word problems involving perimeter and area of rectangles and circles.

Learn How To Write And Solve Polynomial Equations

Learn to write and solve polynomial equations for special integers, consecutive integers.

Example 1: Find a number that is 56 less than its square. Let n be the number. Example 2: Find two consecutive odd integers whose sum is 130.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Polynomial Questions and Problems with Solutions

Polynomial questions and problems related to graphs, x and y intercepts, coefficients, degree, leading coefficients, ... with detailed solutions are presented.

problem solving involving polynomial equation

4.4 Solve Polynomial Equations by Factoring

Learning objectives.

Review general strategies for factoring.
Solve polynomial equations by factoring.
Find roots of a polynomial function.
Find polynomial equations given the solutions.

Reviewing General Factoring Strategies

We have learned various techniques for factoring polynomials with up to four terms. The challenge is to identify the type of polynomial and then decide which method to apply. The following outlines a general guideline for factoring polynomials:

Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF).

Determine the number of terms in the polynomial.

Factor four-term polynomials by grouping.
Factor trinomials (3 terms) using “trial and error” or the AC method.

Factor binomials (2 terms) using the following special products:

Look for factors that can be factored further.
Check by multiplying.

Note : If a binomial is both a difference of squares and a difference cubes, then first factor it as difference of squares. This will result in a more complete factorization. In addition, not all polynomials with integer coefficients factor. When this is the case, we say that the polynomial is prime.

If an expression has a GCF, then factor this out first. Doing so is often overlooked and typically results in factors that are easier to work with. Furthermore, look for the resulting factors to factor further; many factoring problems require more than one step. A polynomial is completely factored when none of the factors can be factored further.

Factor: 54 x 4 − 36 x 3 − 24 x 2 + 16 x .

This four-term polynomial has a GCF of 2 x . Factor this out first.

54 x 4 − 36 x 3 − 24 x 2 + 16 x = 2 x ( 27 x 3 − 18 x 2 − 12 x + 8 )

Now factor the resulting four-term polynomial by grouping and look for resulting factors to factor further.

Answer: 2 x ( 3 x − 2 ) 2 ( 3 x + 2 ) . The check is left to the reader.

Factor: x 4 − 3 x 2 − 4 .

This trinomial does not have a GCF.

x 4 − 3 x 2 − 4 = ( x 2 ) ( x 2 ) = ( x 2 + 1 ) ( x 2 − 4 ) D i f f e r e n c e o f s q u a r e s = ( x 2 + 1 ) ( x + 2 ) ( x − 2 )

The factor ( x 2 + 1 ) is prime and the trinomial is completely factored.

Answer: ( x 2 + 1 ) ( x + 2 ) ( x − 2 )

Factor: x 6 + 6 x 3 − 16 .

Begin by factoring x 6 = x 3 ⋅ x 3 and look for the factors of 16 that add to 6.

The factor ( x 3 − 2 ) cannot be factored any further using integers and the factorization is complete.

Answer: ( x 3 − 2 ) ( x + 2 ) ( x 2 + 2 x + 4 )

Try this! Factor: 9 x 4 + 17 x 2 − 2

Answer: ( 3 x + 1 ) ( 3 x − 1 ) ( x 2 + 2 )

Solving Polynomial Equations by Factoring

In this section, we will review a technique that can be used to solve certain polynomial equations. We begin with the zero-product property A product is equal to zero if and only if at least one of the factors is zero. :

a ⋅ b = 0 if and only if a = 0 or b = 0

The zero-product property is true for any number of factors that make up an equation. In other words, if any product is equal to zero, then at least one of the variable factors must be equal to zero. If an expression is equal to zero and can be factored into linear factors, then we will be able to set each factor equal to zero and solve for each equation.

Solve: 2 x ( x − 4 ) ( 5 x + 3 ) = 0 .

Set each variable factor equal to zero and solve.

2 x = 0 or x − 4 = 0 or 5 x + 3 = 0 2 x 2 = 0 2 x = 4 5 x 5 = − 3 5 x = 0 x = − 3 5

To check that these are solutions we can substitute back into the original equation to see if we obtain a true statement. Note that each solution produces a zero factor. This is left to the reader.

Answer: The solutions are 0, 4, and − 3 5 .

Of course, most equations will not be given in factored form.

Solve: 4 x 3 − x 2 − 100 x + 25 = 0 .

Begin by factoring the left side completely.

4 x 3 − x 2 − 100 x + 25 = 0 F a c t o r b y g r o u p i n g . x 2 ( 4 x − 1 ) − 25 ( 4 x − 1 ) = 0 ( 4 x − 1 ) ( x 2 − 25 ) = 0 F a c t o r a s a d i f f e r e n c e o f s q u a r e s . ( 4 x − 1 ) ( x + 5 ) ( x − 5 ) = 0

Set each factor equal to zero and solve.

4 x − 1 = 0 or x + 5 = 0 or x − 5 = 0 4 x = 1 x = − 5 x = 5 x = 1 4

Answer: The solutions are 1 4 , −5, and 5.

Using the zero-product property after factoring an equation that is equal to zero is the key to this technique. However, the equation may not be given equal to zero, and so there may be some preliminary steps before factoring. The steps required to solve by factoring The process of solving an equation that is equal to zero by factoring it and then setting each variable factor equal to zero. are outlined in the following example.

Solve: 15 x 2 + 3 x − 8 = 5 x − 7 .

Step 1: Express the equation in standard form, equal to zero. In this example, subtract 5 x from and add 7 to both sides.

15 x 2 + 3 x − 8 = 5 x − 7 15 x 2 − 2 x − 1 = 0

Step 2: Factor the expression.

( 3 x − 1 ) ( 5 x + 1 ) = 0

Step 3: Apply the zero-product property and set each variable factor equal to zero.

3 x − 1 = 0 or 5 x + 1 = 0

Step 4: Solve the resulting linear equations.

3 x − 1 = 0 or 5 x + 1 = 0 3 x = 1 5 x = − 1 x = 1 3 x = − 1 5

Answer: The solutions are 1 3 and − 1 5 . The check is optional.

Solve: ( 3 x + 2 ) ( x + 1 ) = 4 .

This quadratic equation appears to be factored; hence it might be tempting to set each factor equal to 4. However, this would lead to incorrect results. We must rewrite the equation equal to zero, so that we can apply the zero-product property.

( 3 x + 2 ) ( x + 1 ) = 4 3 x 2 + 3 x + 2 x + 2 = 4 3 x 2 + 5 x + 2 = 4 3 x 2 + 5 x − 2 = 0

Once it is in standard form, we can factor and then set each factor equal to zero.

( 3 x − 1 ) ( x + 2 ) = 0 3 x − 1 = 0 or x + 2 = 0 3 x = 1 x = − 2 x = 1 3

Answer: The solutions are 1 3 and −2.

Finding Roots of Functions

Recall that any polynomial with one variable is a function and can be written in the form,

f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a 1 x + a 0

A root A value in the domain of a function that results in zero. of a function is a value in the domain that results in zero. In other words, the roots occur when the function is equal to zero, f ( x ) = 0 .

Find the roots: f ( x ) = ( x + 2 ) 2 − 4 .

To find roots we set the function equal to zero and solve.

f ( x ) = 0 ( x + 2 ) 2 − 4 = 0 x 2 + 4 x + 4 − 4 = 0 x 2 + 4 x = 0 x ( x + 4 ) = 0

Next, set each factor equal to zero and solve.

x = 0 or x + 4 = 0 x = − 4

We can show that these x -values are roots by evaluating.

f ( 0 ) = ( 0 + 2 ) 2 − 4 f ( − 4 ) = ( − 4 + 2 ) 2 − 4 = 4 − 4 = ( − 2 ) 2 − 4 = 0 ✓ = 4 − 4 = 0 ✓

Answer: The roots are 0 and −4.

If we graph the function in the previous example we will see that the roots correspond to the x -intercepts of the function. Here the function f is a basic parabola shifted 2 units to the left and 4 units down.

Find the roots: f ( x ) = x 4 − 5 x 2 + 4 .

f ( x ) = 0 x 4 − 5 x 2 + 4 = 0 ( x 2 − 1 ) ( x 2 − 4 ) = 0 ( x + 1 ) ( x − 1 ) ( x + 2 ) ( x − 2 ) = 0

x + 1 = 0 or x − 1 = 0 or x + 2 = 0 or x − 2 = 0 x = − 1 x = 1 x = − 2 x = 2

Answer: The roots are −1, 1, −2, and 2.

Graphing the previous function is not within the scope of this course. However, the graph is provided below:

Notice that the degree of the polynomial is 4 and we obtained four roots. In general, for any polynomial function with one variable of degree n , the fundamental theorem of algebra Guarantees that there will be as many (or fewer) roots to a polynomial function with one variable as its degree. guarantees n real roots or fewer. We have seen that many polynomials do not factor. This does not imply that functions involving these unfactorable polynomials do not have real roots. In fact, many polynomial functions that do not factor do have real solutions. We will learn how to find these types of roots as we continue in our study of algebra.

Find the roots: f ( x ) = − x 2 + 10 x − 25 .

f ( x ) = 0 − x 2 + 10 x − 25 = 0 − ( x 2 − 10 x + 25 ) = 0 − ( x − 5 ) ( x − 5 ) = 0

Next, set each variable factor equal to zero and solve.

x − 5 = 0 or x − 5 = 0 = 5 x = 5

A solution that is repeated twice is called a double root A root that is repeated twice. . In this case, there is only one solution.

Answer: The root is 5.

The previous example shows that a function of degree 2 can have one root. From the factoring step, we see that the function can be written

f ( x ) = − ( x − 5 ) 2

In this form, we can see a reflection about the x -axis and a shift to the right 5 units. The vertex is the x -intercept, illustrating the fact that there is only one root.

Try this! Find the roots of f ( x ) = x 3 + 3 x 2 − x − 3 .

Answer: ±1, −3

Assuming dry road conditions and average reaction times, the safe stopping distance in feet is given by d ( x ) = 1 20 x 2 + x , where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 40 feet.

We are asked to find the speed x where the safe stopping distance d ( x ) = 40 feet.

d ( x ) = 40 1 20 x 2 + x = 40

To solve for x , rewrite the resulting equation in standard form. In this case, we will first multiply both sides by 20 to clear the fraction.

20 ( 1 20 x 2 + x ) = 20 ( 40 ) x 2 + 20 x = 800 x 2 + 20 x − 800 = 0

Next factor and then set each factor equal to zero.

x 2 + 20 x − 800 = 0 ( x + 40 ) ( x − 20 ) = 0 x + 40 = 0 o r x − 20 = 0 x = − 40 x = 20

The negative answer does not make sense in the context of this problem. Consider x = 20 miles per hour to be the only solution.

Answer: 20 miles per hour

Finding Equations with Given Solutions

We can use the zero-product property to find equations, given the solutions. To do this, the steps for solving by factoring are performed in reverse.

Find a quadratic equation with integer coefficients, given solutions − 3 2 and 1 3 .

Given the solutions, we can determine two linear factors. To avoid fractional coefficients, we first clear the fractions by multiplying both sides by the denominator.

x = − 3 2 or x = 1 3 2 x = − 3 3 x = 1 2 x + 3 = 0 3 x − 1 = 0

The product of these linear factors is equal to zero when x = − 3 2 or x = 1 3 .

( 2 x + 3 ) ( 3 x − 1 ) = 0

Multiply the binomials and present the equation in standard form.

6 x 2 − 2 x + 9 x − 3 = 0 6 x 2 + 7 x − 3 = 0

We may check our equation by substituting the given answers to see if we obtain a true statement. Also, the equation found above is not unique and so the check becomes essential when our equation looks different from someone else’s. This is left as an exercise.

Answer: 6 x 2 + 7 x − 3 = 0

Find a polynomial function with real roots 1, −2, and 2.

Given solutions to f ( x ) = 0 we can find linear factors.

x = 1 or x = − 2 or x = 2 x − 1 = 0 x + 2 = 0 x − 2 = 0

Apply the zero-product property and multiply.

( x − 1 ) ( x + 2 ) ( x − 2 ) = 0 ( x − 1 ) ( x 2 − 4 ) = 0 x 3 − 4 x − x 2 + 4 = 0 x 3 − x 2 − 4 x + 4 = 0

Answer: f ( x ) = x 3 − x 2 − 4 x + 4

Try this! Find a polynomial equation with integer coefficients, given solutions 1 2 and − 3 4 .

Answer: 8 x 2 + 2 x − 3 = 0

Key Takeaways

Factoring and the zero-product property allow us to solve equations.
To solve a polynomial equation, first write it in standard form. Once it is equal to zero, factor it and then set each variable factor equal to zero. The solutions to the resulting equations are the solutions to the original.
Not all polynomial equations can be solved by factoring. We will learn how to solve polynomial equations that do not factor later in the course.
A polynomial function can have at most a number of real roots equal to its degree. To find roots of a function, set it equal to zero and solve.
To find a polynomial equation with given solutions, perform the process of solving by factoring in reverse.

Topic Exercises

Part a: general factoring.

Factor completely.

50 x 2 − 18

12 x 3 − 3 x

10 x 3 + 65 x 2 − 35 x

15 x 4 + 7 x 3 − 4 x 2

6 a 4 b − 15 a 3 b 2 − 9 a 2 b 3

8 a 3 b − 44 a 2 b 2 + 20 a b 3

36 x 4 − 72 x 3 − 4 x 2 + 8 x

20 x 4 + 60 x 3 − 5 x 2 − 15 x

3 x 5 + 2 x 4 − 12 x 3 − 8 x 2

10 x 5 − 4 x 4 − 90 x 3 + 36 x 2

x 4 − 23 x 2 − 50

2 x 4 − 31 x 2 − 16

− 2 x 5 − 6 x 3 + 8 x

− 36 x 5 + 69 x 3 + 27 x

54 x 5 − 78 x 3 + 24 x

4 x 6 − 65 x 4 + 16 x 2

x 6 − 7 x 3 − 8

x 6 − 25 x 3 − 54

3 x 6 + 4 x 3 + 1

27 x 6 − 28 x 3 + 1

Part B: Solving Polynomial Equations by Factoring

( 6 x − 5 ) ( x + 7 ) = 0

( x + 9 ) ( 3 x − 8 ) = 0

5 x ( 2 x − 5 ) ( 3 x + 1 ) = 0

4 x ( 5 x − 1 ) ( 2 x + 3 ) = 0

( x − 1 ) ( 2 x + 1 ) ( 3 x − 5 ) = 0

( x + 6 ) ( 5 x − 2 ) ( 2 x + 9 ) = 0

( x + 4 ) ( x − 2 ) = 16

( x + 1 ) ( x − 7 ) = 9

( 6 x + 1 ) ( x + 1 ) = 6

( 2 x − 1 ) ( x − 4 ) = 39

x 2 − 15 x + 50 = 0

x 2 + 10 x − 24 = 0

3 x 2 + 2 x − 5 = 0

2 x 2 + 9 x + 7 = 0

1 10 x 2 − 7 15 x − 1 6 = 0

1 4 − 4 9 x 2 = 0

6 x 2 − 5 x − 2 = 30 x + 4

6 x 2 − 9 x + 15 = 20 x − 13

5 x 2 − 23 x + 12 = 4 ( 5 x − 3 )

4 x 2 + 5 x − 5 = 15 ( 3 − 2 x )

( x + 6 ) ( x − 10 ) = 4 ( x − 18 )

( x + 4 ) ( x − 6 ) = 2 ( x + 4 )

4 x 3 − 14 x 2 − 30 x = 0

9 x 3 + 48 x 2 − 36 x = 0

1 3 x 3 − 3 4 x = 0

1 2 x 3 − 1 50 x = 0

− 10 x 3 − 28 x 2 + 48 x = 0

− 2 x 3 + 15 x 2 + 50 x = 0

2 x 3 − x 2 − 72 x + 36 = 0

4 x 3 − 32 x 2 − 9 x + 72 = 0

45 x 3 − 9 x 2 − 5 x + 1 = 0

x 3 − 3 x 2 − x + 3 = 0

x 4 − 5 x 2 + 4 = 0

4 x 4 − 37 x 2 + 9 = 0

Find the roots of the given functions.

f ( x ) = x 2 + 10 x − 24

f ( x ) = x 2 − 14 x + 48

f ( x ) = − 2 x 2 + 7 x + 4

f ( x ) = − 3 x 2 + 14 x + 5

f ( x ) = 16 x 2 − 40 x + 25

f ( x ) = 9 x 2 − 12 x + 4

g ( x ) = 8 x 2 + 3 x

g ( x ) = 5 x 2 − 30 x

p ( x ) = 64 x 2 − 1

q ( x ) = 4 x 2 − 121

f ( x ) = 1 5 x 3 − 1 x 2 − 1 20 x + 1 4

f ( x ) = 1 3 x 3 + 1 2 x 2 − 4 3 x − 2

g ( x ) = x 4 − 13 x 2 + 36

g ( x ) = 4 x 4 − 13 x 2 + 9

f ( x ) = ( x + 5 ) 2 − 1

g ( x ) = − ( x + 5 ) 2 + 9

f ( x ) = − ( 3 x − 5 ) 2

g ( x ) = − ( x + 2 ) 2 + 4

Given the graph of a function, determine the real roots.

The sides of a square measure x − 2 units. If the area is 36 square units, then find x .

The sides of a right triangle have lengths that are consecutive even integers. Find the lengths of each side. (Hint: Apply the Pythagorean theorem)

The profit in dollars generated by producing and selling n bicycles per week is given by the formula P ( n ) = − 5 n 2 + 400 n − 6000 . How many bicycles must be produced and sold to break even?

The height in feet of an object dropped from the top of a 64-foot building is given by h ( t ) = − 16 t 2 + 64 where t represents the time in seconds after it is dropped. How long will it take to hit the ground?

A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box of height 2 inches is given.

What is the length of each side of the cardboard sheet if the volume of the box is to be 98 cubic inches?

The height of a triangle is 4 centimeters less than twice the length of its base. If the total area of the triangle is 48 square centimeters, then find the lengths of the base and height.

A uniform border is to be placed around an 8 × 10 inch picture.

If the total area including the border must be 168 square inches, then how wide should the border be?

The area of a picture frame including a 3-inch wide border is 120 square inches.

If the width of the inner area is 2 inches less than its length, then find the dimensions of the inner area.

Assuming dry road conditions and average reaction times, the safe stopping distance in feet is given by d ( x ) = 1 20 x 2 + x where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 75 feet.

A manufacturing company has determined that the daily revenue in thousands of dollars is given by the formula R ( n ) = 12 n − 0.6 n 2 where n represents the number of palettes of product sold ( 0 ≤ n < 20 ) . Determine the number of palettes sold in a day if the revenue was 45 thousand dollars.

Part C: Finding Equations with Given Solutions

Find a polynomial equation with the given solutions.

Find a function with the given roots.

2 5 , − 1 3

5 double root

−3 double root

Recall that if | X | = p , then X = − p or X = p . Use this to solve the following absolute value equations.

| x 2 − 8 | = 8

| 2 x 2 − 9 | = 9

| x 2 − 2 x − 1 | = 2

| x 2 − 8 x + 14 | = 2

| 2 x 2 − 4 x − 7 | = 9

| x 2 − 3 x − 9 | = 9

Part D: Discussion Board

Explain to a beginning algebra student the difference between an equation and an expression.

What is the difference between a root and an x -intercept? Explain.

Create a function with three real roots of your choosing. Graph it with a graphing utility and verify your results. Share your function on the discussion board.

Research and discuss the fundamental theorem of algebra.

2 ( 5 x + 3 ) ( 5 x − 3 )

5 x ( x + 7 ) ( 2 x − 1 )

3 a 2 b ( 2 a + b ) ( a − 3 b )

4 x ( x − 2 ) ( 3 x + 1 ) ( 3 x − 1 )

x 2 ( 3 x + 2 ) ( x + 2 ) ( x − 2 )

( x 2 + 2 ) ( x + 5 ) ( x − 5 )

− 2 x ( x 2 + 4 ) ( x − 1 ) ( x + 1 )

6 x ( x + 1 ) ( x − 1 ) ( 3 x + 2 ) ( 3 x − 2 )

( x + 1 ) ( x 2 − x + 1 ) ( x − 2 ) ( x 2 + 2 x + 4 )

( 3 x 3 + 1 ) ( x + 1 ) ( x 2 − x + 1 )

0, 5 2 , − 1 3

− 1 2 , 1, 5 3

− 5 3 , 1 2

0, − 3 2 , 5

± 1 3 , 1 5

−3, −1, 0, 2

20 or 60 bicycles

30 miles per hour

x 2 − 2 x − 15 = 0

3 x 2 − 7 x + 2 = 0

x 2 + 4 x = 0

x 2 − 49 = 0

x 3 − x 2 − 9 x + 9 = 0

f ( x ) = 6 x 2 − 7 x + 2

f ( x ) = 16 x 2 − 9

f ( x ) = x 2 − 10 x + 25

f ( x ) = x 3 − 2 x 2 − 3 x

Answer may vary

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

6.5: Polynomial Equations

Last updated
Save as PDF
Page ID 30868

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

By the end of this section, you will be able to:

Use the Zero Product Property

Solve quadratic equations by factoring
Solve equations with polynomial functions
Solve applications modeled by polynomial equations

Are you ready?

Before you get started, take this readiness quiz.

Solve: $5y−3=0$. If you missed this problem, review [link] .
Factor completely: $n^3−9n^2−22n$. If you missed this problem, review [link] .
If $f(x)=8x−16$, find $f(3)$ and solve $f(x)=0$. If you missed this problem, review [link] .

We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.

A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

POLYNOMIAL EQUATION

A polynomial equation is an equation that contains a polynomial expression.

The degree of the polynomial equation is the degree of the polynomial.

We have already solved polynomial equations of degree one . Polynomial equations of degree one are linear equations are of the form ax+b=c.ax+b=c.

We are now going to solve polynomial equations of degree two . A polynomial equation of degree two is called a quadratic equation . Listed below are some examples of quadratic equations:

\[x^2+5x+6=0 \quad 3y^2+4y=10 \quad 64u^2−81=0 \quad n(n+1)=42 \nonumber\]

The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get n2+n.n2+n.

The general form of a quadratic equation is $ax^2+bx+c=0$, with $a\neq 0$. (If $a=0$, then $0·x^2=0$ and we are left with no quadratic term.)

QUADRATIC EQUATION

An equation of the form $ax^2+bx+c=0$ is called a quadratic equation.

\[a,b,\text{ and }c\text{ are real numbers and }a\neq 0\nonumber\]

To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.

We will first solve some quadratic equations by using the Zero Product Property . The Zero Product Property says that if the product of two quantities is zero, then at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.

ZERO PRODUCT PROPERTY

If $a·b=0$, then either $a=0$ or $b=0$ or both.

We will now use the Zero Product Property, to solve a quadratic equation .

Example $\PageIndex{1}$: How to Solve a Quadratic Equation Using the Zero Product Property

Solve: $(5n−2)(6n−1)=0$.

$The equation is open parentheses 5n minus 2 close parentheses open parentheses 6n minus 1 close parentheses equals 0. The product equals zero, so at least one factor must equal zero. Step 1 is set each factor equal to zero. So, 5n minus 2 equals 0 and 6n minus 1 equals 0.$

Example $\PageIndex{2}$

Solve: $(3m−2)(2m+1)=0$.

$m=\frac{2}{3},\space m=−\frac{1}{2}$

Example $\PageIndex{3}$

Solve: $(4p+3)(4p−3)=0$.

$p=−\frac{3}{4},\space p=\frac{3}{4}$

USE THE ZERO PRODUCT PROPERTY.

Set each factor equal to zero.
Solve the linear equations.

Solve Quadratic Equations by Factoring

The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So we be sure to start with the quadratic equation in standard form , $ax^2+bx+c=0$. Then we factor the expression on the left.

Solve: $2y^2=13y+45$.

$The equation is 2 y squared equals 13y plus 45. Step 1 is to write it in standard form a x squared plus bx plus c. So we have 2 y squared minus 13y minus 45 equals 0.$

Example $\PageIndex{5}$

Solve: $3c^2=10c−8$.

$c=2,\space c=\frac{4}{3}$

Example $\PageIndex{6}$

Solve: $2d^2−5d=3$.

$d=3,\space d=−12$

SOLVE A QUADRATIC EQUATION BY FACTORING.

Write the quadratic equation in standard form, $ax^2+bx+c=0$.
Factor the quadratic expression.
Use the Zero Product Property.
Check. Substitute each solution separately into the original equation.

Before we factor, we must make sure the quadratic equation is in standard form .

Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?

Example $\PageIndex{7}$

Solve: $169q^2=49$.

$\begin{array} {ll} &169x^2=49 \\ \text{Write the quadratic equation in standard form.} &169x^2−49=0 \\ \text{Factor. It is a difference of squares.} &(13x−7)(13x+7)=0 \\ \text{Use the Zero Product Property to set each factor to }0. & \\ \text{Solve each equation.} &\begin{array} {ll} 13x−7=0 &13x+7=0 \\ 13x=7 &13x=−7 \\ x=\frac{7}{13} &x=−\frac{7}{13} \end{array} \end{array}$

We leave the check up to you.

Example $\PageIndex{8}$

Solve: $25p^2=49$.

$p=\frac{7}{5},p=−\frac{7}{5}$

Example $\PageIndex{9}$

Solve: $36x^2=121$.

$x=\frac{11}{6},x=−\frac{11}{6}$

In the next example, the left side of the equation is factored, but the right side is not zero. In order to use the Zero Product Property , one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.

Example $\PageIndex{10}$

Solve: $(3x−8)(x−1)=3x$.

$\begin{array} {ll} &(3x−8)(x−1)=3x \\ \text{Multiply the binomials.} &3x^2−11x+8=3x \\ \text{Write the quadratic equation in standard form.} &3x^2−14x+8=0 \\ \text{Factor the trinomial.} &(3x−2)(x−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {ll} 3x−2=0 &x−4=0 \\ 3x=2 &x=4 \\ x=\frac{2}{3} & \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}$

Example $\PageIndex{11}$

Solve: $(2m+1)(m+3)=12m$.

$m=1,\space m=\frac{3}{2}$

Example $\PageIndex{12}$

Solve: $(k+1)(k−1)=8$.

$k=3,\space k=−3$

In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.

Example $\PageIndex{13}$

Solve: $3x^2=12x+63$.

$\begin{array} {ll} &3x^2=12x+63 \\ \text{Write the quadratic equation in standard form.} &3x^2−12x−63=0 \\ \text{Factor the greatest common factor first.} &3(x^2−4x−21)=0 \\ \text{Factor the trinomial.} &3(x−7)(x+3)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {lll} 3\neq 0 &x−7=0 &x+3=0 \\ 3\neq 0 &x=7 &x=−3 \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}$

Example $\PageIndex{14}$

Solve: $18a^2−30=−33a$.

$a=−\frac{5}{2},a=\frac{2}{3}$

Example $\PageIndex{15}$

Solve: $123b=−6−60b^2$

$b=−2,\space b=−\frac{1}{20}$

The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree greater than two by using the Zero Product Property, just like we solved quadratic equations.

Example $\PageIndex{16}$

Solve: $9m^3+100m=60m^2$

$\begin{array} {ll} & 9m^3+100m=60m^2 \\ \text{Bring all the terms to one side so that the other side is zero.} &9m^3−60m^2+100m=0 \\ \text{Factor the greatest common factor first.} &m(9m^2−60m+100)=0 \\ \text{Factor the trinomial.} &m(3m−10)^2=0 \end{array}\\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} &\begin{array} {lll} m=0 &3m−10=0 &{}\\ m=0 &m=\frac{10}{3} & {} \end{array}\\ \text{Check your answers.} &\text{The check is left to you.} \end{array}$

Example $\PageIndex{17}$

Solve: $8x^3=24x^2−18x$.

$x=0,\space x=\frac{3}{2}$

Example $\PageIndex{18}$

Solve: $16y^2=32y^3+2y$.

$y=0,\space y=14$

Solve Equations with Polynomial Functions

As our study of polynomial functions continues, it will often be important to know when the function will have a certain value or what points lie on the graph of the function. Our work with the Zero Product Property will be help us find these answers.

Example $\PageIndex{19}$

For the function $f(x)=x^2+2x−2$,

ⓐ find $x$ when $f(x)=6$ ⓑ find two points that lie on the graph of the function.

ⓐ $\begin{array} {ll} &f(x)=x^2+2x−2 \\ \text{Substitute }6\text{ for }f(x). &6=x^2+2x−2 \\ \text{Put the quadratic in standard form.} &x^2+2x−8=0 \\ \text{Factor the trinomial.} &(x+4)(x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &x−2=0 \\ x=−4 &\text{or} &x=2 \end{array} \\ \text{Check:} & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \begin{array} {lll} \quad &\hspace{3mm} f(x)=x^2+2x−2 &f(x)=x^2+2x−2 \\ \quad &f(−4)=(−4)^2+2(−4)−2 &f(2)=2^2+2·2−2 \\ \quad &f(−4)=16−8−2 &f(2)=4+4−2 \\ \quad &f(−4)=6\checkmark &f(2)=6\checkmark \end{array} & \end{array} $ ⓑ Since $f(−4)=6$ and $f(2)=6$, the points $(−4,6)$ and $(2,6)$ lie on the graph of the function.

Example $\PageIndex{20}$

For the function $f(x)=x^2−2x−8$,

ⓐ find $x$ when $f(x)=7$ ⓑ Find two points that lie on the graph of the function.

ⓐ $x=−3$ or $x=5$ ⓑ $(−3,7)\space (5,7)$

Example $\PageIndex{21}$

For the function $f(x)=x^2−8x+3$,

ⓐ find $x$ when $f(x)=−4$ ⓑ Find two points that lie on the graph of the function.

ⓐ $x=1$ or $x=7$ ⓑ $(1,−4)\space (7,−4)$

The Zero Product Property also helps us determine where the function is zero. A value of $x$ where the function is $0$, is called a zero of the function .

ZERO OF A FUNCTION

For any function $f$, if $f(x)=0$, then $x$ is a zero of the function .

When $f(x)=0$, the point $(x,0)$ is a point on the graph. This point is an $x$- intercept of the graph. It is often important to know where the graph of a function crosses the axes. We will see some examples later.

Example $\PageIndex{22}$

For the function $f(x)=3x^2+10x−8$, find

ⓐ the zeros of the function, ⓑ any $x$-intercepts of the graph of the function ⓒ any $y$-intercepts of the graph of the function

ⓐ To find the zeros of the function, we need to find when the function value is 0. $\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Substitute }0\text{ for}f(x). &0=3x^2+10x−8 \\ \text{Factor the trinomial.} &(x+4)(3x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &3x−2=0 \\ x=−4 &\text{or} &x=\frac{2}{3} \end{array} \end{array}$ ⓑ An $x$-intercept occurs when $y=0$. Since $f(−4)=0$ and $f(\frac{2}{3})=0$, the points $(−4,0)$ and $(\frac{2}{3},0)$ lie on the graph. These points are $x$-intercepts of the function. ⓒ A $y$-intercept occurs when $x=0$. To find the $y$-intercepts we need to find $f(0)$. $\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Find }f(0)\text{ by substituting }0\text{ for }x. &f(0)=3·0^2+10·0−8 \\ \text{Simplify.} &f(0)=−8 \end{array} $ Since $f(0)=−8$, the point $(0,−8)$ lies on the graph. This point is the $y$-intercept of the function.

Example $\PageIndex{23}$

For the function $f(x)=2x^2−7x+5$, find

ⓐ the zeros of the function ⓑ any $x$-intercepts of the graph of the function ⓒ any $y$-intercepts of the graph of the function.

ⓐ $x=1$ or $x=\frac{5}{2}$ ⓑ $(1,0),\space (\frac{5}{2},0)$ ⓒ $(0,5)$

Example $\PageIndex{24}$

For the function $f(x)=6x^2+13x−15$, find

ⓐ $x=−3$ or $x=\frac{5}{6}$ ⓑ $(−3,0),\space (\frac{5}{6},0)$ ⓒ $(0,−15)$

Solve Applications Modeled by Polynomial Equations

The problem-solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to polynomial equations. We will copy the problem-solving strategy here so we can use it for reference.

USE A PROBLEM SOLVING STRATEGY TO SOLVE WORD PROBLEMS.

Read the problem. Make sure all the words and ideas are understood.
Identify what we are looking for.
Name what we are looking for. Choose a variable to represent that quantity.
Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
Solve the equation using appropriate algebra techniques.
Check the answer in the problem and make sure it makes sense.
Answer the question with a complete sentence.

We will start with a number problem to get practice translating words into a polynomial equation.

Example $\PageIndex{25}$

The product of two consecutive odd integers is 323. Find the integers.

$\begin{array} {ll} \textbf{Step 1. Read }\text{the problem.} & \\ \textbf{Step 2. Identify }\text{what we are looking for.} &\text{We are looking for two consecutive integers.} \\ \textbf{Step 3. Name}\text{ what we are looking for.} &\text{Let } n=\text{ the first integer.} \\ &n+2= \text{ next consecutive odd integer} \\ \begin{array} {l} \textbf{Step 4. Translate }\text{into an equation. Restate the}\hspace{20mm} \\ \text{problem in a sentence.} \end{array} &\begin{array} {l} \text{The product of the two consecutive odd} \\ \text{integers is }323. \end{array} \\ &\quad n(n+2)=323 \\ \textbf{Step 5. Solve }\text{the equation.} n^2+2n=323 \\ \text{Bring all the terms to one side.} &n^2+2n−323=0 \\ \text{Factor the trinomial.} &(n−17)(n+19)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve the equations.} \end{array} &\begin{array} {ll} n−17=0 \hspace{10mm}&n+19=0 \\ n=17 &n=−19 \end{array} \end{array} $ There are two values for $n$ that are solutions to this problem. So there are two sets of consecutive odd integers that will work.

$\begin{array} {ll} \text{If the first integer is } n=17 \hspace{60mm} &\text{If the first integer is } n=-19 \\ \text{then the next odd integer is} &\text{then the next odd integer is} \\ \hspace{53mm} n+2 &\hspace{53mm} n+2 \\ \hspace{51mm} 17+2 &\hspace{51mm} -19+2 \\ \hspace{55mm} 19 &\hspace{55mm} -17 \\ \hspace{51mm} 17,19 &\hspace{51mm} -17,-19 \\ \textbf{Step 6. Check }\text{the answer.} & \\ \text{The results are consecutive odd integers} & \\ \begin{array} {ll} 17,\space 19\text{ and }−19,\space −17. & \\ 17·19=323\checkmark &−19(−17)=323\checkmark \end{array} & \\ \text{Both pairs of consecutive integers are solutions.} & \\ \textbf{Step 7. Answer }\text{the question} &\text{The consecutive integers are }17, 19\text{ and }−19,−17. \end{array} $

Example $\PageIndex{26}$

The product of two consecutive odd integers is 255. Find the integers.

$−15,−17$ and $15, 17$

Example $\PageIndex{27}$

The product of two consecutive odd integers is 483 Find the integers.

$−23,−21$ and $21, 23$

Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give positive results.

In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.

Example $\PageIndex{28}$

A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.

Example $\PageIndex{29}$

A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

The width is 5 feet and length is 6 feet.

Example $\PageIndex{30}$

A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

The length of the patio is 12 feet and the width 15 feet.

In the next example, we will use the Pythagorean Theorem $(a^2+b^2=c^2)$. This formula gives the relation between the legs and the hypotenuse of a right triangle.

$Figure shows a right triangle with the shortest side being a, the second side being b and the hypotenuse being c.$

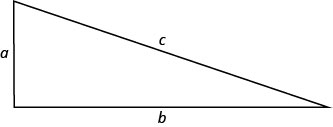
We will use this formula to in the next example.

Example $\PageIndex{31}$

A boat’s sail is in the shape of a right triangle as shown. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the sail.

$Figure shows a right triangle with the shortest side being x, the second side being x minus 7 and the hypotenuse being 17.$

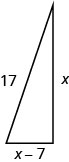
Example $\PageIndex{32}$

Justine wants to put a deck in the corner of her backyard in the shape of a right triangle. The length of one side of the deck is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the deck.

5 feet and 12 feet

Example $\PageIndex{33}$

A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of the other leg. Find the lengths of the hypotenuse and the other leg.

24 feet and 25 feet

The next example uses the function that gives the height of an object as a function of time when it is thrown from 80 feet above the ground.

Example $\PageIndex{34}$

Dennis is going to throw his rubber band ball upward from the top of a campus building. When he throws the rubber band ball from 80 feet above the ground, the function $h(t)=−16t^2+64t+80$ models the height, $h$, of the ball above the ground as a function of time, $t$. Find:

ⓐ the zeros of this function which tell us when the ball hits the ground ⓑ when the ball will be 80 feet above the ground ⓒ the height of the ball at $t=2$ seconds.

ⓐ The zeros of this function are found by solving $h(t)=0$. This will tell us when the ball will hit the ground. $\begin{array} {ll} &h(t)=0 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=0 \\ \text{Factor the GCF, }−16. &−16(t^2−4t−5)=0 \\ \text{Factor the trinomial.} &−16(t−5)(t+1)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.} \end{array} &\begin{array} {ll} t−5=0 &t+1=0 \\ t=5 &t=−1 \end{array} \end{array} $

The result $t=5$ tells us the ball will hit the ground 5 seconds after it is thrown. Since time cannot be negative, the result $t=−1$ is discarded.

ⓑ The ball will be 80 feet above the ground when $h(t)=80$. $\begin{array} {ll} &h(t)=80 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=80 \\ \text{Subtract 80 from both sides.} &−16t^2+64t=0 \\ \text{Factor the GCF, }−16t. &−16t(t−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.}\end{array} &\begin{array} {ll} −16t=0 &t−4=0 \\ t=0 &t=4 \end{array} \\ &\text{The ball will be at 80 feet the moment Dennis} \\ &\text{tosses the ball and then 4 seconds later, when} \\ &\text{the ball is falling.} \end{array} $

ⓒ To find the height ball at $t=2$ seconds we find $h(2)$. $\begin{array} {ll} &h(t)=−16t^2+64t+80 \\ \text{To find }h(2)\text{ substitute }2\text{ for }t. &h(2)=−16(2)^2+64·2+80 \\ \text{Simplify.} &h(2)=144 \\ &\text{After 2 seconds, the ball will be at 144 feet.} \end{array}$

Example $\PageIndex{35}$

Genevieve is going to throw a rock from the top a trail overlooking the ocean. When she throws the rock upward from 160 feet above the ocean, the function $h(t)=−16t^2+48t+160$ models the height, $h$, of the rock above the ocean as a function of time, $t$. Find:

ⓐ the zeros of this function which tell us when the rock will hit the ocean ⓑ when the rock will be 160 feet above the ocean. ⓒ the height of the rock at $t=1.5$ seconds.

ⓐ 5 ⓑ 0;3 ⓒ 196

Example $\PageIndex{36}$

Calib is going to throw his lucky penny from his balcony on a cruise ship. When he throws the penny upward from 128 feet above the ground, the function $h(t)=−16t^2+32t+128$ models the height, $h$, of the penny above the ocean as a function of time, $t$. Find:

ⓐ the zeros of this function which is when the penny will hit the ocean ⓑ when the penny will be 128 feet above the ocean. ⓒ the height the penny will be at $t=1$ seconds which is when the penny will be at its highest point.

ⓐ 4 ⓑ 0;2 ⓒ 144

Access this online resource for additional instruction and practice with quadratic equations.

Beginning Algebra & Solving Quadratics with the Zero Property

Key Concepts

Polynomial Equation: A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

\[a,b,c\text{ are real numbers and } a\neq 0\nonumber\]

Zero Product Property: If $a·b=0$, then either $a=0$ or $b=0$ or both.
Zero of a Function: For any function $f$, if $f(x)=0$, then $x$ is a zero of the function.

Module 7: Polynomials and Polynomial Functions

7.5 – polynomial equations and applications, learning objectives.

The principle of zero products
Projectile motion
Using the Pythagorean theorem to find the lengths of a right triangle

Geometric Applications

Cost, revenue, and profit polynomials

(7.5.1) – Solving polynomial equations

Not all of the techniques we use for solving linear equations will apply to solving polynomial equations. In this section we will introduce a method for solving polynomial equations that combines factoring and the zero product principle.

The Principle of Zero Products

What if we told you that we multiplied two numbers together and got an answer of zero? What could you say about the two numbers? Could they be 2 and 5? Could they be 9 and 1? No! When the result (answer) from multiplying two numbers is zero, that means that one of them had to be zero. This idea is called the zero product principle, and it is useful for solving polynomial equations that can be factored.

Principle of Zero Products

The Principle of Zero Products states that if the product of two numbers is 0, then at least one of the factors is 0. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both [latex]a[/latex] and [latex]b[/latex] are 0.

Let’s start with a simple example. We will factor a GCF from a binomial and apply the principle of zero products to solve a polynomial equation.

[latex]-t^2+t=0[/latex]

Each term has a common factor of [latex]t[/latex], so we can factor and use the zero product principle. Rewrite each term as the product of the GCF and the remaining terms.

[latex]\begin{array}{c}-t^2=t\left(-t\right)\\t=t\left(1\right)\end{array}[/latex]

Rewrite the polynomial equation using the factored terms in place of the original terms.

[latex]\begin{array}{c}-t^2+t=0\\t\left(-t\right)+t\left(1\right)\\t\left(-t+1\right)=0\end{array}[/latex]

Now we have a product on one side and zero on the other, so we can set each factor equal to zero using the zero product principle.

[latex]\begin{array}{c}t=0\,\,\,\,\,\,\,\,\text{ OR }\,\,\,\,\,\,\,\,\,\,\,-t+1=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-1}\,\,\,\underline{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-t=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-t}{-1}=\frac{-1}{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=1\end{array}[/latex]

[latex]t=0\text{ OR }t=1[/latex]

In the following video we show two more examples of using both factoring and the principle of zero products to solve a polynomial equation.

In the next video we show that you can factor a trinomial using methods previously learned to solve a quadratic equation.

You and I both know that it is rare to be given an equation to solve that has zero on one side, so let’s try another one.

Solve: [latex]s^2-4s=5[/latex]

First, move all the terms to one side. The goal is to try and see if we can use the zero product principle, since that is the only tool we know for solving polynomial equations.

[latex]\begin{array}{c}\,\,\,\,\,\,\,s^2-4s=5\\\,\,\,\,\,\,\,s^2-4s-5=0\\\end{array}[/latex]

We now have all the terms on the left side, and zero on the other side. The polynomial [latex]s^2-4s-5[/latex] factors nicely, which makes this equation a good candidate for the zero product principle. (imagine that)

[latex]\begin{array}{c}s^2-4s-5=0\\\left(s+1\right)\left(s-5\right)=0\end{array}[/latex]

We separate our factors into two linear equations using the principle of zero products.

[latex]\begin{array}{c}\left(s-5\right)=0\\s-5=0\\\,\,\,\,\,\,\,\,\,s=5\end{array}[/latex]

[latex]\begin{array}{c}\left(s+1\right)=0\\s+1=0\\s=-1\end{array}[/latex]

[latex]s=-1\text{ OR }s=5[/latex]

We will work through one more example that is similar to the one above, except this example has fractions.

Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]

Start by multiplying the whole equation by 2 to eliminate fractions:

[latex]\begin{array}{ccc}2\left(y^2-5=-\frac{7}{2}y+\frac{5}{2}\right)\\\,\,\,\,\,\,2(y^2)+2(-5)=2\left(-\frac{7}{2}\right)+2\left(-\frac{5}{2}\right)\\2y^2-10=-7y+5\end{array}[/latex]

Now we can move all the terms to one side and see if this will factor so we can use the principle of zero products.

[latex]\begin{array}{c}2y^2-10=-7y-5\\2y^2-10+7y-5=0\\2y^2-15+7y=0\\2y^2+7y-15=0\end{array}[/latex]

We can now check whether this polynomial will factor, using a table we can list factors until we find two numbers with a product of [latex]2\cdot-15=-30[/latex] and a sum of 7.

We have found the factors that will produce the middle term we want,[latex]-3,10[/latex]. We need to place the factors in a way that will lead to a term of [latex]10y[/latex]:

[latex]\left(2y-3\right)\left(y+5\right)=0[/latex]

Now we can set each factor equal to zero and solve:

[latex]\begin{array}{ccc}\left(2y-3\right)=0\text{ OR }\left(y+5\right)=0\\2y=3\text{ OR }y=-5\\y=\frac{3}{2}\text{ OR }y=-5\end{array}[/latex]

You can always check your work to make sure your solutions are correct:

Check [latex]y=\frac{3}{2}[/latex]

[latex]\begin{array}{ccc}\left(\frac{3}{2}\right)^2-5=-\frac{7}{2}\left(\frac{3}{2}\right)+\frac{5}{2}\\\frac{9}{4}-5=-\frac{21}{4}+\frac{5}{2}\\\text{ common denominator = 4}\\\frac{9}{4}-\frac{20}{4}=-\frac{21}{4}+\frac{10}{4}\\-\frac{11}{4}=-\frac{11}{4}\end{array}[/latex]

[latex]y=\frac{3}{2}[/latex] is indeed a solution, now check [latex]y=-5[/latex]

[latex]\begin{array}{ccc}\left(-5\right)^2-5=-\frac{7}{2}\left(-5\right)+\frac{5}{2}\\25-5=\frac{35}{2}+\frac{5}{2}\\20=\frac{40}{2}\\20=20\end{array}[/latex]

[latex]y=-5[/latex] is also a solution, so we must have done something right!

[latex]y=\frac{3}{2}\text{ OR }y=-5[/latex]

In our last video, we show how to solve another quadratic equation that contains fractions.

(7.5.2) – Applications of polynomial equations

Projectile motion.

Projectile motion happens when you throw a ball into the air and it comes back down because of gravity. A projectile will follow a curved path that behaves in a predictable way. This predictable motion has been studied for centuries, and in simple cases it’s height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where h(t) = height of an object at a given time, [latex]t[/latex]. Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile’s motion, as in the image of water in the fountain below.

Water from a fountain shoing classic parabolic motion.

Parabolic WaterTrajectory

Parabolic motion and it’s related functions allow us to launch satellites for telecommunications, and rockets for space exploration. Recently, police departments have even begun using projectiles with GPS to track fleeing suspects in vehicles, rather than pursuing them by high-speed chase [1] .

In this section we will use polynomial functions to answer questions about the parabolic motion of a projectile. The real mathematical model for the path of a rocket or a police GPS projectile may have different coefficients or more variables, but the concept remains the same. We will also learn to interpret the meaning of the variables in a polynomial function that models projectile motion.

A small toy rocket is launched from a 4-foot pedestal. The height ([latex]h[/latex] , in feet) of the rocket [latex]t[/latex] seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?

The rocket will be on the ground when the [latex]h(t)=0[/latex]. We want to know how long, [latex]t[/latex], the rocket is in the air.

[latex]\begin{array}{l}h(t)=−2t^{2}+7t+4=0\\0=−2t^{2}+7t+4\end{array}[/latex]

We can factor the polynomial [latex]−2t^{2}+7t+4[/latex] more easily by first factoring out a [latex]-1[/latex]

[latex]\begin{array}{c}0=-1(2t^{2}-7t-4)\\0=-1\left(2t+1\right)\left(t-4\right)\end{array}[/latex]

Use the Zero Product Property. There is no need to set the constant factor [latex]-1[/latex] to zero, because [latex]-1[/latex] will never equal zero.

[latex]2t+1=0\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t-4=0[/latex]

Solve each equation.

[latex]t=-\frac{1}{2}\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t=4[/latex]

Interpret the answer. Since t represents time, it cannot be a negative number; only [latex]t=4[/latex] makes sense in this context.

[latex]t=4[/latex]

We can check our answer: [latex]\begin{array}{c}h(4)=−2(4)^{2}+7(4)+4=0\\h(4)=-2(16)+28+4=0\\h(4)-32+32=0\\h(4)=0\end{array}[/latex]

The rocket will hit the ground 4 seconds after being launched.

In the next example we will solve for the time that the rocket is at a given height other than zero.

Use the formula for the height of the rocket in the previous example to find the time when the rocket is 4 feet from hitting the ground on it’s way back down. Refer to the image.

[latex]h(t)=−2t^{2}+7t+4[/latex]

Parabolic motion of rocket which starts four feet up from the ground. t=0 is labeled at the starti of hte parabolic motion adn t=? is labeled at four feet from the ground on the other side of the parabola.

We are given that the height of the rocket is 4 feet from the ground on it’s way back down. We want to know how long it has taken the rocket to get to that point in it’s path, we are going to solve for [latex]t[/latex].

Substitute [latex]h(t) = 4[/latex] into the formula for height, and try to get zero on one side since we know we can use the zero product principle to solve polynomials.

Write and Solve:

[latex]\begin{array}{l}h(t)=4=−2t^{2}+7t+4\\4=-2t^2+7t+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\0=-2t^2+7t\end{array}[/latex]

Now we can factor out a [latex]t[/latex] from each term:

[latex]0=t\left(-2t+7\right)[/latex]

Solve each equation for [latex]t[/latex] using the zero product principle:

[latex]\begin{array}{l}t=0\text{ OR }-2t+7=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-7}\,\,\,\,\,\,\,\underline{-7}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-2t}{-2}=\frac{-7}{-2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=\frac{7}{2}=3.5\end{array}[/latex]

It doesn’t make sense for us to choose [latex]t=0[/latex] because we are interested in the amount of time that has passed when the projectile is 4 feet from hitting the ground on it’s way back down. We will choose [latex]t=3.5[/latex]

Check the answer on your own for practice.

[latex]t=3.5\text{ seconds }[/latex]

In the following video we show another example of how to find the time when a object following a parabolic trajectory hits the ground.

In this section we introduced the concept of projectile motion, and showed that it can be modeled with polynomial function. While the models used in these examples are simple, the concepts and interpretations are the same as what would happen in “real life”.

Pythagorean Theorem

The Pythagorean theorem or Pythagoras’s theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to 90 degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the hypotenuse. The hypotenuse is the side opposite to the right angle, and it is always the longest side. The image above shows four common kinds of triangle, including a right triangle.

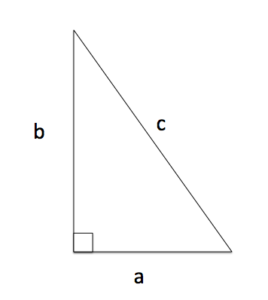
Right Triangle Labeled

The Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the longest leg of a right triangle is labeled c, and the other two a, and b as in the image on teh left, The Pythagorean Theorem states that

[latex]a^2+b^2=c^2[/latex]

Given enough information, we can solve for an unknown length. This relationship has been used for many, many years for things such as celestial navigation and early civil engineering projects. We now have digital GPS and survey equipment that have been programmed to do the calculations for us.

In the next example we will combine the power of the Pythagorean theorem and what we know about solving quadratic equations to find unknown lengths of right triangles.

A right triangle has one leg with length [latex]x[/latex], another whose length is greater by two, and the length of the hypotenuse is greater by four. Find the lengths of the sides of the triangle. Use the image below.

Right triangle with one leg having length = x, one with length= x+2 and the hypotenuse = x+4

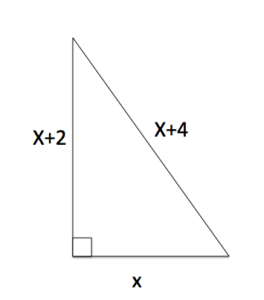
Read and understand: We know the lengths of all the sides of a triangle in terms of one side. We also know that the Pythagorean theorem will give us a relationship between the side lengths of a right triangle.

Translate:

[latex]\begin{array}{l}a^2+b^2=c^2\\x^2+\left(x+2\right)^2=\left(x+4\right)^2\end{array}[/latex]

Solve: If we can move all the terms to one side and factor, we can use the zero product principle to solve. Since this is the only method we know – let’s hope it works!

First, multiply the binomials and simplify so we can see what we are working with.

[latex]\begin{array}{l}x^2+\left(x+2\right)^2=\left(x+4\right)^2\\x^2+x^2+4x+4=x^2+8x+16\\2x^2+4x+4=x^2+8x+16\end{array}[/latex]

Now move all the terms to one side and see if we can factor.

[latex]\begin{array}{l}2x^2+4x+4=x^2+8x+16\\\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\,\,\,\,\,\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\\x^2-4x-12=0\end{array}[/latex]

This went from a messy looking problem to something promising. We can factor using the shortcut:

[latex]-6\cdot{2}=-12,\text{ and }-6+2=-4[/latex]

So we can build our binomial factors with -6 and 2:

[latex]\left(x-6\right)\left(x+2\right)=0[/latex]

Set each factor equal to zero:

[latex]x-6=0, x=6[/latex]

[latex]x+2=0, x=-2[/latex]

Interpret: Ok, it doesn’t make sense to have a length equal to -2, so we can safely throw that solution out. The lengths of the sides are as follows:

[latex]x=6[/latex]

[latex]x+2=6+2=8[/latex]

[latex]x+4=6+4=10[/latex]

Check: Since we know the relationship between the sides of a right triangle we can check that we are correct. Sometimes it helps to draw a picture

We know that [latex]a^2+b^2=c^2[/latex], so we can substitute the values we found:

[latex]\begin{array}{l}6^2+8^2=10^2\\36+64=100\\100=100\end{array}[/latex]

Our solution checks out.

The lengths of the sides of the right triangle are 6, 8, and 10

This video example shows another way a quadratic equation can be used to find and unknown length of a right triangle.

In this section we will explore ways that polynomials are used in applications of area problems.

The length of a rectangle is 3 more than the width. If the area is 40 square inches, what are the dimensions?

[latex]\begin{eqnarray*} x & & \text{ We} \text{ do} \text{ not} \text{ know} \text{ the} \text{ width}, x.\\ x + 3 & & \text{ Length} \text{ is}\, 3 \text{ more}, \text{ or}\, x + 3, \text{ and} \text{ area} \text{ is}\, 40.\\ x (x + 3) = 40 & & \text{ Multiply} \text{ length} \text{ by} \text{ width} \text{ to} \text{ get} \text{ area}\\ x^2 + 3 x = 40 & & \text{ Distribute}\\ \underline{- 40 - 40} & & \text{ Make} \text{ equation} \text{ equal} \text{ zero}\\ x^2 + 3 x - 40 = 0 & & \text{ Factor}\\ (x - 5) (x + 8) = 0 & & \text{ Set} \text{ each} \text{ factor} \text{ equal} \text{ to} \text{ zero}\\ x - 5 = 0 \text{ or}\, x + 8 = 0 & & \text{ Solve} \text{ each} \text{ equation}\\ x = 5 \text{ or}\, x = - 8 & & \text{ Our}\, x \text{ is} a \text{ width}, \text{ cannot} \text{ be} \text{ negative} .\\ (5) + 3 = 8 & & \text{ Length} \text{ is}\, x + 3, \text{ substitute} 5 \text{ for}\, x \text{ to} \text{ find} \text{ length}\\ 5 \text{ in} \text{ by}\, 8 \text{ in} & & \text{ Our} \text{ Solution} \end{eqnarray*}[/latex]

The dimensions of the rectangle are 5 inches by 8 inches.

In the following video you are shown how to find the dimensions of a border around a rectangle.

Cost, Revenue, and Profit Polynomials

In the systems of linear equations section, we discussed how a company’s cost and revenue can be modeled with two linear equations. We found that the profit region for a company was the area between the two lines where the company would make money based on how much was produced. In this section, we will see that sometimes polynomials are used to describe cost and revenue.

Profit is typically defined in business as the difference between the amount of money earned (revenue) by producing a certain number of items and the amount of money it takes to produce that number of items. When you are in business, you definitely want to see profit, so it is important to know what your cost and revenue is.

Cell Phones

For example, let’s say that the cost to a manufacturer to produce a certain number of things is C and the revenue generated by selling those things is R. The profit, P, can then be defined as

The example we will work with is a hypothetical cell phone manufacturer whose cost to manufacture x number of phones is [latex]C=2000x+750,000[/latex], and the Revenue generated from manufacturing x number of cell phones is [latex]R=-0.09x^2+7000x[/latex].

Define a Profit polynomial for the hypothetical cell phone manufacturer.

Read and Understand: Profit is the difference between revenue and cost, so we will need to define P = R – C for the company.

Define and Translate: [latex]\begin{array}{c}R=-0.09x^2+7000x\\C=2000x+750,000\end{array}[/latex]

Write and Solve: Substitute the expressions for R and C into the Profit equation.

[latex]\begin{array}{c}P=R-C\\=-0.09x^2+7000x-\left(2000x+750,000\right)\\=-0.09x^2+7000x-2000x-750,000\\=-0.09x^2+5000x-750,000\end{array}[/latex]

Remember that when you subtract a polynomial, you have to subtract every term of the polynomial.

[latex]P=-0.09x^2+5000x-750,000[/latex]

Mathematical models are great when you use them to learn important information. The cell phone manufacturing company can use the profit equation to find out how much profit they will make given [latex]x[/latex] number of phones are manufactured. In the next example, we will explore some profit values for this company.

Given the following numbers of cell phones manufactured, find the profit for the cell phone manufacturer:

x = 100 phones
x = 25,000 phones
x=60,000 phones

Interpret your results.

Read and Understand: The profit polynomial defined in the previous example,[latex]P=-0.09x^2+5000x-750,000[/latex], gives profit based on x number of phones manufactured. We need to substitute the given numbers of phones manufactured into the equation, then try to understand what our answer means in terms of profit and number of phones manufactured.

We will move straight into write and solve since we already have our polynomial. It is probably easiest to use a calculator since the numbers in this problem are so large.

Write and Solve:

Substitute [latex]x = 100[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(100\right)^2+5000\left(100\right)-750,000\\=-900+500,000-750,000\\=-250,900\end{array}[/latex]

Interpret: When the number of phones manufactured is 100, the profit for the business is $-250,000. This is not what we want! The company must produce more than 100 phones to make a profit.

Substitute [latex]x = 25,000[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(25000\right)^2+5000\left(25000\right)-750,000\\=-6120000+125,000,000-750,000\\=118,130,000\end{array}[/latex]

Interpret: When the number of phones manufactured is 25,000, the profit for the business is $118,130,000. This is more like it! If the company makes 25,000 phones it will make a profit after it pays all it’s bills.

If this is true, then the company should make even more phones so it can make even more money, right? Actually, something different happens as the number of items manufactured increases without bound.

Substitute [latex]x = 60,000[/latex]

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(60000\right)^2+5000\left(60000\right)-750,000\\=-324,000,000+300,000,000-750,000\\=-24,750,000\end{array}[/latex]

Interpret: When the number of phones manufactured is 60,000, the profit for the business is $-24,750,000. Wait a minute! If the company makes 60,000 phones it will lose money, what happened? At some point, the cost to manufacture the phones will overcome the amount of profit that the business can make. If this is interesting to you, you may enjoy reading about Economics and Business models.

In the video that follows, we present another example of finding a polynomial profit equation.

"Cops' Latest Tool in High-speed Chases: GPS Projectiles." CBSNews . CBS Interactive, n.d. Web. 14 June 2016. ↵
Solve a Quadratic Equations with Fractions by Factoring (a not 1). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/kDj_qdKW-ls . License : CC BY: Attribution
Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
Parabolic motion description and example. Provided by : Lumen Learning. License : CC BY: Attribution
Factoring Application - Find the Time When a Projectile Hits and Ground. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/hsWSzu3KcPU . License : CC BY: Attribution
Pythagorean Theorem, Description and Examples. Provided by : Lumen Learning. License : CC BY: Attribution
Screenshot: Thumbsdown. Provided by : Lumen Learning. License : CC BY: Attribution
Screenshot PI. Provided by : Lumen Learning. License : CC BY: Attribution
Polynomial Multiplication Application - Volume of a Cylinder. . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/g-g_nSsfGs4 . License : CC BY: Attribution
Polynomial Subtracton App - Profit Equation from Revene and Cost.. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning.. Located at : https://youtu.be/-TWjDC4g9dU . License : CC BY: Attribution
Screenshot: Cell Phones.. Authored by : Lumen Learning. License : CC BY: Attribution
Profit Polynomial Examples. Provided by : Lumen Learning. License : CC BY: Attribution
Ex: Factor and Solve Quadratic Equation - Greatest Common Factor Only. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/gIwMkTAclw8 . License : CC BY: Attribution
Ex: Factor and Solve Quadratic Equations When A equals 1. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/bi7i_RuIGl0 . License : CC BY: Attribution
Unit 12: Factoring, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
Parabolic water trajectory. Authored by : By GuidoB. Located at : https://commons.wikimedia.org/w/index.php?curid=8015696 . License : CC BY-SA: Attribution-ShareAlike
Pythagorean Theorem. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/Pythagorean_theorem . License : CC BY-SA: Attribution-ShareAlike
Ex: Polynomial Addition Application - Perimeter.. Authored by : James Sousa (Mathispower4u.com). . Located at : . License : CC BY: Attribution
Ex: Find the Area of a Rectangle Using a Polynomial.. Authored by : James Sousa (Mathispower4u.com) .. Located at : . License : CC BY: Attribution
Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. . Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
Applied Optimization Problems. Provided by : OpenStax. Located at : http://cnx.org/contents/svyieFe9@2/Applied-Optimization-Problems . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Download for free at http://cnx.org/contents/b2fca278-57bd-421d-aa85-21f539b4cc6f@2
Applications of Quadratic Equations. Authored by : James Sousa. Located at : http://www.youtube.com/watch?v=AlIoxXQ-V50 . License : CC BY: Attribution
Quadratics - Rectangle. Authored by : Tyler Wallace. Located at : http://wallace.ccfaculty.org/book/book.html . Project : Beginning and Intermediate Algebra. License : Public Domain: No Known Copyright
Question ID#74417. Authored by : Nearing,Daniel. License : CC BY: Attribution

PRACTICE PROBLEMS ON SOLVING POLYNOMIAL EQUATIONS

(1) Solve the cubic equation : 2x 3 − x 2 −18x + 9 = 0, if sum of two of its roots vanishes Solution

(2) Solve the equation 9x 3 − 36x 2 + 44x −16 = 0 if the roots form an arithmetic progression. Solution

(3) Solve the equation 3x 3 − 26x 2 + 52x − 24 = 0 if its roots form a geometric progression. Solution

(4) Determine k and solve the equation 2x 3 − 6x 2 + 3x + k = 0 if one of its roots is twice the sum of the other two roots. Solution

(5) Find all zeros of the polynomial x 6 − 3x 5 − 5x 4 + 22x 3 − 39x 2 − 39x + 135, if it is known that 1 + 2i an d √ 3 are two of its zeros. Solution

(6) Solve the cubic equation

(i) 2x 3 − 9x 2 +10x = 3

(ii) 8x 3 − 2x 2 − 7x + 3 = 0. Solution

(7) Solve the equation x 4 −14x 2 + 45 = 0 Solution

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to [email protected]

We always appreciate your feedback.

Sat Math Practice
SAT Math Worksheets
PEMDAS Rule
BODMAS rule
GEMDAS Order of Operations
Math Calculators
Transformations of Functions
Order of rotational symmetry
Lines of symmetry
Compound Angles
Quantitative Aptitude Tricks
Trigonometric ratio table
Word Problems
Times Table Shortcuts
10th CBSE solution
PSAT Math Preparation
Privacy Policy
Laws of Exponents

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Polynomial Equations

Learning objectives.

By the end of this section, you will be able to:

Use the Zero Product Property

Solve quadratic equations by factoring
Solve equations with polynomial functions
Solve applications modeled by polynomial equations

Before you get started, take this readiness quiz.

We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.

A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

A polynomial equation is an equation that contains a polynomial expression.

The degree of the polynomial equation is the degree of the polynomial.

We are now going to solve polynomial equations of degree two . A polynomial equation of degree two is called a quadratic equation . Listed below are some examples of quadratic equations:

${x}^{2}+5x+6=0\phantom{\rule{3em}{0ex}}3{y}^{2}+4y=10\phantom{\rule{3em}{0ex}}64{u}^{2}-81=0\phantom{\rule{3em}{0ex}}n\left(n+1\right)=42$

To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.

We will now use the Zero Product Property, to solve a quadratic equation .

$\left(5n-2\right)\left(6n-1\right)=0.$

Set each factor equal to zero.
Solve the linear equations.

Solve Quadratic Equations by Factoring

$a{x}^{2}+bx+c=0.$

Factor the quadratic expression.
Use the Zero Product Property.
Check. Substitute each solution separately into the original equation.

Before we factor, we must make sure the quadratic equation is in standard form .

Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?

$169{q}^{2}=49.$

We leave the check up to you.

$25{p}^{2}=49.$

$\left(3x-8\right)\left(x-1\right)=3x.$

In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.

$3{x}^{2}=12x+63.$

$9{m}^{3}+100m=60{m}^{2}.$

Solve Equations with Polynomial Functions

$f\left(x\right)={x}^{2}+2x-2,$

The Zero Product Property also helps us determine where the function is zero. A value of x where the function is 0, is called a zero of the function .

$f\left(x\right)=0,$

ⓐ the zeros of the function,

ⓑ any x -intercepts of the graph of the function

ⓐ To find the zeros of the function, we need to find when the function value is 0.

$\begin{array}{cccccc}& & & & & f\left(x\right)=3{x}^{2}+10x-8\hfill \\ \text{Substitute 0 for}\phantom{\rule{0.2em}{0ex}}f\left(x\right).\hfill & & & & & \phantom{\rule{1.2em}{0ex}}0=3{x}^{2}+10x-8\hfill \\ \text{Factor the trinomial.}\hfill & & & & & \left(x+4\right)\left(3x-2\right)=0\hfill \\ \begin{array}{c}\text{Use the zero product property.}\hfill \\ \text{Solve.}\hfill \end{array}\hfill & & & & & \begin{array}{ccccccccccc}\hfill x+4& =\hfill & 0\hfill & & & \text{or}\hfill & & & \hfill 3x-2& =\hfill & 0\hfill \\ \hfill x& =\hfill & -4\hfill & & & \text{or}\hfill & & & \hfill x& =\hfill & \frac{2}{3}\hfill \end{array}\hfill \end{array}$

ⓐ the zeros of the function

$x=\frac{5}{2}$

Solve Applications Modeled by Polynomial Equations

Read the problem. Make sure all the words and ideas are understood.
Identify what we are looking for.
Name what we are looking for. Choose a variable to represent that quantity.
Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
Solve the equation using appropriate algebra techniques.
Check the answer in the problem and make sure it makes sense.
Answer the question with a complete sentence.

We will start with a number problem to get practice translating words into a polynomial equation.

The product of two consecutive odd integers is 323. Find the integers.

$\begin{array}{cccccc}\mathbf{\text{Step 1. Read}}\phantom{\rule{0.2em}{0ex}}\text{the problem.}\hfill & & & & & \\ \mathbf{\text{Step 2. Identify}}\phantom{\rule{0.2em}{0ex}}\text{what we are looking for.}\hfill & & & & & \text{We are looking for two consecutive integers.}\hfill \\ \mathbf{\text{Step 3. Name}}\phantom{\rule{0.2em}{0ex}}\text{what we are looking for.}\hfill & & & & & \text{Let}\phantom{\rule{0.2em}{0ex}}n=\text{the first integer.}\hfill \\ & & & & & n+2=\phantom{\rule{0.2em}{0ex}}\text{next consecutive odd integer}\hfill \\ \begin{array}{c}\mathbf{\text{Step 4. Translate}}\phantom{\rule{0.2em}{0ex}}\text{into an equation. Restate the}\hfill \\ \text{problem in a sentence.}\hfill \end{array}\hfill & & & & & \begin{array}{c}\text{The product of the two consecutive odd}\hfill \\ \text{integers is 323.}\hfill \end{array}\hfill \\ & & & & & \phantom{\rule{3.47em}{0ex}}n\left(n+2\right)=323\hfill \\ \mathbf{\text{Step 5. Solve}}\phantom{\rule{0.2em}{0ex}}\text{the equation.}\hfill & & & & & \phantom{\rule{3.57em}{0ex}}{n}^{2}+2n=323\hfill \\ \text{Bring all the terms to one side.}\hfill & & & & & \phantom{\rule{0.85em}{0ex}}{n}^{2}+2n-323=0\hfill \\ \text{Factor the trinomial.}\hfill & & & & & \left(n-17\right)\left(n+19\right)=0\hfill \\ \begin{array}{c}\text{Use the Zero Product Property.}\hfill \\ \text{Solve the equations.}\hfill \end{array}\hfill & & & & & \begin{array}{ccccccccc}\hfill n-17& =\hfill & 0\hfill & & & & \hfill n+19& =\hfill & 0\hfill \\ \hfill n& =\hfill & 17\hfill & & & & \hfill n& =\hfill & -19\hfill \end{array}\hfill \end{array}$

There are two values for n that are solutions to this problem. So there are two sets of consecutive odd integers that will work.

$\begin{array}{cccccc}\text{If the first integer is}\phantom{\rule{0.2em}{0ex}}n=17\hfill & & & & & \text{If the first integer is}\phantom{\rule{0.2em}{0ex}}n=-19\hfill \\ \text{then the next odd integer is}\hfill & & & & & \text{then the next odd integer is}\hfill \\ \phantom{\rule{11em}{0ex}}n+2\hfill & & & & & \phantom{\rule{11em}{0ex}}n+2\hfill \\ \phantom{\rule{10.5em}{0ex}}17+2\hfill & & & & & \phantom{\rule{10em}{0ex}}\text{−}19+2\hfill \\ \phantom{\rule{11.5em}{0ex}}19\hfill & & & & & \phantom{\rule{11em}{0ex}}\text{−}17\hfill \\ \phantom{\rule{10.5em}{0ex}}17,19\hfill & & & & & \phantom{\rule{10em}{0ex}}\text{−}17,-19\hfill \\ \mathbf{\text{Step 6. Check}}\phantom{\rule{0.2em}{0ex}}\text{the answer.}\hfill & & & & & \\ \text{The results are consecutive odd integers}\hfill & & & & & \\ 17,19\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\text{−}19,-17.\hfill & & & & & \\ 17·19=323✓\phantom{\rule{4em}{0ex}}\text{−}19\left(\text{−}17\right)=323✓\hfill & & & & & \\ \text{Both pairs of consecutive integers are solutions.}\hfill & & & & & \\ \mathbf{\text{Step 7. Answer}}\phantom{\rule{0.2em}{0ex}}\text{the question}\hfill & & & & & \text{The consecutive integers are 17, 19 and}\phantom{\rule{0.2em}{0ex}}\text{−}19,-17.\hfill \end{array}$

The product of two consecutive odd integers is 255. Find the integers.

The product of two consecutive odd integers is 483 Find the integers.

In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.

A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.

A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

The width is 5 feet and length is 6 feet.

A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

The length of the patio is 12 feet and the width 15 feet.

$\left({a}^{2}+{b}^{2}={c}^{2}\right).$

We will use this formula to in the next example.

Figure shows a right triangle with the shortest side being x, the second side being x minus 7 and the hypotenuse being 17.

5 feet and 12 feet

24 feet and 25 feet

The next example uses the function that gives the height of an object as a function of time when it is thrown from 80 feet above the ground.

$h\left(t\right)=-16{t}^{2}+64t+80$

ⓐ the zeros of this function which tell us when the ball hits the ground

ⓑ when the ball will be 80 feet above the ground

ⓐ the zeros of this function which tell us when the rock will hit the ocean

ⓑ when the rock will be 160 feet above the ocean.

$h\left(t\right)=-16{t}^{2}+32t+128$

ⓐ the zeros of this function which is when the penny will hit the ocean

ⓑ when the penny will be 128 feet above the ocean.

Access this online resource for additional instruction and practice with quadratic equations.

Beginning Algebra & Solving Quadratics with the Zero Property

Key Concepts

Polynomial Equation: A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

$a,b,c\phantom{\rule{0.2em}{0ex}}\text{are real numbers and}\phantom{\rule{0.2em}{0ex}}a\ne 0$

Section Exercises

Practice makes perfect.

In the following exercises, solve.

$\left(3a-10\right)\left(2a-7\right)=0$

In the following exercises, for each function, find: ⓐ the zeros of the function ⓑ the x -intercepts of the graph of the function ⓒ the y -intercept of the graph of the function.

$f\left(x\right)=9{x}^{2}-4$

Solve Applications Modeled by Quadratic Equations

The product of two consecutive odd integers is 143. Find the integers.

The product of two consecutive odd integers is 195. Find the integers.

The product of two consecutive even integers is 168. Find the integers.

The product of two consecutive even integers is 288. Find the integers.

The area of a rectangular carpet is 28 square feet. The length is three feet more than the width. Find the length and the width of the carpet.

A rectangular retaining wall has area 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.

The area of a bulletin board is 55 square feet. The length is four feet less than three times the width. Find the length and the width of the a bulletin board.

A rectangular carport has area 150 square feet. The height of the carport is five feet less than twice its length. Find the height and the length of the carport.

A pennant is shaped like a right triangle, with hypotenuse 10 feet. The length of one side of the pennant is two feet longer than the length of the other side. Find the length of the two sides of the pennant.

A stained glass window is shaped like a right triangle. The hypotenuse is 15 feet. One leg is three more than the other. Find the lengths of the legs.

A reflecting pool is shaped like a right triangle, with one leg along the wall of a building. The hypotenuse is 9 feet longer than the side along the building. The third side is 7 feet longer than the side along the building. Find the lengths of all three sides of the reflecting pool.

A goat enclosure is in the shape of a right triangle. One leg of the enclosure is built against the side of the barn. The other leg is 4 feet more than the leg against the barn. The hypotenuse is 8 feet more than the leg along the barn. Find the three sides of the goat enclosure.

$h\left(t\right)=-16{t}^{2}+32t$

ⓐ the zeros of this function which tells us when the rocket will hit the ground. ⓑ the time the rocket will be 16 feet above the ground.

$h\left(t\right)=-16{t}^{2}+32t+48$

Writing Exercises

Explain how you solve a quadratic equation. How many answers do you expect to get for a quadratic equation?

Answers will vary.

Give an example of a quadratic equation that has a GCF and none of the solutions to the equation is zero.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

This table has 4 columns, 3 rows and a header row. The header row labels each column: I can, confidently, with some help and no, I don’t get it. The first column has the following statements: solve quadratic equations by using the zero product property, solve quadratic equations by factoring and solve applications modeled by quadratic equations.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

Chapter Review Exercises

Greatest common factor and factor by grouping.

Find the Greatest Common Factor of Two or More Expressions

In the following exercises, find the greatest common factor.

$12{a}^{2}{b}^{3},15a{b}^{2}$

Factor the Greatest Common Factor from a Polynomial

In the following exercises, factor the greatest common factor from each polynomial.

Factor by Grouping

In the following exercises, factor by grouping.

Factor Trinomials

${x}^{2}+bx+c$

In the following exercises, factor completely using trial and error.

${x}^{3}+5{x}^{2}-24x$

In the following exercises, factor.

$2{x}^{2}+9x+4$

Factor using substitution

In the following exercises, factor using substitution.

${x}^{4}-13{x}^{2}-30$

Factor Special Products

Factor Perfect Square Trinomials

In the following exercises, factor completely using the perfect square trinomials pattern.

$25{x}^{2}+30x+9$

Factor Differences of Squares

In the following exercises, factor completely using the difference of squares pattern, if possible.

$81{r}^{2}-25$

Factor Sums and Differences of Cubes

In the following exercises, factor completely using the sums and differences of cubes pattern, if possible.

${a}^{3}-125$

General Strategy for Factoring Polynomials

Recognize and Use the Appropriate Method to Factor a Polynomial Completely

In the following exercises, factor completely.

$24{x}^{3}+44{x}^{2}$

In each function, find: ⓐ the zeros of the function ⓑ the x -intercepts of the graph of the function ⓒ the y -intercept of the graph of the function.

$f\left(x\right)=64{x}^{2}-49$

The product of two consecutive numbers is 399. Find the numbers.

The area of a rectangular shaped patio 432 square feet. The length of the patio is 6 feet more than its width. Find the length and width.

A ladder leans against the wall of a building. The length of the ladder is 9 feet longer than the distance of the bottom of the ladder from the building. The distance of the top of the ladder reaches up the side of the building is 7 feet longer than the distance of the bottom of the ladder from the building. Find the lengths of all three sides of the triangle formed by the ladder leaning against the building.

The lengths are 8, 15, and 17 ft.

Chapter Practice Test

$80{a}^{2}+120{a}^{3}$

In the following exercises, solve

$5{a}^{2}+26a=24$

The product of two consecutive integers is 156. Find the integers.

The area of a rectangular place mat is 168 square inches. Its length is two inches longer than the width. Find the length and width of the placemat.

The width is 12 inches and the length is 14 inches.

Solver Title

Generating PDF...

Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
Linear Algebra Matrices Vectors
Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
Physics Mechanics
Chemistry Chemical Reactions Chemical Properties
Finance Simple Interest Compound Interest Present Value Future Value
Economics Point of Diminishing Return
Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
Pre Algebra
One-Step Addition
One-Step Subtraction
One-Step Multiplication
One-Step Division
One-Step Decimals
Two-Step Integers
Two-Step Add/Subtract
Two-Step Multiply/Divide
Two-Step Fractions
Two-Step Decimals
Multi-Step Integers
Multi-Step with Parentheses
Multi-Step Rational
Multi-Step Fractions
Multi-Step Decimals
Solve by Factoring
Completing the Square
Quadratic Formula
Biquadratic
Logarithmic
Exponential
Rational Roots
Floor/Ceiling
Equation Given Roots
Newton Raphson
Substitution
Elimination
Cramer's Rule
Gaussian Elimination
System of Inequalities
Perfect Squares
Difference of Squares
Difference of Cubes
Sum of Cubes
Polynomials
Distributive Property
FOIL method
Perfect Cubes
Binomial Expansion
Negative Rule
Product Rule
Quotient Rule
Expand Power Rule
Fraction Exponent
Exponent Rules
Exponential Form
Logarithmic Form
Absolute Value
Rational Number
Powers of i
Complex Form
Partial Fractions
Is Polynomial
Leading Coefficient
Leading Term
Standard Form
Complete the Square
Synthetic Division
Linear Factors
Rationalize Denominator
Rationalize Numerator
Identify Type
Convergence
Interval Notation
Pi (Product) Notation
Boolean Algebra
Truth Table
Mutual Exclusive
Cardinality
Caretesian Product
Age Problems
Distance Problems
Cost Problems
Investment Problems
Number Problems
Percent Problems
Addition/Subtraction
Multiplication/Division
Dice Problems
Coin Problems
Card Problems
Pre Calculus
Linear Algebra
Trigonometry
Conversions

Most Used Actions

Number line.

x^4-5x^2+4=0
\sqrt{x-1}-x=-7
\left|3x+1\right|=4
\log _2(x+1)=\log _3(27)
3^x=9^{x+5}
What is the completing square method?
Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
What is the golden rule for solving equations?
The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
How do you simplify equations?
To simplify equations, combine like terms, remove parethesis, use the order of operations.
How do you solve linear equations?
To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...

Please add a message.

Message received. Thanks for the feedback.

IMAGES

Problem solving involving polynomial functions
Problem solving involving polynomial functions
5-3 solving polynomial equations
48 Problem Solving Using Polynomial Equations
Problem solving involving polynomial functions
Polynomial Equation

VIDEO

Math 8
Solving Polynomial Equations
Solving Polynomial Equations
2. Solving Polynomial Equations Notes
Solve Polynomial Equations
Solving Polynomial Equations

COMMENTS

1.4: Solving Polynomial Equations
Polynomial equations of degree one are linear equations are of the form ax + b = c. We are now going to solve polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation. Listed below are some examples of quadratic equations: x2 + 5x + 6 = 0 3y2 + 4y = 10 64u2 − 81 = 0 n(n + 1) = 42.
Polynomial Equation Word Problems (Mixed Operations)
Show Video Lesson. How To Solve Word Problems With Polynomial Equations? Examples: The sum of a number and its square is 72. Find the number. The area of a triangle is 44m 2. Find the lengths of the legs if one of the legs is 3m longer than the other leg. The top of a 15-foot ladder is 3 feet farther up a wall than the foo is from the bottom of ...
Polynomial Questions and Problems with Solutions
The remaining zeros may found by solving the equation 3 x 2 + 5 x - 2 = 0 Solve the above equation to find the remaining zeros of f.-2 and 1 / 3 Problem 5: A polynomial of degree 4 has a positive leading coefficient and simple zeros (i.e. zeros of multiplicity 1) at x = 2, x = - 2, x = 1 and x = -1. Is the y intercept of the graph of this ...
Solving Problems Involving Polynomials and Polynomial Equations
For the eighth and ninth week of our lesson in Grade 10 Mathematics we will have discussions on illustrating and finding roots of polynomial equations using ...
Solve real-world applications of polynomial equations
Let's use these tools to solve the bakery problem from the beginning of the section. Example 8: Solving Polynomial Equations. A new bakery offers decorated sheet cakes for children's birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid.
Polynomial expressions, equations, & functions
About this unit. This topic covers: Adding, subtracting, and multiplying polynomial expressions. Factoring polynomial expressions as the product of linear factors. Dividing polynomial expressions. Proving polynomials identities. Solving polynomial equations & finding the zeros of polynomial functions. Graphing polynomial functions.
4.4: Solve Polynomial Equations by Factoring
Solving Polynomial Equations by Factoring. In this section, we will review a technique that can be used to solve certain polynomial equations. We begin with the zero-product property 20: $a⋅b=0$ if and only if $a=0$ or $b=0$ The zero-product property is true for any number of factors that make up an equation.
Polynomial word problem: area of a window (video)
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. ... Polynomial word problem: rectangle and circle area. Polynomial word problem: total value of bills ... Math > Algebra (all content) > Polynomial expressions, equations, & functions > Polynomials word problems ...
Graphs of polynomials: Challenge problems
I assume you are asking about problem 3. The polynomial is in factored form. If you set y=0 to find the x-intercepts, each factor gets set to 0 (using the zero product rule). x-2=0 and x+1=0. Solve them, and you get that the x-intercepts are at x=-2 and x=-1. Next, you look at the exponents on each factor.
PDF Problem Solving Using Polynomial Equations
Plan for Solving a Word Problem, Continued. 3. Reread the problem. Then write an equation that represents relationships among the numbers in the problem. 4. Solve the equation and find the required numbers. 5. Check your results with the original statement of the problem. Give the answer.
Solve Polynomial Equations by Factoring
Solving Polynomial Equations by Factoring. In this section, we will review a technique that can be used to solve certain polynomial equations. We begin with the zero-product property A product is equal to zero if and only if at least one of the factors is zero.. a ⋅ b = 0 if and only if a = 0 or b = 0. The zero-product property is true for any number of factors that make up an equation.
6.5: Polynomial Equations
We are now going to solve polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation. Listed below are some examples of quadratic equations: ... Read the problem. In problems involving geometric figures, a sketch can help you visualize the situation. Step 2. Identify what you are looking for.
(7.5.1)
Learning Objectives. (7.5.1) - Solving polynomial equations. The principle of zero products. (7.5.2) - Applications of polynomial equations. Projectile motion. Using the Pythagorean theorem to find the lengths of a right triangle. Geometric Applications. Cost, revenue, and profit polynomials.
Grade 10 Math
#ProblemSolving #PolynomialEquationsLesson 17: Solving Problems Involving Polynomial EquationMELC Quarter 1 Week 8corrections on 12:39-54 + 80 = 26
PDF 4.8 Applications of Polynomials
Problems involving geometric figures are very common in algebra, as well as in life. So, as we always do in a problem involving geometry, we draw a picture to help us with generating our equation. We will also have to remember our geometry formulas. So, since our length is 2 yards more than twice the width, our rectangle must look like
PRACTICE PROBLEMS ON SOLVING POLYNOMIAL EQUATIONS
PRACTICE PROBLEMS ON SOLVING POLYNOMIAL EQUATIONS. (1) Solve the cubic equation : 2x 3 − x 2 −18x + 9 = 0, if sum of two of its roots vanishes Solution. (2) Solve the equation 9x3 − 36x2 + 44x −16 = 0 if the roots form an arithmetic progression. Solution. (3) Solve the equation 3x 3 − 26x 2 + 52x − 24 = 0 if its roots form a ...
PDF Quarter 2 Module 2: Solving Problems Involving Polynomial Functions
Solving Problems Involving Polynomial Functions 10 ... The aforesaid equations are first degree, second degree, and third degree polynomial functions known as linear, quadratic, and cubic functions, respectively. Take note that, in general, a polynomial function, usually denoted by 𝑃( T) or ( T), is a function defined by ...
Polynomial multiplication word problem (video)
It's squared because you are multiplying 30x and 8x. When multiplying variables, you write the variable, (x), and add what powers that they are each to together, (x^1 times x^1).You will end up with x^2. Here is an example. x^3 times x^2. First, write the variable, (x), and then, add their powers together, (^3+^2)=^5.
Grade 10 Mathematics Module: Solving Problems Involving Polynomial
It is here to help you solve problems involving polynomial functions applying the concepts learned in the previous modules. The scope of this module permits it to be used in many different learning situations. The language used recognizes the diverse vocabulary level of students. The lessons are arranged to follow the standard sequence of the ...
Polynomial Equations
We are now going to solve polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation. Listed below are some examples of quadratic equations: ... Read the problem. In problems involving. geometric figures, a sketch can help you visualize. the situation. Step 2. Identify what you are looking for.
PDF Quarter 1 Module 2 Solving Problems Involving Factors of Polynomials
consecutive values or create an equation that you are going to solve with accuracy and using variety of strategies. This module contains: Lesson 1- Solving Problems Involving Factors of Polynomials After going through this module, you are expected to: 1. recall the different techniques of factoring polynomials; 2. apply the concept of factoring ...
Math 10 q1 WK 9 Module 9 Solving Problems in Polynomials and ...
This document provides an overview of a mathematics module on solving problems involving polynomials and polynomial equations. It begins by explaining the key concepts of polynomials versus polynomial equations. It then outlines the three lessons that make up the module, which are: 1) Solving Problems Involving polynomials, 2) Solving Problems Involving Polynomial Equations, and 3) Factoring ...
Equation Calculator
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Type in any equation to get the solution, steps and graph

Polynomial Equation Word Problems (Mixed Operations)

Polynomial Questions and Problems with Solutions

4.4 Solve Polynomial Equations by Factoring

Reviewing General Factoring Strategies

Solving Polynomial Equations by Factoring

Finding Roots of Functions

Finding Equations with Given Solutions

Key Takeaways

Topic Exercises

Part B: Solving Polynomial Equations by Factoring

Part C: Finding Equations with Given Solutions

Part D: Discussion Board

Margin Size

6.5: Polynomial Equations

Use the Zero Product Property

ZERO PRODUCT PROPERTY

Example \(\PageIndex{1}\): How to Solve a Quadratic Equation Using the Zero Product Property

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

USE THE ZERO PRODUCT PROPERTY.

Solve Quadratic Equations by Factoring

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

SOLVE A QUADRATIC EQUATION BY FACTORING.

Example \(\PageIndex{7}\)

Example \(\PageIndex{8}\)

Example \(\PageIndex{9}\)

Example \(\PageIndex{10}\)

Example \(\PageIndex{11}\)

Example \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Example \(\PageIndex{14}\)

Example \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Example \(\PageIndex{17}\)

Example \(\PageIndex{18}\)

Solve Equations with Polynomial Functions

Example \(\PageIndex{19}\)

Example \(\PageIndex{20}\)

Example \(\PageIndex{21}\)

ZERO OF A FUNCTION

Example \(\PageIndex{22}\)

Example \(\PageIndex{23}\)

Example \(\PageIndex{24}\)

Solve Applications Modeled by Polynomial Equations

USE A PROBLEM SOLVING STRATEGY TO SOLVE WORD PROBLEMS.

Example \(\PageIndex{25}\)

Example \(\PageIndex{26}\)

Example \(\PageIndex{27}\)

Example \(\PageIndex{28}\)

Example \(\PageIndex{29}\)

Example \(\PageIndex{30}\)

Example \(\PageIndex{31}\)

Example \(\PageIndex{32}\)

Example \(\PageIndex{33}\)

Example \(\PageIndex{34}\)

Example \(\PageIndex{35}\)

Example \(\PageIndex{36}\)

Key Concepts

Module 7: Polynomials and Polynomial Functions

Geometric Applications

(7.5.1) – Solving polynomial equations

The Principle of Zero Products

Principle of Zero Products

(7.5.2) – Applications of polynomial equations

Pythagorean Theorem

Cost, Revenue, and Profit Polynomials

PRACTICE PROBLEMS ON SOLVING POLYNOMIAL EQUATIONS

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

The Mean Value Theorem Worksheet

Mean Value Theorem

Polynomial Equations

Solve Applications Modeled by Polynomial Equations

Key Concepts

Section Exercises

Writing Exercises

Chapter Review Exercises

Factor Trinomials

Factor Special Products