problem solving with rational equations

Solving Rational Equations · Examples

Listen up, fraction fans! In today’s lesson, you will learn and practice solving rational equations. As you will see, these are any equation involving a fraction, also known as a rational number in math talk!

By the end, you will know the difference between rational and irrational numbers and have two tricks for solving rational equations.

You could even tackle one of the tricky challenges to form a rational equation using the Pythagorean theorem , or to simplify an expression involving some radicals!

What is a Rational Equation? How to Solve Rational Equations Step 1: Eliminate the Denominators Step 2: Simplify the Equation Step 3: Solve the Equation Step 4: Check Solutions Practice & Challenges Question 1 Question 2 Challenge 1 Challenge 2 Worksheet To Sum Up (Pun Intended!)

What is a Rational Equation?

A rational equation is simply an equation involving a rational number.

A ratio -nal number can be written as a ratio of two integers – an irratio -nal number cannot.

Most of the numbers you know and love such as \(\Large\frac{2}{7}\), \(\Large\frac{1}{2}\) and \(-\Large\frac{20817}{43}\) are rational. Some common irrational numbers are π, \(\sqrt{2}\) and Euler’s number, e. These cannot be written as a fraction of integers.

Numberphile has an interesting video about All the Numbers , which categorizes number types, including rational and irrational numbers .

Technically speaking, basic equations like x+2=5 are rational because each term is a rational number. However, the rational equations you will solve today won’t be so easy!

An example of what you will more likely see in an exam is something like this:

Each term is shown as a fraction.

Rational equations can also include radicals:

Or other operations such as division:

Luckily, the technique you learn now will work for every type of rational equation!

How to Solve Rational Equations

The method to solve these equations is pretty much the same for every type of rational equation. You’ll see questions of varying difficulty in this lesson; don’t be afraid to tackle the challenges later on!

Step 1: The Denominator Elimination Round!

First, you need to deal with the elephant in the room: what should you do with the denominators!?

Solving rational equations is just like solving any other equation once you complete this step.

If it’s a simple case, where you have one fraction being equal to one other fraction, you can cross multiply .

Multiply both sides by the values of both denominators. In this example, both sides are multiplied by 3, then 5.

The 3 cancels with the left denominator and the 5 cancels with the right denominator, leaving you with 5(x+4)=3×2.

See why it’s called cross multiplying?

The product of the left denominator and right numerator equals the product of the right denominator and left numerator !

The more general way to deal with the denominators is to find their lowest common multiple (LCM) . This is the smallest number which all denominators divide neatly, leaving no remainder.

If you cannot find the LCM by inspection – if you cannot “just see it” – you need to factor every denominator like you would with a polynomial.

If you have more than one constant term, you may need to find their prime factors.

The LCM is the smallest combination of each denominator’s factors.

You’ll now see a worked example to illustrate!

Remember, you can only cross multiply when each side has only one fraction, so in this case, your first step is to find the LCM.

The only factors of 3x you know for certain are 3 and x. The only factor you know of x is just x, and 4 is a constant so you can use it as it is.

Write down each denominator’s polynomial factors into rows, with similar terms lined up in the same column.

You need to include both 3 and 4 because neither is a factor of the other. You don’t need both copies of x because x is a factor of itself! So the LCM is 12x.

You might find another example of finding the LCM with the same technique helpful.

You’re now ready to eliminate the denominators by multiplying both sides by the LCM.

Step 2: Simplify the Equation

Multiply each term by the LCM. Continuing from the last example, you have:

You now have a regular equation with no fractions, which should be familiar ground!

Step 3: Solve the Equation

Solving rational equations usually produces a simple polynomial equation. Hopefully, you’ve solved lots of these before!

You could complete the square, factor the terms by inspection, or use the quadratic formula.

This example can be solved by factoring the polynomial, having found that x+2 and x+4 are factors.

You could also solve the equation by completing the square:

Or by using the quadratic formula with a=1, b=6 and c=8:

Each way of solving the simplified rational equation is valid, but you will find that some are quicker than others!

Step 4: Check Every Solution

It is important to check that your solutions are complete, meaning you’ve found all of them and that they don’t give any weird numbers when substituted into the original equation.

In the worked example, you were left with a quadratic equation and found two distinct roots.

Quadratic equations either have two distinct solutions, one repeated solution, or no real solution so the solution x=-2 or x=-4 is complete.

You must be careful that none of the rational terms in the original equation have a zero in the denominator.

Do this by going back to the beginning and substituting your answers into the denominators!

The denominators in the worked example are 3x, x, and 4. Replacing x with -2 or -4 doesn’t give you zero in any of them, so you’re safe here!

A solution that gives a zero-denominator is not allowed. That’s because dividing by zero is “illegal” in math!

Any number divided by zero gives an error on a calculator. Ever wondered why that is?

This is your time to shine – try solving rational equations for yourself and, if you’re feeling confident, tackle the challenges too.

As they say, practice makes perfect! Use the worked example for guidance if you get stuck.

Find x in the following rational equation:

The equation is two equal fractions so you can cross-multiply. You could also simplify \(\Large\frac{15}{3}\normalsize\) to 5, but this does not change the final answer.

Each term is divisible by 9. Simplify the equation by dividing both sides by 9:

This form is called the difference of two squares because it can be factored like this:

So the solution is x=±3.

These must be all the solutions because quadratic equations have a maximum of two distinct real roots.

Neither denominator in the original rational equation has an x term, so substituting any value for x makes no difference to their values – there is no chance of them being zero!

This means the solutions x=3 and x=-3 are valid.

Solve the following rational equation:

There are three fractions so you cannot cross-multiply.

See that the second denominator is the difference of two squares?

Multiply each term by the LCM and simplify.

So its solution is -5, right?… STOP RIGHT THERE! Don’t forget, we can’t divide by zero!

If you put x=±5 into the original equation, at least one of the denominators is always zero, so the original equation has no solutions.

Challenge 1

Can you spot the mistake in the following example? Hint: there has been some cheating with radicals!

If you need a refresher on radicals , check out our lesson on multiplying them. That will get you on the right track!

The mistake is that radicals cannot be subtracted like normal terms.

Instead, you must square both sides of the equation to remove the radical. Similar terms can then be combined as usual.

Still confused? You can find lots of interactive questions on Lumen Learning . Radicals often pop up in rational equations, so getting comfortable with radicals is super helpful for exam success!

Challenge 2

Find the value of x, by using the Pythagorean theorem on the following right-angled triangle:

If you need a refresher on the Pythagorean theorem or are interested in the man himself, check out our lesson. Do the worksheets and you’ll be acing triangle questions in no time !

The Pythagorean theorem states that:

Where c is the length of the hypotenuse, and a and b are the other side lengths.

This gives the rational equation:

Simplifying, you find:

The LCM is 36 so the denominators are removed by dividing each term by this:

It’s always fun when different areas of math link together!

To Sum Up (Pun Intended!)

In today’s lesson on solving rational equations, you first saw the difference between rational and irrational numbers.

Rational numbers are “nice” because they can be written as a fraction of integers. Remember that all integers are rational because they can be written with a denominator of 1!

Irrational numbers are a little more abstract. They include weird but incredibly beautiful numbers like π and e, which cannot be written as a fraction of integers.

Rational equations are solved by eliminating the denominator in every term, then simplifying and solving as normal.

Denominators can be removed by cross-multiplication if there is only one fraction on either side or by finding the LCM if the equation is more complicated.

Don’t be shy, leave a comment below if you have any questions or need help!

Still curious about rational numbers, or eager for an extra challenge? Check out our lesson on the rational root theorem , which combines algebra and equation solving.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

7.5 Solve Applications with Rational Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve proportions

Solve similar figure applications

• Solve uniform motion applications
• Solve work applications
• Solve direct variation problems
• Solve inverse variation problems

Be Prepared 7.13

Before you get started, take this readiness quiz.

Solve: 2 ( n − 1 ) − 4 = −10 . 2 ( n − 1 ) − 4 = −10 . If you missed this problem, review Example 2.13 .

Be Prepared 7.14

An express train and a charter bus leave Chicago to travel to Champaign. The express train can make the trip in two hours and the bus takes five hours for the trip. The speed of the express train is 42 miles per hour faster than the speed of the bus. Find the speed of the bus. If you missed this problem, review Example 2.43 .

Be Prepared 7.15

Solve 1 3 x + 1 4 x = 5 6 . 1 3 x + 1 4 x = 5 6 . If you missed this problem, review Example 2.9 .

Solve Proportions

When two rational expressions are equal, the equation relating them is called a proportion .

A proportion is an equation of the form a b = c d , a b = c d , where b ≠ 0 , d ≠ 0 . b ≠ 0 , d ≠ 0 .

The proportion is read “ a is to b as c is to d. ”

The equation 1 2 = 4 8 1 2 = 4 8 is a proportion because the two fractions are equal. The proportion 1 2 = 4 8 1 2 = 4 8 is read “1 is to 2 as 4 is to 8.”

Since a proportion is an equation with rational expressions, we will solve proportions the same way we solved rational equations. We’ll multiply both sides of the equation by the LCD to clear the fractions and then solve the resulting equation.

Example 7.43

Solve: n n + 14 = 5 7 . n n + 14 = 5 7 .

Try It 7.85

Solve the proportion: y y + 55 = 3 8 . y y + 55 = 3 8 .

Try It 7.86

Solve the proportion: z z − 84 = − 1 5 . z z − 84 = − 1 5 .

Notice in the last example that when we cleared the fractions by multiplying by the LCD, the result is the same as if we had cross-multiplied.

For any proportion, a b = c d , a b = c d , we get the same result when we clear the fractions by multiplying by the LCD as when we cross-multiply.

To solve applications with proportions, we will follow our usual strategy for solving applications But when we set up the proportion, we must make sure to have the units correct—the units in the numerators must match each other and the units in the denominators must also match each other.

Example 7.44

When pediatricians prescribe acetaminophen to children, they prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

Try It 7.87

Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 pounds?

Try It 7.88

For every 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?

When you shrink or enlarge a photo on a phone or tablet, figure out a distance on a map, or use a pattern to build a bookcase or sew a dress, you are working with similar figures . If two figures have exactly the same shape, but different sizes, they are said to be similar. One is a scale model of the other. All their corresponding angles have the same measures and their corresponding sides have the same ratio.

Similar Figures

Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides have the same ratio.

For example, the two triangles in Figure 7.2 are similar. Each side of Δ A B C Δ A B C is four times the length of the corresponding side of Δ X Y Z . Δ X Y Z .

This is summed up in the Property of Similar Triangles.

Property of Similar Triangles

If Δ A B C Δ A B C is similar to Δ X Y Z , Δ X Y Z , then their corresponding angle measure are equal and their corresponding sides have the same ratio.

To solve applications with similar figures we will follow the Problem-Solving Strategy for Geometry Applications we used earlier.

Example 7.45

On a map, San Francisco, Las Vegas, and Los Angeles form a triangle. The distance between the cities is measured in inches. The figure on the left below represents the triangle formed by the cities on the map. If the actual distance from Los Angeles to Las Vegas is 270 miles, find the distance from Los Angeles to San Francisco.

Since the triangles are similar, the corresponding sides are proportional.

On the map, Seattle, Portland, and Boise form a triangle. The distance between the cities is measured in inches. The figure on the left below represents the triangle formed by the cities on the map. The actual distance from Seattle to Boise is 400 miles.

Try It 7.89

Find the actual distance from Seattle to Portland.

Try It 7.90

Find the actual distance from Portland to Boise.

We can use similar figures to find heights that we cannot directly measure.

Example 7.46

Tyler is 6 feet tall. Late one afternoon, his shadow was 8 feet long. At the same time, the shadow of a tree was 24 feet long. Find the height of the tree.

Try It 7.91

A telephone pole casts a shadow that is 50 feet long. Nearby, an 8 foot tall traffic sign casts a shadow that is 10 feet long. How tall is the telephone pole?

Try It 7.92

A pine tree casts a shadow of 80 feet next to a 30 foot tall building which casts a 40 feet shadow. How tall is the pine tree?

Solve Uniform Motion Applications

We have solved uniform motion problems using the formula D = r t D = r t in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

The formula D = r t D = r t assumes we know r and t and use them to find D . If we know D and r and need to find t , we would solve the equation for t and get the formula t = D r . t = D r .

We have also explained how flying with or against the wind affects the speed of a plane. We will revisit that idea in the next example.

Example 7.47

An airplane can fly 200 miles into a 30 mph headwind in the same amount of time it takes to fly 300 miles with a 30 mph tailwind. What is the speed of the airplane?

This is a uniform motion situation. A diagram will help us visualize the situation.

Try It 7.93

Link has an electric bike which runs at a constant speed. That speed will be reduced by the amount of any headwind and increased by the amount of any tailwind. Link can ride his bike 20 miles into a 3 mph headwind in the same amount of time he can ride 30 miles with a 3 mph tailwind. What is Link’s biking speed?

Try It 7.94

On a river that flows at 7 miles per hour, Danica can take a motorboat 5 miles upstream, in the same amount of time she can take her motorboat 12 miles downstream. How fast is Danica's boat in a lake?

In the next example, we will know the total time resulting from travelling different distances at different speeds.

Example 7.48

Jazmine trained for 3 hours on Saturday. She ran 8 miles and then biked 24 miles. Her biking speed is 4 mph faster than her running speed. What is her running speed?

Try It 7.95

Dennis went cross-country skiing for 6 hours on Saturday. He skied 20 mile uphill and then 20 miles back downhill, returning to his starting point. His uphill speed was 5 mph slower than his downhill speed. What was Dennis’ speed going uphill and his speed going downhill?

Try It 7.96

Joon drove 4 hours to his home, driving 208 miles on the interstate and 40 miles on country roads. If he drove 15 mph faster on the interstate than on the country roads, what was his rate on the country roads?

Once again, we will use the uniform motion formula solved for the variable t . t .

Example 7.49

Hamilton rode his bike downhill 12 miles on the river trail from his house to the ocean and then rode uphill to return home. His uphill speed was 8 miles per hour slower than his downhill speed. It took him 2 hours longer to get home than it took him to get to the ocean. Find Hamilton’s downhill speed.

Try It 7.97

Kayla rode her bike 75 miles home from college one weekend and then rode the bus back to college. It took her 2 hours less to ride back to college on the bus than it took her to ride home on her bike, and the average speed of the bus was 10 miles per hour faster than Kayla’s biking speed. Find Kayla’s biking speed.

Try It 7.98

Victoria jogs 12 miles to the park along a flat trail and then returns by jogging on an 20 mile hilly trail. She jogs 1 mile per hour slower on the hilly trail than on the flat trail, and her return trip takes her two hours longer. Find her rate of jogging on the flat trail.

Solve Work Applications

The weekly gossip magazine has a big story about the Princess’ baby and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes 6 hours to do the job and Press #2 takes 12 hours to do the job. How long will it take the printer to get the magazine printed with both presses running together?

This is a typical ‘work’ application. There are three quantities involved here—the time it would take each of the two presses to do the job alone and the time it would take for them to do the job together.

If Press #1 can complete the job in 6 hours, in one hour it would complete 1 6 1 6 of the job.

If Press #2 can complete the job in 12 hours, in one hour it would complete 1 12 1 12 of the job.

We will let t be the number of hours it would take the presses to print the magazines with both presses running together. So in 1 hour working together they have completed 1 t 1 t of the job.

We can model this with the word equation and then translate to a rational equation. To find the time it would take the presses to complete the job if they worked together, we solve for t . t .

A chart will help us organize the information. We are looking for how many hours it would take to complete the job with both presses running together.

Keep in mind, it should take less time for two presses to complete a job working together than for either press to do it alone.

Example 7.50

Suppose Pete can paint a room in 10 hours. If he works at a steady pace, in 1 hour he would paint 1 10 1 10 of the room. If Alicia would take 8 hours to paint the same room, then in 1 hour she would paint 1 8 1 8 of the room. How long would it take Pete and Alicia to paint the room if they worked together (and didn’t interfere with each other’s progress)?

This is a ‘work’ application. A chart will help us organize the information. We are looking for the numbers of hours it will take them to paint the room together.

In one hour Pete did 1 10 1 10 of the job. Alicia did 1 8 1 8 of the job. And together they did 1 t 1 t of the job.

Try It 7.99

One gardener can mow a golf course in 4 hours, while another gardener can mow the same golf course in 6 hours. How long would it take if the two gardeners worked together to mow the golf course?

Try It 7.100

Daria can weed the garden in 7 hours, while her mother can do it in 3. How long will it take the two of them working together?

Example 7.51

Ra’shon can clean the house in 7 hours. When his sister helps him it takes 3 hours. How long does it take his sister when she cleans the house alone?

This is a work problem. A chart will help us organize the information.

We are looking for how many hours it would take Ra’shon’s sister to complete the job by herself.

Try It 7.101

Alice can paint a room in 6 hours. If Kristina helps her it takes them 4 hours to paint the room. How long would it take Kristina to paint the room by herself?

Try It 7.102

Tracy can lay a slab of concrete in 3 hours, with Jordan’s help they can do it in 2 hours. If Jordan works alone, how long will it take?

Solve Direct Variation Problems

When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.

Lindsay gets paid $15 per hour at her job. If we let s be her salary and h be the number of hours she has worked, we could model this situation with the equation

Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.

Direct Variation

For any two variables x and y , y varies directly with x if

The constant k is called the constant of variation.

In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates x and y. Then we can use that equation to find values of y for other values of x .

We’ll list the steps here.

Solve direct variation problems.

• Step 1. Write the formula for direct variation.
• Step 2. Substitute the given values for the variables.
• Step 3. Solve for the constant of variation.
• Step 4. Write the equation that relates x and y using the constant of variation.

Now we’ll solve an application of direct variation.

Example 7.52

When Raoul runs on the treadmill at the gym, the number of calories, c , he burns varies directly with the number of minutes, m , he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.

ⓐ Write the equation that relates c and m . ⓑ How many calories would he burn if he ran on the treadmill for 25 minutes?

Try It 7.103

The number of calories, c , burned varies directly with the amount of time, t , spent exercising. Arnold burned 312 calories in 65 minutes exercising.

ⓐ Write the equation that relates c and t . ⓑ How many calories would he burn if he exercises for 90 minutes?

Try It 7.104

The distance a moving body travels, d , varies directly with time, t , it moves. A train travels 100 miles in 2 hours

ⓐ Write the equation that relates d and t . ⓑ How many miles would it travel in 5 hours?

Solve Inverse Variation Problems

Many applications involve two variable that vary inversely . As one variable increases, the other decreases. The equation that relates them is y = k x . y = k x .

Inverse Variation

For any two variables x and y , y varies inversely with x if

The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is 1 x . 1 x .

We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.

Solve inverse variation problems.

• Step 1. Write the formula for inverse variation.

Example 7.53

The frequency of a guitar string varies inversely with its length. A 26 in.-long string has a frequency of 440 vibrations per second.

ⓐ Write the equation of variation. ⓑ How many vibrations per second will there be if the string’s length is reduced to 20 inches by putting a finger on a fret?

Try It 7.105

The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees Celsius.

ⓐ Write the equation of variation. ⓑ How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?

Try It 7.106

Xander’s new business found that the daily demand for its product was inversely proportional to the price, p . p . When the price is $5, the demand is 700 units.

ⓐ Write the equation of variation. ⓑ What is the demand if the price is raised to $7?

Access this online resource for additional instruction and practice with applications of rational expressions

• Applications of Rational Expressions

Section 7.5 Exercises

Practice makes perfect.

In the following exercises, solve each proportion.

x 56 = 7 8 x 56 = 7 8

56 72 = y 9 56 72 = y 9

98 154 = −7 p 98 154 = −7 p

72 156 = −6 q 72 156 = −6 q

a a + 12 = 4 7 a a + 12 = 4 7

b b − 16 = 11 9 b b − 16 = 11 9

m + 90 25 = m + 30 15 m + 90 25 = m + 30 15

n + 10 4 = 40 − n 6 n + 10 4 = 40 − n 6

2 p + 4 8 = p + 18 6 2 p + 4 8 = p + 18 6

q − 2 2 = 2 q − 7 18 q − 2 2 = 2 q − 7 18

In the following exercises, solve.

Kevin wants to keep his heart rate at 160 beats per minute while training. During his workout he counts 27 beats in 10 seconds.

ⓐ How many beats per minute is this? ⓑ Has Kevin met his target heart rate?

Jesse’s car gets 30 miles per gallon of gas.

ⓐ If Las Vegas is 285 miles away, how many gallons of gas are needed to get there and then home? ⓑ If gas is $3.09 per gallon, what is the total cost of the gas for the trip?

Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Jocelyn, who weighs 45 pounds?

A veterinarian prescribed Sunny, a 65-pound dog, an antibacterial medicine in case an infection emerges after her teeth were cleaned. If the dosage is 5 mg for every pound, how much medicine was Sunny given?

A new energy drink advertises 106 calories for 8 ounces. How many calories are in 12 ounces of the drink?

One 12-ounce can of soda has 150 calories. If Josiah drinks the big 32-ounce size from the local mini-mart, how many calories does he get?

Kyra is traveling to Canada and will change $250 US dollars into Canadian dollars. At the current exchange rate, $1 US is equal to $1.3 Canadian. How many Canadian dollars will she get for her trip?

Maurice is traveling to Mexico and needs to exchange $450 into Mexican pesos. If each dollar is worth 12.29 pesos, how many pesos will he get for his trip?

Ronald needs a morning breakfast drink that will give him at least 390 calories. Orange juice has 130 calories in one cup. How many cups does he need to drink to reach his calorie goal?

Sonya drinks a 32-ounce energy drink containing 80 calories per 12 ounce. How many calories did she drink?

Phil wants to fertilize his lawn. Each bag of fertilizer covers about 4,000 square feet of lawn. Phil’s lawn is approximately 13,500 square feet. How many bags of fertilizer will he have to buy?

An oatmeal cookie recipe calls for 1 2 1 2 cup of butter to make 4 dozen cookies. Hilda needs to make 10 dozen cookies for the bake sale. How many cups of butter will she need?

Solve Similar Figure Applications

In the following exercises, the triangles are similar. Find the length of the indicated side.

ⓐ side x ⓑ side b

ⓐ side d ⓑ side q

In the following exercises, use the map shown. On the map, New York City, Chicago, and Memphis form a triangle. The actual distance from New York to Chicago is 800 miles.

Find the actual distance from New York to Memphis.

Find the actual distance from Chicago to Memphis.

In the following exercises, use the map shown. On the map, Atlanta, Miami, and New Orleans form a triangle. The actual distance from Atlanta to New Orleans is 420 miles.

Find the actual distance from New Orleans to Miami.

Find the actual distance from Atlanta to Miami.

In the following exercises, answer each question.

A 2-foot-tall dog casts a 3-foot shadow at the same time a cat casts a one foot shadow. How tall is the cat ?

Larry and Tom were standing next to each other in the backyard when Tom challenged Larry to guess how tall he was. Larry knew his own height is 6.5 feet and when they measured their shadows, Larry’s shadow was 8 feet and Tom’s was 7.75 feet long. What is Tom’s height?

The tower portion of a windmill is 212 feet tall. A six foot tall person standing next to the tower casts a seven-foot shadow. How long is the windmill’s shadow?

The height of the Statue of Liberty is 305 feet. Nikia, who is standing next to the statue, casts a 6-foot shadow and she is 5 feet tall. How long should the shadow of the statue be?

In the following exercises, solve the application problem provided.

Mary takes a sightseeing tour on a helicopter that can fly 450 miles against a 35-mph headwind in the same amount of time it can travel 702 miles with a 35-mph tailwind. Find the speed of the helicopter.

A private jet can fly 1,210 miles against a 25-mph headwind in the same amount of time it can fly 1694 miles with a 25-mph tailwind. Find the speed of the jet.

A boat travels 140 miles downstream in the same time as it travels 92 miles upstream. The speed of the current is 6mph. What is the speed of the boat?

Darrin can skateboard 2 miles against a 4-mph wind in the same amount of time he skateboards 6 miles with a 4-mph wind. Find the speed Darrin skateboards with no wind.

Jane spent 2 hours exploring a mountain with a dirt bike. First, she rode 40 miles uphill. After she reached the peak she rode for 12 miles along the summit. While going uphill, she went 5 mph slower than when she was on the summit. What was her rate along the summit?

Laney wanted to lose some weight so she planned a day of exercising. She spent a total of 2 hours riding her bike and jogging. She biked for 12 miles and jogged for 6 miles. Her rate for jogging was 10 mph less than biking rate. What was her rate when jogging?

Byron wanted to try out different water craft. He went 62 miles downstream in a motor boat and 27 miles downstream on a jet ski. His speed on the jet ski was 10 mph faster than in the motor boat. Bill spent a total of 4 hours on the water. What was his rate of speed in the motor boat?

Nancy took a 3-hour drive. She went 50 miles before she got caught in a storm. Then she drove 68 miles at 9 mph less than she had driven when the weather was good. What was her speed driving in the storm?

Chester rode his bike uphill 24 miles and then back downhill at 2 mph faster than his uphill. If it took him 2 hours longer to ride uphill than downhill, what was his uphill rate?

Matthew jogged to his friend’s house 12 miles away and then got a ride back home. It took him 2 hours longer to jog there than ride back. His jogging rate was 25 mph slower than the rate when he was riding. What was his jogging rate?

Hudson travels 1080 miles in a jet and then 240 miles by car to get to a business meeting. The jet goes 300 mph faster than the rate of the car, and the car ride takes 1 hour longer than the jet. What is the speed of the car?

Nathan walked on an asphalt pathway for 12 miles. He walked the 12 miles back to his car on a gravel road through the forest. On the asphalt he walked 2 miles per hour faster than on the gravel. The walk on the gravel took one hour longer than the walk on the asphalt. How fast did he walk on the gravel.

John can fly his airplane 2800 miles with a wind speed of 50 mph in the same time he can travel 2400 miles against the wind. If the speed of the wind is 50 mph, find the speed of his airplane.

Jim’s speedboat can travel 20 miles upstream against a 3-mph current in the same amount of time it travels 22 miles downstream with a 3-mph current speed . Find the speed of the Jim’s boat.

Hazel needs to get to her granddaughter’s house by taking an airplane and a rental car. She travels 900 miles by plane and 250 miles by car. The plane travels 250 mph faster than the car. If she drives the rental car for 2 hours more than she rode the plane, find the speed of the car.

Stu trained for 3 hours yesterday. He ran 14 miles and then biked 40 miles. His biking speed is 6 mph faster than his running speed. What is his running speed?

When driving the 9-hour trip home, Sharon drove 390 miles on the interstate and 150 miles on country roads. Her speed on the interstate was 15 more than on country roads. What was her speed on country roads?

Two sisters like to compete on their bike rides. Tamara can go 4 mph faster than her sister, Samantha. If it takes Samantha 1 hours longer than Tamara to go 80 miles, how fast can Samantha ride her bike?

Dana enjoys taking her dog for a walk, but sometimes her dog gets away, and she has to run after him. Dana walked her dog for 7 miles but then had to run for 1 mile, spending a total time of 2.5 hours with her dog. Her running speed was 3 mph faster than her walking speed. Find her walking speed.

Ken and Joe leave their apartment to go to a football game 45 miles away. Ken drives his car 30 mph faster Joe can ride his bike. If it takes Joe 2 hours longer than Ken to get to the game, what is Joe’s speed?

Mike, an experienced bricklayer, can build a wall in 3 hours, while his son, who is learning, can do the job in 6 hours. How long does it take for them to build a wall together?

It takes Sam 4 hours to rake the front lawn while his brother, Dave, can rake the lawn in 2 hours. How long will it take them to rake the lawn working together?

Mia can clean her apartment in 6 hours while her roommate can clean the apartment in 5 hours. If they work together, how long would it take them to clean the apartment?

Brian can lay a slab of concrete in 6 hours, while Greg can do it in 4 hours. If Brian and Greg work together, how long will it take?

Josephine can correct her students test papers in 5 hours, but if her teacher’s assistant helps, it would take them 3 hours. How long would it take the assistant to do it alone?

Washing his dad’s car alone, eight year old Levi takes 2.5 hours. If his dad helps him, then it takes 1 hour. How long does it take Levi’s dad to wash the car by himself?

At the end of the day Dodie can clean her hair salon in 15 minutes. Ann, who works with her, can clean the salon in 30 minutes. How long would it take them to clean the shop if they work together?

Ronald can shovel the driveway in 4 hours, but if his brother Donald helps it would take 2 hours. How long would it take Donald to shovel the driveway alone?

If y y varies directly as x x and y = 14 , ​ y = 14 , ​ when x = 3 . x = 3 . find the equation that relates x x and y . y .

If a a varies directly as b b and a = 16 , ​ ​ a = 16 , ​ ​ when b = 4 . b = 4 . find the equation that relates a a and b . b .

If p p varies directly as q q and p = 9.6 , ​ ​ p = 9.6 , ​ ​ when q = 3 . q = 3 . find the equation that relates p p and q . q .

If v v varies directly as w w and v = 8 , ​ v = 8 , ​ when ​ w = 1 2 . ​ w = 1 2 . find the equation that relates v v and w . w .

The price, P , P , that Eric pays for gas varies directly with the number of gallons, g , g , he buys. It costs him $50 to buy 20 gallons of gas.

ⓐ Write the equation that relates P P and g . g . ⓑ How much would 33 gallons cost Eric?

Joseph is traveling on a road trip. The distance, d , d , he travels before stopping for lunch varies directly with the speed, v , v , he travels. He can travel 120 miles at a speed of 60 mph.

ⓐ Write the equation that relates d d and v . v . ⓑ How far would he travel before stopping for lunch at a rate of 65 mph?

The mass of a liquid varies directly with its volume. A liquid with mass 16 kilograms has a volume of 2 liters.

ⓐ Write the equation that relates the mass to the volume. ⓑ What is the volume of this liquid if its mass is 128 kilograms?

The length that a spring stretches varies directly with a weight placed at the end of the spring. When Sarah placed a 10-pound watermelon on a hanging scale, the spring stretched 5 inches.

ⓐ Write the equation that relates the length of the spring to the weight. ⓑ What weight of watermelon would stretch the spring 6 inches?

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 6 inch will support a maximum load of 108 pounds.

ⓐ Write the equation that relates the load to the diagonal of the cross-section. ⓑ What load will a beam with a 10-inch diagonal support?

The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.

ⓐ Write the equation that relates the area to the radius. ⓑ What is the area of a personal pizza with a radius 4 inches?

If y y varies inversely with x x and y = 5 y = 5 when x = 4 , x = 4 , find the equation that relates x x and y . y .

If p p varies inversely with q q and p = 2 p = 2 when q = 1 q = 1 , find the equation that relates p p and q . q .

If v v varies inversely with w w and v = 6 v = 6 when w = 1 2 , w = 1 2 , find the equation that relates v v and w . w .

If a a varies inversely with b b and a = 12 a = 12 when b = 1 3 , b = 1 3 , find the equation that relates a a and b . b .

In the following exercises, write an inverse variation equation to solve the following problems.

The fuel consumption (mpg) of a car varies inversely with its weight. A Toyota Corolla weighs 2800 pounds getting 33 mpg on the highway.

ⓐ Write the equation that relates the mpg to the car’s weight. ⓑ What would the fuel consumption be for a Toyota Sequoia that weighs 5500 pounds?

A car’s value varies inversely with its age. Jackie bought a 10-year-old car for $2,400.

ⓐ Write the equation that relates the car’s value to its age. ⓑ What will be the value of Jackie’s car when it is 15 years old?

The time required to empty a tank varies inversely as the rate of pumping. It took Ada 5 hours to pump her flooded basement using a pump that was rated at 200 gpm (gallons per minute).

ⓐ Write the equation that relates the number of hours to the pump rate. ⓑ How long would it take Ada to pump her basement if she used a pump rated at 400 gpm?

On a string instrument, the length of a string varies inversely as the frequency of its vibrations. An 11-inch string on a violin has a frequency of 400 cycles per second.

ⓐ Write the equation that relates the string length to its frequency. ⓑ What is the frequency of a 10 inch string?

Paul, a dentist, determined that the number of cavities that develops in his patient’s mouth each year varies inversely to the number of minutes spent brushing each night. His patient, Lori, had four cavities when brushing her teeth 30 seconds (0.5 minutes) each night.

ⓐ Write the equation that relates the number of cavities to the time spent brushing. ⓑ How many cavities would Paul expect Lori to have if she had brushed her teeth for 2 minutes each night?

Boyle’s law states that if the temperature of a gas stays constant, then the pressure varies inversely to the volume of the gas. Braydon, a scuba diver, has a tank that holds air under a pressure of 220 psi.

ⓐ Write the equation that relates pressure to volume. ⓑ If the pressure increases to 330 psi, how much air can Braydon’s tank hold?

The cost of a ride service varies directly with the distance traveled. It costs $35 for a ride from the city center to the airport, 14 miles away.

ⓐ Write the equation that relates the cost, c , with the number of miles, m . m . ⓑ What would it cost to travel 22 miles with this service?

The number of hours it takes Jack to drive from Boston to Bangor is inversely proportional to his average driving speed. When he drives at an average speed of 40 miles per hour, it takes him 6 hours for the trip.

ⓐ Write the equation that relates the number of hours, h , h , with the speed, s . s . ⓑ How long would the trip take if his average speed was 75 miles per hour?

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \frac{5}{x-7}=\frac{2}{x-2}
• \frac{7x+5}{x-4}-\frac{6x-1}{x-3}-\frac{1}{x^{2}-7x+12}=1
• \frac{7}{x-3}-\frac{10}{x-2}-\frac{6}{x-1}=0
• \frac{x-3}{3-x}=2

rational-equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...

Please add a message.

Message received. Thanks for the feedback.

Module 7: Rational Expressions and Equations

Solve rational equations, learning outcomes.

• Solve rational equations by clearing denominators
• Identify extraneous solutions in a rational equation
• Solve for a variable in a rational formula
• Identify the components of a work equation
• Solve a work equation
• Define and write a proportion
• Solve proportional problems involving scale drawings
• Define direct variation, and solve problems involving direct variation
• Define inverse variation and solve problems involving inverse variation
• Define joint variation and solve problems involving joint variation

Equations that contain rational expressions are called rational equations . For example, [latex] \frac{2x+1}{4}=\frac{x}{3}[/latex] is a rational equation. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing a variety of proportional relationships.

One of the most straightforward ways to solve a rational equation is to eliminate denominators with the common denominator, then use properties of equality to isolate the variable. This method is often used to solve linear equations that involve fractions as in the following example:

Solve  [latex]\frac{1}{2}x-3=2-\frac{3}{4}x[/latex] by clearing the fractions in the equation first.

Multiply both sides of the equation by 4, the common denominator of the fractional coefficients.

[latex]\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)+4\left(-\frac{3}{4}x\right)\\2x-12=8-3x\\\underline{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{array}[/latex]

We could have found a common denominator and worked with fractions, but that often leads to more mistakes. We can apply the same idea to solving rational equations.  The difference between a linear equation and a rational equation is that rational equations can have polynomials in the numerator and denominator of the fractions. This means that clearing the denominator may sometimes mean multiplying the whole rational equation by a polynomial. In the next example, we will clear the denominators of a rational equation with a terms that has a polynomial in the numerator.

Solve the equation [latex] \frac{x+5}{8}=\frac{7}{4}[/latex].

[latex]\begin{array}{l}4=2\cdot2\\8=2\cdot2\cdot2\cdot2\\\text{LCM}=2\cdot2\cdot2\\\text{LCM}=8\end{array}[/latex]

The LCM of 4 and 8 is also the lowest common denominator for the two fractions.

Multiply both sides of the equation by the common denominator, 8, to keep the equation balanced and to eliminate the denominators.

[latex]\begin{array}{r}8\cdot \frac{x+5}{8}=\frac{7}{4}\cdot 8\,\,\,\,\,\,\,\\\\\frac{8(x+5)}{8}=\frac{7(8)}{4}\,\,\,\,\,\,\\\\\frac{8}{8}\cdot (x+5)=\frac{7(4\cdot 2)}{4}\\\\\frac{8}{8}\cdot (x+5)=7\cdot 2\cdot \frac{4}{4}\\\\1\cdot (x+5)=14\cdot 1\,\,\,\end{array}[/latex]

Simplify and solve for x .

[latex]\begin{array}{r}x+5=14\\x=9\,\,\,\end{array}[/latex]

Check the solution by substituting 9 for x in the original equation.

[latex]\begin{array}{r}\frac{x+5}{8}=\frac{7}{4}\\\\\frac{9+5}{8}=\frac{7}{4}\\\\\frac{14}{8}=\frac{7}{4}\\\\\frac{7}{4}=\frac{7}{4}\end{array}[/latex]

[latex]x=9[/latex]

In the next example, we show how to solve a rational equation with a binomial in the denominator of one term. We will use the common denominator to eliminate the denominators from both fractions. Note that the LCD is the product of both denominators because they don’t share any common factors.

Solve the equation [latex] \frac{8}{x+1}=\frac{4}{3}[/latex].

[latex]\begin{array}{c}3\left(x+1\right)\left(\frac{8}{x+1}\right)=3\left(x+1\right)\left(\frac{4}{3}\right)\end{array}[/latex]

Simplify common factors.

[latex]\begin{array}{c}3\cancel{\left(x+1\right)}\left(\frac{8}{\cancel{x+1}}\right)=\cancel{3}\left(x+1\right)\left(\frac{4}{\cancel{3}}\right)\\24=4\left(x+1\right)\\24=4x+4\end{array}[/latex]

Now this looks like a linear equation, and we can use the addition and multiplication properties of equality to solve it.

[latex]\begin{array}{c}24=4x+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\20=4x\,\,\,\,\,\,\,\,\\\\x=5\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Check the solution in the original equation.

[latex]\begin{array}{r}\,\,\,\,\,\frac{8}{\left(x+1\right)}=\frac{4}{3}\\\\\frac{8}{\left(5+1\right)}=\frac{4}{3}\\\\\frac{8}{6}=\frac{4}{3}\end{array}[/latex]

Reduce the fraction [latex]\frac{8}{6}[/latex] by simplifying the common factor of 2:

[latex]\large\frac{\cancel{2}\cdot4}{\cancel{2}\cdot3}\normalsize=\large\frac{4}{3}[/latex]

[latex]x=1[/latex]

You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.

Solve the equation [latex]\frac{x}{3}+1=\frac{4}{3}[/latex].

[latex] 3\left( \frac{x}{3}+1 \right)=3\left( \frac{4}{3} \right)[/latex]

Apply the distributive property and multiply 3 by each term within the parentheses. Then simplify and solve for x .

[latex]\begin{array}{r}3\left( \frac{x}{3} \right)+3\left( 1 \right)=3\left( \frac{4}{3} \right)\\\\\cancel{3}\left( \frac{x}{\cancel{3}} \right)+3\left( 1 \right)=\cancel{3}\left( \frac{4}{\cancel{3}} \right)\\\\ x+3=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-3}\,\,\,\,\,\underline{-3}\\\\x=1\end{array}[/latex]

In the video that follows we present two ways to solve rational equations with both integer and variable denominators.

Excluded Values and Extraneous Solutions

Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values . Let’s look at an example.

Solve the equation [latex] \frac{2x-5}{x-5}=\frac{15}{x-5}[/latex].

[latex] \frac{2x-5}{x-5}=\frac{15}{x-5}[/latex]

5 is an excluded value because it makes the denominator [latex]x-5[/latex] equal to 0.

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for x.

[latex]\begin{array}{r}2x-5=15\\2x=20\\x=10\end{array}[/latex]

[latex]\begin{array}{r}\frac{2x-5}{x-5}=\frac{15}{x-5}\,\,\\\\\frac{2(10)-5}{10-5}=\frac{15}{10-5}\\\\\frac{20-5}{10-5}=\frac{15}{10-5}\\\\\frac{15}{5}=\frac{15}{5}\,\,\,\,\,\,\,\,\,\end{array}[/latex]

[latex]x=10[/latex]

In the following video we present an example of solving a rational equation with variables in the denominator.

You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions . That’s why it is always important to check all solutions in the original equations—you may find that they yield untrue statements or produce undefined expressions.

Solve the equation [latex] \frac{16}{m+4}=\frac{{{m}^{2}}}{m+4}[/latex].

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for m.

[latex]\begin{array}{l}16=m^{2}\\\,\,\,0={{m}^{2}}-16\\\,\,\,0=\left( m+4 \right)\left( m-4 \right)\end{array}[/latex]

[latex]\begin{array}{c}0=m+4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,0=m-4\\m=-4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,m=4\\m=4,-4\end{array}[/latex]

Check the solutions in the original equation.

Since [latex]m=−4[/latex] leads to division by 0, it is an extraneous solution.

[latex]\begin{array}{c}\frac{16}{m+4}=\frac{{{m}^{2}}}{m+4}\\\\\frac{16}{-4+4}=\frac{{{(-4)}^{2}}}{-4+4}\\\\\frac{16}{0}=\frac{16}{0}\end{array}[/latex]

[latex]-4[/latex] is excluded because it leads to division by 0.

[latex]\begin{array}{c}\frac{16}{4+4}=\frac{{{(4)}^{2}}}{4+4}\\\\\frac{16}{8}=\frac{16}{8}\end{array}[/latex]

[latex]m=4[/latex]

Rational formulas

Rational formulas can be useful tools for representing real-life situations and for finding answers to real problems. Equations representing direct, inverse, and joint variation are examples of rational formulas that can model many real-life situations. As you will see, if you can find a formula, you can usually make sense of a situation.

When solving problems using rational formulas, it is often helpful to first solve the formula for the specified variable. For example, work problems ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). Using algebra, you can write the work formula 3 ways:

[latex]W=rt[/latex]

Find the time (t): [latex] t=\frac{W}{r}[/latex] (divide both sides by r)

Find the rate (r): [latex] r=\frac{W}{t}[/latex] (divide both sides by t)

The formula for finding the density of an object is [latex] D=\frac{m}{v}[/latex], where D is the density, m is the mass of the object and v is the volume of the object. Rearrange the formula to solve for the mass ( m ) and then for the volume ( v ).

[latex] D=\frac{m}{v}[/latex]

Multiply both side of the equation by v to isolate m.

[latex] v\cdot D=\frac{m}{v}\cdot v[/latex]

Simplify and rewrite the equation, solving for m .

[latex]\begin{array}{l}v\cdot D=m\cdot \frac{v}{v}\\v\cdot D=m\cdot 1\\v\cdot D=m\end{array}[/latex]

To solve the equation [latex] D=\frac{m}{v}[/latex] in terms of v , you will need do the same steps to this point, and then divide both sides by D .

[latex]\begin{array}{r}\frac{v\cdot D}{D}=\frac{m}{D}\\\\\frac{D}{D}\cdot v=\frac{m}{D}\\\\1\cdot v=\frac{m}{D}\\\\v=\frac{m}{D}\end{array}[/latex]

[latex] m=D\cdot v[/latex] and [latex] v=\frac{m}{D}[/latex]

Now let’s look at an example using the formula for the volume of a cylinder.

The formula for finding the volume of a cylinder is [latex]V=\pi{r^{2}}h[/latex], where V is the volume, r is the radius and h is the height of the cylinder. Rearrange the formula to solve for the height ( h ).

[latex] V=\pi{{r}^{2}}h[/latex]

Divide both sides by [latex] \pi {{r}^{2}}[/latex] to isolate h.

[latex] \frac{V}{\pi {{r}^{2}}}=\frac{\pi {{r}^{2}}h}{\pi {{r}^{2}}}[/latex]

Simplify. You find the height, h , is equal to [latex] \frac{V}{\pi {{r}^{2}}}[/latex].

[latex] \frac{V}{\pi {{r}^{2}}}=h[/latex]

[latex] h=\frac{V}{\pi {{r}^{2}}}[/latex]

In the following video we give another example of solving for a variable in a formula, or as they are also called, a literal equation.

Applications of Rational Equations

Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.

A Good Day’s Work

A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. (Notice that the work formula is very similar to the relationship between distance, rate, and time, or [latex]d=rt[/latex].) The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). The work formula has 3 versions.

[latex]\begin{array}{l}W=rt\\\\\,\,\,\,\,t=\frac{W}{r}\\\\\,\,\,\,\,r=\frac{W}{t}\end{array}[/latex]

Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.

Myra takes 2 hours to plant 50 flower bulbs. Francis takes 3 hours to plant 45 flower bulbs. Working together, how long should it take them to plant 150 bulbs?

Myra: [latex] \frac{50\,\,\text{bulbs}}{2\,\,\text{hours}}[/latex], or [latex] \frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Francis: [latex] \frac{45\,\,\text{bulbs}}{3\,\,\text{hours}}[/latex], or [latex] \frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Combine their hourly rates to determine the rate they work together.

Myra and Francis together:

[latex] \frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}+\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}=\frac{40\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]

Use one of the work formulas to write a rational equation, for example [latex] r=\frac{W}{t}[/latex]. You know r , the combined work rate, and you know W , the amount of work that must be done. What you don’t know is how much time it will take to do the required work at the designated rate.

[latex] \frac{40}{1}=\frac{150}{t}[/latex]

Solve the equation by multiplying both sides by the common denominator, then isolating t .

[latex]\begin{array}{c}\frac{40}{1}\cdot 1t=\frac{150}{t}\cdot 1t\\\\40t=150\\\\t=\frac{150}{40}=\frac{15}{4}\\\\t=3\frac{3}{4}\text{hours}\end{array}[/latex]

It should take 3 hours 45 minutes for Myra and Francis to plant 150 bulbs together.

Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.

Joe and John are planning to paint a house together. John thinks that if he worked alone, it would take him 3 times as long as it would take Joe to paint the entire house. Working together, they can complete the job in 24 hours. How long would it take each of them, working alone, to complete the job?

Let x = time it takes Joe to complete the job

3 x = time it takes John to complete the job

The work is painting 1 house or 1. Write an expression to represent each person’s rate using the formula [latex] r=\frac{W}{t}[/latex] .

Joe’s rate: [latex] \frac{1}{x}[/latex]

John’s rate: [latex] \frac{1}{3x}[/latex]

Their combined rate is the sum of their individual rates. Use this rate to write a new equation using the formula [latex]W=rt[/latex].

combined rate: [latex] \frac{1}{x}+\frac{1}{3x}[/latex]

The problem states that it takes them 24 hours together to paint a house, so if you multiply their combined hourly rate [latex] \left( \frac{1}{x}+\frac{1}{3x} \right)[/latex] by 24, you will get 1, which is the number of houses they can paint in 24 hours.

[latex] \begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\frac{24}{x}+\frac{24}{3x}\end{array}[/latex]

Now solve the equation for x . (Remember that x represents the number of hours it will take Joe to finish the job.)

[latex]\begin{array}{l}\,\,\,1=\frac{3}{3}\cdot \frac{24}{x}+\frac{24}{3x}\\\\\,\,\,1=\frac{3\cdot 24}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72+24}{3x}\\\\\,\,\,1=\frac{96}{3x}\\\\3x=96\\\\\,\,\,x=32\end{array}[/latex]

[latex]\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\left[ \frac{\text{1}}{\text{32}}+\frac{1}{3\text{(32})} \right]24\\\\1=\frac{24}{\text{32}}+\frac{24}{3\text{(32})}\\\\1=\frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{3}{3}\cdot \frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{72}{96}+\frac{24}{96}[\end{array}[/latex]

The solution checks. Since [latex]x=32[/latex], it takes Joe 32 hours to paint the house by himself. John’s time is 3 x , so it would take him 96 hours to do the same amount of work.

It takes 32 hours for Joe to paint the house by himself and 96 hours for John the paint the house himself.

In the video that follows, we show another example of finding one person’s work rate given a combined work rate.

As shown above, many work problems can be represented by the equation [latex] \frac{t}{a}+\frac{t}{b}=1[/latex], where t is the time to do the job together, a is the time it takes person A to do the job, and b is the time it takes person B to do the job. The 1 refers to the total work done—in this case, the work was to paint 1 house.

The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t , set it equal to the amount of work done, and solve the rational equation.

We present another example of two people painting at different rates in the following video.

Proportions

Matryoshka, or nesting dolls.

A proportion is a statement that two ratios are equal to each other.  There are many things that can be represented with ratios, including the actual distance on the earth that is represented on a map.  In fact, you probably use proportional reasoning on a regular basis and don’t realize it.  For example, say you have volunteered to provide drinks for a community event.  You are asked to bring enough drinks for 35-40 people.  At the store  you see that drinks come in packages of 12. You multiply 12 by 3 and get 36 – this may not be enough if 40 people show up, so you decide to buy 4 packages of drinks just to be sure.

This process can also be expressed as a proportional equation and solved using mathematical principles. First, we can express the number of drinks in a package as a ratio:

[latex]\frac{12\text{ drinks }}{1\text{ package }}[/latex]

Then we express the number of people who we are buying drinks for as a ratio with the unknown number of packages we need. We will use the maximum so we have enough.

[latex]\frac{40\text{ people }}{x\text{ packages }}[/latex]

We can find out how many packages to purchase by setting the expressions equal to each other:

[latex]\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}[/latex]

To solve for x, we can use techniques for solving linear equations, or we can cross multiply as a shortcut.

[latex]\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\\\text{}\\x\cdot\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{40}{12}=\frac{10}{3}=3.33\end{array}[/latex]

We can round up  to 4 since it doesn’t make sense to by 0.33 of a package of drinks.  Of course, you don’t write out your thinking this way when you are in the grocery store, but doing so helps you to be able to apply the concepts to less obvious problems.  In the following example we will show how to use a proportion to find the number of people on teh planet who don’t have access to a toilet.

As of March, 2016 the world’s population was estimated at 7.4 billion.  [1] .  According to water.org , 1 out of every 3 people on the planet lives without access to a toilet.  Find the number of people on the planet that do not have access to a toilet.

Read and Understand:  We can use a proportion to find the unknown number of people who live without a toilet since we are given that 1 in 3 don’t have access, and we are given the population of the planet.

Define and Translate:  We know that 1 out of every 3 people don’t have access, so we can write that as a ratio (fraction)

[latex]\frac{1\text{ doesn't }}{3\text{ do }}[/latex].

Let the number of people without access to a toilet be x. The ratio of people with and without toilets is then

[latex]\frac{x\text{ don't }}{7.4\text{ billion do}}[/latex]

Notice how it helps to use descriptions or units to know where to place the given numbers in the proportion.

Write and Solve:  Equate the two ratios since they are representing the same fractional amount of the population.

[latex]\frac{1}{3}=\frac{x}{7.4\text{ billion }}[/latex]

[latex]\begin{array}{l}\frac{1}{3}=\frac{x}{7.4}\\\text{}\\7.4\cdot\frac{1}{3}=\frac{x}{7.4}\cdot{7.4}\\\text{}\\2.46=x\end{array}[/latex]

Interpret:  The original units were billions of people, so our answer is [latex]2.46[/latex] billion people don’t have access to a toilet.  Wow, that’s a lot of people.

2.46 billion people don’t have access to a toilet.

In the next example, we will use the length of a person’t femur to estimate their height.  This process is used in forensic science and anthropology, and has been found in many scientific studies to be a very good estimate.

It has been shown that a person’s height is proportional to the length of their femur  [2] . Given that a person who is 71 inches tall has a femur length of 17.75 inches, how tall is someone with a femur length of 16 inches?

Read and Understand:  Height and femur length are proportional for everyone, so we can define a ratio with the given height and femur length.  We can then use this to write a proportion to find the unknown height.

Define and Translate:  Let x be the unknown height.  Define the ratio of femur length and height for both people using the given measurements.

Person 1:  [latex]\frac{\text{femur length}}{\text{height}}=\frac{17.75\text{inches}}{71\text{inches}}[/latex]

Person 2:  [latex]\frac{\text{femur length}}{\text{height}}=\frac{16\text{inches}}{x\text{inches}}[/latex]

Write and Solve:  Equate the ratios, since we are assuming height and femur length are proportional for everyone.

[latex]\frac{17.75\text{inches}}{71\text{inches}}=\frac{16\text{inches}}{x\text{inches}}[/latex]

 Solve by using the common denominator to clear fractions.  The common denominator is [latex]71x[/latex]

[latex]\begin{array}{c}\frac{17.75}{71}=\frac{16}{x}\\\\71x\cdot\frac{17.75}{71}=\frac{16}{x}\cdot{71x}\\\\17.75\cdot{x}=16\cdot{71}\\\\x=\frac{16\cdot{71}}{17.75}=64\end{array}[/latex]

Interpret:  The unknown height of person 2 is 64 inches. In general, we can reduce the fraction [latex]\frac{17.75}{71}=0.25=\frac{1}{4}[/latex] to find a general rule for everyone.  This would translate to saying for every one femur length, a person’s height is 4 times that length.

Another way to describe the ratio of femur length to height that we found in the last example is to say there’s a 1:4 ratio between femur length and height, or 1 to 4.

Ratios are also used in scale drawings. Scale drawings are enlarged or reduced drawings of objects, buildings, roads, and maps. Maps are smaller than what they represent and a drawing of dendritic cells in your brain is most likely larger than what it represents. The scale of the drawing is a ratio that represents a comparison of the length of the actual object and it’s representation in the drawing. The image below shows a map of the us with a scale of 1 inch representing 557 miles. We could write the scale factor as a fraction [latex]\frac{1}{557}[/latex] or as we did with the femur-height relationship, 1:557.

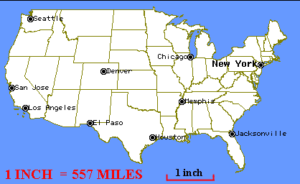
Map with scale factor

In the next example we will use the scale factor given in the image above to find the distance between Seattle Washington and San Jose California.

Given a scale factor of 1:557 on a map of the US, if the distance from Seattle, WA to San Jose, CA is 1.5 inches on the map,  define a proportion to find the actual distance between them.

Read and Understand:  We need to define a proportion to solve for the unknown distance between Seattle and San Jose.

Define and Translate: T he scale factor is 1:557, and we will call the unknown distance x. The ratio of inches to miles is [latex]\frac{1}{557}[/latex].

We know inches between the two cities, but we don’t know miles, so the ratio that describes the distance between them is [latex]\frac{1.5}{x}[/latex].

Write and Solve:  The proportion that will help us solve this problem is [latex]\frac{1}{557}=\frac{1.5}{x}[/latex].

Solve using the common denominator [latex]557x[/latex] to clear fractions.

[latex]\begin{array}{c}\frac{1}{557}=\frac{1.5}{x}\\\\557x\cdot\frac{1}{557}=\frac{1.5}{x}\cdot{557x}\\\\x=1.5\cdot{557}=835.5[/latex]

Interpret:  We used the scale factor 1:557 to find an unknown distance between Seattle and San Jose. We also check our answer of 835.5 miles with Google maps, and found that the distance is 839.9 miles, so we did pretty well!

In the next example, we will find a scale factor given the length between two cities on a map, and their actual distance from each other.

Two cities are 2.5 inches apart on a map.  Their actual distance from each other is 325 miles.  Write a proportion to represent and solve for the scale factor for one inch of the map.

Read and Understand: We know that for each 2.5 inches on the map, it represents 325 actual miles. We are looking for the scale factor for one inch of the map.

Define and Translate:  The ratio we want is [latex]\frac{1}{x}[/latex] where x is the actual distance represented by one inch on the map.  We know that for every 2.5 inches, there are 325 actual miles, so we can define that relationship as [latex]\frac{2.5}{325}[/latex]

Write and Solve:  We can use a proportion to equate the two ratios and solve for the unknown distance.

[latex]\begin{array}{c}\frac{1}{x}=\frac{2.5}{325}\\\\325x\cdot\frac{1}{x}=\frac{2.5}{325}\cdot{325x}\\\\325=2.5x\\\\x=130[/latex]

Interpret:  The scale factor for one inch on the map is 1:130, or for every inch of map there are 130 actual miles.

The video that follows show another example of finding an actual distance using the scale factor from a map.

In the video that follows, we present an example of using proportions to obtain the correct amount of medication for a patient, as well as finding a desired mixture of coffees.

So many cars, so many tires.

Direct Variation

Variation equations are examples of rational formulas and are used to describe the relationship between variables. For example, imagine a parking lot filled with cars. The total number of tires in the parking lot is dependent on the total number of cars. Algebraically, you can represent this relationship with an equation.

[latex]\text{number of tires}=4\cdot\text{number of cars}[/latex]

The number 4 tells you the rate at which cars and tires are related. You call the rate the constant of variation . It’s a constant because this number does not change. Because the number of cars and the number of tires are linked by a constant, changes in the number of cars cause the number of tires to change in a proportional, steady way. This is an example of direct variation , where the number of tires varies directly with the number of cars.

You can use the car and tire equation as the basis for writing a general algebraic equation that will work for all examples of direct variation. In the example, the number of tires is the output, 4 is the constant, and the number of cars is the input. Let’s enter those generic terms into the equation. You get [latex]y=kx[/latex]. That’s the formula for all direct variation equations.

[latex]\text{number of tires}=4\cdot\text{number of cars}\\\text{output}=\text{constant}\cdot\text{input}[/latex]

Solve for k , the constant of variation, in a direct variation problem where [latex]y=300[/latex] and [latex]x=10[/latex].

[latex]y=kx[/latex]

Substitute known values into the equation.

[latex]300=k\left(10\right)[/latex]

Solve for k by dividing both sides of the equation by 10.

[latex]\begin{array}{l}\frac{300}{10}=\frac{10k}{10}\\\\\,\,\,\,30=k\end{array}[/latex]

The constant of variation, k , is 30.

In the video that follows, we present an example of solving a direct variation equation.

Inverse Variation

Another kind of variation is called inverse variation . In these equations, the output equals a constant divided by the input variable that is changing. In symbolic form, this is the equation [latex] y=\frac{k}{x}[/latex].

One example of an inverse variation is the speed required to travel between two cities in a given amount of time.

Let’s say you need to drive from Boston to Chicago, which is about 1,000 miles. The more time you have, the slower you can go. If you want to get there in 20 hours, you need to go 50 miles per hour (assuming you don’t stop driving!), because [latex] \frac{1,000}{20}=50[/latex]. But if you can take 40 hours to get there, you only have to average 25 miles per hour, since [latex] \frac{1,000}{40}=25[/latex].

The equation for figuring out how fast to travel from the amount of time you have is [latex] speed=\frac{miles}{time}[/latex]. This equation should remind you of the distance formula [latex] d=rt[/latex]. If you solve [latex] d=rt[/latex] for r , you get [latex] r=\frac{d}{t}[/latex], or [latex] speed=\frac{miles}{time}[/latex].

In the case of the Boston to Chicago trip, you can write [latex] s=\frac{1,000}{t}[/latex]. Notice that this is the same form as the inverse variation function formula, [latex] y=\frac{k}{x}[/latex].

Solve for k , the constant of variation, in an inverse variation problem where [latex]x=5[/latex] and [latex]y=25[/latex].

[latex] y=\frac{k}{x}[/latex]

[latex] 25=\frac{k}{5}[/latex]

Solve for k by multiplying both sides of the equation by 5.

[latex] \begin{array}{c}5\cdot 25=\frac{k}{5}\cdot 5\\\\125=\frac{5k}{5}\\\\125=k\,\,\,\end{array}[/latex]

The constant of variation, k , is 125.

In the next example, we will find the water temperature in the ocean at a depth of 500 meters.  Water temperature is inversely proportional to depth in the ocean.

Water temperature in the ocean varies inversely with depth.

The water temperature in the ocean varies inversely with the depth of the water. The deeper a person dives, the colder the water becomes. At a depth of 1,000 meters, the water temperature is 5º Celsius. What is the water temperature at a depth of 500 meters?

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=\frac{k}{x}\\\\temp=\frac{k}{depth}\end{array}[/latex]

[latex] 5=\frac{k}{1,000}[/latex]

Solve for k .

[latex]\begin{array}{l}1,000\cdot5=\frac{k}{1,000}\cdot 1,000\\\\\,\,\,\,\,\,\,\,5,000=\frac{1,000k}{1,000}\\\\\,\,\,\,\,\,\,\,5,000=k\end{array}[/latex]

Now that k , the constant of variation is known, use that information to solve the problem: find the water temperature at 500 meters.

[latex]\begin{array}{l}temp=\frac{k}{depth}\\\\temp=\frac{5,000}{500}\\\\temp=10\end{array}[/latex]

At 500 meters, the water temperature is 10º C.

In the video that follows, we present an example of inverse variation.

Joint Variation

A third type of variation is called joint variation . Joint variation is the same as direct variation except there are two or more quantities. For example, the area of a rectangle can be found using the formula [latex]A=lw[/latex], where l is the length of the rectangle and w is the width of the rectangle. If you change the width of the rectangle, then the area changes and similarly if you change the length of the rectangle then the area will also change. You can say that the area of the rectangle “varies jointly with the length and the width of the rectangle.”

The formula for the volume of a cylinder, [latex]V=\pi {{r}^{2}}h[/latex] is another example of joint variation. The volume of the cylinder varies jointly with the square of the radius and the height of the cylinder. The constant of variation is [latex] \pi [/latex].

The area of a triangle varies jointly with the lengths of its base and height. If the area of a triangle is 30 inches[latex]^{2}[/latex] when the base is 10 inches and the height is 6 inches, find the variation constant and the area of a triangle whose base is 15 inches and height is 20 inches.

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=kxz\\Area=k(base)(height)\end{array}[/latex]

Substitute known values into the equation, and solve for k .

[latex]30=k\left(10\right)\left(6\right)\\30=60k\\\\\frac{30}{60}=\frac{60k}{60}\\\\\frac{1}{2}=k[/latex]

Now that k is known, solve for the area of a triangle whose base is 15 inches and height is 20 inches.

[latex]\begin{array}{l}Area=k(base)(height)\\\\Area=(15)(20)(\frac{1}{2})\\\\Area=\frac{300}{2}\\\\Area=150\,\,\text{square inches}\end{array}[/latex]

The constant of variation, k , is [latex] \frac{1}{2}[/latex], and the area of the triangle is 150 square inches.

Finding k to be [latex] \frac{1}{2}[/latex] shouldn’t be surprising. You know that the area of a triangle is one-half base times height, [latex] A=\frac{1}{2}bh[/latex]. The [latex] \frac{1}{2}[/latex] in this formula is exactly the same [latex] \frac{1}{2}[/latex] that you calculated in this example!

In the following video, we show an example of finding the constant of variation for a jointly varying relation.

Direct, Joint, and Inverse Variation

k is the constant of variation. In all cases, [latex]k\neq0[/latex].

• Direct variation: [latex]y=kx[/latex]
• Inverse variation: [latex] y=\frac{k}{x}[/latex]
• Joint variation: [latex]y=kxz[/latex]

Rational formulas can be used to solve a variety of problems that involve rates, times, and work. Direct, inverse, and joint variation equations are examples of rational formulas. In direct variation, the variables have a direct relationship—as one quantity increases, the other quantity will also increase. As one quantity decreases, the other quantity decreases. In inverse variation, the variables have an inverse relationship—as one variable increases, the other variable decreases, and vice versa. Joint variation is the same as direct variation except there are two or more variables.

You can solve rational equations by finding a common denominator. By rewriting the equation so that all terms have the common denominator, you can solve for the variable using just the numerators. Or, you can multiply both sides of the equation by the least common multiple of the denominators so that all terms become polynomials instead of rational expressions.

An important step in solving rational equations is to reject any extraneous solutions from the final answer. Extraneous solutions are solutions that don’t satisfy the original form of the equation because they produce untrue statements or are excluded values that make a denominator equal to 0.

• "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . ↵
• Obialor, Ambrose, Churchill Ihentuge, and Frank Akapuaka. "Determination of Height Using Femur Length in Adult Population of Oguta Local Government Area of Imo State Nigeria." Federation of American Societies for Experimental Biology, April 2015. Accessed June 22, 2016. http://www.fasebj.org/content/29/1_Supplement/LB19.short . ↵
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Solve Basic Rational Equations. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/R9y2D9VFw0I . License : CC BY: Attribution
• Solve Rational Equations with Like Denominators. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/gGA-dF_aQQQ . License : CC BY: Attribution
• Screenshot: A Good Day's Work. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Matroyshka, or nesting dolls.. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: map with scale factor. Provided by : Lumen Learning. License : CC BY: Attribution
• Proportion Applications: Map Scale Factor (Clear Fractions, No Cross Products). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/id3sp4wvmVg . License : CC BY: Attribution
• Screenshot: so many cars, so many tires. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Water temperature in the ocean varies inversely with depth. Provided by : Lumen Learning. License : CC BY: Attribution
• Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution
• Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. License : CC BY: Attribution
• Ex 2: Solve a Literal Equation for a Variable. Authored by : James Sousa (Mathispower4u.com). Located at : https://www.youtube.com/watch?v=ecEUUbRLDQs&feature=youtu.be . License : CC BY: Attribution
• Ex 1: Rational Equation Application - Painting Together. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/SzSasnDF7Ms . License : CC BY: Attribution
• Ex: Rational Equation App - Find Individual Working Time Given Time Working Together. Authored by : James Sousa (Mathispower4u.com) . Located at : https://www.youtube.com/watch?v=kbRSYb8UYqU&feature=youtu.be . License : CC BY: Attribution
• Ex: Proportion Applications - Mixtures . Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/yGid1a_x38g . License : CC BY: Attribution
• Ex: Direct Variation Application - Aluminum Can Usage. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/DLPKiMD_ZZw . License : CC BY: Attribution
• Ex: Inverse Variation Application - Number of Workers and Job Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/y9wqI6Uo6_M . License : CC BY: Attribution

Solving Rational Equations and Applications

Learning Objective(s)

·          Solve rational equations.

·          Check for extraneous solutions.

·          Solve application problems involving rational equations.

Introduction

You can solve these equations using the techniques for performing operations with rational expressions and the procedures for solving algebraic equations. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing distance-speed-time relationships and for modeling work problems that involve more than one person.

Solving Rational Equations

One method for solving rational equations is to rewrite the rational expressions in terms of a common denominator. Then, since you know the numerators are equal, you can solve for the variable. To illustrate this, let’s look at a very simple equation.

Since the denominator of each expression is the same, the numerators must be equivalent. This means that x = 2.

This is true for rational equations with polynomials too.

Since the denominators of each rational expression are the same, x + 4, the numerators must be equivalent for the equation to be true. So, x – 5 = 11 and x = 16.

Just as with other algebraic equations, you can check your solution in the original rational equation by substituting the value for the variable back into the equation and simplifying.

When the terms in a rational equation have unlike denominators, solving the equation will involve some extra steps. One way of solving rational equations with unlike denominators is to multiply both sides of the equation by the least common multiple of the denominators of all the fractions contained in the equation. This eliminates the denominators and turns the rational equation into a polynomial equation. Here’s an example.

Another way to solve a rational equation with unlike denominators is to rewrite each term with a common denominator and then just create an equation from the numerators. This works because if the denominators are the same, the numerators must be equal. The next example shows this approach with the same equation you just solved:

In some instances, you’ll need to take some additional steps in finding a common denominator. Consider the example below, which illustrates using what you know about denominators to rewrite one of the expressions in the equation.

You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.

Excluded Values and Extraneous Solutions

Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values . Let’s look at an example.

Let’s look at an example with a more complicated denominator.

You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions . That's why it is always important to check all solutions in the original equations—you may find that they yield untrue statements or produce undefined expressions.

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for m.

-4 is excluded because

it leads to division by 0.

Check the solutions in the original equation.

Since m = −4 leads to division by 0, it is an extraneous solution.

Solving Application Problems

A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, W = rt . (Notice that the work formula is very similar to the relationship between distance, rate, and time, or d = rt .) The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). The work formula has 3 versions.

Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.

Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.

The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t , set it equal to the amount of work done, and solve the rational equation.

You can solve rational equations by finding a common denominator. By rewriting the equation so that all terms have the common denominator, you can solve for the variable using just the numerators. Or, you can multiply both sides of the equation by the least common multiple of the denominators so that all terms become polynomials instead of rational expressions. Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.

An important step in solving rational equations is to reject any extraneous solutions from the final answer. Extraneous solutions are solutions that don't satisfy the original form of the equation because they produce untrue statements or are excluded values that make a denominator equal to 0.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Rational Equations

Intro Harder Probs Graphs

Solve the following equation:

The rational expressions in this equation have variables in the denominators. So my first step is to check for which x -values are not allowed, because they'd cause division by zero. Setting each denominator equal to zero and solving, I get:

x ≠ −4, −1

Looking at the equation, I notice that this equation is a proportion ; that is, the equation is of the form "(one fraction) equals (another fraction)". So all I need to do here is "cross-multiply"; that is, I can use Method 3:

Content Continues Below

MathHelp.com

10(4( x + 1)) = 15( x + 4)

40 x + 40 = 15 x + 60

25 x + 40 = 60

x = 20 / 25 = 4 / 5

Since this solution won't cause any division-by-zero problems, it is a valid solution to the equation, and my answer is:

There is only one fraction, so the common denominator is the only denominator; namely, x . Also, setting that denominator equal to zero, I see that the solution to this equation cannot be x  = 0 .

Method 1: To solve, I can convert everything to this common denominator, and then solve the numerators:

x 2 + x = 72

x 2 + x − 72 = 0

( x + 9)( x − 8) = 0

x = −9 or x = 8

Method 2: To solve, I can start by multiplying through on both sides by x :

Either way, the solution is the same. Since neither solution causes a division-by-zero problem in the original equation, both solution values are valid.

x = −9, 8

First, I'll solve the denominators. Setting each equal to zero to find the disallowed values, I get:

x ≠ 0, 2

The lowest common denominator of these fractions will be x ( x  − 2) .

Method 1: I can solve the equation by converting all of the rational expressions to the common denominator, and then solving the numerators:

10 + (4 x − 8) = 5 x

10 + 4 x − 8 = 5 x

4 x + 2 = 5 x

Method 2: I can also solve this equation by multiplying through on both sides of the equation by the denominator. (The equation becomes a bit of a mess. I've used color below to highlight which parts cancel off. Use caution! )

10 + 4( x − 2) = 5( x )

Using either method, I get the same answer; namely, x  = 2 . However, checking back to the beginning, where I first noted the disallowed values for the original equation, I see that x  ≠ 2 . In other words, my only solution value would actually cause division by zero. Since the only possible solution causes division by zero, then this equation really has no solution. My answer then is:

no solution

It doesn't look like I did anything wrong, mathematically, in the previous exercise. So how did I end up with an entirely invalid solution?

Advertisement

When dealing with rational expressions and equations, we're not allowed to divide by zero. When there are variables in denominators, we then will have certain values which can cause division by zero. Whichever method one uses to solve a given rational equation, one will, at some point, get rid of those denominators. In other words, at some point, one will, in effect, make those division-by-zero problems magically disappear. But they aren't actually gone; they've merely been ignored at some stage. In the end, one must go back to the beginning and check one's solution against those original disallowed values. And it is perfectly possible that a given equation will have no solution at all.

Whenever you solve a rational equation, always check your (interim) solution against the denominators (and their disallowed values) from the original equation. It is entirely possible that a problem will have an invalid (that is, an "extraneous") solution. This is especially true on tests. So always check!

URL: https://www.purplemath.com/modules/solvrtnl2.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.6: Applications of Rational Equations

• Last updated
• Save as PDF
• Page ID 18373

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve applications involving relationships between real numbers.
• Solve applications involving uniform motion (distance problems).
• Solve work-rate applications.

Number Problems

Recall that the reciprocal of a nonzero number \(n\) is \(\frac{1}{n}\). For example, the reciprocal of \(5\) is \(\frac{1}{5}\) and \(5\cdot \frac{1}{5} = 1\). In this section, the applications will often involve the key word “reciprocal.” When this is the case, we will see that the algebraic setup results in a rational equation.

Example \(\PageIndex{1}\)

A positive integer is \(4\) less than another. The sum of the reciprocals of the two positive integers is \(\frac{10}{21}\). Find the two integers.

Begin by assigning variables to the unknowns.

Let \(n\) represent the larger positive integer.

Let \(n-4\) represent the smallest positive integer.

Next, use the reciprocals \(\frac{1}{n}\) and \(\frac{1}{n−4}\) to translate the sentences into an algebraic equation.

\(\begin{array}{ccc}{\color{Cerulean} { the\:sum\:of\:the\:reciprocals }} & {\color{Cerulean} { is }} \\ {\qquad \frac{1}{n}+\frac{1}{n-4}} & {=} & {\frac{10}{21}}\end{array}\)

We can solve this rational expression by multiplying both sides of the equation by the least common denominator (LCD). In this case, the LCD is \(21n(n−4)\).

\(\begin{array}{cl}{\frac{1}{n}+\frac{1}{n-4}=\frac{10}{21}}&{} \\ {\color{Cerulean}{21n(n-4)} \color{black}{\cdot \left(\frac{1}{n}+\frac{1}{n-4} \right)}=\color{Cerulean}{21n(n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Multiply\:both\:sides}}\\{}&{\color{Cerulean}{by\:the\:LCD.}} \\ {\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n}+}\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n-4}}=\color{Cerulean}{21n (n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Distribute\:and}}\\{}&{\color{Cerulean}{then\:cancel.}} \\ {21(n-4)+21n =10 n(n-4)}\end{array}\)

Solve the resulting quadratic equation.

\(\begin{array}{rlrl}{5 n-6} & {=0} & {\text { or }} & {n-7=0} \\ {5 n} & {=6} && {n=7} \\ {n} & {=\frac{6}{5}}\end{array}\)

The question calls for integers and the only integer solution is \(n=7\). Hence disregard \(\frac{6}{5}\). Use the expression \(n−4\) to find the smaller integer.

\(n-4=7-4=3\)

The two positive integers are \(3\) and \(7\). The check is left to the reader.

Example \(\PageIndex{2}\)

A positive integer is \(4\) less than another. If the reciprocal of the smaller integer is subtracted from twice the reciprocal of the larger, then the result is \(\frac{1}{30}\). Find the two integers.

Let \(n-4\) represent the smaller positive integer.

Set up an algebraic equation.

Solve this rational expression by multiplying both sides by the LCD. The LCD is \(30n(n−4)\).

\(\begin{aligned}\frac{2}{n}-\frac{1}{n-4}&=\frac{1}{30} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{2}{n}-\frac{1}{n-4}\right)}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{2}{n}-}\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{1}{n-4}}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)}\end{aligned}\)

\(\begin{array}{rlrl}{n-10} & {=0 \quad \text { or }} & {n-24} & {=0} \\ {n} & {=10} & { n=24}\end{array}\)

Here we have two viable possibilities for the larger integer. For this reason, we will we have two solutions to this problem.

If \(n=10\), then \(n-4=10-4=6\).

If \(n=24\), then \(n-4=24-4=20\).

As a check, perform the operations indicated in the problem.

\(\begin{array}{r|r}{\text { Check } 6 \text { and } 10 .} &{\text{Check} \:20\:\text{and}\:24.}\\{2\left(\frac{1}{\color{OliveGreen}{10}}\right)-\frac{1}{\color{OliveGreen}{6}}=\frac{1}{5}-\frac{1}{6}}&{2\left(\frac{1}{\color{OliveGreen}{24}}\right)-\frac{1}{\color{OliveGreen}{20}}=\frac{1}{12}-\frac{1}{20}}\\{=\frac{6}{30}-\frac{5}{30}}&{=\frac{5}{60}-\frac{3}{60}}\\{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}}&{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}} \end{array}\)

Two sets of positive integers solve this problem: {\(6, 10\)} and {\(20, 24\)}.

Exercise \(\PageIndex{1}\)

The difference between the reciprocals of two consecutive positive odd integers is \(\frac{2}{15}\). Find the integers.

The integers are \(3\) and \(5\).

Uniform Motion Problems

Uniform motion problems, also referred to as distance problems, involve the formula

where the distance, \(D\), is given as the product of the average rate, \(r\), and the time, \(t\), traveled at that rate. If we divide both sides by the average rate, \(r\), then we obtain the formula

\[t=\frac{D}{r}\]

For this reason, when the unknown quantity is time, the algebraic setup for distance problems often results in a rational equation. Similarly, when the unknown quantity is the rate, the setup also may result in a rational equation.

We begin any uniform motion problem by first organizing our data with a chart. Use this information to set up an algebraic equation that models the application.

Example \(\PageIndex{5}\)

Mary spent the first 120 miles of her road trip in traffic. When the traffic cleared, she was able to drive twice as fast for the remaining 300 miles. If the total trip took 9 hours, then how fast was she moving in traffic?

First, identify the unknown quantity and organize the data.

Let \(x\) represent Mary's average speed (miles per hour) in traffic.

Let \(2x\) represent her average speed after the traffic cleared.

To avoid introducing two more variables for the time column, use the formula \(t=\frac{D}{r}\). Here the time for each leg of the trip is calculated as follows:

\(\begin{array}{c} {\color{Cerulean} { Time\:spent\:in\:traffic:}\:\:\color{black}{ t=\frac{D}{r}=\frac{120}{x}}} \\{\color{Cerulean}{Time\:clear\:of\:traffic:}\:\:\color{black}{t=\frac{D}{r}}=\frac{300}{2x}} \end{array}\)

Use these expressions to complete the chart.

The algebraic setup is defined by the time column. Add the times for each leg of the trip to obtain a total of 9 hours:

\(\begin{array}{ccccc}{\color{Cerulean}{time\:spent\:in\:traffic}}&{}&{\color{Cerulean}{time\:clear\:of\:traffic}}&{}&{\color{Cerulean}{total\:time\:of\:trip}} \\ {\overbrace{\frac{120}{x}}}&{+}&{\overbrace{\frac{300}{2x}}}&{=}&{\overbrace{9}} \end{array}\)

We begin solving this equation by first multiplying both sides by the LCD, \(2x\).

\(\begin{aligned} \frac{120}{x}+\frac{300}{2 x} &=9 \\ \color{Cerulean}{2x }\color{black}{ \cdot\left(\frac{120}{x}+\frac{300}{2 x}\right)} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ \color{Cerulean}{2 x}\color{black}{ \cdot \frac{120}{x}+}\color{Cerulean}{2 x}\color{black}{ \cdot \frac{300}{2 x}} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ 240+300 &=18 x \\ 540 &=18 x \\ 30 &=x \end{aligned}\)

Mary averaged 30 miles per hour in traffic.

Example \(\PageIndex{6}\)

A passenger train can travel, on average, \(20\) miles per hour faster than a freight train. If the passenger train covers \(390\) miles in the same time it takes the freight train to cover \(270\) miles, then how fast is each train?

First, identify the unknown quantities and organize the data.

Let \(x\) represent the average speed of the freight train.

Let \(x+20\) represent the speed of the passenger train.

Next, organize the given data in a chart.

Use the formula \(t=\frac{D}{r}\) to fill in the time column for each train.

\(\begin{array}{c} {\color{Cerulean} { Passenger\: train: }\:\:\color{black}{ t=\frac{D}{r}=\frac{390}{x+20}}} \\ {\color{Cerulean}{Freight\:train:}\:\:\color{black}{t=\frac{D}{r}=\frac{270}{x}}} \end{array}\)

Because the trains travel the same amount of time, finish the algebraic setup by equating the expressions that represent the times:

\(\frac{390}{x+20}=\frac{270}{x}\)

Solve this equation by first multiplying both sides by the LCD, \(x(x+20)\).

\(\begin{aligned} \color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{390}{x+20}\right)} &=\color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{270}{x}\right) }\\ 390 x &=270(x+20) \\ 390 x &=270 x+5400 \\ 120 x &=5400 \\ x &=45 \end{aligned}\)

Use \(x+20\) to find the speed of the passenger train.

\(x+20=\color{OliveGreen}{45}\color{black}{+20=65}\)

The speed of the passenger train is \(65\) miles per hour and the speed of the freight train is \(45\) miles per hour.

Example \(\PageIndex{7}\)

Brett lives on the river \(8\) miles upstream from town. When the current is \(2\) miles per hour, he can row his boat downstream to town for supplies and back in \(3\) hours. What is his average rowing speed in still water?

Let \(x\) represent Brett's average rowing speed in still water.

Rowing downstream, the current increases his speed, and his rate is \(x + 2\) miles per hour. Rowing upstream, the current decreases his speed, and his rate is \(x − 2\) miles per hour. Begin by organizing the data in the following chart:

Use the formula \(t=\frac{D}{r}\) to fill in the time column for each leg of the trip.

\(\begin{array}{c} {\color{Cerulean} { Trip\: downstream: } \:\:\color{black}{ t=\frac{D}{r}=\frac{8}{x+2}}}\\{\color{Cerulean}{Trip\:upstream:}\:\:\color{black}{t=\frac{D}{r}=\frac{8}{x-2}}} \end{array}\)

The algebraic setup is defined by the time column. Add the times for each leg of the trip to obtain a total of 3 hours:

\(\begin{array}{ccccc}{\color{Cerulean}{time\:rowing\:downstream}}&{}&{\color{Cerulean}{time\:rowing\:upstream}}&{}&{\color{Cerulean}{total\:time\:of\:trip}}\\{\overbrace{\frac{8}{x+2}}}&{+}&{\overbrace{\frac{8}{x-2}}}&{=}&{\overbrace{3}} \end{array}\)

Solve this equation by first multiplying both sides by the LCD, \((x+2)(x−2)\).

Next, solve the resulting quadratic equation.

\(\begin{array}{rlrl}{3 x+2} & {=0} & {\text { or }} & {x-6=0} \\ {3 x} & {=-2} & {} & {x=6} \\ {x} & {=\frac{-2}{3}}\end{array}\)

Use only the positive solution, \(x=6\) miles per hour.

His rowing speed is \(6\) miles per hour.

Exercise \(\PageIndex{2}\)

Dwayne drove \(18\) miles to the airport to pick up his father and then returned home. On the return trip he was able to drive an average of \(15\) miles per hour faster than he did on the trip there. If the total driving time was \(1\) hour, then what was his average speed driving to the airport?

His average speed driving to the airport was \(30\) miles per hour.

Work-Rate Problems

The rate at which a task can be performed is called a work rate.

Example \(\PageIndex{8}\)

For example, if a painter can paint a room in 8 hours, then the task is to paint the room, and we can write

\(\frac{1 \text { task }}{8 \text { hours }} \quad \color{Cerulean} { Work\: rate }\)

In other words, the painter can complete \(\frac{1}{8}\) of the task per hour.

If he works for less than 8 hours, then he will perform a fraction of the task. For example,

\(\begin{array}{cc} {\color{Cerulean}{work\:rate}\color{black}{\times}\color{Cerulean}{time}\color{black}{=}\color{Cerulean}{work\:completed}}&{}\\{\frac{1}{8}\times 2\text{hrs}=\frac{1}{4}}&{\color{Cerulean}{One-quarter\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 4\text{hrs}=\frac{1}{2}}&{\color{Cerulean}{One-half\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 8\text{hrs}=1}&{\color{Cerulean}{One\:whole\:room\:painted}} \end{array}\)

Obtain the amount of the task completed by multiplying the work rate by the amount of time the painter works. Typically, work-rate problems involve people working together to complete tasks. When this is the case, we can organize the data in a chart, just as we have done with distance problems.

Suppose an apprentice painter can paint the same room by himself in \(10\) hours. Then we say that he can complete \(\frac{1}{10}\) of the task per hour.

Let \(t\) represent the time it takes both of the painters, working together, to paint the room.

To complete the chart, multiply the work rate by the time for each person.

The portion of the room each can paint adds to a total of \(1\) task completed.

This is represented by the equation obtained from the first column of the chart:

This setup results in a rational equation that can be solved for \(t\) by multiplying both sides by the LCD, \(40\).

\(\begin{aligned} \frac{1}{8}t+\frac{1}{10}t &=1 \\ \color{Cerulean}{40}\color{black}{\cdot \left(\frac{1}{8}t+\frac{1}{10}t\right)}&=\color{Cerulean}{40}\color{black}{\cdot 1} \\ \color{Cerulean}{40}\color{black}{\cdot\frac{t}{8}+}\color{Cerulean}{40}\color{black}{\cdot\frac{t}{10}}&=\color{Cerulean}{40}\color{black}{\cdot 1}\\ 5t+4t &=40 \\ 9t & =40 \\ t & = \frac{40}{9} \\ t & = 4 \frac{4}{9} \end{aligned}\)

Therefore, the two painters, working together, complete the task in \(4 \frac{4}{9}\) hours.

In general, we have the following work-rate formula:

\[\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1\]

Here \(\frac{1}{t_{1}}\) and \(\frac{1}{t_{2}}\) are the individual work rates and \(t\) is the time it takes to complete one task working together. If we factor out the time, \(t\), and then divide both sides by \(t\), we obtain an equivalent work-rate formula:

\(\begin{array}{c} {\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1} \\ {t\left( \frac{1}{t_{1}}+\frac{1}{t_{2}} \right)=1} \\ {\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}} \end{array}\)

In summary, we have the following equivalent work-rate formulas:

\(\begin{array}{ccccc}{}&{}&{\color{Cerulean}{Work\:rate\:formulas:}}&{}&{} \\ {\frac{1}{t_{1}}t}&{\text{or}}&{\frac{t}{t_{1}}+\frac{t}{t_{2}}=1}&{\text{or}}&{\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}}\end{array}\)

Example \(\PageIndex{9}\)

Working alone, Billy’s dad can complete the yard work in 3 hours. If Billy helps his dad, then the yard work takes 2 hours. How long would it take Billy working alone to complete the yard work?

The given information tells us that Billy’s dad has an individual work rate of \(\frac{1}{3}\) task per hour. If we let \(x\) represent the time it takes Billy working alone to complete the yard work, then Billy’s individual work rate is \(\frac{1}{x}\), and we can write

Working together, they can complete the task in \(2\) hours. Multiply the individual work rates by \(2\) hours to fill in the chart.

The amount of the task each completes will total 1 completed task. To solve for \(x\), we first multiply both sides by the LCD, \(3x\).

\(\begin{aligned} \frac{1}{3}\cdot 2+\frac{1}{x}\cdot 2 &=1 \\ \color{Cerulean}{3x}\color{black}{\cdot \left(\frac{2}{3}+\frac{2}{x} \right)}&=\color{Cerulean}{3x}\color{black}{\cdot1} \\ \color{Cerulean}{3x}\color{black}{\cdot \frac{2}{3} +}\color{Cerulean}{3x}\color{black}{\cdot \frac{2}{x}}&=\color{Cerulean}{3x}\color{black}{\cdot 1} \\ 2x+6&=3x \\ 6&=x \end{aligned}\)

It takes Billy \(6\) hours to complete the yard work alone.

Of course, the unit of time for the work rate need not always be in hours.

Example \(\PageIndex{10}\)

Working together, two construction crews can build a shed in \(5\) days. Working separately, the less experienced crew takes twice as long to build a shed than the more experienced crew. Working separately, how long does it take each crew to build a shed?

Let \(x\) represent the time it takes the more experienced crew to build a shed.

Let \(2x\) represent the time it takes the less experienced crew to build a shed.

Working together, the job is completed in \(5\) days. This gives the following setup:

The first column in the chart gives us an algebraic equation that models the problem:

\(\begin{aligned} \frac{1}{x}\cdot 5+\frac{1}{2x}\cdot 5 &=1 \\ \frac{5}{x}+\frac{5}{2x}&=1 \end{aligned}\)

Solve the equation by multiplying both sides by \(2x\).

\(\begin{aligned} \color{Cerulean}{2x}\color{black}{\cdot \left(\frac{5}{x}+\frac{5}{2x} \right)}&=\color{Cerulean}{2x}\color{black}{\cdot 1}\\ \color{Cerulean}{2x}\color{black}{\cdot \frac{5}{x} +}\color{Cerulean}{2x}\color{black}{\cdot \frac{5}{2x}}&=\color{Cerulean}{2x}\color{black}{\cdot 1} \\ 10+5&=2x \\ 15&=2x \\ \frac{15}{2}&=x \quad\text{or}\quad x=7\frac{1}{2}\:\text{days} \end{aligned}\)

To determine the time it takes the less experienced crew, we use \(2x\):

\(\begin{aligned} 2x&= 2\color{black}{\left(\color{OliveGreen}{\frac{15}{2}} \right) } \\ &= 15\:\text{days} \end{aligned}\)

Working separately, the experienced crew takes \(7\frac{1}{2}\) days to build a shed, and the less experienced crew takes \(15\) days to build a shed.

Exercise \(\PageIndex{3}\)

Joe’s garden hose fills the pool in \(12\) hours. His neighbor has a thinner hose that fills the pool in \(15\) hours. How long will it take to fill the pool using both hoses?

It will take both hoses \(6\frac{2}{3}\) hours to fill the pool.

Key Takeaways

• In this section, all of the steps outlined for solving general word problems apply. Look for the new key word “reciprocal,” which indicates that you should write the quantity in the denominator of a fraction with numerator \(1\).
• When solving distance problems where the time element is unknown, use the equivalent form of the uniform motion formula, \(t=\frac{D}{r}\), to avoid introducing more variables.
• When solving work-rate problems, multiply the individual work rate by the time to obtain the portion of the task completed. The sum of the portions of the task results in the total amount of work completed.

Exercise \(\PageIndex{4}\) Number Problems

Use algebra to solve the following applications.

• A positive integer is twice another. The sum of the reciprocals of the two positive integers is \(\frac{3}{10}\). Find the two integers.
• A positive integer is twice another. The sum of the reciprocals of the two positive integers is \(\frac{3}{12}\). Find the two integers.
• A positive integer is twice another. The difference of the reciprocals of the two positive integers is \(\frac{1}{8}\). Find the two integers.
• A positive integer is twice another. The difference of the reciprocals of the two positive integers is \(\frac{1}{18}\). Find the two integers.
• A positive integer is \(2\) less than another. If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is \(\frac{5}{12}\), then find the two integers.
• A positive integer is \(2\) more than another. If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is \(\frac{17}{35}\), then find the two integers.
• The sum of the reciprocals of two consecutive positive even integers is \(\frac{11}{60}\). Find the two even integers.
• The sum of the reciprocals of two consecutive positive odd integers is \(\frac{16}{63}\). Find the integers.
• The difference of the reciprocals of two consecutive positive even integers is \(\frac{1}{24}\). Find the two even integers.
• The difference of the reciprocals of two consecutive positive odd integers is \(\frac{2}{99}\). Find the integers.
• If \(3\) times the reciprocal of the larger of two consecutive integers is subtracted from \(2\) times the reciprocal of the smaller, then the result is \(\frac{1}{2}\). Find the two integers.
• If \(3\) times the reciprocal of the smaller of two consecutive integers is subtracted from \(7\) times the reciprocal of the larger, then the result is \(\frac{1}{2}\). Find the two integers.
• A positive integer is \(5\) less than another. If the reciprocal of the smaller integer is subtracted from \(3\) times the reciprocal of the larger, then the result is \(\frac{1}{12}\). Find the two integers.
• A positive integer is \(6\) less than another. If the reciprocal of the smaller integer is subtracted from \(10\) times the reciprocal of the larger, then the result is \(\frac{3}{7}\). Find the two integers.

1. {\(5, 10\)}

3. {\(4, 8\)}

5. {\(6, 8\)}

7. {\(10, 12\)}

9. {\(6, 8\)}

11. {\(1, 2\)} or {\(−4, −3\)}

13. {\(4, 9\)} or {\(15, 20\)}

Exercise \(\PageIndex{5}\) Uniform Motion Problems

• James can jog twice as fast as he can walk. He was able to jog the first \(9\) miles to his grandmother’s house, but then he tired and walked the remaining \(1.5\) miles. If the total trip took \(2\) hours, then what was his average jogging speed?
• On a business trip, an executive traveled \(720\) miles by jet aircraft and then another \(80\) miles by helicopter. If the jet averaged \(3\) times the speed of the helicopter and the total trip took \(4\) hours, then what was the average speed of the jet?
• Sally was able to drive an average of \(20\) miles per hour faster in her car after the traffic cleared. She drove \(23\) miles in traffic before it cleared and then drove another \(99\) miles. If the total trip took \(2\) hours, then what was her average speed in traffic?
• Harry traveled \(15\) miles on the bus and then another \(72\) miles on a train. If the train was \(18\) miles per hour faster than the bus and the total trip took \(2\) hours, then what was the average speed of the train?
• A bus averages \(6\) miles per hour faster than a trolley. If the bus travels \(90\) miles in the same time it takes the trolley to travel \(75\) miles, then what is the speed of each?
• A passenger car averages \(16\) miles per hour faster than the bus. If the bus travels \(56\) miles in the same time it takes the passenger car to travel \(84\) miles, then what is the speed of each?
• A light aircraft travels \(2\) miles per hour less than twice as fast as a passenger car. If the passenger car can travel \(231\) miles in the same time it takes the aircraft to travel \(455\) miles, then what is the average speed of each?
• Mary can run \(1\) mile per hour more than twice as fast as Bill can walk. If Bill can walk \(3\) miles in the same time it takes Mary to run \(7.2\) miles, then what is Bill’s average walking speed?
• An airplane traveling with a \(20\)-mile-per-hour tailwind covers \(270\) miles. On the return trip against the wind, it covers \(190\) miles in the same amount of time. What is the speed of the airplane in still air?
• A jet airliner traveling with a \(30\)-mile-per-hour tailwind covers \(525\) miles in the same amount of time it is able to travel \(495\) miles after the tailwind eases to \(10\) miles per hour. What is the speed of the airliner in still air?
• A boat averages \(16\) miles per hour in still water. With the current, the boat can travel \(95\) miles in the same time it travels \(65\) miles against it. What is the speed of the current?
• A river tour boat averages \(7\) miles per hour in still water. If the total \(24\)-mile tour down river and \(24\) miles back takes \(7\) hours, then how fast is the river current?
• If the river current flows at an average \(3\) miles per hour, then a tour boat makes the \(9\)-mile tour downstream with the current and back the \(9\) miles against the current in \(4\) hours. What is the average speed of the boat in still water?
• Jane rowed her canoe against a \(1\)-mile-per-hour current upstream \(12\) miles and then returned the \(12\) miles back downstream. If the total trip took \(5\) hours, then at what speed can Jane row in still water?
• Jose drove \(15\) miles to pick up his sister and then returned home. On the return trip, he was able to average \(15\) miles per hour faster than he did on the trip to pick her up. If the total trip took \(1\) hour, then what was Jose’s average speed on the return trip?
• Barry drove the \(24\) miles to town and then back in \(1\) hour. On the return trip, he was able to average \(14\) miles per hour faster than he averaged on the trip to town. What was his average speed on the trip to town?
• Jerry paddled his kayak upstream against a \(1\)-mile-per-hour current for \(12\) miles. The return trip downstream with the \(1\)-mile-per-hour current took \(1\) hour less time. How fast can Jerry paddle the kayak in still water?
• It takes a light aircraft \(1\) hour more time to fly \(360\) miles against a \(30\)- mile-per-hour head wind than it does to fly the same distance with it. What is the speed of the aircraft in calm air?

1. \(6\) miles per hour

3. \(46\) miles per hour

5. Trolley: \(30\) miles per hour; bus: \(36\) miles per hour

7. Passenger car: \(66\) miles per hour; aircraft: \(130\) miles per hour

9. \(115\) miles per hour

11. \(3\) miles per hour

13. \(6\) miles per hour

15. \(40\) miles per hour

17. \(5\) miles per hour

Exercise \(\PageIndex{6}\) Work-Rate Problems

• James can paint the office by himself in \(7\) hours. Manny paints the office in \(10\) hours. How long will it take them to paint the office working together?
• Barry can lay a brick driveway by himself in \(12\) hours. Robert does the same job in \(10\) hours. How long will it take them to lay the brick driveway working together?
• Jerry can detail a car by himself in \(50\) minutes. Sally does the same job in \(1\) hour. How long will it take them to detail a car working together?
• Jose can build a small shed by himself in \(26\) hours. Alex builds the same small shed in \(2\) days. How long would it take them to build the shed working together?
• Allison can complete a sales route by herself in \(6\) hours. Working with an associate, she completes the route in \(4\) hours. How long would it take her associate to complete the route by herself?
• James can prepare and paint a house by himself in \(5\) days. Working with his brother, Bryan, they can do it in \(3\) days. How long would it take Bryan to prepare and paint the house by himself?
• Joe can assemble a computer by himself in \(1\) hour. Working with an assistant, he can assemble a computer in \(40\) minutes. How long would it take his assistant to assemble a computer working alone?
• The teacher’s assistant can grade class homework assignments by herself in \(1\) hour. If the teacher helps, then the grading can be completed in \(20\) minutes. How long would it take the teacher to grade the papers working alone?
• A larger pipe fills a water tank twice as fast as a smaller pipe. When both pipes are used, they fill the tank in \(5\) hours. If the larger pipe is left off, then how long would it take the smaller pipe to fill the tank?
• A newer printer can print twice as fast as an older printer. If both printers working together can print a batch of flyers in \(45\) minutes, then how long would it take the newer printer to print the batch working alone?
• Working alone, Henry takes \(9\) hours longer than Mary to clean the carpets in the entire office. Working together, they clean the carpets in \(6\) hours. How long would it take Mary to clean the office carpets if Henry were not there to help?
• Working alone, Monique takes \(4\) hours longer than Audrey to record the inventory of the entire shop. Working together, they take inventory in \(1.5\) hours. How long would it take Audrey to record the inventory working alone?
• Jerry can lay a tile floor in \(3\) hours less time than Jake. If they work together, the floor takes \(2\) hours. How long would it take Jerry to lay the floor by himself?
• Jeremy can build a model airplane in \(5\) hours less time than his brother. Working together, they need \(6\) hours to build the plane. How long would it take Jeremy to build the model airplane working alone?
• Harry can paint a shed by himself in \(6\) hours. Jeremy can paint the same shed by himself in \(8\) hours. How long will it take them to paint two sheds working together?
• Joe assembles a computer by himself in \(1\) hour. Working with an assistant, he can assemble \(10\) computers in \(6\) hours. How long would it take his assistant to assemble \(1\) computer working alone?
• Jerry can lay a tile floor in \(3\) hours, and his assistant can do the same job in \(4\) hours. If Jerry starts the job and his assistant joins him 1 hour later, then how long will it take to lay the floor?
• Working alone, Monique takes \(6\) hours to record the inventory of the entire shop, while it takes Audrey only \(4\) hours to do the same job. How long will it take them working together if Monique leaves \(2\) hours early?

1. \(4 \frac{2}{17}\) hours

3. \(27 \frac{3}{11}\) minutes

5. \(12\) hours

7. \(2\) hours

9. \(15\) hours

11. \(9\) hours

13. \(3\) hours

15. \(6\frac{6}{7}\) hours

17. \(2 \frac{1}{7}\) hours