

The Math You Need, When You Need It
math tutorials for students majoring in the earth sciences
Scientific Notation - Practice Problems
Solving earth science problems with scientific notation, × div[id^='image-'] {position:static}div[id^='image-'] div.hover{position:static} introductory problems.
These problems cover the fundamentals of writing scientific notation and using it to understand relative size of values and scientific prefixes.
Problem 1: The distance to the moon is 238,900 miles. Write this value in scientific notation.
Problem 2: One mile is 1609.34 meters. What is the distance to the moon in meters using scientific notation?
`1609.34 m/(mi) xx 238","900 mi` = 384,400,000 m
Notice in the above unit conversion the 'mi' units cancel each other out because 'mi' is in the denominator for the first term and the numerator for the second term
Problem 4: The atomic radius of a magnesium atom is approximately 1.6 angstroms, which is equal to 1.6 x 10 -10 meters (m). How do you write this length in standard form?
0.00000000016 m
Fissure A = 40,0000 m Fissure B = 5,0000 m
This shows fissure A is larger (by almost 10 times!). The shortcut to answer a question like this is to look at the exponent. If both coefficients are between 1-10, then the value with the larger exponent is the larger number.
Problem 6: The amount of carbon in the atmosphere is 750 petagrams (pg). One petagram equals 1 x 10 15 grams (g). Write out the amount of carbon in the atmosphere in (i) scientific notation and (ii) standard decimal format.
The exponent is a positive number, so the decimal will move to the right in the next step.
750,000,000,000,000,000 g
Advanced Problems
Scientific notation is used in solving these earth and space science problems and they are provided to you as an example. Be forewarned that these problems move beyond this module and require some facility with unit conversions, rearranging equations, and algebraic rules for multiplying and dividing exponents. If you can solve these, you've mastered scientific notation!
Problem 7: Calculate the volume of water (in cubic meters and in liters) falling on a 10,000 km 2 watershed from 5 cm of rainfall.
`10,000 km^2 = 1 xx 10^4 km^2`
5 cm of rainfall = `5 xx 10^0 cm`
Let's start with meters as the common unit and convert to liters later. There are 1 x 10 3 m in a km and area is km x km (km 2 ), therefore you need to convert from km to m twice:
`1 xx 10^3 m/(km) * 1 xx 10^3 m/(km) = 1 xx 10^6 m^2/(km)^2` `1 xx 10 m^2/(km)^2 * 1 xx 10^4 km^2 = 1 xx 10^10 m^2` for the area of the watershed.
For the amount of rainfall, you should convert from centimeters to meters:
`5 cm * (1 m)/(100 cm)= 5 xx 10^-2 m`
`V = A * d`
When multiplying terms with exponents, you can multiply the coefficients and add the exponents:
`V = 1 xx 10^10 m^2 * 5.08 xx 10^(-2) m = 5.08 xx 10^8 m^3`
Given that there are 1 x 10 3 liters in a cubic meter we can make the following conversion:
`1 xx 10^3 L * 5.08 xx 10^8 m^3 = 5.08 xx 10^11 L`
Step 5. Check your units and your answer - do they make sense?
`V = 4/3 pi r^3`
Using this equation, plug in the radius (r) of the dust grains.
`V = 4/3 pi (2 xx10^(-6))^3m^3`
Notice the (-6) exponent is cubed. When you take an exponent to an exponent, you need to multiply the two terms
`V = 4/3 pi (8 xx10^(-18)m^3)`
Then, multiple the cubed radius times pi and 4/3
`V = 3.35 xx 10^(-17) m^3`
`m = 3.35 xx 10^(-17) m^3 * 3300 (kg)/m^3`
Notice in the equation above that the m 3 terms cancel each other out and you are left with kg
`m = 1.1 xx 10^(-13) kg`

`V = 4/3 pi (2.325 xx10^(15) m)^3`
`V = 5.26 xx10^(46) m^3`
Number of dust grains = `5.26 xx10^(46) m^3 xx 0.001` grains/m 3
Number of dust grains = `5.26xx10^43 "grains"`
Total mass = `1.1xx10^(-13) (kg)/("grains") * 5.26xx10^43 "grains"`
Notice in the equation above the 'grains' terms cancel each other out and you are left with kg
Total mass = `5.79xx10^30 kg`
If you feel comfortable with this topic, you can go on to the assessment . Or you can go back to the Scientific Notation explanation page .
« Previous Page Next Page »
Scientific Notation Calculator
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Example (Click to try)
How to solve your scientific notation problems, scientific notation video lesson.
- Khan Academy Video: Scientific Notation Examples
Need more problem types? Try MathPapa Algebra Calculator
Clear Scientific Notation Calculator »
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Solve Scientific Notation? (+FREE Worksheet!)
Learn how to solve mathematics problems containing scientific notation in a few simple and easy steps.

Related Topics
- How to Solve Powers of Products and Quotients
- How to Multiply Exponents
- How to Divide Exponents
- How to Solve Zero and Negative Exponents
- How to Solve Negative Exponents and Negative Bases
Step by step guide to solve scientific notation problems
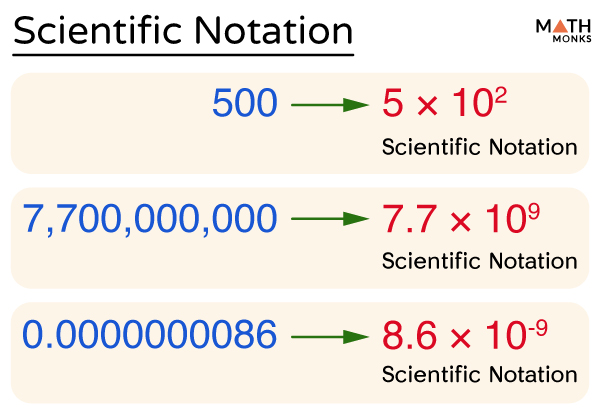
- Scientific notation is used to write very big or very small numbers in decimal form.
- In scientific notation all numbers are written in the form of: \(m×10^n\)
Scientific Notation – Example 1:
Write \(0.00015\) in scientific notation.
First, move the decimal point to the right so that you have a number that is between \(1\) and \(10\). Then: \(N=1.5\) Second, determine how many places the decimal moved in step \(1\) by the power of \(10\). Then: \(10^{ \ -4} →\) When the decimal is moved to the right, the exponent is negative. Then: \(0.00015=1.5×10^{ \ -4} \)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
The Ultimate Algebra Bundle From Pre-Algebra to Algebra II
Scientific notation – example 2:.
Write \(9.5 \times 10^{\ -5}\) in standard notation.
\(10^{-5} →\) When the decimal is moved to the right, the exponent is negative. Then: \(9.5×10^{-5}=0.000095\)
Scientific Notation – Example 3:
Write \(0.00012\) in scientific notation.
First, move the decimal point to the right so that you have a number that is between \(1\) and \(10\). Then: \(N=1.2\) Second, determine how many places the decimal moved in step \(1\) by the power of \(10\). Then: \(10^{-4}→ \) When the decimal is moved to the right, the exponent is negative. Then: \(0.00012=1.2×10^{-4}\)
Scientific Notation – Example 4:
Write \(8.3×10^{-5}\) in standard notation.
\(10^{-5} →\) When the decimal is moved to the right, the exponent is negative. Then: \(8.3×10^{-5}=0.000083\)
Exercises for Solving Scientific Notation
Write each number in scientific notation..
- \(\color{blue}{91 × 10^3}\)
- \(\color{blue}{60}\)
- \(\color{blue}{2000000}\)
- \(\color{blue}{0.0000006}\)
- \(\color{blue}{354000}\)
- \(\color{blue}{0.000325}\)
Download Scientific Notation Worksheet
- \(\color{blue}{9.1 × 10^4}\)
- \(\color{blue}{6 × 10^1}\)
- \(\color{blue}{2 × 10^6}\)
- \(\color{blue}{6 × 10^{–7}}\)
- \(\color{blue}{3.54 × 10^5}\)
- \(\color{blue}{3.25 × 10^{–4}}\)
The Greatest Books for Students to Ace the Algebra
Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests
Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.
by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )
Effortless Math Team
Related to this article, more math articles.
- How to Find Rational and Irrational Numbers?
- Calculations to Help Curb Your Rising Debt
- How to Identify the Value of a Digit on Numbers Up to a Billion
- 6th Grade NYSE Math Worksheets: FREE & Printable
- How to Identify Independent and Dependent Events?
- How to Solve Special Systems
- Algebra Puzzle – Challenge 38
- 4th Grade Wisconsin Forward Math Worksheets: FREE & Printable
- 6th Grade Scantron Math Worksheets: FREE & Printable
- 5 Best Laptops for Math Teachers in 2023
What people say about "How to Solve Scientific Notation? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra
Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra for beginners the ultimate step by step guide to preparing for the pre-algebra test, pre-algebra tutor everything you need to help achieve an excellent score.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy

Learn maths at home
A Complete Guide to Scientific Notation (Standard Form)
Scientific notation: video lesson, what is scientific notation.
Scientific notation can be used to represent both decimals less than one whole and very large whole numbers.
Scientific notation is a concise way to represent both very large or very small numbers. Scientific notation involves a number between 1 and 10 being multiplied to a power of 10. The power of 10 is positive if the number being represented is large and it is negative if the number is small.
- A positive power of 10 tells us how many digits the number has between its first digit and the decimal point
- A negative power of 10 tells us how many zero digits are in front of the non-zero digits.
For example, 6×10 5 is a 6 followed by 5 digits. It represents 600 000.
For example, 6×10 -5 is a 6 with 5 zeros before it. It represents 0.00006.

How Scientific Notation is Used in Real Life
Scientific notation is used whenever very large or very small numbers are involved. For example in physics, astronomy, chemistry and finance.
Some examples of scientific notation used in real-life include:
- The very large distances involved in astronomy. For example, the distance between the Earth and the Sun is said to be 93 million miles, which can be written as 9.3 × 10 7 miles.
- In Physics, very large or very small known constants are represented in scientific notation such as the speed of light (2.998 × 10 8 meters per second) or Planck’s constant (6.63 × 10 -34 joule-seconds).
- In chemistry, the mass of atoms, molecules and molar mass is often written in scientific notation. For example, Avogadro’s number is 6.02 × 10 23 particles per mole.
- In finance and economics, figures such as national debt, gross domestic product (GDP), or market capitalisation are often expressed in scientific notation. For instance, if a country’s GDP is $2.5 trillion, it would be expressed as 2.5 × 10 12 dollars.
- Engineers often work with values that span many orders of magnitude, such as voltage, current, or power.
- In medicine and biology, scientific notation is used to express values like cell counts, DNA base pairs, or concentrations of substances in body fluids.
In science, abbreviations are commonly used to refer to given orders of magnitude such as:
Here are some common values of scientific notation listed on a number line from least to greatest.

Scientific Notation Explained
Scientific notation is used when a very large or very small number is too long to write in the normal manner. In scientific notation numbers are written as a number between 1 and 10 multiplied by a power of 10. For example, 32500 is written as 3.25×10 4 .
Scientific notation is a more concise way to write long numbers whilst indicating their order of magnitude.
Scientific notation is also commonly known as standard form. Both scientific notation and standard form refer to numbers written as a number between 1 and 10 multiplied by 10 to the power of some other positive or negative number.
For example consider the following lists:
- 10 3 = 1000
- 10 4 = 10000
The power that 10 is raised to in each case is equal to the number of digits after the 1.
- 3 × 10 1 = 30
- 3 × 10 2 = 300
- 3 × 10 3 = 3000
- 3 × 10 4 = 30000
The power that 10 is raised to in each case is equal to the number of digits after the 3.

A number written in scientific notation always consists of the following parts:
- A number between the values of 1 and 10
- A multiplication by 10 raised to a power

The name for a number not written in scientific notation is simply ‘standard notation’ or ‘decimal notation’. When comparing a number written in standard notation to a number written in scientific notation, it may also be referred to as ‘expanded form’.
The first step is to write the first part of the number which must always be between 1 and 10.
We take 32500 and write it as 3.25 so that it is now a number that is bigger than 1 and less than 10.
The next step is to find the power of 10 that 3.25 is raised to to make it equal to 32500.
The power that ten is raised to is equal to the number of digits after the first digit.
In 32500, there are 4 digits after the first digit of 3. Therefore the power that 10 is raised to is 4.
32500 can be written as 3.25 × 10 4 .
Scientific notation is often used on calculator displays (since the calculator screen cannot fit very long numbers). On a calculator, scientifi notation is written using ‘E’ to represent × 10^.
For example, 32500 can be written as 3.25 × 10 4 or alternatively as 3.25E4.
In scientific notation, E stands for × 10 raised to the power of the number that comes after the E.

Scientific notation can also be used to write very small numbers by using negative powers of 10.
We can see that the negative power of 10 describes how many zeros are at the start of the decimal number.
For example, 10 -3 has 3 zeros when written as 0.001.

The number 0.000034 can be written as 3.4 × 10 -5 . There are 5 zeros before the digits of 3 and 4.
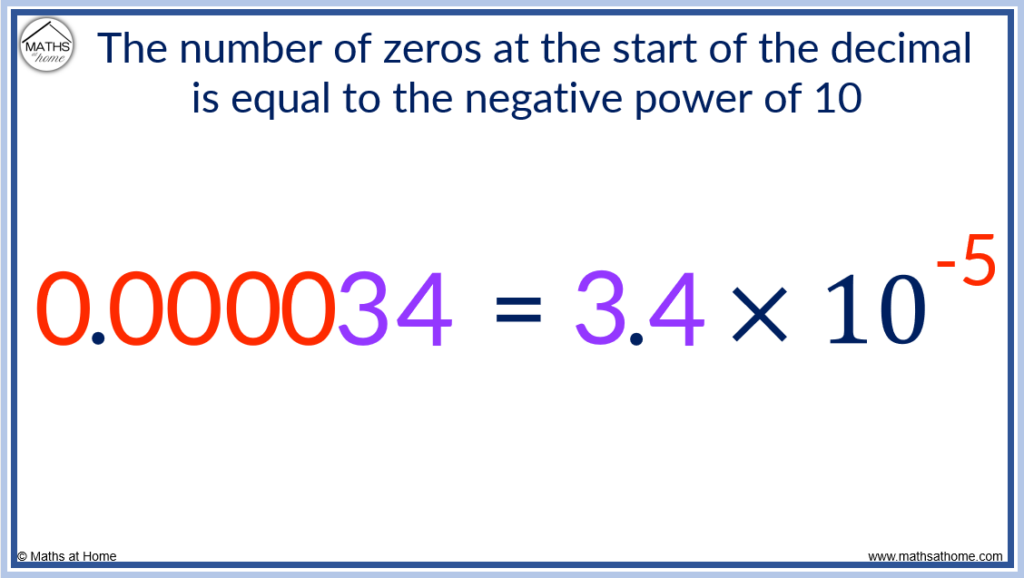
Rules of Scientific Notation
Numbers written in scientific notation must adhere to the following rules:
- The number before the multiplication sign must always be at least 1 and less than 10.
- There is always a multiplication by a power of 10 (as opposed to a multiplication by any other number).
- The power of 10 can be negative, zero or positive.
- If the number being represented is 10 or more, the power of 10 is positive.
- If the number being represented is 10 or more, the power of 10 is equal to the number of digits that come after the first digit of the number.
- If the number being represented is less than 1, the power of 10 is negative.
- If the number being represented is less than 1, the power of 10 is equal to (-1) multiplied by the number of zeros at the start of the number.
- If the number being represented is greater than 1 but less than 10, the power of 10 is zero.
How to Write Large Numbers in Scientific Notation
- Write a decimal point after the first digit of the number to form a number between 1 and 10.
- Multiply this by a power of 10, where the power is equal to the number of digits after the first digit of the large number.
For example, write 630000 in scientific notation:
Step 1. Write a decimal point after the first digit of the number to form a number between 1 and 10
A decimal point is placed after the 6 to make 6.30000 which is just 6.3
6.3 is a number between 1 and 10.
Step 2. Multiply this by a power of 10, where the power is equal to the number of digits after the first digit of the large number
The first digit of 630000 is 6. We count the number of digits after this first digit of 6.
There are 5 digits after the first digit. That is, the 3, 0, 0, 0 and 0.
Therefore we multiply by 10 5 .
630000 is written in scientific notation as 6.3×10 5 .

How to Write Small Numbers in Scientific Notation
- Write the non-zero digits as a number between 1 and 10.
- Multiply this by a negative power of 10 equal to the number of zeros in front of the first non-zero digit.
For example, write 0.000008 in scientific notation.
Step 1. Write the non-zero digits as a number between 1 and 10
The zeros at the start of 0.000008 are ignored to obtain the non-zero digit of 8.
8 is written because it is a number between 1 and 10.
Step 2. Multiply this by a negative power of 10 equal to the number of zeros in front of the first non-zero digit
The first non-zero digit in 0.000008 is the 8.
The number of zeros in front of this non-zero digit is 6.
Since there are 6 zeros, we multiply the 8 by 10 to the power of -6.
0.000008 is written in scientific notation as 8×10 -6 .

Small numbers less than one whole are written in scientific notation with a negative exponent representing the number of zeros at the start of the number.
For example, write the number 0.0257 in scientific notation.
The zeros at the start of 0.0257 are ignored and the decimal point is placed after the first non-zero digit of 2.
This results in 2.57 which is a number between 1 and 10.
The first non-zero digit is 2.
There are 2 zeros before the 2 and so, we multiply 2.57 by 10 to the power of -2.
0.0257 is written in scientific notation as 2.57×10 -2 .
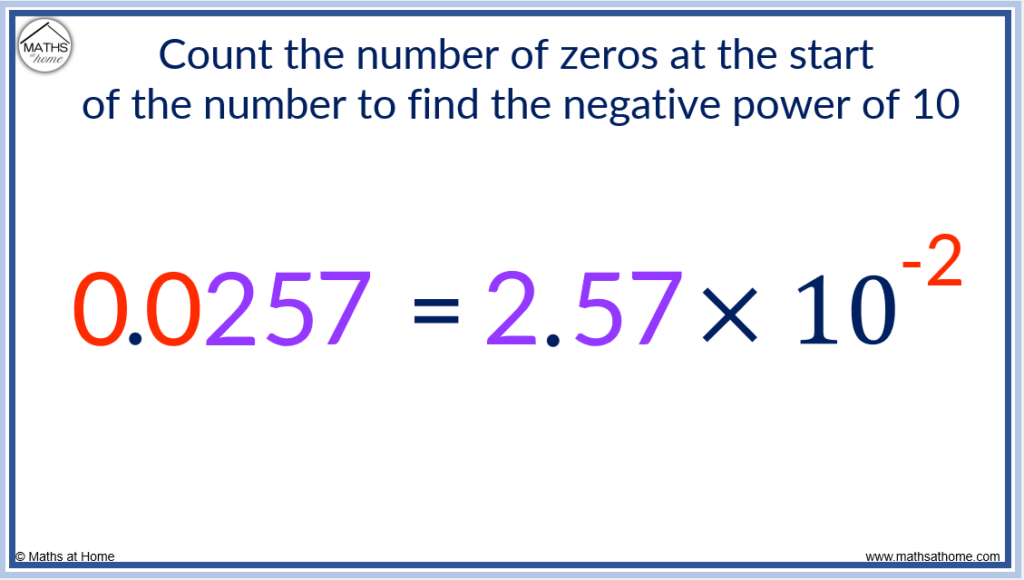
The power of the 10 is equal to the number of zeros at the start of the number multiplied by -1.
How to Read Scientific Notation
- If the power of 10 is positive, this is the number of digits after the first digit. So 2.11×10 6 has 6 digits after the 2. It is written as 2110000.
- If the power of 10 is negative, this is the number of zeros in front of the digits. So 5.3 × 10 -3 has 3 zeros at the start. It is written as 0.0053.
Scientific Notation for a Large Number
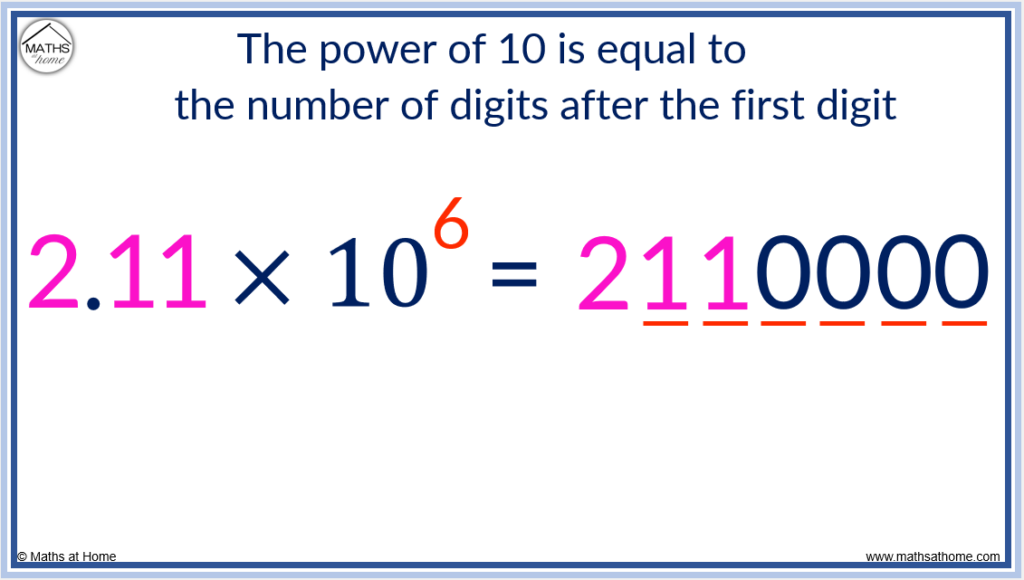
The power of 10 is 6 and so, there are 6 digits after the 2.
We already have two digits of 1 and so, four more 0 digits are needed.
Scientific Notation for a Small Number

The power of 10 is negative 3.
Negative powers tell us how many 0 digits are at the start of the number.
We put three 0 digits and then the 5 and the 3.
The decimal point always comes after the first 0 digit.
For example, 2.93 × 10 4 has 4 digits after the first digit of 2.
Following the 2, there is a 9 then a 3. We need two more 0 digits to obtain 4 digits after the 2.
2.93 × 10 4. = 29300.

For example, 1.04 × 10 -4 has a negative power of 10.
Therefore this power is equivalent to the number of zeros at the start of the number. There will be 4 zeros followed by the digits of 1, 0 and 4.
1.04 × 10 -4 = 0.000104.
Notice that the power of 10 is only equal to the number of zeros at the start of the number, not the total number of zeros in the answer.

Examples of Scientific Notation
Notice that as an extra zero digit is added to the value, the exponent in scientific notation increases by 1.
Notice that as we move from one thousand to one million to one billion to one trillion, three zero digits are added and so, the exponent in scientific notation increases by 3.
Here are some common values listed in scientific notation:
The power of zero in 1×10 0 means that zero tens have been multiplied by.
That is, 10 0 = 1 and so 1×10 0 simply means 1×1 which is just equal to 1.
Here are some examples of numbers written in scientific notation:
How to Round Numbers in Scientific Notation
It is common for numbers to be written to a particular number of significant figures and then written in scientific notation. This is because numbers in scientific notation are very large or very small and so, the final digits do not really impact on the overall size of the number.
Typically, numbers in scientific notation are given to 2 or 3 decimal places although further accuracy may be required.
It is common to round numbers in scientific notation to 3 significant figures.
For example, write 125364 in scientific notation, rounded to 3 significant figures.
The first step is to round the number to 3 significant figures.
That is, we look at the first 3 non-zero digits of the number, which are 1, 2 and 5. We then look at the next digit after this to decide if the 3rd significant figure of 5 remains as a 5 or rounds up to a 6.
Only round up the 3rd significant figure if the 4th significant figure is equal to 5 or more.
Since the digit after the 5 is a 3, we do not round up.
We write 125 and then replace the other digits with zeros, so that 125364 written to 3 significant figures is 125000.
We now write this in scientific notation as 1.25 × 10 5 , since there are 5 digits after the first digit of 1 in the number 125000.

For example, write the number 0.06627 in scientific notation to 3 significant figures.
Significant figures are counted after the zeros at the start of the number.
We look at the first 3 significant figures of the number which are 6, 6 and 2.
We only round up the 3rd significant figure if the 4th significant figure is equal to 5 or more.
The 4th significant figure is a 7 and so, we round the 2 up to a 3.
0.06627 rounded to 3 significant figures is 0.0663.
This number starts with 2 zeros, so writing it in scientific notation we have 6.33 × 10 -2 .

How to Add and Subtract Numbers in Scientific Notation
The ease of adding and subtracting numbers in scientific notation depends on whether the size of the exponents are the same in each number.
To add or subtract numbers in scientific notation that have the same exponent, simply add or subtract the coefficients and keep the exponent the same. For example, 3×10 5 + 4 × 10 5 is (3+4) × 10 5 which equals 7 × 10 5 .
In this example, the exponents on both 3×10 5 and 4×10 5 are both 5.
Therefore, we can simply add the 3 and the 4 together to obtain 7, whilst the exponent in the answer remains as 5.
3×10 5 + 4×10 5 = 7×10 5 .
This addition is essentially the same as 300 000 + 400 000 = 700 000.

For example, 3×10 -4 – 1×10 -4 = (3-1)×10 -4 which is just 2×10 -4 .
In this example, we simply subtract the coefficients and keep the exponent as -4.

To add or subtract numbers in scientific notation that have different exponents, it is easiest to convert the numbers to standard notation first. Then perform the addition or subtraction and write the result back in scientific notation if needed.
In the example of 3.21×10 3 + 2×10 4 , the exponents are different sizes.
- Converting 3.21×10 3 to standard notation, we have 3 210. The exponent of 3 means there are 3 digits after the first digit.
After the 3, we have the 2 then the 1 and so, another digit of 0 is needed to make 3 digits after the first digit in total.
Converting 2×10 4 to standard notation, we have 20 000. That is, we have 4 digits after the first digit of 2.
Now, these numbers can be added following the standard addition process.
3 210 + 20 000 = 23 210.
We can write this in scientific notation if needed as 2.321×10 4 since there are 4 digits after the first digit in 23 210.

Here is an alternate method for adding numbers in scientific notation when they have different exponents.
The same numbers as above are used but here we are demonstrating a different method to solve the problem.
To add or subtract numbers in scientific notation, first convert the numbers to have the same exponent. To do this, multiply the coefficient of the number with the largest exponent by 10 each time the exponent is reduced by 1.
For example, in 3.21×10 3 + 2×10 4 , we wish to reduce the exponent in 2×10 4 from a 4 to a 3 so that it is the same exponent as in 3.21×10 3 .
Since we need to reduce the exponent by 1, we multiply the 2 by 10 to make 20.
2×10 4 is the same as 20×10 3 .
Therefore 3.21×10 3 + 2×10 4 is rewritten as 3.21×10 3 + 20×10 3 .
Now the coefficients can be added so that 3.21×10 3 + 20×10 3 = (3.21+20)×10 3 .
This equals 23.21×10 3 which can be readjusted to 2.321×10 4 as we divide the coefficient by 10 as we increase the exponent of 10 by 1.

Here is an example of subtracting numbers in scientific notation by first converting them to have the same exponents.
In the example of 5.3×10 5 – 7.9×10 4 , we need to change the exponent of 5.3×10 5 to a 4.
To do this, we multiply the 5.3 by 10 to make 53.
5.3×10 5 is the same as 53×10 4 .
Therefore 5.3×10 5 – 7.9×10 4 can be written as 53×10 4 – 7.9×10 4 .
Now the numbers have the same exponent, subtract the coefficients like so:
(53 – 7.9)×10 4 = 45.1×10 4 .
Finally, this is rewritten so that the coefficient is a number between 1 and 10. We divide 45.1 by 10 and increase the exponent by 1 to compensate.
45.1×10 4 = 4.51×10 5 .

How to Multiply and Divide Numbers in Scientific Notation
To multiply numbers in scientific notation, multiply the coefficients and add the exponents. For example, (2×10 3 ) × (3×10 5 ) = 6×10 8 . The coefficients of 2 and 3 were multiplied to make 6 and the exponents of 3 and 5 were added to make 8.
This occurs since exponents are always added when they are multiplied together.

Here is an example of multiplying numbers in scientific notation: (4.5×10 9 ) × (5.2×10 -2 ).
Firstly, the coefficients of 4.5 and 5.2 are multiplied to obtain 23.4.
Secondly, the exponents are added so that 9 + -2 = 7.
Therefore, (4.5×10 9 ) × (5.2×10 -2 ) = 23.4×10 7 .
However, 23.4 must be written as a number between 1 and 10.
We divide 23.4 by 10 to obtain 2.34 and we increase the exponent from 7 to 8 to compensate.
(4.5×10 9 ) × (5.2×10 -2 ) = 2.34×10 8 .

To divide numbers in scientific notation, divide the coefficients and subtract the exponents. For example, (6×10 7 ) ÷ (2×10 2 ) = 3×10 5 . The coefficients of 6 and 2 were divided to obtain 3 and the exponent of 2 was subtracted from the exponent of 7 to obtain 5.
This occurs since exponents are subtracted when they a division takes place.

Here is another example of dividing numbers in scientific notation: (8.4×10 4 ) ÷ (2.5×10 -3 ).
Firstly, the coefficients are divided so 8.4 ÷ 2.5 = 3.36.
Secondly, the exponents are subtracted. 4 – -3 is the same as 4 + 3 which equals 7.
(8.4×10 4 ) ÷ (2.5×10 -3 ) = 3.36×10 7 .

Scientific Notation on Calculator
Scientific notation is commonly used in calculator displays.
To write scientific notation on a calculator, use the button labelled as ‘×10 𝑥 ‘ or just 10 𝑥 ‘.
- Enter the coefficient (the number between 1 and 10)
- Then press the ‘×10 𝑥 ‘ button
- Then enter the power of 10

Here are the instructions for entering scientific notation on some common calculators:
Casio Fx-300
The ‘×10 𝑥 ‘ button is found in the middle of the bottom row.
Casio Fx-82
Casio fx-cg50.
The ’10 𝑥 ‘ option is found above the ‘log’ button. Press ‘2nd’ then ‘log’ to write numbers in scientific notation.
- Press the ‘2nd’ button
- Then press the ‘log’ button to select the ’10 𝑥 ‘ option
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Scientific notation
Here you will learn about scientific notation including how to convert between ordinary numbers and scientific notation and how to calculate with numbers in scientific notation.
Students will first learn about scientific notation as part of expressions and equations in 8 th grade.
What is scientific notation?
Scientific notation is a way of writing very large or very small numbers by using powers of ten.
Numbers in scientific notation are written in this format:
a\times10^{n}
Where a is a number 1\leq{a}<10 and n is an integer (whole number).
To write a number in scientific notation, you need to understand the place value of the number.
For example, let’s look at the number 8,290,000 and write the digits in a place value table:

So 8,290,000 written in scientific notation is 8.29\times10^{6} .
Step-by-step guide: Powers of 10
Scientific notation is a representation of place value which compliments the decimal number system, as shown in the table below.
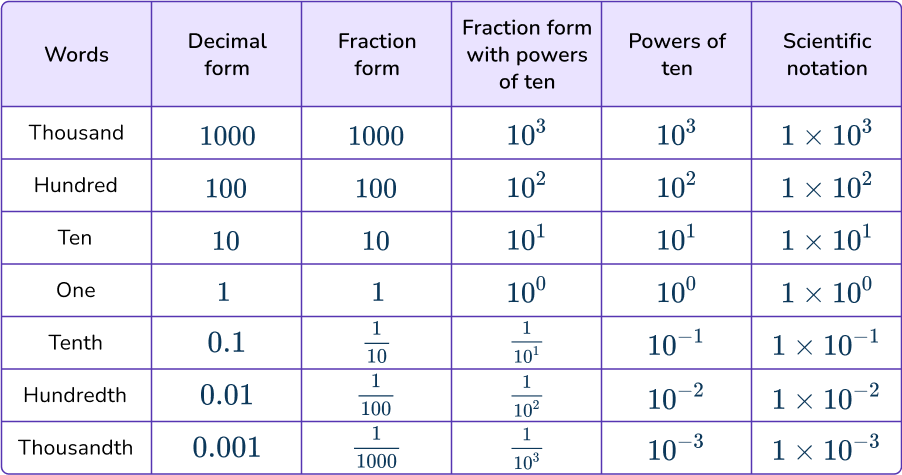
Any integer or terminating decimal can be written using the scientific notation a\times10^{n}. The table below shows how the value of a can remain the same while the power of ten ‘n’ changes the place value of those digits.
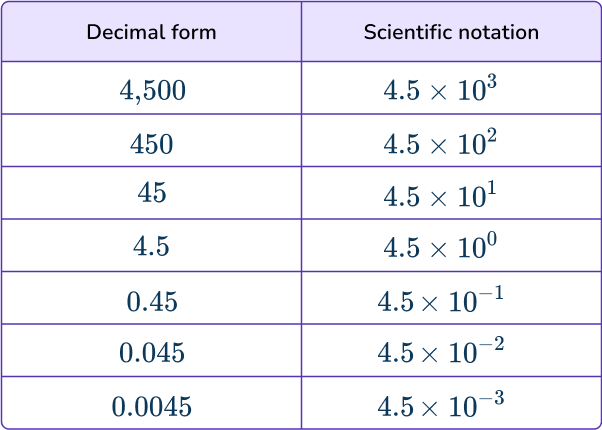
Using scientific notation enables us to write very large or very small numbers.
For example,
Using scientific notation also enables us to compare the size of very large or very small numbers easily.
Which is larger: 8,560,000,000,000 or 45,320,000,000,000?
At a glance, it is difficult to tell which is larger, but written in scientific notation, you can compare these numbers very quickly, as shown.
Instantly you can see that 4.532\times10^{13} is the larger number as it has the higher power of ten.
Scientific notation calculation
When numbers are written in scientific notation it can make some calculations neater and quicker to compute.
For example, solve 8.56\times{10^5}-2.3\times{10^2}.
How do you begin? If you expand each number, the expression is 856,000-230.
Notice that none of the digits are in the same place value. So, to solve using scientific notation, convert so that all numbers have the same power of 10.
Now the expression is 8,560\times{10^2}-2.3\times{10^2}.
Finally, convert 8,557.7\times{10^2} back to scientific notation.
Step-by-step guide: Adding and subtracting scientific notation
Now let’s solve 3.4\times{10^{5}}\times{2}\times{10^{-3}}.
Since multiplication is commutative (the order does not matter), you can reorder this calculation to 3.4\times{2}\times{10^{5}}\times{10^{-3}}.
Hint: Use the rule a^{b}\times{a^{c}}=a^{b+c} to simplify the powers of 10.
Since 6.8 is between 1 and 10, you don’t need to adjust the power of 10.
Step-by-step guide: How to multiply scientific notation
Now let’s solve \left(3.4\times{10^5}\right)\div\left(2\times{10^3}\right).
Re–write this expression as \cfrac{3.4\times{10^5}}{2\times{10^3}}, which equals \cfrac{3.4\times{10}\times{10}\times{10}\times{10}\times{10}}{2\times{10}\times{10}\times{10}}.
Notice how you can divide the corresponding parts to simplify.
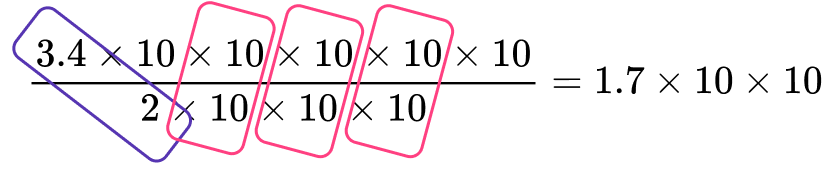
This is the same as solving:
Since 1.7 is between 1 and 10, you don’t need to adjust the power of 10.
Step-by-step guide: How to divide scientific notation

Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8 – Expressions and Equations (8.EE.A.3) Use numbers expressed in the form of a single digit times an integer power of 10 to estimate very large or very small quantities, and to express how many times as much one is than the other. For example, estimate the population of the United States as 3\times{10^8} and the population of the world as 7\times{10^9}, and determine that the world population is more than 20 times larger.
- Grade 8 – Expressions and Equations (8.EE.A.4) Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology.
![solve scientific notation problems [FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
How to write numbers with scientific notation
In order to represent a number in scientific notation:
- Show the number as an expression with multipliers of \bf{10}.
- Determine the power of \bf{10}.
- Write the number.
Scientific notation examples
Example 1: writing numbers in scientific notation.
Write this number in scientific notation: 52,000
Remember the first number is always between 1 and 10 .
2 Determine the power of \bf{10}.
3 Write the equation.
How to convert numbers written in scientific notation to ordinary numbers
In order to solve problems with numbers written in scientific notation:
Use place value reasoning to identify how the power of \bf{10} will change the number.
Shift the digits left if multiplying or right if dividing.
Example 2: writing a number in scientific notation as an ordinary number
Write 9.4\times10^{5} as an ordinary number.
Each digit must move 5 places to the left.
How to add and subtract in scientific notation
In order to add and subtract numbers in scientific notation:
Convert the number(s) to have the same power of \bf{10}.
Add or subtract the non-zero digits.
Check your answer is in scientific notation.
Example 3: adding numbers in scientific notation
Calculate 6\times10^{4}+2\times10^{3}. Write your answer in scientific notation.
Let’s convert 2\times10^{3} to be 10^4.
To do this, multiply it by 10 to add one to the power. To maintain the value of the number you need to divide the non-zero number by 10.
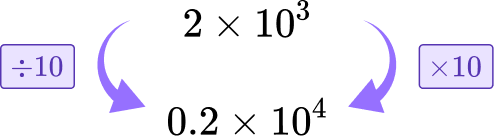
Since 6.2 is between 1 and 10, you don’t need to adjust the power of 10.
Example 4: subtracting numbers in scientific notation
Calculate 5\times{10^8}-4\times{10^6}. Write your answer in scientific notation.
Let’s convert 5\times{10^8} to be 10^6.
5\times{10^8}=50\times{10^7}=500\times{10^6}
496 is not between 1 and 10.
Convert 496\times{10^6} back to scientific notation.
How to multiply and divide in scientific notation
In order to multiply and divide in scientific notation:
Multiply or divide the non-zero numbers.
Multiply or divide the powers of \bf{10} by adding or subtracting the exponents.
Write the solution in scientific notation.
Example 5: multiplying numbers in scientific notation
Calculate \left(5\times{10^4}\right)\times\left(7\times{10^8}\right).
Write your answer in scientific notation.
35 is not between 1 and 10.
Convert 35\times{10^{12}} back to scientific notation.
\left(5\times{10^4}\right)\times\left(7\times{10^8}\right)=3.5\times{10^{13}}
Example 6: dividing numbers in scientific notation
Calculate 8\times{10^7}\div{2}\times{10^2}. Write your answer in scientific notation.
Teaching tips for scientific notation
- Give students real world examples of when scientific notation is useful, such as the distance from the sun to Neptune or the size of a microorganism.
- Start with smaller numbers when students are first learning. This allows students an opportunity to make sense of problems or check their work by expanding numbers written in scientific notation, until they understand the rules for operating.
- Allow struggling students to use a scientific notation calculator.
Easy mistakes to make

- Not converting numbers to the same power of \bf{10} when adding or subtracting Multiplying by different powers of 10 means the first part of the number does not represent the same place value. In order to use the subtraction algorithm, the first number needs to represent the same place value positions. For example, 5.6\times{10^3}+6.7\times{10^2} 5.6\times{10^3} is read as “ 5.6 thousands” and 6.7\times{10^2} is read as “ 6.7 hundreds.” In order to add them, they need to represent the same place value. Since, 5.6\times{10^3}=56\times{10^2}, you can solve 56\times{10^2}+6.7\times{10^2}
- Not converting solutions to scientific notation After calculating with scientific notation, a common mistake is to not check that the first part of the number is 1\leq{n}<10.
- Forgetting the meaning of negative exponents Remember that decimals are represented as smaller powers of 10. The negative exponent represents the equivalent fractional value and is used for every position to the right of the decimal. For example, 10^{-1}=\cfrac{1}{10} 10^{-2}=\cfrac{1}{100} 10^{-3}=\cfrac{1}{1,000} 10^{-4}=\cfrac{1}{10,000}
Practice scientific notation questions
1. Write 86,000 in scientific notation.

The number between 1 and 10 here is 8.6. Since 8 is in the ten thousands column,
2. Write 0.0097 in scientific notation.
The number between 1 and 10 here is 9.7. Since 9 is in the thousandths position
3. Write 5.9\times{10^3} as an ordinary number.
10^{3}=1,000 therefore
4. Solve 7\times{10^5}+2\times{10^4}. Write your answer in scientific notation.
Before adding, the first number needs to have the same place values. To do this, both powers of 10 need to be the same.
Since 2\times{10^4}=0.2\times{10^5}, solve 7\times{10^5}+0.2\times{10^5}.
5. Solve \left(6\times{10^8}\right)\times\left(3\times{10^4}\right). Write your answer in scientific notation.
Use the commutative property to rearrange the expression.
However 18\times{10^{12}} is not in scientific notation since 18 is not between 1 and 10.
6. Solve \left(9\times{10^7}\right)\div(4\times{10^2}). Write your answer in scientific notation.
Re–write this expression as \cfrac{9\times{10^7}}{4\times{10^2}},
which equals \cfrac{9\times{10}\times{10}\times{10}\times{10}\times{10}\times{10}\times{10}}{4\times{10}\times{10}}.
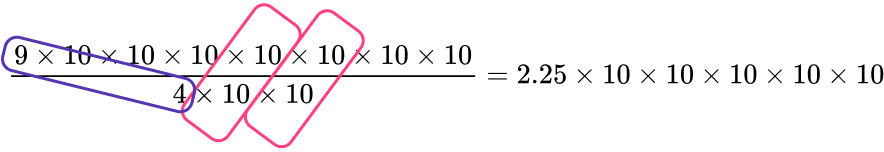
Scientific notation FAQs
Yes. For example, Richard, David and James did a survey, asking people what the best genre of movie was. If 1.3\times{10^4} people said sci-fi and 4\times{10^2} more people said historical fiction, how many people said historical fiction? This word problem can be solved by adding the numbers written in scientific notation.
This and other terms, such as ‘standard index form’ or ‘standard form’ (in the UK), all have the same meaning as scientific notation.
These are the digits used to express a number to the desired form of accuracy.
It is a form of number similar to scientific notation, but each number is written so that the exponents of 10 are always multiples of 3.
Each power of 10 has a prefix in the metric system, since the system is based on powers of 10.
The distance a number is from 0.
The next lessons are
- Quadratic graphs
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
Scientific Notation
Table of Contents
Last modified on August 3rd, 2023
#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
Scientific notation is a special way of representing numbers which are too large or small in a unique way that makes it easier to remember and compare them. They are expressed in the form (a × 10n). Here ‘a’ is the coefficient, and ‘n’ is the power or exponent of the base 10.
The diagram below shows the standard form of writing numbers in scientific notation:
Thus, scientific notation is a floating-point system where numbers are expressed as products consisting of numbers between 1 and 10 multiplied with appropriate power of 10. It helps to represent big and small numbers in a much easier way.
The speed of light(c) measured in a vacuum is approximately 300,000,000 meters per second, which is written as 3 × 10 8 m/s in scientific notation. Again the mass of the sun is written as 1.988 × 10 30 kg. All these values, if written in scientific form, will reduce a lot of space and decrease the chances of errors.
Scientific Notation Rules
We must follow the five rules when writing numbers in scientific notation:
- The base should always be 10
- The exponent (n) must be a non-zero integer, positive or negative
- The absolute value of the coefficient (a) is greater than or equal to 1, but it should be less than 10 (1 ≤ a < 10)
- The coefficient (a) can be positive or negative numbers, including whole numbers and decimal numbers
- The mantissa contains the remaining significant digits of the number
How to Do Scientific Notation with Examples
As we know, in scientific notation, there are two parts:
- Part 1: Consisting of just the digits with the decimal point placed after the first digit
- Part 2: This part follows the first part by × 10 to a power that puts the decimal point where it should be
While writing numbers in scientific notation, we need to figure out how many places we should move the decimal point. The exponent of 10 determines the number of places the decimal point gets shifted to represent the number in long form.
There are two possibilities:

Case 1: With Positive Exponent
When the non-zero digit is followed by a decimal point
For example, if we want to represent 4237.8 in scientific notation, it will be:
- The first part will be 4.2378 (only the digit and the decimal point placed after the first digit)
- The second part following the first part will be × 10 3 (multiplied by 10 having a power of 3)
Case 2: With Negative Exponent
When the decimal point comes first, and the non-zero digit comes next
For example, if we want to represent 0.000082 in scientific notation, it will be:
- The first part will be 8.2 (only the coefficient in decimal form and the decimal point placed after the first digit)
- The second part following the first part will be × 10 -5 (multiplied by 10 having a power of -5)
Here is a table showing some more examples of numbers written in scientific notation:
Let us solve some more word problems involving writing numbers in scientific notation.
Write the number 0.0065 in scientific notation.
0.0065 is written in scientific notation as: 6.5 × 10 -3
Convert 4.5 in scientific notation.
4.5 is written in scientific notation as: 4.5 × 10 0
Write 53010000 in scientific notation.
53010000 is written in scientific notation as: 5.301 ×10 7
Light travels with a speed of 1.86 x 10 5 miles/second. It takes sunlight 4.8 x 10 3 seconds to reach Saturn. Find the approximate distance between Sun and Saturn. Express your answer in scientific notation.
As we know, Distance (d) = Speed (s) × Time (t), here s = 1.86 x 10 5 miles/second, t = 4.8 x 10 3 seconds = 8.928 x 10 8 miles
Other Ways of Writing in Scientific Notation
We sometimes use the ^ symbol instead of power while writing numbers in scientific notation. In such cases, the above number 4237.8, written in scientific notation as 4.2378 × 10 3 , can also be written as 4.2378 × 10^3 Similarly, calculators use the notation 4.2378E; here, E signifies 10 × 10 × 10
- Converting Scientific Notation to Standard Form
- Multiplying Numbers in Scientific Notation
- Dividing Numbers in Scientific Notation
- Adding and Subtracting Numbers in Scientific Notation
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.2: Exponents and Scientific Notation
- Last updated
- Save as PDF
- Page ID 61961

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Various rules of Exponents
Scientific Notation
Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is \(2,048\) pixels by \(1,536\) pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to \(48\) bits per frame, and can shoot the equivalent of \(24\) frames per second. The maximum possible number of bits of information used to film a one-hour (\(3,600\)-second) digital film is then an extremely large number.
Using a calculator, we enter \(2,048×1\), \(536×48×24×3\), \(600\) and press ENTER. The calculator displays \(1.304596316E13\). What does this mean? The “\(E13\)” portion of the result represents the exponent \(13\) of ten, so there are a maximum of approximately \(1.3\times10^{13}\) bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
Using the Product Rule of Exponents
Consider the product \(x^3\times x^4\). Both terms have the same base, \(x\), but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
\[ \begin{align*} x^3 \times x^4 &= \overbrace{x \times x \times x}^{\text{3 factors}} \times \overbrace{ x \times x \times x\times x}^{\text{4 factors}} \\[4pt] &= \overbrace{x\times x\times x\times x\times x\times x\times x}^{\text{7 factors}} \\[4pt] &=x^7 \end{align*}\]
The result is that \(x^3\times x^4=x^{3+4}=x^7\).
Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
\[a^m\times a^n=a^{m+n}\]
Now consider an example with real numbers.
\(2^3\times2^4=2^{3+4}=2^7\)
We can always check that this is true by simplifying each exponential expression. We find that \(2^3\) is \(8\), \(2^4\) is \(16\), and \(2^7\) is \(128\). The product \(8\times16\) equals \(128\), so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
THE PRODUCT RULE OF EXPONENTS
For any real number a and natural numbers \(m\) and \(n\), the product rule of exponents states that
\[a^m\times a^n=a^{m+n} \label{prod}\]
Example \(\PageIndex{1}\): Using the Product Rule
Write each of the following products with a single base. Do not simplify further.
- \(t^5\times t^3\)
- \((−3)^5\times(−3)\)
- \(x^2\times x^5\times x^3\)
Use the product rule (Equation \ref{prod}) to simplify each expression.
- \(t^5\times t^3=t^{5+3}=t^8\)
- \((−3)^5\times(−3)=(−3)^5\times(−3)^1=(−3)^{5+1}=(−3)^6\)
At first, it may appear that we cannot simplify a product of three factors. However, using the associative property of multiplication, begin by simplifying the first two.
\[x^2\times x^5\times x^3=(x^2\times x^5) \times x^3=(x^{2+5})\times x^3=x^7\times x^3=x^{7+3}=x^{10} \nonumber\]
Notice we get the same result by adding the three exponents in one step.
\[x^2\times x^5\times x^3=x^{2+5+3}=x^{10} \nonumber\]
Exercise \(\PageIndex{1}\)
- \(k^6\times k^9\)
- \(\left(\dfrac{2}{y}\right)^4\times\left(\dfrac{2}{y}\right)\)
- \(t^3\times t^6\times t^5\)
\(\left(\dfrac{2}{y}\right)^5\)
Using the Quotient Rule of Exponents
The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. In a similar way to the product rule, we can simplify an expression such as \(\dfrac{y^m}{y^n}\), where \(m>n\). Consider the example \(\dfrac{y^9}{y^5}\). Perform the division by canceling common factors.
\[\begin{align*} \dfrac{y^9}{y^5} &= \dfrac{y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y}{y\cdot y\cdot y\cdot y\cdot y}\\ &= \dfrac{y\cdot y\cdot y\cdot y}{1}\\ &= y^4 \end{align*}\]
Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.
\[\dfrac{a^m}{a^n}=a^{m−n}\]
In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
\(\dfrac{y^9}{y^5}=y^{9−5}=y^4\)
For the time being, we must be aware of the condition \(m>n\). Otherwise, the difference \(m-n\) could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.

THE QUOTIENT RULE OF EXPONENTS
For any real number \(a\) and natural numbers \(m\) and \(n\), such that \(m>n\), the quotient rule of exponents states that
\[\dfrac{a^m}{a^n}=a^{m−n} \label{quot}\]
Example \(\PageIndex{2}\): Using the Quotient Rule
- \(\dfrac{(−2)^{14}}{(−2)^{9}}\)
- \(\dfrac{t^{23}}{t^{15}}\)
- \(\dfrac{(z\sqrt{2})^5}{z\sqrt{2}}\)
Use the quotient rule (Equation \ref{quot}) to simplify each expression.
- \(\dfrac{(−2)^{14}}{(−2)^{9}}=(−2)^{14−9}=(−2)^5\)
- \(\dfrac{t^{23}}{t^{15}}\)=t^{23−15}=t^8\)
- \(\dfrac{(z\sqrt{2})^5}{z\sqrt{2}}=(z\sqrt{2})^{5−1}=(z\sqrt{2})^4\)
Exercise \(\PageIndex{2}\)
- \(\dfrac{s^{75}}{s^{68}}\)
- \(\dfrac{(−3)^6}{−3}\)
- \(\dfrac{(ef^2)^5}{(ef^2)^3}\)
\((−3)^5\)
\((ef^2)^2\)
Using the Power Rule of Exponents
Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents. Consider the expression \((x^2)^3\). The expression inside the parentheses is multiplied twice because it has an exponent of \(2\). Then the result is multiplied three times because the entire expression has an exponent of \(3\).
\[\begin{align*} (x^2)^3 &= (x^2)\times(x^2)\times(x^2)\\ &= x\times x\times x\times x\times x\times x\\ &= x^6 \end{align*}\]
The exponent of the answer is the product of the exponents: \((x^2)^3=x^{2⋅3}=x^6\). In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
\[(a^m)^n=a^{m⋅n}\]
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
THE POWER RULE OF EXPONENTS
For any real number a and positive integers m and n, the power rule of exponents states that
\[(a^m)^n=a^{m⋅n} \label{power}\]
Example \(\PageIndex{3}\): Using the Power Rule
- \((x^2)^7\)
- \(((2t)^5)^3\)
- \(((−3)^5)^{11}\)
Use the power rule (Equation \ref{power}) to simplify each expression.
- \((x^2)^7=x^{2⋅7}=x^{14}\)
- \(((2t)^5)^3=(2t)^{5⋅3}=(2t)^{15}\)
- \(((−3)^5)^{11}=(−3)^{5⋅11}=(−3)^{55}\)
Exercise \(\PageIndex{3}\)
- \(((3y)^8)^3\)
- \((t^5)^7\)
- \(((−g)^4)^4\)
\((3y)^{24}\)
\((−g)^{16}\)
Using the Zero Exponent Rule of Exponents
Return to the quotient rule. We made the condition that \(m>n\) so that the difference \(m−n\) would never be zero or negative. What would happen if \(m=n\) ? In this case, we would use the zero exponent rule of exponents to simplify the expression to \(1\). To see how this is done, let us begin with an example.
\[\dfrac{t^8}{t^8}=1 \nonumber\]
If we were to simplify the original expression using the quotient rule, we would have
\[\dfrac{t^8}{t^8}=t^{8−8}=t^0 \nonumber\]
If we equate the two answers, the result is \(t^0=1\). This is true for any nonzero real number, or any variable representing a real number.
\[a^0=1 \nonumber\]
The sole exception is the expression \(0^0\). This appears later in more advanced courses, but for now, we will consider the value to be undefined.
THE ZERO EXPONENT RULE OF EXPONENTS
For any nonzero real number a, the zero exponent rule of exponents states that
Example \(\PageIndex{4}\): Using the Zero Exponent Rule
Simplify each expression using the zero exponent rule of exponents.
- \(\dfrac{c^3}{c^3}\)
- \(\dfrac{-3x^5}{x^5}\)
- \(\dfrac{(j^2k)^4}{(j^2k)\times(j^2k)^3}\)
- \(\dfrac{5(rs^2)^2}{(rs^2)^2}\)
Use the zero exponent and other rules to simplify each expression.
a. \[\begin{align*} \dfrac{c^3}{c^3} &= c^{3-3}\\ &= c^0\\ &= 1 \end{align*}\]
b. \[\begin{align*} \dfrac{-3x^5}{x^5} &= -3\times\dfrac{x^5}{x^5}\\ &= -3\times x^{5-5}\\ &= -3\times x^0\\ &= -3\times 1\\ &= -3 \end{align*}\]
c. \[\begin{align*} \dfrac{(j^2k)^4}{(j^2k)\times(j^2k)^3} &= \dfrac{(j^2k)^4}{(j^2k)^{1+3}} && \text{ Use the product rule in the denominator}\\ &= \dfrac{(j^2k)^4}{(j^2k)^4} && \text{ Simplify}\\ &= (j^2k)^{4-4} && \text{ Use the quotient rule}\\ &= (j^2k)^0 && \text{ Simplify}\\ &= 1 \end{align*}\]
d. \[\begin{align*} \dfrac{5(rs^2)^2}{(rs^2)^2} &= 5(rs^2)^{2-2} && \text{ Use the quotient rule}\\ &= 5(rs^2)^0 && \text{ Simplify}\\ &= 5\times1 && \text{ Use the zero exponent rule}\\ &= 5 && \text{ Simplify} \end{align*}\]
Exercise \(\PageIndex{4}\)
- \(\dfrac{t^7}{t^7}\)
- \(\dfrac{(de^2)^{11}}{2(de^2)^{11}}\)
- \(\dfrac{w^4\times w^2}{w^6}\)
- \(\dfrac{t^3\times t^4}{t^2\times t^5}\)
\(\dfrac{1}{2}\)
Using the Negative Rule of Exponents
Another useful result occurs if we relax the condition that \(m>n\) in the quotient rule even further. For example, can we simplify \(\dfrac{t^3}{t^5}\)? When \(m<n\) —that is, where the difference \(m−n\) is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
Divide one exponential expression by another with a larger exponent. Use our example, \(\dfrac{t^3}{t^5}\).
\[\begin{align*} \dfrac{t^3}{t^5} &= \dfrac{t\times t\times t}{t\times t\times t\times t\times t} \\ &= \dfrac{1}{t\times t}\\ &= \dfrac{1}{h^2} \end{align*}\]
\[\begin{align*} \dfrac{t^3}{t^5} &= h^{3-5} \\ &= h^{-2} \end{align*}\]
Putting the answers together, we have \(h^{−2}=\dfrac{1}{h^2}\). This is true for any nonzero real number, or any variable representing a nonzero real number.
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.
We have shown that the exponential expression an is defined when \(n\) is a natural number, \(0\), or the negative of a natural number. That means that an is defined for any integer \(n\). Also, the product and quotient rules and all of the rules we will look at soon hold for any integer \(n\).
THE NEGATIVE RULE OF EXPONENTS
For any nonzero real number a and natural number n, the negative rule of exponents states that
\[a^{−n}=\dfrac{1}{a^n}\]
Example \(\PageIndex{5}\): Using the Negative Exponent Rule
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
- \(\dfrac{\theta^3}{\theta^{10}}\)
- \(\dfrac{z^2\times z}{z^4}\)
- \(\dfrac{(-5t^3)^4}{(-5t^3)^8}\)
- \(\dfrac{\theta^3}{\theta^{10}}=\theta^{3-10}=\theta^{-7}=\dfrac{1}{\theta^7}\)
- \(\dfrac{z^2\times z}{z^4}=\dfrac{z^{2+1}}{z^4}=\dfrac{z^3}{z^4}=z^{3-4}=z^{-1}=\dfrac{1}{z}\)
- \(\dfrac{(-5t^3)^4}{(-5t^3)^8}=(-5t^3)^{4-8}=(-5t^3)^{-4}=\dfrac{1}{(-5t^3)^4}\)
Exercise \(\PageIndex{5}\)
- \(\dfrac{(-3t)^2}{(-3t)^8}\)
- \(\dfrac{f^{47}}{f^{49}\times f}\)
- \(\dfrac{2k^4}{5k^7}\)
\(\dfrac{1}{(-3t)^6}\)
\(\dfrac{1}{f^3}\)
\(\dfrac{2}{5k^3}\)
Example \(\PageIndex{6}\): Using the Product and Quotient Rules
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
- \(b^2\times b^{-8}\)
- \((-x)^5\times(-x)^{-5}\)
- \(\dfrac{-7z}{(-7z)^5}\)
- \(b^2\times b^{-8}=b^{2-8}=b^{-6}=\dfrac{1}{b^6}\)
- \((-x)^5\times(-x)^{-5}=(-x)^{5-5}=(-x)^0=1\)
- \(\dfrac{-7z}{(-7z)^5}= \dfrac{(-7z)^1}{(-7z)^5}=(-7z)^{1-5}=(-7z)^{-4}=\dfrac{1}{(-7z)^4}\)
Exercise \(\PageIndex{6}\)
- \(t^{-11}\times t^6\)
- \(\dfrac{25^{12}}{25^{13}}\)
\(t^{-5}=\dfrac{1}{t^5}\)
\(\dfrac{1}{25}\)
Finding the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider \((pq)^3\). We begin by using the associative and commutative properties of multiplication to regroup the factors.
\[\begin{align*} (pq)^3 &= (pq)\times(pq)\times(pq)\\ &= p\times q\times p\times q\times p\times q\\ &= p^3\times q^3 \end{align*}\]
In other words, \((pq)^3=p^3\times q^3\).
THE POWER OF A PRODUCT RULE OF EXPONENTS
For any real numbers a and b and any integer n, the power of a product rule of exponents states that
\[(ab)^n=a^nb^n\]
Example \(\PageIndex{7}\): Using the Power of a Product Rule
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
- \((ab^2)^3\)
- \((2t)^{15}\)
- \((-2w^3)^3\)
- \(\dfrac{1}{(-7z)^4}\)
- \((e^{-2}f^2)^7\)
Use the product and quotient rules and the new definitions to simplify each expression.
a. \((ab^2)^3=(a)^3\times(b^2)^3=a^{1\times3}\times b^{2\times3}=a^3b^6\)
b. \((2t)^{15}=(2)^{15}\times(t)^{15}=2^{15}t^{15}=32,768t^{15}\)
c. \((−2w^3)^3=(−2)^3\times(w^3)^3=−8\times w^{3\times3}=−8w^9\)
d. \(\dfrac{1}{(-7z)^4}=\dfrac{1}{(-7)^4\times(z)^4}=\dfrac{1}{2401z^4}\)
e. \((e^{-2}f^2)^7=(e^{−2})^7\times(f^2)^7=e^{−2\times7}\times f^{2\times7}=e^{−14}f^{14}=\dfrac{f^{14}}{e^{14}}\)
Exercise \(\PageIndex{7}\)
- \((g^2h^3)^5\)
- \((-3y^5)^3\)
- \(\dfrac{1}{(a^6b^7)^3}\)
- \((r^3s^{-2})^4\)
\(g^{10}h^{15}\)
\(-27y^{15}\)
\(\dfrac{1}{a^{18}b^{21}}\)
\(\dfrac{r^{12}}{s^8}\)
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.
\[(e^{−2}f^2)^7=\dfrac{f^{14}}{e^{14}}\]
Let’s rewrite the original problem differently and look at the result.
\[\begin{align*} (e^{-2}f^2)^7 &= \left(\dfrac{f^2}{e^2}\right)^7\\ &= \dfrac{f^{14}}{e^{14}} \end{align*}\]
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.
\[\begin{align*} (e^{-2}f^2)^7 &= \left(\dfrac{f^2}{e^2}\right)^7\\ &= \dfrac{(f^2)^7}{(e^2)^7}\\ &= \dfrac{f^{2\times7}}{e^{2\times7}}\\ &= \dfrac{f^{14}}{e^{14}} \end{align*}\]
THE POWER OF A QUOTIENT RULE OF EXPONENTS
For any real numbers a and b and any integer n, the power of a quotient rule of exponents states that
\[\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}\]
Example \(\PageIndex{8}\): Using the Power of a Quotient Rule
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
- \(\left(\dfrac{4}{z^{11}}\right)^3\)
- \(\left(\dfrac{p}{q^3}\right)^6\)
- \(\left(\dfrac{-1}{t^2}\right)^{27}\)
- \((j^3k^{-2})^4\)
- \((m^{-2}n^{-2})^3\)
a. \(\left(\dfrac{4}{z^{11}}\right)^3=\dfrac{(4)^3}{(z^{11})^3}=\dfrac{64}{z^{11\times3}}=\dfrac{64}{z^{33}}\)
b. \(\left(\dfrac{p}{q^3}\right)^6=\dfrac{(p)^6}{(q^3)^6}=\dfrac{p^{1\times6}}{q^{3\times6}}=\dfrac{p^6}{q^{18}}\)
c. \(\left(\dfrac{-1}{t^2}\right)^{27}=\dfrac{(-1)^{27}}{(t^2)^{27}}=\dfrac{-1}{t^{2\times27}}=\dfrac{-1}{t^{54}}=-\dfrac{1}{t^{54}}\)
d. \((j^3k^{-2})^4=\left(\dfrac{j^3}{k^2}\right)^4=\dfrac{(j^3)^4}{(k^2)^4}=\dfrac{j^{3\times4}}{k^{2\times4}}=\dfrac{j^{12}}{k^8}\)
e. \((m^{-2}n^{-2})^3=\left(\dfrac{1}{m^2n^2}\right)^3=\dfrac{(1)^3}{(m^2n^2)^3}=\dfrac{1}{(m^2)^3(n^2)^3}=\dfrac{1}{m^{2\times3}n^{2\times3}}=\dfrac{1}{m^6n^6}\)
Exercise \(\PageIndex{8}\)
- \(\left(\dfrac{b^5}{c}\right)^3\)
- \(\left(\dfrac{5}{u^8}\right)^4\)
- \(\left(\dfrac{-1}{w^3}\right)^{35}\)
- \((p^{-4}q^3)^8\)
- \((c^{-5}d^{-3})^4\)
\(\dfrac{b^{15}}{c^3}\)
\(\dfrac{625}{u^{32}}\)
\(\dfrac{-1}{w^{105}}\)
\(\dfrac{q^{24}}{p^{32}}\)
\(\dfrac{1}{c^{20}d^{12}}\)
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
Example \(\PageIndex{9}\): Simplifying Exponential Expressions
Simplify each expression and write the answer with positive exponents only.
- \((6m^2n^{-1})^3\)
- \(17^5\times17^{-4}\times17^{-3}\)
- \(\left(\dfrac{u^{-1}v}{v^{-1}}\right)^2\)
- \((-2a^3b^{-1})(5a^{-2}b^2)\)
- \((x^2\sqrt{2})^4(x^2\sqrt{2})^{-4}\)
- \(\dfrac{(3w^2)^5}{(6w^{-2})^2}\)
a. \[\begin{align*} (6m^2n^{-1})^3 &= (6)^3(m^2)^3(n^{-1})^3 && \text{ The power of a product rule}\\ &= 6^3m^{2\times3}n^{-1\times3} && \text{ The power rule}\\ &= 216m^6n^{-3} && \text{ The power rule}\\ &= \dfrac{216m^6}{n^3} && \text{ The negative exponent rule} \end{align*}\]
b. \[\begin{align*} 17^5\times17^{-4}\times17^{-3} &= 17^{5-4-3} && \text{ The product rule}\\ &= 17^{-2} && \text{ Simplify}\\ &= \dfrac{1}{17^2} \text{ or } \dfrac{1}{289} && \text{ The negative exponent rule} \end{align*}\]
c. \[\begin{align*} \left ( \dfrac{u^{-1}v}{v^{-1}} \right )^2 &= \dfrac{(u^{-1}v)^2}{(v^{-1})^2} && \text{ The power of a quotient rule}\\ &= \dfrac{u^{-2}v^2}{v^{-2}} && \text{ The power of a product rule}\\ &= u^{-2}v^{2-(-2)} && \text{ The quotient rule}\\ &= u^{-2}v^4 && \text{ Simplify}\\ &= \dfrac{v^4}{u^2} && \text{ The negative exponent rule} \end{align*}\]
d. \[\begin{align*} \left (-2a^3b^{-1} \right ) \left(5a^{-2}b^2 \right ) &= \left (x^2\sqrt{2} \right )^{4-4} && \text{ Commutative and associative laws of multiplication}\\ &= -10\times a^{3-2}\times b^{-1+2} && \text{ The product rule}\\ &= -10ab && \text{ Simplify} \end{align*}\]
e. \[\begin{align*} \left (x^2\sqrt{2})^4(x^2\sqrt{2} \right )^{-4} &= \left (x^2\sqrt{2} \right )^{4-4} && \text{ The product rule}\\ &= \left (x^2\sqrt{2} \right )^0 && \text{ Simplify}\\ &= 1 && \text{ The zero exponent rule} \end{align*}\]
f. \[\begin{align*} \dfrac{(3w^2)^5}{(6w^{-2})^2} &= \dfrac{(3)^5\times(w^2)^5}{(6)^2\times(w^{-2})^2} && \text{ The power of a product rule}\\ &= \dfrac{3^5w^{2\times5}}{6^2w^{-2\times2}} && \text{ The power rule}\\ &= \dfrac{243w^{10}}{36w^{-4}} && \text{ Simplify}\\ &= \dfrac{27w^{10-(-4)}}{4} && \text{ The quotient rule and reduce fraction}\\ &= \dfrac{27w^{14}}{4} && \text{ Simplify} \end{align*}\]
Using Scientific Notation
Recall at the beginning of the section that we found the number \(1.3\times10^{13}\) when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about \(0.00005\; m\), and the radius of an electron, which is about \(0.00000000000047\; m\). How can we effectively work read, compare, and calculate with numbers such as these?
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of \(10\). To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between \(1\) and \(10\). Count the number of places \(n\) that you moved the decimal point. Multiply the decimal number by \(10\) raised to a power of \(n\). If you moved the decimal left as in a very large number, \(n\) is positive. If you moved the decimal right as in a small large number, \(n\) is negative.
For example, consider the number \(2,780,418\). Move the decimal left until it is to the right of the first nonzero digit, which is \(2\).

We obtain \(2.780418\) by moving the decimal point \(6\) places to the left. Therefore, the exponent of \(10\) is \(6\), and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.
Working with small numbers is similar. Take, for example, the radius of an electron, \(0.00000000000047\; m\). Perform the same series of steps as above, except move the decimal point to the right.

Be careful not to include the leading \(0\) in your count. We move the decimal point \(13\) places to the right, so the exponent of \(10\) is \(13\). The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.
SCIENTIFIC NOTATION
A number is written in scientific notation if it is written in the form \(a\times{10}^n\), where \(1≤|a|<10\) and \(n\) is an integer.
Example \(\PageIndex{10}\): Converting Standard Notation to Scientific Notation
Write each number in scientific notation.
- Distance to Andromeda Galaxy from Earth: \(24,000,000,000,000,000,000,000\; m\)
- Diameter of Andromeda Galaxy: \(1,300,000,000,000,000,000,000\; m\)
- Number of stars in Andromeda Galaxy: \(1,000,000,000,000\)
- Diameter of electron: \(0.00000000000094\; m\)
- Probability of being struck by lightning in any single year: \(0.00000143\)
a. \(24,000,000,000,000,000,000,000\; m\) \(22\) places
\(2.4\times{10}^{22}\; m\)
b. \(1,300,000,000,000,000,000,000\; m\) \(21\) places
\(1.3\times{10}^{21}\; m\)
c. \(1,000,000,000,000\) \(12\) places
\(1\times{10}^{12}\)
d. \(0.00000000000094\; m\) \(13\) places
\(9.4\times{10}^{-13}\; m\)
e. \(0.00000143\) \(6\) places
\(1.43\times{10}^6\)
Observe that, if the given number is greater than \(1\), as in examples a–c, the exponent of \(10\) is positive; and if the number is less than \(1\), as in examples d–e, the exponent is negative.
Exercise \(\PageIndex{10}\)
- U.S. national debt per taxpayer (April 2014): \(\$152,000\)
- World population (April 2014): \(7,158,000,000\)
- World gross national income (April 2014): \(\$85,500,000,000,000\)
- Time for light to travel \(1\; m: 0.00000000334\; s\)
- Probability of winning lottery (match \(6\) of \(49\) possible numbers): \(0.0000000715\)
\(\$1.52\times{10}^5\)
\(7.158\times{10}^9\)
\(\$8.55\times{10}^{13}\)
\(3.34\times{10}^{-9}\)
\(7.15\times{10}^{-8}\)
Converting from Scientific to Standard Notation
To convert a number in scientific notation to standard notation, simply reverse the process. Move the decimal n places to the right if \(n\) is positive or \(n\) places to the left if \(n\) is negative and add zeros as needed. Remember, if \(n\) is positive, the value of the number is greater than \(1\), and if \(n\) is negative, the value of the number is less than one.
Example \(\PageIndex{11}\): Converting Scientific Notation to Standard Notation
Convert each number in scientific notation to standard notation.
- \(3.547\times{10}^{14}\)
- \(−2\times{10}^6\)
- \(7.91\times{10}^{−7}\)
- \(−8.05\times{10}^{−12}\)
a. \(3.547\times{10}^{14}\)
\(3.54700000000000\)
\(\rightarrow14\) places
\(354,700,000,000,000\)
b. \(−2\times{10}^6\)
\(−2.000000\)
\(\rightarrow6\) places
\(−2,000,000\)
c. \(7.91\times{10}^{−7}\)
\(0000007.91\)
\(\rightarrow7\) places
\(0.000000791\)
d. \(−8.05\times{10}^{−12}\)
\(−000000000008.05\)
\(\rightarrow12\) places
\(−0.00000000000805\)
Exercise \(\PageIndex{11}\)
- \(7.03\times{10}^5\)
- \(−8.16\times{10}^{11}\)
- \(−3.9\times{10}^{−13}\)
- \(8\times{10}^{−6}\)
\(703,000\)
\(−816,000,000,000\)
\(−0.00000000000039\)
\(0.000008\)
Using Scientific Notation in Applications
Scientific notation, used with the rules of exponents, makes calculating with large or small numbers much easier than doing so using standard notation. For example, suppose we are asked to calculate the number of atoms in \(1\; L\) of water. Each water molecule contains \(3\) atoms (\(2\) hydrogen and \(1\) oxygen). The average drop of water contains around \(1.32\times{10}{21}\) molecules of water and \(1\; L\) of water holds about \(1.22\times{10}^{4}\) average drops. Therefore, there are approximately \(3⋅(1.32\times{10}^{21})⋅(1.22\times{10}^4)≈4.83\times{10}^{25}\) atoms in \(1\; L\) of water. We simply multiply the decimal terms and add the exponents. Imagine having to perform the calculation without using scientific notation!
When performing calculations with scientific notation, be sure to write the answer in proper scientific notation. For example, consider the product \((7\times{10}^4)⋅(5\times{10}^6)=35\times{10}^{10}\). The answer is not in proper scientific notation because \(35\) is greater than \(10\). Consider \(35\) as \(3.5\times10\). That adds a ten to the exponent of the answer.
\((35)\times{10}^{10}=(3.5\times10)\times{10}^{10}=3.5\times(10\times{10}^{10})=3.5\times{10}^{11}\)
Example \(\PageIndex{12}\): Using Scientific Notation
Perform the operations and write the answer in scientific notation.
- \((8.14\times{10}^{−7})(6.5\times{10}^{10})\)
- \((4\times{10}^5)÷(−1.52\times{10}^{9})\)
- \((2.7\times{10}^5)(6.04\times{10}^{13})\)
- \((1.2\times{10}^8)÷(9.6\times{10}^5)\)
- \((3.33\times{10}^4)(−1.05\times{10}^7)(5.62\times{10}^5)\)
a. \[\begin{align*} (8.14\times{10}^{-7})(6.5\times{10}^{10}) &= (8.14\times6.5)({10}^{-7}\times{10}^{10}) \text{ Commutative and associative properties of multiplication}\\ &= (52.91)({10}^3) \text{ Product rule of exponents}\\ &= 5.291\times{10}^4 \text{ Scientific notation} \end{align*}\]
b. \[\begin{align*} (4\times{10}^5)\div (-1.52\times{10}^{9}) &= \left(\dfrac{4}{-1.52}\right)\left(\dfrac{{10}^5}{{10}^9}\right) \text{ Commutative and associative properties of multiplication}\\ &\approx (-2.63)({10}^{-4}) \text{ Quotient rule of exponents}\\ &= -2.63\times{10}^{-4} \text{ Scientific notation} \end{align*}\]
c. \[\begin{align*} (2.7\times{10}^5)(6.04\times{10}^{13}) &= (2.7\times6.04)({10}^5\times{10}^{13}) \text{ Commutative and associative properties of multiplication}\\ &= (16.308)({10}^{18}) \text{ Product rule of exponents}\\ &= 1.6308\times{10}^{19} \text{ Scientific notation} \end{align*}\]
d. \[\begin{align*} (1.2\times{10}^8)÷(9.6\times{10}^5) &= \left(\dfrac{1.2}{9.6}\right)\left(\dfrac{{10}^8}{{10}^5}\right) \text{ Commutative and associative properties of multiplication}\\ &= (0.125)({10}^3) \text{ Quotient rule of exponents}\\ &= 1.25\times{10}^2 \text{ Scientific notation} \end{align*}\]
e. \[\begin{align*} (3.33\times{10}^4)(-1.05\times{10}^7)(5.62\times{10}^5) &= [3.33\times(-1.05)\times5.62]({10}^4\times{10}^7\times{10}^5)\\ &\approx (-19.65)({10}^{16})\\ &= -1.965\times{10}^{17} \end{align*}\]
Exercise \(\PageIndex{12}\)
- \((−7.5\times{10}^8)(1.13\times{10}^{−2})\)
- \((1.24\times{10}^{11})÷(1.55\times{10}^{18})\)
- \((3.72\times{10}^9)(8\times{10}^3)\)
- \((9.933\times{10}^{23})÷(−2.31\times{10}^{17})\)
- \((−6.04\times{10}^9)(7.3\times{10}^2)(−2.81\times{10}^2)\)
\(−8.475\times{10}^6\)
\(8\times{10}^{−8}\)
\(2.976\times{10}^{13}\)
\(−4.3\times{10}^6\)
\(≈1.24\times{10}^{15}\)
Example \(\PageIndex{13}\): Applying Scientific Notation to Solve Problems
In April 2014, the population of the United States was about \(308,000,000\) people. The national debt was about \(\$17,547,000,000,000\). Write each number in scientific notation, rounding figures to two decimal places, and find the amount of the debt per U.S. citizen. Write the answer in both scientific and standard notations.
The population was \(308,000,000=3.08\times{10}^8\).
The national debt was \($17,547,000,000,000≈$1.75\times{10}^{13}\).
To find the amount of debt per citizen, divide the national debt by the number of citizens.
\[\begin{align*} (1.75\times{10}^{13})\div (3.08\times{10}^8)&=\left(\dfrac{1.75}{3.08}\right)({10}^5)\\ &\approx 0.57\times{10}^5\\ &=5.7\times{10}^4 \end{align*}\]
The debt per citizen at the time was about \($5.7\times{10}^4\), or \($57,000\).
Exercise \(\PageIndex{13}\)
An average human body contains around \(30,000,000,000,000\) red blood cells. Each cell measures approximately \(0.000008\; m\) long. Write each number in scientific notation and find the total length if the cells were laid end-to-end. Write the answer in both scientific and standard notations.
Number of cells: \(3\times{10}^{13}\); length of a cell: \(8\times{10}^{−6}\; m\); total length: \(2.4\times{10}^8\; m\) or \(240,000,000\; m\).
Access these online resources for additional instruction and practice with exponents and scientific notation.
Exponential Notation
Properties of Exponents
Zero Exponent
Simplify Exponent Expressions
Quotient Rule for Exponents
Converting to Decimal Notation
Key Equations
Key concepts.
- Products of exponential expressions with the same base can be simplified by adding exponents. See Example .
- Quotients of exponential expressions with the same base can be simplified by subtracting exponents. See Example .
- Powers of exponential expressions with the same base can be simplified by multiplying exponents. See Example .
- An expression with exponent zero is defined as 1. See Example .
- An expression with a negative exponent is defined as a reciprocal. See Example and Example .
- The power of a product of factors is the same as the product of the powers of the same factors. See Example .
- The power of a quotient of factors is the same as the quotient of the powers of the same factors. See Example .
- The rules for exponential expressions can be combined to simplify more complicated expressions. See Example .
- Scientific notation uses powers of 10 to simplify very large or very small numbers. See Example and Example .
- Scientific notation may be used to simplify calculations with very large or very small numbers. See Example and Example .
HIGH SCHOOL
- ACT Tutoring
- SAT Tutoring
- PSAT Tutoring
- ASPIRE Tutoring
- SHSAT Tutoring
- STAAR Tutoring
GRADUATE SCHOOL
- MCAT Tutoring
- GRE Tutoring
- LSAT Tutoring
- GMAT Tutoring
- AIMS Tutoring
- HSPT Tutoring
- ISAT Tutoring
- SSAT Tutoring
Search 50+ Tests
Loading Page
math tutoring
- Elementary Math
- Pre-Calculus
- Trigonometry
science tutoring
Foreign languages.
- Mandarin Chinese
elementary tutoring
- Computer Science
Search 350+ Subjects
- Video Overview
- Tutor Selection Process
- Online Tutoring
- Mobile Tutoring
- Instant Tutoring
- How We Operate
- Our Guarantee
- Impact of Tutoring
- Reviews & Testimonials
- About Varsity Tutors
HiSET: Math : Solve problems using scientific notation
Study concepts, example questions & explanations for hiset: math, all hiset: math resources, example questions, example question #1 : solve problems using scientific notation.
Simplify the following expression using scientific notation.

You can solve this problem in several ways. One way is to convert each number out of scientific notation and write it out fully, then find the sum of the two values and convert the answer back into scientific notation.

Another, potentially faster, way to solve this problem is to convert one answer into the same scientific-notational terms as the other and then sum them.
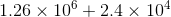
Multiply, and express the product in scientific notation:

Convert 7,200,000 to scientific notation as follows:
Move the (implied) decimal point until it is immediately after the first nonzero digit (the 7). This required moving the point six units to the left:

Rearrange and regroup the expressions so that the powers of ten are together:

Multiply the numbers in front. Also, multiply the powers of ten by adding exponents:

In order for the number to be in scientific notation, the number in front must be between 1 and 10. An adjustment must be made by moving the implied decimal point in 36 one unit left. It follows that

the correct response.

Express the product in scientific notation.

None of the other choices gives the correct response.

Scientific notation refers to a number expressed in the form

Each factor can be rewritten in scientific notation as follows:

Now, substitute:

Apply the Product of Powers Property:

This is in scientific notation and is the correct choice.

Report an issue with this question
If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.
DMCA Complaint
If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.
Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.
Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.
Please follow these steps to file a notice:
You must include the following:
A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.
Send your complaint to our designated agent at:
Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105
Or fill out the form below:
Contact Information
Complaint details.

Objective 3
Problem solving with scientific notation, learning objectives.
- Solve application problems involving scientific notation

Water Molecule
Solve application problems
Learning rules for exponents seems pointless without context, so let’s explore some examples of using scientific notation that involve real problems. First, let’s look at an example of how scientific notation can be used to describe real measurements.
Think About It
Match each length in the table with the appropriate number of meters described in scientific notation below.

Red Blood Cells
One of the most important parts of solving a “real” problem is translating the words into appropriate mathematical terms, and recognizing when a well known formula may help. Here’s an example that requires you to find the density of a cell, given its mass and volume. Cells aren’t visible to the naked eye, so their measurements, as described with scientific notation, involve negative exponents.
Human cells come in a wide variety of shapes and sizes. The mass of an average human cell is about [latex]2\times10^{-11}[/latex] grams [1] Red blood cells are one of the smallest types of cells [2] , clocking in at a volume of approximately [latex]10^{-6}\text{ meters }^3[/latex]. [3] Biologists have recently discovered how to use the density of some types of cells to indicate the presence of disorders such as sickle cell anemia or leukemia. [4] Density is calculated as the ratio of [latex]\frac{\text{ mass }}{\text{ volume }}[/latex]. Calculate the density of an average human cell.
Read and Understand: We are given an average cellular mass and volume as well as the formula for density. We are looking for the density of an average human cell.
Define and Translate: [latex]m=\text{mass}=2\times10^{-11}[/latex], [latex]v=\text{volume}=10^{-6}\text{ meters}^3[/latex], [latex]\text{density}=\frac{\text{ mass }}{\text{ volume }}[/latex]
Write and Solve: Use the quotient rule to simplify the ratio.
[latex]\begin{array}{c}\text{ density }=\frac{2\times10^{-11}\text{ grams }}{10^{-6}\text{ meters }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-11-\left(-6\right)}\frac{\text{ grams }}{\text{ meters }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-5}\frac{\text{ grams }}{\text{ meters }^3}\\\end{array}[/latex]
If scientists know the density of healthy cells, they can compare the density of a sick person’s cells to that to rule out or test for disorders or diseases that may affect cellular density.
The average density of a human cell is [latex]2\times10^{-5}\frac{\text{ grams }}{\text{ meters }^3}[/latex]
The following video provides an example of how to find the number of operations a computer can perform in a very short amount of time.

Light traveling from the sun to the earth.
In the next example, you will use another well known formula, [latex]d=r\cdot{t}[/latex], to find how long it takes light to travel from the sun to the earth. Unlike the previous example, the distance between the earth and the sun is massive, so the numbers you will work with have positive exponents.
The speed of light is [latex]3\times10^{8}\frac{\text{ meters }}{\text{ second }}[/latex]. If the sun is [latex]1.5\times10^{11}[/latex] meters from earth, how many seconds does it take for sunlight to reach the earth? Write your answer in scientific notation.
Read and Understand: We are looking for how long—an amount of time. We are given a rate which has units of meters per second and a distance in meters. This is a [latex]d=r\cdot{t}[/latex] problem.
Define and Translate:
[latex]\begin{array}{l}d=1.5\times10^{11}\\r=3\times10^{8}\frac{\text{ meters }}{\text{ second }}\\t=\text{ ? }\end{array}[/latex]
Write and Solve: Substitute the values we are given into the [latex]d=r\cdot{t}[/latex] equation. We will work without units to make it easier. Often, scientists will work with units to make sure they have made correct calculations.
[latex]\begin{array}{c}d=r\cdot{t}\\1.5\times10^{11}=3\times10^{8}\cdot{t}\end{array}[/latex]
Divide both sides of the equation by [latex]3\times10^{8}[/latex] to isolate t.
[latex]\begin{array}{c}1.5\times10^{11}=3\times10^{8}\cdot{t}\\\text{ }\\\frac{1.5\times10^{11}}{3\times10^{8}}=\frac{3\times10^{8}}{3\times10^{8}}\cdot{t}\end{array}[/latex]
On the left side, you will need to use the quotient rule of exponents to simplify, and on the right, you are left with t.
[latex]\begin{array}{c}\frac{1.5\times10^{11}}{3\times10^{8}}=\frac{3\times10^{8}}{3\times10^{8}}\cdot{t}\\\text{ }\\\left(\frac{1.5}{3}\right)\times\left(\frac{10^{11}}{10^{8}}\right)=t\\\text{ }\\\left(0.5\right)\times\left(10^{11-8}\right)=t\\0.5\times10^3=t\end{array}[/latex]
This answer is not in scientific notation, so we will move the decimal to the right, which means we need to subtract one factor of 10.
[latex]0.5\times10^3=5.0\times10^2=t[/latex]
The time it takes light to travel from the sun to the earth is [latex]5.0\times10^2=t[/latex] seconds, or in standard notation, 500 seconds. That’s not bad considering how far it has to travel!
Scientific notation was developed to assist mathematicians, scientists, and others when expressing and working with very large and very small numbers. Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to one and less than ten, and a power of 10. The format is written [latex]a\times10^{n}[/latex], where [latex]1\leq{a}<10[/latex] and n is an integer. To multiply or divide numbers in scientific notation, you can use the commutative and associative properties to group the exponential terms together and apply the rules of exponents.
- Orders of magnitude (mass). (n.d.). Retrieved May 26, 2016, from https://en.wikipedia.org/wiki/Orders_of_magnitude_(mass) ↵
- How Big is a Human Cell? ↵
- How big is a human cell? - Weizmann Institute of Science. (n.d.). Retrieved May 26, 2016, from http://www.weizmann.ac.il/plants/Milo/images/humanCellSize120116Clean.pdf ↵
- Grover, W. H., Bryan, A. K., Diez-Silva, M., Suresh, S., Higgins, J. M., & Manalis, S. R. (2011). Measuring single-cell density. Proceedings of the National Academy of Sciences, 108(27), 10992-10996. doi:10.1073/pnas.1104651108 ↵
- Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
- Application of Scientific Notation - Quotient 1 (Number of Times Around the Earth). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/15tw4-v100Y . License : CC BY: Attribution
- Application of Scientific Notation - Quotient 2 (Time for Computer Operations). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/Cbm6ejEbu-o . License : CC BY: Attribution
- Screenshot: water molecule. Provided by : Lumen Learning. License : CC BY: Attribution
- Screenshot: red blood cells. Provided by : Lumen Learning. License : CC BY: Attribution
- Screenshot: light traveling from the sun to the earth. Provided by : Lumen Learning. License : CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
- Math Article
- Scientific Notation
Scientific notation

Scientific notation is a form of presenting very large numbers or very small numbers in a simpler form. As we know, the whole numbers can be extended till infinity, but we cannot write such huge numbers on a piece of paper. Also, the numbers which are present at the millions place after the decimal needed to be represented in a simpler form. Thus, it is difficult to represent a few numbers in their expanded form. Hence, we use scientific notations. Also learn, Numbers In General Form .

For example, 100000000 can be written as 10 8 , which is the scientific notation. Here the exponent is positive. Similarly, 0.0000001 is a very small number which can be represented as 10 -8 , where the exponent is negative.
Scientific Notation Definition
As discussed in the introduction, the scientific notation helps us to represent the numbers which are very huge or very tiny in a form of multiplication of single-digit numbers and 10 raised to the power of the respective exponent. The exponent is positive if the number is very large and it is negative if the number is very small. Learn power and exponents for better understanding.
The general representation of scientific notation is:
Also, read:
- Scientific notation formula calculator
- Scientific Notation Calculator
Scientific Notation Rules
To determine the power or exponent of 10, we must follow the rule listed below:
- The base should be always 10
- The exponent must be a non-zero integer, that means it can be either positive or negative
- The absolute value of the coefficient is greater than or equal to 1 but it should be less than 10
- Coefficients can be positive or negative numbers including whole and decimal numbers
- The mantissa carries the rest of the significant digits of the number
Let us understand how many places we need to move the decimal point after the single-digit number with the help of the below representation.
- If the given number is multiples of 10 then the decimal point has to move to the left, and the power of 10 will be positive. Example: 6000 = 6 × 10 3 is in scientific notation.
- If the given number is smaller than 1, then the decimal point has to move to the right, so the power of 10 will be negative. Example: 0.006 = 6 × 0.001 = 6 × 10 -3 is in scientific notation.
Scientific Notation Examples
The examples of scientific notation are: 490000000 = 4.9×10 8 1230000000 = 1.23×10 9 50500000 = 5.05 x 10 7 0.000000097 = 9.7 x 10 -8 0.0000212 = 2.12 x 10 -5
Positive and Negative Exponent
When the scientific notation of any large numbers is expressed, then we use positive exponents for base 10. For example: 20000 = 2 x 10 4 , where 4 is the positive exponent.
When the scientific notation of any small numbers is expressed, then we use negative exponents for base 10. For example: 0.0002 = 2 x 10 -4 , where -4 is the negative exponent.
From the above, we can say that the number greater than 1 can be written as the expression with positive exponent, whereas the numbers less than 1 with negative exponent.
Problems and Solutions
Question 1: Convert 0.00000046 into scientific notation.
Solution: Move the decimal point to the right of 0.00000046 up to 7 places.
The decimal point was moved 7 places to the right to form the number 4.6
Since the numbers are less than 10 and the decimal is moved to the right. Hence, we use a negative exponent here.
⇒ 0.00000046 = 4.6 × 10 -7
This is the scientific notation.
Question 2: Convert 301000000 in scientific notation.
Solution: Move the decimal to the left 8 places so it is positioned to the right of the leftmost non zero digits 3.01000000. Remove all the zeroes and multiply the number by 10.
Now the number has become = 3.01.
Since the number is greater than 10 and the decimal is moved to left, therefore, we use here a positive exponent.
Hence, 3.01 × 10 8 is the scientific notation of the number.
Question 3:Convert 1.36 × 10 7 from scientific notation to standard notation.
Solution: Given, 1.36 × 10 7 in scientific notation.
Exponent = 7
Since the exponent is positive we need to move the decimal place 7 places to the right.
1.36 × 10 7 = 1.36 × 10000000 = 1,36,00,000.
Practice Questions
Problem 1: Convert the following numbers into scientific notation.
Problem 2: Convert the following into standard form.
- 2.89 × 10 -6
- 9.8 × 10 -2
Frequently Asked Questions on Scientific Notation – FAQs
How do you write 0.00001 in scientific notation, what are the 5 rules of scientific notation, what are the 3 parts of a scientific notation, how do you write 75 in scientific notation, how do you put scientific notation into standard form.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.7: Expressing Numbers - Scientific Notation
- Last updated
- Save as PDF
- Page ID 406491
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Express a large number or a small number in scientific notation.
- Convert a number in scientific notation to standard conventional form.
The instructions for making a pot of coffee specified 3 scoops (rather than 12,000 grounds) because any measurement is expressed more efficiently with units that are appropriate in size. In science, however, we often must deal with quantities that are extremely small or incredibly large. For example, you may have 5,000,000,000,000 red blood cells in a liter of blood, and the diameter of an iron atom is 0.000000014 inches. Numbers with many zeros can be cumbersome to work with, so scientists use scientific notation.
Scientific notation is a system for expressing very large or very small numbers in a compact manner. It uses the idea that such numbers can be rewritten as a simple number multiplied by 10 raised to a certain exponent, or power.
Let us look first at very large numbers. Suppose a spacecraft is 1,500,000 miles from Mars. The number 1,500,000 can be thought of as follows:
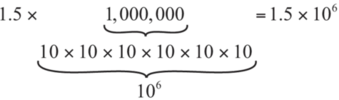
That is, 1,500,000 is the same as 1.5 times 1 million, and 1 million is 10 × 10 × 10 × 10 × 10 × 10, or 10 6 (which is read as “ten to the sixth power”). Therefore, 1,500,000 can be rewritten as 1.5 times 10 6 , or 1.5 × 10 6 . The distance of the spacecraft from Mars can therefore be expressed as 1.5 × 10 6 miles.
Recall that:
- 10 3 = 1,000
- 10 4 = 10,000
- and so forth
The standard convention for expressing numbers in scientific notation is to write a single nonzero first digit, a decimal point, and the rest of the digits, excluding any trailing zeros (see rules for significant figures in the next section for more details on what to exclude). This number is followed by a multiplication sign and then by 10 raised to the power necessary to reproduce the original number. For example, although 1,500,000 can also be written as 15. × 10 5 (which would be 15. × 100,000), the convention is to have only one digit before the decimal point. How do we know to what power 10 is raised? The power is the number of places you have to move the decimal point to the left to place it after the first digit , so that the number being multiplied is between 1 and 10 :
Example \(\PageIndex{1}\): Scientific Notation
Express each number in scientific notation.
- 67,000,000,000
Moving the decimal point 10 places to the left gives 6.7 × 10 10 .
The decimal point is assumed to be at the end of the number, so moving it three places to the left gives 1.689 × 10 3 .
In this case, we need to move the decimal point only one place to the left, which yields 1.26 × 10 1 .
Exercise \(\PageIndex{1}\)
- 102,000,000
Moving the decimal point 3 places to the left gives 1.492 × 10 3 .
The decimal point is assumed to be at the end of the number, so moving it 8 places to the left gives 1.02 × 10 8 .
Moving the decimal point 5 places to the left yields 1.01325 × 10 5 .
To change a number in scientific notation to standard form , we reverse the process, moving the decimal point to the right. Add zeros to the end of the number being converted, if necessary, to produce a number of the proper magnitude. Lastly, we drop the number 10 and its power.

Example \(\PageIndex{2}\)
Express each number in standard, or conventional notation.
- 5.27 × 10 4
- 1.0008 × 10 6
Moving the decimal four places to the right and adding zeros give 52,700.
Moving the decimal six places to the right and adding zeros give 1,000,800.
Exercise \(\PageIndex{2}\)
- \(6.98 \times 10^8\)
- \(1.005 \times 10^2\)
Moving the decimal point eight places to the right and adding zeros give 698,000,000.
Moving the decimal point two places to the right gives 100.5
We can also use scientific notation to express numbers whose magnitudes are less than 1. For example, the quantity 0.006 centimeters can be expressed as follows:
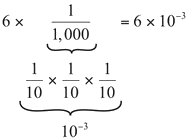
That is, 0.006 centimeters is the same as 6 divided by one thousand, which is the same as 6 divided by 10 x 10 x 10 or 6 times 10 –3 (which is read as "ten to the negative third power"). Therefore, 0.006 centimeters can be rewritten as 6 times 10 –3 , or 6 × 10 –3 centimeters.
- 10 −1 = 1/10
- 10 −2 = 1/100
- 10 −3 = 1/1,000
- 10 −4 = 1/10,000
- 10 −5 = 1/100,000
We use a negative number as the power to indicate the number of places we have to move the decimal point to the right to make it follow the first nonzero digit so that the number is between 1 and 10. This is illustrated as follows:
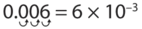
In writing scientific notations, the convention is to have only one digit before the decimal point.
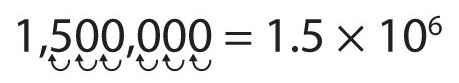
Example \(\PageIndex{3}\)
- 0.000006567
- −0.0004004
- 0.000000000000123
Move the decimal point six places to the right to get 6.567 × 10 −6 .
Move the decimal point four places to the right to get −4.004 × 10 −4 . The negative sign on the number itself does not affect how we apply the rules of scientific notation.
Move the decimal point 13 places to the right to get 1.23 × 10 −13 .
Exercise \(\PageIndex{3}\)
- −0.051204
Moving the decimal point four places to the right gives 3.55 × 10 −4 .
Moving the decimal point one place to the right gives 3.14159 × 10 −1 .
Moving the decimal point one place to the right gives −5.1204 × 10 −2 .
As with numbers with positive powers of 10, when changing from scientific notation to standard or conventional format, we reverse the process.

Changing a number in scientific notation to standard form:
- If the scientific notation has a positive power, the standard number is greater than one. Example: 8 x 10 4 = 80,000
- If the scientific notation has a negative power, then the standard number is less than one. Example: 8 x 10 -2 = 0.08
Example \(\PageIndex{4}\)
Change the number in scientific notation to standard form.
- 6.22 × 10 −2
- 9.9 × 10 −9
0.0000000099
Exercise \(\PageIndex{4}\)
- 9.98 × 10 −5
- 5.109 × 10 −8
0.00000005109
Although calculators can show 8 to 10 digits in their display windows, that is not always enough when working with very large or very small numbers. For this reason, many calculators are designed to handle scientific notation. The method for entering scientific notation differs for each calculator model, so take the time to learn how to do it properly on your calculator, asking your instructor for assistance if necessary . If you do not learn to enter scientific notation into your calculator properly, you will not get the correct final answer when performing a calculation.
Concept Review Exercises
- Why it is easier to use scientific notation to express very large or very small numbers?
- What is the relationship between how many places a decimal point moves and the power of 10 used in changing a conventional number into scientific notation?
- Scientific notation is more convenient than listing a large number of zeros.
- The number of places the decimal point moves equals the power of 10. The power of 10 is positive if the decimal point moves to the left and negative if the decimal point moves to the right.
Key Takeaway
- Large or small numbers are expressed in scientific notation, which use powers of 10.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: 8th grade > Unit 1
- Multiplying & dividing in scientific notation
- Multiplying three numbers in scientific notation
- Subtracting in scientific notation
Adding & subtracting in scientific notation
- Simplifying in scientific notation challenge

IMAGES
VIDEO
COMMENTS
Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to one and less than ten times a power of 10 10. The format is written a×10n a × 10 n, where 1 ≤a < 10 1 ≤ a < 10 and n is an integer. To multiply or divide numbers in scientific notation, you can use the ...
Advanced Problems. Scientific notation is used in solving these earth and space science problems and they are provided to you as an example. Be forewarned that these problems move beyond this module and require some facility with unit conversions, rearranging equations, and algebraic rules for multiplying and dividing exponents.
Scientific notation word problems. Google Classroom. Microsoft Teams. You might need: Calculator. Light travels 9.45 ⋅ 10 15 meters in a year. There are about 3.15 ⋅ 10 7 seconds in a year. How far does light travel per second?
In order to simplify multiplication and division using scientific notation, you should multiply and divide numbers with the same base, and add or subtract the exponents. Through this process, complex expressions can be simplified into a single value multiplied with 10 to a certain power. As an example, 7 times 10 to the fifth over 2 times 10 to ...
How to solve your scientific notation problems. To solve your scientific notation problem, type in your number like 23400. The scientific notation calculator will then show you the steps to help you learn how to convert the number to scientific notation.
Express this number in scientific notation. 0.3643. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Convert 0.82 into scientific notation by moving the decimal point one place to the right and multiplying by 10 − 1. (8.2 × 10 − 1) × 10 − 6. Group the powers of 10 together using the associative property. 8.2 × (10 − 1 × 10 − 6) Multiply the powers of 10 using the Product Rule—add the exponents.
Step by step guide to solve scientific notation problems. Scientific notation is used to write very big or very small numbers in decimal form. In scientific notation all numbers are written in the form of: \(m×10^n\) Scientific Notation
For example, write 630000 in scientific notation: Step 1. Write a decimal point after the first digit of the number to form a number between 1 and 10. A decimal point is placed after the 6 to make 6.30000 which is just 6.3. 6.3 is a number between 1 and 10. Step 2.
Scientific notation - Practice problems. After having reviewed the examples with answers, try to solve the following scientific notation problems. Simply choose an answer and select the "Check" button to check your chosen answer. If you are having trouble with these problems, you can look back at the above examples carefully.
So, to solve using scientific notation, convert so that all numbers have the same power of 10. 8.56\times{10^5}=85.6\times{10^4}=856\times{10^3}=8,560\times{10^2} ... Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used.
Thus, scientific notation is a floating-point system where numbers are expressed as products consisting of numbers between 1 and 10 multiplied with appropriate power of 10. It helps to represent big and small numbers in a much easier way. ... Let us solve some more word problems involving writing numbers in scientific notation. Write the number ...
Scientific notation examples. Scientific notation is a way of writing very large or very small numbers. A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10. For example, 650,000,000 can be written in scientific notation as 6.5 10^8. Created by Sal Khan and CK-12 Foundation.
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10.
In this example scientific notation calculation we're solving 1.225 × 10 5 + 3.655 × 10 3: 1.225 × 10 5 + 3.655 × 10 3 = 1.26155 x 10 5. E Notation. E notation is also known as exponential notation. E notation is the same as scientific notation where a decimal number between 1 and 10 is multiplied by 10 raised to some power.
Correct answer: 1.284 ×106. Explanation: You can solve this problem in several ways. One way is to convert each number out of scientific notation and write it out fully, then find the sum of the two values and convert the answer back into scientific notation. Another, potentially faster, way to solve this problem is to convert one answer into ...
Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to one and less than ten, and a power of 10. The format is written a×10n a × 10 n, where 1 ≤a <10 1 ≤ a < 10 and n is an integer. To multiply or divide numbers in scientific notation, you can use the ...
Problems and Solutions. Question 1: Convert 0.00000046 into scientific notation. Solution: Move the decimal point to the right of 0.00000046 up to 7 places. The decimal point was moved 7 places to the right to form the number 4.6. Since the numbers are less than 10 and the decimal is moved to the right. Hence, we use a negative exponent here.
Multiplying in scientific notation example. Scientific notation shows a number (greater than or equal to 1 and less than 10) times a power of 10. To multiply two numbers in scientific notation, we can rearrange the equation with the associative and commutative properties. If the final product is not in scientific notation, we can regroup a ...
Exercise 1.7.1 1.7. 1. Express each number in scientific notation. To change a number in scientific notation to standard form, we reverse the process, moving the decimal point to the right. Add zeros to the end of the number being converted, if necessary, to produce a number of the proper magnitude.
Scientific notation word problem: speed of light. It is possible to simplify multiplication and division using scientific notation. This can be used to calculate the distance between the sun and the earth, which is 1.5 times 10 to the 11th power meters. This is an incredibly large distance and difficult to visualize.
This video provides a basic introduction into scientific notation as it relates to addition and subtraction. It explains how to add and subtract two numbers...
Express your answer in scientific notation. 8.2 ... Report a problem. Loading... Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.