- Pre-Algebra Topics
- Algebra Topics
- Algebra Calculator
- Algebra Cheat Sheet
- Algebra Practice Test
- Algebra Readiness Test
- Algebra Formulas
- Want to Build Your Own Website?
Sign In / Register

Solving Systems of Equations Real World Problems
Wow! You have learned many different strategies for solving systems of equations! First we started with Graphing Systems of Equations . Then we moved onto solving systems using the Substitution Method . In our last lesson we used the Linear Combinations or Addition Method to solve systems of equations.
Now we are ready to apply these strategies to solve real world problems! Are you ready? First let's look at some guidelines for solving real world problems and then we'll look at a few examples.
Steps For Solving Real World Problems
- Highlight the important information in the problem that will help write two equations.
- Define your variables
- Write two equations
- Use one of the methods for solving systems of equations to solve.
- Check your answers by substituting your ordered pair into the original equations.
- Answer the questions in the real world problems. Always write your answer in complete sentences!
Ok... let's look at a few examples. Follow along with me. (Having a calculator will make it easier for you to follow along.)
Example 1: Systems Word Problems
You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?
1. Let's start by identifying the important information:
- hot dogs cost $1.50
- Sodas cost $0.50
- Made a total of $78.50
- Sold 87 hot dogs and sodas combined
2. Define your variables.
- Ask yourself, "What am I trying to solve for? What don't I know?
In this problem, I don't know how many hot dogs or sodas were sold. So this is what each variable will stand for. (Usually the question at the end will give you this information).
Let x = the number of hot dogs sold
Let y = the number of sodas sold
3. Write two equations.
One equation will be related to the price and one equation will be related to the quantity (or number) of hot dogs and sodas sold.
1.50x + 0.50y = 78.50 (Equation related to cost)
x + y = 87 (Equation related to the number sold)
4. Solve!
We can choose any method that we like to solve the system of equations. I am going to choose the substitution method since I can easily solve the 2nd equation for y.

5. Think about what this solution means.
x is the number of hot dogs and x = 35. That means that 35 hot dogs were sold.
y is the number of sodas and y = 52. That means that 52 sodas were sold.
6. Write your answer in a complete sentence.
35 hot dogs were sold and 52 sodas were sold.
7. Check your work by substituting.
1.50x + 0.50y = 78.50
1.50(35) + 0.50(52) = 78.50
52.50 + 26 = 78.50
35 + 52 = 87
Since both equations check properly, we know that our answers are correct!
That wasn't too bad, was it? The hardest part is writing the equations. From there you already know the strategies for solving. Think carefully about what's happening in the problem when trying to write the two equations.
Example 2: Another Word Problem
You and a friend go to Tacos Galore for lunch. You order three soft tacos and three burritos and your total bill is $11.25. Your friend's bill is $10.00 for four soft tacos and two burritos. How much do soft tacos cost? How much do burritos cost?
- 3 soft tacos + 3 burritos cost $11.25
- 4 soft tacos + 2 burritos cost $10.00
In this problem, I don't know the price of the soft tacos or the price of the burritos.
Let x = the price of 1 soft taco
Let y = the price of 1 burrito
One equation will be related your lunch and one equation will be related to your friend's lunch.
3x + 3y = 11.25 (Equation representing your lunch)
4x + 2y = 10 (Equation representing your friend's lunch)
We can choose any method that we like to solve the system of equations. I am going to choose the combinations method.

5. Think about what the solution means in context of the problem.
x = the price of 1 soft taco and x = 1.25.
That means that 1 soft tacos costs $1.25.
y = the price of 1 burrito and y = 2.5.
That means that 1 burrito costs $2.50.
Yes, I know that word problems can be intimidating, but this is the whole reason why we are learning these skills. You must be able to apply your knowledge!
If you have difficulty with real world problems, you can find more examples and practice problems in the Algebra Class E-course.
Take a look at the questions that other students have submitted:

Problem about the WNBA
Systems problem about ages
Problem about milk consumption in the U.S.
Vans and Buses? How many rode in each?
Telephone Plans problem
Systems problem about hats and scarves
Apples and guavas please!
How much did Alice spend on shoes?
All about stamps
Going to the movies
Small pitchers and large pitchers - how much will they hold?
Chickens and dogs in the farm yard
- System of Equations
- Systems Word Problems

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Privacy Policy
Let Us Know How we are doing!
send us a message to give us more detail!
Would you prefer to share this page with others by linking to it?
- Click on the HTML link code below.
- Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Copyright © 2009-2020 | Karin Hutchinson | ALL RIGHTS RESERVED.
Word Problems on Linear Equations
Worked-out word problems on linear equations with solutions explained step-by-step in different types of examples.
There are several problems which involve relations among known and unknown numbers and can be put in the form of equations. The equations are generally stated in words and it is for this reason we refer to these problems as word problems. With the help of equations in one variable, we have already practiced equations to solve some real life problems.
Steps involved in solving a linear equation word problem: ● Read the problem carefully and note what is given and what is required and what is given. ● Denote the unknown by the variables as x, y, ……. ● Translate the problem to the language of mathematics or mathematical statements. ● Form the linear equation in one variable using the conditions given in the problems. ● Solve the equation for the unknown. ● Verify to be sure whether the answer satisfies the conditions of the problem.
Step-by-step application of linear equations to solve practical word problems:
1. The sum of two numbers is 25. One of the numbers exceeds the other by 9. Find the numbers.
Solution: Then the other number = x + 9 Let the number be x. Sum of two numbers = 25 According to question, x + x + 9 = 25 ⇒ 2x + 9 = 25 ⇒ 2x = 25 - 9 (transposing 9 to the R.H.S changes to -9) ⇒ 2x = 16 ⇒ 2x/2 = 16/2 (divide by 2 on both the sides) ⇒ x = 8 Therefore, x + 9 = 8 + 9 = 17 Therefore, the two numbers are 8 and 17.
2.The difference between the two numbers is 48. The ratio of the two numbers is 7:3. What are the two numbers? Solution: Let the common ratio be x. Let the common ratio be x. Their difference = 48 According to the question, 7x - 3x = 48 ⇒ 4x = 48 ⇒ x = 48/4 ⇒ x = 12 Therefore, 7x = 7 × 12 = 84 3x = 3 × 12 = 36 Therefore, the two numbers are 84 and 36.
3. The length of a rectangle is twice its breadth. If the perimeter is 72 metre, find the length and breadth of the rectangle. Solution: Let the breadth of the rectangle be x, Then the length of the rectangle = 2x Perimeter of the rectangle = 72 Therefore, according to the question 2(x + 2x) = 72 ⇒ 2 × 3x = 72 ⇒ 6x = 72 ⇒ x = 72/6 ⇒ x = 12 We know, length of the rectangle = 2x = 2 × 12 = 24 Therefore, length of the rectangle is 24 m and breadth of the rectangle is 12 m.
4. Aaron is 5 years younger than Ron. Four years later, Ron will be twice as old as Aaron. Find their present ages.
Solution: Let Ron’s present age be x. Then Aaron’s present age = x - 5 After 4 years Ron’s age = x + 4, Aaron’s age x - 5 + 4. According to the question; Ron will be twice as old as Aaron. Therefore, x + 4 = 2(x - 5 + 4) ⇒ x + 4 = 2(x - 1) ⇒ x + 4 = 2x - 2 ⇒ x + 4 = 2x - 2 ⇒ x - 2x = -2 - 4 ⇒ -x = -6 ⇒ x = 6 Therefore, Aaron’s present age = x - 5 = 6 - 5 = 1 Therefore, present age of Ron = 6 years and present age of Aaron = 1 year.
5. A number is divided into two parts, such that one part is 10 more than the other. If the two parts are in the ratio 5 : 3, find the number and the two parts. Solution: Let one part of the number be x Then the other part of the number = x + 10 The ratio of the two numbers is 5 : 3 Therefore, (x + 10)/x = 5/3 ⇒ 3(x + 10) = 5x ⇒ 3x + 30 = 5x ⇒ 30 = 5x - 3x ⇒ 30 = 2x ⇒ x = 30/2 ⇒ x = 15 Therefore, x + 10 = 15 + 10 = 25 Therefore, the number = 25 + 15 = 40 The two parts are 15 and 25.
More solved examples with detailed explanation on the word problems on linear equations.
6. Robert’s father is 4 times as old as Robert. After 5 years, father will be three times as old as Robert. Find their present ages. Solution: Let Robert’s age be x years. Then Robert’s father’s age = 4x After 5 years, Robert’s age = x + 5 Father’s age = 4x + 5 According to the question, 4x + 5 = 3(x + 5) ⇒ 4x + 5 = 3x + 15 ⇒ 4x - 3x = 15 - 5 ⇒ x = 10 ⇒ 4x = 4 × 10 = 40 Robert’s present age is 10 years and that of his father’s age = 40 years.
7. The sum of two consecutive multiples of 5 is 55. Find these multiples. Solution: Let the first multiple of 5 be x. Then the other multiple of 5 will be x + 5 and their sum = 55 Therefore, x + x + 5 = 55 ⇒ 2x + 5 = 55 ⇒ 2x = 55 - 5 ⇒ 2x = 50 ⇒ x = 50/2 ⇒ x = 25 Therefore, the multiples of 5, i.e., x + 5 = 25 + 5 = 30 Therefore, the two consecutive multiples of 5 whose sum is 55 are 25 and 30.
8. The difference in the measures of two complementary angles is 12°. Find the measure of the angles. Solution: Let the angle be x. Complement of x = 90 - x Given their difference = 12° Therefore, (90 - x) - x = 12° ⇒ 90 - 2x = 12 ⇒ -2x = 12 - 90 ⇒ -2x = -78 ⇒ 2x/2 = 78/2 ⇒ x = 39 Therefore, 90 - x = 90 - 39 = 51 Therefore, the two complementary angles are 39° and 51°
9. The cost of two tables and three chairs is $705. If the table costs $40 more than the chair, find the cost of the table and the chair. Solution: The table cost $ 40 more than the chair. Let us assume the cost of the chair to be x. Then the cost of the table = $ 40 + x The cost of 3 chairs = 3 × x = 3x and the cost of 2 tables 2(40 + x) Total cost of 2 tables and 3 chairs = $705 Therefore, 2(40 + x) + 3x = 705 80 + 2x + 3x = 705 80 + 5x = 705 5x = 705 - 80 5x = 625/5 x = 125 and 40 + x = 40 + 125 = 165 Therefore, the cost of each chair is $125 and that of each table is $165.
10. If 3/5 ᵗʰ of a number is 4 more than 1/2 the number, then what is the number? Solution: Let the number be x, then 3/5 ᵗʰ of the number = 3x/5 Also, 1/2 of the number = x/2 According to the question, 3/5 ᵗʰ of the number is 4 more than 1/2 of the number. ⇒ 3x/5 - x/2 = 4 ⇒ (6x - 5x)/10 = 4 ⇒ x/10 = 4 ⇒ x = 40 The required number is 40.
Try to follow the methods of solving word problems on linear equations and then observe the detailed instruction on the application of equations to solve the problems.
● Equations
What is an Equation?
What is a Linear Equation?
How to Solve Linear Equations?
Solving Linear Equations
Problems on Linear Equations in One Variable
Word Problems on Linear Equations in One Variable
Practice Test on Linear Equations
Practice Test on Word Problems on Linear Equations
● Equations - Worksheets
Worksheet on Linear Equations
Worksheet on Word Problems on Linear Equation
7th Grade Math Problems 8th Grade Math Practice From Word Problems on Linear Equations to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
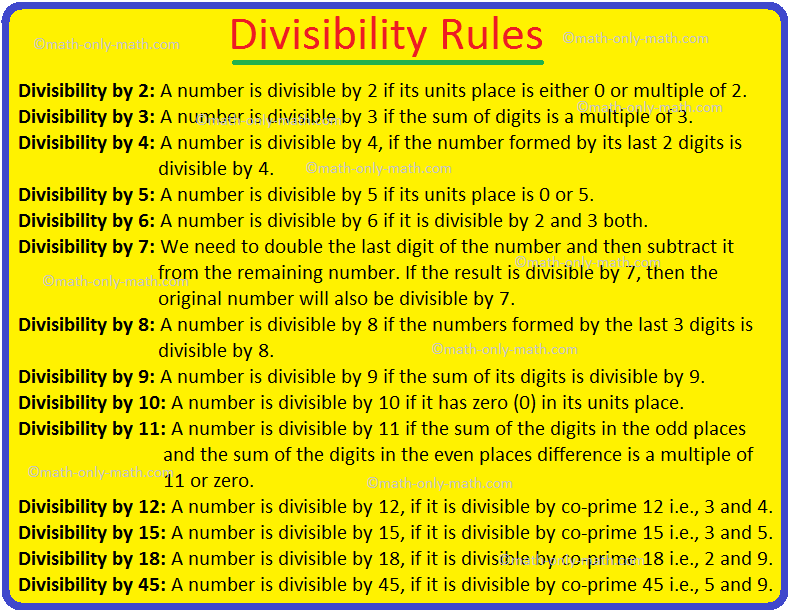
Divisibility Rules | Divisibility Test|Divisibility Rules From 2 to 18
Jun 01, 24 06:41 PM
Consecutive Numbers and Alternate Numbers | Definition | Examples
Jun 01, 24 06:20 PM
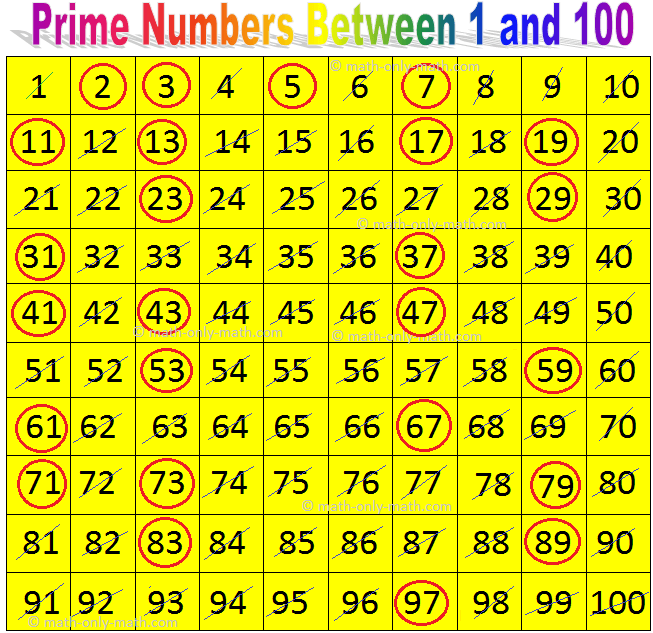
Prime and Composite Numbers | Prime Numbers | Composite Numbers
Jun 01, 24 03:45 PM
Prime Triplet Numbers | Examples on Prime Triplet | Question Answer
Jun 01, 24 11:59 AM
Perfect Numbers | Factors | Solved Examples | Sum of Its Factors |
May 31, 24 07:04 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

2.5: Applications of Linear Equations
- Last updated
- Save as PDF
- Page ID 18337

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Identify key words and phrases, translate sentences to mathematical equations, and develop strategies to solve problems.
- Solve word problems involving relationships between numbers.
- Solve geometry problems involving perimeter.
- Solve percent and money problems including simple interest.
- Set up and solve uniform motion problems.
Key Words, Translation, and Strategy
Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.
Here are some examples of translated key phrases.
When translating sentences into mathematical statements, be sure to read the sentence several times and identify the key words and phrases.
Example \(\PageIndex{1}\)
Four less than twice some number is \(16\).
First, choose a variable for the unknown number and identify the key words and phrases. Let \(x\) represent the unknown indicated by “some number.”
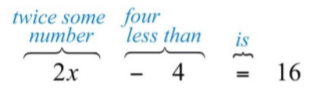.png?revision=1)
Figure \(\PageIndex{1}\)
Remember that subtraction is not commutative. For this reason, take care when setting up differences. In this example, \(4−2x=16\) is an incorrect translation.
\(2x−4=16\)
It is important to first identify the variable— let x represent… —and state in words what the unknown quantity is. This step not only makes your work more readable but also forces you to think about what you are looking for. Usually, if you know what you are asked to find, then the task of finding it is achievable.
Example \(\PageIndex{2}\)
When \(7\) is subtracted from \(3\) times the sum of a number and \(12\), the result is \(20\).
Let \(n\) represent the unknown number.
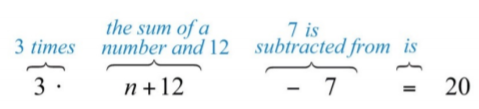.png?revision=1)
Figure \(\PageIndex{2}\)
\(3(n+12)−7=20\)
To understand why parentheses are needed, study the structures of the following two sentences and their translations:
The key is to focus on the phrase “ 3 times the sum .” This prompts us to group the sum within parentheses and then multiply by 3. Once an application is translated into an algebraic equation, solve it using the techniques you have learned.
Guidelines for Setting Up and Solving Word Problems
- Step 1 : Read the problem several times, identify the key words and phrases, and organize the given information.
- Step 2 : Identify the variables by assigning a letter or expression to the unknown quantities.
- Step 3 : Translate and set up an algebraic equation that models the problem.
- Step 4 : Solve the resulting algebraic equation.
- Step 5 : Finally, answer the question in sentence form and make sure it makes sense (check it).
For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.
Problems Involving Relationships between Real Numbers
We classify applications involving relationships between real numbers broadly as number problems. These problems can sometimes be solved using some creative arithmetic, guessing, and checking. Solving in this manner is not a good practice and should be avoided. Begin by working through the basic steps outlined in the general guidelines for solving word problems.
Example \(\PageIndex{3}\)
A larger integer is \(2\) less than \(3\) times a smaller integer. The sum of the two integers is \(18\). Find the integers.
Identify variables : Begin by assigning a variable to the smaller integer.
Let \(x\) represent the smaller integer.
Use the first sentence to identify the larger integer in terms of the variable \(x\): “A larger integer is 2 less than 3 times a smaller.”
Let \(3x-2\) represent the larger integer.
Set up an equation : Add the expressions that represent the two integers, and set the resulting expression equal to \(18\) as indicated in the second sentence: “The sum of the two integers is \(18\).”
\(x+(3x-2)=18\)
Solve : Solve the equation to obtain the smaller integer \(x\).
\(\begin{aligned} x+(3x-2)&=18 \\ x+3x-2&=18 \\ 4x-2&=18 \\ 4x-2\color{Cerulean}{+2}&=18\color{Cerulean}{+2} \\ 4x&=20 \\ \frac{4x}{\color{Cerulean}{4}}&=\frac{20}{\color{Cerulean}{4}} \\ x&=5 \end{aligned}\)
Back substitute : Use the expression \(3x−2\) to find the larger integer—this is called back substituting.
\(3x-2=3(\color{OliveGreen}{5}\color{black}{)-2=15-2=13}\)
Answer the question : The two integers are \(5\) and \(13\).
Check : \(5 + 13 = 18\). The answer makes sense.
Example \(\PageIndex{4}\)
The difference between two integers is \(2\). The larger integer is \(6\) less than twice the smaller. Find the integers.
Use the relationship between the two integers in the second sentence, “The larger integer is 6 less than twice the smaller ,” to identify the unknowns in terms of one variable.
Let \(2x-6\) represent the larger integer.
Since the difference is positive, subtract the smaller integer from the larger.
\((2x-6)-x=2\)
\(\begin{aligned} \color{OliveGreen}{2x}\color{black}{-6}\color{OliveGreen}{-x}&=2 \\ x-6&=2 \\ x-6\color{Cerulean}{+6}&=2\color{Cerulean}{+6} \\ x&=8 \end{aligned}\)
Use \(2x − 6\) to find the larger integer.
\(2x-6=2(\color{Cerulean}{8}\color{black}{)-6=16-6=10}\)
The two integers are \(8\) and \(10\). These integers clearly solve the problem.
It is worth mentioning again that you can often find solutions to simple problems by guessing and checking. This is so because the numbers are chosen to simplify the process of solving, so that the algebraic steps are not too tedious. You learn how to set up algebraic equations with easier problems, so that you can use these ideas to solve more difficult problems later.
Example \(\PageIndex{5}\)
- The sum of two consecutive even integers is \(46\). Find the integers.
The key phrase to focus on is “consecutive even integers.”
Let \(x\) represent the first even integer.
Let \(x+2\) represent the next even integer.
Add the even integers and set them equal to \(46\).
\(x+(x+2)=46\)
\(\begin{aligned}\color{OliveGreen}{x+x}\color{black}{+2}&=46\\2x+2&=46\\2x+2\color{Cerulean}{-2}&=46\color{Cerulean}{-2}\\2x&=44\\x&=22 \end{aligned}\)
Use \(x + 2\) to find the next even integer.
\(x+2=\color{Cerulean}{22}\color{black}{+2=24}\)
The consecutive even integers are \(22\) and \(24\).
It should be clear that consecutive even integers are separated by two units. However, it may not be so clear that odd integers are as well.
.png?revision=1)
Figure \(\PageIndex{3}\)
Example \(\PageIndex{6}\)
The sum of two consecutive odd integers is \(36\). Find the integers.
The key phrase to focus on is “consecutive odd integers.”
Let \(x\) represent the first odd integer.
Let \(x+2\) represent the next odd integer.
Add the two odd integers and set the expression equal to \(36\).
\(x+(x+2)=36\)
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+2}&=36 \\ 2x+2&=36 \\ 2x+2\color{Cerulean}{-2}&=36\color{Cerulean}{-2} \\ 2x&=34 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{34}{\color{Cerulean}{2}} \\ x&=17 \end{aligned}\)
Use \(x + 2\) to find the next odd integer.
\(x+2=\color{OliveGreen}{17}\color{black}{+2=19}\)
The consecutive odd integers are \(17\) and \(19\).
The algebraic setup for even and odd integer problems is the same. A common mistake is to use \(x\) and \(x + 3\) when identifying the variables for consecutive odd integers. This is incorrect because adding 3 to an odd number yields an even number: for example, \(5 + 3 = 8\). An incorrect setup is very likely to lead to a decimal answer, which may be an indication that the problem was set up incorrectly.
Example \(\PageIndex{7}\)
The sum of three consecutive integers is \(24\). Find the integers.
Consecutive integers are separated by one unit.
Let \(x\) represent the first integer.
Let \(x+1\) represent the next integer.
Let \(x+2\) represent the third integer.
Add the integers and set the sum equal to \(24\).
\(x+(x+1)+(x+2)=24\)
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+1}\color{OliveGreen}{+x}\color{black}{+2}&=24\\ 3x+3&=24 \\ 3x+3\color{Cerulean}{-3}&=24\color{Cerulean}{-3} \\ 3x&=21 \\ x&=7 \end{aligned}\)
Back substitute to find the other two integers.
\(x+1=\color{OliveGreen}{7}\color{black}{+1=8}\)
\(x+2=\color{OliveGreen}{7}\color{black}{+2=9}\)
The three consecutive integers are \(7, 8\) and \(9\), where \(7 + 8 + 9 = 24\).
Exercise \(\PageIndex{1}\)
The sum of three consecutive odd integers is \(87\). Find the integers.
The integers are \(27, 29\), and \(31\).
Geometry Problems (Perimeter)
Recall that the perimeter of a polygon is the sum of the lengths of all the outside edges. In addition, it is helpful to review the following perimeter formulas \((π≈3.14159)\).
Keep in mind that you are looking for a relationship between the unknowns so that you can set up algebraic equations using only one variable. When working with geometry problems, it is often helpful to draw a picture.
Example \(\PageIndex{8}\)
A rectangle has a perimeter measuring \(64\) feet. The length is \(4\) feet more than \(3\) times the width. Find the dimensions of the rectangle.
The sentence “The length is 4 feet more than 3 times the width ” gives the relationship between the two variables.
.png?revision=1)
Figure \(\PageIndex{4}\)
Let \(w\) represent the width of the rectangle.
Let \(3w+4\) represent the length.
The sentence “A rectangle has a perimeter measuring \(64\) feet” suggests an algebraic setup. Substitute \(64\) for the perimeter and the expression for the length into the appropriate formula as follows:
\(\begin{aligned} P&=\:\:\:\:\quad 2l + 2w \\ \color{Cerulean}{\downarrow}&\:\:\:\qquad\quad\color{Cerulean}{\downarrow} \\ \color{OliveGreen}{64}&=2(\color{OliveGreen}{3w+4}\color{black}{)+2w} \end{aligned}\)
Once you have set up an algebraic equation with one variable, solve for the width, \(w\).
\(\begin{aligned} 64&=\color{OliveGreen}{6w}\color{black}{+8+}\color{OliveGreen}{2w} \\ 64&=8w+8 \\ 64\color{Cerulean}{-8}&=8w+8\color{Cerulean}{-8} \\ 56&=8w \\ \frac{56}{\color{Cerulean}{8}}&=\frac{8w}{\color{Cerulean}{8}} \\ 7&=w \end{aligned}\)
Use \(3w + 4\) to find the length.
\(l=3w+4=3(\color{OliveGreen}{7}\color{black}{)+4=21+4=25}\)
The rectangle measures \(7\) feet by \(25\) feet. To check, add all of the sides:
\(P=7\text{ ft+}7\text{ ft+}25\text{ ft+}25\text{ ft}=64\text{ ft}\)
Example \(\PageIndex{9}\)
Two sides of a triangle are \(5\) and \(7\) inches longer than the third side. If the perimeter measures \(21\) inches, find the length of each side.
.png?revision=1)
Figure \(\PageIndex{5}\)
The first sentence describes the relationships between the unknowns.
Let \(x\) represent the length of the third side.
Let \(x+5\) and \(x+7\) represent the lengths of the other two sides.
Substitute these expressions into the appropriate formula and use \(21\) for the perimeter \(P\).
\(\begin{aligned} P&=a+b+c \\ \color{OliveGreen}{21}&=\color{OliveGreen}{x}\color{black}{+}\color{OliveGreen}{(x+5)}\color{black}{+}\color{OliveGreen}{(x+7)} \end{aligned}\)
You now have an equation with one variable to solve.
\(\begin{aligned} 21&=x+x+5+x+7 \\ 21&=3x+12 \\ 21\color{Cerulean}{-12}&=3x+12\color{Cerulean}{-12} \\ 9&=3x\\ \frac{9}{\color{Cerulean}{3}}&=\frac{3x}{\color{Cerulean}{3}} \\ 3&=x \end{aligned}\)
Back substitute.
\(x+5=\color{OliveGreen}{3}\color{black}{+5=8}\)
\(x+5=\color{OliveGreen}{3}\color{black}{+7=10}\)
The three sides of the triangle measure \(3\) inches, \(8\) inches, and \(10\) inches. The check is left to the reader.
Exercise \(\PageIndex{2}\)
The length of a rectangle is \(1\) foot less than twice its width. If the perimeter is \(46\) feet, find the dimensions.
Width: \(8\) feet; length: \(15\) feet
Problems Involving Money and Percents
Whenever setting up an equation involving a percentage, we usually need to convert the percentage to a decimal or fraction. If the question asks for a percentage, then do not forget to convert your answer to a percent at the end. Also, when money is involved, be sure to round off to two decimal places.
Example \(\PageIndex{10}\)
If a pair of shoes costs $\(52.50\) including a \(7\frac{1}{4}\)% tax, what is the original cost of the item before taxes are added?
Begin by converting \(7\frac{1}{4}\)% to a decimal.
\(7\frac{1}{4}%=7.25%=0.0725\)
The amount of tax is this rate times the original cost of the item. The original cost of the item is what you are asked to find.
Let \(c\) represent the cost of the item \(\underline{\text{before taxes}}\) are added.
\(\color{Cerulean}{amount\:of\:tax\:=\:tax\:rate\:\cdot\:cost\:of\:item}\)
\(=0.0725\cdot c\)
\(\color{Cerulean}{total\:cost\:=\:cost\:of\:item\:+\:amount\:of\:tax}\)
\(52.50=c+0.0725c\)
Use this equation to solve for \(c\), the original cost of the item.
\(\begin{aligned} 52.50&=\color{OliveGreen}{1c+0.0725c} \\ 52.50&=1.0725c \\ \frac{52.50}{\color{Cerulean}{1.0725}}&=\frac{1.0725c}{\color{Cerulean}{1.0725}} \\ 48.95& \approx c \end{aligned}\)
The cost of the item before taxes is $\(48.95\). Check this by multiplying $\(48.95\) by \(0.0725\) to obtain the tax and add it to this cost.
Example \(\PageIndex{11}\)
Given a \(5\frac{1}{8}\)% annual interest rate, how long will it take $\(1,200\) to yield $\(307.50\) in simple interest?
Let \(t\) represent the time needed to earn $\(307.50\) at \(5.125\)%.
Organize the data needed to use the simple interest formula \(I=prt\).
Next, substitute all of the known quantities into the formula and then solve for the only unknown, \(t\).
\(\begin{aligned} I&=prt \\ \color{OliveGreen}{307.50}&=\color{OliveGreen}{1200}\color{black}{(}\color{OliveGreen}{0.05125}\color{black}{)t} \\ 307.50&=61.5t \\ \frac{307.50}{\color{Cerulean}{61.5}}&=\frac{61.5t}{\color{Cerulean}{61.5}} \\ 5&=t \end{aligned}\)
It takes \(5\) years for $\(1,200\) invested at \(5\frac{1}{8}\)% to earn $\(307.50\) in simple interest.
Example \(\PageIndex{12}\)
Mary invested her total savings of $\(3,400\) in two accounts. Her mutual fund account earned \(8\)% last year and her CD earned \(5\)%. If her total interest for the year was $\(245\), how much was in each account?
The relationship between the two unknowns is that they total $3,400. When a total is involved, a common technique used to avoid two variables is to represent the second unknown as the difference of the total and the first unknown.
Let \(x\) represent the amount invested in the mutual fund at \(8\)%\(=0.08\).
Let \(3,400-x\) represent the remaining amount invested in the CD at \(5\)%\(=0.05\).
The total interest is the sum of the interest earned from each account.
\(\color{Cerulean}{mutual\:fund\:interest\:+\:CD\:interest\:=\:total\:interest}\)
\(0.08x+0.05(3,400-x)=245\)
This equation models the problem with one variable. Solve for \(x\).
\(\begin{aligned} 0.08x+0.05(3,400-x)&=245 \\ \color{OliveGreen}{0.08x}\color{black}{+170}\color{OliveGreen}{-0.05x}&=245 \\ 0.03x+170\color{Cerulean}{-170} &=245\color{Cerulean}{-170} \\ 0.03x&=75 \\ \frac{0.03x}{\color{Cerulean}{0.03}}&=\frac{75}{\color{Cerulean}{0.03}} \\ x&=2,500 \end{aligned}\)
\(3,400-x=3,400-\color{OliveGreen}{2,500}\color{black}{=900}\)
Mary invested $\(2,500\) at \(8\)% in a mutual fund and $\(900\) at \(5\)% in a CD.
Example \(\PageIndex{13}\)
Joe has a handful of dimes and quarters that values $\(5.30\). He has one fewer than twice as many dimes than quarters. How many of each coin does he have?
Begin by identifying the variables.
Let \(q\) represent the number of quarters Joe is holding.
Let \(2q-1\) represent the number of dimes.
To determine the total value of a number of coins, multiply the number of coins by the value of each coin. For example, \(5\) quarters have a value $\(0.25 ⋅ 5 =\) $\(1.25\).
\(\color{Cerulean}{value\:in\:quarters\:+\:value\:in\:dimes\:=\:total\:value\:of\:coins}\)
\(0.25q+0.10(2q-1)=5.30\)
Solve for the number of quarters, \(q\).
\(\begin{aligned} 0.25q+0.10(2q-1)&=5.30 \\ \color{OliveGreen}{0.25q+0.20q}\color{black}{-0.10}&=5.30 \\ 0.45q-0.10&=5.30 \\ 0.45q-0.10\color{Cerulean}{+0.10}&=5.30\color{Cerulean}{+0.10} \\ 0.45q&=5.40 \\ \frac{0.45q}{\color{Cerulean}{0.45}}&=\frac{5.40}{\color{Cerulean}{0.45}} \\ q&=12 \end{aligned}\)
Back substitute into \(2q − 1\) to find the number of dimes.
\(2q-1=2(\color{OliveGreen}{12}\color{black}{)-1=24-1=23}\)
Joe has \(12\) quarters and \(23\) dimes. Check by multiplying $\(0.25 ⋅ 12 = \)$\(3.00\) and $\(0.10 ⋅ 23 = \)$\(2.30\). Then add to obtain the correct amount: $\(3.00 + \)$\(2.30 = \)$\(5.30\).
Exercise \(\PageIndex{3}\)
A total amount of $\(5,900\) is invested in two accounts. One account earns \(3.5\)% interest and another earns \(4.5\)%. If the interest for \(1\) year is $\(229.50\), then how much is invested in each account?
$\(3,600\) is invested at \(3.5\)% and $\(2,300\) at \(4.5\)%.
Uniform Motion Problems (Distance Problems)
Uniform motion refers to movement at a speed, or rate that does not change. We can determine the distance traveled by multiplying the average rate by the time traveled at that rate with the formula \(D=r⋅t\). Applications involving uniform motion usually have a lot of data, so it helps to first organize the data in a chart and then set up an algebraic equation that models the problem.
Example \(\PageIndex{14}\)
Two trains leave the station at the same time traveling in opposite directions. One travels at \(70\) miles per hour and the other at \(60\) miles per hour. How long does it take for the distance between them to reach \(390\) miles?
First, identify the unknown quantity and organize the data.
Let \(t\) represent the time it takes to separate \(390\) miles.
.png?revision=1)
Figure \(\PageIndex{6}\)
The given information is filled in on the following chart. The time for each train is equal.
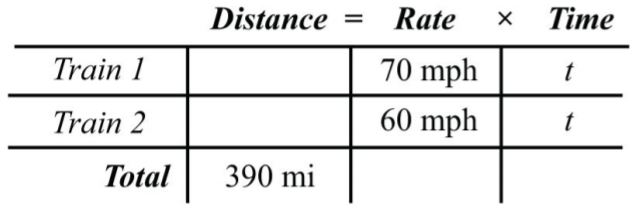.png?revision=1)
Figure \(\PageIndex{7}\)
To avoid introducing two more variables, use the formula \(D=r⋅t\) to fill in the unknown distances traveled by each train.
Distance traveled by train 1: \(D=r\cdot t=70\cdot t\)
Distance traveled by tain 2: \(D=r\cdot t=60\cdot t\)
We can now completely fill in the chart.
.png?revision=1)
Figure \(\PageIndex{8}\)
The algebraic setup is defined by the distance column. The problem asks for the time it takes for the total distance to reach \(390\) miles.
.png?revision=1)
Figure \(\PageIndex{9}\)
Solve for \(t\).
\(\begin{aligned} 70t+60t&=390 \\ 130t&=390 \\ \frac{130t}{\color{Cerulean}{130}}&=\frac{390}{\color{Cerulean}{130}} \\ t&=3 \end{aligned}\)
It takes \(3\) hours for the distance between the trains to reach \(390\) miles.
Example \(\PageIndex{15}\)
A train traveling nonstop to its destination is able to make the trip at an average speed of \(72\) miles per hour. On the return trip, the train makes several stops and is only able to average \(48\) miles per hour. If the return trip takes \(2\) hours longer than the initial trip to the destination, then what is the travel time each way?
Let \(t\) represent the time it takes to arrive at the destination.
Let \(t+2\) represent the time it takes for the return trip.
.png?revision=1)
Figure \(\PageIndex{10}\)
The given information is filled in the following chart:
.png?revision=1)
Figure \(\PageIndex{11}\)
Use the formula \(D=r⋅t\) to fill in the unknown distances.
Distance traveled on the destination: \(D=r\cdot t=72\cdot t\)
Distance traveled on the return trip: \(D=r\cdot t=48\cdot (t+2)\)
Use these expressions to complete the chart.
.png?revision=1)
Figure \(\PageIndex{12}\)
The algebraic setup is again defined by the distance column. In this case, the distance to the destination and back is the same, and the equation is
\(72t=48(t+2)\)
\(\begin{aligned} 72t&=48(t+2) \\ 722&=48t+96 \\ 72t-48t&=48t+96-48t \\ 24t&=96 \\ \frac{24t}{24}&=\frac{96}{24} \\ t&=4 \end{aligned}\)
The return trip takes \(t+2=4+2=6\) hours.
It takes \(4\) hours to arrive at the destination and \(6\) hours to return.
Exercise \(\PageIndex{4}\)
Mary departs for school on a bicycle at an average rate of \(6\) miles per hour. Her sister Kate, running late, leaves \(15\) minutes later and cycles at twice that speed. How long will it take Kate to catch up to Mary? Be careful! Pay attention to the units given in the problem.
It takes \(15\) minutes for Kate to catch up.
Key Takeaways
- Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
- Guessing and checking for solutions is a poor practice. This technique might sometimes produce correct answers, but is unreliable, especially when problems become more complex.
- Read the problem several times and search for the key words and phrases. Identify the unknowns and assign variables or expressions to the unknown quantities. Look for relationships that allow you to use only one variable. Set up a mathematical model for the situation and use algebra to solve the equation. Check to see if the solution makes sense and present the solution in sentence form.
- Do not avoid word problems: solving them can be fun and rewarding. With lots of practice you will find that they really are not so bad after all. Modeling and solving applications is one of the major reasons to study algebra.
- Do not feel discouraged when the first attempt to solve a word problem does not work. This is part of the process. Try something different and learn from incorrect attempts.
Exercise \(\PageIndex{5}\) Translate
Translate the following into algebraic equations.
- The sum of a number and \(6\) is \(37\).
- When \(12\) is subtracted from twice some number the result is \(6\).
- Fourteen less than \(5\) times a number is \(1\).
- Twice some number is subtracted from \(30\) and the result is \(50\).
- Five times the sum of \(6\) and some number is \(20\).
- The sum of \(5\) times some number and \(6\) is \(20\).
- When the sum of a number and \(3\) is subtracted from \(10\) the result is \(5\).
- The sum of three times a number and five times that same number is \(24\).
- Ten is subtracted from twice some number and the result is the sum of the number and \(2\).
- Six less than some number is ten times the sum of that number and \(5\).
1. \(x+6=37\)
3. \(5x−14=1\)
5. \(5(x+6)=20\)
7. \(10−(x+3)=5\)
9. \(2x−10=x+2\)
Exercise \(\PageIndex{6}\) Number Problems
Set up an algebraic equation and then solve.
- A larger integer is \(1\) more than twice another integer. If the sum of the integers is \(25\), find the integers.
- If a larger integer is \(2\) more than \(4\) times another integer and their difference is \(32\), find the integers.
- One integer is \(30\) more than another integer. If the difference between the larger and twice the smaller is \(8\), find the integers.
- The quotient of some number and \(4\) is \(22\). Find the number.
- Eight times a number is decreased by three times the same number, giving a difference of \(20\). What is the number?
- One integer is two units less than another. If their sum is \(−22\), find the two integers.
- The sum of two consecutive integers is \(139\). Find the integers.
- The sum of three consecutive integers is \(63\). Find the integers.
- The sum of three consecutive integers is \(279\). Find the integers.
- The difference of twice the smaller of two consecutive integers and the larger is \(39\). Find the integers.
- If the smaller of two consecutive integers is subtracted from two times the larger, then the result is \(17\). Find the integers.
- The sum of two consecutive even integers is \(238\). Find the integers.
- The sum of three consecutive even integers is \(96\). Find the integers.
- If the smaller of two consecutive even integers is subtracted from \(3\) times the larger the result is \(42\). Find the integers.
- The sum of three consecutive even integers is \(90\). Find the integers.
- The sum of two consecutive odd integers is \(68\). Find the integers.
- The sum of two consecutive odd integers is \(180\). Find the integers.
- The sum of three consecutive odd integers is \(57\). Find the integers.
- If the smaller of two consecutive odd integers is subtracted from twice the larger the result is \(23\). Find the integers.
- Twice the sum of two consecutive odd integers is \(32\). Find the integers.
- The difference between twice the larger of two consecutive odd integers and the smaller is \(59\). Find the integers.
1. \(8, 17\)
3. \(22, 52\)
7. \(69, 70\)
9. \(92, 93, 94\)
11. \(15, 16\)
13. \(118, 120\)
15. \(18, 20\)
17. \(33, 35\)
19. \(17, 19, 21\)
21. \(7, 9\)
Exercise \(\PageIndex{7}\) Geometry Problems
- If the perimeter of a square is \(48\) inches, then find the length of each side.
- The length of a rectangle is \(2\) inches longer than its width. If the perimeter is \(36\) inches, find the length and width.
- The length of a rectangle is \(2\) feet less than twice its width. If the perimeter is \(26\) feet, find the length and width.
- The width of a rectangle is \(2\) centimeters less than one-half its length. If the perimeter is \(56\) centimeters, find the length and width.
- The length of a rectangle is \(3\) feet less than twice its width. If the perimeter is \(54\) feet, find the dimensions of the rectangle.
- If the length of a rectangle is twice as long as the width and its perimeter measures \(72\) inches, find the dimensions of the rectangle.
- The perimeter of an equilateral triangle measures \(63\) centimeters. Find the length of each side.
- An isosceles triangle whose base is one-half as long as the other two equal sides has a perimeter of \(25\) centimeters. Find the length of each side.
- Each of the two equal legs of an isosceles triangle are twice the length of the base. If the perimeter is \(105\) centimeters, then how long is each leg?
- A triangle has sides whose measures are consecutive even integers. If the perimeter is \(42\) inches, find the measure of each side.
- A triangle has sides whose measures are consecutive odd integers. If the perimeter is \(21\) inches, find the measure of each side.
- A triangle has sides whose measures are consecutive integers. If the perimeter is \(102\) inches, then find the measure of each side.
- The circumference of a circle measures \(50π\) units. Find the radius.
- The circumference of a circle measures \(10π\) units. Find the radius.
- The circumference of a circle measures \(100\) centimeters. Determine the radius to the nearest tenth.
- The circumference of a circle measures \(20\) centimeters. Find the diameter rounded off to the nearest hundredth.
- The diameter of a circle measures \(5\) inches. Determine the circumference to the nearest tenth.
- The diameter of a circle is \(13\) feet. Calculate the exact value of the circumference.
1. \(12\) inches
3. Width: \(5\) feet; length: \(8\) feet
5. Width: \(10\) feet; length: \(17\) feet
7. \(21\) centimeters
9. \(21\) centimeters, \(42\) centimeters, \(42\) centimeters
11. \(5\) inches, \(7\) inches, \(9\) inches
13. \(25\) units
15. \(15.9\) centimeters
17. \(15.7\) inches
Exercise \(\PageIndex{8}\) Percent and Money Problems
- Calculate the simple interest earned on a \(2\)-year investment of $\(1,550\) at a \(8\frac{3}{4}\)% annual interest rate.
- Calculate the simple interest earned on a \(1\)-year investment of $\(500\) at a \(6\)% annual interest rate.
- For how many years must $\(10,000\) be invested at an \(8\frac{1}{2}\)% annual interest rate to yield $\(4,250\) in simple interest?
- For how many years must $\(1,000\) be invested at a \(7.75\)% annual interest rate to yield $\(503.75\) in simple interest?
- At what annual interest rate must $\(2,500\) be invested for \(3\) years in order to yield $\(412.50\) in simple interest?
- At what annual interest rate must $\(500\) be invested for \(2\) years in order to yield $\(93.50\) in simple interest?
- If the simple interest earned for \(1\) year was $\(47.25\) and the annual rate was \(6.3\)%, what was the principal?
- If the simple interest earned for \(2\) years was $\(369.60\) and the annual rate was \(5\frac{1}{4}\)%, what was the principal?
- Joe invested last year’s $\(2,500\) tax return in two different accounts. He put most of the money in a money market account earning \(5\)% simple interest. He invested the rest in a CD earning \(8\)% simple interest. How much did he put in each account if the total interest for the year was $\(138.50\)?
- James invested $\(1,600\) in two accounts. One account earns \(4.25\)% simple interest and the other earns \(8.5\)%. If the interest after \(1\) year was $\(85\), how much did he invest in each account?
- Jane has her $\(5,400\) savings invested in two accounts. She has part of it in a CD at \(3\)% annual interest and the rest in a savings account that earns \(2\)% annual interest. If the simple interest earned from both accounts is $\(140\) for the year, then how much does she have in each account?
- Marty put last year’s bonus of $\(2,400\) into two accounts. He invested part in a CD with \(2.5\)% annual interest and the rest in a money market fund with \(1.3\)% annual interest. His total interest for the year was $\(42.00\). How much did he invest in each account?
- Alice puts money into two accounts, one with \(2\)% annual interest and another with \(3\)% annual interest. She invests \(3\) times as much in the higher yielding account as she does in the lower yielding account. If her total interest for the year is $\(27.50\), how much did she invest in each account?
- Jim invested an inheritance in two separate banks. One bank offered \(5.5\)% annual interest rate and the other \(6\frac{1}{4}\)%. He invested twice as much in the higher yielding bank account than he did in the other. If his total simple interest for \(1\) year was $\(4,860\), then what was the amount of his inheritance?
- If an item is advertised to cost $\(29.99\) plus \(9.25\)% tax, what is the total cost?
- If an item is advertised to cost $\(32.98\) plus \(8\frac{3}{4}\)% tax, what is the total cost?
- An item, including an \(8.75\)% tax, cost $\(46.49\). What is the original pretax cost of the item?
- An item, including a \(5.48\)% tax, cost $\(17.82\). What is the original pretax cost of the item?
- If a meal costs $\(32.75\), what is the total after adding a \(15\)% tip?
- How much is a \(15\)% tip on a restaurant bill that totals $\(33.33\)?
- Ray has a handful of dimes and nickels valuing $\(3.05\). He has \(5\) more dimes than he does nickels. How many of each coin does he have?
- Jill has \(3\) fewer half-dollars than she has quarters. The value of all \(27\) of her coins adds to $\(9.75\). How many of each coin does Jill have?
- Cathy has to deposit $\(410\) worth of five- and ten-dollar bills. She has \(1\) fewer than three times as many tens as she does five-dollar bills. How many of each bill does she have to deposit?
- Billy has a pile of quarters, dimes, and nickels that values $\(3.75\). He has \(3\) more dimes than quarters and \(5\) more nickels than quarters. How many of each coin does Billy have?
- Mary has a jar with one-dollar bills, half-dollar coins, and quarters valuing $\(14.00\). She has twice as many quarters than she does half-dollar coins and the same amount of half-dollar coins as one-dollar bills. How many of each does she have?
- Chad has a bill-fold of one-, five-, and ten-dollar bills totaling $\(118\). He has \(2\) more than \(3\) times as many ones as he does five-dollar bills and \(1\) fewer ten- than five-dollar bills. How many of each bill does Chad have?
1. $\(271.25\)
3. \(5\) years
5. \(5.5\)%
7. $\(750.00\)
9. Joe invested $\(2,050\) in the money market account and $\(450\) in the CD.
11. Jane has $\(3,200\) in the CD and $\(2,200\) in savings.
13. Alice invested $\(250\) at \(2\)% and $\(750\) at a \(3\)%.
15. $\(32.76\)
17. $\(42.75\)
19. $\(37.66\)
21. He has \(17\) nickels and \(22\) dimes.
23. Cathy has \(12\) fives and \(35\) ten-dollar bills.
25. Mary has \(7\) one-dollar bills, \(7\) half-dollar coins, and \(14\) quarters.
Exercise \(\PageIndex{9}\) Uniform Motion (Distance Problems)
Set up an algebraic equation then solve.
- Two cars leave a location traveling in opposite directions. If one car averages \(55\) miles per hour and the other averages \(65\) miles per hour, then how long will it take for them to separate a distance of \(300\) miles?
- Two planes leave the airport at the same time traveling in opposite directions. The average speeds for the planes are \(450\) miles per hour and \(395\) miles per hour. How long will it take the planes to be a distance of \(1,478.75\) miles apart?
- Bill and Ted are racing across the country. Bill leaves \(1\) hour earlier than Ted and travels at an average rate of \(60\) miles per hour. If Ted intends to catch up at a rate of \(70\) miles per hour, then how long will it take?
- Two brothers leave from the same location, one in a car and the other on a bicycle, to meet up at their grandmother’s house for dinner. If one brother averages \(30\) miles per hour in the car and the other averages \(12\) miles per hour on the bicycle, then it takes the brother on the bicycle \(1\) hour less than \(3\) times as long as the other in the car. How long does it take each of them to make the trip?
- A commercial airline pilot flew at an average speed of \(350\) miles per hour before being informed that his destination airfield may be closed due to poor weather conditions. In an attempt to arrive before the storm, he increased his speed \(400\) miles per hour and flew for another \(3\) hours. If the total distance flown was \(2,950\) miles, then how long did the trip take?
- Two brothers drove the \(2,793\) miles from Los Angeles to New York. One of the brothers, driving during the day, was able to average \(70\) miles per hour, and the other, driving at night, was able to average \(53\) miles per hour. If the brother driving at night drove \(3\) hours less than the brother driving in the day, then how many hours did they each drive?
- Joe and Ellen live \(21\) miles apart. Departing at the same time, they cycle toward each other. If Joe averages \(8\) miles per hour and Ellen averages \(6\) miles per hour, how long will it take them to meet?
- If it takes \(6\) minutes to drive to the automobile repair shop at an average speed of \(30\) miles per hour, then how long will it take to walk back at an average rate of \(4\) miles per hour?
- Jaime and Alex leave the same location and travel in opposite directions. Traffic conditions enabled Alex to average \(14\) miles per hour faster than Jaime. After \(1\frac{1}{2}\) hours they are \(159\) miles apart. Find the speed at which each was able to travel.
- Jane and Holly live \(51\) miles apart and leave at the same time traveling toward each other to meet for lunch. Jane traveled on the freeway at twice the average speed as Holly. They were able to meet in a half hour. At what rate did each travel?
1. \(2.5\) hours
3. \(6\) hours
5. \(8\) hours
7. \(1\frac{1}{2}\) hours
9. Jaime: \(46\) miles per hour; Alex: \(60\) miles per hour
Exercise \(\PageIndex{10}\) Discussion Board Topics
- Discuss ideas for calculating taxes and tips mentally.
- Research historical methods for representing unknowns.
- Research and compare simple interest and compound interest. What is the difference?
- Discuss why algebra is a required subject.
- Research ways to show that a repeating decimal is rational. Share your findings on the discussion board.
1. Answers may vary
3. Answers may vary
5. Answers may vary
7.2 Systems of Linear Equations: Three Variables
Learning objectives.
In this section, you will:
- Solve systems of three equations in three variables.
- Identify inconsistent systems of equations containing three variables.
- Express the solution of a system of dependent equations containing three variables.
Jordi received an inheritance of $12,000 that he divided into three parts and invested in three ways: in a money-market fund paying 3% annual interest; in municipal bonds paying 4% annual interest; and in mutual funds paying 7% annual interest. Jordi invested $4,000 more in mutual funds than in municipal bonds. He earned $670 in interest the first year. How much did Jordi invest in each type of fund?
Understanding the correct approach to setting up problems such as this one makes finding a solution a matter of following a pattern. We will solve this and similar problems involving three equations and three variables in this section. Doing so uses similar techniques as those used to solve systems of two equations in two variables. However, finding solutions to systems of three equations requires a bit more organization and a touch of visualization.
Solving Systems of Three Equations in Three Variables
In order to solve systems of equations in three variables, known as three-by-three systems, the primary tool we will be using is called Gaussian elimination , named after the prolific German mathematician Karl Friedrich Gauss . While there is no definitive order in which operations are to be performed, there are specific guidelines as to what type of moves can be made. We may number the equations to keep track of the steps we apply. The goal is to eliminate one variable at a time to achieve upper triangular form , the ideal form for a three-by-three system because it allows for straightforward back-substitution to find a solution ( x , y , z ) , ( x , y , z ) , which we call an ordered triple . A system in upper triangular form looks like the following:
The third equation can be solved for z , z , and then we back-substitute to find y y and x . x . To write the system in upper triangular form, we can perform the following operations:
- Interchange the order of any two equations.
- Multiply both sides of an equation by a nonzero constant.
- Add a nonzero multiple of one equation to another equation.
The solution set to a three-by-three system is an ordered triple { ( x , y , z ) } . { ( x , y , z ) } . Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
Number of Possible Solutions
Figure 2 and Figure 3 illustrate possible solution scenarios for three-by-three systems.
- Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple { ( x , y , z ) } . { ( x , y , z ) } . Graphically, the ordered triple defines a point that is the intersection of three planes in space.
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as 0 = 0. 0 = 0. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as 3 = 0. 3 = 0. Graphically, a system with no solution is represented by three planes with no point in common.
Determining Whether an Ordered Triple Is a Solution to a System
Determine whether the ordered triple ( 3 , −2 , 1 ) ( 3 , −2 , 1 ) is a solution to the system.
We will check each equation by substituting in the values of the ordered triple for x , y , x , y , and z . z .
x + y + z = 2 ( 3 ) + ( −2 ) + ( 1 ) = 2 True 6 x −4 y + 5 z = 31 6 ( 3 ) −4 ( −2 ) + 5 ( 1 ) = 31 18 + 8 + 5 = 31 True 5 x + 2 y + 2 z = 13 5 ( 3 ) + 2 ( −2 ) + 2 ( 1 ) = 13 15 −4 + 2 = 13 True x + y + z = 2 ( 3 ) + ( −2 ) + ( 1 ) = 2 True 6 x −4 y + 5 z = 31 6 ( 3 ) −4 ( −2 ) + 5 ( 1 ) = 31 18 + 8 + 5 = 31 True 5 x + 2 y + 2 z = 13 5 ( 3 ) + 2 ( −2 ) + 2 ( 1 ) = 13 15 −4 + 2 = 13 True
The ordered triple ( 3 , −2 , 1 ) ( 3 , −2 , 1 ) is indeed a solution to the system.
Given a linear system of three equations, solve for three unknowns.
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Solving a System of Three Equations in Three Variables by Elimination
Find a solution to the following system:
There will always be several choices as to where to begin, but the most obvious first step here is to eliminate x x by adding equations (1) and (2).
The second step is multiplying equation (1) by −2 −2 and adding the result to equation (3). These two steps will eliminate the variable x . x .
In equations (4) and (5), we have created a new two-by-two system. We can solve for z z by adding the two equations.
Choosing one equation from each new system, we obtain the upper triangular form:
Next, we back-substitute z = 2 z = 2 into equation (4) and solve for y . y .
Finally, we can back-substitute z = 2 z = 2 and y = −1 y = −1 into equation (1). This will yield the solution for x . x .
The solution is the ordered triple ( 1 , −1 , 2 ) . ( 1 , −1 , 2 ) . See Figure 4 .
Solving a Real-World Problem Using a System of Three Equations in Three Variables
In the problem posed at the beginning of the section, Jordi invested his inheritance of $12,000 in three different funds: part in a money-market fund paying 3% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying 7% annually. Jordi invested $4,000 more in mutual funds than he invested in municipal bonds. The total interest earned in one year was $670. How much did he invest in each type of fund?
To solve this problem, we use all of the information given and set up three equations. First, we assign a variable to each of the three investment amounts:
The first equation indicates that the sum of the three principal amounts is $12,000.
We form the second equation according to the information that Jordi invested $4,000 more in mutual funds than he invested in municipal bonds.
The third equation shows that the total amount of interest earned from each fund equals $670.
Then, we write the three equations as a system.
To make the calculations simpler, we can multiply the third equation by 100. Thus,
Step 1. Interchange equation (2) and equation (3) so that the two equations with three variables will line up.
Step 2. Multiply equation (1) by −3 −3 and add to equation (2). Write the result as row 2.
Step 3. Add equation (2) to equation (3) and write the result as equation (3).
Step 4. Solve for z z in equation (3). Back-substitute that value in equation (2) and solve for y . y . Then, back-substitute the values for z z and y y into equation (1) and solve for x . x .
Jordi invested $2,000 in a money-market fund, $3,000 in municipal bonds, and $7,000 in mutual funds.
Solve the system of equations in three variables.
Identifying Inconsistent Systems of Equations Containing Three Variables
Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as 3 = 7 3 = 7 or some other contradiction.
Solving an Inconsistent System of Three Equations in Three Variables
Solve the following system.
Looking at the coefficients of x , x , we can see that we can eliminate x x by adding equation (1) to equation (2).
Next, we multiply equation (1) by −5 −5 and add it to equation (3).
Then, we multiply equation (4) by 2 and add it to equation (5).
The final equation 0 = 2 0 = 2 is a contradiction, so we conclude that the system of equations in inconsistent and, therefore, has no solution.
In this system, each plane intersects the other two, but not at the same location. Therefore, the system is inconsistent.
Solve the system of three equations in three variables.
Expressing the Solution of a System of Dependent Equations Containing Three Variables
We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same, so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. Or two of the equations could be the same and intersect the third on a line.
Finding the Solution to a Dependent System of Equations
Find the solution to the given system of three equations in three variables.
First, we can multiply equation (1) by −2 −2 and add it to equation (2).
We do not need to proceed any further. The result we get is an identity, 0 = 0 , 0 = 0 , which tells us that this system has an infinite number of solutions. There are other ways to begin to solve this system, such as multiplying equation (3) by −2 , −2 , and adding it to equation (1). We then perform the same steps as above and find the same result, 0 = 0. 0 = 0.
When a system is dependent, we can find general expressions for the solutions. Adding equations (1) and (3), we have
We then solve the resulting equation for z . z .
We back-substitute the expression for z z into one of the equations and solve for y . y .
So the general solution is ( x , 5 2 x , 3 2 x ) . ( x , 5 2 x , 3 2 x ) . In this solution, x x can be any real number. The values of y y and z z are dependent on the value selected for x . x .
As shown in Figure 5 , two of the planes are the same and they intersect the third plane on a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.
Does the generic solution to a dependent system always have to be written in terms of x ? x ?
No, you can write the generic solution in terms of any of the variables, but it is common to write it in terms of x and if needed x x and y . y .
Access these online resources for additional instruction and practice with systems of equations in three variables.
- Ex 1: System of Three Equations with Three Unknowns Using Elimination
- Ex. 2: System of Three Equations with Three Unknowns Using Elimination
7.2 Section Exercises
Can a linear system of three equations have exactly two solutions? Explain why or why not
If a given ordered triple solves the system of equations, is that solution unique? If so, explain why. If not, give an example where it is not unique.
If a given ordered triple does not solve the system of equations, is there no solution? If so, explain why. If not, give an example.
Using the method of addition, is there only one way to solve the system?
Can you explain whether there can be only one method to solve a linear system of equations? If yes, give an example of such a system of equations. If not, explain why not.
For the following exercises, determine whether the ordered triple given is the solution to the system of equations.
2 x −6 y + 6 z = −12 x + 4 y + 5 z = −1 − x + 2 y + 3 z = −1 2 x −6 y + 6 z = −12 x + 4 y + 5 z = −1 − x + 2 y + 3 z = −1 and ( 0 , 1 , −1 ) ( 0 , 1 , −1 )
6 x − y + 3 z = 6 3 x + 5 y + 2 z = 0 x + y = 0 6 x − y + 3 z = 6 3 x + 5 y + 2 z = 0 x + y = 0 and ( 3 , −3 , −5 ) ( 3 , −3 , −5 )
6 x −7 y + z = 2 − x − y + 3 z = 4 2 x + y − z = 1 6 x −7 y + z = 2 − x − y + 3 z = 4 2 x + y − z = 1 and ( 4 , 2 , −6 ) ( 4 , 2 , −6 )
x − y = 0 x − z = 5 x − y + z = −1 x − y = 0 x − z = 5 x − y + z = −1 and ( 4 , 4 , −1 ) ( 4 , 4 , −1 )
- x − y + 2 z = 3 5 x + 8 y −3 z = 4 - x + 3 y −5 z = −5 - x − y + 2 z = 3 5 x + 8 y −3 z = 4 - x + 3 y −5 z = −5 and ( 4 , 1 , −7 ) ( 4 , 1 , −7 )
For the following exercises, solve each system by elimination.
3 x −4 y + 2 z = −15 2 x + 4 y + z = 16 2 x + 3 y + 5 z = 20 3 x −4 y + 2 z = −15 2 x + 4 y + z = 16 2 x + 3 y + 5 z = 20
5 x −2 y + 3 z = 20 2 x −4 y −3 z = −9 x + 6 y −8 z = 21 5 x −2 y + 3 z = 20 2 x −4 y −3 z = −9 x + 6 y −8 z = 21
5 x + 2 y + 4 z = 9 −3 x + 2 y + z = 10 4 x −3 y + 5 z = −3 5 x + 2 y + 4 z = 9 −3 x + 2 y + z = 10 4 x −3 y + 5 z = −3
4 x −3 y + 5 z = 31 − x + 2 y + 4 z = 20 x + 5 y −2 z = −29 4 x −3 y + 5 z = 31 − x + 2 y + 4 z = 20 x + 5 y −2 z = −29
5 x −2 y + 3 z = 4 −4 x + 6 y −7 z = −1 3 x + 2 y − z = 4 5 x −2 y + 3 z = 4 −4 x + 6 y −7 z = −1 3 x + 2 y − z = 4
4 x + 6 y + 9 z = 0 −5 x + 2 y −6 z = 3 7 x −4 y + 3 z = −3 4 x + 6 y + 9 z = 0 −5 x + 2 y −6 z = 3 7 x −4 y + 3 z = −3
For the following exercises, solve each system by Gaussian elimination.
2 x − y + 3 z = 17 −5 x + 4 y −2 z = −46 2 y + 5 z = −7 2 x − y + 3 z = 17 −5 x + 4 y −2 z = −46 2 y + 5 z = −7
5 x −6 y + 3 z = 50 − x + 4 y = 10 2 x − z = 10 5 x −6 y + 3 z = 50 − x + 4 y = 10 2 x − z = 10
2 x + 3 y −6 z = 1 −4 x −6 y + 12 z = −2 x + 2 y + 5 z = 10 2 x + 3 y −6 z = 1 −4 x −6 y + 12 z = −2 x + 2 y + 5 z = 10
4 x + 6 y −2 z = 8 6 x + 9 y −3 z = 12 −2 x −3 y + z = −4 4 x + 6 y −2 z = 8 6 x + 9 y −3 z = 12 −2 x −3 y + z = −4
2 x + 3 y −4 z = 5 −3 x + 2 y + z = 11 − x + 5 y + 3 z = 4 2 x + 3 y −4 z = 5 −3 x + 2 y + z = 11 − x + 5 y + 3 z = 4
10 x + 2 y −14 z = 8 −x −2 y −4 z = −1 −12 x −6 y + 6 z = −12 10 x + 2 y −14 z = 8 −x −2 y −4 z = −1 −12 x −6 y + 6 z = −12
x + y + z = 14 2 y + 3 z = −14 −16 y −24 z = −112 x + y + z = 14 2 y + 3 z = −14 −16 y −24 z = −112
5 x −3 y + 4 z = −1 −4 x + 2 y −3 z = 0 −x + 5 y + 7 z = −11 5 x −3 y + 4 z = −1 −4 x + 2 y −3 z = 0 −x + 5 y + 7 z = −11
x + y + z = 0 2 x − y + 3 z = 0 x − z = 0 x + y + z = 0 2 x − y + 3 z = 0 x − z = 0
3 x + 2 y −5 z = 6 5 x −4 y + 3 z = −12 4 x + 5 y −2 z = 15 3 x + 2 y −5 z = 6 5 x −4 y + 3 z = −12 4 x + 5 y −2 z = 15
x + y + z = 0 2 x − y + 3 z = 0 x − z = 1 x + y + z = 0 2 x − y + 3 z = 0 x − z = 1
3 x − 1 2 y − z = − 1 2 4 x + z = 3 − x + 3 2 y = 5 2 3 x − 1 2 y − z = − 1 2 4 x + z = 3 − x + 3 2 y = 5 2
6 x −5 y + 6 z = 38 1 5 x − 1 2 y + 3 5 z = 1 −4 x − 3 2 y − z = −74 6 x −5 y + 6 z = 38 1 5 x − 1 2 y + 3 5 z = 1 −4 x − 3 2 y − z = −74
1 2 x − 1 5 y + 2 5 z = − 13 10 1 4 x − 2 5 y − 1 5 z = − 7 20 − 1 2 x − 3 4 y − 1 2 z = − 5 4 1 2 x − 1 5 y + 2 5 z = − 13 10 1 4 x − 2 5 y − 1 5 z = − 7 20 − 1 2 x − 3 4 y − 1 2 z = − 5 4
− 1 3 x − 1 2 y − 1 4 z = 3 4 − 1 2 x − 1 4 y − 1 2 z = 2 − 1 4 x − 3 4 y − 1 2 z = − 1 2 − 1 3 x − 1 2 y − 1 4 z = 3 4 − 1 2 x − 1 4 y − 1 2 z = 2 − 1 4 x − 3 4 y − 1 2 z = − 1 2
1 2 x − 1 4 y + 3 4 z = 0 1 4 x − 1 10 y + 2 5 z = −2 1 8 x + 1 5 y − 1 8 z = 2 1 2 x − 1 4 y + 3 4 z = 0 1 4 x − 1 10 y + 2 5 z = −2 1 8 x + 1 5 y − 1 8 z = 2
4 5 x − 7 8 y + 1 2 z = 1 − 4 5 x − 3 4 y + 1 3 z = −8 − 2 5 x − 7 8 y + 1 2 z = −5 4 5 x − 7 8 y + 1 2 z = 1 − 4 5 x − 3 4 y + 1 3 z = −8 − 2 5 x − 7 8 y + 1 2 z = −5
− 1 3 x − 1 8 y + 1 6 z = − 4 3 − 2 3 x − 7 8 y + 1 3 z = − 23 3 − 1 3 x − 5 8 y + 5 6 z = 0 − 1 3 x − 1 8 y + 1 6 z = − 4 3 − 2 3 x − 7 8 y + 1 3 z = − 23 3 − 1 3 x − 5 8 y + 5 6 z = 0
− 1 4 x − 5 4 y + 5 2 z = −5 − 1 2 x − 5 3 y + 5 4 z = 55 12 − 1 3 x − 1 3 y + 1 3 z = 5 3 − 1 4 x − 5 4 y + 5 2 z = −5 − 1 2 x − 5 3 y + 5 4 z = 55 12 − 1 3 x − 1 3 y + 1 3 z = 5 3
1 40 x + 1 60 y + 1 80 z = 1 100 − 1 2 x − 1 3 y − 1 4 z = − 1 5 3 8 x + 3 12 y + 3 16 z = 3 20 1 40 x + 1 60 y + 1 80 z = 1 100 − 1 2 x − 1 3 y − 1 4 z = − 1 5 3 8 x + 3 12 y + 3 16 z = 3 20
0.1 x −0.2 y + 0.3 z = 2 0.5 x −0.1 y + 0.4 z = 8 0.7 x −0.2 y + 0.3 z = 8 0.1 x −0.2 y + 0.3 z = 2 0.5 x −0.1 y + 0.4 z = 8 0.7 x −0.2 y + 0.3 z = 8
0.2 x + 0.1 y −0.3 z = 0.2 0.8 x + 0.4 y −1.2 z = 0.1 1.6 x + 0.8 y −2.4 z = 0.2 0.2 x + 0.1 y −0.3 z = 0.2 0.8 x + 0.4 y −1.2 z = 0.1 1.6 x + 0.8 y −2.4 z = 0.2
1.1 x + 0.7 y −3.1 z = −1.79 2.1 x + 0.5 y −1.6 z = −0.13 0.5 x + 0.4 y −0.5 z = −0.07 1.1 x + 0.7 y −3.1 z = −1.79 2.1 x + 0.5 y −1.6 z = −0.13 0.5 x + 0.4 y −0.5 z = −0.07
0.5 x −0.5 y + 0.5 z = 10 0.2 x −0.2 y + 0.2 z = 4 0.1 x −0.1 y + 0.1 z = 2 0.5 x −0.5 y + 0.5 z = 10 0.2 x −0.2 y + 0.2 z = 4 0.1 x −0.1 y + 0.1 z = 2
0.1 x + 0.2 y + 0.3 z = 0.37 0.1 x −0.2 y −0.3 z = −0.27 0.5 x −0.1 y −0.3 z = −0.03 0.1 x + 0.2 y + 0.3 z = 0.37 0.1 x −0.2 y −0.3 z = −0.27 0.5 x −0.1 y −0.3 z = −0.03
0.5 x −0.5 y −0.3 z = 0.13 0.4 x −0.1 y −0.3 z = 0.11 0.2 x −0.8 y −0.9 z = −0.32 0.5 x −0.5 y −0.3 z = 0.13 0.4 x −0.1 y −0.3 z = 0.11 0.2 x −0.8 y −0.9 z = −0.32
0.5 x + 0.2 y −0.3 z = 1 0.4 x −0.6 y + 0.7 z = 0.8 0.3 x −0.1 y −0.9 z = 0.6 0.5 x + 0.2 y −0.3 z = 1 0.4 x −0.6 y + 0.7 z = 0.8 0.3 x −0.1 y −0.9 z = 0.6
0.3 x + 0.3 y + 0.5 z = 0.6 0.4 x + 0.4 y + 0.4 z = 1.8 0.4 x + 0.2 y + 0.1 z = 1.6 0.3 x + 0.3 y + 0.5 z = 0.6 0.4 x + 0.4 y + 0.4 z = 1.8 0.4 x + 0.2 y + 0.1 z = 1.6
0.8 x + 0.8 y + 0.8 z = 2.4 0.3 x −0.5 y + 0.2 z = 0 0.1 x + 0.2 y + 0.3 z = 0.6 0.8 x + 0.8 y + 0.8 z = 2.4 0.3 x −0.5 y + 0.2 z = 0 0.1 x + 0.2 y + 0.3 z = 0.6
For the following exercises, solve the system for x , y , x , y , and z . z .
x + y + z = 3 x −1 2 + y −3 2 + z + 1 2 = 0 x −2 3 + y + 4 3 + z −3 3 = 2 3 x + y + z = 3 x −1 2 + y −3 2 + z + 1 2 = 0 x −2 3 + y + 4 3 + z −3 3 = 2 3
5 x −3 y − z + 1 2 = 1 2 6 x + y −9 2 + 2 z = −3 x + 8 2 −4 y + z = 4 5 x −3 y − z + 1 2 = 1 2 6 x + y −9 2 + 2 z = −3 x + 8 2 −4 y + z = 4
x + 4 7 − y −1 6 + z + 2 3 = 1 x −2 4 + y + 1 8 − z + 8 12 = 0 x + 6 3 − y + 2 3 + z + 4 2 = 3 x + 4 7 − y −1 6 + z + 2 3 = 1 x −2 4 + y + 1 8 − z + 8 12 = 0 x + 6 3 − y + 2 3 + z + 4 2 = 3
x −3 6 + y + 2 2 − z −3 3 = 2 x + 2 4 + y −5 2 + z + 4 2 = 1 x + 6 2 − y −3 2 + z + 1 = 9 x −3 6 + y + 2 2 − z −3 3 = 2 x + 2 4 + y −5 2 + z + 4 2 = 1 x + 6 2 − y −3 2 + z + 1 = 9
x −1 3 + y + 3 4 + z + 2 6 = 1 4 x + 3 y −2 z = 11 0.02 x + 0.015 y −0.01 z = 0.065 x −1 3 + y + 3 4 + z + 2 6 = 1 4 x + 3 y −2 z = 11 0.02 x + 0.015 y −0.01 z = 0.065
Real-World Applications
Three even numbers sum up to 108. The smaller is half the larger and the middle number is 3 4 3 4 the larger. What are the three numbers?
Three numbers sum up to 147. The smallest number is half the middle number, which is half the largest number. What are the three numbers?
At a family reunion, there were only blood relatives, consisting of children, parents, and grandparents, in attendance. There were 400 people total. There were twice as many parents as grandparents, and 50 more children than parents. How many children, parents, and grandparents were in attendance?
An animal shelter has a total of 350 animals comprised of cats, dogs, and rabbits. If the number of rabbits is 5 less than one-half the number of cats, and there are 20 more cats than dogs, how many of each animal are at the shelter?
Your roommate, Shani, offered to buy groceries for you and your other roommate. The total bill was $82. She forgot to save the individual receipts but remembered that your groceries were $0.05 cheaper than half of her groceries, and that your other roommate’s groceries were $2.10 more than your groceries. How much was each of your share of the groceries?
Your roommate, John, offered to buy household supplies for you and your other roommate. You live near the border of three states, each of which has a different sales tax. The total amount of money spent was $100.75. Your supplies were bought with 5% tax, John’s with 8% tax, and your third roommate’s with 9% sales tax. The total amount of money spent without taxes is $93.50. If your supplies before tax were $1 more than half of what your third roommate’s supplies were before tax, how much did each of you spend? Give your answer both with and without taxes.
Three coworkers work for the same employer. Their jobs are warehouse manager, office manager, and truck driver. The sum of the annual salaries of the warehouse manager and office manager is $82,000. The office manager makes $4,000 more than the truck driver annually. The annual salaries of the warehouse manager and the truck driver total $78,000. What is the annual salary of each of the co-workers?
At a carnival, $2,914.25 in receipts were taken at the end of the day. The cost of a child’s ticket was $20.50, an adult ticket was $29.75, and a senior citizen ticket was $15.25. There were twice as many senior citizens as adults in attendance, and 20 more children than senior citizens. How many children, adult, and senior citizen tickets were sold?
A local band sells out for their concert. They sell all 1,175 tickets for a total purse of $28,112.50. The tickets were priced at $20 for student tickets, $22.50 for children, and $29 for adult tickets. If the band sold twice as many adult as children tickets, how many of each type was sold?
In a bag, a child has 325 coins worth $19.50. There were three types of coins: pennies, nickels, and dimes. If the bag contained the same number of nickels as dimes, how many of each type of coin was in the bag?
Last year, at Haven’s Pond Car Dealership, for a particular model of BMW, Jeep, and Toyota, one could purchase all three cars for a total of $140,000. This year, due to inflation, the same cars would cost $151,830. The cost of the BMW increased by 8%, the Jeep by 5%, and the Toyota by 12%. If the price of last year’s Jeep was $7,000 less than the price of last year’s BMW, what was the price of each of the three cars last year?
When his youngest child moved out, Deandre sold his home and made three investments using gains from the sale. He invested $80,500 into three accounts, one that paid 4% simple interest, one that paid 3 1 8 % 3 1 8 % simple interest, and one that paid 2 1 2 % 2 1 2 % simple interest. He earned $2,670 interest at the end of one year. If the amount of the money invested in the second account was four times the amount invested in the third account, how much was invested in each account?
You inherit one million dollars. You invest it all in three accounts for one year. The first account pays 3% compounded annually, the second account pays 4% compounded annually, and the third account pays 2% compounded annually. After one year, you earn $34,000 in interest. If you invest four times the money into the account that pays 3% compared to 2%, how much did you invest in each account?
An entrepreneur sells a portion of their business for one hundred thousand dollars and invests it all in three accounts for one year. The first account pays 4% compounded annually, the second account pays 3% compounded annually, and the third account pays 2% compounded annually. After one year, the entrepreneur earns $3,650 in interest. If they invested five times the money in the account that pays 4% compared to 3%, how much did they invest in each account?
The top three countries in oil consumption in a certain year are as follows: the United States, Japan, and China. In millions of barrels per day, the three top countries consumed 39.8% of the world’s consumed oil. The United States consumed 0.7% more than four times China’s consumption. The United States consumed 5% more than triple Japan’s consumption. What percent of the world oil consumption did the United States, Japan, and China consume? 1
The top three countries in oil production in the same year are Saudi Arabia, the United States, and Russia. In millions of barrels per day, the top three countries produced 31.4% of the world’s produced oil. Saudi Arabia and the United States combined for 22.1% of the world’s production, and Saudi Arabia produced 2% more oil than Russia. What percent of the world oil production did Saudi Arabia, the United States, and Russia produce? 2
The top three sources of oil imports for the United States in the same year were Saudi Arabia, Mexico, and Canada. The three top countries accounted for 47% of oil imports. The United States imported 1.8% more from Saudi Arabia than they did from Mexico, and 1.7% more from Saudi Arabia than they did from Canada. What percent of the United States oil imports were from these three countries? 3
The top three oil producers in the United States in a certain year are the Gulf of Mexico, Texas, and Alaska. The three regions were responsible for 64% of the United States oil production. The Gulf of Mexico and Texas combined for 47% of oil production. Texas produced 3% more than Alaska. What percent of United States oil production came from these regions? 4
At one time, in the United States, 398 species of animals were on the endangered species list. The top groups were mammals, birds, and fish, which comprised 55% of the endangered species. Birds accounted for 0.7% more than fish, and fish accounted for 1.5% more than mammals. What percent of the endangered species came from mammals, birds, and fish?
Meat consumption in the United States can be broken into three categories: red meat, poultry, and fish. If fish makes up 4% less than one-quarter of poultry consumption, and red meat consumption is 18.2% higher than poultry consumption, what are the percentages of meat consumption? 5
- 1 “Oil reserves, production and consumption in 2001,” accessed April 6, 2014, http://scaruffi.com/politics/oil.html.
- 2 “Oil reserves, production and consumption in 2001,” accessed April 6, 2014, http://scaruffi.com/politics/oil.html.
- 3 “Oil reserves, production and consumption in 2001,” accessed April 6, 2014, http://scaruffi.com/politics/oil.html.
- 4 “USA: The coming global oil crisis,” accessed April 6, 2014, http://www.oilcrisis.com/us/.
- 5 “The United States Meat Industry at a Glance,” accessed April 6, 2014, http://www.meatami.com/ht/d/sp/i/47465/pid/47465.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/7-2-systems-of-linear-equations-three-variables
© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
5 Real Life Algebra Problems That You Solve Everyday
Algebra has a reputation for not being very useful in daily life. In fact, in my experience as a high school math teacher, the complaint that I get the most often is that we don’t spend enough time solving real life algebra problems.
You might be surprised to hear that I understand the frustration that my students experience. Unless we are solving real life algebra problems related to money in some way, algebra can feel very “artificial” or disconnected from real life.
My goal here is to walk you through 5 real life algebra problems that will give you a whole new appreciation for the application of algebra to the real-world. I am excited to help you see how many algebraic equations and algebraic concepts are applicable beyond just algebra word problems in your math class!
What is an Example of Algebra in Real Life?
While it is often seen as an abstract branch of mathematics, there are many real-life applications of algebra in everyday life. Now, it is unlikely that you will be solving quadratic equations while walking your dog, or solving real-world problems with linear equations while you play video games. But you can see examples of real life algebra problems all around you!
A simple example is when you want to quickly determine the total cost of a product including taxes, or the total cost after a discount from the original price. Knowing the total amount of money something will cost is a real-life scenario that everyone can relate to!
Depending on your chosen career path, you may see the use of algebra more often than others (I know I see it a lot in my daily life as a math teacher…!).
For example, if you are a business owner, you may use algebra to determine the number of labor hours to spread amongst your staff, or the lowest price you can sell your product for to break even.
For more uses of algebra, check out my list of 20 examples of algebra in real life !
What is an Example of an Algebra Problem in Real Life?
An algebra problem is a mathematical problem that requires the use of algebraic concepts and strategies to determine unknown values or unknown variables. Much like how the order of operations are required to evaluate numerical expressions, algebra problems require the problem solver to apply a set of rules in order to arrive at a solution.
Real world problems that require the use of algebra usually involve modelling real-life situations with algebraic formulas . A formula is a specific equation that can be applied to solve a problem. Formulas make it possible to make predictions about a given real-life scenario.
For example, consider the following problem:
You are saving up for a new smartphone and currently have $200 in your savings account. Your plan is to save a certain amount of money each week from your allowance. If the smartphone costs $600, and you want to have enough money to buy it in 8 weeks, how much money should you save each week?
To solve this problem, we first need to use the information provided in the problem to create an equation that models the real-life scenario. Thinking about the problem in terms of variables, we can define T as the total of the savings, and variable x as the amount saved each week.
Since we know that we have a fixed value of 200, we can use the following equation to model this real world problem:
$$T=200+8x$$
This equation says “the total saved is equal to the original $200 plus whatever amount is saved per week, for 8 weeks”.
Substituting the total of the smartphone allows us to begin solving for the unknown variable x. Remember, when solving algebraic equations, you must apply the same operation to both sides of the equation.
$$ \begin{split} T&=200+8x \\ \\ 600&=200+8x \\ \\ 600-200 &= 8x \\ \\ 400 &= 8x \\ \\ \frac{400}{8} &= \frac{8x}{8} \\\\ 50 &= x \end{split} $$
Therefore, since x = 50, you should save $50 each week in order to save enough money for the smartphone. For more practice with the algebra used in this solution, check out this free collection of solving two step equations worksheets !
5 Real Life Algebra Problems with Step-By-Step Solutions
There are so many real-life examples of algebra problems, but I want to focus on 5 here that I believe will convince you of just how applicable algebra is to the real-world! So let’s dig into these 5 real-world algebraic word problems!
Example #1: Comparing Cell Phone Plans
Link is considering two different cell phone plans. Plan A charges a monthly fee of $30 and an additional $0.10 per minute of talk time. Plan B charges a monthly fee of $45 regardless of how much time is used talking. How many minutes of total time talking will make the plans equal in cost?
The best way to start this problem is by writing two equations to represent each scenario. If C represents total cost, and x represents minutes of talk time used, the equations can be written as follows:
- Plan A: \(C=30+0.1x\)
- Plan B: \(C=45\)
Setting the first equation equal to the second equation will allow us to employ algebra to solve for the number of minutes that makes the two plans equal.
$$ \begin{split} 30+0.1x&=45 \\ \\ 30-30+0.1x&=45-30 \\ \\ 0.1x&=15 \\ \\ \frac{0.1x}{0.1}&=\frac{15}{0.1} \\ \\ x&=150 \end{split} $$
Therefore, the two cell phone plans are equal when 150 minutes of total time talking are used.
Example #2: Calculating Gallons of Gas
Zelda is driving from Hyrule to the Mushroom Kingdom, which are 180 miles apart. Her car can travel 30 miles per gallon of gas. Write an equation to represent the number of gallons of gas, G, that Zelda needs for the trip in terms of the distance, d, she needs to travel. Then calculate how many gallons of gas she needs for this trip.
The number of gallons of gas (G) Zelda needs for any trip can be represented by the equation \(G = \frac{d}{30}\). Since the distance between Hyrule and the Mushroom Kingdom is 180 miles, we can substitute 180 into the equation for d to determine the number of gallons of gas needed:
$$G=\frac{180}{30}=6$$
Therefore, Zelda needs 6 gallons of gas for her trip.

Example #3: Basketball Players in Action!
A basketball player shoots a basketball from a height of 6 feet above the ground. Unfortunately he completely misses the net and the ball bounces off court. A sports analyst models the path of the basketball using the equation \(h(t) = -16t^2 + 16t + 6\), where h(t) represents the height of the basketball above the ground in feet at time t seconds after the shot. Determine the time it takes for the basketball to hit the ground.
Since we are asked for when the ball hits the ground and h(t) is given as the height above the ground, we know that we are looking for the x-intercepts of this quadratic function. We therefore set the equation equal to zero and solve for x.
Note that we cannot use trinomial factoring here since the quadratic is not factorable! Thankfully quadratic equations are solvable using the quadratic formula!
$$ \begin{split} x&=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \\\\ &=\frac{-16 \pm \sqrt{16^2-4(-16)(6)}}{2(-16)}\\\\ &=\frac{-16 \pm \sqrt{640}}{-32}\\\\ x&=-0.291 \\\\ x&=1.291 \end{split}$$
Therefore, the ball hits the ground after approximately 1.3 seconds. Remember that time cannot be negative, so the first answer is inadmissible and rejected!
Example #4: Saving for a Computer Game
You are saving to buy a new computer game that costs $90. You decide to save up for the computer game by depositing some money into a savings account that earns an annual interest rate of 5% (compounded monthly). You start with an initial deposit of $30 and plan to save for 22 months. Will you have enough to purchase the computer game?
This is an example of a math problem that connects to financial problems people encounter everyday! Since the account you chose earns interest , we can apply a compound interest formula to help us out here:
$$A=P(1+i)^n$$
In this formula:
- A(t) is the total amount of money.
- P is the initial deposit (which is $30 in this case).
- i is the monthly interest rate (5% annual interest, compounded monthly means that i is approximately 0.004167).
- n is the time that has elapsed (since we are working with months, we multiply by 12)
We can set up our equation and see if our total amount of money is greater than $90:
$$\begin{split} A(22)&=30(1.004167)^{22 \times 12} \\\\ &=$89.93 \end{split} $$
Remember to always include a dollar sign in your answer and to round to two decimal places when working with money!
Since our answer is approximately equal to $90, we can say that you will have enough money after 22 months! It’s time to get saving!
Example #5: How Many Tickets Did the Movie Theater Sell?
A movie theater charges $10 per ticket for adults and $6 per ticket for children. On a particular day, the theater sold a total of 150 tickets, and the total revenue for the day was $1350. Write a system of equations to represent this real-life scenario and then solve for the number of adult and child tickets sold.
Let’s assume that variable x represents the number of adult tickets sold and variable y represents the number of child tickets sold. We can set up two linear equations as follows:
- First Equation (the total number of tickets sold): \(x+y=150\)
- Second Equation (the total revenue from ticket sales is 1350): \(10x+6y=1350\)
We can use substitution to solve this linear system by rearranging the first equation and substituting it into the second equation. You can catch a quick overview of the substitution process by checking out this substitution video on my YouTube channel!
Rearranging the first equation into a different form to solve for y results in \(y=-x+150\). Substituting this expression for y into the second equation results in:
$$ \begin{split} 10x+6(-x+150)&=1350 \\ \\ 10x-6x+900&=1350 \\ \\ 4x&=450\\ \\ x&=112.5\\ \\ \end{split} $$
We then substitute this value for x into our expression for y:
$$ \begin{split} y&=-x+150 \\ \\ &=-112.50+150 \\ \\ &=37.5\\ \\ \end{split} $$
Since we can’t have fractional ticket sales, we can say that approximately 112 adult tickets were sold and 38 child tickets were sold.
Appreciating Real Life Algebra Problems
While algebra is often seen as an abstract topic, I am hopeful that I have shown you just how applicable it can be to real-life situations! Some of these examples you may have even encountered in your own life!
Even if you aren’t drawing up complex equations and solving them while you are playing basketball, combining basic math and problem solving is one of the most important skills people can have in both their work and their lives.
I hope that I have helped you further your understanding of algebra, while growing an appreciation for the different ways it can be used in your own life!
Did you find this guide to real life algebra problems helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!
RECOMMENDED FOR YOU
Examples of One Solution Equations, Zero, and Infinite
Linear Equations Word Problems Worksheet with Solutions

Systems of Linear Equations
Real World Systems and Solutions
At how many minutes do both companies charge the same amount?

Never, the slope of the graphs of their rates is the same. Parallel lines never intersect.
A Real World Dilemma!
Use your knowledge of solutions of systems of linear equations to solve a real world problem you might have already been faced with: Choosing the best cell phone plan

When is Company T a better Value?
T is a better value from 0 to 20 minutes.
When is Company S a better Value?
S is a better value if you talk more than 20 minutes
The pink region represents the cheaper segment of the chart.
Real World Horror story
A well known real world math incident that almost cost a Verizon customer a large amount of money (Hint: there's a difference between .02 cents and .02 dollars!)

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

Real World Examples of Quadratic Equations
A Quadratic Equation looks like this:
Quadratic equations pop up in many real world situations!
Here we have collected some examples for you, and solve each using different methods:
- Factoring Quadratics
- Completing the Square
- Graphing Quadratic Equations
- The Quadratic Formula
- Online Quadratic Equation Solver
Each example follows three general stages:
- Take the real world description and make some equations
- Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones
When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...
... and a Quadratic Equation tells you its position at all times!
Example: Throwing a Ball
A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.
Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)
Add them up and the height h at any time t is:
h = 3 + 14t − 5t 2
And the ball will hit the ground when the height is zero:
3 + 14t − 5t 2 = 0
Which is a Quadratic Equation !
In "Standard Form" it looks like:
−5t 2 + 14t + 3 = 0
It looks even better when we multiply all terms by −1 :
5t 2 − 14t − 3 = 0
Let us solve it ...
There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :
ac = −15 , and b = −14 .
The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15
By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)
The "t = −0.2" is a negative time, impossible in our case.
The "t = 3" is the answer we want:
The ball hits the ground after 3 seconds!
Here is the graph of the Parabola h = −5t 2 + 14t + 3
It shows you the height of the ball vs time
Some interesting points:
(0,3) When t=0 (at the start) the ball is at 3 m
(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.
(3,0) says that at 3 seconds the ball is at ground level.
Also notice that the ball goes nearly 13 meters high.
Note: You can find exactly where the top point is!
The method is explained in Graphing Quadratic Equations , and has two steps:
Find where (along the horizontal axis) the top occurs using −b/2a :
- t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds
Then find the height using that value (1.4)
- h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters
So the ball reaches the highest point of 12.8 meters after 1.4 seconds.
Example: New Sports Bike

You have designed a new style of sports bicycle!
Now you want to make lots of them and sell them for profit.
Your costs are going to be:
- $700,000 for manufacturing set-up costs, advertising, etc
- $110 to make each bike
Based on similar bikes, you can expect sales to follow this "Demand Curve":
Where "P" is the price.
For example, if you set the price:
- at $0, you just give away 70,000 bikes
- at $350, you won't sell any bikes at all
- at $300 you might sell 70,000 − 200×300 = 10,000 bikes
So ... what is the best price? And how many should you make?
Let us make some equations!
How many you sell depends on price, so use "P" for Price as the variable
Profit = −200P 2 + 92,000P − 8,400,000
Yes, a Quadratic Equation. Let us solve this one by Completing the Square .
Solve: −200P 2 + 92,000P − 8,400,000 = 0
Step 1 Divide all terms by -200
Step 2 Move the number term to the right side of the equation:
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:
(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900
Step 4 Take the square root on both sides of the equation:
Step 5 Subtract (-230) from both sides (in other words, add 230):
What does that tell us? It says that the profit is ZERO when the Price is $126 or $334
But we want to know the maximum profit, don't we?
It is exactly half way in-between! At $230
And here is the graph:
The best sale price is $230 , and you can expect:
- Unit Sales = 70,000 − 200 x 230 = 24,000
- Sales in Dollars = $230 x 24,000 = $5,520,000
- Costs = 700,000 + $110 x 24,000 = $3,340,000
- Profit = $5,520,000 − $3,340,000 = $2,180,000
A very profitable venture.
Example: Small Steel Frame
Your company is going to make frames as part of a new product they are launching.
The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2
The inside of the frame has to be 11 cm by 6 cm
What should the width x of the metal be?
Area of steel before cutting:
Area of steel after cutting out the 11 × 6 middle:
Let us solve this one graphically !
Here is the graph of 4x 2 + 34x :
The desired area of 28 is shown as a horizontal line.
The area equals 28 cm 2 when:
x is about −9.3 or 0.8
The negative value of x make no sense, so the answer is:
x = 0.8 cm (approx.)
Example: River Cruise
A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.
There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:
- Let x = the boat's speed in the water (km/h)
- Let v = the speed relative to the land (km/h)
Because the river flows downstream at 2 km/h:
- when going upstream, v = x−2 (its speed is reduced by 2 km/h)
- when going downstream, v = x+2 (its speed is increased by 2 km/h)
We can turn those speeds into times using:
time = distance / speed
(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)
And we know the total time is 3 hours:
total time = time upstream + time downstream = 3 hours
Put all that together:
total time = 15/(x−2) + 15/(x+2) = 3 hours
Now we use our algebra skills to solve for "x".
First, get rid of the fractions by multiplying through by (x-2) (x+2) :
3(x-2)(x+2) = 15(x+2) + 15(x-2)
Expand everything:
3(x 2 −4) = 15x+30 + 15x−30
Bring everything to the left and simplify:
3x 2 − 30x − 12 = 0
It is a Quadratic Equation!
Let us solve it using the Quadratic Formula :
Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0
Solve 3x 2 - 30x - 12 = 0
Answer: x = −0.39 or 10.39 (to 2 decimal places)
x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!
Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)
And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min
And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min
Example: Resistors In Parallel
Two resistors are in parallel, like in this diagram:
The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.
What are the values of the two resistors?
The formula to work out total resistance "R T " is:
1 R T = 1 R 1 + 1 R 2
In this case, we have R T = 2 and R 2 = R 1 + 3
1 2 = 1 R 1 + 1 R 1 +3
To get rid of the fractions we can multiply all terms by 2R 1 (R 1 + 3) and then simplify:
Yes! A Quadratic Equation!
Let us solve it using our Quadratic Equation Solver .
- Enter 1, −1 and −6
- And you should get the answers −2 and 3
R 1 cannot be negative, so R 1 = 3 Ohms is the answer.
The two resistors are 3 ohms and 6 ohms.
Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.
Quadratic equations are also needed when studying lenses and curved mirrors.
And many questions involving time, distance and speed need quadratic equations.
Zeros of Polynomial Functions
Solve real-world applications of polynomial equations.
We have now introduced a variety of tools for solving polynomial equations. Let’s use these tools to solve the bakery problem from the beginning of the section.
Example 8: Solving Polynomial Equations
A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be four inches longer than the width of the cake and the height of the cake to be one-third of the width. What should the dimensions of the cake pan be?
Begin by writing an equation for the volume of the cake. The volume of a rectangular solid is given by [latex]V=lwh[/latex]. We were given that the length must be four inches longer than the width, so we can express the length of the cake as [latex]l=w+4[/latex]. We were given that the height of the cake is one-third of the width, so we can express the height of the cake as [latex]h=\frac{1}{3}w[/latex]. Let’s write the volume of the cake in terms of width of the cake.
Substitute the given volume into this equation.
Descartes’ rule of signs tells us there is one positive solution. The Rational Zero Theorem tells us that the possible rational zeros are [latex]\pm 3,\pm 9,\pm 13,\pm 27,\pm 39,\pm 81,\pm 117,\pm 351[/latex], and [latex]\pm 1053[/latex]. We can use synthetic division to test these possible zeros. Only positive numbers make sense as dimensions for a cake, so we need not test any negative values. Let’s begin by testing values that make the most sense as dimensions for a small sheet cake. Use synthetic division to check [latex]x=1[/latex].
Since 1 is not a solution, we will check [latex]x=3[/latex].
Since 3 is not a solution either, we will test [latex]x=9[/latex].
Synthetic division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.
The sheet cake pan should have dimensions 13 inches by 9 inches by 3 inches.
A shipping container in the shape of a rectangular solid must have a volume of 84 cubic meters. The client tells the manufacturer that, because of the contents, the length of the container must be one meter longer than the width, and the height must be one meter greater than twice the width. What should the dimensions of the container be?
3 meters by 4 meters by 7 meters
- Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

2.4.6: Applications of Multi-Step Equations
- Last updated
- Save as PDF
- Page ID 4364
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Solving Real-World Problems Using Multi-Step Equations
Real-world application of multi-step equations.
Use strategies for solving multi-step equations to solve real world equations.
Real-World Application: Profit
A growers’ cooperative has a farmer’s market in the town center every Saturday. They sell what they have grown and split the money into several categories. 8.5% of all the money taken in is set aside for sales tax. $150 goes to pay the rent on the space they occupy. What remains is split evenly between the seven growers. How much total money is taken in if each grower receives a $175 share?
Let’s translate the text above into an equation. The unknown is going to be the total money taken in dollars. We’ll call this x.
“8.5% of all the money taken in is set aside for sales tax." This means that 91.5% of the money remains. This is 0.915x.
“$150 goes to pay the rent on the space they occupy.” This means that what’s left is 0.915x−150.
“What remains is split evenly between the 7 growers.” That means each grower gets (0.915x−150)/7.
If each grower’s share is $175, then our equation to find x is (0.915x−150)/7=175.
First we multiply both sides by 7 to get 0.915x−150=1225.
Then add 150 to both sides to get 0.915x=1375.
Finally divide by 0.915 to get x≈1502.7322. Since we want our answer in dollars and cents, we round to two decimal places, or $1502.73.
The workers take in a total of $1502.73.
Real-World Application: Ohm’s Law
The electrical current, I (amps), passing through an electronic component varies directly with the applied voltage, V (volts), according to the relationship V=I⋅R where R is the resistance measured in Ohms (Ω).
A scientist is trying to deduce the resistance of an unknown component. He labels the resistance of the unknown component x Ω. The resistance of a circuit containing a number of these components is (5x+20)Ω. If a 120 volt potential difference across the circuit produces a current of 2.5 amps, calculate the resistance of the unknown component.
To solve this, we need to start with the equation V=I⋅R and substitute in V=120,I=2.5, and R=5x+20. That gives us 120=2.5(5x+20).
Distribute the 2.5 to get 120=12.5x+50.
Subtract 50 from both sides to get 70=12.5x.
Finally, divide by 12.5 to get 5.6=x.
The unknown components have a resistance of 5.6 Ω.
Real-World Application: Distance, Speed and Time
The speed of a body is the distance it travels per unit of time. That means that we can also find out how far an object moves in a certain amount of time if we know its speed: we use the equation “distance=speed×time.”
Shanice’s car is traveling 10 miles per hour slower than twice the speed of Brandon’s car. She covers 93 miles in 1 hour 30 minutes. How fast is Brandon driving?
Here, we don’t know either Brandon’s speed or Shanice’s, but since the question asks for Brandon’s speed, that’s what we’ll use as our variable x.
The distance Shanice covers in miles is 93, and the time in hours is 1.5. Her speed is 10 less than twice Brandon’s speed, or 2x−10 miles per hour. Putting those numbers into the equation gives us 93=1.5(2x−10).
First we distribute, to get 93=3x−15.
Then we add 15 to both sides to get 108=3x.
Finally we divide by 3 to get 36=x.
Brandon is driving at 36 miles per hour.
We can check this answer by considering the situation another way: we can solve for Shanice’s speed instead of Brandon’s and then check that against Brandon’s speed. We’ll use y for Shanice’s speed since we already used x for Brandon’s.
The equation for Shanice’s speed is simply 93=1.5y. We can divide both sides by 1.5 to get 62=y, so Shanice is traveling at 62 miles per hour.
The problem tells us that Shanice is traveling 10 mph slower than twice Brandon’s speed; that would mean that 62 is equal to 2 times 36 minus 10. Is that true? Well, 2 times 36 is 72, minus 10 is 62. The answer checks out.
In algebra, there’s almost always more than one method of solving a problem. If time allows, it’s always a good idea to try to solve the problem using two different methods just to confirm that you’ve got the answer right.
Real-World Application: Speed of Sound
The speed of sound in dry air, v, is given by the equation v=331+0.6T, where T is the temperature in Celsius and v is the speed of sound in meters per second.
Tashi hits a drainpipe with a hammer and 250 meters away Minh hears the sound and hits his own drainpipe. Unfortunately, there is a one second delay between him hearing the sound and hitting his own pipe. Tashi accurately measures the time between her hitting the pipe and hearing Mihn’s pipe at 2.46 seconds. What is the temperature of the air?
This is a complex problem and we need to be careful in writing our equations. First of all, the distance the sound travels is equal to the speed of sound multiplied by the time, and the speed is given by the equation above. So the distance equals (331+0.6T)×time, and the time is 2.46−1 (because for 1 second out of the 2.46 seconds measured, there was no sound actually traveling). We also know that the distance is 250×2 (because the sound traveled from Tashi to Minh and back again), so our equation is 250×2=(331+0.6T)(2.46−1), which simplifies to 500=1.46(331+0.6T).
Distributing gives us 500=483.26+0.876T, and subtracting 483.26 from both sides gives us 16.74=0.876T. Then we divide by 0.876 to get T≈19.1.
The temperature is about 19.1 degrees Celsius.
Example \(\PageIndex{1}\)
A factory manager is packing engine components into wooden crates to be shipped on a small truck. The truck is designed to hold sixteen crates, and will safely carry a 1200 lb cargo. Each crate weighs 12 lbs empty. How much weight should the manager instruct the workers to put in each crate in order to get the shipment weight as close as possible to 1200 lbs?
The unknown quantity is the weight to put in each box, so we’ll call that x.
Each crate when full will weigh x+12 lbs, so all 16 crates together will weigh 16(x+12) lbs.
We also know that all 16 crates together should weigh 1200 lbs, so we can say that 16(x+12)=1200.
To solve this equation, we can start by dividing both sides by 16: x+12=120016=75.
Then subtract 12 from both sides: x=63.
The manager should tell the workers to put 63 lbs of components in each crate.
For 1-6, solve for the variable in the equation.
- (s−4)/11=2/5
- (7x+4)/3=9/2
- (9y−3)/6=5/2
- p/16−2p/3=1/9
- An engineer is building a suspended platform to raise bags of cement. The platform has a mass of 200 kg, and each bag of cement is 40 kg. He is using two steel cables, each capable of holding 250 kg. Write an equation for the number of bags he can put on the platform at once, and solve it.
- A scientist is testing a number of identical components of unknown resistance which he labels xΩ. He connects a circuit with resistance (3x+4)Ω to a steady 12 volt supply and finds that this produces a current of 1.2 amps. What is the value of the unknown resistance?
- Lydia inherited a sum of money. She split it into five equal parts. She invested three parts of the money in a high-interest bank account which added 10% to the value. She placed the rest of her inheritance plus $500 in the stock market but lost 20% on that money. If the two accounts end up with exactly the same amount of money in them, how much did she inherit?
- Pang drove to his mother’s house to drop off her new TV. He drove at 50 miles per hour there and back, and spent 10 minutes dropping off the TV. The entire journey took him 94 minutes. How far away does his mother live?
Review (Answers)
To view the Review answers, open this PDF file and look for section 3.8.
Solver Title
Generating PDF...
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- One-Step Addition
- One-Step Subtraction
- One-Step Multiplication
- One-Step Division
- One-Step Decimals
- Two-Step Integers
- Two-Step Add/Subtract
- Two-Step Multiply/Divide
- Two-Step Fractions
- Two-Step Decimals
- Multi-Step Integers
- Multi-Step with Parentheses
- Multi-Step Rational
- Multi-Step Fractions
- Multi-Step Decimals
- Solve by Factoring
- Completing the Square
- Quadratic Formula
- Biquadratic
- Logarithmic
- Exponential
- Rational Roots
- Floor/Ceiling
- Equation Given Roots
- Newton Raphson
- Substitution
- Elimination
- Cramer's Rule
- Gaussian Elimination
- System of Inequalities
- Perfect Squares
- Difference of Squares
- Difference of Cubes
- Sum of Cubes
- Polynomials
- Distributive Property
- FOIL method
- Perfect Cubes
- Binomial Expansion
- Negative Rule
- Product Rule
- Quotient Rule
- Expand Power Rule
- Fraction Exponent
- Exponent Rules
- Exponential Form
- Logarithmic Form
- Absolute Value
- Rational Number
- Powers of i
- Complex Form
- Partial Fractions
- Is Polynomial
- Leading Coefficient
- Leading Term
- Standard Form
- Complete the Square
- Synthetic Division
- Linear Factors
- Rationalize Denominator
- Rationalize Numerator
- Identify Type
- Convergence
- Interval Notation
- Pi (Product) Notation
- Boolean Algebra
- Truth Table
- Mutual Exclusive
- Cardinality
- Caretesian Product
- Age Problems
- Distance Problems
- Cost Problems
- Investment Problems
- Number Problems
- Percent Problems
- Addition/Subtraction
- Multiplication/Division
- Dice Problems
- Coin Problems
- Card Problems
- Pre Calculus
- Linear Algebra
- Trigonometry
- Conversions
Most Used Actions
Number line.
- \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
- \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
- \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
- \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
- \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
- How do you solve word problems?
- To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
- How do you identify word problems in math?
- Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
- Is there a calculator that can solve word problems?
- Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
- What is an age problem?
- An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.
word-problems-calculator
- Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...
Please add a message.
Message received. Thanks for the feedback.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: Algebra 1 > Unit 6
- Age word problem: Imran
- Age word problem: Ben & William
- Age word problem: Arman & Diya
- Age word problems
- System of equations word problem: walk & ride
- Systems of equations word problems
- System of equations word problem: no solution
System of equations word problem: infinite solutions
- Systems of equations word problems (with zero and infinite solutions)
- Systems of equations with elimination: TV & DVD
- Systems of equations with elimination: apples and oranges
- Systems of equations with substitution: coins
- Systems of equations with elimination: coffee and croissants
- Systems of equations: FAQ
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
Top 10 Challenges to Teaching Math and Science Using Real Problems

- Share article
Nine in ten educators believe that using a problem-solving approach to teaching math and science can be motivating for students, according to an EdWeek Research Center survey.
But that doesn’t mean it’s easy.
Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures—eats up too many precious instructional minutes.
Other challenges: About another third of educators said they weren’t given sufficient professional development in how to teach using a real-world problem-solving approach. Nearly a third say reading and writing take priority over STEM, leaving little bandwidth for this kind of instruction. About a quarter say that it’s tough to find instructional materials that embrace a problem-solving perspective.
Nearly one in five cited teachers’ lack of confidence in their own problem solving, the belief that this approach isn’t compatible with standardized tests, low parent support, and the belief that student behavior is so poor that this approach would not be feasible.
The nationally representative survey included 1,183 district leaders, school leaders, and teachers, and was conducted from March 27 to April 14. (Note: The chart below lists 11 challenges because the last two on the list—dealing with teacher preparation and student behavior—received the exact percentage of responses.)
Trying to incorporate a problem-solving approach to tackling math can require rethinking long-held beliefs about how students learn, said Elham Kazemi, a professor in the teacher education program at the University of Washington.
Most teachers were taught math using a procedural perspective when they were in school. While Kazemi believes that approach has merit, she advocates for exposing students to both types of instruction.
Many educators have “grown up around a particular model of thinking of teaching and learning as the teacher in the front of the room, imparting knowledge, showing kids how to do things,” Kazemi said.
To be sure, some teachers have figured out how to incorporate some real-world problem solving alongside more traditional methods. But it can be tough for their colleagues to learn from them because “teachers don’t have a lot of time to collaborate with one another and see each other teach,” Kazemi said.
What’s more, there are limited instructional materials emphasizing problem solving, Kazemi said.
Though that’s changing, many of the resources available have “reinforced the idea that the teacher demonstrates solutions for kids,” Kazemi said.
Molly Daley, a regional math coordinator for Education Service District 112, which serves about 30 districts near Vancouver, Wash., has heard teachers raise concerns that teaching math from a problem-solving perspective takes too long—particularly given the pressure to get through all the material students will need to perform well on state tests.
Daley believes, however, that being taught to think about math in a deeper way will help students tackle math questions on state assessments that may look different from what they’ve seen before.
“It’s myth that it’s possible to cover everything that will be on the test,” as it will appear, she said. “There’s actually no way to make sure that kids have seen every single possible thing the way it will show up. That’s kind of a losing proposition.”
But rushing through the material in a purely procedural way may actually be counterproductive, she said.
Teachers don’t want kids to “sit down at the test and say, ‘I haven’t seen this and therefore I can’t do it,’” Daley said. “I think a lot of times teachers can unintentionally foster that because they’re so urgently trying to cover everything. That’s where the kind of mindless [teaching] approaches come in.”
Teachers may think to themselves: “’OK, I’m gonna make this as simple as possible, make sure everyone knows how to follow the steps and then when they see it, they can follow it,” Daley said.
But that strategy might “take away their students’ confidence that they can figure out what to do when they don’t know what to do, which is really what you want them to be thinking when they go to approach a test,” Daley said.

Data analysis for this article was provided by the EdWeek Research Center. Learn more about the center’s work.
Sign Up for EdWeek Update
Edweek top school jobs.

Sign Up & Sign In

- Integrations
Ultralytics Solutions: Harness YOLOv8 to Solve Real-World Problems
Ultralytics Solutions provide cutting-edge applications of YOLO models, offering real-world solutions like object counting, blurring, and security systems, enhancing efficiency and accuracy in diverse industries. Discover the power of YOLOv8 for practical, impactful implementations.
Here's our curated list of Ultralytics solutions that can be used to create awesome computer vision projects.
- Object Counting 🚀 NEW: Learn to perform real-time object counting with YOLOv8. Gain the expertise to accurately count objects in live video streams.
- Object Cropping 🚀 NEW: Master object cropping with YOLOv8 for precise extraction of objects from images and videos.
- Object Blurring 🚀 NEW: Apply object blurring using YOLOv8 to protect privacy in image and video processing.
- Workouts Monitoring 🚀 NEW: Discover how to monitor workouts using YOLOv8. Learn to track and analyze various fitness routines in real time.
- Objects Counting in Regions 🚀 NEW: Count objects in specific regions using YOLOv8 for accurate detection in varied areas.
- Security Alarm System 🚀 NEW: Create a security alarm system with YOLOv8 that triggers alerts upon detecting new objects. Customize the system to fit your specific needs.
- Heatmaps 🚀 NEW: Utilize detection heatmaps to visualize data intensity across a matrix, providing clear insights in computer vision tasks.
- Instance Segmentation with Object Tracking 🚀 NEW: Implement instance segmentation and object tracking with YOLOv8 to achieve precise object boundaries and continuous monitoring.
- VisionEye View Objects Mapping 🚀 NEW: Develop systems that mimic human eye focus on specific objects, enhancing the computer's ability to discern and prioritize details.
- Speed Estimation 🚀 NEW: Estimate object speed using YOLOv8 and object tracking techniques, crucial for applications like autonomous vehicles and traffic monitoring.
- Distance Calculation 🚀 NEW: Calculate distances between objects using bounding box centroids in YOLOv8, essential for spatial analysis.
- Queue Management 🚀 NEW: Implement efficient queue management systems to minimize wait times and improve productivity using YOLOv8.
- Parking Management 🚀 NEW: Organize and direct vehicle flow in parking areas with YOLOv8, optimizing space utilization and user experience.
- Analytics 📊 NEW: Conduct comprehensive data analysis to discover patterns and make informed decisions, leveraging YOLOv8 for descriptive, predictive, and prescriptive analytics.
Contribute to Our Solutions
We welcome contributions from the community! If you've mastered a particular aspect of Ultralytics YOLO that's not yet covered in our solutions, we encourage you to share your expertise. Writing a guide is a great way to give back to the community and help us make our documentation more comprehensive and user-friendly.
To get started, please read our Contributing Guide for guidelines on how to open up a Pull Request (PR) 🛠️. We look forward to your contributions!
Let's work together to make the Ultralytics YOLO ecosystem more robust and versatile 🙏!

COMMENTS
Steps For Solving Real World Problems. Highlight the important information in the problem that will help write two equations. Define your variables. Write two equations. Use one of the methods for solving systems of equations to solve. Check your answers by substituting your ordered pair into the original equations.
Worksheet on real world linear equations. Linear Equations: slope of a line. y-intercept. interactive linear equation. equation given slope and a point. equation from graph of a line. real world applications. images.
Given a real-world problem, model a linear equation to fit it. Identify known quantities. Assign a variable to represent the unknown quantity. If there is more than one unknown quantity, find a way to write the second unknown in terms of the first. Write an equation interpreting the words as mathematical operations. Solve the equation.
Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions. ... Using inequalities to solve problems Get 3 of 4 questions to level up! Compound inequalities. Learn. Compound inequalities: OR ... world-class education to anyone, anywhere. Khan ...
Step-by-step application of linear equations to solve practical word problems: 1. The sum of two numbers is 25. One of the numbers exceeds the other by 9. Find the numbers. Let the number be x. Therefore, the two numbers are 8 and 17. 2.The difference between the two numbers is 48. The ratio of the two numbers is 7:3.
We can write an equation using two variables. We will use f for temperature in Fahrenheit, and c for temperature in Celsius. First we take the temperature in Fahrenheit and subtract 32. f − 32 Then divide by 1.8. f − 32 1.8 This equals the temperature in Celsius. c = f − 32 1.8.
If time allows, it's always a good idea to try to solve the problem using two different methods just to confirm that you've got the answer right. Real-World Application: Speed of Sound. The speed of sound in dry air, v, is given by the equation v = 331 + 0.6 T, where T is the temperature in Celsius and v is the speed of sound in meters per ...
Systems of equations can be used to solve many real-world problems. In this video, we solve a problem about distances walking and riding bus to school. Questions Tips ... I like to use substitution when solving problems with multiple equations. Is there a preferred method? w = time walking, b = time riding the bus w + b = 1.5, w = 1.5 - b, b ...
This webpage introduces how to use linear systems to model and solve real-world problems, such as mixture, distance, rate, and cost scenarios. It provides examples, exercises, and solutions to help students practice their algebra skills. It is part of the Mathematics LibreTexts library, which offers free and open-access resources for various levels and topics of mathematics.
Learn how to solve systems of equations with two or more variables, and apply them to real-world problems. Khan Academy offers free online math lessons and exercises.
Guidelines for Setting Up and Solving Word Problems. Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.; Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.; Step 3: Translate and set up an algebraic equation that models the problem.; Step 4: Solve the resulting algebraic equation.
Solving a Real-World Problem Using a System of Three Equations in Three Variables. In the problem posed at the beginning of the section, Jordi invested his inheritance of $12,000 in three different funds: part in a money-market fund paying 3% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying 7% annually.
Plan B: C = 45. Setting the first equation equal to the second equation will allow us to employ algebra to solve for the number of minutes that makes the two plans equal. 30 + 0.1x 30 − 30 + 0.1x 0.1x 0.1x 0.1 x = 45 = 45 − 30 = 15 = 15 0.1 = 150. Therefore, the two cell phone plans are equal when 150 minutes of total time talking are used.
Step 1: Identify the known and unknown quantities from the problem statement. Step 2: Determine the relationship between the known and unknown quantities using keywords. Step 3: Write an equation ...
A Real World Dilemma! Use your knowledge of solutions of systems of linear equations to solve a real world problem you might have already been faced with: Choosing the best cell phone plan
Step 1 Divide all terms by -200. P 2 - 460P + 42000 = 0. Step 2 Move the number term to the right side of the equation: P 2 - 460P = -42000. Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation: (b/2) 2 = (−460/2) 2 = (−230) 2 = 52900.
In this concept, you will learn to solve real-world problems by using rational numbers and simple equations. Using Rational Numbers and Equations in Real World Problems. You can use fractions, decimals, and integers to solve real-world problems. Let's look at an example. Candy is 5 years older than one-third Liam's age.
Today we will do this using straight lines as our equations, and we will solve the problem by drawing these lines (graphing). Creating a mathematical model: We are given a word problem. Determine what question we are to answer. Assign variables to quantities in the problem so that you can answer the question using these variables.
Algebraic word problems are questions that require translating sentences to equations, then solving those equations. The equations we need to write will only involve. basic arithmetic operations. and a single variable. Usually, the variable represents an unknown quantity in a real-life scenario.
Solution. Begin by writing an equation for the volume of the cake. The volume of a rectangular solid is given by \displaystyle V=lwh V = lwh. We were given that the length must be four inches longer than the width, so we can express the length of the cake as \displaystyle l=w+4 l = w + 4.
Solving Real-World Problems Using Multi-Step Equations. Real-World Application of Multi-Step Equations . Use strategies for solving multi-step equations to solve real world equations. Real-World Application: Profit . A growers' cooperative has a farmer's market in the town center every Saturday. They sell what they have grown and split the ...
An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.
This problem-solving or open-ended approach, which emphasizes flexible thinking and real-world situations, is a powerful strategy for engaging the youngest learners in math. Kindergarten through ...
The easiest way to deal with it is to eliminate the fractions. You can multiply the 1st equation by 6: 6 (1/6x) - 6 (3y) = 6 (-58) You get: x - 18y = -348. For the 2nd equation, multiply it by 4 to eliminate the fraction. One the fractions are gone, use elimination or substitution to solve the system.
Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures ...
Here's our curated list of Ultralytics solutions that can be used to create awesome computer vision projects. Object Counting 🚀 NEW: Learn to perform real-time object counting with YOLOv8. Gain the expertise to accurately count objects in live video streams. Object Cropping 🚀 NEW: Master object cropping with YOLOv8 for precise extraction ...